MATLAB数学实验作业

Matlab数学实验

一、求下列方程的根1、5510x x ++=7、42254x dx x+⎰8.0sin 2x e xdx +∞-⎰二、综合题1.求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。

2.设函数y =f (x )由方程xy +e y = e 所确定，求y ′(x )。

3. 08x =展开（最高次幂为）4.求变上限函数x x ⎰对变量x 的导数。

5.求点(1,1,4)到直线L :31102x y z --==- 的距离 6、求矩阵211020413A -⎛⎫ ⎪= ⎪ ⎪-⎝⎭的逆矩阵1A - 及特征值和特征向量。

7、求二重极限1y x y →→《Matlab 数学实验》一、求下列方程的根1、5510x x ++=a=solve('x^5+5*x+1',0);a=vpa(a,6)a =1.10447+1.05983*i-1.00450+1.06095*i-.199936-1.00450-1.06095*i1.10447-1.05983*i7、42254x dx x+⎰ >> sym x;>> int(x^4/(25+x^2),x)ans =125*atan(x/5) - 25*x + x^3/38.0sin 2x e xdx +∞-⎰>> syms x;>> y=exp(-x)*sin(2*x);>> int(y,0,inf)ans =2/5二、综合题1求由参数方程arctan x y t ⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。

>> syms t>> x=log(sqrt(1+t^2));y=atan(t);>> diff(y,t)/diff(x,t)ans =1/t2.设函数y =f (x )由方程xy +e y = e 所确定，求y ′(x )。

(完整版)MATLAB)课后实验[1]

实验一 MATLAB 运算基础1. 先求以下表达式的值，尔后显示 MATLAB 工作空间的使用情况并保存全部变量。

(1)2sin 85 z1 21 e(2) 12z ln( x 1 x ) ，其中22 x2 1 2i5(3)ae e az sin( a 0.3) ln , a 3.0, 2.9, L , 2.9, 32 22t 0 t 1(4) 2z t 1 1 t 242t 2t 1 2 t 3，其中解：M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4. 完成以下操作：(1) 求[100,999] 之间能被 21 整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

解：(1) 结果：m=100:999;n=find(mod(m,21)==0);length(n)ans =43(2). 建立一个字符串向量比方：ch='ABC123d4e56Fg9'; 那么要求结果是：ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch =123d4e56g9实验二 MATLAB矩阵解析与办理1. 设有分块矩阵 A E R3 3 3 2O S2 3 2 2，其中 E、R、O、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试经过数值计算考据 2A E R RS2O S。

MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算（1）设A=15；B=20；求C=A+B与c=a+b？（2）设A=[1 2 3;4 5 6;7 8 9]，B=[9 8 7;6 5 4;3 2 1]；求A*B与A.*B？A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘（3）设a=10，b=20；求i=a/b=0.5与j=a\b=2？（4）设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序，分别找出小于0的矩阵元素及其位置（单下标、全下标的形式），并将其单下标转换成全下标。

clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc（5）在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8]；看结果如何？如果改成运行A=[1,2;3,4]+i[5,6;7,8]，结果又如何？前面那个是虚数矩阵，后面那个出错（6）请写出完成下列计算的指令：a=[1 2 3;3 4 2;5 2 3]，求a^2=？,a.^2=？a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9（7）有一段指令如下，请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量（8）使用三元组方法，创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一：clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二：不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a（9）写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、已知⎪⎭⎫⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1]，取间隔为0.01，试计算出相对应的y 值。

matlab数学实验练习题

Matlab 数学实验实验一插值与拟合实验内容：预备知识：编制计算拉格朗日插值的M 文件。

1. 选择一些函数，在n 个节点上（n 不要太大，如5 ~ 11）用拉格朗日、分段线性、三次样条三种插值方法，计算m 个插值点的函数值（m 要适中，如50~100）。

通过数值和图形输出，将三种插值结果与精确值进行比较。

适当增加n ，再做比较，由此作初步分析。

下列函数任选一种。

（1）、 ;20,sin π≤≤=x x y （2）、;11,)1(2/12≤≤--=x x y （3）、;22,c o s10≤≤-=x x y（4）、22),exp(2≤≤--=x x y2.用电压V=10伏的电池给电容器充电，电容器上t 时刻的电压为)(0)()(t eV V V t v ---=，其中0V 是电容器的初始电压，τ是充电常数。

试由下面一组t ，V 数据确定0V 和τ。

实验二常微分方程数值解试验实验目的：1. 用MATLAB 软件求解微分方程，掌握Euler 方法和龙格-库塔方法；2. 掌握用微分方程模型解决简化的实际问题。

实验内容：实验三地图问题1.下图是一个国家的地图，为了计算出它的国土面积，首先对地图作如下测量：以由西向东方向为x轴，由南到北方向为y轴，选择方便的原点，并将从最西边界点到最东边界点在x轴上的区间适当地划分为若干段，在每个分点的y方向测出南边界点和北边界点的y坐标y1和y2，这样就得到了表中的数据（单位mm）。

根据地图的比例我们知道18mm相当于40km，试由测量数据计算该国土的近似面积，并与它的精确值41288km2比较。

实验四狼追兔问题狼猎兔问题是欧洲文艺复兴时代的著名人物达.芬奇提出的一个数学问题。

当一个兔子正在它的洞穴南面60码处觅食时，一只恶狼出现在兔子正东的100码处。

当两只动物同时发现对方以后，兔子奔向自己的洞穴，狼以快于兔子一倍的速度紧追兔子不放。

狼在追赶过程中所形成的轨迹就是追击曲线。

实验1 MATLAB使用作业

谢谢大家！
3. 输入20个数，求其中最大数和最小数。要求分别用循环结构和调用MATLAB的 max函数、min函数来实现。 4. 求Fibonacci数列 (1)大于4000的最小项。 (2)5000之内的项数。
5、已知矩阵A,线性方程组Ax=b,其中
1 1 1 A 5 4 3 2 1 1
2 b 3 1
试编程求一下问题： 1) 求矩阵A的行列式 2）求矩阵A的特征值和特征向量 3）就矩阵A的逆矩阵 4）求线性方程组的解
6、已知某班的5名学生的三门课成绩列表如下：学生序号 1 2 4 7 8 高等数学 78 89 64 73 68 外语 83 77 80 78 70 MATLAB语言 82 91 78 82 68 试出三门课总分的最高分及其学生序号。 7、针对上小题的成绩表，求出其三门课总分存入数组ZF，再利用SORT命令对之按降序排序，同时把相应的学生序号存入数组XH。
1求矩阵a的行列式2求矩阵a的特征值和特征向量3就矩阵a的逆矩阵4求线性方程组的解下问题????????????112345111a???????????132b6已知某班的5名学生的三门课成绩列表如下
实验一 MATLAB使用实验
作业
1 、在 [0 2π ] 范围内绘制二维曲线图 y=sin(x)*cos(5x)。 2、在[0 2π ]范围内绘制以Y轴为对数的二维曲线图。 y=|1000sin(4x)|+1 3、在[–6 2]范围内用plot和fplot函数分别绘制二维曲线图。 4、绘制z=sin(x)*cos(y)的三维网格和三维曲面图，x,y变化范围均为 [0 2π ]。

MATLAB数学实验答案（全）

MATLAB数学实验答案（全）第⼀次练习教学要求：熟练掌握Matlab 软件的基本命令和操作，会作⼆维、三维⼏何图形，能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。

补充命令vpa(x,n) 显⽰x 的n 位有效数字，教材102页fplot(‘f(x)’,[a,b]) 函数作图命令，画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位（1-9班）或4位（10班以上） 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =，求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项（要求将结果⽤向量的形式给出）。

数学实验(MATLAB版韩明版)5.1,5.3,5.5,5.6部分答案

数学实验(M A T L A B版韩明版)5.1,5.3,5.5,5.6部分答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN练习5.1B的分布规律和分布函数的图形，通过观1、仿照本节的例子，分别画出二项分布()7.0,20察图形，进一步理解二项分布的性质。

解：分布规律编程作图：>> x=0:1:20;y=binopdf(x,20,0.7);>> plot(x,y,'*')图像：yx分布函数编程作图：>> x=0:0.01:20;>>y=binocdf(x,20,0.7)>> plot(x,y)图像：1x观察图像可知二项分布规律图像像一条抛物线，其分布函数图像呈阶梯状。

2、仿照本节的例子，分别画出正态分布()25,2N的概率密度函数和分布函数的图形，通过观察图形，进一步理解正态分布的性质。

解：概率密度函数编程作图：>> x=-10:0.01:10;>> y=normpdf(x,2,5);>> plot(x,y)图像：00.010.020.030.040.050.060.070.08x y分布函数编程作图：>> x=-10:0.01:10;>> y=normcdf(x,2,5);>> plot(x,y)图像：01x y观察图像可知正态分布概率密度函数图像像抛物线，起分布函数图像呈递增趋势。

3、设()1,0~N X ，通过分布函数的调用计算{}11<<-X P ,{}22<<-X P , {}33<<-X P .解：编程求解：>> x1=normcdf(1)-normcdf(-1),x2=normcdf(2)-normcdf(-2),x3=normcdf(3)-normcdf(-3) x1 = 0.6827x2 = 0.9545x3 = 0.9973即：{}6827.011=<<-X P ，{}9545.022=<<-X P ，{}9973.033=<<-X P .4、设()7.0,20~B X ,通过分布函数的调用计算{}10=X P 与{}10<X P .解：编程求解：>> x1=binopdf(10,20,0.7),x2=binocdf(10,20,0.7)-binopdf(10,20,0.7) x1 = 0.0308x2 = 0.0171即：{}0308.010==X P ，{}0171.010=<X P5、设()8~P X ,求：（1）{}4≤X P ;(2){}52≤<X P .解：（1）编程求解：>> p=poisscdf(4,8)p = 0.0996即：{}0996.04=≤X P（2）编程求解：>> p=poisscdf(5,8)-poisscdf(2,8)p = 0.1775即：{}1775.052=≤<X P6、（1）设()1,0~N X ,求01.0z ；（2）对2χ分布，求()8205.0χ；（3）对()1305.0t ；（4）对F 分布，求()10,1505.0F 。

MATLAB数学实验第二版课后练习题含答案

MATLAB数学实验第二版课后练习题含答案课后练习题MATLAB数学实验第二版的课后练习题如下：第一章课后练习题1.编写MATLAB程序，计算并输出下列公式的结果：y = \\frac{1}{\\sqrt{2\\pi\\sigma^2}} e^{-\\frac{(x-\\mu)^2}{2\\sigma^2}}其中，x, $\\mu$, $\\sigma$ 分别由用户输入。

要求输出结果精确至小数点后两位。

答案如下：x=input('请输入 x 的值:');mu=input('请输入 mu 的值:');sigma=input('请输入 sigma 的值:');y=1/sqrt(2*pi*sigma^2) *exp(-(x-mu)^2/ (2*sigma^2));fprintf('y = %.2f\', y);2.编写MATLAB程序，求解下列方程的解：4x + y = 11\\\\x + 2y = 7答案如下：A= [4,1;1,2];B= [11;7];X=inv(A) *B;fprintf('x = %.2f, y = %.2f\', X(1), X(2));第二章课后练习题1.编写MATLAB程序，计算下列多项式的值：P(x) = x^4 - 2x^3 + 3x^2 - x + 1其中，x 由用户输入。

要求输出结果精确至小数点后两位。

答案如下：x=input('请输入 x 的值:');y=x^4-2*x^3+3*x^2-x+1;fprintf('P(%.2f) = %.2f\', x, y);2.编写MATLAB程序，绘制下列函数的图像：f(x) = \\begin{cases} x + 1, & x < 0 \\\\ x^2, & 0 \\leq x < 1 \\\\ 2x - 1, & x \\geq 1 \\end{cases}答案如下：x=-2:0.01:2;y1=x+1;y2=x.^2.* ((x>=0) & (x<1));y3=2*x-1;plot(x,y1,x,y2,x,y3);legend('y1 = x + 1','y2 = x^2','y3 = 2x - 1');总结本文提供了《MATLAB数学实验第二版》的部分课后练习题及其答案。

MATLAB数学实验100例题解

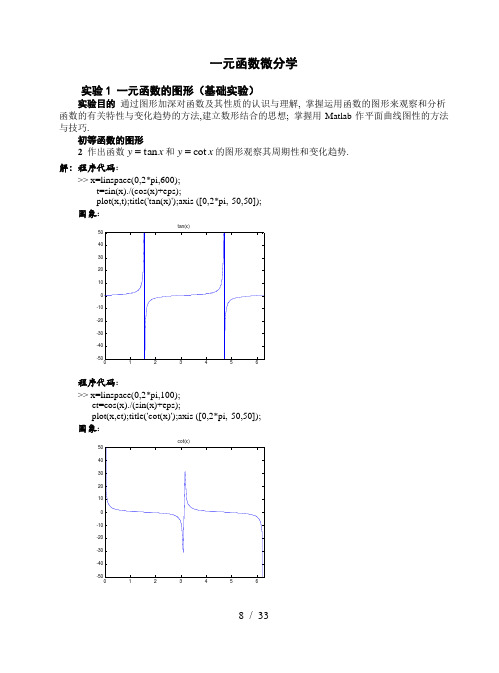
一元函数微分学实验1 一元函数的图形（基础实验）实验目的通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧.初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势. 解：程序代码：>> x=linspace(0,2*pi,600); t=sin(x)./(cos(x)+eps);plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]); 图象：程序代码：>> x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps);plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]); 图象：4在区间]1,1[-画出函数xy 1sin =的图形. 解：程序代码：>> x=linspace(-1,1,10000);y=sin(1./x); plot(x,y);axis([-1,1,-2,2]) 图象：二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形：解：程序代码：>> t=linspace(0,2*pi,100);plot(cos(t).*cos(5*t),sin(t).*cos(3*t)); 图象：极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解：程序代码：>> t=0:0.01:2*pi; r=exp(t/10);polar(log(t+eps),log(r+eps)); 图象：90270分段函数作图10 作出符号函数x y sgn =的图形. 解：程序代码：>> x=linspace(-100,100,10000); y=sign(x); plot(x,y);axis([-100 100 -2 2]);函数性质的研究12研究函数)3(log 3)(35x e x x f x -++=在区间]2,2[-上图形的特征. 解：程序代码：>> x=linspace(-2,2,10000);y=x.^5+3*exp(x)+log(3-x)/log(3); plot(x,y); 图象：实验2 极限与连续（基础实验）实验目的通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用 Matlab 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形特征,理解闭区间上连续函数的几个重要性质.作散点图14分别画出坐标为)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图, 并画出折线图. 解：散点图程序代码： >> i=1:10; plot(i,i.^2,'.')或：>> x=1:10;y=x.^2;for i=1:10;plot(x(i),y(i),'r')hold onend折线图程序代码：>> i=1:10;plot(i,i.^2,'-x')程序代码：>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'.')>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'-x')数列极限的概念16通过动画观察当∞→n 时数列21n a n =的变化趋势.解：程序代码： >> n=1:100; an=(n.^2); n=1:100; an=1./(n.^2); n=1:100; an=1./(n.^2); for i=1:100plot(n(1:i),an(1:i)),axis([0,100,0,1]) pause(0.1) end 图象：函数的极限18在区间]4,4[-上作出函数xx xx x f --=339)(的图形, 并研究 )(lim x f x ∞→ 和 ).(lim 1x f x →解：作出函数x x xx x f --=339)(在区间]4,4[-上的图形 >> x=-4:0.01:4;y=(x.^3-9*x)./(x.^3-x+eps); plot(x,y)从图上看，()f x 在x →1与x →∞时极限为0两个重要极限 20计算极限⎪⎭⎫⎝⎛+→x x x x x sin 11sin lim )1(0 x x e x 2lim )2(+∞→30sin tan lim )3(xx x x -→ x x x 0lim )4(+→ x xx ln cot ln lim )5(0+→ x x x ln lim )6(20+→ xx xx x x sin cos sin lim)7(20-→ 125523lim )8(323+++-∞→x x x x x xx x e e x x x sin 2lim )9(0----→ xx x x cos 110sin lim )10(-→⎪⎭⎫ ⎝⎛ 解：（1）>> limit(x*sin(1/x)+1/x*sin(x))ans =1(2) >> limit(x^2/exp(x),inf) ans = 0(3) >> limit((tan(x)-sin(8))/x^3) ans =NaN(4) >> limit(x^x,x,0,'right') ans =1(5) >> limit(log(cot(x))/log(x),x,0,'right') ans =-1(6) >> limit(x^2*log(x),x,0,'right') ans =0(7) >> limit((sin(x)-x.*cos(x))./(x.^2.*sin(x)),x,0) ans =1/3(8) >> limit((3*x.^3-2*x.^2+5)/(5*x.^3+2*+1),x,inf) ans =3/5(9) >> limit((exp(x)-exp(-x)-2*x)./(x-sin(x))) ans =2(10) >> limit((sin(x)/x).^(1/(1-cos(x)))) ans =exp(-1/3)实验3 导数（基础实验）实验目的深入理解导数与微分的概念, 导数的几何意义. 掌握用Matlab 求导数与高阶导数的方法. 深入理解和掌握求隐函数的导数, 以及求由参数方程定义的函数的导数的方法. 导数概念与导数的几何意义22作函数71232)(23+-+=x x x x f 的图形和在1-=x 处的切线. 解：作函数71232)(23+-+=x x x x f 的图形程序代码： >> syms x;>> y=2*x^3+3*x^2-12*x+7; >> diff(y) ans =6*x^2+6*x-12 >> syms x;y=2*x^3+3*x^2-12*x+7; >> f=diff(y) f =6*x^2+6*x-12 >> x=-1;f1=6*x^2+6*x-12 f1 = -12>> f2=2*x^3+3*x^2-12*x+7 f2 = 20>> x=linspace(-10,10,1000);y1=2*x.^3+3*x.^2-12*x+7; y2=-12*(x+1)+20; plot(x,y1,'r',x,y2,'g')求函数的导数与微分24求函数bx ax x f cos sin )(=的一阶导数. 并求.1⎪⎭⎫⎝⎛+'b a f解：求函数bx ax x f cos sin )(=的一阶导数程序代码： >> syms a b x y;y= sin(a*x)*cos(b*x); D1=diff(y,x,1) 答案：D1 =cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b求.1⎪⎭⎫ ⎝⎛+'b a f程序代码： >> x=1/(a+b);>> cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b 答案：ans =cos(a/(a+b))*a*cos(b/(a+b))-sin(a/(a+b))*sin(b/(a+b))*b 拉格朗日中值定理26对函数),2)(1()(--=x x x x f 观察罗尔定理的几何意义. (1) 画出)(x f y =与)(x f '的图形, 并求出1x 与.2x 解：程序代码：>> syms x;f=x*(x-1)*(x-2); f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-10,10,1000); y1=x.*(x-1).*(x-2);y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); plot(x,y1,x,y2)(2)画出)(x f y 及其在点))(,(11x f x 与))(,(22x f x 处的切线. 程序代码：>> syms x; >> f=x*(x-1)*(x-2); >> f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-3,3,1000); >> y1=x.*(x-1).*(x-2);>> y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); >> plot(x,y1,x,y2) >> hold on>> x=1+1/3*3^(1/2); >> yx1=x*(x-1)*(x-2) yx1 =-0.3849>> x=1-1/3*3^(1/2); >> yx2=x*(x-1)*(x-2) yx2 =0.3849x=linspace(-3,3,1000); yx1 =-0.3849*x.^0; yx2 =0.3849*x.^0; plot(x,yx1,x,yx2)28求下列函数的导数:(1) 31+=x e y ; 解：程序代码：>> syms x y; y=exp((x+1)^3); D1=diff(y,1) 答案：D1 =3*(x+1)^2*exp((x+1)^3)(2) )]42ln[tan(π+=x y ;解：程序代码：>> syms x;y=log(tan(x/2+pi/4)); D1=diff(y,1) 答案：D1 =(1/2+1/2*tan(1/2*x+1/4*pi)^2)/tan(1/2*x+1/4*pi)(3) x x y sin ln cot 212+=;解：程序代码：>> syms x;y=1/2*(cot(x))^2+log(sin(x)); D1=diff(y,1) 答案：D1 =cot(x)*(-1-cot(x)^2)+cos(x)/sin(x) (4) xy 2arctan21=. 解：程序代码：>> syms x;>> y=sqrt(2)*atan(sqrt(2)/x); >> D1=diff(y,1) 答案：D1 =-2/x^2/(1+2/x^2)一元函数积分学与空间图形的画法实验4 一元函数积分学(基础实验)实验目的掌握用Matlab 计算不定积分与定积分的方法. 通过作图和观察, 深入理解定积分的概念和思想方法. 初步了解定积分的近似计算方法. 理解变上限积分的概念. 提高应用定积分解决各种问题的能力.不定积分计算30求.)1(532⎰-dx x x解：程序代码：>> syms x y;>> y=x^2*(1-x^3)^5; >> R=int(y,x) 答案：R =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^332求.arctan 2⎰xdx x解：程序代码：>> syms x y;>> y=x^2*atan(x); >> R=int(y,x) 答案：R =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1)定积分计算34 求.)(102⎰-dx x x解：程序代码：>> syms x y; >> y=x-x^2;>> R=int(y,x,0,1) 答案： R =1/6变上限积分 36 画出变上限函数⎰x dt t t 02sin 及其导函数的图形.解：程序代码：>> syms x y t; >> y=t*sin(t^2); >> R=int(y,x,0,x) 答案：R =t*sin(t^2)*x 再求导函数程序代码：>> DR=diff(R,x,1) 答案：DR =t*sin(t^2)实验5 空间图形的画法(基础实验)实验目的掌握用Matlab 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.一般二元函数作图38作出函数2214y x z ++=的图形.解：程序代码：>> x=linspace(-5,5,500); [x,y]=meshgrid(x); z=4./(1+x.^2+y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')40作出函数)94cos(22y x z +=的图形. 解：程序代码：>> x=-10:0.1:10;[x,y]=meshgrid(x);z=cos(4*x.^2+9*y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')讨论：坐标轴选取范围不同时，图形差异很大，对本题尤为明显，如右图为坐标轴[-1，1]二次曲面42作出单叶双曲面1941222=-+z y x 的图形.(曲面的参数方程为 ,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u ))解：程序代码：>> v=0:pi/100:2*pi; >> u=-pi/2:pi/100:pi/2; >> [U,V]=meshgrid(u,v); >> x=sec(U).*sin(V); >> y=2*sec(U).*cos(V); >> z=3*tan(U); >> surf(x,y,z)44 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.解：程序代码：>> x=-2:0.01:2;[x,y]=meshgrid(x); >> z=x.*y;>> mesh(x,y,z);46 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π 的图形.解：程序代码：>> v=0.001:0.001:2; >> u=0:pi/100:4*pi;>> [U,V]=meshgrid(u,v); >> x=cos(U).*sin(V); >> y=sin(U).*sin(V);>> z=cos(V)+log(tan(V/2)+U/5); >> mesh(x,y,z);空间曲线48 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 解：程序代码：>> syms t;ezplot3(t*cos(t),t*sin(t),2*t,[0,6*pi])-1010-20-100100xx = t cos(t), y = t sin(t), z = 2 tz50绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.解：程序代码：>> t=-2*pi:pi/100:2*pi;x=cos(t).*cos(t);y=1./(1+2*t);z=atan(t); plot3(x,y,z);grid;xlabel('x'),ylabel('y'),zlabel('z')xyz多元函数微积分实验6 多元函数微分学（基础实验）实验目的掌握利用Matlab 计算多元函数偏导数和全微分的方法, 掌握计算二元函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元函数的性质、方向导数、梯度和等高线的概念.求多元函数的偏导数与全微分52设),(cos )sin(2xy xy z +=求.,,,222yx zx z y z x z ∂∂∂∂∂∂∂∂∂解：程序代码：>> syms x y;S=sin(x*y)+(cos(x*y))^2; D1=diff(S,'x',1); D2=diff(S,'y',1); D3=diff(S,'x',2); D4=diff(S,'y',2); D1,D2,D3,D4答案： D1 = cos(x*y)*y-2*cos(x*y)*sin(x*y)*yD2 = cos(x*y)*x-2*cos(x*y)*sin(x*y)*xD3 =-sin(x*y)*y^2+2*sin(x*y)^2*y^2-2*cos(x*y)^2*y^2 D4 = -sin(x*y)*x^2+2*sin(x*y)^2*x^2-2*cos(x*y)^2*x^2实验7 多元函数积分学（基础实验）实验目的掌握用Matlab 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.计算重积分54计算,2dxdy xyD⎰⎰ 其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.解：程序代码：>> syms x y;int(int(x*y^2,x,2-y,sqrt(y)),y,1,2) 答案：ans =193/120 重积分的应用56求旋转抛物面224y x z --=在Oxy 平面上部的面积.S 解：程序代码：>> int(2*pi*r,r,0,2) 答案： ans =4*pi无穷级数与微分方程实验8 无穷级数（基础实验）实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近. 掌握用Matlab 求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法.数项级数58(1) 观察级数∑∞=121n n的部分和序列的变化趋势.解：程序代码：for i=1:100 s=0; for n=1:i s=s+1/n^2; endplot(i,s,'.');hold on; end(2) 观察级数∑∞=11n n 的部分和序列的变化趋势.>> for i=1:100 s=0; for n=1:i s=s+1/n; endplot(i,s,'.'); hold on; end60 求∑∞=++123841n n n的值.解：程序代码：>> syms n;score=symsum(1/(4*n^2+8*n+3),1,inf) 答案： score =1/6函数的幂级数展开62求x arctan 的5阶泰勒展开式. >> syms x;>> T5=taylor(atan(x),6)答案：T5 =x-1/3*x^3+1/5*x^5实验9 微分方程（基础实验）实验目的理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用 Matlab 求微分方程及方程组解的常用命令和方法.求解微分方程64求微分方程 22x xe xy y -=+'的通解. 解：程序代码：>> y=dsolve('Dy+2*x*y=x*exp(-x^2)','x') 答案：y =(1/2*x^2+C1)*exp(-x^2)66求微分方程x e y y y x 2cos 52=+'-''的通解. 解：程序代码：>> y=dsolve('D2y-2*Dy+5*y=exp(x)*cos(2*x)','x') 答案： y =exp(x)*sin(2*x)*C2+exp(x)*cos(2*x)*C1+1/4*exp(x)*sin(2*x)*x68求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dxt 在初始条件0,100====t t y x 下的特解.解：程序代码：>> [x,y]=dsolve('Dx+x+2*y-exp(t)','Dy-x-y','x(0)=1','y(0)=0','t') 答案： x = cos(t)y = 1/2*sin(t)-1/2*cos(t)+1/2*exp(t)70求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 解：程序代码：>> syms x yy=dsolve('Dy-2*y/(x+1)-(x+1)^(5/2)','x') 答案：y =(2/3*(x+1)^(3/2)+C1)*(x+1)^2 做积分曲线由>> syms x yx=linspace(-5,5,100); C=input('请输入C 的值:'); y=(2/3*(x+1).^(3/2)+C).*(x+1).^2; plot(x,y)例如对应有：请输入C 的值:2 请输入C 的值:20矩阵运算与方程组求解实验10 行列式与矩阵实验目的掌握矩阵的输入方法. 掌握利用Matlab 对矩阵进行转置、加、减、数乘、相乘、乘方等运算, 并能求矩阵的逆矩阵和计算方阵的行列式.矩阵A 的转置函数Transpose[A]72 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛411365243271的转置. 解：程序代码：>> A=[1,7,2;3,4,2;5,6,3;1,1,4]; >> Sove=A' 答案：Sove =1 3 5 1 7 4 6 12 234 矩阵线性运算 73设,291724,624543⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=B A 求.24,A B B A -+ 解：程序代码：>> A=[3,4,5;4,2,6]; B=[4,2,7;1,9,2];S1=A+BS2=4*B-2*A答案：S1 =7 6 125 11 8S2 =10 0 18-4 32 -474设,148530291724,36242543⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=mb ma 求矩阵ma 与mb 的乘积. 解：程序代码：>> ma=[3,4,5,2;4,2,6,3];>> mb=[4,2,7;1,9,2;0,3,5;8,4,1];>> Sove=ma*mb答案：Sove =32 65 5642 56 65矩阵的乘法运算 75设,101,530291724⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A 求AB 与,A B T 并求.3A解：程序代码：>> A=[4 2 7;1 9 2;0 3 5];B=[1;0;1];>> AB=A*BAB =1135>> BTA=B'*ABTA =4 5 12>> A3=A^3A3 =119 660 555141 932 44454 477 260求方阵的逆76 设,5123641033252312⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A 求.1-A 解：程序代码：>> A=[2,1,3,2;5,2,3,3;0,1,4,6;3,2,1,5];Y=inv(A)答案：Y =-1.7500 1.3125 0.5000 -0.68755.5000 -3.6250 -2.0000 2.37500.5000 -0.1250 0.0000 -0.1250-1.2500 0.6875 0.5000 -0.312577 设,221331317230,5121435133124403⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=B A 求.1B A - 解：程序代码：>> A=[3 0 4 4 ;2 1 3 3 ;1 5 3 4;1 2 1 5];B=[0 3 2 ;7 1 3;1 3 3 ;1 2 2];Solve=A'*B答案：Solve =16 16 1714 20 2225 26 2830 37 3978 解方程组⎪⎩⎪⎨⎧-=-+=+-=++.2442,63,723z y x z y x z y x解：程序代码：>> A=[3 2 1;1 -1 3;2 4 -4];b=[7 6 -2];>> A\b'答案：ans =1.00001.00002.0000求方阵的行列式79 求行列式 .3351110243152113------=D 解：程序代码：>> A=[3,1,-1,2;-5,1,3,-4;2,0,1,-1;1,-5,3,-3];D=det(A)答案：D =4080求.11111111111122222222d d d d c c c c b b b b a a a a D ++++= 解：程序代码：>> syms a b c d;D=[a^2+1/a^2 a 1/a 1;b^2+1/b^2 b 1/b 1;c^2+1/c^2 c 1/c 1;d^2+1/d^2 d 1/d 1];det(D)答案：ans =-(-c*d^2*b^3+c^2*d*b^3-c^3*d^2*a+c^3*d*a^2*b^4+c*d^2*a^3-c^3*d^2*a*b^4-c^2*d*a^3-c*d^2*b^3*a^4+c^2*d*b^3*a^4+c^3*d^2*b*a^4-c^3*d*b^2*a^4-c^2*d^3*b*a^4+c*d^3*b^2*a^4+c*d ^2*a^3*b^4-c^2*d*a^3*b^4+c^3*d^2*b-c^3*d*b^2-c^2*d^3*b+c*d^3*b^2+c^3*d*a^2+c^2*d^3*a-c *d^3*a^2-b*d^2*a^3+b^2*d*a^3+b^3*d^2*a-b^3*d*a^2-b^2*d^3*a+b*d^3*a^2+b*c^2*a^3-b^2*c*a ^3-b^3*c^2*a+b^3*c*a^2+b^2*c^3*a-b*c^3*a^2+c^2*d^3*a*b^4-c*d^3*a^2*b^4-b*d^2*a^3*c^4+b ^2*d*a^3*c^4+b^3*d^2*a*c^4-b^3*d*a^2*c^4-b^2*d^3*a*c^4+b*d^3*a^2*c^4+b*c^2*a^3*d^4-b^2*c*a^3*d^4-b^3*c^2*a*d^4+b^3*c*a^2*d^4+b^2*c^3*a*d^4-b*c^3*a^2*d^4)/a^2/c^2/d^2/b^281 计算范德蒙行列式.1111145444342413534333231252423222154321x x x x x x x x x x x x x x x x x x x x 解：程序代码：>> syms x1 x2 x3 x4 x5; >> A=[1,1,1,1,1;x1,x2,x3,x4,x5;x1^2,x2^2,x3^2,x4^2,x5^2;x1^3,x2^3,x3^3,x4^3,x5^3;x1^4,x2^4,x3^4,x4^4,x5^4];>> DC=det(A);>> DS=simple(DC)答案：DS =(-x5+x4)*(x3-x5)*(x3-x4)*(-x5+x2)*(x2-x4)*(x2-x3)*(-x5+x1)*(x1-x4)*(x1-x3)*(x1-x2)82 设矩阵 ,60975738723965110249746273⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=A 求.),(|,|3A A tr A 解：程序代码：>> A=[3,7,2,6,-4;7,9,4,2,0;11,5,-6,9,3;2,7,-8,3,7;5,7,9,0,-6];>> D=det(A),T=trace(A),A3=A^3答案：D =11592T =3A3=726 2062 944 294 -3581848 3150 26 1516 2281713 2218 31 1006 4041743 984 -451 1222 384801 2666 477 745 -125向量的内积83 求向量}3,2,1{=u 与}0,1,1{-=v 的内积.解：程序代码：>> u=[1 2 3];v=[1 -1 0];solve=dot(u,v)答案：solve =-184设,001001⎪⎪⎪⎭⎫⎝⎛=λλλA 求.10A 一般地?=k A (k 是正整数).解：程序代码：>> syms r;>> A=[r,1,0;0,r,1;0,0,r];>> A^10答案：ans =[ r^10, 10*r^9, 45*r^8][ 0, r^10, 10*r^9][ 0, 0, r^10]85.求⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+++++a a a a a 1111111111111111111111111的逆.解：程序代码：>> syms aA=[1+a,1,1,1,1;1,1+a,1,1,1;1,1,1+a,1,1;1,1,1,1+a,1;1,1,1,1,1+a];solve=inv(A)答案：solve =[ 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5),-1/a/(a+5)] [ -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5),-1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5)] 实验11 矩阵的秩与向量组的极大无关组实验目的学习利用Matlab 求矩阵的秩,作矩阵的初等行变换; 求向量组的秩与极大无关组. 求矩阵的秩86 设,815073*********⎪⎪⎪⎭⎫ ⎝⎛-------=M 求矩阵M 的秩.解：程序代码：>> M=[3,2,-1,-3,-2;2,-1,3,1,-3;7,0,5,-1,-8];R=rank(M)答案：R=2向量组的秩87求向量组)0,3,0,2(),2,5,4,0(),1,1,2,1(231=--=-=ααα的秩.解：程序代码：>> A=[1,2,-1,1;0,-4,5,-2;2,0,3,0];R=rank(A)答案：R =288向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关?解：由>> A=[1 1 2 3;1 -1 1 1;1 3 4 5;3 1 5 7];rank(A)ans = 3即rank(A)=3 小于阶数489向量组)3,1,1(),2,1,3(),7,2,2(321=-==ααα是否线性相关?解：由>> A3=[2,2,7;3,-1,2;1,1,3];R=rank(A3)得 R = 3即rank(A3)=3 等于阶数3故向量组线性无关。

大学数学matlab实验作业1

重庆大学学生实验报告实验课程名称数学实验开课实验室学院年级专业班学生姓名学号开课时间至学年第学期数理学院制开课学院、实验室：实验时间：年月日2）比较函数33)(,)(,)(xxhxxxgxxf=+==在x→0时函数的性态。

观察到什么现象？从观察到的现象，反映了什么结论。

程序：x=-1:0.0001:1;y1=x;y2=x.^3;y3=y1+y2;plot(x,y1,x,y2,x,y3)结果：结论：当x→0时，f(x)与g(x)很接近，而h(x)与前两个函数都不接近。

3）比较函数33)(,)(,)(xxhxxxgxxf=+==在x→∞时函数的性态。

程序如下所示：x=linspace(-100000,100000,30); y1=x;y2=x+x.^3;y3=x.^3;subplot(2,2,1),plot(x,y1),title('f(x)=x'),xlabel('x');ylabel('f(x)'); grid; subplot(2,2,2),plot(x,y2),title('g(x)=x+x^3'),xlabel('x');ylabel('g(x)'); grid;subplot(2,2,3),plot(x,y3),title('h(x)=x^3'),xlabel('x');ylabel('h(x)');grid ；结果：4）在日常生活中我们有这样的经验：与幂函数相比，指数函数是急脾气，对数函数是慢性子。

这就是说，当x→∞时，再小的指数函数也比幂函数变化快，再大的对数函数也比幂函数变化慢。

当x→∞时,比较10xy=与xy1.1=的大小.当x→∞时,比较001.0xy=与xy lg1000=的大小.程序如下所示：x=linspace(5000,8000,500);y1=x.^10;y2=1.1.^x;Subplot(1,2,1),plot(x,y1),xlabel('x');ylabel('y)'); grid; title('y=x^1^0');Subplot(1,2,2),plot(x,y2),xlabel('x');ylabel('y)'); grid; title('y=1.1^x');结果：从上图可以看出来指数函数变化快程序如下所示：x=linspace(5000,8000,500);y1=x.^0.001;y2=1000.*log(x);Subplot(1,2,1),plot(x,y1),xlabel('x');ylabel('y)'); grid; title('y=x^0.001');Subplot(1,2,2),plot(x,y2),xlabel('x');ylabel('y)'); grid; title('y=1000.*log(x)');结果：分析：由以上函数图形可知对数函数变化比幂函数慢。

MATLAB数学实验100例题解

一元函数微分学实验1 一元函数的图形（基础实验）实验目的通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧.初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势. 解：程序代码：>> x=linspace(0,2*pi,600); t=sin(x)./(cos(x)+eps);plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]); 图象：程序代码：>> x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps);plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]); 图象：4在区间]1,1[-画出函数xy 1sin =的图形. 解：程序代码：>> x=linspace(-1,1,10000);y=sin(1./x); plot(x,y);axis([-1,1,-2,2]) 图象：二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形：解：程序代码：>> t=linspace(0,2*pi,100);plot(cos(t).*cos(5*t),sin(t).*cos(3*t)); 图象：极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解：程序代码：>> t=0:0.01:2*pi; r=exp(t/10);polar(log(t+eps),log(r+eps)); 图象：90270分段函数作图10 作出符号函数x y sgn =的图形. 解：程序代码：>> x=linspace(-100,100,10000); y=sign(x); plot(x,y);axis([-100 100 -2 2]);函数性质的研究12研究函数)3(log 3)(35x e x x f x -++=在区间]2,2[-上图形的特征. 解：程序代码：>> x=linspace(-2,2,10000);y=x.^5+3*exp(x)+log(3-x)/log(3); plot(x,y); 图象：实验2 极限与连续（基础实验）实验目的通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用 Matlab 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形特征,理解闭区间上连续函数的几个重要性质.作散点图14分别画出坐标为)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图, 并画出折线图. 解：散点图程序代码： >> i=1:10; plot(i,i.^2,'.')或：>> x=1:10;y=x.^2;for i=1:10;plot(x(i),y(i),'r')hold onend折线图程序代码：>> i=1:10;plot(i,i.^2,'-x')程序代码：>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'.')>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'-x')数列极限的概念16通过动画观察当∞→n 时数列21n a n =的变化趋势.解：程序代码： >> n=1:100; an=(n.^2); n=1:100; an=1./(n.^2); n=1:100; an=1./(n.^2); for i=1:100plot(n(1:i),an(1:i)),axis([0,100,0,1]) pause(0.1) end 图象：函数的极限18在区间]4,4[-上作出函数xx xx x f --=339)(的图形, 并研究 )(lim x f x ∞→ 和 ).(lim 1x f x →解：作出函数x x xx x f --=339)(在区间]4,4[-上的图形 >> x=-4:0.01:4;y=(x.^3-9*x)./(x.^3-x+eps); plot(x,y)从图上看，()f x 在x →1与x →∞时极限为0两个重要极限 20计算极限⎪⎭⎫⎝⎛+→x x x x x sin 11sin lim )1(0 x x e x 2lim )2(+∞→30sin tan lim )3(xx x x -→ x x x 0lim )4(+→ x xx ln cot ln lim )5(0+→ x x x ln lim )6(20+→ xx xx x x sin cos sin lim)7(20-→ 125523lim )8(323+++-∞→x x x x x xx x e e x x x sin 2lim )9(0----→ xx x x cos 110sin lim )10(-→⎪⎭⎫ ⎝⎛ 解：（1）>> limit(x*sin(1/x)+1/x*sin(x))ans =1(2) >> limit(x^2/exp(x),inf) ans = 0(3) >> limit((tan(x)-sin(8))/x^3) ans =NaN(4) >> limit(x^x,x,0,'right') ans =1(5) >> limit(log(cot(x))/log(x),x,0,'right') ans =-1(6) >> limit(x^2*log(x),x,0,'right') ans =0(7) >> limit((sin(x)-x.*cos(x))./(x.^2.*sin(x)),x,0) ans =1/3(8) >> limit((3*x.^3-2*x.^2+5)/(5*x.^3+2*+1),x,inf) ans =3/5(9) >> limit((exp(x)-exp(-x)-2*x)./(x-sin(x))) ans =2(10) >> limit((sin(x)/x).^(1/(1-cos(x)))) ans =exp(-1/3)实验3 导数（基础实验）实验目的深入理解导数与微分的概念, 导数的几何意义. 掌握用Matlab 求导数与高阶导数的方法. 深入理解和掌握求隐函数的导数, 以及求由参数方程定义的函数的导数的方法. 导数概念与导数的几何意义22作函数71232)(23+-+=x x x x f 的图形和在1-=x 处的切线. 解：作函数71232)(23+-+=x x x x f 的图形程序代码： >> syms x;>> y=2*x^3+3*x^2-12*x+7; >> diff(y) ans =6*x^2+6*x-12 >> syms x;y=2*x^3+3*x^2-12*x+7; >> f=diff(y) f =6*x^2+6*x-12 >> x=-1;f1=6*x^2+6*x-12 f1 = -12>> f2=2*x^3+3*x^2-12*x+7 f2 = 20>> x=linspace(-10,10,1000);y1=2*x.^3+3*x.^2-12*x+7; y2=-12*(x+1)+20; plot(x,y1,'r',x,y2,'g')求函数的导数与微分24求函数bx ax x f cos sin )(=的一阶导数. 并求.1⎪⎭⎫⎝⎛+'b a f解：求函数bx ax x f cos sin )(=的一阶导数程序代码： >> syms a b x y;y= sin(a*x)*cos(b*x); D1=diff(y,x,1) 答案：D1 =cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b求.1⎪⎭⎫ ⎝⎛+'b a f程序代码： >> x=1/(a+b);>> cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b 答案：ans =cos(a/(a+b))*a*cos(b/(a+b))-sin(a/(a+b))*sin(b/(a+b))*b 拉格朗日中值定理26对函数),2)(1()(--=x x x x f 观察罗尔定理的几何意义. (1) 画出)(x f y =与)(x f '的图形, 并求出1x 与.2x 解：程序代码：>> syms x;f=x*(x-1)*(x-2); f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-10,10,1000); y1=x.*(x-1).*(x-2);y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); plot(x,y1,x,y2)(2)画出)(x f y 及其在点))(,(11x f x 与))(,(22x f x 处的切线. 程序代码：>> syms x; >> f=x*(x-1)*(x-2); >> f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-3,3,1000); >> y1=x.*(x-1).*(x-2);>> y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); >> plot(x,y1,x,y2) >> hold on>> x=1+1/3*3^(1/2); >> yx1=x*(x-1)*(x-2) yx1 =-0.3849>> x=1-1/3*3^(1/2); >> yx2=x*(x-1)*(x-2) yx2 =0.3849x=linspace(-3,3,1000); yx1 =-0.3849*x.^0; yx2 =0.3849*x.^0; plot(x,yx1,x,yx2)28求下列函数的导数:(1) 31+=x e y ; 解：程序代码：>> syms x y; y=exp((x+1)^3); D1=diff(y,1) 答案：D1 =3*(x+1)^2*exp((x+1)^3)(2) )]42ln[tan(π+=x y ;解：程序代码：>> syms x;y=log(tan(x/2+pi/4)); D1=diff(y,1) 答案：D1 =(1/2+1/2*tan(1/2*x+1/4*pi)^2)/tan(1/2*x+1/4*pi)(3) x x y sin ln cot 212+=;解：程序代码：>> syms x;y=1/2*(cot(x))^2+log(sin(x)); D1=diff(y,1) 答案：D1 =cot(x)*(-1-cot(x)^2)+cos(x)/sin(x) (4) xy 2arctan21=. 解：程序代码：>> syms x;>> y=sqrt(2)*atan(sqrt(2)/x); >> D1=diff(y,1) 答案：D1 =-2/x^2/(1+2/x^2)一元函数积分学与空间图形的画法实验4 一元函数积分学(基础实验)实验目的掌握用Matlab 计算不定积分与定积分的方法. 通过作图和观察, 深入理解定积分的概念和思想方法. 初步了解定积分的近似计算方法. 理解变上限积分的概念. 提高应用定积分解决各种问题的能力.不定积分计算30求.)1(532⎰-dx x x解：程序代码：>> syms x y;>> y=x^2*(1-x^3)^5; >> R=int(y,x) 答案：R =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^332求.arctan 2⎰xdx x解：程序代码：>> syms x y;>> y=x^2*atan(x); >> R=int(y,x) 答案：R =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1)定积分计算34 求.)(102⎰-dx x x解：程序代码：>> syms x y; >> y=x-x^2;>> R=int(y,x,0,1) 答案： R =1/6变上限积分 36 画出变上限函数⎰x dt t t 02sin 及其导函数的图形.解：程序代码：>> syms x y t; >> y=t*sin(t^2); >> R=int(y,x,0,x) 答案：R =t*sin(t^2)*x 再求导函数程序代码：>> DR=diff(R,x,1) 答案：DR =t*sin(t^2)实验5 空间图形的画法(基础实验)实验目的掌握用Matlab 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.一般二元函数作图38作出函数2214y x z ++=的图形.解：程序代码：>> x=linspace(-5,5,500); [x,y]=meshgrid(x); z=4./(1+x.^2+y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')40作出函数)94cos(22y x z +=的图形. 解：程序代码：>> x=-10:0.1:10;[x,y]=meshgrid(x);z=cos(4*x.^2+9*y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')讨论：坐标轴选取范围不同时，图形差异很大，对本题尤为明显，如右图为坐标轴[-1，1]二次曲面42作出单叶双曲面1941222=-+z y x 的图形.(曲面的参数方程为 ,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u ))解：程序代码：>> v=0:pi/100:2*pi; >> u=-pi/2:pi/100:pi/2; >> [U,V]=meshgrid(u,v); >> x=sec(U).*sin(V); >> y=2*sec(U).*cos(V); >> z=3*tan(U); >> surf(x,y,z)44 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.解：程序代码：>> x=-2:0.01:2;[x,y]=meshgrid(x); >> z=x.*y;>> mesh(x,y,z);46 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π 的图形.解：程序代码：>> v=0.001:0.001:2; >> u=0:pi/100:4*pi;>> [U,V]=meshgrid(u,v); >> x=cos(U).*sin(V); >> y=sin(U).*sin(V);>> z=cos(V)+log(tan(V/2)+U/5); >> mesh(x,y,z);空间曲线48 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 解：程序代码：>> syms t;ezplot3(t*cos(t),t*sin(t),2*t,[0,6*pi])-1010-20-100100xx = t cos(t), y = t sin(t), z = 2 tz50绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.解：程序代码：>> t=-2*pi:pi/100:2*pi;x=cos(t).*cos(t);y=1./(1+2*t);z=atan(t); plot3(x,y,z);grid;xlabel('x'),ylabel('y'),zlabel('z')xyz多元函数微积分实验6 多元函数微分学（基础实验）实验目的掌握利用Matlab 计算多元函数偏导数和全微分的方法, 掌握计算二元函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元函数的性质、方向导数、梯度和等高线的概念.求多元函数的偏导数与全微分52设),(cos )sin(2xy xy z +=求.,,,222yx zx z y z x z ∂∂∂∂∂∂∂∂∂解：程序代码：>> syms x y;S=sin(x*y)+(cos(x*y))^2; D1=diff(S,'x',1); D2=diff(S,'y',1); D3=diff(S,'x',2); D4=diff(S,'y',2); D1,D2,D3,D4答案： D1 = cos(x*y)*y-2*cos(x*y)*sin(x*y)*yD2 = cos(x*y)*x-2*cos(x*y)*sin(x*y)*xD3 =-sin(x*y)*y^2+2*sin(x*y)^2*y^2-2*cos(x*y)^2*y^2 D4 = -sin(x*y)*x^2+2*sin(x*y)^2*x^2-2*cos(x*y)^2*x^2实验7 多元函数积分学（基础实验）实验目的掌握用Matlab 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.计算重积分54计算,2dxdy xyD⎰⎰ 其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.解：程序代码：>> syms x y;int(int(x*y^2,x,2-y,sqrt(y)),y,1,2) 答案：ans =193/120 重积分的应用56求旋转抛物面224y x z --=在Oxy 平面上部的面积.S 解：程序代码：>> int(2*pi*r,r,0,2) 答案： ans =4*pi无穷级数与微分方程实验8 无穷级数（基础实验）实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近. 掌握用Matlab 求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法.数项级数58(1) 观察级数∑∞=121n n的部分和序列的变化趋势.解：程序代码：for i=1:100 s=0; for n=1:i s=s+1/n^2; endplot(i,s,'.');hold on; end(2) 观察级数∑∞=11n n 的部分和序列的变化趋势.>> for i=1:100 s=0; for n=1:i s=s+1/n; endplot(i,s,'.'); hold on; end60 求∑∞=++123841n n n的值.解：程序代码：>> syms n;score=symsum(1/(4*n^2+8*n+3),1,inf) 答案： score =1/6函数的幂级数展开62求x arctan 的5阶泰勒展开式. >> syms x;>> T5=taylor(atan(x),6)答案：T5 =x-1/3*x^3+1/5*x^5实验9 微分方程（基础实验）实验目的理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用 Matlab 求微分方程及方程组解的常用命令和方法.求解微分方程64求微分方程 22x xe xy y -=+'的通解. 解：程序代码：>> y=dsolve('Dy+2*x*y=x*exp(-x^2)','x') 答案：y =(1/2*x^2+C1)*exp(-x^2)66求微分方程x e y y y x 2cos 52=+'-''的通解. 解：程序代码：>> y=dsolve('D2y-2*Dy+5*y=exp(x)*cos(2*x)','x') 答案： y =exp(x)*sin(2*x)*C2+exp(x)*cos(2*x)*C1+1/4*exp(x)*sin(2*x)*x68求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dxt 在初始条件0,100====t t y x 下的特解.解：程序代码：>> [x,y]=dsolve('Dx+x+2*y-exp(t)','Dy-x-y','x(0)=1','y(0)=0','t') 答案： x = cos(t)y = 1/2*sin(t)-1/2*cos(t)+1/2*exp(t)70求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 解：程序代码：>> syms x yy=dsolve('Dy-2*y/(x+1)-(x+1)^(5/2)','x') 答案：y =(2/3*(x+1)^(3/2)+C1)*(x+1)^2 做积分曲线由>> syms x yx=linspace(-5,5,100); C=input('请输入C 的值:'); y=(2/3*(x+1).^(3/2)+C).*(x+1).^2; plot(x,y)例如对应有：请输入C 的值:2 请输入C 的值:20矩阵运算与方程组求解实验10 行列式与矩阵实验目的掌握矩阵的输入方法. 掌握利用Matlab 对矩阵进行转置、加、减、数乘、相乘、乘方等运算, 并能求矩阵的逆矩阵和计算方阵的行列式.矩阵A 的转置函数Transpose[A]72 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛411365243271的转置. 解：程序代码：>> A=[1,7,2;3,4,2;5,6,3;1,1,4]; >> Sove=A' 答案：Sove =1 3 5 1 7 4 6 12 234 矩阵线性运算 73设,291724,624543⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=B A 求.24,A B B A -+ 解：程序代码：>> A=[3,4,5;4,2,6]; B=[4,2,7;1,9,2];S1=A+BS2=4*B-2*A答案：S1 =7 6 125 11 8S2 =10 0 18-4 32 -474设,148530291724,36242543⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=mb ma 求矩阵ma 与mb 的乘积. 解：程序代码：>> ma=[3,4,5,2;4,2,6,3];>> mb=[4,2,7;1,9,2;0,3,5;8,4,1];>> Sove=ma*mb答案：Sove =32 65 5642 56 65矩阵的乘法运算 75设,101,530291724⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A 求AB 与,A B T 并求.3A解：程序代码：>> A=[4 2 7;1 9 2;0 3 5];B=[1;0;1];>> AB=A*BAB =1135>> BTA=B'*ABTA =4 5 12>> A3=A^3A3 =119 660 555141 932 44454 477 260求方阵的逆76 设,5123641033252312⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A 求.1-A 解：程序代码：>> A=[2,1,3,2;5,2,3,3;0,1,4,6;3,2,1,5];Y=inv(A)答案：Y =-1.7500 1.3125 0.5000 -0.68755.5000 -3.6250 -2.0000 2.37500.5000 -0.1250 0.0000 -0.1250-1.2500 0.6875 0.5000 -0.312577 设,221331317230,5121435133124403⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=B A 求.1B A - 解：程序代码：>> A=[3 0 4 4 ;2 1 3 3 ;1 5 3 4;1 2 1 5];B=[0 3 2 ;7 1 3;1 3 3 ;1 2 2];Solve=A'*B答案：Solve =16 16 1714 20 2225 26 2830 37 3978 解方程组⎪⎩⎪⎨⎧-=-+=+-=++.2442,63,723z y x z y x z y x解：程序代码：>> A=[3 2 1;1 -1 3;2 4 -4];b=[7 6 -2];>> A\b'答案：ans =1.00001.00002.0000求方阵的行列式79 求行列式 .3351110243152113------=D 解：程序代码：>> A=[3,1,-1,2;-5,1,3,-4;2,0,1,-1;1,-5,3,-3];D=det(A)答案：D =4080求.11111111111122222222d d d d c c c c b b b b a a a a D ++++= 解：程序代码：>> syms a b c d;D=[a^2+1/a^2 a 1/a 1;b^2+1/b^2 b 1/b 1;c^2+1/c^2 c 1/c 1;d^2+1/d^2 d 1/d 1];det(D)答案：ans =-(-c*d^2*b^3+c^2*d*b^3-c^3*d^2*a+c^3*d*a^2*b^4+c*d^2*a^3-c^3*d^2*a*b^4-c^2*d*a^3-c*d^2*b^3*a^4+c^2*d*b^3*a^4+c^3*d^2*b*a^4-c^3*d*b^2*a^4-c^2*d^3*b*a^4+c*d^3*b^2*a^4+c*d ^2*a^3*b^4-c^2*d*a^3*b^4+c^3*d^2*b-c^3*d*b^2-c^2*d^3*b+c*d^3*b^2+c^3*d*a^2+c^2*d^3*a-c *d^3*a^2-b*d^2*a^3+b^2*d*a^3+b^3*d^2*a-b^3*d*a^2-b^2*d^3*a+b*d^3*a^2+b*c^2*a^3-b^2*c*a ^3-b^3*c^2*a+b^3*c*a^2+b^2*c^3*a-b*c^3*a^2+c^2*d^3*a*b^4-c*d^3*a^2*b^4-b*d^2*a^3*c^4+b ^2*d*a^3*c^4+b^3*d^2*a*c^4-b^3*d*a^2*c^4-b^2*d^3*a*c^4+b*d^3*a^2*c^4+b*c^2*a^3*d^4-b^2*c*a^3*d^4-b^3*c^2*a*d^4+b^3*c*a^2*d^4+b^2*c^3*a*d^4-b*c^3*a^2*d^4)/a^2/c^2/d^2/b^281 计算范德蒙行列式.1111145444342413534333231252423222154321x x x x x x x x x x x x x x x x x x x x 解：程序代码：>> syms x1 x2 x3 x4 x5; >> A=[1,1,1,1,1;x1,x2,x3,x4,x5;x1^2,x2^2,x3^2,x4^2,x5^2;x1^3,x2^3,x3^3,x4^3,x5^3;x1^4,x2^4,x3^4,x4^4,x5^4];>> DC=det(A);>> DS=simple(DC)答案：DS =(-x5+x4)*(x3-x5)*(x3-x4)*(-x5+x2)*(x2-x4)*(x2-x3)*(-x5+x1)*(x1-x4)*(x1-x3)*(x1-x2)82 设矩阵 ,60975738723965110249746273⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=A 求.),(|,|3A A tr A 解：程序代码：>> A=[3,7,2,6,-4;7,9,4,2,0;11,5,-6,9,3;2,7,-8,3,7;5,7,9,0,-6];>> D=det(A),T=trace(A),A3=A^3答案：D =11592T =3A3=726 2062 944 294 -3581848 3150 26 1516 2281713 2218 31 1006 4041743 984 -451 1222 384801 2666 477 745 -125向量的内积83 求向量}3,2,1{=u 与}0,1,1{-=v 的内积.解：程序代码：>> u=[1 2 3];v=[1 -1 0];solve=dot(u,v)答案：solve =-184设,001001⎪⎪⎪⎭⎫⎝⎛=λλλA 求.10A 一般地?=k A (k 是正整数).解：程序代码：>> syms r;>> A=[r,1,0;0,r,1;0,0,r];>> A^10答案：ans =[ r^10, 10*r^9, 45*r^8][ 0, r^10, 10*r^9][ 0, 0, r^10]85.求⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+++++a a a a a 1111111111111111111111111的逆.解：程序代码：>> syms aA=[1+a,1,1,1,1;1,1+a,1,1,1;1,1,1+a,1,1;1,1,1,1+a,1;1,1,1,1,1+a];solve=inv(A)答案：solve =[ 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5),-1/a/(a+5)] [ -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5),-1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5)] 实验11 矩阵的秩与向量组的极大无关组实验目的学习利用Matlab 求矩阵的秩,作矩阵的初等行变换; 求向量组的秩与极大无关组. 求矩阵的秩86 设,815073*********⎪⎪⎪⎭⎫ ⎝⎛-------=M 求矩阵M 的秩.解：程序代码：>> M=[3,2,-1,-3,-2;2,-1,3,1,-3;7,0,5,-1,-8];R=rank(M)答案：R=2向量组的秩87求向量组)0,3,0,2(),2,5,4,0(),1,1,2,1(231=--=-=ααα的秩.解：程序代码：>> A=[1,2,-1,1;0,-4,5,-2;2,0,3,0];R=rank(A)答案：R =288向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关?解：由>> A=[1 1 2 3;1 -1 1 1;1 3 4 5;3 1 5 7];rank(A)ans = 3即rank(A)=3 小于阶数489向量组)3,1,1(),2,1,3(),7,2,2(321=-==ααα是否线性相关?解：由>> A3=[2,2,7;3,-1,2;1,1,3];R=rank(A3)得 R = 3即rank(A3)=3 等于阶数3故向量组线性无关。

数学实验(matlab)样题及参考解答

东华大学高等数学实验试题A考试时间：90分钟（附参考解答）班级学号姓名得分上机考试说明：1. 开考前可将准备程序拷到硬盘, 开考后不允许用移动盘，也不允许上网；2. 领座考生试卷不同，开卷，可利用自己备用的书和其他资料，但不允许讨论，也不允许借用其他考生的书和资料。

3. 解答(指令行，答案等)全部用笔写在考卷上。

一、计算题（70分）要求：写出M 函数（如果需要的话）、MATLAB 指令和计算结果。

1．解线性方程组⎪⎪⎩⎪⎪⎨⎧-=+=+--=-+=-+14235231543421431321x x x x x x x x x x x 并求系数矩阵的行列式。

指令行：A=[5 1 –1 0;1 0 3 –1;-1 –1 0 5;0 0 2 4];b=[1;2;3;-1]; x=A\b,d=det(A) 结果：x 1=1.4, x 2= -5.9, x 3=0.1, x 4= -0.3. 行列式=70.2．设 f(x,y) = 4 sin (x 3y)，求 3,22==∂∂∂y x y x f 。

指令行：syms x y; f=diff(4*sin(x^3*y),x); f=diff(f,y); f=subs(f,x,2); f=subs(f,y,3)结果：1063.63．求方程 3x 4+4x 3-20x+5 = 0 的所有解。

指令行：roots([3 4 0 –20 5])结果：-1.5003 - 1.5470i, -1.5003 + 1.5470i, 1.4134, 0.25394．使用两种方法求积分dx e x 210221-⎰π的近似值。

方法一：指令行：syms x; s=int(1/sqrt(2*pi)*exp(-x^2/2),0,1); vpa(s,5)结果：0.34135方法二：指令行：x=0:0.01:1; y=1/sqrt(2*pi)*exp(-x.^2/2);trapz(x,y)结果：0.3413方法三：M 函数ex4fun.mfunction f=ex4fun(x)f=1/sqrt(2*pi)*exp(-x.^2/2);指令行：s=quadl(@ex4fun,0,1)结果：0.34135．求函数 f(x,y) = 3x 2+10y 2+3xy-3x +2y 在原点附近的一个极小值点和极小值。

MATELAB与数学实验第三次作业

《数学实验》报告实验名称 matlab作业 3 学院专业班级姓名学号2011年 10月一、【实验目的】学习编辑程序来绘制几何立体图等.二、【实验任务】（一）P79 习题5绘制圆锥螺线的图像并加各种标注，圆锥螺线的参数方程为x=tcos(π/6)ty=tsin(π/6)t， (0<=t<=20π)z=2t绘制由函数x^2/9+y^2/16+z^2/4=1形成的立体图，并通过改变观测点获得该图形在各个坐标平面上的投影。

画三维曲面z=5-x^2-y^2(-2<=x,y<=2)与平面z=3的交线.（二）P79 习题7用mesh与surf命令绘制三维曲面z=x^2+3y^2的图像，并使用不同的着色效果及光照效果。

（三）P79习题8绘制由函数x^2/9+y^2/16+z^2/4=1形成的立体图，并通过改变观测点获得该图形在各个坐标平面上的投影。

（四）P79习题9画三维曲面z=5-x^2-y^2(-2<=x,y<=2)与平面z=3的交线.【实验程序】（一）t=0:pi/50:20*pi;x=t.*cos((pi/6)*t);y=t.*sin((pi/6)*t);z=2*t;plot3(x,y,z)title('ÇúÏß4x^2+4y^2=z^2')xlabel('txÖá'),ylabel('tyÖá'),zlabel('tzÖá')（二）t=-5:0.1:5;[x,y]=meshgrid(t);z=x.^2+3*y^2;%meshÃüÁîsubplot(121);mesh(x,y,z);title('meshÃüÁî');shading flat;light('position',[0,0,10])%surfÃüÁîsubplot(1,2,2);surf(x,y,z);title('surfÃüÁî');shading faceted;light('position',[0,2,10])（三）a=3;b=4;c=2;[X,Y,Z]=ellipsoid(0,0,0,a,b,c,400);subplot(221),mesh(X,Y,Z)view(3)subplot(222),mesh(X,Y,Z)view(30,30)subplot(223),mesh(X,Y,Z)view(30,0)subplot(224),mesh(X,Y,Z)view(-120,30)axis equalaxis image(四)t=-2:0.1:2;[x,y]=meshgrid(t);z1=5-x.^2-y.^2;subplot(131)mesh(x,y,z1),title('z=5-x^2-y^2')z2=3*ones(size(x));subplot(132)mesh(x,y,z2),title('z=3')r0=abs(z1-z2)<=1;zz=r0.*z2;yy=r0.*y;xx=r0.*x;subplot(133),plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'x')三、【实验结果】（一）（二）（三）(四)【实验总结】学会使用关键字来绘制函数图象,包括加各种标注,画圆锥螺线,使用着色效果、光照效果,画椭球，并改变观测点获得不同坐标平面的投影，画曲面与平面的交线等。

清华大学MATLAB数学实验作业参考

数学实验内容及目的(作业参考)实验1 一元函数的图形实验目的１．学习 matlab一元函数绘图命令.２．进一步理解函数概念.实验内容１．学习matlab命令.matlab绘图命令比较多，我们选编一些常用命令，并简单说明其作用，这些命令的调用格式，可参阅例题及使用帮助help查找.表1.1 二维绘图函数表1.2 基本线型和颜色表1.3 二维绘图工具表1.4 axis 命令linspace 创建数组命令，调用格式为:x=linspace(x1，x2，n)，创建了x 1到x2之间有n 个数据的数组.funtool 函数工具，在matlab 指令窗键入funtool 可打开“函数计算器”图形用户界面.２．绘制函数图形举例. 例1.1.画出x y sin =的图形解:首先建立点的坐标，然后用plot 命令将这些点绘出并用直线连接起来，采用中学五点作图法，选取五点)0,0(、)1,2(π、)0,(π、)1,23(-π、)0,2(π.输入命令:x=[0，pi/2，pi ，3*pi/2，2*pi]；y=sin(x)；plot(x ，y) 这里分号表示该命令执行结果不显示.可以想象，随点数增加，图形越来越接近x y sin =的图象.例如，在0到π2之间取30个数据点，绘出的图形与x y sin =的图象已经非常接近了． x=linspace(0，2*pi ，30)；y=sin(x)；plot(x ，y) 也可以如下建立该图形.x=0:0.1:2*pi ；y=sin(x)；plot(x ，y) 还可以给图形加标记、格栅线. x=0:0.1:2*pi ； y=sin(x)；plot(x ，y ，’r—‘) title(‘正弦曲线’) xlabel(‘自变量 x’) ylabel(‘函数y=sinx’) text(5.5，0，’y=sinx’) grid 上述命令第三行选择了红色虚线，第四行给图加标题“正弦曲线”，第五行给x 轴加标题“自变量x ”，第六行给y 轴加标题“函数x y sin =”，第七行在点)0,5.5(处放置文本“x y sin =”，第八行给图形加格栅线.例1.2.画出xy 2=和xy )2/1(=的图象.解:输入命令:x=-4:0.1:4；y1=2.^x ；y2=(1/2).^x ；plot(x ，y1，x ，y2)； axis([-4，4，0，8])matlab 允许在一个图形中画多条曲线.plot(x1，y1，x2，y2，x3，y3)指令绘制)2(2),1(1x f y x f y ==等多条曲线.matlab 自动给这些曲线以不同颜色.例1.3.画出arctgx y =的图象. 解: 输入命令:x=-20:0.1:20；y=atan(x)；plot(x ，y ，[-20，20]，[pi/2，pi/2]，[-20，20]，[-pi/2，-pi/2]) grid从图上看，arctgx y =是有界函数，2π±=y 是其水平渐近线. 例1.4.在同一坐标系中画出tgx y x y x y ===,,sin 的图象.解:输入命令:x=-pi/2:0.1:pi/2；y1=sin(x)；y2=tan(x)； plot(x ，x ，x ，y1，x ，y2) axis equalaxis([-pi/2，pi/2，-3，3]) grid从图上看，当0>x 时，tgx x x <<sin ，当0<x 时，tgx x x >>sin ，x y =是x y sin =和tgx y =在原点的切线，因此，当1<<x 时，x tgx x x ≈≈,sin .例1.5.画出110-=xy 及)1lg(+=x y 的图形.解:输入命令:x1=-1:0.1:2；y1=10.^x1-1；x2=-0.99:0.1:2；y2=log10(x2+1)； plot(x1，y1，x2，y2)从图上看，这两条曲线与我们所知的图象相差很远，这是因为坐标轴长度单位不一样的缘故.110-=xy 与)1lg(+=x y 互为反函数，图象关于x y =对称，为更清楚看出这一点，我们再画出x y =的图象. hold onx=-1:0.01:2；y=x ；plot(x ，y ，’r’) axis([-1，2，-1，2]) axis square ；hold offplot 语句清除当前图形并绘出新图形，hold on 语句保持当前图形.例1.6.画出心形线)cos 1(3a r +=的图象. 解:输入命令:x=-2*pi:0.1:2*pi ；r=3*(1+cos(x))；polar(x ，r)例1.7.画出星形线t y t x 33sin 3,cos 3==的图象. 解:这是参数方程，可化为极坐标方程.233232)sin (cos 3a a r +=输入命令:x=0:0.01:2*pi ；r=3./(((cos(x)).^2).^(1/3)+((sin(x)).^2).^(1/3)).^(3/2)； polar(x ，r)注意，如果建立r 与t 的关系，此时t 只是参数，不是极坐标系下的极角.实验2 函数极限实验目的１．理解极限概念.２．掌握用matlab 软件求函数极限的方法.实验内容１．学习matlab 命令.matlab 求极限命令可列表如下:表2.1matlab 代数方程求解命令solve 调用格式. solve (函数)(x f ) 给出0)(=x f 的根.２．理解极限概念.数列}{n x 收敛或有极限是指当n 无限增大时，n x 与某常数无限接近或n x 趋向于某一定值，就图形而言，也就是其点列以某一平行与y 轴的直线为渐近线.例2.1.观察数列}1{+n n 当∞→n 时的变化趋势.解:输入命令:n=1:100；xn=n./(n+1)得到该数列的前100项，从这前100项看出，随n 的增大，1+n n与1非常接近，画出nx 的图形.stem(n ，xn) 或for i=1:100;plot(n(i),xn(i),’r’) hold on end其中for … end 语句是循环语句,循环体内的语句被执行100次,n(i)表示n 的第i 个分量.由图可看出，随n 的增大，点列与直线1=y 无限接近，因此可得结论:1lim+∞→n nn =１.对函数的极限概念，也可用上述方法理解.例2.2.分析函数x x x f 1sin )(=，当0→x 时的变化趋势. 解:画出函数)(x f 在]1,1[-上的图形.x=-1:0.01:1；y=x.*sin(1./x)；plot(x ，y)从图上看，x x 1sin 随着x 的减小，振幅越来越小趋近于0，频率越来越高作无限次振荡.作出x y ±=的图象.hold on ；plot(x ，x ，x ，-x)例2.3.分析函数x x f 1sin )(=当0→x 时的变化趋势. 解:输入命令:x=-1:0.01:1；y=sin(1./x)；plot(x ，y)从图上看，当0→x 时，x 1sin 在-1和1之间无限次振荡，极限不存在.仔细观察该图象，发现图象的某些峰值不是１和-１，而我们知道正弦曲线的峰值是１和-１，这是由于自变量的数据点选取未必使x 1sin 取到１和-１的缘故，读者可试增加数据点，比较它们的结果．例2.4.考察函数x xx f sin )(=当0→x 时的变化趋势. 解:输入命令:x=linspace(-2*pi ，2*pi ，100)；y=sin(x)./x ；plot(x ，y)从图上看，x xsin 在0=x 附近连续变化，其值与1无限接近，可见x xx sin lim 0→=1.例2.5.考察xx x f )11()(+=当∞→x 时的变化趋势. 解:输入命令:x=1:20:1000；y=(1+1./x).^x ；plot(x ，y)从图上看，当∞→x 时，函数值与某常数无限接近，我们知道，这个常数就是e . ３．求函数极限例2.6.求)1311(lim 31+-+-→x x x .解:输入命令:syms x ；f=1/(x+1)-3/(x^3+1)；limit(f ，x ，-1) 得结果ans=-1.画出函数图形.ezplot(f)；hold on ；plot(-1，-1，’r.’)例2.7.求30sin limx xtgx x -→.解:输入命令:limit((tan(x)-sin(x))/x^3) 得结果:ans=1/2例2.8.求xx x x )11(lim -+∞→.解:输入命令:limit(((x+1)/(x-1))^x ，inf) 得结果:ans=exp(2)例2.9.求xx x +→0lim . 解:输入命令:limit(x^x ，x ，0，’right’) 得结果:ans =1 例2.10.求x ctgx 10)(lim+→.解:输入命令:limit((cot(x))^(1/log(x))，x ，0，’right’) 得结果:ans=exp(-1)４．求方程的解. 例2.11.解方程02=++c bx ax . 解:输入命令:syms a b c x ；f=a*x^2+b*x+c ；solve(f) 得结果:ans=[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]如果不指明自变量，系统默认为x ，也可指定自变量，比如指定b 为自变量. solve(f ，b)得结果:ans=-(a*x^2+c)/x例2.12.解方程0155=--x x . 解:输入命令:f=x^5-5*x-1；solve(f) 得结果:ans=[ -1.4405003973415600893186320629653] [ -.20006410262997539129073370075959] [.49456407933505360591791681140791e-1 -1.4994413672391491358223492788056*i] [.49456407933505360591791681140791e-1 +1.4994413672391491358223492788056*i] [ 1.5416516841045247594257824014433] 画出图象ezplot(f ，[-2，2])；hold on ；plot([-2，2]，[0，0])实验3 导数及偏导数计算实验目的１．进一步理解导数概念及其几何意义. ２．学习matlab 的求导命令与求导法.实验内容１．学习matlab 命令.建立符号变量命令sym 和syms 调用格式: x=sym(｀x ｀)，建立符号变量x ；syms x y z ，建立多个符号变量x ，y ，z ； matlab 求导命令diff 调用格式:diff (函数)(x f ) ，求)(x f 的一阶导数)(x f '； diff (函数)(x f ， n ) ，求)(x f 的n 阶导数)()(x fn (n 是具体整数)；diff (函数),(y x f ，变量名x )，求),(y x f 对x 的偏导数x f∂∂；diff (函数),(y x f ，变量名x ，n ) ，求),(y x f 对x 的n 阶偏导数n n x f∂∂；matlab 求雅可比矩阵命令jacobian ，调用格式:jacobian ([函数),,(z y x f ；函数),,(z y x g ；函数),,(z y x h ]， [z y x ,,])给出矩阵:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂z h yh xh z g y g x g z f y f x f２．导数概念.导数是函数的变化率，几何意义是曲线在一点处的切线斜率. （１）点导数是一个极限值.例3.1.设xe xf =)(，用定义计算)0(f '.解:)(x f 在某一点0x 的导数定义为极限:x x f x x f x ∆-∆+→∆)()(lim000我们记x h ∆=，输入命令:syms h ；limit((exp(0+h)-exp(0))/h ，h ，0) 得结果:ans=１．可知1)0(='f（２）导数的几何意义是曲线的切线斜率.例3.2.画出xe xf =)(在0=x 处()1,0(P )的切线及若干条割线，观察割线的变化趋势.解:在曲线x e y =上另取一点),(he h M ，则PM 的方程是:011--=--h e x y h .即 11+-=x h e y h取01.0,1.0,1,2,3=h ，分别作出几条割线.h=[3，2，1，0.1，0.01]；a=(exp(h)-1)./h ；x=-1:0.1:3； plot(x ，exp(x)，’r’)；hold on for i=1:5；plot(h(i)，exp(h(i))，’r.’) plot(x ，a(i)*x+1) endaxis square作出xe y =在0=x 处的切线1+=x yplot(x ，x+1，’r’)从图上看，随着M 与P 越来越接近，割线PM 越来越接近曲线的割线．３．求一元函数的导数.（１）)(x f y =的一阶导数.例3.3.求x x y )sin(=的导数.解:打开matlab 指令窗，输入指令:dy_dx=diff(sin(x)/x). 得结果:dy_dx=cos(x)/x-sin(x)/x^2.matlab 的函数名允许使用字母、空格、下划线及数字，不允许使用其他字符，在这里我们用dy_dx 表示x y '. 例3.4.求)ln(sin x y =的导数.解: 输入命令:dy_dx=diff(log(sin(x))). 得结果:dy_dx=cos(x)/sin(x).在matlab 中，函数x ln 用log(x)表示，而log10(x)表示x lg . 例3.5.求202)2(x x y +=的导数.解: 输入命令:dy_dx=diff((x^2+2*x)^20). 得结果:dy_dx=20*(x^2+2*x)^19*(2*x+2).注意x 2输入时应为2*x.例3.6.求xx y =的导数. 解: 输入命令:dy_dx=diff(x^x). 得结果:dy_dx =x^x*(log(x)+1).利用matlab 命令diff 一次可以求出若干个函数的导数. 例3.7.求下列函数的导数:1.5221+-=x x y .2.x x y 2cos 2cos 22+=. 3.xy sin 34=.4.x y ln ln 4=. 解: 输入命令:a=diff([sqrt(x^2- 2*x+5)，cos(x^2)+2*cos(2*x)，4^(sin(x))， log(log(x))]). 得结果: a=[1/2/(x^2-2*x+5)^(1/2)*(2*x-2)，-2*sin(x^2)*x-4*sin(2*x)， 4^sin(x)*cos(x)*log(4)， 1/x/log(x)]. dy1_dx=a(1)↵.dy1_dx=1/2/(x^2-2*x+5)^(1/2)*(2*x-2). dy2_dx=a(2)↵.dy2_dx=-2*sin(x^2)*x-4*sin(2*x). dy3_dx=a(3)↵.dy3_dx=4^sin(x)*cos(x)*log(4).dy4_dx=a(4)↵.dy4_dx=1/x/log(x).由本例可以看出，matlab 函数是对矩阵或向量进行操作的，a(i)表示向量a 的第i 个分量.（２）参数方程所确定的函数的导数.设参数方程⎩⎨⎧==)()(t y y t x x 确定函数)(x f y =，则y 的导数)()(t x t y dx dy ''=. 例3.8.设⎩⎨⎧-=-=)cos 1()sin (t a y t t a x ，求dx dy .解: 输入命令:dx_dt=diff(a*(t-sin(t)))；dy_dt=diff(a*(1-cos(t)))； dy_dx=dy_dt/dx_dt. 得结果:dy_dx=sin(t)/(1-cos(t)). 其中分号的作用是不显示结果. ４．求多元函数的偏导数.例3.9.设 u=222z y x ++求 u 的一阶偏导数.解: 输入命令:diff((x^2+y^2+z^2)^(1/2)， x). 得结果:ans=1/(x^2+y^2+z^2)^(1/2)*x. 在命令中将末尾的x 换成y 将给出y 的偏导数:ans=1/(x^2+y^2+z^2)^(1/2)*y. 也可以输入命令:jacobian((x^2+y^2+z^2)^(1/2)，[x y]). 得结果:ans=[1/(x^2+y^2+z^2)^(1/2)*x ， 1/(x^2+y^2+z^2)^(1/2)*y]给出矩阵⎪⎭⎫ ⎝⎛∂∂∂∂y u x u ,.例3.10.求下列函数的偏导数:1.)(1x yarctg z =. 2.yx z =2.解: 输入命令:diff(atan(y/x). 得结果:ans=-y/x^2/(1+y^2/x^2). 输入命令:diff(atan(y/x)， y). 得结果:ans=1/x/(1+y^2/x^2). 输入命令:diff(x^y ， x). 得结果:ans=x^y*y/x . 输入命令:diff(x^y ， y). 得结果:ans=x^y*log(x).使用jacobian 命令求偏导数更为方便. 输入命令:jacobian([atan(y/x)，x^y]，[x ，y]). 得结果:ans=[ -y/x^2/(1+y^2/x^2)， 1/x/(1+y^2/x^2)] [ x^y*y/x ， x^y*log(x)]. ５．求高阶导数或高阶偏导数.例3.11.设xe x xf 22)(=，求)()20(x f.解:输入指令:diff(x^2*exp(2*x)，x ，20). 得结果: ans =99614720*exp(2*x)+20971520*x*exp(2*x)+1048576*x^2*exp(2*x)例3.12.设224623y x y x z +-=，求y x z y z x z ∂∂∂∂∂∂∂22222,,.解:输入命令:diff(x^6-3*y^4+2*x^2*y^2，x ，2)可得到22x z ∂∂:ans=30*x^4+4*y^2.将命令中最后一个x 换为y 得22y z ∂∂:ans=-36*y^2+4*x^2. 输入命令:diff(diff(x^6-3*y^4+2*x^2*y^2，x)，y)可得y x z ∂∂∂2:ans=8*x*y同学们可自己计算x y z∂∂∂2比较它们的结果.注意命令:diff(x^6-3*y^4+2*x^2*y^2，x ，y)，是对y 求偏导数，不是求y x z∂∂∂2.６．求隐函数所确定函数的导数或偏导数例3.13.设e e x xy =+-ln ，求dx dy解:e ex y x F xy -+=-ln ),(，先求x F '，再求y F '. 输入命令:df_dx=diff(log(x)+exp(-y/x)-exp(1)，x)得到x F ':df_dx=1/x+y/x^2*exp(-y/x). 输入命令:df_dy=diff(log(x)+exp(-y/x)-exp(1)，y) 得到y F ':df_dy=-1/x*exp(-y/x) 输入命令:dy_dx=-df_dx/df_dy 可得所求结果:dy_dx=-(-1/x-y/x^2*exp(-y/x))*x/exp(-y/x).例3.14.设0)()cos()sin(=++xz tg yz xy ，求y zx z ∂∂∂∂,解:)()cos()sin()(xz tg yz xy x F ++=输入命令:a=jacobian(sin(x*y)+cos(y*z)+tan(z*x)，[x ，y ，z])可得矩阵()z y x F F F ''',,a=[cos(x*y)*y+(1+tan(z*x)^2)*z ，cos(x*y)*x-sin(y*z)*z ， -sin(y*z)*y+(1+tan(z*x)^2)*x]. 输入命令:dz_dx=-a(1)/a(3) 得:dz_dx=(-cos(x*y)*y-(1+tan(z*x)^2)*z)/(-sin(y*z)*y+(1+tan(z*x)^2)*x) 输入命令:dz_dy=-a(2)/a(3) 得:dz_dy=(-cos(x*y)*x+sin(y*z)*z)/(-sin(y*z)*y+(1+tan(z*x)^2)*x)实验4 积分计算实验目的１．通过本实验加深理解积分理论中分割、近似、求和、取极限的思想方法. ２．学习并掌握用matlab 求不定积分、定积分、二重积分、曲线积分的方法. ３．学习matlab 命令sum 、symsum 与int . 实验内容１．学习matlab 命令（１）求和命令sum 调用格式.sum(x)，给出向量x 的各个元素的累加和，如果x 是矩阵，则sum(x)是一个元素为x 的每列列和的行向量.例4.1.x=[1，2，3，4，5，6，7，8，9，10]；↵ sum(x)↵ ans=55例4.2.x=[1，2，3；4，5，6；7，8，9]↵ x=1 2 3 4 5 6 7 8 9 sum(x)↵ans=12 15 18（２）求和命令symsum 调用格式.symsum(s ，n)，求∑nssymsum(s ，k ，m ，n)，求∑=nm k s当x 的元素很有规律，比如为表达式是)(k s 的数列时，可用symsum 求得x 的各项和，即 symsum ),1),((n k s =)()2()1(n s s s +++symsum )()1()(),,),((n s m s m s n m k k s ++++= 例4.3.syms k n ↵ symsum(k ，1，10)↵ ans=55symsum(k^2，k ，1，n)↵ans=1/3*(n+1)^3-1/2*(n+1)^2+1/6*n+1/6 （３）matlab 积分命令int 调用格式int (函数)(x f ) 计算不定积分⎰dx x f )(int (函数),(y x f ，变量名x ) 计算不定积分⎰dx y x f ),(int (函数b a x f ,),() 计算定积分⎰badxx f )(int (函数),,(y x f 变量名b a x ,,) 计算定积分⎰badxy x f ),(２．计算不定积分例4.4.计算xdxx ln 2⎰解:输入命令:int(x^2*log(x)) 可得结果:ans=1/3*x^3*log(x)-1/9*x^3 注意设置符号变量.例4.5.计算下列不定积分: 1.dxx a ⎰-222.⎰++dx x x 31313.⎰xdxx arcsin 2解:首先建立函数向量. syms xsyms a realy=[sqrt(a^2-x^2)，(x-1)/(3*x-1)^(1/3)，x^2*asin(x)]；然后对y 积分可得对y 的每个分量积分的结果.int(y ，x)↵ ans =[1/2*x*(a^2-x^2)^(1/2)+1/2*a^2*asin((1/a^2)^(1/2)*x)， -1/3*(3*x-1)^(2/3)+1/15*(3*x-1)^(5/3)，1/3*x^3*asin(x)+1/9*x^2*(1-x^2)^(1/2)+2/9*(1-x^2)^(1/2)] ３．定积分的概念.定积分是一个和的极限.取xe xf =)(，积分区间为]1,0[，等距划分为20个子区间. x=linspace(0，1，21)；选取每个子区间的端点，并计算端点处的函数值. y=exp(x)；取区间的左端点乘以区间长度全部加起来. y1=y(1:20)；s1=sum(y1)/20 s1=1.6757s1可作为⎰10dx e x 的近似值.若选取右端点:y2=y(2:21)；s2=sum(y2)/20 s2=1.7616s2也可以作为⎰10dx e x 的近似值.下面我们画出图象.plot(x ，y)；hold onfor i=1:20 fill([x(i)，x(i+1)，x(i+1)，x(i)，x(i)]，[0，0，y(i)，y(i)，0]，’b’)end如果选取右端点，则可画出图象. for i=1:20； fill([x(i)，x(i+1)，x(i+1)，x(i)，x(i)]，[0，0，y(i+1)，y(i+1)，0]，’b’) hold on endplot(x ，y ，’r’)在上边的语句中，for … end 是循环语句，执行语句体内的命令20次，fill 命令可以填充多边形，在本例中，用的是兰色(blue)填充.从图上看211s dx e s x <<⎰，当分点逐渐增多时，12s s -的值越来越小，读者可试取50个子区间看一看结果怎样.下面按等分区间计算∑∑=∞→=∞→=∆ξn i n i n ni i n n ex f 111lim)(limsyms k ns=symsum(exp(k/n)/n ，k ，1，n)； limit(s ，n ，inf) 得结果ans=exp(1)-1４．计算定积分和广义积分.例4.6.计算⎰10dx e x .解:输入命令:int(exp(x)，0，1)得结果ans=exp(1)-1.这与我们上面的运算结果是一致的. 例4.7.计算⎰-201dxx解:输入命令:int(abs(x-1)，0，2)得结果ans =1.本例用mathematica 软件不能直接求解. 例4.8.判别广义积分⎰+∞11dx x p 、⎰+∞∞--πdx e x 2221与⎰-202)1(1dx x 的敛散性，收敛时计算积分值.解:对第一个积分输入命令:syms p real ；int(1/x^p ，x ，1，inf)得结果ans =limit(-1/(p-1)*x^(-p+1)+1/(p-1)，x = inf).由结果看出当1<p 时，x^(-p+1)为无穷，当1>p 时，ans=1/(p-1)，这与课本例题是一致的.对第二个积分输入命令:int(1/(2*pi)^(1/2)*exp(-x^2/2)，-inf ，inf) 得结果:ans=7186705221432913/18014398509481984*2^(1/2)*pi^(1/2) 由输出结果看出这两个积分收敛.对后一个积分输入命令:int(1/(1-x)^2，0，2)结果得ans=inf .说明这个积分是无穷大不收敛. 例4.9.求积分⎰t dxxx 0sin解:输入命令:int(sin(x)/x ，0，t)，可得结果sinint(t)，通过查帮助(help sinint )可知sinint(t)=⎰t dxxx 0sin，结果相当于没求!实际上matlab 求出的只是形式上的结果，因为这类积分无法用初等函数或其值来表示.尽管如此，我们可以得到该函数的函数值.输入vpa(sinint(0.5))可得sinint(0.5)的值.５．二重积分计算例4.10.求二次积分⎰⎰+12102x x xydydx解:输入命令:int(int(x*y ，y ，2*x ，x^2+1)，x ，0，1) 得结果ans=1/12. 例4.11.求⎰⎰≤++π12222))(sin(y x dxdyy x解:积分区域用不等式可以表示成2211,11x y x x -≤≤--≤≤-，二重积分可化为二次积分⎰⎰----+π22112211)(sin(x x dyy x dx，输入命令:int(int(sin(pi*(x^2+y^2))，y ，-sqrt(1-x^2)，sqrt(1-x^2))，x ，-1，1) 由输出结果可以看出，结果中仍带有int ，表明matlab 求不出这一积分的值.采用极坐标可化为二次积分⎰⎰ππ20102)sin(drr r da ，输入命令:int(int(r*sin(pi*r^2)，r ，0，1)，a ，0，2*pi) 可得结果为ans=2.６．曲线积分例4.12.求曲线积分⎰L xyds ，其中L 为曲线122=+y x 在第一象限内的一段.解:曲线的参数方程是)20(,sin ,cos π≤≤==t t y t x 曲线积分可以化为⎰π⋅0s i n c o s t d tt .输入命令:int(cos(t)*sin(t)，0，pi/2) 执行后即可求出曲线积分结果1/2.实验5 matlab 自定义函数与导数应用实验目的１．学习matlab 自定义函数.２．加深理解罗必塔法则、极值、最值、单调性. 实验内容１．学习matlab 自定义函数及求函数最小值命令.函数关系是指变量之间的对应法则，这种对应法则需要我们告诉计算机，这样，当我们输入自变量时，计算机才会给出函数值，matlab 软件包含了大量的函数，比如常用的正弦、余弦函数等.matlab 允许用户自定义函数，即允许用户将自己的新函数加到已存在的matlab 函数库中，显然这为matlab 提供了扩展的功能，无庸置疑，这也正是matlab 的精髓所在.因为matlab 的强大功能就源于这种为解决用户特殊问题的需要而创建新函数的能力.matlab 自定义函数是一个指令集合，第一行必须以单词function 作为引导词，存为具有扩展名“.m ”的文件，故称之为函数M －文件.函数M －文件的定义格式为：function 输出参数＝函数名（输入参数）函数体 …… 函数体一旦函数被定义，就必须将其存为M －文件，以便今后可随时调用.比如我们希望建立函数12)(2++=x x x f ，在matlab 工作区中输入命令：syms x ；y=x^2+2*x+1；不能建立函数关系，只建立了一个变量名为y 的符号表达式，当我们调用y 时，将返回这一表达式.y ↵y=x^2+2*x+1当给出x 的值时，matlab 不能给出相应的函数值来. x=3；y ↵y=x^2+2*x+1 如果我们先给x 赋值.x=3；y=x^2+2*x+1 得结果：y=16若希望得出2|=x y 的值，输入： x=2；y ↵得结果：y=16，不是2=x 时的值.读者从这里已经领悟到在matlab 工作区中输入命令：y=x^2+2*x+1不能建立函数关系，如何建立函数关系呢？我们可以点选菜单Fill\New\M-fill 打开matlab 文本编辑器，输入： function y=f1(x) y=x^2+2*x+1；存为f1.m .调用该函数时，输入： syms x ；y=f1(x)↵ 得结果：y= x^2+2*x+1.输入: y1=f1(3)↵ 得结果：y1=16matlab 求最小值命令fmin 调用格式：fmin(‘fun’，a ，b) 给出)(x f 在),(b a 上的最小值点. ２．自定义函数例5.1.建立正态分布的密度函数22)(21),.,(μ--σπ=μσx e x f解：打开文本编辑器，输入：function y=zhengtai(x ，a ，b)y=1/sqrt(2*pi)/a*exp(-(x-b).^2/2/a^2)；存为zhengtai.m .调用时可输入命令： y=zhengtai(1，1，0)得结果：y=0.2420.此即)0,1,1(f 的值.如果想画出标准正态分布的密度函数的图象，输入： ezplot(zhengtai(x ，1，0))例5.2.解一元二次方程02=++c bx ax .解：我们希望当输入c b a ,,的值时，计算机能给出方程的两个根.在文本编辑器中建立名为rootquad.m 的文件.function [x1，x2]=rootquad(a ，b ，c) d=b*b-4*a*c ；x1=(-b+sqrt(d))/(2*a) x2=(-b-sqrt(d))/(2*a) 比如求方程07322=-+x x 的根，可用语句： [r1，r2]=rootquad(2，3，-7)得结果：r1=1.2656 r2=-2.7656２．验证罗必塔法则.罗必塔法则是指在求00及∞∞的极限时，可用导数之比的极限来计算（如果导数之比的极限存在或∞）例5.3.以x ba xx x -→0lim 为例验证罗必塔法则.解：这是00型极限f=a^x-b^x ；g=x ；L=limit(f/g ，x ，0)得结果：L=log(a)-log(b)df=diff(f ，x)；dg=diff(g ，x)；L1=limit(df/dg ，x ，0) 得结果：L1=log(a)-log(b) 从结果看出：L=L1，即x b a x x x -→0lim=x b a x x x '-→'0)(lim４．函数的单调性与极值.例5.4.求函数396)(23++-=x x x x f 的单调区间与极值.解：求可导函数的单调区间与极值，就是求导函数的正负区间与正负区间的分界点，利用matlab 解决该问题，我们可以先求出导函数的零点，再画出函数图象，根据图象可以直观看出函数的单调区间与极值．输入命令：f=x^3-6*x^2+9*x+3；df=diff(f ，x)；s=solve(df) 得结果：ans=[1，3]，画出函数图象． ezplot(f ，[0，4])从图上看，)(x f 的单调增区间为)1,(-∞、),1(+∞，单调减区间是)3,1(，极大值7)1(=f ，极小值3)3(=f .我们可以建立一个名为dandiao.m 的M —文件，用来求求函数的单调区间. disp(‘输入函数（自变量为x ）’) syms xf=input('函数f(x)=') df=diff(f)； s=solve(df) a=[]；for i=1:size(s)； a(i)=s(i)； endezplot(f ，[min(a)-1，max(a)+1])要求函数)1ln(x x y +-=的单调区间与极值，可调用dandiao.m .输入： dandiao ↵在matlab 工作区出现以下提示：输入函数（自变量为x ）函数f(x)=在光标处输入：x-log(1+x)，可得结果s=0.从图上看，)(x f 的单调增区间为),0(+∞，单调减区间是)0,(-∞，极小值0)0(=f . ５．函数的最值调用求函数最小值命令fmin 时，可得出函数的最小值点，为求最小值，必须建立函数M —文件.例5.5.求函数1)3()(2--=x x f 在区间)5,0(上的最小值. 解：我们可以建立一个名为f.m 的函数M －文件. function y=f(x) y=(x-3).^2-1；并且调用fminx=fmin((‘f’，0，5)得：x=3，)(x f 在最小值点处的值（函数最小值）是1)3(-=f .求最大值时可用x=fmin(‘-f(x)’，a ，b)实验6 matab 矩阵运算与数组运算实验目的：１．理解矩阵及数组概念．２．掌握matlab 对矩阵及数组的操作命令．实验内容：１．矩阵与数组的输入．对于较小较简单的矩阵，从键盘上直接输入矩阵是最常用的数值矩阵创建方法．用这种方法输入矩阵时注意以下三点：（1）整个输入矩阵以方括号“[ ]”为其首尾；（2）矩阵的元素必须以逗号“，”或空格分隔；（3）矩阵的行与行之间必须用分号“；”或回车键隔离．例１：下面的指令可以建立一个3行4列的矩阵 a ． a=[1 2 3 4;5 6 7 8;9 10 11 12] (下面是屏幕的显示结果) a =1 2 3 4 5 6 7 8 9 10 11 12 分号“；”有三个作用：（1）在“[ ]”方括号内时它是矩阵行间的分隔符．例子如上．（2）它可用作指令与指令间的分隔符．（3）当它存在于赋值指令后时，该指令执行后的结果将不显示在屏幕上．例如，输入指令：b=[1 2 0 0;0 1 0 0;1 1 1 1];矩阵b 将不被显示，但b 已存放在matlab 的工作内存中，可随时被以后的指令所调用或显示．例如，输入指令： b得结果： b =1 2 0 0 0 1 0 0 1 1 1 1数值矩阵的创建还可由其他方法实现．如：利用matlab 函数和语句创建数值矩阵；利用m 文件创建数值矩阵；从其他文件获取数值矩阵．有兴趣的读者可参阅其他参考书．数组可以看成特殊的矩阵，即1行n列的矩阵，数组的输入可以采用上面矩阵的输入方法．例２：输入以下指令以建立数组c．c=[1 2 3 4 5 6 7 8]c =1 2 3 4 5 6 7 8另外还有两种方法输入数组．请看下面两个例子．例３：在0和2中间每隔0.1一个数据建立数组d．解：输入指令：d=0:0.1:2d =Columns 1 through 70 0.1000 0.2000 0.3000 0.4000 0.50000.6000Columns 8 through 140.7000 0.8000 0.9000 1.0000 1.1000 1.20001.3000Columns 15 through 211.4000 1.5000 1.6000 1.7000 1.8000 1.90002.0000注意“：”的使用方法.例４：在0和2之间等分地插入一些分点，建立具有10个数据点的数组e．解：输入指令：e=linspace(0,2,10)e =Columns 1 through 70 0.2222 0.4444 0.6667 0.8889 1.11111.3333Columns 8 through 101.5556 1.77782.0000linspace(a,b,n)将建立从a到b有n个数据点的数组.２．常用矩阵的生成．matlab为方便编程和运算，提供了一些常用矩阵的生成指令：n⨯单位矩阵eye(n) nn⨯全1矩阵ones(n) nn⨯零矩阵zeros(n) nm⨯标准型矩阵eye(m,n) nm⨯全1矩阵ones(m,n) nm⨯零矩阵zeros(m,n) neye(size(A)) 与A同型的标准型矩阵ones(size(A)) 与A同型的全1矩阵zeros(size(A))与A同型的零矩阵其中指令size(A)给出矩阵A的行数和列数．例５：生成以下矩阵．3⨯零矩阵．(1)33 全1矩阵．(2)6(3)与例1中矩阵a同型的标准型矩阵．解：输入下面指令：d=zeros(3)d =0 0 00 0 00 0 0e=ones(3,6)e =1 1 1 1 1 11 1 1 1 1 11 1 1 1 1 1f=eye(size(a))f =1 0 0 00 1 0 00 0 1 0３．矩阵元素的标识矩阵的元素、子矩阵可以通过标量、向量、冒号的标识来援引和赋值．(1)矩阵元素的标识方式A(ni,nj)．ni,nj都是标量．若它们不是整数，则在调用格式中会自动圆整到最临近整数．ni指定元素的行位置，nj指定元素的列位置．(2)子矩阵的序号向量标识方式A(v,w)．v,w是向量，v,w中的任意一个可以是冒号“：”，他表示取全部行(在v位置)或全部列(在w位置)．v,w中所用序号必须大于等于1且小于等于矩阵的行列数．例６：元素和矩阵的标识a=[1 2 3 4;5 6 7 8;9 10 11 12]a =1 2 3 45 6 7 89 10 11 12a24=a(2,4)a24 =8a1=a([1,2],[2,3,4])a1 =2 3 46 7 8a2=a([1,2],[2,3,1])a2 =2 3 16 7 5a3=a([3,1],:)a3 =9 10 11 121 2 3 4a([1,3],[2,4])=zeros(2)a =1 0 3 05 6 7 89 0 11 0４．矩阵运算和数组运算．矩阵运算的指令和意义如下：A' 矩阵A的共轭转置矩阵，当A是实矩阵时，A'是A的转置矩阵．A+B 两个同型矩阵A与B相加．A-B 两个同型矩阵A与B相减．A*B 矩阵A与矩阵B相乘，要求A的列数等于B的行数．s+B 标量和矩阵相加（matlab约定的特殊运算，等于s加B的每一个分量）．s-B B-s 标量和矩阵相减（matlab约定的特殊运算，含意同上）．s*A 数与矩阵A相乘．例７：a=[1 2 3;4 5 6]a =1 2 34 5 6b=[-1 0 1;3 1 2]b =-1 0 13 1 2a'ans =1 42 53 6a+bans =0 2 47 6 8a-bans =2 2 21 4 41+aans =2 3 45 6 7a-1ans =0 1 23 4 52*bans =-2 0 26 2 4c=[2 4;1 3;0 1]c =2 41 30 1a*cans =4 1313 37数组可以看成特殊矩阵即一行n列的矩阵，矩阵运算的指令和含意同样适用于数组运算．如果在运算符前加“．”，含意将有所不同．A.*B 同维数组或同型矩阵对应元素相乘．A./B A的元素被B的元素对应除．A.^n A的每个元素n次方．p.^A 以p为底，分别以A的元素为指数求幂．例８：a=[1 2 3;4 5 6]a =1 2 34 5 6b=[-1 0 1;3 1 2]b =-1 0 13 1 2a.*bans =-1 0 312 5 12a./bWarning: Divide by zero.ans =-1.0000 Inf 3.00001.3333 5.0000 3.0000a.^2ans =1 4 916 25 362.^aans =2 4 816 32 64实验7矩阵与线性方程组实验目的：１．掌握matlab求矩阵的秩命令．２．掌握matlab求方阵的行列式命令．３．理解逆矩阵概念，掌握matlab求逆矩阵命令．４．会用matlab求解线性方程组．实验内容：１．矩阵的秩.指令rank(A)将给出矩阵A的秩．例１：a=[3 2 -1 -3 -2;2 -1 3 1 -3;7 0 5 -1 -8]a =3 2 -1 -3 -22 -13 1 -37 0 5 -1 -8rank(a)ans =2２．方阵的行列式.指令det(A)给出方阵A的行列式.例２：b=[1 2 3 4;2 3 4 1;3 4 1 2;4 1 2 3];det(b)ans =160det(b')ans =160c=b;c(:,1)=2*b(:,1);det(c)ans =320det(b(:,[3 2 1 4]))ans =-160d=b;d(2,:);det(d)ans =160你能解释上例中的运算结果吗?在这里我们实际上验证了行列式的性质．３．逆矩阵指令inv(A)给出方阵A的逆矩阵，如果A不可逆，则inv(A)给出的矩阵的元素都是Inf．例３：设⎪⎪⎪⎭⎫⎝⎛=343122321A，求A的逆矩阵．解：输入指令：A=[1 2 3;2 2 1;3 4 3];B=inv(A)B =1.0000 3.0000 -2.0000-1.5000 -3.0000 2.50001.0000 1.0000 -1.0000还可以用伴随矩阵求逆矩阵，打开m 文件编辑器，建立一个名为companm 的M-文件文件内容为：function y=companm(x)[n,m]=size(x);y=[];for j=1:n;a=[];for i=1:n;x1=det(x([1:i-1,i+1:n],[1:j-1,j+1:n]))*(-1)^(i+j);a=[a,x1];endy=[y;a];end利用该函数可以求出一个矩阵的伴随矩阵．输入命令：C=1/det(A)*companm(A)C =1.0000 3.0000 -2.0000-1.5000 -3.0000 2.50001.0000 1.0000 -1.0000利用初等变换也可以求出逆矩阵，构造n 行2n 列的矩阵(A E)，并进行行初等变换，当把A 变为单位矩阵时，E 就变成了A 的逆矩阵．利用matlab 命令rref 可以求出矩阵的行简化阶梯形．输入命令：D=[A,eye(3)]D =1 2 3 1 0 02 2 1 0 1 03 4 3 0 0 1rref(D)ans =1.0000 0 0 1.0000 3.0000 -2.0000 0 1.0000 0 -1.5000 -3.0000 2.5000 0 0 1.0000 1.0000 1.0000 -1.0000n m ⨯线性方程组B AX =的求解是用矩阵除来完成的,B A X \=，当n m =且A 可逆时，给出唯一解．这时矩阵除B A \相当于B A inv *)(；当m n >时，矩阵除给出方程的最小二乘解；当m n <时，矩阵除给出方程的最小范数解．例４：解方程组：⎪⎪⎩⎪⎪⎨⎧=-+=++=+-+=++-12121243132143214321x x x x x x x x x x x x x x 解：输入命令：a=[1 -1 1 2;1 1 -2 1;1 1 1 0;1 0 1 -1];b=[1;1;2;1];x=a\bx =0.83330.75000.41670.2500输入命令：z=inv(a)*bz =0.83330.75000.41670.2500例５：解方程组：⎪⎩⎪⎨⎧=-++-=-++-=--++8343242222543215432154321x x x x x x x x x x x x x x x解：方程的个数和未知数不相等，用消去法，将增广矩阵化为行简化阶梯形，如果系数矩阵的秩不等于增广矩阵的秩，则方程组无解；如果系数矩阵的秩等于增广矩阵的秩，则方程组有解，方程组的解就是行简化阶梯形所对应的方程组的解．输入命令：a=[2 1 1 -1 -2 2;1 -1 2 1 -1 4;2 -3 4 3 -1 8];rref(a)ans =1 0 0 0 0 00 1 0 -1 -1 00 0 1 0 -1 2由结果看出，4x ,5x 为自由未知量，方程组的解为：01=x542x x x +=532x x +=例６：解方程组：⎪⎪⎩⎪⎪⎨⎧=+--=--=-+-=+--0320030432142143214321x x x x x x x x x x x x x x x解：输入命令：a=[1 -1 -1 1;1 -1 1 -3;1 -1 0 -1;1 -1 -2 3];rref(a)ans =1 -1 0 -10 0 1 -20 0 0 00 0 0 0由结果看出，2x ,4x 为自由未知量，方程组的解为：421x x x +=432x x =实验8 常微分方程与级数实验目的：１．学习用matlab求解微分方程命令dsolve.２．学习matlab泰勒级数展开命令.３．巩固幂级数的收敛半径、和等概念.实验内容：１．学习matlab命令.matlab求解微分方程命令dsolve，调用格式为：dsolve(‘微分方程’)给出微分方程的解析解，表示为t的函数.dsolve(‘微分方程’，‘初始条件’)给出微分方程初值问题的解，表示为t的函数.dsolve(‘微分方程’，‘变量x’)给出微分方程的解析解，表示为x的函数.dsolve(‘微分方程’，‘初始条件’，‘变量x’)给出微分方程初值问题的解，表示为x的函数.求已知函数的taylor展开式taylor命令，调用格式为：taylor(函数f(x)) f(x)的5次taylor多项式.taylor(函数f(x)，n) f(x)的n-1次taylor多项式.taylor(函数f(x)，a) f(x)在a点的taylor多项式.求级数的和命令symsum调用格式为：symsum(S,n)，求∑n Ssymsum(S,k,m,n),求∑=nmkSmatlab求极限命令limit调用格式为：limit(函数f(x)，变量x，自变量的趋向值)２．求解一阶微分方程.微分方程在输入时，y'应输入Dy，y''应输入D2y等，D应大写．例１：求微分方程22xxexydxdy-=+的通解．解：输入命令：dsolve('Dy+2*x*y=x*exp(-x^2)')结果为ans =1/2*(1+2*exp(-2*x*t)*C1*exp(x^2))/exp(x^2)系统默认的自变量是t，显然系统把x当作常数，把y当作t的函数求解．输入命令：dsolve('Dy+2*x*y=x*exp(-x^2)','x')得正确结果：ans =1/2*(x^2+2*C1)/exp(x^2)例２：求微分方程0=-+'x e y y x 在初始条件e y x 21==下的特解．解：输入命令：dsolve('x*Dy+y-exp(x)=0','y(1)=2*exp(1)','x')得结果为：ans =1/x*(exp(x)+exp(1))例３：求微分方程0cos 2)1(2=-+-x xy dx dy x 在初始条件10==x y 下的特解．解：输入命令：dsolve('(x^2-1)*Dy+2*x*y-cos(x)=0','y(0)=1','x')得结果为ans =1/(x^2-1)*(sin(x)-1)３．求解二阶微分方程．例４：求03=+'+''x e y y 的通解．解：输入命令：dsolve('D2y+3*Dy+exp(x)=0','x')得结果：ans =-1/4*exp(x)+C1+C2*exp(-3*x)例５：求解微分方程．02='-''y e y y 解：输入命令：dsolve('D2y-exp(2*y)*Dy=0','x')得结果：ans =1/2*log(-2*C1/(-1+exp(2*x*C1+2*C2*C1)))+x*C1+C2*C1４．taylor 展开式．例６：求函数y=cosx 在x=0点处的5阶taylor 展开式及在3π=x 处的6阶taylor 展开式．解：输入命令：syms x;taylor(cos(x))得结果：ans =1-1/2*x^2+1/24*x^4输入命令：taylor(cos(x),pi/3,7)得结果：ans =1/2-1/2*3^(1/2)*(x-1/3*pi)-1/4*(x-1/3*pi)^2+1/12*3^(1/2)*(x- 1/3*pi)^3+1/48*(x-1/3*pi)^4-1/240*3^(1/2)*(x-1/3*pi)^5-1/1440*(x-1/3*pi)^6 ５．级数求和．例７：求∑∞=121n n ．解：输入命令：syms n;symsum(1/2^n,1,inf) 得结果：ans =1例８：求幂级数∑∞=⨯12nnnnx的和函数．解：输入命令：symsum(x^n/(n*2^n),n,1,inf) 得结果ans =-log(1-1/2*x)例９：求幂级数∑∞=1nnnx的和函数．解：输入命令：symsum(n*x^n,n,1,inf) 得结果：ans =x/(x-1)^2６．判别级数敛散性．例１０：判断数项级数∑∞=+1)1(1nnn的收敛性．解：输入求和命令：symsum(1/(n*(n+1)),n,1,inf) 得结果：ans =1求和得是1，说明该级数收敛．例１１：判别级数∑∞=+1)1(sinnnnπ的敛散性．解：输入命令：symsum(sin(pi/(n*(n+1))),1,inf)得结果：ans =sum(sin(pi/n/(n+1)),pi = 1 .. inf)由执行结果看出仍含有sum，说明用matlab不能求出其和，可采用比较判别法，取比较级数为P级数∑∞=121nn,取二者通项比值的极限．输入命令：limit(sin(pi/(n*(n+1)))/(1/n^2),n,inf)得结果：ans =pi得值为pi,由所取P级数收敛，得知所要判别的级数也收敛．例１２：判别级数∑∞=⎪⎭⎫⎝⎛143nnn的敛散性．解：用比值判别法，输入命令：limit((n+1)*(3/4)^(n+1)/(n*(3/4)^n),n,inf)得结果：ans =3/4极限值小于1，由比值判别法知级数收敛．实际上输入求和命令：symsum(n*(3/4)^n,n,1,inf)得结果：ans =12。

Matlab实验作业

MATLAB实验报告姓名：学号：学院：专业：任课老师：日期：Matlab 实验报告一、选择题目所选题目为MATLAB 试题中的第二题，题目内容如下：B 、设计遗传算法求解f (x)极小值，具体表达式如下：321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。

二、问题分析本题目是一个很简单的数学问题，很显然f (x)的最小值为0。

但是本次实验要求为必须以matlab 为实验平台，设计遗传算法对问题进行求解。

遗传算法是一种现代智能算法，实际上它的功能十分强大，能够用于求解一些难以用常规数学手段进行求解的问题，尤其适用于求解多目标、多约束，且目标函数形式非常复杂的优化问题。

但是遗传算法也有一些缺点，最为关键的一点，即没有任何理论能够证明遗传算法一定能够找到最优解，算法主要是根据概率论的思想来寻找最优解。

因此，遗传算法所得到的解只是一个近似解，而不一定是最优解。

鉴于遗传算法在求解上的巨大优势，现在对于遗传算法的研究也越来越多。

Matlab 中有专门的遗传算法工具箱，我们只需要按照一定的格式将目标函数、约束条件进行输入，同时根据问题的需要对其中的一些参数进行设置，即可以运行遗传算法对问题进行求解。

在本实验中，要求我们自行设计遗传算法，因此，首先我们必须要弄懂遗传算法的基本原理，之后才能将问题转化成遗传算法能够处理的形式。

例如，我们需要知道怎么表达自变量，怎么表达目标函数，怎么对目标函数进行优化，等等。

在此基础上，我们才能够运用matlab 编写正确的程序，对问题进行求解。

Matlab 实验报告三、遗传算法简介遗传算法是美国Michigan 大学的Holland 教授在20世纪60年代所提出来的。

遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化算法，它借鉴了达尔文的进化论和孟德尔的遗传学说。

遗传算法操作借鉴适者生存的原则，在每一代的进化中，得到的新个体比原个体更能适应环境，就像自然界中的改造一样。

Matlab绘图数学实验作业

《数学实验》报告Matlab绘图学院：冶金与生态工程学院班级：冶金0702姓名：路松斌学号：40721034实验日期： 2009 年 11月 5 日Matlab基础知识一、目的：(1)熟悉MATLAB的具体操作与操作键。

(2)掌握MATLAB中二维曲线绘图，空间曲线、曲面绘图的方法。

二、任务完成P80第5,6(2),8题5、试绘出颜色为黄色、数据点用钻石形标出的函数y=3cosx e sinx在[0，5]上的虚线形程序：x=0:0.1:5;y=3.*exp(sin(x)).*cos(x);plot(x,y,'yd'),grid on, ,title('y=3cosxexp(sinx)') 运行结果：6(2)、绘制图形，练习使用gtext，axis，legend，title，xlable ，ylable。

程序：x=pi:pi/50:4*pi;y=x2.*tan(1./x).*sin(x.^3);plot(x,y,'g-',x,y,'bp')axis([3 12.8 -1.1 1.1])legend('点图 ','星图')ylabel('年份')xlabel('产量')gtext('最高点')grid on,title('y=xtan(1/x)sin(x^3)')运行结果：8、在一个图形窗口画半径为1的球面、z=4的平面以及马鞍面z=2x2-y2。

程序：t=-10:0.1:10;[x,y]=meshgrid(t);z1=(2*x.^2-y.^2)+eps;subplot(1,3,1),mesh(x,y,z1),title('马鞍面');z2=4*ones(size(x));subplot(1,3,2),mesh(x,y,z2),title(' 平面');subplot(1,3,3),sphere(30),title('球面')运行结果：。

MATLAB数学实验课后答案

数学实验MATLAB参考答案（重要部分）P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值，b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明：编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明：编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1，但数据类型分别为数值，字符，逻辑，注意a与c相等，但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 40 98 80 7 14 16 73 55 57 64 41 4 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 34 17 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数，保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37P 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16]; >> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1]; >> rank(A), rank([A,b])ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]'; >> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95]; >> x1=a*x, x2=a^2*x, x10=a^10*x >> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例，说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i -0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000 -41.0000 25.0000 10.0000 -6.0000 -17.0000 10.0000 5.0000 -3.0000 10.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一（三个for）n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二（一个for）n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三（不用for）n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286 -0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771 -0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628 -0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关，可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关，不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的，所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\b ans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);1 6*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置，然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小，x(2)(4)(6)是局部极大，从最后一句知道x(1)全局最小，x(2)最大。

数学实验（MATLAB版韩明版）2.1-2.4部分答案

数学实验（MATLAB版韩明版）2.1-2.4部分答案练习2.1画出下列常见曲线的图形（其中a=1,b=2,c=3)1.31xy =的图像：()55≤≤-x编程：>> x=-5:0.1:5; >> y=x.^(1/3); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y') >> legend('y=x.^(1/3)') >> title('y=x.^(1/3)') 图像：-5-4-3-2-101234500.20.40.60.811.21.41.61.8xyy=x.(1/3)y=x.(1/3)2.e x y -=2的图像：()55≤≤-x 编程：>> x=-5:0.1:5; >> y=exp(-x.^2); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y') >> legend('y=e^(-x^2)'); >> title('y=e^(-x^2)') 图像：-5-4-3-2-101234500.10.20.30.40.50.60.70.80.91xyy=e (-x 2)y=e (-x 2)=++=+=axy a y at x yx tt t313,1333222的图像：()55≤≤-x ，a=1编程：>> t=-5:0.1:5;>> x=3*t./(1+t.^2);y=3*t.^2./(1+t.^2); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y')>> title('x=3*t./(1+t.^2);y=3*t.^2./(1+t.^2)') >> legend('x=3*t./(1+t.^2);y=3*t.^2./(1+t.^2)') 图像：-1.5-1-0.500.51 1.500.511.522.53xyx=3*t./(1+t.2);y=3*t.2./(1+t.2)4.?+=+=x a a y a x xyt tt t3223221,1的图像: ()55≤≤-t ,a=1 编程：>> t=-5:0.1:5;>> x=t.^2./(1+t.^2);y=t.^3./(1+t.^2); >> plot(x,y)>> xlabel('x');ylabel('y')>> title('x=t.^2./(1+t.^2);y=t.^3./(1+t.^2)') >> legend('x=t.^2./(1+t.^2);y=t.^3./(1+t.^2)') >> grid on 图像：0.10.20.30.40.50.60.70.80.91-5-4-3-2-1012345xyx=t.2./(1+t.2);y=t.3./(1+t.2)5.()()t b y t t a x cos 1,sin -=-=的图像：pi t pi *2*2≤≤-,a=1,b=2 编程：>> t=-2*pi:0.1:2*pi; >> x=t-sin(t);y=2*(1-cos(t)); >> plot(x,y) >> grid on>> xlabel('x');ylabel('y')>> legend('x=t-sin(t);y=2*(1-cos(t))') >> title('x=t-sin(t);y=2*(1-cos(t))') 图像：-8-6-4-20246800.511.522.533.54xyx=t-sin(t);y=2*(1-cos(t))x=t-sin(t);y=2*(1-cos(t))6.=+==ayx t a y t a x 32323233sincos ,的图像：pi t pi *2*2≤≤-,a=1 编程：>> t=-2*pi:0.1:2*pi; >> x=(cos(t)).^3;y=(sin(t)).^3; >> plot(x,y) >> grid on>> xlabel('x');ylabel('y')>> title('x=(cos(t)).^3;y=(sin(t)).^3') 图像：-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81xyx=(cos(t)).3;y=(sin(t)).3x=(cos(t)).3;y=(sin(t)).37.ct z t b y t a x ===,sin ,cos 的图像：()pi t pi c b a *2*2,3,2,1≤≤-=== 编程：>> t=-2*pi:0.1:2*pi; >> x=cos(t);y=2*sin(t);z=3*t; >> plot3(x,y ,z)>> xlabel('x');ylabel('y');zlabel('z') >> grid on>> legend('x=cos(t);y=2*sin(t);z=3*t') >> title('x=cos(t);y=2*sin(t);z=3*t') 图像：-101-2-1012-20-101020xx=cos(t);y=2*sin(t);z=3*tyzx=cos(t);y=2*sin(t);z=3*t8.θa r =的图像：()pi a *20,1≤≤=θ编程：>> theta=0.0:0.1:2*pi; >> r=theta; >> polar(theta,r) >> grid on>> legend('r=theta') >> title('r=theta') 图像：24 68302106024090270120300150330180r=theta r=theta9.e a r θ=的图像：()pi a *20,1≤≤=θ编程：>> theta=-2*pi:0.1:2*pi; >> r=exp(theta); >> polar(theta,r) >> grid on >> title('r=exp(theta)') >> legend('r=exp(theta)') 图像：100200 300400 5003021060240902701203001503301800r=exp(theta)r=exp(theta)10.()?-==+yx ayxar 22222222,2cos θ的图像：1=a 编程：>> theta=0:0.1:2*pi;>> r=sqrt(abs(cos(2*theta))); >> polar(theta,r) >> grid on>> title('r=sqrt(abs(cos(2*theta)))'); >> legend('r=sqrt(abs(cos(2*theta)))') 图像：0.20.4 0.60.8 13021060240902701203001503301800r=sqrt(abs(cos(2*theta)))11.()==+xy a yxar 2222*222,2sin θ的图像：a=1编程：>> theta=0:0.1:2*pi;>> r=sqrt(abs(sin(2*theta))); >> polar(theta,r) >> grid on>> title('r=sqrt(abs(sin(2*theta)))') >> legend('r=sqrt(abs(sin(2*theta)))') 图像：0.4 0.60.8 13021060240902701203001503301800r=sqrt(abs(sin(2*theta)))12.)cos 1(θ+=a r 的图像：a=1 编程：>> theta=0:0.1:2*pi; >> r=1+cos(theta); >> polar(theta,r) >> grid on >> legend('r=1+cos(theta)') >> title('r=1+cos(theta)') 图像：0.51 1.52302106024090270120300150330180r=1+cos(theta)r=1+cos(theta)练习2.21.求出下列极限值. （1）nnn n33+∞→；（2）()n n n n ++-+∞→122lim；（3）x x x 2cot lim→；（4）??? ?→x m xx cos lim 0；（5）--→111lim1e xx x ；（6）??-+∞→x x xx 2lim .解：（1）编程：>> syms n >> limit((n^3+3^n)^(1/n),n,inf) ans = 3（2）编程：>> syms n>> limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf) ans =0（3）编程：>> syms x >> limit(x*cot(2*x),x,0) ans = 1/2（4）编程：>> syms x m >> limit((cos(m/x))^x,x,inf) ans =1（5）编程：>> syms x>> limit(1/x-1/(exp(x)-1),x,1) ans = (exp(1)-2)/(exp(1)-1) （6）编程：>> syms x >> limit(sqrt(x^2+x)-x,x,1) ans = 2^(1/2)-1 2.有个客户看中某套⾯积为180m 2，每平⽅⽶7500元的房⼦。

MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案

“”练习题要求：抄题、写出操作命令、运行结果，并根据要求，贴上运行图。

1、求230x e x -=的所有根。

（先画图后求解）（要求贴图）>> ('(x)-3*x^2',0)=-2*(-1/6*3^(1/2))-2*(-11/6*3^(1/2))-2*(1/6*3^(1/2))3、求解下列各题：1）30sin lim x x x x->->> x;>> (((x))^3)=1/62） (10)cos ,x y e x y =求 >> x;>> ((x)*(x),10)=(-32)*(x)*(x)3）21/20(17x e dx ⎰精确到位有效数字）>> x;>> ((((x^2),0,1/2)),17)=0.544987104183622224）42254x dx x+⎰>> x;>> (x^4/(25^2))=125*(5) - 25*x + x^3/35）求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。

>> t;>> ((1^2))(t);>> ()()=16）设函数(x)由方程e所确定，求y′(x)。

>> x y;*(y)(1);>> ()()=(x + (y))7）sin2xe xdx+∞-⎰>> x;>> ()*(2*x); >> (y,0)=2/58）08x =展开（最高次幂为）>> x(1);taylor(f,0,9)=- (429*x^8)/32768 + (33*x^7)/2048 - (21*x^6)/1024 + (7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + 2 + 19） 1sin (3)(2)x y e y =求>> x y;>> ((1));>> ((y,3),2)=-0.582610）求变上限函数x⎰对变量x的导数。