面面垂直证明例题
立体几何第六讲面面垂直练习题(含答案)
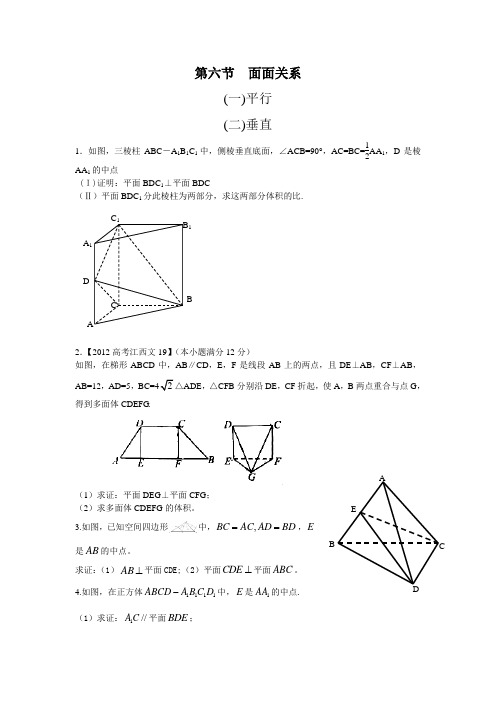
第六节 面面关系(一)平行 (二)垂直1.如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(I)证明:平面BDC 1⊥平面BDC(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.2.【2012高考江西文19】(本小题满分12分)如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,BC=42△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合与点G ,得到多面体CDEFG .(1)求证:平面DEG ⊥平面CFG ; (2)求多面体CDEFG 的体积。
3.如图,已知空间四边形中,,BC AC AD BD ==,E是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
4.如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点. (1)求证:1//A C 平面BDE ;B 1C BADC 1A 1AEDBCA AC⊥平面BDE.(2)求证:平面15.已知四棱锥P—ABCD,底面ABCD是菱形,∠PDDAB,60平面ABCD,PD=AD,=⊥︒点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值第六节 面面关系答案(一)平行 (二)垂直1.【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.【解析】(Ⅰ)由题设知BC ⊥1CC ,BC ⊥AC ,1CC AC C ⋂=,∴BC ⊥面11ACC A , 又∵1DC ⊂面11ACC A ,∴1DC BC ⊥,由题设知01145A DC ADC ∠=∠=,∴1CDC ∠=090,即1DC DC ⊥,又∵DC BC C ⋂=, ∴1DC ⊥面BDC , ∵1DC ⊂面1BDC , ∴面BDC ⊥面1BDC ;(Ⅱ)设棱锥1B DACC -的体积为1V ,AC =1,由题意得,1V =1121132+⨯⨯⨯=12,由三棱柱111ABC A B C -的体积V =1,∴11():V V V -=1:1, ∴平面1BDC 分此棱柱为两部分体积之比为1:1.2.【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG GF ⊥又因为CF EGF ⊥底面,可得CF EG ⊥,即EG CFG ⊥面所以平面DEG ⊥平面CFG . (2)过G 作GO 垂直于EF ,GO 即为四棱锥G-EFCD 的高,所以所求体积为11125520335DECF S GO ⋅=⨯⨯⨯=正方形3.证明:(1)BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理,AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE又∵AB ⊆平面ABC , ∴平面CDE ⊥平面ABC 4.证明:(1)设AC BD O ⋂=,∵E 、O 分别是1AA 、AC 的中点,∴1A C ∥EO又1AC ⊄平面BDE ,EO ⊂平面BDE ,∴1A C ∥平面BDE (2)∵1AA ⊥平面ABCD ,BD ⊂平面ABCD ,1AA BD ⊥ 又BD AC ⊥,1AC AA A⋂=,∴BD ⊥平面1A AC ,BD ⊂平面BDE ,∴平面BDE ⊥平面1A AC5.(1)证明:连接BD.ADB DAB AD AB ∆∴︒=∠=,60, 为等边三角形.E 是AB 中点,.DE AB ⊥∴⊥PD 面ABCD ,AB ⊂面ABCD ,.PD AB ⊥∴⊂DE 面PED ,PD ⊂面PED ,⊥∴=AB D PD DE , 面PED. ⊂AB 面PAB ,⊥∴PED 面面PAB.(2)解:⊥AB 平面PED ,PE ⊂面PED ,.PE AB ⊥∴ 连接EF ,⊂EF PED ,.EF AB ⊥∴PEF ∠∴为二面角P —AB —F 的平面角. 设AD=2,那么PF=FD=1,DE=3. 在,1,2,7,===∆PF EF PE PEF 中,147572212)7(cos 22=⨯-+=∠∴PEF 即二面角P —AB —F 的平面角的余弦值为.1475立体几何练习题1.设α、β、γ为两两不重合的平面,l 、m 、n 为两两不重合的直线,给出下列四个命题: 若α⊥γ,β⊥γ,则α∥β;②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β;③若α∥β,l ⊂α,则l ∥β;④若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n . 其中真命题的个数是( ) A .1 B .2 C .3 D .42.正方体ABCD ﹣A 1B 1C 1D 1中,BD 1与平面ABCD 所成角的余弦值为() A .B .CD .3.三棱柱ABC ﹣A 1B 1C 1中,AA 1=2且AA 1⊥平面ABC ,△ABC 是 边长为的正三角形,该三棱柱的六个顶点都在一个球面上,则这个球的体积为() A . 8πB .C .D . 8π4.三个平面两两垂直,它们的三条交线交于点O ,空间一点P 到三个平面的距离分别为3、4、5,则OP 长为()A . 5B . 2C . 3D . 55.如图,四棱锥S ﹣ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是() A . AC⊥SB B .AB∥平面SCDC . SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D . AB 与SC 所成的角等于DC 与SA 所成的角6.如图,四棱锥P ﹣ABCD 的底面为正方形,PD ⊥底面ABCD ,PD=AD=1,设点CG 到平面PAB 的距离为d 1,点B 到平面PAC 的距离为d 2,则有( ) A . 1<d 1<d 2 B . d 1<d 2<1C . d 1<1<d 2D . d 2<d 1<17.在锐角的二面角βα--EF ,A EF ∈,AG α⊂, 45=∠GAE ,若AG 与β所成角为 30,则二面角βα--EF 为__________. 8.给出下列四个命题:(1)若平面α上有不共线的三点到平面β的距离相等,则βα//; (2)两条异面直线在同一平面内的射影可能是两条平行直线;(3)两条异面直线中的一条平行于平面α,则另一条必定不平行于平面α; (4)b ,a 为异面直线,则过a 且与b 平行的平面有且仅有一个. 其中正确命题的序号是_______________________9.已知正方体 1111ABCD A B C D -中,点E 是棱 11A B 的中点,则直线AE 与平而 11BDD B 所成角的正弦值是_________.EFA Gαβ10.已知直三棱柱111ABC A B C -中,090ABC ∠=,122AC AA ==,2AB =,M 为1BB 的中点,则1B 与平面ACM 的距离为______11.边长分别为a 、b 的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则ba的取值范围是 . 12.已知矩形ABCD 的长4AB =,宽3AD =,将其沿对角线BD 折起,得到四面体A BCD -,如图所示, 给出下列结论:①四面体A BCD -体积的最大值为725; ②四面体A BCD -外接球的表面积恒为定值;③若E F 、分别为棱AC BD 、的中点,则恒有EF AC ⊥且EF BD ⊥; ④当二面角A BD C --为直二面角时,直线AB CD 、所成角的余弦值为1625; ⑤当二面角A BD C --的大小为60︒时,棱AC 的长为145. 其中正确的结论有 (请写出所有正确结论的序号). 13.如图,在直三棱柱ABC ﹣A 1B 1C 1中,∠BAC=90°,AB=BB 1,直线B 1C 与平面ABC 成30°角.(I )求证:平面B 1AC⊥平面ABB 1A 1;(II )求直线A 1C 与平面B 1AC 所成角的正弦值.14.如图,在三棱锥P ﹣ABC 中,D ,E ,F 分别为棱PC ,AC ,AB 的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5. (1)若PB⊥BC,证明平面BDE⊥平面ABC . (2)求直线BD 与平面ABC 所成角的正切值.15.如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 为DD 1的中点. (1)求证:直线BD 1∥平面PAC ;4343AB CD4334DCBA(2)求证:平面PAC⊥平面BDD1B1;(3)求CP与平面BDD1B1所成的角大小.16.如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上(1)求证:AC⊥平面PDB(2)当PD=AB且E为PB的中点时,求AE与平面PDB所成的角的大小.17.在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.(Ⅰ)求证:PB∥平面ACM;(Ⅱ)求证:AD⊥平面PAC;(Ⅲ)求二面角M﹣AC﹣D的正切值.18.如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.(1)证明:BD⊥平面PAC;(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.19.如图,直三棱柱ABC﹣A1B1C1中,CA⊥CB,AA1=AC=CB=2,D是AB的中点.(1)求证:BC1∥平面A1CD;(2)求证:A1C⊥AB1;(3)若点E在线段BB1上,且二面角E﹣CD﹣B的正切值是,求此时三棱锥C﹣A1DE的体积.20.如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.(1)求证:AC⊥SD;(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小;(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由.试卷答案1.B:解:若α⊥γ,β⊥γ,则α与β可能平行也可能相交,故①错误;由于m,n不一定相交,故α∥β不一定成立,故②错误;由面面平行的性质定理,易得③正确;由线面平行的性质定理,我们易得④正确;故选B2.D考点:棱柱的结构特征.专题:空间角.分析:找出BD1与平面ABCD所成的角,计算余弦值.解答:解:连接BD,;∵DD1⊥平面ABCD,∴BD是BD1在平面ABCD的射影,∴∠DBD1是BD1与平面ABCD所成的角;设AB=1,则BD=,BD1=,∴cos∠DBD1===;故选:D.点评:本题以正方体为载体考查了直线与平面所成的角,是基础题.3.C考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:根据题意,正三棱柱的底面中心的连线的中点就是外接球的球心,求出球的半径即可求出球的体积.解答:解:由题意可知:正三棱柱的底面中心的连线的中点就是外接球的球心,因为△ABC是边长为的正三角形,所以底面中心到顶点的距离为:1;因为AA1=2且AA1⊥平面ABC,所以外接球的半径为:r==.所以外接球的体积为:V=πr3=π×()3=.故选:C.点评:本题给出正三棱柱有一个外接球,在已知底面边长的情况下求球的体积.着重考查了正三棱柱的性质、正三角形的计算和球的体积公式等知识,属于中档题.4.D考点:平面与平面垂直的性质.专题:计算题;空间位置关系与距离.分析:构造棱长分别为a,b,c的长方体,P到三个平面的距离即为长方体的共顶点的三条棱的长,OP为长方体的对角线,求出OP即可.解答:构造棱长分别为a,b,c的长方体,P到三个平面的距离即为长方体的共顶点的三条棱的长,则a2+b2+c2=32+42+52=50因为OP为长方体的对角线.所以OP=5.故选:D.点评:本题考查点、线、面间的距离计算,考查计算能力,是基础题.5.D考点:直线与平面垂直的性质.专题:综合题;探究型.分析:根据SD⊥底面ABCD,底面ABCD为正方形,以及三垂线定理,易证AC⊥SB,根据线面平行的判定定理易证AB∥平面SCD,根据直线与平面所成角的定义,可以找出∠ASO是SA与平面SBD所成的角,∠CSO是SC与平面SBD所成的角,根据三角形全等,证得这两个角相等;异面直线所成的角,利用线线平行即可求得结果.解答:解:∵SD⊥底面ABCD,底面ABCD为正方形,∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;∵AB∥CD,AB⊄平面SCD,CD⊂平面SCD,∴AB∥平面SCD,故B正确;∵SD⊥底面ABCD,∠ASO是SA与平面SBD所成的角,∠DSO是SC与平面SBD所成的,而△SAO≌△CSO,∴∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,而这两个角显然不相等,故D不正确;故选D.点评:此题是个中档题.考查线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角等问题,综合性强.6.D考点:点、线、面间的距离计算.专题:综合题;空间位置关系与距离;空间角.分析:过C做平面PAB的垂线,垂足为E,连接BE,则三角形CEB为直角三角形,根据斜边大于直角边,再根据面PAC和面PAB与底面所成的二面角,能够推导出d2<d1<1.解答:解:过C做平面PAB的垂线,垂足为E,连接BE,则三角形CEB为直角三角形,其中∠CEB=90°,根据斜边大于直角边,得CE<CB,即d2<1.同理,d1<1.再根据面PAC和面PAB与底面所成的二面角可知,前者大于后者,所以d2<d1.所以d2<d1<1.故选D.点评:本题考查空间距离的求法,解题时要认真审题,仔细解答,注意空间角的灵活运用.7.48.(2)(4)10.111.1 (,) 212.②③④13.考点:平面与平面垂直的判定;直线与平面所成的角.专题:证明题.分析:(I)欲证平面B1AC⊥平面ABB1A1,关键是寻找线面垂直,而AC⊥平面ABB1A1,又AC⊂平面B1AC,满足面面垂直的判定定理;(II)过A1做A1M⊥B1A1,垂足为M,连接CM,∠A1CM为直线A1C与平面B1AC所成的角,然后在三角形A1CM 中求出此角的正弦值即可.解答:解:(I)证明:由直三棱柱性质,B1B⊥平面ABC,∴B1B⊥AC,又BA⊥AC,B1B∩BA=B,∴AC⊥平面ABB1A1,又AC⊂平面B1AC,∴平面B1AC⊥平面ABB1A1.(II)解:过A1做A1M⊥B1A1,垂足为M,连接CM,∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A,∴A1M⊥平面B1AC.∴∠A1CM为直线A1C与平面B1AC所成的角,∵直线B1C与平面ABC成30°角,∴∠B1CB=30°.设AB=BB1=a,可得B1C=2a,BC=,∴直线A1C与平面B1AC所成角的正弦值为点评:本题主要考查了平面与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力.14.考点:直线与平面所成的角;平面与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)由已知得DE⊥AC,DE2+EF2=DF2,从而DE⊥平面ABC,由此能证明平面BDE⊥平面ABC.(2)由DE⊥平面ABC,得∠DBE是直线BD与平面ABC所成的角,由此能求出直线BD与平面ABC所成角的正切值.解答:(1)证明:∵在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点.PA⊥AC,PA=AB=6,BC=8,DF=5,∴DE⊥AC,DE=3,EF=4,DF=5,∴DE2+EF2=DF2,∴DE⊥EF,又EF∩AC=F,∴DE⊥平面ABC,又DE⊂平面BDE,∴平面BDE⊥平面ABC.(2)∵DE⊥平面ABC,∴PA⊥平面ABC,∴PA⊥AB,∵PB⊥BC,∴AB⊥BC,∴AC==10,∴,由DE⊥平面ABC,得∠DBE是直线BD与平面ABC所成的角,tan∠DBE==.∴直线BD与平面ABC所成角的正切值为.点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.15.考点:直线与平面平行的判定;平面与平面垂直的判定;直线与平面所成的角.专题:证明题.分析:(1)设AC和BD交于点O,由三角形的中位线的性质可得PO∥BD1,从而证明直线BD1∥平面PAC.(2)证明AC⊥BD,DD1⊥AC,可证AC⊥面BDD1B1,进而证得平面PAC⊥平面BDD1B1 .(3)CP在平面BDD1B1内的射影为OP,故∠CPO是CP与平面BDD1B1所成的角,在Rt△CPO中,利用边角关系求得∠CPO的大小.解答:(1)证明:设AC和BD交于点O,连PO,由P,O分别是DD1,BD的中点,故PO∥BD1,∵PO⊂平面PAC,BD1⊄平面PAC,所以,直线BD1∥平面PAC.(2)长方体ABCD﹣A1B1C1D1中,AB=AD=1,底面ABCD是正方形,则AC⊥BD,又DD1⊥面ABCD,则DD1⊥AC.∵BD⊂平面BDD1B1,D1D⊂平面BDD1B1,BD∩D1D=D,∴AC⊥面BDD1B1.∵AC⊂平面PAC,∴平面PAC⊥平面BDD1B1 .(3)由(2)已证:AC⊥面BDD1B1,∴CP在平面BDD1B1内的射影为OP,∴∠CPO是CP与平面BDD1B1所成的角.依题意得,,在Rt△CPO中,,∴∠CPO=30°∴CP与平面BDD1B1所成的角为30°.点评:本题考查证明线面平行、面面垂直的方法,求直线和平面所称的角的大小,找出直线和平面所成的角是解题的难点,属于中档题.16.考点:直线与平面所成的角;直线与平面垂直的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)根据题意证明AC⊥BD,PD⊥AC,可得AC⊥平面PDB;(2)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.解答:(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,∵PD⊥底面ABCD,∴PD⊥AC,又BD∩PD=D∴AC⊥平面PDB,(3分)(2)设AC∩BD=O,连接OE,由(1)知AC⊥平面PDB于O,∴∠AEO为AE与平面PDB所的角,(5分)又O,E分别为DB、PB的中点,∴OE∥PD,OE=PD,在Rt△AOE中,OE=PD=AB=AO,∴∠AEO=45°,(7分)即AE与平面PDB所成的角的大小为45°.(8分)点评:本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于中档题.17.考点:与二面角有关的立体几何综合题;直线与平面平行的判定;直线与平面垂直的判定.专题:计算题.分析:(Ⅰ)连接OM,BD,由M,O分别为PD和AC中点,知OM∥PB,由此能够证明PB∥平面ACM.(Ⅱ)由PO⊥平面ABCD,知PO⊥AD,由∠ADC=45°,AD=AC=1,知AC⊥AD,由此能够证明AD⊥平面PAC.(Ⅲ)取DO中点N,连接MN,由MN∥PO,知MN⊥平面ABCD.过点N作NE⊥AC于E,由E为AO中点,连接ME,由三垂线定理知∠MEN即为所求,由此能求出二面角M﹣AC﹣D的正切值.解答:(Ⅰ)证明:连接OM,BD,∵M,O分别为PD和AC中点,∴OM∥PB,∵OM⊂平面ACM,PB⊄ACM平面,∴PB∥平面ACM….(4分)(Ⅱ)证明:由已知得PO⊥平面ABCD∴PO⊥AD,∵∠ADC=45°,AD=AC=1,∴AC⊥AD,∵AC∩PO=O,AC,PO⊂平面PAC,∴AD⊥平面PAC.…..(8分)(Ⅲ)解:取DO中点N,连接MN,则MN∥PO,∴MN⊥平面ABCD过点N作NE⊥AC于E,则E为AO中点,连接ME,由三垂线定理可知∠MEN即为二面角M﹣AC﹣D的平面角,∵MN=1,NE=∴tan∠MEN=2…..(13分)点评:本题考查直线与平面平行、直线现平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,仔细解答,注意三垂直线定理的合理运用.18.考点:二面角的平面角及求法;直线与平面垂直的判定.专题:空间位置关系与距离;空间角;立体几何.分析:(1)由题设条件及图知,可先由线面垂直的性质证出PA⊥BD与PC⊥BD,再由线面垂直的判定定理证明线面垂直即可;(2)由图可令AC与BD的交点为O,连接OE,证明出∠BEO为二面角B﹣PC﹣A的平面角,然后在其所在的三角形中解三角形即可求出二面角的正切值.解答:(1)∵PA⊥平面ABCD∴PA⊥BD∵PC⊥平面BDE∴PC⊥BD,又PA∩PC=P∴BD⊥平面PAC(2)设AC与BD交点为O,连OE∵PC⊥平面BDE∴PC⊥平面BOE∴PC⊥BE∴∠BEO为二面角B﹣PC﹣A的平面角∵BD⊥平面PAC∴BD⊥AC∴四边形ABCD为正方形,又PA=1,AD=2,可得BD=AC=2,PC=3∴OC=在△PAC∽△OEC中,又BD⊥OE,∴∴二面角B﹣PC﹣A的平面角的正切值为3点评:本题考查二面角的平面角的求法及线面垂直的判定定理与性质定理,属于立体几何中的基本题型,二面角的平面角的求法过程,作,证,求三步是求二面角的通用步骤,要熟练掌握19.考点:棱柱、棱锥、棱台的体积;空间中直线与直线之间的位置关系;直线与平面平行的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)连接AC1交A1C于点F,由三角形中位线定理得BC1∥DF,由此能证明BC1∥平面A1CD.(2)利用线面垂直的判定定理证明A1C⊥平面AB1C1,即可证明A1C⊥AB1;(3)证明∠BDE为二面角E﹣CD﹣B的平面角,点E为BB1的中点,确定DE⊥A1D,再求三棱锥C﹣A1DE 的体积.解答:(1)证明:连结AC1,交A1C于点F,则F为AC1中点,又D是AB中点,连结DF,则BC1∥DF,因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.…(3分)(2)证明:直三棱柱ABC﹣A1B1C1中,因为AA1=AC,所以AC1⊥A1C…(4分)因为CA⊥CB,B1C1∥BC,所以B1C1⊥平面ACC1A1,所以B1C1⊥A1C…(6分)因为B1C1∩AC1=C1,所以A1C⊥平面AB1C1所以A1C⊥AB1…(8分)(3)在直三棱柱ABC﹣A1B1C1中,AA1⊥CD,因为AC=CB,D为AB的中点,所以CD⊥AB,CD⊥平面ABB1A1.所以CD⊥DE,CD⊥DB,所以∠BDE为二面角E﹣CD﹣B的平面角.在Rt△DEB中,.由AA1=AC=CB=2,CA⊥CB,所以,.所以,得BE=1.所以点E为BB1的中点.…(11分)又因为,,,A1E=3,故,故有DE⊥A1D所以…(14分)点评:本题主要考查直线与平面平行、垂直等位置关系,考查线面平行、二面角的概念、求法、三棱锥C﹣A1DE的体积等知识,考查空间想象能力和逻辑推理能力,是中档题.20.考点:直线与平面平行的判定;直线与平面垂直的判定;与二面角有关的立体几何综合题.专题:计算题;证明题;压轴题.分析:(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.以O为坐标原点,分别为x轴、y轴、z轴正方向,建立坐标系O﹣xyz,设底面边长为a,求出高SO,从而得到点S与点C 和D的坐标,求出向量与,计算它们的数量积,从而证明出OC⊥SD,则AC⊥SD;(2)根据题意先求出平面PAC的一个法向量和平面DAC的一个法向量,设所求二面角为θ,则,从而求出二面角的大小;(3)在棱SC上存在一点E使BE∥平面PAC,根据(Ⅱ)知是平面PAC的一个法向量,设,求出,根据可求出t的值,从而即当SE:EC=2:1时,,而BE不在平面PAC内,故BE∥平面PAC解答:证明:(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.以O为坐标原点,分别为x轴、y轴、z轴正方向,建立坐标系O﹣xyz如图.设底面边长为a,则高.于是,,,,故OC⊥SD从而AC⊥SD(2)由题设知,平面PAC的一个法向量,平面DAC的一个法向量.设所求二面角为θ,则,所求二面角的大小为30°.(3)在棱SC上存在一点E使BE∥平面PAC.由(Ⅱ)知是平面PAC的一个法向量,且设,则而即当SE:EC=2:1时,而BE不在平面PAC内,故BE∥平面PAC点评:本题主要考查了直线与平面平行的判定,以及空间两直线的位置关系的判定和二面角的求法,涉及到的知识点比较多,知识性技巧性都很强.。
面面垂直的性质习题详细答案

变种2
如果一个平面内的两条相 交直线与另一个平面垂直, 求证这两个平面垂直。
提高题
如果一个平面内的两条相 交直线与另一个平面垂直, 求证这两个平面的交线与 原直线垂直。
综合பைடு நூலகம்解析与解答
• 综合题1:已知一个平面内的两条相交直线与另一个 平面垂直,求证这两个平面的交线与原直线垂直。
综合题解析与解答
面面垂直的性质习题详细答案
contents
目录
• 面面垂直的性质概述 • 习题解析 • 习题解答技巧 • 面面垂直的性质习题答案 • 习题拓展与提高
01 面面垂直的性质概述
定义与定理
定义
两个平面互相垂直,当且仅当一 个平面内的任意直线都与另一个 平面垂直。
定理
如果两个平面互相垂直,那么其 中一个平面内的任意直线都与另 一个平面垂直。
机械工程
在机械设计中,面面垂直的性质 常常用于确定零件的安装角度和 位置,以确保机器的正常运转。
地理学
在地理学中,地球的经纬线分布 和角度计算也涉及到面面垂直的 性质,例如在计算地球上的纬度、 经度等数值时,需要利用到面面
垂直的性质。
02 习题解析
基础习题解析
总结词
掌握基础概念
题目
两个平面垂直,其中一个平面内有一条直线,那么这条直线与另一个平面的关 系是什么?
由于直线a⊥平面α,且直线b⊥直线a,根 据面面垂直的性质定理,直线b必然在平面 α内。
中等难度习题答案
总结词
中等难度习题在考察面面垂直性质的基础上,增加了对空间想象能力和推理能力的考察。
题目3
已知平面α与平面β互相垂直,点A属于平面α,点B属于平面β,且AB与两平面的交线分别交 于C和D两点,若AC=CD,求证线段BD的长度。
面面垂直证明例题
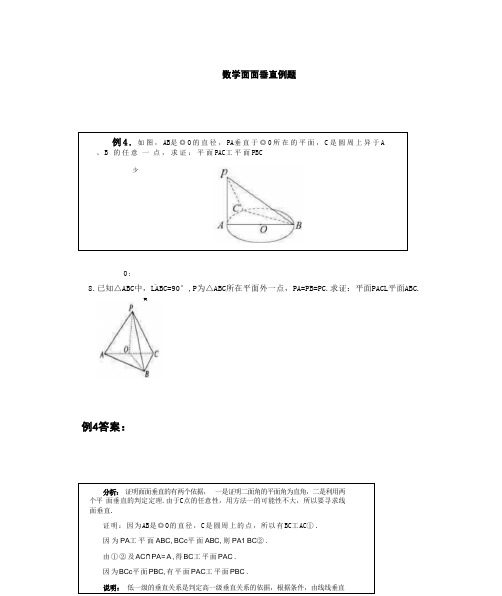
例4.如图,AB是◎O的直径,PA垂直于◎0所在的平面,C是圆周上异于A、B的任意一点,求证:平面PAC工平面PBC
少
8.已知△ABC中,LABC=90°,P为△ABC所在平面外一点,PA=PB=PC.求个依据,一是证明二面角的平面角为直角,二是利用两个平面垂直的判定定理.由于C点的任意性,用方法一的可能性不大,所以要寻求线面垂直.
证明:因为AB是◎O的直径,C是圆周上的点,所以有BC工AC①.
因为PA工平面ABC,BCc平面ABC,则PA1BC②.
由①②及AC∩PA=A,得BC工平面PAC.
因为BCc平面PBC,有平面PAC工平面PBC.
说明:低一级的垂直关系是判定高一级垂直关系的依据,根据条件,由线线垂直一线面垂直→面面垂直.通过这个例题展示了空间直线与平面的位置关系的内在联系,垂直关系的判定和性质共同构成了一个完整的知识体系.
例8答案:取AC的中点为O,连接OP、OB。
AO-OC,PA=PC,故PO垂直AC
证明面面垂直的经典例题

证明面面垂直的经典例题题目:证明面面垂直的经典例题解答:面面垂直的概念是指两个平面的法线互相垂直。
在几何学中,我们可以通过证明两个平面的法线向量的数量积为零来证明面面垂直的关系。
设两个平面为平面α和平面β,且分别由法线向量n1和n2所决定。
为了证明平面α和平面β垂直,我们需要证明n1·n2=0。
根据向量的数量积的定义,n1·n2=|n1|·|n2|·cosθ,其中θ为n1和n2之间的夹角。
根据平面的法向量的定义,平面α上的任意一条法线向量n1与平面β上的任意一条法线向量n2的夹角θ是相等的。
因此,我们只需在平面α上选取一条法线向量n1,并在平面β上选取与n1垂直的一条法线向量n2,计算它们的数量积即可。
下面通过三个经典例题来具体证明两个平面的法线向量的数量积为零,从而证明两个平面垂直的关系。
例题1:已知平面α过点A(1,2,3),法线向量为n1=(2,-1,3),平面β过点B(4,5,6),法线向量为n2=(1,-2,1)。
证明平面α和平面β垂直。
解析:首先计算n1·n2=(2,-1,3)·(1,-2,1),其结果为2×1 + (-1)×(-2) + 3×1=2+2+3=7≠0。
所以n1·n2 ≠ 0,即两个平面α和β不垂直。
例题2:已知平面α过点A(1,-2,0),法线向量为n1=(2,1,-1),平面β过点B(0,-6,3),法线向量为n2=(3,-1,-2)。
证明平面α和平面β垂直。
解析:先计算n1·n2=(2,1,-1)·(3,-1,-2),其结果为2×3 + 1×(-1) + (-1)×(-2)=6-1+2=7。
所以n1·n2 ≠ 0,即两个平面α和β不垂直。
例题3:已知平面α过点A(2,-1,4),法线向量为n1=(1,0,1),平面β过点B(-1,3,2),法线向量为n2=(1,-1,-1)。
线面垂直及面面垂直典型例题

线面垂直与面面垂直 基础要点1、若直线a 与平面,αβ所成的角相等,则平面α与β的位置关系是( B ) A 、//αβB 、α不一定平行于βC 、α不平行于β D 、以上结论都不正确2、在斜三棱柱111ABC A B C -,90BAC ∠=o,又1BC AC ⊥,过1C 作1C H ⊥底面ABC ,垂足为H ,则H 一定在( B ) A 、直线AC 上B 、直线AB 上C 、直线BC 上D 、△ABC 的内部3、如图示,平面α⊥平面β,,,A B AB αβ∈∈与两平面,αβ所成的角分别为4π和6π,过A 、B 分别作两平面交线的垂线,垂足为,A B '',则:AB A B ''=( A ) A 、2:1 B 、3:1 C 、3:2 D 、4:34、如图示,直三棱柱11ABB DCC -中,190,4ABB AB ∠==o,12,1BC CC ==DC 上有一动点P ,则△1APC 周长的最小值是5.已知长方体1111D C B A ABCD -中,21==AB A A ,若棱AB 上存在点P ,使得PC P D ⊥1,则棱AD 长的取值范围是 。
B`A`BAαβABCD 1B 1C 1D A B题型一:直线、平面垂直的应用1.(2014,江苏卷)如图,在三棱锥P-ABC 中,D ,E ,F 分别为棱PC ,AC ,AB 的中点. 已知,685PA AC PA BC DF ⊥===,,. 求证:(1) PA DEF P 平面;(2) BDE ABC ⊥平面平面 . 证明: (1) 因为D ,E 分别为棱PC ,AC 的中点, 所以DE ∥PA.又因为PA ⊄ 平面DEF ,DE 平面DEF , 所以直线PA ∥平面DEF.(2) 因为D ,E ,F 分别为棱PC ,AC ,AB 的中点,PA =6,BC =8,所以DE ∥PA ,DE =12PA =3,EF =12BC =4. 又因 DF =5,故DF 2=DE 2+EF 2, 所以∠DEF =90°,即DE 丄EF. 又PA ⊥AC ,DE ∥PA ,所以DE ⊥AC.因为AC∩EF =E ,AC 平面ABC ,EF 平面ABC ,所以DE ⊥平面ABC. 又DE 平面BDE ,所以平面BDE ⊥平面ABC.2. (2014,北京卷,文科)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面,AB BC ⊥,12AA AC ==,E 、F 分别为11A C 、BC 的中点. (1)求证:平面ABE ⊥平面11B BCC ;(2)求证:1//C F 平面ABE . 证明:(1)在三棱柱111ABC A B C -中,11,,BB ABC BB AB ⊥∴⊥底面11,,AB BC AB B BCC ∴⊥∴⊥平面,AB ABE ⊂Q 平面11ABE B BCC ∴⊥平面平面.(2)取AB 的中点G ,连接EG ,FGQ E 、F 分别为11A C 、BC 的中点, 1,2FG AC FG AC ∴=P , 111111AC AC AC AC FG EC FG EC =∴=Q P P ,,,,则四边形1FGEC 为平行四边形,111,,,C F EG EG ABE C F ABE C F ABE ∴⊂⊄∴P Q P 平面平面平面.3.如图,P 是ABC ∆所在平面外的一点,且⊥PA 平面ABC ,平面⊥PAC 平面PBC .求证AC BC ⊥.分析:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直..证明:在平面PAC 内作PC AD ⊥,交PC 于D .因为平面⊥PAC 平面PBC 于PC ,⊂AD 平面PAC ,且PC AD ⊥,所以PBC AD 平面⊥.又因为⊂BC 平面PBC ,于是有BC AD ⊥①.另外⊥PA 平面ABC ,⊂BC 平面ABC ,所以BC PA ⊥.由①②及A PA AD =I ,可知⊥BC 平面PAC .因为⊂AC 平面PAC ,所以AC BC ⊥.说明:在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直⇒线面垂直⇒线线垂直.4. 过点S 引三条不共面的直线SA 、SB 、SC ,如图,︒=∠90BSC ,︒=∠=∠60ASB ASC ,若截取a SC SB SA ===(1)求证:平面ABC ⊥平面BSC ; (2)求S 到平面ABC 的距离.分析:要证明平面ABC ⊥平面BSC ,根据面面垂直的判定定理,须在平面ABC 或平面BSC 内找到一条与另一个平面垂直的直线.(1)证明:∵a SC SB SA ===, 又︒=∠=∠60ASB ASC ,∴ASB ∆和ASC ∆都是等边三角形, ∴a AC AB ==,取BC 的中点H ,连结AH ,∴BC AH ⊥. 在BSC Rt ∆中,a CS BS ==,∴BC SH ⊥,a BC 2=,∴2)22(222222a a a CH AC AH =-=-=,∴222a SH =. 在SHA ∆中,∴222a AH =,222a SH =,22a SA =,∴222HA SH SA +=,∴SH AH ⊥,∴⊥AH 平面SBC . ∵⊂AH 平面ABC ,∴平面ABC ⊥平面BSC .或:∵AB AC SA ==,∴顶点A 在平面BSC 内的射影H 为BSC ∆的外心,又BSC ∆为∆Rt ,∴H 在斜边BC 上,又BSC ∆为等腰直角三角形,∴H 为BC 的中点,∴⊥AH 平面BSC .∵⊂AH 平面ABC ,∴平面ABC ⊥平面BSC . (2)解:由前所证:AH SH ⊥,BC SH ⊥,∴⊥SH 平面ABC , ∴SH 的长即为点S 到平面ABC 的距离,a BC SH 222==, ∴点S 到平面ABC 的距离为a 22. 5、如图示,ABCD 为长方形,SA 垂直于ABCD 所在平面,过A 且垂直于SC 的平面分别交SB 、SC 、SD 于E 、F 、G ,求证:AE ⊥SB ,AG ⊥SDDCBASG EF6.在四棱锥P-ABCD 中,侧面PCD 是正三角形,且与底面ABCD 垂直,已知底面是面积为32的菱形,︒=∠60ADC ,M 是PB 中点。
面面垂直的性质

小结
1、这节课我们学习了哪些内容,我们是如何得到这些结论的?
2、空间垂直关系有哪些?如何实现垂直关系的相互转化?指出下 图中空间垂直关系转化的依据.
面面垂直
线面垂直
线线垂直
3、平面 ⊥平面β,要过平面 内一点引平面β的垂线, 只需过这一点在平面 内作交线的垂线。
平面与平面垂直的性质定理:
如果两个平面相互垂直,那么在一个平面内垂 直于它们交线的直线垂直于另一个平面。
图像语言:
文字语言:
α C
B
D A
β
CD AB
CD
AB CD
AB CD D
说明:(1)此题运用了“同一法”证明.
(2)这个结论是面面垂直的另一个性质,它的 作用是判定直线在平面内。 文字语言:
如果两个平面垂直,那么经过第一个平面 内的一点垂直于第二个平面的直线,在第一 个平面内。
思考:
设 ,点P , P a, a , 请同学们讨论直线a 与平面的关系
求证:如果两个平面互相垂直,那么经过第一个平面
内的一点垂直于第二个平面的直线在第一个平面内
已知 ,P , P a, a ,求证:a
A1
C1 B1
A
C
B
把等腰直角三角形ABC沿斜边AB旋转至ABD的位置, 使CD AC,(1)平面ABD 平面ABC (2)求二面角C BD A的余弦值
D
A
B
C
在矩形ABCD中,AB 3 3,BC 3,沿对角线BD把BCD 折起,使C移到C,且C在面ABC内的射影O恰好落在AB 上(1)求证:AC BC (2)求AB与平面BCD所成的角的正弦值 (3)求二面角C BD A的正切值
α C
B
如何证明面面垂直(精选多篇)

如何证明面面垂直(精选多篇)第一篇:如何证明面面垂直如何证明面面垂直设p是三角形abc所在平面外的一点,p到a,b,c 三点的距离相等,角bac为直角,求证:平面pcb垂直平面abc过p作pq⊥面abc于q,则q为p在面abc的投影,因为p到a,b,c的距离相等,所以有qa=qb=qc,即q为三角形abc的中心,因为角bac为直,所以q在线段bc上,所以在面pcb上有线段pq⊥平面abc,故平面pcb⊥平面abc2证明一个面上的一条线垂直另一个面;首先可以转化成一个平面的垂线在另一个平面内,即一条直线垂直于另一个平面然后转化成一条直线垂直于另一个平面内的两条相交直线也可以运用两个面的法向量互相垂直。
这是解析几何的方法。
2一、初中部分1利用直角三角形中两锐角互余证明由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°,即直角三角形的两个锐角互余。
2勾股定理逆定理3圆周角定理的推论:直径所对的圆周角是直角,一个三角形的一边中线等于这边的一半,则这个三角形是直角三角形。
二、高中部分线线垂直分为共面与不共面。
不共面时,两直线经过平移后相交成直角,则称两条直线互相垂直。
1向量法两条直线的方向向量数量积为02斜率两条直线斜率积为-13线面垂直,则这条直线垂直于该平面内的所有直线一条直线垂直于三角形的两边,那么它也垂直于另外一边4三垂线定理在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
5三垂线定理逆定理如果平面内一条直线和平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
3高中立体几何的证明主要是平行关系与垂直关系的证明。
方法如下(难以建立坐标系时再考虑):ⅰ.平行关系:线线平行:1.在同一平面内无公共点的两条直线平行。
2.公理4(平行公理)。
3.线面平行的性质。
4.面面平行的性质。
5.垂直于同一平面的两条直线平行。
面面垂直的判定与性质定理

面面垂直的判定与性质定理一.面面垂直的判定定理:符号表示:1.(2013年高考陕西卷(文))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,1AB AA==1A(Ⅰ) 证明: A1BD // 平面CD1B1;(Ⅱ) 求三棱柱ABD-A1B1D1的体积.2.(2013年高考北京卷(文))如图,在四棱锥P ABCD-中,//AB CD,AB AD⊥,2CD AB=,平面PAD⊥底面ABCD,PA AD⊥,E和F分别是CD和PC的中点,求证:(1)PA⊥底面ABCD;(2)//BE平面PAD;(3)平面BEF⊥平面PCD3.(2013年高考山东卷(文))如图,四棱锥P ABCD -中,,AB AC AB PA ⊥⊥,,2AB CD AB CD =∥,,,,,E F G M N分别为,,,,PB AB BC PD PC 的中点(Ⅰ)求证:CE PAD ∥平面;(Ⅱ)求证:EFG EMN ⊥平面平面4.(2013年高考天津卷(文))如图, 三棱柱ABC -A 1B 1C 1中, 侧棱A 1A ⊥底面ABC ,且各棱长均相等. D , E , F 分别为棱AB , BC , A 1C 1的中点.(Ⅰ) 证明EF //平面A 1CD ; (Ⅱ) 证明平面A 1CD ⊥平面A 1ABB 1;ABCD 图2BACD 图1二. 面面垂直的性质定理:符号表示:5. 如图所示,正方形ABCD 与直角梯形ADEF 所在平面互相垂直,90ADE ∠=,DE AF //,22===AF DA DE .(Ⅰ)求证:AC ⊥平面BDE ; (Ⅱ)求证://AC 平面BEF ; (Ⅲ)求四面体BDEF 的体积.6.如图1,在直角梯形A B C D 中,90ADC ∠=︒,//CD AB ,4,2AB AD CD ===.将ADC ∆沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示.(Ⅰ) 求证:BC ⊥平面ACD ;(Ⅱ) 求几何体D ABC -的体积.CDFE。
专题51 由“面面垂直”引发的证明问题案例

1.在如图如示的多面体中,平面AEFD ⊥平面BEFC ,四边形AEFD 是边长为2的正方形,EF ∥BC ,且122BE CF BC ===. (1)若,M N 分别是,AE CF 中点,求证: MN ∥平面ABCD(2)求此多面体ABCDEF 的体积【答案】(1)见解析(2)83V =试题解析:(1)证明:在平面CDF 中,作NH CF ⊥交DC 于H ,连接AH .,M N 是,AE CF 中点,且AEFD 是正方形,NH ∴∥DF , 12NH DF =, 又AM ∥DF , 12AM DF =, ,NH AM NH ∴=∥AM ,∴四边形AMNH 是平行四边形,MN ∴∥AH ,又AH⊂平面ABCD,MN⊄平面ABCD,(2)解:如图,连BD,BF,过F作FG⊥EF,交BC于点G.2.如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角,AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。
E是线段BC1上一点,且BE=BC1.(1)求证:GE∥侧面AA1B1B ;(2)求平面B1GE与底面ABC所成锐二面角的正切值.【答案】(Ⅰ)见解析; 23.【解析】试题分析:(1)延长B 1E 交BC 于F ,根据所得的ΔB 1EC 1∽ΔFEB 可证得F 为BC 的中点,结合G 为ΔABC的重心,可得GE ∥AB 1,根据线面平行的判定定理可得结论成立.(2)在侧面AA 1B 1B 内,过B 1作B 1H⊥AB于H,过H作HT⊥AF于T,连B 1T,根据二面角的定义可得1B TH ∠即为所求,解三角形可得正切值为23.∴GE ∥侧面AA 1B 1B .(2)在侧面AA 1B 1B 内,过B 1作B 1H⊥AB,垂足为H,∵侧面AA 1B 1B ⊥底面ABC ,侧面AA 1B 1B ⋂底面ABC AB =,∴B 1H⊥底面ABC .又侧棱AA 1与底面ABC 成600的角, AA 1= 2,∴∠B 1BH=600,BH=1,B 13在底面ABC 内,过H作HT⊥AF于T,连B 1T.3.如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD , AB BC ⊥, AD BC , 3AD =, 22PA BC AB ===, 3PB =.(Ⅰ)求证: BC PB ⊥;(Ⅱ)求二面角P CD A --的余弦值;(Ⅲ)若点E 在棱PA 上,且BE 平面PCD ,求线段BE 的长.【答案】(Ⅰ)见解析. (Ⅱ)10.(Ⅲ)7. 【解析】试题分析:第一问根据面面垂直的性质和线面垂直的性质得出线线垂直的结论,注意在书写的时候条件不要丢就行;第二问建立空间直角坐标系,利用法向量所成角的余弦值来求得二面角的余弦值;第三问利用向量共线的关系,得出向量的坐标,根据线面平行得出向量垂直,利用其数量积等于零,求得结果.(Ⅰ)证明:因为平面PAB ⊥平面ABCD ,且平面PAB ⋂平面ABCD AB =,因为BC ⊥AB ,且BC ⊂平面ABCD所以BC ⊥平面PAB .因为PB ⊂平面PAB ,(Ⅱ)解:在△PAB 中,因为2PA =, 3PB =, 1AB =,所以222PA AB PB =+,所以PB ⊥AB .令2z =,则()3,3,2m =. 设二面角P CD A --的平面角为α,可知α为锐角,则10cos cos ,334n m n m n m α⋅====⋅++, 即二面角P CD A --的余弦值为105.4.如图所示的几何体中,四边形BCC 1B 1为正方形,AD ∥BB 1,平面ABC ⊥平面BCC 1B 1,AB=AC=2,AD=1,∠ABC=45°。
线面垂直证明面面垂直专题 3

立体几何平行与垂直专题(附经典解析)1垂直证明习题——线面垂直⇒面面垂直1. 如图所示,三棱柱中,,平面.证明:平面平面.2. 如图,在四棱锥中,底面是菱形,且,,,分别为,的中点,且.求证:平面平面.3. 如图所示,△ABC 为正三角形,CE ⊥平面ABC ,BD ∥CE ,且CE =AC =2BD ,M 是AE 的中点.求证:平面BDM ⊥平面ECA .111ABC A B C -90BCA ∠=°1AC ⊥1A BC ABC ⊥11ACCA P ABCD -ABCD 2PA AD ==120PAD BAD ∠=∠=︒E FPDBD 2EF =PAD ⊥ABCD垂直证明习题——线面垂直⇒面面垂直(教师版)1. 如图所示,三棱柱中,,平面.证明:平面平面.【解析】证明:平面,.,,平面.又平面,平面平面.2. 如图,在四棱锥中,底面是菱形,且,,,分别为,的中点,且.求证:平面平面.【解析】过P 作PO ⊥AD ,垂足为O ,连结AO ,BO , 由∠PAD=120°,得∠PAO=60°,111ABC A B C -90BCA ∠=°1AC ⊥1A BC ABC ⊥11ACCA 1AC ⊥1A BC 1AC BC ∴⊥90BCA ∠︒=BC AC ∴⊥BC ∴⊥11ACC A BC ⊂ABC ∴ABC ⊥11ACC A P ABCD -ABCD 2PA AD ==120PAD BAD ∠=∠=︒E FPDBD EF =PAD ⊥ABCD立体几何平行与垂直专题(附经典解析)3∴在Rt △PAO 中,PO=PAsin ∠PAO=2sin60°=2×,∵∠BAO=120°,∴∠BAO=60°,AO=AO ,∴△PAO ≌△BAO ,∴∵E ,F 分别是PA ,BD 的中点,EF=∴EF是△PBD 的中位线,∴PB=2EF=2×,∴PB 2=PO 2+BO 2,∴PO ⊥BO ,∵AD∩BO=O ,∴PO ⊥平面ABCD , 又PO ⊂平面PAD ,∴平面PAD ⊥平面ABCD .3. 如图所示,△ABC 为正三角形,CE ⊥平面ABC ,BD ∥CE ,且CE =AC =2BD ,M 是AE 的中点.求证:平面BDM ⊥平面ECA .【解析】取AC 的中点N ,连接MN 、BN ,则MN //CF .∵BD //CF ,∴MN //BD , ∴N ∈平面BDM .∵EC ⊥平面ABC ,∴EC ⊥BN .又∵AC ⊥BN ,EC ∩AC =C ,∴BN ⊥平面ECA . 又∵BN ⊂平面BDM ,∴平面BDM ⊥平面ECA .222。
线面垂直与面面垂直典型例题

线面垂直与面面垂直基础要点1、若直线a与平而40所成的角相等,则平而a与0的位置关系是(B )A、alipB、a不一定平行于0 C. a不平行于0 D、以上结论都不正确2、在斜三棱柱ABC-A{B}C^ZBAC = 90\又BC』AC,过G作C"丄底而救;垂足为H ,则F—定在(B )A.直线AC上B、直线AB上C、直线BC上D、'ABC的部3、如图示,平而a丄平面0, Aea.Be/3.AB与两平而Z0所成的角分别为冬和冬,4 6 过A. B分别作两平而交线的垂线,垂足为则4 B: A B f =a (A )A. 2:1 B、3:1 C、3:2 D、4:34、如图示,直三棱柱ABB'—DCq中,ZABB l =90=BC = 2,CC,= 1 DC上有一动点P,则厶APC}周长的最小值是 _______________5•已知长方体ABCD_A"GD】中,A l A = AB = 2f若棱AB上存在点P,使得0P丄PC,则棱AD长的取值围是 ____________ 。
题型一:直线、平而垂直的应用1.(2014,卷)如图,在三棱锥P-ABC中,D, E, F分别为棱PC, AC, AB的中点.已知P4丄AC,PA = 6, BC = 8, DF = 5.求证:(1) PA||平而DEF; (2)平面BDE丄平面ABC・证明:(1)因为D, E分别为棱PC, AC的中点,所以DE〃PA・又因为PA 0平而DEF, DEc平而DEF,所以直线PA〃平而DEF.(2)因为D, E, F 分别为棱PC, AC, AB 的中点,PA=6, BC=8,所以DE〃PA, DE= 1PA=3>EF=1BC=4.2 2又因DF=5,故DF2 = DE2+EF2^所以ZDEF=90°,即DE 丄EF.又PA丄AC, DE〃PA,所以DE丄AC.因为ACC1EF=E,ACu平面ABC.EFc平而ABC,所以DE丄平而ABC. 又DEu平而BDE,所以平面BDE丄平而ABC.2.(2014、卷,文科)如图,在三棱柱ABC — A&C中,侧棱垂直于底面, 48丄BC, AA}=AC = 29 E、F分别为、3C的中点.(1)求证:平而丄平而dBCq: (2)求证:Cf〃平而ABE.它二B 证明:(1)在三棱柱ABC — AQC]中,BB l丄底面ABC;BB、丄AB, :. AB丄BC、:. AB丄平面B^BCC^•・• AB u平面ABE 平面ABE丄平面B、BCC\.⑵取AB的中点G,连接EG, FG•;E、F 分别为BC的中点,.•.FG||AC,FG =丄AC,2•.•AC || 4G,AC = A i C l,:.FG\\EC e FG = EC;,则四边形FGEC,为平行四边形,C,F || EG,・.・ EG u 平面<z 平面ABE: C,F || 平.3.如图,P是AAZ?C所在平面外的一点,且PA丄平而A3C,平而PAC丄平而PBC.求证丄AC.分析:已知条件是线而垂直和而而垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平而中,使另一条直线与该平而垂直,即从线而垂直得到线线垂直..证明:在平而PAC作AD丄PC,交PC于D.因为平WPAC丄平面P3C于PC, 4Du平而PAC,且AD丄PC,所以AD丄平面PBC.又因为BCu平而PBC,于是有力D丄①.另外PA丄平而ABC, BCu 平而A3C,所以PA丄BC.由①②及AD[}PA=A,可知BC丄平而PAC.因为ACu平面P4C,所以丄AC.说明:在空间图形中,髙一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面而垂直二>线而垂直二*线线垂直.4.过点S引三条不共面的直线SA、SB、 SC,如图,/BSC=90。
面面垂直答案

1.已知如图,Pe 平面 ABC, PA=PB 二PC, ZAPB=ZAPC=60° , ZBPC 二90 ° 求证:平而 ABe 丄平而PBC【答案】【解析】要证明面面垂直,只 线,然后证明直线与另一平面∏,证明An 垂直平PBC 即可 证明:取BC 中点D 连结Am PnTPA=PB; Z APB=6O β .,.ΔPAB 为正三角形 同≡ΔPAC 为正三角形 设 PA=a在RTΔBPC 中,PB=PC=aBC=∖2a √2 .,.p∏=——a 2 ⅛ΔABC 中AΓ)=√AB 2-BD 2=a 2=AP 2.∙∙ΔAP∏为直角三角形即AD 丄DP 又 √AΓ)±BC.,.AΓ)丄平面PBC・・・平面ABC 丄平面PBC2.如图 ⑴ 在直角梯形ABCr)中,AB∕∕CP, AB 丄AD 且AB=AD=-CP=I, ≡以2AD 为一边向梯形外作正方形ADEF,然后沿AD 将正方形翻拆,使平面AnEF 与平面 ABCr)互相垂直如图(2)o要在其呈平面内找一条 垂直即可。
显然BC 中点√2 VEE(1)求证平面BDE丄平面BEC(2)求直线BD与平面BEF所成角的正弦值。
AH 1【答案】⑴证见解析⑵Sin^ =-DD 2【解析】(1)由折前折后线面的位直关系得ED丄平面ABCD^ UED丄BC, 又在MCD中,DB = BC =近,DC = 2,三边满足勾股定理,:.BC丄BD°由线面垂宜的判定定理即证得结论。
(2)因为DB = Jl,只雲求出点D到平面BEF的距离也是点A到平面BEF的距宵,易证出AD//EF , AQ丄平面B由面面垂直的判定定理得平面A3F丄平面BEF y WF中3F边上的高就是点A到平面BEF的距离。
根据线面角的定义可求直线Bn与平面BEF所成角的正弦值。
3・(本小题满分14分)如图,在正方体ABCD-A X B X C X n X中,E、F为棱人∕λ的中点・(1)求证:EF"平面CB(2)求证:平面CAA}C}丄平面CB I D}・【答案】(I )晒(∏ )略【解析】(1 )证明:连结处在长方体AG中,BDHB x D x. ......... 2 分又・・・E、F为棱AD. AB的中点,/. EFIIBD . . EFI IBp・........ 4分又民D平面CB l D l, EFg平面CBwEFH平面CBa. .......... 7分(2)•••在长方体AC中,£4】丄平面AAGr>、,而厲门平面A l B I C.∖AA l丄Bm…9分又・・•在正方形 Zee中,内G丄5C,・・・5C丄平面CAA I C l・又・・・51P1平面CBU・平面CAA X G丄平面CB X D X・……14分4 .如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB = 2AD=2i BD =忑,PD丄底面ABCD.⑴证明:平面PBC 丄平面PBZ );(2)若二面角P-BC-D 为2,求4P 与平面PBC 所成角的正弦值。
面面垂直的判定习题详细答案

题目二解析
题目二
在四面体$P-ABC$中,已知$angle APB = angle BPC = angle CPA = 90^{circ}$, 求证:平面$PAB perp$平面$PBC$。
解析
首先,由于$angle APB = angle BPC = angle CPA = 90^{circ}$,我们可以得出$PA perp PB$、$PB perp PC$和$PC perp PA$。根据空间直线与平面的垂直关系,我们可以得出$PA perp$平面$PBC$、$PB perp$平面$PAC$和$PC perp$平面$PAB$。由于平面$PAB cap$平面$PBC = PB$,根据两平面垂直于第三
解析
题目三
对于结论$①$
由于正方体的性质,我们知道AC₁和AE都 经过点A,所以它们是共面的。因此,
AC₁E不是异面直线。结论$①$不正确。
对于结论$③$
由于正方体的性质,我们知道AC₁不在平 面ABCD内。所以结论$③$是正确的。
对于结论$②$
由于AC₁不在平面BDE内,所以结论$②$ 是正确的。
平面内的直线
一条直线如果在某个平面上, 则称这条直线为该平面的内直
线。
THANKS FOR WATCHING
感谢您的观看
质,我们可以得出平面 ABDtextsuperscript{⊥}平面BCD。
04 知识点总结
面面垂直的判定定理
判定定理
如果一个平面内的一条直线与另 一个平面垂直,则这两个平面互 相垂直。
推论
如果两个平面互相垂直,则其中 一个平面内的一条直线与另一个 平面垂直。
解题技巧和注意事项
技巧
在解题时,首先确定已知条件和未知 量,然后根据判定定理和推论,构建 数学模型和方程。
面面垂直的判定及性质
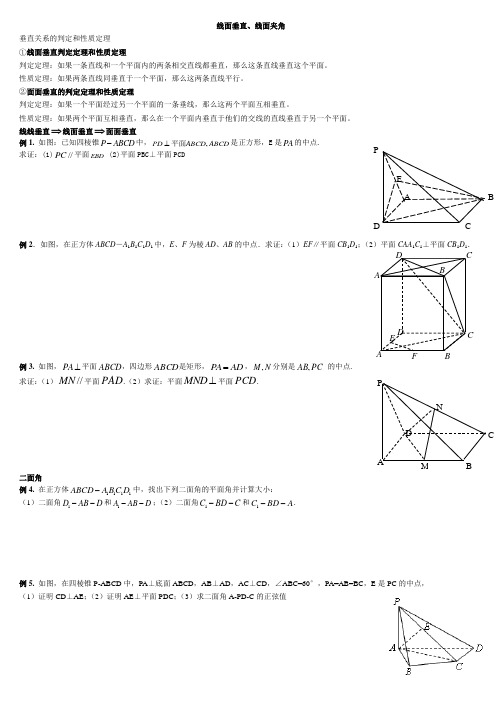
ED C BA PABCDABC DE F 线面垂直、线面夹角垂直关系的判定和性质定理 ①线面垂直判定定理和性质定理判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
②面面垂直的判定定理和性质定理判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。
线线垂直⇒线面垂直⇒面面垂直例1. 如图:已知四棱锥P ABCD -中,,PD ABCD ABCD ⊥平面是正方形,E 是PA 的中点. 求证:(1)//PC 平面EBD (2)平面PBC ⊥平面PCD例2.如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点.求证:(1)EF ∥平面CB 1D 1;(2)平面CAA 1C 1⊥平面CB 1D 1.例3. 如图,⊥PA 平面ABCD ,四边形ABCD 是矩形,PA AD =,,M N 分别是PC AB , 的中点. 求证:(1)//MN 平面PAD .(2)求证:平面⊥MND 平面PCD . 二面角例4. 在正方体1111ABCD A B C D -中,找出下列二面角的平面角并计算大小: (1)二面角1D AB D --和1A AB D --;(2)二面角1C BD C --和1C BD A --.例5. 如图,在四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC=60°,PA=AB=BC ,E 是PC 的中点, (1)证明CD ⊥AE ;(2)证明AE ⊥平面PDC ;(3)求二面角A-PD-C 的正弦值 DNCBMAP新课标高考真题例6. (2011.18.)如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥; (II )设PD=AD=1,求棱锥D-PBC 的高.例7. (2012全国)如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(1)证明:平面BDC 1⊥平面BDC ;(2)平面BDC 1分此棱柱为两部分,求这两部分体积的比。
面面垂直的证明方法

面面垂直的证明方法
要证明两个面面垂直,可以通过以下步骤进行推导:
1. 假设有两个平面P和Q,要证明它们垂直。
2. 选择P上的一条直线AB和Q上的一条直线CD,使得它们相交于点O。
3. 假设P和Q不垂直,即它们存在一个倾斜角度θ。
4. 在P上选择点E,使得OE与AB垂直,并延长OE到与Q 的交点为F。
5. 由于AB与OE垂直,所以角AOE = 90°。
6. 由于θ不等于90°,所以角DOF也不等于90°。
7. 由于P和Q是平面,所以它们的任意两条交线也在同一平面上。
8. 我们可以在这个平面上选择一条直线EF,使得它与CD相交于点G,并且EF与OE垂直。
9. 由于OE与EF垂直,所以角EOF = 90°。
10. 由于角DOF和角EOF不等于90°,所以角DOF不等于角EOF。
11. 根据直线与平面垂直的性质,角AOE和角DOF相等,角EOF和角DOF相等。
12. 由于角AOE和角EOF同时等于90°,所以角AOE等于角EOF。
13. 由于角AOE等于角EOF,同时不等于角DOF,所以假设不成立。
14. 因此,P和Q垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
