第三讲 面板类操作函数
面板数据的操作方法

面板数据的操作方法面板数据是管理和操作数据的一种常见方式,通常用于数据分析和数据可视化。
面板数据可以在数据中心中进行操作,以便更好地理解和利用数据。
下面将介绍一些面板数据的常用操作方法。
1. 数据清洗:面板数据通常包含大量的原始数据,需要进行数据清洗。
数据清洗可以包括删除重复数据、填补缺失值、处理异常值等。
通过数据清洗,可以确保面板数据的质量和准确性。
2. 数据合并:面板数据通常由多个数据源组成,需要将这些数据源合并为一个面板数据集。
数据合并可以通过数据表连接、字段匹配等方式进行。
合并后的面板数据可以更好地反映数据的整体情况。
3. 数据变换:面板数据可以进行数据变换,以便更好地理解和利用数据。
常见的数据变换方法包括数据聚合、数据透视等。
通过数据变换,可以从不同角度和维度分析数据。
4. 数据分析:面板数据可以进行各种数据分析。
常见的数据分析方法包括描述性统计、回归分析、时间序列分析等。
通过数据分析,可以发现数据的规律和趋势,提供决策支持。
5. 数据可视化:面板数据可以通过数据可视化的方式呈现。
数据可视化可以使用折线图、柱状图、饼图等。
通过数据可视化,可以更直观地展示数据的特征和关系,帮助用户更好地理解数据。
6. 数据挖掘:面板数据可以进行数据挖掘,以发现隐藏在数据中的规律和模式。
常见的数据挖掘方法包括聚类分析、关联规则挖掘、预测建模等。
通过数据挖掘,可以发现数据的潜在价值。
7. 数据导出:面板数据可以导出为其他格式,如Excel、CSV等。
导出后的数据可以在其他平台或软件中使用。
通过数据导出,可以更灵活地利用面板数据。
8. 数据更新:面板数据通常会不断更新,需要进行数据更新。
数据更新可以通过定期采集新数据、增量更新等方式进行。
通过数据更新,可以保证面板数据的时效性和完整性。
9. 数据权限管理:面板数据通常需要设置数据权限,以控制数据的访问和使用。
数据权限管理可以包括用户身份认证、数据访问控制等。
通过数据权限管理,可以保护面板数据的安全和隐私。
面板数据基本知识

5678.195
5955.045
6747.152
IP-HLJ(黑龙江)
3518.497
3918.314
4251.494
4747.045
4997.843
5382.808
6143.565
IP-JL(吉林)
3549.935
4041.061
4240.565
4571.439
4878.296
5271.925
图2 15个省级地区的人均消费序列(纵剖面)图3 15个省级地区的人均收入序列(file:4panel02)
图4 15个省级地区的人均消费散点图 图5 15个省级地区的人均收入散点图(7个横截面叠加)
(每条连线表示同一年度15个地区的消费值) (每条连线表示同一年度15个地区的收入值)
用CP表示消费,IP表示收入。AH, BJ, FJ, HB, HLJ, JL, JS, JX, LN, NMG, SD, SH, SX, TJ, ZJ分别表示安徽省、北京市、福建省、河北省、黑龙江省、吉林省、江苏省、江西省、辽宁省、内蒙古自治区、山东省、上海市、山西省、天津市、浙江省。
5133.978
6203.048
6807.451
7453.757
8206.271
8654.433
10473.12
CP-FJ(福建)
4011.775
4853.441
5197.041
5314.521
5522.762
6094.336
6665.005
CP-HB(河北)
3197.339
3868.319
3896.778
图8 北京和内蒙古1996-2002年消费对收入时序图 图9 1996和2002年15个地区的消费对收入散点图
面板数据的常见处理

面板数据的常见处理引言概述:面板数据是一种经济学和社会科学研究中常用的数据形式,它包含了多个个体(如个人、家庭、公司等)在多个时间点上的观测值。
面板数据的处理对于研究者来说至关重要,它可以匡助我们揭示出个体之间的差异以及随时间的变化趋势。
本文将介绍面板数据的常见处理方法,以匡助读者更好地理解和分析面板数据。
正文内容:1. 面板数据的描述统计分析1.1 平均值和标准差面板数据中,我们可以计算每一个个体在不同时间点上的平均值和标准差。
通过比较不同个体之间的平均值和标准差,我们可以了解到个体之间的差异程度。
1.2 相关系数面板数据中,我们可以计算不同个体之间的相关系数,以了解它们之间的相关性。
通过相关系数的分析,我们可以发现个体之间的相互关系,进而对面板数据进行更深入的研究。
2. 面板数据的固定效应模型2.1 固定效应模型的基本概念固定效应模型是一种常用的面板数据分析方法,它通过引入个体固定效应来控制个体特征对结果变量的影响。
通过固定效应模型,我们可以更准确地估计个体之间的差异。
2.2 固定效应模型的估计方法固定效应模型的估计方法有不少种,如最小二乘法、广义最小二乘法等。
通过选择适当的估计方法,我们可以得到更准确的参数估计结果。
2.3 固定效应模型的解释和应用固定效应模型的估计结果可以用来解释个体之间的差异,进而匡助我们理解面板数据中的变化趋势。
固定效应模型在经济学和社会科学研究中有着广泛的应用。
3. 面板数据的随机效应模型3.1 随机效应模型的基本概念随机效应模型是另一种常用的面板数据分析方法,它通过引入个体随机效应来控制个体特征对结果变量的影响。
通过随机效应模型,我们可以更好地理解个体之间的差异。
3.2 随机效应模型的估计方法随机效应模型的估计方法有不少种,如极大似然法、广义矩估计法等。
通过选择适当的估计方法,我们可以得到更准确的参数估计结果。
3.3 随机效应模型的解释和应用随机效应模型的估计结果可以用来解释个体之间的差异,进而匡助我们理解面板数据中的变化趋势。
面板数据的常见处理

面板数据的常见处理面板数据是一种特殊的数据结构,它包含了多个个体(例如个人、公司等)在多个时间点上的观测值。
在经济学、社会学和其他领域的研究中,面板数据时常被使用,因为它可以提供更多的信息和更准确的结果。
在处理面板数据时,以下是一些常见的方法和技巧。
1. 面板数据的导入和整理首先,将面板数据导入到统计软件中,如R、Python等。
然后,对数据进行整理,确保每一个个体和时间点都有对应的观测值。
可以使用数据框或者矩阵等数据结构来存储面板数据。
2. 面板数据的描述性统计面板数据通常具有多个维度,可以通过计算每一个维度的描述性统计量来了解数据的特征。
例如,可以计算每一个个体和时间点的平均值、标准差、最大值、最小值等。
3. 面板数据的平衡性检验面板数据可能存在缺失值或者不平衡的情况,即某些个体或者时间点上缺少观测值。
为了确保数据的可靠性和准确性,可以进行平衡性检验。
可以计算每一个个体和时间点的观测数量,并查看是否存在缺失值或者不平衡的情况。
4. 面板数据的面板效应分析面板效应是指个体固有的特征或者个体之间的异质性对观测结果的影响。
可以通过面板数据模型来分析面板效应。
常见的面板数据模型包括固定效应模型和随机效应模型。
5. 面板数据的时间序列分析面板数据具有时间维度,可以进行时间序列分析。
可以使用时间序列模型来研究个体在时间上的变化趋势和关联性。
常见的时间序列模型包括ARIMA模型、VAR模型等。
6. 面板数据的面板单位根检验面板单位根检验用于检验面板数据中变量是否具有单位根(非平稳性)。
可以使用单位根检验方法,如ADF检验、PP检验等,来判断变量是否具有单位根。
7. 面板数据的固定效应模型固定效应模型是一种常见的面板数据模型,用于控制个体固有的特征对观测结果的影响。
可以使用固定效应模型来估计个体的固定效应,并得到相应的系数估计值和显著性检验结果。
8. 面板数据的随机效应模型随机效应模型是另一种常见的面板数据模型,用于控制个体之间的异质性对观测结果的影响。
面板数据的常见处理

面板数据的常见处理引言概述:面板数据是一种由时间序列和横截面数据组成的数据结构,常用于经济学和社会科学研究中。
由于其特殊的数据结构,面板数据的处理方法与传统的时间序列或者横截面数据有所不同。
本文将介绍面板数据的常见处理方法,包括数据清洗、面板单位根检验、面板回归分析和面板数据的固定效应模型。
一、数据清洗1.1 缺失值处理:面板数据中往往存在缺失值,处理缺失值的方法包括删除缺失观测、插补缺失值和使用面板数据的特征进行缺失值预测。
1.2 异常值处理:面板数据中可能存在异常值,可以通过箱线图、离群值检测方法等进行识别和处理。
1.3 数据平滑:面板数据中的变量可能存在噪声,可以使用平滑方法如挪移平均、指数平滑等对数据进行平滑处理。
二、面板单位根检验2.1 单位根概念:单位根是时间序列分析中的重要概念,用于判断变量是否具有非平稳性。
对于面板数据,我们需要进行面板单位根检验,判断变量的平稳性。
2.2 常见的面板单位根检验方法包括Levin-Lin-Chu(LLC)检验、Im-Pesaran-Shin(IPS)检验和Maddala-Wu(MW)检验等。
2.3 单位根检验的结果可以匡助我们选择合适的模型和估计方法,避免估计结果的偏误。
三、面板回归分析3.1 固定效应模型:面板数据的回归分析中,固定效应模型是常用的方法之一。
该模型可以控制个体间的异质性,并通过固定效应项捕捉个体固定的影响。
3.2 随机效应模型:随机效应模型是另一种常用的面板回归模型,它假设个体效应项与解释变量无关,通过随机效应项来捕捉个体间的异质性。
3.3 混合效应模型:混合效应模型是固定效应模型和随机效应模型的组合,它可以同时考虑个体效应和时间效应。
四、面板数据的固定效应模型4.1 模型假设:固定效应模型假设个体效应是固定的,即个体效应项与解释变量无关。
4.2 估计方法:固定效应模型的估计方法包括最小二乘法和差分法。
最小二乘法可以直接估计固定效应模型的参数,而差分法则通过对数据进行差分来消除个体效应。
第三讲 Scilab程序文件
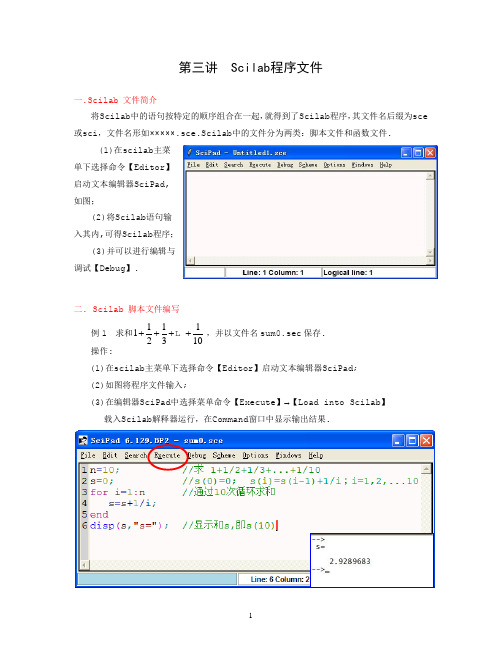
第三讲 Scilab程序文件一.Scilab 文件简介将Scilab中的语句按特定的顺序组合在一起,就得到了Scilab程序,其文件名后缀为sce 或sci,文件名形如×××××.sce.Scilab中的文件分为两类:脚本文件和函数文件.(1)在scilab主菜单下选择命令【Editor】启动文本编辑器SciPad,如图;(2)将Scilab语句输入其内,可得Scilab程序;(3)并可以进行编辑与调试【Debug】.二. Scilab 脚本文件编写例1 求和11112310++++,并以文件名sum0.sec保存.操作:(1)在scilab主菜单下选择命令【Editor】启动文本编辑器SciPad;(2)如图将程序文件输入;(3)在编辑器SciPad中选择菜单命令【Execute】→【Load into Scilab】载入Scilab解释器运行,在Command窗口中显示输出结果.三. Scilab 函数文件编写例2 编写求和111123n++++,并求当10n =的值,并以文件名sum1.sec 保存. 操作如例1,略.函数文件结构函数文件与脚本文件比较1. 脚本文件与函数文件最大的区别是脚本文件内部没有函数,无输入输出变量;2. 脚本文件内的变量不是函数体内部的局部变量,而是基本工作空间内(调用脚本文件的工作空间内)的变量.例3 将上述例子改造成具有多个返回值的情况.四.控制程序流的常用指令return 指令返回到引用函数input 指令请求用户输入pause 指令暂停执行break 指令强行终止其所在for或while循环体error和warning 指令显示出错和警告信息例3 求11a =,21a =的Fibonacci 数组中第一个满足大于10000的元素.例4 输入项数n ,编写求和111123n++++,并求当10n =的值, 并以文件名sum3.sec 保存.。
面板数据的常见处理

面板数据的常见处理引言概述:面板数据是指在一定时间跨度内,对多个个体单位进行观察和测量得到的数据集合。
面板数据具有时间序列和横截面数据的特点,因此在处理面板数据时需要采取一些特定的方法和技巧。
本文将介绍面板数据的常见处理方法,包括数据清洗、平衡面板处理、面板数据变换、面板数据建模以及固定效应和随机效应模型。
一、数据清洗:1.1 缺失值处理:面板数据中常常存在缺失值,需要进行处理。
可以采用删除法、替代法和插补法等方法。
删除法是直接删除含有缺失值的观测值,但会导致样本减少;替代法是用平均值、中位数等代替缺失值,但可能引入估计偏误;插补法是利用其他变量的信息进行插补,如回归插补、多重插补等。
1.2 异常值处理:面板数据中可能存在异常值,需要进行识别和处理。
可以通过箱线图、散点图等方法进行异常值检测,然后采取删除、替代或修正等方式进行处理。
1.3 数据转换:面板数据中的变量可能需要进行转换,以满足建模的要求。
常见的数据转换包括对数变换、差分变换、标准化等。
对数变换可以使数据更加符合正态分布,差分变换可以消除时间序列相关性,标准化可以消除不同变量单位的影响。
二、平衡面板处理:2.1 平衡面板的定义:平衡面板是指在面板数据中,每个个体单位在每个时间点都有观测值的情况。
然而,实际面板数据中往往存在非平衡面板的情况,即某些个体单位在某些时间点没有观测值。
2.2 面板数据的平衡化方法:对于非平衡面板数据,可以采用删除法、插补法或加权法等方法进行平衡化处理。
删除法是直接删除非平衡的观测值,但会导致样本减少;插补法是利用已有观测值进行插补,如线性插值、多重插补等;加权法是给予有观测值的个体单位更大的权重,以弥补非平衡带来的偏误。
2.3 面板数据平衡性的检验:平衡面板处理后,需要对平衡性进行检验。
可以通过计算面板数据的平衡率、面板数据的观测数等指标进行检验,以确保平衡面板的有效性。
三、面板数据变换:3.1 横向平均化:对于面板数据中的个体单位,可以计算它们在不同时间点上的平均值,以得到横向平均化的结果。
面板数据的常见处理

面板数据的常见处理标题:面板数据的常见处理引言概述:面板数据是经济学和统计学中常见的一种数据类型,通常包含了多个单位(如个人、公司)在不同时间点上的观测。
对于处理面板数据,需要采取一些特定的方法和技巧,以确保数据的准确性和可靠性。
一、面板数据的合并1.1 将不同时间点的数据合并在处理面板数据时,通常需要将不同时间点上的数据合并在一起。
这可以通过使用merge函数或者concat函数来实现,确保数据的完整性和一致性。
1.2 将不同单位的数据合并除了时间点上的数据合并,还需要将不同单位(如个人、公司)的数据合并在一起。
这可以通过使用merge函数或者join函数来实现,确保数据的完整性和一致性。
1.3 处理缺失值在合并面板数据时,可能会出现一些缺失值。
需要采取一些方法来处理这些缺失值,如填充均值、中位数或者使用插值方法进行填充,确保数据的完整性和准确性。
二、面板数据的筛选和排序2.1 筛选特定时间点的数据在处理面板数据时,可能需要筛选出特定时间点上的数据。
可以使用条件筛选的方法,如使用loc函数或者query函数来实现,确保数据的准确性和完整性。
2.2 筛选特定单位的数据除了时间点上的筛选,还可能需要筛选出特定单位(如个人、公司)的数据。
可以使用条件筛选的方法,如使用loc函数或者query函数来实现,确保数据的准确性和完整性。
2.3 数据的排序在处理面板数据时,可能需要对数据进行排序。
可以使用sort_values函数或者sort_index函数来实现,确保数据的顺序性和可读性。
三、面板数据的计算和分组3.1 计算变量的平均值在处理面板数据时,通常需要对变量进行计算,如计算平均值、总和等。
可以使用mean函数或者sum函数来实现,确保数据的准确性和可靠性。
3.2 变量的分组除了计算变量的总体统计量,还可能需要对数据进行分组分析。
可以使用groupby函数来实现,确保数据的准确性和可靠性。
3.3 数据的透视表在处理面板数据时,可以使用透视表来进行数据分析。
面板数据的常见处理

面板数据的常见处理面板数据是一种特殊的数据结构,它包含了多个个体(如个人、家庭、公司等)在不同时间点上的观测值。
在经济学、社会学等领域,面板数据被广泛应用于研究个体和时间的关系。
本文将介绍面板数据的常见处理方法,包括数据清洗、平衡性检验、面板回归等。
一、数据清洗1. 缺失值处理:面板数据中往往存在缺失值,可以使用插补方法(如均值插补、回归插补等)来填补缺失值,以保证数据的完整性和准确性。
2. 异常值处理:通过观察数据的分布和统计指标,可以识别和处理异常值,以避免其对分析结果的影响。
二、平衡性检验1. 时间平衡性检验:检验面板数据中每一个个体的观测时间点是否彻底相同,可以使用面板数据的描述性统计方法(如计数、频率分布等)来检验时间平衡性。
2. 个体平衡性检验:检验面板数据中每一个时间点上观测到的个体是否彻底相同,可以使用面板数据的描述性统计方法(如计数、频率分布等)来检验个体平衡性。
三、面板回归面板回归是一种常见的面板数据分析方法,用于研究个体和时间的关系。
常见的面板回归模型包括固定效应模型和随机效应模型。
1. 固定效应模型:固定效应模型假设个体间的差异是固定的,通过引入个体固定效应来控制个体间的差异。
可以使用最小二乘法(OLS)估计固定效应模型。
2. 随机效应模型:随机效应模型假设个体间的差异是随机的,通过引入个体随机效应来控制个体间的差异。
可以使用广义最小二乘法(GLS)估计随机效应模型。
在进行面板回归分析之前,需要进行一些前提检验,如异方差检验、序列相关检验等,以确保模型的有效性和可靠性。
四、面板数据的可视化面板数据的可视化可以匡助我们更直观地理解个体和时间的关系。
常见的面板数据可视化方法包括折线图、散点图、热力图等。
通过可视化分析,我们可以发现数据中的规律和趋势,并作出相应的结论和决策。
总结:面板数据的常见处理包括数据清洗、平衡性检验、面板回归等。
在处理面板数据时,需要注意缺失值和异常值的处理,以及时间平衡性和个体平衡性的检验。
STATA面板数据模型操作命令讲解(word文档良心出品)

STATA 面板数据模型估计命令一览表一、静态面板数据的 STATA 处理命令固定效应模型随机效应模型(一)数据处理输入数据• tsset code year 该命令是将数据定义为“面板”形式 • xtdes该命令是了解面板数据结构・ xtdescode: 1i 2, ■■■( 20n 工 20 year : 3004, 2005, ■…,2014T =11Delta(year) =1 unit span(year) =11 periods(code*year uniquely identifies eachobservation)Distribution of:min 8%2璃50^ 75% 95%max1111 11111111 11Freq. Percent Cum. Pattern20 100.00 100.00 1111111111120100.00XXXXXXXXXXX・ summarize sc I cpi unem gse5 InvariableObs Mean Std ・ Dev.Mi nMax sq 220 .Q142798 2.9303464.75e-0626.22301cpi2201*10655 *032496 1.045 1. 25 unem22Q .0349455 .0071556 .012 ,046 g220,10907 .0427523 0246 .2357220 .0268541 011671? .0053.0693220.1219364.0240077,074,203• summarize sq cpi unem g se5 In各变量的描述性统计(统计分析)• gen lag_y=L.y ///////产生一个滞后一期的新变量*= Xitit• ;itto U 一 if对于固定效应模型而言,回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。
面板数据的常见处理

面板数据的常见处理面板数据是一种特殊的数据结构,通常用于描述在不同时间和不同实体(例如公司、个人等)上的观察结果。
在处理面板数据时,需要采取一些特殊的方法和技术。
本文将介绍面板数据的常见处理方法,帮助读者更好地理解和分析这种数据结构。
一、面板数据的概述1.1 面板数据的定义:面板数据是一种包含多个实体和多个时间点观察结果的数据结构,通常以二维表格的形式呈现。
1.2 面板数据的特点:面板数据具有时间序列和截面数据的特点,能够捕捉实体间的变化和时间上的趋势。
1.3 面板数据的应用:面板数据在经济学、金融学、社会学等领域广泛应用,用于分析实体间的关系和趋势。
二、面板数据的清洗和准备2.1 缺失值处理:面板数据中常常存在缺失值,需要采取合适的方法填充或删除缺失值。
2.2 异常值处理:对于异常值,需要进行识别和处理,以保证数据的准确性和可靠性。
2.3 数据格式转换:将面板数据转换成适合分析的格式,例如长格式或宽格式,以便进行后续的数据分析和建模。
三、面板数据的描述性统计分析3.1 平均值和标准差:计算面板数据的平均值和标准差,了解数据的中心趋势和离散程度。
3.2 相关系数和协方差:计算面板数据的相关系数和协方差,分析不同实体间的关系和趋势。
3.3 可视化分析:利用图表和图形展示面板数据的分布和趋势,帮助更直观地理解数据的特征和规律。
四、面板数据的面板回归分析4.1 固定效应模型:利用固定效应模型分析面板数据中实体间的固定效应,探讨不同实体对因变量的影响。
4.2 随机效应模型:利用随机效应模型分析面板数据中实体间的随机效应,探讨不同实体对因变量的随机影响。
4.3 混合效应模型:结合固定效应和随机效应模型,分析面板数据中实体间的混合效应,更全面地理解实体间的影响。
五、面板数据的时间序列分析5.1 时间序列趋势分析:分析面板数据中时间序列的趋势和周期性,了解时间上的变化和规律。
5.2 季节性分析:分析面板数据中季节性的影响,探讨不同季节对因变量的影响。
面板数据操作方法

面板数据操作方法
面板数据操作方法有很多种,以下是几种常见的操作方法:
1. 增加数据:可以通过新增一行或一列的方式增加数据到面板中。
例如,可以使用df.loc或df.iloc方法在面板中增加一行或一列数据。
2. 删除数据:可以通过删除一行或一列的方式删除面板中的数据。
例如,可以使用df.drop方法删除面板中的一行或一列数据。
3. 修改数据:可以通过选择某个位置并赋新值的方式修改面板中的数据。
例如,可以使用df.loc或df.iloc方法选择特定位置并赋予新的值。
4. 重塑数据:可以通过重新排列面板中的数据来重塑数据。
例如,可以使用df.pivot_table方法将行和列进行重塑。
5. 过滤数据:可以通过选择符合特定条件的数据来过滤面板中的数据。
例如,可以使用df.loc或df.iloc方法选择符合特定条件的数据。
6. 排序数据:可以通过对面板中的数据按照某个标准进行排序。
例如,可以使用df.sort_values方法对面板中的数据进行排序。
这些方法只是面板数据操作的一部分,具体的使用方法可以根据具体的需求和数
据类型来选择。
STATA面板数据模型操作命令讲解

STATA面板数据模型操作命令讲解STATA是一种常用的统计分析软件,可以用于面板数据模型的操作。
面板数据模型是一种用来分析涉及多个单位和多个时间点的数据的统计模型,其主要特点是能够考虑单位间和时间间的相关性。
在STATA中,可以使用一系列命令来进行面板数据模型的操作,包括数据导入、数据清洗、模型估计和结果展示等。
下面将详细介绍STATA中面板数据模型操作的常用命令。
首先,要进行面板数据模型的操作,首先需要将数据导入到STATA中。
STATA支持多种数据格式的导入,包括Excel、CSV和数据库等。
常用的导入命令包括:1. use命令:用于导入STATA格式的数据文件。
例如:use data.dta2. import命令:用于导入其他格式的数据文件。
例如:import excel data.xlsx, firstrow导入数据后,接下来需要进行数据清洗和变量定义。
可以使用一系列命令对数据进行操作,例如生成新变量、删除缺失值和标识变量等。
常用的数据清洗命令包括:1. generate命令:用于生成新变量。
例如:generate log_y = log(y)2. drop命令:用于删除变量。
例如:drop x3. replace命令:用于替换变量值。
例如:replace y = 0 if y < 0数据清洗完成后,就可以开始估计面板数据模型。
常用的估计命令包括固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)。
下面分别介绍这两种模型的估计命令。
1.固定效应模型的估计命令:xtreg y x1 x2, fe其中,xtreg表示面板数据的回归命令,y为因变量,x1和x2为自变量,fe为固定效应模型的选项。
2.随机效应模型的估计命令:xtreg y x1 x2, re其中,re表示随机效应模型的选项。
除了固定效应模型和随机效应模型,STATA还支持其他面板数据模型的估计方法,如差分估计(Difference-in-Differences)、合成控制法(Synthetic Control Method)等。
面板数据的常见处理

面板数据的常见处理面板数据(Panel Data)是一种包含多个个体(cross-section)和多个时间观测(time series)的数据结构。
在经济学、社会科学和其他领域中,面板数据常被用于研究个体间的动态变化和相关关系。
为了有效地分析和处理面板数据,以下是一些常见的处理方法和技巧。
一、面板数据的基本特征面板数据通常由个体和时间两个维度组成。
个体维度表示不同的个体或观测单位,例如企业、家庭或个人,而时间维度表示观测的时间点或时间段。
面板数据的基本特征包括个体固定效应(individual fixed effects)、时间固定效应(time fixed effects)、个体异质性(individual heterogeneity)和序列相关性(serial correlation)等。
二、面板数据的清洗和准备1. 缺失值处理:面板数据中常常存在缺失值,可以采用多种方法进行处理,如删除包含缺失值的观测、使用插补方法填补缺失值或者利用面板数据的特征进行缺失值推断。
2. 异常值处理:对于异常值,可以通过检查数据分布或者利用统计方法进行识别和处理。
3. 数据平衡性检验:面板数据的平衡性指的是每个个体在每个时间点都有观测值。
如果数据不平衡,可能需要进行样本选择或者采用面板数据模型来处理。
三、面板数据的描述性统计分析1. 汇总统计量:可以计算面板数据的平均值、标准差、最小值、最大值等描述性统计量,以了解数据的整体特征。
2. 相关性分析:可以计算个体间和时间间的相关系数,以探索个体间和时间间的关系。
四、面板数据的面板效应模型面板效应模型(Panel Effects Model)是一种常用的面板数据分析方法,用于探索个体固定效应和时间固定效应对因变量的影响。
面板效应模型可以通过固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)来估计。
1. 固定效应模型:固定效应模型通过个体固定效应来控制个体间的异质性,同时估计时间固定效应和其他解释变量对因变量的影响。
Stata之动态面板数据操作

Stata之动态⾯板数据操作对于⾯板数据,如果观测到被解释变量随时间⽽改变,则开启了动态⾯板对参数估计的可能性。
动态⾯板模型设定了⼀个个体的被解释变量部分取决于前⼀期的值。
当被解释变量的滞后⼀期或者多期出现在解释变量中。
对于短⾯板数据来说,需要研究短⾯板的固定效应模型估计,使⽤⼀阶差分消除固定效应。
通过解释变量的适当滞后期作为⼯具变量对⼀阶差分模型中的参数进⾏IV估计可以得到⼀致估计量。
但是Stata有⼀些固定的命令,可以直接进⾏动态⾯板估计。
如:xtabond、xtdpdsys、xtdpd。
以上这些命令使得模型更加容易估计,同时也提供了相关的⼀些检验。
来源 | 计量经济学(id:Mr-lufly),转载已获授权(⼀)xtbaond语法格式:xtabond depvar [indepvars] [if] [in] [,option]注意:1、严格外⽣的解释变量与e不相关,所以可以作为⾃⾝的⼯具变量,它被指定在indepvars中。
2、先决变量或者弱外⽣的解释变量与前期误差项相关,但是与下期误差项不相关,这些变量可以作为共江湖变量。
⼀般设置在pre(varlist)中。
3、⼀个解释变量可能是⼀个同期内⽣性解释变量。
⼀般设置在endogensous(varlist)。
4、可以把其他⼯具变量设置在inst(varlist)中。
对于⼀些T较⼤的⾯板数据,如果将其直接设置为⼯具变量,可能会导致过度识别的问题。
maxldags(#)为先决变量和内⽣变量设置⼯具变量的最⾼滞后期数;maxldags(#)sub选项可以设定先决变量和内⽣变量的最⼤滞后期数。
此外可以将lagstruct(lag,endlags)单独对应⽤于pre(varlist)和endogenous(varlist)中。
其中2SLS为估计量称为⼀阶估计量,如果不附加其它选项为默认估计。
由于模型是过度识别的,建议使⽤⼴义矩估计⽅法(GMM),因为她对模型的估计是更为有效的,附加选项twostep可以实现。
Excel常用函数完全手册(完善版)

Excel 2003函数应用完全手册目录一、函数应用基础 (1)(一)函数和公式 (1)1.什么是函数 (1)2.什么是公式 (1)(二)函数的参数 (1)1.常量 (1)2.逻辑值 (1)3.数组 (1)4.错误值 (1)5.单元格引用 (1)6.嵌套函数 (2)7.名称和标志 (2)(三)函数输入方法 (2)1.“插入函数”对话框 (2)2.编辑栏输入 (3)二、函数速查一览 (3)(一)数据库函数 (3)1.DA VERAGE (3)2.DCOUNT (3)3.DCOUNTA (3)4.DGET (3)5.DMAX (3)6.DMIN (3)7.DPRODUCT (3)8.DSTDEV (3)9.DSTDEVP (4)10.DSUM (4)11.DV AR (4)12.DV ARP (4)13.GETPIVOTDATA (4)(二)日期与时间函数 (4)1.DATE (4)2.DATEV ALUE (4)3.DAY (4)4.DAYS360 (5)5.EDA TE (5)6.EOMONTH (5)14.TIMEV ALUE (6)15.TODAY (6)16.WEEKDAY (6)17.WEEKNUM (6)18.WORKDAY (6)19.YEAR (7)20.YEARFRAC (7)(三)外部函数 (7)1.EUROCONVERT (7)2.SQL.REQUEST (7)(四)工程函数 (7)1.BESSELI (7)2.BESSELJ (8)3.BESSELK (8)4.BESSELY (8)5.BIN2DEC (8)6.BIN2HEX (8)7.BIN2OCT (8)PLEX (8)9.CONVERT (8)10.DEC2BIN (8)11.DEC2HEX (8)12.DEC2OCT (8)13.DELTA (8)14.ERF (8)15.ERFC (9)16.GESTEP (9)17.HEX2BIN (9)18.HEX2DEC (9)19.HEX2OCT (9)20.IMABS (9)21.IMAGINARY (9)22.IMARGUMENT (9)23.MCONJUGA TE (9)24.IMCOS (9)25.IMDIV (9)26.IMEXP (9)27.IMLN (9)28.IMLOG10 (10)29.IMLOG2 (10)30.IMPOWER (10)36.IMSUM (10)37.OCT2BIN (10)38.OCT2DEC (10)39.OCT2HEX (10)(五)财务函数 (10)1.ACCRINT (10)2.ACCRINTM (11)3.AMORDEGRC (11)4.AMORLINC (11)5.COUPDAYBS (11)6.COUPDAYS (11)7.COUPDAYSNC (11)8.COUPNUM (11)9.COUPPCD (11)10.CUMIPMT (11)11.CUMPRINC (12)12.DB (12)13.DDB (12)14.DISC (12)15.DOLLARDE (12)16.DOLLARFR (12)17.DURA TION (12)18.EFFECT (12)19.FV (12)20.FVSCHEDULE (12)21.INTRA TE (13)22.IPMT (13)23.IRR (13)24.ISPMT (13)25.MDURATION (13)26.MIRR (13)27.NOMINAL (13)28.NPER (13)29.NPV (13)30.ODDFPRICE (13)31.ODDFYIELD (14)32.ODDLPRICE (14)33.ODDL YIELD (14)34.PMT (14)35.PPMT (14)36.PRICE (14)37.PRICEDISC (14)43.SYD (15)44.TBILLEQ (15)45.TBILLPRICE (15)46.TBILL YIELD (15)47.VDB (15)48.XIRR (16)49.XNPV (16)50.YIELD (16)51.YIELDDISC (16)52.YIELDMAT (16)(六)信息函数 (16)1.CELL (16)2.ERROR.TYPE (16) (16)4.IS 类函数 (17)5.ISEVEN (17)6.ISODD (17)7.N (17)8.NA (17)9.TYPE (18)(七)逻辑运算符 (18)1.AND (18)2.FALSE (18)3.IF (18)4.NOT (18)5.OR (18)6.TRUE (18)(八)查找和引用函数 (19)1.ADDRESS (19)2.AREAS (19)3.CHOOSE (19)4.COLUMN (19)5.COLUMNS (19)6.HLOOKUP (19)7.HYPERLINK (19)8.INDEX (20)9.INDIRECT (20)10.LOOKUP (20)11.MATCH (20)12.OFFSET (21)(九)数学和三角函数 (21)1.ABS (21)2.ACOS (21)3.ACOSH (22)4.ASIN (22)5.ASINH (22)6.ATAN (22)7.ATAN2 (22)8.ATANH (22)9.CEILING (22)BIN (22)11.COS (22)12.COSH (23)13.COUNTIF (23)14.DEGREES (23)15.EVEN (23)16.EXP (23)17.FACT (23)18.FACTDOUBLE (23)19.FLOOR (23)20.GCD (23)21.INT (23)22.LCM (24)23.LN (24)24.LOG (24)25.LOG10 (24)26.MDETERM (24)27.MINVERSE (24)28.MMULT (24)29.MOD (24)30.MROUND (24)31.MULTINOMIAL (25)32.ODD (25)33.PI (25)34.POWER (25)35.PRODUCT (25)36.QUOTIENT (25)37.RADIANS (25)38.RAND (25)39.RANDBETWEEN (25)40.ROMAN (26)41.ROUND (26)47.SINH (26)48.SQRT (26)49.SQRTPI (27)50.SUBTOTAL (27)51.SUM (27)52.SUMIF (27)53.SUMPRODUCT (27)54.SUMSQ (27)55.SUMX2MY2 (27)56.SUMX2PY2 (27)57.SUMXMY2 (28)58.TAN (28)59.TANH (28)60.TRUNC (28)(十)统计函数 (28)1.A VEDEV (28)2.A VERAGE (28)3.A VERAGEA (28)4.BETADIST (28)5.BETAINV (28)6.BINOMDIST (29)7.CHIDIST (29)8.CHIINV (29)9.CHITEST (29)10.CONFIDENCE (29)11.CORREL (29)12.COUNT (29)13.COUNTA (30)14.COUNTBLANK (30)15.COUNTIF (30)16.COV AR (30)17.CRITBINOM (30)18.DEVSQ (30)19.EXPONDIST (30)20.FDIST (30)21.FINV (30)22.FISHER (31)23.FISHERINV (31)24.FORECAST (31)25.FREQUENCY (31)26.FTEST (31)27.GAMMADIST (31)33.HYPGEOMDIST (32)34.INTERCEPT (32)35.KURT (32)RGE (32)37.LINEST (32)38.LOGEST (33)39.LOGINV (33)40.LOGNORMDIST (33)41.MAX (33)42.MAXA (33)43.MEDIAN (33)44.MIN (33)45.MINA (33)46.MODE (33)47.NEGBINOMDIST (34)48.NORMDIST (34)49.NORMSINV (34)50.NORMSDIST (34)51.NORMSINV (34)52.PEARSON (34)53.PERCENTILE (34)54.PERCENTRANK (34)55.PERMUT (35)56.POISSON (35)57.PROB (35)58.QUARTILE (35)59.RANK (35)60.RSQ (35)61.SKEW (35)62.SLOPE (35)63.SMALL (36)64.STANDARDIZE (36)65.STDEV (36)66.STDEV A (36)67.STDEVP (36)68.STDEVPA (36)69.STEYX (36)70.TDIST (37)71.TINV (37)72.TREND (37)73.TRIMMEAN (37)74.TTEST (37)75.V AR (37)(十一)文本和数据函数 (38)1.ASC (38)2.CHAR (38)3.CLEAN (38)4.CODE (38)5.CONCATENATE (38)6.DOLLAR 或RMB (38)7.EXACT (39)8.FIND (39)9.FINDB (39)10.FIXED (39)11.JIS (39)12.LEFT 或LEFTB (39)13.LEN 或LENB (39)14.LOWER (40)15.MID 或MIDB (40)16.PHONETIC (40)17.PROPER (40)18.REPLACE 或REPLACEB (40)19.REPT (40)20.RIGHT 或RIGHTB (40)21.SEARCH 或SEARCHB (41)22.SUBSTITUTE (41)23.T (41)24.TEXT (41)25.TRIM (41)26.UPPER (41)27.V ALUE (41)28.WIDECHAR (41)三、函数应用案例──算账理财 (42)1.零存整取储蓄 (42)2.还贷金额 (42)3.保险收益 (42)4.个税缴纳金额 (43)四、函数应用案例──信息统计 (43)1.性别输入 (43)2.出生日期输入 (44)3.职工信息查询 (44)4.职工性别统计 (45)5.年龄统计 (45)7.位次阈值统计 (46)五、函数应用案例──管理计算 (46)1.授课日数 (46)2.折旧值计算 (46)3.客流均衡度计算 (47)4.销售额预测 (47)5.客流与营业额的相关分析 (47)一、函数应用基础( 一) 函数和公式1 .什么是函数Excel 函数即是预先定义,执行计算、分析等处理数据任务的特殊公式。
面板数据的常见处理

面板数据的常见处理面板数据(Panel Data)是一种包含多个时间点和多个个体的数据形式,常见于经济学、社会学等领域的研究中。
在处理面板数据时,常常需要进行一系列的数据处理和分析,以便得到准确的结果和有意义的结论。
下面将介绍面板数据的常见处理方法和步骤。
一、数据清洗和准备1. 缺失值处理:面板数据中常常存在缺失值,可以选择删除缺失值较多的个体或时间点,或者使用插补方法填补缺失值。
2. 异常值处理:检查面板数据中是否存在异常值,可以通过箱线图、离群值检测等方法进行识别和处理。
3. 数据格式转换:将面板数据转换为适合进行面板数据分析的格式,如将数据按照个体和时间点进行排序。
二、面板数据的描述性统计分析1. 个体维度的描述性统计:计算每个个体在不同时间点上的均值、标准差、最大值、最小值等统计指标,以了解个体的变化趋势和差异。
2. 时间维度的描述性统计:计算每个时间点上个体的均值、标准差、最大值、最小值等统计指标,以了解时间的变化趋势和差异。
3. 相关性分析:计算个体之间或时间点之间的相关系数,了解个体之间或时间点之间的相关关系。
三、面板数据的面板回归分析1. 固定效应模型:通过引入个体固定效应,控制个体间的不可观测因素对因变量的影响。
2. 随机效应模型:通过引入个体随机效应,控制个体间的随机因素对因变量的影响。
3. 差分法:通过计算变量的差分,消除个体固定效应和个体间的相关性,以控制个体间的不可观测因素。
四、面板数据的动态面板模型1. AR模型:引入滞后因变量作为解释变量,分析因变量的动态调整过程。
2. GMM模型:通过广义矩估计方法,估计面板数据的动态调整模型。
3. 常用动态面板模型:如Arellano-Bond模型、Blundell-Bond模型等,用于分析面板数据的动态调整过程。
五、面板数据的固定效应和随机效应检验1. Hausman检验:用于检验固定效应模型和随机效应模型哪个更适合面板数据的分析。
面板数据的常见处理

面板数据的常见处理面板数据(Panel Data)是一种在经济学和社会科学研究中常用的数据类型,它包含了多个观察单位(如个人、家庭、公司等)在多个时间点上的观测值。
面板数据具有时间序列和横截面数据的特点,可以提供更多的信息和更准确的估计结果。
在进行面板数据的分析前,常常需要对数据进行一些常见的处理,以确保数据的准确性和适用性。
下面将介绍几种常见的面板数据处理方法。
1. 数据清洗和变量选择在进行面板数据分析前,首先需要对数据进行清洗和变量选择。
数据清洗包括处理缺失值、异常值和重复观测等。
可以使用插补方法填补缺失值,剔除异常值和重复观测。
变量选择是指从众多可能的解释变量中选择出最具解释力和相关性的变量。
可以使用相关系数、方差膨胀因子等指标进行变量选择。
2. 平稳性检验和差分处理面板数据中的变量可能存在非平稳性,即变量的均值和方差随时间变化。
为了确保模型的准确性,需要对变量进行平稳性检验。
常用的平稳性检验方法有ADF检验、单位根检验等。
如果变量存在非平稳性,可以进行差分处理,将变量转化为平稳序列。
3. 固定效应模型和随机效应模型面板数据分析中常用的模型有固定效应模型和随机效应模型。
固定效应模型假设个体效应与解释变量无关,而随机效应模型允许个体效应与解释变量存在相关性。
可以使用Hausman检验来选择合适的模型。
固定效应模型可以通过固定效应法或者差分法进行估计,随机效应模型可以通过随机效应法进行估计。
4. 异质性和固定效应面板数据中的个体可能存在异质性,即个体之间存在差异。
为了解决异质性问题,可以引入固定效应。
固定效应模型可以控制个体固定效应,从而减少异质性的影响。
可以使用固定效应模型对个体固定效应进行估计。
5. 面板数据的时间序列分析面板数据同时包含了时间序列和横截面数据,可以进行时间序列分析。
可以使用滞后变量、滚动回归等方法进行时间序列分析。
时间序列分析可以揭示变量之间的动态关系和长期趋势。
总结:面板数据的常见处理方法包括数据清洗和变量选择、平稳性检验和差分处理、固定效应模型和随机效应模型、异质性和固定效应以及面板数据的时间序列分析。
面板数据的常见处理

面板数据的常见处理面板数据,也称为长期面板数据或平衡面板数据,是一种涵盖多个时间周期和多个个体(如个人、家庭、公司等)的数据集。
面板数据通常用于经济学、社会科学和市场研究等领域的研究分析。
在处理面板数据时,常见的任务包括数据清洗、数据转换、数据分析和模型建立等。
一、数据清洗1. 缺失值处理:面板数据中常常存在缺失值,可以通过填充、删除或插值等方法进行处理。
常见的填充方法包括均值填充、中位数填充和回归填充等。
2. 异常值处理:对于异常值,可以通过设定阈值或使用统计方法进行识别和处理。
常见的方法包括箱线图、标准差方法和离群点分析等。
3. 数据格式转换:将面板数据转换为适合分析的格式,如将宽格式转换为长格式或将长格式转换为宽格式。
可以使用reshape、melt和pivot等函数进行转换。
二、数据转换1. 变量构建:根据研究需要,可以构建新的变量。
例如,计算增长率、差分变量或指标变量等。
2. 数据排序:按照时间和个体进行排序,以确保数据的时间顺序和个体顺序正确。
3. 数据合并:将不同数据源的面板数据进行合并,可以使用merge或concat等函数进行合并。
三、数据分析1. 描述性统计分析:对面板数据进行描述性统计,如均值、标准差、最大值、最小值等。
可以使用describe函数进行分析。
2. 面板数据可视化:通过绘制折线图、柱状图、散点图等,对面板数据进行可视化分析。
可以使用matplotlib或seaborn等库进行数据可视化。
3. 面板数据分析方法:面板数据通常需要考虑时间和个体的固定效应、随机效应或混合效应。
可以使用固定效应模型、随机效应模型或混合效应模型进行分析。
四、模型建立1. 面板数据回归模型:根据研究问题,建立适合的面板数据回归模型。
常见的模型包括固定效应模型、随机效应模型、混合效应模型和面板ARMA模型等。
2. 模型估计与检验:使用合适的估计方法对模型进行估计,并进行模型诊断和检验。
常见的估计方法包括最小二乘法、广义最小二乘法和极大似然法等。
面板数据的常见处理

面板数据的常见处理引言概述:面板数据是一种特殊的数据格式,它包含了多个个体(如个人、公司等)在不同时间点上的观测值。
面板数据在经济学、社会学、金融学等领域中被广泛应用,但其处理和分析也面临着一些挑战。
本文将介绍面板数据的常见处理方法,帮助读者更好地理解和分析面板数据。
一、面板数据的基本特征1.1 个体特征:面板数据由多个个体组成,每个个体在观测期内都有多个时间点的观测值。
个体可以是个人、公司、国家等,每个个体都有自己的特征和行为。
1.2 时间特征:面板数据涉及到多个时间点的观测值,这些时间点可以是连续的,也可以是离散的。
时间特征可以帮助我们观察个体在不同时间点上的变化和趋势。
1.3 面板数据的维度:面板数据通常以二维矩阵的形式呈现,其中行表示个体,列表示时间。
这种数据结构使得我们可以同时考虑个体和时间的影响。
二、面板数据的清洗和准备2.1 缺失值处理:面板数据中常常存在缺失值,我们需要对缺失值进行处理。
可以采用删除缺失值的方法,但这可能会导致样本减少;也可以采用插补方法,如均值插补、回归插补等。
2.2 异常值处理:面板数据中可能存在异常值,这些异常值可能会对分析结果产生影响。
我们可以通过观察和分析来判断异常值,并进行处理,如删除或替换。
2.3 数据规范化:面板数据中的变量往往具有不同的量纲和取值范围,为了进行比较和分析,我们需要对数据进行规范化。
常见的方法包括标准化、归一化等。
三、面板数据的描述统计分析3.1 平均值和标准差:面板数据可以计算每个个体在不同时间点上的平均值和标准差,这可以帮助我们了解个体的整体水平和变异程度。
3.2 相关性分析:面板数据中的个体之间可能存在相关关系,我们可以计算个体之间的相关系数,如皮尔逊相关系数、斯皮尔曼相关系数等,来研究个体之间的关联性。
3.3 面板数据的可视化:通过绘制折线图、散点图等方式,我们可以直观地展示面板数据的变化趋势和分布情况,帮助我们更好地理解数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 3.1 MessagePopup 弹出式面板 该函数原形为: int status = MessagePopup ( char title [ ] , char message [ ]); 参数 char title [ ]为对话框的标题;char message [ ]为对话框中显示的消息内容,如果要显示 多行内容, 在消息的字符串中插入“\n”的换行标志。 函数程序举例:
MessagePopup ( “出错”,“用户词库错误! ”); 调用函数后,弹出一个名称为“出错”的对话框,内容为“用户词库错误!” (4)确认框 ConfirmPopup ()函数
ConfirmPopup 函数的功能是显示一个即时的消息对话框,显示文本消息并且输入布尔值, 对话框中有两个按钮。等待用户选择“Yes”或 “No”按钮,来使用户对某一行为进行确认。
第三讲 面板类操作函数(续)
3.1 用户界面管理类函数
用户界面管理类函数(User Interface Management)
1. RunUserInterface 函数
RunUserInterface 函数的功能是运行用户接口界面。该函数原形为:
int status = RunUserInterface (void);
图 3.4 Generic Message Popup 弹出面板 在弹出式面板中显示一个设定的信息,同时面板上还有一个字符串文本框接收响应的字 符串。 函数原型为: int Generic Message Popup (char title[ ], char message[ ], char buttonLabel1[ ], char buttonLabeI2[ ], char buttonLabel3[ ], char responseBuffer[ ], int maxResponseLength, int buttonAlignment, int activeControl, int enterButton, int escapeButton); • Title[ ]:对话框的标题。 • Message[ ]:对话框里显示的提示信息。 • buttonLabel1[ ]:按钮 1 的标题。 • buttonLabel2[ ]:按钮 2 的标题。如果不需要显示按钮 2 和按钮 3,可以输入 0。 • buttonLabel3[]:按钮 3 如标题。如果不需要显示按钮 3,可以输入 0。 • maxResponseLength:向文本框中输入的最大字节数。 • responseBuffer[ ]:为用户输入的字符串。其存储空间要大于 maxResponseLength 设置的 数值,再加上 ASCII 码结束符(NULL)。如果不需要显示文本框,输入 0。 • buttonAlignment:按钮的位置。如果值为 0,则将按钮放置在下方;如果输入的是一个不 为 0 的数值,则将按钮放置在对话框的右侧。 • activeControl:弹出面板后在对话框中被激活的控件。四个控件的常量名分别为: VAL_GENERIC_POPUP_BTN1:按钮 1。 VAL_GENERIC_POPUP_BTN2:按钮 2。 VAL_GENERIC_POPUP_BTN3:按钮 3。 VAL_GENERIC_POPUP_INPUT_STRING:在弹出面板上供用户输入字符的文本框。 • enterButton:确定以 Enter 键作为快捷键的按钮。如取消按钮以 Enter 键作为快捷键,则 可以输入常量名 VAL_GENERIC_POPUP_NO_CTRL。 • escapeButton:确定以 Esc 键作为快捷键的按钮。如取消按钮以 Esc 键作为快捷键,则可 以输入常量名 VAL_GENERIC_POPUP_NO_CTRL。 (7)文件选择框 FileSelect Popup 函数 文件选择框用来选择文件。等待用户选择一个文件或退出,显示的是用户选择的磁盘上 所存储的文件名和路径名。一个文件路径弹出式面板如图 3.5 所示。
表 3. 1 buttonLabel 的可选值
值
显示标签
VAL_OK_BUTTON
OK
VAL_SAVE_BUTTON
Save
VAL_SELECT_BUTTON Select
VAL_LOAD_BUTTON Load • restrictDirectory:用于限定路径,如果设置的数值不为 0,用户不能改变文件路径和驱动器。
(6) 通用消息框 Generic Message Popup 函数 通用消息框可以实现包含以上三者的功能,Generic Message Popup 弹出面板通用消息框
可以包含三个按钮和一个输入框,可输入信息字符串, 并且最多可设置三个按钮。一个简 单的输入信息弹出式面板如图。如图 3.4 所示
函数程序举例说明:
如在上一讲主函数中的应用:
int main (int argc, char *argv[])
{
if (InitCVIRTE (0, argv, 0) == 0)
return -1; /* out of memory */
if ((parent = LoadPanel (0, "pc.uir", PARENT)) < 0)
如:在关闭 LabWindows/CVI 程序时,系统会弹出一 个是否真的退出 LabWindows/CVI 的对话框,这样的设计可以减少用户的误操作。一个简单的确认信息弹出式面板如图 3.2 所 示
图 3.2 Confirm Popup 弹出式面板 该函数原形为: int status = ConfirmPopup ( char title [ ] , char message [ ]); 参数 char title [ ]为对话框的标题;char message [ ]为对话框中显示的消息内容,如果要显示 多行内容, 在消息的字符串中插入“\n”的换行标志,返回代码为 1 时,表示选择“Yes”,返 回代码 为 0 时,表示选择“No”。 函数程序举例:
函数程序举例说明:
如在上一讲 QuitCB 回调函数中的应用:
int CVICALLBACK QuitCB (int panel, int control, int event,
void *callbackData, int eventData1, int eventData2)
{ switch (event)
在文件列表中初始显示所有以.c 为扩展名的 文件。 • FileTypeList[ ]:文件类型列表。当 restrictExtension 设置为“FALSE”(0)时,能够包含在 文件类型列表 “File Type List” 选择框的字符串,不同类型之间用分号(;)分开,分割文件 类型字符串,例如,“*.c;*.h”允许用户从“File Type List”中 选择“*.c” 或“*.h”类型; 在程序运行时,输入的类型将在文件类型列表下拉框中出现。允许用户从文件类型列表中选 择“*.c ”或“*.h”; 输入“*.*”则表示可以选择所有文件。文件列表可输入的最大长度为 255 字节。 • title[ ]:对话框的标题。 • buttonLable:为文件选择按钮的标签,有如下选择值:
InstallPopup 函数的功能是显示并激活一个弹出面板。
该函数原形为:
int status = InstallPopup (int panelHandle);
(2)RemovePopup 函数 RemovePopup 函数的功能是删除弹出面板。 该函数原形为: int status = RemovePopup (int removePopup); 其中,参数 removePopup 决定是否删除所有的弹出面板(设置为 1),还是只删除激活面板 (设置为 0)。 (3)消息框 MessagePopup()函数
return -1;
child=LoadPanel(parent,"pc.uir",CHILD);/*加载子面板到内存,并将子面板的句柄赋值给
child 变量*/
DisplayPanel (parent);
RunUserInterface ();//调用该函数后,运行用户界面。
DiscardPanel(parent);
对话框是常用的一种界面元素,可以不必编辑面板,利用简单的参数来实现一个交互式 界面。对话框通常有一个或多个控件及一些文本,其中文本用来解释程序需要提供什么样的 信息。在 LabWindows/CVI 的用户界面库中提供了 11 种对话框(面板)函数。利用这些函 数可以生成常用的对话框。本讲主要内容是学会如何调用用户界面库中的函数,来生成各种 类型的对话框。这些对话框函数包括: (1)InstallPopup 函数
显示一个提示信息等待用户进行输入信息操作。提示式信息弹出面板要求用户进行输入 操作,如图 3.3 所示。
图 3.3 Prompt Popup 弹出面板 该函数原形为: int PromptPopup (char title[ ], char message[ ], char responseBuffer[ ], int maxResponseLength); Title[ ]:对话框的标题。 Message[ ]:在对话框里显示的信息。 responseBuffer[ ]:为用户输入的字符串。 maxResponseLength:允许用户输入的最大字节数。
return 0;
}
2、QuitUser Interface () 函数
QuitUserInterface ()函数的功能是退出用户接口界面。该函数原形为:
ini status = QuitUserInterface () (int returnCode);
其中,参数 returnCode 为调用 RunUserInterface 函数返回的值,传递参数大于或等于 0。
