模式分解
模式分解例题

模式分解例题设有关系模式R(U, F),其中U={A ,B, C, D, E } , F = {AB C,B D, D E, C B },试问R最高为第几范式,并解释原因?如果R不是3NF或BCNF,要求将其分解为3NF和BCNF关系R中的函数依赖如下图表示R :A,B C ;B D ;D E ;C B第一范式规定关系的每一个分量必须是一个不可分的数据项。
可以看出,该关系满足第一范式。
如果关系模式R满足第一范式,且它的任何一个非主属性都完全函数依赖于任一个候选码,则R满足第二范式(简记为2NF)。
所以不是第二范式分解成第二范式R1 :A,B C ;C BR2:B D ;D E ;如果关系模式R满足2NF,并且它的任何一个非主属性都不传递依赖于任何候选码,则称R是第三范式(3NF),记作R 3NF。
分解成第三范式R1 :A,B C ;C BR21:B DR22:D E? 如果关系模式R是1NF,且每个属性都不传递依赖于R的候选码,那么称R是BCNF的模式。
R1 :A ,B C;C BR21:B DR22:D ER1中属性B传递依赖于R的候选码AB,故R1不是BCNF范式关系模式R 1NF,若X Y,且Y X时,X必含有候选码,则R BCNF。
R1中C B,且B C,但B不含有任何候选码,故R1不是BCNF范式分解成BCNF范式R11 :A,BR12 :C BR21:B DR22:D E候选码是什么?能够唯一标识一个元组的某一属性或属性组。
候选码:(A,B)和(A,C)假设有一个名为参加的关系,该关系有属性:职工(职工名)、工程(工程名)、时数(花费在工程上的小时数)和工资(职工的工资);一个参加记录描述一个职工花费在一个工程上的总时数和他的工资;另外,一个职工可以参加多个工程,多个职工可以参加同一个工程(用A、B、C、D 分别代表属性职工、工程、时数和工资)。
请回答如下各问题:1)确定这个关系的关键字;AB2)找出这个关系中的所有函数依赖;AB->C , A->D3)指出这个关系上的哪些函数依赖会带来操作异常现象;D对关键字AB的部分函数依赖可能会带来如下问题:数据冗余:一个职工参加多个工程,则职工的工资值会重复;更新异常:当改变职工的工资时,可能会只修改了一部分,从而造成数据不一致;插入异常:当一个职工尚未承担工程,但要插入职工信息(如工资)则不允许(因为没有完整的关键字);删除异常:当某个工程结束,删除工程信息时,可能会将职工信息(如工资)一同删除(如果职工只参加了一项工程)。
《关系模式分解》课件

索引优化
通过合理的关系模式分解,可以 为查询语句创建更有效的索引, 提高查询效率。
查询优化
分解后的关系模式可以简化查询 逻辑,减少查询复杂度,提高查 询效率。
缓存策略应用
利用数据库的缓存策略,可以减 少对物理存储的访问次数,提高 数据查询效率。
05
CATALOGUE
关系模式分解的挑战与未来发展
数据冗余问题
数据完整性维护
主键和外键约束
01
关系模式分解后,可以通过主键和外键约束来维护数据的完整
性,确保数据的准确性和一致性。
数据完整性检查
02
通过定期的数据完整性检查,可以及时发现并修复数据异常,
保证数据的可靠性。
事务处理能力
03
关系模式分解后,可以利用数据库的事务处理能力,确保数据
的完整性和一致性。
数据查询效率提升
案例二
总结词
数据安全与隐私保护
详细描述
某银行客户信息管理系统涉及到客户、账户、交易等多个实体的关系,这些关系中包含敏感信息。通 过关系模式分解,可以将敏感信息隐藏在虚拟属性中,降低数据泄露的风险,提高数据的安全性和隐 私保护。
案例三:某社交网络的关系模式分解
总结词
网络结构分析
详细描述
社交网络中存在着各种复杂的关系,如用户之间的关注关系、互动关系等。通过关系模 式分解,可以深入分析这些关系的结构特征,挖掘网络中的核心节点和社区结构,为社
关系模式分解
目录
• 关系模式分解简介 • 关系模式分解的基本概念 • 关系模式分解的方法 • 关系模式分解的应用 • 关系模式分解的挑战与未来发展 • 关系模式分解的案例分析
01
CATALOGUE
模式分解——无损连接分解
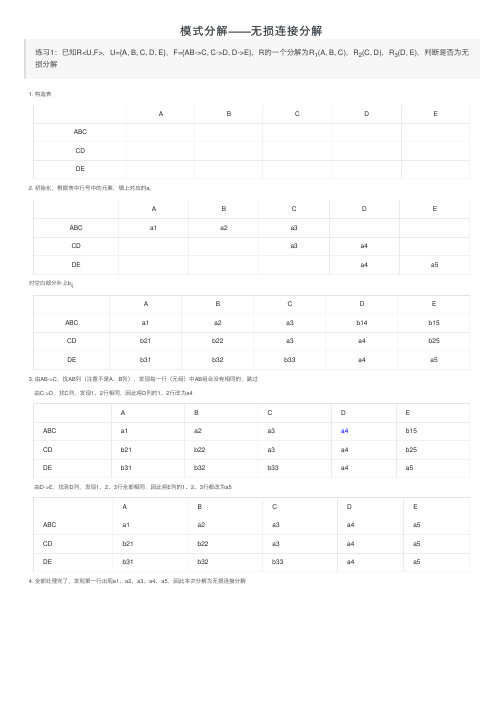
模式分解 ——无损连接分解
练习1:已知R<U,F>,U={A, B, C, D, E},F={AB->C, C->D, D->E},R的一个分解为R1(A, B, C),R2(C, D),R3(D, E),判断是否为无 损分解
1. 构造表
D
E
D
E
a4
a4Βιβλιοθήκη a5DEb14
b15
a4
b25
a4
a5
D a4 a4 a4
D a4 a4 a4
E b15 b25 a5
E a5 a5 a5
A
B
C
ABC
CD
DE
2. 初始化,根据表中行号中的元素,填上对应的ai
A
B
C
ABC
a1
a2
a3
CD
a3
DE
对空白部分补上bij
A
B
C
ABC
a1
a2
a3
CD
b21
b22
a3
DE
b31
b32
b33
3. 由AB->C,找AB列(注意不是A、B列),发现每一行(元组)中AB组合没有相同的,跳过 由C->D,找C列,发现1、2行相同,因此将D列的1、2行改为a4
A
B
C
ABC
a1
a2
a3
CD
b21
b22
a3
DE
b31
b32
b33
由D->E,找到D列,发现1、2、3行全部相同,因此将E列的1、2、3行都改为a5
A
模式分解

2.保持FD (函数依赖)的分解定义1:设F 是属性集U 上的FD 集,Z 是U 的子集,F 在Z 上的投影用πZ (F)表示,定义为πZ (F)={X →Y|X →Y ∈F +,且XY ⊆Z}定义2. 设},...{1K R R =ρ 是R 的一个分解,F 是R 上的FD 集,如果有)(1F R i ki π=Y ╞ F ,那么称分解ρ保持函数依赖集F 。
根据定义1,测试一个分解是否保持FD ,比较可行的方法是逐步验证F 中的每个FD 是否被)(1F R i ki π=Y 逻辑蕴涵。
如果F 的投影不蕴涵F ,而我们又用},...{1K R R =ρ表达R ,很可能会找到一个数据库实例σ 满足投影后的依赖,但不满足F 。
对σ的更新也有可能使r 违反FD 。
案例1:R (T#,TITLE ,SALARY )。
如果规定每个教师只有一个职称,并且每个职称只有 一个工资数目,那么R 上的FD 有T#→TITLE 和TITLE →SALARY 。
如果R 分解成ρ={R 1,R 2},其中R 1={T#,TITLE},R 2={T#,SALARY }。
则该分解具有无损连接性,但未保持函数依赖,丢失了依赖TITLE →SALARY 。
习题1:设关系模式R (ABC ),ρ={AB ,AC}是R 的一个分解。
试分析分别在F 1={A →B};F 2={A →C ,B →C},F 3={B →A},F 4={C→B,B→A}情况下, 是否具有无损分解和保持FD的分解特性。
算法1:分解成2NF模式集的算法设关系模式R(U),主码是W,R上还存在FD X→Z,并且Z是非主属性和X⊂W,那么W→Z就是非主属性对码的部分依赖。
此时,应把R分解成两个关系模式:R1(XZ),主码是X;R2(Y),其中Y=U-Z,主码仍为W,外码是X(参照R1)利用外码和主码的连接可以从R1和R2重新得到R。
如果R1和R2还不是2NF,则重复上述过程,一直到数据库模式中的每个关系模式都是2NF为止。
模式的分解

}
2018/10/5
11
判断无损连接的算法
算法6.2 判断一个分解的无损连接性 {R1 U1, F1 , R2 U2 , F2 ,..., Rk Uk , Fk是 }R<U,F〉的一 个分解,U={A1,A2,…,An},F={FD1,FD2,…, FDm},这里我们设F是一个极小依赖集,记FDi为 Xi→Ali。 (1)建立一张n列k行的表。一列对应一个属 性,一行对应一个分解后的模式;在i行j列中的空白 处,若属性Aj属于Ui,则填上aj,否则填上bij。
2018/10/5
8
6.4.2.1 分解的“无损连接性”
我们先来定义几个符号: 分解: {R1 U1, F1 , R2 U2 , F2 ,..., Rk Uk , Fk } 其中r是R<U,F>的一个关系。 再定义: m = ( r ) Ri 也就是说 是r在各个模式分解上的投 m 影的连接。
2018/10/5 3
本小节要讨论的内容
• “无损连接性”和“保持函数依赖”的含 义; • 对于这三种角度的分解可以达到的分离程 度,即可以达到第几范式; • 对于这几种分离的分解算法;
下面用一个实际分解的例子来引出本小 节的内容。
2018/10/5 4
一个分解实例
例4:一个关系模式R<U,F>,其中U={Sno,Sdept, Mn},F={Sno→Sdept,Sdept →Mn}。 如果我们把它分解成:
我们从r1,r2和r3这三个关系中已经不能回 答“某个学生在哪个系学习”了,显然这样的分 解是失败的。这是由于失去了关原来的关系。 而我们把r1,r2和r3做自然连接(它们的笛卡 尔积)后,我们得到的是一个具有4*4*4=64行的 没有实际意义的关系表。不能恢复表5.3所示的 含义了。
6.4模式的分解

算法6.5:(分解法)转换为BCNF的 无损连接分解*
例:R(U,F),U={X,Y,Z},F={Y→Z,XZ→Y}, 在保持无 损连接的情况下分解为BCNF。 解答:R的侯选码为XY和XZ;R为3NF。
由于存在着Y→Z,而Y不是码,根据算法6.5将R 分解为R1{(Y,Z),(Y→Z)}
分析两种分解的依赖保持性?
分解1:只有AB,显然,分解1不具有依赖保持性 分解2:保留了所有函数依赖,具有依赖保持性
简单练习: 判定无损连接性和函数依赖性
设S-C-M(S学号,C班级,M班主任)
F={S学号C班级,C班级M班主任,S学号M班主任}
1 {S C (学号,班级),C M (班级,班主任)} 2 {S C (学号,班级),S M (学号,班主任)} 3 {S M (学号,班主任),C M (班级,班主任)}
求得F ' F {S D, I B, IS Q, B O}, 故可得R的保持函数依赖的 3NF分解 {SD, IB, ISQ, BO}, 另外,F '中L, N类属性为I , S , 且( IS ) ISDBOQ 包含所有属性 , 故IS为唯一的候选码。在 的基础上增加IS即为R的无损连接 且保持函数依赖的 3NF分解。
分别求解F 和( Fi ) , 若两者相等,则表示分 解
i 1 k
前后的函数依赖集是等 价的,即具有保持函数 依赖性
例子
R(A,B,C), F={AB, C B}
分解1={(A,B) {AB},
分解2={(A,B) {AB}),
(A,C) }
(B,C) {C B}}
关系模式分解

举例:
例 5.8 设 有 关 系 模 式 R(A,B,C) , 函 数 依 赖 集
F={A→B , C→B} , 分 解 ρ ={R1,R2} , 其 中 R1=AB , R2=BC 。检验分解 ρ 是否具有无损联 接性。 分解ρ不具有无损联接性
三、保持函数依赖集
1、定义
设有关系模式 R(U,F) , F 是 R 的函数依赖集, ρ ={R1,R2,…,Rk}是R上的一个分解。如果所有函 数依赖集πRi(F)(i=1,2,…,k)的并集逻辑蕴 含 F 中的每一个函数依赖,则称分解 ρ 具有依赖 保持性,也即分解ρ 保持依赖集F。即
A R1 R2 R3 R4 R5 a1 a1 a1 a1 a1 B b12 a2 a2 b42 b52 C b13 b13 a3 a3 a3 D a4 a4 a4 a4 a4 E b15 b25 a5 a5 a5
例 5.7 设R(ABCDE),F={A→C,B→C,C→D,DE→C,
CE→A},ρ={R1(AD),R2(AB),R3(BE),R4(CDE), R5(AE)},检验分解ρ是否具有无损联接性。 第三步:判断
2、算法5.2 判断一个分解的无损联接性 输入:关系模式R(A1,…,An),
函数依赖集F,
R的一个分解ρ =(R1,…,Rk)。
输出:ρ 是否为无损联接的判断。 方法:
2、算法5.2 判断一个分解的无损联接性(续1)
(1)构造一个k行n列表S,其中:
A1 R1 … Ri … Rk … Aj … An
例 5.7 设R(ABCDE),F={A→C,B→C,C→D,DE→C,
CE→A},ρ={R1(AD),R2(AB),R3(BE),R4(CDE), R5(AE)},检验分解ρ是否具有无损联接性。 第二步:修正②B→C
第13讲模式分解

第13讲模式分解第13讲的主题是模式分解。
在这一讲中,我将向你介绍什么是模式分解,以及如何使用模式分解来解决问题。
首先,让我们来了解一下什么是模式。
模式是一种可重复的结构或行为方式,可以在不同的问题或情境中重复使用。
模式可以是实际存在的实体或过程,也可以是思维模式或行为模式。
模式分解是一种分析问题的方法,通过将问题分解成更小的、更具体的子问题来解决问题。
这种方法可以使复杂的问题变得更加可管理,并帮助我们更好地理解问题的本质。
模式分解的过程通常包括以下几个步骤:1.确定大问题:首先,我们需要明确整个问题的大框架和目标。
这有助于我们保持对问题的整体认识,并指导我们进行模式分解的过程。
2.列举模式:接下来,我们需要在问题中识别出重复出现的模式。
这些模式可能是具体的步骤、观念、数字等等。
列举这些模式有助于我们识别问题中的重点,并为下一步的分解提供线索。
3.分解子问题:一旦我们明确了模式,我们就可以将整个问题切分成更小的、更具体的子问题。
这可以通过将具有共同模式的元素归为一组来实现。
每个子问题都可以独立地解决,并且通过组合子问题的解决方案,可以获得整个问题的解决方案。
4.解决子问题:然后,我们需要逐个解决子问题。
这可能需要使用之前学到的其中一种解决技术,例如算法、数学公式、模拟等。
在解决子问题的过程中,我们可以进一步细化问题,并将其分解成更小的更具体的部分。
5.合并子问题:最后,我们需要将解决子问题的结果合并起来,以获得整个问题的解决方案。
这可以通过将子问题的解决方案进行组合操作来实现。
在合并子问题时,我们还需要确保解决方案的一致性和有效性。
通过模式分解,我们可以将复杂的问题分解成更小的、更容易处理的子问题,从而简化问题的解决过程,并提高解决问题的效率。
此外,模式分解还可以帮助我们深入了解问题的本质,识别出隐藏的模式和规律。
总结来说,模式分解是一种分析和解决问题的方法,通过将问题分解成更小的、更具体的子问题,并逐个解决这些子问题,最终得到整个问题的解决方案。
经验模式分解

经验模式分解摘要近些年来,随着计算机技术的高速发展与信号处理技术的不断提高,人们对图像的分析结构的要求也越来越高。
目前图像处理已经发展出很多分支,包括图像分割、边缘检测、纹理分析、图像压缩等.经验模式分解(EMD)是希尔伯特—黄变换(Hilbert—HuangTransform)中的一部分,它是一种新的信号处理方法,并且在非线性、非平稳信号处理中取得了重大进步,表现出了强大的优势与独特的分析特点.该方法主要是将复杂的非平稳信号分解成若干不同尺度的单分量平稳信号与一个趋势残余项,所以具有自适应性、平稳化、局部性等优点。
鉴于EMD方法在各领域的成功应用以及进一步的发展,国内外很多学者开始将其扩展到了二维信号分析领域中,并且也取得的一定的进展.但是由于二维信号不同于一种信号,限于信号的复杂性和二维数据的一些处理方法的有限性,二维经验模式分解(BEMD)在信号分析和处理精度上还存在一些问题,这也是本文要研究和改善的重点.关键词:图像处理;信号分解;BEMDAbstractIn recent years,with the rapid development of computer technology and the continuous improvement of signal processing technology,the demand for the analysis structure of the image is becoming more and more high. At present, many branches have been developed in image processing, including image segmentation, edge detection,texture analysis, image compression and so on。
Empirical mode decomposition (EMD) is a part of Hilbert Huang transform (Hilbert—HuangTransform). It is a new signal processing method, and has made significant progress in nonlinear and non—stationary signal processing, showing strong advantages and unique analysis points。
模式分解算法

函数依赖的公理系统:设有关系模式R(U),X,Y,Z,W均是U的子集,F是R上只涉及到U中属性的函数依赖集,推理规则如下:∙自反律:如果Y X U,则X→Y在R上成立。
∙增广律:如果X→Y为F所蕴涵,Z U,则XZ→YZ在R上成立。
(XZ表示X∪Z,下同)∙传递律:如果X→Y和Y→Z在R上成立,则X→Z在R上成立。
以上三条为Armstrong公理系统∙合并律:如果X→Y和X→Z成立,那么X→YZ成立。
∙伪传递律:如果X→Y和WY→Z成立,那么WX→Z成立。
∙分解律:如果X→Y和Z Y成立,那么X→Z成立。
这三条为引理注意:∙函数依赖推理规则系统(自反律、增广律和传递律)是完备的。
∙由自反律所得到的函数依赖均是平凡的函数依赖。
模式分解的几个重要事实:∙若只要求分解具有“无损连接性”,一定可以达到4NF;∙若要求分解要“保持函数依赖”,可以达到3NF,但不一定能达到BCNF;∙若要求分解既要“保持函数依赖”,又要具有“无损连接性”,可以达到3NF,但不一定能达到BCNF;试分析下列分解是否具有无损联接和保持函数依赖的特点:设R(ABC),F1={A→B} 在R上成立,ρ1={AB,AC}。
首先,检查是否具有无损联接特点:第1种解法--算法4.2:(1) 构造表(2)根据A→B进行处理结果第二行全是a行,因此分解是无损联接分解。
第2种解法:(定理4.8)R1(AB)∩R2(AC)=AR2- R1=B∵A→B,∴该分解是无损联接分解。
然后,检查分解是否保持函数依赖πR1(F1)={A→B,以及按自反率推出的一些函数依赖}πR2(F1)={按自反率推出的一些函数依赖}F1被πR1(F1)所蕴涵,∴所以该分解保持函数依赖。
保持函数依赖的模式分解一、转换成3NF的保持函数依赖的分解算法:ρ={R1<U1,F1>,R2<U2,F2>,...,R k<U k,F k>}是关系模式R<U,F>的一个分解,U={A1,A2,...,An},F={FD1,FD2,...,FDp},并设F是一个最小依赖集,记FDi为X i →Alj,其步骤如下:① 对R<U,F>的函数依赖集F进行极小化处理(处理后的结果仍记为F);② 找出不在F中出现的属性,将这样的属性构成一个关系模式。
经验模式分解

经验模式分解集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988)经验模式分解摘要近些年来,随着计算机技术的高速发展与信号处理技术的不断提高,人们对图像的分析结构的要求也越来越高。
目前图像处理已经发展出很多分支,包括图像分割、边缘检测、纹理分析、图像压缩等。
经验模式分解(EMD)是希尔伯特-黄变换(Hilbert-HuangTransform)中的一部分,它是一种新的信号处理方法,并且在非线性、非平稳信号处理中取得了重大进步,表现出了强大的优势与独特的分析特点。
该方法主要是将复杂的非平稳信号分解成若干不同尺度的单分量平稳信号与一个趋势残余项,所以具有自适应性、平稳化、局部性等优点。
鉴于EMD方法在各领域的成功应用以及进一步的发展,国内外很多学者开始将其扩展到了二维信号分析领域中,并且也取得的一定的进展。
但是由于二维信号不同于一种信号,限于信号的复杂性和二维数据的一些处理方法的有限性,二维经验模式分解(BEMD)在信号分析和处理精度上还存在一些问题,这也是本文要研究和改善的重点。
关键词:图像处理;信号分解;BEMDAbstractIn recent years, with the rapid development of computer technology and the continuous improvement of signal processing technology, the demand for the analysis structure of the image is becoming more and more high. At present, many branches have been developed in image processing, including image segmentation, edge detection, texture analysis, image compression and so on. Empirical mode decomposition (EMD) is a part of Hilbert Huang transform (Hilbert-HuangTransform). It is a new signal processing method, and has made significant progress in nonlinear and non-stationary signal processing,showing strong advantages and unique analysis points. This method mainly decomposes the complex non-stationary signals into several single scale stationary signals with different scales and a trend residual term, so it has the advantages of adaptability, stationarity and locality. In view of the successful application and further development of EMD method in many fields, many scholars at home and abroad have expanded it to the two-dimensional signal analysis field, and have made some progress. However, because two dimensional signal is different from one signal, it is limited to the complexity of signal and the processing methods of two-dimensional data. Two-dimensional empirical mode decomposition (BEMD) still has some problems in the accuracy of signal analysis and processing, which is also the important point of research and improvement in this paper.Key words: image processing; signal decomposition; BEMD目录第一章概况随着计算机技术的不断发展和其应用领域的不断扩展,数字图像处理技术得到了迅猛的发展,涉及信息科学、计算机科学、数学、物理学以及生物学等学科,因此数理及相关的边缘学科对图像处理科学的发展有越来越大的影响。
简述关系模式分解的两大准则

简述关系模式分解的两大准则
关系模式分解是数据库设计中的重要步骤之一,它通过将一个大型关系模式分解成多个较小的、相关的关系模式,来提高数据库的性能和可维护性。
关系模式分解需要遵循以下两大准则:
第一,无损连接(Lossless Join)准则。
即分解后所得到的关系模式能够保持对原始关系模式中所有可能连接的支持,即能够无损地连接起来。
这意味着分解后的关系模式能够通过连接操作得到与原始关系模式相同的结果,不会因为分解而引入额外的元组或导致遗失某些元组。
无损连接准则确保了数据的完整性和一致性。
第二,函数依赖(Functional Dependency)准则。
即分解后的关系模式要能够保持原始关系模式中的所有函数依赖。
对于给定的关系模式R,如果存在函数依赖A → B,那么在分解后的关系模式中,A和B仍然在同一个关系模式中,并且该函数依赖仍然有效。
这意味着分解后的关系模式要能够保持数据的一致性和完整性。
通过遵循无损连接和函数依赖准则,关系模式分解能够确保分解结果的数据完整性和一致性,提高数据库的性能和可维护性。
数据库模式的分解

15
R1
R2
SNO
S1
SDEPT
D1
SNO S1 S2
SMN 张五 张五
S2 S3
S4
D1 D2
D3
S3
S4
李四
王一
16
以后可以证明ρ2对R的分解是可恢复的,
但是前面提到的插入和删除异常仍然没 有解决,原因就在于原来在R中存在的 函数依赖 SDEPT→MN,现在在R1和R2 中都不再存在了。因此人们又要求分解 具有"保持函数依赖"的特性。
答案:R1=({ST,ZIP},{Φ }) R2=(CITY,ZIP,{ZIP→CITY}) ρ是无损分解,但不具有函数依赖保持性。
40
模式分解的算法
若要求分解保持函数依赖,那么模式分解总可以 达到3NF,但不一定能达到BCNF; 若要求分解既保持函数依赖,又具有无损连接性, 可以达到3NF,但不一定能达到BCNF; 若要求分解具有无损连接性,那一定可达到4NF.
41
算法6.3 (合成法)转换为3NF的保持函数依赖的 分解。 算法6.4 转换为3NF既有无损连接性又保持函数依 赖的分解 算法6.5 转换为BCNF的无损连接分解(分解法)
A a1 a2 B b1 b1
r2=πR2(r)
B b1 b1 C c1 c2
A a1 mρ (r) a1 a2 a2
B b1 b1 b1 b1
C c1 c2 c1 c2
r2=πR2(mρ (r)) A a1 a2 B b1 b1 B b1 b1 C c1 c2
27
r1=πR1(mρ (r))
结论:分解后的关系做自然联接必包含 分解前的关系,即分解不会丢失信息, 但可能增加信息,只有r=mρ (r)时,分解 才具有无损联接性
判断模式分解是否为无损连接例题

判断模式分解是否为无损连接例题
模式分解是一种将数字信号分解为一系列正弦和余弦函数的方法,通常用于信号处理和数据压缩。
无损连接是指在压缩数据时不
丢失任何信息的过程。
在这种情况下,我们需要判断模式分解是否
为无损连接的例题。
首先,我们需要理解模式分解的原理。
模式分解将信号分解为
一系列正弦和余弦函数的叠加,通过保留足够数量的这些函数,可
以准确地重建原始信号。
因此,模式分解本身并不会丢失任何信息,因为它提供了原始信号的完整表示。
其次,我们需要考虑信号的重建过程。
如果我们使用足够数量
的正弦和余弦函数进行模式分解,并且在重建过程中没有丢失任何
信息,那么模式分解就可以被认为是无损连接的例题。
这意味着即
使对信号进行了压缩,我们仍然可以准确地恢复原始信号,而不会
丢失任何细节或精度。
从数学角度来看,如果模式分解的逆变换能够完全恢复原始信号,那么我们可以说模式分解是无损连接的例题。
这意味着在信号
经过模式分解和逆变换后,与原始信号没有任何差异。
综上所述,模式分解可以被认为是无损连接的例题,前提是在分解和重建过程中没有丢失任何信息。
因此,我们需要在具体的情况下对模式分解的参数和重建过程进行仔细的分析和评估,以确定它是否满足无损连接的要求。
模式分解教案幼儿园

模式分解教案幼儿园一、教学目标1.能够对具有相同特征的形状进行分类,归纳出相似规律,培养幼儿的分类思维能力。
2.能够通过观察、比较、归纳、推理等活动,认识和掌握图形的要素——变形、拼凑、重复。
3.通过自主操作的方式体验模式分解的过程,从中探究规律,激发幼儿的逻辑思维能力。
4.提高幼儿的观察能力、逻辑思维能力、归纳总结能力,为幼儿将来的学习打下良好基础。
二、教学内容1.形状识别和分类2.图形的变形、拼凑、重复3.模式分解三、教学方法1.观察法:通过图形的观察,引导幼儿归纳出规律。
2.对比法:将相似和不相似的图案放在一起对比,引导幼儿找出不同之处。
3.游戏法:通过游戏的形式,让幼儿主动参与,加深对图形的认知。
4.体验法:通过模式分解的实际操作,让幼儿体验模式分解的过程,探究规律。
四、教学步骤1. 形状识别和分类1.1 教师出示几种不同形状的图形,如正方形、长方形、圆形、三角形等,引导幼儿进行观察,发现它们的相同点和不同点,并归纳出它们的分类规律。
1.2 教师出示一些形状相同但大小不同的图形,引导幼儿进行比较和分类,加深形状分类的认知。
2. 图形的变形、拼凑、重复2.1 教师出示相同形状的两个图形,一个完整的图形,一个部分缺失的图形,引导幼儿尝试将缺失部分补充完整,培养幼儿的空间想象力。
2.2 教师出示由相同形状拼接而成的图形,引导幼儿通过观察和比较发现相同的形状和不同的部分,加深对形状之间联系的认识。
2.3 教师出示由相同形状重复而成的图形,引导幼儿通过观察和比较发现重复的规律,加深对形状重复的认知。
3. 模式分解3.1 教师介绍模式分解的概念和方法。
3.2 教师出示一个图案,例如红色正方形、蓝色正方形、黄色三角形、绿色圆形,引导幼儿观察并找出其中的规律,将图案分解成几个相同或相似的部分。
3.3 教师出示另一个图案,引导幼儿运用已掌握的模式分解方法,将图案分解成几个相同或相似的部分。
3.4 教师提供多个具有相同特征的图案,让幼儿自行分解模式,发现图案之间的关系并归纳出模式的规律。
数据库模式的分解

泛关系假设下的投影联接变换示意图
关系模式R R的一个实例r
模式分解
π Ri(r)
ρ ={R1,R2,..Rk} r1,r2,..rk
S=mρ (r)
π Ri(s)
23
2引理6.4
设 ρ={R1<U1,F1>, R2<U2,F2>,...Rk<Uk,Fk>} 为关系模
式R的一个分解,r为R的任一个关系,ri=π Ri(r), 则
①r mρ (r)(即r的投影连接包含r) ② 如果s=mρ (r) ,则π Ri(S)=ri ③ mρ (mΡ (r))=mρ (r)
24
①r mρ (r)
r的投影连接包含r,分解后再连接起来的r肯定不
会比原来的r小;
② 如果s=mρ (r) ,则π Ri(S)=ri, 投影连接后再投影到子关系模式 = 直接投影到该 子关系模式。即π Ri(r)= π Ri(mρ (r) ), ③ mρ (mΡ (r))=mρ (r) 多次投影连接的结果等于一次投影连接后的结果 25 .
A a1 a2 B b1 b1
r2=πR2(r)
B b1 b1 C c1 c2
A a1 mρ (r) a1 a2 a2
B b1 b1 b1 b1
C c1 c2 c1 c2
r2=πR2(mρ (r)) A a1 a2 B b1 b1 B b1 b1 C c1 c2
27
r1=πR1(mρ (r))
结论:分解后的关系做自然联接必包含 分解前的关系,即分解不会丢失信息, 但可能增加信息,只有r=mρ (r)时,分解 才具有无损联接性
把低一级的关系模式分解为若干个高一级的关系模式的方法并不是唯一的只有能够保证分解后的关系模式与原关系模式等价分解方法才有意义关系模式分解的标准三种模式分解的等价定义分解具有无损连接性分解要保持函数依赖分解既要保持函数依赖又要具有无损连接性无损连接性是指分解后所得到的各个关系可以通过自然连接来实现还原
关系模式分解的依据

关系模式分解的依据1.引言1.1 概述关系模式分解是数据库设计中的一个重要步骤,旨在将复杂的关系模式分解为更小的关系模式,以提高数据库的性能和管理效率。
在关系模型中,数据以表的形式组织,每个表代表一个实体或关系。
本文将探讨关系模式分解的依据,即为何需要对关系模式进行分解。
关系模式分解的目的是消除数据冗余和数据更新异常,提高数据库的运行效率和数据的一致性。
本文将分为引言、正文和结论三部分。
在引言部分,将对关系模式分解的概述进行阐述,介绍文章的结构和目的。
接下来的正文部分将详细探讨关系模式分解的定义和背景,并重点讨论关系模式分解的两个主要依据:数据冗余和数据更新异常。
在结论部分,将对关系模式分解的依据进行总结,并展望关系模式分解在未来的意义和应用。
通过本文的探讨,读者将能够理解关系模式分解的重要性和必要性,以及在数据库设计和管理中的实际应用价值。
本文的内容将为数据库设计师和管理者提供指导,帮助他们更好地进行数据库设计和优化。
文章结构部分应该介绍本文的结构和各章节的内容,可以使用如下方式进行编写:1.2 文章结构本文分为引言、正文和结论三个部分,具体的章节结构如下所示:1. 引言部分1.1 概述在本部分,我们将介绍关系模式分解的背景和定义,以及本文的目的。
1.2 文章结构在本部分,我们将展示本文的章节结构和各章节的内容,帮助读者了解文章的整体组织。
1.3 目的在本部分,我们将说明本文的目的是为了探讨关系模式分解的依据,并展望其意义和应用。
2. 正文部分2.1 关系模式分解的定义和背景在本部分,我们将介绍关系模式分解的定义,并概述其背景和发展历程。
2.2 关系模式分解的依据在本部分,我们将详细讨论关系模式分解的依据,包括数据冗余和数据更新异常等方面。
2.2.1 数据冗余在本小节,我们将解释数据冗余在关系模式中的含义和问题,并说明为什么需要对其进行分解。
2.2.2 数据更新异常在本小节,我们将介绍数据更新异常的概念和原因,并说明为什么需要通过分解关系模式来解决它。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判断无损分解的方法。
原来数据库所有信息为前提来实现。其根本目标是节省存储空间, 避免数据不一致性,提高对关系的操作效率,同时满足应用需求。 实 际上,并不一定要求全部模式都达到BCNF不可。有时故意保留 部分 冗余可能更方便数据查询。尤其对于那些更新频度不高,查询 频度极 高的数据库系统更是如此。
小结
模式分解的定义。 无 损分解的定义。
i=l
•保持函数依赖分解还牵涉到其它相关的基本知识,在这里我们不作为 重 点来讲解。
6・6模式分解
回算法6.3判定分解的无损连接性
输入
关系模式R<U, F>的的一个分解p = (R1<U1, F1>, R2<U2, F2>,…,Rk<Uk, Fk>}
6・6模式分解
输出
•P是否为无损连接分解的判定
设关系模式RvU, F> ,如果把它分解为两 个 或多个子模式R1和R2,相应一个R关 系中 的数据就要被分解成R1、R2两个或 多个子 表。假如将这些子表自然连接, 即进行 R18R2操作,得到的结果与原来 关系中的 数据一致,信息并没有丢失,则 称该分解 具有无损连接性,否则如果R示 18R2,则 称该分解不具有无损连接性。
•重复如下过程,直到表不发生变化或一行成为a〔a2... ano
6・6模式分解
例:设关系模式R (ABCD), R分解成p=(AB, BC, CD}。如果R上成立的函 数依赖
集F1={B—A, C一D},那么p相对于F1是否为无损分解?如果R上成立的 函数
依赖集F2={A—B, C-D}呢? 解:利用算法6.3进行判断,在依赖集F1 上有: 1,利用算法6.3第一步,求出初始表格如图:
6・6模式分解
定义
•如果我们对折分后的子表进行复原工作,原表中所存在的函数依赖关 系 仍然存在,我们就说模式分解是保持了函数依赖的。
•设p={R1<U1, F1>, R2<U2, F2>z ... , Rn<Un, Fn> }是关系模式 RvU, F>的一个分解,p是保持函数依赖的分解,如果:
kstem
数据库系统概论
Introduction to Database Systems
主讲人:王岩 河南理工大学
知
第六章关系的规范化理论
识
点
\1 )模式设计中存的问题
2)函数依赖
❸第一范式和第二范式
(4 )第三范式
(5 ) BC范式
6)模式分解
6・6模式分解
定义
设有关系模式R (U)和R1 (U1) , R2 (U2) , Rk (Uk), 其中U={A1, A2, ......, An}, Ui包含于U (i=1, 2, k)且U =U1 o 令p={R1 (U1) , R2 (U2) , R (Uk) ), 则称p为R (U)的一个分解,也称为数据库模式,有时也称为模式 集。用p代替R (U)的过程称为关系模式的分解。
解:利用算法6.3进行判断,在依赖集F2上有: 1,利用算法6.3第一步,求出初始表格如图:
6・6模式分解
解:利用算法6.3进行判断
2,根据C一D,可把b24改成a4。据ATB,不能修改表格。此时表格没有一行 全 a行,因此相对于F2,R分解成p是损失分解。示意图如表所示。
6・6模式分解
注意:
一个关系模式分解可以得到不同关系模式集合,也就是说分解 方法不是唯一的。最小冗余的要求必须以分解后的数据库能够表达
从定义中可以看出模式分解的结果就是把表折分为多个表的,相应的原来 存 储在一张二维表中的数据就要分散存储到多张二维表中去。
6・6模式分解
\=\无损连接分解
般定义
形式化定义
对折分结果最基本的要求肯定是不能丢 失原来的信息。也就是说,我们所拆分 的这些子表应该能通过自然连接所得到 的结果与原来的表中的数据一致,如果 能达到这个要求,我们称该分解是无损 连接性的。
6・6模式分解
解:利用算法6.3进行判断 2,对函数依赖集F1,因为BTA,可以把改成al,据CTD,可把b24改成 a4o些时第 二行已是全a行,因此相对F1, R分解成p是无损分解。示意图如 表所示。
6・6模式分解
例:设关系模式R (ABCD), R分解成p={AB, BC, CD)。如果R上成立的函数依赖 集 F1={BTA, CTD},那么p相对于F1是否为无损分解?如果R上成立的函数依赖 集 F2={ATB, CTD}呢?
