2020中考模拟试卷
2020年江西省中考化学模拟试卷(解析版)

2020年江西省中考化学模拟试卷一、选择题(本大题包括10小题,每小题2分,共20分.每小题只有一个选项正确,请将正确选项的序号填在题后括号内)1.下列变化属于物理变化的是()A.水果榨汁B.粮食酿酒C.塑料降解D.盐酸除锈2.在物质分类中,氯气属于()A.氧化物B.金属单质C.非金属单质D.混合物3.为除去某化工厂车间排放的废水中的色素,可采取的合理措施是()A.静置沉淀B.加入明矾处理C.蒸馏D.经活性炭层吸附4.试管是常见的仪器,下列与试管相关的操作中,正确的是()A.塞紧橡胶塞B.倾倒液体C.加热固体D.振荡试管5.火神山医院是为抗击新型冠状病毒而赶建的临时医院,但在废水处理上一点都不“临时”,铺设了3万平方米的HDPE(高密度聚乙烯)防渗膜,防止污水渗入地下。
HDPE防渗膜属于()A.天然材料B.合成材料C.金属材料D.无机非金属材料6.高氯酸盐主要作为火箭、导弹、焰火等的固体氧化剂等。
已知高氯酸盐中氯元素显+7价,则高氯酸镁的化学式为()A.Mg(ClO4)2B.Mg(ClO3)2C.MgClO4D.MgClO27.铯原子钟是一种精密的计时器具,它的稳定程度很高,目前最好的铯原子钟达到2000万年才相差1秒。
已知某种铯原子的相对原子质量为134,核外电子数为55,则该原子的中子数为()A.34B.55C.79D.1348.将棉手帕放入白酒中浸湿,再用坩埚钳夹住,从下方点燃,待火焰熄灭后棉手帕依然完好。
下列有关“烧不坏的棉手帕”实验的叙述正确的是()A.手帕不是可燃物,不能燃烧B.手帕被白酒浸湿,导致着火点降低C.手帕接触不到氧气,不燃烧D.白酒中的水蒸发使手帕的温度达不到着火点9.如图是离子五角星示意图。
五角星上每个角的阳离子与中间的阴离子R结合若不产生沉淀或气体或水,则称为共存离子对。
要使共存离子对数目最大,则R应该是()A.OH﹣B.NO3﹣C.Cl﹣D.CO32﹣10.下列实验方案的设计没有正确体现对比这种科学思想的是()A.验证二氧化碳的密度比空气大且不支持燃烧的性质B.探究氧气浓度对燃烧剧烈程度的影响C.验证反应物间接触面积对反应速率的影响D.比较温度对反应速率的影响二、选择填充题(本大题包括5小题,每小题3分,共15分.先在A、B、C中选择一个正确选项将序号填在题后括号内,然后在D处再补充一个符合题意的答案.每小题的选择2分,填充1分)11.(3分)下列属于氢氧化钠化学性质的是A、易潮解B.腐蚀性C.易溶于水D.12.(3分)下列事实的解释中合理的是选项事实解释A氧气和液氧都能使带火星的木条复燃同种分子的化学性质相同B金刚石质硬,石墨质软碳原子的结构不同C洗涤剂和汽油都能除油污都利用了其乳化作用D稀盐酸与稀硫酸的化学性质相似13.(3分)向盛有一定量金属X粉末的烧杯中加入适量的硝酸铜溶液恰好完全反应,得到无色溶液和不溶物,再向烧杯中加入适量的硝酸银溶液,恰好完全反应,过滤,得到滤渣和蓝色溶液。
2020年浙江省宁波市中考数学模拟试卷(三) 解析版

2020年浙江省宁波市中考数学模拟试卷(三)一.选择题1.在﹣3,﹣1,0,1这四个数中,最小的数是()A.﹣3B.﹣1C.0D.12.在平面直角坐标系中,点P(1,2)关于原点的对称点P'的坐标是()A.(1,2)B.(﹣1,2)C.(1,﹣2)D.(﹣1,﹣2)3.研究表明,可燃冰是一种可替代石油的新型清洁能源,在我国某海域已探明的可燃冰储存量达150000000000立方米,其中数字150000000000用科学记数法可表示为()A.15×1010B.0.15×1012C.1.5×1011D.1.5×10124.有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的()A.方差B.中位数C.众数D.平均数5.一元一次不等式组的解集是()A.x>﹣1B.x≤2C.﹣1<x≤2D.x>﹣1或x≤2 6.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是()A.主视图B.左视图C.俯视图D.主视图和左视图7.一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球都是红球的概率是()A.B.C.D.8.如果三角形的两边分别为4和6,那么连接该三角形三边中点所得三角形的周长可能是()A.6B.8C.10D.129.如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC 于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE 10.下列关于函数y=x2﹣6x+10的四个命题:①当x=0时,y有最小值10;②n为任意实数,x=3+n时的函数值大于x=3﹣n时的函数值;③若n>3,且n是整数,当n≤x≤n+1时,y的整数值有(2n﹣4)个;④若函数图象过点(a,y0)和(b,y0+1),其中a>0,b>0,则a<b.其中真命题的序号是()A.①B.②C.③D.④11.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为()A.8B.﹣8C.4D.﹣412.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧,,,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为()A.(﹣6,24)B.(﹣6,25)C.(﹣5,24)D.(﹣5,25)二.填空题13.把多项式x2﹣3x因式分解,正确的结果是.14.已知扇形的面积为3π,圆心角为120°,则它的半径为.15.若分式的值为0,则x的值为.16.如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC 上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=(k≠0)的图象恰好经过点A′,B,则k的值为.17.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B 在同一水平直线上,则这条江的宽度AB为米(结果保留根号).18.如图,已知点A,C在反比例函数y=(a>0)的图象上,点B,D在反比例函数y =(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB 与CD的距离为5,则a﹣b的值是.三.解答题19.先化简,再求值:(a+2)(a﹣2)+a(1﹣a),其中a=5.20.一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为.(1)布袋里红球有多少个?(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表法或画树状图等方法求出两次摸到的球都是白球的概率.21.如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA =37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.(1)求改直的公路AB的长;(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)22.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.23.如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).(1)求b,m的值;(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD长为2,求a 的值.24.计划在某广场内种植A、B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.(1)A、B两种花木的数量分别是多少棵?(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?25.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC.∠ABC=90°,①若AB=CD=1,AB∥CD,求对角线BD的长;②若AC⊥BD,求证:AD=CD;(2)如图2.在矩形ABCD中,AB=5.BC=9,点P是对角线BD中点,过点P作直线分别交边AD,BC于点E,F.使四边形ABFE是等腰直角四边形,求四边形DPFC的面积.26.如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是P A,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.(1)当∠APB=28°时,求∠B和的度数;(2)求证:AC=AB.(3)在点P的运动过程中①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.2020年浙江省宁波市中考数学模拟试卷(三)参考答案与试题解析一.选择题1.在﹣3,﹣1,0,1这四个数中,最小的数是()A.﹣3B.﹣1C.0D.1【分析】根据正数大于零,零大于负数,可得答案.【解答】解:由正数大于零,零大于负数,得﹣3<﹣1<0<1,最小的数是﹣3,故选:A.2.在平面直角坐标系中,点P(1,2)关于原点的对称点P'的坐标是()A.(1,2)B.(﹣1,2)C.(1,﹣2)D.(﹣1,﹣2)【分析】关于原点对称的点,横坐标与纵坐标都互为相反数,可得答案.【解答】解:点P(1,2)关于原点的对称点P'的坐标是(﹣1,﹣2),故选:D.3.研究表明,可燃冰是一种可替代石油的新型清洁能源,在我国某海域已探明的可燃冰储存量达150000000000立方米,其中数字150000000000用科学记数法可表示为()A.15×1010B.0.15×1012C.1.5×1011D.1.5×1012【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:150000000000=1.5×1011,故选:C.4.有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的()A.方差B.中位数C.众数D.平均数【分析】根据各自的定义判断即可.【解答】解:有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的方差,故选:A.5.一元一次不等式组的解集是()A.x>﹣1B.x≤2C.﹣1<x≤2D.x>﹣1或x≤2【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式2x>x﹣1,得:x>﹣1,解不等式x≤1,得:x≤2,则不等式组的解集为﹣1<x≤2,故选:C.6.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是()A.主视图B.左视图C.俯视图D.主视图和左视图【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:从上边看是一个田字,“田”字是中心对称图形,故选:C.7.一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球都是红球的概率是()A.B.C.D.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出红球情况,再利用概率公式即可求得答案.【解答】解:画树状图得:∵共有16种等可能的结果,两次摸出红球的有9种情况,∴两次摸出红球的概率为;故选:D.8.如果三角形的两边分别为4和6,那么连接该三角形三边中点所得三角形的周长可能是()A.6B.8C.10D.12【分析】本题依据三角形三边关系,可求第三边大于2小于10,原三角形的周长大于12小于20,连接中点的三角形周长是原三角形周长的一半,那么新三角形的周长应大于6而小于10,看哪个符合就可以了.【解答】解:设三角形的三边分别是a、b、c,令a=4,b=6,则2<c<10,12<三角形的周长<20,故6<中点三角形周长<10.故选:B.9.如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC 于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE 【分析】利用等腰三角形的性质分别判断后即可确定正确的选项.【解答】解:∵AB=AC,∴∠ABC=∠ACB,∵以点B为圆心,BC长为半径画弧,交腰AC于点E,∴BE=BC,∴∠ACB=∠BEC,∴∠BEC=∠ABC=∠ACB,∴∠A=∠EBC,故选:C.10.下列关于函数y=x2﹣6x+10的四个命题:①当x=0时,y有最小值10;②n为任意实数,x=3+n时的函数值大于x=3﹣n时的函数值;③若n>3,且n是整数,当n≤x≤n+1时,y的整数值有(2n﹣4)个;④若函数图象过点(a,y0)和(b,y0+1),其中a>0,b>0,则a<b.其中真命题的序号是()A.①B.②C.③D.④【分析】分别根据二次函数的图象与系数的关系、抛物线的顶点坐标公式及抛物线的增减性对各选项进行逐一分析.【解答】解:∵y=x2﹣6x+10=(x﹣3)2+1,∴当x=3时,y有最小值1,故①错误;当x=3+n时,y=(3+n)2﹣6(3+n)+10,当x=3﹣n时,y=(n﹣3)2﹣6(3﹣n)+10,∵(3+n)2﹣6(3+n)+10﹣[(n﹣3)2﹣6(3﹣n)+10]=0,∴n为任意实数,x=3+n时的函数值等于x=3﹣n时的函数值,故②错误;∵抛物线y=x2﹣6x+10的对称轴为x=3,a=1>0,∴当x>3时,y随x的增大而增大,当x=n+1时,y=(n+1)2﹣6(n+1)+10,当x=n时,y=n2﹣6n+10,(n+1)2﹣6(n+1)+10﹣[n2﹣6n+10]=2n﹣5,∵n是整数,∴2n﹣5是整数,∴y的整数值有(2n﹣4)个;故③正确;∵抛物线y=x2﹣6x+10的对称轴为x=3,1>0,∴当x>3时,y随x的增大而增大,x<3时,y随x的增大而减小,∵y0+1>y0,∴当0<a<3,0<b<3时,a>b,当a>3,b>3时,a<b,当0<a<3,b>3时,a<b,故④错误,故选:C.11.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为()A.8B.﹣8C.4D.﹣4【分析】设A(a,h),B(b,h),根据反比例函数图象上点的坐标特征得出ah=k1,bh =k2.根据三角形的面积公式得到S△ABC=AB•y A=(a﹣b)h=(ah﹣bh)=(k1﹣k2)=4,求出k1﹣k2=8.【解答】解:∵AB∥x轴,∴A,B两点纵坐标相同.设A(a,h),B(b,h),则ah=k1,bh=k2.∵S△ABC=AB•y A=(a﹣b)h=(ah﹣bh)=(k1﹣k2)=4,∴k1﹣k2=8.故选:A.12.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧,,,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为()A.(﹣6,24)B.(﹣6,25)C.(﹣5,24)D.(﹣5,25)【分析】观察图象,推出P9的位置,即可解决问题.【解答】解:由题意,P5在P2的正上方,推出P9在P6的正上方,且到P6的距离=21+5=26,所以P9的坐标为(﹣6,25),故选:B.二.填空题13.把多项式x2﹣3x因式分解,正确的结果是x(x﹣3).【分析】直接提公因式x即可.【解答】解:原式=x(x﹣3),故答案为:x(x﹣3).14.已知扇形的面积为3π,圆心角为120°,则它的半径为3.【分析】根据扇形的面积公式,可得答案.【解答】解:设半径为r,由题意,得πr2×=3π,解得r=3,故答案为:3.15.若分式的值为0,则x的值为2.【分析】根据分式的值为零的条件可以得到,从而求出x的值.【解答】解:由分式的值为零的条件得,由2x﹣4=0,得x=2,由x+1≠0,得x≠﹣1.综上,得x=2,即x的值为2.故答案为:2.16.如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC 上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=(k≠0)的图象恰好经过点A′,B,则k的值为.【分析】设B(m,1),得到OA=BC=m,根据轴对称的性质得到OA′=OA=m,∠A′OD=∠AOD=30°,求得∠A′OA=60°,过A′作A′E⊥OA于E,解直角三角形得到A′(m,m),列方程即可得到结论.【解答】解:∵四边形ABCO是矩形,AB=1,∴设B(m,1),∴OA=BC=m,∵四边形OA′B′D与四边形OABD关于直线OD对称,∴OA′=OA=m,∠A′OD=∠AOD=30°,∴∠A′OA=60°,过A′作A′E⊥OA于E,∴OE=m,A′E=m,∴A′(m,m),∵反比例函数y=(k≠0)的图象恰好经过点A′,B,∴m•m=m,∴m=,∴k=.故答案为:.17.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B 在同一水平直线上,则这条江的宽度AB为1200(﹣1)米(结果保留根号).【分析】在Rt△ACH和Rt△HCB中,利用锐角三角函数,用CH表示出AH、BH的长,然后计算出AB的长.【解答】解:由于CD∥HB,∴∠CAH=∠ACD=45°,∠B=∠BCD=30°在Rt△ACH中,∵∴∠CAH=45°∴AH=CH=1200米,在Rt△HCB,∵tan∠B=∴HB====1200(米).∴AB=HB﹣HA=1200﹣1200=1200(﹣1)米故答案为:1200(﹣1)18.如图,已知点A,C在反比例函数y=(a>0)的图象上,点B,D在反比例函数y =(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB 与CD的距离为5,则a﹣b的值是6.【分析】利用反比例函数k的几何意义,结合相关线段的长度来求a﹣b的值.【解答】解:如图,设CD交y轴于E,AB交y轴于F.连接OD、OC.由题意知:DE•OE=﹣b,CE•OE=a,∴a﹣b=OE(DE+CE)=OE•CD=2OE,同法:a﹣b=3•OF,∴2OE=3OF,∴OE:OF=3:2,又∵OE+OF=5,∴OE=3,OF=2,∴a﹣b=6.故答案是:6.三.解答题19.先化简,再求值:(a+2)(a﹣2)+a(1﹣a),其中a=5.【分析】先用平方差公式和单项式乘以多项式的方法将代数式化简,然后将a的值代入化简的代数式即可求出代数式的值.【解答】解:(a+2)(a﹣2)+a(1﹣a)=a2﹣4+a﹣a2=a﹣4将a=5代入上式中计算得,原式=a﹣4=5﹣4=120.一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为.(1)布袋里红球有多少个?(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表法或画树状图等方法求出两次摸到的球都是白球的概率.【分析】(1)设红球的个数为x,根据白球的概率可得关于x的方程,解方程即可;(2)画出树形图,即可求出两次摸到的球都是白球的概率.【解答】解:(1)设红球的个数为x,由题意可得:,解得:x=1,经检验x=1是方程的根,即红球的个数为1个;(2)画树状图如下:∴P(摸得两白)==.21.如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA =37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.(1)求改直的公路AB的长;(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)【分析】(1)作CH⊥AB于H.在Rt△ACH中,根据三角函数求得CH,AH,在Rt△BCH中,根据三角函数求得BH,再根据AB=AH+BH即可求解;(2)在Rt△BCH中,根据三角函数求得BC,再根据AC+BC﹣AB列式计算即可求解.【解答】解:(1)作CH⊥AB于H.在Rt△ACH中,CH=AC•sin∠CAB=AC•sin25°≈10×0.42=4.2(千米),AH=AC•cos∠CAB=AC•cos25°≈10×0.91=9.1(千米),在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),∴AB=AH+BH=9.1+5.6=14.7(千米).故改直的公路AB的长14.7千米;(2)在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米),则AC+BC﹣AB=10+7﹣14.7=2.3(千米).答:公路改直后比原来缩短了2.3千米.22.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.【分析】(1)根据∠ACD=∠ADC,∠BCD=∠EDC=90°,可得∠ACB=∠ADE,进而运用SAS即可判定全等三角形;(2)根据全等三角形对应角相等,运用五边形内角和,即可得到∠BAE的度数.【解答】(1)证明:∵AC=AD,∴∠ACD=∠ADC,又∵∠BCD=∠EDC=90°,∴∠ACB=∠ADE,在△ABC和△AED中,,∴△ABC≌△AED(SAS);(2)解:当∠B=140°时,∠E=140°,又∵∠BCD=∠EDC=90°,∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.23.如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).(1)求b,m的值;(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD长为2,求a的值.【分析】(1)由点P(1,b)在直线l1上,利用一次函数图象上点的坐标特征,即可求出b值,再将点P的坐标代入直线l2中,即可求出m值;(2)由点C、D的横坐标,即可得出点C、D的纵坐标,结合CD=2即可得出关于a 的含绝对值符号的一元一次方程,解之即可得出结论.【解答】解:(1)∵点P(1,b)在直线l1:y=2x+1上,∴b=2×1+1=3;∵点P(1,3)在直线l2:y=mx+4上,∴3=m+4,∴m=﹣1.(2)当x=a时,y C=2a+1;当x=a时,y D=4﹣a.∵CD=2,∴|2a+1﹣(4﹣a)|=2,解得:a=或a=.∴a的值为或.24.计划在某广场内种植A、B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.(1)A、B两种花木的数量分别是多少棵?(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?【分析】(1)首先设A种花木的数量为x棵,B种花木的数量为y棵,根据题意可得等量关系:①A、B两种花木共6600棵;②A花木数量=B花木数量的2倍﹣600棵,根据等量关系列出方程,再解即可;(2)首先设应安排a人种植A花木,则安排(26﹣a)人种植B花木,由题意可等量关系:种植A花木所用时间=种植B花木所用时间,根据等量关系列出方程,再解即可.【解答】解:(1)设A种花木的数量为x棵,B种花木的数量为y棵,由题意得:,解得:,答:A种花木的数量为4200棵,B种花木的数量为2400棵;(2)设应安排a人种植A花木,由题意得:=,解得:a=14,经检验:a=14是原方程的解,26﹣a=12,答:应安排14人种植A花木,应安排,12人种植B花木,才能确保同时完成各自的任务.25.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC.∠ABC=90°,①若AB=CD=1,AB∥CD,求对角线BD的长;②若AC⊥BD,求证:AD=CD;(2)如图2.在矩形ABCD中,AB=5.BC=9,点P是对角线BD中点,过点P作直线分别交边AD,BC于点E,F.使四边形ABFE是等腰直角四边形,求四边形DPFC的面积.【分析】(1)①只要证明四边形ABCD是正方形即可解决问题;②只要证明△ABD≌△CBD,即可解决问题;(2)若EF⊥BC,则AE≠EF,BF≠EF,推出四边形ABFE表示等腰直角四边形,不符合条件.若EF与BC不垂直,①当AE=AB时,如图2中,此时四边形ABFE是等腰直角四边形,②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,分别求解即可;【解答】解:(1)①∵AB=CD=1,AB∥CD,∴四边形ABCD是平行四边形,∵AB=BC,∴四边形ABCD是菱形,∵∠ABC=90°,∴四边形ABCD是正方形,∴BD=AC==.②如图1中,连接AC、BD.∵AB=BC,AC⊥BD,∴∠ABD=∠CBD,∵BD=BD,∴△ABD≌△CBD(SAS),∴AD=CD.(2)若EF⊥BC,则四边形ABFE是矩形,AE=BF=BC=4.5,∵AB=5,∴AE≠AB∴四边形ABFE表示等腰直角四边形,不符合条件.若EF与BC不垂直,①当AE=AB时,如图2﹣1中,此时四边形ABFE是等腰直角四边形,∴AE=AB=5,∴S△PDCF=S△BDC﹣S△BPF=×5×9﹣×4×=.②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,∴BF=AB=5,∴S△PDCF=S△BDC﹣S△BPF=×5×9﹣×5×=,综上所述,四边形DPFC的面积为或.26.如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是P A,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.(1)当∠APB=28°时,求∠B和的度数;(2)求证:AC=AB.(3)在点P的运动过程中①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.【分析】(1)根据三角形ABP是等腰三角形,可得∠B的度数,再连接MD,根据MD 为△P AB的中位线,可得∠MDB=∠APB=28°,进而得到=2∠MDB=56°;(2)根据∠BAP=∠ACB,∠BAP=∠B,即可得到∠ACB=∠B,进而得出AC=AB;(3)①记MP与圆的另一个交点为R,根据AM2+MR2=AR2=AC2+CR2,即可得到PR =,MR=,再根据Q为直角三角形锐角顶点,分四种情况进行讨论:当∠ACQ =90°时,当∠QCD=90°时,当∠QDC=90°时,当∠AEQ=90°时,即可求得MQ 的值为或或;②先判定△DEG是等边三角形,再根据GMD=∠GDM,得到GM=GD=1,过C作CH ⊥AB于H,由∠BAC=30°可得CH=AC=1=MG,即可得到CG=MH=﹣1,进而得出S△ACG=CG×CH=,再根据S△DEG=,即可得到△ACG和△DEG 的面积之比.【解答】解:(1)∵MN⊥AB,AM=BM,∴P A=PB,∴∠P AB=∠B,∵∠APB=28°,∴∠B=76°,如图1,连接MD,∵MD为△P AB的中位线,∴MD∥AP,∴∠MDB=∠APB=28°,∴=2∠MDB=56°;(2)∵∠BAC=∠MDC=∠APB,又∵∠BAP=180°﹣∠APB﹣∠B,∠ACB=180°﹣∠BAC﹣∠B,∴∠BAP=∠ACB,∵∠BAP=∠B,∴∠ACB=∠B,∴AC=AB;(3)①如图2,记MP与圆的另一个交点为R,∵MD是Rt△MBP的中线,∴DM=DP,∴∠DPM=∠DMP=∠RCD,∵∠ACR=∠AMR=90°,∴AM2+MR2=AR2=AC2+CR2,∴12+MR2=22+PR2,∴12+(4﹣PR)2=22+PR2,∴PR=,∴MR=,Ⅰ.当∠ACQ=90°时,AQ为圆的直径,∴Q与R重合,∴MQ=MR=;Ⅱ.如图3,当∠QCD=90°时,在Rt△QCP中,PQ=2PR=,∴MQ=;Ⅲ.如图4,当∠QDC=90°时,∵BM=1,MP=4,∴DP=BP=,∵cos∠MPB==,∴PQ=,∴MQ=;Ⅳ.如图5,当∠AEQ=90°时,由对称性可得∠AEQ=∠BDQ=90°,∴MQ=;综上所述,MQ的值为或或;②△ACG和△DEG的面积之比为.理由:如图6,∵DM∥AF,DE∥AB,∴四边形AMDE是平行四边形,四边形AMDF是等腰梯形,∴DF=AM=DE=1,又由对称性可得GE=GD,∴△DEG是等边三角形,∴∠EDF=90°﹣60°=30°,∴∠DEF=75°=∠MDE,∴∠GDM=75°﹣60°=15°,∴∠GMD=∠PGD﹣∠GDM=15°,∴∠GMD=∠GDM,过C作CH⊥AB于H,由∠BAC=30°可得CH=AC=AB=1=MG,AH=,∴CG=MH=﹣1,∴S△ACG=CG×CH=,∵S△DEG=,∴S△ACG:S△DEG=.。
2020中考考前模拟测试《语文试卷》附答案解析

部编版语文中考模拟测试卷第一部分积累与运用(共30分)一、(6小题,20分)1.下列词语中,每对加点字读音都相同的一项是()(3分)A.折.本/折.扣游弋./摇曳.生姿B.挟.持/协.助拮据./不足为据.C.调.和/调.停雷.霆/自吹自擂.D.轻觑./吹嘘.冠.冕/免冠.徒跣2.下列词语中,没有错别字的一项是()(3分)A.罔然自惭形秽亵渎与日巨增B.嘻闹舍身求法别墅如雷灌耳C.端祥间不容发鄙夷丰功伟迹D.贸然走投无路浑家不言而喻3.依次填入下面横线处的词语,恰当的一组是()(3分)倾听使人,你将不再囿于一己的狭隘;倾听使人,你将懂得山外有山天外有天;倾听使人,你会知道孤独和苦难并非只莅临你的屋檐;倾听使人,你会觉察此时此刻有多少大脑飞速运转,有多少巧手翻飞不息。
A.谦虚安宁警醒丰富B.丰富谦虚安宁警醒C.警醒丰富谦虚安宁D.安宁警醒丰富谦虚4.下列句子没有语病的一项是()(3分)A.在国人的期待中,国产大型客机C919圆满完成了第一趟蓝天首飞之旅。
B.学校开展与策划的“经典诵读”活动,有助于更多同学了解中华优秀传统文化。
C.“一带一路”的倡议获得了世界各国的高度评价,并得到了沿线国家的热烈响应。
D.共享单车管理难题能否得到解决,关键在于有关部门制定有效的管理措施。
5.与下面句子衔接最恰当的一项是()(3分)梅花和雪花都是文学作品中经常描写的对象,它们各有所长:A.梅花没有雪花那么素雅,雪花没有梅花那么芬芳。
B.雪花没有梅花那么芬芳,但它比梅花素雅。
C.雪花比梅花素雅,但它没有梅花那么芬芳。
D.梅花比雪花芬芳,雪花比梅花素雅。
6.名著阅读(5分)A亦垂泪道:“罢,罢,罢!生时服侍哥哥,死了也只是哥哥部下一个小鬼!”言讫泪下,便觉身体有些沉重。
当时泪洒,拜别了宋江下船。
回到润州,果然药发身死。
A临死之时,嘱咐从人:“我死了,可千万将我灵柩去楚州南门外蓼儿洼和哥哥一处埋葬。
”嘱罢而死。
(1)这段文字节选自《水浒传》,选段中的A是____________________。
湖北省2020年中考语文模拟试卷(含答案)

湖北省中考语文模拟试卷一、语文基础知识。
(共12分)1、下列词语中加点字的注音完全正确..的一项是( )(2分)A.牟.取(móu) 叱咤.(chà) 匀称.(chèn) 忍俊不禁.(jīn)B.禁锢.(gù) 酝酿.(niàng)追溯.(shuò) 义愤填膺.(yīng)C.恻.隐(cè) 恣睢.(suī)蓦.然(mò) 惟妙惟肖.(xiào)D.阔绰.(chuò) 琐屑.(xiè) 炽.热(zhì)鳞次栉.比(zhì)2、下列词语中书写正确无误..的一项是( ) (2分)‘A.沉湎幅射名列前茅语无伦次B.震撼荫庇通宵达旦厉行节约C.馈赠文采眼花缭乱物竟天择D.踌躇娴熟题纲挈领月明风清3、下列句子中加点的成语使用不正确...的一项是()(2分)A、在基础教育较为薄弱的地区,任何一分钱都应用在“刀刃”上,如此败家的行为,怎能不让人义愤..填膺..?B、一场春雨之后,那雪白的梨花漫山遍野,绽放出五彩缤纷....的美丽。
C、如果孩子缺乏危机意识,当突然受到外来伤害时,往往会手足无措,呆若木鸡....。
D、制止违法犯罪,我们不应该成为无动于衷....的旁观者。
4、下列句子,没有语病....的一句是( ) (2分)A.南充的金秋时节是旅游休闲的好去处。
B.马航MH370失踪后,许多中国大陆的游客纷纷取消去马来西亚旅游的预约。
C.根治“中国式过马路”的陋习,完善道路设施,增强法律意识才是根本途径。
D.在学校开设的选修课中,同学们尤其更喜欢“生活中的法律”“电脑制作”等课程。
5、下列有关文学常识的表述有误..的一项是()(2分)A、《沁园春雪》的作者是毛泽东,这首词写于1945年国共两党重庆谈判期间。
B、《左迁至蓝关示侄孙湘》的作者是唐朝的韩愈。
C、老舍,原名舒庆春,现代小说家、戏剧家。
2020年河北省石家庄市中考数学模拟试卷 (解析版)
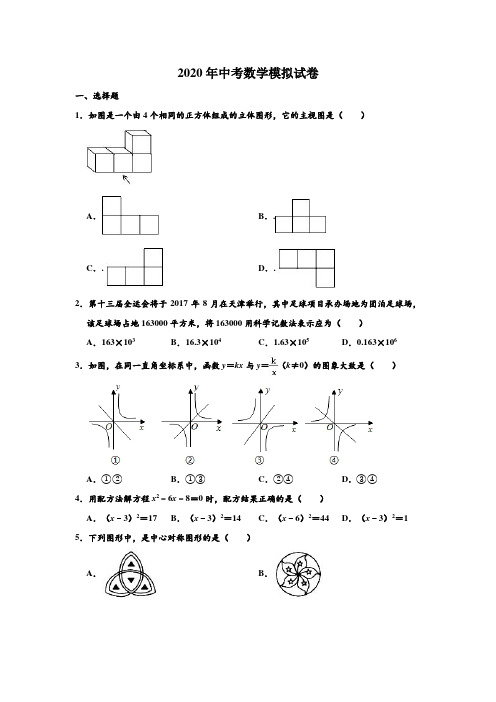
2020年中考数学模拟试卷一、选择题1.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()A.B..C..D..2.第十三届全运会将于2017年8月在天津举行,其中足球项目承办场地为团泊足球场,该足球场占地163000平方米,将163000用科学记数法表示应为()A.163×103B.16.3×104C.1.63×105D.0.163×106 3.如图,在同一直角坐标系中,函数y=kx与y=(k≠0)的图象大致是()A.①②B.①③C.②④D.③④4.用配方法解方程x2﹣6x﹣8=0时,配方结果正确的是()A.(x﹣3)2=17B.(x﹣3)2=14C.(x﹣6)2=44D.(x﹣3)2=1 5.下列图形中,是中心对称图形的是()A.B.C.D.6.计算2sin30°﹣2cos60°+tan45°的结果是()A.2B.C.D.17.计算的结果为()A.B.C.D.8.抛物线y=﹣(x+2)2﹣3向右平移了3个单位,那么平移后抛物线的顶点坐标是()A.(﹣5,﹣3)B.(1,﹣3)C.(﹣1,﹣3)D.(﹣2,0)9.已知线段AB=8cm,在直线AB上画线BC,使它等于3cm,则线段AC等于()A.11cm B.5cm C.11cm或5cm D.8cm或11cm 10.如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为()A.15°B.10°C.20°D.25°11.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于()A.30°B.40°C.35°D.45°12.已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为()A.(1,﹣5)B.(3,﹣13)C.(2,﹣8)D.(4,﹣20)二.填空题(本大题共6小题,每小题3分,共18分)13.计算:3x2•5x3的结果为.14.已知点P(a,﹣6)与点Q(﹣5,3b)关于原点对称,则a+b=.15.如图,坡角为30°的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为16.若关于x、y的方程组的解是,则mn的值为.17.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=EH,那么EH的长为.18.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,且过点(3,0),则下列结论:①abc<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③2a+b=0;④4a2+2b+c<0.其中正确结论的序号是.三.解答题(本大题共5小题,共46分.解答应写出文字说明、演算步骤或推理过程)19.解不等式组请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得;(Ⅱ)解不等式②,得;(Ⅲ)把不等式①和②的解集在数轴上表示出来;(Ⅳ)原不等式组的解集为.20.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学横顶部D 处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)21.如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.(1)求证:点D是AB的中点;(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.22.每年十月的第二个周四是世界爱眼日,为预防近视,超市决定对某型号护眼台灯进行降价销售.降价前,进价为50元的护眼台灯以80元售出,平均每月能售出120盏,调查表明:这种护眼台灯每盏售价每降低1元,其月平均销售量将增加10盏.(1)写出月销售利润y(单位:元)与销售价x(单位:元/盏)之间的函数表达式:(2)当销售价定为多少元时,所得月利润最大?最大月利润为多少元?23.如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.(Ⅰ)求该抛物线的解析式和顶点坐标;(Ⅱ)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?(Ⅲ)在(Ⅱ)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程).四.选做题(本题不计入总成绩)24.如图所示,在平面直角坐标系中A(0,2),点B(﹣3,0).△AOB绕点O逆时针旋转30°得到△A1OB1.(1)直接写出点B1的坐标;(2)点C(2,0),连接CA1交OA于点D,求点D的坐标.参考答案一、选择题1.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()A.B..C..D..【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.解:该立体图形主视图的第1列有1个正方形、第2列有1个正方形、第3列有2个正方形,故选:C.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.2.第十三届全运会将于2017年8月在天津举行,其中足球项目承办场地为团泊足球场,该足球场占地163000平方米,将163000用科学记数法表示应为()A.163×103B.16.3×104C.1.63×105D.0.163×106【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解:将163000用科学记数法表示为:1.63×105.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.如图,在同一直角坐标系中,函数y=kx与y=(k≠0)的图象大致是()A.①②B.①③C.②④D.③④【分析】利用反比例函数的图象及正比例函数的图象分别判断后即可确定正确的选项.解:当k>0时,反比例函数的图象位于一、三象限,正比例函数的图象位于一三象限,②正确;当k<0时,反比例函数的图象位于二、四象限,正比例函数的图象位于二四象限,④正确;故选:C.【点评】本题考查了反比例函数及正比例函数的图象,属于函数的基础知识,难度不较大.4.用配方法解方程x2﹣6x﹣8=0时,配方结果正确的是()A.(x﹣3)2=17B.(x﹣3)2=14C.(x﹣6)2=44D.(x﹣3)2=1【分析】方程利用完全平方公式变形即可得到结果.解:用配方法解方程x2﹣6x﹣8=0时,配方结果为(x﹣3)2=17,故选:A.【点评】此题考查了解一元二次方程﹣配方法,熟练掌握完全平方公式是解本题的关键.5.下列图形中,是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的概念即可求解.解:A、不是中心对称图形,不符合题意;B、不是中心对称图形,不符合题意;C、是中心对称图形,符合题意;D、不是中心对称图形,不符合题意.故选:C.【点评】本题考查了中心对称的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合,难度一般.6.计算2sin30°﹣2cos60°+tan45°的结果是()A.2B.C.D.1【分析】直接利用特殊角的三角函数值分别代入求出答案.解:2sin30°﹣2cos60°+tan45°=2×﹣2×+1=1﹣1+1=1.故选:D.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.7.计算的结果为()A.B.C.D.【分析】根据分式的运算法则即可求出答案.【解答】原式==,故选:A.【点评】本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型8.抛物线y=﹣(x+2)2﹣3向右平移了3个单位,那么平移后抛物线的顶点坐标是()A.(﹣5,﹣3)B.(1,﹣3)C.(﹣1,﹣3)D.(﹣2,0)【分析】根据二次函数图象左加右减,上加下减的平移规律进行解答.解:抛物线y=﹣(x+2)2﹣3的顶点坐标是(﹣2,﹣3),向右平移3个单位后,所得抛物线的顶点坐标是(﹣2+3,﹣3),即(1,﹣3).故选:B.【点评】主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.9.已知线段AB=8cm,在直线AB上画线BC,使它等于3cm,则线段AC等于()A.11cm B.5cm C.11cm或5cm D.8cm或11cm 【分析】由于C点的位置不能确定,故要分两种情况考虑AC的长,注意不要漏解.解:由于C点的位置不确定,故要分两种情况讨论:(1)当C点在B点右侧时,如图所示:AC=AB+BC=8+3=11cm;(2)当C点在B点左侧时,如图所示:AC=AB﹣BC=8﹣3=5cm;所以线段AC等于5cm或11cm,故选C.【点评】本题考查了比较线段的长短,注意点的位置的确定,利用图形结合更易直观地得到结论.10.如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为()A.15°B.10°C.20°D.25°【分析】由旋转前后的对应角相等可知,∠DFC=∠BEC=60°;一个特殊三角形△ECF 为等腰直角三角形,可知∠EFC=45°,把这两个角作差即可.解:∵△BCE绕点C顺时针方向旋转90°得到△DCF,∴CE=CF,∠DFC=∠BEC=60°,∠EFC=45°,∴∠EFD=60°﹣45°=15°.【点评】本题考查旋转的性质和正方形的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.11.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于()A.30°B.40°C.35°D.45°【分析】先撸垂径定理的推论得到CD⊥EF,再根据垂径定理得到=,然后利用圆周角定理确定∠EOD的度数.解:∵直径CD经过弦EF的中点G,∴CD⊥EF,∴=,∴∠EOD=2∠DCF=2×20°=40°.故选:B.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.12.已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为()A.(1,﹣5)B.(3,﹣13)C.(2,﹣8)D.(4,﹣20)【分析】先利用配方法求得点M的坐标,然后利用关于原点对称点的特点得到点M′的坐标,然后将点M′的坐标代入抛物线的解析式求解即可.解:y=x2﹣2mx﹣4=x2﹣2mx+m2﹣m2﹣4=(x﹣m)2﹣m2﹣4.∴点M(m,﹣m2﹣4).∴点M′(﹣m,m2+4).∴m2+2m2﹣4=m2+4.解得m=±2.∴m=2.∴M(2,﹣8).故选:C.【点评】本题主要考查的是二次函数的性质、关于原点对称的点的坐标特点,求得点M′的坐标是解题的关键.二.填空题(本大题共6小题,每小题3分,共18分)13.计算:3x2•5x3的结果为15x5.【分析】直接利用单项式乘以单项式运算法则求出即可.解:3x2•5x3=15x5.故答案是:15x5.【点评】此题主要考查了整式的乘法运算,熟练掌握相关运算法则是解题关键.14.已知点P(a,﹣6)与点Q(﹣5,3b)关于原点对称,则a+b=7.【分析】直接利用关于原点对称点的性质得出a,b的值,即可得出答案.解:∵点P(a,﹣6)与点Q(﹣5,3b)关于原点对称,∴a=5,3b=6,解得:b=2,故a+b=7.故答案为:7.【点评】此题主要考查了关于原点对称点的性质,正确记忆横纵坐标的关系是解题关键.15.如图,坡角为30°的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为m【分析】根据余弦的定义计算,得到答案.解:在Rt△ABC中,cos A=,∴AB==,故答案为:m.【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握坡度坡角的概念、锐角三角函数的定义是解题的关键.16.若关于x、y的方程组的解是,则mn的值为﹣2.【分析】将代入方程组即可求出m与n的值.解:将代入,∴,∴,∴mn=﹣2,故答案为:﹣2.【点评】本题考查二元一次方程组,解题的关键是正确理解二元一次方程组的解的定义,本题属于基础题型.17.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=EH,那么EH的长为.【分析】设EH=3x,表示出EF,由AD﹣EF表示出三角形AEH的边EH上的高,根据三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,即为EH的长.解:如图所示:∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC,∵AM⊥EH,AD⊥BC,∴,设EH=3x,则有EF=2x,AM=AD﹣EF=2﹣2x,∴,解得:x=,则EH=.故答案为:.【点评】此题考查了相似三角形的判定与性质,以及矩形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.18.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,且过点(3,0),则下列结论:①abc<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③2a+b=0;④4a2+2b+c<0.其中正确结论的序号是①②③.【分析】由抛物线对称轴的位置确定ab的符号,由抛物线与y轴的交点在x轴上方得c >0,则可对A进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点为(﹣1,0),则可对B选项进行判断;由对称轴公式可结C进行判断;由于x=2时,函数值大于0,则有4a+2b+c>0,于是可对D选项进行判断.解:①∵抛物线与y轴的交点在x轴上方,∴c>0,∵对称轴为直线x=1,∴ab<0,∴abc<0,所以此选项正确;②∵抛物线过点A(3,0),二次函数图象的对称轴是x=1,∴抛物线与x轴的另一个交点为(﹣1,0),∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;所以此选项正确;③∵对称轴为直线x=1,∴﹣=1,b=﹣2a,∴2a+b=0,所以此选项正确;④∵当x=2时,y>0,∴4a+2b+c>0,所以此选项错误;其中正确结论的序号是①②③;故答案为:①②③.【点评】本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=﹣;抛物线与y轴的交点坐标为(0,c),熟练掌握二次函数的性质是关键.三.解答题(本大题共5小题,共46分.解答应写出文字说明、演算步骤或推理过程)19.解不等式组请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得x≤2;(Ⅱ)解不等式②,得x>﹣1;(Ⅲ)把不等式①和②的解集在数轴上表示出来;(Ⅳ)原不等式组的解集为﹣1<x≤2.【分析】先求出不等式组中的每一个不等式的解集,然后取其交集即为不等式组的解集;最后根据在数轴上表示不等式的解集的方法将其表示在数轴上.解:(Ⅰ)解不等式①,得x≤2;(Ⅱ)解不等式②,得x>﹣1;(Ⅲ)把不等式①和②的解集在数轴上表示出来;(Ⅳ)原不等式组的解集为﹣1<x≤2.故答案为:x≤2;x>﹣1;﹣1<x≤2.【点评】本题考查了在数轴上表示不等式的解集、解一元一次不等式组.把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.20.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学横顶部D 处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)【分析】作CM⊥BD,在Rt△CDM中DM=CM tan∠DCM,在Rt△BCM中BM=CM tan ∠BCM,根据DM+BM=BD可得CM tan18°+CM tan20°=21,解之即可得.解:过点C作CM⊥BD于点M,在Rt△CDM中,∵tan∠DCM=,∴DM=CM tan∠DCM=CM tan18°;在Rt△BCM中,∵tan∠BCM=,∴BM=CM tan∠BCM=CM tan20°,∵DM+BM=BD,∴CM tan18°+CM tan20°=21,解得:CM=≈31(m),则AB=31m,答:AB的长约为31m.【点评】此题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.21.如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.(1)求证:点D是AB的中点;(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.【分析】(1)由于AC=AB,如果连接CD,那么只要证明出CD⊥AB,根据等腰三角形三线合一的特点,我们就可以得出AD=BD,由于BC是圆的直径,那么CD⊥AB,由此可证得.(2)连接OD,再证明OD⊥DE即可.【解答】证明:(1)如图1,连接CD,∵BC为⊙O的直径,∴CD⊥AB.∵AC=BC,∴AD=BD.(2)如图2,连接OD;∵AD=BD,OB=OC,∴OD是△BCA的中位线,∴OD∥AC.∵DE⊥AC,∴DF⊥OD.∵OD为半径,∴DE是⊙O的切线.【点评】本题主要考查了切线的判定,等腰三角形的性质等知识点.要注意的是要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.22.每年十月的第二个周四是世界爱眼日,为预防近视,超市决定对某型号护眼台灯进行降价销售.降价前,进价为50元的护眼台灯以80元售出,平均每月能售出120盏,调查表明:这种护眼台灯每盏售价每降低1元,其月平均销售量将增加10盏.(1)写出月销售利润y(单位:元)与销售价x(单位:元/盏)之间的函数表达式:(2)当销售价定为多少元时,所得月利润最大?最大月利润为多少元?【分析】(1)根据“总利润=单件利润×销售量”可得;(2)利用配方法求出二次函数最值即可得出答案.解:(1)设售价为x元/盏,月销售利润y元,根据题意得:y=(x﹣50)[120+10(80﹣x)]=﹣10x2+1420x﹣46000;(2)∵y=﹣10x2+1420x﹣46000=﹣10(x﹣71)2+96410,∴当销售价定为71元时,所得月利润最大,最大月利润为96410元.【点评】此题主要考查了二次函数的应用以及二次函数最值求法,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系.23.如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.(Ⅰ)求该抛物线的解析式和顶点坐标;(Ⅱ)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?(Ⅲ)在(Ⅱ)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程).【分析】(Ⅰ)把A、B两点坐标代入抛物线y=﹣x2+bx+c得关于b、c方程组,则解方程组即可得到抛物线解析式;然后把一般式配成顶点式得到抛物线的顶点坐标;(Ⅱ)先利用待定系数法求出直线AB的解析式为y=﹣x+2,设N(t,﹣t2+t+2)(0<t<4),则N(t,﹣t+2),则MN=﹣t2+t+2﹣(﹣t+2),然后利用二次函数的性质解决问题;(Ⅲ)由(Ⅱ)得N(2,5),M(2,1),如图,利用平行四边形的性质进行讨论:当MN为平行四边形的边时,利用MN∥AD,MN=AD=4和确定定义D点坐标,当MN为平行四边形的对角线时,利用AN∥MN,AN=MD和点平移的坐标规律写出对应D点坐标.解:(Ⅰ)把A(0,2)、B(4,0)代入抛物线y=﹣x2+bx+c得,解得,∴抛物线解析式为y=﹣x2+x+2;∵y=﹣x2+x+2=﹣(x﹣)2+,∴抛物线的顶点坐标为(,);(Ⅱ)设直线AB的解析式为y=mx+n,把A(0,2)、B(4,0)代入得,解得,∴直线AB的解析式为y=﹣x+2,设N(t,﹣t2+t+2)(0<t<4),则N(t,﹣t+2),∴MN=﹣t2+t+2﹣(﹣t+2)=﹣t2+4t=﹣(t﹣2)2+4,当t=2时,MN有最大值,最大值为4;(Ⅲ)由(Ⅱ)得N(2,5),M(2,1),如图,当MN为平行四边形的边时,MN∥AD,MN=AD=4,则D1(0,6),D2(0,﹣2),当MN为平行四边形的对角线时,AN∥MN,AN=MD,由于点A向右平移2个单位,再向上平移3个单位得到N点,则点M向右平移2个单位,再向上平移3个单位得到D 点,则D3的坐标为(4,4),综上所述,D点坐标为(0,6)或(0,﹣2)或(4,4).【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求函数解析式;会利用点平移的坐标规律求平行四边形第四个顶点的坐标;理解坐标与图形性质;会运用分类讨论的思想解决思想问题.四.选做题(本题不计入总成绩)24.如图所示,在平面直角坐标系中A(0,2),点B(﹣3,0).△AOB绕点O逆时针旋转30°得到△A1OB1.(1)直接写出点B1的坐标;(2)点C(2,0),连接CA1交OA于点D,求点D的坐标.【分析】(1)过点B1作B1E⊥y轴于点E,根据△AOB绕点O逆时针旋转30°得到△A1OB1,即可求出点B1坐标;(2)根据题意可得OA1=OC=2,由旋转可得∠AOA1=30°,进而得∠A1OC=120°,所以可得∠A1CO=30°.从而可求出OD的长,即可得点D的坐标.解:(1)如图,过点B1作B1E⊥y轴于点E,∵△AOB绕点O逆时针旋转30°得到△A1OB1,∴∠BOB1=30°,∴∠B1OE=60°,∵B(﹣3,0),∴OB=OB1=3,∴OE=,B1E=,∴点B1的坐标为:(﹣,﹣);(2)∵点C(2,0),∴OC=2,∵A(0,2),∴OA=OA1=2,∴OA1=OC=2,∵∠AOA1=30°,∠DOC=90°,∴∠A1OC=120°,∴∠A1CO=30°.∴OD=OC•tan30°=2×=.∴点D的坐标为:(0,).【点评】本题考查了坐标与图形变化﹣旋转,解决本题的关键是掌握旋转的性质.。
2020年河南省中考数学模拟考试试卷(经典一) (解析版)

2020年河南省中考数学模拟试卷(经典一)一.选择题(共10小题)1.﹣2020的绝对值是()A.﹣2020B.2020C.﹣D.2.2019年上半年,河南接待海内外旅游人数4.9亿人次,旅游总收入5150亿元,数据“5150亿”用科学记数法表示为()A.5150×108B.5.15×1011C.515×109D.0.515×1013 3.下列四个图案中,是轴对称图形,但不是中心对称图形的是()A.B.C.D.4.下列运算结果正确的是()A.(﹣a3)2=﹣a6B.a8÷a2=a4C.(a+b)2=a2+b2D.(﹣)﹣2=45.如图由6个等大的小立方体搭成的,有关三视图的说法正确的是()A.正视图(主视图)面积最大B.左视图面积最大C.俯视图面积最大D.三种视图面积一样大6.一元二次方程(2x+1)(2x﹣1)=8x+15的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根7.某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95,90,85.则小桐这学期的体育成绩是()A.88.5B.86.5C.90D.90.58.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=(x<0)的图象经过点C,则k的值为()A.﹣12B.﹣6C.6D.129.如图,已知∠AOB.按照以下步骤作图:①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD.②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE.③连接OE交CD于点M.下列结论中错误的是()A.∠CEO=∠DEO B.CM=MDC.∠OCD=∠ECD D.S=CD•OE四边形OCED10.如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O…依此规律,得到等腰直角三角形A2020OB2020,则点B2020的坐标为()A.(22019,22019)B.(﹣22019,22019)C.(﹣22020,22020)D.(22020,22020)二.填空题(共5小题)11.﹣3﹣1=.12.不等式组的解集是.13.同时掷两枚普通的骰子,“出现数字之积为奇数”的概率为.14.如图,Rt△ABC中,∠BCA=90°,∠BAC=30°,AB=6.△ABC以点B为中心逆时针旋转,使点C旋转至AB边延长线上的C′处,那么AC边转过的图形(图中阴影部分)的面积是.15.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE 折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为.三.解答题(共8小题)16.先化简,再从2、3、4中选一个合适的数作为x的值代入求值.()÷17.在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,P为AC延长线上一点,且∠PBC=∠BAC,连接DE,BE.(1)求证:BP是⊙O的切线;(2)若sin∠PBC=,AB=10,求BP的长.18.九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的条形统计图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:(1)在这次评价中,一共抽查了名学生;(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)请将条形统计图补充完整;(4)如果全市有6000名九年级学生,那么在试卷评讲课中,“独立思考”的约有多少人?19.如图,山顶有一塔AB,塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°,从与F点相距50m的D 处测得A的仰角为45°.求隧道EF的长度.(参考数据:tan22°≈0.40,tan27°≈0.51.)20.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A 型节能灯和2只B型节能灯共需29元.(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.21.如图,反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于点A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°.(1)求k的值及B点坐标;(2)求△ABC的面积.22.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.23.如图,直线y=﹣2x+12与x轴交于点C,与y轴交于点B,抛物线y=3ax2+10x+3c经过B,C两点,与x轴交于另一点A,点E是直线BC上方抛物线上的一动点,过E作EF∥y轴交x轴于点F,交直线BC于点M.(1)求抛物线的解析式;(2)求线段EM的最大值;(3)在(2)的条件下,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,A,M为顶点的四边形为平行四边形?如果存在,请直接写出P 点坐标;如果不存在,请说明理由.参考答案与试题解析一.选择题(共10小题)1.﹣2020的绝对值是()A.﹣2020B.2020C.﹣D.【分析】根据绝对值的定义直接进行计算.【解答】解:根据绝对值的概念可知:|﹣2020|=2020,故选:B.2.2019年上半年,河南接待海内外旅游人数4.9亿人次,旅游总收入5150亿元,数据“5150亿”用科学记数法表示为()A.5150×108B.5.15×1011C.515×109D.0.515×1013【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:5150亿=515000000000=5.15×1011.故选:B.3.下列四个图案中,是轴对称图形,但不是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、是轴对称图形,不是中心对称图形,符合题意;B、不是轴对称图形,也不是中心对称图形,不符合题意;C、不是轴对称图形,是中心对称图形,不符合题意;D、是轴对称图形,也是中心对称图形,不符合题意.故选:A.4.下列运算结果正确的是()A.(﹣a3)2=﹣a6B.a8÷a2=a4C.(a+b)2=a2+b2D.(﹣)﹣2=4【分析】分别根据积的乘方运算法则,同底数幂的除法法则,完全平方公式以及负整数指数幂的定义逐一判断即可.【解答】解:A.(﹣a3)2=a6,故本选项不合题意;B.a8÷a2=a6,故本选项不合题意;C.(a+b)2=a2+2ab+b2,故本选项不合题意;D.(﹣)﹣2=,符合题意.故选:D.5.如图由6个等大的小立方体搭成的,有关三视图的说法正确的是()A.正视图(主视图)面积最大B.左视图面积最大C.俯视图面积最大D.三种视图面积一样大【分析】根据三视图可得主视图,左视图,俯视图都是4个正方形,因此面积一样大.【解答】解:正视图(主视图),左视图,俯视图都是4个正方形,因此面积一样大,故选项A、B、C错误,D正确;故选:D.6.一元二次方程(2x+1)(2x﹣1)=8x+15的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根【分析】先把方程化为一般式,再计算判别式的值,然后根据判别式的意义判断方程根的情况.【解答】解:方程化为x2﹣2x﹣4=0,∵△=(﹣2)2﹣4×(﹣4)=20>0,∴方程有两个不相等的实数根.故选:A.7.某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95,90,85.则小桐这学期的体育成绩是()A.88.5B.86.5C.90D.90.5【分析】直接利用每部分分数所占百分比进而计算得出答案.【解答】解:由题意可得,小桐这学期的体育成绩是:95×20%+90×30%+85×50%=19+27+42.5=88.5(分).故选:A.8.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=(x<0)的图象经过点C,则k的值为()A.﹣12B.﹣6C.6D.12【分析】设菱形的两条对角线相交于点D,如图,根据菱形的性质得OB⊥AC,BD=OD =2,CD=AD=3,再由菱形ABCD的对角线OB在y轴上得到AC∥x轴,则可确定C (﹣3,2),然后根据反比例函数图象上点的坐标特征求k的值.【解答】解:设菱形的两条对角线相交于点D,如图,∵四边形ABCD为菱形,∴OB⊥AC,BD=OD=2,CD=AD=3,∵菱形ABCO的对角线OB在y轴上,∴AC∥x轴,∴C(﹣3,2),∴k=﹣3×2=﹣6.故选:B.9.如图,已知∠AOB.按照以下步骤作图:①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD.②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE.③连接OE交CD于点M.下列结论中错误的是()A.∠CEO=∠DEO B.CM=MDC.∠OCD=∠ECD D.S=CD•OE四边形OCED【分析】利用基本作图得出角平分线的作图,进而解答即可.【解答】解:由作图步骤可得:OE是∠AOB的角平分线,∴∠CEO=∠DEO,CM=MD,S=CD•OE,四边形OCED但不能得出∠OCD=∠ECD,故选:C.10.如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O…依此规律,得到等腰直角三角形A2020OB2020,则点B2020的坐标为()A.(22019,22019)B.(﹣22019,22019)C.(﹣22020,22020)D.(22020,22020)【分析】根据题意得出B点坐标变化规律,进而得出点B2020的坐标位置,进而得出答案.【解答】解:∵△AOB是等腰直角三角形,OA=1,∴AB=OA=1,∴B(1,1),将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,∴每4次循环一周,B1(2,﹣2),B2(﹣4,﹣4),B3(﹣8,8),B4(16,16),∵2020÷4=505,∴点B2020与B同在一个象限内,∵﹣4=﹣22,8=23,16=24,∴点B2020(22020,22020).故选:D.二.填空题(共5小题)11.﹣3﹣1=.【分析】首先计算乘方、开方,然后计算减法,求出算式的值是多少即可.【解答】解:﹣3﹣1=3﹣=故答案为:.12.不等式组的解集是x<5.【分析】此题可通过对不等式组里的两个一元一次不等式求解,再写出两个不等式的公共解集.【解答】解:解不等式①得:x<5,解不等式②得:x≤9,∴不等式组的解集为x<5,故答案为:x<5.13.同时掷两枚普通的骰子,“出现数字之积为奇数”的概率为.【分析】列举出所有情况,看出现数字之积为奇数的情况数占所有情况数的多少即可.【解答】解:根据题意列表得:(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)共有36种等情况数,其中数字之积为奇数的有9种情况,所以“出现数字之积为奇数”的概率是=;故答案为:.14.如图,Rt△ABC中,∠BCA=90°,∠BAC=30°,AB=6.△ABC以点B为中心逆时针旋转,使点C旋转至AB边延长线上的C′处,那么AC边转过的图形(图中阴影部分)的面积是9π.【分析】根据旋转变换的性质可得△ABC与△A′BC′全等,从而得到阴影部分的面积=扇形ABA′的面积﹣小扇形CBC′的面积.【解答】解:根据旋转变换的性质,△ABC≌△A′BC′,∵∠BCA=90°,∠BAC=30°,AB=6,∴BC=AB=3,∴阴影面积=﹣=9π.15.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE 折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为3或6.【分析】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时四边形ABEB′为正方形.【解答】解:当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,在Rt△ABC中,AB=6,BC=8,∴AC==10,∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,∴EB=EB′,AB=AB′=6,∴CB′=10﹣6=4,设BE=x,则EB′=x,CE=8﹣x,在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+42=(8﹣x)2,解得x=3,∴BE=3;②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形,∴BE=AB=6.综上所述,BE的长为3或6.故答案为:3或6.三.解答题(共8小题)16.先化简,再从2、3、4中选一个合适的数作为x的值代入求值.()÷【分析】首先计算括号里面的减法,然后再算括号外的除法,化简后,根据分式有意义的条件确定x的取值,再代入x的值即可.【解答】解:原式=[﹣]•,=(﹣)•,=•,=x+2,∵x﹣2≠0,x﹣4≠0,x+2≠0,∴x≠2或4或﹣2,∴x取3,当x=3时,原式=3+2=5.17.在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,P为AC延长线上一点,且∠PBC=∠BAC,连接DE,BE.(1)求证:BP是⊙O的切线;(2)若sin∠PBC=,AB=10,求BP的长.【分析】(1)连接AD,求出∠PBC=∠ABC,求出∠ABP=90°,根据切线的判定得出即可;(2)解直角三角形求出BD,求出BC,根据勾股定理求出AD,根据相似三角形的判定和性质求出BE,根据相似三角形的性质和判定求出BP即可.【解答】(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分∠BAC,∴∠BAD=∠BAC,∵∠ADB=90°,∴∠BAD+∠ABD=90°,∵∠PBC=∠BAC,∴∠PBC+∠ABD=90°,∴∠ABP=90°,即AB⊥BP,∴PB是⊙O的切线;(2)解:∵∠PBC=∠BAD,∴sin∠PBC=sin∠BAD,∵sin∠PBC==,AB=10,∴BD=2,由勾股定理得:AD==4,∴BC=2BD=4,∵由三角形面积公式得:AD×BC=BE×AC,∴4×4=BE×10,∴BE=8,∴在Rt△ABE中,由勾股定理得:AE=6,∵∠BAE=∠BAP,∠AEB=∠ABP=90°,∴△ABE∽△APB,∴=,∴PB===.18.九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的条形统计图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:(1)在这次评价中,一共抽查了560名学生;(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为54度;(3)请将条形统计图补充完整;(4)如果全市有6000名九年级学生,那么在试卷评讲课中,“独立思考”的约有多少人?【分析】(1)根据专注听讲的人数是224人,所占的比例是40%,即可求得抽查的总人数;(2)利用360乘以对应的百分比即可求解;(3)利用总人数减去其他各组的人数,即可求得讲解题目的人数,从而作出频数分布直方图;(4)利用6000乘以对应的比例即可.【解答】解:(1)调查的总人数是:224÷40%=560(人),故答案是:560;(2)“主动质疑”所在的扇形的圆心角的度数是:360×=54°,故答案是:54;(3)“讲解题目”的人数是:560﹣84﹣168﹣224=84(人).(4)6000×=1800(人),答:在试卷评讲课中,“独立思考”的初三学生约有1800人.19.如图,山顶有一塔AB,塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°,从与F点相距50m的D 处测得A的仰角为45°.求隧道EF的长度.(参考数据:tan22°≈0.40,tan27°≈0.51.)【分析】延长AB交CD于H,利用正切的定义用CH表示出AH、BH,根据题意列式求出CH,计算即可.【解答】解:延长AB交CD于H,则AH⊥CD,在Rt△AHD中,∠D=45°,∴AH=DH,在Rt△AHC中,tan∠ACH=,∴AH=CH•tan∠ACH≈0.51CH,在Rt△BHC中,tan∠BCH=,∴BH=CH•tan∠BCH≈0.4CH,由题意得,0.51CH﹣0.4CH=33,解得,CH=300,∴EH=CH﹣CE=220,BH=120,∴AH=AB+BH=153,∴DH=AH=153,∴HF=DH﹣DF=103,∴EF=EH+FH=323,答:隧道EF的长度为323m.20.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A 型节能灯和2只B型节能灯共需29元.(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.【分析】(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元,根据:“1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元”列方程组求解即可;(2)首先根据“A型节能灯的数量不多于B型节能灯数量的3倍”确定自变量的取值范围,然后得到有关总费用和A型灯的只数之间的关系得到函数解析式,确定函数的最值即可.【解答】解:(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元,根据题意,得:,解得:,答:一只A型节能灯的售价是5元,一只B型节能灯的售价是7元;(2)设购进A型节能灯m只,总费用为W元,根据题意,得:W=5m+7(50﹣m)=﹣2m+350,∵﹣2<0,∴W随m的增大而减小,又∵m≤3(50﹣m),解得:m≤37.5,而m为正整数,∴当m=37时,W=﹣2×37+350=276,最小此时50﹣37=13,答:当购买A型灯37只,B型灯13只时,最省钱.21.如图,反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于点A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°.(1)求k的值及B点坐标;(2)求△ABC的面积.【分析】(1)先把A(1,a)代入y=2x中求出a得到A(1,2);再把A点坐标代入y=中可确定k的值,然后利用反比例函数和正比例函数图象的性质确定B点坐标;(2)设C(1,t),根据两点间的距离公式和勾股定理得到(1+1)2+(t+2)2+(1+1)2+(2+2)2=(2﹣t)2,求出t得到C(1,﹣3),从而得到AC的长,然后关键三角形面积公式求得即可.【解答】解:(1)把A(1,a)代入y=2x得a=2,则A(1,2);把A(1,2)代入y=得k=1×2=2,∵点A与点B关于原点对称,∴B(﹣1,﹣2);(2)∵CA∥y轴,∴C点的横坐标为1,设C(1,t),∵∠ABC=90°.∴BC2+AC2=AB2,即(1+1)2+(t+2)2+(1+1)2+(2+2)2=(2﹣t)2,解得t=﹣3,∴C(1,﹣3),∴AC=5,=AC(x A﹣x B)==5.∴S△ABC22.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=1;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.【分析】(1)先用等量代换判断出∠ADE=∠CDF,∠A=∠DCB,得到△ADE∽△CDF,再判断出△ADC∽△CDB即可;(2)方法和(1)一样,先用等量代换判断出∠ADE=∠CDF,∠A=∠DCB,得到△ADE ∽△CDF,再判断出△ADC∽△CDB即可;(3)由(2)的结论得出△ADE∽△CDF,判断出CF=2AE,求出DE,再利用勾股定理,计算出即可.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴=1,∴=1(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴②成立.如图,∵∠ACB=90°,∴∠A+∠ABC=90°,又∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE+∠CDE=∠ADC+∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴.(3)由(2)有,△ADE∽△CDF,∵=,∴=,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF=2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,②当E在AC延长线上时,在Rt△CEF中,CF=2AE=2(AC+CE)=2(+CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(+CE)]2=40,∴CE=,或CE=﹣2(舍),③如图1,当点E在CA延长线上时,CF=2AE=2(CE﹣AC)=2(CE﹣),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(CE﹣)]2=40,∴CE=2,或CE=﹣(舍)即:CE=2或CE=.23.如图,直线y=﹣2x+12与x轴交于点C,与y轴交于点B,抛物线y=3ax2+10x+3c经过B,C两点,与x轴交于另一点A,点E是直线BC上方抛物线上的一动点,过E作EF∥y轴交x轴于点F,交直线BC于点M.(1)求抛物线的解析式;(2)求线段EM的最大值;(3)在(2)的条件下,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,A,M为顶点的四边形为平行四边形?如果存在,请直接写出P 点坐标;如果不存在,请说明理由.【分析】(1)点C、B的坐标分别为:(6,0)、(0,12),抛物线y=3ax2+10x+3c 经过B,C两点,则3c=12,将点C的坐标代入抛物线表达式,即可求解;(2)设点E(x,﹣2x2+10x+12),则点M(x,﹣2x+12),EM=﹣2x2+12x,即可求解;(3)分AM是边、AM是对角线两种情况,分别求解即可.【解答】解:(1)直线y=﹣2x+12与x轴交于点C,与y轴交于点B,则点C、B的坐标分别为:(6,0)、(0,12),抛物线y=3ax2+10x+3c经过B,C两点,则3c=12,故抛物线的表达式为:y=3ax2+10x+12,将点C的坐标代入上式并解得:a=﹣,故抛物线的表达式为:y=﹣2x2+10x+12;(2)设点E(x,﹣2x2+10x+12),则点M(x,﹣2x+12),EM=(﹣2x2+10x+12)﹣(﹣2x+12)=﹣2x2+12x,∵﹣2<0,故EM有最大值,最大值为18,此时x=3;(3)y=﹣2x2+10x+12,令y=0,则x=﹣1或6,故点A(﹣1,0),由(2)知,x=3,则点M(3,6),设点P的横坐标为:m,点Q的坐标为:(,s),①当AM是边时,当点A向右平移4个单位向上平移6个单位得到点M,同样,点P(Q)向右平移4个单位向上平移6个单位得到点得到点Q(P),即m±4=,解得:m=﹣或,故点P(﹣,﹣)或(,﹣);②当AM是对角线时,由中点公式得:﹣1+2=m+,解得:m=﹣,故点P(﹣,);综上,点P的坐标为:(﹣,﹣)或(,﹣)或(﹣,).。
2020年中考语文模拟试题

广西上思县2020年中考语文模拟试题温馨提示:(1)本学科试卷分试题卷和答题卷两部分,考试时量为120分钟,满分为120分。
(2)请你将姓名、准考证号等相关信息按要求填涂在答题卡上。
(3)请你在答题卡上作答,答在本试题卷上无效。
一、积累与运用(共30分)1.对下边的宣传语中字形纠错最准确的一项是()(2分)A.精采人生责无旁待科学至贫宏扬雷锋精神B.一成不变责无旁贷科学治贫参预志愿服务C.一成不变责无旁贷科学治贫参与志愿服务D.精彩人生责无旁待科学至贫宏扬雷锋精神2.下列句子中加点的词语运用正确的一项是()(2分)A.两位阔别多年的老朋友意外地在异国他乡萍水相逢....,又是握手,又是拥抱,别提有多高兴了。
B.邵阳市交警支队招聘了许多交通协管员,在他们的协助下,交通拥堵的现象戛然而止....。
C.做一个人,我们要行使自己的权力;做一个公民,我们要恪尽职守....。
D.李红经常为孤寡老人做好事,她的事迹真是罄竹难书....。
3.下列句子没有语病的一项是()(2分)A.作家杨绛先生的晚年,仍然精力充沛,充满了创作的激情。
B. 对于新冠肺炎感染源是不是动物以及可能有哪些动物等问题,目前还在调查中。
C.能否彻底治理环境污染,留住碧水蓝天,关键在于有关部门严格执法。
D. 疫情面前,请广大市民注意防护,不要恐慌,切忌不要造谣传谣。
4.依次填入下列句子横线处的词语,最恰当的一项是()(2分)宝庆艺术展开设了雕塑展览专场,展出的大量雕塑作品非常精美,尤其是木雕,以其_________的雕刻技艺吸引了众多参观者。
这些作品有的简练粗放,有的,其中最为突出的是“三英战吕布”组雕,人物,令人惊叹。
A.巧夺天工具体而微引人入胜 B.美不胜收精雕细刻引人入胜C.巧夺天工精雕细刻惟妙惟肖 D.美不胜收具体而微惟妙惟肖5.下列句子变换后意思发生变化的一项是()(2分)A.原句:如果宇宙没有生命,怎么会从中开出灿烂的生命之花?改句:如果宇宙没有生命,就不会从中开出灿烂的生命之花。
2020年地理中考模拟试卷(含答案)-2020地生中考模拟卷

2020年地理中考模拟试卷(含答案)-2020地生中考模拟卷2020年地理中考模拟试卷一、选择题(2×3=60分)1.下列山脉中,既是我国第一、二级阶梯分界线,又是东西走向的山脉是()A.XXXD.祁连山脉2.我国水能资源十分丰富,居世界第一位,其最主要原因是()A.地形多种多样B.地势西高东低,呈斜坡状分布C.山地面积广大D.地势西高东低,呈阶梯状分布3.下列不位于我国第二阶梯的是()A.云贵高原、黄土高原B.长江中下游平原、东北平原C.黄土高原、塔里木盆地D.塔里木盆地、准噶尔盆地4.下列山脉中属于东西走向的一组是()A.大兴安岭、太行山、天山B.长白山、武夷山、昆仑山C.武夷山、喜马拉雅山、祁连山D.天山、秦岭、南岭5.关于山区说法正确的是()A.在山区可以大力发展种植业B.在山区最适合发展林业C.山区交通便利,基础设施较好D.山区多发生干旱、地震等自然灾害6.下列符号中,正确表示风力4级东南风的()A.B.C.D.7.降水几率为100%和降水几率为分别表示()A.大概有雨肯定无雨B.肯定有雨大概无雨C.大概有雨大概无雨D.肯定有雨肯定无雨8.对天气状况的描述,正确的一项是()A.今天下这么大的雨,明天肯定还有雨B.适才还晴得好好的,突然狂风暴雨,真是“天有意外风云”C.今年夏季天气多云到暴雨D.我们这里天气这么晴朗,北京也一定是晴天9.下列选项不是天气特性的是()A.人们经常用阴晴、风雨、冷热来描述天气B.天气反映一个地方短工夫内的大气状况C.天气是经常变化的D.同一时刻,不同的地方天气可能差别很大10.XXX小朋友已经10岁了,可他在家乡从未见过下雪,他的家乡最可能在()A.XXX11.我国内流区大抵位于()A.东南部季风区B.西北部非季风区C.南部湿润地区D.北部半湿润地区12.诗“更立西江石壁,截断巫山云雨,高峡出平湖”,是对哪一条河流与水电站的描述()A.雅砻江二滩水电站B.珠江天生桥水电站C.黄河小浪底三峡水电站13.关于黄河的叙述,正确的是()A.黄河流经四川盆地,上游多高山、峡谷B.黄河的泥沙主要来自中游的黄土高原C.从河流的长度、水量来看均为我国第二大河D.黄河下游为“地上河”,易决口成灾,加固防洪大堤是治理黄河的根本14.“一江春水向东流”“滚滚长江东逝水”反映了()A.我国地势西高东低B.我国地势东高西低C.我国阵势南高北低D.我国阵势北高南低15.下列对于南方地区地理事物的叙述,正确的选项是()A.南方地区属于湿润的亚热带和热带季风气候B.长江三角洲地区是我国最大的重工业基地C.香港和澳门自然资源丰富,成为我国经济发展水平最高的地区D.台湾目前的经济发展特点为:以农业和农产品加工为主16.当自然灾害来临时,个人采取适当的方法,可以有效避灾.下列说法中,不正确的是()A.当地震发生时,乘电梯迅速离开B.台风降临,渔船进港避风C.当发生泥石流时,应向垂直于泥石流流动方向的山坡上跑D.在室外时,到空旷的地方17.长江中下游地区最集中、最严重、最频仍的自然灾祸是()A.泥石流B.洪涝C.寒潮D.酸雨18.(学好地理可以有效地帮助我们合理安排出产、糊口.下列行为较合理的是()A.陡坡地种水稻,平原地栽果树B.雾霾发生时,尽量减少户外活动C.夏季去新疆带雨伞,冬季游海南穿羽绒服D.遭遇泥石流时,沿着泥石流流动方向往山谷快跑19.下列现象不属于自然灾祸的是()A.洪涝B.泥石流C.工厂废水污染水源D.地动20.图示漫画《自毁家园》,告诉我们的道理是()A.背景吃山B.合理利用水资源C.砍树拓荒,扩大耕地面积D.保护森林资源,爱惜人类家园2、综合题(每空1分,共40分)21.读黄河水系示意图,回答题目。
陕西省2020年中考数学模拟试卷(三)及解析

2020年陕西省中考数学模拟试卷(三)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)9的倒数是()A.9B.C.﹣9D.2.(3分)如图所示,该几何体的俯视图是()A.B.C.D.3.(3分)下列计算正确的是()A.2x+3y=5xy B.(﹣2x2)3=﹣6x6C.3y2•(﹣y)=﹣3y2D.6y2÷2y=3y4.(3分)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为()A.75°B.65°C.45°D.30°5.(3分)已知:点A(a,b),B(a+1,b﹣2)均在正比例函数y=kx(k≠0)的图象上,则k值为()A.﹣1B.﹣2C.﹣3D.﹣46.(3分)如图,在Rt△ABC中,∠C=30°,AB=4,D,F分别是AC,BC的中点,等腰直角三角形DEH的边DE经过点F,EH交BC于点G,且DF=2EF,则CG的长为()A.2B.2﹣1C.D.+17.(3分)直线y=﹣x+1与y=2x+a的交点在第一象限,则a的取值不可能是()A.B.﹣C.﹣D.﹣8.(3分)如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为()A.3B.C.D.49.(3分)如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E,则tan∠OEA的值是()A.B.C.D.10.(3分)在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距6个单位长度,若其中一条抛物线的函数表达式为y=﹣x2+4x+m,则m的值是()A.1或7B.﹣1或7C.1或﹣7D.﹣1或﹣7二、填空题(共4小题,每小题3分,计12分)11.(3分)在﹣2,,,,这5个数中,无理数有个.12.(3分)在正六边形中,其较短对角线与较长对角线的比值为.13.(3分)如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(8,4),反比例函数y=(k >0)的图象分别交边BC、AB于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是.14.(3分)如图,在正方形ABCD中,AB=4,E,F分别为BC,AD上的点,过点E,F的直线将正方形ABCD 的面积分为相等的两部分,过点A作AG⊥EF于点G,连接DG,则线段DG的最小值为.三、解答题(共11小题,计78分.解答应写出过程)15.(5分)计算:(π﹣2020)0+|1﹣|+2﹣1﹣2sin60°.16.(5分)化简:(x)17.(5分)赵凯想利用一块三角形纸片ABC裁剪一个菱形ADEF,要求一个顶点为A,顶点D在三角形的AC边上,点E在三角形的BC边上,点F在三角形的AB边上,请你利用尺规作图把这个菱形作出来.(不写作法,保留作图痕迹)18.(5分)如图,点A、E、F、C在一直线上,DE∥BF,DE=BF,AE=CF.求证:AB∥CD.19.(7分)为了给顾客提供更好的服务,某商场随机对部分顾客进行了关于“商场服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.满意度人数所占百分比非常满意1210%满意54m比较满意n40%不满意65%根据图表信息,解答下列问题:(1)本次调查的总人数为,表中m的值为;(2)请补全条形统计图;(3)根据统计,该商场平均每天接待顾客约3600名,若将“非常满意”和“满意”作为顾客对商场服务工作的肯定,请你估计该商场服务工作平均每天得到多少名顾客的肯定.20.(7分)为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为多少米(精确到0.1米).21.(7分)春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.(1)求甲、乙两种商品每件的进价分别是多少元?(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.22.(7分)小明最喜欢吃芝麻馅的汤圆了,一天早晨小明妈妈给小明下了四个大汤圆,一个花生馅,一个水果馅,两个芝麻馅,四个汤圆除内部馅料不同外,其他一切均相同.(1)求小明吃第一个汤圆恰好是芝麻馅的概率;(2)请利用树状图或列表法,求小明吃前两个汤圆恰好是芝麻馅的概率.23.(8分)如图,已知⊙O经过平行四边形ABCD的顶点A,B及对角线的交点M,交AD于点E且圆心〇在AD 边上,∠BCD=45°.(1)求证:BC为⊙O的切线;(2)连接ME,若ME=﹣1,求⊙O的半径.24.(10分)综合与探究:如图,抛物线y=ax2+bx﹣4与x轴交于A(﹣3,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线解析式;(2)抛物线对称轴上存在一点H,连接AH、CH,当|AH﹣CH|值最大时,求点H坐标;(3)若抛物线上存在一点P(m,n),mn>0,当S△ABC=S△ABp时,求点P坐标;(4)若点M是∠BAC平分线上的一点,点N是平面内一点,若以A、B、M、N为顶点的四边形是矩形,请直接写出点N坐标.25.(12分)问题提出(1)如图1,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有处.问题探究(2)如图2,在△ABC中,内角∠ABC的平分线BE和外角∠ACF的平分线CE,相交于点E,连接AE,若∠BEC=40°,请求出∠EAC的度数.问题解决(3)如图3,某地在市政工程施工中需要对一直角区域(∠AOB=90°)内部进行围挡,直角区域∠AOB内部有一棵大树(点P),工作人员经过测量得到点P到OA的距离PC为10米,点P到OB的距离PD为20米,为了保护大树及节约材料,设计要求围挡牌要经过大树位置(点P)并且所用材料最少,即围挡区域△EOF周长最小,请你根据以上信息求出符合设计的△EOF周长的最小值,并说明理由.参考答案与试题解析1.B.2.C.3.D.4.A.5.B.6.B.7.D.8.C.9.D.10.D.11.3.12.:2.13.12.14.2﹣2.15.解:原式=1+﹣1+﹣2×=.16.解:原式=•=•=x(x﹣1)=x2﹣x.17.解:如图所示:先作∠BAC的平分线交BC边于点E,再作线段AE的垂直平分线交AC于点D,交AB于点F 连接DE、EF,易证△EAD≌△EAF(SAS),则F A=DA而由线段的垂直平分线的性质可得DA=DE、F A=FE∴F A=DA=DE=FE∴四边形ADEF为菱形则菱形ADEF即为所求作的菱形.18.证明:∵DE∥BF∴∠DEF=∠BFE∵AE=CF∴AF=CE,且DE=BF,∠DEF=∠BFE∴△AFB≌△CED(SAS)∴∠A=∠C∴AB∥CD19.解:(1)本次调查的总人数为:12÷10%=120,m=54÷120×100%=45%,故答案为:120,45%;(2)比较满意的人数为:120×40%=48,补全的条形统计图如右图所示;(3)3600×(10%+45%)=3600×55%=1980(名),答:该商场服务工作平均每天得到1980名顾客的肯定.20.解:∵∠CED=∠AEB,CD⊥DB,AB⊥BD,∴△CED∽△AEB,∴=,∵CD=1.6米,DE=2.4米,BE=8.4米,∴=,∴AB==5.6米.故答案为:5.6米.21.解:(1)设甲、乙两种商品每件的进价分别是x元、y元,,解得,,即甲、乙两种商品每件的进价分别是30元、70元;(2)设购买甲种商品a件,获利为w元,w=(40﹣30)a+(90﹣70)(100﹣a)=﹣10a+2000,∵a≥4(100﹣a),解得,a≥80,∴当a=80时,w取得最大值,此时w=1200,即获利最大的进货方案是购买甲种商品80件,乙种商品20件,最大利润是1200元.22.解:(1)小明吃第一个汤圆,可能的结果有4种,其中是芝麻馅的结果有2种,∴小明吃第一个汤圆恰好是芝麻馅的概率==;(2)分别用A,B,C表示花生馅,水果馅,芝麻馅的大汤圆,画树状图得:∵共有12种等可能的结果,小明吃前两个汤圆恰好是芝麻馅的有2种情况,∴小明吃前两个汤圆恰好是芝麻馅的概率为=.23.(1)证明:连接OB,∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=45°,∴∠BOD=2∠BAD=90°,∵AD∥BC,∴∠DOB+∠OBC=180°,∴∠OBC=90°,∴OB⊥BC,∴BC为⊙O切线;(2)解:连接OM,∵四边形ABCD是平行四边形,∴BM=DM,∵∠BOD=90°,∴OM=BM,∵OB=OM,∴OB=OM=BM,∴∠OBM=60°,∴∠ADB=30°,连接EM,过M作MF⊥AE于F,∵OM=DM,∴∠MOF=∠MDF=30°,设OM=OE=r,∴FM=r,OF=r,∴EF=r﹣r,∵EF2+FM2=EM2,∴(r﹣r)2+(r)2=(﹣1)2,解得:r=(负值舍去),∴⊙O的半径为.24.解:(1)∵抛物线与y轴交于点C,∴点C坐标为(0,﹣4),把A(﹣3,0)、B(4,0)坐标代入y=ax2+bx﹣4得解得∴抛物线解析式为:.(2)抛物线的对称轴为:x=,由三角形任意两边之差小于第三边,可知抛物线对称轴上存在一点H,连接AH、CH,当|AH﹣CH|值最大时,点H为AC直线与对称轴的交点,由A(﹣3,0)、C(0,﹣4)易得直线AC解析式为:,当x=时,y=,故点H的坐标为:(,﹣).(3)∵抛物线上存在一点P(m,n),mn>0,当S△ABC=S△ABp时,∴点P(m,n)只能位于第一象限,C(0,﹣4)∴n=4∴由4=﹣4解得x=或x=(舍)故点P坐标为(,4).(4)若以A、B、M、N为顶点的四边形是矩形,则点M和点N的位置有两种如图所示点M和点M’点N和点N’易得OA=3,OC=4,AC=5,点M是∠BAC平分线上的一点,作QF⊥AC,则OQ=QF,∴OQ=QF=1.5,∴在直角三角形AOQ和直角三角形ABM中,,∴,∴BM=3.5,∴点N(﹣3,﹣3.5)同理在直角三角形AEN’和直角三角形ABN’中,可解得点N’(﹣,).故点N的坐标为(﹣3,﹣3.5)或(﹣,).25.解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.故答案为:4;(2)解:∵∠ABC与∠ACD的角平分线相交于点E,∴∠CBE=∠ABC,∠ECD=∠ACD,由三角形的外角性质得,∠ACD=∠ABC+∠BAC,∠ECD=∠BEC+∠CBE,∴∠ACD=∠BEC+∠ABC,∴(∠ABC+∠BAC)=∠BEC+∠ABC,整理得,∠BAC=2∠BEC,∵∠BEC=40°,∴∠BAC=2×40°=80°,过点E作EH⊥BA交延长线于H,作EG⊥AC于G,作EF⊥BC于F,∵BE平分∠ABC,∴EF=EH,∵CE平分∠ACD,∴EG=EF,∴EH=EG,∴AE是∠CAF的平分线,∴∠CAE=(180°﹣∠BAC)=(180°﹣80°)=50°;(3)如图,设∠AOB、∠AEF、∠BFE的角平分线交于点Q,作QN⊥OB于N,QM⊥OA于M,QH⊥EF于H.连接QP.则QN=QH=QM=y,FH=FN,EH=EM,∴△OEF的周长:OE+OF+EF=OF+FN+OE+EM=ON+OM=QN+QM=2QN=2y,∵PDOC是矩形,且PD=20,PC=10,∴ND=y﹣10,CM=y﹣20,∴QP2=(y﹣10)2+(y﹣20)2∵PQ≥QH,∴(y﹣10)2+(y﹣20)2≥y2∴y2﹣60y+500≥0,∴(y﹣30)2≥400,∴y≥50或y≤10(舍),∴2y≥100,当且仅当P、H重合时取等号.即△OEF的周长的最小值为100.。
山西2020中考语文模拟测试卷 (含答案)

山西省2020高中阶段教育学校招生统一考试语文模拟试题(含答案全解全析)(满分150分)一、基础(20分)1.默写。
(10分)(1)山重水复疑无路, 。
(陆游《游山西村》)(2) ,长河落日圆。
(王维《使至塞上》)(3)乱花渐欲迷人眼, 。
(白居易《钱塘湖春行》)(4) ,西北望,射天狼。
(苏轼《江城子·密州出猎》)(5)《岳阳楼记》中传诵千古,表达范仲淹宏伟抱负的警句是: , 。
(6)请从下面两首古诗中任选一首,完整默写。
杜牧《赤壁》王安石《登飞来峰》2.下列归类有误的一项是(2分)( )A.喜盈盈雄赳赳堂堂正正彬彬有礼(叠音词)B.真挚挺拔英姿飒爽顶天立地(褒义词)C.扑哧哗啦喵呜呼噜(拟声词)D.平坦—崎岖茂密—稀疏寂静—安宁清澈—浑浊(反义词)3.下列判断有误的一项是(2分)( )A.“我们忘不了同窗三载的情谊。
”“一手好字让人赏心悦目。
”两句都是陈述句。
B.“20多年的农村生活体验是2012年诺贝尔文学奖获得者莫言的创作资源。
”一句的主干是“体验是资源”。
C.“河,莱茵,江声浩荡……钟声复起,天已黎明……中国正到了‘复旦’的黎明时期,但愿你做中国的——新中国的——钟声,响遍世界,响遍每个人的心!”一句中破折号的作用是:话题突然转变。
D.“聪明人无论在哪里跌倒,都会捡点有用的东西。
”一句是条件复句。
4.杜甫有句名言曰:语不惊人死不休!语若惊人,须要炼字。
下面的对联别出心裁,上联中“读”字,人格化地活现出水中景,请你在下联中填写一个动词,与“读”相对,拟人化地表现出山里的情趣。
(2分)5.诺贝尔文学奖获得者泰戈尔是一个多才多艺的诗人,文、史、哲、艺等几乎无所不精。
他父亲是一个受人尊敬的智者。
父亲对他的教育概括起来就是:潜移默化、身体力行。
泰戈尔12岁那年,父亲就带他去喜马拉雅山旅游。
白天他们或步行或骑马,徜徉于自然美景和人文胜境之间;晚上则是坐在星空下,听父亲讲天文知识,欣赏美丽迷人的夜色。
浙江省杭州市萧山区2020年中考数学模拟试卷(含答案解析)

2020年浙江省杭州市萧山区中学中考数学模拟试卷选择题(共10小题,满分30分,每小题3分)一.1.函数y=(x+1)°-2的最小值是()A.1B.-1C.2D.-22.从1978年12月18日党的^一届三中全会决定改革开放到如今已经40周年了,我国GDP(国内生产总值)从1978年的1495亿美元到2017年已经达到了122400亿美元,全球排名第二,将122400用科学记数法表示为(A.12.24X104B. 1.224X105C.0.1224X106D. 1.224X1063.若2'〃=5,4"=3,则4in m的值是()A•会C.2D.44.“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表7K了寓言中的龟、兔的路程S和时间,的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是()B.乌龟在这次比赛中的平均速度是0.1米/分钟C.兔子比乌龟早到达终点10分钟D.乌龟追上兔子用了20分钟5.一组数据:201、200、199、202、200,分别减去200,得到另一组数据:1、0、-1、2、0,其中判断错误的是()A.前一组数据的中位数是200B.前一组数据的众数是200C.后一组数据的平均数等于前一组数据的平均数减去200D.后一组数据的方差等于前一组数据的方差减去2006.如图,己知直线AB、CD被直线AC所截,AB//CD,E是平面内任意一点(点E不在直线AB、CD、AC_b),设/BAE=a,ZDCE=^.下列各式:①a+8,②a",③&-a,④360。
-a-p, ZAEC 的度数可能是( )A.①②③B.①②④C.①③④D.①②③④7.把抛物线y= - 2x 向上平移1个单位,再向右平移1个单位,得到的抛物线是()A. y= - 2 (x+1) ?+1B. y= -2 (x- 1) 2+1C. y= - 2 (x- 1) 2 - 1D. y= - 2 (x+1) 2 - 18.现在把一张正方形纸片按如图方式剪去一个半径为40柄厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,插F.41,寸*1.73)A. 6470 D. 739.如图,^ABCD 的对角线AC 、BD 交于点O, DE 平分ZAD C 交AB 于点E, ZBCD=60° , AD =*43,连接 OE.下列结论:①S°abcd =AD・BD ;②DB 平分ZCDE ; @AO=DE ; @S a ADE =5S m )fe ,其中正确的个数有()A. 9AB. 10 人C. 3个D. 4个如果一共碰杯55次,则参加酒会的人数为(c. II A D. 12 A二.填空题(共6小题,满分24分,每小题4分)11.若二次函数y=2 (x+1) 2+3的图象上有三个不同的点A (xi ,4)、B (羽+电,n )、C (电,4),则〃的值为.12,某次数学测试,某班一个学习小组的六位同学的成绩如下:84、75、75、92、86、99,则这六位同学成绩的中位数是13.如图,已知函数y=x+2的图象与函数尸直•(切0)的图象交于A、B两点,连接80并延长交X函数y=—Ck^O)的图象于点C,连接AC,若△ABC的面积为8.则k的值为.x14.如图1为两个边长为1的正方形组成的2X1格点图,点A,B,C,£>都在格点上,AB,CD交于点P,则tanZBPD=,如果是"个边长为1的正方形组成的“X1格点图,如图2,那15.如图,动点。
2020年九年级中考语文模拟试卷含答案

2020年九年级中考语⽂模拟试卷含答案2020年九年级中考语⽂模拟试卷含答案(满分 150分,考试时间 150分钟)说明:1.本试卷共6页,计22题(包含单项选择题第1~4题),满分150分,考试时间150分钟。
考试结束后,请将本试卷和答题卡⼀并交回。
2.答题前,考⽣务必将本⼈的姓名、准考证号准确⽆误地填写在答题卡相应的位置上,同时务必在试卷的装订线内将本⼈的姓名、准考证号、毕业学校填好。
3.所有的试题都必须在专⽤的“答题卡”上作答,选择题⽤2B 铅笔作答,⾮选择题在指定位置⽤0.5毫⽶⿊⾊⽔笔作答。
在试卷或草稿纸上答题⽆效。
⼀、积累运⽤(33分)1.下列加点字读⾳完全正确的⼀项是(2分)()A .⽢霖.(l íng )腼腆.(ti ǎn )绯.红(f ēi )深恶.痛疾(è)B .呻吟.(y íng )荫.蔽(y īn )和煦.(x ù)风姿绰.约(zhu ó)C .酝酿.(ni àng )贮.蓄(zh ù)惩.罚(ch ěng )不谙.世故(àn )D .倜.傥(t ì)风靡.(m ǐ)蜿.蜒(w ān )罄.⽵难书(q ìng ) 2.下列句⼦中加点成语使⽤正确的⼀项(2分)()A. 短短⼀个世纪,中国从⼀⽂不名....的穷⼩⼦摇⾝⼀变成了世界银⾏家,⽽欧洲正截然相反。
B. 七⽉的扬州,⽓温居⾼不下,室外暑热如⽕,我们坐在室内,吹着空调,却如坐春风....,⼗分惬意。
C. 武磊在西甲联赛中的出⾊表现,让所有质疑他的⼈噤若寒蝉....。
D. 电影《红海⾏动》在社会上引起不⼩的轰动,观看者趋之若骜....。
3.下列解说有误的⼀项是(2分)()A .芳草如茵⼼旷神怡独占鳌头坚决⽀持解说:这四个短语结构各不相同。
B .失败不是⼈⽣的绊脚⽯,⽽是⼈⽣的垫脚⽯。
解说:“不是……⽽是……”是表⽰递进关系的复句。
2020年内蒙古省包头市中考数学(4月份)模拟试卷(Word 含解析)

2020年内蒙古省包头市中考数学模拟试卷(4月份)一、选择题1.计算|﹣2020|的结果是()A.﹣2020B.2020C.﹣D.2.如图,a∥b,若∠1=110°,则∠2的度数是()A.110°B.80°C.70°D.60°3.将一副三角板(∠A=30°,∠E=45°)按如图所示方式摆放,使得BA∥EF,则∠AOF 等于()A.75°B.90°C.105°D.115°4.下列运算正确的是()A.3x3﹣5x3=﹣2x B.8x3÷4x=2xC.=D.+=5.不等式1﹣2x≥0的解集是()A.x≥2B.x≥C.x≤2D.x6.已知正比例函数y=kx(k≠0)经过第二、四象限,点(k﹣1,3k+5)是其图象上的点,则k的值为()A.3B.5C.﹣1D.﹣37.篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分,某队在10场比赛中得到16分.若设该队胜的场数为x,负的场数为y,则可列方程组为()A.B.C.D.8.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c <0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是()A.1B.2C.3D.49.一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为()A.24B.24πC.96D.96π10.从1,2,3,4中任取两个不同的数,分别记为a和b,则a2+b2>19的概率是()A.B.C.D.11.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是()A.0.5B.1C.1.5D.212.下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是()A.图象经过第一、二、四象限B.y随x的增大而减小C.图象与y轴交于点(0,b)D.当x>﹣时,y>0二、填空题:(本大题共8小题,每小题3分,合计24分)13.计算:×﹣tan45°=.14.2019年1月12日,“五指山”舰正式入列服役,是我国第六艘071型综合登陆舰艇,满载排水量超过20000吨,20000用科学记数法表示为.15.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是.16.东营市某中学为积极响应“书香东营,全民阅读”活动,助力学生良好阅读习惯的养成,形成浓厚的阅读氛围,随机调查了部分学生平均每天的阅读时间,统计结果如表所示,则在本次调查中,学生阅读时间的中位数是.时间(小时)0.51 1.52 2.5人数(人)1222105317.如图,在正方形ABCD中,AB=1,点E、F分别在边BC和CD上,AE=AF,∠EAF =60°,则CF的长是.18.已知等腰三角形的底角是30°,腰长为2,则它的周长是.19.用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品;要生产甲种产品37件,乙种产品18件,则恰好需用A、B两种型号的钢板共块.20.不等式组的解集为.三、解答题:(本大题共6小题,合计60分)21.化简:1﹣.22.如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(﹣2,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是2.(1)求m、n的值;(2)求直线AC的解析式.23.某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:(1)计算样本中,成绩为98分的教师有人,并补全两个统计图;(2)样本中,测试成绩的众数是,中位数是;(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?24.如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为3,求图中阴影部分的面积.25.已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.(1)求直线的解析式;(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.26.如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.参考答案一、选择题:(本大题共12小题,每小题3分,合计36分)1.计算|﹣2020|的结果是()A.﹣2020B.2020C.﹣D.【分析】根据绝对值的性质直接解答即可.解:|﹣2020|=2020;故选:B.2.如图,a∥b,若∠1=110°,则∠2的度数是()A.110°B.80°C.70°D.60°【分析】根据两直线平行,同位角相等,即可求得∠3的度数,进而得出∠2的度数.解:∵a∥b,∴∠1=∠3=110°.∵∠2+∠3=180°,∴∠2=180°﹣∠3=70°,故选:C.3.将一副三角板(∠A=30°,∠E=45°)按如图所示方式摆放,使得BA∥EF,则∠AOF 等于()A.75°B.90°C.105°D.115°【分析】依据AB∥EF,即可得∠FCA=∠A=30°,由∠F=∠E=45°,利用三角形外角性质,即可得到∠AOF=∠FCA+∠F=30°+45°=75°.解:∵BA∥EF,∠A=30°,∴∠FCA=∠A=30°.∵∠F=∠E=45°,∴∠AOF=∠FCA+∠F=30°+45°=75°.故选:A.4.下列运算正确的是()A.3x3﹣5x3=﹣2x B.8x3÷4x=2xC.=D.+=【分析】直接利用合并同类项法则以及单项式除以单项式、分式的约分、二次根式的加减运算法则分别化简得出答案.解:A、3x3﹣5x3=﹣2x3,故此选项错误;B、8x3÷4x=2x2,故此选项错误;C、=,正确;D、+无法计算,故此选项错误.故选:C.5.不等式1﹣2x≥0的解集是()A.x≥2B.x≥C.x≤2D.x【分析】先移项,再系数化为1即可.解:移项,得﹣2x≥﹣1系数化为1,得x≤;所以,不等式的解集为x≤,故选:D.6.已知正比例函数y=kx(k≠0)经过第二、四象限,点(k﹣1,3k+5)是其图象上的点,则k的值为()A.3B.5C.﹣1D.﹣3【分析】把x=k﹣1,y=3k+5代入正比例函数y=kx解答即可.解:把x=k﹣1,y=3k+5代入正比例函数的y=kx,可得:3k+5=k(k﹣1),解得:k1=﹣1,k2=5,因为正比例函数的y=kx(k≠0)的图象经过二,四象限,所以k<0,所以k=﹣1,故选:C.7.篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分,某队在10场比赛中得到16分.若设该队胜的场数为x,负的场数为y,则可列方程组为()A.B.C.D.【分析】设这个队胜x场,负y场,根据在10场比赛中得到16分,列方程组即可.解:设这个队胜x场,负y场,根据题意,得.故选:A.8.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c <0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是()A.1B.2C.3D.4【分析】由抛物线与x轴有两个交点得到b2﹣4ac>0,可判断①;根据对称轴是x=﹣1,可得x=﹣2、0时,y的值相等,所以4a﹣2b+c>0,可判断③;根据﹣=﹣1,得出b=2a,再根据a+b+c<0,可得b+b+c<0,所以3b+2c<0,可判断②;x=﹣1时该二次函数取得最大值,据此可判断④.解:∵图象与x轴有两个交点,∴方程ax2+bx+c=0有两个不相等的实数根,∴b2﹣4ac>0,∴4ac﹣b2<0,①正确;∵﹣=﹣1,∴b=2a,∵a+b+c<0,∴b+b+c<0,3b+2c<0,∴②是正确;∵当x=﹣2时,y>0,∴4a﹣2b+c>0,∴4a+c>2b,③错误;∵由图象可知x=﹣1时该二次函数取得最大值,∴a﹣b+c>am2+bm+c(m≠﹣1).∴m(am+b)<a﹣b.故④正确∴正确的有①②④三个,故选:C.9.一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为()A.24B.24πC.96D.96π【分析】由已知三视图为圆柱,首先得到圆柱底面半径,从而根据圆柱体积=底面积乘高求出它的体积.解:由三视图可知圆柱的底面直径为4,高为6,∴底面半径为2,∴V=πr2h=22×6•π=24π,故选:B.10.从1,2,3,4中任取两个不同的数,分别记为a和b,则a2+b2>19的概率是()A.B.C.D.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与a2+b2>19的情况,再利用概率公式即可求得答案.解:画树状图得:∵共有12种等可能的结果,任取两个不同的数,a2+b2>19的有4种结果,∴a2+b2>19的概率是=,故选:D.11.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是()A.0.5B.1C.1.5D.2【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=4,CF=3,即可求线段DB的长.解:∵CF∥AB,∴∠A=∠FCE,∠ADE=∠F,在△ADE和△FCE中,∴△ADE≌△CFE(AAS),∴AD=CF=3,∵AB=4,∴DB=AB﹣AD=4﹣3=1.故选:B.12.下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是()A.图象经过第一、二、四象限B.y随x的增大而减小C.图象与y轴交于点(0,b)D.当x>﹣时,y>0【分析】由k<0,b>0可知图象经过第一、二、四象限;由k<0,可得y随x的增大而减小;图象与y轴的交点为(0,b);当x>﹣时,y<0;解:∵y=kx+b(k<0,b>0),∴图象经过第一、二、四象限,A正确;∵k<0,∴y随x的增大而减小,B正确;令x=0时,y=b,∴图象与y轴的交点为(0,b),∴C正确;令y=0时,x=﹣,当x>﹣时,y<0;D不正确;故选:D.二、填空题:(本大题共8小题,每小题3分,合计24分)13.计算:×﹣tan45°=﹣1.【分析】根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.解:×﹣tan45°=﹣1=﹣1,故答案为:﹣1.14.2019年1月12日,“五指山”舰正式入列服役,是我国第六艘071型综合登陆舰艇,满载排水量超过20000吨,20000用科学记数法表示为2×104.【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.解:20000用科学记数法表示为2×104.故答案是:2×104.15.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是(﹣2,2).【分析】先求出点P到直线x=1的距离,再根据对称性求出对称点P′到直线x=1的距离,从而得到点P′的横坐标,即可得解.解:∵点P(4,2),∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,∴点P′的横坐标为1﹣3=﹣2,∴对称点P′的坐标为(﹣2,2).故答案为:(﹣2,2).16.东营市某中学为积极响应“书香东营,全民阅读”活动,助力学生良好阅读习惯的养成,形成浓厚的阅读氛围,随机调查了部分学生平均每天的阅读时间,统计结果如表所示,则在本次调查中,学生阅读时间的中位数是1.时间(小时)0.51 1.52 2.5人数(人)12221053【分析】由统计表可知总人数为52,得到中位数应为第26与第27个的平均数,而第26个数和第27个数都是1,即可确定出中位数为1.解:由统计表可知共有:12+22+10+5+3=52人,中位数应为第26与第27个的平均数,而第26个数和第27个数都是1,则中位数是1.故答案为:1.17.如图,在正方形ABCD中,AB=1,点E、F分别在边BC和CD上,AE=AF,∠EAF =60°,则CF的长是.【分析】在AD上取一点G,使∠GFA=∠DAF,先证明Rt△ABE≌Rt△ADF,得∠DAF 的度数,设DF=x,用x表示DG,AG,再由正方形的边长列出x的方程求得x,便可求得结果.解:∵四边形ABCD是正方形,∴∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴∠BAE=∠DAF,∵∠EAF=60°,∴∠BAE+∠DAF=30°,∴∠DAF=15°,在AD上取一点G,使∠GFA=∠DAF=15°,如图所示,∴AG=FG,∠DGF=30°,∴DF=FG=AG,DG=DF,设DF=x,则DG=x,AG=FG=2x,∵AG+DG=AD,∴2x+x=1,解得:x=2﹣,∴DF=2﹣,∴CF=CD﹣DF=1﹣(2﹣)=﹣1;故答案为.18.已知等腰三角形的底角是30°,腰长为2,则它的周长是6.【分析】作AD⊥BC于D,根据直角三角形的性质求出AD,根据勾股定理求出BD,根据三角形的周长公式计算即可.解:作AD⊥BC于D,∵AB=AC,∴BD=DC,在Rt△ABD中,∠B=30°,∴AD=AB=,由勾股定理得,BD==3,∴BC=2BD=6,∴△ABC的周长为:6+2+2=6+4,故答案为:6+4.19.用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品;要生产甲种产品37件,乙种产品18件,则恰好需用A、B两种型号的钢板共11块.【分析】设需用A型钢板x块,B型钢板y块,根据“用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品”,可得出关于x,y的二元一次方程组,用(①+②)÷5可求出x+y的值,此题得解.解:设需用A型钢板x块,B型钢板y块,依题意,得:,(①+②)÷5,得:x+y=11.故答案为:11.20.不等式组的解集为﹣7≤x<1.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.解:解不等式x﹣3(x﹣2)>4,得:x<1,解不等式≤,得:x≥﹣7,则不等式组的解集为﹣7≤x<1,故答案为:﹣7≤x<1.三、解答题:(本大题共6小题,合计60分)21.化简:1﹣.【分析】直接利用分式的混合运算法则计算得出答案.解:原式=1﹣=1﹣=﹣.22.如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(﹣2,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是2.(1)求m、n的值;(2)求直线AC的解析式.【分析】(1)根据反比例函数的对称性可得点A与点B关于原点中心对称,则B(2,a),由于BC⊥x轴,所以C(2,0),先利用三角形面积公式得到×2×a=2,解得a=2,则可确定A(﹣2,2),然后把A点坐标代入y=mxy=mx和y=中即可求出m,n;(2)根据待定系数法即可得到直线AC的解析式.解:(1)∵直线y=mx与双曲线y=相交于A(﹣2,a)、B两点,∴点A与点B关于原点中心对称,∴B(2,﹣a),∴C(2,0);∵S△AOC=2,∴×2×a=2,解得a=2,∴A(﹣2,2),把A(﹣2,2)代入y=mx和y=得﹣2m=2,2=,解得m=﹣1,n=﹣4;(2)设直线AC的解析式为y=kx+b,∵直线AC经过A、C,∴,解得∴直线AC的解析式为y=﹣x+1.23.某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:(1)计算样本中,成绩为98分的教师有14人,并补全两个统计图;(2)样本中,测试成绩的众数是98,中位数是100;(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?【分析】(1)先根据96分人数及其百分比求得总人数,再根据各组人数之和等于总数可得98分的人数;(2)根据中位数和众数的定义可得;(3)利用样本中100分人数所占比例乘以总人数可得.解:(1)本次调查的人数共有10÷20%=50人,则成绩为98分的人数为50﹣(20+10+4+2)=14(人),补全统计图如下:故答案为:14;(2)本次测试成绩的中位数为=98分,众数100分,故答案为:98,100;(3)∵6880×=2752,∴估计该区大约有2752名教师已全部掌握扫黑除恶专项斗争应知应会知识.24.如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为3,求图中阴影部分的面积.【分析】(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.【解答】(1)证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.∵OA=OC,∴∠ACO=∠A=30°.∴∠OCD=∠ACD﹣∠ACO=90°.即OC⊥CD,∴CD是⊙O的切线.(2)解:∵∠A=30°,∴∠COB=2∠A=60°.∴S扇形BOC=,在Rt△OCD中,CD=OC,∴,∴,∴图中阴影部分的面积为.25.已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.(1)求直线的解析式;(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.【分析】(1)根据点A,B的坐标,利用待定系数法即可求出直线AB的解析式;(2)设平移后抛物线的解析式为y=(x﹣m)2(m>0),则平移后抛物线的对称轴为直线x=m,点C的坐标为(0,m2),由CD∥x轴,可得出点C,D关于直线x=m对称,进而可得出点D的坐标,再利用一次函数图象上点的坐标特征即可得出关于m的一元二次方程,解之取其正值即可得出结论;(3)设点P的坐标为(a,a2﹣4a+4),则PQ=|a﹣2|,EQ=a2﹣4a+4,由∠PQE=90°可得出△EQP∽△AOB或△PQE∽△AOB,①当△EQP∽△AOB时,利用相似三角形的性质可得出关于a的方程,解之即可得出a值,将其代入点P的坐标即可得出结论;②当△PQE∽△AOB时,利用相似三角形的性质可得出关于a的方程,解之即可得出a 值,将其代入点P的坐标即可得出结论.综上,此题得解.解:(1)将A(0,2),B(﹣4,0)代入y=kx+b,得:,解得:,∴直线AB的解析式为y=x+2.(2)如图1,设平移后抛物线的解析式为y=(x﹣m)2(m>0),则平移后抛物线的对称轴为直线x=m,点C的坐标为(0,m2).∵CD∥x轴,∴点C,D关于直线x=m对称,∴点D的坐标为(2m,m2).∵点D在直线y=x+2上,∴m2=×2m+2,解得:m1=﹣1(舍去),m2=2,∴平移后抛物线的解析式为y=(x﹣2)2,即y=x2﹣4x+4.(3)存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似.设点P的坐标为(a,a2﹣4a+4),则PQ=|a﹣2|,EQ=a2﹣4a+4.∵∠PQE=90°,∴分两种情况考虑,如图2所示.①当△EQP∽△AOB时,=,即=,化简,得:|a﹣2|=,解得:a1=,a2=,∴点P的坐标为(,)或(,);②当△PQE∽△AOB时,=,即=,化简,得:|a﹣2|=2,解得:a1=0,a2=4,∴点P的坐标为(0,4)或(4,4).综上所述:存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似,点P的坐标为(,),(,),(0,4)或(4,4).26.如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.【分析】(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出的值是多少.②α=180°时,可得AB∥DE,然后根据=,求出的值是多少即可.(2)首先判断出∠ECA=∠DCB,再根据==,判断出△ECA∽△DCB,然后由相似三角形的对应边成比例,求得答案.(3)分两种情形:①如图3﹣1中,当点E在AV的延长线上时,②如图3﹣2中,当点E在线段AB上时,分别求解即可.解:(1)①当α=0°时,∵Rt△ABC中,∠B=90°,∴AC===2,∵点D、E分别是边BC、AC的中点,∴AE=AC=,BD=BC=1,∴=.②如图1﹣1中,当α=180°时,可得AB∥DE,∵=,∴==.故答案为:①,②.(2)如图2,当0°≤α<360°时,的大小没有变化,∵∠ECD=∠ACB,∴∠ECA=∠DCB,又∵==,∴△ECA∽△DCB,∴==..(3)①如图3﹣1中,当点E在AB的延长线上时,在Rt△BCE中,CE=,BC=2,∴BE===1,∴AE=AB+BE=5,∵=,∴BD==.②如图3﹣2中,当点E在线段AB上时,易知BE=1,AE=4﹣1=3,∵=,∴BD=,综上所述,满足条件的BD的长为或.。
2020年上海中考英语仿真模拟试卷(含听力材料与答案)

上海中考英语模拟试卷(满分150分,考试时间100分钟)考生注意:本卷有7大题,共94小题。
试题均采用连续编号,所有答案务必按照规定在答题纸上完成,做在试卷上不给分。
Part l Listening (第一部分听力)I.Listening Comprehension (听力理解) (共30分)A. Listen and choose the right picture (根据你听到的内容,选出相应的图片) (6分)B.Listen to the dialogue and choose the best answer to the question you hear (根据你听到的对话和问题,选出最恰当的答案) (8分)7. A) Blue. B) Yellow. C) Green. D) Red.8. A) Betty. B) Sharon. C) Sue. D) John.9. A) 7:00. B) 7:30. C) 8:00. D) 8:30.10. A) By bus. B) By bike. C) By car. D) By underground.11. A) At a restaurant. B) At a library. C) At a store. D) At a school.12. A) She will watch a TV program. B) She will watch a football match.C) She will visit her friends. D) She will sing in the program.13. A) He doesn’t want to help.B) He isn’t able to work.C) He’ll help the woman later.D) He’d like to work here.14. A) He found it interesting. B) He found it enjoyable.C) He found it boring. D) He found it amazing.C. Listen to the passage and tell whether the following statements are true or false (判断下列句子是否符合你听到的短文内容,符合的用“T”表示,不符合的用“F”表示) (6分)15. The writer and his parents stayed in an Australian hotel last summer.16. The hotel where they stayed was very big and comfortable.17. Though the hotel was small, it had many lifts.18. The writer had to spend a long time waiting for the lift each day.19. One morning the writer went back to his room for his jacket.20. When the writer took the lift, it suddenly stopped halfway down.D.Listen to the passage and complete the following sentences. (听短文,完成下列内容。
河南省2020年中考模拟数学试卷及答案参考(一) 解析版 (1)
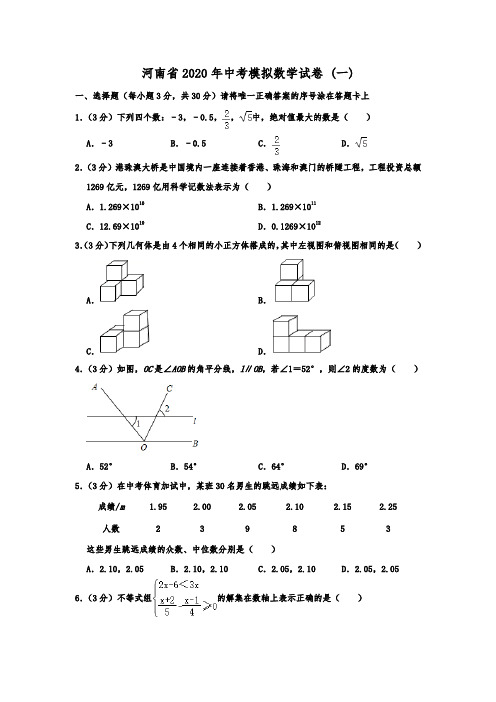
河南省2020年中考模拟数学试卷 (一)一、选择题(每小题3分,共30分)请将唯一正确答案的序号涂在答题卡上1.(3分)下列四个数:﹣3,﹣0.5,,中,绝对值最大的数是()A.﹣3 B.﹣0.5 C.D.2.(3分)港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程,工程投资总额1269亿元,1269亿用科学记数法表示为()A.1.269×1010B.1.269×1011C.12.69×1010D.0.1269×10123.(3分)下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是()A.B.C.D.4.(3分)如图,OC是∠AOB的角平分线,l∥OB,若∠1=52°,则∠2的度数为()A.52°B.54°C.64°D.69°5.(3分)在中考体育加试中,某班30名男生的跳远成绩如下表:成绩/m 1.95 2.00 2.05 2.10 2.15 2.25人数 2 3 9 8 5 3 这些男生跳远成绩的众数、中位数分别是()A.2.10,2.05 B.2.10,2.10 C.2.05,2.10 D.2.05,2.05 6.(3分)不等式组的解集在数轴上表示正确的是()A.B.C.D.7.(3分)如图,正比例函数y=x的图象与一次函数y=x+的图象交于点A,若点P 是直线AB上的一个动点,则线段OP长的最小值为()A.1 B.C.D.28.(3分)如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为()A.140°B.100°C.50°D.40°9.(3分)如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON 分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE ≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG•OC.其中正确的是()A.①②③④B.①②③C.①②④D.③④10.(3分)在边长为的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为()A.B.C.D.二、填空题(每小题3分,共15分)11.(3分)计算:﹣()﹣1+=.12.(3分)2019年永州市初中体育学业水平考试实行改革,增加了两类自选类项目:一类是运动技能测试,学生可以从篮球、足球、排球向上垫球三个项目中必须自选一项;另一类是身体力量测试,学生从一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远四个项目中再选一项,则某一初三男学生同时选择篮球和立定跳远这两项的概率是.13.(3分)关于x的一元二次方程a(x﹣h)2+k=x+n两根为x1=﹣1,x2=3,则方程a(x﹣h﹣3)2+k+3=x+n的两根为.14.(3分)如图,7个腰长为1的等腰直角三角形(Rt△B1AA1,Rt△B2A1A2,Rt△B3A2A3…)有一条腰在同一条直线上,设△A1B2C1的面积为S1,△A2B3C2的面积为S2,△A3B4C3的面积为S3,则S1+S2+S3+S4+S5+S6=.15.(3分)如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:,其中a是方程a2+a﹣6=0的解.17.(9分)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D为圆心,DB长为半径作作⊙D.(1)求证:AC是⊙D的切线.(2)设AC与⊙D切于点E,DB=1,连接DE,BF,EF.①当∠BAD=时,四边形BDEF为菱形;②当AB=时,△CDE为等腰三角形.18.(9分)设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级;75≤x<85为B级;60≤x<75为C级;x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:(1)在这次调查中,一共抽取了名学生,A级人数占本次抽取人数的百分比为%;(2)补全条形统计图;(3)扇形统计图中C级对应的圆心角为度;(4)若该校共有1000名学生,请你估计该校D级学生有多少名?19.(9分)如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)(2)求景点C与景点D之间的距离.(结果精确到1km)(参考数据:=1.73,=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)20.(9分)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB 于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)观察图象,直接写出当x>0时,不等式2x+6<0的解集;(3)当n为何值时,△BMN的面积最大?最大值是多少?21.(10分)某商场计划经销A,B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.A型B型进价(元/盏)40 65售价(元/盏)60 100(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?(3)若该商场预计用不多于2600元的资金购进这批台灯,其中A种台灯不超过30盏,为了打开B种台灯的销路,商场决定每售出一盏B种台灯,返还顾客现金a元(10<a <20),问该商场该如何进货,才能获得最大的利润?22.(10分)(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D 时线段AB上一动点,连接BE.填空:①的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D 是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.23.(11分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(﹣1,0),(0,﹣3),直线x=1为抛物线的对称轴.点D为抛物线的顶点,直线BC与对称轴相交于点E.(1)求抛物线的解析式并直接写出点D的坐标;(2)点P为直线x=1右方抛物线上的一点(点P不与点B重合).记A、B、C、P四点所构成的四边形面积为S,若S=S△BCD,求点P的坐标;(3)点Q是线段BD上的动点,将△DEQ延边EQ翻折得到△D′EQ,是否存在点Q使得△D′EQ与△BEQ的重叠部分图形为直角三角形?若存在,请求出BQ的长,若不存在,请说明理由.参考答案与试题解析一、选择题(每小题3分,共30分)请将唯一正确答案的序号涂在答题卡上1.(3分)下列四个数:﹣3,﹣0.5,,中,绝对值最大的数是()A.﹣3 B.﹣0.5 C.D.【分析】根据绝对值的性质以及正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小判断即可.【解答】解:∵|﹣3|=3,|﹣0.5|=0.5,||=,||=且0.5<<<3,∴所给的几个数中,绝对值最大的数是﹣3.故选:A.2.(3分)港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程,工程投资总额1269亿元,1269亿用科学记数法表示为()A.1.269×1010B.1.269×1011C.12.69×1010D.0.1269×1012【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:1269亿=126900000000,用科学记数法表示为1.269×1011.故选:B.3.(3分)下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是()A.B.C.D.【分析】根据图形、找出几何体的左视图与俯视图,判断即可.【解答】解:A、左视图第一层两个小正方形,俯视图第一层一个小正方形,故A不符合题意;B、左视图和俯视图相同,故B符合题意;C、左视图第一层两个小正方形,俯视图第一层一个小正方形,故C不符合题意;D、左视图是一列两个小正方形,俯视图一层三个小正方形,故D不符合题意;故选:B.4.(3分)如图,OC是∠AOB的角平分线,l∥OB,若∠1=52°,则∠2的度数为()A.52°B.54°C.64°D.69°【分析】依据平行线的性质以及角平分线的定义,即可得到∠BOC=64°,再根据平行线的性质,即可得出∠2的度数.【解答】解:∵l∥OB,∴∠1+∠AOB=180°,∴∠AOB=128°,∵OC平分∠AOB,∴∠BOC=64°,又l∥OB,且∠2与∠BOC为同位角,∴∠2=64°,故选:C.5.(3分)在中考体育加试中,某班30名男生的跳远成绩如下表:成绩/m 1.95 2.00 2.05 2.10 2.15 2.25人数 2 3 9 8 5 3 这些男生跳远成绩的众数、中位数分别是()A.2.10,2.05 B.2.10,2.10 C.2.05,2.10 D.2.05,2.05 【分析】中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.【解答】解:由表可知,2.05出现次数最多,所以众数为2.05;由于一共调查了30人,所以中位数为排序后的第15人和第16人的平均数,即:2.10.故选:C.6.(3分)不等式组的解集在数轴上表示正确的是()A.B.C.D.【分析】分别解不等式进而得出不等式组的解集,进而得出答案.【解答】解:,解①得:x>﹣6,解②得:x≤13,故不等式组的解集为:﹣6<x≤13,在数轴上表示为:.故选:B.7.(3分)如图,正比例函数y=x的图象与一次函数y=x+的图象交于点A,若点P 是直线AB上的一个动点,则线段OP长的最小值为()A.1 B.C.D.2【分析】判断出OP⊥AB时,OP最小,利用三角形的面积建立方程求解即可得出结论.【解答】解:由得,∴A(2,3),由一次函数y=x+,令y=0,解得x=﹣2,∴(﹣2,0),∴S△AOB=OB•|y A|==3,AB==5,∵当OP⊥AB时,OP最小,∴S△AOB=AB•OP最小,∴×5OP最小=3∴OP最小=,故选:C.8.(3分)如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为()A.140°B.100°C.50°D.40°【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后得到等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,即可得出∠MPN =∠OPM+∠OPN=∠OP1M+∠OP2N=100°.【解答】解:分别作点P关于OA、OB的对称点P1、P2,连接P1P2,交OA于M,交OB于N,则OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,根据轴对称的性质,可得MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2,∴∠P1OP2=2∠AOB=80°,∴等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100°,故选:B.9.(3分)如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON 分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE ≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG•OC.其中正确的是()A.①②③④B.①②③C.①②④D.③④【分析】①由正方形证明OC=OD,∠ODF=∠OCE=45°,∠COM=∠DOF,便可得结论;②证明点O、E、C、F四点共圆,得∠EOG=∠CFG,∠OEG=∠FCG,进而得OGE∽△FGC便可;③先证明S△COE=S△DOF,∴便可;④证明△OEG∽△OCE,得OG•OC=OE2,再证明OG•AC=EF2,再证明BE2+DF2=EF2,得OG•AC=BE2+DF2便可.【解答】解:①∵四边形ABCD是正方形,∴OC=OD,AC⊥BD,∠ODF=∠OCE=45°,∵∠MON=90°,∴∠COM=∠DOF,∴△COE≌△DOF(ASA),故①正确;②∵∠EOF=∠ECF=90°,∴点O、E、C、F四点共圆,∴∠EOG=∠CFG,∠OEG=∠FCG,∴OGE∽△FGC,故②正确;③∵△COE≌△DOF,∴S△COE=S△DOF,∴,故③正确;④)∵△COE≌△DOF,∴OE=OF,又∵∠EOF=90°,∴△EOF是等腰直角三角形,∴∠OEG=∠OCE=45°,∵∠EOG=∠COE,∴△OEG∽△OCE,∴OE:OC=OG:OE,∴OG•OC=OE2,∵OC=AC,OE=EF,∴OG•AC=EF2,∵CE=DF,BC=CD,∴BE=CF,又∵Rt△CEF中,CF2+CE2=EF2,∴BE2+DF2=EF2,∴OG•AC=BE2+DF2,故④错误,故选:B.10.(3分)在边长为的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为()A.B.C.D.【分析】分析,EF与x的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.【解答】解:∵四边形ABCD是正方形,∴AC=BD=2,OB=OD=,①当P在OB上时,即0≤x≤1,∵EF∥AC,∴△BEF∽△BAC,∴EF:AC=BP:OB,∴EF=2BP=2x,∴y=EF•OP=×2x(1﹣x)=﹣x2+x;②当P在OD上时,即1<x≤2,∵EF∥AC,∴△DEF∽△DAC,∴EF:AC=DP:OD,即EF:2=(2﹣x):1,∴EF=4﹣2x,∴y=EF•OP==﹣x2+3x﹣2,这是一个二次函数,根据二次函数的性质可知:二次函数的图象是一条抛物线,开口方向取决于二次项的系数.当系数>0时,抛物线开口向上;系数<0时,开口向下.根据题意可知符合题意的图象只有选项B.故选:B.二、填空题(每小题3分,共15分)11.(3分)计算:﹣()﹣1+=0 .【分析】直接利用负指数幂的性质以及二次根式的性质分别化简得出答案.【解答】解:原式=﹣4+4=0.故答案为:0.12.(3分)2019年永州市初中体育学业水平考试实行改革,增加了两类自选类项目:一类是运动技能测试,学生可以从篮球、足球、排球向上垫球三个项目中必须自选一项;另一类是身体力量测试,学生从一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远四个项目中再选一项,则某一初三男学生同时选择篮球和立定跳远这两项的概率是.【分析】用A、B、C分别表示篮球、足球、排球向上垫球三个项目,用a、b、c、d分别表示一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远四个项目,画树状图展示所有9种等可能的结果数,找出某一初三男学生同时选择篮球和立定跳远这两项的结果数,然后根据概率公式求解.【解答】解:用A、B、C分别表示篮球、足球、排球向上垫球三个项目,用a、b、c、d 分别表示一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远四个项目,画树状图为:共有12种等可能的结果数,其中某一初三男学生同时选择篮球和立定跳远这两项的结果数为1,所以某一初三男学生同时选择篮球和立定跳远这两项的概率=.故答案为.13.(3分)关于x的一元二次方程a(x﹣h)2+k=x+n两根为x1=﹣1,x2=3,则方程a(x ﹣h﹣3)2+k+3=x+n的两根为2或6 .【分析】根据函数与方程的关系及函数平移的规律,变形要求的方程,利用平移规律可解.【解答】解:由方程a(x﹣h﹣3)2+k+3=x+n得a(x﹣h﹣3)2+k=x+n﹣3①方程①可看作左边是二次函数y=a(x﹣h﹣3)2+k,右边是一次函数y=x+n﹣3根据平移知识,可知方程①相当于关于x的一元二次方程a(x﹣h)2+k=x+n②,左右两边都向右平移3个单位而方程②的两根为x1=﹣1,x2=3∴方程①的两根为x1=2,x2=6故答案为2或6.14.(3分)如图,7个腰长为1的等腰直角三角形(Rt△B1AA1,Rt△B2A1A2,Rt△B3A2A3…)有一条腰在同一条直线上,设△A1B2C1的面积为S1,△A2B3C2的面积为S2,△A3B4C3的面积为S3,则S1+S2+S3+S4+S5+S6=.【分析】连接B1、B2、B3、B4点,显然它们共线且平行于AC1,依题意可知△B1B2C1与△C1AA1相似,求出相似比,根据三角形面积公式可得出S1,同理:B2B3:AA2=1:2,所以B2C2:C2A=1:2,进而S2的值可求出,同样的道理,即可求出S3,S4…S6的值,即可求解.【解答】解:解:连接B1、B2、B3、B4.∵n+1个边长为1的等腰三角形有一条边在同一直线上,∴=×1×1=,=×2×1=1,=×3×1=,…==3,连接B1、B2、B3点,显然它们共线且平行于AA1易知S1=,∵B2B3∥AA2,∴△B2C2B3∽△A2C2A,∴=,∴S2==,同理可求,S3==,S4=×2=,S5==,S6==,∴S1+S2+S3+S4+S5+S6==,故答案为:.15.(3分)如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=1或﹣.【分析】分两种情形:①如图1中,当∠DGF=90°时,作DH⊥BC于H.②如图2中,当∠GDF=90°,作DH⊥BC于H,DK⊥FG于K.【解答】解:①如图1中,当∠DGF=90°时,作DH⊥BC于H.在Rt△ACB中,∵∠ACB=90°,AC=2,BC=4,∴AB===2,∵AD=DB,∴CD=AB=,∵DH∥AC,AD=DB,∴CH=BH,∴DH=DG=AC=1,∴CG=﹣1,∵DC=DB,∴∠DCB=∠B,∴cos∠DCB=cos∠B=,∴CE=CG÷cos∠DCB=﹣.②如图2中,当∠GDF=90°,作DH⊥BC于H,DK⊥FG于K.易证四边形DKEH是正方形,可得EH=DH=1,∵CH=BH=2,∴CE=1,综上所述,满足条件的CE的值为1或﹣.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:,其中a是方程a2+a﹣6=0的解.【分析】根据分式的减法和除法可以化简题目中的式子,然后由方程a2+a﹣6=0可以求得a的值,然后将a的值代入化简后的式子即可解答本题,注意代入a的值必须使得原分式有意义.【解答】解:====,由a2+a﹣6=0,得a=﹣3或a=2,∵a﹣2≠0,∴a≠2,∴a=﹣3,当a=﹣3时,原式==.17.(9分)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D为圆心,DB长为半径作作⊙D.(1)求证:AC是⊙D的切线.(2)设AC与⊙D切于点E,DB=1,连接DE,BF,EF.①当∠BAD=30°时,四边形BDEF为菱形;②当AB=+1 时,△CDE为等腰三角形.【分析】(1)作DM⊥AC于M,由角平分线的性质可得DM=DB,由切线的判定可证AC是⊙D的切线;(2)①由菱形的性质可得BD=BF,且BD=DF,可证△BDF是等边三角形,可得∠ADB=60°,即可求解;②由切线的性质可得DE⊥AC,由等腰直角三角形的性质可得CD=DE=,∠C=45°,可证AB=BC=+1.【解答】证明:(1)如图1,作DM⊥AC于M,∵∠B=90°,AD平分∠BAC,DM⊥AC,∴DM=DB,∵DB是⊙D的半径,∴AC是⊙D的切线;(2)①如图2,∵四边形BDEF是菱形,∴BD=DE=EF=BF,∵BD=DF=DE,∴BD=DF=DE=EF=BF,∴△BDF,△DEF是等边三角形,∴∠ADB=∠ADE=60°,∵∠ABC=90°,∴∠BAD=30°,∴当∠BAD=30°时,四边形BDEF是菱形,故答案为:30°;②∵AC与⊙D切于点E,∴DE⊥AC,∵△DEC是等腰三角形,且DE⊥AC,∴DE=EC,∠C=∠EDC=45°,∴DC=DE,∵∠ABC=90°,∠C=45°,∴∠BAC=∠C=45°,∴AB=BC,∵BD=DE=EC=1,∴DC=x,∴AB=BC=+1,∴当AB=+1时,△CDE为等腰三角形,故答案为:+1.18.(9分)设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级;75≤x<85为B级;60≤x<75为C级;x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:(1)在这次调查中,一共抽取了50 名学生,A级人数占本次抽取人数的百分比为24 %;(2)补全条形统计图;(3)扇形统计图中C级对应的圆心角为72 度;(4)若该校共有1000名学生,请你估计该校D级学生有多少名?【分析】(1)根据B级的人数和所占的百分比求出抽取的总人数,再用A级的人数除以总数即可求出α;(2)用抽取的总人数减去A、B、D的人数,求出C级的人数,从而补全统计图;(3)用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数;(4)用D级所占的百分比乘以该校的总人数,即可得出该校D级的学生数.【解答】解:(1)在这次调查中,一共抽取的学生数是:24÷48%=50(人),α=×100%=24%;故答案为:50,24;(2)等级为C的人数是:50﹣12﹣24﹣4=10(人),补图如下:(3)扇形统计图中C级对应的圆心角为×360°=72°;故答案为:72;(4)根据题意得:1000×=80(人),答:该校D级学生有80人.19.(9分)如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)(2)求景点C与景点D之间的距离.(结果精确到1km)(参考数据:=1.73,=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)【分析】过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,求DE的问题就可以转化为求∠DBE的度数或三角函数值的问题.Rt△DCE中根据三角函数就可以求出CD的长.【解答】解:(1)如图,过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,在Rt△DAF中,∠ADF=30°,∴AF=AD=×8=4,∴DF=,在Rt△ABF中BF==3,∴BD=DF﹣BF=4﹣3,sin∠ABF=,在Rt△DBE中,sin∠DBE=,∵∠ABF=∠DBE,∴sin∠DBE=,∴DE=BD•sin∠DBE=×(4﹣3)=≈3.1(km),∴景点D向公路a修建的这条公路的长约是3.1km;(2)由题意可知∠CDB=75°,由(1)可知sin∠DBE==0.8,所以∠DBE=53°,∴∠DCB=180°﹣75°﹣53°=52°,在Rt△DCE中,sin∠DCE=,∴DC=≈4(km),∴景点C与景点D之间的距离约为4km.20.(9分)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB 于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)观察图象,直接写出当x>0时,不等式2x+6<0的解集;(3)当n为何值时,△BMN的面积最大?最大值是多少?【分析】(1)求出点A的坐标,利用待定系数法即可解决问题;(2)结合函数图象找到直线在双曲线下方对应的x的取值范围;(3)构建二次函数,利用二次函数的性质即可解决问题.【解答】解:(1)∵直线y=2x+6经过点A(1,m),∴m=2×1+6=8,∴A(1,8),∵反比例函数经过点A(1,8),∴k=8,∴反比例函数的解析式为y=;(2)不等式2x+6<0的解集为0<x<1;(3)由题意,点M,N的坐标为M(,n),N(,n),∵0<n<6,∴<0,∴>0∴S△BMN=|MN|×|y M|==(n﹣3)2+,∴n=3时,△BMN的面积最大,最大值为.21.(10分)某商场计划经销A,B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.A型B型进价(元/盏)40 65售价(元/盏)60 100(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?(3)若该商场预计用不多于2600元的资金购进这批台灯,其中A种台灯不超过30盏,为了打开B种台灯的销路,商场决定每售出一盏B种台灯,返还顾客现金a元(10<a <20),问该商场该如何进货,才能获得最大的利润?【分析】(1)首先设该商场购进A种台灯x盏,购进B种台灯(50﹣x)盏,然后根据题意,即可得方程,解方程即可求得答案;(2)设至少需购进B种台灯x盏,然后由该商场销售这批台灯的总利润不少于1400元,即可得一元一次不等式35y+20(50﹣y)≥1400,解此不等式即可求得答案;(3)首先设该商场购进A种台灯m盏,由该商场预计用不多于2600元的资金购进这批台灯,可通过不等式组求得m的取值范围,然后求得该商场获得的总利润与该商场购进A种台灯的盏数的一次函数,由10<a<20,根据一次函数的增减性即可求得答案.【解答】解:(1)设该商场购进A种台灯x盏,购进B种台灯(50﹣x)盏,由题意得:40x+65(50﹣x)=2500,解得:x=30,∴该商场购进A种台灯30盏,购进B种台灯20盏.(2)设购进B种台灯y盏,由题意得:35y+20(50﹣y)≥1400,解得:y≥,∴y的最小整数解为27,∴至少需购进B种台灯27盏;(3)设该商场购进A种台灯m盏,由题意得:40m+65(50﹣m)≤2600,解得:m≥26,∴26≤m30,设该商场获得的总利润为w元,则w=20m+(35﹣a)(50﹣m)=(a﹣15)m+1750﹣50a,∵10<a<20,∴当10<a≤15时,m=26,即购进A种台灯26盏,购进B种台灯24盏,该商场获得的总利润最大,当15<a<20时,m=30,即购进A种台灯30盏,购进B种台灯20盏,该商场获得的总利润最大.22.(10分)(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D 时线段AB上一动点,连接BE.填空:①的值为 1 ;②∠DBE的度数为90°.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D 是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.【分析】(1)由直角三角形的性质可得∠ABC=45°,可得∠DBE=90°,通过证明△ACD ∽△BCE,可得的值;(2)通过证明△ACD∽△BCE,可得的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;(3)分点D在线段AB上和BA延长线上两种情况讨论,由直角三角形的性质可证CM=BM=,即可求DE=2,由相似三角形的性质可得∠ABE=90°,BE=AD,由勾股定理可求BE的长.【解答】解:(1)∵∠ACB=90°,∠CAB=45°∴∠ABC=∠CAB=45°∴AC=BC,∠DBE=∠ABC+∠CBE=90°∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,且∠CAB=∠CDE=45°,∴△ACD∽△BCE∴故答案为:1,90°(2),∠DBE=90°理由如下:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴∠ACD=∠BCE,∠CED=∠ABC=30°∴tan∠ABC=tan30°==∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴Rt△ACB∽Rt△DCE∴∴,且∠ACD=∠BCE∴△ACD∽△BCE∴=,∠CBE=∠CAD=60°∴∠DBE=∠ABC+∠CBE=90°(3)若点D在线段AB上,如图,由(2)知:=,∠ABE=90°∴BE=AD∵AC=2,∠ACB=90°,∠CAB=90°∴AB=4,BC=2∵∠ECD=∠ABE=90°,且点M是DE中点,∴CM=BM=DE,且△CBM是直角三角形∴CM2+BM2=BC2=(2)2,∴BM=CM=∴DE=2∵DB2+BE2=DE2,∴(4﹣AD)2+(AD)2=24∴AD=+1∴BE=AD=3+若点D在线段BA延长线上,如图同理可得:DE=2,BE=AD∵BD2+BE2=DE2,∴(4+AD)2+(AD)2=24,∴AD=﹣1∴BE=AD=3﹣综上所述:BE的长为3+或3﹣23.(11分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(﹣1,0),(0,﹣3),直线x=1为抛物线的对称轴.点D为抛物线的顶点,直线BC与对称轴相交于点E.(1)求抛物线的解析式并直接写出点D的坐标;(2)点P为直线x=1右方抛物线上的一点(点P不与点B重合).记A、B、C、P四点所构成的四边形面积为S,若S=S△BCD,求点P的坐标;(3)点Q是线段BD上的动点,将△DEQ延边EQ翻折得到△D′EQ,是否存在点Q使得△D′EQ与△BEQ的重叠部分图形为直角三角形?若存在,请求出BQ的长,若不存在,请说明理由.【分析】(1)利用抛物线的对称性得到B(3,0),则设交点式为y=a(x+1)(x﹣3),把C(0,﹣3)代入求出a即可得到抛物线解析式,然后把解析式配成顶点式即可得到D 点坐标;(2)设P(m,m2﹣2m﹣3),先确定直线BC的解析式y=x﹣3,再确定E(1,﹣2),则可根据三角形面积公式计算出S△BDC=S△BDE+S△CDE=3,然后分类讨论:当点P在x轴上方时,即m>3,如图1,利用S=S△PAB+S△CAB=S△BCD得到2m2﹣4m=;当点P在x轴下方时,即1<m<3,如图2,连结OP,利用S=S△AOC+S△COP+S△POB=S△BCD得到﹣m2+m+6=,再分别解关于m的一元二次方程求出m,从而得到P点坐标;(3)存在.直线x=1交x轴于F,利用两点间的距离公式计算出BD=2,分类讨论:①如图3,EQ⊥DB于Q,证明Rt△DEQ∽Rt△DBF,利用相似比可计算出DQ=,则BQ=BD﹣DQ=;②如图4,ED′⊥BD于H,证明Rt△DEQ=H∽Rt△DBF,利用相似比计算出DH=,EH=,在Rt△QHD′中,设QH=x,D′Q=DQ=DH﹣HQ=﹣x,D′H=D′E﹣EH=DE﹣EH=2﹣,则利用勾股定理可得x2+(2﹣)2=(﹣x)2,解得x=1﹣,于是BQ=BD﹣DH+HQ﹣=+1;③如图5,D′Q⊥BC于G,作EI⊥BD于I,利用①得结论可得EI=,BI=,而BE=2,则BG=BE﹣EG=2﹣,根据折叠性质得∠EQD=∠EQD′,则根据角平分线性质得EG=EI=,接着证明△BQG∽△BEI,利用相似比可得BQ=﹣,所以当BQ为或+1或﹣时,将△DEQ沿边EQ翻折得到△D′EQ,使得△D′EQ与△BEQ 的重叠部分图形为直角三角形.【解答】解:(1)∵点A与点B关于直线x=1对称,∴B(3,0),设抛物线解析式为y=a(x+1)(x﹣3),把C(0,﹣3)代入得﹣3a=﹣3,解得a=1,∴抛物线就笑着说为y=(x+1)(x﹣3)=x2﹣2x﹣3,∵y=(x﹣1)2﹣4,∴抛物线顶点D的坐标为(1,﹣4);(2)设P(m,m2﹣2m﹣3),易得直线BC的解析式为y=x﹣3,当x=1时,y=x﹣3=﹣3,则E(1,﹣2),∴S△BDC=S△BDE+S△CDE=×3×(﹣2+4)=3,当点P在x轴上方时,即m>3,如图1,S=S△PAB+S△CAB=•3•(3+1)+•(3+1)•(m2﹣2m﹣3)=2m2﹣4m,∵S=S△BCD,∴2m2﹣4m=,整理得4m2﹣8m﹣15=0,解得m1=,m2=(舍去),∴P点坐标为(,);当点P在x轴下方时,即1<m<3,如图2,连结OP,S=S△AOC+S△COP+S△POB=•3•1+•3•m+•3•(﹣m2+2m+3)=﹣m2+m+6,∵S=S△BCD,∴﹣m2+m+6=,整理得m2﹣3m+1=0,解得m1=,m2=(舍去)∴P点坐标为(,),综上所述,P点坐标为(,)或(,);(3)存在.直线x=1交x轴于F,BD==2,①如图3,EQ⊥DB于Q,△DEQ沿边EQ翻折得到△D′EQ,∵∠EDQ=∠BDF,∴Rt△DEQ∽Rt△DBF,∴=,即=,解得DQ=,∴BQ=BD﹣DQ=2﹣=;②如图4,ED′⊥BD于H,∵∠EDH=∠BDF,∴Rt△DEQ=H∽Rt△DBF,∴==,即==,解得DH=,EH=,在Rt△QHD′中,设QH=x,D′Q=DQ=DH﹣HQ=﹣x,D′H=D′E﹣EH=DE﹣EH=2﹣,∴x2+(2﹣)2=(﹣x)2,解得x=1﹣,∴BQ=BD﹣DQ=BD﹣(DH﹣HQ)=BD﹣DH+HQ=2﹣+1﹣=+1;③如图5,D′Q⊥BC于G,作EI⊥BD于I,由①得EI=,BI=,∵BE==2,∴BG=BE﹣EG=2﹣,∵△DEQ沿边EQ翻折得到△D′EQ,∴∠EQD=∠EQD′,∴EG=EI=,∵∠GBQ=∠IBE,∴△BQG∽△BEI,∴=,即=,∴BQ=﹣,综上所述,当BQ为或+1或﹣时,将△DEQ沿边EQ翻折得到△D′EQ,使得△D′EQ与△BEQ的重叠部分图形为直角三角形.。
2020届中考语文模拟试卷

重庆市2020届中考语文模拟试卷(满分:150分时间:120分钟)一、语文知识及运用(30分)1.下列句子中加点字注音有误的一项是(3分)( )A.先生棱.(léng)角分明的脸上,有一双洞察世事的眼睛。
B.尚武敢为、负重自强的巴文化与绚丽浪漫的楚文化、文静兼容的蜀文化在这里交错共生,成就了重庆独特的自然景观和文化精神,滋养和哺.(pǔ)育了重庆独特的文学景观。
C.历史的星空,因有众多叱咤.(zhà)风云的人物而熠熠生辉。
D.铭记历史,不是为了憎恶.(wù),而是为了知盛衰兴替,明是非得失。
2.下列词语书写全部正确的一项是(3分)( )A.蜷缩娉婷不修边幅怒不可遏B.推搡诘问鞠躬尽萃鸠占鹊巢C.烦躁斡旋珊珊来迟狗皮膏药D.徙峭虔诚李代桃僵接踵而至3.下列句子中加点词语使用不恰当的一项是(3分)( )A.一年只能种植一季水稻的冬水田里,农户们以拓荒牛的执着酝酿..着一年更比一年好的美好生活。
B.重庆收藏家陈斌嵩收藏的“同治大婚瓷”在《舌尖上的中国3》里出镜,20余件藏品是他辗转..美、英、法等国搜集到的。
C.在国学知识竞赛的陈述环节,西南大学的选手们口若悬河,寻章摘句....,尽显才情。
D.不管我们宣传教育改革的成果多么辉煌,不管我们宣传学校的课程改革突破了什么,只要我们学生的睡眠得不到满足,体质在下降,近视在增加,我们的教育改革就黯然失色....。
4.依次填入下面文段横线处的语句,衔接最恰当的一项是(3分)( )数据加密是信息安全的核心技术之一,它主要用于保障数据在不安全环境中的安全存储和通信。
________。
________。
________。
________。
①在这一过程中,敏感信息就是待加密的数据,专业术语称为明文,被公布的乱码称为密文,从密文恢复出明文的过程称为解密②通过数据加密,我们手机里的敏感信息将变成一堆乱码③显然,加密过程必须是可逆的,即从密文一定能够正确地恢复出明文④即使公布这堆乱码,也只有你的那个他才能读懂它的真正含义A.①③②④B.①②④③C.②④①③D.②①③④5.请参照画线部分,再补写两个句子。
江苏省扬州市广陵区2020届中考数学模拟试卷(含解析)

江苏省扬州市广陵区2020届中考模拟试卷数学一.选择题(共8小题)1.﹣的倒数是()A. B.﹣ C.﹣ D.2.给出一列数,在这列数中,第50个值等于1的项的序号是()A.4900 B.4901 C.5000 D.50013.(3分)若二次根式有意义,则a的取值范围是()A.a≥2 B.a≤2 C.a>2 D.a≠24.(3分)下列图形中,属于中心对称图形的是()A. B. C. D.5.(3分)如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为()A.36° B.42° C.45° D.48°6.(3分)某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是()捐款(元)10 15 20 50人数 1 5 4 2A.15,15 B.17.5,15 C.20,20 D.15,207.(3分)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是()A.12cm2 B.(12+π)cm2 C.6πcm2 D.8πcm28.(3分)如图,有一住宅小区呈三角形ABC形状,且周长为2 000m,现规划沿小区周围铺上宽为3m的草坪,则草坪的面积(精确到1)是()A.6000m2 B.6016m2 C.6028m2 D.6036m2二.填空题(共10小题,满分30分,每小题3分)9.(3分)科学家发现,距离地球2540000光年之遥的仙女星系正在向银河系靠近.其中2540000用科学记数法表示为.10.(3分)分解因式:a2﹣a+2= .11.(3分)反比例函数和一次函数y=k2x+b的图象交于点M(3,﹣)和点N(﹣1,2),则k1= ,k2= ,一次函数的图象交x轴于点.12.(3分)某电信局现有300部已申请装机的电话等待装机.假设每天新申请装机的电话部数相同,该电信局每个电话装机小组每天装的电话部数也相同,那么安排3个装机小组,恰好30天可将需要装机的电话全部装完;如果安排5个装机小组,则恰好10天可将需要装机的电话全部装完.试求每个电话装机小组每天装机多少部?每天有多少部新申请装机的电话?13.(3分)抛物线y=ax2+bx+c(a≠0)过点A(1,﹣3)、B(3,﹣3)、C(﹣1,5),顶点为M点.在抛物线上是找一点P使∠POM=90°,则P点的坐标.14.(3分)某市对九年级学生进行“综合素质”评价,评价结果分为A,B,C,D,E五个等级.现随机抽取了500名学生的评价结果作为样本进行分析,绘制了如图所示的统计图.已知图中从左到右的五个长方形的高之比为2:3:3:1:1,据此估算该市80000名九年级学生中“综合素质”评价结果为“A”的学生约为人.15.(3分)如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,第n次操作,分别作∠ABE n﹣1和∠DCE n﹣1的平分线,交点为E n.若∠E n=1度,那∠BEC等于度16.(3分)如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于.17.(3分)如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC= .18.(3分)如图,直线y1=kx+b与直线y2=mx交于点P(1,m),则不等式mx>kx+b的解集是.三.解答题(共10小题,满分96分)19.(8分)(1)(﹣2)﹣1﹣|﹣|+(3.14﹣π)0+4cos45°(2)已知x2﹣2x﹣7=0,求(x﹣2)2+(x+3)(x﹣3)的值.20.(8分)当x满足条件时,求出方程x2﹣2x﹣4=0的根.21.(8分)某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.(1)求共抽取了多少名学生的征文;(2)将上面的条形统计图补充完整;(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.22.(8分)小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图(1)若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;(2)若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同时时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)23.(10分)列方程解应用题:某城市为了治理污水,需要铺设一条全长为3000米的污水排放管道.为使工程提前10天完成,在保证质量的前提下,必须把工作效率提高25%.问原计划每天铺设管道多少米?24.(10分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,延长BE到F,使BE=EF,连接AF、CF、DF.(1)求证:AF=BD;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.25.(10分)有一个二次函数满足以下条件:①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);②对称轴是x=3;③该函数有最小值是﹣2.(1)请根据以上信息求出二次函数表达式;(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.26.(10分)如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB于点E,OE:EA=1:2,PA=6,∠POC=∠PCE.(1)求证:PC是⊙O的切线;(2)求⊙O的半径;(3)求sin∠PCA的值.27.(12分)在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=,连接PB,试探究PA、PB、PC满足的等量关系.(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为;(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;(3)PA、PB、PC满足的等量关系为.28.(12分)如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.请从下列A、B两题中任选一题作答,我选择题.A:①求线段AD的长;②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.B:①求线段DE的长;②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC 全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.2020年江苏省扬州市广陵区中考数学模拟试卷参考答案与试题解析一.选择题(共8小题,满分18分)1.【解答】解:﹣的倒数是﹣,故选:B.2.【解答】解:第50个值等于1的项的分子分母的和为2×50=100,由于从分子分母的和为2到分子分母的和为99的分数的个数为:1+2+…+98=4851.第50个值等于1的项为.故4851+50=4901.故选:B.3.【解答】解:∵二次根式有意义,∴a﹣2≥0,即a≥2,则a的范围是a≥2,故选:A.4.【解答】解:A、不是中心对称图形,故此选项错误;B、不是中心对称图形,故此选项错误;C、不是中心对称图形,故此选项错误;D、是中心对称图形,故此选项正确,故选:D.5.【解答】解:如图,梅花扇的内角的度数是:360°÷3=120°,180°﹣120°=60°,正五边形的每一个内角=(5﹣2)•180°÷5=108°,∴梅花图案中的五角星的五个锐角均为:108°﹣60°=48°.故选:D.6.(15+20)【解答】解:共有数据12个,第6个数和第7个数分别是15元,20元,所以中位数是:÷2=17.5(元);捐款金额的众数是15元.故选:B.7.【解答】解:先由三视图确定该几何体是圆柱体,底面半径是2÷2=1cm,高是3cm.所以该几何体的侧面积为2π×1×3=6π(cm2).故选:C.8.【解答】解:∵如图:草坪是由长分别为AB、BC、AC,宽为3m的3个矩形与三个半径为3m 的扇形组成的,又∵AB+AC+BC=2000m,三个扇形正好组成一个圆,∴草坪的面积为:S=2000×3+9π=6000+9π=6028m2.故选:C.二.填空题(共10小题,满分30分,每小题3分)9.【解答】解:2540000用科学记数法表示为2.54×106.故答案为:2.54×106.10.【解答】解:a2﹣a+2=(a2﹣6a+9)=(a﹣3)2.故答案为:(a﹣3)2.11.【解答】解:∵M(3,﹣)和点N(﹣1,2)为两函数的交点,∴x=﹣1,y=2代入反比例函数y=中得:2=,即k1=﹣2;将两点坐标代入y=k2x+b得:,解得:k1=﹣,b=,∴一次函数解析式为y=﹣x+,令y=0,解得:x=2,∴一次函数与x轴交点为(2,0).故答案为:﹣2;﹣;(2,0)12.【解答】解:设每个电话装机小组每天装机x部,每天有y部新申请装机的电话,根据题意得:,解得:,答:每个装机小组每天装机10部,每天有20部新申请装机的电话.13.【解答】解:抛物线y=ax2+bx+c(a≠0)过点A(1,﹣3)、B(3,﹣3)、C(﹣1,5),所以,解得:,所以抛物线的解析式为:y=x2﹣4x=(x﹣2)2﹣4,顶点M坐标是(2,﹣4),因此直线OM的解析式为y=﹣2x,由于直线PO与直线OM垂直,因此直线PO的解析式为y=x,联立抛物线的解析式有:,解得,,因此P点坐标为(,).14.【解答】解:该市80000名九年级学生中“综合素质”评价结果为“A”的学生约为,故答案为:1600015.【解答】解:如图①,过E作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;如图②,∵∠ABE和∠DCE的平分线交点为E1,∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BE C.∵∠ABE1和∠DCE1的平分线交点为E2,∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;…以此类推,∠E n=∠BE C.∴当∠E n=1度时,∠BEC等于2n度.故答案为:2n.16.【解答】解:将线段AP绕点A顺时针旋转60°得到线段AM,连接PM,作AH⊥BP于H.∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∵AM=AP,∠MAP=60°,∴△AMP是等边三角形,∵∠MAP=∠BAC,∴∠MAB=∠PAC,∴△MAB≌△PAC,∴BM=PC=10,∵PM2+PB2=100,BM2=100,∴PM2+PB2=BM2,∴∠MPB=90°,∵∠APM=60°,∴∠APB=150°,∠APH=30°,∴AH=PA=3,PH=3,BH=8+3,∴AB2=AH2+BH2=100+48,∴菱形ABCD的面积=2•△ABC的面积=2××AB2=50+72,故答案为50+72.17.【解答】解:∵AB为⊙O直径,∴∠ACB=90°,∴BC==12,∴tan∠ADC=tanB===,故答案为.18.【解答】解:∵直线y1=kx+b与直线y2=mx交于点P(1,m),∴不等式mx>kx+b的解集是x>1,故答案为:x>1.三.解答题(共10小题,满分96分)19.【解答】解:(1)原式=﹣﹣2+1+2=;(2)原式=x2﹣4x+4+x2﹣9=2x2﹣4x﹣5=2(x2﹣2x)﹣5,∵x2﹣2x﹣7=0,即x2﹣2x=7,∴原式=14﹣5=9.20.【解答】解:解不等式x+1<3x﹣3,得:x>2,解不等式3(x﹣4)<2(x﹣4),得:x<4,则不等式组的解集为2<x<4,∵x2﹣2x=4,∴x2﹣2x+1=4+1,即(x﹣1)2=5,则x﹣1=±,∴x=1或x=1﹣,∵2<x<4,∴x=1.21.【解答】解:(1)本次调查共抽取的学生有3÷6%=50(名).(2)选择“友善”的人数有50﹣20﹣12﹣3=15(名),条形统计图如图所示:(3)∵选择“爱国”主题所对应的百分比为20÷50=40%,∴选择“爱国”主题所对应的圆心角是40%×360°=144°;(4)该校九年级共有1200名学生,估计选择以“友善”为主题的九年级学生有1200×30%=360名.22.【解答】解:(1)一共有四个开关按键,只有闭合开关按键K2,灯泡才会发光,所以P(灯泡发光)=(2)用树状图分析如下:一共有12种不同的情况,其中有6种情况下灯泡能发光,所以P(灯泡发光)=.23.【解答】解:设原计划每天铺设多长管道设原计划每天铺设x米管道,根据题意得.解得x=60,经检验x=60是原分式方程的解.答:原计划每天铺设60米长的管道.24.【解答】(1)证明:∵AE=ED,BE=EF,∴四边形ABDF是平行四边形,∴AF=B D.(2)结论:四边形ADCF是菱形.理由:∵AB⊥AC,∴∠CAB=90°,∵CD=DB,∴AD=BC=DC,∵四边形ABDF是平行四边形,∴AF∥CD,AF=BD,∴AF=CD,∴四边形AFCD是平行四边形,∵DA=DC,∴四边形AFCD是菱形.25.【解答】解:(1)有上述信息可知该函数图象的顶点坐标为:(3,﹣2)设二次函数表达式为:y=a(x﹣3)2﹣2.∵该图象过A(1,0)∴0=a(1﹣3)2﹣2,解得a=.∴表达式为y=(x﹣3)2﹣2(2)如图所示:由已知条件可知直线与图形“G”要有三个交点1当直线与x轴重合时,有2个交点,由二次函数的轴对称性可求x3+x4=6,∴x3+x4+x5>11.当直线过y=(x﹣3)2﹣2的图象顶点时,有2个交点,由翻折可以得到翻折后的函数图象为y=﹣(x﹣3)2+2∴令(x﹣3)2+2=﹣2时,解得x=3+2或x=3﹣2(舍去)∴x3+x4+x5<9+2.综上所述11<x3+x4+x5<9+2.26.【解答】解:(1)证明:∵弦CD⊥AB于点E,∴在Rt△COE中∠COE+∠OCE=90°,∵∠POC=∠PCE,∴∠PCE+∠OCE=90°,即PC⊥OC,∴PC是⊙O的切线;(2)∵OE:EA=1:2,PA=6,∴可设OE=k,EA=2k,则半径r=3k,在Rt△COP中,∵CE⊥PO垂足为E,∴△COE∽△POC,∴CO2=OE•OP即(3k)2=k•(3k+6),解得k=0(舍去)或k=1,∴半径r=3;(3)过A作AH⊥PC,垂足为H,∵PC⊥OC∴AH∥OC,∴,即,解得AH=2,在Rt△COE中,由OC=3,OE=1,解得CE=,在Rt△ACE中,由CE=,AE=2,解得AC=,在Rt△ACH中,由AC=,AH=2,∴sin∠PCA===.27.【解答】解:(1)∵△ABP≌△ACP′,∴AP=AP′,由旋转变换的性质可知,∠PAP′=60°,P′C=PB,∴△PAP′为等边三角形,∴∠APP′=60°,∵∠PAC+∠PCA==30°,∴∠APC=150°,∴∠P′PC=90°,∴PP′2+PC2=P′C2,∴PA2+PC2=PB2,故答案为:150,PA2+PC2=PB2;(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,作AD⊥PP′于D,由旋转变换的性质可知,∠PAP′=120°,P′C=PB,∴∠APP′=30°,∵∵∠PAC+∠PCA==60°,∴∠APC=120°,∴∠P′PC=90°,∴PP′2+PC2=P′C2,∵∠APP′=30°,∴PD=PA,∴PP′=PA,∴3PA2+PC2=PB2;(3)如图2,与(2)的方法类似,作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,作AD⊥PP′于D,由旋转变换的性质可知,∠PAP′=α,P′C=PB,∴∠APP′=90°﹣,∵∵∠PAC+∠PCA=,∴∠APC=180°﹣,∴∠P′PC=(180°﹣)﹣(90°﹣)=90°,∴PP′2+PC2=P′C2,∵∠APP′=90°﹣,∴PD=PA•cos(90°﹣)=PA•sin,∴PP′=2PA•sin,∴4PA2sin2+PC2=PB2,故答案为:4PA2sin2+PC2=PB2.28.【解答】解:(1)∵一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,∴A(4,0),C(0,8),∴OA=4,OC=8,∵AB⊥x轴,CB⊥y轴,∠AOC=90°,∴四边形OABC是矩形,∴AB=OC=8,BC=OA=4,在Rt△ABC中,根据勾股定理得,AC==4,故答案为:8,4,4;(2)A、①由(1)知,BC=4,AB=8,由折叠知,CD=AD,在Rt△BCD中,BD=AB﹣AD=8﹣AD,根据勾股定理得,CD2=BC2+BD2,即:AD2=16+(8﹣AD)2,∴AD=5,②由①知,D(4,5),设P(0,y),∵A(4,0),∴AP2=16+y2,DP2=16+(y﹣5)2,∵△APD为等腰三角形,∴Ⅰ、AP=AD,∴16+y2=25,∴y=±3,∴P(0,3)或(0,﹣3)Ⅱ、AP=DP,∴16+y2=16+(y﹣5)2,∴y=,∴P(0,),Ⅲ、AD=DP,25=16+(y﹣5)2,∴y=2或8,∴P(0,2)或(0,8).B、①、由A①知,AD=5,由折叠知,AE=AC=2,DE⊥AC于E,在Rt△ADE中,DE==,②、∵以点A,P,C为顶点的三角形与△ABC全等,∴△APC≌△ABC,或△CPA≌△ABC,∴∠APC=∠ABC=90°,∵四边形OABC是矩形,∴△ACO≌△CAB,此时,符合条件,点P和点O重合,即:P(0,0),如图3,过点O作ON⊥AC于N,易证,△AON∽△ACO,∴,∴,∴AN=,过点N作NH⊥OA,∴NH∥OA,∴△ANH∽△ACO,∴,∴,∴NH=,AH=,∴OH=,∴N(,),而点P2与点O关于AC对称,∴P2(,),同理:点B关于AC的对称点P1,同上的方法得,P1(﹣,),即:满足条件的点P的坐标为:(0,0),(,),(﹣,).。
苏教版2020年中考数学模拟卷(含答案解析)
2020年中考数学模拟试卷一.选择题(共8小题)1.下列各数中最小的数为()A.﹣3 B.﹣1 C.0 D.12.下列运算正确的是()A.3x2•4x2=12x2B.x3+x5=x8C.x4÷x=x3D.(x5)2=x73.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示为()A.0.3×105B.3×105C.0.3×106D.3×1064.下图几何体的主视图是()A.B.C.D.5.某小组7名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是()劳动时间(小时) 3 3.5 4 4.5人数 1 1 3 2A.中位数是4,众数是4 B.中位数是3.5,众数是4C.平均数是3.5,众数是4 D.平均数是4,众数是3.56.受益于电子商务发展和法治环境改善等多重因素,“快递业”成为我国经济的一匹“黑马”,2016年我国快递业务量为300亿件,2018年快递量将达到450亿件,若设快递量平均每年增长率为x,则下列方程中,正确的是()A.300(1+x)=450 B.300(1+2x)=450C.300(1+x)2=450 D.450(1﹣x)2=3007.某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是()A.打六折B.打七折C.打八折D.打九折8.如图,▱ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为()A.﹣4tanαB.﹣2sinαC.﹣4cosαD.﹣2tanα二.填空题(共8小题)9.=.10.分解因式:x3﹣x=.11.已知一个多边形的内角和为540°,则这个多边形是边形.12.从长度分别是3,4,5的三条线段中随机抽出一条,与长为2,3的两条线段首尾顺次相接,能构成三角形的概率是.13.小亮测得一圆锥模型的底面直径为10cm,母线长为7cm,那么它的侧面展开图的面积是cm2.14.如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为.15.抛物线y=﹣x2+2x+8与x轴交于B、C两点,点D平分BC,且点A为抛物线上的点,且∠BAC为锐角,则AD的值范围为.16.如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,若BD=3,CD=2.则△ABC的面积为.三.解答题(共10小题)17.计算或化简:(1)(2)18.解方程:+=1.19.图书馆是一个很好的学习平台,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图.(1)在统计的这段时间内,共有万人次到图书馆阅读,其中商人占百分比为%.(2)将条形统计图补充完整.(3)5月份到图书馆的读者共有24000人次,根据以上调查结果,估计24000人次中是职工的人次.20.如图,E是AC上一点,AB=CE,AB∥CD,AC=CD.求证:BC=ED.21.有四张仅一面分别标有1,2,3,4的不透明纸片,除所标数字不同外,其余都完全相同.(1)将四张纸片分成两组,标有1、3的为第一组,标有2、4的为第二组,背面向上,放在桌上,从两组中各随机抽取一张,求两次抽取数字和为5的概率;(2)将四张纸片洗匀后背面向上,放在桌上,一次性从中随机抽取两张,用树形图法或列表法,求所抽取数字和为5的概率.22.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sin A=时,求AF的长.23.如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(1)求DE与水平桌面(AB所在直线)所成的角;(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)24.近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%.某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的,两种猪肉销售的总金额比5月20日提高了a%,求a的值.25.如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.(1)求二次函数的解析式;(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.①求点P的运动路程;②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结EF,求△PEF周长的最小值.26.(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①的值为;②∠AMB的度数为.(2)类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.参考答案与试题解析一.选择题(共8小题)1.下列各数中最小的数为()A.﹣3 B.﹣1 C.0 D.1【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.【解答】解:根据有理数比较大小的方法,可得﹣3<﹣1<0<1,∴各数中最小的数是﹣3.故选:A.2.下列运算正确的是()A.3x2•4x2=12x2B.x3+x5=x8C.x4÷x=x3D.(x5)2=x7【分析】A、利用单项式乘单项式法则计算得到结果,即可做出判断;B、原式不能合并,本选项错误;C、原式利用同底数幂的除法法则计算得到结果,即可做出判断;D、原式利用幂的乘方运算法则计算得到结果,即可做出判断.【解答】解:A、3x2•4x2=12x4,本选项错误;B、原式不能合并,错误;C、x4÷x=x3,本选项正确;D、(x5)2=x10,本选项错误,故选:C.3.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示为()A.0.3×105B.3×105C.0.3×106D.3×106【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将300 000用科学记数法表示为:3×105.故选:B.4.下图几何体的主视图是()A.B.C.D.【分析】找到从正面看所得到的图形即可.【解答】解:从正面可看到的几何体的左边有3个正方形,中间只有2个正方形,右边有1个正方形.故选:C.5.某小组7名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是()劳动时间(小时) 3 3.5 4 4.5人数 1 1 3 2A.中位数是4,众数是4 B.中位数是3.5,众数是4C.平均数是3.5,众数是4 D.平均数是4,众数是3.5【分析】根据众数和中位数的概念求解.【解答】解:这组数据中4出现的次数最多,众数为4,∵共有7个人,∴第4个人的劳动时间为中位数,所以中位数为4,故选:A.6.受益于电子商务发展和法治环境改善等多重因素,“快递业”成为我国经济的一匹“黑马”,2016年我国快递业务量为300亿件,2018年快递量将达到450亿件,若设快递量平均每年增长率为x,则下列方程中,正确的是()A.300(1+x)=450 B.300(1+2x)=450C.300(1+x)2=450 D.450(1﹣x)2=300【分析】设快递量平均每年增长率为x,根据我国2016年及2018年的快递业务量,即可得出关于x的一元二次方程,此题得解.【解答】解:设快递量平均每年增长率为x,依题意,得:300(1+x)2=450.故选:C.7.某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是()A.打六折B.打七折C.打八折D.打九折【分析】根据题意和函数图象中的数据可以列出相应的方程,从而可以求得超过500元的部分可以享受的优惠,本题得以解决.【解答】解:设超过500元的部分可以享受的优惠是x折,(1000﹣500)×+500=900,解得,x=8,故选:C.8.如图,▱ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为()A.﹣4tanαB.﹣2sinαC.﹣4cosαD.﹣2tanα【分析】过点C作CE⊥OA于E,过点D作DF⊥x轴于F,根据平行四边形的对边相等可得OC=AB,然后求出OC=2AD,再求出OE=2AF,设AF=a,表示出点C、D的坐标,然后根据CE、DF的关系列方程求出a的值,再求出OE、CE,然后利用∠COA的正切值列式整理即可得解.【解答】解:如图,过点C作CE⊥OA于E,过点D作DF⊥x轴于F,在▱OABC中,OC=AB,∵D为边AB的中点,∴OC=AB=2AD,CE=2DF,∴OE=2AF,设AF=a,∵点C、D都在反比例函数上,∴点C(﹣2a,﹣),∵A(3,0),∴D(﹣a﹣3,),∴=2×,解得a=1,∴OE=2,CE=﹣,∵∠COA=∠α,∴tan∠COA=tan∠α=,即tanα=﹣,k=﹣4tanα.故选:A.二.填空题(共8小题)9.= 2 .【分析】如果一个数x的平方等于a,那么x是a的算术平方根,由此即可求解.【解答】解:∵22=4,∴=2.故答案为:210.分解因式:x3﹣x=x(x+1)(x﹣1).【分析】本题可先提公因式x,分解成x(x2﹣1),而x2﹣1可利用平方差公式分解.【解答】解:x3﹣x,=x(x2﹣1),=x(x+1)(x﹣1).故答案为:x(x+1)(x﹣1).11.已知一个多边形的内角和为540°,则这个多边形是五边形.【分析】利用n边形的内角和可以表示成(n﹣2)•180°,结合方程即可求出答案.【解答】解:根据多边形的内角和可得:(n﹣2)180°=540°,解得:n=5.则这个多边形是五边形.故答案为:五.12.从长度分别是3,4,5的三条线段中随机抽出一条,与长为2,3的两条线段首尾顺次相接,能构成三角形的概率是.【分析】先写出3种等可能的结果数,然后根据三角形三边的关系确定三条线段能构成三角形的结果数,再根据概率公式求解.【解答】解:共有3种等可能的结果数,它们是:2、3、3,2、3、4,2、3、5,其中三条线段能构成三角形的结果数为2种,所以能构成三角形的概率=.故答案为:.13.小亮测得一圆锥模型的底面直径为10cm,母线长为7cm,那么它的侧面展开图的面积是35πcm2.【分析】首先求得圆锥的底面周长,然后利用扇形的面积公式S=lr即可求解.【解答】解:底面周长是:10π,则侧面展开图的面积是:×10π×7=35πcm2.故答案是:35π.14.如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为.【分析】分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,先根据全等三角形的判定定理得出△BCE≌△ACF,故可得出CF及CE的长,在Rt△ACF中根据勾股定理求出AC的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD的长,在Rt△BCD中根据勾股定理即可求出BD的长.【解答】解:别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,∵△ABC是等腰直角三角形,∴AC=BC,∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,∴∠EBC=∠ACF,∠BCE=∠CAF,在△BCE与△ACF中,∴△BCE≌△ACF(ASA)∴CF=BE,CE=AF,∵l1与l2的距离为1,l2与l3的距离为3,∴CF=BE=3,CE=AF=3+1=4,在Rt△ACF中,∵AF=4,CF=3,∴AC=5,∵AF⊥l3,DG⊥l3,∴△CDG∽△CAF,∴,∴∴在Rt△BCD中,∵CD=,BC=5,所以BD==.故答案为:.15.抛物线y=﹣x2+2x+8与x轴交于B、C两点,点D平分BC,且点A为抛物线上的点,且∠BAC为锐角,则AD的值范围为3<x≤9 .【分析】由“∠BAC为锐角”可知点A在以定线段BC为直径的圆外,又点A在x轴上侧,从而可确定动点A的范围.【解答】解:如图,∵抛物线y=﹣x2+2x+8,∴抛物线的顶点为A0(1,9),对称轴为x=1,与x轴交于两点B(﹣2,0)、C(4,0),分别以BC、DA为直径作⊙D、⊙E,则两圆与抛物线均交于两点P(1﹣2,1)、Q(1+2,1).可知,点A在不含端点的抛物线内时,∠BAC<90°,且有3=DP=DQ<AD≤DA0=9,即AD的取值范围是3<AD≤9.则A的横坐标取值范围是3<x≤9.故答案为:3<x≤9.16.如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,若BD=3,CD=2.则△ABC的面积为15 .【分析】将△ABD绕着点A逆时针旋转90°,得△AFQ,延长FQ,BC,交于点E,连接CQ,判定△BAC≌△QAC(SAS),得到BC=CQ=BD+CD=5,再设AD=x,在Rt△CQE中,运用勾股定理列出关于x的方程,求得x的值,最后根据△ABC的面积=×BC×AD,进行计算即可【解答】解:如图,将△ABD绕着点A逆时针旋转90°,得△AFQ,延长FQ,BC,交于点E,连接CQ,由旋转可得,△ABD≌△AQF,∴AB=AQ,∠BAD=∠FAQ,BD=QF=3,∠F=∠ADC=∠DAF=90°=∠E,∵∠BAC=45°,∴∠BAD+∠DAC=45°,∴∠DAC+∠FAQ=45°,又∵∠DAF=90°,∴∠CAQ=45°,∴∠BAC=∠CAQ.且AB=AQ,AC=AC∴△BAC≌△QAC(SAS),∴BC=CQ=BD+CD=5,设AD=x,则QE=x﹣3,CE=x﹣2.在Rt△CQE中,CE2+QE2=CQ2∴(x﹣2)2+(x﹣3)2=52解得:x1=6,x2=﹣1(舍去),∴AD=6,∴△ABC的面积为=×BC×AD=15故答案为:15三.解答题(共10小题)17.计算或化简:(1)(2)【分析】(1)直接利用特殊角的三角函数值以及零指数幂的性质、二次根式的性质分别化简得出答案;(2)首先利用分式的混合运算法则进而化简得出答案.【解答】解:(1)原式=﹣2+2×+1=﹣2++1=1;(2)原式=1﹣×=1﹣=﹣.18.解方程:+=1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:(x+1)(x+1)﹣4=x2﹣1,解得:x=1,经检验x=1是分式方程的增根,∴原分式方程无解.19.图书馆是一个很好的学习平台,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图.(1)在统计的这段时间内,共有16 万人次到图书馆阅读,其中商人占百分比为12.5 %.(2)将条形统计图补充完整.(3)5月份到图书馆的读者共有24000人次,根据以上调查结果,估计24000人次中是职工的人次.【分析】(1)利用到图书馆阅读的人数=学生的人数÷学生的百分比求解,商人占百分比=商人数÷总人数求解即可,(2)求出职工到图书馆阅读的人数,作图即可,(3)利用总人数乘读者是职工的人数所占的百分比求解即可.【解答】解:(1)在统计的这段时间内,到图书馆阅读的人数为4÷25%=16(万人),其中商人占百分比为×100%=12.5%;故答案为:16;12.5;(2)职工:16﹣4﹣2﹣4=6(万人),如图所示:(3)估计24000人次中是职工的人次为24000×=9000(人次).20.如图,E是AC上一点,AB=CE,AB∥CD,AC=CD.求证:BC=ED.【分析】要证明BC=ED,只要证明△ABC≌△CED即可,根据题意目中的条件和平行线的性质可以得到证明两个三角形全等的条件,本题得以解决.【解答】证明:∵AB∥CD,∴∠A=∠ECD,在△ABC和△CED中,,∴△ABC≌△CED(SAS),∴BC=ED.21.有四张仅一面分别标有1,2,3,4的不透明纸片,除所标数字不同外,其余都完全相同.(1)将四张纸片分成两组,标有1、3的为第一组,标有2、4的为第二组,背面向上,放在桌上,从两组中各随机抽取一张,求两次抽取数字和为5的概率;(2)将四张纸片洗匀后背面向上,放在桌上,一次性从中随机抽取两张,用树形图法或列表法,求所抽取数字和为5的概率.【分析】(1)应用列表法,求出两次抽取数字和为5的概率是多少即可.(2)应用列表法,求出所抽取数字和为5的概率是多少即可.【解答】解:(1)1 32 (1,2)(3,2)4 (1,4)(3,4)∵共有4种可能性,且每种可能性都相同,数字和为5有两种可能性,∴两次抽取数字和为5的概率为:=.(2)1 2 3 41 ﹣﹣(2,1)(3,1)(4,1)2 (1,2)﹣﹣(3,2)(4,2)3 (1,3)(2,3)﹣﹣(4,3)4 (1,4)(2,4)(3,4)﹣﹣∵共有12种可能性,且每种可能性都相同,数字和为5的有4种可能性,∴抽取数字和为5概率为:=.22.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sin A=时,求AF的长.【分析】(1)连接OE,BE,因为DE=EF,所以=,从而易证∠OEB=∠DBE,所以OE∥BC,从可证明BC⊥AC;(2)设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sin A===,从而可求出r的值.【解答】解:(1)连接OE,BE,∵DE=EF,∴=,∴∠OBE=∠DBE,∵OE=OB,∴∠OEB=∠OBE,∴∠OEB=∠DBE,∴OE∥BC,∵⊙O与边AC相切于点E,∴OE⊥AC,∴BC⊥AC,∴∠C=90°;(2)在△ABC,∠C=90°,BC=3,sin A=,∴AB=5,设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sin A===,∴r=,∴AF=5﹣2×=.23.如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(1)求DE与水平桌面(AB所在直线)所成的角;(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)【分析】(1)直接作出平行线和垂线进而得出∠EDF的值;(2)利用锐角三角函数关系得出DN以及EF的值,进而得出答案.【解答】解:(1)如图所示:过点D作DF∥AB,过点D作DN⊥AB于点N,EF⊥AB于点M,由题意可得,四边形DNMF是矩形,则∠NDF=90°,∵∠A=60°,∠AND=90°,∴∠ADN=30°,∴∠EDF=135°﹣90°﹣30°=15°,即DE与水平桌面(AB所在直线)所成的角为15°;(2)如图所示:∵∠ACB=90°,∠A=60°,AB=16cm,∴∠ABC=30°,则AC=AB=8cm,∵灯杆CD长为40cm,∴AD=48cm,∴DN=AD•cos30°≈41.76cm,则FM=41.76cm,∵灯管DE长为15cm,∴sin15°===0.26,解得:EF=3.9,故台灯的高为:3.9+41.76≈45.7(cm).24.近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%.某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的,两种猪肉销售的总金额比5月20日提高了a%,求a的值.【分析】(1)设今年年初猪肉价格为每千克x元;根据题意列出一元一次不等式,解不等式即可;(2)设5月20日两种猪肉总销量为1;根据题意列出方程,解方程即可.【解答】解:(1)设今年年初猪肉价格为每千克x元;根据题意得:2.5×(1+60%)x≥100,解得:x≥25.答:今年年初猪肉的最低价格为每千克25元;(2)设5月20日两种猪肉总销量为1;根据题意得:40(1﹣a%)×(1+a%)+40×(1+a%)=40(1+a%),令a%=y,原方程化为:40(1﹣y)×(1+y)+40×(1+y)=40(1+y),整理得:5y2﹣y=0,解得:y=0.2,或y=0(舍去),则a%=0.2,∴a=20;答:a的值为20.25.如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.(1)求二次函数的解析式;(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.①求点P的运动路程;②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结EF,求△PEF周长的最小值.【分析】(1)利用tan∠ABC=3,得出C点坐标,再利用待定系数法求出二次函数解析式;(2)①当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC中点K,则P的运动路程为△ABC的中位线HK,再利用勾股定理得出答案;②首先利用等腰三角形的性质得出∠PAE=∠PEA=∠EPD,同理可得:∠PAF=∠PFA=∠DPF,进而求出∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即可得出答案;(3)首先得出C△PEF=AD+EF,进而得出EG=PE,EF=PE=AD,利用C△PEF=AD+EF =(1+)AD=AD,得出最小值即可.【解答】解:(1)∵函数y=ax2+bx+c与x轴交于A、B两点,且一元二次方程ax2+bx+c =0两根为:﹣8,2,∴A(﹣8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,﹣6),将A(﹣8,0)、B(2,0)代入y=ax2+bx﹣6中,得:,解得:,∴二次函数的解析式为:y=x2+x﹣6;(2)①如图1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC中点K,∴P的运动路程为△ABC的中位线HK,∴HK=BC,在Rt△BOC中,OB=2,OC=6,∴BC=2,∴HK=,即P的运动路程为:;②∠EPF的大小不会改变,理由如下:如图2,∵DE⊥AB,∴在Rt△AED中,P为斜边AD的中点,∴PE=AD=PA,∴∠PAE=∠PEA=∠EPD,同理可得:∠PAF=∠PFA=∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;(3)设△PEF的周长为C,则C△PEF=PE+PF+EF,∵PE=AD,PF=AD,∴C△PEF=AD+EF,在等腰三角形PEF中,如图2,过点P作PG⊥EF于点G,∴∠EPG=∠EPF=∠BAC,∵tan∠BAC==,∴tan∠EPG==,∴EG=PE,EF=PE=AD,∴C△PEF=AD+EF=(1+)AD=AD,又当AD⊥BC时,AD最小,此时C△PEF最小,又S△ABC=30,∴BC×AD=30,∴AD=3,∴C△PEF最小值为:AD=.26.(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①的值为 1 ;②∠AMB的度数为40°.(2)类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.【分析】(1)①证明△COA≌△DOB(SAS),得AC=BD,比值为1;②由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理得:∠AMB=180°﹣(∠DBO+∠OAB+∠ABD)=40°;(2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则=,由全等三角形的性质得∠AMB的度数;(3)正确画图形,当点C与点M重合时,有两种情况:如图3和4,同理可得:△AOC ∽△BOD,则∠AMB=90°,,可得AC的长.【解答】解:(1)问题发现①如图1,∵∠AOB=∠COD=40°,∴∠COA=∠DOB,∵OC=OD,OA=OB,∴△COA≌△DOB(SAS),∴AC=BD,∴=1,②∵△COA≌△DOB,∴∠CAO=∠DBO,∵∠AOB=40°,∴∠OAB+∠ABO=140°,在△AMB中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD)=180°﹣(∠DBO+∠OAB+∠ABD)=180°﹣140°=40°,故答案为:①1;②40°;(2)类比探究如图2,=,∠AMB=90°,理由是:Rt△COD中,∠DCO=30°,∠DOC=90°,∴,同理得:,∴,∵∠AOB=∠COD=90°,∴∠AOC=∠BOD,∴△AOC∽△BOD,∴=,∠CAO=∠DBO,在△AMB中,∠AMB=180°﹣(∠MAB+∠ABM)=180°﹣(∠OAB+∠ABM+∠DBO)=90°;(3)拓展延伸①点C与点M重合时,如图3,同理得:△AOC∽△BOD,∴∠AMB=90°,,设BD=x,则AC=x,Rt△COD中,∠OCD=30°,OD=1,∴CD=2,BC=x﹣2,Rt△AOB中,∠OAB=30°,OB=,∴AB=2OB=2,在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,,x2﹣x﹣6=0,(x﹣3)(x+2)=0,x1=3,x2=﹣2,∴AC=3;②点C与点M重合时,如图4,同理得:∠AMB=90°,,设BD=x,则AC=x,在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,+(x+2)2=x2+x﹣6=0,(x+3)(x﹣2)=0,x1=﹣3,x2=2,∴AC=2;综上所述,AC的长为3或2.。
2020届陕西省中考数学模拟试卷(有答案)(Word版)(已审阅)

陕西省中考数学试卷一、选择题(本大题共10小题,每小题3分,共30分)1.计算:21()12--==( ) A .54-B .14-C .34- D .0 【答案】C . 【解析】 试题分析:原式=14﹣1=34-,故选C . 考点:有理数的混合运算.2.如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )A .B .C .D .【答案】B . 【解析】试题分析:从正面看下边是一个较大的矩形,上便是一个角的矩形,故选B . 考点:简单组合体的三视图.3.若一个正比例函数的图象经过A (3,﹣6),B (m ,﹣4)两点,则m 的值为( ) A .2 B .8 C .﹣2 D .﹣8 【答案】A . 【解析】考点:一次函数图象上点的坐标特征.4.如图,直线a ∥b ,Rt △ABC 的直角顶点B 落在直线a 上,若∠1=25°,则∠2的大小为( )A .55°B .75°C .65°D .85°【答案】C . 【解析】试题分析:∵∠1=25°,∴∠3=90°﹣∠1=90°﹣25°=65°.∵a ∥b ,∴∠2=∠3=65°.故选C .考点:平行线的性质. 5.化简:x xx y x y--+,结果正确的是( ) A .1 B .2222x y x y +- C . x y x y-+ D .22x y + 【答案】B . 【解析】试题分析:原式=2222x xy xy y x y +-+- =2222x y x y +-.故选B .考点:分式的加减法.6.如图,将两个大小、形状完全相同的△ABC 和△A ′B ′C ′拼在一起,其中点A ′与点A 重合,点C ′落在边AB 上,连接B ′C .若∠ACB =∠AC ′B ′=90°,AC =BC =3,则B ′C 的长为( )A .33B .6C . 32D 21 【答案】A . 【解析】试题分析:∵∠ACB =∠AC ′B ′=90°,AC =BC =3,∴AB 22AB BC +=32CAB =45°,∵△ABC和△A ′B ′C ′大小、形状完全相同,∴∠C ′AB ′=∠CAB =45°,AB ′=AB =32,∴∠CAB ′=90°,∴B ′C 22'CA B A +33A . 考点:勾股定理.7.如图,已知直线l 1:y =﹣2x +4与直线l 2:y =kx +b (k ≠0)在第一象限交于点M .若直线l 2与x 轴的交点为A (﹣2,0),则k 的取值范围是( )A.﹣2<k<2B.﹣2<k<0C.0<k<4D.0<k<2【答案】D.【解析】考点:两条直线相交或平行问题;一次函数图象上点的坐标特征.8.如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为()A.3102B.3105C.105D.355【答案】B.【解析】考点:相似三角形的判定与性质;矩形的性质.9.如图,△ABC 是⊙O 的内接三角形,∠C =30°,⊙O 的半径为5,若点P 是⊙O 上的一点,在△ABP 中,PB =AB ,则P A 的长为( )A .5B .532C . 52D .53 【答案】D . 【解析】试题分析:连接OA 、OB 、OP ,∵∠C =30°,∴∠APB =∠C =30°,∵PB =AB ,∴∠P AB =∠APB =30° ∴∠ABP =120°,∵PB =AB ,∴OB ⊥AP ,AD =PD ,∴∠OBP =∠OBA =60°,∵OB =OA ,∴△AOB 是等边三角形,∴AB =OA =5,则Rt △PBD 中,PD =cos30°•PB =32×5=532,∴AP =2PD =53,故选D .考点:三角形的外接圆与外心;等腰三角形的性质.10.已知抛物线224y x mx =--(m >0)的顶点M 关于坐标原点O 的对称点为M ′,若点M ′在这条抛物线上,则点M 的坐标为( )A .(1,﹣5)B .(3,﹣13)C .(2,﹣8)D .(4,﹣20) 【答案】C . 【解析】试题分析:224y x mx =--=22()4x m m ---,∴点M (m ,﹣m 2﹣4),∴点M ′(﹣m ,m 2+4),∴m 2+2m 2﹣4=m 2+4.解得m =±2.∵m >0,∴m =2,∴M (2,﹣8).故选C . 考点:二次函数的性质.二、填空题(本大题共4小题,每小题3分,共12分)11.在实数﹣5,﹣3,0,π,6中,最大的一个数是 . 【答案】π. 【解析】考点:实数大小比较.12.请从以下两个小题中任选一个作答,若多选,则按第一题计分.A.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠1+∠2的度数为.B.317tan38°15′≈.(结果精确到0.01)【答案】A.64°;B.2.03.【解析】考点:计算器—三角函数;计算器—数的开方;三角形内角和定理.13.已知A,B两点分别在反比例函数3myx=(m≠0)和25myx-=(m≠52)的图象上,若点A与点B 关于x轴对称,则m的值为.【答案】1.【解析】试题分析:设A(a,b),则B(a,﹣b),依题意得:325mbamba⎧=⎪⎪⎨-⎪-=⎪⎩,所以325m ma+-=0,即5m﹣5=0,解得m=1.故答案为:1.考点:反比例函数图象上点的坐标特征;关于x轴、y轴对称的点的坐标.14.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为.【答案】18. 【解析】∴四边形ABCD 的面积=正方形AMCN 的面积; 由勾股定理得:AC 2=AM 2+MC 2,而AC =6; ∴2λ2=36,λ2=18,故答案为:18.考点:全等三角形的判定与性质.三、解答题(本大题共11小题,共78分)15.计算:11(2)6|32|()2---. 【答案】33- 【解析】试题分析:根据二次根式的性质以及负整数指数幂的意义即可求出答案. 试题解析:原式=12232+=233-=33- 考点:二次根式的混合运算;负整数指数幂. 16.解方程:32133x x x +-=-+. 【答案】x =﹣6.【解析】试题分析:利用解分式方程的步骤和完全平方公式,平方差公式即可得出结论.试题解析:去分母得,(x+3)2﹣2(x﹣3)=(x﹣3)(x+3),去括号得,x2+6x+9﹣2x+6=x2﹣9,移项,系数化为1,得x=﹣6,经检验,x=﹣6是原方程的解.考点:解分式方程.17.如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)【答案】作图见解析.【解析】考点:作图—基本作图.18.养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.请你根据以上提供的信息,解答下列问题:(1)补全频数分布直方图和扇形统计图;(2)所抽取的七年级学生早锻炼时间的中位数落在区间内;(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)【答案】(1)作图见解析;(2)C;(3)1020.【解析】百分比为1﹣(5%+10%+65%)=20%,补全图形如下:(2)由于共有200个数据,其中位数是第100、101个数据的平均数,则其中位数位于C区间内,故答案为:C;(3)1200×(65%+20%)=1020(人).答:估计这个年级学生中约有1020人一天早锻炼的时间不少于20分钟.考点:频数(率)分布直方图;用样本估计总体;扇形统计图;中位数.19.如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.【答案】证明见解析.【解析】试题分析:根据正方向的性质,可得∠ADF=CDE=90°,AD=CD,根据全等三角形的判定与性质,可得答案.考点:正方形的性质;全等三角形的判定与性质.20.某市一湖的湖心岛有一颗百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A 处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)【答案】34米.【解析】试题分析:作BD⊥MN,CE⊥MN,垂足分别为点D、E,设AN=x米,则BD=CE=x米,再由锐角三角函数的定义即可得出结论.试题解析:如图,作BD⊥MN,CE⊥MN,垂足分别为点D、E,设AN=x米,则BD=CE=x米,在Rt△MBD 中,MD=x•tan23°,在Rt△MCE中,ME=x•tan24°,∵ME﹣MD=DE=BC,∴x•tan24°﹣x•tan23°=1.7﹣1,∴x=0.7tan24tan23o o,解得x≈34(米).答:“聚贤亭”与“乡思柳”之间的距离AN的长约为34米.考点:解直角三角形的应用﹣仰角俯角问题.21.在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.根据以上提供的信息,请你解答下列问题:(1)求出y与x之间的函数关系式;(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.【答案】(1)y=7500x+68000;(2)5.【解析】试题分析:(1)利用总利润=种植香瓜的利润+种植甜瓜的利润即可得出结论;(2)利用(1)得出的结论大于等于100000建立不等式,即可确定出结论.试题解析:(1)由题意得,y=(2000×12﹣8000)x+(4500×3﹣5000)(8﹣x)=7500x+68000;(2)由题意得,7500x+6800≥100000,∴x≥4415,∵x为整数,∴李师傅种植的8个大棚中,香瓜至少种植5个大棚.考点:一次函数的应用;最值问题.22.端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.根据以上情况,请你回答下列问题:(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.【答案】(1)12;(2)316.【解析】(A,A)、(A,B)、(A,C)、(A,C)、(A,A)、(A,B)、(A,C)、(A,C)、(B,A)、(B,B)、(B,C)、(B,C)、(C,A)、(C,B)、(C,C)、(C,C),∴小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率是:3 16.考点:列表法与树状图法;概率公式.23.如图,已知⊙O的半径为5,P A是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时.(1)求弦AC的长;(2)求证:BC∥P A.【答案】(1)53;(2)证明见解析.【解析】在Rt△ODA中,AD=OA•sin6053,∴AC=2AD=53;(2)∵AC⊥PB,∠P=30°,∴∠P AC=60°,∵∠AOP=60°,∴∠BOA=120°,∴∠BCA=60°,∴∠P AC=∠BCA,∴BC∥P A.考点:切线的性质.24.在同一直角坐标系中,抛物线y=ax2﹣2x﹣3与抛物线y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.(1)求抛物线C1,C2的函数表达式;(2)求A、B两点的坐标;(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q 四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.【答案】(1)C1的函数表示式为y=x2﹣2x﹣3,C2的函数表达式为y=x2+2x﹣3;(2)A(﹣3,0),B(1,0);(3)存在满足条件的点P、Q,其坐标为P(﹣2,5),Q(2,5)或P(﹣2,﹣3),Q(2,﹣3).【解析】试题分析:(1)由对称可求得a、n的值,则可求得两函数的对称轴,可求得m的值,则可求得两抛物线的函数表达式;(2)由C2的函数表达式可求得A、B的坐标;(3)由题意可知AB只能为平行四边形的边,利用平行四边形的性质,可设出P点坐标,表示出Q点坐标,代入C2的函数表达式可求得P、Q的坐标.试题解析:(t+4,t2﹣2t﹣3)或(t﹣4,t2﹣2t﹣3),①当Q(t+4,t2﹣2t﹣3)时,则t2﹣2t﹣3=(t+4)2+2(t+4)﹣3,解得t=﹣2,∴t2﹣2t﹣3=4+4﹣3=5,∴P(﹣2,5),Q(2,5);②当Q(t﹣4,t2﹣2t﹣3)时,则t2﹣2t﹣3=(t﹣4)2+2(t﹣4)﹣3,解得t=2,∴t2﹣2t﹣3=4﹣4﹣3=﹣3,∴P(﹣2,﹣3),Q(2,﹣3),综上可知存在满足条件的点P、Q,其坐标为P(﹣2,5),Q(2,5)或P(﹣2,﹣3),Q(2,﹣3).考点:二次函数综合题;存在型;分类讨论;轴对称的性质.25.问题提出(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为;问题探究(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.问题解决(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.»AB于点E,如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交又测得DE=8m.请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)【答案】(1)43;(2)PQ =122;(3)喷灌龙头的射程至少为19.71米.【解析】试题分析:(1)构建Rt △AOD 中,利用cos ∠OAD =cos30°=AD OA,可得OA 的长; (2)经过矩形对角线交点的直线将矩形面积平分,根据此结论作出PQ ,利用勾股定理进行计算即可;(3)如图3,作辅助线,先确定圆心和半径,根据勾股定理计算半径:在Rt △AOD 中,由勾股定理解得:r =13根据三角形面积计算高MN 的长,证明△ADC ∽△ANM ,列比例式求DC 的长,确定点O 在△AMB 内部,利用勾股定理计算OM ,则最大距离FM 的长可利用相加得出结论. 试题解析:(1)如图1,过O 作OD ⊥AC 于D ,则AD =12AC =12×12=6,∵O 是内心,△ABC 是等边三角形,∴∠OAD =12∠BAC =12×60°=30°,在Rt △AOD 中,cos ∠OAD =cos30°=AD OA,∴OA =6÷32=43,故答案为:43;(r ﹣8)2,解得:r =13,∴OD =5,过点M 作MN ⊥AB ,垂足为N ,∵S △ABM =96,AB =24,∴12AB •MN =96,12×24×MN =96,∴MN =8,NB =6,AN =18,∵CD ∥MN ,∴△ADC ∽△ANM ,∴DC AD MN AN =,∴12818DC ,∴DC =163,∴OD <CD ,∴点O 在△AMB 内部,∴连接MO 并延长交»AB 于点F ,则MF 为草坪上的点到M 点的最大距离,∵在»AB 上任取一点异于点F 的点G ,连接GO ,GM ,∴MF =OM +OF =OM +OG >MG ,即MF >MG ,过O 作OH ⊥MN ,垂足为H ,则OH =DN =6,MH =3,∴OM 22MH OH +2236+=35,∴MF=OM+r=35+13≈19.71(米).答:喷灌龙头的射程至少为19.71米.考点:圆的综合题;最值问题;存在型;阅读型;压轴题.。
2020年中考语文模拟试卷3(部编版,含答案)

2020年中考语文模拟试卷3(部编版,含答案)2020年中考语文模拟试卷3一、积累和运用(共6小题,计17分)1.下列各组词语中,加点字读音全都正确的一组是(2分)()..A.糟糕(zāo)坎坷(kē)服侍(sì)任劳任怨(yuàn)....B.游弋(yì)囫囵(hú)阔绰(chuò)随声附和(hé)....C.哄笑(hōng)XXX(wā)束缚(fú)诲人不倦(huǐ)....D.模拟(mó)洗涤(dí)枯燥(zào)大发雷霆(tíng)....2.下列各组词语中,汉字书写全都正确的一组是(2分)()..A.愕然滞碍抑扬顿挫浑为一谈B.筹画怅惘巧妙绝伦物竟天择C.热忱隽刻草长莺飞根深谛固D.妩媚旁骛沥尽心血混乱无章3.请从所给的三个词语中,选出一个最符合语境的填写在横线上。
(2分)(1)感动书香,薄薄的书页间是千年文化的浓缩和________(沉淀积累积淀),浓浓的墨香中承载着历史的厚重与古朴。
(2)中国进入高铁时代,不断增长的大长隧道建设,呼唤着一场________(百废待兴如火如荼风云突变)的技术革命。
4.经典诗文默写。
[在第(1)~(7)题中,任选五题;在第(8)~(10)题中,任选一题](6分)........(1)安得广厦千万间,________________!(XXX《茅屋为秋风所破歌》)(2)晴川历历汉阳树,________________。
(XXX《黄鹤楼》)(3)________________,风掣红旗冻不翻。
(XXX《白雪歌送武判官归京》)(4)半卷红旗临易水,________________。
(XXX《雁门太守行》)(5)千古兴亡多少事?悠悠。
________________。
(XXX《南乡子·登京口北固亭有怀》)(6)____________________________,必先苦其心志,劳其筋骨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考冲刺试卷
*考试时间120分钟 试卷满分150分
一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分) 1.|65-|=( ) A .65+
B .65-
C .-65-
D .56-
2.如果一个四边形ABCD 是中心对称图形,那么这个四边形一定是( ) A .等腰梯形 B .矩形 C .菱形 D .平行四边形 3. 下面四个数中,最大的是( )
A .35-
B .sin88°
C .tan46°
D .
2
1
5- 4.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( ) A .4 B .5 C .6 D .10 5.二次函数y=(2x-1)2
+2的顶点的坐标是( ) A .(1,2) B .(1,-2) C .(
21,2) D .(-2
1
,-2) 6.足球比赛中,胜一场可以积3分,平一场可以积1分,负一场得0分,
某足球队最后的积分是17分,他获胜的场次最多是( ) A .3场 B .4场 C .5场 D .6场 7. 如图,四边形ABCD 的对角线AC 和BD 相交于点E ,如果△CDE 的面积为3,△BCE 的面积为4,△AED 的面积为6,那么△ABE 的面积为
( ) A .7 B .8 C .9 D .10
8. 如图,△ABC 内接于⊙O,AD 为⊙O 的直径,交BC 于点E ,
若DE =2,OE =3,则tanC·tanB = ( )
A .2
B .3
C .4
D .5 二、填空题(每小题3分,共24分)
9.写出一条经过第一、二、四象限,且过点(1-,3)的直线解析式 . 10.一元二次方程x2
=5x的解为 .
11. 凯恩数据是按照某一规律排列的一组数据,它的前五个数是:26
9
,177,21,53,31,按照
这样的规律,这个数列的第8项应该是 . 12.一个四边形中,它的最大的内角不能小于 . 13.二次函数x x y 22
12
+-=,当x 时,0<y ;且y 随x 的增大而减小.
14. 如图,△ABC 中,BD 和CE 是两条高,如果∠A =45°,则BC
DE
= . 15.如图,已知A 、B 、C 、D 、E 均在⊙O 上,且AC 为 ⊙O 的直径,则∠A +∠B +∠C =__________度. 16.如图,矩形ABCD 的长AB =6cm ,宽AD =3cm. O 是AB 的中点,OP ⊥AB ,两半圆的直径分别为AO 与OB .抛物线y=ax2
经过C 、D 两点,则图中阴影部分 的面积是 cm 2.
三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分) 17.计算:01
)32009(22
1
245cos 4)
2
1
(8--⨯÷-︒-+-
18.计算:2211
1211x x x x ⎛⎫-+÷ ⎪
-+-⎝⎭
O
E
D
C
B A A
C B
D P
O
x
y
19.已知:如图,梯形ABCD 中,A B ∥CD ,E 是BC 的中点,直线AE 交DC 的延长线于点F .
(1)求证:△ABE ≌△FCE ; (2)若BC ⊥AB ,且BC =16,AB =17,求AF 的长.
20.观察下面方程的解法 x4-13x2
+36=0
解:原方程可化为(x2-4)(x2
-9)=0 ∴(x+2)(x-2)(x+3)(x-3)=0 ∴x+2=0或x-2=0或x+3=0或x-3=0 ∴x1=2,x2=-2,x3=3,x4=-3 你能否求出方程x2
-3|x|+2=0的解?
四、(每小题10分,共20分)
21.(1)顺次连接菱形的四条边的中点,得到的四边形是.(2)顺次连接矩形的四条边的中点,得到的四边形是.
(3)顺次连接正方形的四条边的中点,得到的四边形是.
(4)小青说:顺次连接一个四边形的各边的中点,得到的一个四边形如果是正方形,那么原来的四边形一定是正方形,这句话对吗?请说明理由.
22.下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
(1)李刚同学6次成绩的极差是.
(2)李刚同学6次成绩的中位数是.
(3)李刚同学平时成绩的平均数是.
(4)如果用右图的权重给李刚打分,他应该得多少分?
(满分100分,写出解题过程)
23.(本题12分)某射击运动员在一次比赛中,前6次射击已经得到52环,该项目的记录是89环(10次射击,每次射击环数只取1~10中的正整数).
(1)如果他要打破记录,第7次射击不能少于多少环?
(2)如果他第7次射击成绩为8环,那么最后3次射击中要有几次命中10环才能打破记录?
(3)如果他第7次射击成绩为10环,那么最后3次射击中是否必须至少有一次命中10环才有可能打破记录?
24.(本题12分)甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C 处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离
(2)甲轮船后来的速度.
25.(本题12分)如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒. (1) 求直线AB 的解析式;
(2) 当t 为何值时,△APQ 与△AOB 相似?
(3) 当t 为何值时,△APQ 的面积为
524个平方单位?
26.(本题14分)如图,直线y= -x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线与x轴的另一交点为A,顶点为P,且
对称轴为直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、
B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q
的坐标;若不存在,请说明理由.。
