化学晶胞计算
化学晶胞计算知识点归纳

1.“均摊法”确定晶体的化学式
(1)原则:晶胞任意位置上的一个粒子如果是被n个晶胞所共有,那么每个晶胞对这个粒子分得的份额就是1/n
①长方体(包括立方体)晶胞中不同位置的粒子数的计算
顶点:为8个晶胞共有,1/8属于该晶胞。
棱:为4个晶胞共有,1/4属于该晶胞。
面心:为2个晶胞共有,1/2属于该晶胞
体心:处于晶胞内部,全部属于该晶胞
②非长方体晶胞中粒子视具体情况而定。
如石墨晶胞每一层内碳原子排成六边形,其顶点(1个碳原子)被三个六边形共有,每个六边形占1/3;当晶胞为六棱柱时,其顶点上的粒子被6个晶胞共用,每个粒子属于该晶胞的部分为1/6,而不是1/8。
注意:审题时一定要注意是“分子结构”还是“晶体结构”,若是分子结构,其化学式由图中所有实际存在的原子个数决定,且原子个数可以不互质(即原子个数比可以不约简)。
2.晶体密度、晶胞体积和晶胞参数(晶胞边长)的求算
对于立方晶胞,可建立如下求算途径:。
晶胞摩尔体积计算公式

晶胞摩尔体积计算公式晶胞摩尔体积计算公式是一个用来计算晶体原子数密度和晶体容积的公式。
许多科学家和工程师都熟悉这个公式,但它也有一些令人混淆的方面。
本文旨在介绍这种公式,以深入了解它的基本原理和应用。
晶胞摩尔体积的概念是由P.W. Anderson在1937年提出的,它是一种在晶体中表示原子数密度的方法,可以用于预测晶体容积。
它通过描述晶体中固定晶胞的体积来计算晶体的原子数密度。
具体来说,它的公式为:V=(N/4π) * (a/h)^3其中,V表示晶胞体积,N表示晶体中原子的数量,a表示晶体中原子半径,h表示晶体中晶胞间距。
在计算晶胞摩尔体积时,最重要的一点就是准确估算晶体原子的数量。
为了确定此值,最常用的方法是从晶体样品中提取一枚样本,然后使用X射线衍射原理来确定原子数。
计算晶胞摩尔体积时还需要正确确定晶体原子的半径。
关于这一值,能够提供有效的估算值的有效工具是无结构X射线衍射(USAXS)仪器。
另外,X射线吸收光谱(XAS)也可以用来推断晶体原子半径。
最后,晶胞摩尔体积的计算还需要正确确定晶体的晶胞间距。
在这一步中,X射线衍射也起到了相当重要的作用。
X射线衍射可以用来确定晶胞间距,以及晶体的物相。
综上所述,可以看出,晶胞摩尔体积计算公式是一个重要的工具,它可以用来正确估算晶体容积和原子数密度。
它所用的各种技术也可以应用于原子结构的研究,如确定原子半径和晶体的物相,从而更深入地了解晶体结构。
此外,晶胞摩尔体积计算公式可以用于实际工程中,例如在石油、化学和建筑领域中,它可以帮助研究人员更准确地计算物质的容积和重量以及晶体原子数密度,从而更好地控制生产活动。
综上所述,晶胞摩尔体积计算公式是一种重要的工具,它可以准确估算晶体容积和原子数密度。
它的使用需要对晶体原子的数量、半径和晶胞间距有一个准确的估计。
在实际工程中,这种公式有助于计算物质的容积和重量,从而更好地控制生产活动。
高考化学大题逐空突破系列(全国通用)有关晶胞参数的计算 (附答案解析)
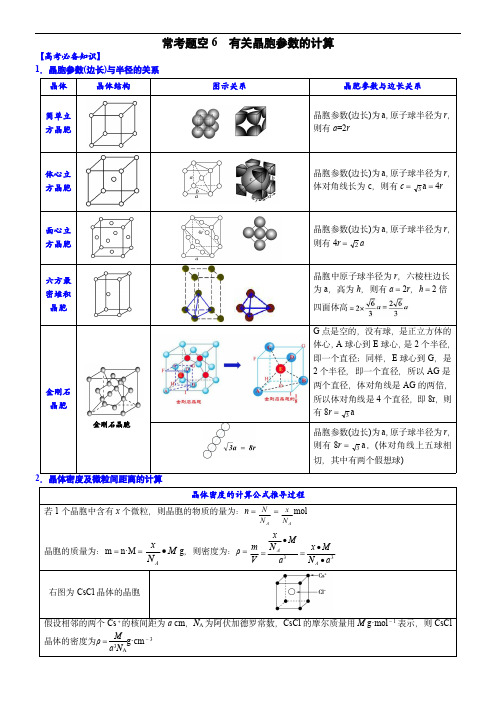
常考题空6有关晶胞参数的计算【高考必备知识】1.晶胞参数(边长)与半径的关系晶体晶体结构图示关系晶胞参数与边长关系简单立方晶胞晶胞参数(边长)为a ,原子球半径为r ,则有a =2r体心立方晶胞晶胞参数(边长)为a ,原子球半径为r ,体对角线长为c ,则有c =3a =4r面心立方晶胞晶胞参数(边长)为a ,原子球半径为r ,则有4r =2a六方最密堆积晶胞晶胞中原子球半径为r ,六棱柱边长为a ,高为h ,则有a =2r ,h =2倍四面体高金刚石晶胞金刚石晶胞G 点是空的,没有球,是正立方体的体心,A 球心到E 球心,是2个半径,即一个直径;同样,E 球心到G ,是2个半径,即一个直径,所以AG 是两个直径,体对角线是AG 的两倍,所以体对角线是4个直径,即8r ,则有8r =3a晶胞参数(边长)为a ,原子球半径为r ,则有8r =3a 。
(体对角线上五球相切,其中有两个假想球)2.晶体密度及微粒间距离的计算晶体密度的计算公式推导过程若1个晶胞中含有x 个微粒,则晶胞的物质的量为:n =AN N =AN x mol晶胞的质量为:m =n·M =M N x A g ,则密度为:ρ=33aN M x a MN xV m A A 右图为CsCl 晶体的晶胞假设相邻的两个Cs +的核间距为a cm ,N A 为阿伏加德罗常数,CsCl 的摩尔质量用M g·mol -1表示,则CsCl 晶体的密度为ρ=Ma 3N Ag·cm -33.金属晶体空间利用率的计算方法(1)空间利用率的定义及计算步骤①空间利用率(η):指构成晶体的原子、离子或分子总体积在整个晶体空间中所占有的体积百分比②%1003433a r V V 球数空间利用率晶胞球类型晶体结构示意图图示关系简单立方堆积原子的半径为r ,立方体的棱长为2r ,则V 球=43πr 3,V 晶胞=(2r )3=8r 3,空间利用率=V 球V 晶胞×100%=43πr 38r 3×100%=6 ≈52%体心立方晶胞原子的半径为r ,体对角线c 为4r ,面对角线b 为2a ,由(4r )2=a 2+b 2得a =43r 。
晶胞的计算

晶胞的计算一、晶胞在高考中的地位分析:2008、2009年新课标,未对晶胞的计算进行考查;2010年新课标:37(4),一空,化学式的计算;2011年新课标:37(5),三空,晶胞中原子个数及密度的计算;2012年新课标:37(6),两空,晶胞密度、离子距离的计算。
二、常见的晶胞计算题:第一类:金属堆积方式的简单计算(空间利用率和密度)[选三P76] 晶胞密度 =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100%【注】1m=10dm=102 cm=103 mm=106 um=109 nm=1012 pm①简单立方堆积:假设球的半径为r cm,则该堆积方式的空间利用率为:②体心立方堆积:假设球的半径为r cm,则该堆积方式的空间利用率为:③面心立方最密堆积:假设球的半径为r cm,则该堆积方式的空间利用率为:再假设该金属的摩尔质量为Mg/mol,N A为阿伏伽德罗常数的数值,试计算该晶胞的密度:【总结】必须掌握的常见晶胞及晶体结构分子晶体:干冰、冰晶胞图形、晶胞组成特点;原子晶体:金刚石(晶体硅)、二氧化硅晶胞组成特点、边长(体积、密度、原子最近距离)的计算方式;金属晶体:四种堆积方式的名称、图形、代表金属、边长(体积、密度、原子最近距离)的计算方式;离子晶体:NaCl、CsCl、CaF2晶胞图形、晶胞组成、边长(体积、密度、原子最近距离)的计算方式。
【练习】中学化学教材中展示了NaCl晶体结构,它向三维空间延伸得到完美晶体。
NiO(氧化镍)晶体的结构与NaCl 相同,Ni2+与最临近O2-的核间距离为 a cm,计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g/mol)。
(2)天然和绝大部分人工制备的晶体都存在各种缺陷,例如在某氧化镍晶体中就存在如图所示的缺陷:一个Ni2+空缺,另有两个Ni2+被两个Ni3+所取代。
其结果为晶体仍呈电中性,但化合物中Ni 和O的比值却发生了变化。
晶胞的计算

晶胞的计算一、晶胞在高考中的地位分析:2008、2009年新课标,未对晶胞的计算进行考查;2010年新课标:37(4),一空,化学式的计算;2011年新课标:37(5),三空,晶胞中原子个数及密度的计算;2012年新课标:37(6),两空,晶胞密度、离子距离的计算。
二、常见的晶胞计算题:第一类:金属堆积方式的简单计算(空间利用率和密度)[选三P76]晶胞密度 =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100%【注】1m=10dm=102 cm=103 mm=106 um=109 nm=1012 pm①简单立方堆积:假设球的半径为r cm,则该堆积方式的空间利用率为:②体心立方堆积:假设球的半径为r cm,则该堆积方式的空间利用率为:③面心立方最密堆积:假设球的半径为r cm,则该堆积方式的空间利用率为:再假设该金属的摩尔质量为Mg/mol,N A为阿伏伽德罗常数的数值,试计算该晶胞的密度:【总结】必须掌握的常见晶胞及晶体结构分子晶体:干冰、冰晶胞图形、晶胞组成特点;原子晶体:金刚石(晶体硅)、二氧化硅晶胞组成特点、边长(体积、密度、原子最近距离)的计算方式;金属晶体:四种堆积方式的名称、图形、代表金属、边长(体积、密度、原子最近距离)的计算方式;离子晶体:NaCl、CsCl、CaF2晶胞图形、晶胞组成、边长(体积、密度、原子最近距离)的计算方式。
【练习】中学化学教材中展示了NaCl晶体结构,它向三维空间延伸得到完美晶体。
NiO(氧化镍)晶体的结构与NaCl 相同,Ni2+与最临近O2-的核间距离为a cm,计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g/mol)。
(2)天然和绝大部分人工制备的晶体都存在各种缺陷,例如在某氧化镍晶体中就存在如图所示的缺陷:一个Ni2+空缺,另有两个Ni2+被两个Ni3+所取代。
其结果为晶体仍呈电中性,但化合物中Ni 和O的比值却发生了变化。
晶胞计算

1、顶点:一个立 方体的顶点由八 个相同的立方体 在共用,则平均 每个立方体只分 到其1/8.
晶胞中金属原子数目的计算方法(平均值)
1、顶点:一个立 方体的顶点由八 个相同的立方体 在共用,则平均 每个立方体只分 到其1/8. 2、面:1/2
晶胞中金属原子数目的计算方法(平均值)
例1:
右图是石英晶 体平面示意图(它实 际上是立体的网状结 构),其中硅、氧原 子数之比为____.
1:2
例2:
如图直线交点处 的圆圈为NaCl晶体中 Na+或Cl-所处位置, 晶体中,每个Na+周 围与它最接近的且距 离相等的Na+个数为: ____ 12
例3:
金刚石晶体中 含有共价键形成的 C原子环,其中最
钇________ 个
巩固练习五:
(1) 平均每个正六边形拥有_____个锗原2子, _____个氧原子.3
(2) 化学式为:_____(_G_e_C_H__2C__H_2_C_O_O__H_)2O3
或Ge2C6H10O7
巩固练习六:
某离子晶体的晶胞结构如右 图所示: ●表示X离子,位于立 方体的顶点;○表示Y离子,位 于立方体的中心。试分析: ①该晶体的化学式为 Y2X 。 ②晶体中距离最近的2个X与一 个Y形成的夹角为109028′ _____________
已知晶体的基本单元 是由12个硼原子构成的 (如右图),每个顶点上 有一个硼原子,每个硼原 子形成的化学键完全相同, 通过观察图形和推算,可 知此基本结构单元是一个 正_2_0__面体。
巩固练习四:
某晶胞结 构如图所示, 晶胞中各微粒 个数分别为:
铜___3_____ 个2
pm、nm、um、mm、cm间的换算及f读法

pm、nm、μm、mm、cm等之间的换算及读法现在重点记(化学晶胞计算用):1毫米(m m)=10丝米(dmm)1丝米(dmm)=10忽米(cmm)1忽米(cmm)=10微米(μm)1微米(μm)=1000纳米(nm)1纳米(n m)=1000皮米(pm)规律自上而下丝忽微纳皮3个10 两个千(1000)...以后记1:1毫米(m m)=10丝米(dmm)1丝米(dmm)=10忽米(cmm)1忽米(cmm)=10微米(μm)1微米(um)=1000纳米(nm)1纳米(nm)=1000皮米(pm)1皮米(pm)=1000飞米(fm)1飞米(f m)=1000阿米(am)复习记1米(m)=10分米(dm)1分米(dm)=10厘米(cm)1厘米(cm)=10毫米(mm)1毫米(m m)=10丝米(dmm)1丝米(dmm)=10忽米(cmm)1忽米(cmm)=10微米(μm)1微米(um)=1000纳米(nm)1纳米(nm)=1000皮米(pm)1皮米(pm)=1000飞米(fm)1飞米(f m)=1000阿米(am)1米(m)=10分米(dm)1分米(dm)=10厘米(cm)1厘米(cm)=10毫米(mm)1毫米(mm)=1000微米(μm)1微米(um)=1000纳米(nm)1纳米(nm)=1000皮米(pm)1皮米(pm)=1000飞米(fm)1飞米(fm)=1000阿米(am)简记2 ........1厘米(cm)=10毫米(mm)1毫米(mm)=1000微米(um)1微米((μm)=1000纳米(nm)1纳米(nm)=1000皮米(pm)1皮米(pm)=1000飞米(fm)1飞米(fm)=1000阿米(am)再说(下条较全).......1米(m)=10分米(dm)1分米(dm)=10厘米(cm)1厘米(cm)=10毫米(mm)1毫米(mm)=10丝米(dmm)1丝米(dmm)=10忽米(cmm)1忽米(cmm)=10微米(μm)1微米(μm)=1000纳米(nm)1纳米(nm)=1000皮米(pm)1皮米(pm)=1000飞米(fm)1飞米(fm)=1000阿米(am)其他回答1米(m)=10分米(dm)=10^2厘米(cm)=10^3毫米(mm)=10^6微米(um)= 10^9纳米(nm)=10^10埃米(A)=10^12皮米(pm)傻蛋二35 |发布于2014-06-20 22:52举报|评论最佳答案1(m)=10(dm)=10^2(cm)=10^3(mm)=10^6(um)=10^9(nm)=10^10(A)=10^12(pm)举报|评论怎么倒换算xibeizi122 |浏览2349 次发布于2011-10-21 08:50最佳答案m,dm,=10^-1mcm,=10^-2mμm,=10^-6mnm,=10^-9mpm,=10^-12m埃=10^-10m=0.1纳米满意请采纳O(∩_∩)O~本回答由提问者推荐评论180氯金酸采纳率:84% 来自团队:数学百分百擅长:教育/科学化学理工学科其他回答1厘米(cm)=10毫米(mm)1毫米(mm)=1000微米(um)1微米((μm)=1000纳米(nm)1纳米(nm)=1000皮米(pm)1皮米(pm)=1000飞米(fm)1飞米(fm)=1000阿米(am)长度是国际单位制(SI)中的七个基本物理量的量纲之一,符号L。
2024届高三化学二轮复习 热点强化练16 晶胞的相关计算

,则 Bi
1
2
3
4
5
6
2.(2023·河南商丘模拟节选)CIGS靶材是一种主要含铜、铟(In)、镓(Ga)、硒
(Se)的合金,由于其良好的电学传导和光学透明性被广泛用于薄膜太阳能电池
领域。回答下列问题。
四方晶系CuInSe2的晶胞结构如图所示,晶胞参数为a=b=m pm,c=2m pm,晶胞棱边
1
2
3
4
5
6
3.(2023·陕西铜川质量检测节选)钙钛矿型太阳能电池近年越来
越受到科学界的关注,其效率提升速度超越过去任何一类电池。某
种钙钛矿晶胞如图所示,则钙原子的配位数是 12 ,若阿伏加德
罗常数的值为NA,晶胞中钙原子与氧原子的最近距离为 a pm。则
+ + ×
该晶体的密度为
cm3。
解析:(3)氮化铁的化学式为 Fe4N,则晶胞质量 m=
3
则晶胞质量 m=ρV=ρa g=
3
g,a =
g,若晶胞边长为 a cm,
,Fe(Ⅱ)围成的八面体相当于两个正
四棱锥,底面为正方形,对角线长为晶胞边长,并且两对角线相互垂直,S 底=
2
2
3
与单个In键合的Se有 4 个。
1
2
3
4
5
6
解析:Cu 原子有 4 个位于棱上、6 个位于面上,故 Cu 原子的个数为 6× +4× =4,In 原
子有 8 个位于顶点上、4 个位于面上、1 个位于体心,故 In 原子的个数为 8× +4×
微专题19 晶胞参数、坐标参数的分析与应用

(2)晶胞有两个基本要素:①原子坐标参数,表示晶胞内部各 原子的相对位置,如图 2、3 为 Ge 单晶的晶胞,其中原子坐标参 数 A 为(0,0,0),B 为12,0,12 ,C 为12,12,0 。则 D 原子的
②体心立方堆积
设原子半径为 R,由于原子在晶胞体对角线方向上相切,可
以计算出晶胞参数:a=b=c=433 R,α=β=γ=90°。每
个晶胞中包含两个原子。
η=2×a433πR3 ×100%=24×433πRR33 ×100%≈68%。
3
③面心立方最密堆积
设原子半径为 R,由于原子在晶胞面对角线方向上相切,可 以计算出晶胞参数:a=b=c=2 2 R,α=β=γ=90°。每 个晶胞中包含四个原子。 η=4×a433πR3 ×100%=(42×432πRR)3 3 ×100%≈74%。 ④六方最密堆积
2.金属晶体空间利用率的计算方法
(1)空间利用率的定义及计算步骤
空间利用率(η):指构成晶体的原子、离子或分子总体积在整
个晶体空间中所占有的体积百分比。
晶胞中原子所占的总体积
空间利用率=
晶胞体积
×100%
(2)金属晶体空间利用率分类简析 ①简单立方堆积
设原子半径为R,由于原子在晶胞棱的方向上相切,可以计 算出晶胞参数:a=b=c=2R,α=β=γ=90°。每个晶胞中 包含一个原子。 η=1×a433πR3 ×100%=1(×243Rπ)R33 ×100%≈52%。
精彩三年选考尖峰 化学2023
第十四章 晶体结构与性质
微专题十九 晶胞参数、坐标参数的分析与应用
1. 晶胞参数的相关计算 (1)晶胞参数 晶胞的形状和大小可以用6个参数来表示,包 括晶胞的3组棱长a、b、c和3组棱相互间的夹 角α、β、γ,即晶格特征参数,简称晶胞参数。 (2)晶胞参数的计算方法
晶胞的计算

晶胞的计算
化学晶胞计算公式:M=Na×N。
构成晶体的最基本的几何单元称为晶胞(Unit Cell),其形状、大小与空间格子的平行六面体单位相同,保留了整个晶格的所有特征。
晶胞是能完整反映晶体内部原子或离子在三维空间分布之化学-结构特征的平行六面体最小单元。
分子是由组成的原子按照一定的键合顺序和空间排列而结合在一起的整体,这种键合顺序和空间排列关系称为分子结构。
由于分子内原子间的相互作用,分子的物理和化学性质不仅取决于组成原子的种类和数目,更取决于分子的结构。
3.3微专题2晶胞参数的相关计算讲义高二化学人教版选择性必修2

3.Zn与S所形成化合物晶体的晶胞如图所示。Zn2+的配位数是________,S2-填充在Zn2+形成的正四面体空隙中。若该晶体的密度为dg·cm-3,阿伏加德罗常数的值为NA,则该晶胞参数a=________ nm
7.研究发现,氨硼烷在低温高压条件下为正交晶系结构,晶胞参数分别为apm、bpm、cpm,α=β=γ=90°。氨硼烷的2×2×2超晶胞结构如图所示,氨硼烷晶体的密度ρ=________g·cm-3(列出计算式,设NA为阿伏加德罗常数的值)
8.用晶体的X-射线衍射法对Cu的测定得到以下结果:Cu的晶胞为面心立方最密堆积(如下图),已知该晶体的密度为9.00 g·cm-3,晶胞中该原子的配位数为________;Cu的原子半径为_______cm。(阿伏加德罗常数为NA,要求列式计算)
面心立方最密堆积
原子的半径为r,面对角线为4r,a=2 r,V晶胞=a3=(2 r)3=16 r3,1个晶胞中有4个原子,则空间利用率= ×100%= ×100%= ≈74%
六方最密堆积
原子的半径为r,底面为菱形(棱长为2r,其中一个角为60°),则底面面积S=2r× r=2 r2,h= r,V晶胞=S×2h=2 r2×2× r=8 r3,1个晶胞中有2个原子,则空间利用率= ×100%= ×100%= ≈74%
13.Zn与S形成的某种化合物的晶胞结构如图所示,S2-填入由Zn2+围成的________空隙中,若晶胞参数为540 pm,Zn2+和S2-间的最短距离为________pm
14.两种含硅化合物的晶胞结构如图所示
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有,每个离子有1/2属于晶胞。
3、在面上: 处于面上的离子,同时为2 个晶胞共
4、在棱上
处于棱上的离子,同时为4 个晶胞共 有,每个离子有1/4属于晶胞。
返回 TO模型
三、晶体化学式推导 1、氯化钠化学式推导
Cl -
+ Na
继续
1
顶点:8× 8 =1 一个 Na+
1
TO 三维位置
距离最近的分子的位置
2 1
ห้องสมุดไป่ตู้
TO目录
思考:三维 立体中,与 一个二氧化 碳分子距离 最近的二氧 化碳有几个?
12个
3
返回
金刚石晶体
基本单元: 六元环
观察,一个碳原子与多 少个碳原子相连,多少 个碳原子形成一个环? 一个碳被几个环共有?
TO目录
碳原子与键数比是
?
与4个碳相连,呈空间正四面体形
解:在该晶体中最小正方体中所含
的Ni2+、O2-个数均为:
4×
1 8
=
1 (个) 2 1 2
即晶体中每个小正方体中平均含有
74.7g
个
8 8
3
NiO.其质量为:
而此小正方体体积为
6.02×10
× 23
1 2
7
4
(a×10-8㎝)3
74.7g
5
1
6
2
,故NiO晶体密度为:
6.02×1023
× 1 2
(a×10-8㎝)3
对每个小立方体而言,若铯离子 位于顶点,则氯离子位于体心, 反之依然
二氧化碳晶体—面心立方体
观察后回答题:
1、二氧化碳分 子处于立方体 的什么位置?
顶点和面心
2、一个立方体 中含有多少个 二氧化碳分子?
8×1/8+6×1/2 = 4
代表一个 二氧化碳分子
同一平面内二氧化碳分子的位置
观察:
在同一 平面上与一个二氧化 碳分子距离最近的二氧化碳 分子有多少个? 4个 TO CO2晶体
A.TiC B.Ti4C4, C.Ti14C13 D.Ti13C14
课 堂 练 习 题
• 中学教材上图示的NaCl晶体结构,它向三维空
间沿伸得到完美晶体。NiO晶体结构与NaCl相同, Ni2+与邻近的O2-核间距为a×10-8 ㎝,计算NiO晶 体密度(已知NiO摩尔质量为74.7g· -1) mol
③ 用X射线测得NaCl晶体中靠得最近的Na+与Cl-间的平均距离为a cm,用上述测定方法测得的阿伏加德罗常数NA的表达式为NA=
8a3m/v=58.5/NA×4 NA=58.5V/2ma3
返回
6个碳原子形成一个环 一个碳被12个环共有 碳原子与键数比是( 1:2 )
二氧化硅晶体
每个硅连4个氧原子, 每个氧原子连2个硅原子, 最小环为12元环 一个硅原子被12个环共有 一个氧原子被6个环共有
石墨晶体结构
TO层移动
石墨晶体 TO目录
可移动的电子:
石墨的晶体结构俯视图
石墨的层状结构
层状结构的基本单元
顶点 棱上
钠离子
氯离子
观察:氯化钠晶体中钠离子和氯 离子分别处于晶胞的什么位置?
体心
顶点和面心是氯离子 棱上和体心是钠离子 面心
氯化钠晶体结构
6
4 1 3 5 2
TO目录 TO模型
思考:
与一个钠离 子相邻最近 且距离相等 的氯离子有 多少个? a 6个
距离是多少? (图示距离 为a)
a
氯化钠晶体结构
返回
3、二氧化硅化学式推导
金刚石的结构
白球表示硅原子
6 6 十二元环 SiO2最小的环为___,其中有___个Si原子__个O原子 6×1/6=1 6×1/12=1/2 每个环实际占有______个Si原子______个O原子 1/2 12 每个 Si原子被__个环所占有,一个环占有一个Si原子的__ 1/6 6 每个 O原子i被__个环所占有,一个环占有一个O原子的__
SiO2平面结构
4 1molSiO2拥有___mol Si-O键.
4、练习推导化学式
C
B A
A:B:C=1:1:3 ABC3
A:B:C=1:1:3 ABC3
确定化学式
A2 B
AB
A2BC2
ABC
防止类推中的失误
题目:最近科学家发现一种由钛原子和碳原子构成的 气态团簇分子,如右图所示。顶角和面心的原于是钛 原子,棱的中心和体心的原子是碳原子,则它的分子 式是 ( D )
碳原子与键数比是( 2:3 )
石墨的层间移动
TO结构 石墨晶体
可自由移动的电子:
石墨晶体
TO结构
TO目录
石墨的六方晶胞
用隧道扫描显微镜放 大后的石墨层状结构
二、晶胞中含微粒个数比的计算方法:
1、在内部:处于内部的离子,完全属于该晶胞,该离子
按1计入晶胞。
2、在顶点: 处于顶点的离子,同时为8 个晶胞共
=
62. 0 a3
g. ㎝-3
氯化钠晶胞有关综合计算
随着科学技术的发展,阿伏加德罗常数的测定手段越来越多,测 定精确度也越来越高,现有一种简单可行的测定方法,具体步骤 为:(1)将固体NaCl研细、干燥后,准确称取mg NaCl固体并转 移到定容仪器A中(2) 用一个能计量所加液体体积多少的仪器, 向A仪器中滴加苯,不断振荡,继续加苯至A仪器的刻度线,计算 出 NaCl 固 体 的 体 积 Vcm3① 测 步 骤 ( 1 ) 中 A 仪 器 最 好 用 容量瓶 _______________(填仪器名称) ② 能否用水代替苯?,理由 不能,NaCl溶于水,分子间有间隙,测得体积偏小 _______________________
11 5 9 2 8
TO目录 TO模型
思考: 与一个钠离 子相邻最近 且距离相等 的钠离子有 多少个? 12个
4
a 3 10 7 12 6 1
距离是多少? (图示距离 为a)
2 a
氯化铯晶体 (体心立方体)
铯离子: 氯离子:
观察:氯化铯 晶体中氯离子 和铯离子分别 处于晶胞的什 么位置?
氯化铯的小晶胞
离子晶体、分子晶体 和原子晶体
——-晶胞中微粒的计算及化学式推导
晶胞中微粒的计算
TO总结
TO目录
思考:处于晶胞顶 点上、棱上、面上 的离子分别被多少 个晶胞共用? 处于晶胞面上粒子 被2个晶胞共用 处于晶胞棱上粒子 被4个晶胞共用
处于晶胞顶点上 粒子被8个晶胞 共用
一、典型的各种晶体结构特点
氯化钠晶体模型—面心立方体
NaCl
晶胞 Cl-
面点:6 × 2 =3 线点: 12 ×
1 4
=3
心点:1 × 1=1
Na+
Na+:Cl-==1:1 Cl-- 一个大NaCl晶胞包含4个NaCl
一个小NaCl晶胞包含4个NaCl
21、氯化铯化学式推导
氯化铯
1 个CS+,有 1 个Cl -。 每个CSCl晶胞中有 一个CSCl l晶胞包含1个CSCl
