压缩弹簧疲劳强度安全系数计算
弹簧压缩计算公式

弹簧压缩计算公式弹簧压缩计算公式在物理学中可是个相当重要的知识点。
咱们先来说说啥是弹簧压缩。
想象一下,你有一个弹簧,然后你用力把它压短,这就是弹簧压缩啦。
那怎么去算这个压缩的程度呢?这就得靠弹簧压缩计算公式了。
弹簧压缩的计算公式通常是 F = kx ,这里的 F 代表施加在弹簧上的力,k 呢是弹簧的劲度系数,x 就是弹簧的压缩量。
给您说个我之前碰到的事儿吧。
有一次我带着一群小朋友做实验,就是研究这个弹簧压缩的问题。
我给每个小组都发了一个弹簧和一些测量工具。
小朋友们可兴奋了,一个个摩拳擦掌准备大干一场。
其中有个小组,特别有意思。
他们一开始都没搞清楚怎么测量弹簧的原始长度,拿着尺子在那比划半天,急得小脸通红。
我在旁边看着,心里觉得又可爱又好笑。
等他们好不容易量好了原始长度,开始施力压缩弹簧的时候,问题又来了。
他们不知道怎么去确定施加的力的大小。
我就引导他们去看测力计的读数。
这几个小家伙,眼睛瞪得大大的,特别认真。
经过一番努力,他们终于算出了弹簧的压缩量。
那兴奋的样子,就好像发现了新大陆一样。
咱们再回到这个公式啊。
这个劲度系数 k 可重要了。
它反映了弹簧的“倔强程度”,有的弹簧软一些,k 值就小;有的弹簧硬邦邦的,k 值就大。
比如说,床垫里的弹簧和圆珠笔里的弹簧,劲度系数就差别很大。
床垫里的弹簧得能承受人的重量,所以相对较软,k 值小;圆珠笔里的弹簧得能把笔芯顶回去,就比较硬,k 值大。
在实际生活中,这个弹簧压缩计算公式用处可多啦。
像汽车的减震系统,就是利用弹簧的压缩和伸展来减少颠簸。
工程师们就得根据车辆的重量和行驶条件,计算出合适的弹簧参数,保证乘车的舒适性和安全性。
还有那些机械玩具,里面也少不了弹簧的身影。
要想让玩具动起来恰到好处,也得靠这个公式来帮忙。
总之,弹簧压缩计算公式虽然看起来简单,但它的应用可是非常广泛的。
无论是在科学研究中,还是在我们的日常生活里,都能发挥重要的作用。
希望通过我的讲解,您对弹簧压缩计算公式能有更清楚的理解和认识。
压缩弹簧弹簧系数

压缩弹簧弹簧系数摘要:一、压缩弹簧的概念与原理1.压缩弹簧的定义2.压缩弹簧的工作原理二、压缩弹簧的弹簧系数1.弹簧系数的定义2.弹簧系数的影响因素3.弹簧系数的计算方法三、压缩弹簧的应用领域1.汽车行业的应用2.电子行业的应用3.工业设备领域的应用四、弹簧系数的实际应用案例分析1.案例一:汽车减震器中的压缩弹簧2.案例二:电子设备中的压缩弹簧正文:压缩弹簧是一种常见的弹性元件,它主要通过弹簧的弹性变形来产生弹力,从而对物体施加压力。
压缩弹簧广泛应用于各个领域,如汽车、电子和工业设备等。
了解压缩弹簧的弹簧系数对于设计和使用压缩弹簧至关重要。
弹簧系数是一个重要的参数,用于描述弹簧的弹性特性。
它反映了弹簧在受到外力作用时的变形程度,以及弹簧产生的弹力大小。
弹簧系数受到许多因素的影响,如弹簧的材料、截面形状、长度和加载方式等。
计算压缩弹簧的弹簧系数需要知道弹簧的材料和几何参数。
一般来说,弹簧系数的计算公式为:弹簧系数= 弹性模量× 截面积× 弹簧长度其中,弹性模量是弹簧材料的弹性特性,截面积是弹簧的横截面积,弹簧长度是弹簧的初始长度。
压缩弹簧在实际应用中有很多优势。
例如,在汽车行业,压缩弹簧被广泛应用于减震器,可以有效减轻车辆在行驶过程中产生的震动,提高驾驶舒适性。
在电子行业,压缩弹簧可用于微型电子设备,如手机、平板电脑等,提供良好的缓冲和抗冲击性能。
此外,在工业设备领域,压缩弹簧可用于各种自动化设备和机器人,实现精确控制和高效操作。
在实际应用案例中,弹簧系数对于优化产品性能起到关键作用。
例如,在汽车减震器中,通过调整弹簧系数,可以实现对车辆震动的优化控制,提高驾驶舒适性。
在电子设备中,合适的弹簧系数能确保设备在受到外力冲击时,弹簧能够有效地保护设备内部的元器件。
总之,压缩弹簧的弹簧系数对于弹簧的设计和应用具有重要意义。
压缩弹簧疲劳强度安全系数计算

压缩弹簧疲劳强度安全系数计算
压缩弹簧的疲劳强度安全系数是指弹簧的疲劳强度与设计荷载之比。
疲劳强度是指弹簧承受循环荷载时,不发生破坏的最大应力水平。
设计荷
载则是根据实际工作条件和需求确定的。
计算压缩弹簧的疲劳强度安全系数需要以下步骤:
1.确定工作条件和设计荷载。
包括使用环境的温度、压力、振动等因
素以及弹簧承受的荷载大小和循环次数等。
2.选择合适的弹簧材料。
根据工作条件和要求,选择具有较好耐疲劳
性能的材料,如高强度钢材等。
3.计算弹簧的疲劳强度。
根据弹簧的几何形状和材料特性,使用经验
公式或有限元分析等方法计算出弹簧在工作循环次数下的应力水平。
4.确定疲劳极限。
测试或参考材料数据库,确定所选材料的疲劳极限。
5.计算疲劳强度安全系数。
将弹簧的疲劳强度除以设计荷载,得到疲
劳强度安全系数。
一般要求安全系数大于1,通常为2-4
6.分析和评估结果。
根据计算结果和实际需求,对疲劳强度安全系数
进行评估,如是否满足设计要求、是否需要采取进一步措施提高强度等。
需要注意的是,压缩弹簧的疲劳寿命受多种因素影响,如弹簧形状、
材料、制造工艺等,而疲劳强度安全系数只是其中之一、因此,在实际设
计中,还需要综合考虑其他因素,如弹簧的疲劳曲线、应力集中因素、弹
簧预紧量等,以综合评估弹簧的可靠性和寿命。
弹簧计算公式

调压弹簧旋绕比 C D/d 3.9曲度系数 k1(4C-1)/(4C-4) +0.615/C 1.415弹簧刚度 K G×d4/(8×n×D3)36.4予压缩量H1P/(K*π*(d2*d2-d1*d1)/4)0.010最小工作载荷 F1K×H10.4最大工作载荷F2K×(H1+△H) 2.18平均载荷Fm(F2+F1)/2 1.27载荷幅Fa(F2-F1)/20.91平均剪切应力τm8 *k1*D*F m/π*d314.75切应力幅τa8 *k1*D*F a/π*d310.59 最大切应力τmaxτm+τa25.34最小切应力τmixτm-τa 4.16疲劳强度安全系数S(τo+0.75τmix)/ τmax27.21弹簧的高径比b H0/D 2.56弹簧的自振频率γn 3.56×105 ×d/n D24235.80弹簧的强迫机械振动频率γr油泵转速/6030.00γn/γr141.19工作时最小高度Hb1H0-△H -H110.94压并高度Hb n1*d7.7弹簧节距t(Ho-1.5×d)/n 1.87螺旋角 αarctg(t/(Dπ))7.9弹簧展开长度LπDn1/cos(α)95.42临界载荷Fc Cb*K*H00电磁阀弹簧项目调压弹簧电磁阀弹簧3.5#DIV/0!钢丝直径 d 1.111.476#DIV/0!弹簧中径 D 4.3 3.546.1#DIV/0!有效圈数 n550.000#DIV/0!总圈数 n1770.0#DIV/0!自由高度 H01110.82.30#DIV/0!升程 △H0.050.051.15#DIV/0!抗拉强度 σb196119611.15#DIV/0!许用剪切应力τ0686.35686.3515.15#DIV/0!发动机转速3600360015.15#DIV/0!开启压力 P 3.0030.31#DIV/0!针阀密封交线直径 d1 2.30.00#DIV/0!针阀导向直径 d2422.65#DIV/0!切变模量 G79000790003.09#DIV/0!弹簧安装高度8.958.975812.24#DIV/0!不稳定系数Cb30.000.00193.74#DIV/0!10.75#DIV/0!701.86#DIV/0!9.6#DIV/0!78.02#DIV/0!。
弹簧疲劳强度的计算方法.

对于循环次数较多、工作在变应力下的重要弹簧,还应该进一步对疲劳强度进行 计算。如果变应力的循环次数NK103,或应力变化幅度不大时,应进行静强度计 算。如果上述两种情况不能明确区分时,则应同时进行这两种强度的计算。
1、疲劳强度计算
一般受变应力作用的弹簧,其应力变化规律有tmax常数和tmin常数两种。因
7
t00.45erB0.35erB0.33crB0.30cB
注:1.经喷丸处理的弹簧,t可提高20%;
2.对于硅青铜丝、不锈钢丝,取r。
tmintmax--最小、最大切应力(MPa);
Fmin、Fmax ---最小、最大工作载荷(N);
[S]-许用安全系数,当弹簧计算和材料的性能数据精确度高时,取1.3〜1.7;精
此,可根据力学疲劳强度理论与相应计算公式,进行应力幅安全系数、最大应力 安全系数的计算。对于弹簧钢丝也可按下述简化公式进行计算
max
如2
min厂
式中,T0--弹簧材料的脉动循环剪切疲劳极限(MPa),当弹簧材料为碳素钢 丝、不锈钢丝、铍青铜丝等材料时,可根据循环次数N由表中查取。
表20-4弹簧材料的脉动疲劳极限t0N<10410510610
确度较低时,取1.8〜2.2。
2、静强度计算
弹簧的静强度安全系数Ss的计算式为
压缩弹簧压力计算公式

压缩弹簧压力计算公式F=k*x其中,F表示弹力,k表示弹簧的弹性系数,x表示弹簧的形变量。
弹簧的弹性系数k是表示弹簧刚度的一个常数,其单位是N/m。
弹性系数的大小与弹簧的刚度成正比。
刚度越大,弹性系数就越大,弹簧变形越小;反之亦然。
形变量x是指弹簧的变形量。
当外力作用于弹簧时,弹簧会因而发生形变,形变量表示弹簧的压缩或伸展的程度。
形变量的单位通常是米。
1.弹簧受力平衡原理当外力作用于弹簧时,弹簧内部各点受到的应力和变形都保持平衡。
根据受力平衡原理,可以得到其中一截面上的外力与内力之间的关系式。
2.应力-应变关系根据胡克定律,应力与应变之间的关系式可以写为:σ=E*ε其中,σ表示应力,E表示弹簧的杨氏模量,ε表示应变。
应力是单位面积上的力,单位是帕斯卡(Pa),表示为N/m²。
杨氏模量是描述固体材料弹性性能的物理量,单位是帕斯卡(Pa)。
应变是单位长度上的变形量,是一个无量纲量。
3.弹簧变形与应变的关系由于弹簧在压缩过程中无法保持完全均匀形变,故无法应用长度不变原理。
我们可以假设弹簧的变形是线弹性的,且弹簧截面积保持不变。
这样,弹簧的应变与形变量之间可以表示为:ε=ΔL/L其中,ΔL表示弹簧的变形量,L表示弹簧的原始长度。
4.弹性系数k的计算根据弹性系数的定义,该值可以表示为应力与应变的比例系数。
由应力-应变关系式,我们可以得到:σ=E*εk*x/A=E*ΔL/Lk=E*A/L其中,A表示弹簧的截面积。
5.弹簧的压力计算将弹性系数k的计算结果代入弹簧的压力计算公式,可以得到:F=k*xF=E*A*ΔL/L以上就是压缩弹簧压力计算公式的推导过程。
根据此公式,我们可以通过测量弹簧的形变量和已知的材料参数,计算出弹簧所产生的压力。
这个公式在设计和选择弹簧系统时非常有用,可以帮助工程师确定所需的弹簧参数,以满足特定的压力需求。
圆柱螺旋压缩(拉伸)弹簧的设计计算

圆柱螺旋压缩(拉伸)弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有:外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。
由下图圆柱螺旋弹簧的几何尺寸参数图可知,它们的关系为:式中弹簧的螺旋升角α,对圆柱螺旋压缩弹簧一般应在5°~9°范围内选取。
弹簧的旋向可以是右旋或左旋,但无特殊要求时,一般都用右旋。
圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸(mm)计算公式)。
普通圆柱螺旋压缩及拉伸弹簧的结构尺寸(mm)计算公式质量m sm s=γ为材料的密度,对各种钢,γ=7700kg/;对铍青•(二)特性曲线弹簧应具有经久不变的弹性,且不允许产生永久变形。
因此在设计弹簧时,务必使其工作应力在弹性极限范围内。
在这个范围内工作的压缩弹簧,当承受轴向载荷P时,弹簧将产生相应的弹性变形,如右图a所示。
为了表示弹簧的载荷与变形的关系,取纵坐标表示弹簧承受的载荷,横坐标表示弹簧的变形,通常载荷和变形成直线关系(右图b)。
这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。
对拉伸弹簧,如图<圆柱螺旋拉伸弹簧的特性曲线>所示,图b为无预应力的拉伸弹簧的特性曲线;图c为有预应力的拉伸弹簧的特性曲线。
右图a中的H0是压缩弹簧在没有承受外力时的自由长度。
弹簧在安装时,通常预加一个压力F min,使它可靠地稳定在安装位置上。
F min称为弹簧的最小载荷(安装载荷)。
在它的作用下,弹簧的长度被压缩到H1其压缩变形量为λmin。
F max为弹簧承受的最大工作载荷。
在F max作用下,弹簧长度减到H2,其压缩变形量增到λmax。
λmax与λmin的差即为弹簧的工作行程圆柱螺旋压缩弹簧的特性曲线h,h=λmax-λmin。
F lim为弹簧的极限载荷。
在该力的作用下,弹簧丝内的应力达到了材料的弹性极限。
《机械优化设计》第6章习题解答-2资料

8. 有一汽门用弹簧,已知安装高度H1=50.8mm,安装(初始)载荷F1=272N ,最大工作载荷F2=680N ,工作行程h=10.16mm 弹簧丝用油淬火的50CrV A 钢丝,进行喷丸处理; 工作温度126°C ;要求弹簧中径为20mm ≤D2≤50mm ,弹簧总圈数4≤n1≤50,支 承圈数n2=1.75,旋绕比C ≥6;安全系数为1.2;设计一个具有重量最轻的结构方案。
[解] 1.设计变量:影响弹簧的重量的参数有弹簧钢丝直径:d ,弹簧中径D1和弹簧总圈数n1,可取这三个参数作为设计变量:即:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=H D x x x 212.目标函数:弹簧的重量为式中 ρ――钢丝材料的容重,目标函数的表达式为3221611262101925.0108.725.0)(x x x n D d x F --⨯=⨯⨯=π3.约束条件:1)弹簧的疲劳强度应满足min S S ≥式中 2.1m i n m i n =--S S ,可取最小安全系数,按题意S ――弹簧的疲劳安全系数,由下式计算:m s s s S ττττττττα⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-=002式中 :劳极限,计算方法如下弹簧实际的脉动循环疲--0τ初选弹簧钢丝直径:4mm ≤d ≤8mm ,其抗拉强度MPa b 1480=σ,取弹簧的循环工作次数大于710,则材料的脉动循环疲劳极限为MPa b 44414803.03.0'0=⨯==στ设可靠度为90%,可靠性系数 868.0=r k ; 工作温度为126°C ,温度修正系数 862.0126273344273344=+=+=T k t再考虑到材料经喷丸处理,可提高疲劳强度10%,则弹簧实际的脉动循环疲劳极限为MPa k k t r 4.365444862.0868.01.1)1.01('00=⨯⨯⨯=+=ττ36/107.8mm kg -⨯=ρρπ12220.25n D d W =--s τ弹簧材料的剪切屈服极限,计算公式为MPa b s 74014805.05.0=⨯==στ--ατ弹簧的剪应力幅,计算公式为328dD F ka πτα=式中 k ――曲度系数,弹簧承受变应力时,计算公式为14.02)(6.1615.04414d D C C C k ≈+--=a F ――载荷幅,其值为N F F F a 2042/)272680(2/)(12=-=-=m τ――弹簧的平均剪应力,计算公式为328dD F k m sm πτ=式中s k ――应力修正系数,计算公式为dD C k s /615.01615.012+=+= m F ――平均载荷,其值为N F F F m 4762/)272680(2/)(12=+=+=由此,得到弹簧疲劳强度的约束条件为 计算剪应力幅ατ:86.2186.023214.023.8308)/(6.1x x d D F d D dD F ka a =⋅==ππτα328 计算平均应力幅m τ:21312246.74512.1212615.01x x x d D F Dd dD F k m m sm +=⎪⎪⎭⎫ ⎝⎛+==33288ππτ 计算弹簧的实际疲劳安全系数S :mms s s S τττττττττταα494.0506.14.365+=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=0002从而得到弹簧的疲劳强度约束条件为012.1)(min 1≤-=-=SS S S x g 2)根据旋绕比的要求,得到约束条件016)(21min 2≤-=-=x x C C C x g3)根据对弹簧中径的要求,得到约束条件50222≤-=-=≤-=-=1)4(0120)3(max max 242min 3x D D D g x D D D g4)根据压缩弹簧的稳定性条件,要求:c F F ≤2式中 c F ――压缩弹簧稳定性的临界载荷,可按下式计算:K H D H F C ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛--=2022085.611813.0μ 式中 K ――要求弹簧具有的刚度,按下式计算:mm N h F F K /2.4016.1027268012=-=-=0H ――弹簧的自由高度,按下式计算: 当mm K F 16.9240.26802===λ 时, 304.20)5.0(2.1)5.0(310+-=+-=x n H λμ――长度折算系数,当弹簧一端固定,一端铰支时,取 7.0=μ;则:[][]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+---+-=221398.1311304.20)5.0(268.320.3040.5)(13x x x x x F C于是得 01680)(25≤-=-=CC C F F F F x g5)为了保证弹簧在最大载荷作用下不发生并圈现象,要求弹簧在最大载荷2F 时的高度2H 应大于压并高度b H ,由于13112)5.0()5.0(64.4016.108.50x x d n H h H H b -=-==-=-=于是得到010123.00246.0)(131226≤--=-=x x x H H H x g b6)为了保证弹簧具有足够的刚度,要求弹簧的刚度αK 与设计要求的刚度K 的误差小于1/100,其误差值用下式计算:401.02.40)75.1(8100/)(33241---=--=x x Gx K K K αθ式中 G ――弹簧材料的剪切弹性模量,取G=80000Mpa 。
压缩弹簧压力计算公式

压缩弹簧压力通常是指弹簧力。
其计算公式为k = gd ^ 4 / 8nd ^ 3。
压缩弹簧(压缩弹簧)是承受压力的螺旋弹簧。
所使用的材料部分大部分为圆形,并且也由矩形和多股钢制成。
弹簧通常是等距的。
压缩弹簧压力计算公式压缩弹簧力的公式公式:k = gd ^ 4 / 8nd ^ 3上式中的每个术语表示:G =剪切弹性模量[mpa](g值:碳钢80000,不锈钢72000)D =线的直径[mm,in]N =有效圈数[-]D =中心直径[mm,in]K =弹簧系数[n / mm,lb / in]该公式是用于计算弹簧刚度的公式。
刚度乘以工作冲程等于弹簧的工作力。
通过以上公式可以得出,压缩弹簧的参数必须由材料,线径,中心直径,有效环数,弹簧总长,工作高度和要求强度组成。
如果对弹簧强度没有特殊要求,则无法提供工作高度和所需力的参数。
什么是弹性物体在力的作用下的形状或体积变化称为变形。
外力停止后,可以恢复到原始状态的变形称为弹性变形。
变形的物体必须对与其接触的物体施加力,因为它要恢复到其原始状态。
这称为弹性。
即,在弹性极限内,由物体产生的力对施加到物体的力引起的物体变形的力称为弹力。
在日常生活中观察到的相互作用,无论是推,拉,举,举,还是牵引火车,锻造工件,击球,射箭等,都仅在物体接触物体时发生。
这种相互作用可以称为接触力。
根据其性质,接触力可分为弹力和摩擦力。
它们本质上是由电磁力引起的。
弹力是接触力,并且弹力只能存在于物体的接触位置,但是彼此接触的物体之间没有弹性作用。
因为弹力不仅需要接触,而且具有相互作用。
弹簧设计及验证计算方法

型众多 , 然而在工程实 际工作 中使用最多的是圆柱形 压缩弹簧。弹簧在设计时 , 通常是根据其所承受 的最 大载荷 、 最大变形量以及结构尺寸要求来决定弹簧的 外径 、 中径 、 工作 圈数 、 螺旋 升角 和高度 等参 数 。
1 基本 设计I 盱卜 可将 1 系 公式化, 碳素弹簧钢 I 一 、 对于 、 .
丝 0 m≤d m的钢 I l .m 5 ≤4m \ \
丝, 抗拉强度 - o 可表示 f l 为: 司
- 34 9 6. d 7 7 ; o= 0 . —7 1+ . t 8 6 6
\\ 、
l I
对于 6 n 1 m ≤ d≤ 5M , m
卜— - -
l二] =
压 缩 弹 簧 在设 计 阶段 , 一般 给 出最 大 工作 载 荷 F 和需 要 的变 形 量 入 要 求 根 据 工 况 条 件 选 定 材 料并 确 ,
48mm 的 钢 丝 , 叮l 图 弹簧工作受力示意图 . 其 l : 107 — 1. 一01 。同时工程 已证 明 : 动循 环疲 9. 9 11 1 . 2 脉
弹簧设计及验证计算方法
孙 畅
( 中国船舶重_ 丁集团公司 第七一 0研究所 , 湖北 宜昌 4 30 ) 4 0 3
【 摘
要 1 文章从弹簧的设计阶段 入手 , 对所 涉及的 主要参数的进行 了扼要说 明, 并对弹簧在使 用过 程 中产生的共
振性 问题进行 了简要 的验 算 , 同时结合工程经验对弹簧结构参数的确定作 了初步探 讨。
表 1 脉 动 循 环 疲 劳 极 限 T。
rk8 ( )k8 / d ( =x 耵 =x C( [ 1  ̄) F )
变 形计 算式 :A= 8 D3 G 4 8 Cn G F 2 d= F S/d r d
圆柱螺旋拉伸弹簧的设计计算

15.3 圆柱螺旋压缩(拉伸)弹簧的设计计算(三) 圆柱螺旋压缩(拉伸)弹簧受载时的应力及变形圆柱螺旋弹簧受压或受拉时,弹簧丝的受力情况是完全一样的。
现就下图<圆柱螺旋压缩弹簧的受力及应力分析>所示的圆形截面弹簧丝的压缩弹簧承受轴向载荷P的情况进行分析。
由图<圆柱螺旋压缩弹簧的受力及应力分析a>(图中弹簧下部断去,末示出)可知,由于弹簧丝具有升角α,故在通过弹簧轴线的截面上,弹簧丝的截面A-A呈椭圆形,该截面上作用着力F及扭矩。
因而在弹簧丝的法向截面B-B上则作用有横向力Fcosα、轴向力Fsinα、弯矩M=Tsinα及扭矩Tˊ= T cosα。
由于弹簧的螺旋升角一般取为α=5°~9°,故sinα≈0;cosα≈1(下图<圆柱螺旋压缩弹簧的受力及应力分析b>),则截面B-B上的应力(下图<圆柱螺旋压缩弹簧的受力及应力分析c>)可近似地取为式中C=D2/d称为旋绕比(或弹簧指数)。
为了使弹簧本身较为稳定,不致颤动和过软,C值不能太大;但为避免卷绕时弹簧丝受到强烈弯曲,C值又不应太小。
C值的范围为4~16(表<常用旋绕比C值>), 常用值为5~8。
圆柱螺旋压缩弹簧的受力及应力分析常用旋绕比C值为了简化计算,通常在上式中取1+2C≈2C(因为当C=4~16时,2C>>l,实质上即为略去了τp),由于弹簧丝升角和曲率的影响,弹簧丝截面中的应力分布将如图<圆柱螺旋压缩弹簧的受力及应力分析>c 中的粗实线所示。
由图可知,最大应力产生在弹簧丝截面内侧的m点。
实践证明,弹簧的破坏也大多由这点开始。
为了考虑弹簧丝的升角和曲率对弹簧丝中应力的影响,现引进一个补偿系数K(或称曲度系数),则弹簧丝内侧的最大应力及强度条件可表示为式中补偿系数K,对于圆截面弹簧丝可按下式计算: 圆柱螺旋压缩(拉伸)弹簧受载后的轴向变形量λ可根据材料力学关于圆柱螺旋弹簧变形量的公式求得:式中:n—弹簧的有效圈数;G—弹簧材料的切变模量,见前一节表<弹簧常用材料及其许用应力>。
弹簧计算公式

弹簧应力:弹簧的压缩应力、拉伸 应力等
工作环境:温度、湿度、腐蚀性等
弹簧制造工艺:热处理、表面处理 等
提高弹簧疲劳寿命的方法
选用优质材料: 选用高强度、高 韧性的材料,提 高弹簧的疲劳寿 命
优化设计:优化弹 簧的形状、尺寸和 结构,提高弹簧的 疲劳寿命
控制加工工艺:控 制弹簧的加工工艺, 提高弹簧的疲劳寿 命
计算。
添加标题
弹簧应力和应变 的计算公式:弹 簧应力和应变的 计算公式可以通 过弹簧的弹性模 量、截面尺寸和 弹簧的刚度等参
数来计算。
添加标题
弹簧应力和应变的计算公式
弹簧应力计算公式:σ = F/A 弹簧应变计算公式:ε = ΔL/L 弹簧应力和应变的关系:σ = Eε 弹簧应力和应变的物理意义:应力表示弹簧受力大小,应变表示弹簧形变量大小。
热处理:对弹簧进 行热处理,提高弹 簧的疲劳寿命
润滑:对弹簧进行 润滑,减少摩擦, 提高弹簧的疲劳寿 命
定期维护:定期对 弹簧进行检查和维 护,及时发现和处 理问题,提高弹簧 的疲劳寿命
感谢观看
汇报人:
弹簧应力和应变的影响因素
弹簧的材料:材料 的弹性模量、屈服
强度等
弹簧的形状:弹簧 的直径、长度、线
径等
弹簧的载荷:弹簧 所承受的力大小和
方向
弹簧的温度:温度 对弹簧的弹性模量 和屈服强度的影响
05
弹簧振动频率和阻尼比计算
弹簧振动频率和阻尼比的定义
弹簧振动频率:弹簧在振动过程中,单位时间内振动的次数,单位为赫兹(Hz)。
1/2π√(k/m尼比的应用场景
汽车悬挂系统:弹簧振动频率和阻尼比直接影响汽车的舒适性和操控性 机械设备:弹簧振动频率和阻尼比影响设备的稳定性和寿命 建筑结构:弹簧振动频率和阻尼比影响建筑的抗震性能和稳定性 航空航天:弹簧振动频率和阻尼比影响飞行器的稳定性和操控性
压缩弹簧力值计算

压缩弹簧力值计算
《压缩弹簧力值计算》
压缩弹簧力值是指弹簧在压缩时所受的力。
计算压缩弹簧力值需要考虑弹簧的材料、形状、尺寸和压缩量等因素。
首先,确定弹簧的材料,如钢、铝、铜等。
其次,确定弹簧的形状,如圆簧、螺旋簧等。
再次,确定弹簧的尺寸,如外径、内径、高度等。
最后,确定弹簧的压缩量。
根据上述信息,可以使用弹簧力学公式计算压缩弹簧力值。
该公式为:F=k*x,其中F为
弹簧力值,k为弹簧刚度,x为压缩量。
因此,计算压缩弹簧力值需要考虑弹簧的材料、形状、尺寸和压缩量等因素,并使用弹簧力学公式计算。
压缩弹簧疲劳强度安全系数计算

压缩弹簧疲劳强度安全系数计算压缩弹簧是一种能够储存和释放能量的机械元件,通常由金属线材弯曲而成,用于各种机械设备和结构中的弹簧元件。
压缩弹簧主要承受压缩载荷,并通过压缩变形存储弹性势能,在释放力的作用下恢复原始形状。
疲劳强度是指弹簧在循环变形加载下的抗疲劳能力,也就是弹簧在受到循环应力作用下能够一直保持正常工作的能力。
弹簧在长期的使用中会经历很多循环载荷作用,如果应力过大或过小都会导致弹簧的疲劳强度下降,最终导致失效。
安全系数是指实际工作载荷与弹簧的设计载荷之间的比值,用来衡量弹簧的安全性能,也是在设计弹簧时需要考虑的重要指标。
安全系数越高,表示弹簧的承载能力越大,安全性能越高。
1.弹簧参数确定:包括弹簧的材料、几何尺寸和工作条件等。
2.设计载荷计算:根据实际工作条件和要求,确定弹簧的设计载荷。
3.弹簧材料的疲劳强度计算:根据弹簧材料的相关材料特性和应力应变曲线等数据,计算材料的疲劳强度。
4.弹簧的疲劳强度计算:根据弹簧的几何尺寸和工作条件,结合材料的疲劳强度,计算弹簧的疲劳强度。
5.安全系数计算:根据实际工作载荷和设计载荷,计算弹簧的安全系数。
具体计算步骤如下:1.弹簧参数确定:包括弹簧的线径、外径、活圈数、刚度和工作长度等。
2.设计载荷计算:根据实际工作条件和要求,确定弹簧的设计载荷,包括载荷的大小和载荷的作用方式。
3.弹簧材料的疲劳强度计算:根据弹簧材料的相关材料特性和应力应变曲线等数据,计算材料的疲劳强度,包括疲劳强度极限和疲劳寿命。
4.弹簧的疲劳强度计算:根据弹簧的几何尺寸和工作条件,结合材料的疲劳强度,计算弹簧的疲劳强度。
常用的计算方法包括史密斯修正方法、赫尔曼-斯特雷斯曲线法和b模型法等。
5.安全系数计算:根据实际工作载荷和设计载荷,计算弹簧的安全系数。
安全系数的计算公式为安全系数=实际工作载荷/设计载荷。
安全系数大于1表示设计合理,安全系数越大表示弹簧的安全性能越高。
需要注意的是,在计算过程中需要准确获取弹簧材料的疲劳强度参数,并结合材料的应力应变曲线、弹簧的几何尺寸和工作条件,进行严谨的计算和分析。
弹簧的强度计算
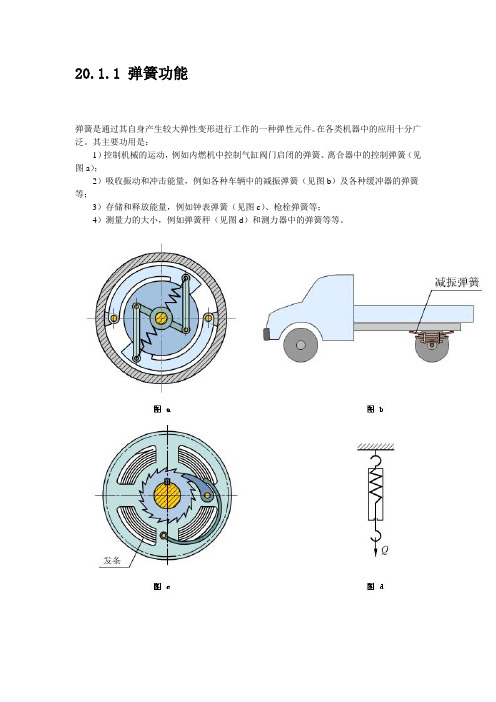
20.1.1 弹簧功能弹簧是通过其自身产生较大弹性变形进行工作的一种弹性元件。
在各类机器中的应用十分广泛。
其主要功用是:1)控制机械的运动,例如内燃机中控制气缸阀门启闭的弹簧、离合器中的控制弹簧(见图a);2)吸收振动和冲击能量,例如各种车辆中的减振弹簧(见图b)及各种缓冲器的弹簧等;3)存储和释放能量,例如钟表弹簧(见图c)、枪栓弹簧等;4)测量力的大小,例如弹簧秤(见图d)和测力器中的弹簧等等。
20.2.1 弹簧材料为了保障弹簧能够可靠地工作,其材料除应满足具有较高的强度极限和屈服极限外,还必须具有较高的弹性极限、疲劳极限、冲击韧性、塑性和良好的热处理工艺性等。
表20-2列出了几种主要弹簧材料及其使用性能。
实践中应用最广泛的就是弹簧钢,其品种又有碳素弹簧钢、低锰弹簧钢、硅锰弹簧钢和铬钒钢等。
图20-2给出了碳素弹簧钢丝的抗拉强度极限。
图20-2 碳素钢丝直径与强度的关系表20-2主要弹簧材料及其许用应力表20-2 主要弹簧材料及其许用应力注:1.按受力循环次数N不同,弹簧分为三类:Ⅰ类N>106;Ⅱ类N=103~105以及受冲击载荷的场合;Ⅲ类N<103。
2.碳素弹簧钢丝按机械性能不同分为Ⅰ、Ⅱ、Ⅱa、Ⅲ四组,Ⅰ组强度最高,依次为Ⅱ、Ⅱa、Ⅲ组。
3.弹簧的工作极限应力τlim:Ⅰ类≤1.67[τ];Ⅱ类≤1.25[τ];Ⅲ类≤1.12[τ]。
4.轧制钢材的机械性能与钢丝相同。
5.碳素钢丝的切变模量和弹性模量对0.5~4mm直径有效,>4mm取下限。
20.2.2 弹簧材料选择弹簧材料选择必须充分考虑到弹簧的用途、重要程度与所受的载荷性质、大小、循环特性、工作温度、周围介质等使用条件,以及加工、热处理和经济性等因素,以便使选择结果与实际要求相吻合。
钢是最常用的弹簧材料。
当受力较小而又要求防腐蚀、防磁等特性时,可以采用有色金属。
此外,还有用非金属材料制做的弹簧,如橡胶、塑料、软木及空气等。
压缩弹簧设计计算

25 7.94813
1056.3 132.9
37.7448 15.0979
7.64 1.64
200 22.6469
159 67.1005 162.255 184.902 3.47914 125.896
27 3399.18
计算项目 三.稳定性验算 1.稳定性临界负荷
不稳定性系数 2.稳定性条件 四.疲劳强度验算
压缩弹簧设计计算
计算项目 一.已知条件
最大工作负荷 最小工作负荷 工作行程 变载荷作用次数 弹簧材料 端部型式 端部固定状态 稳定性措施 二.几何计算 1.弹簧丝直径 1.弹簧许用应力 2.弹簧中径 3.曲度系数 4.旋绕比 5.要求的弹簧刚度 6.弹簧单圈刚度 7.有效圈数 8.弹簧刚度 9.工作极限负荷 10.工作极限负荷下变形 11.最大工作负荷下变形 12.最小工作负荷下变形 13.节距 14.间距 15.自由高度 16.工作行程 17.压并高度 10.工作极限负荷下高度 11.最大工作负荷下高度 12.最小工作负荷下高度 13.螺旋角 14.弹簧单圈展开长度 15.总圈数 16.展开长度
τmax=8KDPn/(πd3) τmin=8KDP1/(πd3) 表:11-1-7
s≥[s]
结果
1271.7 0.8
满足
2.62386
402.6 173.246 69.2984
1.7 满足
符号 单位
公式及数据来源
结果
Pn N P1 N Hn mm
次
300 120
25 1000000 碳素弹簧钢丝B级 端部并紧,磨平,支撑圈为1圈 两端固定
无
d mm 按GB1358-78试取
[τp] MPa 表:11-1-2
压缩弹簧压力计算公式

压缩弹簧压力计算公式
压缩弹簧压力通常指弹簧力。
计算公式为k=gd^4/8nd^3。
压缩弹簧(压缩弹簧)是受压的螺旋弹簧。
使用的大多数材料是圆形的,也由矩形钢和多股钢制成。
弹簧通常是等距的。
压缩弹簧压力计算公式
压缩弹簧力公式
公式:k=gd^4/8nd^3
上述公式中的每一项是指:
G=剪切弹性模量[mpa](G值:碳钢80000,不锈钢72000)
D=钢丝直径[mm,in]
N=有效圈数[-]
D=中心直径[mm,in]
K=弹簧常数[n/mm,lb/in]
该公式用于计算弹簧刚度。
刚度乘以工作行程等于弹簧的工作力。
由上式可知,压缩弹簧的参数必须由材料、线径、中心直径、有效圈数、弹簧总长度、工作高度和所需强度组成。
如果弹簧强度没有特殊要求,则无法提供工作高度和所需力的参数。
什么是灵活性
物体在力的作用下形状或体积的变化称为变形。
外力停止后,能恢复原状的变形称为弹性变形。
变形的物体必须对与其接触的物体施加力,因为它必须回到原来的状态。
这叫做弹性。
也就是说,在弹性极限内,物体所产生的使物体变形的力被称为弹性力。
日常生活中观察到的相互作用,无论是推、拉、举、拉火车、锻造工件、打球、射箭等,都只有在物体与物体接触时才会发生。
这种相互作用可以称为接触力。
接触力按其性质可分为弹性力和摩擦力。
它们基本上是由电磁力引起的。
弹性力就是接触力,弹性力只能存在于物体的接触部位,而相互接触的物体之间不存在弹性效应。
因为弹性不仅需要接触,还需要相互作用。
圆柱螺旋压缩(拉伸)弹簧的设计计算
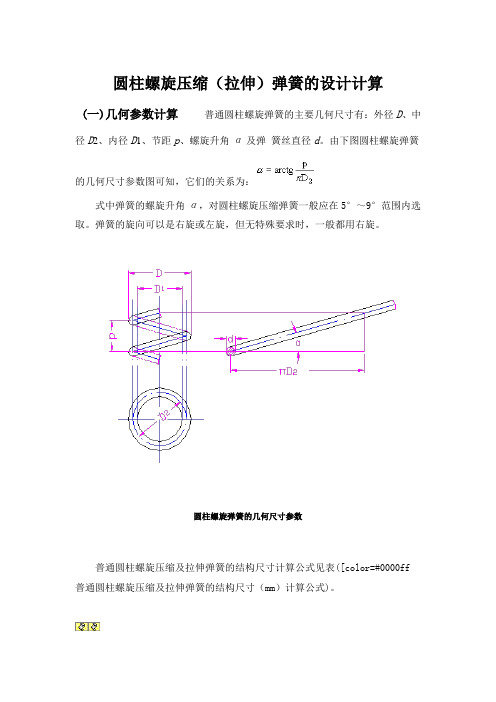
圆柱螺旋压缩(拉伸)弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有:外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。
由下图圆柱螺旋弹簧的几何尺寸参数图可知,它们的关系为:式中弹簧的螺旋升角α,对圆柱螺旋压缩弹簧一般应在5°~9°范围内选取。
弹簧的旋向可以是右旋或左旋,但无特殊要求时,一般都用右旋。
圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸(mm)计算公式)。
普通圆柱螺旋压缩及拉伸弹簧的结构尺寸(mm)计算公式参数名称及代号计算公式备注压缩弹簧拉伸弹簧中径D2D2=Cd 按普通圆柱螺旋弹簧尺寸系列表取标准值内径D1D1=D2-d外径D D=D2+d旋绕比C C=D2/d 压缩弹簧长细比b b=H0/D2b在1~5.3的范围内选取自由高度或长度H0H0≈pn+(1.5~2)d(两端并紧,磨平)H0≈pn+(3~3.5)d(两端并紧,不磨H0=nd+钩环轴向长度平)工作高度或长度H1,H2,…,H nH n=H0-λn H n=H0+λnλn--工作变形量有效圈数n根据要求变形量按式(16-11)计算n≥2总圈数n1n1=n+(2~2.5)(冷卷)n1=n+(1.5~2)(YII型热卷)n1=n拉伸弹簧n1尾数为1/4,1/2,3/4整圈。
推荐用1/2圈节距p p=(0.28~0.5)D2p=d轴向间距δδ=p-d展开长度L L=πD2n1/cosαL≈πD2n+钩环展开长度螺旋角αα=arct g(p/πD2) 对压缩螺旋弹簧,推荐α=5°~9°质量m sm s=γ为材料的密度,对各种钢,γ=7700kg/;对铍青(二)特性曲线弹簧应具有经久不变的弹性,且不允许产生永久变形。
因此在设计弹簧时,务必使其工作应力在弹性极限范围内。
在这个范围内工作的压缩弹簧,当承受轴向载荷P时,弹簧将产生相应的弹性变形,如右图a所示。
压缩弹簧压力计算公式

压缩弹簧压力通常指弹簧力。
计算公式为k=gd^4/8nd^3。
压缩弹簧(压缩弹簧)是受压的螺旋弹簧。
使用的大多数材料是圆形的,也由矩形钢和多股钢制成。
弹簧通常是等距的。
压缩弹簧压力计算公式
压缩弹簧力公式
公式:k=gd^4/8nd^3
上述公式中的每一项是指:
G=剪切弹性模量[mpa](G值:碳钢80000,不锈钢72000)
D=钢丝直径[mm,in]
N=有效圈数[-]
D=中心直径[mm,in]
K=弹簧常数[n/mm,lb/in]
该公式用于计算弹簧刚度。
刚度乘以工作行程等于弹簧的工作力。
由上式可知,压缩弹簧的参数必须由材料、线径、中心直径、有效圈数、弹簧总长度、工作高度和所需强度组成。
如果弹簧强度没有特殊要求,则无法提供工作高度和所需力的参数。
什么是灵活性
物体在力的作用下形状或体积的变化称为变形。
外力停止后,能恢复原状的变形称为弹性变形。
变形的物体必须对与其接触的物体施加力,因为它必须回到原来的状态。
这叫做弹性。
也就是说,在弹性极限内,物体所产生的使物体变形的力被称为弹性力。
日常生活中观察到的相互作用,无论是推、拉、举、拉火车、锻造工件、打球、射箭等,都只有在物体与物体接触时才会发生。
这种相互作用可以称为接触力。
接触力按其性质可分为弹性力和摩擦力。
它们基本上是由电磁力引起的。
弹性力就是接触力,弹性力只能存在于物体的接触部位,而相互接触的物体之间不存在弹性效应。
因为弹性不仅需要接触,还需要相互作用。
