圆柱螺旋压缩弹簧计算公式

圆柱螺旋压缩弹簧计算

D+d 265 D-d 175 arc tan t/πD 0.10002485 0.1003598 0.001447 691.15 πDn1 / cosα 16671 1.005 0.995002 1447.54 1101.38 1059.00 346.1681845 0.3 0.9 7.245454545 2.6 1 / Pj 1/D 1.09E-05 0.004545 P1/ P' Pn / P' Pj / P' 146.4558 492.624 535.0029
圆柱弹簧设计计算
最小输出扭矩M（Nm）最大输出扭矩M（Nm）驱动半径R（m）驱动半径R（mm）弹簧最小输出力 P1（N）弹簧最大输出力 Pn（N）工作行程 L（m）工作行程 h（mm）最大最小输出力差 Δ P（N）初算弹簧刚度 P'（N/mm）工作的极限载荷 Pj（N）初选材料直径d及中径D 弹簧有效圈数 n 总圈数 n1 弹簧刚度 P'（N/mm）工作极限载荷下的变形量 Fj 节距 t（mm）自由高度 H0（mm）取标准值 H0（mm）弹簧外径 D2（mm）弹簧内径 D1（mm）螺旋角 α （弧度）展开长度 L（mm） Mmin Mmax R R P1 Pn L h Pn-P1 ΔP / h K × Pn d 45 P'd / P' n+2 P'd / n n × fj Fj / n+d nt + 1.5d 5500 18500 0.22 倒数 1/R 4.545455 220 25000 84090.90909 0.3454 345 倒数 1/h 0.002895 59090.90909 171.0796442 倒数 1/P' 0.005845 92500 D 220 21.94884154 24 170.6818182 535.04 69.36363636 1593.5 1594 系数 K Pj 91325 取整取整取整 Fj / n nt 1.1 fj 24.32 22 170.7 536 24.36364 1526 P'd 3755 倒数倒数倒数 1.5d 0.045455 0.005858 0.001866 67.5

圆柱螺旋压缩弹簧计算公式

圆柱螺旋压缩弹簧计算
公式
-CAL-FENGHAI.-(YICAI)-Company One1
普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式
参数名称及代号计算公式备注
压缩弹簧拉伸弹簧
中径D2 D2=Cd 按普通圆柱螺旋弹簧尺寸系列表取标准值
内径D1 D1=D2-d
外径D D=D2+d
旋绕比C C=D2/d压缩弹簧长细比b b=H0/D2 b在1～的范围内选取自由高度或长度H0 H0≈pn+～2)d（两端并紧，磨平）H0≈pn+(3～d（两端并紧，不磨平） H0=nd+钩环轴向长度工作高度或长度H1,H2,…,Hn Hn=H0-λn Hn= H0+λn λn--工作变形量有效圈数n 根据要求变形量按式（16-11）计算n≥2总圈数n1 n1=n+(2～（冷卷）n1=n+～2) （YII型热卷） n1=n 拉伸弹簧n1尾数为1/4,1/2,3/4整圈。

推荐用1/2圈节距p p=～D2 p=d 轴向间距δ δ=p
-d 展开长度L L=πD2n1/cosα L≈πD2n+钩环展开长度螺旋角α α=arctg(p/πD 2) 对压缩螺旋弹簧，推荐α=5°～9°质量ms ms= γ为材料的密度，对各种钢，γ=7700kg/ ；对铍青铜，γ=8100kg/。

圆柱螺旋弹簧一般计算公式

1. 弹簧刚度：
2. 力值：其中：G 为材料剪切模量，一般不锈钢取71500Mpa,碳钢取
78500Mpa ；
d 为材料直径；
D 为弹簧中径；
n 为弹簧有效圈数；
f 为变形量（拉压行程）。

3. 应力： K 为曲度系数，公式为：其中C 为弹簧旋绕比，是弹簧中径与线径的比值，即
4. 下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力，加上初拉力就行。

初拉力：其中初拉力τ0按初切应力图选取，见下图。

三．扭簧：
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径；
E---材料的弹性模量，一般不锈钢丝取188000Mpa ，碳素钢丝
取206000Mpa ；
D---弹簧外径；
ϕ---弹簧的扭转行程（角度）；
4. 应力： K1为曲度系数，顺旋向扭转取1，逆旋向扭转时按下式：
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。

弹簧设计计算

圆柱螺旋压缩弹簧设计计算
项目最小工作载荷P1 最大工作载荷Pn 工作行程h 弹簧中径D 弹簧直径d 原弹簧类别始条端部结构件旋绕比C 曲度系数K 弹簧材料材料极限切应力材料切变模量初算弹簧刚度P' 工作极限载荷Pj 单位 N N mm mm mm 公式及数据 2000 7570 170 80 14 III类端部并紧、磨平，两端支承圈各1圈 C= 5.714285714 K= 1.266715909 60Si2Mn MPa τj= 740 MPa G= 79000 N/mm P'= 32.76470588 N Pj= 7868.763643 P1= Pn= h= D= d= fj= 10.62006597 P'd= 740.9335938 n= 22.613772 取 n= n1= 30 P‘= 26.46191406 Fj= t= H0= D2= D1= α= L= H1= Hn= Hj= h= 下限上限 b= 297 24.61 710.08 取H0= 94 66 5.592578199 7576 634.42 423.93 412.64 210.49 0.25 0.96 81、根据弹簧套筒内径以及旋绕比C 5～8初步确定弹簧直径与中径； d 3 j 2、由极限载荷公式 Pj 8DK 可知，极限载荷只由中径、直径以及材料有关，与施加的外力无关。故一旦中径、直径以及材料确定后，弹簧的极限载荷就是一定值； 3、根据弹簧的工作范围为20%～80%初步确定最小工作载荷以及最大工作载荷；最小工作载荷应大于推动侧护板所需要的力； 4、根据以上最终验算结果，对以上各值进行调整
工作极限载荷下的 mm 单圈变形量fj 单圈弹性刚度P'd N/mm 有效圈数n 圈总圈数n1 圈 N/mm 参数弹簧刚度P’ 计算工作极限载荷下的变形量Fj mm 节距t mm 自由度高H0 mm 弹簧外径D2 mm 弹簧内径D1 mm 螺旋角α (°) 展开长度L mm 最小载荷时高度H1 mm 最大载荷时高度Hn mm 极限载荷时高度Hj mm mm 验算实际工作行程h 工作范围高径比b

圆柱螺旋压缩弹簧计算公式

圆柱螺旋压缩弹簧计算公式
弹簧常量（Spring Constant）是指单位压缩或拉伸长度下所储存的能量。

它是衡量弹簧刚性和柔性的重要指标。

圆柱螺旋压缩弹簧的弹簧常量可以通过以下公式计算：
k=(Gd^4)/(8D^3n)
其中，k为弹簧常量，G为弹簧材料的剪切模量，d为弹簧线圈的直径，D为弹簧线圈的平均直径，n为弹簧线圈的总数。

F = kx
其中，F为受到的力，k为弹簧常量，x为弹簧的位移。

Fmax = kxmax
其中，Fmax为最大力，k为弹簧常量，xmax为允许的最大位移。

Lmax = Ln - (D/2 + d/2 + c)
其中，Lmax为最大压缩长度，Ln为弹簧线圈的总长度，D为弹簧线圈的平均直径，d为弹簧线圈的直径，c为线圈间的缝隙。

x_max = (Ln - L0) / n
其中，x_max为最大位移，Ln为弹簧线圈的总长度，L0为弹簧的初始长度，n为弹簧线圈的总数。

S=F/x
其中，S为刚度，F为受到的力，x为位移。

E = (1/2)kx^2
其中，E为弹性能量，k为弹簧常量，x为位移。

以上就是关于圆柱螺旋压缩弹簧的计算公式。

通过这些公式，我们可以准确地计算弹簧的性能参数，为机械设计提供依据，并确保弹簧在实际使用中能够正常工作。

当然，在实际设计中，还需要考虑许多其他因素，如疲劳寿命、可靠性和安全系数等，并结合实际应用需求进行综合设计。

弹簧计算

=

′
13.73239437
mm
= +d
5.068
自由高度H0
mm
H0=nt+1.5d
75.452
弹簧外径D2
mm
D2=D+d
19
弹簧内径D1
mm
D1=D-d
13
mm
最小载荷时的高
度H1
mm
最大载荷时的高
度Hn
mm
极限载荷时的高
度Hj
mm
实际工作行程h
mm
工作区范围
高径比 b
Fj=nfj

α =
π
πD1
=

1
1 = 0 −
′

′

= 0 −
′
= 0 −
h=H1-Hn
1
; ;

0
=

根据机械设计手册表查得标准
值
14
取标准值
75
12.1875
节距t
展开长度 L
根据机械设计手册表查得
16
mm
（°）
弹簧类别Ⅱ时 Pj≥1.25Pn
弹簧类别Ⅲ时 Pj≥Pn
195
′
= ′

工作载荷下的变
形量Fj
螺旋角α
算
N/mm
碳素弹簧钢丝C级
− 1
′ =
14.2
ℎ
N
单圈刚度 P＇d
验
1000000
工作极限载荷Pj
所选弹簧工作极限载荷Pj
数据
工作极限载荷下
的单圈变形量fj
28.952
5.763193109

圆柱螺旋压缩弹簧计算全过程—Richard Deng

γ
判断
弹簧稳定性校核
弹簧的高径比b
Mpa
τ2=K*(8DF2/πd^3）
γ=τ1/τ2
τ1/Rm
0.2
τ2/Rm
查阅图1 若点（0.2,0.4）在γ=0.5和10^7作用线的交点以下表明弹簧的疲劳寿命N＞10^7次，反之不然
b=H0/D 一端固定一端回转：b≤2.6
自振频率fe
Hz
fe=3.56d/nD^2*√(G/ρ)
C=D/d 推荐值范围参照表7
K=4C-1/4C-4+0.615/C
mm
调整后必须满足 d≥（8KFD/π[τ]）^1/3
弹簧中径D
mm由上Biblioteka 1所得弹簧线径dmm
弹簧直径
弹簧外径D2
mm
由上表1所得 D2=D+d
弹簧内径D1
mm
D1=D-d
所需刚度F'
N/mm
由上表1决定
弹簧所需刚度和圈数有效圈数n
24.5454545
簧外径≤34.8mm
34.8
据F2确定
4.1
VDCrSi
78500
5*10^-6
0.00000785
d决定附录F =F1/F2
1810 表2
0.5
环次数）交点的纵坐标大致为 0.41
1（上值）
0.41 742.1
D=D2-d-0.3(公差) 荐值范围参照表7
C-4+0.615/C ≥（8KFD/π[τ]）^1/3
压并时负荷Fb
N
试验负荷和试验负荷
下的高度和变形量
实际试验负荷Fs
N
Fb=F'*fb 如果Fs＞Fb则Fs取Fb值，否则取原值

圆柱螺旋压缩(拉伸)弹簧的设计计算

圆柱螺旋压缩（拉伸）弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。

由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。

圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青•(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。

因此在设计弹簧时，务必使其工作应力在弹性极限范围内。

在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。

为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系(右图b)。

这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。

对拉伸弹簧，如图<圆柱螺旋拉伸弹簧的特性曲线>所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。

右图a中的H0是压缩弹簧在没有承受外力时的自由长度。

弹簧在安装时，通常预加一个压力F min，使它可靠地稳定在安装位置上。

F min称为弹簧的最小载荷(安装载荷)。

在它的作用下，弹簧的长度被压缩到H1其压缩变形量为λmin。

F max为弹簧承受的最大工作载荷。

在F max作用下，弹簧长度减到H2，其压缩变形量增到λmax。

λmax与λmin的差即为弹簧的工作行程圆柱螺旋压缩弹簧的特性曲线h,h=λmax-λmin。

F lim为弹簧的极限载荷。

在该力的作用下，弹簧丝内的应力达到了材料的弹性极限。

圆柱螺旋压缩弹簧计算公式

圆柱螺旋压缩弹簧计算公式圆柱螺旋压缩弹簧是机械中常用的一种元件，可以用于各种机械装置中，用于提供压缩力、缓冲力和储能等功能。

圆柱螺旋压缩弹簧的设计和计算公式一般包括弹簧刚度、载荷、工作长度、自由长度等参数的计算。

下面将详细介绍圆柱螺旋压缩弹簧的计算公式。

1.弹簧刚度：弹簧刚度是指弹簧在单位长度内所产生的载荷与该长度内的变形之比，用符号C表示，其单位为N/mm。

弹簧刚度可以通过几何参数和材料的弹性模量来计算。

若弹簧线直径为d，弹簧线直径外形半径为D，圈数为n，弹簧长度为L，则弹簧刚度C的计算公式为：C=(Gd^4)/(8D^3n)其中，G为弹簧材料的剪切模量，d和D的单位为mm，n为无量纲。

2.载荷：载荷是指施加在弹簧上的力或重量，用符号F表示，其单位为N。

载荷的大小会影响到弹簧的变形和工作性能。

3.工作长度：工作长度是指弹簧在工作状态下的长度，也称为工作高度，用符号H表示，其单位为mm。

工作长度的大小与弹簧的刚度和载荷有关。

4.自由长度：自由长度是指弹簧在无外力作用时的长度，用符号L0表示，其单位为mm。

自由长度的大小与弹簧线直径、圈数和线径外径有关。

根据载荷、工作长度和自由长度，可以计算出弹簧的变形量。

变形量是指弹簧在工作状态下相对于自由状态下的变化长度，用符号δ表示，其单位为mm。

5.弹簧力：弹簧力是指弹簧在工作状态下所产生的力，用符号Fspring表示，其单位为N。

弹簧力可以通过弹簧刚度和变形量的乘积来计算。

Fspring = C * δ其中C为弹簧刚度，δ为变形量。

综上所述，圆柱螺旋压缩弹簧的计算公式包括弹簧刚度、载荷、工作长度、自由长度和弹簧力等参数的计算公式。

这些参数的计算可以帮助工程师根据具体的需求来选择和设计合适的圆柱螺旋压缩弹簧，以满足机械装置的要求。

圆柱螺旋压缩弹簧设计计算

% 圆柱螺旋压缩弹簧设计计算% M文件中的表16-3和表16-5见参考文献[1]% 已知条件：最小和最大弹簧载荷、工作行程、剪切弹性模量、许用应力、最小内径F1=500;F2=1200;h=60;G=7.85e4;sigma=1420;D1_min=50;% 1-按照强度条件确定弹簧丝直径% 由于弹簧丝材料强度与它的直径相关，需要采用试算法ds=input(' 试选弹簧丝直径(mm) ds = ');sigma_b=input(' 按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = ');tau_p=0.45*sigma_b;fprintf(' 许用剪切应力tau_p = %3.4f MPa \n',tau_p);Cj=D1_min/ds+1;fprintf(' 计算弹簧指数Cj = %3.4f \n',Cj);C=input(' 按照表16-5，选择弹簧指数C = ');Kq=(4*C-1)/(4*C-4)+0.615/C;fprintf(' 计算曲度系数Kq = %3.4f \n',Kq);dj=sqrt(8*Kq*F2*C/(pi*tau_p));fprintf(' 计算簧丝直径dj = %3.4f mm \n',dj);if dj>dsdisp ' 不安全，需要重选弹簧丝直径'elsedisp ' 安全'd=ds; % 确定弹簧丝直径end第1次试算：试选弹簧丝直径(mm) ds = 6按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = 1420许用剪切应力tau_p = 639.0000 MPa计算弹簧指数Cj = 9.3333按照表16-5，选择弹簧指数C = 9计算曲度系数Kq = 1.1621计算簧丝直径dj = 7.0721 mm不安全，需要重选弹簧丝直径第2次试算：试选弹簧丝直径(mm) ds = 7按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = 1370许用剪切应力tau_p = 616.5000 MPa计算弹簧指数Cj = 8.1429按照表16-5，选择弹簧指数C = 8计算曲度系数Kq = 1.1840计算簧丝直径dx = 6.8520 mm安全% 2-按照刚度条件确定弹簧工作圈数Kj=(F2-F1)/h;fprintf(' 计算弹簧刚度Kj = %3.4f N/mm \n',Kj);nj=G*d/(8*C^3*Kj);fprintf(' 计算弹簧圈数nj = %3.4f \n',nj);n=input(' 选取弹簧工作圈数n = ');n2=input(' 选取弹簧支承圈数n2 = ');n1=n+n2;fprintf(' 弹簧总圈数n1 = %3.4f \n',n1);% 计算弹簧的刚度和变形量Kp=G*d/(8*C^3*n);f1=F1/Kp;f2=F2/Kp;fprintf(' 弹簧实际刚度Kp = %3.4f N/mm \n',Kp);fprintf(' 弹簧最小变形量f1 = %3.4f mm \n',f1);fprintf(' 弹簧最大变形量f2 = %3.4f mm \n',f2);计算结果：计算弹簧刚度Kj = 11.6667 N/mm计算弹簧圈数nj = 11.4990选取弹簧工作圈数n = 12选取弹簧支承圈数n2 = 2弹簧总圈数n1 = 14.0000弹簧实际刚度Kp = 11.1796 N/mm弹簧最小变形量f1 = 44.7243 mm弹簧最大变形量f2 = 107.3383 mm% 3-弹簧稳定性校核D2=C*d;fprintf(' 弹簧中径D2 = %3.4f mm \n',D2);delta=input(' 选取相邻两圈弹簧丝间隙系数delta = ');t=(1+delta)*d+f2/n; % 圆柱螺旋压缩弹簧fprintf(' 弹簧节距t = %3.4f mm \n',t);Y=input(' 选取弹簧端部结构类型Y = '); % 弹簧端部结构类型:1或是2if Y==1H0=n*t+(n2-0.5)*d;elseif Y==2H0=n*t+(n2+1)*d;endfprintf(' 弹簧自由高度H0 = %3.4f mm \n',H0);b=H0/D2;fprintf(' 弹簧高径比 b = %3.4f \n',b);% 采用3次样条插值确定圆柱螺旋弹簧不稳定系数CbDBZC=input(' 选取弹簧端部支承类型DBZC = '); % 弹簧端部支承类型:1、2、3 switch DBZCcase 1 % 1-弹簧两端固定支承bx=[5.3 5.4 5.5 5.75 6 6.5 7 7.5 8 8.5 9 10];Cby=[0.80 0.65 0.60 0.45 0.40 0.325 0.265 0.225 0.19 0.165 0.145 0.125];case 2 % 2-弹簧一端固定、一端自由支承bx=[3.7 3.85 4 4.5 5 5.5 6 6.5 7 8 9 10];Cby=[0.80 0.60 0.50 0.31 0.24 0.20 0.17 0.15 0.13 0.105 0.08 0.075];case 3 % 3-弹簧两端自由支承bx=[2.6 2.8 3 3.5 4 4.5 5 5.5 6 7 8 9 10];Cby=[0.8 0.5 0.4 0.27 0.21 0.15 0.12 0.09 0.075 0.05 0.04 0.03 0.025]; endCb=interp1(bx,Cby,b,'spline'); % 3次样条插值fprintf(' 弹簧不稳定系数Cb = %3.4f \n',Cb);% 绘制圆柱螺旋弹簧不稳定系数Cb线图plot(bx,Cby,'ro',bx,Cby);grid on;xlabel('\bf\it b');ylabel('\bf\it Cb');title('\bf 弹簧不稳定系数线图');switch DBZCcase 1gtext('\bf 1-弹簧两端固定支承')case 2gtext('\bf 2-弹簧一端固定、一端自由支承')case 3gtext('\bf 3-弹簧两端自由支承')endFc=Cb*Kp*H0;fprintf(' 弹簧稳定临界载荷Fc = %3.4f N \n',Fc);if Fc<F2disp ' 弹簧工作不稳定，需要改变参数或是加装导向装置'elsedisp ' 弹簧工作稳定'end计算结果：弹簧中径D2 = 56.0000 mm选取相邻两圈弹簧丝间隙系数delta = 0.15弹簧节距t = 16.9949 mm选取弹簧端部结构类型Y = 1弹簧自由高度H0 = 214.4383 mm弹簧高径比 b = 3.8293选取弹簧端部支承类型DBZC = 3弹簧不稳定系数Cb = 0.2278弹簧稳定临界载荷Fc = 546.0792 N弹簧工作不稳定，需要改变参数或是加装导向装置。

汽车用螺旋弹簧设计和制造知识概述

可参照表3计算：
总圈数n1
n+1.5 n+2 n+2.5 n+2 n+2.5
自有高度H0 nt+d
nt+1.5d nt+2d nt+3d nt+3.5d
端部形式
两端圈磨平两端圈不磨
压缩弹簧的典型图样
以下两种表达方式皆可：
弹簧技术要求含：
1. 总圈数 2. 工作圈数 3. 绕制方向 4. 表面处理 5. 制造技术条件 6. 设计计算参数
C
旋绕比
K
应力修正系数
K 4C 1 0.615
t
弹簧节距
4C 4 C
mm
F1 Ip
弹簧安装时的予加载荷 N 材料截面极惯性矩，圆形截面为
Ip
d 4
32
mm4
圆柱螺旋压缩弹簧的计算公式
1. 载荷 F 与变形 f 的简化计算式：
f
FD3n
4GI p
8FD3n Gd 4
8FC 3n Gd
2. 载荷与应力的计算式：
除此之外，喷丸处理还可消除弹簧表面的疵点、脱碳（严重降低弹簧的疲劳强度）和微小缺陷，从而消除或减少了疲劳源。
应当指出，喷丸后的弹簧长度会变短，制定工艺时应予以考虑。喷丸处理和强化处理可同时在重要弹簧上采用，譬如悬架弹簧。
弹簧的表面处理
1.弹簧的金属保护层：镀锌处理：锌在干燥空气中较安定，不变化。在潮湿空气中会产生一层氧化锌白色薄膜，它可阻止弹簧继续遭受腐蚀，可用于弹簧在一般大气条件下防腐。凡是与硫酸、盐酸和苛性钠相接触的弹簧则不宜用镀锌处理。镀锌后的弹簧还可经钝化处理，藉以进一步提高保护性能和增加美观。镀锌层厚一般在6-24微米范围内选取。

弹簧失稳计算公式

弹簧失稳计算公式弹簧在我们的日常生活和工业生产中都有着广泛的应用，从小小的玩具到大型的机械装置，都能看到它的身影。

而要确保弹簧能够稳定可靠地工作，了解弹簧失稳的计算公式就显得尤为重要啦。

咱们先来说说弹簧失稳到底是咋回事。

想象一下，一根弹簧被过度压缩或者拉伸，它可能就会突然弯曲、扭曲，不再能正常发挥作用，这就是弹簧失稳啦。

就好像有一次我在修理一辆老旧自行车的时候，发现车座下面的减震弹簧好像有点不对劲。

我一用力压下去，它居然歪歪扭扭的，完全不像正常弹簧那样有规律地伸缩。

这可把我急坏了，后来才意识到可能是这弹簧长期使用，已经接近失稳的状态。

那弹簧失稳的计算公式是啥呢？一般来说，对于圆柱螺旋压缩弹簧，其失稳的临界载荷可以用下面这个公式计算：$F_{cr} = C_{B} \times k \times H_{0}$ 。

这里面，$F_{cr}$ 表示临界载荷，$C_{B}$ 是一个和弹簧端部支撑条件有关的系数，$k$ 是弹簧的刚度，$H_{0}$ 则是自由高度。

咱们来具体解释解释这些参数。

先说 $C_{B}$ 这个系数，它会根据弹簧两端的固定方式有所不同。

比如说，如果弹簧两端是固定的，那$C_{B}$ 的值就会比较大；要是一端固定一端自由，那 $C_{B}$ 的值就小很多啦。

刚度 $k$ 呢，它等于弹簧所受的载荷变化量除以相应的变形量。

而自由高度 $H_{0}$ 就比较好理解啦，就是弹簧在没有受到任何载荷时的高度。

再举个例子哈，假如有一个弹簧，它的端部是固定的，$C_{B}$ 取2，刚度 $k$ 是 100 N/mm，自由高度 $H_{0}$ 是 50mm ，那通过公式算出来，它的临界载荷 $F_{cr}$ 就是 2×100×50 = 10000 N 。

这就意味着，当对这个弹簧施加的压力超过 10000 N 时，它就可能会失稳啦。

在实际应用中，计算弹簧失稳可不是简单地套个公式就行。

还得考虑很多其他因素，比如说材料的疲劳、环境的温度和湿度等等。

弹簧参数、尺寸及计算公式

弹簧参数、尺寸及计算公式弹簧参数及尺寸一、小型圆柱螺旋拉伸弹簧尺寸及参数1、弹簧的工作图及形式1.1 工作图样的绘制按GB4459、4规定。

1.2 弹簧的形式分为A型和B型两种。

2、材料弹簧材料直径为0.16~0.45mm，并规定使用GB4357中B组钢丝或YB(T)11中B组钢丝。

采用YB(T)11中B组钢丝时，需在标记中注明代号“S”。

3、制造精度弹簧的刚度、外径、自由长度按GB1973规定的3级精度制造。

如需按2级精度制造时，加注符号“2”，但钩环开口尺寸均按3级精度制造。

4、旋向弹簧的旋向规定为右旋。

如需左旋应在标记中注明“左”。

5、钩环开口弹簧钩环开口宽度a为0.25D~0.35D。

注：D为弹簧中径。

6、表面处理6.1采用碳素弹簧钢丝制造的弹簧，表面一般进行氧化处理，但也可进行镀锌、镀镉、磷化等金属镀层及化学处理。

其标记方法应按GB1238的规定。

6.2采用弹簧用不锈钢丝制造的弹簧，必要时可对表面进行清洗处理，不加任何标记。

7、标记7.1标记的组成弹簧的标记由名称、型式、尺寸、标准编号、材料代号(材料为弹簧用不锈钢丝时)以及表面处理组成。

规定如下：7.2标记示例例1:A型弹簧，材料直径0.20mm，弹簧中径3.20mm，自由长度8.80mm，左旋，刚度、外径和自由长度的精度为2级，材料为碳素弹簧钢丝B组，表面镀锌处理。

标记:拉簧A0.20*3.20*8.80-2左GB1973.2——89-D-Zn例2：B型弹簧，材料直径0.40mm，弹簧中径5.00mm，自由长度17.50mm，右旋，刚度、外径和自由长度的精度为3级，材料为弹簧用不锈钢丝B组。

标记：拉簧B0.40*5.00*17.50 GB1973.2--89-S8、计算依据标准中的计算采用如下基本公式：切应力(N/mm²)：τ=(8PDK)/(πd³)变形量(mm)：F=(8PD³n)/ Gd4弹簧钢度(N/mm):P′=P/ F=(Gd4)/(8D³n)曲度系数：K =(4C-1)/(4C-4)+ (0.615)/C旋转比：C =D/d 自由长度(mm)：H。

弹簧的极限压缩力计算公式

弹簧的极限压缩力计算公式弹簧是一种能够储存和释放机械能的装置，它常常用于各种机械装置中，如汽车悬挂系统、工业机械、家用电器等。

弹簧的一个重要参数就是极限压缩力，它反映了弹簧在最大压缩状态下所能承受的力量。

在工程设计和制造中，了解弹簧的极限压缩力是十分重要的，因为它直接关系到弹簧的使用寿命和安全性。

本文将介绍弹簧的极限压缩力计算公式以及相关知识。

首先，我们来看一下弹簧的基本结构和工作原理。

弹簧通常由金属丝或钢带制成，其形状可以是螺旋形、圆柱形或其他形状。

当外力作用于弹簧时，它会发生弹性变形，存储能量。

当外力消失时，弹簧会恢复原状，并释放储存的能量。

在弹簧的工作过程中，极限压缩力是一个重要的参数，它决定了弹簧在最大压缩状态下所能承受的力量。

弹簧的极限压缩力与弹簧的材料、尺寸和形状等因素有关。

一般来说，弹簧的极限压缩力可以通过以下公式来计算：F = kx。

其中，F表示弹簧的极限压缩力，k表示弹簧的弹簧系数，x表示弹簧的压缩量。

弹簧系数是一个反映弹簧刚度的参数，它与弹簧的材料和形状等因素有关。

压缩量是指弹簧在受力作用下的压缩程度，它与外力的大小和弹簧的刚度有关。

在实际工程中，我们可以通过测量弹簧的弹簧系数和压缩量来计算弹簧的极限压缩力。

通常情况下，弹簧系数可以通过实验测量得到，而压缩量可以通过对弹簧的压缩测试来得到。

通过这些数据，我们就可以利用上述公式来计算弹簧的极限压缩力。

除了弹簧的极限压缩力，我们还需要关注弹簧的安全性和使用寿命。

弹簧在工作过程中可能会受到一些外部因素的影响，如温度变化、外部振动等，这些因素都可能影响弹簧的性能和寿命。

因此，在工程设计和制造中，我们需要对弹簧进行全面的考虑和分析，以确保其安全可靠地工作。

在实际工程中，我们还需要考虑弹簧的安装和使用环境等因素。

弹簧的安装方式和使用环境可能会对其性能和寿命产生影响，因此我们需要在设计和选择弹簧时，充分考虑这些因素。

总之，弹簧的极限压缩力是一个重要的参数，它直接关系到弹簧的使用寿命和安全性。

弹簧计算公式

0.55 0.83 20.50 87
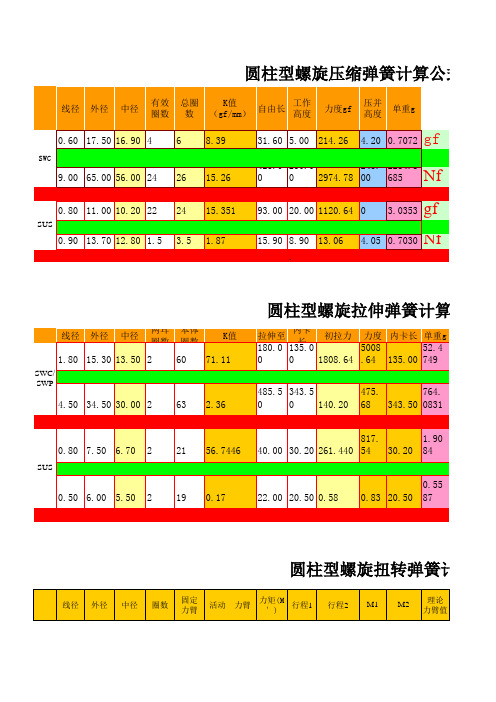
圆柱型螺旋扭转弹簧计算公式
线径外径
中径
圈数
固定力臂
活动
力臂
力矩(M ′)
行程1
行程2
M1
理论 M2 力臂值
6.80 28.30 21.50 4.25 15.00 20.00
SWC/
SWP 6.80 28.30 21.50 4.25 10.00 14.00
130.1 2
76
253.2942 1.079708 17.68889
1580 0.160313
1664.27 7.20
gf 1.2345
301.8053 1.162083 9
1700 0.177533
18.83
10.50
Nf 2.3539
181.0261 1.212857 7
1680 0.107754
243. 2284.8
0
Nf 0 2974.78 00 685
0.80 11.00 10.20 22 24 15.351
SUS
0.90 13.70 12.80 1.5 3.5 1.87
20.0
gf 93.00 20.00 1120.64 0 3.0353
Nf 15.90 8.90 13.06 4.05 0.7030
2.00
30.00
17.3 5
260.24
25.8 2
1275. 18
6.00
24.00
7651 30604. 25.8 .09 37 2
0.65 10.50 9.85 2 5.00 12.00 SUS
1.80 7.40 5.60 4.7 11.00 20.00

圆柱螺旋压缩（拉伸）弹簧的设计计算

圆柱螺旋压缩（拉伸）弹簧的设计计算(⼀)⼏何参数计算普通圆柱螺旋弹簧的主要⼏何尺⼨有：外径D、中径D2、内径D1、节距p、螺旋升⾓α及弹簧丝直径d。

由下图圆柱螺旋弹簧的⼏何尺⼨参数图可知，它们的关系为：式中弹簧的螺旋升⾓α，对圆柱螺旋压缩弹簧⼀般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但⽆特殊要求时，⼀般都⽤右旋。

圆柱螺旋弹簧的⼏何尺⼨参数普通圆柱螺旋压缩及拉伸弹簧的结构尺⼨计算公式见表(普通圆柱螺旋压缩及拉伸弹簧的结构尺⼨（mm ）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺⼨（mm）计算公式参数名称及代号计算公式备注压缩弹簧拉伸弹簧中径D2D2=Cd按普通圆柱螺旋弹簧尺⼨系列表取标准值内径D1D1=D2-d外径D D=D2+d旋绕⽐C C=D2/d压缩弹簧长细⽐bb=H0/D2b在1～5.3的范围内选取⾃由⾼度或长度H0H0≈pn+(1.5～2)d（两端并紧，磨平）H0≈pn+(3～3.5)d（两端并紧，不磨平）H0=nd+钩环轴向长度⼯作⾼度或长度H1,H2,…,HnHn=H0-λn Hn=H0+λnλn--⼯作变形量有效圈数n根据要求变形量按式（16-11）计算n≥2总圈数n1n1=n+(2～2.5)（冷卷）n1=n+(1.5～2) （YII型热卷）n1=n拉伸弹簧n1尾数为1/4,1/2,3/4整圈。

推荐⽤1/2圈节距p p=(0.28～0.5)D2p=d 轴向间距δδ=p-d展开长度L L=πD2n1/cosαL≈πD2n+钩环展开长度螺旋⾓αα=arctg(p/πD2)对压缩螺旋弹簧，推荐α=5°～9°(⼆)特性曲线弹簧应具有经久不变的弹性，且不允许产⽣永久变形。

因此在设计弹簧时，务必使其⼯作应⼒在弹性极限范围内。

在这个范围内⼯作的压缩弹簧，当承受轴向载荷P时，弹簧将产⽣相应的弹性变形，如右图a所⽰。

为了表⽰弹簧的载荷与变形的关系，取纵坐标表⽰弹簧承受的载荷，横坐标表⽰弹簧的变形，通常载荷和变形成直线关系(右图b)。

弹簧螺旋角计算公式

弹簧螺旋角计算公式弹簧螺旋角是在弹簧设计和制造中一个非常重要的参数。

它的计算对于确保弹簧能够正常工作，满足特定的性能要求具有关键意义。

咱们先来说说弹簧螺旋角到底是啥。

想象一下一个弹簧，就像咱们常见的那种压缩弹簧或者拉伸弹簧，它一圈一圈绕起来的那个角度，就是螺旋角啦。

这个角度的大小会影响弹簧的很多性能，比如它的弹性、承载能力等等。

那怎么计算这个螺旋角呢？一般来说，我们可以用下面这个公式：tanα = p / (πd)这里的α就是螺旋角，p 是弹簧的螺距，d 是弹簧的中径。

可能有人会问，啥是螺距？啥又是中径？别着急，咱们一个一个来解释。

螺距呢，就是弹簧相邻两圈对应点之间的轴向距离。

比如说，你拿一个弹簧，从这一圈的某个点，到相邻的下一圈的对应点，这之间的距离就是螺距。

中径呢，就是弹簧钢丝中心线所在圆柱的直径。

我给您举个例子哈。

比如说有一个弹簧，它的螺距是 10 毫米，中径是 50 毫米。

那咱们来算算它的螺旋角。

tanα = 10 / (π×50) ，算出来之后，再用反正切函数就可以求出螺旋角α啦。

在实际的工程应用中，弹簧螺旋角的计算可不是这么简单就完事儿的。

还得考虑很多其他的因素，比如说材料的特性、工作环境的要求等等。

我记得有一次，我们工厂要生产一批特殊规格的弹簧，用于一种新型的机械设备。

客户对弹簧的性能要求特别高，其中就包括对螺旋角的精确控制。

我们的工程师们可真是费了好大的劲儿，反复计算、试验，不断调整参数，就为了能让弹簧达到最佳的性能。

那几天，整个车间都弥漫着紧张的气氛。

大家都知道，这批弹簧要是做不好，不仅影响订单，还可能影响咱们厂的声誉。

最后，经过大家的努力，终于算出了合适的螺旋角，生产出了让客户满意的弹簧。

所以说啊，别看这小小的弹簧螺旋角，里面的学问可大着呢！它需要我们仔细计算，精心设计，才能让弹簧发挥出最好的作用。

总之，弹簧螺旋角的计算公式虽然看起来不复杂，但要真正运用好，还得结合实际情况，综合考虑各种因素。