湖北省广水市马坪镇中心中学2014-2015学年八年级上期中考试数学试题
【数学】2014-2015年湖北省随州市广水市马坪镇中学七年级上学期期中数学试卷与解析PDF

2014-2015学年湖北省随州市广水市马坪镇中学七年级(上)期中数学试卷一、精心选一选(每小题3分,共30分,请将答案写在表中.)1.(3分)﹣0.2的相反数是()A.B.C.﹣5 D.52.(3分)下列计算正确的是()A.23=6 B.﹣42=﹣16 C.﹣8﹣8=0 D.﹣5﹣2=﹣33.(3分)在有理数(﹣1)2、、﹣|﹣2|、(﹣2)3中负数有()个.A.4 B.3 C.2 D.14.(3分)下列说法中正确的是()A.没有最小的有理数B.0既是正数也是负数C.整数只包括正整数和负整数D.﹣1是最大的负有理数5.(3分)2010年5月1日至2010年10月31日期间在上海举行的世界博览会总投资约450亿元人民币,其中“450亿”用科学记数法表示为()元.A.4.5×1010B.4.5×109C.4.5×108D.0.45×1096.(3分)下列说法错误的是()A.2x2﹣3xy﹣1是二次三项式B.﹣x+1不是单项式C.的系数是D.﹣22xab2的次数是67.(3分)下列各式中与多项式2x﹣(﹣3y﹣4z)相等的是()A.2x+(﹣3y+4z)B.2x+(3y﹣4z)C.2x+(﹣3y﹣4z)D.2x+(3y+4z)8.(3分)若﹣3x2m y3与2x4y n是同类项,那么m﹣n=()A.0 B.1 C.﹣1 D.﹣29.(3分)有理数a、b、c的大小关系为:c<b<0<a,则下面的判断正确的是()A.abc<0 B.a﹣b>0 C.D.c﹣a>010.(3分)下列方程中,是一元一次方程的是()A.x2﹣4x=3 B.C.x+2y=3 D.x=0二、耐心填一填(每题3分,共24分)11.(3分)如果+20%表示增加20%,那么﹣6%表示.12.(3分)比较大小:(用“>或=或<”填空).13.(3分)若a与b互为相反数,c与d互为倒数,则(a+b)3﹣4(cd)5=.14.(3分)一个单项式加上﹣y2+x2后等于x2+y2,则这个单项式为.15.(3分)长方形的长为acm,宽为bcm,若长增加了3cm,面积比原来增加了cm2.16.(3分)已知|a+1|=0,b2=9,则a+b=.17.(3分)老师的生日那天的上、下、左、右4个日期的和为80,老师的生日是号.18.(3分)观察一列数:﹣,,,,﹣,…根据规律,请你写出第9个数是.三、细心解一解(本大题66分)19.(16分)计算(1)﹣15﹣(﹣8)+(﹣11)﹣12(2)(﹣)××÷(﹣)(3)(﹣2)2+4×(﹣3)2﹣(﹣4)2÷(﹣2)(4)﹣ab﹣a2+a2﹣(﹣ab)20.(8分)解下列方程:(1)0.3x+1.2﹣2x=1.2﹣27x(2)40×10%•x﹣5=100×20%+12x.21.(8分)先化简,再求值:5(3a2b﹣ab2﹣1)﹣(ab2+3a2b﹣5),其中a=,b=.22.(8分)当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m 的解大2?23.(8分)如图所示:(1)用代数式表示阴影部分的面积;(2)当a=1,b=4时,求阴影部分的面积.24.(8分)已知蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“﹣”,从开始到结束爬行的各段路程(单位:cm)依次为:+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4(1)若A点在数轴上表示的数为﹣3,则蜗牛停在数轴上何处,请通过计算加以说明;(2)若蜗牛的爬行速度为每秒,请问蜗牛一共爬行了多少秒?25.(10分)某农户承包荒山若干亩,投资7800元改造一种果树2000棵.今年水果总产量为18000千克.目前有两种销售方式:一、此水果在市场上每千克售a元,该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天需付工资25元,农用车运费及其他各项税费平均每天100元.二、直接在果园每千克售b元(b<a).(1)分别用a,b表示两种方式出售水果的收入?(2)若a=1.5元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?2014-2015学年湖北省随州市广水市马坪镇中学七年级(上)期中数学试卷参考答案与试题解析一、精心选一选(每小题3分,共30分,请将答案写在表中.)1.(3分)﹣0.2的相反数是()A.B.C.﹣5 D.5【解答】解:﹣0.2的相反数是,故选:A.2.(3分)下列计算正确的是()A.23=6 B.﹣42=﹣16 C.﹣8﹣8=0 D.﹣5﹣2=﹣3【解答】解:A、23=8≠6,错误;B、﹣42=﹣16,正确;C、﹣8﹣8=﹣16≠0,错误;D、﹣5﹣2=﹣7≠﹣3,错误;故选:B.3.(3分)在有理数(﹣1)2、、﹣|﹣2|、(﹣2)3中负数有()个.A.4 B.3 C.2 D.1【解答】解:(﹣1)2=1是正数,﹣(﹣)=是正数,﹣|﹣2|=﹣2是负数,(﹣2)3=﹣8是负数,所以负数有﹣|﹣2|,(﹣2)32个,故选:C.4.(3分)下列说法中正确的是()A.没有最小的有理数B.0既是正数也是负数C.整数只包括正整数和负整数D.﹣1是最大的负有理数【解答】解:A、没有最大的有理数,也没有最小的有理数;故本选项正确;B、0既不是正数,也不是负数,而是整数;故本选项错误;C、整数包括正整数、负整数和零;故本选项错误;D、比﹣1大的负有理数可以是﹣;故本选项错误;故选:A.5.(3分)2010年5月1日至2010年10月31日期间在上海举行的世界博览会总投资约450亿元人民币,其中“450亿”用科学记数法表示为()元.A.4.5×1010B.4.5×109C.4.5×108D.0.45×109【解答】解:将450亿用科学记数法表示为:4.5×1010.故选:A.6.(3分)下列说法错误的是()A.2x2﹣3xy﹣1是二次三项式B.﹣x+1不是单项式C.的系数是D.﹣22xab2的次数是6【解答】解:A、2x2﹣3xy﹣1是二次三项式,故本选项不符合题意;B、﹣x+1不是单项式,故本选项不符合题意;C、的系数是,故本选项不符合题意;D、﹣22xab2的次数是4,故本选项符合题意.故选:D.7.(3分)下列各式中与多项式2x﹣(﹣3y﹣4z)相等的是()A.2x+(﹣3y+4z)B.2x+(3y﹣4z)C.2x+(﹣3y﹣4z)D.2x+(3y+4z)【解答】解:2x﹣(﹣3y﹣4z)=2x+3y+4z=2x+(3y+4z),故选:D.8.(3分)若﹣3x2m y3与2x4y n是同类项,那么m﹣n=()A.0 B.1 C.﹣1 D.﹣2【解答】解:∵﹣3x2m y3与2x4y n是同类项,∴2m=4,n=3,解得:m=2,n=3,∴m﹣n=﹣1.故选:C.9.(3分)有理数a、b、c的大小关系为:c<b<0<a,则下面的判断正确的是()A.abc<0 B.a﹣b>0 C.D.c﹣a>0【解答】解:A、∵c<b<0<a,∴a,b,c中有2个负数,一个正数,∴abc>0,故错误;B、∵a>b,∴a﹣b>0,故正确;C、∵分子均为1,两个负分数,分母的绝对值大的数就大,∴>,故错误;D、∵c<a,∴c﹣a<0,故错误;故选:B.10.(3分)下列方程中,是一元一次方程的是()A.x2﹣4x=3 B.C.x+2y=3 D.x=0【解答】解;A、是一元二次方程,故A错误;B、是分式方程,故B错误;C、是二元一次方程,故C错误;D、是一元一次方程,故D正确;故选:D.二、耐心填一填(每题3分,共24分)11.(3分)如果+20%表示增加20%,那么﹣6%表示减少6%.【解答】解:根据正数和负数的定义可知,﹣6%表示减少6%.故答案为:减少6%.12.(3分)比较大小:<(用“>或=或<”填空).【解答】解:∵>,∴<;故答案为:<.13.(3分)若a与b互为相反数,c与d互为倒数,则(a+b)3﹣4(cd)5=﹣4.【解答】解:∵a与b互为相反数,c与d互为倒数,∴a+b=0,cd=1.∴(a+b)3﹣4(cd)5=0﹣4×1=﹣4.故答案是:﹣4.14.(3分)一个单项式加上﹣y2+x2后等于x2+y2,则这个单项式为2y2.【解答】解:设所求单项式为A,根据题意得:A+(﹣y2+x2)=x2+y2,可得:A=(x2+y2)﹣(﹣y2+x2)=x2+y2+y2﹣x2=2y2.故答案为:2y215.(3分)长方形的长为acm,宽为bcm,若长增加了3cm,面积比原来增加了3b cm2.【解答】解:(a+3)b﹣ab=ab+3b﹣ab=3b(cm2).故答案为:3b.16.(3分)已知|a+1|=0,b2=9,则a+b=2或﹣4.【解答】解:∵|a+1|=0,∴a+1=0,a=﹣1,∵b2=9,∴b=±3,∴当a=﹣1,b=3时,a+b=﹣1+3=2,当a=﹣1,b=﹣3时,a+b=﹣1﹣3=﹣4,故答案为:2或﹣4.17.(3分)老师的生日那天的上、下、左、右4个日期的和为80,老师的生日是20号.【解答】解:设老师生日为x号,由题意得,x﹣1+x+1+x﹣7+x+7=80,解得:x=20.故答案为:20.18.(3分)观察一列数:﹣,,,,﹣,…根据规律,请你写出第9个数是﹣.【解答】解:﹣,,,,﹣,…第n个数为(﹣1)n.所以第9个数为﹣.故答案为:﹣.三、细心解一解(本大题66分)19.(16分)计算(1)﹣15﹣(﹣8)+(﹣11)﹣12(2)(﹣)××÷(﹣)(3)(﹣2)2+4×(﹣3)2﹣(﹣4)2÷(﹣2)(4)﹣ab﹣a2+a2﹣(﹣ab)【解答】解:(1)原式=﹣15+8﹣11﹣12=﹣38+8=﹣30;(2)原式=﹣×(﹣)××(﹣2)=﹣;(3)原式=4+36+8=48;(4)原式=﹣ab﹣a2+a2+ab=﹣a2+ab.20.(8分)解下列方程:(1)0.3x+1.2﹣2x=1.2﹣27x(2)40×10%•x﹣5=100×20%+12x.【解答】解:(1)方程移项合并得:25.3x=0,解得:x=0;(2)方程整理得:400x﹣500=2000+1200x,移项合并得:800x=﹣2500,解得:x=﹣.21.(8分)先化简,再求值:5(3a2b﹣ab2﹣1)﹣(ab2+3a2b﹣5),其中a=,b=.【解答】解:原式=15a2b﹣5ab2﹣5﹣ab2﹣3a2b+5=12a2b﹣6ab2;当a=﹣,b=时,原式=12××﹣6×(﹣)×=1+=.22.(8分)当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m 的解大2?【解答】解:解方程5m+3x=1+x得:x=,解2x+m=3m得:x=m,根据题意得:﹣2=m,解得:m=﹣.23.(8分)如图所示:(1)用代数式表示阴影部分的面积;(2)当a=1,b=4时,求阴影部分的面积.【解答】解:(1)S阴影部分=S矩形﹣S半圆=ab﹣πb2;(2)当a=4,b=1时,S阴影部分=1×4﹣π×12=4﹣.24.(8分)已知蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“﹣”,从开始到结束爬行的各段路程(单位:cm)依次为:+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4(1)若A点在数轴上表示的数为﹣3,则蜗牛停在数轴上何处,请通过计算加以说明;(2)若蜗牛的爬行速度为每秒,请问蜗牛一共爬行了多少秒?【解答】解:(1)依题意得﹣3+(+7)+(﹣5)+(﹣10)+(﹣8)+(+9)+(﹣6)+(+12)+(+4)=0,∴蜗牛停在数轴上的原点;(2)(|+7|+|﹣5|+|﹣10|+|﹣8|+|+9|+|+12|+|+4|+|﹣6|)÷=122秒.∴蜗牛一共爬行了122秒.25.(10分)某农户承包荒山若干亩,投资7800元改造一种果树2000棵.今年水果总产量为18000千克.目前有两种销售方式:一、此水果在市场上每千克售a元,该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天需付工资25元,农用车运费及其他各项税费平均每天100元.二、直接在果园每千克售b元(b<a).(1)分别用a,b表示两种方式出售水果的收入?(2)若a=1.5元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?【解答】解:(1)将这批水果拉到市场上出售收入为:18000a﹣×8×25﹣×100=18000a﹣3600﹣1800=18000a﹣5400(元).在果园直接出售收入为:18000b元.(2)当a=1.5时,市场收入为18000a﹣5400=18000×1.5﹣5400=216000(元).当b=1.1时,果园收入为18000b=18000×1.1=19800(元).因为2160019800,所以应选择在市场销售.。
湖北广水市马坪镇中心中学2014-2015学年八年级上学期期中考试语文试卷(纯word解析)人教版

2014-2015学年湖北广水市马坪镇中心中学八年级上期中考试语文试卷(解析版)1、将下面文字抄写在方格中,要求:规范、正确、美观。
(2分)让预言的号角奏鸣!哦,西风啊,冬天已经到来,春天还会远吗?—雪莱【答案】规范、正确、美观【解析】试题分析:要求学生在课下,在平时养成认真书写的习惯,练习硬笔书法。
做到书写认真,字体美观大方。
考点:识记并正确书写现代常用规范汉字。
能力层级为识记A。
2、下列加点字字音全对的一项是()(2分)A.辟头pì交卸xiè镂空lóu豁然开朗huòB.阻遏è匀称chèng伛偻yǔyǚ转弯抹角mǒC.瓦砾lì疮疤chuāng文绉绉zhōu锐不可当dāngD.疟子yào珐琅fàng蟠桃pān惟妙惟肖xiào【答案】C【解析】试题分析:此类型的题目考查学生对字词的理解识记能力,考查等级为A。
需要学生在平时多读课文,养成熟练地语感,注意读准拼音,多读课下注释,多查字典等工具书。
A.镂空lòu B.匀称chèn伛偻lǚ 转弯抹角mò D.珐琅fà 蟠桃pán考点:识记并正确书写现代汉语普通话常用字的字音。
能力层级为识记A。
3、下面字形全对的一项是()(2分)A.寒噤愧怍击磐巧妙绝论B.尴尬蹒跚噩耗穷困缭倒C.吊唁帷幕唏嘘微不足道D.骷髅狼藉杀戳张皇失措【答案】C【解析】试题分析:此题考查学生的词语辨析能力,考查等级为A。
需要学生在平时多读课文,多积累词语,多查工具书,注意易错字。
A:巧妙绝伦C:穷困潦倒D:杀戮考点:识记并正确书写现代常用规范汉字。
能力层级为识记A。
4、下列加点词语运用恰当的一项是()(2分)A.我家这个孩子呀,基础不太好,读书又无动于衷,这样的学习态度,怎能指望他的成绩会提高呢?B.一座座新建的楼房,一排排电视天线,短短三年,故乡已经面目全非了。
2014-2015年湖北省随州市广水市马坪镇中学八年级上学期期中数学试卷和答案

2014-2015学年湖北省随州市广水市马坪镇中学八年级(上)期中数学试卷一、选择题(每小题3分,共36分)1.(3分)下列交通标志是轴对称图形的是()A.B.C. D.2.(3分)点M(1,2)关于y轴对称点的坐标为()A.(﹣1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)3.(3分)若一个三角形三个内角度数的比为2:3:4,那么这个三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形4.(3分)下列各组图形中,是全等形的是()A.两个含60°角的直角三角形B.腰对应相等的两个等腰直角三角形C.边长为3和4的两个等腰三角形D.一个钝角相等的两个等腰三角形5.(3分)下列说法正确的是()A.等腰三角形的高、中线、角平分线互相重合B.顶角相等的两个等腰三角形全等C.等腰三角形一边不可以是另一边的二倍D.等腰三角形的两个底角相等6.(3分)若等腰三角形一腰上的高等于腰长的一半,则此三角形的底角等于()A.75°B.15°C.75°或15°D.30°7.(3分)如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC8.(3分)如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD 的周长是()A.22cm B.16cm C.23cm D.25cm9.(3分)一个多边形内角和是1080°,则这个多边形的对角线条数为()A.26 B.24 C.22 D.2010.(3分)把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是()A.B. C.D.11.(3分)下列计算错误的是()A.(﹣2x)3=﹣2x3B.﹣a2•a=﹣a3C.(﹣x)9÷(﹣x)3=x6D.(﹣2a3)2=4a6 12.(3分)以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是()A.1个 B.2个 C.3个 D.4个二、填空题(每小题3分,共18分)13.(3分)三角形一边长为40,一边长为50,求第三边a的取值范围.14.(3分)计算(直接写出结果)①a•a3=;②(b3)4=;③(2ab)3=.15.(3分)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=度.16.(3分)如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB 上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D 恰好落在BC上,则AP的长是.17.(3分)如图,PM⊥OA,PN⊥OB,垂足分别为M、N.PM=PN,若∠BOC=30°,则∠AOB=.18.(3分)如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件时,就可得到△ABC≌△FED.(只需填写一个即可)三、计算题(每小题20分,共20分)19.(20分)(1)x n•x n+1(2)﹣82013×(﹣0.125)2014(3)(﹣2x4)4+2x10•(﹣2x2)3﹣2x4•5(﹣x4)3(4)0.251999×42000﹣8100×0.5300.四、解答题(共46分)20.(8分)求出下列各题中正整数的值(1)若(9m+1)2=316,求正整数m的值.(2)若2×8n×16n=222,求正整数n的值.21.(8分)如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.22.(10分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴对称的△A1B1C1.(2)写出A1,B1,C1的坐标(直接写出答案),A1;B1;C1.(3)△A1B1C1的面积为.23.(10分)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.24.(10分)如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水.(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?请将上述两种情况下的自来水厂厂址标出,并保留作图痕迹.2014-2015学年湖北省随州市广水市马坪镇中学八年级(上)期中数学试卷参考答案与试题解析一、选择题(每小题3分,共36分)1.(3分)下列交通标志是轴对称图形的是()A.B.C. D.【解答】解:A、不是轴对称图形,故错误;B、不是轴对称图形,故错误;C、是轴对称图形,故正确;D、不是轴对称图形,故错误.故选:C.2.(3分)点M(1,2)关于y轴对称点的坐标为()A.(﹣1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)【解答】解:点M(1,2)关于y轴对称点的坐标为(﹣1,2).故选:A.3.(3分)若一个三角形三个内角度数的比为2:3:4,那么这个三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形【解答】解:∵三角形三个内角度数的比为2:3:4,∴三个内角分别是180°×=40°,180°×=60°,180°×=80°.所以该三角形是锐角三角形.故选:B.4.(3分)下列各组图形中,是全等形的是()A.两个含60°角的直角三角形B.腰对应相等的两个等腰直角三角形C.边长为3和4的两个等腰三角形D.一个钝角相等的两个等腰三角形【解答】解:A、两个含60°角的直角三角形,缺少对应边相等,所以不是全等形;B、腰对应相等的两个等腰直角三角形,符合AAS或ASA,或SAS,是全等形;C、边长为3和4的两个等腰三角形有可能是3,3,4或4,4,3不一定全等对应关系不明确不一定全等;D、一个钝角相等的两个等腰三角形.缺少对应边相等,不是全等形.故选:B.5.(3分)下列说法正确的是()A.等腰三角形的高、中线、角平分线互相重合B.顶角相等的两个等腰三角形全等C.等腰三角形一边不可以是另一边的二倍D.等腰三角形的两个底角相等【解答】解:A、应为等腰三角形底边上的高、中线、顶角平分线互相重合,故错误;B、顶角相等的两个等腰三角形,若对应边不等,则不全等,故错误;C、等腰三角形中腰可以是底边的2倍的,故错误;D、等腰三角形的两个底角相等是正确.故选:D.6.(3分)若等腰三角形一腰上的高等于腰长的一半,则此三角形的底角等于()A.75°B.15°C.75°或15°D.30°【解答】解:当高在三角形内部时,由已知可求得三角形的顶角为30°,则底角是75°;当高在三角形外部时,三角形顶角的外角是30°,则底角是15°;所以此三角形的底角等于75°或15°,故选C.7.(3分)如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC【解答】解:A、∵在△ABD和△ACD中∴△ABD≌△ACD(SSS),故本选项错误;B、∵在△ABD和△ACD中∴△ABD≌△ACD(SAS),故本选项错误;C、∵在△ABD和△ACD中∴△ABD≌△ACD(AAS),故本选项错误;D、不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项正确;故选:D.8.(3分)如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD 的周长是()A.22cm B.16cm C.23cm D.25cm【解答】解:∵DE⊥AC,垂足为E,CE=AE,AB=12cm,BC=10cm,∴CD=AD,∴BC+BD+CD=BC+AB=10+12=22cm.故选:A.9.(3分)一个多边形内角和是1080°,则这个多边形的对角线条数为()A.26 B.24 C.22 D.20【解答】解:设多边形的边数是n,则(n﹣2)•180°=1080°,解得n=8,∴多边形的对角线的条数是:==20.故选:D.10.(3分)把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是()A.B. C.D.【解答】解:从折叠的图形中剪去8个等腰直角三角形,易得将从正方形纸片中剪去4个小正方形,故选C.11.(3分)下列计算错误的是()A.(﹣2x)3=﹣2x3B.﹣a2•a=﹣a3C.(﹣x)9÷(﹣x)3=x6D.(﹣2a3)2=4a6【解答】解:A、应为(﹣2x)3=﹣8x3,故本选项错误;B、﹣a2•a=﹣a3,正确;C、(﹣x)9÷(﹣x)3=(﹣x)9﹣3=x6,正确;D、(﹣2a3)2=(﹣2)2(a3)2=4a6,正确.故选:A.12.(3分)以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是()A.1个 B.2个 C.3个 D.4个【解答】解:首先可以组合为13,10,5;13,10,7;13,5,7;10,5,7.再根据三角形的三边关系,发现其中的13,5,7不符合,则可以画出的三角形有3个.故选:C.二、填空题(每小题3分,共18分)13.(3分)三角形一边长为40,一边长为50,求第三边a的取值范围10<a <90.【解答】解:根据三角形的三边关系,得50﹣40<a<50+40,解得10<a<90.故答案为:10<a<90.14.(3分)计算(直接写出结果)①a•a3=a4;②(b3)4=b12;③(2ab)3=8a3b3.【解答】解:①a•a3=a1+3=a4;②(b3)4=b3×4=b12;③(2ab)3=8a3b3.故答案是:a4,b12,8a3b3.15.(3分)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=74度.【解答】解:∵∠A=40°,∠B=72°,∴∠ACB=68°,∵CE平分∠ACB,CD⊥AB于D,∴∠BCE=34°,∠BCD=90﹣72=18°,∵DF⊥CE,∴∠CDF=90°﹣(34°﹣18°)=74°.故答案为:74.16.(3分)如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB 上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D 恰好落在BC上,则AP的长是6.【解答】解:∵∠A+∠APO=∠POD+∠COD,∠A=∠POD=60°,∴∠APO=∠COD,在△APO和△COD中,,∴△APO≌△COD(AAS),即AP=CO,∵CO=AC﹣AO=6,∴AP=6.故答案为6.17.(3分)如图,PM⊥OA,PN⊥OB,垂足分别为M、N.PM=PN,若∠BOC=30°,则∠AOB=60°.【解答】解:∵PM⊥OA,PN⊥OB,PM=PN,∴OC平分∠AOB,∴∠AOB=2∠BOC=2×30=60°.故答案为:60°.18.(3分)如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件BC=ED 或∠A=∠F或AB∥EF时,就可得到△ABC≌△FED.(只需填写一个即可)【解答】解:AD=FC⇒AC=FD,又AB=EF,加BC=DE就可以用SSS判定△ABC≌△FED;加∠A=∠F或AB∥EF就可以用SAS判定△ABC≌△FED.故答案为:BC=ED或∠A=∠F或AB∥EF.三、计算题(每小题20分,共20分)19.(20分)(1)x n•x n+1(2)﹣82013×(﹣0.125)2014(3)(﹣2x4)4+2x10•(﹣2x2)3﹣2x4•5(﹣x4)3(4)0.251999×42000﹣8100×0.5300.【解答】解:(1)原式=x2n+1;(2)原式=﹣82013×0.1252014=﹣(8×0.125)2013×0.125=﹣1×0.125=﹣0.125;(3)原式=16x16+2x10•(﹣8x6)﹣2x4•5(﹣x12)=16x16﹣16x16+10x16=10x16;(4)原式=(0.25×4)1999×4﹣8100×0.125100=4﹣1=3.四、解答题(共46分)20.(8分)求出下列各题中正整数的值(1)若(9m+1)2=316,求正整数m的值.(2)若2×8n×16n=222,求正整数n的值.【解答】解:(1)(9m+1)2=【(32)m+1】2=3 4(m+1)=316,则4(m+1)=16,解得:m=3;(2)2×8n×16n=2×23n×24n=21+3n+4n=27n+1=222,则7n+1=22,解得:n=3.21.(8分)如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.【解答】解:∵两个四边形关于直线l对称,∴四边形ABCD≌四边形FEHG,∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,∴∠G=360°﹣∠H﹣∠A﹣∠F=55°,∴a=5cm b=4cm.22.(10分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴对称的△A1B1C1.(2)写出A1,B1,C1的坐标(直接写出答案),A1(﹣1,2);B1(﹣3,1);C1(2,﹣1).(3)△A1B1C1的面积为 4.5.【解答】解:(1)△A1B1C1如图所示;(2)△A1(﹣1,2),B1(﹣3,1),C1(2,﹣1);(3)△A1B1C1的面积=5×3﹣×1×2﹣×2×5﹣×3×3,=15﹣1﹣5﹣4.5,=15﹣10.5,=4.5.故答案为:(2)(﹣1,2),(﹣3,1),(2,﹣1);(3)4.5.23.(10分)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.【解答】证明:∵∠BAC=∠DAE,∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,即∠BAD=∠CAE,在△ABD和△AEC中,,∴△ABD≌△AEC(SAS).24.(10分)如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水.(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?请将上述两种情况下的自来水厂厂址标出,并保留作图痕迹.【解答】解:(1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等知,作出AB的中垂线与河岸交于点P,则点P满足到AB的距离相等.(2)作出点A关于河岸的对称点C,连接CB,交于河岸于点P,连接AP,则点P能满足AP+PB最小,理由:AP=PC,三角形的任意两边之和大于第三边,当点P在CB的连线上时,CP+BP是最小的.赠送初中数学几何模型【模型一】“一线三等角”模型:图形特征:运用举例:1.如图,若点B在x轴正半轴上,点A(4,4)、C(1,-1),且AB=BC,AB⊥BC,求点B的坐标;xyBCAO2.如图,在直线l上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是1S、2S、3S、4S,则14S S+=.ls4s3s2s13213. 如图,Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC上运动(不与点B,C重合),过D作∠ADE=45°,DE交AC于E.(1)求证:△ABD∽△DCE;(2)设BD=x,AE=y,求y关于x的函数关系式,并写出自变量x的取值范围;(3)当△ADE是等腰三角形时,求AE的长.B4.如图,已知直线112y x=+与y轴交于点A,与x轴交于点D,抛物线212y x bx c=++与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0)。
数学八上期中卷

2014—2015学年度第一学期期中考试八年级数学试题亲爱的同学,你好!本学期进行了一半了,今天是展示你才华的时候了,只要你仔细审题、认真答题,把平常的水平发挥出来,你就会有出色的表现!一、选择(本大题共12小题,每小题2分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的,把这个正确的选项填在括号中).1.下列图形是轴对称图形的有( )A.2B.3个C.4个D.5个2.下面各组线段中,能组成三角形的是( )A .4,10,6B .7,8,16C .10,5,4D .6,9,14 3下列图形中具有稳定性的是( )A .梯形B 长方形C .三角形D .正方形4.如图,若△ABC ≌△DEF ,则∠E 等于( ) A .30° B .50° C .60°D .100°5.正多边形的一个外角为36度,则它的边数是( ) (A) 10 (B) 6 (C)5 (D)8 6..和点P (2,5-)关于x 轴对称的点是( ) A (-2,5-) B (2,5-) C (2,5) D (-2,5)(第4题图)A BC ( )50° 30° DEF(30°7、如右图,图中显示的是从镜子中看到背后墙上的电子钟读数,由此你可以推断这时的实际时间是( )A 、10:05B 、20:01C 、20:10 D 、10:02 8.如图,△ABC 中,AB=AC,∠A=30°,DE 垂直平分AC ,则∠BCD 的度数为() A .80° B .75° C .65° D .45°9.等腰三角形的两边分别为3和6,则这个三角形的周长是 ( ) A. 12 B. 15 C. 9 D .12或15 10、如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2013个三角形,那么这个多边形是( ) A 、2013边形 B 、2014边形 C 、2015边形 D 、2016边形 11.如图,已知∠1=∠2,AC =AD ,增加下列条件:①∠C =∠D ;②∠B =∠E ;③AB =AE ;④BC =ED .其中能使△ABC ≌△AED 的条件有( )A .4个B .3个C .2个D .1个12.如图,在△ABC 中,AB=AC ,∠C=30°,∠BAD=90°,AD=4cm ,则BC 的长为( )A .4cmB .8cmC .10cmD .12cm(第8题图)(第11题图)A BE CD1 2 ABCD图4N MDCBA D 图3A CFEB二、填一填,看看谁仔细(本大题共8小题,每小题3分,共24分).13. 等腰三角形的底角为40°,则它的顶角是14.一个多边形的内角和是它外角和的8倍,则这个多边形是 边形。
初中数学八年级2014—2015第一学期期中学业水平测试卷附参考答案

2014—2015 第一学期初二数学期中学业水平测试、选一选,牛刀初试露锋芒!(每小题3分,共42分)1.下列图形中,轴对称图形的个数是()A. 4个2 .下列说法正确的是()A .三角形的角平分线是射线。
B.三角形三条高都在三角形内。
C. 三角形的三条角平分线有可能在三角形内,也可能在三角形外。
D. 三角形三条中线相交于一点。
3 .两根木棒长分别为5cm和7cm,要选择第三根,将它们钉成一个三角形,?如果第三根木棒长为偶数, 则组成方法有b5E2RGbCAPA. 3种B. 4种C. 5种D. 6种4. 下列各组条件中,不能判定△AB4A A/B/C/的一组是()/ / / / / //—”//A、/ A=Z A,/B=Z B ,AB= A BB、/ A=Z A , AB= A B , AC=A C/ / / J / / / / / / /C、/ A=/ A , AB= A B , BC= B CD、AB= A B , AC=A C ,BC= B C5. 如图,已知△ ABC的六个元素,则下面甲、乙、丙三个三角形中和△ ABC全等的图形是(D.只有丙6.如图1,将长方形ABCD纸片沿对角线BD折叠,使点C落在C •处,BC交AD于丘,若• DBC =22.5 °,贝恠不添加任何辅助线的情况下, 则图中45的角(虚线也视为角的边)的个数是()A. 5个E 22.12.如图5,△ ABC 的三边 AB 、BC CA 长分别是 20、30、40,其三条 角平分线将△ ABC 分为三个三角形,则 S A ABO : S A BCO:CAO 等于( )A . 1 : 1 : 1B . 1 : 2 : 3C . 2 : 3 : 4D . 3 : 4 : 513.如图6, 一圆柱高8cm,底面半径2cm,—只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程 (二 取 3)是() DXDiTa9E3dA.20cm;B.10cm;C.14cm;D. 无法确定.7•如图2,有一张直角三角形纸片,两直角边 △ ABC 折叠,使点B 与点A 重合,折痕为DE 为( )A. 10 cm B . 12cmC8、若等腰三角形的腰长为10,底边长为12,A 、6B 、7C 、8AC=5cm BC=10cm则厶ACD 的周长盒命 图2 E.15cmD . 20cm则底边上的高为()D 、99.如图3,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事 的办法是()p1EanqFDPwA.带①去B.带②去C.带③去D.带①和②去10、下列条件中,不能确定三角形是直角三角形的是(A.三角形中有两个角是互为余角; B.三角形三个内角之比为3 : 2 : 1; C.三角形的三边之比为3 : 2 : 1 ; D.三角形中有两个内角的差等于第三个内角 11.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图 4所示的图形,两条直角边在同一直线上.则图中等腰三角形有( )个. A. 1个B . 2个C.3 个D.4 个F C D图4图5A图614.如图7所示,已知△ ABC和厶BDE都是等边三角形。
2014——2015学年度第一学期八年级数学期中考试卷(含答案)

2014——2015学年度第一学期 八年级数学期中考试卷(含答案)(考试时间:100分钟 满分:120分)一、选择题:(每小题3分,共42分)下列各题都有A 、B 、C 、D 四个答案供选择,其中只有一个答案是正确的,请把认为正确1、4的算术平方根是A . 2B . 2-C . 2±D . 2±2、与数轴上的点成一一对应关系的数是A . 有理数B . 无理数C . 实数D . 整数 3、下列从左边到右边的变形,属于因式分解的是A . 1)1)(1(2-=-+x x x B . 1)2(122+-=+-x x x xC . )4)(4(422y x y x y x -+=-D . 22)3(96-=+-x x x4、下列命题中是真命题的是A .三角形的内角和为180°B .同位角相等C .三角形的外角和为180°D .内错角相等 5、使式子32+x 有意义的实数x 的取值范围是A .32>x B . 23>x C . 23-≥x D . 32-≥x6、在实数73,1+π,4,3.14,38,8,0, 11.21211211中,无理数有A . 2个B . 3个C . 4个D . 5个7、一个正方形的边长增加了cm 2,面积相应增加了232cm ,则这个正方形的边长为 A . 6cm B . 5cm C . 8cm D . 7cm8、计算:()20132013125.08-⨯等于A . 1-B . 1C . 2013D . 2013- 9、下列条件中,不能证明△ABC ≌△'''C B A 的是 A .''''C A AC B B A A =∠=∠∠=∠,,学校:班别: 姓名: 座号:………………………………………………………………装………………订………………线………………………………………………得分 B'C BB .''''B A AB B B A A =∠=∠∠=∠,,C .'''''C A AC A A B A AB =∠=∠=,,D .'''''C B BC B A AB A A ==∠=∠,, 10、下列算式计算正确的是A .523a a a =+B .623a a a =⋅C .923)(a a =D . a a a =÷2311、估计15的大小在A . 2和3之间B . 3和4之间C . 4和5之间D . 5和6之间12、若(x+a)(x-5)展开式中不含有x 的一次项,则a 的值为A . 5-B . 5C . 0D . 5± 13、如右图,△ABC ≌△EDF ,DF =BC ,AB=ED ,AF =20,EC =10,则AE 等于 A . 5 B . 8 C .10 D . 15 14、如果则的值分别是A . 2 和 3B . 2和-3C . 2和D .二、填空题:(每小题4分,共16分) 15、计算:=⨯-2016201020132________。
湖北省广水市马坪镇中心中学八年级地理上学期期中试题 新人教版
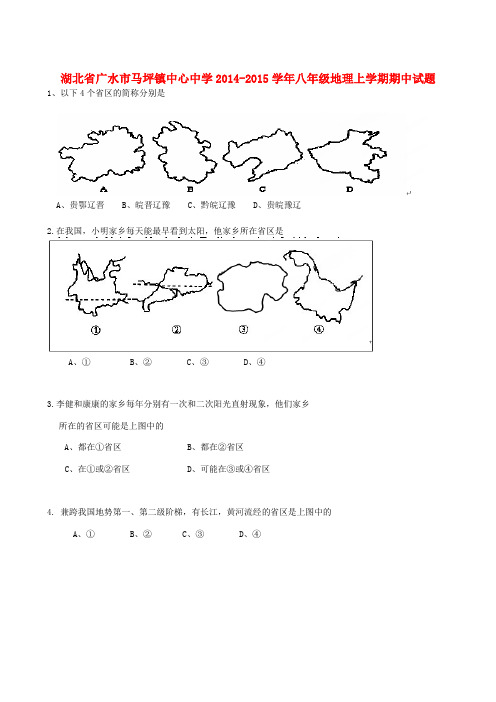
湖北省广水市马坪镇中心中学2014-2015学年八年级地理上学期期中试题1、以下4个省区的简称分别是
A、贵鄂辽晋
B、皖晋辽豫
C、黔皖辽豫
D、贵皖豫辽
2.在我国,小明家乡每天能最早看到太阳,他家乡所在省区是
A、①
B、②
C、③
D、④
3.李健和康康的家乡每年分别有一次和二次阳光直射现象,他们家乡
所在的省区可能是上图中的
A、都在①省区
B、都在②省区
C、在①或②省区
D、可能在③或④省区
4. 兼跨我国地势第一、第二级阶梯,有长江,黄河流经的省区是上图中的
A、①
B、②
C、③
D、④
5.读下图,回答图中山脉属于我国第二和第三级阶梯分界线的是
A、①
B、④
C、②③
D、①④
6..放寒假的时候,小明去了哈尔滨滑雪,小刘则去了海南岛领略海岛风情,下面是他们拍摄的两幅照片,你认为造成两地气候差异的最主要因素是
A.地形
B.海陆位
置 C.纬度位置 D.地势
二、读图
7.读沿某纬线我国地势剖面图,回答问题。
(3分)
①据图可以推出我国地势特征是。
(2分)
②这种地势特征对我国河流流向影响是?河流向流。
(1分)
8、读“中国地形图”,写出图中序号代表的地形区名称:
A、山脉 C、山脉 M、山脉
N、山脉 P、山脉 L、山脉
B、盆地 D、盆地E、_ _高原
F、高原
G、高原
H、 _高原
I、平原 J、_ _平原 K、平原
八年级地理期中试题答案
每题2分
7题西高东低,呈阶梯状分布。
(2分)东(或自西向东)。
2014-2015学年八年级上学期期中联考数学试题(含答案)
2014-2015学年八年级上学期期中联考 数学试题(含答案)(时间:100分钟,满分:100分)一、选择题(每题3分,共30分)1、下面各组线段中,能组成三角形的是( )A .5,11,6B .8,8,16C .10,5,4D .6,9,142、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A.3个B.2个C.1个D.0个 3、一个多边形内角和是10800,则这个多边形的边数为 ( ) A 、 6 B 、 7 C 、 8 D 、 9 4、等腰三角形的一个角是50,则它的底角是( ) A. 50 B. 50或65 C 、80 D 、65 5、和点P (2,5-)关于x 轴对称的点是( )A (-2,5-)B (2,5-)C (2,5)D (-2,5) 6、已知直角三角形中30°角所对的直角边为2 cm ,则斜边的长为( ). A .2 cm B .4 cm C .6 cm D .8 cm7、如图,已知12=∠∠,AC AD =,增加下列条件:①AB AE =;②BC ED =;③C D =∠∠;④B E =∠∠.其中能使ABC AED △≌△的条件有( )A.4个 B.3个 C.2个 D.个8、如图,先将正方形纸片对折,折痕为MN ,再把B 点折叠在折痕MN 上,折痕为AE ,点B 在MN 上的对应点为H ,沿AH 和DH 剪下,这样剪得的三角形中 ( ) A .AD DH AH ≠= B .AD DH AH ==C .DH AD AH ≠= D .AD DH AH ≠≠9、如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,∠A 与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) A .∠A =∠1+∠2 B .2∠A =∠1+∠2 C .3∠A =2∠1+∠2 D .3∠A =2(∠1+∠2)10、把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( ) A .对应点连线与对称轴垂直 B .对应点连线被对称轴平分C .对应点连线被对称轴垂直平分D .对应点连线互相平行二、填空题(每题3分,共24分)11、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根 木条这样做的道理是_______________。
2014-2015年湖北省随州市广水市杨寨中学八年级(上)数学期中试卷及参考答案

2014-2015学年湖北省随州市广水市杨寨中学八年级(上)期中数学试卷一、选择题(每小题4分,共40分)1.(4分)在实数﹣,0.21,,,,0.20202中,无理数的个数为()A.1 B.2 C.3 D.42.(4分)下列说法错误的是()A.1的平方根是±1B.只有非负数才有平方根和算术平方根C.2的平方根是D.±3是的平方根3.(4分)若,则a的取值范围是()A.a>3 B.a≥3 C.a<3 D.a≤34.(4分)使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等 D.两条边对应相等5.(4分)如果等腰三角形的两边长是6cm和3cm,那么它的周长是()A.9cm B.12cm C.12cm或15cm D.15cm6.(4分)如图是小亮在某时从镜子里看到镜子对面电子钟的像,则这个时刻是()A.10:21 B.10:51 C.21:10 D.12:017.(4分)如图,在△ABC中,AB=AC,BD平分∠ABC,若∠BDC=120°,则∠A 的度数为()A.110°B.100°C.80°D.60°8.(4分)下列图案是轴对称图形的有( )个.A .1B .2C .3D .49.(4分)如图,△ABC 的三边AB ,BC ,CA 长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,则S △ABO :S △BCO :S △CAO 等于( )A .1:1:1B .1:2:3C .2:3:4D .3:4:510.(4分)如图,AB=AC ,BD=CE ,DF ⊥CB 于F ,若BC=a ,则GF=( )A .B .C .D .二、填空题(每小题4分,共24分)11.(4分)若有意义,则x 的取值范围是 .12.(4分)等腰三角形的底角是15°,腰长为10,则其腰上的高为 .13.(4分)已知(2a +1)2+=0,则﹣a 2+b 2004= .14.(4分)已知点P (a +1,2a ﹣1)关于x 轴的对称点在第一象限,则|a +2|﹣|1﹣a |= .15.(4分)如图,已知DE ∥BC ,AB ∥CD ,E 为AB 的中点,∠A=∠B .下列结论: ①AC=DE ;②CD=AE ;③AC 平分∠BCD ;④O 点是DE 的中点;⑤AC=AB .其中正确的番号有 .16.(4分)如图,Rt△ABC≌Rt△ADE中,∠C=∠AED=90°,且EF=2,BF=3,则DE=.三、解答题(8小题,共86分)17.(8分)(1)计算:(2)求x的值:(3x﹣1)2=(﹣5)2.18.(8分)在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E,若∠CAE=∠B+30°,求∠AEC.19.(6分)如图,M,N分别为△ABC边AB,AC上的点,在BC边上求作一点P,使△MNP的周长最小.(保留作图痕迹)20.(8分)已知的的小数部分为a,的小部分为b,求a+b的值.21.(10分)如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?22.(10分)如图,在四边形ABCD中,AD∥BC,∠DAB=90°,E为CD的中点,作EG⊥CD交CB的延长线于点G,连AG,在GE上取点F使GF=GA,CF=AD,(1)求证:∠GFC=∠GAD;(2)若∠GFC=120°,GB=2,求GF的长.23.(10分)如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(﹣2,﹣2).(1)请在图中作出△ABC关于直线x=﹣1的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出D、E、F的坐标;(2)求四边形ABED的面积.24.(12分)如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.(1)若BE平分∠CBA,求证:BD=2EC;(2)若D为AC上一动点(不与C,A重合),则∠AED的大小是否变化?若变化,求出变化范围;若不变,求出大小.25.(14分)如图,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)(1)求B点坐标;(2)若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD,求∠AOD的度数;(3)过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式=1是否成立?若成立,请证明:若不成立,说明理由.2014-2015学年湖北省随州市广水市杨寨中学八年级(上)期中数学试卷参考答案与试题解析一、选择题(每小题4分,共40分)1.(4分)在实数﹣,0.21,,,,0.20202中,无理数的个数为()A.1 B.2 C.3 D.4【解答】解:在实数﹣,0.21,,,,0.20202中,根据无理数的定义可得其中无理数有﹣,,三个.故选:C.2.(4分)下列说法错误的是()A.1的平方根是±1B.只有非负数才有平方根和算术平方根C.2的平方根是D.±3是的平方根【解答】解:A、1的平方根是±1,故A不正确;B、只有非负数才有平方根和算术平方根,故B不正确;C、2的平方根±,故C正确;D、±3是的平方根,故D不正确;故选:C.3.(4分)若,则a的取值范围是()A.a>3 B.a≥3 C.a<3 D.a≤3【解答】解:,即a﹣3≥0,解得a≥3;故选:B.4.(4分)使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等 D.两条边对应相等【解答】解:A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错误;D、两条边对应相等,若是两条直角边相等,可利用SAS证全等;若一直角边对应相等,一斜边对应相等,也可证全等,故D选项正确.故选:D.5.(4分)如果等腰三角形的两边长是6cm和3cm,那么它的周长是()A.9cm B.12cm C.12cm或15cm D.15cm【解答】解:当腰为3cm时,3+3=6,不能构成三角形,因此这种情况不成立.当腰为6cm时,6﹣3<6<6+3,能构成三角形;此时等腰三角形的周长为6+6+3=15cm.故选:D.6.(4分)如图是小亮在某时从镜子里看到镜子对面电子钟的像,则这个时刻是()A.10:21 B.10:51 C.21:10 D.12:01【解答】解:在镜子上看到的数字是12:01,那么真实数字应该是将此数字反转为:10:51.故选:B.7.(4分)如图,在△ABC中,AB=AC,BD平分∠ABC,若∠BDC=120°,则∠A的度数为( )A .110°B .100°C .80°D .60°【解答】解:∵AB=AC∴∠C=∠ABC∵BD 平分∠ABC∴∠ABD=∠DBC=∠ABC=∠C ,∴∠ADB=∠C +∠DBC=3∠DBC=60°∴∠DBC=∠ABD=20°∴∠A=180°﹣20°﹣60°=100°.故选:B .8.(4分)下列图案是轴对称图形的有( )个.A .1B .2C .3D .4【解答】解:第一个图形是轴对称图形,第二个图形不是轴对称图形,第三个图形不是轴对称图形,第四个图形是轴对称图形,综上所述,轴对称图形共有2个.故选:B .9.(4分)如图,△ABC 的三边AB ,BC ,CA 长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,则S △ABO :S △BCO :S △CAO 等于( )A .1:1:1B .1:2:3C .2:3:4D .3:4:5【解答】解:过点O 作OD ⊥AC 于D ,OE ⊥AB 于E ,OF ⊥BC 于F ,∵点O 是内心,∴OE=OF=OD ,∴S △ABO :S △BCO :S △CAO =•AB•OE :•BC•OF :•AC•OD=AB :BC :AC=2:3:4, 故选:C .10.(4分)如图,AB=AC ,BD=CE ,DF ⊥CB 于F ,若BC=a ,则GF=( )A .B .C .D .【解答】解:作EH ⊥BC 的延长线与H 点,∵AB=AC ,∴∠B=∠ACB=∠HCE ,在Rt △BDF 和Rt △CEH 中,,∴Rt △BDF ≌Rt △CEH (AAS ),∴BF=CH ,∴BC=FH=a ,∴FG=FH=.故选:A .二、填空题(每小题4分,共24分)11.(4分)若有意义,则x的取值范围是≤x≤2.【解答】解:根据题意得:,解得≤x≤2.故答案为:≤x≤2.12.(4分)等腰三角形的底角是15°,腰长为10,则其腰上的高为5.【解答】解:如图,△ABC中,∠B=∠ACB=15°,∴∠BAC=180°﹣15°×2=150°,∴∠CAD=180°﹣150°=30°,∵CD是腰AB边上的高,∴CD=AC=×10=5cm.故答案为:5.13.(4分)已知(2a+1)2+=0,则﹣a2+b2004=.【解答】解:已知(2a+1)2+=0,2a+1=0,b﹣1=0,a=﹣,b=1,﹣a2+b2004=﹣(﹣)2+12004=﹣+1=,故答案为:.14.(4分)已知点P(a+1,2a﹣1)关于x轴的对称点在第一象限,则|a+2|﹣|1﹣a|=2a+1.【解答】解:∵点P(a+1,2a﹣1)关于x轴的对称点在第一象限,∴点P(a+1,2a﹣1)在第四象限,∴,解得﹣1<a<,∴|a+2|﹣|1﹣a|=a+2﹣1+a=2a+1,故答案为2a+1.15.(4分)如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:①AC=DE;②CD=AE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的番号有①②④.【解答】解:∵已知DE∥BC,AB∥CD,∴四边形BCDE为平行四边形,∴CB=DE;∵∠A=∠B,∴AC=BC,∴AC=DE,即可得①正确;根据平行线等分线段性质可得AO=CO,∵AB∥CD,∴∠A=∠DCO,又∵∠AOE=∠COD,∴△AOE≌△COD(ASA),∴AE=CD,即可得②正确;OE=OD,O点是DE的中点;即可得④正确;结论③⑤无法证明.故答案填:①②④.16.(4分)如图,Rt△ABC≌Rt△ADE中,∠C=∠AED=90°,且EF=2,BF=3,则DE=5.【解答】解:如图,连结AF.∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE.在Rt△AFC与Rt△AFE中,∠C=∠AEF=90°,,∴Rt△AFC≌Rt△AFE(HL),∴CF=EF=2,∴BC=CF+BF=2+3=5,∴DE=BC=5.故答案为5.三、解答题(8小题,共86分)17.(8分)(1)计算:(2)求x的值:(3x﹣1)2=(﹣5)2.【解答】解:(1)原式=2﹣﹣2+2﹣3=﹣3;(2)开方得,3x﹣1=±5,x=,x1=2,x2=﹣.18.(8分)在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E,若∠CAE=∠B+30°,求∠AEC.【解答】解:ED垂直平分AB,∴AE=EB,∴∠EAB=∠B(1分),∴∠AEC=∠EAB+∠B=2∠B(2分),∵在△ACE中,∠C=90°,∴∠CAE+∠AEC=90°,∵∠CAE=∠B+30°,∴∠B+30°+2∠B=90°(4分),∴∠B=20°,∴∠AEC=2∠B=40°(6分).19.(6分)如图,M,N分别为△ABC边AB,AC上的点,在BC边上求作一点P,使△MNP的周长最小.(保留作图痕迹)【解答】解:如图所示:20.(8分)已知的的小数部分为a,的小部分为b,求a+b的值.【解答】解:∵3<<4,∴8<5+<9,∴a=5+﹣8=﹣3,(4分)∵1<5﹣<2∴b=4﹣(8分)∴a+b=1.(10分)21.(10分)如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?【解答】解:根据三角形全等的判定方法HL可知:①当P运动到BP=AC时,∵∠A=∠QBP=90°,在Rt△ABC与Rt△BQP中,,∴Rt△ABC≌Rt△BQP(HL),即BP=AC=6;②当P运动到与A点重合时,BP=AB,在Rt△ABC与Rt△BPQ中,,∴Rt△BPQ≌Rt△ABC(HL),即AB=BP=8,∴当点P与点A重合时,△ABC才能和△BPQ全等.22.(10分)如图,在四边形ABCD中,AD∥BC,∠DAB=90°,E为CD的中点,作EG⊥CD交CB的延长线于点G,连AG,在GE上取点F使GF=GA,CF=AD,(1)求证:∠GFC=∠GAD;(2)若∠GFC=120°,GB=2,求GF的长.【解答】解:(1)连接GD,∵E为DC的中点,GF⊥CD,∴GF垂直平分CD,∴GD=GC,在△DAG和△CFG中,,∴△DAG≌△CFG(SSS),∴∠GFC=∠GAD;(2)∵∠GFC=120°,∴∠GAD=120°,∵AD∥GC,∴∠AGB=60°,∵GB=2,∴AG=4,∴GF=AG=4.23.(10分)如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(﹣2,﹣2).(1)请在图中作出△ABC关于直线x=﹣1的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出D、E、F的坐标;(2)求四边形ABED的面积.【解答】解:(1)D(﹣4,3);E(﹣5,1);F(0,﹣2);(5分)(2)AD=6,BE=8,=(AD+BE)•2=AD+BE=14.(8分)∴S四边形ABED24.(12分)如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.(1)若BE平分∠CBA,求证:BD=2EC;(2)若D为AC上一动点(不与C,A重合),则∠AED的大小是否变化?若变化,求出变化范围;若不变,求出大小.【解答】解(1)延长BA、CE相交于点F,∵BE平分∠CBA,BE⊥CE,∴BC=BF,在△BEC与△BEF中,,∴△BEC≌△BEF(HL),∴CE=FE,∴CE=CF,∵∠BAC是直角,∴∠BAD=∠CAF=90°,∵∠F+∠FBE=∠FCA+∠F=90°,∴∠ACF=∠FBE,即∠ACF=∠ABD,又∵AC=AB,在△BAD与△CAF中,,∴△BAD≌△CAF(ASA),∴BD=CF,即CE=BD.(2)∠AEB不变为45°.理由如下:过点A作AH⊥BE垂足为H,作AG⊥CE交CE延长线于G,由(1)知∠ACF=∠ABD,在△BAH与△CAG中,,∴△BAH≌△CAG(AAS)∴AH=AG,∵AH⊥EB,AG⊥EG,∴EA平分∠BEF,∴∠BEA=∠BEG=45°.25.(14分)如图,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)(1)求B点坐标;(2)若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD,求∠AOD的度数;(3)过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式=1是否成立?若成立,请证明:若不成立,说明理由.【解答】解:(1)作AE⊥OB于E,∵A(4,4),∴OE=4,∵△AOB为等腰直角三角形,且AE⊥OB,∴OE=EB=4,∴OB=8,∴B(8,0);(2)作AE⊥OB于E,DF⊥OB于F,∵△ACD为等腰直角三角形,∴AC=DC,∠ACD=90°即∠ACF+∠DCF=90°,∵∠FDC+∠DCF=90°,∴∠ACF=∠FDC,在△DFC和△CEA中,∴△DFC≌△CEA,∴EC=DF,FC=AE,∵A(4,4),∴AE=OE=4,∴FC=OE,即OF+EF=CE+EF,∴OF=CE,∴OF=DF,∴∠DOF=45°,∵△AOB为等腰直角三角形,∴∠AOB=45°,∴∠AOD=∠AOB+∠DOF=90°;方法一:过C作CK⊥x轴交OA的延长线于K,则△OCK为等腰直角三角形,OC=CK,∠K=45°,又∵△ACD为等腰Rt△,∴∠ACK=90°﹣∠OCA=∠DCO,AC=DC,∴△ACK≌△DCO(SAS),∴∠DOC=∠K=45°,∴∠AOD=∠AOB+∠DOC=90°;(3)成立,理由如下:在AM上截取AN=OF,连EN.∵A(4,4),∴AE=OE=4,又∵∠EAN=∠EOF=90°,AN=OF,∴△EAN≌△EOF(SAS),∴∠OEF=∠AEN,EF=EN,又∵△EGH为等腰直角三角形,∴∠GEH=45°,即∠OEF+∠OEM=45°,∴∠AEN+∠OEM=45°又∵∠AEO=90°,∴∠NEM=45°=∠FEM,又∵EM=EM,∴△NEM≌△FEM(SAS),∴MN=MF,∴AM﹣MF=AM﹣MN=AN,∴AM﹣MF=OF,即;方法二:在x轴的负半轴上截取ON=AM,连EN,MN,则△EAM≌△EON(SAS),EN=EM,∠NEO=∠MEA,即∠NEF+∠FEO=∠MEA,而∠MEA+∠MEO=90°,∴∠NEF+∠FEO+∠MEO=90°,而∠FEO+∠MEO=45°,∴∠NEF=45°=∠MEF,∴△NEF≌△MEF(SAS),∴NF=MF,∴AM=ON=OF+NF=OF+MF,即.注:本题第(3)问的原型:已知正方形AEOP,∠GEH=45°,将∠GEH的顶点E与正方形的顶点E重合,∠GEH的两边分别交PO、AP的延长线于F、M,求证:AM=MF+OF.。
2015八年级上学期期中数学试卷(含答案)

第1页 共6页 第2页 共6页2015-2016学年上学期八年级期中考试数学试卷(满分120分,考试时间120分钟) 座位号_______一、选择题(每题3分,共30分)1、下列“QQ 表情”中属于轴对称图形的是( )2、一个多边形的内角和与外角和相等,则这个多边形是( ) A 、四边形 B 、五边形 C 、六边形 D 、八边形3、等腰三角形中有一个角是40o ,则另外两个角的度数是( ) A 、70 o ,70 o B 、40 o ,100 o C 、70 o ,40 o D 、70 o ,70 o 或40 o ,100 o4、在平面直角坐标系中,O 为坐标原点,已知点(1,1),在x 轴上确定点P ,使△AOP 为等腰三角形,则符合条件的点P 共有( ) A 、1个 B 、2个 C 、3 个 D 、4个5、如图1,工人师傅常用角尺平分一个任意角,做法:在∠AOB 的边OA ,OB 上分别取OM=ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合,得到∠AOB 的平分线OP ,做法中用到三角形全等的判定方法是( ) A 、SSS B 、SAS C 、ASA D 、HL6、在△ABC 和△DEF 中,下列条件①AB=DE ②BC=EF ③AC=DF ④∠A=∠D ,⑤∠B=∠E ⑥∠C=∠F 其中不能保证△ABC ≌△DEF 的是( ) A 、①②③ B 、①②⑤ C 、①③⑤ D 、②⑤⑥ 7 、下列各组条件中,能决定△ABC ≌△DEF 的是( )A 、AB=DE ,BC=EF ,∠A=∠DB 、∠A=∠D ,∠C=∠FC 、 AB=DE ,BC=EF ,△ABC 的周长=△DEF 的周长D 、∠A =∠D ,∠B=∠E ,∠C=∠F 8、如图2,直线1l ,2l ,3l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A 、1处B 、2处C 、3处D 、4处 9、下列说法中,正确的是( )A 、如果两个三角形全等,则它们必是关于某直线成轴对称的图形B 、如果两个三角形关于某直线成轴对称,那么它们是全等三角形C 、等腰三角形是关于底边中线成轴对称的图形D 、一条线段是关于经过该线段中点的直线成轴对称的图形 10、如图3,已知△ABC 中,AC+BC=24,AO ,BO 分别是角平分线,且MN ∥BA ,分别交 AC 于N ,BC 于M ,则△CMN 的周长为( ) A 、12 B 、24 C 、36 D 、不确定二、填空题(每题4分,共32分)11、点P (-1,2)关于x 轴的对称点的坐标是 ,关于y 轴的对称点的坐标是 。
2014-2015八年级第一学期期中试卷(含答案)

ACB D E 人教版2014-2015学年度第一学期八年级数学期中考试试卷(含参考答案)一、选择题:(本题满分24分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填在题后的括号内。
......... 1.下列各组线段能组成一个三角形的是( ).(A)5cm ,8cm ,12cm (B)2cm ,3cm ,6cm (C)3cm ,3cm ,6cm (D)4cm ,7cm ,11cm 2.下列图案是轴对称图形的有( )。
A.(1)(2)B.(1)(3)C.(1)(4)D.(2)(3)(1) (2) (3) (4)3.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形一定重合。
其中正确的是( )。
A. ①② B. ②③ C. ③④ D. ①④ 4.已知直角三角形中30°角所对的直角边为2㎝,则斜边的长为( )。
A. 2 ㎝B. 4 ㎝C. 6 ㎝D. 8㎝ 5.点M (1,2)关于y 轴对称的点的坐标为 ( )。
A.(—1,2)B.(-1,-2)C. (1,-2)D. (2,-1) 6.如图,∠B=∠D=90°,CB=CD ,∠1=40°,则∠2=( )。
A .40° B. 45° C. 60° D. 50°7. 如图所示,在△ABC 中,已知点D,E,F 分别为边BC,AD,CE 的中点,且S △ABC=4cm 2,则阴影部分的面积等于( )A.2cm 2B.1cm 2C.12cm 2D.1 4 cm 28.已知等腰三角形一个内角是70°,则另外两个内角的度数是( )A.55°, 55°B.70°, 40°C.55°, 55°或70°, 40°D.以上都不对 二 、填空题:(本题满分24分,每小题3分)9.一扇窗户打开后,用窗钩可将其固定,这里运用的几何原理为 。
【新精品卷】湖北省马坪镇中心中学八年级(下)第一次月考数学试卷(内含答案详析)

湖北省马坪镇中心中学八年级(下)第一次月考数学试卷(考试时间共分钟,满分分)准考证号:__________ 姓名:________ 座位号:_________【请考生认真审题,争取会做的不要错,不会做的冷静思考】一.选择题(共10小题)1.在下列代数式中,不是二次根式的是()A. B. C.D.2.如果y=+3,那么yx的算术平方根是()A.2 B.3 C.9 D.±33.下列计算正确的是()A.2+3=5 B.÷=2 C.5×5=5 D.=24.如果二次根式有意义,那么x的取值范围是()A.x≥3 B.x≥0 C.x>3 D.x≠35.在化简时,甲、乙两位同学的解答如下:甲:===﹣乙:===﹣.A.两人解法都对B.甲错乙对C.甲对乙错D.两人都错6.下列各组数中,能作为直角三角形的三边长的是()A.1,2,3 B.,,C.3,3,5 D.6,8,97.如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为()A.8 B.9 C.D.108.如图,某小区有一块直角三角形的绿地,量得两直角边AC=4m,B C=3m,考虑到这块绿地周围还有足够多的空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以AC为一直角边的直角三角形,则扩充方案共有()A.2种B.3种C.4种D.5种9.如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若AC=3,BC=4.则BD的长是()A.2 B.3 C.4 D.510.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2EF,则正方形ABCD的面积为()A.14S B.13S C.12S D.11S二.填空题(共5小题)11.若二次根式有意义,则x的取值范围是.12.化简二次根式:=.13.计算:(2+)(﹣2)=.14.如图,6×6正方形网格(每个小正方形的边长为1)中,网格线的交点称为格点,△ABC的顶点都在格点上,D是BC的中点.则AC=;AD=.15.如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑米.三.解答题(共7小题)16.完成下列两道计算题:(1)﹣15+;(2)(﹣)+.17.在计算的值时,小亮的解题过程如下:解:原式==2……①=2……②=(2﹣1)……③=……④(1)老师认为小亮的解法有错,请你指出:小亮是从第步开始出错的;(2)请你给出正确的解题过程.18.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?19.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.(1)求这个梯子顶端A距地面有多高;(2)如果梯子的顶端A下滑4m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4m吗?为什么?20.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.21.如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点都在格点上.(1)求四边形ABCD的周长;(2)连接AC,试判断△ACD的形状,并说明理由.22.在△ABC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中a,b为常数,且a<b.将△ABD沿射线BC方向平移,得到△FCE,点A、B、D的对应点分别为点F、C、E.连接BE.(1)如图1,若D在△ABC内部,请在图1中画出△FCE;(2)在(1)的条件下,若AD⊥BE,求BE的长(用含a,b的式子表示);(3)若∠BAC=α,当线段BE的长度最大时,则∠BAD的大小为;当线段BE的长度最小时,则∠BAD的大小为(用含α的式子表示).参考答案与试题解析一.选择题(共10小题)1.在下列代数式中,不是二次根式的是()A. B. C.D.【解答】解:A、,是二次根式,故此选项错误;B、,是二次根式,故此选项错误;C、,是二次根式,故此选项错误;D、,不是二次根式,故此选项正确;故选:D.2.如果y=+3,那么yx的算术平方根是()A.2 B.3 C.9 D.±3【解答】解:由题意得,x﹣2≥0,2﹣x≥0,解得,x=2,∴y=3,则yx=9,9的算术平方根是3.故选:B.3.下列计算正确的是()A.2+3=5 B.÷=2 C.5×5=5 D.=2【解答】解:A、2与3不能合并,所以A选项错误;B、原式==2,所以B选项正确;C、原式=25=25,所以C选项错误;D、原式==,所以D选项错误.故选B.4.如果二次根式有意义,那么x的取值范围是()A.x≥3 B.x≥0 C.x>3 D.x≠3【解答】解:二次根式有意义,则x的取值范围是:x≥3.故选:A.5.在化简时,甲、乙两位同学的解答如下:甲:===﹣乙:===﹣.A.两人解法都对B.甲错乙对C.甲对乙错D.两人都错【解答】解:甲进行分母有理化时不能确定﹣≠0,故不能直接进行分母的有理化,故甲错误;乙分子因式分解,再与分母约分,故乙正确.故选B.6.下列各组数中,能作为直角三角形的三边长的是()A.1,2,3 B.,,C.3,3,5 D.6,8,9【解答】解:A、12+22≠32,根据勾股定理的逆定理不是直角三角形,故此选项错误;B、()2+2=2,根据勾股定理的逆定理是直角三角形,故此选项正确;C、32+32≠52,根据勾股定理的逆定理不是直角三角形,故此选项错误;D、82+62≠92,根据勾股定理的逆定理不是直角三角形,故此选项错误.故选B.7.如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为()A.8 B.9 C.D.10【解答】解:∵AB=8,BC=10,AC=6,∴62+82=102,∴△ABC是直角三角形,∠BAC=90°,则由面积公式知,S△ABC=AB•AC=BC•AD,∴AD=.故选C.8.如图,某小区有一块直角三角形的绿地,量得两直角边AC=4m,BC=3m,考虑到这块绿地周围还有足够多的空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以AC为一直角边的直角三角形,则扩充方案共有()A.2种B.3种C.4种D.5种【解答】解:如图所示:故答案为:B.9.如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若AC=3,BC=4.则BD的长是()A.2 B.3 C.4 D.5【解答】解:∵AC=3,BC=4,∴AB===5,∵以点A为圆心,AC长为半径画弧,交AB于点D,∴AD=AC,∴AD=3,∴BD=AB﹣AD=5﹣3=2.故选A.10.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2EF,则正方形ABCD的面积为()A.14S B.13S C.12S D.11S【解答】解:设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2由题意可知EF=(2a﹣b)﹣2(a﹣b)=2a﹣b﹣2a+2b=b,∵AM=2EF,∴2a=2b,∴a=b,∵正方形EFGH的面积为S,∴b2=S,∴正方形ABCD的面积=4a2+b2=13b2=13S,故选B.二.填空题(共5小题)11.若二次根式有意义,则x的取值范围是x≤3.【解答】解:∵二次根式有意义,∴3﹣x≥0,解得:x≤3.故答案为:x≤3.12.化简二次根式:=±.【解答】解:原式==,当a>0时,原式=,当a<0时,原式=﹣,故答案为:±.13.计算:(2+)(﹣2)=﹣1.【解答】解:原式=3﹣4=﹣1.故答案为﹣1.14.如图,6×6正方形网格(每个小正方形的边长为1)中,网格线的交点称为格点,△ABC的顶点都在格点上,D是BC的中点.则AC=2;AD=.【解答】解:由题意得,BD=CD=,由勾股定理得,AC==2,AD==,故答案为:2;.15.如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑0.8米.【解答】解:∵AB=2.5米,AC=0.7米,∴BC==2.4(米),∵梯子的顶部下滑0.4米,∴BE=0.4米,∴EC=BC﹣0.4=2米,∴DC==1.5米.∴梯子的底部向外滑出AD=1.5﹣0.7=0.8(米).故答案是:0.8.三.解答题(共7小题)16.完成下列两道计算题:(1)﹣15+;(2)(﹣)+.【解答】(1)解:原始=3﹣15×+×=3+=;(2)原=(5﹣2)=417.在计算的值时,小亮的解题过程如下:解:原式==2……①=2……②=(2﹣1)……③=……④(1)老师认为小亮的解法有错,请你指出:小亮是从第①步开始出错的;(2)请你给出正确的解题过程.【解答】解:(1)①(2)原式=2﹣=6﹣2=418.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?【解答】解:连接BD,在Rt△ABD中,BD2=AB2+AD2=32+42=52,在△CBD中,CD2=132BC2=122,而122+52=132,即BC2+BD2=CD2,∴∠DBC=90°,S四边形ABCD=S△BAD+S△DBC=,==36.所以需费用36×200=7200(元).19.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.(1)求这个梯子顶端A距地面有多高;(2)如果梯子的顶端A下滑4m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4m吗?为什么?【解答】解:(1)∵AO⊥DO,∴AO=,=,=12m,∴梯子顶端距地面12m高;(2)滑动不等于4m,∵AC=4m,∴OC=AO﹣AC=8m,∴OD=,=,∴BD=OD﹣OB=,∴滑动不等于4m.20.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.【解答】解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE,∵CD=3,∴DE=3;(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,由勾股定理,得AB═10,∴△ADB的面积为S=AB•DE=×10×3=15.21.如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点都在格点上.(1)求四边形ABCD的周长;(2)连接AC,试判断△ACD的形状,并说明理由.【解答】解:(1)由题意可知AB==3,AD==,DC==2,BC==,∴四边形ABCD的周长=AB+BC+CD+AD=+3+3;(2)△ACD是直角三角形,理由如下:∵AD=,DC=2,AC=5,∴AD2+CD2=AC2,∴△ACD是直角三角形.22.在△A BC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中a,b为常数,且a<b.将△ABD沿射线BC方向平移,得到△FCE,点A、B、D的对应点分别为点F、C、E.连接BE.(1)如图1,若D在△ABC内部,请在图1中画出△FCE;(2)在(1)的条件下,若AD⊥BE,求BE的长(用含a,b的式子表示);(3)若∠BAC=α,当线段BE的长度最大时,则∠BAD的大小为180°﹣α;当线段BE的长度最小时,则∠BAD的大小为α(用含α的式子表示).【解答】解:(1)如图,(2)连接BF.∵将△ABD沿射线BC方向平移,得到△FCE,∴AD∥EF,AD=EF;AB∥FC,AB=FC.∵∠ABC=90°,∴四边形ABCF为矩形.∴AC=BF.∵AD⊥BE,∴EF⊥BE.∵AD=a,AC=b,∴EF=a,BF=b.∴.(3)①如图,当线段BE的长度最大时,E点在B F的延长线上,∵四边形ABCF是矩形,∠BAC=α,∴∠BFC=α,∴∠EFC=180°﹣α.∴∠BAD=180°﹣α.②如图,当线段BE的长度最小时,E点在BF上,∵四边形ABCF是矩形,∠BAC=α,∴AC=BF,且互相平分,∴∠BAC=∠ABF,∠BFC=∠ACF,∵∠AOB=∠COF,∴∠BAC=∠ABF=∠BFC=∠ACF,∴∠BFC=∠BAC=α,∴∠BAD=α.故答案为:180°﹣α,α.。
2014-2015学年新人教版八年级上期中数学试卷及答案解析

2014-2015学年八年级(上)期中数学试卷一、选择题(本大题共12个小题,每小题3分,共36分.)1.下列交通标志是轴对称图形的是( )A.B.C. D.2.三角形的一个外角小于和它相邻的内角,这个三角形为( )A.锐角三角形B.直角三角形C.钝角三角形D.以上三种都有可能3.已知图中的两个三角形全等,则∠1等于( )A.72°B.60°C.50°D.58°4.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )A.13cm B.6cm C.5cm D.4cm5.下列等式成立的是( )A.(﹣3)﹣2=﹣9 B.m•m﹣2•m3=m5C.(﹣a﹣1b﹣3)﹣2=﹣a2b6D.(﹣2m)2÷2m3=6.若b为常数,要使16x2+bx+1成为完全平方式,那么b的值是( )A.4 B.8 C.±4 D.±87.若分式的值为零,则x的值为( )A.0 B.﹣3 C.3 D.3或﹣38.已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC 是( )A.直角三角形B.等腰三角形C.钝角三角形D.锐角三角形9.如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,线段DE=1cm,则BD 的长为( )A.6cm B.8cm C.3cm D.4cm10.随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,若设乘公交车平均每小时走x千米,根据题意可列方程为( )A.B.C.D.11.如图,设k=(a>b>0),则有( )A.k>2 B.1<k<2 C.D.12.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )A.B.3 C.4 D.二、填空题(本大题共5小题,每小题3分,共18分)13.一生物教师在显微镜下发现某种植物的细胞直径约为0.000000102mm,用科学记数法表示这个数为__________.14.分解因式:ab2﹣4ab+4a=__________.15.若3x=4,9y=7,则3x﹣2y的值为__________.16.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,则底角∠B=__________.17.如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:①Rt△ABC≌Rt△CDA;②S△AEF<S△BCE;③∠DAE+∠DFE=180°;④∠AFB>∠ACB 其中正确命题的代号是__________.三、解答题:(本大题共6小题,共46分)18.(1)解不等式:(2x﹣5)2+(3x+1)2>13(x2﹣10)(2)解分式方程:.19.先化简:÷(a+),当b=﹣1时,请你为a任选一个适当的数代入求值.20.如图,∠1=∠2,∠3=∠4,求证:AC=AD.21.如图,已知△ABC,P为内角平分线AD,BE,CF的交点,过点P作PG⊥BC于G,试说明∠BPD与∠CPG的大小关系,并说明理由.22.用电脑程序控制小型赛车进行50m比赛,“畅想号”和“和谐号”两辆赛车进入了决赛.比赛前的练习中,两辆车从起点同时出发,“畅想号”到达终点时,“和谐号”离终点还差3m.已知“畅想号”的平均速度为2.5m/s.(1)求“和谐号”的平均速度;(2)如果两车重新开始比赛,“畅想号”从起点向后退3m,两车同时出发,两车能否同时到达终点?若能,求出两车到达终点的时间;若不能,请重新调整一辆车的平均速度,使两车能同时到达终点.23.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.(1)在图①中,求∠AFB的度数;(2)在图②中,∠AFB的度数为__________,图③中,∠AFB的度数为__________;(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.2014-2015学年四川省绵阳中学八年级(上)期中数学试卷一、选择题(本大题共12个小题,每小题3分,共36分.)1.下列交通标志是轴对称图形的是( )A.B.C. D.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:A、不是轴对称图形,故错误;B、不是轴对称图形,故错误;C、是轴对称图形,故正确;D、不是轴对称图形,故错误.故选C.【点评】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.三角形的一个外角小于和它相邻的内角,这个三角形为( )A.锐角三角形B.直角三角形C.钝角三角形D.以上三种都有可能【考点】三角形的外角性质.【分析】此题依据三角形的外角性质,即三角形的外角与它相邻的内角互为邻补角,可判断出此三角形有一内角为钝角,从而得出这个三角形是钝角三角形的结论.【解答】解:∵三角形的一个外角与它相邻的内角和为180°,而题中说这个外角小于它相邻的内角,∴与它相邻的这个内角是一个大于90°的角即钝角,∴这个三角形就是一个钝角三角形.故选C.【点评】本题考查的是三角形的外角性质,解题的关键是熟练掌握三角形的外角与它相邻的内角互为邻补角.3.已知图中的两个三角形全等,则∠1等于( )A.72°B.60°C.50°D.58°【考点】全等三角形的性质.【分析】根据三角形内角和定理求得∠2=58°;然后由全等三角形是性质得到∠1=∠2=58°.【解答】解:如图,由三角形内角和定理得到:∠2=180°﹣50°﹣72°=58°.∵图中的两个三角形全等,∴∠1=∠2=58°.故选:D.【点评】本题考查了全等三角形的性质,解题的关键是找准对应角.4.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )A.13cm B.6cm C.5cm D.4cm【考点】三角形三边关系.【分析】此题首先根据三角形的三边关系,求得第三边的取值范围,再进一步找到符合条件的数值.【解答】解:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,即9﹣4=5,9+4=13.∴第三边取值范围应该为:5<第三边长度<13,故只有B选项符合条件.故选:B.【点评】本题考查了三角形三边关系,一定要注意构成三角形的条件:两边之和>第三边,两边之差<第三边.5.下列等式成立的是( )A.(﹣3)﹣2=﹣9 B.m•m﹣2•m3=m5C.(﹣a﹣1b﹣3)﹣2=﹣a2b6D.(﹣2m)2÷2m3=【考点】负整数指数幂;整式的除法.【分析】根据负整数指数幂、同底数幂的乘法以及整式的除法运算法则进行计算.【解答】解:A、原式=9,故本选项错误;B、原式=m(1﹣2+3)=m2,故本选项错误;C、原式=(﹣1)﹣2•a﹣1×(﹣2)•b(﹣3)×(﹣2)=a2b6,故本选项错误;D、原式==,故本选项正确.‘故选:D.【点评】本题考查了负整数指数幂、整式的除法.掌握运算法则的解题的关键.6.若b为常数,要使16x2+bx+1成为完全平方式,那么b的值是( )A.4 B.8 C.±4 D.±8【考点】完全平方式.【专题】常规题型.【分析】先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定b的值.【解答】解:16x2+bx+1=(4x)2+bx+1,∴bx=±2×4x×1,解得b=±8.故选D.【点评】本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.7.若分式的值为零,则x的值为( )A.0 B.﹣3 C.3 D.3或﹣3【考点】分式的值为零的条件.【专题】计算题.【分析】根据分式的值为零的条件得到当x2﹣9=0且x+3≠0时,分式的值为零,然后解方程和不等式即可得到x的值.【解答】解:∵分式的值为零,∴x2﹣9=0且x+3≠0,∴x=3.故选C.【点评】本题考查了分式的值为零的条件:分式的分子为零且分母不为零时,分式的值为零.也考查了解方程与不等式.8.已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC 是( )A.直角三角形B.等腰三角形C.钝角三角形D.锐角三角形【考点】轴对称的性质.【分析】作出图形,根据轴对称的性质可得∠BAC=∠DAC,∠ACB=∠ACD,然后求出∠BAC+∠ACB,再根据三角形的内角和定理求出∠B,然后判断三角形的形状即可.【解答】解:如图,∵△ABC和△ADC关于直线AC轴对称,∴∠BAC=∠DAC,∠ACB=∠ACD,∴∠BAC+∠ACB=(∠BAD+∠BCD)=×160°=80°,在△ABC中,∠B=180°﹣(∠BAC+∠ACB)=180°﹣80°=100°,∴△ABC是钝角三角形.故选C.【点评】本题考查了轴对称的性质,根据成轴对称的两个图形能够完全重合得到相等的角是解题的关键,作出图形更形象直观.9.如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,线段DE=1cm,则BD 的长为( )A.6cm B.8cm C.3cm D.4cm【考点】线段垂直平分线的性质;含30度角的直角三角形;三角形中位线定理.【专题】计算题.【分析】过A作AF∥DE交BD于F,则DE是△CAF的中位线,根据线段垂直平分线的性质,即可解答.【解答】解:过A作AF∥DE交BD于F,则DE是△CAF的中位线,∴AF=2DE=2,又∵DE⊥AC,∠C=30°,∴FD=CD=2DE=2,在△AFB中,∠1=∠B=30°,∴BF=AF=2,∴BD=4.故选D.【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段两个端点的距离相等.10.随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,若设乘公交车平均每小时走x千米,根据题意可列方程为( )A.B.C.D.【考点】由实际问题抽象出分式方程.【分析】根据乘私家车平均速度是乘公交车平均速度的2.5倍,乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,利用时间得出等式方程即可.【解答】解:设乘公交车平均每小时走x千米,根据题意可列方程为:=+,故选:D.【点评】此题主要考查了由实际问题抽象出分式方程,解题关键是正确找出题目中的相等关系,用代数式表示出相等关系中的各个部分,把列方程的问题转化为列代数式的问题.11.如图,设k=(a>b>0),则有( )A.k>2 B.1<k<2 C.D.【考点】分式的乘除法.【专题】计算题.【分析】分别计算出甲图中阴影部分面积及乙图中阴影部分面积,然后计算比值即可.【解答】解:甲图中阴影部分面积为a2﹣b2,乙图中阴影部分面积为a(a﹣b),则k====1+,∵a>b>0,∴0<<1,∴1<+1<2,∴1<k<2故选B.【点评】本题考查了分式的乘除法,会计算矩形的面积及熟悉分式的运算是解题的关键.12.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )A.B.3 C.4 D.【考点】轴对称-最短路线问题;正方形的性质.【分析】由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE 最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为16,可求出AB的长,从而得出结果.【解答】解:设BE与AC交于点P',连接BD.∵点B与D关于AC对称,∴P'D=P'B,∴P'D+P'E=P'B+P'E=BE最小.∵正方形ABCD的面积为16,∴AB=4,又∵△ABE是等边三角形,∴BE=AB=4.故选C.【点评】本题考查的是正方形的性质和轴对称﹣最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.二、填空题(本大题共5小题,每小题3分,共18分)13.一生物教师在显微镜下发现某种植物的细胞直径约为0.000000102mm,用科学记数法表示这个数为1.02×10﹣7.【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000000102=1.02×10﹣7.故答案为:1.02×10﹣7.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.14.分解因式:ab2﹣4ab+4a=a(b﹣2)2.【考点】提公因式法与公式法的综合运用.【专题】因式分解.【分析】先提取公因式a,再根据完全平方公式进行二次分解.完全平方公式:a2﹣2ab+b2=(a﹣b)2.【解答】解:ab2﹣4ab+4a=a(b2﹣4b+4)﹣﹣(提取公因式)=a(b﹣2)2.﹣﹣(完全平方公式)故答案为:a(b﹣2)2.【点评】本题考查了提公因式法,公式法分解因式,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.15.若3x=4,9y=7,则3x﹣2y的值为.【考点】同底数幂的除法;幂的乘方与积的乘方.【分析】根据3x﹣2y=3x÷32y=3x÷9 y即可代入求解.【解答】解:3x﹣2y=3x÷32y=3x÷9 y=.故答案是:.【点评】本题考查了同底数的幂的除法运算,正确理解3x﹣2y=3x÷32y=3x÷9 y是关键.16.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,则底角∠B=70°或20°.【考点】线段垂直平分线的性质;等腰三角形的性质.【分析】由于△ABC的形状不能确定,故应分△ABC是锐角三角形与钝角三角形两种情况进行讨论.【解答】解:如图①,当AB的中垂线与线段AC相交时,则可得∠ADE=50°,∵∠AED=90°,∴∠A=90°﹣50°=40°,∵AB=AC,∴∠B=∠C==70°;如图②,当AB的中垂线与线段CA的延长线相交时,则可得∠ADE=50°,∵∠AED=90°,∴∠DAE=90°﹣50°=40°,∴∠BAC=140°,∵AB=AC,∴∠B=∠C==20°.∴底角B为70°或20°.故答案为:70°或20°.【点评】本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.17.如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:①Rt△ABC≌Rt△CDA;②S△AEF<S△BCE;③∠DAE+∠DFE=180°;④∠AFB>∠ACB 其中正确命题的代号是①③④.【考点】矩形的性质;全等三角形的判定与性质.【分析】由矩形的性质得出∠ABC=∠D=∠BCD=∠BAD=90°,BC=DA,AB=CD,由SAS 证明△ABC≌△CDA,①正确;由△ABF的面积=△ABC的面积,得出△AEF的面积=△BCE的面积,②不正确;证明A、E、F、D四点共圆,得出∠DAE+∠DFE=180°,③正确;延长AF交矩形ABCD的外接圆于G,连接BG,由圆周角定理得出∠AGB=∠ACB,由三角形的外角性质得出∠AFB>∠AGB,得出∠AFB>∠ACB,④正确;即可得出结论.【解答】解:∵四边形ABCD是矩形,∴∠ABC=∠D=∠BCD=∠BAD=90°,BC=DA,AB=CD,在△ABC和△CDA中,,∴△ABC≌△CDA(SAS),∴①正确;∵△ABF的面积=△ABC的面积=AB•BC,∴△AEF的面积=△BCE的面积,∴②不正确;∵BE⊥AC,∴∠AEF=90°,∴∠AEF+∠D=180°,∴A、E、F、D四点共圆,∴∠DAE+∠DFE=180°,∴③正确;∵A、B、C、D四点共圆,如图所示:延长AF交矩形ABCD的外接圆于G,连接BG,则∠AGB=∠ACB,∵∠AFB>∠AGB,∴∠AFB>∠ACB,∴④正确;正确的代号是①③④;故答案为:①③④.【点评】本题考查了矩形的性质、全等三角形的判定与性质、四点共圆、圆周角定理、圆内接四边形的性质;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.三、解答题:(本大题共6小题,共46分)18.(1)解不等式:(2x﹣5)2+(3x+1)2>13(x2﹣10)(2)解分式方程:.【考点】整式的混合运算;解分式方程;解一元一次不等式.【分析】(1)直接利用完全平方公式化简求出即可;(2)首先去分母进而合并同类项求出即可.【解答】解:(1)(2x﹣5)2+(3x+1)2>13(x2﹣10)去括号得:4x2+25﹣20x+9x2+1+6x>13x2﹣130整理得:﹣14x>﹣156解得:x<11;(2)去分母得:x(x+2)﹣(x﹣1)(x+2)=3(x﹣1),x2+2x﹣(x2+2x﹣x﹣2)=3x﹣3,则﹣2x=﹣5,解得:x=,检验:当x=时,(x﹣1)(x+2)≠0,则x=是原方程的根.【点评】此题主要考查了整式的混合运算以及分式方程的解法,正确利用乘法公式是解题关键.19.先化简:÷(a+),当b=﹣1时,请你为a任选一个适当的数代入求值.【考点】分式的化简求值.【专题】开放型.【分析】主要考查了分式的化简求值,其关键步骤是分式的化简.要熟悉混合运算的顺序,正确解题.注意化简后,代入的数不能使分母的值为0.【解答】解:原式=÷==,∵a≠0、a≠±1,∴答案不唯一.当a=2时,原式=1.【点评】本题主要考查分式的化简求值,式子化到最简是解题的关键.20.如图,∠1=∠2,∠3=∠4,求证:AC=AD.【考点】全等三角形的判定与性质.【专题】证明题.【分析】先证出∠ABC=∠ABD,再由ASA证明△ABC≌△ABD,得出对应边相等即可.【解答】证明:∵∠3=∠4,∴∠ABC=∠ABD,在△ABC和△ABD中,,∴△ABC≌△ABD(ASA),∴AC=AD.【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.21.如图,已知△ABC,P为内角平分线AD,BE,CF的交点,过点P作PG⊥BC于G,试说明∠BPD与∠CPG的大小关系,并说明理由.【考点】三角形内角和定理.【分析】利用AD平分∠BAC,BE平分∠ABC,CF平分∠ACB,得出∠BAD=∠BAC,∠ABE=∠ABC,∠BCF=∠ACB,再利用三角形的外角意义得出∠BPD=∠BAD+∠ABE 等量代换得出∠BPD=90°﹣∠ACB;再利用PG⊥BC,得出三角形CPG是直角三角形,利用三角形的内角和表示出∠CPG=90°﹣∠ACB,证明结论成立.【解答】∠BPD=∠CPG证明:∵AD平分∠BAC,BE平分∠ABC,CF平分∠ACB,∴∠BAD=∠BAC,∠ABE=∠ABC,∠BCF=∠ACB,∴∠BPD=∠BAD+∠ABE=(∠BAC+∠ABC),∵∠BAC+∠ABC=180﹣∠ACB,∴∠BPD=(180﹣∠ACB)=90°﹣∠ACB;∵PG⊥BC,∴∠PGC=90°,∴∠BCP+∠CPG=180°﹣∠PGC=90°,∴∠CPG=90°﹣∠BCP=90°﹣∠ACB,∴∠BPD=∠CPG.【点评】此题考查角平分线的性质,三角形内角和定理,三角形外角的意义,垂直的性质等知识点.22.用电脑程序控制小型赛车进行50m比赛,“畅想号”和“和谐号”两辆赛车进入了决赛.比赛前的练习中,两辆车从起点同时出发,“畅想号”到达终点时,“和谐号”离终点还差3m.已知“畅想号”的平均速度为2.5m/s.(1)求“和谐号”的平均速度;(2)如果两车重新开始比赛,“畅想号”从起点向后退3m,两车同时出发,两车能否同时到达终点?若能,求出两车到达终点的时间;若不能,请重新调整一辆车的平均速度,使两车能同时到达终点.【考点】分式方程的应用.【分析】(1)设“和谐号”的平均速度为x,根据,“畅想号”运动50m与“和谐号”运动47m所用时间相等,可得方程,解出即可.(2)不能同时到达,设调整后“和谐号”的平均速度为y,根据时间相等,得出方程求解即可.【解答】解:(1)设“和谐号”的平均速度为x,由题意得,=,解得:x=2.35,经检验x=2.35是原方程的解.答:“和谐号”的平均速度2.35m/s.(2)不能同时到达.设调整后“和谐号”的平均速度为y,=,解得:y=.答:调整“畅想号”的车速为m/s可使两车能同时到达终点.【点评】本题考查了分式方程的应用,解答本题的关键是仔细审题,找到等量关系,建立方程,难度一般.23.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB 的延长线交AE于点F.(1)在图①中,求∠AFB的度数;(2)在图②中,∠AFB的度数为90°,图③中,∠AFB的度数为108°;(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.【考点】正多边形和圆;全等三角形的判定与性质;相似三角形的判定与性质.【分析】(1)先根据等边三角形的性质得出∠AC=60°,再由补角的定义可得出∠ABE与∠BCD的度数,根据△ABE与△BCD能相互重合可得出∠E=∠D,∠DBC=∠BAE,由三角形外角的性质可得出结论;(2)根据(1)中的方法可得出△BEF∽△BDC,进而可得出结论;(3)根据(1)(2)的结论找出规律即可.【解答】解:(1)∵△ABC是等边三角形,∴AB=BC,∠ABC=∠ACB=60°,∴∠ABE=∠BCD=120°.∵△ABE与△BCD能相互重合,∴∠E=∠D,∠DBC=∠BAE.∵∠FBE=∠CBD,∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°;(2)图②中,∵△ABE与△BCD能相互重合,∴∠E=∠D.∵∠FBE=∠CBD,∠D+∠CBD=90°,∴∠AFB=∠E+∠FBE=∠D+∠CBD=90°;同理可得,图③中∠AFB=108°.故答案为:90°,108°;(3)由(1)(2)可知,在正n边形中,∠AFB=.【点评】本题考查的是正多边形和圆,在解答此题时要注意正三角形、正四边形及正五边形的性质的应用,根据题意找出规律是解答此题的关键.。
2015年八年级(上)数学期中考试数学试卷(人教版)(含答案)

八年级(上)数学期中考试试卷 (人教版)一、选择题(本大题共6小题,每小题3分,共18分) 1.下列四个图形中是轴对称图形的是( )2.如图,已知MB =ND ,∠MBA =∠NDC ,下列条件中不能判定△ABM ≌△CDN 的是( )A .∠M =∠NB . AM ∥CNC .AB = CD D . AM =CN 3.能将三角形面积平分的是三角形的( )A 、 角平分线B 、 高C 、 中线D 、外角平分线 4.下面各角能成为某多边形的内角和的是( )A.430°B.4343°C.4320°D.4360°5.等腰三角形的底角为15°,腰长为a ,则此三角形的面积是( ).A 、a 2B 、½a 2C 、¼a 2D 、2a 26.如下图,直线L 是一条河,P,Q 是两个村庄。
欲在L 上的某处修建一个水泵站M ,向P,Q 两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )二、填空题(本大题共8小题,每小题3分,共24分)7.等腰三角形的腰长是8,则底长a 的取值范围是 ;8.若三角形三个内角度数的比为2:3:4,则相应的外角比是 . 9.一辆汽车的车牌号在水中的倒影是那么它的实际车牌号是.10.已知点A (a ,2)、B (-3,b ),关于X 轴对称,求a +b=___________.11.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a 的取值范围是 .12.如图是一个等边三角形木框,甲虫P 在边框AC 上爬行(A ,C端点除外),设甲虫P 到另外两边的距离之和为d ,等边三角形ABC 的高为h ,则d 与h 的大小关系是d h (填“>、<或=)13.如图所示,AD 是△ABC 中BC 边上的中线,若AB=2,AC=4,则AD 的取值范围是__________ 14.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下五个结论:① AD=BE ;② PQ ∥AE ;③ AP=BQ;④ DE=DP;⑤ ∠AOB=60°.恒成立的有 . 三、(本大题共3个小题,每小题5分,共15分)15. 如图,(1)过点A 画高AD ;(2)过点B 画中线BE ;(3)过点C 画角平分线CF .16.雨伞的中截面如图所示,伞骨AB=AC ,支撑杆OE=OF ,AE=31AB ,AF=31AC ,当O 沿AD 滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD 与∠CAD 有何关系?说明理由.17. 小华从点A 出发向前走10m ,向右转36°然后继续向前走第13题ABMN第2题第12题 A B C E DO P Q 第14题10m ,再向右转36°,他以同样的方法继续走下去,他能回到点A 吗?若能,当他走回到点A 时共走多少米?若不能,写出理由。
湖北省广水市马坪镇中心中学七年级数学上学期期中试题

湖北省广水市马坪镇中心中学2014-2015学年七年级数学上学期期中试题一、精心选一选(每小题3分,共30分,请将答案写在表中。
) 题号 1 2 3 4 5 6 7 8 9 10 答案1、-0.2的相反数是 A 、15 B 、15- C 、-5 D 、5 2、下列计算正确的是A 、326= B 、2416-=- C 、880--= D 、523--=- 3、在有理数2(1)-、3()2--、|2|--、3(2)-中负数有( )个A 、4B 、3C 、2D 、14、下列说法中正确的是A 、没有最小的有理数B 、0既是正数也是负数C 、整数只包括正整数和负整数D 、1-是最大的负有理数5、上海举行的世界博览会总投资约450亿元人民币,其中“450亿”用科学计数法表示为( )元 A 、104.510⨯ B 、94.510⨯ C 、84.510⨯ D 、90.4510⨯ 6、下列说法错误..的是 A 、2231x xy --是二次三项式 B 、1x -+不是单项式C 、223xy π-的系数是23π- D 、222xab -的次数是67、下列各式中与多项式2(34)x y z ---相等的是A 、2(34)x y z +-+B 、2(34)x y z +-C 、2(34)x y z +--D 、2(34)x y z ++8、若233m x y -与42nx y 是同类项,那么m n -=( )A 、0B 、1C 、-1D 、-29、有理数a 、b 、c 的大小关系为:c<b<0<a ,则下面的判断正确的是 A 、0abc < B 、0a b -> C 、11c b< D 、0c a -> 10、下列方程中,是一元一次方程的是 A.B.C.D二、耐心填一填(每题3分,共24分) 11、如果表示增加,那么表示12、比较大小12-_________13-(填“<”或“>”) 13、若a 与b 互为相反数,c 与d 互为倒数,则35()4()a b cd +-=___________14、一个单项式加上22y x -+后等于22x y +,则这个单项式为______________ 15、长方形的长为a cm ,宽为b cm ,若长增加了3 cm ,面积比原来增加 了________ 2cm16、已知|1|0a +=,29b =,则a b +=______________17、老师的生日那天的上、下、左、右4个日期的和为80, 老师的生日是________号 18、观察一列数:21-,52,103-,174,265-,376……根据规律,请你写出第9个数是________三、细心解一解(本大题66分) 19、计算(每小题4分,共16分)(1)15(8)(11)12---+-- (2)71131()()()262142-⨯-⨯÷-(3)222(2)4(3)(4)(2)-+⨯---÷- (4)221112()3233ab a a ab --+--20、解下列方程: (每小题4分,共8分)(1)0.3x+1.2-2x=1.2-27x (2)40×10%·x -5=100×20%+12x21、(8分)先化简,再求值22225(31)(35)a b ab ab a b ---+-,其中12a =-,13b =22.(8分)当m 为何值时,关于x 的方程x x m +=+135的解比关于x 的方程 的解大2?23、(8分)如图所示:(1) 用代数式表示阴影部分的面积; (2) 当10=a ,b =4时,求阴影部分的面积.24、(8分)已知蜗牛从A 点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位:cm )依次为:7,5,10,8,9,6,12,4+---+-++ (1)若A 点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明(2)若蜗牛的爬行速度为每秒12cm ,请问蜗牛一共爬行了多少秒? 25、(10分)某农户承包荒山若干亩,投资7800元改造—种果树2000棵.今年水果总产量为18000千克。
湖北省随州市广水市2024-2025学年八年级上学期期中数学试题
湖北省随州市广水市2024-2025学年八年级上学期期中数学试题一、单选题1.判断下列几组数据中,不可以作为三角形的三条边的是()A .6,8,10B .7,12,15C .5,15,20D .7,24,252.画ABC V 的边AB 上的高,下列画法中,正确的是()A .B .C .D .3.下列图案是轴对称图形的是()A .B .C .D .4.在ABC V 中,若3615A B C ∠=︒∠∠=,::,则C ∠等于()A .120︒B .100︒C .24︒D .20︒5.如图,1∠是在五边形ABCDE 的一个外角,若140∠=︒,则A B C D ∠+∠+∠+∠的度数是()A .300︒B .400︒C .500︒D .540︒6.如图,AD 是ABC V 的角平分线,DE AB ⊥于点E ,9ABC S = ,2DE =,5AB =,则AC的长是()A .2B .3C .4D .57.如图,在ABC V 中,AB AC =,AB 的垂直平分线DE 交AC 于点E ,CE 的垂直平分线正好经过点B ,与AC 相交于点F ,则A ∠的度数是()A .28︒B .35︒C .36︒D .45︒8.如图在ABC V 中,已知点D 、E 、F 分别为边BC 、AD 、CE 的中点,且ABC V 的面积是8,则BEF △的面积是()A .2B .4C .6D .79.如图,四边形ABCD 中,7AD =,2BC =,30A ∠=︒,90B Ð=°,120ADC ∠=︒,则CD 的长为()A .2B .3C .4D .510.如图,在ABC V 中,60BAC ∠=︒,BE CD 、为ABC V 的角平分线.BE 与CD 相交于点F ,FG 平分BFC ∠,有下列四个结论:①120BFC ∠=︒;②BD CE =;③BC BD CE =+;④若BE AC ⊥,BDF CEF ≌△△.其中正确的是()A .①③B .②③④C .①③④D .①②③④二、填空题11.若a 、b 、c 为三角形的三边,且a 、b220()b -=,第三边c 为奇数,则c =.12.如图AB =AD ,∠BAE =∠DAC ,要使△ABC ≌△ADE ,可补充的条件是(写一个即可).13.如图,小明从A 点出发,向前走30m 后向右转36︒,继续向前走30m ,再向右转36︒,他回到A 点时共走了米.14.等腰三角形一腰上的高与另一腰的夹角为60︒,则顶角的度数为.15.如图,在ABC V 中,10128AB AC BC AD ====,,,AD 是BAC ∠的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC PQ +的最小值是.三、解答题16.一个多边形的内角和比它的外角和的3倍少180︒,求这个多边形的边数和总对角线条数.17.如图,90ACB ∠=︒,AC AD =,DE AB ⊥,求证:CE DE =.18.如图,在△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE 于E ,AD ⊥CE 于D .(1)求证:△ADC ≌△CEB .(2)AD =5cm ,DE =3cm ,求BE 的长度.19.如图,已知四边形ABCD 中,12AB =厘米,8BC =厘米,13CD =厘米,B C ∠=∠,点E 为AB 的中点.如果点P 在线段BC 上以2厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CD 上由C 点向D 点运动.当点Q 的运动速度为多少厘米/秒时,能够使BPE 与COP 全等.20.如图,在等腰ABC V 中,AB AC =,8BC =,90BAC ∠=︒,AD 是BAC ∠的平分线,交BC 于D ,4=AD ,点E 是AB 的中点,连接DE .(1)求B ∠的度数;(2)求三角形BDE 的面积.21.如图所示,在平面直角坐标系xOy 中,△ABC 的顶点坐标分别是A (-2,3),B (m-1,1),C (1,-2),点B 关于x 轴的对称点P 的坐标为(-3,n-2).(1)求m ,n 的值;(2)画出△ABC ,并求出它的面积;(3)画出与△ABC 关于y 轴成轴对称的图形△A 1B 1C 1,并写出△A 1B 1C 1,各个顶点的坐标.22.如图,在等边ABC V 中,6AB =,过AB 边上一点D 作DH AC ⊥于点H ,点E 为BC 延长线上一点,且=AD CE ,连接DE 交AC 于点F ,求HF 的长.23.如图,点A 在y 轴的正半轴上,点B 在x 轴的负半轴上,过点A 作CA AB ⊥,且AB AC =.(1)若点()()0,41,0A B -,,求点C 的坐标;(2)点D 在x 轴的负半轴上且OA OD =,连接DC 交y 轴的正半轴于点E ,求证:2DB OE =.24.(1)【感悟】如图1,AD 是ABC V 的高线,2C B ∠=∠,若2CD =,5AC =,求BC 的长.小明同学的解法是:将ABC V 沿AD 折叠,则点C 刚好落在BC 边上的点E 处.请你画出图形并写出完整的解题过程;(2)【探究】如图2,2ACB B ∠=∠,AD 为ABC V 的外角CAF ∠的平分线,交BC 的延长线于点D ,则线段AB 、AC 、CD 又有怎样的数量关系?请写出你的猜想并证明;(3)【拓展】如图3,在四边形ABCD 中,AC 平分BAD ∠,8AD =,10DC BC ==,2D B ∠=∠,则AB 的长为__________.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(每小题3分,共36分)
1.下列交通标志是轴对称图形的是( )
B
C
D
2.点M (1,2)关于x 轴对称的点的坐标为( )
A.
(—1,2) B.(-1,-2) C.(1,-2) D.(2,-1)
3. 一个三角形三个内角的度数之比为2:3:4,这个三角形是( ) A. 直角三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形
4.下列各组图形中,是全等形的是( )
A.两个含60°角的直角三角形
B.腰对应相等的两个等腰直角三角形
C.边长为3和4的两个等腰三角形
D.一个钝角相等的两个等腰三角形
5.下列说法正确的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.顶角相等的两个等腰三角形全等
C.等腰三角形一边不可以是另一边的二倍
D.等腰三角形的两个底角相等 6. 若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角为( ) A. 75°或15° B. 75° C. 15° D. 75°或30°
7.如图,在下列条件中,不能证明△ABD ≌△ACD 的是( ) A.BD =DC ,AB =AC B.∠ADB =∠ADC ,BD =DC C.∠B =∠C ,∠BAD =∠CAD D.∠B =∠C ,BD =DC
8.如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD的周长是()
A.22cm
B.16cm
C.23cm
D.25cm
9、一个多边形内角和是1080º,则这个多边形的对角线条数为()
A.26
B. 24
C.22
D.20
10、如图,把一个正方形三次对折后沿虚线剪下,则所得图形大致是()
11、下列计算错误的是( ).
A.(-2)x3=-2x3 B.-a2•a=-a3
C.(-x)9+(-x)9=-2x9 D.(-2a3)2=4a6
12.以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是()
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共18分)
1.三角形一边长为40,一边长为50,求第三边a的取值范围_______________。
2、计算(直接写出结果)
①a•a3=_______ ②(b3)4=_______ ③(2ab)3=______
3.如图,⊿ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF = 度。
4.如图,在等边△ABC 中,AC=9,点O 在AC 上,且AO=3,点P 是AB 上一动点,连结OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD .要使点D 恰好落在BC 上,则AP 的长是 。
5.如图,PM ⊥OA ,PN ⊥OB ,垂足分别为M 、N.PM =PN ,若∠BOC =30°,则∠AOB = .
6.如图,在△ABC 和△FED 中,AD =FC ,AB =FE ,当添加条件 时,就可得到 △ABC ≌△FED.(只需填写一个你认为正确的条件) 三、计算题(每小题5分,共20分) (1) x n
· x n+1
(2)-82013
x(-0.125)
2014
(3)(-2x 4
)4
+2x 10
·(-2x 2)3
-2x 4
·5(-x 4)3
(4)0.25
1999
x4
2000
-8100x0.5300
第5题 第6题
四、解答题(共46分)
1,(共8分)求出下列各题中正整数的值 (1)若(9m+1)2
=316
求正整数m 的值。
(2)若2x8n
x16n
=222
求正整数n 的值。
2,(8分)如图,两个四边形关于直线 对称,∠C =90°,试写出a ,b 的长度,并求出∠G 的度数.
3.(10分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1). (1)在图中作出△ABC 关于y 轴对称的△A 1B 1C 1. (2)写出点A 1,B 1,C 1的坐标(直接写出答案). A 1 B 1 C 1 (3)△A 1B 1C 1的面积为 .
第2题
4.(10分)如图:△ABC和△EAD中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.
求证:△ABD≌△AEC.
5.(10分)如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水.(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?
请将上述两种情况下的自来水厂厂址标出,并保留作图痕迹.
.B
A .。
