三年级奥数乘法简便运算及答案
三年级奥数题及答案:乘法竖式的乘积

编者导语:题海无边,题型有限。
学习数学必须要有扎实的基本功,有了扎实的基本功再进行奥数的学习就显得水到渠成了。
希望查字典数学网小编整理的三年级奥数题及参考答案:乘法竖式的乘积,可以帮助到你们,一分耕耘一分收获,相信大家通过自己的努力,一定能够取得优异的成绩!!难度:★★图7-4是一个残缺的乘法竖式,那么乘积是多少?此主题相关图片如下:【答案】由乘积的最高位不难看出积应该是10?2,且在它上面的乘积应该是9?;因为加2后有进位,所以,个位只有8、9两种可能;又第一个乘积的十位为2,个位也是2,说明被乘数为22,乘数个位为1;或者被乘数为11,乘数个位为2;如果被乘数为22,乘数个位为1,乘数的个位只能是4,显然不行;那么,被乘数为11,乘数个位为2,这样,乘数个位就为9,即整个算式为11*92=1012。
所以,乘积是1012。
三年级奥数,乘除法巧算,带答案

答案:A 解析:有公因数76,所以提取公因数即76×(153-53)。
错因分析:对提取公因数的应用不理解。
4. (25+20)×4用乘法分配律应该怎么计算呢?下列哪个方法是符合的? A. (25+20)×4=25×4+20×4 B. (25+20)×4=25×4×20×4 C. (25+20)×4=25+20×4
答案:A 解析:由乘法分配律可知A项是正确的。
5. 下面的算式你会计算吗:380÷(38÷125) A. 38不能除以125,所以不能计算。
2013) + 2015 = 6043
.
28. 计算:25 × 13 × 2 + 15 × 13 × 7 =
。
答案:2015
解析:25 × 13 × 2 + 15 × 13 × 7
= 5 × 13 × 10 + 5 × 13 × 21
= 5 × 13 × (10 + 21)
= 5 × 13 × 31
18. 计算:125×1700×8 A. 1550000 B. 1700000 C. 1890000 D. 2380000
答案:B 解析:125×1700×8
=1700×(125×8) =1700×1000 =1700000
19. 计算:125×78 A. 9750 B. 9650 C. 9550
答案:A 解析:当两个数相乘时,有时可以运用乘法分配律把一个因数变成两个数的差与另一个因数相乘。
三年级奥数题及参考答案:乘法巧算

三年级奥数题及参考答案:乘法巧算
编者导语:“题海无边,题型有限”。学习数学必须要有扎实的基本功,有了扎实的基本功再进行“奥数”的学习就显得水到渠成了。查字典数学网为大家准备了小学三年级奥数题,希望小编整理的三年级奥数题及参考答案:乘法巧算,可以帮助到你们,助您快速通往高分之路!!
=125×40+125&ti
=6000;
(3)2019×25
=(2019+4)×25
=2019×25+4×25
=50000+100
=50100;
(4)125×792
=125×(800-8)
要练说,得练看。看与说是统一的,看不准就难以说得好。练看,就是训练幼儿的观察能力,扩大幼儿的认知范围,让幼儿在观察事物、观察生活、观察自然的活动中,积累词汇、理解词义、发展语言。在运用观察法组织活动时,我着眼观察于观察对象的选择,着力于观察过程的指导,着重于幼儿观察能力和语言表达能力的提高。=1000×(100-1)
计算下列各题:(1)125×(40+8); (2)(100-4)×25;(3)2019×25; (4)125×792。
解答:
(1)125×(40+8)
=125×40+125×8
三年级奥数乘法简便运算及答案

2018 秋季数学集训三队 A 教材每周习题 (6) 参考答案星期一简便计算。
125 X 4X 8X 25 X 5 X 21200=(125 X 8) X (4 X 25) X (5 X 2)=1000 X 100X 10 =600000 - (125 X 8) - (25 X 4) =600000 - 1000 - 1008- 7+ 9 - 7 + 11-7125X 40121X 73+26X 21 +21 =(8 + 9 + 11) - 7=125X (400 + 1)=21 X (73 + 26 + 1) =28 - 7=125X 400 + 125=21X 100 =4=50000+125=2100=50125=1000000=48=6或:原式=12 X (100 - 25)=12 X 4=48600000=(1200 X 4) - (25 X 4)=4800 - 100 372- 162X 54=372 - (162 - 54) =372 - 3 =1242222X 9998981+5X 9810+49X 981 =2222 X (10000 — 2) =981 + 50X 981 + 49X 981=2222X 10000—2222 X 2 =981 X (1 + 50 + 49)=22220000—4444 =981X 100=22215556=98100简便计算。
222X 444+222X 556=222 X (444 + 556) =222X 1000=2220001440X 976 - 488=1440 X (976 - 488) =1440X 2 =288028 - 3 X 54 X 15 -54 - 14(48=(28 - 14) X (54 - 54) X (15 - 3) =2X 1X 5 X 75 X 81) - (25 X 24 X 27) =(48 - 24) X (75 - 25) X (81 - 27) =2 X 3 X 3 =10=18(720 — 180-450) - 972=720 - 9— 180 - 9 — 450 - 9 =80 — 20 —50=10X 108+108X 46— 118X 142+118X 134 =108 X (72 + 46) — 118 X (142 — 134) =108X 118 — 118X 8 =118 X (108 — 8) =11800星期二星期三简便计算。
小学三年级(奥数)专项训练 乘法巧算

三年级专项训练乘法巧算[知识概述]:1.乘法的运算律乘法交换律:两个数相乘,交换两个数的位置,其积不变。
即a×b=b×a。
其中,a,b为任意数。
例如,35×12=12×35=420。
2、乘法结合律:三个数相乘,可以先把前两个数相乘后,再与后一个数相乘,或先把后两个数相乘后,再与前一个数相乘,积不变。
即a×b×c=(a×b)×c=a×(b×c)。
注意:(1)这两个运算律中数的个数可以推广到更多个的情形。
即多个数连乘中,可以任意交换其中各数的位置,积不变;多个数连乘中,可以任意先把几个数结合起来相乘后,再与其它数相乘,积不变。
(2)这两个运算律常一起并用。
例如,并用的结果有 a×b×c=b ×(a×c)等。
3、乘法分配律:两个数之和(或差)与一数相乘,可用此数先分别乘和(或差)中的各数,然后再把这两个积相加(或减)。
即(a+b)×c=a×c+b×c, (a-b)×c=a×c-b×c。
例1计算下列各题:(1)17×4×25; (2)125×19×8;=17×(4×25) =125×8×19(3)125×72; (4)25×125×16。
=125×8×9 =(125×8)×(25×2)变式练习:(1)12×4×25; (2)125×13×8;(3)125×56; (4)25×32×125。
例2:计算下列各题(1)125×(40+8); (2)(100-4)×25;=125×40+125×8 =100×25-4×25 (3)2004×25; (4)125×792=25×2000+25×4=125×(800-8)变式练习:(1)125×(80+4); (2)(100-8)×25;(3)180×125; (4)125×88。
三年级奥数12-巧算乘除法

速算
(3)11125-125
13.用简便方法计算。
⑵5600-(28北)
(6)8100廿TOX15
作业
1•巧算(提示:特殊数的计算)
125x16x5
240x5
4804x25
2.速算下列各题(提示:头同尾合十、尾同头合十)
29x21
31x71
3.用简便方法计算
72x32
84x999
100+76x73
4.用巧妙的方法计算。
(1)37x48x625
(2)25x19x64x 125
6.用简便方法进行计算。
(3)36024x125
⑵427 x25
8.巧算。
(1)1295x11
(2)3782 x 11
9.计算下列各题。
(1)84x86
(2)34X74
11.速算下列各题。
(9+99+999)x9999
(1)25X13X4
(3)27X50X2
⑷5X25X4X20
例2运用简便方法计算。
(1)44X25
⑷64X25X125
(5)75X16
例3乘数是5 ,25、125 ,625的乘法
(1)12X5
(2)24X25
(3)48x125
⑷64X625
例4速算下列各题
⑵382X41十58X382+382
(3)102X19
⑸67X33+68 X67一67
例5用简便方法计算下列各题。
(1)13X5(2)26X25
(3)97X125
⑷34X625
例6一个数乘以11的速算
(1)45362X11
例7用简便方法计算下列各题
小学三年级奥数乘法速算例题练习题答案

小学三年级奥数乘法速算例题练习题答案练习一【题目】很快算出下面各题的结果:1,321×5 25×5 41×52,470×5 629×5 546×53,1032×5 4832×5 7326×5【解析】⑴321×5 = 321×10÷2 = 3210÷2 = 160525×5 = 25×10÷2 = 250÷2 = 12541×5 = 41×10÷2 =410÷2 = 205⑵470×5 = 470×10÷2 = 4700÷2 = 2350629×5 = 629×10÷2 = 6290÷2 = = 3145546×5= 546×10÷2 = 5460÷2 = 2730⑶1032×5 = 10320×10÷2 = 10320÷2 = 51604832×5 = = 4832×10÷2 = 48320÷2 = 241607326×5 = 7326×10÷2 = 73260÷2 = 36630练习二【题目】很快算出下面各题的结果。
1,12×11 23×11 45×11 35×112,47×11 11×65 11×96 87×113,135×11 603×11 329×11 872×11【解析】AB×11 = 100A +10〔A+B〕+B⑴AB两数和小于10。
小学奥数简便计算:乘除法篇

以下是为⼤家整理的关于⼩学奥数简便计算:乘除法篇的⽂章,供⼤家学习参考!⼀、乘法:1.因数含有25和125的算式:例如①:25×42×4我们牢记25×4=100,所以交换因数位置,使算式变为25×4×42.同样含有因数125的算式要先⽤125×8=1000。
例如②:25×32此时我们要根据25×4=100将32拆成4×8,原式变成25×4×8。
例如③:72×125我们根据125×8=1000将72拆成8×9,原式变成8×125×9。
重点例题:125×32×25=(125×8)×(4×25)2.因数含有5或15、35、45等的算式:例如:35×16我们根据需要将16拆分成2×8,这样原式变为35×2×8。
因为这样就可以先得出整⼗的数,运算起来⽐较简便。
3.乘法分配率的应⽤:例如:56×32+56×68我们注意加号两边的算式中都含有56,意思是32个56加上68个56的和是多少,于是可以提出56将算式变成56×(32+68)如果是56×132—56×32⼀样提出56,算是变成56×(132-32)注意:56×99+56应想99个56加上1个56应为100个56,所以原式变为56×(99+1)或者56×101-56=56×(101-1)另外注意综合运⽤,例如:36×58+36×41+36=36×(58+41+1)47×65+47×36-47=47×(65+36-1)4.乘法分配率的另外⼀种应⽤:例如:102×47我们先将102拆分成100+2算式变成(100+2)×47然后注意将括号⾥的每⼀项都要与括号外的47相乘,算式变为:100×47+2×47例如:99×69我们将99变成100-1算式变成(100-1)×69然后将括号⾥的数分别乘上69,注意中间为减号,算式变成:100×69-1×69⼆、除法:1.连续除以两个数等于除以这两个数的乘积:例如:32000÷125÷8我们可以将算式变为32000÷(125×8)=32000÷10002.例如:630÷18我们可以将18拆分成9×2这时原式变为630÷(9×2)注意要加括号,然后打开括号,原式变成630÷9÷2=70÷2三、乘除综合:例如6300÷(63×5)我们需要打开括号,此时要将括号⾥的乘号变为除号,原式变为6300÷63÷5。
高思奥数导引小学三年级含详解答案第18讲 简单乘除法竖式.
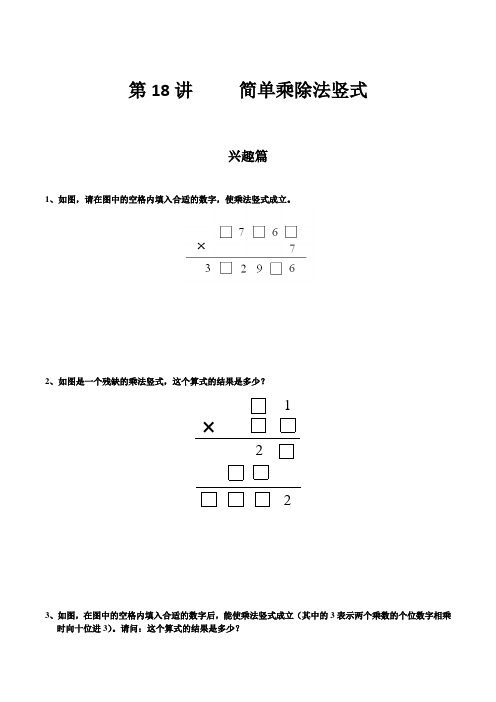
第18讲简单乘除法竖式兴趣篇1、如图,请在图中的空格内填入合适的数字,使乘法竖式成立。
2、如图是一个残缺的乘法竖式,这个算式的结果是多少?1×223、如图,在图中的空格内填入合适的数字后,能使乘法竖式成立(其中的3表示两个乘数的个位数字相乘时向十位进3)。
请问:这个算式的结果是多少?×4134、如图,在图中的空格内填入合适的数字,使乘法竖式成立。
81645×5、如图是一个残缺的乘法算式。
现在知道其中一个位置上的数字为8,这个算式的结果是多少?8×6、在如图所示的乘法竖式中,、、、分别代表不同的数字。
问:这个三位数是多少?×7447、如图,在图中的空格内填入合适的数字,使除法竖式成立。
8538、如图,在图中的空格内填入合适的数字,使除法竖式成立。
4127519、如图,在图中的空格内填入合适的数字,使除法竖式成立。
10、如图,在图中的空格内填入合适的数字,使乘法竖式成立。
5拓展篇1、如图,在图中的空格内填入合适的数字,使乘法竖式成立。
744881×72、如图,在图中的空格内填入合适的数字,使乘法竖式成立。
6529×3、如图,在图中的空格内填入合适的数字,使乘法竖式成立。
08×7 4、如图,在图中的空格内填入合适的数字,使乘法竖式成立。
3812132×23355、在如图所示的乘法竖式中,有些数字被三角形纸片盖住了。
请问:算式的结果是多少?82×56、如图是一个残缺的乘法算式,请补充完整并求出这个算式的结果。
8×87、如图所示的竖式中,不同的汉字代表不同的数字。
“车”、“马”、“炮”分别代表什么数字?车车马炮车车×车炮马马8、如图,在图中的空格内填入合适的数字,使除法竖式成立。
76919、如图,在图中的空格内填入合适的数字,使除法竖式成立。
210、如图,在图中的空格内填入合适的数字,使除法竖式成立。
高斯小学奥数含答案三年级(上)第01讲 乘除法巧算

6基础例题:这一讲介绍的是乘法巧算和除法巧算的一些基本方法.在计算乘法时,一个数与10、100、1000这样的数相乘,很容易算出结果,例如2310230⨯=,231002300⨯=,23100023000⨯=等.有三组乘法在巧算时也经常用到:2510⨯=,425100⨯=,81251000⨯=.第一讲乘除法巧算7加减法里有带符号搬家,乘法中也有.在计算多个数相乘时,我们可以通过带符号搬家改变运算顺序,简化计算.例题1计算:(1)2135⨯⨯; (2)41125⨯⨯.分析:仔细观察算式,如何改变一下运算顺序来变得简单些呢?练习1计算:(1)41725⨯⨯;(2)125108⨯⨯.有时题目中没有明确给出2与5、4与25、8与125相乘,我们可以通过拆数的方法凑出10、100、1000,例如:18592590⨯=⨯⨯=.例题2计算:(1)532125⨯⨯; (2)801625⨯⨯.分析:这两个小题中有25或者125,这两个数能够如何巧算呢?练习2 计算:(1)25532⨯⨯; (2)56125⨯.下面介绍的是乘除法巧算的一些基本方法,同加减法一样,通过“带符号搬家”来适当改变运算顺序,像漫画中那样配对进行简化计算.例题3 乘法中常见运算技巧➢ 乘法中的凑整:25⨯;425⨯;8125⨯.➢ 带符号搬家:在只有乘除运算的算式里,每个数前面的运算符号是这个数的符号.不论数移动到哪个位置,它前面的运算符号不变.带符号搬家依据的运算律是:(1) 乘法交换律:⨯=⨯a b b a .(2) 乘法结合律:()()⨯⨯=⨯⨯a b c a b c .小 总 结8 计算:(1)36119⨯÷; (2)4000125÷.分析:如何利用除号后面的数进行除法凑整呢?练习3计算:(1)28114⨯÷;(2)30025÷.在计算连续乘除法运算时,式子中经常会出现括号.在乘除法去括号时,同加减法去括号时类似,要注意变号的问题,具体来说,乘除法中去括号的法则是: 括号前面是乘号,去掉括号不变号;括号前面是除号,去掉括号变符号. 例题4计算:(1)()72072513÷⨯÷; (2)()()()81123123363÷⨯÷÷-.分析:在去括号的时候要注意些什么?去掉括号后算式变成了什么样?能够如何巧算? 练习4计算:(1)()13013315÷÷⨯;(2)()3631111÷⨯⨯.挑战极限:除了去括号之外,有时候还需要添括号来简化运算.例题5计算:(1)310008125÷÷; (2)333155÷⨯.分析:第一问中看到8和125,能不能让它俩相乘呢?第二问中15和5处能不能加个括号呢?加括号时要注意什么呢?例题6计算:()()()()262527172591739÷⨯÷⨯÷⨯÷.分析:在去括号的时候要注意些什么?去掉括号后算式变成了什么样?能够如何巧算?9运算符号的来历 同学们每天都与+、-、×、÷打交道,做起题来也已经习惯了有它们的帮助,但你们一定还不知道它们来到这个世界上的时间可比数字晚多了. 大约五百年前,德国科学家魏特曼在横线上加上一竖来表示增加的意思,在加号上去掉一竖来表示减少的意思,从此,数学这一学科就多了两个新成员,这就是“+”、“-”的来历. “×”是英国的数学家欧德艾在三百多年前提出来的,他认为乘法是一种特殊的加法,于是把“+”斜过来写,也就是我们今天的“×”,“÷”是瑞士数学家拉哈提出来的,他在两点中间放上一横,表示平均分的意思.同学们,现在我们不仅会使用这些数学运算符号,而且还了解了它们的来历,以后算题的时候就会辨别的更清楚,计算的更仔细了. 课堂内外 去括号和添括号原则在只有乘除运算的算式里,如果括号的前面是“÷”,那么不论是去掉括号或添上括号,括号里面运算符号都要改变,即“×”号变“÷”,“÷”变“×”;如果括号的前面是“×”,那么不论是去掉括号或添上括号,括号里面运算符号都不改变.例如:○1 ()a b c a b c ⨯÷=⨯÷○2 ()a b c a b c ⨯÷=⨯÷ ○3 ()a b c a b c ÷÷=÷⨯ ○4 ()a b c a b c ÷÷=÷⨯ 小 总 结10 作业1. 计算:(1)295⨯⨯; (2)25194⨯⨯.2. 计算:(1)2512⨯; (2)12532⨯.3. 计算:(1)20025÷; (2)3000125÷;(3)121437⨯÷÷; (4)12253⨯÷.4. 计算:()()()220887227÷⨯÷÷÷.5. 计算:420002425÷÷÷.11第一讲 乘除法巧算1. 例题1答案:(1)130;(2)1100详解:(1)213525*********⨯⨯=⨯⨯=⨯=;(2)4112542511100111100⨯⨯=⨯⨯=⨯=.2. 例题2答案:(1)20000;(2)32000详解:(1)53212554812554812554100020000⨯⨯=⨯⨯⨯=⨯⨯⨯=⨯⨯=;(2)80162580442580442580410032000⨯⨯=⨯⨯⨯=⨯⨯⨯=⨯⨯=.3. 例题3答案:(1)44;(2)32详解:(1)361193691141144⨯÷=÷⨯=⨯=;(2)400012541000125410001254832÷=⨯÷=⨯÷=⨯=().4. 例题4答案:(1)26;(2)9详解:(1)72072513720725131051321326÷⨯÷=÷÷⨯=÷⨯=⨯=();(2)81123123363811231233381331231239÷⨯÷÷=÷⨯÷÷=÷÷⨯÷=()()(-).5. 例题5答案:(1)31;(2)111详解:(1)31000812531000100031÷⨯=÷=();(2)3331553331553333111÷⨯=÷÷=÷=().6. 例题6答案:2详解:2625271725917392627252591717392627252591717392627939262793132633132613332=÷⨯÷⨯÷⨯÷=⨯⨯÷÷⨯÷÷=⨯⨯÷÷⨯÷÷=⨯÷÷=⨯÷÷⨯=⨯÷÷=÷⨯÷=原式()()()()()(). 7. 练习1答案:(1)1700;(2)10000简答:(1)425171700=⨯⨯=原式;(2)12581010000=⨯⨯=原式.8. 练习2答案:(1)4000;(2)7000简答:(1)25548254584000=⨯⨯⨯=⨯⨯⨯=原式;(2)781257000=⨯⨯=原式.9. 练习3答案:(1)77;(2)12简答:(1)2841171177=÷⨯=⨯=原式;(2)3100253412=⨯÷=⨯=原式.10. 练习4答案:(1)2;(2)12简答:(1)13013315103152=÷⨯÷=⨯÷=原式;(2)3631111363111112=÷÷⨯=÷⨯÷=原式.11. 作业1答案:(1)90;(2)1700简答:(1)29525990⨯⨯=⨯⨯=;(2)25194254191900⨯⨯=⨯⨯=.12 12. 作业2答案:(1)300;(2)4000简答:(1)25122543300⨯=⨯⨯=;(2)12532125844000⨯=⨯⨯=.13. 作业3答案:(1)8;(2)24;(3)8;(4)100简答:(1)20025210025248÷=⨯÷=⨯=;(2)3000125310001253824÷=⨯÷=⨯=;(3)121437123147428⨯÷÷=÷⨯÷=⨯=;(4)1225312325425100⨯÷=÷⨯=⨯=.14. 作业4答案:10简答:2208872272202210=÷⨯÷÷⨯=÷=原式.15. 作业5答案: 210简答:()42000242542000242542000200210÷÷÷=÷⨯⨯=÷=.。
三年级奥数乘除法巧算

1、乘除法巧算这一讲介绍的是乘除法巧算的一些基本方法,同加减法一样,通过“带符号搬家”来适当改变运算顺序。
例题1计算:(1)2×13×5(2)51÷17×17÷51(3)12×7÷3÷7分析:仔细观察算式,如何改变运算顺序来使得计算简单些呢?练习1、计算:(1)4×7×25 (2)21×19÷7÷19 .在乘法巧算时,有三组乘法在巧算时经常用到:2×5=10,4×25=100, 8×125=1000 .还有许多两位数乘法中的乘数,十位相同,个位相加得10,例如:47和43,72和78、65和65等,我们把这样的情况称为“头同尾合十”。
对于“头同尾合十”的两个数可以这样进行计算:把“尾×尾”的结果作为得数的末两位,“头×(头+1)”的结果作为得数的头。
例题2计算:(1)25×28 ;125×24 ;(2)300÷25 ;8000÷125 ;(3)45×45 ;41×49 .分析:前两个小题中都有25或者125,这两个数能够如何巧算呢?第3小题的每组数有什么特点?练习:2、计算:(1)25×24 ;(2)2000÷125 ;(3)88×82 .在计算连续乘除法运算时,式子中经常会出现括号。
在乘除法中去括号同在加减法中去括号类似,要注意变号的问题,具体来说,乘除法中去括号的法则是:例题3计算:(1)(126÷9)×(9÷3)÷(6÷3);(2)512÷(512÷16×8).分析:在去括号的时候要注意些什么?去括号后算式变成了什么样?能够如何巧算?练习3、计算:(10÷7)×(7÷6)×(6÷5)例题4计算:(1)23×70×22÷11÷7 ;(2)300×13÷4÷25分析:(1)算式中有几个数有倍数关系,该如何计算?(2)看到4和25,能不能让它俩相乘呢?练习4、计算:3000×28÷125÷8÷14除了“带符号搬家”、“添、脱括号”等巧算方法之外,还有一个非常重要的方法,那就是运用乘法分配律进行巧算。
小学三年级数学简便运算方法归类 及练习(含答案)

小学三年级数学简便运算方法归类一、带符号搬家法(根据:加法交换律和乘法交换率)当一个计算题只有同一级运算(只有乘除或只有加减运算)又没有括号时,我们可以“带符号搬家”。
(a+b+c=a+c+b,a+b-c=a-c+b,a-b+c=a+c-b,a-b-c=a-c-b;a×b×c=a×c×b,a÷b÷c=a÷c÷b,a×b÷c=a÷c×b,a÷b×c=a×c÷b)二、结合律法(一)去括号法1.当一个计算题只有加减运算又有括号时,我们可以将加号后面的括号直接去掉,原来是加现在还是加,是减还是减。
但是将减号后面的括号去掉时,原来括号里的加,现在要变为减;原来是减,现在就要变为加。
(现在没有括号了,可以带符号搬家了哈) (注:去掉括号是添加括号的逆运算)a+(b+c)= a+b+c a +(b-c)= a+b-c a- (b-c)= a-b+c a-( b +c)= a-b-c2.当一个计算题只有乘除运算又有括号时,我们可以将乘号后面的括号直接去掉,原来是乘还是乘,是除还是除。
但是将除号后面的括号去掉时,原来括号里的乘,现在就要变为除;原来是除,现在就要变为乘。
(现在没有括号了,可以带符号搬家了哈) (注:去掉括号是添加括号的逆运算)a×(b×c) = a×b×c, a×(b÷c) = a×b÷c, a÷(b×c) = a÷b÷c , a÷(b÷c) = a÷b ×c(二)加括号法1.当一个计算题只有加减运算又没有括号时,我们可以在加号后面直接添括号,括到括号里的运算原来是加还是加,是减还是减。
三年级奥数

华西英语培训学校——三年级奥数一、简便运算一、加减的简便运算1、加法交换律:交换两个加数的位置,和不变。
即:a+=a+bb例如:3+9=9+32、加法结合律:三个数连续相加,可以先前两个数相加,得到的和再与第三个数相加;也可以后两个数相加,得到的和再与第一个数相加;也可以第一个数和第三个数相加,得到的和再与第二个数相加,它们的和不变。
即:()()b++=+++=ccababca+例如:23+168+32 34+71+66=23+(168+32)=(34+66)+71=23+200 =100+71=223 =1713、一个数连续减去两个数,等于这个数减去这两个减数的和,差不变。
即:()c-=--bba+ac168-79-21=168-(79+21)=168-100=684、)-=-+a-bb(cca例如:489-298+198=489-(298-198)=489-100=3895、b+=+a--bacc例如:245-168+155=245+155-168=400-168=2326、)=++a--(cbbac例如:345+478-278=345+(478-278)=345+200=545练习:933-157-43 106-72-28 788-367+267834+267-167 1123+73+127 206+507+294 3034+976-1034 179+86-79 147-50-47274+98 587-99 361+102 456-10353+99 346+98 126-99 154-98二、乘法的简便运算1、乘交换律:交换两个因数的位置,分数的积不变。
即:a b b a ⨯=⨯例如: 3×4=4×32、乘法结合律:三个数连续相乘,可以先前两个数相乘,得到的积再与第三个数相乘;也可以后两个数相乘,得到的积再与第一个数相乘;也可以第一个数和第三个数相乘,得到的积再与第二个数相乘,它们的积不变。
三年级数学 奥数讲解 乘法与除法

三年级数学奥数讲解乘法与除法1.算式333×625×125×25×5×16×8×4×2的结果中末尾有多少个零?解答:找出算式中含有5的是:625×125×25×5=(5×5×5×5)×(5×5×5)×(5×5)×5,共10个5;找出算式中含有2的是:16×8×4×2=(2×2×2×2)×(2×2×2)×(2×2)×2,共10个2。
每一组5×2=10,产生1个0,所以共有10个0。
答:结果中末尾有10个零。
2.如果n=2×3×5×7×11×13×17×125。
那么n的各位数字的和是多少?解答:2×3×5×7×11×13×17×125=(7×11×13) ×(3×17) ×(2×5×125)=1001×51×1250=1001×(50×1250+1×1250)=1001×(12500÷2+1250)=1001×(62500+1250)=(1000+1)×63750=63750000+63750=638137506+3+8+1+3+7+5+0=33答:n的各位数字的和是33.3.(1)计算:5÷(7÷11)÷(11÷15)÷(15÷21),(2)计算:(11×10×9…×3×2×1)÷(22×24×25×27).解答:(1)5÷(7÷11)÷(11÷15)÷(15÷21)=5×11÷7×15÷11×21÷15=5×11÷11×15÷15×21÷7=5×21÷7=5×3×7÷7=5×3=15(2)(11×10×9…×3×2×1)÷(22×24×25×27)=(11×10×9…×3×2×1)÷22÷24÷25÷27)=(11×2÷22) ×(10×5÷25) ×(9×6 ÷27) ×(8×3÷24) ×7×4=1×2×2×1×7×4=4×28=1124.在算式(□□-7×□)÷16=2的各个方框内填入相同的数字后可使等式成立,求这个数字.解答:□□-7×□=11×□-7×□=□×(11-7)=□×4,因为□×4÷16=2,所以□×4=32,□=8答:□=8.5. 计算:9×17+91÷17-5×17+45÷17.解答:9×17+91÷17-5×17+45÷17=9×17-5×17+91÷17+45÷17=(9-5)×17+(91+45)÷17=4×17+136÷17=68+8=766. 计算:567×142+426×811-8520×50.解答:567×142+426×811-8520×50=567×142+3×142×811-8520×100÷2 .=142×(567+3×811)-852000÷2=142×3000-426000=426000-426000=07. 计算:28×5+2×4×35+21×20+14×40+8×62.解答:28×5+2×4×35+21×20+14×40+8×62=2×2×7×5+2×4×5×7+3×7×4×5+2×7×5×2×4+8×62=2×2×7×5×(1+2+3+4)+496=10×14×10+496=1400+496=18968. 计算:55×66+66×77+77×88+88×99.解答:55×66+66×77+77×88+88×99=(11×5)×(11×6)+(11×6)×(11×7)+(11×7)×(11×8)+(11×8)×(11×9)=11×11×(5×6+6×7+7×8+8×9)=11×(10+1)×(30+42+56+72)=(110+11)×200=121×200=242009. 计算:(123456+234561+345612+456123+561234+612345) ÷7.解答:(123456+234561+345612+456123+561234+612345) ÷7=[(1×100000+2×10000+3×1000+4×100+5×10+6)+(2×100000+3×10000+4×1000+5×100+6×10+1)+(3×100000+4×10000+5×1000+6×100+1×10+2)+(4×100000+5×10000+6×1000+1×100+2×10+3)+(5×100000+6×10000+1×1000+2×100+3×10+4)+(6×100000+1×10000+2×1000+3×100+4×10+5)] ÷7=[1+2+3+4+5+6]×100000+(2+3+4+5+6+1)×10000+(3+4+5+6+1+2)×1000+(4+5+6+1+2+3)×100+(5+6+1+2+3+4)×10+(6+1+2+3+4+5)×1] ÷7=(21×100000+21×10000+21×1000+21×100+21×10+21×1)÷7=21×100000÷7+21×10000÷7+21×1000÷7+21×100÷7+21×10÷7+21×1÷7=300000+30000+3000+300+30+3=33333310. (87+56+73+75+83+63+57+53+67+78+65+77+84+62) ÷14.解答:(87+56+73+75+83+63+57+53+67+78+65+77+84+62) ÷14=[(8+5+7+7+8+6+5+5+6+7+6+7+8+6)×10+(7+6+3+5+3+3+7+3+7+8+5+7+4+2)]÷14=[(14×7-7)×10+(14×7-28)] ÷14=[(13×7)×10+(10×7)]÷14=(130+10)×7÷14=140×7÷14=10×7=7011.在算是12345679×□=888888888,12345679×○=555555555的方框和圆圈内分别填入恰当的数后可使两个等式都成立,求所填的两个数之和.解答:□×9个位是8,○×9个位是5,所以□的个位是2,○的个位是5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018秋季数学集训三队A教材每周习题(6)参考答案星期一简便计算。
125×4×8×25×5×2 1200÷25 600000÷125÷8÷25÷4=(125×8)×(4×25)×(5×2) =(1200×4)÷(25×4) =600000÷(125×8)÷(25×4) =1000×100×10 =4800÷100 =600000÷1000÷100=1000000 =48 =6或:原式=12×(100÷25)=12×4=488÷7+9÷7+11÷7 125×401 21×73+26×21+21=(8+9+11)÷7 =125×(400+1) =21×(73+26+1)=28÷7 =125×400+125 =21×100=4 =50000+125 =2100=50125372÷162×54 2222×9998 981+5×9810+49×981=372÷(162÷54) =2222×(10000-2) =981+50×981+49×981=372÷3 =2222×10000-2222×2 =981×(1+50+49)=124 =22220000-4444 =981×100=22215556 =98100星期二简便计算。
222×444+222×556 1440×976÷488=222×(444+556) =1440×(976÷488)=222×1000 =1440×2=222000 =288028÷3×54×15÷54÷14 (48×75×81)÷(25×24×27)=(28÷14)×(54÷54)×(15÷3) =(48÷24)×(75÷25)×(81÷27)=2×1×5 =2×3×3=10 =18(720-180-450)÷9 72×108+108×46-118×142+118×134=720÷9-180÷9-450÷9 =108×(72+46)-118×(142-134)=80-20-50 =108×118-118×8=10 =118×(108-8)=11800星期三简便计算。
450000÷(25×45) 3333×2222÷6666=45×10000÷25÷45 =1111×(3×2222÷6666)=(45÷45)×(10000÷25) =1111×1=1×400 =1111=40013÷9+5÷9+21÷5-6÷5 25×77+55×14+15×77=(13+5)÷9+(21-6)÷5 =25×77+10×77+15×77=18÷9+15÷5 =77×(25+10+15)=2+3 =77×50=5 =3850999×999+1999 125×36÷(18÷8)=999×999+999+1000 =125×36÷18×8=999×(999+1)+1000 =(125×8)×(36÷18)=1000×(999+1) =1000×2=1000000 =2000333×666+999×778 234×566-233×567=333×3×222+999×778 =(233+1)×566-233×(566+1)=999×(222+778) =233×566+566-233×566-233=999×1000 =566-233=999000 =333星期四1.简便计算。
12345×99+12345×999-98×12345 209209209×803-803803803×209=12345×(99+999-98) =209×1001001×803-803×1001001×209=12345×1000 =0=12345000189+188+187×98 3÷(5÷7)÷(7÷9)÷(9÷11)÷…÷(2013÷2015) =187×2+2+1+187×98 =3÷5×7÷7×9÷9×11÷…÷2013×2015=187×(2+98)+3 =3×(2015÷5)=18700+3 =3×403=18703 =120954×36×56÷36 (123456+234561+345612+456123+561234+612345)÷7 =(54×56)×(36÷36) =(111111+222222+333333+444444+555555+666666)÷7 =5×(5+1)×100+4×6 =(111111+666666)×3÷7=3000+24 =777777÷7×3=3024 =3333332.1234567654321×(1+2+3+4+5+6+7+6+5+4+3+2+1)是什么平方数?解:原式=1111111×1111111×7×7=(1111111×7)×(1111111×7)=77777772答:该平方数是77777772。
星期五1.简便计算。
5432×9090+5432×909 9×17+91÷17-5×17+45÷17=5432×(9090+909) =(9-5)×17+(91+45)÷17=5432×(10000-1) =4×17+136÷17=5432×10000-5432 =68+8=54320000-5432 =76=543145682997×729÷(81×81) 3861÷39+8613÷87=(2997÷81)×(729÷81) =(3900-39)÷39+(8700-87)÷87=37×3×3 =3900÷39-39÷39+8700÷87-87÷87=111×3 =100-1+100-1=333 =1981997×1999-1996×2000 1÷(3÷5)÷(5÷7)÷(7÷9)÷…÷(998÷999) =1997×(2000-1)-1996×2000 =1÷3×5÷5×7÷7×9÷…÷998×999=1997×2000-1997-1996×2000 =1×999÷3=2000×(1997-1996)-1997 =333=2000-1997=32.计算:36×34= 1224 ;27×23= 621 ;69×61= 4209 ;52×58= 3016 。
(1)根据上面的计算,请总结出这类“头同尾合十”的简便算法。
先将两个因数的个位数相乘,并把积写在末尾,如果积不满10,十位上要补写0;然后再将两个因数的十位数乘它本身加1的和,积写在两个个位数积的前面。
(2)利用上面的结论计算:18×12= 216 ;72×78= 5616 ;91×99= 9009 。
3.计算:63×43= 2709 ;72×32= 2304 ;96×16= 1536 ;25×85= 2125 。
(1)根据上面的计算,请总结出这类“尾同头合十”的简便算法。
先将两个因数的个位数相乘,并把积写在末尾,如果积不满10,十位上要补写0;然后再将两个因数的十位数相乘后再加上个位数,和写在两个个位数积的前面。
(2)利用上面的结论计算:81×21= 1701 ;27×87= 2349 ;19×99= 1881 。
