2019年上海市各区一模压轴题图文解析
上海市各区2019届物理中考一模试卷按考点分类汇编 压强计算含答案

压强计算宝山:21.如图所示,高为1.3米,底面积分别为0.15米2和0.05米2的甲、乙两个轻质薄壁圆柱形容器在下部用轻质细管连通后放在水平地面上,且容器内盛有1米深的水.(1)求水对甲容器底部的压强p甲.(2)若将一体积为0.04米3的实心小球慢慢地放到甲容器中的水里(已知ρ球=1×103千克/米3),求:直到小球在水中不动为止,水对乙容器底部压力的增加量△F乙.嘉定:22.如图14所示,甲、乙两圆柱形容器(容器足够高)放在水平桌面上,甲的底面积为9S,乙的底面积为10S,分别盛有1.8×10-3米3体积的水和0.25米高的酒精。
(ρ3千克/米3)求:酒=0.8×10(1)水的质量m水。
(2)若甲容器的质量为0.2千克,底面积为1×10-2米2,求甲容器对水平桌面的压强p甲。
(3)若水和酒精对甲、乙容器底部的压强相等,为了使甲、乙容器底部受到的水和酒精的压力相等,以下方法可行的是(选填“A”、“B”或“C”)。
并计算出抽出(或加入)的ΔV或Δh。
图14闵行:25.质量为 0.2 千克、底面积为 0.01 米2、容积为 2×10-3米3的薄壁容器内装入0.15 米深的某液体后,容器对桌面的压力与液体对容器底部的压力恰好为 11.76 牛。
(1)求该液体对容器底的压强。
(2)求该液体的密度、体积。
(3)若在容器内再放入一质量为 1.5 千克、体积为1.5×10-1米3的实心物块,且物块浸没。
求物块静止后容器对桌面压强的增加量。
黄浦:21.如图11所示,薄壁圆柱形容器甲和均匀圆柱体乙置于水平地面上。
①若甲中盛有质量为3千克的水,求水的体积V 1及水对甲底部的压力F 1。
②若容器甲足够高、底面积为2S ,其内装有深为H 、密度为ρ的液体;圆柱体乙的底面积为S 高h 。
现将乙沿水平方向在上部切去一半,并将切去部分浸没在甲的液体中,此时液体对甲底部压强P恰等于乙剩余部分对水平地面压强P1。
2019年上海初三所有区一模数学压轴题详解

25题汇编1. 相似三角形的分类讨论(宝山)25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图10,已知:梯形ABCD 中,∠ABC =90°,∠A =45°,AB ∥DC ,DC =3,AB =5,点 P 在AB 边上,以点A 为圆心AP 为半径作弧交边DC 于点E ,射线EP 与射线CB 交于点F .(1)若,求DE 的长; (2)联结CP ,若CP=EP ,求AP 的长;(3)线段CF 上是否存在点G ,使得△ADE 与△FGE 相似,若相似,求FG 的值;若不相似,请说明理由.【答案】(1) DE =1;(2);(3) 【解析】(1)过点A 作AG ⊥CD 交CD 的延长线于点M ……………………… … …1分梯形ABCD 中,∠ABC =90°,∠A =45°∴∠DAM =45°∵AB //CD ,AM=CD 且∠ADM =∠DAM =45°,DM=AM =2……… … …1分 ∴Rt △AEM 中,AE=AP =√13,ME =√AE 2−AG 2=3…………… ……1分 ∴DE =1 ……………………………………………………………… ……1分 (2)过点P 作PH ⊥CD ,垂足是点H∵CP=EP ∴EC =2CH ……………………………………… …… 1分 设AE=AP=x ,PB =5-x ,EC =10-2x , BC =2∴Rt △PBC 中,PE=PC=√PB 2+BC 2=√(5−x )2+22=√x 2−10x +29 …… 1分由题意可知AE=AP ,∴∠AEP =∠APE ,∵CP=EP ,∴∠PEC =∠PCE …… …1分13AP =31310+133-PEABCDF(图10)∵AB //CD ∴∠PEC =∠APE ,∴∠PEC =∠APE 且∠PCE =∠AEP ∴△APE ∽△PCE …………………………………………………………1分∴ 即 ……………… ……1分化简得解得,(不合题意舍去) ………………………1分∴当CP=EP 时,AD 为. (3)∵△ADE 是钝角三角形,当点G 在CF 上时,∠GEF 、∠F 必是锐角,∴若△ADE ∽△FGE ,只能∠ADE =∠FGE =135°…………………………… ……1分 ∵Rt △PBF 中,∠F +∠FPB =90° 又∵∠EAP +∠APE +∠AEP =180° ∵∠FPB =∠APE ,∠APE =∠AEP ∴∠EAP =2∠F ∵AB//CD ∴∠DEA =∠EAP ∴∠DEA =2∠F∴必有∠DAE =∠F …………………………………………………………… …… …1分 ∴∠EAP =2∠DAE ∴∠EAP =30°,∠F=∠DAE =15°∴AE=AP =2AM =4,PB =1,EM =,CG=CE=……………… ………1分 ∴EG=∵△ADE ∽△FGE∴∴FG=………………………………1分 ∴当FG =时,△ADE ∽△FGE .ECEPEP AP =x x x x x x2102910291022-+-=+-0292032=+-x x 313101+=x 313-102=x 31310+3232-56225-FGADEG DE =133-133-(奉贤)25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =4,26AB CD ==,E 是边BC 上一点,过点D 、E 分别作BC 、CD 的平行线交于点F ,联结AF 并延长,与射线DC 交于点G . (1)当点G 与点C 重合时,求:CE BE 的值;(2)当点G 在边CD 上时,设CE m =,求△DFG 的面积;(用含m 的代数式表示) (3)当AFD ∆∽ADG ∆时,求∠DAG 的余弦值.【答案】(1) :1CE BE;(2)26255DFGm S m∆=-;(3) 3cos 5DAG ∠= 【解析】(1)∵CD ∥EF ,DF ∥CE ,∴四边形DFEC 是平行四边形. ······················································ (1分) ∴EF=DC . ················································································ (1分) ∵26AB CD ==,∴3CD EF ==.∵AB ∥CD ,∴AB ∥EF . ∵点G 与点C 重合,∴12EF CE AB BC ==.∴:1CE BE . ····················· (2分) (2)过点C 作CQ ∥AG ,交AB 于点Q ,交EF 于点P . 过点C 作CM ⊥AB ,交AB 于点M ,交EF 于点N . 在Rt △BCM 中,90CMB ,4CM AD ==,3BM AB CD =-=,∴5BC =.∵AB ∥EF ∥CD ,∴GC=PF =AQ . ∴EP CEBQ BC =.又3EF =,∴365GC m CG -=-. ∴1565mGC m-=-.········································································ (2分) ∴35mDG DC GC m=-=-. ····························································· (1分)∵NE ∥MB ,∴CN CECM BC=. 又4CM AD ==,∴45CN m =,45mCN =. ········································ (1分) 图11ABC D FEG 备用图ABCD∴2113462254255DFGm m m S DG CN m m∆=••=••=--. ································· (1分) (3)当AFD ∆∽ADG ∆时,∵∠DAB =90°,∴ADG ∆是直角三角形,∴AFD ∆也是直角三角形. ∵90DAF ,90FDA ,∴90DFA. ····························· (1分) ∵90FADADF,90FDC ADF,∴FAD FDC .∵AB ∥EF ,∴BCEF .∵四边形DFEC 是平行四边形,∴FDC CEF .∴BFDC FAD . ······························································ (1分) 在Rt △BCM 中, 90CMB ,3BM AB CD =-=,5BC =,∴3cos 5BM B BC ==. ········································································ (2分) ∴3cos 5DAG ∠=. ·········································································· (1分)(嘉定)25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在矩形ABCD 中,6=AB ,8=AD ,点E 是边AD 上一点,EC EM ⊥交AB 于点M ,点N 在射线MB 上,且AE 是AM 和AN 的比例中项. (1)如图8,求证:DCE ANE ∠=∠;(2)如图9,当点N 在线段MB 之间,联结AC ,且AC 与NE 互相垂直,求MN 的长; (3)联结AC ,如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似,求DE 的长.【答案】(1) 略;(2) 2449=MN ;(3) 29或3【解析】(1)证明:∵AE 是AM 和AN 的比例中项∴ANAEAE AM =……………………1分 ∵A A ∠=∠∴△AME ∽△AEN ∴ANE AEM ∠=∠……………………1分 ∵︒=∠90D ∴︒=∠+∠90DEC DCE ∵EC EM ⊥∴︒=∠+∠90DEC AEM ∴DCE AEM ∠=∠……………………1分 ∴DCE ANE ∠=∠ ………1分(2)∵AC 与NE 互相垂直∴︒=∠+∠90AEN EAC ∵︒=∠90BAC ∴︒=∠+∠90AEN ANE ∴EAC ANE ∠=∠ 由(1)得DCE ANE ∠=∠ ∴EAC DCE ∠=∠ ∴DAC DCE ∠=∠tan tan∴ADDCDC DE =……………………1分 ∵6==AB DC , 8=AD , ∴29=DE∴27298=-=AE ……………………1分A 图8BMEDCNA备用图BDCM ENA 图9BDC由(1)得DCE AEM ∠=∠ ∴DCE AEM ∠=∠tan tan ∴DCDEAE AM =∴821=AM ……………………1分 ∵AN AE AE AM = ∴314=AN ……………………1分 ∴2449=MN ……………………1分(3)∵AEM MAE NME ∠+∠=∠,DCE D AEC ∠+∠=∠又︒=∠=∠90D MAE ,由(1)得DCE AEM ∠=∠∴ NME AEC ∠=∠ …………………………1分 当△AEC 与以点E 、M 、N 为顶点所组成的三角形相似时 1)EAC ENM ∠=∠,如图9 ∴EAC ANE ∠=∠ 由(2)得:29=DE ……………………2分 2)ECA ENM ∠=∠,如图10 过点E 作AC EH ⊥,垂足为点H由(1)得DCE ANE ∠=∠ ∴DCE ECA ∠=∠ ∴DE HE =又86tan ===∠AD DC AH HE HAE 设x DE 3=,则x HE 3=,x AH 4=,x AE 5= 又AD DE AE =+ ∴835=+x x ,解得1=x∴33==x DE ……………………2分综上所述,DE 的长分别为29或3.A 图10B MEDCNH25(青浦).(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)如图,在梯形ABCD 中,AD//BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF =5. AE 的延长线交边BC 于点G , AF 交BD 于点N 、其延长线交BC 的延长线于点H . (1)求证:BG =CH ;(2)设AD =x ,△ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域; (3)联结FG ,当△HFG 与△ADN 相似时,求AD 的长.【答案】(1) 略;(2)()22096x y x x =<≤+;(3) 3或2 【解析】(1)∵AD//BC ,∴=AD DE BG EB ,=AD DFCH FC. ····················································· (2分) ∵DB =DC =15,DE =DF =5, ∴12==DE DF EB FC ,∴=AD ADBG CH. ············································· (1分) ∴BG =CH . ············································································ (1分) (2)过点D 作DP ⊥BC ,过点N 作NQ ⊥AD ,垂足分别为点P 、Q .∵DB =DC =15,BC =18,∴BP = CP =9,DP =12. ······························ (1分)∵12==AD DE BG EB ,∴BG = CH =2x ,∴BH =18+2x . ·························· (1分) ∵AD ∥BC ,∴=AD DN BH NB ,∴182=+x DN x NB ,∴182+15==++x DN DNx x NB DN , ∴56=+xDN x . ······································································ (1分)∵AD ∥BC ,∴∠ADN =∠DBC ,∴sin ∠ADN =sin ∠DBC , ∴=NQ PD DN BD ,∴46=+xNQ x . ················································· (1分) NHG FEDC AB (第25题图)∴()21142092266=⋅=⋅=<≤++x x y AD NQ x x x x .························· (2分) (3)∵AD ∥BC ,∴∠DAN =∠FHG .(i )当∠ADN =∠FGH 时,∵∠ADN =∠DBC ,∴∠DBC =∠FGH ,∴BD ∥FG , ············································································ (1分) ∴=BG DF BC DC ,∴51815=BG ,∴BG =6,∴AD =3.·························· (1分) (ii )当∠ADN =∠GFH 时, ∵∠ADN =∠DBC=∠DCB , 又∵∠AND =∠FGH ,∴△ADN ∽△FCG . ································································· (1分) ∴=AD FC DN CG ,∴()5182106⋅-=⋅+xx x x ,整理得23290--=x x ,解得 =x =x . ································· (1分)综上所述,当△HFG 与△ADN 相似时,AD 的长为3(长宁)25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)已知锐角MBN ∠的余弦值为53,点C 在射线BN 上,25=BC ,点A 在MBN ∠的内部, 且︒=∠90BAC ,MBN BCA ∠=∠.过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E . 点F 在线段BE 上(点F 不与点B 重合),且MBN EAF ∠=∠. (1)如图1,当BN AF ⊥时,求EF 的长;(2)如图2,当点E 在线段BC 上时,设x BF =,y BD =,求y 关于x 的函数解析式并写出函数定义域;(3)联结DF ,当ADF ∆与ACE ∆相似时,请直接写出BD 的长.【答案】(1) 16=EF ;(2)157400x y -=(2250≤<x );(3) 596或 1172000【解析】(1)∵在 BAC Rt ∆中 ︒=∠90BAC∴53cos cos ==∠=∠BC AC MBN BCA ∵25=BC ∴15=AC2022=-=AC BC AB∵AF BC AC AB S ABC ⋅=⋅=∆2121 ∴12=AF ∵BC AF ⊥ ∴︒=∠90AFC ∴ 34tan tan ==∠=∠AF EF BCA FAE ∴16=EF (2)过点A 作EF AH ⊥于点H ∴ ︒=∠90AHB ∴ 1622=-=AH AB BH∵x BF =,x FH -=16,x FC -=25第25题图如图2BF EC N DA MB FC E N AD M如图1备用图BC NAM∴ 40032)16(122222+-=-+=x x x AF ∵ BCA MBN ∠=∠,EAF MBN ∠=∠∴BCA EAF ∠=∠ 又∵CFA AFE ∠=∠ ∴AFE ∆∽CFA ∆ ∴AFEFCF AF =,FAC AEF ∠=∠, ∴EF FC AF ⋅=2∴EF x x x ⋅-=+-)25(400322∴xx x EF -+-=25400322,xxx x x x BF EF BE --=+-+-=+=25740025400322∵ ACB MBN ∠=∠,FAC AEF ∠=∠,∴BDE ∆∽CFA ∆∴ACBEFC BD =∴1525740025x x x y --=- ∴157400x y -=(2250≤<x )(3)596或 11720002. 等腰三角形的分类讨论(虹口)25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,在四边形ABCD 中,AD ∥BC ,∠A =90°,AB =6,BC =10,点E 为边AD 上一点,将△ABE 沿BE 翻折,点A 落在对角线BD 上的点G 处,联结EG 并延长交射线BC 于点F . (1)如果cos ∠DBC =23,求EF 的长;(2)当点F 在边BC 上时,联结AG ,设AD=x ,ABG BEF S y S ∆∆= ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CG ,如果△FCG 是等腰三角形,求AD 的长.【答案】(1) 9;(2)2236x y x =+(92x ≥);(3) 454AD =或189191【解析】(1)根据题意得△ABE ≌△GBE ∴BG=AB=6在Rt △BGF 中,BF = 9cos BGDBC=∠ …………………………………………(2分)由△ABE ≌△GBE得∠AEB =∠BEG ∵AD ∥BC ∴∠AEB =∠EBF∴∠BEF =∠EBF∴FE=FB =9………………………………………………………………………(2分) (2)∵AD ∥BC ∴∠ADB =∠GBF 又∵∠A =∠BGF =90° ∴△ABD ∽△GFB∴AD BD BG BF =即2366x x BF+= ∴2636x BF x +=………………………………………………………………(2分)EABCFG∵AD ∥BC ∠A =90° ∴∠ABF =90° ∴∠ABG+∠GBF=90° 又∵∠GBF+∠EFB =90° ∴∠ABG =∠EFB 根据题意得AB=BG 又∵FE=FB∴AB BG FB FE =∴△ABG ∽△EFB …………………………………………………………………(1分)∴2222236()36(36)36ABG BEF S AB x x S BF x x ∆∆===++…………………………………(1分)∴2236x y x =+(92x ≥) ………………………………………………(1分,1分)(3)①点F 在BC 上 ∵∠GFC =∠AEG >90°∵△FCG 是等腰三角形 ∴FG=FC 设FG=FC=a ,则BF=10-a由题意得a 2+62=(10-a )2 解得165a =∵∠ADB=∠GBF ∴tan ∠ADB = tan ∠GBF即16656AD = 解得454AD = ………………………………………………(2分)②点F 在BC 的延长线上 ∵∠GCF >∠DCF >90°∵△FCG 是等腰三角形 ∴CG=CF∴易得在Rt △BGF 中,BC=CF =10∴FG =∵∠ADB=∠GBF ∴tan ∠ADB = tan ∠GBF即6AD =解得AD =…………………………………………(2分)综合①②,454AD =(黄浦)25.(本题满分14分)在ABC ∆中,90ACB ∠=︒,3BC =,4AC =,点O 是AB 的中点,点D 是边AC 上一点,DE BD ⊥,交BC 的延长线于点E ,OD DF ⊥,交BC 边于点F ,过点E 作EG AB ⊥,垂足为点G ,EG 分别交BD 、DF 、DC 于点M 、N 、H .(1)求证:DE NEDB OB=; (2)设CD x =,NE y =,求y 关于x 的函数关系式及其定义域; (3)当DEF ∆是以DE 为腰的等腰三角形时,求线段CD 的长.【答案】(1) 略;(2);(3) 或【解析】(1)证明:∵,,,,.------------------------------------------------------------------------------------------(1分),,,又,∴,-------------------------------------------------------------------------------------(1分) ∽,---------------------------------------------------------------------------------------(1分).---------------------------------------------------------------------------------------------------(1分) (2),在Rt 中,tan DEDBE BD∠=,在Rt 中,tan DC DBE BC ∠=,.----------------------------------------------------(1分) 又,.--------------------------------------------------------------------------------(1分)∵,,,,,.-------------(2分) (3)∵,,,∵,90ADO FDC ∴∠+∠=︒, ∵90ACB ∠=︒,90CFD FDC ∴∠+∠=︒,ADO CFD ∴∠=∠,∽.---(1分) ()5026y x x ∴=<≤7843OD DF ⊥90ODB BDF ∴∠+∠=︒DE BD ⊥90EDF BDF ∴∠+∠=︒ODB EDF ∴∠=∠DE BD ⊥EG AB ⊥90BGM EDM ∴∠=∠=︒GMB DME ∠=∠GBM DEM ∠=∠∴NDE ∆ODB ∆DE NEDB OB∴=90BDE BCD ∠=∠=︒BDE ∆BCD ∆DE DC DB BC ∴=DE NEDB OB =NE DC OB BC∴=3BC =4AC =CD x =NE y =532y x∴=()5026y x x ∴=<≤EG AB ⊥90ACB ∠=︒GEB A ∴∠=∠OD DF ⊥∴AOD ∆ENF ∆ABCDOEF HGM N(第25题图),∵∽,,,.------------(1分)若,,90AOD DNF ∴∠=∠=︒,,∴.-----(2分) 若,∴点H 是重心,.∵tan tan CEH A ∠=∠,,,,,.-----------------------(2分)综上所述,线段CD 的长为或.(徐汇)25. (本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD 中,AD //BC ,AC =BC =10,54cos =∠ACB ,点E 在对角线AC 上(不与点A 、C 重合),EDC ACB ∠=∠,DE 的延长线与射线CB 交于点F ,设AD 的长为x . (1)如图1,当DF BC ⊥时,求AD 的长;(2)设EC 的长为y ,求y 关于x 的函数解析式,并直接写出定义域; (3)当△DFC 是等腰三角形时,求AD 的长.【答案】(1) 72AD =;(2)21610010x x y -+=(016x <<且10)x ≠;(3) 3964或.【解析】(1)过A 作AH ⊥BC ,垂足为H ,∵=CH AHC ACB AC ∆∠在Rt 中,cos ,且4=,105ACB AC ∠=cos ,∴8CH =. ∵222AHC AH CH AC ∆+=在Rt 中,,∴6AH = ……………………………(1分) ∴34AHC ACB ∆∠在Rt 中,tan =,∵AD ∥,,BC DF BC AH BC ⊥⊥且, ∴90AHF HFD DFH ∠=∠=∠=︒,∴四边形AHFD 是矩形,∴6DF AH ==AO OD EN NF ∴=NDE ∆ODB ∆BO ODEN ND∴=AO BO =NF ND ∴=DE EF =NE DF ∴⊥OA AC AD AB ∴=78CD =DE DF =1133HC CD x ==HC BCCE AC∴=49CE x ∴=tan tan CDE DBE ∠=∠CE DC DC BC ∴=43CD ∴=7843(第25题图1)(第25题图)CBB∵,CFDFC DEC EDC ACB DF∆∠∠=∠在Rt 中,tan =且…………………………(1分) ∴39tan ,42CF ACB CF DF =∠==得: ……………………………………………(1分) ∴97822AD HF ==-= ……………………………………………………………(1分)(2)∵AD ∥BC ,∴DAC ACB ∠=∠. ∵EDC ACB ∠=∠,∴EDC DAC ∠=∠.∵ACD ACD ∠=∠,∴CAD ∽CDE ………………………………………(1分) ∴CA CDCD CE=, ∵10,AC EC y ==,∴210CD CA CE y =⋅= …………………………………(1分) ∵222226(8)DFC CD DF FC x ∆=+=+-在Rt 中,∴221610010(8)36,10x x y x y -+=-+=即(016x <<且10)x ≠ ……………(2分)(3)由EDC ACB ∠=∠,EFC EFC ∠=∠得:FCE ∆∽FDC ∆, 又AD ∥BC 有FCE ∆∽DAE ∆,∴DAE ∆∽FDC ∆∴当FDC ∆是等腰三角形时,DAE ∆也是等腰三角形 ………………………(1分)∴1,DA DE ︒=当时不存在; ………………………………………………………(1分)2,10AD AE x y ︒==-当时得:120(),6x x ==解得:舍……………………………………………………………(2分)3,sin AMEA ED AME MAE ACB AE︒=∆∠=∠当时在Rt 中由=sin 12143920(),1054xx x y ===-得:,解得:舍………………………………………(2分)∴综上所述,当DFC ∆是等腰三角形时,AD 的长是3964或.3. 直角三角形存在性分类讨论 (静安)25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图11,在ABC ∆中,6AB =,9AC =,tan 22ABC ∠=.过点B 作BM //AC ,动点P 在射线BM 上(点P 不与点B 重合),联结PA 并延长到点Q ,使AQC ABP ∠=∠. (1)求ABC ∆的面积;(2)设BP x =,AQ y =,求y 关于x 的函数解析式,并写出x 的取值范围; (3)联结PC ,如果PQC ∆是直角三角形,求BP 的长.【答案】(1) 略;(2);(3) 或【解析】(1)过点A 作AH ⊥BC ,交BC 于点H . ············· (1分)在Rt ABH ∆中,tan 22AHABC BH∠==. 设22,AH x BH x ==,由勾股定理得36AB x ==.∴2,42BH x AH === ····················· (1分) 在Rt AHC ∆中,∴22229(42)7HC AC AH =-=-=,∴279BC BH HC =+=+=, ·················· (1分) ∴1194218222ABC S BC AH ∆=⋅=⨯⨯=.…………………(1分) (2) 过点A 作AG ⊥BM ,交BM 于点G . ∵AC BC =, ∴CAB CBA ∠=∠ ∵BM //AC , ∴ABP CAB ∠=∠∴ABP CBA ∠=∠∴42AG AH ==,即2BG BH ==………(1分) ∴2PG x =- 在Rt AGP ∆中,22222(42)(2)436AP AG PG x x x =+=+-=-+(1分)∵BAQ BAC CAQ ∠=∠+∠,BAQ ABP APB ∠=∠+∠,∴APB CAQ ∠=∠又AQC ABP ∠=∠ ················ (1分)()5026y x x ∴=<≤7843 图11ABCPQM第25题ABCPQM GH∴ABP ∆∽CQA ∆ ∴AP BPAC AQ=∴9x y=, 即0)y x => ·········· (2分)(3) 由题意得PQ AP AQ =+=2=由ABP ∆∽CQA ∆得AB APCQ AC= 得 CQ = ········ (1分)如果PCQ ∆是直角三角形,又90AQC ABP ∠=∠≠,故只有两种可能:……(1分) ①90PCQ ∠=,则1cos 3CQ AQC PQ ∠==,即3PQ CQ =, 23=,解得129,14x x ==-(舍); (2分)②90CPQ ∠=,则1cos 3PQ AQC CQ ∠==,即3CQ PQ =, 23=(1分)综上所述,如果PCQ ∆是直角三角形,BP 的长为9.4. 其他求线段长或线段之比 (闵 行)25.(本题满分14分,其中第(1)小题4分、第(2)、(3)小题各5分)如图,在梯形ABCD 中,AD // BC ,AB = CD ,AD = 5,BC = 15,5cos 13ABC ∠=.E 为射线CD 上任意一点,过点A 作AF // BE ,与射线CD 相交于点F .联结BF ,与直线AD 相交于点G .设CE = x ,AGy DG=. (1)求AB 的长;(2)当点G 在线段AD 上时,求y 关于x 的函数解析式,并写出函数的定义域; (3)如果23ABEF ABCDS S =四边形四边形,求线段CE 的长.【答案】(1) AB = 13;(2)3923x y x -=(3902x <<);(3) 136522CE =或【解析】(1)分别过点A 、D 作AM ⊥BC 、DN ⊥BC ,垂足为点M 、N .∵ AD // BC ,AB = CD ,AD = 5,BC = 15,∴ 11()(155)522BM BC AD =-=-=.……………………………(2分)在Rt △ABM 中,∠AMB = 90°,∴ 55cos 13BM ABM AB AB ∠===. ∴ AB = 13.……………………………………………………………(2分) (2)∵AG y DG =,∴ 1AG DGy DG+=+.即得 51DG y =+.………(1分) ∵ ∠AFD =∠BEC ,∠ADF =∠C .∴ △ADF ∽△BCE . ∴51153FD AD EC BC ===.……………………………………………(1分) 又∵ CE = x ,13FD x =,AB = CD = 13.即得 1133FC x =+.ABCDEFG(第25题图)ABCD(备用图)∵ AD // BC ,∴ FD DGFC BC =.∴ 5113115133x y x +=+.……………(1分) ∴ 3923xy x-=. ∴ 所求函数的解析式为3923x y x -=,函数定义域为3902x <<.(2分) (3)在Rt △ABM 中,利用勾股定理,得12AM =.∴ 11()(515)1212022ABCD S AD BC AM =+⋅=+⨯=梯形.∵23ABEF ABCDS S =四边形四边形,∴ 80ABEF S =四边形. …………………………(1分) 设ADFS S =.由 △ADF ∽△BCE ,13FD EC =,得 9BECS S =.过点E 作EH ⊥BC ,垂足为点H . 由题意,本题有两种情况:(ⅰ)如果点G 在边AD 上,则 840ABCD ABEF S S S -==四边形四边形.∴ S = 5.∴ 945BECS S ==.∴ 11154522BECSBC EH EH =⋅=⨯⋅=.∴ 6EH =. 由 DN ⊥BC ,EH ⊥BC ,易得 EH // DN . ∴61122CE EH CD DN ===. 又 CD = AB = 13,∴ 132CE =.…………………………………(2分) (ⅱ)如果点G 在边DA 的延长线上,则 9ADFABCD ABEF S S SS ++=四边形四边形.∴ 8200S =.解得 25S =.∴ 9225BECS S ==.∴ 111522522BECS BC EH EH =⋅=⨯⋅=.解得 30EH =. ∴305122CE EH CD DN ===.∴ 652CE =.……………………………(2分) ∴ 136522CE =或.(松江)25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)如图,已知△ABC 中,∠ACB =90°,D 是边AB 的中点,P 是边AC 上一动点,BP 与CD 相交于点E . (1)如果BC =6,AC =8,且P 为AC 的中点,求线段BE 的长; (2)联结PD ,如果PD ⊥AB ,且CE =2,ED =3,求cosA 的值; (3)联结PD ,如果222BP CD =,且CE =2,ED =3,求线段PD 的长.【答案】(1) 241333BE BP ==;(2)6cos 3A =;(3) 15=PD 【解析】(1)∵P 为AC 的中点,AC =8,∴CP =4……………………………(1分)∵∠ACB =90°,BC =6,∴BP =213……………………………………………(1分) ∵D 是边AB 的中点,P 为AC 的中点,∴点E 是△ABC 的重心……………(1分) ∴241333BE BP ==…………………………………………………………(1分) (2)过点B 作BF ∥CA 交CD 的延长线于点F ………………………………(1分) ∴CABFDC FD DA BD ==………………………………(1分) ∵BD=DA ,∴FD=DC ,BF=AC …………………(1分) ∵CE=2,ED=3,则CD =5,∴EF =8∴4182===EF CE BF CP …………………………(1分) ∴41=CA CP ,∴13CP PA =,设CP=k ,则P A=3k ,∵PD ⊥AB ,D 是边AB 的中点,∴P A=PB=3k∴k BC 22=,∴k AB 62=,∵k AC 4=,∴6cos 3A =…………(1分) (3)∵∠ACB =90°,D 是边AB 的中点,∴12CD BD AB ==∵222BP CD =,∴22BP CD CD BD AB =⋅=⋅……………(1分)(备用图2)ABCD(备用图1)ABCD(第25题图)ABPC DEPE (备用图ABCD F∵∠PBD=∠ABP ,∴△PBD ∽△ABP …………………………(1分) ∴∠BPD=∠A ……………………………………………………(1分) ∵∠A=∠DCA ,∴∠DPE=∠DCP ,∵∠PDE=∠CDP ,△DPE ∽△DCP ,∴DC DE PD ⋅=2…………………………(1分) ∵DE=3,DC=5,∴15=PD …………………………………(1分)(普陀)25.(本题满分14分)如图11,点O 在线段AB 上,22AO OB a ==,60BOP ∠=︒,点C 是射线OP 上的一个动点. (1)如图11①,当90ACB ∠=︒,2OC =,求a 的值;(2)如图11②,当AC =AB 时,求OC 的长(用含a 的代数式表示);(3)在第(2)题的条件下,过点A 作AQ ∥BC ,并使∠QOC=∠B ,求:AQ OQ 的值.【答案】(1) 1334a +=;(2)6OC a a =-+;(3) 165AQ OQ +=【解析】(1)过点C 作CH AB ⊥,H 为垂足. ············································· (1分)∴90CHO CHB ∠=∠=.在Rt △COH 中,60COB ∠=,2OC =.∴1OH =,3CH =. ································································ (1分) ∵22AO OB a ==, ∴21AH a =+,1BH a =-.∵90ACB ∠=,∴90ACH HCB ∠+∠=.A BCPOABCPO图11①图11②∵CH AB ⊥,∴90ACH A ∠+∠=. ∴A HCB ∠=∠.∵90CHA BHC ∠=∠=︒,∴△ACH ∽△CBH . ·································································· (1分) ∴AH CHCH BH=. ∴2CH AH BH =⋅.∴2(21)(1)a a =+⋅-. ···························································· (1分)∴a =,a =.∴14a =. ············································································ (1分)(2)过点C 作CH AB ⊥,H 为垂足.设OC m =. 在Rt △COH 中,60COB ∠=,OC m =.∴12OH m =,2CH =. ·························································· (2分) 在Rt △ACH 中,90CHA ∠=︒, ∴222AC AH CH =+.∴2221(3)(2)()22a a m =++. ···················································· (2分)得m a =-,m a =-(不合题意,舍去).即OC a =-. ······································································ (1分) (3)延长QA 、CO 交于点E . ∵AQ //BC ,∴E OCB ∠=∠.∵COA AOQ QOC ∠=∠+∠,COA OCB B ∠=∠+∠,QOC B ∠=∠, ∴AOQ OCB ∠=∠.∵QOA E ∠=∠.又∵Q Q ∠=∠,∴△QOA ∽△QEO . ············································ (1分) ∴AQ AOOQ OE=. ············································································ (1分) ∵AQ //BC ,∴AO EO OB OC =.∴AO OBEO OC=.∴AQ OB OQ OC =. ················· (1分)。
2019-2020年上海各区数学中考一模压轴题分类汇编-23题含详解

专题2020分类汇编-23题专题一相似三角形之等量代换【知识梳理】【历年真题】1.(2019秋•奉贤区期末)如图,在平行四边形ABCD中,点E在边AD上,点F在边CB 的延长线上,联结CE、EF,CE2=DE•CF.(1)求证:∠D=∠CEF;(2)联结AC,交EF于点G,如果AC平分∠ECF,求证:AC•AE=CB•CG.2(2019秋•浦东新区期末)如图,已知△ABC和△ADE,点D在BC边上,DA=DC,∠ADE=∠B,边DE与AC相交于点F.(1)求证:AB•AD=DF•BC;(2)如果AE∥BC,求证:BD DF DC FE.3.(2019秋•长宁区、金山区期末)如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD交于点F,若AE平分∠BAC,AB•AF=AC•AE.(1)求证:∠AFD=∠AEC;(2)若EG∥CD,交边AC的延长线于点G,求证:CD•CG=FC•BD.4.(2019秋•静安区期末)如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,点E在线段OB上,AE的延长线与BC相交于点F,OD2=OB•OE.(1)求证:四边形AFCD是平行四边形;(2)如果BC=BD,AE•AF=AD•BF,求证:△ABE∽△ACD.5.(2019秋•青浦区期末)已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G,AF2=FG⋅FE.(1)求证:△CAD∽△CBG;(2)联结DG,求证:DG•AE=AB•AG.6.(2019秋•杨浦区期末)如图,已知在△ABC中,AD是△ABC的中线,∠DAC=∠B,点E在边AD上,CE=CD.(1)求证:AC BD AB AD;(2)求证:AC2=2AE•AD.7.(2019秋•宝山区期末)如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得BD ADDE DC=,联结CE.求证:(1)∠ECD=2∠BAM;(2)BF是DF和EF的比例中项.8.(2019秋•嘉定区期末)已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE ∥BC,∠ABE=∠C.(1)求证:BE2=DE•BC;(2)当BE平分∠ABC时,求证:BD AE BE AB=.专题二相似三角形之面积比【知识梳理】【历年真题】1.(2019秋•黄浦区期末)已知:如图,在平行四边形ABCD中,过点C分别作AD、AB 的垂线,交边AD、AB延长线于点E、F.(1)求证:AD•DE=AB•BF;(2)联结AC,如果CF ACDE CD=,求证:22AC AFBC BF=.2.(2019秋•黄浦区期末)已知:如图,四边形ABCD的对角线AC、BD相交于点O,S△AOD=S△BOC·(1)求证:DO CO OB OA=;(2)设ΔOAB的面积为S,CDAB=k,求证:S四边形ABCD=(k+1)2S.专题三相似三角形综合题【知识梳理】【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.(1)求证:BD2=DE•AD;(2)如果∠ABC=∠DCE,求证:BD•CE=BE•DE.2.(2019秋•闵行区期末)如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且AD•OC=AB•OD,AF是∠BAC的平分线,交BC于点F,交DE 于点G.求证:(1)CE⊥AB;(2)AF•DE=AG•BC.3.(2019秋•崇明区期末)如图,△ABC中,AD⊥BC,E是AD边上一点,连接BE,过点D作DF⊥BE,垂足为F,且AE•DF=EF•CD,联结AF、CF,CF与边AD交于点O.求证:(1)∠EAF=∠DCF;(2)AF•BD=AC•DF.4.(2019秋•松江区期末)已知:如图,点D,F在△ABC边AC上,点E在边BC上,且DE∥AB,CD2=CF•CA.(1)求证:EF∥BD;(2)如果AC•CF=BC•CE,求证:BD2=DE•BA.5.(2019秋•徐汇区期末)如图,在△ABC中,点D,E,F,G分别在AB、AC、BC上,AB=3AD,CE=2AE,BF=FG=CG,DG与EF交于点H.(1)求证:FH•AC=HG•AB;(2)联结DF,EG,求证:∠A=∠FDG+∠GEF.专题2020分类汇编-23题专题一相似三角形之等量代换【历年真题】1.(2019秋•奉贤区期末)如图,在平行四边形ABCD中,点E在边AD上,点F在边CB的延长线上,联结CE、EF,CE2=DE•CF.(1)求证:∠D=∠CEF;(2)联结AC,交EF于点G,如果AC平分∠ECF,求证:AC•AE=CB•CG.【考点】平行四边形的性质;相似三角形的判定与性质.【专题】证明题;多边形与平行四边形;图形的相似;推理能力.【分析】(1)根据CE2=DE•CF且∠DEC=∠ECF可证明△CDE∽△CEF,即可得结论;(2)根据AC平分∠ECF,AD∥BC,可得∠EAC=∠ECA,进而得E=EC,再证明△CGE∽△CAB,对应边成比例即可.【解答】(1)证明:∵CE2=DE•CF,即CE CF DE CE=∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DEC=∠ECF,∴△CDE∽△CEF,∴∠D=∠CEF.(2)如图所示:∵AC平分∠ECF,∴∠ECA=∠BCA,∵∠D=∠CEF,∠D=∠B,∴∠CEF=∠B,∴△CGE∽△CAB,∴CG CE AC CB=,∵AD∥BC,∴∠DAC=∠BCA,∵∠ECA=∠DAC,∴AE=CE,∴CG AEAC CB=,即AC•AE=CB•CG.【点评】本题考查了平行四边形的性质、相似三角形的判定和性质,解决本题的关键是综合运用平行四边形的性质、相似三角形的判定和性质、等腰三角形的性质.2(2019秋•浦东新区期末)如图,已知△ABC和△ADE,点D在BC边上,DA=DC,∠ADE=∠B,边DE与AC相交于点F.(1)求证:AB•AD=DF•BC;(2)如果AE∥BC,求证:BD DF DC FE=.【考点】相似三角形的判定与性质.【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;图形的相似;推理能力.【分析】(1)由等腰三角形的性质得出∠DAC=∠C,由已知∠ADE=∠B,证明△ABC∽△FDA,得出AB BC DF AD=,即可得出结论;(2)由三角形的外角性质得出∠CDF=∠BAD,由平行线的性质得出∠E=∠CDF,∠C=∠EAF,证出∠BAD=∠E,证明△ABD∽△EDA,得出BD ADAD AE=,证出∠EAF=∠DAC,即AC平分∠DAE,作FM⊥AD于M,FN⊥AE于N,则FM=FN,求出ADF DF=AEFADEF AE=△的面积△的面积,即可得出结论.【解答】(1)证明:∵DA=DC,∴∠DAC=∠C,又∵∠ADE=∠B,∴△ABC∽△FDA,∴AB BC DF AD=,∴AB•AD=DF•BC;(2)证明:∵∠ADE+∠CDF=∠B+∠BAD,∠ADE=∠B,∴∠CDF=∠BAD,∵AE∥BC,∴∠E=∠CDF,∠C=∠EAF,∴∠BAD=∠E,又∵∠ADE=∠B,∴△ABD∽△EDA,∴BD AD AD AE=,∵DA=DC,∴∠DAC=∠C,∴∠EAF=∠DAC,即AC平分∠DAE,作FM⊥AD于M,FN⊥AE于N,则FM=FN,∵1ADF DF2=1AEF2AD FM ADEF AEAE FN⨯==⨯△的面积△的面积,∴BD DF DC FE=.方法二:∵∠B=∠ADE,∠BAD=∠CDF=∠E,∴△ABD∽△EDA,∴AD BD AE AD=,∵DA=DC,∴BD AD CDCD AE AE==①,又∵AE∥BC,∴△DFC∽△EFA,∴CD DFAE FE=②,由①②得:BD DF DC FE=.【点评】本题考查了相似三角形的判定与性质、等腰三角形的性质、三角形的外角性质、平行线的性质、角平分线的性质等知识;证明三角形相似是解题的关键.3.(2019秋•长宁区、金山区期末)如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD交于点F,若AE平分∠BAC,AB•AF=AC•AE.(1)求证:∠AFD=∠AEC;(2)若EG∥CD,交边AC的延长线于点G,求证:CD•CG=FC•BD.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)先证△BAE∽△CAF,推出∠AEB=∠AFC,由等角的补角相等可得出结论;(2)先后证明∠DCB=∠CEG,∠G=∠ACF=∠B,推出△BDC∽△GCE,由相似三角形的性质可得出结论.【解答】(1)证明:∵AB•AF=AC•AE,∴AB AC AE AF=,∵AE平分∠BAC,∴∠BAE=∠CAE,∴△BAE∽△CAF,∴∠AEB=∠AFC,∴180°﹣∠AEB=180°﹣∠AFC,∴∠AEC=∠AFD;(2)证明:∵∠CFE=∠AFD=∠CEF,∴CE=CF,∵DC ∥EG ,∴∠DCB =∠CEG ,∠G =∠ACF =∠B ,∴△BDC ∽△GCE ,∴BD GC GC DC CE CF==,∴CD •CG =FC •BD .【点评】本题考查了相似三角形的判定与性质,解题关键是能够灵活运用相似三角形的判定与性质.4.(2019秋•静安区期末)如图,在梯形ABCD 中,AD ∥BC ,AC 与BD 相交于点O ,点E 在线段OB 上,AE 的延长线与BC 相交于点F ,OD 2=OB •OE .(1)求证:四边形AFCD 是平行四边形;(2)如果BC =BD ,AE •AF =AD •BF ,求证:△ABE ∽△ACD .【考点】相似三角形的判定;平行四边形的判定与性质;梯形.【专题】等腰三角形与直角三角形;多边形与平行四边形;梯形;图形的相似;推理能力.【分析】(1)由已知得出OE OD OD OB =,由平行线得出△AOD ∽△COB ,得出OA OD OC OB =,证出OA OE OC OD=,得出AF ∥CD ,即可得出结论;(2)由平行线得出∠AED =∠BDC ,△BEF ∽△BDC ,得出BE BF BD BC =,证出∠AEB =∠ADC .由已知得出AE AD BF AF =,由平行四边形的性质得出AF =CD ,得出AE AD BE DC=,由相似三角形的判定定理即可得出结论.【解答】(1)证明:∵OD 2=OE •OB ,∴OE OD OD OB=,∵AD ∥BC ,∴△AOD ∽△COB ,∴OA OD OC OB =∴OA OE OC OD=∴AF ∥CD ,∴四边形AFCD 是平行四边形;(2)证明:∵AF ∥CD ,∴∠AED =∠BDC ,△BEF ∽△BDC ,∴BE BF BD BC =,∵BC =BD ,∴BE =BF ,∠BDC =∠BCD ,∴∠AED =∠BCD .∵∠AEB =180°﹣∠AED ,∠ADC =180°﹣∠BCD ,∴∠AEB =∠ADC .∵AE •AF =AD •BF ,∴AE AD BF AF=,∵四边形AFCD 是平行四边形,∴AF =CD ,∴AE AD BE DC =,∴△ABE∽△ADC.【点评】本题考查了相似三角形的判定与性质、平行四边形的判定与性质、梯形的性质、等腰三角形的性质等知识;熟练掌握相似三角形的判定与性质和平行四边形的判定是解题的关键.5.(2019秋•青浦区期末)已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G,AF2=FG⋅FE.(1)求证:△CAD∽△CBG;(2)联结DG,求证:DG•AE=AB•AG.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)通过证明△FAG∽△FEA,可得∠FAG=∠E,由平行线的性质可得∠E=∠EBC=∠FAG,且∠ACD =∠BCG,可证△CAD∽△CBG;(2)由相似三角形的性质可得CA CDCB CG=,且∠DCG=∠ACB,可证△CDG∽△CAB,可得DG CGAB CB=,由平行线分线段成比例可得AE AGCB GC=,可得结论.【解答】证明:(1)∵AF2=FG⋅FE.∴AF EFFG AF=,且∠AFG=∠EFA,∴△FAG∽△FEA,∴∠FAG=∠E,∵AE∥BC,∴∠E=∠EBC,∴∠EBC=∠FAG,且∠ACD=∠BCG,∴△CAD∽△CBG;(2)∵△CAD∽△CBG,∴CA CDCB CG=,且∠DCG=∠ACB,∴△CDG∽△CAB,∴DG CGAB CB=,∵AE∥BC,∴AE AGCB GC=∴AG GCAE BC=,∴DG AGAB AE=,∴DG•AE=AB•AG.【点评】本题考查了相似三角形的判定和性质,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.6.(2019秋•杨浦区期末)如图,已知在△ABC中,AD是△ABC的中线,∠DAC=∠B,点E在边AD上,CE=CD.(1)求证:AC BD AB AD=;(2)求证:AC2=2AE•AD.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】(1)先利用等腰三角形的性质,由CD=CE得到∠CED=∠EDC,则可根据等角的补角相等得到∠AEC=∠ADB,加上∠DAC=∠B,于是可根据有两组角对应相等的两个三角形相似判断△ACE∽△BAD.(2)由∠DAC=∠B及公共角相等证明△ACD∽△BCA,利用相似比即可得到结论.【解答】(1)证明:∵CD=CE,∴∠CED=∠EDC,∵∠AEC+∠CED=180°,∠ADB+∠EDC=180°,∴∠AEC=∠ADB,∵∠DAC=∠B,∴△ACE∽△BAD;∴AC CE AB AD=,∵BD=CD=CE,∴AC BD AB AD=;(2)∵∠DAC=∠B,∠ACD=∠BCA,∴△ACD∽△BCA,∴AC CBCD CA=,∴AC2=CD•CB,∵△ACE∽△BAD,∴AE CEBD AD=,∴AE•AD=BD•CE,∴2AE•AD=2BD•CE=BC•CD,∴AC2=2AE•AD.7.(2019秋•宝山区期末)如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得BD ADDE DC=,联结CE.求证:(1)∠ECD=2∠BAM;(2)BF是DF和EF的比例中项.【考点】相似三角形的判定与性质;等腰三角形的性质.【专题】图形的全等;等腰三角形与直角三角形;图形的相似;推理能力.【分析】(1)由等腰三角形的性质可得∠BAC=2∠BAM,通过证明△ADB∽△CDE,可得∠BAC=∠ECD=2∠BAM;(2)由等腰三角形的性质可得BF=CF,通过证明△DCF∽△CEF,可得DF CFCF EF=,可得结论.【解答】证明:(1)∵AB=AC,AM为BC边的中线,∴∠BAC=2∠BAM,∵BD ADDE DC=,∠ADB=∠CDE,∴△ADB∽△CDE,∴∠BAC=∠ECD,∴∠ECD=2∠BAM;(2)如图,连接CF,∵AB=AC,AM为BC边的中线,∴AM是BC的垂直平分线,∴BF=CF,且AB=AC,AF=AF,∵△ABF≌△ACF(SSS)∴∠ABF=∠ACF,由(1)可知:△ADB∽△CDE,∴∠ABF=∠E,∴∠ACF=∠E,且∠EFC=∠DFC,∴△DCF∽△CEF,∴DF CFCF EF=,且BF=CF,∴BF2=DF•EF,∴BF是DF和EF的比例中项.【点评】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,等腰三角形的性质,证明△DCF∽△CEF 是本题的关键.8.(2019秋•嘉定区期末)已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ABE=∠C.(1)求证:BE2=DE•BC;(2)当BE平分∠ABC时,求证:BD AE BE AB=.【考点】相似三角形的判定与性质.【专题】图形的相似;应用意识.【分析】(1)证明△BDE∽△CEB,推出DE BEBE BC=可得结论.(2)利用相似三角形的性质以及平行线分线段成比例定理即可解决问题.【解答】证明:(1)∵DE∥BC,∴∠BED=∠CBE,又∵∠ABE=∠C,∴△BDE∽△CEB,∴DE BE BE BC=,∴BE2=DE•BC.(2)∵DE∥BC,∴∠AED=∠C.又∠ABE=∠C,∴∠AED=∠ABE,又∵∠EAD=∠BAE,∴△ADE∽△AEB,∴AE AD AB AE=,∵DE∥BC,∴AD AEBD CE=,即AD BEAE CE=,∴AE BDAB CE=,∵BE平分∠ABC,∴∠ABE=∠CBE,又∵∠ABE=∠C,∴∠CBE=∠C,∴BE=CE,∴BD AE BE AB=.【点评】本题考查相似三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.专题二相似三角形之面积比【历年真题】1.(2019秋•黄浦区期末)已知:如图,在平行四边形ABCD中,过点C分别作AD、AB的垂线,交边AD、AB延长线于点E、F.(1)求证:AD •DE =AB •BF ;(2)联结AC ,如果CF AC DE CD=,求证:22AC AF BC BF =.【考点】相似三角形的判定与性质;平行四边形的性质.【专题】图形的相似;应用意识.【分析】(1)证明想办法证明四边形ABCD 是平行四边形即可解决问题.(2)由△ACF ∽△CDE ,△CDE ∽△CBF ,推出△ACF ∽△CBF ,可得2ACF 2CBF S AC S BC =△△,又△ACF 与△CBF 等高,推出ACF CBF S AF S BF =△△,可得结论.【解答】解:(1)∵四边形ABCD 是平行四边形,∴CD ∥AB ,AD ∥BC ,∴∠CDE =∠DAB ,∠CBF =∠DAB ,∴∠CDE =∠CBF ,∵CE ⊥AE ,CF ⊥AF ,∴∠CED =∠CFB =90°,∴△CDE ∽△CBF ,∴BC CD BF DE=,∵四边形ABCD 是平行四边形,∴BC =AD ,CD =AB ,∴AD AB BF DE =,∴AD •DE =AB •BF .(2)连接AC .∵CF AC DE CD =,∴CF DE AC CD=,设1CF DE AC CD k==,∴AC =kCF ,CD =kDE ,∴AF=•CF ,CE=•DE ,∴AF CF AC CE DE CD==,∴△ACF ∽△CDE ,又∵△CDE ∽△CBF ,∴△ACF ∽△CBF ,∴2ACF 2CBF S AC S BC=△△,∵△ACF 与△CBF 等高,∴ACF CBF S AF S BF=△△,∴22AC AF BC BF =.【点评】本题考查相似三角形的判定和性质,平行四边形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.2.(2019秋•黄浦区期末)已知:如图,四边形ABCD 的对角线AC 、BD 相交于点O ,S △AOD =S △BOC ·(1)求证:DO CO OB OA=;(2)设ΔOAB 的面积为S,CD AB =k,求证:S 四边形ABCD =(k+1)2S.【考点】相似三角形的判定与性质,等线段替换法【专题】图形的相似;推理能力.【分析】(1)由S △AOD =S △BOC 易得S △ADB =S △ACB ,根据三角形面积公式得到点D 和点C 到AB 的距离相等,则CD//AB,于是可判断△DOC∽△BOA,然后利用相似比即可得到结论;(2)利用相似三角形的性质可得结论.【解答】证明:(1)S △AOD =S △BOC ,∴S △AOD +S △AOB =S △BOC +S △AOB ,即=S △ACB ∴CD//A B,∴△DOC ∽△BOA ,DO CO OB OA =(2)∵△DOC ∽△BOA ∴CD DO CO k AB BO AO ===,22COD AOB S DO k S BO==△△(∴DO=kOB ,CO=kAO ,S △ACB =k 2S ,∴S △AOD =kS △AOD =kS ,S △co B =kS △o AB =kS ,∴S 四边形ABCD =S+kS+kS+k 2S=(k+1)2S.【点评】本题考查了相似三角形的判定和性质,证明△DOC ∽△BOA 是本题的关键。
2019年上海市黄浦区高考数学一模试卷(含解析版)

2019年上海市黄浦区高考数学一模试卷一、填空题1.(3分)不等式<0的解集为.2.(3分)双曲线x2﹣=1的渐近线方程为.3.(3分)若复数z=1﹣i(i为虚数单位),则z2的共轭复数为.4.(3分)记等差数列{a n}(n∈N*)的前n项和为S n,若a5=1,则S9=.5.(3分)若函数y=f(x)是函数y=a x(a>0,且a≠1)的反函数,且f(2)=1,则f (x)=.6.(3分)已知a>0,b>0,若a+b=4,则a2+b2的最小值为.7.(3分)已知三阶行列式,元素8的余子式的值与代数余子式的值之和.8.(3分)设a∈R,若(2+)(1+x)5展开式中x2的系数为10,则a=.9.(3分)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有种.(用数字作答).10.(3分)已知数列{a n}(n∈N*),若a1=1,a n+1+a n=()n,则a2n=.11.(3分)在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为,,,,,若与的夹角记为θij,其中i,j∈{1,2,3,4,5},且i≠j,则||cosθij的最大值为.12.(3分)如图,l1、l2是过点M夹角为的两条直线,且与圆心为O,半径长为1的圆分别相切,设圆周上一点P到l1、l2的距离分比为d1、d2,那么2d1+d2的最小值为.二、选择题13.(3分)设函数y=f(x),“该函数的图象过点(1,1)”是“该函数为幂函数”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件14.(3分)下列关于函数y=sin x与y=arcsin x的命题中正确的是()A.它们互为反函数B.都是增函数C.都是周期函数D.都是奇函数15.(3分)如图,在正方体ABCD﹣A1B1C1D1的八个顶点中任取两个点作直线,与直线A1B 异面且夹角成60°的直线的条数为()A.3B.4C.5D.616.(3分)如图,平面直角坐标系中,曲线(实线部分)的方程可以是()A.(|x|﹣y﹣1)•(1﹣x2+y2)=0B.()•(1﹣x2+y2)=0C.(|x|﹣y﹣1)•()=0D.()•()=0三.解答题17.如图,一个圆锥形量杯的高为12厘米,其母线与轴的夹角为30°.(1)求该量杯的侧面积S;(2)若要在圆锥形量杯的一条母线P A上,刻上刻度,表示液面到达这个刻度时,量杯里的液体的体积是多少?当液体体积是100立方厘米时,刻度的位置B与顶点P之间的距离是多少厘米(精确到0.1厘米)?18.已知函数f(x)=sin2x+2cos2x﹣1,x∈(0,π).(1)求函数y=f(x)的单调递减区间;(2)在△ABC中,若f(A)=f(B),且A≠B,AB=,求△ABC外接圆半径的长.19.已知函数f(x)=+b,其中a,b∈R.(1)当a=6,b=0时,求满足f(|x|)=2x的x的值;(2)若f(x)为奇函数且非偶函数,求a与b的关系式.20.椭圆Γ:+=1.(1)若抛物线C的焦点与Γ的焦点重合,求C的标准方程;(2)若Γ的上顶点A、右焦点F及x轴上一点M构成直角三角形,求点M的坐标;(3)若O为Γ的中心,P为Γ上一点(非Γ的顶点),过Γ的左顶点B,作BQ∥OP,BQ交y轴于点Q,交Γ于点N,求证:•=22.21.给定整数n(n≥4),设集合A={a1,a2,…,a n}.记集合B={a i+a j|a i,a j∈A,1≤i≤j≤n}.(1)若A={﹣3,0,1,2},求集合B;(2)若a1,a2,…a n构成以a1为首项,d(d>0)为公差的等差数列,求证:集合B中的元素个数为2n﹣1;(3)若a1,a2,…,a n构成以3为首项,3为公比的等比数列,求集合B中元素的个数及所有元素之和.2019年上海市黄浦区高考数学一模试卷参考答案与试题解析一、填空题1.(3分)不等式<0的解集为(0,1).【考点】7E:其他不等式的解法.【专题】59:不等式的解法及应用.【分析】由不等式<0可得x(x﹣1)<0,由此解得不等式的解集.【解答】解:由不等式<0可得x(x﹣1)<0,解得0<x<1,故答案为:(0,1).【点评】本题主要考查分式不等式的解法,体现了等价转化的数学思想,属于基础题.2.(3分)双曲线x2﹣=1的渐近线方程为y=±x.【考点】KC:双曲线的性质.【专题】34:方程思想;48:分析法;5D:圆锥曲线的定义、性质与方程.【分析】由双曲线的方程﹣=1的渐近线方程为y=±x,求得a,b,即可得到渐近线方程.【解答】解:双曲线x2﹣=1的a=1,b=,可得渐近线方程为y=±x,即有y=±x.故答案为:y=±x.【点评】本题考查双曲线的渐近线方程的求法,注意运用双曲线的性质,考查运算能力,属于基础题.3.(3分)若复数z=1﹣i(i为虚数单位),则z2的共轭复数为2i.【考点】A5:复数的运算.【专题】11:计算题;38:对应思想;4O:定义法;5N:数系的扩充和复数.【分析】然后利用复数代数形式的乘除运算化简得答案.【解答】解:若复数z=1﹣i(i为虚数单位),则z2=(1﹣i)2=﹣2i,则共轭复数为2i,故答案为:2i.【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.4.(3分)记等差数列{a n}(n∈N*)的前n项和为S n,若a5=1,则S9=9.【考点】85:等差数列的前n项和.【专题】34:方程思想;4R:转化法;54:等差数列与等比数列.【分析】由a5=1,利用等差数列的性质可得a1+a9=2a5.再利用求和公式即可得出.【解答】解:∵a5=1,∴a1+a9=2a5.则S9==9a5=9.故答案为:9.【点评】本题考查了等差数列的性质与求和公式,考查了推理能力与计算能力,属于中档题.5.(3分)若函数y=f(x)是函数y=a x(a>0,且a≠1)的反函数,且f(2)=1,则f (x)=log2x.【考点】4R:反函数.【分析】欲求函数y=a x的反函数,先由原函数式解出x,后将x,y互换即得.最后根据f(2)=1求出a值.【解答】解:f(x)=log2x函数y=a x(a>0,且a≠1)的反函数是f(x)=log a x,又f(2)=1,即log a2=1,所以,a=2,故f(x)=log2x.故答案是:log2x.【点评】本题主要考查了反函数的求法,属于基础题.6.(3分)已知a>0,b>0,若a+b=4,则a2+b2的最小值为.【考点】7F:基本不等式及其应用.【专题】11:计算题;59:不等式的解法及应用.【分析】利用基本不等式,可求.【解答】解:∵a>0,b>0,a+b=4,又,则a2+b2≥8,即最小值为8.故答案为:8.【点评】本题主要考查了利用基本不等式,求解最值的应用.7.(3分)已知三阶行列式,元素8的余子式的值与代数余子式的值之和0.【考点】OM:二阶行列式的定义.【专题】11:计算题;34:方程思想;4O:定义法;5R:矩阵和变换.【分析】元素8的余子式为:=﹣6,元素8的代数余子式为:(﹣1)5×=6,由此能求出元素8的余子式的值与代数余子式的值之和.【解答】解:∵三阶行列式,∴元素8的余子式为:=﹣6,元素8的代数余子式为:(﹣1)5×=6,∴元素8的余子式的值与代数余子式的值之和为:﹣6+6=0.故答案为:0.【点评】本题考查行列式的余子式与代数余子式之和的求法,考查余子式、代数余子式的定义等基础知识,考查运算求解能力,是基础题.8.(3分)设a∈R,若(2+)(1+x)5展开式中x2的系数为10,则a=﹣1.【考点】DA:二项式定理.【专题】35:转化思想;49:综合法;5P:二项式定理.【分析】把(1+x)5按照二项式定理展开,可得x2的系数,再根据x2的系数为10,求得实数a的值.【解答】解:∴(2+)(1+x)5=(2+)(1+5x+10x2+10x3+5x4+x5),故x2的系数为20+10a=10,∴a=﹣1,故答案为:﹣1.【点评】本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.9.(3分)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有96种.(用数字作答).【考点】D9:排列、组合及简单计数问题.【专题】11:计算题;16:压轴题.【分析】根据题意,如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生;按第一棒是丙或甲、乙中一人,分为两类,分别计算其情况数目,结合分类计数原理,计算可得答案.【解答】解:分两类:第一棒是丙有C11•C21•A44=48,第一棒是甲、乙中一人有C21•C11•A44=48因此共有方案48+48=96种;故答案为96.【点评】本题考查排列、组合的综合应用,注意优先分析有特殊要求的元素,对于本题,注意分类的标准前后统一,要做到不重不漏.10.(3分)已知数列{a n}(n∈N*),若a1=1,a n+1+a n=()n,则a2n=.【考点】8H:数列递推式;8J:数列的极限.【专题】33:函数思想;49:综合法;55:点列、递归数列与数学归纳法.【分析】由已知推导出,,从而,由此能求出a2n.【解答】解:∵数列{a n}(n∈N*)满足a1=1,a n+1+a n=()n,∴(a1+a2)+(a3+a4)+…+(a2n﹣1+a2n)=,∴.又a1+(a2+a3)+(a4+a5)+…+(a2n﹣2﹣a2n﹣1)==.即.∴.∴.【点评】本题考查由数列递推式求数列的通项公式,考查数列极限的求法,是中档题.11.(3分)在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为,,,,,若与的夹角记为θij,其中i,j∈{1,2,3,4,5},且i≠j,则||cosθij的最大值为.【考点】9H:平面向量的基本定理.【专题】13:作图题;5A:平面向量及应用.【分析】由向量的投影的几何意义有:||cosθij的几何意义为向量在向量方向上的投影,由图可知:在直角三角形AED中,向量在向量方向上的投影最大,即可得解.【解答】解:由向量的投影的几何意义有:||cosθij的几何意义为向量在向量方向上的投影,由图可知:在向量方向上的投影最大,且为,故答案为:.【点评】本题考查了向量的投影的几何意义,属简单题.12.(3分)如图,l1、l2是过点M夹角为的两条直线,且与圆心为O,半径长为1的圆分别相切,设圆周上一点P到l1、l2的距离分比为d1、d2,那么2d1+d2的最小值为3﹣.【考点】J9:直线与圆的位置关系;JE:直线和圆的方程的应用.【专题】11:计算题;34:方程思想;35:转化思想;51:函数的性质及应用.【分析】根据题意,分析可得|OM|=2,建立坐标系,分析可得l1、l2的关于y轴对称,据此设出直线l1与l2的方程,P(cosθ,sinθ),由此表示2d1+d2,结合三角函数的性质分析可得答案.【解答】解:根据题意,l1、l2是过点M夹角为的两条直线,且与圆心为O,半径r =1的圆分别相切,则|OM|=2r=2,如图建立坐标系,以圆心O为坐标原点,OM为y轴建立坐标系,M(0,2),又由l1、l2是过点M夹角为的两条直线,则l1、l2的关于y轴对称,易得l1、l2的倾斜角为和,则设l1的方程为y=x+2,l2的方程为y=﹣x+2,P是圆周上的一个动点,设P(cosθ,sinθ),则d1===1+,d2===1﹣,则2d1+d2=2+(cosθ﹣sinθ)+1﹣×(cosθ+sinθ)=3+=3+sin(﹣θ)≥3﹣;即2d1+d2的最小值为3﹣;故答案为:3﹣.【点评】本题考查直线与圆方程的应用,注意建立坐标系,表示2d1+d2.二、选择题13.(3分)设函数y=f(x),“该函数的图象过点(1,1)”是“该函数为幂函数”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【考点】29:充分条件、必要条件、充要条件.【专题】49:综合法;51:函数的性质及应用;5L:简易逻辑.【分析】若函数f(x)为幂函数,利用性质可的该函数的图象过点(1,1).反之不成立.即可判断出关系.【解答】解:若函数f(x)为幂函数,则该函数的图象过点(1,1).反之不成立.∴“该函数的图象过点(1,1)”是“该函数为幂函数”的必要非充分条件.故选:B.【点评】本题考查了幂函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.14.(3分)下列关于函数y=sin x与y=arcsin x的命题中正确的是()A.它们互为反函数B.都是增函数C.都是周期函数D.都是奇函数【考点】3K:函数奇偶性的性质与判断;4R:反函数.【专题】11:计算题;57:三角函数的图象与性质.【分析】根据正弦函数y=sin x的性质可得A,B不正确,反正弦函数不是周期函数得C 不正确.【解答】解:y=sin x在R内不存在反函数,且不具有单调性,故A,B不正确;y=arcsin x不是周期函数,故C不正确;故选:D.【点评】本题考查了反函数,属基础题.15.(3分)如图,在正方体ABCD﹣A1B1C1D1的八个顶点中任取两个点作直线,与直线A1B 异面且夹角成60°的直线的条数为()A.3B.4C.5D.6【考点】LM:异面直线及其所成的角.【专题】11:计算题;37:集合思想;44:数形结合法;5F:空间位置关系与距离.【分析】结合图形,利用异面直线所称的角的概念,把与A1B成60°角的异面直线一一列出,即得答案.【解答】解:在正方体ABCD﹣A1B1C1D1的八个顶点中任取两个点作直线,与直线A1B异面且夹角成60°的直线有:AD1,AC,D1B1,B1C,共4条.故选:B.【点评】本题考查异面直线的定义域判断方法,异面直线成的角的定义,体现了数形结合的数学思想,是基础题.16.(3分)如图,平面直角坐标系中,曲线(实线部分)的方程可以是()A.(|x|﹣y﹣1)•(1﹣x2+y2)=0B.()•(1﹣x2+y2)=0C.(|x|﹣y﹣1)•()=0D.()•()=0【考点】KE:曲线与方程.【专题】34:方程思想;48:分析法;5D:圆锥曲线的定义、性质与方程.【分析】由图象可得曲线表示折线段的一部分和双曲线,对照选项一一分析,方程表示的图形,注意绝对值和根式的意义,即可得到正确选项.【解答】解:如图曲线表示折线段的一部分和双曲线,选项A等价于|x|﹣y﹣1=0或1﹣x2+y2=0,表示折线y=|x|﹣1的全部和双曲线,故错误;选项B等价于,或|x|﹣y﹣1=0,|x|﹣y﹣1=0表示折线y=|x|﹣1的全部,故错误;选项C等价于或1﹣x2+y2=0,表示折线y=|x|﹣1在双曲线的外部(包括有原点)的一部分,1﹣x2+y2=0表示双曲线,符合题中图象,故正确;选项D等价于或,表示表示折线y=|x|﹣1在双曲线的外部(包括有原点)的一部分,表示双曲线在x轴下方的一部分,故错误.故选:C.【点评】本题考查曲线的方程和方程的曲线概念,关键在于考虑问题要周全,即在每个因式等于0时,需保证另一个因式有意义,此题是个中档题,也是易错题.三.解答题17.如图,一个圆锥形量杯的高为12厘米,其母线与轴的夹角为30°.(1)求该量杯的侧面积S;(2)若要在圆锥形量杯的一条母线P A上,刻上刻度,表示液面到达这个刻度时,量杯里的液体的体积是多少?当液体体积是100立方厘米时,刻度的位置B与顶点P之间的距离是多少厘米(精确到0.1厘米)?【考点】5C:根据实际问题选择函数类型.【专题】11:计算题;38:对应思想;4R:转化法;5Q:立体几何.【分析】(1)设底面圆的半径为r,根据侧面积公式即可求出,(2)根据体积公式计算即可.【解答】解:(1)设底面圆的半径为r,∵h=12,∠OP A=30°,∴AP==8,r=12×=4,∴量杯的侧面积S=πrl=4×8π=96πcm2,(2)V=Sh=πr2h=×48×12π=196cm2,设PB=x,则BC=x,PC=x,∴V′=×π(x)2•x=πx3=100,解得x≈7.6【点评】本题考查了圆锥的侧面积和体积,考查了运算能力,属于基础题.18.已知函数f(x)=sin2x+2cos2x﹣1,x∈(0,π).(1)求函数y=f(x)的单调递减区间;(2)在△ABC中,若f(A)=f(B),且A≠B,AB=,求△ABC外接圆半径的长.【考点】GS:二倍角的三角函数.【专题】33:函数思想;4A:数学模型法;58:解三角形.【分析】(1)利用倍角公式降幂,再由辅助角公式化积,由复合函数的单调性求函数y =f(x)的单调递减区间;(2)由f(A)=f(B),且A≠B,求得A+B=,得C=,结合c=AB=,再由正弦定理求得△ABC外接圆半径的长.【解答】解:(1)f(x)=sin2x+2cos2x﹣1=sin2x+cos2x=,由,得,k∈Z.取k=0,可得.∴函数y=f(x)的单调递减区间为();(2)由f(A)=f(B),得,∵A≠B,∴,则A+B=,∴C=,∵c=AB=.∴,即R=1.【点评】本题考查三角函数的恒等变换应用,考查三角形的解法,是中档题.19.已知函数f(x)=+b,其中a,b∈R.(1)当a=6,b=0时,求满足f(|x|)=2x的x的值;(2)若f(x)为奇函数且非偶函数,求a与b的关系式.【考点】3N:奇偶性与单调性的综合.【专题】11:计算题;34:方程思想;35:转化思想;51:函数的性质及应用.【分析】(1)根据题意,当a=6,b=0时,f(x)=,若f(|x|)=2x,则=2x,解可得x的值,即可得答案;(2)根据题意,由奇函数的定义可得f(﹣x)+f(x)=0,即(+b)+(+b)=0,变形分析可得a、b的关系,即可得答案.【解答】解:(1)根据题意,当a=6,b=0时,f(x)=,若f(|x|)=2x,则=2x,又由2x>0,则2x=3,则x=log23,(2)若f(x)为奇函数且非偶函数,则f(﹣x)+f(x)=0,即(+b)+(+b)=0,变形可得:a﹣2b=0,即a=2b(a≠0).【点评】本题考查函数的奇偶性的应用,涉及函数值的计算,属于基础题.20.椭圆Γ:+=1.(1)若抛物线C的焦点与Γ的焦点重合,求C的标准方程;(2)若Γ的上顶点A、右焦点F及x轴上一点M构成直角三角形,求点M的坐标;(3)若O为Γ的中心,P为Γ上一点(非Γ的顶点),过Γ的左顶点B,作BQ∥OP,BQ交y轴于点Q,交Γ于点N,求证:•=22.【考点】KL:直线与椭圆的综合.【专题】15:综合题;38:对应思想;4R:转化法;5E:圆锥曲线中的最值与范围问题.【分析】(1)根据椭圆的方程和抛物线的性质即可求出,(2)根据勾股定理即可求出,(3)由B(﹣3,0),BQ∥OP,设直线BQ的方程为x=my﹣3,直线OP的方程为x=my,分别于椭圆的方程联立,求出点Q,N,P的坐标,在根据向量的运算即可证明【解答】解:(1)椭圆Γ:+=1中a2=9,b2=4,∴c2=a2﹣b2=5,∴c=,∴Γ的焦点坐标为(,0),(﹣,0),∵抛物线C的焦点与Γ的焦点重合,∴p=2,且抛物线的焦点在x轴上,∴C的标准方程y2=±4;(2)∵Γ的上顶点A、右焦点F及x轴上一点M构成直角三角形,∴A(0,2),F(,0),设M(t,0),显然t<0,∵|MA|2+|AF|2=|MF|2,∴t2+4+5+4=(﹣t)2,解得t=﹣,∴M(﹣,0),证明(3)由B(﹣3,0),BQ∥OP,设直线BQ的方程为x=my﹣3,直线OP的方程为x=my,由,消x可得(4m2+9)y2﹣24my=0,解得y=0,或y=,则x N=﹣3=则N点的坐标为(,),对于直线方程x=my﹣3,令x=0,可得y=∴Q(0,),∴•=(+3,)•(3,)=+=由,解得y p2=,x p2=解得或,∴22=2(x p2+y p2)=2(+)=,∴•=22.【点评】本题考查直线与椭圆的位置关系的综合应用,抛物线方程的求法,向量的运算,考查计算能力,属于中档题.21.给定整数n(n≥4),设集合A={a1,a2,…,a n}.记集合B={a i+a j|a i,a j∈A,1≤i≤j≤n}.(1)若A={﹣3,0,1,2},求集合B;(2)若a1,a2,…a n构成以a1为首项,d(d>0)为公差的等差数列,求证:集合B中的元素个数为2n﹣1;(3)若a1,a2,…,a n构成以3为首项,3为公比的等比数列,求集合B中元素的个数及所有元素之和.【考点】8M:等差数列与等比数列的综合.【专题】35:转化思想;48:分析法;54:等差数列与等比数列.【分析】(1)由新定义和集合的列举法,可得所求集合;(2)运用等差数列为递增数列,以及性质,即可得到所求个数;(3)由等比数列的通项公式和性质,结合新定义计算可得所求结论.【解答】解:(1)A={﹣3,0,1,2},由题意可得集合B={﹣6,﹣3,﹣2,﹣1,0,1,2,3,4};(2)证明:若a1,a2,…a n构成以a1为首项,d(d>0)为公差的等差数列,可得等差数列{a n}为递增数列,由等差数列的性质a m+a n=a p+a q,可得B中的元素个数为n+﹣=2n﹣1;(3)a1,a2,…,a n构成以3为首项,3为公比的等比数列,可得a n=3n,由3n为奇数,即有3m+3n=2•3k,m.n,k为不相等的正整数,则方程无实数解,3m+3n=3l+3k,m.n,k,l为不相等的正整数,则方程无实数解,若a i,a j相等,可得a1,a2,…,a n中取两个相等的,和为n个;若a i,a j不相等,可得a1,a2,…,a n中取两个,和为C=个;B中的元素个数为n+=个;则B中元素的和为2(3+32+…+3n)+(n﹣1)(3+32+…+3n)=(n+1)(3+32+…+3n)=(n+1)•=.【点评】本题考查新定义的理解和运用,考查等差数列和等比数列的通项公式和求和公式的运用,考查运算能力,属于中档题.。
2019年上海市宝山区中考数学一模试卷解析版

2019年上海市宝山区中考数学一模试卷一、选择题(本大题共6小题,共24.0分)1.如图,已知AB∥CD∥EF,BD:DF=1:2,那么下列结论正确的是()A. AC:AE=1:3B. CE:EA=1:3C. CD:EF=1:2D. AB:CD=1:2【答案】A【解析】解:∵AB∥CD∥EF,∴AC:CE=BD:DF=1:2,即CE=2AC,∴AC:CE=1:3,CE:EA=2:3.故选:A.根据平行线分线段成比例定理得到AC:CE=BD:DF=1:2,然后利用比例性质对各选项进行判断.本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.2.下列命题中,正确的是()A. 两个直角三角形一定相似B. 两个矩形一定相似C. 两个等边三角形一定相似D. 两个菱形一定相似【答案】C【解析】解:两个直角三角形不一定相似,两个矩形不一定相似,两个菱形不一定相似,而两个等边三角形一定相似.故选:C.根据相似三角形的判定方法对A、C进行判断;利用反例可对B、D进行判断.本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.3.已知二次函数y=ax2-1的图象经过点(1,-2),那么a的值为()A. a=-2B. a=2C. a=1D. a=-1【答案】D【解析】解:把(1,-2)代入y=ax2-1得a-1=-2,解得a=-1.故选:D.把已知点的坐标代入抛物线解析式可得到a的值.本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.4.如图,直角坐标平面内有一点P(2,4),那么OP与x轴正半轴的夹角α的余切值为()A. 2B.C.D.【答案】B【解析】解:过点P作PA⊥x轴于点A.由于点P(2,4),∴PA=4,OA=2∴cotα==.故选:B.过点P作PA⊥x轴于点A.由P点的坐标得PA、OA的长,根据余切函数的定义得结论.本题考查了点在平面直角坐标系里的意义及解直角三角形.解决本题的关键是构造直角三角形.5.设m,n为实数,那么下列结论中错误的是()A. m(n)=(mn)B. (m+n)=m+nC. m()=m+mD. 若m=,那么=【答案】D【解析】解:A、如果m、n为实数,那么m(n)=(mn),故本选项结论正确;B、如果m、n为实数,那么(m+n)=m+n,故本选项结论正确;C、如果m、n为实数,那么m()=m+m,故本选项结论正确;D、如果m为实数,那么若m=,那么m=0或=,故本选项结论错误.故选:D.根据平面向量的性质,即可判断A、B,C正确,根据向量的计算法则即可得D错误.此题考查了平面向量的性质.题目比较简单,注意向量是有方向性的,掌握平面向量的性质是解此题的关键.6.若⊙A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为()A. 在⊙A内B. 在⊙A上C. 在⊙A外D. 不能确定【答案】A【解析】解:∵圆心A的坐标是(1,2),点P的坐标是(5,2),∴AP==4<5,∴点P在⊙A内,故选:A.先根据两点间的距离公式计算出PA的长,然后比较PA与半径的大小,再根据点与圆的关系的判定方法进行判断.本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.也考查了坐标与图形性质.二、填空题(本大题共12小题,共48.0分)7.抛物线y=x2-1的顶点坐标是______.【答案】(0,-1)【解析】解:抛物线y=x2-1的顶点坐标为(0,-1).故答案是:(0,-1).形如y=ax2+k的顶点坐标为(0,k),据此可以直接求顶点坐标.本题考查了二次函数的性质.二次函数的顶点式方程y=a(x-k)2+h的顶点坐标是(k,h),对称轴方程是x=k.8.将二次函数y=2x2的图象向右平移3个单位,所得图象的对称轴为______.【答案】直线x=3【解析】解:将二次函数y=2x2的图象向右平移3个单位,所得解析式为:y=2(x-3)2,故其图象的对称轴为:直线x=3.故答案为:直线x=3.直接利用二次函数平移规律得出平移后解析式进而得出答案.此题主要考查了二次函数图象与几何变换,正确记忆平移规律是解题关键.9.请写出一个开口向下且过点(0,2)的抛物线解析式:______.【答案】y=-x2+2(答案不唯一)【解析】解:∵开口向下且过点(0,2)的抛物线解析式,∴可以设顶点坐标为(0,2),故解析式为:y=-x2+2(答案不唯一).故答案为:y=-x2+2(答案不唯一).根据二次函数的性质,二次项系数小于0时,函数图象的开口向下,再利用过点(0,2)得出即可.本题考查了二次函数图象的性质,是开放型题目,答案不唯一.10.若2||=3,那么3||=______.【答案】【解析】解:由2||=3得到:||=,故3||=3×=.故答案是:.实数的乘除运算法则同样适用于向量的运算.考查了平面向量的知识,解题时,可以与实数的运算法则联系起来考虑,属于基础题.11.甲、乙两地的实际距离为500千米,甲、乙两地在地图上的距离为10cm,那么图上4.5cm的两地之间的实际距离为______千米.【答案】225【解析】解:∵甲、乙两地的实际距离为500千米,甲、乙两地在地图上的距离为10cm,∴比例尺==,设图上4.5cm的两地之间的实际距离为xcm,则解得x=22500000,∵22500000cm=225km,∴图上4.5cm的两地之间的实际距离为225千米.故答案为:225.依据甲、乙两地的实际距离为500千米,甲、乙两地在地图上的距离为10cm,即可得到比例尺,即可得出图上4.5cm的两地之间的实际距离.本题主要考查了比例线段,解题时注意:比例尺等于图上距离与实际距离的比值.12.如果两个相似三角形的周长的比等于1:4,那么它们的面积的比等于______.【答案】1:16【解析】解:∵两个相似三角形的周长的比等于1:4,∴它们的相似比为1:4,∴它们的面积的比等于1:16.故答案为:1:16.由两个相似三角形的周长的比等于1:4,即可求得它们的相似比,根据相似三角形的面积比等于相似比的平方,即可求得它们的面积的比.此题考查了相似三角形的性质.注意相似三角形的面积比等于相似比的平方,相似三角形的对应高线、角平分线、中线的比等于相似比.13.Rt△ABC中,∠C=90°,AB=2AC,那么sin B=______.【答案】【解析】解:由题意,得sin B==,故答案为:.根据锐角的正弦等于对边比斜边,可得答案.本题考查了锐角三角函数的定义,利用锐角的正弦等于对边比斜边是解题关键.14.直角三角形的重心到直角顶点的距离为4cm,那么该直角三角形的斜边长为______.【答案】12cm【解析】解:由题意得,CG=4,∵点G是△ABC的重心,∴CD=CG=6,CD是△ABC的中线,在Rt△ACB中,∠ACB=90°,CD是△ABC的中线,∴AB=2CD=12(cm),故答案为:12cm.根据三角形的重心的性质求出CD,根据直角三角形的性质计算即可.本题考查的是三角形的重心的概念和性质,直角三角形的性质,掌握三角形的重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.15.如图,四边形ABCD中,AB∥DC,点E在CB延长线上,∠ABD=∠CEA,若3AE=2BD,BE=1,那么DC=______.【解析】解:∵AB∥DC,∴∠ABD=∠BDC,∵∠ABD=∠CEA,∴∠AEB=∠BDC,∴∠EAB=180°-∠AEB-∠ABE,∠CBD=180°-∠ABD-∠ABE,∴∠EAB=∠CBD,∴△AEB∽△BDC,∴=,∵3AE=2BD,BE=1,∴CD=,故答案为:.根据平行线的性质得到∠ABD=∠BDC,推出△AEB∽△BDC,根据相似三角形的性质即可得到结论.本题考查了平行线的性质,相似三角形的判定和性质,证得△AEB∽△BDC是解题的关键.16.⊙O的直径AB=6,C在AB延长线上,BC=2,若⊙C与⊙O有公共点,那么⊙C的半径r的取值范围是______.【答案】2≤r≤8【解析】解:∵⊙O的直径AB=6,C在AB延长线上,BC=2,∴CA=8,∵⊙C与⊙O有公共点,即⊙C与⊙O相切或相交,∴r=2或r=8或2<r<8,即2≤r≤8.故答案为2≤r≤8.利用⊙C与⊙O相切或相交确定r的范围.本题考查了圆与圆的位置关系:两圆的圆心距为d、两圆的半径分别为r、R:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R-r<d<R+r(R≥r);④两圆内切⇔d=R-r(R>r);⑤两圆内含⇔d<R-r(R>r).17.我们将等腰三角形腰长与底边长的差的绝对值称为该三角形的“边长正度值”,若等腰三角形腰长为5,“边长正度值”为3,那么这个等腰三角形底角的余弦值等于______.【答案】或【解析】解:设等腰三角形的底边长为a,|5-a|=3,解得,a=2或a=8,当a=2时,这个等腰三角形底角的余弦值是:,当a=8时,这个等腰三角形底角的余弦值是:,故答案为:或根据题意,可以求得底边的长,然后利用分类讨论的方法和锐角三角函数可以求得相应的角的三角函数值.本题考查解直角三角形、等腰三角形的性质、锐角三角函数,解答本题的关键是明确题意,求出相应的角的三角函数值.18.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=5,点P为AC上一点,将△BCP沿直线BP翻折,点C落在C′处,连接AC′,若AC′∥BC,那么CP的长为______.【答案】【解析】解:过点C'作C'D⊥BC于点D,∵A'C∥BC,∠ACB=90°,∴∠C'AC=∠ACB=90°,且C'D⊥BC,∴四边形C'DCA是矩形,∴CD=AC',C'D=AC=4,∵折叠∴BC'=BC=5,CP=C'P,在Rt△BDC'中,BD==3∴CD=BC-BD=2∴AC'=2,在Rt△AC'P中,C'P2=C'A2+AP2,∴CP2=4+(4-CP)2,∴CP=故答案为:过点C'作C'D⊥BC于点D,通过题意可证四边形C'DCA是矩形,可得CD=AC',C'D=AC=4,根据勾股定理可求BD=3,即CD=AC'=2,根据勾股定理可求CP的长.本题是翻折变换,考查了矩形的判定和性质,折叠的性质,勾股定理,添加恰当辅助线构造全等三角形是本题的关键.三、计算题(本大题共1小题,共10.0分)19.如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.(1)求CF的长;(2)求∠D的正切值.【答案】解:(1)∵∠ACB=90°,∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,∵AD⊥AB,∴∠BAC+∠CAF=90°,∴∠B=∠CAF,∴△ABC∽△FAC,∴=,即=,解得CF=;(2)如图,过点C作CH⊥AB于点H,∵AC=3,BC=4,∴AB=5,则CH==,∴AH==,EH=AE-AH=,∴tan D=tan∠ECH==.【解析】(1)证△ABC∽△FAC,得=,将相关线段的长代入计算可得;(2)作CH⊥AB,先计算AB=5,据此可得CH==,AH==,EH=AE-AH=,依据tan D=tan∠ECH=可得答案.本题主要考查解直角三角形与相似三角形的判定和性质,解题的关键是添加辅助线构造与∠D相等的角,并熟练掌握相似三角形的判定与性质、勾股定理等知识点.四、解答题(本大题共6小题,共68.0分)20.计算:sin30°tan30°+cos60°cot30°.【答案】解:原式=×+×=.【解析】直接利用特殊角的三角函数值把相关数据代入进而得出答案.此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.21.已知:如图,在△ABC中,AB=AC,点E、F在边BC上,∠EAF=∠B.求证:BF•CE=AB2.【答案】证明:∵∠AEC=∠B+∠BAE=∠EAF+∠BAE=∠BAF,又∵AB=AC,∴∠B=∠C,∴△ABF∽△ECA,∴AB:CE=BF:AC,∴BF•EC=AB•AC=AB2.【解析】利用两角对应成比例可得△ABF∽△ECA,对应边成比例可得相应的比例式,整理可得所求的乘积式.此题考查了相似三角形的判定与性质.注意证得△ABF∽△ECA是解此题的关键.22.如图,已知:△ABC中,点D、E分别在AB、AC上,AB=9,AC=6,AD=2,AE=3.(1)求的值;(2)设=,=,求(用含、的式子表示).【答案】解:(1)∵∠AED=∠ABC,∠A=∠A∴△ADE∽△ACB,∴===,即=.(2)=+=-+.【解析】(1)根据已知∠AED=∠ABC,∠A=∠A,进而得出△ADE∽△ACB,由该相似三角形的性质解答;(2)由三角形法则解答即可.考查了平面向量和相似三角形的判定与性质.注意:平面向量是有方向的.23.地铁10号线某站点出口横截面平面图如图所示,电梯AB的两端分别距顶部9.9米和2.4米,在距电梯起点A端6米的P处,用1.5米的测角仪测得电梯终端B处的仰角为14°,求电梯AB的坡度与长度.参考数据:sin14°≈0.24,tan14°≈0.25,cos14°≈0.97.【答案】解:作BC⊥PA交PA的延长线于点C,作QD∥PC交BC于点D,由题意可得,BC=9.9-2.4=7.5米,QP=DC=1.5米,∠BQD=14°,则BD=BC-DC=7.5-1.5=6米,∵tan∠BQD=,∴tan14°=,即0.25=,解得,ED=18,∴AC=ED=18,∵BC=7.5,∴tan∠BAC==,即电梯AB的坡度是5:12,∵BC=7.5,AC=18,∠BCA=90°,∴AB==19.5,即电梯AB的坡度是5:12,长度是19.5米.【解析】根据题意作出合适的辅助线,然后根据锐角三角函数即可求得电梯AB的坡度,然后根据勾股定理即可求得AB的长度.本题考查解直角三角形的应用-仰角俯角问题、坡度坡角问题,解答本题的关键是明确题意,利用锐角三角函数和数形结合的思想解答.24.如图,已知:二次函数y=x2+bx的图象交x轴正半轴于点A,顶点为P,一次函数y=x-3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为.(1)求二次函数的解析式与顶点P坐标;(2)将二次函数图象向下平移m个单位,设平移后抛物线顶点为P′,若S△ABP=S△BCP,求m的值.【答案】解:(1)∵y=x-3,∴x=0时,y=-3,当y=0时,x-3=0,解得x=6,∴点B(6,0),C(0,-3),∵tan∠OCA==,∴OA=2,即A(2,0),将A(2,0)代入y=x2+bx,得4+2b=0,解得b=-2,∴y=x2-2x=(x-1)2-1,则抛物线解析式为y=x2-2x,顶点P的坐标为(1,-1);(2)如图,由平移知点P′坐标为(1,-1-m),设抛物线对称轴与x轴交于点H,与BC交于点M,则M(1,-),S△ABP′=AB•P′H=×4(m+1)=2(m+1),S△BCP′=S△P′MC+S△P′MB=P′M•OB=|-1-m+|×6=3|-m|,∴2(m+1)=3|-m|,解得m=或m=.【解析】(1)先由直线解析式求出点B,C坐标,利用∠OCA正切值求得点A坐标,再利用待定系数法求解可得;(2)由平移知点P′坐标为(1,-1-m),设抛物线对称轴与x轴交于点H,与BC交于点M,知M(1,-),先得出S△ABP′=AB•P′H=2(m+1),S△BCP′=S△P′MC+S△P′MB=P′M•OB=3|-m|,根据S△ABP=S△BCP列出方程求解可得.本题主要考查抛物线与x轴的交点,解题的关键是掌握待定系数法求函数解析式,二次函数的图象与性质及三角函数的应用等知识点.25.如图,已知:梯形ABCD中,∠ABC=90°,∠DAB=45°,AB∥DC,DC=3,AB=5,点P在AB边上,以点A为圆心AP为半径作弧交边DC于点E,射线EP于射线CB 交于点F.(1)若AP=,求DE的长;(2)联结CP,若CP=EP,求AP的长;(3)线段CF上是否存在点G,使得△ADE与△FGE相似?若相似,求FG的值;若不相似,请说明理由.【答案】解:(1)如图1中,过点A,作AH∥BC,交CD的延长线于点H.∵AB∥CD,∴∠ABC+∠C=180°,∵∠ABC=90°,∴∠C=∠ABC=∠H=90°,∴四边形AHCB是矩形,∴DH=CH-CD=2,∵∠HAB=90°,∠DAB=45°,∴∠HAD=∠HDA=45°∴HD=AH=2,AE=AP=,根据勾股定理得,HE==3,则ED=1;(2)连接CP,设AP=x.∵AB∥CD,∴∠EPA=∠CEP,即等腰△APE、等腰△PEC两个底角相等,∴△APE∽△PEC,∴=,即:PE2=AE•CE,而EC=2PB=2(5-x),即:PC2=CE•AP=2(5-x)x,而PC2=PB2+BC2,即:PC2=(5-x)2+22,∴2(5-x)x=(5-x)2+22,解得:x=(不合题意值已舍去),即:AP=;(3)如图3中,在线段CF上取一点G,连接EG.设∠F=α,则∠APE=∠AEP=∠BPF=90°-α,则:∠EAP=180°-2∠APE=2α,∵△ADE∽△FGE,设∠DAE=∠F=α,由∠DAB=45°,可得3α=45°,2α=30°,在Rt△ADH中,AH=DH=2,在Rt△AHE中,∠HEA=∠EAB=2α=30°,∠HAE=60°,∴HE=AH•tan∠HAE=2,EC=HC-HE=5-2,∵△ADE∽△FGE,∴∠ADC=∠EGF=135°,则∠CEG=45°,∴EG=EC=5-2,∴=,即:=,解得:FG=3-1.【解析】(1)如图,过点A,作AH∥BC,交CD的延长线于点H,在Rt△AHE中求出AE,即可求求解;(2)设:AP=x,利用△APE∽△PEC,得出PC2=CE•AP,利用勾股定理得出PC2=PB2+BC2,即可求解;(3)利用△ADE∽△FGE,得到3α=45°,进而求出相应线段的长度,再利相似比=,即可求解.本题属于三角形相似综合题,涉及到解直角三角形、勾股定理等知识点,其中(3)中,利用三角形相似,确定α的大小,是本题的突破点,属于中考压轴题.。
2019上海各区中考数学一模压轴题18题图文解析

例2015年上海市宝山区中考一模第18题如图1,在直角梯形ABCD中,AD//BC,CD=2,AB=BC,AD=1.动点M、N分别在AB边和BC的延长线上运动,且AM=CN,联结AC交MN于点E,MH⊥AC于H,则EH=____ _____.图1动感体验图2例2015年上海市崇明县中考一模第18题如图1,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C 落在点Q处,EQ与BC交于点G,那么△EBG的周长是________.图1 图2动感体验请打开几何画板文件名“14崇明一模18”,可以体验到,FB=FD,△FAE与△EBQ相解得△EBG的周长=12.例2015年上海市奉贤区中考一模第18题在△ABC中,∠C=90°,AC=3,BC=4.在平面内将△ABC绕点B旋转,点A落到点A′,点C落到点C′,若旋转后点C的对应点C′和点A、B正好在同一直线上,那么∠A′AC′的正切值等于________.动感体验请打开几何画板文件名“14奉贤一模18”,拖动点C′绕着点B旋转,可以体验到,点C′可以落在线段AB上(如图1),也可以落在AB的延长线上(如图2).答案3或1.思路如下:3如图1,当点C′落在线段AB上时,AC′=AB-BC′=5-4=1,A′C′=3.如图2,当点C′落在线段AB的延长线上时,AC′=AB+BC′=5+4=9,A′C′=3.图1 图2例 2015年上海市虹口区中考一模第18题如图1,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,联结DE ,点F 为线段DE 上一点,且∠AFE =∠B .若AB =5,AD =8,AE =4,则AF 的长为________.图1动感体验请打开几何画板文件名“14虹口一模18”,可以体验到,在△AEF 中,已知两个角和其中一个角的对边,求AF 的长,AF 是直角三角形AFH 的斜边.在Rt △AFH 中,AH ,sin ∠AFE =sin ∠B =45,所以AF =sin AH B=图2 图3例 2015年上海市黄浦区中考一模第18题如图1,在梯形ABCD 中,AD //BC ,BE ⊥CD ,垂足为E ,联结AE ,∠AEB =∠C ,且2cos 5C ∠=,若AD =1,则AE 的长是______.图1动感体验请打开几何画板文件名“14黄浦一模18”,拖动点A 运动,可以体验到,△ADE 、例2015年上海市嘉定区中考一模第18题如图1,在△ABC中,AB=9,AC=5,AD是∠BAC的平分线,交BC于点D.△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=12∠BAC,那么BD=_______.图1动感体验请打开几何画板文件名“14嘉定一模18”,拖动点C绕点A旋转,可以体验到,AB1与A图2例2015年上海市金山区中考一模第18题如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3.将△ABC绕着点C旋转90°,点A、B的对应点分别为D、E,那么tan∠ADE的值为_________.图1动感体验请打开几何画板文件名“14金山18”,拖动点D绕着点C旋转,可以体验到,旋转90°存在顺时针和逆时针两种情况,因此∠ADE的大小存在两种情况.在Rt△ADH中,DH=DE-EH=5-215=45,所以tan∠ADE=AHDH=7.图2 图3例2015年上海市浦东新区中考一模第18题把一个三角形绕其中一个顶点逆时针旋转并放大或缩小(这个顶点不变),我们把这样的三角形运动称为三角形的T-变换,这个顶点称为T-变换中心,旋转角称为T-变换角,放大或缩小的三角形与原三角形的对应边之比称为T-变换比.已知△ABC在直角坐标平面内,点A(0,-1),B(,C(0, 2),将△ABC进行T-变换,T-变换中心为点A,T-变换角为60°,T-变换比为23,那么经过T-变换后点C所对应的点的坐标为________.图1 图2动感体验请打开几何画板文件名“14浦东新区18”,拖动点B′绕着点A逆时针旋转,可以体验到此时点H与点O重合,所以点C′′的坐标为(,0).图1 图2例2015年上海市普陀区中考数学一模第18题如图1,已知△ABC中,AB=AC,tan B=2,AD⊥BC于D,G是△ABC的重心.将△ABC绕着重心G旋转,得到三角形A′B′C′,并且点B′在直线AD上,联结CC′,那么tan∠CC′B′的值等于________________.图1动感体验打开几何画板文件名“15普陀一模18”,拖动点在B′绕重心G旋转,可以体验到,当B′落在直线AD上时,C、C′、D′三点共线,∠CC ′B′就是Rt△CC′D′的一个锐角(如图2,图3).图2 图3 图4例 2015年上海市徐汇区中考数学一模第18题如图1,△ABC 中,∠ABC =90°,AB =6,BC =8.点M 、N 分别在边AB 、BC 上,沿直线MN 将△ABC 折叠.点B 落在点P 处,如果AP //BC 且AP =4,那么BN =_____.图1动感体验打开几何画板文件名“15徐汇一模18”,可以体验到,△BAP 与△NBM 相似,△MAP图2 图3 图4【方法2】如图4,作NH ⊥AP ,垂足为H ,那么△MAP ∽△PHN .所以MA AP PM PH HN NP==.设BN =PN =n ,那么PH =AH -AP =n -4.所以446MA PM n n ==-.所以+446MA PM n n =-+,即4246AB n =-.所以64246n =-.解得n =132.例 2015年上海市闸北区中考一模第18题如图1,在Rt △ABC 中,∠C =90°,点D 在边AB 上,线段DC 绕点D 逆时针旋转,端点C 恰好落在边AC 上的点E 处.如果AD DB =m ,AE EC=n ,那么m 与n 满足的关系式是m =_______(用含n 的代数式表示m).图1动感体验请打开几何画板文件名“14闸北一模18”,拖动点D 在AB 上运动,观察m 随n 变化的函数图像,可以体验到,m 是n 的一次函数.答案 2n +1.思路如下:如图2,作DH ⊥AC ,垂足为H .由于DC =DE ,所以H 是EC 的中点.已知AE EC =n =1n ,所以122+112n AH n HC+==.因此m =AD DB =2+1AH n HC =. 图2例 2015年上海市长宁区中考一模第18题如图1,正方形ABCD 绕点A 逆时针旋转,得到正方形AB ′C ′D ′.当两正方形重叠部分的面积是原正方形面积的14时,1sin '2B AD =_________.图1当重叠部分的面积等于原正方形面积的14时,DE 的长等于正方形边长的14.设正方形的边长为4,此时DE =1,所以sin ∠EAD .图2。
2019年上海市16区中考数学一模压轴题赏析

2019年上海市16区中考数学一模压轴题赏析作者:马学斌,民进会员,上海市中学数学高级教师,几何画板爱好者,专注中考数学压轴题15年,华东师范大学出版社《挑战中考数学压轴题》的作者,年读者量逾30万。
《中学数学教学参考》、《中小学数学·初中版》、《青少年科技报》中考频道特约撰稿人。
“中考数学压轴题解题策略12讲”累计听众超过一万人。
为“国培计划”初中数学教师班做过压轴题、几何画板讲座多次。
2015年,在华东师范大学出版社的支持下,为师范大学数学系学生送教“几何画板”三场。
2017年、2018年暑假,参与策划、组织了全国新青年数学教师发展(西部)论坛暨青年数学教师中考数学压轴题讲题比赛。
全国青年教师中考数学压轴题讲题比赛已经成为一个品牌活动,成为解题爱好者的狂欢节,数学压轴题的嘉年华,2019年在长春市举办了第三届,2020年将在沈阳市举办第四届。
2018年3、4月份,在华东师范大学出版社的支持下,“中考数学压轴题公益行”行程25天跨越6个省,做压轴题讲课15场。
2019年10月份,马学斌老师又历经20天时间,在沈阳市、长春市、呼和浩特市、长沙市开展了压轴题巡讲之旅。
12019松江区一模压轴题赏析22019黄埔区一模压轴题赏析32019静安区一模压轴题赏析42019徐汇区一模压轴题赏析52019杨浦区一模压轴题赏析62019浦东区一模压轴题赏析72019闵行区一模压轴题赏析82019青浦区一模压轴题赏析92019宝山区一模压轴题赏析102019金山区一模压轴题赏析112019奉贤区一模压轴题赏析。
2019年上海市普陀区中考数学一模试卷及答案(word解析版)

上海市普陀区2019年中考数学一模试卷一.选择题:(本大题共6题,每题4分,满分24分)B2.(4分)(2019•普陀区一模)某一时刻,身髙1.6m的小明在阳光下的影长是0.4m,同一3.(4分)(2019•普陀区一模)若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k4.(4分)(2019•普陀区一模)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()5.(4分)(2019•普陀区一模)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()=;=;==6.(4分)(2019•普陀区一模)已知线段a、b、c,求作第四比例线段x,下列作图正确的..二.填空题:(本大题共12题,每题4分,满分48分)7.(4分)(2019•普陀区一模)如果在比例尺为1:1 000 000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是34千米.÷8.(4分)(2019•普陀区一模)把长为10cm的线段进行黄金分割,那么较长线段长为5﹣5cm.线段分割叫做黄金分割,他们的比值(×﹣原线段的9.(4分)(2019•普陀区一模)如果两个相似三角形的对应角平分线之比为1:4,那么它们的周长之比是1:4.10.(4分)(2019•普陀区一模)如果抛物线y=(k﹣1)x2+4x的开口向下,那么k的取值范围是k<1.11.(4分)(2019•普陀区一模)把抛物线y=x2的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=(x﹣3)2﹣2.12.(4分)(2019•普陀区一模)二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表,则m的值为﹣1.13.(4分)(2019•普陀区一模)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,则BC= 2.14.(4分)(2019•普陀区一模)如图,点D、E、F分别是△ABC三边的中点,那么与相等的向量是和.相等的向量.相等的向量是和.故答案为:和.15.(4分)(2019•普陀区一模)如图,G是△ABC的重心,AG⊥GC,AC=4,则BG的长为4.16.(4分)(2019•普陀区一模)如图,△ABC中,∠C=90°,BC=4cm,tanB=,则△ABC 的面积是12cm2.tanB===tanB==,17.(4分)(2019•普陀区一模)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是210cm.18.(4分)(2019•普陀区一模)如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,那么四边形MABN的面积是.=),即可求得四边形)NC=22,=24﹣=18.三、解答题:(本大题共7题,满分78分)19.(10分)(2019•普陀区一模)计算:.,﹣20.(10分)(2019•普陀区一模)如图,已知两个不平行的向量、.先化简,再求作:(不要求写作法,但要指出图中表示结论的向量).21.(10分)(2019•普陀区一模)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.(1)求证:△ABE∽△DBC;(2)求线段AE的长.22.(10分)(2019•普陀区一模)一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北63.5°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?(参考数据:sin21.3°≈,tan21.3°≈,sin63.5°≈,tan63.5°≈2)CBD=,,,﹣=60=1523.(12分)(2019•普陀区一模)如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.(1)求证:△ABE∽△ECF;(2)找出与△ABH相似的三角形,并证明;(3)若E是BC中点,BC=2AB,AB=2,求EM的长.EM=,即可求得答案.EM=24.(12分)(2019•普陀区一模)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.×=2,)代入,得﹣+时,在POD==不符合题意,舍去,2|2|2)25.(14分)(2019•普陀区一模)将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].(1)如图①,对△ABC作变换[60°,]得△AB′C′,则S△AB′C′:S△ABC=3;直线BC 与直线B′C′所夹的锐角为60度;(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.)(=2=。
2019年上海市松江区高考数学一模试卷及解析〔精品解析版〕

.
6.(4 分)已知双曲线标准方程为 ﹣y2=1,则其焦点到渐近线的距离为
.
7.(5 分)若向量 , 满足( + ) =7,且| |= ,| |=2,则向量 与 夹角为
.
8.(5 分)在△ABC 中,内角 A,B,C 所对应的边分别是 a,b,c,若 c2=(a﹣b)2+6,
C= ,则△ABC 的面积是
.
9.(5 分)若函数 f(x)=
,则 y=f(x)图象上关于原点 O 对称的点
共有
对.
10.(5 分)已知 A、B、C 是单位圆上三个互不相同的点,若| |=| |,则 • 的最小
值是
.
11.(5 分)已知向量 , 是平面 α 内的一组基向量,O 为 α 内的定点,对于 α 内任意
一点 P,当 =x +y 时,则称
其中的真命题是
.(请写出所有真命题的序号)
12.(5 分)已知函数 f(x)的定义域为 R,且 f(x)•f(﹣x)=1 和 f(1+x)•f(1﹣x)=4
对任意的 x∈R 都成立.若当 x∈[0,1],f(x)的值城为[1,2],则当 x∈[﹣100,100]时,
函数 f(x)的值域为
.
二、选择题(本大题满分 20 分)本大题共有 4 题,每题有且只有一个正确答案,选对得 5
2019 年上海市松江区高考数学一模试卷
一、填空题(本大题满分 54 分),本大题共有 12 题,第 1-6 题每个空格填对得 4 分,第 7-12 题每个空格得 5 分,否则一律得零分
1.(4 分)设集合 A={x|x>1},B={x| <0},则 A∩B=
.
2.(4 分)若复数 z 满足(3﹣4i)•z═4+3i,则|z|=
2019-2020年上海各区数学中考一模压轴题分类汇编-25题含详解

专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【知识梳理】【历年真题】1.(2019秋•奉贤区期末)如图,已知平行四边形ABCD中,AD AB=5,tan A=2,点E在射线AD上,过点E作EF⊥AD,垂足为点E,交射线AB于点F,交射线CB于点G,联结CE、CF,设AE=m.(1)当点E在边AD上时,①求△CEF的面积;(用含m的代数式表示)②当S△DCE=4S△BFG时,求AE:ED的值;(2)当点E在边AD的延长线上时,如果△AEF与△CFG相似,求m的值.2.(2019秋•杨浦区期末)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.专题二动点函数背景下的面积问题【知识梳理】【历年真题】1.(2019秋•黄浦区期末)如图,△ABC 是边长为2的等边三角形,点D 与点B 分别位于直线AC 的两侧,且AD =AC ,联结BD 、CD ,BD 交直线AC 于点E .(1)当∠CAD =90°时,求线段AE 的长.(2)过点A 作AH ⊥CD ,垂足为点H ,直线AH 交BD 于点F ,①当∠CAD <120°时,设AE =x ,y =BCE AEFS S ∆∆(其中S △BCE 表示△BCE 的面积,S △AEF 表示△AEF 的面积),求y 关于x 的函数关系式,并写出x 的取值范围;②当BCE AEFS S ∆∆=7时,请直接写出线段AE 的长.2.(2019秋•松江区期末)已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.(1)如图(1),作AE⊥ON,垂足为点E,当m=2时,求线段EF的长度.(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;(3)如图(3),当△AFD与△CDF相似时,求m的值.专题三动点函数背景下的等腰三角形【知识梳理】【历年真题】1.(2019秋•浦东新区期末)在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.(1)如图,当ED=EB时,求AD的长;(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.2.(2019秋•青浦区期末)如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.(1)求证:EQ∥DC;(2)当BP>BQ时,如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)3.(2019秋•闵行区期末)已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.(1)求证:∠DAB=∠DCF;(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.4.(2019秋•崇明区期末)如图,在△ABC中,AB=AC=10,BC=16,点D为BC边上的一个动点(点D不与点B、点C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F.(1)求证:AB•CE=BD•CD;(2)当DF平分∠ADC时,求AE的长;(3)当△AEF是等腰三角形时,求BD的长.5.(2019秋•宝山区期末)如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=k⋅OC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;(3)写出当△ONB为等腰三角形时,旋转角α的度数.专题四动点函数背景下的线段问题【知识梳理】【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=3 5,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;=y,求y关于x的函数关系式(不需要写函数的定义域);(2)当点D在BC的延长线上时,设AG=x,S△DAF(3)如果AG=8,求DE的长.2.(2019秋•静安区期末)已知:如图1,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2=BE•DC,DE:EC=3:1,F是边AC上的一点,DF与AE交于点G.(1)找出图中与△ACD相似的三角形,并说明理由;(2)当DF平分∠ADC时,求DG:DF的值;(3)如图2,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.专题四动点函数背景下四边形【知识梳理】【历年真题】1.(2019秋•长宁、金山区期末)如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.2.(2019秋•嘉定区期末)已知:点P在△ABC内,且满足∠APB=∠APC(如图),∠APB+∠BAC=180°.(1)求证:△PAB∽△PCA;(2)如果∠APB=120°,∠ABC=90°,求PCPB的值;(3)如果∠BAC=45°,且△ABC是等腰三角形,试求tan∠PBC的值.3.(2019秋•徐汇区期末)如图,在△ABC中,AB=AC=5,BC=6,点D是边AB上的动点(点D不与点AB重合),点G在边AB的延长线上,∠CDE=∠A,∠GBE=∠ABC,DE与边BC交于点F.(1)求cos A的值;(2)当∠A=2∠ACD时,求AD的长;(3)点D在边AB上运动的过程中,AD:BE的值是否会发生变化?如果不变化,请求AD:BE的值;如果变化,请说明理由.4.(2019秋•普陀区期末)如图,在梯形ABCD中,AD//BC,∠C=90°,AD=2,BC=5,DC=3,点E在边BC上,tan∠AEC=3,点M是射线DC上一个动点(不与点D、C重合),联结BM交射线AE于点N,设DM=x,AN=y.(1)求BE的长;(2)当动点M在线段DC上时,试求y与x之间的函数解析式,并写出函数的定义域;(3)当动点M运动时,直线BM与直线AE的夹角等于45°,请直接写出这时线段DM的长.专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【历年真题】1.(2019秋•奉贤区期末)如图,已知平行四边形ABCD 中,AD AB =5,tan A =2,点E 在射线AD 上,过点E 作EF ⊥AD ,垂足为点E ,交射线AB 于点F ,交射线CB 于点G ,联结CE 、CF ,设AE =m .(1)当点E 在边AD 上时,①求△CEF 的面积;(用含m 的代数式表示)②当S △DCE =4S △BFG 时,求AE :ED 的值;(2)当点E 在边AD 的延长线上时,如果△AEF 与△CFG 相似,求m 的值.【考点】相似形综合题.【专题】综合题;运算能力;推理能力.【分析】(1)①先根据三角函数表示出EF ,再用勾股定理表示出AF ,再判断出△AEF ∽△BGF ,得出比例式表示出CG ,即可得出结论;②先表示出FG ,再用S △DCE =4S △BFG 建立方程求出m ,即可得出结论;(2)分两种情况:①当△AEF ∽△CGF 时,得出∠AFE =∠CFG ,进而得出BG =12BC =52,FG =BG tan ∠CBFBF =52,进而得出AF =AB +BF =5+52=152,最后判断出△BGF ∽△AEF ,得出比例式建立方程求解即可得出结论;②当△AEF ∽△CGF 时,先判断出∠AFC =90°,进而得出CF =2BF ,再根据勾股定理得,求出BF =1,得出AF =AB +BF =6,同理:BG =,再判断出△BGF ∽△AEF ,得出比例式建立方程求解即可得出结论.【解答】解:(1)①∵EF ⊥AD ,∴∠AEF =90°,在Rt △AEF 中,tan A =2,AE =m ,∴EF =AE tan A =2m ,根据勾股定理得,AF ,∵AB =5,∴BF =5,∵四边形ABCD 是平行四边形,∴BC =AD AD ∥BC ,∴∠G =∠AEF =90°,∴△AEF ∽△BGF ,∴AE AFBG BF =,∴m BG =,∴BG m ,∴CG =BC +BG =m =m ,∴S △CEF =12EF •CG =12•2m •(m )=m ﹣m 2;②由①知,△AEF ∽△BGF ,∴BF FG AF EF =,∴FG =BFAF •EF •2m =2m ),∴EG =EF +FG =2m +2﹣m )=∴S △CDE =12DE •EG =12(m )•5,S △BFG =12BG •FG =12m )•2m ﹣m )2,S △DCE =4S △BFG 时,∴5=4m )2,∴m m =354,∴DE =AD ﹣AE ﹣4=4,∴AE :ED =354:54=3,即:AE :ED 的值为3;(2)∵四边形ABCD 是平行四边形,∴BC =AD ,AD ∥BC ,∵EF ⊥AD ,∴EF ⊥BC ,∴∠AEF =∠CGF =90°,∵△AEF 与△CFG 相似,∴①当△AEF ∽△CGF 时,如图1,∴∠AFE =∠CFG ,∵EF ⊥BC ,∴BG =12BC =52,∵AD ∥BC ,∴∠CBF =∠A ,∵tan A =2,∴tan ∠CBF =2,在Rt △BGF 中,FG =BG tan ∠CBF根据勾股定理得,BF 52,∴AF =AB +BF =5+52=152,∵BC∥AD,∴△BGF∽△AEF,∴BG BFAE AF=,∴,∴m =35 2;②当△AEF∽△CGF时,如图2,∴∠EAF=∠GFC,∵∠EAF+∠AFE=90°,∴∠GFC+∠AFE=90°,∴∠AFC=90°,∵AD∥BC,∴∠CBF=∠A,∴tan∠CBF=tan A=2,在Rt△BFC中,CF=BF•∠CBF=2BF,根据勾股定理得,BF2+CF2=BC2,∴BF2+4BF2)2,∴BF=1,∴AF=AB+BF=6,在Rt△BGF中,同理:BG =5 5,∵AD∥BC,∴△BGF∽△AEF,∴AE AFBG BF=6155=,∴m =655.即:如果△AEF与△CFG相似,m 的值为35 2或.【点评】此题是相似形综合题,主要考查了平行四边形的性质,锐角三角函数,三角形的面积公式,相似三角形的判定和性质,用方程的思想解决问题是解本题的关键.2.(2019秋•杨浦区期末)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ ,直线PQ 与直线BC 交于点E ,如果△QCE 与△BCP 相似,求线段BP 的长.【考点】相似形综合题.【专题】几何综合题;应用意识.【分析】(1)如图1中,作PH ⊥BC 于H .解直角三角形求出BH ,PH ,在Rt △PCH 中,理由勾股定理即可解决问题.(2)如图1中,作PH ⊥BC 于H ,连接PQ ,设PC 交BD 于O .证明△POQ ∽△BOC ,推出∠OPQ =∠OBC =30°=∠PCQ ,推出PQ =CQ =y ,推出PC ,在Rt △PHB 中,BH =12x ,PH =2x ,根据PC 2=PH 2+CH 2,可得结论.(3)分两种情形:①如图2中,若直线QP 交直线BC 于B 点左侧于E .②如图3中,若直线QP 交直线BC 于C 点右侧于E .分别求解即可.【解答】解:(1)如图1中,作PH ⊥BC 于H .∵四边形ABCD 是菱形,∴AB =BC =4,AD ∥BC ,∴∠A +∠ABC =180°,∵∠A =120°,∴∠PBH =60°,∵PB =3,∠PHB =90°,∴BH =PB •cos60°=32,PH =PB •sin60°=332,∴CH =BC ﹣BH =4﹣32=52,∴PC =.(2)如图1中,作PH ⊥BC 于H ,连接PQ ,设PC 交BD 于O .∵四边形ABCD 是菱形,∴∠ABD =∠CBD =30°,∵∠PCQ =30°,∴∠PBO =∠QCO ,∵∠POB=∠QOC,∴△POB∽△QOC,∴PO BOQO CO=,∴PO QOBO CO=,∵∠POQ=∠BOC,∴△POQ∽△BOC,∴∠OPQ=∠OBC=30°=∠PCQ,∴PQ=CQ=y,∴PC y,在Rt△PHB中,BH=12x,PH=32x,∵PC2=PH2+CH2,∴3y2=(2x)2+(4﹣12x)2,∴y=3(0≤x<8).(3)①如图2中,若直线QP交直线BC于B点左侧于E.此时∠CQE=120°,∵∠PBC=60°,∴△PBC中,不存在角与∠CQE相等,此时△QCE与△BCP不可能相似.②如图3中,若直线QP交直线BC于C点右侧于E.则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,∵∠PCB>∠E,∴只可能∠BCP=∠QCE=75°,作CF⊥AB于F,则BF=2,CF=PCF=45°,∴PF=CF=,此时PB=2+2,③如图4中,当点P在AB的延长线上时,∵△QCE 与△BCP 相似,∴∠CQE =∠CBP =120°,∴∠QCE =∠PCB =15°,作CF ⊥AB 于F .∵∠FCB =30°,∴∠FCP =45°,∴BF =12BC =2,CF =PF =23∴PB =3﹣2.综上所述,满足条件的PB 的值为3或232.【点评】本题考查相似形综合题,考查了菱形的性质,解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.专题二动点函数背景下的面积问题【历年真题】1.(2019秋•黄浦区期末)如图,△ABC 是边长为2的等边三角形,点D 与点B 分别位于直线AC 的两侧,且AD =AC ,联结BD 、CD ,BD 交直线AC 于点E .(1)当∠CAD =90°时,求线段AE 的长.(2)过点A 作AH ⊥CD ,垂足为点H ,直线AH 交BD 于点F ,①当∠CAD <120°时,设AE =x ,y =BCE AEFS S ∆∆(其中S △BCE 表示△BCE 的面积,S △AEF 表示△AEF 的面积),求y 关于x 的函数关系式,并写出x 的取值范围;②当BCE AEFS S ∆∆=7时,请直接写出线段AE的长.【考点】三角形综合题.【专题】等腰三角形与直角三角形;应用意识.【分析】(1)过点E 作EG ⊥BC ,垂足为点G .AE =x ,则EC =2﹣x .根据BG =EG 构建方程求出x 即可解决问题.(2)①证明△AEF ∽△BEC ,可得22BCE AEF S BE S AE∆∆=,由此构建关系式即可解决问题.②分两种情形:当∠CAD <120°时,当120°<∠CAD <180°时,分别求解即可解决问题.【解答】解:(1)∵△ABC 是等边三角形,∴AB =BC =AC =2,∠BAC =∠ABC =∠ACB =60°.∵AD =AC ,∴AD =AB ,∴∠ABD =∠ADB ,∵∠ABD +∠ADB +∠BAC +∠CAD =180°,∠CAD =90°,∠ABD =15°,∴∠EBC =45°.过点E 作EG ⊥BC ,垂足为点G.设AE =x ,则EC =2﹣x .在Rt △CGE 中,∠ACB =60°,∴3sin ACB=)2EG EC x =- ∠,1cos ACB=12CG EC x =- ∠,∴BG =2﹣CG =1+12x ,在Rt △BGE 中,∠EBC =45°,∴131)22x x +=-,解得4x =-.所以线段AE的长是4-.(2)①设∠ABD =α,则∠BDA =α,∠DAC =∠BAD ﹣∠BAC =120°﹣2α.∵AD =AC ,AH ⊥CD ,∴1CAF=DAC=60-2α ∠∠,又∵∠AEF =60°+α,∴∠AFE =60°,∴∠AFE =∠ACB ,又∵∠AEF =∠BEC ,∴△AEF ∽△BEC ,∴22BCE AEF S BE S AE∆∆=,由(1)得在Rt △CGE 中,BG =1+12x,EG )2x =-,∴BE 2=BG 2+EG 2=x 2﹣2x +4,∴2224x x y x-+=(0<x <2).②当∠CAD <120°时,y =7,则有7=2224x x x-+,整理得3x 2+x ﹣2=0,解得x =23或﹣1(舍弃),2AE=3.当120°<∠CAD <180°时,同法可得22+24x x y x +=当y=7时,7=22+24x xx,整理得3x2﹣x﹣2=0,解得x=﹣23(舍弃)或1,∴AE=1.【点评】本题属于三角形综合题,考查了等边三角形的性质,解直角三角形,相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考常考题型.2.(2019秋•松江区期末)已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.(1)如图(1),作AE⊥ON,垂足为点E,当m=2时,求线段EF的长度.(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;(3)如图(3),当△AFD与△CDF相似时,求m的值.【考点】相似形综合题.【专题】分类讨论;图形的相似;推理能力.【分析】(1)如图1,延长FC交OM于点G,证∠BCG=∠MON,在Rt△AOE中,设OE=a,可求得OA,OG,OF的长,则EF=OF﹣OE=65 5;(2)如图2,延长FC交OM于点G,由(1)得CG=5,推出CO=CG=5,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;(3)需分情况讨论:当D在∠MON内部时,△FDA∽△FDC时,此时CD=AD=2,m=2;当△FDA∽△CDF 时,延长CD交ON于点Q,过F作FP⊥CQ于P,可利用三角函数求出m的值;当D在∠MON外部时,可利用相似的性质等求出m的值.【解答】解:(1)如图1,延长FC交OM于点G,∵∠BCG+∠CGB=90°,∠MON+∠CGB=90°,∴∠BCG=∠MON,则tan∠BCG=tan∠MON=2,∴BG=2BC=4,CG=,在Rt△AOE中,设OE=a,由tan∠MON=2,可得OA a,则OG+6,OF=OG=a+,∴EF=OF﹣OE=65 5;(2)如图2,延长FC交OM于点G,由(1)得CG=∵CD平分∠FCO,∴∠FCD=∠DCO,∵CD∥OM,∴∠FCD=∠CGO,∠DCO=∠COG,∴∠CGO=∠COG,∴CO=CG=在Rt△COB中,由BC2+BO2=OC2,得22++2)2=(2,解得a1=﹣655(舍去),a2=255,∴OF=a+5=5,cos∠COF=45 OFOC=,∴sin∠COF=3 5;(3)当D在∠MON内部时,①如图3﹣1,△FDA∽△FDC时,此时CD=AD=2,∴m=2;②当△FDA∽△CDF时,如图3﹣2,延长CD交ON于点Q,过F作FP⊥CQ于P,则∠FDC=∠FDA=135°,∴∠FDP=45°,∵PC=FP•tan∠PFC=FP•tan∠MON=2FP=2DP=CD+DP,∴FP=PD=CD=m,∴FD m,∵△FDA∽△CDF,∴FD CD DA FD=,∴FD==,∴m=1;当D在∠MON外部时,∠ADF>90°,∠DFC>90°,∴∠ADF =∠DFC ,∴∠DFI =∠FDI ,ID =IF ,①如图3﹣3,△FDA ∽△DFC 时,此时△FDA ≌△DFC ,∴CF =AD =2,∵∠DAF =∠FCD =∠FHD ,∴A 、O 重合,延长BC 交ON 于R ,∴FR =2CF =4,CR =BR =,∴m =CD =AB =12BR =;②如图3﹣4,△FDA ∽△CFD 时,设CF =(t >0),延长BC 交ON 于R ,过F 作FS ⊥CD 于S ,∵△DFC ≌△FDH ,∴DH =FC ,∴ID =IF =12CF ,∴IS =t ,FS =2t ,CS =4t ,DS )t ,DH =FC =,∵△FDA ∽△CFD ,∴AD DF DF FC=,∴DF 2=AD •FC =2DH =t ,∵DF 2=DS 2+FS 2,∴=4t 2+)2t 2,解得t 1=512-,t 2=0(舍去),∴DH =t =52=AD ,矛盾,综上所述:m =1或m =2,或m =【点评】本题考查了解直角三角形,等腰三角形的性质,相似三角形的判定与性质等,解题关键是注意分类讨论思想的运用.专题三动点函数背景下的等腰三角形【历年真题】1.(2019秋•浦东新区期末)在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.(1)如图,当ED=EB时,求AD的长;(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.【考点】几何变换综合题.【专题】几何综合题;应用意识.【分析】(1)证明∠ACD=∠EDB=∠B,推出tan∠ACD=tan∠B,可得AD ACAC AB=,由此构建方程即可解决问题.(2)如图1中,作EH⊥BD于H.证明△ACD∽△HDE,推出AC ADDH EH=,由此构建关系式即可解决问题.(3)分两种情形:①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N.利用角平分线的性质定理求出BD即可.②如图3﹣2中,当CB′交BA的延长线于K时,同法可得BD.【解答】解:(1)∵ED=EB,∴∠EDB=∠B,∵CD⊥DE,∴∠CDE=∠A=90°,∵∠ACD+∠ADC=90°,∠ADC+∠EDH=90°,∴∠ACD=∠EDB=∠B,∴tan∠ACD=tan∠B,∴AD ACAC AB=,∴334AD=,∴94AD=.(2)如图1中,作EH⊥BD于H.在Rt△ACB中,∵∠A=90°,AC=3,AB=4,∴BC=5,∵BE=y,∴EH=35y,BH=45y,DH=AB﹣AD﹣BH=4﹣x﹣45y,∵∠A=∠DHE=90°,∠ACD=∠EDH,∴△ACD∽△HDE,∴AC AD=DH EH,∴3x=434-x-55y y,∴220594x xyx-=+(0<x<4).(3)①如图3﹣1中,设CB′交AB于K,作AE⊥CK于E,DM⊥CB′于M,DN⊥BC于N∵AC =AB ′=3,AE ⊥CB ′,∴CE ='EB ='12CB =52,∴AE 22225113()22AC CE -=-,由△ACE ∽△KCA ,可得AK =3115,CK =185,∴BK =AB ﹣AK =4﹣3115,∵∠DCK =∠DCB ,DM ⊥CM ,DN ⊥CB ,∴DM =DN ,∴181185215252CDK CDB CK DM S DK CK S DB CB BC DN ∆∆===== ,∴BD =2543BK =10043151143,∴AD =AB ﹣BD =4﹣(10043151143)=7242151143.②如图3﹣2中,当CB ′交BA 的延长线于K 时,同法可得BD =2543BK =10043151143,∴AD =AB ﹣BD =7242﹣151143.【点评】本题属于几何变换综合题,考查了解直角三角形,相似三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.2.(2019秋•青浦区期末)如图,在梯形ABCD 中,AD ∥BC ,BC =BD =10,CD =4,AD=6.点P 是线段BD 上的动点,点E 、Q 分别是线段DA 、BD 上的点,且DE =DQ =BP ,联结EP 、EQ .(1)求证:EQ ∥DC ;(2)当BP >BQ 时,如果△EPQ 是以EQ 为腰的等腰三角形,求线段BP 的长;(3)当BP =m (0<m <5)时,求∠PEQ 的正切值.(用含m 的式子表示)【考点】相似形综合题.【专题】综合题;运算能力;推理能力.【分析】(1)先利用两边对应成比例,夹角相等,判断出△DEQ ∽△BCD ,得出∠DQE =∠BDC ,即可得出结论;(2)先用△DEQ ∽△BCD ,得出比例式表示出EQ ,再分两种情况,建立方程求解,即可得出结论;(3)先判得出△PHQ ∽△BGD ,得出PH PQ HQ BG BD GD ==,进而表示出HQ =1025m -,PH =26(102)5m -,即可得出结论.【解答】解:(1)∵AD ∥BC ,∴∠EDQ =∠DBC ,∵DE =DQ ,BD =BC ,∴1DE DQ =,BD BC =1,∴DE BD DQ BC=,∴△DEQ ∽△BCD ,∴∠DQE =∠BDC ,∴EQ ∥CD ;(2)设BP =x ,则DQ =x ,QP =2x ﹣10,∵△DEQ∽△BCD,∴EQ QDDC BC=,∴410EQ x=,∴EQ=25x,∵△EPQ是以EQ为腰的等腰三角形,∴Ⅰ、当EQ=EP时,∴∠EQP=∠EPQ,∵DE=DQ,∴∠EQP=∠QED,∴∠EPQ=∠QED,∴△EQP∽△DEQ,∴,∴EQ2=DE•QP,∴(25x)2=(2x﹣10)•x,解得,x=0(舍)或x=12523<6,即:BP=12523,Ⅱ、当QE=QP时,25x=2x﹣10,解得,x=254>6,此种情况不存在,即:BP=125 23;(3)如图,过点P作PH⊥EQ,交EQ的延长线于点H,过点B作BG⊥DC,垂足为点G,∵BD=BC,BG⊥DC,∴DG=2,BG=,∵BP=DQ=m,∴PQ=10﹣2m,∵EQ∥DC,∴∠PQH=∠BDG,∵∠PHQ=∠BGD=90°,∴△PHQ∽△BGD,∴PH PQ HQBG BD GD==102102m HQ-==,∴HQ=1025m-,PH=2)5m-,∴EH=102255m m-+=2,∴tan∠PEQ=PHEH=2)5m-12⨯=﹣5m.【点评】此题是相似形综合题,主要考查了相似三角形的判定和性质,平行线的性质,锐角三角函数,用方程的思想解决问题是解本题的关键.3.(2019秋•闵行区期末)已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.(1)求证:∠DAB=∠DCF;(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.【考点】相似形综合题.【专题】图形的相似;推理能力.【分析】(1)由点G是Rt△ABC的重心,证明CF⊥AB,即∠AFC=90°,利用外角的性质即可证明结论;(2)过点B作BH⊥CD于点H,先证△CAD≌△BCH,得出BH=CD=2,CH=AD=x,DH=2﹣x,再证△ADE ∽△BHE,利用合比性质即可求出结论;(3)分两种情况讨论,当GC=GD时,如图2﹣1,取AC的中点M,联结MD,可证AD=CH=12CD=1;当CG=CD时,如图2﹣2,可由重心分别求出CF,AC,CD的长,可由勾股定理求出AD的长.【解答】(1)证明:∵点G是Rt△ABC的重心,∴CF是Rt△ABC的中线,又∵在Rt△ABC中,AC=BC,∠ACB=90°,∴CF⊥AB,即∠AFC=90°,∵∠DEF=∠ADE+∠DAE=∠EFC+∠ECF,且∠ADE=∠EFC=90°,∴∠DAB=∠DCF;(2)解:如图1,过点B作BH⊥CD于点H,则∠CBH+∠BCH=90°,又∵∠BCH+∠ACD=90°,∴∠ACD=∠CBH,又∵∠ADC=∠CHB=90°,AC=CB,∴△CAD≌△BCH,∴BH=CD=2,CH=AD=x,DH=2﹣x,∵∠ADC=∠CHB=∠BHD=90°,∴AD∥BH,∴△ADE∽△BHE,∴AD DEBH EH=,∴2x DEEH=,∴22x DE EH DHEH EH++==,∴4-2xEH=x+2,∴2424(02)22x xy CE CH HE x xx x-+==+=+=<≤++;(3)解:当GC=GD时,如图2﹣1,取AC的中点M,联结MD,那么MD=MC,联结MG,MG⊥CD,且直线MG经过点B,那么BH与MG共线,又CH =AD ,那么AD =CH =12CD =1;当CG =CD 时,如图2﹣2,即CG =2,点G 为△ABC 的重心,∴332CF CG ==,∴AB =2CF =6,∴22AC AB ==,∴AD ==;综上所述,AD =1【点评】本题考查了函数,相似三角形的判定与性质,重心的性质等,解题关键是熟练掌握重心的性质.4.(2019秋•崇明区期末)如图,在△ABC 中,AB =AC =10,BC =16,点D 为BC 边上的一个动点(点D 不与点B 、点C 重合).以D 为顶点作∠ADE =∠B ,射线DE 交AC 边于点E ,过点A 作AF ⊥AD 交射线DE 于点F .(1)求证:AB •CE =BD •CD ;(2)当DF 平分∠ADC 时,求AE 的长;(3)当△AEF 是等腰三角形时,求BD 的长.【考点】相似形综合题.【专题】几何综合题;图形的相似;推理能力.【分析】(1)根据等腰三角形的性质得到∠B =∠C ,根据三角形的外角性质得到∠BAD =∠CDE ,得到△BAD ∽△CDE ,根据相似三角形的性质证明结论;(2)证明DF ∥AB ,根据平行线的性质得到AE BD AC BC =,证明△BDA ∽△BAC ,根据相似三角形的性质列式计算,得到答案;(3)分点F 在DE 的延长线上、点F 在线段DE 上两种情况,根据等腰三角形的性质计算即可.【解答】(1)证明:∵AB =AC ,∴∠B =∠C ,∠ADC =∠BAD +∠B ,∠ADE =∠B ,∴∠BAD =∠CDE ,又∠B =∠C ,∴△BAD ∽△CDE ,∴AB BD CD CE=,即AB •CE =BD •CD ;(2)解:∵DF 平分∠ADC ,∴∠ADE =∠CDE ,∵∠CDE =∠BAD ,∴∠ADE =∠BAD ,∴DF ∥AB ,∴AE BD AC BC=,∵∠BAD =∠ADE =∠B ,∴∠BAD =∠C ,又∠B =∠B ,∴△BDA ∽△BAC ,∴BD BA BA BC =,即101016BD =解得,254BD =,∴2541016AE =,解得,AE =12532;(3)解:作AH ⊥BC 于H ,∵AB =AC ,AH ⊥BC ,∴BH =HC =12BC =8,由勾股定理得,AH 22221086AB BH -=-=,∴tan B =AH BH =34,∴tan ∠ADF =AF AD =34,设AF =3x ,则AD =4x ,由勾股定理得,DF 22AD AF +=5x ,∵△BAD ∽△CDE ,∴AD AB DE CD =,当点F在DE的延长线上,FA=FE时,DE=5x﹣3x=2x,∴1042xCD x=,解得,CD=5,∴BD=BC﹣CD=11,当EA=EF时,DE=EF=2.5x,∴1042.5xCD x=,解得,CD=254,∴BD=BC﹣CD=39 4;当AE=AF=3x时,DE=75x,∴10475xCD x=,解得,CD=72,∴BD=BC﹣CD=252;当点F在线段DE上时,∠AFE为钝角,∴只有FA=FE=3x,则DE=8x,∴1048x CD x=,解得,CD=20>16,不合题意,∴△AEF是等腰三角形时,BD的长为11或394或252.【点评】本题考查的是相似三角形的判定和性质、等腰三角形的性质,掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.5.(2019秋•宝山区期末)如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=k⋅OC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;(3)写出当△ONB为等腰三角形时,旋转角α的度数.【考点】几何变换综合题.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】(1)通过证明△ODE ∽△OCA ,可得2()DEO OAC S OD S OC∆∆=,即可求解;(2)通过证明△OEM ∽△BAC ,可得∠EOM =∠ABC =36°,分两种情况讨论可求解;(3)分四种情况讨论,由等腰三角形的性质可求解.【解答】解:(1)∵OC 是△ABC 中AB 边的中线,△ABC 的面积为26,∴S △OAC =13,∵DE ∥AC ,∴△ODE ∽△OCA ,∠OEM =∠OAC ,∴2()DEO OAC S OD S OC∆∆=,且OD =k ⋅OC ,∴S △ODE =13k 2,(2)∵△ODE ∽△OCA ,∴OE OD DE k OA OC AC ===,∵OC 是△ABC 中AB 边的中线,点M 是DE 的中点,∴AB =2AO ,EM =12DE ,∴2OE k EM AB AC==,且∠OEM =∠OAC ,∴△OEM ∽△BAC ,∴∠EOM =∠ABC =36°,如图2,当0<α<144°时,∵∠AON =∠B +∠ONB ,∴∠AOE +∠EOM =∠B +∠ONB ∴y =α如图3,当144°<α<180°时,∵∠BON =∠EOM ﹣∠BOE =36°﹣(180°﹣α)∴∠NOB =α﹣144°,∵∠BNO =∠ABC ﹣∠NOB =36°﹣(α﹣144°)=180°﹣α;(3)当0<α<144°时,若OB=ON,则∠ABC=∠BNO=36°=α,若OB=BN,则∠ONB=180362-=72°=α,若ON=BN,则∠ABC=∠BON=36°,∴∠ONB=180°﹣2×36°=108°=α,当144°<α<180°时,若OB=BN,则∠N=∠NOB=18°=180°﹣α,∴α=162°.【点评】本题是几何变换综合题,考查了相似三角形的判定和性质,旋转的性质,等腰三角形的性质等知识,证明△OEM∽△BAC是本题的关键.专题四动点函数背景下的线段问题【历年真题】1.(2019秋•虹口区期末)如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=3 5,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;(2)当点D在BC的延长线上时,设AG=x,S△DAF=y,求y关于x的函数关系式(不需要写函数的定义域);(3)如果AG=8,求DE的长.【考点】三角形综合题.【专题】几何综合题;等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力;应用意识.【分析】(1)求出AC=3,可得∠DAC=∠FBC,则tan∠FBC=tan∠DAC=23 DCAC=;(2)由条件可得∠AGF=∠CBF,可得AF CFAG BC=,可用x表示CF和AF的长,求出CD,则S△DAF=12AF CD,可用x表示结果;(3)分两种情况,①当点D 在BC 的延长线上时,②当点D 在BC 的边上时,可求出AE 长AD 的长,则DE =AD ﹣AE 可求出.【解答】解:(1)∵∠ACB =90°,BC =4,sin ∠ABC =35,∴设AC =3x ,AB =5x ,∴(3x )2+16=(5x )2,∴x =1,即AC =3,∵BE ⊥AD ,∴∠AEF =90°,∵∠AFE =∠CFB ,∴∠DAC =∠FBC ,∴tan ∠FBC =tan ∠DAC =23DC AC =;(2)∵AG ∥BD ,∴∠AGF =∠CBF ,∴tan ∠AGF =tan ∠CBF ,∴AF CF AG BC =,AG AF BC CF =,∴34x CF CF-=,∴124CF x =+.∴12334AF CF x =-=-+=34x x+.∵∠EAF =∠CBF ,∴CD CF AC BC =,∴94CD x =+,∴S △DAF =12AF CD =2193272442(4)x x x x x ⨯⨯=+++;(3)①当点D 在BC 的延长线上时,如图1,∵AG =8,BC =4,AG ∥BD ,∴21AG AF BC CF ==,∴AF =2CF ,∵AC =3,∴AF =2,CF =1,∴CF 1tan AGE=tan CBF==BC 4∠∠,∴AE 1=GE 4,设AE =x ,GE =4x ,∴x 2+16x 2=82,解得x =,即AE .同理tan ∠DAC =tan ∠CBF ,∴DC 1=AC 4,∴DC =34,∴AD∴DE AD AE=-=②当点D在BC的边上时,如图2,∵AG∥BD,AG=8,BC=4,∴8241AG AFBC CF===.∴AF=6,∵∠EAF=∠CBF=∠ABC,∴cos∠EAF=cos∠ABC,∴654AE=,∴245AE=,同理AC BCAD AB=,∴345AD=,∴154AD=.∴DE=AE﹣AD=241521 5420-=.综合以上可得DE的长为191768或2120.【点评】本题是三角形综合题,考查了勾股定理,平行线的性质,三角形的面积,锐角三角函数等知识,熟练掌握锐角三角函数的定义是解题的关键.2.(2019秋•静安区期末)已知:如图1,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2=BE•DC,DE:EC=3:1,F是边AC上的一点,DF与AE交于点G.(1)找出图中与△ACD相似的三角形,并说明理由;(2)当DF平分∠ADC时,求DG:DF的值;(3)如图2,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.【考点】相似三角形的判定与性质;等腰三角形的判定与性质.【专题】等腰三角形与直角三角形;图形的相似;推理能力.【分析】(1)根据相似三角形的判定定理进行判定即可;(2)由相似三角形的性质即可得出答案;(3)由等腰直角三角形的性质、相似三角形的判定与性质即可得出答案.【解答】解:(1)与△ACD 相似的三角形有:△ABE 、△ADE ,理由如下:∵AB 2=BE •DC ,∴BE AB AB DC=,∵AB =AC ,∴∠B =∠C ,BE AC AB DC =,∴△ABE ∽△DCA .∵△ABE ∽△DCA ,∴∠AED =∠DAC .∵∠AED =∠C +∠EAC ,∠DAC =∠DAE +∠EAC ,∴∠DAE =∠C .∴△ADE ∽△CDA ;(2)∵△ADE ∽△CDA ,又∵DF 平分∠ADC ,∴DG DE AD DF AD CD==,设CE =a ,则DE =3CE =3a ,CD =4a ,∴34a AD AD a=,解得:AD =23a ,∴23342DG AD a DF CD a ===;(3)∵∠BAC =90°,AB =AC ,∴∠B =∠C =45°,∴∠DAE =∠C =45°∵DG ⊥AE ,∴∠DAG =∠ADF =45°,∴AG =DG =22AD =22×236a ,∴EG 2222(3)(6)3DE DG a a -=-a ,∴AE =AG +EG =(63)a ,∵∠AED =∠DAC ,∴△ADE ∽△DFA ,∴AD AE DF AD=,∴22AD AE ==a ,∴24DG DF +==.【点评】本题考查了相似三角形的判定与性质、等腰直角三角形的性质、勾股定理等知识;熟记相似三角形的判定定理是解题的关键.专题四动点函数背景下四边形【历年真题】1.(2019秋•长宁、金山区期末)如图,已知在Rt △ABC 中,∠C =90°,AC =8,BC =6,点P 、Q 分别在边AC 、射线CB 上,且AP =CQ ,过点P 作PM ⊥AB ,垂足为点M ,联结PQ ,以PM 、PQ 为邻边作平行四边形PQNM ,设AP =x ,平行四边形PQNM 的面积为y .(1)当平行四边形PQNM 为矩形时,求∠PQM 的正切值;(2)当点N 在△ABC 内,求y 关于x 的函数解析式,并写出它的定义域;(3)当过点P 且平行于BC 的直线经过平行四边形PQNM 一边的中点时,直接写出x 的值.【考点】四边形综合题.【专题】几何综合题;应用意识.【分析】(1)当四边形PQMN 是矩形时,PQ ∥AB .根据tan ∠PQM =PM PQ求解即可.(2)如图1中,延长QN 交AB 于K .求出MK ,PM ,根据y =PM •MK 求解即可.(3)分两种情形:①如图3﹣1中,当平分MN 时,D 为MN 的中点,作NE ∥BC 交PQ 于E ,作NH ⊥CB 交CB 的延长线于H ,EG ⊥BC 于G .根据EG =12PC 构建方程求解.②如图3﹣2中,当平分NQ 时,D 是NQ 的中点,作DH ⊥CB 交CB 的延长线于H .根据PC =GH 构建方程求解即可.【解答】解:(1)在Rt △ACB 中,∵∠C =90°,AC =8,BC =6,∴AB ==10,当四边形PQMN是矩形时,PQ∥AB.∴tan∠PQM=PMPQ=3955253PACQ=.(2)如图1中,延长QN交AB于K.由题意BQ=6﹣x,QN=PM=35x,AM=45x,KQ=45BQ=2445x-,BK=35BQ=1835x-,∴MK=AB﹣AM﹣BK=325x-,∵QN<QK,∴35x<2445x-,∴x<247,∴y=PM•MK=296325x x-(0<x<247).(3)①如图3﹣1中,当平分MN时,D为MN的中点,作NE∥BC交PQ于E,作NH⊥CB交CB的延长线于H,EG⊥BC于G.∵PD∥BC,EN∥BC,∴PD∥NE,∵PE∥DN,∴四边形PDNE是平行四边形,∴PE=DN,∵DN=DM,PQ=MN,∴PE=EQ,∵EG∥PC,∴CG=GQ,∴EG=12PC,∵四边形EGHN是矩形,∴NH=EG=35NQ=35PM=925x,PC=8﹣x,∴925x=12•(8﹣x),解得x=20043.②如图3﹣2中,当平分NQ时,D是NQ的中点,作DH⊥CB交CB的延长线于H.∵DH=PC,∴8﹣x=12•925x,解得x=40059,综上所述,满足条件x的值为20043或40059.【点评】本题属于四边形综合题,考查了平行四边形的性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.2.(2019秋•嘉定区期末)已知:点P在△ABC内,且满足∠APB=∠APC(如图),∠APB+∠BAC=180°.(1)求证:△PAB∽△PCA;(2)如果∠APB=120°,∠ABC=90°,求PCPB的值;(3)如果∠BAC=45°,且△ABC是等腰三角形,试求tan∠PBC的值.【考点】相似三角形的判定与性质;解直角三角形;等腰三角形的性质.【专题】图形的相似;应用意识.【分析】(1)根据两角对应相等的两个三角形相似证明即可.(2)证明△PAB∽△PCA,利用相似三角形的性质解决问题即可.(3)分三种情形:AB=AC,AB=BC,AC=BC分别求解即可解决问题.【解答】证明:(1)∵∠ABP +∠BAP +∠APB =180°,∠APB +∠BAC =180°,∴∠ABP +∠BAP +∠APB =∠APB +∠BAC ,即∠ABP +∠BAP +∠APB =∠APB +∠BAP +∠CAP ,∴∠ABP =∠CAP ,又∵∠APB =∠APC ,∴△PAB ∽△PCA .(2)如图1中,∵∠APB +∠BAC =180°,∠APB =120°,∴∠BAC =60°,在△ABC 中,∵∠ABC =90°,∠BAC =60°,∴,又∵△PAB ∽△PCA ,∴12PB PA AB PA PC AC ===,∴14PB PB PA PC PA PC == ,即4PC PB =.(3)∵∠BAC =45°,∠APB +∠BAC =180°,∠APB =∠APC ,∴∠APB =∠APC =135°.∴∠BPC =360°﹣∠APB ﹣∠APC =360°﹣135°﹣135°=90°,∵△PCA ∽△PAB ,∴PA PC AC PB PA AB==,∴163.①如图2中,当△ABC 是等腰三角形,且AB =AC 时,2tan PBC=()=1PC AC PB AB =∠.②如图3中,当△ABC 是等腰三角形,且AB =BC 时,∠ACB =∠BAC =45°,∠ABC =90°,易得2AC AB ,∴2tan PBC=()=2PC AC PB AB=∠.③如图10﹣4,当△ABC 是等腰三角形,且AC =BC 时,∠ABC =∠BAC =45°,∠ACB =90°,易得2=2AC AB ,∴21tan PBC=()=2PC AC PB AB =∠.【点评】本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.3.(2019秋•徐汇区期末)如图,在△ABC 中,AB =AC =5,BC =6,点D 是边AB 上的动点(点D 不与点AB 重合),点G 在边AB 的延长线上,∠CDE =∠A ,∠GBE =∠ABC ,DE 与边BC 交于点F .(1)求cos A 的值;(2)当∠A =2∠ACD 时,求AD 的长;(3)点D 在边AB 上运动的过程中,AD :BE 的值是否会发生变化?如果不变化,请求AD :BE 的值;如果变化,请说明理由.【考点】三角形综合题.。
2019-2021年上海各区数学中考一模压轴题分类汇编18题-定义新图形及其他题型含详解

专题定义新图形及其他题型【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2021秋•浦东新区期末)如图,a ∥b ∥c ,直线a 与直线b c与直线b 之间的距离为,等边△ABC 的三个顶点分别在直线a 、直线b 、直线c 上,则等边三角形的边长是.2.(2021秋•宝山区期末)如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征三角形”.已知y =x 2+bx (b >0)的“特征三角形”是等腰直角三角形,那么b 的值为.3.(2021秋•青浦区期末)如图,一次函数y =ax +b (a <0,b >0)的图象与x 轴,y 轴分别相交于点A ,点B ,将它绕点O 逆时针旋转90°后,与x 轴相交于点C ,我们将图象过点A ,B ,C 的二次函数叫做与这个一次函数关联的二次函数.如果一次函数y =﹣kx +k (k >0)的关联二次函数是y =mx 2+2mx +c (m ≠0),那么这个一次函数的解析式为.4.(2021秋•青浦区期末)若抛物线y 1=ax 2+b 1x+c 1的顶点为A ,抛物线y 2=ax 2+b 1x+c 1的顶点为B ,且满足顶点A 在抛物线y 2上,顶点B 在抛物线y 1上,则称抛物线y 1与抛物线y 2互为“关联抛物线”已知顶点为M 的抛物线y=(x-2)2+3与顶点为N 的抛物线互为“关联抛物线”,直线MN 与x 轴正半轴交于点D ,如果3tan MDO=4∠,那么顶点为N 的抛物线的表达式为5.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC AD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.6.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=.7.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为.8.(2020秋•徐汇区期末)如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=45,ED=5,如果△ECD的面积是6,那么BC的长是.9.(2020秋•金山区期末)已知在Rt△ABC中,∠C=90°,BC=1,AC=2,以点C为直角顶点的Rt△DCE的顶点D在BA的延长线上,DE交CA的延长线于点G,若tan∠CED=12,CE=GE,那么BD的长等于.10.(2020秋•黄浦区期末)已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为.11.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是.12.(2019秋•宝山区期末)如图,点A在直线34y x上,如果把抛物线y=x²沿OA方向平移5个单位,那么平移后的抛物线的表达式为__.专题定义新图形及其他题型【历年真题】1.(2021秋•浦东新区期末)如图,a ∥b ∥c ,直线a 与直线b c与直线b 之间的距离为,等边△ABC 的三个顶点分别在直线a 、直线b 、直线c 上,则等边三角形的边长是【考点】相似三角形的判定与性质;等边三角形的性质.【专题】图形的相似;模型思想.【分析】过点A 作AD ⊥直线b 于D ,将△ABD 绕点A 逆时针旋转60°得到△ACE ,作EG ⊥直线c 于G 交直线a 于F .想办法求出AE ,EC 即可解决问题.【解答】解:如图,过点A 作AD ⊥直线b 于D ,将△ABD 绕点A 逆时针旋转60°得到△ACE ,作EG ⊥直线c 于G 交直线a 于F .则有∠AEC =∠ADB =∠AFE =∠EGC =90°,AE =AD ,∠EAF =∠CEG =30°,∴EF =12AE =2,∴EG =2,CG =3EG =52,CE =2CG =5,∴AC =.∴等边△ABC 的边长为.故答案为:.【点评】本题考查了相似三角形的性质与判定,勾股定理的运用,直角三角形的性质的运用,相似三角形的性质的运用,解答时构造相似三角形是关键.2.(2021秋•宝山区期末)如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征三角形”.已知y =x 2+bx (b >0)的“特征三角形”是等腰直角三角形,那么b 的值为2.【考点】抛物线与x 轴的交点;等腰直角三角形;二次函数的性质;二次函数图象上点的坐标特征.【专题】二次函数图象及其性质;应用意识.【分析】根据抛物线的“特征三角形”是等腰直角三角形建立方程求解即可.【解答】解:设抛物线y =x 2+bx 与x 轴的交点坐标为A ,B ,顶点为D ,∴A (0,0),B (﹣b ,0),D (﹣2b ,﹣24b ),∵抛物线y =x 2+bx 对应的“特征三角形”是等腰直角三角形,∴AB 2=AD 2+BD 2=2AD 2,∴b 2=2(24b +416b ),解得:b =±2,∵b >0,∴b =2,故答案为:2.【点评】本题考查抛物线与x 轴的交点和抛物线的“特征三角形”的特点,关键是利用“特征三角形”是等腰直角三角形建立等量关系.3.(2021秋•青浦区期末)如图,一次函数y =ax +b (a <0,b >0)的图象与x 轴,y 轴分别相交于点A ,点B ,将它绕点O 逆时针旋转90°后,与x 轴相交于点C ,我们将图象过点A ,B ,C 的二次函数叫做与这个一次函数关联的二次函数.如果一次函数y =﹣kx +k (k >0)的关联二次函数是y =mx 2+2mx +c (m ≠0),那么这个一次函数的解析式为y =﹣3x +3.【考点】抛物线与x 轴的交点;坐标与图形变化﹣旋转;一次函数的性质;一次函数图象上点的坐标特征;待定系数法求一次函数解析式;待定系数法求二次函数解析式.【专题】一次函数及其应用;二次函数图象及其性质;平移、旋转与对称;推理能力.【分析】先由直线y =﹣kx +k 求得点A 和点B 的坐标,然后求得点C 的坐标,最后将点A 、B 、C 的坐标分别代入函数y =mx 2+2mx +c 中求得m 、k 、c 的值,即可得到一次函数的解析式.【解答】解:对y =﹣kx +k ,当x =0时,y =k ,当y =0时,x =1,∴A (1,0),B (0,k ),∴C (﹣k ,0),将A 、B 、C 的坐标代入y =mx 2+2mx +c 得,22020m m c c k mk mk c ⎧++=⎪=⎨⎪++=⎩,解得:000m k c =⎧⎪=⎨⎪=⎩或133m k c =-⎧⎪=⎨⎪=⎩或1311m k c ⎧=⎪⎪=-⎨⎪=-⎪⎩,∵m ≠0,k >0,∴m =﹣1,k =3,c =3,∴一次函数的解析式为y =﹣3x +3,故答案为:y =﹣3x +3.【点评】本题考查了一次函数图象上点的坐标特征、二次函数的解析式、旋转的特征,解题的关键是会求点B 经过逆时针旋转90°后的点的坐标.4.(2021秋•青浦区期末)若抛物线y 1=ax 2+b 1x+c 1的顶点为A ,抛物线y 2=ax 2+b 2x+c 2的顶点为B ,且满足顶点A 在抛物线y 2上,顶点B 在抛物线y 1上,则称抛物线y 1与抛物线y 2互为“关联抛物线”已知顶点为M 的抛物线y=(x-2)2+3与顶点为N 的抛物线互为“关联抛物线”,直线MN 与x 轴正半轴交于点D ,如果3tan MDO=4∠,那么顶点为N 的抛物线的表达式为2557(416y x =--+.【考点】待定系数法求二次函数解析式.【专题】二次函数图象及其性质;;推理能力.【分析】设顶点为N 的抛物线顶点坐标N 为(a ,b ),由题意可知34M M N y x x =-,即可求得D 点坐标为(6,0),则有直线MD 解析式为3(6)4y x =--,因为N 点过直线MD ,N 点也过抛物线y=(x-2)2+3,故有()23(6)423b a b a ⎧=--⎪⎨⎪=-+⎩,解得545716a b ⎧=⎪⎪⎨⎪=⎪⎩,故N 点坐标为(54,5716),可设顶点为N 的抛物线的表达式为2557(416y a x =-+,又因为M 点过2557()416y a x =-+,即可解得a=-1,故顶点为N 的抛物线的表达式为2557()416y x =--+.【解答】设顶点为N 的抛物线顶点坐标N 为(a ,b )已知抛物线y=(x-2)2+3的顶点坐标M 为(2,3)∵3tan 4MDO ∠=∴34M M N y x x =-即3324D x =-解得24D x =±∵直线MN 与x 轴正半轴交于点D ∴D 点坐标为(6,0)则直线MD 解析式为3(6)4y x =--N 点在直线MD 3(6)4y x =--上,N 点也在抛物线y=(x-2)2+3故有()23(6)423b a b a ⎧=--⎪⎨⎪=-+⎩化简得2394247b a b a a ⎧=-+⎪⎨⎪=-+⎩联立得2394742a a a --=-+化简得2135042a a -+=解得a=54或a=2(舍)将a=54代入3942b a =-有359157257442161616b =-⨯+=-+=解得545716a b ⎧=⎪⎪⎨⎪=⎪⎩故N 点坐标为(54,5716)则顶点为N 的抛物线的表达式为2557()416y a x =-+将(2,3)代入2557(416y a x =-+有25573(2)416a =-+化简得95731616a =+解得a=-1故顶点为N 的抛物线的表达式为2557(416y x =--+故答案为:2557(416y x =--+.【点评】本题考察了二次函数的图象及其性质,三角函数的应用.理解题意所述“关联抛物线”的特点,即若抛物线y 1=ax 2+b 1x+c 1的顶点为A ,抛物线y 2=ax 2+b 2x+c 2的顶点为B ,且满足顶点A 在抛物线y 2上,顶点B 在抛物线y 1上是解题的关键.5.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD 中,AB =ACAD=CD =32,点E 、点F 分别是边AD ,边BC 上的中点.如果AC 是凸四边形ABCD 的相似对角线,那么EF 的长等于414.【考点】相似图形;三角形中位线定理.【专题】图形的相似;推理能力.【分析】利用相似三角形的性质求出BC 长,再利用等腰三角形的性质和勾股定理计算出EF 的长即可.【解答】解:如图所示:∵AB=AC,AD=CD,△ABC∽△DAC,∴AC2=BC•AD,∵AC AD=32,∴CB=2,∵△ABC∽△DAC,∴∠ACB=∠CAD,∴CB∥AD,∵AB=AC,F为BC中点,∴AF⊥CB,BF=CF=1,∴∠AFC=90°,∵CB∥AD,∴∠FAE=∠AFC=90°,∵AC Rt△AFC中AF==,∵AD=32,E为AD中点,∴AE=34,∴EF414 =.故答案为:41 4.【点评】此题主要考查了相似三角形的性质,以及等腰三角形的性质和勾股定理,关键是掌握相似三角形对应边成比例、对应角相等.6.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=或.【考点】相似图形.【专题】图形的相似;推理能力.【分析】如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.利用相似三角形的性质,构建方程求解即可.【解答】解:如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.过点A作AE⊥BC于E,过点D作DF⊥BC于F,则四边形AEFD是矩形,∴AD=EF,∵AB=CD=2,AD∥BC,∴四边形ABCD是等腰梯形,∴∠ABE=∠DCF=60°,BE=AB•cos60°=1,CF=CD•cos60°=1,∴EF=BC﹣BE﹣CF=6,∴AD=EF=6,DQ=6﹣x,∵△BAQ∽△QDC,∴AB AQ=QD CD,∴x(6﹣x)=4,解得x=3±5,∴AQ=3±5故答案为:5或3-5【点评】本题考查相似三角形的判定和性质,等腰梯形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.7.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为2.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】先求出BD=8,CD=4,再求出MH=4,DH=2,设BE=x,得出CE=12﹣x,CF=3+x,EH=10﹣x,再判断出△EHM∽△ECF,得出比例式,建立方程求解,即可得出结论.【解答】解:如图,∵点D是BC上一点,BC=12,∴BD:CD=2:1,∴BD=8,CD=4,过点M作MH∥AC交CD于H,∴△DHM∽△DCA,∴MH DH=ACDMCD AD=,∴点M是AD的中点,∴AD=2DM,∵AC=8,∴MH DH1=842=,∴MH=4,DH=2,过点M 作MG ∥AB 交BD 于G ,同理得,BG =DG =4,∵AB =10,BC =12,AC =8,∴△ABC 的周长为10+12+8=30,∵过AD 中点M 的直线将△ABC 分成周长相等的两部分,∴CE +CF =15,设BE =x ,则CE =12﹣x ,∴CF =15﹣(12﹣x )=3+x ,EH =CE ﹣CH =CE ﹣(CD ﹣DH )=12﹣x ﹣2=10﹣x ,∵MH ∥AC ,∴△EHM ∽△ECF ,∴MH EH =CF CE ,∴410-=3+12x x x,∴x =2或x =9,当x =9时,CF =12>AC ,点F 不在边AC 上,此种情况不符合题意,即BE =x =2,故答案为:2.【点评】此题主要考查了相似三角形的判定和性质,构造出相似三角形是解本题的关键.8.(2020秋•徐汇区期末)如图,在△ABC 中,∠ABC =120°,AB =12,点D 在边AC 上,点E 在边BC 上,sin ∠ADE =45,ED =5,如果△ECD 的面积是6,那么BC 的长是﹣6.【考点】解直角三角形;三角形的面积.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .解直角三角形求出BH ,CH 即可解决问题.【解答】解:如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .∵∠ABC =120°,∴∠ABH =180°﹣∠ABC =60°,∵AB =12,∠H =90°,∴BH =AB •cos60°=6,AH =AB •sin60°=,∵EF ⊥DF ,DE =5,∴sin ∠ADE =EF DE =45,∴EF =4,∴DF 3==,∵S △CDE =6,∴12•CD •EF =6,∴CD =3,∴CF =CD +DF =6,∵tan C =EF AH CF CH =,∴4636CH=,∴CH =,∴BC =CH ﹣BH =6.故答案为:﹣6.【点评】本题考查解直角三角形,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.9.(2020秋•金山区期末)已知在Rt △ABC 中,∠C =90°,BC =1,AC =2,以点C 为直角顶点的Rt △DCE 的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若tan ∠CED=12,CE =GE ,那么BD 的长等于2+【考点】解直角三角形;勾股定理.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点A 作AH ⊥CE 于H .想办法证明AK =AC ,推出HK =CH ,推出AK =AD =2,即可解决问题.【解答】解:如图,过点A 作AH ⊥CE 于H .∵tan ∠CED =12=tan ∠BAC ,∴∠E =∠BAC ,∵CE =EG ,∴∠CGE =∠ECG ,∵∠BAC +∠GAK =180°,∴∠E +∠GAK =180°,∴∠AGE +∠AKE =180°,∵∠AKE +∠AKC =180°,∴∠AKC =∠CGE ,∴∠AKC =∠ACK ,∴AC =AK =2,∵AH ⊥CK ,∴KH =CH ,∵∠AHE =∠DCK =90°,∴AH ∥CD ,∴KA =AD ,∴DK =2AK =4,AD =AK =2,∵∠ACB =90°,BC =1,AC =2,∴AB =∴BD =AB +AD =,故答案为:【点评】本题考查解直角三角形,勾股定理,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.10.(2020秋·黄浦区期末)已知一个矩形的两邻边长之比为1:2.5.一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为2:1或1:2或1:1.【考点】相似多边形的性质;矩形的性质,四手拉手模型【专题】图形的相似;推理能力.【分析】如图,设AB=a,AD=2.5a,AE=x,则DE=2.5a-x,利用相似多边形的性质,构建方程求解,另外两个矩形全等也符合题意.【解答】解:如图,设AB=a,AD=2.5a,,AE=x,则DE=2.5a-x.∵矩形ABFE∽矩形EDCF∴AE EF=EF DE∴=2.5x aa a x整理得,x2-2.5xa+a2=0,解得x=2a或0.5a,∴矩形ABFE与矩形EDCF相似,相似比为2:1或1:2.当E,F分别是AD,BC的中点时,两个矩形全等,也符合题意,相似比为:1:1故答案为:2:1或1:2或1:1.【点评】本题考查相似多边形的性质,解题的关键是学会利用参数构建方程求解,属干电考常考题型11.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是13318﹣1.【考点】等腰三角形的性质;相似三角形的判定与性质.【专题】等腰三角形与直角三角形;图形的相似;推理能力.【分析】证明△ADE∽△BAE,得出AE2=DE×BE,同理△ADE∽△CDA,得出AD2=DE×CD,得出2294AD CD AE BE ==,设CD =9x ,则BE =4x ,求出AB =AD AE×BE =6x ,作AM ⊥BC 于M ,由等腰三角形的性质得出BM =CM =12BC ,由直角三角形的性质得出AM =12AB =3x ,BM AM =x ,得出BC =2BM =,求出DE =BE +CD ﹣BC =13x ﹣x ,即可得出答案.【解答】解:∵AB =AC ,∴∠C =∠B =30°,∵∠DAE =∠B =30°,∴∠DAE =∠B =∠C ,∵∠AED =∠BEA ,∴△ADE ∽△BAE ,∴AD AE DE ==AB BE AE,∴AE 2=DE ×BE ,同理:△ADE ∽△CDA ,∴AD DE =CD AD ,∴AD 2=DE ×CD ,∴22239()24AD CD AE BE ===,设CD =9x ,则BE =4x ,∵AD AE AB BE =,∴AB =AD AE ×BE =32×4x =6x ,作AM ⊥BC 于M ,如图所示:∵AB =AC ,∴BM =CM =12BC ,∵∠B =30°,∴AM =12AB =3x ,BM AM =,∴BC =2BM =,∴DE =BE +CD ﹣BC =13x ﹣x ,∴13318DE EC ==﹣1;故答案为:13318﹣1.【点评】本题考查了等腰三角形的性质、相似三角形的判定与性质、直角三角形的性质等知识;证明三角形相似是解题的关键.12.(2019秋•宝山区期末)如图,点A 在直线34y x =上,如果把抛物线y=x ²沿OA 方向平移5个单位,那么平移后的抛物线的表达式为_y=(x-4)2+3_.【考点】二次函数图象与几何变换;一次函数图象上点的坐标特征,四二次函数的平移【专题】二次函数图象及其性质;运算能力;推理能力.【分析】过点A作AB丄x轴于B,求出OB、AB,然后写出点A的坐标,再利用顶点式解析式写出即可.【解答】解:如图,过点A作AB丄x轴于B,∵点A在直线34y x上,OA=5,∴OB=4,AB=3,∵点A的坐标为(4,3),∴平移后的抛物线解析式是y=(x-4)2+3故答案为y=(x-4)2+3.【点评】本题考查了二次函数图象与几何变换,平移的规律:左加右减,上加下减,此类题目,利用顶点的变化求解更简便.。
2019年上海市普陀区中考数学一模考试卷含逐题详解

2019年上海市普陀区中考数学一模试卷一、选择题:(本大题共6题,每题4分,满分24分)下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]1.(4分)已知二次函数y=(a﹣1)x2+3的图象有最高点,那么a的取值范围是()A.a>0B.a<0C.a>1D.a<12.(4分)下列二次函数中,如果图象能与y轴交于点A(0,1),那么这个函数是()A.y=3x2B.y=3x2+1C.y=3(x+1)2D.y=3x2﹣x3.(4分)如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,如果添加下列其中之一的条件,不一定能使△ADE与△ABC相似,那么这个条件是()A.∠AED=∠B B.∠ADE=∠C C.=D.=4.(4分)已知、、都是非零向量,如果=2,=﹣2,那么下列说法中,错误的是()A.∥B.||=||C.=0D.与方向相反5.(4分)已知⊙O1和⊙O2,其中⊙O1为大圆,半径为3.如果两圆内切时圆心距等于2,那么两圆外切时圆心距等于()A.1B.4C.5D.86.(4分)如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE经过重心G,在下列四个说法中①=;②=;③=;④=,正确的个数是()A.1个B.2个C.3个D.4个二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)如果=,那么的值是.8.(4分)化简:3()﹣2()=.9.(4分)如果抛物线y=2x2+x+m﹣1经过原点,那么m的值等于.10.(4分)将抛物线y=(x+3)2﹣4先向右平移2个单位,再向上平移3个单位,那么平移后所得新抛物线的表达式是.11.(4分)已知抛物线y=2x2+bx﹣1的对称轴是直线x=1,那么b的值等于.12.(4分)已知△ABC三边的比为2:3:4,与它相似的△A′B′C′最小边的长等于12,那么△A′B′C′最大边的长等于.13.(4分)在Rt△ABC中,∠ACB=90°,AB=3,BC=1,那么∠A的正弦值是.14.(4分)正八边形的中心角为度.15.(4分)如图,在梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,tan∠ABD=,BC=5,那么DC的长等于.16.(4分)如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于.17.(4分)已知二次函数y=ax2+c(a>0)的图象上有纵坐标分别为y1、y2的两点A、B,如果点A、B到对称轴的距离分别等于2、3,那么y1y2(填“<”、“=”或“>”)18.(4分)如图,△ABC中,AB=AC=8,cos B=,点D在边BC上,将△ABD沿直线AD翻折得到△AED,点B的对应点为点E,AE与边BC相交于点F,如果BD=2,那么EF=.三、解答题:(本大题共7题,满分78分)19.(10分)计算:4sin45°+cos230°﹣.20.(10分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E在边BC上,AE与BD相交于点G,AG:GE=3:1.(1)求EC:BC的值;(2)设=,=,那么=,=(用向量、表示)21.(10分)如图,⊙O1和⊙O2相交于A、B两点,O1O2与AB交于点C,O2A的延长线交⊙O1于点D,点E为AD的中点,AE=AC,联结OE.(1)求证:O1E=O1C;(2)如果O1O2=10,O1E=6,求⊙O2的半径长.22.(10分)如图,小山的一个横断面是梯形BCDE,EB∥DC,其中斜坡DE的坡长为13米,坡度i=1:2.4,小山上有一座铁塔AB,在山坡的坡顶E处测得铁塔顶端A的仰角为45°,在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°(点F、D、C在一直线上),求铁塔AB的高度.(参考数值:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)23.(12分)已知:如图,△ADE的顶点E在△ABC的边BC上,DE与AB相交于点F,AE2=AF•AB,∠DAF=∠EAC.(1)求证:△ADE∽△ACB;(2)求证:=.24.(12分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0)和点B,且OB=3OA,与y轴交于点C,此抛物线顶点为点D.(1)求抛物线的表达式及点D的坐标;(2)如果点E是y轴上的一点(点E与点C不重合),当BE⊥DE时,求点E的坐标;(3)如果点F是抛物线上的一点.且∠FBD=135°,求点F的坐标.25.(14分)如图,点O在线段AB上,AO=2OB=2a,∠BOP=60°,点C是射线OP上的一个动点.(1)如图①,当∠ACB=90°,OC=2,求a的值;(2)如图②,当AC=AB时,求OC的长(用含a的代数式表示);(3)在第(2)题的条件下,过点A作AQ∥BC,并使∠QOC=∠B,求AQ:OQ的值.2019年上海市普陀区中考数学一模试卷参考答案与试题解析一、选择题:(本大题共6题,每题4分,满分24分)下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]1.(4分)已知二次函数y=(a﹣1)x2+3的图象有最高点,那么a的取值范围是()A.a>0B.a<0C.a>1D.a<1【分析】根据二次函数的图象与性质即可求出答案.【解答】解:由题意可知:a﹣1<0,∴a<1,故选:D.【点评】本题考查二次函数,解题的关键是熟练运用二次函数的图象与性质,本题属于中等题型.2.(4分)下列二次函数中,如果图象能与y轴交于点A(0,1),那么这个函数是()A.y=3x2B.y=3x2+1C.y=3(x+1)2D.y=3x2﹣x【分析】根据y轴上点的坐标特征,分别计算出x=0时四个函数对应的函数值,然后根据函数值是否为1来判断图象能否与y轴交于点A(0,1).【解答】解:当x=0时,y=3x2=0;当x=0时,y=3x2+1=1;当x=0时,y=3(x+1)2=9;当x=0时,y =3x2﹣x=0,所以抛物线y=3x2+1与y轴交于点(0,1).故选:B.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.3.(4分)如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,如果添加下列其中之一的条件,不一定能使△ADE与△ABC相似,那么这个条件是()A.∠AED=∠B B.∠ADE=∠C C.=D.=【分析】由已知及三角形相似的判定方法,对每个选项分别分析、判断解答出即可.【解答】解:由题意得,∠A=∠A,A、当∠ADE=∠B时,△ADE∽△ABC;故本选项不符合题意;B、当∠ADE=∠C时,△ADE∽△ABC;故本选项不符合题意;C、当=时,△ADE∽△ABC;故本选项不符合题意;D、当=时,不能推断△ADE与△ABC相似;故选项符合题意;故选:D.【点评】本题考查了直角三角形相似的判定:①有两个对应角相等的三角形相;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似.4.(4分)已知、、都是非零向量,如果=2,=﹣2,那么下列说法中,错误的是()A.∥B.||=||C.=0D.与方向相反【分析】根据平面相等向量的定义、共线向量的定义以及向量的模的计算方法解答.【解答】解:A、因为=2,=﹣2,所以∥,且与方向相反,故本选项说法正确;B、因为=2,=﹣2,所以||=||=|2|,故选项说法正确;C、因为=2,=﹣2,所以∥,则•=0,故本选项说法错误;D、因为=2,=﹣2,所以∥,且与方向相反,故本选项说法正确;故选:C.【点评】考查了向量,向量是既有方向又有大小的.5.(4分)已知⊙O1和⊙O2,其中⊙O1为大圆,半径为3.如果两圆内切时圆心距等于2,那么两圆外切时圆心距等于()A.1B.4C.5D.8【分析】根据两圆位置关系是内切,则圆心距=两圆半径之差,以及外切时,r+R=d,分别求出即可.【解答】解:∵两圆相内切,设小圆半径为x,圆心距为2,∴3﹣x=2,∴x=1,∴小圆半径为1,这两圆外切时,圆心距为:1+3=4.故选:B.【点评】此题主要考查了两圆的位置关系,用到的知识点为:两圆内切,圆心距=两圆半径之差,外切时,r+R =d.6.(4分)如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE经过重心G,在下列四个说法中①=;②=;③=;④=,正确的个数是()A.1个B.2个C.3个D.4个【分析】连接AG并延长,交BC于F,依据DE∥BC,且DE经过重心G,即可得到△ADE∽△ABC,且相似比为2:3,依据相似三角形的性质,即可得到正确结论.【解答】解:如图所示,连接AG并延长,交BC于F,∵DE∥BC,且DE经过重心G,∴△ADE∽△ABC,∴===,故①正确;∴=,故③正确;∵DG∥BF,∴==,故②错误;∵△ADE∽△ABC,=,∴=,∴=,故④正确;故选:C.【点评】本题考查相似三角形的判定和性质以及三角形重心的性质的运用,解决问题的关键是知道相似三角形的对应边对应成比例.二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)如果=,那么的值是.【分析】直接根据已知用同一未知数表示出各数,进而得出答案.【解答】解:∵=,∴设x=7a,则y=2a,那么==.故答案为:.【点评】此题主要考查了比例的性质,正确表示出x,y的值是解题关键.8.(4分)化简:3()﹣2()=.【分析】平面向量的运算法则也符合实数的运算法则.【解答】解:3()﹣2()=3+﹣2+2=(3﹣2)+(+2)=.故答案是:.【点评】考查了平面向量,解题的关键是掌握平面向量的计算法则.9.(4分)如果抛物线y=2x2+x+m﹣1经过原点,那么m的值等于1.【分析】把原点坐标代入抛物线解析式即可得到对应m的值.【解答】解:把(0,0)代入y=2x2+x+m﹣1得m﹣1=0,解得m=1,故答案为1.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.10.(4分)将抛物线y=(x+3)2﹣4先向右平移2个单位,再向上平移3个单位,那么平移后所得新抛物线的表达式是(x+1)2﹣1.【分析】根据“左加右减、上加下减”的原则进行解答即可.【解答】解:将抛物线y=(x+3)2﹣4向右平移2个单位所得直线解析式为:y=(x+3﹣2)2﹣4=(x+1)2﹣4;再向上平移3个单位为:y=(x+1)2﹣4+3,即y=(x+1)2﹣1.故答案是:y=(x+1)2﹣1.【点评】此题主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.11.(4分)已知抛物线y=2x2+bx﹣1的对称轴是直线x=1,那么b的值等于﹣4.【分析】由对称轴公式可得到关于b的方程,可求得答案.【解答】解:∵y=2x2+bx﹣1,∴抛物线对称轴为x=﹣=﹣,∴﹣=1,解得b=﹣4,故答案为:﹣4.【点评】本题主要考查二次函数的性质,掌握二次函数的对称轴公式是解题的关键,即y=ax2+bx+c的对称轴为x=﹣.12.(4分)已知△ABC三边的比为2:3:4,与它相似的△A′B′C′最小边的长等于12,那么△A′B′C′最大边的长等于24.【分析】由于△A′B′C′∽△ABC,因此它们各对应边的比都相等,可据此求出△A′B′C′的最大边的长.【解答】解:设△A′B′C′的最大边长是x,根据相似三角形的对应边的比相等,可得:=,解得:x=24,∴△A′B′C′最大边的长等于24.故答案为:24.【点评】本题主要考查了相似三角形的性质:相似三角形的对应边成比例.13.(4分)在Rt△ABC中,∠ACB=90°,AB=3,BC=1,那么∠A的正弦值是.【分析】我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sin A.代入数据直接计算得出答案.【解答】解:∵∠ACB=90°,AB=3,BC=1,∴∠A的正弦值sin A==,故答案为:.【点评】本题考查了锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.14.(4分)正八边形的中心角为45度.【分析】根据中心角是正多边形相邻的两个半径的夹角来解答.【解答】解:正八边形的中心角等于360°÷8=45°;故答案为45.【点评】本题考查了正多边形和圆的知识,解题的关键是牢记中心角的定义及求法.15.(4分)如图,在梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,tan∠ABD=,BC=5,那么DC的长等于2.【分析】根据垂直的定义得到∠ABD=∠C,根据正切的定义得到BD=CD,根据勾股定理计算即可.【解答】解:∵AB⊥BC,∴∠ABD+∠DBC=90°,∵BD⊥DC,∴∠C+∠DBC=90°,∴∠ABD=∠C,∴tan C==,∴BD=CD,由勾股定理得,BD2+CD2=BC2,即(CD)2+CD2=52,解得,CD=2,故答案为:2.【点评】本题考查的是梯形的性质,正切的定义,勾股定理,掌握梯形的性质,正切的定义是解题的关键.16.(4分)如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于15.【分析】由△ABE∽△DCE,推出==,可得=,再证明△BEF∽△BCD,可得==,由此即可解决问题.【解答】解:∵AB∥CD,∴△ABE∽△DCE,∴==,∴=,∵EF∥CD,∴△BEF∽△BCD,∴==,∵EF=6,∴CD=15,故答案为15.【点评】本题考查平行线的性质,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.17.(4分)已知二次函数y=ax2+c(a>0)的图象上有纵坐标分别为y1、y2的两点A、B,如果点A、B到对称轴的距离分别等于2、3,那么y1<y2(填“<”、“=”或“>”)【分析】由于二次函数y=2(x﹣1)2+k的图象的开口向上,然后根据点A和点B离对称轴的远近可判断y1与y2的大小关系.【解答】解:∵二次函数y=ax2+c(a>0),∴抛物线开口向上,∵点A、B到对称轴的距离分别等于2、3,∴y1<y2.故答案为<.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足解析式y=ax2+bx+c(a、b、c为常数,a≠0).18.(4分)如图,△ABC中,AB=AC=8,cos B=,点D在边BC上,将△ABD沿直线AD翻折得到△AED,点B的对应点为点E,AE与边BC相交于点F,如果BD=2,那么EF=.【分析】过A作AH⊥BC于H,依据等腰三角形的性质即可得到BH=6=CH,由折叠可得,BD=DE=2,∠E =∠ABC=∠C,AB=AE=6,依据△AFC∽△DFE,即可得到===,设EF=x,则CF=4x,AF =8﹣x,DF=AF=2﹣x,依据BD+DF+CF=BC,可得x的值,进而得出EF的长.【解答】解:如图所示,过A作AH⊥BC于H,∵AB=AC=8,cos B=,∴BH=6=CH,BC=12,由折叠可得,BD=DE=2,∠E=∠ABC=∠C,AB=AE=6,又∵∠AFC=∠DFE,∴△AFC∽△DFE,∴===,设EF=x,则CF=4x,AF=8﹣x,∴DF=AF=2﹣x,∵BD+DF+CF=BC,∴2+2﹣x+4x=12,解得x=,∴EF=,故答案为:.【点评】本题主要考查了相似三角形的判定与性质,等腰三角形的性质的运用,解决问题的关键是利用相似三角形的对应边成比例,列方程求解.三、解答题:(本大题共7题,满分78分)19.(10分)计算:4sin45°+cos230°﹣.【分析】直接利用特殊角的三角函数值分别代入求出答案.【解答】解:原式=4×+()2﹣=2+﹣2(+)=.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.20.(10分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E在边BC上,AE与BD相交于点G,AG:GE=3:1.(1)求EC:BC的值;(2)设=,=,那么=+,=﹣﹣(用向量、表示)【分析】(1)根据平行四边形的性质,平行线分线段成比例定理即可解决问题;(2)利用三角形法则计算即可;【解答】解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴==3,∴=3,∴EC:BC=2:3.(2)∵=,AC=2AO,∴=2,∵=+=+2,EC=BC,∴=+,∵AD∥BE,∴==,∴BG=BD,∵=+=+=++2=2+2,∴=(2+2)=+,∴=﹣﹣故答案为+,﹣﹣.【点评】本题考查平行四边形的性质,平行线分线段成比例定理,平面向量等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.21.(10分)如图,⊙O1和⊙O2相交于A、B两点,O1O2与AB交于点C,O2A的延长线交⊙O1于点D,点E为AD的中点,AE=AC,联结OE.(1)求证:O1E=O1C;(2)如果O1O2=10,O1E=6,求⊙O2的半径长.【分析】(1)连接O1A,根据垂径定理得到O1E⊥AD,根据相交两圆的性质得到O1C⊥AB,证明Rt△O1EA≌Rt△O1CA,根据全等三角形的性质证明结论;(2)设⊙O2的半径长为r,根据勾股定理列出方程,解方程得到答案.【解答】(1)证明:连接O1A,∵点E为AD的中点,∴O1E⊥AD,∵⊙O1和⊙O2相交于A、B两点,O1O2与AB交于点C,∴O1C⊥AB,在Rt△O1EA和Rt△O1CA中,,∴Rt△O1EA≌Rt△O1CA(HL)∴O1E=O1C;(2)解:设⊙O2的半径长为r,∵O1E=O1C=6,∴O2C=10﹣6=4,在Rt△O1EO2中,O2E==8,则AC=AE=8﹣r,在Rt△ACO2中,O2A2=AC2+O2C2,即r2=(8﹣r)2+42,解得,r=5,即⊙O2的半径长为5.【点评】本题考查的是相交两圆的性质,全等三角形的判定和性质,垂径定理,勾股定理的应用,掌握相交两圆的连心线,垂直平分两圆的公共弦是解题的关键.22.(10分)如图,小山的一个横断面是梯形BCDE,EB∥DC,其中斜坡DE的坡长为13米,坡度i=1:2.4,小山上有一座铁塔AB,在山坡的坡顶E处测得铁塔顶端A的仰角为45°,在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°(点F、D、C在一直线上),求铁塔AB的高度.(参考数值:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)【分析】延长AB交DC于G,过E作EH⊥CD于H,则四边形EHGB是矩形,根据勾股定理得到EH=5,DH =12根据三角函数的定义列方程即可得到结论.【解答】解:延长AB交DC于G,过E作EH⊥CD于H,则四边形EHGB是矩形,∵斜坡DE的坡长为13米,坡度i=1:2.4,∴设EH=5x,DH=12x,∵EH2+DH2=DE2,∴(5x)2+(12x)2=132,∴x=1,∴EH=5,DH=12,∵EB∥DC,∴∠ABE=∠AGH=90°,∵∠AEB=45°,∴AB=BE,∴HG=AB,∴FG=5+12+AB,AG=AB+5,∵∠F=31°,∴tan F=tan31°===0.6,∴AB=13米,答:铁塔AB的高度是13米.【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,解直角三角形的应用﹣坡度坡角问题,矩形的性质,掌握的作出辅助线是解题的关键.23.(12分)已知:如图,△ADE的顶点E在△ABC的边BC上,DE与AB相交于点F,AE2=AF•AB,∠DAF=∠EAC.(1)求证:△ADE∽△ACB;(2)求证:=.【分析】(1)由AE2=AF•AB,推出△AEF∽△ABE,推出∠AEF=∠B,再证明∠DAE=∠BAC,即可解决问题;(2)由△ADE∽△ACB,推出=,∠D=∠C,再证明△ADF∽△ACE,可得=,由此即可解决问题;【解答】证明:(1)∵AE2=AF•AB,∴=,∵∠EAF=∠BAE,∴△AEF∽△ABE,∴∠AEF=∠B,∵∠DAF=∠EAC,∴∠DAE=∠BAC,∴△ADE∽△ACB.(2)∵△ADE∽△ACB,∴=,∠D=∠C,∵∠DAF=∠EAC,∴△ADF∽△ACE,∴=,∴=,∴=.【点评】本题考查相似三角形的判定和性质,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.24.(12分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0)和点B,且OB=3OA,与y轴交于点C,此抛物线顶点为点D.(1)求抛物线的表达式及点D的坐标;(2)如果点E是y轴上的一点(点E与点C不重合),当BE⊥DE时,求点E的坐标;(3)如果点F是抛物线上的一点.且∠FBD=135°,求点F的坐标.【分析】(1)把点A、B的坐标代入二次函数表达式,即可求解;(2)设:OE=m,则EL=4﹣m,OB=3,DL=1,利用∠LED=∠OBE,即可求解;(3)延长BD交y轴于点H,将△BCH围绕点B顺时针旋转135°至△BC′H′的位置,延长BH′交抛物线于点F.确定直线BH′的表达式,即可求解.【解答】解:(1)OB=3OA=3,则点B的坐标为(3,0),点A(﹣1,0),则函数的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),则﹣3a=﹣3,解得:a=1,则抛物线的表达式为:y=x2﹣2x﹣3…①函数对称轴为x=﹣=1,则点D的坐标为(1,﹣4);(2)如图,过点D作DL⊥y轴,交于点L,设:OE=m,则EL=4﹣m,OB=3,DL=1,∵∠LED+∠OEB=90°,∠OEB+∠OBE=90°,∴∠LED=∠OBE,∴tan∠LED=tan∠OBE,即:=,=,解得:m=1或3(舍去x=3),则点E的坐标为(0,﹣1);(3)延长BD交y轴于点H,将△BCH围绕点B,顺时针旋转135°至△BC′H′的位置,延长BH′交抛物线于点F,∵OB=OC=3,∴∠OCB=∠OBC=45°,则∠FBD=135°,BC′⊥x轴,则点C′(3,3),∠H′C′B=∠HCB=180°﹣45°=135°,tan∠ABD===2,OH=OB•tan∠ABD=2×3=6,则:HC=6﹣3=3=H′C′,过点C′作C′G⊥GH′交于点G,在△BGH′中,GC′=H′C′cos45°==GH′,则点H′的坐标为(3﹣,),将点H′、B的坐标代入一次函数表达式y=kx+b得:,解得:,则直线BH′的表达式为:y=﹣3x+9…②,联立①②并解得:x=3或﹣4(x=3舍去),故点F的坐标为(﹣4,21).【点评】本题考查的是二次函数综合运用,涉及到解直角三角形、图形旋转等知识,其中(3)用图形旋转的方法,确定旋转后图形的位置时本题的难点.25.(14分)如图,点O在线段AB上,AO=2OB=2a,∠BOP=60°,点C是射线OP上的一个动点.(1)如图①,当∠ACB=90°,OC=2,求a的值;(2)如图②,当AC=AB时,求OC的长(用含a的代数式表示);(3)在第(2)题的条件下,过点A作AQ∥BC,并使∠QOC=∠B,求AQ:OQ的值.【分析】(1)如图①中,作CH⊥AB于H.证明△ACH∽△CBH,可得=,由此构建方程即可解决问题.(2)如图②中,设OC=x.作CH⊥AB于H,则OH=,CH=x.在Rt△ACH中,根据AC2=AH2+CH2,构建方程即可解决问题.(3)如图②﹣1中,延长QC交CB的延长线于K.利用相似三角形的性质证明=,即可解决问题.【解答】解:(1)如图①中,作CH⊥AB于H.∵CH⊥AB,∴∠AHC=∠BHC=90°,∵∠ACB=90°,∴∠ACH+∠BCH=90°,∵∠ACH+∠A=90°,∴∠BCH=∠A,∴△ACH∽△CBH,∴=,∵OC=2,∠COH=60°,∴∠OCH=30°,∴OH=OC=1,CH=,∴=,整理得:2a2﹣a﹣4=0,解得a=或(舍弃).经检验a=是分式方程的解.∴a=.(2)如图②中,设OC=x.作CH⊥AB于H,则OH=,CH=x.在Rt△ACH中,∵AC2=AH2+CH2,∴(3a)2=(x)2+(2a+x)2,整理得:x2+ax﹣5a2=0,解得x=(﹣1)a或(﹣﹣1)a(舍弃),∴OC=(﹣1)a,(3)如图②﹣1中,延长QC交CB的延长线于K.∵∠AOC=∠∠AOQ+∠QOC=∠ABC+∠OCB,∠QOC=∠ABC,∴∠AOQ=∠KCO,∵AQ∥BK,∴∠Q=∠K,∴△QOA∽△KCO,∴=,∴=,∵∠K=∠K,∠KOB=∠AOQ=∠KCO,∴△KOB∽△KCO,∴=,∴===【点评】本题属于相似形综合题,考查了相似三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.。
上海市2019届初三数学一模提升题汇编第25题(压轴题)(word版含答案)
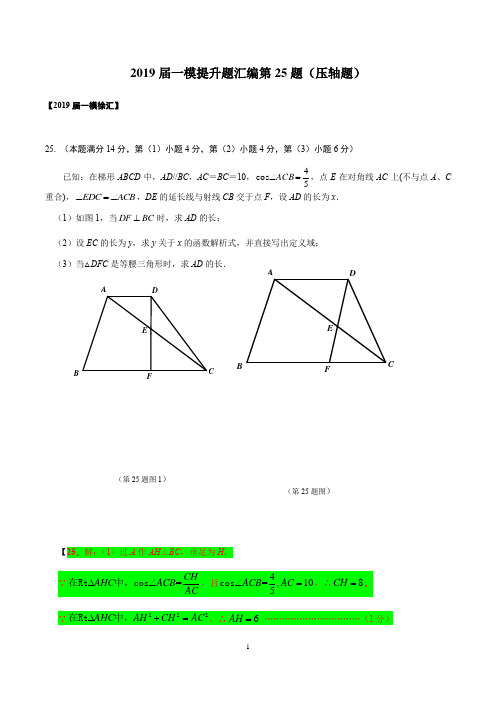
BB2019届一模提升题汇编第25题(压轴题)【2019届一模徐汇】25. (本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD 中,AD //BC ,AC =BC =10,54cos =∠ACB ,点E 在对角线AC 上(不与点A 、C 重合),EDC ACB ∠=∠,DE 的延长线与射线CB 交于点F ,设AD 的长为x . (1)如图1,当DF BC ⊥时,求AD 的长;(2)设EC 的长为y ,求y 关于x 的函数解析式,并直接写出定义域; (3)当△DFC 是等腰三角形时,求AD 的长.【25.解:(1)过A 作AH ⊥BC ,垂足为H ,∵222AHC AH CH AC ∆+=在Rt 中,,∴6AH = ……………………………(1分)(第25题图1)(第25题图)∴90AHF HFD DFH ∠=∠=∠=︒,∴四边形AHFD 是矩形,∴6DF AH ==(2)∵AD ∥BC ,∴DAC ACB ∠=∠. ∵EDC ACB ∠=∠,∴EDC DAC ∠=∠.∵ACD ACD ∠=∠,∴CAD ∽CDE ………………………………………(1分)∵10,AC EC y ==,∴210CD CA CE y =⋅= …………………………………(1分)∵222226(8)DFC CD DF FC x ∆=+=+-在Rt 中,(3)由EDC ACB ∠=∠,EFC EFC ∠=∠得:FCE ∆∽FDC ∆, 又AD ∥BC 有FCE ∆∽DAE ∆,∴DAE ∆∽FDC ∆∴当FDC ∆是等腰三角形时,DAE ∆也是等腰三角形 ………………………(1分) ∴1,DA DE ︒=当时不存在; ………………………………………………………(1分)2,10AD AE x y︒==-当时得:120(),6x x ==解得:舍……………………………………………………………(2分)【2019届一模浦东】25. (本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)将大小两把含30°角的直角三角尺按如图10-1位置摆放,即大小直角三角尺的直角顶点C 重合,小三角尺的顶点D 、E 分别在大三角尺的直角边AC 、BC 上, 此时小三角尺的斜边DE 恰好经过大三角尺的重心G . 已知∠A =∠CDE =30°,AB =12. (1)求小三角尺的直角边CD 的长;(2)将小三角尺绕点C 逆时针旋转,当点D 第一次落在大三角尺的边AB 上时(如图10-2),求点B 、E 之间的距离;(3)在小三角尺绕点C 旋转的过程中,当直线DE 经过点A 时,求∠BAE 的正弦值.(图10-1)(图10-2)DCABBAE【2019届一模杨浦】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)已知:梯形ABCD 中,AD //BC ,AB ⊥BC ,AD =3,AB =6,DF ⊥DC 分别交射线AB 、射线CB 于点E 、F .(1)当点E 为边AB 的中点时(如图1),求BC 的长;(2)当点E 在边AB 上时(如图2),联结CE ,试问:∠DCE 的大小是否确定?若确定,请求出∠DCE 的正切值;若不确定,则设AE =x ,∠DCE 的正切值为y ,请求出y 关于x 的函数解析式,并写出定义域; (3)当△AEF 的面积为3时,求△DCE 的面积.【 25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分) 解:(1)∵AD //BC ,∴DEAE ADEF EB BF.∵E 为AB 中点,∴AE =BE . ∴AD = BF ,DE = EF . ∵AD =3,AB =6,∴BF =3,BE =3. ∴BF =BE .∵AB ⊥BC ,∴∠F =45°且EF =32. ··················· (1分) ∴DF =2EF =62. ···························· (1分) ∵DF ⊥DC ,∠F =45°,∴CF =12. ···················· (1分) ∴BC = 1239CFBF . ······················(1分) A BCD E F(图1)(第25题图)A BCDEF (图2)(2)∠DCE的大小确定,1tan2DCE. ·················(1分)作CH⊥AD交AD的延长线于点H,∴∠HCD+∠HDC=90°.∵DF⊥DC,∴∠ADE+∠HDC=90°. ∴∠HCD=∠ADE.又∵AB⊥AD,∴∠A=∠CHD. ∴△AED∽△HDC. ·············(2分)∴DE ADDC CH. ·····························(1分)∵AB⊥AD,CH⊥AD,AD//BC,∴CH=AB=6.∵AD=3,CH=6,∴12DEDC.即1tan2DCE. ··············(1分)(3)当点E在边AB上,设AE=x,∵AD//BC,∴AD AEBF EB,即36xBF x.∴183xBFx.∵△AEF的面积为3,∴11833 2xxx.∴4x. ·······························(1分)∵AD=3,AB⊥AD,∴DE=5. ∵12DEDC,∴DC=10.∵DF⊥DC,∴1510252DCES. ··················(1分)当点E在边AB延长线上,设AE=y,∵AD//BC,∴AD AEBF EB,即36yBF y.∴318yBFy.∵△AEF的面积为3,∴131832yyy.∴8y. ·············(1分)∵AD=3,AB⊥AD,∴DE=73.联结CE,作CH⊥AD交AD的延长线于点H,同(1)可得12DEDC. ·····(1分)AB CDEF∴DC =273∵DF ⊥DC ,∴173273732DCES.················(1分) 综上,当△AEF 的面积为3时,△DCE 的面积为25或73.】【2019届一模普陀】25.(本题满分14分)如图11,点O 在线段AB 上,22AO OB a ==,60BOP ∠=︒,点C 是射线OP 上的一个动点. (1)如图11①,当90ACB ∠=︒,2OC =,求a 的值;(2)如图11②,当AC =AB 时,求OC 的长(用含a 的代数式表示);(3)在第(2)题的条件下,过点A 作AQ ∥BC ,并使∠QOC=∠B ,求:AQ OQ 的值.【 25.解:ABCPO ABCPO图11①图11②(1)过点C 作CH AB ⊥,H 为垂足. ·················· (1分)∴90CHO CHB ∠=∠=.在Rt △COH 中,60COB ∠=,2OC =.∵22AO OB a ==, ∴21AH a =+,1BH a =-.∵90ACB ∠=,∴90ACH HCB ∠+∠=. ∵CH AB ⊥,∴90ACH A ∠+∠=. ∴A HCB ∠=∠.∵90CHA BHC ∠=∠=︒,∴△ACH ∽△CBH . ······················· (1分)∴2CH AH BH =⋅.(2)过点C 作CH AB ⊥,H 为垂足.设OC m =. 在Rt △COH 中,60COB ∠=,OC m =.在Rt △ACH 中,90CHA ∠=︒, ∴222AC AH CH =+.(3)延长QA 、CO 交于点E .∵AQ //BC ,∴E OCB ∠=∠.∵COA AOQ QOC ∠=∠+∠,COA OCB B ∠=∠+∠,QOC B ∠=∠, ∴AOQ OCB ∠=∠. ∵QOA E ∠=∠.又∵Q Q ∠=∠,∴△QOA ∽△QEO . ················ (1分)【2019届一模奉贤】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =4,26AB CD ==,E 是边BC 上一点,过点D 、E 分别作BC 、CD 的平行线交于点F ,联结AF 并延长,与射线DC 交于点G . (1)当点G 与点C 重合时,求:CE BE 的值;(2)当点G 在边CD 上时,设CE m =,求△DFG 的面积;(用含m 的代数式表示) (3)当AFD ∆∽ADG ∆时,求∠DAG 的余弦值.【25.解:(1)∵CD ∥EF ,DF ∥CE ,∴四边形DFEC 是平行四边形. ····················· (1分) ∴EF =DC . ······························ (1分) ∵26AB CD ==,∴3CD EF ==.∵AB ∥CD ,∴AB ∥EF .∵点G 与点C 重合,∴12EF CE AB BC ==.∴:1CE BE .··········· (2分) (2)过点C 作CQ ∥AG ,交AB 于点Q ,交EF 于点P . 过点C 作CM ⊥AB ,交AB 于点M ,交EF 于点N . 在Rt △BCM 中, 90CMB,4CM AD ==,3BM AB CD =-=,∴5BC =.∵AB ∥EF ∥CD ,∴GC =PF =AQ . ∴EP CEBQ BC=. 图11ABCDFEG备用图ABCD(3)当AFD ∆∽ADG ∆时,∵∠DAB =90°,∴ADG ∆是直角三角形,∴AFD ∆也是直角三角形. ∵90DAF ,90FDA ,∴90DFA. ············(1分) ∵90FADADF,90FDC ADF,∴FAD FDC .∵AB ∥EF ,∴BCEF .∵四边形DFEC 是平行四边形,∴FDC CEF .∴BFDC FAD . ·······················(1分) 在Rt △BCM 中, 90CMB ,3BM AB CD =-=,5BC =,【2019届一模松江】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)如图,已知△ABC 中,∠ACB =90°,D 是边AB 的中点,P 是边AC 上一动点,BP 与CD 相交于点E . (1)如果BC =6,AC =8,且P 为AC 的中点,求线段BE 的长; (2)联结PD ,如果PD ⊥AB ,且CE =2,ED =3,求cosA 的值; (3)联结PD ,如果222BP CD =,且CE =2,ED =3,求线段PD 的长.【25.解:(1)∵P 为AC 的中点,AC =8,∴CP =4……………………………(1分) ∵∠ACB =90°,BC =6,∴BP =213……………………………………………(1分) ∵D 是边AB 的中点,P 为AC 的中点,∴点E 是△ABC 的重心……………(1分) ∴241333BE BP ==…………………………………………………………(1分) (2)过点B 作BF ∥CA 交CD 的延长线于点F ………………………………(1分)(备用图2)ABCD(备用图1)ABCD(第25题图)ABPCDE∴CABFDC FD DA BD ==………………………………(1分) ∵BD =DA ,∴FD =DC ,BF =AC …………………(1分) ∵CE =2,ED =3,则CD =5,∴EF =8 ∴4182===EF CE BF CP …………………………(1分) ∴41=CA CP ,∴13CP PA =,设CP =k ,则P A =3k ,∵PD ⊥AB ,D 是边AB 的中点,∴P A =PB =3k∴k BC 22=,∴k AB 62=,∵k AC 4=,∴6cos 3A =…………(1分)(3)∵∠ACB =90°,D 是边AB 的中点,∴12CD BD AB ==∵222BP CD =,∴22BP CD CD BD AB =⋅=⋅……………(1分) ∵∠PBD =∠ABP ,∴△PBD ∽△ABP …………………………(1分) ∴∠BPD =∠A ……………………………………………………(1分) ∵∠A =∠DCA ,∴∠DPE =∠DCP ,∵∠PDE =∠CDP ,△DPE ∽△DCP ,∴DC DE PD ⋅=2…………………………(1分)∵DE =3,DC =5,∴15=PD …………………………………………………(1分)】【2019届一模嘉定】25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)(备用图2)ABC DPE PE (备用图1)AB C DF在矩形ABCD 中,6=AB ,8=AD ,点E 是边AD 上一点,EC EM ⊥交AB 于点M ,点N 在射线MB 上,且AE 是AM 和AN 的比例中项. (1)如图8,求证:DCE ANE ∠=∠;(2)如图9,当点N 在线段MB 之间,联结AC ,且AC 与NE 互相垂直,求MN 的长; (3)联结AC ,如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似,求DE 的长.【25.(1)证明:∵AE 是AM 和AN 的比例中项∴ANAE AE AM = ……………………1分 ∵A A ∠=∠∴△AME ∽△AEN ∴ANE AEM ∠=∠……………………1分 ∵︒=∠90D ∴︒=∠+∠90DEC DCE ∵EC EM ⊥∴︒=∠+∠90DEC AEM ∴DCE AEM ∠=∠……………………1分 ∴DCE ANE ∠=∠ ………1分A备用图 BDCA备用图BDCA 图8B MEDCNA 备用图BDCM EN A 图9BDCA图8 BM EDC N(2)解:∵AC 与NE 互相垂直∴︒=∠+∠90AEN EAC∵︒=∠90BAC ∴︒=∠+∠90AEN ANE ∴EAC ANE ∠=∠ 由(1)得DCE ANE ∠=∠ ∴EAC DCE ∠=∠ ∴DAC DCE ∠=∠tan tan ∴ADDCDC DE =……………………1分 ∵6==AB DC , 8=AD , ∴29=DE ∴27298=-=AE ……………………1分 由(1)得DCE AEM ∠=∠ ∴DCE AEM ∠=∠tan tan ∴DCDEAE AM =∴821=AM ……………………1分 ∵AN AE AE AM =∴314=AN ……………………1分 ∴2449=MN ……………………1分 (3)∵AEM MAE NME ∠+∠=∠,DCE D AEC ∠+∠=∠ 又︒=∠=∠90D MAE ,由(1)得DCE AEM ∠=∠∴ NME AEC ∠=∠ …………………………1分 当△AEC 与以点E 、M 、N 为顶点所组成的三角形相似时 1)EAC ENM ∠=∠,如图9 ∴EAC ANE ∠=∠由(2)得:29=DE ……………………2分2)ECA ENM ∠=∠,如图10 过点E 作AC EH ⊥,垂足为点H由(1)得DCE ANE ∠=∠ ∴DCE ECA ∠=∠M EN A 图9 BDCA 图10B MEDCNH设x DE 3=,则x HE 3=,x AH 4=,x AE 5= 又AD DE AE =+ ∴835=+x x ,解得1=x∴33==x DE……………………2分 【2019届一模青浦】25.(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)如图,在梯形ABCD 中,AD//BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF =5. AE 的延长线交边BC 于点G , AF 交BD 于点N 、其延长线交BC 的延长线于点H . (1)求证:BG =CH ;(2)设AD =x ,△ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域; (3)联结FG ,当△HFG 与△ADN 相似时,求AD 的长.【25.解:(1)∵AD //BC ,∵DB =DC =15,DE =DF =5,∴BG =CH . ························· (1分)NHG FED C AB(第25题图)(2)过点D作DP⊥BC,过点N作NQ⊥AD,垂足分别为点P、Q.∵DB=DC=15,BC=18,∴BP=CP=9,DP=12.··········(1分)∵AD∥BC,∴∠ADN=∠DBC,∴sin∠ADN=sin∠DBC,(3)∵AD∥BC,∴∠DAN=∠FHG.(i)当∠ADN=∠FGH时,∵∠ADN=∠DBC,∴∠DBC =∠FGH,∴BD∥FG,·························(1分)(ii)当∠ADN=∠GFH时,∵∠ADN=∠DBC=∠DCB,又∵∠AND =∠FGH,∴△ADN∽△FCG.·····················(1分)图11ABCPQM【2019届一模静安】25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图11,在ABC∆中,6AB =,9AC =,tan ABC ∠=B 作BM //AC ,动点P 在射线BM 上(点P 不与点B 重合),联结PA 并延长到点Q ,使AQC ABP ∠=∠. (1)求ABC ∆的面积;(2)设BP x =,AQ y =,求y 关于x 的函数解析式,并写出x 的取值范围; (3)联结PC ,如果PQC ∆是直角三角形,求BP 的长.【 25.解:(1)过点A 作AH ⊥BC ,交BC 于点H . ···············(1分)∴279BC BH HC =+=+=, ··················· (1分) ∴1194218222ABC S BC AH ∆=⋅=⨯⨯=.…………………(1分) (2) 过点A 作AG ⊥BM ,交BM 于点G . ∵AC BC =, ∴CAB CBA ∠=∠ ∵BM //AC , ∴ABP CAB ∠=∠ ∴ABP CBA ∠=∠∴42AG AH ==,即2BG BH ==………(1分) ∴2PG x =- 在Rt AGP ∆中,22222(42)(2)436AP AG PG x x x =+=+-=-+ (1分)∵BAQ BAC CAQ ∠=∠+∠,BAQ ABP APB ∠=∠+∠,∴APB CAQ ∠=∠又AQC ABP ∠=∠ ················· (1分) ∴ABP ∆∽CQA ∆ ∴AP BPAC AQ= ∴24369x x x y-+=, 即29(0)436x y x x x =>-+ ·········· (2分)(3) 由题意得PQ AP AQ =+=22229536436436436x x x x x x x x x ++-++=-+-+由ABP ∆∽CQA ∆得AB APCQ AC= 得 254436CQ x x =-+ ········ (1分)如果PCQ ∆是直角三角形,又90AQC ABP ∠=∠≠,故只有两种可能:……(1分)①90PCQ ∠=,则1cos 3CQ AQC PQ ∠==,即3PQ CQ =, 222536543436436x x x x x x ++=⨯-+-+,解得129,14x x ==-(舍); (2分)②90CPQ ∠=,则1cos 3PQ AQC CQ ∠==,即3CQ PQ =, 第25题ABCPQMGH222536543436436x x x x x x ++⨯=-+-+,该方程无解; (1分)综上所述,如果PCQ ∆是直角三角形,BP 的长为9.】【2019届一模宝山】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图10,已知:梯形ABCD 中,∠ABC =90°,∠A =45°,AB ∥DC ,DC =3,AB =5,点 P 在AB 边上,以点A 为圆心AP 为半径作弧交边DC 于点E ,射线EP 与射线CB 交于点F .(1)若,求DE 的长; (2)联结CP ,若CP=EP ,求AP 的长;(3)线段CF 上是否存在点G ,使得△ADE 与△FGE 相似,若相似,求FG 的值;若不相似,请说明理由.【25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 解:(1)过点A 作AG ⊥CD 交CD 的延长线于点M ……………………… … …1分梯形ABCD 中,∠ABC =90°,∠A =45°∴∠DAM =45°13AP =备用图A BCD PEABCDF(图10)∵AB //CD ,AM =CD 且∠ADM =∠DAM =45°,DM =AM =2……… … …1分 ∴Rt △AEM 中,AE =AP =√13,ME =√AE 2−AG 2=3…………… ……1分 ∴DE =1 ……………………………………………………………… ……1分 (2)过点P 作PH ⊥CD ,垂足是点H∵CP =EP ∴EC =2CH ……………………………………… …… 1分 设AE =AP =x ,PB =5-x ,EC =10-2x , BC =2∴Rt △PBC 中,PE =PC =√PB 2+BC 2=√(5−x )2+22=√x 2−10x +29 …… 1分由题意可知AE =AP ,∴∠AEP =∠APE ,∵CP =EP ,∴∠PEC =∠PCE …… …1分∵AB //CD ∴∠PEC =∠APE ,∴∠PEC =∠APE 且∠PCE =∠AEP ∴△APE ∽△PCE …………………………………………………………1分化简得(3)∵△ADE 是钝角三角形,当点G 在CF 上时,∠GEF 、∠F 必是锐角,∴若△ADE ∽△FGE ,只能∠ADE =∠FGE =135°…………………………… ……1分 ∵Rt △PBF 中,∠F +∠FPB =90° 又∵∠EAP +∠APE +∠AEP =180° ∵∠FPB =∠APE ,∠APE =∠AEP ∴∠EAP =2∠F ∵AB //CD ∴∠DEA =∠EAP ∴∠DEA =2∠F∴必有∠DAE =∠F …………………………………………………………… …… …1分0292032=+-x x∴∠EAP =2∠DAE ∴∠EAP =30°,∠F =∠DAE =15°∴AE =AP =2AM =4,PB =1,EM =,CG =CE =……………… ………1分 ∴EG =∵△ADE ∽△FGE ∴∴FG =………………………………1分 ∴当FG =时,△ADE ∽△FGE .】【2019届一模长宁】25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)已知锐角MBN ∠的余弦值为53,点C 在射线BN 上,25=BC ,点A 在MBN ∠的内部, 且︒=∠90BAC ,MBN BCA ∠=∠.过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E . 点F 在线段BE 上(点F 不与点B 重合),且MBN EAF ∠=∠. (1)如图1,当BN AF ⊥时,求EF 的长;(2)如图2,当点E 在线段BC 上时,设x BF =,y BD =,求y 关于x 的函数解析式并写出函数定义域;(3)联结DF ,当ADF ∆与ACE ∆相似时,请直接写出BD 的长.3232-56225-FGADEG DE =133-133-如图2BF EC ND AMB FC E N ADM如图1备用图BC NAM【25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分) 解:(1)∵在 BAC Rt ∆中 ︒=∠90BAC∵25=BC ∴15=AC (1分)∵BC AF ⊥ ∴︒=∠90AFC∴16=EF (1分)(2)过点A 作EF AH ⊥于点H ∴ ︒=∠90AHB∵x BF =,x FH -=16,x FC -=25∴ 40032)16(122222+-=-+=x x x AF (1分) ∵ BCA MBN ∠=∠,EAF MBN ∠=∠∴BCA EAF ∠=∠ 又∵CFA AFE ∠=∠ ∴AFE ∆∽CFA∆ ∴EF FC AF ⋅=2第25题图∴EF x x x ⋅-=+-)25(400322(1分)∴xx x EF -+-=25400322,xxx x x x BF EF BE --=+-+-=+=25740025400322 (1分)∵ ACB MBN ∠=∠,FAC AEF ∠=∠,∴BDE ∆∽CFA ∆ ∴ACBEFC BD =(1分) ∴1525740025x xx y--=- ∴157400x y -=(2250≤<x ) (1分+1分) (3)596或 1172000(2分+2分)】 【2019届一模金山】25.已知多边形ABCDEF 是⊙O 的内接正六边形,联结AC 、FD ,点H 是射线AF 上的一个动点,联结CH ,直线CH 交射线DF 于点G ,作CH MH ⊥交CD 的延长线于点M ,设⊙O 的半径为()0>r r . (1)求证:四边形ACDF 是矩形.(2)当CH 经过点E 时,⊙M 与⊙O 外切,求⊙M 的半径(用r 的代数式表示).(3)设()900<<=∠ααHCD ,求点C 、M 、H 、F 构成的四边形的面积(用r 及含α的三角比的式子表示).AB CDEFGOHM第25题图第25题备用图ABCD EFO【25.(1)证明:∵多边形ABCDEF 是⊙O 的内接正六边形,∴BCA BAC ∠=∠,∵180=∠+∠+∠ABC BCA BAC ,∴ 30=∠BAC ,得90=∠CAF , (1分)同理 90=∠ACD ,90=∠AFD ,(1分) ∴四边形ACDF 是矩形. (1分)∴OCD ∆为等边三角形,∴r OC CD ==,60=∠OCD , 作CD ON ⊥垂足为N ,即ON 为CD 弦的弦心距,作AC OP ⊥垂足为P ,即OP 为AC 弦的弦心距,当CH 经过点E 时,可知30=∠ECD , ∵四边形ACDF 是矩形,∴CD AF //,∴30=∠=∠ECD AHC ,∵CH MH ⊥,∵⊙M 与⊙O 外切,(3)作CM HQ ⊥垂足为Q ,由α=∠HCD ,CH MH ⊥可得α=∠QHM , ∵CD AF //,CD AC ⊥①当600<<α时,点H 在边AF 的延长线上,此时点C 、M 、H 、F 构成的四边形为梯形,②当60=α时,点H 与点F 重合,此时点C 、M 、H 、F 构成三角形,非四边形,所以舍去. (1分)③当9060<<α时,点H 在边AF 上,此时点C 、M 、H 、F 构成的四边形为梯形,∴()()2tan 3322r HQ CM FH S ⋅+=⋅+=α. (1分)综上所述,当()900<<=∠ααHCD 时,点C 、M 、H 、F 构成的四边形的面积为()23tan 3cot 62r S ⋅-+=αα或()2tan 332r S ⋅+=α.(备注:若求出ααcos sin 3⋅=r CM ,可得当600<<α2cos sin 2323cot 23r S ⋅⎪⎪⎭⎫ ⎝⎛⋅+-=ααα, 当9060<<α时2cos sin 23cot 2323r S ⋅⎪⎪⎭⎫⎝⎛⋅+-=ααα.】【2019届一模闵行】25.(本题满分14分,其中第(1)小题4分、第(2)、(3)小题各5分)如图,在梯形ABCD 中,AD // BC ,AB = CD ,AD = 5,BC = 15,5cos 13ABC ∠=.E 为射线CD 上任意一点,过点A 作AF // BE ,与射线CD 相交于点F .联结BF ,与直线AD 相交于点G .设CE = x ,AGy DG=.(1)求AB 的长;(2)当点G 在线段AD 上时,求y 关于x 的函数解析式,并写出函数的定义域; (3)如果23ABEF ABCDS S =四边形四边形,求线段CE 的长.F【25.解:(1)分别过点A、D作AM⊥BC、DN⊥BC,垂足为点M、N.∵AD // BC,AB = CD,AD = 5,BC = 15,在Rt△ABM中,∠AMB = 90°,∴AB = 13.……………………………………………………………(2分)∵∠AFD=∠BEC,∠ADF=∠C.∴△ADF∽△BCE.ADFSS =9BECS =过点E 作EH ⊥BC ,垂足为点H . 由题意,本题有两种情况:(ⅰ)如果点G 在边AD 上,则 840ABCD ABEF S S S -==四边形四边形.∴ S = 5. ∴ 945BECS S ==.12BECS=∴ 6EH =.由 DN ⊥BC ,EH ⊥BC ,易得 EH // DN .(ⅱ)如果点G 在边DA 的延长线上,则 9ADFABCD ABEF S S SS ++=四边形四边形.∴ 8200S =.解得 25S =. ∴ 9225BECS S ==.12BECS=∴305122CE EH CD DN ===.∴ 652CE =.……………………………(2分) ∴ 136522CE =或.】【2019届一模虹口】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,在四边形ABCD 中,AD ∥BC ,∠A =90°,AB =6,BC =10,点E 为边AD 上一点,将△ABE 沿BE 翻折,点A 落在对角线BD 上的点G 处,联结EG 并延长交射线BC 于点F . (1)如果cos ∠DBC =23,求EF 的长;(2)当点F 在边BC 上时,联结AG ,设AD=x ,ABG BEF S y S ∆∆= ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CG ,如果△FCG 是等腰三角形,求AD 的长.第25题备用图ABC第25题图EABCFDG【25.(1)根据题意得△ABE≌△GBE∴BG=AB=6由△ABE≌△GBE得∠AEB=∠BEG∵AD∥BC∴∠AEB=∠EBF∴∠BEF=∠EBF∴FE=FB=9………………………………………………………………………(2分)(2)∵AD∥BC∴∠ADB=∠GBF又∵∠A=∠BGF=90°∴△ABD∽△GFB∵AD∥BC∠A=90°∴∠ABF=90°∴∠ABG+∠GBF=90°又∵∠GBF+∠EFB =90°∴∠ABG =∠EFB根据题意得AB=BG又∵FE=FB∴△ABG∽△EFB…………………………………………………………………(1分)(3)①点F在BC上∵∠GFC=∠AEG>90°∵△FCG是等腰三角形∴FG=FC设FG=FC=a,则BF=10-atan∠GBF∵∠ADB=∠GBF∴tan∠ADB=②点F在BC的延长线上∵∠GCF>∠DCF >90°∵△FCG是等腰三角形∴CG=CF∵∠ADB=∠GBF∴tan∠ADB= tan∠GBF31。
上海市普陀区2019届高考数学一模试题卷及答案解析

上海市普陀区2019届高考数学一模试题卷一、填空题(本大题共12小题,共60.0分)1.函数f(x)=1−x+2x的定义城为______.2.若sinα=13,则cos(π2+α)=______.3.设α∈{13,12,−1,−2,3},若f(x)=xα为偶函数,则α=______.4.若直线l经过抛物线C:y2=4x的焦点且其一个方向向量为d=(1,1),则直线l的方程为______.5.若一个球的体积是其半径的43倍,则该球的表面积为______.6.在一个袋中装有大小、质地均相同的9只球,其中红色、黑色、白色各3只,若从袋中随机取出两个球,则至少有一个红球的概率为______.(结果用最简分数表示)7.设(x−1)(x+1)5=a0+a1x+a2x2+a3x3+…+a6x6,则a3=______(结果用数值表示)8.设a>0且a≠1,若log a(sinx−cosx)=0,则sin8x+cos8x=______.9.如图,正四棱柱ABCD−A1B1C1D1的底面边长为4,记A1C1∩B1D1=F,BC1∩B1C=E,若AE⊥BF,则此棱柱的体积为______.10.某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的110%.照此推算,此人2019年的年薪为______万元(结果精确到0.1) 11.已知点A(−2,0),设B、C是圆O:x2+y2=1上的两个不同的动点,且向量OB= tOA+(1−t)OC(其中t为实数),则AB⋅AC=______.12.设a为常数记函数f(x)=12+log a xa−x(a>0且a≠1,0<x<a)的反函数为f−1(x),则f−1(12a+1)+f−1(22a+1)+f−1(32a+1)+……+f−1(2a2a+1)=______.二、选择题(本大题共4小题,共20.0分)13.下列关于双曲线Γ:x26−y23=1的判断,正确的是()A.渐近线方程为x±2y=0B.焦点坐标为(±3,0)C.实轴长为12D.顶点坐标为(±6,0)14.函数y=2cos(2x+π4)的图象()A.关于原点对称B.关于点(−3π8,0)C.关于y轴对称 D.关于直线x=π4轴对称15.若a、b、c表示直线,α、β表示平面,则“a//b”成立的一个充分非必要条件是()A.a⊥b,b⊥cB.a//α,b//αC.a⊥β,b⊥βD.a//c,b⊥c16.设f(x)是定义在R上的周期为4的函数,且f(x)=2log2x,1<x<4sin2πx,0≤x≤1,记g(x)=f(x)−a,若0<a≤12则函数g(x)在区间[−4,5]上零点的个数是()A.5B.6C.7D.8三、解答题(本大题共5小题,共70.0分)17.在△ABC中,三个内角A,B,C所对的边依次为a,b,c,且cosC=14.(1)求2cos2A+B2+2sin2C的值;(2)设c=2,求a+b的取值范围.18.已知曲线Γ:x216+y212=1的左、右顶点分别为A,B,设P是曲线Γ上的任意一点.(1)当P异于A,B时,记直线PA,PB的斜率分别为k1,k2,求证:k1⋅k2是定值;(2)设点C满足AC=λCB(λ>0),且|PC|的最大值为7,求λ的值.19.如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为O,钉尖为A i(i=1,2,3,4).(1)设OA1=a(a>0),当A1,A2,A3在同一水平面内时,求OA1与平面A1A2A3所成角的大小(结果用反三角函数值表示).(2)若该“钉”的三个钉尖所确定的三角形的面积为32cm2,要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料多少米?20.设数列{a n}满足a1=35,a n+1=3a n an+2(n∈N∗).(1)求a2,a3的值;(2)求证:{1a n −1}是等比数列,并求n→∞lim(1a1+1a2+…+1a n−n)的值;(3)记{a n}的前n项和为S n,是否存在正整数k,使得对于任意的n(n∈N∗且n≥2)均有S n≥k成立?若存在,求出k的值:若不存在,说明理由.21.已知函数f(x)=2x(x∈R),记g(x)=f(x)−f(−x).(1)解不等式:f(2x)−f(x)≤6;(2)设k为实数,若存在实数x0∈(1,2],使得g(2x0)=k⋅g2(x0)−1成立,求k的取值范围;(3)记h(x)=f(2x+2)+a⋅f(x)+b(其中a,b均为实数),若对于任意的x∈[0,1],均有|h(k)|≤12,求a,b的值.上海市普陀区2019届高考数学一模试卷及解析一、填空题(本大题共12小题,共60.0分)1.函数f(x)=1−x+2x的定义城为______.【答案】(−∞,0)∪(0,1]【解析】解:由x≠01−x≥0解得:x≤1且x≠0,故答案为:(−∞,0)∪(0,1]根据偶次根式中被开方非负,分母不为0列式解得.本题考查了函数的定义域及其求法.属基础题.2.若sinα=13,则cos(π2+α)=______.【答案】−13【解析】解:∵sinα=1,∴cos(π+α)=−sinα=−1.故答案为:−1.由已知直接利用三角函数的诱导公式化简求值.本题考查三角函数的化简求值,考查诱导公式的应用,是基础题.3.设α∈{1,1,−1,−2,3},若f(x)=xα为偶函数,则α=______.【答案】−2【解析】解:f(x)=x−2是偶函数;∴α=−2.故答案为:−2.可以看出,只有α=−2时,f(x)为偶函数,从而得出α=−2.考查偶函数的定义,偶函数图象的特点.4.若直线l经过抛物线C:y2=4x的焦点且其一个方向向量为d=(1,1),则直线l的方程为______.【答案】x−y−1=0【解析】解:抛物线y2=4x的焦点为(1,0),方向向量为d=(1,1)的直线l的斜率为1,故直线l的方程是y−0=1⋅(x−1),即y=x−1,故答案为:x−y−1=0.求出抛物线y2=4x的焦点,求出直线l的斜率,用点斜式求直线方程,并化为一般式.本题考查用点斜式求直线方程的方乘,抛物线的简单性质,确定斜率是解题的关键.5.若一个球的体积是其半径的43倍,则该球的表面积为______.【解析】解:设球的半径为R,则43πR3=43R,∴πR2=1,球的表面积为:4πR2=4,故答案为:4.设球的半径为R,根据题意列方程可得.本题考查了球的体积和表面积,属中档题.6.在一个袋中装有大小、质地均相同的9只球,其中红色、黑色、白色各3只,若从袋中随机取出两个球,则至少有一个红球的概率为______.(结果用最简分数表示)【答案】712【解析】解:在一个袋中装有大小、质地均相同的9只球,其中红色、黑色、白色各3只,从袋中随机取出两个球,基本事件总数n=C92=36,至少有一个红球的对立事件是没有红球,∴至少有一个红球的概率为P=1−C6236=712.故答案为:712.从袋中随机取出两个球,基本事件总数n=C92=36,至少有一个红球的对立事件是没有红球,由此能求出至少有一个红球的概率.本题考查概率的求法,考查对立事件概率计算公式等基础知识,考查运算求解能力,是基础题.7.设(x−1)(x+1)5=a0+a1x+a2x2+a3x3+…+a6x6,则a3=______(结果用数值表示)【答案】0【解析】解:∵(x−1)(x+1)5=(x−1)(x5+5x4+10x3+10x2+5x+1)=a0+a1x+a2x2+ a3x3+…+a6x6,则a3=10−10=0,故答案为:0.把(x+1)5按照二项式定理展开,可得a3的值.本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.8.设a>0且a≠1,若log a(sinx−cosx)=0,则sin8x+cos8x=______.【答案】1【解析】解:设a>0且a≠1,若log a(sinx−cosx)=0,所以:sinx−cosx=a0=1,所以:sinx⋅cosx=0,则:sinx−cosx=1,则:sin8x+cos8x=(sin4x−cos4x)2+2sin4x⋅cos4x,=[(sin2x+cos2x)(sin2x−cos2x)]2+2sin4x⋅cos4x,=[(sinx+cosx)(sinx−cosx)]2−0,=1,故答案为:1.直接利用三角函数关系式的恒等变变换和对数的应用求出结果.本题考查的知识要点:三角函数关系式的恒等变变换的应用,主要考查学生的运算能力和转化能力,属于基础题型.9.如图,正四棱柱ABCD−A1B1C1D1的底面边长为4,记A1C1∩B1D1=F,BC1∩B1C=E,若AE⊥BF,则此棱柱的体积为______.【答案】322【解析】解:建立如图所示空间直角坐标系,设DD1=h,又AB=BC=4,),B(4,4,0),F(2,2,h),则A(4,0,0),E(2,4,h2∴AE =(−2,4,h 2),BF =(−2,−2,h),∵AE ⊥BF ,∴4−8+h 22=0,即h =22.∴此棱柱的体积为4×4×22=322.故答案为:322.建立空间直角坐标系,设出直四棱柱的高h ,求出AE,BF 的坐标,由数量积为0求得h ,则棱柱的体积可求.本题考查棱柱体积的求法,考查利用空间向量求解线线垂直问题,是中档题.10.某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的110%.照此推算,此人2019年的年薪为______万元(结果精确到0.1)【答案】10.4【解析】解:由题意可得,基础工资是以2100元为首项,以210元公差的等差数列,绩效工资以为2000元首项,以公比为1.1的等比数列,则此人2019年每月的基础工资为2100+210(10−1)=3990元,每月的绩效工资为2000×1.19≈4715.90元,则此人2019年的年薪为12(3990+4715.90)≈10.4万元,故答案为:10.4.由题意可得,基础工资是以2100元为首项,以210元公差的等差数列,绩效工资以为2000元首项,以公比为1.1的等比数列,即可求出2019年的每月的工资,即可求出年薪本题考查了等差数列和等比数列在实际生活中的应用,属于中档题.11.已知点A(−2,0),设B 、C 是圆O :x 2+y 2=1上的两个不同的动点,且向量OB =tOA +(1−t)OC(其中t 为实数),则AB ⋅AC =______.【答案】3【解析】解:由向量OB =tOA +(1−t)OC(其中t 为实数),可得:A ,B ,C 三点共线,且AB ,AC 同向,设圆O 与x 轴正半轴交于点E ,由圆的割线定理可得,|AB||AC|=|AO||AE|,∴AB ⋅AC =|AB||AC|cos0=|AB||AC|=|AO||AE|=1×3=3故答案为:3由向量OB =tOA +(1−t)OC(其中t 为实数),可得:A ,B ,C 三点共线,且AB ,AC 同向,设圆O 与x 轴正半轴交于点E ,由割线定理可得,|AB||AC|=|AO||AE|=1×3=3本题考查了向量中三点共线的判断,及圆的割线定理,属中档题12.设a 为常数记函数f(x)=12+log a x a−x (a >0且a ≠1,0<x <a)的反函数为f −1(x),则f −1(12a+1)+f −1(22a+1)+f −1(32a+1)+……+f −1(2a 2a+1)=______.【答案】a 2【解析】解:由f(x)=12+log a x a−x ,得f −1(x)=a x+12a x−12+1,∴f −1(1−x)=a 1−x+12a 1−x−12+1=a 1+a x−12,∴f −1(x)+f −1(1−x)=a x+12a x−12+1+a 1+a x−12=a ,∴原式=a ⋅a =a 2,故答案为:a 2先求出反函数,然后求出f −1(x)+f −1(1−x)=a ,所以等于a 个a .本题考查了反函数,属基础题.二、选择题(本大题共4小题,共20.0分)13.下列关于双曲线Γ:x 26−y 23=1的判断,正确的是()A.渐近线方程为x ±2y =0B.焦点坐标为(±3,0)C.实轴长为12D.顶点坐标为(±6,0)【答案】B【解析】解:关于双曲线Γ:x 26−y 23=1,a 2=6,b 2=3,c 2=9,则渐近线方程为x ±2y =0;焦点为(±3,0);实轴2a =26,顶点坐标为(±6,0).故选:B .关于双曲线Γ:x 26−y 23=1,a 2=6,b 2=3,c 2=9,即可得答案.本题考查双曲线的方程、几何性质,属于基础题.14.函数y =2cos(2x +π4)的图象()A.关于原点对称B.关于点(−3π8,0)C.关于y 轴对称D.关于直线x =π4轴对称【答案】B【解析】解:对于选项:A ,当x =0时y =2,故错误.对于选项C :当x =0时,y =2≠2,故错误.对于选项D :当x =π4时,y =−2≠±2,故错误.故选:B .直接利用余弦函数的性质求出结果.本题考查的知识要点:三角函数关系式的恒等变变换,正弦型函数的性质的应用,主要考查学生的运算能力和转化能力,属于基础题型.15.若a 、b 、c 表示直线,α、β表示平面,则“a//b ”成立的一个充分非必要条件是()A.a ⊥b ,b ⊥cB.a//α,b//αC.a ⊥β,b ⊥βD.a//c ,b ⊥c【答案】C【解析】解:由a 、b 、c 表示直线,α、β表示平面,在A 中,a ⊥b ,b ⊥c ,则a 与b 相交、平行或异面,故A 错误;在B中,a//α,b//α,则a与b相交、平行或异面,故B错误;在C中,a⊥β,b⊥β,则a//b,反之a//b,不一定得到a⊥β,b⊥β,故C正确;在D中,a//c,b⊥c,则a与b相交或异面,故D错误.故选:C.在A中,a与b相交、平行或异面;在B中,a与b相交、平行或异面;在C中,a⊥β,b⊥β,则a//b,反之a//b,不一定得到a⊥β,b⊥β;在D中,a与b相交或异面.本题考查命题成立的一个充分非必要条件的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是基础题.16.设f(x)是定义在R上的周期为4的函数,且f(x)=2log2x,1<x<4sin2πx,0≤x≤1,记g(x)=f(x)−a,若0<a≤12则函数g(x)在区间[−4,5]上零点的个数是()A.5B.6C.7D.8【答案】D【解析】解:由图可知:直线y=a(0<a≤12)与y=f(x)在区间[−4,5]上的交点有8个,故选:D.分别作出y=f(x)与直线y=a(1<a≤12)的图象,观察交点个数即可本题考查了数形结合的思想及作图能力.三、解答题(本大题共5小题,共70.0分)17.在△ABC中,三个内角A,B,C所对的边依次为a,b,c,且cosC=14.(1)求2cos2A+B2+2sin2C的值;(2)设c=2,求a+b的取值范围.【答案】解:(1)∵cosC=14,∴sinC=1−cos2C=154,∴2cos2A+B2+2sin2C=1+cos(A+B)+2sin2C=1−cosC+4sinCcosC=1−1+4×1×15 4=3+154.…(6分)(2)∵c=2,cosC=14,∴由余弦定理可得:4=a2+b2−12ab=(a+b)2−52ab,∵a2+b2≥2ab,可得:ab≤8,当且仅当a=b时等号成立,∴可得:(a+b)2=4+52ab≤323,可得:a+b≤463,当且仅当a=b时等号成立,∵a+b>c=2,∴a+b的取值范围为:(2,463].…(12分)【解析】(1)利用同角三角函数基本关系式可求sinC,利用三角函数恒等变换的应用即可计算得解.(2)由余弦定理,基本不等式可求a+b的最大值,利用三角形两边之和大于第三边可求a+b>c=2,即可得解a+b的取值范围.本题主要考查了同角三角函数基本关系式,三角函数恒等变换的应用,余弦定理,基本不等式,三角形两边之和大于第三边等知识的应用,考查了计算能力和转化思想,属于中档题.18.已知曲线Γ:x216+y212=1的左、右顶点分别为A,B,设P是曲线Γ上的任意一点.(1)当P异于A,B时,记直线PA,PB的斜率分别为k1,k2,求证:k1⋅k2是定值;(2)设点C满足AC=λCB(λ>0),且|PC|的最大值为7,求λ的值.【答案】(1)证明:由椭圆方程可得A(−4,0),B(4,0),设P(x 0,y 0)(−4≤x 0≤4),则k 1=y 0x 0+4,k 2=y 0x 0−4,∴k 1⋅k 2=y 02x 02−16=12(1−x 0216)x 02−16=−1216=−34为定值;(2)解:设C(m,0)(−4<m <4),则|PC|=(x 0−m)2+y 02=x 02−2mx 0+m 2+12(1−x 0216)=14(x 0−4m)2+12−3m 2.若m ≥0,则|PC|max =14(−4−4m)2+12−3m 2=7,解得m =3.此时AC =(7,0),CB =(1,0),AC =7CB ,由AC =λCB ,得λ=7;同理,若m <0,可得m =−3,此时求得λ=17.故λ的值为7或17.【解析】(1)由已知椭圆方程求出A ,B 的坐标,设P(x 0,y 0)(−4≤x 0≤4),由斜率公式及点P 在椭圆上即可证明k 1⋅k 2是定值;(2)设C(m,0)(−4<m <4),写出两点间的距离公式,分类利用配方法求最值,可得m 值,结合AC =λCB(λ>0),求得λ的值.本题考查椭圆的简单性质,考查两点间距离公式的应用,训练了利用配方法求最值,是中档题.19.如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为O,钉尖为A i(i=1,2,3,4).(1)设OA1=a(a>0),当A1,A2,A3在同一水平面内时,求OA1与平面A1A2A3所成角的大小(结果用反三角函数值表示).(2)若该“钉”的三个钉尖所确定的三角形的面积为32cm2,要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料多少米?【答案】解:(1)根据题意,可知组成该种钉的四条线段长必相等,且两两所成的角相等,A1,A2,A3,A4两两连结后得到的四面体A1A2A3A4为正四面体,延长A4O交平面A1A2A3于B,则A4B⊥平面A1A2A3,连结A1B,则A1B是OA1在平面A1A2A3上的射影,∴∠OA1B就是OA1与平面A1A2A3所成角,设A1A4=l,则A1B=33l,在Rt△A4A1B中,A1A42=A1B2+A4B2,即l2=(33l)2++a)2,∴l=263a,∴A1B=33×263a=223a,cos∠OA1B=A1BOA1=223(其中0<∠OA1B<π2),∴∠OA1B=223,∴OA1与平面A1A2A3所成角的大小为arccos223.(2)12A1A22⋅32=32,根据(1)可得A1A2=263a,∴a=4272cm,∴要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料:1100⋅100⋅(4a)=4a =24216(米).∴要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料24216米.【解析】(1)组成该种钉的条线段长必相等,且两两所成的角相等,A 1,A 2,A 3,A 4两两连结后得到的四面体A 1A 2A 3A 4为正四面体,延长A 4O 交平面A 1A 2A 3于B ,则A 4B ⊥平面A 1A 2A 3,连结A 1B ,则∠OA 1B 就是OA 1与平面A 1A 2A 3所成角,由此能求出OA 1与平面A 1A 2A 3所成角的大小.(2)推导出12A 1A 22⋅32=32,A 1A 2=263a ,从而a =4272cm ,由此能求出要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料的长度.本题考查线面角的求法,考查需要材料数量的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理能力与计算能力,是中档题.20.设数列{a n }满足a 1=35,a n+1=3a n a n +2(n ∈N ∗).(1)求a 2,a 3的值;(2)求证:{1a n −1}是等比数列,并求n →∞lim (1a 1+1a 2+…+1a n −n)的值;(3)记{a n }的前n 项和为S n ,是否存在正整数k ,使得对于任意的n(n ∈N ∗且n ≥2)均有S n ≥k 成立?若存在,求出k 的值:若不存在,说明理由.【答案】解:(1)数列{a n }满足a 1=35,a n+1=3a n a n +2(n ∈N ∗).所以:a 2=3a 1a 1+2=95135=913,a 3=3a 2a 2+2=2735,(2)由于数列{a n }满足a 1=35,a n+1=3a n a n +2(n ∈N ∗).所以:1a n+1−11a n −1=13a n a n +2−11a n −1=23(常数),所以::{1a n −1}是以23为首项,23为公比的等比数列.所以:1n −1=2⋅(2)n−1=(2)n ,所以:1a n =(23)n +1,故:n →∞lim (1a 1+1a 2+…+1a n −n),=n →∞lim 23[1−(23)n ]1−23,=2.(3)由于:1a n =(23)n +1,所以,a n =1(23)n +1,a n+1=1(23)n+1+1,所以:a n+1−a n =1(23)n+1+1−1(23)n +1<0,所以:数列{a n }为递减数列,则:当n ≥2时,k ≤S 2=a 1+a 2=35+913=8465,所以:k =1.所以:存在k =1,使得对于任意的n(n ∈N ∗且n ≥2)均有S n ≥k 成立.【解析】(1)直接利用关系式求出结果.(2)利用定义证明数列{1a n −1}是等比数列,并求出极限值.(3)首先求出数列的关系式,进一步利用数列的单调性求出函数的存在问题的条件,进一步确定k 的值.1本题考查的知识要点:数列的通项公式的求法及应用,叠加法在求数列的通项公式中的应用,主要考查学生的运算能力和转化能力,属于基础题型.21.已知函数f(x)=2x (x ∈R),记g(x)=f(x)−f(−x).(1)解不等式:f(2x)−f(x)≤6;(2)设k 为实数,若存在实数x 0∈(1,2],使得g(2x 0)=k ⋅g 2(x 0)−1成立,求k 的取值范围;(3)记h(x)=f(2x +2)+a ⋅f(x)+b(其中a ,b 均为实数),若对于任意的x ∈[0,1],均有|h(k)|≤12,求a ,b 的值.【答案】解:(1)函数f(x)=2x ,f(2x)−f(x)≤6,即为22x −2x −6≤0,即为(2x +2)(2x −3)≤0,即有2x ≤3,解得x ≤log 23,即解集为(−∞,log 23];(2)存在实数x0∈(1,2],使得g(2x0)=k⋅g2(x0)−1成立,即为1+22x0−2−2x0=k(2x0−2−x0)2,设t=2x0−2−x0,在(1,2]递增,可得32<t≤154,(2x0+2−x0)2=22x0+2−2x0+2=t2+4,即有1+4+t2=kt2,则k=1t2+设m=1t2,m∈[16225,49),即有y=m+m+4m2,在m∈[16225,49)递增,可得y∈(2125,273 289],即有k∈(2125,273289],(3)h(x)=f(2x+2)+a⋅f(x)+b=22x+2+a⋅2x+b=4(2x)2+a⋅2x+b,令v=2x,∵x∈[0,1],∴v∈[1,2],∴h(x)=φ(v)=4v2+av+b.若对于任意的x∈[0,1],均有|h(x)|≤12,即对任意v∈[1,2],|φ(v)|=|4v2+av+b|≤12.∴|4+a+b|≤12①|16+2a+b|≤12②|16b−a216|≤12③,解得:a=−12,b=13.5.【解析】(1)函数f(x)=2x,f(2x)−f(x)≤6,即为22x−2x−6≤0,即为(2x+2)(2x−3)≤0,可得解集;(2)根据g(2x0)=k⋅g2(x0)−1,利用换元法,求解最值,即可求解k的取值范围;(3)根据h(x)=f(2x+2)+a⋅f(x)+b(其中a,b均为实数),x∈[0,1],均有|h(k)|≤12,建立关系即可求解a,b的值.本题主要考查了函数恒成立问题的求解,分类讨论以及转化思想的应用,二次函数闭区间是的最值以及单调性的应用.。
2018-2019学年上海中考数学各区一模压轴题汇编

目录Ⅰ第18题(填空小压轴) (2)【2019届一模徐汇】 (2)【2019届一模浦东】 (2)【2019届一模杨浦】 (3)【2019届一模普陀】 (3)【2019届一模奉贤】 (3)【2019届一模松江】 (3)【2019届一模嘉定】 (4)【2019届一模青浦】 (4)【2019届一模青浦】 (4)【2019届一模静安】 (5)【2019届一模宝山】 (5)【2019届一模长宁】 (5)【2019届一模金山】 (6)【2019届一模闵行】 (6)【2019届一模虹口】 (6)Ⅱ第23题(几何证明题) (7)【2019届一模徐汇】 (7)【2019届一模浦东】 (7)【2019届一模杨浦】 (7)【2019届一模普陀】 (8)【2019届一模奉贤】 (8)【2019届一模松江】 (9)【2019届一模嘉定】 (9)【2019届一模青浦】 (10)【2019届一模静安】 (10)【2019届一模宝山】 (11)【2019届一模长宁】 (11)【2019届一模金山】 (12)【2019届一模闵行】 (12)【2019届一模虹口】 (13)Ⅲ第24题(二次函数综合) (13)【2019届一模徐汇】 (13)【2019届一模浦东】 (14)【2019届一模普陀】 (16)【2019届一模奉贤】 (16)【2019届一模松江】 (17)【2019届一模嘉定】 (18)【2019届一模青浦】 (19)【2019届一模静安】 (20)【2019届一模宝山】 (21)【2019届一模长宁】 (22)【2019届一模金山】 (23)【2019届一模闵行】 (24)【2019届一模虹口】 (25)Ⅳ第25题(压轴题) (25)【2019届一模徐汇】 (25)【2019届一模浦东】 (26)【2019届一模杨浦】 (27)【2019届一模普陀】 (28)【2019届一模奉贤】 (29)【2019届一模松江】 (30)【2019届一模嘉定】 (31)【2019届一模青浦】 (32)【2019届一模静安】 (33)【2019届一模宝山】 (33)【2019届一模长宁】 (34)【2019届一模金山】 (35)【2019届一模闵行】 (36)【2019届一模虹口】 (37)Ⅰ第18题(填空小压轴)【2019届一模徐汇】18.在梯形ABCD中,AB∥DC,∠B=90°,BC=6,CD=2,3tan4A=.点E为BC上一点,过点E作EF∥AD交边AB于点F.将△BEF沿直线EF翻折得到△GEF,当EG过点D时,BE的长为▲ .【2019届一模浦东】18. 将矩形纸片ABCD沿直线AP折叠,使点D落在原矩形ABCD的边BC上的点E处,如果∠AED的余弦值为35,那么ABBC=__________.(第18题图)【2019届一模杨浦】18.Rt △ABC 中,∠C =90°,AC =3,BC =2,将此三角形绕点A 旋转,当点B 落在直线BC 上的点D 处时,点C 落在点E 处,此时点E 到直线BC 的距离为 ▲ .【2019届一模普陀】18.如图5,△ABC 中,8AB AC ==,3cos 4B =,点D 在边BC 上,将△ABD 沿直线AD 翻折得到△AED ,点B 的对应点为点E ,AE 与边BC 相交于点F ,如果2BD =,那么EF = ▲ .【2019届一模奉贤】18.如图5,在△ABC 中,AB =AC =5,3sin =5C ,将△ABC 绕点A 逆时针旋转得到△ADE ,点B 、C 分别与点D 、E 对应,AD 与边BC 交于点F .如果AE //BC ,那么BF 的长是 ▲ .【2019届一模松江】18.如图,在直角坐标平面xoy 中,点A 坐标为(3,2),∠AOB =90°,∠OAB =30°,ABACB(第18题图)图 5ABCD图5ABC与x 轴交于点C ,那么AC :BC 的值为______.【2019届一模嘉定】18.在△ABC 中,°=∠90ACB ,点D 、E 分别在边BC 、AC 上,AE AC 3=,°=∠45CDE (如图3),△DCE沿直线DE 翻折,翻折后的点C 落在△ABC 内部的点F ,直线AF 与边BC 相交于点G ,如果AE BG =,那么=B tan ▲ .【2019届一模青浦】17.如图,在Rt △ABC 中,∠ACB=90°,AC=1,tan ∠CAB=2,将△ABC 绕点A 旋转后,点B 落在AC 的延长线上的点D ,点C 落在点E ,DE 与直线BC 相交于点F ,那么CF= ▲ .【2019届一模青浦】18.对于封闭的平面图形,如果图形上或图形内的点S 到图形上的任意一点P 之间的线段都在图形内或图形上,那么这样的点S 称为“亮点”. 如图,对于封闭图形ABCDE ,S 1是“亮点”,S 2不是“亮点”,如果AB ∥DE ,AE ∥DC , AB=2,AE=1,∠B=∠C= 60°,那么该图形中所有“亮点” 组成的图形的面积为 ▲ .【2019届一模静安】18.如图6,将矩形ABCD 沿对角线BD 所在直线翻折后,点A 与点E 重合,且ED 交BC 于点F ,联结AE .如果2tan 3DFC ∠=,那么BDAE的值是 ▲ .【2019届一模宝山】18.如图4,Rt △ABC 中,∠ACB =90°,AC =4,BC =5,点P 为AC 上一点,将△BCP 沿直线BP 翻折,点C 落在C ’处,连接AC ’,若AC ’∥BC ,则CP 的长为 ▲ .【2019届一模长宁】18.如图,点P 在平行四边形ABCD 的边BC 上,将ABP ∆沿直线AP 翻折,点B 恰好落在边AD 的垂直平分线上,如果5=AB ,8=AD ,34tan =B ,那么BP 的长为 ▲ . AC(图4)B(第18题图)图6F BA CDEA【2019届一模金山】18.如图,在ABC Rt ∆中,o90=∠C ,8=AC ,6=BC .在边AB 上取一点O ,使BC BO =,以点O 为旋转中心,把ABC ∆逆时针旋转o90,得到C B A ′′′∆(点A 、B 、C 的对应点分别是点A ′、B ′、C ′),那么ABC ∆与C B A ′′′∆的重叠部分的面积是 ▲ .【2019届一模闵行】18.如图,在Rt △ABC 中,∠ACB = 90°,BC = 3,AC = 4,点D 为边AB 上一点.将△BCD 沿直线CD 翻折,点B 落在点E 处,联结AE .如果AE // CD ,那么BE = ▲ .【2019届一模虹口】18.如图,正方形ABCD 的边长为4,点O 为对角线AC 、BD 的交点,点E 为边AB 的中点,△BED 绕着点B 旋转至△BD 1E 1,如果点D 、E 、D 1在同一直线上,那么EE 1的长为 ▲ .ABC第18题OABC (第18题图)A DE OⅡ第23题(几何证明题)【2019届一模徐汇】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,已知菱形ABCD,点E是AB的中点,AF BC⊥于点F,联结EF、ED、DF,DE交AF于点G,且2AE EG ED=⋅.(1) 求证:DE EF⊥;(2) 求证:22BC DF BF=⋅.【2019届一模浦东】23.(本题满分12分,其中每小题各6分)已知:如图8,在平行四边形ABCD中,M是边BC的中点,E是边BA延长线上的一点,联结EM,分别交线段AD于点F、AC于点G.(1)求证:GF EF GM EM=;(2)当22BC BA BE=⋅时,求证:∠EMB=∠ACD.【2019届一模杨浦】23.(本题满分12分,每小题各6分)B(第23题图)(图8)D B已知:如图,在△ABC 中,点D 在边AB 上,点E 在线段CD 上,且∠ACD =∠B =∠BAE. (1)求证:AD DEBC AC=; (2)当点E 为CD 中点时,求证:22AE ABCE AD=.【2019届一模普陀】23.(本题满分12分)已知:如图9,△ADE 的顶点E 在△ABC 的边BC 上,DE 与AB 相交于点F ,AE AF AB =⋅2,DAF EAC ∠=∠.(1)求证:△ADE ∽△ACB ;(2)求证:DF CE DE CB=.【2019届一模奉贤】23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图9,在△ABC 中,点D 在边AC 上,BD 的垂直平分线交CA 的延长线于点E , (第23题图)ECF图9ABDE交BD 于点F ,联结BE ,EC EA ED •=2. (1)求证:∠EBA =∠C ;(2)如果BD =CD ,求证:AC AD AB •=2.【2019届一模松江】23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:如图,在梯形ABCD 中,AD ∥BC ,AB=DC ,E 是对角线AC 上一点,且AC ·CE=AD ·BC . (1)求证:∠DCA=∠EBC ;(2)延长BE 交AD 于F ,求证:AB 2=AF ·AD .【2019届一模嘉定】23.(本题满分12分,每小题6分)如图6,已知点D 在△ABC 的外部,AD //BC ,点E 在边AB 上,AE BC AD AB ⋅=⋅. (1)求证:AED BAC ∠=∠;(2)在边AC 取一点F ,如果D AFE ∠=∠,ABCDEF图9(第23题图)EDCBAF(第23题图)EDCBAD A求证:ACAFBC AD =.【2019届一模青浦】23.(本题满分12分,第(1)小题7分,第(2)小题5分)已知:如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,点F 在DE 的延长线上,AD=AF ,AE CE DE EF ⋅=⋅.(1)求证:△ADE ∽△ACD ;(2)如果AE BD EF AF ⋅=⋅,求证:AB=AC .【2019届一模静安】23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)已知:如图9,在ABC ∆中,点D 、E 分别在边BC 和AB 上,且AD AC =,EB ED =,分别延长ED 、AC 交于点F .(1)求证:ABD ∆∽FDC ∆;(2)求证:2AE BE EF =⋅.ABCDEF(第23题图) 图9AC BDEF【2019届一模宝山】23.(本题满分12分)地铁10号线某站点出口横截面平面图如图8所示,电梯AB 的两端分别距顶部9.9米和2.4米,在距电梯起点A 端6米的P 处,用1.5米的测角仪测得电梯终端B 处的仰角为14°,求电梯AB 的坡度与长度. 参考数据:,,.【2019届一模长宁】23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,点D 、E 分别在ABC ∆的边AC 、AB 上,延长DE 、CB 交 于点F ,且AC AD AB AE ⋅=⋅. (1)求证:C FEB ∠=∠;(2)联结AF ,若FD CD AB FB =,求证:FB AC AB EF ⋅=⋅.24.014sin ≈°25.014tan ≈°97.014cos ≈°Q 9.9米 B出口顶部1.5米(图8) AP 6米 2.4米°14 第23题图CEDABF【2019届一模金山】23.如图,M 是平行四边形ABCD 的对角线上的一点,射线AM 与BC 交于点F ,与DC 的延长线交于点H .(1)求证:MH MF AM ⋅=2.(2)若DM BD BC ⋅=2,求证:ADC AMB ∠=∠.【2019届一模闵行】23.(本题共2小题,每小题6分,满分12分)如图,在△ABC 中,点D 为边BC 上一点,且AD = AB ,AE ⊥BC ,垂足为点E .过点D 作DF // AB ,交边AC 于点F ,联结EF ,212EF BD EC =⋅. (1)求证:△EDF ∽△EFC ; (2)如果14EDF ADC S S =V V ,求证:AB = BD .ABCD HF M第23题ABCDE F(第23题图)【2019届一模虹口】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,在△ABC 中,AB=AC ,D 是边BC 的中点,DE ⊥AC ,垂足为点E . (1)求证:DE CD AD CE ⋅=⋅;(2)设F 为DE 的中点,联结AF 、BE ,求证:=AF BC AD BE ⋅⋅.Ⅲ第24题(二次函数综合)【2019届一模徐汇】24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图,在平面直角坐标系xoy 中,顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ,AO =OB =2,120AOB ∠=o .(1)求该抛物线的表达式; (2)联结AM ,求AOM S V ;(3)将抛物线C 1向上平移得到抛物线C 2,抛物线C 2与x 轴分别交于点E 、F (点E 在点F 的左侧),如果△MBF 与△AOM 相似,求所有符合条件的抛物线C 2的表达式.(第24题图)第23题图E【2019届一模浦东】24. (本题满分12分,其中每小题各4分)已知:如图9,在平面直角坐标系xOy 中,直线12y x b =−+与x 轴相交于点A ,与y 轴相交于点B . 抛物线244y ax ax =−+经过点A 和点B ,并与x 轴相交于另一点C ,对称轴与x 轴相交于点D .(1)求抛物线的表达式; (2)求证: △BOD ∽△AOB ;(3)如果点P 在线段AB 上,且∠BCP =∠DBO , 求点P 的坐标.【2019届一模杨浦】24.(本题满分12分,每小题各4分)在平面直角坐标系xOy 中,抛物线2(0)y ax bx c a =++?与y 轴交于点C (0,2), 它的顶点为D (1,m ),且1tan 3COD ?. (1)求m 的值及抛物线的表达式;(2)将此抛物线向上平移后与x 轴正半轴交于点A ,与y 轴交于点B ,且OA =OB .若点A 是由原抛物线上的点E 平移所得,求点E 的坐标;(3)在(2)的条件下,点P 是抛物线对称轴上的一点(位于x 轴上方),且∠APB =45°.求P 点的坐标.O xy 1 2 3 4 1 2 3 45-1-2 -3-1 -2 -3 (第24题图)【2019届一模普陀】24.(本题满分12分)如图10,在平面直角坐标系中,抛物线23y ax bx =+−(0)a ≠与x 轴交于点A ()1,0−和点B ,且3OB OA =,与y 轴交于点C ,此抛物线顶点为点D .(1)求抛物线的表达式及点D 的坐标;(2)如果点E 是y 轴上的一点(点E 与点C 不重合),当BE DE ⊥时,求点E 的坐标; (3)如果点F 是抛物线上的一点,且135FBD ∠=o ,求点F 的坐标.【2019届一模奉贤】24.(本题满分12分,每小题满分6分)如图10,在平面直角坐标系中,直线AB 与抛物线2y ax bx =+交于点A (6,0)和点B (1,-5). (1)求这条抛物线的表达式和直线AB 的表达式; xOy xOy 图10(2)如果点C 在直线AB 上,且∠BOC 的正切值是32, 求点C 的坐标.【2019届一模松江】24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图,抛物线c bx x y ++−=221经过点A (﹣2,0),点B (0,4). (1)求这条抛物线的表达式;(2)P 是抛物线对称轴上的点,联结AB 、PB ,如果∠PBO=∠BAO ,求点P 的坐标;(3)将抛物线沿y 轴向下平移m 个单位,所得新抛物线与y 轴交于点D ,过点D 作DE ∥x 轴交新抛物线于点E ,射线EO 交新抛物线于点F ,如果EO =2OF ,求m 的值.【2019届一模嘉定】24.(本题满分12分,每小题4分)在平面直角坐标系xOy (如图7)中,抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ,与y 轴的交点为C .(1)试求这个抛物线的表达式;(2)如果这个抛物线的顶点为M ,求△AMC(3)如果这个抛物线的对称轴与直线BC 交于点D (第24题图)y xOBA在线段AB 上,且°=∠45DOE ,求点E 的坐标.【2019届一模青浦】24.(本题满分12分, 其中第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,将抛物线2y x =−平移后经过点A (-1,0)、B (4,0),且平移后的抛物线与y 轴交于点C (如图).(1)求平移后的抛物线的表达式;(2)如果点D 在线段CB 上,且CD CAD 的正弦值;(3)点E 在y 轴上且位于点C 的上方,点P 在直线BC 上,点Q 在平移后的抛物线上,如果四边形ECPQ 是菱形,求点Q 的坐标.【2019届一模静安】24.(本题满分12分,其中第(1)小题4分,第(2)小题3分,第(3)小题5分)在平面直角坐标系xOy 中(如图10),已知抛物线2(0)y ax bx c a ++≠的图像经过点(40)B ,、(53)D ,,设它与x 轴的另一个交点为A (点A 在点B 的左侧),且ABD ∆的面积是3. (1)求该抛物线的表达式; (2)求ADB ∠的正切值;(3)若抛物线与y 轴交于点C ,直线CD 交x 轴于点E ,点P 在射线AD 上,当APE ∆与ABD ∆相似时,求点P 的坐标.(第24题图)(备用图)BD ﹒﹒【2019届一模宝山】24.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图9,已知:二次函数的图像交x 轴正半轴于点A ,顶点为P ,一次函数的图像交x 轴于点B ,交y 轴于点C , ∠OCA 的正切值为. (1)求二次函数的解析式与顶点P 坐标;(2)将二次函数图像向下平移m 个单位,设平移后抛物线顶点为P ’,若,求m 的值.2y x bx =+132y x =−23A CO (图9)【2019届一模长宁】24.(本题满分12分,每小题4分)如图,在直角坐标平面内,抛物线经过原点O 、点)3,1(B ,又与x 轴正半轴相交于点A ,°=∠45BAO ,点P 是线段AB 上的一点,过点P 作OB PM //,与抛物线交于点M ,且点M 在第一象限内. (1)求抛物线的表达式;(2)若AOB BMP ∠=∠,求点P 的坐标;(3)过点M 作x MC ⊥轴,分别交直线AB 、x 轴于点N 、C ,若ANC ∆的面积等于PMN ∆的面积的2倍,求NCMN 的值. 第24题图xO A By备用图xO A By【2019届一模金山】24.已知抛物线c bx x y ++=2经过点()6,0A ,点()3,1B ,直线1l :()0≠=k kx y ,直线2l :2−−=x y ,直线1l 经过抛物线c bx x y ++=2的顶点P ,且1l 与2l 相交于点C ,直线2l 与x 轴、y 轴分别交于点D 、E .若把抛物线上下平移,使抛物线的顶点在直线2l 上(此时抛物线的顶点记为M ),再把抛物线左右平移,使抛物线的顶点在直线1l 上(此时抛物线的顶点记为N ). (1)求抛物线c bx x y ++=2的解析式.(2)判断以点N 为圆心,半径长为4的圆与直线2l 的位置关系,并说明理由.(3)设点F 、H 在直线1l 上(点H 在点F 的下方),当MHF ∆与OAB ∆相似时,求点F 、H 的坐标(直接写出结果). 第24题【2019届一模闵行】24.(本题共3小题,每小题4分,满分12分)已知:在平面直角坐标系xOy中,抛物线2y a x b x=+经过点A(5,0)、B(-3,4),抛物线的对称轴与x 轴相交于点D.(1)求抛物线的表达式;(2)联结OB、BD.求∠BDO的余切值;(3)如果点P在线段BO的延长线上,且∠PAO =∠BAO,求点P的坐标.xO(第24题图)【2019届一模虹口】24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)如图,在平面直角坐标系xOy 中,抛物线2y x bx c =−++与x 轴相交于原点O 和点B (4,0),点A (3,m )在抛物线上.(1)求抛物线的表达式,并写出它的对称轴; (2)求tan ∠OAB 的值;(3)点D 在抛物线的对称轴上,如果∠BAD =45°,求点D 的坐标.Ⅳ第25题(压轴题)【2019届一模徐汇】25. (本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD 中,AD //BC ,AC =BC =10,54cos =∠ACB ,点E 在对角线AC 上(不与点A 、C 重合),EDC ACB ∠=∠,DE 的延长线与射线CB 交于点F ,设AD 的长为x . (1)如图1,当DF BC ⊥时,求AD 的长;(2)设EC 的长为y ,求y 关于x 的函数解析式,并直接写出定义域;(3)当△DFC 是等腰三角形时,求AD 的长.OAy xB【2019届一模浦东】25. (本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)将大小两把含30°角的直角三角尺按如图10-1位置摆放,即大小直角三角尺的直角顶点C重合,小三角尺的顶点D、E分别在大三角尺的直角边AC、BC上,此时小三角尺的斜边DE恰好经过大三角尺的重心G. 已知∠A=∠CDE=30°,AB=12.(1)求小三角尺的直角边CD的长;(2)将小三角尺绕点C逆时针旋转,当点D第一次落在大三角尺的边AB上时(如图10-2),求点B、E之间的距离;(3)在小三角尺绕点C旋转的过程中,当直线DE经过点A时,求∠BAE的正弦值.(第25题图1)(第25题图)CE【2019届一模杨浦】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)已知:梯形ABCD 中,AD //BC ,AB ⊥BC ,AD =3,AB =6,DF ⊥DC 分别交射线AB 、射线CB 于点E 、F . (1)当点E 为边AB 的中点时(如图1),求BC 的长;(2)当点E 在边AB 上时(如图2),联结CE ,试问:∠DCE 的大小是否确定?若确定,请求出∠DCE 的正切值;若不确定,则设AE =x ,∠DCE 的正切值为y ,请求出y 关于x 的函数解析式,并写出定义域; (3)当△AEF 的面积为3时,求△DCE 的面积.A BC D EF (图1) (第25题图) A B C D E F (图2)【2019届一模普陀】25.(本题满分14分)如图11,点O 在线段AB 上,22AO OB a ==,60BOP ∠=°,点C 是射线OP 上的一个动点. (1)如图11①,当90ACB ∠=°,2OC =,求a 的值;(2)如图11②,当AC =AB 时,求OC 的长(用含a 的代数式表示);(3)在第(2)题的条件下,过点A 作AQ ∥BC ,并使∠QOC=∠B ,求:AQ OQ 的值.A BCP OABCPO图11①图11②【2019届一模奉贤】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =4,26AB CD ==,E 是边BC 上一点,过点D 、E 分别作BC 、CD 的平行线交于点F ,联结AF 并延长,与射线DC 交于点G . (1)当点G 与点C 重合时,求:CE BE 的值;(2)当点G 在边CD 上时,设CE m =,求△DFG 的面积;(用含m 的代数式表示) (3)当AFD ∆∽ADG ∆时,求∠DAG 的余弦值.图11ABC D F E G 备用图ABC D【2019届一模松江】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)如图,已知△ABC 中,∠ACB =90°,D 是边AB 的中点,P 是边AC 上一动点,BP 与CD 相交于点E . (1)如果BC =6,AC =8,且P 为AC 的中点,求线段BE 的长; (2)联结PD ,如果PD ⊥AB ,且CE =2,ED =3,求cosA 的值; (3)联结PD ,如果222BP CD =,且CE =2,ED =3,求线段PD 的长. (备用图2)ABCD(备用图1)ABCD(第25题图)ABPCD E【2019届一模嘉定】25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在矩形ABCD 中,6=AB ,8=AD ,点E 是边AD 上一点,EC EM ⊥交AB 于点M ,点N 在射线MB 上,且AE 是AM 和AN 的比例中项. (1)如图8,求证:DCE ANE ∠=∠;(2)如图9,当点N 在线段MB 之间,联结AC ,且AC 与NE 互相垂直,求MN 的长; (3)联结AC ,如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似,求DE 的长.A 备用图BDCA 图8B M E DC N A 备用图 BD C ME N A 图9 B D C【2019届一模青浦】25.(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)如图,在梯形ABCD 中,AD//BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF =5. AE 的延长线交边BC 于点G , AF 交BD 于点N 、其延长线交BC 的延长线于点H . (1)求证:BG =CH ;(2)设AD =x ,△ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域; (3)联结FG ,当△HFG 与△ADN 相似时,求AD 的长. NHGFEDC AB (第25题图)图11ABCPQM【2019届一模静安】25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图11,在ABC ∆中,6AB =,9AC=,tan ABC ∠.过点B 作BM //AC ,动点P 在射线BM 上(点P 不与点B 重合),联结PA 并延长到点Q ,使AQC ABP ∠=∠. (1)求ABC ∆的面积;(2)设BP x =,AQ y =,求y 关于x 的函数解析式,并写出x 的取值范围; (3)联结PC ,如果PQC ∆是直角三角形,求BP 的长.【2019届一模宝山】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图10,已知:梯形ABCD 中,∠ABC =90°,∠A =45°,AB ∥DC ,DC =3,AB =5,点 P 在AB 边上,以点A 为圆心AP 为半径作弧交边DC 于点E ,射线EP 与射线CB 交于点F .(1)若DE 的长; (2)联结CP ,若CP=EP ,求AP 的长;(3)线段CF 上是否存在点G ,使得△ADE 与△FGE 相似,若相似,求FG 的值;若不相似,请说明理由.【2019届一模长宁】25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)已知锐角MBN ∠的余弦值为53,点C 在射线BN 上,25=BC ,点A 在MBN ∠的内部, 且°=∠90BAC ,MBN BCA ∠=∠.过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E . 点F 在线段BE 上(点F 不与点B 重合),且MBN EAF ∠=∠. (1)如图1,当BN AF ⊥时,求EF 的长;(2)如图2,当点E 在线段BC 上时,设x BF =,y BD =,求y 关于x 的函数解析式并写出函数定义域; AP 备用图A BCD A(图10)(3)联结DF ,当ADF ∆与ACE ∆相似时,请直接写出BD 的长.【2019届一模金山】25.已知多边形ABCDEF 是⊙O 的内接正六边形,联结AC 、FD ,点H 是射线AF 上的一个动点,联结CH ,直线CH 交射线DF 于点G ,作CH MH ⊥交CD 的延长线于点M ,设⊙O 的半径为()0>r r . (1)求证:四边形ACDF 是矩形.(2)当CH 经过点E 时,⊙M 与⊙O 外切,求⊙M 的半径(用r 的代数式表示).(3)设()o900<<=∠ααHCD ,求点C 、M 、H 、F 构成的四边形的面积(用r 及含α的三角比的式子表示). 第25题图图2 BFEC NDA MB FCE N A DM图1备用图BC NAMA B FOHEO【2019届一模闵行】25.(本题满分14分,其中第(1)小题4分、第(2)、(3)小题各5分)如图,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,5cos13ABC∠=.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,AG yDG=.(1)求AB的长;(2)当点G在线段AD上时,求y关于x的函数解析式,并写出函数的定义域;(3)如果23ABEFABCDSS=四边形四边形,求线段CE的长.A DFGA D【2019届一模虹口】25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,在四边形ABCD 中,AD ∥BC ,∠A =90°,AB =6,BC =10,点E 为边AD 上一点,将△ABE 沿BE 翻折,点A 落在对角线BD 上的点G 处,联结EG 并延长交射线BC 于点F . (1)如果cos ∠DBC =23,求EF 的长;(2)当点F 在边BC 上时,联结AG ,设AD=x ,ABG BEFS y S ∆∆= ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CG ,如果△FCG 是等腰三角形,求AD 的长. 第25题备用图第25题图EABCFDG。
2019年上海市虹口区中考数学一模考试卷含逐题详解

2019年上海市虹口区中考数学一模试卷一、选择题1.抛物线y=x2﹣1与y轴交点的坐标是()A.(﹣1,0)B.(1,0)C.(0,﹣1)D.(0,1)2.如果抛物线y=(a+2)x2开口向下,那么a的取值范围为()A.a>2B.a<2C.a>﹣2D.a<﹣23.如图,在Rt△ABC中,∠C=90°,如果AC=5,AB=13,那么cos A的值为()A.B.C.D.4.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为()A.5米B.5米C.2米D.4米5.如果向量与单位向量的方向相反,且长度为3,那么用向量表示向量为()A.=3B.=﹣3C.=3D.=﹣36.如图,在△ABC中,AD平分∠BAC交BC于点D,点E在AD上,如果∠ABE=∠C,AE=2ED,那么△ABE 与△ADC的周长比为()A.1:2B.2:3C.1:4D.4:9二、填空题7.如果=,那么的值为.8.计算:2﹣(3﹣)=9.如果抛物线y=ax2+2经过点(1,0),那么a的值为.10.如果抛物线y=(m﹣1)x2有最低点,那么m的取值范围为.11.如果抛物线y=(x﹣m)2+m+1的对称轴是直线x=1,那么它的顶点坐标为.12.如果点A(﹣5,y1)与点B(﹣2,y2)都在抛物线y=(x+1)2+1上,那么y1y2(填“>”、“<”或“=”)13.在Rt△ABC中,∠C=90°,如果sin A=,BC=4,那么AB=.14.如图,AB∥CD∥EF,点C、D分别在BE、AF上,如果BC=6,CE=9,AF=10,那么DF的长为.15.如图,在△ABC中,点G为ABC的重心,过点G作DE∥AC分别交边AB、BC于点D、E,过点D作DF∥BC交AC于点F,如果DF=4,那么BE的长为.16.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD交BC于点E,如果AC=2,BC=4,那么cot∠CAE=.17.定义:如果△ABC内有一点P,满足∠PAC=∠PCB=∠PBA,那么称点P为△ABC的布罗卡尔点,如图,在△ABC中,AB=AC=5,BC=8,点P为△ABC的布罗卡尔点,如果PA=2,那么PC=.18.如图,正方形ABCD的边长为4,点O为对角线AC、BD的交点,点E为边AB的中点,△BED绕着点B旋转至△BD1E1,如果点D、E、D1在同一直线上,那么EE1的长为.三、解答题19.(10分)计算:20.(10分)已知抛物线y=2x2﹣4x﹣6.(1)请用配方法求出顶点的坐标;(2)如果该抛物线沿x轴向左平移m(m>0)个单位后经过原点,求m的值.21.(10分)如图,在Rt△ABC中,∠C=90°,cot A=,BC=6,点D、E分别在边AC、AB上,且DE∥BC,tan∠DBC=.(1)求AD的长;(2)如果=,=,用、表示.22.(10分)如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)23.(12分)如图,在△ABC中,AB=AC,D是边BC的中点,DE⊥AC,垂足为点E.(1)求证:DE•CD=AD•CE;(2)设F为DE的中点,连接AF、BE,求证:AF•BC=AD•BE.24.(12分)如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴相交于原点O和点B(4,0),点A(3,m)在抛物线上.(1)求抛物线的表达式,并写出它的对称轴;(2)求tan∠OAB的值.25.(14分)如图,在四边形ABCD中AD∥BC,∠A=90°,AB=6,BC=10,点E为边AD上一点,将ABE沿BE翻折,点A落在对角线BD上的点G处,连接EG并延长交射线BC于点F.(1)如果cos∠DBC=,求EF的长;(2)当点F在边BC上时,连接AG,设AD=x,=y,求y关于x的函数关系式并写出x的取值范围;(3)连接CG,如果△FCG是等腰三角形,求AD的长.2019年上海市虹口区中考数学一模试卷参考答案与试题解析一、选择题1.抛物线y=x2﹣1与y轴交点的坐标是()A.(﹣1,0)B.(1,0)C.(0,﹣1)D.(0,1)【分析】通过计算自变量为对应的函数值可得到抛物线y=x2﹣1与y轴交点的坐标.【解答】解:当x=0时,y=x2﹣1=﹣1,所以抛物线y=x2﹣1与y轴交点的坐标为(0,﹣1).故选:C.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.2.如果抛物线y=(a+2)x2开口向下,那么a的取值范围为()A.a>2B.a<2C.a>﹣2D.a<﹣2【分析】由抛物线的开口向下可得出a+2<0,解之即可得出结论.【解答】解:∵抛物线y=(a+2)x2开口向下,∴a+2<0,∴a<﹣2.故选:D.【点评】本题考查了二次函数图象与系数的关系,牢记“a>0时,抛物线向上开口;当a<0时,抛物线向下开口.”是解题的关键.3.如图,在Rt△ABC中,∠C=90°,如果AC=5,AB=13,那么cos A的值为()A.B.C.D.【分析】锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cos A.【解答】解:∵∠C=90°,AC=5,AB=13,∴cos A==,故选:A.【点评】本题主要考查了锐角三角函数的定义,锐角A的邻边b与斜边c的比叫做∠A的余弦.4.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为()A.5米B.5米C.2米D.4米【分析】作BC⊥地面于点C,根据坡度的概念、勾股定理列式计算即可.【解答】解:作BC⊥地面于点C,设BC=x米,∵传送带和地面所成斜坡AB的坡度为1:2,∴AC=2x米,由勾股定理得,AC2+BC2=AB2,即(2x)2+x2=102,解得,x=2,即BC=2米,故选:C.【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握坡度坡角的概念是解题的关键.5.如果向量与单位向量的方向相反,且长度为3,那么用向量表示向量为()A.=3B.=﹣3C.=3D.=﹣3【分析】根据平面向量的定义即可解决问题.【解答】解:∵向量为单位向量,向量与向量方向相反,∴=﹣3.故选:B.【点评】本题考查平面向量的性质,解题的关键是灵活运用所学知识解决问题,属于中考基础题.6.如图,在△ABC中,AD平分∠BAC交BC于点D,点E在AD上,如果∠ABE=∠C,AE=2ED,那么△ABE与△ADC的周长比为()A.1:2B.2:3C.1:4D.4:9:S△BED=2:1,再根据三角形相似求得S△ACD=S△ABE即可求得.【分析】根据已知条件先求得S△ABE【解答】解:∵AD:ED=3:1,∴AE:AD=2:3,∵∠ABE=∠C,∠BAE=∠CAD,∴△ABE∽△ACD,:L△ACD=2:3,∴L△ABE故选:B.【点评】本题考查了相似三角形的判定和性质,不同底等高的三角形面积的求法等,等量代换是本题的关键.二、填空题7.如果=,那么的值为.【分析】直接利用已知把a,b用同一未知数表示,进而计算得出答案.【解答】解:∵=,∴设a=2x,则b=3x,那么==.故答案为:.【点评】此题主要考查了比例的性质,正确表示出a,b的值是解题关键.8.计算:2﹣(3﹣)=3﹣3【分析】实数的加减计算法则同样适用于平面向量的加减计算法则.【解答】解:原式=2﹣3+=3﹣3.故答案是:3﹣3.【点评】考查了平面向量,掌握平面向量的加减计算法则即可解题,属于基础计算题.9.如果抛物线y=ax2+2经过点(1,0),那么a的值为﹣2.【分析】把已知点的坐标代入抛物线解析式可求出a的值.【解答】解:把(1,0)代入y=ax2+2得a+2=0,解得a=﹣2.故答案为﹣2.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.10.如果抛物线y=(m﹣1)x2有最低点,那么m的取值范围为m>1.【分析】由于抛物线y=(m﹣1)x2有最低点,这要求抛物线必须开口向上,由此可以确定m的范围.【解答】解:∵抛物线y=(m﹣1)x2有最低点,∴m﹣1>0,即m>1.故答案为m>1.【点评】本题主要考查二次函数的最值的知识点,解答此题要掌握二次函数图象的特点,本题比较基础.11.如果抛物线y=(x﹣m)2+m+1的对称轴是直线x=1,那么它的顶点坐标为(1,2).【分析】首先根据对称轴是直线x=1,从而求得m的值,然后根据顶点式直接写出顶点坐标;【解答】解:∵抛物线y=(x﹣m)2+m+1的对称轴是直线x=1,∴m=1,∴解析式y=(x﹣1)2+2,∴顶点坐标为:(1,2),故答案为:(1,2).【点评】本题主要考查了二次函数的性质,熟练掌握顶点式是解题的关键,难度适中.12.如果点A(﹣5,y1)与点B(﹣2,y2)都在抛物线y=(x+1)2+1上,那么y1>y2(填“>”、“<”或“=”)【分析】利用二次函数的性质得到当x<﹣1时,y随x的增大而减小,然后利用自变量的大小关系得到y1与y2的大小关系.【解答】解:抛物线的对称轴为直线x=﹣1,而抛物线开口向上,所以当x<﹣1时,y随x的增大而减小,所以y1>y2.故答案为>.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.13.在Rt△ABC中,∠C=90°,如果sin A=,BC=4,那么AB=6.【分析】由sin A=知AB=,代入计算可得.【解答】解:∵在Rt△ABC中,sin A==,且BC=4,∴AB===6,故答案为:6.【点评】本题主要考查解直角三角形,解题的关键是熟练掌握三角函数的定义.14.如图,AB∥CD∥EF,点C、D分别在BE、AF上,如果BC=6,CE=9,AF=10,那么DF的长为6.【分析】根据平行线分线段成比例、比例的基本性质解答即可.【解答】解:∵AB∥CD∥EF,∴=,∴=,∴DF=6,故答案为:6.【点评】本题考查了平行线分线段成比例、比例的性质;由平行线分线段成比例定理得出比例式求出AF是解决问题的关键.15.如图,在△ABC中,点G为ABC的重心,过点G作DE∥AC分别交边AB、BC于点D、E,过点D作DF∥BC交AC于点F,如果DF=4,那么BE的长为8.【分析】连接BG并延长交AC于H,根据G为ABC的重心,得到=2,根据平行四边形的性质得到CE=DF =4,根据相似三角形的性质即可得到结论【解答】解:连接BG并延长交AC于H,∵G为ABC的重心,∴=2,∵DE∥AC,DF∥BC,∴四边形DECF是平行四边形,∴CE=DF=4,∵GE∥CH,∴△BEG∽△CBH,∴=2,∴BE=8,故答案为:8.【点评】本题考查了三角形重心的性质,平行线分线段成比例定理,相似三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.16.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD交BC于点E,如果AC=2,BC=4,那么cot∠CAE=2.【分析】根据直角三角形的性质得到AD=CD=BD,根据等腰三角形的性质得到∠ACD=∠CAD,∠DCB=∠B,根据余角的性质得到∠CAE=∠B,于是得到结论.【解答】解:∵∠ACB=90°,CD为AB边上的中线,∴AD=CD=BD,∴∠ACD=∠CAD,∠DCB=∠B,∵AE⊥CD,∴∠CAE+∠ACD=∠B+∠CAD=90°,∴∠CAE=∠B,∴cot∠CAE=cot B===2,故答案为:2.【点评】本题考查了解直角三角形,直角三角形斜边上的中线定义斜边的一半,余角的性质,等腰三角形的性质,熟练掌握直角三角形的性质是解题的关键.17.定义:如果△ABC内有一点P,满足∠PAC=∠PCB=∠PBA,那么称点P为△ABC的布罗卡尔点,如图,在△ABC中,AB=AC=5,BC=8,点P为△ABC的布罗卡尔点,如果PA=2,那么PC=.【分析】根据两角对应相等的两三角形相似得出△ACP∽△CBP,利用相似三角形对应边的比相等即可求出PC.【解答】解:∵AB=AC,∴∠ACB=∠ABC,∵∠PCB=∠PBA,∴∠ACB﹣∠PCB=∠ABC﹣∠PBA,即∠ACP=∠CBP.在△ACP与△CBP中,,∴△ACP∽△CBP,∴=,∵AC=5,BC=8,PA=2,∴PC==.故答案为.【点评】本题考查等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是证明△ACP∽△CBP,属于中考常考题型.18.如图,正方形ABCD的边长为4,点O为对角线AC、BD的交点,点E为边AB的中点,△BED绕着点B旋转至△BD1E1,如果点D、E、D1在同一直线上,那么EE1的长为.【分析】根据正方形的性质得到AB=AD=4,根据勾股定理得到BD=AB=4,==2,过B作BF⊥DD1于F,根据相似三角形的性质得到EF=,求得DF=2+=,根据旋转的性质得到BD1=BD,∠D1BD=∠E1BE,BE1=BE,根据相似三角形的性质即可得到结论.【解答】解:∵正方形ABCD的边长为4,∴AB=AD=4,∴BD=AB=4,∵点E为边AB的中点,∴AE=AB=2,∵∠EAD=90°,∴DE==2,过B作BF⊥DD1于F,∴∠DAE=∠EFB=90°,∵∠AED=∠BEF,∴△ADE∽△FEB,∴,∴=,∴EF=,∴DF=2+=,∵△BED绕着点B旋转至△BD1E1,∴BD1=BD,∠D1BD=∠E1BE,BE1=BE,∴DD1=2DF=,△D1BD∽△E1BE,∴=,∴=,∴EE1=,故答案为:.【点评】本题考查了旋转的性质,正方形的性质,相似三角形的判定和性质,勾股定理,正确的作出图形是解题的关键.三、解答题19.(10分)计算:【分析】直接利用特殊角的三角函数值代入进而得出答案.【解答】解:原式====3+2.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.20.(10分)已知抛物线y=2x2﹣4x﹣6.(1)请用配方法求出顶点的坐标;(2)如果该抛物线沿x轴向左平移m(m>0)个单位后经过原点,求m的值.【分析】(1)直接利用配方法求出二次函数的顶点坐标即可;(2)直接求出图象与x轴的交点,进而得出平移规律.【解答】解:(1)y=2x2﹣4x﹣6=2(x2﹣2x)﹣6=2(x﹣1)2﹣8,故该函数的顶点坐标为:(1,﹣8);(2)当y=0时,0=2(x﹣1)2﹣8,解得:x1=﹣1,x2=3,即图象与x轴的交点坐标为:(﹣1,0),(3,0),故该抛物线沿x轴向左平移3个单位后经过原点,即m=3.【点评】此题主要考查了二次函数图象与几何变换,正确得出顶点坐标是解题关键.21.(10分)如图,在Rt△ABC中,∠C=90°,cot A=,BC=6,点D、E分别在边AC、AB上,且DE∥BC,tan∠DBC=.(1)求AD的长;(2)如果=,=,用、表示.【分析】(1)通过解Rt△ABC求得AC=8,解Rt△BCD得到CD=3,易得AD=AC﹣CD=5;(2)由平行线截线段成比例求得DE的长度,利用向量表示即可.【解答】解:(1)∵在Rt△ABC中,∠C=90°,cot A=,BC=6,∴==,则AC=8.又∵在Rt△BCD中,tan∠DBC=,∴==,∴CD=3.∴AD=AC﹣CD=5.(2)∵DE∥BC,∴==.∴DE=BC.∵=,=,∴=﹣=﹣.∴=﹣.【点评】考查了平面向量,解直角三角形,平行线的性质.注意:向量是有方向的.22.(10分)如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【分析】过点C作CG⊥AB于G,得到四边形CFEG是矩形,根据矩形的性质得到EG=CF=0.45,设AD=x,求得AE=1.8﹣x,AC=AB=AE﹣BE=1.6﹣x,AG=AE﹣CF=1.35﹣x,根据三角函数的定义列方程即可得到结论.【解答】解:过点C作CG⊥AB于G,则四边形CFEG是矩形,∴EG=CF=0.45,设AD=x,∴AE=1.8﹣x,∴AC=AB=AE﹣BE=1.6﹣x,AG=AE﹣CF=1.35﹣x,在Rt△ACG中,∠AGC=90°,∠CAG=37°,cos∠CAG===0.8,解得:x=0.35,∴AD=0.35米,AB=1.25米,答:AB和AD的长分别为1.25米,0.35米.【点评】此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.23.(12分)如图,在△ABC中,AB=AC,D是边BC的中点,DE⊥AC,垂足为点E.(1)求证:DE•CD=AD•CE;(2)设F为DE的中点,连接AF、BE,求证:AF•BC=AD•BE.【分析】(1)由AB=AC,D是边BC的中点,利用等腰三角形的性质可得出∠ADC=90°,由同角的余角相等可得出∠ADE=∠DCE,结合∠AED=∠DEC=90°可证出△AED∽△DEC,再利用相似三角形的性质可证出DE•CD=AD•CE;(2)利用等腰三角形的性质及中点的定义可得出CD=BC,DE=2DF,结合DE•CD=AD•CE可得出=,结合∠BCE=∠ADF可证出△BCE∽△ADF,再利用相似三角形的性质可证出AF•BC=AD•BE.【解答】证明:(1)∵AB=AC,D是边BC的中点,∴AD⊥BC,∴∠ADC=90°,∴∠ADE+∠CDE=90°.∵DE⊥AC,∴∠CED=90°,∴∠CDE+∠DCE=90°,∴∠ADE=∠DCE.又∵∠AED=∠DEC=90°,∴△AED∽△DEC,∴=,∴DE•CD=AD•CE;(2)∵AB=AC,∴BD=CD=BC.∵F为DE的中点,∴DE=2DF.∵DE•CD=AD•CE,∴2DF•BC=AD•CE,∴=.又∵∠BCE=∠ADF,∴△BCE∽△ADF,∴=,∴AF•BC=AD•BE.【点评】本题考查了相似三角形的判定与性质、等腰三角形的性质以及余角,解题的关键是:(1)利用相似三角形的判定定理证出△AED∽△DEC;(2)利用相似三角形的判定定理证出△BCE∽△ADF.24.(12分)如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴相交于原点O和点B(4,0),点A(3,m)在抛物线上.(1)求抛物线的表达式,并写出它的对称轴;(2)求tan∠OAB的值.【分析】(1)把点O(0,0),点B(4,0)分别代入y=﹣x2+bx+c,解之,得到b和c的值,即可得到抛物线的表达式,根据抛物线的对称轴x=﹣,代入求值即可,(2)把点A(3,m)代入y=﹣x2+4x,求出m的值,得到点A的坐标,过点B作BD⊥OA,交OA于点D,过点A作AE⊥OB,交OB于点E,根据三角形的面积和勾股定理,求出线段BD和AD的长,即可得到答案.【解答】解:(1)把点O(0,0),点B(4,0)分别代入y=﹣x2+bx+c得:,解得:,即抛物线的表达式为:y=﹣x2+4x,它的对称轴为:x=﹣=2,(2)把点A(3,m)代入y=﹣x2+4x得:m=﹣32+4×3=3,即点A的坐标为:(3,3),过点B作BD⊥OA,交OA于点D,过点A作AE⊥OB,交OB于点E,如下图所示,AE=3,OE=3,BE=4﹣3=1,OA==3,AB==,S△OAB=×OB×AE=×OA×BD,BD===2,AD==,tan∠OAB==2.【点评】本题考查了抛物线与x轴的交点,二次函数的性质,二次函数图象上点的坐标特征,待定系数法求二次函数解析式,解直角三角形,解题的关键:(1)正确掌握代入法和抛物线的对称轴公式,(2)正确掌握三角形面积公式和勾股定理.25.(14分)如图,在四边形ABCD中AD∥BC,∠A=90°,AB=6,BC=10,点E为边AD上一点,将ABE沿BE翻折,点A落在对角线BD上的点G处,连接EG并延长交射线BC于点F.(1)如果cos∠DBC=,求EF的长;(2)当点F在边BC上时,连接AG,设AD=x,=y,求y关于x的函数关系式并写出x的取值范围;(3)连接CG,如果△FCG是等腰三角形,求AD的长.=BF•AB=EF•BG,即可求解;【分析】(1)利用S△BEF(2)y====,tanα===,即可求解;(3)分GF=FC、CF=CG两种情况,求解即可.【解答】解:(1)将ABE沿BE翻折,点A落在对角线BD上的点G处,∴BG⊥EF,BG=AB=6,cos∠DBC===,则:BF=9,S△BEF=BF•AB=EF•BG,即:9×6=6×EF,则EF=9;(2)过点A作AH⊥BG交于点H,连接AG,设:BF=a,在Rt△BGF中,cos∠GBF=cosα==,则tanα=,sinα=,y====…①,tanα===,解得:a2=36+()2…②,把②式代入①式整理得:y=(x);(3)①当GF=FC时,FC=10﹣a=GF=a sinα=,把②式代入上式并解得:x=,②当CF=CG时,同理可得:x=;故:AD的长为或.【点评】本题为四边形综合题,基本方法是利用解直角三角形的方法,确定相应线段间的关系,此类题目难度较大.。
17--19上海各区一模压轴题(2)
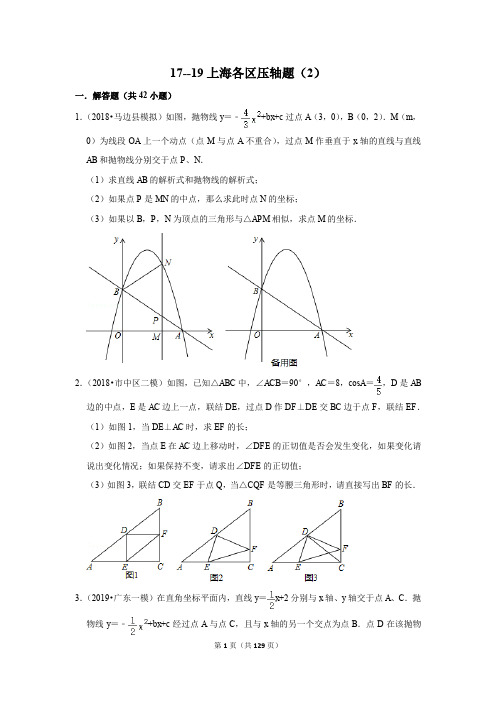
17--19上海各区压轴题(2)一.解答题(共42小题)1.(2018•马边县模拟)如图,抛物线y=﹣+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)求直线AB的解析式和抛物线的解析式;(2)如果点P是MN的中点,那么求此时点N的坐标;(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.2.(2018•市中区二模)如图,已知△ABC中,∠ACB=90°,AC=8,cos A=,D是AB 边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.(1)如图1,当DE⊥AC时,求EF的长;(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.3.(2019•广东一模)在直角坐标平面内,直线y=x+2分别与x轴、y轴交于点A、C.抛物线y=﹣+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.4.(2018•长宁区一模)已知在矩形ABCD中,AB=2,AD=4.P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F.联结AP,画∠FPE =∠BAP,PE交BF于点E.设PD=x,EF=y.(1)当点A、P、F在一条直线上时,求△ABF的面积;(2)如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;(3)联结PC,若∠FPC=∠BPE,请直接写出PD的长.5.(2018•松江区一模)如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.(1)求点A的坐标和抛物线的表达式;(2)当AE:EP=1:2时,求点E的坐标;(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t 的值.6.(2018•松江区一模)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠P AB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.7.(2019•富顺县三模)在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;(2)如图2,试探索:的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.8.(2018•嘉定区一模)已知在平面直角坐标系xOy(如图)中,已知抛物线y=+bx+c 点经过A(1,0)、B(0,2).(1)求该抛物线的表达式;(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.9.(2018•奉贤区一模)如图,在平面直角坐标系xOy中,已知抛物线y=+bx+c与x 轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且.(1)求这条抛物线的表达式,并写出它的对称轴;(2)求∠F AB的余切值;(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.10.(2019•莲湖区模拟)已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD =2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.(1)用含x的代数式表示线段CF的长;(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设=y,求y 关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是时,求AB的长.11.(2018•虹口区一模)如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(﹣2,0)、B(4,0),与y轴交于点C(0,﹣4),BC与抛物线的对称轴相交于点D.(1)求该抛物线的表达式,并直接写出点D的坐标;(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;(3)在(2)的条件下,点F在射线AE上,若△ADF∽△CBA,求点F的坐标.12.(2018•虹口区一模)已知AB=5,AD=4,AD∥BM,cos B=(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,=y.(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.13.(2018•普陀区一模)如图,已知在平面直角坐标系中,已知抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A,它的坐标是(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4(1)求抛物线的表达式;(2)求∠CAB的正切值;(3)如果点P是抛物线上的一点,且∠ABP=∠CAO,试直接写出点P的坐标.14.(2018•普陀区一模)如图1,∠BAC的余切值为2,AB=2,点D是线段AB上的一动点(点D不与点A、B重合),以点D为顶点的正方形DEFG的另两个顶点E、F都在射线AC上,且点F在点E的右侧,联结BG,并延长BG,交射线EC于点P.(1)点D在运动时,下列的线段和角中,是始终保持不变的量(填序号);①AF;②FP;③BP;④∠BDG;⑤∠GAC;⑥∠BP A;(2)设正方形的边长为x,线段AP的长为y,求y与x之间的函数关系式,并写出定义域;(3)如果△PFG与△AFG相似,但面积不相等,求此时正方形的边长.15.(2018•金山区一模)平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.(1)求这条抛物线的表达式和顶点P的坐标;(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.16.(2018•五通桥区模拟)如图,已知在△ABC中,AB=AC=5,cos B=,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.(1)求△ABC的面积;(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△APD是直角三角形,求PB的长.17.(2019•禄劝县一模)如图,二次函数y=ax2﹣x+2(a≠0)的图象与x轴交于A、B 两点,与y轴交于点C,已知点A(﹣4,0).(1)求抛物线与直线AC的函数解析式;(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.18.(2017•宝山区一模)如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段).(1)试根据图(2)求0<t≤5时,△BPQ的面积y关于t的函数解析式;(2)求出线段BC、BE、ED的长度;(3)当t为多少秒时,以B、P、Q为顶点的三角形和△ABE相似;(4)如图(3)过E作EF⊥BC于F,△BEF绕点B按顺时针方向旋转一定角度,如果△BEF中E、F的对应点H、I恰好和射线BE、CD的交点G在一条直线,求此时C、I 两点之间的距离.19.(2017•静安区一模)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x 轴,且∠DCB=∠DAB,AB与CD相交于点E.(1)求证:△BDE∽△CAE;(2)已知OC=2,tan∠DAC=3,求此抛物线的表达式.20.(2017•静安区一模)如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC=.(1)求证:BC2=CD•BE;(2)设AD=x,CE=y,求y与x之间的函数解析式,并写出定义域;(3)如果△DBC∽△DEB,求CE的长.21.(2017•浦东新区一模)已知顶点为A(2,﹣1)的抛物线经过点B(0,3),与x轴交于C、D两点(点C在点D的左侧);(1)求这条抛物线的表达式;(2)联结AB、BD、DA,求△ABD的面积;(3)点P在x轴正半轴上,如果∠APB=45°,求点P的坐标.22.(2017•浦东新区一模)如图,矩形ABCD中,AB=3,BC=4,点E是射线CB上的动点,点F是射线CD上一点,且AF⊥AE,射线EF与对角线BD交于点G,与射线AD 交于点M;(1)当点E在线段BC上时,求证:△AEF∽△ABD;(2)在(1)的条件下,联结AG,设BE=x,tan∠MAG=y,求y关于x的函数解析式,并写出x的取值范围;(3)当△AGM与△ADF相似时,求BE的长.23.(2018•邵阳模拟)已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x 轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.(1)求这个抛物线的表达式;(2)求点P的坐标;(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.24.(2017•青浦区一模)已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD=.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.(1)求证:AE=CE;(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.25.(2017•松江区一模)如图,抛物线y=﹣x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.(1)求抛物线的解析式以及顶点坐标;(2)点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点,联结BC,BE,求∠CBE 的正切值;(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标.26.(2017•阳谷县一模)如图,已知四边形ABCD是矩形,cot∠ADB=,AB=16.点E 在射线BC上,点F在线段BD上,且∠DEF=∠ADB.(1)求线段BD的长;(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;(3)当△DEF为等腰三角形时,求线段BE的长.27.(2017•闵行区一模)如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.(1)求这个二次函数的解析式并写出其图象顶点D的坐标;(2)求∠CAD的正弦值;(3)设点P在线段DC的延长线上,且∠P AO=∠CAD,求点P的坐标.28.(2017•闵行区一模)如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC =.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=.(1)求BD的长;(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.29.(2017•黄浦区一模)平面直角坐标系xOy中,对称轴平行于y轴的抛物线过点A(1,0)、B(3,0)和C(4,6);(1)求抛物线的表达式;(2)现将此抛物线先沿x轴方向向右平移6个单位,再沿y轴方向平移k个单位,若所得抛物线与x轴交于点D、E(点D在点E的左边),且使△ACD∽△AEC(顶点A、C、D依次对应顶点A、E、C),试求k的值,并注明方向.30.(2017•黄浦区一模)如图,△ABC边AB上点D、E(不与点A、B重合),满足∠DCE =∠ABC,∠ACB=90°,AC=3,BC=4;(1)当CD⊥AB时,求线段BE的长;(2)当△CDE是等腰三角形时,求线段AD的长;(3)设AD=x,BE=y,求y关于x的函数解析式,并写出定义域.31.(2017•普陀区一模)如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x﹣c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;(2)求∠CAB的正切值;(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.32.(2017•普陀区一模)如图,在直角三角形ABC中,∠ACB=90°,AB=10,sin B=,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.(1)当CM=2时,求线段CD的长;(2)设CM=x,BN=y,试求y与x之间的函数解析式,并写出定义域;(3)如果△OMN是以OM为腰的等腰三角形,请直接写出线段CM的长.33.(2017•杨浦区一模)在直角坐标系xOy中(如图),抛物线y=ax2﹣4ax+4a+3(a<0)的顶点为D,它的对称轴与x轴交点为M.(1)求点D、点M的坐标;(2)如果该抛物线与y轴的交点为A,点P在抛物线上且AM∥DP,AM=2DP,求a 的值.34.(2017•杨浦区一模)在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为边BC上的一动点(不与B、C重合),点P关于直线AC、AB的对称点分别为M、N,连接MN交边AB于点F,交边AC于点E.(1)如图1,当点P为边BC的中点时,求∠M的正切值;(2)连接FP,设CP=x,S△MPF=y,求y关于x的函数关系式,并写出定义域;(3)连接AM,当点P在边BC上运动时,△AEF与△ABM是否一定相似?若是,请证明;若不是,请求出当△AEF与△ABM相似时CP的长.35.(2017•奉贤区一模)如图,在平面直角坐标系中xOy中,抛物线y=﹣x2+bx+c与x轴相交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D,联结AC、BC、DB、DC.(1)求这条抛物线的表达式及顶点D的坐标;(2)求证:△ACO∽△DBC;(3)如果点E在x轴上,且在点B的右侧,∠BCE=∠ACO,求点E的坐标.36.(2017•奉贤区一模)已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC=,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F 在线段AE上,∠ACF=∠B.设BD=x.(1)若点F恰好是AE的中点,求线段BD的长;(2)若y=,求y关于x的函数关系式,并写出它的定义域;(3)当△ADE是以AD为腰的等腰三角形时,求线段BD的长.37.(2017•金山区一模)在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B (点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0)(1)当B(﹣4,0)时,求抛物线的解析式;(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心,OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.38.(2017•金山区一模)已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.(1)求证:△BDE∽△CFD;(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;(3)当△AOF是等腰三角形时,求BE的长.39.(2017•嘉定区一模)已知在平面直角坐标系xOy(如图)中.已知抛物线y=﹣x2+bx+4与X轴的一个交点为A(﹣1,0),与y轴的交点记为点C(1)求该抛物线的表达式以及顶点D的坐标;(2)如果点E在这个抛物线上,点F在x轴上,且以点O、C、E、F为顶点的四边形是平行四边形.直接写出点F的坐标(写出两种情况即可);(3)点P与点A关于y轴对称,点B与点A关于抛物线的对称轴对称,点Q在抛物线上,且∠PCB=∠QCB.求点Q的坐标.40.(2017•嘉定区一模)已知点P不在⊙O上,点Q是⊙O上任意一点,将线段PQ的长度中最小的值定义为点P到⊙O的“最近距离”;将线段PQ的长度的最大的值定义为点P到⊙O的“最远距离”.(1)(尝试)已知点P到⊙O的“最近距离”为2,点P到⊙O的“最远距离”为6,求⊙O的半径长(不需要解题过程,直接写出答案).(2)(证明)如图,已知点P在⊙O外,试在⊙O上确定一点Q,使得PQ最短,并简要说明PQ最短的理由.(3)(应用)已知⊙O的半径长为5,点P到⊙O的“最近距离”为1,以点P为圆心,以线段PO为半径画圆.⊙P交⊙O于点A、B,联结OA、P A.求∠OAP的余弦值.41.(2017•虹口区一模)如图,抛物线y=x2+bx+5与x轴交于点A和点B(5,0),与y轴交于点C,抛物线的顶点为点P.(1)求抛物线的表达式并写出顶点P的坐标;(2)在x轴上方的抛物线上有一点D,若∠ABD=∠ABP,试求出点D的坐标;(3)设在直线BC下方的抛物线上有一点Q,若S△BCQ=15,试求出点Q的坐标.42.(2017•虹口区一模)如图,在Rt△ABC,∠ACB=90°,AC=4,BC=3,点D为边BC上一动点(不与点B、C重合),联结AD,过点C作CF⊥AD,分别交AB、AD于点E、F设,DC=x,=y.(1)当x=1时,求tan∠BCE的值;(2)求y关于x的函数关系式,并写出x的取值范围;(3)当x=1时,在边AC上取点G,联结BG,分别交CE、AD于点M、N.当△MNF ∽△ABC时,请直接写出AG的长.17--19上海各区压轴题(2)参考答案与试题解析一.解答题(共42小题)1.(2018•马边县模拟)如图,抛物线y=﹣+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)求直线AB的解析式和抛物线的解析式;(2)如果点P是MN的中点,那么求此时点N的坐标;(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.【分析】(1)利用待定系数法求直线和抛物线解析式;(2)先表示出N(m,﹣m2+m+2),P(m,﹣m+2),则计算出NP=﹣m2+4m,PM=﹣m+2,则利用NP=PM得到﹣m2+4m=﹣m+2,然后解方程求出m即可得到N点坐标;(3)利用两点间的距离公式计算出AB=,BP=m,NP=﹣m2+4m,由于∠BPN=∠ABO,利用相似三角形的判定方法,当=时,△BPN∽△OBA,则△BPN ∽△MP A,即m:2=(﹣m2+4m):;当=时,△BPN∽△ABO,则△BPN∽△APM,即m:=(﹣m2+4m):2,然后分别解关于m的方程即可得到对应的M点的坐标.【解答】解:(1)设直线AB的解析式为y=px+q,把A(3,0),B(0,2)代入得,解得,∴直线AB的解析式为y=﹣x+2;把A(3,0),B(0,2)代入y=﹣+bx+c得,解得,∴抛物线解析式为y=﹣x2+x+2;(2)∵M(m,0),MN⊥x轴,∴N(m,﹣m2+m+2),P(m,﹣m+2),∴NP=﹣m2+4m,PM=﹣m+2,而NP=PM,∴﹣m2+4m=﹣m+2,解得m1=3(舍去),m2=,∴N点坐标为(,);(3)∵A(3,0),B(0,2),P(m,﹣m+2),∴AB==,BP==m,而NP=﹣m2+4m,∵MN∥OB,∴∠BPN=∠ABO,当=时,△BPN∽△OBA,则△BPN∽△MP A,即m:2=(﹣m2+4m):,整理得8m2﹣11m=0,解得m1=0(舍去),m2=,此时M点的坐标为(,0);当=时,△BPN∽△ABO,则△BPN∽△APM,即m:=(﹣m2+4m):2,整理得2m2﹣5m=0,解得m1=0(舍去),m2=,此时M点的坐标为(,0);综上所述,点M的坐标为(,0)或(,0).【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质;会利用待定系数法求函数解析式;灵活应用相似比表示线段之间的关系;理解坐标与图形的性质;会利用分类讨论的思想解决数学问题.2.(2018•市中区二模)如图,已知△ABC中,∠ACB=90°,AC=8,cos A=,D是AB 边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.(1)如图1,当DE⊥AC时,求EF的长;(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.【分析】(1)先求出BC=6,AB=10,再判断出四边形DECF是矩形,即可用勾股定理求出EF;(2)先判断出四边形DHCG是矩形,进而判断出△EDH∽△FDG,即可得出结论;(3)分三种情况,利用等腰三角形的性质和相似三角形得出比例式建立方程即可得出结论.【解答】解:(1)∵∠ACB=90°,∴,∵AC=8,∴AB=10,∵D是AB边的中点,∴,∵DE⊥AC,∴∠DEA=∠DEC=90°,∴,∴AE=4,∴CE=8﹣4=4,∵在Rt△AED中,AE2+DE2=AD2,∴DE=3,∵DF⊥DE,∴∠FDE=90°,又∵∠ACB=90°,∴四边形DECF是矩形,∴DF=EC=4,∵在Rt△EDF中,DF2+DE2=EF2,∴EF=5(2)不变如图2,过点D作DH⊥AC,DG⊥BC,垂足分别为点H、G,由(1)可得DH=3,DG=4,∵DH⊥AC,DG⊥BC,∴∠DHC=∠DGC=90°又∵∠ACB=90°,∴四边形DHCG是矩形,∴∠HDG=90°,∵∠FDE=90°,∴∠HDG﹣∠HDF=∠EDF﹣∠HDF,即∠EDH=∠FDG,又∵∠DHE=∠DGF=90°∴△EDH∽△FDG,∴,∵∠FDE=90°,∴,(3)①当QF=QC时,∴∠QFC=∠QCF,∵∠EDF+∠ECF=180°,∴点D,E,C,F四点共圆,∴∠ECQ=∠DFE,∠DFE+∠QFC=∠ECQ+∠QCF=∠ACB=90°,即∠DFC=90°,又∵∠ACB=90°,D是AB的中点,∴,∴,②当FQ=FC时,∴∠BCD=∠CQF,∵点D是AB的中点,∴BD=CD=AB=5,∴∠BDC=∠BCD,∴∠BCD=∠FCQ,∠BDC=∠CFQ,∴△FQC∽△DCB,由①知,点D,E,C,F四点共圆,∴∠DEF=∠DCF,∵∠DQE=∠FQC,∴△FQC∽△DEQ,即:△FQC∽△DEQ∽△DCB∵在Rt△EDF中,,∴设DE=3k,则DF=4k,EF=5k,∵∠DEF=∠DCF=∠CQF=∠DQE,∴DE=DQ=3k,∴CQ=5﹣3k,∵△DEQ∽△DCB,∴,∴,∴,∵△FQC∽△DCB,∴,∴,解得,∴,∴,③当CF=CQ时,如图3,∴∠BCD=∠CQF,由②知,CD=BD,∴∠BDC=∠BCD,∵△EDQ∽△BDK,在BC边上截取BK=BD=5,过点D作DH⊥BC于H,∴DH=AC=4,BH=BC=3,由勾股定理得,同②的方法得,△CFQ∽△EDQ,∴设DE=3m,则EQ=3m,EF=5m,∴FQ=2m,∵△EDQ∽△BDK,∴,∴DQ=m,∴CQ=FC=5﹣m,∵△CQF∽△BDK,∴,∴,解得m=,∴,∴.即:△CQF是等腰三角形时,BF的长为3或或.【点评】此题是三角形综合题,主要考查了相似三角形的判定和性质,锐角三角函数,勾股定理,矩形的判定和性质,等腰三角形的性质,解本题的关键是判断出相似三角形得出比例式建立方程求解.3.(2019•广东一模)在直角坐标平面内,直线y=x+2分别与x轴、y轴交于点A、C.抛物线y=﹣+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.【分析】(1)先利用一次函数解析式确定A(﹣4,0),C(0,2),然后利用待定系数法求抛物线解析式;(2)过点E作EH⊥AB于点H,如图1,先解方程﹣﹣x+2=0得B(1,0),设E(x,x+2),再计算出△ABC的面积为5,则△ABE的面积为4,所以•(1+4)•(x+2)=4,解得x=﹣,则E(﹣,),然后利用余切的定义求解;(3)利用∠AOC=∠DFC=90°进行讨论:若∠DCF=∠ACO时,△DCF∽△ACO,如图2,过点D作DG⊥y轴于点G,过点C作CQ⊥DC交x轴于点Q,先证明QA=QC,设Q(m,0),解方程m+4=可确定Q(﹣,0),再证明Rt△DCG∽Rt△CQO,利用相似比得到=,设DG=4t,CG=3t,可表示出D(﹣4t,3t+2),然后把D(﹣4t,3t+2)代入抛物线解析式得到﹣8t2+6t+2=3t+2,解方程求出t即可得到此时D点坐标;当∠DCF=∠CAO时,△DCF∽△CAO,则CD∥AO,利用D点的纵坐标与C点的纵坐标相同可确定此时点D的纵坐标.【解答】解:(1)当y=0时,x+2=0,解得x=﹣4,则A(﹣4,0);当x=0时,y=x+2=2,则C(0,2),把A(﹣4,0),C(0,2)代入y=﹣+bx+c得,解得,∴抛物线的解析式为y=﹣﹣x+2;(2)过点E作EH⊥AB于点H,如图1,当y=0时,﹣﹣x+2=0,解得x1=﹣4,x2=1,则B(1,0)设E(x,x+2),∵S△ABC=•(1+4)•2=5,而△ABE的面积与△ABC的面积之比为4:5,∴S△AEB=4,∴•(1+4)•(x+2)=4,解得x=﹣,∴E(﹣,),∴BH=1+=,在Rt△BHE中,cot∠EBH===,即∠DBA的余切值为;(3)∠AOC=∠DFC=90°,若∠DCF=∠ACO时,△DCF∽△ACO,如图2,过点D作DG⊥y轴于点G,过点C作CQ⊥DC交x轴于点Q,∵∠DCQ=∠AOC,∴∠DCF+∠ACQ=90°,即∠ACO+∠ACQ=90°,而∠ACO+∠CAO=90°,∴∠ACQ=∠CAO,∴QA=QC,设Q(m,0),则m+4=,解得m=﹣,∴Q(﹣,0),∵∠QCO+∠DCG=90°,∠QCO+∠CQO=90°,∴∠DCG=∠CQO,∴Rt△DCG∽Rt△CQO,∴=,即===,设DG=4t,CG=3t,则D(﹣4t,3t+2),把D(﹣4t,3t+2)代入y=﹣﹣x+2得﹣8t2+6t+2=3t+2,整理得8t2﹣3t=0,解得t1=0(舍去),t2=,∴D(﹣,);当∠DCF=∠CAO时,△DCF∽△CAO,则CD∥AO,∴点D的纵坐标为2,把y=2代入y=﹣﹣x+2得﹣﹣x+2=2,解得x1=﹣3,x2=0(舍去),∴D(﹣3,2),综上所述,点D的坐标为(﹣,)或(﹣3,2).【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质;会利用待定系数法求函数解析式;灵活应用相似比表示线段之间的关系;理解坐标与图形的性质;会利用分类讨论的思想解决数学问题.4.(2018•长宁区一模)已知在矩形ABCD中,AB=2,AD=4.P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F.联结AP,画∠FPE =∠BAP,PE交BF于点E.设PD=x,EF=y.(1)当点A、P、F在一条直线上时,求△ABF的面积;(2)如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;(3)联结PC,若∠FPC=∠BPE,请直接写出PD的长.【分析】(1)首先证明∠ADB=∠BAF,由tan∠ADB===,推出tan∠BAF==,可得BF=1,根据S△ABF=•AB•BF计算即可;(2)首先证明△BAP∽△BAP,可得=,由AD∥BC,推出∠ADB=∠PBF,tan ∠PBF=tan∠ADB=,即=,由BP=2﹣x,可得PF=(2﹣x),代入比例式即可解决问题;(3)分两种情形分别求解:①当点F在线段BC上时,如图1﹣1中;②如图2中,当点F在线段BC的延长线上时,作PH⊥AD于H,连接DF.寻找相似三角形,构建方程即可解决问题;【解答】解:(1)如图,∵矩形ABCD,∴∠BAD=∠ABF=90°,∴∠ABD+∠ADB=90°,∵A、P、F在一条直线上,且PF⊥BD,∴∠BP A=90°,∴∠ABD+∠BAF=90°,∴∠ADB=∠BAF,∵tan∠ADB===,∴tan∠BAF==,∴BF=1,∴S△ABF=•AB•BF=×2×1=1.(2)如图1中,∵PF⊥BP,∴∠BPF=90°,∴∠PFB+∠PBF=90°,∵∠ABF=90°,∴∠PBF+∠ABP=90°,∴∠ABP=∠PFB,又∵∠BAP=∠FPE∴△BAP∽△FPE,∴=,∵AD∥BC,∴∠ADB=∠PBF,∴tan∠PBF=tan∠ADB=,即=,∵BP=2﹣x,∴PF=(2﹣x),∴=,∴y=(≤x<2).(3)①当点F在线段BC上时,如图1﹣1中,∵∠FPB=∠BCD=90°,∴∠1+∠2=90°,∠1+∠3=90°,∴∠2=∠3,∵∠4=∠5,∠4+∠7=90°,∠5+∠6=90°,∴∠6=∠7,∴△PEF∽△PCD,∴=,∴=,整理得:x2﹣2x+4=0,解得x=±1.②如图2中,当点F在线段BC的延长线上时,作PH⊥AD于H,连接DF.由△APH∽△DFC,可得=,∴=,解得x=或(舍弃),综上所述,PD的长为±1或.【点评】本题考查四边形综合题.相似三角形的判定和性质、锐角三角函数、矩形的性质等知识,解题的关键是正确寻找相似三角形解决问题,学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.5.(2018•松江区一模)如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.(1)求点A的坐标和抛物线的表达式;(2)当AE:EP=1:2时,求点E的坐标;(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t 的值.【分析】(1)依据抛物线的对称性可得到A、B的坐标,利用抛物线的交点式可得到抛物线的解析式;(2)过点P作PF∥y轴,交x轴与点F,则△AEG∽△APF,从而可得到AF=6,然后可求得PF的长,从而可得到EG的长,故此可得到点E的坐标;(3)先证明∠ADO=∠CME,然后,再求得点C和点M的坐标,从而可得到tan∠ADO =1,于是可得到OD=AO=1,故此可得到AP的解析式,最后求得直线AP与抛物线的交点坐标即可.【解答】解:(1)∵AB=4,抛物线y=x2+bx+c的对称轴为直线x=1,∴点A到对称轴的距离为2,∴A(﹣1,0),B(3,0),∴y=(x+1)(x﹣3)整理得:y=x2﹣2x﹣3;(2)如下图所示:过点P作PF⊥x轴,垂足为F.∵EG∥PF,AE:EP=1:2,∴==.又∵AG=2,∴AF=6,∴F(5,0).当x=5时,y=12,∴EG=4,∴E(1,4).(3)∵CD∥EM,∴∠ADO=∠AEM.又∵四边形CDEM是等腰梯形,∴∠ADO=∠CME.∴∠ADO=∠CME.∵y=x2﹣2x﹣3,∴C(0,﹣3),M(1,﹣4)∴tan∠DAO=tan∠CME=1.∴OA=OD=1.∴直线AP的解析式为y=x+1.把y=x+1代入y=x2﹣2x﹣3得:x+1=x2﹣2x﹣3,解得:x=4或x=﹣1(舍去)∴点P的横坐标为4,即t=4.【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,相似三角形的性质和判定、等腰梯形的性质、求得AF的长是解答问题(2)的关键;求得AP的解析式是解答问题(3)的关键.6.(2018•松江区一模)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠P AB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.【分析】(1)作辅助线,证明四边形ECFD是正方形,设DF=x,则CF=x,BF=2﹣x,由△BDF∽△BAC,得,可得CD的长;(2)如图2,作辅助线,构建全等三角形,先根据C、B、P、A四点共圆,得∠APB=90°,可知AP=BP,由角平分线性质得:PM=PN,根据HL证明Rt△PMA≌Rt△PNB (HL),得AM=BN,设AM=x,则PM=CM=x+1,CN=2﹣x,由CM=CN列方程可得x的值,可得CD的长;(3)存在三种情况:①当PM=CM时,如图3,同理作出辅助线,根据△PCM是等腰直角三角形,可得CP的长;②先根据勾股定理求AB=,根据直角三角形斜边中线等于斜边一半可得CP的长;③由△CPN∽△CMH,列比例式结合①可得CP的长.【解答】解:(1)如图1,过D作DE⊥AC于E,DF⊥BC于F,∵CD平分∠ACB,∠ACB=90°,∴DE=DF,∵∠DEC=∠ACB=∠CFD=90°,∴四边形ECFD是正方形,设DF=x,则CF=x,BF=2﹣x,∵DF∥AC,∴△BDF∽△BAC,∴,∴,∴x=,∵△CDE是等腰直角三角形,∴CD=;(2)如图2,∵∠P AB=∠PCB=45°,∴C、B、P、A四点共圆,∴∠ACB+∠APB=180°,∵∠ACB=90°,∴∠APB=90°,∴△APB是等腰直角三角形,∴AP=BP,过P作PM⊥AC于M,PN⊥BC于N,连接PB,∵PM=PN,∴Rt△PMA≌Rt△PNB(HL),∴AM=BN,由(1)知:四边形MCNP是正方形,∴CM=CN,设AM=x,则PM=CN=x+1,CN=2﹣x,∴x+1=2﹣x,x=,∴CM=,∴CP=;(3)若△CMP是等腰三角形,存在三种情况:①当PM=CM时,如图3,同理作出辅助线,∵∠PCN=45°,∴△PCN是等腰直角三角形,∴CN=PN,同(2)得Rt△PGA≌Rt△PNB(HL),∴AG=BN,设AG=x,则PN=CG=x+1,CN=2﹣x,∴x+1=2﹣x,x=,∴CN=,∴CP=;②Rt△ACB中,AC=1,BC=2,∴AB=,∵M是AB的中点,∴CM=CP=AB=;③作CM的中垂线交CD于P,则CP=PM,过M作MH⊥CD于H,由①知:CG(就是CP=)=,CH=,∵△CPN∽△CMH,∴,∴=,CP=,综上所述,CP的长是或或.【点评】本题考查的是直角三角形的性质、三角形相似的性质和判定、正方形的判定和性质、等腰三角形的判定和性质等知识,与方程相结合,设未知数,列方程解决问题.7.(2019•富顺县三模)在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;(2)如图2,试探索:的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.【分析】(1)先求出PC=6、PB=10、RP=2,再证△PBC∽△PRQ得,据此可得;(2)证△RMQ∽△PCB得,根据PC=6、BC=8知,据此可得答案;(3)由PD∥AB知,据此可得、PN=,由、RM=y知,根据PD∥MQ得,即,整理可得函数解析式,当点R与点A重合。
2019年上海市静安区中考数学一模考试卷含逐题详解

2019年上海市静安区中考数学一模试卷一、选择题(本大题共6题,每题4分)1.化简(﹣x3)2的结果是()A.﹣x6B.﹣x5C.x6D.x52.下列抛物线中,顶点坐标为(2,1)的是()A.y=(x+2)2+1B.y=(x﹣2)2+1C.y=(x+2)2﹣1D.y=(x﹣2)2﹣13.在Rt△ABC中,∠C=90°,如果∠A=α,AB=3,那么AC等于()A.3sinαB.3cosαC.D.4.点P把线段AB分割成AP和PB两段,如果AP是PB和AB的比例中项,那么下列式子成立的是()A.=B.=C.=D.=5.如图,点D、E分别在△ABC的边AB、AC上,且DE与BC不平行.下列条件中,能判定△ADE与△ACB相似的是()A.=B.=C.=D.=6.下列说法不正确的是()A.设为单位向量,那么||=1B.已知、、都是非零向量,如果=2,=﹣4,那么∥C.四边形ABCD中,如果满足AB∥CD,||=||,那么这个四边形一定是平行四边形D.平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解二、填空题(本大题共12题,每题4分)7.不等式2x﹣1>0的解是.8.方程=的根是.9.已知=,那么的值是.10.△ABC∽△A1B1C1,其中点A,B,C分别与点A1,B1,C1对应,如果AB:A1B1=2:3,AC=6,那么A1C1=.11.如图,在点A处测得点B处的仰角是.(用“∠1,∠2,∠3或∠4”表示)12.如图,当小明沿坡度i=1:的坡面由A到B行走了6米时,他实际上升的高度BC=米.13.抛物线y=ax2+(a﹣1)(a≠0)经过原点,那么该抛物线在对称轴左侧的部分是的.(填“上升”或“下降”)14.如图4,AD∥BC,AC、BD相交于点O,且S△AOD:S△BOC=1:4.设=,=,那么向量=.(用向量、表示)15.在中△ABC,∠C=90°,AC=8,BC=6,G是重心,那么G到斜边AB中点的距离是.16.抛物线y=ax2(a≠0)沿某条直线平移一段距离,我们把平移后得到的新抛物线叫做原抛物线的“同簇抛物线”.如果把抛物线y=x2沿直线y=x向上平移,平移距离为时,那么它的“同簇抛物线”的表达式是.17.如图,梯形ABCD中,AB∥CD,BE∥AD,且BE交CD于点E,∠AEB=∠C.如果AB=3,CD=8,那么AD的长是.18.如图,将矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,且ED交BC于点F,连接AE.如果tan∠DFC=,那么的值是.三、解答题(本大题共7题,满分78分)19.(10分)计算:20.(10分)先化简,再求值:(2﹣)÷,其中x=2.21.(10分)已知:如图,反比例函数的图象经过点A、P,点A(6,),点P的横坐标是2.抛物线y=ax2+bx+c (a≠0)经过坐标原点,且与x轴交于点B,顶点为P.求:(1)反比例函数的解析式;(2)抛物线的表达式及B点坐标.22.(10分)2018年首届“进博会”期间,上海对周边道路进行限速行驶.道路AB段为监测区,C、D为监测点(如图).已知C、D、B在同一条直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.(1)求道路AB段的长;(精确到1米)(2)如果AB段限速为60千米/时,一辆车通过AB段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:sin35°≈0.57358,cos35°≈0.8195,tan35°≈0.7)23.(12分)已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC 交于点F.(1)求证:△ABD∽△FDC;(2)求证:AE2=BE•EF.24.(12分)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+c(a≠0)的图象经过点B(4,0)、D(5,3),设它与x轴的另一个交点为A(点A在点B的左侧),且△ABD的面积是3.(1)求该抛物线的表达式;(2)求∠ADB的正切值;(3)若抛物线与y轴交于点C,直线CD交x轴于点E,点P在射线AD上,当△APE与△ABD相似时,求点P 的坐标.25.(14分)已知:如图,在△ABC中,AB=6,AC=9,tan∠ABC=2.过点B作BM∥AC,动点P在射线BM 上(点P不与B重合),连结PA并延长到点Q,使∠AQC=∠ABP.(1)求△ABC的面积;(2)设BP=x,AQ=y,求y关于x的函数解析式,并写出x的取值范围;(3)连接PC,如果△PQC是直角三角形,求BP的长.2019年上海市静安区中考数学一模试卷参考答案与试题解析一、选择题(本大题共6题,每题4分)1.化简(﹣x3)2的结果是()A.﹣x6B.﹣x5C.x6D.x5【分析】原式利用幂的乘方与积的乘方运算法则计算即可求出值.【解答】解:原式=x6,故选:C.【点评】此题考查了幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键.2.下列抛物线中,顶点坐标为(2,1)的是()A.y=(x+2)2+1B.y=(x﹣2)2+1C.y=(x+2)2﹣1D.y=(x﹣2)2﹣1【分析】根据各个选项中的函数解析式可以直接写出它们的顶点坐标,从而可以解答本题.【解答】解:y=(x+2)2+1的顶点坐标是(﹣2,1),故选项A不符合题意,y=(x﹣2)2+1的顶点坐标是(2,1),故选项B符合题意,y=(x+2)2﹣1的顶点坐标是(﹣2,﹣1),故选项C不符合题意,y=(x﹣2)2﹣1的顶点坐标是(2,﹣1),故选项D不符合题意,故选:B.【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.3.在Rt△ABC中,∠C=90°,如果∠A=α,AB=3,那么AC等于()A.3sinαB.3cosαC.D.【分析】根据三角函数的定义即可得到结论.【解答】解:∵∠A=α,AB=3,∴cosα=,∴AC=AB•cosα=3cosα,故选:B.【点评】本题考查了锐角三角函数的定义的应用,熟记三角函数的定义是解题的关键.4.点P把线段AB分割成AP和PB两段,如果AP是PB和AB的比例中项,那么下列式子成立的是()A.=B.=C.=D.=【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值()叫做黄金比.【解答】解:∵点P把线段AB分割成AP和PB两段,AP是PB和AB的比例中项,∴根据线段黄金分割的定义得:=.故选:D.【点评】考查了黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.5.如图,点D、E分别在△ABC的边AB、AC上,且DE与BC不平行.下列条件中,能判定△ADE与△ACB相似的是()A.=B.=C.=D.=【分析】根据两边对应成比例且夹角相等的两个三角形相似即可求解.【解答】解:在△ADE与△ACB中,∵=,且∠A=∠A,∴△ADE∽△ACB.故选:A.【点评】此题考查了相似三角形的判定:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.6.下列说法不正确的是()A.设为单位向量,那么||=1B.已知、、都是非零向量,如果=2,=﹣4,那么∥C.四边形ABCD中,如果满足AB∥CD,||=||,那么这个四边形一定是平行四边形D.平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解【分析】根据单位向量的定义,向量平行的定义以及平行四边形的判定进行判断.【解答】解:A、设为单位向量,那么||=1,故本选项说法正确.B、已知、、都是非零向量,如果=2,=﹣4,那么、方向相反,则∥,故本选项说法正确.C、四边形ABCD中,如果满足AB∥CD,||=||即AD=BC,不能判定这个四边形一定是平行四边形,故本选项说法错误.D、由平面向量的平行四边形法则可以推知,平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解,故本选项说法正确.故选:C.【点评】此题考查了平面向量的知识,属于基础题,解答本题的关键是明确平面向量的表示形式,难度一般.二、填空题(本大题共12题,每题4分)7.不等式2x﹣1>0的解是x>.【分析】先移项,再系数化为1即可.【解答】解:移项,得2x>1,系数化为1,得x>.【点评】注意移项要变号.8.方程=的根是x=﹣1.【分析】按分式方程的解法,去分母化分式方程为整式方程求解即可.【解答】解:方程的两边都乘以(x﹣1),得x2=1所以x=±1.当x=1时,x﹣1=0,所以1不是原方程的根;当x=﹣1时,x﹣1=﹣2≠0,所以﹣1是原方程的根.所以原方程的解为:x=﹣1.故答案为:x=﹣1.【点评】本题考查了分式方程的解法.题目比较简单,解分式方程易忘记检验而出错.9.已知=,那么的值是.【分析】直接根据已知用同一未知数表示出各数,进而得出答案.【解答】解:∵=,∴设x=2a,则y=5a,那么==.故答案为:.【点评】此题主要考查了比例的性质,正确表示出x,y的值是解题关键.10.△ABC∽△A1B1C1,其中点A,B,C分别与点A1,B1,C1对应,如果AB:A1B1=2:3,AC=6,那么A1C1=9.【分析】根据相似三角形的性质即可得到结论.【解答】解:∵△ABC∽△A1B1C1,AB:A1B1=2:3,∴==,∵AC=6,∴=∴A1C1=9,故答案为:9.【点评】本题主要考查了相似三角形的性质,熟记相似三角形的性质是解题的关键.11.如图,在点A处测得点B处的仰角是∠4.(用“∠1,∠2,∠3或∠4”表示)【分析】根据仰角的定义即可得到结论.【解答】解:在点A处测得点B处的仰角是∠4,故答案为:∠4.【点评】本题考查了解直角三角形的应用﹣仰角和俯角,熟记仰角和俯角的定义是解题的关键.12.如图,当小明沿坡度i=1:的坡面由A到B行走了6米时,他实际上升的高度BC=3米.【分析】根据坡度的概念求出∠A,根据直角三角形的性质解答.【解答】解:∵i=1:,∴tan A==,∴∠A=30°,∴BC=AB=3(米),故答案为:3.【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握锐角三角函数的定义、坡度坡角的概念是解题的关键.13.抛物线y=ax2+(a﹣1)(a≠0)经过原点,那么该抛物线在对称轴左侧的部分是下降的.(填“上升”或“下降”)【分析】根据抛物线y=ax2+(a﹣1)(a≠0)经过原点,从而可以求得a的值,进而得到该抛物线在对称轴左侧的部分是上升还是下降,本题得以解决.【解答】解:∵抛物线y=ax2+(a﹣1)(a≠0)经过原点,∴0=a×02+(a﹣1),得a=1,∴y=x2,∴该函数的顶点坐标为(0,0),函数图象的开口向上,∴该抛物线在对称轴左侧的部分是下降的,故答案为:下降.【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.14.如图4,AD∥BC,AC、BD相交于点O,且S△AOD:S△BOC=1:4.设=,=,那么向量=+.(用向量、表示)【分析】根据已知条件得到△ADO∽△CBO,根据相似三角形的性质得到=()2=,得到=,求得=,根据已知条件得到=+,于是得到结论.【解答】解:∵AD∥BC,∴△ADO∽△CBO,∴=()2=,∴=,∴=,∵=,=,∴=+,∴==+,故答案为:+.【点评】本题考查了相似三角形的判定和性质,平面向量,熟练掌握相似三角形的判定和性质是解题的关键.15.在中△ABC,∠C=90°,AC=8,BC=6,G是重心,那么G到斜边AB中点的距离是.【分析】根据勾股定理可求得AB=10,再根据直角三角形斜边上的中线等于斜边的一半可得CD=5,最后根据重心的性质可求DG.【解答】解:∵∠C=90°,AC=8,BC=6,∴AB==10,∵CD为AB边上的中线,∴CD=AB=5,∵点G是重心,∴DG=CD=.故答案为:.【点评】本题考查的是三角形的重心的概念和性质,掌握三角形的重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.16.抛物线y=ax2(a≠0)沿某条直线平移一段距离,我们把平移后得到的新抛物线叫做原抛物线的“同簇抛物线”.如果把抛物线y=x2沿直线y=x向上平移,平移距离为时,那么它的“同簇抛物线”的表达式是y=(x﹣1)2+1.【分析】沿直线y=x向上平移,平移距离为则相当于抛物线y=ax2(a≠0)向右平移1个单位,向上平移1个单位,即可得到平移后抛物线的表达式.【解答】解:∵抛物线y=x2沿直线y=x向上平移,平移距离为,相当于抛物线y=ax2(a≠0)向右平移1个单位,向上平移1个单位,∴根据平移的规律得到:“同簇抛物线”的表达式是y=(x﹣1)2+1.故答案为:y=(x﹣1)2+1.【点评】本题考查了二次函数的几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式只考虑平移后的顶点坐标,即可求出解析式.17.如图,梯形ABCD中,AB∥CD,BE∥AD,且BE交CD于点E,∠AEB=∠C.如果AB=3,CD=8,那么AD的长是.【分析】根据平行四边形的判定得到四边形ABED是平行四边形,由平行四边形的性质得到BE=AD,DE=AB =3,根据相似三角形的性质即可得到结论.【解答】解:∵AB∥CD,BE∥AD,∴四边形ABED是平行四边形,∴BE=AD,DE=AB=3,∵CD=8,∴CE=CD﹣DE=5,∵AB∥CD,∴∠ABE=∠BEC,∵∠AEB=∠C,∴△AEB∽△BCE,∴,∴,∴BE=,故答案为:.【点评】本题考查了相似三角形的判定和性质,平行四边形的判定和性质,平行线的性质,正确的识别图形是解题的关键.18.如图,将矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,且ED交BC于点F,连接AE.如果tan∠DFC=,那么的值是.【分析】根据矩形的性质得到BC=AD,∠DAB=∠C=90°,AD∥BC,根据折叠的性质得到DE=AD,∠BED=∠DAB=90°,∠ADB=∠BDE,设CD=BE=2x,CF=EF=3x,根据勾股定理得到BF=CF==x,求得BC=(+3)x,根据勾股定理得到BD==x,根据三角形的面积公式得到AH=,求得AE=2AH=,于是得到结论.【解答】解:∵四边形ABCD是矩形,∴BC=AD,∠DAB=∠C=90°,AD∥BC,∴∠ADB=∠DBC,∵矩形ABCD沿对角线BD所在直线翻折后,点A与点E重合,∴DE=AD,∠BED=∠DAB=90°,∠ADB=∠BDE,∴∠DBF=∠FDB,∴BF=DF,∴EF=CF,∵tan∠DFC=∠BFE=,∴设CD=BE=2x,CF=EF=3x,∴BF=CF==x,∴BC=(+3)x,∴BD==x,∵AE⊥BD,∴AH=,∴AE=2AH=,∴===,故答案为:.【点评】本题考查了翻折变换(折叠问题),矩形的性质,解直角三角形,正确的识别图形是解题的关键.三、解答题(本大题共7题,满分78分)19.(10分)计算:【分析】直接利用特殊角的三角函数值代入进而得出答案.【解答】解:原式====3﹣2.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.20.(10分)先化简,再求值:(2﹣)÷,其中x=2.【分析】根据分式的减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.【解答】解:(2﹣)÷====,当x=2时,原式=.【点评】本题考查分式的混合运算,解答本题的关键是明确分式混合运算的计算方法.21.(10分)已知:如图,反比例函数的图象经过点A、P,点A(6,),点P的横坐标是2.抛物线y=ax2+bx+c (a≠0)经过坐标原点,且与x轴交于点B,顶点为P.求:(1)反比例函数的解析式;(2)抛物线的表达式及B点坐标.【分析】(1)设反比例函数的解析式为:y=,把点A(6,)代入,得到关于k的一元一次方程,解之得到k的值,即可得到答案,(2)把x=2代入(1)的解析式,得到点P的坐标,根据抛物线过坐标原点,利用待定系数法,求得抛物线的表达式,把y=0代入抛物线的表达式,解之即可得到答案.【解答】解:(1)设反比例函数的解析式为:y=,把点A(6,)代入得:=,解得:k=8,即反比例函数的解析式为:y=,(2)把x=2代入y=得:y==4,即点P的坐标为:(2,4),设抛物线的表达式为:y=a(x﹣2)2+4,把点O(0,0)代入得:4a+4=0,解得:a=﹣1,即抛物线的表达式为:y=﹣(x﹣2)2+4,把y=0代入得:﹣(x﹣2)2+4=0,解得:x1=0,x2=4,即B点的坐标为:(4,0).【点评】本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征,二次函数的性质,二次函数图象上点的坐标特征,待定系数法求二次函数解析式,抛物线与x轴的交点,解题的关键:(1)正确掌握待定系数法求反比例函数解析式,(2)正确掌握待定系数法求二次函数解析式,根据抛物线解析式,求抛物线与x 轴的交点.22.(10分)2018年首届“进博会”期间,上海对周边道路进行限速行驶.道路AB段为监测区,C、D为监测点(如图).已知C、D、B在同一条直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.(1)求道路AB段的长;(精确到1米)(2)如果AB段限速为60千米/时,一辆车通过AB段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:sin35°≈0.57358,cos35°≈0.8195,tan35°≈0.7)【分析】(1)由AC⊥BC,得到∠C=90°,根据三角函数的定义得到AC=800,在Rt△ABC中根据三角函数的定义得到AB==≈1395米;(2)求得该车的速度==55.8km/h<60千米/时,于是得到结论.【解答】解:(1)∵AC⊥BC,∴∠C=90°,∵tan∠ADC==2,∵CD=400,∴AC=800,在Rt△ABC中,∵∠ABC=35°,AC=800,∴AB==≈1395米;(2)∵AB=1395,∴该车的速度==55.8km/h<60千米/时,故没有超速.【点评】此题主要考查了解直角三角形的应用,关键是掌握三角函数定义.23.(12分)已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC 交于点F.(1)求证:△ABD∽△FDC;(2)求证:AE2=BE•EF.【分析】(1)根据等腰三角形的性质得到∠ADC=∠ACD,∠B=∠BDE,根据三角形的外角的性质得到∠BAD =∠F,于是得到结论;(2)根据相似三角形的性质得到=,等量代换即可得到结论.【解答】证明:(1)∵AD=AC,∴∠ADC=∠ACD,∵BE=DE,∴∠B=∠BDE,∵∠BDE=∠CDF,∴∠CDF=∠B,∵∠BAD=∠ADC﹣∠B,∠F=∠ACD﹣∠CDF,∴∠BAD=∠F,∴△ABD∽△FDC;(2)∵∠EAD=∠F,∠AED=∠FEA,∴△AED∽△FEA,∴=,∴AE2=DE•EF,∵BE=DE,∴AE2=BE•EF.【点评】本题考查了相似三角形的判定和性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.24.(12分)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+c(a≠0)的图象经过点B(4,0)、D(5,3),设它与x轴的另一个交点为A(点A在点B的左侧),且△ABD的面积是3.(1)求该抛物线的表达式;(2)求∠ADB的正切值;(3)若抛物线与y轴交于点C,直线CD交x轴于点E,点P在射线AD上,当△APE与△ABD相似时,求点P 的坐标.【分析】(1)设A(m,0),由△ABD的面积是3可求得m=2,再利用待定系数法求解可得;(2)作DF⊥x轴,BF⊥AD,由A,B,D坐标知DF=AF=3,据此可求得AD=3,∠DAF=45°,继而可得AE=BE=,DE=2,再依据正切函数的定义求解可得;(3)先求出直线AD解析式为y=x﹣2,直线BD解析式为y=3x﹣12,直线CD解析式为y=﹣x+8,①△ADB ∽△APE时BD∥PE,此条件下求得PE解析式,连接直线PE和直线AD解析式所得方程组,解之求得点P坐标;②△ADB∽△AEP时∠ADB=∠AEP,依据tan∠ADB=tan∠AEP=求解可得.【解答】解:(1)设A(m,0),则AB=4﹣m,由△ABD的面积是3知(4﹣m)×3=3,解得m=2,∴A(2,0),设抛物线解析式为y=a(x﹣2)(x﹣4),将D(5,3)代入得:3a=3,解得a=1,∴y=(x﹣2)(x﹣4)=x2﹣6x+8;(2)如图1,过点D作DF⊥x轴于点F,∵A(2,0),B(4,0),D(5,3),∴DF=3,AF=3,则AD=3,∠DAF=45°,过点B作BE⊥AD于E,则AE=BE=,∴DE=2,∴tan∠ADB===;(3)如图2,由A(2,0),D(5,3)得直线AD解析式为y=x﹣2,由B(4,0),D(5,3)可得直线BD解析式为y=3x﹣12,由C(0,8),D(5,3)可得直线CD解析式为y=﹣x+8,当y=0时,﹣x+8=0,解得x=8,∴E(8,0),①若△ADB∽△APE,则∠ADB=∠APE,∴BD∥PE,设PE所在直线解析式为y=3x+m,将点E(8,0)代入得24+m=0,解得m=﹣24,∴直线PE解析式为y=3x+24,由得,∴此时点P(11,9);②若△ADB∽△AEP,则∠ADB=∠AEP,∴tan∠ADB=tan∠AEP=,设P(n,n﹣2),过点P作PG⊥AE于点G,则OG=n,PG=n﹣2,∴GE=8﹣n,由tan∠AEP===求得n=4,∴P(4,2);综上,P(11,9)或(4,2).【点评】本题是二次函数的综合问题,解题的关键是掌握三角形的面积公式、待定系数法求二次函数和一次函数的解析式、一次函数和二次函数的交点问题等知识点.25.(14分)已知:如图,在△ABC中,AB=6,AC=9,tan∠ABC=2.过点B作BM∥AC,动点P在射线BM 上(点P不与B重合),连结PA并延长到点Q,使∠AQC=∠ABP.(1)求△ABC的面积;(2)设BP=x,AQ=y,求y关于x的函数解析式,并写出x的取值范围;(3)连接PC,如果△PQC是直角三角形,求BP的长.【分析】(1)用解直角三角形的方法,求出AH和BC长即可求解;(2)证明△ABP∽△CQA,利用,即可求解;(3)连接PC,△PQC是直角三角形,即∠PCQ=90°,利用cos∠PQC=cosα==,即可求解.【解答】解:(1)过点A作AH⊥BC交于点H,在Rt△ABH中,tan∠ABC==2,设BH=m,∴AH=2m,根据勾股定理得,m2+(2m)2=36,∴m=﹣2(舍)或m=2,∴BH=2,AH=2m=4,在Rt△AHC中,AC=9,根据勾股定理得,CH==7,∴BC=BH+CH=9,S△ABC=AH•BC=×4×9=18;(2)过点A作AG⊥PA交于点G,由(1)知,BC=9,∵AC=9,∴AC=BC,∴∠ABC=∠BAC,∵BM∥AC,∴∠BAC=∠ABP,∴∠ABP=∠ABC,∵AH⊥BC,AG⊥BP,∴AG=AH=4,BG=BH=2,∴PG=BP﹣BG=x﹣2根据勾股定理得,AP==,∵BM∥AC,∴∠QAC=∠APB,又∠AQC=∠ABP,∴△ABP∽△CQA,∴,其中:AB=6,BP=x,QA=y,AP =,AC=9,∴,∴CQ =,y =①(x>0);(3)连接PC,△PQC是直角三角形,即∠PCQ=90°,在Rt△ABH中,cos∠ABH ==,∴cos∠PQC=cosα==其中CQ =,PQ=AP+AQ=y+AP,AP =,∴=②联立①②解得:x=﹣14(舍)或x=9,即BP的长为9.【点评】本题为三角形综合题,重点是确定三角形相似,利用解直角三角形和三角形相似的方法,求出对应线段长度是解题的关键,本题难度较大.第21页(共21页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 PH 3
4
①当点 P 在 x 轴上方时, 1 (x 2)(x 6) 3 (6 x) .
2
4
解得 x= 1 ,或 x=6(与 B 重合,舍去).此时 P ( 1 , 39) .
2
28
②当点 P 在 x 轴下方时, 1 (x 2)(x 6) 3 (6 x) .
图1
动感体验
请打开几何画板文件名“19 宝山一模 24”,拖动点 P′在抛物线的对称轴上运动,观察面
积比的度量值,可以体验到,有两个时刻,△ABP′与△BCP′的面积相等.
满分解答
(1)由 y 1 x 3 ,得 B(6, 0),C(0,-3). 2
由 tan∠OCA= OA = 2 ,得 OA= 2 OC=2,A(2, 0).
①如图 3,当点 P′在 CB 上方时,
此时 S△BCP′=S△OCB-S△OBP′-S△OCP′= 1 6 3 1 6n 1 31 15 3n .
2
2
2
2
解方程 2n 15 3n ,得 n 3 .
2
2
图2
图3
2
所以点 P(1,-1)向下平移到点 P′ (0, 3) ,平移距离 m 1 .
所以 P ' M 3 5 15 .此时所以 P′ (0, 15) .
22
2
图5
图6
3
例
2019 年上海市宝山区中考一模第 25 题
如图 1,已知梯形 ABCD 中,∠ABC=90°,∠A=45°,AB//DC,DC=3,AB=5,
点 P 在 AB 边上,以点 A 为圆心、AP 为半径作弧交 DC 于点 E,射线 EP 与射线 CB 交于点
3
3
BM=4,所以 cot∠BNM= 4 . 3
所以 cot∠CBD=cot∠BNM= 4 . 3
图2
6
(3)如图 3,设 P (x, 1 (x 2)(x 6)) .作 PH⊥x 轴于 H. 2
由 cot∠PBA=cot∠CBD= 4 ,得 BH 4 .所以 PH 3 BH .
F.
(1)若 AP= 13 ,求 DE 的长;
(2)联结 CP,若 CP=EP,求 AP 的长; (3)线段 CF 上是否存在点 G,使得△ADE 与△FGE 相似,若相似,求 FG 的值;若 不相似,请说明理由.
图1
动感体验
请打开几何画板文件名“19 宝山一模 25”,拖动点 P 在线段 AB 上运动,可以体验到, 当 CP=EP 时,等腰三角形 APE 与等腰三角形 PEC 相似.点击屏幕左下方的按钮“第(3) 题”,拖动点 P 运动,可以体验到,当∠DEA=30°时,△DAE∽△GFE.
(2)过点 B 的直线 y 1 x 3交抛物线的对称轴于点 D,联结 BC,求∠CBD 的余切 2
值;
(3)点 P 为抛物线上一个动点,当∠PBA=∠CBD 时,求点 P 的坐标.
图1
动感体验
请打开几何画板文件名“19 崇明一模 24”,可以体验到,△CNB∽△CBD.点击屏幕左
下方的按钮“第(3)题”,可以体验到,点 P 存在两种情况,射线 BO 平分∠PBP′.
2 3 2 2(5 2 3)
解得 GF= 3 3 1 .
图4
5
例
2019 年上海市崇明区中考一模第 24 题
如图 1,在平面直角坐标系中,二次函数 y=ax2+bx+6(a、b 当时常数,且 a<0)的
图像与 x 轴交于 A(-2, 0)、B(6, 0),顶点为 C.
(1)求这个二次函数的解析式及点 C 的坐标;
BG 5
33
所以 DG=BG-BD= 5 x 3. 3
图2
图3
图4
(2)如图 4,由 PF//AC,得 BP BA 5 .所以 BF 6 BP 6 x .
BF BC 6
5
5
所以 FD=BD-BF= 3 6 x . 5
8
如图 3,在 Rt△EDG 中,tan∠EGD= ED 3 ,所以 ED 3 DG 3 (5 x 3) .
PEF 存在两种情况.每种情况下,直角三角形 EDF 的两条直角边的比都是 3∶4.
满分解答
(1)如图 2,因为 AB=AC,AD⊥BC,所以 AD 垂直平分 BC.
在 Rt△ABD 中,AB=5,BD=3,所以 AD=4,cos∠B= 3 . 5
如图 3,在 Rt△PBG 中,由 cos∠B= BP 3 ,得 BG 5 BP 5 x .
距离相等,所以点 P′恰好是 AC 的中点.此时△ABP′与△BCP′是等底同高的三角形.
所以 P′ (0, 3) . 2
②如图 6,当点 P′在 CB 下方时,△ABP′与△BCP′有公共底边 BP′,如果面积相等,那
么 AC//P′B.所以∠OAC=∠MBP′.
由 tan∠OAC=tan∠MBP′,得 P ' M CO 3 . BM AO 2
解得 m 5 13 ,或 m 5 13 (此时 EC=2m>3,舍去).
3
3
所以 AP=5-m= 5 5 13 = 10 13 .
3
3
(3)作 AM⊥PE 于 M.设∠F=α,那么∠PAM=∠EAM=α. 由 DE//AP,得∠DEA=∠EAP=2α. 在△ADE 中,∠ADE=135°为定值. 如果△ADE 与△FGE 相似,那么∠EGF=135°,∠DAE=∠GFE=α. 此时在△ADE 中,3α=45°.所以 α=15°.
例
2019 年上海市宝山区中考一模第 24 题
如图 1,已知二次函数 y=x2+bx 的图像交 x 轴正半轴于点 A,顶点为 P,一次函数
y 1 x 3 的图像交 x 轴于点 B,交 y 轴于点 C,∠OCA 的正切值为 2 .
2
3
(1)求二次函数的解析式与顶点 P 的坐标;
(2)将二次函数的图像向下平移 m 个单位,设平移后抛物线的顶点为 P′,如果 S△ABP′ =S△BCP′,求 m 的值.
在 Rt△HAE 中,∠DEA=30°,所以 AE=2HA=4,HE= 2 3 .
所以 DE= 2 3 2 .
在等腰直角三角形 CEG 中,CE=HC-HE= 5 2 3 .所以 GE= 2(5 2 3) .
由△DAE∽△GFE,得 DA GF .所以 2 2 GF .
DE GE
DG 4
4
43
如图 5,y=S△DEF= 1 FD ED = 1 (3 6 x) 3 (5 x 3) = 3 x2 129 x 27 .
2
2
②如图 4,当点 P′在 CB 下方时,此时 S△BCP′=S△OBP′+S△OCP′-S△OCB= 3n 15 . 2
解方程 2n 3n 15 ,得 n 15 .
2
2
所以点 P(1,-1)向下平移到点 P′ (0, 15) ,平移距离 m 13 .
2
2
图4
【另解】①如图 5,当点 P′在 CB 上方时,联结 AC,因为 A、C 两点到对称轴 x=1 的
满分解答
(1)因为抛物线与 x 轴交于 A(-2, 0)、B(6, 0)两点,设 y=a(x+2)(x-6).
对照 y=ax2+bx+6,根据常数项相等,得-12a=6.解得 a 1 . 2
所以 y 1 (x 2)(x 6) 1 x2 2x 6 1 (x 2)2 8 .
满分解答
(1)如图 2,作 AH⊥DC,垂足为 H,那么四边形 HABC 是矩形. 在等腰直角三角形 HAD 中,HD=HA=2.
当 AP= 13 时,在 Rt△HAE 中,HA=2,AE=AP= 13 ,所以 HE=3.
所以 DE=HE-HD=3-2=1.
图2
图3
(2)如图 3,如果 CP=EP,那么点 P 在 EC 的垂直平分线上.所以 EC=2PB.
设 PB=m,那么 AP=5-m,EC=2m,PE2=PC2=m2+22=m2+4.
由 CP=EP,AP=AE,得∠1=∠2,∠3=∠4.
因为 DC//AB,所以∠2=∠3.所以△APE∽△PEC.
所以 AP PE .所以 PE2 EC AP . PE EC
4
解方程 m2+4=2m(5-m),整理,得 3m2-10m+4=0.
G.
(1)用含 x 的代数式表示线段 DG 的长;
(2)设△DEF 的面积为 y,求 y 与 x 之间的函数关系式,并写出定义域;
(3)△PEF 能否为直角三角形?如果能,求出 BP 的长;如果不能,请说明理由.
图1
动感体验
请打开几何画板文件名“19 崇明一模 25”,拖动来自 P 运动,可以体验到,直角三角形
2
4
解得 x= 7 ,或 x=6(与 B 重合,舍去).此时 P ( 7 , 57) .
2
28
图3
7
例
2019 年上海崇明区市中考一模第 25 题
如图 1,在△ABC 中,AB=AC=5,BC=6,AD⊥BC,垂足为 D,点 P 是边 AB 上的
一个动点,过点 P 作 PF//AC 交线段 BD 于点 F,作 PG⊥AB 交 AD 于点 E,交线段 CD 于点
OC 3
3
因为抛物线 y=x2+bx 与 x 轴交于 O、A(2, 0)两点,所以 y=x (x-2)=x2-2x.
(2)由 y=x2-2x=(x-2)2-1,得顶点 P 的坐标为(1,-1).
如图 2,设抛物线的对称轴与 x 轴交于点 M.
设 P′M=n,那么 S△ABP′= 1 AB P ' M =2n. 2
