第2章思考题参考答案_58809914
数值分析第二章复习与思考题

数值分析第二章复习与思考题P k L X =P k X a k 1 X - X oX - X k ,第 1 页,共 7 页 26298o288.doc第二章复习与思考题1?什么是拉格朗日插值基函数?它们是如何构造的?有何重要性质?答:若n 次多项式I j X (j =0,1,…,n)在n 1个节点x ° ::: x 1 :::…:::X n上满足条件H k=j, Ij (X k )=JI . j,k = 0,1,…,n, 0, 2j,则称这n ? 1个n 次多项式∣o X ,∣1 x ,…,l n X 为节点X o ,/,…,x n 上的n 次拉格朗日插值基函数.以I k X 为例,由I k X 所满足的条件以及I k X 为n 次多项式,可设I k X =Ax-X oX-X k 」X-X k ?1 X-X n ,其中A 为常数,利用I k X k =1得1 =AX k -X o X^X kd X k-X k ?i X^-X n ,1X k —X oX^X kJ X k —X k 1X k —X nI k (X)X xoX" X" X J(Xk -Xo 丿(X^-XkJL I xk —Xk* ) (xk —X|j-kn对于I i X (i =o,1,…,n),有 V x i kI i X =X kk = o,1,…,n ,特别当 k = o 时,有i=on ■- Ii X= 1 ?i =o2.什么是牛顿基函数?它与单项式基1,X,…,X nf 有何不同?答:称 1,X-X o , X-X o X-X 1,i,X-Xo^ X-X nd f 为节点 X o ,X 1 ,…,X n 上的牛顿基函数,利用牛顿基函数,节点x o ,x 1,…,X n 上的n 次牛顿插值多项式 P n X 可以表示为=πj ≡o X k _ X jP n X i=a o a1 X — X o 厂亠a n X - X o ^X n^其中a k = f l X o ,X1Λ' ,X k , k =o,1,…,n.与拉格朗日插值多项式不同,牛顿插值基函数在增加节点时可以通过递推逐步得到高次的插值多项式,例如其中a k ι是节点X o ,X ι,…,X k.ι上的k 1阶差商,这一点要比使用单项式基1,x,…,χn{方便得多?3?什么是函数的n 阶均差?它有何重要性质?答:称f ∣x 0,x ∣J = f~x-- L XL 为函数 fx 关于点 x 0, x k 的一阶均差,xk _x丄丄也心泌]为f X 的二阶均差?一般地,称Xk - xI均差具有如下基本性质:(3)若f X 在a,b 上存在n 阶导数,且节点X o , %,…,X n ■ a,b 1,则n 阶均差与n 阶导数的关系为f l -X 0,X i Λ' X nL f ' ,- l a,b In!4?写出n 1个点的拉格朗日插值多项式与牛顿均差插值多项式,它们有何异同?答:给定区间 ?,b 1上n ?1a _ X o 叮%叮…叮X n _ b上的函数值y^ f X i (i =0,1/ ,n),则这n 1个节点上的拉格朗日插值多项式为nL n x [= Y k l k X ,k =0i Vn1X -X i其中 Ik (X )= 口 -------UIX k 一 X jj ^k这n ? 1个节点上的牛顿插值多项式为f x °,X ι,X k X θ,X i ,…X nI=fk ,,x n 2, X nX n -X ndL fX 0,X i「,X n」I 为f X 的n 阶均差.(1) n 阶均差可以表示为函数值f x 0 , f x 1 Λ , f x n 的线性组合,即 nf X θ, X i,…X ndvf (X j )j=0X j —Xo …X j —Xj 」X j —X j 1 … X j —X n 该性质说明均差与节点的排列次序无关,即均差具有对称性I-f l -X θ,X iΛ' ,X njlf X, x l ,X nl =f X 1,X 2, ,X nX n _Xok =0,1, ,n .Pn X=a° y x-x 。
北师大版八年级数学上册第2章 回顾与思考

回顾与思考
10.比较大小: 52-1____<____58.
5-1 5 4 5-4 5 4 5-9 [解析] 2 -8= 8 -8= 8 ,因为 5<2.25,所以 4
4 5-9
5-1 5
5-1 5
所以 8 <0,所以 2 -8<0,故 2 <8.
5<9,
回顾与思考
类型之四 二次根式的有关概念及性质
回顾与思考
解:(1)有理数集合0,-7.5,4,23,3 -27,0.31,
6.7·89·,(3 5- 2)0,-|-4|,…;
(2)无理数集合 15,
197,-π3 ,…;
(3)正实数集合{ 15,4, 197,32,0.31,6.7·89·,(3 5- 2)0,…};
回顾与思考
18.已知 x= 3+ 2,y= 3- 2,求 x2+y2-xy-3x+3y 的 值.
解:因为 x= 3+ 2,y= 3- 2, 所以 x-y= 3+ 2- 3+ 2=2 2, xy=( 3+ 2)( 3- 2)=1, 所以原式=(x-y)2-3(x-y)+xy=(2 2)2-3×2 2+1=9-6 2.
5. 3- 2的相反数是__2_-__3___,绝对值是__3_-__2___.
回顾与思考
6.在实数-
2
,
π 3
,
0.50105
,
1 7
,
-
3
125 中 , 无 理 数 是
___-___2,__π3____.
7.2016·黄山校级期中如图 2-X-1 所示,数轴上点 A 所表 示的数为 a,则 a 的值是-__1+___5___.
第二章 实数
回顾与思考
回顾与思考
第2章思考题及习题2参考答案

第2章思考题及习题2参考答案一、填空1. 在AT89S52单片机中,如果采用6MHz晶振,一个机器周期为。
答:2µs2. AT89S52单片机的机器周期等于个时钟振荡周期。
答:123. 内部RAM中,位地址为40H、88H的位,该位所在字节的字节地址分别为和。
答:28H,88H4. 片内字节地址为2AH单元最低位的位地址是;片内字节地址为A8H单元的最低位的位地址为。
答:50H,A8H5. 若A中的内容为63H,那么,P标志位的值为。
答:06. AT89S52单片机复位后,R4所对应的存储单元的地址为,因上电时PSW= 。
这时当前的工作寄存器区是组工作寄存器区。
答:04H,00H,0。
7. 内部RAM中,可作为工作寄存器区的单元地址为 H~ H。
答:00H,1FH8. 通过堆栈操作实现子程序调用时,首先要把的内容入栈,以进行断点保护。
调用子程序返回指令时,再进行出栈保护,把保护的断点送回到,先弹出的是原来中的内容。
答:PC, PC,PCH9. AT89S52单片机程序存储器的寻址范围是由程序计数器PC的位数所决定的,因为AT89S52单片机的PC是16位的,因此其寻址的范围为 KB。
答:6410. AT89S52单片机复位时,P0~P3口的各引脚为电平。
答:高11. AT89S52单片机使用片外振荡器作为时钟信号时,引脚XTAL1接,引脚XTAL2的接法是。
答:片外振荡器的输出信号,悬空12. AT89S52单片机复位时,堆栈指针SP中的内容为,程序指针PC中的内容为。
答:07H,0000H二、单选1. 程序在运行中,当前PC的值是。
A.当前正在执行指令的前一条指令的地址 B.当前正在执行指令的地址。
C.当前正在执行指令的下一条指令的首地址 D.控制器中指令寄存器的地址。
答:C2. 判断下列哪一种说法是正确的?A.PC是一个可寻址的寄存器 B.单片机的主频越高,其运算速度越快。
C.AT89S52单片机中的一个机器周期为1µsD.特殊功能寄存器SP内存放的是堆栈栈顶单元的内容。
第2章习题+答案-PDF

,
E1′
=
e r′
−π a2ρ0 2πε 0 r ′
=
−
ρ0a2r′ 2ε 0 r ′2
E
=
E1
+
E 1′
=
ρ 2ε 0
(
b2r r2
−
a2r r′2
′
)
在 r < b 且 r′ > a 区域中,同理可求得大、小圆柱中的正、负电荷在点 P 产生的电场分别为
点 P 处总的电场为
E2
=
er
πr2ρ 2πε 0 r
ε0 d
解:
E
=
−∇ϕ
=
−
∂ϕ ∂x
ex
=
−⎜⎜⎝⎛
2x ε0
+
U d
⎟⎟⎠⎞e x
V/m
ρ
= ∇ ⋅ D = −ε 0∇ ⋅ E
= −ε 0
∂E x ∂x
=
−ε
0
⎜⎜⎝⎛
2 ε0
⎟⎟⎠⎞ = −2
C/m2
2-4 半径为 a 的圆面上均匀带电,电荷面密度为 σ ,试求:(1)轴线上离圆心为 z 处的场强,(2)在保持 σ 不变的情况下,当 a → 0 和 a → ∞ 时结果如何?(3)在保持总电荷不变的情况下,当 a → 0 和 a → ∞ 时
说明 在给定 E 或ϕ = 分布,可应用 ρ = ε∇ ⋅ E 或 ρ = −ε∇2ϕ 求电荷分布。但应注意:在 E 或ϕ 的 奇异点处可能有点电荷,而在 E 的突变面上,可能有面分布的自由电荷。
2-13 一个半径为 a 的导体球,要使得它在空气中带点且不放电,试求它所能带点最大电荷量级表面电
位各是多少?已知空气的击穿场强为 3×106 V/m。
理论力学课后习题第二章思考题答案

理论力学课后习题第二章思考题解答2.1.答:因均匀物体质量密度处处相等,规则形体的几何中心即为质心,故先找出各规则形体的质心把它们看作质点组,然后求质点组的质心即为整个物体的质心。
对被割去的部分,先假定它存在,后以其负质量代入质心公式即可。
2.2.答:物体具有三个对称面已足以确定该物体的规则性,该三平面的交点即为该物体的几何对称中心,又该物体是均匀的,故此点即为质心的位置。
2.3.答:对几个质点组成的质点组,理论上可以求每一质点的运动情况,但由于每一质点受到周围其它各质点的相互作用力都是相互关联的,往往其作用力难以n3预先知道;再者,每一质点可列出三个二阶运动微分方程,各个质点组有个相互关联的三个二阶微分方程组,难以解算。
但对于二质点组成的质点组,每一质点的运动还是可以解算的。
若质点组不受外力作用,由于每一质点都受到组内其它各质点的作用力,每一质点的合内力不一定等于零,故不能保持静止或匀速直线运动状态。
这表明,内力不改变质点组整体的运动,但可改变组内质点间的运动。
2.4.答:把碰撞的二球看作质点组,由于碰撞内力远大于外力,故可以认为外力为零,碰撞前后系统的动量守恒。
如果只考虑任一球,碰撞过程中受到另一球的碰撞冲力的作用,动量发生改变。
2.5.答:不矛盾。
因人和船组成的系统在人行走前后受到的合外力为零(忽略水对船的阻力),且开船时系统质心的初速度也为零,故人行走前后系统质心相对地面的位置不变。
当人向船尾移动时,系统的质量分布改变,质心位置后移,为抵消这种改变,船将向前移动,这是符合质心运动定理的。
2.6.答:碰撞过程中不计外力,碰撞内力不改变系统的总动量,但碰撞内力很大,使物体发生形变,内力做功使系统的动能转化为相碰物体的形变能(分子间的结合能),故动量守恒能量不一定守恒。
只有完全弹性碰撞或碰撞物体是刚体时,即相撞物体的形变可以完全恢复或不发生形变时,能量也守恒,但这只是理想情况。
2.7.答:设质心的速度,第个质点相对质心的速度,则,代入质点组动量定理可得这里用到了质心运动定理。
第2章思考题答案
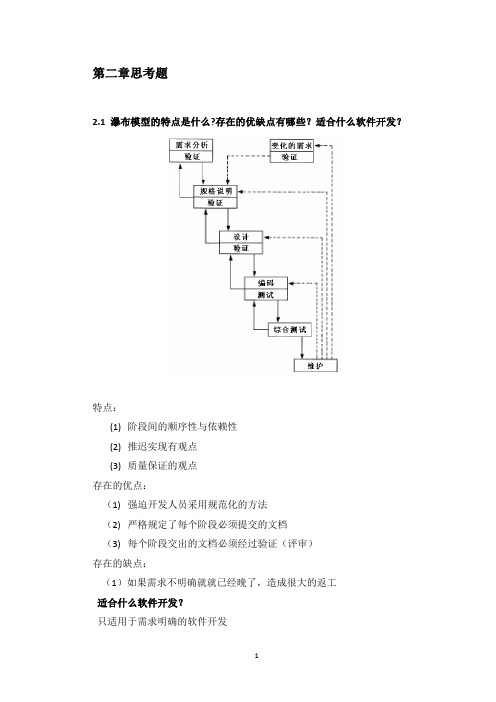
第二章思考题2.1 瀑布模型的特点是什么?存在的优缺点有哪些?适合什么软件开发?特点:(1)阶段间的顺序性与依赖性(2)推迟实现有观点(3)质量保证的观点存在的优点:(1)强迫开发人员采用规范化的方法(2)严格规定了每个阶段必须提交的文档(3)每个阶段交出的文档必须经过验证(评审)存在的缺点:(1)如果需求不明确就就已经晚了,造成很大的返工适合什么软件开发?只适用于需求明确的软件开发2.2 快速原型的优点?怎么样体现出快速的意思?适合什么软件开发?何为快速原型:由于种种原因,在需求分析阶段得到完全、一致、准确、合理的需求说明是很困难的,在获得一组基本需求说明后,就快速地使其"实现",通过原型反馈,加深对系统的理解,并满足用户基本要求,使用户在试用过程中受到启发,对需求说明进行补充和精确化,消除不协调的系统需求,逐步确定各种需求,从而获得合理、协调一致、无歧义的、完整的、现实可行的需求说明。
又把快速原型思想用到软件开发的其他阶段,向软件开发的全过程扩展。
即先用相对少的成本,较短的周期开发一个简单的、但可以运行的系统原型向用户演示或让用户试用,以便及早澄清并检验一些主要设计策略,在此基础上再开发实际的软件系统。
优点:(1)有助于满足用户的真实需求。
(2)原型系统已经通过与用户的交互而得到验证,据此产生的规格说明文档能够正确地描述用户需求。
(3)软件产品的开发基本上是按线性顺序进行。
(4)因为规格说明文档正确地描述了用户需求,因此,在开发过程的后续阶段不会因为发现规格说明文档的错误而进行较大的返工。
(5)开发人员通过建立原型系统已经学到了许多东西,因此,在设计和编码阶段发生错误的可能性也比较小,这自然减少了在后续阶段需要改正前面阶段所犯错误的可能性。
(6) 快速原型的突出特点是“快速”。
开发人员应该尽可能快地建造出原型系统,以加速软件开发过程,节约软件开发成本。
原型的用途是获知用户的真正需求,一旦需求确定了,原型可以抛弃,当然也可以在原型的基础上进行开发。
高等数学第2章课后习题及答案

-----高等数学第2章课后习题及答案习题211 设物体绕定轴旋转 在时间间隔 [0 t]内转过的角度为从而转角是 t 的函数(t) 如果旋转是匀速的 那么称为该物体旋转的角速度 如果旋转t是非匀速的 应怎样确定该物体在时刻t 0 的角速度?解 在时间间隔 [t 0 t 0t] 内的平均角速度为(t 0t ) (t 0 )tt故 t 0 时刻的角速度为l i ml i m l i m(tt) (t 0) (t )t 0t 0 tt 0t2 当物体的温度高于周围介质的温度时物体就不断冷却 若物体的温度 T与时间 t 的函数关系为 T T(t) 应怎样确定该物体在时刻t 的冷却速度?解 物体在时间间隔 [t 0 t 0t]内 温度的改变量为T T(tt) T(t)平均冷却速度为T T (t t) T(t) t t故物体在时刻 t 的冷却速度为limT lim T (t t ) T (t ) T (t) t 0t t 0 t 3 设某工厂生产 x 单位产品所花费的成本是 f(x)元 此函数 f(x)称为成本函数成本函数 f(x)的导数 f (x)在经济学中称为边际成本 试说明边际成本 f (x)的实际意义解 f(x x)f(x)表示当产量由 x 改变到 x x 时成本的改变量f (x x) f (x)表示当产量由 x 改变到 x x 时单位产量的成本xf (x)lim 0f (x x) f ( x)表示当产量为 x 时单位产量的成本x x4 设 f(x)10x 2 试按定义 求 f ( 1)解 f ( 1)limf ( 1 x) f ( 1)10( 1x)2 10( 1)2xlimxxx 010 lim0 2 xx 2 10 lim ( 2x) 20xxx 05 证明 (cos x) sin x解 (cosx) limcos(x x) cosxxx2s i nx(x) s i nxlim2 2x 0 xlim [ s i nx(x ) s i n x] s i nx 2 x 0 2x26 下列各题中均假定 f (x 0)存在 按照导数定义观察下列极限指出 A 表示什么(1) lim f ( x 0x) f ( x 0 ) A xx 解 Alim0f (x 0x) f (x 0)xxl i mf ( xx) f (x 0) f ( x 0 )x 0x(2) lim f (x)A 其中 f(0) 0 且 f (0)存在x 0 x解 Alim f ( x) lim f (0 x) f (0) f (0)x 0 x x 0x (3) lim f (x 0 h) f (x 0 h)Ah 0h解A lim f ( x 0 h 0 lim[ f (xh 0limf (xh 0h)f (x 0 h) hh) f ( x 0 )] [ f (x 0 h) f (x 0)]h h) f (x 0)limf (xh) f ( x 0 ) hh 0hf (x 0) [ f (x 0)] 2f (x 0)7 求下列函数的导数(1)y x 4(2) y 3 x 2(3) y x1 6-----(4) y1 x(5) y1x23 5 x(6) y x232(7) y x x解 (1)y (x 4) 4x 4 1 4x 322 1 2 x (2) y (3 x 2 ) ( x 3 )2x 3331 3(3)y (x 1 6) 1 6x 1 6 1 1 6x 0 61 1 x(4) y ( 1) (x 2)x21 121 x 23 2(5) y(1)( x 2 )2x 3x 23 516 16 16 116 11 (6) y (x x) (x 5)x 5 x 555(7) y ( x2 3 x21 111 x ) (x 6) 1 x 6x 5665 68 已知物体的运动规律为 s t 3(m) 求这物体在 t 2 秒 (s)时的速度解 v(s) 3t 2 v|t 2 12(米 /秒)9 如果 f(x)为偶函数且 f(0)存在 证明 f(0)证明 当 f(x)为偶函数时 f( x) f(x)所以f (0) l i mf (x)f (0) l i m f (x) f (0) l i m f ( x) f (0)x 0xx 0x 0x 0x 0从而有 2f (0) 0 即 f (0) 010 求曲线 ysin x 在具有下列横坐标的各点处切线的斜率x 解 因为 y cos x 所以斜率分别为2 1k 1 c o sk 2 cos 13 2f (0)2x311 求曲线 y cos x 上点 ( , 1) 处的切线方程和法线方程式3 2解 ysin x ysin3x3 23故在点 (, 1) 处 切线方程为 y 1 3(x)3 22 23法线方程为 y 1 2(x )23 312 求曲线 y e x在点 (0 1)处的切线方程 解 y e xy |x 0 1 故在 (0 1)处的切线方程为y 1 1 (x 0)即 y x 113 在抛物线 y x 2上取横坐标为 x 1 1 及 x 2 3 的两点 作过这两点的割线问该抛物线上哪一点的切线平行于这条割线?解 yy(3) y(1)9 1 42x 割线斜率为 k132令 2x 4 得 x 2因此抛物线 y x 2 上点 (2 4)处的切线平行于这条割线 14 讨论下列函数在 x 0 处的连续性与可导性(1)y |sin x| (2) yx 2sin 1x 0xx 0解 (1)因为y(0) 0 lim y lim |sin x | lim ( sin x) 0x 0x 0x 0 lim ylim |sin x|lim sin xx 0x 0x所以函数在 x 0 处连续又因为y (0)l i m y( x)y(0) l i m |si nx | |si n0 |l i m s i nx1x 0x 0x 0x 0x 0xy (0) lim y( x) y(0) lim |sin x | |sin0|lim s i nx 1x 0 x 0 x 0x 0 x 0 x而 y (0) y (0) 所以函数在 x 0 处不可导-----解 因为 lim y(x) lim x 2sin10 又 y(0)0 所以函数在 x 0 处连续x 0 x 0x 又因为21 0y(x) y(0)xs i n1 l i mx l i ml i mxs i n 0 x 0xx 0xx 0x所以函数在点 x 0 处可导 且 y (0) 015 设函数 f (x)x 2x 1为了使函数 f(x)在 x 1 处连续且可导a b 应取什ax b x 1么值?解 因为lim f ( x) lim x 21 limf (x) lim (ax b)a b f(1) a bx 1x 1x1x 1所以要使函数在 x1 处连续 必须 a b 1 又因为当 a b1 时f (1)x 2 12l i m1x 1 xf (1) lim ax b 1 lim a( x 1) a b 1 lim a(x 1) ax 1 x 1 x 1 x 1 x 1x 1 所以要使函数在 x 1 处可导 必须 a 2 此时 b 116已知 f (x)x 2x 0求 f (0)及 f(0) 又 f (0)是否存在?x x 0解 因为f(0) lim f (x) f (0)lim x 0x 0 x x 0x f(0) lim f (x) f (0)lim x 2 0xxx 0x 而 f (0) f (0) 所以 f (0)不存在17 已知 f(x)sin x x0 求 f (x)x x解 当 x<0 时 f(x) sin x f (x) cos x 当x>0 时 f(x) x f (x) 11因为 f (0) lim f (x) f (0) lim sin x 0 1x 0 x x 0xf (0) lim f (x)f (0) lim x 0 1所以 f (0) 1 从而x 0x x 0x f (x)cosx x1 x18 证明 双曲线 xy a 2 上任一点处的切线与两坐标轴构成的三角形的面积都等于 2a 2解 由 xy a 2得 ya 2k ya 2xx 2设 (x 0 y 0)为曲线上任一点则过该点的切线方程为y a2x 0 ) y 02 ( xx 02y x 2令 y 0并注意 x 0y 0a 解得 xx 0 2x 0为切线在 x 轴上的距 a 2令 x 0并注意 x 0y 0 a 2 解得 y a 2y 2 y0 为切线在 y 轴上的距x 0 0此切线与二坐标轴构成的三角形的面积为S1|2x 0 ||2y 0 | 2|x 0 y 0 | 2a 22习题221 推导余切函数及余割函数的导数公式(cot x)csc 2x(csc x)csc xcot x解 (cot x)(cosx )sin x sin x cosx cosxsin xsin 2 x2 21 2s i nx c o s x2 2 c s cxs i nxs i nx( c sxc) ( 1 ) c o xsc s cx c o xt s i nx 2s i n x 2 求下列函数的导数(1) y4 7 2 12x 5 x 4x-----(2) y 5x 3 2x 3e x (3) y 2tan x sec x 1 (4) y sin x cos x (5) y x 2ln x (6) y 3e x cos x(7) yln xxx(8) y e 2 ln 3x(9) y x 2ln x cos x(10) s 1 sint1 cost解 (1) y ( 4 7 2 12)(4x 5 7x 4 2x 112)x 5 x 4 x20x628x52x220282x6x5x2(2) y (5x 32x 3e x ) 15x22xln2 3ex(3) y (2tan x sec x 1)2sec x tan x sec x(2sec x tan x)2sec x (4) y (sin x cos x) (sin x) cos x sin x (cos x)cos x cos x sin x ( sin x) cos 2x(5) y (x 2ln x) 2x ln x x 21 x(2ln x 1)x(6) y (3e x cos x) 3e x cos x 3e x ( sin x) 3e x(cos x sin x)ln x1 x ln x1 ln x(7) y ( ) xx x 2 x 2(8) y ( e x ln 3) e x x 2 e x 2x e x ( x 2)x 2 x 43x(9) y221cos x x 2ln x ( sin x)(x ln x cos x) 2x ln x cos x x x2x ln x cos x x cos x x 2 ln x sin x(10) s (1sin t ) cost(1 cost) (1 sin t)( sin t)1 sin t cost1 cost(1 cost)2(1 cost)23 求下列函数在给定点处的导数(1) y sin x cos x 求 y和 yxx46(2)sin1cos 求d2d4(3) f (x)3 x 2求 f (0)和 f (2)5 x 5解 (1)ycos x sin xyc o s s i n3 1 3 1x22266 6yc o s s i n22 2x2 244 4(2)dsincos1sin1sincosd22d1s i nc o s 1 2 422(1)d4 244 4 2 22 42(3) f (x)32x f (0)3 f (2) 17(5 x)2525154 以初速 v 0 竖直上抛的物体其上升高度 s 与时间 t 的关系是 s v 0t 1gt 22求(1)该物体的速度 v(t)(2)该物体达到最高点的时刻解 (1)v(t) s (t) v 0 gt(2)令 v(t) 0 即 v 0 gt 0 得 t v 0这就是物体达到最高点的时刻g5 求曲线 y 2sin x x 2 上横坐标为 x 0 的点处的切线方程和法线方程 解 因为 y 2cos x 2x y |x 0 2又当 x 0 时 y 0 所以所求的切线方程为y 2x所求的法线方程为-----y 1x即x 2y 0 26求下列函数的导数(1)y (2x 5)4(2)y cos(4 3x)(3) y e 3x 2(4)y ln(1x2)(5)y sin2x(6) y a2x2(7)y tan(x2)(8)y arctan(e x)(9)y(arcsin x)2(10) y lncos x解 (1) y4(2x 5)4 1 (2x5) 4(2x 5)3 2 8(2x 5)3 (2)y sin(4 3x) (4 3x)sin(4 3x) ( 3) 3sin(4 3x)(3) y e 3 x2 ( 3x2 )(4)y1 (1 x2)1x2(5)y 2sin x (sin x) e 3x 2(6x)6xe 3x212x2x1 x2 1 x22sin x cos x sin 2x(6) y [( a21] 1 (a211(a2 x2 ) x2) 2x2) 221 (a2x2 )1x2 ( 2x)x2 2a2 (7) y sec2(x2) (x2)2xsec2(x2)(8) y1x2 (e x)e x2x1(e ) 1 e2 arcsin x (9) y2arcsin x (arcsin x)1x2(10) y1 (cosx)1( sin x) tan xcosx cosx 7 求下列函数的导数(1) y arcsin(1 2x)(2) y11 x 2x(3) y e 2 cos3x(4) y arccos 1x(5) y1 ln x1 ln x (6) y sin 2xx(7) y arcsin x(8) y ln(x a 2 x 2 ) (9) y ln(sec x tan x)(10) y ln(csc x cot x)解 (1) y1(1 2x)21 1 (1 2x)2x x 21 (1 2x) 2(2) y [(111 1 x 2)x 2) 2]1(1 x 2) 2(1213x(1 x 2 ) 2 ( 2x)x 22(1 x 2 ) 1xxxx) cos3xx(3) y (e 2) cos3x e 2(cos3x) e 2(e 2( sin 3x)(3x)21 e xxx2 c o 3sx 3e 2 s i n3x 1e 2( c o3sx6s i n3x)22-----(4) y1 1 (1)1 1 ( 1 )|x|1 (2 x 1 ( ) 2x2x 2x21)xx1(1 l n x) (1 ln x)12(5) yxx(1ln x) 2x(1 ln x)2(6) ycos2x 2 x sin 2x 1 2x cos2x sin2xx2x2(7) y1( x)1111 ( x)21 ( x )22 x 2 x x 2(8) y1x 2 (xa 2x 2 )1x 2 [1 1(a 2 x 2) ]xa 2x a 22 a 2 x 21[112 (2x)]1x a 2 22 a 2x a 2x 2x(9) y1(secx tan x) secxtan x(10) y1(csc x cot x)csc x cot xsecx tan x sec 2x secxsecx tan x cscx cot x csc 2 x cscxcscx cot x8 求下列函数的导数(1) y (arcsin x )22(2) y ln tan x2(3) y 1 ln 2 x(4) y e arctan x(5) y sin nxcos nx(6) y arctanx 1x 1(7) y arcsinxarccosx(8) y=ln[ln(ln x)](9) y1x 1 x 1 x1 x(10) y arcsin1 x1 x解 (1) y2(arcsin x ) (arcsin x)2 22( a r c s xi)n 1( x)2 1 ( x )2 222( a r c s xi) n1 x 12 1 ( ) 222x2a r c s i n24 x 2(2) y1x (tan x) 1 x sec 2 x( x)tan 2 tan2 22 2(3) y(4) y1 2 x 1x s e c2 c s cxt a n 22 1 ln 2 x 2 1 (1 ln 2 x)1 ln2 x1 2ln x ( l nx)12ln x12 1 ln 2x2 1 ln 2xxln xx1 ln2 xearctan x(arctan x)e arctan x1 x) 2( x)1 (-----e a r c t axn11x e a r c t axn1( x)2 2 2 x(1 x)(5) y n sin n 1x (sin x) cos nx sin n x ( sin nx) (nx)n sin n 1x cos x cos nx sin n x ( sin nx) nn sin n 1x (cos x cos nx sin x sin nx) n sin n 1xcos(n 1)x(6) y1( x 1) 1(x 1) ( x 1)11 ( x 1) 2x 11 (x 1)2(x 1)2 1 x 2x 1x 11arccosx 1 arcsin x1 x2 1 x 2(7) y(arccos x)21 a r c c oxs a r c s ixn1 x22( ar c c ox)s2 1 x 2 ( a r c cxo)2s(8) y1 ln(ln x)1ln(ln x)[ln(ln x)] 11(ln x)ln(ln x) ln x 1 1 1 ln x x xln x l n ( lxn)(1 1 )( 1 x1 x) ( 1 x1 x)(1 1)(9) y2 1 x 2 1 x2 1 x 2 1 x( 1 x1 x)211 x 21 x2(10) y1 (1 x) 1 (1 x) (1 x)1 1 x 1 x 1 1 x(1 x)21 x1 x1(1 x) 2x(1 x)9. 设函数 f(x)和 g(x)可导且 f 2(x) g 2(x) 0 试求函数 y f 2 (x) g 2 (x) 的导数解 yf 1[ f 2(x) g2 (x)]22 (x)g 2(x)1[2 f (x) f ( x) 2g(x) g ( x)] 2f 2(x)g2(x)f (x) f (x)g(x)g (x)f 2 (x)g 2 (x)10设 f(x)可导求下列函数 y 的导数dy dx(1) y f(x2)(2)y f(sin2x) f(cos2x)解 (1) y f (x2) (x2)f(x2) 2x 2x f (x2)(2)y f(sin2x) (sin2x) f (cos2x) (cos2x)f(sin2x) 2sin x cos x f (cos2x) 2cosx ( sin x)sin 2x[f (sin2x)f(cos2x)]11求下列函数的导数(1)y ch(sh x )(2)y sh x e ch x(3)y th(ln x)(4)y sh3x ch2x(5)y th(1 x2)(6)y arch(x2 1)(7)y arch(e2x)(8)y arctan(th x)(9)y ln chx12 x 2ch(10)y ch2( x 1) x 1解 (1) y sh(sh x) (sh x) sh(sh x) ch x(2) y ch x e ch x sh x e ch x sh x e ch x(ch x sh2x)(3) y1(ln x)12 (ln x)2 (ln x)ch x ch-----(4) y3sh 2x ch x 2ch x sh x sh x ch x (3sh x 2) (5) ych 21 2 (1 x 2)2 2xx 2 )(1 x )ch (1 (6) y1 1(x 2 1)2x( x 2 1)x 4 2x 2 2(7) y1(e 2x)2e2x(e 2x )21 e 4 x 1 (8) y 1(th x) 1 1 1 1 1 (thx) 2 1 th 2 x ch 2 x 1 2 2sh x ch xch 2x 1 1ch 2 x sh 2x 1 2sh 2 x(9) y1 (ch x) 1 (ch 2x)ch x2ch 4 xsh x 1 2ch x shxch x2ch 4 xsh x shx sh x ch 2x shxch xch 3x ch 3xsh x (ch 2 x 1) sh 3x th 3xch 3xch 3x(10) y2ch(x1) [ch(x1)] 2ch(x1) sh(x1) ( x 1)x 1x 1x 1 x 1 x 1sh(2x 1(x 1) (x 1)2sh(2 x 1)(x 1)2( x 1)2 )x 1x 112 求下列函数的导数(1) y e x (x 2 2x 3)(2) y sin 2x sin(x 2) (3) y (arctan x )22(4) yln xx ne t e (5) ye t ett(6) y ln cos 1x(7) y e sin 2 1x(8) y x x(9) yxarcsinx4 x 22(10) y arcsin2t1 t 2解 (1) y e x (x 2 2x 3) e x (2x 2) ex( x 2 4x 5)(2) y2 222sin x cos x sin(x ) sin x cos(x ) 2xsin2x sin(x 2) 2x sin 2x cos(x 2)(3) y 2arctanx1 1 4 arctan x2 1 x 2 2 x 2 4 241 xnln x nxn 11 n ln x(4) yxx 2nx n 1(5) y(e te t )(e t e t ) (e t e t )(e te t )4e 2t(e t e t )2(e 2t 1) 211111 1 1(6) y sec x (cos x ) sec x ( sin x ) ( x 2 ) x 2tanx(7) y esin 21 ( sin 21) e sin 21xxx( 2sin 1) cos1( 1 ) xxx2122 1s i nx 2 s i nexx(8) y1x (x x )2 1 (1 1 ) 2 xxx2 x2 x 1 4 xxx(9) y arcsinxx1 12 1 ( 2x) arcsin x21 x2 2 4 x 2 24-----(10) y1 ( 2t ) 12 (1 t 2) 2t (2t) 1 (2t)2 1 t 21 ( 2t )2 (1 t 2) 21 t21 t21 t22(1 t 2)2(1 t 2)(1 t 2)2 (1 t 2 )2 |1 t 2 |(1 t 2 )习题231 求函数的二阶导数(1) y 2x 2ln x (2) y e2x 1(3) y xcos x (4) y e t sin t (5) y a 2 x 2 (6) y ln(1 x 2)(7) y tan x1(8) yx 3 12(9) y (1 x )arctan x(10) ye xx(11) y x 2xe(12) y ln( x 1 x 2 )解 (1) y 4x1 y4 1xx2(2) y e 2x 12 2e 2x 1y 2e2x 1 2 4e 2x 1(3) y xcos x y cos x xsin xy sin x sin x xcos x2sin x xcos x(4) ye tsin t e tcos t e t(cos t sin t)ye t (cos t sin t) e t ( sin t cos t) 2e t cos t(5) y21x2(a2x2)xx2a2a2a2x2x xa2ya2x2a2 x2(a2 x2 ) a2 x2(6) y11(1x2 )12x x2x2y 2(1x2 )2x (2x)2(1 x2)(1 x2 )2(1x2 )2(7) y sec2 xy2sec x (sec x)2sec x sec x tan x2sec2x tan x(8) y(x31)3x2 (x31) 2(x31)2y 6x ( x31)23x22( x31) 3x6x(2x3 1) (x3 1)4(x31)3(9) y2xarctanx(1x2)112xarctanx1 x2y2a r c t xa n2x1 x2(10)y e x x e x 1e x( x 1)x2x2y [e x( x 1) e x] x2 e x( x 1) 2x e x(x2 2x 2)x4x3(11)y e x 2x e x2(2x)e x2(12x2 )yx22x24xx22 e2x (12x )e2xe(32x )(12)y12( x1x2 )12(12x 2 )12x 1 x x 1 x 2 1 x 1 x y1(1 x2 )12x x1 x2 1 x22 1 x2)(1 x) 2 1 x-----2 设 f(x)(x6(2)?10)f解 f(x) 6(x5f(x)43 10)30(x 10) f (x) 120(x 10)f(2)120(210)32073603若 f (x)存在求下列函数 y 的二阶导数d2ydx2(1)y f(x2)(2)y ln[ f(x)]解 (1)y f(x2) (x2) 2xf(x2)y2f(x2)2x 2xf(x2)2f(x2) 4x2f(x2)(2) y1 f (x)f (x)f(x) f (x) f ( x) f(x)f( x) f (x)[ f ( x)] 2 y[ f ( x)]2[ f ( x)]24试从dx 1导出dy y(1) d 2 x ydy 2( y ) 3(2)d 3x3( y )2y y dy3( y )5解(1) d 2x d dx d1d1dx y1ydy2dy dy dy y dx y dy( y )2y( y )3(2) d3x d y d y dxdy3dy y 3dx y 3dyy ( y )3 y 3( y )2 y13( y )2 y y(y )6y(y )55已知物体的运动规律为s Asin t(A、是常数 )求物体运动的加速度并验证d 2s2 s 0dt 2解dsA cos t dt d2 s A 2 sin t dt 22d s就是物体运动的加速度dt2d2 s 2 s A 2 s i n t2 As i n t 0dt 2C1e x C2e x(6验证函数 y C1 C2是常数 )满足关系式y2y 0解y C1 e x C2 e xy C12e x C22e xy2y (C12e x C22e x)2(C1e x C2e x)(C12e x C22e x) (C12e x C22e x) 0 7验证函数 y e x sin x 满足关系式y2y2y 0解 y e x sin x e x cos x e x(sin x cos x)y e x(sin x cos x)e x(cos x sin x) 2e x cos xyx xcos x)x2y 2y 2e cos x2e (sin x2e sin x 2e x cos x2e x sin x2e x cos x2e x sin x 08求下列函数的 n 阶导数的一般表达式(1) y x n1n 12n 2n 1n 12n 都是常数)a x a x a x a (a a a(2)y sin2x(3)y xln x(4)y xe x解 (1) y nx n 1(n1)a1x n 2 (n2)a2x n 3a n 1y n(n1)x n 21 n 32n 4n 2 (n 1)(n2)a x(n 2)(n 3)a x ay(n) n(n 1)(n 2) 2 1x0 n!(2) y 2sin x cos x sin2xy 2c o 2sx 2s i n2(x)2-----y22 c o s2x()22 s i n2x( 2)22y(4)23 c o s2x(2) 23 s i n2(x 3 )22y(n)2n 1s i n2x[ (n 1)]2(3)y ln x 1y 1 x1xy ( 1)x 2y(4) ( 1)( 2)x 3y(n)(1)( 2)( 3) ( n 2)x n 1( 1)n 2(n 2)!( 1)n (n 2)!x n 1x n 1(4) y e x xe xy e x e x xe x 2e x xe xy 2e x e x xe x 3e x xe xy(n) ne x xe x e x(n x)9求下列函数所指定的阶的导数(1)y e x cos x 求 y(4)(2)y xsh x 求 y(100)(3) y x2sin 2x求y(50) .xv cos x有解 (1)令 u eu u u u(4)e xv sin x v cos x v sin x v(4) cos x所以y(4)u(4) v4u v6u v4u v u v(4)e x[cos x4(sin x)6(cos x)4sin x cos x] 4e x cos x(2)令 u x v sh x则有u 1 u0v ch x v sh x v(99)ch x v(100) sh x所以y(100)u(100)v C1 u(99) v C2u(98) v C 98 u v(98) C99 u v(99)u v(100)100100100100100ch x xsh x(3)令 u x2 v sin 2x则有u2x u 2 u0v(48)248 sin(2x48)248 s i n2x2v(49)249cos 2x v(50)250sin 2x所以y(50)u(50)v C1501u(49) v C502u(48) v C5048u v(48) C5049u v(49) u v(50)C5048u v(48)C5049u v(49) u v(50)50 492 228 sin 2x50 2x 249 c o 2sx x2 (250 s i n2x)250x2sin 2x50xc o 2sx12252 (s i n2x)2习题231求函数的二阶导数(1)y 2x2 ln x(2)y e2x 1(3)y xcos x(4)y e t sin t(5)y a2 x2(6)y ln(1 x2)(7)y tan x1(8) yx3 1(9) y (1 x2)arctan x(10) y e xx-----(11) y xe x2(12) y ln( x1x2 )解 (1) y4x1y41x x2(2) y e2x 1 2 2e2x 1y2e2x 1 2 4e2x 1(3) y xcos x y cos x xsin xy sin x sin x xcos x2sin x xcos x(4) y e t sin t e t cos t e t (cos t sin t)y e t(cos t sin t) e t (sin t cos t)2e t cos t(5) y21x2(a2x2)xx2a2a2a2x2x xx2a2ya2a2 x2(a2 x2 ) a2 x2(6) y11(1x2 )12x x2x2y 2(1x2 )2x (2x)2(1x2)(1 x2 )2(1x2 )2(7) y sec2 xy2sec x (sec x)2sec x sec x tan x2sec2x tan x(8) y(x31)3x2 (x31) 2(x31)2y 6x ( x31)23x22( x31) 3x 6x(2x3 1) (x31)4(x31)3(9) y2xarctanx(1x2)112xarctanx1 x2y2a r c t xa n 2x21 x(10)y e x x e x1 e x( x 1)x2x2y[e x ( x 1) e x ] x 2 e x ( x 1) 2x e x (x 2 2x 2)x4x3(11) ye x 2 x e x 2 (2x) e x 2 (1 2x 2 )yx 22x (1 2x 2x22e 2x ) e4x 2xe (3 2x )(12) y1( x1x 2 ) 1 (1 2x ) 1x 1 x 2x 1 x 22 1 x 21 x 2y1(1 x 2) 12xx1 x21 x 22 1 x 2)(1 x) 21 x2 设 f(x) (x 10)6f (2) ?解 f (x) 6(x 10)5 f (x) 30(x 10)4f (x) 120(x 10)3f(2) 120(2 10)3 2073603 若 f (x)存在 求下列函数(1) y f(x 2)(2) y ln[ f(x)]解 (1)yf(x 2) (x 2) 2xf (x 2) y 2f(x 2) 2x 2xf (x 2) (2) y1 f (x)f (x)f (x) f (x) f( x) f (x) y2[ f ( x)]4 试从dx 1导出dy y(1) d 2xydy 2( y ) 3(2)d 3x 3( y )2 y ydy3( y )5解 (1) d 2xd dxd 1dy2dy dydyyd 2 yy的二阶导数d x 22f (x 2) 4x 2f (x 2)f ( x) f (x) [ f ( x)] 2[ f ( x)]2d1dx y 1y dx y dy( y )2 y( y )3(2) d3x d y d y dxdy3dy y 3dx y 3dyy ( y )3 y 3( y )2 y13( y )2 y y(y )6y(y )55已知物体的运动规律为s Asin t(A、是常数 )求物体运动的加速度并验证d 2s2s 0dt 2解dsA cos t dt d2 s A 2 sin t dt 22d s就是物体运动的加速度dt2d2 s 2 s A 2 s i n t2 As i n t 0dt 2C1e x C2e x(6验证函数 y C1 C2是常数 )满足关系式y2y 0解y C1 e x C2 e xy C12e x C22e xy212e x C22x21x2e x)y (C e ) (C e C(C12e x C22e x) (C12e x C22e x) 0 7验证函数 y e x sin x 满足关系式y2y2y 0解 y e x sin x e x cos x e x(sin x cos x)y e x(sin x cos x)e x(cos x sin x) 2e x cos xyx xcos x)x2y 2y 2e cos x2e (sin x2e sin x 2e x cos x2e x sin x2e x cos x2e x sin x 08求下列函数的 n 阶导数的一般表达式(1) y x n1n 12n 2n 1n 12n 都是常数)a x a x a x a (a a a(2) y sin2x-----(3)y xln x(4)y xe x解 (1) y n 11n 2(n2 n 3n 1nx(n 1)a x2)a x ay n(n1)x n 2 (n1)(n2)a1x n 3(n 2)(n 3)a2x n 4a n 2y(n) n(n 1)(n 2) 2 1x0 n!(2) y2sin x cos x sin2xy2c o 2sx 2s i n2(x)2y22 c o s2x() 22 s i n2x( 2)22y(4) 23 cos(2x2) 23 sin(2x 3 )22(n)n 1y 2 s i n2x[ (n 1)](3)y ln x 1y 1x 1 xy ( 1)x 2y(4) ( 1)( 2)x 3(n)( 1)( 2)( 3)( n 2)x n 1( 1)n 2 (n 2)!( 1)n (n 2)!y x n 1x n 1 (4)y e x xe xy e x e x xe x 2e x xe xy 2e x e x xe x 3e x xe xy(n) ne x xe x e x(n x)9求下列函数所指定的阶的导数(1)y e x cos x 求 y(4)(2)y xsh x 求 y(100)(3)y x2sin 2x 求 y(50) .所以所以xv cos x有解 (1)令 u eu u u u(4)e xv sin x v cos x v sin x v(4)cos xy(4)u(4) v4u v6u v4u v u v(4)e x[cos x4(sin x)6(cos x)4sin x cos x] 4e x cos x(2)令 u x v sh x则有u 1 u0v ch x v sh x(99)ch x(100)sh xv vy(100) u(100) v C1 u(99)v C2u(98)v C 98 u v(98)C99 u v(99)u v(100) 100100100100(3)令 u x2u 2xv(48)100ch x xsh xv sin 2x 则有u 2 u0248 sin(2x 48 )248 s i n2x2v(49)249cos 2x v(50)250sin 2x所以y(50)u(50)v C1501u(49) v C502u(48) v C5048u v(48) C5049u v(49) u v(50) C5048u v(48) C5049u v(49) u v(50)50 492 228 sin 2x50 2x 249 c o 2sx x2 (250 s i n2x)250x 2sin 2x50xc o 2sx1 2 2 52 (2s i n2x)习题241求由下列方程所确定的隐函数 y 的导数dydx(1)y2 2x y 9 0(2)x3 y3 3axy 0(3)xy e x y(4)y 1 xe y解 (1)方程两边求导数得-----2y y 2y 2x y 0于是(y x)y yyyy x(2)方程两边求导数得3x 2 3y 2y 2ay 3axy 0于是(y 2 ax)y ayx 2yay x 2y2ax(3)方程两边求导数得y xy e x y (1 y )于是(x e x y )y e x y ye x yyyx e x y(4)方程两边求导数得y e y xe yy于是(1 xe y )y e yyey1 xey222在点 ( 2a, 2a) 处的切线方程和法线方程2 求曲线 x3y 3a34 4解 方程两边求导数得 2 x31 13 2y 3 y 031于是yx31y3在点 (2a,2a) 处 y 144所求切线方程为y2a ( x2a) 即 x y 2 a442所求法线方程为y2a (x2a) 即 x y 04423 求由下列方程所确定的隐函数 y 的二阶导数d ydx22 2(1) x y 1(2) b 2x 2 a 2y 2 a 2b 2 (3) y tan(x y)(4) y 1 xe y解 (1)方程两边求导数得2x 2yy 0yx yy ( x)y xxy xy y y 2x 21yy 2y 2y 3 y 3(2)方程两边求导数得2b 2 x 2a 2 yy 0yb 2 xa2yy x( b 2 x)b 2 y xy b 2 a 2 y ya2y2a2y 2b 2 a 2 y 2 b 2 x 2b 4a2a 2 y3a 2 y3(3)方程两边求导数得y sec 2(x y) (1 y )2y)1y s e c( x2y) 2y) 11 s e c(xc o s( x2y)21s i n(xc o s(x y)12y)y 2s i n( xy23 y23( 112 )2(1 y 2 )y 5yyy(4)方程两边求导数得yyy e xe y-----yeyeyey1 xe y1 (y 1)2 yye y y (2 y) e y ( y ) e y (3 y) y e 2 y (3 y)(2 y)2(2 y)2(2 y)34 用对数求导法求下列函数的导数(1) y ( x )x1 x (2) y5x 525 x2(3) yx 2(3 x)4( x 1)5(4) y xsin x 1e x解 (1)两边取对数得ln y xln|x| xln|1 x|,两边求导得1 y ln x x 1 l n1( x) x 1y x 1 x 于是y ( x)x[ l nx1 ]1 x 1 x 1x(2)两边取对数得ln y1ln |x 5|1l nx(22)两边求导得5251 y1 1 12x2y5 x 525 x 2于是y 1 5x 5[11 2x ]5 5 x 2 2x 5 5 x 2 2(3)两边取对数得ln y1l nx( 2) 4 l n3( x) 5l n x( 1)2两边求导得1 y 1 3 45y 2(x 2)x x 1于是yx 2(3x)4 [ 12)4 5 ](x 1)52(x x 3 x 1(4)两边取对数得ln y1ln x1ln s i nx1l n1( e x )两边求导得22 41 y1 1 c o xte xy 2x24(1 e x )于是yxs i nx 1 e x[11c o xte x]2x 2 4(1 e x )1 x 22c o tx e x ]4 xs i nx 1 e [ x e x1 dy5求下列参数方程所确定的函数的导数dxx at 2(1)y bt2x (1 sin ) (2)ycos解 (1)dyy t 3bt 2 3b tdxx t 2at 2ady ycos sin(2) dx x 1 sincos6 已知xe tsin t, 求当 t 3 时 dy的值y e tcost. dx解dy y te t cost e t sin t costsin t dxx t e tsin t e tcost sintcostdy 1 3 1 3 当 t 时 2 2 3 2dx 1 3 1 3 32 27 写出下列曲线在所给参数值相应的点处的切线方程和法线方程(1)x sin t在 t处y cos2t4x3at (2)1 t 2在 t=2 处y 3at 21 t 2解 (1) dyy t2sin 2tdxx tcost-----dy 2sin(2)当 t时42 2 2 x02y0 0 dx4cos2242所求切线方程为y 2 2(x2) 即2 2x y 2 0 2所求法线方程为y1(x 2 )即 2x 4y1222(2) y t 6at (1t2 )3at 2 2t6at(1t 2 )2(1t 2 )2x t 3a(1t 2)3at2t3a3at 2 (1t 2 )2(1t 2)2dy y t6at2tdx x t3a3at 21t 2当 t 2 时dy 2 24x 6a ydx1223050所求切线方程为012a 5y12 a 4(x6a)即 4x 3y 12a 0535所求法线方程为y12 a3(x 6a)即 3x 4y 6a 0545d 2 y8求下列参数方程所确定的函数的二阶导数dx2 x t 2(1)2y 1 t. xacost(2)y bsin t(3)x3e t y2e t(4)x f t (t )设 f(t)存在且不为零y tf t (t) f (t)dy y t1 d 2 y(y x)t1解 (1)t 21 dx x t t dx2x t t t3(2) dy y tbcostbcot tdx x t asin t ab 2 d 2 y (y x )t a csc t b dx 2 x t asin ta 2 sin 3 tdy y t 2e t22t(3) dx x t3e t3ed 2y( y x )t2 2t3 2e4 3tdx 2x t3e te9 (4) dy y t f (t) tf (t) f (t)dx x tf (t)td 2 y ( y x )t 1dx 2x tf (t)9 求下列参数方程所确定的函数的三阶导数(1) x 1 t 2y t t3(2)x ln(1 t 2) y t arctan t解 (1)dy (t t 3)1 3t2dx (1 t 2 )2t1 3t 2d 2y ( 2t )1 ( 1 3) dx 22t4 t 3 t1 1 3d 3y 4 ( t 3t )3(1 t 2)dx 32t8t 5dy (t arctan t)11(2)1 t 21 tdx [ln(1 t 2)]2t 21 t21d 2 y ( 2t) 1 t 2 dx 22t 4t1 t 23d y-----1 t 2d 3 y ( 4t ) t 4 1dx 3 2t 8t 31t 210 落在平静水面上的石头 产生同心波纹 若最外一圈波半径的增大率总是6m/s 问在 2 秒末扰动水面面积的增大率为多少?解 设波的半径为 r 对应圆面积为 S 则 S r 2 两边同时对 t 求导得S t 2 rr当 t 2 时 r 6 2 12 r t 6故 S t t 22 126 144( 米 2 秒)| 其速率为 4m 2/min11 注水入深 8m 上顶直径 8m 的正圆锥形容器中 当水深为 5m 时 其表面上升的速度为多少?解水深为 h 时 水面半径为 r1 h 水面面积为 S 1 h 21hS 1 h 1 h 224水的体积为 Vh 33 34 12dV 12 3h 2dh dh 4 dVdt dt dt h 2 dt已知 h 5(m), dV 4 (m 3/min) 因此 dh 4 dV 4 4 16(m/min)dtdt h 2 dt252512 溶液自深 18cm 直径 12cm 的正圆锥形漏斗中漏入一直径为 10cm 的圆柱形筒中 开始时漏斗中盛满了溶液 已知当溶液在漏斗中深为 12cm 时 其表面下 降的速率为 1cm/min 问此时圆柱形筒中溶液表面上升的速率为多少?解 设在 t 时刻漏斗在的水深为 y 圆柱形筒中水深为 h 于是有1 62 18 1r 2 y 52hy 3y3由 r得 r 代入上式得 6 18 31 62 18 1 ( y ) 2 y 23 3 3 5 h即162 18 1y 3 52 h 两边对 t 3 33求导得1 y2 y 52 h32t当 y 12 时 y t1 代入上式得1 122( 1) 16h t32 52 0.64 (cm/min).25。
曼昆微观经济学第二章课后答案

第二章像经济学家一样思考复习题1.经济学如何像一门科学?答:经济学家努力以科学家的客观态度来探讨经济问题。
用科学的方法提出理论、收集资料,并分析这些资料以努力证明或否定他们提出的理论来研究社会。
经济学家研究经济的过程和方法与自然科学的科学家研究自然是一样的。
所以说经济学也是一门科学。
2.为什么经济学家要做出假设?答:假设可以使解释这个世界更为容易。
对不同的问题作出不同的假设,略去对问题的答案没有实质影响的因素,突出实质性的内容,使我们可以集中进行思考。
3.经济模型应该准确地描述现实吗?答:经济模型不需要准确地描述现实。
所有的模型都是建立在假设的基础上的,它们忽略掉了大量不会对研究结果有实质性影响的细节,向我们说明什么是真正重要的。
模型是为了增进我们对现实的理解而简化了现实。
4.说出你的家庭参与要素市场的一种方式,以及参与产品市场的一种方式。
答:略。
5.举出一种没有包括在简单的循环流量图中的经济关系。
答:略。
6.画出并解释一个生产牛奶与点心的经济的生产可能性边界。
如果一场瘟疫使该经济中的一半奶牛死亡,这条生产可能性边界会发生怎样的变动?答:假设在正常情况下,将可能得到的所有资源用于生产点心,可以生产300 千克,如果全用于生产牛奶,可以生产1 000 升。
L1 表示正常情况下该经济的生产可能性边界。
如果一场疾病造成该经济一半的奶牛死亡,生产可能性边界会向内移,即L2 线。
因为在生产率不变的情况下,可用于生产点心和牛奶的经济资源减少了。
5图2—1 生产可能性边界7.用生产可能性边界描述“效率”的思想。
答:如果经济可以利用它所得到的全部稀缺资源,就可以说这种结果是有效率的。
西方经济学第02章复习思考题参考答案

第二章习题答案一、名词解释(略)二、问答题1.什么是供求规律?影响供给及需求的因素各有哪些?答:供求规律是商品经济的基本规律。
它是指商品的供求关系与价格变动之间的相互制约的必然性。
当商品供不应求,价格上涨,会刺激供给增加,抑制需求;而当商品供过于求,价格下降,又引起供给减少,刺激需求,从而使市场价格趋向稳定,供求实现平衡。
引起需求变化的因素有:(1)该商品的价格水平;(2)消费者的收入水平;(3)消费者的偏好;(4)相关商品的价格;(5)消费者的预期等。
引起供给变动的其他因素:(1)该商品的价格水平;(2)技术因素;(3)资源和其他投入要素的价格变化;(4)相关商品的价格;(5)生产者对未来价格的预期2.请画图说明需求、供给的变动对均衡价格和均衡产量变动影响的几种情形,并作扼要说明。
答:(1)图1为供给不变条件下需求变动对均衡价格的影响。
当需求因受该商品自身价格以外的因素变化(如收入、相关商品价格或突发性事件等)使该商品的需求发生变化,则会引起需求曲线的变动:需求增加,则需求曲线向右平移,从而使均衡价格和均衡数量都增加;反之,需求减少,则需求曲线向左平移,从而使均衡价格和均衡数量都减少,如图1中所示的需求曲线由D1变动到D3,均衡点由E1移至E3,相应,均衡价格由1P下降至3P,均衡数量由1Q减少至3Q。
所以在其他条件不变的前提下,需求变动分别引起均衡价格和均衡数量的同向变动。
(2)图2为需求不变条件下供给变动对均衡价格的影响。
在需求不变的前提下,因受该商品自身价格以外的因素变化(如成本、技术因素变化或突发性事件等)使该商品的供给发生变化,则会引起供给曲线的变动:供给减少,则供给曲线向左平移,从而使均衡价格上升和均衡数量减少;反之,供给增加,则供给曲线向右平移,从而使均衡价格下降和均衡数量增加,如图中的供给增加,供给曲线由S1变动到S3,均衡点由E1移至E3,相应地,均衡价格由1P下降至3P,均衡数量由1Q增加至3Q。
金融学第二版课后复习思考题参考答案

第一章货币与货币制度一、单项选择题1.B2.C3.B4.C5.A6.B7.C二、多项选择题1.ACDE2.CDE3.CD4.ABCD5.ABCDE6.ABCD三、简答题1. 货币的职能有哪些?价值尺度;流通手段;支付手段;贮藏手段;世界货币2. 人民币制度包括哪些内容?(1)人民币是我国的法定货币;(2)人民币是我国唯一的合法通货;(3)人民币的发行权集中于中央银行;(4)人民币以商品物资作为发行的首要保证,也以大量的政府政府债券、商业票据、商业银行票据等为发行的信用保证,还有黄金、外汇储备等也是人民币发行的现金保证;(5)人民币实行有管理的货币制度;(6)人民币称为可兑换货币。
3. 货币制度的构成要素是什么?货币材料;货币单位;各种通货的铸造、发行和流通程序;准备制度4. 不兑现的信用货币制度有哪些特点?(1)不兑现信用货币一般由中央银行发行,并由国家赋予其无限法偿能力,这是不兑现信用货币制度最基本的特点;(2)信用货币不与任何金属保持等价关系,也不能兑换黄金;(3)货币通过信用程序投入流通领域;(4)信用货币制度是一种管理货币制度;5. 钱、货币、通货、现金是一回事吗?银行卡是货币吗?不一样。
(1)钱的概念在不同场景下有很多不同的意思。
可以是个收入的概念、也可以是个财富的概念,也可以特指现金货币;(2)货币是在商品劳务交换与债券债务清偿时,被社会公众所普遍接受的东西。
(3)通货是流通中的货币,指流通与银行体系之外的货币。
范围小于货币。
(4)现金就是现钞,包括纸币、硬币。
现金是货币的一部分,流动性很强,对人们的日常消费影响很大。
(5)银行卡本身也称为“塑料货币”,包括信用卡、支票卡,记账卡、自动出纳机卡等。
银行卡可以用于存取款和转账支付。
在发达西方国家,各种银行卡正在取代现钞和支票,称为经济生活中广泛的支付工具,因此现代社会银行卡也是货币6.社会经济生活中为什么离不开货币?为什么自古至今,人们又往往把金钱看做说万恶之源?(1)社会经济生活离不开货币,货币的产生和发展都有其客观必然性。
.微观第二章 思考题答案详解

第二章思考题详解一、思考题A:基础知识题1.1 A答案详解:只有实际价格低于均衡价格时,供给者因为无利可图就会减少生产,从而减少供给1.2 A答案详解:总需求曲线的形状是向右下方倾斜,随着价格提高,需求是递减的。
1.3 B答案详解:如果其它各种条件均保持不变,当X商品的互补品Y商品的价格上升时,对X商品的需求减少。
1.4D答案详解:土壤的肥沃程度、技术水平、棉花的种植面积在影响供给曲线时,均保持常数。
1.5 B答案详解:对一般的商品来说,当其供给不变时,如果其需求增加,则该商品的均衡价格上升和均衡数量增加。
1.6 C答案详解:需求定理表明计算机的价格下降会引起其需求量增加。
1.7 BCD答案详解:下列各项中会引起厂商劳动需求曲线移动的因素是企业产品的价格、其他投入品的价格、生产技术二、思考题B:名校历年考研真题2.1 B答案详解:在消费者收入与商品价格既定时,消费者所能购买到的两种商品数量的最大组合的线叫做消费可能线。
2.2 B答案详解:一种商品价格下降对其互补品最直接的影响是互补品的需求曲线向右移动。
2.3 CDE答案详解:某种商品的供给曲线的移动是由于生产技术条件的变化、生产这种商品的成本的变化、政府向生产企业提供补贴。
2.4 B答案详解:消费者收入变化、消费者偏好变化、其他相关商品价格变化等因素都会使需求曲线移动。
2.5 B答案详解:当价格高于均衡价格时需求量小于供给量。
2.6 B答案详解:某月内,X商品的替代品的价格上升和互补品的价格上升,分别引起X商品的需求变动量为30单位和90单位,则在它们共同作用下该月X 商品需求数量减少60单位。
2.7 C答案详解:农产品市场上均衡价格下降,均衡数量增加的原因必定是.开发出了高产的新品种。
2.8√答案详解:提高水价,人们会减少水的使用,达到节约的效果。
2.9√答案详解:某地区的荔枝树被毁,市场上的荔枝少了,意味着市场供给减少。
2.10╳答案详解:一般来说,商品的需求量随着商品价格的上升而减少,因此相应地,需求曲线是向右下方倾斜的。
第2章-习题解答_final.pdf

∑∑ ij
i =1 j =1
n
n
b.
∑1 / i(i + 1)
i =1
n
c.
k −1
| 找到 nk-1 多项式的下界
上式, A = a k −1 + a k − 2 + ... + a ⇒ A ≥ 0 因此,
a k n k + a k −1 n k −1 + ... + a 0 ≥ a k n k − An k −1 a k n k − An k −1 ≥ C1 n k ⇐ (a k − C1 )n k ≥ An k −1 ⇐ (a k − C1 )n ≥ A ⇐ n≥ A A ∧ a k − C1 > 0 ⇐ n ≥ ∧ 0 < C1 < a k a k − C1 a k − C1
(
)
4. 计算增长次数(即写出下列和的 Θ( g (n)) ) a. 解: a.
∑ (i
i =0
n −1
2
+ 1)
b.
∑ lg i
i=2
n −1
2
c.
∑ (i + 1)2
i =2
n
i −1
d.
∑∑ (i + j )
i =0 j =0
n −1 i −1
∑ (i
i =0 n −1 i =0
n −1
2
+ 1) ≥ ∑ i 2 =
第2章习题答案 (2)

第2章习题答案
一、思考题(略)
二、选择题
1、B;
2、ABCE;
3、C;
4、A;
5、B;
6、B;
7、C;
8、ABCE;
9、ABCD;
10、ABCDEF;
三、分析题
1、(1) 数值型,定比;
(2) 品质型,定序;
(3) 数值型,定比;
(4) 品质型,定类。
2、(1)上市公司披露的反应独立董事专业能力与履职情况、独立董事身份的数据,调研获取反应独立董事社会关系的数据等;
(2)专门设计的统计研究。
4、(1)产品的口味检验与市场检验;
(2)专门设计的统计研究。
5、(1)时序数据;
(2)2003大中型工业企业科技统计口径作了调整,表中列示两列2003年的数据,是为调整前(老口径)后(新口径)的数据连续可比之需要;
(3)浙江省企业R&D投入情况,其统计范围应该包括浙江省所有大中小型企业,表中
数据仅仅是浙江省大中型工业企业,缺所有小型企业与大中型非工业企业的R&D投入数据。
需要专门设计的统计研究来获取缺失的数据。
四、案例分析(略)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 思考题参考答案
1. 工质膨胀时是否必须对工质加热?工质边膨胀边放热可能否?工质边被压
缩边吸入热量可以否?工质吸热后内能一定增加?对工质加热,其温度反而降低,有否可能?
答:由闭口系统热力学第一定律关系式:
Q U W =∆+
规定吸热0Q >,对外做功0W >。
(1) 不一定;工质膨胀对外做功,0W >,由于可以使0U ∆<,因此可能出现
0Q <,即对外放热;
(2) 能,如(1)中所示;
(3) 能;工质被压缩,对内做功,0W <,由于可以使0U ∆>,因此可能出现
0Q >,即吸入热量;
(4) 不一定;工质吸热,0Q >,由于可以使0W >,即工质对外做功,因此
可能出现0U ∆<,即工质内能减小;
(5) 可能;对工质加热,0Q >,由于可以使0W >,即工质对外做功,因此
可能出现0U ∆<,对于理想气体,其内能仅为温度的单值函数,因此对于理想气体来说温度可能降低。
2. 一绝热刚体容器,用隔板分成两个部分,左边贮有高压气体,右边为真空。
抽去隔板时,气体立即充满整个容器。
问工质内能、温度将如何变化?如该刚体容器为绝对导热的,则工质内能、温度又如何变化?
答:对于绝热刚体容器,以高压气体为对象。
由闭口系统热力学第一定律:Q =∆U +W (式1)。
其中容器绝热,则Q=0;且右边为真空,高压气体没有对外做功对象,即自由膨胀,有0W =。
所以:∆U =0,即工质的内能不发生变化。
如果工质为理想气体,那么其温度也不变;
如果工质为实际气体,则温度未必不变。
如果该刚体容器为绝对导热,那么初始状态下容器内工质与外界环境等温,而自由膨胀过程终了时容器内工质仍旧与外界环境等温。
当外界环境温度不发生变化时,容器内工质温度在整个自由膨胀过程中温度不变。
自由膨胀0W =,所以Q =∆U 。
如果工质为理想气体,其温度不变则内能也不变,∆U =0,所以Q =0; 如果工质为实际气体,Q =∆U ,无法进一步推断。
3. 图2-9 中,过程1-2与过程1-a-2 有相同的初、终点,试比较: 12W 与12a W ,12U ∆与12a U ∆,12Q 与12a Q
答:根据图2-9,由于是p-v 图,因此有:0〈12W 〈12a W (对外做功);
12U ∆=12a U ∆;
由闭口系统热力学第一定律,Q U W =∆+,有0〈12Q 〈12a Q (吸热)。
4. 推进功与过程有无关系?
答:推进功是因工质出、入开口系统而传递的功。
推进功是工质在流动中向前方传递的功,并且只有在工质的流动过程中才出现。
当系统出口处工质状态为(out p ,out v )时,1kg 工质流出系统,系统所需要做出的推进功为out out p v 。
推进功的大小仅与选取出口处的压力和比容数值的乘积有关,因此是状态参数,且为广延参数。
5. 你认为“任何没有体积变化的过程就一定不对外做功”的说法是否正确? 答:错误。
体积变化仅产生容积变化功。
除了容积变化功外,还有电功、推进功等等,这些功不需要体积发生变化。
6. 说明下述说法是否正确:
(1) 气体膨胀时一定对外做功。
(2) 气体压缩时一定消耗外功。
答:对“功”的理解,功可以分为有用功和无用功,有用功是指有目的且产生有用效果的功。
(1)气体膨胀时不一定对外做功,如气体的自由膨胀,由于气体没有做功对象,因此气体对外做功为零;(2)不一定。
当热气体冷却时,如果外界大气做的功为有用功,则(2)成立,但是如果外界大气做的功为无用功,则(2)不成立。
7. 下列各式是否正确:
q du w δδ=+ (1)
q du pdv δ=+ (2)
()q du d pv δ=+
(3) 各式的适用条件是什么?
答:三个式子都针对1kg 工质。
(1)式是针对闭口系的能量方程,且忽略闭口系的位能和动能变化,w δ为闭口系统与外界交换的净功。
(2)式是针对简单可压缩系统准静态过程(或可逆过程)的能量方程,pdv 为系统与外界交换的容积变化功。
(3)式是针对技术功为零的稳定流动能量方程,即()q dh du d pv δ==+,且0t w δ=。
8. 试写出表2-1内所列四种过程的各种功计算式。
注:低压气体可以认为是理想气体,且内能仅为温度的单值函数。
计算依据:
(1) q u w =∆+
(2) t q h w =∆+
(3) ()h u pv ∆=∆+∆
(4) ()t w pv w =∆+。
