中考数学专题训练——专题一 几何题型( 中点M型)(无答案)
中考数学几何专项——中点专题

中点专题【类型一】见中线 可倍长例1、如图,已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 点F ,AF=EF ,求证:A C=BE.变式、如下图所示,在△ABC 中,AD 交BC 于点D ,点E 是BC 中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,若AD 为△ABC 的角平分线,求证:BG =CF.例2、如图,在ABC Rt ∆中,︒=∠90BAC ,点D 为BC 中点,点E 、F 分别为AB 、AC 上的点,且FD ED ⊥.以线段BE 、EF 、FC 为边能否构成一个三角形?若能,请判断此三角形的形状.变式1、 如图所示,已知M 为△ABC 中BC 边上的中点,∠AMB 、 ∠AMC 的平分线分别交AB 、AC 于点E 、F ,连接EF .求证:BE+CF>EF .4例3、已知:ABC ∆和ADE ∆是两个不全等的等腰直角三角形,其中BC BA =,DE DA =,连接EC,取EC 的中点M,连接BM 和DM.(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是____________;(2)将图1中的ADE ∆绕点A 旋转到图2的位置,此时DE AC //判断(1)中的结论是否仍然成立,并说明理由.检测1、在ABC ∆中,AD 是边BC 上的中线,已知4=AB ,6=AC ,则中线AD 的取值范围是___________。
检测2、如图,在△ABC 中,D 是BC 边上的中点,DE ⊥DF ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF 。
①求证:BE +CF >EF 。
(4分)【类型二】见等腰三角形,想“三线合一”例4、如图所示:一幅三角板如图放置,等腰直角三角板ABC 固定不动,另一块三角板的直角顶点放在等腰直角三角形的斜边中点D 处,且可以绕点D 旋转,在旋转过程中,两直角边的交点G 、H 始终在边AB 、BC 上.(1)在旋转过程中线段BG 和CH 大小有何关系?证明你的结论.(2)若cm BC AB 4==,在旋转过程中四边形GBHD 的面积是否改变?若不变,求出它的值;若改变,求出它的取值范围.(3)若交点G 、H 分别在边AB 、BC 的延长线上,则(1)中的结论仍然成立吗?请画出相应的图形,直接写出结论.例5、如图,点P 是等腰Rt △ABC 底边BC 上一点,过点P 作BA 、AC 的垂线,垂足为E 、F ,设点D 为BC 中点,求证:△DEF 是等腰直角三角形.检测1、如图,ABC ∆是等腰直角三角形,AC AB =,D 是斜边BC 的中点,E 、F 分别是AB 、AC 边上的点,且.(1)请说明:DF DE =;(2)请说明:222EF CF BE =+;(3)若6=BE ,8=CF ,求DEF ∆的面积(直接写结果).【类型三】见斜边 想中线例6、如图,在ABC ∆中,若C B ∠=∠2,BC AD ⊥,E 为BC 边中点,求证:DE AB 2=.例7、 如图,在ABC Rt ∆中,︒=∠90ACB ,点D 、E 分别为AB 、BC 的中点,点F 在AC 的延长线上,B FEC ∠=∠.请问DE CF =成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)检测2、如图在Rt △ACB 中,C 为直角顶点,∠ABC=25°,O 为斜边中点,将OA 绕着点O 逆时针旋转θ°(0<θ<180)至OP ,当△BCP 恰为轴对称图形时,θ的值为 .【类型四】见多个中点,想中位线例8、如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,证得HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF交延长,与BA的延长线交于点G,若∠EFC=60°,连结GD,判断△AGD的形状并证明.检测1、如图,在ABC ∆中,点O 是重心,10=BC ,连接AO 并延长交BC 于点D,连接BO 并延长交AC 于点E,BE AD ⊥.若62==OD BE ,6=AO ,则AC 的值为________。
中考数学基本模型—中点模型,初三数学专题复习总结倍长中线练习题
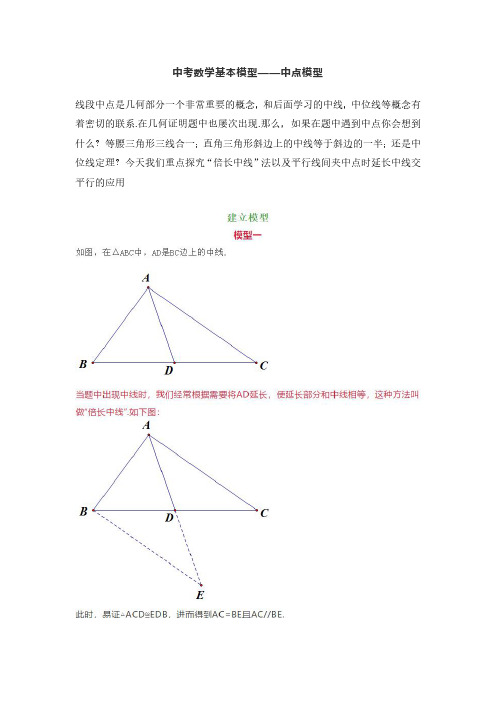
中考数学基本模型——中点模型线段中点是几何部分一个非常重要的概念,和后面学习的中线,中位线等概念有着密切的联系.在几何证明题中也屡次出现.那么,如果在题中遇到中点你会想到什么?等腰三角形三线合一;直角三角形斜边上的中线等于斜边的一半;还是中位线定理?今天我们重点探究“倍长中线”法以及平行线间夹中点时延长中线交平行的应用线相交.即“延长中线交平行”此时,易证△BEF≌△CED模型三如图,在△ABC中,点D是AB边的中点.可作另一边AC的中点,构造三角形中位线.如下图所示:时,只需将AE延长和DC的延长线相交,就一定会得到全等三角形,进而得到我们需要的结果.证明:如图,延长AE交DC的延长线于点F.∵四边形ABCD是平行四边形∴AB//CD,即AB//DF∴∠BAE=∠CFE,∠B=∠FCE又∵点E是BC中点∴BE=CE∴△ABE≌△FCE∴CF=AB=CD,AE=FE∴DF=2CD,又∵AD=2CD∴AD=DF,又因为点E是AF的中点∴DE⊥AF即∠AED=90°.反思:对于本题,还可以延长AE至点F使EF=AE,连接CF.通过证明△ABE ≌△FCE得到AB//CF,利用经过直线外一点有且只有一条直线与已知直线平行,得到D、C、F三点共线.再证明△DAF是等腰三角形,利用等腰三角形三线合一得到结论.对于第二种方法,同学们可以自己尝试.例2、在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.分析:由题可知,DE//BF,且点G是BE的中点,满足平行线间夹中点,所以可将DG延长与BF相交.证明:(1)AG=DG,且AG⊥DG.如图,延长DG交BF于点H,连接AH,AD.∵四边形CDEF是正方形,∴DE//CF即DE//BC∴∠GBH=∠GED,∠GHB=∠GDF又∵点G是BF的中点∴GB=GF∴△GBH≌△GDF(AAS)∴GD=GH,BH=DF∵DE=DC,∴BH=CD因为△ABC是等腰直角三角形∴AB=AC,∠ACD=180°-45°-90°=45°=∠ABC∴△ABH≌△ACD∴AH=AD,∠BAH=∠CAD∴∠DAH=∠CAD+∠CAH=∠BAH+∠CAH=∠BAC=90°∴△DAH是等腰直角三角形,又∵点G是DH的中点∴AG=DG且AG⊥DG.反思:若将正方形绕点C旋转任意角度,在旋转的过程中,上述结论还成立吗?试试看(2)AG⊥DG,AG=√3DG如图,延长DG交BF于点H,连接AH,AD.∵四边形CDEF是菱形,∴DE//CF即DE//BC∴∠GBH=∠GED,∠GHB=∠GDF又∵点G是BF的中点∴GB=GF∴△GBH≌△GDF(AAS)∴GD=GH,BH=DF∵DE=DC,∴BH=CD因为△ABC是等边三角形∴AB=AC,∠ACD=180°-60°-60°=60°=∠ABC∴△ABH≌△ACD∴AH=AD,∠BAH=∠CAD∴∠DAH=∠CAD+∠CAH=∠BAH+∠CAH=∠BAC=60°∴△DAH是等边三角形,又∵点G是DH的中点∴AG⊥DG.∠DAG=1/2∠DAH=30°∴AG=√3DG(3)AG⊥DG,DG=AG×tan(α/2)证明:延长DG与BC交于H,连接AH、AD,∵四边形CDEF是菱形,∴DE=DC,DE∥CF,∴∠GBH=∠GED,∠GHB=∠GDE,∵G是BE的中点,∴BG=EG,∴△BGH≌△EGD(AAS),∴BH=ED,HG=DG,∴BH=DC,∵AB=AC,∠BAC=∠DCF=α,∴∠ABC=90°﹣α/2,∠ACD=90°﹣α/2,∴∠ABC=∠ACD,∴△ABH≌△ACD(SAS),∴∠BAH=∠CAD,AH=AD,∴∠BAC=∠HAD=α;∴AG⊥HD,∠HAG=∠DAG=α/2,∴tan∠DAG=tan(α/2),∴DG=AGtan(α/2).反思:在本题的证明中,我们结合题目中给出的平行线间夹中点这一条件,将DG进行延长和BC相交,通过全等使问题得证.对于本题我们也可以采用倍长中线法进行证明.下面用倍长中线法对第一种情况加以证明.证明:如图,延长AG至点H,使GH=AG.连接EH,AD,DH.在△ABG和△HEG中BG=EG,∠AGB=∠HGE,AG=HG∴△ABG≌△HEG∴AB=HE,∠ABG=∠HEG∵AB=AC∴AC=HE∵DE//BC∴∠DEG=∠EBC∴∠HED=∠HEB+∠DEG=∠ABG+∠EBC=∠ABC=45°又∠ACD=180°-45°-90°=45°∴∠ACD=∠HED在△ACD和△HED中AC=HE,∠ACD=∠HED,DC=DE∴△ACD≌△HEDDA=DH,∠ADC=∠HDE∴∠ADC-∠HDC=∠HDE-∠HDC即∠ADH=∠CDE=90°所以△ADH是等腰直角三角形又因为点G是AH的中点所以DG=AG,DG⊥AG.上面我们用倍长中线证明了第一种情况,请你对第二三问加以证明.反思:在本题的证明过程中,容易犯的一个错误是,许多同学看到HE经过点C,就说∠HED=45°.而这一结论是需要证明的.小试身手如图1,在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG.易证:EG=CG且EG⊥CG.(1)将△BEF绕点B逆时针旋转90°,如图2所示,则线段EG和CG有怎样的数量和位置关系?请直接写出你的猜想.(2)将△BEF绕点B逆时针旋转180°,如图3所示,则线段EG和CG又有怎样的数量和位置关系?请写出你的猜想,并加以证明.(3)将△BEF绕点B旋转一个任意角度α,如图4所示,则线段EG和CG 有怎样的数量和位置关系?请直接写出结论.前两问较简单,请同学们自行完成,这里只给出第三问的几种解法,仅供大家参考.解法一:如图,延长EG至点H,使GH=EG.连接DH,CE,CH.因为点G是DF的中点,所以GF=GD.根据SAS易证△GEF≌△GHDEF=HD且∠GEF=∠GHD,所以EF//DH.分别延长HD与EB交于点K,HD的延长线交BC于点M.如下图:因为EB⊥EF,而EF//DH,所以EK⊥HK,即∠BKM=∠MCD=90°.又∠BMK=∠CMD.根据三角形的内角和,可得∠KBM=∠MDC.所以∠EBC=∠HDC.又EB=HD,BC=DC所以△EBC≌△HDC.所以CE=CB且∠ECB=∠HCD.所以∠ECB=90°,即△BCE是等腰直角三角形,又因为点G是斜边EB的中点,所以CG⊥GE且CG=GE.解法二:如图,延长CG至点N,是GN=CG.连接FN,EN,EC.以下过程可参照解法一自行完成解法三:延长FE至点P使得EP=EF,连接BP;延长DC至点Q,使得CQ=CD,连接BQ.连接FQ,DP。
中考数学压轴题《中点模型》

解题方法一. 倍长中线在△遊中•”为證边的中点.图1(1) 如图1,连结川/并延长至点尸,使得ME=AM.连结⑦ 则△月&溜(2) 如图2,点。
在初边上,连结6/并延长至点呂使得\fF=DM.连结⑦ 则△血孑 Q'CEH 、遇到线段的中点问题,常借助倍长中线的方法还原中心对称图形,利用“8”字形全等 将题中条件集中,达到解题的目的,这种方法是最常用的也是最重要的方法.二. 构造中位线在△磁中.Q 为初边的中点,图1 图2(1) 如图1,取M 边的中点伐 连结比 则DE//BC.且DF=-BC ・2(2) 如图2・延长證至点尸.使得CF=BC ・连结AF.则DC//AF.且DC=-AE.三角形的中位线从位置关系和数量关系两方而将将图形中分散的线段关系集中起来•通 常需要再找一个中点来构造中位线,或者倍长某线段构造中位线,三. 等腰三角形“三线合一”《中点模型》 A AE如图,在△磁中,若AB=AC・通常取底边氏的中点D・则初丄万G且肋平分ZBAC.事实上,在△磁中:(£)AB=AC;②初平分ZBAC;③BD=CD、④初丄反・对于以上四条语句,任意选择两个作为条件,就可以推出另两条结论,即“知二得二”・B u四・直角三角形斜边中线如图,在△遊看,Z磁=90°,取胚的中点Q,连结助,则有BD=AD=CD=-AC. 2反过来,/£AABC中,点Q在川7边上,若BD=AD=CD=、AC,则有ZABC=90Q例题讲解例1如图,在四边形丽G?中,E、尸分别是曲、仞的中点,过点疋作曲的垂线,过点尸作切的垂线,两垂线交于点G,连结/1G、BG、CG且ZAGD=ZBGC,若肋、證所在直线互相垂直,求呼的值EF解由题意可得阳和为共顶点等顶角的两个等腰三角形,所以△必谑△07G HEGF.方法一:如图1,连结传并延长到F,使曲=云7,连EH、AH,则AH//BC. AH=BC、而/1P=万G ADLBC所以肋=加肋丄加连结加则△妙为等腰直角三角形,又因为E尸分别为阳、CD的中点,所停益皿2方法二:如图2,连结助并取中点/连结胡FH.则EH= ' AD,孔EH"AD 、FH= 1 BC. 2 2而AD=BC. ADLBC.所以△砂为等腰直角三角形,所以巴=空=迈 EF EF解:连结曰DF >由题意可得厅、ZF 分别为砒△亦G A7△磁斜边的中线,所以DF=EF 存“,而6沁的中点,所以心心仆丄加所以刃△磁中,心阿F =4\/6如图,在△磁中,氏=22,BD 丄AC 于点D, CE 丄AB 于E, F 、G 分别是应; 眩的中点,若劭=10,求尺;的长.例3 已知:在RT/^ACB和斤7△遁■中.ZACB=ZAEF=9,若尸是莎的中点,连结FGPE(1)如图1,若点忒尸分别落在边仙、/1Q上,请直接写出此时陽与肱的数量关系.(2)如图2,把图1中的△川莎绕着点£顺时针旋转,当点f落在边©的延长线上时,上述结论是否成立?若成立,请给予证明;若不成立,请说明理由.(3)如图3,若点尸落在边丽上,则上述结论是否仍然成立?若成立,请给予证明:若不解(1)易得PC=PE=、BF、即尸0与胶"相等.2(2)结论成立.理由如下:如图4,延长6P交疗的延长线于点Q,则證〃刊,易证△毋倶所以PC=PD.而Z㈤=90°,所以PE=-CD=PC2cD(3)结论仍成立,理由如下:如图5,过点F作FD//BC,交疗的延长线于点Q,易得PD=PC, FD=BC 所以兰=空=空AC BC FD而ZAFE= ZPBC= ZPFD.所以ZEAC=\8”一2ZAFE= ZEFD、如图,连结比ED、则△內,所以ZAEC= ZFED,乙CED=乙AEF=90 所以PE=、CD=PC2例4已知:△遊是等腰三角形,ZBAC=900, DELCE. DE=CE=-AC,连结個"是处2的中点(1)如图1,若0在△磁的内部,连结助,.V是別的中点,连结NE.求ilE:MN1.AE <2)如图2,将图1中的△宓绕点C逆时针旋转,使ZBCD= 30°,连结加,A•是勿的中点,连结血;求竺ACD解:(1)如图3,延长少至点尸,使得肿=\5;连结尬易证△加胫△"';从而可得BF//DE. BF= DE.延长胁CE 交于点G,则ZG=9Q\从而小B、G、Q四点共圆所以ZABF= ZACE、连结胪所以△ ABf陛“ACE (SAS),所以加=広AFLAE.而燃〃肿所以MN= 1AE. MN LAE2G(2)如图4,同(1)可得•亞V=1也 MV •丄也由题意可得AC=2CE.作EHLAC 于",则 2MN _打 AC =T【答案】略【提示】延长饰场交于点尸,则ZCBF=90c , \CME3\FMD 、从而BM=-CF=CM. 22. 我们把两条中线互相垂直的三角形称为”中垂三角形”・如图b AF.亦是△月證的中 线,且处丄庞于点只像△磁这样的三角形均称为“中垂三角形”,设BC=a, AC=b, AB=c ・(1) 猜想a‘,歹,£三者之间的关系,并加以证明;(2) 如图2,在平行四边形月万G?中,E. F, G 分别是月必BC 、切上的中点.BE LEG.AD=2y/5 . AB=3.求府的长.Eg 所以防弓◎抄'盼纠°从而近妬 F进阶训练1. 如图,△.血和△月他都是直角三角形, 曲上,连结眩”为亦的中点,连结 英中Z ABD =ZACE=90° ,且点C 在,所以PE PF EF【提示】⑴如图,连结肿,由中位线定理可得莎=莎=丽飞•在Rt △遊,Rt △加近和Rt △咖中,利用勾股怎理即可得到』+歹=5c ;(2)如图,取M 的中点〃,连结曲,AC,由中位线泄理可得FH//AC//EG.从而必 丄亦,於込APE^'FPB 、所以莎=〃,所以△月肿是"中垂三角形"从而利用(1)中结 论求得£尸的长・3. 巳知:△磁和是等腰直角三角形,ZACB=ZADE=9Q° ,尸为亦的中点・连结 DF 、CF.(1) 如图,当点D^AB 上,点疋在EC 上时,请直接写出此时线段力;G 7的数量关系 和位宜关系(不用证明);(2) 如图2.在(1)的条件下将△/!%绕点月顺时针旋转45° .请你判断此时(1) 中的结论是否仍然成立,并证明你的判断:(3) 如图3.在(1)的条件下将△川疋绕点月顺时针旋转角",请你判断此时(1) 中的结论是否仍然成立,井证明你的判断.【答案】 (1) J+F =5c\ 证明略: (2) £F=4・EB图1 B 图2【答案】(1)DF= CF. DFLCFx(2)成立:(3)成立.【提示】(2)延长DF交氏于点G,则咤△如,从而得DF=GF, CD=CG,即得证・(3)延长G7至点G使得尸片G7,连结%,则GE=CB=CA, GE LAC.可得乙CAD=乙必D・连结QG, CD.从而△ ADX'EDG JSAS)•即得证.4. 匚知:F是平行四边形对角线“所在直线上的一个动点(不与点丛Q重合)・分别过点川、Q向直线歹作垂线,垂足分别为E F, 0为川6•的中点,如图1.将直线册绕点万逆时针旋转,当ZOFE= 30°时,如图2所示,请你猜想线段併,AE,处之间有怎样的数量关系,并给予证明.[答案]图]中处二/一处:图2中OE=CF+AE・【提示】如图1,延长丹交尸C于点G,易证莎=&, AE=CG.从而R也GFE中,OF=OG=OE.而ZOFE=30° ,所U OE=CF-AE・如图2,同理可得处。
中点问题练习题

中点问题练习题在这篇文章中,将深入讨论中点问题以及与之相关的练习题。
中点问题是数学中的一个重要概念,在几何和代数中均有广泛应用。
我们将从基本概念入手,逐步深入,帮助您更好地理解和应用中点问题。
一、基本概念中点是指位于一条线段中间的点,其距离两个端点的距离相等。
假设线段AB上有一个中点M,那么AM的长度等于MB的长度。
这是中点的基本定义。
对于任意线段,都存在唯一的中点。
二、中点的性质中点具有一些重要的性质,如下所示:1. 中点将线段分为两个等长的部分。
即AM = MB。
2. 连接中点和端点的线段两边是平行的,且长度相等。
即AM || BC,且AM = BC。
3. 连接线段两个端点的线段与中点的连线相交于中点。
即∠AMB = 90°。
三、练习题1. 已知线段AB的长度为10cm,C是线段AB上的一个点,AC的长度为4cm。
求C到线段AB的中点的距离。
解析:首先找到AB的中点,记为M。
由于M是AB的中点,所以AM = MB。
然后计算AC的长度,得到AC = 4cm。
利用中点的性质2,我们知道MC = BC。
从而MC的长度为10cm - 4cm = 6cm。
2. 线段CD平分线段EF,并且EF的长度为14cm。
已知CE = 6cm,求DF的长度。
解析:线段CD平分线段EF,意味着D是EF的中点。
首先找到EF的中点,记为D。
根据题目给出的信息可知,CE = 6cm,EF = 14cm。
利用中点的性质1,我们知道CD = DE。
从而CE + ED = 6cm + DE =EF = 14cm。
解方程可得DE = 8cm。
又知DF = EF - DE = 14cm - 8cm =6cm。
3. 线段GH上有一个中点M,GM的长度为8cm,且GM与线段GH交于点K。
求KH的长度。
解析:我们已知线段GM的长度为8cm,并且GM是线段GH的中点。
利用中点的性质3,我们知道∠GKM = 90°。
由此可知,三角形GKM是直角三角形。
初中几何中点专题练习

中点一、线段的中点把线段分成相等的两部分,图形中出现的中点,可以引起丰富的联想 1、 三角形,梯形的中位线定理 2、 斜边上的中线是斜边的一半 3、 平行线等分线段定理 4、 等腰三角形的三线合一定理 5、 以中点为对称中心的对称图形二、解答中点问题的关键是恰当地添加辅助线 1、 利用中点构造“X ”型全等(倍长中线) 2、 作直角三角形斜边上的中线 3、 构造梯形,三角形的中位线 4、 构造中心对称图形5、 利用等腰三角形的三线合一定理构造辅助线 三、常见图形 练习1、如图:若E ,F ,G ,H 分别是四边形ABCD 各边中点,则四边形EFGH 是 。
2、如果把条件中的四边形ABCD 依次改为矩形,菱形,正方形,等腰梯形,其他条件不,那么,所得的四边形分别为 。
3、如果把结论中的平行四边形EFGH 依次改为矩形,菱形,正方形,那么原四边形ABCD 应具备的条件 。
4、如图:把长为8cm 的长方形纸片对折,按图中的虚线煎出一个梯形并打开,则打开后梯形中位线的长为 。
5、如图:在△ABC 中,AB=AC ,AD ⊥BC 于D ,E 是AC 的中点,若BC=16,DE=5,则AD= 。
6、 如图,在△ABC 中,∠B=2∠C ,AD ⊥BC ,M 是BC 的中点,求证DM=1/2AB7、在△ABC 中,BD=CE ,BE ,CD 的中点分别是M ,N ,直线MN 分别交AB ,AC 于P ,Q ,求证:AP=AQ8、如图,在△ABC 的边长分别为AB=14,BC=16,AC=26,P 为∠A 的平分线AD 上一点,BP ⊥AD ,M 为BC 的中点,求PM 的值9、如图,□ABCD 中,∠ABC=75°,AF ⊥BC 于F ,AF 交BD 于E ,若DE=2AB ,求∠AED 的度数 10、正方形ABCD 的两条对角线相交于E ,∠CAD 的平分线AF 交DE 于G ,交DC 于F ,若GE=24,求FC 的大小11、如图:在△ABC 中,∠BAC=120°,以AB ,AC 为边分别形外作正三角形ABD ,ACE ,M 为AD 中点,N 为AE中点,P 为BC 中点,求∠MPN12、在梯形ABCD 中,AB ∥CD ,M 为DC 的中点,N 为AB 的中点,求证:MN <1/2(AD+BC )13、如图,△ABC 的∠B 的角平分线BE 与BC 边上的中线AD 垂直且相等,已知BE=AD=4,求△ABC 的三边长 14、锐角三角形ABC 中,作高BD ,CE ,过顶点B ,C 分别作ED 的垂线BF 和CG ,求证:EF=DG15、在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在在AC 边,且∠MDN= 90°,如果BM 2+CN 2=DM 2+DN 2,求证:)(41222AC AB AD +=16、请选择恰当的方法将如图的梯形分割成面积相等的四块。
中考数学几何专项——中点专题

中考数学几何专项——中点专题中点专题类型一:见中线可倍长例1:在△ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC点F,且AF=EF,证明AC=BE。
我们可以利用中线的性质,即AD=DC,BE=EC,来证明AC=BE。
首先,连接AE和CF,因为AF=EF,所以∠AFE=∠AEF,又因为∠AFE+∠BFC=180°,所以∠XXX∠AFE=∠AEF。
由此可知,△BFC与△AED相似,所以BC/AB=AC/AD,即AC=BC*AD/AB=BE。
变式:在△ABC中,AD交BC于点D,点E是BC中点,EF∥AD交CA的延长线于点F,交AB于点G。
若AD为△ABC的角平分线,证明BG=CF。
因为AD是角平分线,所以XXX。
又因为EF∥AD,所以XXX。
所以BE/AB=EC/AC,即△BEG与△CEA相似。
因此,BG/AC=BE/AB=EC/AC,所以BG=CF。
例2:在直角三角形ABC中,∠BAC=90°,D为BC的中点,E、F分别为AB、AC上的点,且ED⊥FD。
以线段BE、EF、FC为边能否构成一个三角形?若能,请判断此三角形的形状。
我们可以利用勾股定理和中线的性质来判断。
首先,因为D为BC的中点,所以BD=DC,即△ABD与△ACD相似。
又因为ED⊥FD,所以△EDF为直角三角形,所以DE²+EF²=DF²。
由△ABD与△ACD相似可得,AB²=BD·BC,AC²=DC·BC,所以AB²+AC²=BC²。
因此,DE²+EF²=DF²=AB²+AC²-2AB·AC·cos∠BAC=BC²-2AB·AC=BC²-2BC²/4=BC²/2.所以DE²+EF²<BC²/2,即XXX<BC,所以以线段BE、EF、FC为边的三角形一定存在。
中考数学与中点有关的问题试题(24题)

〔二讲〕与中点有关的几何题〔2014年昌平二模〕24.[探究]如图1,在△ABC 中, D 是AB 边的中点,AE ⊥BC 于点E ,BF ⊥AC 于点F ,AE ,BF 相交于点M ,连接DE ,DF . 则DE ,DF 的数量关系为.[拓展]如图2,在△A B C 中,C B = C A ,点D 是AB 边的中点,点M 在△A B C 的内部,且∠MBC =∠MAC . 过点M 作ME ⊥BC 于点E ,MF ⊥AC 于点F ,连接DE ,DF . 求证:DE =DF ;[推广]如图3,若将上面[拓展]中的条件"CB =CA "变为"CB ≠CA ",其他条件不变,试探究DE 与DF 之间的数量关系,并证明你的结论.ADBE CM F A D BECMF MABCDFE图3图2图1海淀2-海淀25. 在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中 点, 点E 在直线CF 上〔点E 、C 不重合〕.〔1〕如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系与BMCE的值, 并证明你的结论; 〔2〕如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在〔1〕中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;〔3〕如图3,若点M 、A 不重合,BN =NE ,你在〔1〕中得到的结论两个是否成立, 请直接写出你的结论.丰台1-24.已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .〔1〕如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是;〔2〕将图1中的△ADE 绕点A 旋转到图2的位置时,判断〔1〕中的结论是否仍然成立,并说明理由.海淀1-24. 在□ABCD 中,∠A =∠DBC , 过点D 作DE =DF , 且∠EDF=∠ABD , 连接EF 、 EC ,N 、P 分别为EC 、BC 的中点,连接NP .〔1〕如图1,若点E 在DP 上, EF 与DC 交于点M , 试探究线段NP 与线段NM 的数量关系与∠ABD 与∠MNP 满足的等量关系,请直接写出你的结论;〔2〕如图2,若点M 在线段EF 上, 当点M 在何位置时,你在〔1〕中得到的结论仍然成立,写出你确定的点M 的位置,并证明〔1〕中的结论.图1图213、〔2014燕山一模〕24.如图1,已知ABC ∆是等腰直角三角形,︒=∠90BAC ,点D 是BCD C B A EMMEA B C DMBDCFE ANPPN AEFCDBEDMBCAEDMBCAMBCA的中点.作正方形DEFG ,使点A 、C 分别在DG 和DE 上,连接 AE ,BG .〔1〕试猜想线段BG 和AE 的数量关系是;〔2〕将正方形DEFG 绕点D 逆时针方向旋转)3600(︒≤<︒αα, ①判断〔1〕中的结论是否仍然成立?请利用图2证明你的结论; ②若4==DE BC ,当AE 取最大值时,求AF 的值.1、〔2014年门头沟二模〕24. 在△ABC 中,AB=AC ,分别以AB 和AC 为斜边,向△ABC 的外侧作等腰直角三角形,M 是BC 边中点中点,连接MD 和ME〔1〕如图24-1所示,若AB=AC ,则MD 和ME 的数量关系是〔2〕如图24-2所示,若AB ≠AC 其他条件不变,则MD 和ME 具有怎样的数量和位置关系?请给出证明过程; 〔3〕 在任意△ABC 中,仍分别以AB 和AC 为斜边,向△ABC 的内侧..作等腰直角三角形,M 是BC 的中点,连接MD 和ME ,请在图24-3中补全图形,并直接判断△MED 的形状.〔2014年昌平二模〕24.[探究]DE =DF . …………………………………………………………………………………1分[拓展]如图2,连接CD . ∵在△A B C 中 ,C B = C A , ∴∠CAB =∠CBA . ∵∠MBC =∠MAC ,∴∠MAB =∠MBA . ……………………………2分 ∴AM =BM .∵点 D 是 边 AB 的 中点 ,∴点M 在CD 上. ………………………………………3分 ∴CM 平分∠FCE . ∴∠FCD =∠ECD .∵ME ⊥BC 于E ,MF ⊥AC 于F , ∴MF =ME . 又∵CM =CM , ∴△CMF ≌△CME . ∴CF =CE . ∵CD =CD ,∴△CFD ≌△CED .∴DE =DF .………………………………………4分 [推广] DE =DF .如图3,作AM 的中点G ,BM 的中点H .∵点 D 是 边 AB 的 中点 , ∴1//,.2DG BM DG BM =同理可得:1//,.2DH AM DH AM = ∵ME ⊥BC 于E ,H 是BM 的中点, ∴在Rt △BEM 中, 1.2HE BM BH ==∴DG =HE . ……………………………………………………5分 同理可得:.DH FG = ∵DG //BM ,DH //GM ,∴四边形DHMG 是平行四边形.图2F MCE BD A图3H GF M CE BD A∴∠DGM =∠DHM .∵∠MGF =2∠MAC ,∠MHE =2∠MBC , 又∵∠MBC =∠MAC , ∴∠MGF =∠MHE .∴∠DGM +∠MGF =∠DHM +∠MHE .∴∠DGF =∠DHE . ……………………………………6分 ∴△DHE ≌△FGD .∴DE =DF . ……………………………………………………7分〔海淀二模〕25. 解:〔1〕BN 与NE 的位置关系是BN ⊥NE ;CE BM.证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中,AB =BC , ∴ 矩形ABCD 为正方形.∴AB=AD =CD ,∠A =∠ADC =∠DCB =90°. ∴EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵E 为CF 的中点,EG//CD ,∴GF =DG =11.22DF CD =∴1.2GE CD =∵N 为MD <AD >的中点, ∴AN =ND =11.22AD CD =∴GE =AN , NG=ND+DG=ND+AN=AD=AB .……………………………2分∴△NGE ≌△BAN . ∴∠1=∠2. ∵∠2+∠3=90°, ∴∠1+∠3=90°. ∴∠BNE =90°.∴BN ⊥NE .……………………………………………………………3分 ∵∠CDF =90°, CD =DF , 可得 ∠F =∠FCD =45°,2.CF CD .于是122.2CF CECE CE BMBACDCD……………………………………4分 〔2〕在〔1〕中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .∵ 四边形ABCD 是矩形,∴AB ∥CG .∴∠MBN =∠DGN ,∠BMN =∠GDN .∵N 为MD 的中点, H A BC DEM NF 321GFEA (M )CDNB∴MN=DN.∴△BMN≌△GDN.∴MB=DG,BN=GN.∵BN=NE,∴BN=NE=GN.∴∠BEG=90°.……………………………………………5分∵EH⊥CE,∴∠CEH=90°.∴∠BEG=∠CEH.∴∠BEC=∠GEH.由〔1〕得∠DCF=45°.∴∠CHE=∠HCE=45°.∴EC=EH,∠EHG=135°.∵∠ECB=∠DCB+∠HCE=135°,∴∠ECB=∠EHG.∴△ECB≌△EHG.∴EB=EG,CB=HG.∵BN=NG,∴BN⊥NE. ……………………………………………6分∵BM =DG= HG-HD= BC-HD=CD-HD =CH=2CE,∴CEBM =22. ……………………………………………7分〔3〕BN⊥NE;CEBM 不一定等于22. …………………………………………8分〔2012丰台一模〕24.解:〔1〕BM=DM且BM⊥DM.………2分〔2〕成立.……………3分理由如下:延长DM至点F,使MF=MD,联结CF、BF、BD.易证△EMD≌△CMF.………4分∴ED=CF,∠DEM=∠1.∵AB=BC,AD=DE,且∠ADE=∠ABC=90°,∴∠2=∠3=45°,∠4=∠5=45°.∴∠BAD=∠2+∠4+∠6=90°+∠6.∵∠8=360°-∠5-∠7-∠1,∠7=180°-∠6-∠9,∴∠8=360°-45°-〔180°-∠6-∠9〕-〔∠3+∠9〕=360°-45°-180°+∠6+∠9- 45°-∠9=90°+∠6 .∴∠8=∠BAD.………5分又AD=CF.∴△ABD≌△CBF.∴BD=BF,∠ABD=∠CBF.………6分∴∠DBF=∠ABC=90°.∵MF=MD,∴BM=DM且BM⊥DM.〔海淀一模〕9解:〔1〕 NP =MN ,∠ABD +∠MNP =180︒<或其它变式与文字叙述,各1分>.………2分 〔2〕点M 是线段EF 的中点<或其它等价写法>. 证明:如图, 分别连接BE 、CF .∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥DC ,∠A =∠DCB , ∴∠ABD =∠BDC . ∵∠A =∠DBC , ∴∠DBC =∠DCB . ∴ DB =DC .①………………………3分 ∵∠EDF =∠ABD ,∴∠EDF =∠BDC .∴∠BDC-∠EDC =∠EDF-∠EDC .即∠BDE =∠CDF .②又 DE =DF ,③由①②③得△BDE ≌△CDF .…………………………………………4分 ∴ EB =FC , ∠1=∠2.∵N 、P 分别为EC 、BC 的中点, ∴NP ∥EB , NP =EB 21.同理可得 MN ∥FC ,MN =FC 21.∴NP = NM . …………………………………………………5分∵NP ∥EB , ∴∠NPC =∠4.∴∠ENP =∠NCP +∠NPC =∠NCP +∠4. ∵MN ∥FC ,∴∠MNE =∠FCE =∠3+∠2=∠3+∠1.∴∠MNP =∠MNE +∠ENP =∠3+∠1+∠NCP +∠4=∠DBC +∠DCB =180︒-∠BDC =180︒-∠ABD .∴∠ABD +∠MNP =180︒.……………………………………7分〔2014燕山一模〕解析:24. 解:〔1〕AE BG =; …………………2分 〔2〕①成立.以下给出证明: 如图,连接AD ,∵在 Rt BAC ∆中,D 为斜边BC 中点,∴BD AD =,BC AD ⊥,∴︒=∠+∠90GDB ADG . …………………3分 ∵四边形EFGD 为正方形, ∴DG DE =,且︒=∠90GDE , ∴︒=∠+∠90ADE ADG , ∴ADE BGD ∠=∠. ……4分 在BDG ∆和ADE ∆中, ⎪⎩⎪⎨⎧=∠=∠=,,,ED GD ADE BDG AD BD ∴BDG ∆≌ADE ∆,M 1 32 4P N A EF C DB BACDEGFEDMBC∴AE BG =.……………………5分②由①可得AE BG =,当BG 取得最大值时,AE 取得最大值.当旋转角为︒270时,AE BG =,最大值为642=+. ………6分 如图,此时13222=+=EF AE AF . ……………………7分〔2014年门头沟二模〕24. 〔1〕MD =ME ……………1分〔2〕如图,作DF ⊥AB ,EG ⊥AC ,垂足分别为F 、G . 因为DF 、EG 分别是等腰直角三角形ABD 和等腰直角三角形ACE 斜边上的高,所以F 、G 分别是AB 、AC 的中点.又∵M 是BC 的中点,所以MF 、MG 是△ABC 的中位线. ∴12MF AC =,12MG AB =,MF //AC ,MG //AB .∴∠BFM =∠BAC ,∠MGC =∠BAC .∴∠BFM =∠MGC .所以∠DFM =∠MGE .……………2分∵DF 、EG 分别是直角三角形ABD 和直角三角形ACE 斜边上的中线, ∴12EG AC =,12DF AB =. ∴MF =EG ,DF =NG .……………3分∴△DFM ≌△MGE .∴DM =ME .……………4分 ∠FMD=∠GEM∴∠DME =∠FMD+∠FMG+∠GME=∠GEM+∠MGC +∠GME ∵EG ⊥AC ∴∠EGC=900∵∠GEM+∠MGC +∠GME+∠EGC=1800∴∠DME=900……………5分〔3〕作图正确得一分……………6分△MDE 是等腰直角三角形.……………7分BA CDE GF。
【数学中考一轮复习】中点问题常考模型(含答案)
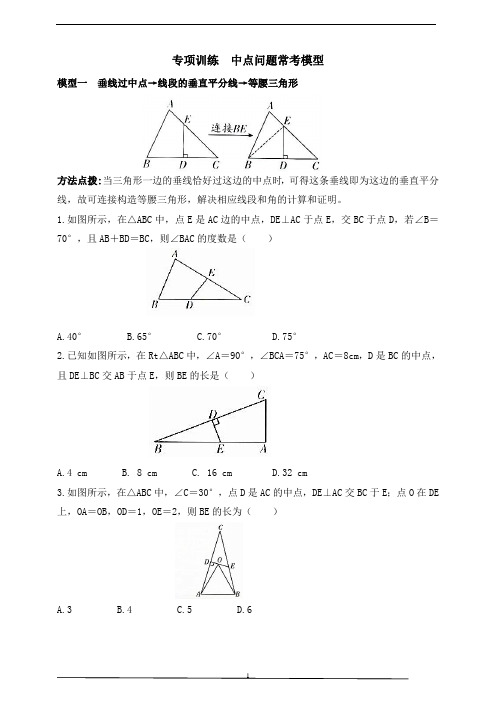
专项训练中点问题常考模型模型一垂线过中点→线段的垂直平分线→等腰三角形方法点拨:当三角形一边的垂线恰好过这边的中点时,可得这条垂线即为这边的垂直平分线,故可连接构造等腰三角形,解决相应线段和角的计算和证明。
1.如图所示,在△ABC中,点E是AC边的中点,DE⊥AC于点E,交BC于点D,若∠B=70°,且AB+BD=BC,则∠BAC的度数是()A.40°B.65°C.70°D.75°2.已知如图所示,在Rt△ABC中,∠A=90°,∠BCA=75°,AC=8cm,D是BC的中点,且DE⊥BC交AB于点E,则BE的长是()A.4 cmB. 8 cmC. 16 cmD.32 cm3.如图所示,在△ABC中,∠C=30°,点D是AC的中点,DE⊥AC交BC于E;点O在DE 上,OA=OB,OD=1,OE=2,则BE的长为()A.3B.4C.5D.6模型二等腰三角形+底边中点→三线合一如图所示,在△ABC中,若AB=AC.通常取底边BC的中点D,则AD⊥BC,且AD平分∠BAC.方法点拨:当等腰三角形有底边上的中点时,常作出底边上的中线,利用等腰三角形底边上的中线、底边上的高和顶角的平分线“三线合一”的性质,证明线段相等、角的相等及线段的垂直、平分关系.4.如图所示,在△ABC中,AB=AC,D是BC的中点,∠B=35°,则∠BAD=()A.110°B.70°C.55°D.35°5.如图所示,在△ABC中,AE⊥BC于点E,点D为BC边中点,AF⊥AB交BC边于点F,∠C=2∠B,若DE=4CF=2,则CE=_________.模型三见三角形的中线或过中点的线段→加倍延长构造全等在△ABC中,M为BC边的中点.在△ABC中,点M为BC边上中点.(1)如图1,连接中线AM 并延长到点E ,使得ME =AM 连接CE ,则△ABM ≌△ECM.(2)如图2,连接过中点的线段DM 并延长到点E ,使得ME =DM.连接CE ,则△BDM ≌△CEM.方法点拨:遇到线段中点问题,常借助倍长中线的方法还原中心对称图形,利用“8”字形全等将题中条件集中,达到解题的目的,这种方法是最常用的也是最重要的方法.6.如图所示,已知AB =12,AB ⊥BC 于B ,AB ⊥AD 于A ,AD =5,BC =10.点E 是CD 的中点,则AE 的长为( )A.6B.213C.5D.4123 7.已知三角形两边分别为6和9,求第三边上中线的取值范围是___________.8.(1)如图1所示,若△ABC 是直角三角形,∠BAC =90°,点D 是BC 的中点,延长AD 到点E ,使DE =AD ,连接CE ,可以得到△ABD ≌△ECD ,这种作辅助线的方法我们通常叫做“倍长中线法”.求证:△ACE 是直角三角形.(2)如图2所示,△ABC 是直角三角形,∠BAC =90°,D 是斜边BC 的中点,E ,F 分别是AB ,AC 边上的点,且DE ⊥DF.试说明BE 2+CF 2=EF 2;(3)如图3所示,在(2)的条件下,若AB =AC ,BE =12,CF =5,求△DEF 的面积.模型四 直角三角形+斜边中点→直角三角形斜边中线如图所示,在△ABC 中,∠ACB =90°,取AB 的中点D ,连接CD ,则有BD =AD =CD. 反过来,在△ABC 中,点D 在AB 边上,若BD =AD =CD ,则有∠ABC =90°.方法点拨:在直角三角形中,当有斜边中点时,常连斜边的中线,利用直角三角形斜边上的中线等于斜边的一半,来证明线段的数量关系,同时得两个等腰三角形,为角的计算提供了条件,该模型经常和三角形的中位线连用,更具综合性.9.如图所示,在△ABC 中,D ,E ,F 分别是AB ,CA ,BC 的中点,若CF =3,CE =4,EF =5,则CD 的长为( )A.5B.6C.8D.1010.如图所示,在Rt △ABC 中,∠ACB =90°,点D ,E 分别是边AB ,AC 的中点,延长BC 至F ,使CF =21BC ,若AB =10,则 EF 的长是( )A.5B.4C.3D.211.如图所示,DE 为△ABC 的中位线,点F 在DE 上,且∠AFC 为直角,若DF =2cm.BC =16cm ,则AC 的长为__________.→连接或作平行构造中位线方法点拨:在三角形中,如果有两个中点,往往直接连接两中点构造三角形的中位线;如果只有一个中点,可以取另一边的中点相连接,也可以过已知中点作另一边的平行线,都能构造三角形的中位线,然后利用三角形的中位线平行于第三边,并且等于第三边的一半,得到两线段的平行和倍分关系,从而进行相应的计算和证明.12.如图所示,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是()A.2.2 cmB.2.3 cmC.2.4 cmD. 2.5 cm13.如图所示,在矩形ABCD中,E,F分别是AB,BC的中点,BD=12,则EF的长为()A.6B.5C.4D.314.如图所示,在四边形ABCD中,P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是()A.50°B.40°C.30°D.20°模型六圆+弦(或弧)的中点→垂径定理或圆周角定理方法点拨:(1)圆心O是直径的中点,常和弦的两个端点相连接,构造等腰三角形或直角三角形解决问题。
中考数学专题训练专题一几何题型(中点M型)

( 2) 将直线 EF绕点 F 逆时针旋转 90°,得到直线 m,直线 m交 y 轴于点 D,求点 D 的坐标。
C
B
E D
O
FA
x
1. 如图,在△ ABC中, AB=AC,∠ BAC=α,点 D 为 BC边的中点, BE⊥ AC于 E, DF⊥ AB 于 F. (1) 当 0<α< 90,(如图 1),求证: AE+ 2BF= AB;
特例二:条件:①等腰直角△ ABC, AC=BC,∠ C= 90°;②∠ EDF=45°;③点 D 是 AB 的中点。特例
三:条件:① AB= AC;②∠ BAC= 120°,∠ EDF=30°,③ D 是 BC的中点。
特例四:条件:①矩形 ABCD;②∠ GEF= 90°,③ E 是 AB 的中点。
C D
G F
A
E
B
图1
C D
G
A
F
E
B
图2
3. 已知,在△ ABC中, BC= AC,∠ MCN=∠ ACB, CM交 AB 于点 E,过点 B 作 BF⊥ CB 交 CN
于点 F. ( 1) 当 ∠ ACB=90°(如图 1 所示)时,求证: BE-AE= BF;
1. 已知, A、 C 分别为∠ BOE两边上的两点, D 为∠ BOE内一点, DC∥OB, DA∥OE,连接 OD、 AC相交 于点 F, G为 FD上一点,过点 G的直线交 OE于 Q,交 CD于点 P,交 AD于点 N,交 OB于点 M.
特例五:条件:①直角梯形 ABCD中, AB∥ CD,∠ A= 90°;② E 是 AD的中点;③∠ BEC= 90°。
MA D
N E
B
P
C
中考数学压轴题专项汇编专题之19中点模型

专题1 中点模型破解策略 1.倍长中线在△ABC 中.M 为BC 边的中点.MECB AEMCAB De图1 图2(1)如图1,连结AM 并延长至点F ,使得ME =AM .连结CE .则△ABM ≌△ECM .(2)如图2,点D 在AB 边上,连结DM 并延长至点E .使得MF =DM .连结CE ,则△BDM ≌△CEM ,遇到线段的中点问题,常借助倍长中线的方法还原中心对称图形,利用“8”字形全等将题中条件集中,达到解题的目的,这种方法是最常用的也是最重要的方法. 2.构造中位线在△ABC 中.D 为AB 边的中点,图1 图2(1)如图1,取AC 边的中点E ,连结DE .则DE ∥BC ,且DF =12B C . (2)如图2.延长BC 至点F .使得CF =B C .连结CD ,AF .则DC ∥AF ,且DC =12AE . 三角形的中位线从位置关系和数量关系两方面将将图形中分散的线段关系集中起来.通常需要再找一个中点来构造中位线,或者倍长某线段构造中位线, 3.等腰三角形“三线合一”如图,在△ABC 中,若AB =A C .通常取底边BC 的中点D .则AD ⊥BC ,且AD 平分∠BA C . 事实上,在△ABC 中:①AB =AC ;②AD 平分∠BAC ;③BD =CD ,④AD ⊥B C .对于以上四条语句,任意选择两个作为条件,就可以推出另两条结论,即“知二得二”.AB DCCFABDABDEC4. 直角三角形斜边中线如图,在△ABC 看,∠ABC =900,取AC 的中点D ,连结BD ,则有BD =AD =CD =12AC . 反过来,在△ABC 中,点D 在AC 边上,若BD =AD =CD =12AC ,则有∠ABC =900例题讲解例1 如图,在四边形ABCD 中,E 、F 分别是AB 、CD 的中点,过点E 作AB 的垂线,过点F 作CD 的垂线,两垂线交于点G ,连结AG 、BG 、CG 且∠AGD =∠BGC ,若AD 、BC 所在直线互相垂直,求ADEF的值例2 如图,在△ABC 中,BC =22,BD ⊥AC 于点D ,CE ⊥AB 于E ,F 、G 分别是BC 、DE 的中点,若ED =10,求FG 的长.进阶训练I .如图,△ABD 和△ACE 都是直角三角形,其中∠ABD =∠ACE =90°,且点C 在AB 上,连结DE ,M 为DE 的中点,连结BM ,CM ,(1)求证:BM =CM .(2)设∠BAD=∠CAE ,固定△ABD ,让Rt △ACE 绕顶点A 在平面内旋转到图乙的位置,试问:MB=MC 是否还能成立?并证明其结论.3.巳知:△ABC 和△ADE 是等腰直角三角形,∠ACB =∠ADE =90°,F 为BE 的中点.连结DF ,CF .图3图2图1FEFEBBFEB AAACD CCDD(1)如图,当点D 在AB 上,点E 在AC 上时,请直接写出此时线段DF ,CF 的数量关系和位置关系(不用证明); (2)如图2.在(1)的条件下将△ADE 绕点A 顺时针旋转45°.请你判断此时(1)中的结论是否仍然成立,并证明你的判断;(3)如图3.在(1)的条件下将△ADE 绕点A 顺时针旋转角α,请你判断此时(1)中的结论是否仍然成立,井证明你的判断.5.巳知:P 是平行四边形ABCD 对角线AC 所在直线上的一个动点(不与点A 、C 重合).分别过点A 、C 向直线BP 作垂线,垂足分别为E ,F ,O 为AC 的中点,如图1.将直线BP 绕点B 逆时针旋转,当∠OFE = 30°时,如图2所示,请你猜想线段CF ,AE ,OE 之间有怎样的数量关系,并给予证明.图1OE FCABDP 图2EFOCABDP6.已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,AO=4,CO=2,接连接AD,BC、点H为BC中点,连接OH.(1)如图1所示,求证:OH=AD且OH⊥AD;(2)将△COD绕点O旋转到图2所示位置时,线段OH与AD又有怎样的关系,证明你的结论;(3)请直接写出线段OH的取值范围.如图1,四边形ABCO为正方形。
(完整版)中考数学压轴题专项汇编专题之19中点模型

专题1 中点模型破解策略 1.倍长中线在△ABC 中.M 为BC 边的中点.MECB AEMCAB De图1 图2(1)如图1,连结AM 并延长至点F ,使得ME =AM .连结CE .则△ABM ≌△ECM .(2)如图2,点D 在AB 边上,连结DM 并延长至点E .使得MF =DM .连结CE ,则△BDM ≌△CEM ,遇到线段的中点问题,常借助倍长中线的方法还原中心对称图形,利用“8”字形全等将题中条件集中,达到解题的目的,这种方法是最常用的也是最重要的方法. 2.构造中位线在△ABC 中.D 为AB 边的中点,图1 图2(1)如图1,取AC 边的中点E ,连结DE .则DE ∥BC ,且DF =12B C . (2)如图2.延长BC 至点F .使得CF =B C .连结CD ,AF .则DC ∥AF ,且DC =12AE . 三角形的中位线从位置关系和数量关系两方面将将图形中分散的线段关系集中起来.通常需要再找一个中点来构造中位线,或者倍长某线段构造中位线, 3.等腰三角形“三线合一”如图,在△ABC 中,若AB =A C .通常取底边BC 的中点D .则AD ⊥BC ,且AD 平分∠BA C . 事实上,在△ABC 中:①AB =AC ;②AD 平分∠BAC ;③BD =CD ,④AD ⊥B C .对于以上四条语句,任意选择两个作为条件,就可以推出另两条结论,即“知二得二”.AB DCCFABDABDEC4.直角三角形斜边中线如图,在△ABC看,∠ABC=900,取AC的中点D,连结BD,则有BD=AD=CD=12 AC.反过来,在△ABC中,点D在AC边上,若BD=AD=CD=12AC,则有∠ABC=900例题讲解例1 如图,在四边形ABCD中,E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结AG、BG、CG且∠AGD=∠BGC,若AD、BC所在直线互相垂直,求ADEF的值例2 如图,在△ABC中,BC=22,BD⊥AC于点D,CE⊥AB于E,F、G分别是BC、DE的中点,若ED=10,求FG的长.进阶训练I.如图,△ABD和△ACE都是直角三角形,其中∠ABD =∠ACE=90°,且点C在AB上,连结DE,M为DE的中点,连结BM,CM,(1)求证:BM=CM.(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图乙的位置,试问:MB=MC是否还能成立?并证明其结论.3.巳知:△ABC 和△ADE 是等腰直角三角形,∠ACB =∠ADE =90°,F 为BE 的中点.连结DF ,CF .图3图2图1EEE(1)如图,当点D 在AB 上,点E 在AC 上时,请直接写出此时线段DF ,CF 的数量关系和位置关系(不用证明); (2)如图2.在(1)的条件下将△ADE 绕点A 顺时针旋转45°.请你判断此时(1)中的结论是否仍然成立,并证明你的判断;(3)如图3.在(1)的条件下将△ADE 绕点A 顺时针旋转角α,请你判断此时(1)中的结论是否仍然成立,井证明你的判断.5.巳知:P 是平行四边形ABCD 对角线AC 所在直线上的一个动点(不与点A 、C 重合).分别过点A 、C 向直线BP 作垂线,垂足分别为E ,F ,O 为AC 的中点,如图1.将直线BP 绕点B 逆时针旋转,当∠OFE = 30°时,如图2所示,请你猜想线段CF ,AE,OE 之间有怎样的数量关系,并给予证明.图1图26.已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,AO=4,CO=2,接连接AD,BC、点H为BC中点,连接OH.(1)如图1所示,求证:OH=AD且OH⊥AD;(2)将△COD绕点O旋转到图2所示位置时,线段OH与AD又有怎样的关系,证明你的结论;(3)请直接写出线段OH的取值范围.如图1,四边形ABCO为正方形。
最新-中考数学和中点有关的几何综合题20道

1、(2014 年丰台一模)24.在等腰直角△ ABC 中,/ BAC=90° , AB=AC,(1)如图1 ,点D、E分别是AB、AC边的中点,AF± BE交BC于点F,连结EF、CD交于点H.求证,EFLCD;(2)如图2, AD=AE, AF± BE于点G交BC于点F,过F作FP± CD交BE的延长线于点P,试探究线段BP,FP,AF之间的数量关系,并说明理由。
2、(2014年西城一模)24.四边形ABCD是正方形,ABEF是等腰直角三角形,/BEF =90、BE =EF ,连接DF , G 为DF 的中点,连接EG , CG , EC。
(1)如图24-1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及空的值;GC(2)将图24-1中的ABEF绕点B顺时针旋转至图24-2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图24-1中的ABEF绕点B顺时针旋转久(0口<a <90。
),若BE =1 , AB = J2 ,当E , F , D三点共线时,求DF的长及tan/ABF的值。
图24-1 图24-23、(2014年通州一模)24.已知:等边三角形AB8,点H E、F分别为边AB AC BC的中点,点M在直线BC上,以点M为旋转中心,将线段MU顶时针旋转60o至MD、连接ED〔(1)如图1,当点M在点B左侧时,线段ED”与MF的数量关系是 ;(2)如图2,当点M在BC边上时,(1)中的结论是否依然成立?如果成立,请利用图 2 证明,如果不成立,请说明理由;(3)当点M在点C右侧时,请你在图3中画出相应的图形,直接判断(1)中的结论是否依然成立?不必给出证明或说明理由.4(2014年燕山一模)24.如图1,已知AABC是等腰直角三角形,/BAC =90',点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE , BG .(1)试猜想线段BG和AE的数量关系是 ;(2)将正方形DEFG绕点D逆时针方向旋转«(0°<« < 360)),①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;②若BC = DE = 4 ,当AE取最大值时,求AF的值.5 .(平谷22.)如图1,若点A 、B 在直线l 同侧,在直线l 上找一点P,使AP+BP 的值最 小,做法是:作点 B 关于直线l 的对称点B',连接AB,与直线l 的交点就是所求的点 P, 线段AB'的长度即为AP+ BP 的最小值.(1)如图2,在等边三角形 ABC 中,AB=2,点E 是AB 的中点,AD 是高,在 AD 上找一 点P,使BP+PE的值最小.做法是:作点 B 关于AD 的对称点,恰好与点 C 重合,连接 CE 交AD 于一点,这点就是所求的点 P,故BP+PE 的最小值为 ;(2)如图3,已知。
2024学年初中数学几何(中点问题一倍长中线)模型专项练习(附答案)

2024学年初中数学几何(中点问题一倍长中线)模型专项练习1.如图在△ABC中,AD为BC边上的中线,E是线段AD上一点,且AE=BC,BE的延长线交AC于F,若AF=EF.求证:(1)AC=BE(2)∠ADC=60°.2.【证明体验】(1)如图1,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连结BE.求证:△ACD≌△EBD.【迁移应用】(2)如图2,在△ABC中,AC=5,BC=13,D为AB的中点,DC⊥AC.求△ABC面积. 【拓展延伸】(3)如图3,在△ABC中,∠ABC=90°,D是BC延长线上一点,BC=CD,F是AB上一点,连结FD交AC于点E,若AF=EF=2,BD=6,求ED的长.3.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA 的延长线于点F,交EF于点G.若BG=CF,求证:AD为△ABC的角平分线.4.已知:如图所示,AB=BC,AD为△ABC中BC边的中线,延长BC至E点,使CE=BC,连接AE.求证:∠DAC=∠CAE.5.在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,若AB=10,BF=4,求PG的长;(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想;并给予证明.(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.6.已知:在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,连接EC,取EC的中点M,连接DM和BM.(1)若点D在边AC上,点E在边AB上且与点B不重合,如图1,探索BM、DM的关系并给予证明;(2)如果将图1中的△ADE绕点A逆时针旋转小于45°的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.7.如图1,在△ABC中,∠BAC=90°,AB=AC.(1)若点M为AC上的任意一点,过M作MN⊥BC于点N,连接BM,取BM的中点D,连接AD、DM,求证:AD=DN.(2)如图2,若M为BC上的任意一点,以线段CM为底边作等腰Rt△MCN,此时,取BM的中点D,连接AD、DN,则AD与DN有怎样的数量关系?说明理由.(3)如图3,在(2)的条件下将Rt△MNC绕C点旋转任意角度,连接BM,取BM的中点D,再连接AD、DN,则(2)中的结论仍然成立吗,它们之间又有怎样的位置关系?请说明理由.8.△ABC中,点D为BC上一点,E为AC上一点,连接AD,BE,DE,已知BD=DE,AD=DC,∠ADB=∠EDC.(1)如图1,若∠ACB=40°,求∠BAC的度数;(2)如图2,F是BE的中点,过点F作AD的垂线,分别交AD、AC于点G、H.求证:AH=CH.9.直角三角形有一个非常重要的性质:直角三角形斜边上的中线等于斜边的一半,比如:如图1,Rt△ABC中,∠C=90°,D为斜边AB中点,则CD=AD=BD=AB.请你利用该定理和以前学过的知识解决下列问题:如图2,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(1)求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明:若不成立,请说明理由;(3)如图4,∠BAC=90°,a旋转到与BC垂直的位置,E为BC上一点且AE =AC,EN⊥a于N,连接EC,取EC中点P,连接PM,PN,求证:PM⊥PN.参考答案1.如图在△ABC中,AD为BC边上的中线,E是线段AD上一点,且AE=BC,BE的延长线交AC于F,若AF=EF.求证:(1)AC=BE(2)∠ADC=60°.【过程解答】证明:(1)倍长AD至点T,连BT.在△ACD和△TBD中,∴△ACD≌△TBD,∴AC=BT,∠CAD=∠T,又∵AF=EF,∴∠CAD=∠AEF=∠BET,∴BT=BE,∴BE=AC.(2)在DT上取DM=DC,连接BM.∴AE+ED=ED+DM即AD=EM∴△DAC≌△MEB(SAS),∴BM=CD=BD,∴△BDM为正三角形,∴∠ADC=∠BDM=60°.2.【证明体验】(1)如图1,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连结BE.求证:△ACD≌△EBD.【迁移应用】(2)如图2,在△ABC中,AC=5,BC=13,D为AB的中点,DC⊥AC.求△ABC面积.【拓展延伸】(3)如图3,在△ABC中,∠ABC=90°,D是BC延长线上一点,BC=CD,F是AB 上一点,连结FD交AC于点E,若AF=EF=2,BD=6,求ED的长.【过程解答】(1)证明:如图1中,在△ACD和△EBD中,,∴△ACD≌△EBD(SAS);(2)解:如图2中,延长CD到T,使得DT=CD,连接BT.由(1)可知△ADC≌△BDT,∴AC=BT=5,∠ACD=∠T=90°,∴CT===12,∴CD=DT=6,∴S△ACB=S△ADC+S△CDB=•AC•DC+•BT•CD=×5×6+×5×6=30;(3)解:如图3中,延长AC到R,使得CR=CA,连接DR.由(1)可知,△ACB≌△RCD,∴AB=DR,∠A=∠R,∵FE=F A,∴∠A=∠AEF,∵∠AEF=∠DER,∴∠DER=∠R,∴DE=DR=AB,设DE=DR=AB=x,则BF=x﹣2,DF=x+2,在Rt△DBF中,BF2+BD2=DF2,∴(x﹣2)2+62=(x+2)2,∴x=,∴DE=.3.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交EF于点G.若BG=CF,求证:AD为△ABC的角平分线.【过程解答】解:延长FE,截取EH=EG,连接CH,∵E是BC中点,∴BE=CE,在△BEG和△CEH中,,∴△BEG≌△CEH(SAS),∴∠BGE=∠H,BG=CH,∴∠BGE=∠FGA=∠H,∵CF=BG,∴CH=CF,∴∠F=∠H=∠FGA,∵EF∥AD,∴∠F=∠CAD,∠BAD=∠FGA,∴∠CAD=∠BAD,∴AD平分∠BAC.4.已知:如图所示,AB=BC,AD为△ABC中BC边的中线,延长BC至E点,使CE=BC,连接AE.求证:∠DAC=∠CAE.【过程解答】解:延长AD到F,使得DF=AD,连接CF.∵AD=DF,∠ADB=∠FDC,BD=DC,∴△ADB≌△FDC(SAS),∴AB=CF,∠B=∠DCF,∵BA=BC,CE=CB∴∠BAC=∠BCA,CE=CF,∵∠ACE=∠B+∠BAC,∠ACF=∠DCF+∠ACB,∴∠ACF=∠ACE,∵AC=AC,∴△ACF≌△ACE(SAS),∴∠CAD=∠CAE.5.在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,若AB=10,BF=4,求PG的长;(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想;并给予证明.(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.【过程解答】(1)解:如图1:延长GP交DC于点E,利用△PED≌△PGF,得出PE=PG,DE=FG,∵△BGF是等边三角形,∴FG=BG,又∵四边形ABCD是菱形,∴CD=CB,∴CE=CG,∴CP是EG的中垂线,在Rt△CPG中,∠PCG=60°,∵AB=10,BF=4;∴CG=6∴PG=3(2)如图2,证明:延长GP交DA于点E,连接EC,GC,∵∠ABC=60°,△BGF正三角形∴GF∥BC∥AD,∴∠EDP=∠GFP,在△DPE和△FPG中∴△DPE≌△FPG(ASA)∴PE=PG,DE=FG=BG,∵∠CDE=∠CBG=60°,CD=CB,在△CDE和△CBG中,∴△CDE≌△CBG(SAS)∴CE=CG,∠DCE=∠BCG,∴∠ECG=∠DCB=120°,∵PE=PG,∴CP⊥PG,∠PCG=∠ECG=60°∴PG=PC.(3)猜想:PG=PC.证明:如图3,延长GP到H,使PH=PG,连接CH,CG,DH,作FE∥DC∵P是线段DF的中点,∴FP=DP,∵∠GPF=∠HPD,∴△GFP≌△HDP,∴GF=HD,∠GFP=∠HDP,∵∠GFP+∠PFE=120°,∠PFE=∠PDC,∴∠CDH=∠HDP+∠PDC=120°,∵四边形ABCD是菱形,∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上, ∴∠GBC=120°,∵△BFG是等边三角形,∴GF=GB,∴HD=GB,∴△HDC≌△GBC,∴CH=CG,∠DCH=∠BCG,∴∠DCH+∠HCB=∠BCG+∠HCB=120°,即∠HCG=120°∵CH=CG,PH=PG,∴PG⊥PC,∠GCP=∠HCP=60°,∴PG=PC.6.已知:在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,连接EC,取EC的中点M,连接DM和BM.(1)若点D在边AC上,点E在边AB上且与点B不重合,如图1,探索BM、DM的关系并给予证明;(2)如果将图1中的△ADE绕点A逆时针旋转小于45°的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.【过程解答】解:(1)BM=DM,BM⊥DM,在Rt△EBC中,M是斜边EC的中点,∴BM=EC=EM=MC,∴∠EMB=2∠ECB.在Rt△EDC中,M是斜边EC的中点,∴DM=EC=EM=MC.∴∠EMD=2∠ECD.∴BM=DM,∠EMD+∠EMB=2(∠ECD+∠ECB),∵∠ECD+∠ECB=∠ACB=45°,∴∠BMD=2∠ACB=90°,即BM⊥DM.(2):(1)中的结论仍成立,延长DM至点F,使得DM=MF,连接CD和EF,连接BD,连接BF、FC,延长ED交AC于点H.∵DM=MF,EM=MC,∴四边形CDEF是平行四边形,∴DE∥CF,ED=CF,∵ED=AD,∴AD=CF.∵DE∥CF,∴∠AHE=∠ACF.∵∠BAD=45°﹣∠DAH=45°﹣(90°﹣∠AHE)=∠AHE﹣45°,∠BCF=∠ACF ﹣45°,∴∠BAD=∠BCF.又∵AB=BC,∴△ABD≌△CBF,∴BD=BF,∠ABD=∠CBF,∵∠ABD+∠DBC=∠CBF+∠DBC,∴∠DBF=∠ABC=90°.在Rt△DBF中,由BD=BF,DM=MF,得BM=DM且BM⊥DM.7.如图1,在△ABC中,∠BAC=90°,AB=AC.(1)若点M为AC上的任意一点,过M作MN⊥BC于点N,连接BM,取BM的中点D,连接AD、DM,求证:AD=DN.(2)如图2,若M为BC上的任意一点,以线段CM为底边作等腰Rt△MCN,此时,取BM的中点D,连接AD、DN,则AD与DN有怎样的数量关系?说明理由.(3)如图3,在(2)的条件下将Rt△MNC绕C点旋转任意角度,连接BM,取BM的中点D,再连接AD、DN,则(2)中的结论仍然成立吗,它们之间又有怎样的位置关系?请说明理由.【过程解答】(1)证明:解法一:如图1中,延长AD到K,使得DK=AD,连接AN、KN、KM.在△ADB和△KDM中,,∴△ADB≌△KDM,∴AB=KM=AC,∠BAD=∠MKD,∴AB∥KM,∴∠KMC=∠BAC=90°,∵AB=AC,∠BAC=90°,∴∠C=45°,∵MN⊥BC,∴∠MNC=90°,∠NMC=45°=∠KMC=∠C,∴MN=NC,在△ANC和△KNM中,,∴△ANC≌△KNM,∴AN=KN,∠ANC=∠KNM,∴∠KNA=∠MNC=90°∵AD=DK,∴DN=AD=DK,即AD=DN.解法二:根据直角三角形斜边中线性质,可知AD=BM,DN=BM,由此即可证明.(2)如图2中,结论:AD=DN.理由:延长AD到K,使得DK=AD,连接AN、KN、KM.在△ADB和△KDM中,,∴△ADB≌△KDM,∴AB=KM=AC,∠BAD=∠MKD,∴AB∥KM,∴∠KMD=∠B=45°,∵∠NMC=∠NCM=∠ACB=45°∴MN=NC,∠KMN=∠ACN=90°在△ANC和△KNM中,,∴△ANC≌△KNM,∴AN=KN,∠ANC=∠KNM,∴∠KNA=∠MNC=90°∵AD=DK,∴DN=AD=DK,即AD=DN.(3)如图3中,结论:AD=DN,AD⊥DN.理由:延长AD到K,使得DK=AD,连接AN、KN、KM,延长KN交AC于G.在△ADB和△KDM中,,∴△ADB≌△KDM,∴AB=KM=AC,∠BAD=∠MKD,∴AB∥KM,∴∠KGC=∠BAC=90°,∴∠ACN+∠NMG=180°,∵∠KMN+∠NMG=180°,∴∠ACN=∠NMK,在△ANC和△KNM中,,∴△ANC≌△KNM,∴AN=KN,∠ANC=∠KNM,∴∠KNA=∠MNC=90°∵AD=DK,∴DN=AD=DK,DN⊥AK,即AD=DN.AD⊥DN.8.△ABC中,点D为BC上一点,E为AC上一点,连接AD,BE,DE,已知BD=DE,AD=DC,∠ADB=∠EDC.(1)如图1,若∠ACB=40°,求∠BAC的度数;(2)如图2,F是BE的中点,过点F作AD的垂线,分别交AD、AC于点G、H.求证:AH=CH.【过程解答】解:(1)如图1,∵AD=DC,∠ACB=40°,∴∠DAC=∠ACB=40°,∴∠ADB=∠C+∠DAC=80°,在△ADB和△CDE中,∵,∴△ADB≌△CDE(SAS),∴∠BAD=∠ACB=40°,∴∠BAC=40°+40°=80°;(2)如图2,过B作BN∥AC,交HF的延长线于N,直线HF交AB于M,连接DH、DM,∴∠BNM=∠EHF,∵BF=EF,∠BFN=∠EFH,∴△EFH≌△BFN(AAS),∴BN=EH,由(1)得:∠BAD=∠DAC,∵FH⊥AD,∴∠AGF=∠AGH=90°,∵AG=AG,∴△AMG≌△AHG(ASA),∴AH=AM,∠AHM=∠AMH,∵∠AMH=∠BMN,∴∠BNM=∠BMN,∴BN=BM,∵△ABD≌△CED,∴∠ABD=∠CED,∵BD=DE,∴△DEH≌△DBM,∴∠BMD=∠AHD,∵AM=AH,∠BAD=∠DAH,AD=AD,∴△AMD≌△AHD,∴∠AMD=∠AHD,∴∠AMD=∠BMD,∵∠AMD+∠BMD=180°,∴∠AMD=90°,∴∠AHD=90°,∵AD=CD,∴AH=CH.9.直角三角形有一个非常重要的性质:直角三角形斜边上的中线等于斜边的一半,比如:如图1,Rt△ABC中,∠C=90°,D为斜边AB中点,则CD=AD=BD=AB.请你利用该定理和以前学过的知识解决下列问题:如图2,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(1)求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明:若不成立,请说明理由;(3)如图4,∠BAC=90°,a旋转到与BC垂直的位置,E为BC上一点且AE=AC,EN⊥a于N,连接EC,取EC中点P,连接PM,PN,求证:PM⊥PN.【过程解答】(1)证明:如图2中,延长NP交BM的延长线于G.∵BM⊥AM,CN⊥AM,∴BG∥CN,∴∠PCN=∠PBG,在△PNC和△PGB中,,∴△PNC≌△PGB,∴PN=PG,∵∠NMG=90°,∴PM=PN=PG.(2)解:结论:PM=PN.如图3中,延长NP交BM于G.∵BM⊥AM,CN⊥AM,∴BM∥CN,∴∠PCN=∠PBG,在△PNC和△PGB中,,∴△PNC≌△PGB,∴PN=PG,∵∠NMG=90°,∴PM=PN=PG.(3)如图4中,延长NP交BM于G.∵∠EAN+∠CAM=90°,∠CAM+∠ACM=90°, ∴∠EAN=∠ACM,在△EAN和△CAM中,,∴△EAN≌△CAM,∴EN=AM,AN=CM,∵EN∥CG,∴∠ENP=∠CGP,在△ENP和△CGP中,,∴△ENP≌△CGP,∴EN=CG=AM,PN=PG, ∵AN=CM,∴MG=MN,∴PM⊥PN.。
中考数学基本模型—中点模型,初三数学专题复习总结倍长中线练习题

中考数学基本模型——中点模型线段中点是几何部分一个非常重要的概念,和后面学习的中线,中位线等概念有着密切的联系.在几何证明题中也屡次出现.那么,如果在题中遇到中点你会想到什么?等腰三角形三线合一;直角三角形斜边上的中线等于斜边的一半;还是中位线定理?今天我们重点探究“倍长中线”法以及平行线间夹中点时延长中线交平行的应用线相交.即“延长中线交平行”此时,易证△BEF≌△CED模型三如图,在△ABC中,点D是AB边的中点.可作另一边AC的中点,构造三角形中位线.如下图所示:时,只需将AE延长和DC的延长线相交,就一定会得到全等三角形,进而得到我们需要的结果.证明:如图,延长AE交DC的延长线于点F.∵四边形ABCD是平行四边形∴AB//CD,即AB//DF∴∠BAE=∠CFE,∠B=∠FCE又∵点E是BC中点∴BE=CE∴△ABE≌△FCE∴CF=AB=CD,AE=FE∴DF=2CD,又∵AD=2CD∴AD=DF,又因为点E是AF的中点∴DE⊥AF即∠AED=90°.反思:对于本题,还可以延长AE至点F使EF=AE,连接CF.通过证明△ABE ≌△FCE得到AB//CF,利用经过直线外一点有且只有一条直线与已知直线平行,得到D、C、F三点共线.再证明△DAF是等腰三角形,利用等腰三角形三线合一得到结论.对于第二种方法,同学们可以自己尝试.例2、在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.分析:由题可知,DE//BF,且点G是BE的中点,满足平行线间夹中点,所以可将DG延长与BF相交.证明:(1)AG=DG,且AG⊥DG.如图,延长DG交BF于点H,连接AH,AD.∵四边形CDEF是正方形,∴DE//CF即DE//BC∴∠GBH=∠GED,∠GHB=∠GDF又∵点G是BF的中点∴GB=GF∴△GBH≌△GDF(AAS)∴GD=GH,BH=DF∵DE=DC,∴BH=CD因为△ABC是等腰直角三角形∴AB=AC,∠ACD=180°-45°-90°=45°=∠ABC∴△ABH≌△ACD∴AH=AD,∠BAH=∠CAD∴∠DAH=∠CAD+∠CAH=∠BAH+∠CAH=∠BAC=90°∴△DAH是等腰直角三角形,又∵点G是DH的中点∴AG=DG且AG⊥DG.反思:若将正方形绕点C旋转任意角度,在旋转的过程中,上述结论还成立吗?试试看。
中点有关的几何题

安徽中考中与中点有关的几何题【08安徽】 10.如图,在厶ABC 中, AB=AC=5 ,BC=6,点M 为BC 中点, MN 丄AC 于点N ,则MN等于 ............. 【 】A691216/\A.-B.C. —D./ \5 5 55/ \NCBMC【08安徽】 20.如图四边形 ABCD 和四边形 ACED 都是平行四边形,点 R 为DE 的中点,BR 分别交AC 、CD 于点P 、Q 。
⑴请写出图中各对相似三角形 (相似比为1除外); 【解】(2)求 BP : PQ : QR【解】【09安徽】22、如图,M 为线段 AB 的中点,AE 与BD 交于点C , / DME M A= / B= a ,且DM 交AC 于F ,ME 交BC 于G.(1) 写出图中两对相似三角形,并证明其中的一对;(2) 请连接 FG.如果 a =45 ° AB=4 2 , AF=3,求 FG 长.【11安徽】6.如图,D 是厶ABC 内一点,BD 丄CD , AD = 6,E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点,则四边形 的周长是【 】第20题图BD = 4, EFGHBC . 10 【11安徽】22.在厶ABC 中,/ ACB = 90° / ABC = 30°将厶ABC 绕顶点C 顺时针旋转, 旋转角为r(O°VrV 180°,得到△ A 1B 1C .(1)如图1,当AB // CB 1时,设A 1B 1与BC 相交于点D •证明:△ AQD 是等边三角形; 【证】(2)如图2,连接 AA 1、BB 1,设△ ACA 1和厶BCB j 的面积分别为 S 1、S ?.求证:S 1 : S 2 =1 : 3;【证】(3)如图3,设AC 的中点为E , A 1B 1的中点为P , AC = a ,连接EP -当二= _______________________时,EP 的长度最大,最大值为 ____________ .【12安徽】10.在一张直角三角形纸片的两直角边上各取一点,分别 沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图 所示的直角梯形,其中三边长分别为 2、4、3,则原直角三角形纸 片的斜边长是( )A.10B.4.5C. 10 或 4.5D.10 或 2、17上, △ BDG 与四边形 ACDG 的周长相等,设 BC=a 、AC=b 、AB=c. (1) 求线段BG 的长; 解:D . 11【12安徽】22.如图1,在厶ABC 中, D 、E 、F 分别为三边的中点, G 点在边ABB 图2B第1U 题囹(2)求证:DG平分/ EDF;证:(3)连接CG,如图2,若厶BDG与厶DFG相似,求证: 证:PEF △ PDC、△ PAB的面积分别为S、S、S。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页/共4页专题一 中点M 型基本条件:①∠PMQ =∠B =∠C ;②M 是BC 的中点 基本结论:①△EMF ∽△EBM ∽△MCF. ②EM 平分∠BEF ,FM 平分∠EFC. ③EM 2=EB ·EF ,FM 2=FC ·EF. 常见特例:特例一:条件:①等边△ABC ;②∠MPN =60°,③P 是BC 的中点。
特例二:条件:①等腰直角△ABC ,AC =BC ,∠C =90°;②∠EDF =45°;③点D 是AB 的中点。
特例三:条件:①AB =AC ;②∠BAC =120°,∠EDF =30°,③D 是BC 的中点。
特例四:条件:①矩形ABCD ;②∠GEF =90°,③E 是AB 的中点。
特例五:条件:①直角梯形ABCD 中,AB ∥CD ,∠A =90°;②E 是AD 的中点;③∠BEC =90°。
巩固练习:1. 已知:梯形ABCD 中,AD ∥BC ,∠A =90°,E 为AB 的中点,若AD =2, BC =4,∠CED =90°,则CD 长为 。
2. 如图,在正方形ABCD 中,点E 、F 在边BC 、CD 上,若 AE =2,EF =1,AF =5 ,则正方形的边长为 。
3. 已知:等边 △ABC 中,AB =8,点D 为AB 的中点,点M 为BC 上一动点,以DM 为一边,在点B 异侧作等边△DMN 。
DN 交AC 于点F ,当∠DAN =90°时,则FN 的长为 。
4. 如图,以矩形OABC 的邻边OA 、OC 分别为x 轴、yOA 上的一点,将△COF 沿直线CF 翻折,点O 落在AB 的中点E 处,且OC =(1) 求直线EF 的解析式;(2) 将直线EF 绕点F逆时针旋转90°,得到直线m ,直线m 交y 轴于点D ,求点D 的坐标。
1. 如图,在△ABC 中,AB =AC ,∠BAC =α,点D 为BC 边的中点,BE ⊥AC 于E ,DF ⊥AB于F.(1) 当00<α<900,(如图1),求证:AE +2BF =AB ;(2) 当900<α<1800,(如图2),则AE 、BF 、AB 之间的数量关系 ; (3) 在(1)的条件下,过点D 作DG ∥AB ,交AC 于G ,且DF =GE =3时(如图3),求BF 的值。
2. 已知:直角梯形ABCD ,AB ∥CD ,∠ABC =90°,AB =BC ,E 为射线BC 上一点,连接AE ,过点E 作AE 的垂线,分别交直线AB 、直线CD 于点G 和F. (1) 当点E 在BC 上时(如图1),求证:BE =BG +CF.(2) 当点E 在BC 的延长线上时(如图2),猜想BE 、BG 和CF 的数量关系,并证明你的猜想; (3) 在(2)的条件下,设AE 交CD 于点H ,若CH =92BE ,AB =2,且CD <34,求EG 的长。
“A ”字型专题1. 已知,在正方形ABCD 中,点E 是边AB 上一点,点G 在边=DG ,作EF ⊥EG ,交边BC 于点F(图1)。
(1) 求证:AE +CF =EF ;(2) 连接正方形ABCD 的对角线AC ,连接DF ,线段AC 2),探究线段AE 、AD 、AK 之间的数量关系,直接写出你的结论 。
(3) 在(2)的条件下,连接线段DE 与线段AC 相交于点P ,(图3)若AK =82,△BEF 的周长为24,求PK 的长。
2. 如图,在△ABC 中,AB =2AC ,点D 在BC 上,且∠CAD =∠连接CE ,CE 与AD 交于点G ,点F 在BC 上,且∠CEF =∠(1) 若∠BAC =90°,如图1,求证:EG +EF =2AC ;(2) 若∠BAC =120°,如图2,此时线段EG 、EF 、AC 为 ;(3) 在(2)的条件下,在∠BAD 的内部作∠DAM =60°,∠DAM 的一边AM 交BC 于巩固1巩固2巩固3图1图1E第2页/共4页点M ,AM 与CE 交于点N ,若AC =2,求线段MN 的长。
3. 已知,在△ABC 中, BC =AC ,∠MCN =21∠ACB ,CM 交AB 于点E ,过点B 作BF ⊥CB 交CN 于点F.(1) 当 ∠ACB =90°(如图1所示)时,求证:BE -AE =2BF ;(2) 当∠ACB =120°(如图2所示)时,线段BE 、AE 与BF 之间的数量关系为 ;(3) 在(2)的条件下,FB 、CE 的延长线相交于点G ,连接AG 、FE ,直线AG 、FE 交于点H ,若AC =6,BF =BE ,求AH 的长。
“X ”字型专题1. 已知,A 、C 分别为∠BOE 两边上的两点,D 为∠BOE 内一点,DC ∥AC 相交于点F ,G 为FD 上一点,过点G 的直线交OE 于Q ,交CD OB 于点M. (1) 若FG =31FD 时(如图1),求证:PQ +MN =PN ; (2) 若FG =21FD 时(如图1),且△OAC 为等边三角形,OC =4,CQ =3,现将∠DAC 绕点A顺时针旋转,旋转后AD 所在边交OC 于S ,AC 所在边交CD 于点T ,当旋转到AT ∥MQ 时,连接ST , 求:ST 长。
2. 如图,已知Rt △ABC 中,∠C =90°,AD 平分∠BAC ,AB边上一点,过点P 作PM ⊥BC ,PN ⊥AD 垂足为M 、N 。
(1) 当点M 与点D 重合时,求证:PM =5P N.(2) 当点N 与点重合时,连接AM 交PD 于点E ,将射线于点F ;若AC =3,求EF 的长。
“M ”字型专题1. 已知,四边形ABCD 中,AD =AB ,AD ∥BC ,∠A =90°,M 为AD 连接MF ,过M 点作ME ⊥MF ,交边AB 于点E 。
(1) 如图1,当∠ADC =90°时,求证:4AE +2CF =CD.(2) 如图2,当∠ADC =135°时,线段AE 、CF 、CD 的数量关系为 . (3) 如图3,在(1)的条件下,连接EF 、EC 、EC 与FM 相交于点K ,线段FM 关于FE 对称的线段与AB 相交于点N ,若NE =310,FC =AE ,求MK 的长。
2.如图,已知Rt △ABC 中,∠C =90°,过点B 作∠BAC 平分线AD 的垂线,垂足为D ,AD 交BC 于点E.(1)当AC BC =53时,求证:DE =81AE ; (2)当AC BC =54时,判断DE 、AE 的关系 ;(3)在(2)的条件下,取CD 中点F ,连结EF 并延长交AC 延长线于点G ,交CD 于F ,现有一个45°角顶点与F 重合,将它旋转一边交CG 于点M ,另一边交BC 于点N ,若CM =MG ,AC =3,求CN 的长。
2. 如图1,在△ABC 中,AC =BC ,∠ACB =90°,点D 为AB 边中点,以点D 为顶点,作∠PDQ=90°,DP 、DQ 分别交直线AC 、BC 于E 、F ,分别过点E 、F 作AB 的垂线,垂足分别为M 、N.(1) 求证:EM +FN =22AC. (2) 把∠PDQ 绕点D 旋转,当点E 在线段AC 的延长线上时(如图2)特别资料一、基本图形:“A ”字型1. 计算,已知:△ABC 中,DA 交BF 于点E ,AE =ED ,BD :CD =1:2,AC =4,求AF 的值。
2. 已知,△ABC 中,AD 平分∠BAC ,∠BAC =120°,若AC =6,BC =37,求AD 的长。
3. 已知,△ABC 中,AD 平分∠BAC ,DE ∥AC ,EF ∥BC ,AF =2,AB =215,求DE 的长度。
4.已知,D 在BC 的延长线上,DF 交AC 于点E ,E 为AC 的中点,BF =3AF.图1M ()第3页/共4页求证:BC =2CD.5.已知:△AB C 、△BCE 均为等边三角形,且A 、B 、求证:(1)MN ∥AC (2)MNBCAB 111=+ 6.已知,△ABC 中,AD 、CE 分别平分∠BAC ,∠ACB 求证:(1)AE +CD =AC(2)若AD =5,PC 二、基本图形:“X ”字型1.已知:Rt △ABC 中,∠ACB =90°,CD ⊥DE ,且DB =BC ,若AE:EC =1:3,AB =5,求AD 的长。
2.已知: △ABC 中,AD ⊥BC ,BE ⊥AC 交AD 于点F ,若∠BAC =45°,CD =1,BD =23求AD 的长。
3. 已知,矩形ABCD 沿BE 折叠后C 与G 重合,若DE =1,CE =2,4. 已知:Rt △ABC 中,∠BAC =90°,AD ⊥BC ,BF 平分∠ABC ,且5. 已知:△ABC 中,AB =AC ,∠BAC =120°,AB ⊥BD ,∠DAE =60AC.6.已知:矩形ABCD 沿AE 折叠后B 与G 重合,且CE:BE =1:27. 已知:矩形ABCD 中,B (8,5),点P (m ,0)且0<m <8,点O ',直线CO '交直线AB 于Q ,求m 为何值时,△PCQ 是以PQ 三、基本图形“直射影、斜射影”1. 已知:△ABC 中,∠BAD =∠C , 若AB =4,BD =2,求2.已知:△ABC 中,AD ⊥AC , 若AB =AC =6,BD =1,求BC 的长。
3.已知:AB ⊥CD ,∠CED =90°,DF ⊥AC 交BE 于点G ,若BG =3,AE =6,求EG 的长。
4.已知:AD 平分∠BAC ,E 在BC 的延长线上,EF 垂直平分AD 且CE =2CD , 求证:DE =2BD.5.已知:Rt △ABC 中,∠BAC =90°,AD ⊥BC ,延长AC AC =CE .6. 已知:Rt △ABC 中,∠BAC =90°,AD ⊥BC ,E 为AD 中点,且EF ⊥EC ,求证:BF =3DF .7.已知:梯形OABC 中,BC ∥OA ,B (3,6),A (8,0)点P(m ,n)在AB 边上(3<m <8),过P 作OA 平行线OA ,交AC 于D ,过P 作OA 的垂线交OA 于点E ,求,当m 为何值时,△ODE 为直角三角形?8.已知:△ABC 中,BC =2AB ,P 为BC 中点,∠ABC =∠APF =(1)求证:PF =AE (2)若AD =7,求DE 四、基本图形“M ”型①直M 型②斜M 型1.已知:Rt △ABC 中,∠C =90°,D 为BC 中点,∠ADE =∠B ,若AC =2,BC =4,求BE 的长。
