力学8-质心,质心运动定理,质点动力学习题课
质点动力学2019习题解析

(m1
m2 )g m1 m2
2m2a
a2
a
a
(m1 m2 )g 2m1a
m m 1
2大学物理教学中心
Northeastern University
7.一质量为0.05 kg、速率为10 m·s -1的刚球,以与钢板法线呈45º角
的方向撞击在钢板上,并以相同的速率和角度弹回来;设碰撞时间
1
和m2
的星球,原来为静止,且相
距为无穷远,后在引力的作用下,互相接近 ,到相距为r 时。 求它
们之间的相对速率为多少?
解 由动量守恒,机械能守恒
mv1 mv2 0
1 2
m1v12
1 2
m2v22
G
m1m2 r
0
m1 v 1
v m2 2
解得
v1 m2
2G (m1 m2)r
v2 m1
2G (m1 m2 )r
相对速率 vr v1 v2 m2
2G m (m1 m2 )r 1
2G (m1 m2)r
大学物理教学中心
Northeastern University
x
F
m(x)
mg
o
9.一人从10m深的井中提水,开始桶连 水共10kg,由于水桶漏水,每升高1m 漏去0.2kg的水。水桶被匀速地从井底 提到井口,则人所做的功为多少?重 力做功为多少?(g=9.8m/s2)
m
dt
v dv
t 3t 2dt
2
0
v 2 t3 dx , v(1) 3 dt
x dx
t (2 t 3 )dt
5
0
x 5 2t 1 t 4; x(1) 7.25
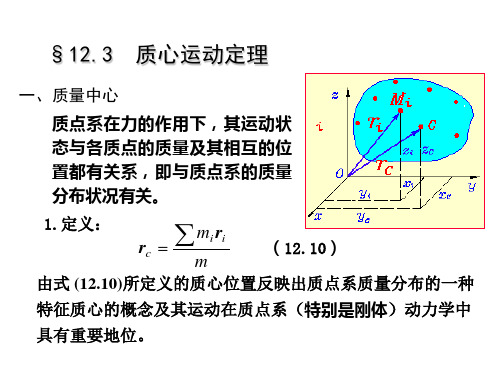
质心运动(课堂PPT)

m1 x1
l1
xC
l2
m2 x2
x
xC就是m1和m2的质心位置
m 1 (x C x 1) m 2(x 2 x C ) xCm 1 m x1 1 m m 2 2x2m 1x1M m 2x 4 2
二.质心坐标
推广到3维质点系,若n个质点的位矢为
r1,r2, rn,
质点系总质量 Mmi
作用在质点系上的合外力等于质点系 的总质量与质心加速度的乘积
质心的运动状态变化只由系统所受 的合外力决定,与内力无关。
(质心运动定理本身只对惯性系成立!)
10
质心的运动满足: F r合外Marc
质心能作为质点系 整体运动的代表!
11
五.质心动量变化定理
质心运动定理:
F 合 外 d(M dv C t)M a c
2
旋轮线:教材P25习题1.4
• 质点系运动 质心运动+各质点相对于质心的运动3
§6-1 质心动量定理
一. 质心
质心 — 质点系统的质量中心
对质点系, 总有一特殊点,其运动和质点系的所 有质量集中于该处的质点运动相同 质心
以质点系各点质量为权重的系统位置的平均值
以两质点系统为例:
若有一点xC,使
若质心系是非惯性系,则质心系中有:
F 合 F 外 惯 m a '(c质心系中的质心运动定律) 而a 'c0(质 心系中质心的加速度为零)
F 合 外 F 惯 0
在质心非惯性系中惯性力和外力完全抵消,
故系统总动量守恒,且恒为零。
16
§6-2. 质心动能定理
M aCF 合 外
若F合
外 0x,则 a C0
质点动量定理.pptx

1
Yc m
1 yCdm m
R
0 y边 (2x边dy边)
1 R
m
0
y边 (2
R2
y边2 dy边 )
4R 3π
dy边
yC
y边
即质心位置为
0,
4R 3π
。
8
第9页/共47页
(4) 多个规则形状物体组成系统的质心 多个规则形状物体组成系统的质心,可先找到每
个物体的质心,再用分立质点系质心的求法,求出公 共质心。
它们置于一质量也为 m 的槽的底部。槽置于光滑的水
平面上。释放后,球最终静止于槽的底部,问此时槽移
动了多远?
解:水平方向动量守恒,质心位置不变
xC0 xC
xC 0
2m 0 3m
mR
3mx xC 3m
解得: x 1 R 0 向右移动
3 27 第28页/共47页
例4.1.2-2 一物体在光滑水平面上以 5m/s的速度沿 x
由牛顿第二定律原始表达式:
对上式积分得:
F d(mv) dt
定义:
t t
Fdt mv(t t) mv(t) t P mv 称为质点的动量
tt
I Fdt
称为力在 t 时间内的冲量
t
质点的动量定理: 外力冲量等于质点动量的改变量
16
第17页/共47页
例4.2.1-1 一质量为 0.15 千克的棒球以 v0 40m/s 的
(3)
1
yc
mA yA mB yB mD yD mA mB mD
4mD (2) 2mD (1) mD (8) 4mD 2mD mD
2
zc
mA zA mB zB mD mA mB mD
大学物理章质点动力学习题答案

第二章 质点动 力学2-1一物体从一倾角为30︒的斜面底部以初速v 0=10m·s -1向斜面上方冲去,到最高点后又沿斜面滑下,当滑到底部时速率v =7m·s -1,求该物体与斜面间的摩擦系数;解:物体与斜面间的摩擦力f =uN =umgcos30︒物体向斜面上方冲去又回到斜面底部的过程由动能定理得220112(1)22mv mv f s -=-⋅物体向斜面上方冲到最高点的过程由动能定理得2010sin 302mv f s mgh f s mgs -=-⋅-=-⋅-2(2)s ∴=把式2代入式1得,220.198u =2-2如本题图,一质量为m 的小球最初位于光滑圆形凹槽的A 点,然后沿圆弧ADCB 下滑,试求小球在C 点时的角速度和对圆弧表面的作用力,圆弧半径为r ;解:小球在运动的过程中受到重力G 和轨道对它的支持力T .取如图所示的自然坐标系,由牛顿定律得22sin (1)cos (2)t n dv F mg mdt v F T mg mR αα=-==-=由,,1ds rd rd v dt dt dt vαα===得代入式(), A 并根据小球从点运动到点C 始末条件进行积分有,902n (sin )m cos 3cos '3cos ,e v vdv rg d v vrv mg mg rmg αααωααα=-===+==-=-⎰⎰得则小球在点C 的角速度为=由式(2)得 T 由此可得小球对园轨道得作用力为T T 方向与反向2-3如本题图,一倾角为θ的斜面置于光滑桌面上,斜面上放一质量为m 的木块,两者间摩习题2-2图擦系数为μ,为使木块相对斜面静止,求斜面的加速度a 应满足的条件;解:如图所示()1212min max sin ,cos cos sin (1)sin cos 2(1)(2)(sin cos )(cos sin )(sin cos )()(cos sin )1(2)(1)(sin cos )(cos sin )(sin cos a a a a N mg ma ma mg uN m a ma u g u a u g u g tg u a u utg u g u a u g u a θθθθθθθθθθθθθθθθθθθθθ==∴-==±==⨯+-=+--∴==++-⨯+=-+∴=得,得,)()(cos sin )1()()11g tg u u utg g tg u g tg u a utg utg θθθθθθθθθ+=---+∴≤≤+- 2-4如本题图,A 、B 两物体质量均为m,用质量不计的滑轮和细绳连接,并不计摩擦,则A和B 的加速度大小各为多少 ; 解:如图由受力分析得(1)(2)2(3)2(4)ggA AB B A B A BA B mg T ma T mg ma a a T T a a -=-===1解得=-52=-52-5如本题图所示,已知两物体A 、B 的质量均为m=,物体A 以加速度a =s 2 运动,求物体B 与桌面间的摩擦力;滑轮与连接绳的质量不计解:分别对物体和滑轮受力分析如图,由牛顿定律和动力学方程得,()()()1f 111f (1)''(2)2'(3)'2(4)5'6'7(4)7.22A T A TB T T A B T T T T m g F m a F F m a a a F F m m m F F F F mg m m aF N-=-======-+===解得2-6质量为M 的三角形木块,放在光滑的水平桌面上,另一质量为m 的木块放在斜面上如本题图所示;如果所有接触面的摩擦均可忽略不计,求M 的加速度和m 相对M 的加速度;AB 习题2-4图习题2-5图aθ习题2-3图ma AmgT A T B a Bmg解:如图m 相对M 的相对加速度为m a ',则 cos ,sin ,mxm my m a a a a θθ''''== 在水平方向,cos mxmx Mx mx mxMx m M a a a a a a a a θ'=-''∴=+=-+在竖直方向sin mymy myma a a a θ'='∴=由牛顿定律可得,sin cos cos sin sin mx mM my m MN ma ma ma mg N ma ma N Ma θθθθθ'-==-+'-===解得θ+θθ=2sin cos sin m M mg a M , 2()sin sin m M m g a M m θθ++= 2-7在一只半径为R 的半球形碗内,有一粒质量为m 的小钢球;当钢球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高解:取钢球为隔离体,受力分析如图所示,在图示坐标中列动力学方程得,2sin sin cos cos ()/n F ma mR F mg R h Rθωθθθ====-解得钢球距碗底的高度2ω-=g R h2-8光滑的水平面上放置一半径为R 的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦系数为μ;物体的初速率为v 0,求:1t 时刻物体的速率;2当物体速率从v 0减少到v 0/2时,物体所经历的时间及经过的路程;解:1设物体质量为m,取图示的自然坐标系,由牛顿定律得,02222tv 2v (1)(2)(3)4dv 4dt u v N n f t f Nv F ma m R dv F m a m dtF uF v dvu R dt ===-=-=-⎰⎰0由上三式可得=()R 对()式积分得=-习题2-6图00Rv v R v tμ∴=+(2) 当物体速率从v 0减少到v 0/2时,由上式00Rv vR v tμ∴=+可得物体所经历的时间0t R v μ'=经过的路程t t 000vdt dt ln 2Rv Rs R v t μμ''=+⎰⎰==2-9从实验知道,当物体速度不太大时,可以认为空气的阻力正比于物体的瞬时速度,设其比例常数为k;将质量为m 的物体以竖直向上的初速度v 0抛出; 1试证明物体的速度为t m ktm ke v e kmg v --+-=0)1(2证明物体将达到的最大高度为)1ln(020mgkv k g m k mv H +-=3证明到达最大高度的时间为)1ln(0mgkv k mt H +=证明:由牛顿定律可得0000220200ln (1)(2),()ln(13tvv mmt t k kx mg mg kv mdv dt mg kvmg kv m mg t v e v e k mg kv kmvdvdx mg kvmg kv u du kdvk mgdu k mgdudx mdu dx mdu m u m u mv kv m g x k k mg m t k --+-=++∴==-++=-++==∴=-+=-+∴=-+=⎰⎰⎰⎰dv(1)-mg-kv=m ,dt,dv -mg-kv=mv ,dx 令,)()0ln0t ln mg kv mg kvmg kv m v k mg k +++∴=+当时,=即为到达最高点的时间2-10质量为m 的跳水运动员,从距水面距离为h 的高台上由静止跳下落入水中;把跳水运动员视为质点,并略去空气阻力;运动员入水后垂直下沉,水对其阻力为-b v 2,其中b 为一常yf =-kvmgv量;若以水面上一点为坐标原点O,竖直向下为Oy 轴,求:1运动员在水中的速率v 与y 的函数关系;2跳水运动员在水中下沉多少距离才能使其速率v 减少到落水速率v 0的1/10假定跳水运动员在水中的浮力与所受的重力大小恰好相等解:运动员入水可视为自由落体运动,所以入水时的速度为0v =入水后如图由牛顿定律的0220//0100mg-f-F=ma mg=F f=bv dv a=dt v dy (2)0.4,0.1m vy ln 5.76m b y v v by m by m dv v dy dvb mv dyb dv m vv v e m v v v ---=∴-=-=====⎰⎰b将已知条件代入上式得,m=-=2-11一物体自地球表面以速率v 0竖直上抛;假定空气对物体阻力的值为f =-km v 2,其中k 为常量,m 为物体质量;试求:1该物体能上升的高度;2物体返回地面时速度的值;解:分别对物体上抛和下落时作受力分析如图,h120m 1ln()2v 01ln()2(2)m v=v 1gyvv vvdv dy g k g k y k g k g k k g vdvdy g k k =-++∴=-+∴+=-∴+⎰⎰⎰⎰222220max 222-/0dv mvdv (1)-mg-k v =m=,dt dy v v v 物体达到最高点时,=,故v h=y =dv mvdv下落过程中,-mg+k v =m=dt dy-v v ()2-12长为60cm 的绳子悬挂在天花板上,下方系一质量为1kg 的小球,已知绳子能承受的最大张力为20N ;试求要多大的水平冲量作用在原来静止的小球上才能将绳子打断解:由动量定理得000I mv I v m∆=-∆∴=,如图受力分析并由牛顿定律得,2020220/202.47mv T mg l mv T mg lmg I l I Ns-==+≥∴+∆≥∆≥2-13一作斜抛运动的物体,在最高点炸裂为质量相等的两块,最高点距离地面为;爆炸后,第一块落到爆炸点正下方的地面上,此处距抛出点的水平距离为100m;问第二块落在距抛出点多远的地面上 设空气的阻力不计解:取如图示坐标系,根据抛体运动规律,爆炸前,物体在最高点得速度得水平分量为()1010x 2x 12y 2x 0x (1),v 2mv mv 30mv mv 414v v 100x x v x t==+=2111121物体爆炸后,第一块碎片竖直下落的运动方程为1y =h-v t-gt 2当碎片落地时,y =0,t=t 则由上式得爆炸后第一块碎片抛出得速度为1h-gt 2=()t 又根据动量守恒定律,在最高点处有1=()211=-22联立以上()-()式得爆炸后第二块碎片抛出时的速度分量分别为=2=2x 11212x 2222y 222214.7v t 5y =h+v t -60,x 500my ms v v ms gt y --====21211h-gt 2t 爆炸后第二块碎片作斜抛运动,其运动方程为x =x +()1()2落地时由式(5)和(6)可解得第二块碎片落地点得水平位置=2-14质量为M 的人手里拿着一个质量为m 的物体,此人用与水平面成θ角的速率v 0向前跳去;当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出;问:由于人抛出物体,他跳跃的距离增加了多少假设人可视为质点解:取如图所示坐标,把人和物视为一系统,当人跳跃到最高点处,在向左抛物得过程中,满足动量守恒,故有()00000m cos ()v u mu v cos m mu v v- cos m sin t g m sin x vt um gv Mv m v u v v v v v θθθθθ=+-∆∆∆+M 式中为人抛物后相对地面的水平速率,-为抛出物对地面得水平速率,得=++M人的水平速率得增量为==+M而人从最高点到地面得运动时间为=所以人跳跃后增加的距离为==(+M )2-15铁路上有一静止的平板车,其质量为M,设平板车可无摩擦地在水平轨道上运动;现有N 个人从平板车的后端跳下,每个人的质量均为m,相对平板车的速度均为u;问:在下列两种情况下,1N 个人同时跳离;2一个人、一个人地跳离,平板车的末速是多少所得的结果为何不同,其物理原因是什么解:取平板车及N 个人组成的系统,以地面为参考系,平板车的运动方向为正方向,系统在该方向上满足动量守恒;考虑N 个人同时跳车的情况,设跳车后平板车的速度为v,则由动量守恒定律得 0=Mv+Nmv -uv =Nmu/Nm+M 1又考虑N 个人一个接一个的跳车的情况;设当平板车上商有n 个人时的速度为v n ,跳下一个人后的车速为v n -1,在该次跳车的过程中,根据动量守恒有M+nmv n =M v n -1+n-1m v n -1+mv n -1-u 2 由式2得递推公式v n -1=v n +mu/M+nm 3当车上有N 个人得时即N =n,v N =0;当车上N 个人完全跳完时,车速为v 0, 根据式3有,v N-1=0+mu/Nm+Mv N-2= v N-1+mu/N-1m+M ………….v 0= v 1+mu/M+nm将上述各等式的两侧分别相加,整理后得,0n 0mu v nm,1,2,3....v vM nm M Nm n N N +≤+=∑N=1=M+由于故有,即个人一个接一个地跳车时,平板车的末速度大于N 个人同时跳下车的末速度。
第二章质点运动学(2)

F
F
t1
t2 t
例 质量M=3t的重锤,从高度h=1.5m处自由落 到受锻压的工件上,工件发生形变。如果作用 的时间 (1) =0.1s, (2) =0.01s 。试求锤对工件 的平均冲力。 解法一利用动量定理,取竖 直向上为正。
( N Mg ) Mv Mv0
初状态动量为 M 2 gh , 末状态动量为 0。
第二章 质点动力学
(2) 动量守恒定律 火箭运动 质心运动定律
2-3 冲量‧动量定理
1、冲量
dp 把牛顿第二定律的微分形式 F dt 改写为 F d t d p
考虑一过程,力对质点的作用时间从t1 — t2, t2 p2 两端积分 Fdt dp p 2 p1 mv2 mv1
mi ri
d vi mi d vc dt ac dt mi
由牛顿第二定律得
mi ai
m
i
m1a1 m2 a2 mn an
d v1 m1 F1 f12 f13 f1n dt d v2 m2 F2 f 21 f 23 f 2 n dt d vn mn Fn f n 2 f n 3 f n ( n 1) dt
x g v x g 2 gx 3x g 所以桌面受的压力 N N 3x g
2
例 2 一柔软链条长为 l ,单位长度的质量为。 链条放在桌上,桌上有一小孔,链条一端由小孔稍 伸下,其余部分堆在小孔周围。由于某种扰动,链 条因自身重量开始落下。求链条下落速度与落下距 离之间的关系。设链与各处的摩擦均略去不计,且 认为链条软得可以自由伸开。 解 以竖直悬挂的链条 m2 和桌面上的链条为一系统, O 建立如图坐标。 则 F m1 g yg 动量定理 m1
理论力学总复习(3)

二、选择题
1、已知刚体质心 C 到相互平行的 、
z ′、z
轴的距离分别为
a、b
,刚体的质量为 m ② 的计算公式为__________________。 的计算公式为 。 ① ② ③
,对 z 轴的转动惯量为 J z ,则
Jz
′
′ J z = J z + m( a 2 − b 2 )
′ ② J z = J z − m (a 2 − b 2 )
& −ω2x = 0 & x
摆锤质量m,悬挂点O以加速度 2、已知摆长 OM = L ,摆锤质量 ,悬挂点 以加速度 a0 、 ' ' 向上运动, 向上运动,则相对于 Ox y 坐标系的相对运动动力学方程为 _________________________。 。
& & φ + (a0+g) sin φ / L = 0
p A > pB
p A < pB
p A = pB
3、 3、质量分别为 m1 = m2 = 2m 的两个小球 M 1 , M 2 用长为L而重量不计的刚杆相连 而重量不计的刚杆相连。 用长为 而重量不计的刚杆相连。现将 M 1 置于光滑水平面上, 置于光滑水平面上,且 M 1 M 2 与水平面成 则当无初速释放、 球落地时, 60° 角,则当无初速释放、M 2 球落地时, ② M 1 球移动的水平距离为 球移动的水平距离为___________。 。 ① L/3; ; ② L/4; ; ③ L/6; ; ④ 0。 。
① 30N; ; ② 20N; ; ③ 16N; ; ④ 24N。 。
三、填空题 1、光滑细管绕铅垂轴 以匀角速度 ω 转动。管内有一小球以相对于管 、光滑细管绕铅垂轴z以匀角速度 点运动, 的初速度 v r 0 朝O点运动,则小球相对细管的相对运动微分方程为 点运动 __________________。 。
质心运动定理

质心运动定理3、质心运动定理质心运动定理问题:内力是否影响质心的运动?(e)1d ()d n C ii mv F t==∑由(e)1d d n C ii v m F t ==∑得(e)1nC ii ma F ==∑或质点系的质量与质心加速度的乘积等于作用于质点系外力的矢量和.--质心运动定理质心运动定理与动力学基本方程有何相似与不同之处?质心运动定理常量质心运动定理质心运动定理内力不能改变质心的运动汽车发动机的气体压力是原动力通过传动机构使主动轮转动地面摩擦力(e)1nC ii ma F ==∑ma F=质点系质心的运动可看成质点的运动,此质点集中了质点系的质量及其所受的力爆破山石通过质心运动轨迹, 确定石块堆落地点 ma F=是公理,描述质点运动状态变化规律(e)1nC ii ma F ==∑是导出定理,描述质心运动状态变化规律质心运动守恒定律(e)Cx xma F=∑(e)Cy yma F=∑(e)Cz zma F=∑2(e)Cnv m F ρ=∑(e)C t v m F t =∑d d (e)0bF=∑在直角坐标轴上的投影式为:在自然轴上的投影式为:(e)F ∑≡若 则 常矢量 C v =(e)0xF∑≡若 则 常量 =Cxv若初始静止,质心位置不变 若初始速度投影等于0, 质心在该轴坐标不变质心运动定理均质曲柄AB长为r,质量为m1,假设受力偶作用以不变的角速度ω转动,并带动滑槽连杆以及与它固连的活塞D ,如图所示.滑槽、连杆、活塞总质量为m2,质心在点C .在活塞上作用一恒力F .不计摩擦及滑块B的质量,求:作用在曲柄轴A处的最大水平约束力Fx .例1t m m m m r t x a C Cxωωcos 2d d 2121222⎪⎭⎫⎝⎛++-==tm m r F F x ωωcos 2212⎪⎭⎫⎝⎛+-=⎪⎭⎫⎝⎛++=212m ax2m m r F F ω最大水平约束力为应用质心运动定理()FF a m m x Cx -=+21()21211cos cos 2m m b r m r m x C +⋅⎥⎦⎤⎢⎣⎡++=ϕϕ分析整体,受力如图所示。
力学习题-第4章质点组动量定理(含答案)

已知 B 的质量是 A 的两倍,而 C 的质量是 A 的三倍,此时由此三质点组成的体
系的质心的位置为
1 28 A. ( 3 , - 3 , 3) ; B. (1, -1, 2) ; C. (1, - 2, 8) ; D. (1, 2, 3)
答案:B
解:根据题中给定的坐标系,由质心计算公式可知:
rc
M月l 81M 月 M 月
l 82
4.68 106
m.
2. 已知质点质量 m = 5kg,运动方程 r = 2ti + t2j . 则质点在 0~2 秒内受的冲量大 小为 N·s. 答案:20 解:F = ma = 10j ;
I = FΔt = 20j; 所以冲量大小为 20Ns.
3. 沿 x 方向的力 F = 12t (SI)作用在质量 m = 2kg 的物体上,使物体从静止开始 运动,则它在 3 秒末的动量大小为 kg·m/s. 答案:54 解:力 F 的冲量大小为
2. 无论质心系是否是惯性系,质心系下质点组的总动量始终为零. 答案:对 解释:对质心系下的观测者而言,质点组所受的合外力与总的惯性力相等,即, 质点组所受合外力为零,动量守恒. 其守恒值为质点组的总质量与质心速度的 乘积。而对质心系下的观测者而言,观测的质点组的质心速度始终为零. 因此, 出现质心系下质点组总动量为零的结果. 这也是质心系的特点之一.
第四章 质点组动量定理与守恒定律 单元测验题
一、选择题
1. 作用在质点上的力对时间的累积称为力的 ,其效果等于质点
的
改变.
A. 冲量、动量;B. 功、动量;C. 功、动能;D. 冲量、动能
答案:A
2. 某一时刻 A、B、C 三质点的位置坐标分别为:(-3, 4, 3)、(3, -8, 6)、(1, 2, -1),
质心运动定理

质点动量
p mv
质点系动量
P
mivi mvC
问:刚体系动量?
元冲量
dI F dt
冲量
t2 t2
I dI F dt
t1
t1
§3 动量(冲量)定理
质点 质点系
d
mv
F
mv2
mv1
t2
Fdt
dt
i
dmivi
dt
Fi E
Fi I
t1
dmivi
dt
FiE
Fi I
F
问题2:AB、AC为两相同的均质杆,每根质量为m。 系统初始时刻静止于光滑的水平桌面,受大小为F的力 作用如图示。问A点的加速度等于?
B
A
C
F
例1:图示机构,地面光滑,初始时刻系统静止。问 m1下降h时,m4水平移动多少?
解: 1.建立坐标架
记四个物块的质心初始时刻坐标 分别为x1、 x2、 x3、 x4。
ABab和CDcd流体质点系的质量为
m g Qt
g
P2
P1
PCDcd
PABab
g
g
Qt
(v2
v1 )
g
P2 P1 PCDcd PABab g Qt(v2 v1 )
F1
v1
P2 P1 t
g
g
Q(v2
v1 )
dP dt
W
受力分析画示力图,建立动量 定理方程:
v2
dP dt
O
450
1m
A
C
450
B
同样,如果方程完整了,B点 的速度和加速度不必知道。
例4.质量1kg,长度2m的均质杆被绳索和光滑地面约束。已 知在图示位置时B点的速度为 2 m/s,加速度 2 / 2 m/s2。 试求绳索的拉力。
4.4 质心 质心运动定理

大学物理 第三次修订本
17
第4章 冲量和动量
在第二级火箭燃料耗尽时, 火箭主体的 速度达到了v2 , 由公式得
v v0 uln
M0 M
v2 v1 uln N 2
在第三级火箭燃料耗尽时, 火箭主体最后 达到的速度为v, 应满足
M v [(M dM )(v dv) (dM )(v dv u )]
即
M dv udM 0
v
0
积分得 v
dv u
M
dM M
0
M0
v v 0 u(ln M ln M 0 ) 0 v v 0 u ln
M0 M
12
大学物理 第三次修订本
第4章 冲量和动量
16
第4章 冲量和动量
例3有一个三级火箭, 第一级火箭脱落前的质量 比为 N1 , 第二级火箭刚发动时火箭的质量与第 二级火箭燃料耗尽时火箭的质量之比为 N2 , 第 三级火箭刚点燃时火箭的质量与燃料耗尽时火 箭的质量之比为N3 。 若取N1 = N2 = N3 = 7.4;各级火箭的喷射速 度都为u =2.5kms-1。不计重力影响, 求该火箭最 后达到的速度。
第4章 冲量和动量
各级火箭中燃料烧完后, 火箭的速率为
v1 u ln N1
v2 v1 u ln N 2
v3 v2 u ln N 3
若火箭粒子流的喷射速率u=2.5kms-1,每 一级的质量比分别为N1=4, N2=3, N3=2, 可得: v3=7.93kms-1。
大学物理 第三次修订本
ri
rc
mi
质点力学教案8:质心

M
M
的大小的增量为负
的大小的增量为正,但cos< 10 0
三. 几个守恒定律 研究对象:物体系
※守恒条件要在体系 运动过程中时时刻刻 都满足
四. 动力学做题时,必建立坐标
分清矢量和标量,具体运算时化成标量式求解 在直角坐标系中:
一维运动: Fx——力在x轴上的分量(可正可负) dx——x的微分(沿x轴正方向的增量,取正) x1 ——运动初点 11 x2 ——运动终点
例 用一弹簧(k)将二木板(m1、m2)水平连接如图,以上 板在弹簧上的平衡位置为重力势能和弹性势能零点,试求:上 板在某一位置x时,上板、弹簧及地球这个系统的总势能 x m1 x x0 o
势能 零点
m2 结论:若势能零点取在平衡 位置处,则总势能以弹力势 能的单一形式出现(mg和 12 kx0时时平衡)
m
弹力 重力 势能 零点
x M
x M压缩过程,E守恒,则:
14
m
弹力 势能 零点
o x0 x M
重力 势能 零点
若弹力势能零点取原长端点处, 重力势能零点取M最低处,则压 缩过程中,E守恒:
x
15
例 二带弹簧的小车A、B,质量分别为m1 m2,B静止,A以速 度 与B相碰,求:二车相对静止时,两车的相互作用力为多 大?( k1 k2已知) A k1 k2 B 完全弹性碰撞,从碰 前到形变最大只有压缩, 没有恢复
例 如图,已知 k m M h, m从h处自由下落与M做弹性碰撞, 求:碰后小球m上升的最大高度,碰后弹簧压缩的最大长度 m自由下落 m与M做弹性碰撞 o x0 x M m
x m以v竖直上抛:
13
M向下压缩x 若重、弹势能零点均取在M放 在弹簧上的平衡位置处,则 弹簧压缩的最大长度时总势 能: o x0
质心运动课件

一.质心动能定理 (科尼希定理)
一个质点组的质心在C,如图.
z S
ric C
mi
rc
对某参照系S, 定义:
O
ri
EC
1 2
MvC2
——质心动能
x
y
是否相等?
Ek
i
1 2
mi
vi2——质点组总动能
可以证明:
对 质某点参组照 总系 动, 能:Ek EC ErC
——质心动能定理 (科尼希定理)
质点组总动能 = 质心动能 + 质点组相对质心的动能
ErC
vrriiCC
i
1 2
mi
vi2C
是质点组相对质心的总动能
是第i个质点相对于质心C的位 速率矢
18
科尼希定理: Ek EC ErC 证明如下: z
r riC
是第i
个质点相对于质心C的位矢
如图:对某参照系S,
ri
v
2 i
rC
i
1 2
mi vi2C
i
1 2
mi
2vC
viC
19
Ek
i
1 2
mi vC2
i
1 2
mi vi2C
i
rr mivC viC
r r r mivC viC vC
r mi viC
vC
0
0
i
i
质心系中质点组总动量
=质心系中的质心动量
Ek
i
1 2
dLrC dt
M rC
质点组对质心的 角动量变化定理
质点组的角动
质点组相对于质心的角动量的时间 量变化定理在
变化率 = 各外力对质心的总力矩
大学物理第2章 质点动力学习题(含解答)

第2章质点动力学习题解答2-1 如图所示,电梯作加速度大小为a 运动。
物体质量为m ,弹簧的弹性系数为k ,•求图示三种情况下物体所受的电梯支持力(图a 、b )及电梯所受的弹簧对其拉力(图c )。
解:(a )ma mg N =- )(a g m N += (b )ma N mg =- )(a g m N -= (c )ma mg F =- )(a g m F +=2-2 如图所示,质量为10kg 物体,•所受拉力为变力2132+=t F (SI ),0=t 时物体静止。
该物体与地面的静摩擦系数为20.0=s μ,滑动摩擦系数为10.0=μ,取10=g m/s 2,求1=t s 时,物体的速度和加速度。
解:最大静摩擦力)(20max N mg f s ==μmax f F >,0=t 时物体开始运动。
ma mg F =-μ,1.13.02+=-=t mmgF a μ 1=t s 时,)/(4.12s m a =dtdv a =Θ,adt dv =,⎰⎰+=t v dt t dv 0201.13.0t t v 1.11.03+=1=t s 时,)/(2.1s m v =2-3 一质点质量为2.0kg ,在Oxy 平面内运动,•其所受合力j t i t F ρρρ232+=(SI ),0=t 时,速度j v ρρ20=(SI ),位矢i r ρρ20=。
求:(1)1=t s 时,质点加速度的大小及方向;(2)1=t s 时质点的速度和位矢。
解:j t i t m Fa ρρρρ+==223 223t a x =,00=x v ,20=x ⎰⎰=tv x dt t dv x0223,23t v x =⎰⎰⎰==txtx dt t dt v dx 03202,284+=t xt a y =,20=y v ,00=y⎰⎰=tv y tdt dv y02,222+=t v y⎰⎰⎰+==tyty dt t dt v dy 020)22(,t t y 263+=(1)1=t s 时,)/(232s m j i a ρρρ+=(2)j t i t v ρρρ)22(223++=,1=t s 时,j i v ρρρ2521+= j t t i t r ρρρ)26()28(34+++=,1=t s 时,j i r ρρρ613817+=2-4 质量为m 的子弹以速度0v 水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为k ,忽略子弹的重力,求:(1)子弹射入沙土后,速度随时间变化的关系;(2)子弹射入沙土的最大深度。
§4.4 质心 质心运动定理

例 水平桌面上有一张纸,上面放一个m=0.5kg的均质圆盘, 将纸右拉,会有f=0.1N的力作用在圆盘上. 。 求 2s内圆盘 质心移动的距离 S 解 质心运动定理
f maC
质心运动距离 1 S aC t 2 0.4 2
aC
f
例 设有一质量为2m的弹丸,从地面斜抛出去,他飞行到最高点时爆炸成
y l y dy N
质心运动定理
y2 m 质心高度 yC 0 ydm 0 ydy 2l l dyC y dy vC 质心速度 dt l dt dv dy g v 2 g(l-y) 自有落体 dt dt dv C d y v 2 y dv ( v) 质心加速度 aC dt dt l l l dt y y y 2 g (1 ) g 2 g 3 g l l l m N 3g (l y ) N mg maC l
M
二. 质心运动定理
• 质心的速度
rc
mi r i m
dri mi dt miv i drc d mi ri vc ( ) dt m dt m m mv c miv i P 质点系动量 P mv c
质点系动量等于总质量与质心速度的积
说明
• 质心的加速度及其动力学规律
质点系动量定理
质点系动量
dP F外 dt P mv c
dv c F外 m mac dt
说明
质心运动状态只取决于外力,与内力无关
水平纸面
质心
运动 状态 只取 决于 外力 ,与 内力 无关
质量相等的两个碎片,其中一个 碎片垂直自由下落,到发射点的距离为L.
12.3质心运动定理(理论力学课件).
(12.10)
mi ri rc
2.质心的力学意义
m
① 若质点系中各质点的质量相等,则:
m r1 m r2 ...... m rn rc m m ...... m r1 r2 ...... rn 1 ri n n
1/n 与 i 无关,为公因子。
e F ix 0, px cont
运动分析:t=0 时系统静止; t时刻:车v,人v+vr
可知
t 0
px 0 0
y
车重W,人重Q,某瞬时人相对小 车的速度为vr,试求此时的车速v?
e F ix 0, px cont
vr Q
v
o
N1
W
N2
x
t=0时系统静止; t:车v,人v+vr 可知
(3)
将质心c的运动方程等式两端微分得:
y
m2 2 x e cos t c m1 m2 (4) y m2 e 2 sin t c m1 m2
c1
m 1g m2g
c
c2 e
x
t
Rx Ry
(4)质心运动微分方程:
m1 m2 xc m2e 2 cos t Rx 2 m m y m e sin 1 2 c 2 Ry m1 g m2 g
习题12.19 均质杆AB,长2L,铅直地静置于光滑
水平面上受到微小扰动后,无初速地倒下。求杆AB在
倒下过程中,点A的轨迹方程。
y A Co , C B , FN B mg , A
x
解:以均质杆AB为研究对象,并以杆AB铅直时的 轴线为 y轴,建立图示坐标系。AB杆倒下过程中所受外力 有:重力mg,光滑水平面的法向反力FN, 杆在倒下的过程中有:
《理论力学》第十章 质心运动定理 动量定理 习题共7页

第十章 质心运动定理 动量定理 习题解[习题10-1] 船A 、B 的重量分别为kN 4.2及kN 3.1,两船原处于静止间距m 6。
设船B 上有一人,重N 500,用力拉动船A ,使两船靠拢。
若不计水的阻力,求当两船靠拢在一起时,船B 移动的距离。
解:以船A 、B 及人组成的物体系统为质点 系。
因为质点系在水平方向不受力。
即:设B 船向左移动了S 米, 则A 船向右移动了6-S 米。
由质点系的动量定理得:[习题10-2] 电动机重1P ,放置在光滑的水平面上,另有一匀质杆,长L 2,重2P ,一端与电动机机轴固结,并与机轴的轴线垂直,另一端则刚连一重3P 的物体,设机轴的角速度为ω(ω为常量),开始时杆处于铅垂位置并且系统静止。
试求电动机的水平运动。
解:以电动机、匀质杆和球构成的质点系为研究对象。
其受力与运动分析如图所示。
匀质杆作平面运动。
因为质点系在水平方向上不受力,所以 由动量定理得:这就是电动机的水平运动方程。
[习题10-3] 浮动起重机起吊重kN P 201=的重物,起重机重kN P 2002=,杆长m OA 8=,开始时杆与铅垂位置成060角,忽略水的阻力,杆重不计,当起重杆OA 转到与铅垂位置成030角时,求起重机的位移。
解:以重物和起重机构成的物体系统为质系。
因为质点系在水平方向不受力,所以0=x Fconst x C =。
即OA 运动前后,质点系的质心保持不变。
也就是质心守恒。
当OA 杆转到与铅垂位置成030角时,质点系质心的横坐标为: 当OA 杆转到与铅垂位置成030角时, 质点系质心的横坐标为: 因为质心守恒,所以21C C x x =,即:故,当起重杆OA 转到与铅垂位置成030角时,起重机向左移动了0.2662米。
[习题10-4] 匀质圆盘绕偏心轴O 以匀角速度ω转动。
重P 的夹板借右端弹簧推压面顶在圆盘上,当圆盘转动时,夹板作住复运动。
设圆盘重W ,半径为r ,偏心距为e ,求任一瞬时作用于基础和别螺栓的动反力。
第八讲 质点组的质心运动

u×r× 解释:由于质点组中各质点所受惯性力 -mi rc 彼此平行,方向相同,且大小只取决于各质点
ur 的质量,这与质点组中各质点所受重力 mi g 相似,矢量和必通过质心,力矩必为零。
2)如果动系原点不建立在质心上,而是其他运动的质点上,一般没有上述的动量矩定理形 式,因为这时惯性力矩的矢量和不一定为零。
=
ur ( e ) F
,即
d
ur P
=
ur ( e ) F
dt
dt
dt
或
d
ur P
=
ur ( e ) F dt
-
- 质点组动量定理的微分形式
。
其中
ur F
(e)
dt
-
-在dt时间内外力主矢的冲量
。
å ì
ï ï
d dt
(
mvcx
)
ห้องสมุดไป่ตู้
=
d dt
æ çè
i
mi
×
xi
ö ÷
=
Fx( e )
ø
( ) å 直角坐标系的分量式
可以相互传递。
五、 质点组的动量矩定理和守恒律
(一) 对固定点的动量矩定理和守恒律(即在 L —系中)
1、 引入两个概念
1) 质点组对固定点的动量矩——质点组中各质点对同一固定点的动量矩的矢量和。
uur ur ur
第 i 个质点对固定点的动量矩 Ji = ri ´ mi vi
å å( ) ur uur
i
ur ri
uur ur ur rji = rj - ri
零。
证明:根据牛顿第三定律,就一对质点而言,
uur uur
o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2)质量均匀分布的物体,质心在几何中心 )质量均匀分布的物体, 均匀分布的物体 质量中心不一定有质量 中心不一定有质量) (质量中心不一定有质量) 3)质心与重心不是同一概念 ) 重心——地球对物体系各部分引力的合力的作用点 地球对物体系各部分引力的合力的作用点 重心 质心——由质量分布确定的一个点 质心 由质量分布确定的一个点 不太大物体
π
几何对称性
2011-5-16
第四章 冲量和动量
3
三、质心运动定理
r dr r r r mi i ∑mivi ∑p v drc ∑ dt i 质心速度: = = 质心速度: vc = = dt M M M
v v 质心位置: 质心位置: rc = ∑mdr M i i
r r p = m c —— 质点系的总动量 v r r dvc ac = 质心的加速度 dt r r r dp dvc r F= =m = mac —— 质心运动定理 dt dt
A + A =0 外 内
5、势能计算 、
Ek 守恒
mgz
A + A = 0 E 守恒 外 非
(注意参考点的选取) 注意参考点的选取)
−G Mm r
2011-5-16
≠
第四章 冲量和动量
8
例 从地球表面以一定速度发射卫星,υ0多大时,卫星在距地 从地球表面以一定速度发射卫星, 多大时, 处的圆轨道上运动? 心 r 处的圆轨道上运动? 解 研究对象:卫星+ 研究对象:卫星+地球 分析力:万有引力(保守内力) 分析力:万有引力(保守内力) ∴ 系统机械能守恒 状态1 状态
力的持续作用规律
力的持续作用规律(动能、动量定理) 力的持续作用规律(动能、动量定理) 描 述了某一过程的过程量和始末状态相应的状态 量之间的联系
2011-5-16
第四章 冲量和动量
6
二、动力学问题
1、两类问题 、 直线运动: 直线运动: 已知状态求力 已知力求状态 微分法 积分法
x
υ υ
ω
a
an = υ
质心加速度取决系统所受外力,而内力不改变质心的运动状态。 质心加速度取决系统所受外力,而内力不改变质心的运动状态。
2011-5-16 4
第四章 冲量和动量
如:抛出去在空中翻滚的手榴弹 运动员: 运动员:
(1)上例中,质心均沿抛物线运动,为什么? )上例中,质心均沿抛物线运动,为什么? (2)使自行车前进的力是什么力? )使自行车前进的力是什么力? (3)揪着自己的头发向上,使身体离开座 )揪着自己的头发向上, 脚不能沾地)。 为什么? 椅(脚不能沾地 。可能吗 为什么 脚不能沾地 可能吗?为什么
1 m 2 − G Mm υ0 2 R
R
O
r
=
状态2 状态 1 m 2 − G Mm υ 2 r ②
2
①
由牛二律
Mm = mυ2 G 2 r r
υ0 = 2GM − GM = 2gR − gR ∴ R r r
2011-5-16
第四章 冲量和动量
9
例 用一弹簧 将二木板 1=m2=m) 连接如图,以上板在弹 用一弹簧(k) 将二木板(m 连接如图, 簧上的平衡点为势能(重力、弹力)零点。 簧上的平衡点为势能(重力、弹力)零点。试写出上板在某一 位置x时 上板、弹簧及地球这个系统的总势能。 位置 时,上板、弹簧及地球这个系统的总势能。 x 0 解 EP弹 = −k(x − x0 )dx x x x0 1 2
i i
z
O
rc
c
x
zc = ∑mi zi / M
i
2011-5-16
第四章 冲量和动量
质量连续分布的物体: 质量连续分布的物体:
xc = ∫ xdm M yc = ∫ ydm M
m
r r rc = ∫dmr / ∫dm
m
zc = ∫ zdm M
说明 1) )
v rc与坐标选取有关,但对物体系的相对位置不变 与坐标选取有关,
b
v v F = ma
v v 1 2 1 2 ∫a F ⋅ dr = 2 mυ2 − 2 mυ1 = ∆Ek
∫
3、功能原理 、 4、守恒定律 、
b
a
v r v v F ⋅ dt = m 2 − m 1 = ∆p υ υ
A + A = ∆Ek A + A = ∆E 外 外 内 非 v r ∑F外 = 0 p 守恒
2011-5-16
质心与重心重合
第四章 冲量和动量
2
例 已知一半圆环半径为 R,质量为 ,质量为M 求 它的质心位置 解 建坐标系如图 取 dl
y
dθ
dm = λ dl
dm
θ
dl = Rdθ
M dm= Rdθ πR
O
x
x = Rcosθ y = Rsinθ
xc = 0
M ydm ∫ 0 Rsinθ π R Rdθ 2R ∫ = = yc = M M π
∫
= kx − kxx0 2
EP = EP弹 + mgx 1 2 = kx − kxx0 + mgx 2 由已知条件 mg = kx0
∴
2011-5-16
o
1 2 EP = kx 2
结论: 结论: 若势能取在平衡位 置,则总势能以弹性势 能的单一形式出现。 能的单一形式出现。
10
第四章 冲量和动量
F
F τ
v v v F = F + Fn τ
平面曲线运动: 平面曲线运动: s
aτ
2
ρ
Fn
aτ = rβ
圆周运动: 圆周运动:
θ
β
an = rω2
根据已知条件选取积分变量, 根据已知条件选取积分变量,确定上下限
2011-5-16
第四章 冲量和动量
F τ Fn
7
2、求力的瞬时作用规律 、 求力的持续作用规律
2011-5-16
第四章 冲量和动量
第4章结束 章结束
5
质点动力学小结
从不同角度描述了力的作用规律。 从不同角度描述了力的作用规律。
一、基本定理
1、牛顿运动定律 、
b
r r dp F= dt
力的瞬时作用规律
v v 1 2 1 2 υ υ 2、动能定理 ∫a F ⋅ dr = m 2 − m 1 、 2 2 b v v v F ⋅ dt = m 2 − m 1 υ υ 3、动量定理 ∫a 、
§4-4 质心运动定理
一、质心的概念
质量中心, 质量中心,可以代表整个物体的运动
二、质心位置的确定
N个质点的系统(质点系)的质心位置 个质点的系统(质点系) 个质点的系统
质点系
y
r r rc = ∑mri / ∑mi i
i i
mi
r ri r
分量式: 分量式:
xc = ∑mi xi / M yc = ∑mi yi / M
