长方体的表面积计算公式 (2)

合集下载

长方体和正方体表面积计算公式

长方体和正方体表面积计算公式长方体和正方体是我们生活中常见的几何体，无论是在建筑、设计、制造还是日常生活中，都有广泛的应用。

在计算长方体和正方体的表面积时，我们需要根据其特定的公式进行计算。

本文将介绍长方体和正方体的表面积计算公式及其应用。

一、长方体表面积计算公式长方体是一种具有六个矩形面的立体几何体，其表面积的计算公式为：长方体表面积 = 2(长×宽 + 长×高 + 宽×高)其中，长、宽、高分别代表长方体的三个边长。

上述公式中，2表示长方体的前后两个面、左右两个面、上下两个面，共六个面，每个面的面积都是长乘宽，因此需要将其相加。

例如，如果一个长方体的长、宽、高分别为3厘米、4厘米、5厘米，则其表面积为：长方体表面积 = 2(3 × 4 + 3 × 5 + 4 × 5) = 2(12 + 15 +20) = 94平方厘米二、正方体表面积计算公式正方体是一种具有六个正方形面的立体几何体，其表面积的计算公式为：正方体表面积 = 6 ×边长其中，边长代表正方体的边长。

上述公式中，6表示正方体有六个面，每个面的面积都是边长的平方，因此需要将其相加。

例如，如果一个正方体的边长为3厘米，则其表面积为：正方体表面积 = 6 × 3 = 6 × 9 = 54平方厘米三、长方体和正方体表面积的应用长方体和正方体的表面积计算公式在实际生活中有广泛的应用。

以下是一些例子：1. 在建筑设计中，建筑师需要计算建筑物的表面积，以确定需要使用的建筑材料的数量和成本。

例如，一个长方体的房间的墙壁和天花板的表面积可以用长方体表面积的公式来计算。

2. 在制造业中，工程师需要计算机器和设备的表面积，以确定需要使用的材料的数量和成本。

例如，一个正方体的箱子的表面积可以用正方体表面积的公式来计算。

3. 在日常生活中，我们可以用长方体和正方体表面积的公式来计算一些日常用品的表面积。

长方体五个面的表面积公式

长方体五个面的表面积公式篇一：长方体有五个面，每个面都是一个长方形。

计算长方体五个面的表面积时，可以使用以下公式:表面积 = 2 × (长面面积 + 宽面面积 + 高面面积)其中，长面、宽面、高面分别指长方体的一个长面、一个宽面和一个高面。

长方体的各个面的特征如下:- 长面：通常是长方形，长度是长方体的长度。

- 宽面：通常是长方形，宽度是长方体的宽度。

- 高面：通常是长方形，高度是长方体的高度。

根据长方体的特征，可以推导出长方体表面积的公式:表面积 = 2 × (长面面积 + 宽面面积 + 高面面积)= 2 × (长度×宽度 + 长度×高度 + 宽度×高度)= 2 × (长度×宽度 + 宽度×高度 + 长度×高度)= 2 × (长度 + 宽度 + 高度) ×长度×宽度= (长度 + 宽度 + 高度) × 2 ×长方体的长度×宽度因此，长方体五个面的表面积公式可以表示为:表面积 = (长面面积 + 宽面面积 + 高面面积) ×长方体的长度×宽度拓展：长方体表面积的计算方法计算长方体的表面积时，可以使用多种方法。

其中，最常见的方法是使用公式计算法，也称为“面积公式法”。

方法一：面积公式法1. 确定长方体的长、宽、高，并计算出每个面的面积。

2. 将每个面的面积乘以长方体的长、宽、高，得到总表面积。

方法二：折叠法1. 将长方体展开，并折叠成一个平面图形。

2. 计算每个面的面积，并将所有面积相加得到长方体的表面积。

无论使用哪种方法，计算长方体的表面积都需要一定的数学知识和技巧。

在实际生产和生活中，人们常常需要快速、准确地计算长方体的表面积，因此需要熟悉各种表面积计算方法和技巧。

篇二：长方体是由三个轴对称的平面组成的三维多面体，因此它有五个面。

长方体表面积和体积的公式

长方体表面积和体积的公式一、长方体表面积公式。

1. 公式内容。

- 长方体的表面积S = 2(ab+bc + ac)，其中a、b、c分别为长方体的长、宽、高。

2. 推导过程。

- 长方体有6个面，相对的面面积相等。

- 前面和后面的面积都为ac（长×高），左面和右面的面积都为bc（宽×高），上面和下面的面积都为ab（长×宽）。

- 所以长方体的表面积S=2ac + 2bc+2ab = 2(ab + bc+ac)。

3. 示例。

- 一个长方体，长a = 5厘米，宽b = 3厘米，高c = 4厘米。

- 根据表面积公式S = 2(ab+bc + ac)，可得S=2×(5×3 + 3×4+5×4)- 先计算括号内的值：5×3 = 15，3×4 = 12，5×4 = 20，15+12 + 20=47。

- 再乘以2，S = 2×47 = 94平方厘米。

二、长方体体积公式。

1. 公式内容。

- 长方体的体积V=abc（长×宽×高）。

2. 推导过程。

- 可以把长方体看作是由许多个单位小正方体组成的。

- 沿着长的方向有a个小正方体，沿着宽的方向有b个小正方体，沿着高的方向有c个小正方体。

- 那么总的小正方体个数（也就是长方体的体积）就是a× b× c。

3. 示例。

- 对于上述长a = 5厘米，宽b = 3厘米，高c = 4厘米的长方体。

- 根据体积公式V = abc，可得V=5×3×4 = 60立方厘米。

长正方体表面积计算公式

长方体的表面积
（1）前面的面积＝后面的面积＝长×高，
左面的面积＝右边的面积＝宽×高，
上面的面积＝下面的面积＝长×宽。

所以，长方体的表面积＝(前面的面积＋右面的面积＋上面的面积)×2
长方体的表面积＝（长×高＋宽×高＋长×宽）×2
通常我们用字母a表示长，用字母b表示宽，用字母h表示高，用S表示图形的面积。

长方体的表面积是：S＝2（ah＋bh＋ab）。

（2）长方体的表面积=侧面积+底面积×2
侧面积=底面周长×高
长方形的表面积=底面周长×高＋底面积×2
正方体的表面积
正方体的表面积是指围成正方体的6个正方形的面积之和，也就是说，要求一个正方体的表面积，我们只需要求出正方体的一个面的面积，再乘6就可以了。

正方体的表面积＝棱长×棱长×6
通常我们用字母a表示正方体的棱长，用S表示正方体的表面积，所以正方体的表面积是：
S＝6a²。

长方体表面面积公式

长方体表面面积公式长方体是我们日常生活中常见的一个几何体。

它有六个面，分别是两个底面和四个侧面。

这六个面中，除了底面是相同的矩形，其它的五个面都是相同的长方形。

想要计算长方体的表面积，我们需要知道各个面的面积，并将它们加起来。

长方体表面积的公式是：S=2ab+2ac+2bc，其中a、b、c分别代表长方体的三个棱长。

根据公式，我们可以把长方体表面积分成三部分。

第一部分是两个底面的面积，每个底面的面积都是ab。

由于底面相同，所以两个底面的面积相加就是2ab。

第二部分是长方体前后面以及左右两侧面的面积。

这四个面的面积都相等，都为ac，bc。

所以这部分的表面积应该是2ac+2bc。

第三部分是长方体上下两个面的面积。

这两个面的面积也相等，都为ab。

所以这部分的表面积也是2ab。

通过这个公式，我们可以为各种长方体计算表面积。

例如一个长方体的棱长分别为3 cm、4 cm和5 cm，那么它的表面积就是2×3×4+2×3×5+2×4×5=94 (cm²)。

也就是说，这个长方体的表面积是94平方厘米。

除此之外，这个公式也可以拓展到其他类似的几何体。

例如，如果我们希望计算正方体的表面积，即六个面中每个面都是正方形，那么我们可以将a、b、c这三个棱长看成相等的边长s。

这样，公式就变成了S=6s²。

当然，在计算长方体表面积时，还有一些可以简化的优化。

比如我们可以把公式写成S=2（ab+ac+bc），这样的话就可以省略重复计算两次的2ab。

另外，如果长方体的两个棱长相等，那么其中的一些项也可以简化。

总的来说，长方体表面积公式是一种非常重要的数学知识。

在我们进行日常生活、学术研究和工程设计等场景下都有广泛的应用。

通过熟练掌握这个公式，我们不仅可以准确地计算长方体的表面积，也能更好地理解其它几何体的表面积。

数学人教版五年级下册长、正方体公式集合

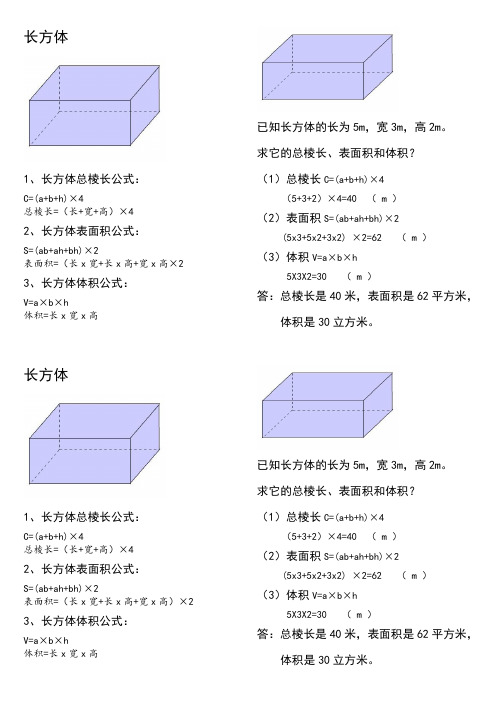
1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高×2 3、长方体体积公式：V=a×b×h体积=长x宽x高长方体1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高）×2 3、长方体体积公式：V=a×b×h体积=长x宽x高已知长方体的长为5m，宽3m，高2m。

求它的总棱长、表面积和体积？（1）总棱长C=(a+b+h)×4（5+3+2）×4=40 （ m ）（2）表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 （ m ）（3）体积V=a×b×h5X3X2=30 （ m ）答：总棱长是40米，表面积是62平方米，体积是30立方米。

已知长方体的长为5m，宽3m，高2m。

1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长正方体1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长已知正方体的棱长为5m。

长方体表面积的公式

长方体表面积的公式
长方体表面积的公式
长方体是我们日常生活中经常会见到的一种几何体，因其外表形状而得名。

它
由六个面所组成，三个面是正方形，另三个面是长方形，计算长方体表面积是很有用的。

长方体表面积的公式为：S=2a2+2ab+2bc，其中a，b，c分别代表长方体的长，宽和高。

比如我们有一个长10厘米，宽5厘米，高4厘米的长方体，那么它的表面积
就是：S=2*(10*10+5*10+5*4)=440平方厘米。

由此可见，几何中计算长方体表面积的公式非常重要，它不仅能够帮助我们评
估物品体积，而且能够为工程计算提供参考。

同时，在进行投影计算时，也能够让我们更好地评估大自然的形状变化，从而更好地学习自然现象。

综上所述，计算长方体表面积的公式是一个重要的科学公式，它不仅在几何中
发挥着重要的作用，同时还在工程计算和投影计算中大有用途。

它让人们更加了解自己身处的物理世界，同时又为中小学生学习几何提供了有益的参考。

长方体的表面公式

长方体的表面公式
长方体是一种三维基本体，其英文名为rectangular prism，也称
正方体。

它具有6个相对的端面，以及6条边。

每条边的长度均相等，两个相邻的边之间的夹角均相等。

因此，长方体的表面积公式为：
表面积 S = 2(lw + wh + lh)
其中，l为长方体的长度，w为长方体的宽度，h为长方体的高度。

要计算长方体的表面积，需要先确定其尺寸，即长宽和高，以及
其六个表面的组成，从而得到其表面积的计算公式。

正方体是特殊的
长方体，其表面积公式为：
表面积 S = 6a^2
其中，a为正方体单边的长度。

在一般情况下，长方体表面积可以通过以下步骤计算：
第一步：准备必要数据（长宽高）；
第二步：采用公式S=2（lw+wh+hl）计算出长方体表面积值（使用
双重循环计算）；
第三步：根据计算结果，用实际长度、宽度和高度计算出长方体
表面积值；
第四步：将双重循环计算的长方体表面积值和实际计算的表面积
值进行比较，确保两者完全相同。

长方体表面积公式是通过计算长度、宽度和高度和其相互连接的
方式设定的，可以帮助计算出体积的表面积。

此外，长方体的表面积
公式可以帮助使用者在计算长方体的表面积时，更加精确快速地进行
计算。

长方体无盖的表面积公式

无盖的长方体表面积=长×宽+（长×高+宽×高）×2，即S=2(ab+ah)+bh。

长方体的表面积因为相对的2个面面积相等，所以先算上下两个面，再算前后两个面，最后算左右两个面。

设一个长方体的长、宽、高分别为a、b、c，则它的表面积为S = (ab+bc+ca)×2，也等于2ab+2bc+2ca，还等于2（ab+bc+ca）；
公式：长方体的表面积=长×宽×2+宽×高×2+长×高×2，或：长方体的表面积=（长×宽+宽×高+长×高）×2。

扩展资料
长方体的特征
(1) 长方体有6个面。

每组相对的面完全相同。

(2) 长方体有12条棱，相对的四条棱长度相等。

按长度可分为三组，每一组有4条棱。

(3) 长方体有8个顶点。

每个顶点连接三条棱。

三条棱分别叫做长方体的长，宽，高。

(4) 长方体相邻的两条棱互相垂直。

长方体的体积=长×宽×高。

设一个长方体的长、宽、高分别为a、b、c，则它的体积：
因为长方体也属于棱柱的一种，所以棱柱的体积计算公式它也同样适用。

长方体体积=底面积×高，即。

长方体的表面积计算公式

上
右
前
长方体的表面积=（长×宽+长×高+高×宽）×2
＝（ab＋bh＋ah）×2
上
后
前
正方体的表面积＝棱长×棱长×6
＝棱长2×6
＝a×a×6＝6a2
说一说该求哪部分的面积
制一个长方体无盖鱼缸，求所需玻璃的面积。

粉刷教室时，粉刷教室四面墙壁，求粉刷的面积。

说一说该求哪部分的面积
给一个长方体罐头盒贴包装纸，求包装纸的面积。

给一个长方体的领操台刷上油漆，求粉刷的面积。

做一个包装箱（如下图），至少要用多少平方米的硬纸板？
上下每个面,长
,宽,面积是。

前后每个面,长,宽,面积是。

左右每个面,长
,宽,面积是。

0.7m 0.5m 0.35m 20.7m 0.4m 0.28m 20.5m 0.4m 0.2m 2
做一个包装箱（如下图），至少要用多少平方米的硬纸板？
这个包装箱的表面积是：
（0.7×0.5+0.7×0.4+0.5×0.4）×2
=0.83×2
=1.66（m2）
答：至少需要1.66平方米的硬纸板。

一个正方体礼品盒，棱长1.2dm，包装这个礼品盒至少用多少平方分米的包装纸？
几何学和欧几里得
几何学是数学学科的一个重要分支，它主要研究空间图形的有关
问题。

古希腊数学家欧几里
得的著作《几何原本》在数
学发展史上有着深远的影响。

该书从１７世纪初开始传入
我国。

长方体的表面积计算公式

长方体的表面积计算公式长方体的表面积公式长方体的体积计算公式正方体的体积计算公式圆柱的表面积计算公式长方体表面积计算公式求长方体的表面积公式长方体表面积公式长方体表面积计算器圆的表面积计算公式
上右
前
长方体的表面积=（长×宽+长×高+高×宽）×2
＝（ab＋bh＋ah）×2
.
上后
前
正方体的表面积＝棱长×棱长×6 ＝棱长2×6 ＝a×a×6＝6a2
.
说一说该求哪部分的面积
制一个长方体无盖鱼缸，求所需
玻璃的面积。
粉刷教室时，粉刷教室四面墙壁，求粉刷的面积。。
.
说一包装纸的面积。
给一个长方体的领操台刷上油漆，求粉刷的面积。。
.
做一个包装箱（如下图），至少要用多少平方米的硬纸板？
.
上下每个面,长 0.7m ,宽 0.5m ,面积是 0.35m2 。前后每个面,长 0.7m ,宽 0.4m ,面积是 0.28m2 。左右每个面,长 0.5m ,宽 0.4m ,面积是 0.2m2 。
.
做一个包装箱（如下图），至少要用多少平方米的硬纸板？
这个包装箱的表面积是：
（0.7×0.5+0.7×0.4+0.5×0.4）×2 =0.83×2 =1.66（m2）
答：至少需要1.66平方米的硬纸板。
.
一个正方体礼品盒，棱长 1.2dm，包装这个礼品盒至少用多少平方分米的包装纸？
.
几何学和欧几里得
几何学是数学学科的一个重要分支，它主要研究空间图形的有关问题。古希腊数学家欧几里得的著作《几何原本》在数学发展史上有着深远的影响。该书从１７世纪初开始传入我国。

长方体表面积公式计算公式

长方体表面积公式计算公式长方体表面积公式计算公式在学习几何学的时候，长方体一定是我们必须学会的一个几何体。

无论是在各种工程中，还是在我们的日常生活中，长方体都随处可见。

长方体的表面积公式是一个非常基本的公式，本文将为大家详细介绍长方体表面积公式的计算方法。

定义：首先，我们需要了解长方体的定义。

长方体是一个拥有六个矩形面的几何体。

计算方法：了解了长方体的定义之后，我们可以使用公式计算它的表面积了。

长方体表面积的计算公式为：2*(a*b+b*c+c*a)。

其中，a、b、c分别代表长方体的三个不同的边长。

在本公式中，我们需要计算长方体的各个面的面积，即六个矩形的面积。

如何计算矩形的面积：接下来，我们需要了解如何计算矩形的面积。

一个矩形的面积等于它的长乘以宽。

所以，要计算出长方体的各个面的面积，我们需要知道长方体的各个面的长和宽。

比如，对于一个长方体，它有一个长方形的面。

那么我们需要知道这个长方形的长和宽。

我们可以将这个面划分成两个长方形，在计算它们的乘积时再将它们相加。

这样就可以计算出矩形的面积。

当然，如果我们使用公式计算长方体的表面积，我们不需要知道矩形的长和宽具体数值，只需要知道长方体的三个边长就行了。

实例：假设一个长方体的长为5、宽为3、高为2，那么我们就可以使用上面的公式来计算这个长方体的表面积了。

我们将5、3、2代入公式，进行计算。

最终得出的结果是：2*(5*3+3*2+2*5)=62。

因此，这个长方体的表面积是62平方单位。

结尾：通过本文，我们介绍了长方体的定义、长方体表面积的计算公式以及如何计算矩形的面积。

当然，这个公式只是一个基本的公式。

针对不同特殊情况，计算表面积的方法也会有所不同。

希望本文能够帮助大家掌握计算长方体表面积的基本方法。