桁架单元例子MATLAB 1
桁架优化matlab算法

桁架优化matlab算法桁架优化Matlab 算法【引言】桁架是一种常见的结构体系,它由连接节点的杆件构成。
桁架通常在工程设计中用于支撑、加固或分散载荷。
优化桁架结构对于减少材料使用、提高结构强度和降低成本非常重要。
Matlab 是一种功能强大的计算软件,它提供了许多优化算法和工具。
本文将介绍如何使用Matlab 进行桁架优化的算法实现。
【第一步- 建立力学模型】桁架的力学模型是优化过程的基础。
在Matlab 中,可以使用矩阵表示力学模型。
首先,我们需要定义桁架的节点和杆件。
节点用坐标表示,杆件用节点之间的连接关系表示。
根据节点和杆件的定义,可以构建节点坐标矩阵和链接关系矩阵。
【第二步- 约束条件和目标函数】在进行桁架优化时,通常会遇到一些约束条件和目标函数。
典型的约束条件可能包括杆件的最大和最小尺寸限制、节点的最大和最小高度限制等。
目标函数可以是桁架的重量、刚度或模态频率等。
根据具体问题,我们需要定义合适的约束条件和目标函数。
【第三步- 优化算法】Matlab 提供了许多优化算法,如遗传算法、粒子群优化算法等。
我们需要选择合适的算法来解决桁架优化问题。
对于离散变量的优化,可以使用遗传算法。
对于连续变量的优化,可以使用粒子群优化算法。
选择合适的算法后,可以将约束条件和目标函数输入优化算法,得到优化结果。
【第四步- 结果分析】优化算法完成后,我们需要对结果进行分析。
可以通过绘制优化后的桁架结构来比较与原始结构的差异。
此外,还可以从目标函数的值来评估优化结果。
如果目标函数的值较小,则说明优化结果较优。
【第五步- 进一步优化】根据结果的分析,我们可以进一步优化桁架结构。
可以尝试使用不同的约束条件和目标函数,或者尝试其他优化算法。
通过多次迭代优化,逐步优化桁架结构,以得到更好的结果。
【第六步- 结论】通过以上的一步一步的回答,我们可以得出结论,桁架优化的Matlab 算法是一个有效的方法。
通过建立力学模型、定义约束条件和目标函数、选择合适的优化算法,我们可以获得优化后的桁架结构。
matlab桁架结构有限元计算

matlab桁架结构有限元计算摘要:一、引言- 介绍MATLAB在桁架结构有限元计算中的应用- 说明本文的主要内容和结构二、有限元计算原理- 有限元方法的背景和基本原理- 有限元方法在桁架结构分析中的应用三、MATLAB实现桁架结构有限元计算- MATLAB的基本操作和编程基础- 使用MATLAB进行桁架结构有限元计算的步骤和示例四、MATLAB桁架结构有限元计算的应用- 分析不同桁架结构的特点和计算结果- 探讨MATLAB在桁架结构有限元计算中的优势和局限五、结论- 总结MATLAB在桁架结构有限元计算中的应用和优势- 展望MATLAB在桁架结构分析中的未来发展方向正文:一、引言随着计算机技术的不断发展,有限元方法已经成为工程界解决复杂问题的重要手段。
MATLAB作为一款功能强大的数学软件,可以方便地实现桁架结构的有限元计算。
本文将介绍MATLAB在桁架结构有限元计算中的应用,并详细阐述其操作方法和计算原理。
二、有限元计算原理1.有限元方法的背景和基本原理有限元法是一种数值分析方法,通过将连续的求解域离散为离散的单元,将复杂的问题转化为求解单元的线性或非线性方程组。
有限元方法具有适应性强、精度高、计算效率高等优点,广泛应用于固体力学、流体力学、传热等领域。
2.有限元方法在桁架结构分析中的应用桁架结构是一种由杆件组成的结构,其节点只有三个自由度。
有限元方法可以有效地分析桁架结构的强度、刚度和稳定性,为工程设计提供理论依据。
三、MATLAB实现桁架结构有限元计算1.MATLAB的基本操作和编程基础MATLAB是一种功能强大的数学软件,可以进行矩阵运算、绘制图形、编写程序等操作。
在MATLAB中,用户可以通过编写脚本文件或使用图形界面进行各种计算和分析。
2.使用MATLAB进行桁架结构有限元计算的步骤和示例(1) 建立桁架结构模型:根据实际结构绘制桁架的节点和杆件,确定各节点的三自由度。
(2) 离散化:将桁架结构离散为有限个单元,每个单元包含若干个节点。
平面桁架结构matlab

桁架结构计算第四章P56******************************************************************************* function y=plane_truss_element_stiffness(E,A,L,theta) %平面桁架单元刚度x=theta*pi/180;C=cos(x);S=sin(x);y=E*A/L*[C*C C*S -C*C -C*S;C*S S*S -C*S -S*S;-C*C -C*S C*C C*S;-C*S -S*S C*S S*S];%平面桁架刚度矩阵*******************************************************************************function y=plane_truss_assemble(K,k,i,j) %平面桁架组装K(2*i-1,2*i-1)=K(2*i-1,2*i-1)+k(1,1);K(2*i-1,2*i)=K(2*i-1,2*i)+k(1,2);K(2*i-1,2*j-1)=K(2*i-1,2*j-1)+k(1,3);K(2*i-1,2*j)=K(2*i-1,2*j)+k(1,4);K(2*i,2*i-1)=K(2*i,2*i-1)+k(2,1);K(2*i,2*i)=K(2*i,2*i)+k(2,2);K(2*i,2*j-1)=K(2*i,2*j-1)+k(2,3);K(2*i,2*j)=K(2*i,2*j)+k(2,4);K(2*j-1,2*i-1)=K(2*j-1,2*i-1)+k(3,1);K(2*j-1,2*i)=K(2*j-1,2*i)+k(3,2);K(2*j-1,2*j-1)=K(2*j-1,2*j-1)+k(3,3);K(2*j-1,2*j)=K(2*j-1,2*j)+k(3,4);K(2*j,2*i-1)=K(2*j,2*i-1)+k(4,1);K(2*j,2*i)=K(2*j,2*i)+k(4,2);K(2*j,2*j-1)=K(2*j,2*j-1)+k(4,3);K(2*j,2*j)=K(2*j,2*j)+k(4,4);y=K;*******************************************************************************function y=plane_truss_element_force(E,A,L,theta,u)%力的表达式x=theta*pi/180;C=cos(x);S=sin(x);y=E*A/L*[-C -S C S]*u;*******************************************************************************function y=plane_truss_element_stress(E,L,theta,u) %应力表达式x=theta*pi/180;C=cos(x);S=sin(x);y=E/L*[-C -S C S]*u;***************************************************************************************************** *****************************************************************************************************clear;clc;E= ;A= ;L1= ;%杆长度L2= ;L3= ;L4= ;%杆长度L5= ;L6= ;L7= ;L8= ;t1= ;%杆角度t2= ;t3= ;t4= ;%杆角度t5= ;t6= ;t7= ;t8= ;k1=plane_truss_element_stiffness(E,A,L1,t1) % 单位刚度矩阵k2=plane_truss_element_stiffness(E,A,L2,t2)k3=plane_truss_element_stiffness(E,A,L3,t3)k4=plane_truss_element_stiffness(E,A,L4,t4);% 单位刚度矩阵k5=plane_truss_element_stiffness(E,A,L5,t5); % 单位刚度矩阵k6=plane_truss_element_stiffness(E,A,L6,t6)k7=plane_truss_element_stiffness(E,A,L7,t7)k8=plane_truss_element_stiffness(E,A,L8,t8) % 单位刚度矩阵K=zeros( );%组装矩阵大小,节点位移个数Q,节点数乘以2K=plane_truss_assemble(K,k1, , ); %刚度矩阵的组装K=plane_truss_assemble(K,k2, , ); %后边为单元连接关系图中杆的指向顺序K=plane_truss_assemble(K,k3, , );K=plane_truss_assemble(K,k4, , );K=plane_truss_assemble(K,k5, , ); %刚度矩阵的组装K=plane_truss_assemble(K,k6, , ); %后边为单元连接关系图中杆的指向顺序K=plane_truss_assemble(K,k7, , );K=plane_truss_assemble(K,k8, , ) %注意( )中的数字参数B=K([ , , , , , , , ,],:) ; %取特定的行5 6 7 8 9 10 11 12k=B(:,[ , , , , , , , ]) %取特定的列5 6 7 8 9 10 11 12%得到k矩阵f=[ ]';u=k\f***************************************************************************** ***************************************************************************** 求得位移列矩阵为:u = [0 0 0 0 0.2133 0.4083 -0.1600 0.4617 0.4267 1.5008 -0.0533 1.6608]’;以下为求各个杆的应力大小:u1=[u( );u( );u( );u( )];%后边为单元连接关系图中杆的指向顺序sigma1=plane_truss_element_stress(E,L1,t1,u1) %element stress,u1是Q列向量u2=[u( );u( );u( );u( )];sigma2=plane_truss_element_stress(E,L2,t2,u2)u3=[u( );u( );u( );u( )];sigma3=plane_truss_element_stress(E,L3,t3,u3) %element stress,u1是Q列向量u4=[u( );u( );u( );u( )];sigma4=plane_truss_element_stress(E,L4,t4,u4)u5=[u( );u( );u( );u( )];sigma5=plane_truss_element_stress(E,L5,t5,u5) %element stress,u1是Q列向量u6=[u( );u( );u( );u( )];sigma6=plane_truss_element_stress(E,L6,t6,u6)u7=[u( );u( );u( );u( )];sigma7=plane_truss_element_stress(E,L7,t7,u7) %element stress,u1是Q列向量u8=[u( );u( );u( );u( )];sigma8=plane_truss_element_stress(E,L8,t8,u8)*******************************************************************************R=K*u; %求得支反力,从中选取支反力处的值R=[R( );R( );R( );R( )] %填入位置坐标。
MATLAB平面桁架算例

陈继乐专业:工程力学学号:1120150528SummaryIn this term, I have learned professional English class of Mr. Sun. There are five students in this class. Each of us would make a presentation in class. I have learned a lot. Here is the main content of my presentations.1. The Introduction of mechanics of materialsThe research object of mechanics of materials is structure member. Structure members include bar,rod,plate,shell and clump body. Bar and rod are the main objects of mechanic of material. The task of mechanics of materials is as following. Under the request that the strength, rigidity, stability is satisfied, offering the necessary theoretical foundation and calculation method for determining reasonable shapes and dimensions, choosing proper materials for the components at the most economic price. There are four assumptions of the solid deformable bodies including continuity, homogeneity, isotropy and small deformations. Basic types of the deformation of rods are axial tension, shear, torsion and bending.2.Statically determinate problemsIf forces act on a body, the lines of action of these forces are in the same place, which called coplanar forces system. To a general coplanar force system, there are three independent equations which can determine 3 unknown quantities. That are 0=∑X , 0=∑Y , ∑=0)(F m o , whichmean the total force in x axis and y axis are equal to zero and the total moment of point O is equal to zero. When the number of equations is larger than or equal to the number of unknown quantities, it is a statically determinate problem. When the number of equations is less than to the number of unknown quantities, it is a statically indeterminate problem. And statically indeterminate problems can be solved by the conditions of compatibility.3.Plane trussesA truss is a structure that is made of straight, slender bars that are joined together to form a pattern of triangles. There are three assumptions of plane trusses. 1. the weights of the members are negligible.2 . all joints are pin. 3 .the applied forces act at joints.According to three assumptions, we can get conclusion that each member of a truss is a two-force body. And there are two methods of calculation of the forces in the members ofa truss,1. Method of joint. 2 .Method of section.positive Motion of a ParticleIn practice, we often observe the motion with respect to a moving body. There may exist relationship between two different objects.There are two coordinate systems. A coordinate system fixed to the earth ground is called static coordinate system (SCS). A coordinate system fixed to a moving object relative to the earth ground is called moving coordinate system (MCS). There are three kinds of motion andtheir velocities. The motion of the moving point relative to the SCS is called absolute motion. The motion of the moving point relative to the MCS is called relative motion. The motion of the MCS relative to the SCS is called converted motion. The velocity and acceleration of the moving point in its absolute motion are called absolute velocity. The velocity of the convected point in its absolute motion is called convected velocity. The velocity of the moving point in its relative motion is called relative velocity.There exists relationship among the three velocities. At any instant of time, the absolute velocity of a moving point equals the geometric sum of its relative velocity and convected velocity. This is the theorem of composition of velocities of a particle.Those are the main contents of my presentations.I have learned a lot from the professional English class. When I do my first presentation, I was nervous and I didn’t do well. But I made progress in the following class. After each presentation, Mr. Sun would tell me how I should do to do better. I find many shortcoming of mine. And I have learned the advantages of my classmates. I will study harder and I hope I can do better in the future.总结在本学期,我学习了孙老师的专业英语这门课程。
基于MATLAB的三维桁架有限元分析

cx Z m
Cy CY CZ
CZ CZ
CX Cy
CX CZ
C CZ
CZ 66 ×
—
CX CZ
一
一
其 中 ,足 ]为二 力杆单 元 轴 向 刚度 矩阵 , [ 愚
EA
L 。
2 编 程 思 路
2 1 工 程 实 例 .
如 图 2所示 , 一机 架 由空间桁 架杆组 成 , 其杆 件单 元 的横 截面 积为 1 m。 由钢制 成 ( 5c , E一 2 0GP ) 试 0 a ,
C 0 OS y
_—
—
[ 卅 尼]
—
C xC SO OSO O z
—
C S0 o 0 O yc s z
。— —
CS z O O
—
—
C S0 C SO — OS0 OSO O x O z —C yC z
CS x O 0 C xC r OS0 OSO C S0 O O xC S
C S0 O z O xC S 0
C y O z OS0 C S O
—
一
CS x O O
。 O xC y — —C S O OS0
—
・—
—
C SO O z O xC S O C S 0 C SO O y O z
—
C Se O y O xC S 0
—
—
CX z
一
CX, CY
CX CZ I
CX CYm
CX CZ CX 。
一
C CZ
CZ
CZ
。
[ 。 r K ]= - ] k
一
有限元方法与MATLAB程序设计 第3章 桁架和刚架

Fe keUe
Ue TUe
结构坐标系下的 单元刚度方程
9
结构坐标系下单元刚度矩阵 ke T TkeT
c cos s sin
y
Fe keUe
y
i (xi , yi )
(xj, yj ) x j
x
结构坐标系
cos sin 0
0 1 0 1 0 e cos sin 0
0
ke
EA sin
Fyi
Fxj Fyj
EA l
0
1
0
0 0 0
0 1 0
0
vi
0 0
u v
j j
单元坐标系下的 1 0 1 0
单元刚度矩阵
ke
EA l
0
1
0 0
0 1
0 0
0
0
0
0
7
§3.1.3 整体坐标系下的单元刚度方程
Fxi Fxi cos Fyi sin Fyi Fxi sin Fyi cos Fxj Fxj cos Fyj sin
是结构坐标系x轴正方 向至单元坐标轴x 的角度
y
x
y Fxi i
Fxi Fyi Fyi
x
结构(整体)坐标系
Fyj Fxj sin Fyj cos
Fxi Fyi
Fxj
Fyj
e
cos
sin
0
0
sin cos
0 0
0 0
cos sin
0
e
Fxi
e0Fyi源自sin cosFxj
Fyj
Fe TFe Ue TUe
cos
T sin
0
0
sin cos
1D truss单元理论公式

基于MATLAB和ANSYS的有限元分析一维Truss桁架单元理论公式案例代码5.一维Truss桁架单元:公式5.1. 桁架单元?5.2.形函数5.3.应变位移矩阵5.4.单元刚度矩阵5.5.全局刚度矩阵1221N 1N 25.1. 什么是桁架单元?销接头(自由旋转)N 2N 1•只能承受张力或压力•内力始终与桁架平行•只有平移自由度(u ,v ,w ),没有旋转自由度N1ξ=121−ξ;N2ξ=12(1+ξ)ξ=0ξ=1/2+Atξ=0,N1=N2=12uξ=0=12u1+12u2=12(u1+u2)+Atξ=12,N1=14,N2=34uξ=1/2=14u1+34u2=14(u1+3u2)5.2. 形函数x=全局坐标ξ=自然坐标:−1≤ξ≤11D中, 我们假设:ξ≡x示例:位于两个节点之间的轴向位移扇形点可以计算为u=N1ξu1+N2ξu2其中N1和N2是可定义的函数B=1detJN′=1detJðN1ðξðN2ðξx=Jξ=L2ξ, with J=L2⇒detJ=L2N1ξ=121−ξ;N2ξ=121+ξ⇒ðN1ðξ=−12,ðN2ðξ=12B=2L−1212=1L−11应变-位移矩阵可以定义为:e=B u 其中e单元应变,u为节点位移的矢量.应变-位移矩阵,B, 可以计算为:J=雅可比矩阵,可以定义为注:detJ的出现是由于坐标系(从全局坐标系到自然坐标系)的变换。
5.3. 应变位移矩阵: Bk e=A i න−11BiT C (B (i))detJ dξdetJ =L i2,B (i)=1L i−11,k e=A i න−111L i −11E i 1L i −11L i 2dξ=න−11E i A i 2L i 1−1−11dξC =E i (弹性模量)*L i = i tℎ单元长度通过detJ ,B ,C , 我们得到单元刚度矩阵为其中k e=න−11E i A i 2L i 1−1−11dξI =න−11f(ξ)dξ=i=1nωi f(ξi )I =i=11ω1f(ξ1=0)=2f ξ1=0⇒k e=2E i A i 2L i 1−1−11=E i A i L i 1−1−11ቚ−11−1/3+ቚE i A i 2L i1−1−111/3.If E i Ai 2L =const ⇒k e =2E i A i2L 1−1=E i A i L1−1Points , ξiWeights, ωi122±1/31−11ξ1=0−11ξ1=−13ξ2=13单元刚度矩阵高斯求积:+ 一高斯点积分:1个高斯点:2个高斯点:高斯点数,n+ 两个高斯点积分:I =σi=21ωi f(ξi )=1f −1/3+1f 1/3⇒k e=E i A i 12L i−11st element2nd element3rd elementN th elementK =i=1Nk (i)e k e=E i A i L i 1−1−11注:右侧的整体刚度矩阵是针对均匀网格尺寸获得的 (L 1=L 2=⋯=L N ), 均匀截面面积 (A 1=A 2=⋯=A N ), 均匀材料特性 (E 1=E 2=⋯=E N ).K =E1A1L1−E1A1L100−E1A1L1E1A1L1+E2A2L2−E2A2L2...0 0−E2A2L2E2A2L2+E3A3L3...0 ............ ........... ...........E N−1A N−1L N−1+E N A NL N−E N A NL N00............−E N A NL NE N A NL N一般情况下的刚度矩阵K:L = 1mE = 2e11 N/m 2, A = 1 m 2F = 1e8 Nk (i)e =A i න−11BiT C(B (i))detJdξwheredetJ =L i 2,C =E i ,B (i)=1detJ ðN 1ðξðN 2ðξ=1L i −11K =Nk (i)e N 1ξ=121−ξ;N 2ξ=12(1+ξ)F EAx 应力:σ=F A=1081=108N/m 2应变:e =FEA=1082×1011×1=5×10−4k (i)e =න−11E i A i 2L i 1−1−11dξ6-8.一维桁架(Truss)单元:示例1解析解:位移:U =116-8. 2345 MATLAB 和 ANSYS 有限元分析1节点1固定.一维Truss 单元:示例1function d isp = solution(nDof,fixedDof,K,force)%%%%% This function is to solve: K*U=F to obtain U activeDof =s etdiff((1:nDof)',fixedDof);U = K(activeDof,activeDof)\force(activeDof);disp = zeros(nDof,1);disp(activeDof) = U;endMatlab 代码+ 我们有5个节点,每个节点有1个自由度=> 自动度总数:n Dof =5×1=5+ 我们固定了节点1。
桁架矩阵位移法matlab计算程序

%% Yjj 211908214006clear all;clc;jd=input('请输入节点数量');free=input('请输入自由度');gj=input('请输入杆件数量');P=zeros(free,1);P=input('请输入外荷载矩阵([x;y;z])');d=zeros(free,1);member=zeros(1,4,gj);K=zeros(4,4,gj);for i=1:1:gjangle(i)=input(sprintf('请输入第%d杆件角度(角度制)',i));E(i)=input(sprintf('请输入第%d杆件弹性模量(N/mm2)',i));A(i)=input(sprintf('请输入第%d杆件截面面积(mm2)',i));L(i)=input(sprintf('请输入第%d杆件长度(mm)',i));member(:,:,i)=input(sprintf('请输入第%d杆件定位向量([1 2 3 4])',i));endfor i=1:1:gjK(:,:,i)=[cosd(angle(i))*cosd(angle(i)) cosd(angle(i))*sind(angle(i)) -cosd(angle(i))*cosd(angle(i)) -cosd(angle(i))*sind(angle(i));cosd(angle(i))*sind(angle(i)) sind(angle(i))*sind(angle(i)) cosd(angle(i))*sind(angle(i)) -sind(angle(i))*sind(angle(i));-cosd(angle(i))*cosd(angle(i)) -cosd(angle(i))*sind(angle(i)) cosd(angle(i))*cosd(angle(i)) cosd(angle(i))*sind(angle(i));-cosd(angle(i))*sind(angle(i)) -sind(angle(i))*sind(angle(i)) cosd(angle(i))*sind(angle(i)) sind(angle(i))*sind(angle(i))]*E(i)*A(i)/L(i);endSs=zeros(free);S=zeros(free);for i=1:1:gjfor n=1:1:4for j=1:1:4if (member(1,n,i)<=free && member(1,j,i)<=free)Ss(member(1,n,i),member(1,j,i))=K(n,j,i);endendendS=S+Ss ;endd=S\Pv=zeros(4,1,gj);for i=1:1:gjc=1;for j=1:1:4if(member(1,j,i)<free+1)v(j,1,i)=d(c,1);c=c+1;endendendT=zeros(4,4,gj);for i=1:1:gjT(:,:,i)=[cosd(angle(i)) sind(angle(i)) 0 0;-sind(angle(i)) cosd(angle(i)) 0 0;0 0 cosd(angle(i)) sind(angle(i));0 0 -sind(angle(i)) cosd(angle(i))]; endu=zeros(4,1,gj)for i=1:1:gju(:,:,i)=T(:,:,i)*v(:,:,i);endk=zeros(4,4,gj);for i=1:1:gjk(:,:,i)=[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0]*E(i)*A(i)/L(i); endQ=zeros(4,1,gj);for i=1:1:gjQ(:,:,i)=k(:,:,i)*u(:,:,i)endF=zeros(4,1,gj);for i=1:1:gjF(:,:,i)=T(:,:,i)'*Q(:,:,i);endzfl=jd*2;r=zeros(zfl,1);for i=1:1:gjfor j=1:1:4r(member(1,j,i),1)=F(j,1,i);endendzfl=zfl-free;R=r(free+1:end)。
桁架结构MATLAB编程

桁架结构% 变量说明% NPOIN NELEM NVFIX NFPOIN NFPRES% 总结点数,单元数, 约束个数, 受力结点数, 非结点力数% COORD LNODS YOUNG% 结构节点坐标数组, 单元定义数组, 弹性模量% FPOIN FPRES FORCE FIXED% 结点力数组,非结点力数组,总体荷载向量, 约束信息数组% HK DISP% 总体刚度矩阵,结点位移向量%**************************************************format short e%设定输出类型clear %清除内存变量FP1=fopen('6-6.txt','rt'); %打开初始数据文件%读入控制数据NELEM=fscanf(FP1,'%d',1); %单元数NPOIN=fscanf(FP1,'%d',1); %结点数NVFIX=fscanf(FP1,'%d',1); %约束数NFPOIN=fscanf(FP1,'%d',1); %结点荷载数NFPRES=fscanf(FP1,'%d',1); %非结点荷载数YOUNG=fscanf(FP1,'%f',1); %弹性模量% 读取结构信息LNODS=fscanf(FP1,'%f',[4,NELEM])'% 单元定义:左、右结点号,面积,惯性矩(共计 NELEM组)COORD=fscanf(FP1,'%f',[2,NPOIN])'% 坐标: x,y坐标(共计 NPOIN 组)FPOIN=fscanf(FP1,'%f',[3,NFPOIN])'% 节点力(共计 NFPOIN 组):结点号、X方向力(向右正),% Y方向力(向上正),FPRES=fscanf(FP1,'%f',[4,NFPRES])' % 均布力(共计% NFPRES 组):单元号、荷载类型、荷载大小、距离左端长度FIXED=fscanf(FP1,'%f',NVFIX)'% 约束信息:约束对应的位移编码(共计 NVFIX 组)%---------------------------------------------------------HK=zeros(2*NPOIN,2*NPOIN); % 张成总刚矩阵并清零FORCE=zeros(2*NPOIN,1); % 张成总荷载向量并清零%形成总刚for i=1:NELEM % 对单元个数循环% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵EKT=T'*EK*T; % 生成整体单刚(整体坐标系)% 组成总刚按2*2子块加入总刚中(共计4块)for j=1:2 %对行进行循环---按结点号循环N1=LNODS(i,j)*2; % j结点第2个位移的整体编码for k=1:2 %对列进行循环---按结点号循环N2=LNODS(i,k)*2; % k结点第2个位移的整体编码HK((N1-1):N1,(N2-1):N2)=HK((N1-1):N1,(N2-1):N2)...+EKT(j*2-1:j*2,k*2-1:k*2);endendend% 由结点力与非结点力生成总荷载向量列阵for i=1:NFPOIN % 对结点荷载个数进行循环N1=FPOIN(i,1); % 作用荷载的结点号N1=N1*2-2; % 该结点号对应第一个位移编码 - 1for j=1:2FORCE(N1+j)=FORCE(N1+j)+FPOIN(i,j+1);%取结点荷载endend% 计算由非结点荷载引起的等效结点荷载for i=1:NFPRES % 对非结点荷载个数进行循环F0=ele_FPRES(i,FPRES,LNODS,COORD); %计算单元固端力% 对单元局部杆端力要进行坐标转换T=zbzh(i,LNODS,COORD); % 坐标转换矩阵F0=T'*F0;ele=FPRES(i,1); % 取荷载所在的单元号NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号% 将单元固端力变成等效结点荷载(注意固端力与等效结点荷载符号相反)FORCE((3*NL-2):3*NL)=FORCE((3*NL-2):3*NL)-F0(1:3);FORCE((3*NR-2):3*NR)=FORCE((3*NR-2):3*NR)-F0(4:6);end% 总刚、总荷载进行边界条件处理for j=1:NVFIX % 对约束个数进行循环N1=FIXED(j);HK(1:2*NPOIN,N1)=0; HK(N1,1:2*NPOIN)=0; HK(N1,N1)=1;% 将零位移约束对应的行、列变成零,主元变成1FORCE(N1)=0;end%---------------------------------------------------------DISP=HK\FORCE % 方程求解,HK先求逆再与力向量左乘%---------------------------------------------------------% 求结构各个单元内力EDISP=zeros(4,1); % 单元位移列向量清零for i=1:NELEM % 对单元个数进行循环for j=1:2 %对杆端循环% i单元左右端结点号*2 = 该结点的最后一个位移编码N1=LNODS(i,j)*2;% 取一端的单元位移列向量EDISP(2*j-1:2*j)=DISP(N1-1:N1);end% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵FE=EK*T*EDISP; %计算局部坐标杆端力(由结点位移产生)for j=1:NFPRESif FPRES(j,1) == i %成立时,当前单元上有非结点荷载F0=ele_FPRES(j,FPRES,LNODS,COORD);%单元固端力FE=FE+F0; % 考虑由非结点荷载引起的杆端力endendFE % 打印杆端力end%-------------------------------------------------------------------------------- % 计算桁架单元刚度矩阵函数 EK% 入口参数:单元号、单元信息数组、结点坐标、弹性模量% 出口参数:局部桁架单元刚度矩阵EKfunction EK=ele_EK(i,LNODS,COORD,YOUNG)NL=LNODS(i,1); NR=LNODS(i,2); %左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度A=LNODS(i,3); %面积;E=YOUNG;% 生成单刚(局部坐标) 右手坐标系EK =[E*A/L 0 -E*A/L 0 ;...0 0 0 0 ;...-E*A/L 0 E*A/L 0 ;...0 0 0 0 ];return%---------------------------------------------------------------------------------%计算单元固端力函数(正方向:X向右 Y向上 M逆时针)% 入口参数:荷载序号,荷载信息,单元信息,结点坐标% 出口参数:单元固端力——左右两端的轴力、剪力、弯矩function F0=ele_FPRES(iFPRES,FPRES,LNODS,COORD)ele=FPRES(iFPRES,1); %取荷载所在的单元号G=FPRES(iFPRES,3); %单元荷载大小C=FPRES(iFPRES,4); %单元荷载与左端距离NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度% 计算公式中一些常出现的项D=L-C; C1=C/L; C2=C1*C1; C3=C1*C2;B1=D/L; B2=B1/L;F0=[0;0;0;0;0;0]; %单元固端力清零switch FPRES(iFPRES,2)case 1 %均布荷载F0(2)=-G*C*(2-2*C2+C3)/2.0;F0(3)=-G*C*C*(6-8*C1+3*C2)/12.0;F0(5)=-G*C-F0(2);F0(6)=G*C*C*C1*(4-3*C1)/12.0;case 2 %横向集中力F0(2)=-G*B1*B2*(L+2*C);F0(3)=-G*C*B1*B1;F0(5)=-G*C2*(L+2*D)/L;F0(6)=G*D*C2;case 3 %纵向集中力F0(1)=-G*B1;F0(4)=-G*C1;endreturn%-------------------------------------------------------------------------------- % 形成第i单元的坐标转换矩阵函数 T(4,4)% 入口参数:单元号,单元信息,结点坐标% 出口参数:坐标转换矩阵(整体向局部投影)function T=zbzh(i,LNODS,COORD)NL=LNODS(i,1); %左结点号NR=LNODS(i,2); %右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); % 单元长度c=dx/L; % cos a (与 x 轴夹角余弦) s=dy/L; % sin aT=[ c s 0 0;...-s c 0 0;...0 0 c s0 0 -s c ];return6-6.txt文件数据:4 45 2 0 2.95e111 2 0.001 13 2 0.001 11 3 0.001 14 3 0.001 10 00.4 00.4 0.30 0.32 2e4 03 0 -2.5e41 2 4 7 8。
运用MATLAB对桁架单元进行有限元分析

np=3; ne=2; nload=1; nb=4; nu=0;% np为节点数,ne为单元数,nload为外力数,nb为约束数,nu 为泊松比np2=np*2; np3=np2-nb;% np2为不受约束时自由度是节点的两倍 ,np3为不受约束的节点自由度个数K=sym(zeros(np2,np2));% 定义受整体刚度空数组F=sym(zeros(np2,1));% 定义节点外力空数组KK=sym(zeros(np3,np3));% 预置自由度刚度空数组FF=sym(zeros(np3,1));% 预置自由度外力空数组syms h A P E L% 定义未知正常数为变量xy=[0,h;sqrt(3)*h,0;0,0];% 节点横纵坐标数组AA=[A;A];% 单元杆件面积load=[2,2,-P];% 荷载数组bound=[1,1,0;1,2,0;3,1,0;3,2,0];% 边界条件数组IJ=[1,2;3,2];% 各杆单元节点编号DW=zeros(1,4);for ie =1:neip=IJ(ie,1);jp=IJ(ie,2);DW(1)=ip*2-1; DW(2)=ip*2; DW(3)=jp*2-1; DW(4)=jp*2; % 给单元节点横纵方向编号x1=xy(ip,1); x2=xy(jp,1); y1=xy(ip,2); y2=xy(jp,2); % 杆单元节点x,y坐标L=sqrt((x2-x1)^2+(y2-y1)^2);% 杆单元长度c=(x2-x1)/L; s=(y2-y1)/L;% c为余弦, s为正弦T=[c,s,0,0;-s,c,0,0;0,0,c,s;0,0,-s,c];% 坐标转换矩阵(将局部坐标转换为整体坐标)A1=AA(ie);ke=[E*A1/L,0,-E*A1/L,0;0,0,0,0;-E*A1/L,0,E*A1/L,0;0,0,0,0];k=T.'*ke*T;% 将局部坐标下单元刚度转换为整体坐标下单元刚度 (转置后面加.可以去掉结果中的虚数)for i =1:4i1=DW(i);for j =1:4j1=DW(j);K(i1,j1)=K(i1,j1)+k(i,j);% 集成整体刚度矩阵endendendfor i =1:nloadi1=(load(i,1)-1)*2+load(i,2);F(i1,1)=F(i1,1)+load(i,3);% 将荷载按节点方向代码累加,计入外力荷载endFuu=sym(zeros(np2,1));% 节点位移NR=zeros(np2,1);for i =1:nbi1=(bound(i,1)-1)*2+bound(i,2);NR(i1)=-i1;% 将有约束的节点的横纵节点编号挑出来变为负数uu(i1)=bound(i,3);% 有约束的四个方向位移为0endj=0;for i =1:np2i1=NR(i);if i1==0j=j+1;NR(i)=j;endend% 此循环目的是为了将没有约束的节点以及方向挑出来for i =1:np2i1=NR(i);if i1>0FF(i1)=F(i);end% 将没有约束的节点方向的外力储存下来for j =1:np2j1=NR(j);if (i1>0 & j1>0)KK(i1,j1)=K(i,j);end% 将没有约束的节点的刚度储存下来endendKKFFfor i =1:np2i1=NR(i);for j =1:np2j1=NR(j);if (i1>0 & j1<0)jj1=abs(j1);FF(i1)=FF(i1)-K(i,jj1)*uu(jj1);end% 由于有约束方向的位移为0,所以无位移的地方FF[i1]不变endendu=sym(zeros(np2,1));u=KK\FF% 求解线性方程for i =1:np2i1=NR(i);if i1>0uu(i)=u(i1);end% 将求解的无约束方向的位移放进总的位移数组相应的位置中去enduudisp('位移')for ip =1:npstr=[ip;uu(ip*2-1);uu(ip*2)];disp(str)% 输出节点位移endfor ie =1:neip=IJ(ie,1);jp=IJ(ie,2);DW(1)=ip*2-1; DW(2)=ip*2; DW(3)=jp*2-1; DW(4)=jp*2; x1=xy(ip,1); x2=xy(jp,1); y1=xy(ip,2); y2=xy(jp,2);L=sqrt((x2-x1)^2+(y2-y1)^2);c=(x2-x1)/L; s=(y2-y1)/L;T=[c,s,0,0;-s,c,0,0;0,0,c,s;0,0,-s,c];A1=AA(ie);ke=[E*A1/L,0,-E*A1/L,0;0,0,0,0;-E*A1/L,0,E*A1/L,0; 0,0,0,0];d=sym(zeros(4,1));for i=1:4d(i)=uu(i);endde=T*d;% 将整体坐标位移转换为局部坐标位移Fe=ke*de;% 杆单元力for j=1:4N=Fe((ie-1)*2+1);% 杆单元轴力sigma=N/A1;enddisp('单元,轴力,应力')str=[ie;N;sigma];disp(str)endF3=K*uu;R=F3-F;disp('支反力');for i =1:nbi1=(bound(i,1)-1)*2+bound(i,2);str=[bound(i,1);bound(i,3);simplify(R(i1))]; disp(str)end。
matlab桁架结构有限元计算

matlab桁架结构有限元计算摘要本文介绍了使用M ATL A B进行桁架结构有限元计算的方法。
首先,我们将讨论桁架结构的基本概念和有限元分析的原理。
然后,我们将详细介绍如何使用MA TL AB建立桁架结构的有限元模型,并进行力学分析。
最后,我们将通过一个案例演示如何使用MA TL AB进行桁架结构的有限元计算,以及如何分析结果。
1.引言桁架结构是一种由杆件和节点组成的空间结构。
它具有轻巧、刚性和稳定等特点,在工程领域中得到了广泛应用。
有限元方法是一种常用的工程分析方法,可以用于求解桁架结构的应力、变形等问题。
MA T LA B是一个功能强大的计算软件,具有丰富的工具箱和便于使用的界面,可以用于桁架结构的有限元分析。
2.桁架结构的基本概念桁架结构由若干杆件和节点组成,杆件可以看作是刚性杆,节点是杆件的连接点。
桁架结构常用于承受桥梁、建筑物等结构的荷载。
桁架结构的节点可以是固定支撑、铰支撑或滑动支撑等。
杆件可以是直杆、曲杆或弯曲杆等。
桁架结构的力学行为可以通过有限元方法进行分析。
3.有限元分析的原理有限元分析是一种将复杂结构离散化为单元,通过对单元的力学计算得到整体结构的力学行为的方法。
有限元分析的基本步骤包括离散化、建立单元模型、求解节点位移和计算单元力等。
在桁架结构的有限元分析中,常用的单元类型有一维梁单元和杆单元。
4.使用MAT LAB进行桁架结构有限元分析使用MA TL AB进行桁架结构有限元分析的步骤如下:4.1建立有限元模型首先,需要根据实际情况确定桁架结构的几何尺寸和材料属性,然后使用MA TL AB的有限元建模工具箱创建桁架结构的有限元模型。
模型的建立包括定义节点、杆件和单元,设置边界条件和加载。
4.2求解节点位移和单元力通过求解有限元方程,可以得到桁架结构的节点位移和单元力。
M A TL AB提供了一系列用于求解线性方程组的函数,可以快速得到结果。
4.3分析结果得到节点位移和单元力后,可以进行进一步的分析。
桁架结构的有限元分析MATLAB

桁架结构的有限元分析MATLAB桁架结构是一种由直杆或斜杆连接而成的稳定结构,在工程应用中较为常见。
有限元分析(Finite Element Analysis,FEA)是一种利用数值方法解决结构力学问题的工具。
本文将介绍如何使用MATLAB进行桁架结构的有限元分析,并对其进行1200字以上的详细描述。
在进行桁架结构有限元分析前,需要先进行结构建模以及材料属性和加载条件的定义。
这些定义可以通过MATLAB命令行或者编写MATLAB脚本文件实现。
首先,我们需要定义桁架结构的节点和单元。
节点用于表示桁架结构的连接点,单元用于表示相邻节点之间的连接关系。
可以使用MATLAB中的矩阵表示节点和单元,如下所示:nodes = [x1, y1; x2, y2; ...; xn, yn];elements = [n1, n2; n3, n4; ...; nm, np];```其中,`nodes`是一个n行2列的矩阵,表示n个节点的坐标;`elements`是一个m行2列的矩阵,表示m个单元的节点连接关系。
接下来,我们需要定义材料属性和加载条件。
材料属性包括杨氏模量和截面面积等参数,加载条件包括节点的约束和外部加载。
可以使用MATLAB中的矩阵或者结构体表示材料属性和加载条件,如下所示:materials = struct('E', E1, 'A', A1; 'E', E2, 'A', A2; ...);constraints = [n1, d1x, d1y; ...; nm, dmx, dmy];loads = [n1, F1x, F1y; ...; nl, Flx, Fly];```其中,`materials`是一个结构体数组,每个结构体包含材料的杨氏模量(E)和截面面积(A);`constraints`是一个m行3列的矩阵,表示m个节点的约束,其中d1x和d1y分别表示节点的x方向和y方向位移约束;`loads`是一个l行3列的矩阵,表示l个节点的外部加载,其中F1x和F1y分别表示节点的x方向和y方向外部力。
桁架单元例子ANSYS 1
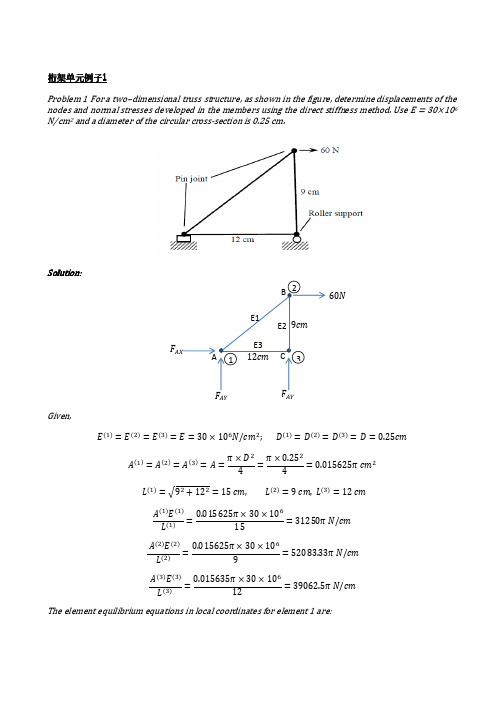
݂ۍଵሺ௫ଵሻې
݂ێێଵሺ௬ଵሻ
ۑ ۑ
݂݂ێێۏଶଶሺሺ௫௬ଵଵሻሻ
ۑ ۑ
ے
=
ܣሺଵሻܧሺଵሻ ܮሺଵሻ
1 ൦−01
0
0 0 0 0
−1 0 1 0
0 00൪ 0
ݑۍଵሺଵ௫ሻې ݒێێଵሺଵ௬ሻۑۑ ݑݒێێۏଶଶሺሺଵଵ௬௫ሻሻۑۑے
桁架单元例子1
Problem 1 For a two–dimensional truss structure, as shown in the figure, determine displacements of the nodes and normal stresses developed in the members using the direct stiffness method. Use E = 30×106 N/cm2 and a diameter of the circular cross-section is 0.25 cm.
0
߶݊݅ݏଵ ܿ߶ݏଵ
0
0
0
0
ܿ߶ݏଵ −߶݊݅ݏଵ
0
0 ߶݊݅ݏଵ
൪
ܿ߶ݏଵ
For element 1, ߶ଵ = ି݊ܽݐଵሺ9/12ሻ = 36.87°, putting this value of ߶ଵin the above matrix we get,
0.8 0.6 0 0
Solution:
B2
60ܰ
E1 E2 9ܿ݉
ܨ
E3 A 1 12ܿ݉ C 3
Given,
matlab桁架结构有限元计算

matlab桁架结构有限元计算摘要:一、引言二、MATLAB 在桁架结构有限元计算中的应用1.桁架结构的离散化与编号2.组装刚度矩阵3.求解器求解4.后处理三、MATLAB 桁架有限元分析实例1.空间桁架有限元分析2.基于MATLAB 的三维桁架有限元分析3.五杆桁架有限元分析四、用MATLAB 编写程序求解桁架结构内力问题1.静定结构绘制简图2.计算结构力学3.机动分析五、结论正文:一、引言在工程领域中,桁架结构由于其优越的力学性能和简单的结构形式,被广泛应用于桥梁、塔架等大型建筑结构中。
为了确保桁架结构的安全性和稳定性,对其进行有限元分析是非常必要的。
MATLAB 作为一种强大的数学软件,可以方便地进行桁架结构的有限元计算。
本文将介绍如何使用MATLAB 进行桁架结构有限元计算。
二、MATLAB 在桁架结构有限元计算中的应用1.桁架结构的离散化与编号在进行有限元分析之前,首先需要对桁架结构进行离散化处理,将连续的桁架杆件划分为有限个小杆件。
同时,为了方便后续计算,需要对各个杆件和节点进行编号。
2.组装刚度矩阵根据桁架结构的几何参数和材料性能,可以计算出各个杆件的刚度矩阵。
将这些刚度矩阵组装成一个总的刚度矩阵,用于描述整个桁架结构的刚度特性。
3.求解器求解利用MATLAB 的求解器,可以对桁架结构进行有限元求解。
求解器会根据刚度矩阵和施加的边界条件,计算出节点的位移和单元的应力。
4.后处理在求解完成后,需要对计算结果进行后处理。
这包括对计算结果的保存、可视化以及结果的验证等。
三、MATLAB 桁架有限元分析实例1.空间桁架有限元分析例如,可以针对一个空间桁架结构,使用MATLAB 进行有限元分析。
假设该桁架结构由铝制成的垂直和水平部分和钢制成的对角桁架构件组成。
结构承受荷载P,需要计算节点位移、单元应力以及支反力。
2.基于MATLAB 的三维桁架有限元分析还可以利用MATLAB 进行三维桁架有限元分析。
matlab刚架计算编程
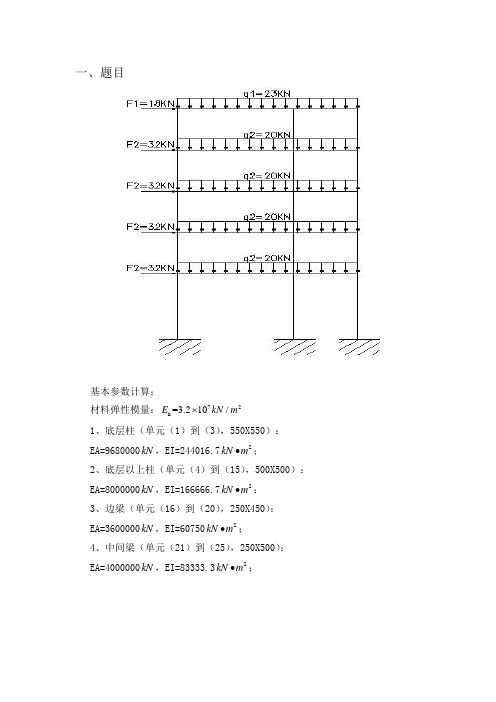
一、题目基本参数计算:材料弹性模量:72h =3.210/E kN m ⨯1、底层柱(单元(1)到(3),550X550): EA=9680000kN ,EI=244016.72kN m ∙;2、底层以上柱(单元(4)到(15),500X500): EA=8000000kN ,EI=166666.72kN m ∙;3、边梁(单元(16)到(20),250X450): EA=3600000kN ,EI=607502kN m ∙;4、中间梁(单元(21)到(25),250X500): EA=4000000kN ,EI=83333.32kN m ∙;节点编号及单元编号二、计算结果对比1.竖向均布荷载作用下的杆端内力计算输入底层柱高h1:4.8输入二至五层柱高h2:3输入左梁跨度L1:4.8输入右梁跨度L2:2.7输入底层柱子的抗弯刚度EIc1:244016.7输入二至五层柱子的抗弯刚度EIc2:166666.7输入底层柱子的抗压刚度EAc1:9680000输入二至五层柱子的抗压刚度EAc2:8000000输入左梁的抗弯刚度EIb1:60750输入右梁的抗弯刚度EIb2:83333.3输入左梁的抗压刚度EAb1:3600000输入右梁的抗压刚度EAb2:4000000输入顶层竖向均布荷载集度q1:23输入一至四层均布荷载集度q2:20输入顶层水平集中力F1:0输入一至四水平集中力F2:0Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 3.812489e-019.> In gangjia at 125第1节点的位移是-0.000312 0.000320 0.000158第2节点的位移是-0.000255 0.000299 0.000004第3节点的位移是-0.000139 0.000260 0.000032第4节点的位移是-0.000058 0.000201 0.000036第5节点的位移是-0.000024 0.000125 0.000066第6节点的位移是-0.000000 0.000000 0.000000第7节点的位移是-0.000341 0.000471 -0.000125第8节点的位移是-0.000243 0.000438 -0.000063第9节点的位移是-0.000140 0.000380 -0.000072第10节点的位移是-0.000059 0.000296 -0.000057第11节点的位移是-0.000012 0.000185 -0.000054第12节点的位移是0.000000 0.000000 -0.000000第13节点的位移是-0.000347 0.000189 -0.000090第14节点的位移是-0.000241 0.000177 -0.000058第15节点的位移是-0.000140 0.000154 -0.000057第16节点的位移是-0.000058 0.000119 -0.000045第17节点的位移是-0.000010 0.000073 -0.000032第18节点的位移是0.000000 0.000000 -0.000000第1单元节点内力是55.676623 22.120376 41.726078 -55.676623 -22.120376 24.635050第2单元节点内力是105.531000 12.618842 17.368689 -105.531000 -12.618842 20.487837第3单元节点内力是154.956696 13.495898 20.022904 -154.956696 -13.495898 20.464789第4单元节点内力是203.914370 13.818765 19.057567 -203.914370 -13.818765 22.398728第5单元节点内力是86.165797 -13.600544 -23.843462 -86.165797 13.600544 -16.958168第6单元节点内力是154.343865 -7.348932 -10.545483 -154.343865 7.348932 -11.501313第7单元节点内力是225.186314 -8.283039 -13.237518 -225.186314 8.283039 -11.611598第8单元节点内力是297.205484 -8.885450 -13.512019 -297.205484 8.885450 -13.144331第9单元节点内力是30.657580 -8.519833 -14.535293 -30.657580 8.519833 -11.024205第10单元节点内力是62.625136 -5.269910 -7.987274 -62.625136 5.269910 -7.822456 第11单元节点内力是92.356990 -5.212859 -8.482119 -92.356990 5.212859 -7.156458 第12单元节点内力是121.380147 -4.933315 -8.107970 -121.380147 4.933315 -6.691976第13单元节点内力是252.113359 4.837824 14.964088 -252.113359 -4.837824 8.257469第14单元节点内力是372.232119 -3.084712 -10.134383 -372.232119 3.084712-4.672235第15单元节点内力是148.154523 -1.753112 -5.827793 -148.154523 1.753112 -2.587145第16单元节点内力是22.120376 -55.676623 -41.726078 -22.120376 -54.723377 39.438288第17单元节点内力是-9.501534 -49.854377 -42.003740 9.501534 -46.145623 33.102731第18单元节点内力是0.877056 -49.425696 -40.510741 -0.877056 -46.574304 33.667399第19单元节点内力是0.322867 -48.957674 -39.522356 -0.322867 -47.042326 34.925521第20单元节点内力是-8.980941 -48.198989 -37.362816 8.980941 -47.801011 36.407668第21单元节点内力是8.519833 -31.442420 -15.594826 -8.519833 -30.657580 14.535293第22单元节点内力是-3.249922 -22.032445 -5.599080 3.249922 -31.967555 19.011480 第23单元节点内力是-0.057051 -24.268146 -8.928568 0.057051 -29.731854 16.304575第24单元节点内力是-0.279544 -24.976843 -9.801904 0.279544 -29.023157 15.264428第25单元节点内力是-3.180203 -27.225624 -13.128954 3.180203 -26.774376 12.519769Matlab计算弯矩图力矩分配法计算弯矩图8.87最终8.8715.1020.7518.2218.2518.2418.2415.3521.8538.2138.2166.2444.1837.2057.6039.0036.4838.7436.4738.7557.6057.6035.8557.6038.474.821.794.253.813.138.5118.2318.4118.2318.2318.2320.9610.48 3.807.617.3817.7811.5510.4910.4812.2825.535.695.6919.2517.197.749.53 3.604.1417.787.623.813.8110.48结构力学求解器计算弯矩图2.水平荷载作用下的杆端内力计算输入底层柱高h1:4.8输入二至五层柱高h2:3输入左梁跨度L1:4.8输入右梁跨度L2:2.7输入底层柱子的抗弯刚度EIc1:244016.7输入二至五层柱子的抗弯刚度EIc2:166666.7输入底层柱子的抗压刚度EAc1:9680000输入二至五层柱子的抗压刚度EAc2:8000000输入左梁的抗弯刚度EIb1:60750输入右梁的抗弯刚度EIb2:83333.3输入左梁的抗压刚度EAb1:3600000输入右梁的抗压刚度EAb2:4000000输入顶层竖向均布荷载集度q1:0输入一至四层均布荷载集度q2:0输入顶层水平集中力F1:18输入一至四水平集中力F2:32Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 3.812489e-019.> In gangjia at 125第1节点的位移是0.010766 -0.000078 0.000176第2节点的位移是0.009966 -0.000076 0.000321第3节点的位移是0.008565 -0.000070 0.000521第4节点的位移是0.006503 -0.000058 0.000714第5节点的位移是0.003785 -0.000039 0.000935第6节点的位移是-0.000000 -0.000000 0.000000第7节点的位移是0.010747 -0.000138 0.000165第8节点的位移是0.009932 -0.000137 0.000284第9节点的位移是0.008530 -0.000132 0.000432第10节点的位移是0.006464 -0.000115 0.000589第11节点的位移是0.003772 -0.000079 0.000689第12节点的位移是0.000000 -0.000000 0.000000第13节点的位移是0.010745 0.000216 0.000205第14节点的位移是0.009924 0.000213 0.000312第15节点的位移是0.008522 0.000202 0.000483第16节点的位移是0.006456 0.000173 0.000651第17节点的位移是0.003765 0.000118 0.000796第18节点的位移是-0.000000 0.000000 0.000000第1单元节点内力是-5.788617 -4.001579 -14.039455 5.788617 4.001579 2.034718第2单元节点内力是-15.767839 -10.233070 -26.449395 15.767839 10.233070 -4.249815第3单元节点内力是-31.245046 -15.512425 -34.021177 31.245046 15.512425-12.516099第4单元节点内力是-52.244156 -18.146548 -39.461868 52.244156 18.146548 -14.977776第5单元节点内力是-1.562581 -10.530910 -22.438577 1.562581 10.530910 -9.154153 第6单元节点内力是-14.655617 -24.288069 -44.629714 14.655617 24.288069 -28.234493第7单元节点内力是-44.997366 -39.528302 -68.050342 44.997366 39.528302 -50.534563第8单元节点内力是-94.445810 -57.286585 -91.484591 94.445810 57.286585 -80.375163第9单元节点内力是7.351198 -3.467511 -11.155563 -7.351198 3.467511 0.753031第10单元节点内力是30.423456 -15.478861 -32.749852 -30.423456 15.478861 -13.686732第11单元节点内力是76.242412 -26.959273 -49.759213 -76.242412 26.959273 -31.118606第12单元节点内力是146.689967 -38.566867 -65.888400 -146.689967 38.566867 -49.812202第13单元节点内力是-78.206852 -40.813457 -50.436253 78.206852 40.813457 -145.468339第14单元节点内力是-160.306021 -56.066694 -99.510204 160.306021 56.066694 -169.609927第15单元节点内力是238.512872 -49.119849 -77.431186 -238.512872 49.119849 -158.344090第16单元节点内力是13.998421 5.788617 14.039455 -13.998421 -5.788617 13.745907 第17单元节点内力是25.768509 9.979222 24.414677 -25.768509 -9.979222 23.485589 第18单元节点内力是26.720645 15.477207 38.270992 -26.720645 -15.477207 36.019600第19单元节点内力是29.365877 20.999110 51.977967 -29.365877 -20.999110 48.817762第20单元节点内力是9.333091 25.962695 65.414029 -9.333091 -25.962695 59.206909 第21单元节点内力是3.467511 7.351198 8.692670 -3.467511 -7.351198 11.155563第22单元节点内力是12.011350 23.072259 30.298277 -12.011350 -23.072259 31.996821第23单元节点内力是11.480412 45.818955 60.265235 -11.480412 -45.818955 63.445944第24单元节点内力是11.607594 70.447555 93.201392 -11.607594 -70.447555 97.007006第25单元节点内力是10.552982 91.822906 120.678459 -10.552982 -91.822906 127.243387Matlab计算弯矩图D 值法计算弯矩图9.239.230.0020.5220.525.1330.3725.2416.8248.9932.1726.3273.6247.30141.915.1212.4917.6113.7213.7214.307.5534.8341.5841.335.8835.4526.4127.7264.3663.0568.2019.0949.1142.8451.59104.3795.62114.6740.1874.4950.0463.75108.20121.91134.0449.6684.38157.00162.31结构力学求解器计算弯矩图三、程序代码h1=input('输入底层柱高h1:');h2=input('输入二至五层柱高h2:');L1=input('输入左梁跨度L1:');L2=input('输入右梁跨度L2:');EIc1=input('输入底层柱子的抗弯刚度EIc1:');EIc2=input('输入二至五层柱子的抗弯刚度EIc2:');EAc1=input('输入底层柱子的抗压刚度EAc1:');EAc2=input('输入二至五层柱子的抗压刚度EAc2:');EIb1=input('输入左梁的抗弯刚度EIb1:');EIb2=input('输入右梁的抗弯刚度EIb2:');EAb1=input('输入左梁的抗压刚度EAb1:');EAb2=input('输入右梁的抗压刚度EAb2:');q1=input('输入顶层竖向均布荷载集度q1:');q2=input('输入一至四层均布荷载集度q2:');F1=input('输入顶层水平集中力F1:');F2=input('输入一至四水平集中力F2:');T=[0,1,0,0,0,0;-1,0,0,0,0,0;0,0,1,0,0,0;0,0,0,0,1,0;0,0,0,-1,0,0;0,0,0,0,0,1];%角度为90°的转换矩阵%左梁的单元刚度矩阵Kb1=[EAb1/L1 0 0 -EAb1/L1 0 0;0 12*EIb1/(L1*L1*L1) 6*EIb1/(L1*L1) 0 -12*EIb1/(L1*L1*L1) 6*EIb1/(L1*L1);0 6*EIb1/(L1*L1) 4*EIb1/L1 0 -6*EIb1/(L1*L1) 2*EIb1/L1;-EAb1/L1 0 0 EAb1/L1 0 0;0 -12*EIb1/(L1*L1*L1) -6*EIb1/(L1*L1) 0 12*EIb1/(L1*L1*L1) -6*EIb1/(L1*L1);0 6*EIb1/(L1*L1) 2*EIb1/L1 0 -6*EIb1/(L1*L1) 4*EIb1/L1];%右梁的单元刚度矩阵Kb2=[EAb2/L2 0 0 -EAb2/L2 0 0;0 12*EIb2/(L2*L2*L2) 6*EIb2/(L2*L2) 0 -12*EIb2/(L2*L2*L2) 6*EIb2/(L2*L2);0 6*EIb2/(L2*L2) 4*EIb2/L2 0 -6*EIb2/(L2*L2) 2*EIb2/L2;-EAb2/L2 0 0 EAb2/L2 0 0;0 -12*EIb2/(L2*L2*L2) -6*EIb2/(L2*L2) 0 12*EIb2/(L2*L2*L2) -6*EIb2/(L2*L2);0 6*EIb2/(L2*L2) 2*EIb2/L2 0 -6*EIb2/(L2*L2) 4*EIb2/L2];%底层柱子的单元刚度矩阵Kc1=[EAc1/h1 0 0 -EAc1/h1 0 0;0 12*EIc1/(h1*h1*h1) 6*EIc1/(h1*h1) 0 -12*EIc1/(h1*h1*h1) 6*EIc1/(h1*h1);0 6*EIc1/(h1*h1) 4*EIc1/h1 0 -6*EIc1/(h1*h1) 2*EIc1/h1;-EAc1/h1 0 0 EAc1/h1 0 0;0 -12*EIc1/(h1*h1*h1) -6*EIc1/(h1*h1) 0 12*EIc1/(h1*h1*h1) -6*EIc1/(h1*h1);0 6*EIc1/(h1*h1) 2*EIc1/h1 0 -6*EIc1/(h1*h1) 4*EIc1/h1];%二至五层柱子的单元刚度矩阵Kc2=[EAc2/h2 0 0 -EAc2/h2 0 0;0 12*EIc2/(h2*h2*h2) 6*EIc2/(h2*h2) 0 -12*EIc2/(h2*h2*h2) 6*EIc2/(h2*h2);0 6*EIc2/(h2*h2) 4*EIc2/h2 0 -6*EIc2/(h2*h2) 2*EIc2/h2;-EAc2/h2 0 0 EAc2/h2 0 0;0 -12*EIc2/(h2*h2*h2) -6*EIc2/(h2*h2) 0 12*EIc2/(h2*h2*h2) -6*EIc2/(h2*h2);0 6*EIc2/(h2*h2) 2*EIc2/h2 0 -6*EIc2/(h2*h2) 4*EIc2/h2];Kc11=T'*Kc1*T;%总体坐标下底层柱子的单元刚度矩阵Kc22=T'*Kc2*T;%总体坐标下二至五层柱子的单元刚度矩阵X=zeros(54,54);K1=zeros(54,54);K2=zeros(54,54);%定义54阶0矩阵%把梁杆单元矩阵整合到总体刚度矩阵的循环语句for ii=1:5X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb1(1:3,1:3);K1=K1+X;X=zeros(54,54);endfor ii=7:11X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb1(4:6,4:6);K1=K1+X;X=zeros(54,54);endfor ii=7:11X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb2(1:3,1:3);K1=K1+X;X=zeros(54,54);endfor ii=13:17X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb2(4:6,4:6);K1=K1+X;X=zeros(54,54);endfor ii=1:5X(3*ii-2:3*ii,3*ii+16:3*ii+18)=Kb1(1:3,4:6);K1=K1+X;X=zeros(54,54);endfor ii=1:5X(3*ii+16:3*ii+18,3*ii-2:3*ii)=Kb1(4:6,1:3);K1=K1+X;X=zeros(54,54);endX(3*ii-2:3*ii,3*ii+16:3*ii+18)=Kb2(1:3,4:6);K1=K1+X;X=zeros(54,54);endfor ii=7:11X(3*ii+16:3*ii+18,3*ii-2:3*ii)=Kb2(4:6,1:3);K1=K1+X;X=zeros(54,54);end%把柱杆单元矩阵整合到总体刚度矩阵的循环语句for jj=1:4X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc22;K2=K2+X;X=zeros(54,54);endfor jj=7:10X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc22;K2=K2+X;X=zeros(54,54);endfor jj=13:16X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc22;K2=K2+X;X=zeros(54,54);endfor jj=5:6:17X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc11;K2=K2+X;X=zeros(54,54);endK=K1+K2;for i=6:6:18K(3*i-2:3*i,3*i-2:3*i)=Kc11(4:6,4:6).*10.^15;endP=zeros(54,1);Y=zeros(54,1);Z=zeros(54,1);P(1,1)=F1;P(2,1)=q1*L1/ 2;P(3,1)=q1*L1*L1/12;P(20,1)=q1*L1/2+q1*L2/2;P(21,1)=-q1*L1*L1/12 +q1*L2*L2/12;P(38,1)=q1*L2/2;P(39,1)=-q1*L2*L2/12;%定义荷载列阵for i=2:5Y(3*i-2,1)=F2;P=P+Y;Y=zeros(54,1);endfor i=2:5Y(3*i-1,1)=q2*L1/2;Z(3*i,1)=q2*L1*L1/12;P=P+Y+Z;Y=zeros(54,1);Z=zeros(54,1);endfor i=8:11Y(3*i-1,1)=q2*L1/2+q2*L2/2;Z(3*i,1)=-q2*L1*L1/12+q2*L2*L2/12;P=P+Y+Z;Y=zeros(54,1);Z=zeros(54,1);endY(3*i-1,1)=q2*L2/2;Z(3*i,1)=-q2*L2*L2/12;P=P+Y+Z;Y=zeros(54,1);Z=zeros(54,1);endA=K\P;%结构位移LOC=zeros(25,2);LOC(1,1)=1;LOC(1,2)=2;LOC(2,1)=2;LOC(2,2)=3;LOC(3,1)=3;LOC(3,2)=4 ;LOC(4,1)=4;LOC(4,2)=5;LOC(5,1)=7;LOC(5,2)=8;LOC(6,1)=8;LOC(6,2)= 9;LOC(7,1)=9;LOC(7,2)=10;LOC(8,1)=10;LOC(8,2)=11;LOC(9,1)=13;LOC(9,2)=14;LOC(10,1)=14;LOC(10,2)=15;LOC(11,1)=15;LO C(11,2)=16;LOC(12,1)=16;LOC(12,2)=17;LOC(13,1)=5;LOC(13,2)=6;LOC( 14,1)=11;LOC(14,2)=12;LOC(15,1)=17;LOC(15,2)=18;LOC(16,1)=1;LOC(1 6,2)=7;LOC(17,1)=2;LOC(17,2)=8;LOC(18,1)=3;LOC(18,2)=9;LOC(19,1)=4;LOC(1 9,2)=10;LOC(20,1)=5;LOC(20,2)=11;LOC(21,1)=7;LOC(21,2)=13;LOC(22, 1)=8;LOC(22,2)=14;LOC(23,1)=9;LOC(23,2)=15;LOC(24,1)=10;LOC(24,2) =16;LOC(25,1)=11;LOC(25,2)=17;a=zeros(6,1);M=zeros(6,25);MT=zeros(6,25);FE1=[0;q1*L1/2;q1*L1*L1/12;0;q1*L1/2;-q1*L1*L1/12];FE2=[0;q2*L1/2;q2*L1*L1/12;0;q2*L1/2;-q2*L1*L1/12];FE3=[0;q1*L2/2;q1*L2*L2/12;0;q1*L2/2;-q1*L2*L2/12];FE4=[0;q2*L2/2;q2*L2*L2/12;0;q2*L2/2;-q2*L2*L2/12];for i=1:12I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kc2*T*a;M=M+MT;MT=zeros(6,25);a=zeros(6,1);endfor i=13:15I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kc1*T*a;M=M+MT;MT=zeros(6,25);a=zeros(6,1);endfor i=16:16I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb1*a-FE1;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=17:20I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb1*a-FE2;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=21:21I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb2*a-FE3;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=22:25I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb2*a-FE4;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=1:18m=i;fprintf('第%d节点的位移是%f %f %f\n',i,A(3*m-2:3*m,1))endfor i=1:25m=i;fprintf('第%d单元节点内力是%f %f %f %f %f %f\n',i,M(:,m)) end。
matlab中关于桁架问题的程序

clear; %清除内存变量ss1=input('give a data filename:','s');fp1=fopen(ss1,'r');ss2=input('give a result filename:','s');fp2=fopen(ss2,'w');%1.读入结构数据、建立累积约束表向量、建立结构刚度矩阵%1.1.结构参数和弹性模量[m,c]=fscanf(fp1,'%u',[1]); %杆件数[nj,c]=fscanf(fp1,'%u',[1]); %节点数[nrj,c]=fscanf(fp1,'%u',[1]); %约束节点[e,c]=fscanf(fp1,'%e',[1]); %弹性模量fprintf(fp2,'(1)结构参数和弹性模量\n');fprintf(fp2,'杆件数节点数约束节点数弹性模量\n');fprintf(fp2,'%3u %8u %8u %13.3e\n',m,nj,nrj,e);fprintf(fp2,'\n');%1.2. 节点坐标pc(1:2,1:nj)=0for jx=1:nj[k,c]=fscanf(fp1,'%u',[1]); %节点号[pc(:,k),c]=fscanf(fp1,'%f',[2]); %x坐标、y坐标endfprintf(fp2,'(2)节点坐标\n');fprintf(fp2,'节点号x坐标y坐标\n');fprintf(fp2,'%3u %13.3e %13.3e\n',[1:nj;pc(:,1:nj)]);fprintf(fp2,'\n');%1.3.杆件标号与截面特性jj(1:m)=0; jk(1:m)=0; ax(1:m)=0; iz(1:m)=0;for imx=1:m[k,c]=fscanf(fp1,'%u',[1]); %杆件号[jj(k),c]=fscanf(fp1,'%u',[1]); %j端点号[jk(k),c]=fscanf(fp1,'%u',[1]); %k端点号[ax(k),c]=fscanf(fp1,'%f',[1]); %截面积[iz(k),c]=fscanf(fp1,'%f\n',[1]); %杆件号endfprintf(fp2,'(3)杆件标号与截面特性\n');fprintf(fp2,'杆件号j端点号k端点号截面积截面惯性矩\n');fprintf(fp2,'%3u %8u%8u %13.3e%13.3e\n',[1:m;jj(1:m);jk(1:m);ax(1:m);iz(1:m)]); fprintf(fp2,'\n');%1.4.di和dj取值di(1:m)=0; dj(1:m)=0;for imx=1:m[k1(imx),c]=fscanf(fp1,'%u',[1]);[di(k1(imx)),c]=fscanf(fp1,'%f',[1]);[dj(k1(imx)),c]=fscanf(fp1,'%f',[1]);endfprintf(fp2,'(4)杆件标号与两端刚域\n');fprintf(fp2,'杆件号j端刚域k端刚域\n');fprintf(fp2,'%3u %13.3e %13.3e\n',[1:m;di(1:m);dj(1:m)]);fprintf(fp2,'\n');%1.5.节点约束情况fprintf(fp2,'(5)节点约束情况\n');fprintf(fp2,'受约束点号x向约束情况y向约束情况z约束情况\n');rl(1:3*nj)=0;for jx=1:nrj[k,c]=fscanf(fp1,'%u',[1]); %受约束节点号[rl(3*k-2:3*k),c]=fscanf(fp1,'%f',[3]); %x向约束情况y向约束情况z约束情况fprintf(fp2,'%5u %12u%12u%12u\n',k,rl(3*k-2:3*k));endfprintf(fp2,'\n');%1.6.建立累积约束表向量crl(1:3*nj)=0;[n,nr,crl]=Cu(3*nj,rl);fprintf(fp2,'(5)非约束位移数约束位移数\n');fprintf(fp2,'%10u %10u\n',n,nr);fprintf(fp2,'\n');H(1:6,1:6)=0;%1.7. 装配总节点刚度矩阵sj(1:3*nj,1:3*nj)=0;for imx=1:mH(1:6,1:6)=[1 0 0 0 0 0;0 1 di(k1(imx)) 0 0 0;0 0 1 0 0 0;0 0 0 1 0 0;0 0 0 0 1 -dj(k1(imx));0 0 0 0 0 1];sm=Psm(pc(:,jj(imx)),pc(:,jk(imx)),ax(imx),iz(imx),e);sm2=H(1:6,1:6)'*sm*H(1:6,1:6);RT=PRT(pc(:,jj(imx)),pc(:,jk(imx)));smd=RT'*sm2*RT;j=[3*jj(imx)-2:3*jj(imx),3*jk(imx)-2:3*jk(imx)]; %计算杆端位移对应的总节点位移标号sj(j(1:6),j(1:6))= sj(j(1:6),j(1:6))+smd(1:6,1:6);end%1.8. 对应非约束位移、约束位移、将总节点刚度矩阵sj重新排列s(crl(1:3*nj),crl(1:3*nj))=sj(1:3*nj,1:3*nj);%2. 读入荷载数据、构建约束杆端力、构建综合节点荷载%2.1. 读入荷载节点数、集中荷载杆件数、分布荷载杆件数[nlj,c]=fscanf(fp1,'%u',[1]); %荷载节点数[nla,c]=fscanf(fp1,'%u',[1]); %集中荷载杆件数[nlq,c]=fscanf(fp1,'%u',[1]); %分布荷载杆件数fprintf(fp2,'(7)荷载节点数集中荷载杆件数分布荷载杆件数\n');fprintf(fp2,'%10u %10u %10u\n',nlj,nla,nlq);fprintf(fp2,'\n');%2.2. 节点荷载fprintf(fp2,'(8)节点荷载\n');fprintf(fp2,'节点号x向线力y向线力z向力偶\n');ac(1:3*nj,1:1)=0;for jx=1:nlj[k,c]=fscanf(fp1,'%u',[1]); %受荷载节点号[aj,c]=fscanf(fp1,'%f',[3]); %x向线力y向线力z向力偶fprintf(fp2,'%3u %13.3e%13.3e%13.3e\n',k,aj);ac(3*k-2:3*k)=ac(3*k-2:3*k)+aj(1:3);endfprintf(fp2,'\n');%2.3.杆件上集中荷载fprintf(fp2,'(9)杆件上集中荷载\n');fprintf(fp2,'杆件号x向线力y向线力z向力偶作用点距杆j端距离\n');aml(1:6,1:m)=0;for imx=1:nla[ia,c]=fscanf(fp1,'%u',[1]); %杆件号[as,c]=fscanf(fp1,'%f',[3]); %x向线力y向线力z向力偶[xa,c]=fscanf(fp1,'%f',[1]); %集中荷载杆端距fprintf(fp2,'%3u %13.3e%13.3e%13.3e%13.3e\n',ia,as,xa);amx=PamlC(pc(:,jj(ia)),pc(:,jk(ia)),as,di(k1(imx)),dj(k1(imx)),xa);aml(:,ia)=aml(:,ia)+amx(:); %累加约束杆端力endfprintf(fp2,'\n');%2.4.杆件上分布荷载fprintf(fp2,'(10)杆件上分布荷载\n');fprintf(fp2,'杆件号起点x向集度终点x向集度起点y向集度终点y向集度起点距j端距离终点距j端距离\n');for imx=1:nlq[iq,c]=fscanf(fp1,'%u',[1]); %杆件号[q,c]=fscanf(fp1,'%f',[4]); %起点x向集度终点x向集度起点y向集度终点y向集度[xq,c]=fscanf(fp1,'%f',[2]); %起点距j端距离终点距j端距离fprintf(fp2,'%3u %14.3e%14.3e%14.3e%14.3e%14.3e\n',iq,q,xq);amx=PamlD(pc(:,jj(iq)),pc(:,jk(iq)),q,xq);aml(:,iq)=aml(:,iq)+amx(:); %累加约束杆端力endfprintf(fp2,'\n');fclose(fp1); %关闭输入数据文件fprintf(fp2,'(111)约束杆端力\n');fprintf(fp2,'杆件号j/k端号xm向线约束力ym向线约束力zm向约束弯矩\n');fprintf(fp2,'%3u %6u %14.3e%14.3e%14.3e\n %6u %14.3e%14.3e%14.3e\n',[1:m;jj(1:m);aml( 1:3,1:m);jk(1:m);aml(4:6,1:m)]);fprintf(fp2,'\n');%2.5.计算等效节点荷载,累加到综合节点荷载中for im=1:mRT=PRT(pc(:,jj(im)),pc(:,jk(im)));j=[3*jj(im)-2:3*jj(im) 3*jk(im)-2:3*jk(im)];ac(j(1:6))=ac(j(1:6))-RT'*aml(1:6,im);endfprintf(fp2,'(12)综合节点荷载\n');fprintf(fp2,'节点号x向线力y向线力z向力偶\n');for ja=1:njfprintf(fp2,'%3u %13.3e%13.3e%13.3e\n',ja,ac(3*ja-2:3*ja));endfprintf(fp2,'\n');%2.6.对应非约束位移、约束位移,将综合节点荷载ac重新排列ac(crl(1:3*nj))=ac(1:3*nj);%3.计算非约束位移、支座反力,并构建总节点位移向量[d,r]=St(n,nr,s,ac,crl);fprintf(fp2,'(13)节点位移与支座反力\n');fprintf(fp2,'节点号x向线位移y向线位移z向角位移x向支座反力y向支座反力z向支座反力矩\n');for je=1:njfprintf(fp2,'%3u %13.3e%13.3e%13.3e%13.3e%13.3e%13.3e\n',je,d(3*je-2:3*je),r(3*je-2:3*je)); endfprintf(fp2,'\n');%4.计算最终杆端力for im=1:mRT=PRT(pc(:,jj(im)),pc(:,jk(im)));j=[3*jj(im)-2:3*jj(im),3*jk(im)-2:3*jk(im)];aml(:,im)=aml(:,im)+sm2*RT*d(j(1:6));endfprintf(fp2,'(14)最终杆端力\n');fprintf(fp2,'杆件号j/k端号xm向轴力ym向剪力zm向弯矩\n');fprintf(fp2,'%3u %7u %14.3e%14.3e%14.3e\n %7u %14.3e%14.3e%14.3e\n',[1:m;jj(1:m);aml( 1:3,1:m);jk(1:m);aml(4:6,1:m)]);fclose(fp2); %关闭计算结果数据文件。
2D四杆桁架结构的有限元分析实例学习资料

2D四杆桁架结构的有限元分析实例实例:2D四杆桁架结构的有限元分析学习有限元方法的一个最佳途径,就是在充分掌握基本概念的基础上亲自编写有限元分析程序,这就需要一个良好的编程环境或平台。
MATLAB软件就是这样一个平台,它以功能强大、编程逻辑直观、使用方便见长。
将提供有限元分析中主要单元完整的MATLAB程序,并给出详细的说明。
1D杆单元的有限元分析MATLAB程序(Bar1D2Node)最简单的线性杆单元的程序应该包括单元刚度矩阵、单元组装、单元应力等几个基本计算程序。
下面给出编写的线性杆单元的四个MATLAB函数。
Bar1D2Node _Stiffness(E,A,L)该函数计算单元的刚度矩阵,输入弹性模量E,横截面积A和长度L,输出单元刚度矩阵k(2×2)。
Bar1D2Node _Assembly(KK,k,i,j)该函数进行单元刚度矩阵的组装,输入单元刚度矩阵k,单元的节点编号i、j,输出整体刚度矩阵KK。
Bar1D2Node _Stress(k,u,A)该函数计算单元的应力,输入单元刚度矩阵k、单元的位移列阵u(2×1)以及横截面积A计算单元应力矢量,输出单元应力stress。
Bar1D2Node_Force(k,u)收集于网络,如有侵权请联系管理员删除该函数计算单元节点力矢量,输入单元刚度矩阵k和单元的位移列阵u(2×1),输出2×1的单元节点力矢量forces。
基于1D杆单元的有限元分析的基本公式,写出具体实现以上每个函数的MATLAB程序如下。
%%%%%%%%%%% Bar1D2Node %% begin %%%%%%%%%function k=Bar1D2Node_Stiffness(E, A, L)%该函数计算单元的刚度矩阵%输入弹性模量E,横截面积A和长度L%输出单元刚度矩阵k(2×2)%---------------------------------------k=[E*A/L -E*A/L; -E*A/L E*A/L];%%%%%%%%%%%%%%%%%%%%%%%%%%function z=Bar1D2Node_Assembly(KK,k,i,j)%该函数进行单元刚度矩阵的组装%输入单元刚度矩阵k,单元的节点编号i、j%输出整体刚度矩阵KK%-----------------------------------DOF(1)=i;DOF(2)=j;for n1=1:2for n2=1:2收集于网络,如有侵权请联系管理员删除KK(DOF(n1), DOF(n2))= KK(DOF(n1), DOF(n2))+k(n1, n2);endendz=KK;%------------------------------------------------------------function stress=Bar1D2Node_Stress(k, u, A)%该函数计算单元的应力%输入单元刚度矩阵k, 单元的位移列阵u(2×1)%输入横截面积A计算单元应力矢量%输出单元应力stress%-----------------------------------stress=k*u/A;%-----------------------------------------------------------%%%%%%%%%%%%%%%%%%%%%%%%%function forces=Bar1D2Node_Force(k, u)%该函数计算单元节点力矢量%输入单元刚度矩阵k和单元的位移列阵u(2×1)%输出2×1的单元节点力分量forces%-----------------------------------------forces=k*u;%%%%%%%%%%% Bar1D2Node %% end %%%%%%%%%收集于网络,如有侵权请联系管理员删除【四杆桁架结构的有限元分析—数学推导】如图所示的结构,各杆的弹性模量和横截面积都为E=29.54×10N/mm2,A=100mm 2,试求解该结构的节点位移、单元应力以及支反力。
有限元的matlab编程

本程序的网架位移求解函数附在主程序后面,主程序运行时调用该函数。
完整ppt
14
几何建模 定义荷载
用自定义输入
加下划线的为单元编号
完整ppt
5
形成等效荷载列阵
f=[0;0;0;a;0;0;0;a;0;0;0;a;0;0;0;a;0;0;0;a];%每个节点两个自由度,a 为之前输入的节点力
集成总刚:
获取单元两端节点坐标
xi = Node( Element( ie, 1 ), 1 ) ;%ie为单元号,以下相同 yi = Node( Element( ie, 1 ), 2 ) ; xj = Node( Element( ie, 2 ), 1 ) ; yj = Node( Element( ie, 2 ), 2 ) ;
节点号:',num2str(Element(ie,2)),' 轴力:',num2str(nodef(1))] ) ;
完整ppt
12
end
例二:网架
完整ppt
13
思路分析
几点说明
网架是由多根杆件按照一定的网格形式通过节点连结而成的空间结构。构成 网架的基本单元有三角锥,三棱体,正方体,截头四角锥等。鉴于网架的形 式较多,本程序提供一种通用的网架输入方法,但录入较为繁琐,同时提供 一种正放四角锥网架的简易输入方法作为典型。
有限元编程示例
完整ppt
1
例一:桁架
题目描述:
如下图所示的平面桁架,杆件长度、弹性模量、截 面积以及所受节点力P的大小可以自行定义。求节 点位移及杆件轴力。
桁架结构的有限元分析MATLAB

然后根据各杆的节点号对单刚进行叠加得到总刚
根据位移向量,对总刚划行划列。对1、3节点上的力进行分解,分解成X、Y方向的位移,得到力矩阵, 。由方程 求得未知的节点位移。最后可根据公式 求得各杆的内力如下:
, , ,
,
改变力的大小,重新对桁架进行内力分析,由于杆件尺寸没有变化,所以总刚不变,只需改变力矩阵即可得到结果。
在建筑结构中,桁架结构是一种应用比较普遍的结构形式,在桥梁工程、大型建筑、船舶工程、港口机械等工程领域均有广泛应用。在我国桁架结构发展迅速且应用最为广泛,如屋架、网架结构等。为了增加建筑的表现力,近些年来管桁架结构得到了许多业主的青睐,在大量的屋面结构中采用。
2.目前问题的研究现状
目前在普遍刚桁架的结构设计中,工程中普遍采用的发放时按理想铰接模型进行计算,并很据计算出的杆件界面应力选择合适的杆件型号。计算桁架结构内力时,一般采用如下基本假定:(1)接单均为铰接;(2)杆件轴线平直相交于节点中心;(3)荷载作用线通过桁架的节点。对于平面桁架还要求所有杆件轴线及荷载作用线在同一平面内。
关键词:有限元法、MATLAB、桁架结构、内力分析
一、引言
1.工程背景及重要性
桁架结构(Truss structure)中的桁架指的是桁架梁,是格构化的一种梁式结构。桁架结构常用于大跨度的厂房、展览馆、体育馆和桥梁等公共建筑中。由于大多用于建筑的屋盖结构,桁架通常也被称作屋架。
各杆件受力均以单向拉、压为主,通过对上下弦杆和腹杆的合理布置,可适应结构内部的弯矩和剪力分布。由于水平方向的拉、压内力实现了自身平衡,整个结构不对支座产生水平推力。结构布置灵活,应用范围非常广。桁架梁和实腹梁(即我们一般所见的梁)相比,在抗弯方面,由于将受拉与受压的截面集中布置在上下两端,增大了内力臂,使得以同样的材料用量,实现了更大的抗弯强度。在抗剪方面,通过合理布置腹杆,能够将剪力逐步传递给支座。这样无论是抗弯还是抗剪,桁架结构都能够使材料强度得到充分发挥,从而适用于各种跨度的建筑屋盖结构。更重要的意义还在于,它将横弯作用下的实腹梁内部复杂的应力状态转化为桁架杆件内简单的拉压应力状态,使我们能够直观地了解力的分布和传递,便于结构的变化和组合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The deflection for the 1st element of the beam can be written in terms of the shape functions as,
ݒ = )ݏ(ݒଵܰଵ( )ݏ+ ߠଵܰଶ( )ݏ+ ݒଶܰଷ( )ݏ+ ߠଶܰସ( )ݏെ െ െ െ െ െ െ െ െ (2.1) The deflection for the 2nd element of the beam can be written in terms of the shape functions as,
0
=
0.5
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ
െ(4)
(ݒ0.5) = ݒଵܰଵ(0.5) + ߠଵܰଶ(0.5) + ݒଶܰଷ(0.5) + ߠଶܰସ(0.5) = 0.01ܰଷ(0.5) = 0.0417(3 × 0.5ଶ െ 2 × 0.5ଷ) = 0.021݉
From (3.1),
ߠ(0.5)
ݏ
=
ݔെ ݔଶ (ܮଶ)
=
ݔ
ݒଶ = 0.0417 ݉ ܽ݊݀ ߠଶ = 0 ݀ܽݎ, which are the deflection and slope at the midpoint of the beam, that is at x=1m.
The deflections and slopes at points in between nodes can be interpolated using the shape functions.
Solution:
Element 1
Element 2
(a) Given, (ܮଵ) = (ܮଶ) = = ܮ1݉; = ܫܧ1000ܰ݉; =of length L, the structural stiffness matrix is defined as,
=
1 (ܮଶ)
(ݒଶ
݀ܰଵ ݀ݏ
+
ߠଶ
݀ܰଶ ݀ݏ
+
ݒଷ
݀ܰଷ ݀ݏ
+ ߠଷ ݀݀ܰݏସ)
െ െ െ െ(3.2)
The point x=0.5m is in the 1st element.
From (2.1),
ݏ
=
ݔെ ݔଵ (ܮଵ)
=
0.5 െ 1
ܰଶ((ܮ = )ݏଵ)( ݏെ 2ݏଶ + ݏଷ) െ െ െ െ(ܾ) ܰସ((ܮ = )ݏଵ)(െݏଶ + ݏଷ) െ െ െ െ െ (݀)
݀ ݏ݀ )ݏ(ݒ݀ )ݏ(ݒ1 ݀)ݏ(ݒ ߠ((ܮ = ݔ݀ ݏ݀ = ݔ݀ = )ݏଵ) ݀ݏ
=
1 (ܮଵ)
(ݒଵ
݀ܰଵ ݀ݏ
+
ߠଵ
݀ܰଶ ݀ݏ
+
ݒଶ
݀ܰଷ ݀ݏ
+ ߠଶ ݀݀ܰݏସ)
െെ
െ െ(3.1)
The slope for 2nd element of a beam is,
Deflection and slope at x=0.5m:
݀ ݏ݀ )ݏ(ݒ݀ )ݏ(ݒ1 ݀)ݏ(ݒ ߠ((ܮ = ݔ݀ ݏ݀ = ݔ݀ = )ݏଶ) ݀ݏ
=
1 (ܮଵ)
݀(ݒ0.5) ݀ݏ
=
1 (ܮଵ)
(ݒଵ
݀ܰଵ(0.5) ݀ݏ
+
ߠଵ
݀ܰଶ(0.5) ݀ݏ
+
ݒଶ
݀ܰଷ(0.5) ݀ݏ
+
ߠଶ
݀ܰସ(0.5) ݀ݏ
=
1 (ܮଵ)
(ݒଶ
݀ܰଷ݀(ݏ0.5))
=
1
×
0.0417
×
(6
×
0.5
െ
6
×
0.5ଶ)
×
(െ6
×
0.5
+
6
×
0.5ଶ)
=
െ0.063
݀ܽݎ
(a) Deflection and slopes = ݔ ݐܣ0.5݉ (ݒ0.5) = 0.021݉ ߠ(0.5) = 0.063 ݀ܽݎ
= ݔ ݐܣ1݉ (ݒ1) = 0.0417 ݉
ߠ(1) = 0 ݀ܽݎ
= ݔ ݐܣ1.5݉ (ݒ1.5) = 0.021݉ ߠ(1.5) = −0.063 ݀ܽݎ
=
ܫܧ ሾ(ܮଶ)ሿଷ
൦െ612
4 െ6
െ6 12
െ26൪ = 1000 ൦െ612
4 െ6
െ6 12
െ26൪
6 2 െ6 4
6 2 െ6 4
Assembling the element stiffness matrices above, we obtain the following matrix equation,
12 6 ܮെ12 6ܮ
ሾ݇ሿ
=
ܫܧ ܮଷ
൦െ61ܮ2
4ܮଶ െ6ܮ
െ6ܮ 12
െ2ܮ6ଶܮ൪
6 ܮ2ܮଶ െ6 ܮ4ܮଶ
The element stiffness matrix for element 1 is:
12 6 െ12 6
12 6 െ12 6
桁架单元例子 MATLAB 1
Problem 1: Consider the clamped-clamped beam shown below. Assume there are no axial forces acting on the beam. Use two elements to solve the problem. (a) Determine the deflection and slope at x = 0.5, 1 and 1.5 m; (b) Draw the bending moment and shear force diagrams for the entire beam; (c) What are the support reactions? (d) Use the beam element shape functions to plot the deflected shape of the beam. Use EI = 1,000 Nm, L = 1 m, and F = 1,000 N.
(b) The bending moment and shear force diagrams for the entire beam: The bending moment can be found from,
݀ ܫܧଶݒ ܮ = )ݏ(ܯଶ ቆ݀ݏଶቇ
For the 1st element:
We have to express these moments in terms of x to plot the results. For the first element,
For the second element,
ݏ
=
ݔെ ݔଵ (ܮଵ)
=
ݔ
െ 1
0
;
⇒ ݔ = ݏെ െ െ െ െ െ െ (8)
݀ܰଷ ݀ݏ
+
ߠଷ
݀݀ܰݏସ൰൱
= 1000ሾݒଶ(െ6 + 12)ݏ+ ߠଶ(െ4 + 6(ܮ)ݏଶ) + ݒଷ(6 െ 12)ݏ+ ߠଷ(െ2 + 6(ܮ)ݏଶ)ሿ = 1000ሾ0.0417(െ6 + 12 )ݏ+ 0 + 0 + 0ሿ
= െ250.2 + 500.4 ݉ܰ ݏെ െ െ െ െ െ െ െ െ െ(7)
From (3.2),
ߠ(1.5)
=
1 (ܮଶ)
݀(ݒ0.5) ݀ݏ
=
1 (ܮଶ)
(ݒଶ
݀ܰଵ(0.5) ݀ݏ
+
ߠଶ
݀ܰଶ(0.5) ݀ݏ
+
ݒଷ
݀ܰଷ(0.5) ݀ݏ
+
ߠଷ
݀ܰସ(0.5) ݀ݏ
=
1 ܮ
(ݒଶ
݀ܰଵ݀(ݏ0.5))
=
1
×
0.0417
ۏ0 0 6 2 െ6 4 ۏ ے0 ܥ ۏ ےଷ ے
Striking out the rows and columns of zero elements, (1) reduces to,
1000 ቂ204 80ቃ ቂߠݒଶଶቃ = ቂ10000ቃ
Solving the above set of equations we get,
(ܯଵ)()ݏ
=
ܫܧ ሾ(ܮଵ)ሿଶ
݀ଶݒ ݀ݏଶ
=
1000
݀ ൭݀ݏ
൬ݒଵ
݀ܰଵ ݀ݏ
+
ߠଵ
݀ܰଶ ݀ݏ
+
ݒଶ
݀ܰଷ ݀ݏ
+
ߠଶ
݀݀ܰݏସ൰൱
