2016基本平面刚架各种荷载MATLAB程序
第2章++MATLAB2016程序设计基础

2.1 MATLAB的程序界面
2.1.4当前文件夹窗口
当前文件夹(Current Folder)窗口显示了MATLAB在对文件 操作(保存、打开等)时默认的工作目录,显示的文件信 息包括文件名称、文件类型、修改日期、内容描述等。 该窗口相当于是一个资源管理器。在当前文件夹窗口中的 某一文件上单击鼠标右键,会弹出上下文菜单,可通过此 菜单实现对文件的打开、运行、重命名、复制、删除等操 作
7
2.1 MATLAB的程序界面
键
↑ ↓ ← → Ctrl+← Ctrl+ → Home
功能
重调前一行 重调下一行 左移一个字符 右移一个字符 左移一个字 右移一个字 移动到行首
8
键
End ESC Backspace PageUp PageDown Ctrl+Home Ctrl+End
功能
移动到行尾 清除一行 删除光标左侧一个字符 向前翻页 向后翻页 光标移到命令窗口首 光标移到命令窗口尾
10
2.1 MATLAB的程序界面
2.1.2 工作区窗口
工作区窗口是MATLAB的变量管理中心,每次启动 MATLAB,都会自动建立一个工作区,运行MATLAB 的程序或命令时产生的变量被加入到工作区中,除 非用特殊的命令删除某变量,否则该变量在关闭 MATLAB之前一直保存在工作区,工作区在MATLAB 运行期间一直存在,关闭MATLAB后,工作区才会自 动消除。
27
2.4 数据与数据类型
例2-3创建变量并赋值为数组。
在命令行窗口依次输入下面命令:
>>x=[1 2 3 4 5 6 7 8 9] >> y=[1,2,3;4,5,6;7,8,9] 注2: 在赋值过程中,如果变量已存在,MATLAB将使用 新值代替旧值,并以新的变量类型代替旧的变量类型。
MATLAB2016基础实例教程 第1章 MATLAB入门

1.1.4 MATLAB系统
MATLAB系统主要包括以下5个部分 桌面 数学函数库工具和开发环境 语言 图形处理 外部接口
1.2 MATLAB 2016的用户界面
MATLAB 2016的工作界面主要由标题栏、菜单栏、 工具栏、当前工作目录窗口、命令窗口、工作空 间管理窗口和历史命令窗口等组成。
1.2.5 历史窗口
选择“命令历史记录”→“停靠”命令,在显示界 面上固定显示命令历史窗口,如图所示。
在历史窗口中双击某一命令,命令窗口中将执行该 命令。
1.2.6 当前目录窗口
当前目录窗口显示如图所示,可显示或改变当前目 录,查看当前目录下的文件,单击 按钮可以在当 前目录或子目录下搜索文件。
(3)缺少步骤,未定义变量
(4)正确格式
1.3.2 功能符号
除了命令输入必须的符号外,MATLAB为了解决命 令输入过于繁琐、复杂的问题,采取了分号、续行 符及插入变量等方法。
1.分号 一般情况下,在MATLAB中命令窗口中输入命令,
则系统随机根据指令给出计算结果。若不想让 MATLAB每次都显示运算结果,只需在运算式最后加 上分号(;)。 2.续行号
1.1.3 MATLAB的特点
MATLAB的一个重要特色是它具有一系列称为工 具 箱 ( Toolbox ) 的 特 殊 应 用 子 程 序 。 工 具 箱 是 MATLAB函数的子程序库,可以分为功能性工具 箱和学科性工具箱。
所有MATLAB核心文件和各种工具箱文件都是可 读可修改的源文件,用户可通过对源程序进行修 改或加入自己编写的程序来构造新的专用工具箱。
1.2.2 功能区
MATLAB 2016将所有的功能命令分类别放置在三 个选项卡中,下面分别介绍这3个选项卡。 “主页”选项卡:单击标题栏下方的“主页” 选项卡,显示基本的“新建脚本”“新建变量” 等命令。
实验一 Matlab基本操作(2016)

实验一 MATLAB 基本操作一、实验目的1. 学习和掌握MA TLAB 的基本操作方法2. 掌握命令窗口的使用3. 熟悉MATLAB 的数据表示、基本运算二、实验内容和要求1. 实验内容1) 练习MATLAB7.0或以上版本2) 练习矩阵运算与数组运算2. 实验要求1) 每位学生独立完成,交实验报告2) 禁止玩游戏!三、实验主要软件平台装有MATLAB7.0或以上的PC 机一台四、实验方法、步骤及结果测试1. 实验方法:上机练习。
2. 实验步骤:1) 开启PC ,进入MA TLAB 。
2) 使用帮助命令,查找sqrt 函数的使用方法答: help sqrt3) 矩阵、数组运算a) 已知 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=963852741B ,求)2()(A B B A -⋅+ 答: A=[1, 2, 3; 4, 5, 6; 7, 8, 9]; B=[1, 4, 7; 2, 5, 8; 3, 6, 9]; (A+B)*(2*B-A)b) 已知⎥⎦⎤⎢⎣⎡-=33.1x ,⎥⎦⎤⎢⎣⎡=π24y ,求T xy ,y x T c) 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=300020001B ,求A/B, A\B. d) 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A ,求:(1) A 中第三列前两个元素;(2) A 中所有第二行元素;(3) A 中四个角上的元素;(4) 交换A 的第1、3列。
(5) 交换A 的第1、2行。
(6) 删除A 的第3列。
e) 已知[]321=x ,[]654=y ,求:y x *.,y x /.,y x \.,y x .^,2.^x ,x .^2。
f) 给出x=1,2,…,7时,xx sin 的值。
3)常用的数学函数a )随机产生一个3x3的矩阵A ,求:(1) A 每一行的最大、最小值,以及最大、最小值所在的列;(2) A 每一列的最大、最小值,以及最大、最小值所在的行;(3) 整个矩阵的最大、最小值;(4) 每行元素之和;(5) 每列元素之和;(6) 每行元素之积;(7) 每列元素之积。
平面刚架电算程序说明(供阅读、熟悉程序、编程使用)

平面刚架电算程序说明一.本程序适用范围1.结构形式:刚架可具有任意几何形状,刚架结点全部为刚性结点,各杆为等截面杆。
2.支承方式:支座形式可以是固定端、铰支座、沿垂直或水平方向的棍轴支座。
3.荷载类型:荷载包括结点荷载和非结点荷载。
结点荷载包括三种:水平集中力、垂直集中力、集中力偶。
非结点荷载包括三种情况:部分均布荷载、垂直集中荷载和平行集中荷载。
二.数据符号说明1.输入基本参数:ne——单元数nj——结点数nz——支承数,为支承对应的位移分量总个数npj——结点荷载数npf——非结点荷载数e0——弹性模量nj3——位移分量总个数 nj3=nj×32.输入其它数据jm(1 to ne,1 to 2)——杆端结点码数组。
由全部NE个单元的两个端点的结点码组成。
Jm(e,1)——表示第E号单元的始端结点码Jm(e,2)——表示第E号单元的末端结点码l(1 to ne)——杆长数组an(1 to ne)——杆角数组h(1 to ne)——杆件截面高度数组b(1 to ne)——杆件截面宽度数组mj(1 to ne)——杆件截面面积数组i(1 to ne)——截面惯性距数组zc(1 to nz)——支承数组。
由全部NZ个支承对应的位移分量的编码组成。
ZC(I)——表示第I号支承对应的位移分量的编码pj(0 to npj,1 to 2)——由全部NPJ个结点荷载的数值及对应位移分量的编码组成。
当NPJ=0时,可将PJ(0,1)与PJ(0,2)设为0。
当NPJ>0时,PJ(I,1)——第I号结点荷载的数值PJ(I,2)——第I号结点荷载对应的位移分量编码pf(0 to npf,1 to 4) ——由全部NPF个非结点荷载的四种数据组成(荷载数值、位置参数、作用杆码、荷载类型码)。
当NPF=0时,可将第0行的四个元素设为0。
当NPF>0时,PF(I,1)——第I号非结点荷载的数值PF(I,2)——第I号非结点荷载的位置参数。
刚架矩阵位移法matlab计算程序

clc;%输入基本信息jd=input('请输入节点数量');free=input('请输入自由度');gj=input('请输入杆件数量');P=zeros(free,1);P=input('请输入外荷载矩阵([x;y;z])');d=zeros(free,1);member=zeros(1,6,gj);K=zeros(6,6,gj);k=zeros(6,6,gj)for i=1:1:gjangle(i)=input(sprintf('请输入第%d杆件角度(角度制)',i));E(i)=input(sprintf('请输入第%d杆件弹性模量(N/mm2)',i));A(i)=input(sprintf('请输入第%d杆件截面面积(mm2)',i));L(i)=input(sprintf('请输入第%d杆件长度(mm)',i));member(:,:,i)=input(sprintf('请输入第%d杆件定位向量([1 2 3 4 5 6])',i)); end%计算局部坐标系下单元刚度矩阵kfor i=1:1:gjk=(:,:,i)=E(i)*I(i)/L(i)^3*[A(i)*L(i)^2/I(i) 0 0 -A(i)*L(i)^2/I(i) 0 0;0 12 6*L(i) 0 -12 6*L(i);0 6*L(i) 4*L(i)^2 0 -6*L(i) 2*L(i)^2;-A(i)*L(i)^2/I(i) 0 0 A(i)*L(i)^2/I(i) 0 0;0 -12 -6*L(i) 0 12 -6*L(i);0 6*L(i) 2*L(i)^2 0 -6*L(i) 4*L(i)^2 ];end%计算各杆件转换矩阵TT=zeros(6,6,gj);for i=1:1:gjT=(:,:,i)=[cosd(angle(i)) sind(angle(i)) 0 0 0 0;-sind(angle(i)) cosd(angle(i)) 0 0 0 0;0 0 1 0 0 0;0 0 0 cosd(angle(i)) sind(angle(i)) 0;0 0 0 -sind(angle(i)) cosd(angle(i)) 0;0 0 0 0 0 1];end%计算整体坐标系下单元刚度矩阵KK(:,:,i)=T(:,:,i)'*k(:,:,i)*T(:,:,i);end%形成SSs=zeros(free);S=zeros(free);for i=1:1:gjfor n=1:1:6for j=1:1:6if (member(1,n,i)<=free && member(1,j,i)<=free)Ss(member(1,n,i),member(1,j,i))=K(n,j,i);endendendS=S+Ss ;Ss=zeros(free);end%计算杆间荷载作用PfFf=[FAbcosd-FSbsind;FAbsind+FSbcosd;FMb;FAecosd-FSbsind;FAesind+FSecosd;FMe]for i=1:1:gjgjl=input('请输入杆间力数量');ppp=zeros(1,4,gjl);for j=1:1:gjlppp(:,:,i)=input(sprintf('请输入第%d杆件l1,l2,W,a ([1 2 3 4])',i));l1=ppp(1,1,i);l2=ppp(1,2,i);W=ppp(1,3,i);a=ppp(1,3,i);if a==0,l1+l2==L(i)pd=1else if a==0,l1+l2<L(i)pd=2else if a>0,l1+l2==L(i)pd=3elsepf=4endendendswitch pdcase 1Qf(:,:,gjl)=[0;W*l2^2*(3*l1+l2);W*l1*l2^2;0;W*l1^2*(l1+3*l2);-W*l1^2*l2/L(i)^2]case 2Qf(:,:,gjl)=[W*cosd(a);W*sind(a)*l2^2*(3*l1+l2);W*sind(a)*l1*l2^2;W*cosd(a);W*sin(a)*l1^2*(l1+3*l2);-W*l1^2*l2/L(i)^2]case 3Qf(:,:,gjl)=[0;W*L(i)/2*(1-l1/L(i)^4*(2*L(i)^3-2*l1^2*L(i)+l1^3)-l2^3/L(i)^4*(2*L(i)-l2));W*L(i)^2/12*(1-l1^2/L(i)^4*(6*L(i)^2-8*l1*L(i)+3*l1^2)-l2^3/L(i)^4*(4*L(i)-3*l2));W*L(i)/2*(1-l1^3/L(i)^4*(2*L(i)-l1)-l2/L(i)^4*(2*L(i)^3-2*l2^2+l2^3));0;-W*L(i)^2/12*(1-l1^3/L(i)^4*(4*L(i)-3*l1)-l2^2/L(i)^4*(6*L(i)^2-8*l2*L(i)+3*l2^2))]case 4Qf(:,:,gjl)=[W*cosd(a)*(L(i)-l1-l2);W*sind(a)*L(i)/2*(1-l1/L(i)^4*(2*L(i)^3-2*l1^2*L(i)+l1^3)-l2^3/L(i)^4*(2*L(i)-l2));W*sind(a)*L(i)^2/12*(1-l1^2/L(i)^4*(6*L(i)^2-8*l1*L(i)+3*l1^2)-l2^3/L(i)^4*(4*L(i)-3*l2));W*sind(a)*L(i)/2*(1-l1^3/L(i)^4*(2*L(i)-l1)-l2/L(i)^4*(2*L(i)^3-2*l2^2+l2^3));W*sind(a)*cosd(a)*(L(i)-l1-l2);-W*sind(a)*L(i)^2/12*(1-l1^3/L(i)^4*(4*L(i)-3*l1)-l2^2/L(i)^4*(6*L(i)^2-8*l2*L(i)+3*l2^2)) ]endendFf(:,:,i)=T(:,:,i)'*Qf(:,:,i);endPf=zeros(free,1);for i=1:1:gjpfp=zeros(free,1);for j=1:1:6if member(1,j,i)<=freePfp(member(1,j,i),1)=Pf(j,1,i);endendPf=Pf+Pfp;end%P-Pf=S*dd=S\(P-Pf);%计算位移和内力v=zeros(6,1,gj);u=zeros(6,1,gj)Q=zeros(6,1,gj);F=zeros(6,1,gj);for i=1:1:gjc=1;for j=1:1:6if(member(1,j,i)<free+1)v(j,1,i)=d(c,1);c=c+1;endendendfor i=1:1:gju(:,:,i)=T(:,:,i)*v(:,:,i);endfor i=1:1:gjQ(:,:,i)=k(:,:,i)*u(:,:,i)endfor i=1:1:gjF(:,:,i)=T(:,:,i)'*Q(:,:,i);endzfl=jd*2;r=zeros(zfl,1);for i=1:1:gjfor j=1:1:4r(member(1,j,i),1)=F(j,1,i);endend%计算支座反力zfl=zfl-free;R=r(free+1:end)。
matlab连续梁程序的编制与使用
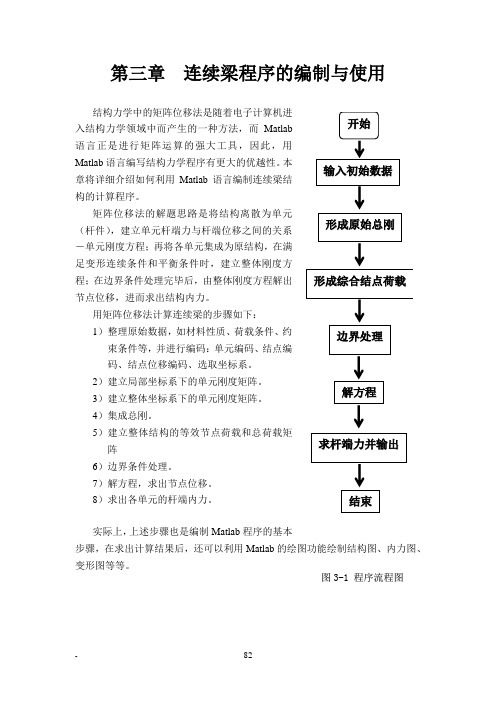
第三章连续梁程序的编制与使用入结构力学领域中而产生的一种方法,而Matlab语言正是进行矩阵运算的强大工具,因此,用Matlab语言编写结构力学程序有更大的优越性。
本章将详细介绍如何利用Matlab语言编制连续梁结构的计算程序。
矩阵位移法的解题思路是将结构离散为单元(杆件),建立单元杆端力与杆端位移之间的关系-单元刚度方程;再将各单元集成为原结构,在满足变形连续条件和平衡条件时,建立整体刚度方程;在边界条件处理完毕后,由整体刚度方程解出节点位移,进而求出结构内力。
用矩阵位移法计算连续梁的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,并进行编码:单元编码、结点编码、结点位移编码、选取坐标系。
2)建立局部坐标系下的单元刚度矩阵。
3)建立整体坐标系下的单元刚度矩阵。
4)集成总刚。
5)建立整体结构的等效节点荷载和总荷载矩阵6)边界条件处理。
7)解方程,求出节点位移。
8)求出各单元的杆端内力。
实际上,上述步骤也是编制Matlab程序的基本步骤,在求出计算结果后,还可以利用Matlab的绘图功能绘制结构图、内力图、变形图等等。
图3-1程序流程图3.1 程序说明%******************************************************************* % 矩阵位移法解连续梁主程序%******************************************************************* ●功能:运用矩阵位移法解连续梁的基本原理编制的计算主程序。
●基本思想:结点(结点位移)编码默认为从左至右,从1开始顺序进行;杆端弯矩的方向默认为逆时针。
●荷载类型:可计算结点荷载,每单元作用的跨中集中力和均布荷载。
●说明:主程序的作用是通过赋值语句、读取和写入文件、函数调用等完成算法的全过程,即实现程序流程图的程序表达。
%----------------------------------------------------------------------------------------------------- 1 程序准备format short e %设定输出类型clear all %清除所有已定义变量clc %清屏●说明:format short e -设定计算过程中显示在屏幕上的数字类型为短格式、科学计数法;clear all -清除所有已定义变量,目的是在本程序的运行过程中,不会发生变量名相同等可能使计算出错的情况;clc -清屏,使屏幕在本程序运行开始时%----------------------------------------------------------------------------------------------------- 2 打开文件FP1=fopen('input.txt','rt'); %打开输入数据文件存放初始数据FP2=fopen('output.txt','wt'); %打开输出数据文件存放计算结果●说明:FP1=fopen('input.txt','rt'); -打开已存在的输入数据文件input.txt,且设置其为只读格式,使程序在执行过程中不能改变输入文件中的数值,并用文件句柄FP1来FP2=fopen('output.txt','wt'); -打开输出数据文件,该文件不存在时,通过此命令创建新文件,该文件存在时则将原有内容全部删除。
平面杆件结构计算 matlab

⎡µ1⎤ ⎡0⎤
∆1
=
⎢⎢υ1
⎥ ⎥
=
⎢⎢0⎥⎥
⎢⎣θ1 ⎥⎦ ⎢⎣0⎥⎦
⎡µ10 ⎤ ⎡0⎤
∆10
=
⎢⎢υ1
0
⎥ ⎥
=
⎢⎢0⎥⎥
⎢⎣θ10 ⎥⎦ ⎢⎣0⎥⎦
-4-
修改刚度方程有划行划列法和乘大数法,划行划列法是在原始刚度矩阵中删
去 0 位移对应的行和列,即分别划去 1 号和 10 号结点各自对应的三行和三列,
②形成局部坐标系中的单元刚度矩阵 k (e ) 和整体坐标系中的单元刚度矩阵 k (e ): 对于单元(1):
⎡ 1.260
0
0 -1.2600
0
0⎤
⎢ ⎢
0 0.1008 0.1008
0
- 0.1008
0.1008
⎥ ⎥
k
(1
)
=
1×
109
⎢0 ⎢⎢-1.260
0.1008 0
0.1344 0
0 - 0.1008 0.0672 ⎥
i=EN(ND(id,1),1);
j=EN(ND(id,1),2);
F(((i-1)*3+1):((i-1)*3+3))=F(((i-1)*3+1):((i-1)*3+3))+EF(1:3); %等效结点力集成
F(((j-1)*3+1):((j-1)*3+3))=F(((j-1)*3+1):((j-1)*3+3))+EF(4:6); %等效结点力集成
=
(e )
kT
(e )∆(e )
−
F
(e )
E
对于单元(1)
MATLAB基本操作及环境设置

MATLAB基本操作及环境设置1.MATLAB的基本操作:-启动MATLAB:在计算机上安装MATLAB软件后,可以从开始菜单中或桌面图标启动MATLAB。
-MATLAB命令窗口:启动MATLAB后,可以看到一个命令窗口。
在命令窗口中,可以输入MATLAB命令,并执行它们。
- 基本算术操作:MATLAB可以进行基本的算术操作,如加减乘除。
例如,输入"2+3",然后按Enter键,MATLAB将计算并显示结果。
- 变量:在MATLAB中,可以定义变量,并将值赋给它们。
例如,输入"x = 5",然后按Enter键,MATLAB将创建变量x,并将值设为5 - 矩阵操作:MATLAB是以矩阵为基础的语言。
可以使用MATLAB的矩阵操作函数创建、修改和操作矩阵。
例如,可以使用"zeros"函数创建由0组成的矩阵,使用"eye"函数创建单位矩阵,以及使用"inv"函数计算矩阵的逆矩阵。
2.MATLAB的环境设置:- 工作目录:工作目录是MATLAB文件的位置。
可以使用"cd"命令更改工作目录。
可以使用"pwd"命令查看当前工作目录。
- 文件管理:MATLAB提供了一些函数来管理和操作文件。
可以使用"dir"函数列出当前目录中的文件和文件夹,使用"mkdir"函数创建新文件夹,使用"delete"函数删除文件等。
-图形界面:MATLAB还提供了一个图形用户界面(GUI),可以通过点击菜单和按钮来执行操作。
GUI提供了更直观和交互式的方式来使用MATLAB。
- 图形绘制:MATLAB具有强大的图形绘制功能。
可以使用"plot"函数绘制二维曲线,使用"mesh"函数绘制三维曲面等。
matlab有限元编程荷载

matlab有限元编程荷载-概述说明以及解释1.引言1.1 概述概述部分的内容可以包括以下内容:有限元方法是一种广泛应用于工程领域的数值计算方法,它通过将复杂的连续体结构分割为一系列简单的子结构,然后利用数学方法为每个子结构建立相应的数学模型,从而得到整个结构的行为特性。
这种分割的过程通常被称为网格划分,而每个子结构则称为有限元。
MATLAB作为一种功能强大的数学软件工具,被广泛应用于有限元方法的编程与分析。
MATLAB提供了大量的工具箱和函数,可以方便地实现有限元方法的各个步骤,包括网格划分、单元构造、边界条件的施加以及结果的可视化分析等。
本文将重点介绍MATLAB在有限元编程中的应用,特别是在荷载分析方面的应用。
荷载分析是有限元分析的核心内容之一,它通过施加不同的荷载条件,分析结构在荷载作用下的变形、位移和应力等。
荷载分析的准确性对于工程设计以及结构安全性的评估至关重要。
文章将首先介绍有限元方法的基本原理,包括对结构的离散化、单元的建立和组装,以及求解过程中的矩阵运算等。
然后,针对荷载分析的特点,将详细介绍MATLAB有限元编程中的荷载处理方法,包括荷载的施加、荷载类型的选择以及荷载与结构响应的耦合关系等。
通过本文的学习,读者可以了解到MATLAB在有限元编程中的应用,并且掌握荷载分析的基本原理和方法。
同时,也可以对MATLAB有限元编程在实际工程问题中的应用进行进一步的探索和研究。
总而言之,本文将为读者提供一个全面而系统的MATLAB有限元编程荷载分析的引导,帮助读者理解有限元方法的基本原理和应用,提高工程设计和结构安全性评估的能力。
1.2 文章结构本文旨在介绍MATLAB在有限元编程中的应用,重点讲解荷载分析的基本原理以及MATLAB有限元编程中的荷载处理方法。
该文章分为引言、正文和结论三个部分。
引言部分对文章进行了概述,包括本文的目的和总结。
在概述中,我们会介绍有限元方法的简要背景和意义,以及MATLAB在该领域中的重要性。
《MATLAB仿真技术》实验指导书2016附问题详解

实验项目及学时安排实验一 MATLAB环境的熟悉与基本运算 2学时实验二 MATLAB数值计算实验 2学时实验三 MATLAB数组应用实验 2学时实验四 MATLAB符号计算实验 2学时实验五 MATLAB的图形绘制实验 2学时实验六 MATLAB的程序设计实验 2学时实验七 MATLAB工具箱Simulink的应用实验 2学时实验八 MATLAB图形用户接口GUI的应用实验 2学时实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、 exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
MATLAB 2016基础实例教程 第1章 MATLAB入门

《MATLAB 2016 基础实例教程》
1.2.4 命令窗口
2.基本操作 在命令窗口的右上角,用户可以单击相应的按钮进行最大化、还原
或关闭窗口。单击右上角的 按钮,出现一个下拉菜单,如图所示。在 该下拉菜单中,单击“ ”按钮,可将命令窗口最小化到主窗口左侧,以 页签形式存在,当鼠标指针移到上面时,显示窗口内容。此时单击 下拉 菜单中的 按钮,即可恢复显示。
1983-2006年间相继发布了多个版本的MATLAB。 2016年3月,MathWorks正式发布了R2016a版MATLAB和Simulink
产品系列的Release 2016(R2016)版本。
《MATLAB 2016 基础实例教程》
1.1.2 MATLAB的应用
其典型的应用主要包括如下8个方面 数值分析和计算 算法开发 数据采集 系统建模、仿真和原型化 数据分析、探索和可视化 工程和科学绘图 数字图像处理 应用软件开发,包括图形用户界面的建立
《MATLAB 2016 基础实例教程》
1.1.1 MATLAB的发展历程
20 世 纪 70 年 代 中 期 , Cleve Moler 博 士 及 其 同 事 开 发 了 调 用 EISPACK和LINPACK的FORTRAN子程序库。
70 年 代 后 期 ,Cleve Moler 教 授 设 计 了 一 组 调 用 LINPACK 和 EISPACK库程序的“通俗易用”的接口,此即用FORTRAN编写的 萌芽状态的MATLAB。
《MATLAB 2016 基础实例教程》
1.2.2 功能区
MATLAB 2016将所有的功能命令分类别放置在三个选项卡中,下面 分别介绍这3个选项卡。 “主页”选项卡:单击标题栏下方的“主页”选项卡,显示基本 的“新建脚本”“新建变量”等命令。
MATLAB 2016基础实例教程 第5章 程序设计基础

《MATLAB 2016 基础实例教程》
5.2.5 程序的信息诊断
在MATLAB编程中,使用break命令、pause命令、continue命令、 return命令、echo命令、error命令与warning命令等可以实现程序 流程控制命令。
1.break命令 该命令一般用来终止for或while循环,通常与if条件语句在一起用,
该命令用来显示错误信息,同时返回键盘控制。
5.2.6
《MATLAB 2016 基础实例教程》
操作实例
例1:计算平方根函数。 例2:编写一个求两矩阵之和的程序。 例3:编写一个求 的函数。
《MATLAB 2016 基础实例教程》
5.2.7 程序调试
最常用的调试方式有两种:一种是根据程序运行时系统给出的错误 信息或警告信息进行相应的修改;另一种是通过用户设置断点来对 程序进行调试。
《MATLAB 2016 基础实例教程》
第5章 程序设计基础
MATLAB提供特有的函数功能可以解决许多复杂的科学计算,工 程设计问题,但在很多情况下利用函数无法解决复杂问题,或者解 决方法过于繁琐,因此需要编写专门的程序。本节以M文件为基础, 详细介绍程序的基本编写流程。
《MATLAB 2016 基础实例教程》
《MATLAB 2016 基础实例教程》
5.2.7 程序调试
2.清除断点 与设置断点一样,清除断点同样有三种实现方法:最简单的就是
将光标放在断点所在行,然后按F12便可清除断点;第二种方法同样 是利用“Debug”菜单下拉菜单中的“Set/Clear Breakpoint”选项;第 三种方法是利用dbclear命令来清除断点。 3.列出全部断点
函数的加载方式只有当函数类型为overloaded时才存在。
matlab刚架计算编程
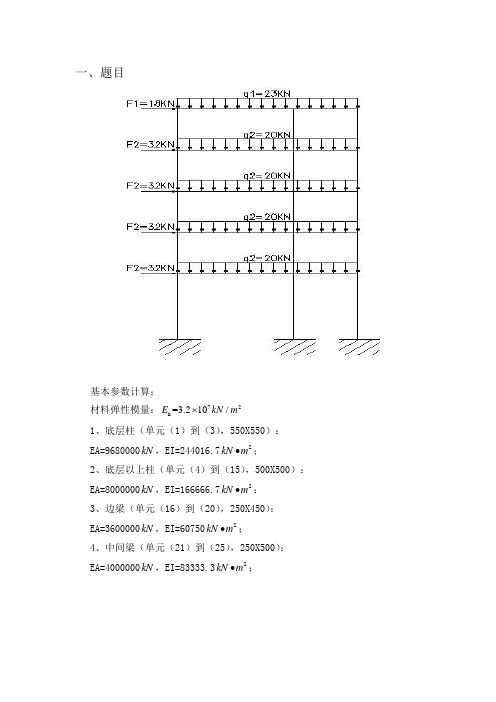
一、题目基本参数计算:材料弹性模量:72h =3.210/E kN m ⨯1、底层柱(单元(1)到(3),550X550): EA=9680000kN ,EI=244016.72kN m ∙;2、底层以上柱(单元(4)到(15),500X500): EA=8000000kN ,EI=166666.72kN m ∙;3、边梁(单元(16)到(20),250X450): EA=3600000kN ,EI=607502kN m ∙;4、中间梁(单元(21)到(25),250X500): EA=4000000kN ,EI=83333.32kN m ∙;节点编号及单元编号二、计算结果对比1.竖向均布荷载作用下的杆端内力计算输入底层柱高h1:4.8输入二至五层柱高h2:3输入左梁跨度L1:4.8输入右梁跨度L2:2.7输入底层柱子的抗弯刚度EIc1:244016.7输入二至五层柱子的抗弯刚度EIc2:166666.7输入底层柱子的抗压刚度EAc1:9680000输入二至五层柱子的抗压刚度EAc2:8000000输入左梁的抗弯刚度EIb1:60750输入右梁的抗弯刚度EIb2:83333.3输入左梁的抗压刚度EAb1:3600000输入右梁的抗压刚度EAb2:4000000输入顶层竖向均布荷载集度q1:23输入一至四层均布荷载集度q2:20输入顶层水平集中力F1:0输入一至四水平集中力F2:0Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 3.812489e-019.> In gangjia at 125第1节点的位移是-0.000312 0.000320 0.000158第2节点的位移是-0.000255 0.000299 0.000004第3节点的位移是-0.000139 0.000260 0.000032第4节点的位移是-0.000058 0.000201 0.000036第5节点的位移是-0.000024 0.000125 0.000066第6节点的位移是-0.000000 0.000000 0.000000第7节点的位移是-0.000341 0.000471 -0.000125第8节点的位移是-0.000243 0.000438 -0.000063第9节点的位移是-0.000140 0.000380 -0.000072第10节点的位移是-0.000059 0.000296 -0.000057第11节点的位移是-0.000012 0.000185 -0.000054第12节点的位移是0.000000 0.000000 -0.000000第13节点的位移是-0.000347 0.000189 -0.000090第14节点的位移是-0.000241 0.000177 -0.000058第15节点的位移是-0.000140 0.000154 -0.000057第16节点的位移是-0.000058 0.000119 -0.000045第17节点的位移是-0.000010 0.000073 -0.000032第18节点的位移是0.000000 0.000000 -0.000000第1单元节点内力是55.676623 22.120376 41.726078 -55.676623 -22.120376 24.635050第2单元节点内力是105.531000 12.618842 17.368689 -105.531000 -12.618842 20.487837第3单元节点内力是154.956696 13.495898 20.022904 -154.956696 -13.495898 20.464789第4单元节点内力是203.914370 13.818765 19.057567 -203.914370 -13.818765 22.398728第5单元节点内力是86.165797 -13.600544 -23.843462 -86.165797 13.600544 -16.958168第6单元节点内力是154.343865 -7.348932 -10.545483 -154.343865 7.348932 -11.501313第7单元节点内力是225.186314 -8.283039 -13.237518 -225.186314 8.283039 -11.611598第8单元节点内力是297.205484 -8.885450 -13.512019 -297.205484 8.885450 -13.144331第9单元节点内力是30.657580 -8.519833 -14.535293 -30.657580 8.519833 -11.024205第10单元节点内力是62.625136 -5.269910 -7.987274 -62.625136 5.269910 -7.822456 第11单元节点内力是92.356990 -5.212859 -8.482119 -92.356990 5.212859 -7.156458 第12单元节点内力是121.380147 -4.933315 -8.107970 -121.380147 4.933315 -6.691976第13单元节点内力是252.113359 4.837824 14.964088 -252.113359 -4.837824 8.257469第14单元节点内力是372.232119 -3.084712 -10.134383 -372.232119 3.084712-4.672235第15单元节点内力是148.154523 -1.753112 -5.827793 -148.154523 1.753112 -2.587145第16单元节点内力是22.120376 -55.676623 -41.726078 -22.120376 -54.723377 39.438288第17单元节点内力是-9.501534 -49.854377 -42.003740 9.501534 -46.145623 33.102731第18单元节点内力是0.877056 -49.425696 -40.510741 -0.877056 -46.574304 33.667399第19单元节点内力是0.322867 -48.957674 -39.522356 -0.322867 -47.042326 34.925521第20单元节点内力是-8.980941 -48.198989 -37.362816 8.980941 -47.801011 36.407668第21单元节点内力是8.519833 -31.442420 -15.594826 -8.519833 -30.657580 14.535293第22单元节点内力是-3.249922 -22.032445 -5.599080 3.249922 -31.967555 19.011480 第23单元节点内力是-0.057051 -24.268146 -8.928568 0.057051 -29.731854 16.304575第24单元节点内力是-0.279544 -24.976843 -9.801904 0.279544 -29.023157 15.264428第25单元节点内力是-3.180203 -27.225624 -13.128954 3.180203 -26.774376 12.519769Matlab计算弯矩图力矩分配法计算弯矩图8.87最终8.8715.1020.7518.2218.2518.2418.2415.3521.8538.2138.2166.2444.1837.2057.6039.0036.4838.7436.4738.7557.6057.6035.8557.6038.474.821.794.253.813.138.5118.2318.4118.2318.2318.2320.9610.48 3.807.617.3817.7811.5510.4910.4812.2825.535.695.6919.2517.197.749.53 3.604.1417.787.623.813.8110.48结构力学求解器计算弯矩图2.水平荷载作用下的杆端内力计算输入底层柱高h1:4.8输入二至五层柱高h2:3输入左梁跨度L1:4.8输入右梁跨度L2:2.7输入底层柱子的抗弯刚度EIc1:244016.7输入二至五层柱子的抗弯刚度EIc2:166666.7输入底层柱子的抗压刚度EAc1:9680000输入二至五层柱子的抗压刚度EAc2:8000000输入左梁的抗弯刚度EIb1:60750输入右梁的抗弯刚度EIb2:83333.3输入左梁的抗压刚度EAb1:3600000输入右梁的抗压刚度EAb2:4000000输入顶层竖向均布荷载集度q1:0输入一至四层均布荷载集度q2:0输入顶层水平集中力F1:18输入一至四水平集中力F2:32Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 3.812489e-019.> In gangjia at 125第1节点的位移是0.010766 -0.000078 0.000176第2节点的位移是0.009966 -0.000076 0.000321第3节点的位移是0.008565 -0.000070 0.000521第4节点的位移是0.006503 -0.000058 0.000714第5节点的位移是0.003785 -0.000039 0.000935第6节点的位移是-0.000000 -0.000000 0.000000第7节点的位移是0.010747 -0.000138 0.000165第8节点的位移是0.009932 -0.000137 0.000284第9节点的位移是0.008530 -0.000132 0.000432第10节点的位移是0.006464 -0.000115 0.000589第11节点的位移是0.003772 -0.000079 0.000689第12节点的位移是0.000000 -0.000000 0.000000第13节点的位移是0.010745 0.000216 0.000205第14节点的位移是0.009924 0.000213 0.000312第15节点的位移是0.008522 0.000202 0.000483第16节点的位移是0.006456 0.000173 0.000651第17节点的位移是0.003765 0.000118 0.000796第18节点的位移是-0.000000 0.000000 0.000000第1单元节点内力是-5.788617 -4.001579 -14.039455 5.788617 4.001579 2.034718第2单元节点内力是-15.767839 -10.233070 -26.449395 15.767839 10.233070 -4.249815第3单元节点内力是-31.245046 -15.512425 -34.021177 31.245046 15.512425-12.516099第4单元节点内力是-52.244156 -18.146548 -39.461868 52.244156 18.146548 -14.977776第5单元节点内力是-1.562581 -10.530910 -22.438577 1.562581 10.530910 -9.154153 第6单元节点内力是-14.655617 -24.288069 -44.629714 14.655617 24.288069 -28.234493第7单元节点内力是-44.997366 -39.528302 -68.050342 44.997366 39.528302 -50.534563第8单元节点内力是-94.445810 -57.286585 -91.484591 94.445810 57.286585 -80.375163第9单元节点内力是7.351198 -3.467511 -11.155563 -7.351198 3.467511 0.753031第10单元节点内力是30.423456 -15.478861 -32.749852 -30.423456 15.478861 -13.686732第11单元节点内力是76.242412 -26.959273 -49.759213 -76.242412 26.959273 -31.118606第12单元节点内力是146.689967 -38.566867 -65.888400 -146.689967 38.566867 -49.812202第13单元节点内力是-78.206852 -40.813457 -50.436253 78.206852 40.813457 -145.468339第14单元节点内力是-160.306021 -56.066694 -99.510204 160.306021 56.066694 -169.609927第15单元节点内力是238.512872 -49.119849 -77.431186 -238.512872 49.119849 -158.344090第16单元节点内力是13.998421 5.788617 14.039455 -13.998421 -5.788617 13.745907 第17单元节点内力是25.768509 9.979222 24.414677 -25.768509 -9.979222 23.485589 第18单元节点内力是26.720645 15.477207 38.270992 -26.720645 -15.477207 36.019600第19单元节点内力是29.365877 20.999110 51.977967 -29.365877 -20.999110 48.817762第20单元节点内力是9.333091 25.962695 65.414029 -9.333091 -25.962695 59.206909 第21单元节点内力是3.467511 7.351198 8.692670 -3.467511 -7.351198 11.155563第22单元节点内力是12.011350 23.072259 30.298277 -12.011350 -23.072259 31.996821第23单元节点内力是11.480412 45.818955 60.265235 -11.480412 -45.818955 63.445944第24单元节点内力是11.607594 70.447555 93.201392 -11.607594 -70.447555 97.007006第25单元节点内力是10.552982 91.822906 120.678459 -10.552982 -91.822906 127.243387Matlab计算弯矩图D 值法计算弯矩图9.239.230.0020.5220.525.1330.3725.2416.8248.9932.1726.3273.6247.30141.915.1212.4917.6113.7213.7214.307.5534.8341.5841.335.8835.4526.4127.7264.3663.0568.2019.0949.1142.8451.59104.3795.62114.6740.1874.4950.0463.75108.20121.91134.0449.6684.38157.00162.31结构力学求解器计算弯矩图三、程序代码h1=input('输入底层柱高h1:');h2=input('输入二至五层柱高h2:');L1=input('输入左梁跨度L1:');L2=input('输入右梁跨度L2:');EIc1=input('输入底层柱子的抗弯刚度EIc1:');EIc2=input('输入二至五层柱子的抗弯刚度EIc2:');EAc1=input('输入底层柱子的抗压刚度EAc1:');EAc2=input('输入二至五层柱子的抗压刚度EAc2:');EIb1=input('输入左梁的抗弯刚度EIb1:');EIb2=input('输入右梁的抗弯刚度EIb2:');EAb1=input('输入左梁的抗压刚度EAb1:');EAb2=input('输入右梁的抗压刚度EAb2:');q1=input('输入顶层竖向均布荷载集度q1:');q2=input('输入一至四层均布荷载集度q2:');F1=input('输入顶层水平集中力F1:');F2=input('输入一至四水平集中力F2:');T=[0,1,0,0,0,0;-1,0,0,0,0,0;0,0,1,0,0,0;0,0,0,0,1,0;0,0,0,-1,0,0;0,0,0,0,0,1];%角度为90°的转换矩阵%左梁的单元刚度矩阵Kb1=[EAb1/L1 0 0 -EAb1/L1 0 0;0 12*EIb1/(L1*L1*L1) 6*EIb1/(L1*L1) 0 -12*EIb1/(L1*L1*L1) 6*EIb1/(L1*L1);0 6*EIb1/(L1*L1) 4*EIb1/L1 0 -6*EIb1/(L1*L1) 2*EIb1/L1;-EAb1/L1 0 0 EAb1/L1 0 0;0 -12*EIb1/(L1*L1*L1) -6*EIb1/(L1*L1) 0 12*EIb1/(L1*L1*L1) -6*EIb1/(L1*L1);0 6*EIb1/(L1*L1) 2*EIb1/L1 0 -6*EIb1/(L1*L1) 4*EIb1/L1];%右梁的单元刚度矩阵Kb2=[EAb2/L2 0 0 -EAb2/L2 0 0;0 12*EIb2/(L2*L2*L2) 6*EIb2/(L2*L2) 0 -12*EIb2/(L2*L2*L2) 6*EIb2/(L2*L2);0 6*EIb2/(L2*L2) 4*EIb2/L2 0 -6*EIb2/(L2*L2) 2*EIb2/L2;-EAb2/L2 0 0 EAb2/L2 0 0;0 -12*EIb2/(L2*L2*L2) -6*EIb2/(L2*L2) 0 12*EIb2/(L2*L2*L2) -6*EIb2/(L2*L2);0 6*EIb2/(L2*L2) 2*EIb2/L2 0 -6*EIb2/(L2*L2) 4*EIb2/L2];%底层柱子的单元刚度矩阵Kc1=[EAc1/h1 0 0 -EAc1/h1 0 0;0 12*EIc1/(h1*h1*h1) 6*EIc1/(h1*h1) 0 -12*EIc1/(h1*h1*h1) 6*EIc1/(h1*h1);0 6*EIc1/(h1*h1) 4*EIc1/h1 0 -6*EIc1/(h1*h1) 2*EIc1/h1;-EAc1/h1 0 0 EAc1/h1 0 0;0 -12*EIc1/(h1*h1*h1) -6*EIc1/(h1*h1) 0 12*EIc1/(h1*h1*h1) -6*EIc1/(h1*h1);0 6*EIc1/(h1*h1) 2*EIc1/h1 0 -6*EIc1/(h1*h1) 4*EIc1/h1];%二至五层柱子的单元刚度矩阵Kc2=[EAc2/h2 0 0 -EAc2/h2 0 0;0 12*EIc2/(h2*h2*h2) 6*EIc2/(h2*h2) 0 -12*EIc2/(h2*h2*h2) 6*EIc2/(h2*h2);0 6*EIc2/(h2*h2) 4*EIc2/h2 0 -6*EIc2/(h2*h2) 2*EIc2/h2;-EAc2/h2 0 0 EAc2/h2 0 0;0 -12*EIc2/(h2*h2*h2) -6*EIc2/(h2*h2) 0 12*EIc2/(h2*h2*h2) -6*EIc2/(h2*h2);0 6*EIc2/(h2*h2) 2*EIc2/h2 0 -6*EIc2/(h2*h2) 4*EIc2/h2];Kc11=T'*Kc1*T;%总体坐标下底层柱子的单元刚度矩阵Kc22=T'*Kc2*T;%总体坐标下二至五层柱子的单元刚度矩阵X=zeros(54,54);K1=zeros(54,54);K2=zeros(54,54);%定义54阶0矩阵%把梁杆单元矩阵整合到总体刚度矩阵的循环语句for ii=1:5X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb1(1:3,1:3);K1=K1+X;X=zeros(54,54);endfor ii=7:11X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb1(4:6,4:6);K1=K1+X;X=zeros(54,54);endfor ii=7:11X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb2(1:3,1:3);K1=K1+X;X=zeros(54,54);endfor ii=13:17X(3*ii-2:3*ii,3*ii-2:3*ii)=Kb2(4:6,4:6);K1=K1+X;X=zeros(54,54);endfor ii=1:5X(3*ii-2:3*ii,3*ii+16:3*ii+18)=Kb1(1:3,4:6);K1=K1+X;X=zeros(54,54);endfor ii=1:5X(3*ii+16:3*ii+18,3*ii-2:3*ii)=Kb1(4:6,1:3);K1=K1+X;X=zeros(54,54);endX(3*ii-2:3*ii,3*ii+16:3*ii+18)=Kb2(1:3,4:6);K1=K1+X;X=zeros(54,54);endfor ii=7:11X(3*ii+16:3*ii+18,3*ii-2:3*ii)=Kb2(4:6,1:3);K1=K1+X;X=zeros(54,54);end%把柱杆单元矩阵整合到总体刚度矩阵的循环语句for jj=1:4X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc22;K2=K2+X;X=zeros(54,54);endfor jj=7:10X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc22;K2=K2+X;X=zeros(54,54);endfor jj=13:16X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc22;K2=K2+X;X=zeros(54,54);endfor jj=5:6:17X(3*jj-2:3*jj+3,3*jj-2:3*jj+3)=Kc11;K2=K2+X;X=zeros(54,54);endK=K1+K2;for i=6:6:18K(3*i-2:3*i,3*i-2:3*i)=Kc11(4:6,4:6).*10.^15;endP=zeros(54,1);Y=zeros(54,1);Z=zeros(54,1);P(1,1)=F1;P(2,1)=q1*L1/ 2;P(3,1)=q1*L1*L1/12;P(20,1)=q1*L1/2+q1*L2/2;P(21,1)=-q1*L1*L1/12 +q1*L2*L2/12;P(38,1)=q1*L2/2;P(39,1)=-q1*L2*L2/12;%定义荷载列阵for i=2:5Y(3*i-2,1)=F2;P=P+Y;Y=zeros(54,1);endfor i=2:5Y(3*i-1,1)=q2*L1/2;Z(3*i,1)=q2*L1*L1/12;P=P+Y+Z;Y=zeros(54,1);Z=zeros(54,1);endfor i=8:11Y(3*i-1,1)=q2*L1/2+q2*L2/2;Z(3*i,1)=-q2*L1*L1/12+q2*L2*L2/12;P=P+Y+Z;Y=zeros(54,1);Z=zeros(54,1);endY(3*i-1,1)=q2*L2/2;Z(3*i,1)=-q2*L2*L2/12;P=P+Y+Z;Y=zeros(54,1);Z=zeros(54,1);endA=K\P;%结构位移LOC=zeros(25,2);LOC(1,1)=1;LOC(1,2)=2;LOC(2,1)=2;LOC(2,2)=3;LOC(3,1)=3;LOC(3,2)=4 ;LOC(4,1)=4;LOC(4,2)=5;LOC(5,1)=7;LOC(5,2)=8;LOC(6,1)=8;LOC(6,2)= 9;LOC(7,1)=9;LOC(7,2)=10;LOC(8,1)=10;LOC(8,2)=11;LOC(9,1)=13;LOC(9,2)=14;LOC(10,1)=14;LOC(10,2)=15;LOC(11,1)=15;LO C(11,2)=16;LOC(12,1)=16;LOC(12,2)=17;LOC(13,1)=5;LOC(13,2)=6;LOC( 14,1)=11;LOC(14,2)=12;LOC(15,1)=17;LOC(15,2)=18;LOC(16,1)=1;LOC(1 6,2)=7;LOC(17,1)=2;LOC(17,2)=8;LOC(18,1)=3;LOC(18,2)=9;LOC(19,1)=4;LOC(1 9,2)=10;LOC(20,1)=5;LOC(20,2)=11;LOC(21,1)=7;LOC(21,2)=13;LOC(22, 1)=8;LOC(22,2)=14;LOC(23,1)=9;LOC(23,2)=15;LOC(24,1)=10;LOC(24,2) =16;LOC(25,1)=11;LOC(25,2)=17;a=zeros(6,1);M=zeros(6,25);MT=zeros(6,25);FE1=[0;q1*L1/2;q1*L1*L1/12;0;q1*L1/2;-q1*L1*L1/12];FE2=[0;q2*L1/2;q2*L1*L1/12;0;q2*L1/2;-q2*L1*L1/12];FE3=[0;q1*L2/2;q1*L2*L2/12;0;q1*L2/2;-q1*L2*L2/12];FE4=[0;q2*L2/2;q2*L2*L2/12;0;q2*L2/2;-q2*L2*L2/12];for i=1:12I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kc2*T*a;M=M+MT;MT=zeros(6,25);a=zeros(6,1);endfor i=13:15I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kc1*T*a;M=M+MT;MT=zeros(6,25);a=zeros(6,1);endfor i=16:16I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb1*a-FE1;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=17:20I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb1*a-FE2;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=21:21I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb2*a-FE3;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=22:25I1=LOC(i,1);I2=LOC(i,2);a(1,1)=A(3*I1-2,1);a(2,1)=A(3*I1-1,1);a(3,1)=A(3*I1,1);a(4,1)=A(3*I2-2,1);a(5,1)=A(3*I2-1,1);a(6,1)=A(3*I2,1);MT(1:6,i)=Kb2*a-FE4;M=M+MT;MT=zeros(6,25);a=zeros(6,1); endfor i=1:18m=i;fprintf('第%d节点的位移是%f %f %f\n',i,A(3*m-2:3*m,1))endfor i=1:25m=i;fprintf('第%d单元节点内力是%f %f %f %f %f %f\n',i,M(:,m)) end。
平面刚架MATLAB程序

% 平面刚架MATLAB程序% 2003.9.16 2007.2.28 2008.4.1 2009.10 2011.10 2013.9%*************************************************% 变量说明% NPOIN NELEM NVFIX NFPOIN NFPRES% 总结点数,单元数, 约束个数, 受力结点数, 非结点力数% COORD LNODS YOUNG% 结构节点坐标数组, 单元定义数组, 弹性模量% FPOIN FPRES FORCE FIXED% 结点力数组,非结点力数组,总体荷载向量, 约束信息数组% HK DISP% 总体刚度矩阵,结点位移向量%**************************************************format short e %设定输出类型clear all %清除内存变量clcFP1=fopen('6-6.txt','rt'); %打开初始数据文件%读入控制数据NELEM=fscanf(FP1,'%d',1); %单元数NPOIN=fscanf(FP1,'%d',1); %结点数NVFIX=fscanf(FP1,'%d',1); %约束数NFPOIN=fscanf(FP1,'%d',1); %作用荷载的结点个数NFPRES=fscanf(FP1,'%d',1); %非结点荷载数YOUNG=fscanf(FP1,'%f',1); %弹性模量% 读取结构信息LNODS=fscanf(FP1,'%f',[4,NELEM])';% 单元定义:左、右结点号,面积,惯性矩(共计NELEM组)COORD=fscanf(FP1,'%f',[2,NPOIN])';% 坐标:x,y坐标(共计NPOIN 组)FPOIN=fscanf(FP1,'%f',[4,NFPOIN])';% 节点力(共计NFPOIN 组):受力结点号、X方向力(向右正),% Y方向力(向上正),M力偶(逆时针正)FPRES=fscanf(FP1,'%f',[4,NFPRES])'; % 均布力(共计% NFPRES 组):单元号、荷载类型、荷载大小、距离左端长度FIXED=fscanf(FP1,'%f',NVFIX)';% 约束信息:约束对应的位移编码(共计NVFIX 组)%---------------------------------------------------------HK=zeros(3*NPOIN,3*NPOIN); % 张成总刚矩阵并清零FORCE=zeros(3*NPOIN,1); % 张成总荷载向量并清零%形成总刚for i=1:NELEM % 对单元个数循环% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵EKT=T’*EK*T; % 生成整体单刚(整体坐标系)% 组成总刚按3*3子块加入总刚中(共计4块)for j=1:2 %对行进行循环---按结点号循环N1=LNODS(i,j)*3; % j结点第3个位移的整体编码for k=1:2 %对列进行循环---按结点号循环N2=LNODS(i,k)*3; % k结点第3个位移的整体编码HK((N1-2):N1,(N2-2):N2)=HK((N1-2):N1,(N2-2):N2)...+EKT(j*3-2:j*3,k*3-2:k*3);end % 单刚3 x 3子块叠加到总刚中endend% 由结点力与非结点力生成总荷载向量列阵for i=1:NFPOIN % 对结点荷载个数进行循环N1=FPOIN(i,1); % 作用荷载的结点号N1=N1*3-3; % 该结点号对应第一个位移编码- 1for j=1:3FORCE(N1+j)=FORCE(N1+j)+FPOIN(i,j+1);%取结点荷载endend% 计算由非结点荷载引起的等效结点荷载for i=1:NFPRES % 对非结点荷载个数进行循环F0=ele_FPRES(i,FPRES,LNODS,COORD); %计算单元固端力% 对单元局部杆端力要进行坐标转换ele=FPRES(i,1); % 取荷载所在的单元号T=zbzh(ele,LNODS,COORD); % 坐标转换矩阵F0=T’ *F0;NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号% 将单元固端力变成等效结点荷载(注意固端力与等效结点荷载符号相反)FORCE((3*NL-2):3*NL)=FORCE((3*NL-2):3*NL)-F0(1:3);FORCE((3*NR-2):3*NR)=FORCE((3*NR-2):3*NR)-F0(4:6);end% 总刚、总荷载进行边界条件处理for j=1:NVFIX % 对约束个数进行循环N1=FIXED(j);HK(1:3*NPOIN,N1)=0; HK(N1,1:3*NPOIN)=0; HK(N1,N1)=1;% 将零位移约束对应的行、列变成零,主元变成1FORCE(N1)=0;end%---------------------------------------------------------DISP=HK\FORCE; % 方程求解,HK先求逆再与力向量左乘%---------------------------------------------------------% 求结构各个单元内力EDISP=zeros(6,1); % 单元位移列向量清零for i=1:NELEM % 对单元个数进行循环for j=1:2 %对杆端循环% i单元左右端结点号*3 = 该结点的最后一个位移编码N1=LNODS(i,j)*3;% 取一端的单元位移列向量EDISP(3*j-2:3*j)=DISP(N1-2:N1);end% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵FE=EK*T*EDISP; %计算局部坐标杆端力(由结点位移产生)for j=1:NFPRESif FPRES(j,1) == i %成立时,当前单元上有非结点荷载F0=ele_FPRES(j,FPRES,LNODS,COORD);%单元固端力FE=FE+F0; % 考虑由非结点荷载引起的杆端力endendFE % 打印杆端力end%-------------------------------------------------------ele_FPRES.m %计算单元固端力函数(正方向:X向右Y向上M逆时针)% 入口参数:荷载序号,荷载信息,单元信息,结点坐标% 出口参数:单元固端力——左右两端的轴力、剪力、弯矩function F0=ele_FPRES(iFPRES,FPRES,LNODS,COORD)ele=FPRES(iFPRES,1); %取荷载所在的单元号G=FPRES(iFPRES,3); %单元荷载大小C=FPRES(iFPRES,4); %单元荷载与左端距离NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度% 计算公式中一些常出现的项D=L-C; C1=C/L; C2=C1*C1; C3=C1*C2;B1=D/L; B2=B1/L;F0=[0;0;0;0;0;0]; %单元固端力清零switch FPRES(iFPRES,2)case 1 %均布荷载F0(2)=-G*C*(2-2*C2+C3)/2.0;F0(3)=-G*C*C*(6-8*C1+3*C2)/12.0;F0(5)=-G*C-F0(2);F0(6)=G*C*C*C1*(4-3*C1)/12.0;case 2 %横向集中力F0(2)=-G*B1*B2*(L+2*C);F0(3)=-G*C*B1*B1;F0(5)=-G*C2*(L+2*D)/L;F0(6)=G*D*C2;case 3 %纵向集中力F0(1)=-G*B1;F0(4)=-G*C1;endreturnele_EK.m % 计算单元刚度矩阵函数EK% 入口参数:单元号、单元信息数组、结点坐标、弹性模量% 出口参数:局部单元刚度矩阵EKfunction EK=ele_EK(i,LNODS,COORD,E)NL=LNODS(i,1); NR=LNODS(i,2); %左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度A=LNODS(i,3); I=LNODS(i,4); %面积;惯性矩% 生成单刚(局部坐标) 右手坐标系EK =[E*A/L 0 0 -E*A/L 0 0;...0 12*E*I/L^3 6*E*I/L^2 0 -12*E*I/L^3 6*E*I/L^2;...0 6*E*I/L^2 4*E*I/L 0 -6*E*I/L^2 2*E*I/L;...-E*A/L 0 0 E*A/L 0 0;...0 -12*E*I/L^3 -6*E*I/L^2 0 12*E*I/L^3 -6*E*I/L^2;...0 6*E*I/L^2 2*E*I/L 0 -6*E*I/L^2 4*E*I/L]; return%--------------------------------------------------------zbzh.m % 形成第i单元的坐标转换矩阵函数T(6,6)% 入口参数:单元号,单元信息,结点坐标% 出口参数:坐标转换矩阵(整体向局部投影)function T=zbzh(i,LNODS,COORD)NL=LNODS(i,1); %左结点号NR=LNODS(i,2); %右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); % 单元长度c=dx/L; % cos a (与x 轴夹角余弦)s=dy/L; % sin aT=[ c s 0 0 0 0;...-s c 0 0 0 0;...0 0 1 0 0 0;...0 0 0 c s 0;...0 0 0 -s c 0;...0 0 0 0 0 1];return。
有限元钢架结构分析手算matlabansys模拟

有限元大作业——钢架结构分析选题人:日期:2016年6月2日目录:第一章:问题重述 ...................................................................................................................... 错误!未定义书签。
一、题目内容: .................................................................................................................. 错误!未定义书签。
二、题目要求: .................................................................................................................. 错误!未定义书签。
第二章:有限元法手工求解 ...................................................................................................... 错误!未定义书签。
一、平面两单元离散化 ...................................................................................................... 错误!未定义书签。
二、单元分析 ...................................................................................................................... 错误!未定义书签。
matlab钢架结构

matlab钢架结构
在MATLAB中,可以使用矩阵位移法来分析钢架结构的位移和内力。
具体步骤如下:
1. 对结构进行离散化,对结点和单元进行编号,建立结构(整体)坐标系和单元(局部)坐标系,并对结点位移进行编号。
2. 对结点位移分量进行编码,形成单元定位向量。
3. 建立按结构整体编码顺序排列的结点位移列向量,计算固端力、等效结点荷载及综合结点荷载列向量。
4. 计算各单元局部坐标系的刚度矩阵,通过坐标变换矩阵形成整体坐标系下的单元刚度矩阵。
5. 利用单元定位向量形成结构刚度矩阵。
6. 按式求解未知结点位移。
7. 计算各单元的杆端力。
需要注意的是,在MATLAB中,可以使用矩阵运算和编程语言来处理这些计算过程,因此需要具备一定的编程基础和数学基础。
同时,对于复杂的钢架结构,可能需要使用更高级的有限元分析软件来进行精确的分析和计算。
MATLAB 2016基础实例教程 第5章 程序设计基础

(2)用命令式M文件的简单形式来创建大型矩阵。编制一个名为 new.m的M文件。在M文件编辑器中输入程序,创建简单矩阵。
《MATLAB 2016 基础实例教程》
《MATLAB 2016 基础实例教程》
第5章 程序设计基础
MATLAB提供特有的函数功能可以解决许多复杂的科学计算,工 程设计问题,但在很多情况下利用函数无法解决复杂问题,或者解 决方法过于繁琐,因此需要编写专门的程序。本节以M文件为基础, 详细介绍程序的基本编写流程。
《MATLAB 2016 基础实例教程》
例3:利用try-catch-end结构调试10!。
的值。
5.2.3
《MATLAB 2016 基础实例教程》
程序的注解
1.disp命令 该命令用来展示变量的内容,可以是数值、字符串或表达式,可
以输出几乎所有类型的变量。它的使用格式如下: disp(X):在屏幕上显示任何输入的变量。
2.input命令 该命令用来提示用户从键盘输入数值、字符串或表达式,并将相
《MATLAB 2016 基础实例教程》
函数文件
《MATLAB 2016 基础实例教程》
5.1.4 操作实例
例1:编写矩阵的加法文件。 例2:编写矩阵的重组文件。 例3:编写复数的加法函数。
《MATLAB 2016 基础实例教程》
5.1.5 课堂练习——求解函数表达式
当a取-3,5,8,9,45时,求
《MATLAB 2016 基础实例教程》
5.2.5 程序的信息诊断
平面刚架程序设计

第五章平面刚架程序设计第一节 概述一、计算模型及计算方法 1.计算模型以杆件联结点、支座结点、截面突变电和外伸端点作为计算结点,任意两结点件的杆件作为计算单元。
在局部坐标系下单元两端杆端力、杆端位移列阵如式(1-15)、式(1-16)所示,即:[]TjjjiiieMYX MY XF =[]Tjjj i iiev u v u θθδ=在局部坐标系下,单元刚度矩阵如式(1-19)所示,即:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------=lEI lEI lEI lEI l EIl EI l EIl EI l EA l EA l EI l EI l EI lEI l EI l EI l EI l EI l EA l EAke4602606120612000002604606120612000002223232223232.坐标变换杆端力和杆端位移的坐标变换是通过式(1-26)所示的单元坐标变换矩阵eT 完成的。
⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=1000cos sin 0000sin cos 0000001000000cos sin 0000sin cos ααααααααeT局部坐标单元杆端力、杆端位移与整体坐标系下单元杆端力、杆端位移之间的关系分别为式(1-25)和式(1-28),即eeeTeee eTk TF T F==δ整体坐标系下的单元刚度矩阵为ee eTeT k Tk=这里ek为式(1-19)所示的6阶方阵。
3.支承条件的引入集整体刚度矩阵的组集整体刚度矩阵得组集采用“直接刚度法”。
整体坐标系下单元刚度矩阵个元素的下标有单元定位数组确定,即在组集整体刚度矩阵之前已引入了支承条件。
确定单元定位数组适应注意以下两个问题(1)支座结点的位置位移分量编号若单元的某一端与支座相联,则该单元支座结点的位移分量信息应按表5-1输入。
(2)杆件联结点未知位移分量编号若单元的某一端与其它杆件相联,则应首先根据联结情况确定结点编码,而后再确定与结点相应的单元未知位移分量编码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
% 平面刚架MATLAB程序% 2003.9.16 2007.2.28 2008.4.1 2009.10 2011.10 2013.9 2014.09 2016.03%*************************************************% 变量说明% NPOIN NELEM NVFIX NFPOIN NFPRES% 总结点数,单元数, 约束个数, 受力结点数, 非结点力数% COORD LNODS YOUNG% 结构节点坐标数组, 单元定义数组, 弹性模量% FPOIN FPRES FORCE FIXED% 结点力数组,非结点力数组,总体荷载向量, 约束信息数组% HK DISP% 总体刚度矩阵,结点位移向量%**************************************************format short e %设定输出类型clear %清除内存变量FP1=fopen('6-6.txt','rt') %打开初始数据文件%读入控制数据NELEM=fscanf(FP1,'%d',1); %单元数NPOIN=fscanf(FP1,'%d',1); %结点数NVFIX=fscanf(FP1,'%d',1); %约束数NFPOIN=fscanf(FP1,'%d',1); %作用荷载的结点个数NFPRES=fscanf(FP1,'%d',1); %非结点荷载数YOUNG=fscanf(FP1,'%f',1); %弹性模量% 读取结构信息LNODS=fscanf(FP1,'%f',[6,NELEM])'% 单元定义:左、右结点号,面积,惯性矩,线膨胀系数,截面高度(共计NELEM组)COORD=fscanf(FP1,'%f',[2,NPOIN])'% 坐标:x,y坐标(共计NPOIN 组)FPOIN=fscanf(FP1,'%f',[4,NFPOIN])'% 节点力(共计NFPOIN 组):受力结点号、X方向力(向右正),% Y方向力(向上正),M力偶(逆时针正)FPRES=fscanf(FP1,'%f',[7,NFPRES])' % 均布力(共计% NFPRES 组):单元号、荷载类型、荷载大小、距离左端长度,温差=(下端-上端)梯形上边。
下边(改)% 荷载类型1-均布荷载2-横向集中力3-纵向集中力4-三角形荷载5-温度荷载6-梯形荷载FIXED=fscan f(FP1,'%f',NVFIX)'% 约束信息:约束对应的位移编码(共计NVFIX 组)%---------------------------------------------------------HK=zeros(3*NPOIN,3*NPOIN); % 张成总刚矩阵并清零FORCE=zeros(3*NPOIN,1); % 张成总荷载向量并清零%形成总刚for i=1:NELEM % 对单元个数循环% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD);% 坐标转换矩阵EKT=T’*EK*T;% 生成整体单刚(整体坐标系)% 组成总刚按3*3子块加入总刚中(共计4块)for j=1:2 %对行进行循环---按结点号循环N1=LNODS(i,j)*3; % j结点第3个位移的整体编码for k=1:2 %对列进行循环---按结点号循环N2=LNODS(i,k)*3; % k结点第3个位移的整体编码HK((N1-2):N1,(N2-2):N2)=HK((N1-2):N1,(N2-2):N2)...+EKT(j*3-2:j*3,k*3-2:k*3);% 单刚3 x 3子块叠加到总刚中endend% 由结点力与非结点力生成总荷载向量列阵for i=1:NFPOIN % 对结点荷载个数进行循环N1=FPOIN(i,1); % 作用荷载的结点号N1=N1*3-3; % 该结点号对应第一个位移编码- 1for j=1:3FORCE(N1+j)=FORCE(N1+j)+FPOIN(i,j+1);%取结点荷载endend% 计算由非结点荷载引起的等效结点荷载for i=1:NFPRES % 对非结点荷载个数进行循环F0=ele_FPRES(i,FPRES,LNODS,COORD,YOUNG); %计算单元固端力% 对单元局部杆端力要进行坐标转换ele=FPRES(i,1); % 取荷载所在的单元号T=zbzh(ele,LNODS,COORD); % 坐标转换矩阵F0=T’*F0;NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号% 将单元固端力变成等效结点荷载(注意固端力与等效结点荷载符号相反)FORCE((3*NL-2):3*NL)=FORCE((3*NL-2):3*NL)-F0(1:3);FORCE((3*NR-2):3*NR)=FORCE((3*NR-2):3*NR)-F0(4:6);end% 总刚、总荷载进行边界条件处理for j=1:NVFIX % 对约束个数进行循环N1=FIXED(j);HK(1:3*NPOIN,N1)=0; HK(N1,1:3*NPOIN)=0; HK(N1,N1)=1;% 将零位移约束对应的行、列变成零,主元变成1FORCE(N1)=0;end%---------------------------------------------------------DISP=HK\FORCE % 方程求解,HK先求逆再与力向量左乘% 求结构各个单元内力EDISP=zeros(6,1); % 单元位移列向量清零for i=1:NELEM % 对单元个数进行循环for j=1:2 %对杆端循环% i单元左右端结点号*3 = 该结点的最后一个位移编码N1=LNODS(i,j)*3;% 取一端的单元位移列向量EDISP(3*j-2:3*j)=DISP(N1-2:N1);end% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵FE=EK*T*EDISP; %计算局部坐标杆端力(由结点位移产生)for j=1:NFPRESif FPRES(j,1) == i %成立时,当前单元上有非结点荷载F0=ele_FPRES(j,FPRES,LNODS,COORD,YOUNG);%单元固端力FE=FE+F0; % 考虑由非结点荷载引起的杆端力endendFE % 打印杆端力endend%-------------------------------------------------------ele_FPRES.m %计算单元固端力函数(正方向:X向右Y向上M逆时针)% 入口参数:荷载序号,荷载信息,单元信息,结点坐标% 出口参数:单元固端力——左右两端的轴力、剪力、弯矩function F0=ele_FPRES(iFPRES,FPRES,LNODS,COORD, E)ele=FPRES(iFPRES,1); %取荷载所在的单元号G=FPRES(iFPRES,3); %单元荷载大小C=FPRES(iFPRES,4); %单元荷载与左端距离W= FPRES(iFPRES,5); %单元下上端温差S= FPRES(iFPRES,6); %梯形长边荷载X= FPRES(iFPRES,6); %梯形短边荷载H= LNODS(ele,6);%单元截面高度P = LNODS(ele,5);%单元截面线膨胀系数NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度% 计算公式中一些常出现的项D=L-C; C1=C/L; C2=C1*C1; C3=C1*C2;B1=D/L; B2=B1/L;F0=[0;0;0;0;0;0]; %单元固端力清零switch FPRES(iFPRES,2)case 1 %均布荷载F0(2)=-G*C*(2-2*C2+C3)/2.0;F0(3)=-G*C*C*(6-8*C1+3*C2)/12.0;F0(5)=-G*C-F0(2);F0(6)=G*C*C*C1*(4-3*C1)/12.0;case 2 %横向集中力F0(2)=-G*B1*B2*(L+2*C);F0(3)=-G*C*B1*B1;F0(5)=-G*C2*(L+2*D)/L;F0(6)=G*D*C2;case 3 %纵向集中力F0(1)=-G*B1;F0(4)=-G*C1;case 4 %三角形荷载F0(2)=-7*G*L/20;F0(3)=G*L^2/20;F0(5)=3*G*L/20;F0(6)=G*L*L/30;case 5 %温度荷载F0(3)=E*I*W*P/H;F0(6)=-E*I*W*P/H;case 6 %梯形荷载(改)F1(2)=-X*C*(2-2*C2+C3)/2.0;F1(3)=-X*C*C*(6-8*C1+3*C2)/12.0;F2(5)=-X*C-F0(2);F2(6)=X*C*C*C1*(4-3*C1)/12.0;F3(2)=-7*(S-G)*L/20;F3(3)=(S-G)*L^2/20;F4(5)=3*(S-G)*L/20;F4(6)=(S-G)*L*L/30;F0(2)= F1(2)+ F3(2);F0(3)= F1(3)+ F3(3);F0(5)= F2(5)+ F4(5);F0(6)= F2(6)+ F4(6);endreturnele_EK.m % 计算单元刚度矩阵函数EK% 入口参数:单元号、单元信息数组、结点坐标、弹性模量% 出口参数:局部单元刚度矩阵EKfunction EK=ele_EK(i,LNODS,COORD,E)NL=LNODS(i,1); NR=LNODS(i,2); %左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度A=LNODS(i,3); I=LNODS(i,4); %面积;惯性矩% 生成单刚(局部坐标) 右手坐标系EK =[E*A/L 0 0 -E*A/L 0 0;...0 12*E*I/L^3 6*E*I/L^2 0 -12*E*I/L^3 6*E*I/L^2;...0 6*E*I/L^2 4*E*I/L 0 -6*E*I/L^2 2*E*I/L;...-E*A/L 0 0 E*A/L 0 0;...0 -12*E*I/L^3 -6*E*I/L^2 0 12*E*I/L^3 -6*E*I/L^2;...0 6*E*I/L^2 2*E*I/L 0 -6*E*I/L^2 4*E*I/L]; return%--------------------------------------------------------zbzh.m % 形成第i单元的坐标转换矩阵函数T(6,6)% 入口参数:单元号,单元信息,结点坐标% 出口参数:坐标转换矩阵(整体向局部投影)function T=zbzh(i,LNODS,COORD)NL=LNODS(i,1); %左结点号NR=LNODS(i,2); %右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); % 单元长度c=dx/L; % cos a (与x 轴夹角余弦)s=dy/L; % sin aT=[ c s 0 0 0 0;...-s c 0 0 0 0;...0 0 1 0 0 0;...0 0 0 c s 0;...0 0 0 -s c 0;...0 0 0 0 0 1];return。
