电子电路基础第六章复习题答案
电路与电子技术基础总复习题及解

《电路与电子技术基础》总复习题及解2013.11《电路与电子技术基础》总复习题及解2013.11一、问 答第一章答题1. 电流与电压为关联参考方向是指什么?答:电流参考方向(箭头方向)与电压降参考方向(“+”到“-”的方向)一致的方向。
第二章答题1. 应用叠加定理时,理想电压源不作用时视为短路,理想电流源不作用时视为 开路。
2、求含有受控源单口网络的戴维南(诺顿)等效电路的内阻时,屏蔽掉电源后须用 外施电压、电流 法求得。
第三章答题1、对于电容C 和电感L ,电压和电流间的关系为:,2、换路定律是指: 3、全响应解的两种表达式: (1)全响应=(零输入响应)+(零状态响应)(2)三要素法:第四章答题1、直流电路中,感抗为0,容抗为无穷大。
2、正弦电压 u (t ) =2U cos (?t + ?u )对应的相量表示为 u U U θ∠=•。
3、任意一个相量乘以j相当于该相量逆时针旋转90o 。
1倍,4、三相对称电源星型联结,相、线电压的关系为相电压是线电压的3且相电压滞后对应线电压30°。
对称电源△接线时,线电流、相电流之间关系为线电流等于3倍相电流,相位滞后对应相电流30°。
5、电阻元件的电压电流的有效值满足:U=IR,关联参考方向下电压和电流同相位,即第五章答题无第六章答题1、本征半导体电子浓度等于空穴浓度;N型半导体的电子浓度大于空穴浓度;P型半导体的电子浓度小于空穴浓度。
2、场效应管属于电压控制型器件,晶体三极管则属于电流控制器件。
3、晶体三极管工作在放大状态时,应使发射结正向偏置;集电结反向偏置。
4、稳定二极管稳压时是处于反向偏置状态,而二极管导通时是处于正向偏置状态。
5、 PN结的单向导电性,就是PN结正偏时导通,反偏时截止。
6、当温度升高时,三极管的集电极电流Ic 增加,发射结压降U BE减小。
第七章答题1、共模抑制比K CMR是差模放大倍数与共模放大倍数(绝对值)之比。
电子电路基础第六章习题答案

第六章习题6. 1求习题图6・1所示的电路的传递函数H(a)) = V o/V t•习题图6. 1•• RH ——解:(%-匕)-MC 八V jwLjcoL - 3、RLCR + jcoL-cerRLCjcoCR一ja)CR — e f CL6・2对于习题图6. 2所示的电路,求传递函数二丿6. 3串联RLC网络有R二5G, L二10川H, C二1 “F,求该电路的谐振角频率.特征阻抗和品质因数。
当外加电压有效值为24V时,求谐振电流、电感和电容上的电压值。
解:电路的谐振角频率卧忌一皿特征阻抗0二姑= 100。
品质因数0二二20谐振电流人吕十A电感和电容上的电压值U L = U c = U a Q = 480V 6・4设计一个串联RLC电路,使其谐振频率q 二50m〃/“品质因数为80,且谐振时的阻抗为10Q,并求英带宽。
解:B 二色=0. 625rad / 56. 5对于习题图6. 5所示的电路,求和,(/)为同相时的频率解••阶S叫+盏血5将厶二1乩厶二\H、C =一"+ y(w_ ♦W 1 + M rIQ F卜I w谐振时虚部为零,沙——+——二0W 1 +讥厂得出,W二0・7861 6. 6并联RLC网络有R二50G, L二4〃M・C二160 “八求并联电路谐振频率和品质因数。
若外接电流源有效值为2A,求谐振时电阻、电感及电容上的电流值。
解:电路的谐振角频率%二二I・25xl0rad/s4LC品质因数Q二毬CR ==10谐振时电阻、电感及电容上的电流值h二2AJ L二Ic二I K・Q = 2OA6. 7并联谐振电路,其品质因数为120,谐振频率是6x10%/ 〃/ “计算其带宽。
6・8计算习题图6. 8所示的电路的谐振角频率叫,品质因数Q和带宽Bo3好20m H 冒2jfcQ i6“戸〒习题图6・81 1 1 c C 1解:y 二 >・(5//C2)+一+— = 一+7 (=_)谐振时Y的虚部为0沙• g-一丄=0 C] + C、wL得出w =Q = qRC = CD O R(C( //CJ 二20B二八二2^0rad/.y 6. 9习题图6. 9所示的电路,已知电容值C为固圧,欲使电路在© 时发生并联谐振,而在©时发生串联谐振,求厶、乙的值。
现代电子线路基础(新版教材)_第六章习题答案

第六章习题答案6.1在题图6.1所示调谐放大器中,工作频率 f o =10.7MHz,L I -3=4^ H,Q =100, N -3=20匝,N+5匝,N”5匝,晶体管3DG39在 f o =10.7MHz 时测得 g ie =2860^ S,C e =18pF, g oe =200^ S, C oe =7pF,| y fe |= 45mS, y 「e =O,试求放大器的电压增益 A 。
和通频带BW总电容 C 1/((2 f 0)2* L) 55.4pFLC 振荡回路电容 C Cp 2c °e P ;Ge 53.8pF注:由上述计算可以看出,f 。
'和f 。
相差不大,即部分接入后对谐振频率影响较小,但概念要清楚。
另外,这里给出了 y fe (即认为是g m )不要通过I EQ 来计算g m6.2题图6.2是某中放单级电路图。
已知工作频率f o =30MHz 回路电感L =1.5卩H, Q =100, N /N =4, C ~C 均为耦合电容 和旁路电容。
晶体管在工作条件下的y 参数为y ie(2.8 j3.5)mS;y 「e 0y fe (36 j27)mS y °e (0.2 j2)mS试解答下列问题: (1) 画出放大器y 参数等效电路; (2) 求回路谐振电导g 2; (3) 求回路总电容C 2;(4) 求放大器电压增益 A 。
和通频带BV y(5)当电路工作温度或电源电压变化时,A vo 和BW 是否变化?解:M~3N4~ 5NT ;5200.25 LC 振荡回路固有谐振频率f 0固有损耗电导:901— 10.85(MHz)2 . LC1 1Q 0 0 L 2 Q 0 f ° L36.7 10 6(S)222 6266G p g oe P 2 g ie g o0.25 200 100.252860 1036.7 100.228(mS)Q L1 16.32G 0LB W 邑 107656(KHz),Q L 16.3A V 00.25 0.25 45 10 0.228 1012RN2~35 20 0.25,F 2交流等效电路I C折合后的等效电路R2 2P 22C ie 18.78 10.6 o.252 18.58 7.02( pF )11rw2J1.5 106 7.02 m2491(MHz)固有损耗电导:RRdZJ 1O.25 V 362 10 328.4G0.396 10解:(1) y 参数等效电路如上图:由f o2LC 得 C1 2 2 4 Lfo42;0 621218.78( pF )P 2也丄0.25N 14 由y 参数得C ie33.5 10 3 6230 1018.58( pF),C oe3盘帝 10.6(pF)RS g oQ o o L 2 Q o f o L2 3.14 100 49.1 10*^2「6 106(S)R goe2 3P 2 gieg o 0.2 10230.252.8 1021.4 10 0.396( mS)Q L1366G 0L 0.396 102 30 101.5 108.9Q L竺 3.37( MHz )8.9AV 0C NNC 6 输入IIC 1D8上R JIA输入LN C NC 2 二 R 2V DD------- •GSL 1A C 3”2输出某场效应管调谐放大器电路如题图 6.3所示,为提高放大器稳定性,消除管子极间电容C D G 引起的部反馈,电路中分析其它各元件的作用; 画出放大器的交流等效电路; 导出放大器电压增益 A/o 表达式解:(1) L N 、C N 与C dg 组成并联谐振回路,使得漏栅之间的反馈阻抗为 ,故消除了漏栅之间的反馈,即消除了 C dg 引起得部反馈,实现了单向化。
《电工电子学》第6章习题答案

第6章习题答案6.1.1 选择题(1)在LC并联谐振回路谐振时,若电感的中间抽头交流接地,则首端与尾端的信号电压相位_B __________ 。
A. 相同B. 相反C. 90 。
D. -90 。
(2)在LC并联谐振回路谐振时,若电感的首端或尾端交流接地,则电感其它两个端点的信号电压相位A __________ 。
A. 相同B. 相反C. 90 。
D. -90 。
(3)自激振荡是电路在__B—的情况下,产生了有规则的、持续存在的输出波形的现象。
A.外加输入激励B.没有输入信号C.没有反馈信号(4)正反馈是放大电路产生自激振荡的 A QA.必要条件B. 充分条件C.充要条件(5)在正弦波振荡电路中,能产生等幅振荡的幅度条件是 A QA.丄- .B.丄-■ .C. .5 ■- 1(6)正弦波振荡电路的起振条件是__B QA.丄口 - *B.丄口 -■ *C. 匸■- 1(7)在RC型正弦波振荡器中,通常是利用—B ■来自动的稳定振荡器输出的幅度。
A.线性特性元件B. 非线性特性元件C. 电抗特性元件(8)在题图6.1.1所示电路中,谐振回路由A元件组成。
A. . 1B. “、1C. = 7 =1 1 1纭爲C. 河石B.(10)电路如题图6.1.2所示,设运放是理想器件,厂二1小「,为使该电路能产生正弦波, 则要求C _________ 。
a.Ry = 10kQ+4?kQ(可调)b.=100kQ+4.7kQ (可调)c.$=18kQ+47kfi (可调)题图6.1.2(11)对于LC正弦波振荡电路,若已满足相位平衡条件,则反馈系数越大, A QA.越容易起振B. 越不容易起振错误C.输出越小6.1.2判断下列说法是否正确,在括号中画上“V”或“X” Q(1)在反馈电路中,只要安排有LC谐振回路,就一定能产生正弦波振荡。
(x )(2)对于LC正弦波振荡电路,若已满足相位平衡条件,则反馈系数越大,越容易起振。
范世贵 电路基础2版 答案(第6章)

第六章 三相电路6-1 已知对称三相电源线,平衡三项负载每相的阻抗。
求负载为星形连接和三角形连接时的相电流,线电流和三相总功率,并画出相量图。
答案解:设则:相量图如图6-27(a )所示。
380U V=线1053.1Z ︒=∠Ω380U V = 11053.1Z ︒=∠Ω(1)∴负载为星形联结时:220p U V=22p l I I A==cos 8718.1p p P U I Wϕ==2200AC U V∙︒=∠2253.1A I A ∙︒=∠-22173.1B I A ∙︒=∠-2266.9c I A ∙︒=∠220120BC U V ∙︒=∠-220120COU V ∙︒=∠(2)当负载为三角形联接时:设, 则:相量如图6-27(b )所示。
6-2 两组平衡负载并联如图题6-2所示。
三角形联接的负载功率为10千瓦,功率因数为0.8(电感性);星形联接的负载功率为10千瓦,功率因数为0.855;端线阻抗。
欲使负载端的线电压有效值保持为380V ,求电源线电压应为多少?图题6-2 答案解: 三角形负载380l p U U V ==38p I A=66l p I A==3cos 26010.2p p P U I Wϕ==3800AB U V ∙︒=∠380120BC U V ∙︒=∠-380120CA U V ∙︒=∠3853.1AB I A ∙︒=∠-38173.1BC I A ∙︒=∠-3866.9CA I A ∙︒=∠6683.1A I A ∙︒=∠-66203.1B I A ∙︒=∠-6636.9C I A ∙︒=∠(0.10.2)l Z j =+Ω119l I A===星形负载电路为对称三相电路,将形联接负载变换为星形联接负载。
并可取出一相计算,现取A 相,设A 相负载相电压则电源相电压电源线电压117.77l I A=== '2200AO U V ∙︒=∠11936.9I A ∙︒=∠-217.7731.2I A∙︒=∠-1236.6534.16A I I I A ∙∙∙︒=+=∠-'AO A l AO U I Z U ∙∙∙=+(0.10.2)2200A j I V ∙︒=++∠227.070.99V ︒=∠∴227.07393.3()l U V ==。
电路理论基础第三版陈希有第六章答案

第六章答案6.1解:将2i 和3i 改写为余弦函数的标准形式,即234cos(190)A 4cos(190180)A 4cos(10)A5sin(10)A 5cos(1090)A 5cos(80)Ai t t t i t t t ωωωωωω=-+︒=+︒-︒=+︒=+︒=+︒-︒=-︒电压、电流的有效值为12370.7V, 1.414A 2.828A, 3.54A U I I I ======== 初相位12310,100,10,80u i i i ψψψψ====-相位差111010090u i ϕψψ=-=-=- 11u i u i 与正交,滞后于; 2210100u i ϕψψ=-=︒-︒= u 与2i 同相; 3310(80)90u i ϕψψ=-=︒--︒= u 与3i 正交,u 超前于3i答案6.2()()()().a 10cos(10)V-8b arctg 10233.1V,233.1)V -6-20.8c arctg 20.889.4A,20.8cos(89.4)A 0.2d 30180A,180)A m u t U u t I i t I i t ωωωω=-︒==∠︒=+︒==∠-︒=-︒=∠︒=+︒答案6.3解:(a)利用正弦量的相量表示法的线性性质得:11221,U I n U I n ==- (b)磁通相量通常用最大值表示,利用正弦量的相量表示法的微分性质得:mj m U N ω=Φ (c) 利用正弦量的相量表示法的线性性质与微分性质得:j URI LI ω=+答案6.4解:由KCL 得电流i 的振幅相量m 1m 2m 3mI I I I =++ (2100410580)A =∠︒+∠︒+∠-︒(0.347j 1.97 3.939j0.6950.868j4.924)A =-++++-A 86.265︒-∠=电流i 的瞬时值为5cos(26.86)A i t ω=-︒答案6.5解:电压表和电流表读数为有效值,其比值为阻抗模,即/U I =将已知条件代入,得100V 15A 100V10⎧=⎪⎪=Ω 联立方程,解得13.7mH, 5.08L R ==Ω答案6.6解:(a) RC 串联电路中电阻电压与电容电压相位正交,各电压有效值关系为30V U ===电流i 的有效值为30V 3A 10C C U I I X ====Ω(b)302A 60V C C U X I ==Ω⨯=60V 1.2A 50R U I R ===ΩRC 并联电路中电阻电流与电容电流相位正交,总电流有效值为2.33I A === (c)30130C C C U X I A V ==Ω⨯=由30215C L C L L L U V U U X I I A X ==⇒===Ω并联电容、电感上电流相位相反,总电流为1L C I I I A =-= 电阻电压与电容电压相位正交,总电压为:50U V ===答案6.7解:感抗()3210rad/s 0.1H 200L X L ω==⨯⨯=Ω容抗()()3611100210rad/s 510FC X C ω--=-==-Ω⨯⨯⨯ 图(a)电路的相量模型如图(b)所示。
电子电路基础_刘京南_课后习题解答

第一章例题分析题1.1 电路如题图1.1所示,试判断图中二极管是导通还是截止,并求出AO两端的电压UAO。
设二极管是理想的。
解:分析:二极管在外加正偏电压时是导通,外加反偏电压时截止。
正偏时硅管的导通压降为0.6~0.8V 。
锗管的导通压降为0.2~0.3V 。
理想情况分析时正向导通压降为零,相当于短路;反偏时由于反向电流很小,理想情况下认为截止电阻无穷大,相当于开路。
分析二极管在电路中的工作状态的基本方法为“开路法”,即:先假设二极管所在支路断开,然后计算二极管的阳极(P 端)与阴极(N 端)的电位差。
若该电位差大于二极管的导通压降,该二极管处于正偏而导通,其二端的电压为二极管的导通压降;如果该电位差小于导通压降,该二极管处于反偏而截止。
如果电路中存在两个以上的二极管,由于每个二极管的开路时的电位差不等,以正向电压较大者优先导通,其二端电压为二极管导通压降,然后再用上述“开路法”法判断其余二极管的工作状态。
一般情况下,对于电路中有多个二极管的工作状态判断为:对于阴极(N 端)连在一起的电路,只有阳极(P 端)电位最高的处于导通状态;对于阳极(P 端)连在一起的二极管,只有阴极(N 端)电位最低的可能导通。
图(a )中,当假设二极管的VD 开路时,其阳极(P 端)电位P U 为-6V ,阴极(N 端)电位N U 为-12V 。
VD 处于正偏而导通,实际压降为二极管的导通压降。
理想情况为零,相当于短路。
所以V U AO 6-=;图(b )中,断开VD 时,阳极电位V U P 15-=,阴极的电位V U N 12-=, ∵ N PUU < ∴ VD 处于反偏而截止∴ VU AO 12-=; 图(c ),断开VD1,VD2时∵ V U P 01= V U N 121-= 11N P U U >V U P 152-= V U N 122-= 22N P U U<∴ VD1处于正偏导通,VD2处于反偏而截止V U AO 0=;或,∵ VD1,VD2的阴极连在一起∴ 阳极电位高的VD1就先导通,则A 点的电位V U AO 0=,而 A N P U UV U =<-=2215∴ VD2处于反偏而截止 图(d ),断开VD1、VD2,∵ V U P 121-= V U N 01= 11N P U U < V U P 122-= VU N 62-= 22N P U U <;∴ VD1、VD2均处于反偏而截止。
数字电子技术基础第四版课后答案6

数字电子技术基础第四版课后答案6第六章脉冲波形的产生和整形[题6.1]用施密特触发器能否寄存1位二值数据,说明理由。
[解]不能,因为施密特触发器不具备记忆功能。
[题6.2]在图P6.2(a)所示的施密特触发器电路中,已知R110k,R230kG1和G2为CMOS反相器,VDD=15V。
(1)试计算电路的正向阈值电压VT+、负向阈值电压VT-和回差电压△VT。
(2)若将图P6.2(b)给出的电压信号加到P6.2(a)电路的输入端,试画出输出电压的波形。
[解]R11015VT1VRTH1302V10V2(1)R11015VT1VRTH1302V5V2VTVTVT5V(2)见图A6.2。
[题6.3]图P6.3是用CMOS反相器接成的压控施密特触发器电路,试分析它的转换电平VT+、VT-以及回差电压△VT与控制电压VCO的关系。
,则根据叠加定理得到[解]设反相器G1输入端电压为IR2//R3R1//R3R1//R2VCO0R1R2//R3R3R1//R2R2R1//R3VTH时,IVT,因而得到(1)在I升高过程中00。
当升至IIIVTHVTR2//R3R1//R2VCOR1R2//R3R3R1//R2R1R1R1R1//R2R1R2//R3VTVTHVCOVTH1RVCORRRR//RR//R32331223 VTH时,IVT,于是可得(2)在I降低过程中0VDD。
当降至I VTHVTR2//R3R1//R3R1//R2VCOVDDR1R2//R3R3R1//R2R2R1//R3 R1//R3R1R2//R3R1//R2VVVCODDTHR3R1//R2R2R1//R3R2//R3VTR1R1R1VTH1RRRVCO323RRVTVTVT21VTH1VDDR2R2(3)(与VCO无关)根据以上分析可知,当Vco变小时,VT+和VT-均增大,但回差电压△VT不变。
[题6.4]在图P6.4施密特触发器电路中,若G1和G2为74LS系列与非门和反相器它们的阈值电压VTH=1.1V,R1=1KΩ,二极管的导通压降VD=0.7V,试计算电路的正向阈值电压VT+、负向阈值电压VT-和回差电压△VT。
电子电路基础第六章习题答案

第六章习题6.1 求习题图6.1所示的电路的传递函数()/o i H V V ω=gg。
习题图6.1解:1//()i o oR V V jwCjwLV -=g gg22()oi V j L RLCH R j L RLCV ωωωωω-==+-gg 6.2 对于习题图6.2所示的电路,求传递函数()o iI H I ω=gg。
习题图6.2解:2()11o iI R j CRH j CR CL I jwL R jwCωωωω===-+++gg6.3 串联RLC 网络有R=5Ω,L=10mH ,C=1F μ,求该电路的谐振角频率、特征阻抗和品质因数。
当外加电压有效值为24V 时,求谐振电流、电感和电容上的电压值。
解:电路的谐振角频率4010/rad s LCω== 特征阻抗100LCρ==Ω 品质因数020LQ Rω==谐振电流0 4.8mU I A R== 电感和电容上的电压值L 480V C m U U U Q ===6.4 设计一个串联RLC 电路,使其谐振频率050/rad s ω=,品质因数为80,且谐振时的阻抗为10Ω,并求其带宽。
解:00.625rad /B s Qω==6.5 对于习题图6.5所示的电路,求()v t 和()i t 为同相时的频率ω。
习题图6.5解:12()1Z (//)()v t jwL R L i t jwC==++ 121,1,1,1L H L H C F R ====Ω将代入2221Z ()11w w j w w w w-=+-+++谐振时虚部为零,2101w w w w -+=+ 0.7861w =得出,6.6 并联RLC 网络有R=50Ω,L 4mH =,C=160F μ,求并联电路谐振频率和品质因数。
若外接电流源有效值为2A ,求谐振时电阻、电感及电容上的电流值。
解:电路的谐振角频率30 1.2510rad /s LCω==⨯ 品质因数010LQ CR RCω=== 谐振时电阻、电感及电容上的电流值2A,20A R L C R I I I I Q ====g6.7 并联谐振电路,其品质因数为120,谐振频率是6610/rad s ⨯,计算其带宽。
电路分析基础第6章习题答案 ppt课件
7
dt
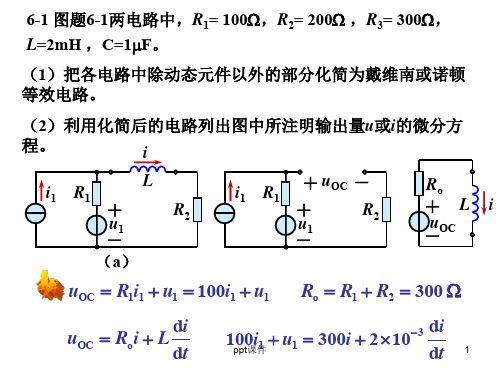
6-4 图题6-4所示电路中,各电源均在 t =0时开始作用于电路,
求 i (t),已知电容电压初始值为零。
i(t)
i(t)
4k +
1V -
1mA
4k
+
6k
+
uOC
2F
1V-
-
1mA 6k
把除电容元件以外的电路进行戴维南变换
(1 4k
1 6k
)uOC
10 3
1 4k
uOC 3 V
+
4
u
i1(t)
-
18
6-9 电路如图题6-8所示,电压源于 t =0 时开始作用于电路,试 求i (t),t≥0。
-10i1(t)+
4A 4 2H i1(t) i(t)
14
+
2H
-56V i(t)
时间常数为: 2 1 s
14 7
稳态时 i() 56 4 A 14
t
i(t) i()(1 e ) 4(1 e 7t ) V t≥0
4
103
ppt课件
(0.5
0.75e
208.3t
)
mA
t≥0
9
6-5 电路如图题6-5所示,开关在 t =0时闭合,求t=15s时ua及
各支路电流。 设电容的初始储能为零
+200V 60k 40k
6k 1000pF
+ ua uC -
-300V
时间常数为: RoC (60k // 40k 6k)109 3105 s
1.5 1.25 1.2 16
6-8 电路如图题6-7所示,电压源于 t =0 时开始作用于电路,试
电路与模拟电子技术基础(第2版)_习题解答_第6章习题解答
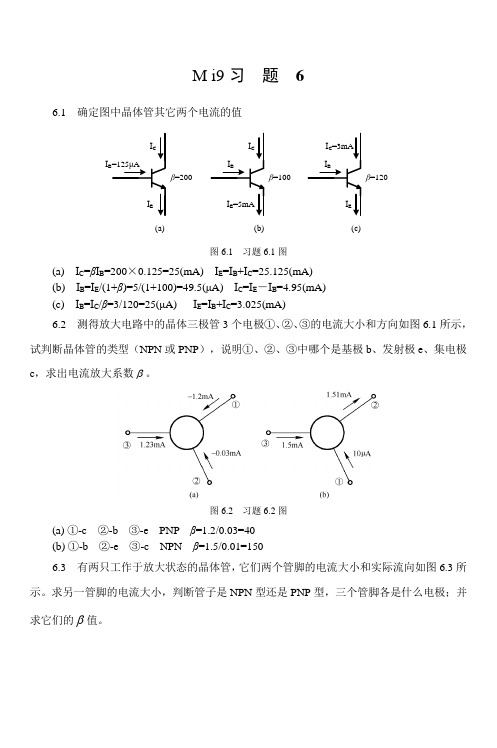
M i9习 题 66.1 确定图中晶体管其它两个电流的值β=200Iβ=100β=120(a)(b)(c)图6.1 习题6.1图(a) I C =βI B =200×0.125=25(mA) I E =I B +I C =25.125(mA) (b) I B =I E /(1+β)=5/(1+100)=49.5(μA) I C =I E -I B =4.95(mA) (c) I B =I C /β=3/120=25(μA) I E =I B +I C =3.025(mA)6.2 测得放大电路中的晶体三极管3个电极①、②、③的电流大小和方向如图6.1所示,试判断晶体管的类型(NPN或PNP ),说明①、②、③中哪个是基极b 、发射极e 、集电极c ,求出电流放大系数β。
图6.2 习题6.2图(a) ①-c ②-b ③-e PNP β=1.2/0.03=40 (b) ①-b ②-e ③-c NPN β=1.5/0.01=1506.3 有两只工作于放大状态的晶体管,它们两个管脚的电流大小和实际流向如图6.3所示。
求另一管脚的电流大小,判断管子是NPN 型还是PNP 型,三个管脚各是什么电极;并求它们的β值。
①② ③(a)①② ③(b)图6.3 习题6.3图(a) ①-c ②-e ③-b NPN I E =I B +I C =4+0.1=4.1(mA) β=4/0.1=40 (b) ①-e ②-c ③-b NPN I C =I E -I B =5.1-0.1=5(mA) β=5/0.1=506.4 试判断图6.4所示电路中开关S 放在1、2、3哪个位置时的I B 最大;放在哪个位置时的I B 最小,为什么?+V CC图6.4 习题6.4图在①时,发射极相当于一个二级管导通,此时I B 就等于此导通电流。
在②时,三极管相当于两个并联的二极管,此时I B 等于两个二级管导通电流之和,所以此时的电流最大。
万里学院-数字电子技术基础-第六章习题及参考答案

第六章习题一、选择题 1. PROM和 PAL的结构是。
A.PROM的与阵列固定,不可编程B. PROM 与阵列、或阵列均不可编程C.PAL 与阵列、或阵列均可编程D. PAL 的与阵列可编程 2. PAL是指。
A.可编程逻辑阵列B. 可编程阵列逻辑C. 通用阵列逻辑D. 只读存储器 3.当用异步 I/O 输出结构的 PAL 设计逻辑电路时,它们相当于。
A. 组合逻辑电路B. 时序逻辑电路C. 存储器D. 数模转换器 4. PLD器件的基本结构组成有。
A. 输出电路B. 或阵列C. 与阵列D. 输入缓冲电路5. PLD器件的主要优点有。
A. 集成密度高B. 可改写C. 可硬件加密D. 便于仿真测试 6. GAL的输出电路是。
A.OLMCB. 固定的C. 只可一次编程D. 可重复编程7. PLD开发系统需要有。
A. 计算机B. 操作系统C. 编程器D. 开发软件 8.只可进行一次编程的可编程器件有。
A.PALB.GALC.PROMD.PLD 9.可重复进行编程的可编程器件有。
A.PALB.GALC.PROMD.ISP-PLD 10. ISP-PLD 器件开发系统的组成有。
A. 计算机B. 编程器C. 开发软件D. 编程电缆 11.全场可编程(与、或阵列皆可编程)的可编程逻辑器件有。
A.PALB.GALC.PROMD.PLA12.GAL16V8 的最多输入输出端个数为。
A.8 输入 8 输出B.10 输入 10 输出C.16 输入 8 输出D.16 输入 1 输出 13 一个容量为 1K×8 的存储器有个存储单元。
A.8B. 8192C.8000D. 8K14.要构成容量为 4K× 8 的 RAM,需要片容量为 256× 4 的 RAM。
A. 8B.4C. 2D.32 15.寻址容量为 16K× 8 的 RAM需要根地址线。
A. 8B. 4C.14D.16KE. 1616.RAM的地址码有 8 位,行、列地址译码器输入端都为 4 个,则它们的字线加条。
电路与电子技术基础第6章习题参考答案

习题六6-1 (1) A; (2) C; (3) B; (4) C; (5) A6-2,黑表笔插入COM,红表笔插入V/Ω(红笔的极性为“+”),将表笔连接在二极管,其读数为二极管正向压降的近似值。
用模拟万用表测量二极管时,万用表内的电池正极与黑色表笔相连;负极与红表笔相连。
测试二极管时,将万用表拨至R×1k档,将两表笔连接在二极管两端,然后再调换方向,若一个是高阻,一个是低阻,则证明二极管是好的。
当确定了二极管是好的以后就非常容易确定极性,在低阻时,与黑表笔连接的就是二极管正极。
6-3 什么是PN结的击穿现象,击穿有哪两种。
击穿是否意味着PN结坏了?为什么?答:当PN结加反向电压(P极接电源负极,N极接电源正极)超过一定的时候,反向电流突然急剧增加,这种现象叫做PN结的反向击穿。
击穿分为齐纳击穿和雪崩击穿两种,齐纳击穿是由于PN结中的掺杂浓度过高引起的,而雪崩击穿则是由于强电场引起的。
PN 结的击穿并不意味着PN结坏了,只要能够控制流过PN结的电流在PN结的允许范围内,不会使PN结过热而烧坏,则PN结的性能是可以恢复正常的,稳压二极管正式利用了二极管的反向特性,才能保证输出电压的稳定。
对于图(a)假定D1、D2、D3截止,输出端的电位为-18V,而D1、D2、D3的阳极电位分别是-6V、0V、-6V,因此,理论上D1、D2、D3都能导通,假定D1导通,则输出点的电位为-6V,由于该点电位也是D2的阴极电位,因此D2会导通,一旦D2导通,u O点的电位就为0V,因此,D1、D3的阴极电位为0V,而阳极端为-6V,这样D1、D3必定截止,所以输出电压u o=0V(这就是脉冲数字电路中的或门,0V为高电平,-6V为低电平,只要输入端有一个高电平,输出就为高电平)。
对于图(b)依同样的道理可知:D1、D2、D3的阳极电位都低于+18V,所以三个二极管均截止,流过R的电流为0,故输出电位u o=18V试分析图(b)中的三个二极管极性都反过来,输出电压u o=?6-5 现有两只稳压二极管,它们的稳定电压分别为5V和9V,正向导通电压为0.7V。
技校电工基础习题及答案(第六章 三相交流电路)

第六章三相交流电路§6-1 三相交流电源一、填空题1.三相交流电源是三个大小相等、频率相同而相位互差120°的单相交流电源按一定方式的组合。
2.由三根相线和一根中性线所组成的供电线路,称为三相四线制电网。
三相电动势到达最大值的先后次序称为相序。
3.三相四线制供电系统可输出两种电压供用户选择,即线电压和相电压。
这两种电压的数值关系是U线=U相,相位关系是U线超前U相30°。
4.如果对称三相交流电源的U相电动势e u=E m sin (314t+)V,那么其余两相电动势分别为ev= E m sin (314t-90°)V,ew =E m sin (314t+150°) V。
二、判断题1.一个三相四线制供电线路中,若相电压为220 V,则电路线电压为311 V。
( × )2.三相负载越接近对称,中线电流就越小。
( √ )3.两根相线之间的电压叫相电压。
( × )4.三相交流电源是由频率、有效值、相位都相同的三个单个交流电源按一定方式组合起来的。
( × )三、选择题1.某三相对称电源电压为380 V,则其线电压的最大值为( A )V。
A.380 B.380 c.380 D.2.已知在对称三相电压中,V相电压为u v=220sin(314t+π)V,则U相和W相电压为(B)V。
A. U u=220sin (314t+) u w=220sin (314t-)B.u u=220sin (314t-) u w=220 sin (314t+)C.u u=220sin (314t+) uw=220sin (314t-)3.三相交流电相序U-V-W-U属( A )。
A.正序 B.负序 C.零序4.在如图6-1所示三相四线制电源中,用电压表测量电源线的电压以确定零线,测量结果U12=380 V,U23 =220 V,则( B )。
A.2号为零线B.3号为零线 C.4号为零线5.已知某三相发电机绕组连接成星形时的相电压u u=220sin(314t+300)V,u v=220sin(314t - 900)V,u w=220sin (314t+1500)V,则当t=10 s时,它们之和为(B)V。
电路与电子技术——电路基础知到章节答案智慧树2023年中国石油大学(华东)

电路与电子技术——电路基础知到章节测试答案智慧树2023年最新中国石油大学(华东)第一章测试1.在图示电路中,器件A两端的电压和电流参考方向属于()。
参考答案:关联参考方向2.使用理想独立电压源的定义判断下列那个选项的电压源连接是被允许()。
参考答案:3.图中流过电阻的电流I=( )A。
参考答案:24.某电阻R两端的电压u与流过该电阻的电流i为非关联参考方向时,令u=-10V,消耗功率为0.5W,则电阻R为()。
参考答案:200Ω5.电路如图所示,流过受控源两端的电流I=( )A。
参考答案:26.图示电路中I = 0 A 时,电位UA=()。
参考答案:60 V7.沿顺时针和逆时针列写KVL方程,其结果是相同的。
()参考答案:对8.电路如图所示,已知U s=3V,I s=2A,则U AB=( )V;I=( )A。
参考答案:1;59.图示电路中,正确的电压方程是()。
参考答案:U S1-R1I1-U S2-R2I2=010.已知图中的I=3A,I2=1A,R1=2Ω,则R2=()Ω。
参考答案:4第二章测试1.下列说法中错误的是()。
参考答案:两个电路N1、N2等效时,电路内部的同一元件的功率一定相同2.ab端口的等效电阻为()Ω。
参考答案:103.对称Y形和对称Δ形纯电阻网络等效变换的公式为R Y=3RΔ。
参考答案:错4.ab在下图电路中,电流源与1欧姆电阻的串联电路等效为()。
参考答案:4A电流源5.图示电路中,对负载R而言,虚线框中的电路可以等效为()。
参考答案:10V电压源6.理想电压源和理想电流源间()。
参考答案:没有等效变换关系7.图示两个电路是等效的。
()参考答案:错8.若图示两电路等效,则U s=()V,R s=()Ω。
参考答案:8;29.一个含独立源的电阻性线性二端网络(可以含受控源)总可以等效为一个电压源与一个电阻串联或一个电流源与一个电阻并联。
()参考答案:错10.如图所示电路的等效电阻为参考答案:对第三章测试1.现用支路电流法求解图示电路,下面描述正确的是()。
电路分析基础(第四版)张永瑞答案第6章

29
第6 章
电路频率响应
题6.6图
30
第6 章
电路频率响应
解 并接Yx前电路处于谐振, 电容上电压应是电源电
压Q倍, 所以
U C 10 Q 100 U s 0.1
r 1 Q0C 1 20 6 12 100 2 3.14 10 80 10
31
第6 章
电路频率响应
H (j )
1 1 2 2
解得
c
R12 R2 2 2 R1 R2 rad/ s R1 R2C
28
第6 章
电路频率响应
6.6 在图示的rLC串联谐振电路中, 电源频率为1 MHz, 电源有效值Us=0.1 V, 当可变电容器调到C=80 pF时, 电路达 谐振。 此时, ab端的电压有效值UC=10 V。 然后, 在ab端之 间接一未知的导纳Yx, 并重新调节C使电路谐振, 此时电容 值为60 pF, 且UC=8 V。 试求所并接Yx中的电导Gx、 电容Cx, 电路中电感L和并接Yx前、 后的电路通频带BW。
10
第6 章
电路频率响应
题解6.2图
11
第6 章
电路频率响应
所以欲满足上述条件, 必须使
R RL 2 ( ) 1 cCRRL
则该网络的截止角频率
R RL c rad/ s RRLC
(3)
12
第6 章
电路频率响应
将式(3)代入H(jω)式中, 得
H (j )
c 1 j( )
电路频率响应
6.11 某电视接收机输入电路的次级为并联谐振电路,
如题6.11图所示。 已知电容C=10 pF, 回路的谐振频率f0=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章习题6.1 求习题图6.1所示的电路的传递函数()/o i H V V ω=gg。
习题图6.1解:1//()i o oR V V jwCjwLV -=g gg22()oi V j L RLCH R j L RLCV ωωωωω-==+-gg 6.2 对于习题图6.2所示的电路,求传递函数()o iI H I ω=gg。
习题图6.2解:2()11o iI R j CRH j CR CL I jwL R jwCωωωω===-+++gg6.3 串联RLC 网络有R=5Ω,L=10mH ,C=1F μ,求该电路的谐振角频率、特征阻抗和品质因数。
当外加电压有效值为24V 时,求谐振电流、电感和电容上的电压值。
解:电路的谐振角频率4010/rad s LCω== 特征阻抗100LCρ==Ω 品质因数020LQ Rω==谐振电流0 4.8mU I A R== 电感和电容上的电压值L 480V C m U U U Q ===6.4 设计一个串联RLC 电路,使其谐振频率050/rad s ω=,品质因数为80,且谐振时的阻抗为10Ω,并求其带宽。
解:00.625rad /B s Qω==6.5 对于习题图6.5所示的电路,求()v t 和()i t 为同相时的频率ω。
习题图6.5解:12()1Z (//)()v t jwL R L i t jwC==++ 121,1,1,1L H L H C F R ====Ω将代入2221Z ()11w w j w w w w-=+-+++谐振时虚部为零,2101w w w w -+=+ 0.7861w =得出,6.6 并联RLC 网络有R=50Ω,L 4mH =,C=160F μ,求并联电路谐振频率和品质因数。
若外接电流源有效值为2A ,求谐振时电阻、电感及电容上的电流值。
解:电路的谐振角频率30 1.2510rad /s LCω==⨯ 品质因数010LQ CR RCω=== 谐振时电阻、电感及电容上的电流值2A,20A R L C R I I I I Q ====g6.7 并联谐振电路,其品质因数为120,谐振频率是6610/rad s ⨯,计算其带宽。
解:40510rad /B s Qω==⨯6.8 计算习题图6.8所示的电路的谐振角频率0ω,品质因数Q 和带宽B 。
习题图6.8解:1212121111(//)()C C Y jw C C j w jwL R R C C wL=++=+-+ 谐振时Y 的虚部为0121210C C wC C wL-=+得出5krad /s w ==0012(//)20Q RC R C C ωω===250rad /B s Qω==6.9 习题图6.9所示的电路,已知电容值C 为固定,欲使电路在1ω时发生并联谐振,而在2ω时发生串联谐振,求12L L 、的值。
习题图6.9解:12w w ==得出,1222221111,L ()CL w w C w ==- 6.10 一个电子检测电路产生的谐振曲线其半功率频率是432Hz 和454Hz ,若Q=20,求电路的谐振频率是多少?解:1222,f B f f kHZ B Q=-==得出,电路的谐振频率440f Hz =6.11 一台电子设备中,用了一个串联的RLC 电路,其电阻为100Ω,在2MHz 时的容抗是3.6k Ω,感抗是100Ω,求电路的谐振频率。
解:2,2f MH w f π==13.6,100L C X wL k X wC==Ω==Ω那么012MHz w == 6.12 如习题图6.12所示的滤波器,确实该滤波器的类型,并计算其截止频率。
习题图 6.12解:()o iV j LH R j LV ωωω==+gg(0)0,()1,H H =∞=该滤波器的类型为高通滤波器,2,318.47Hz 2c c C C R R w w f f L Lππ==== 6.13 如习题图 6.13所示的RL 串联高通滤波器,其截止频率为100kHz ,L=40mH ,求R 。
习题图 6.13解:,2,225.12k c c C C Rw w f R f L Lππ====Ω 6.14 设计一个RLC 串联带通滤波器,通带带宽为1kHz ,中心频率为10kHz ,假定C=80pF ,求R ,L 。
解:010kHzf =0002w w f π== 得出2013.169H (2)L f Cπ== 1,B kHZ R B L ==⋅得出 3.169k R =Ω6.15 求习题图6.15所示的有源滤波器的传递函数,并确定其滤波器的类型。
习题图 6.14解:01()1f i if i f i i fV H C R V j C R R C j C R ωωω==-++gg,带通滤波器6.16 设计一个有源低通滤波器,直流幅度增益为0.25,截止频率为500Hz 。
解:20k f R =Ω选取0.25,80k f i iR k R ===Ω则R1500Hz,2,c c c c f ff w f w R C π===115.92nF 2f c fC f R π==则6.17 设计一个有源高通滤波器,高频幅度增益为5,截止频率为200Hz 。
解:10k f R =Ω选取5,2k f i iR k R ===Ω则R1200Hz,2,c c c c i if w f w R C π===10.398F 2i c iC f R μπ==则6.18 对于习题图6.18所示的电路,计算三个串联电感的总电感量。
习题图 6.18解:1231238H,10H,6H,3H,3H,2H L L L M M M ======121323L L L L L L 与,与不是同名端,与互为同名端那么三个串联电感的总电感量:123123222L L L L M M M =++-+-20H L =6.19 对于习题图6.19所示的电路,计算耦合线圈的总电感量。
(a) (b)习题图 6.19解:(a)2 12121214.875H112L L ML ML L ML M L M-=+==+-+-+(b)212122.46H2L L MLL L M-==++6.20 对于习题6.20所示的电路,写出1212V V I Ig g gg和与和的关系式。
习题图 6.20解:对于线圈1、2所在的回路,分别列基尔霍夫电压方程(向量形式)11112()V I R j L I j Mωω=+-g g g21222()V I j M I R j Lωω=-++g g g6.21 求习题图6.21所示的电路中的oIg。
习题图6.21解:011()()m I R j L I j L j C j Cωωωω++=+gg 0(1/)1/m j I L C I R j L j Cωωωω-=++gg6.22 求习题图6.22所示的电路中的o I g。
习题图6.22解:12(506040202)(60203010)(40201030)0o I j j j j I j j j j I j j j j -++-⨯---+---+=g g g102(6010080302)(60203010)(80301020)0I j j j I j j j j I j j j j ++-⨯---+---+=ggg210(4080102)50(80103020)(40201030)0I j j j I j j j j I j j j j +-⨯----+---+=g g g3.199175.2A o o I =∠-g得出6.23 求习题图6.23所示的电路中的o I g。
习题图6.23解:120.601k L L == 17jwM j =得出01(1040)170I j I j +-=gg101(2030)17(4)500I j j I j I --+-=ggg得出0 3.75536.34A oI =∠-g6.24 求习题图6.24中a ,b 两端的戴维南等效电路。
习题图6.24解:2(625)//(8232) 2.33268.39oTh Z j j j j j j =+-+--+=∠-Ω(86223)2402109050I j j j j I I +-⨯--⨯∠++∠+=gggoo(562)10 5.5434.51V o Th V I j j j =+--=∠gg( 5.34934.11V oTh V =∠g 2.33250o Th Z =∠Ω)6.25 求习题图6.25中a ,b 两端的诺顿等效电路。
习题图6.25解: 4(20105)(205)600Th Th I j j I j j +-+-=∠ggo0.68723.63A o Th I =∠-g,(205)(20105)//(205)19.52666.37oTh Z j j j j j j =-++--=∠-(0.68723.63A o Th I =∠-g,24.5239.21o Th Z =∠)6.26 求习题图6.26电路中的1I g和2I g。
习题图6.26解:122:3:1,2N N R ==Ω2i 2318R ==Ω归算到一次侧的入端阻抗R1114A 0.5A1018s i U R R ===++gg则一次侧的电流I 123I I =-g g得出120.5A, 1.5A I I ==-gg6.27 对于习题图6.27所示的电路,求o V g。
习题图6.27解:3111052010j jwC j -==-⨯⨯11s 2020I V -+=gg00100s I j V u -+-=ggg123u u =gg123I I =-g g02.96332.9V o V =∠g得出,6.28 对于习题图6.28所示的电路。
(1)求给负载200Ω提供最大功率时,匝数2N 的值。
(2)若210N =,求200Ω负载的功率。
习题图6.28解:(1) 22200I u =gg110130I I V u -+=gggg(4-)5 212N u u =gg122N I I =gg20022Ω2002N 5P Ω=得出,取最大值时,(2)若210N =,可得20.2A,800W I P ==g6.29 对于习题图6.29所示的电路,求传送到s Z 上的平均功率。
习题图6.29解:12:1:10,500200s N N Z j ==-Ω2i s /1052Z Z j ==-Ω归算到一次侧的入端阻抗114.5514si pU Z Z ==∠-+ggo则一次侧的电流I 传送到s Z 上的平均功率2211114.555W=529.4W 22s i i P P I Z ===⨯⨯ 6.30 求习题图6.30所示的电路中传送到每个电阻的平均功率。
