统计学第四章测试答案
人大版统计学 习题加答案第四章 假设检验

第四章 假设检验填空(5题/章),选择(5题/章),判断(5题/章),计算(3题/章) 一、填空1、在做假设检验时容易犯的两类错误是 和2、如果提出的原假设是总体参数等于某一数值,这种假设检验称为 ,若提出的原假设是总体参数大于或小于某一数值,这种假设检验称为3、假设检验有两类错误,分别是 也叫第一类错误,它是指原假设H0是 的,却由于样本缘故做出了 H0的错误;和 叫第二类错误,它是指原假设H0是 的, 却由于样本缘故做出 H0的错误。
4、在统计假设检验中,控制犯第一类错误的概率不超过某个规定值α,则α称为 。
5、 假设检验的统计思想是小概率事件在一次试验中可以认为基本上是不会发生的,该原理称为 。
6、从一批零件中抽取100个测其直径,测得平均直径为5.2cm ,标准差为1.6cm ,想知道这批零件的直径是否服从标准直径5cm ,在显著性水平α下,否定域为7、有一批电子零件,质量检查员必须判断是否合格,假设此电子零件的使用时间大于或等于1000,则为合格,小于1000小时,则为不合格,那么可以提出的假设为 。
(用H 0,H 1表示)8、一般在样本的容量被确定后,犯第一类错误的概率为α,犯第二类错误的概率为β,若减少α,则β9、某厂家想要调查职工的工作效率,用方差衡量工作效率差异,工厂预计的工作效率为至少制作零件20个/小时,随机抽样30位职工进行调查,得到样本方差为5,试在显著水平为0.05的要求下,问该工厂的职工的工作效率 (有,没有)达到该标准。
KEY: 1、弃真错误,纳伪错误 2、双边检验,单边检验3、拒真错误,真实的,拒绝,取伪错误,不真实的,接受4、显著性水平5、小概率事件6、1.25>21α-z7、H 0:t≥1000 H 1:t <1000 8、增大 9、有二、 选择1、假设检验中,犯了原假设H 0实际是不真实的,却由于样本的缘故而做出的接受H 0的错误,此类错误是( )A 、α类错误B 、第一类错误C 、取伪错误D 、弃真错误 2、一种零件的标准长度5cm ,要检验某天生产的零件是否符合标准要求,建立的原假设和备选假设就为( )A 、0:5H μ=,1:5H μ≠B 、0:5H μ≠,1:5H μ>C 、0:5H μ≤,1:5H μ>D 、0:5H μ≥,1:5H μ< 3、一个95%的置信区间是指( ) A 、总体参数有95%的概率落在这一区间内 B 、总体参数有5%的概率未落在这一区间内C 、在用同样方法构造的总体参数的多个区间中,有95%的区间包含该总体参数D 、在用同样方法构造的总体参数的多个区间中,有95%的区间不包含该总体参数4、假设检验中,如果增大样本容量,则犯两类错误的概率( ) A 、都增大 B 、都减小 C 、都不变 D 、一个增大一个减小5、一家汽车生产企业在广告中宣称“该公司的汽车可以保证在2年或24000公里内无事故”,但该汽车的一个经销商认为保证“2年”这一项是不必要的,因为汽车车主在2年内行驶的平均里程超过24000公里。
统计学第四章课后题及答案解析

第四章一、单项选择题1.由反映总体单位某一数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占比重之和等于1或100%的相对数()A.比例相对数B.比较相对数C.结构相对数D.动态相对数3.某企业工人劳动生产率计划提高5%,实际提高了10%,则提高劳动生产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A.只存在一个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.大量的B.同质的C.有差异的D.不同总体的7.几何平均数的计算适用于求()A.平均速度和平均比率B.平均增长水平C.平均发展水平D.序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.方差B.极差C.标准差D.变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采用()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。
《统计学原理》第四章习题及答案

111%
111%
113%
17:权数对算术平均数的影响作用,实质上取 决于( A)。 A、作为权数的各组单位数占总体单位数比重的 大小 B、各组标志值占总体标志总量比重的大小 C、标志值本身的大小 D、标志值数量的多少
《统计学原理》第四章习题
一.判断题部分 1:同一个总体,时期指标值的大小与时期 长短成正比,时点指标值的大小与时点间 隔成反比。( × ) 2:全国粮食总产量与全国人口对比计算的 人均粮食产量是平均指标。( × )
3:根据分组资料计算算术平均数,当各组 单位数出现的次数均相等时,按加权算数 平均数计算的结果与按简单算数平均数计 算的结果相同。( √ ) 4:同一总体的一部分数值与另一部分数值 对比得到的相对指标是比较相对指标。 (×)
26、第一批产品废品率1%,第二批产品 废品率1.5%,第三批产品废品率2%, 第一批产品数量占总数的25%,第二批 产品数量占总数的30%,则平均废品率 为(C)。
A、1.5% C、1.6% B、4% D、4.5%
27、某企业工人劳动生产率,计划提高5 %,实际提高了10%,则提高劳动生产 率的计划完成程度为(A)。 A、104.76% B、95.45% C、200% D、76%
A . 500 700 600 500 700 600 110 % 115 % 105 %
110 % 500 115 % 700 105 % 600 B . 500 700 600
110 % 115 % 105 % C . 3 10 % 15 % 5 % D . 3
第四章统计学基础课后习题答案

第四章综合指标一、单选题1.B 2.D 3.D 4.D 5.B二、多选题1.BDE 2.BCE 3.AC三、简答题1.总量指标是反映现象总体在一定时间、地点条件下的总规模和总水平的指标。
总量指标的作用:(1)反映社会经济现象总体的基本状况和基本实力;(2)计算相对指标和平均指标的基础。
2.结构相对指标将总体分为性质不同的部分,用各部分和总体数值对比;比例相对指标是同一总体两个不同部分之间的数值对比;比较相对指标是用两个不同总体的同类指标数值对比。
3.强度相对指标是对两个性质不同而又有密切联系的指标进行对比,反映现象强度、密度、或普及程度的相对指标。
在表现形式上同平均指标类似,单平均指标是总体标志总量处以总体单位个数,强度相对指标是两个不同性质单密切联系的总体指标之比。
4.时点指标和时期指标的区别:(1)时期指标具有可加性,不同时期的指标数值相加表明较长时期的总量。
时点指标不具有可加性;(2)时期指标的数值大小和时间长短有关,时点指标则无关;(3)时期指标的数值可以连续计数,时点指标的数值只能间断计数。
5.权数可理解为对计算结果的影响因素,在数据未分组时可用简单算术平均,对分组数据适用加权算术平均。
在各数据的权数都为1时两者相等。
6.联系:两者都是平均指标的一种,调和平均数作为算术平均数的变形使用区别:(1)变量不同:算术平均数是x,调和平均数是1/x 。
(2)权数不同:算术平均数是f或n,代表次数(单位数),调和平均数是xf 或M,代表标志总量。
四、计算题1.(1)结构指标:男性人口(女性人口)/人口总数×100%(2)比例指标:男性人口/女性人口×100%、女性人口/男性人口×100%(3)动态指标:1990年人口总数/1982年人口总数×100%-1等2.3.单位成本的计划数=520×(1-5%)=494 元单位成本的实际数=520×(1-6%)=488.8元降低成本计划完成程度=(1-6%)/(1-5%)×100%=98.95%超额完成了1.05%。
《统计学原理》第四章习题

《统计学原理》第四章习题及答案一.判断题部分题目1:同一个总体,时期指标值的大小与时期长短成正比,时点指标值的大小与时点间隔成反比。
()题目2:全国粮食总产量与全国人口对比计算的人均粮食产量是平均指标。
()题目3:根据分组资料计算算术平均数,当各组单位数出现的次数均相等时,按加权算数平均数计算的结果与按简单算数平均数计算的结果相同。
()题目4:同一总体的一部分数值与另一部分数值对比得到的相对指标是比较相对指标。
()题目5:某年甲、乙两地社会商品零售额之比为1:3,这是一个比例相对指标。
()题目6:某企业生产某种产品的单位成本,计划在上年的基础上降低2%,实际降低了3%,则该企业差一个百分点,没有完成计划任务。
()题目7:标准差系数是标准差与平均数之比,它说明了单位标准差下的平均水平。
()题目8:1999年与1998年相比,甲企业工人劳动生产率是乙企业的一倍,这是比较相对指标。
()题目9:中位数与众数都是位置平均数,因此用这两个指标反映现象的一般水平缺乏代表性。
()题目10:对两个性质相同的变量数列比较其平均数的代表性,都可以采用标准差指标。
()题目11:利用变异指标比较两总体平均数的代表性时,标准差越小,说明平均数的代表性越大;标准差系数越小,则说明平均数的代表性越小。
()题目12:标志变异指标数值越大,说明总体中各单位标志值的变异程度越大,则平均指标的代表性越小。
()题目13:权数对算数平均数的影响作用只表现为各组出现次数的多少,与各组次数占总次数的比重无关。
()题目14;能计算总量指标的总体必须是有限总体。
()二.单项选择题题目1:反映社会经济现象发展总规模、总水平的综合指标是()。
A、质量指标B、总量指标C、相对指标D、平均指标题目2:总量指标按反映时间状况的不同,分为()。
A、数量指标和质量指标B、时期指标和时点指标C、总体单位总量和总体标志总量D、实物指标和价值指标题目3:总量指标是用()表示的。
统计学第四章习题答案
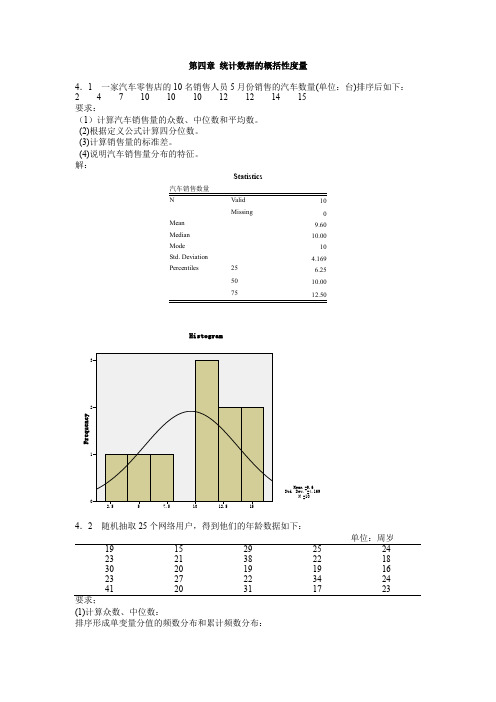
第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing0Mean9.60Median10.00Mode10Std. Deviation 4.169Percentiles25 6.255010.0075单位:周岁19152925242321382218302019191623272234244120311723要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客。
《统计学》题库第四章

一、单项选择题1. 设B A 、表示事件,则=+B A ( )A.B AB.B AC.ABD.B A +答案:B2. 某人射击三次,以A i 表示事件“第i 次击中目标”(i=1,2,3),则事件“至多击中目标一次”的正确表达式为( )A.321A A AB.313221A A A A A AC.321321321A A A A A A A A AD.321A A A答案:B3. 袋中有10个形状相同的小球,其中4白6黑,现随机地将球一个一个地取出,则第4次取得白球的概率为( )A.101 B.102C.103D.104 答案:D 4. 线路由A ,B 两元件并联组成(如图)A ,B 元件独立工作,A 正常工作的概率为p ,B 正常工作的概率为q ,则此线路正常工作的概率为( )A. pqB. p+qC. p+q-pqD.1-pq答案:C 5. 设A ,B ,C 表示三个事件,则C B A 表示( )A.A ,B ,C 中有一个发生B.A ,B ,C 中不多于一个发生C.A ,B ,C 中恰有两个发生D.A ,B ,C 都不发生答案:D6. 设随机变量ξ可取无穷多个值:0,1,2,…,其概率分布为P (K ;3)=3k e !k 3- (即ξ~P (3))则下式成立的是( )A.E ξ=D ξ=3B.E ξ=D ξ=31 C.E ξ=3,D ξ=31D.E ξ=31,D ξ=3 答案:A7. 设随机变量ξ的分布列为P{ξ=k}=Ak,k=1,2,3,4,5,则常数A=( ) A.5 B.10C.15D.20答案:C 8. 设ξ的分布为则常数α=( ) A.0.1B.0.2C.0.3D.0.4答案:A9. 设ζ的分布列为则E ζ2=( ) A.-0.2 B.0.2 C.2.76 D.2.8答案:D10. 设随机变量ξ的密度函数p(x)=⎪⎩⎪⎨⎧∈ 其它 ,x ,Cx 0[0,1]4,则常数C =( )A .51B .41 C .4D .5答案:D11.设随机变量ζ的概率密度为p(x)=⎪⎩⎪⎨⎧<<-其他,0,21a x a a,其中A>0,要使P{ζ>1}=31,则A=( ) A.1B.2C.3D.4答案:C12.设ζ的分布函数为F(x)=A++∞<<∞-πx x arctan 1,则常数A=( )A.21B.1C.2D.π答案:A13. 独立随机变量ξ,η,若ξ~N (1,4),η~N (3,16),下式中不成立...的是( ) A .E (ξ+η)=4B .E (ξη)=3C .D (ξ-η)=12D .D (η+2)=16答案:C14.将一枚均匀硬币反复抛掷10次,已知前三次抛掷中恰出现了一次正面,则第二次出现正面的概率为( )A.31B.21C.41D.103 答案:A15. 13.设随机变量ζ的密度函数p(x)=⎩⎨⎧π∈其他,0],0[x ,ASinx ,则常数A=( )A.41B.21 C.1D.2答案:B16.设试验成功概率是p(0<p<1),则在三次重复独立试验中至少失败一次的概率是( ) A. (1-p)3 B. 1-p 3C. 3(1-p)D. (1-p)3+p(1-p)2+p 2(1-p)答案:B 17.设随机变量X 在[A ,B]上服从均匀分布,则其标准差)(X D 为 A.12/)(2a b -B. 6/)(2a b -C. 32/)(a b -D. 6/)(a b -答案:C18.设),(~2σμN X ,则=)(2X E A.22σμ+B. 2σμ+C.σμ+2D. σμ+答案:A19.若,2)(=X D 则=-)14(X D A.32B.8C. 2D. 31答案:A20.若,2)(,1)(==Y E X E 则=-)2(Y X E A.0B.-1C. 1D. 2答案:A二、多项选择题(略) 三、名词解释1.古典概型2.随机事件的独立性3.分布函数4.依概率收敛[参考答案]1.古典概型:古典概型是指满足下面两个特征的随机试验模型:1)样本空间是有限的,{}n ωωω,,,21 =Ω其中),,2,1(n i i =ω是样本点(基本随机事件);2)各基本事件的出现是等可能的,即它们发生的概率相同; 3)各基本事件互不相容,即);,,2,1,(j i n j i j i ≠=Φ= ωω2.随机事件的独立性:若事件A 、B 满足)()()(B P A P AB P =,称A 、B 相互独立。
统计学第4章练习题及答案

第4章 练习题 一、单项选择题1.平均指标反映了( )①总体次数分布的集中趋势 ②总体分布的特征③总体单位的集中趋势 ④总体次数分布的离中趋势2.某单位的生产小组工人工资资料如下:90元、100元、110元、120元、128元、148元、200元,计算结果均值为128=X 元,标准差为( )①σ=33 ②σ=34 ③σ=34.23 ④σ=35 3.众数是总体中下列哪项的标志值( ) ①位置居中 ②数值最大 ③出现次数较多 ④出现次数最多4.某工厂新工人月工资400元,工资总额为200000元,老工人月工资800元,工资总额80000元,则平均工资为( )①600元 ②533.33元 ③466.67元 ④500元5.标志变异指标说明变量的( )①变动趋势 ②集中趋势 ③离中趋势 ④一般趋势 6.标准差指标数值越小,则反映变量值( )①越分散,平均数代表性越低 ②越集中,平均数代表性越高 ③越分散,平均数代表性越高 ④越集中,平均数代表性越低 7.在抽样推断中应用比较广泛的指标是( )①全距 ②平均差 ③标准差 ④标准差系数二、多项选择题1.根据标志值在总体中所处的特殊位置确定的平均指标有( ) ①算术平均数 ②调和平均数 ③几何平均数 ④众数 ⑤中位数2.影响加权算术平均数的因素有( )①总体标志总量 ②分配数列中各组标志值③各组标志值出现的次数 ④各组单位数占总体单位数比重 ⑤权数3.标志变异指标有( )①全距 ②平均差 ③标准差 ④标准差系数 ⑤相关系数 4.在组距数列的条件下,计算中位数的公式为( )①i f S fL M mm e ⋅-+=+∑12②i f S fU M m m e ⋅-=∑12--③i f S fL M mm e ⋅-+=∑12- ④i f S fU M mm e ⋅-=+∑12-⑤i f S fU M mm e ⋅-=∑12-+5.几何平均数的计算公式有( )①n n n X X X X ⋅⋅⋅121-Λ ②nX X X X nn ⋅⋅⋅121-Λ③122121-++++n X X X X nn -Λ ④∑f fIIX ⑤n IIX三、计算题1.某企业360名工人生产某种产品的资料如表1:试分别计算7、8月份平均每人日产量,并简要说明8月份平均每人日产量变化的原因。
统计学课后习题答案第四章动态数列

精选文档第四章动态数列一﹑单项选择题以下动向数列中属于时点数列的是A.历年在校学生数动向数列B.历年毕业生人数动向数列C.某厂各年工业总产值数列D.某厂各年劳动生产率数列组成动向数列的两个基本因素是A. 主词和宾词B. 变量和次数C. 分组和次数D. 现象所属的时间及其指标值动向数列中各项指标数值能够相加的是A.相对数动向数列B.均匀数动向数列C. 期间数列D. 时点数列最基本的动向数列是A.指数数列B.相对数动向数列C. 均匀数动向数列D. 绝对数动向数列动向数列中,指标数值的大小与其时间长短没有直接关系的是A. 期间数列B. 时点数列C. 相对数动向数列D. 均匀数动向数列动向数列中,指标数值是经过连续不停登记获得的数列是A.期间数列B.时点数列C. 相对数动向数列D. 均匀数动向数列以下动向数列中属于期间数列的是A.公司历年员工人数数列B.公司历年劳动生产率数列C.公司历年利税额数列D.公司历年单位产品成本数列动向数列中,各项指标数值不可以够相加的是A. 相对数动向数列B. 绝对数动向数列C. 期间数列D. 时点数列动向数列中,指标数值大小与其时间长短相关的是A.相对数动向数列B.绝对数动向数列C. 期间数列D. 时点数列动向数列中,指标数值是经过一次登记获得的数列是A.相对数动向数列B.绝对数动向数列C. 期间数列D. 时点数列编制动向数列的最基来源则是保证数列中各项指标一定拥有A. 可加性B. 可比性C. 连续性D. 一致性基期为某一固准期间水平的增添量是A.累计增添量B.逐期增添量C.均匀增添量D. 年距增添量基期为先期水平的增添量是A.累计增添量B.逐期增添量C.均匀增添量D. 年距增添量累计增添量与逐期增添量之间的关系是A.累计增添量等于相应的各个逐期增添量之和.A.精选文档B.C.累计增添量等于相应的各个逐期增添量之差D.累计增添量等于相应的各个逐期增添量之商E.累计增添量等于相应的各个逐期增添量之积F.均匀增添量等于G. A.累计增添量 B. 逐期增添量H. C.逐期增添量之和除以逐期增添量的项 D. 以上均不对I.动向数列中的发展水平是指J. A.总量指标B.相对指标K. C.均匀指标 D. 以上指标均可L.进行动向剖析的基础指标是M. A.发展水平B.均匀发展水平N. C. 增添量 D. 均匀增添量O.动向数列的剖析指标主要包含两个类型,即P.发展水平易发展速度B.水平指标和速度指标Q. C.均匀发展水平易均匀发展速度D.增添量和增添速度R.序时均匀数和一般均匀数的共同点在于二者S.都是依据动向数列计算B.都是依据变量数列计算T.都是反应现象的一般水平D.均能够除去现象颠簸的影响U.依据期间数列计算序时均匀数应采纳V. A.简单算术均匀法B.加权算术均匀法W. C.简单序时均匀法 D. 加权序时均匀法X.依据间隔相等连续时点数列计算序时均匀数应采纳Y.简单算术均匀法B.加权算术均匀法Z.简单序时均匀法D.加权序时均匀法AA.依据间隔不相等连续时点数列计算序时均匀数应采纳BB.简单算术均匀法B.加权算术均匀法CC.简单序时均匀法D.加权序时均匀法DD.依据间隔相等中断时点数列计算序时均匀数应采纳EE.简单算术均匀法B.加权算术均匀法FF. C.简单序时均匀法 D. 加权序时均匀法GG.依据间隔不相等中断时点数列计算序时均匀数应采纳HH. A.简单算术均匀法B.加权算术均匀法II. C. 简单序时均匀法 D. 加权序时均匀法JJ.序时均匀数计算中,“首未折半法”运用于KK. A.期间数列的资料B.间隔相等的时点数列资料LL.间隔不等的时点数列资料MM. D.由两个时点数列组成的相对数动向数列NN.将研究对象在不一样时间上的数目差异抽象化,从动向上说明现象在某一期间内发展的一般水平的方法是OO. A.一般均匀数B.序时均匀数PP. C. 均匀发展速度 D. 均匀增添速度QQ.间隔不相等的中断时点数列计算均匀发展水平,应采纳RR.以每次改动连续的时间长度对各时点水平加权均匀SS.用各间隔长度对各间隔的均匀水平加权均匀.精选文档对各时点水平简单算术均匀以数列的总速度按几何均匀法计算依据采纳的对照基期不一样发展速度有环比发展速度与定基发展速度环比发展速度与环比增添速度C.定基发展速度与定基增添速度环比增添速度与定基增添速度发展速度的计算方法能够表述为报告期水平与基期水平之差B.增添量与基期水平之差C.报告期水平与基期水平之比D. 增添量与基期水平之比基期为前一期水平的发展速度是A.定基发展速度B.环比发展速度C.年距发展速度D. 均匀发展速度基期为某一固按期水平的发展速度是A.定基发展速度B.环比发展速度C.年距发展速度D. 均匀发展速度定基发展速度和环比发展速度的关系是两个相邻期间的定基发展速度之商等于相应的环比发展速度之差等于相应的环比发展速度C.之和等于相应的环比发展速度D.之积等于相应的环比发展速度增添速度是A.动向数列水平之差B.动向数列水平之比增添量同发展速度之比增添量同作为比较基准的数列水平之比定基增添速度与环比增添速度的关系表现为定基增添速度等于各环比增添速度的连乘积B.定基增添速度等于各环比增添速度的连乘积的n次方根各环比增添速度连乘积加一等于定基增添速度加一定基增添速度等于各环比增添速度加一后的连乘积减一既然总速度是环比发展速度的连乘积,那么均匀发展速度就应按A. 简单算术均匀数计算B. 加权算术均匀数计算C.几何均匀数计算D. 调解均匀数计算发展速度与增添速度的关系是定基发展速度等于环比增添速度加一环比增添速度等于环比发展速度减一C.定基增添速度的连乘积等于定基发展速度D.环比增添速度的连乘积等于环比发展速度动向数列中的均匀增添速度是各个期间环比增添速度的算术均匀数各个期间环比增添速度的调解均匀数C.各个期间环比增添速度的几何均匀数.精选文档D.各个期间环比增添速度的序时均匀数采纳几何均匀法计算均匀发展速度的原因是各期环比发展速度之积等于总速度各期环比发展速度之和等于总速度各期环比增添速度之积等于总速度各期环比增添速度之和等于总速度已知各期定基发展速度和期间数,而不知道各期水平要计算均匀发展速度A.只好用水平法计算B.只好用累计法计算C. 两种方法皆能计算D. 两种方法都没法计算已知各期间发展水平之和与最先水平实期间数,要计算均匀发展速度A.只好用水平法计算B.只好用累计法计算C. 两种方法皆能计算D. 两种方法都没法计算当动向数列剖析目的是重视于观察期未发展水平,则均匀发展速度A.应采纳算术均匀法计算B.应采纳调解均匀法计算C. 应采纳几何均匀法计算D. 应采纳方程式法计算当动向数列剖析目的是重视于观察整个期间中各年发展水平的总和,则均匀发展速度A.应采纳算术均匀法计算B.应采纳调解均匀法计算应采纳几何均匀法计算D.应采纳方程式法计算动向数列中的均匀发展速度等于各期间定基发展速度的序时均匀数各期间环比发展速度的序时均匀数各期间环比发展速度的算术均匀数D.各期间定基发展速度的算术均匀数几何均匀数所计算的均匀发展速度的数值大小不受最先水平易最未水平的影响只受中间各期发展水平的影响只受最先水平易最未水平的影响既受最先水平易最未水平的影响,又受中间各期发展水平的影响累计法计算均匀发展速度的本质是从最先水平出发按均匀增添量增添,经过n期,正好达到最未水平B.按均匀发展速度发展,经过n期,正好达到第n期本质水平按均匀发展速度计算获得的各期理论水平之和正好等于各期的本质水平总和按均匀发展速度发展获得的各期理论水平之和正好等于最未期的本质水平直线趋向方程YC=a+bx中a和b的意义是是截距,b表示X=0的趋向值表示最先发展水平的趋向值,b表示均匀发展水平表示最先发展水平的趋向值,b表示均匀发展速度.是直线的截距,表示最先发展水平的趋向值;b是直线的斜率,表示按最小平方法计算的均匀增添量47. 用最小平方法配合趋向直线方程Y C=a+bx在什么条件下,a=Y;b=ΣXY/ΣX2A.ΣX=0B.Σ(Y-Y)=0C.ΣY=0D.Σ(Y-Y)2=最小值二﹑多项选择题组成动向数列的两个基本因素是A.变量B.次数C.现象所属的时间D.现象所属的范围E.反应现象的统计指标数值动向数列按研究任务不一样能够分为A.绝对数动向数列B.均匀数动向数列C.相对数动向数列D.期间数列E.时点数列动向数列的作用表此刻A.描绘现象变化的过程B.说明现象发展的速度和趋向探究现象发展变化的规律性对现象的发展进行展望反应现象整体的散布特色期间数列的特色数列中各个指标数值能够相加数列中指标数值大小与其期间长短无直接关系数列中各个指标数值不可以相加数列中指标数值大小与其期间长短有直接关系数列中指标数值往常是经过连续不停登记而获得的时点数列的特色数列中各个指标数值能够相加数列中指标数值大小与此间隔长短无直接关系数列中各个指标数值不可以相加数列中指标数值大小与此间隔长短有直接关系E.数列中指标数值往常是经过中断登记而获得的以下动向数列中,各项指标数值不可以相加的有A.绝对数动向数列B.相对数动向数列B.均匀数动向数列 D.期间数列时点数列以下数列中,属于两个期间对照组成的相对数动向数列有A.全员劳动生产率动向数列B.百元产值收益率动向数列C.员工人数动向数列D.计划达成程度动向数列出勤率动向数列以下数列中属于期间数列的有A.历年年未人口总数B.历年出生人数B.历年工业增添值 D.各月商品库存量各月未银行存款余额以下数列中属于时点数列的有A.高校每年毕业生人数B.高校每年在校学生数C.银行每个月未银行存款余额D.商铺各月商品库存额.我国历年外汇贮备量编制动向数列应依照的原则有期间长短应当相等B.指标的经济内容应当同样C.整体范围应当一致D.指标的计算方法应当一致E.指标的计算价钱和计量单位应当一致动向数列中的水平剖析指标有A.发展水平B.均匀发展水平C.增添量D.均匀增添量E.均匀发展速度动向数列中的速度剖析指标有A.均匀发展水平B.增添速度C.均匀发展速度D.均匀增添速度E.发展速度以下指标中属于序时均匀数的有A.均匀发展水平B.均匀增添量C.均匀发展速度D.均匀增添速度E.均匀指标动向数列中的发展水平包含A.期初水平B.期未水平C.中间水平D.报告期水平E.基期水平将不一样期间的发展水平加以均匀所获得的均匀数称为A.一般均匀数B.算术均匀数C.序时均匀数D.动向均匀数E.均匀发展水平均匀增添量的计算公式是逐期增添量之和/逐期增添量项数逐期增添量的序时均匀数C.累计增添量/动向数列项数-1D.累计增添量/动向数列项数累计增添量/动向数列项数+1定基发展速度与环比发展速度之间的关系表现为A.两个相邻期间的定基发展速度之商等于相应的环比发展速度定基发展速度等于相应的各个环比发展速度的连乘积C.定基发展速度等于环比发展速度加一D.定基发展速度等于环比增添速度加一后的连乘积环比发展速度乘积等于总速度增添速度和发展速度的关系为A.仅差一个基数B.发展速度=增添速度+1C.定基增添速度=各环比增添速度的连乘积C.定基发展速度=定基增添速度+1定基增添速度=各环比发展速度的连乘积-1定基增添速度等于A.累计增添量除以基期发展水平B.定基发展速度减去一C.总速度减去一D.环比增添速度的连乘积逐期增添量除从先期发展水平环比增添速度等于A累计增添量除以基期发展水平 B.环比发展速度减去一.精选文档C.定基发展速度减去一D.环比增添速度的连乘积逐期增添量除从先期发展水平动向数列中的发展水平能够是A.总量指标B.相对指标C.均匀指标D.变异指标E.样本指标增添1%的绝对值等于累计增添量除以定基发展速度逐期增添量除以环比发展速度C.逐期增添量除以环比增添速度×100D.累计增添量除以定基增添速度×100E. 固按期水平除以100计算均匀发展速度的方法有A.几何均匀法B.水平法C.方程式法D.累计法E.序时均匀法均匀发展速度从广义上讲属于A.静态均匀数B.动向均匀数C.序时均匀数D.几何均匀数E.调解均匀数计算均匀发展速度的几何均匀法和方程式法的差异是A.数理依照不一样B.重视点不一样C.合用条件不一样D.合用范围不一样E.对资料要求不一样常用的长久趋向测定的方法有A.时距扩大法B.挪动均匀法C.分段均匀法D.最小平方法E.季节比率法直线趋向方程Y c=a+bx的参数b是表示A.趋向值B.趋向线的截距C.趋向线的斜率D.当X=0时的Y c的数值当X每改动一个单位时Y c均匀增减的数值三﹑填空题1.动向数列一般由两个基本因素组成,即和。
统计学第四章、第十章课后练习答案贾俊平第四版

?统计学?第四版统计学? 第四章练习题答案4.1 〔1 〕众数:M0=10; 中位数:中位数位置=n+1/2=5.5 ,Me=10 ;平均数:x=∑xni=96 = 9 .6 102(2)QL 位置=n/4=2.5, QL=4+7/2=5.5;QU 位置=3n/4=7.5,QU=12 〔3〕s =∑( xi ? x )n ?1=156.4 = 4.2 9〔4〕由于平均数小于中位数和众数,所以汽车销售量为左偏分布。
4.2 〔1〕从表中数据可以看出,年龄出现频数最多的是19 和23,故有个众数,即M0=19 和M0=23。
将原始数据排序后,计算中位数的位置为:中位数位置= n+1/2=13,第13 个位置上的数值为23,所以中位数为Me=23 〔2〕QL 位置=n/4=6.25, QL==19;QU 位置=3n/4=18.75,QU=26.5 ∑x (3)平均数x =ni= 600/25=24,标准差s =∑( xi ? x )n ?12=1062 = 6.65 25 ? 1〔4〕偏态系数SK=1.08,峰态系数K=0.77 〔5〕分析:从众数、中位数和平均数来看,网民年龄在23-24 岁的人数占多数。
由于标准差较大,说明网民年龄之间有较大差异。
从偏态系数来看,年龄分布为右偏,由于偏态系数大于1,所以,偏斜程度很大。
由于峰态系数为正值,所以为尖峰分布。
4.3 〔1〕茎叶图如下:茎 5 6 7 叶5 678 13488 频数1 3 52∑x 〔2〕x =ni= 63/9=7, s =∑( xi ? x )n ?1=4.08 = 0.714 8〔3〕由于两种排队方式的平均数不同,所以用离散系数进展比拟。
第一种排队方式:v1=1.97/7.2=0.274;v2=0.714/7=0.102.由于v1>v2,说明第一种排队方式的离散程度大于第二种排队方式。
〔4〕选方法二,因为第二种排队方式的平均等待时间较短,且离散程度小于第一种排队方式。
统计学课后第四章习题答案

第4章练习题1、一组数据中出现频数最多的变量值称为()A。
众数 B.中位数 C。
四分位数 D.平均数2、下列关于众数的叙述,不正确的是()A。
一组数据可能存在多个众数 B.众数主要适用于分类数据C。
一组数据的众数是唯一的 D。
众数不受极端值的影响3、一组数据排序后处于中间位置上的变量值称为()A。
众数 B.中位数 C。
四分位数 D.平均数4、一组数据排序后处于25%和75%位置上的值称为()A.众数 B。
中位数 C。
四分位数 D。
平均数5、非众数组的频数占总频数的比例称为()A.异众比率 B。
离散系数 C.平均差 D.标准差6、四分位差是()A.上四分位数减下四分位数的结果 B。
下四分位数减上四分位数的结果C。
下四分位数加上四分位数 D.下四分位数与上四分位数的中间值7、一组数据的最大值与最小值之差称为()A.平均差 B。
标准差 C.极差 D.四分位差8、各变量值与其平均数离差平方的平均数称为()A.极差B.平均差C.方差 D。
标准差9、变量值与其平均数的离差除以标准差后的值称为()A.标准分数B.离散系数 C。
方差 D.标准差10、如果一个数据的标准分数—2,表明该数据()A。
比平均数高出2个标准差 B.比平均数低2个标准差C。
等于2倍的平均数 D。
等于2倍的标准差11、经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围之内大约有()A.68%的数据B.95%的数据C.99%的数据D。
100%的数据12、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=4,其意义是()A。
至少有75%的数据落在平均数加减4个标准差的范围之内B。
至少有89%的数据落在平均数加减4个标准差的范围之内C. 至少有94%的数据落在平均数加减4个标准差的范围之内D。
至少有99%的数据落在平均数加减4个标准差的范围之内13、离散系数的主要用途是()A。
反映一组数据的离散程度 B。
反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平14、比较两组数据离散程度最适合的统计量是()A.极差B.平均差C.标准差 D。
统计学第四章在线作业

统计学第四章在线作业单选题1、男女性别比是一个( )A、比例相对指标B、比较相对指标C、强度相对指标D、结构相对指标你的答案: A2、下面属于时点指标的是( )A、商品销售额B、商品销售量C、商品价格D、营业员人数你的答案: D3、对甲、乙两个工厂生产的饮料进行质量检查,不合格率分别为5%和8%,则甲、乙两厂饮料的不合格品数量为( )A、无法判断B、甲>乙C、甲<乙D、甲=乙你的答案: A4、将不同地区、部门、单位之间同类指标进行对比所得的综合指标称为( )A、动态相对指标B、结构相对指标C、比例相对指标D、比较相对指标你的答案: D5、某地区人口普查结果显示,每10万人口中有大学文化程度的为7532人.该数字是( )A、比较相对指标值B、结构相对指标值C、绝对指标值D、强度相对指标值你的答案: B6、就业人数增减量指标属于( )A、总量指标B、平均指标C、变异指标D、相对指标你的答案: A7、结构相对指标是( )A、总体某部分数值与总体全部数值之比B、甲单位水平与乙单位水平之比C、实际数与计划数之比D、报告期水平与基期水平之比你的答案: A8、指标值会随研究范围的大小而增减的综合指标是( )A、平均指标B、质量指标C、相对指标D、总量指标你的答案: D9、下列属于比例相对指标的是( )A、每百元产值利税额B、第一、第二、第三产业的产值比C、净产值占总产值的比重D、工人出勤率你的答案: B10、某商场上半年销售了彩色电视机8800台,其年初库存量为1500台,这两个总量指标是( ).A、时期指标B、前者是时点指标,后者是时期指标C、前者是时期指标,后者是时点指标D、时点指标你的答案: C11、某商场计划6月份销售利润比5月份提高2%,实际却下降了3%,则销售利润计划完成程度为( )A、95.10%B、66.70%C、99.00%D、105.10%你的答案: A12、某地区有10万人口,拥有80个医院.平均每个医院要服务1250人,这个指标是( )A、总量指标B、平均指标C、强度相对指标D、发展水平指标你的答案: C13、人均粮食产量是( )A、相对指标B、平均指标C、总量指标D、数量指标14、下面指标中,属于时期指标的是( )A、产品产量B、商品库存量C、某地区人口数D、中小企业数你的答案: A15、计算计划完成情况相对指标时,分子和分母的数值( )A、只能是平均指标B、只能是相对指标C、既可以是绝对指标,也可以是相对指标或平均指标D、只能是绝对指标你的答案: C多选题16、总量指标的计量单位主要有( )A、实物单位B、劳动单位C、度量衡单位D、货币单位E、自然单位你的答案: A,B,D17、在检查长期计划执行情况时,常使用的方法有( )A、平均法B、累计法C、综合法D、比例法E、水平法你的答案: B,E18、在相对指标中,分子和分母可以互换位置的有( )A、计划完成相对指标B、比例相对指标C、结构相对指标D、动态相对指标E、比较相对指标你的答案: B,E19、时点指标的特点是( )A、指标数值大小与时期长短直接相关B、不同时点上的数值可以相加C、调查资料需连续登记D、指标数值大小与时点间隔长短无直接关系E、不同时点上的数值不可以相加20、总量指标按其反映时间状态的不同,可分为( )A、总体单位总量指标B、时点指标C、总体标志总量指标D、时期指标E、总体总量指标你的答案: B,D21、以下指标中属于比较相对指标的有( ).A、三次产业结构比一B、城乡收入比C、中美GDP增速比D、东西部工业劳动生产率比E、男女性别比你的答案: B,C,D22、在相对指标中,属于不同总体数值对比的指标有( )A、比较相对指标B、动态相对指标C、强度相对指标D、结构相对指标E、比例相对指标你的答案: A,B,C23、总量指标按其反映总体的内容不同,可分为( )A、总体总量指标B、时点指标C、时期指标D、总体单位总量指标E、总体标志总量指标你的答案: D,E24、以下指标中属于强度相对指标的有( )A、耕地亩产量B、人均粮食产量C、人均耕地面积D、万元产值利税率E、单位成本你的答案: B,C,D25、计算计划完成程度相对指标,其分子、分母可以是( )A、相对数B、0C、强度相对数D、绝对数E、平均数你的答案: A,C,D,E判断题26、按人口平均的粮食产量是一个平均数( )对错你的答案: 错27、所有的强度相对指标都有正逆指标之分.( )对错你的答案: 错28、检查长期计划时,选择水平法还是累计法是依据计划指标的情况而定的. ( )对错你的答案: 对29、反映总体内部构成特征的指标只能是结构相对数.( )对错你的答案: 错30、结构相对数的数值只能小于1( )对错你的答案: 对31、男女性别比为107.98:100,这说明以男性为100,女性人口是男性人口数的1.0798倍.( )对错你的答案: 错32、强度相对数与平均数不同,因为它不是同质总体的标志总量与总体单位数之比.()对错你的答案: 对33、一个总量指标究竟应属于总体单位总量还是总体标志总量,应视研究目的的不同和研究对象的变化而定()对错你的答案: 对34、只有当计划完成程度相对数大于100%时,表示超额完成计划.( )对错你的答案: 错35、甲企业完成产值50万元,刚好完成计划;乙企业完成产值88万元,超额10%完成计划,则甲、乙两企业共超额5%完成计划.( )对错你的答案: 错。
统计学第四章

统计学第四章1.动态数列的构成要素是()。
[单选题] *A)变量和次数B)时间和指标数值(正确答案)C)时间和次数D)主词和宾词2.动态数列中,每个指标数值可以相加的是()。
[单选题] *A)相对数动态数列B)时期数列(正确答案)C)间断时点数列D)平均数动态数列4.定基增长速度与环比增长速度的关系为()。
[单选题] *A)定基增长速度等于相应的各个环比增长速度的算术和B)定基增长速度等于相应的各个环比增长速度的连乘积C)定基增长速度等于相应的各个环比增长速度加1后的连乘积再减1(正确答案)D)定基增长速度等于相应的各个环比增长速度连乘积加1(或100%)5.按季平均法测定季节比率时,各季的季节比率之和应等于() [单选题] *A)100%B)400%(正确答案)C)120%D)1200%9.某城市2016年末有人口750万人,有零售商业网点3万个,则该市的商业网点密度指标是()。
[单选题] *A)2.5千人/个B)250人/个(正确答案)C)0.25个/千人D)250个/人10.按水平法计算的平均发展速度推算可以使() [单选题] *A)推算的各期水平之和等于各期实际水平之和B)推算的期末水平等于实际期末水平(正确答案)C)推算的各期定基发展速度等于实际的各期定基发展速度D)推算的各期增长量等于实际的逐期增长量11.增长1%的绝对值是()。
[单选题] *A)水平指标B)速度指标C)水平与速度相结合的指标(正确答案)D)什么也不是12.评比城市间的社会发展状况,将各城市每人分摊的绿化面积按年排列的动态数列是属于()。
[单选题] *A)总量指标的时期数列B)总量指标的时点数列C)相对指标动态数列(正确答案)D)平均指标动态数列13.年距增长速度的计算公式是()。
[单选题] *A)年距增长量÷最初水平B)逐期增长量÷最初水平C)逐期增长量÷前期水平D)年距增长量÷上年同期发展水平(正确答案)14.动态数列中的发展水平()。
统计学第四章测试答案

第四章1、一组数据中出现频数最多的变量值称为()A.众数B.中位数C.四分位数D.平均数2、下列关于众数的叙述,不正确的是()A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响3、一组数据排序后处于中间位置上的变量值称为()A.众数B.中位数C. 四分位数D.平均数4、一组数据排序后处于25%和75%位置上的值称为()A.众数B.中位数C. 四分位数D.平均数5、非众数组的频数占总频数的比例称为()A.异众比率B.离散系数C.平均差D.标准差6、四分位差是()A.上四分位数减下四分位数的结果B.下四分位数减下四分位数的结果C.下四分位数加上四分位数D.下四分位数与上四分位数的中间值7、一组数据的最大值与最小值之差称为()A.平均差B.标准差C.极差D.四分位差8、各变量值与其平均数离差平方的平均数称为()A.极差B.平均差C.方差D.标准差9、变量值与其平均数的离差除以标准差后的值称为()A.标准分数B.离散系数C.方差D.标准差10、如果一个数据的标准分数是-2,表明该数据()A.比平均数高出2个平均差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差11-15AABCA11、如果一个数据的标准分数是3,表明该数据()A.比平均数高出3个标准差B. 比平均数低3个标准差C.等于3倍的平均数D.等于3倍的标准差12、经验法则表明,当一组数据对称分布时,在平均数加减1个标准差的范围内大约有()A.68%的数据B.95%的数据C.99%的数据D.100%的数据13、经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围内大约有()A.68%的数据B.95%的数据C.99%的数据D.100%的数据14、经验法则表明,当一组数据对称分布时,在平均数加减3个标准差的范围内大约有()A.68%的数据B.95%的数据C.99%的数据D.100%的数据15、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=2,其意义是()A.至少有75%的数据落在平均数加减2个标准差的范围之内B.至少有89%的数据落在平均数加减2个标准差的范围之内C. 至少有94%的数据落在平均数加减2个标准差的范围之内D. 至少有99%的数据落在平均数加减2个标准差的范围之内16-20BCCDA16、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=3,其意义是()A.至少有75%的数据落在平均数加减2个标准差的范围之内B.至少有89%的数据落在平均数加减2个标准差的范围之内C.至少有94%的数据落在平均数加减2个标准差的范围之内D.至少有99%的数据落在平均数加减2个标准差的范围之内17、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=3,其意义是()A.至少有75%的数据落在平均数加减2个标准差的范围之内B.至少有89%的数据落在平均数加减2个标准差的范围之内C.至少有94%的数据落在平均数加减2个标准差的范围之内D.至少有99%的数据落在平均数加减2个标准差的范围之内18、离散系数的主要用途是()A.反映一组数据的离散水平B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平19、比较两组数据的离散程度最适合的统计量是()A.极差B.平均差C.标准差D.离散系数20、偏态系数测度了数据分布的非对称性程度。
统计学第四章课后题及答案解析

第四章一、单项选择题1.由反映总体单位某一数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占比重之和等于1或100%的相对数()A.比例相对数 B.比较相对数 C.结构相对数 D.动态相对数3.某企业工人劳动生产率计划提高5%,实际提高了10%,则提高劳动生产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A.只存在一个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.大量的B.同质的C.有差异的D.不同总体的7.几何平均数的计算适用于求()A.平均速度和平均比率B.平均增长水平C.平均发展水平D.序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.方差B.极差C.标准差D.变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采用()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。
统计学第四章练习题 答案

统计学第四章练习题一、 选择题(一个或一个以上答案)(不用做)1、 研究某超市的经营情况,则销售额是 ABCEA 总量指标B 时期指标C 数量指标D 时点指标E 绝对指标 2、 劳动生产率是 CA 两个时期指标之比B 两个时点指标之比C 一个时期指标和一个时点指标之比D 一个时点指标和一个时期指标之比3、 下面属于时间数列基本分析的方法有 BCA 移动平均法B 水平分析法C 速度分析法D 长期趋势外推法E 季节分析4、 下列属于时点数列的是 ABDA 库存B 人数C 死亡人口D 资产E 销售量5、 下列属于时期数列的有 ABCDEA 存款增长量B 收入C 收入增加额D 产值E 现金流量 6、 下列说法不正确的是 ABCE A 环比增长量之和等于累计增长量B 环比增长速度的连乘机等于定基增长速度C 定基发展速度的连乘机等于环比发展速度D 逐期增长量之和等于累计增长量E 环比发展速度之和等于定基发展速度 7、 月度资料的季节比率之和等于 BA 400B 1200C 100D 2400E 无法计算二、 计算题1、某家具厂木材仓库2008年7月记录显示,7月初木材库存为100立方,7月3日入库20立方,7月10日出库34立方,7月24日入库15立方,计算该月木材的平均库存。
(保留1位小数)2、某超市2004-2007年营业额的增长速度分别为10%,8%,15%,20%,计算2004-2007年的年平均增长速度。
(保留1位小数)%.%%%%%213100201151811014=-++++=∆))()()((δ(立方))()(平均库存98.5 8147281534-120143412071202100 =+++⨯++⨯-+⨯+⨯==∑∑f af3、进入21世纪以来,中国经济发展迅速。
根据名义GDP 资料(《中国统计年鉴2008》)年份 2000 2001 2002 2003 2004 2005 2006 2007 GDP (亿元)980011)计算逐期和累计增长量 2)计算环比和定基发展速度 3)计算环比和定基增长速度4)计算平均增长量、平均增长速度4、已知某种产品产量有关资料(产量取整数,其他保留1位小数): 年份 2001 2002 2003 2004 2005 2006 产量(吨)20 增长量(吨) 逐期 — 5 累计 10 发展速度(%) 定基 180 环比 — 150 增长速度(%)定基12514.3%1254.621647181515297=-==-=%平均增长速度(亿元)平均增长量环比—1)根据已知资料填空2)计算平均增长量、平均发展速度和平均增长速度。
统计学习题第四章数据分布特征的描述习题答案

第四章 静态指标分析法(一)一、填空题1、数据分布集中趋势的测度值(指标)主要有、和。
其中和用于测度品质数据集中趋势的分布特征,用于测度数值型数据集中趋势的分布特征。
2、标准差是反映的最主要指标(测度值)。
3、几何平均数是计算和的比较适用的一种方法。
4、当两组数据的平均数不等时,要比较其数据的差异程度大小,需要计算。
5、在测定数据分布特征时,如果M M e X 0==,则认为数据呈分布。
6、当一组工人的月平均工资悬殊较大时,用他们工资的比其算术平均数更能代表全部工人工资的总体水平。
二.选择题单选题:1.反映的时间状况不同,总量指标可分为( )A 总量指标和时点总量指标B 时点总量指标和时期总量指标C 时期总量指标和时间指标D 实物量指标和价值量指标2、某厂1999年完成产值200万元,2000年计划增长10%,实际完成了231万元,超额完成( )A 5.5%B 5%C 115.5%D 15.5%3、在同一变量数列中,当标志值(变量值)比较大的次数较多时,计算出来的平均数( )A 接近标志值小的一方B 接近标志值大的一方C 接近次数少的一方D 接近哪一方无法判断4、在计算平均数时,权数的意义和作用是不变的,而权数的具体表现( )A 可变的B 总是各组单位数C 总是各组标志总量D 总是各组标志值 5、1998年某厂甲车间工人的月平均工资为520元,乙车间工人的月平均工资为540元,1999年各车间的工资水平不变,但甲车间的工人占全部工人的比重由原来的40%提高到了60%,则1999年两车间工人的总平均工资比1998年( )A 提高B 不变C 降低D 不能做结论 6、在变异指标(离散程度测度值)中,其数值越小,则( )A 说明变量值越分散,平均数代表性越低B 说明变量值越集中,平均数代表性越高C 说明变量值越分散,平均数代表性越高D 说明变量值越集中,平均数代表性越低7、有甲、乙两数列,已知甲数列:07.7,70==甲甲σX ;乙数列:41.3,7==乙乙σX 根据以上资料可直接判断( )A 甲数列的平均数代表性大B 乙数列的平均数代表性大C 两数列的平均数代表性相同D 不能直接判别8、杭州地区每百人手机拥有量为90部,这个指标是 ( )A 、比例相对指标B 、比较相对指标C 、结构相对指标D 、强度相对指标 9、某组数据呈正态分布,计算出算术平均数为5,中位数为7,则该数据分布为 ( ) A 、左偏分布 B 、右偏分布 C 、对称分布 D 、无法判断10、加权算术平均数的大小 ( )A 主要受各组标志值大小的影响,与各组次数多少无关;B 主要受各组次数多少的影响,与各组标志值大小无关;C 既与各组标志值大小无关,也与各组次数多少无关;D 既与各组标志值大小有关,也受各组次数多少的影响11、已知一分配数列,最小组限为30元,最大组限为200元,不可能是平均数的为 ( ) A 、50元 B 、80元 C 、120元 D 、210元12、比较两个单位的资料,甲的标准差小于乙的标准差,则 ( ) A 两个单位的平均数代表性相同 B 甲单位平均数代表性大于乙单位C 乙单位平均数代表性大于甲单位D 不能确定哪个单位的平均数代表性大 13、若单项数列的所有标志值都增加常数9,而次数都减少三分之一,则其算术平均数 ( ) A 、增加9 B 、增加6C 、减少三分之一 D 、增加三分之二 14、如果数据分布很不均匀,则应编制( )A 开口组B 闭口组C 等距数列D 异距数列 15、计算总量指标的基本原则是:( ) A 总体性B 全面性C 同质性D 可比性16、某企业的职工工资分为四组:800元以下;800-1000元;1000—1500元;1500以上,则1500元以上这组组中值应近似为()A1500元 B 1600元 C 1750元D 2000元 17、统计分组的首要问题是( )A 选择分组变量和确定组限B 按品质标志分组C 运用多个标志进行分组,形成一个分组体系D 善于运用复合分组18、某连续变量数列,其末组为开口组,下限为200,又知其邻组的组中值为170,则末组组中值为( )A 230B 260C 185D 215 19、分配数列中,靠近中间的变量值分布的次数少,靠近两端的变量值分布的次数多,这种分布的类型是( )A 钟型分布B U 型分布C J 型分布D 倒J 型分布 20、要了解上海市居民家庭的开支情况,最合适的调查方式是:() A 普查B 抽样调查C 典型调查D 重点调查21、已知两个同类企业的职工平均工资的标准差分别为5元和6元,而平均工资分别为3000元,3500元则两企业的工资离散程度为 ( )A 甲大于乙B 乙大于甲C 一样的D 无法判断 22、加权算术平均数的大小取决于( )A 变量值B 频数C 变量值和频数D 频率23、如果所有标志值的频数都减少为原来的1/5,而标志值仍然不变.那么算术平均数( ) A 不变 B 扩大到5倍 C 减少为原来的1/5 D 不能预测其变化 24、 计算平均比率最好用 ( )A 算术平均数B 调和平均数C 几何平均数D 中位数25、若两数列的标准差相等而平均数不同,在比较两数列的离散程度大小时,应采用() A 全距 B 平均差 C 标准差 D 标准差系数26、若n=20,∑∑==2080,2002x x ,标准差为( )A 2B 4C 1.5D 327、已知某总体3215,3256==eMM,则数据的分布形态为( )A左偏分布B正态分布 C 右偏分布DU型分布28、一次小型出口商品洽谈会,所有厂商的平均成交额的方差为156.25万元,标准差系数为14.2%,则平均成交额为( )万元A11 B 177.5 C 22.19 D 8826、欲粗略了解我国钢铁生产的基本情况,调查了上钢、鞍钢等十几个大型的钢铁企业,这是()A普查B重点调查C典型调查D抽样调查多选题:1.某企业计划2000年成本降低率为8%,实际降低了10%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学第四章测试答案第四章1、一组数据中出现频数最多的变量值称为()A.众数B.中位数C.四分位数D.平均数2、下列关于众数的叙述,不正确的是()A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响3、一组数据排序后处于中间位置上的变量值称为()A.众数B.中位数C. 四分位数D.平均数4、一组数据排序后处于25%和75%位置上的值称为()A.众数B.中位数C. 四分位数D.平均数5、非众数组的频数占总频数的比例称为()A.异众比率B.离散系数C.平均差D.标准差6、四分位差是()A.上四分位数减下四分位数的结果B.下四分位数减下四分位数的结果C.下四分位数加上四分位数D.下四分位数与上四分位数的中间值7、一组数据的最大值与最小值之差称为()A.平均差B.标准差C.极差D.四分位差8、各变量值与其平均数离差平方的平均数称为()A.极差B.平均差C.方差D.标准差9、变量值与其平均数的离差除以标准差后的值称为()A.标准分数B.离散系数C.方差D.标准差10、如果一个数据的标准分数是-2,表明该数据()A.比平均数高出2个平均差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差11-15AABCA11、如果一个数据的标准分数是3,表明该数据()A.比平均数高出3个标准差B. 比平均数低3个标准差C.等于3倍的平均数D.等于3倍的标准差12、经验法则表明,当一组数据对称分布时,在平均数加减1个标准差的范围内大约有()A.68%的数据B.95%的数据C.99%的数据D.100%的数据13、经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围内大约有()A.68%的数据B.95%的数据C.99%的数据D.100%的数据14、经验法则表明,当一组数据对称分布时,在平均数加减3个标准差的范围内大约有()A.68%的数据B.95%的数据C.99%的数据D.100%的数据15、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=2,其意义是()A.至少有75%的数据落在平均数加减2个标准差的范围之内B.至少有89%的数据落在平均数加减2个标准差的范围之内C. 至少有94%的数据落在平均数加减2个标准差的范围之内D. 至少有99%的数据落在平均数加减2个标准差的范围之内16-20BCCDA16、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=3,其意义是()A.至少有75%的数据落在平均数加减2个标准差的范围之内B.至少有89%的数据落在平均数加减2个标准差的范围之内C.至少有94%的数据落在平均数加减2个标准差的范围之内D.至少有99%的数据落在平均数加减2个标准差的范围之内17、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=3,其意义是()A.至少有75%的数据落在平均数加减2个标准差的范围之内B.至少有89%的数据落在平均数加减2个标准差的范围之内C.至少有94%的数据落在平均数加减2个标准差的范围之内D.至少有99%的数据落在平均数加减2个标准差的范围之内18、离散系数的主要用途是()A.反映一组数据的离散水平B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平19、比较两组数据的离散程度最适合的统计量是()A.极差B.平均差C.标准差D.离散系数20、偏态系数测度了数据分布的非对称性程度。
如果一组数据的分布是对称的,则偏态系数()A.等于0B.等于1C.大于0D.大于121-25 BAABB21、如果一组数据分布的偏态系数在0.5~1或-1~-0.5之间,则表明该组数据属于()A.对称分布B.中等偏态分布C.高度偏态分布D.轻微偏态分布22、峰态通常是与标准正态分布相比较而言的。
如果一组数据服从标准正态分布,则峰态系数的值()A. 等于0B.等于1C.大于0D.大于123、如果峰态系数k>0,表明该组数据是()A.尖峰分布B.扁平分布C.左偏分布D.右偏分布24,某大学经济管理学院有1200名学生,法学院有800名学生,医学院有320名学生,理学院有200学生。
在上面的描述中,众数是()A.1200B.经济管理学院C.200D.理学院25,某小区准备采取新的物业管理措施,随机抽取了100户居民进行调查,其中赞成的有69户,中立的有22户,反对的有9户,描述该组数据的集中趋势宜采用()A.众数B.中位数C.四分位数D.平均数26-30AABAC26. 某小区准备采取新的物业管理措施,随机抽取了100户居民进行调查,其中赞成的有69户,中立的有22户,反对的有9户,该组数据的中位数是()A.赞成B.69 C。
中立 D.2227.某班有25名学生,期末统计学课程的考试分数分别为:68,73,66,76,86,74,61,89,65,90,69,67,76,62,81,63,68,81,70,73,60,87,75,64,56,该班考试分数的下四分位数和上四分位数分别为()A.64.5和78.5B.67.5和71.5C.64.5和71.5D.64.5和67.528.假定一个样本由5个数据组成:3,7,8,9,13,该样本的方差为()A.8B.13C.9.7D.10.429.对于右偏分布,平均数、中位数和众数之间的关系是()A.平均数>中位数>众数 B.中位数>平均数>众数C. 众数>中位数>平均数D.众数>平均数>中位数30.在某行业中随机抽取10家企业,第一季度的利润额(万元)分别为:72,63.1,54.7,54.3,29,26.9,25,23.9,23,20.该组数据的中位数为()A.28.46B.30.20C.27.95D.28.1231-35DBBAC31. 在某行业中随机抽取10家企业,第一季度的利润额(万元)分别为:72,63.1,54.7,54.3,29,26.9,25,23.9,23,20.该组数据的平均数为()A.28.46B.30.20C.27.95D.39.1932. 在某行业中随机抽取10家企业,第一季度的利润额(万元)分别为:72,63.1,54.7,54.3,29,26.9,25,23.9,23,20.该组数据的平均数为()A.28.46B.19.54C.27.95D.381.9433.某班学生的统计学平时成绩是70分,最高96,最低62,根据这些信息,可以计算的测度离散程度的统计量是()A.方差B.极差C.标准差 D.变异系数34.某班学生的平均成绩为80分,标准差是10分,如果已知该班学生的考试分数对称分布,可以判断成绩在60~100分之间的学生大约占()A. 95%B.89%C.68%D.99%35. 某班学生的平均成绩为80分,标准差是10分,如果已知该班学生的考试分数对称分布,可以判断成绩在70~90分之间的学生大约占()A. 95%B.89%C.68%D.99%36-40DBBDA36. 某班学生的平均成绩为80分,标准差是5分,如果已知该班学生的考试分数非对称分布,可以判断成绩在70~90分之间的学生至少占()A.95%B.89%C.68%D.75%37.在某公司进行的计算机水平测试中,新员工的平均分为80分,标准差是5分,假设新员工得分的分布是未知的,则得分在65~95分的新员工至少占()A.75%B.89%C.94%D.95%38. 在某公司进行的计算机水平测试中,新员工的平均分为80分,标准差是5分,中位数是86分,则新员工得分的分布形状是()A.对称的B.左偏得C.右偏的 D.无法确定39.对某个高速公路段行驶过的120辆汽车的车速进行测量后发现,平均车速是85公里/小时,标准差是4公里/小时,下列哪个车速可以看做异常值()A.78公里/小时B.82公里/小时C.91公里/小时D.98公里/小时40.下列叙述中正确的是()A.如果计算每个数据与平均数的离差,则这些离差的和总是等于零B.如果考试成绩的分布是对称的,平均数为75,标准差为12,则考试成绩在63-75分之间的比例大约为95%C.平均数和中位数相等D.中位数大于平均数41-46DADDDA41.一组样本数据为3,3,1,5,13,12,11,9,7.这组数据的中位数是()A.3B.13C.7.1D.742.在离散程度得测度中,最容易受极端值影响的是()A.极差B.四分位差C.标准差D.平均差43.测度数据离散程度的相对统计量是()A.极差B.平均差C.标准差D.离散系数44.一组数据的离散系数为0.4,平均数为20,则标准差为()A.80B.0.02C.4D.845.在比较两组数据的离散程度时,不能直接比较它们的标准差,因为两组数据的()不同A.标准差B.方差C.数据个数D.计量单位46.两组数据的平均数不等,但标准差相等,则()A.平均数小的,离散程度大B.平均数大的,离散程度大C.平均数小的,离散程度小D.两组数据的离散程度相同答案:1-5 ACBCA 6-10 ACCAB 11-15AABCA 16-20BCCDA21-25 BAABB 26-30AABAC 31-35DBBAC 36-40DBBDA41-46DADDDA。
