杨辉三角的各种算法实现
杨辉三角的规律公式

杨辉三角的规律公式杨辉三角,又称帕斯卡三角,是古代数学中一种重要的图形。
它的构造方法非常简单:从第一行开始,每一行的两端都是1,其余的数是上一行相邻两个数的和。
下面我们将深入探讨杨辉三角的规律和公式。
1. 杨辉三角的构造让我们以一个简单的示例来说明杨辉三角的构造过程。
首先是第一行的唯一元素1。
然后,每一行的两端都是1,如下所示:11 1接着,根据规则,我们可以继续构造出下一行:11 11 2 1依此类推,我们可以继续构造出更多行,形成完整的杨辉三角。
2. 杨辉三角的规律杨辉三角不仅仅是一种几何图形,它还蕴含着许多有趣的规律。
其中最引人注目的规律之一就是每一行的数字都遵循一定的数学公式。
首先,每一行的数字个数是递增的,从1开始逐渐增加;其次,除了两端的数字是1之外,其他数字都是其上一行相邻两个数字之和。
这一规律可以用数学公式表示如下:考虑第n行的第k个数字,我们记为T(n, k)。
根据规律,有:T(n, k) = T(n-1, k-1) + T(n-1, k)当k等于1或n时,T(n, k)为1。
这个公式描述了杨辉三角中每个数字的生成过程。
3. 应用与拓展杨辉三角虽然看似简单,却有着丰富的应用。
在数学领域,它与组合数学和多项式有着密切的联系;在计算机科学领域,它则与动态规划等算法密切相关。
此外,杨辉三角还有不少拓展和变体。
例如,帕斯卡梯形(Pascal’s Trapezium)就是杨辉三角的一个拓展形式,每一行的元素都是由对应的斜线上的元素之和得到。
结语杨辉三角作为古代数学的经典之作,展现了数学中的奇妙规律和美丽结构。
通过对其规律和公式的探究,我们可以更深入地理解其内在的数学之美。
愿每一个探索者在这个数学的世界里都能发现属于自己的精彩之处!。
研究性学习课题:杨辉三角

THANKS
感谢观看
杨辉三角在其他数学领域的应用研究
总结词
杨辉三角在组合数学、概率论、数论等领域 都有广泛的应用,研究这些应用有助于深入 理解相关数学领域的基本原理。
详细描述
杨辉三角是组合数学中的重要工具,它可以 用来计算组合数、排列数等。此外,杨辉三 角在概率论中也有应用,如计算概率的加法 定理等。同时,杨辉三角在数论中也有应用 ,如计算质因数分解等。研究这些应用有助 于深入理解相关数学领域的基本原理和应用
杨辉三角在计算机科学中的应用
总结词
杨辉三角在计算机科学中也有着广泛的应用,它为计算机算法设计和数据结构提供了重 要的启示。
详细描述
杨辉三角的规律性和高效性使得它在计算机科学中有着广泛的应用。例如,利用杨辉三 角可以设计高效的算法来计算组合数、排列数等,同时也可以利用杨辉三角来设计一些 特殊的数据结构,如动态规划等。此外,杨辉三角在计算机图形学、加密算法等领域也
3
杨辉三角的数字排列方式具有对称性、规律性和 高效性等特点,使得它在解决一些数学问题时具 有独特的优势。
杨辉三角的性质和特点
杨辉三角的每一行数字都是上 一行相邻两个数字之和,这种 递推关系使得杨辉三角具有高
度的自相似性。
杨辉三角的数字排列具有规律 性,如每一行的数字个数、对 称性等,这些规律使得杨辉三 角在解决数学问题时具有高效
杨辉三角在数学归纳法中的应用
总结词
数学归纳法是一种证明与自然数有关的命题的数学方法,而 杨辉三角为其提供了一种有效的工具。
详细描述
在数学归纳法的应用过程中,杨辉三角可以提供组合数的一 些性质和关系,从而简化了归纳法的证明过程。例如,利用 杨辉三角可以证明组合数的递推公式,进而证明与自然数有 关的命题。
杨辉三角形的六种解法

杨辉三角形的六种解法杨辉三角形是形如11 11 2 11 3 3 11 4 6 4 1的三角形,其实质是二项式(a+b)的n次方展开后各项的系数排成的三角形,它的特点是左右两边全是1,从第二行起,中间的每一个数是上一行里相邻两个数之和。
这个题目常用于程序设计的练习。
下面给出六种不同的解法。
解法一#include <stdio.h>main(){ int i,j,n=0,a[17][17]={0};while(n<1 || n>16){ printf("请输入杨辉三角形的行数:");scanf("%d",&n);}for(i=0;i<n;i++)a[i][0]=1; /*第一列全置为一*/for(i=1;i<n;i++)for(j=1;j<=i;j++)a[i][j]=a[i-1][j-1]+a[i-1][j];/*每个数是上面两数之和*/for(i=0;i<n;i++) /*输出杨辉三角*/{ for(j=0;j<=i;j++)printf("%5d",a[i][j]);printf("\n");}}点评:解法一是一般最容易想到的解法,各部分功能独立,程序浅显易懂。
解法二#include <stdio.h>main(){ int i,j,n=0,a[17][17]={1};while(n<1 || n>16){ printf("请输入杨辉三角形的行数:");scanf("%d",&n);}for(i=1;i<n;i++){ a[i][0]=1; /*第一列全置为一*/for(j=1;j<=i;j++)a[i][j]=a[i-1][j-1]+a[i-1][j]; /*每个数是上面两数之和*/}for(i=0;i<n;i++) /*输出杨辉三角*/{ for(j=0;j<=i;j++)printf("%5d",a[i][j]);printf("\n");}}点评:解窢二是在解法一的基础上,把第一列置为1的命令移到下面的双重循环中,减少了一个循环。
C语言杨辉三角两种实现方法

C语⾔杨辉三⾓两种实现⽅法⽬录杨辉三⾓——C语⾔实现⽅法⼀:利⽤⼆维数组实现⽅法⼆(对⽅法⼀的改进):总结杨辉三⾓——C语⾔实现杨辉三⾓:在屏幕上打印杨辉三⾓。
11 11 2 11 3 3 1……根据上述例⼦可知:1.每⼀⾏的第⼀个和第⼆个数为1;2.其余的数为正上⽅和左边数字之和。
⽅法⼀:利⽤⼆维数组实现解题思路:根据杨辉三⾓的规律,我们可以定义⼀个⼆维数组来实现杨辉三⾓的打印,其中数字的规律为:data[i][j] = data[i - 1][j] + data[i - 1][j - 1],所以我们按照这个⽅法将数据填⼊⼆维数组之后打印即可。
代码如下:#include <stdio.h>int main(){int n;int data[30][30] = {1};//将第⼀⾏直接填好,为1printf("请输⼊要打印的⾏数:>");scanf("%d", &n);for (int i = 1; i < n; i++)//从第⼆⾏开始填{data[i][0] = 1;//将每⼀⾏第⼀列先初始化为1,防⽌越界for (int j = 1; j < i + 1; j++){data[i][j] = data[i - 1][j] + data[i - 1][j - 1];}}for (int i = 0; i < n; i++)//打印⼆维数组{for (int j = 0; j < i + 1; j++){printf("%d ", data[i][j]);}printf("\n");}return 0;}运⾏结果:⽅法⼆(对⽅法⼀的改进):由于我在填第n⾏的杨辉三⾓时,只跟第n-1⾏的杨辉三⾓产⽣联系,不会跟之前的有联系,所以没必要保存每⼀⾏的杨辉三⾓,利⽤⼀维数组,填⼀⾏打⼀⾏即可,这样能让空间复杂度从O(n^2)降低到O(n)。
三角计数算法

三角计数算法三角计数算法是指一种用于求解排列组合问题的算法,在数学和计算机领域均有广泛应用。
下面我们来分步骤介绍三角计数算法的原理和实现方法。
一、杨辉三角杨辉三角,又称帕斯卡三角,是三角计数算法的重要组成部分。
杨辉三角的每一行都是一个排列组合系数,其计算方法如下:1.每一行左右两端的值都为1;2.每一个数是上一行中左右两个数之和。
例如,杨辉三角的前五行如下:11 11 2 11 3 3 11 4 6 4 1二、排列组合问题排列组合问题指的是从给定的n个不同元素中选取r个元素的排列或组合方式的数量。
其中,排列指选取后的元素有顺序,组合指选取后的元素无顺序。
例如,从a、b、c、d四个字母中选取两个字母的排列和组合分别如下:排列:ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc,共12种方式。
组合:ab, ac, ad, bc, bd, cd,共6种方式。
三、组合计数组合计数的公式为:C(n, r) = n!/(r!*(n-r)!),其中,n为总数,r为选取的数量。
通过杨辉三角可以容易地得出n取不同值时,一些组合数量的系数。
例如,计算C(5,2)时,从杨辉三角的第五行中取得第三个数6,即C(5,2)=6。
四、排列计数排列计数的公式为:P(n, r) = n!/(n-r)!,其中,n为总数,r 为选取的数量。
通过将组合计数乘以选取数量的阶乘,可以得到排列计数的公式:P(n, r) = C(n, r)*r!。
五、三角计数算法三角计数算法的核心思想在于利用杨辉三角的规律解决排列组合问题。
算法分为以下两个步骤:1.确定组合或排列的数量。
首先,根据所求问题和已知条件确定有多少种组合或排列方式。
2.计算组合或排列的具体情况。
利用杨辉三角,将组合或排列的数量系数乘以相应的元素个数,得出具体的组合或排列方式。
例如,计算从1到10的数列中选取4个数的组合方式,可以先确定组合数量为C(10,4)=210。
杨辉三角的规律公式6种

杨辉三角的规律公式6种
1、每个数等于它上方两数之和。
2、每行数字左右对称,由1 开始逐渐变大。
3、第n 行的数字有n+1 项。
4、第n 行数字和为2(n-1) (2 的(n-1) 次方)。
5 (a+b) n 的展开式中的各项系数依次对应杨辉三角的第(n+1) 行中的每一项。
6、第n 行的第m个数和第n-m 个数相等,即C(n,m)=C(n,n-m) 。
数在杨辉三角中的出现次数。
由1开始,正整数在杨辉三角形出现的次数为∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4。
除了1之外,所有正整数都出现有限次,只有2出现刚好一次,6,20,70等出现三次;出现两次和四次的数很多,还未能找到出现刚好五次的数。
120,210,1540等出现刚好六次。
队列实现杨辉三角的算法原理

队列实现杨辉三角的算法原理
杨辉三角是一种数学模式,每个位置上的数字等于它上方两个数字之和。
队列可以用来实现杨辉三角的算法,其原理如下:
1. 首先,创建一个空的队列。
2. 将1入队列,作为第一行的元素。
3. 进行循环,从第二行开始到第n行:
- 将当前队列中的元素依次出队,并将它们存储在一个临时数组temp中。
- 在temp数组末尾添加一个0,作为哨兵元素。
- 再将temp数组中的元素依次相加,并将结果入队列。
4. 打印队列中的元素,即可得到杨辉三角的结果。
这个算法的基本思路是利用队列先进先出的特性,每次处理一行的数据。
在处理每一行时,将队列中的元素依次出队,并计算它们的和,然后将和再次入队,作为下一行的元素。
通过不断重复这个过程,最终得到的队列中的元素就是杨辉三角的结果。
python中递归函数实现杨辉三角

一、概述随着计算机编程的发展和普及,对于递归函数的应用也越来越广泛。
递归函数是一种自身调用自身的函数,它在编程领域中有着重要的应用。
而在Python语言中,递归函数的应用可以实现许多有趣和复杂的算法,比如杨辉三角。
本文将介绍如何使用Python中的递归函数来实现杨辉三角。
二、杨辉三角的定义杨辉三角,又称帕斯卡三角,是我国古代数学家杨辉在《详解九章算术》一书中首次介绍的一种数学图形。
它有着许多有趣的性质和应用,是数学中的一个经典问题。
杨辉三角的具体定义如下:1. 第n行有n个数;2. 每一行的首尾数字都是1;3. 从第三行开始,对于非首尾的位置,其值等于其上一行的前一个数与后一个数之和。
下面是杨辉三角的前几行:11 11 2 11 3 3 11 4 6 4 1...三、Python递归函数实现杨辉三角在Python语言中,可以使用递归函数来实现杨辉三角。
递归函数的定义如下:```pythondef yanghui_triangle(row, col):if col == 1 or col == row:return 1else:return yanghui_triangle(row-1, col-1) +yanghui_triangle(row-1, col)```其中,row表示杨辉三角的行数,col表示杨辉三角的列数。
递归函数首先判断当前位置是否为首尾位置,如果是,则直接返回1;否则,利用递归函数计算当前位置的值,即上一行的前一个数与后一个数之和。
四、Python程序实现使用递归函数实现杨辉三角的Python程序如下:```pythondef yanghui_triangle(row, col):if col == 1 or col == row:return 1else:return yanghui_triangle(row-1, col-1) +yanghui_triangle(row-1, col)def print_yanghui_triangle(n):for i in range(1, n+1):for j in range(1, i+1):print(yanghui_triangle(i, j), end=" ")print()n = 10print_yanghui_triangle(n)```在上面的程序中,首先定义了递归函数`yanghui_triangle`来计算杨辉三角的每一个位置的值,然后定义了一个打印函数`print_yanghui_triangle`来打印杨辉三角的前n行。
杨辉三角形最简单的c语言

杨辉三角形最简单的c语言杨辉三角形是指首先在平行于水平的一条直线上绘制出一个等边三角形,然后再分别在其三个内角所在的三条边上下绘制出三角形,其顶点恰好与上层三角形的相邻三角形的顶点相连,重复此过程可以形成杨辉三角形。
杨辉三角形具有一些特殊的特性,例如,在水平中间有一条对角线,同一对角线上的数值相等;在垂直中部有一条对角线,同一对角线上的数值相等。
杨辉三角形也被用作许多数学领域的组合数学,例如排列组合、组合统计等的基础理论。
C语言是一种比较流行的高级编程语言,它具有简单、灵活、功能强大的特点,是应用于软件设计、开发等方面的优秀工具。
运用c 语言实现杨辉三角形也是一门很有价值的学问,有利于我们更好地理解这种数学结构,为数学计算和后续运算奠定基础。
本文拟从两方面,介绍杨辉三角形的c语言实现方式:一、利用数组实现杨辉三角形在C语言中,可以通过定义一个整型数组的方式来实现杨辉三角形。
具体的步骤如下:1.创建一个二维数组,其中根据需要定义行数和列数,以实现所需的杨辉三角形尺寸。
2.通过循环,遍历该二维数组:a)第一行和第一列设置为1;b)其他单元格设置为上一行上一列的数值加上上一行当前列的数值,即y[i][j]=y[i-1][j-1]+y[i-1][j];c)后输出数组中的每一个值,即为所求杨辉三角。
二、采用T型算法实现杨辉三角形本文将介绍采用T型算法实现杨辉三角形的方法,参照如下: 1.首先,定义一个变量t,用于记录杨辉三角中元素的值,初始值设为1;2.下一步,输出t的值,即该元素值;3.然后,更新t的值,t=t*(row-i)/(i+1),其中row表示本行列数,i表示第i列;4.继续输出新t的值,即可获得下一个元素值;5.重复此过程,直到达到本行的最后一个元素为止。
上述算法可以很好地实现杨辉三角形,可以说是一种简单、高效的c语言实现方式。
总之,利用c语言实现杨辉三角的方法有很多种,本文介绍的只是其中的两种方法,还可以采用递归法来实现,通过这种方法我们可以更深入地理解杨辉三角形以及数学原理。
队列实现杨辉三角形(数据结构)(c语言)

用队列实现杨辉三角形在数据结构中,队列是一种非常常用的数据结构,其基本操作包括入队、出队、队列大小等。
利用队列的先进先出的特性,我们不仅可以解决简单的数据存储问题,还可以实现许多更加复杂的算法。
其中,一道有趣的题目就是用队列实现杨辉三角形。
首先,我们需要了解杨辉三角形的概念和特点。
杨辉三角形是一个数列,其每一行由从左到右逐渐增加的数字组成,而且每一行的首尾都是1。
中间的数字由上一行相邻的两个数字相加得到。
以下是杨辉三角形的前几行:11 11 2 11 3 3 11 4 6 4 1在实现杨辉三角形的过程中,我们可以利用队列的特性来存储每个数字。
具体来说,我们可以每次将一行的数字存储到一个队列中,并且在生成下一行数字时,根据队列中上一行的数字求出新的一行数字。
具体实现过程如下:1. 定义一个队列,并将1入队。
2. 对于每一行,我们可以先将1入队,然后根据上一行计算新的数字序列,将其逐一入队。
3. 每次生成新行数字序列时,都需要更新队列中的数据,即出队首元素,插入新的末尾元素。
4. 重复2-3步,直到生成的行数达到指定数目。
通过以上过程,我们就可以用队列实现杨辉三角形了。
实际上,在这个过程中,我们让每一行的数字序列都成为了队列中的元素,而依次入队出队的过程,也相当于在按照规律生成每一行数字序列。
这种算法虽然看似复杂,但实际上非常巧妙,也能够充分发挥队列数据结构的优势。
综上所述,用队列实现杨辉三角形是一道很有意思的题目,不仅能够锻炼我们的编程能力,还可以让我们更深入地理解队列数据结构和算法的本质。
如果你正在学习数据结构和算法,不妨尝试一下这道题目,相信它会给你带来更多的收获。
java实现杨辉三角的三种方法(含代码和解析且全面)

前言既然是实现杨辉三角,就要知道什么是杨辉三角。
如下图,就是两种杨辉三角。
(1)等边形状的杨辉三角(2)直角形状的杨辉三角在知道这两种都是杨辉三角之后,我们就来实现利用java语言打印出杨辉三角。
杨辉三角的规律:(1)第n行有n个数字.(2)每一行的开始和结尾数字都为1.用二维数组表示就是a[i][0]=1; a[i][j]=1(当i==j时);(3)第n+1行的第i个数字等于第n行的i-1个数字加上第n行的i个数字。
用二维数组表示就是a[i+1][j]=a[i][j-1]+a[i][j];代码部分(1)创建一个长度为10,宽度为10的二维数组,但赋值和输出时只输出杨辉三角那个范围的数。
首先,我们得理解定义一个长度和高度都为10的二维数组时,他到底做了什么。
数组的图为可以看出,实际是给每个位置上都赋值为0;而我们要做的是给A部分的位置赋值并且输出,而B部分的位置不用管。
A部分与B部分的区别在于:A部分的横坐标大于等于纵坐标。
用数组中的话就是i<=j;知道要赋值的范围,那么for循环的语句就知道了啦,就为而接下来就是利用杨辉三角的特点实现赋值并输出,这里就直接看下面的完整代码吧。
第一种该方法完整代码:最后的实现效果就是下图。
(2)直接创建一个和杨辉三角形状一样的数组再赋值输出。
在前面我们使用了一个长10高10的数组,但是最后我们只用了它的A部分,思考一下,为什么我们不直接创建一个和前面那个A部分形状一样的数组呢?形状如下图:知道基本的概念之后,我们先创建该数组,首先可以确定的是这里的高度还是为10,也就是横坐标最大还是为10,但是纵坐标就是小于等于该行的横坐标。
用代码表示就是:在数组创建好之后,再就是赋值了,之前赋值用的是j<=i,但是此处数组的范围就是杨辉三角的范围,所以可以直接对数组进行内外两层循环。
用代码表示就是:而赋值的代码也是一样,不过这种方法就可以赋值完再输出,不用像第一种一样赋值时输出。
杨辉三角python经典算法例题

杨辉三角python经典算法例题全文共四篇示例,供读者参考第一篇示例:杨辉三角是一种经典的数学问题,也被称为帕斯卡三角形,灵感源自中国历史上著名的数学家杨辉。
在这篇文章中,我们将探讨杨辉三角的基本概念,以及如何利用Python编程语言来实现这一经典算法。
首先让我们了解一下什么是杨辉三角。
杨辉三角是一个数字排列成三角形的数列,其特点是每一行的端点数字都是1,而且每个数等于它上方两个数之和。
第一行只有一个数字1,第二行有两个数字1,第三行有三个数字1,依次类推。
在第四行中,中间的数字3是由上一行的相邻两个数字1和2相加而来。
整个三角形的结构如下所示:```11 11 2 11 3 3 11 4 6 4 1```接下来我们将使用Python来实现杨辉三角的经典算法。
下面是一个简单的Python代码示例:```pythondef generate_triangle(num_rows):triangle = []for i in range(num_rows):row = [1] * (i + 1)for j in range(1, i):row[j] = triangle[i-1][j-1] + triangle[i-1][j]triangle.append(row)return triangle在上面的代码中,我们首先定义了一个函数`generate_triangle`来生成杨辉三角。
该函数接受一个参数`num_rows`表示要生成的杨辉三角的行数。
然后我们使用两层循环来逐行生成杨辉三角的数字,并将其存储在一个二维列表`triangle`中。
我们定义了一个函数`print_triangle`来打印出生成的杨辉三角。
该函数遍历每一行,并使用`center`方法来保持数字的对齐。
接着我们调用`generate_triangle`函数生成了一个5行的杨辉三角,然后调用`print_triangle`函数将其打印出来。
杨辉三角的规律公式4种初中

杨辉三角的规律公式4种初中
杨辉三角,是一种有规律的数列,它同时具有非常丰富的结构和几何模型,在数学上有着独特的含义。
研究杨辉三角的四种规律公式可以帮助我们更好地理解它。
首先我们重点来讲一下杨辉三角第一规律,即第一和最后一个元素等于1。
它
体现在任一行的首尾都是1,而其他的元素由他的上两个支配并以此衍生出来,即任一行的元素都可由上一行的两个元素得出,即“用上一行的两个元素相加得到下
一行的元素”。
其次引入的是第二规律,即它的对角元素均为1,这个规律关系到了二项式定理,二项式定理推出杨辉三角形、杨辉三角也是由二项式定理推出来的。
它由真子集和虚子集进行组合组成,真子集和虚子集其实就是两条对角线。
紧接着是第三规律,即每行元素之和等于改行第一个元素的平方,这明确了杨辉三角是一种对称性物体,这表示任一行的元素之和等于首元素的平方,即p 1 = 1^2 、p 2 = 2^2 、p 3 = 3^2,以此类推。
最后一规律是任一行的元素的积为改行第一个元素的次方,即任一行的元素的乘积等于首元素的数量,即P 1 = 1^1 、P 2 = 2^2 、P 3 = 3^3,以此类推。
显然,杨辉三角是一种有特殊规律、有充分结构和几何模型的数列,它的四种规律公式使我们可以更加深入地理解它,从而在数学研究和想象上开阔视野,获得新的启发与收获。
JS实现的杨辉三角【帕斯卡三角形】算法示例

JS实现的杨辉三⾓【帕斯卡三⾓形】算法⽰例本⽂实例讲述了JS实现的杨辉三⾓【帕斯卡三⾓形】算法。
分享给⼤家供⼤家参考,具体如下:杨辉三⾓,是⼆项式系数在三⾓形中的⼀种⼏何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》⼀书中出现。
在欧洲,帕斯卡(1623-1662)在1654年发现这⼀规律,所以这个表⼜叫做帕斯卡三⾓形。
帕斯卡的发现⽐杨辉要迟393年,⽐贾宪迟600年。
题⽬:给定⾮负整数numRows,⽣成Pascal三⾓形的第⼀个numRows。
在Pascal的三⾓形中,每个数字是它上⾯两个数字的总和。
输⼊: 5输出:[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]JS代码如下:<script>var generate = function(numRows) {if (numRows) {var result = [[1]];for(var i = 1;i < numRows;i++) {result[i] = [];for(var j = 0; j < i + 1;j++) {result[i][j] = (result[i - 1][j] || 0) + (result[i - 1][j - 1] || 0);}}return result;}else {return [];}};console.log(generate(1000));</script>由于数据⽐较多,这⾥仅展⽰⼀部分运算结果,感兴趣的朋友可以⾃⼰动⼿测试⼀下,看看运⾏效果。
更多关于JavaScript相关内容感兴趣的读者可查看本站专题:《》、《》、《》、《》、《》、《》及《》希望本⽂所述对⼤家JavaScript程序设计有所帮助。
杨辉三角-蓝桥杯python解法

杨辉三角-蓝桥杯python解法杨辉三角是一种古老的数学结构,它由二项式系数形成,从而展示了二项式定理。
这个三角形的第n行由n+1个元素组成,其中第k个元素等于(n choose k),即从n个元素中选取k个元素的组合个数。
杨辉三角的命名源自于17世纪的法国数学家Blaise Pascal(1623-1662),他在研究二项式定理时首先描述了该结构。
下面,我们通过Python实现一个生成杨辉三角的程序。
首先,我们来看一下已知杨辉三角第n行,如何生成第n+1行的算法。
对于第n行,我们需要取任意两个相邻的数相加,将结果插入到下一行中,组成较小的一个杨辉三角。
这个操作可以看作是将杨辉三角中的“骨架”沿着中轴线翻转所得到的结果。
同时,我们知道杨辉三角中间对称的两个数之和等于该行的奇数项数列,也就是说,如果我们知道了一个杨辉三角的奇数项数列,那么我们就可以推出该杨辉三角。
接下来,我们来看一下具体的实现:```pythondef pascal_triangle(n):if n == 0: # 第一行只有一个1return [[1]]elif n == 1: # 第二行是两个1return [[1], [1, 1]]else:# 生成上一行的奇数项数列row = pascal_triangle(n-1)[-1]odd_row = [row[i] + row[i+1] for i in range(len(row)-1)]# 将奇数项数列转换为新的一行new_row = [1] + odd_row + [1]# 递归生成下一行return pascal_triangle(n-1) + [new_row]```我们可以看到,如果n为0或1,则直接返回对应的两个行。
对于一般的n,我们递归生成该杨辉三角的前n-1行,得到第n-1行的奇数项数列。
然后将这个数列左右各加一个1,就得到了第n行的所有元素。
最后,将该行加入到当前的杨辉三角中,递归生成下一行。
用Python生成N层的杨辉三角的实现方法
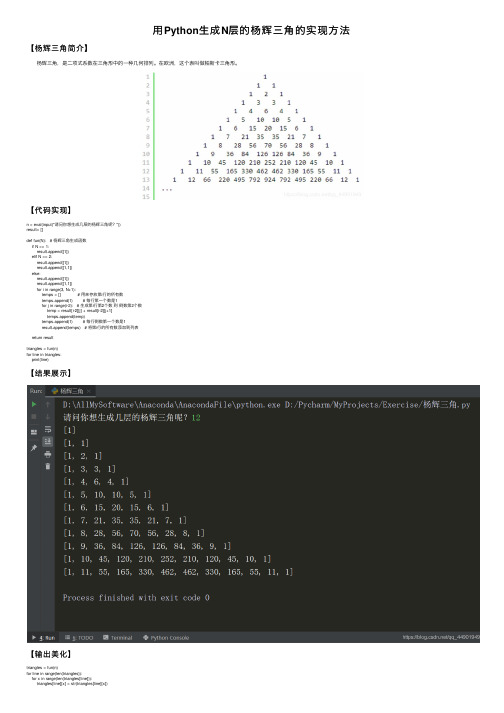
⽤Python⽣成N层的杨辉三⾓的实现⽅法【杨辉三⾓简介】 杨辉三⾓,是⼆项式系数在三⾓形中的⼀种⼏何排列。
在欧洲,这个表叫做帕斯卡三⾓形。
【代码实现】n = eval(input("请问你想⽣成⼏层的杨辉三⾓呢?"))result= []def fun(N): # 杨辉三⾓⽣成函数if N == 1:result.append([1])elif N == 2:result.append([1])result.append([1,1])else:result.append([1])result.append([1,1])for i in range(3, N+1):temps = [] # ⽤来存放第i⾏的所有数temps.append(1) # 每⾏第⼀个数是1for j in range(i-2): # ⽣成第i⾏第2个数到倒数第2个数temp = result[i-2][j] + result[i-2][j+1]temps.append(temp)temps.append(1) # 每⾏倒数第⼀个数是1result.append(temps) # 将第i⾏的所有数添加到列表return resulttriangles = fun(n)for line in triangles:print(line)【结果展⽰】【输出美化】triangles = fun(n)for line in range(len(triangles)):for x in range(len(triangles[line])):triangles[line][x] = str(triangles[line][x])triangles[line] = ' '.join(triangles[line])print("第{:>2}⾏ {:^100}".format(line+1, triangles[line]))到此这篇关于⽤Python⽣成N层的杨辉三⾓的实现⽅法的⽂章就介绍到这了,更多相关Python 杨辉三⾓内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持!。
杨辉三角算法集锦

/*Name: 杨辉三角算法集锦分别使用了二维数组,一维数组,队列,二项式公式,组合公式推论和递归方法等9种算法*/#include<iostream>#include<iomanip>using namespace std;const int MAXROW = 40;void PrintBlank(int n);int Com(int n, int m);int Try(int row, int cel);void Fun_1(int row);void Fun_2(int row);void Fun_3(int row);void Fun_4(int row);void Fun_5(int row);void Fun_6(int row);void Fun_7(int row);void Fun_8(int row);void Fun_9(int row);int main(){int row;cin >> row;Fun_1(row);cout << endl;Fun_2(row);cout << endl;Fun_3(row);cout << endl;Fun_4(row);cout << endl;Fun_5(row);cout << endl;Fun_6(row);cout << endl;Fun_7(row);cout << endl;Fun_8(row);cout << endl;Fun_9(row);system("pause");return 0;}//输出n个空格void PrintBlank(int n){for (int i=0; i<n; i++)cout << ' ';}//使用二维数组输出杨辉三角void Fun_1(int row){const int DIS = 6;int blank = 32;int a[MAXROW][MAXROW] = {0};for (int i=0; i<row; i++){PrintBlank(blank-=DIS/2);//输出第i行空格 for (int j=0; j<=i; j++){if (j == 0 || j == i)a[i][j] = 1;else //规律: 左上与正上元素之和a[i][j] = a[i-1][j-1] + a[i-1][j];cout << setw(DIS) << a[i][j];if (j == i)cout << endl;}}}//使用队列输出杨辉三角void Fun_2(int row){const int DIS = 6;int max = row + 2;int blank = 30;int *a = new int[max];int front, rear;front = 0; a[0] = 1;rear = 1; a[1] = 1;PrintBlank(blank);//输出第一行空格while (front != (rear+1)%max){if (a[front] == 1 && a[(front+1)%max] == 1)//到i-1行尾部{rear = (rear+1)%max; a[rear] = 1; //第i行尾部rear = (rear+1)%max; a[rear] = 1; //队尾进入第i+1行cout << setw(DIS) << 1 << endl; //输出第i-1行尾部front = (front+1)%max; //对头进入第i行PrintBlank(blank-=DIS/2);//输出第i行空格}//处理中间数据rear = (rear+1)%max; a[rear] = a[front] + a[(front+1)%max]; if (front != rear)//队列非空时输出cout << setw(DIS) << a[front]; //输出对头front = (front+1)%max; //删除对头元素}delete []a;}//使用两个一维数组代替二维数组输出杨辉三角void Fun_3(int row){const int DIS = 6;int blank = 33;int *a = new int[row]; //存储下一行int *b = new int[row];//存储输出行b[0] = 1;for (int n=1; n<=row; n++){//输出第n行PrintBlank(blank-=DIS/2);cout << setw(DIS) << b[i];cout << endl;if (n == row)//已经到最后一行则不再复制continue;//生成第n+1行数据a[0] = b[0];for (int i=1; i<n; i++)a[i] = b[i] + b[i-1];a[n] = 1;//复制第n+1行数据for (int i=0; i<=n; i++)b[i] = a[i];}delete []a;delete []b;}//使用一个一维数组和两个临时变量代替二维数组输出杨辉三角:很巧妙void Fun_4(int row){const int DIS = 6;int blank = 30;int *a = new int[row]; //存储输出行int left, right;//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;a[0] = 1;//左侧数据永远为1for (int n=1; n<row; n++){left = a[0];//生成第n行数据for (int i=1; i<n; i++)//设置中间数据{right = a[i];a[i] = left + right;//left=a[i-1],right=a[i]left = right;}a[n] = 1;//设置右侧的数据1//输出第n行PrintBlank(blank-=DIS/2);cout << setw(DIS) << a[i];cout << endl;}delete []a;}//使用一个一维数组和两个临时变量代替二维数组输出杨辉三角:方法同Fun_4,但更具有技巧,有点难懂void Fun_5(int row){const int DIS = 6;int blank = 33;int *a = new int[row]; //存储输出行for (int i=1; i<row; i++)//赋初值0,这个很重要,因为后面有用到 a[i] = 0;a[0] = 1;int left, right;for (int n=1; n<=row; n++){left = 0;//生成第n行数据for (int i=0; i<n; i++){right = a[i];a[i] = left + right;//left=a[i-1],right=a[i]left = right;}//输出第n行PrintBlank(blank-=DIS/2);for (int i=0; i<n; i++)cout << setw(DIS) << a[i];cout << endl;}delete []a;}//使用一个一维数组输出杨辉三角;两侧的1不变,计算中间的元素void Fun_6(int row){const int DIS = 6;int blank = 30;int *a = new int[row];//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;a[0] = 1;//最左侧为1,永远不变for (int n=1; n<row; n++){a[n] = 1; //设置最右侧的1for (int i=n-1; i>0; i--)//设置中间的元素,由于a[i]的值变化,故应从右到左计算{a[i] += a[i-1]; //杨辉三角的规律}//输出第n+1行PrintBlank(blank-=DIS/2);for (int i=0; i<=n; i++)cout << setw(DIS) << a[i];cout << endl;}delete []a;}//使用二项式定理输出杨辉三角void Fun_7(int row){const int DIS = 6;int blank = 30;//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;for (int i=1; i<row; i++){PrintBlank(blank-=DIS/2);//输出第i行空格for (int j=0; j<i; j++){cout << setw(DIS) << Com(i, j);}cout << setw(DIS) << 1 << endl;//输出每行最后一个1}}//输出组合c(n,m)int Com(int n, int m){int s1 = 1;int s2 = 1;m = (m > n/2) ? (n - m) : m;//取小的,以减少计算量for (int i=1; i<=m; i++){s1 *= n;s2 *= i;if (s1 % s2 == 0)//防止溢出{s1 /= s2;s2 = 1;}n--;}return s1;}//使用组合公式推论输出杨辉三角 :C(n,m) = (n-m+1)/m * C(n,m-1) void Fun_8(int row){const int DIS = 6;int blank = 30;//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;for (int n=1; n<row; n++){int c = 1;PrintBlank(blank-=DIS/2);//输出第i行空格cout << setw(DIS) << c; //输出每行第一个1for (int m=1; m<n; m++)//输出中间元素{c = c * (n - m + 1) / m;cout << setw(DIS) << c;}cout << setw(DIS) << 1 << endl;//输出每行最后一个1 }}//使用递归方法输出杨辉三角 :C(n,k) = 1 (k=0或者n=k);C(n,k) = C(n-1,k-1) + C(n-1,k)void Fun_9(int row){const int DIS = 6;int blank = 33;for (int n=0; n<row; n++){PrintBlank(blank-=DIS/2);//输出第i行空格for (int m=0; m<=n; m++)//输出中间元素{cout << setw(DIS) << Try(n, m);}cout << endl;//输出每行最后一个1}}//递归函数,输出杨辉三角 :C(n,k) = 1 (k=0或者n=k);C(n,k) = C(n-1,k-1) + C(n-1,k)int Try(int n, int k){if (k == 0 || k == n)//在左右两侧返回1return 1;return Try(n-1,k-1) + Try(n-1,k);//递推公式}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/*Name: 杨辉三角算法集锦Copyright: 始发于goal00001111的专栏;允许自由转载,但必须注明作者和出处Author: goal00001111Date: 27-11-08 19:04Description:分别使用了二维数组,一维数组,队列,二项式公式,组合公式推论和递归方法等9种算法算法思路详见代码注释——注释很详细,呵呵*/#include<iostream>#include<iomanip>using namespace std;const int MAXROW = 40;void PrintBlank(int n);int Com(int n, int m);int Try(int row, int cel);void Fun_1(int row);void Fun_2(int row);void Fun_3(int row);void Fun_4(int row);void Fun_5(int row);void Fun_6(int row);void Fun_7(int row);void Fun_8(int row);void Fun_9(int row);int main(){int row;cin >> row;Fun_1(row);cout << endl;Fun_2(row);cout << endl;Fun_3(row);cout << endl;Fun_4(row);cout << endl;Fun_5(row);cout << endl;Fun_6(row);cout << endl;Fun_7(row);cout << endl;Fun_8(row);cout << endl;Fun_9(row);system("pause");return 0;}//输出n个空格void PrintBlank(int n){for (int i=0; i<n; i++)cout << ' ';}//使用二维数组输出杨辉三角void Fun_1(int row){const int DIS = 6;int blank = 32;int a[MAXROW][MAXROW] = {0};for (int i=0; i<row; i++){PrintBlank(blank-=DIS/2);//输出第i行空格for (int j=0; j<=i; j++){if (j == 0 || j == i)a[i][j] = 1;else //规律: 左上与正上元素之和a[i][j] = a[i-1][j-1] + a[i-1][j];cout << setw(DIS) << a[i][j];if (j == i)cout << endl;}}}//使用队列输出杨辉三角void Fun_2(int row){const int DIS = 6;int max = row + 2;int blank = 30;int *a = new int[max];int front, rear;front = 0; a[0] = 1;rear = 1; a[1] = 1;PrintBlank(blank);//输出第一行空格while (front != (rear+1)%max){if (a[front] == 1 && a[(front+1)%max] == 1)//到i-1行尾部{rear = (rear+1)%max; a[rear] = 1; //第i行尾部rear = (rear+1)%max; a[rear] = 1; //队尾进入第i+1行cout << setw(DIS) << 1 << endl; //输出第i-1行尾部front = (front+1)%max; //对头进入第i行PrintBlank(blank-=DIS/2);//输出第i行空格}//处理中间数据rear = (rear+1)%max; a[rear] = a[front] + a[(front+1)%max];if (front != rear)//队列非空时输出cout << setw(DIS) << a[front]; //输出对头front = (front+1)%max; //删除对头元素}delete []a;}//使用两个一维数组代替二维数组输出杨辉三角void Fun_3(int row){const int DIS = 6;int blank = 33;int *a = new int[row]; //存储下一行int *b = new int[row];//存储输出行b[0] = 1;for (int n=1; n<=row; n++){//输出第n行PrintBlank(blank-=DIS/2);cout << setw(DIS) << b[i];cout << endl;if (n == row)//已经到最后一行则不再复制continue;//生成第n+1行数据a[0] = b[0];for (int i=1; i<n; i++)a[i] = b[i] + b[i-1];a[n] = 1;//复制第n+1行数据for (int i=0; i<=n; i++)b[i] = a[i];}delete []a;delete []b;}//使用一个一维数组和两个临时变量代替二维数组输出杨辉三角:很巧妙void Fun_4(int row){const int DIS = 6;int blank = 30;int *a = new int[row]; //存储输出行int left, right;//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;a[0] = 1;//左侧数据永远为1for (int n=1; n<row; n++){left = a[0];//生成第n行数据for (int i=1; i<n; i++)//设置中间数据{right = a[i];a[i] = left + right;//left=a[i-1],right=a[i]left = right;}a[n] = 1;//设置右侧的数据1//输出第n行PrintBlank(blank-=DIS/2);cout << setw(DIS) << a[i];cout << endl;}delete []a;}//使用一个一维数组和两个临时变量代替二维数组输出杨辉三角:方法同Fun_4,但更具有技巧,有点难懂void Fun_5(int row){const int DIS = 6;int blank = 33;int *a = new int[row]; //存储输出行for (int i=1; i<row; i++)//赋初值0,这个很重要,因为后面有用到a[i] = 0;a[0] = 1;int left, right;for (int n=1; n<=row; n++){left = 0;//生成第n行数据for (int i=0; i<n; i++){right = a[i];a[i] = left + right;//left=a[i-1],right=a[i]left = right;}//输出第n行PrintBlank(blank-=DIS/2);for (int i=0; i<n; i++)cout << setw(DIS) << a[i];cout << endl;}delete []a;}//使用一个一维数组输出杨辉三角;两侧的1不变,计算中间的元素void Fun_6(int row){const int DIS = 6;int blank = 30;int *a = new int[row];//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;a[0] = 1;//最左侧为1,永远不变for (int n=1; n<row; n++){a[n] = 1; //设置最右侧的1for (int i=n-1; i>0; i--)//设置中间的元素,由于a[i]的值变化,故应从右到左计算{a[i] += a[i-1]; //杨辉三角的规律}//输出第n+1行PrintBlank(blank-=DIS/2);for (int i=0; i<=n; i++)cout << setw(DIS) << a[i];cout << endl;}delete []a;}//使用二项式定理输出杨辉三角void Fun_7(int row){const int DIS = 6;int blank = 30;//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;for (int i=1; i<row; i++){PrintBlank(blank-=DIS/2);//输出第i行空格for (int j=0; j<i; j++){cout << setw(DIS) << Com(i, j);}cout << setw(DIS) << 1 << endl;//输出每行最后一个1}}//输出组合c(n,m)int Com(int n, int m){int s1 = 1;int s2 = 1;m = (m > n/2) ? (n - m) : m;//取小的,以减少计算量for (int i=1; i<=m; i++){s1 *= n;s2 *= i;if (s1 % s2 == 0)//防止溢出{s1 /= s2;s2 = 1;}n--;}return s1;}//使用组合公式推论输出杨辉三角:C(n,m) = (n-m+1)/m * C(n,m-1) void Fun_8(int row){const int DIS = 6;int blank = 30;//输出第一行PrintBlank(blank);//输出第1行空格cout << setw(DIS) << 1 << endl;for (int n=1; n<row; n++){int c = 1;PrintBlank(blank-=DIS/2);//输出第i行空格cout << setw(DIS) << c; //输出每行第一个1for (int m=1; m<n; m++)//输出中间元素{c = c * (n - m + 1) / m;cout << setw(DIS) << c;}cout << setw(DIS) << 1 << endl;//输出每行最后一个1 }}//使用递归方法输出杨辉三角:C(n,k) = 1 (k=0或者n=k);C(n,k) = C(n-1,k-1) + C(n-1,k) void Fun_9(int row){const int DIS = 6;int blank = 33;for (int n=0; n<row; n++){PrintBlank(blank-=DIS/2);//输出第i行空格for (int m=0; m<=n; m++)//输出中间元素{cout << setw(DIS) << Try(n, m);}cout << endl;//输出每行最后一个1}}//递归函数,输出杨辉三角:C(n,k) = 1 (k=0或者n=k);C(n,k) = C(n-1,k-1) + C(n-1,k) int Try(int n, int k){if (k == 0 || k == n)//在左右两侧返回1return 1;return Try(n-1,k-1) + Try(n-1,k);//递推公式}。
