新版递归算法课件.ppt
合集下载
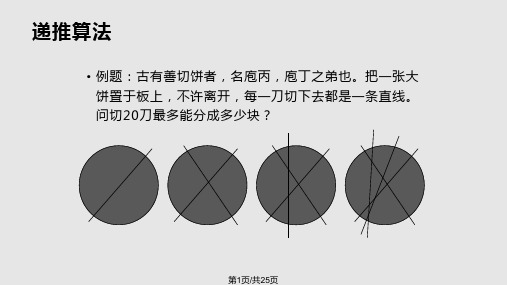
递归算法 ppt课件

ppt课件
14
int fib(int n) { if (n==0) return 0; if (n==1) return 1; return (fib(n-1)+fib(n-2)); }
输入 15 输出 fib(15)=610
//满足边界条件,递归返回 //满足边界条件,递归返回 //递归公式,进一步递归
//调用下一层递归
}
int main()
{
int n,k;
cin >> n >> k;
cout << s(n,k);
return 0;
}
ppt课件
19
【例6】数的计数(Noip2001)
【问题描述】
我们要求找出具有下列性质数的个数(包括输入的自然数n)。先输入一 个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:
8
ppt课件
9
假设把第3步,第4步,第7步抽出来就相当于N=2的情况(把上面2片 捆在一起,视为一片):
ppt课件
10
所以可按“N=2”的移动步骤设计:
①如果N=0,则退出,即结束程序;否则继续往下执行;
②用C柱作为协助过渡,将A柱上的(N-1)片移到B柱上,调用过程mov(n-1,
a,b,c);
本题是典型的递归程序设计题。 (1)当N=1 时,只有一个盘子,只需要移动一次:A—>C; (2)当N=2时,则需要移动三次:
A------ 1 ------> B, A ------ 2 ------> C, B ------ 1------> C. (3)如果N=3,则具体移动步骤为:
递归与分治ppt课件

C三个柱子间移动。}
2023/10/8
计算机算法设计与分析
3
Hanoi塔问题的时间复杂性
n Hanoi塔问题的时间复杂性为O(2n)。 n 证明:对n归纳证明move(n) = 2n – 1。 n 归纳基础:当n = 1, move(1) = 1 = 21 – 1。 n 归纳假设:当n k, move(n) = 2n – 1。 n 归纳步骤:当n= k + 1,移动次数为
2、除法,即n / b,的形式
2023/11/4
计算机算法设计与分析
21
递归算法的时间复杂性
n 若~为减法,即n – b,则有:
T(n) = aT(n – b) + D(n)
= a(aT(n – 2b) + D(n – b)) + D(n) =
k–1
k–1
= akT(1) + ai D(n – ib) = ak + ai D(n – ib)
n q最(n简, m单)情{ 形1:(1) q(n, 1)=1, q(1, mn)==1 n或, mm≥1=;1 n 递q(iin归ff,((mnn关)<=系==1):1q1)||(|((+|nm2(,)qmm<(qn=–(1,n1=)n,)–+1n1)q))(=rrnee–1ttmuu+rr,nqnm(01n);;, nnn>–≤1m)m,>n1>1; n 产i生f (n的=新= 情1) 况|| (:n < m) return 1 + q(n, n–1); n (3r)eqtu(nr,nmq)(n=,qm(n–,1m) +–1q)(n+–qm(,nm–m);, m} ), n>m>1 n (整4)数q(nn的, m划)分= q数(nρ,(n),=nq<(nm, n。)。
2023/10/8
计算机算法设计与分析
3
Hanoi塔问题的时间复杂性
n Hanoi塔问题的时间复杂性为O(2n)。 n 证明:对n归纳证明move(n) = 2n – 1。 n 归纳基础:当n = 1, move(1) = 1 = 21 – 1。 n 归纳假设:当n k, move(n) = 2n – 1。 n 归纳步骤:当n= k + 1,移动次数为
2、除法,即n / b,的形式
2023/11/4
计算机算法设计与分析
21
递归算法的时间复杂性
n 若~为减法,即n – b,则有:
T(n) = aT(n – b) + D(n)
= a(aT(n – 2b) + D(n – b)) + D(n) =
k–1
k–1
= akT(1) + ai D(n – ib) = ak + ai D(n – ib)
n q最(n简, m单)情{ 形1:(1) q(n, 1)=1, q(1, mn)==1 n或, mm≥1=;1 n 递q(iin归ff,((mnn关)<=系==1):1q1)||(|((+|nm2(,)qmm<(qn=–(1,n1=)n,)–+1n1)q))(=rrnee–1ttmuu+rr,nqnm(01n);;, nnn>–≤1m)m,>n1>1; n 产i生f (n的=新= 情1) 况|| (:n < m) return 1 + q(n, n–1); n (3r)eqtu(nr,nmq)(n=,qm(n–,1m) +–1q)(n+–qm(,nm–m);, m} ), n>m>1 n (整4)数q(nn的, m划)分= q数(nρ,(n),=nq<(nm, n。)。
教科版选修1《递归法》ppt课件

题的运行效率较低。所以一般不提倡用递归算法 设计程序
递归法的归纳2:
递归算法所体现的“重复”一般有三个要求: 一是每次调用在规模上都有所缩小(通常是减半); 二是相邻两次重复之间有紧密的联系,前一次要为
后一次做准备(通常前一次的输出就作为后一次的 输入); 三是在问题的规模极小时必须用直接给出解答而不 再进行递归调用,因而每次递归调用都是有条件 的(以规模未达到直接解答的大小为条件),无条 件递归调用将会成为死循环而不能正常结束。
• 注意:必须要有一个结束递归的条件,不 得无限递归。
分析步骤:
• 1.决定问题规模的参数。 • 2.问题的边界条件及边界值。 • 3.解决问题的通式。
例:计算一个数的阶乘
• 1!=1 • 2!=1*2 • 3!=1*2*3 • 4!=1*2*3*4 • 5!=1*2*3*4*5 • ……. • n!=1*2*3*4*5*….*n
函数是为了实现某种功能而编写的一段相对独立 的程序。
• 标准函数
Abs( ) 、len( )、mid( )、chr( )、asc( )……
• 自定义函数
自定义函数是指我们自己编写的函数。
自定义函数:
• 在VB中,自定义函数形式如下: • [Public|Private] Function <函数名称> ([参数列表]) [As
f(1)=1 f(2)=f(1)*2 f(3)=f(2)*3 f(4)=f(3)*4 f(5)=f(4)*5 …….. f(n)=f(n-1)*n
递归函数求5!
• Public Function s(n As Integer) As Long
• If n = 1 Then
• s =1
• Else
递归法的归纳2:
递归算法所体现的“重复”一般有三个要求: 一是每次调用在规模上都有所缩小(通常是减半); 二是相邻两次重复之间有紧密的联系,前一次要为
后一次做准备(通常前一次的输出就作为后一次的 输入); 三是在问题的规模极小时必须用直接给出解答而不 再进行递归调用,因而每次递归调用都是有条件 的(以规模未达到直接解答的大小为条件),无条 件递归调用将会成为死循环而不能正常结束。
• 注意:必须要有一个结束递归的条件,不 得无限递归。
分析步骤:
• 1.决定问题规模的参数。 • 2.问题的边界条件及边界值。 • 3.解决问题的通式。
例:计算一个数的阶乘
• 1!=1 • 2!=1*2 • 3!=1*2*3 • 4!=1*2*3*4 • 5!=1*2*3*4*5 • ……. • n!=1*2*3*4*5*….*n
函数是为了实现某种功能而编写的一段相对独立 的程序。
• 标准函数
Abs( ) 、len( )、mid( )、chr( )、asc( )……
• 自定义函数
自定义函数是指我们自己编写的函数。
自定义函数:
• 在VB中,自定义函数形式如下: • [Public|Private] Function <函数名称> ([参数列表]) [As
f(1)=1 f(2)=f(1)*2 f(3)=f(2)*3 f(4)=f(3)*4 f(5)=f(4)*5 …….. f(n)=f(n-1)*n
递归函数求5!
• Public Function s(n As Integer) As Long
• If n = 1 Then
• s =1
• Else
高二年级 信息技术 递归算法课件

什么是递归算法? 递归算法:是一种直接或者间接地调用自身 的算法。在计算机编写程序中,递归算法对 解决一大类问题是十分有效的,它往往使算 法的描述简洁而且易于理解。
斐波那契的兔子问题 某人有一对兔子饲养在围墙中,如果 它们每个月生一对兔子,且新生的兔子 在第二个月后也是每个月生一对兔子, 问一年后围墙中共有多少对兔子。
递 归 算 法
主讲人:位胜楠
老师今天在查看英文文献的时候,遇 到了一些问题。 每次遇到不懂的单词都头痛不已,但是 老师只有英译英的词典,那么,可想而知, 遇到第一个不懂的单词时,查看词典,词 典的解释又全是英文,看第一个单词的解 释时,又遇到第二个不懂的单词,就这样, 继续查看第二个单词的解释, 同样的情况,在第二个单词解释中又遇到 第三个不认识的单词,幸运的是第三个单 词的解释老师全都认识,那么,很明显知 道了第三个解释,就知道了第二个,知道 了第二个就知道了第一个, 最后不认识的单词都知道了。这个过程, 就是递归。
Private Sub Command1_Click()
n = Val(Text1.Text)
If n < 3 Then c = 1 Else a = 1: b = 1 For i = 3 To n
c=Text = "第" & n & "月的兔子数目是:" & c End Sub
递归算法的特点
递归过程一般通过函数或子过程来实 现。
递归算法:
在函数或子过程的内部,直接或者间 接地调用自己的算法。
递归算法的实质:是把问题转
化为规模缩小了的同类问题的子问题。 然后递归调用函数(或过程)来表示问 题的解。
列函数
运用学过的自定义函数知识,结合之前分析的递归思想列出函数,更 加深入理解递归的特点。
递归算法课件

写成函数形式,则为:
当n 0时 1 f ( n) n * f (n 1) 当n 0时
这种函数定义的方法是用阶乘函数自己本身定义了 阶乘函数,称上式为阶乘函数的递推定义式。
数学归纳法表明,如果我们知道某个论点对最小的情 形成立,并且可以证明一个情形暗示着另一个情形,那么我 们就知道该论点对所有情形都成立。 数学有时是按递归方式定义的。 例1:假设S(n)是前n个整数的和,那么S(1)= 1,并且 我们可以将S(n)写成S(n)= S(n-1)+ n。 根据递归公式,我们可以得到对应的递归函数: int S(int n) { if (n == 1) return 1; else return S(n-1) + n; } 函数由递归公式得到,应该是好理解的,要想求出S (n),得先求出S(n-1),递归终止的条件(递归出口)是(n == 1)。
↑
low 第二次: 下标 元素值 0 1 1 3 2 4
↑
mid 3 5 4 17 5 18 6 31
↑
high 7 33
↑
low 第三次: 下标 元素值 0 1 1 3 2 4 3 5 4 17
↑
mid 5 18 6 31
↑
high 7 33
↑
low high mid
• Public static void main(String args[]) •{ • int[] shus={1,3,4,5,17,18,31,33};
求Fib(5)的递归计算过程如图所示。
Fib(5) Fib(4) Fib(3) Fib(2) Fib(1) Fib(2) Fib(3) Fib(2) Fib(1) Fib(0)
Fib(1) Fib(0) Fib(1)
当n 0时 1 f ( n) n * f (n 1) 当n 0时
这种函数定义的方法是用阶乘函数自己本身定义了 阶乘函数,称上式为阶乘函数的递推定义式。
数学归纳法表明,如果我们知道某个论点对最小的情 形成立,并且可以证明一个情形暗示着另一个情形,那么我 们就知道该论点对所有情形都成立。 数学有时是按递归方式定义的。 例1:假设S(n)是前n个整数的和,那么S(1)= 1,并且 我们可以将S(n)写成S(n)= S(n-1)+ n。 根据递归公式,我们可以得到对应的递归函数: int S(int n) { if (n == 1) return 1; else return S(n-1) + n; } 函数由递归公式得到,应该是好理解的,要想求出S (n),得先求出S(n-1),递归终止的条件(递归出口)是(n == 1)。
↑
low 第二次: 下标 元素值 0 1 1 3 2 4
↑
mid 3 5 4 17 5 18 6 31
↑
high 7 33
↑
low 第三次: 下标 元素值 0 1 1 3 2 4 3 5 4 17
↑
mid 5 18 6 31
↑
high 7 33
↑
low high mid
• Public static void main(String args[]) •{ • int[] shus={1,3,4,5,17,18,31,33};
求Fib(5)的递归计算过程如图所示。
Fib(5) Fib(4) Fib(3) Fib(2) Fib(1) Fib(2) Fib(3) Fib(2) Fib(1) Fib(0)
Fib(1) Fib(0) Fib(1)
迭代与递归 递归的概念与特征 课件(20张PPT)

2022
JUNE 17th
适用情况
一、每次计算在规模上都有所缩小。二、可以通过同一套规则(即相同的程序)转化为比该问题更为简单的子问题。比如: 三、问题的规模极小时必须用直接给出解答。比如:
Coding is FUN
总结
Summarize
#04
2022
JUNE 17th
Informatics Olympiad
递归算法的条件
Conditions for recursive algorit来自ms#022022
JUNE 17th
Informatics Olympiad
2022
JUNE 17th
递归条件
使用递归解决的问题都可以通过同一套规则转化为比该问题更为简单的子问题,这套规则被称为该问题的递归定义或递归公式。例如,在计算阶乘问题中,就是计算阶乘的递归公式。
递归的概念与特征
The concept and characteristics of recursion
2022 JUNE 17th
讲课人:XXX
引 入
introduce
从前有座山,山上有座庙,庙里有个老和尚在讲故事,讲的是什么呢?从前有座山,山上有座庙……
Coding is FUN
什么是递归
JUNE 17th
2022
JUNE 17th
分析问题
如果用表示计算斐波纳奇数列的函数,那么根据定义我们可以知道, 当 或者 的时候 为 ,此时直接返回结果就可以。与刚刚计算阶乘一样,我们可以得到以下表达式:
Coding is FUN
2022
JUNE 17th
适用情况
Coding is FUN
我们已经用递归算法解决了两个问题,那在什么情况下可以使用递归算法来解决问题的?
递归软件学院PPT课件

HR(n-1, i, k, j). MOVE(i, k). HR(n-1, j, i, k).▌
27
第27页/共39页
例如HR(3,1,2,3),递归算法的执行过程及结果如 下:
1→3 1→2 3→2 1→3 2→1
28
第28页/共39页
递归过程的实现与堆栈
实现递归的系统工作栈由系统管理; 也可自己设计基于栈的非递归程序。
24
第24页/共39页
例:汉诺塔游戏
一块铜板上有三根金刚石柱,柱上放有N个大小 不等的金盘。目标是把左面柱上的金盘移动到右 面柱上,移动过程中一次只能移动一个盘子,不 允许大盘放在小盘上面,只能借助中间柱。
25
第25页/共39页
递归算法的思想: 1. 以C柱为临时柱,从A柱将1至N-1号盘移至B
堆栈常用的操作: 1)CREATS ( S ):建立一个堆栈 S; 2)S x : 元素 x 进栈; 3)x S : 元素 x 出栈; 4)StackEmpty(S): 若 S 为空,返回1.
29
第29页/共39页
基于堆栈的非递归算法
堆栈存储递归调用的返回路径 堆栈元素为四元组(n,i,j,k)
16
第16页/共39页
递归过程的调用分为外部调用和内部调用。
main() f(n) f(0)
f(n-1)
f(1)
调用
调用点 Pn
Pn-1
Pn-2
P0
…
返回
17
第17页/共39页
为保证递归调用正确,要解决参数传递和返回地址问题,系统使用 “递 归工作栈” 来解决。
调用时执行入栈操作保存现场,返回时执行出栈操作恢复现场。 现场(工作记录):
18
27
第27页/共39页
例如HR(3,1,2,3),递归算法的执行过程及结果如 下:
1→3 1→2 3→2 1→3 2→1
28
第28页/共39页
递归过程的实现与堆栈
实现递归的系统工作栈由系统管理; 也可自己设计基于栈的非递归程序。
24
第24页/共39页
例:汉诺塔游戏
一块铜板上有三根金刚石柱,柱上放有N个大小 不等的金盘。目标是把左面柱上的金盘移动到右 面柱上,移动过程中一次只能移动一个盘子,不 允许大盘放在小盘上面,只能借助中间柱。
25
第25页/共39页
递归算法的思想: 1. 以C柱为临时柱,从A柱将1至N-1号盘移至B
堆栈常用的操作: 1)CREATS ( S ):建立一个堆栈 S; 2)S x : 元素 x 进栈; 3)x S : 元素 x 出栈; 4)StackEmpty(S): 若 S 为空,返回1.
29
第29页/共39页
基于堆栈的非递归算法
堆栈存储递归调用的返回路径 堆栈元素为四元组(n,i,j,k)
16
第16页/共39页
递归过程的调用分为外部调用和内部调用。
main() f(n) f(0)
f(n-1)
f(1)
调用
调用点 Pn
Pn-1
Pn-2
P0
…
返回
17
第17页/共39页
为保证递归调用正确,要解决参数传递和返回地址问题,系统使用 “递 归工作栈” 来解决。
调用时执行入栈操作保存现场,返回时执行出栈操作恢复现场。 现场(工作记录):
18
递归及递归算法分析课件

A(1,1)=2故A(n,1)=2*n ❖ M=2时,A(n,2)=A(A(n-1,2),1)=2A(n-1,2),和
A(1,2)=A(A(0,2),1)=A(1,1)=2,故A(n,2)= 2^n 。
2 222
❖ M=3时,类似的可以推出
n
❖ M=4时,A(n,4)的增长速度非常快,以至于没有适当的数 学式子来表示这一函数。
❖
move(a,b);
❖
hanoi(n-1, c, b, a);
❖
}
❖}
❖ T(n)=2T(n-1)+O(1) n≥1
T(n)=2n-1
0
n=0
4
27
简单递归式的求解
1.T(n)=T(n-1)+c1 n>1
c2
n=1
2. T(n)=2T(n/2)+c1 n ≥2
c2
n<2
3. T(n)=2T(n/2)+Θ(n) n ≥2
O(1)
n<2
28
T( n/2 ) + T( n/2 ) + 1
例1 T(n) =
0
(n = 1)
解 :T(n)=2T(n/2)+1
=22T(n/22)+2+1
=23T(n/23)+22+2+1
令2r=n =2rT(1)+2r-1+。。。+2+1
=(1-2r)/(1-2)=n-1
∴ T( n ) = n - 1
25
递归算法的时间复杂度分析
❖ 递归函数求解
简单递归式求解 master method 递推方程的特征方程求解
A(1,2)=A(A(0,2),1)=A(1,1)=2,故A(n,2)= 2^n 。
2 222
❖ M=3时,类似的可以推出
n
❖ M=4时,A(n,4)的增长速度非常快,以至于没有适当的数 学式子来表示这一函数。
❖
move(a,b);
❖
hanoi(n-1, c, b, a);
❖
}
❖}
❖ T(n)=2T(n-1)+O(1) n≥1
T(n)=2n-1
0
n=0
4
27
简单递归式的求解
1.T(n)=T(n-1)+c1 n>1
c2
n=1
2. T(n)=2T(n/2)+c1 n ≥2
c2
n<2
3. T(n)=2T(n/2)+Θ(n) n ≥2
O(1)
n<2
28
T( n/2 ) + T( n/2 ) + 1
例1 T(n) =
0
(n = 1)
解 :T(n)=2T(n/2)+1
=22T(n/22)+2+1
=23T(n/23)+22+2+1
令2r=n =2rT(1)+2r-1+。。。+2+1
=(1-2r)/(1-2)=n-1
∴ T( n ) = n - 1
25
递归算法的时间复杂度分析
❖ 递归函数求解
简单递归式求解 master method 递推方程的特征方程求解
C语言递推与递归PPT课件
• 使用递归函数编程
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
VB递归算法 PPT课件

End Sub
Function f(n as integer)as integer if n<=1 then f=1
Else f=n* f(n-1)
End if End function
观察如下VB程序段:
Function fx(n As Integer) As Long
If n = 1 Then
练习题
➢ 用递归算法求 1~n 个连续自然数的和
Function sum(n As Integer) As Integer If n = 1 Then sum = 1 Else sum = sum(n - 1) + n End If End Function
Private Sub Command1_Click() Dim n As Integer n = Val(Text1.Text) Text2.Text = Str(sum(n)) End Sub
fact = 1 ……
fact (3)=6 返回
fact (2)=2 返回
fact (1)=1 返回
递归算法的实现要点
➢ (1)有明确的结束递归的边界条件(又称终止条件)以及结束 时的边界值,可以通过条件语句(If语句)来实现
➢ (2)函数的描述中包含其本身,即能用递归形式表示,且递 归终止条件的发展。
If n <= 1 Then
fact = 1
Else
fact = n * fact (n - 1)
End If
End Function
Private Sub Command1_Click()
Dim y As Integer y = fact(3) Print y
End Sub
Function f(n as integer)as integer if n<=1 then f=1
Else f=n* f(n-1)
End if End function
观察如下VB程序段:
Function fx(n As Integer) As Long
If n = 1 Then
练习题
➢ 用递归算法求 1~n 个连续自然数的和
Function sum(n As Integer) As Integer If n = 1 Then sum = 1 Else sum = sum(n - 1) + n End If End Function
Private Sub Command1_Click() Dim n As Integer n = Val(Text1.Text) Text2.Text = Str(sum(n)) End Sub
fact = 1 ……
fact (3)=6 返回
fact (2)=2 返回
fact (1)=1 返回
递归算法的实现要点
➢ (1)有明确的结束递归的边界条件(又称终止条件)以及结束 时的边界值,可以通过条件语句(If语句)来实现
➢ (2)函数的描述中包含其本身,即能用递归形式表示,且递 归终止条件的发展。
If n <= 1 Then
fact = 1
Else
fact = n * fact (n - 1)
End If
End Function
Private Sub Command1_Click()
Dim y As Integer y = fact(3) Print y
End Sub
《递归算法梁》PPT课件_OK

的问题求解和从原 点到(m-1,n)的走法 数的问题求解
15
田字表中路径数函数
//计算从原点到达(m,n)的走法数 int road(int m,int n) {
如果 m=0 或n=0; 返回1; //递归出口
否则 返回 road(m-1,n)+road(m,n-1);
}
2021/9/1
16
//计算从原点到达(m,n)的走法数 int road ( int m,int n) {
当P(1)在委员中时,则需要在P(2)~P(n)中选举k-1个人
当P(1)在委员中时,则需要在P(2)~P(n)中选举k个人
2021/9/1
25
委员会选举
2021/9/1
26
委员会选举
//委员会选举函数
int comm(n,k)//在n个人种选举k个委员的方法数
{ if (n==k||k==0) return 1; else return comn(n-1,k-1)+comnn(n-1,k);
2021/9/1
13
田字表中路径数
• 如下图所示,田字表由m*n个1*1的方格所组成,在 田字表右下角原点处(0,0)处有一小人,该小人需 要可以沿着表中框线向上或向右前进。则小人从原 点出发,到达(m,n)定点可以有多少中走法。
(m,n)
2021/9/1 (0,0)
14
算法分析:小人只能向上或向右前进,则小人需要到
20
一、 用循环结构的算法消除
//二分查找法算法的非递归实现
int bin_search (int a[ ],int low,int high,int k)
{ int mid;
while(low<=high) {
15
田字表中路径数函数
//计算从原点到达(m,n)的走法数 int road(int m,int n) {
如果 m=0 或n=0; 返回1; //递归出口
否则 返回 road(m-1,n)+road(m,n-1);
}
2021/9/1
16
//计算从原点到达(m,n)的走法数 int road ( int m,int n) {
当P(1)在委员中时,则需要在P(2)~P(n)中选举k-1个人
当P(1)在委员中时,则需要在P(2)~P(n)中选举k个人
2021/9/1
25
委员会选举
2021/9/1
26
委员会选举
//委员会选举函数
int comm(n,k)//在n个人种选举k个委员的方法数
{ if (n==k||k==0) return 1; else return comn(n-1,k-1)+comnn(n-1,k);
2021/9/1
13
田字表中路径数
• 如下图所示,田字表由m*n个1*1的方格所组成,在 田字表右下角原点处(0,0)处有一小人,该小人需 要可以沿着表中框线向上或向右前进。则小人从原 点出发,到达(m,n)定点可以有多少中走法。
(m,n)
2021/9/1 (0,0)
14
算法分析:小人只能向上或向右前进,则小人需要到
20
一、 用循环结构的算法消除
//二分查找法算法的非递归实现
int bin_search (int a[ ],int low,int high,int k)
{ int mid;
while(low<=high) {
递归算法设计技术47页PPT

。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
递归算法设计技术
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
递归算法设计技术
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)问题的解法存在自调用
一个典型的例子是在有序数组中查找一个数据元素是否 存在的折半查找算法。
精选
4
精选
5
6.2递归算法的执行过程
例6-1 给出按照公式6-3计算阶乘函数的递归算法, 并给出n = 3时递归算法的执行过程。
设计:按照公式6-3计算阶乘函数的递归算法如下:
精选
6
long int Fact(int n)
当一个问题存在上述两个基本要素时,该问题的递归算 法的设计方法是:
(1)把对原问题的求解设计成包含有对子问题求解的形 式。
(2)设计递归出口。
精选
16
例6-3 设计模拟汉诺塔问题求解过程的算法。汉诺塔问题的 描述是:设有3根标号为A,B,C的柱子,在A柱上放着n个盘子, 每一个都比下面的略小一点,要求把A柱上的盘子全部移到C柱 上,移动的规则是:
fromPeg, " to peg ", toPeg);
return;
}
//把n-1个圆盘从fromPeg借助toPeg移至auxPeg
towers(n-1,fromPeg,auxPeg,toPeg);
//把圆盘n由fromPeg直接移至toPeg printf("%s%d%s%c%s%c\n", "move disk ", n,
Move Disk i from Peg X to Peg Y
这样,汉诺塔问题的递归算法可设计如下:
精选
20
void towers(int n, char fromPeg, char toPeg, char auxPeg)
{ if(n==1)
//递归出口
{ printf("%s%c%s%c\n", "move disk 1 from peg ",
}
精选
11
测试主函数设计如下: # include <stdio.h> main(void) { int a[] = {1, 3, 4, 5, 17, 18, 31, 33};
int x = 17; int bn; bn = BSearch(a, x, 0,7); if(bn == -1) printf("x不在数组a中"); else printf("x在数组a的下标%d中", bn); }
long int fn; fn = Fact(3); }
主函数用实参n= 3调用了递归算法Fact(3),而 Fact(3)要通过调用Fact(2)、Fact(2)要通过调用Fact(1)、 Fact(1)要通过调用Fact(0)来得出计算结果。Fact(3)的 递归调用过程如图6-2所示。
精选
8
图6-2 Fact(3)的递归调用执行过程
精选
18
图6-4 汉诺塔问题的递归求解示意图
精选
19
算法设计:首先,盘子的个数n是必须的一个输入参数, 对n个盘子,我们可从上至下依次编号为1,2,…,n;其次, 输入参数还需有3个柱子的代号,我们令3个柱子的参数名分 别为fromPeg,auxPeg和toPeg;最后,汉诺塔问题的求解 是一个处理过程,因此算法的输出是n个盘子从柱子 fromPeg借助柱子auxPeg移动到柱子toPeg的移动步骤,我 们设计每一步的移动为屏幕显示如下形式的信息:
精选
12
BSearch(a, x, 0,7)的递归调用过程如图6-3所示, 其中,实箭头表示函数调用,虚箭头表示函数的返回值。
图6-3 BSearch(a, x, 0,7)的递归调用过程
精选
13
精选
14
6.3递归算法的设计方法
递归算法既是一种有效的算法设计方法,也是一种有效的 分析问题的方法。
6.1递归的概念
若一个算法直接的或间接的调用自己本身,则称这 个算法是递归算法。 存在算法调用自己的情况: (1)问题的定义是递推的
阶乘函数的常见定义是:
精选
2
也可定义为:
写成函数形式,则为:
这种函数定义的方法是用阶乘函数自己本身定义了阶 乘函数,称公式(6 – 3)是阶乘函数的递推定义式。
精选
3
递归算法求解问题的基本思想是:对于一个较为复杂的问 题,把原问题分解成若干个相对简单且类同的子问题,这样,原 问题就可递推得到解。
精选
15
适宜于用递归算法求解的问题的充分必要条件是: (1)问题具有某种可借用的类同自身的子问题描述的性 质; (2)某一有限步的子问题(也称作本原问题)有直接的 解存在。
(1)一次只能移动一个盘子;
(2)移动过程中大盘子不能放在小盘子上面;
(3)在移动过程中盘子可以放在A,B,C的任意一个柱子 上。
精选
17
问题分析:
可以用递归方法求解n个盘子的汉诺塔问题。
基本思想:
1个盘子的汉诺塔问题可直接移动。n个盘子的汉诺 塔问题可递归表示为,首先把上边的n-1个盘子从A柱移 到B柱,然后把最下边的一个盘子从A柱移到C柱,最后把 移到B柱的n-1个盘子再移到C柱。4个盘子汉诺塔问题的 递归求解示意图如图6-4所示。
{ int x;
long int y; if(n < 0)
//n < 0时阶乘无定义
{ printf(“参数错!”);
return -1;
}
if(n == 0) return 1;
else
{ y = Fact(n - 1);
//递归调用
return n * y;
void main(void) {
精选
9
例6-2 给出在有序数组a中查找数据元素x是否存在的 递归算法,并给出如图6-1所示实际数据的递归算法的 执行过程。递归算法如下:
精选
10
int BSearch(int a[], int x, int low, int high)
{
int mid;
if(low > high) return -1;
//查找不成功
mid = (low + high) / 2;
if(x == a[mid]) return mid; //查找成功
else if(x < a[mid])
return BSearch(a, x, low, mid-1);
//在下半区查找
else
return BSearch(a, x, mid+1, high); //在上半区查找
" from peg ", fromPeg, " to peg ", toPeg);
//把n-1个圆盘从auxPeg借助fromPeg移至toPeg
