递归算法(C++版)PPT课件
合集下载
C++函数、递推、递归ppt课件

i = 7 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(7) = 2 * (S(8) + 1) // s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
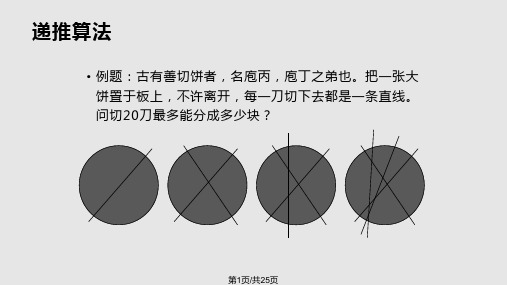
看一个简单的例子:
1 4
第九讲——函数、递推、递归
递归
有 5 个人坐在一起,问第 5 个人多少岁? 他说比第 4 个人 大两岁。问第 4 个人岁数,他说比第 3 个人大两岁。问第 3 个人,又说比第 2 个人大两岁。问第 2 个人,说比第 1 个人 大两岁。最后问第 1 个人,他说是 10 岁。请问第 5 个人多 大?
3
第九讲——函数、递推、递归
解题思路:
假设用 S(i) 表示第 i 天没吃之前的桃子数目;
则
S(1) 即为第 1 天所摘的桃子数; S(2) = S(1) * 1/2 – 1 第 2 天没吃之前的桃子数
S(3) = S(2) * 1/2 - 1 第 3 天没吃之前的桃子数
…
…
S(9) = S(8) * 1/2 - 1 第 9 天没吃之前的桃子数
= age(2) + 2 + 2 + 2 // c = age(2) + 2
= age(1) + 2 + 2 + 2 + 2;// c = 10;
2 2
计算年龄程序
第九讲——函数、递推、递归
2 3
第九讲——函数、递推、递归
递归算例(2)
用递归方法计算 n! 算法思路:
《c语言递归算法》课件

《C语言递归算法》PPT 课件
C语言递归算法是一种强大的编程技巧,通过函数自身调用实现问题的解决。 本课件将介绍递归算法的概念、实现方式、应用场景、优缺点以及与循环的 区别,同时还会通过案例演示帮助理解。
什么是递归算法?
基本概念
递归是指函数直接或间接地调用自身的过程。
递归特点
递归算法需要有基准条件和递推关系,用于结 束递归和推进递归过程。
递归算法的实现方式
递归函数
通过函数自身调用实现递归,需要定义递归函数和 递归终止条件。
递归流程图
通过流程图展示递归算法的执行过程,帮助理解递 归逻辑。
递归算法的应用场景
1 数学计算
递归算法可以用于解决数学问题,如斐波那契数列、阶乘等。
2 数据结构
递归算法在树、图等数据结构的遍历和搜索中有广泛应用。
递归算法的优点和缺点
优点
• 简化问题复杂度 • 代码结构清晰
缺点
• 执行效率较低 • 内存占用较高
递归算法与循环的区别
1
循环
2
迭代操作
3
递归
函数自身调用
区别
递归更直观,但消耗资源较多;循环更 高效,但代码可读性差。
递归算法的注意事项
1 递归终止条件
保证递归过程能够结束,否则可能导致死循 环。
2 堆栈溢出
过深的递归调用可能导致堆栈溢出,需要注 意递归深度。
递归算法的案例演示
斐波那契数列
通过递归实现斐波那契数列的计算。
二叉树遍历
通过递归遍历二叉树的各种方式。
C语言递归算法是一种强大的编程技巧,通过函数自身调用实现问题的解决。 本课件将介绍递归算法的概念、实现方式、应用场景、优缺点以及与循环的 区别,同时还会通过案例演示帮助理解。
什么是递归算法?
基本概念
递归是指函数直接或间接地调用自身的过程。
递归特点
递归算法需要有基准条件和递推关系,用于结 束递归和推进递归过程。
递归算法的实现方式
递归函数
通过函数自身调用实现递归,需要定义递归函数和 递归终止条件。
递归流程图
通过流程图展示递归算法的执行过程,帮助理解递 归逻辑。
递归算法的应用场景
1 数学计算
递归算法可以用于解决数学问题,如斐波那契数列、阶乘等。
2 数据结构
递归算法在树、图等数据结构的遍历和搜索中有广泛应用。
递归算法的优点和缺点
优点
• 简化问题复杂度 • 代码结构清晰
缺点
• 执行效率较低 • 内存占用较高
递归算法与循环的区别
1
循环
2
迭代操作
3
递归
函数自身调用
区别
递归更直观,但消耗资源较多;循环更 高效,但代码可读性差。
递归算法的注意事项
1 递归终止条件
保证递归过程能够结束,否则可能导致死循 环。
2 堆栈溢出
过深的递归调用可能导致堆栈溢出,需要注 意递归深度。
递归算法的案例演示
斐波那契数列
通过递归实现斐波那契数列的计算。
二叉树遍历
通过递归遍历二叉树的各种方式。
C++递归函数ppt课件

有3对(1+2=3)兔子。 到第五个月,第一对兔子又生了一对小兔而在第三
个月出生的小兔也生下了一对小兔。所以,这个月共 有5对(2+3=5)兔子。……
规律:从三月份开始兔子总对数,恰好等于前面两个月
份兔子总对数的和。因为该月的兔子对总数应该等于上
个月的兔子对数加上新出生的小兔对数,而新出生的小
兔对数恰好为上上个月的兔子对数(因上上个月的每对
兔子到该月都会生出一对新兔子)
20
于是得到每个月的兔子对数: 1,1,2,3,5,8,13,21,34,55,
89,144,233,377…… 人们为了纪念这位数学家,就把上面
这样的一串数称作斐波那契数列,把这 个数列中的每一项数称作斐波那契数。 斐波那契数列的递归定义:
{ fib(n)=
1
1 fib (n1) fib (n2)
第一次调用:n为4 第二次调用:n为3 第三次调用:n为2 第四次调用:n为1
int fac(int n) { if(n==1)
return(1); else
return(fac(n-1)*n);
} 返回1*2*3*4
int fac(int n) { if(n==1)
return(1); else
return(fac(n-1)*n);
} 以上函数用递归算法实现了求解以head做表头指 针的链表的所有结点数据的和。
10
问题求解过程是递归的 如,前面数组一章中介绍的在有序数组 中查找某一数据是否存在于数组中的折 半查找算法,其求解过程便是一个递归 求解的过程。即不断在前一次区间一半 的搜索区间范围内重复着与前一次搜索 相同的操作。具体实现后面给出。
其中,指针域next是指向自身类型的指针, 故该数据结构是一种递归数据结构。
个月出生的小兔也生下了一对小兔。所以,这个月共 有5对(2+3=5)兔子。……
规律:从三月份开始兔子总对数,恰好等于前面两个月
份兔子总对数的和。因为该月的兔子对总数应该等于上
个月的兔子对数加上新出生的小兔对数,而新出生的小
兔对数恰好为上上个月的兔子对数(因上上个月的每对
兔子到该月都会生出一对新兔子)
20
于是得到每个月的兔子对数: 1,1,2,3,5,8,13,21,34,55,
89,144,233,377…… 人们为了纪念这位数学家,就把上面
这样的一串数称作斐波那契数列,把这 个数列中的每一项数称作斐波那契数。 斐波那契数列的递归定义:
{ fib(n)=
1
1 fib (n1) fib (n2)
第一次调用:n为4 第二次调用:n为3 第三次调用:n为2 第四次调用:n为1
int fac(int n) { if(n==1)
return(1); else
return(fac(n-1)*n);
} 返回1*2*3*4
int fac(int n) { if(n==1)
return(1); else
return(fac(n-1)*n);
} 以上函数用递归算法实现了求解以head做表头指 针的链表的所有结点数据的和。
10
问题求解过程是递归的 如,前面数组一章中介绍的在有序数组 中查找某一数据是否存在于数组中的折 半查找算法,其求解过程便是一个递归 求解的过程。即不断在前一次区间一半 的搜索区间范围内重复着与前一次搜索 相同的操作。具体实现后面给出。
其中,指针域next是指向自身类型的指针, 故该数据结构是一种递归数据结构。
C++递归函数ppt课件

n=0 n=1 n>1
21
f(1)=1, f(2)=1 f(n)=f(n-1)+f(n-2)
递归出口
问题 f(n)
递归体 与的关系: 子问题解决了,大问题就解决了
子问 题1
f(n-1)
与
子问 题2
f(n-2)
int fib(int n) {
if( n==1 || n==2 ) return(1);
} 返回1*2*3
int fac(int n) { if(n==1)
return(1); else
return(fac(n-1)*n);
} 返回1*2
int fac(int n) { if(n==1)
return(1); else
return(fac(n-1)*n);
} 返回1
15
? 递归函数反映一种什么样的思维
问题 n!
分 解
(n-1)!
小问题
问题 n!
分 解
小问题 (n-1)!
分 解
更小
问题 (n-2)!
分 解 ┆
最小 问题1! 不能再分解
16
四、递归与迭代
用迭代法求n! s=1; for(i=1;i<=n;i++) s=s*i;
迭代过程: 1!=1 2!=1!*2 3!=2!*3 …… n!=(n-1)!*n
有3对(1+2=3)兔子。 到第五个月,第一对兔子又生了一对小兔而在第三
个月出生的小兔也生下了一对小兔。所以,这个月共 有5对(2+3=5)兔子。……
规律:从三月份开始兔子总对数,恰好等于前面两个月
份兔子总对数的和。因为该月的兔子对总数应该等于上
递归算法课件

写成函数形式,则为:
当n 0时 1 f ( n) n * f (n 1) 当n 0时
这种函数定义的方法是用阶乘函数自己本身定义了 阶乘函数,称上式为阶乘函数的递推定义式。
数学归纳法表明,如果我们知道某个论点对最小的情 形成立,并且可以证明一个情形暗示着另一个情形,那么我 们就知道该论点对所有情形都成立。 数学有时是按递归方式定义的。 例1:假设S(n)是前n个整数的和,那么S(1)= 1,并且 我们可以将S(n)写成S(n)= S(n-1)+ n。 根据递归公式,我们可以得到对应的递归函数: int S(int n) { if (n == 1) return 1; else return S(n-1) + n; } 函数由递归公式得到,应该是好理解的,要想求出S (n),得先求出S(n-1),递归终止的条件(递归出口)是(n == 1)。
↑
low 第二次: 下标 元素值 0 1 1 3 2 4
↑
mid 3 5 4 17 5 18 6 31
↑
high 7 33
↑
low 第三次: 下标 元素值 0 1 1 3 2 4 3 5 4 17
↑
mid 5 18 6 31
↑
high 7 33
↑
low high mid
• Public static void main(String args[]) •{ • int[] shus={1,3,4,5,17,18,31,33};
求Fib(5)的递归计算过程如图所示。
Fib(5) Fib(4) Fib(3) Fib(2) Fib(1) Fib(2) Fib(3) Fib(2) Fib(1) Fib(0)
Fib(1) Fib(0) Fib(1)
当n 0时 1 f ( n) n * f (n 1) 当n 0时
这种函数定义的方法是用阶乘函数自己本身定义了 阶乘函数,称上式为阶乘函数的递推定义式。
数学归纳法表明,如果我们知道某个论点对最小的情 形成立,并且可以证明一个情形暗示着另一个情形,那么我 们就知道该论点对所有情形都成立。 数学有时是按递归方式定义的。 例1:假设S(n)是前n个整数的和,那么S(1)= 1,并且 我们可以将S(n)写成S(n)= S(n-1)+ n。 根据递归公式,我们可以得到对应的递归函数: int S(int n) { if (n == 1) return 1; else return S(n-1) + n; } 函数由递归公式得到,应该是好理解的,要想求出S (n),得先求出S(n-1),递归终止的条件(递归出口)是(n == 1)。
↑
low 第二次: 下标 元素值 0 1 1 3 2 4
↑
mid 3 5 4 17 5 18 6 31
↑
high 7 33
↑
low 第三次: 下标 元素值 0 1 1 3 2 4 3 5 4 17
↑
mid 5 18 6 31
↑
high 7 33
↑
low high mid
• Public static void main(String args[]) •{ • int[] shus={1,3,4,5,17,18,31,33};
求Fib(5)的递归计算过程如图所示。
Fib(5) Fib(4) Fib(3) Fib(2) Fib(1) Fib(2) Fib(3) Fib(2) Fib(1) Fib(0)
Fib(1) Fib(0) Fib(1)
C语言与程序设计ppt-第12章递归

第12章 递 归
华中科技大学计算机学院 卢萍
华中科技大学计算机学院C语言课
2021/4/25
程组
1
本章讲授内容
递归(recursion)是一项非常重要的编 程技巧,可以使程序变得简洁和清晰,是 许多复杂算法的基础。本章介绍 递归、递归函数的概念; 递归的执行过程; 典型问题的递归函数设计; 分治法与快速排序; 回溯法; 递归在动态规划等算法中的应用。
12
【例12.3】 设计一个求解汉诺塔问题的算法。
这是一个典型的用递归方法求解的问题。要移动n个 盘子,可先考虑如何移动n 1个盘子。分解为以下3 个步骤:
(1)把A上的n-1个盘子借助C移到B。 (2)把A上剩下的盘子(即最大的那个)移到C。 (3)把B上的n-1个盘子借助A移到C。 其中,第(1)步和第(3)步又可用同样的3步继
2021/4/25
华中科技大学计算机学院C语言课程组
2
12.1 递归概述
递归是一种函数在其定义中直接或间接调用 自己的编程技巧。递归策略只需少量代码就 可描述出解题过程所需要的多次重复计算, 十分简单且易于理解。
递归调用:函数直接调用自己或通过另一函 数间接调用自己的函数调用方式
递归函数:在函数定义中含有递归调用的函 数
续分解,依次分解下去,盘子数目n每次减少1,直 至n为1结束。这显然是一个递归过程,递归结束条 件是n为1。
2021/4/25
华中科技大学计算机学院C语言课程组
13
函数move(n,a,b,c)
为了更清楚地描述算法,可以定义一个函数 move(n,a,b,c)。该函数的功能是:将n个盘 子从木桩a上借助木桩b移动到木桩c上。算法 的第(1)步和第(3)步的实现都是递归调 用,分别为move(n-1,a,c,b)和move(n1,b,a,c)。
高中信息技术课件:递归算法 (共19张PPT)

(3)编写程序 窗ຫໍສະໝຸດ 中开设一个文本框Text1用于填 人月数N,设置命令框Commandl,点击 它即执行程序求出第N月的兔子数。然后用 文本框Text2输出答案。
根据递推式可以写出递归程序如下:
Function Fib(ByVal N As Integer) As Long If N < 3 Then Fib = 1 Else Fib = Fib(N - 1) + Fib(N - 2) End Function Private Sub Command1_Click() N = Val(Text1.Text) Text2.Text = "第" & N & "月的兔子数目是:" & Fib(N) End Sub
递 归 算 法
什么是递归算法?
递归算法:是一种直接或者间接地调 用自身的算法。在计算机编写程序中,递 归算法对解决一大类问题是十分有效的, 它往往使算法的描述简洁而且易于理解。
斐波那契的兔子问题
某人有一对兔子饲养在围墙中,如 果它们每个月生一对兔子,且新生的兔子 在第二个月后也是每个月生一对兔子,问 一年后围墙中共有多少对兔子。
算法:
① ② ③ ④ ⑤ ⑥ 输入计算兔子的月份数:n If n < 3 Then c = 1 Else a = 1: b = 1 i=3 c = a + b:a = b:b = c i=i+1,如果i≤n则返回④ 结束
Private Sub Command1_Click() n = Val(Text1.Text) If n < 3 Then c = 1 Else a = 1: b = 1 For i = 3 To n c=a+b a=b b=c Next i Text2.Text = "第" & n & "月的兔子数目是:" &c End Sub
C语言递推与递归PPT课件
• 使用递归函数编程
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
C语言递归算法ppt课件

因此,我们可以得出划分数S(n,k)的递归关系式为:
S(n,k)=S(n-1,k-1) + k * S(n-1,k) (n>k,k>0)
S(n,k)=0
(n<k)或(k=0)
S(n,k)=1
(k=1)或(k=n)
ppt课件完整
18
【参考程序】
#include<iostream>
using namespace std;
}
int fac(int n)
{
if (n==1) return 1;
return(fac(n-1)+n);
/p/p调t课用件完下整一层递归
3
}
运行程序,当T=5时,输出结果:S=15,其递归调用执行过程是: (设T=3)
递归调用过程,实质上是不断调用过程或函数的过程,由于递归调 用一次,所有子程序的变量(局部变量、变参等)、地址在计算机内部 都有用特殊的管理方法——栈(先进后出)来管理,一旦递归调用结束, 计算机便开始根据栈中存储的地址返回各子程序变量的值,并进行相应 操作。
mov过程中出现了自己调用自己的情况,在Pascal中称为递归调用,这 是Pascal语言的一个特色。对于没有递归调用功能的程序设计语言,则需 要将递归过程重新设计为非递归过程的程序。
ppt课件完整
13
【例4】用递归的方法求斐波那契数列中的第N个数
【参考程序】 #include<iostream> using namespace std; int a[11]; int fib(int); int main() { int m; cin>>m; cout<<"fib("<<m<<")="<<fib(m); }
C语言递归函数调用PPT课件

知识点精讲
【解析】第10天:1个桃子。第9天:设第9天有x个桃子,x-(x/2+1)= 1,解x=4。以此类推计算 出10、22、46、…,得出第n项等于(前一项+1)*2.
列出求某一天桃子数的公式:
#include <stdio.h> int fun(int day) { if(day==1) return 1; /*最后一天桃子的数量为1*/ return(fun(day-1)+1)*2;
知识点精讲
s=f(&a[0],3); printf("%d\n" ,s); } 4.下列程序的运行结果是___f_(_n_)_=_2________ #include″stdio.h″ int f(int n){ if(n<=2) return 1; else return f(n-1)+f(n-2); } main(){ int n=5; printf(″f(n)=%d\n″,f(3)); }
第八章 递归函数调用
考纲要求
递归函数编程方法。
知识准备
高频考点:递归函数调用、用递归函数设计算法。 重难点分析:用递归函数设计算法。
知识点精讲
知识点1 递归函数
知识点分析 在调用一个函数的过程中出现直接或间接地调用该函数本身,称为函数的递归调用。C语言的 特点之一就在于允许函数的递归调用。 巩固提高 1.下列程序的运行结果是_____5_5______ L1 #include <stdio.h> L2 int fun(int n) L3 { L4 if(n==1) return 1; /*当n==1时,函数调用结束*/ L5 return fun(n-1)+n; /*前n项的和等于前n-1项的和再加上n*/ L6 } L7 void main( ) L8 {
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
【例2】 设有N个数已经按从大到小的顺序排列,现在输入X,判断它是 否在这N个数中,如果存在则输出:“YES” 否则输出“NO”。 【算法分析】
该问题属于数据的查找问题,数据查找有多种方法,通常方法是:顺 序查找和二分查找,当N个数排好序时,用二分查找方法速度大大加快。 二分查找算法:
(1) 设有N个数,存放在A数组中,待查找数为X,用L指向数据的高 端,用R指向数据的低端,MID指向中间:
【参考程序】
#include<iostream>
using namespace std;
int k=0,n;
void mov(int n,char a,char c,char b)
//用b柱作为协助过渡,将a柱上的(n)移到c柱上
{
if (n==0) return;
//如果n=0,则退出,即结束程序
10
所以可按“N=2”的移动步骤设计:
①如果N=0,则退出,即结束程序;否则继续往下执行;
②用C柱作为协助过渡,将A柱上的(N-1)片移到B柱上,调用过程mov(n-1,
a,b,c);
③将A柱上剩下的一片直接移到C柱上;
④用A柱作为协助过渡,将B柱上的(N-1)移到C柱上,调用过程mov (n-
1,b,c,a)。
for (k=1;k<=10;k++)
cin>>a[k];
cin>>x;
search(x,L,R);
system("pause");
} void search(int x,int top,int bot) //二分查找递归过程
{
int mid;
if (top<=bot)
{ mid=(top+bot)/2;
5
【参考程序】
#include<iostream>
#include<cstdlib>
using namespace std;
int a[11];
void search(int,int,int); int main()
//主程序
{
int k,x,L=1,R=10; cout<<"输入10个从大到小顺序的数:"<<endl;
7
【例3】Hanoi汉诺塔问题
有N个圆盘,依半径大小(半径都不同),自下而上套在A柱上,每次只允 许移动最上面一个盘子到另外的柱子上去(除A柱外,还有B柱和C柱,开始时这 两个柱子上无盘子),但绝不允许发生柱子上出现大盘子在上,小盘子在下的情 况,现要求设计将A柱子上N个盘子搬移到C柱去的方法。 【算法分析】
return(fac(n-1)+n);
//调用下一层递归
3
}
运行程序,当T=5时,输出结果:S=15,其递归调用执行过程是: (设T=3)
递归调用过程,实质上是不断调用过程或函数的过程,由于递归调 用一次,所有子程序的变量(局部变量、变参等)、地址在计算机内部 都有用特殊的管理方法——栈(先进后出)来管理,一旦递归调用结束, 计算机便开始根据栈中存储的地址返回各子程序变量的值,并进行相归方法求解,其原因在于它符合递归的三个条件:
(1)本题是累加问题:当前和=前一次和+当前项,而前一次和的计算方法与其 相同,只是数据不同s(n)=s(n-1)+n;
(2)给定n,所以是有限次的递归调用; (3)结束条件是当n=1,则s=1。 【参考程序】
#include<iostream>
//求中间数的位置
6
if (x==a[mid]) cout<<"YES"<<endl; else if (x<a[mid]) search(x,mid+1,bot); else search(x,top,mid-1);
} else cout<<"NO"<<endl;
}
//找到就输出 //判断在前半段还是后半段查找
mov(n-1,a,b,c );
//用c柱作为协助过渡,将a柱上的(n-1)片移到b柱上
k++;
cout <<k<<" :from "<<a <<"-->"<<c<<endl;
mov(n-1,b,c,a );
//用a柱作为协助过渡,将b柱上的(n-1)移到c柱上
}
11
int main() { cout<<"n="; cin>>n; mov(n,'a','c','b'); }
本题是典型的递归程序设计题。 (1)当N=1 时,只有一个盘子,只需要移动一次:A—>C; (2)当N=2时,则需要移动三次:
A------ 1 ------> B, A ------ 2 ------> C, B ------ 1------> C. (3)如果N=3,则具体移动步骤为:
8
9
假设把第3步,第4步,第7步抽出来就相当于N=2的情况(把上面2片 捆在一起,视为一片):
(2) 若X=A[MID] 输出 “YES”; (3)若X<A[MID]则到数据后半段查找:R不变,L=MID+1,计算新的 MID值,并进行新的一段查找; (4) 若X>A[MID]则到数据前半段查找:L不变,R=MID-1,计算新的 MID值,并进行新的一段查找; (5)若L>R都没有查找到,则输出“NO”。 该算法符合递归程序设计的基本规律,可以用递归方法设计。
第四章 递归算法
1
前面已经介绍了关于递归调用这样一种操作,而递归 程序设计是C++语言程序设计中的一种重要的方法,它使许 多复杂的问题变得简单,容易解决了。递归特点是:函数 或过程调用它自己本身。其中直接调用自己称为直接递归, 而将A调用B,B以调用A的递归叫做间接递归。
2
【例1】 给定n(n>=1),用递归的方法计算1+2+3+4+...+(n-1)+n。
12
程序定义了把n片从A柱移到C柱的过程mov (n,a,c,b),这个过程把移动 分为以下三步来进行:
①先调用过程mov (n-1, a, b, c),把(n-1)片从A柱移到B柱, C柱作为过 渡柱;
②直接执行 writeln(a, ’-->’, c),把A柱上剩下的一片直接移到C柱 上,;
using namespace std; int fac(int);
//递归函数
int main()
{
int t; cin>>t; cout<<"s="<<fac(t)<<endl;
//输入t的值 //计算1到t的累加和,输出结果
}
int fac(int n)
{
if (n==1) return 1;
【例2】 设有N个数已经按从大到小的顺序排列,现在输入X,判断它是 否在这N个数中,如果存在则输出:“YES” 否则输出“NO”。 【算法分析】
该问题属于数据的查找问题,数据查找有多种方法,通常方法是:顺 序查找和二分查找,当N个数排好序时,用二分查找方法速度大大加快。 二分查找算法:
(1) 设有N个数,存放在A数组中,待查找数为X,用L指向数据的高 端,用R指向数据的低端,MID指向中间:
【参考程序】
#include<iostream>
using namespace std;
int k=0,n;
void mov(int n,char a,char c,char b)
//用b柱作为协助过渡,将a柱上的(n)移到c柱上
{
if (n==0) return;
//如果n=0,则退出,即结束程序
10
所以可按“N=2”的移动步骤设计:
①如果N=0,则退出,即结束程序;否则继续往下执行;
②用C柱作为协助过渡,将A柱上的(N-1)片移到B柱上,调用过程mov(n-1,
a,b,c);
③将A柱上剩下的一片直接移到C柱上;
④用A柱作为协助过渡,将B柱上的(N-1)移到C柱上,调用过程mov (n-
1,b,c,a)。
for (k=1;k<=10;k++)
cin>>a[k];
cin>>x;
search(x,L,R);
system("pause");
} void search(int x,int top,int bot) //二分查找递归过程
{
int mid;
if (top<=bot)
{ mid=(top+bot)/2;
5
【参考程序】
#include<iostream>
#include<cstdlib>
using namespace std;
int a[11];
void search(int,int,int); int main()
//主程序
{
int k,x,L=1,R=10; cout<<"输入10个从大到小顺序的数:"<<endl;
7
【例3】Hanoi汉诺塔问题
有N个圆盘,依半径大小(半径都不同),自下而上套在A柱上,每次只允 许移动最上面一个盘子到另外的柱子上去(除A柱外,还有B柱和C柱,开始时这 两个柱子上无盘子),但绝不允许发生柱子上出现大盘子在上,小盘子在下的情 况,现要求设计将A柱子上N个盘子搬移到C柱去的方法。 【算法分析】
return(fac(n-1)+n);
//调用下一层递归
3
}
运行程序,当T=5时,输出结果:S=15,其递归调用执行过程是: (设T=3)
递归调用过程,实质上是不断调用过程或函数的过程,由于递归调 用一次,所有子程序的变量(局部变量、变参等)、地址在计算机内部 都有用特殊的管理方法——栈(先进后出)来管理,一旦递归调用结束, 计算机便开始根据栈中存储的地址返回各子程序变量的值,并进行相归方法求解,其原因在于它符合递归的三个条件:
(1)本题是累加问题:当前和=前一次和+当前项,而前一次和的计算方法与其 相同,只是数据不同s(n)=s(n-1)+n;
(2)给定n,所以是有限次的递归调用; (3)结束条件是当n=1,则s=1。 【参考程序】
#include<iostream>
//求中间数的位置
6
if (x==a[mid]) cout<<"YES"<<endl; else if (x<a[mid]) search(x,mid+1,bot); else search(x,top,mid-1);
} else cout<<"NO"<<endl;
}
//找到就输出 //判断在前半段还是后半段查找
mov(n-1,a,b,c );
//用c柱作为协助过渡,将a柱上的(n-1)片移到b柱上
k++;
cout <<k<<" :from "<<a <<"-->"<<c<<endl;
mov(n-1,b,c,a );
//用a柱作为协助过渡,将b柱上的(n-1)移到c柱上
}
11
int main() { cout<<"n="; cin>>n; mov(n,'a','c','b'); }
本题是典型的递归程序设计题。 (1)当N=1 时,只有一个盘子,只需要移动一次:A—>C; (2)当N=2时,则需要移动三次:
A------ 1 ------> B, A ------ 2 ------> C, B ------ 1------> C. (3)如果N=3,则具体移动步骤为:
8
9
假设把第3步,第4步,第7步抽出来就相当于N=2的情况(把上面2片 捆在一起,视为一片):
(2) 若X=A[MID] 输出 “YES”; (3)若X<A[MID]则到数据后半段查找:R不变,L=MID+1,计算新的 MID值,并进行新的一段查找; (4) 若X>A[MID]则到数据前半段查找:L不变,R=MID-1,计算新的 MID值,并进行新的一段查找; (5)若L>R都没有查找到,则输出“NO”。 该算法符合递归程序设计的基本规律,可以用递归方法设计。
第四章 递归算法
1
前面已经介绍了关于递归调用这样一种操作,而递归 程序设计是C++语言程序设计中的一种重要的方法,它使许 多复杂的问题变得简单,容易解决了。递归特点是:函数 或过程调用它自己本身。其中直接调用自己称为直接递归, 而将A调用B,B以调用A的递归叫做间接递归。
2
【例1】 给定n(n>=1),用递归的方法计算1+2+3+4+...+(n-1)+n。
12
程序定义了把n片从A柱移到C柱的过程mov (n,a,c,b),这个过程把移动 分为以下三步来进行:
①先调用过程mov (n-1, a, b, c),把(n-1)片从A柱移到B柱, C柱作为过 渡柱;
②直接执行 writeln(a, ’-->’, c),把A柱上剩下的一片直接移到C柱 上,;
using namespace std; int fac(int);
//递归函数
int main()
{
int t; cin>>t; cout<<"s="<<fac(t)<<endl;
//输入t的值 //计算1到t的累加和,输出结果
}
int fac(int n)
{
if (n==1) return 1;
