最新整理小学五年级奥数组合图形的面积
五年级奥数专题组合图形面积

五年级奥数专题组合图形面积(一)1、一根铁丝长12厘米,要围成两个整厘米数的正方形,这两个正方形的面积分别是多少?1、有两个相同的长方形,长7厘米,宽3厘米,把它们按下图的样子重叠在一起,这个图形的面积是多少?3、有一个梯形,它的上底是6厘米,下底8厘米,如果只把上底增加4厘米,那么面积就增加6平方厘米。
求原来梯形的面积。
4、求下图长方形ABCD的面积。
(单位:厘米)5、如图,已知四条线段的长度分别是:AB=4厘米,CE=12厘米,CD=10厘米,AF=8厘米,并且有两个直角。
求四边形ABCD的面积。
6、图中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
7、图中,ABCD是长方形,E、F分别是AB、DA的中点,G是BF和DE的交点,四边形BCDG的面积是40平方厘米,那么ABCD的面积是多少平方厘米?组合图形面积(二)【一】一个正方形被分成3个大小、形状完全一样的长方形,每个小长方形的周长都是24厘米,求这个正方形的面积。
练习1、一个正方形被分成6个大小、形状完全一样的长方形,每个长方形的周长都是14厘米。
原来正方形的面积是多少?2、一块长方形布,周长是18米,长比宽多1米。
这块布的面积是多少?【二】下图是由6个相等的三角形拼成的图形,求这这图像的面积。
练习1、ABCD是正方形,求阴影部分的面积。
(单位:厘米)2、下图中,E、F分别是长和宽的中点,求阴影部分的面积。
(单位:厘米)【三】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习1、求下图中阴影部分的面积和。
2、求下图中阴影部分的面积。
(单位:厘米)【四】下图中,边长为10和15的两个正方形并放在一起,求三角形ABC(阴影部分)的面积。
练习1、下图中,三角形ABC的面积是72平方厘米,三角形ABE与三角形AEC面积相等,如果AB=18厘米,FB=FE,求三角形AFE的面积。
小学五年级奥数-第19讲 组合图形的面积(二)

小学奥数发散思维-掌握解题技巧-提高运算效率和准确率第19讲组合图形的面积(二)一、知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点:1.两个三角形等底、等高,其面积相等;2.两个三角形底相等,高成倍数关系,面积也成倍数关系;3.两个三角形高相等,底成倍数关系,面积也成倍数关系。
二、精讲精练【例题1】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习1:1.求下图中阴影部分的面积。
2.求图中阴影部分的面积。
(单位:厘米)3.下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
【例题2】下图中,边长为10和15的两个正方体并放在一起,求三角形ABC (阴影部分)的面积。
练习2:1.下图中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
2.图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
3.图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积(ADFC不是正方形)。
【例题3】两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)练习3:1.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?2.下图的梯形ABCD中,下底是上底的2倍,E是AB的中点。
那么梯形ABCD的面积是三角形BDE面积的多少倍?3.下图梯形ABCD中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的面积比三角形AOD的面积大多少平方厘米?【例题4】在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
练习4:1.把下图三角形的底边BC四等分,在下面括号里填上“>”、“<”或“=”。
甲的面积()乙的面积。
五年级奥数11组合图形的面积

五年级奥数11组合图形的面积第十一讲 组合图形的面积教学目标1、 切实掌握有关简单图形的概念、面积公式,牢固建立空间观念 ;2、 切实掌握有关概念,利用“割补”、“平移”、“旋转”等方法,使复杂的问题转化为普通的求长方形、正方形面积的问题,教学重难点在组合图形中,三角形的面积出现的机会很多,解题时我们要记住下面三点 :1、 两个三角形等底、等高,其面积相等;2、 两个三角形底相等,高成倍数关系,面积也成倍数关系 ;3、 两个三角形高相等,底成倍数关系,面积也成倍数关系。
新课导入组合图形是由两个或两个以上的简单的几何图形组合成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得 问题的解决无从下手。
今天我们就一起来学习组合图形的面积的计算方法。
新知传授例题1 一个等腰直角三角形,最长的边是 12厘米,这个三角形的面积是多少 解:由于此三角形中只知道最长的边是 12厘米,所以,不能用三角形的面积公 式来计算它的面积。
我们可以假设有 4个这样的三角形,且拼成了下图正方形。
显然,这个正方形的面积是12X12.那么,一个三角形的面积就是12X 12?4=36平方厘米。
练习1正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
解:图中的两个小三角形平移后可拼得一个小正方形,两个大三角形平移后可拼得一个大正方形。
这两个正方形的边长分别是12?(1,2)=4(厘米)和4 X 2=8(厘米)。
中间长方形的面积只要用总面积减去这两个拼起来的正方形的面积就可以得到。
即:12 X 12,(4 X 4,8X 8)=64(平方厘米)例题2四边形ABC丙四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH勺面积是多少平方厘米,解:设大正方形的边长是a,小正方形的边长是b o(1)梯形EFAM面积是(a+b) X b?2.三角形EFC的面积也是(a+b) X b?2。
小学五年级奥数第19讲 组合图形的面积(二)(含答案分析)

第19讲组合图形的面积(二)一、知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点:1.两个三角形等底、等高,其面积相等;2.两个三角形底相等,高成倍数关系,面积也成倍数关系;3.两个三角形高相等,底成倍数关系,面积也成倍数关系。
二、精讲精练【例题1】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习1:1.求下图中阴影部分的面积。
2.求图中阴影部分的面积。
(单位:厘米)3.下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
【例题2】下图中,边长为10和15的两个正方体并放在一起,求三角形ABC (阴影部分)的面积。
练习2:1.下图中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
2.图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
3.图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积(ADFC不是正方形)。
【例题3】两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)练习3:1.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?2.下图的梯形ABCD中,下底是上底的2倍,E是AB的中点。
那么梯形ABCD的面积是三角形BDE面积的多少倍?3.下图梯形ABCD中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的面积比三角形AOD的面积大多少平方厘米?【例题4】在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
练习4:1.把下图三角形的底边BC四等分,在下面括号里填上“>”、“<”或“=”。
甲的面积()乙的面积。
2.如图,在三角形ABC中,D是BC的中点,E、F是AC的三等分点。
五年级奥数组合图形面积

组合图形面积
1、求四边形ABCD的面积。
(单位:厘米)
2、下图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点。
求AEF的面积。
3、图中的甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)
4、求图中阴影部分的面积。
5、图中ABCD是长方形,三角形EFD的面积比ABF的面积大6平方厘米,求ED的长。
6、下图中三个正方形的边长分别是1厘米、2厘米和3厘米。
求图中阴影部分的面积。
7、求下图长方形ABCD的面积。
(单位:厘米)
8、如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。
求四边
形ABCD的面积。
9、正方形的边长是2(a+b),已知图中阴影部分B的面积是7平方厘米,求阴影部分A和C的和是多少平方厘
米?。
五年级奥数组合图形面积

挑战练习题
总结词
思维训练与难题攻克
详细描述
挑战练习题旨在培养学生的思维能力和解题 技巧,题目难度较大,需要学生具备一定的 数学思维和创新能力。这类题目通常涉及多 个知识点的综合运用,需要学生通过观察、
分析、推理等手段寻找解题思路。
感谢您的观看
THANKS
五年级奥数组合图形面积
汇报人: 202X-01-03
目录
• 组合图形面积概述 • 常见组合图形及面积计算 • 组合图形面积的解题技巧 • 组合图形面积的实际应用 • 练习与巩固
01
组合图形面积概述
组合图形的定义
01
组合图形是由两个或两个以上的 基本图形通过一定的方式组合而 成的图形。
02
常见的组合图形有平行四边形、 三角形、梯形等。
03
组合图形面积的解题技巧
分割法
总结词
将复杂的组合图形分割成几个简单的规 则图形,分别求出各部分的面积,最后 相加。
VS
详细描述
分割法是解决组合图形面积问题的一种常 用方法。通过合理分割,将复杂的图形拆 分成几个简单的图形,如三角形、长方形 、平行四边形等,这些图形的面积计算相 对简单。在分割后,分别计算各部分的面 积,最后将各部分面积相加即可得到整个 组合图形的面积。
填补法
总结词
将组合图形补全为一个完整的规则图形,然后计算整个图形的面积,再减去填补的部分。
详细描述
填补法是通过将组合图形补全为一个完整的规则图形,如长方形、平行四边形等,然后计算整个图形的面积。再 从总面积中减去填补的部分,即可得到组合图形的面积。这种方法适用于不规则图形,通过填补的方式将其转化 为规则图形,便于计算。
02
常见组合图形及面积计算
【小学五年级奥数讲义】组合图形的面积(二)

【小学五年级奥数讲义】组合图形的面积(二)一、知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点:1.两个三角形等底、等高,其面积相等;2.两个三角形底相等,高成倍数关系,面积也成倍数关系;3.两个三角形高相等,底成倍数关系,面积也成倍数关系。
二、精讲精练【例题 1】如图, ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习 1:1.求下图中阴影部分的面积。
2.求图中阴影部分的面积。
(单位:厘米)3. 下图的长方形是一块草坪,中间有两条宽 1 米的走道,求植草的面积。
【例题 2】下图中,边长为10 和 15 的两个正方体并放在一起,求三角形ABC (阴影部分)的面积。
练习 2:1.下图中,三角形 ABC的面积是 36 平方厘米,三角形 ABE与三角形 AEC的面积相等,如果 AB=9厘米, FB=FE,求三角形 AFE的面积。
2. 图中两个正方形的边长分别是10 厘米和 6 厘米,求阴影部分的面积。
3.图中三角形 ABC的面积是 36 平方厘米, AC长 8 厘米, DE长 3 厘米,求阴影部分的面积( ADFC不是正方形)。
【例题 3】两条对角线把梯形 ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)练习 3:1.如下图,图中 BO=2DO,阴影部分的面积是 4 平方厘米,求梯形 ABCD的面积是多少平方厘米?2.下图的梯形 ABCD中,下底是上底的 2 倍, E 是 AB的中点。
那么梯形 ABCD的面积是三角形 BDE面积的多少倍?3.下图梯形 ABCD中, AD=7厘米, BC=12厘米,梯形高 8 厘米,求三角形 BOC 的面积比三角形 AOD的面积大多少平方厘米?【例题 4】在三角形 ABC中,DC=2BD,CE=3AE,阴影部分的面积是 20 平方厘米,求三角形 ABC的面积。
练习 4:1.把下图三角形的底边 BC四等分,在下面括号里填上“>”、“<”或“ =”。
五年级数学奥数专题组合图形面积

组合图形面积(一)【知识点击】组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
【典型例题1】一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?【对点演练1】1.求四边形ABCD的面积。
(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
【典型例题2】正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
【对点演练2】1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
【典型例题3】四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH 的面积是多少平方厘米?【对点演练3】1.图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
2.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)【典型例题4】下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?【对点演练4】1.如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
2.在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)【典型例题5】图中ABCD是长方形,三角形EFD的面积比三角形ABF的面积大6平方厘米,AB=4厘米,BC=6厘米。
最新五年级组合图形面积解析及一题多解大全(重磅推出)

组合图形面积应知应会基础图形的面积:【1】平行四边形的面积=底×高,【2】三角形的面积=底×高用字母表示的三角形面积计算公式是:S=ah÷2【3】梯形的面积=(上底+下底)×高÷2s梯形=(a+b)×h÷2a=s梯形×2÷h-bb=s梯形×2÷h-ah=s梯形×2÷(a+b)二、组合图形(一)组合图形:计算时需转化成已学的基本图形,通过加、减进行计算。
(二)求组合图形的方法:1、分割法:将组合图形分成几个基本图形,通过加,求几个基本图形的和。
2、填补法:将组合图形补成一个基本图形,通过大面积减小面积,求两个基本图形的差。
组合图形的面积直接计算:根据公式计算图形的面积【1】分析:梯形的高等于三角形的高解:S阴影三角形=底×高÷2=14×12÷2=84(平方厘米)直接计算:S 阴影=S 三角形甲+S 三角形乙 【2】求阴影部分的面积。
解:S 阴影=S 三角形甲+S 三角形乙 =5×3÷2+3×3÷2 =7.5+4.5=12(平方厘米)直接计算:S 组合图形=S 平行四边形+S 三角形 【3】求组合图形的面积。
解:S 组合图形=S 平行四边形+S 三角形 =24×8+10×24÷2 =192+120 =312(平方米)直接计算:S 组合图形=S 平行四边形+S 三角形 【4】求组合图形的面积。
解:S 组合图形=S 平行四边形+S 三角形 =50×33+35×12÷2 =1650+210 =1860(平方米)直接计算:S 组合图形=S 长方形+S 三角形【5】下图为一个游泳馆的标识牌,求黄色标识牌的面积。
S 组合图形=S 长方形+S 三角形 =20×10+20×10÷ 253 甲乙单位:厘米=200+100=300(平方厘米)直接计算:S组合图形=S长方形+S三角形【6】下图为一个墙面的平面图,求这面墙面的面积。
小学五年级奥数第18讲 组合图形的面积(含答案分析)

第18讲组合图形面积(一)一、知识要点组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
二、精讲精练【例题1】一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习1:1.求四边形ABCD的面积。
(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
【例题2】正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习2:1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3.求下图(上右图)长方形ABCD的面积(单位:厘米)。
【例题3】四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习3:1.图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
2.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)3.下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?【例题4】下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?练习4:1.如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
五年级奥数-组合图形的面积(一)

分析 :
要求梯形的面积,关键是要求出上底 FD的长度。连接FC后就能得到一个 三角形EFC,用三角形EBC的面积减 去三角形FBC的面积就能得到三角形 EFC的面积: 8×20÷2-8×8÷2=48平方厘米。 FD=48×2÷20=4.8厘米, 所求梯形的面积就是: (4.8+8)×8÷2=51.2平方厘米。
练 习 五
1,如图,平行四边形BCEF中,BC=8厘米, 直角三角形中,AC=10厘米,阴影部分面积比 三角形ADH的面积大8平方厘米。 求AH长多少厘米?
2,图中三个正方形的边长分别是1厘米、2厘米和3厘米,求 图中阴影部分的面积。
3,正方形的边长是2(a+b),已知图中阴影部分B的面积是7 平方厘米,求阴影部分A和C的和 是多少平方厘米?
专题简析:组合图形是由两个或两个以上的
简单的几何图形组合而成的。组合的形式分为两种: 一是拼合组合,二是重叠组合。由于组合图形具有 条件相等的特点,往往使得问题的解决无从下手。 要正确解答组合图形的面积,应该注意以下几点: 1,切实掌握有关简单图形的概念、公式,牢固建立 空间观念; 2,仔细观察,认真思考,看清所求图形是由哪几个 基本图形组合而成的; 3,适当采用增加辅助线等方法帮助解题; 4,采用割、补、分解、代换等方法,可将复杂问题 变得简单。
例5 、 图中ABCD是长方形,三
角形EFD的面积比三角形ABF的面 积大6平方厘米,求ED的长。
分析: 因为三角形EFD的面积比三角形ABF 的面积大6平方厘米,所以,三角形 BCE的面积比长方形ABCD的面积大 6平方厘米。三角形BCE的面积是 6×4+6=30平方厘米,EC的长则是 30×2÷6=10厘米。 因此,ED的长是10-4=6厘米。
例1 、一个等腰直角三角 形,最长的边是12厘米, 这个三角形的面积是多少 平方厘米?
(完整)五年级奥数组合图形的面积

组合图形的面积1.基本平面图形特征及面积公式特征面积公式正方形①四条边都相等。
②四个角都是直角。
③有四条对称轴。
S=a2长方形①对边相等。
②四个角都是直角。
③有二条对称轴。
S=ab平行四边形①两组对边平行且相等。
②对角相等,相邻的两个角之和为180°③平行四边形容易变形。
S=ah三角形①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角,具有稳定性。
S=ah ÷2梯形①只有一组对边平行。
②中位线等于上下底和的一半。
S=(a+b)h÷22.基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
1.已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
2.右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内阴影部分的面积。
4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分别为6厘米、4厘米,DF的长是多少厘米?5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求阴影部分的面积。
6.右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少?8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中间有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大?9.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。
问原来的三角形的面积是多少平方米?1米组合图形的面积作业1.在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是多少厘米?2.如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
2022-2023学年小学五年级奥数(全国通用)测评卷24《组合图形的面积》(解析版)

【五年级奥数举一反三—全国通用】测评卷24《组合图形的面积》试卷满分:100分考试时间:100分钟姓名:_________班级:_________得分:_________ 一.选择题(共8小题,满分16分,每小题2分)1.(2分)如图中长方形的面积相等,则图中阴影部分面积相比较,()A.甲的面积大B.乙的面积大C.甲和乙的面积相等D.无法确定【解答】解:甲的面积=长方形的长⨯长方形的宽2÷;乙的面积=长方形的长⨯长方形的宽2÷;即:甲乙的面积都是长方形面积的一半,它们的面积一样大.故选:C。
2.(2分)在图中,平行线间的三个图形,它们的面积()A.平行四边形最大B.三角形最大C.梯形最大D.一样大【解答】解:设他们的高为h,平行四边形的面积4h=三角形的面积184 2h h =⨯⨯=梯形面积(26)24h h=+⨯÷=所以它们的面积相比,都相等;故选:D。
3.(2分)甲长方形包含16个小正方形,乙长方形包含12个小正方形.甲长方形与乙长方形的面积相比,结果是什么?()A.甲的面积大B.乙的面积大C.无法确定【解答】解:因为不能确定甲、乙长方形包含的小正方形的面积是否相等,所以无法比较甲长方形与乙长方形面积的大小;故选:C.4.(2分)如图所示,把一个长方形分成一个梯形和一个三角形.已知梯形的面积比三角形的面积大18厘米2,那么梯形的上底长为()厘米.A.2 B.3 C.4 D.6【解答】解:设梯形的上底为a厘米,那么三角形的底为(12)a-厘米,根据题意可得:+⨯÷--⨯÷=(12)62(12)6218a a+⨯--⨯=a a(12)3(12)318+-+=a a33636318a=618a=3答:梯形的上底是3厘米.故选:B.5.(2分)如图,甲、乙两个平行四边形中阴影部分面积的大小为()A.甲>乙B.甲=乙C.甲<乙D.无法确定【解答】解:如图:甲+丙=乙+丙,丙是公共部分,所以甲=乙,答:甲的面积等于乙的面积.故选:B .6.(2分)如图的长方形中有三个三角形,它们面积间的关系是( )A .123S S S +=B .13S S =C .23S S =D .321S S S =-【解答】解:由图可知:2S 的面积是长方形形面积的一半,3S 和1S 的面积和也是长方形面积的一半,由此可得:132S S S +=,即:321S S S =-.故选:D .7.(2分)图中,直线//a b ,比较三角形ADC 和三角形ABD 面积的大小,结果是( )A .三角形ADC 面积大B .三角形ABD 面积大C .它们的面积相等D .无法比较【解答】解:由题意可知:三角形ADC 和三角形ABD 等底等高,所以角形ADC 和三角形ABD 面积相等. 故选:C .8.(2分)如图ABCD 是长方形,已知4AB =厘米,6BC =厘米,三角形EFD 的面积比三角形ABF 的面积大6平方厘米,求(ED = )厘米.A .9B .7C .8D .6【解答】解:长方形ABCD 的面积:4624⨯=(平方厘米);三角形EBC的面积:+=(平方厘米);24630⨯÷=(厘米);CE的长:302610DE的长:1046-=(厘米).故选:D.二.填空题(共9小题,满分18分,每小题2分)9.(2分)如图,图中2=,阴影部分的面积是6平方厘米,求梯形ABCD的面积是27平方厘米.BO DO【解答】解:因为2=,BO DO所以三角形CDO的面积=三角形BCO面积的一半,即三角形CDO的面积3=平方厘米;三角形BCD与三角形ACD同底等高,所以三角形BCD与三角形ACD的面积相等,三角形AOD的面积=三角形BCO的面积,即三角形AOD的面积6=平方厘米;=,三角形ABO的面积是三角形AOD面积的2倍,BO DO2即三角形AOB的面积12=平方厘米;梯形ABCD的面积为:6361227+++=(平方厘米),答:梯形ABCD的面积为27平方厘米.故答案为:27.10.(2分)如图涂色部分的面积是322cm.【解答】解:8866⨯+⨯=+6436=(平方厘米)100(86)62882+⨯÷+⨯÷=+423274=(平方厘米)⨯-÷6(86)2=⨯÷6226=(平方厘米)-+100746=+266=(平方厘米)32答:涂色部分的面积是232cm.故答案为:32.11.(2分)如图,它是由两个正方形拼成的,小正方形的边长为2厘米,大正方形的边长为4厘米,阴影部分的面积为6平方厘米.【解答】解:(24)22+⨯÷=⨯÷622=(平方厘米)6答:阴影部分的面积是6平方厘米.故答案为:6.12.(2分)六个等腰三角形如图摆放,那么四个空白三角形的面积和是两个阴影三角形的面积和的6倍.【解答】解:如下图:把这六个等腰直角三角形从小到大分别编号为①②③④⑤⑥,设①号三角形的面积为1,则②号的面积为2,③号的面积为4,④号的面积为8,⑤号的面积为16,⑥号的面积为32,+++÷+(241632)(18)=÷5496=答:四个空白三角形的面积和是两个阴影三角形的面积和的6倍.故答案为:6.13.(2分)如图,梯形的面积是18.【解答】解:如图:已知45BAC∠=︒,90ABC∠=︒,所以180904545ACB∠=︒-︒-︒=︒,所以AB BC=;因为90ACE∠=︒,所以180904545ECD∠=︒-︒-︒=︒,则45DEC∠=︒,所以DE CD=,梯形的面积()62DE AB=+⨯÷()62BC CD=+⨯÷662=⨯÷18=.故答案为:18.14.(2分)如图:ABCD是一个面积为36平方厘米的长方形,E为BC中点,则阴影部分的面积是15平方厘米.【解答】解:据分析可知:三角形ABE的面积为13694⨯=(平方厘米);三角形DHC的面积和三角形ADH的面积比是1:2,而三角形ADC的面积是36218÷=(平方厘米),所以三角形DHC 的面积为18(12)6÷+=(平方厘米),则三角形AHE 的面积也是6平方厘米.所以阴影部分的面积是9615+=(平方厘米).答:阴影部分的面积是15平方厘米.故答案为:15.15.(2分)如图,ABCD 是直角梯形,5AD =厘米,3DC =厘米,三角形DOC 的面积是1.5平方厘米,则阴影部分的面积是 6 平方厘米.【解答】解:352 1.5⨯÷-,7.5 1.5=-,6=(平方厘米); 答:阴影部分的面积是6平方厘米.故答案为:6.16.(2分)图中直角三角形里有3个正方形,已知25AD cm =,100BD cm =,阴影部分的面积是 10754 2cm .【解答】解:100:25100254=÷=4BC AB =4(25100)=⨯+500=(厘米)设最小正方形的边长为x 厘米4()1005004x x x x ++++= 6.25100500x ++=6.25100100500100x +-=-6.25400x =6.25 6.25400 6.25x ÷=÷64x =中正方形的边长:4x x + 64644=+6416=+80=(厘米)500(25100)2(10010080806464)⨯+÷-⨯+⨯+⨯5001252(1000064004096)=⨯÷-++3125020496=-10754=(平方厘米)答:阴影部分的面积是10754平方厘米.故答案为:10754.17.(2分)如图,已知正方形ABCD 的周长是40厘米, 6.4DE =厘米,阴影部分的面积是 32 平方厘米.【解答】解:由分析可知阴影部分的面积为:6.4(404)2⨯÷÷6.4102=⨯÷642=÷32=(平方厘米); 答:阴影部分的面积是32平方厘米.故答案为:32.三.计算题(共3小题,满分18分,每小题6分)18.(6分)求阴影部分面积.【解答】解:(1)222+=,空白三角形是一个直角三角形,304050空白三角形的面积:30402⨯÷=÷12002=(平方分米)600斜边上的高:⨯÷600250=÷120050=(分米)24+⨯÷(4050)242=⨯÷90242=(平方分米)1080-=(平方分米)1080600480答:阴影部分的面积是480平方分米.(2)40403030⨯+⨯=+1600900=(平方分米)2500⨯÷=(平方分米)40402800+⨯÷(4030)302=⨯÷70302=÷21002=(平方分米)1050--25008001050=-17001050=(平方分米)650答:阴影部分的面积是650平方分米.19.(6分)平行四边形ABCD的边BC长10厘米,直角三角形的直角边EC长8厘米.已知阴影部分的面积比三角形EGF的面积大9平方厘米.求CF的长.【解答】解:设EF长为x厘米,则CF就是8x-厘米,根据题干分析可得方程:x⨯-=⨯÷+10(8)10829-=801049xx=1031x=3.1-=(厘米);8 3.1 4.9答:CF长为4.9厘米.20.(6分)求图中阴影部分的面积.【解答】解:6644662(64)42⨯+⨯-⨯÷-+⨯÷3616181042=+--⨯÷=+--36161820=(平方厘米)14答:阴影部分的面积是14平方厘米.四.应用题(共5小题,满分29分)21.(5分)如图是一幢楼房占地的平面图,算一算它的占地面积有多大?(单位:)m你能想出几种算法?【解答】解:方法一如图:⨯+-⨯-÷6048(6030)(7248)2=+⨯÷288030242=+28803603240=(平方米)方法二如图:⨯-+⨯-÷7260(6030)(7248)2432090242=-⨯÷=-43201080=(平方米)3240答:它的占地面积有3240平方米。
五年级上册奥数(课件)第12讲:组合图形的面积

答:阴影部分的面积为140平方厘米。
米德思考
总结
(一)组合图形面积的计算方法: 1.分割法:把一个复杂的组合图形分割成我们学过的几 个简单的基本图形,通过求这几个简单的基本图形的面积来 得到组合图形的面积。 2.添补法:充分利用已知的数据,恰当地使用辅助线, 用添补的方法,把复杂的组合图形转化为简单的图形,从而 计算出组合图形的面积。
3.挖空法:就是把多边形看成是一个完整的规则图 形,计算它的面积以后,再减去空缺部分的面积。
天每
开个
放孩
;子
有的
的花
孩期
子不
是一
菊样
花,
,有
选的
择孩
在子
秋是
天牡
开丹
放花
;,
而选
有择
的在
孩春
➢ He who falls today may rise tomorrow.
子天
是开
梅放
花;
,有
选的
择孩
在子
例题三
求下面图形的面积(单位:m)
把它看成一个 三角形和梯形 的面积组合
三角形面积:11×8÷2=44(平方米) 梯形的面积:(11+22)×10÷2=165(平方米) 图形的面积:165+44=209(平方米)
答:这个图形的面积是209平方米。
练习三
求下面图形的面积。(单位:m)
8.5 4
13
答:图形的面积为525平方米。
练习一
求下面图形的面积。(单位:m)
22
52
20
31
48
上面为三角形, 下面为梯形。
三角形的面积:52×22÷2=572(平方米) 梯形的面积:(31+20)×48÷2=1224(平方米) 图形的面积:1224+572=1796(平方米)
五年级奥数 第19讲 组合图形的面积(2)
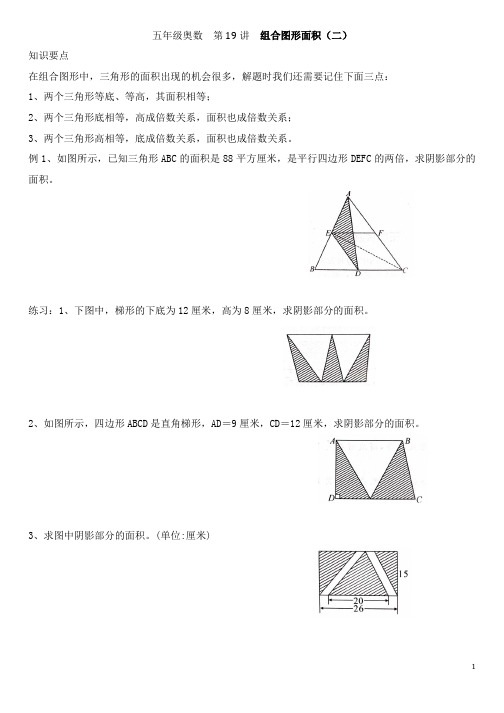
五年级奥数第19讲组合图形面积(二)知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还需要记住下面三点:1、两个三角形等底、等高,其面积相等;2、两个三角形底相等,高成倍数关系,面积也成倍数关系;3、两个三角形高相等,底成倍数关系,面积也成倍数关系。
例1、如图所示,已知三角形ABC的面积是88平方厘米,是平行四边形DEFC的两倍,求阴影部分的面积。
练习:1、下图中,梯形的下底为12厘米,高为8厘米,求阴影部分的面积。
2、如图所示,四边形ABCD是直角梯形,AD=9厘米,CD=12厘米,求阴影部分的面积。
3、求图中阴影部分的面积。
(单位:厘米)例2、下图中,边长为10和15的两个正方形并放在一起,求三角形ABC(阴影部分)的面积。
练习:1、下图中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB =9厘米,FB=FE,求三角形AFE的面积。
2、图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
3、图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米。
求阴影部分的面积(ADFC是长方形)。
例3、下图中每个长方形小格的面积都是1平方厘米,求阴影部分的面积练习:1、下图中每个长方形小格的面积都是1平方厘米,求阴影部分的面积。
2、把等边三角形ABC的每条边6等分,组成如下图所示的三角形网。
如果图中每个小三角形的面积都是1平方厘米,求图中三角形DEF的面积。
3、如图所示,在长方形ABCD中,AD=15厘米,AB=8厘米图中阴影部分面积为68平方厘米,四边形EFGO的面积是多少平方厘米?例4、在三角形ABC中(如下图所示),DC=2BD,CE=3AE,阴影部分的面积是20平方厘米。
求三角形ABC的面积。
练习:1、把下图三角形的底边BC四等分,在下面括号里填上“>”“<”或“=”。
2、如图所示,在三角形ABC中,D是BC的中点,E、F是AC的三等分点。
五年级数学《组合图形的面积》试题及答案

五年级数奥数:《组合图形的面积》1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×÷2 12×3÷2= 20×÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积: 85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2) = 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= ×2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×÷2= 45÷12×2 = 17×÷2= ×2 = ÷2= (cm2) = (cm2)阴影部分面积=梯形面积–空白部分面积: - 45 = (cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8(m2) = 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形的面积
十一右图正方形边长为12厘米,四边形EFGH面积是6平方厘米,那么阴影面积是多少平方厘
米?
分析:S阴影=S AFC+S BDF-2*S EFGH
=FC*AB÷2+BF*AB÷2-2*S EFGH
=(FC+ BF)*AB÷2-2*S EFGH =BC*AB÷2-2*S EFGH
=12*12÷2-2*6=60平方厘米
十二如图,正方形ABCD的边长是12厘米,CE=4厘米。
求阴影部分的面积。
分析:△CEF与△AFB相似;CE:AB=4:12=1:3 EF:BF=1:3
S BCE=CE*BC÷2=4*12÷2=24平方厘米,EF:BF=1:3,所以S BCF=3S CFE
S CFE=6平方厘米S BCF=18平方厘米;S AFE=18平方厘米
S阴影= S BCF + S AFE
=36平方厘米
十三在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD 的边长为15厘米,DF的长是多少厘米?
分析:S ACF=(CD+DF)*AC÷2=(15+DF)*15÷2
S ABCD=AB*AC=15*15=225平方厘米
S ACF-S ABCD=(S ACDE+S EDF)-(S ACDE+S ABE)
S ACF-S ABCD= S EDF-S ABE=75
(15+DF)*15÷2-225=75
DF=25厘米
十四如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
分析:过E点做S AEC的高,其值等于CD,为55厘米
S AEC=AC*CD÷2=12*5÷2=30平方厘米
十五已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中阴影部分的面积
是多少?
分析:S阴影=(8*8+6*6 )-{(6+8)*8÷2+6*6÷2+8*2÷2} =100-82
=18平方厘米
十六如图,A、B两点是长方形长和宽的中点,那么阴影部分占长方形的面积是多少?
分析:长方形的长和宽为a,b;S阴影=a×b-( a×b÷2+ a×b÷8)
=3/8 a×b
十七、在正方形ABCD中,AB是4厘米,三角形BCF比三角形DEF的面积多2平方厘米,求DE的长。
分析:S ABE=(AD+DE)*AB÷2=(4+DE)*4÷2
S ABCD=AB*AB=4*4=16平方厘米
S ABE=S ABDF+S DEF
S ABCD= S ABDF+S BCF
S ABCD-S ABE= S BCF-S DEF=2平方厘米
(4+DE)*4÷2-16=2
DE=5厘米
十八、平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,平行四边形的面积是多少平方厘米?
分析:AE=EF=FB,S AGE=S EGF=S FGB=6平方厘米;S ABG=18平方厘米
AG=2CG;S ABG=2 S BGC;S BGC=9平方厘米
S ABC= S ABG+ S BGC
=27平方厘米
S ABCD=2 S ABC
=54平方厘米
十九下图大正方形边长为3厘米,小正方形边长为2厘米,求阴影部分面积?
分析:S阴影=(3*3+2*2)-(3*3÷2+5*2÷2)-
=3.5平方厘米
二十如下图,ABCD是长8厘米、宽6厘米的长方形,AF是4厘米,求阴影部分(三角形AEF)的面积。
分析:
S阴影=(AB*AD)÷2-(AB*AF)÷2
=8平方厘米
二十一、三角形ABO的面积为9平方厘米,线段BO的长度为OD的3倍,梯形ABCD的面积是多少平方厘米?
分析:BO=3OD,S ABO=3*S AOD
S AOD=3平方厘米;S ABO= S COD=9平方厘米
BO=3OD,S BOC=3*S COD S BOC=27平方厘米
S ABCD= S AOD+ S ABO+ S COD+ S BOC
=3+9+9+27
=48平方厘米
二十二、图中ABCD是直角梯形,两条对角线把梯形分为4个三角形(O是AC和BD的交点)。
已知其中两个三角形的面积为3平方厘米和6平方厘米,求直角梯形ABCD的面积。
分析:S COD= S AOB=3平方厘米
S COD:S BOC=3:6=1:2
DO:BO=1:2
S AOD= 1.5平方厘米
SABCD= S AOD+ S COD+S BOC+S AOC=1.5+3+3+6=13.5平方厘米。
