山东省章丘绣江中学2014年推荐生考试数学模拟试题(3)及答案
最新人教版2014年中考模拟题 数学(三)(山东卷)

2014年中考模拟数学试题(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至10页.共120分.考试时间120分钟.第Ⅰ卷(选择题共42分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案.不能答在试卷上.3.考试结束,答题卡和卷Ⅱ一并交回.一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的4个选项中,只有一项是符合题目要求的.1.﹣2014的倒数是()A. 2014B.﹣2014C.12014D.120142.下列运算正确的是()A.3x2﹣2x2=x2B.﹣(2a)2=﹣2a2C. (a+b)2=a2+b2D. ﹣2(a﹣1)=﹣2a﹣13.已知⊙O1与⊙O2的半径分别为3cm和5cm,若圆心距O1O2=8cm,则⊙O1与⊙O2的位置关系是()A.相交, B.相离, C.内切, D.外切6.若关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是()A.k<1, B.k>1, C.k=1, D.k≥07.如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是()A.45°B.85°C.90°D.95°8.如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )1111A. B. C. D.34569.不等式组211420x x ->⎧⎨-⎩,≤的解在数轴上表示为( )10.计算1÷()2111mm m+∙--的结果果( ) A .-m 2-2m -1B .-m 2+2m -1C .m 2-2m -1D .m 2-111.下列说法正确的是( )A .事件“如果a 是实数,那么0 a ”是必然事件;B .在一次抽奖活动中,“中奖的概率是1001”表示抽奖100次就一定会中奖; C .随机抛一枚均匀硬币,落地后正面一定朝上;D .在一副52张扑克牌(没有大小王)中任意抽一张,抽到的牌是6的概率是131. 12.如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙述正确的是( ) A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形MBCO 和四边形NDCO 都是等腰梯形D .四边形AMON 与四边形ABCD 是位似图形13.如图,是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费( )A 、0.4元B 、0.45 元C 、约0.47元D 、0.5元 13.下列说法正确的是( )A .事件“如果a 是实数,那么0 a ”是必然事件;B .在一次抽奖活动中,“中奖的概率是1001”表示抽奖100次就一定会中奖; C .随机抛一枚均匀硬币,落地后正面一定朝上;D .在一副52张扑克牌(没有大小王)中任意抽一张,抽到的牌是6的概率是131. 14.如图,已知AB 、CD 是⊙O 的两条直径,∠ABC =28°,那么∠BAD =( ) A.28° B.42° C.56° D.84°14.如图,菱形ABCD 的边长为2,∠B =30°. 动点P 从点B 出发,沿B →C →D 的路线向点D 运动.设△ABP 的面积为y (B 、P 两点重合时,△ABP 的面积可以看做0),点P 运动的路程为x ,则y 与x 之间函数关系的图象大致为( )2014年中考模拟数学试题(一)第Ⅱ卷(非选择题 共78分)注意事项:1.第Ⅱ卷共8页,用蓝黑钢笔或圆珠笔直接答在试卷上.2.答卷前将密封线内的项目填写清楚.二. 填空题:(本大题共5个小题.每小题3分,共15分)把答案填在题中横线上.15.因式分解:++-2244a a b =.16.计算()))cos -⎛⎫---- ⎪⎝⎭121311452π=_________.17.如图,在△ABC 中,D 是BC 边上的中点,∠BDE =∠CDF ,请你添加一个..条件,使DE =DF 成立.你添加的条件是 .(不再添加辅助线和字母)18.如图,两个反比例函数10y =x 和5y =x在第一象限内的图象分别是1C 和2C ,设点P 是1C 上的一个动点,PA x ⊥轴于点A ,交2C 于点B ,则△POB 的面积为19.若x 是不等于1的实数,我们把11x -称为x 的差倒数,如2的差倒数是112-=-1,-1的差倒数为()11112=--,现已知121x x 3=-,是x 1的差倒数,x 3是x 2的差倒数,x 4是x 3的差倒数,…,依次类推,则x 2 013=____________.三、开动脑筋,你一定能做对!(本大题共3小题,共20分)20.(本小题满分6分)为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:(1)在这次调查中共调查了多少名学生?(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图; (3)求表示户外活动时间1小时的扇形圆心角的度数;(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?21.(本小题满分8分)如图,E 是正方形ABCD 的边DC 上的一点,过A 作AF ⊥AE ,交CB 延长线于点F 。
【解析版】济南市绣惠中学2014-2015年八年级上期末模拟试卷

A. 10 B. 16 C. 18 D. 20 9.根据下边流程图中的程序,当输入数值 x 为﹣2 时,输出数值 y 为( )
A. 4 B. 6 C. 8 D. 10 10.若等腰三角形的周长为 60cm,底边长为 x cm,一腰长为 y cm,则 y 与 x 的函数关系 式及自变量 x 的取值范围是( )
A. y=60﹣2x(0<x<60) B. y=60﹣2x(0<x<30) C. y= (60﹣x)(0<x<60) D. y= (60﹣x)(0<x<30) 11.Rt△ABC中,AB=AC,点 D 为 BC中点.∠MDN=90°,∠MDN绕点 D 旋转,DM、DN分别 与边 AB、AC交于 E、F 两点.下列结论: ①(BE+CF)= BC; ②S△AEF≤ S△ABC ; ③S 四边形 AEDF=AD•EF; ④AD≥EF; ⑤AD与 EF可能互相平分, 其中正确结论的个数是( )
2.如图,点 A1,A2,A ,A4 是某市正方形道路网的部分交汇点,且它们都位于同一对角线 上.某人从点 A1 出发,3规定向右或向下行走,那么到达点 A 的走法共有( )
3
A. 4 种 B. 6 种 C. 8 种 D. 10种
3.在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点.设 k 为整数,当直线 y=x﹣2 与 y=kx+k的交点为整点时,k 的值可以取( )
A. 4 个 B. 5 个 C. 6 个 D. 7 个
4.在所给的数: , , ,π,0.57.0.585 885 888 588 885…(相邻两个 5 之间
的 8 的个数逐次增加 1)中,无理数的个数是( ) A. 2 B. 3 C. 4 D. 5
5.下列说法正确的是( ) A. 无限小数是无理数 B. 不循环小数是无理数 C. 无理数的相反数还是无理数 D. 两个无理数的和还是无理数
山东省章丘市明水街道办事处绣江中学2014届推荐生考试模拟语文试题

············绝密★启用前山东省章丘市明水街道办事处绣江中学2014届推荐生考试模拟语文试题说明:1.答卷前将密封线内的项目用钢笔或圆柱笔填写清楚。
2.本试卷共8页四个大题,21个小题,全部答在试卷上。
3.全卷满分120分,考试时间120分钟。
一、积累与运用(15分)1.按要求默写。
(6分)A. ,到乡翻似烂柯人。
(刘禹锡《酬乐天扬州初逢席上见赠》)B.鸡声茅店月,。
(温庭筠《商山早行》)C. ,芳草萋萋鹦鹉洲。
(崔颢《黄鹤楼》)D.无言独上西楼,月如钩,。
(李煜《相见欢》)E. 野芳发而幽香,,风霜高洁,水落而石出者,山间之四时也。
(欧阳修《醉翁亭记》)F. 春天像健壮的青年,。
(朱自清《春》)2.阅读下面这则材料,按要求回答问题。
(5分)济南自然风光秀丽,自古素有“泉城”之美称。
城内百泉争涌。
尤以趵突泉、黑虎泉、五龙潭、珍珠泉四大名泉久负盛名,自古享有“家家泉水,户户垂杨”之誉。
众泉汇流成的大明湖周围千佛山、五峰山、灵岩寺云山等构成了“一城山色半城湖”的独特风光。
济南的2000多年的历史,是闻名世界的史前文化-龙山文化的发祥地,城区内有新石器时代的遗址城子崖,有先于秦长城的齐长城,有现在中国最古老的地面房屋建筑汉代孝堂山郭氏墓,单层古塔四门塔,有被誉为“海内第一名塑”的灵岩寺宋代彩塑罗汉等。
济南诞生了许多中国历史上的著名人物,像中医科学的奠基人扁鹊,阴阳五行学派大师邹衍,唐代开国元勋房玄龄、秦琼,中国著名文学家李清照、辛弃疾等。
另外,李白、杜甫、苏轼、曾巩等历代杰出的作家学者,都先后在济南生活游历,故有“济南名士多”的佳誉。
①文中画线句有语病,请用所给的修改符号(不必全部使用)直接在原文上进行修改。
(2分)换用号增补号删除号调位号②把下面的对联或诗句补充完整。
(任选一句作答,两句都做只按A句计分)(1分)A ,一城山色半城湖。
2014年中考数学模拟试卷含答案(精选3套)

济南市2014年初三年级学业水平考试数学全真模拟试卷(时间:120分钟 满分:120分)第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题所给的四个选项中,只有一项是符合题目要求的.) 1.-2的绝对值是( )11A. B.2 C. D.222- -2.我国第一艘航母“辽宁舰”最大排水量为67 500吨,用科学记数法表示这个数字是( )A.6.75×103 吨B.67.5×103吨C.6.75×104 吨D.6.75×105吨 3.16的平方根是( )A.4B.±4C.8 D .±84.如图,直线l ∥m ,将含有45°角的三角板ABC 的直角顶点C 放在直线m 上,若∠1=25°,则∠2的度数为( )A.20°B.25°C.30°D.35° 5.下列等式成立的是( )A.a 2×a 5=a 10B.a b a b +=+C.(-a 3)6=a 18D.2a a =6.一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回)其数字记为p ,再随机摸出另一个小球其数字记为q ,则满足关于x 的方程x 2+px+q=0有实数根的概率是( )1125A. B. C. D.23367.分式方程12x 1x 1=-+的解是( ) A.1 B.-1 C.3 D.无解8.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )111A. B. C. D.248π π π π9.如图,数轴上表示某不等式组的解集,则这个不等式组可能是( )x 10x 10A. B.2x 02x 0x 10x 10C. D.x 20x 20+≥+≤⎧⎧ ⎨⎨-≥-≥⎩⎩+≤+≥⎧⎧ ⎨⎨-≥-≥⎩⎩10.如图是一个正方体被截去一角后得到的几何体,它的俯视图是( )11.化简2(21)÷-的结果是( )A.221B.22C.12D. 22- - - +12.如图,在Rt △ABC 中,∠BAC=90°,D 、E 分别是AB 、BC 的中点,F 在CA 的延长线上,∠FDA=∠B ,AC=6,AB=8,则四边形AEDF 的周长为( )A.22B.20C.18D.1613.如图,过x 轴正半轴上的任意一点P ,作y 轴的平行线,分别与反比例函数64y y x x=-=和的图象交于A 、B 两点.若点C 是y 轴上任意一点,连接AC 、BC ,则△ABC的面积为( )A.3B.4C.5D.1014.如图,已知AB、CD是⊙O的两条直径,∠ABC=28°,那么∠BAD=( )A.28°B.42°C.56°D.84°15.如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B→C→D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )第Ⅱ卷(非选择题共75分)二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上.)16.分解因式:(a+2)(a-2)+3a=________.17.已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则ab的值为_________.18.如图,两建筑物的水平距离BC为18 m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为________ m(结果不作近似计算).19.三棱柱的三视图如图所示,△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为______cm.20.如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为_______.21.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是________.三、解答题(本大题共7个小题,共57分.解答应写出文字说明、证明过程及演算步骤.)22.(本小题满分7分)(1)化简222x1x2x1. x1x x--+÷+-(2)解方程:15x2(x1)8x. 24++=+23.(本小题满分7分)(1)如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.(2)如图所示,已知在平行四边形ABCD中,BE=DF.求证:AE=CF.24.(本小题满分8分)五一期间某校组织七、八年级的同学到某景点郊游,该景点的门票全票票价为15元/人,若为50~99人可以八折购票,100人以上则可六折购票.已知参加郊游的七年级同学少于50人、八年级同学少于100人.若七、八年级分别购票,两个年级共计应付门票费1 575元,若合在一起购买折扣票,总计应付门票费1 080元.(1)请你判断参加郊游的八年级同学是否也少于50人.(2)求参加郊游的七、八年级同学各为多少人?25.(本小题满分8分)某市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽取了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14∶9∶6∶1,评价结果为D等级的有2人,请你回答以下问题:(1)共抽取了多少人?(2)样本中B等级的频率是多少?C等级的频率是多少?(3)如果要绘制扇形统计图,A、D两个等级在扇形统计图中所占的圆心角分别是多少度?(4)该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有多少名学生可以报考示范性高中?26.(本小题满分9分)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.(1)求证:直线BF是⊙O的切线;(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长;(3)填空:在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O 的距离为5,则r的取值范围为_________.27.(本小题满分9分)已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).(1)求二次函数的解析式并写出D点坐标;(2)点E是BD的中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标;(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.28.(本小题满分9分)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于点F,∠1=∠2,连接CB与DG交于点N.(1)求证:CF 是⊙O 的切线; (2)求证:△ACM ∽△DCN ;(3)若点M 是CO 的中点,⊙O 的半径为4,cos ∠BOC=14,求BN 的长.参考答案1.D2.C3.B4.A5.C6.A7.C8.A9.A 10.A 11.D 12.D 13.C 14.A 15.C 16.(a-1)(a+4) 17.-10 18.123 19.6 20.n 13-()21.25522.(1)解:原式=()()()2x 1x 1x x 1x.x 1x 1+--=+- () (2)解:原方程可化为3x+2=8+x,合并同类项得:2x=6, 解得:x=3.23.(1)证明:∵∠1=∠2, ∴∠1+∠EAC=∠2+∠EAC, 即∠BAC=∠EAD.∵在△ABC 中和△AED 中,D C,BAC EAD,AB AE,∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△AED(AAS) (2)证明:∵BE=DF,∴BE-EF=DE-EF,∴DE=BF.∵四边形ABCD 是平行四边形, ∴AD=BC,AD ∥BC, ∴∠ADE=∠CBF,在△ADE 和△CBF 中,DE BF,ADE CBF,AD BC,=⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CBF(SAS), ∴AE=CF. 24.解:(1)全票为15元,则八折票价为12元,六折票价为9元. ∵100×15=1 500<1 575,∴参加郊游的七、八年级同学的总人数必定超过100人,∴由此可判断参加郊游的八年同学不少于50人.(2)设七、八年级参加郊游的同学分别有x 人、y 人. 由(1)及已知可得,x<50,50<y<100,x+y>100. 依题意可得:()15x 12y 1 575,9x y 1 080,+=⎧⎨+=⎩ 解得:x 45,y 75.=⎧⎨=⎩答:参加郊游的七、八年级同学分别为45人和75人. 25.解:(1)D 等级所占比例为:111496130=+++,则共抽取的人数为:1260().30÷=人 (2)样本中B 等级的频率为:9100%30%;14961⨯=+++C 等级的频率为:6100%20%.14961⨯=+++ (3)样本中A 等级在扇形统计图中所占圆心角度数为:1430×360=168(度); D 等级在扇形统计图中所占圆心角度数为:130×360=12(度). (4)可报考示范性高中的总人数: 300×149()3030+=230(名). 26.(1)证明:∵∠CBF=∠CFB , ∴BC=CF. ∵AC=CF , ∴AC=BC ,∴∠ABC=∠BAC.在△ABF 中,∠ABC+∠CBF+∠BAF+∠F=180°, 即2(∠ABC+∠CBF)=180°, ∴∠ABC+∠CBF=90°, ∴BF 是⊙O 的切线;(2)解:连接BD.∵点D ,点E 是弧AB 的三等分点,AB 为直径, ∴∠ABD=30°,∠ADB=90°,∠A=60°. ∵AD=5,∴AB=10,()BFtan603ABBF 103;3535r 53 5.∴︒==∴=-<<+,27.解:(1)设二次函数的解析式为:y=ax 2+bx+c.221a c 4216a 4b c 0b 1b c 4,12a 1y x x 4.21D(2m)m 224 4.2⎧⎧=-⎪⎪=⎪⎪++==⎨⎨⎪⎪=⎪⎪-=⎩⎩=-++=-⨯++= ,,由题意有:,解得:,,所以,二次函数的解析式为:点,在抛物线上,即∴点D 的坐标为(2,4);(2)作DG 垂直于x 轴,垂足为G ,因为D (2,4),B (4,0), 由勾股定理得:BD=25,∵E 是BD 的中点, ∴BE=5.BE BQ 1QBE ABD BD BA 2AB 2BQ Q 10BQ BE 5QBE DBA BD BA 6557BQ 25OQ 6337Q 0.3==∴=∴==∴=⨯==∴ 当≌时,,,点的坐标为(,);当≌时,,,则,点的坐标(,) (3)如图,由A(-2,0),D(2,4),可求得直线AD 的解析式为:y=x+2,则点F 的坐标为:F(0,2).过点F作关于x轴的对称点F′,即F′(0,-2),连接CD,再连接DF′交对称轴于M′,交x轴于N′.由条件可知,点C,D关于对称轴x=1对称,∴DF′=210,F′N′=FN′,DM′=CM′,∴CF+FN′+M′N′+M′C=CF+DF′=2210+,∴四边形CFNM的周长=CF+FN+NM+MC≥CF+FN′+M′N′+M′C=2210+,即四边形CFNM的最短周长为:2210+,此时直线DF′的解析式为:y=3x-2,所以存在点N的坐标为2(,0)3,点M的坐标为(1,1)使四边形CMNF周长取最小值.28.(1)证明:∵△BCO中,BO=CO,∴∠B=∠BCO,在Rt△BCE中,∠2+∠B=90°,又∵∠1=∠2,∴∠1+∠BCO=90°,即∠FCO=90°,∴CF是⊙O的切线;(2)证明:∵AB是⊙O直径,∴∠ACB=∠FCO=90°,∴∠ACB-∠BCO=∠FCO-∠BCO,即∠ACO=∠1,∴∠ACO=∠2,∵∠CAM=∠D,∴△ACM∽△DCN;(3)解:∵⊙O的半径为4,即AO=CO=BO=4,在Rt△COE中,cos∠BOC=1 4,∴OE=CO ·cos ∠BOC=4×14=1, 由此可得:BE=3,AE=5,由勾股定理可得:222222222222CE CO OE 4115AC CE AE (15)5210,BC CE BE (15)326,=-=-==+=+==+=+= ∵AB 是⊙O 直径,AB ⊥CD , ∴由垂径定理得:CD=2CE=215,∵△ACM ∽△DCN ,∴CM AC,CN CD= ∵点M 是CO 的中点,11CMOA 42,22==⨯= CM CD 2215CN 6,AC 210BN BC CN 266 6.⨯∴===∴=-=-=济南市2014年初三年级学业水平考试数学全真模拟试卷2第Ⅰ卷(选择题共45分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题所给的四个选项中,只有一项是符合题目要求的).1.如果+30 m表示向东走30 m,那么向西走40 m表示为( )A.+40 mB.-40 mC.+30 mD.-30 m2.若实数a、b满足a+b=5,a2b+ab2=-10,则ab的值是( )A.-2B.2C.-50D.503.图中几何体的主视图是( )4.英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯目前是世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )A.0.34×10-9B.3.4×10-9C.3.4×10-10D.3.4×10-115.已知圆锥的底面半径为6 cm,高为8 cm,则这个圆锥的母线长为( )A.12 cmB.10 cmC.8 cmD.6 cm6.如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )1111A. B. C. D.34567.假期到了,17名女教师去外地培训,住宿时有2人间和3人间可供租住,每个房间都要住满,她们有几种租住方案( )A.5种B.4种C.3种D.2种8.某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1 225元,设其中有x张成人票,y张儿童票.根据题意,下列方程组正确的是( )9.如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )A.18°B.24°C.30°D.36°10.如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为( )A.4B. 22C.1D.211.如图,数轴上a,b两点表示的数分别为3和-1,点a关于点b的对称点为c,则点c所表示的数为( )A.23B.13C.23D.13-- -- -+ +12.如图,A、B、C是反比例函数kyx=(x<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3∶1∶1,则满足条件的直线l共有( )A.4条B.3条C.2条D.1条13.在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表所示:这8名同学捐款的平均金额为( )A.3.5元B.6元C.6.5元D.7元14.已知关于x 的不等式组()4x 123x,6x ax 1,7⎧-+⎪⎨+-⎪⎩><有且只有三个整数解,则a 的取值范围是( )A.-2≤a-1B.-2≤a <-1C.-2<a ≤-1D.-2<a <-1 15.如图,直线l :y=-x-2与坐标轴交于A 、C 两点,过A 、O 、C 三点作⊙O 1,点E 为劣弧 AO上一点,连接EC 、EA 、EO ,当点E 在劣弧上运动时(不与A 、O 两点重合),EC EA EO-的值是( )A.2 B.3 C.2 D.变化的第Ⅱ卷(非选择题 共75分)二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上.)16.分解因式:a 3-ab 2=________. 17.计算124183-⨯=_________. 18.如图,在Rt △ABC 中,∠C=90°,∠B=60°,点D 是BC 边上的点,CD=1,将△ABC 沿直线AD 翻折,使点C 落在AB 边上的点E 处,若点P 是直线AD 上的动点,则△PEB 的周长的最小值是______.19.如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P ,则tan ∠APD 的值是______.20.某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示,那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为_____________.21.若x 是不等于1的实数,我们把11x -称为x 的差倒数,如2的差倒数是112-=-1,-1的差倒数为()11112=--,现已知121x x 3=-,是x 1的差倒数,x 3是x 2的差倒数,x 4是x 3的差倒数,…,依次类推,则x 2 013=____________.三、解答题(本大题共7个小题,共57分.解答应写出文字说明、证明过程及演算步骤.) 22.(本小题满分7分)(1)解方程组2x 3y 3x 2y 2.-=⎧⎨+=-⎩,(2)化简:1a a ().22a 2a 1-÷++23.(本小题满分7分)(1)如图,在四边形ABCD 中,AB=BC ,∠ABC=∠CDA=90°,BE ⊥AD ,垂足为E. 求证:BE=DE.(2)如图,AB 是⊙O 的直径,DF ⊥AB 于点D ,交弦AC 于点E ,FC=FE. 求证:FC 是⊙O 的切线.24.(本小题满分8分)小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).25.(本小题满分8分)某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.(1)将条形统计图补充完整;(2)本次抽样调查的样本容量是____________;(3)已知该校有1 200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.26.(本小题满分9分)如图,O是菱形ABCD对角线AC与BD的交点,CD=5 cm,OD=3 cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.(1)求OC的长;(2)求证:四边形OBEC为矩形;(3)求矩形OBEC的面积.27.(本小题满分9分)如图,直线1yx 4=与双曲线ky x =相交于A 、B 两点,BC ⊥x 轴于点C (-4,0).(1)求A 、B 两点的坐标及双曲线的解析式;(2)若经过点A 的直线与x 轴的正半轴交于点D ,与y 轴的正半轴交于点E ,且△AOE 的面积为10,求CD 的长.28.(本小题满分9分) 如图,抛物线21y x 1=-交x 轴的正半轴于点A ,交y 轴于点B ,将此抛物线向右平移4个单位得抛物线y 2,两条抛物线相交于点 C.(1)请直接写出抛物线y 2的解析式;(2)若点 P 是x 轴上一动点,且满足∠CPA=∠OBA ,求出所有满足条件的P 点坐标; (3)在第四象限内抛物线y 2上,是否存在点Q ,使得△QOC 中OC 边上的高h 有最大值,若存在,请求出点Q 的坐标及h 的最大值;若不存在,请说明理由.参考答案1.B2.A3.D4.C5.B6.B7.C8.B9.A10.D 11.A 12.A 13.C 14.C 15.A19.2 20.40% 21.416.a(a+b)(a-b) 17.618.1323.(1)证明:作CF⊥BE,垂足为F.∵BE⊥AD,∴∠AEB=90°,∴∠FED=∠D=∠CFE=90°,∠CBE+∠ABE=90°,∠BAE+∠ABE=90°,∴∠BAE=∠CBF,∵四边形EFCD为矩形,∴DE=CF.在△BAE和△CBF中,有∠CBE=∠BAE,∠BFC=∠BEA=90°,AB=BC,∴△BAE≌△CBF,∴BE=CF=DE,即BE=DE.(2)证明:连接OC.∵FC=FE,∴∠FCE=∠FEC.又∵∠AED=∠FEC,∴∠FCE=∠AED.∵OC=OA,∴∠OCA=∠OAC,∴∠FCO=∠FCE+∠OCA=∠AED+∠OAC=180°-∠ADE.∵DF⊥AB,∴∠ADE=90°,∴∠FCO=90°,即OC⊥FC.又∵点C在⊙O上,∴FC是⊙O的切线;24.解法一:解:设上月萝卜的单价是x 元/斤,排骨的单价是y 元/斤,根据题意得:()()3x 2y 363150%x 2120%y 45x 2:y 15.+=⎧⎨+++=⎩=⎧⎨=⎩,,,解得这天萝卜的单价是(1+50%)x=(1+50%)×2=3(元/斤), 这天排骨的单价是(1+20%)y=(1+20%)×15=18(元/斤). 答:这天萝卜的单价是3元/斤,排骨的单价是18/斤. 解法二:解:设这天萝卜的单价是x 元/斤,排骨的单价是y 元/斤,根据题意得:32x y 36150%120%3x 2y 45x 3:y 18.⎧+=⎪++⎨⎪+=⎩=⎧⎨=⎩,,,解得 答:这天萝卜的单价是3元/斤,排骨的单价18元/斤. 25.解:(1)∵根据扇形统计图可得出女生喜欢武术的占20%, 利用条形图中喜欢武术的女生有10人, ∴女生总人数为:10÷20%=50(人),∴女生中喜欢舞蹈的人数为:50-10-16=24(人). 补充条形统计图,如图所示:(2)100(3)∵样本中喜欢剪纸的人数为30人,样本容量为100, ∴估计全校学生中喜欢剪纸的人数:1 200×30100=360人. 答:全校学生中喜欢剪纸的有360人. 26.解:(1)∵四边形ABCD 是菱形, ∴AC ⊥BD ,∴直角△OCD 中,2222OC CD OD 53 4 cm =-=-=;(2)∵CE ∥DB ,BE ∥AC , ∴四边形OBEC 为平行四边形, 又∵AC ⊥BD ,即∠COB=90°, ∴平行四边形OBEC 为矩形; (3)∵OB=OD ,∴S 矩形OBEC =OB ·OC=4×3=12(cm 2). 27.解:(1)∵BC ⊥x 轴,C (-4,0),∴B 的横坐标是-4,代入y=14x 得:y=-1,∴B 的坐标是(-4,-1). ∵把B 的坐标代入ky k 4x==得:, ∴反比例函数的解析式是4y .x=∵解方程组12121y x x 4x 444y 1y 1y x⎧=⎪==-⎧⎧⎪⎨⎨⎨==-⎩⎩⎪=⎪⎩,,,得:,,,∴A 的坐标为(4,1),B 的坐标为(-4,-1);(2)设OE=a ,OD=b ,则△AOE 面积S △AOE =S △EOD -S △AO D,AOE 1110ab b 1,221S a 410,2=- == 即:①并且,②由①,②可解得:a=5,b=5,即OD=5. ∵OC=|-4|=4,∴CD 的长为:4+5=9.28.解:(1)y=x 2-8x+15;(2)当 y 1= y 2,即x 2-1 =x 2-8x+15, ∴x=2,y=3, ∴C (2,3).由题可知, A ( 1 , 0 ) , B ( 0 ,-1), ∴OA =OB= 1 ,∴∠OBA= 45°. 过点 C 作CD ⊥x 轴于点D, ∴D(2,0),∴CD=3.当∠CPA=∠OBA=45°时,∴PD=CD=3 ,∴满足条件的点P有2个,分别为P1 (5,0),P2(-1,0);(3)存在.过点C作CE⊥y轴于点E,过点Q作QF⊥y轴于点F,连接OC、QC、 OQ. 设Q (x0,y0) ,∵Q在y2上,∴y0=x02-8x0+15,∴CE=2,QF=x0,EF=3-y0,OE=3,OF=-y0.∵在△QOC中,OC边长为定值,∴当S△QOC取最大值时,OC边上的高h也取最大值.2014届中考数学模拟测试卷(本试卷满分150分,考试时间120分钟)一、选择题(本题有8小题,每小题3分,共24分) 1.12-的倒数为【 】 A .12B .2C .2-D .1-2.下列图形中,既是轴对称图形,又是中心对称图形的是【 】 A .平行四边形 B .等边三角形 C .等腰梯形 D .正方形3.已知地球距离月球表面约为383900千米,那么这个距离用科学记数法表示为(保留三个有效数字)【 】A .3.84×104千米B .3.84×105千米C .3.84×106千米D .38.4×104千米 4.已知⊙O 1与⊙O 2的半径分别为5cm 和3cm ,圆心距0102=7cm ,则两圆的位置关系为【 】 A .外离 B .外切 C .相交 D .内切5.如图是由七个相同的小正方体堆成的几何体,这个几何体的俯视图是【 】6.某校在开展“爱心捐助”的活动中,初三(一)班六名同学捐款的数额分别为:8,10,10,4,8,10(单位:元),这组数据的众数是【 】A .10B .9C .8D .4 7.如图7,AB 是⊙O 的直径,点D 在AB 的延长线上, DC 切⊙O 于点C ,若∠A=25°,则∠D 等于【 】 A .20°B .30°C .40° D.50°8.已知二次函数2(0)y ax bx c a =++≠的图象如右图8所示,下列结论①abc >0 ②b<a+c③2a-b=0 ④4a+2b+c >0 ⑤2c<3b⑥a+b >m(am+b)(m 为任意实数), 其中正确的结论有【 】 A . 1个 B .2个 C . 3个D .4个二、填空题(本大题共10小题,每小题3分,共30分)9.扬州市某天的最高气温是6℃,最低气温是-3℃,那么当天的日温差是 ▲ .10.函数12-+=x x y 中自变量x 的取值范围是 ▲ . 11.如图11,四边形ABCD 中,AB//CD ,要使四边形ABCD 为平行四边形,则可添加的条件为 ▲ .(填一个即可).12.因式分解:m 3n -9mn= ▲ .13.已知25-是一元二次方程240x x c -+=的一个根,则方程的另一个根是▲ .14.在平面直角坐标系中,如果抛物线y=3x 2不动,而把x 轴、y 轴分别向上、向右平移3个单位,那么在新坐标系中此抛物线的解析式是 ▲ . 15.已知关于x 的不等式组0521x a x -⎧⎨->⎩≥,只有四个整数解,则实数a 的取值范围是 ▲ .16.已知一个圆锥的母线长为10cm ,将侧面展开后所得扇形的圆心角是144°,则这个圆锥的底面圆的半径是 ▲ cm .17.如图,线段AB 的长为2,C 为AB 上一个动点,分别以AC 、BC 为斜边在AB 的同侧作两个等腰直角三角形△ACD 和△BCE ,那么DE 长的最小值是 ▲ . 18.观察分析下列方程:①,②,③;请利用它们所蕴含的规律,求关于x 的方程(n 为正整数)的根,你的答案是: ▲ .(用n 的代数式 )三、解答题(本大题共有10小题,共96分) 19.(本题8分)(1) (4分)解方程组 ⎩⎨⎧=-=-;1383,32y x y x(2) (4分)821)14.3(45sin 2)31(02+-+︒--π 20.(本题8分)先化简:22a 1a 11a a +2a---÷,再选取一个合适的 a 值代入计算.21.(本题8分)如图,在△ABC 中,∠ACB=90°,AC=BC ,BE ⊥CE 于点E ,AD ⊥CE 于点D 。
山东省章丘市明水街道办事处绣江中学2014届九年级下学期第一次月考语文试题

山东省章丘市明水街道办事处绣江中学2014届九年级下学期第一次月考语文试题一、积累与运用。
(21分)1.按照要求默写.(共10分)A.雪暗凋旗画, ___风多杂鼓声 _。
B.吊影分为千里雁,____辞根散作九秋蓬______。
C.__举杯邀明月_____,对影成三人。
D. 君不见走马川行雪海边, 平沙莽莽黄入天。
F.无限山河泪, __ 谁言天地宽______。
G.水是眼波横,__山是眉峰聚____,欲问行人去哪边,___眉眼盈盈处_____。
H.故曰,域民不以封疆之界,固国不以山溪之险,威天下不以兵革之利。
I.人恒过然后能改,困于心衡于虑而后作,征于色发于声而后喻。
J.为什么我的眼里常含泪水?___因为我对这土地爱得深沉 _ 。
2.阅读下列文字,按要求作答。
(共7分)①随着电脑文字入录技术的应用,使人们逐渐不喜欢用笔写字了。
这一问题已经引起了有关部门的高度重视。
我国正在制订中小学生汉字书写等级标准,要求学生不仅会认会写,还要写得规范和美观。
学校也要加强宣传,②提高同学们对汉字书写的重要性。
A文中划横线的两个句子有语病,请用恰当的修改符号直接在原句上修改。
①随着电脑文字入录技术的应用,使人们逐渐不喜欢用笔写字了。
(去掉“随着”或者去掉“使”。
)②提高同学们对汉字书写的重要性。
(在“重要性”的后面加上“的认识”。
)B. 根据文段,为学校拟写一则宣传语,宣传汉字书写的重要性。
(不超过20字)示例:写规范美观的汉字,做堂堂正正的好人。
书写规范美观汉字,弘扬中华传统文化。
3.名著阅读。
(5分)“不过人不是为失败而生的,”他说“一个人可以被毁灭,但不能给打败”不过,我很痛心,把这条鱼给杀了,他想。
现在倒霉的时候要来了,可我连鱼叉也没有了。
这条登多索鲨鱼是残忍,能干,强壮而聪明的。
但我比他更聪明。
也许并不,他想,也许仅仅是武器比它强。
A.选文选自__《老人与海》__,是__美国_国作家__海明威___的经典之作。
山东省章丘绣江中学2014年推荐生考试数学模拟试题及答案

2014.5章丘市推荐生考试倒计时11、如图,在平面直角坐标系中,已知点A (-2,-4),OB =2,抛物线y =ax 2+bx +c 经过点A 、O 、B 三点.(1)求抛物线的函数表达式;(2)若点M 是抛物线对称轴上一点,试求AM +OM 的最小值;(3)在此抛物线上,是否存在点P ,使得以点P 与点O 、A 、B 为顶点的四边形是梯形.若存在,求点P 的坐标;若不存在,请说明理由.解:(1)由OB =2,可知B(2,0)将A (-2,-4),B(2,0),O(0,0)三点坐标代入抛物线y =ax 2+bx +c ,得4420420a b c a b c c -=-+⎧⎪=++⎨⎪=⎩解得:1102a b c =-==,,∴抛物线的函数表达式为212y x x =-+。
(2)由22111(1)222y x x x =-+=--+,可得,抛物线的对称轴为直线1x =,且对称轴1x =是线段OB 的垂直平分线,连结AB 交直线1x =于点M ,即为所求。
∴MO=MB ,则MO+MA=MA+MB=AB作AC ⊥x 轴,垂足为C ,则AC=4,BC=4,∴AB=∴MO+MA的最小值为(3)①若OB ∥AP ,此时点A 与点P 关于直线1x =对称, 由A (-2,-4),得P(4,-4),则得梯形OAPB 。
②若OA ∥BP ,设直线OA 的表达式为y kx =,由A (-2,-4)得,2y x =。
设直线BP 的表达式为2y x m =+,由B(2,0)得,04m =+,即4m =-, ∴直线BP 的表达式为24y x =-由22412y x y x x =-⎧⎪⎨=-+⎪⎩,解得14x =-,22x =(不合题意,舍去) 当4x =-时,12y =-,∴点P(412--,),则得梯形OAPB 。
③若AB ∥OP ,设直线AB 的表达式为y kx m =+,则 4202k m k m -=-+⎧⎨=+⎩,解得12k m =⎧⎨=-⎩,∴AB 的表达式为2y x =-。
山东省章丘市明水街道办事处绣江中学2014届中考模拟语文考试试题

**学校2014年学业水平模拟考试语 文 试 题亲爱的同学们:考试中请一定静心阅读、仔细审题,认真答卷。
语文试卷还要特别做到:字迹美观....(一.律用钢笔或签字笔书写)...........、卷面整洁....、文笔优美....、谢绝空题....。
希望你能够交上一份满意的答卷。
题号一二三(1) 三(2)四总分得分一、积累与运用(15分) 1.请用正楷字,笔画清晰........地填写相应的诗文名句。
(6分,每小题1分) A.春潮带雨晚来急, 。
(韦应物《滁州西涧》) B. ,似曾相识燕归来,小园香径独徘徊。
(晏殊《浣溪沙》) C. ,欲语泪先流。
(李清照《武陵春》) D.其间千二百里, ,不以疾也。
(郦道元《三峡》) E.入则无法家拂士, ,国恒亡。
(孟子《生于忧患,死于安乐》) F .假如生活欺骗了你, , 。
(普希金《假如生活欺骗了你》)2.阅读下面的新闻,按要求回答问题。
(4分)经过3个月改造,4月18日天桥区无影山东路垃圾压缩转运站正式投入使用。
这是济南首个已建成使用的环保型垃圾压缩转运站,也是目前唯一的济南的环保型垃圾压缩转运站。
据济南市城管部门介绍,改造前,无影山垃圾转运站采用的是地埋式垃圾转运箱收集方式,站内垃圾外露,倾倒时扬尘漫天。
同时,地埋式垃圾箱存在垃圾清运成本较高、转运效率较低、二次污染等问题。
新的垃圾压缩转运站集成系统采用水平式固定压缩机和密闭式垃圾转运箱,垃圾不外露,单机日处理量达50吨。
A .画线的句子有语病,请选用恰当的修改符号直接在原句上修改。
(2分)B .请在下面的空格内为这则新闻拟写标题。
(15个字以内)(2分)3.名著阅读。
(5分)[A]第一条鲨鱼飞速逼近船艄,袭击大马林鱼。
老人使出全身力气,用鱼叉猛扎鲨鱼的脑袋,鲨鱼翻了几个身,自己缠上了老人准备好的绳子,老人知道鲨鱼快不行了,它越挣扎绳子绷得越紧直到断裂。
鲨鱼在水面上静静躺了片刻,老人盯着它,然后它慢慢沉入海底。
山东省章丘绣江中学2014年推荐生数学模拟试题3及答案
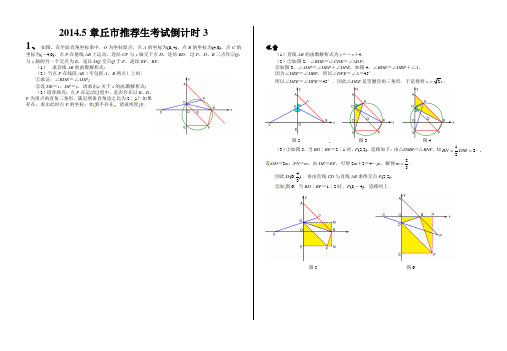
(0,连结ADP,请求出y的函1果不存在,请说明理由.图2 图3 图4(3)①如图5,当BD∶BF=2∶1时,P(2,2).思路如下:由△DMB∽△BNF,知12B N=.设OD=2m,FN=m,由DE=EF,可得2m+2=4-m.解得23m=.因此4(0,)3D.再由直线CD与直线AB求得交点P(2,2).②如图6,当BD∶BF=1∶2时,P(8,-4).思路同上.图5 图6的边长为2A都停止运动长为半径作圆,请问:在整个运动过程中,个公共点?Q=A B的中如图重合时图2 图3 图4 图5P°得到(径的⊙图1 图2 图3的三角比反复OB N OB分割为两个具有公共直角边直线在4105x y--,由勾股定理得ON2=OF2+NF2.2.整理,得25050xy-=.定义域为0<x<5.第(2,=1,35PQ=,45BQ=.=4461055x x--=-,所以222463()()55OP x=-+.①当MO时,方程22426()()155x-+=没有实数根.PM0)AB点)以点Pt的值.图2 图3,当⊙P与直线BC相切时,t=1;如图与直线DC相切时,t=4;与直线AD相切时,t=5.6.图4 图5 图6两点的坐标;的坐标;若不存在,请说明理由;BDM的周长最小,求出点的图1′2′,联结x轴于=4.所以点图2 图3考点伸展是平行四边形的对角线时,点,抛物线213922y xx =--与x 轴交于A 、B 两点,与y 轴交于点联结AB 和OC 的长;E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点于点D .设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变m 的取值范围;CDE 面积的最大值;此时,求出以点图1AC 1,所以图2 图3)如图2,因为DE //CB ,所以9CD BE mAD AE m-==.DE在CDE1(0,的式子表示)条抛物线被,0)等?若存在备用图(仅供草稿使用).本题写在卷面的文.最大的纠结莫过于对字母意义的理解,这道题的复杂性就体现在数形结合上.2+)题得到,第2)得的线段的长度都相等.图1考点伸展我们一起来梳理一下这道题目的备用图怎么用.x-a n)2+a n,得抛物线的顶点坐标为(a n, a n).顶点的横坐标和纵坐标相等,而且,因此先画出顶点所在的射线y=x(x>0).,画抛物线y1的顶点、与x轴的右交点.,画抛物线y2的顶点、与x轴的右交点.,在△ABC中,AB=13,BC=14,5 cos13ABC∠=.⊥BC于点H,则AH=_____,AC=______,△ABC的面积_______D在AC上(可与点A、C重合),分别过点A、C作直线BD,CF=n.(当点D与点A重合时,我们认为S△ABD=0)或n的代数式表示S△ABD及S△CBD;x的函数关系式,并求(m+n)的最大值和最小值;x值,有时只能确定唯一的点D,指出这样的x的取值范围.请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程)图1 图2图3 图4答案AH=12,AC=15,S△ABC=84.ABD=12mx,S△CBD=12nx.=S△ABD+S△CBD,得118422mx nx+=.所以168m nx+=.边上的高56BG=,所以x的取值范围是56≤x≤14.BC的中点,连结,连结的形状.答:_______图1的作用重大,既能产生中位线,又是直角三角形斜边上的中线.2AB EGF,MGDF图4 图5考点伸展2)题和第(3)题证明△DFM≌△MGE的思路是相同的,不同的是证明∠DFM=∠MGE 程有一些不同.4,如图5,∠BFM=∠BAC=∠MGC.4,∠DFM=90°+∠BFM,∠MGE=90°+∠MGC,所以∠DFM=∠MGE.5,∠DFM=90°-∠BFM,∠MGE=90°-∠MGC,所以∠DFM=∠MGE.BC为底边的等腰三角形,点y轴、,同时动点运动到何处时,四边形图1.求抛物线的解析式需要代入.4,0),在△APQ图2 图3②如图3,过点Q 作QH ⊥AD ,垂足为H . 由于S △A PQ =2111333sin (5)2225102AP QH AP AQ PAQ t t t t ⋅=⋅∠=-⨯=-+, S △ACD =11831222AD OA ⋅=⨯⨯=,所以S 四边形PDCQ =S △ACD -S △APQ =2233358112()()1021028t t t --+=-+.所以当AP =52时,四边形PDCQ 的最小值是818. 考点伸展如果把第(2)①题改为“当P 运动到何处时,△APQ 是直角三角形?” 除了PQ ⊥AC 这种情况,还有QP ⊥AD 的情况. 这时45AP AQ =,所以455t t =-.解得209t =(如图4所示).图4。
山东省章丘市明水街道办事处绣江中学2014届九年级下学期期中考试语文试题

山东省章丘市明水街道办事处绣江中学2014届九年级下学期期中考试语文试题胸存自信,手书华章;努力表现,永不言弃亲爱的同学们:考试中请一定静心阅读、仔细审题,认真答卷。
语文试卷还要特别做到:字迹美观....(一.律用钢笔或签字笔........书写..).、卷面整洁....、文笔优美....、谢绝空题....。
希望你能够交上一份满意的答卷。
题号 一二三(1) 三(2) 四总分得分一、积累与运用(15分)1.请用正楷字,笔画清晰........地填写相应的诗文名句。
(6分,每小题1分) A.无可奈何花落去, 。
(晏殊《浣溪沙》) B. ,何人不起故园情。
(李白《春夜洛城闻笛》) C.衣沾不足惜, 。
(陶渊明《归园田居》) D. ,松柏有本性!(刘桢《赠从弟》)E.游鱼细石,直视无碍。
, 。
(吴均《与朱元思书》)F.母亲啊!你是荷叶,我是红莲,心中的雨点来了,除了你, ?(冰心《荷叶 母亲》) 2.阅读下面这则新闻,按要求作答。
(4分)2011年3月11日13点46分,日本北部发生里氏9级强烈地震。
地震引发了海啸,造成巨大破坏,人员伤亡人数在不断上升。
消息传来,中国人民上至总理下至普通百姓,都怀着焦急关注着日本地震灾区的状况。
国务院总理温家宝致电日本首相菅直人,代表中国政府向日本政府和人民致以深切慰问,表示中方愿向日方提供必要的帮助。
中国国际救援队高度关注日本震灾,人员、装备、物资、医疗物品等都已经到位,只要日本方面有需求,就可以第一时间出发前往参与人道主义救援。
自然灾难面前人类是一家人。
我们为日本人民祈福!A .画线的句子有语病,请选用恰当的修改符号直接在原句上修改。
(2分)B .请在下面的空格内为这则新闻拟写标题。
(12个字以内)(2分)3.名著阅读。
(5分)A 睁圆环眼,隐隐见后军青罗伞盖、旄钺旌旗来到,料得是B 心疑,亲自来看。
A 乃厉声大喝曰:“我乃 A 也!谁敢与我决一死战?”声如巨雷。
山东省济南市章丘区绣惠中学2023-2024学年七年级下学期期末数学模拟试题

山东省济南市章丘区绣惠中学2023-2024学年七年级下学期期末数学模拟试题一、单选题1.下列图案中.是轴对称图形的是( )A .B .C .D .2.下列计算正确的是( )A .321mn mn -=B .()22346m n m n = C .()34m m m -⋅= D .()222m n m n +=+ 3.已知三角形的两边长分别为5cm 和8cm ,则第三边的长可以是( )A .2cmB .3cmC .6cmD .13cm4.某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )A .抛一枚硬币,出现正面朝上B .掷一个正六面体的骰子,出现3点朝上C .一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃D .从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球5.如图,AB CD ∥,61BED ∠=︒,ABE 的平分线与CDE ∠的平分线交于点F ,则DFB ∠=( )A .149︒B .149.5︒C .150︒D .150.5︒6.已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x 表示时间,y 表示林茂离家的距离.依据图中的信息,下列说法错误的是( )A .体育场离林茂家2.5kmB .体育场离文具店1kmC .林茂从体育场出发到文具店的平均速度是50min mD .林茂从文具店回家的平均速度是60min m7.如图,//AB CD ,点,E F 在AC 边上,已知70,130CED BFC ∠=︒∠=︒,则B D ∠+∠的度数为( )A .40︒B .50︒C .60︒D .70︒8.已知5x =3,5y =2,则52x ﹣3y =( )A .34B .1C .23D .989.如图,两个正方形的边长分别为a, b,如果a+b=ab=9,则阴影部分的面积为( )A .36B .27C .18D .910.选择计算()()224343xy xy xy xy -++的最佳方法是( )A .运用多项式乘多项式法则B .运用平方差公式C .运用单项式乘多项式法则D .运用完全平方公式11.如图,在△ABC 中,AB =20cm ,AC =12cm ,点P 从点B 出发以每秒3cm 速度向点A 运动,点Q 从点A 同时出发以每秒2cm 速度向点C 运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ 是以PQ 为底的等腰三角形时,运动的时间是( )秒A .2.5B .3C .3.5D .412.已知多项式x -a 与2x 2-2x+1的乘积中不含x 2项,则常数a 的值是( )A .-1B .0C .1D .213.已知3325198,16,32a b c ===,则有( )A .a b c <<B .c b a <<C .c a b <<D .a c b <<14.如图,有两个正方形A ,B ,现将B 放在A 的内部得图甲,将A ,B 并列放置后构造新的正方形得图乙.若留甲和图乙中阴影部分的面积分别为3和30,则正方形A 、B 的面积之和为( )A .33B .30C .27D .2415.如图,是三个等边三角形(注:等边三角形的三个内角都相等)随意摆放的图形,则123∠+∠+∠等于A .90°B .120°C .150°D .180°二、填空题16.计算10120222-⎛⎫-= ⎪⎝⎭. 17.最薄的金箔厚度约为0.000000091m ,将0.000000091用科学记数法表示为. 18.一天,小明洗手后没有把水龙头拧紧,如果该水龙头每分钟约滴出100滴水,每滴水约0.04毫升,那么所滴出的水的总量y (毫升)与小明离开的时间x (分钟)之间的关系式可以表示为19.如图,在△ABC 中,将△ABC 沿直线m 翻折,点B 落在点D 的位置,若∠1−∠2=60°,则∠B 的度数是.20.用一水管向某容器内持续注水,设单位时间内注入的水量保持不变;在注水过程中,表示容器内水深h 与注水时间t 的关系有如图所示的A,B,C,D 四个图象,它们分别与E,F ,G,H 四种容器中的其中一种相对应,请你把相对应容器的字母填在下面的横线上.A→;B→;C→; D→.21.若 ()31m m -= 成立,则 m 的值为.22.如图,在四边形ABCD 中:AB AD =,140BAD ∠=︒,AB CB ⊥于点B ,AD CD ⊥于点D ,E 、F 分别是CB 、CD 上的点,且70EAF ∠=︒,下列说法:①DF BE =.②ADF ABE △≌△.③FA 平分DFE ∠;④AE 平分FAB ∠;⑤BE DF EF +=;⑥CF CE FD EB +>+.其中正确的是:(填写正确的序号)23.如图,已知等边三角形ABC 的边长为12cm ,甲,乙两动点同时从顶点A 出发,甲以1厘米/秒的速度沿等边三角形的边按顺时针方向移动,乙以3厘米/秒的速度沿等边三角形的边按逆时针方向移动,相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动.则第二次相遇时乙与最近顶点的距离是厘米.三、解答题24.解答下列各题(1)()0123π20223-+-+- (2)()()231231x y x y +--+(3)()()22482x y y y x x x ⎡⎤+-+-÷⎣⎦(4)111162233a b a b ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭ 25.先化简,再求值:已知2x 4x 2-=,求代数式()()()2223x x y x y y --+--的值. 26.甲骑摩托车从A 地去B 地,乙开汽车从B 地去A 地,同时出发,匀速行驶,各自到达终点后停止,甲、乙两人间的距离为s (km )与甲行驶的时间为t (h )之间的关系如图所示.(1)以下是点M 、点N 、点P 所代表的实际意义,请将M 、N 、P 填入对应的括号里. ①甲到达终点②甲乙两人相遇③乙到达终点(2)AB 两地之间的路程为千米:(3)求甲、乙各自的速度;(4)甲出发多长时间后,甲、乙两人相距180千米?27.阅读并完成下列证明:如图,已知180B BCD ∠+∠=︒,B D ∠=∠.求证:E DFE ∠=∠.证明:∵180B BCD ∠+∠=︒.∴AB CD ∥()∴B ∠=()又∵B D ∠=∠∴D ∠=()∴AD BE ∥()∴E DFE ∠=∠().28.如图,点A 、E 、F 、B 在同一条直线上,且AE =BF ,AC ∥BD ,∠C =∠D .求证:DE ∥CF .29.某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.(1)转动一次转盘,获得50元、30元、10元购物券的概率分别是多少?(2)如果有一名顾客在商场消费了200元,通过计算说明转转盘和直接获得购物券,哪种方式对这位顾客更合算?30.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD ,以D 为顶点作MDN ∠,交边AC 、BC 于M 、N .(1)若30ACD ∠=︒,60MDN ∠=︒,当MDN ∠绕点D 旋转时, AM 、MN 、BN 三条线段之间有何种数量关系?证明你的结论;(2)当90ACD MDN ∠+∠=︒时,AM 、MN 、BN 三条线段之间有何数量关系?证明你的结论;(3)如图③,在(2)的条件下,若将M 、N 改在CA 、BC 的延长线上,完成图③,其余条件不变,则AM 、MN 、BN 之间有何数量关系?(直接写出结论,不必证明)31.如图1,O 为数轴原点,在数轴上摆放一个长方形ABCD ,使得AB 、CD 的中点E 、G 恰好落在数轴上,AB =16,BC =EG =6,点H 为数轴上的点,HE =2GO ,HO =3EG .(1)点H 所表示的数为;(2)若动点M 以每秒3个单位的速度从H 出发沿折线H →E →B →C 运动,动点N 同时以每秒2个单位的速度从点O 出发沿折线O →G →D 运动,当一个点到达终点时,另一个点随之停止运动,设两个点运动时间为t 秒,记M 、N 、A 三点所形成的三角形的面积为S ,试用时间t 表示S ;(3)如图2,点F 对应的数为﹣13,蚂蚁甲以每秒5个单位的速度从点F 开始沿折线F →E →B →C 运动,同时蚂蚁乙从点O 出发沿折线O →G →D →A 运动,乙在线段OG 、DA 上的速度是每秒4个单位,在线段GD 上的速度则是每秒7个单位.当一只蚂蚁到达终点时,另一只蚂蚁也随之停止运动,记运动时间为t ,是否存在某一时刻t 使得两只蚂蚁在长方形ABCD 上走过的路程恰好相等?若存在,请直接写出t 的值;若不存在,请说明理由.。
章丘市2014年推荐生考试(自主招生)模拟试题

章丘市2013年初三年级推荐生考试英语模拟试题II.读音选词根据所给句意和音标,从每题A、B、C、D四个选项中选出一个最佳答案(5分)petition should beat the [prais]down.A.prizeB. pieceC. pleaseD.price:t].A.dissertB.dessertC. desertD. deside23.I wonder who will play in the basketball [mæt∫]A.murderB. marchC. matchD. mathɔ:t] my answer was correct, but it was erroneous.A.thoughB. caughtC.boughtD. thoughtΛŋki] house at the zoo.A.monkeyB.donkeyC.moneyD. memeryIII.单项选择。
从A B C D 四个选项中选出一个最佳答案。
(30分)26.Every year ______ Mother’s Day is on ________ second Sunday in May.A. the, theB. /, theC. the, /D. /, /27.Could you say _________ about it, please ? I’d like to know more.A. nothing elseB. anything elseC. something elseD. something other28.I don’t have a present, _______ everyone else brings a present?A. what ifB. ifC. how ifD. how29.I enjoy the popular dance “hip-hop” ,but ___ my father ___my mother likes it.A. both ;andB. ont only; but alsoC. either ;orD. neither ;nor30._______of the money_______been spent recycling the rubbish.A. three fourths; hasB. three fourths; haveC. three fourth; hasD. three fourth; have31.—How do you like the film Titanic?—I must say it’s _______ film I _______.A. the better; have seenB. good; had seenC. the best; have seenD. the best; had seenA. canB. mayC. mustD. need32.There is a backpack _________ on the floor.A. lyingB. liesC. lieD. to lie33.Two mirrors are placed right angles(直角)to each other, and a clock is put in front of the mirrorlike the picture. The clock is placed facing the mirror like the picture. A person standing in front of the other mirror will see the time is ________.A. 2∶35B. 9∶25C. 1l∶20D. 5∶5034.—My sports shoes are _____ out.—How long have you_____them?A. worn; boughtB. wearing; hadC. wearing; boughtD. worn; had35.His father and mother often argue _______ what TV programmes _________.A. with; watchingB. about; watchingC. with; to watchD. about; to watch36.Eating a ________diet helps us to keep a _________of yin and yang.A. balanced; balanceB. balance; balanceC. balancing; balancingD. balance; balanced37.--- What a beautiful city our hometown is! There are many trees ______ of the road!--- Yes, and ____________ of the trees is growing larger and larger.A. on both side; a numberB. on each sides; a numberC. on both sides; the numberD. on every side; the number38. Lucy______here two years ago, she______here for about two years.A. got, has gotB. got, has beenC. got, gotD. has got, got39. She was seen______paper planes in the room.A. madeB. to makeC. makesD. making40. Though the old woman lives______, she doesn’t feel______.A. alone, aloneB. alone, lonelyC. lonely, lonelyD. lonely, alone41. I like to keep the windows______. It’s raining heavily outside.A. closedB. openedC. openD. closing42.----Will you___us about your trip to Tokyo?----Ok. Shall I___it in English or Japanese?A. talk, sayB. tell, sayC. talk, speakD. tell, speak43._____Lily_____Lucy may go with you because one of them must stay at home.A. Not, butB. Neither, norC. Both, andD. Either, or44. The weather in Changsha is different______in Beijing.A. than thatB. to itC. fromD. from that45. The dictionary _______ well.A. is soldB. is selledC. sellsD. was sold46.----What is _______ the people in the village ?----I am sorry. I don’t know. I only know that _____people like living in village.A. the number of , the number ofB. a number of , the number ofC. the number of , a number ofD. a number of , a number of47.We have 3 rooms ____________ , but I can't decide ____________ .A. to live, to choose which oneB. lived, choose which oneC. to live in, which one to chooseD. live, which one48.—Amy has made great progress recently.—and .A. So she has; so have youB. So she has; so you haveC. So has she; so have youD. So has she; so you have49.What______it is to go swimming in ________weather!A. a great fun, so fineB. a great fun, such a fineC. great fun, so fine aD. great fun, such fine50.— Could you tell me_____ ?— About half an hour.A. how long it takes to walk to the Science and Technology Museum from schoolB. how long it took to walk to the Science and Technology Museum from schoolC. how far was it to walk to the Science and Technology Museum from schoolD. how far it was to walk to the Science and Technology Museum from schoolIV.完形填空阅读下面短文,从每小题A B C D四个选项中,选出一个能填入文章中相应空白处的最佳答案。
2024届山东省济南市章丘市初中数学毕业考试模拟冲刺卷含解析

2024届山东省济南市章丘市初中数学毕业考试模拟冲刺卷注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.下列图形中,既是中心对称图形又是轴对称图形的是()A.B.C.D.2.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若2(,大正方形的面积为13,则小正方形的面积为()+=a b)21A.3 B.4 C.5 D.63.长城、故宫等是我国第一批成功入选世界遗产的文化古迹,长城总长约6 700 000米,将6 700 000用科学记数法表示应为()A.6.7×106B.6.7×10﹣6C.6.7×105D.0.67×1074.已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如右图所示,则该封闭图形可能是( )A.B.C.D.5.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为().A.60 °B.75°C.85°D.90°6.如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE7.在△ABC中,∠C=90°,tan A=,△ABC的周长为60,那么△ABC的面积为()A.60 B.30 C.240 D.1208.若2m﹣n=6,则代数式m-12n+1的值为()A.1 B.2 C.3 D.49.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF 的长度是()A .3cmB .6 cmC .2.5cmD .5 cm10.在平面直角坐标系中,若点A(a ,-b)在第一象限内,则点B(a ,b)所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 二、填空题(共7小题,每小题3分,满分21分)11.长城的总长大约为6700000m ,将数6700000用科学记数法表示为______12.若将抛物线y=﹣4(x+2)2﹣3图象向左平移5个单位,再向上平移3个单位得到的抛物线的顶点坐标是_____. 13.分解因式:24xy x -=____14.计算(a 3)2÷(a 2)3的结果等于________ 15.下面是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:第n 个“上”字需用_____枚棋子. 16.已知二次函数y=x 2,当x >0时,y 随x 的增大而_____(填“增大”或“减小”). 173a 的正确结果是_____.三、解答题(共7小题,满分69分)18.(10分)某食品厂生产一种半成品食材,产量p(百千克)与销售价格x(元/千克)满足函数关系式1p x 82=+,从市场反馈的信息发现,该半成品食材的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,如下表: 销售价格x(元/千克)24⋯ 10市场需求量q /(百千克)12 10 ⋯4已知按物价部门规定销售价格x 不低于2元/千克且不高于10元/千克()1求q 与x 的函数关系式;()2当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x 的取值范围;()3当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.若该半成品食材的成本是2元/千克.①求厂家获得的利润y(百元)与销售价格x 的函数关系式;②当厂家获得的利润y(百元)随销售价格x 的上涨而增加时,直接写出x 的取值范围.(利润=售价-成本)19.(5分)如图1,点D 为正ABC ∆的BC 边上一点(D 不与点,B C 重合),点,E F 分别在边,AB AC 上,且EDF B ∠=∠.(1)求证:~BDE CFD ∆∆;(2)设,BD a CD b ==,BDE ∆的面积为1S ,CDF ∆的面积为2S ,求12S S ⋅(用含,a b 的式子表示); (3)如图2,若点D 为BC 边的中点,求证: 2DF EF FC =⋅.图1 图220.(8分)如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC (顶点是网格线的交点)的坐标分别是A (﹣2,2),B (﹣3,1),C (﹣1,0). (1)将△ABC 绕点O 逆时针旋转90°得到△DEF ,画出△DEF ;(2)以O 为位似中心,将△ABC 放大为原来的2倍,在网格内画出放大后的△A 1B 1C 1,若P (x ,y )为△ABC 中的任意一点,这次变换后的对应点P 1的坐标为 .21.(10分)定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图. A B C 笔试 85 95 90 口试8085(1)请将表和图中的空缺部分补充完整;图中B 同学对应的扇形圆心角为 度;竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为,B同学得票数为,C同学得票数为;若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断当选.(从A、B、C、选择一个填空)22.(10分)随着社会经济的发展,汽车逐渐走入平常百姓家.某数学兴趣小组随机抽取了我市某单位部分职工进行调查,对职工购车情况分4类(A:车价40万元以上;B:车价在20—40万元;C:车价在20万元以下;D:暂时未购车)进行了统计,并将统计结果绘制成以下条形统计图和扇形统计图.请结合图中信息解答下列问题:(1)调查样本人数为__________,样本中B类人数百分比是_______,其所在扇形统计图中的圆心角度数是________;(2)把条形统计图补充完整;(3)该单位甲、乙两个科室中未购车人数分别为2人和3人,现从中选2人去参观车展,用列表或画树状图的方法,求选出的2人来自不同科室的概率.23.(12分)如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.当α=125°时,∠ABC=°;求证:AC=CE;若△ABC的外心在其内部,直接写出α的取值范围.24.(14分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=1OD,OE=1OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;(1)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图1.①在旋转过程中,当∠OAG′是直角时,求α的度数;②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1、D【解题分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.【题目详解】解:A. ∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;B. ∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误;C. ∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;D. ∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.【题目点拨】本题考查了中心对称图形与轴对称图形的定义,解题的关键是熟练的掌握中心对称图形与轴对称图形的定义.2、C【解题分析】如图所示,∵(a+b)2=21∴a2+2ab+b2=21,∵大正方形的面积为13,2ab=21﹣13=8,∴小正方形的面积为13﹣8=1.故选C.考点:勾股定理的证明.3、A【解题分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【题目详解】解:6 700 000=6.7×106,故选:A【题目点拨】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4、A【解题分析】解:分析题中所给函数图像,-段,AP随x的增大而增大,长度与点P的运动时间成正比.O E-段,AP逐渐减小,到达最小值时又逐渐增大,排除C、D选项,E F-段,AP逐渐减小直至为0,排除B选项.F G故选A.【题目点拨】本题考查了动点问题的函数图象,函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.5、C【解题分析】试题分析:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.如图,设AD⊥BC于点F.则∠AFB=90°,∴在Rt△ABF中,∠B=90°-∠BAD=25°,∴在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,即∠BAC的度数为85°.故选C.考点: 旋转的性质.6、C【解题分析】解:∵AB=AC,∴∠ABC=∠ACB.∵以点B为圆心,BC长为半径画弧,交腰AC于点E,∴BE=BC,∴∠ACB=∠BEC,∴∠BEC=∠ABC=∠ACB,∴∠BAC=∠EBC.故选C.点睛:本题考查了等腰三角形的性质,当等腰三角形的底角对应相等时其顶角也相等,难度不大.7、D【解题分析】由tanA的值,利用锐角三角函数定义设出BC与AC,进而利用勾股定理表示出AB,由周长为60求出x的值,确定出两直角边,即可求出三角形面积.【题目详解】如图所示,由tan A=,设BC=12x,AC=5x,根据勾股定理得:AB=13x,由题意得:12x+5x+13x=60,解得:x=2,∴BC=24,AC=10,则△ABC面积为120,故选D.【题目点拨】此题考查了解直角三角形,锐角三角函数定义,以及勾股定理,熟练掌握勾股定理是解本题的关键.8、D【解题分析】先对m-12n+1变形得到12(2m﹣n)+1,再将2m﹣n=6整体代入进行计算,即可得到答案.【题目详解】m12n+1=12(2m﹣n)+1当2m﹣n=6时,原式=12×6+1=3+1=4,故选:D.【题目点拨】本题考查代数式,解题的关键是掌握整体代入法.9、D【解题分析】分析:根据垂径定理得出OE的长,进而利用勾股定理得出BC的长,再利用相似三角形的判定和性质解答即可.详解:连接OB,∵AC是⊙O的直径,弦BD⊥AO于E,BD=1cm,AE=2cm.在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2解得:OE=3,∴OB=3+2=5,∴EC=5+3=1.在Rt△EBC中,==∵OF⊥BC,∴∠OFC=∠CEB=90°.∵∠C=∠C,∴△OFC∽△BEC,∴OF OCBE BC=,即4OF=,解得:故选D.点睛:本题考查了垂径定理,关键是根据垂径定理得出OE的长.10、D【解题分析】先根据第一象限内的点的坐标特征判断出a、b的符号,进而判断点B所在的象限即可.【题目详解】∵点A(a,-b)在第一象限内,∴a>0,-b>0,∴b<0,∴点B((a,b)在第四象限,故选D.【题目点拨】本题考查了点的坐标,解决本题的关键是牢记平面直角坐标系中各个象限内点的符号特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.二、填空题(共7小题,每小题3分,满分21分)11、6.7×106【解题分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【题目详解】解:6700000用科学记数法表示应记为6.7×106,故选6.7×106. 【题目点拨】本题考查科学记数法的表示方法.科学记数法的表示形式为ax10n 的形式,其中1≤|a|<10,n 为整数;表示时关键要正确确定a 的值以及n 的值.12、(﹣7,0)【解题分析】直接利用平移规律“左加右减,上加下减”得出平移后的解析式进而得出答案.【题目详解】∵将抛物线y=-4(x+2)2-3图象向左平移5个单位,再向上平移3个单位,∴平移后的解析式为:y=-4(x+7)2,故得到的抛物线的顶点坐标是:(-7,0).故答案为(-7,0).【题目点拨】此题主要考查了二次函数与几何变换,正确掌握平移规律是解题关键.13、x(y+2)(y-2)【解题分析】原式提取x ,再利用平方差公式分解即可.【题目详解】原式=x (y 2-4)=x (y+2)(y-2),故答案为x (y+2)(y-2).【题目点拨】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.14、1【解题分析】根据幂的乘方, 底数不变, 指数相乘; 同底数幂的除法, 底数不变, 指数相减进行计算即可.【题目详解】解:原式=6601a a a ÷==【题目点拨】本题主要考查幂的乘方和同底数幂的除法,熟记法则是解决本题的关键, 在计算中不要与其他法则相混淆. 幂的乘方, 底数不变,指数相乘; 同底数幂的除法, 底数不变, 指数相减.15、4n+2【解题分析】∵第1个有:6=4×1+2;第2个有:10=4×2+2; 第3个有:14=4×3+2; ……∴第1个有: 4n +2;故答案为4n +216、增大.【解题分析】根据二次函数的增减性可求得答案【题目详解】∵二次函数y=x 2的对称轴是y 轴,开口方向向上,∴当y 随x 的增大而增大.故答案为:增大.【题目点拨】本题考查的知识点是二次函数的性质,解题的关键是熟练的掌握二次函数的性质.17、﹣【解题分析】30a -≥ ,0a ∴≤ .== .三、解答题(共7小题,满分69分)18、(1) q x 14=-+;(2)2x 4≤≤;(3)213105y (x )24=--+①;②当134x 2<≤时,厂家获得的利润y 随销售价格x 的上涨而增加.【解题分析】(1)直接利用待定系数法求出一次函数解析式进而得出答案;(2)由题意可得:p ≤q ,进而得出x 的取值范围;(3)①利用顶点式求出函数最值得出答案;②利用二次函数的增减性得出答案即可.【题目详解】(1)设q=kx+b(k,b为常数且k≠0),当x=2时,q=12,当x=4时,q=10,代入解析式得:212 410 k bk b+=⎧⎨+=⎩,解得:114kb=-⎧⎨=⎩,∴q与x的函数关系式为:q=﹣x+14;(2)当产量小于或等于市场需求量时,有p≤q,∴12x+8≤﹣x+14,解得:x≤4,又2≤x≤10,∴2≤x≤4;(3)①当产量大于市场需求量时,可得4<x≤10,由题意得:厂家获得的利润是:y=qx﹣2p=﹣x2+13x﹣16=﹣(x132-)21054+;②∵当x132≤时,y随x的增加而增加.又∵产量大于市场需求量时,有4<x≤10,∴当4<x132≤时,厂家获得的利润y随销售价格x的上涨而增加.【题目点拨】本题考查了待定系数法求一次函数解析式以及二次函数最值求法等知识,正确得出二次函数解析式是解题的关键.19、(1)详见解析;(1)详见解析;(3)详见解析.【解题分析】(1)根据两角对应相等的两个三角形相似即可判断;(1)如图1中,分别过E,F作EG⊥BC于G,FH⊥BC于H,S1=12•BD•EG=12•BD•EG=12•a•BE•sin60°=34•a•BE,S1=12•CD•FH=34•b•CF,可得S1•S1=316ab•BE•CF,由(1)得△BDE∽△CFD,BD FCBE CD=,即BE•FC=BD•CD=ab,即可推出S1•S1=316a1b1;(3)想办法证明△DFE∽△CFD,推出EF DFDF FC=,即DF1=EF•FC;【题目详解】(1)证明:如图1中,在△BDE中,∠BDE+∠DEB+∠B=180°,又∠BDE+∠EDF+∠FDC=180°,∴∠BDE+∠DEB+∠B=∠BDE+∠EDF+∠FDC,∵∠EDF=∠B,∴∠DEB=∠FDC,又∠B=∠C,∴△BDE∽△CFD.(1)如图1中,分别过E,F作EG⊥BC于G,FH⊥BC于H,S1=12•BD•EG=12•BD•EG=123,S1=123,∴S1•S1=316ab•BE•CF由(1)得△BDE∽△CFD,∴BD FCBE CD=,即B E•FC=BD•CD=ab,∴S1•S1=316a1b1.(3)由(1)得△BDE∽△CFD,∴BD FC BE CD=,又BD=CD,∴CD FC DE DF=,又∠EDF=∠C=60°,∴△DFE∽△CFD,∴F DFDF FC=,即DF1=EF•FC.【题目点拨】本题考查了相似形综合题、等边三角形的性质、相似三角形的判定和性质、三角形的面积等知识,解题的关键是正确寻找相似三角形的相似的条件.20、(1)见解析;(2)见解析,(﹣2x,﹣2y).【解题分析】(1)利用网格特点和旋转的性质画出点A、B、C的对应点D、E、F,即可得到△DEF;(2)先根据位似中心的位置以及放大的倍数,画出原三角形各顶点的对应顶点,再顺次连接各顶点,得到△A1B1C1,根据△A1B1C1结合位似的性质即可得P1的坐标.【题目详解】(1)如图所示,△DEF即为所求;(2)如图所示,△A1B1C1即为所求,这次变换后的对应点P1的坐标为(﹣2x,﹣2y),故答案为(﹣2x,﹣2y).【题目点拨】本题主要考查了位似变换与旋转变换,解决问题的关键是先作出图形各顶点的对应顶点,再连接各顶点得到新的图形.在画位似图形时需要注意,位似图形的位似中心可能在两个图形之间,也可能在两个图形的同侧.21、(1)90;(2)144度;(3)105,120,75;(4)B【解题分析】(1)由条形图可得A演讲得分,由表格可得C笔试得分,据此补全图形即可;(2)用360°乘以B对应的百分比可得答案;(3)用总人数乘以A、B、C三人对应的百分比可得答案;(4)根据加权平均数的定义计算可得.【题目详解】解:(1)由条形图知,A演讲得分为90分,补全图形如下:故答案为90;(2)扇图中B同学对应的扇形圆心角为360°×40%=144°,故答案为144;(3)A同学得票数为300×35%=105,B同学得票数为300×40%=120,C同学得票数为300×25%=75,故答案为105、120、75;(4)A的最终得分为854903105310⨯+⨯+⨯=92.5(分),B的最终得分为954803120310⨯+⨯+⨯=98(分),C的最终得分为90485375310⨯+⨯+⨯=84(分),∴B最终当选,故答案为B.【题目点拨】本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.22、(1)50,20%,72°.(2)图形见解析;(3)选出的2人来自不同科室的概率=.【解题分析】试题分析:(1)根据调查样本人数=A类的人数除以对应的百分比.样本中B类人数百分比=B类人数除以总人数,B 类人数所在扇形统计图中的圆心角度数=B类人数的百分比×360°.(2)先求出样本中B类人数,再画图.(3)画树状图并求出选出的2人来自不同科室的概率.试题解析:(1)调查样本人数为4÷8%=50(人),样本中B类人数百分比(50﹣4﹣28﹣8)÷50=20%,B类人数所在扇形统计图中的圆心角度数是20%×360°=72°;(2)如图,样本中B类人数=50﹣4﹣28﹣8=10(人);(3)画树状图为:共有20种可能的结果数,其中选出选出的2人来自不同科室占12种,所以选出的2人来自不同科室的概率=.考点:1.条形统计图2.扇形统计图3.列表法与树状图法.23、(1)125;(2)详见解析;(3)45°<α<90°.【解题分析】(1)利用四边形内角和等于360度得:∠B+∠ADC=180°,而∠ADC+∠EDC=180°,即可求解;(2)证明△ABC≌△EDC(AAS)即可求解;(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,∠ABC=α>90°时,△ABC的外心在其外部,即可求解.【题目详解】(1)在四边形BADC中,∠B+∠ADC=360°﹣∠BAD﹣∠DCB=180°,而∠ADC+∠EDC=180°,∴∠ABC=∠PDC=α=125°,故答案为125;(2)∠ECD+∠DCA=90°,∠DCA+∠ACB=90°,∴∠ACB=∠ECD,又BC=DC,由(1)知:∠ABC=∠PDC,∴△ABC ≌△EDC (AAS ),∴AC =CE ;(3)当∠ABC =α=90°时,△ABC 的外心在其斜边上;∠ABC =α>90°时,△ABC 的外心在其外部,而45°<α<135°,故:45°<α<90°.【题目点拨】本题考查圆的综合运用,解题的关键是掌握三角形全等的判定和性质(AAS )、三角形外心.24、(1)见解析;(1)①30°或150°,②AF '的长最大值为222+,此时0315α=. 【解题分析】(1)延长ED 交AG 于点H ,易证△AOG ≌△DOE ,得到∠AGO=∠DEO ,然后运用等量代换证明∠AHE=90°即可;(1)①在旋转过程中,∠OAG′成为直角有两种情况:α由0°增大到90°过程中,当∠OAG′=90°时,α=30°,α由90°增大到180°过程中,当∠OAG′=90°时,α=150°;②当旋转到A 、O 、F′在一条直线上时,AF′的长最大,AF′=AO+OF′=22+1,此时α=315°. 【题目详解】(1)如图1,延长ED 交AG 于点H,∵点O 是正方形ABCD 两对角线的交点,∴OA=OD ,OA ⊥OD ,∵OG=OE ,在△AOG 和△DOE 中,90OA OD AOG DOE OG OE =⎧⎪∠=∠=︒⎨⎪=⎩,∴△AOG ≌△DOE ,∴∠AGO=∠DEO ,∵∠AGO+∠GAO=90°,∴∠GAO+∠DEO=90°,∴∠AHE=90°,即DE⊥AG;(1)①在旋转过程中,∠OAG′成为直角有两种情况:(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,∵OA=OD=12OG=12OG′,∴在Rt△OAG′中,sin∠AG′O=OAOG=12,∴∠AG′O=30°,∵OA⊥OD,OA⊥AG′,∴OD∥AG′,∴∠DOG′=∠AG′O=30°∘,即α=30°;(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,同理可求∠BOG′=30°,∴α=180°−30°=150°.综上所述,当∠OAG′=90°时,α=30°或150°.②如图3,当旋转到A. O、F′在一条直线上时,AF′的长最大,∵正方形ABCD的边长为1,∴,∵OG=1OD,∴∴OF′=1,+1,∴AF′=AO+OF′=2∵∠COE′=45°,∴此时α=315°.【题目点拨】本题考查的是正方形的性质、旋转变换的性质以及锐角三角函数的定义,掌握正方形的四条边相等、四个角相等,旋转变换的性质是解题的关键,注意特殊角的三角函数值的应用.。
章丘市绣江中学2013-2014学年第二学期综合素质测试七年级数学试题

章丘市绣江中学2013-2014学年第二学期综合素质测试七年级数学试题章丘市绣江中学2013-2014学年第二学期综合素质测试七年级数学试题一、选择题(每小题3分,共30分) 1、计算()32a -的结果是()A .5a -B .5aC .6aD .6a - 2、如右图,Rt ABC △中,90ACB ∠=°,DE 过点C 且平行于AB ,若35BCE ∠=°,则A ∠的度数为()A .55°B .45°C .35°D .65°3、下列条件中能判定△ABC ≌△DEF 的是 ( ) A .AB =DE ,BC =EF ,∠A =∠D B .∠A =∠D ,∠B =∠E ,∠C =∠FC .AC =DF ,∠B =∠F ,AB =DED .∠B =∠E ,∠C =∠F ,AC =DF4、下列运算正确的是( )A 、3a-(2a-b)=a-bB 、(a 3b 2-2a 2b)÷ab=a 2b-2C 、(a+2b)(a-2b)=a 2-2b 2D 、(-12a 2b)3=-18a 6b 35、如图,AB ∥CD ,CE ∥BF ,A ,E ,F ,D 在一条直线上,BC 与AD 交于点O 且OE=OF ,则图中有全等三角形的对数为( )(A)2 (B)3 (C)4 (D)56、从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张.下列事件中,必然事件是( )(A)标号小于6 (B)标号大于6 (C)标号是奇数 (D)标号是37、图(1)是一个长为2m ,宽为2n(m >n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样C的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( ) (A)2mn (B)(m+n)2 (C)(m-n)2 (D)m 2-n 28、根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )(A)男生在13岁时身高增长速度最快(B)女生在10岁以后身高增长速度放慢(C)11岁时男女生身高增长速度基本相同(D)女生身高增长的速度总比男生慢 9、如图,AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为50和39,则△EDF 的面积为()10、如图,如果一只蚂蚁以均匀的速度沿台阶12345A A A A A →→→→爬行,那么蚂蚁爬行的高度..h 随时间t 变化的图象大致是().1A 2A 3A4A 5AA .B .C .D .二、填空题(每小题3分,共24分)11、若3=a m ,2=a n ,则a n m +=________.12、如图所示,在△ABC 中,∠B=90°,AB=3,AC=5,将△ABC 折叠,使点C 与点A 重合,折痕为DE ,则△ABE 的周长为.13、如果x 2+2(k-3)x+25是一个用完全平方公式得到的结果, 则k 的值是 .14、一个三角形的两边长分别是2和7,另一边长a 为偶数,且2<a <8,则这个三角形的周长为★ .15、若代数式x 2+3x+2可以表示为(x-1)2+a(x-1)+b 的形式,则a+b 的值是____. 16、定义:如果一个数的平方等于–1,记为i 2=–1,这个数i 叫做虚数单位.那么,1i i =12-=i ,i i -=3,1,,1654-===i i i i ,…那么=2011i . 17、已知:直线l1∥l 2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于 18、在全民健身环城越野赛中,甲乙两选手的行程y (千米)随时间(时)变化的图象(全程)如图所示.则根据图像,起跑后1小时内,跑在前面的是;最终先到达终点;整个赛程是公里.三、解答题(第19、20题每小题4分,第21、22、23、24、25、26、27题每题6分,共66分) 19、计算与化简(1))6(3)2(3322b a ab b a -÷?-(2)(3)()()()p p p p 3645?+?--- (4)运用乘法公式计算:1992-120、先化简,再求值:(1)[]22(2)()(4)5(2)x y x y x y y x +-+--÷,其中1,22x y ==-(2)化简求值()()()()222b a b a b a b a a ++-++-;其中1,21=-=b a)3)(2(2)4)(32(-+--+x x x x21、如图所示,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC 的交点,点E是AB 的中点.(1)图中有哪几对全等三角形,请写出来;(2)试判断OE和AB的位置关系,并给予证明.22、如图,△ABC中,∠BAC=90°,AC=2AB,D为AC的中点,E为△ABC 外一点,且EA=ED,EA⊥ED,试猜想线段BE和CE的数量关系和位置关系,并证明.B23、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?24、甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”“石头”“剪子”“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.(1)若甲先摸,则他摸出“石头”的概率是多少?(2)若甲先摸出了“石头”,则乙获胜的概率是多少?(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?25、如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).(1)在图中作出△ABC 关于直线l 对称的△A 1B 1C 1.(要求:A 与A 1,B 与B 1,C 与C 1相对应)(2)在(1)问的结果下,连接BB 1,CC 1,求四边形BB 1C 1C 的面积.26、如图,已知:BC AD ⊥于D ,BC EG ⊥于G ,1∠=∠E 。
山东省绣江中学2013-2014学年八年级上数学期中试题及答案

A EFB DCD C B AE 八年级数学期中测试题一、选择题(每小题3分,共30分) 1、、三角形的三边长a 、b 、c 满足ab c b 2)a (22+=+,则这个三角形是 A 、 等边三角形 B 、 钝角三角形 C 、 直角三角形 D 、 锐角三角形2、在5,0.1,-π,25,327-,722,8,73八个实数中,无理数有A 、5 个B 、4个C 、3个D 、2个3、如图,在高为5m ,坡面长为13m 的楼梯表面铺地毯,地毯的长度至少需要 A 、17m B 、18m C 、25m D 、26m4、下列平方根中, 已经简化的是( )A. 31B. 20C. 22D. 1215、下列结论正确的是( ) A.6)6(2-=-- B.9)3(2=- C.16)16(2±=-D.251625162=⎪⎪⎭⎫ ⎝⎛-- 6、如图1-6,等边△ABC 边长为3cm ,将△ABC 沿AC 向右平移 1cm ,得到△DEF ,则四边形ABEF 的周长( )A .11cmB .12cmC .13cmD .14cm 7、在如图1-5所示的网格中,△MNP 绕某点旋转一定角度,得到 △111M N P ,其旋转中心可能是( )A .点AB .点BC .点CD .点D8、如图,在△ABC 中,AB=AC=5,D 为BC 上的一点,DE ∥AB ,DF ∥AC ,那么四边形AFDE 的周长是A.5B.10C. 15D.20 9、下列说法中,正确的是 ( ) A.两条对角线相等的四边形是平行四边形B.两条对角线相等且互相垂直的四边形是矩形C.两条对角线互相垂直平分的四边形是菱形D.两条对角线互相垂直平分且相等的四边形是菱形 10、如图,在▱ABCD 中, E ,F 是对角线AC 上的两点且AE=CF ,在①BE=DF ②BE ∥DF ③AB=DE ④四边形EBFD 为平行四边形⑤S △ADE=S △ABE ⑥AF=CE 这些结论中正确的个数是( )A.3B.4C.5D.6题号 12 3 4 5 6 7 8 9 10 答案11、32-的相反数是 ,绝对值是 。
济南市绣江中学八年级(下)第三次段考数学试卷

2013-2014学年山东省济南市绣江中学八年级(下)第三次段考数学试卷一、填空题(3’×9=27’)1.在平行四边形中,若一个角为其邻角的2倍,则这个平行四边形中两邻角的度数分别是________.2.设点O是ABCD对角线的交点,如果ABCD的面积为20cm2,则△AOB的面积为________cm2.3.若平行四边形的一边长为8cm,一条对角线长为6cm,则另一条对角线长x(cm)的取值范围为________.4.ABCD的周长为36cm,AB=8cm,则BC=________cm;当∠B=60∘时,AD、BC间的距离AE=________cm,ABCD的面积S ABCD=________cm2.5.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是________.6.已知a、b、c、d为四边形的四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是________四边形.7.已知,EF过ABCD对角线的交点O,交AD于E,交BC于F,若AB=4,BC=5,OE=2,则四边形EFCD的周长为________.8.在△ABC中,∠C=90∘,AC=3,AB=5,若以A、B、C、P四点为顶点组成一个平行四边形,则这个平行四边形的周长为________.9.如图,P为ABCD的对角线BD上一点,过P作GH // CD,EF // BC,写出图中你认为面积相等的平行四边形有________.二、单项选择题(3’×7=21’)10.如图,在ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为()A.1:2:3B.2:1:3C.3:2:1D.3:1:211.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是()A.88∘,108∘,88∘B.88∘,104∘,108∘C.88∘,92∘,92∘D.88∘,92∘,88∘12.平行四边形的一边长为10,那么它的两条对角线的长度可以是()A.8和12B.4和16C.20和30D.8和613.A,B,C,D在同一平面内,从①AB // CD,②AB=CD,③BC // AD,④BC=AD 这四个中任选两个作为条件,能使四边形ABCD为平行四边形的选法有()A.6种B.5种C.4种D.3种14.如图,△ABC是等边三角形,P是形内一点,PD // AB,PE // BC,PF // AC,若△ABC 的周长为18,则PD+PE+PF=()A.18B.9√3C.6D.条件不够,不能确定15.已知线段a=10cm,b=14cm,c=8cm,以其中两条为对角线,另一条为边画平行四边形,可以画出不同形状的平行四边形的个数为()A.0个B.1个C.2个D.3个三、多项选择题(4′×2=8′)16.已知四边形ABCD,AC与BD相交于点O,如果给出条件AB // CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是()①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.A.①④B.①③④C.②③D.②③④17.下列条件中不能判定一定是平行四边形的有()A.一组对角相等,一组邻角互补B.一组对边平行,另一组对边相等C.一组对边相等,一组对角相等D.一组对边平行,且一条对角线平分另一条对角四、解答题18.如图,已知E、F分别为ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:EF与MN互相平分.19.已知,如图,在ABCD中,AB=8cm,BC=10cm,∠C=120∘,(1)求BC边上的高AH的长;(2)求ABCD的面积.20.已知,△ABC的中线为BD,过B作BE // AC,过A作AE // BD,AE与BE相交于点E,连结CE交BD于点O.(1)画出图,猜想BD与CE间的关系________;(2)证明你的结论.21.如图,在△ABC中,AB=AC,点D在BC上,DE // AC,DF // AB,(1)求证:FD=FC;(2)若AC=6cm,试求四边形AEDF的周长.22.如图,ABCD中,E、F分别是AB、CD上的点,且AE=CF,M、N分别为DE、BF的中点,连结MF、NE,求证:MF // EN.23.如图,已知在ABCD中,对角线AC、BD相交于点O,AE⊥BD,BM⊥AC、DN⊥AC,CF⊥BD垂足分别是E、M、N、F,求证:EN // MF.答案1. 【答案】120∘,60∘【解析】根据平行四边形的性质,在平行四边形中,若一个角为其邻角的2倍,设一个角x,由四边形的内角和定理得到方程2x+4x=360∘,解得x=60∘,则它的邻角是2x=120∘【解答】解:设一个角x,则另一个角为2x.∵平行四边形∴2(x+2x)=360∘,即x=60∘,则2x=120∘∴这个平行四边形中两邻角的度数分别是120∘,60∘.故答案为120∘,60∘.2. 【答案】5【解析】因为平行四边形的对角线互相平分,所以对角线分成的四个三角形的面积相等,所以△AOB的面积为20÷4=5cm2.【解答】解:∵ABCD的面积为20cm2∴S△ABC=S△ADC∵△AOB≅△DOC,△AOD≅△BOC∴S△AOB=S△DOC,S△AOD=S△BOC∵OA=OC∴S△AOB=S△BOCS ABCD=5cm2故答案为5.∴S△AOB=S△BOC=S△DOC=S△AOD∴S△AOB=143. 【答案】10<x<22组成的三角形,【解析】平行四边形的对角线互相平分,那么一边是8cm,另两边是3cm和x2结合三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围即可.<8+3,【解答】解:由题意得:8−3<x2解得:10<x<22.故答案为:10<x<22.4. 【答案】10,4√3,40√3【解析】首先根据平行四边形对边相等的性质可求得BC的长度,又由∠B=60∘,即可求得AD与BC的距离AE的长,继而求得S▫ABCD的值.【解答】解:∵ABCD的周长为36cm,AB=8cm,∴CD=AB=8cm,AD=BC=10cm,∵∠B=60∘,AE⊥BC,∴∠BAE=30∘,AB=4(cm),∴BE=12∴AE=√AB2−BE2=4√3(cm),∴S▫ABCD=BC⋅AE=10×4√3=40√3(cm2).故答案为:10;4√3;40√3.5. 【答案】68【解析】由平行四边形的面积是144,相邻两边上的高分别为8和9,即可求得其相邻两边的长,继而求得它的周长.【解答】解:∵平行四边形的面积是144,相邻两边上的高分别为8和9,∴相邻两边长分别为:144÷8=18,144÷9=16,∴它的周长是:18+16+18+16=68.故答案为:68.6. 【答案】平行【解析】首先配方可得(a−b)2+(c−d)2=0,再根据偶次幂的非负性可得a−b=0,c−d=0,进而得到a=b,c=d,然后再根据两组对边分别相等的四边形是平行四边形可得答案.【解答】解:∵a2+b2+c2+d2=2ac+2bd∴a2+b2+c2+d2−2ac−2bd=0∴(a−b)2+(c−d)2=0解得:a=b,c=d,∴这个四边形的形状是平行四边形.故答案为:平行.7. 【答案】13【解析】先利用平行四边形的性质求出AB、CD、BC、AD的值,可利用AAS判定△AEO≅△CFO,即可求出四边形的周长.【解答】解:∵四边形ABCD为平行四边形,∴AB=CD=4,BC=AD=5,在△AEO和△CFO中,{∠OAE=∠OCF ∠AOE=∠COF OA=OC,∴△AEO≅△CFO(AAS),∴AE=CF,OE=OF=2,则EFCD的周长=ED+CD+CF+EF=(DE+CF)+AB+EF=5+4+4=13.则EFCD的周长是13.故答案为:13.8. 【答案】14或16或18【解析】先利用勾股定理求出BC的长,然后分类讨论即可确定答案.【解答】解:∵△ABC中,∠C=90∘,AC=3,AB=5,∴BC=4,当以AB为对角线时,此时ACBP的周长为(3+4)×2=14;当以AC为对角线时,此时APCB的周长为(5+4)×2=18;当以BC为对角线时,此时ACPB的周长为(5+3)×2=16;故答案为:14或16或18.9. 【答案】S ABHG=S BCFE,S AGPE=S HCFP,S AEFD=S HCDG【解析】根据平行四边形的性质证全等三角形,然后利用等量关系推出面积相等.【解答】解:∵四边形ABCD是平行四边形∴S△ABD=S△CBD.∵BP是平行四边形BEPH的对角线,∴S△BEP=S△BHP,∵PD是平行四边形GPFD的对角线,∴S△GPD=S△FPD.∴S△ABD−S△BEP−S△GPD=S△BCD−S△BHP−S△PFD,即S AEPG=S HCFP,∴S ABHG=S BCFE,同理S AEFD=S HCDG.即:S ABHG=S BCFE,S AGPE=S HCFP,S AEFD=S HCDG.故答案为S ABHG=S BCFE,S AGPE=S HCFP,S AEFD=S HCDG.10. 【答案】A【解析】根据题意可知,∠DCE=∠BEC=∠BCE,所以BE=BC=5,则AE=AB−BE=6−5=1,EF=AF−AE=3−1=2,所以FB=AF=3,所以AE:EF:FB=1:2:3.【解答】解:∵四边形ABCD是平行四边形,∴∠DCE=∠BEC,∵CE是∠DCB的平分线,∴∠DCE=∠BCE,∴∠CEB=∠BCE,∴BC=BE=5,∵F是AB的中点,AB=6,∴FB=3,∴EF=BE−FB=2,∴AE=AB−EF−FB=1,∴AE:EF:FB=1:2:3,故选A.11. 【答案】D【解析】两组对角分别相等的四边形是平行四边形,根据所给的三个角的度数可以求出第四个角,然后根据平行四边形的判定方法验证即可.【解答】解:两组对角分别相等的四边形是平行四边形,故B不是;当三个内角度数依次是88∘,108∘,88∘时,第四个角是76∘,故A不是;当三个内角度数依次是88∘,92∘,92∘,第四个角是88∘,而C中相等的两个角不是对角故C 错,D中满足两组对角分别相等,因而是平行四边形.故选D.12. 【答案】C【解析】平行四边形的长为10的一边,与两条对角线的一半构成的三角形的另两边应满足三角形的三边关系,即两边之和大于第三边,两边之差小于第三边.根据这个结论可以判断选择哪一个.【解答】解:如图,设两条对角线的长度是x ,y ,即三角形的另两边是12x ,12y ,那么得到不等式组{12x +12y >1012x −12y <10, 解得{x +y >20x −y <20, 所以符合条件的对角线只有20和30它的两条对角线的长度可以是20和30.故选C .13. 【答案】C【解析】平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据判定方法依次组合即可.【解答】解:根据平行四边形的判定,可以有四种:①与②,③与④,①与③,②与④都能判定四边形是平行四边形,故选C .14. 【答案】C【解析】因为要求证明PD +PE +PF 的值,而PD 、PE 、PF 并不在同一直线上,构造平行四边形,求出等于AB ,根据三角形的周长求出AB 即可.【解答】解:延长EP 交AB 于点G ,延长DP 交AC 与点H ,∵PD // AB ,PE // BC ,PF // AC ,∴四边形AFPH 、四边形PDBG 均为平行四边形,∴PD =BG ,PH =AF .又∵△ABC 为等边三角形,∴△FGP 和△HPE 也是等边三角形,∴PE =PH =AF ,PF =GF ,∴PE +PD +PF =AF +BG +FG =AB =183=6,故选C .15. 【答案】C【解析】根据平行四边形性质得出OA =OC =12AC ,BO =OD =12BD ,分为三种情况:①AC =10,BD =14,AB =8时,②AC =10,BD =8,AB =14时,③AC =8,BD =14,AB =10时,求出AO 和BO 的值,根据三角形的三边关系定理看看△AOB 是否存在即可.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC=12AC,BO=OD=12BD,分为三种情况:①AC=10,BD=14,AB=8时,AO=5,BO=7,则5+7>8,符合三角形三边关系定理;能组成平行四边形;②AC=10,BD=8,AB=14时,AO=5,BO=4,则5+4<14,不符合三角形三边关系定理;不能组成平行四边形;③AC=8,BD=14,AB=10时,AO=4,BO=7,则4+7>10,符合三角形三边关系定理;能组成平行四边形;可以画出不同形状的平行四边形的个数是2,故选C.16. 【答案】C【解析】根据已知,结合题意,画出图形,再根据平行四边形的判定,逐一判断即可.【解答】解:①也可能是等腰梯形.②可得AD // BC,故正确.③可判定△ABO≅△CDO,就有AB=CD,故可判定为平行四边形,正确.④也可能是等腰梯形.故选C.17. 【答案】B【解析】平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定逐一验证.【解答】解:A、能用两组对角相等的四边形是平行四边形判定平行四边形;B、不能判定平行四边形,如等腰梯形;C、能用两组对边相等的四边形是平行四边形判定平行四边形;D、能用两组对边分别平行的四边形是平行四边形判定平行四边形;故选B.18. 【答案】证明:连接EN、FM,∵EM⊥AC,FN⊥AC,∴∠AME=∠EMN=∠FNC=∠FNM=90∘,∴EM // FN,∵四边形ABCD是平行四边形,∴AD // BC,AD=BC,∴∠EAM=∠FCN,∵DE=BF,∴AE=CF,在△AEM和△CFN中{∠EANM=∠FCN ∠AME=∠CNF AE=CF∴△AEM≅△CFN(AAS),∴EM=FN,∵EM // FN,∴四边形EMFN是平行四边形,∴EF与MN互相平分.【解析】连接EN、FM,求出EM=FN,EM // FN,得出平行四边形EMFN,根据平行四边形的性质得出即可.【解答】证明:连接EN、FM,∵EM⊥AC,FN⊥AC,∴∠AME=∠EMN=∠FNC=∠FNM=90∘,∴EM // FN,∵四边形ABCD是平行四边形,∴AD // BC,AD=BC,∴∠EAM=∠FCN,∵DE=BF,∴AE=CF,在△AEM和△CFN中{∠EANM=∠FCN ∠AME=∠CNF AE=CF∴△AEM≅△CFN(AAS),∴EM=FN,∵EM // FN,∴四边形EMFN是平行四边形,∴EF与MN互相平分.19. 【答案】解:(1)∵在ABCD中,AB // CD∴∠B=180∘−120∘=60∘在直角三角形ABH中,AH=AB⋅sinB=8×√32=4√3.; (2)S平行四边形ABCD=BC⋅AH= 40√3.【解析】(1)根据平行四边形的邻角互补,得到∠B=60∘,再根据直角三角形的知识进行求解;; (2)根据平行四边形的面积等于底乘以高进行计算.【解答】解:(1)∵在ABCD中,AB // CD∴∠B=180∘−120∘=60∘=4√3.; (2)S平行四边形ABCD=BC⋅AH=在直角三角形ABH中,AH=AB⋅sinB=8×√3240√3.20. 【答案】BD和CE互相平分;; (2)证明:连接DE,∵AE // BD,BE⊥AC,∴四边形AEBD是平行四边形,∴BE=AD,∵BD是△ABC的中线,∴AD=DC,∴BE=CD,∵BE // AC,∴四边形EBCD是平行四边形,∴BD和CE互相平分,故答案为:BD和CE互相平分.【解析】(1)根据平行四边形的性质得出BD和CE互相平分;; (2)先证四边形AEBD是平行四边形,推出BE=AD=CD,再证四边形EBCD是平行四边形,即可得出答案.【解答】(1)解:如图,BD和CE互相平分,; (2)证明:连接DE,∵AE // BD,BE⊥AC,∴四边形AEBD是平行四边形,∴BE=AD,∵BD是△ABC的中线,∴AD=DC,∴BE=CD,∵BE // AC,∴四边形EBCD是平行四边形,∴BD和CE互相平分,21. 【答案】(1)证明:∵AB=AC,∴∠B=∠C.∵DF // AB,∴∠FDC=∠B.∴∠FDC=∠C.∴FD=FC.; (2)解:∵DE // AC,DF // AB,∴四边形AEDF是平行四边形.∴C AEDF=2AC=12cm.【解析】(1)利用△FDC中:等角对等边可证明ED=FC.先根据等腰三角形的性质和平行的性质得到∠EDC=∠C,再证明ED=FC;; (2)直接利用平行四边形的性质可知:平行四边形的周长正好是AC的2倍,即C AEDF=2AC=12cm.【解答】(1)证明:∵AB=AC,∴∠B=∠C.∵DF // AB,∴∠FDC=∠B.∴∠FDC=∠C.∴FD=FC.; (2)解:∵DE // AC,DF // AB,∴四边形AEDF是平行四边形.∴C AEDF=2AC=12cm.22. 【答案】证明:∵四边形ABCD为平行四边形,∴CD // AB,CD=AB,∵AE=CF,∴CD−CF=AB−AE,即DF=EB,∴四边形DEBF为平行四边形,∴DE // BF,DE=BF,∵M、N分别为DE、BF的中点,∴ME=FN=12DE=12BF,∴四边形MENF为平行四边形,则MF // EN.【解析】由四边形ABCD为平行四边形,利用平行四边形的对边平行且相等得到CD平行且相等于AB,再由AE=CF,得到DF与BE平行且相等,得到四边形DEBF为平行四边形,进而得到DE与BF平行且相等,根据M、N分别为DE、BF的中点,得到ME与FN平行且相等,确定出四边形MENF为平行四边形,利用平行四边形的对边平行即可得证.【解答】证明:∵四边形ABCD为平行四边形,∴CD // AB,CD=AB,∵AE=CF,∴CD−CF=AB−AE,即DF=EB,∴四边形DEBF为平行四边形,∴DE // BF,DE=BF,∵M、N分别为DE、BF的中点,∴ME=FN=12DE=12BF,∴四边形MENF为平行四边形,则MF // EN.23. 【答案】证明:连接ME,FN,∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,∵AE⊥BD,CF⊥BD,在△AOE和△COF中,{∠AEO=∠CFO=90∘∠AOE=∠COFOA=OC,∴△AOE≅△COF(AAS),∴OE=OF,同理△BOM≅△DON,得到OM=ON,∴四边形EMFN为平行四边形,∴EN // MF.【解析】连接ME,FN,由四边形ABCD为平行四边形,得到对角线互相平分,利用AAS得到三角形AOE与三角形COF全等,利用全等三角形对应边相等得到OE=OF,同理得到三角形BOM与三角形DON全等,得到OM=ON,进而确定出四边形MEFN为平行四边形,利用平行四边形的对边平行即可得证.【解答】证明:连接ME,FN,∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,∵AE⊥BD,CF⊥BD,在△AOE和△COF中,{∠AEO=∠CFO=90∘∠AOE=∠COFOA=OC,∴△AOE≅△COF(AAS),∴OE=OF,同理△BOM≅△DON,得到OM=ON,∴四边形EMFN为平行四边形,∴EN // MF.。
山东省章丘三中2013-2014学年八年级寒假结束检测考试数学试卷

ABOC D八年级数学试题注意事项:本试卷分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,共36分,答案请填在题后答题栏内;第Ⅱ卷为非选择题,共64分.Ⅰ、Ⅱ卷合计100分,考试时间为90分钟.第Ⅰ卷(选择题 共36分)一.选择题(每小题3分,共36分,在每小题的四个选项中,只有一项是符合要求的) 1、9的平方根是( ).A 、3B 、-3C 、±3D 、81 2、将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( ) A 、1、2、3 B 、2、3、4 C 、3、4、5 D 、4、5、6 3、内角和与外角和相等的多边形是( ) A 、三角形 B 、四边形C 、五边形D 、六边形4、随着人们生活水平的不断提高,汽车越来越普及,在下面的汽车标志图形中,是中心对称图形又是轴对称图形有( )A 、2 个B 、3个C 、4个D 、5个 5、如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC 、BD 相交于点O .下列结论不一定正确.....的是( ) A 、AC =BD B 、∠OBC =∠OCB C 、S △AOB =S △COD D 、∠BCD =∠BDC 6、下列四点中,在函数y =3x +2的图象上的点是( )A 、(-1,1)B 、(-1,-1)C 、(2,0)D 、(0,-1.5) 7、10名初中毕业生的中考体育考试成绩如下: 26 ,29 ,26 ,25 ,26, 26, 27, 28, 29, 30 ,这些成绩的中位数是( )A 、25B 、26C 、26.5D 、30(图1)8、已知正比例函数kx y =(0≠k )的函数值y 随x 的增大而减小,则一次函数k x y +=的图象大致是( )A B C D 9、点M (-5,12)离原点的距离是( )A 、3B 、13C 、17D 、 7 10、已知11x y =⎧⎨=-⎩是方程230x my --=的一个解,那么m 的值是( )A 、1B 、3C 、-3D 、 -1 11、如图,AB ⊥BC ,∠ABD 的度数比∠DBC 的度数的两倍少15°,设∠ABD 和∠DBC 的度数分别为x °、y °,那么下面可以求出这两个角的度数的方程组是( )A 、9015x y x y +=⎧⎨=-⎩B 、90215x y x y +=⎧⎨=-⎩C 、90152x y x y +=⎧⎨=-⎩D 、290215x x y =⎧⎨=-⎩12、如图1,在矩形MNPQ 中,动点R 从点N 出发,沿N →P →Q →M 方向运动至点M 处停止.设点R 运动的路程为x ,MNR △的面积为y ,如果y 关于x 的函数图象如图2所示,则当9x =时,点R 应运动到( ) A 、N 处 B 、P 处 C 、Q 处 D 、M 处 第Ⅱ卷(非选择题 共64分)A DBy°x° CFEC B 第19题图AB D13、若无理数a 满足14a <<,请你写出一个满足条件的无理数a 是14、已知直角三角形两边的长分别为3和4, 则第三边长为15、有一块直角三角形纸片,两直角边AB =6,BC=8,将该纸片折叠, 使直角边AB 落在斜边AC 上,折痕为AD ,则BD =___________16、如图,在R t △ABC 中,∠C =90°,AC =4,将△ABC 沿BC向右平移得到△DEF ,若平移的距离为2,则四边形ABED 的面积等于.17、如图,作一矩形,以数轴的原点为旋转中心,将过原点的对角线逆时针旋转,使对角线的另一端点落在数轴负半轴的点A 处,则点A 表示的数是 .18、如图所示为一程序框图,若开始输入的数为24,我们发现第一次得到的结果为12,第二次得到的结果为6,……,请问第4次得到的结果为 ,第2013次得到的结果为三.解答题(本大题共7个小题,满分46分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014.5章丘市推荐生考试倒计时31、如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P、D、B三点作⊙Q,与y轴的另一个交点为E,延长DQ交⊙Q于F,连结EF、BF.(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A、B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y,请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B、D、F为顶点的直角三角形,满足两条直角边之比为2∶1?如果存在,求出此时点P的坐标;如果不存在,请说明理由.答案(1)直线AB的函数解析式为y=-x+4.(2)①如图2,∠BDE=∠CDE=∠ADP;②如图3,∠ADP=∠DEP+∠DPE,如图4,∠BDE=∠DBP+∠A,因为∠DEP=∠DBP,所以∠DPE=∠A=45°.所以∠DFE=∠DPE=45°.因此△DEF是等腰直角三角形.于是得到y=.图2 图3 图4(3)①如图5,当BD∶BF=2∶1时,P(2,2).思路如下:由△DMB∽△BNF,知122B N D M==.设OD=2m,FN=m,由DE=EF,可得2m+2=4-m.解得23m=.因此4(0,)3D.再由直线CD与直线AB求得交点P(2,2).②如图6,当BD∶BF=1∶2时,P(8,-4).思路同上.图5 图62、如图,菱形ABCD的边长为2厘米,∠DAB=60°.点P从AAC 向C作匀速运动;与此同时,点Q也从点A出发,以每秒1厘米的速度沿射线作匀速运动.当点P到达点C时,P、Q都停止运动.设点P运动的时间为t秒.(1)当P异于A、C时,请说明PQ//BC;(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?答案(1)因为2AQ tAB=,2AP tAC==,所以AQ APAB AC=.因此P Q//BC.(2)如图2,由PQ=PH=12PC,得1)2t=.解得6t=.如图3,由PQ=PB,得等边三角形PBQ.所以Q是A B的中点,t=1.如图4,由PQ=PC,得t=.解得3t=如图5,当P、C重合时,t=2.因此,当6t=或1<t≤3t=2时,⊙P与边BC有1个公共点.当6<t≤1时,⊙P与边BC有2个公共点.图2 图3 图4 图53、在Rt △ABC 中,∠C =90°,AC =6,53sin =B ,⊙B 的半径长为1,⊙B 交边CB 于点P ,点O是边AB 上的动点.(1) 如图1,将⊙B 绕点P 旋转180°得到⊙M ,请判断⊙M 与直线AB 的位置关系; (2) 如图2,在(1)的条件下,当△OMP 是等腰三角形时,求OA 的长;(3)如图3,点N 是边BC 上的动点,如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切,设NB =y ,OA =x ,求y 关于x 的函数关系式及定义域.图1 图2 图3思路点拨1.∠B 的三角比反复用到,注意对应关系,防止错乱.2.分三种情况探究等腰△OMP ,各种情况都有各自特殊的位置关系,用几何说理的方法比较简单. 3.探求y 关于x 的函数关系式,作△OB N 的边OB 上的高,把△OBN 分割为两个具有公共直角边的直角三角形.满分解答(1) 在Rt △ABC 中,AC =6,53sin =B , 所以AB =10,BC =8.过点M 作MD ⊥AB ,垂足为D .在Rt △BMD 中,BM =2,3sin 5MD B BM ==,所以65MD =.因此MD >MP ,⊙M 与直线AB 相离.(2)①如图4,MO ≥MD >MP ,因此不存在MO =MP 的情况.②如图5,当PM =PO 时,又因为PB =PO ,因此△BOM 是直角三角形. 在Rt △BOM 中,BM =2,4cos 5BO B BM ==,所以85BO =.此时425OA =.③如图6,当OM =OP 时,设底边MP 对应的高为OE .在Rt △BOE 中,BE =32,4cos 5BE B BO ==,所以158BO =.此时658OA =.(3)如图7,过点N 作NF ⊥AB ,垂足为F .联结ON .当两圆外切时,半径和等于圆心距,所以ON =x +y .在Rt △BNF 中,BN =y ,3sin 5B =,4cos 5B =,所以35NF y =,45BF y =.在Rt △ONF 中,4105OF AB AO BF x y =--=--,由勾股定理得ON 2=OF 2+NF 2.于是得到22243()(10)()55x y x y y +=--+.整理,得2505040x y x -=+.定义域为0<x <5.考点伸展第(2)题也可以这样思考:如图8,在Rt △BMF 中,BM =2,65MF =,85BF =.在Rt △OMF 中,OF =8421055x x --=-,所以222426()()55OM x =-+.在Rt △BPQ 中,BP =1,35PQ =,45BQ =.在Rt △OPQ 中,OF =4461055x x --=-,所以222463()()55OP x =-+.①当MO =MP =1时,方程22426()()155x -+=没有实数根.②当PO =PM =1时,解方程22463()()155x -+=,可得425x OA ==③当OM =OP 时,解方程22426()()55x -+22463()()55x =-+,可得658x OA ==.4、如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD//AB,∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长的速度运动,运动时间为t秒.(1)求点C的坐标;(2)当∠BCP=15°时,求t的值;(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.(1)点C的坐标为(0,3).(2)如图2,当P在B的右侧,∠BCP=15°时,∠PCO=30°,4t=如图3,当P在B的左侧,∠BCP=15°时,∠CPO=30°,4t=+图2 图3 (3)如图4,当⊙P与直线BC相切时,t=1;如图5,当⊙P与直线DC相切时,t=4;如图6,当⊙P与直线AD相切时,t=5.6.图4 图5 图65、如图1,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上的一个动点,过P作直线l//AC交抛物线于点Q.试探究:随着点P的运动,在抛物线上是否存在点Q,使以A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;(3)请在直线AC上找一点M,使△BDM的周长最小,求出点M的坐标.图1 思路点拨1.第(2)题探究平行四边形,按照AP为边或者对角线分两种情况讨论.2.第(3)题是典型的“牛喝水”问题,构造点B关于“河流”AC的对称点B′,那么M落在B′D 上时,MB+MD最小,△MBD的周长最小.满分解答(1)由y=-x2+2x+3=-(x+1)(x-3)=-(x-1)2+4,得A(-1, 0)、B(3, 0)、C(0, 3)、D(1, 4).直线AC的解析式是y=3x+3.(2)Q1(2, 3),Q2(13-),Q3(13-).(3)设点B关于直线AC的对称点为B′,联结BB′交AC于F.联结B′D,B′D与交AC的交点就是要探求的点M.作B′E⊥x轴于E,那么△BB′E∽△BAF∽△CAO.在Rt△BAF中,13AF BF==AB=4,所以BF=.在Rt△BB′E中,'13B E BE=='2BB BF==,所以12'5B E=,365BE=.所以3621355OE BE OB=-=-=.所以点B′的坐标为2112(,)55-.因为点M在直线y=3x+3上,设点M的坐标为(x, 3x+3).由''''''DD MMB D B M=,得''''yD yB yM yBxD xB xM xB--=--.所以1212433552121155xx-+-=++.解得935x=.所以点M的坐标为9132(,)3535.图2 图3考点伸展第(2)题的解题思路是这样的:①如图4,当AP 是平行四边形的边时,CQ //AP ,所以点C 、Q 关于抛物线的对称轴对称,点Q 的坐标为(2, 3).②如图5,当AP 是平行四边形的对角线时,点C 、Q 分居x 轴两侧,C 、Q 到x 轴的距离相等. 解方程-x 2+2x +3=-3,得1x =Q 的坐标为(13-)或(13-).6、如图1,抛物线213922y xx =--与x 轴交于A 、B 两点,与y 轴交于点C ,联结BC 、AC . (1) 求AB 和OC 的长;(2) 点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点E 作BC 的平行线交AC 于点D .设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围;(3)在(2)的条件下,联结CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π).图1思路点拨1.△ADE 与△AC B 相似,面积比等于对应边的比的平方.2.△CDE 与△ADE 是同高三角形,面积比等于对应底边的比.满分解答(1)由21319(3)(6)222y x x x x =--=+-,得A (-3,0)、B (6,0)、C (0,-9). 所以AB =9,OC =9.(2)如图2,因为DE //CB ,所以△ADE ∽△ACB .所以2()ADE ACB S AE S AB∆∆=.而18122ACB S AB OC ∆=⋅=,AE =m ,所以222811()()922ADE ACB AE m s S S m AB ∆∆==⨯=⨯=.m 的取值范围是0<m <9.图2 图3(3)如图2,因为DE //CB ,所以9CD BE mAD AE m-==.因为△C DE 与△ADE 是同高三角形,所以9CDE ADE S CD m S AD m∆∆-==.所以22291191981()222228CDE m S m m m m m ∆-=⨯=-+=--+.当92m =时,△CDE 的面积最大,最大值为818.此时E 是AB 的中点,92BE =.如图3,作EH ⊥CB ,垂足为H .在Rt △BOC 中,OB =6,OC =9,所以sin B =在Rt △BEH中,9sin 2EH BE B =⋅==. 当⊙E 与BC 相切时,r EH =.所以272952S r ππ==.考点伸展在本题中,△CDE 与△BEC 能否相似?如图2,虽然∠CED =∠BCE ,但是∠B >∠BCA ≥∠ECD ,所以△CDE 与△BEC 不能相似.7、已知抛物线y n=-(x -a n )2+a n(n 为正整数,且0<a 1<a 2<…<a n)与x 轴的交点为An -1(b n -1,0)和A n (b n ,0).当n =1时,第1条抛物线y 1=-(x -a 1)2+a 1与x 轴的交点为A 0(0,0)和A 1(b 1,0),其他依此类推(1) 求a 、b 的值及抛物线y 2的解析式; (2)抛物线y 3的顶点坐标为(_____,_____);依此类推第n 条抛物线y n 的顶点坐标为(_____,_____)(用含n 的式子表示); 所有抛物线的顶点坐标满足的函数关系式是________________; (3)探究下列结论:①若用A n -1 A n 表示第n 条抛物线被x 轴截得的线段的长,直接写出A 0A 1的值,并求出A n -1 A n ; ②是否存在经过点A (2,0)的直线和所有抛物线都相交,且被每一条抛物线截得的线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.备用图(仅供草稿使用)思路点拨1.本题写在卷面的文字很少很少,可是卷外是大量的运算.2.最大的纠结莫过于对字母意义的理解,这道题的复杂性就体现在数形结合上. 3.这个备用图怎么用?边画边算,边算边画.满分解答(1)将A 0(0,0)代入y 1=-(x -a 1)2+a 1,得-a 12+a 1=0. 所以符合题意的a 1=1.此时y 1=-(x -1)2+1=-x (x -2).所以A 1的坐标为(2,0),b 1=2. 将A 1(2,0)代入y 2=-(x -a 2)2+a 2,得-(2-a 2)2+a 2=0. 所以符合题意的a 2=4.此时y 2=-(x -4)2+4=-(x -2)(x -6). (2)抛物线y 3的顶点坐标为(9,9); 第n 条抛物线y n 的顶点坐标为(n 2,n 2);所有抛物线的顶点坐标满足的函数关系式是y =x . (3)①如图1,A 0A 1=2.由第(2)题得到,第n 条抛物线y n =-(x -a n )2+a n 的顶点坐标为(n 2,n 2). 所以y n =-(x -n 2)2+n 2=n 2-(x -n 2)2=(n -x +n 2)(n +x -n 2).所以第n 条抛物线与x 轴的交点坐标为A n -1(n 2-n ,0)和A n (n 2+n ,0). 所以A n -1 A n =(n 2+n )-(n 2-n )=2n .②如图1,直线y =x -2和所有抛物线都相交,且被每一条抛物线截得的线段的长度都相等.图1考点伸展我们一起来梳理一下这道题目的备用图怎么用.第一步,由y n =-(x -a n )2+a n ,得抛物线的顶点坐标为(a n , a n ).顶点的横坐标和纵坐标相等,而且已知a n >0,因此先画出顶点所在的射线y =x (x >0).第二步,计算出y 1,画抛物线y 1的顶点、与x 轴的右交点. 第三步,计算出y 2,画抛物线y 2的顶点、与x 轴的右交点.8、如图1,图2,在△ABC 中,AB =13,BC =14,5cos 13ABC ∠=.探究 如图1,AH ⊥BC 于点H ,则AH =_____,AC =______,△ABC 的面积S △ABC =________.拓展 如图2,点D 在AC 上(可与点A 、C 重合),分别过点A 、C 作直线BD 的垂线,垂足为E 、F .设BD =x ,AE =m ,CF =n .(当点D 与点A 重合时,我们认为S △ABD =0)(1) 用含x ,m 或n 的代数式表示S △ABD 及S △CBD ;(2) 求(m +n )与x 的函数关系式,并求(m +n )的最大值和最小值;(3)对给定的一个x 值,有时只能确定唯一的点D ,指出这样的x 的取值范围.发现 请你确定一条直线,使得A 、B 、C 三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.图1 图2图3 图4答案 探究 AH =12,AC =15,S△ABC=84.拓展 (1)S △ABD =12mx ,S △CBD =12nx .(2)由S △ABC =S △ABD +S △CBD ,得118422mx nx +=.所以168m n x+=.由于AC 边上的高565BG =,所以x 的取值范围是565≤x ≤14.所以(m +n )的最大值为15,最小值为12.(3)x 的取值范围是x =565或13<x ≤14.发现 A 、B 、C 三点到直线AC 的距离之和最小,最小值为565.9、某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:(1)操作发现:在等腰△ABC中,AB=AC,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连结MD和ME,则下列结论正确的是__________(填序号即可).①AF=AG=12AB;②MD=ME;③整个图形是轴对称图形;④MD⊥ME.(2)数学思考:在任意△ABC中,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M 是BC的中点,连结MD和ME,则MD与ME有怎样的数量关系?请给出证明过程;(3)类比探究:在任意△ABC中,仍分别以AB、AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M 是BC的中点,连结MD和ME,试判断△MDE的形状.答:_________.图1 思路点拨1.本题图形中的线条错综复杂,怎样寻找数量关系和位置关系?最好的建议是按照题意把图形规范、准确地重新画一遍.2.三个中点M、F、G的作用重大,既能产生中位线,又是直角三角形斜边上的中线.3.两组中位线构成了平行四边形,由此相等的角都标注出来,还能组合出那些相等的角?满分解答(1)填写序号①②③④.(2)如图4,作DF⊥AB,EG⊥AC,垂足分别为F、G.因为DF、EG分别是等腰直角三角形ABD和等腰直角三角形ACE斜边上的高,所以F、G分别是AB、AC的中点.又已知M是BC的中点,所以MF、MG是△ABC的中位线.所以12MF AC=,12MG AB=,MF//AC,MG//AB.所以∠BFM=∠BAC,∠MGC=∠BAC.所以∠BFM=∠MGC.所以∠DFM=∠MGE.因为DF、EG分别是直角三角形ABD和直角三角形ACE斜边上的中线,所以12EG AC=,12DF AB=.所以MF=EG,DF=NG.所以△DFM≌△MGE.所以DM=ME.(3)△MDE是等腰直角三角形.图4 图5考点伸展第(2)题和第(3)题证明△DFM ≌△MGE 的思路是相同的,不同的是证明∠DFM =∠MGE 的过程有一些不同.如图4,如图5,∠BFM =∠BAC =∠MGC .如图4,∠DFM =90°+∠BFM ,∠MGE =90°+∠MGC ,所以∠DFM =∠MGE . 如图5,∠DFM =90°-∠BFM ,∠MGE =90°-∠MGC ,所以∠DFM =∠MGE .10如图1, △ABC 是以BC 为底边的等腰三角形,点A 、C 分别是一次函数334y x =-+的图像与y 轴、x 轴的交点,点B 在二次函数218y x bx c =++的图像上,且该二次函数图像上存在一点D 使四边形ABCD 能构成平行四边形.(1) 试求b 、c 的值,并写出该二次函数的解析式;(2)动点P 从A 到D ,同时动点Q 从C 到A 都以每秒1个单位的速度运动,问: ①当P 运动到何处时,由PQ ⊥AC ?②当P 运动到何处时,四边形PDCQ 的面积最小?此时四边形PDCQ 的面积是多少?图1思路点拨1.求抛物线的解析式需要代入B 、D 两点的坐标,点B 的坐标由点C 的坐标得到,点D 的坐标由AD =BC 可以得到.2.设点P 、Q 运动的时间为t ,用含有t 的式子把线段AP 、CQ 、AQ 的长表示出来. 3.四边形PDCQ 的面积最小,就是△APQ 的面积最大.满分解答(1)由334y x =-+,得A (0,3),C (4,0).由于B 、C 关于OA 对称,所以B (-4,0),BC =8. 因为AD //BC ,AD =BC ,所以D (8,3).将B (-4,0)、D (8,3)分别代入218y x bx c =++,得240,883.b c b c -+=⎧⎨++=⎩解得14b =-,c =-3.所以该二次函数的解析式为211384y x x =--.(2)①设点P 、Q 运动的时间为t .如图2,在△APQ 中,AP =t ,AQ =AC -CQ =5-t ,cos ∠P AQ =cos ∠ACO =45. 当PQ ⊥AC 时,45AQ AP =.所以545t t -=.解得259AP t ==.2014.5章丘市推荐生考试倒计时3第 11 页 共 11 页图2 图3②如图3,过点Q 作QH ⊥AD ,垂足为H . 由于S △A PQ =2111333sin (5)2225102AP QH AP AQ PAQ t t t t ⋅=⋅∠=-⨯=-+, S △ACD =11831222AD OA ⋅=⨯⨯=,所以S 四边形PDCQ =S △ACD -S △APQ =2233358112()()1021028t t t --+=-+.所以当AP =52时,四边形PDCQ 的最小值是818. 考点伸展如果把第(2)①题改为“当P 运动到何处时,△APQ 是直角三角形?” 除了PQ ⊥AC 这种情况,还有QP ⊥AD 的情况. 这时45AP AQ =,所以455t t =-.解得209t =(如图4所示).图4。
