线路板的打孔机工作流程设计
pcb背钻孔工艺流程

pcb背钻孔工艺流程
PCB背钻孔工艺流程是指在PCB板的背面钻孔的工艺流程,一般包括以下几个步骤:
1. 材料准备:准备好需要钻孔的PCB板和背钻孔用的钻头。
2. 设计钻孔布局:在PCB设计时,在背面的相应位置安排好需要钻孔的位置和大小。
3. 钻孔定位:使用精确的钻孔机来对PCB板进行定位。
可以使用自动对位系统或者人工对位。
4. 钻孔加工:将PCB板放置在钻孔机上,根据钻孔布局,使用钻头对PCB背面进行钻孔操作。
钻孔机可以是CNC钻孔机或者半自动钻孔机,根据生产需求选择。
5. 清洁处理:钻孔完成后,需要进行清洁处理,以便去除可能产生的残渣和污染物。
6. 检查质量:对钻孔的质量进行检查,包括孔径、孔壁平整度和孔位置偏差等。
7. 防腐处理:有些需要防腐的PCB板,在背部钻孔完成后,需要进行防腐处理,以防止氧化和腐蚀。
8. 清洁再检查:最后,对PCB板进行再次清洁和检查,确保钻孔工艺完成后的质量符合要求。
这是一个基本的PCB背钻孔工艺流程,具体的操作方法和设备选择还会因实际情况而有所不同。
线路板的打孔机工作流程设计

C题线路板的打孔机工作流程设计摘要本文讨论了电路板的打孔机工作流程中的费用及时间问题,在已知孔型、刀具及行走费用和转刀费用的前提下,综合考虑成本和时间,设计行走路线及换刀方案,使生产效率最高。
本文中首先采用了0-1整数规划方法(模型一),再采用二次逐边修正法(模型二),之后采用了贪心算法(模型三)。
在求解过程中,我们先考虑只打孔的情况,即遇到孔便打完,同时以最少费用为目标,对这三个模型进行比较,结果如下:模型一:该模型的变量较多,且使用0-1规划法,对matlab以及lingo的要求较高,鉴于我们的计算机条件,该模型只有理论上的意义。
模型二:在以最少费用为目标的条件下,费用为79232元,时间为49188秒(约合13.66小时)。
模型三:在以最少费用为目标的条件下,费用为44708元,时间为48665秒(约合13.5小时)。
在以最少时间为目标的条件下,费用为374090元,时间为56298秒(约合15.6小时)。
在模型的优化部分,本文将需要两种刀具(或三种)的孔视为两种孔型(或三种),如C型孔,视为C1和C2两种孔型,分别用a刀和c刀(有下刀顺序),D型孔视为两个独立的孔D1和D2(无下刀顺序)。
同时综合考虑费用和时间,建立适合大规模生产的模型,取合适的权值(以费用60%、时间40%为例),费用为49276元,时间为21272秒(约合5.9小时)。
一、问题的重述过孔是印刷线路板(也称为印刷电路板)的重要组成部分之一,过孔的加工费用通常占制板费用的30%到40%,打孔机主要用于在制造印刷线路板流程中的打孔作业。
本问题旨在提高某类打孔机的生产效能。
打孔机的生产效能主要取决于以下几方面:(1)单个过孔的钻孔作业时间,这是由生产工艺决定,为了简化问题,这里假定对于同一孔型钻孔作业时间都是相同的;(2)打孔机在加工作业时,钻头的行进时间;(3)针对不同孔型加工作业时,刀具的转换时间。
目前,实际采用的打孔机普遍是单钻头作业,即一个钻头进行打孔。
线路板钻孔流程及注意事项

线路板钻孔流程及注意事项下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!线路板钻孔是印刷电路板(PCB)制造过程中的重要步骤,主要作用是在电路板的铜箔上钻孔,以便于形成连接线路。
pcb钻孔工作计划

pcb钻孔工作计划
1. 确定钻孔需求:根据PCB设计文件,确定需要进行钻孔的
位置、尺寸和数量。
2. 确定钻孔机器和工具:选择适合钻孔PCB的机器和工具,
如钻床、钻头、冷却液等。
3. 准备工作:清洁工作台,确保工作环境整洁,安全且易于操作。
4. 校准机器:检查钻床的准确性和稳定性,校准钻头的位置和深度。
5. 准备PCB材料:确保PCB材料干燥和平整,检查是否有损
坏或缺陷。
6. 设置工作参数:根据PCB设计要求,设置钻孔机器的速度、深度和间距等参数。
7. 开始钻孔:将PCB材料放置于工作台上,并根据设计要求
逐个进行钻孔。
8. 定期检查和维护:在钻孔过程中,定期检查钻头的状态,及时更换损坏的钻头,并清洁切屑。
9. 质量控制:钻孔完成后,检查每个孔的质量,确保孔径和位置的准确性。
10. 清理工作:清除PCB上的切屑和残留物,清理工作台,将废弃物进行分类和处理。
11. 记录和报告:记录钻孔的工作量、工时和质量控制结果,并报告给相关人员。
12. 维护设备:钻孔机器使用完毕后,进行日常维护,保证设备的使用寿命和性能。
13. 改进和优化:根据钻孔工作的经验和反馈,及时总结经验教训,寻找改进和优化的方法。
pcb钻孔流程

pcb钻孔流程PCB钻孔流程。
PCB(Printed Circuit Board)即印刷电路板,是电子元器件的支撑体,是各种电子设备中不可或缺的一部分。
而PCB的制作过程中,钻孔是一个非常重要的环节,下面将介绍PCB钻孔的流程及注意事项。
首先,PCB钻孔的流程可以分为以下几个步骤:1. 设计钻孔位置,在PCB设计阶段,需要确定钻孔的位置和大小。
这些信息将在制造阶段被用来定位和钻孔。
2. 制作钻孔文件,根据设计要求,制作出钻孔文件。
这些文件将包含每个钻孔的坐标和直径。
3. 准备钻孔设备,将制作好的PCB放在钻孔机上,准备进行钻孔。
4. 钻孔,根据钻孔文件的要求,使用钻头逐个在PCB上进行钻孔。
这个过程需要非常精准和小心,以确保每个孔的位置和大小都符合要求。
5. 检查和清洁,完成钻孔后,需要对PCB进行检查,确保没有漏孔或者钻孔偏位。
然后使用清洁工具清洁PCB,确保孔壁干净。
6. 表面处理,最后,对PCB进行表面处理,以保护钻孔和提高PCB的耐久性。
在进行PCB钻孔的过程中,需要注意以下几点:1. 钻头选择,根据PCB设计要求选择合适的钻头,确保钻孔的大小和形状符合要求。
2. 钻孔精度,钻孔的精度直接影响到PCB的质量,因此在钻孔过程中需要严格控制钻头的位置和深度。
3. 钻孔速度,钻孔速度过快会导致PCB表面损伤,速度过慢则会影响效率,需要根据实际情况选择合适的钻孔速度。
4. 孔壁清洁,钻孔后需要及时清洁孔壁,以防止残留的金属屑或碎屑影响PCB的使用。
5. 表面处理,表面处理可以采用镀铜、喷锡等方式,以保护钻孔和提高PCB的稳定性。
总之,PCB钻孔是PCB制作过程中不可或缺的一环,需要在设计、制作和加工过程中严格控制每一个环节,以确保PCB的质量和稳定性。
希望本文对PCB钻孔流程有所帮助,谢谢阅读!。
电路板钻孔操作方法

电路板钻孔操作方法
电路板钻孔操作方法如下:
1. 准备工具和材料:钻床、电路板、钻头、标尺、磁铁、胶带等。
2. 将电路板固定在钻床上,可以使用夹具或胶带将其稳定在钻床台面上。
3. 根据需要,在电路板上标记出要钻孔的位置,可以使用标尺和铅笔进行标记。
4. 选择合适的钻头,一般选择直径略大于要钻孔的孔径,例如选择铣刀钻头或碳化钨钻头。
5. 设置钻床的转速和进给速度,根据钻头和电路板的材质进行调整,一般来说,转速较高、进给速度较低可以更好地控制钻孔质量。
6. 开始钻孔,将钻头缓慢地放在标记位置上,用手指轻轻按压,使钻头与电路板接触,然后启动钻床,有节奏地向下加压并旋转钻头,直至钻孔完成。
7. 注意控制钻孔深度,以免穿透电路板或损坏底部元件。
8. 钻孔结束后,可以使用吹风机或气压枪等清除孔中产生的切屑,保持孔洞的清洁和平整。
9. 最后,检查钻孔质量,确保孔径与要求一致,没有明显的倾斜、破损或毛刺等问题。
10. 如果需要,可以进行除毛刺或抛光等后续处理。
完成以上步骤后,即可完成电路板钻孔操作。
戴上必要的防护眼镜和手套、注意操作安全。
PCB钻孔流程1

PCB钻孔流程(一)一、目的:1.1提高员工对制程的了解及品质意识,使其能迅速上岗,达成产能及品质目标。
二、适用范围:2.1 仅适用于PCB钻孔的工程师与领班。
三、相关权责:3.1 PCB钻孔。
四、名词定义:4.1无五、相关文件:5.1无六、培训内容:6.1钻孔的作用及细步流程介绍6.2各流程的作用及注意事项6.3制程控制的工艺参数6.4品质检测与处理6.5技术员工作职掌6.6不良板重工流程6.7 保养规范6.8不良原因及改善对策6.9点检项目记录表单PCB钻孔流程(二)6.1钻孔的作用及细步流程介绍:6.1.1钻孔作用:用来对PCB进行切削孔位,便于插件及导通之作业。
6.1.2钻孔的细步流程介绍:进料→准备PCB钻咀→钻孔→检验→出货6.1.3钻孔的环境要求:温度:20±2℃相对湿度:50±5%6.1.4钻孔的主物料介绍:6.1.4.1垫板(2.5mm):6.1.4.1.1作用:a.防止钻机台面受损;b.减少出口性毛头;c.减少钻咀扭断;d.降低钻咀温度;e.清洁钻咀沟槽中之胶渣。
6.1.4.1.2板材种类:a.复合材料——其制造法与纸质基板类似,但木屑为基础,再混合含酸或盐类的粘著剂,高温高压下压合硬化成为一体而硬度很高的板子。
b.酚醛树脂板——价格比上述的合板要贵一些,也就是一般单面板的基材。
c.铝箔压合板——同盖板一样。
d.Vbu垫板——是指Vented Back up垫板,上、下两面铝箔,中层为折曲同质的纯铝箔,空气可以自由流通其间,如石棉浪一样。
垫板的选择一样依各厂条件来评估,其重点在:不含有机油脂,屑够软不伤孔壁,表面够硬,板厚均匀、平整等。
操作CNC控制现有CAD/CAM工作站都可直接转换钻孔机接受之语言只要设定一些参数如各孔代号代表之孔径即可。
6.1.4.2铝片(0.2mm),也称盖板:6.1.4.2.1作用:a.防止压力脚直接压伤铜面;b.使钻尖容易中心定位;c.减少进口性毛头;d.利于散热;e.钻咀进、退时的清洁。
线路板钻孔流程及注意事项

英文回答:The drilling process for circuit boards involves several key steps and considerations. Here's a breakdown:Drilling Process:Design the Hole Locations: During the design phase of the circuit board, it's crucial to predetermine the exact locations for the holes to ensure smooth connections for the components and wires.Select and Install the Drill Bit: Choose a drill bit that is slightly smaller than the diameter of the component pins to ensure a snug fit. Then, securely install the bit onto the drilling machine.Perform the Drilling: With the circuit board securely fixed, begin drilling at the designated locations, ensuring each hole is drilled accurately and smoothly. Precautions:Safety First: Wear protective gear, such as safety glasses, to avoid any debris or splinters. Ensure the drilling machine is properly grounded and in good working condition.Accuracy Matters: Use a precision drilling machine and ensure the board is firmly clamped to prevent any movement during the drilling process.Cleanliness: After drilling, clean the holes to remove any debris or residue. This ensures a clean and reliable connection for the components.中文回答:线路板钻孔流程涉及几个关键步骤和注意事项,具体如下:钻孔流程:设计孔位:在电路板的设计阶段,需要预先确定孔的确切位置,以确保元件和导线能够顺利连接。
线路板钻孔工艺

线路板钻孔工艺线路板钻孔工艺是电子制造过程中关键的组成部分之一,它对于电子产品的性能和质量具有重要影响。
本文将详细介绍线路板钻孔工艺的步骤和技术要点。
一、工艺步骤1. 钻前准备:在进行线路板钻孔之前,需要进行一系列的准备工作。
首先,将待钻孔的线路板放置在钻孔机的工作台上。
然后,根据实际需要选择合适的钻头,并进行安装和调试。
2. 调试参数:钻孔机需要根据不同线路板的要求进行参数调试。
这些参数包括钻头的转速、进给速度、润滑液的类型和流量等。
调试参数的目的是保证钻孔的精度和效率。
3. 钻孔操作:开始钻孔之前,操作人员需要根据线路板上的设计要求,确定钻孔位置和孔径。
然后,将钻头对准待钻孔的位置,开始钻孔操作。
操作过程中需要注意控制钻头的进给速度和转速,以确保钻孔质量。
4. 检查和修整:钻孔完成后,需要对钻孔质量进行检查。
检查的主要内容包括孔径是否满足要求、孔壁是否平整等。
如果发现问题,需要及时进行修整,以保证钻孔质量达到标准要求。
二、技术要点1. 选择合适的钻头:不同的线路板钻孔需求不同,因此需要选择合适的钻头。
钻头的材质、形状和尺寸等要与线路板的材料和设计要求相匹配。
2. 控制钻头转速:钻头的转速对钻孔的质量和进度有着重要影响。
一般来说,转速过快容易引起钻孔毛刺和孔壁破损,而转速过慢则会降低钻孔效率。
3. 控制钻孔进给速度:钻孔的进给速度也会影响钻孔质量和进度。
过快的进给速度可能导致钻孔偏斜或者钻头折断,而过慢的进给速度则会造成钻孔时间过长。
4. 使用合适的润滑液:润滑液在钻孔过程中起到冷却和润滑的作用,能够减少钻头的磨损和提高钻孔效果。
不同材质的线路板可能需要使用不同类型的润滑液。
5. 定期检查和维护钻头:钻头是易损件,需要定期进行检查和维护。
检查的内容包括钻头的磨损情况和钻孔质量。
如果钻头磨损严重或者钻孔质量不合格,需要及时更换钻头。
三、注意事项1. 操作人员需要熟悉钻孔机的操作要点,并严格按照操作规程进行操作,确保人员安全和产品质量。
pcb钻孔机的操作技术及流程详解

pcb钻孔机的操作技术及流程详解pcb钻孔机的操作技术及流程详解6.1 制程目的单面或双面板的制作都是在下料之后直接进行非导通孔或导通孔的钻孔, 多层板则是在完成压板之后才去钻孔。
传统孔的种类除以导通与否简单的区分外,以功能的不同尚可分:零件孔,工具孔,通孔(Via),盲孔(Blind hole),埋孔(Buried hole)(后二者亦为via hole的一种).近年电子产品'轻.薄.短.小.快.'的发展趋势,使得钻孔技术一日千里,机钻,雷射烧孔,感光成孔等,不同设备技术应用于不同层次板子.本章仅就机钻部分加以介绍,其它新技术会在20章中有所讨论.6.2 流程上PIN→钻孔→检查6.3上PIN作业钻孔作业时除了钻盲孔,或者非常高层次板孔位精准度要求很严,用单片钻之外,通常都以多片钻,意即每个stack两片或以上.至于几片一钻则视1.板子要求精度2.最小孔径3.总厚度4.总铜层数.来加以考虑. 因为多片一钻,所以钻之前先以pin将每片板子固定住,此动作由上pin机(pinning maching)执行之. 双面板很简单,大半用靠边方式,打孔上pin 连续动作一次完成.多层板比较复杂,另须多层板专用上PIN机作业.6.4. 钻孔6.4.1钻孔机钻孔机的型式及配备功能种类非常多,以下List评估重点A. 轴数:和产量有直接关系B. 有效钻板尺寸C. 钻孔机台面:选择振动小,强度平整好的材质。
D. 轴承(Spindle)E. 钻盘:自动更换钻头及钻头数F. 压力脚G. X、Y及Z轴传动及尺寸:精准度,X、Y独立移动H. 集尘系统:搭配压力脚,排屑良好,且冷却钻头功能I. Step Drill的能力J. 断针侦测K. RUN OUT6.4.1.1钻孔房环境设计A. 温湿度控制B. 干净的环境C. 地板承受之重量D. 绝缘接地的考虑E. 外界振动干扰6.4.2 物料介绍钻孔作业中会使用的物料有钻针(Drill Bit),垫板(Back-up board),盖板(Entry board)等.以下逐一介绍:图6.1为钻孔作业中几种物料的示意图.6.4.2.1 钻针(Drill Bit), 或称钻头,其质量对钻孔的良窳有直接立即的影响, 以下将就其材料,外型构、及管理简述之。
电路板镭射钻孔流程

电路板镭射钻孔流程
激光钻孔技术是一种高精度、高效率的加工方法,广泛应用于电路板制造行业。
电路板镭射钻孔是一种使用激光束将孔洞精确地加工在电路板上的加工技术。
下面介绍电路板镭射钻孔的流程:
1. 设计:首先,根据电路板的设计图纸确定需要加工的孔洞位置、尺寸和数量等参数。
2. 设备准备:确定采用的激光钻孔设备,并进行设备的调试和检查,确保设备能够正常工作。
3. 材料准备:准备待加工的电路板材料,确保电路板表面平整、清洁,并放置在设备工作台上。
4. 参数设置:根据设计要求和实际情况,设置激光钻孔设备的加工参数,包括激光功率、激光脉冲频率、加工速度等。
5. 对准定位:利用设备上的光学对准系统,将激光束精确对准待加工的位置,并调整好加工头的位置。
6. 开始加工:启动设备,让激光束按照设定的参数和位置进行钻孔加工,通过在电路板材料上聚焦高能量的激光束来熔化和蒸发材料,形成孔洞。
7. 检验质量:完成钻孔后,对加工得到的孔洞进行检查和测试,确保孔洞尺寸和位置精确符合设计要求。
8. 清洗处理:清洁电路板表面和孔洞,去除激光加工时留下的残留物和污垢,保证电路板的表面质量。
9. 检验验证:经过清洗处理后,再次对孔洞进行检验和验证,确保整个加工过程
完成并且符合质量要求。
10. 完成:当电路板上所有需要的孔洞都完成加工后,整个镭射钻孔流程就完成了。
电路板镭射钻孔技术具有高加工精度、加工效率高、操作简便、适应性强等优点,被广泛应用于电子产品的生产制造过程中。
随着激光技术的不断发展和完善,电路板镭射钻孔技术也将会得到进一步提升和发展,为电路板制造业带来更多的发展机遇和挑战。
电路板的打孔机工作流程设计(DOC 41页)

电路板的打孔机工作流程设计摘要打孔机完成的打孔作业在印刷电路板的生产过程中占有极其重要的地位,通过合理优化打孔路线,进而减少生产时间及生产成本,提高生产效能,是生产作业过程中必须解决的问题。
论文以总工作时间最短为目标函数,建立数序模型,寻找最优路径,最短工作时间以及最少生产成本。
忽略打孔时间,认为总的工作时间为钻孔行进时间和刀具转换时间的叠加。
总的作业成本为行进成本和刀具转换成本之和。
为了解决问题,建立了以下三种模型:模型一:机械模型,按照所需刀具种类和打孔次序,将孔进行分类,并合理安排打孔刀具的顺序,进行分块局部优化。
认为用一种刀具打完相应所有孔后,再换刀;通过蚁群算法解得最短路径62480000mil,最短工作时间:2.46h,加工过程总费用95999.328(元)。
模型二:简化模型,以所有点为研究对象,进行全局优化。
假定钻孔行进过程中不进行换刀操作,打完某一孔后,先换刀,再行进。
利用贪婪算法和蚁群算法的混合算法解得,最短路径为54941000mil,最短工作时间:2.60h,加工过程总费用84570(元)。
模型三:改进模型,认为钻孔行进过程中进行换刀操作,通过引入有效换刀时间,将总的工作时间分为钻头行进时间和有效换刀时间。
利用贪婪算法和蚁群算法的混合算法解得,最短路径为55231000mil,最短工作时间:2.347h,加工过程总费用84570(元) ,经分析该模型精确度更高,具体的刀具转换方案及最优路径见附录(一)。
在模型二和模型三建立的过程中,将衡量孔的坐标由原始的二维空间坐标,扩充为四维坐标:二维空间坐标,所需刀具种类坐标,加工次序坐标。
这样将一个需要多种刀具才能打完的孔型,扩充为多个只需一种刀具的孔,有效的解决了不必一次性打完一个孔型的问题。
关键词:蚁群算法贪婪算法坐标维度扩充群孔加工路线设计Ⅰ问题的提出与重述印刷电路板(PCB)制造技术是电子信息制造业的重要基础和组成部分,而由打孔机完成的过孔作业在其生产中占有重要的地位。
电路板的打孔机工作流程设计

电路板的打孔机工作流程设计引言电路板的打孔是在电路板制造过程中的重要步骤之一。
打孔机的工作流程设计对于提高生产效率、保证打孔质量具有重要意义。
本文将介绍电路板的打孔机工作流程设计的相关内容。
打孔机工作流程设计的目标电路板的打孔机工作流程设计的目标是在保证产品质量的前提下,提高生产效率。
具体目标如下: 1. 提高打孔机的操作简便性,减少人员培训时间。
2. 保证打孔孔径的准确性和一致性。
3. 最大限度地减少打孔机故障和维修时间,提高设备可靠性和稳定性。
4. 提高打孔机的自动化程度,减少人工干预。
5. 确保打孔机工作流程的可追溯性,方便质量管理和问题排查。
打孔机工作流程设计的关键步骤电路板的打孔机工作流程设计包括以下关键步骤:1. 工艺参数设置在进行打孔机工作流程设计之前,首先需要对打孔工艺参数进行设置。
根据电路板的设计要求和材料特性,确定打孔孔径、孔距、孔排布方式等参数。
2. 材料准备在进行打孔之前,需要对电路板进行材料准备。
包括清洁电路板表面,去除杂质和污垢,确保电路板表面光滑,以便于打孔过程中的准确定位。
3. 机器调试在正式进行打孔之前,需要对打孔机进行调试和参数设置。
确保打孔机的正常运行和准确性。
调试包括打孔头的安装、打孔压力和速度的调整等。
4. 打孔操作在进行打孔操作时,首先需要对电路板进行定位,将电路板放置到打孔机的工作台上,并进行固定。
然后,通过操作界面输入打孔参数,并启动打孔机进行打孔操作。
5. 质量检查打孔完成后,需要进行质量检查。
检查包括对打孔孔径、孔距和孔排布的准确性进行验证。
可使用光学显微镜或其他检测仪器进行检查。
6. 数据记录和分析为了确保打孔机工作流程的可追溯性,需要对每次打孔的相关数据进行记录和分析。
包括打孔时间、打孔参数、质检结果等信息。
通过数据分析,可以对打孔机性能进行评估,并进行优化。
打孔机工作流程设计的优化方案为了进一步提高打孔机的工作效率和质量,可以采取以下优化方案:1. 引入自动化设备,减少人工干预。
PCB钻孔的流程、分类和技巧
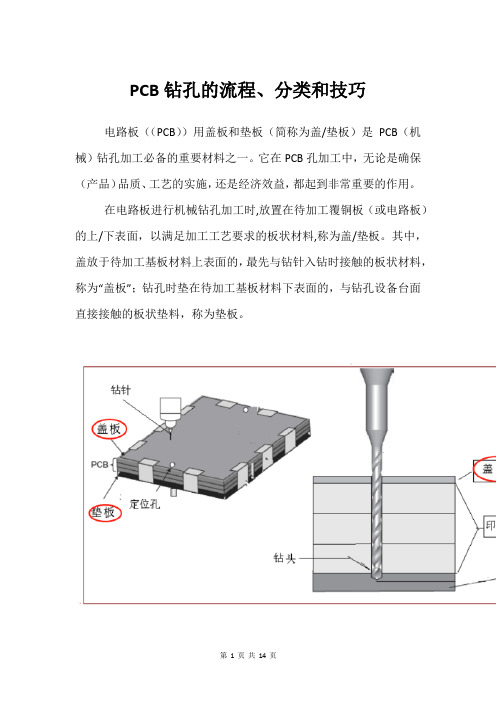
PCB钻孔的流程、分类和技巧电路板((PCB))用盖板和垫板(简称为盖/垫板)是PCB(机械)钻孔加工必备的重要材料之一。
它在PCB孔加工中,无论是确保(产品)品质、工艺的实施,还是经济效益,都起到非常重要的作用。
在电路板进行机械钻孔加工时,放置在待加工覆铜板(或电路板)的上/下表面,以满足加工工艺要求的板状材料,称为盖/垫板。
其中,盖放于待加工基板材料上表面的,最先与钻针入钻时接触的板状材料,称为“盖板”;钻孔时垫在待加工基板材料下表面的,与钻孔设备台面直接接触的板状垫料,称为垫板。
钻孔是PCB制造中最昂贵和最耗时的过程。
PCB钻孔过程必须小心实施,因为即使是很小的错误也会导致很大的损失。
钻孔工艺是PCB制造过程中最关键的工艺。
钻孔工艺是通孔和不同层之间连接的基础,因此钻孔技巧十分重要。
PCB钻孔一、PCB钻孔技术主要有2 种PCB 钻孔技术:机械钻孔和激光钻孔。
PCB钻孔技术1、机械钻孔机械钻头的精度较低,但易于执行。
这种钻孔技术实现了钻头。
这些钻头可以钻出的最小孔径约为6密耳(0.006 英寸)。
机械钻孔的局限性当用于FR4 等较软的材料时,机械钻可用于800 次冲击。
对于密度比较大的材料,寿命会减少到200 计数。
如果PCB 制造商忽视这一点,则会导致出现错误的孔,从而导致电路板报废。
2、激光钻孔另一方面,激光钻可以钻出更小的孔。
激光钻孔是一种非接触式工艺,工件和工具不会相互接触。
激光束用于去除电路板材料并创建精确的孔,可以毫不费力地控制钻孔深度。
激光技术用于轻松钻出受控深度的过孔,可以精确钻出最小直径为2 密耳(0.002”)的孔。
激光钻孔限制电路板由铜、玻璃纤维和树脂制成,这些PCB 材料具有不同的(光学)特性,这使得激光束很难有效地烧穿电路板。
在激光钻孔的情况下,该过程的成本也相对较高。
二、PCB钻孔流程对于PCB(工程师)来说,如果设计电路板,也必须要了解PCB 的制造。
这样才能保证(PCB设计)是可制造,也是可靠的,反过来如果在设计时就注意到制造上的工艺,可以降低成本,并且可以在规定的时间内交付产品。
PCB(印刷线路板) 钻孔流程简介

3-3 鑽孔
L 全長 overall length
柄 部 shank 斜 鑽針中心線 導腳 chamfer
Φ 0.005m/m 部
Φ 0.005m/m
பைடு நூலகம்
盤旋角 Helixangle
鑽部:主要功能為刺入、切削及退屑。 退屑溝:排除廢屑用,需平滑,以減少阻力。 尖部:是最先碰觸板材之處, 具定位功用。 斜部:主要功能為應力分散之用。 柄部:被 Spindle 夾具夾住的部份,而其尾部之導角為上套環所用 。 盤旋角:角度小時, 螺紋較少, 但廢屑退出以及鑽針之進入所受阻力較大, 容易升溫 造成尖部積屑積熱,形成樹脂之軟化而在孔壁上形成膠渣 (smear)。此螺旋角大 時鑽針的進入及退屑所受之磨擦阻力較小而不易發熱, 但退料太慢。
Margin
後讓腹地 第二面 第一面
鑽尖側面放大圖
第二面 (secondary facet ):為支撑第一面 : 的腹地。 刃角 ( corner ):為孔璧最後切削整修
鑽尖角 :130 ℃
鑽尖橫斷面放大圖
刃角
對孔璧品質影響最大,超過使用壽 命時會崩會變圓。 鑿刀 (chisel edge ):為最先在板材上定 位用。
靶距 Step 2 基準Pin上擺放以 “ 鑽靶 ” 完成之 “ 待鑽孔板 ”
三、鑽 孔 :
Step 3 此為上Pin作業之示意圖
3-2 上 Pin
推Pin氣壓缸 震動盤
Pin
常用之規格 Φ:3.175±0.025mm L:15.8±0.025mm
基準PIN
Step 4 上Pin完成後之情形
+
Step 5
PCB各製程介紹 各製程介紹
电路板钻孔制程介绍

六、鑽孔6.1製程目的單面或雙面板的製作都是在下料之後直接進行非導通孔或導通孔的鑽孔,多層板則是在完成壓板之後才去鑽孔。
傳統孔的種類除以導通與否簡單的區分外,以功能的不同尚可分:零件孔,工具孔,通孔(Via),盲孔(Blind hole),埋孔(Buriedhole)(後二者亦為via hole的一種).近年電子產品'輕.薄.短.小.快.'的發展趨勢,使得鑽孔技術一日千里,機鑽,雷射燒孔,感光成孔等,不同設備技術應用於不同層次板子.本章僅就機鑽部分加以介紹,其他新技術會在20章中有所討論.6.2流程上PIN→鑽孔→檢查6.3上PIN作業鑽孔作業時除了鑽盲孔,或者非常高層次板孔位精準度要求很嚴,用單片鑽之外,通常都以多片鑽,意即每個stack兩片或以上.至於幾片一鑽則視1.板子要求精度2.最小孔徑3.總厚度4.總銅層數.來加以考量.因為多片一鑽,所以鑽之前先以pin將每片板子固定住,此動作由上pin機(pinning maching)執行之.雙面板很簡單,大半用靠邊方式,打孔上pin連續動作一次完成.多層板比較複雜,另須多層板專用上PIN機作業.6.4.鑽孔6.4.1鑽孔機鑽孔機的型式及配備功能種類非常多,以下List評估重點A.軸數:和產量有直接關係B.有效鑽板尺寸C.鑽孔機檯面:選擇振動小,強度平整好的材質。
D.軸承(Spindle)E.鑽盤:自動更換鑽頭及鑽頭數F.壓力腳G.X、Y及Z軸傳動及尺寸:精準度,X、Y獨立移動H.集塵系統:搭配壓力腳,排屑良好,且冷卻鑽頭功能I.Step Drill的能力J.斷針偵測K.RUN OUT6.4.1.1鑽孔房環境設計A.溫濕度控制B.乾淨的環境C.地板承受之重量D.絕緣接地的考量E.外界振動干擾6.4.2物料介紹鑽孔作業中會使用的物料有鑽針(Drill Bit),墊板(Back-up board),蓋板(Entry board)等.以下逐一介紹:圖6.1為鑽孔作業中幾種物料的示意圖.圖6.16.4.2.1鑽針(Drill Bit),或稱鑽頭,其品質對鑽孔的良窳有直接立即的影響,以下將就其材料,外型構、及管理簡述之。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C题线路板的打孔机工作流程设计摘要本文讨论了电路板的打孔机工作流程中的费用及时间问题,在已知孔型、刀具及行走费用和转刀费用的前提下,综合考虑成本和时间,设计行走路线及换刀方案,使生产效率最高。
本文中首先采用了0-1整数规划方法(模型一),再采用二次逐边修正法(模型二),之后采用了贪心算法(模型三)。
在求解过程中,我们先考虑只打孔的情况,即遇到孔便打完,同时以最少费用为目标,对这三个模型进行比较,结果如下:模型一:该模型的变量较多,且使用0-1规划法,对matlab以及lingo的要求较高,鉴于我们的计算机条件,该模型只有理论上的意义。
模型二:在以最少费用为目标的条件下,费用为79232元,时间为49188秒(约合13.66小时)。
模型三:在以最少费用为目标的条件下,费用为44708元,时间为48665秒(约合13.5小时)。
在以最少时间为目标的条件下,费用为374090元,时间为56298秒(约合15.6小时)。
在模型的优化部分,本文将需要两种刀具(或三种)的孔视为两种孔型(或三种),如C型孔,视为C1和C2两种孔型,分别用a刀和c刀(有下刀顺序),D型孔视为两个独立的孔D1和D2(无下刀顺序)。
同时综合考虑费用和时间,建立适合大规模生产的模型,取合适的权值(以费用60%、时间40%为例),费用为49276元,时间为21272秒(约合5.9小时)。
一、问题的重述过孔是印刷线路板(也称为印刷电路板)的重要组成部分之一,过孔的加工费用通常占制板费用的30%到40%,打孔机主要用于在制造印刷线路板流程中的打孔作业。
本问题旨在提高某类打孔机的生产效能。
打孔机的生产效能主要取决于以下几方面:(1)单个过孔的钻孔作业时间,这是由生产工艺决定,为了简化问题,这里假定对于同一孔型钻孔作业时间都是相同的;(2)打孔机在加工作业时,钻头的行进时间;(3)针对不同孔型加工作业时,刀具的转换时间。
目前,实际采用的打孔机普遍是单钻头作业,即一个钻头进行打孔。
现有某种钻头,上面装有8种刀具a ,b ,c ,… , h ,依次排列呈圆环状,如图1所示。
图1:某种钻头上8种刀具的分布情况而且8种刀具的顺序固定,不能调换。
在加工作业时,一种刀具bc dfh a使用完毕后,可以转换使用另一种刀具。
相邻两刀具的转换时间是18 s,例如,由刀具a转换到刀具b所用的时间是18s,其他情况以此类推。
作业时,可以采用顺时针旋转的方式转换刀具,例如,从刀具a转换到刀具b;也可以采用逆时针的方式转换刀具,例如,从刀具a转换到刀具h。
将任一刀具转换至其它刀具处,所需时间是相应转换时间的累加,例如,从刀具a转换到刀具c,所需的时间是36s (采用顺时针方式)。
为了简化问题,假定钻头的行进速度是相同的,为180 mm/s,行进成本为0.06元/mm,刀具转换的时间成本为7元/min。
刀具在行进过程中可以同时进行刀具转换,但相应费用不减。
不同的刀具加工不同的孔型,有的孔型只需一种刀具来完成,如孔型A只用到刀具a。
有的孔型需要多种刀具及规定的加工次序来完成,如孔型C需要刀具a和刀具c,且加工次序为a,c。
表1列出了10种孔型所需加工刀具及加工次序(标*者表示该孔型对刀具加工次序没有限制)。
表1:10种孔型所需加工刀具及加工次序一块线路板上的过孔全部加工完成后,再制作另一线路板。
但在同一线路板上的过孔不要求加工完毕一个孔,再加工另一个孔,即对于须用两种或两种以上刀具加工的过孔,只要保证所需刀具加工次序正确即可。
请建立相应的数学模型,并完成以下问题:(1)附件1提供了某块印刷线路板过孔中心坐标的数据,单位是密尔(mil)(也称为毫英寸,1 inch=1000 mil),请给出单钻头作业的最优作业线路(包括刀具转换方案)、行进时间和作业成本。
二、问题的分析本题的主要问题,是考虑行走的费用、时间以及转刀的费用、时间,找到一条遍历所有点的合适的行走路径,使生产的效率达到最高。
在MATLAB软件中,我们画出了这十种孔型的坐标(见附录1),发现孔的数目很多,既有集中的孔,也有相对分散的孔。
因此,所建的模型,应该要将所有的点都走遍,这一点可以参照TSP的相关算法,同时考虑到各种换刀问题。
从收集的资料可以看出,解决TSP问题的一般算法有遗传算法,模拟退火算法,贪心算法,二次逐边修正法等等。
考虑到本题并不是完全意义上的TSP问题,本文对使用的方法进行了一定程度改进,例如考虑将路程和转刀的因素统一成时间或是费用,使其更适合本题的要求。
考虑到本题要求得出打孔的费用和时间,因此有不同生产效率的生产线,对费用和时间有不同的要求,因此在模型求解的过程中应该要考虑到对费用和时间赋予不同的权数,得出不同的行走方案,最终确定符合要求且效率高的行走路径和转刀方案。
三、模型假设1、加工每块板工作过程中,无刀具磨损、损坏情况,中途无间断。
2、钻头钻孔、刀具加工的结果均合格,不存在残品孔。
3、钻头钻孔时间及费用固定,不予考虑。
4、刀具行进速度保持恒定。
5、周围环境对钻头和刀具没有干扰。
6、钻头和刀具可以按照设定的路程准确行走和换刀。
7、刀具行进过程中两点之间所走路径为直线。
四、符号说明m:点的数目(2124个)。
M: 将孔拆分后点的数目(2814个)。
Wij :为0-1变量,Wij=1表示,i点可到达j点,Wij=0表示,i点不能到达j点。
Lij :移动的费用加换刀具的费用。
Ni :为0-1变量,保证有m-1条折线。
mm:转刀费用矩阵(10*10)。
mm1:转刀费用矩阵(18*18)。
x :点的横坐标。
y :点的纵坐标。
S1 :i点到j点的费用(包括路程费和转刀费)。
S2 :i+1点到j+1点的费用(包括路程费和转刀费)。
S3 :i 点到i+1点的费用(包括路程费和转刀费)。
S4 :j 点到j+1点的费用(包括路程费和转刀费)。
S(i): i 点到i+1点的费用(包括路程费和转刀费)。
F(i): i 到i+1点所用时间(路程所用时间和转刀所用时间中较大的一个)。
fare :总费用。
V1:fare 权数。
time :总时间。
V2:time 权数。
五、模型的建立和求解(1),模型一的建立(0-1规划模型)通过以上分析,我们建立了模型一,综合考虑总路程与总费用,通过0-1规划思想来求取最优解。
11ij 11**min 11111-=<=+==∑∑∑∑∑=====m Ni Wji W Wij Wij NiLij Wij mi mj mi mi mj其中∑∑-=m11**min i mj NiLij Wij 表示最小费用的目标函数。
1m1=∑=i Wij 表示回路只能到达各顶点一次。
1m1=∑=j Wij 表示回路只能从各顶点出发一次。
1<=+Wji Wij 表示两点之间只有一条路径连接。
模型一从0-1 整数规划角度给出了一个只考虑总回路路程最短的M-TSP 问题模型。
对于这样一个规划问题,每个分组对应着一个TSP 问题,相关资料显示,由于数据量特别大现有的Lingo 和Matlab 软件不能求解或不能精确求解,故该模型只有理论意义,不能在现有的软件下实现。
下面讨论用一些简化的方法来求得问题的近似解。
(2)模型二的建立(二边逐次修正法)1、按照附件中给定点的顺序在坐标纸上将各点依次连接,命名为路径a1。
2、对所有的i 、j ,1<i+1<j<m,若S1+S2<S3+S4,则在a1中删去路径i 到i+1和j 到j+1两条路径,而选择i 到j 和i+1到j+1两条路径,形成新的路径a2。
3、重复步骤(2),直到满足条件,最后的路径即为所求的路径a 。
4、计算总的费用:1.2*)1,(001524.0*2))^(y -)1((2))^()1(()i (++++-+=i i mm i i y i x i x S∑==1-m 1i )i (fare S其中mm 矩阵如下(不考虑换刀时的转刀费(从竖列到横行)): D C ,表示D 打完到C 打完,需要换刀六次。
取得路径a 之后即可求解出最小费用。
结果表明:以最小费用为目标,需要79232元,时间为 49188秒(约合13.66小时),具体的行走路径、路径图及程序见附件1(按点给出初始顺序依次排序为1号到2124号,打孔的顺序即按编号排列,附件2、3同样)。
(3)模型三的建立(贪心算法)1、选择一个起点,计算这个起点到其它各点的费用(路程费加转刀费),选择费用最小的一个点作为下一个起点,计算费用S(1)。
2、计算新的起点到其它点的费用(不包括已选定的点),选择费用最小的点作为下一个起点,计算费用S(2)。
3、重复步骤2,直到遍历各点,求出相应费用S(i)。
4、计算总的费用:1.2*)1,(001524.0*2))^(y -)1((2))^()1(()i (++++-+=i i mm i i y i x i x S∑==1-m 1i )i (fare S)18*)1,(,180/0254.0*2))^(y -)1((2))^()1((max ()i (+++-+=i i mm i i y i x i x F∑==1-m 1i )i (time F结果表明:在以最少费用为目标的条件下,费用为44708元,时间为48665秒(约合13.5小时)。
同模型二相比,该模型所需的费用更少。
具体的行走路径、路径图及程序见附件2。
考虑到本设计方案要应用于大规模工业生产,故而对单个板加工时间有一定要求。
基于这种考虑,本文对费用和时间进行加权。
在以最少时间为目标的条件下,费用为374090元,时间为56298秒(约合15.6小时)。
具体的行走路径、路径图及程序见附件3。
六、模型的优化由原题可知,当需要两种(或三种)刀具的孔型,过孔不要求加工完毕一个孔,再加工另一个孔,即对于须用两种或两种以上刀具加工的过孔,只要保证所需刀具加工次序正确即可。
故而将两种刀具(或三种)的孔视为两种孔型(或三种),则可得到18*18种换刀的情况,即mm1矩阵:针对这种方法,结合贪心算法,给出优化模型,如下:1、选择一个起点,计算这个起点到其它各点的费用(路程费加转刀费),选择费用最小的一个点作为下一个起点,计算费用S(1)。
2、计算新的起点到其它点的费用(不包括已选定的点和某些有下刀顺序限制的点),选择费用最小的点作为下一个起点,计算费用S(2)。
3、重复步骤2,直到遍历各点,求出相应费用S(i)。
4、计算总的费用:+=i imm+++-i)i(+ xSxiiyi2.0*2001524,(11.2*)1))^(y-)1)1(())^(((∑==1-M 1i )i (fare S)18*)1,(1,180/0254.0*2))^(y -)1((2))^()1((max()i (+++-+=i i mm i i y i x i x F∑==1-M 1i )i (time FV1、V2求一些值时的结果如下:由上表可以看出,优化后最小费用为4.4万元较优化前的4.5万元降低了。
