贪心算法程序设计
程序设计五大算法

程序设计五大算法算法是计算机程序设计中非常重要的概念,它是一系列解决问题的步骤和规则。
在程序设计中,有许多经典的算法被广泛应用于各种领域。
下面将介绍程序设计中的五大算法,包括贪心算法、分治算法、动态规划算法、回溯算法和图算法。
1. 贪心算法贪心算法是一种简单而高效的算法,它通过每一步都选择当前最优解来达到全局最优解。
贪心算法通常适用于那些具有最优子结构的问题,即问题的最优解可以通过子问题的最优解来推导。
例如,找零钱问题就可以使用贪心算法来解决,每次选择面额最大的硬币进行找零。
2. 分治算法分治算法将问题分解成更小的子问题,然后递归地求解这些子问题,最后将子问题的解合并起来得到原问题的解。
分治算法通常适用于那些可以被划分成多个相互独立且相同结构的子问题的问题。
例如,归并排序就是一种典型的分治算法,它将待排序的数组不断划分成两个子数组,然后分别对这两个子数组进行排序,最后将排序好的子数组合并成一个有序数组。
3. 动态规划算法动态规划算法通过将问题划分成多个重叠子问题,并保存子问题的解来避免重复计算,从而提高算法的效率。
动态规划算法通常适用于那些具有最优子结构和重叠子问题的问题。
例如,背包问题就可以使用动态规划算法来解决,通过保存每个子问题的最优解,可以避免重复计算,从而在较短的时间内得到最优解。
4. 回溯算法回溯算法是一种穷举法,它通过尝试所有可能的解,并回溯到上一个步骤来寻找更好的解。
回溯算法通常适用于那些具有多个决策路径和约束条件的问题。
例如,八皇后问题就可以使用回溯算法来解决,通过尝试每个皇后的位置,并检查是否满足约束条件,最终找到所有的解。
5. 图算法图算法是一类专门用于处理图结构的算法,它包括图的遍历、最短路径、最小生成树等问题的解决方法。
图算法通常适用于那些需要在图结构中搜索和操作的问题。
例如,深度优先搜索和广度优先搜索就是两种常用的图遍历算法,它们可以用于解决迷宫问题、图的连通性问题等。
贪心算法(4):活动选择问题
贪⼼算法(4):活动选择问题我们继续回到上⼀堂课留下的课外习题:活动选择问题。
活动选择问题是很常见的场景。
例如各个部门共享⼀个会议室,利⽤该算法能使会议室安排尽量多的会议。
【问题】给你n个活动的开始时间和结束时间,从中选择你可以参与的活动,但是同⼀时间你只能参与⼀个活动,请找出你可以参与的最多活动数。
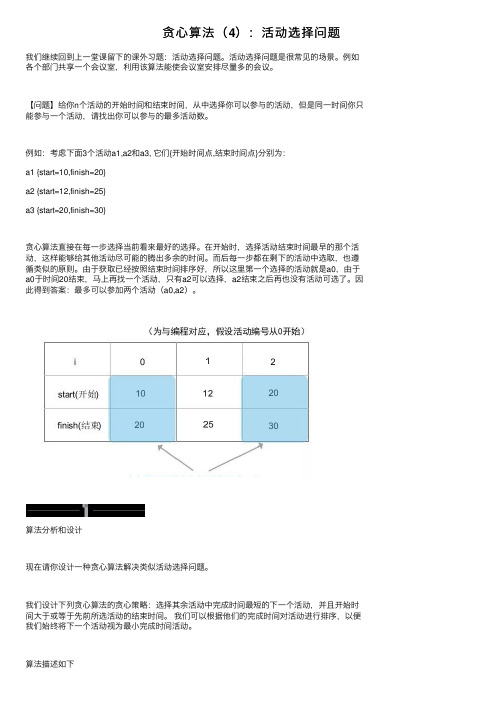
例如:考虑下⾯3个活动a1,a2和a3, 它们{开始时间点,结束时间点}分别为:a1 {start=10,finish=20}a2 {start=12,finish=25}a3 {start=20,finish=30}贪⼼算法直接在每⼀步选择当前看来最好的选择。
在开始时,选择活动结束时间最早的那个活动,这样能够给其他活动尽可能的腾出多余的时间。
⽽后每⼀步都在剩下的活动中选取,也遵循类似的原则。
由于获取已经按照结束时间排序好,所以这⾥第⼀个选择的活动就是a0,由于a0于时间20结束,马上再找⼀个活动,只有a2可以选择,a2结束之后再也没有活动可选了。
因此得到答案:最多可以参加两个活动(a0,a2)。
算法分析和设计现在请你设计⼀种贪⼼算法解决类似活动选择问题。
我们设计下列贪⼼算法的贪⼼策略:选择其余活动中完成时间最短的下⼀个活动,并且开始时间⼤于或等于先前所选活动的结束时间。
我们可以根据他们的完成时间对活动进⾏排序,以便我们始终将下⼀个活动视为最⼩完成时间活动。
算法描述如下{k}}U{1},必定仍然是⼀个最佳解决⽅案,说明如下:因为S 中的活动是独⽴的,⽽在排序队列中,【活动1】在所有活动中具有最⼩的结束时间,因为k不等于1,【活动k】的完成时间必定是⼤于等与【活动1】的完成时间,因此把【活动k】换成【活动1】后的新⽅案S‘必定也是最佳解决⽅案。
算法实现在以下C/C++代码实现中,假设活动已根据其完成时间进⾏了排序。
#include<stdio.h>// n --> 活动个数// s[] --> 数组保存所有活动的开始时间// f[] --> 数组保存所有活动的结束时间void printMaxActivities(int s[], int f[], int n){int i, j;printf ('选择以下的活动\n');// 第⼀个活动总是选中i = 0;printf('%d ', i);// 依次检查余下的活动for (j = 1; j < n; j++){//如果某活动在之前选择的活动结束之后开始if (s[j] >= f[i]){printf ('%d ', j);i = j;}}}//主程序int main(){int s[] = {1, 3, 0, 5, 8, 5};int f[] = {2, 4, 6, 7, 9, 9};int n = sizeof(s)/sizeof(s[0]);printMaxActivities(s, f, n);return 0;}注意:若是finish数组没有排序,需要先对它进⾏排序。
贪心算法程序设计

贪心算法程序设计贪心算法程序设计1. 什么是贪心算法贪心算法(Greedy Algorithm)是一种常见的算法思想,它在每一步选择中都采取当前状态下的最优选择,从而希望最终达到全局最优解。
贪心算法的核心思想是局部最优解能导致全局最优解。
2. 贪心算法的基本步骤贪心算法的基本步骤如下:1. 定义问题的优化目标。
2. 将问题分解成子问题。
3. 选择当前最优的子问题解,将子问题的解合并成原问题的解。
4. 检查是否达到了问题的优化目标,如果没有达到,则回到第二步,继续寻找下一个最优子问题解。
5. 在所有子问题解合并成原问题解后,得到问题的最优解。
3. 贪心算法的应用场景贪心算法的应用非常广泛,几乎可以用于解决各种优化问题。
以下几个常见的应用场景:1. 零钱找零问题:给定一定面额的纸币和硬币,如何找零使得所需纸币和硬币的数量最小?2. 区间调度问题:给定一些活动的开始时间和结束时间,如何安排活动使得可以办理的活动数量最大?3. 背包问题:给定一些具有重量和价值的物品,如何选择物品使得背包的总价值最大?4. 最小树问题:给定一个带权无向图,如何找到一棵树,使得它的边权之和最小?5. 哈夫曼编码问题:给定一组字符和相应的频率,如何构造一个满足最低编码长度限制的二进制编码?4. 贪心算法的优缺点贪心算法的优点是简单、高效,可以快速得到一个近似最优解。
而且对于一些问题,贪心算法能够得到全局最优解。
贪心算法的缺点在于它不一定能够得到全局最优解,因为在每一步只考虑局部最优解,无法回溯到之前的选择。
5. 贪心算法的程序设计在使用贪心算法进行程序设计时,通常需要以下几个步骤:1. 定义问题的优化目标。
2. 将问题分解成子问题,并设计子问题的解决方案。
3. 设计贪心选择策略,选择局部最优解。
4. 设计贪心算法的递推或迭代公式。
5. 判断贪心算法是否能够得到全局最优解。
6. 编写程序实现贪心算法。
6.贪心算法是一种常见的算法思想,它在每一步选择中都采取当前状态下的最优选择,从而希望最终达到全局最优解。
程序设计竞赛常用算法

程序设计竞赛常用算法1.排序算法:排序是一个基本的算法问题,常见的排序算法有冒泡排序、选择排序、插入排序、快速排序、归并排序等。
这些排序算法有各自的优势和适用场景,需要根据具体问题需求选择合适的算法。
2.图论算法:图论是程序设计竞赛中经常出现的重要领域。
常见的图论算法有深度优先(DFS)、广度优先(BFS)、Dijkstra算法、Floyd-Warshall算法、拓扑排序、最小生成树等。
这些算法可以用于解决最短路径、连通性、最大流最小割等问题。
3.动态规划:动态规划是一种常用于解决优化问题的算法。
该算法通过将问题分解成子问题,并记录子问题的解来求解原问题的最优解。
常见的动态规划算法有背包问题、最长公共子序列(LCS)、最大子序列和等。
4.字符串处理算法:字符串处理是程序设计竞赛中常见的问题。
常见的字符串处理算法有KMP算法、哈希算法、字符串匹配等。
这些算法可以用于解决模式匹配、字符串、字符统计等问题。
5.数学算法:数学算法在程序设计竞赛中也经常被使用。
常见的数学算法有质因数分解、素数筛、快速乘法、高精度计算等。
这些算法可以用于解决数论、计算几何、概率等问题。
6.图形算法:图形算法主要用于处理图像和几何图形。
常见的图形算法有扫描线算法、凸包算法、几何运算等。
这些算法可以用于解决图像处理、三维建模等问题。
7.树和图的遍历算法:树和图的遍历算法是程序设计竞赛中常用的算法之一、常见的树和图的遍历算法有先序遍历、中序遍历、后序遍历、深度优先(DFS)、广度优先(BFS)等。
这些算法可以用于解决树和图的构建、路径等问题。
8.最大匹配和最小割算法:最大匹配算法用于求解二分图的最大匹配问题,常见的算法有匈牙利算法。
最小割算法用于求解图的最小割问题,常见的算法有Ford-Fulkerson算法。
这些算法可以用于解决网络流和二分图匹配等问题。
9.贪心算法:贪心算法是一种常用于优化问题的算法。
该算法通过每一步选择局部最优解来达到全局最优解。
软件设计师下午题算法技巧

软件设计师下午题算法技巧下午题算法技巧包括如下几种常见的算法技巧:1. 贪心算法(Greedy Algorithm):贪心算法是一种基于局部最优选择的算法策略,每一步都选择当前最优解,最终得到全局最优解。
例如,找零钱问题可以使用贪心算法,每次尽可能选择面额最大的零钱来找零。
2. 动态规划(Dynamic Programming):动态规划是一种将原问题分解为子问题求解的方法,将子问题的解保存下来,避免重复计算。
例如,背包问题可以使用动态规划来求解,通过构建一个二维数组保存每个子问题的解,避免重复计算。
3. 分治算法(Divide and Conquer):分治算法将原问题分解成相互独立且相同的子问题,然后将子问题的解合并得到原问题的解。
例如,归并排序就是一种典型的分治算法。
4. 回溯算法(Backtracking):回溯算法通过递归地尝试所有可能解,并在不满足条件时进行回溯,尝试其他解。
例如,八皇后问题可以使用回溯算法来求解,在每个位置上尝试放置一个皇后,如果不满足条件则回溯,尝试其他位置。
5. 搜索算法(Search):搜索算法通常用于在大规模的搜索空间中找到目标解。
例如,深度优先搜索(DFS)和广度优先搜索(BFS)都是常见的搜索算法。
6. 排序算法(Sorting):排序算法用于将一组数据按照某个规则进行排序。
例如,快速排序、归并排序、堆排序等都是常见的排序算法。
7. 图算法(Graph):图算法用于解决与图相关的问题,例如最短路径、最小生成树等。
例如,Dijkstra算法用于求解带权图中的最短路径问题。
这些算法技巧在软件设计中经常会用到,根据具体的问题场景选择合适的算法技巧可以提高程序的效率和准确性。
Rectangle Packing问题的程序设计

Rectangle Packing问题贪心算法的Pascal程序设计报告Flowers bi**a*c**b【摘要】本文主要阐述了基于贪心算法的Rectangle Packing问题的Pascal程序实现方法,介绍了程序主要procedure的作用和部分功能模块的实现算法。
【关键词】贪心算法;Rectangle Packing;Pascal;程序;回溯。
一. 程序设计任务及要求设计一个程序利用贪心算法对Rectangle Packing问题进行求解。
输入容器和各个待填矩形块的长宽,输出尽可能高空间利用率的装填方法,填入矩形块数和空间未利用率。
二. Rectangle Packing问题的贪心算法简介基本原理在某一时刻,已经按放置规则向矩形容器中放置了若干矩形块,对将要放入的矩形块,最好是占据某个角,其次是贴边,最差的是悬空。
用贪心的思路,找到合适的矩形块并按合适的位置放入使其占角最多,贴边最多,剩余角点数最少,并用回溯对这种放置方法进行评估,以找到这一时刻最适合的放法。
基本流程1.对容器状态进行初始化。
2.按照规则选择一个最优的矩形块放入容器。
如果这个放置动作的穴度为1,则继续进行下一个放置动作,否则通过回溯找到当前最优的放置位置。
3.重复2步骤,直至所有矩形块都已经放入容器或者容器中已无法再放入任何矩形。
4.对容器中矩形放置状态进行分析,求出放入矩形块数和空间未利用率。
三. 需求分析根据算法的基本需求和流程,用程序实现时,总体应分为输入、初始化、放置矩形、结果分析、输出五个基本步骤来对问题进行求解,其流程方框图如下:四. 用Pascal实现Rectangle Packing问题的贪心算法1. 程序定义的主要的数组型变量:w,h:array [1..300] of integer; {width and height of each rectangles}used:array [1..300] of boolean; {Hash table for used rectangles}state:array [1..300,1..4] of integer; {location of put rectangles}legalpos:array [1..10000,1..7] of integer; {legal position of newly put rectangle} dmin:array [1..10000] of integer; {min distance of put rectangle and others} c:array [1..10000] of real; {caving degree of each rectangles}c1:array [1..1000] of integer; {rectangles of 1 caving degree} cornercheck:array [1..4,1..2] of boolean; {Hash table for occupied corners} corners:array [1..300] of integer; {occupied corners of each coa}2. 程序中主要的procedure的作用:procedure init “输入”——用于读入容器和各个矩形的长宽。
“知乎杯”2018CCF大学生计算机系统与程序设计竞赛贪心算法(greedy)

“知乎杯”2018CCF⼤学⽣计算机系统与程序设计竞赛贪⼼算法(greedy)-->贪⼼算法1)题解•分别⽤V0、V1和V>=2表⽰度为0、1以及⾄少为2的顶点集合•对于每个顶点,维护三个属性:•degree 邻居的个数•degree2邻居中度为2的顶点数•id 编号Pseudo-code•initialize V0, V1, V>=2 and (degree, degree2, id) of each node•while G is not empty•if V0 is not empty•choose v ∈ V0 with the smallest id•output v, delete v from V0 and G•else if V1 is not empty•choose v ∈ V1 with the smallest id, and find the neighbor u of v•output v, delete v from V0 and G, delete u from V1(or V>=2) and G•else•choose v ∈ V>=2 with the largest (degree, degree2, id)•delete v from V>=2 and G索引的维护•需要注意的是,每个顶点的属性以及顶点集合V0、V1和V>=2并⾮⼀成不变。
•当从图中删去某个顶点u时,u邻居的degree均会减⼀;如果u的degree恰好为2,那么u邻居的degree2也会减⼀。
•如果某个邻居v的degree恰好从3减少到2或从2减到1,那么还会进⼀步影响到v的邻居的degree2属性。
•对于那些degree减⼀的顶点,还需要相应地更新V0、V1和V>=2。
Delete Node u from G•for v ∈ Neighbor(u)•v.degree decreases by one•if u.degree == 2 then v.degree2 decreases by one•if v.degree == 0•move v from V1 to V0•else if v.degree == 1•move v from V>=2 to V1•find the only neighbor w of v•w.degree2 decreases by one•else if v.degree == 2•for w ∈ Neighbor(v) do w.degree2 increases by one2)复杂度分析V0和V1 {node_id}•插⼊、删除顶点,但每个顶点最多⼀次;•查询id最⼩的顶点。
实验项目名称∶用贪心算法解单源最短路径问题

实验项目名称:用贪心算法解单源最短路径问题一、实验目的:明确单源最短路径问题的概念;利用贪心算法解决单源最短路径问题;并通过本例熟悉贪心算法在程序设计中的应用方法。
二、实验原理:贪心算法原理:在贪婪算法(greedy method)中采用逐步构造最优解的方法。
在每个阶段,都作出一个看上去最优的决策(在一定的标准下)。
决策一旦作出,就不可再更改。
作出贪婪决策的依据称为贪婪准则(greedy criterion)。
三、实验内容与步骤:问题描述:求网(带权有向图)中从一个顶点到其余各顶点间的最短路径。
一个有向图G,它的每条边都有一个非负的权值c[i,j],“路径长度”就是所经过的所有边的权值之和。
对于源点需要找出从源点出发到达其他所有结点的最短路径。
基本思想分步求出最短路径,每一步产生一个到达新目的顶点的最短路径。
下一步所能达到的目的顶点通过如下贪婪准则选取:在未产生最短路径的顶点中,选择路径最短的目的顶点。
设置顶点集合S并不断作贪心选择来扩充这个集合。
当且仅当顶点到该顶点的最短路径已知时该顶点属于集合S。
初始时S中只含源。
设u为G中一顶点,我们把从源点到u 且中间仅经过集合S中的顶点的路称为从源到u特殊路径,并把这个特殊路径记录下来(例如程序中的dist[i])。
每次从V-S选出具有最短特殊路径长度的顶点u,将u添加到S中,同时对特殊路径长度进行必要的修改。
一旦V=S,就得到从源到其他所有顶点的最短路径,也就得到问题的解。
如上图所示,编程实现求从任一顶点出发到其它顶点的最短路径长度。
如下:please input the first number:00->0:00->1:450->2:100->3:250->4:450->5:50please input the first number:11->0:351->1:01->2:151->3:181->4:101->5:15please input the first number:22->0:202->1:352->2:02->3:152->4:452->5:50please input the first number:33->0:553->1:203->2:353->3:03->4:303->5:35please input the first number:44->0:634->1:284->2:434->3:84->4:04->5:5please input the first number:55->0:585->1:235->2:385->3:35->4:335->5:0四实验结果与结论自己总结五实验中遇到的问题及解决办法自己总结六实验结论自己总结参考程序段如下#include<stdio.h>#define MAX 10000int main(){int cost[6][6]={{0,50,10,MAX,45,MAX},{MAX,0,15,MAX,10,MAX},{20,MAX,0,15,MAX,MAX},{MAX,20,MAX,0,35,MAX},{MAX,MAX,MAX,30,0,5},{MAX,MAX,MAX,3,MAX,0}};int s[6],dist[6];int n;int i,j,k,m,min;clrscr();printf("please input the first number:");while(scanf("%d",&n)&&n>=0&&n<6){for(i=0;i<6;i++){s[i]=0;dist[i]=cost[n][i];}s[n]=1,dist[n]=0;for(j=1;j<6;j++){min=MAX;for(k=0;k<6;k++){if(s[k]==0&&min>dist[k]){min=dist[k];m=k;}}if(min==MAX)break;s[m]=1,dist[m]=min;for(k=0;k<6;k++){if(s[k]==0)dist[k]=(dist[k]<(dist[m]+cost[m][k]))?dist[k]:(dist[m]+cost[m ][k]);}}for(i=0;i<6;i++){if(dist[i]<MAX)printf("%d->%d:%d\n",n,i,dist[i]);}printf("please input the first number:");}}。
著名算法matlab编程 贪心算法 背包问题 递归算法 Hanoi塔问题 回溯算法 n皇后问题

10/22
在命令窗口输入:>> [n,s]=hanoi(3,1,2,3) n= 7 s= 1 2 1 3 1 2 1 1 1 3 1 2 2 1 3 2 2 3 1 3 3
1
1 2 3
2 3 3 3 1
2
3
1
2 1 2
1
1 2
2
3
3
1
2 3
1 2 3
11/22
5/22
A
B
C
1
2
n
6/22
问题分析: 把柱C作为目标柱子,设an为n块金片从其中一柱移 到另一柱的搬运次数,则把n块金片从A移到C,可 以先把前n-1片移到B,需搬an-1次;接着把第n片从 A称到C,再从B把剩下的n-1片搬到C,又需搬an-1 次。所以从A到n块金片称到柱C,共需次数为: 2an-1+1次。 显然,当n=1时,a1=1,所以Hanoi塔的移动次数相 当于一个带初值的递归关系:
有 旅 行 者 要 从 n 种 物 品 中 选 取 不 超 过 b公 斤 的 物 品 放 入 背 包 , 要 求 总 价 值 最 大 。 设 第 i 种 物 品 的 重 量 为 a i, 价 值 为 c i,i 1, 2 , n )。 定 义 向 量 [ x 1 , x 2 , , x n ], 当 选 第 i ( 种 物 品 往 背 包 放 时 取 x i 1, 否 则 取 x i 0。 于 是 所 有 选 取 的 物 品 的 总 价 值 为 : c 1 x 1 c 2 x 2 c n x n, 总 的 重 量 为 : a 1 x 1 a 2 x 2 a n x n。 问 题 可 描 述 为
贪心算法设计实验报告

A
B
C
D
E
F
G
0
0
0
0
1
0
0
0
对表进行维护(维护后仍同上表,因为还没有两个集合合并)
0
A
B
C
D
E
F
G
0
0
0
0
1
0
0
0
C,选择第二条边 C----E (修改上表)
0
A
B
C
D
E
F
G
0
0
0
0
1
3
0
0
对上表进行维护(任同上表,因为还没有两个集合合并)
0
A
B
C
D
E
F
G
0
0
0
0
1
3
0
0
D,选择第三条边( D-----F ) (根据条件 DF 两点不再同一集合,改边可选 ) 然后就合并 DF 两点所在的集合 D 的前去是 1,即 A 标记为 0, E 的标记也为 0,合并因为 6>1 所以表修改如下
Edge* selectionsort(Edge *array,int n)// 选择排序(对边按权重由高到低排序) {
int i,j,min,temp; for(i=0;i<n;i++) {
min=i; for(j=i+1;j<n;j++)
if(array[min].weight>array[j].weight) min=j;
在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直至森林中
只有一棵树,也即子图中含有
浙江大学 算法与程序设计 贪心算法

13
Planning of schools
A collection of towns. We want to plan schools in towns.
Each school should be in a town No one should have to travel more than 30 miles to reach one of them.
9
Analysis – exact solution cont.
Let A {A1,, Ak } and OPT {B1,, Bm} be sorted. By definition of OPT we have k ≤ m Fact: for every i ≤ k, Ai finishes not later than Bi. Pf. by induction.
nt 1 nt 1 nt nt (1 ) k k
17
Upper bound con.
Then , since 1 x e x for all x, with equality if and only if x=0.
1 t nt n0 (1 ) k
Thus
1 t nt n0 (1 ) n0 (e 1/ k )t ne t / k k
Analyzing optimal greedy algorithms by showing that:
in every step it is not worse than any other algorithm, or every algorithm can be gradually transformed to thegreedy one without hurting its quality
贪心算法----删数问题

贪⼼算法----删数问题
⼀、问题描述
给定n位整数a,去掉其中任意k<=n个数字后,剩下的数字按原次序排列组成⼀个新的正整数。
如输⼊⼀个正整数:178543;
删除其中4个数
得到:13
⼆、解决思路--贪婪算法
这⾥先介绍之前错误的思路:
找出数字中n-k个最⼩的数,组成新的正整数;
但是很快就有问题出现,虽然每次都找的是整数各个位置中最⼩的数,但是忽略掉了位置的相对关系,如以下的例⼦:
输⼊的⼀个整数:178906; 6位数的整数
删除其中4个数;
按照这个思路,即要选择6-4=2个最⼩的数,即0 和1,按照数中原有的次序,得到的是10;
但是事实上,应该是06,即6
所以换个思路,叫“最近下降点”优先。
利⽤“最陡下降点”优先,即每次找到第⼀个元素,使其满⾜⼤于下⼀个元素。
正如上述的那个例⼦,第⼀个删除的是9,因为9>0;
得到的整数是17806;第⼆个删除的是8,因为8>0,得到的整数是1706,第三个删除的是7,因为7>0,得到的整数是106;
第四个删除的是1,因为1>0,得到的是06,为正确的答案。
三、程序设计
(1)同样,给出错误的设计思路的程序:
(2)正确的设计思路的程序:。
贪心算法实现背包问题算法设计与分析实验报告

算法设计与分析实验报告实验名称贪心算法实现背包问题评分实验日期年月日指导教师姓名专业班级学号一.实验要求1. 优化问题有n个输入,而它的解就由这n个输入满足某些事先给定的约束条件的某个子集组成,而把满足约束条件的子集称为该问题的可行解。
可行解一般来说是不唯一的。
那些使目标函数取极值(极大或极小)的可行解,称为最优解。
2.贪心法求优化问题算法思想:在贪心算法中采用逐步构造最优解的方法。
在每个阶段,都作出一个看上去最优的决策(在一定的标准下)。
决策一旦作出,就不可再更改。
作出贪心决策的依据称为贪心准则(greedy criterion)。
3.一般方法1)根据题意,选取一种量度标准。
2)按这种量度标准对这n个输入排序3)依次选择输入量加入部分解中。
如果当前这个输入量的加入,不满足约束条件,则不把此输入加到这部分解中。
procedure GREEDY(A,n) /*贪心法一般控制流程*///A(1:n)包含n个输入//solutions←φ //将解向量solution初始化为空/for i←1 to n dox←SELECT(A)if FEASIBLE(solution,x)then solutions←UNION(solution,x)endifrepeatreturn(solution)end GREEDY4. 实现典型的贪心算法的编程与上机实验,验证算法的时间复杂性函数。
二.实验内容1. 编程实现背包问题贪心算法。
通过具体算法理解如何通过局部最优实现全局最优,并验证算法的时间复杂性。
2.输入5个的图的邻接矩阵,程序加入统计prim算法访问图的节点数和边数的语句。
3.将统计数与复杂性函数所计算比较次数比较,用表格列出比较结果,给出文字分析。
三.程序算法1.背包问题的贪心算法procedure KNAPSACK(P,W,M,X,n)//P(1:n)和W(1;n)分别含有按P(i)/W(i)≥P(i+1)/W(i+1)排序的n件物品的效益值和重量。
03贪心算法

第3章贪心算法贪心算法一般来说是解决“最优问题”,具有编程简单、运行效率高、空间复杂度低等特点。
是程序竞赛中的一个有力武器,受到广大同学们的青睐。
贪心算法一般是求“最优解”这类问题的。
最优解问题可描述为:有n个输入,它的解是由这n个输入的某个子集组成,并且这个子集必须满足事先给定的条件。
这个条件称为约束条件。
而把满足约束条件的子集称为该问题的可行解。
这些可行解可能有多个。
为了衡量可行解的优劣,事先给了一个关于可行解的函数,称为目标函数。
目标函数最大(或最小)的可行解,称为最优解。
贪心算法的正确性证明虽然不容易,但一些常见的方法还是值得总结的。
1.构造法根据描述的算法,用贪心的策略,依次构造出一个解,可证明一定是合法的解。
即用贪心法找可行解。
2.反证法用贪心的策略,依次构造出一个解S1。
假设最优解S2不同与S1,可以证明是矛盾的。
从而S1就是最优解。
3.调整法用贪心的策略,依次构造出一个解S1。
假设最优解S2不同与S1,找出不同之处,在不破坏最优性的前提下,逐步调整S2,最终使其变为S1。
从而S1也是最优解。
3.1 构造法构造法就是从一个空的解开始,根据贪心策略,逐步将新的内容加入原有的解中,直到满足要求或无法将新的元素加入为止。
也可以将使用相反的手段,即先将整个解设定为一个最大的集合,然后,用贪心策略逐步从原有解中取出元素,直至满足要求或无法取出元素为止。
本节例题将介绍第一种贪心的例子。
3.1.1 〖案例1〗订票一家票务办公室为音乐会售票。
它们以出售某一固定数量的连号票(简称套票)来替代常见的单张票销售。
票务办收到了大量的购票订单。
套票的订单以该套票中最小的座位号作为标识。
然而票务办并不能满足所有的订单,而且如果他们完全按照观众的要求来分·60· ACM 程序设计培训教程配座位,就会出现很多空位。
为此票务办采取了如下的座位分配和价格策略:如果一个订单被接受且完全按照观众的要求安排座位,那么观众就要付全价(每套票2 petaks);如果一个订单虽被接受但是至少有一个座位与观众的要求不同,那么顾客只需付半价(每套票1 petaks)。
贪心算法设计及其实际应用研究

哈尔滨师范大学学年论文题目关于贪心算法研究学生***指导教师年级2009级专业计算机科学与技术系别计算机科学与技术学院计算机科学与信息工程学院哈尔滨师范大学年月论文提要为满足人们对大数据量信息处理的渴望,解决各种实际问题,计算机算法学得到了飞速的发展。
设计一个好的求解算法更像是一门艺术而不像是技术。
当一个问题具有最优子结构性质和贪心选择性质时,贪心算法通常会给出一个简单、直观、高效的解法。
贪心算法通过一系列的选择来得到一个问题的解。
它所作的每一个选择都是在当前状态下具有某种意义的最好选择,即贪心选择;并且每次贪心选择都能将问题化简为一个更小的与原问题具有相同形式的子问题。
尽管贪心算法对许多问题不能总是产生整体最优解,但对诸如最短路径问题、最小生成树问题,以及哈夫曼编码问题等具有最优子结构和贪心选择性质的问题却可以获得整体最优解。
而且所给出的算法一般比动态规划算法更加简单、直观和高效。
贪心算法设计及其实际应用研究***摘要:在求最优解问题的过程中,依据某种贪心标准,从问题的初始状态出发,直接去求每一步的最优解,通过若干次的贪心选择,最终得出整个问题的最优解,这种求解方法就是贪心算法。
从贪心算法的定义可以看出,贪心法并不是从整体上考虑问题,它所做出的选择只是在某种意义上的局部最优解,而由问题自身的特性决定了该题运用贪心算法可以得到最优解。
贪心算法所作的选择可以依赖于以往所作过的选择,但决不依赖于将来的选择,也不依赖于子问题的解,因此贪心算法与其它算法相比具有一定的速度优势。
如果一个问题可以同时用几种方法解决,贪心算法应该是最好的选择之一。
本文讲述了贪心算法的含义、基本思路及实现过程,贪心算法的核心、基本性质、特点及其存在的问题。
并通过贪心算法的特点举例列出了以往研究过的几个经典问题,对于实际应用中的问题,也希望通过贪心算法的特点来解决。
关键词:贪心算法;哈夫曼编码;最小生成树;多处最优服务次序问题;删数问题一、贪心算法的基本知识概述(一)贪心算法的核心贪心算法的核心问题是选择能产生问题最优解的最优度量标准,即具体的贪心策略。
大学计算机数学的算法设计与分析

大学计算机数学的算法设计与分析在现代社会中,计算机技术的发展日新月异,成为了人们生活中不可或缺的一部分。
而计算机数学作为计算机科学的基础,对于计算机技术的发展和应用起着至关重要的作用。
算法作为计算机数学的一个重要组成部分,它的设计与分析对计算机的性能和效率起着决定性的影响。
本文将围绕大学计算机数学的算法设计与分析展开讨论。
第一部分:算法设计算法设计是指根据问题需求和计算机的特点,设计出能够解决问题的一系列有序可行的操作步骤。
一个好的算法设计可以提高程序运行的效率和稳定性。
以下是一些常见算法设计的方法:1. 贪心算法:贪心算法是一种以局部最优解为基础,逐步得到全局最优解的策略。
它的设计思想是在每一步都做出当时看起来最优的选择,从而希望最终能够达到全局最优解。
该算法的一个典型应用是霍夫曼编码。
2. 分治算法:分治算法将一个大问题划分为若干个规模较小的子问题,然后分别解决这些子问题,最后将子问题的解合并为原问题的解。
经典的分治算法有快速排序和归并排序。
3. 动态规划算法:动态规划算法常用于求解最优解的问题。
它将原问题划分为若干个子问题,并保存子问题的解,通过递归或迭代的方式求解出最优解。
动态规划算法的一个著名应用是背包问题。
第二部分:算法分析算法分析是指对算法的性能进行评估和分析,主要包括时间复杂度和空间复杂度。
了解算法的时间和空间耗费情况,可以选择更加高效的算法,提高程序的性能。
以下是一些常见的算法分析方法:1. 时间复杂度:时间复杂度是指算法所需要的计算时间和问题规模之间的关系。
常见的时间复杂度有常数阶O(1)、对数阶O(logn)、线性阶O(n)、平方阶O(n^2)等。
通过时间复杂度的分析,可以评估算法的执行效率。
2. 空间复杂度:空间复杂度是指算法在运行过程中所需的内存空间和问题规模之间的关系。
常见的空间复杂度有常数阶O(1)、线性阶O(n)、对数阶O(logn)等。
通过空间复杂度的分析,可以评估算法的内存占用情况。
课程设计--贪心算法

课程设计--贪心算法数据结构课程设计贪心算法专业软件工程班级B软件121 学号1210701132 学生姓名目录1设计题目 (1)2设计分析 (1)3设计实现 (4)4测试方法 (7)4.1测试目的 (7)4.2 测试输入 (7)4.3 正确输出 (7)4.4 实际输出 (8)5分析与探讨 (8)5.1 测试结果分析 (8)5.2 探讨与改进 (8)6设计小结 (8)1 设计题目有n项任务,要求按顺序执行,并设定第i项任务需要t[i]单位时间。
如果任务完成的顺序为1,2,…,n,那么第i项任务完成的时间为c[i]=t[1]+…+t[i],平均完成时间(Average Completion Time,ACT)即为(c[1]+…+c[n])/n。
本题要求找到最小的任务平均时间。
输入要求:输入数据中包含几个测试案例。
每一个案例的第一行给出一个不大于2000000的整数n,接着下面一行开始列出n个非负整数t(t<=1000000000),每个数之间用空格相互隔开,以一个负数来结束输入。
输出要求:对每一个测试案例,打印它的最小平均完成时间,并精确到0.01。
每个案例对应的输出结果都占一行。
若输入某一个案例中任务数目n=0,则对应输出一个空行。
输入例子:44 2 8 1-1表示有四个任务,各自完成需要的时间单位分别是4,2,8,1,第三行输入-1表示结束。
输出例子:要求程序运行后的输出结果为:6.50。
2 设计分析算法是为了求解一个问题需要遵循的,被青春地指定的简单指令的集合。
任何程序基本上都是要用特点的算法来实现的。
算法性能的好坏,直接决定了所实现程序性能的优劣。
贪心算法通过一系列的选择来的得到一个问题的解。
它所做的每一个选择都是当前的状态下某种意义的最好选择,即贪心选择。
希望通过每次所做的贪心选择导致最终结果问题的一个最优解。
这种启发式的策略并不总能奏效,然而在许多情况下能达到预期的目的。
这个题目属于贪心算法应用中的任务调度问题。
结构选择程序设计实验报告

结构选择程序设计实验报告一、引言本实验旨在设计一个结构选择程序,通过输入不同的参数,能够根据给定的条件选择出最优的结构。
结构选择是一种重要的工程和科学问题,它涉及到在满足一定的约束条件下,选择出最佳的结构设计方案。
本实验采用了贪心算法作为结构选择的基本策略,并通过程序设计实现。
二、贪心算法概述贪心算法是一种基于局部最优选择的算法策略。
它每次选取当前状态下最优的选择,并以此迭代地求解问题的最优解。
贪心算法常用于在限定条件下选择出局部最优解的问题。
三、程序设计本程序设计采用Python语言进行开发。
下面分别介绍程序的输入、输出和算法设计。
1. 输入程序需要输入以下几个参数:- 结构类型:输入结构的类型,例如:桥梁、建筑物等。
- 结构规模:输入结构的规模,例如:桥梁的跨度、建筑物的楼层数等。
- 约束条件:输入结构选择的约束条件,例如:成本、强度等。
2. 算法设计本程序采用以下步骤设计贪心算法:1. 针对给定的结构类型和规模,预先定义不同结构的选择策略,并将其按照优先级排序。
2. 针对给定的约束条件,将不满足条件的结构筛选掉。
3. 从排好序的选择策略中,依次选择满足约束条件的结构方案,直到满足所有约束条件。
3. 输出程序输出最优的结构方案,包括结构类型、规模以及满足所有约束条件的最优方案。
四、实验结果本次实验我们设计了一个结构选择程序,并进行了多组测试。
以下是其中一组测试的结果。
输入参数:- 结构类型:桥梁- 结构规模:100米- 约束条件:成本不超过100万元,强度不低于5000N输出结果:- 结构方案:拱桥- 成本:80万元- 强度:5500N五、总结与讨论本次实验通过贪心算法设计了一个结构选择程序,并在多组测试中获得了较好的结果。
贪心算法在解决结构选择问题上具有较高的效率和可行性,但其结果可能并不是全局最优解。
未来可以进一步改进程序的算法策略,例如采用动态规划算法,以获得更优的结构方案。
另外,程序的输入和输出界面也可以进行优化,提升用户体验。
算法设计与分析论文(贪心算法)

贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪 心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划 算法的主要区别。
贪心选择是采用从顶向下、以迭代的方法做出相继选择,每做一次贪心选择 就将所求问题简化为一个规模更小的子问题。对于一个具体问题,要确定它是否 具有贪心选择的性质,我们必须证明每一步所作的贪心选择最终能得到问题的最 优解。通常可以首先证明问题的一个整体最优解,是从贪心选择开始的,而且作 了贪心选择后,原问题简化为一个规模更小的类似子问题。然后,用数学归纳法 证明,通过每一步贪心选择,最终可得到问题的一个整体最优解。
物品超出背包容量为止。伪代码如下:
public static void DepWePr(double[][] a, double c, int[] ans) { // depend on
// the // weight // and price double[] w = new double[a[0].length]; // the weight of goods System.arraycopy(a[0], 0, w, 0, w.length); // copy the array
贪心算法
——不在贪心中爆发,就在贪心中灭亡 徐晓龙 武汉理工大学计算机科学与技术学院软件 ZY1101 班
摘要
本文介绍贪心算法的基本意义以及算法的使用范围,并通过具体的案例来分 析贪心算法的具体应用,从而指出其特点和存在问题。 关键字:贪心算法,贪心策略,TSP、0/1 背包
引言
我们用了 13 周的时间学完了《算法设计与分析》这本书。这本书中涵盖了 大量的常见算法,包括蛮力法、分治法、动态规划法、贪心算法等等。我最有印 象的就是贪心算法。贪心算法是一种有合理的数据组织和清晰高效的算法,它简 单有效。下面我们来详细解读一下这个算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贪心算法程序设计
实验目的:掌握贪心算法。
实验内容:设n是一个正整数。
现在要求将n分解为若干个互不相同的自然数的和,且使这些自然数的乘积最大。
对于给定的正整数n,编程计算最优分解方案。
实验要求:利用贪心算法思想写出算法的伪代码和C程序代码。
(一)算法思想
1)把一个正整数从中间分开(如果是偶数,直接除以2;如果是奇数,分别加1除以2,减1除以2)
2)其中一部分保留在A[]数组中(奇数的话,比较大的那一部分保留给A[]数组),另一部分赋给temp,并重复1,2 步骤
3)最后把temp赋给A[]数组
(二)程序代码
//贪心算法
import java.io.*;
public class Testsuanfa {
public int N = this.GetN();
public int[] A = new int[100];
// 取得用户需要实现算法的一个正整数
public int GetN() {
int dvalue = 0;
String value;
System.out.println("请输入一个正整数: ");
BufferedReader bfr = new BufferedReader(
new InputStreamReader(System.in));
try {
value = bfr.readLine();
dvalue = Integer.parseInt(value);
//如果输入的不是数字,系统自动退出,并提示:“输入正确的数值!”。
} catch (IOException e) {
System.out.println("输入出错了,请重新输入:");
System.exit(0);
} catch (NumberFormatException e2) {
System.out.println("请输入正确的数字!!");
System.exit(0);
}
return dvalue;
}
public void f() {
int count = 0;
int sum = 0;
// 将这个数分解:从2到i(直到这些数的和sum大于N)
for (int i = 0; sum < N; i++) {
sum = 2 + i + sum;
A[i] = 2 + i;
count++;
}
// 如果sum比N大1,即把2去掉,其他数在数组的位置往前移,最后一个数加1。
if ((sum - N) == 1) {
for (int i = 0; i < count - 1; i++) {
A[i] = A[i + 1];
}
A[count - 2] = A[count - 1] + 1;
A[count - 1] = 0;
count--;
//如果sum比N大k,只需把2到i中等于k的那个数去掉,k后面在数组的位置往前移。
} else if ((sum - N) > 1) {
int temp = sum - N;
for (int i = 0; i <= count; i++) {
if (A[i] == temp) {
for (int j = i; j < count; j++) {
A[j] = A[j + 1];
}
A[count] = 0;
count--;
}
}
}
// 输出分解后的数,和最大积MAX.
double temp = 1;
System.out.println(N + "分解为" + count + "个不同的自然数:");
System.out.println();
System.out.print(N + "=");
for (int i = 0; i < count; i++) {
if (i < (count - 1)) {
System.out.print(A[i] + "+");
} else if (i == (count - 1)) {
System.out.println(A[i]);
}
}
System.out.println();
System.out.print("时,可得最大积MAX=");
for (int i = 0; i < count; i++) {
temp = temp * A[i];
if (i < (count - 1)) {
System.out.print(A[i] + "*");
} else if (i == (count - 1)) {
System.out.println(A[i]);
}
}
System.out.println();
System.out.println("MAX=" + temp);
}
public static void main(String[] args) {// 主函数定义一个对象,调用f()方法,实现贪心算法
Testsuanfa tsf = new Testsuanfa();
tsf.f();
}
}
(三)运行结果
Java工作环境:。
