矩阵分析Chapter TwoSummary - 北京理工大学研究生课程
《矩阵分析》教学大纲.doc

《矩阵分析》教学大纲(Matrix Analysis, 14xs20012)一、前言1、课程概述本课程内容包括线性空间与线性变换,矩阵的Jordan标准型,内积空间,正规矩阵,Hermite矩阵,二次型,矩阵分解,特征值的估计与计算,矩阵的扰动问题,向量范数与矩阵范数,矩阵序列和级数,广义逆矩阵,矩阵函数等内容。
《矩阵分析》的特点之一是在介绍矩阵论有关基础理论的同时,引入用MATLAB进行计算的相关内容,使读者能将理论与实践相结合,在培养学生理论水平、演绎推理能力的同时还培养了学生的实际动手能力。
实践内容包括MATLAB软件的讲解和实际动手操作。
2、课程性质专业基础课3、学分与学时本课程总学分:6学分,总学时:48学时。
其中理论课40学时;实践:8学时。
本课程针对计算机应用技术专业研究牛的知识结构背景,在其本科阶段所学的《线性代数》的基础之上,进一步深化和提高矩阵理论的相关知识,并着重培养学生运用矩阵分析的知识和方法解决计算机应用领域相关问题的能力。
通过本课程的学习,使学生掌握矩阵理论的基本概念,基本理论和基本方法,全面了解和掌握矩阵的标准形、特征值与特征向量、矩阵分解、范数与矩阵函数等重点内容,了解近代矩阵理论中十分活跃的若干分支,为今后的进一步学习和研究打下扎实的基础。
5、使用对象计算机应用技术专业一年级学历硕士研究生6、知识背景要求线性代数,程序设计二、讲授提纲第1章线性空间与线性变换(-)本章概述本章首先从线性空间的基本概念讲起,逐步介绍基与坐标、坐标变换,线性子空间, 线性映射,线性映射的值域、核,线性变换的矩阵与线性变换的运算,门维线性空间的结构,线性变换的特征值与特征向量,线性变换的不变子空间,矩阵的相似形等重要概念和方法,同时还要对线性方程组解的结构定理进行复习。
实践环节讲解用MATLAB求解线性方程组的方法和技巧。
(二)教学目标介绍教材及全课程内容,使学生对本课有一个总体的印象,对进一步的学习起到提纲挈领的作用。
北京理工大学出版社矩阵分析习题解答

2005级电路与系统矩阵分析作业3-1已知)(ij a A =是n 阶正定Hermite 矩阵,在n 维线性空间nC 中向量[]n x x x ,,,21 =α ,[]n y y y ,,,21 =β定义内积*),(βαβαA =。
(1)证明在上述定义下,nC 是酉空间;(2)写出nC 中的Canchy -Schwarz 不等式。
(1)证明:),(αβ=H A αβ=H H A )(βα=H A βα ,(βα,k )=),(βαβαk A k H =),(),()(),(γβγαγβγαγβαγβα+=+=+=+H H H A A AH A αααα=),(,因为A 为正定H 矩阵,所以0),(≥αα,当且仅当0),(0==ααα时,由上可知cn是酉空间。
証毕。
(2)解: ∑∑==n jnij ij i Hy a x A |||),(|βαβα∑∑==n jnij ijix ax ),(||||ααα,∑∑==n jnij ijiy ay ),(||||βββ由Cauchy-Schwarz 不等式有:∑∑∑∑∑∑≤n jnij ijin jnin jnij ijij ijiy ay x ax y ax *3-3(1)已知.A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡502613803---,试求酉矩阵U,使得U*AU 是上三角矩阵 解:由|λE-A| = (λ+1)3得 λ= -1是A 的特征值,当λ=-1时,可得|λE-A|=000000201于是ε1=(0,1,0)T是A 的特征向量。
选择与ε1正交,并且互相也正交两个向量组成酉阵:U 1= ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001010则U 1*A U 1= ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---520830631 取A 1= ⎥⎦⎤⎢⎣⎡--5283,|λE- A 1| = (λ+1)2λ= -1是A 1的特征值。
当λ=-1时,可得|λE- A 1|=0021,于是,α1 =( --52,51)T是A 的特征向量,选择与α1正交的向量组成酉阵U 2 = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡52515152 -,U 2*A 1U 2 = 51⎥⎦⎤⎢⎣⎡-2112⎥⎦⎤⎢⎣⎡--5283⎥⎦⎤⎢⎣⎡-2112 =⎥⎦⎤⎢⎣⎡---10101 3-9若S ,T 分别是实对称矩阵和反实对称矩阵,且0)det(≠--iS T E ,试证:1))((---++iS T E iS T E 是酉矩阵,。
矩阵分析 - 北京理工大学研究生院

课程名称:矩阵分析一、课程编码:1700002课内学时: 32 学分: 2二、适用学科专业:计算机、通信、软件、宇航、光电、生命科学等工科研究生专业三、先修课程:线性代数,高等数学四、教学目标通过本课程的学习,要使学生掌握线性空间、线性变换、Jordan标准形,及各种矩阵分解如QR分解、奇异值分解等,正规矩阵的结构、向量范数和矩阵范数、矩阵函数,广义逆矩阵、Kronecker积等概念和理论方法,提升研究生的数学基础,更好地掌握矩阵理论,在今后的专业研究或工作领域中熟练应用相关的矩阵分析技巧与方法,让科研结果有严格的数学理论依据。
五、教学方式教师授课六、主要内容及学时分配1、线性空间和线性变换(5学时)1.1线性空间的概念、基、维数、基变换与坐标变换1.2子空间、线性变换1.3线性变换的矩阵、特征值与特征向量、矩阵的可对角化条件2、λ-矩阵与矩阵的Jordan标准形(4学时)2.1 λ-矩阵及Smith标准形2.2 初等因子与相似条件2.3 Jordan标准形及应用;3、内积空间、正规矩阵、Hermite 矩阵(6学时)3.1 欧式空间、酉空间3.2标准正交基、Schmidt方法3.3酉变换、正交变换3.4幂等矩阵、正交投影3.5正规矩阵、Schur 引理3.6 Hermite 矩阵、Hermite 二次齐式3.7.正定二次齐式、正定Hermite 矩阵3.8 Hermite 矩阵偶在复相合下的标准形4、矩阵分解(4学时)4.1矩阵的满秩分解4.2矩阵的正交三角分解(UR、QR分解)4.3矩阵的奇异值分解4.4矩阵的极分解4.5矩阵的谱分解5、范数、序列、级数(4学时)5.1向量范数5.2矩阵范数5.3诱导范数(算子范数)5.4矩阵序列与极限5.5矩阵幂级数6、矩阵函数(4学时)6.1矩阵多项式、最小多项式6.2矩阵函数及其Jordan表示6.3矩阵函数的多项式表示6.4矩阵函数的幂级数表示6.5矩阵指数函数与矩阵三角函数7、函数矩阵与矩阵微分方程(2学时)7.1 函数矩阵对纯量的导数与积分7.2 函数向量的线性相关性7.3 矩阵微分方程(t)()() dXA t X t dt=7.4 线性向量微分方程(t)()()() dxA t x t f t dt=+8、矩阵的广义逆(3学时)8.1 广义逆矩阵8.2 伪逆矩阵8.3 广义逆与线性方程组课时分配说明:第一章的课时根据学生的数学基础情况可以调整,最多5学时,如学生线性代数的基础普遍较高,可以分配3学时,剩余2学时可在最后讲解第九章部分内容(Kronecker 积的概念和基本性质)。
北京理工大学硕士研究生培养方案

车辆工程080204(一级学科:机械工程)本学科1981年获得硕士学位和博士学位授予权,1988年设立博士后流动站,1987年和2001年两次被评为国家级重点学科。
本学科在机械学科的基础上拓宽和发展,涉及动力、控制、电子、计算机、信息、材料、能源等学科领域,具有多学科交叉的特点。
主要研究军用车辆、汽车及其它工程车辆。
主要研究方向有:1.车辆总体理论与现代设计:车辆动力学,车辆系统优化;车辆设计专家系统,车辆虚拟技术;车辆试验与测试技术,车辆可靠性与故障诊断技术等。
2.车辆传动系统理论与技术:车辆动力传动理论与控制,车辆传动系统动态仿真与优化匹配,推进系统集成理论与技术,多流传动与转向,液力液压传动,车辆自动变速和无级变速,车辆新型传动。
3.车辆信息技术:车辆信息网络化技术,车辆电子系统可靠性与故障诊断,智能车辆,车载信息系统,主动和半主动悬挂,车辆安全行驶控制,车辆通过性控制等。
4.新能源车辆与电驱动技术:电动车辆及其它新能源车辆理论与技术,电机驱动系统,车辆能量管理系统,车辆电气综合控制等。
5.车辆安全与人机工程:车辆安全性,车辆安全行驶装置,车辆振动噪声控制,车辆人机工程,车身结构与造型等。
一、培养目标热爱祖国,有社会主义觉悟和较高道德修养,在车辆工程领域掌握坚实的基础理论和系统的专门知识,具有从事本领域科学研究工作或独立担负专门技术工作的能力,能够胜任科研院所、企业、高校的科学研究、工程设计、产品开发和教学工作。
二、课程设置·139·三、必修环节1.文献综述报告(1学分):本学科硕士研究生的文献阅读要结合课题研究方向和具体的研究领域进行,文献综述报告的参考文献应不少于20篇,文献综述报告要反映国内外相关领域的研究历史、现状和发展趋势,不少于4000汉字。
2.学术活动(1学分):在学期间至少应参加6次以上学术活动(含现代数学系列讲座、跨学科或晓外的学术活动3次),其中本人进行正规性的学术报告1次以上。
《矩阵分析》课程教案

讨 论
练 习
作 业
作业:第3章练习题中任选5题
教学要求
熟练掌握线性空间与线性变换,矩阵的Jordan标准型,内积空间,正规矩阵,Hermite矩阵,二次型,矩阵分解,特征值的估计与计算,矩阵的扰动问题,向量范数与矩阵范数,矩阵序列和级数,广义逆矩阵,矩阵函数等基本概念和基本方法。
教学方法
课堂讲述+实验演示+实际动手操作+作业+研究报告
教学手段
多媒体课件+案例+理论推导+编程实现
考核方式
结合课堂所学写一篇论文/开卷考试二者选一
教学参考资料
[1]《矩阵分析》,史荣昌,魏丰编著,北京理工大学出版社,2010.6,第3版
[2]《Matrix Methods in Data Mining and Pattern Recognition》,Lars Eldén,The SIAM series on Fundamentals of Algorithms,2007.2
本课程针对计算机应用技术专业研究生的知识结构背景,在其本科阶段所学的《线性代数》的基础之上,进一步深化和提高矩阵理论的相关知识,并着重培养学生运用矩阵分析的知识和方法解决计算机应用领域相关问题的能力。通过本课程的学习,使学生掌握矩阵理论的基本概念,基本理论和基本方法,全面了解和掌握矩阵的标准形、特征值与特征向量、矩阵分解、范数与矩阵函数等重点内容,了解近代矩阵理论中十分活跃的若干分支,为今后的进一步学习和研究打下扎实的基础。
山西财经大学研究生课程教案
课程名称
矩阵分析
课程编码
北理版矩阵分析课件 共101页

1 ,2 , ,n 1 ,2 ,n P
定理:过渡矩阵 P 是可逆的。
任取 V ,设 在两组基下的坐标分别为
x1,x2,
,xn
T
与
y1,y2,
,yn
T
,那么我们有:
x1 y1
x
2
P
y
2
的为极向大量线 组性无关组,span1,2, ,s的维数即
的秩。
1,2, ,s
例 4 实数域 R 上的线性空间 R n n 中全体上三角矩
阵集合,全体下三角矩阵集合,全体对称矩阵集合,
全体反对称矩阵集合分别都构成 R n n 的子空间,
问题:这几个子空间的基底与维数分别时什么?
(2) 加法结合律 ( ) ( )
(3) 零元素 在 V 中存在一个元素 0 ,使得对
于任意的 V 都有
0
(4) 负元素
对于 V 中的任意元素 都存
在一个元素 使得
0
(5) 1
(6) k(l)(kl)
(7) (kl)kl
与向量组
(0,1,1),(1,0,1),(1,1,0)
都是 R 3 的基。R 3 是3维线性空间。
例 2 实数域 R 上的线性空间R 2 2 中的向量组
0 1
1 1,1 1
10,10
1 1,1 1
1 0
与向量组
1 0
0 0,10
例 4 R 表示实数域 R 上的全体无限序列组成的
的集合。即
R [a1,a2,a3,]iai 1,F 2,,3,
在 R 中定义加法与数乘:
北京理工大学研究生培养方案

控制科学与工程共济网081100网络督察(一级学科:控制科学与工程)kaoyantj共济控制科学与工程学科具有博士学位授予权并设博士后流动站,在2006年全国一级学科评估中综合排名第10。
下设“控制理论与控制工程(081101)”、“检测技术与自动化装置(081102)”、“系统工程(081103)”、“模式识别与智能系统(081104)”、“导航、制导与控制(081105)”、“运动驱动与控制”六个二级学科,其中,“控制理论与控制工程”是国家级重点学科,“模式识别与智能系统”是北京市和科工委重点学科。
kaoyantj控制科学与工程是研究控制的理论、方法、技术及其工程应用的学科。
控制科学以控制论、系统论、信息论为基础,研究各应用领域内的共性问题,即为了实现控制目标,应如何建立系统的模型,分析其内部与环境信息,采取何种控制与决策行为;而与各应用领域的密切结合,又形成了控制工程丰富多样的内容。
本学科点在理论研究与工程实践相结合、学科交叉和军民结合等方面具有明显的特色与优势,对我国国民经济发展和国家安全发挥了重大作用。
本学科主要研究方向有:3362 30391.控制理论与控制工程:复杂系统的建模、控制、优化、决策与仿真;鲁棒控制与非线性控制;工程系统的综合控制与优化;运动控制系统设计与分析;先进控制理论与方法。
112室2.模式识别与智能系统:智能控制与智能系统;专家系统与智能决策;模式识别理论与应用;智能信息处理与计算机视觉;生物信息学。
课3.导航、制导与控制:惯性定位导航技术;组合导航及智能导航技术;飞行器制导、控制与仿真技术;惯性器件及系统测试技术;火力控制技术。
共济网4.检测技术与自动化装置:先进传感与检测技术;新型执行机构与自动化装置;智能仪表及控制器;测控系统集成与网络化;测控系统的故障诊断与容错技术。
课5.系统工程:系统工程理论及应用;系统分析、设计与集成;系统预测、决策、仿真与性能评估;网络信息技术、火控与指控系统技术;复杂系统信息处理、控制与应用技术。
《矩阵分析》课件

Gauss消元法原理
LU分解求解线性方程组
通过行变换将矩阵化为上三角矩阵, 从而解线性方程组。
将Ax=b转化为LUx=b,通过前向替 换和后向替换求解。
LU分解定义
将矩阵分解为一个下三角矩阵L和一个 上三角矩阵U的乘积。
QR分解原理及实现
QR分解定义
将矩阵分解为一个正交矩阵Q和 一个上三角矩阵R的乘积。
Jordan标准型及其性质
Jordan标准型定义: 设A是n阶方阵,如果 存在一个可逆矩阵P, 使得P^(-1)AP为 Jordan矩阵,则称A 可以相似对角化为 Jordan标准型。
Jordan标准型的性质
Jordan标准型是唯一 的,即对于给定的方 阵A,其Jordan标准 型是唯一的。
Jordan标准型中的每 个Jordan块对应A的 一个特征值。
非零行的首非零元所在列在上一行的 首非零元所在列的右边。
同一行的所有非零元均在首非零元的 右边。
线性无关组与基础解系
线性无关组:一组向量线性无关当且仅当它们不 能由其中的部分向量线性表示出来。换句话说, 只有当这组向量中任何一个向量都不能由其余向 量线性表示时,这组向量才是线性无关的。
基础解系中的解向量线性无关。
初等变换和行阶梯形式
初等变换:对矩阵进行以下三种变换称为初等变 换 对调两行(列)。
以数k≠0乘某一行(列)中的所有元。
初等变换和到另一行(列)的对应元上去。
02
行阶梯形式:一个矩阵经过初等行变换可以化为行阶梯形式,
其特点是
非零行在零行的上面。
03
初等变换和行阶梯形式
方阵
行数和列数相等的矩阵称为方阵。
01
对角矩阵
除主对角线外的元素全为零的方阵称 为对角矩阵。
矩阵分析_第一章 北京理工大学

(5)
1
(6)
(7)
k (l ) (kl ) (k l ) k l
(8)
k ( ) k k
V中的元素称 为向量
称这样的 V 为数域
F 上的线性空间。
R
例 1 全体实函数集合 R 构成实数域 线性空间。 按函数的加法和数乘函数
R上的
例 2 复数域 C上的全体 m n 型矩阵构成 的集合为 C上的线性空间。
A线性表示, 且表示式是唯一的.
最大(线性)无关向量组
定义3 设有向量组A,如果在A中能选出r个向量
A0 : 1 , 2 ,, r,满足 (1)向量组 A0 : 1 , 2 ,, r 线性无关; (2)向量组A中任意r 1个向量(如果A中有
r 1个向量的话)都线性相关, 那末称向量组A0是
定理:过渡矩阵
P 是可逆的。
提示PX=0 只有零解
任取
V
,设 在两组基下的坐标分别为
T
x1 , x2 ,, xn
与
y1 , y2 ,, yn ,那么我们有:
T
x1 x 2 (1 , 2 , , n ) xn y1 y1 y y 2 ( , , , ) P 2 ( 1 , 2 , , n ) 1 2 n yn yn
按矩阵的加法和数乘矩阵
ห้องสมุดไป่ตู้
例 3 实数域 R 上全体次数小于或等于 n 的多项 式集合 R[ x ]n 构成实数域 R上的线性空间 例 4 全体正的实数 R 在下面的加法与数乘的 定义下也构成线性空间:
a b : ab, a , b R k a : a , a , k R
矩阵分析_第三章 北京理工大学

(4) ( , ki i ) ki ( , i )
i 1 i 1
t
酉空间的性质:
(1) ( , k ) k ( , ), (k , ) k ( , ) (2) ( , ) ( , ) ( , ) (3) ( ki i , ) ki ( i , )
b
2
a
f ( x) d ( x)
b
2
a
g ( x) d ( x)
定义:设 V 为欧氏空间,两个非零向量 , 的夹角定义为
, : arccos
于是有
( , )
2
0 ,
定理:
,
2
( , ) 0
因此我们引入下面的概念; 定义:在酉空间 V 中,如果 称 与 正交。
(1) ( , ) ( , ) (2) (k , ) k ( , ) (3) ( , ) ( , ) ( , ) (4) ( , ) 0
k 这里 , , 是 V 中任意向量, 为任意复数
,只有当 0 时 ( , ) 0 ,我们称带有 这样内积的 n 维线性空间 V 为酉空间。 欧氏空间与酉空间通称为内积空间。
1 2i 3i 6 1 2i (2) 9 1 i 3i 1 i 7
1 2i 3i 1 2i 3i 6 6 1 2i 1 2i 9 1 i 9 1 i 3i 1 i 7 3i 1 i 7
n
2
维线性空间
n n
酉空间。
内积空间的基本性质:
欧氏空间的性质:
教学日历-北京理工大学研究生院

北京理工大学研究生课程教学日历周 次 上课方式时数授 课 内 容课外阅读和书面的作业 学习检查参考书名和章节时数内 容 检查方式 所需时间4 讲授 6 Chapter1.LinearSpace and Mapping1. Basic abstractalgebra2. Linear space3. Basis of Linearspace4. Linear subspace5. Linear transfo-rmations3课外阅读:参考书第一章第六节作业:Example 1.8Example 1.27Example 1.30批阅 2小时LinearAlgebrawithApplications inAutomaticControl第一章5 讲授6 Chapter2.Polynomials and matrixpolynomials1. Linear algebras2. Polynomial ring3.Ideals ofpolynomials4.Matrixpolynomials-Smithcanonical form4课外阅读:参考书第二章第八节作业:Example 2.17Example 2.25Example 2.26批阅2小时LinearAlgebrawithApplications inAutomaticControl第二章6 讲授 6 Chapter3. Lineartransformation1.The eigenvalues oflinear transformation2. Similarityreduction, theNatural normal form4课外阅读:矩阵分析特征值相关内容作业:Example 3.2Example 3.4批阅2小时LinearAlgebrawithApplications inAutomaticControl第三章第一、二节7 讲授 6 Chapter3. Lineartransformation3. The JordanCanonical forms4 . Minimalpolynomials and thefirst decompositionof a linear space5. The cyclicinvariant subspacesand the seconddecomposition of alinear space4课外阅读:线性系统理论中约旦标准型及应用相关内容作业:Example 3.5-3.9批阅4小时LinearAlgebrawithApplications inAutomaticControl第三章第三、四、五节8 讲授 6 Chapter4.Lineartransformation inunitary spaces1.Euclidean andunitary spaces2. Orthonormal basisand the Gram-Smithprocess3.Unitarytransformations4. Projectors andidempotent matrices5. Adjointtransformation4课外阅读:矩阵分析同构变换、酉矩阵相关内容作业:Example 4.3-4.5批阅2小时LinearAlgebrawithApplications inAutomaticControl第四章前五节9 讲授 6 Chapter4.Lineartransformation inunitary spaces6.Normaltransformations andnormal matrices7.Hermitian matricesand Hermitian formsChapter5.Decomposition of lineartransformations andmatrices1.Spectraldecomposition ofsimple lineartransformation andmatrices4课外阅读:矩阵分析正定矩阵及Lyapunov稳定性理论相关内容Example 4.11Example 5.2-5.3批阅2小时LinearAlgebrawithApplications inAutomaticControl第四章第六节至第五章第一节10 讲授 6 Chapter5.Decomposition of lineartransformations andmatrices2. Singular valuedecomposition oflineartransformationsbetween unitaryspaces and theassociated matrices3.Full rankfactorization oflineartransformations andmatrices4.UR and QRfactorization ofmatrices5课外阅读:奇异值在鲁棒与非线性控制中的应用相关内容Example 5.4-5.7批阅2小时LinearAlgebrawithApplications inAutomaticControl第五章第二节至第四节11 讲授和答疑6Chapter6.Norms forvectors and matrices1.Norms for vectors2. Norms of matrices3. Induced norms ofmatricesReview and exercise4课外阅读:矩阵分析中矩阵范数相关内容Theorem6.6证明推导及Example6.6批阅3小时LinearAlgebrawithApplications inAutomatic Control第一章至第六章一、 教学目的The Linear Algebra with Applications in Automatic Control is one of the main specialized core courses for master students majoring in Automation and Electrical Engineering & Automation. The objective of this course is to familiarize students with the basic concepts and knowledge of linear algebra and matrices and background material that is useful in systems and control theory.This course consists of two parts: The first part includes a thorough treatment of material in standard courses on linear algebra, and the main topics for this part include linear space and mapping, polynomials and matrix polynomials, linear transformations and the canonical forms for the corresponding matrix representations, linear transformations in unitary spaces; the second part is devoted to develop material that is useful in systems and control theory, the main topics of this part include decomposition of linear transformations and matrices, norms for vectors and matrices, short introduction of function of matrices and matrix-valued functions and applications to differential equations.二、 授课方法和方式Classroom teaching and discussions三、 成绩评定方式English problems and English answers. The final score is made up of daily performance (30%) and final exam performance (70%).四、 教材和必读参考资料1.Defense Industry Press, 20112. 黄琳. 系统与控制理论中的线性代数,科学出版社,19843. Roger A. Horn, Charles R. Johnson, Matrix Analysis, The Cambridge University Press,(1985-1st Edition, 2013-2nd Edition)4. Lancaster, Peter, & Tismenetsky, Miron. The Theory of Matrices (2nd Edition). AcademicPress: Orlando San Diego 19975. MIT-open course on linear algebra任课教师年月日教学院长年月日注:1.此教学日历由授课教师填写,教学院长签字后执行,学院留存一份。
北京理工大学研究生课程教学日历-BeijingInstituteof

北京理工大学研究生课程教学日历课程名称财务管理课程代码2100009课程性质必修课主讲教师肖淑芳2017—2018学年第一学期辅导教师无院授课对象MBA周次上课方式时数授课内容课外阅读和书面的作业学习检查参考书名和章节时数内容检查方式所需时间1课堂讲授4●财务管理决策财务管理的目标●企业组织形式●委托代理问题与公司治理●资金时间价值2阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第1、3章2课堂讲授+课堂讨论4●投资组合的风险与收益●资本资产定价模型●债券与股票估价4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第4、5章3课堂讲授+课堂小案例4●投资决策方法●项目现金流量的估计4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第9、10章4课堂讲授+课堂小案例4●项目现金流量分析的一些特殊情况●项目进一步分析与评估●如何考虑项目的风险4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第10、11章5课堂讲授+课堂讨论4●权益资本成本的估计●债务资本成本●加权平均资本成本●发行成本和加权平均资本成本4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第14章6课堂讲授+课堂小案例4●资本结构与杠杆效应●资本结构、公司价值与资本成本●最优资本结构决策4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第16章7课堂讲授+课堂讨论4●股利分配类型与股利支付程序●现金股利与股票股利●股票股利与资本公积转增●现金股利与股票回购●股利政策4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第17章8课堂讲授+课堂讨论4●经营周期和现金周转期●短期财务政策●现金预算与短期财务计划●现金与流动性管理应收账款与存货管理4阅读教材相关章节完成课后作业课堂提问检查作业2公司理财(精要版)第18、19、20章一、教学目的本课程主要以资本市场为背景,在管理学、会计学、统计学等课程基础之上,学生通过本课程的学习,掌握企业筹资、投资、收益分配等资金管理的理论与方法,提升学生在企业筹资、投资、收益分配等方面的财务管理决策能力。
电路与系统北京理工大学研究生培养方案

080902电路与系统——北京理工大学硕士研究生培养方案(2009版)2009-12-19 18:39:43 北京理工大学考研共济网点击浏览:256次·[考研一站式]北京理工大学硕士招生相关文章索引·[考研一站式]北京理工大学硕士专业课试题、[订购]考研参考书、专业目录电路与系统专080902彰武(一级学科:电子科学与技术)研网络督察电路与系统学科研究电路与系统的理论、分析、测试、设计和物理实现,它是信息与通信工程和电子科学与技术两个学科之间的桥梁,它又是信号与信息处理、通信、控制、计算机乃至电力、电子等诸方面研究和发展的理论与技术基础。
由于电路与系统学科的有力支持,才可能最有效地利用现代的电子科学技术和最新的器件实现复杂的、高性能的各种信息和通信网络与系统。
济近二十年来因为信息与系统产业的高速发展以及微电子器件集成规模的迅速增大,使电子电路与系统走向数字化、集成化、多维化。
电路与系统的经典理论向现代化理论过度,而且与信息和通讯工程、计算机学科与技术、生物电子学等学科交叠,相互渗透,形成一系列的边缘、交叉学科,如新的微处理器设计、各种数字信号处理系统、人工神经网络等。
本学科主要研究方向有:专1.信息处理与传输:信号采集与处理,网络数据融合,现代通信传输理论与技术研究。
济2.应用电子电路与系统:智能与虚拟仪器技术,综合传感器检测技术,多媒体技术、嵌入式技术,电路系统集成技术的应用性研究。
研3.功率电子学:功率控制与驱动技术,电力伺服传动技术,现代电源理论与应用技术研究。
336260 37济一、培养目标112室热爱祖国,有社会主义觉悟和较高道德修养;掌握坚实的数字、模拟、线性和非线性电路与系统的基础理论与技术,信号处理理论与技术,电路与系统的计算机辅助设计,现代信息与通信网络的理论与技术;在本研究方向有系统和深入的专门知识与实验技术;较为熟练地掌握一门外国语,能阅读本专业的外文资料;具有从事科学研究工作和独立担负专门技术工作的能力;能胜任在科研单位、生产部门或高等院校从事有关方面的研究、科技开发、教学和管理工作。
矩阵分析_第二章 北京理工大学

要(2)式成立,取
Q0 D0 , Q1 D1 AQ0 , Q2 D2 AQ1 , , Qk Dk AQk 1 , , Qm 1 Dm 1 AQm 2 ,U 0 Dm AQm 1
定理 A ~ B E A E B 的证明
0 A2 ( ) 0
0 0 A3 ( )
对于 A3 ( ) ,其初等因子为 , 1, 1 由上面的定理可知 A( ) 的初等因子为
, , , 1, 1, 1
的秩为4,故
因为
A( )
A( )
的不变因子为
d 4 ( 1)( 1), d 3 ( 1), d 2 , d1 1
1 0 0, D3 ( ) 1 1
D3 ( ) 1 D2 ( ) 1, D1 ( ) 1
1 0 0 1 D4 ( ) 0 0
5
4 3
0 0 1
4
2
3
2
2 3 4 5
d1 ( ) 1, d2 ( ) 1, d3 ( ) 1 4 3 2 d 4 ( ) 2 3 4 5
例 如果 5 6 矩阵 A( ) 的秩为4,其初等因
子为 , , , 1,( 1) ,( 1) ,( i )
2 2 3 3
( i ) 求 A( ) 的Smith标准形。
3
解:首先求出 A( ) 的不变因子
d 4 ( 1) ( i ) ( i )
E U ( ) P ( E A)V 1 ( ) R( ) [( E A)Q( ) U 0 ]P ( E A)V 1 ( ) R( ) U 0 P ( E A)[Q( ) P V ( ) R( )]
矩阵分析-(1)(终)

《矩阵分析》 · 徐赐文
《矩阵分析》
1.教材:
《矩阵分析》史荣昌编,北京理工大学出版社
2.参考书:
《矩阵分析学习指导》魏丰,史荣昌等编, 北京理工大学出版社
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
难点: 求线性映射的值域、核的基与维数
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
首先, 我们回忆一下《线性代数》中的向量.
向量的运算及性质
负向量: 向量 ( a1 , a2 ,, an ) 称为向量 的负向量
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
向量的差: ( )
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
第一章 线性空间和线性映射
《矩阵分析》 · 徐赐文
2014-3-16
北京理工大学-2016版专业学位硕士研究生培养方案(2017年修订)-安全工程
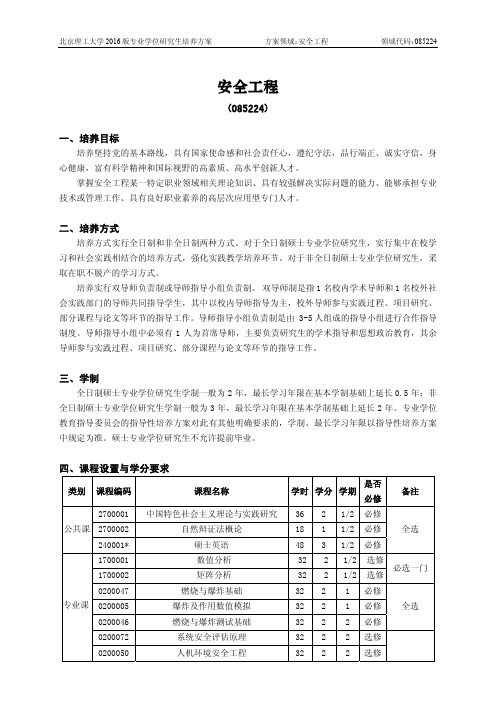
0200032
化学物质安全技术
32 2 1 选修
0200001
安全生产技术
32 2 2 选修
0200082
消防工程
32 2 2 选修
注:1. 研究生在入学当年达到免修条件者,可以申请免修外国语。以研究生院发布的最新“研
究生英语免修条件”为准。
2.数值分析和矩阵分析指由数学与统计学院针对研究生开设的课程,至少选修 1 门。
北京理工大学 2016 版专业学位研究生培养方案
方案领域:安全工程
领域代码:224
六、培养环节及学位论文相关工作
1.文献综述(0.5学分) 硕士专业学位研究生在学期间应结合学位论文任务,至少阅读 20 篇在研究领域内以行业技术发
展与工程应用为主要内容的国内外文献,了解、学习本领域新技术、新工艺、新方法、新材料的应
北京理工大学 2016 版专业学位研究生培养方案
方案领域:安全工程
领域代码:085224
安全工程
(085224)
一、培养目标
培养坚持党的基本路线,具有国家使命感和社会责任心,遵纪守法,品行端正、诚实守信,身 心健康,富有科学精神和国际视野的高素质、高水平创新人才。
掌握安全工程某一特定职业领域相关理论知识、具有较强解决实际问题的能力、能够承担专业 技术或管理工作、具有良好职业素养的高层次应用型专门人才。
32 2 2 选修
北京理工大学 2016 版专业学位研究生培养方案
方案领域:安全工程
领域代码:085224
类别 课程编码
课程名称
是否 学时 学分 学期
必修
备注
0200031
化学物理效应
32 2 1 选修
0200057
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个。
(2)不变因子与行列式因子的关系:
d1() D1()
d2 ( )
X i1, X i2 , , X ini
(4)Jordan标准形的某些应用 a)求一个给定的矩阵的高次幂 b) 求解一个常微分方程组 c) 判断两个矩阵是否相似 d) 待补充…☺
J1
J
J2
J
s
为Jordan标准形矩阵。
定理: 设 A C nn , A的初等因子为
( a1)n1 , ( a2 )n2 ,
则
AJ
, ( as )ns
,这里
J1
J
J2
J
s
其中
ai 1
ai 1
Ji
,(i 1,2, , s)
1
ai ni ni
我们称 J 是矩阵 A 的Jordan标准形。
0
பைடு நூலகம்
0
其中 r 1, di ()是首项系数为1的多项式且
di () di1() (i 1,2, , r 1)
称这种形式的 矩阵为 A( ) 的Smith标准形。 d1(), d2(), , dr ()称为 A()的不变因子。
矩阵Smith标准形的唯一性
(1) 行列式因子
定 义: A()为一个 矩阵且 rank( A()) r 对
(2)用特征矩阵秩的方法求数字矩阵的Jordan标 准形. 具体操作步骤: (1)先求出该矩阵的特征多项式及其特征值;
(2)以 i为主对角元的 阶 t Jordan 块的个数等
于
rank(i E A)t1 rank(i E A)t
(3)如何求相似变换矩阵?
设 ACnn,则存在 n 阶可逆矩阵 P 使得
J1
P1AP
J2
J
t
其中
这里
Ji
为Jordan块,记
Pi C nni
P
P1, P2,
, Pt
那么有
AP1, AP2, , APt P1J1, P2J2, , Pt Jt
APi Pi Ji , i 1, 2, ,t
记 Pi Xi1, Xi2, , Xini ,又可得
D2 () D1 ( )
D1() d1() D2 () d1()d2 ()
dr ()
Dr () Dr 1 ( )
Dr () d1()d2() dr ()
二、初等因子和矩阵的相似
(1)初等因子
设 矩阵 A() 的不变因子为
d1(), d2(), , dr ()
在复数域内将它们分解成一次因式的幂的乘积:
AX i1 i X i1 AX i2 X i1 i X i2
AX ini
X X ini 1
i ini
注意: X i1 是矩阵 A
特征向量,特征向量
的对应于特征值 i 的
X i1的选取应该保证向
量 Xi2
可以求出,同样向量
X
i
的选取应该保证
2
向量 Xi3可以求出,依此类推,并且使得
线性无关。
d1
(
a )e11 1
(
a2
)e12
d2
(
a )e21 1
(
a2
)e22
( as )e1s ( as )e2s
dr
(
a )er1 1
(
a2
)er
2
( as )ers
其中 a1, as 是互异的复数,eij 是非负整数。因
为 di | di1()(i 1, , r 1) ,所以满足如下关系
0 e11 e21 0 e12 e22
er1 er2
0 e1s e2s ers
定义 在上式中,所以指数大于零的因子
( aj )eij , eij 0,i 1, , r, j 1, , s
称为 矩阵 A() 的初等因子
(2)数字矩阵的相似与 矩阵的等价
定理: 设 A, B 是两个n 阶的数字矩阵,那么
总结: - 矩阵与矩阵的Jordan标准形 一、 -矩阵的Smith标准形
(1) 存在性 (2) 唯一性
(3) 求一个给定的 -矩阵的Smith标准形的方法
矩阵Smith标准形的存在性
定 理 任意一个非零的m n型的 矩阵都等价于
一个“对角矩阵”,即
d1 ( )
d2()
A( )
dr ( )
条件是它们有相同的初等因子。
定理:两个同阶的方阵 A, B 相似的充分必要
条件是它们有相同的不变因子。
三、数字矩阵的Jordan标准形 (1)用初等因子求数字矩阵的Jordan标准形
ai 1
ai 1
Ji
1
ai ni ni
为Jordan块。设 对角形矩阵
J1,
J
2,
, J s 为Jordan块,称准
A与B 相似的充分必要条件为它们的特征矩
阵
I A
与
I B
等价。
定义: 对于数字矩阵A ,我们称 I A 的 不变因子为 A 的不变因子,称 I A的初等
因子为 A 的初等因子。
对于任何一个数字矩阵 A, I A 0 所以 rank(I A) n ,于是可得下面两
个定理
定理: 两个同阶的方阵 A, B 相似的充分必要
