2019普通高中学业水平考试
2019年辽宁省普通高中学业水平考试英语卷真题(附答案)

2019年辽宁省普通高中学业水平考试英语卷真题(本试卷分第I卷和第II卷两部分。
满分100分,考试时间90分钟)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.答案一律写在答题卡上,写在本试卷上无效。
考试结束后,将本试卷和答题卡一并交回。
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
第I卷(选择题满分60分)第一部分阅读理解(共两节;满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项。
AWelcome to Haneul’s Blogging WorldMay 23, 2028I saw it in my favorite science magazine: “Win a five-day vacation to a space hotel, 300 km (186 mi.) above Earth.” A vacation like that costs more than $1 million. Of course I entered the competition! I’m crazy about space. And ... can you believe it? I won! Now, I am in a rocket with five billionaires on our way to space!May 24, 2028The journey on the rocket yesterday was pretty scary and very noisy. It only took ten minutes to get into space, but it took six hours to connect with our space hotel. The space hotel is amazing! We all have our own bedrooms, and we have special belts to hold us onto our beds so we don’t float away when we’re asleep! Being in zero gravity(重力)is so strange!May 25, 2028I took a lot of photos today. Earth is the most beautiful and the most colourful thing in space. We’re travelling around Eart h at 27,000 km (16,777 mi.) per hour, and we can watch the sun rise and set 16 times a day!May 26, 2028Some of the other guests in this space hotel complain about everything! They don’t like the food or the beds. But I think we are the luckiest people in the universe!May 27, 2028Today was our last day in the space hotel. Now I just need to find $1 million for my next trip.1.What do we know about the author?A.He went to space by himself.B.He is craze about space.C.He took a plane to a space hotel.D.He failed to enter the competition.2.According to Paragraph 2, the journey on the rocket was _______.A.scary and noisyB. strange and quietC. boring and tiringD. long and dengerous3. Why do the guests have special belts in the space hotel?A. To make them wake early.B. To help them float away easily.C. To hold them onto their beds.D. To fasten them to their chairs.4. How many times can they watch the sun rise and set a day in space?A.186.B.27.C.16.D.65.Which of the following is true according to the text?A. Pilots are pleased with the view outside their rooms.B. Organizers like the elegant design of their bedroomsC. Waiters think they have provided the best service.D. Some guests complain about the food or the beds.BImagine stepping out your front door and standing in the middle of a national park. Daniel Raven-Ellison hopes this might soon be possible for millions of London residents (居民). Daniel is leading a campaign to make London a national park city.Although London has much more concrete than a national park usually would, it is home to more than 13,000 kinds of wildlife. These species live in its 3,000 parks, along with 15,000 varieties of flowering plants, and more than 300 species of birds. In fact, 47 percent of the land in London is green space.“We have eight million trees in London; it’s the world’s largest urban forest,” Daniel says. That’s almost one tree for every person living in London! Yet, even though London has thousands of outdoor spaces, one in seven children living there have n’t visited a green space in the past year.Daniel believes that making London into a national park will protect the animal life and green spaces in London. He hopes it will also encourage people, especially young people, to spend more time outdoors. Daniel takes his own son out to explore in London, and he thinks that other parents should do the same. Daniel believes that people who spend a lot of time in nature live happier and healthier lives. What do you think?6.What’s the purpose of the campaign led by Daniel?A.To build a modern town in England.B. To attract more visitors to parks.B.C.To create a new beautiful village. D. To make London a national park city.7.What does the underlined word “concrete” mean in Paragraph 2?A.大理石B. 混凝土C. 玻璃D. 塑料8.We can learn from Paragraph 2 and 3 that _______.A.London has 8 million treesB.London is small urban forestC.There few park in LondonD.More than 50% of London is green space9.In Daniel’s opinion, other parents should ______.A.take care of themselvesB.help their children with their schoolworkC.spend a lot of time indoorsD.take their children out to explore in London10.What can be the best title for the text?A.A New Type of ParkB. People’s Busy LifeC.A Traditional FestivalD. Children`s MuseumCAt a high school graduation, each graduating senior was asked to tell of their future plans. A girl named Dolly said she planned to become a country music singer. The audience laughed at her answer, which caused her to become determined to complete her dream and in the end, she became one of the stars of country music.This kind of persistence (执着) teaches all of us that we need to set goals and try our best to achieve them. Someone has said you can’t hit a target unless you aim for it. A goal is like a target where one takes steady aim to hit it.A famous bridge in New York connects the island of Manhattan to the city of Brooklyn so it is called the Brooklyn Bridge. The idea of building this bridge came to Ruebling in 1883. However, experts thought the distance across the river was too great and that Ruebling’s design would not work. Ruebling asked his son, Washington, who was also an engineer, to help him build the bridge. One day, Ruebling was killed at the bridge site and Washington was injured so badly that he couldn’t talk or walk.Everyone thought that the bridge construction would have to stop because the design of the bridge was understood only by Ruebling and Washington. As he thought about his situation, Washington decided his brain could still think how the bridge could be completed.As he lay in his hospital bed, he asked his wife to come and sit beside him. He began to communicate to her by tapping out a code on his wife’s arm. From this code, she was able to tell the bridge construction engineers what they should do next. This process took 13 years and today the Brooklyn Bridge is one of the wonders of New York.11.What caused the audience to laugh at Dolly?A.Her dream.B. Her kindness.C. Her beauty.D. Her honesty.12.Who came up with the idea of building the Brooklyn Bridge?A.DollyB. RueblingC. WashingtonD. Washington’s wife13.Experts thought John Ruebling’s design was ______A.realisticB. practicalC. impossibleD. necessary14.After he was injured, Washington decided ______.A.to take up writingB.to give up building the bridgeC.to leave his hometownD.to complete the Brooklyn Bridge15. How did Washington communicate to his wife?A. By drawing.B. By talking.C. By tappingD. By nodding.第二节(共5小题;每小题2分,满分10分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
海南省2019年普通高中学业水平合格性考试真题含答案

海南省2019年普通高中学业水平合格性考试生物注意事项:1.本试卷分为第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷共6页,满分100分,考试时间60分钟。
答卷前,考生务必在试卷和答题卡指定位置填写本人的姓名和准考证号,在答题卡上粘贴条形码。
2.选择题的答题,必须使用2B铅笔将所选项方框涂黑。
如果修改答案应使用橡皮将错选项方框的涂点擦干净,并将改选项的方框涂黑。
3.非选择题的答题,使用黑色签字笔在答题卡上题号指定的区域书写答案,在题号指定答题区域以外及草稿纸、试卷上书写的答案无效。
4.考试结東后,将本试卷和答题卡一并交回。
第I卷选择题(80分)本卷共30题,其中第1至20题,每题3分;第21至30题,每题2分。
在每道题给出的四个选项中,只有一项符合题意。
1.以碳链为骨架的多糖、蛋白质、核酸等生物大分子,构成了细胞生命大厦的基本框架。
这说明生命的核心元素是A.碳B.氢C.氧D.氮2.真核细胞和原核细胞的主要区别是有无成形的A.细胞壁B.细胞膜C.细胞质D.细胞核3.某同学在鉴定牛奶中的化学成分时,向牛奶样液中加入双缩脲试剂,摇匀后,观察到样液颜色变成紫色,据此推测该样液中含有A.蔗糖B.脂肪C.蛋白质D.淀粉4.细胞中绝大多数需要能量的生命活动都是由A TP直接提供能量的。
下列生命活动不需要ATP提供能量的是A.人脑思考B.肌肉收缩C.萤火虫发光D.水分子进出细胞1 2 5.刚收获的玉米种子在阳光下晒干,重量会有所减轻。
这个过程种子减少的物质主要是刚收获的玉米种子在阳光下晒干,重量会有所减轻。
这个过程种子减少的物质主要是A.水B.无机盐无机盐C.糖类糖类D.蛋白质蛋白质 6.2019年4月19日,经有关部门确诊,我省发生非洲猪瘟疫情。
当地政府迅速启动应急响应机制,采取有效措施,疫情及时得到控制。
非洲猪瘟是由非洲猪瘟病毒感染家猪和野猪引起的一种急性、出血性、烈性传染病。
非洲猪瘟病毒属于出血性、烈性传染病。
2019年6月广西壮族自治区普通高中学业水平考试数学试题(含答案)

7分
综上所述,a 的取值范围是(一∞,3].
8分
第3页 共3页
好
记
星
书
签
2019 年 6 月广西壮族自治区普通高中学业水平考试
数学
参考答案及评分标准
一、选择题(共 30 小题,每小题 2 分,共 60 分)
题号 1
2
3
4
5
6
7
8
9
10
答案 A
C
A
A
B
B
C
D
C
BHale Waihona Puke 题号 111213
14
15
16
17
18
19
20
答案 A
C
B
D
A
A
D
B
D
C
题号 21
22
23
2分
又∵f(2)=4-8ln2,
3分
∴y=x+2-8ln2,即 x-y+2-8ln2=0 为所求曲线的切线方程.
4分
第2页 共3页
好
记
星
书
签
(2)f’(x)=2x+1- =
,
令 g(x)=2x2+x-a,对称轴为 x=- ,
易知 g(x)在(1,+∞)上单调递增.
5分
又 g(1)=3-a,
①当 a<3 时,g(x)>g(1)=3-a>0,∴f(x)>0 在(1,+∞)上恒成立.
5分
EF 的长为点 E 到面 ABCD 的距离.
当 F 与 O 重合时,EF 取到最大值 EO=1.
6分
∴几何体 ABCDE 体积的最大值为:
2019年山西省普通高中学业水平考试数学试卷真题(含解析)
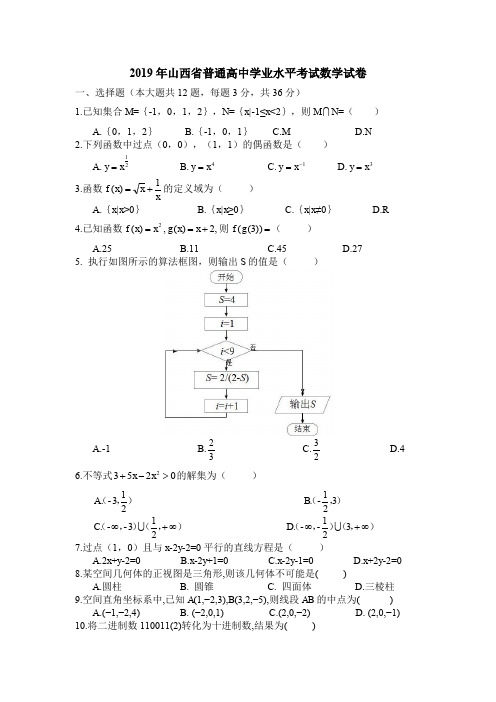
2019年山西省普通高中学业水平考试数学试卷一、选择题(本大题共12题,每题3分,共36分)1.已知集合M ={-1,0,1,2},N ={x|-1≤x <2},则M N =( ) A.{0,1,2} B.{-1,0,1} C.M D.N2.下列函数中过点(0,0),(1,1)的偶函数是( )A.21x y =B.4y x =C.1y -=xD.3x y =3.函数xx x f 1)(+=的定义域为( ) A.{x|x >0} B.{x|x ≥0} C.{x|x ≠0}D.R4.已知函数2)(x x f =,,2)(+=x x g 则=))3((g f ( ) A.25 B.11 C.45 D.275. 执行如图所示的算法框图,则输出S 的值是( )A.-1B.32 C.23D.46.不等式02532>-+x x 的解集为( )),(213-.A ),(321-B. ),(),(∞+∞213--.C),(),(∞+∞321--.D7.过点(1,0)且与x -2y -2=0平行的直线方程是( )A.2x +y -2=0B.x -2y +1=0C.x -2y -1=0D.x +2y-2=08.某空间几何体的正视图是三角形,则该几何体不可能是( )A.圆柱B. 圆锥C. 四面体D.三棱柱 9.空间直角坐标系中,已知A (1,−2,3),B (3,2,−5),则线段AB 的中点为( )A.(−1,−2,4)B. (−2,0,1)C.(2,0,−2)D. (2,0,−1) 10.将二进制数110011(2)转化为十进制数,结果为( )A.51B.52C.53D.5411.某自行车存车处在某一天总共存放车辆4000辆次,存车费为:电动自行车0.3元/辆,普通自行车0.2元/辆.若该天普通自行车存车x 辆次,存车费总收入为y 元,则y 与x 的函数关系式为( ).A.y =0.2x (0≤x ≤4000)B.y=0.5x (0≤x ≤4000)C.y =-0.1x +1200(0≤x ≤4000)D.y =0.1x +1200(0≤x ≤4000)12.若实数x ,y 满足⎪⎩⎪⎨⎧≤≥≥0001x x+y x-y+,则z=x−2y 的最小值是( )A.0B. −1C. −23D.−2二、填空题(本大题共4题,每题3分,共12分.请将答案填在题中横线上) 13.点(2,1)到直线3x +4y -2=0的距离是______.14.笔筒中放有2支黑色和1支红色,共3支签字笔,先从笔筒中随机取出一支笔,使用后放回笔筒,第二次再从笔筒中随机取出一支笔使用,则两次使用的都是黑色笔的概率为_______.15.已知向量a =(2,3),b =(−1,2),若m a +b 与a −2b 平行,则实数m 等于_______. 16.已知△ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,且(a 2+b 2−c 2)·(a cos B +b cos A )=abc ,若a +b =2,则c 的取值范围为________.三、解答题(本大题共5题,17-20题每题10分,21题12分,共52分) 17.某次运动会甲、乙两名射击运动员的成绩如下:甲:9.4 8.7 7.5 8.4 10.1 10.5 10.7 7.2 7.8 10.8 乙:9.1 8.7 7.1 9.8 9.7 8.5 10.1 9.2 10.1 9.1 (1)用一个茎叶图表示甲、乙两人的成绩;(2)计算平均值,并根据茎叶图的方差、中位数以及单峰与多峰分析甲、乙两人的成绩的集中程度和稳定情况;(甲方差为1.3,乙方差为0.9)18.设数列{a n}的前n项和为S n=2n2,{b n}为等比数列,且a1=b1,b2(a2−a1)=b1, (1)求数列{a n}和{b n}的通项公式,(2)若{b n}的前n项和为T n,求T2019。
2019年6月福建省普通高中学业水平合格性考试(会考)数学试题 含答案

机密★2019年6月17日 启用前2019年福建省普通高中学生学业基础会考数学试题考试时间:90分钟;满分:100分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷4至6页.考生注意:1.答题前,考生务必将自己的考生号、姓名填写在试题卷、答题卡上.考生要认真核对答题卡上粘贴的条形码的“考生号、姓名”与考生本人考生号、姓名是否一致.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.第Ⅱ卷用黑色字迹签字笔在答题卡上作答.在试题卷上作答,答案无效.3.考试结束,监考员将试题卷和答题卡一并收回.参考公式:样本数据12,,,n x x x 的标准差(n s x =+− 其中x 为样本平均数柱体体积公式V Sh =,其中S 为底面面积,h 为高台体体积公式()13V S S h '=+, 其中S ',S 分别为上、下底面面积,h 为高锥体体积公式13V Sh =, 其中S 为底面面积,h 为高球的表面积公式24S R π=,球的体积公式343V R π=, 其中R 为球的半径第Ⅰ卷 (选择题45分) 一、选择题(本大题有15小题,每小题3分,共45分,每小题只有一个选项符合题意)1.若集合{0,1},{1,2}A B ==,则A B ⋃=( )A .{0,1,2}B .{}0,1C .{}1,2D .{}12.若角50α=−︒,则角α是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角3.如图是一个底面边长为2的正三棱柱,当侧面水平放置时,它的俯视图...是( )A .B .C .D .4.若三个数1,2,m 成等比数列,则实数m =( )A .8B .4C .3D .25.一组数据3,4,5,6,7的中位数是( )A .7B .6C .5D .46.函数2sin y x =的最小值是( )A .2−B .1−C .1D .27.直径..为2的球的表面积是( ) A .2π B .4π C .8π D .16π8.从a ,b ,c ,d 四个字母中,随机抽取一个字母,则抽到字母a 的概率是( )A .14B .13C .12D .1 9.已知向量()()1,2,2,1a b ==−,则a b −=( )A .()1,3−B .()3,1−−C .()1,3D .()3,110.已知直线l 的斜率是1,且在y 轴上的截距是1−,则直线l 的方程是( )A .1y x =−−B .1y x =−+C .1y x =−D .1y x =+11.不等式220x x −>的解集是( )A .{}|0x x <B .{|2}x x >C .{|02}x x <<D .{|0,2}x x x <>或12.下列图象表示的函数中,在R 上是增函数的是( )A .B .C .D .13.不等式组0,0,20x y x y ≥⎧⎪≥⎨⎪+−≤⎩表示的平面区域的面积是( )A .4B .2C .1D .1214.某公司市场营销部员工的个人月收入与月销售量成一次函数关系,其对应关系如图所示.由图示信息可知,月销售量为3百件时员工的月收入是( )A .2100元B .2400元C .2700元D .3000元15.函数2lg ,0,()2,0x x f x x x x >⎧=⎨−≤⎩的零点个数是( ) A .1 B .2 C .3 D .4第Ⅱ卷 (非选择题55分)(请考生在答题卡上作答)二、填空题(本大题有5小题,每小题3分,共15分)16.若幂函数()f x x α=的图象过点(,则这个函数的解析式()f x =____________.17.执行右边的程序框图,当输入m 的值为3时,则输出的m 值是___________.18.函数6()([3,5])2f x x x =∈−的最小值是___________. 19.已知向量(1,1),(,1)a b x ==,且a b ⊥,则x =___________.20.设ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若1,6a c B π===,则b =________.三、解答题(本大题有5小题,共40分.解答应写出文字说明、证明过程或演算步骤)21.(本小题满分6分) 已知4sin ,5αα=是第一象限角. (Ⅰ)求cos α的值;(Ⅱ)求sin 4πα⎛⎫+ ⎪⎝⎭的值. 22.(本小题满分8分)甲、乙两人玩投掷骰子游戏,规定每人每次投掷6枚骰子,将掷得的点数和...记为该次成绩.进行6轮投掷后,两人的成绩用茎叶图表示,如图.(Ⅰ)求乙成绩的平均数;(Ⅱ)规定成绩在27点以上(含27点)为高分,根据两人的成绩,估计掷得高分的概率.23.(本小题满分8分)一辆汽车在某段路程中的行驶速率v 与时间t 的关系如图所示.(Ⅰ)求图中阴影部分的面积,并说明所求面积的实际含义;(Ⅱ)根据图示,求该汽车在这段路的行驶路程km s 关于时间h t 的函数解析式.24.(本小题满分8分)如图,长方体1111ABCD ABC D −中,AB BC =,E 为1CC 的中点. (Ⅰ)求证:1AC ∥平面BDE ;(Ⅱ)求证:1AC BD ⊥.25.(本小题满分10分)已知圆22:(2)16C x y +−=.(Ⅰ)写出圆C 的圆心坐标及半径长;(Ⅱ)已知圆C 与x 轴相交于A 、B 两点,试问在圆C 上是否存在点P ,使ABP 的面积等于请求出点P 的坐标;若不存在,请说明理由.2019年福建省普通高中学生学业基础会考数学试题参考答案与评分标准说明:1.本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容、比照评分标准酌情给分.2.对计算题,当考生的解答在某一步骤出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答所得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.解答題只给整数分,填空题不给中间分数.第Ⅰ卷 (选择题45分)一、选择题(本大题主要考查基础知识和基本运算.每小题3分,满分45分)1.A 2.D 3.A 4.B 5.C 6.A 7.B 8.A 9.D 10.C 11.D 12.D 13.B 14.C15.B第Ⅱ卷 (非选择题55分)二、填空题(本大题主要考查基础知识和基本运算.每小题3分,满分15分)16.12x 17.4 18.2 19.1− 20.1三、解答题(本大题有5小题,共40分.解答应写出文字说明、证明过程或演算步骤)21.本小题主要考查同角三角函数的基本关系,三角函数的符号,两角和的正弦等基础知识;考查运算求解能力、化归与转化思想.满分6分.解:(Ⅰ)∵4sin 5α=,且22sin cos 1αα+=,α为第一象限角, (1分)∴cos α= (2分)35==. (3分) (Ⅱ)sin sin cos cos sin 444πππααα⎛⎫+=+ ⎪⎝⎭(4分)3455=⨯+ (5分)=. (6分) 22.本小题主要考查茎叶图、特征数、概率等基础知识;考查数据处理能力、运算求解能力和应用意识.满分8分.解:(Ⅰ)由茎叶图得815151923286x +++++= (2分) 18=. (3分)∴乙成绩的平均数为18. (4分)(Ⅱ)由茎叶图知,掷得的12个数据中得高分的有3个, (6分) ∴据此估计得高分的概率30.2512P ==. (8分) 23.本小题主要考查函数有关概念、分段函数等基础知识;考查读图能力、运算求解能力、数学建模能力,考查函数思想、化归与转化思想和运用意识.满分8分.解:(Ⅰ)阴影部分的面积为601801901701300⨯+⨯+⨯+⨯=. (2分) 阴影部分的面积表示该汽车在这4小时内行驶的路程为300km . (4分)(Ⅱ)根据图形有:60,01,80(1)60,12,90(2)140,23,70(3)230,3 4.t t t t s t t t t ≤<⎧⎪−+≤<⎪=⎨−+≤<⎪⎪−+≤≤⎩ (注:按段给分)(8分) 或60,01,8020,12,9040,23,7020,3 4.t t t t s t t t t ≤<⎧⎪−≤<⎪=⎨−≤<⎪⎪+≤≤⎩ (8分)24.本小题主要考查空间直线、平面的位置关系等基础知识;考查空间想象能力、推理论证能力,考查化归与转化思想.满分8分.(Ⅰ)证明:连接AC 交BD 于O ,连接OE .在长方体1111ABCD ABC D −中,AB BC =, ∴底面ABCD 是正方形,∴AO OC =. (1分)∵1CE EC =,∴1OE AC ∥. (3分)又∵OE ⊂平面BDE ,1AC ⊄平面BDE ,∴1AC ∥平面BDE . (4分)(Ⅱ)证明:在长方体1111ABCD ABC D −中,1CC ⊥平面ABCD , 又BD ⊂平面ABCD ∴1CC BD ⊥. (5分)由(Ⅰ)知,ABCD 是正方形,∴AC BD ⊥.又1AC CC C ⋂=,∴BD ⊥平面1ACC . (7分)∵1AC ⊂平面1ACC ,∴1AC BD ⊥. (8分)25.本小题考查圆的方程、点与圆的位置关系、一元二次方程、三角形的面积等基础知识;考查逻辑推理能力和运算求解能力,考查数形结合思想、化归与转化思想、方程思想.满分10分.解:(Ⅰ)圆心()0,2C , (2分)半径4r =. (4分)(Ⅱ)对于方程22(2)16x y +−=,令0y =,解得x =±∴(A B −,∴||AB = (5分)假设圆C 上存在点()()000,26P x y y −≤≤,使得PAB 的面积等于即0011||22PAB S AB y y =⨯=⨯= 解得04y =,∴04y =(04y =−舍去). (7分) 将04y =代入方程22(2)16x y +−=,解得0x =± (9分)∴圆C 上存在点12(P P −满足题意.(10分)。
2019年山东省普通高中学业水平合格考试数学试卷(附详解)
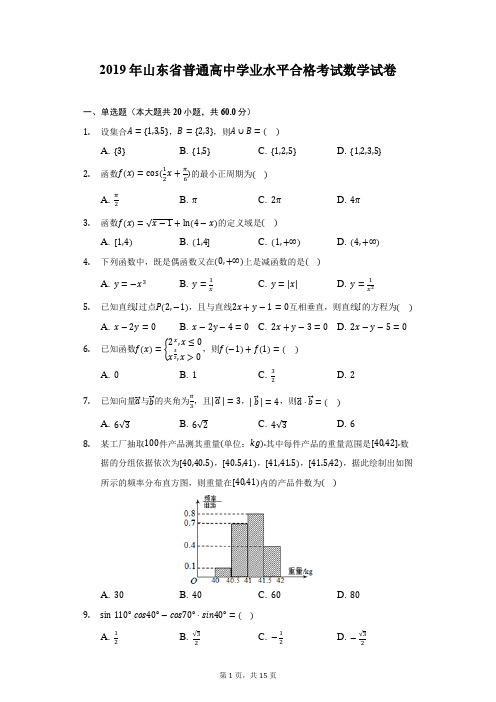
2019年山东省普通高中学业水平合格考试数学试卷一、单选题(本大题共20小题,共60.0分) 1. 设集合A ={1,3,5},B ={2,3},则A ∪B =( )A. {3}B. {1,5}C. {1,2,5}D. {1,2,3,5}2. 函数f(x)=cos(12x +π6)的最小正周期为( )A. π2B. πC. 2πD. 4π3. 函数f(x)=√x −1+ln(4−x)的定义域是( )A. [1,4)B. (1,4]C. (1,+∞)D. (4,+∞)4. 下列函数中,既是偶函数又在(0,+∞)上是减函数的是( )A. y =−x 3B. y =1xC. y =|x|D. y =1x 25. 已知直线l 过点P(2,−1),且与直线2x +y −1=0互相垂直,则直线l 的方程为( )A. x −2y =0B. x −2y −4=0C. 2x +y −3=0D. 2x −y −5=06. 已知函数f(x)={2x ,x ≤0x 32,x >0,则f(−1)+f(1)=( )A. 0B. 1C. 32D. 27. 已知向量a ⃗ 与b ⃗ 的夹角为π3,且|a ⃗ |=3,|b ⃗ |=4,则a ⃗ ⋅b ⃗ =( )A. 6√3B. 6√2C. 4√3D. 68. 某工厂抽取100件产品测其重量(单位:kg).其中每件产品的重量范围是[40,42].数据的分组依据依次为[40,40.5),[40.5,41),[41,41.5),[41.5,42),据此绘制出如图所示的频率分布直方图,则重量在[40,41)内的产品件数为( )A. 30B. 40C. 60D. 809. sin 110° cos40°−cos70°⋅sin40°=( )A. 12B. √32C. −12D. −√3210. 在平行四边形ABCD 中,AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ −AC⃗⃗⃗⃗⃗ =( ) A. DC⃗⃗⃗⃗⃗ B. BA⃗⃗⃗⃗⃗ C. BC⃗⃗⃗⃗⃗ D. BD⃗⃗⃗⃗⃗⃗ 11. 某产品的销售额y(单位:万元)与月份x 的统计数据如表.用最小二乘法求出y 关于x的线性回归方程为y ̂=7x +a ̂,则实数a ̂=( ) x 3 4 5 6 y25304045A. 3B. 3.5C. 4D. 10.512. 下列结论正确的是( )A. 若a <b ,则a 3<b 3B. 若a >b ,则2a <2bC. 若a <b ,则a 2<b 2D. 若a >b ,则lna >lnb13. 圆心为M(1,3),且与直线3x −4y −6=0相切的圆的方程是( )A. (x −1)2+(y −3)2=9B. (x −1)2+(y −3)2=3C. (x +1)2+(y +3)2=9D. (x +1)2+(y +3)2=314. 已知袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片,则下列判断不正确的是( )A. 事件“都是红色卡片”是随机事件B. 事件“都是蓝色卡片”是不可能事件C. 事件“至少有一张蓝色卡片”是必然事件D. 事件“有1张红色卡片和2张蓝色卡片”是随机事件15. 若直线(a −1)x −2y +1=0与直线x −ay +1=0垂直,则实数a =( )A. −1或2B. −1C. 13D. 316. 将函数y =sinx 的图象上所有的点的横坐标缩短到原来的13(纵坐标不变),再将得到的图象向右平移π12个单位,得到的图象对应的函数解析式为( )A. y =sin(3x −π4) B. y =sin(3x −π12) C. y =sin(13x −π4)D. y =sin(13x −π12)17. 3名同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( )A. 14B. 23C. 12D. 3418. 如图,在正方体ABCD −A 1B 1C 1D 1中,下列判断正确的是( )A. A 1D ⊥C 1CB. BD 1⊥ADC. A 1D ⊥ACD. BD 1 ⊥AC19. 已知向量a ⃗ ,b ⃗ 不共线,若AB ⃗⃗⃗⃗⃗ =a ⃗ +2b ⃗ ,BC ⃗⃗⃗⃗⃗ =−3a ⃗ +7b ⃗ ,CD ⃗⃗⃗⃗⃗ =4a ⃗ −5b ⃗ ,则( )A. A ,B ,C 三点共线B. A ,B ,D 三点共线C. A ,C ,D 三点共线D. B ,C ,D 三点共线20. 在三棱锥P −ABC 中,PA ,PB ,PC 两两垂直,且PA =1,PB =PC =2,则该三棱锥的外接球体的体积为( )A. 9π2B.27π2C. 9πD. 36π二、单空题(本大题共5小题,共15.0分)21. 某校田径队共有男运动员45人,女运动员36人.若采用分层抽样的方法在全体运动员中抽取18人进行体质测试,则抽到的女运动员人数为______. 22. α为第二象限角sinα=35,则tanα= ______ .23. 已知圆锥底面半径为1,高为√3,则该圆锥的侧面积为______.24. 已知函数f(x)=x 2+x +a 在区间(0,1)内有零点,则实数a 的取值范围为______. 25. 若P 是圆C 1:(x −4)2+(y −5)2=9上一动点,Q 是圆C 2:(x +2)2+(y +3)2=4上一动点,则|PQ|的最小值是______.三、解答题(本大题共3小题,共25.0分)26. 如图,在四棱锥P −ABCD 中,四边形ABCD 是平行四边形,E 、F 分别是AB 、PC 中点,求证:EF//面PAD .27.在△ABC中,a,b,c分别是角A,B,C的对边,且a=6,cosB=1.3(1)若sinA=3,求b的值;5(2)若c=2,求b的值及△ABC的面积S.28.已知函数f(x)=ax+log3(9x+1)(a∈R)为偶函数.(1)求a的值;(2)当x∈[0,+∞)时,不等式f(x)−b≥0恒成立,求实数b的取值范围.答案和解析1.【答案】D【解析】解:∵A={1,3,5},B={2,3},∴A∪B={1,2,3,5}.故选:D.进行并集的运算即可.本题考查了列举法的定义,并集的定义及运算,考查了计算能力,属于基础题.2.【答案】D【解析】解:由三角函数的周期公式得T=2π12=4π,故选:D.根据三角函数的周期公式直接进行计算即可.本题主要考查三角函数周期的计算,结合周期公式是解决本题的关键,比较基础.3.【答案】A【解析】解:∵函数f(x)=√x−1+ln(4−x),∴{x−1≥04−x>0,解得1≤x<4;∴函数f(x)的定义域是[1,4).故选A.根据函数f(x)的解析式,列出使解析式有意义的不等式组,求出解集即可.本题考查求定义域,是基础题.4.【答案】D【解析】解:由幂函数的性质可知,y=−x3,y=1x为奇函数,不符合题意,y=|x|为偶函数且在(0,+∞)上单调递增,不符号题意,y =1x 2为偶函数且在(0,+∞)上单调递减,符合题意. 故选:D .结合基本初等函数的单调性及奇偶性对选项分别进行判断即可. 本题主要考查了基本初等函数的奇偶性及单调性的判断,属于基础试题.5.【答案】B【解析】 【分析】本题考查了直线的一般式方程,是基础题.根据题意设出直线l 的方程,把点P(2,−1)代入方程求出直线l 的方程. 【解答】解:根据直线l 与直线2x +y −1=0互相垂直,设直线l 为x −2y +m =0, 又l 过点P(2,−1), ∴2−2×(−1)+m =0, 解得m =−4,∴直线l 的方程为x −2y −4=0. 故选:B .6.【答案】C【解析】解:∵函数f(x)={2x ,x ≤0x 32,x >0,∴f(−1)=2−1=12,f(1)=132=1,∴f(−1)+f(1)=12+1=32. 故选:C .推导出f(−1)=2−1=12,f(1)=132=1,由此能求出f(−1)+f(1)的值.本题考查函数值的求法,考查函数性质等基础知识,考查运算求解能力,是基础题.7.【答案】D【解析】解:∵向量a⃗与b⃗ 的夹角为π3,且|a⃗|=3,|b⃗ |=4,∴a⃗⋅b⃗ =|a⃗||b⃗ |cosπ3=3×4×12=6.故选:D.进行数量积的运算即可.本题考查了向量数量积的计算公式,考查了计算能力,属于基础题.8.【答案】B【解析】解:由频率分布直方图得:重量在[40,41)内的频率为:(0.1+0.7)×0.5=0.4.∴重量在[40,41)内的产品件数为0.4×100=40.故选:B.由频率分布直方图得重量在[40,41)内的频率为0.4.由此能求出重量在[40,41)内的产品件数.本题考查产品件数的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,是基础题.9.【答案】A【解析】解:sin110°cos40°−cos70°⋅sin40°=sin70°cos40°−cos70°⋅sin40°=sin(70°−40°)=sin30°=12.故选:A.利用诱导公式以及两角和的正弦函数化简求解即可.本题考查两角和与差的三角函数,特殊角的三角函数求值,考查计算能力.10.【答案】B【解析】解:在平行四边形ABCD 中, AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ +CA ⃗⃗⃗⃗⃗ =CD ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ . 故选:B .利用平面向量加法法则直接求解.本题考查向量的求法,考查平面向量加法法则等基础知识,考查运算求解能力,是基础题.11.【答案】B【解析】解:x −=3+4+5+64=4.5,y −=25+30+40+454=35,∴样本点的中心坐标为(4.5,35),代入y ̂=7x +a ̂,得35=7×4.5+a ̂,即a ̂=3.5. 故选:B .由已知求得样本点的中心坐标,代入线性回归方程即可求得实数a ^.本题考查线性回归方程,明确线性回归方程恒过样本点的中心是关键,是基础题.12.【答案】A【解析】解:A.a <b ,可得a 3<b 3,正确; B .a >b ,可得2a >2b ,因此B 不正确;C .a <b ,a 2与b 2大小关系不确定,因此不正确;D .由a >b ,无法得出lna >lnb ,因此不正确. 故选:A .利用函数的单调性、不等式的性质即可判断出正误.本题考查了函数的单调性、不等式的性质,考查了推理能力与计算能力,属于基础题.13.【答案】A【解析】解:由题意可知,圆的半径r =|3−12−6|5=3,故所求的圆的方程为(x −1)2+(y −3)2=9. 故选:A .由题意可知,圆的半径即为圆心M 到直线的距离,根据点到直线的距离公式即可求解. 本题主要考查了圆的方程的求解,解题的关键是直线与圆相切性质的应用.14.【答案】C【解析】解:袋中有大小、形状完全相同的5张红色、2张蓝色卡片,从中任取3张卡片, 在A 中,事件“都是红色卡片”是随机事件,故A 正确; 在B 中,事件“都是蓝色卡片”是不可能事件,故B 正确; 在C 中,事件“至少有一张蓝色卡片”是随机事件,故C 错误;在D 中,事件“有1张红色卡片和2张蓝色卡片”是随机事件,故D 正确. 故选:C .利用随机事件的定义直接求解.本题考查命题真假的判断,考查随机事件等基础知识,考查运算求解能力,是基础题.15.【答案】C【解析】解:根据题意,若直线(a −1)x −2y +1=0与直线x −ay +1=0垂直, 必有(a −1)+2a =0,解可得a =13; 故选:C .根据题意,分析可得(a −1)+2a =0,解可得a 的值,即可得答案.本题考查直线平行的判断方法,注意直线的一般式方程的形式,属于基础题.16.【答案】A【解析】解:将函数y =sinx 的图象上所有的点的横坐标缩短到原来的13(纵坐标不变),可得y =sin3x 的图象;再将得到的图象向右平移π12个单位,得到的图象对应的函数解析式为y =sin3(x −π12)=sin(3x −π4), 故选:A .由题意利用函数y =Asin(ωx +φ)的图象变换规律,得出结论.本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.17.【答案】D【解析】【分析】本题考查古典概型,是一个古典概型与排列组合结合的问题,解题时先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.求得3位同学各自在周六、周日两天中任选一天参加公益活动、周六、周日都有同学参加公益活动的情况,利用古典概型概率公式求解即可.【解答】解:3位同学各自在周六、周日两天中任选一天参加公益活动,共有23=8种情况,周六、周日都有同学参加公益活动,共有23−2=8−2=6种情况,∴所求概率为68=34.故选D.18.【答案】D【解析】解:因为AC⊥BD,AC⊥DD1;BD∩DD1=D;BD⊆平面DD1B1B,DD1⊆平面DD1B1B,∴AC⊥平面DD1B1B;BD1⊆平面DD1B1B;∴AC⊥BD1;即D对.故选:D.直接可以看出A,B,C均不成立,用线线垂直来推线面垂直进而得到线线垂直.本题主要考查平面中的线线垂直的证明,属于对基础知识的考查.19.【答案】B【解析】解:向量a ⃗ ,b ⃗ 不共线,AB ⃗⃗⃗⃗⃗ =a ⃗ +2b ⃗ ,BC ⃗⃗⃗⃗⃗ =−3a ⃗ +7b ⃗ ,CD ⃗⃗⃗⃗⃗ =4a ⃗ −5b⃗ , ∴BD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =(−3a ⃗ +7b ⃗ )+(4a ⃗ −5b ⃗ )=a ⃗ +2b ⃗ =AB ⃗⃗⃗⃗⃗ , ∴BD ⃗⃗⃗⃗⃗⃗ //AB ⃗⃗⃗⃗⃗ ,∴A ,B ,D 三点共线. 故选:B .BD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =(−3a ⃗ +7b ⃗ )+(4a ⃗ −5b ⃗ )=a ⃗ +2b ⃗ =AB ⃗⃗⃗⃗⃗ ,从而BD ⃗⃗⃗⃗⃗⃗ //AB ⃗⃗⃗⃗⃗ ,进而A ,B ,D 三点共线.本题考查命题真假的判断,考查向量加法法则、向量共线等基础知识,考查运算求解能力,是基础题.20.【答案】A【解析】解:由三棱锥中PA ,PB ,PC 两两垂直,且PA =1,PB =2,PC =2将此三棱锥放在长方体中,由题意知长方体的长宽高分别是:1,2,2.设外接球的半径为R ,则2R =√12+22+22=3所以R =32, 所以外接球的体积V =43πR 3=92π, 故选:A .由题意将此三棱锥放在长方体中,可得长方体的长宽高,再由长方体的对角线等于外接球的直径求出外接球的体积.考查三棱锥的棱长与外接球的半径之间的关系及球的体积公式,属于基础题.21.【答案】8【解析】解:∵某校田径队共有男运动员45人,女运动员36人, ∴这支田径队共有45+36=81人,用分层抽样的方法从该队的全体运动员中抽取一个容量为18的样本, ∴每个个体被抽到的概率是1881=29, ∵女运动员36人,∴女运动员要抽取36×29=8人, 故答案为:8.根据田径队的男女运动员数目和用分层抽样要抽取的数目,得到每个个体被抽到的概率值,利用每个个体被抽到的概率乘以女运动员的数目,得到女运动员要抽取得人数. 本题考查分层抽样,本题解题的关键是在抽样过程中每个个体被抽到的概率相等,本题是一个基础题.22.【答案】−34【解析】解:∵α为第二象限角sinα=35, ∴cosα=−45,则tanα=sinαcosα=−34, 故答案为:−34.由条件利用同角三角函数的基本关系求得cosα的值,从而求得tanα的值. 本题主要考查同角三角函数的基本关系的应用,属于基础题.23.【答案】2π【解析】解:由已知可得r =1,ℎ=√3,则圆锥的母线长l =√12+(√3)2=2. ∴圆锥的侧面积S =πrl =2π. 故答案为:2π.由已知求得母线长,代入圆锥侧面积公式求解.本题考查圆锥侧面积的求法,关键是对公式的记忆,是基础题.24.【答案】(−2,0)【解析】解:函数f(x)=x2+x+a在区间(0,1)内有零点,f(0)=a,f(1)=2+a,由零点存在性定理得f(0)⋅f(1)=a(a+2)<0,得−2<a<0,经验证a=−2,a=0均不成立,故答案为:(−2,0)由零点存在性定理得f(0)⋅f(1)=a(a+2)<0,求出即可.考查函数零点存在性定理的应用,中档题.25.【答案】5【解析】解:圆C1:(x−4)2+(y−5)2=9的圆心C1(4,5),半径r=3,圆C2:(x+2)2+(y+3)2=4的圆心C2(−2,−3),半径r=2,d=|C1C2|=√(4+2)2+(5+3)2=10>2+3=r+R,所以两圆的位置关系是外离,又P在圆C1上,Q在圆C2上,则|PQ|的最小值为d−(r+R)=10−(2+3)=5,故答案为:5.分别找出两圆的圆心坐标,以及半径r和R,利用两点间的距离公式求出圆心间的距离d,根据大于两半径之和,得到两圆的位置是外离,又P在圆C1上,Q在圆C2上,则|PQ|的最小值为d−(r+R),即可求出答案.本题考查圆与圆的位置关系,属于中档题.26.【答案】证明:取PD的中点G,连接FG、AG.因为PF=CF,PG=DG,CD.所以FG//CD,且FG=12又因为四边形ABCD是平行四边形,且E是AB的中点.CD.所以AE//CD,且AE=12所以FG//AE,且FG=AE,所以四边形EFGA是平行四边形,所以EF//AG.又因为EF⊄平面PAD,AG⊂平面PAD,所以EF//平面PAD .【解析】本题考查直线与平面平行的证明,是基础题.取PD 的中点G ,连接FG 、AG ,由PF =CF ,PG =DG ,所以FG//CD ,且FG =12CD.又因为四边形ABCD 是平行四边形,且E 是AB 的中点.所以AE//CD ,且AE =12CD.证得四边形EFGA 是平行四边形,所以EF//AG ,由线面平行的判定定理即可得证.27.【答案】解:(1)由cosB =13可得sinB =2√23, 由正弦定理可得,a sinA =bsinB , 所以b =asinB sinA=6×2√2335=20√23,(2)由余弦定理可得,cosB =13=a 2+c 2−b 22ac=36+4−b 22×2×6,解可得,b =4√2, S =12acsinB =12×6×2×2√23=4√2.【解析】(1)先根据同角平方关系求出sinB ,然后结合正弦定理即可求解, (2)结合余弦定理及三角形的面积公式即可求解.本题主要考查了正弦定理,余弦定理及三角形的面积公式在求解三角形中的应用,属于基础试题.28.【答案】解:(1)根据题意可知f(x)=f(−x),即ax +log 3(9x+1)=−ax +log 3(9−x+1),整理得log 39x +19−x +1=−2ax ,即−2ax =log 39x =2x ,解得a =−1;(2)由(1)可得f(x)=−x +log 3(9x +1)=log 3(3x +13x ),令ℎ(x)=3x +13x ,x ∈[0,+∞),任取x 1、x 2∈[0,+∞),且x 2>x 1, 则ℎ(x 2)−ℎ(x 1)=3x 2+13x 2−(3x 1+13x 1)=(3x 2−3x 1)⋅3x 1+x 2−13x 1+x 2因为x 2>x 1≥0,所以3x 2−3x 1≥0,3x 1+x 2>1,则3x 1+x 2−1>0, 所以ℎ(x)在[0,+∞)上单调递增,故f(x)在[0,+∞)上单调递增, 因为f(x)−b ≥0对x ∈[0,+∞)恒成立,即−x+log3(9x+1)≥b对x∈[0,+∞)恒成立,因为函数g(x)=−x+log3(9x+1)在[0,+∞)上是增函数,所以g(x)min=g(0)=log32,则b≤log32.【解析】(1)根据偶函数性质f(x)=f(−x),化简整理可求得a的取值;(2)根据条件可知x+log3(9x+1)≥b对x∈[0,+∞)恒成立,求出函数g(x)=x+ log3(9x+1)在[0,+∞)上的最小值即可本题考查利用函数奇偶性求参数值,利用函数增减性求参数取值范围,属于中档题.。
2019年安徽省普通高中学业水平考试英语试题含答案

2019年安徽省普通高中学业水平考试英语本试卷分第Ⅰ卷和第Ⅱ卷,共四部分,八大题,共8页。
第Ⅰ卷为选择题,第Ⅱ卷为非选择题。
全卷满分100分,考试时间为90分钟。
第Ⅰ卷(选择题)注意事项:1. 答题前,请将自己的姓名、座位号用钢笔或黑色水笔填写在答题卡上,并用2B铅笔在答题卡规定位置上将自己的座位号、考试科目涂黑。
考试结束时,请将试卷和答题卡一并交回。
2. 请将所有选择题的答案涂在答题卡上。
每一小题只能从所给选项中挑选一个选项,并用2B铅笔在答题卡上把该题对应的答案标号涂黑。
如需改动,要用橡皮擦干净后,再涂另一个答案。
选对得分;不选、错选或多选均不得分。
第一部分听力(共三大题,满分20分)Ⅰ. 关键词语选择(共5小题;每小题1分,满分5分)听下面五个句子。
从每小题所给的A、B、C三个选项中选出你所听到的单词或短语。
每个句子读两遍。
1. A. devote B. demand C. defend2. A. lecture B. licence C. lesson3. A. feeding B. feeling C. fixing4. A. single B. simple C. similar5. A. set about B. set out C. set upⅡ. 短对话理解(共5小题;每小题1分,满分5分)听下面五段对话。
每段对话后有一个小题,从每小题所给的A、B、C三个选项中选出一个最佳选项。
每段对话读两遍。
6. What will the man do today?A. Take the day off.B. Go to a meeting.C. See a doctor.7. What is the man’s advice on losing weight?A. To take exercise.B. To go on a diet.C. To eat healthily.8. What time is it now?A. 8:30.B. 9:00.C. 11:00.9. Where does the conversation probably take place?A. In a supermarket.B. In a restaurant.C. In a library.10. What are the two speakers talking about?A. The air pollution.B. The man’s illness.C. The government’s policy.Ⅲ. 长对话和独白理解(共10小题;每小题1分,满分10分)听下面三段对话或独白。
2019年普通高中学业水平合格性考试(会考)数学试卷三(含答案)

2019年普通高中学业水平合格性考试数学试卷(考试时间:90分钟满分:100分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至4页,第Ⅱ卷5至6页。
考生注意:1.答题前,考生务必将自己的考生号、姓名填写在试题卷答题卡上。
考生要认真核对答题卡上粘贴的条形码的“考生号、姓名”与考生本人考生号、姓名是否一致。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
第Ⅱ卷用黑色字迹签字笔在答题卡上作答。
在试题卷上作答,答案无效。
3.考试结束,监考员将试题卷和答题卡一并收回。
第Ⅰ卷(选择题45分)一、选择题(本大题有15小题,每小题3分,共45分。
每小题只有一个选项符合题目要求)1.已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩C uA=9)A.{1,6}B.{1,7}C.{6,7}D.{1,6,7}2.某学校为了解1000名新生的身体素质,将这些学生编号为1,2,...1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验。
若46号学生被抽到,则下面4名学生中被抽到的是()A.8号学生B.200号学生C.616号学生D.815号学生3.等差数列{a n}中,a1+a5=10,a4=7,则数列{a n}的公差为()A.1B.2C.3D.44.甲、乙两人下棋,两人下成和棋的概率是12,甲获胜的概率是13,则甲不输的概率为()A.56B.25C.16D.135.幂函数y=f(x)的图象经过点(8,22),则f(x)的图象是()6.经过点A(8,-2),斜率为.−12的直线方程为()A.x+2y-4=0B.x-2y-12=0C.2x+y-14=0D.x+2y+4=07.设f(x)为奇函数,且当x≥0时,f(x)=e-X-1.则当x<0时,f(x)=()A.e-X-1B.e-X+1C.-e-X-1D.-e-X+18.在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,AB =(1,-2),AD =(2,1),则AB ·AD =()A.5B.4C.3D.29.函数f(x)=1X—x3的图像关于()A.x轴对称B.y轴对称C.直线y=x对称D.坐标原点对称10.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于()A.2πB.πC.2D.111.设m,n是两条不同的直线,α,β是两个不同的平面,下列说法正确的是()A.若m⊥n,n//α,则m⊥αB.若m//β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α12.直线3x+4y=b与圆x2+y2-2x-2y+1=0相切,则b的值是()A.-2或12B.2或一12C.-2或-12D.2或1213.在区间[o,2]上随机地取一个数x,则事件“-1≤log1(x+12)≤1发生的概率为()2A.34B.23C.13D.1414.为了得到函数y=sin2x的图象,只要把函数y=sin x的图象上所有点()A.横坐标缩短到原来的12,纵坐标不变B.横坐标伸长到原来的2倍,纵坐标不变C.纵坐标缩短到原来的12,横坐标不变D.纵坐标伸长到原来的2倍,横坐标不变15.已知{a n}是首项为1的等比数列,s n是{a n}的前n项和,且9S3=S6,则数列{1a n}的前5项和为()A.158或5B.3116或5C.3116D.158第Ⅱ卷(非选择题55分)二、填空题(本大题共5小题,每小题3分,共15分)16.函数y=7+6x−x2的定义域是。
山东省2019年冬季普通高中学业水平合格考试生物真题卷精选全文完整版

可编辑修改精选全文完整版山东省2019年冬季普通高中学业水平合格考试生物真题卷学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 组成细胞的元素大多以化合物的形式存在。
下列关于化合物中所含元素的叙述,错误的是()A.ATP与核酸中都含磷元素B.胰岛素中含氮元素C.脂肪与脂肪酶中含硫元素D.血红蛋白中含铁元素2. 蛋白质是生命活动的主要承担者。
下列关于人体血浆中蛋白质的叙述,正确的是()A.都由相同数目的氨基酸组成B.都是在核糖体上合成的C.都是由内质网直接分泌的D.都具有运输氧气的作用3. 为了研究细胞膜的化学组成,需要把细胞膜与细胞的其他组分离开。
下列细胞中最容易获得较纯细胞膜的是()A.酵母菌细胞B.动物的卵细胞C.植物细胞D.哺乳动物成熟的红细胞4. 下列关于麦芽糖、蔗糖和乳糖的叙述,错误的是()A.都广泛分布于动物细胞中B.都由两分子单糖组成C.都需水解成单糖才能被细胞吸收D.都只含有C、H、O三种元素5. 如图为某细胞局部结构模式图,①~④表示不同的结构。
下列叙述错误的是()A.①是双层膜结构B.②与核糖体的形成有关C.③主要由RNA和蛋白质组成D.④是某些大分子物质的运输通道6. 蓝细菌和玉米叶肉细胞在结构上最主要的区别是()A.有无细胞器B.有无细胞壁C.有无DNA和RNA D.有无核膜包被的细胞核7. 在观察洋葱根尖分生组织细胞有丝分裂的实验中,用盐酸和酒精混合液处理根尖的目的是()A.将染色体染成深色B.促进根尖分生组织细胞的分裂C.抑制细胞内纺锤体的形成D.使组织中的细胞相互分离开来8. 肺泡是人体与外界环境进行气体交换的场所,氧气进入肺泡细胞的方式是()A.自由扩散(单纯扩散)B.协助扩散C.主动运输D.胞吞9. 将紫色洋葱鳞片叶外表皮置于质量浓度为0.3g/mL的蔗糖溶液中,细胞不会出现的变化是()A.细胞的体积增大B.液泡的体积变小C.原生质层与细胞壁分离D.液泡的颜色变深10. 唾液中的淀粉酶会随食物一起进入胃,胃内能催化唾液淀粉酶水解的酶是()A.淀粉酶B.蛋白酶C.麦芽糖酶D.脂肪酶11. 人体的生命活动需要消耗能量。
2019年山东省普通高中学业水平考试数学试题(带答案)

2019年山东省普通高中学业水平考试数学试题(带答案)2019年山东省普通高中学业水平考试数学试题(带答案)一、选择题(共20小题,每小题3分,共60分)1.已知集合 $A=\{2,4,8\}$,$B=\{1,2,4\}$,则 $A\capB=$()A。
{4} B。
{2} C。
{2,4} D。
{1,2,4,8}2.周期为 $\pi$ 的函数是()A。
$y=\sin x$ B。
$y=\cos x$ C。
$y=\tan 2x$ D。
$y=\sin2x$3.在区间 $(1,2)$ 上为减函数的是()A。
$y=x$ B。
$y=x^2$ C。
$y=\frac{1}{x}$ D。
$y=\ln x$4.若角 $\alpha$ 的终边经过点 $(-1,2)$,则 $\cos\alpha=$()A。
$-\frac{5}{13}$ B。
$\frac{5}{13}$ C。
$-\frac{1}{13}$ D。
$\frac{1}{13}$5.把红、黄两张纸牌随机分给甲、乙两个人,每人分得一张,设事件 $P$ 为“甲分得黄牌”,设事件 $Q$ 为“乙分得黄牌”,则()A。
$P$ 是必然事件 B。
$Q$ 是不可能事件 C。
$P$ 与$Q$ 是互斥但不对立事件 D。
$P$ 与 $Q$ 是互斥且对立事件6.在数列 $\{a_n\}$ 中,若 $a_{n+1}=3a_n$,$a_1=2$,则$a_4=$()A。
18 B。
36 C。
54 D。
1087.采用系统抽样的方法,从编号为1~50的50件产品中随机抽取5件进行检验,则所选取的5件产品的编号可以是()A。
1,2,3,4,5 B。
2,4,8,16,32 C。
3,13,23,33,43 D。
5,10,15,20,258.已知 $x,y\in (0,+\infty)$,且 $x+y=1$,则 $xy$ 的最大值为()A。
1 B。
$\frac{1}{3}$ C。
$\frac{1}{4}$ D。
四川省成都市2019-2020学年普通高中学生学业水平测试数学试题-含答案

四川省成都市2019-2020学年普通高中学生学业水平测试数学试题-含答案2019年四川省成都市普通高中生学业水平考试数学试题注意事项:1.考生在答题前需使用0.5毫米黑色签字笔填写姓名、座号、考生号、县区和科类到答题卡和试卷规定的位置上。
2.选择题需使用2B铅笔将答案标号涂黑,如需改动,需使用橡皮擦干净后再涂其他答案标号。
在试卷上作答无效。
3.答案必须使用0.5毫米黑色签字笔写在答题卡各题目指定区域内相应的位置,如需改动,需先划掉原来的答案,再写上新的答案。
不能使用涂改液、胶带纸、修正带。
不按要求作答的答案无效。
一、选择题1.把复数z的共轭复数记为-z,i为虚数单位,若z=1+i,则(1+z)·-z=()A.3-i。
B.3+1.C.1+3i。
D.3- 解析:(1+z)·z=(2+i)(1-i)=3-i。
答案:A2.设U=R,M={x|x^2-2x>0},则∁U M=()A.[0,2]。
B.(0,2)。
C.(-∞,0)∪(2,+∞)。
D.(-∞,0]∪[2,+∞)解析:因为M={x|x^2-2x>0}={x|x>2或x<0},所以∁UM={x|0≤x≤2}.答案:A3.若函数f(x)=(2x+1)(x-a)/(x+1)(x+2),为奇函数,则a=()A.1.B.2.C.-1.D.-2解析:因为f(x)为奇函数,所以f(-1)=-f(1),即(-1-a)/(1-a)=-1,解得a=1.答案:A4.命题“∀x>0,x^2+x>0”的否定是()A.∃x>0,x^2+x≤0.B.∃x>0,x+x≤0C.∀x>0,x^2+x≤0.D.∀x≤0,x^2+x>0解析:根据全称命题的否定是特称命题,可知该命题的否定是:∃x>0,x^2+x≤0.答案:B5.若等比数列{an}满足an·an+1=16n,则公比为()A.2.B.4.C.8.D.16解析:由an·an+1=an^2·q=16n,得q>0,又an+1/an=q,所以q^2=an+1/an=16,所以q=4.答案:B6.根据图中的三视图,可以确定多面体的形状。
【学业水平】北京2019年普通高中第一次合格性学业水平考试英语试题

2019年北京市第一次普通高中学业水平合格性考试第一节:听下面十段对话或独白,从各题A、B、C三个选项中每段对话或独白你将听两遍。
听第1段材料,回答第1题。
1.What is the man going to听第2段材料,回答第2题。
2.Where was the man born?4.How doe the woman feel?听第5段材料,回答第5题至第6题。
选出能回答问题的最佳答案。
do this Saturday?A. Go hiking.B. Visit his grandparents.C. Have a picnic.A. In England.B. In New Zealand.C. In Russia.听第3段材料,回答第3题。
3. When will the speakers leave for the airport?A.At 1:30.B.At 2:00.C. At 4:30.听第4段材料,回答第4题。
A. Interested.B. Nervous.C. Happy.5. What is the man doing?A. Making an invitation.B. Asking for help.C. Talking about the weather.6. What does the woman need to take for camping?A. A tent.B. Warm clothes.C. Some food.听第6段材料回答第7题至第8题。
7. What will the speakers do tomorrow evening?A. Watch a film.B. See friends off.C. Put on a show.8. Where will the speakers meet?A. At the airport.B. At the cinema.C. At the cafe.听第7段材料,回答第9题至第11题。
2019年安徽省普通高中学业水平考试数学试题(解析版)

2019年安徽省普通高中学业水平考试数学试题一、单选题1.已知集合{}13,5A =,,{}0,1,2B =,则=A B I ( ) A .∅ B .{}1C .{0,1}D .{}1,2,3【答案】B【解析】直接根据交集的定义计算可得; 【详解】解:{}13,5A =Q ,,{}0,1,2B =, {}1A B ∴⋂=故选:B 【点睛】本题考查集合的运算,属于基础题. 2.下列函数中为偶函数的是( )A .y =B .1y x =-C .2y x =D .3y x =【答案】C【解析】利用偶函数的定义判断即可. 【详解】解:y =[)0,+∞,不关于原点对称,不是偶函数;1y x =-是非奇非偶函数;2y x =是偶函数,3y x =是奇函数;故选:C . 【点睛】本题考查常见函数的奇偶性的判断,属于基础题.3.立德中学男子篮球队近5场比赛得分情况如茎叶图所示,则这5场比赛的平均得分是( ) 茎叶3 84 2 65 0 4A .42B .44C .46D .48【答案】C【解析】根据茎叶图读取数据,再计算平均数即可; 【详解】解:由茎叶图可得这5场比赛得分分别为:38、42、46、50、54, 则平均数3842465054465++++==故选:C 【点睛】本题考查茎叶图的应用,几个数的平均数的计算,属于基础题. 4.不等式(1)(3)0x x +-<的解集为( ) A .{|13}x x -<< B .{|31}x x -<< C .{|1x x <-,或3}x > D .{|3x x <-,或1}x >【答案】A【解析】直接根据一元二次不等式的解法求解即可; 【详解】解:因为(1)(3)0x x +-< 所以13x -<<即不等式的解集为{|13}x x -<< 故选:A 【点睛】本题考查一元二次不等式的解法,属于基础题.5.函数()1x f x a =+(0a >,且1a ≠)的图象经过定点( ) A .(0,1)B .(01)-,C .(0,2)D .(1,1)【答案】C【解析】由指数函数的定义可知,当指数为0时,指数式的值为1即可得解. 【详解】解:因为()1xf x a =+(0a >,且1a ≠) 令0x =,则()0012f a =+=,故函数过点()0,2,故选:C 【点睛】本题考查指数函数过定点问题,属于基础题.6.一支田径队有男运动员56人,女运动员42人,若用分层抽样的方法从全体运动员中抽取一个容量为28的样本,则在男运动员中需要抽取的人数为( ) A .12 B .14C .16D .18【答案】C【解析】若用分层抽样的方法,则样本中男运动员与所有运动员的人数之比与总体的男运动员与所有运动员的人数之比相同,由此求解即可 【详解】由题,男运动员占总体运动员的56456427=+,所以男运动员中需要抽取的人数为428167⨯=,故选:C 【点睛】本题考查分层抽样的应用,属于基础题7.如图,分别以正方形ABCD 的两条边AB 和CD 为直径,向此正方形内作两个半圆(阴影部分),在正方形内随机取一点,则此点取自阴影部分的概率是( )A .12πB .8πC .6π D .4π 【答案】D【解析】首先求出正方形的面积以及阴影部分的面积,再根据几何概型的概率公式计算可得; 【详解】解:设正方形的边长为2,则正方形的面积为224=,阴影部分恰可拼成一个直径为2的圆,则阴影部分的面积为21ππ⨯=,根据几何概型的概率公式可得,在正方形内随机取一点,则此点取自阴影部分的概率4P π=,故选:D 【点睛】本题考查面积型几何概型的概率计算,属于基础题.8.在平面直角坐标系中,已知角α的终边经过点(3,4),则cos α=( )A .43B .34C .45D .35【答案】D【解析】先求出点P 到原点的距离r ,然后按照cos α的定义:cos xrα=求出结果. 【详解】解:3x =Q ,4y =,5r ==,∴由任意角的三角函数的定义知,3cos 5x r α==, 故选:D . 【点睛】本题考查任意角的三角函数的定义:在角的终边上任取一点(除原点外),求出此点到原点的距离r ,该角的余弦值等于所取点的横坐标除以此点到原点的距离r .9.已知直线l 10y -+=,则直线l 的倾斜角是 A .23πB .56π C .3π D .6π 【答案】C【解析】直线方程即:1y =+ ,直线的斜率k =,则直线的倾斜角为3π .本题选择C 选项.10.已知(2,2)a m =-r ,(4,)b m =r ,且//a b r r,则m =( )A .4B .-4C .6D .-6【答案】A【解析】根据平面向量共线定理的坐标表示得到方程,解得即可; 【详解】解:因为(2,2)a m =-r ,(4,)b m =r ,且//a b r r,所以()242m m ⨯=⨯-, 解得4m = 故选:A 【点睛】本题考查平面向量共线定理的应用,属于基础题. 11.5sin6π=( )A .12 B .12-C D . 【答案】A【解析】根据诱导公式及特殊角的三角函数值计算可得; 【详解】 解:51sinsin sin 6662ππππ⎛⎫=-== ⎪⎝⎭ 故选:A 【点睛】本题考查诱导公式及特殊角的三角函数值,属于基础题.12.已知点(4,9)A ,(6,3)B ,则以线段AB 为直径的圆的标准方程是( ) A .22(5)(6)40x y +++=B .22(5)(6)40x y -+-=C .22(5)(6)10x y +++=D .22(5)(6)10x y -+-=【答案】D【解析】利用中点坐标公式求出AB 的中点坐标即为圆心,再根据平面直角坐标系上两点间的距离公式求出AB 的长即直径,最后写出圆的标准方程. 【详解】解:因为(4,9)A ,(6,3)B ,所以AB 的中点坐标为()5,6,AB ==,则以线段AB 为直径的圆的圆心坐标为()5,6,半径r =,故圆的标准方程为22(5)(6)10x y -+-=,故选:D 【点睛】本题考查了中点坐标公式,两点间的距离公式以及圆的标准方程,解答本题的关键是灵活运用已知条件确定圆心坐标及圆的半径.同时要求学生会根据圆心与半径写出圆的标准方程.13.函数()ln 3f x x x =+-的零点的个数是( ) A .0 B .1C .2D .3【答案】B【解析】首先可以判断函数的单调性,再根据零点存在性定理判断可得; 【详解】解:因为ln y x =与3y x =-在()0,∞+上单调递增, 所以()ln 3f x x x =+-也在()0,∞+上单调递增,又()1ln11320f =+-=-<Q ,()3ln333ln30f =+-=> 所以()()130f f <,故函数在()1,3上存在唯一零点, 故选:B 【点睛】本题考查函数的单调性的判断及应用,零点存在性定理的应用,属于基础题.14.我国古代数学专著《九章算术》中的“堑堵”是指底面为直角三角形的直棱柱.如图,三棱柱111ABC A B C -为堑堵,其中AB AC ⊥,AB =1AC =,则直线BC 与11A B 所成角是( )A .60°B .30°C .120°D .150°【答案】B【解析】由三棱柱的定义可得11//AB A B ,则ABC ∠为异面直线11A B 与BC 所成的角,在ABC ∆中利用三角函数计算可得; 【详解】解:在三棱柱111ABC A B C -中,11//AB A B , 所以ABC ∠为异面直线11A B 与BC 所成的角, 在ABC ∆中,AB AC ⊥,3AB =1AC =, 所以3tan 33AC ABC AB ∠===, 所以30ABC ︒∠=,故异面直线11A B 与BC 所成的角为30︒, 故选:B 【点睛】本题考查异面直线所成的角,属于中档题.15.某人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( ) A .至多有一次中靶 B .只有一次中靶 C .两次都中靶 D .两次都不中靶 【答案】D【解析】根据互斥事件的定义逐个分析即可. 【详解】“至少有一次中靶”与 “至多有一次中靶”均包含中靶一次的情况.故A 错误. “至少有一次中靶”与“只有一次中靶” 均包含中靶一次的情况.故B 错误.“至少有一次中靶”与“两次都中靶” 均包含中靶两次的情况.故C错误.根据互斥事件的定义可得,事件“至少有一次中靶”的互斥事件是“两次都不中靶”.故选:D【点睛】本题主要考查了互斥事件的辨析,属于基础题型.16.如图,在ABCV中,CD是AB边上的中线,点P是CD的中点,则()A.1142AP AB AC=+u u u r u u u r u u u rB.1124AP AB AC=+u u u r u u u r u u u rC.1132AP AB AC=+u u u r u u u r u u u rD.1123AP AB AC=+u u u r u u u r u u u r【答案】A【解析】根据平面向量的加法和数乘运算法则计算可得;【详解】解:依题意可得()12AP AC AD=+u u u r u u u r u u u r,12AD AB=u u u r u u u r所以()1111122224AP AC AD AC AB AC AB⎛⎫=+=+=+⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r u u u r故选:A【点睛】本题考查平面向量的线性运算的几何表示,属于基础题.17.不等式组20210x yx y+->⎧⎨--<⎩表示的平面区域是()A.B.C .D .【答案】B【解析】由线定界,由点定域,即可画出线性约束条件所表示的平面区域; 【详解】解: 首先在平面直角坐标系中画出直线20x y +-=,将()0,0代入20x y +->,不等式不成立,可得20x y +->所表示的平面区域在直线20x y +-=的右上方, 同理可得210x y --<所表示的平面区域在直线210x y --=的左上方,即可得到线性约束条件所表示的平面区域为:故选:B 【点睛】本题考查根据线性约束条件画出可行域,属于基础题.18.如图,树人中学欲利用原有的墙(墙足够长)为背面,建造一间长方体形状的房屋作为体育器材室.房屋地面面积为218m ,高度为3m .若房屋侧面和正面每平方米的造价均为1000元,屋顶的造价为6000元,且不计房屋背面和地面的费用,则该房屋的最低总造价为( )A .40000元B .42000元C .45000元D .48000元【答案】B【解析】设房屋的长为xm ,则宽为18m x ,则总造价1860001000323y x x ⎛⎫=+⨯+⨯⨯ ⎪⎝⎭再利用基本不等式求出最小值即可得解; 【详解】解:设房屋的长为xm ,则宽为18m x ,则总造价1860001000323y x x ⎛⎫=+⨯+⨯⨯ ⎪⎝⎭36366000300060003000242000y x x x x ⎛⎫∴=+⨯+≥+⨯⋅= ⎪⎝⎭,当且仅当36x x =,即6x =时取等号;故当长等于6m ,宽等于3m 时,房屋的最低总造价为42000元, 故选:B 【点睛】本题考查函数的应用,基本不等式的应用,属于基础题.二、填空题19.从甲、乙、丙三名学生中任选一名学生参加某项活动,则甲被选中的概率是_______. 【答案】13【解析】由题意可得总的方法种数为133C =,甲被选中只有1种选择方法,由古典概型的概率公式可得. 【详解】解:从甲、乙、丙三人中,任选一人参加某项活动共有133C =种不同的选择方法,而甲被选中,只有1种选择方法,由古典概型的概率公式可得甲被选中的概率13P =,故答案为:13. 【点睛】本题考查古典概型及其概率公式,涉及排列组合简单计数,属于基础题. 20.点M (2,-2)到直线210x y --=的距离为______.【解析】直接利用点到直线的距离公式d =计算可得;【详解】解:点()2,2M -到直线210x y --=的距离d==【点睛】本题考查点到直线的距离公式的应用,属于基础题. 21.2lg2lg25+=______. 【答案】2【解析】通过同底对数的运算法则,求得结果. 【详解】2lg2lg25lg4lg25lg1002+=+==本题正确结果:2 【点睛】本题考查对数的运算,属于基础题.22.如图,设Ox 、Oy 是平面内相交成60︒角的两条数轴,1e u v 、2e u u v分别是与x 轴、y 轴正方向同向的单位向量.若向量12OP xe ye =+u u u v u v u u v ,则把有序实数对,x y 叫做向量OPuuu v在斜坐标系xOy 中的坐标,记作,OP x y =u u u v .在此斜坐标系xOy 中,已知2,3a =v,5,2b =-v , ,a b v v夹角为θ,则θ=______.【答案】23π 【解析】由题意,1223a e e =+u r u u r r ,1252b e e =-+u r u u r r ,分别求出a b ⋅r r ,a r ,b r ,进而利用数量积求出夹角即可 【详解】由题,1223a e e =+u r u u r r,1252b e e =-+u r u u r r ,所以()()21221211221195210116101162223a b e e e e e e e e ⋅=⋅-+=--⋅+=--⨯+=+-u r u u r u r u u r u r u r u u r u u r rr()212112222214129412931922e e e e e e a ==+⋅+=++⨯+=u r u u r u r u r u u r u u r r ,则19a =r()22221211221522520425204192b e e e e e e =-+=-⋅+=-⨯+=u r u u r u r u r u u r u u r r ,则19b =r 所以1912cos 21919a b a bθ-⋅===-⨯⋅r r r r ,则23θπ= 故答案为:23π 【点睛】本题考查平面向量基本定理的应用,考查利用数量积求向量的夹角,考查运算能力三、解答题23.ABC V 中的内角A ,B ,C 所对的边分别为a ,b ,c .已知sin 30A A -=. (1)求角A ;(2)若4b =,2c =,求a . 【答案】(1)3π(2)23【解析】(1)由同角三角函数的基本关系求出角A ; (2)由余弦定理即可求出边a 的值; 【详解】解:(1)由sin 3cos 0A A -=,易知cos 0A ≠,则tan 3A =.因为0A π<<,所以3A π=.(2)由余弦定理得22212cos 164242122a b c bc A =+-=+-⨯⨯⨯=,所以23a =.【点睛】本题考查同角三角函数的基本关系及余弦定理的应用,属于基础题.24.如图,AB 是半圆O 的直径,C 是半圆上一点,M 是PB 的中点,PA ⊥平面ABC ,且23PA =,4AB =,30ABC ︒∠=.(1)求证:BC ⊥平面PAC ; (2)求三棱锥M —ABC 体积. 【答案】(1)证明见解析(2)2【解析】(1)依题意可得AC BC ⊥,再由PA ⊥平面ABC ,得到PA BC ⊥,即可证明BC ⊥平面PAC ;(2)连接OM ,可证//OM PA ,即可得到OM ⊥平面ABC ,OM 为三棱锥M ABC -的高,再根据锥体的体积公式计算可得; 【详解】(1)证明:因为AB 是半圆O 的直径,所以AC BC ⊥. 因为PA ⊥平面ABC ,BC ⊂平面ABC ,所以PA BC ⊥, 又因为AC ⊂平面PAC ,PA ⊂平面PAC ,且AC PA A ⋂= 所以BC ⊥平面PAC .(2)解:因为30ABC ∠=︒,4AB =,所以23BC =,1sin 30232ABC S AB BC ︒=⋅⋅⋅=V .连接OM .因为O 、M 分别是AB ,PB 的中点,所以//OM PA ,132OM PA ==.又PA ⊥平面ABC .所以OM ⊥平面ABC .因此OM 为三棱锥M ABC -的高.所以123323M ABC V -=⨯⨯=.【点睛】本题考查线面垂直的证明,锥体的体积的计算,属于中档题. 25.已知数列{}n a 是等差数列,n S 是其前n 项的和,且11a =,23211a a +=.(1)求数列{}n a 的通项公式; (2)求数列{}n a 的前n 项和n S ; (3)求证:123111174n S S S S +++⋯+<. 【答案】(1)21n a n =-(2)2n S n =(3)证明见解析【解析】(1)设等差数列{}n a 的公差为d ,由题意得方程组,解得1a ,d ,即可求出通项公式;(2)由等差数列的前n 项和公式直接可得;(3)利用()()22111111n n n n =--<+放缩,再利用裂项相消法求和即可得证; 【详解】解:(1)设等差数列{}n a 的公差为d ,由题意得()1111,2211.a a d a d =⎧⎨+++=⎩解得11a =,2d =.所以21n a n =-.(2)由(1)知21n a n =-,21(21)2n n S n n +-∴=⨯=. (3)①当1n =时,左边714=<,原不等式成立. ②当2n …时,左边22222111111234n =+++++L 2222111112131411n <++++⋯+----11111132435(1)(1)n n =++++⋯+⨯⨯⨯-⨯+111171171122142224n n n n ⎛⎫=+⨯+--=--< ⎪++⎝⎭. 综上可得,123111174n S S S S +++⋯+<. 【点睛】本题考查等差数列的通项公式及求和公式的应用,放缩法证明数列不等式及裂项相消法求和,属于中档题.。
2019年江苏省普通高中学业水平测试试题及答案(word版)

本卷可能用到的相对原子质量 H :1 C :12 N :14 O :16 S :32 Fe :56 Cu :641.现代社会,人们越来越关注饮食中的营养成分。
肉、鱼和红枣等食物含有丰富的铁,这里的铁应理解 为A .单质B .分子C .元素D .同位素2.当光束通过鸡蛋清水溶液时,从侧面观察到一条光亮的“通路” ,说明鸡蛋清水溶液是 A .溶液 B .胶体 C .悬浊液 D .乳浊液3.体操运动员比赛时为了防滑。
常在手掌上涂抹碳酸镁粉末。
碳酸镁属于 A .酸 B .碱 C .盐 D .氧化物 4.下列关于二氧化硫的说法错误的是 A .无色无味 B .有毒 C .密度比空气大 D .氧化物5.(2019 ·江苏省学业水平测试真题 )石墨烯是仅由一层碳原子构成的新型材料,具有超强的导电性。
下列 元素与碳元素处于同一主族的是 A .He B .O C .Si D . P 6.下列各组物质互为同分异构体的是12 13 A .O 2和 O 3B .CH 3CH 2CH 2CH 3和 CH (CH 3)3C . 12C 和 13C7.某溶液中存在大量的 H +、Cl 一、 SO 42 一,该溶液中还可能大量存在的是A . HCO 3 一2+ B .Ba 2+C . Al 3+ +D .Ag + 8下列物质含有离子键的是A . C12B . NaClC .CO 2D .H 2O 9. 下列试剂需要用棕色试剂瓶保存的是A .浓硫酸B .浓硝酸C .浓盐酸D .碳酸钠溶10.2019 年诺贝尔化学奖授予在“钯催化交叉偶联反应”领域作出突出贡献的三位化学家。
下列有关钯原 子 (46 Pd ) 的说法错误的是A .原子序数为 46B .质子数为 46C .电子数为 46 11.用下列方法制取氢气,反应速率最大的是A .冬天,块状锌与 2 mol ·L 一1硫酸溶液反应C .夏天,块状锌与 2 mol ·L 一1硫酸溶液反应 12 下列离子方程式正确的是一A .稀硝酸与氢氧化钾溶液反应 H ++OH 一=H 2OB .铝与稀盐酸反应 Al+2H +=Al 3++H 2↑C .三氯化铁溶液与氢氧化钠溶液反应 FeCl 3+3OH 一D .CH 3 和 CH 3CH 3 D .中子数为 46 B .冬天,粉末状锌与 D .夏天,粉末状2 mol ·L 一1硫酸溶液反应 2mol · L 一 1 硫酸溶=Fe(OH)3 ↓ +3C1一一2D .二氧化碳与石灰水反应CO2+2OH 一=CO32一+ H2OA .用蒸馏法淡化海水B .用铁矿石冶炼铁 13.下列反应属于吸热反应的是 A .金属钠与水反应C .盐酸与氢氧化钠溶液反应14 下列说法正确的是A .含碳元素的化合物都是有机物C .乙酸的酸性比碳酸弱 15.下列反应属于取代反应的是16.下列有关实验原理或操作正确的是B .甲烷在空气中燃烧D .石灰石高温分解 B .乙醇难溶于水 D .乙烯分子中含有碳碳双键喷泉实验收集氯化氢气体 分离苯和水17.制太阳能电池需要高纯硅,工业上用粗硅制高纯硅可通过以下反应实现: ① Si+3HCl ( 气3)0=0S ℃iHCl 3(气)+H 2 对上述两个反应的叙述错误的是 A .都是置换反应 C .反应中硅元素都被还原 18.下列化② SiHCl 3(气)+H 2=S ℃i+3HCl ( 气) B .都是氧化还原反应 D .都不是离子反应A .氯化氢的电子式 C .乙酸的结构简式 C 2H 4O 2+ 2D .碳酸钠的电离方程式 Na 2CO 3=Na ++CO 32-19.用 N A 表示阿伏加德罗常数的值。
2019年12月广东省普通高中学业水平考试英语试卷(含答案)

机密★启用前试卷类型:B2019年12月广东省普通高中学业水平考试英语试卷本试卷共6页,60小题,满分100分。
考试用时90分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.每题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
Ⅰ.情景交际(共5小题:每小题2分,满分10分)阅读下列简短对话,从A、B、C和D选出最佳答案,将对对话补全。
1.—Could you lend me some books?—.I have a lot of books here.A. Excuse meB. SorryC. SureD. No way2. —Tell me about your stay in London. Did you enjoy it—Yes,.A. it was boringB. it was pleasantC. it was terribleD. it was expensive3. —,sir?—A glass of milk, please.A. What would you likeB. What is it over thereC. What day is it todayD. What's the matter with you4. —My wife and I are going to Paris.—.A. Never mindB. No problemC. Have a good tripD. It's my pleasure5. —Would you like to see a movie with me tonight?—Great!.A. I’m not freeB. We'd better notC. We'll be fineD. I'd love toⅡ.阅读理解(共15小题:每小题2分,满分30分)阅读下列短文,掌握其大意,然后从每题所给的A、B、C和D项中选出最佳选项。
山东省2019年冬季普通高中学业水平考试

山东省2019年冬季普通高中学业水平考试一、考试概况山东省2019年冬季普通高中学业水平考试是山东省教育厅主管,旨在全面评价高中学生的学业水平。
该考试主要考察学生在各个学科领域的知识掌握、能力运用和学科思维等方面的综合能力,对学生的综合素质进行综合评定和学业水平定级。
二、考试时间和科目1.考试时间:2019年12月1日至12月3日;2.考试科目:语文、数学、英语、物理、化学、生物、历史、地理、政治、技术等10门学科。
三、考试形式1.考试分为单项选择题、填空题、解答题等不同形式;2.每门学科的考试时间为120分钟;3.考试使用纸质试卷,学生需使用2B铅笔进行作答;4.考试题目按照学科教学大纲的相关要求编写,力求考查学生的综合能力。
四、考试内容和考查重点1.各学科考试内容和考查重点由山东省教育厅制定,并按照学科教学大纲进行设计;2.考试内容以知识点、思维能力和实践能力为主线,注重对学生实际掌握情况的考查。
五、考试评分和评价方式1.考试采取阅卷与电子扫描相结合的方式;2.阅卷由专业教师和教育专家进行,保证评分的公正性和客观性;3.评价方式采用等级制,将学生的成绩分为优秀、良好、合格和不合格等多个等级;4.考试成绩将作为学生普通高中学业水平评价的重要依据,决定学生的学业水平定级。
六、考试后的后续处理1.考试结束后,学生的试卷将由考试中心进行收集、整理和保管;2.学生可通过所在学校了解自己的考试成绩和学业水平等级;3.考试成绩和学业水平等级将被用于高考志愿填报、升学和就业等方面。
七、备考建议1.提前规划备考时间,合理安排学科复习;2.重点关注各学科的基础知识和考点;3.多做模拟试题,熟悉考试形式和题型;4.加强解题思路和答题技巧的训练;5.保持良好的心态,保证体力和精力的充足。
八、注意事项1.参加考试的学生需携带准考证、身份证等有效证件;2.考试期间需遵守考场纪律和考试规则;3.在规定的时间内完成试卷,严禁迟到或提前交卷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市普通高中学业水平考试数学试卷一、选择题(每小题3分,共75分)1.(3分)已知集合A={0,1},B={﹣1,1,3},那么A∩B等于()A.{0} B.{1} C.{0,1} D.{0,1,3} 2.(3分)平面向量,满足=2,如果=(1,2),那么等于()A.(﹣2,﹣4)B.(﹣2,4)C.(2,﹣4)D.(2,4)3.(3分)如果直线y=kx﹣1与直线y=3x平行,那么实数k的值为()A.﹣1 B.C.D.34.(3分)如图,给出了奇函数f(x)的局部图象,那么f(1)等于()A.﹣4 B.﹣2 C.2 D.45.(3分)如果函数f(x)=a x(a>0,且a≠1)的图象经过点(2,9),那么实数a等于()A.2 B.36.(3分)某中学现有学生1800人,其中初中学生1200人,高中学生600人.为了解学生在“阅读节”活动中的参与情况,决定采用分层抽样的方法从全校学生中抽取一个容量为180的样本,那么应从高中学生中抽取的人数为()A.60 B.90 C.100 D.1107.(3分)已知直线l经过点O(0,0),且与直线x﹣y﹣3=0垂直,那么直线l的方程是()A.x+y﹣3=0 B.x﹣y+3=0 C.x+y=0 D.x﹣y=08.(3分)如图,在矩形ABCD中,E为CD中点,那么向量等于()A.B.C.D.9.(3分)实数的值等于()A.1 B.2 C.3 D.410.(3分)函数y=x2,y=x3,,y=lgx中,在区间(0,+∞)上为减函数的是()A.y=x2B.y=x3C.D.y=lgx11.(3分)某次抽奖活动共设置一等奖、二等奖两类奖项.已知中一等奖的概率为,中二等奖的概率为,那么本次活动中,中奖的概率为()A.B.C.D.12.(3分)如果正△ABC的边长为1,那么?等于()A.B.C.1 D.213.(3分)在△ABC中,角A,B,C所对的边分别为a,b,c,如果a=10,A=45°,B =30°,那么b等于()A.B.C.D.14.(3分)已知圆C:x2+y2﹣2x=0,那么圆心C到坐标原点O的距离是()A.B.C.1 D.15.(3分)如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是正方形,A1A⊥底面ABCD,A1A=2,AB=1,那么该四棱柱的体积为()A.1 B.2 C.4 D.816.(3分)函数f(x)=x3﹣5的零点所在的区间是()A.(1,2)B.(2,3)C.(3,4)D.(4,5)17.(3分)在sin50°,﹣sin50°,sin40°,﹣sin40°四个数中,与sin130°相等的是()A.sin50°B.﹣sin50°C.sin40°D.﹣sin40°18.(3分)把函数y=sin x的图象向右平移个单位得到y=g(x)的图象,再把y=g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),所得到图象的解析式为()A.B.C.D.19.(3分)函数的最小值是()A.﹣1 B.0 C.1 D.220.(3分)在空间中,给出下列四个命题:①平行于同一个平面的两条直线互相平行;②垂直于同一个平面的两条直线互相平行;③平行于同一条直线的两个平面互相平行;④垂直于同一个平面的两个平面互相平行.其中正确命题的序号是()A.①B.②C.③D.④21.(3分)北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况.2018年1月份各区域的浓度情况如表:各区域1月份浓度(单位:微克/立方米)表区域浓度区域浓度区域浓度怀柔27海淀34平谷40密云31延庆35丰台42门头沟32西城35大兴46顺义32东城36开发区46昌平32石景山37房山47朝阳34通州39从上述表格随机选择一个区域,其2018年1月份的浓度小于36微克/立方米的概率是()A.B.C.D.22.(3分)已知,那么=()A.B.C.D.23.(3分)在△ABC中,角A,B,C所对的边分别为a,b,c,如果,那么△ABC的最大内角的余弦值为()A.B.C.D.24.(3分)北京故宫博物院成立于1925年10月10日,是在明、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆,每年吸引着大批游客参观游览.下图是从2012年到2017年每年参观人数的折线图.根据图中信息,下列结论中正确的是()A.2013年以来,每年参观总人次逐年递增B.2014年比2013年增加的参观人次不超过50万C.2012年到2017年这六年间,2017年参观总人次最多D.2012年到2017年这六年间,平均每年参观总人次超过160万25.(3分)阅读下面题目及其证明过程,在横线处应填写的正确结论是()如图,在三棱锥P﹣ABC中,平面P AC⊥平面ABC,BC⊥AC求证:BC⊥P A证明:因为平面P AC⊥平面ABC平面P AC∩平面ABC=ACBC⊥AC,BC?平面ABC所以______.因为P A?平面P AC.所以BC⊥P AA.AB⊥底面P AC B.AC⊥底面PBC C.BC⊥底面P AC D.AB⊥底面PBC 二、解答题(共4小题,满分25分)26.(7分)已知函数(Ⅰ)A=;(将结果直接填写在答题卡的相应位置上)(Ⅱ)函数f(x)的最小正周期T=(将结果直接填写在答题卡的相应位置上)(Ⅲ)求函数f(x)的最小值及相应的x的值.27.(7分)如图,在三棱锥P﹣ABC中,P A⊥底面ABC,AB⊥BC,D,E,分别为PB,PC 的中点.(Ⅰ)求证:BC∥平面ADE;(Ⅱ)求证:BC⊥平面P AB.28.(6分)已知圆O:x2+y2=r2(r>0)经过点A(0,5),与x轴正半轴交于点B.(Ⅰ)r=;(将结果直接填写在答题卡的相应位置上)(Ⅱ)圆O上是否存在点P,使得△P AB的面积为15若存在,求出点P的坐标;若不存在,说明理由.29.(5分)种植于道路两侧、为车辆和行人遮阴并构成街景的乔木称为行道树.为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离.按照北京市《行道树修剪规范》要求,当树木与原有电力线发生矛盾时,应及时修剪树枝.《行道树修剪规范》中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表电力线安全距离(单位:m)水平距离垂直距离≤1KV≥1≥1 3KV~10KV≥3≥335KV~110KV≥≥4154KV~220KV≥4≥330KV≥5≥500KV≥7≥7现有某棵行道树已经自然生长2年,高度为2m.据研究,这种行道树自然生长的时间x (年)与它的高度y(m)满足关系式(Ⅰ)r=;(将结果直接填写在答题卡的相应位置上)(Ⅱ)如果这棵行道树的正上方有35kV的电力线,该电力线距地面20m.那么这棵行道树自然生长多少年必须修剪(Ⅲ)假如这棵行道树的正上方有500kV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少m北京市普通高中学业水平考试数学试卷参考答案与试题解析一、选择题(每小题3分,共75分)1.(3分)已知集合A={0,1},B={﹣1,1,3},那么A∩B等于()A.{0} B.{1} C.{0,1} D.{0,1,3}【考点】1E:交集及其运算.【专题】11:计算题;37:集合思想;4O:定义法;5J:集合.【分析】利用交集定义直接求解.【解答】解:∵集合A={0,1},B={﹣1,1,3},∴A∩B={1}.故选:B.【点评】本题考查交集的求法,考查交集定义、不等式等基础知识,考查运算求解能力,是基础题.2.(3分)平面向量,满足=2,如果=(1,2),那么等于()A.(﹣2,﹣4)B.(﹣2,4)C.(2,﹣4)D.(2,4)【考点】96:平行向量(共线).【专题】11:计算题;34:方程思想;4O:定义法;5A:平面向量及应用.【分析】利用数乘向量运算法则直接求解.【解答】解:∵平面向量,满足=2,=(1,2),∴=2(1,2)=(2,4).故选:D.【点评】本题考查向量的求法,考查数乘向量运算法则等基础知识,考查运算求解能力,是基础题.3.(3分)如果直线y=kx﹣1与直线y=3x平行,那么实数k的值为()A.﹣1 B.C.D.3【考点】II:直线的一般式方程与直线的平行关系.【专题】11:计算题;34:方程思想;4O:定义法;5B:直线与圆.【分析】利用两条直线相互平行的充要条件即可得出.【解答】解:∵直线y=kx﹣1与直线y=3x平行,∴k=3,经过验证满足两条直线平行.故选:D.【点评】本题考查了两条直线相互平行的充要条件,考查了推理能力与计算能力,属于基础题.4.(3分)如图,给出了奇函数f(x)的局部图象,那么f(1)等于()A.﹣4 B.﹣2 C.2 D.4【考点】3K:函数奇偶性的性质与判断.【专题】11:计算题;34:方程思想;35:转化思想;51:函数的性质及应用.【分析】根据题意,由函数的图象可得f(﹣1)的值,结合函数的奇偶性可得f(1)的值,即可得答案.【解答】解:根据题意,由函数的图象可得f(﹣1)=2,又由函数为奇函数,则f(1)=﹣f(﹣1)=﹣2,故选:B.【点评】本题考查函数的奇偶性的性质,关键是掌握函数单调性的性质,属于基础题.5.(3分)如果函数f(x)=a x(a>0,且a≠1)的图象经过点(2,9),那么实数a等于()A.2 B.3【考点】4B:指数函数的单调性与特殊点.【专题】38:对应思想;4R:转化法;51:函数的性质及应用.【分析】由题意代入点的坐标,即可求出a的值.【解答】解:指数函数f(x)=a x(a>0,a≠1)的图象经过点(2,9),∴9=a2,解得a=3,故选:B.【点评】本题考查了指数函数的图象和性质,属于基础题.6.(3分)某中学现有学生1800人,其中初中学生1200人,高中学生600人.为了解学生在“阅读节”活动中的参与情况,决定采用分层抽样的方法从全校学生中抽取一个容量为180的样本,那么应从高中学生中抽取的人数为()A.60 B.90 C.100 D.110【考点】B3:分层抽样方法.【专题】11:计算题;38:对应思想;4O:定义法;5I:概率与统计.【分析】根据分层抽样的定义和题意知,抽样比例是,根据样本的人数求出应抽取的人数【解答】解:根据分层抽样的定义和题意,则高中学生中抽取的人数600×=60(人).故选:A.【点评】本题的考点是分层抽样方法,根据样本结构和总体结构保持一致,求出抽样比,再求出在所求的层中抽取的个体数目.7.(3分)已知直线l经过点O(0,0),且与直线x﹣y﹣3=0垂直,那么直线l的方程是()A.x+y﹣3=0 B.x﹣y+3=0 C.x+y=0 D.x﹣y=0【考点】IJ:直线的一般式方程与直线的垂直关系.【专题】11:计算题;34:方程思想;4O:定义法;5B:直线与圆.【分析】由题意可求出直线l的斜率,由点斜式写出直线方程化简即可.【解答】解:∵直线l与直线x﹣y﹣3=0垂直,∴直线l的斜率为﹣1,则y﹣0=﹣(x﹣0),即x+y=0故选:C.【点评】本题考查了直线方程的求法,属于基础题.8.(3分)如图,在矩形ABCD中,E为CD中点,那么向量等于()A.B.C.D.【考点】9H:平面向量的基本定理.【专题】35:转化思想;5A:平面向量及应用.【分析】直接利用向量的线性运算求出结果.【解答】解:在矩形ABCD中,E为CD中点,所以:,则:=.故选:A.【点评】本题考查的知识要点:向量的线性运算的应用,主要考查学生的运算能力和转化能力,属于基础题型.9.(3分)实数的值等于()A.1 B.2 C.3 D.4【考点】41:有理数指数幂及根式;4H:对数的运算性质.【专题】33:函数思想;4A:数学模型法;51:函数的性质及应用.【分析】直接利用有理指数幂及对数的运算性质求解即可.【解答】解:=2+0=2.故选:B.【点评】本题考查了有理指数幂及对数的运算性质,是基础题.10.(3分)函数y=x2,y=x3,,y=lgx中,在区间(0,+∞)上为减函数的是()A.y=x2B.y=x3C.D.y=lgx【考点】3E:函数单调性的性质与判断.【专题】11:计算题;34:方程思想;35:转化思想;51:函数的性质及应用.【分析】根据题意,依次分析4个函数在区间(0,+∞)的单调性,综合即可得答案.【解答】解:根据题意,函数y=x2,为二次函数,在区间(0,+∞)为增函数;y=x3,为幂函数,在区间(0,+∞)为增函数;,为指数函数,在区间(0,+∞)上为减函数;y=lgx中,在区间(0,+∞)为增函数;故选:C.【点评】本题考查函数单调性的判定,关键是掌握常见函数的单调性,属于基础题.11.(3分)某次抽奖活动共设置一等奖、二等奖两类奖项.已知中一等奖的概率为,中二等奖的概率为,那么本次活动中,中奖的概率为()A.B.C.D.【考点】C2:概率及其性质.【专题】38:对应思想;4R:转化法;5I:概率与统计.【分析】根据互斥事件概率加法公式即可得到其发生的概率的大小.【解答】解:由于中一等奖,中二等奖,为互斥事件,故中奖的概率为+=,故选:B.【点评】此题考查概率加法公式及互斥事件,是一道基础题.12.(3分)如果正△ABC的边长为1,那么?等于()A.B.C.1 D.2【考点】9O:平面向量数量积的性质及其运算.【专题】38:对应思想;4R:转化法;5A:平面向量及应用.【分析】根据向量的数量积的运算性质计算即可.【解答】解:∵正△ABC的边长为1,∴?=||?||cos A=1×1×cos60°=,故选:B.【点评】本题考查了向量的数量积的运算,是一道基础题.13.(3分)在△ABC中,角A,B,C所对的边分别为a,b,c,如果a=10,A=45°,B =30°,那么b等于()A.B.C.D.【考点】HP:正弦定理.【专题】38:对应思想;4R:转化法;58:解三角形.【分析】根据正弦定理直接代入求值即可.【解答】解:由正弦定理==,得=,解得:b=5,故选:B.【点评】本题考查了正弦定理的应用,考查解三角形问题,是一道基础题.14.(3分)已知圆C:x2+y2﹣2x=0,那么圆心C到坐标原点O的距离是()A.B.C.1 D.【考点】J2:圆的一般方程.【专题】11:计算题;34:方程思想;35:转化思想;5B:直线与圆.【分析】根据题意,由圆的一般方程分析可得圆心C的坐标,进而由两点间距离公式,计算可得答案.【解答】解:根据题意,圆C:x2+y2﹣2x=0,其圆心C为(1,0),则圆心C到坐标原点O的距离d==1;故选:C.【点评】本题考查圆的一般方程,涉及两点间距离公式,属于基础题.15.(3分)如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是正方形,A1A⊥底面ABCD,A1A=2,AB=1,那么该四棱柱的体积为()A.1 B.2 C.4 D.8【考点】LF:棱柱、棱锥、棱台的体积.【专题】11:计算题;31:数形结合;4O:定义法;5F:空间位置关系与距离.【分析】该四棱柱的体积为V=S正方形ABCD×AA1,由此能求出结果.【解答】解:∵在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是正方形,A1A⊥底面ABCD,A1A=2,AB=1,∴该四棱柱的体积为V=S正方形ABCD×AA1=12×2=2.故选:B.【点评】本题考查该四棱柱的体积的求法,考查四棱柱的性质等基础知识,考查运算求解能力,是基础题.16.(3分)函数f(x)=x3﹣5的零点所在的区间是()A.(1,2)B.(2,3)C.(3,4)D.(4,5)【考点】52:函数零点的判定定理.【专题】11:计算题;34:方程思想;35:转化思想;49:综合法;51:函数的性质及应用.【分析】求得f(1)f(2)<0,根据函数零点的判定定理可得函数f(x)的零点所在的区间.【解答】解:由函数f(x)=x3﹣5可得f(1)=1﹣5=﹣4<0,f(2)=8﹣5=3>0,故有f(1)f(2)<0,根据函数零点的判定定理可得,函数f(x)的零点所在区间为(1,2),故选:A.【点评】本题主要考查函数的零点的判定定理的应用,属于基本知识的考查.17.(3分)在sin50°,﹣sin50°,sin40°,﹣sin40°四个数中,与sin130°相等的是()A.sin50°B.﹣sin50°C.sin40°D.﹣sin40°【考点】GF:三角函数的恒等变换及化简求值.【专题】35:转化思想;56:三角函数的求值.【分析】利用诱导公式化简可得答案.【解答】解:由sin130°=sin(180°﹣50°)=sin50°.∴与sin130°相等的是sin50°故选:A.【点评】题主要考察了诱导公式的应用,属于基本知识的考查.18.(3分)把函数y=sin x的图象向右平移个单位得到y=g(x)的图象,再把y=g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),所得到图象的解析式为()A.B.C.D.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【专题】35:转化思想;49:综合法;57:三角函数的图象与性质.【分析】由题意利用函数y=A sin(ωx+φ)的图象变换规律,得出结论.【解答】解:把函数y=sin x的图象向右平移个单位得到y=g(x)=sin(x﹣)的图象,再把y=g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),所得到图象的解析式为y=2sin(x﹣),故选:A.【点评】本题主要考查函数y=A sin(ωx+φ)的图象变换规律,属于基础题.19.(3分)函数的最小值是()A.﹣1 B.0 C.1 D.2【考点】3H:函数的最值及其几何意义.【专题】33:函数思想;48:分析法;51:函数的性质及应用.【分析】分别讨论两段函数的单调性和最值,即可得到所求最小值.【解答】解:当x>﹣1时,f(x)=x2的最小值为f(0)=0;当x≤﹣1时,f(x)=﹣x递减,可得f(x)≥1,综上可得函数f(x)的最小值为0.故选:B.【点评】本题考查分段函数的最值求法,注意分析各段的单调性和最值,考查运算能力,属于基础题.20.(3分)在空间中,给出下列四个命题:①平行于同一个平面的两条直线互相平行;②垂直于同一个平面的两条直线互相平行;③平行于同一条直线的两个平面互相平行;④垂直于同一个平面的两个平面互相平行.其中正确命题的序号是()A.①B.②C.③D.④【考点】2K:命题的真假判断与应用.【专题】38:对应思想;48:分析法;5F:空间位置关系与距离.【分析】由线面平行的性质可判断①;由线面垂直的性质定理可判断②;由两个平面的位置关系可判断③;由面面平行的判定定理可判断④.【解答】解;对于①,平行于同一个平面的两条直线互相平行或相交或异面,故①错误;对于②,垂直于同一个平面的两条直线互相平行,故②正确;对于③,平行于同一条直线的两个平面互相平行或相交,故③错误;对于④,垂直于同一个平面的两个平面互相平行或相交,故④错误.故选:B.【点评】本题考查空间线线和面面的位置关系的判断,考查平行和垂直的判断和性质定理的运用,属于基础题.21.(3分)北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况.2018年1月份各区域的浓度情况如表:各区域1月份浓度(单位:微克/立方米)表区域浓度区域浓度区域浓度怀柔27海淀34平谷40密云31延庆35丰台42门头沟32西城35大兴46顺义32东城36开发区46昌平32石景山37房山47朝阳34通州39从上述表格随机选择一个区域,其2018年1月份的浓度小于36微克/立方米的概率是()A.B.C.D.【考点】CB:古典概型及其概率计算公式.【专题】11:计算题;38:对应思想;4O:定义法;5I:概率与统计.【分析】由表可知从上述表格随机选择一个区域,共有17种情况,其中2018年1月份的浓度小于36微克/立方米的地区有9个,根据概率公式计算即可.【解答】解:从上述表格随机选择一个区域,共有17种情况,其中2018年1月份的浓度小于36微克/立方米的地区有9个,则2018年1月份的浓度小于36微克/立方米的概率是,故选:D.【点评】本题主要考查频率分布表、古典概型、统计等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等22.(3分)已知,那么=()A.B.C.D.【考点】GP:两角和与差的三角函数.【专题】35:转化思想;36:整体思想;56:三角函数的求值.【分析】直接利用同角三角函数关系式的应用求出结果.【解答】解:知,那么,则:=sin==,故选:D.【点评】本题考查的知识要点:三角函数关系式的恒等变变换,主要考查学生的运算能力和转化能力,属于基础题型.23.(3分)在△ABC中,角A,B,C所对的边分别为a,b,c,如果,那么△ABC的最大内角的余弦值为()A.B.C.D.【考点】HR:余弦定理.【专题】38:对应思想;4O:定义法;58:解三角形.【分析】先判断△ABC的最大内角为A,再利用余弦定理计算cos A的值.【解答】解:△ABC中,,∴a>c>b,∴△ABC的最大内角为A,且cos A===.故选:A.【点评】本题考查了余弦定理的应用问题,是基础题.24.(3分)北京故宫博物院成立于1925年10月10日,是在明、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆,每年吸引着大批游客参观游览.下图是从2012年到2017年每年参观人数的折线图.根据图中信息,下列结论中正确的是()A.2013年以来,每年参观总人次逐年递增B.2014年比2013年增加的参观人次不超过50万C.2012年到2017年这六年间,2017年参观总人次最多D.2012年到2017年这六年间,平均每年参观总人次超过160万【考点】F4:进行简单的合情推理.【专题】11:计算题;31:数形结合;44:数形结合法;5I:概率与统计.【分析】由从2012年到2017年每年参观人数的折线图,得2012年到2017年这六年间,2017年参观总人次最多.【解答】解:由从2012年到2017年每年参观人数的折线图,得:在A中,2013年以来,2015年参观总人次比2014年参观人次少,故A错误;在B中,2014年比2013年增加的参观人次超过50万,故B错误;在C中,2012年到2017年这六年间,2017年参观总人次最多,故C正确;在D中,2012年到2017年这六年间,平均每年参观总人次不超过160万,故D错误.故选:C.【点评】本题考查命题真假的判断,考查折线图的应用,考查运算求解能力,考查数形结合思想,是基础题.25.(3分)阅读下面题目及其证明过程,在横线处应填写的正确结论是()如图,在三棱锥P﹣ABC中,平面P AC⊥平面ABC,BC⊥AC求证:BC⊥P A证明:因为平面P AC⊥平面ABC平面P AC∩平面ABC=ACBC⊥AC,BC?平面ABC所以______.因为P A?平面P AC.所以BC⊥P AA.AB⊥底面P AC B.AC⊥底面PBC C.BC⊥底面P AC D.AB⊥底面PBC 【考点】LW:直线与平面垂直.【专题】38:对应思想;4R:转化法;5F:空间位置关系与距离.【分析】根据面面垂直的性质定理判断即可.【解答】解:根据面面垂直的性质定理判定得:BC⊥底面P AC,故选:C.【点评】本题考查了面面垂直的性质定理,考查数形结合思想,是一道基础题.二、解答题(共4小题,满分25分)26.(7分)已知函数(Ⅰ)A=2;(将结果直接填写在答题卡的相应位置上)(Ⅱ)函数f(x)的最小正周期T=2π(将结果直接填写在答题卡的相应位置上)(Ⅲ)求函数f(x)的最小值及相应的x的值.【考点】HW:三角函数的最值.【专题】33:函数思想;4O:定义法;57:三角函数的图象与性质.【分析】(Ⅰ)由f(0)=1求得A的值;(Ⅱ)由正弦函数的周期性求得f(x)的最小正周期;(Ⅲ)由正弦函数的图象与性质求得f(x)的最小值以及对应x的值.【解答】解:(Ⅰ)函数由f(0)=A sin=A=1,解得A=2;(Ⅱ)函数f(x)=2sin(x+),∴f(x)的最小正周期为T=2π;(Ⅲ)令x+=2kπ﹣,k∈Z;x=2kπ﹣,k∈Z;此时函数f(x)取得最小值为﹣2.故答案为:(Ⅰ)2,(Ⅱ)2π.【点评】本题考查了正弦函数的图象与性质的应用问题,是基础题.27.(7分)如图,在三棱锥P﹣ABC中,P A⊥底面ABC,AB⊥BC,D,E,分别为PB,PC 的中点.(Ⅰ)求证:BC∥平面ADE;(Ⅱ)求证:BC⊥平面P AB.【考点】LS:直线与平面平行;LW:直线与平面垂直.【专题】14:证明题;31:数形结合;49:综合法;5F:空间位置关系与距离.【分析】(Ⅰ)由D、E分别为PB、PC的中点,得DE∥BC,由此能证明BC∥平面ADE.(Ⅱ)推导出P A⊥BC,AB⊥BC,由此能证明BC⊥平面P AB.【解答】证明:(Ⅰ)在△PBC中,∵D、E分别为PB、PC的中点,∴DE∥BC,∵BC?平面ADE,DE?平面ADE,∴BC∥平面ADE.(Ⅱ)∵P A⊥平面ABC,BC?平面ABC,∴P A⊥BC,∵AB⊥BC,P A∩AB=A,∴BC⊥平面P AB.【点评】本题考查线面平行、线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.28.(6分)已知圆O:x2+y2=r2(r>0)经过点A(0,5),与x轴正半轴交于点B.(Ⅰ)r=5;(将结果直接填写在答题卡的相应位置上)(Ⅱ)圆O上是否存在点P,使得△P AB的面积为15若存在,求出点P的坐标;若不存在,说明理由.【考点】J9:直线与圆的位置关系.【专题】34:方程思想;4R:转化法;5B:直线与圆.【分析】(Ⅰ)直接由已知条件可得r;(Ⅱ)存在.由(Ⅰ)可得圆O的方程为:x2+y2=25,依题意,A(0,5),B(5,0),求出|AB|=,直线AB的方程为x+y﹣5=0,又由△P AB的面积,可得点P到直线AB 的距离为,设点P(x0,y0),解得x0+y0=﹣1或x0+y0=11(显然此时点P不在圆上,故舍去),联立方程组,求解即可得答案.【解答】解:(Ⅰ)r=5;(Ⅱ)存在.∵r=5,∴圆O的方程为:x2+y2=25.依题意,A(0,5),B(5,0),∴|AB|=,直线AB的方程为x+y﹣5=0,又∵△P AB的面积为15,∴点P到直线AB的距离为,设点P(x0,y0),∴,解得x0+y0=﹣1或x0+y0=11(显然此时点P不在圆上,故舍去),联立方程组,解得或.∴存在点P(﹣4,3)或P(3,﹣4)满足题意.【点评】本题考查直线与圆的位置关系,考查点到直线的距离公式,是中档题.29.(5分)种植于道路两侧、为车辆和行人遮阴并构成街景的乔木称为行道树.为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离.按照北京市《行道树修剪规范》要求,当树木与原有电力线发生矛盾时,应及时修剪树枝.《行道树修剪规范》中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表电力线安全距离(单位:m)水平距离垂直距离≤1KV≥1≥13KV~10KV≥3≥335KV~110KV≥≥4154KV~220KV≥4≥330KV≥5≥500KV≥7≥7现有某棵行道树已经自然生长2年,高度为2m.据研究,这种行道树自然生长的时间x (年)与它的高度y(m)满足关系式(Ⅰ)r=;(将结果直接填写在答题卡的相应位置上)(Ⅱ)如果这棵行道树的正上方有35kV的电力线,该电力线距地面20m.那么这棵行道树自然生长多少年必须修剪(Ⅲ)假如这棵行道树的正上方有500kV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少m【考点】5C:根据实际问题选择函数类型.【专题】11:计算题;33:函数思想;4A:数学模型法;51:函数的性质及应用.【分析】(Ⅰ)将x=2,y=2代入计算即可,(Ⅱ)函数解析式为y=,令y=20﹣4=16,解得x=10,问题得以解决,(Ⅲ)根据指数函数的性质可得y=<30,问题得以解决【解答】解:(Ⅰ)r=,故答案为:(Ⅱ)根据题意,该树木的高度为16米时需要及时修剪这颗行道数,函数解析式为y=,令y=20﹣4=16,解得x=10,故这棵行道树自然生长10年必须修剪;(Ⅲ)因为>0,所以1+28×>1,所以y=<30,所以该电力线距离地面至少37米,这这棵行道树一直自然生长,始终不会影响电力线段安全.【点评】本题考查了函数在实际生活中的应用,考查了分析问题解决问题的能力,属于中档题.。
