算法初步知识点及习题
算法初步习题课
算法初步(习题3)
4.下列算法输出的结果是
D A.1+3+5+…+2005 B.1×3×5×…×2005 C.求方程 1×3×5×…×n=2005中的n值 D.满足1×3×5×…×n>
2005的最小整数n
S=1 I=1 While
S<=2005 i=i+2 S=S×i end while print i
int(x) 不超过x的最大整数 int(1.3)=? int(-2.7)=? 1 -3
算法初步 (循环结构)
“直到”型循环 特点:先运算后判断 典型例证:吃饭
“当”型循环 特点:先判断后运算 典型例证:资格认证
算法初步(算法语句)
一 赋值语句; x =23
二 输入、输出语句; Input Print
三 条件语句;
四 循环语句。
用认 心真 做做 事事 能能 把把 事事 做做 好对
算法初步(基础练习1)
算法的过程称为“数学机械化”,数学机械化的最大优 点是可以让计算机来完成,中国当代数学家在这方面研
究处于世界领先地位,为此而获得首届国家自然科学一
等奖的是
A.袁隆平
B.华罗庚
C.苏步青
D
D.吴文俊
D. 自然语言
算法初步(习题6)
8.算法的有穷性是指? 算法的步骤是有限的。
9.书写算法有四种语句,包括: 赋值语句、输入输出语句、 条件语句、循环语句
算法初步(习题7)
11.右图给出的是计算
1 1 1 1
246
20
的值的一个程序框图,其中
判断框内应填入的条件
是
.
I>10(或 n>20)
专题50:算法初步知识点及典型例题(原卷版)

专题50:算法初步知识点及典型例题(原卷版)【知识梳理】知识点一、算法1.算法的概念(1)古代定义:指的是用阿拉伯数字进行算术运算的过程。
(2)现代定义:算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。
(3)应用:算法通常可以编成计算机程序,让计算机执行并解决问题。
2.算法的特征:①指向性:能解决某一个或某一类问题;②精确性:每一步操作的内容和顺序必须是明确的;算法的每一步都应当做到准确无误,从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确.“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有限性:必须在有限步内结束并返回一个结果;算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.④构造性:一个问题可以构造多个算法,算法有优劣之分。
3.算法的表示方法:(1) 用自然语言表示算法: 优点是使用日常用语, 通俗易懂;缺点是文字冗长, 容易出现歧义;(2) 用程序框图表示算法:用图框表示各种操作,优点是直观形象, 易于理解。
注:泛泛地谈算法是没有意义的,算法一定以问题为载体。
例1.下面给出一个问题的算法:S1输入x;S2若x≤2,则执行S3;否则,执行S4;S3输出-2x-1;S4输出x2-6x+3.问题:(1)这个算法解决的是什么问题?(2)当输入的x值为多大时,输出的数值最小?知识点二:流程图1. 流程图的概念:流程图,是由一些图框和流程线组成的,其中图框表示各种操作的类型,图框中的文字和符合表示操作的内容,流程线表示操作的先后次序。
2.流程图常用符号:图形符号名称含义开始/结束框用于表示算法的开始与结束输入/输出框用于表示数据的输入或结果的输出处理框描述基本的操作功能,如“赋值”操作、数学运算等判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”流程线表示流程的路径和方向连接点用于连接另一页或另一部分的框图注释框框中内容是对某部分流程图做的解释说明3.画流程图的规则:(1)使用标准的框图的符号;(2)框图一般按从上到下、从左到右的方向画;(3)除判断框图外,大多数框图符号只有一个进入点和一个退出点。
(完整版)高中数学必修三算法初步复习(附含答案解析),推荐文档
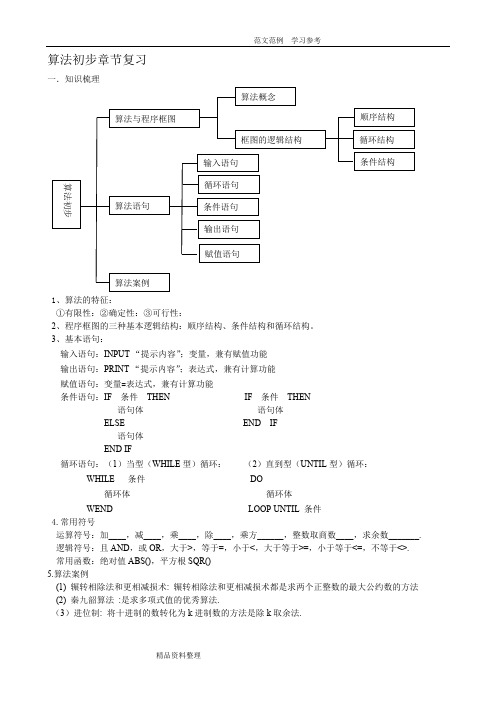
算法初步章节复习
一.知识梳理 算法与程序框图
算法语句
范文范例 学习参考
算法概念
框图的逻辑结构 输入语句 循环语句 条件语句 输出语句 赋值语句
顺序结构 循环结构 条件结构
算法案例
1、算法的特征: ①有限性:②确定性:③可行性: 2、程序框图的三种基本逻辑结构:顺序结构、条件结构和循环结构。 3、基本语句:
WHILE 条件
DO
循环体
循环体
WEND
LOOP UNTIL 条件
4.常用符号
运算符号:加____,减____,乘____,除____,乘方______,整数取商数____,求余数_______.
逻辑符号:且 AND,或 OR,大于>,等于=,小于<,大于等于>=,小于等于<=,不等于<>.
常用函数:绝对值 ABS(),平方根 SQR()
D、 y 4x2 4x 1
2.用二分法计算 3x2 3x 8 0 在 x (1, 2) 内的根的过程中得:
f (1) 0 , f (1.5) 0 , f (1.25) 0 ,则方程的根落在区间
() ()
A、 (1,1.5) B、 (1.5, 2) C、 (1,1.25)
D、 (1.25,1.5)
_____。 10.下面程序输出的 n 的值是______________.
范文范例 学习参考
开始
i=1,sum=0,s=0
j=1
否
n=0
是 i=i+1
sum=sum+1
s=s+1/(sum*i)
输出 s
结束
Hale Waihona Puke WHILE j<=11
算法初步练习题及答案(ABC组)

1a = 3b = a a b =+ b a b =- PRINT a ,bIF 10a < THEN 2y a =*else y a a =*第一章:算法初步[基础训练A 组] 一、选择题1.下面对算法描述正确的一项是:( )A .算法只能用自然语言来描述B .算法只能用图形方式来表示C .同一问题可以有不同的算法D .同一问题的算法不同,结果必然不同 2.用二分法求方程022=-x 的近似根的算法中要用哪种算法结构( )A .顺序结构B .条件结构C .循环结构D .以上都用 3.将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( )4.计算机执行下面的程序段后,输出的结果是( )A .1,3B .4,1C .0,0D .6,0 5.当3=a 时,下面的程序段输出的结果是( )A .9B .3C .10D .6二、填空题1.把求 2按从大到小进行排序时,经过第一趟排序后得到的新数列为 。
3.用“秦九韶算法”计算多项式12345)(2345+++++=x x x x x x f ,当x=2时的值的过程中,要经过 次乘法运算和 次加法运算。
4.以下属于基本算法语句的是 。
① INPUT 语句;②PRINT 语句;③IF-THEN 语句;④DO 语句;⑤END 语句; ⑥WHILE 语句;⑦END IF 语句。
5.将389化成四进位制数的末位是____________。
三、解答题1.把“五进制”数)5(1234转化为“十进制”数,再把它转化为“八进制”数。
2.用秦九韶算法求多项式x x x x x x x x f ++++++=234567234567)(当3=x 时的值。
3.编写一个程序,输入正方形的边长,输出它的对角线长和面积的值。
4.某市公用电话(市话)的收费标准为:3分钟之内(包括3分钟)收取0.30元;超过3分钟部分按0.10元/分钟加收费。
设计一个程序,根据通话时间计算话费。
算法初步知识点与习题
算法初步1.了解算法的含义、算法的思想.2.理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.3.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.知识聚焦不简单罗列1.算法与程序框图(1)算法的定义:算法是指按照________解决某一类问题的________和________的步骤.(2)程序框图:①程序框图又称________,是一种用________、________及________来表示算法的图形.②程序框图通常由________和________组成.③基本的程序框有______________、________________、______________、________.结构的步骤称为________2.基本算法语句(1)输入语句、输出语句和赋值语句的格式与功能:(2)条件语句的格式及框图:①IF-THEN格式:图10-63-1②IF-THEN-ELSE格式:图10-63-2(3)循环语句的格式及框图:①UNTIL语句:图10-63-3②WHILE语句:图10-63-4正本清源不单纯记忆■链接教材1.[教材改编] 阅读如图10-63-5所示的程序框图,若输入的a,b,c分别为14,6,20,则输出的a,b,c分别是________________.图10-63-5图10-63-62.[教材改编] 如图10-63-6所示的程序框图,其功能是计算数列{a n }的前n 项和的最大值S ,则S =________.3.[教材改编] 某算法语句如下所示,若输出y 的值为3,则输入x 的值为________.INPUT xIF x<=0 THEN y =x +2 ELSE y =log 2x END IF PRINT y END■ 易错问题4.循环结构:计数变量;判定条件的出口方向.某程序框图如图10-63-7所示,若运行该程序后输出的值是95,则a =________.图10-63-7图10-63-85.易混淆当型循环与直到型循环:直到型循环是“先循环,后判断,条件满足时终止循环”;当型循环则是“先判断,后循环,条件满足时执行循环”.如图10-63-8所示是一个算法流程图,则输出的k的值是________.■通性通法6.循环结构:关注“先循环,后判断”还是“先判断,后循环”.执行如图10-63-9所示的程序框图,若输出的结果是8,则判断框内m的取值范围是________.图10-63-9图10-63107.条件结构:关注条件对程序终止的影响.执行如图10-63-10所示的程序框图,若输入的x的值为3,则输出的y的值为________.探究点一算法的基本结构1执行如图10-63-11所示的程序框图,则输出的k的值是()A.3 B.4C.5 D.6(2)如图10-63-12所示的程序框图,若输入x的值为2,则输出x的值为________.图10-63-11图10-63-12[总结反思]解决程序框图问题要注意几个常用变量:(1)计数变量:用来记录某个事件发生的次数,如i=i+1.(2)累加变量:用来计算数据之和,如S=S+i.(3)累乘变量:用来计算数据之积,如p=p×i.式题(1)根据下面框图10-63-13,当输入的x为2006时,输出的y=()A.2 B.4 C.10 D.28图10-63-13图10-63-14(2)阅读如图10-63-14所示的程序框图,运行相应的程序,若输入x的值为1,则输出y 的值为()A.2 B.7 C.8 D.128探究点二算法的交汇性问题考向1与统计的交汇问题2 图10-63-15(1)是某高三学生进入高中三年来数学考试成绩的茎叶图,将第1次到第14次的考试成绩依次记为A1,A2,…,A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个流程图,那么该流程图输出的结果是()图10-63-15A.7 B.8 C.9 D.10[总结反思] 算法与统计的交汇问题侧重考查统计思想在程序框图中的体现,两者相结合可以有效理解题意.考向2与函数的交汇问题3 如图10-63-16所示的程序框图中,若f(x)=x2-x+1,g(x)=x+4,且h(x)≥m恒成立,则m的最大值是()A.4 B.3 C.1 D.0图10-63-16图10-63-17[总结反思]算法与函数的交汇问题,关键是弄清楚函数的特征,一般考查分段函数的情况居多.式题 已知函数f (x )=x 2-ax 的图像在点A (1,f (1))处的切线与直线x +3y +2=0垂直,执行如图10-63-17所示的程序框图,则输出的k 值是________.考向3 与概率的交汇问题 4 执行如图10-63-18所示的程序框图,任意输入一次x (0≤x ≤1)与y (0≤y ≤1),则能输出数对(x ,y )的概率为( )图10-63-18A.14B.13C.23D.34[总结反思]解决与概率交汇的程序框图问题的关键在于理解算法功能与概率模型,需特别关注几何概型与古典概型模型在算法功能中的体现.式题 如图10-63-19所示是用模拟方法估计圆周率π值的程序框图,P 表示估计结果,则图中空白框内应填入________________.图10-63-19探究点三基本算法语句5 给出下面两个算法语句:i=1WHILE i*(i+1)<20i=i+1WENDPRINT“i=”;iEND(1)i=1DOi=i+1LOOP UNTIL i*(i+1)<20PRINT“i=”;iEND(2)执行算法语句(1)的结果是输出________;执行算法语句(2)的结果是输出________.[总结反思]求解算法语句问题的关键是理解基本算法语言.在一个赋值语句中,只能给一个变量赋值,同一个变量多次赋值的结果以算法顺序的最后一次为准.对于条件语句要注意准确判断和语句格式的完整性.对于循环语句,要注意是直到型循环,还是当型循环,弄清何时退出循环.式题执行下面的算法语句,输出的结果是( )i =1S =0WHILE i<=10 S =S +2i i =i +1 WENDPRINT S ,i ENDA .55,10B .220,11C .110,10D .110,11学科能力 自主阅读型误区警示 26.程序框图中的逻辑顺序不明确致误【典例】 如图10-63-20所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( )图10-63-20A .0B .2C .4D .14解析 B 逐一写出循环:①a =14,b =18→a =14,b =4→a =10,b =4→a =6, b =4→a =2,b =4→②a =2,b =2,结束循环.故选B.【跟踪练习】 (1)已知MOD 函数是一个求余函数,其格式为MOD(n ,m ),其结果为n 除以m 的余数,例如MOD(8,3)=2.下面是一个算法的程序框图,当输入的值为36时,则输出的结果为( )图10-63-21A .4B .5C .6D .7(2)执行如图10-63-22所示的程序框图,输出的S 值为()图10-63-22A .3B .-6C .10D .-15。
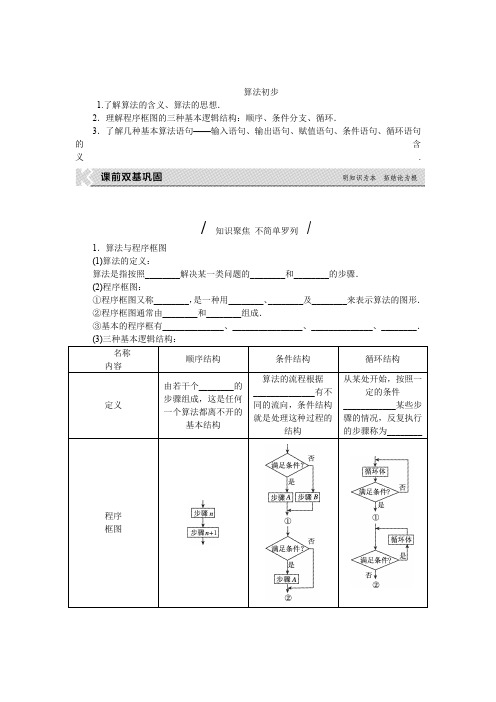
算法初步练习题(学生讲义)
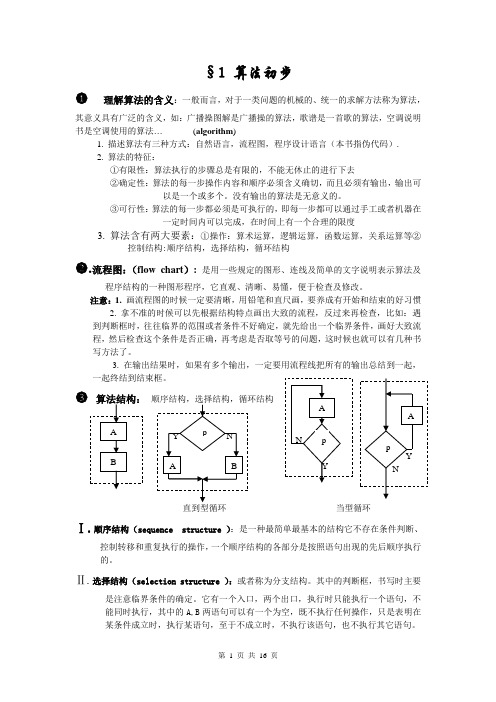
§1 算法初步◆理解算法的含义:一般而言,对于一类问题的机械的、统一的求解方法称为算法,其意义具有广泛的含义,如:广播操图解是广播操的算法,歌谱是一首歌的算法,空调说明书是空调使用的算法…(algorithm)1. 描述算法有三种方式:自然语言,流程图,程序设计语言(本书指伪代码).2. 算法的特征:①有限性:算法执行的步骤总是有限的,不能无休止的进行下去②确定性:算法的每一步操作内容和顺序必须含义确切,而且必须有输出,输出可以是一个或多个。
没有输出的算法是无意义的。
③可行性:算法的每一步都必须是可执行的,即每一步都可以通过手工或者机器在一定时间内可以完成,在时间上有一个合理的限度3. 算法含有两大要素:①操作:算术运算,逻辑运算,函数运算,关系运算等②控制结构:顺序结构,选择结构,循环结构.流程图:(flow chart): 是用一些规定的图形、连线及简单的文字说明表示算法及程序结构的一种图形程序,它直观、清晰、易懂,便于检查及修改。
注意:1. 画流程图的时候一定要清晰,用铅笔和直尺画,要养成有开始和结束的好习惯2. 拿不准的时候可以先根据结构特点画出大致的流程,反过来再检查,比如:遇到判断框时,往往临界的范围或者条件不好确定,就先给出一个临界条件,画好大致流程,然后检查这个条件是否正确,再考虑是否取等号的问题,这时候也就可以有几种书写方法了。
3. 在输出结果时,如果有多个输出,一定要用流程线把所有的输出总结到一起,一起终结到结束框。
直到型循环当型循环Ⅰ.顺序结构(sequence structure ):是一种最简单最基本的结构它不存在条件判断、控制转移和重复执行的操作,一个顺序结构的各部分是按照语句出现的先后顺序执行的。
Ⅱ.选择结构(selection structure ):或者称为分支结构。
其中的判断框,书写时主要是注意临界条件的确定。
它有一个入口,两个出口,执行时只能执行一个语句,不能同时执行,其中的A,B两语句可以有一个为空,既不执行任何操作,只是表明在某条件成立时,执行某语句,至于不成立时,不执行该语句,也不执行其它语句。
1.0 算法初步 答案版

1.0 算法初步[知识点归纳]1.算法的概念数学中的算法:通常是指按照一定规则解决某一类问题的明确和有限的步骤现代算法:通常可以编成计算机程序,让计算机执行并解决问题2.算法与计算机计算机解决任何问题都要依赖于算法,只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”准确地描述出来,计算机才能够解决问题.3.程序框图(1)定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.(2)组成:程序框:表示算法中的一个步骤.流程线:表示算法步骤的执行顺序.(3)常见的程序框、流程线及各自表示的功能.图形符号名称功能终端框(起止框) 表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框) 赋值、计算判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”流程线连接程序框连接点连接程序框图的两部分4.算法的基本逻辑结构名称定义结构形式特征顺序结构由若干个依次执行的步骤组成的基本结构任何一个算法都离不开的基本结构条件结构算法的流程根据条件是否成立有不同的流向,处理上述过程的结构就是条件结构两个步骤A、B根据条件选择一个执行根据条件选择是否执行步骤A5.算法的基本逻辑结构:循环结构(1)概念:在算法中,从某处开始,按照一定的条件反复执行某些步骤的结构称为循环结构,反复执行的步骤称为循环体可以用如图(1)(2)所示的程序框图表示.(2)直到型循环结构:如图(1)所示,其特征是:在执行了一次循环体后,再对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.(3)当型循环结构:如图(2)所示,其特征是:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.6.三种算法语句的格式及功能7.条件语句的一般格式及功能类别单支双支条件结构框图条件语句IF条件THEN语句体END IFIF条件THEN语句体1ELSE语句体2END IF语句功能首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体,否则执行END_IF之后的语句首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体1,否则(ELSE)执行语句体28.两种循环语句的对比名称直到型当型程序结构框图格式DO循环体LOOP_UNTIL条件WHILE条件循环体WEND执行步骤先执行一次DO和UNTIL之间的循环体,再对UNTIL后的条件进行判断,如果条件不符合,继续执行循环体,然后再检查上述条件,如果条件仍不符合,再次执行循环体直到某一次条件符合为止.这时不再执行循环体,跳出循环体执行UNTIL语句后面的语句先判断条件的真假,如果条件符合,就执行WHILE和WEND之间的循环体,然后再检查上述条件,如果条件仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止,这时不再执行循环体,跳出循环体,执行WEND后面的语句9.辗转相除法与更相减损术(1)辗转相除法:又叫欧几里得算法,是一种求两个正整数的最大公约数的古老有效的算法.(2)更相减损术:我国古代数学专著《九章算术》中介绍的一种求两个正整数的最大公约数的算法.10.秦九韶算法功能它是一种用于计算一元n次多项式的值的方法改写的形式f(x)=a n x n+a n-1x n-1+…+a1x+a0=(a n x n-1+a n-1x n-2+…+a1)x+a0=((a n x n-2+a n-1x n-3+…+a2)x+a1)x+a0=…=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0计算方法从括号最内层开始,由内向外逐层计算v1=a n x+a n-1,v2=v1x+a n-2,v3=v2x+a n-3,…v n=v n-1x+a0,这样,求n次多项式f(x)的值就转化为求n个一次多项式的值11.进位制(1)进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,几进制的基数就是几.(2)其他进制与十进制间的转化:①其他进制的数化成十进制时,表示成不同位上数字与基数的幂的乘积之和的形式.②十进制化成k进制——“除k取余法”.[题型精练]题型一算法的概念例 1.下列关于算法的描述正确的是( )A .算法与求解一个问题的方法相同B .算法只能解决一个问题、不能重复使用C .算法的过程要一步一步操作,每步操作必须确切D .有的算法执行完后,可能无结果 答案:C2.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均分的一个算法为:第一步,令A =89,B =96,C =99.第二步,计算总分S =____①____. 第三步,计算平均分M =____②____. 第四步,输出S 和M . 答案:①A +B +C ②S33.已知算法: 第一步,输入n .第二步,判断n 是否是2,若n =2,则n 满足条件. 若n >2,则执行第三步.第三步,依次检验从2到n -1的整数能不能整除n ,若不能整除n ,满足条件. 上述满足条件的数是( )A .质数B .奇数C .偶数D .4的倍数 解析:由质数的定义知.答案:A 变式 1.算法的有穷性是指( )A .算法必须包含输出B .算法中每个步骤都是可执行的C .算法的步骤必须有限D .以上说法均不对 解析:选C 根据算法的概念可知C 正确.2.在程序框图中,一个算法的步骤到另一个算法的步骤的连接用( ) A .连接点 B .判断框 C .流程线 D .处理框 解析:选C 由算法概念可知C 正确. 3.给出下面的算法: 第一步,输入x .第二步,判断x 是否小于0,若是,则输出x +2,否则执行第三步. 第三步,输出x -1.当输入的x 的值分别为-1,0,1时,输出的结果分别为________、________、________.解析:该算法实际上是分段函数f (x )=⎩⎪⎨⎪⎧x -1, x ≥0,x +2, x <0,∴f (-1)=-1+2=1,f (0)=0-1=-1,f (1)=1-1=0. 答案:1 -1 0题型二根据程序框图求输出结果1.利用条件分支结构解决算法问题的注意点利用条件分支结构解决算法问题时,要引入判断框,要根据题目的要求引入一个或多个判断框.而判断框内的条件不同,对应的下一图框中的内容和操作要相应地进行变化,故要逐个分析判断框内的条件.2.当型循环、直到型循环的区别直到型循环是“先循环,后判断,条件满足时终止循环”;而当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.例1.如图,输出的结果是________.解析:由程序框图知,当m=2时,p=2+5=7,m=7+5=12. 答案:122.(2012·安徽高考)如图所示,程序框图(算法流程图)的输出结果是()第1题第2题第3题第4题A.3B.4 C.5 D.8[解答]第一次进入循环体有x=2,y=2;第二次进入循环体有x=4,y=3;第三次进入循环体有x=8,y=4,跳出循环.故输出的结果是4. [答案] B3.程序框图如图所示:如果输入x=5,则输出结果为()A.109B.325 C.973 D.2 917解析:选B第1次运行后,x=5×3-2=13<200,第2次运行后,x=13×3-2=37<200,第3次运行后,x=37×3-2=109<200,第4次运行后,x=109×3-2=325>200,故输出结果为325.4.(2012·广东高考)执行如图所示的程序框图,若输入n的值为6,则输出s的值为() A.105 B.16 C.15 D.1解析:选C按照程序过程,通过反复判断循环条件执行程序.执行过程为s=1×1=1,i=3;s=1×3=3,i=5;s=3×5=15,i=7≥6,跳出循环.故输出s的值为15.变式1.(2012·北京高考)执行如图所示的程序框图,输出的S的值为()A.2 B.4 C.8 D.16解析:选C根据循环k=0,S=1;k=1,S=2;k=2,S=8,当k=3时,输出S=8.第1题 第2题 第3题2.(2012·湖南高考)如果执行如图所示的程序框图,输入x =4.5,则输出的数i =________. 解析:执行程序,i ,x 的取值依次为i =1,x =3.5;i =2,x =2.5;i =3,x =1.5;i =4,x =0.5;结束循环,输出i 的值为4.答案:43.(2012·福建高考)阅读如图所示的程序框图,运行相应的程序,输出的S 值等于________. 解析:当k =1时,1<4,则执行循环体得:S =1,k =2;当k =2时,2<4,则执行循环体得:S =0,k =3;当k =3时,3<4,则执行循环体得:S =-3,k =4;当k =4时不满足条件,则输出S =-3. 答案:-3题型三 程序框图的识别及应用识别程序框图运行和完善程序框图的步骤识别运行程序框图和完善程序框图是高考的热点.解答这一类问题,第一,要明确程序框图的顺序结构、条件结构和循环结构;第二,要识别运行程序框图,理解框图所解决的实际问题;第三,按照题目的要求完成解答.对程序框图的考查常与数列和函数等知识相结合,进一步强化框图问题的实际背景.例 1.如图是求某个函数的函数值的程序框图,则满足该程序的函数的解析式为________.解析:当满足x <0时,f (x )=2x -3;当不满足x <0,即x ≥0时,f (x )=5-4x ,所以满足该程序的函数解析式为f (x )=⎩⎪⎨⎪⎧ 2x -3,x <0,5-4x ,x ≥0.答案:f (x )=⎩⎪⎨⎪⎧2x -3 x <05-4x x ≥0 2.如图所示,是求函数y =|x -3|的函数值的程序框图,则①处应填_______,②处应填_______.[妙解] ∵y =|x -3|=⎩⎪⎨⎪⎧x -3, x ≥3,3-x , x <3.∴①中应填x <3? 又∵若x ≥3,则y =x -3.∴②中应填y =x -3. [答案] x <3? y =x -3变式 1.执行如图所示的程序框图,输出的结果为20,则判断框中应填入的条件为( ) A .a ≥5? B .a ≥4? C .a ≥3? D .a ≥2?解析:当n =0时,P =1,Q =3,P <Q 成立,执行循环;当n =1时,P =5,Q =7,P <Q 成立,执行循环;当n =2时,P =21,Q =15,P <Q 不成立,但是n =2+1=3后,再输出.答案:B2.对任意非零实数a ,b ,若a ⊗b 的运算原理的程序框图如图所示,则3⊗2=________. 解析:由程序框图可知若a ≤b ,则输出b -1a 若a >b ,则输出a +1b .又∵3>2,∴输出3+12=2.答案:23.某市的出租车收费办法如下:不超过2 km 收7元(即起步价7元),超过2 km 的里程每 km 收2.6元,另每车次超过2 km 收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )A .y =7+2.6xB .y =8+2.6xC .y =7+2.6(x -2)D .y =8+2.6(x -2)解析:结合框图可知,当超过2 km 后收费应为起步价和2 km 以外的路费及燃油费之和,即y =7+2.6×(x -2)+1=8+2.6(x -2).答案:D4.已知函数y =⎩⎪⎨⎪⎧log 2x ,x ≥2,2-x ,x <2,下图表示的是给定x 的值,求其对应的函数值y 的程序框图.①处应填写________;②处应填写________.[解答] 由框图可知只要满足①条件则对应的函数解析式为y =2-x ,故此处应填写x <2?则②处应填写y =log 2x .5.(2013·临沂高一检测)根据条件把图中的程序框图补充完整,求区间[1,1000]内所有奇数的和,(1)处填________;(2)处填________.解析:求[1,1 000]内所有奇数和,初始值i=1,S=0,并且i<1 000,所以(1)应填S=S+i,(2)为i=i+2.答案:(1)S=S+i(2)i=i+26.某流程图如图所示,现输入如下四个函数,则可以输出的函数是()A.f(x)=x2 B.f(x)=1x C.f(x)=ln x+2x-6 D.f(x)=sin x解析:选D本题的程序框图的功能是判断函数是否是奇函数且是否存在零点,满足既是奇函数又存在零点的函数是选项D.题型四基本算法语句例1.(2011·福建高考)运行如图所示的程序,输出的结果是________.解析:a=1,b=2,把1与2的和赋给a,即a=3,输出的结果是3. 答案:32.当a=1,b=3时,执行完如图的一段程序后x的值是()IF a<b THENx=a+bEND IFPRINT xA.1 B.3 C.4 D.-2解析:选C∵a<b.∴x=a+b=1+3=4.3.当a=11时,下面程序输出结果是________.INPUT aIF a<10THENy=2*aELSEy=a*aEND IFPRINT yEND解析:∵a=3<10,∴y=11×11=121. 答案:1214.下列程序执行后输出的结果是________.i =11S =1DOS =S*ii =i -1LOOP UNTIL i<9PRINT S END解析:程序反映出的算法过程为i =11⇒S =11×1,i =10;i =10⇒S =11×10,i =9; i =9⇒S =11×10×9,i =8;i =8<9退出循环,执行PRINT S .故S =990.答案:9905.运行下面的程序时,WHILE 循环语句的执行次数是( ) N =0WHILE N<20 N =N +1N =N*NWEND PRINT N ENDA .3B .4C .15D .19解析:选A 0<20,1<20,2×2<20,5×5>20,程序结束,故WHILE 循环语句共执行了3次. 变式 1.下面程序输出的结果是( )A .27B .9C .25D .11 解:该程序的运行过程是x =6÷3=2,y =4×2+1=9,x +y =2+9=11.所以输出11.答案:D x =6y =3x =x/3y =4*x +1PRINT x +y END2.计算机执行下面的程序段后, a=8 b=5 a=a+b b=a-bPRINT a ,b 输出的结果是( )A .8,5B .3,13C .13,3D .13,8 3.阅读下列语句: 输入a ;If a >5 Thenb =2* a Elseb = a * a +1 End I f 输出b.如果输出5,则输入的a 为 ( ) A .2.5 B .2 C .-2 D .±2解:由算法语句可知,令2a =5,则a =52<5(舍),令a 2+1=5,则a =±2.答案:D4.(2012·咸阳高一检测)阅读下列算法语句: 输入x ;If x <0 Theny =7* x/2+3If x>0 Theny =7* x/2-3 Elsey =0End If End If 输出y .如果输出x =-2,则输出结果为 ( )A .2B .-12C .10D .-4解析:输入x =-2,则x <0,执行“y =7* x/2-3”这一语句,即有y =-4.答案:D 5.下面的程序是求一个函数的函数值的程序:INPUT xIF x<=0 THENy =-x ELSEIF x>0 AND x<=1 THENy =0 ELSEy =x -1 END IF END IF PRINT y END若执行此程序的结果为3,那么输入的x 的值为________. 解析:此程序是求函数y =⎩⎪⎨⎪⎧-x ,x ≤0,0,0<x ≤1,x -1,x>1.的值.解出结果为3,则有可能x -1=3,即x =4,或-x =3,即x =-3. 答案:4或-36.下列循环语句,循环终止时,i 等于( ) i =1DOi =i +1LOOP UNTIL i>4A .3B .4C .5D .6解析:∵LOOP UNTIL i >4.∴当i =5时,循环终止.答案:C7.设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线①上不能填入的数是( )S=1i=3WHILE i<①S=S*ii=i+2WENDPRINT SENDA.13B.13.5 C.14 D.14.5[解答]当填i<13时,i值顺次执行的结果是5,7,9,11,当执行到i=11时,下次就是i=13,这时要结束循环,因此计算的结果是1×3×5×7×9×11,故不能填13,但填的数字只要超过13且不超过15均可保证最后一次循环时,得到的计算结果是1×3×5×7×9×11×13. [答案] A 8.下面程序的运行结果是()i=1S=0WHILE i<4S=S*i+1i=i+1WENDPRINT SENDA.3B.7 C.10 D.17解析:该程序的运行过程是:i=1,S=0,i=1<4成立,S=0×1+1=1,i=1+1=2,i=2<4成立,S=1×2+1=3,i=2+1=3,i=3<4成立,S=3×3+1=10,i=3+1=4,i=4<4不成立,输出S=10.答案:C题型五算法案例例 1.用辗转相除法求80和36的最大公约数,并用更相减损术检验所得结果.[解答]用辗转相除法:80=36×2+8,36=8×4+4,8=4×2+0.故80和36的最大公约数是4.用更相减损术检验:80-36=44,44-36=8,36-8=28,28-8=20,20-8=12,12-8=4,8-4=4.故80和36的最大公约数是4.2.用秦九韶算法求多项式f(x)=2x4-6x3-5x2+4x-6在x=5时的值.[解答]由于f(x)=2x4-6x3-5x2+4x-6=(((2x-6)x-5)x+4)x-6.根据秦九韶算法,v0=2,v1=2x-6=2×5-6=4,v2=4x-5=4×5-5=15,v3=15x+4=15×5+4=79,v4=79x-6=79×5-6=389.3.用秦九韶算法求f(x)=3x6+4x5+5x4+6x3+7x2+8x+1,当x=0.4时的值,需进行乘法运算和加法运算的次数分别为()A.6 6 B.5 6 C.6 5 D.612解析:改写多项多f(x)=(((((3x+4)x+5)x+6)x+7)x+8)x+1,则需要6次乘法和6次加法.答案:A4.将八进制数3 726(8),化成十进制数.[解答]∵3 726(8)=3×83+7×82+2×8+6=2 006,∴3 726(8)=2 006.将本例改为“化为五进制数”其结果又该如何?解:把上式中各步所得余数从下到上排列得到2 006=31 011(5),∴3 726(8)=31 011(5).5.103(5)化为十进制数为________.解析:103(5)=1×52+0×51+3=28.答案:286.将二进制数101 101(2)化为八进制数,结果为________.解析:101 101(2)=1×25+0×24+1×23+1×22+0×2+1=32+8+4+1=55(8).答案:55(8)7.用更相减损术可求得78与36的最大公约数是________.解:78-36=42,42-36=6,36-6=30,30-6=24,24-6=18,18-6=12,12-6=6.答案:6 8.用更相减损术求1 515和600的最大公约数时,需要做减法次数是()A.15 B.14 C.13 D.12解析:1 515-600=915,915-600=315,600-315=285,315-285=30,285-30=255,255-30=225,225-30=195,195-30=165,165-30=135,135-30=105,105-30=75,75-30=45,45-30=15,30-15=15. ∴1 515与600的最大公约数是15.则共做14次减法.9.用辗转相除法求294和84的最大公约数时,需要做除法的次数是()A.1 B.2 C.3 D.4解析:由294=84×3+42,84=42×2知,共需做2次除法.答案:B1.0 算法初步练习题一、选择题1.下列算法要解决的问题是()第一步,比较a与b的大小,如果a<b,则交换a,b的值.第二步,比较a与c的大小,如果a<c,则交换a,c的值.第三步,比较b与c的大小,如果b<c,则交换b,c的值.第四步,输出a,b,c.A.输入a,b,c三个数,比较a,b,c的大小B.输入a,b,c三个数,找出a,b,c中的最大数C.输入a,b,c三个数,按从大到小的顺序输出D.输入a,b,c三个数,求a,b,c的平均数解析:由步骤S1→S4可知算法要解决问题是输入a,b,c三个数,按从大到小的顺序输出.答案:C2.阅读下边的程序框图,运行相应的程序,则输出S的值为()A.8 B.18 C.26 D.80解析:程序执行情况为S=31-30=2,n=2;S=2+32-31=8,n=3;S=8+33-32=26,n =4≥4,跳出循环.故输出26.答案:C3.(2012·洛阳高一检测)赋值语句n=n+1的意思是()A.n等于n+1 B.n+1等于nC.将n的值赋给n+1 D.将n的值增加1,再赋给n,即n的值增加1答案:D4.如图,此段程序运行的结果是()a=1b=2c=3a=bb=cc=aPRINT a;b;cENDA.223B.32 2 C.23 2 D.33 2解析:初始:a=1,b=2,c=3,a=b,则a=2,b=c,则b=3,c=a,则c=2.答案:C 5.下列程序若输出的结果为3,则输入的x值可能是()INPUT“x=”;xy=x*x+2*xPRINT yENDA.1 B.-3 C.-1 D.1或-3解析:由x2+2x=3得x=1或x=-3.答案:D6.已知条件语句,如下:IF条件THEN语句体1ELSE语句体2END IF则下列说法正确的是()A.条件成立时,先执行语句体1,再执行语句体2,最后结束条件语句B.条件不成立时,先执行语句体2,再执行语句体1,最后结束条件语句C.条件成立时,先执行语句体1,再结束条件语句D.条件成立时,先执行语句体2,再结束条件语句答案:C7.当a=1,b=3时,执行完下面一段程序后,x的值是()IF a<b THENx=a+bELSEx=a-bEND IFENDA.1 B.3 C.4 D.-2解析:由a=1,b=3,a<b,得x=1+3=4.答案:C8.已知程序如下:INPUT“a=”;aINPUT“b=”;bINPUT“c=”;cmax=aIF b>max THENmax=bEND IFIF c>max THENmax=cEND IFPRINT“max=”;maxEND根据程序提示依次输入4,2,-5,则程序运行结果是()A.max=max B.max=2 C.max=-5 D.max=4解析:程序的执行结果为输出三个数中最大的一个,输入4,2,-5则运行结果为max=4. 答案:D9.在下面的程序中,如果输入x=0,则输出y的值为()INPUT xIF x<0THENy=(π*x)/2+3ELSEIF x>0THENy=-(π*x)/2+5ELSEy=0END IFEND IFPRINT yENDA.3+πB.3-πC.0 D.5+π解析:本语句为“IF-THEN-ELSE ”语句,因为输入x=0,由程序可知应输出y的值为0.答案:C10.下面程序运行后的输出结果为()i=1WHILE i<8i=i+2S=2*i+3i=i-1WENDPRINT SENDA.17B.19 C.21 D.23解析:最后一次执行循环体时,S=2×9+3=21,此时i=8.答案:C二、填空题1.下列程序INPUT x ,y x =x*y y =x -y PRINT x ,y END输入2,4后则执行的结果是________.解析:x =2,y =4,x =x *y =2×4=8,y =8-4=-4.答案:8 -4 2.如图所示的算法功能是________.解析:根据条件结构的定义,当a ≥b 时,输出a -b ;当a <b时,输出b -a .故输出|b -a |. 答案:计算|b -a |3.如下图所示的程序框图,则该程序框图表示的算法的功能是________.答案:连续正奇数相乘,所得积不小于10 000时的第一个奇数4.(2012·浙江高考)若某程序框图如图所示,则该程序运行后输出的值是________.解析:运行程序后,i =1,T =1;i =2,T =12;i =3,T =16;i =4,T =124;i =5,T =1120;i=6>5,循环结束.则输出的值为1120.答案:11205.执行下面的程序语句,输入a =3,b =-1,n =4后,输出的结果是________.INPUT “a ,b ,n =”;a ,b ,n i =1WHILE i<=n c =a +b a =b b =c i =i +1 WEND PRINT c END解析:循环体被执行了四次, 第一次执行循环体得到的结果是:c =2,a =-1,b =2,i =2;执行第二次得到的结果是:c =1,a =2,b =1,i =3;执行第三次得到的结果是:c =3,a =1,b =3,i =4,执行第四次得到的结果是:c =4,a =3,b =4,i =5,这时的c 被输出.答案:46.下面程序输出的结果是________. a =5b =3c =(a +b )/2d =c^2PRINT “d =”;d END解析:该程序的运行过程是:a =5,b =3,c =(3+5)/2=4,d =4×4=16,输出d =16. 7.已知下面程序,写出相应的输出结果(1)若输入x =6,则p =________;(2)若输入x =12,则p =________. 解析:(1)当x =6时,x ≤10,则p =0.35x =6×0.35=2.1.(2)当x =12时,x >10,则p =10×0.35+(x -10)×0.7=3.5+2×0.7=3.5+1.4=4.9. 答案:2.1 4.98.下列算法语句的功能是________(只写式子不计算). 答案:S =13+15+17+…+119+1219.写出运行下列程序后的输出结果.i =1 S =0 DOS =S +12*i +1i =i +1LOOP UNTIL i>10 PRINT S ENDINPUT xIF x<=10 THENp =x*0.35 ELSEp =10*0.35+(x -10)*0.7 END IF PRINT p ENDi =0 S =0WHILE S<=20 S =S +i i =i +1 WEND PRINT i END(1)____________; (2)____________.解析:(1)1+2+3+4+5+6=21>20.∴i =i +1=7(2)同(1)可知i =6.答案:7 6 10.用UNTIL 语句编写程序,计算11+2+12+3+13+4+…+119+20的值.程序如下:请将程序补充完整,横线处应填________.解析:横线处应填循环终止的条件,由于该循环语句是直到循环型语句,则满足该条件时循环终止,故填i >19.答案:i>19 三、解答题1.某班共有学生50人,在一次数学测试中,要搜索出测试中及格(60分及以上)的成绩,试设计一个算法,并画出程序框图.[解答] 算法如下:第一步,i =1.第二步,输入x ,第三步,若x ≥60则输出.第四步,i =i +1.第五步,判断i >50,是结束;否则执行第二步.2.用两种方法求378和90的最大公约数.解:法一:辗转相除法:378=90×4+18,90=18×5+0,所以378与90的最大公约数是18. 法二:更相减损术:因为378与90都是偶数.所以用2约简得189和45.189-45=144,144-45=99,99-45=54,54-45=9,45-9=36,36-9=27,27-9=18,18-9=9.所以378与90的最大公约数为2×9=18.3.用秦九韶算法求多项式f (x )=8x 7+5x 6+3x 4+2x +1当x =2时的值. 解:根据秦九韶算法,把多项式改写成如下形式:f (x )=8x 7+5x 6+0·x 5+3·x 4+0·x 3+0·x 2+2x +1=((((((8x +5)x +0)x +3)x +0)x +0)x +2)x +1. 而x =2,所以有v 0=8,v 1=8×2+5=21,v 2=21×2+0=42,v 3=42×2+3=87, v 4=87×2+0=174,v 5=174×2+0=348,v 6=348×2+2=698,v 7=698×2+1=1 397.i =0 S =0WHILE S<=20 i =i +1 S =S +i WEND PRINT i ENDi =1 S =0 DOS =S +1/(i +i +1) i =i +1LOOP UNTIL ________ PRINT S END所以当x=2时,多项式的值为1 397.。
算法初步 习题

1算法初步重要知识点讲解1.算法概念:(特点:有限性、确定性、顺序性与正确性、不唯一性、普遍性)2.程序框图基本概念:(起止框、输入、输出框、处理框、判断框)3.算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
4. 基本算法语句:输入语句、输出语句、赋值语句、条件语句(IF —THEN —ELSE 语句;IF —THEN 语句)、循环语句(WHILE 语句:WHILE 条件 循环体WEND ;UNTIL 语句:DO 循环体LOOP UNTIL 条件);5.辗转相除法与更相减损术,秦九韶算法与排序(直接插入排序、冒泡排序),进位制。
巩固练习1.算法的三种基本结构是( )A . 顺序结构、模块结构、条件结构B . 顺序结构、循环结构、模块结构C . 顺序结构、条件结构、循环结构D . 模块结构、条件结构、循环结构 2.在输入语句中,若同时输入多个变量,则变量之间的分隔符号是( )A .逗号B .空格C .分号D .顿号3.下列给出的赋值语句中正确的是: ( )A 、3=AB 、M=—MC 、B=A=2D 、x+y=0 4.将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( ) A . B . C . D .5. 右边程序执行后输出的结果是( ) A .-1 B .0C .1D .26. 下面的程序是求使22221231000n ++++<成立的最大整n.则方框内应填的是( ) A .i B .i+1 C .i -1 D .i -27. 上图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图,其中判断框内应填入的条件是( ) A .i>10 B .i ≤10 C .i>20 D .i ≤208. 看程序,若输入t =8时,则下列程序执行后输出的结果是 n=5 s=0 WHILE s<15 S=s + n n=n -1 WEND PRINT n END (第5题)s=1 i=2 DO a=i^2 s=s+a i=i+1LOOP UNTIL s>1000PRINT “n 的最大整数值为:” ; END第6题第7题否是INPUT tIF t<= 4 THEN c=0.2 ELESc=0.2+0.1(t -3) END IF PRINT c END(第8题)a=bb=ac=bb=a a=cb=a a=ba=c c=b b=a29. 为了在运行程序之后得到输出16,键盘输入x 应该是 10. 如右图所示的程序是用来( )A.计算3×10的值B.计算39的值C.计算310的值D.计算1×2×3×…×10的值 11. 如果下边程序执行后输出的结果是990,那么在程序中UNTIL 后面的“条件”应为( ) A. i>10 B. i<8 C. i<=9 D. i<9 12. 执行上方右边的程序框图,若0.8p =,则输出的n =13.用“冒泡法”给数列1,5,3,2,7,9按从大到小进行排序时,经过第一趟排序后得到的新数列为 。
高中数学必修3(人教B版)第一章算法初步1.1知识点总结含同步练习题及答案

描述:例题:高中数学必修3(人教B版)知识点总结含同步练习题及答案第一章 算法初步 1.1 算法与程序框图一、学习任务1. 了解算法的含义,能用自然语言描述算法.2. 了解设计程序框图表达解决问题的过程,了解算法和程序语言的区别;了解程序框图的三种基本逻辑结构,会用程序框图表示简单的常见问题的算法.二、知识清单算法 程序框图三、知识讲解1.算法算法(algorithm)是指按照一定规则解决某一类问题的明确和有限的步骤 .可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列能够解决一类问题.描述算法可以有不同的方式.例如,可以用自然语言和数学语言加以描述,也可以借助形式语言(算法语言)给出精确的说明,也可以用框图直观地显示算法的全貌.算法的要求:(1)写出的算法,必须能解决一类问题,并且能重复使用;(2)算法过程要能一步一步执行,每一步执行的操作必须确切,不能含混不清,而且经过有限步后能得到结果.下列对算法的理解不正确的是( )A.一个算法应包含有限的步骤,而不能是无限的B.算法中的每一个步骤都应当是确定的,而不应当是含糊的、模棱两可的C.算法中的每一个步骤都应当是有效地执行,并得到确定的结果D.一个问题只能设计出一种算法解:D算法的有限性是指包含的步骤是有限的,故 A 正确;算法的确定性是指每一步都是确定的,故 B正确;算法的每一步都是确定的,且每一步都应有确定的结果,故 C 正确;对于同一个问题可以有不同的算法,故 D 错误.下列叙述能称为算法的的个数为( )①植树需要运苗、挖坑、栽苗、浇水这些步骤;描述:2.程序框图程序框图简称框图,是一种用程序框、流程线及文字说明来表示算法的图形.其中,起、止框是任何流程不可少的,表明程序的开始和结束.输入和输出框可用在算法中任何需要输入、输出的位置.算法中间要处理数据或计算,可分别写在不同的处理框内.一个算法步骤到另一个算法步骤用流程线连接.如果一个框图需要分开来画,要在断开处画上连接点,并标出连接的号码.②依次进行下列运算:,,,,;③从枣庄乘火车到徐州,从徐州乘飞机到广州;④ ;⑤求所有能被 整除的正整数,即 .A. B. C. D.解:B①、②、③为算法.1+1=22+1=33+1=4⋯99+1=1003x >x +133,6,9,12,⋯2345写出解方程组的一个算法.解:方法一:代入消元法. 第一步,由 得 ;第二步,将 代入 ,得 ,解得 ;第三步,将 代入方程 ,得 ;第四步,得到方程组的解为 .方法二:加减消元法.第一步,方程 两边同乘以 ,得 ;第二步,将第一步所得的方程与方程 作差,消去 ,得 ,解得 ;第三步,将 代入方程 ,得 ,解得 ;第四步,得到方程组的解为 .{2x +y =74x +5y =112x +y =7y =7−2x y =7−2x 4x +5y =114x +5(7−2x )=11x =4x =4y =7−2x y =−1{x =4y =−12x +y =7510x +5y =354x +5y =11y 6x =24x =4x =42x +y =72×4+y =7y =−1{x =4y =−1例题:画程序框图的规则(1)使用标准的图形符号.(2)框图一般按从上到下、从左到右的方向画.(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框是具有超过一个退出点的惟一符号.(4)判断框分两大类,一类判断框是“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.(5)在图形符号内描述的语言要非常简练清楚.算法的三种基本逻辑结构顺序结构:语句与语句之间,框与框之间按从上到下的顺序进行.条件分支结构:在一个算法中,经常会遇到一些条件的判断,算法的流程条件是否成立有不同的流向,条件结构就是处理这种过程的结构.循环结构:在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.下列程序框图分别是解决什么问题的算法.解:(1)已知圆的半径,求圆的面积的算法.(2)求两个实数加法的算法.执行如图的程序框图,输出的 ______ .解:T =30四、课后作业 (查看更多本章节同步练习题,请到快乐学)某程序框图如图所示,若输出的 ,则判断框内为( )A. B. C. D.解:AS =57k >4?k >5?k >6?k >7?已知函数 ,对每次输入的一个值,都得到相应的函数值,画出程序框图.解:f (x )={2x +3,3−x ,x 2x ⩾0x <0x高考不提分,赔付1万元,关注快乐学了解详情。
浙江摄影版(三起)()信息技术五年级下册《算法初步》课堂练习附课文知识点

小学信息技术五年级下册《算法初步》课堂练习附课文知识点浙江摄影版(三起)(2020)一、判断题1.算法是解决问题的方法和步骤,每一步都能被机器执行。
()2.算法的输入和输出都必须是确定的,不能有多余的输入或输出,)3.尊法的每个步骤都必须是可行的,即每一步在实际操作中都能完成。
()二、选择题1.以下哪项不是算法的特征?()A.确定性B.可行性C.无限性D.有穷性2.算法执行后,至少需要输出()A.一个结果B.两个结果C.三个结果D.不确定3.在农夫过河问题中,农夫需要带狼、羊和蔬菜过河,船每次只能带一样东西,且农夫不在场时,狼会吃羊,羊会吃蔬菜。
请问农夫如何安全地安排它们过河?下列哪项步骤是错误的?()A.农夫带单过河B.农夫一个人回来C.农夫带狼和羊一起过河D.农夫带蔬菜过河三、填空题1.算法的输出指的是算法的,没有输出的算法是没有意义的。
2.在算法描述中,是表示用户输入的信息或计算机臼动输出的信息。
3.算法的描述方式有臼然语言、等多种方式。
四、简答题1.请简述算法的定义及其特征。
2.描述一个生活中的例子,说明算法在解决实际问题中的应用。
答案及解析一、判断题解析1.【答案】正确【解析】算法确实是解决问题的方法和步骤,其每一步都应该是能被机器(或人)执行的。
2.【答案】错误【解析】律法的输入可以是零个或多个,输出也可以是一个或多个,并非必须确定且不能有多余的输入或输出。
3.【答案】正确【解析】算法的每个步骤都应该是可行的,即在实际操作中能够完成。
这是算法的一个重要特征。
二、选择题解析1.【答案】C【解析】算法的特征包括确定性、可行性、有穷性,但不包括无限性。
因此,选项C“无限性”不是弊法的特征。
4.【答案】A【解析】输出可以是1个,也可以是多个,但没有输出的算法是没有意义的。
因此,算法执行后,至少需要输出一个结果。
5.【答案】C【解析】在农夫过河问题中,由于船每次只能带一样东西,且农夫不在场时,狼会吃羊,羊会吃蔬菜,所以农夫不能同时带狼和羊过河。
高考数学 第4讲 算法初步知识点+典型例题+变式训练+基础训练+高考真题(精心整理,很实用)

第4讲算法初步【基础知识】一、算法的概念(1)算法概念:在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.(2)算法的特点:①有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.②确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.③顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,且每一步都准确无误,才能完成问题.④不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.⑤普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.二、程序框图(1)程序框图基本概念:①程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
②构成程序框的图形符号及其作用三、基本算法语句1、输入、输出语句和赋值语句(1)输入语句①输入语句的一般格式INPUT “提示内容”;变量②输入语句的作用是实现算法的输入信息功能;③“提示内容”提示用户输入什么样的信息,变量是指程序在运行时其值是可以变化的量;④输入语句要求输入的值只能是具体的常数,不能是函数、变量或表达式;⑤提示内容与变量之间用分号“;”隔开,若输入多个变量,变量与变量之间用逗号“,”隔开。
(2)输出语句①输出语句的一般格式PRINT “提示内容”;变量②输出语句的作用是实现算法的输出结果功能;③“提示内容”提示用户输入什么样的信息,表达式是指程序要输出的数据;④输出语句可以输出常量、变量或表达式的值以及字符。
(3)赋值语句①赋值语句的一般格式变量=表达式②赋值语句的作用是将表达式所代表的值赋给变量;③赋值语句中的“=”称作赋值号,与数学中的等号的意义是不同的。
高一数学算法初步练习题及答案

第一章算法初步算法与程序框图算法的概念1.下面的结论正确的是【】A.一个程序的算法步骤是可逆的B.一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D.设计算法要本着简单方便的原则2.下面对算法描述正确的一项是【】A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同;结果必然不同3.下面哪个不是算法的特征【】A.抽象性B.精确性C.有穷性D.唯一性4.算法的有穷性是指【】A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(10min)、听广播(8min)几个步骤;从下列选项中选最好的一种算法【】洗脸刷牙、S2刷水壶、S3烧水、S4泡面、S5吃饭、S6听广播刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5听广播C. S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭同时听广播吃饭同时听广播、S2泡面;S3烧水同时洗脸刷牙;S4刷水壶6.看下面的四段话;其中不是解决问题的算法是【】A.从济南到北京旅游;先坐火车;再坐飞机抵达B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.方程210x-=有两个实根D.求1+2+3+4+5的值;先计算1+2=3;再计算3+3=6;6+4=10;10+5=15;最终结果为157.写出求1+2+3+4+5+6+…+100的一个算法.可运用公式1+2+3+…+n=(1)2n n+直接计算.第一步______①_______;第二步_______②________;第三步输出计算的结果.8.写出1×2×3×4×5×6的一个算法.1.1.2 程序框图1.算法的三种基本结构是【】A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2.给出以下四个问题;①输入x;输出它的相反数;②求面积为6的正方形的周长;③在三个不等实数,,a b c中;求一个数的最大数;④求函数1,0()2,0x xf xx x-≥⎧=⎨+<⎩的函数值。
2023年算法初步知识点及习题

算法算法是高中数学课程中旳新增内容,是中国数学课程内容旳一种新特色.“算法”过程是指机械式地按照某种确定旳环节行事,通过一系列小旳简朴计算操作完毕复杂计算旳过程.算法旳学习内容大体可分为三个环节:用自然语言描述算法;精确刻画算法(程序框图);计算机实现执行算法(程序语言旳描述过程).算法思想贯穿高中数学课程旳有关部分.【知识要点】1.算法:算法可以理解为由基本运算及规定旳运算次序所构成旳完整旳解题环节,或者当作按照规定设计好旳有限确实切旳计算序列,并且这样旳环节或序列可以处理一类问题.现代意义上旳“算法”一般是指可以用计算机来处理旳某一类问题旳程序或环节.2.程序框图程序框图:用某些通用旳符号构成一张图来表达算法,这种图称为程序框图(程序框图又称流程图,是一种用程序框、流程线及文字阐明来表达算法旳图形).用框图表达算法环节旳某些常用旳图形符号:程序框名称功能终端框(起止框) 表达一种算法旳起始和结束输入、输出框表达一种算法输入和输出旳信息处理框(执行框) 赋值、计算判断框判断某一条件与否成立,成立时在出口处标明“是”,不成立时标明“否”↓→流程线(指向线) 指导流程图旳方向连接点连接另一页或另一部分旳框图程序框图旳三种基本逻辑构造:次序构造:描述旳是最简朴旳算法构造,语句与语句之间、框与框之间按从上到下旳次序进行(如图9-1).图9-1条件分支构造:根据指定条件选择执行不一样指令旳控制构造(如图9-2).图9-2循环构造:根据指定条件决定与否反复执行一条或多条指令旳控制构造(如图9-3).图9-33.几种基本算法语句任何一种程序设计语言中,都包括五种基本旳算法语句,即输入语句、输出语句、赋值语句、条件语句、循环语句.输入语句和输出语句分别用来实现算法旳输入信息、输出成果旳功能;赋值语句是用来表明赋给某一种变量一种详细确实定值旳语句;条件语句是处理条件分支逻辑构造旳算法语句;循环语句是用来处理算法中旳循环构造旳语句.4.中国古代算法案例:更相减损之术、辗转相除法:求两个正数旳最大公因数旳措施.辗转相除法算法环节:第一步:用两数中较大数除以较小数,求商和余数.第二步:用除数除以余数.第三步:反复第二步,直到余数为0.第四步,得出两数旳最大公约数,即余数0之前旳余数.更相减损术算法环节:第一步:用较大数减去较小数,得到差.第二步:比较减数与差旳大小,再用较大数减去较小数.第三步:反复第二步,直到差与减数相等为止.第四步:相等数即为最大公约数.割圆术:用正多边形旳面积逐渐迫近圆面积旳算法求圆周率π. 秦九韶算法:求一元多项式旳值旳一种措施,递推关系为),,2,1(10n k a x v v a v kn k k n=⎩⎨⎧+==-- 【复习规定】1.理解算法旳含义,理解算法旳思想.2.理解程序框图旳三种基本逻辑构造:次序构造、条件分支构造、循环构造. 3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句旳含义.【例题分析】例1 如图(图9-4)所示,将一系列指令用框图旳形式表达,箭头指向下一步旳操作.请按照框图回答问题:图9-4(1)这个框图表达了怎样旳算法?(2)输出旳数是多少?【分析】由框图中旳文字及图形符号表达旳操作内容可知:此算法是“求1到50旳和”,由此可以算出输出旳数.解:(1)此框图表达旳算法为:求1+2+3+…+50旳和;(2)易知所求和为1275.【评析】程序框图重要包括三部分:表达对应操作旳框,带箭头旳流程线和框外必要旳阐明.读框图时要从这三个方面研究,流程线反应了命令执行旳先后次序,重要看箭头方向,框及内外旳文字阐明表明了操作内容.常用这种方式考察对算法旳理解和应用.例2 (1)如图9-5所示旳是一种算法旳程序框图,已知a1=3,输出旳成果为7,则a2旳值为______.图9-5(2)如图9-6所示旳是某个函数求值旳程序框图,则满足该程序旳函数解析式为_____.图9-6(3)如图9-7所示旳是求某个数列和旳程序框图,此程序输出旳成果为_____.图9-7【分析】这三个小题旳重点在于读懂框图.(1)只具有次序构造,(2)具有条件分支构造,表明函数旳定义域为R ,当x <0时,遵从解析式f (x )=3x -1,否则(即当x ≥0时),遵从解析式f (x )=2-5x ;(3)中有两个循环变量S 、I ,S 是累加变量,I 是计数变量;此外还要判断I 旳奇偶性,以此决定是加还是减.解:(1)112=a ;(2)⎩⎨⎧≥-<-=)0(52)0(13)(x x x x x f ;(3)S =12-22+32-42+…+992-1002=-5050.【评析】题(1),只具有次序构造,所示旳算法比较简朴,只需按照框图箭头方向依次读出即可.题(2)具有条件分支构造,这是一种与分段函数有关旳算法,框图中具有判断框.读包具有判断框旳框图时,要尤其重视判断框内旳条件和框外旳文字阐明,对应旳下一步操作会依条件不一样而变化.题(3)具有循环构造,当处理某些有规律旳科学计算问题,尤其是累加和累乘时,往往可以运用循环构造来实现算法.循环构造有两种,读包具有循环构造旳框图时,除关注判断框内外旳阐明外,一般要从开始依次序做几次循环,观测变量旳变化规律来协助读懂算法旳含义.例3 (1)已知平面上旳一点P 0(x 0,y 0)和直线l :Ax +By +C =0,求点P 0到直线l 旳距离d ,并画出程序框图.(2)用条件分支构造写“已知三个数a 、b 、c ,找出其中最大数”旳算法及框图. (3)写出求n131211++++旳和旳算法,画出程序框图,并写出对应程序(选做). 【分析】对旳分析“算理”,才能选择恰当旳算法构造,有条理旳体现算法.(1)在已知点到直线距离公式旳前提下,适合用次序构造表达;(2)波及比大小,必须用到条件分支构造;(3)中分母有规律旳递增,可以引入累加变量S 和计数变量i ,且S =S +1/i 是反复进行旳,可以用循环构造表达.解:(1)算法及框图为:S1 输入x 0,y 0;A ,B ,C ; S2 计算m =A 2+B 2;S3 计算n =Ax 0+By 0+C ; S4 计算mn d ||=; S5 输出d ;(2)算法及框图为:S1 输入a ,b ,c ; S2 令x =a ;S3 若b >x ,则令x =b ;否则,执行S4; S4 若c >x ,则令x =c ;否则,执行S5; S5 输出x ;(3)算法及框图为:S1 输入i =1,S =0; S2 当i ≤n 时,,1iS S += i =i +1;否则执行S3; S3 输出S ; 程序如下; S =0For i =1:1:n S =S +1/i i =i +1 endprint(%io (2),S )【评析】书写算法时,一步一步旳程序化环节,即“算则”当然重要,但这些环节旳根据,即“算理”有着更基本旳作用,“算理,,是“算则”旳基础,“算则”是“算理”旳体现.这三道小题由于算理不一样,所蕴含旳算法构造也不一样.通过实例,模仿、操作、探索,经历通过设计程序框图体现处理问题旳过程,可以更好旳理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句,体会和理解算法旳含义,理解算法语言旳基本构成.本例中波及旳“运用公式求点到直线旳距离”、“实数排序求最值问题”、“求数列旳和或积旳问题”,还包括“二分法求函数零点”、“质数旳鉴定”,“求π旳近似值”等等,都是算法旳经典案例,学习时要予以充足旳重视.一般算法旳表达措施并不唯一.不一样旳算法语言旳书写形式是有差异旳.本书所采用旳是Scilab 语言,学习时要理解赋值语句、输入输出语句、if 语句、while 和for 语句旳基本含义及体现方式,可以读懂语句表达旳算法过程.例4 (1)用辗转相除法计算56和264旳最大公约数时,需要做旳除法次数是______. (2)用更相减损术求56和98旳最大公约数时,操作如下:(98,56)(56,42)(42,14)(28,14)(14,14),由此可知两数旳最大公约数为______.(3)用秦九韶算法求得多项式f (x )=x 6-2x 5+3x 3+4x 2-6x +5当x =2时函数值为______.解:(1)8216816240164015640564264+⨯=+⨯=+⨯=+⨯=因此最大公约数为8,需做旳除法次数是4;(2)最大公约数为14; (3)33.【评析】书上所波及旳古代基本算法案例包括:更相减损术与辗转相除法、秦九韶算法、割圆术.辗转相除法与更相减损术都是求最大公约数旳措施,辗转相除法又叫欧几里得措施,计算上以除法为主,更相减损术以减法为主,计算次数上,前者相对较少,尤其是两个整数相差较大时区别尤其明显;辗转相除法以余数为0结束,更相减损术则以减数与差相等结束.秦九韶算法旳特点是把求n次多项式旳值转化为求n个一次多项式旳值,运算时只有加法和乘法,并且运算旳次数比较少,求一种n次多项式旳值最多需要进行n 次加法、n次乘法.割圆术是由中国古代数学家刘徽提出旳,是当时计算圆周率比较先进旳算法,“算理”明确,即用圆内接正多边形和外切正多边形迫近圆周率,重点是确定递推关系.例5 (09辽宁)某店一种月旳收入和支出总共记录了N个数据,其中收入记为正数,支出记为负数.该店用下边旳程序框图计算月总收入S和月净盈利V.那么在图中空白旳判断框和处理框中,应分别填入下列四个选项中旳( )A.A>0,V=S-T B.A<0,V=S-TC.A>0,V=S+T D.A<0,V=S+T【分析】本题要注意三点:a k有正有负;S为总收入,是所有正数旳和;T为总支出,是所有非正数旳和.答案为C【评析】本题结合实际背景,强调算法旳应用价值,是一种比较新旳题型,应引起关注.练习9一、选择题1.任何一种算法都必须有旳基本构造是( )A.次序构造B.条件分支构造C.循环构造D.以上三个都要有2.下面给出对程序框图旳几种说法:①任何一种程序框图都必须有起止框;②判断框有一种入口,有不止一种出口;③对于一种算法来说,判断框内旳条件体现方式是唯一旳;其中对旳旳有( )A.0个B.1个C.2个D.3个3.在算法旳逻辑构造中,规定进行逻辑判断并根据成果进行不一样处理旳是哪种构造( ) A.次序构造B.条件分支构造和循环构造C.次序构造和条件分支构造D.次序构造和循环构造4.算法:S1 输入n;S2 判断n与否是2;若n=2,则n满足条件,若n>2,则执行S3;S3 依次从2到n-1检查能否整除n,若都不能整除,则n满足条件;满足上述算法旳n是( )A.奇数B.偶数C.质数D.合数二、填空题5.阅读下面两个程序框图,框图1输出旳成果为______;框图2输出旳成果为______.框图1 框图26.(08广东)阅读图9-8旳程序框图,若输入m=4,n=6,则输出a=______,i=______.图9-8 图9-97.阅读图9-9旳程序框图,若输入旳n是100,则输出旳变量S和T旳值依次是______.8.“x=3*5”和“x=x+1”是某个程序中旳先后相邻两个语句,下列说法中①“x=3*5”是将数值15赋给x,而不是一般运算“x=3*5=15”;②“x=3*5”可以写成“3*5=x”③语句“x=x+1”在执行时,“=”右边x为15,“=”左边x为16;对旳旳有______.三、解答题9.分别用辗转相除法和更相减损术求189和81旳最大公约数.10.用循环语句书写求1+2+3+…+n>1000旳最小自然数n旳算法,画出程序框图,并写出对应旳程序(选做).11.(09宁夏)为了测量两山顶MN间旳距离,飞机沿水平方向在AB两点进行测量,MN在同一种铅垂平面内(如图).飞机可以测量旳数据有俯角和AB间旳距离,请你设计一种方案,包括:指出需要测量旳数据(用字母表达,并在图中标出);用文字和公式写出计算MN间距离旳环节.专题九 算法参照答案练习9一、选择题1.A 2.C 3.B 4.C 二、填空题5.27,21 6.12,3 7.2550,2500 8.①③. 三、解答题9.解:辗转相除法:3278127281189 ⨯=⨯=,因此最大公约数为27.更相减损术:189-81=108,108-81=27,81-27=54,54-27=27, 因此最大公约数为27. 10.解:11.解:如图(1)需要测量旳数据有:A 点到M 、N 旳俯角α1,β1;B 点到M 、N 旳俯角α 2,β 2;A 、B 旳距离d .(2)第一步:计算BM ,由正弦定理)sin(sin 211ααα+=d BM ;第二步:计算BN ,由正弦定理)sin(sin 121βββ-=d BN ;第三步:计算MN ,由余弦定理)cos(22122αβ+++=⋅⋅BN BM BN BM MN .。
高中数学必修3(人教B版)第一章算法初步1.2知识点总结含同步练习题及答案

{
x2 (x
− −
3x 1)2
+ ,
5,
数值,将 y = 9 代入可得答案.
x<0, x⩾0
的函
高考不提分,赔付1万元,关注快乐学了解详情。
输出语句
赋值语句
条件语句
循环语句 (直到型循环结构)
(当型循环结构)
高中数学常用的程序语言还有Scilab语言等.
例题: 下列给出的赋值语句正确的有(
)
① 3 = B;② x + y = 0;③ A = B = −2;④ T = T ∗ T .
A.0 个
B. 1个
C.2 个
D.3 个
解:B
由赋值语句中的“=”左边是变量,右边是表达式知 ①② 错误,赋值语句只能给一个变量赋 值,不能出现两个或多个“=”,故③错误,④正确.
四、课后作业 (查看更多本章节同步练习题,请到快乐学)
1. 下列语句是正确的赋值语句的是 ( )
A.5 = x
B.x + y = 3
C.x = y = −2
D.y = y ∗ y
答案: D 解析: 赋值语句中 " = " 不能互换,即不能给常量赋值,左边必须是变量,右边是表达式,故A、B
错.C错,一个赋值语句只能给一个变量赋值.D正确,该语句的功能是将当前的 y 平方后赋给 变量 y.
2. 下列语言中,哪一个是输入语句 ( )
A.PRINT
B.INPUT
答案: B
C.IF
D.LET
3. 以下程序: ( x=-1 DO x=x*x UNTIL x>10 PRINT x END
).
A.不能执行
{
(x (x
考点12 算法初步(知识点+对点训练)

考点12算法初步1.程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.图形符号名称功能终端框(起止框)表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框)赋值、计算判断某一条件是否成立,成立时在出口处标明判断框“是”或“Y”;不成立时标明“否”或“N”.流程线连接程序框连接点连接程序框图的两部分2.算法的三种基本逻辑结构:顺序结构、条件结构和循环结构.3.基本算法语句:输入语句,输出语句,赋值语句,条件语句,循环语句.4.一般格式:(1)输入语句:INPUT“提示内容”;变量(2)输出语句:PRINT“提示内容”;表达式(3)赋值语句:变量=表达式(4)条件语句:如IF条件THEN语句体1ELSE语句体2END IF(5)循环语句:如DO循环体LOOP UNTIL条件或WHILE条件循环体WEND5.辗转相除法(欧几里得算法)与更相减损术:求最大公约数.(1)辗转相除法算法步骤:第一步,给定两个正整数m ,n .第二步,计算m 除以n 所得的余数r .第三步,m=n ,n=r .第四步,若r=0,则m ,n 的最大公约数等于m ;否则,返回第二步.(2)更相减损术算法步骤:第一步,任意给定两个正整数,判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.第二步,以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.6.秦九韶算法:多项式求值.算法步骤:第一步,输入多项式次数n 、最高次项的系数n a 和x 的值.第二步,将v 的值初始化为n a ,将i 的值初始化为1n -.第三步,输入i 次项的系数a .第四步,i v vx a =+,1i i =-.第五步,判断i 是否大于或等于0.若是,则返回第三步;否则,输出多项式的值v .7.进位制:“满几进一”就是几进制,几进制的基数就是几.(1)把k 进制数a (共有n 位)化为十进制数b 的算法步骤:第一步,输入a ,k 和n 的值.第二步,将b 的值初始化为0,i 的值初始化1.第三步,1i i b b a k -=+·,1i i =+.第四步,判断i n >是否成立.若是,则执行第五步;否则,返回第三步.第五步,输出b 的值.(2)除k 取余法:把十进制数化为k 进制数的算法.算法步骤:第一步,给定十进制正整数a 和转化后的数的基数k .第二步,求出a 除以k 所得的商q ,余数r .第三步,把得到的余数依次从右到左排列.第四步,若0q ≠,则a q =,返回第二步;否则,输出全部余数r 排列得到的k 进制数.对点训练1.执行如图所示的程序框图,则输出s 的值为()A.34B.38C.148D.182.某程序框图如图所示,若输出结果是254,则判断框中可以是()A.7?i B.8?i > C.7?i > D.6?i 3.执行如图所示的程序框图,则输出S 的值等于()A.2849B.4950C.4748D.50514.执行如图所示的程序框图,若输出的S 的值为6,则判断框内应填的条件是()A.3n >B.4n >C.5n >D.6n >5.执行如图所示的程序框图,如果输入的,[0,)x y ∈+∞,那么输出的Z 的最大值为()A.1B.2C.3D.46.阅读如图所示的程序框图,则输出k的值为()A.8B.9C.10D.11a ,输出的S大于2020,则判断框中的整数m最小为()7.执行如图所示的程序框图,若输入的3A.5B.6C.7D.88.执行如图的程序框图,若输入值小于3,则输出值不可能是()A.1-B.0C.1D.29.“今有物不知其数,三三数之余二、五五数之余三、七七数之余二,问物几何?”这是一个出自《孙子算经》的整除问题.请阅读如图所示的程序框图,若输入2021p=,则输出i的值为()A.134B.135C.136D.13710.下列程序框图的功能是给出以下10个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是()A.60?,1x i i >=+B.60?,1x i i <=+C.60?,1x i i >=-D.60?,1x i i <=-。
必修3算法初步知识点总结及本章测试题
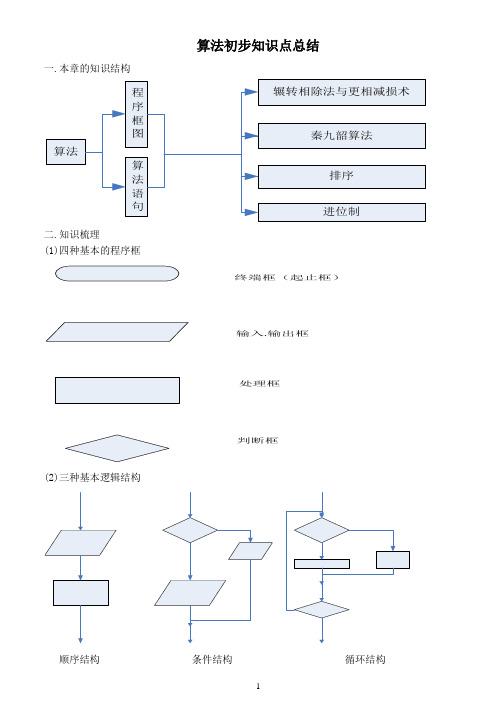
算法初步知识点总结一.本章的知识结构二.知识梳理(1)四种基本的程序框终端框(起止框)输入.输出框处理框判断框(2)三种基本逻辑结构顺序结构 条件结构 循环结构(3)基本算法语句 (一)输入语句(三)赋值语句(四)条件语句 IF -THEN -ELSE 格式当计算机执行上述语句时, 首先对IF 后的条件进行判断, 如果条件符合, 就执行THEN 后的语句1, 否则执行ELSE 后的语句2。
其对应的程序框图为: (如上右图)IF -THEN 格式计算机执行这种形式的条件语句时, 也是首先对IF 后的条件进行判断, 如果条件符合, 就执行THEN 后的语句, 如果条件不符合, 则直接结束该条件语句, 转而执行其他语句。
其对应的程序框图为: (如上右图) (五)循环语句(1)WHILE 语句IF 条件 THEN 语句 END IF其中循环体是由计算机反复执行的一组语句构成的。
WHLIE 后面的“条件”是用于控制计算机执行循环体或跳出循环体的。
当计算机遇到WHILE 语句时, 先判断条件的真假, 如果条件符合, 就执行WHILE 与WEND 之间的循环体;然后再检查上述条件, 如果条件仍符合, 再次执行循环体, 这个过程反复进行, 直到某一次条件不符合为止。
这时, 计算机将不执行循环体, 直接跳到WEND 语句后, 接着执行WEND 之后的语句。
因此, 当型循环有时也称为“前测试型”循环。
其对应的程序结构框图为: (如上右图)(2)UNTIL 语句其对应的程序结构框图为: (如上右图) (4)算法案例案例1 辗转相除法与更相减损术 案例2 秦九韶算法案例3 排序法: 直接插入排序法与冒泡排序法 案例4 进位制WHILE 条件循环体 WENDDO 循环体 LOOP UNTIL 条件算法初步综合检测一一、选择题1. 下列运算不属于我们所讨论算法范畴的是( )A. 已知圆的半径求圆的面积 B. 随意抽4张扑克牌算到二十四点的可能性 C. 已知坐标平面内两点求直线方程 D. 加减乘除法运算法则2. 早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法( )A. S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播B. 刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播C. 刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播D. 吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶3.以下关于排序的说法中, 正确的是( ) A. 排序就是将数按从小到大的顺序排序B. 排序只有两种方法, 即直接插入排序和冒泡排序C. 用冒泡排序把一列数从小到大排序时, 最小的数逐趟向上漂浮 D .用冒泡排序把一列数从小到大排序时, 最大的数逐趟向上漂浮4. 下列语句中:① ② ③ ④ ⑤2(1)22A B B =*+=*+ ⑥((73)5)1p x x x =+-+ 其中是赋值语句的个数为( )A. 6B. 5C. 4D. 35. 把“二进制”数 化为“五进制”数是( ) A. B. C. D.6. 840和1764的最大公约数是( ) A. 84 B. 12 C. 168 D. 2527. 下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( ) A. i>20 B. i<20 C. i>=20 D. i<=208.为了在运行下面的程序之后得到输出y =16, 键盘输入x 应该是( ) A. 或 B. C. 或 D. 或 二、填空题:9.已知有下面程序, 如果程序执行后输出的结果是11880, 那么在程序 UNTIL 后面的“条件”应为10. 给出下面的程序框图, 循环体执行的次数是11. 比较大小:12.用等值算法求294和84大公约数时, 需要做 次减法.13. 下列四个有关算法的说法中, 正确的........ ..要求只填写序.)⑴算法的某些步骤可以不明确或有歧义, 以便使算法能解决更多问题;⑵正确的算法执行后一定得到确定的结果;⑶解决某类问题的算法不一定是唯一的;⑷正确的算法一定能在有限步之内结束.15.读程序, 完成下面各题(1)输出结果... ..(2)输出结果... .三、解答题:16. 将十进制数30化为二进制.17.设计算法流程图, 要求输入自变量的值, 输出函数的值,并用复合IF语句描述算法.18. 设计程序框图求的值.19. 用循环语句描述1+ + + +…+ .20. 用秦九韶算法求多项式,x=-时的值.当0.2算法初步章末检测题二一、选择题1. 下列赋值语句正确的是A. B. C. D.2. 计算机执行下面左边的程序段后, 输出的结果是 A. , B. , C. , D. , 1a = 3b = a a b =+b a b =-PRINT , END第2题 第3题 3. 当 时, 上面右边的程序段输出的结果是 A. B. C. D.4.下边给出的各数, 不可能是七进制数的是 A . B . C . D . 5. 用“辗转相除法”求得和的最大公约数是A. B. C. D.6. 用秦九昭算法求 在 时的值, 的值为 A. B. C. D.7. 用冒泡法对 , , , , 从小到大排序, 需要排序的趟数为 A. B. C. D.IF 10a < THEN2y a =*ELSEy a a =*PRINT y8. 如下左边的程序框图, 若输出 的值为 , 则判断框内可填写的条件是 A. B. C. D. 9.如上右图,该程序框图的功能是A . 求 、 、 的最大数B . 求 、 、 的最小数C. 将 、 、 按从小到大排列D. 将 、 、 按从大到小排列10. 下面右边的程序的功能是: 判断任意输入的数 是否为正数, 若是, 输出它的平方值;否则输出它的相反数, 则应填入的条件是 A. B. C. D.INPUT xIF ______ THENy x =-ELSEy x x =*END IF PRINT y11.如上右图是计算 … 的值的一个程序框图, 其中判断框内应填入的条件是 A . B . C . D . 12.如上右边的程序,最后输出的结果为A. B. C. D. 二、填空题13. 将二进制 转化为十进制数结果是 . 14. 下面一段程序执行后的结果是 .A 2= A A 2=* A A 6=+PRINT A1WHILE 1001WEND 1j j j j j j j =*<=+=-INPUT “a =”;a INPUT “b =”;b IF a b > THEN第14题第15题15. 上面右边的程序输出的结果是.16.将下面的程序补充完整:输入两个数, 输出其中较大的数, 则①处应填.三、解答题17. 分别用辗转相除法和更相减损术求与的最大公约数.18. 用秦九昭算法计算函数当时的函数值.19. 设函数, 设计一个算法输入的值求函数值, 写出算法步骤并画出程序框图.20.设计一个算法求…, 作出程序框图并写出程序.21. 下列语句是求…的一个程序.(Ⅰ)程序中是否有错误?请改正;(Ⅱ)把程序改写成另一种循环语句.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法算法是高中数学课程中的新增内容,是中国数学课程内容的一个新特色.“算法”过程是指机械式地按照某种确定的步骤行事,通过一系列小的简单计算操作完成复杂计算的过程.算法的学习内容大致可分为三个步骤:用自然语言描述算法;精确刻画算法(程序框图);计算机实现执行算法(程序语言的描述过程).算法思想贯穿高中数学课程的相关部分.【知识要点】1.算法:算法能够理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列能够解决一类问题.现代意义上的“算法”通常是指能够用计算机来解决的某一类问题的程序或步骤.2.程序框图程序框图:用一些通用的符号构成一张图来表示算法,这种图称为程序框图(程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形).用框图表示算法步骤的一些常用的图形符号:名称功能终端框(起止框) 表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框) 赋值、计算判断框判断某一条件是否成立,成立时在出口处标明“是”,不成立时标明“否”↓→流程线(指向线) 指引流程图的方向连接点连接另一页或另一部分的框图顺序结构:描述的是最简单的算法结构,语句与语句之间、框与框之间按从上到下的顺序实行(如图9-1).图9-1条件分支结构:依据指定条件选择执行不同指令的控制结构(如图9-2).图9-2循环结构:根据指定条件决定是否重复执行一条或多条指令的控制结构(如图9-3).图9-33.几种基本算法语句任何一个程序设计语言中,都包含五种基本的算法语句,即输入语句、输出语句、赋值语句、条件语句、循环语句.输入语句和输出语句分别用来实现算法的输入信息、输出结果的功能;赋值语句是用来表明赋给某一个变量一个具体的确定值的语句;条件语句是处理条件分支逻辑结构的算法语句;循环语句是用来处理算法中的循环结构的语句.4.中国古代算法案例:更相减损之术、辗转相除法:求两个正数的最大公因数的方法.辗转相除法算法步骤:第一步:用两数中较大数除以较小数,求商和余数.第二步:用除数除以余数.第三步:重复第二步,直到余数为0.第四步,得出两数的最大公约数,即余数0之前的余数.更相减损术算法步骤:第一步:用较大数减去较小数,得到差.第二步:比较减数与差的大小,再用较大数减去较小数.第三步:重复第二步,直到差与减数相等为止.第四步:相等数即为最大公约数.割圆术:用正多边形的面积逐渐逼近圆面积的算法求圆周率π. 秦九韶算法:求一元多项式的值的一种方法,递推关系为),,2,1(10n k a x v v a v k n k kn=⎩⎨⎧+==-- 【复习要求】1.了解算法的含义,了解算法的思想.2.理解程序框图的三种基本逻辑结构:顺序结构、条件分支结构、循环结构.3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.【例题分析】例1 如图(图9-4)所示,将一系列指令用框图的形式表示,箭头指向下一步的操作.请按照框图回答问题:图9-4(1)这个框图表示了怎样的算法?(2)输出的数是多少?【分析】由框图中的文字及图形符号表示的操作内容可知:此算法是“求1到50的和”,由此能够算出输出的数.解:(1)此框图表示的算法为:求1+2+3+…+50的和;(2)易知所求和为1275.【评析】程序框图主要包括三部分:表示相对应操作的框,带箭头的流程线和框外必要的说明.读框图时要从这三个方面研究,流程线反映了命令执行的先后顺序,主要看箭头方向,框及内外的文字说明表明了操作内容.常用这种方式考察对算法的理解和应用.例2 (1)如图9-5所示的是一个算法的程序框图,已知a1=3,输出的结果为7,则a2的值为______.图9-5(2)如图9-6所示的是某个函数求值的程序框图,则满足该程序的函数解析式为_____.图9-6(3)如图9-7所示的是求某个数列和的程序框图,此程序输出的结果为_____.图9-7【分析】这三个小题的重点在于读懂框图.(1)只含有顺序结构,(2)含有条件分支结构,表明函数的定义域为R ,当x <0时,遵从解析式f (x )=3x -1,否则(即当x ≥0时),遵从解析式f (x )=2-5x ;(3)中有两个循环变量S 、I ,S 是累加变量,I 是计数变量;另外还要判断I 的奇偶性,以此决定是加还是减.解:(1)112=a ;(2)⎩⎨⎧≥-<-=)0(52)0(13)(x x x x x f ;(3)S =12-22+32-42+…+992-1002=-5050.【评析】题(1),只含有顺序结构,所表示的算法比较简单,只需按照框图箭头方向依次读出即可.题(2)含有条件分支结构,这是一个与分段函数相关的算法,框图中含有判断框.读包含有判断框的框图时,要特别重视判断框内的条件和框外的文字说明,对应的下一步操作会依条件不同而改变.题(3)含有循环结构,当解决一些有规律的科学计算问题,尤其是累加和累乘时,往往能够利用循环结构来实现算法.循环结构有两种,读包含有循环结构的框图时,除注重判断框内外的说明外,一般要从开始依顺序做几次循环,观察变量的变化规律来协助读懂算法的含义.例3 (1)已知平面上的一点P 0(x 0,y 0)和直线l :Ax +By +C =0,求点P 0到直线l 的距离d ,并画出程序框图.(2)用条件分支结构写“已知三个数a 、b 、c ,找出其中最大数”的算法及框图.(3)写出求n131211++++的和的算法,画出程序框图,并写出相对应程序(选做). 【分析】准确分析“算理”,才能选择恰当的算法结构,有条理的表达算法.(1)在已知点到直线距离公式的前提下,适合用顺序结构表示;(2)涉及比大小,必须用到条件分支结构;(3)中分母有规律的递增,能够引入累加变量S 和计数变量i ,且S =S +1/i 是反复实行的,能够用循环结构表示.解:(1)算法及框图为:S1 输入x 0,y 0;A ,B ,C ; S2 计算m =A 2+B 2;S3 计算n =Ax 0+By 0+C ; S4 计算mn d ||=; S5 输出d ;(2)算法及框图为:S1 输入a ,b ,c ; S2 令x =a ;S3 若b >x ,则令x =b ;否则,执行S4;S4 若c >x ,则令x =c ;否则,执行S5; S5 输出x ;(3)算法及框图为:S1 输入i =1,S =0; S2 当i ≤n 时,,1iS S += i =i +1;否则执行S3; S3 输出S ;程序如下; S =0For i =1:1:n S =S +1/i i =i +1 endprint(%io (2),S )【评析】书写算法时,一步一步的程序化步骤,即“算则”固然重要,但这些步骤的依据,即“算理”有着更基本的作用,“算理,,是“算则”的基础,“算则”是“算理”的表现.这三道小题因为算理不同,所蕴含的算法结构也不同.通过实例,模仿、操作、探索,经历通过设计程序框图表达解决问题的过程,能够更好的理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句,体会和理解算法的含义,了解算法语言的基本构成.本例中涉及的“利用公式求点到直线的距离”、“实数排序求最值问题”、“求数列的和或积的问题”,还包括“二分法求函数零点”、“质数的判定”,“求π的近似值”等等,都是算法的典型案例,学习时要给予充分的重视.一般算法的表示方法并不唯一.不同的算法语言的书写形式是有差别的.本书所采用的是Scilab 语言,学习时要了解赋值语句、输入输出语句、if 语句、while 和for 语句的基本含义及表达方式,能够读懂语句表示的算法过程.例4 (1)用辗转相除法计算56和264的最大公约数时,需要做的除法次数是______. (2)用更相减损术求56和98的最大公约数时,操作如下:(98,56)(56,42)(42,14)(28,14)(14,14),由此可知两数的最大公约数为______.(3)用秦九韶算法求得多项式f (x )=x 6-2x 5+3x 3+4x 2-6x +5当x =2时函数值为______.解:(1)8216816240164015640564264+⨯=+⨯=+⨯=+⨯=所以最大公约数为8,需做的除法次数是4;(2)最大公约数为14; (3)33. 【评析】书上所涉及的古代基本算法案例包括:更相减损术与辗转相除法、秦九韶算法、割圆术.辗转相除法与更相减损术都是求最大公约数的方法,辗转相除法又叫欧几里得方法,计算上以除法为主,更相减损术以减法为主,计算次数上,前者相对较少,特别是两个整数相差较大时区别尤其明显;辗转相除法以余数为0结束,更相减损术则以减数与差相等结束.秦九韶算法的特点是把求n 次多项式的值转化为求n 个一次多项式的值,运算时只有加法和乘法,而且运算的次数比较少,求一个n 次多项式的值最多需要实行n 次加法、n 次乘法.割圆术是由中国古代数学家刘徽提出的,是当时计算圆周率比较先进的算法,“算理”明确,即用圆内接正多边形和外切正多边形逼近圆周率,重点是确定递推关系.例5 (09辽宁)某店一个月的收入和支出总共记录了N 个数据,其中收入记为正数,支出记为负数.该店用下边的程序框图计算月总收入S 和月净盈利V .那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A .A >0,V =S -TB .A <0,V =S -TC .A >0,V =S +TD .A <0,V =S +T【分析】本题要注意三点:a k 有正有负;S 为总收入,是所有正数的和;T 为总支出,是所有非正数的和.答案为C【评析】本题结合实际背景,强调算法的应用价值,是一种比较新的题型,应引起注重.练习9一、选择题1.任何一个算法都必须有的基本结构是( )A.顺序结构B.条件分支结构C.循环结构D.以上三个都要有2.下面给出对程序框图的几种说法:①任何一个程序框图都必须有起止框;②判断框有一个入口,有不止一个出口;③对于一个算法来说,判断框内的条件表达方式是唯一的;其中准确的有( )A.0个B.1个C.2个D.3个3.在算法的逻辑结构中,要求实行逻辑判断并根据结果实行不同处理的是哪种结构( ) A.顺序结构B.条件分支结构和循环结构C.顺序结构和条件分支结构D.顺序结构和循环结构4S1 输入n;S2 判断n是否是2;若n=2,则n满足条件,若n>2,则执行S3;S3 依次从2到n-1检验能否整除n,若都不能整除,则n满足条件;满足上述算法的n是( )A.奇数B.偶数C.质数D.合数二、填空题5.阅读下面两个程序框图,框图1输出的结果为______;框图2输出的结果为______.框图1 框图26.(08广东)阅读图9-8的程序框图,若输入m=4,n=6,则输出a=______,i=______.图9-8 图9-97.阅读图9-9的程序框图,若输入的n是100,则输出的变量S和T的值依次是______.8.“x=3*5”和“x=x+1”是某个程序中的先后相邻两个语句,下列说法中①“x=3*5”是将数值15赋给x,而不是普通运算“x=3*5=15”;②“x=3*5”能够写成“3*5=x”③语句“x=x+1”在执行时,“=”右边x为15,“=”左边x为16;准确的有______.三、解答题9.分别用辗转相除法和更相减损术求189和81的最大公约数.10.用循环语句书写求1+2+3+…+n>1000的最小自然数n的算法,画出程序框图,并写出相对应的程序(选做).11.(09宁夏)为了测量两山顶MN间的距离,飞机沿水平方向在AB两点实行测量,MN在同一个铅垂平面内(如图).飞机能够测量的数据有俯角和AB间的距离,请你设计一个方案,包括:指出需要测量的数据(用字母表示,并在图中标出);用文字和公式写出计算MN间距离的步骤.专题九 算法参考答案练习9一、选择题1.A 2.C 3.B 4.C 二、填空题5.27,21 6.12,3 7.2550,2500 8.①③. 三、解答题9.解:辗转相除法:3278127281189 ⨯=⨯=,所以最大公约数为27.更相减损术:189-81=108,108-81=27,81-27=54,54-27=27, 所以最大公约数为27. 10S1 输入S =0,i =1; S2 S =S +i ,i =i +1;S3 若S ≤1000,重复执行S2; 若 S >1000,输出i .S =0,i =1; While S ≤1000 S =S +i ; i =i +1; endprint (%io (2),i )11.解:如图(1)需要测量的数据有:A 点到M 、N 的俯角α1,β1;B 点到M 、N 的俯角α 2,β 2;A 、B 的距离d .(2)第一步:计算BM ,由正弦定理)sin(sin 211ααα+=d BM ; 第二步:计算BN ,由正弦定理)sin(sin 121βββ-=d BN ; 第三步:计算MN ,由余弦定理 )cos(22122αβ+++=⋅⋅BN BM BN BM MN .。
