华科电气MATLAB大作业
matlab大作业实验报告,《Matlab程序设计》期末实验报告-大作业2015.doc

matlab⼤作业实验报告,《Matlab程序设计》期末实验报告-⼤作业2015.doc《MATLAB程序设计》实验报告学院: 学号: 姓名:⼀、题⽬:1、(10分)已知矩阵,⽤Matlab代码实现以下要求:(1)将矩阵赋给变量A,并在屏幕上显⽰A;(2)将A按列进列逆序重排,重排后的矩阵赋给变量B,并在屏幕上显⽰B;(3)⽤reshape命令将A重排为⼀个2⾏6列矩阵并赋给变量C;(4)将A重排为⼀个列向量,将其赋给变量D,求D的平均值,在屏幕上显⽰D和它的平均值;(5)⽤命令查看变量A的维数,并显⽰运⾏结果。
2、(10分)写代码实现以下要求:构造菜单项‘Plot’,菜单项Plot有两个⼦菜单项Plot sin(选择此项后执⾏画出曲线,线型为虚线,线条颜⾊为红⾊)和Plot cos(选择此项后执⾏画出曲线 ,线型为实线,线条宽度为2)。
3、(20分)已知,实现下列操作:(1)在同⼀个图形窗⼝,同⼀坐标系下⽤不同的颜⾊和线型绘制三条曲线,并添加图例来区分三条曲线(5分)。
(2)⽤subplot命令,以⼦图的⽅式绘制三条曲线,图形排列⽅式为三⾏⼀列(5分)。
(3) 分别⽤直⽅图(bar)、棒状图(stem)和填充图(fill)绘制三条曲线,以⼦图⽅式绘制,排列⽅式为3⾏3列,共9幅⼦图(10分)。
4、(10分)⽤surf命令绘制曲⾯图形,⽤shading interp命令进⾏插值着⾊处理并添加垂直颜⾊棒。
5、(15分)⾃2011年9⽉1⽇起,我国实⾏新的个⼈所得税征收办法,起征点为3500元,请⽤If-else if-else-end结构实现⼈⼯输⼊⽉收⼊后能计算出个⼈所得税的缴纳额并显⽰⽉收⼊10000元时应缴纳的税款。
级数应纳税所得额x(元)税率备注1x<=15003%x指⽉收⼊扣除起征点3500元之后的余额;215008000045%同上6. (10分)⽤while-end循环结构计算级数和的值,输⼊n值,能计算出f的值,并显⽰结果。
MATLAB大作业

M A T L A B大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
这方面的资料很多(如),请分析构图原理并用MATLAB 实现。
问题四:模拟掷骰子游戏:掷1000次骰子,统计骰子各个点出现的次数,将结果以下表的形式显示,并绘制出直方图。
华科电气matlab第一次作业

第一次作业(2015.10.27)目的:熟悉MA TLAB 的基本应用要求:用editor 对程序进行编辑和调试,形成相应的脚本文件(*.m )。
1.1若已知某电路参数,输入电压,绘制其输出电压的波形如图1,已知:R1=3Ω,R3=6Ω,C=1uF ;us=18V ,is=3A 。
在零初始条件下,开关s 开路,当t=0时,开关S 闭合,求uc ,并画出波形;图1下列程序仅供参考(注:本例中的RC 电路非图1所示的电路):已知一阶RC 电路的端电压的表达式为 10s ~0 ,62==-t e u t ,试绘制电压波形u 。
t=0:0.1:10;u=6*exp(-2*t);plot(t,u);title('RC response');xlabel('t/s');ylabel('V/V')grid解得u = -12+12/exp(t/(2*(e - 6)))t=0:1e-8:1e-5; %以10-8为间隔,在0到10-5区间内取点u=12*exp(-2e 6*t)-12; %算出t 时刻对应的电压值plot(t,u); %以t 为横坐标,u 为纵坐标画图title('RC response'); %以RC response 为标题xlabel('t/s'); %以t/s 为横坐标ylabel('V/V') %以V/V 为纵坐标grid2. 已有两组测试数据不等的曲线,对其进行拟合和插值处理。
2.1给例程2.1加入注释,说明程序的用途和调试结果,尝试修改x,y,或polyfit的不同设置。
熟悉fitting工具例程2.1:clear;clc;close;%删除工作空间的所有变量,删除命令窗口的所有变量,关掉图形x=0:0.1:2*pi; %在0到2pi范围内,以0.1为步长,随机生成样本点y = sin(x)+0.5*rand(size(x)); %随机矩阵生成yp = polyfit(x,y,4) %拟合成4阶多项式y1= polyval(p,x); %求多项式y1的值plot(x,y, '+',x,y1, '-r') %绘制y与x的函数关系曲线title('fitting')%曲线命名为fitting2.2 给例程2.2加入注释,说明程序的用途和调试结果,尝试修改xs,ys,或xi,或interp1的不同设置,熟悉插值的用法。
Matlab电气仿真实验作业

Matlab电气仿真实验指导老师:学生姓名:爸爸专业班级:电气工程及其自动化1班学号:222012!!!!本课程设计的目的:1、掌握Matlab/Simulink中SimPowerSystems 工具箱的基本建模方法;2、掌握Matlab/Simulink 电气仿真的基本步骤;3、利用Matlab/Simulink 在基本电路与磁路、电力电子技术、电气传动等方面的仿真设计。
实验一设计任务:单相桥式整流加LC滤波电路,电源为220V,50Hz,整流电路输入为24V,负载为10Ω阻性负载,滤波电感L=100mH,滤波电容C=200uF。
实验步骤:在matlab/simulink中选取相应的器件,如图连接运行。
注意事项:将全部示波器scope中的“limit data point to the last”选项应该去掉。
参数设置:交流电压源幅值:220*sqrt(2),频率:50HZ。
变压器参数,容量S=200V A,变比k=220V/24V。
电感:100mH;电容:200uF;电阻:10欧。
实验结果:二极管Diode3电流电压曲线第一个图显示的为二极管电流I ,第二个图显示为二极管电压U 。
当diode3导通时其电压接近为0V (管压降为0.7V ),其电流有值;当diode3关断时,其电流值为0A ,此时功率二极管承受反向电压,承受的最大反向电压幅值为24*sqrt (2)=33.94V 。
而电流图像上出现波动是因为电感L 的值不是无穷大,会受频率电压幅值的影响,所以如图所示。
二极管Diode4电压电流曲线结论分析:第一个图显示的为二极管电流I ,第二个图显示为二极管电压U 。
当diode3导通时其电压接近为0V (管压降为0.7V ),其电流有值;当diode3关断时,其电流值为0A ,此时功率二极管承受反向电压,承受的最大反向电压幅值为24*sqrt (2)=33.94V 。
而电流图像上出现波动是因为电感L 的值不是无穷大,会受频率电压幅值的影响,所以如图所示。
Matlab大作业

Matlab的基本操作一、使用函数实现对下列矩阵的左旋和右旋以及反转已知答案:如图:矩阵如图矩阵的左旋如图一矩阵的右旋如图二矩阵的左右反转如图三矩阵的上下反转如图四二、已知A=[8 9 5 ] B=[-1 3 -2][36 -7 11] [2 0 3][21 -8 5] [-3 1 9 ]计算:1)A+5*B;2)A*B和A.*B3)A^3和A.^34)A/B和B\A5)[A,B]答案:A=[8 9 5;36 -7 11;21 -8 5];B=[-1 3 -2;2 0 3;-3 1 9];A+5*BA*BA.*BA^3A.^3A/BA\B[A,B]程序运行结果如下:第二章、Matlab程序设计一、已知S=1+2+22+23+…+263求S的值答案:代码如下:ClearClcs=0,j=2for i=1:63s=s+j^iends程序运行结果如下:二、第三章、Matlab绘图一、在同一坐标系中画出下列函数的图像:x2,-x2,xsin(x)在[0,2π]上的函数图像程序代码如下:clearclcx=0:pi/100:2*pi;y1=x.^2;y2=-x.^2;y3=x.*sin(x);title('同一坐标下的函数图像')plot(x,y1,':',x,y2,'h',x,y3,'--')程序运行结果如下:二、绘制极坐标图像:程序代码如下:clearclcx=0:0.01:2*pi;y=2*cos(2*(x-pi/8));title('极坐标图像')xlabel('x')ylabel('y')polar(x,y)程序运行结果如下:第四章、Matlab符号运算一、求函数y=e-x2 的傅立叶变换及其逆变换程序代码如下:clearclcsyms x t;y=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)程序运行结果如下:二、求下列极限值:答案:1、程序代码:clearclcsyms x;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)程序运行结果如下:第五章、Matlab数值运算一、建立一个3*4阶随机矩阵,求矩阵的最大值、最小值、方差和标准差、极差、协方差,和自相关阵程序代码如下:clearclcA=rand(3,4)B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)程序运行结果如下:二、求函数f(x)=x3-2x+1在x=[-1 1]之间的极小值和x=-1附近的零点程序代码如下:clearclc[x,y]=fminbnd('x.^3-2.*x+1',-1,1)[x,y]=fzero('x.^3-2.*x+1',-1)程序运行结果如下:第六章、Matlab图形用户界面一、建立一个具有三个输入框的窗口对话框程序代码如下:clearclcprompt={'姓名','年龄','班级'};DTitle='注册学生信息';line[1;1;1];def{'乔阳','18','100412105'};info=inputdlg(prompt,DTitle,line,def,'ON')程序运行结果如下:二、设计一个表现下载进度的进度条程序代码如下:clearclch = waitbar(0,'正在下载,请稍等……');for i=1:1000waitbar(i/10000,h)endclose(h)程序运行结果如下:第七章、Matlab Simulink 仿真一、仿真信号x(t)=sin(t)sin(10t)的波形仿真步骤:1.建立模型窗口:生成无标题(intitled)的模型窗口;2.添加信号源模块(sine)、输出模块(scope)、数学模块(Dot product)3.设置模块参数:如下图:4.编辑模块即将各个模块连接起来。
华科电气MATLAB大作业

华中科技大学电气与电子工程学院《MATLAB课程作业》班级学号姓名时间2014年12月25日目录一.概述 (2)二.设计要求 (2)三.设计分析 (2)1.系统的稳态误差理论分析 (3)2.系统稳态误差仿真分析 (3)3.阶跃响应仿真分析 (4)四.根轨迹法设计相位滞后环节 (9)1.相位滞后环节设计 (9)2.加入相位滞后环节的仿真分析 (10)五.超前校正设计 (11)1.超前校正器设计 (11)2.超前校正仿真分析 (13)六.滞后校正设计 (17)1.滞后校正器设计 (17)2.仿真分析 (18)七.总结 (20)参考文献 (21)反馈控制系统设计—铣床控制系统设计一.概述铣床是指主要用铣刀在工件上加工各种表面的机床。
通常铣刀旋转运动为主运动,工件和铣刀的移动为进给运动。
它可以加工平面、沟槽,也可以加工各种曲面、齿轮等。
铣床是用铣刀对工件进行铣削加工的机床。
铣床除能铣削平面、沟槽、轮齿、螺纹和花键轴外,还能加工比较复杂的型面,效率较刨床高,在机械制造和修理部门得到广泛应用。
铣床的自动控制系统的设计直接影响到加工的精度,影响产品的工艺。
所以,本文通过利用MATLAB 和Simulink 对铣床的控制系统做一个校正设计,使其具有相应的性能.二.设计要求1、单位斜坡输入21()R s s作用下 ,速度误差不大于18; 2、阶跃输入时的超调量小于20%.三.设计分析用Visio 画出一个简化的铣床闭环控制系统的方框图如图二所示.图1. 简单的铣床闭环控制系统图1中,D(s )为外部扰动,N(s )为测量噪声干扰。
铣床的传递函数为:2()(1)(5)G s s s s =++首先,在没有控制器()C G s 的情况下,看看系统的输出结果。
1. 系统的稳态误差理论分析系统的稳态误差为:()1()()()()()()1()1()G s E s R s Y s R s R s R s G s G s =-=-=++式中,2()(1)(5)G s s s s =++,21()R s s=。
Matlab作业电气工程专业试题及答案

江苏大学京江学院《电气工具软件训练Ⅲ》课程设计报告设计题目:MATLAB专业班级:学生姓名:学生学号:指导老师:完成日期:江苏大学·电气信息工程学院一MATLAB课程设计的目的和要求1.MATLAB软件功能简介MATLAB的名称源自Matrix Laboratory,1984年由美国Mathworks公司推向市场。
它是一种科学计算软件,专门以矩阵的形式处理数据。
MATLAB将高性能的数值计算和可视化集成在一起,并提供了大量的内置函数,从而被广泛的应用于科学计算、控制系统和信息处理等领域的分析、仿真和设计工作。
MATLAB软件包括五大通用功能,数值计算功能(Nemeric)、符号运算功能(Symbolic)、数据可视化功能(Graphic)、数字图形文字统一处理功能(Notebook)和建模仿真可视化功能(Simulink)。
其中,符号运算功能的实现是通过请求MAPLE内核计算并将结果返回到MATLAB命令窗口。
该软件有三大特点,一是功能强大;二是界面友善、语言自然;三是开放性强。
目前,Mathworks公司已推出30多个应用工具箱。
MATLAB 在线性代数、矩阵分析、数值及优化、数值统计和随机信号分析、电路与系统、系统动力学、次那好和图像处理、控制理论分析和系统设计、过程控制、建模和仿真、通信系统以及财政金融等众多领域的理论研究和工程设计中得到了广泛应用。
2.MATLAB课程设计的目的本次课程设计主要是为了使学生了解MATLAB软件的基本知识,熟悉MATLAB的上机环境,掌握MATLAB数值运算、程序设计、二维/三维绘图、符号运算、Simulink仿真等相关知识,并初步具备将一般数学问题转化为对应的计算机进行处理的能力,以便为今后进一步的学习打下坚定基础。
二 MATLAB 课程内容1 MATLAB 语言基础实验目的:基本掌握 MATLAB 向量、 矩阵、 数组的生成及其基本运算(区分数组运算和矩阵运算)、常用的数学函数。
matlab大作业实验报告

matlab大作业学号姓名:年级:专业:1、产生一个10 10的随机矩阵A,要求A中元素均为整数,范围[1,50]。
1)求出A中所有元素之和S,平均值M。
2)找到所有小于平均值,且能被3整除的元素。
3)绘制出A的二维纵向柱状图,横坐标为[8 5 9 1 2 3 4 7 10 13],条形宽度为0.7的“stacked”样式。
代码如下:clc,clear all,close allA=round(rand(10,10)*50);disp(A)S=sum(sum(A));P=mean(mean(A));disp(S)disp(P)disp('所有小于平均数且能被三整除的元素')XPS=H((mod(H,3)==0)&(H<P));disp(XPS')subplot(1,1,1),bar(A,0.7,'stacked'),title('ygh');set(gca,'XTickLabel',{'8','5','9','1','2','3','4','7','10','13'})2、产生一个随机四位密码。
用户用“input”进行输入对比。
猜错提示“WRONG”,正确提示“RIGHT”同时退出程序,最多五次机会。
代码如下:clc,clear all,close alldisp('请输入密码')A=round(8999*rand(1,1))+1000;m=1;while m<=5N=input('请输入一个四位数:');if A==N;disp('RIGHT');breakelsedisp('WRONG');endm=m+1;enddisp('密码是:')disp(A)disp('输入结束')3、按照脚本文件的编程风格,用for和while循环嵌套输出如下的乘法口诀表。
MATLAB大作业

贵州大学实验报告姓名学号实验组实验时间指导教师成绩实验项目名称MATLAB大作业实验通过综合考察,让同学们能对学到的知识综合运用,更好地灵活地解决问题目的实验利用matlab提供的一些函数实现数据分析和数值计算。
原理实验运行MATLAB7.0或以上的计算机一台仪器实验内容实验数据1、试编写名为test01.m的MATLAB函数,用以计算下述的值:⎪⎩⎪⎨⎧-<->=ttntttntf的)4/sin()(si对所有)4/sin(其他情况)sin(的)4/sin()(si对所有)4/sin()(ππππ要绘制t关于函数f(t)的图形,其中t的取值范围为ππ66≤≤-t,间距为10/π。
(提示:注意要产生一系列的点,这里可考虑t的输入是向量形式,可以利用find函数找出所需限定值的元素的位置,对其按需要赋值后,再进行绘图;其次,另外一种思路,也可考虑使用循环的形式来实现)①test01.m代码如下:function y=test01(t)if sin(t)>sin(pi/4)y=sin(pi/4);elseif sin(t)<sin(-pi/4)y=sin(-pi/4);elsey=sin(t);end②调用test01函数计算值③绘制t关于函数f(t)的图形,其中t的取值范围为ππ66≤≤-t,间距为10/π代码如下:t=-6*pi:pi/10:6*pi;y=sin(t);y(find(y>sin(pi/4)))=sin(pi/4);%f(t)=sin(pi/4),y>sin(pi/4) y(find(y<sin(-pi/4)))=sin(-pi/4);%f(t)=sin(pi/4),y>sin(pi/ 4)plot(t,y) %绘制图形title('t from -6{\pi} to 6{\pi}') %添加图形标题xlabel('t') %x轴标签ylabel('f(t)') %y轴标签实验结果:2、编写函数,在同一窗口的4个子图中利用plot等语句绘制y=at2图像,其中a=[1 2 5 10],t范围[-2,5]。
华科Matlab大作业_铣床控制器设计说明

引言铣床是以各类电动机为动力的传动装置与系统的对象以实现生产过程自动化的技术装置。
电气系统是其中的主干部分,在国民经济各行业中的许多部门得到广泛应用。
自动铣床具有工作平稳可靠,操作维护方便,运转费用低的特点,已成为现代生产中的主要设备。
自动铣床控制系统的设计是一个很传统的课题,现在随着各种先进精确的诸多控制仪器的出现,铣床控制的设计方案也越来越先进,越来越趋于完美。
我们之前学习了自动控制原理,要学会把学习的知识用在现实生活的具体设计之中,才能更深的体会和理解这些知识。
这次我们通过Matlab仿真工具Simulink,完成对该控制系统仿真简单建模,进行简单仿真分析和研究。
一、设计要求图1铣床的基本模型现有一个控制器的传递函数为的磨床,要对它进行校正,使它达到以下的要求:1、对于斜坡输入R(s)=,输出地稳态误差为。
2、对于阶跃输入,输出的超调量要小于20%。
图2系统的抽象框图图2系统的开环传递函数G(s):二、设计原理及思路控制系统的动态性能、稳定性和稳态性能通常是矛盾的:增大系统开环增益可使系统稳态误差减小,但是也将减小系统的阻尼比,是系统的超调量和振荡增加;同样,增加开环积分环节可以提高系统类型,是系统跟踪输入信号的能力加强,却有可能导致系统动态性能恶化,甚至不稳定。
因此,为了使控制系统同时具有满意的动态性能和稳态性能,就需要对系统加入一些校正环节。
校正的基本思想就是:低频段具有足够高的增益值,以保证稳态误差足够小;中频段具有-20dB/dec的斜率,保证系统的稳定性;高频段具有足够负的斜率,保证抑制噪声干扰能力。
本次实验采用超前校正环节改善系统性能,观察它的阶跃响应和斜坡响应,确定需要采用哪几个参数来描述这个校正器,再根据题目的各个条件,分别算出各个参数需要满足的范围,最后用Matlab对经过校正后的系统进行仿真,如果发现波形还有些不够满足题目要求,再对参数进行微小的调整,最终使得它满足题目的要求。
matlab作业电气工程及其自动化专业

电气工程工具软件课程作业1. matlab 软件主要功能是什么?电气工程及其自动化专业本科生主要用到哪些工具箱,各有什么功能?Matlab 的主要功能有:1 数值计算和符号计算功能 Matlab 以矩阵作为数据操作的基本单位,这使得矩阵运算变得非常简洁,方便,高效。
Matlab 还可以提供非常丰富的数值计算函数,而且采用的都是国际通用的数值计算算法;其程序由国际一流的专家编制优化,计算功能为 matlab 赢得了良好的口碑。
2 绘图功能利用 matlab 绘图十分方便,它可以绘制各种图像,囊括了 2d 和 3d 图形,也可以对图像进行修饰控制,以增强图像的表现效果。
Matlab 提供两个层次的绘图操作,一种是对图形句柄进行的底层绘图操作;另一种是建立在低层绘图之上的高层绘图,利用 matlabu 的高层绘图,用户不需要考虑过多的细节,只要给出一个剧本参数就能会出图像。
3 汇编语言功能 Matlab 具有程序结构控制,函数调用,数据结构,输出输入。
面向对象的程序设计语言特征。
不仅简单易学,而且操作简便,对于数值结算,程序仿真,计算机辅助设计等领域的人来说 matlab 是个理想的选择。
4 扩展功能 Matlab 包括基本部分和各种选择工具箱。
工具箱扩展了matlab 的其他功能。
Matlab 工具箱分为两大类:功能类工具箱和学科类工具箱。
功能类工具箱主要是用来扩充其符号计算功能,可视建模仿真及文字处理功能,学科性工具专业性比较强,如控制系统工具箱、神经网络工具箱,金融工具箱等。
工具箱包括:1.DSP Blockset(数字信号处理模块库)2.Control System Toolbox(控制系统模块库)3.Simulink(系统仿真模块库)munications Blockset(通信模块库)5.Control System Toolbox(控制系统工具箱)6. Signal Processing Toolbox(信号处理工具箱)7. Image Processing Toolbox(图象处理工具箱)2. 在matlab/simulink 中绘制三相电机的双闭环控制系统,采用PID 闭环综合。
华中科技大学电气学院matlab选修课大作业__PI控制器

2008 级《MATAB语言与控制系统仿真》课程大作业姓名赖智鹏学号 u200811806所在院系电气与电子工程学院班级电气0809日期 1月16日同组人员作业评分评阅人设计报告评分表DOC.PI控制器设计与讨论1.引言本文讨论的对象是智能交通/高速公路系统IVHS(习题7.3),系统通过电子技术为驾驶者和控制系统提供实时路面情况,该系统还提供更方便服务,驾驶者可不用自己操纵驾驶,而系统自动控制车辆,且保持车相对速度,以实现交通的有序进展。
本文前半局部讨论了PI 控制器参数的设计问题,根据性能指标推导控制器参数的约束条件,通过相关算法找到问题的解,后半局部讨论系统参数变化时对系统性能的影响,通过比拟得出综合性能较优的控制器参数。
2.给定系统的控制器设计2.1性能分析:〔1〕阶跃响应零稳态误差。
由原系统为零型系统,故必须通过控制器在原点参加至少一个开环极点,可选择的由PI 控制器、PID 控制器等,而单独使用比例控制器已达不到目标。
〔2〕要求系统对爬坡响应的跟踪误差小于25%,故Kv>4,从而有:001416s s Kv sGcG sGc ->->==>∑∑。
〔3〕阶跃响应的超调量小于5%,所以如果校正后系统近似为2阶系统,要求阻尼比ξ>0.7。
〔4〕调节时间Ts=4/n ξω<1.5s 〔2%〕,所以有n ξω>4/1.5=2.67。
就目前分析,单独使用比例控制器不能满足要求,而在考虑选择PID 控制器之前我们选择相对简单的PI 控制器:iP KGc K S =+。
图 1 原系统做出根轨迹图并作出满足性能指标的区域:rlocus(G); hold on;plot([-2.66 -2.66],[-20 20]);%指定性能指标在根轨迹图中所在区域 zeta=0.7;plot([0 -20*zeta],[0 20*sqrt(1-zeta^2)],[0 -20*zeta],[0 -20*sqrt(1-zeta^2)]); %指定性能指标在根轨迹图中所在区域。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
华科matlab大作业铣床(themillingmachine)的系统设计资料

铣床(the milling machine)的系统设计一、引言本学期开始学习《MATLAB语言、控制系统分析与设计》,其实最早接触matlab是在学习概率论时。
在老师的讲解与自己平时的练习中,不断地使用和学习matlab软件。
其实一开始学习的目标就不局限于控制系统领域,希望了解该软件的各种用途。
当然了,最基本的用途是绘图。
经过半个学期的汲取,觉得它用途广泛,功能强大。
我最喜欢的就是它的仿真(simulink),也许是对于初学者来说最简单的操作。
学习matlab的同时,也同时加深了对控制系统知识的掌握。
自控中的绘图可以在matlab下的响应分析的图形用户界面(ltiview)中建立。
此外还有sisotool等自控方面的超强工具箱。
图10.1铣床模型图10.2铣床系统方框图铣床系统的开环传递函数2()(1)(5)G s s s s =++ (10.1)设计要求:重新设计滞后校正器参数1)对于斜坡输入2()aR s s =,稳态误差小于8a2)使校正后系统的阶跃响应超调量..20%P O ≤对于(1)参数a 不影响系统的设计,在以下分析中作为‘1’处理本章的核心是滞后校正系统,但之所以对铣床系统采用滞后校正,理由见(四)深入探讨中频域下的分析。
另外我们超前校正器、超前-滞后校正器、PI 校正器、PD 校正器、PID 校正器。
二、设计方法以运用matlab 编程为主,其他各种工具箱为辅助根据极点、零点、增益输入原系统开环传递函数,并加入单位负反馈构成闭环系统 程序1G=zpk([],[0,-1,-5],2);%原系统开环传递函数 sys=feedback(G,1);%单位负反馈,构成闭环 得到2()(1)(5)G s s s s =++ (10.2)22( 5.096)(0.90420.3925)sys s s s =+++ (10.3)第一个要求稳态误差小于a/8 程序2 tf1=10; a=1;t=[0:0.1:tf1];u=a*t;%斜坡输入y_t=lsim(sys,u,t);plot(t,y_t,'b-',t,u,'r:') yss=y_t(length(t));y_deta=t(length(t))-yssif y_deta<(a/8)%稳态误差小于a/8disp('yes')elsedisp('no')end图10.3原系统单位斜坡输入的稳态误差得到原系统E(s)=2.500 no根据闭环传递函数求原系统性能程序3step(sys);%加阶跃响应Step ResponseTime (sec)A m p l i t u d e051015图10.4原系统阶跃响应第二个要求超调量小于20%,则根据阻尼比与超调量的函数关系..100*P O = (10.4)程序4sigmaN=0.2;%要求超调上限 A=log(1/sigmaN);zeta=sqrt((A^2)/(pi^2+A^2)); 得到阻尼比0.4559ξ= 引入滞后校正系统(),c K s z G s p z s p α+=<+,zp α=(10.5) 先考虑要求(1)lim ()lim ()()8s c s a asE s sG s G s →→=<(10.6)lim ()()8c sG s G s ⇒> (10.7)22855vcomp K z z K K p p α⎛⎫⎛⎫⎛⎫⎛⎫⇒==> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ (10.8)210(1)(5)Ks s s ⇒+=++ (10.9)画出其根轨迹并且找到满足0.4559ξ>的点,程序5n=[2];d=[1 6 5 0]; rlocus(n,d),hold on gridz=0.4559; hs=12*z;hc=12*sqrt(1-z^2);plot([0 -hs],[0 hc],'--',[0 -hs],[0 -hc],'--') text(-9.5,1,'Desired performance region')会显示Select a point in the graphics window 之后在图上找符合条件的点Root LocusReal AxisI m a g i n a r y A x i s图10.5原系统的根轨迹来求取K 的临界值为了精确性采用Data Cursor ,得到闭环极点p=-0.401+0.782i2.02K =Root LocusReal AxisI m a g i n a r y A x i s图10.6找寻K 临界值仅当引入增益K 下,系统的阶跃响应程序6G=zpk([],[0,-1,-5],2);%原系统开环传递函数 G2=2.02*G;%引入K/alphasys2=feedback(G2,1);%单位负反馈,构成闭环 step(sys2)Step ResponseTime (sec)A m p l i t u d e0510150.20.40.60.811.21.4图10.7引入增益2.02下的阶跃响应要满足要求一则:22855vcomp K z z K K p p α⎛⎫⎛⎫⎛⎫⎛⎫⇒==> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ (10.10)根据K ,并取10vcomp K =程序7Kvc=10;%Kvcopm>8 Kgang=2.02;%K/alpha Kvu=2*Kgang/5;alpha=Kvc/Kvu %alpha 即z/p 得到零点与极点的倍数12.3762α=得到了校正后系统开环传递函数0.012382() 4.04(1)(5)(0.001)s G s s s s s +=+++ (10.11)看系统是否符合要求(1)程序8G=zpk([],[0,-1,-5],2);%原系统开环传递函数p=0.001;z=alpha*p;nc=[1 z];dc=[1,p];Gc=2.02*tf(nc,dc);G2=G*Gc;%引入K/alphasys2=feedback(G2,1);%单位负反馈,构成闭环系统建立后,输入斜坡信号程序9tf1=10000;a=1;t=[0:0.1:tf1];u=a*t;%斜坡输入y_t=lsim(sys2,u,t);plot(t,y_t,'b-',t,u,'r:')yss=y_t(length(t));y_deta=u(length(t))-yssif y_deta<(a/8)%稳态误差小于a/8disp('yes')%符合要求(1)elsedisp('no')%不符合end得到==yesE s y a()_det0.100图10.8第一次校正后系统斜坡响应接着检验其阶跃响应程序10G=zpk([],[0,-1,-5],2);%原系统开环传递函数p=0.001;z=alpha*p;nc=[1 z];dc=[1,p]; Gc=2.02*tf(nc,dc);G2=G*Gc;%引入K/alphasys2=feedback(G2,1);%单位负反馈,构成闭环 step(sys2)Step ResponseTime (sec)A m p l i t u d e01020304050600.20.40.60.811.21.4图10.9第一次校正后的系统阶跃响应超调21.2%,需要继续调整令参数稍微改变, 2.02,1.90,2.1K程序11G=zpk([],[0,-1,-5],2);%原系统开环传递函数 p=0.001;z=alpha*p; nc=[1 z];dc=[1,p]; Gca=2.02*tf(nc,dc); Gcb=1.90*tf(nc,dc);Gcc=2.1*tf(nc,dc);%引入K/alpha G2a=G*Gca; G2b=G*Gcb; G2c=G*Gcc;sys2a=feedback(G2a,1);%单位负反馈,构成闭环 sys2b=feedback(G2b,1); sys2c=feedback(G2c,1); step(sys2a,'b--') hold onstep(sys2b,'r:') step(sys2c,'y-')Step ResponseTime (sec)A m p l i t u d e0.20.40.60.811.21.4图10.10对参数稍作调整的系统阶跃响应当 1.90K 时才能使超调降低到20%以下 再次使用求K 临界值的程序验证程序12 hold off clgn=[2];d=[1 6 5 0]; rlocus(n,d),hold on gridz=0.4559; hs=12*z;hc=12*sqrt(1-z^2);plot([0 -hs],[0 hc],'--',[0 -hs],[0 -hc],'--') text(-9.5,1,'Desired performance region') rlocfind(n,d)-0.42-0.415-0.41-0.405-0.4-0.395-0.39-0.385-0.380.770.7750.780.7850.79Root LocusReal AxisI m a g i n a r y A x i s图10.11在根轨迹上调整参数探索验证可以看出 2.02K ≤的点满足要求(2) 对0.12.0K =进行探索程序13G=zpk([],[0,-1,-5],2);%原系统开环传递函数 Kvc=10;%Kvcopm>8 y=zeros(200,1);i=0;for K=0.1:0.1:2%K/alpha Kvu=2*K/5;alpha=Kvc/Kvu;%alpha 即z/p p=0.001;z=alpha*p; nc=[1 z];dc=[1,p];Gc=K*tf(nc,dc);%引入K/alpha G2=G*Gc;sys2=feedback(G2,1);%单位负反馈,构成闭环 t=[0:0.1:19.9]; i=i+1;y(:,i)=step(sys2,t); endplot(y)legend('K=0.1','K=0.2','K=0.3','K=0.4','K=0.5','K=0.6','K=0.7','K=0.00.511.5图10.12不同取值下的阶跃响应求各曲线超调量,先将时间范围扩大到200程序14G=zpk([],[0,-1,-5],2);%原系统开环传递函数 Kvc=10;%Kvcopm>8 y=zeros(200,1);i=0;for K=0.1:0.1:2%K/alpha Kvu=2*K/5;alpha=Kvc/Kvu;%alpha 即z/p p=0.001;z=alpha*p; nc=[1 z];dc=[1,p];Gc=K*tf(nc,dc);%引入K/alpha G2=G*Gc;sys2=feedback(G2,1);%单位负反馈,构成闭环 t=[0:1:199];%改变时间长度 i=i+1;y(:,i)=step(sys2,t); endplot(y)legend('K=0.1','K=0.2','K=0.3','K=0.4','K=0.5','K=0.6','K=0.7','K=0.00.20.40.60.811.21.41.61.8图10.13时间轴扩大100观察分布情况 程序15sigma=zeros(20,20);j=0;Kgan=zeros(20,20); for i=1:1:20;[mp,tf]=max(y(:,i));%求最大幅值点 yss=y(length(t));%求稳态值 tp=t(tf);%峰值时间 j=j+1;Kgan(j,1)=j/10;%K/alphasigma(j,1)=100*(mp-yss)/yss;%超调量 endplot(Kgan,sigma,[0 2],[20 20]) gridxlabel('K/alpha') ylabel('Overshoot')K/alphaO v e r s h o o t图10.14K 与..P O 的关系若找到K 的取值范围,问题就比较清晰程序16n=find(sigma(:,1)<20);%找满足要求二的K/alpha Kn=Kgan(n,1)0.5 1.9K <<再考虑0.12.0K =的情况下的单位斜坡输入的稳态误差程序17G=zpk([],[0,-1,-5],2);%原系统开环传递函数 Kvc=10;%Kvcopm>8y=zeros(200,1);i=0;y_deta=zeros(20,1);Kgan=zeros(20,1); for K=0.1:0.1:2%K/alpha Kvu=2*K/5;alpha=Kvc/Kvu;%alpha 即z/p p=0.001;z=alpha*p; nc=[1 z];dc=[1,p];Gc=K*tf(nc,dc);%引入K/alpha G2=G*Gc;sys2=feedback(G2,1);%单位负反馈,构成闭环 t=[0:1:199]; i=i+1;Kgan(i,1)=i/10;u=t;y(:,i)=lsim(sys2,u,t); yss=y(length(t),i);y_deta(i,1)=u(length(t))-yss if y_deta(i,1)<(1/8)%稳态误差小于a/8 disp('yes')%符合要求(1) elsedisp('no')%不符合 end endplot(Kgan,y_deta,[0 2],[0.125 0.125])%找到误差小于a/8的直线 gridxlabel('K/alpha') ylabel('E(s)')K/alphaE (s )图10.15K 与稳态误差的关系程序18m=find(y_deta<0.125);%找满足要求一的K/alpha Km=Kgan(m,1) 得到0.2 1.1K <<综合上述两个范围0.5 1.1K <<三、结果分析令1K=程序19Kvc=10;%Kvcopm>8Kgang=1;%K/alphaKvu=2*Kgang/5;alpha=Kvc/Kvu;%alpha即z/p将参数带入校正后系统程序20G=zpk([],[0,-1,-5],2);%原系统开环传递函数p=0.001;z=alpha*p;nc=[1 z];dc=[1,p];Gc=1*tf(nc,dc);G2=G*Gc;%引入K/alphasys2=feedback(G2,1);%单位负反馈,构成闭环求单位斜坡响应程序21tf1=1000;a=1;t=[0:0.1:tf1];u=a*t;%斜坡输入y_t=lsim(sys2,u,t);plot(t,y_t,'b-',t,u,'r:')gridyss=y_t(length(t));y_deta=u(length(t))-yss;if y_deta<(a/8)%稳态误差小于a/8disp('yes')%符合要求(1)elsedisp('no')%不符合end得到()_det0.1000.125E s y a==<,yes,校正系统为100025()10001csG ss+=+(10.12)然后求单位阶跃响应step(sys2)Step ResponseTime (sec)A m p l i t u d e0204060801001200.20.40.60.81.21.4图10.16K =1的系统阶跃响应再讨论0.5K 程序23Kvc=10;%Kvcopm>8 Kgang=0.5;%K/alpha Kvu=2*Kgang/5;alpha=Kvc/Kvu;%alpha 即z/pG=zpk([],[0,-1,-5],2);%原系统开环传递函数 p=0.001;z=alpha*p; nc=[1 z];dc=[1,p]; Gc=Kgang*tf(nc,dc);G2=G*Gc;%引入K/alphasys2=feedback(G2,1);%单位负反馈,构成闭环 tf1=1000; a=1;t=[0:0.1:tf1];u=a*t;%斜坡输入y_t=lsim(sys2,u,t);plot(t,y_t,'b-',t,u,'r:')yss=y_t(length(t));y_deta=u(length(t))-yss; if y_deta<(a/8)%稳态误差小于a/8 disp('yes')%符合要求(1) elsedisp('no')%不符合 end得到()_det 0.1000.125E s y a ==<,yes50025()10001c s G s s +=+ (10.13)程序24step(sys2)Step ResponseTime (sec)A m p l i t u d e01020304050607080900.20.40.60.811.21.4图10.17K =0.5的系统阶跃响应四、深入探讨从频域下分析 先做原系统的伯德图程序25G=zpk([],[0,-1,-5],2);%原系统开环传递函数bode(G);%原系统伯德图 gridFrequency (rad/sec)M a g n i t u d e (d B)1010101010P h a s e (d e g )图10.18原系统伯德图程序26G=zpk([],[0,-1,-5],2);%原系统开环传递函数 [mag,phase,w]=bode(G);%原系统伯德图 m=find(phase>=-135); w1=w(max(m))得到当0.6877/sec w rad =,相位等于45deg 频率穿越点0.374/sec w rad =系统已经满足要求二,而且有23.5dB 的增益裕度 若利用增益K 来调节系统使其满足要求:2()(1)(5)KG s s s s =++ (10.14)对于要求一:01/5()0.125lim1()2s s aess t a G s K →===+ (10.15)得到K=20程序28G=zpk([],[0,-1,-5],2);%原系统开环传递函数 bode(G);%原系统伯德图 hold onbode(20*G)%引入增益K gridlegend('K=1','K=20')Frequency (rad/sec)M a g n i t u d e (d B)P h a s e (d e g )图10.19增益校正前后系统伯德图虽然K=20满足条件一可是相位裕度为负,闭环系统不稳定 所以不能用使用单一的增益校正。
华科电磁场matlab仿真作业
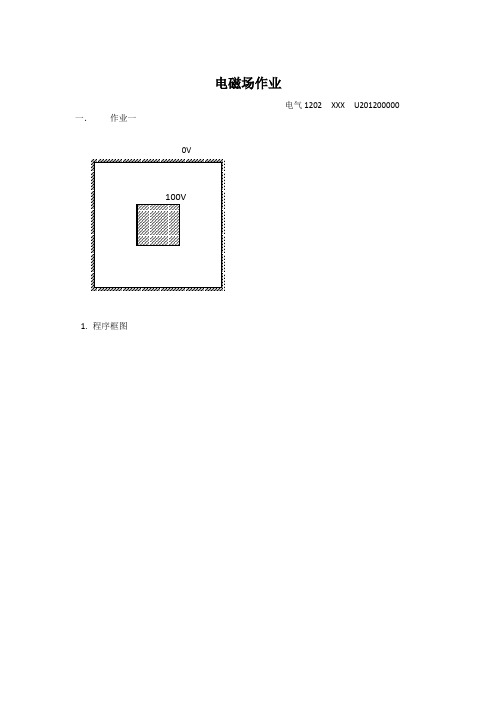
电磁场作业电气1202 XXX U201200000一.作业一1.程序框图2.程序clear;col = 61; %第一行点数row = col; %行数span = 0.3/(col-1); %步长End = ones(1,col)*col; %每一行的终止点Start = ones(1,col); %每一行的起始点A = zeros(row,col); %A矩正存储每点电势for i = (col-1)/3+1:(col-1)*2/3+1for j = (col-1)/3+1:(col-1)*2/3+1A(i,j) =100;endend %初始化电势完毕temp = A;for n= 1:500 %迭代次数for i = 2:row-1if ( i<((col-1)/3+1)||i>( (col-1)*2/3+1 ) )for j = Start(i)+1:End(i)-1temp(i,j)=(A(i-1,j) +A(i+1,j) +A(i,j-1) +A(i,j+1))/4;endelsefor j = 2:(col-1)/3temp(i,j)=(A(i-1,j) +A(i+1,j) +A(i,j-1) +A(i,j+1))/4;endfor j = 2*(col-1)/3+2:col-1temp(i,j)=(A(i-1,j) +A(i+1,j) +A(i,j-1) +A(i,j+1))/4;endendA = temp;endendX = row:-1:1;Y = col:-1:1;[X,Y] = meshgrid(X,Y);figure(1);surf(rot90(A,2));figure(2);contour(rot90(A,2));hold on;[Gx,Gy] = gradient(A,1,1);quiver(Gx,Gy);3.计算机绘图二.作业二1.程序框图2.程序100V0Vclear;col=101;row=101;A=zeros(row,col);for i=11:101A(i,11)=100;endfor j=11:101A(11,j)=100;endfor i=2:10A(i,col)=10*i-10;endfor j=2:10A(row,j)=10*j-10;endA1=A;x=1;t=0;while x>0.1x=0;for i=2:100for j=2:100if (i>1&&i<11)||(j>1&&j<11)A1(i,j)=(A(i,j-1)+A(i,j+1)+A(i-1,j)+A(i+1,j))/4;t=abs(A(i,j)-A1(i,j));if (t>x)x=t;endendendendA=A1;endX = 1:1:row;Y = 1:1:col;[X,Y] = meshgrid(X,Y);figure(1);surf(rot90(A,4));figure(2);contour(rot90(A,4));hold on;[Gx,Gy] = gradient(A,1,1);quiver(Gx,Gy);3.计算机绘图三.作业三1.程序框图2.程序clear;N = 41; %第一行点数h = 0.2/(N-1); %步长row = (N+1)/2; %行数E = N:-1:N-row+1;%每一行的终止点S = 1:1:N-row+1;%每一行的起始点A = zeros(row,N); %A矩阵存储每点电势A(1,:)=ones(1,E(1))*100; %初始化电势for i = 1:rowA(i,S(i)) = 0;A(i,E(i)) = 0;end %初始化电势完毕temp = A;for n= 1:600 %迭代次数for i = 2:rowfor j = S(i):E(i)if j ==S(i) || j==E(i)temp(i,j)=0;elsetemp(i,j)=(3*A(i-1,j) +3*A(i+1,j) +A(i,j-1) +A(i,j+1))/8;endendendA = temp;endX = row:-1:1;Y = N:-1:1;[X,Y] = meshgrid(X,Y);figure(1);surf(rot90(A,2));figure(2);contour(rot90(A,2));3.计算机绘图。
matlab大作业-平衡杆小球位置控制系统-华中科技大学精选全文

可编辑修改精选全文完整版MATLAB语言、控制系统分析与设计大作业平衡杆小球位置控制系统设计与仿真专业:电气工程及其自动化班级:设计者:学号:华中科技大学电气与电子工程学院2008年1月平衡杆小球位置控制系统设计与仿真一、问题描述与实验要求A ball is placed on a beam, see figure below, where it is allowed to roll with 1 degree of freedom along the length of the beam. A lever arm is attached to the beam at one end and a servo gear at the other. As the servo gear turns by an angle theta, the lever changes the angle of the beam by alpha. When the angle is changed from the vertical position, gravity causes the ball to roll along the beam. A controller will be designed for this system so that the ball's position can be manipulated.For this problem, we will assume that the ball rolls without slipping and friction between the beam and ball is negligible. The constants and variables for this example are defined as follows:M mass of the ball 0.11 kgR radius of the ball 0.015 mD lever arm offset 0.03 mG gravitational acceleration 9.8 m/s^2L length of the beam 1.0 mJ ball's moment of inertia 9.99e-6 kgm^2R ball position coordinate Alpha beam angle coordinate Theta servo gear angleSystem EquationsThe Lagrangian equation of motion for the ball is given by the following:Linearization of this equation about the beam angle, alpha = 0, gives us the following linear approximation of the system:The equation which relates the beam angle to the angle of the gear can be approximated as linear by the equation below:Substituting this into the previous equation, we get:Design requirementsThe design criteria for this problem are: •Settling time less than 3 seconds • Overshoot less than 5%1.数学模型的建立将上面推导的简化式做拉普拉斯变换,得到: 22()()()J d m R s s mg s R Lθ+=- 变化后得到:22()()()dmgR s lJ s m s Rθ=-+ 化简为:222()()()R s mgdR s J mR ls θ=-+2.设计目标希望能精确小球的位置,即要求小球的稳态误差为零,同时希望因扰动引起的稳态误差也能为零。
MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华科电气MATLAB大作业————————————————————————————————作者:————————————————————————————————日期:华中科技大学电气与电子工程学院《MATLAB课程作业》班级学号姓名时间2014年12月25日目录一.概述 (2)二.设计要求 (2)三.设计分析 (2)1.系统的稳态误差理论分析 (3)2.系统稳态误差仿真分析 (3)3.阶跃响应仿真分析 (4)四.根轨迹法设计相位滞后环节 (9)1.相位滞后环节设计 (9)2.加入相位滞后环节的仿真分析 (10)五.超前校正设计 (11)1.超前校正器设计 (11)2.超前校正仿真分析 (13)六.滞后校正设计 (17)1.滞后校正器设计 (17)2.仿真分析 (18)七.总结 (20)参考文献 (21)反馈控制系统设计—铣床控制系统设计一.概述铣床是指主要用铣刀在工件上加工各种表面的机床。
通常铣刀旋转运动为主运动,工件和铣刀的移动为进给运动。
它可以加工平面、沟槽,也可以加工各种曲面、齿轮等。
铣床是用铣刀对工件进行铣削加工的机床。
铣床除能铣削平面、沟槽、轮齿、螺纹和花键轴外,还能加工比较复杂的型面,效率较刨床高,在机械制造和修理部门得到广泛应用。
铣床的自动控制系统的设计直接影响到加工的精度,影响产品的工艺。
所以,本文通过利用MATLAB 和Simulink 对铣床的控制系统做一个校正设计,使其具有相应的性能。
二.设计要求1、单位斜坡输入21()R s s作用下 ,速度误差不大于18;2、阶跃输入时的超调量小于20%。
三.设计分析用Visio 画出一个简化的铣床闭环控制系统的方框图如图二所示。
ContollerGc(s)Plant G(s)+-++++D(s)N(s)R (s )Desired depth-of-cutY (s )Actual depth-of-cut图1. 简单的铣床闭环控制系统图1中,D(s)为外部扰动,N(s)为测量噪声干扰。
铣床的传递函数为:2()(1)(5)G s s s s =++首先,在没有控制器()C G s 的情况下,看看系统的输出结果。
1. 系统的稳态误差理论分析系统的稳态误差为:()1()()()()()()1()1()G s E s R s Y s R s R s R s G s G s =-=-=++式中,2()(1)(5)G s s s s =++,21()R s s=。
利用终值定理,系统斜坡响应的稳态误差为:220011(1)(5)15lim ()lim ()lim lim 2(1)(5)221(1)(5)ss t s s s s s s e e t sE s ss s s s s s s s s →∞→→→++=====++++++ 显然速度误差52远大于18,误差太大,不满足要求。
2. 系统稳态误差仿真分析用Simulink 画出校正前的斜坡输入仿真图如图2所示。
图2. 校正前的Simulink 斜坡输入仿真设输入斜坡为()r t t =,利用Simulink 仿真,在同一示波器中记录了输入()r t 和输出()y t 的波形图。
为方便观察,把示波器中的曲线用MATLAB 命令画出如图3所示。
其中,画图代码如下:curve=plot(ry(:,1),ry(:,2),'-g',ry(:,1),ry(:,3),'-r') set(curve(1),'linewidth',2) %设置曲线r(t)的粗细为2 set(curve(2),'linewidth',2) %设置曲线y(t)的粗细为2legend('y(t)','r(t)') %设置曲线名称人r(t),y(t) xlabel('仿真时间(s )') %X 坐标轴名称标注 ylabel('幅值') %Y 轴坐标轴标注 title('稳态误差') %所画图的名称 grid on %添加网格 axis([0 25 0 25]); %坐标范围控制 set(gca,'xtick',[0 1 2 ...25]); set(gca,'ytick',[0 1 2 ...25]);图3. 校正前斜坡输入仿真结果图3中红色为斜坡输入()r t t ,绿色为输出()y t ,为方便观察系统的稳态误差,把坐标控制在[0,25]区间,可以看出,在25S 时,已经基本达到稳态,此时的误差可从图中得到约为2.5左右,可见与理论相符。
3. 阶跃响应仿真分析5101520250510152025仿真时间(s )幅值稳态误差y(t)r(t)图4. 校正前系统的Simulink 阶跃输入仿真用同样的方法可以得到阶跃响应的仿真曲线如图5所示。
图5. 校正前的阶跃输入仿真结果从图5中可以大致的看出该系统的阶跃响应的各个性能指标。
为了更加方便准确的获得阶跃响应的各个性能指标,下面利用传递函数和MATLAB 代码仿真。
代码如下:51015202500.20.40.60.81仿真时间(s )幅值阶跃响应y(t)u(t)图6. 无控制器时的阶跃输入仿真结果num=[2];den=conv(conv([1, 0],[1,1]),[1,5]) G=tf(num,den) Gf=feedback(G,1); t=[0:0.01:20]; u=1; plot(t,u,'-r'); hold on step(Gf,'-b') den =1 6 5 0 G =2 ----------------- s^3 + 6 s^2 + 5 sStep ResponseTime (seconds)A m p l i t u d e0510150.20.40.60.811.21.4System: GfP eak amplitude: 1.04Overshoot (%): 3.75At time (seconds): 7.44Continuous-time transfer function.从图6中可以看出,在没有控制器时,系统的阶跃响应的超调量为3.75%,符合系统要求。
但是,总体来说,由于系统的速度稳态误差太大,此系统需要改进。
由系统的传递函数221()(1)(5)5(1)(1)5G s s s s s s s ==++++ 可知,该系统为1型系统,根据系统的型别与稳态误差的关系可知,1型系统的单位斜坡响应稳态误差为1v ess K =,其中25v K =为速度误差系数。
所以,为减小系统的斜坡响应稳态误差,需要适当的增大v K 的值。
根据要求,要使稳态误差小于18,也就是要求8v K >,则根轨迹增益要求540v K K =>。
下面画出根轨迹增益为1的开环传递函数'1()(1)(5)G s s s s =++的根轨迹如图7所示。
图7. 开环传递函数的根轨迹画根轨迹代码如下:Root LocusReal Axis (seconds -1)I m a g i n a r y A x i s (s e c o n d s -1)-20-15-10-50510-15-10-551015System: G Gain: 30.7P ole: 0.00837 + 2.26i Damping: -0.00371Overshoot (%): 101Frequency (rad/s): 2.26num=[1];den=conv(conv([1, 0],[1,1]),[1,5]); G=tf(num,den); rlocus(G)由图7可以看出,根轨迹过虚轴时的根轨迹增益约为30.7,所以,当根轨迹增益大于30.7时,系统不稳定,这与上面分析的540v K K =>矛盾。
所以,只靠增大系统增益,并不能满足系统的性能要求。
根据上面分析, 为使系统满足性能要求,必须要更进一步改进。
首先,我们看到,为满足斜坡响应 稳态误差的要求,则需要8v K >,即根轨迹增益540v K K =>,于是,我们不妨取10v K =,即根轨迹增益50K =来看看怎样改进这个新的系统。
四.根轨迹法设计相位滞后环节为了使系统满足超调量小于20%的要求,在10v K =的前提下,采用根轨迹的方法来设计滞后环节,使其满足要求。
1. 相位滞后环节设计滞后环节的传递函数为()c K s zG s s pα+=+于是有()20111lim 1()()lim ()()8s c c s a E s s s sG s G s sG s G s →→=⋅⋅=<+ 即lim ()()8c s sG s G s →>将()c G s ,()G s 代入易得21085v K zK pα==> 下面画出开环传递函数2()(1)(5)G s s s s =++的根轨迹如图所示。
画根轨迹代码如下: num=[2];den=conv(conv([1, 0],[1,1]),[1,5]); G=tf(num,den); rlocus(G); grid on图8. 校正前系统根轨迹根据超调量低于20%,则要求阻尼比大于0.45。
为留足够裕度,于是取阻尼比为0.6。
由图8可知,当阻尼比为0.601时,系统的增益为1.35,即 1.35Kα=。
于是根据2105v K zK pα== 可以得到18.52zp= 取0.01z =,则0.00054p =Root LocusReal Axis (seconds -1)I m a g i n a r y A x i s (s e c o n d s -1)-20-15-10-5510-15-10-5510150.160.340.50.640.760.860.940.985 2.557.51012.51517.5200.160.340.50.640.760.860.940.985System: G Gain: 1.35P ole: -0.436 + 0.58i Damping: 0.601Overshoot (%): 9.43Frequency (rad/s): 0.726于是滞后环节的传递函数为()0.011.350.00054c K s z s G s s p s α++==++于是,整个系统的传递函数为()()()()()20.01 2.7(0.01)() 1.35150.00054150.00054c s s G G s G s s s s s s s s s ++===++++++()2. 加入相位滞后环节的仿真分析利用MATLAB 程序可以获得新系统的阶跃响应如图9所示。
