MATLAB期末大作业模版
MATLAB期末大作业

MATLAB期末⼤作业学号:姓名:《Matlab/Simulink在数学计算与仿真中的应⽤》⼤作业1.假设地球和⽕星绕太阳运转的半径分别为r和2r,利⽤comet指令动画显⽰从地球到⽕星的转移轨迹(r可以任意取值,要求实时显⽰探测器、太阳、地球和⽕星的位置)。
解函数function comet(varargin)[ax,args,nargs] = axescheck(varargin{:});error(nargchk(1,3,nargs,'struct'));% Parse the rest of the inputsif nargs < 2, x = args{1}; y = x; x = 1:length(y); endif nargs == 2, [x,y] = deal(args{:}); endif nargs < 3, p = 0.10; endif nargs == 3, [x,y,p] = deal(args{:}); endif ~isscalar(p) || ~isreal(p) || p < 0 || p >= 1error('MATLAB:comet:InvalidP', ...'The input ''p'' must be a real scalar between 0 and 1.'); End指令 %particle_motiont = 0:5:16013;r1=6.7e6;%随便给定参数%---------------------------r2=2*r1;g=9.8;R=6.378e6;m=g*R^2;%内轨道v_inner=sqrt(m/r1);w_inner=v_inner/r1;x_inter=r1*cos(w_inner*t);y_inter=r1*sin(w_inner*t);%外轨道v_outer=sqrt(m/r2);w_outer=v_outer/r2;x_outer=r2*cos(w_outer*t);y_outer=r2*sin(w_outer*t);%控制器转移轨道a=(r1+r2)/2;E=-m/(2*a);V_near=sqrt(m*(2/r1-2/(r1+r2)));%转移轨道在近地点的速度V_far=sqrt(m*(2/r2-2/(r1+r2)));%转移轨道在远地点的速度h=r1*V_near;%由于在近地点的速度垂直于位置失量, h是转移轨道的⽐动量矩e=sqrt(1+2*E*h^2/m^2);%e为椭圆轨迹的偏⼼率TOF=pi*sqrt(a^3/m);%转移轨道是椭圆的⼀半及飞⾏时间是周期的⼀半(开普勒第三定律) w=pi/TOF;%椭圆轨迹的⾓速度c=a*e;b=sqrt(a^2-c^2);x_ellipse=a*cos(w*t)-0.5*r1;y_ellipse=b*sin(w*t);%动画显⽰运动轨迹x=[x_inter;x_outer;x_ellipse]';y=[y_inter;y_outer;y_ellipse]';comet(x,y)%---------------------------动态图像如下:2.利⽤两种不同途径求解边值问题dfdxf gdgdxf g f g=+=-+==34430001,,(),()的解.途径⼀:指令syms f g[f,g]=dsolve('Df=3*f+4*g,Dg=-4*f+3*g','f(0)=0,g(0)=1'); disp('f=');disp(f)disp('g=');disp(g)结果(Matlab 7.8版本)f=i/(2*exp(t*(4*i - 3))) - (i*exp(t*(4*i + 3)))/2g=exp(t*(4*i + 3))/2 + 1/(2*exp(t*(4*i - 3)))(Matlab 6.5版本)f=exp(3*t)*sin(4*t)g=exp(3*t)*cos(4*t)>>途径⼆:%problem2function dy=problem2(t,y)dy = zeros(2,1);dy(1) = 3*y(1)+4*y(2);dy(2) = -4*y(1)+3*y(2);[t,y] = ode45('problem2',[0 2],[0 1]);plot(t,y(:,1),'r',t,y(:,2),'b');图23.假设著名的Lorenz 模型的状态⽅程表⽰为-+-=+-=+-=)()()()()()()()()()()()(322133223211t x t x t x t x t x t x t x t x t x t x t x t x σρρβ其中,设28,10,3/8===σρβ。
MATLAB期末大作业模板

MATLAB应用技术期末大作业专业:姓名:学号:分数一、在一个图形窗口中以子图形式同时绘制正弦、余弦、正切、余切曲线。
请写下完整代码,展示图形结果。
(请标注题图和坐标轴,用不同颜色和不同线型分别绘制以上曲线)。
(15分)二、某公司员工的工资计算方法如下。
(1)工作时数超过120小时者,超过部分加发15%。
(2)工作时数低于60小时者,扣发700元。
(3)其余按每小时84元发。
根据员工的工时数,计算应发工资。
请写下完整的程序代码,并任意输入一工时数(使用input 函数),将结果展示(使用disp 函数)利用该代码进行计算工资,请写下计算结果。
(15分)三、编写一个函数文件,使其能够产生如下的分段函数:⎪⎩⎪⎨⎧≥<<≤-=66225.0,25.05.15.0)(x x x x xx f请编写完整的函数文件(保存函数文件名为hanshu.m ),并编写脚本文件代码,任意输入x 值(使用input 函数),在脚本文件中调用函数文件求)(x f ,展示结果(使用disp 函数),请写下计算结果。
(15分)四、将5个学生的6门功课的成绩存入矩阵P 中,进行如下处理:(1)分别求每门课的最高分、最低分及相应学生的序号。
(2)分别求每门课的平均分和标准差。
(3)5门课总分的最高分、最低分及相应学生序号。
(4)将5门课总分按从大到小顺序存入score 中,相应学生序号存入num 。
请将各小题的运行代码完整写下来,并写下运行结果。
(20分)五、请利用所学的MATLAB 知识,自主设计一个图形用户界面,请完整记录它的设计过程,需提供文字、代码和图片,以充分说明设计的图形用户界面可实现的功能。
(35分)。
matlab期末大作业

matlab期末⼤作业MATLAB语⾔及控制系统仿真期末⼤作业姓名:熊睿班级:K0312417学号:K031241742⽇期:2014/10/18⼤作业题⽬:⼀、已知单位负反馈系统的开环传递函数为)10)(5(100)(++=s s s Ks G ,K 分别取0.5和3两种情况。
1、分别在MATLAB 命令窗⼝或Simulink 模型窗⼝,建⽴K 取不同值时控制系统的模型;2、在第1问建⽴的模型基础上,要求分别在MATLAB 命令窗⼝或Simulink 模型窗⼝中绘制并观察该系统的单位阶跃响应曲线、单位斜坡响应曲线和单位加速度响应曲线;(注意:要求将K 取不同值时系统的单位阶跃响应绘制在⼀张图中并进⾏必要的标注)3、计算两种K 值所对应系统的时域性能指标(包括调节时间、上升时间、超调量、峰值时间);4、绘制系统的伯德图和奈奎斯特曲线;5、判断当K 取7.8时系统的稳定性,如果不稳定,进⾏校正直到系统稳定为⽌。
(提⽰:可使⽤rltool ⼯具)要求:有详细的建模过程、绘图过程和分析过程,最后要求进⾏总结。
⼆、写⼀份800字左右的MATLAB 学习体会和总结。
⼀、已知单位负反馈系统的开环传递函数为)10)(5(100)(++=s s s Ks G ,K 分别取0.51、分别在MATLAB 命令窗⼝或Simulink 模型窗⼝,建⽴K 取不同值时控制系统的模型;根据题⽬,在simulink 中建⽴程序图,如图○1,利⽤To workspace 将数据导⼊workspace 中,在cammond window 中⽤plot 函数画出两个不同增益的系统的阶跃响应。
如图○2 命令窗⼝中的程序:plot(tout,Y,’r ’,tout ’Y2,’k ’)图○11234567891000.511.5时间(秒)幅值阶跃响应曲线K=0.5K=3图○22、在第1问建⽴的模型基础上,要求分别在MATLAB命令窗⼝或Simulink模型窗⼝中绘制并观察该系统的单位阶跃响应曲线、单位斜坡响应曲线和单位加速度响应曲线;(注意:要求将K取不同值时系统的单位阶跃响应绘制在⼀张图中并进⾏必要的标注)根据题⽬:在1中所创建的程序图的基础下,对K=0.5的系统分别接⼊单位阶跃、单位斜坡和单位加速度输⼊。
MATLAB期末大作业

学号:姓名:《Matlab/Simulink在数学计算与仿真中的应用》大作业1.假设地球和火星绕太阳运转的半径分别为r和2r,利用comet指令动画显示从地球到火星的转移轨迹(r可以任意取值,要求实时显示探测器、太阳、地球和火星的位置)。
解函数function comet(varargin)[ax,args,nargs] = axescheck(varargin{:});error(nargchk(1,3,nargs,'struct'));% Parse the rest of the inputsif nargs < 2, x = args{1}; y = x; x = 1:length(y); endif nargs == 2, [x,y] = deal(args{:}); endif nargs < 3, p = 0.10; endif nargs == 3, [x,y,p] = deal(args{:}); endif ~isscalar(p) || ~isreal(p) || p < 0 || p >= 1error('MATLAB:comet:InvalidP', ...'The input ''p'' must be a real scalar between 0 and 1.'); End指令 %particle_motiont = 0:5:16013;r1=6.7e6;%随便给定参数%---------------------------r2=2*r1;g=9.8;R=6.378e6;m=g*R^2;%内轨道v_inner=sqrt(m/r1);w_inner=v_inner/r1;x_inter=r1*cos(w_inner*t);y_inter=r1*sin(w_inner*t);%外轨道v_outer=sqrt(m/r2);w_outer=v_outer/r2;x_outer=r2*cos(w_outer*t);y_outer=r2*sin(w_outer*t);%控制器转移轨道a=(r1+r2)/2;E=-m/(2*a);V_near=sqrt(m*(2/r1-2/(r1+r2)));%转移轨道在近地点的速度V_far=sqrt(m*(2/r2-2/(r1+r2)));%转移轨道在远地点的速度h=r1*V_near;%由于在近地点的速度垂直于位置失量, h是转移轨道的比动量矩e=sqrt(1+2*E*h^2/m^2);%e为椭圆轨迹的偏心率TOF=pi*sqrt(a^3/m);%转移轨道是椭圆的一半及飞行时间是周期的一半(开普勒第三定律)w=pi/TOF;%椭圆轨迹的角速度c=a*e;b=sqrt(a^2-c^2);x_ellipse=a*cos(w*t)-0.5*r1;y_ellipse=b*sin(w*t);%动画显示运动轨迹x=[x_inter;x_outer;x_ellipse]';y=[y_inter;y_outer;y_ellipse]';comet(x,y)%---------------------------动态图像如下:2.利用两种不同途径求解边值问题dfdxf gdgdxf g f g=+=-+==34430001,,(),()的解.途径一:指令syms f g[f,g]=dsolve('Df=3*f+4*g,Dg=-4*f+3*g','f(0)=0,g(0)=1');disp('f=');disp(f)disp('g=');disp(g)结果(Matlab 7.8版本)f=i/(2*exp(t*(4*i - 3))) - (i*exp(t*(4*i + 3)))/2g=exp(t*(4*i + 3))/2 + 1/(2*exp(t*(4*i - 3)))(Matlab 6.5版本)f=exp(3*t)*sin(4*t)g=exp(3*t)*cos(4*t)>>途径二:%problem2function dy=problem2(t,y)dy = zeros(2,1);dy(1) = 3*y(1)+4*y(2);dy(2) = -4*y(1)+3*y(2);[t,y] = ode45('problem2',[0 2],[0 1]);plot(t,y(:,1),'r',t,y(:,2),'b');图23.假设著名的Lorenz 模型的状态方程表示为⎪⎩⎪⎨⎧-+-=+-=+-=)()()()()()()()()()()()(322133223211t x t x t x t x t x t x t x t x t x t x t x t x σρρβ 其中,设28,10,3/8===σρβ。
MATLAB期末大作业

1.龟兔赛跑本题旨在可视化龟兔赛跑的过程。
比赛的跑道由周长为P面积为A的矩形构成。
每单位时间,乌龟沿跑道缓慢前进一步,而兔子信心满满,每次以一个固定的概率决定走或不走。
如果选择走,就从2-10步中等概率选择一个步长。
每个单位时间用一个循环表示。
赛跑从矩形跑道左上点(0,0)开始,并沿顺时针方向进行。
不管是乌龟或兔子,谁先到达终点,比赛就告结束。
要求:编写MATLAB程序可视化上述过程。
程序以P,A以及兔子每次休息或前进的概率为输入参量。
程序必须可视化每个时刻龟兔赛跑的进程,并以红色“*”表示乌龟,蓝色的“—”表示兔子。
测试时可取P=460,A=9000。
通过上述例子,可否从理论和实验角度估计兔子休息或前进的概率,是的兔子和乌龟在概率意义下打平手。
2.黄金分割Fibonacci数列F n通过如下递推格式定义F n=F n-1+F n-2,其中F0=F1=1要求:1.计算前51项Fibonacci数,并存入一个向量2.利用上述向量计算比值F n/F n-13.验证该比值收敛到黄金比例(1+5)/23.图像处理此题旨在熟悉图像处理的基本操作,请各位自己选择一张彩色图像pMATLAB以三维数组读取一张彩图。
该彩图上每个像素位置分别存放一个取值0-255的三维向量,其三个分量分别表示该点的红(R)绿(G)蓝(B)强度信息。
要求:编写MATLAB程序,读入原始彩色图像,并且在一个图形窗口界面下显示六张图像。
这六张图分别是原始RGB彩图,及其5各变形:RBG,BRG,BGR,GBR和GRB。
每张子图要求以其对应变形命名。
最后将图像以a.jpg形式保存并黏贴至报告中。
提示:imread, imshow, cat。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
《科学计算与MATLAB》期末大作业

杭州电子科技大学信息工程学院《科学计算与MATLAB》期末大作业给出程序、图、作业分析,程序需加注释。
1. 试编写名为fun.m 的MATLAB 函数,用以计算下述的值:⎪⎩⎪⎨⎧-<->=t t n t t t n t f 的)4/sin()(si 对所有)4/sin(其他情况)sin(的)4/sin()(si 对所有)4/sin()(ππππ绘制t 关于函数f(t)的图形,其中t 的取值范围为ππ66≤≤-t ,间距为10/π。
function y=fun()%定义函数%t=-6*pi:pi/10:6*pi; %定义变量范围 y =(sin(pi/4)).*(sin(t)>sin(pi/4))+(sin(-pi/4)).*(sin(t)<sin(-pi/4))+(sin(t)).*((sin(t)<=sin(pi/4))&(sin(t)>=sin(-pi/4)));%函数表示 plot(t,y); %画图 end2.解以下线性方程组⎪⎩⎪⎨⎧=+=++=--353042231321321x x x x x x x xA=[2 -1 -1;1 1 4;3 0 5];%输入矩阵 B=[2;0;3]; %输入矩阵 X = A\B %计算结果3.已知矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44434241343332312423222114131211A 求: (1)A(2:3,2:3)(2)A(:,1:2) (3)A(2:3,[1,3])(4)[A,[ones(2,2);eye(2)]]A=[11 12 13 14;21 22 23 24;31 32 33 34;41 42 43 44];%输入矩阵A(2:3,2:3) %输出矩阵A(:,1:2) %输出矩阵A(2:3,[1,3]) %输出矩阵[A,[ones(2,2);eye(2)]] %输出矩阵4.数学函数()2222sinyxyxz++=定义在区域[-8,8]×[-8,8]上。
matlab期末大作业题目及答案

matlab 期末大作业(30分,每题6分)1. 积分运算(第四数值和五章符号)(1)定积分运算:分别采用数值法(quad ,dblquad )和符号运算(syms, int )一重定积分π⎰1. 数值法(quad )a) 运行代码:b) 运行结果:2. 符号运算(syms )a) 运行代码:b) 运行结果:二重定积分112200()x y dxdy+⎰⎰1.数值法(dblquad):a)运行代码:b)运行结果:2.符号运算(syms):a)运行代码:b)运行结果:(2) 不定积分运算sin dxdy ⎰⎰((x/a)+b/y) i.运行代码:ii.运行结果:2. 用符号法和数值法求解线性代数方程 (第五章和第二章)⎩⎨⎧=+=+12*22x *213*12x *a11y a a y a (1) 用syms 定义待解符号变量x,y 和符号参数a11,a12,a21,a22,用符号solve 求x,y 通解 1. 运行代码:2. 运行结果:(2) 用subs 带入a11=2,a12=4,a21=6,a22=8,求x 和y 特解,用vpa 输出有效数值4位的结果 1. 运行代码:2. 运行结果:(3) 采用左除(\)和逆乘法求解符号参数赋值后的方程 ⎩⎨⎧=+=+12*8x *63*4x *2y y1. 运行代码:2. 运行结果:3.数值法和符号法求解非线性方程组(第四数值和五章符号 )(1)采用数值法(fsolve )求解初始估计值为x0 = [-5; -5]的数值解1. 运行代码:2. 运行结果:21x 21x 21e x 2x e x x 2--=+-=-(2)符号法(solve )的符号结果用eval 或double 转化为数值结果.1. 运行代码:2. 运行结果:4. 解二阶微分方程 (第四数值和五章符号 )⎪⎩⎪⎨⎧===++6)0(',0)0(09322y y y dx dy dx y d(1)数值ode 求特解,用plot (x,y) 画t 在[0,10]范围内(x ,y )数值曲线 1. 运行代码:2. 运行结果:(2)符号运算dsolve求通解,用ezplot画t在[0,10]范围内(x,y)符号曲线1. 运行代码:2. 运行结果:5. 三维绘图(第六章)已知:x和y都在[-8,8]范围内,采用subplot(3,1,x)绘制三个子图,它们分别是用meshgrid和mesh绘制网格图、用c=contour 绘制等位线和用surf 绘制曲面图1.运行代码:2.运行结果:。
杭州电子科技大学matlab期末作业

Matlab课程设计作业机械三班一、(1)建立数学模型>> num=[1];>> den=conv([0.2 1 0],[0.15 1]); >> G=tf(num,den)Transfer function:1-----------------------0.03 s^3 + 0.35 s^2 + s(2)根轨迹(3)K值的确定>> K=0:0.05:200;rlocus(G,K)[K,POLES]=rlocfind(G)selected_point =0.0059 + 5.7764iK =11.6902POLES =-11.67130.0023 + 5.7782i0.0023 - 5.7782i(4)超前校正>>sigma=0.2 ;zeta=((log(1/sigma))^2/((pi)^2+(log(1/sigma))^2))^(1/2); wn=3/zeta;p=[1 2*zeta*wn wn*wn];s=roots(p)>> s1=s(1);ng=1;dg=[0.03 0.35 1 0];ngv=polyval(ng,s1);dgv=polyval(dg,s1);g=ngv/dgv;theta=angle(g);phic=pi-theta;phi=angle(s1);thetaz=(phi+phic)/2;thetap=(phi-phic)/2;zc=real(s1)-imag(s1)/tan(thetaz);pc=real(s1)-imag(s1)/tan(thetap);nc=[1 -zc];dc=[1 -pc];Gc=tf(nc,dc)>> G=tf(ng,dg);rlocus(Gc*G)sgrid(0.4559,[])>> step(feedback(19.9*Gc*G,1))4)校正前后的simulink仿真模型1)校正前2)校正后(5)校正前单位响应曲线和单位脉冲曲线:>> num=[0 1];>> den=[0.03 0.35 1 0];>> G=tf(num,den);>> G0=feedback(G,1);>> step(G0)校正前单位响应>>impulse(G0)校正前单位脉冲响应校正后单位响应曲线和单位脉冲曲线:>> num=[19.9 57.6416];>> den=[0.03 0.809 6.355 15.3 0];>> G=tf(num,den);>> G0=feedback(G,1)>> step(G0)校正后单位响应>> impulse(G0) 校正后单位脉冲响应第二题:(1):>> num=10;den=[0.1 0.7 1 0];G=tf(num,den);nyquist(G)>>delta=11.1;s=tf('s');G=10/(s*(0.2*s+1)*(0.5*s+1)); margin(G)[gm,pm]=margin(G)phim1=50;phim=phim1-pm+delta;phim=phim*pi/180;alfa=(1+sin(phim))/(1-sin(phim))a=10*log10(alfa);[mag,phase,w]=bode(G);adB=20*log10(mag);wm=spline(adB,w,-a);t=1/(wm*sqrt(alfa));Gc=(1+alfa*t*s)/(1+t*s)/alfa;[gmc,pmc]=margin(G*Gc)figure;margin(G*Gc)前:后:、>> figure;step(feedback(G,1))>> figure;step(feedback(G*Gc,1))。
matlab期末作业_附源代码

clc f=[-11,-9]'; A=[6,5;10,20]; B=[60,150]; Ae=[]; Be=[]; xm=[0,0]; xM=[8,Inf]; [x,f_opt]=linprog(f,A,B,Ae,Be,xm,xM)
6
③结果如下:
Optimization terminated. x= 8.0000 2.4000 f_opt = -109.6000
⑤结果分析: 生产甲800箱,生产乙240箱,获利最多为109.6万元。 显然应该是要改变生产计划的,改变计划获利增加。
7
②编写 m 文件
function y = myodefun(t,x ) y=[-x(1)^3-x(2);x(1)-x(2)^3]; end
0<t<30
③在 command 窗口中输入:
>> tspan=[0,30]; >> x0=[1;0.5]; >> [t,x]=ode45('myodefun',tspan,x0); >> plot(t,x(:,1),'g*',t,x(:,2),'b-.');
②Matlab源代码
clc f=[-10,-9]'; A=[6,5;10,20]; B=[60,150]; Ae=[]; Be=[]; xm=[0,0]; xM=[8,Inf]; [x,f_opt]=linprog(f,A,B,Ae,Be,xm,xM)
③结果如下:
Optimization terminated. x= 6.4286 4.2857 f_opt = -102.8571
1
1.求解微分方程组,画出解函数图。
(完整版)武汉大学matlab期末课程作业

(完整版)武汉⼤学matlab期末课程作业“MATLAB及其应⽤”课程作业院系:姓名:学号:联系⽅式:1. 请指出如下5个变量名中,哪些是合法的? abcd-2 xyz_3 3chan a 变量 ABCDefgh答:xyz_3,ABCDefgh 是合法的。
2. 在命令窗中,运⾏命令a=sqrt(2)。
然后请回答以下问题:计算结果a吗?该计算结果只是5近似吗?请在命令窗中,显⽰出具有最多位有MATLAB 数值结果显⽰的默认设置。
该计算结果只是5近似。
3. 命令clear, clf, clc 各有什么⽤处?答:clear 可以清除matlab ⼯作空间中保持的变量。
clf 可以清除图形窗。
clc 清除命令窗中显⽰内容。
4. 想要在MATLAB 中产⽣⼆维数组=987654321S ,下⾯哪些命令能实现⽬的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个命令在中⽂状态下输⼊答:第⼆条S=[1 2 3;4 5 6;7 8 9]能实现⽬的。
中⽂状态下逗号不是有效字符。
1.说出以下四条命令产⽣的结果各属于哪种数据类型,是“双精度”对象,还是“符号”对象?3/7+0.1, sym(3/7+0.1), vpa(sym(3/7+0.1),4), vpa(sym(3/7+0.1))答:3/7+0.1结果是双精度。
sym(3/7+0.1)结果是符号。
vpa(sym(3/7+0.1),4)结果是符号。
vpa(sym(3/7+0.1))结果是符号。
过程如图:2.已知a1=sin(sym(pi/4)+exp(sym(0.7)+sym(pi/3)))产⽣精准符号数字,请回答:以下产⽣的各种符号数哪些是精准的?若不精准,误差⼜是多少?能说出产⽣误差的原因吗?a2=sin(sym(pi/4)+exp(sym(0.7))*exp(sym(pi/3)))a3=sin(sym('pi/4')+exp(sym('0.7'))*exp(sym('pi/3')))a4=sin(sym('pi/4')+exp(sym('0.7+pi/3')))a5=sin(sym(pi/4)+exp(sym(0.7+pi/3)))a6=sin(sym(pi/4)+sym(exp(0.7+pi/3)))a7=sin(sym(pi/4+exp(0.7+pi/3)))a8=sym(sin(pi/4+exp(0.7+pi/3)))(提⽰:可⽤vpa观察误差;注意数位的设置)。
matlab大作业例子
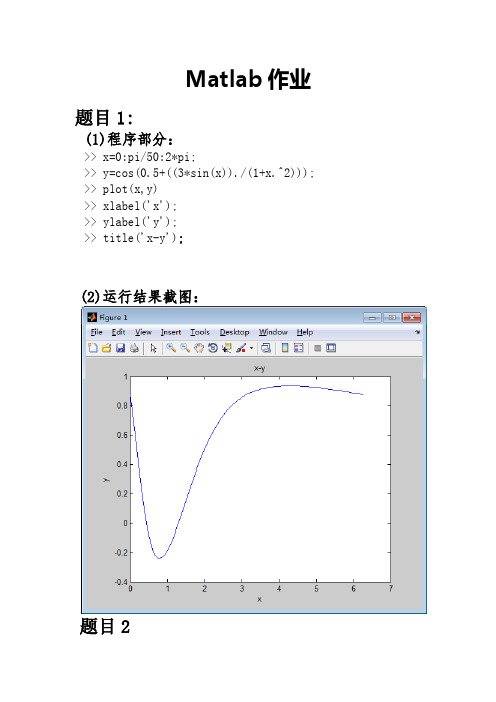
Matlab作业题目1:(1)程序部分:>> x=0:pi/50:2*pi;>> y=cos(0.5+((3*sin(x))./(1+x.^2))); >> plot(x,y)>> xlabel('x');>> ylabel('y');>> title('x-y');(2)运行结果截图:(1)程序部分:>> clear>> clc>> x=0:pi/100:4*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,'r-',x,y2,'g:') >> hold on>> y3=x(find(abs(y1-y2)<0.001)); >> plot(y3,sin(y3),'*')(2)运行结果截图:(1)程序部分:>> t=(0:2*pi/100:2*pi)'; >> y1=sin(t)*[1,-1]; >> y2=sin(t).*sin(9*t); >> subplot(2,1,1);>> plot(t,[y1,y2]);>> subplot(2,1,2);>> plot(t,[y1,y2]) (2)运行结果截图:题目4(1)程序部分:>> t=0:pi/50:4*pi;>> y=exp(-t/3);>> y0=exp(-t/3).*sin(3*t); >> plot(t,y,'r-',t,y0,'b:') >> xlabel('\bf\it t')>> ylabel('\bf\it y')>> grid on;(2)运行结果截图:题目5(1)程序部分:>> n=0;>> sum=0;>> while sum<2000n=n+1;sum=sum+n;end>> n(2)运行结果截图:题目6(1)程序部分:for j=1:3n=input('n='); sum=0;for i=1:na=1/(i.^2);sum=sum+a;endPI=sqrt(6*sum) end(2)运行结果截图:题目7(1)程序部分:n0=0;y0=0;while 3*y0<5n0=n0+1;y0=y0+1/(2*n0-1);y=y0-1/(2*n0-1);n=n0-1;endn(2)运行结果截图:题目8(1)程序部分:for i=1:7x=input('put x:');if x<0&x~-3y=x^2+x-6;elseif x>=0&x<5&x~=3&x~=2 y=x*x-5*x+6;elsey=x*x-x-1;endend(2)运行结果截图:题目9①switch语句(1)程序部分:>> score=input('请输入成绩'); switch fix(score/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {0,5}disp('E');otherwisedisp('error');end(2)运行结果截图:如右图②if语句(1)程序部分:score=input('请输入成绩:') n=score/10;if n>=9&n<10disp Aelseif n>=8&n<9disp Belseif n>=7&n<8disp Celseif n>=6&n<7disp Delseif n>=0&n<6disp Eelsedisp errorend(2)运行结果截图:题目10(1)程序部分:t=input('员工的工作时间:')if t<60m=84*t-700;elseif t>120m=84*(t-120)*1.15+84*120;elsem=84*t;endm2)运行结果截图:题目11(1)程序部分:a=round(20*rand(5,6))n=input('请输入n的值:') tryb=a(n,:);catchb=a(5,:);endblasterr(2)运行结果截图:。
MATLAB期末大作业模版

学号:《MATLAB》期末大作业学院土木工程与建筑学院专业班级姓名指导教师李琳2018年5月16日题目2:问题描述:在[0 2π]范围内绘制二维曲线图y=cos(5x)*sin(x)(1)问题分析这是一个二维绘图问题,先划定x的范围与间距,再列出y的表达式,利用plot函数绘制二维曲线。
(2)软件说明及源代码>> x = 0:pi/10:2*pi;>>y = cos(5*x).*sin(x);>>plot(x,y)(3)实验结果题目4:问题描述:创建符号函数并求解,要求写出步骤和运行结果(1)创建符号函数f=ax2+bx+c(2)求f=0的解(1)问题分析这是一个符号函数显示以及符号函数的求解问题,第一问先定义常量与变量,在写出f表达式,利用pretty函数显示f。
第二问利用solve函数求解f=0时的解。
(2)软件说明及源代码第一问>> syms a b c x;>> f=a*x^2+b*x+c;>> pretty(f)第二问>>syms a b c x;>>f=a*x^2+b*x+c;>> solve(f)(3)实验结果1、2、题目5:问题描述:求积分(1)问题分析这是一个利用符号函数求积分的问题,先定义变量x,再列出I1表达式,利用int函数求在范围0到Pi/2上的积分。
(2)软件说明及源代码>> syms x;>> I1=(1-2*sin(2*x))^0.5;>> int(I1,0,0.5*pi)(3)实验结果题目6:问题描述:分别随机产生一个6×6的整数矩阵(元素可在[-20,20]之间),求该随机阵的秩,特征值和特征向量。
(1)问题分析这是一个矩阵运算问题,先利用rand函数产生一个6*6的元素在-20到20之间的整形矩阵,再利用rank、eig两个函数分别求该随机阵的秩,特征值和特征向量。
期末matlab考试题及答案

期末matlab考试题及答案注意:以下内容为虚构的期末MATLAB考试题目及答案,并非真实情况。
一、选择题1. 在MATLAB中,以下哪个命令可以将矩阵A的第一列元素求和?A) sum(A(:,1))B) sum(A(1,:))C) sum(A(1))D) sum(A(:,1))答案:A) sum(A(:,1))2. 对于向量x = [1, 2, 3, 4],以下哪个命令可以将x的元素逆序排列?A) flip(x)B) reverse(x)C) sort(x,'descend')D) sort(x,'ascend')答案:A) flip(x)3. 如果一个函数文件的文件名为"myFunction.m",那么在MATLAB中如何调用该函数?A) myFunction.mB) call myFunctionC) run myFunctionD) myFunction答案:D) myFunction4. 在MATLAB中,以下哪个命令可以生成一个在-1到1范围内均匀分布的10个数的向量?A) linspace(-1, 1, 10)B) rand(1, 10)*2-1C) linspace(1, 10, -1)D) randi([-1, 1], 1, 10)答案:B) rand(1, 10)*2-15. 对于矩阵A和B,以下哪个命令可以将它们进行垂直方向的拼接?A) vertcat(A, B)B) concat(A, B, 'vertical')C) merge(A, B, 'vertical')D) [A; B]答案:D) [A; B]二、填空题1. 假设有一个向量x = [1, 2, 3, 4],使用MATLAB命令求x的最大值。
答案:max(x)2. 假设有一个矩阵A = [1, 2, 3; 4, 5, 6; 7, 8, 9],使用MATLAB命令求A的行数。
上海电院Matlab大作业

1、编写Matlab函数命令M文件,完成下列功能,要求程序语句尽可能简洁:(1)函数输入参数为正整数n,要求3<n<10,如果输入的参数不符合3<n<10,则给出提示。
(2)生成n阶随机矩阵A;(3)生成n阶矩阵B,B的每个元素是对应位置上A矩阵元素的自然对数;(4)求矩阵B的所有对角线元素之和m。
(5)返回值为矩阵B和m。
(6)要求:进行上机编程,调试完成后将程序书写在大作业报告中、并加以注释,将调试结果截图打印粘贴在大作业报告中。
解:①根据题目要求编写一个函数文件,设函数名为heer ,则函数文件名为heer.m②因为题目要求最终的返回值为B和m,故在定义函数时可设置为 function [B,m]=heer(n)③根据要求,矩阵的阶数n是有限定范围(3<n<10)的,故可采用if语句实现④在这个大前提下,矩阵A是系统产生的,且矩阵B在A的基础上进行对数运算,可以直接用赋值语句实现:A=rand(n,n)B=log(A)⑤因为题目还要求矩阵B的所有对角线上的元素和,考虑到对角线上元素为B[i,i], 即元素下标相等,则可以用for 循环语句实现:for i=1:1:nsum=sum+B(i,i);end这样,整个M文件的内容就确定下来,只需在软件中先编写好该文件,再保存,即可在命令窗口直接调用该文件。
下面为M文件的截图如下图所示,设置n=2,则系统显示错误信息如下图所示,设置n=7.,程序运行结果如下2、一个50Hz的简单电力系统如下图所示,试在Simulink中建立仿真模型研究该系统性能。
k1GTLD2LLD1系统建模要求如下:(1) 发电机G 采用“Synchronous Machine pu Fundamental ”模型,变压器T 采用“Three-Phase Transformer (Two Windings)”模型,输电线路L 采用“Three-Phase Series RLC Branch ”模型,负荷LD1、LD2采用“Three-Phase Parelell RLC Load ”模型。
MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
MATLAB 大作业

MATLAB 大作业请各位同学,自己完成matlab 大作业的内容。
禁止相互抄袭,如有雷同,零分计算。
大作业的格式按照实验报告的格式书写,务必标明题号,作业完成后,将生成的报告打印出来提交。
正文的字号以宋体五号字,1.5倍行距的格式打印。
请与18周五前将大作业报告由班级负责人统一收齐交给我,过期不收。
1、 试编写名为test01.m 的MATLAB 函数,用以计算下述的值:⎪⎩⎪⎨⎧-<->=t t n t t t n t f 的对所有其他情况的对所有)4/sin()(si )4/sin()sin()4/sin()(si )4/sin()(ππππ要绘制t 关于函数f (t )的图形,其中t 的取值范围为ππ66≤≤-t ,间距为10/π。
(提示:注意要产生一系列的点,这里可考虑t 的输入是向量形式,可以利用find 函数找出所需限定值的元素的位置,对其按需要赋值后,再进行绘图;其次,另外一种思路,也可考虑使用循环的形式来实现)2、 编写函数,在同一窗口的4个子图中利用plot 等语句绘制y=at 2图像,其中a=[1 2 5 10],t 范围[-2,5]。
3、 求函数32)(3-+=x x x f 在区间[-5,5]上的最大值和最小值。
4、 求解函数⎰102dx e x 的数值积分和符号积分,并比较结果。
5、 求解微分方程3|;1|2)1(002='='=''+==x x y y y x y x 的精确解和解析解,并绘制图形。
假设求解区间为[0,10] 。
6、 说说你对MATLAB 及应用这门课程学习后的体会,另外请说明在所学章节中哪一章的内容你最感兴趣,为什么?哪一章的内容你认为是没有必要学习的,为什么?如果可以选择MATLAB 的学习的内容的话,谈谈你所期望学到的知识类别的前三种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学号:
《MATLAB》
期末大作业
学院土木工程与建筑学院
专业
班级
姓名
指导教师李琳
2018年5月16日
题目2:问题描述:在[0 2π]范围内绘制二维曲线图y=cos(5x)*sin(x)
(1)问题分析
这是一个二维绘图问题,先划定x的范围与间距,再列出y的表达式,利用plot函数绘制二维曲线。
(2)软件说明及源代码
>> x = 0:pi/10:2*pi;
>>y = cos(5*x).*sin(x);
>>plot(x,y)
(3)实验结果
题目4:问题描述:创建符号函数并求解,要求写出步骤和运行结果
(1)创建符号函数f=ax2+bx+c
(2)求f=0的解
(1)问题分析
这是一个符号函数显示以及符号函数的求解问题,第一问先定义常量与变量,在写出f表达式,利用pretty函数显示f。
第二问利用solve函数求解f=0时的解。
(2)软件说明及源代码
第一问
>> syms a b c x;
>> f=a*x^2+b*x+c;
>> pretty(f)
第二问
>>syms a b c x;
>>f=a*x^2+b*x+c;
>> solve(f)
(3)实验结果
1、
2、
题目5:问题描述:求积分
(1)问题分析
这是一个利用符号函数求积分的问题,先定义变量x,再列出I1表达式,利用int函数求在范围0到Pi/2上的积分。
(2)软件说明及源代码
>> syms x;
>> I1=(1-2*sin(2*x))^0.5;
>> int(I1,0,0.5*pi)
(3)实验结果
题目6:问题描述:分别随机产生一个6×6的整数矩阵(元素可在[-20,20]之间),求该随机阵的秩,特征值和特征向量。
(1)问题分析
这是一个矩阵运算问题,先利用rand函数产生一个6*6的元素在-20到20
之间的整形矩阵,再利用rank、eig两个函数分别求该随机阵的秩,特征值和特征向量。
(2)软件说明及源代码
>> a=round(-20+40*rand(6));
>> rank(a);
>> [X,B]=eig(a)
(3)实验结果
题目9:问题描述:按水平和竖直方向分别合并下述两个矩阵:
(1)问题分析
这是一个矩阵基本操作问题,先输入矩阵A与B,再使用水平和竖直方向合并矩阵。
(2)软件说明及源代码
>> A=[1 0 0;1 1 0;0 0 1];
>> B=[2 3 4;5 6 7;8 9 10];
>> C=[A,B];
>> D=[A;B]
(3)实验结果
题目12:问题描述:读入RGB图像pepper.png,并把它转换为灰度图,在同一个图像窗口的第一个子图显示原图,在第二个子图显示其灰度图。
(1)问题分析
这是一个三维绘图问题,先用imread函数读取图片,再利用figure生成一个窗口,利用subplot函数使在一个窗口里显示两个子图,利用imshow显示图片。
(2)软件说明及源代码
>> peppers = imread ('F:\Desktop\peppers.png');
>> figure;
>> I = rgb2gray(peppers);
>> subplot(1,2,1);imshow(peppers);
>> subplot(1,2,2);imshow(I)
(3)实验结果
题目14:问题描述:利用switch函数编写脚本文件。
用户输入ch值,当ch=1时,产生[-1, 1]之间均匀分布的随机数;ch=2时,产生大小为5x5的对角阵,其中每个元素在[0, 1]之间随机数;当ch=3时,产生大小为5x5的单位矩阵;当ch=4时,产生3阶魔方阵;当ch=5时,直接退出。
(1)问题分析
这是一个脚本编辑与矩阵基本操作的问题,先利用input函数获取用户输入的ch值,再在使用switch判断用户输入的值,1时,利用randi产生[-1, 1]之间均匀分布的随机数;2时,利用diag函数与rand函数,产生大小为5x5的对角阵,其中每个元素在[0, 1]之间随机数;3时,利用eye函数产生大小为5x5的单位矩阵;4时,利用magic函数,产生3阶魔方阵。
(2)软件说明及源代码
ch = input('Enter the value of "ch":');
switch ch
case 1
y = randi([-1,1]);
case 2
y = diag(rand(1,5));
case 3
y = eye(5);
case 4
题目18:问题描述:编制m文件,等待键盘输入,输入密码20171026,密码正确,显示输入密码正确,程序结束;否则提示,重新输入。
(1)问题分析
这是一个while循环编程问题,先利用input获取用户输入的a的值,利用while循环判断a是否等于20171026,错误时重新输入,正确时退出循环,利用if语句判断a值并输出密码正确。
(2)软件说明及源代码
a=input('输入密码:')
while a~=20171026
disp('密码错误:')
clear
a=input('输入密码:')
end
if a==20171026
disp('密码正确·!')
end
题目21:问题描述:从键盘输入若干个数,当输入0时结束输入,求这些数的平均值以及平方和。
(1)问题分析
这是一个数组操作问题,先生成一个空数组,再利用input函数获取用户输入的值,利用while循环来使用户输入更多的值,并将值放入数组末端,当用
户输入0则循环停止,利用mean函数求平均值,利用sum求数值的平方和。
(2)软件说明及源代码
data=[];%建立空数组
in=input('输入数据:');%输入一个数据
while (isempty(in)||in~=0)%空数据或数值不为0进入循环
data=[data in];%将新数据放入原来数据的末端
in=input('输入数据:');%要求再次输入数据
end
mean(data)%求平均
sum(data.^2)%求平方和
题目3:某河流边有两个化工厂,流经第一座化工厂的河水流量是每天500万立方米,在两个工厂之间有一条流量为200万立方米的支流,如下图所示。
第一个化工厂每天排放工业污水2万立方米,第二个化工厂每天排放工业污水1.4万立方米,从第一个化工厂排出的污水流到第二个化工厂之前,有20%可以自然进化,根据环保要求,河流中工业污水的含量不应大于0.2%。
因此两个化工厂都必须各自处理净化一部分污水,第一个化工厂处理污水的成本是0.1元每立方米,第二个化工厂处理污水的成本是0.08元每立方米,问在满足环保要求的条件下,各化工厂每天应处理多少污水,才能使两厂总的处理污水费用最少?
(1)问题分析:这是一个单目标优化问题。
设x1,x2分别表示第一第二化工厂每天处理的污水量,则易得目标函数为f=1000x1+800x2。
约束条件为
{(2−x1)
500
≤0.2%
0.8(2−x1)+(1.4−x2)
700≤0.2%
x1≤2
x2≤1.4
可将该题线性规划模型归结为:minf=1000x1+800x2
s.t.
{−x1≤−1
−0.8x1−x2≤−1.6
x1≤2
x2≤1.4
x1,x2≥0
输入参数f,A,b,lb;利用linprog函数求解(2)软件说明及源代码
>> f=[1000 800];
A=[-1 0;-0.8 -1;1 0;0 1];
b=[-1;-1.6;2;1.4];
lb=zeros(2,1);。
