几个基本常数弹性模量-泊松比-应力应变曲线
杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度

杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度、柔度、刚性、柔性、泊松比、剪切应变、体积应变“模量”可以理解为是一种标准量或指标。
材料的“模量”一般前面要加说明语,如弹性模量、压缩模量、剪切模量、截面模量等。
这些都是与变形有关的一种指标。
杨氏模量(Young's Modulus):杨氏模量是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量,也是材料力学中的名词。
1807年因英国医生兼物理学家托马斯·杨(Thomas Young, 1773-1829) 所得到的结果而命名。
根据胡克定律,在物体的弹性限度内,应力与应变成正比,比值被称为材料的杨氏模量,它是表征材料性质的一个物理量,仅取决于材料本身的物理性质。
杨氏模量的大小标志了材料的刚性,杨氏模量越大,越不容易发生形变。
对于线弹性材料有公式σ(正应力)=Eε(正应变)成立,式中σ为正应力,ε为正应变,E为弹性模量,是与材料有关的常数,与材料本身的性质有关。
在材料力学方面,研究了剪形变,认为剪应力是一种弹性形变。
钢的杨氏模量大约为2×1011N·m-2,铜的是1.1×1011 N·m-2。
弹性模量和杨氏模量很相似,弹性模量有拉伸和剪切的两个方向,杨氏主要指的是拉伸的。
测量杨氏模量的方法一般有拉伸法、梁弯曲法、振动法、内耗法等,还出现了利用光纤位移传感器、莫尔条纹、电涡流传感器和波动传递技术(微波或超声波)等实验技术和方法测量杨氏模量。
弹性模量(Elastic Modulus):弹性模量E是指材料在弹性变形范围内(即在比例极限内),作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力如拉伸,压缩,弯曲,扭曲,剪切等)与材料产生的相应应变之比。
弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结构不敏感参数。
在工程上,弹性模量则是材料刚度的度量,是物体变形难易程度的表征。
材料的弹性变形

47
1.2.2 广义胡克定律(各向异性体)
❖各向异性材料的各个方向的弹性模量都不相同; ❖当各向异性材料同时受到三向应力作用时,各个方向的形
C B A
D K
O
29
三、应力与应变曲线
C
B A
D K
➢ A(A点):比例极限;E(B点):弹性极限;P(C点 ):屈服极限;U(D点):断裂极限。
➢ 应力E,可逆线性正比例关系,当应力在E和P之间, 外力去除后有一定程度的永久变形,即发生塑性变形。
➢ 陶瓷材料一般没有塑性变形,发生脆性断裂。
力不能是任意的,内力与变形有关,必须满足 平衡条件。
12
3.工程构件受力模型 拉伸
压缩
13
3.工程构件受力模型 剪切
14
3.工程构件受力模型
扭转
15
3.工程构件受力模型 弯曲
16
3.工程构件受力模型 弯曲
17
3.工程构件受力模型 组合受力
18
4.强度、刚度和稳定性问题
强度—不因发生断裂或塑性变形而失效; 刚度—不因发生过大的弹性变形而失效; 稳定性—不因发生因平衡形式的突然转变而失效。
材料物理性能
第一部分:材料的力学性能
1
高温蠕变
2
第一章:材料的弹性变形
主要内容:
一.应力和应变; 二.胡克定律; 三.弹性模量; 四.滞弹性。
要求:
从微观的角度来理解宏观性能、掌握解决问题的 关键。
3
1. 基本概念
变形:材料在受到外力作用时产生的形状和体积 的变化;
应力应变曲线弹性模量切变模量泊松比等

低碳钢、铸铁拉伸、压缩曲线的比较
5. 轴向拉压破坏现象分析
观察拉、压破坏试件的断口方向:
拉伸
低碳钢 铸铁 与轴线成45º 斜面 剪断! 与轴线垂直
压缩
与轴线成45º 斜面
剪断!
拉断! 横截面上 最大 与轴线成45º 斜面上 最大
轴向拉压
拉伸
低碳钢 铸铁 与轴线成45º 斜面 剪断! 与轴线垂直
4P/3
D
P
E
-
F
2P/3
a
a
P 1 F 10 4 N 3 3 4P 4 E FN 2 10 4 N 3 3 2P 2 FN 1 10 4 N 3 3
C N2
画出轴力图。从图中可知:
2 F 10 4 N 3 (拉力)
N 1max
F
N 2 max
低碳钢拉伸实验:
低碳钢拉伸曲线的4个阶段、3个特征点
b s e P
OB:弹性阶段(卸载可逆) A:比例极限P
D E
C B A
B:弹性极限e
(两者很接近) =E E=tan BC’:屈服阶段 (出现塑性变形) C:屈服极限s
C’
=E
O
C’D:强化阶段 D:强度极限b ,在C’D段内卸载曲线为弹性直线 e:弹性应变 ,p:塑性应变(不可逆的残余应变) b
W FN ( x) Wx qdx x l
FN
A
W
EA
FN x
l
W q l
x
B
Wx
max W A A
FN max W
2. 杆中应力
FN ( x) Wx ( x) A Al
弹性力学基本概念

弹性力学基本概念弹性力学是力学的一个分支领域,研究材料在受力时的弹性变形和恢复变形的行为规律。
本文将介绍弹性力学的基本概念,包括应力、应变、胡克定律和杨氏模量等。
一、应力和应变在弹性力学中,应力和应变是两个基本的物理量,用来描述物体在受力时的变形情况。
应力是单位面积上的力,通常用希腊字母σ表示。
应力可以分为正应力和剪应力两种。
正应力是指垂直于受力面的力,它可以通过力的大小和受力面的面积计算得到。
正应力的单位是帕斯卡(Pa),1Pa等于1牛顿/平方米。
剪应力是指平行于受力面的力,它也可以通过力的大小和受力面的面积计算得到。
剪应力的单位也是帕斯卡(Pa)。
应变是物体由于受力而发生的变形程度,通常用希腊字母ε表示。
应变可以分为线性应变和剪切应变两种。
线性应变是指物体在受力下发生的长度变化与原长度之比。
线性应变的计算公式为:ε = ΔL / L,其中ΔL表示长度变化,L表示原长度。
剪切应变是指物体在受到剪应力时,各层之间相对位置的变化。
剪切应变的计算公式为:γ = Δx / h,其中Δx表示位置变化,h表示物体的厚度。
二、胡克定律胡克定律是弹性力学的基本定律之一,描述了材料的应力和应变之间的关系。
胡克定律可以用公式表示为:σ = Eε,其中σ表示应力,E表示杨氏模量,ε表示应变。
杨氏模量是衡量材料硬度和刚度的重要物理量,表示单位应力下材料的单位应变。
杨氏模量的单位是帕斯卡(Pa)。
胡克定律表明,当材料处于弹性变形状态时,应力和应变之间成正比。
杨氏模量越大,材料的刚度越高,抵抗变形的能力也越强。
三、弹性常数除了杨氏模量,弹性力学还有其他一些描述材料力学性质的常数。
泊松比是描述材料在受到正应力时,在垂直方向上的应变情况的比值。
泊松比的计算公式为:ν = -ε_2 / ε_1,其中ε_1表示垂直方向上的线性应变,ε_2表示平行方向上的线性应变。
弹性体模量是描述材料在受力时的刚度的物理量,定义为单位体积的材料在受力时所发生的应变与应力之比。
常用工程材料属性弹性模量泊松比质量密度抗剪模张力强度屈服度度

常用工程材料属性弹性模量泊松比质量密度抗剪模张力强度屈服度度1. 弹性模量(Young's modulus):弹性模量反映了材料在外力作用下的变形程度。
它定义为材料在线性弹性阶段的应力与应变的比值。
单位为帕斯卡(Pa)或兆帕(MPa)。
弹性模量越大,材料的刚度越高,抗变形能力越强。
典型弹性模量值:金属约为100-400GPa,钢约为200-210GPa,铝约为70GPa。
2. 泊松比(Poisson's ratio):泊松比定义为材料纵向(拉伸方向)的应变与横向(垂直拉伸方向)应变之比。
它是衡量材料的压缩性和延展性的能力的参数。
泊松比一般介于0和0.5之间,无量纲。
对于大多数金属材料,泊松比约为0.33. 质量密度(Density):质量密度是指物质的质量与体积的比值,单位为千克每立方米(kg/m³)或克每立方厘米(g/cm³)。
质量密度是衡量材料重量的参数,越大则材料越重。
4. 抗剪模量(Shear modulus):抗剪模量是材料在纵向剪切应力作用下的刚度指标。
它描述了材料的剪切刚度。
单位为帕斯卡(Pa)或兆帕(MPa)。
典型抗剪模量值:金属约为1/3-1/4弹性模量。
5. 张力强度(Tensile strength):张力强度指材料在拉伸过程中所能承受的最大应力。
单位为帕斯卡(Pa)或兆帕(MPa)。
张力强度较高的材料具有抵抗拉伸破坏的能力。
典型张力强度值:钢的张力强度约为300-400MPa,铝的张力强度约为150-300MPa。
6. 屈服度(Yield strength):屈服度是指材料在拉伸过程中从线性弹性阶段到塑性变形阶段的变化点,也称为屈服点。
屈服度是标志材料开始塑性变形的临界应力。
单位为帕斯卡(Pa)或兆帕(MPa)。
通常屈服度值会低于张力强度,典型屈服度值:钢的屈服度约为200-400MPa,铝的屈服度约为50-250MPa。
总结:以上所介绍的常用工程材料属性包括弹性模量、泊松比、质量密度、抗剪模量、张力强度和屈服度等,它们对于材料的应用、设计和性能具有重要意义,不同材料的这些属性值也有很大的差异。
几个基本常数弹性模量-泊松比-应力应变曲线

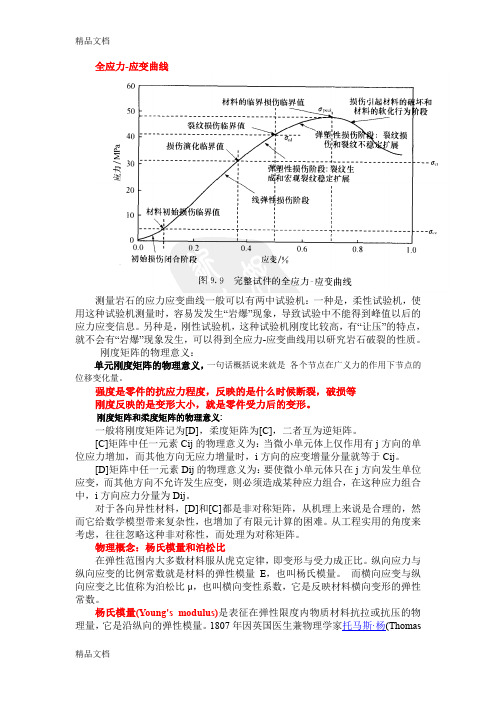
全应力-应变曲线测量岩石的应力应变曲线一般可以有两中试验机:一种是,柔性试验机,使用这种试验机测量时,容易发发生“岩爆”现象,导致试验中不能得到峰值以后的应力应变信息。
另种是,刚性试验机,这种试验机刚度比较高,有“让压”的特点,就不会有“岩爆”现象发生,可以得到全应力-应变曲线用以研究岩石破裂的性质。
刚度矩阵的物理意义:单元刚度矩阵的物理意义,一句话概括说来就是各个节点在广义力的作用下节点的位移变化量。
强度是零件的抗应力程度,反映的是什么时候断裂,破损等刚度反映的是变形大小,就是零件受力后的变形。
刚度矩阵和柔度矩阵的物理意义:一般将刚度矩阵记为[D],柔度矩阵为[C],二者互为逆矩阵。
[C]矩阵中任一元素Cij的物理意义为:当微小单元体上仅作用有j方向的单位应力增加,而其他方向无应力增量时,i方向的应变增量分量就等于Cij。
[D]矩阵中任一元素Dij的物理意义为:要使微小单元体只在j方向发生单位应变,而其他方向不允许发生应变,则必须造成某种应力组合,在这种应力组合中,i方向应力分量为Dij。
对于各向异性材料,[D]和[C]都是非对称矩阵,从机理上来说是合理的,然而它给数学模型带来复杂性,也增加了有限元计算的困难。
从工程实用的角度来考虑,往往忽略这种非对称性,而处理为对称矩阵。
物理概念:氏模量和泊松比在弹性围大多数材料服从虎克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E,也叫氏模量。
而横向应变与纵向应变之比值称为泊松比μ,也叫横向变性系数,它是反映材料横向变形的弹性常数。
氏模量(Young's modulus)是表征在弹性限度物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·(ThomasYoung, 1773-1829) 所得到的结果而命名。
根据胡克定律,在物体的弹性限度,应力与应变成正比,比值被称为材料的氏模量,它是表征材料性质的一个物理量,仅取决于材料本身的物理性质。
(完整版)材料力学简答题

(完整版)材料力学简答题1、(中)材料的三个弹性常数是什么?它们有何关系?材料的三个弹性常数是弹性模量E,剪切弹性模量G和泊松比μ,它们的关系是G=E/2(1+μ)。
2、何谓挠度、转角?挠度:横截面形心在垂直于梁轴线方向上的线位移。
转角:横截面绕其中性轴旋转的角位移。
3、强度理论分哪两类?最大应切力理论属于哪一类强度理论?Ⅰ.研究脆性断裂力学因素的第一类强度理论,其中包括最大拉应力理论和最大伸长线应变理论;Ⅱ. 研究塑性屈服力学因素的第二类强度理论,其中包括最大切应力理论和形状改变能密度理论。
4、何谓变形固体?在材料力学中对变形固体有哪些基本假设?在外力作用下,会产生变形的固体材料称为变形固体。
变形固体有多种多样,其组成和性质是复杂的。
对于用变形固体材料做成的构件进行强度、刚度和稳定性计算时,为了使问题得到简化,常略去一些次要的性质,而保留其主要性质。
根据其主要的性质对变形固体材料作出下列假设。
1.均匀连续假设。
2.各向同性假设。
3.小变形假设。
5、为了保证机器或结构物正常地工作,每个构件都有哪些性能要求?强度要求、刚度要求和稳定性要求。
6、用叠加法求梁的位移,应具备什么条件?用叠加法计算梁的位移,其限制条件是,梁在荷载作用下产生的变形是微小的,且材料在线弹性范围内工作。
具备了这两个条件后,梁的位移与荷载成线性关系,因此梁上每个荷载引起的位移将不受其他荷载的影响。
7、列举静定梁的基本形式?简支梁、外伸梁、悬臂梁。
8、列举减小压杆柔度的措施?(1)加强杆端约束(2)减小压杆长度,如在中间增设支座(3)选择合理的截面形状,在截面面积一定时,尽可能使用那些惯性矩大的截面。
9、欧拉公式的适用范围?=只适用于压杆处于弹性变形范围,且压杆的柔度应满足:λ≥λ110、列举图示情况下挤压破坏的结果?一种是钢板的圆孔局部发生塑性变形,圆孔被拉长;另一种是铆钉产生局部变形,铆钉的侧面被压扁。
11、简述疲劳破坏的特征?(1)构件的最大应力在远小于静应力的强度极限时,就可能发生破坏;(2)即使是塑性材料,在没有显著的塑性变形下就可能发生突变的断裂破坏;(3)断口明显地呈现两具区域:光滑区和粗糙区。
《应力应变曲线》课件

结果输出
绘制应力应变曲线,并分 析材料的弹塑性行为。
实验结果与分析
要点一
实验结果
通过实验获得一组应力应变数据,可以绘制出应力应变曲 线。
要点二
结果分析
根据应力应变曲线,可以分析材料的弹塑性行为,包括屈 服点、弹性极限、应变硬化等特性。这些特性对于材料的 选择和应用具有重要意义。例如,在机械设计中,需要选 择具有合适弹塑性行为的材料来保证结构的稳定性和安全 性。同时,通过分析材料的弹塑性行为,可以为材料的进 一步改性或优化提供理论依据。
理论计算方法
弹性力学公式
根据材料的弹性常数和几何形状,利用弹性力学公式计 算应力应变关系。
塑性力学公式
在达到屈服点后,材料进入塑性阶段,此时需要利用塑 性力学公式计算应力应变关系。
数值模拟方法
01
有限元分析
利用有限元分析软件建立材料的有限元模型,通 过模拟加载过程得到应力应变曲线。
02
有限差分法
06
应变曲线的理论计算
弹性力学基础
弹性力学定义
弹性力学是研究物体在弹性介质中受 到外力作用时的应力、应变和位移的 学科。
基本假设
弹性力学的基本方程
包括平衡方程、几何方程、物理方程 等。
连续性、均匀性、各向同性、小变形 等假设。
应变曲线的理论模型
应变曲线的基本形式
描述了应力与应变之间的关系,通常呈现非线性的特点。
通过建立材料的有限元模型,模拟材料的 应力应变行为,可以得到材料的应力应变 曲线。
材料模型的建立
根据材料的性质和实验数据,建立材料的 本构方程或材料模型,如弹性模型、弹塑 性模型、粘塑性模型等。
边界条件的设定
求解方法的选择
(整理)几个基本常数弹性模量-泊松比-应力应变曲线.
全应力-应变曲线测量岩石的应力应变曲线一般可以有两中试验机:一种是,柔性试验机,使用这种试验机测量时,容易发发生“岩爆”现象,导致试验中不能得到峰值以后的应力应变信息。
另种是,刚性试验机,这种试验机刚度比较高,有“让压”的特点,就不会有“岩爆”现象发生,可以得到全应力-应变曲线用以研究岩石破裂的性质。
刚度矩阵的物理意义:单元刚度矩阵的物理意义,一句话概括说来就是各个节点在广义力的作用下节点的位移变化量。
强度是零件的抗应力程度,反映的是什么时候断裂,破损等刚度反映的是变形大小,就是零件受力后的变形。
刚度矩阵和柔度矩阵的物理意义:一般将刚度矩阵记为[D],柔度矩阵为[C],二者互为逆矩阵。
[C]矩阵中任一元素Cij的物理意义为:当微小单元体上仅作用有j方向的单位应力增加,而其他方向无应力增量时,i方向的应变增量分量就等于Cij。
[D]矩阵中任一元素Dij的物理意义为:要使微小单元体只在j方向发生单位应变,而其他方向不允许发生应变,则必须造成某种应力组合,在这种应力组合中,i方向应力分量为Dij。
对于各向异性材料,[D]和[C]都是非对称矩阵,从机理上来说是合理的,然而它给数学模型带来复杂性,也增加了有限元计算的困难。
从工程实用的角度来考虑,往往忽略这种非对称性,而处理为对称矩阵。
物理概念:杨氏模量和泊松比在弹性范围内大多数材料服从虎克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E,也叫杨氏模量。
而横向应变与纵向应变之比值称为泊松比μ,也叫横向变性系数,它是反映材料横向变形的弹性常数。
杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·杨(ThomasYoung, 1773-1829) 所得到的结果而命名。
根据胡克定律,在物体的弹性限度内,应力与应变成正比,比值被称为材料的杨氏模量,它是表征材料性质的一个物理量,仅取决于材料本身的物理性质。
(完整版)高分子材料的拉伸性能.doc

《高分子材料的拉伸性能测试》实验指导书一、实验目的1、测试热塑性塑料拉伸性能。
2、掌握高分子材料的应力—应变曲线的绘制。
4、了解塑料抗张强度的实验操作。
二、实验原理拉伸试验是材料最基本的一种力学性能试验方法,可以得到材料的各种拉伸性能,包括拉伸强度、弹性模量、泊松比、伸长率、应力 -应变曲线等。
拉伸试验是指在规定的温度、湿度和试验速度下,在试样上沿纵轴方向施加拉伸载荷使其破坏,此时材料的性能指标如下:1.拉伸强度为:(1)式中σ -- 拉伸强度, MPa;P--- 破坏载荷(或最大载荷),N;b--- 试样宽度, cm;h--- 试样厚度, cm.2. 拉伸破坏 ( 或最大载荷处 ) 的伸长率为:(2)式中ε ---试样拉伸破坏(或最大载荷处)伸长率,%;L0- 破坏时标距内伸长量, cm;L0--- 测量的标距,cm,3.拉伸弹性模量为:(3)式中E t---拉伸弹性模量,MPa;P—荷载-变形曲线上初始直线段部分载荷量,N;L0—与载荷增量对应的标距内变形量,cm。
4. 拉伸应力- 应变曲线如果材料是理想弹性体,抗张应力与抗张应变之间的关系服从胡克定律,即:σ= E ε式中: E-杨氏模量或拉伸模量;σ-应力;ε-应变聚合物材料由干本身长链分子的大分子结构持点,使其具有多重的运动单元,因此不是理想的弹性体,在外力作用下的力学行为是一个松弛过程,具有明显的粘弹性质。
拉伸试验时因试验条件的不同,其拉伸行为有很大差别。
起始时,应力增加,应变也增加,在 A 点之前应力与应变成正比关系,符合胡克定律,呈理想弹性体。
A点叫做比例极限点。
超过A点后的一段,应力增大,应变仍增加,但二者不再成正比关系,比值逐渐减小;当达到Y点时,其比值为零。
Y点叫做屈服点。
此时弹性模最近似为零,这是一个重要的材料持征点。
对塑料来说,它是使用的极限。
如果再继续拉伸,应力保持不变甚至还会下降,而应变可以在一个相当大的范围内增加,直至断裂。
五种家具常用木材弹性常数及力学性能参数的测定

五种家具常用木材弹性常数及力学性能参数的测定张帆,李黎,张立,徐卓(北京林业大学材料科学与技术学院,北京100083)摘要:采用电测法和三点弯曲法对5种家具常用木材的弹性常数及主要力学性能参数进行了试验测定,并根据木材的正交异性原理对试验结果进行了统计分析。
对木材物理力学性能参数测定的试验方法进行研究和探讨,为实木家具结构力学设计提供材料性能参考数据。
关键词:木材弹性常数;力学性能;家具结构设计中图分类号:TS 612文献标识码:A文章编号:2095-2953(2012)01-0016-04Study of the Determination of the Elastic Constants and Mechanical PropertyParameters of Five Kinds of Wood Commonly Used in FurnitureZHANG Fan,LI Li,ZHANG Li,XU Zhuo(College of Materials Science and Technology,Beijing Forestry University,Beijing 100083,China )Abstract :The te s t de te rm ina tio n o f the e las tic co ns tants a nd m e cha nica l pro pe rty pa ra m e te rs o f five kinds o f wo o d co m m o nly us ed in furniture is co nducted us ing a n e le ctrical m ea s ure m e nt m e thod a nd a thre e po int bending m etho d a nd a s ta tis tica l a na lys is o f the te s t re s ult is m a de acco rding to the o rtho tro pic principle o f w o od.The te s t m e thod fo r de term ining the phys ica l a nd m echanical pro pe rty pa ra m e te rs o f wo o d is s tudie d a nd dis cus s e d,which pro vide s a re fe re nce bas is fo r the s tructure m e cha nica l de s ig n of s olid furniture.Key words :wo o d e la s tic co ns ta nt;m e cha nica l pro perty;s tructura l de s ig n o f furniture木材的物理力学特性对实木家具构件的强度、刚度及稳定性具有重要的意义。
abaqus 金属材料参数 应力应变曲线

abaqus 金属材料参数应力应变曲线abaqus 金属材料参数应力应变曲线1. 引言金属材料的力学性质对于工程设计和材料研究至关重要。
在工程应用中,了解金属材料的力学行为可以帮助我们预测材料在加载条件下的性能和可靠性。
而abaqus作为一款常用的有限元分析软件,能够通过建立合适的材料模型,模拟材料的力学响应。
在abaqus中,金属材料参数的设定是非常重要的,其中最基本和常用的参数之一是应力应变曲线。
本文将深入探讨abaqus中金属材料参数的设置与应力应变曲线的关系,为读者提供有关abaqus金属材料参数应用的深入理解。
2. 金属材料参数的设置2.1 弹性模量与泊松比金属材料的弹性模量是一个关键参数,描述了材料在弹性阶段的应力-应变行为。
弹性模量可以通过材料的压缩试验或拉伸试验得到。
在abaqus中,可以通过输入杨氏模量和泊松比来定义材料的弹性行为。
对于弹性完全线性的材料,可以简单地输入杨氏模量和泊松比即可。
2.2 屈服强度与应变硬化模型金属材料在受到一定应力时会发生塑性变形,而塑性变形的起始点就是屈服强度。
在abaqus中,屈服强度可以通过输入屈服应力和屈服应变来定义。
一般来说,屈服应力可以通过材料的拉伸试验曲线得到。
而屈服应变可以通过使用应变硬化模型来描述。
应变硬化模型是用来描述金属材料在塑性变形过程中硬化的机理。
abaqus中提供了多种应变硬化模型,如线性硬化模型、赫希方程模型和拉曼方程模型等。
不同的模型适用于不同的材料和力学行为。
我们需要根据具体的材料性质和实验数据,选择最适合的应变硬化模型,并确定相应的参数。
3. 应力应变曲线的建立在abaqus中,通过建立材料模型和输入相应的材料参数,可以生成应力应变曲线。
在进行有限元分析时,abaqus会根据设定的材料参数,结合加载条件,自动生成材料的应力应变曲线。
通过abaqus生成的应力应变曲线可以帮助我们深入理解金属材料的力学行为。
通过观察应力应变曲线的特征,我们可以了解金属材料的强度、塑性、韧性等性能。
实验5 拉伸性能测定 (2)

试验五 拉伸性能测定一、 目的要求1. 明确试验条件。
2. 测试热塑性塑料和玻璃纤维增强塑料拉伸性能。
二、 原理拉伸试验是最基本的一种力学性能试验方法。
测定塑料、玻璃纤维织物增强塑料板材和短切玻璃纤维增强塑料的拉伸性能,包括拉伸强度、弹性模量、泊松比、伸长率、应力-应变曲线等。
拉伸试验是指在规定的温度、湿度和试验速度下,在试样上沿纵轴方向施加载荷使其破坏,此时材料的性能指标如下:1. 拉伸强度为hb P t ⋅=σ 式中 t σ——拉伸强度,Mpa ;P ——破坏载荷(或最大载荷),N ;b ——试样宽度,cm ;h ——试样厚度,cm 。
2. 拉伸破坏(或最大载荷处)的伸长率为1000⨯∆=L L b t ε 式中 t ε——试样拉伸破坏(或最大载荷处)伸长率,%;b L ∆——试样破坏时(或最大载荷处)标距0L 内伸长量,cm ; 0L ——测量的标距,cm 。
3. 拉伸弹性模量为t E =L h b PL ∆⋅⋅∆⋅0式中 t E ——拉伸弹性模量,Mpa ;P ∆——载荷-变形曲线上初始直线段的载荷增量,N ;L ∆ ——与载荷增量P ∆对应的标距0L 内的变形增量,cm 。
4. 泊松比为μ =12εε-式中 μ——泊松比;21,εε ——分别为载荷增量P ∆对应的纵向应变和横向应变。
222111/,/L L L L ∆=∆=εε式中 21,L L ——分别为纵向和横向的测量标距,cm21,L L ∆∆——分别为与载荷增量P ∆对应的标距21,L L 的变形增,cm5. 拉伸应力-应变曲线图玻璃纤维增强塑料拉伸应力-应变曲线由折线组成,折线的拐点出现在强度极限的三分之一处附近,试样拉伸过程达到此处时,可听到有开裂声,并伴随在试样表面上出现白斑。
由于折线的存在,就形成了所谓第一弹性模量和第二弹性模量问题。
形成第二弹性模量是复合材料的特点,这主要是由于在受力状况下树脂和纤维延伸率不同,在界面处出现开裂(热固性树脂延伸率仅1%左右,玻璃纤维延伸率:有碱纤维为2.7%,无碱纤维为3%),此时复合材料中有缺陷的纤维先行断裂,致使纤维总数少于起始状态,相应每根纤维上受力增加,形变也就增加,这是弹性模量降低的缘故。
材料力学应力应变部分

材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力 表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力) 体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p 应分解为正应力σ ,切应力τ 。
→应力单位pa ,1pa=1N/m 2;常用Mpa ,1Mpa=106pa 。
第二章 拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→F N =σA ;σ(x)=F N (x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力 α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,σα=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A ,45°斜截面上,力→√22,面积→√22。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取n s =1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取n b =2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
σ=Eε ,弹性模量E 的值随材料而不同。
∆l l=ε=σE =F AE ;∆l =FLAE即,对长度相同,受力相等的杆件,有EA 越大则变形Δl越小,所以称EA 为杆件的抗拉/压刚度。
泊松比、弹性模量、剪切模量

目录泊松比 (1)杨氏模量 (1)弹性模量 (2)剪切模量 (3)基本概念 (3)纤维复合材料层间剪切模量测试 (3)筑坝堆石料的剪切模量 (4)弹性模量和切变模量 (7)弹簧钢的切变模量取值 (8)泊松比法国数学家 Simeom Denis Poisson 为名。
在材料的比例极限内,由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。
比如,一杆受拉伸时,其轴向伸长伴随着横向收缩(反之亦然),而横向应变 e' 与轴向应变 e 之比称为泊松比 V。
材料的泊松比一般通过试验方法测定。
可以这样记忆:空气的泊松比为0,水的泊松比为0.5,中间的可以推出。
主次泊松比的区别Major and Minor Poisson's ratio主泊松比PRXY,指的是在单轴作用下,X方向的单位拉(或压)应变所引起的Y 方向的压(或拉)应变次泊松比NUXY,它代表了与PRXY成正交方向的泊松比,指的是在单轴作用下,Y 方向的单位拉(或压)应变所引起的X方向的压(或拉)应变。
PRXY与NUXY是有一定关系的: PRXY/NUXY=EX/EY对于正交各向异性材料,需要根据材料数据分别输入主次泊松比,但是对于各向同性材料来说,选择PRXY或NUXY来输入泊松比是没有任何区别的,只要输入其中一个即可杨氏模量杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·杨(Thomas Young, 1773-1829) 所得到的结果而命名。
根据胡克定律,在物体的弹性限度内,应力与应变成正比,比值被称为材料的杨氏模量,它是表征材料性质的一个物理量,仅取决于材料本身的物理性质。
杨氏模量的大小标志了材料的刚性,杨氏模量越大,越不容易发生形变。
杨氏弹性模量是选定机械零件材料的依据之一是工程技术设计中常用的参数。
杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度,泊松比

杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度,泊松比“模量”可以理解为是一种标准量或指标。
材料的“模量”一般前面要加说明语,如弹性模量、压缩模量、剪切模量、截面模量等。
这些都是与变形有关的一种指标。
杨氏模量(Young'sModulus)——杨氏模量就是弹性模量,这是材料力学里的一个概念。
对于线弹性材料有公式σ(正应力)=Eε(正应变)成立,式中σ为正应力,ε为正应变,E为弹性模量,是与材料有关的常数,与材料本身的性质有关。
杨(ThomasYoung1773~1829)在材料力学方面,研究了剪形变,认为剪应力是一种弹性形变。
1807年,提出弹性模量的定义,为此后人称弹性模量为杨氏模量。
钢的杨氏模量大约为2×1011N∙m-2,C30混凝土是3.00×1010N∙m-2。
弹性模量(ElasticModulus)E——弹性模量E是指材料在弹性变形范围内,作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力(如拉伸,压缩,弯曲,剪切等)与材料产生的相应应变之比。
弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结构不敏感参数。
在工程上,弹性模量则是材料刚度的度量,是物体变形难易程度的表征。
弹性模量E是在比例极限内,应力与材料相应的应变之比。
对于有些材料在弹性范围内应力-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的办法来代替它的弹性模量值。
根据不同的受力情况,有相应的拉伸弹性模量(杨氏模量)、剪切弹性模量(刚性模量)、体积弹性模量、压缩弹性模量等。
剪切模量G(ShearModulus)——剪切模量是指剪切应力与剪切应变之比,它表征材料抵抗切应变的能力。
模量大,则表示材料的刚性强。
剪切模数G是材料的基本物理特性参数之一,可表示材料剪切变形的难易程度;与杨氏(压缩、拉伸)弹性模量E、泊桑比ν并列为材料的三项基本物理特性参数,在材料力学、弹性力学中有广泛的应用。
结构力学形常数和载常数表

结构力学形常数和载常数表1. 形常数形常数是指描述材料在变形过程中的力学行为的常数。
在结构力学中,常见的形常数有弹性模量、剪切模量、泊松比等。
弹性模量是衡量材料抗弯曲和拉伸变形能力的常数。
它描述了材料在受力后产生的应力与应变之间的关系。
弹性模量越大,材料的刚度越高,抗弯曲和拉伸能力越强。
剪切模量是衡量材料抗剪切变形能力的常数。
它描述了材料在受到剪切力时产生的剪切应力与剪切应变之间的关系。
剪切模量越大,材料的刚度越高,抗剪切能力越强。
泊松比是衡量材料在受力时体积变化与横向应变之间的关系的常数。
它描述了材料在受到拉伸或压缩力时纵向应变与横向应变之间的比例关系。
泊松比的取值范围在0到0.5之间,常见材料的泊松比一般在0.25左右。
2. 载常数载常数是指结构在受到外部荷载时所产生的应力与应变之间的关系的常数。
在结构力学中,常见的载常数有抗弯强度、抗剪强度、抗压强度等。
抗弯强度是材料在受到弯曲力时能够抵抗变形和破坏的能力。
它描述了材料在弯曲过程中所能承受的最大应力。
抗弯强度越大,材料的抗弯能力越强。
抗剪强度是材料在受到剪切力时能够抵抗剪切变形和破坏的能力。
它描述了材料在剪切过程中所能承受的最大应力。
抗剪强度越大,材料的抗剪能力越强。
抗压强度是材料在受到压缩力时能够抵抗压缩变形和破坏的能力。
它描述了材料在压缩过程中所能承受的最大应力。
抗压强度越大,材料的抗压能力越强。
形常数和载常数是结构力学中非常重要的参数,它们直接影响着结构的性能和安全性。
在设计和分析结构时,我们需要准确地了解材料的形常数和载常数,以确保结构的稳定性和承载能力。
除了这些常见的形常数和载常数之外,还有许多其他的参数和常数在结构力学中起着重要的作用,如杨氏模量、体积模量、屈服强度等。
这些参数的取值与材料的性质和结构的要求有关,不同的材料和结构可能有不同的形常数和载常数。
形常数和载常数是结构力学中不可或缺的概念和参数。
它们描述了材料和结构在受力时的力学行为,对于结构的设计和分析起着重要的指导作用。
材料力学线弹性材料知识点总结

材料力学线弹性材料知识点总结材料力学是工程学科中的重要分支,它研究物质在外力作用下的力学性质和变形行为。
其中,线弹性材料是一类具有线弹性特性的材料,其力学性能相对简单,因此被广泛应用于各个领域。
在本篇文章中,将对线弹性材料的相关知识进行总结和归纳。
I. 弹性模量弹性模量是衡量材料抵抗单位面积应力的能力,常用符号为E。
根据胡克定律,线弹性材料的应力和应变之间存在线性关系,即应力等于弹性模量与应变的乘积:σ = Eε。
II. 线弹性材料的应力应变关系线弹性材料的应力应变关系可以用杨氏模量和泊松比来描述。
杨氏模量表示材料在拉伸或压缩时的刚度,泊松比则表示材料在轴向受力时的横向收缩程度。
1. 杨氏模量杨氏模量是衡量材料单位应变下的应力增量,常用符号为E。
一般情况下,材料越硬,杨氏模量越大,说明材料具有较高的刚度。
2. 泊松比泊松比是衡量材料在轴向受力时横向收缩程度的比例系数,常用符号为ν。
泊松比的取值范围在0和0.5之间,其中,当材料不发生体积变化时,泊松比为0.5;当材料完全不会发生横向收缩时,泊松比为0。
III. 应力应变曲线应力应变曲线是反映材料在外力作用下应力和应变的关系的曲线图。
对于线弹性材料,应力应变曲线呈线性关系,分为弹性阶段和屈服阶段。
1. 弹性阶段在弹性阶段,材料的应变与应力之间存在线性关系,即材料会随着外力的撤离而恢复最初的形状。
该阶段的应力应变曲线为直线,呈比例关系。
2. 屈服阶段当材料受到较大的外力时,会超出其弹性限度,材料将出现应力和应变不再成比例的情况,即开始进入屈服阶段。
屈服阶段的应力应变曲线为弯曲线,曲线上的点称为屈服点。
IV. 各向同性与各向异性各向同性和各向异性是描述材料力学性质的两个重要概念。
1. 各向同性材料各向同性材料是指材料的性质在各个方向上具有相同的特性。
这意味着,在任何方向上施加的外力和应变对材料的响应都是相同的。
大部分金属和合金都属于各向同性材料。
2. 各向异性材料各向异性材料是指材料的性质在不同的方向上具有差异。
泊松比、弹性模量、剪切模量

目录泊松比 (1)杨氏模量 (1)弹性模量 (2)剪切模量 (3)基本概念 (3)纤维复合材料层间剪切模量测试 (3)筑坝堆石料的剪切模量 (4)弹性模量和切变模量 (7)弹簧钢的切变模量取值 (8)泊松比法国数学家 Simeom Denis Poisson 为名。
在材料的比例极限内,由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。
比如,一杆受拉伸时,其轴向伸长伴随着横向收缩(反之亦然),而横向应变 e' 与轴向应变 e 之比称为泊松比 V。
材料的泊松比一般通过试验方法测定。
可以这样记忆:空气的泊松比为0主次泊松比的区别Major and Minor Poisson's ratio主泊松比PRXY,指的是在单轴作用下,X方向的单位拉(或压)应变所引起的Y 方向的压(或拉)应变次泊松比NUXY,它代表了与PRXY成正交方向的泊松比,指的是在单轴作用下,Y 方向的单位拉(或压)应变所引起的X方向的压(或拉)应变。
PRXY与NUXY是有一定关系的: PRXY/NUXY=EX/EY对于正交各向异性材料,需要根据材料数据分别输入主次泊松比,但是对于各向同性材料来说,选择PRXY或NUXY来输入泊松比是没有任何区别的,只要输入其中一个即可杨氏模量杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·杨(Thomas Young, 1773-1829) 所得到的结果而命名。
根据胡克定律,在物体的弹性限度内,应力与应变成正比,比值被称为材料的杨氏模量,它是表征材料性质的一个物理量,仅取决于材料本身的物理性质。
杨氏模量的大小标志了材料的刚性,杨氏模量越大,越不容易发生形变。
杨氏弹性模量是选定机械零件材料的依据之一是工程技术设计中常用的参数。
杨氏模量的测定对研究金属材料、光纤材料、半导体、纳米材料、聚合物、陶瓷、橡胶等各种材料的力学性质有着重要意义,还可用于机械零部件设计、生物力学、地质等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全应力-应变曲线测量岩石的应力应变曲线一般可以有两中试验机:一种是,柔性试验机,使用这种试验机测量时,容易发发生“岩爆”现象,导致试验中不能得到峰值以后的应力应变信息。
另种是,刚性试验机,这种试验机刚度比较高,有“让压”的特点,就不会有“岩爆”现象发生,可以得到全应力-应变曲线用以研究岩石破裂的性质。
刚度矩阵的物理意义:单元刚度矩阵的物理意义,一句话概括说来就是各个节点在广义力的作用下节点的位移变化量。
强度是零件的抗应力程度,反映的是什么时候断裂,破损等刚度反映的是变形大小,就是零件受力后的变形。
刚度矩阵和柔度矩阵的物理意义:一般将刚度矩阵记为[D],柔度矩阵为[C],二者互为逆矩阵。
[C]矩阵中任一元素Cij的物理意义为:当微小单元体上仅作用有j方向的单位应力增加,而其他方向无应力增量时,i方向的应变增量分量就等于Cij。
[D]矩阵中任一元素Dij的物理意义为:要使微小单元体只在j方向发生单位应变,而其他方向不允许发生应变,则必须造成某种应力组合,在这种应力组合中,i方向应力分量为Dij。
对于各向异性材料,[D]和[C]都是非对称矩阵,从机理上来说是合理的,然而它给数学模型带来复杂性,也增加了有限元计算的困难。
从工程实用的角度来考虑,往往忽略这种非对称性,而处理为对称矩阵。
物理概念:杨氏模量和泊松比在弹性范围内大多数材料服从虎克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E,也叫杨氏模量。
而横向应变与纵向应变之比值称为泊松比μ,也叫横向变性系数,它是反映材料横向变形的弹性常数。
杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·杨(Thomas Young, 1773-1829) 所得到的结果而命名。
根据胡克定律,在物体的弹性限度内,应力与应变成正比,比值被称为材料的杨氏模量,它是表征材料性质的一个物理量,仅取决于材料本身的物理性质。
杨氏模量的大小标志了材料的刚性,杨氏模量越大,越不容易发生形变。
FL/EA=△L,其中F是力,L是长度,E是弹性模量,A是截面积,△L是长度变化量,也就是形变。
弹性模量可视为衡量材料产生弹性变形难易程度的指标,其值越大,使材料发生一定弹性变形的应力也越大,即材料刚度越大,亦即在一定应力作用下,发生弹性变形越小。
弹性模量E是指材料在外力作用下产生单位弹性变形所需要的应力。
它是反映材料抵抗弹性变形能力的指标,相当于普通弹簧中的刚度。
力学里没有弹性系数这个物理量。
杨氏弹性模量是选定机械零件材料的依据之一是工程技术设计中常用的参数。
杨氏模量的测定对研究金属材料、光纤材料、半导体、纳米材料、聚合物、陶瓷、橡胶等各种材料的力学性质有着重要意义,还可用于机械零部件设计、生物力学、地质等领域。
测量杨氏模量的方法一般有拉伸法、梁弯曲法、振动法、内耗法等,还出现了利用光纤位移传感器、莫尔条纹、电涡流传感器和波动传递技术(微波或超声波)等实验技术和方法测量杨氏模量。
胡克定律和杨氏弹性模量固体在外力作用下将发生形变,如果外力撤去后相应的形变消失,这种形变称为弹性形变。
如果外力后仍有残余形变,这种形变称为范性形变。
应力(σ)单位面积上所受到的力(F/S)。
应变(ε ):是指在外力作用下的相对形变(相对伸长DL/L)它反映了物体形变的大小。
胡克定律:在物体的弹性限度内,应力与应变成正比,其比例系数称为杨氏模量(记为Y)。
用公式表达为:Y=(F·L)/(S·△L)Y在数值上等于产生单位应变时的应力。
它的单位是与胁力的单位相同。
杨氏弹性模量是材料的属性,与外力及物体的形状无关。
杨氏模数(Young's modulus )是材料力学中的名词,弹性材料承受正向应力时会产生正向应变,定义为正向应力与正向应变的比值。
公式记为E = σ / ε其中,E 表示杨氏模数,σ 表示正向应力,ε 表示正向应变。
杨氏模量大,说明压缩或拉伸该材料,材料的形变小。
一般的如楼上所说但是有些是各向异性的及各个方向的弹性模量不同用矩阵表示弹性模量英文名称:Elastic Modulus,又称 Young 's Modulus(杨氏模量)定义:材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。
单位:达因每平方厘米。
意义:弹性模量可视为衡量材料产生弹性变形难易程度的指标,其值越大,使材料发生一定弹性变形的应力也越大,即材料刚度越大,亦即在一定应力作用下,发生弹性变形越小。
弹性模量E是指材料在外力作用下产生单位弹性变形所需要的应力。
它是反映材料抵抗弹性变形能力的指标,相当于普通弹簧中的刚度。
说明:又称杨氏模量。
弹性材料的一种最重要、最具特征的力学性质。
是物体弹性t变形难易程度的表征。
用E表示。
定义为理想材料有小形变时应力与相应的应变之比。
E以单位面积上承受的力表示,单位为牛/米^2。
模量的性质依赖于形变的性质。
剪切形变时的模量称为剪切模量,用G表示;压缩形变时的模量称为压缩模量,用K表示。
模量的倒数称为柔量,用J表示。
拉伸试验中得到的屈服极限бb和强度极限бS ,反映了材料对力的作用的承受能力,而延伸率δ 或截面收缩率ψ,反映了材料缩性变形的能力,为了表示材料在弹性范围内抵抗变形的难易程度,在实际工程结构中,材料弹性模量E的意义通常是以零件的刚度体现出来的,这是因为一旦零件按应力设计定型,在弹性变形范围内的服役过程中,是以其所受负荷而产生的变形量来判断其刚度的。
一般按引起单为应变的负荷为该零件的刚度,例如,在拉压构件中其刚度为:式中 A0为零件的横截面积。
由上式可见,要想提高零件的刚度E A0,亦即要减少零件的弹性变形,可选用高弹性模量的材料和适当加大承载的横截面积,刚度的重要性在于它决定了零件服役时稳定性,对细长杆件和薄壁构件尤为重要。
因此,构件的理论分析和设计计算来说,弹性模量E是经常要用到的一个重要力学性能指标。
在弹性范围内大多数材料服从胡克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E,也叫杨氏模量。
弹性模量在比例极限内,材料所受应力如拉伸,压缩,弯曲,扭曲,剪切等)与材料产生的相应应变之比,用牛/米^2表示。
弹性模量:材料的抗弹性变形的一个量,材料刚度的一个指标。
它只与材料的化学成分有关,与其组织变化无关,与热处理状态无关。
各种钢的弹性模量差别很小,金属合金化对其弹性模量影响也很小。
关于剪切模量,参考: ... urse/8_2.html切线模量好像是塑性阶段的曲线斜率;切变弹性模量;切变弹性模量G,材料的基本物理特性参数之一,与杨氏(压缩、拉伸)弹性模量E、泊桑比ν并列为材料的三项基本物理特性参数,在材料力学、弹性力学中有广泛的应用。
其定义为:G=τ/γ,其中G(Mpa)为切变弹性模量;τ为剪切应力(Mpa);γ为剪切应变(弧度)。
泊松比法国数学家 Simeom Denis Poisson 为名。
在材料的比例极限内,由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。
比如,一杆受拉伸时,其轴向伸长伴随着横向收缩(反之亦然),而横向应变 e' 与轴向应变 e 之比称为泊松比 V。
材料的泊松比一般通过试验方法测定。
(在弹性范围内大多数材料服从虎克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E,也叫杨氏模量。
横向应变与纵向应变之比值称为泊松比µ,也叫横向变性系数,它是反映材料横向变形的弹性常数。
)(一种物质在固体状态下一个方向有拉(或压)形变伸长 l 时,与之垂直的方向就会出现缩小(或增加)l' 泊松比是指形变量的比正负之比取负值;对一根杆件来说,横向伸长那么轴向必然缩短,所以出现正应变的比值为负的情况,一般我们取的泊松比是横向正应变与轴向正应变的比值的绝对值。
)可以这样记忆:空气的泊松比为0,水的泊松比为0.5,中间的可以推出。
主次泊松比的区别Major and Minor Poisson's ratio主泊松比PRXY,指的是在单轴作用下,X方向的单位拉(或压)应变所引起的Y方向的压(或拉)应变次泊松比NUXY,它代表了与PRXY成正交方向的泊松比,指的是在单轴作用下,Y方向的单位拉(或压)应变所引起的X方向的压(或拉)应变。
PRXY与NUXY是有一定关系的: PRXY/NUXY=EX/EY对于正交各向异性材料,需要根据材料数据分别输入主次泊松比,但是对于各向同性材料来说,选择PRXY或NUXY来输入泊松比是没有任何区别的,只要输入其中一个即可“模量”可以理解为是一种标准量或指标。
材料的“模量”一般前面要加说明语,如弹性模量、压缩模量、剪切模量、截面模量等。
这些都是与变形有关的一种指标。
杨氏模量(Young's Modulus):杨氏模量就是弹性模量,这是材料力学里的一个概念。
对于线弹性材料有公式σ(正应力)=Eε(正应变)成立,式中σ为正应力,ε为正应变,E为弹性模量,是与材料有关的常数,与材料本身的性质有关。
杨(ThomasYoung1773~1829)在材料力学方面,研究了剪形变,认为剪应力是一种弹性形变。
1807年,提出弹性模量的定义,为此后人称弹性模量为杨氏模量。
钢的杨氏模量大约为2×1011N·m-2,铜的是1.1×1011 N·m-2。
弹性模量(Elastic Modulus)E:弹性模量E是指材料在弹性变形范围内(即在比例极限内),作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力如拉伸,压缩,弯曲,扭曲,剪切等)与材料产生的相应应变之比。
弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结构不敏感参数。
在工程上,弹性模量则是材料刚度的度量,是物体变形难易程度的表征。
弹性模量E在比例极限内,应力与材料相应的应变之比。
对于有些材料在弹性范围内应力-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的办法来代替它的弹性模量值。
根据不同的受力情况,分别有相应的拉伸弹性模量modulus of elasticity for tension (杨氏模量)、剪切弹性模量shear modulus of elasticity (刚性模量)、体积弹性模量、压缩弹性模量等。
剪切模量G(Shear Modulus):剪切模量是指剪切应力与剪切应变之比。
剪切模数G=剪切弹性模量G=切变弹性模量G 切变弹性模量G,材料的基本物理特性参数之一,与杨氏(压缩、拉伸)弹性模量E、泊桑比ν并列为材料的三项基本物理特性参数,在材料力学、弹性力学中有广泛的应用。
