2020年九年级中考数学专题复习 几何:三角形综合(包含答案)
2020年中考数学三角形专题练习(含答案)

2020年中考数学三角形专题练习【名师精选全国真题,值得下载练习】一.选择题(每题3分,共30分)1.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的()A.三边中线的交点B.三条角平分线的交点C.三边高的交点D.三边垂直平分线的交点2.如图,在△ABC中,∠C=90°,AD是△ABC的一条角平分线.若AC=6,AB=10,则点D到AB边的距离为()A.2 B.2.5 C.3 D.43.如图,在△ABC中,AB=AC,∠A=40°,DE垂直平分AC,则∠BCD的度数等于()A.20°B.30°C.40°D.50°4.若等腰△ABC中有一个内角为40°,则这个等腰三角形的一个底角的度数为()A.40°B.100°C.40°或100°D.40°或70°5.适合下列条件的△ABC中,直角三角形的个数为()(1)a=b,∠A=45°(2)∠A=32°,∠B=58°,(3)a=5,b=12,c=13,(4)a=52,b=122,c=132,A.1个B.2个C.3个D.4个6.如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,若∠A=40°,∠P=38°,则∠C的度数为()A.36°B.39°C.38°D.40°7.如图是由11个等边三角形拼成的六边形,若最小等边三角形的边长为a,最大等边三角形的边长为b,则a与b的关系为()A.b=3a B.b=5a C.b=a D.b=a8.如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是()A.36 B.24 C.18 D.169.如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB的中点,E为线段AD上一点,过E点的线段FG交CD的延长线于G点,交AC于F点,且EG=AE.分别延长CE,BG交于点H,若EH平分∠AEG,HD平分∠CHG则下列说法:①∠GDH =45°;②GD=ED;③EF=2DM;④CG=2DE+AE,正确的是()A.①②③B.①②④C.②③④D.①②③④10.如图,在Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P 作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=P A;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是()A.①②③B.①②④C.①③④D.①②③④二.填空题(每题3分,共30分)11.如图,△ABC为等边三角形,D、E分別是AC、BC上的点,且AD=CE,AE与BD 相交于点P,BF⊥AE于点F.若PF=4,PD=1,则AE的长为.12.已知等腰△ABC中,顶角∠A为36°,BD平分∠ABC交AC于D,那么AD:AC =.13.如图,等边△ABC外一点P,连接AP、BP、CP,AH垂直平分PC于点H,∠BAP 的平分线交PC于点D,连接BD,有以下结论:①DP=DB;②DA+DB=DC;③DA ⊥BP;④若连接BH,当△BDH为等边三角形时,则CP=3DP,其中正确的有.(只需要填写序号)14.已知点O是三角形ABC的重心,DE经过点O且平行于BC,则△ADE与四边形DBCE的面积比为.15.如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且AB =5cm,AC=3cm,BC=4cm,则△DEB的周长为.16.如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半,已知BC=2,△ABC平移的距离为.17.在△ABC中,边BC、AC上的中线AD、BE相交于点G,AD=6,那么AG=.18.如图,在△ABC中,中线BD,CE相交于点O,若S△ABC=4,则S△DOE=.19.在△ABC中,AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,则AC=,AB=.20.如图,∠MAN是一个钢架结构,已知∠MAN=15°,在角内部构造钢条BC,CD,DE,……且满足AB=BC=CD=DE=……则这样的钢条最多可以构造根.三.解答题(每题8分,共40分)21.如图,△ABC中,∠ABC=90°,AB=BC,D在边AC上,AE⊥BD于E.(1)如图1,作CF⊥BD于F,求证:CF﹣AE=EF;(2)如图2,若BC=CD,求证:BD=2AE;(3)如图3,作BM⊥BE,且BM=BE,AE=2,EN=4,连接CM交BE于N,请直接写出△BCM的面积为.22.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.(1)求证:DE=CE.(2)若∠CDE=25°,求∠A的度数.23.已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC 于E,点F是AE的中点.(1)线段FD与线段FC的数量关系,位置关系;(2)如图2,将△BDE绕点B逆时针旋转a(0°<a<90°),其它条件不变,线段FD 与线段FC的关系是否变化,写出你的结论并证明;(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2,直接写出线段BF的范围.24.已知,如图,∠C=∠D=90°,E是CD上一点,AE、BE分别平分∠DAB、∠ABC.求证:E是CD的中点.25.△ABC是等边三角形,BD是角平分线,过点D作DE⊥AB于E,交BC边的延长线于点F,AE=2.(1)求证:△DCF是等腰三角形;(2)求BF的长.参考答案一.选择题1.解:∵支撑点应是三角形的重心,∴三角形的重心是三角形三边中线的交点,故选:A.2.解:作DE⊥AB于E,如图,在Rt△ABC中,BC==8,∵AD是△ABC的一条角平分线,DC⊥AC,DE⊥AB,∴DE=DC,设DE=DC=x,S△ABD=DE•AB=AC•BD,即10x=6(8﹣x),解得x=3,即点D到AB边的距离为3.故选:C.3.解:∵AB=AC,∠A=40°,∴∠ABC=∠ACB=70°.∵DE垂直平分AC,∴AD=CD,∴∠A=∠ACD=40°∴∠BCD=∠ACB﹣∠ACD=30°.故选:B.4.解:当40°的角为等腰三角形的顶角时,底角的度数==70°;当40°的角为等腰三角形的底角时,其底角为40°,故它的底角的度数是70°或40°.故选:D.5.解:(1)∵a=b,∠A=45°,∴∠A=∠B=45°,∴∠C=90°,∴△ABC是直角三角形;(2)∵∠A=32°,∠B=58°,∴∠C=90°,∴△ABC是直角三角形;(3)a=5,b=12,c=13,∴a2+b2=c2,∴∠C=90°,△ABC是直角三角形;(4)a=52,b=122,c=132,∴a2+b2≠c2,∴△ABC不是直角三角形.∴是直角三角形的有(1)(2)(3).故选:C.6.解:∵BP平分∠ABC,DP平分∠ADC,∴∠ADP=∠PDF,∠CBP=∠PBA,∵∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,∴∠A+∠C=2∠P,∵∠A=40°,∠P=38°,∴∠C=2×38°﹣40°=36°,故选:A.7.解:设第二个小的等边三角形的边长为x,则第三个小的等边三角形的边长为:x+a,第四个小的等边三角形的边长为:x+2a,最大的个小的等边三角形的边长b=x+3a,又∵b=3x,∴3x=x+3a,∴x=a,∴b=3x=a,故选:D.8.解:∵直线ME为线段AB的垂直平分线,∴MA=MB(线段垂直平分线上的点到线段两端点的距离相等),又直线NF为线段BC的垂直平分线,∴NB=NC(线段垂直平分线上的点到线段两端点的距离相等),∴△BMN的周长=BM+MN+BN=AM+MN+NC=AC=24(等量代换),故选:B.9.解:∵AC=BC,∠ACB=90°,AD=DB,∴CD⊥AB,CD=AD=DB,∠A=∠CBD=45°,∵EH平分∠AEG,∴∠AEH=∠GEH∵∠AEH+∠AEC=180°,∠GEH+∠CEG=180°,∴∠AEC=∠CEG,∵AE=GE,EC=EC,∴△AEC≌△GEC(SAS),∴CA=CG,∠A=∠CGE=45°,∵∠EDG=90°,∴∠DEG=∠DGE=45°,∴DE=DG,∠AEF=∠DEG=∠A=45°,故②正确,∴∠AFE=∠CFG=90°,∴∠FCG=∠FGC=45°,∴CF=FG,∵∠ADC=∠GFC=90°,∠ACD=∠GCF,AC=GC,∴△ADC≌△GFC(AAS),∴AD=CF=FG,∵AE=EG,∴EF=DE,∵DE=DG,∠CDE=∠BDG=90°,DC=DB,∴△EDC≌△GDB(SAS),∴∠ECD=∠DBG,EC=GB,∵∠DHC=∠DHB,∠HCD=∠HBD,HD=HD,∴△HDC≌△HDB(AAS),∴HC=HB,∴HE=EG,∵∠DHE=∠DHG,DH=DH,∴△HDE≌△HDG(SAS),∴∠HDG=∠HDE=45°,故①正确,∴DE=DM,EF=DE≠2DM,故③错误,作ET∥AC交CD于T.∵∠DET=∠A=45°,∠DTE=∠ACD=45°,∴DE=DT=DG,∵DA=DC,∴AE=CT,∴CG=CT+TG=AE+2DG,故④正确,故选:B.10.解:在△ABC中,∵∠ACB=90°,∴∠BAC+∠ABC=90°,又∵AD、BE分别平分∠BAC、∠ABC,∴∠BAD+∠ABE=(∠BAC+∠ABC)=45°,∴∠APB=135°,故①正确.∴∠BPD=45°,又∵PF⊥AD,∴∠FPB=90°+45°=135°,∴∠APB=∠FPB,在△ABP和△FBP中,,∴△ABP≌△FBP(ASA),∴∠BAP=∠BFP,AB=FB,P A=PF,故②正确.在△APH和△FPD中,∴△APH≌△FPD(ASA),∴PH=PD,故③正确.∵△ABC的角平分线AD、BE相交于点P,∴点P到AB、AC的距离相等,点P到AB、BC的距离相等,∴点P到BC、AC的距离相等,∴点P在∠ACB的平分线上,∴CP平分∠ACB,故④正确.故选:D.二.填空题(共10小题)11.解:∵△ABC是等边三角形,∴AB=AC.∴∠BAC=∠C.在△ABD和△CAE中,,∴△ABD≌△CAE(SAS).∴∠ABD=∠CAE,BD=AE,∴∠APD=∠ABP+∠P AB=∠BAC=60°.∴∠BPF=∠APD=60°.∵∠BFP=90°,∠BPF=60°,∴∠PBF=30°.∴BP=2PF=8,∵PD=1,∴BD=BP+PD=9,∴AE=BD=9.故答案为9.12.解:假设AB=AC=1,那么在△ACB和△BCD中,∠C=∠C,∠A=∠CBD=36°,∴△ACB∽△BCD,∴AC:BC=BC:DC,∴AC:BC=BC:DC,而BC=BD=DA(等腰的性质)所以设AD=x,那么CD=1﹣x,1:x=x:(1﹣x),所以舍负根,得到:x=,∴AD:AC=.13.解:①∵AH是PC的垂直平分线,∴P A=AC=AB,∵AD平分∠P AB,∴∠P AD=∠BAD,在△P AD和△BAD中,,∴△P AD≌△BAD(SAS),∴DP=DB;故①符合题意;②在CP上截取CQ=PD,连接AQ,如图所示:∵AP=AC,∴∠APD=∠ACQ,在△APD和△ACQ中,,∴△APD≌△ACQ(SAS),∴AD=AQ,∠CAQ=∠P AD,∴∠BAC=∠CAQ+∠BAQ=∠P AD+∠BAQ=∠BAD+∠BAQ=∠DAQ=60°,∴△ADQ为等边三角形,∴DA=DQ,∴DC=DQ+CQ=DA+DB,即DA+DB=DC.故②符合题意;③∵AB=AP,AD平分∠P AB,∴AD⊥PB,故③符合题意;④∵AH垂直平分PC,∴PH=CH,∵△BDH为等边三角形,∴DB=DH,∵PD=DB,∴PD=DH,∴PH=2PD,∴CP=4PD,故④不合题意,故答案为:①②③.14.解:连接AO并延长交BC于F,如图,∵点O是三角形ABC的重心,∴OA=2OF,∴AO:AF=2:3,∵DE∥BC,∴△ADE∽△ABC,∴=()2=,∴△ADE与四边形DBCE的面积比为4:5.故答案为4:5.15.解:∵AD平分∠CAB交BC于D,DE⊥AB,DC⊥AC,∴DC=DE,在Rt△ADC和△ADE中,∴Rt△ADC≌△ADE(HL),∴AE=AC=3,∴BE=AB=5﹣3=2,∴△DEB的周长=BE+BD+DE=BE+BD+CD=BE+BC=2+4=6(cm).故答案为6cm.16.解:∵△ABC沿BC边平移到△DEF的位置,∴AB∥EG,∴△ABC∽△GEC,∴=()2=,∴BC:EC=:1,∵BC=2,∴EC=,∴△ABC平移的距离为:BE=2﹣,故答案为2﹣.17.解:∵AD、BE为△ABC的中线,且AD与BE相交于点G,∴G点是三角形ABC的重心,∴AG===4,故答案为4.18.解:∵BD,CE分别是边AC,AB上的中线,∴DE是△ABC的中位线,∴DE∥BC,DE=,∴△DOE∽△BOC,,∴S△DOE=S△BDE=S△ABD=S△ABC==,故答案为.19.解:∵AD是BC边上的中线,AC=2BC,∴BD=CD,设BD=CD=x,AB=y,则AC=4x,分为两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得:x=12,y=28,即AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得:x=8,y=52,即AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系定理;综合上述:AC=48,AB=28.故答案为:48;28.20.解:∵BC=AB,∴∠BCA=∠A=15°,∴∠DBC=∠BCA+∠A=30°.同理,∠CDB=∠DBC=30°,∴∠DCE=∠CDB+∠A=45°,∠DEC=∠DCE=45°,∴∠FDE=∠DEC+∠A=60°,∠DFE=∠FDE=60°,∴∠FEM=∠DFE+∠A=90°.再作与AB相等的线段时,90°的角不能是底角,则最多能作出的线段是:BC、CD、DE、EF共有5条.故答案是:5.三.解答题(共5小题)21.(1)证明:∵CF⊥BD于点F,AE⊥BD,∴∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,又∵∠ABC=90°,∴∠ABE+∠CBF=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(AAS),∴BE=CF,AE=BF,∴CF﹣AE=BE﹣BF=EF;(2)证明:如图1,过点C作CF⊥BD于点F,∵BC=CD,∴BF=DF,由(1)得AE=BF,∴AE=DF,∴BD=2AE;(3)解:如图2,过点C作CG⊥MB,交MB的延长线于点G,过点C作CH⊥BE,交BE于点H,∵BM⊥BE,CH⊥BE,CG⊥MB,∴∠NBG=∠CHB=∠CGB=90°,∴四边形BGCH为矩形,∴BG=HC,BH=GC,由(1)得△AEB≌△BHC,∴AE=BH,BE=CH,∵BM=BE,∴BM=CH,∵∠MBN=∠CHN=90°,∠MNB=∠CNH,∴△BMN≌△HCN(AAS),∴BM=CH,BN=HN,∵AE=BH=2,∴BN=1,∴BE=BM=BN+EN=1+4=5,∴=.故答案为:5.22.(1)证明:∵CD是∠ACB的平分线,∴∠BCD=∠ECD,∵DE∥BC,∴∠EDC=∠BCD,∴∠EDC=∠ECD,∴DE=CE.(2)解:∵∠ECD=∠EDC=25°,∴∠ACB=2∠ECD=50°,∵AB=AC,∴∠ABC=∠ACB=50°,∴∠A=180°﹣50°﹣50°=80°.23.解:(1)如图1中,∵∠ADE=∠ACE=90°,AF=FE,∴DF=AF=EF=CF,∴∠F AD=∠FDA,∠F AC=∠FCA,∴∠DFE=∠FDA+∠F AD=2∠F AD,∠EFC=∠F AC+∠FCA=2∠F AC,∵CA=CB,∠ACB=90°,∴∠BAC=45°,∴∠DFC=∠EFD+∠EFC=2(∠F AD+∠F AC)=90°,∴DF=FC,DF⊥FC,故答案为:DF=FC,DF⊥FC.(2)结论不变.理由:如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.∵BC⊥AM,AC=CM,∴BA=BM,同法BE=BN,∵∠ABM=∠EBN=90°,∴∠NBA=∠EBM,∴△ABN≌△MBE,∴AN=EM,∴∠BAN=∠BME,∵AF=FE,AC=CM,∴CF=EM,FC∥EM,同法FD=AN,FD∥AN,∴FD=FC,∵∠BME+∠BOM=90°,∠BOM=∠AOH,∴∠BAN+∠AOH=90°,∴∠AHO=90°,∴AN⊥MH,FD⊥FC.(3)如图3中,当点E落在AB上时,BF的长最大,最大值=3如图4中,当点E落在AB的延长线上时,BF的值最小,最小值=.综上所述,≤BF≤3.24.证明:作EF⊥AB于点F,∵∠C=∠D=90°,E是CD上一点,AE、BE分别平分∠DAB、∠ABC,∴EF=ED,EF=EC,∴ED=EC,∴点E为CD的中点.25.证明:(1)∵△ABC是等边三角形,BD是中线,∴∠A=∠ACB=60°,AC=BC,AD=CD=AC,∵DE⊥AB于E,∴∠ADE=90°﹣∠A=30°,∴CD=AD=2AE=4,∴∠CDF=∠ADE=30°,∴∠F=∠ACB﹣∠CDF=30°,∴∠CDF=∠F,∴DC=CF,∴△DCF是等腰三角形,(2)∵DC=CF,∴BF=BC+CF=2AD+AD=12。
2020年中考数学复习专题练:《三角形综合 》(含答案)

2020年中考数学复习专题练:《三角形综合》1.如图:在四边形ABCD中,AB∥CD,∠BCD=90°,且AB=2,DC=BC=4.(1)求sin∠ADC的值.(2)E是四边形内一点,F是四边形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF 的形状.(等腰直角三角形)(3)在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.2.如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.(1)当∠BAM=°时,AB=2BM;(2)请添加一个条件:,使得△ABC为等边三角形;①如图1,当△ABC为等边三角形时,求证:CN+CM=AC;②如图2,当点M运动到线段BC之外(即点M在线段BC的延长线上时),其它条件不变(△ABC仍为等边三角形),请写出此时线段CN、CM、AC满足的数量关系,并证明.3.综合与实践:操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;(2)在(1)的条件下,求∠BEC的度数;拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.4.如图,在△ABC中,AB=AC=5,BC=6,点D是边AB上的动点(点D不与点AB重合),点G在边AB的延长线上,∠CDE=∠A,∠GBE=∠ABC,DE与边BC交于点F.(1)求cos A的值;(2)当∠A=2∠ACD时,求AD的长;(3)点D在边AB上运动的过程中,AD:BE的值是否会发生变化?如果不变化,请求AD:BE的值;如果变化,请说明理由.5.如图1,OA=2,OB=4,以点A为顶点,AB为腰在第三象限作等腰直角△ABC.(Ⅰ)求C点的坐标;(Ⅱ)如图2,OA=2,P为y轴负半轴上的一个动点,若以P为直角顶点,PA为腰等腰直角△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;(Ⅲ)如图3,点F坐标为(﹣4,﹣4),点G(0,m)在y轴负半轴,点H(n,0)x 轴的正半轴,且FH⊥FG,求m+n的值.6.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点P从点A出发沿线段AB以每秒3个单位长的速度运动至点B,过点P作PQ⊥AB射线AC于点Q.设点P的运动时间为t秒(t>0).(1)线段CQ的长为(用含t的代数式表示)(2)当△APQ与△ABC的周长的比为1:4时,求t的值.(3)设△APQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式.(4)当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时,直接写出t的值.7.如图,在平面内给定△ABC,AB=AC,点O到△ABC的三个顶点的距离均等于c(c为常数),到点O的距离等于c的所有点组成图形G,过点A作AB的垂线交BC于点E,交图形G于点D,延长DA,在DA的延长线上存在一点F,使得∠ABF=∠ABC.(1)依题意补全图形;(2)判断直线BF与图形G交点的个数并证明;(3)若AD=4,cos∠ABF=,求DE的长.8.如图,△ABC是等边三角形,AB=8,AH⊥BC,垂足为H点,点D是射线AH上的动点,连接CD,以CD为边在CD的下方作等边△CDE,连接BE.(1)当点D在线段AH上时,设AD=x,△CDE的面积为y,求y关于x的函数解析式,并求出自变量x的取值范围;(2)当△CDE的面积等于△ABC的面积的时,判断线段CE与△ABC的边是否存在特殊的位置关系?若存在,说出是什么关系并证明;若不存在,请说明理由.9.如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为圆心以AM为半径作圆弧,以B为圆心以BN为半径作圆弧,两圆弧相交于点C构成△ABC,设AB=x.(1)求x的取值范围;(2)若△ABC为直角三角形,求x的值;(3)当∠CAB是锐角时,求△ABC的最大面积?10.如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,D是边AC上一点,且CD=1cm.动点P从点D出发,以1cm/s的速度沿D→A向终点A匀速运动;同时动点Q从点B出发,以1m/s的速度沿B→C向终点C匀速运动,连结PQ,设点P的运动时间为ts,△CPQ的面积为Scm2(1)当PQ=3时,求t的值;(2)求S与t之间的函数关系式,并写出自变量t的取值范围;(3)连结DQ,当直线DQ将△CPQ分成面积比为1:2两部分时,直接写出t的值,并写出此时S的值.11.如图,△ABC是边长为2的等边三角形,点D与点B分别位于直线AC的两侧,且AD=AC,联结BD、CD,BD交直线AC于点E.(1)当∠CAD=90°时,求线段AE的长.(2)过点A作AH⊥CD,垂足为点H,直线AH交BD于点F,①当∠CAD<120°时,设AE=x,y=(其中S△BCE 表示△BCE的面积,S△AEF表示△AEF的面积),求y关于x的函数关系式,并写出x的取值范围;②当=7时,请直接写出线段AE的长.12.如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d)(1)当a=2时,则C点的坐标为(,);(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由;(3)当a=2时,在第一象限内是否存在一点P,使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由13.平面直角坐标系中,若点A(a,b),且+=0,点B(m,m),其中m>1,R点在x轴正半轴上,RA⊥RB(1)求a、b的值;(2)连接AB交y轴于E,连接ER,若∠ARO=15°,求的值;(3)点D(﹣1,0)、C(0,1),射线DC分别交线段AR、AB于点S、T,若SC=n,CT =k,试用含n的式子表示k.14.在平面直角坐标系中,A(﹣3,﹣2),B(2,4).(1)如图1,求△AOB的面积;(2)如图2,求AB与两坐标轴的交点C,D坐标;(3)在坐标轴上求作点P,使△ABP的面积为6,求P点坐标,利用图3解答.15.如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,4),点B在x的负半轴上,△AOB的面积为8,作△AOB关于y轴的对称图形,点B的对应点为C.(1)求线段OC的长;(2)点D从A点出发,沿线段AO向终点O运动,同时点E从点C出发,沿x轴的正方向运动,且CE=AD,连接DE交AC于点G,判断DG和EG的数量关系,并说明理由.(3)在(2)的条件下,当∠CEG=∠ABD时,求点G点坐标.16.在Rt△ABC中,AC=BC,∠ACB=90°,点D是BC上一点.(1)如图1,AD平分∠BAC,求证:AB=AC+CD;(2)如图2,点E在线段AD上,且∠CED=45°,∠BED=30°,求证:BE=2AE;(3)如图3,CD=BD,过B点作BM⊥AD交AD的延长线于点M,连接CM,过C点作CN⊥CM交AD于N,求证:DN=3DM.17.如图,在Rt△ABC中,=nM为BC上的一点,连接BM.(1)如图1,若n=1,①当M为AC的中点,当BM⊥CD于H,连接AH,求∠AHD的度数;②如图2,当H为CD的中点,∠AHD=45°,求的值和∠CAH的度数;(2)如图3,CH⊥AM于H,连接CH并延长交AC于Q,M为AC中点,直接写出tan∠BHQ 的值(用含n的式子表示).18.如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.(1)求∠AFE的度数;(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=CP,求的值.(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)19.在等边△ABC中,点E,F分别在边AB,BC上.(1)如图1,若AE=BF,以AC为边作等边△ACD,AF交CE于点O,连接OD.求证:①AF=CE;②OD平分∠AOC;(2)如图2,若AE=2CF,作∠BCP=∠AEC,CP交AF的延长线于点P,求证:CE=CP.20.已知等边△ABC和等腰△CDE,CD=DE,∠CDE=120°.(1)如图1,点D在BC上,点E在AB上,P是BE的中点,连接AD,PD,则线段AD与PD之间的数量关系为;(2)如图2,点D在△ABC内部,点E在△ABC外部,P是BE的中点,连接AD,PD,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)如图3,若点D在△ABC内部,点E和点B重合,点P在BC下方,且PB+PC为定值,当PD最大时,∠BPC的度数为.参考答案1.解:(1)如图1,过点A作AM⊥DC于M,∵∠BCD=90°,AM⊥CD,∴AM∥BC,AB∥CD,∴四边形ABCM是平行四边形,且∠BCD=90°,∴四边形ABCM是矩形,∴AM=CB=4,AB=CM=2,∴DM=2,∴AD===2,∴sin∠ADC===;(2)△DEF是等腰直角三角形,理由如下:∵∠EDC=∠FBC,DE=BF,BC=CD,∴△CDE≌△CBF(SAS)∴∠DCE=∠BCF,CE=CF,∴∠DCE+∠ECB=∠BCF+∠BCE,∴∠DCB=∠ECF=90°,且CE=CF,∴△DEF是等腰直角三角形;(3)设BE=k,则CE=CF=2k,∴EF=2k,∵∠BEC=135°,又∠CEF=45°,∴∠BEF=90°,∴BF===3k,∴sin∠BFE=.2.解:(1)当∠BAM=30°时,∴∠AMB=180°﹣60°﹣30°=90°,∴AB=2BM;故答案为:30;(2)添加一个条件AB=AC,可得△ABC为等边三角形;故答案为:AB=AC;①如图1中,∵△ABC与△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAC﹣∠MAC=∠MAN﹣∠MAC,即∠BAM=∠CAN,在△BAM与△CAN中,,∴△BAM≌△CAN(SAS),∴BM=CN;②成立,理由:如图2中,∵△ABC与△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAC+∠MAC=∠MAN+∠MAC,即∠BAM=∠CAN,在△BAM与△CAN中,,∴△BAM≌△CAN(SAS),∴BM=CN.3.(1)证明:如图1中,∵∠ABC=∠ACB=∠ADE=∠AED,∴∠EAD=∠CAB,∴∠EAC=∠DAB,∵AE=AD,AC=AB,∴△BAD≌△CAE(SAS).(2)解:如图1中,设AC交BE于O.∵∠ABC=∠ACB=55°,∴∠BAC=180°﹣110°=70°,∵△BAD≌△CAE,∴∠ABO=∠ECO,∵∠EOC=∠AOB,∴∠CEO=∠BAO=70°,即∠BEC=70°.(3)解:如图2中,∵∠CAB=∠EAD=120°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴∠BAD=∠ACE,BD=EC=4,同法可证∠BEC=∠BAC=120°,∴∠FEC=60°,∵CF⊥EF,∴∠F=90°,∴∠FCE=30°,∴EF=EC=2.4.解:(1)作AH⊥BC于H,BM⊥AC于M.∵AB=AC,AH⊥BC,∴BH=CH=3,∴AH===4,=•BC•AH=•AC•BM,∵S△ABC∴BM==,∴AM===,∴cos A==.(2)设AH交CD于K.∵∠BAC=2∠ACD,∠BAH=∠CAH,∴∠CAK=∠ACK,∴CK=AK,设CK=AK=x,在Rt△CKH中,则有x2=(4﹣x)2+32,解得x=,∴AK=CK=,∵∠ADK=∠ADC,∠DAK=∠ACD,∴△ADK∽△CDA,∴====,设AD=m,DK=n,则有,解得m=,n=.∴AD=.(3)结论:AD:BE=5:6值不变.理由:∵∠GBE=∠ABC,∠BAC+2∠ABC=180°,∠GBE+∠EBC+∠ABC=180°,∴∠EBC=∠BAC,∵∠EDC=∠BAC,∴∠EBC=∠EDC,∴D,B,E,C四点共圆,∴∠EDB=∠ECB,∵∠EDB+∠EDC=∠ACD+∠DAC,∠EDC=∠DAC,∴∠EDB=∠ACD,∴∠ECB=∠ACD,∴△ACD∽△BCE,∴==.5.解:(Ⅰ)如图1,过C作CM⊥x轴于M点,如图1所示:∵CM⊥OA,AC⊥AB,∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,∴∠MAC=∠OBA,在△MAC和△OBA中,,∴△MAC≌△OBA(AAS),∴CM=OA=2,MA=OB=4,∴OM=6,∴点C的坐标为(﹣6,﹣2),故答案为(﹣6,﹣2);(Ⅱ)如图2,过D作DQ⊥OP于Q点,则四边形OEDQ是矩形,∴DE=OQ,∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,∴∠QPD=∠OAP,在△AOP和△PDQ中,,∴△AOP≌△PDQ(AAS),∴AO=PQ=2,∴OP﹣DE=OP﹣OQ=PQ=OA=2;(Ⅲ)如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,则∠HSF=∠GTF=90°=∠SOT,∴四边形OSFT是正方形,∴FS=FT=4,∠EFT=90°=∠HFG,∴∠HFS=∠GFT,在△FSH和△FTG中,,∴△FSH≌△FTG(AAS),∴GT=HS,又∵G(0,m),H(n,0),点F坐标为(﹣4,﹣4),∴OT═OS=4,∴GT=﹣4﹣m,HS=n﹣(﹣4)=n+4,∴﹣4﹣m=n+4,∴m+n=﹣8.6.解:(1)在Rt△ABC中,tan A===,由题意得,AP=3t,在Rt△APQ中,tan A==,∴PQ=AP=4t,根据勾股定理得,AQ===5t.当0<t≤时,如图1所示:CQ=AC﹣AQ=6﹣5t;当<t≤时,如图2所示:CQ=AQ﹣AC=5t﹣6;故答案为:6﹣5t或5t﹣6;(2)∵PQ⊥AB,∴∠APQ=90°=∠ACB,∵∠A=∠A,∴△APQ∽△ACB,∴==,即=,解得:t=,即当△APQ与△ABC的周长的比为1:4时,t为秒.(3)分两种情况:①当0<t≤时,如图1所示:△APQ与△ABC重叠部分图形的面积为S=△APQ的面积=×3t×4t=6t2;即S=6t2(0<t≤);②当<t≤时,如图2所示:由(1)得:PQ=3t,PQ=4t,AQ=5t,同(2)得:△CDQ∽△PAQ,∴==,即==,解得:CD=(5t﹣6),∴△APQ与△ABC重叠部分图形的面积为S=△APQ的面积﹣△CDQ的面积=×3t×4t ﹣×(5t﹣6)×(5t﹣6)=﹣t2+t﹣;即S=﹣t2+t﹣(<t≤);(4)由(1)知,AQ=5t,PQ=4t,CQ=6﹣5t或CQ=5t﹣6,当CQ=PQ时,四边形BCQP是轴对称图形,则4t=6﹣5t,∴t=;当<t≤时,设PQ和BC相交于D,当AC=AP时,四边形ACDP是轴对称图形,则6=3t,∴t=2.综上所述,当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时,t的值为秒或2秒.7.解:(1)如图,作AB,AC的垂直平分线交于点O,以O为圆心,OB长为半径作圆,⊙O 为图形G;(2)直线BF与图形G交点只有一个,理由如下:∵AD⊥AB,∴∠BAD=90°,∴BD是直径,∠ADB+∠ABD=90°,∵AB=AC,∴∠ACB=∠ABC,∵∠ACB=∠ADB,∠ABF=∠ABC,∴∠ABF=∠ADB,∴∠ABF+∠ABD=90°,∴∠DBF=90°,∴BD⊥BF,且OB是半径,∴BF是圆O的切线,∴直线BF与图形G交点的只有一个;(3)∵cos∠ABF=cos∠ADB==,∴BD=5,∴AB===3,∵∠ABE=∠ADB,∠BAE=∠BAD=90°,∴△ABE∽△ADB,∴,∴∴AE=,∴DE=AD﹣AE=.8.解:(1)∵△ABC是等边三角形,AB=8,AH⊥BC,∴BC=AC=AB=8,BH=HC=4,∠HAC=30°,∴AH=HC=4,∴DH=4﹣x,∴DC2=DH2+CH2=(4﹣x)2+16∵△CDE是等边三角形,=CD2=[(4﹣x)2+16]=x2﹣6x+16(0≤x≤4)∴y=S△CDE(2)∵当△CDE的面积等于△ABC的面积的,∴x2﹣6x+16=××64,∴x=或,当x=时,即AD=,如图1,∴DH=AH﹣AD=,∵tan∠DCH===,∴∠DCH=30°,∴∠ACD=∠ACB﹣∠DCH=30°,∴∠ACE=∠DCE+∠ACD=90°,∴CE⊥AC;当x=时,即AD=,如图2,∴DH=AD﹣AH=,∵tan∠DCH===,∴∠DCH=30°,∴∠BCE=∠DCH+∠DCE=90°,∴CE⊥BC.9.解:(1)∵在△ABC中,AC=1,AB=x,BC=3﹣x.,解得1<x<2;(2)①若AC为斜边,则1=x2+(3﹣x)2,即x2﹣3x+4=0,无解,②若AB为斜边,则x2=(3﹣x)2+1,解得x=,满足1<x<2,③若BC为斜边,则(3﹣x)2=1+x2,解得x=,满足1<x<2,综上,x=或;(3)在△ABC中,作CD⊥AB于D,设CD=h,△ABC的面积为S,则S=xh,①若点D在线段AB上,则+=x,∴(3﹣x)2﹣h2=x2﹣2x+1﹣h2,即x=3x﹣4,∴x2(1﹣h2)=9x2﹣24x+16,即x2h2=﹣8x2+24x﹣16.∴S2=x2h2=﹣2x2+6x﹣4=﹣2(x﹣)2+(≤x<2),当x=时(满足≤x<2),S2取最大值,从而S取最大值;②若点D在线段MA上,则﹣=x,同理可,得S2=x2h2=﹣2x2+6x﹣4=﹣2(x﹣)2+(1<x≤),易知此时S<,综合①②得,△ABC的最大面积为.10.解:(1)由题意PC=1+t,CQ=3﹣t,在Rt△PQC中,∵∠C=90°,PQ=3,PC=1+t,CQ=3﹣t,∴32=(1+t)2+(3﹣t)2,解得t=.∴PQ=3时,t的值为.(2)S=•PC•CQ=•(1+t)(3﹣t)=﹣t2+t+(0≤t≤3).(3)∵直线DQ将△CPQ分成面积比为1:2两部分,∴CD=2PD或PD=2CD,∴1=2t或t=2,解得t=或2,当t=时,S=﹣×++=,当t=2时,S=﹣×4+2+=,∴t=s或2s时,直线DQ将△CPQ分成面积比为1:2两部分.11.解:(1)∵△ABC是等边三角形,∴AB=BC﹣AC=2,∠BAC=∠ABC=∠ACB=60°.∵AD=AC,∴AD=AB,∴∠ABD=∠ADB,∵∠ABD+∠ADB+∠BAC+∠CAD=180°,∠CAD=90°,∠ABD=15°,∴∠EBC=45°.过点E作EG⊥BC,垂足为点G.设AE=x,则EC=2﹣x.在Rt△CGE中,∠ACB=60°,∴,,∴BG=2﹣CG=1+x,在Rt△BGE中,∠EBC=45°,∴,解得.所以线段AE的长是.(2)①设∠ABD=α,则∠BDA=α,∠DAC=∠BAD﹣∠BAC=120°﹣2α.∵AD=AC,AH⊥CD,∴,又∵∠AEF=60°+α,∴∠AFE=60°,∴∠AFE=∠ACB,又∵∠AEF=∠BEC,∴△AEF∽△BEC,∴,由(1)得在Rt△CGE中,,,∴BE2=BG2+EG2=x2﹣2x+4,∴(0<x<2).②当∠CAD<120°时,y=7,则有7=,整理得3x2+x﹣2=0,解得x=或﹣1(舍弃),.当120°<∠CAD<180°时,同法可得y=当y=7时,7=,整理得3x2﹣x﹣2=0,解得x=﹣(舍弃)或1,∴AE=1.12.解:(1)如图1中,过点C作CE⊥y轴于E,则∠CEB=∠AOB.∵△ABC是等腰直角三角形,∴BC=BA,∠ABC=90°,∴∠BCE+∠CBE=90°=∠BAO+∠CBE,∴∠BCE=∠ABO,在△BCE和△BAO中,,∴△CBE≌△BAO(AAS),∵A(﹣1,0),B(0,2),∴AO=BE=1,OB=CE=2,∴OE=1+2=3,∴C(﹣2,3),故答案为:﹣2,3;(2)动点A在运动的过程中,c+d的值不变.过点C作CE⊥y轴于E,则∠CEA=∠AOB,∵△ABC是等腰直角三角形,∴BC=BA,∠ABC=90°,∴∠BCE+∠CBE=90°=∠ABO+∠CBE,∴∠BCE=∠ABO,在△BCE和△BAO中,,∴△CBE≌△BAO(AAS),∵B(﹣1,0),A(0,a),∴BO=AE=1,AO=CE=a,∴OE=1+a,∴C(﹣a,1+a),又∵点C的坐标为(c,d),∴c+d=﹣a+1+a=1,即c+d的值不变;(3)存在,使△PAB与△ABC全等,如图2中,过C作CM⊥x轴于M,过P作PE⊥x轴于E则∠CMB=∠PEB=90°,∵△CAB≌△PAB,∴∠PBA=∠CBA=45°,BC=BP,∴∠CBP=90°,∴∠MCB+∠CBM=90°,∠CBM+∠PBE=90°,∴∠MCB=∠PBE,在△CMB和△BEP中,,∴△CMB≌△BEP(AAS),∴PE=BM,CM=BE,∵C(﹣2,3),B(﹣1,0),∴PE=1,OE=BE﹣BO=3﹣1=2,即P的坐标是(2,1).13.解:(1)∵+=0,又∵≥0,≥0,∴a=﹣1,b=1.(2)如图1中,作AM⊥x轴于M,AH⊥y轴于H,在RM上取一点K,使得AK=KR,连接AK,AO.∵A(﹣1,1),∴AM=AH=1,∵AK=KR,∴∠KRA=∠KAR=15°,∴∠AKM=∠KAR+∠KRA=30°,∴AK=KR=2AM=2,MK=,∴MR=2+,∴AR===+,∵B(m,m),∴OB平分∠EOB,∵OA平分∠EOM,∴OA⊥OB,∴∠AOB=∠ARB=90°,∴A,O,R,B四点共圆,∴∠BAR=∠BOR=45°,∴△ABR是等腰直角三角形,∴AB=AR=2+2,∵AH∥MR,∴∠HAR=∠ARM=15°,∴∠EA=30°,∴AE==,∴==.(3)如图,作SH⊥AD于H.由题意四边形ADOC是正方形,∴∠ACD=45°=∠CAT+∠ATC,∵∠CAT+∠SAC=45°,∴∠SAC=∠ATC,∵∠ASC=∠TSA,∴△SAC∽△STA,∴=,∴SA2=SC•ST,∵CS=n,CT=k,CD=,∴SH=DH=(﹣n),AH=n,∴AS2=AH2+HS2=n2+(﹣n)2=n(n+k),∴k=(0<n<).14.解:(1)如图1,过A作AC∥x轴,过B作BC⊥AC于C,BC交x轴于E,AC交y轴于D,∵A (﹣3,﹣2),B (2,4),∴△AOB 的面积=S △ACB ﹣S △AOD ﹣S △BOE ﹣S 长方形ODCE ,=﹣﹣﹣2×2,=15﹣3﹣4﹣4,=4;(2)设直线AB 的解析式为:y =kx +b (k ≠0),则,解得:,∴直线AB 的解析式为:y =x +,当x =0时,y =,∴C (0,),当y =0时,x +=0,解得:x =﹣,∴D (,0);(3)①当点P 在x 轴上时,∵△ABP 的面积为6,∴=6,∴PD =2,如图3,点P 在x 轴的正半轴上,P (,0);同理得当点P在x轴的负半轴上,P(﹣,0);②当点P在y轴上时,=6,∴CP=,∴P(0,4)或(0,﹣);综上,点P的坐标是(,0)或(,0)或(0,4)或(0,).15.解:(1)如图1中,∵A(0,4),∴OA=4,=×OB×OA=8,∵S△AOB∴OB=4,∵△AOB与△AOC关于y轴对称,∴OC=OB=4.(2)如图2中,结论:DG=GE.理由:作DH∥EC交AC于H.∵OA=OC,∠AOC=90°,∴∠DAH=∠ACO=45°,∵DH∥OC,∴∠AHD=∠ACO=45°,∴∠DAH=∠AHD,∴AD=DH,∵AD=EC,∴DH=EC,∵∠DHG=∠GCE,∠DGH=∠CGE,∴△DGH≌△EGC(AAS),∴DG=EG.(3)如图3中,连接DB,DC,作DH∥EC交AC于H.设AD=DH=x,则AH=x,HC=4﹣x,∵HG=CG,∴HG=HC=2﹣x,∵OA⊥BC,OB=OC,∴AB=AC,DB=DC,∴∠ABC=∠ACB,∠DBO=∠DCO,∴∠ABD=∠ACD,∵∠CEG=∠ABD,∴∠ACD=∠CEG,∵DH∥CE,∴∠HDG=∠CEG=∠DCH,∵∠DHG=∠DHC,∴△DHG∽△CHD,∴=,∴=,解得x=2,∴AH=CH=2,∴H(2,2),∵GH=GC,∴G(3,1).16.证明:(1)如图1中,作DH⊥AB于H.∵∠ACD=∠AHD=90°,AD=AD,∠DAC=∠DAH,∴△ADC≌△ADH(ASA),∴AC=AH,DC=DH,∵CA=CB,∠C=90°,∴∠B=45°,∵∠DHB=90°,∴∠HDB=∠B=45°,∴HD=HB,∴BH=CD,(2)如图2中,作BM⊥AD交AD的延长线于M,连接CM.∵∠ACB=∠AMB=90°,∴C,A,B,M四点共圆,∴∠AMC=∠ABC=45°,∵∠CEM=45°,∴∠CEM=∠CME,∴CE=CM,∴∠ECM=∠ACB=90°,∴∠ACE=∠BCM,∵CA=CB,CE=CM,∴△ACE≌△BCM(SAS),∴AE=BM,∵在Rt∠EMB中,∠MEB=30°,∵BE=2BM=2AE.(3)如图3中,作CH⊥MN于H.∵∠ACB=∠AMB=90°,∴C,A,B,M四点共圆,∵CN⊥CM,∴∠NCM=90°∴∠CNM=∠CMN,∴CN=CM,∵CH⊥MN,∴HN=HM.∵CD=DB,∠CHD=∠BMD=90°,∠ADH=∠BDM,∴△CHD≌△BMD(AAS),∴DH=DM,∵HN=HM,∴DN=3DM.17.解:(1)①如图1中,作AK⊥CD交CD的延长线于K.∵CD⊥BM,AK⊥CK,∠ACB=90°,∴∠CHB=∠K=90°,∠CBH+∠BCH=90°,∠BCH+∠ACK=90°,∴∠CBH=∠ACK,∵CB=CA,∴△CHB≌△AKC(AAS),∴AK=CH,∵∠CHM=∠K=90°,∴MH∥AK,∵AM=BM,∴CH=KH,∴AK=KH,∵∠K=90°,∴∠AHD=45°.②如图2中,作AK⊥CD交CD的延长线于K,作CM⊥AB于M.设DH=CH=a.∵CA=CB,∠ACB=90°,∴∠CAB=45°,∵∠AHD=45°,∠AHD=∠ACH+∠CAH,∴∠ACH+∠CAH=∠CAH+∠DAH,∴∠DAH=∠ACD,∵∠ADH=∠CAD,∴△ADH∽△CDA,∴=,∴=,∴AD=a,∵CA=CB,∠ACB=90°,CM⊥AB,∴AM=BM,∴CM=AM=BM,设AM=CM=BM=x,在Rt△CMD中,∵CM2=DM2+CD2,∴x2+(x﹣a)2=4a2,解得x=a(负根已经舍弃).∴BD=AB﹣AD=(+)a﹣a=a,∴==.∵△ADH∽△CDA,∴==,设AH=m,则AC=m,AK=KH=m,∴tan∠ACK==,∴∠ACH=30°,∴∠CAH=∠AHD﹣∠ACH=45°﹣30°=15°.(2)作AJ⊥BM交BM的延长线于J.设AM=CM=y,则BC=2yn.∵CH⊥BM,BM===•y,∴CH===•y,∴HM==•y,∵AJ⊥BJ,CH⊥BJ,∴∠J=∠CHM=90°,∵∠AMJ=∠CMH,AM=CM,∴△AMJ≌△CMH(AAS),∴AJ=CH=•y,HM=JM=•y,∵∠BHQ=∠AHJ,∴tan∠BHQ=tan∠AHJ===n.18.(1)解:如图1中.∵△ABC为等边三角形,∴AC=BC,∠BAC=∠ABC=∠ACB=60°,在△EBC和△DCA中,,∴△EBC≌△DCA(SAS),∴∠BCE=∠DAC,∵∠BCE+∠ACE=60°,∴∠DAC+∠ACE=60°,∴∠AFE=60°.(2)证明:如图1中,∵AH⊥EC,∴∠AHF=90°,在Rt△AFH中,∵∠AFH=60°,∴∠FAH=30°,∴AF=2FH,∵△EBC≌△DCA,∴EC=AD,∵AD=AF+DF=2FH+DF,∴2FH+DF=EC.(3)解:在PF上取一点K使得KF=AF,连接AK、BK,∵∠AFK=60°,AF=KF,∴△AFK为等边三角形,∴∠KAF=60°,∴∠KAB=∠FAC,在△ABK和△AFC中,,∴△ABK≌△AFC(SAS),∴∠AKB=∠AFC=120°,∴∠BKE=120°﹣60°=60°,∵∠BPC=30°,∴∠PBK=30°,∴FP=CK,∴PK=CK,∵FP=FK+PK∴FP=AF+CF,∵CF=CP,设CP=9a,∵CF=2a,∴FP=7a,∴AF=5a,∴==.19.(1)证明:①如图1中,∵△ABC是等边三角形,∴AB=BC,∠B=∠BAC=60°,∵AE=BF,∴△ABF≌△CAE(SAS),∴AF=EC.②如图1中,∵△ABF≌△CAE,∴∠BAF=∠ACE,∵∠AOE=∠OAC+∠ACO=∠OCA+∠BAF=∠BAC=60°,又∵△ACD是等边三角形,∴∠ADC=∠DAC=∠DCA=60°,∴∠AOE=∠ADC,∵∠AOE+∠AOC=180°,∴∠ADC+∠AOC=180°,∴A,D,C,O四点共圆,∴∠AOD=∠ACD=60°,∠COD=∠CAD=60°,∴∠AOD=∠COD,∴OD平分∠AOC.(2)证明:如图2中,取AE的中点M,连接CM.∵AE=2CF,AM=ME,∴AM=CF,∵∠CAM=∠ACF=60°,AC=CA,∴△ACM≌△CAF(SAS),∴∠ACM=∠CAF,∵∠CME=∠CAM+∠ACM=60°+∠ACM,∠CFP=∠ACF+∠CAF=60°+∠CAF,∴∠CME=∠CFP,∵EM=CF,∠PCF=∠CEM,∴△CME≌△PFC(ASA),∴CE=PC.20.解:(1)结论:AD=2PD.理由:如图1中,∵△ABC是等边三角形,∴∠B=60°,∵∠EDC=120°,∴∠EDB=180°﹣120°=60°,∴∠B=∠EDB=∠BED=60°,∴△BDE是等边三角形,∵BP=PE,∴DP⊥AB,∴∠APD=90°,∵DE=DC,DE=DB,∴BD=CD,∵AB=AC,∠BAC=60°,∴∠PAD=∠BAC=30°,∴AD=2PD.(2)结论成立.理由:延长DP到N,使得PN=PD,连接BN,EN,延长ED到M,使得DM=DE,连接BD,BM,CM.∵DE=DC=DM,∠MDC=180°﹣∠EDC=60°,∴△DCM是等边三角形,∵CA=CB,CM=CD,∠DCM=∠ACB=60°,∴∠BCM=∠ACD,∴△BCM≌△ACD(SAS),∴AD=BM,∵PB=PE,PD=PN,∴四边形BNED是平行四边形,∴BN∥DE,BN=DE,∵DE=DM,∴BN=DM,BN∥DM,∴四边形BNDM是平行四边形,∴BM=DN=2PD,∴AD=2PD.(3)如图3中,作∠PDK=∠BDC=120°,且PD=PK,连接PK,CK.∵DB=DC,DP=DK,∠BDC=∠PDK,∴∠BDP=∠CDK,∴△PDB≌△KDC(SAS),∴PB=CK,∵PB+PC=PC+CK=定值,∴P,C,K共线时,PK定值最大,此时PD的值最大,此时,∠DPB=∠DKP=∠DPK=30°,∠BPC=∠DPB+∠DPK=60°.故答案为60°.。
人教版2020年九年级中考数学一轮复习 第15讲 三角形(有答案)

第十五节三角形【知识点梳理】一、三角形1、三角形中的主要线段(1)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做。
(2)在三角形中,连接一个顶点和它对边的中点的线段叫做。
(3)从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做(简称)。
2.三角形的中位线三角形的中位线平行于,并且等于.3.三角形的三边关系定理及推论三角形三边关系:任意两边之和第三边;任意两边之差第三边.4、三角形的内角和定理及推论1.三角形内角和:三角形三内角之和等于.2.三角形外角的性质:(1)三角形的一个外角任何一个和它不相邻的内角;(2)三角形的一个外角与它不相邻的两内角之和.1.三角形的分类:(1)按边分:三角形分为和等腰三角形;等腰三角形又分为及 .(2)按角分:三角形和斜三角形;斜三角形又分为:和 .答案:一、三角形1、三角形中的主要线段(1)三角形的角平分线。
(2)三角形的中线。
(3)三角形的高线(简称三角形的高)。
2.三角形的中位线:三角形的第三边,并且等于第三边长的一半.3.三角形的三边关系定理及推论:任意两边之和大于第三边;任意两边之差小于第三边.4、三角形的内角和定理及推论1. 180°.2.三角形外角的性质:(1)大于;(2)等于.1.三角形的分类:(1)按边分:三角形分为不等边三角形和等腰三角形;等腰三角形又分为底和腰不等的三角形及等边三角形.(2)按角分:三角形直角三角形和斜三角形;斜三角形又分为:锐角三角形和钝角三角形.【课堂练习】一.选择题(共9小题)1.三角形的下列线段中能将三角形的面积分成相等两部分的是()A.中线B.角平分线C.高D.中位线【考点】K3:三角形的面积;K2:三角形的角平分线、中线和高.【分析】根据等底等高的三角形的面积相等解答.【解答】解:∵三角形的中线把三角形分成两个等底同高的三角形,∴三角形的中线将三角形的面积分成相等两部分.故选A.2.如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为()A.3:5 B.4:5 C.9:10 D.15:16【考点】K3:三角形的面积.【分析】根据三角形面积求法进而得出S△BDC:S△ADC=3:2,S△BDE:S△DCE=3:2,即可得出答案.【解答】解:∵AD:DB=CE:EB=2:3,∴S△BDC:S△ADC=3:2,S△BDE:S△DCE=3:2,∴设S△BDC=3x,则S△ADC=2x,S△BED=1.8x,S△DCE=1.2x,故△DBE与△ADC的面积比为:1.8x:2x=9:10.故选:C.3.如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于()A.1 B.3C.32D.2【考点】K5:三角形的重心;KW:等腰直角三角形.【分析】连接CP并延长,交AB于D,根据重心的性质得到CD是△ABC的中线,PD=CD,根据直角三角形的性质求出CD,计算即可.【解答】解:连接CP并延长,交AB于D,∵P是Rt△ABC的重心,∴CD是△ABC的中线,PD=CD,∵∠C=90°,∴CD=AB=3,∵AC=BC,CD是△ABC的中线,∴CD⊥AB,∴PD=1,即点P到AB所在直线的距离等于1,故选:A.4.三角形的重心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平行线的交点【考点】K5:三角形的重心.【分析】根据三角形的重心是三条中线的交点解答.【解答】解:三角形的重心是三条中线的交点,故选:A.5.如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则MOMF的值为()A.12B.54C.23D.33【考点】K5:三角形的重心;S9:相似三角形的判定与性质.【分析】根据三角形的重心性质可得OC=CE,根据直角三角形的性质可得CE=AE,根据等边三角形的判定和性质得到CM=CE,进一步得到OM=CE,即OM=AE,根据垂直平分线的性质和含30°的直角三角形的性质可得EF=AE,MF=EF,依此得到MF=AE,从而得到的值.【解答】解:∵点O是△ABC的重心,∴OC=CE,∵△ABC是直角三角形,∴CE=BE=AE,∵∠B=30°,∴∠FAE=∠B=30°,∠BAC=60°,∴∠FAE=∠CAF=30°,△ACE是等边三角形,∴CM=CE,∴OM=CE﹣CE=CE,即OM=AE,∵BE=AE,∴EF=AE,∵EF⊥AB,∴∠AFE=60°,∴∠FEM=30°,∴MF=EF,∴MF=AE,∴==.故选:D.6.长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是()A.4 B.5 C.6 D.9【考点】K6:三角形三边关系.【分析】已知三角形的两边长分别为2和7,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围,再结合选项选择符合条件的.【解答】解:由三角形三边关系定理得7﹣2<x<7+2,即5<x<9.因此,本题的第三边应满足5<x<9,把各项代入不等式符合的即为答案.4,5,9都不符合不等式5<x<9,只有6符合不等式,故选:C.7.已知a,b,c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为()A.2a+2b﹣2c B.2a+2b C.2c D.0【考点】K6:三角形三边关系.【分析】先根据三角形的三边关系判断出a﹣b﹣c与c﹣b+a的符号,再去绝对值符号,合并同类项即可.【解答】解:∵a、b、c为△ABC的三条边长,∴a+b﹣c>0,c﹣a﹣b<0,∴原式=a+b﹣c+(c﹣a﹣b)=0.故选D.8.若一个三角形的两边长分别为2和4,则该三角形的周长可能是()A.6 B.7 C.11 D.12【考点】K6:三角形三边关系.【分析】首先求出三角形第三边的取值范围,进而求出三角形的周长取值范围,据此求出答案.【解答】解:设第三边的长为x,∵三角形两边的长分别是2和4,∴4﹣2<x<2+4,即2<x<6.则三角形的周长:8<C<12,C选项11符合题意,故选C.9.如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为()A.54°B.62°C.64°D.74°【考点】K7:三角形内角和定理;JA:平行线的性质.【分析】根据平行线的性质得到∠C=∠AED=54°,根据三角形的内角和即可得到结论.【解答】解:∵DE∥BC,∴∠C=∠AED=54°,∵∠A=62°,∴∠B=180°﹣∠A﹣∠C=64°,故选C.二.填空题(共5小题)10.在△ABC中,已知BD和CE分别是边AC、AB上的中线,且BD⊥CE,垂足为O.若OD=2cm,OE=4cm,则线段AO的长度为cm.【考点】K5:三角形的重心;KQ:勾股定理.【分析】连接AO并延长,交BC于H,根据勾股定理求出DE,根据三角形中位线定理求出BC,根据直角三角形的性质求出OH,根据重心的性质解答.【解答】解:连接AO并延长,交BC于H,由勾股定理得,DE==2,∵BD和CE分别是边AC、AB上的中线,∴BC=2DE=4,O是△ABC的重心,∴AH是中线,又BD⊥CE,∴OH=BC=2,∵O是△ABC的重心,∴AO=2OH=4,故答案为:4.11.在△ABC中,∠A:∠B:∠C=2:3:4,则∠A的度数为.【考点】K7:三角形内角和定理.【分析】直接用一个未知数表示出∠A,∠B,∠C的度数,再利用三角形内角和定理得出答案.【解答】解:∵∠A:∠B:∠C=2:3:4,∵∠A+∠B+∠C=180°,∴2x+3x+4x=180°,解得:x=20°,∴∠A的度数为:40°.故答案为:40°.12.如图,BC∥EF,AC∥DF,添加一个条件,使得△ABC≌△DEF.【考点】KB:全等三角形的判定.【分析】本题要判定△ABC≌△DEF,易证∠A=∠EDF,∠ABC=∠E,故添加AB=DE、BC=EF或AC=DF根据ASA、AAS即可解题.【解答】解:∵BC∥EF,∴∠ABC=∠E,∵AC∥DF,∴∠A=∠EDF,∵在△ABC和△DEF中,,∴△ABC≌△DEF,同理,BC=EF或AC=DF也可证△ABC≌△DEF.故答案为AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可).13.如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S=12 AC•BD.正确的是(填写所有正确结论的序号)【考点】KD:全等三角形的判定与性质;KG:线段垂直平分线的性质.【分析】①证明△ABC≌△ADC,可作判断;②③由于AB与BC不一定相等,则可知此两个选项不一定正确;④根据面积和求四边形的面积即可.【解答】解:①在△ABC和△ADC中,∵,∴△ABC≌△ADC(SSS),∴∠ABC=∠ADC,故①结论正确;②∵△ABC≌△ADC,∴∠BAC=∠DAC,∵AB=AD,∴OB=OD,AC⊥BD,而AB与BC不一定相等,所以AO与OC不一定相等,故②结论不正确;而AB与BC不一定相等,所以BD不一定平分四边形ABCD的对角;故③结论不正确;④∵AC⊥BD,∴四边形ABCD的面积S=S△ABD+S△BCD=BD•AO+BD•CO=BD•(AO+CO)=AC•BD.故④结论正确;所以正确的有:①④;故答案为:①④.14.如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.【考点】KI:等腰三角形的判定.【分析】分三种情况讨论:先确定特殊位置时成立的x值,①如图1,当M与O重合时,即x=0时,点P恰好有三个;②如图2,构建腰长为4的等腰直角△OMC,和半径为4的⊙M,发现M在点D的位置时,满足条件;③如图3,根据等腰三角形三种情况的画法:分别以M、N为圆心,以MN为半径画弧,与OB的交点就是满足条件的点P,再以MN为底边的等腰三角形,通过画图发现,无论x取何值,以MN为底边的等腰三角形都存在一个,所以只要满足以MN为腰的三角形有两个即可.【解答】解:分三种情况:①如图1,当M与O重合时,即x=0时,点P恰好有三个;②如图2,以M为圆心,以4为半径画圆,当⊙M与OB相切时,设切点为C,⊙M与OA交于D,∴MC⊥OB,∵∠AOB=45°,∴△MCO是等腰直角三角形,∴MC=OC=4,∴OM=4,当M与D重合时,即x=OM﹣DM=4﹣4时,同理可知:点P恰好有三个;③如图3,取OM=4,以M为圆心,以OM为半径画圆,则⊙M与OB除了O外只有一个交点,此时x=4,即以∠PMN为顶角,MN为腰,符合条件的点P有一个,以N圆心,以MN为半径画圆,与直线OB相离,说明此时以∠PNM为顶角,以MN为腰,符合条件的点P不存在,还有一个是以NM为底边的符合条件的点P;点M沿OA运动,到M1时,发现⊙M1与直线OB有一个交点;综上所述,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是:x=0或x=4﹣4或4.故答案为:x=0或x=4﹣4或4.三.解答题(共9小题)15.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.【考点】KB:全等三角形的判定.【分析】根据全等三角形的判定即可求证:△ADF≌△BCE【解答】解:∵AE=BF,∴AE+EF=BF+EF,在△ADF与△BCE中,∴△ADF≌△BCE(SAS)16.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.【考点】KD:全等三角形的判定与性质.【分析】可通过证△ABF≌△DCE,来得出∠A=∠D的结论.【解答】证明:∵BE=FC,∴BE+EF=CF+EF,即BF=CE;又∵AB=DC,∠B=∠C,∴△ABF≌△DCE;(SAS)17.如图,已知AB∥DE,AB=DE,BE=CF,求证:AC∥DF.【考点】KD:全等三角形的判定与性质.【分析】首先由BE=CF可以得到BC=EF,然后利用边角边证明△ABC≌△DEF,最后利用全等三角形的性质和平行线的判定即可解决问题.【解答】证明:∵AB∥CD,∴∠ABC=∠DEF,又∵BE=CF,∴BE+EC=CF+EC,即:BC=EF,在△ABC和△DEF中∴△ABC≌△DEF(SAS),∴∠ACB=∠DFE,∴AC∥DF.18.已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.(1)如图1,求证:AE=BD;(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.【考点】KD:全等三角形的判定与性质;KW:等腰直角三角形.【分析】(1)根据全等三角形的性质即可求证△ACE≌△BCD,从而可知AE=BD;(2)根据条件即可判断图中的全等直角三角形;【解答】解:(1)∵△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,∴AC=BC,DC=EC,∴∠ACB+∠ACD=∠DCE+∠ACD,∴∠BCD=∠ACE,在△ACE与△BCD中,∴△ACE≌△BCD(SAS),∴AE=BD,(2)∵AC=DC,∴AC=CD=EC=CB,△ACB≌△DCE(SAS);由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC∴∠DOM=90°,∵∠AEC=∠CAE=∠CBD,∴△EMC≌△BCN(ASA),∴CM=CN,∴DM=AN,△AON≌△DOM(AAS),∵DE=AB,AO=DO,∴△AOB≌△DOE(HL)19.如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.(1)如图1,若AB=4,BE=5,求AE的长;(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.【考点】KD:全等三角形的判定与性质;KQ:勾股定理.【分析】(1)根据等腰直角三角形的性质得到AC=BC=AB=4,根据勾股定理得到CE==3,于是得到结论;(2)根据等腰直角三角形的性质得到∠CAB=45°,由于∠AFB=∠ACB=90°,推出A,F,C,B四点共圆,根据圆周角定理得到∠CFB=∠CAB=45°,求得∠DFC=∠AFC=135°,根据全等三角形的性质即可得到结论.【解答】解:(1)∵∠ACB=90°,AC=BC,∴AC=BC=AB=4,∵BE=5,∴CE==3,∴AE=4﹣3=1;(2)∵∠ACB=90°,AC=BC,∴∠CAB=45°,∵AF⊥BD,∴∠AFB=∠ACB=90°,∴A,F,C,B四点共圆,∴∠CFB=∠CAB=45°,∴∠DFC=∠AFC=135°,在△ACF与△DCF中,,∴△ACF≌△DCF,∴CD=AC,∵AC=BC,∴AC=BC.20.在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示).(2)用等式表示线段MB与PQ之间的数量关系,并证明.【考点】KD:全等三角形的判定与性质;KW:等腰直角三角形.【分析】(1)由等腰直角三角形的性质得出∠BAC=∠B=45°,∠PAB=45°﹣α,由直角三角形的性质即可得出结论;(2)连接AQ,作ME⊥QB,由AAS证明△APC≌△QME,得出PC=ME,△MEB是等腰直角三角形,由等腰直角三角形的性质即可得出结论.【解答】解:(1)∠AMQ=45°+α;理由如下:∵∠PAC=α,△ACB是等腰直角三角形,∴∠BAC=∠B=45°,∠PAB=45°﹣α,∵QH⊥AP,∴∠AHM=90°,∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α;(2)PQ=MB;理由如下:连接AQ,作ME⊥QB,如图所示:∵AC⊥QP,CQ=CP,∴∠QAC=∠PAC=α,∴∠QAM=45°+α=∠AMQ,∴AP=AQ=QM,在△APC和△QME中,,∴△APC≌△QME(AAS),∴PC=ME,∴△MEB是等腰直角三角形,∴PQ=MB,∴PQ=MB.21.如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.(1)判断∠ABE与∠ACD的数量关系,并说明理由;(2)求证:过点A、F的直线垂直平分线段BC.【考点】KH:等腰三角形的性质;KG:线段垂直平分线的性质.【分析】(1)证得△ABE≌△ACD后利用全等三角形的对应角相等即可证得结论;(2)利用垂直平分线段的性质即可证得结论.【解答】解:(1)∠ABE=∠ACD;在△ABE和△ACD中,,∴△ABE≌△ACD,∴∠ABE=∠ACD;(2)∵AB=AC,∴∠ABC=∠ACB,由(1)可知∠ABE=∠ACD,∴∠FBC=∠FCB,∴FB=FC,∵AB=AC,∴点A、F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.22.如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中:(1)求证:△APR,△BPQ,△CQR的面积相等;(2)求△PQR面积的最小值;(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.【考点】KY:三角形综合题.【分析】(1)先利用锐角三角函数表示出QE=4t,QD=3(2﹣t),再由运动得出AP=3t,CR=4t,BP=3(2﹣t),AR=4(2﹣t),最后用三角形的面积公式即可得出结论;(2)借助(1)得出的结论,利用面积差得出S△PQR=18(t﹣1)2+6,即可得出结论;(3)先判断出∠DQR=∠EQP,用此两角的正切值建立方程求解即可.【解答】解:(1)如图,在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,sin∠B===,sin∠C=,过点Q作QE⊥AB于E,在Rt△BQE中,BQ=5t,∴sin∠B==,∴QE=4t,过点Q作QD⊥AC于D,在Rt△CDQ中,CQ=BC﹣BQ=10﹣5t,∴QD=CQ•sin∠C=(10﹣5t)=3(2﹣t),由运动知,AP=3t,CR=4t,∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),∴S△APR=AP•AR=×3t×4(2﹣t)=6t(2﹣t),S△BPQ=BP•QE=×3(2﹣t)×4t=6t(2﹣t),S△CQR=CR•QD=×4t×3(2﹣t)=6t(2﹣t),∴S△APR=S△BPQ=S△CQR,∴△APR,△BPQ,△CQR的面积相等;(2)由(1)知,S△APR=S△BPQ=S△CQR=6t(2﹣t),∵AB=6,AC=8,∴S△PQR=S△ABC﹣(S△APR+S△BPQ+S△CQR)=×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,∵0≤t≤2,∴当t=1时,S△PQR最小=6;(3)存在,由(1)知,QE=4t,QD=3(2﹣t),AP=3t,CR=4t,AR=4(2﹣t),∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),过点Q作QD⊥AC于D,作QE⊥AB于E,∵∠A=90°,∴四边形APQD是矩形,∴AE=DQ=3(2﹣t),AD=QE=4t,∴DR=|AD﹣AR|=|4t﹣4(2﹣t)|=|4(2t﹣2)|,PE=|AP﹣AE|=|3t﹣3(2﹣t)|=|3(2t﹣2)|∵∠DQE=90°,∠PQR=90°,∴∠DQR=∠EQP,∴tan∠DQR=tan∠EQP,在Rt△DQR中,tan∠DQR==,在Rt△EQP中,tan∠EQP==,∴,∴16t=9(2﹣t),∴t=.23.如图1,在△ABC中,设∠A、∠B、∠C的对边分别为a,b,c,过点A作AD⊥BC,垂足为D,会有sin∠C=,则S△ABC=BC×AD=×BC×ACsin∠C=absin∠C,即S△ABC=absin∠C同理S△ABC=bcsin∠AS△ABC=acsin∠B通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理:如图2,在△ABC中,若∠A、∠B、∠C的对边分别为a,b,c,则a2=b2+c2﹣2bccos∠Ab2=a2+c2﹣2accos∠Bc2=a2+b2﹣2abcos∠C用上面的三角形面积公式和余弦定理解决问题:(1)如图3,在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8.求S△DEF和DE2.解:S△DEF=EF×DFsin∠F=;DE2=EF2+DF2﹣2EF×DFcos∠F=.(2)如图4,在△ABC中,已知AC>BC,∠C=60°,△ABC'、△BCA'、△ACB'分别是以AB、BC、AC为边长的等边三角形,设△ABC、△ABC'、△BCA'、△ACB'的面积分别为S1、S2、S3、S4,求证:S1+S2=S3+S4.【考点】KY:三角形综合题.【分析】(1)直接利用正弦定理和余弦定理即可得出结论;(2)方法1、利用正弦定理得出三角形的面积公式,再利用等边三角形的性质即可得出结论;方法2、先用正弦定理得出S1,S2,S3,S4,最后用余弦定理即可得出结论.【解答】解:(1)在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8,∴EF=3,DF=8,∴S△DEF=EF×DFsin∠F=×3×8×sin60°=6,DE2=EF2+DF2﹣2EF×DFcos∠F=32+82﹣2×3×8×cos60°=49,故答案为:6,49;(2)证明:方法1,∵∠ACB=60°,∴AB2=AC2+BC2﹣2AC•BCcos60°=AC2+BC2﹣AC•BC,两边同时乘以sin60°得,AB2sin60°=AC2sin60°+BC2sin60°﹣AC•BCsin60°,∵△ABC',△BCA',△ACB'是等边三角形,∴S1=AC•BCsin60°,S2=AB2sin60°,S3=BC2sin60°,S4=AC2sin60°,∴S2=S4+S3﹣S1,∴S1+S2=S3+S4,方法2、令∠A,∠B,∠C的对边分别为a,b,c,∴S1=absin∠C=absin60°=ab∵△ABC',△BCA',△ACB'是等边三角形,∴S2=c•c•sin60°=c2,S3=a•a•sin60°=a2,S4=b•b•sin60°=b2,∴S1+S2=(ab+c2),S3+S4=(a2+b2),∵c2=a2+b2﹣2ab•cos∠C=a2+b2﹣2ab•cos60°,∴a2+b2=c2+ab,∴S1+S2=S3+S4.。
2020年中考数学九年级三轮冲刺:《三角形综合》(四)

三轮冲刺:《三角形综合》(四)1.已知△ABC中,AB=AC.(1)如图1,在△ADE中,AD=AE,连接BD、CE,若∠DAE=∠BAC,求证:BD=CE;(2)如图2,在△ADE中,AD=AE,连接BE、CE,若∠DAE=∠BAC=60°,CE⊥AD于点F,AE=4,,求BE的长;(3)如图3,在△BCD中,∠CBD=∠CDB=45°,连接AD,若∠CAB=45°,求的值.2.在等边△ABC中,点E,F分别在边AB,BC上.(1)如图1,若AE=BF,以AC为边作等边△ACD,AF交CE于点O,连接OD.求证:①AF=CE;②OD平分∠AOC;(2)如图2,若AE=2CF,作∠BCP=∠AEC,CP交AF的延长线于点P,求证:CE=CP.3.如图(1),在Rt△ABC中,∠C=90°,∠ABC=30°,点D,E分别是AB,AC的中点,过点B作直线DE的垂线段BM,垂足为M,点F是直线ED上一动点,作Rt△BFG,使∠BFG =90°,∠FGB=30°,连接GD.【观察猜想】如图(2),当点F与点D重合时,则的值为.【问题探究】如图(1),当点F与点D不重合时,请求出的值及两直线GD、ED夹角锐角的度数,并说明理由.【问题解决】如图(3),当点F、G、A在同一直线上时,请直接写出的值.4.△ABC中,AB=AC,∠BAC=120°,AD,BE分别为△ABC的高与中线.(1)如图1,求证:AE=AD;(2)如图2,点F在AD的延长线上,连接BF,CF,若BE=CF,求证:∠AEB=∠AFB;(3)在(2)的条件下,如图3,过点A作BF的平行线交CF于点G,若FG=6,求BE 的长.5.如图1,在直角三角形ABC中,∠BAC=90°,AD为斜边BC上的高线.(1)求证:AD2=BD⋅CD;(2)如图2,过A分别作∠BAD,∠DAC的角平分线,交BC于E,M两点,过E作AE的垂线,交AM于F.①当tan C=时,求的值;②如图3,过C作AF的垂线CG,过G点作GN∥AD交AC于M点,连接MN.若∠EAD=15°,AB=1,直接写出MN的长度.6.已知等边△ABC和等腰△CDE,CD=DE,∠CDE=120°.(1)如图1,点D在BC上,点E在AB上,P是BE的中点,连接AD,PD,则线段AD与PD之间的数量关系为;(2)如图2,点D在△ABC内部,点E在△ABC外部,P是BE的中点,连接AD,PD,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)如图3,若点D在△ABC内部,点E和点B重合,点P在BC下方,且PB+PC为定值,当PD最大时,∠BPC的度数为.7.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.动点P从点A出发,沿AB以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作PD⊥AC于点D、PE ∥AC,过点D作DE∥AB,DE与PE交于点E.设点P的运动时间为t秒.(1)线段AD的长为.(用含t的代数式表示).(2)当点E落在BC边上时,求t的值.(3)设△DPE与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式.(4)若线段PE的中点为Q,当点Q落在△ABC一边垂直平分线上时,直接写出t的值.8.在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB 于点E,DF∥AB交边AC于点F.(1)如图1,试判断四边形AEDF的形状,并说明理由;(2)如图2,若AD=4,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.(i)求EN•EG的值;(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上9.已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.10.如图1,△ABC为等腰直角三角形,∠BAC=90°,AD⊥BC于D.(1)点E、F分别在DA、DC的延长线上,且AE=CF,连接BE、AF,猜想线段BE和AF 的数量关系和位置关系,并证明你的结论;(2)如图2,连接EF,将△DEF绕点D顺时针旋转角α(0°<α<90°),连接AE、CE,若四边形ABCE恰为平行四边形,求DA与DE的数量关系;(3)如图3,连接EF,将△DEF绕点D逆时针旋转,当点A落在线段EF上时,设DE与AB交于点G,若AE:AF=3:4,求的值.参考答案1.(1)证明:如图1中,∵∠DAE=∠BAC,∴∠EAC=∠DAB,∵AE=AD,AC=AB,∴△EAC≌△DAB(SAS),∴EC=BD.(2)解:如图2中,连接BD.∵AE=AD,∠EAD=60°,∴△AED是等边三角形,∴∠DEA=∠CDE=60°,∵EF⊥AD,∴∠FEA=∠DEA=30°∵∠DAE=∠BAC,∴∠EAC=∠DAB,∵AE=AD,AC=AB,∴△EAC≌△DAB(SAS),∴∠BDA=∠AEC=30°,EC=BD,∴∠EDB=90°,∵AE=4,AF=2,AC=,∠EFA=∠AFC=90°,∴EF===2,CF===,∴EC=BD=3,∴BE===.(3)解:如图3中,作CM⊥CA,使得CM=CA,连接AM,BM.∵CA=CM,∠ACM=90°,∴∠CAM=45°,∵∠CAB=45°,∴∠MAB=45°+45°=90°,设AB=AC=m,则AM=m,BM==m,∵∠ACM=∠BCD=90°,∴∠BCM=∠ACD,∵CA=CM,CB=CD,∴△ACD≌△MCB(SAS),∴AD=BM=m,∴==.2.(1)证明:①如图1中,∵△ABC是等边三角形,∴AB=BC,∠B=∠BAC=60°,∵AE=BF,∴△ABF≌△CAE(SAS),∴AF=EC.②如图1中,∵△ABF≌△CAE,∴∠BAF=∠ACE,∵∠AOE=∠OAC+∠ACO=∠OCA+∠BAF=∠BAC=60°,又∵△ACD是等边三角形,∴∠ADC=∠DAC=∠DCA=60°,∴∠AOE=∠ADC,∵∠AOE+∠AOC=180°,∴∠ADC+∠AOC=180°,∴A,D,C,O四点共圆,∴∠AOD=∠ACD=60°,∠COD=∠CAD=60°,∴∠AOD=∠COD,∴OD平分∠AOC.(2)证明:如图2中,取AE的中点M,连接CM.∵AE=2CF,AM=ME,∴AM=CF,∵∠CAM=∠ACF=60°,AC=CA,∴△ACM≌△CAF(SAS),∴∠ACM=∠CAF,∵∠CME=∠CAM+∠ACM=60°+∠ACM,∠CFP=∠ACF+∠CAF=60°+∠CAF,∴∠CME=∠CFP,∵EM=CF,∠PCF=∠CEM,∴△CME≌△PFC(ASA),∴CE=PC.3.解:【观察猜想】如图(2)中,结论:当点F与点D重合时,则的值为2.理由:设BM=a.∵AE=EC,AD=DB,∴DE∥BC,∴∠BDM=∠ABC=30°,∵BM⊥EM,∴∠BMD=90°,∴BD=2BM=2a,DM=BM=a,在Rt△GDB中,∵∠GDB=90°,∠G=30°,∴GD=BD=2a,∴==2.故答案为2.【问题探究】如图(1)中,结论:的值为2,两直线GD、ED夹角锐角的度数为60°.理由:延长GD交BF的延长线于P.在Rt△BDM中,设BM=a,则BD=2a,DM=a,在Rt△BGF中,设BF=b,则BG=2b,FG=,在△BGD与△BFM中,∵BG:BF=2b:b=2a:a=BF:BM,∠DBG=60°﹣∠FBD=∠FBM,∴△BGD∽△BFM,∴DG:FM=BD:BM=2a:a=2:1,即的值为2,∵△BGD∽△BFM,∴∠PFD=∠MFB=∠BGD,则在△PDF与△PBG中,∠PDF=∠PBG=60°.故的值为2,两直线GD、ED夹角锐角的度数为60°.【问题解决】结论:的值为4+或4﹣.如图(3)﹣1中,当点G在线段AF上时,∵△BDG∽△BMF,∴∠BDG=∠BMF=90°,∴GD⊥AB,∵AD=BD,∴GD垂直平分线段AB,∴GA=GB,设BF=x,则BG=2x=AG,FG=,∴BG:AF=2x:=4﹣.如图(3)﹣2中,当点G在线段AF的延长线上时,设BF=x,同法可得:BG=AG=2x,GF=x,∴AF=2x﹣x,∴BG:AF=2x:(2x﹣x)=4+.∴的值为4+或4﹣.4.(1)证明:如图1中,∵AB=AC,∠BAC=120°,∴∠ABC=∠C=30°,∵BD=CD,∴AD⊥BC,∴AD=AC,∵BE是△ABC的中线,∴AE=EC=AC,∴AD=AE.(2)证明:如图2中,作BP⊥CA交CA的延长线于P.∵∠P=90°,∠BCP=30°,∴BP=BC=CD,∵∠FDC=∠P=90°,BE=CF,BP=CD,∴Rt△BPE≌Rt△CDF(HL),∴∠BEP=∠CFD,∵DF⊥BC,CD=DB,∴FB=FC,∴∠BFD=∠CFD,∴∠AEB=∠AFB.(3)解:如图3中,设AG交BE于H,交BC于M,作CN∥AD交AM的延长线于G.∵AG∥BF,∴∠GAF=∠AFB,∵∠FAB=∠AFC,∴∠GAF=∠AFG,∴GA=GF=6,∵CN∥AF,∴∠N=∠FAG,∠GCN=∠AFG,∴∠N=∠GCN,∴CG=GN,∴CF=AN=BE,∵∠ACB=30°,∠DCN=90°,∴∠BAE=∠ACN=120°,∵∠AEB=∠AFC=∠N,∴△BAE≌△ACN(AAS),∴AE=CN=AD,∵∠ADM=∠MCN=90°,AMD=∠CMN,∴△ADM≌△NCM(AAS),∴AM=MN,∵∠N+∠NMG=90∠NCG+∠MCG=90°,∴∠GMC=∠GCM,∴CG=GM=GN,∴AG=3GN=6,∴CG=GN=2,∴BE=CF=FG+CG=6+2=8.5.(1)证明:如图1中,∵AD⊥BC,∴∠ADB=∠ADC=90°,∵∠BAC=90°,∴∠B+∠C=90°,∵∠B+∠BAD=90°,∴∠BAD=∠C,∴△BAD∽△ACD,∴=,∴AD2=BD•CD.(2)①解:如图2中,作EH⊥AB于H,MG⊥AC于G.∵AD⊥BC,∴∠tan C==,∴可以假设AD=3k,CD=4k,则AC=5k,BD=k,AB=k,∵MA平分∠CAD,MD⊥AD,MG⊥AC,∴DM=MG,∵∠ADM=∠AGM=90°,AM=AM,∴Rt△MAD≌Rt△MAG(HL)∴AD=AG=3k,设MD=MG=x,则CG=2k,CM=4k﹣x,在Rt△CMG中,∵CM2=MG2+CG2,∴(4k﹣x)2=x2+(2k)2,∴x=k,∴DM=k,同法可得DE=k,∴==.②如图3中,∵AE平分∠BAD,∠EAD=15°,∴∠BAD=30°,∵AD⊥BC,∠BAC=90°,∴∠B=∠DAC=60°,∠C=30°,∵MA平分∠CAD,∴∠MAC=∠MAD=30°,∴∠MAC=∠MCA=30°,∴∠AMB=∠MAC+∠MCA=60°=∠B=∠BAM,∴MA=MC,△ABM是等边三角形,∴AM=BM,∵GN∥AD,∴∠GNC=∠DAC=60°,∵CG⊥AG,∴∠AGC=90°,∴∠ACG=60°=∠CNG,∴△CGN是等边三角形,∴NC=CG,∵AC=2CG,∴AN=CN,∵BM=MC,∴MN=AB=.6.解:(1)结论:AD=2PD.理由:如图1中,∵△ABC是等边三角形,∴∠B=60°,∵∠EDC=120°,∴∠EDB=180°﹣120°=60°,∴∠B=∠EDB=∠BED=60°,∴△BDE是等边三角形,∵BP=PE,∴DP⊥AB,∴∠APD=90°,∵DE=DC,DE=DB,∵AB=AC,∠BAC=60°,∴∠PAD=∠BAC=30°,∴AD=2PD.(2)结论成立.理由:延长DP到N,使得PN=PD,连接BN,EN,延长ED到M,使得DM=DE,连接BD,BM,CM.∵DE=DC=DM,∠MDC=180°﹣∠EDC=60°,∴△DCM是等边三角形,∵CA=CB,CM=CD,∠DCM=∠ACB=60°,∴∠BCM=∠ACD,∴△BCM≌△ACD(SAS),∴AD=BM,∵PB=PE,PD=PN,∴四边形BNED是平行四边形,∴BN∥DE,BN=DE,∵DE=DM,∴BN=DM,BN∥DM,∴四边形BNDM是平行四边形,∴BM=DN=2PD,∴AD=2PD.(3)如图3中,作∠PDK=∠BDC=120°,且PD=PK,连接PK,CK.∵DB=DC,DP=DK,∠BDC=∠PDK,∴∠BDP=∠CDK,∴△PDB≌△KDC(SAS),∴PB=CK,∵PB+PC=PC+CK=定值,∴P,C,K共线时,PK定值最大,此时PD的值最大,此时,∠DPB=∠DKP=∠DPK=30°,∠BPC=∠DPB+∠DPK=60°.故答案为60°.7.解:(1)如图1中,在Rt△ACB中,∵∠C=90°,AC=8,BC=6,∴AB===10,∵PD⊥AC,∴cos A==,∴=,∴AD=4t,故答案为4t.(2)如图2中,当点E落在BC上时,∵DE∥AB,PE∥AD,∴四边形APED是平行四边形,∴DE=AP=5t,AD=PE=4t,∴=,∴=,解得t=1,∴当点E落在BC边上时,t的值为1.(3)①如图1中,当0<t≤1时,重叠部分是△PDE,∵PE∥AD,∴∠DPE=∠ADP=90°,∵DE=5t,PE=4t,∴PD=3t,∴S=•PD•PE=×3t×4t=6t2.②如图3中,当1<t≤2时,S=•(MN+PD)•PN=[3t+3t﹣(10﹣5t)]•(10﹣5t)=﹣18t2+48t﹣24.综上所述,S=.(4)①如图4﹣1中,当点Q落在线段AC的垂直平分线MN上时,由题意:=,可得=,解得t=.②如图4﹣2中,当点Q落在线段AB的垂直平分线MN上时,由题意:=,可得=,解得t=③如图4﹣3中,当点Q落在线段BC的垂直平分线上时,AP=PB,此时t=1,综上所述,满足条件的t的值为或或1.8.(1)解:四边形AEDF的形状是菱形;理由如下:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∵AD平分∠BAC,∴∠EAD=∠FAD,∵DE∥AC,∴∠EDA=∠FAD,∴∠EAD=∠EDA,∴AE=DE,∴四边形AEDF是菱形;(2)(i)解:连接EF交AD于点Q,如图2所示:∵∠BAC=60°,四边形AEDF是菱形,∴∠EAD=30°,AD、EF相互垂直平分,△AEF是等边三角形,∴∠EAF=∠AEF=∠AFE=60°,∵AD=4,∴AQ=2,在Rt△AQE中,cos∠EAQ=,即cos30°=,∴AE===4,∴AE=AF=EF=4,在△AEG和△EFH中,,∴△AEG≌△EFH(SAS),∴∠AEG=∠EFH,∴∠ENH=∠EFH+∠GEF=∠AEG+∠GEF=60°,∴∠ENH=∠EAG,∵∠AEG=∠NEH,∴△AEG∽△NEH,∴=,∴EN•EG=EH•AE=3×4=12;(ii)证明:如图3,连接FM',∵DE∥AC,∴∠AED=180°﹣∠BAC=120°,由(1)得:△EDF是等边三角形,∴DE=DF,∠EDF=∠FED=∠EFD=60°,由旋转的性质得:∠MDM'=60°,DM=DM',∴∠EDM=∠FDM',在△EDM和△FDM'中,,∴△EDM≌△FDM'(SAS),∴∠MED=∠DFM',由(i)知,∠AEG=∠EFH,∴∠DFM'+∠EFH=∠MED+∠AEG=∠AED=120°,∴∠HFM'=∠DFM'+∠HFE+∠EFD=120°+60°=180°,∴H,F,M′三点在同一条直线上.9.提出问题:解:在△DBA和△CAB中,∵.∴△DBA≌△CAB(AAS),∴AD=BC;类比探究:结论仍然成立.理由:作∠BEC=∠BCE,BE交AC于E.∵∠ADB+∠ACB=∠AEB+∠BEC=180°,∴∠ADB=∠AEB.∵∠CAB=∠DBA,AB=BA,∴△DBA≌△EAB(AAS),∴BE=AD,∵∠BEC=∠BCE,∴BC=BE,∴AD=BC.综合运用:作∠BEC=∠BCE,BE交AC于E.由(2)得,AD=BC=BE=1.在Rt△ACB中,∠CAB=18°,∴∠C=72°,∠BEC=∠C=72°.由∠CFB=∠CAB+∠DBA=36°,∴∠EBF=∠CEB﹣∠CFB=36°,∴EF=BE=1.在△BCF中,∠FBC=180°﹣∠BFC﹣∠C=72°,∴∠FBC=∠BEC,∠C=∠C,∴△CBE∽△CFB.∴=,令CE=x,∴1=x(x+1).解得,x=,∴CF=.由∠FBC=∠C,∴BF=CF.又AF=BF,∴AC=2CF=+1.10.解:(1)BE=AF,BE⊥AF,理由如下:延长FA交BE于H,∵△ABC为等腰直角三角形,∠BAC=90°,AD⊥BC,∴∠BAD=∠ACD=45°,AB=AC,∴∠BAE=∠ACF=135°,又∵AB=AC,AE=CF,∴△ABE≌△CAF(SAS),∴AF=BE,∠EBA=∠FAC,∵∠BAF=∠ABE+∠BHA=∠BAC+∠CAF,∴∠BAC=∠BHA=90°,∴BE⊥AF;(2)∵△ABC为等腰直角三角形,∠BAC=90°,AD⊥BC,∴AD=BC,∵四边形ABCE恰为平行四边形,∴AE=BC=2AD,AE∥BC,∴∠EAD=∠ADB=90°,∴DE===AD;(3)如图3,连接BE,过点E作EH⊥AB于H,DN⊥AB于N,由图1可得:∵△ABC为等腰直角三角形,∠BAC=90°,AD⊥BC,∴AD=BD=CD,AD⊥CD,又∵AE=CF,∴DE=DF,∴△DEF是等腰直角三角形,∴∠DFE=∠DEF=45°由图3可得:∠EDF=∠BDA=90°,∴∠ADF=∠BDE,又∵AD=BD,DE=DF,∴△ADF ≌△BDE (SAS ), ∴BE =AF ,∠DFE =∠BED =45°, ∴∠AEB =90°, ∵AE :AF =3:4,∴设AE =3a ,AF =BE =4a , ∴AB ===5a ,∵AD =BD ,∠ADB =90°,DN ⊥AB , ∴DN =BN =AN =a ,∵S △ABE =AE ×BE =AB ×EH , ∴EH ==a ,∴AH ==a ,∵∠BED =∠AED =45°, ∴, ∴BG =,AG =,∴GH =a ,GN =a ,∴EG ==a ,DG ==a ,∴==.1、在最软入的时候,你会想起谁。
2020年数学中考复习专题:《三角形综合》(后附解析)

中考复习冲刺:《三角形综合》1.如图,在三角形ABC 中,AB =8,BC =16,AC =12.点P 从点A 出发以2个单位长度/秒的速度沿A →>B →C →A 的方向运动,点Q 从点B 沿B →C →A 的方向与点P 同时出发;当点P 第一次回到A 点时,点P ,Q 同时停止运动;用t (秒)表示运动时间.(1)当t = 秒时,P 是AB 的中点.(2)若点Q 的运动速度是23个单位长度/秒,是否存在t 的值,使得BP =2BQ . (3)若点Q 的运动速度是a 个单位长度/秒,当点P ,Q 是AC 边上的三等分点时,求a 的值.2.如图,在△ABC 中,BC =7cm ,AC =24cm ,AB =25cm ,P 点在BC 上,从B 点到C 点运动(不包括C 点),点P 运动的速度为2cm /s ;Q 点在AC 上从C 点运动到A 点(不包括A 点),速度为5cm /s .若点P 、Q 分别从B 、C 同时运动,请解答下面的问题,并写出探索主要过程:(1)经过多少时间后,P 、Q 两点的距离为5cm ?(2)经过多少时间后,S △PCQ 的面积为15cm 2?(3)用含t 的代数式表示△PCQ 的面积,并用配方法说明t 为何值时△PCQ 的面积最大,最大面积是多少?3.定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.(1)如图1,△ABC中,AB=AC,∠A=36°,求证:△ABC是倍角三角形;(2)若△ABC是倍角三角形,∠A>∠B>∠C,∠B=30°,AC=4 2 ,求△ABC面积;(3)如图2,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.4.如图,如图1,在平面直角坐标系中,已知点A(﹣4,﹣1)、B(﹣2,1),将线段AB 平移至线段CD,使点A的对应点C在y轴的正半轴上,点D在第一象限.(1)若点C的坐标(k,0),求点D的坐标(用含k的式子表示);(2)连接BD、BC,若三角形BCD的面积为5,求k的值;(3)如图2,分别作∠ABC和∠ADC的平分线,它们交于点P,请写出∠A、和∠P和∠BCD 之间的一个等量关系,并说明理由.5.如图1,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.(1)求证:S△ABD =S△ACE;(2)如图2,AM是△ACE的中线,MA的延长线交BD于N,求证:MN⊥BD.6.已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出的值.7.定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“和美三角形”,这条边称为“和美边”,这条中线称为“和美中线”.理解:(1)请你在图①中画一个以AB为和美边的和美三角形,使第三个顶点C落在格点上;(2)如图②,在Rt△ABC中,∠C=90°,tan A=.求证:△ABC是“和美三角形”.运用:(3)已知,等腰△ABC是“和美三角形”,AB=AC=20,求底边BC的长(画图解答).8.【问题提出】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC =α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)【特例探究】小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是三角形;∠ADB的度数为.【问题解决】在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;【拓展应用】在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC =7,AD=2.请直接写出线段BE的长为.9.如图,已知A(3,0),B(0,﹣1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC.(1)如图1,求C点坐标;(2)如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;(3)在(2)的条件下若C、P,Q三点共线,求此时∠APB的度数及P点坐标.10.问题原型:如图①,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,在AD上取点E,使DE=CD,连结BE.求证:BE=AC.问题拓展:如图②,在问题原型的条件下,F为BC的中点,连结EF并延长至点M,使FM =EF,连结CM.(1)判断线段AC与CM的大小关系,并说明理由.(2)若AC=,直接写出A、M两点之间的距离.11.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C 不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q 不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)证明:在运动过程中,点D是线段PQ的中点;(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.12.如图,AC平分钝角∠BAE交过B点的直线于点C,BD平分∠ABC交AC于点D,且∠BAD+∠ABD=90°.(1)求证:AE∥BC;(2)点F是射线BC上一动点(点F不与点B,C重合),连接AF,与射线BD相交于点P.(ⅰ)如图1,若∠ABC=45°,AF⊥AB,试探究线段BF与CF之间满足的数量关系;=30,∠CAF=∠ABD,求线段BP的长.(ⅱ)如图2,若AB=10,S△ABC13.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC=°,∠DEC=°;点D从B向C的运动过程中,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由.(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.14.如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,过点C作CG⊥AD于点G,过点B作FB⊥CB于点B,交CG的延长线于点F,连接DF交AB于点E.(1)求证:△ACD≌△CBF;(2)求证:AB垂直平分DF;(3)连接AF,试判断△ACF的形状,并说明理由.15.【阅读理解】截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD =∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是;【拓展延伸】(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC =90°,探索线段DA、DB、DC之间的数量关系,并说明理由;【知识应用】(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长分别为cm.16.如图,△ABC中,∠ABC=90°,AB=BC,D在边AC上,AE⊥BD于E.(1)如图1,作CF⊥BD于F,求证:CF﹣AE=EF;(2)如图2,若BC=CD,求证:BD=2AE;(3)如图3,作BM⊥BE,且BM=BE,AE=2,EN=4,连接CM交BE于N,请直接写出△BCM的面积为.17.已知△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,M为CE中点.(1)如图1,若D点在BA延长线上,直接写出BM与DM的数量关系与位置关系不必证明.(2)如图2,当C,E,D在同直线上,连BE,探究BE与AB的的数量关系,并加以证明.(3)在(2)的条件下,若AB=AE=2.求BD的长.18.如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P(1)观察猜想:①线段AE与BD的数量关系为.②∠APC的度数为.(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为.19.(1)已知:如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C 重合),以AD为边作等边△ADE,连接CE.求证:①BD=CE,②∠DCE=120°;(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:①∠DCE的度数;②线段BD、CD、DE之间的关系,并说明理由;(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE.①则题(2)的结论还成立吗?请直接写出,不需论证;②连结BE,若BE=10,BC=6,直接写出AE的长.20.思维启迪:(1)如图①,A,B两点分别位于一个池塘的两端,小亮想用绳子测量A,B间的距离,但绳子不够长,他出一个办法:先在地上取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),利用工具过点C作CD∥AB交AP的延长线于点D,此时测得CD=200米,那么A,B间的距离是米.思维探索:(2)在△ABC和△ADE中,AC=BC=4,AE=DE=,∠ACB=∠AED=90°,将△ADE 绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE.①如图②,当△ADE在起始位置时,求证:PC⊥PE,PC=PE.②如图③,当α=90°时,点D落在AB边上,PC与PE的数量关系和位置关系分别为.③当α=135°时,直接写出PC的值.参考答案1.解:(1)∵AB=8,点P的运动速度为2个单位长度/秒,∴当P为AB中点时,即4÷2=2(秒);故答案为:2.(2)由题意可得:当BP=2BQ时,P,Q分别在AB,BC上,∵点Q的运动速度为个单位长度/秒,∴点Q只能在BC上运动,∴BP=8﹣2t,BQ=t,则8﹣2t=2×t,解得t=,当点P运动到BC和AC上时,不存在BP=2BQ;(3)当点P为靠近点A的三等分点时,如图1,AB+BC+CP=8+16+8=32,此时t=32÷2=16,∵BC+CQ=16+4=20,∴a=20÷16=,当点P为靠近点C的三等分点时,如图2,AB +BC +CP =8+16+4=28,此时t =28÷2=14,∵BC +CQ =16+8=24,∴a =24÷14=.综上可得:a 的值为或.2.解:(1)连接PQ ,设经过ts 后,P 、Q 两点的距离为5cm ,ts 后,PC =7﹣2tcm ,CQ =5tcm ,根据勾股定理可知PC 2+CQ 2=PQ 2,代入数据(7﹣2t )2+(5t )2=(5)2; 解得t =1或t =﹣(不合题意舍去);(2)设经过ts 后,S △PCQ 的面积为15cm 2 ts 后,PC =7﹣2tcm ,CQ =5tcm ,S △PCQ =×PC ×CQ =×(7﹣2t )×5t =15解得t 1=2,t 2=1.5,经过2或1.5s 后,S △PCQ 的面积为15cm 2.(3)设经过ts 后,△PCQ 的面积最大,ts 后,PC =7﹣2tcm ,CQ =5tcm ,S △PCQ =×PC ×CQ =×(7﹣2t )×5t =×(﹣2t 2+7t ).=﹣5.∴当t=s时,△PCQ的面积最大,最大值为cm2.3.(1)证明:∵AB=AC,∴∠B=∠C,∵∠A+∠B+∠C=180°,∠A=36°,∴∠B=∠C=72°,∴∠A=2∠C,即△ABC是倍角三角形,(2)解:∵∠A>∠B>∠C,∠B=30°,①当∠B=2∠C,得∠C=15°,过C作CH⊥直线AB,垂足为H,可得∠CAH=45°,∴AH=CH=AC=4.∴BH=,∴AB=BH﹣AH=﹣4,∴S=.②当∠A=2∠B或∠A=2∠C时,与∠A>∠B>∠C矛盾,故不存在.综上所述,△ABC面积为.(3)△ADC和△ABC是倍角三角形,证明如下:∵AD平分∠BAE,∴∠BAD=∠EAD,∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),∴∠ADE=∠ADB,BD=DE.又∵AB +AC =BD ,∴AE +AC =BD ,即CE =BD .∴CE =DE .∴∠C =∠BDE =2∠ADC .∴△ADC 是倍角三角形.∵△ABD ≌△AED ,∴∠E =∠ABD ,∴∠E =180°﹣∠ABC ,∵∠E =180°﹣2∠C ,∴∠ABC =2∠C .∴△ABC 是倍角三角形.4.解:(1)∵点A (﹣4,﹣1)、B (﹣2,1),C (k ,0),将线段AB 平移至线段CD , ∴点B 向上平移一个单位,向右平移(k +4)个单位到点D ,∴D (k +2,2);(2)如图1,过点B 作BE ⊥x 轴于点E ,过点D 作DF ⊥x 轴于点F ,∵A (﹣4,﹣1)、B (﹣2,1),C (k ,0),D (k +2,2),∴BE =1,CE =k +2,DF =2,EF =k +4,CF =2,∵S 四边形BEFD =S △BEC +S △DCF +S △BCD , ∴=+,解得:k =2.(3)∠BPD =∠BCD +∠A ;理由如下:过点P 作PE ∥AB ,如图2所示:∴∠PBA=∠EPB,∵线段AB平移至线段CD,∴AB∥CD,∴PE∥CD,∠ADC=∠A,∠ABC=∠BCD,∴∠EPD=∠PDC,∴∠BPD=∠PBA+∠PDC,∵BP平分∠ABC,DP平分∠ADC,∴∠PBA=∠ABC,∠PDC=∠ADC,∴∠BPD=∠ABC+∠ADC=∠BCD+∠A.5.证明:(1)过B作BM⊥DA于M,过C作CN⊥EA交EA的延长线于N,如图,∵∠BAC=∠DAE=90°,∴∠BAD+∠CAE=180°,∵∠CAN+∠CAE=180°,∴∠BAD=∠CAN∵sin∠BAD=,sin∠CAN=,又∵AB=AC,∴BM=CN,∵DA=AE,S△ABD =DN×BM,S△ACE=AE×CN,∴S△ADB =S△ACE.(2)延长AM到Q使AM=QM,连接CQ、EQ,如图,∵AM是△ACE中线,∴CM=EM,∴四边形ACQE是平行四边形,∴AC=EQ=AB,AE=CQ=AD,AC∥EQ,∴∠CAE+∠AEQ=180°,∵∠BAD+∠CAE=180°,∴∠BAD=∠AEQ,∵在△BAD和△QEA中∴△BAD≌△QEA,∴∠BDA=∠EAM,∵∠DAE=90°,∴∠NAD+∠QAE=90°,∴∠BDA+∠NAD=90°,∴∠DNA=180°﹣90°=90°,∴MN⊥BD.6.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC =∠AEH ,∵AD =AE ,∴△ACD ≌△EHA ,∴CD =AH ,EH =AC =BC ,∵CB =CA ,∴BD =CH ,∵∠EHF =∠BCF =90°,∠EFH =∠BFC ,EH =BC ,∴△EHF ≌△BCF ,∴FH =CF ,∴BD =CH =2CF .(3)如图3中,同法可证BD =2CM .∵AC =3CM ,设CM =a ,则AC =CB =3a ,BD =2a , ∴==.7.解:(1)如图①中,△ABC 1,△ABC 2即为所求.(2)证明:如图②,根据定义Rt △ABC 中,和美中线一定是较长直角边上的中线. 理由:取AC 的中点D ,连结BD ,设AC =2x ,则CD =AD =x ,∵,∴,∴,在Rt△BCD中,∴BD=AC,∴△ABC是“和美三角形:.(3)分两种情况:如图③,当腰上的中线BD=AC时,则AB=BD,过B作BE⊥AD于E,∵AB=AC=20,∴BD=20,,∴CE=10+5=15,∴Rt△BDE中,BE2=BD2﹣DE2=375,∴Rt△BCE中,;如图④,当底边上的中线AD=BC时,则AD⊥BC,且AD=2BD,设BD=x,则x2+(2x)2=202,∴x2=80,又∵x>0,∴,∴.综上所述,底边BC的长为或.8.解:【特例探究】①如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,∵AB=AC,∠BAC=90°,∴∠ABC=45°,∵∠DBC=30°,∴∠ABD=∠ABC﹣∠DBC=15°,在△ABD和△ABD′中,∴△ABD≌△ABD′,∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,∴∠D′BC=∠ABD′+∠ABC=60°,∵BD=BD′,BD=BC,∴BD′=BC,∴△D′BC是等边三角形,②∵△D′BC是等边三角形,∴D′B=D′C,∠BD′C=60°,在△AD′B和△AD′C中,∴△AD′B≌△AD′C,∴∠AD′B=∠AD′C,∴∠AD′B=∠BD′C=30°,∴∠ADB=30°.故答案为:等边,30°;【问题解决】解:∵∠DBC<∠ABC,∴60°<α≤120°,如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,∵AB=AC,∴∠ABC=∠ACB,∵∠BAC=α,∴∠ABC=(180°﹣α)=90°﹣α,∴∠ABD=∠ABC﹣∠DBC=90°﹣α﹣β,同(1)①可证△ABD≌△ABD′,∴∠ABD=∠ABD′=90°﹣α﹣β,BD=BD′,∠ADB=∠AD′B∴∠D′BC=∠ABD′+∠ABC=90°﹣α﹣β+90°﹣α=180°﹣(α+β),∵α+β=120°,∴∠D′BC=60°,由(1)②可知,△AD′B≌△AD′C,∴∠AD′B=∠AD′C,∴∠AD′B=∠BD′C=30°,∴∠ADB=30°.【拓展应用】第①情况:当60°<α<120°时,如图3﹣1,由(2)知,∠ADB=30°,作AE⊥BD,在Rt△ADE中,∠ADB=30°,AD=2,∴DE=,∵△BCD'是等边三角形,∴BD'=BC=7,∴BD=BD'=7,∴BE=BD﹣DE=7﹣;第②情况:当0°<α<60°时,如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.同理可得:∠ABC=(180°﹣α)=90°﹣α,∴∠ABD=∠DBC﹣∠ABC=β﹣(90°﹣α),同(1)①可证△ABD≌△ABD′,∴∠ABD=∠ABD′=β﹣(90°﹣α),BD=BD′,∠ADB=∠AD′B,∴∠D′BC=∠ABC﹣∠ABD′=90°﹣α﹣[β﹣(90°﹣α)]=180°﹣(α+β),∴D′B=D′C,∠BD′C=60°.同(1)②可证△AD′B≌△AD′C,∴∠AD′B=∠AD′C,∵∠AD′B+∠AD′C+∠BD′C=360°,∴∠ADB=∠AD′B=150°,在Rt△ADE中,∠ADE=30°,AD=2,∴DE=,∴BE=BD+DE=7+,故答案为:7+或7﹣.9.解:(1)作CH⊥y轴于H,则∠BCH+∠CBH=90°,∵AB⊥BC,∴∠ABO+∠CBH=90°,∴∠ABO=∠BCH,在△ABO和△BCH中,,∴△ABO≌△BCH,∴BH=OA=3,CH=OB=1,∴OH=OB+BH=4,∴C点坐标为(1,﹣4);(2)∵∠PBQ=∠ABC=90°,∴∠PBQ﹣∠ABQ=∠ABC﹣∠ABQ,即∠PBA=∠QBC,在△PBA和△QBC中,,∴△PBA≌△QBC,∴PA=CQ;(3)∵△BPQ是等腰直角三角形,∴∠BQP=45°,当C、P,Q三点共线时,∠BQC=135°,由(2)可知,△PBA≌△QBC,∴∠BPA=∠BQC=135°,∴∠OPB=45°,∴OP=OB=1,∴P点坐标为(1,0).10.解:问题原型:∵AD⊥BC,∴∠ADB=∠ADC=90°,∵∠ABC=45°,∴∠BAD=45°,∴∠ABC=∠BAD,∴AD=BD,在△BDE和△ADC中,∵,∴△BDE≌△ADC(SAS),∴BE=AC,问题拓展:(1)AC=CM,理由:∵点F是BC中点,∴BF=CF,在△BEF和△CMF中,∵,∴△BEF≌△CMF(SAS),∴BE=CM,由(1)知,BE=AC,∴AC=CM;(2)如图②,连接AM,由(1)知,△BDE≌△ADC,∴∠BED=∠ACD,由(2)知,△BEF≌△CMF,∴∠EBF=∠BCM,∴∠ACM=∠ACD+∠BCM=∠BED+∠EBF=90°,∵AC=CM,∴AM=AC=.11.(1)解:设AP=x,则BQ=x,∵∠BQD=30°,∠C=60°,∴∠QPC=90°,∴QC=2PC,即x+6=2(6﹣x),解得x=2,即AP=2.(2)证明:如图,过P点作PF∥BC,交AB于F,∵PF∥BC,∴∠PFA=∠FPA=∠A=60°,∴PF=AP=AF,∴PF=BQ,又∵∠BDQ=∠PDF,∠DBQ=∠DFP,∴△DQB≌△DPF,∴DQ=DP即D为PQ中点,(3)运动过程中线段ED的长不发生变化,是定值为3,理由:∵PF=AP=AF,PE⊥AF,∴,又∵△DQB≌△DPF,∴,∴.12.(1)证明:∵AC平分钝角∠BAE,BD平分∠ABC,∴∠BAE=2∠BAD,∠ABC=2∠ABD,∴∠BAE+∠ABC=2(∠BAD+∠ABD)=2×90°=180°,∴AE∥BC;(2)解:(ⅰ)BF=(2+)CF;理由如下:∵∠BAD+∠ABD=90°,∴BD⊥AC,∴∠CBD+∠BCD=90°,∵∠ABD=∠CBD,∴∠BAD=∠BCD,∴AB=BC,过点A作AH⊥BC于H,如图1所示:∵∠ABC=45°,AF⊥AB,∴△ABH、△BAF是等腰直角三角形,∴AH=BH=HF,BC=AB=BH,BF=AB=×BH=2BH,∴CF=BF﹣BC=2BH﹣BH=(2﹣)BH,∴BH==(1+)CF,∴BF=2(1+)CF=(2+)CF;(ⅱ)当点F在点C的左侧时,如图2所示:同(ⅰ)得:∠BAD=∠BCD,∴AB=BC=10,∵∠CAF=∠ABD,∠BAD+∠ABD=90°,∴∠BCD+∠CAF=90°,∴∠AFC=90°,∴AF⊥BC,=BC•AF=×10×AF=30,则S△ABC∴AF=6,∴BF==8,∴CF=BC﹣BF=10﹣8=2,∴AC==2,=AC•BD=×2×BD=30,∵S△ABC∴BD=3,作PG⊥AB于G,则PG=PF,在Rt△BPG和Rt△BPF中,,∴Rt△BPG≌Rt△BPF(HL),∴BG=BF=8,∴AG=AB﹣BG=2,∵AB=CB,BD⊥AC,∴AD=CD=AC=,设AP=x,则PG=PF=6﹣x,在Rt△APG中,由勾股定理得:22+(6﹣x)2=x2,解得:x=,∴AP=,∴PD===,∴BP=BD﹣PD=3﹣=;当点F在点C的右侧时,则∠CAF=∠ACF',∵BD⊥AC,∴∠APD=∠AP'D,∴AP=AP',PD=P'D=,∴BP=+2×=;综上所述,线段BP的长为或.13.解:(1)∵∠ADB+∠ADE+∠EDC=180°,且∠ADE=40°,∠BDA=110°,∴∠EDC=30°,∵∠AED=∠EDC+∠ACB=30°+40°=70°∴∠EDC=180°﹣∠AED=110°,故答案为:30,110,∵∠BDA+∠B+∠BAD=180°,∴∠BDA=140°﹣∠BAD∵点D从B向C的运动过程中,∠BAD逐渐变大∴∠BDA逐渐变小,故答案为:小(2)当DC=2时,△ABD≌△DCE,理由如下:∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,∠B=∠ADE=40°,∴∠BAD=∠CDE,且AB=CD=2,∠B=∠C=40°,∴△ABD≌△DCE(ASA)(3)若AD=DE时,∵AD=DE,∠ADE=40°∴∠DEA=∠DAE=70°∵∠DEA=∠C+∠EDC∴∠EDC=30°∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣30°=110°若AE=DE时,∵AE=DE,∠ADE=40°∴∠ADE=∠DAE=40°,∴∠AED=100°∵∠DEA=∠C+∠EDC∴∠EDC=60°∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣60°=80°综上所述:当∠BDA=80°或110°时,△ADE的形状可以是等腰三角形14.证明:(1)∵CG⊥AD,∴∠AGC=90°,∴∠GCA+∠CAD=90°,∵∠GCA+∠FCB=90°,∴∠CAD=∠FCB,∵FB⊥BC,∴∠CBF=90°,∵Rt△ABC是等腰三角形,∠ACB=90°,∴AC=BC,∠CBF=∠ACB,在△ACD和△CBF中,∴△ACD≌△CBF(ASA);(2)∵△ACD≌△CBF,∴CD=BF,∵D为BC的中点,∴CD=BD,∴BD=BF,∵△ABC是等腰直角三角形,∠ACB=90°,∴∠DBE=45°,∵∠CBF=90°,∴∠DBE=∠FBE=45°,在△DBE和△FBE中,∴△DBE≌△FBE(SAS),∴DE=FE,∠DEB=∠FEB=90°,∴AB垂直平分DF;(3)△ACF是等腰三角形,理由为:连接AF,如图所示,由(1)知:△CBF≌△ACD,∴CF=AD,由(2)知:AB垂直平分DF,∴AF=AD,∵CF=AD,∴CF=AF,∴△ACF是等腰三角形.15.解:(1)如图1,延长DC到点E,使CE=BD,连接AE,∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵∠BDC=120°,∴∠ABD+∠ACD=180°,又∵∠ACE+∠ACD=180°,∴∠ABD=∠ACE,∴△ABD≌△ACE(SAS),∴AD=AE,∠BAD=∠CAE,∵∠ABC=60°,即∠BAD+∠DAC=60°,∴∠DAC+∠CAE═60°,即∠DAE=60°,∴△ADE是等边三角形,∴DA=DE=DC+CE=DC+DB,即DA=DC+DB,故答案为:DA=DC+DB;(2)DA=DB+DC,如图2,延长DC到点E,使CE=BD,连接AE,∵∠BAC=90°,∠BDC=90°,∴∠ABD+∠ACD=180°,∵∠ACE+∠ACD=180°,∴∠ABD=∠ACE,∵AB=AC,CE=BD,∴△ABD≌△ACE,∴AD=AE,∠BAD=∠CAE,∴∠DAE=∠BAC=90°,∴DA2+AE2=DE2,∴2DA2=(DB+DC)2,∴DA=DB+DC;(3)如图3,连接PQ,∵MN=14,∠QMN=30°,∴QN=MN=7,∴MQ===7,由(2)知PQ=QN+QM=7+7,∴PQ==,故答案为:.16.(1)证明:∵CF⊥BD于点F,AE⊥BD,∴∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,又∵∠ABC=90°,∴∠ABE+∠CBF=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(AAS),∴BE=CF,AE=BF,∴CF﹣AE=BE﹣BF=EF;(2)证明:如图1,过点C作CF⊥BD于点F,∵BC=CD,∴BF=DF,由(1)得AE=BF,∴AE=DF,∴BD=2AE;(3)解:如图2,过点C作CG⊥MB,交MB的延长线于点G,过点C作CH⊥BE,交BE于点H,∵BM⊥BE,CH⊥BE,CG⊥MB,∴∠NBG=∠CHB=∠CGB=90°,∴四边形BGCH为矩形,∴BG=HC,BH=GC,由(1)得△AEB≌△BHC,∴AE=BH,BE=CH,∵BM=BE,∴BM=CH,∵∠MBN=∠CHN=90°,∠MNB=∠CNH,∴△BMN≌△HCN(AAS),∴BM=CH,BN=HN,∵AE=BH=2,∴BN=1,∴BE=BM=BN+EN=1+4=5,∴=.故答案为:5.17.解:(1)BM=DM,BM⊥DM;如图1,连接AM,∵△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,∴∠CAE=90°,∵M为CE中点.∴CM=AM,∵BM=BM,BC=BA,∴△BCM≌△BAM(SSS),∴∠CBM=∠MBA=45°,同理可得∠MDA=45°,∴∠BMD=90°,∴BM=DM,BM⊥DM;(2)如图2,延长BM到N,使BM=MN,连EN,DN,BD,BE,∵∠CMB=∠EMN,CM=ME,∴△CBM≌△ENM(SAS),∴BC=EN,∠BCM=∠MEN,∴EN=AB,∵∠CBA=∠ADE=90°,∴∠BCM+∠BAD=180°,∵∠NED+∠MEN=180°,∴∠NED=∠BAD,又∵AD=DE,∴△END≌△ABD(SAS),∴DB=DN,∠NDE=∠BDA,∴∠NDE+∠BDE=90°,∴∠NDB=90°,∴DB⊥DN,∴DM⊥BN,∴BE=EN=BC=AB;(3)如图3,连BE,BD交AE于N,在(2)的条件下,CM=ME,DM⊥BM,∴BE=BC=AE=AB=2,DE=DA=2,∴BD为AE的垂直平分线,∴EN=DN=AN=,∴BN==,∴BD=+.18.解:(1)观察猜想:①如图1,设AE交CD于点O.过点C作CH⊥AE,CG⊥BD,∵△ADC,△ECB都是等边三角形,∴CA=CD,∠ACD=∠ECB=60°,CE=CB,∴∠ACE=∠DCB,∴△ACE≌△DCB(SAS),∴AE=BD,∠CAO=∠ODP,S△ACE =S△BCD,∴∠DPO=∠ACO=60°,∴∠APB=120°,∵S△ACE =S△BCD,∴×AE×CH=×BD×CG,∴CH=CG,且CH⊥AE,CG⊥BD,∴CP平分∠APB,∴∠APC=60°,故答案为AE=BD,60°.(2)数学思考::①成立,②不成立,理由:设AC交BD于点O.过点C作CH⊥AE,CG⊥BD,∵△ADC,△ECB都是等边三角形,∴CA=CD,∠ACD=∠ECB=60°,CE=CB,∴∠ACE=∠DCB∴△ACE≌△DCB(SAS),∴AE=BD,∠PAO=∠ODC,∵∠AOP=∠DOC,∴∠APO=∠DCO=60°,∴∠DPE=120°,∵S△ACE =S△BCD,∴×AE×CH=×BD×CG,∴CH=CG,且CH⊥AE,CG⊥BD,∴∠DPC=60°,∴∠APC=120°,∴①成立,②不成立;拓展应用:设AC交BD于点O.∵∠ACD=∠BCE=90°,CA=CD,CB=CE,∴∠ACE=∠DCB∴△AEC≌△DBC(SAS),∴AE=BD,∠CDB=∠CAE,∵∠AOP=∠COD,∠CDB=∠CAE,∴∠DCO=∠APO=90°,∴AE⊥BD,故答案为:AE=BD,AE⊥BD.19.证明:(1)①如图1,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠ACB=∠B=60°,∠BAC=∠DAE=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠BAD=∠EAC.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE;②∵△ABD≌△ACE,∴∠ACE=∠B=60°,∴∠DCE=∠ACE+∠ACB=60°+60°=120°;(2)∠DCE=90°,BD2+CD2=DE2.证明:如图2,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE=45°,BD=CE,∴∠B+∠ACB=∠ACE+∠ACB=90°,∴∠BCE=90°,∴Rt△DCE中,CE2+CD2=DE2,∴BD2+CD2=DE2;(3)①(2)中的结论还成立.理由:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABC=∠ACE=45°,BD=CE,∴∠ABC+∠ACB=∠ACE+∠ACB=90°,∴∠BCE=90°=∠ECD,∴Rt△DCE中,CE2+CD2=DE2,∴BD2+CD2=DE2;②∵Rt△BCE中,BE=10,BC=6,∴CE===8,∴BD=CE=8,∴CD=8﹣6=2,∴Rt△DCE中,DE===,∵△ADE是等腰直角三角形,∴.20.(1)解:∵CD∥AB,∴∠ABP=∠C,∵P是BC的中点,∴PB=PC,在△ABP和△DCP中,,∴△ABP≌△DCP(ASA),∴AB=CD=200米;故答案为:200;(2)①证明:延长EP交BC于F,如图②所示:∵∠ACB=∠AED=90°,∴DE∥BC,∴∠EDP=∠FBP,∠DEP=∠BFP,∵点P是线段BD的中点,∴PB=PD,在△FBP和△EDP中,,∴△FBP≌△EDP(AAS),∴PF=PE,BF=DE,∵AC=BC,AE=DE,∴FC=EC,又∵∠ACB=90°,∴△EFC是等腰直角三角形,∵PE=PF,∴PC⊥EF,PC=EF=PE;②解:PC⊥PE,PC=PE;理由如下:延长ED交BC于H,如图③所示:由旋转的性质得:∠CAE=90°,∵∠AED=∠ACB=90°,∴四边形ACHE是矩形,∴∠BHE=∠CHE=90°,AE=CH,∵AE=DE,∴CH=DE,∠ADE=45°,∴∠EDP=135°,∵∠ACB=90°,AC=BC,∴∠ABC=45°,∵∠BHE=90°,点P是线段BD的中点,∴PH⊥BD,PH=BD=PD,△BPH是等腰直角三角形,∴∠BHP=45°,∴∠CHP=135°=∠EDP,在△CPH和△EPD中,,∴△CPH≌△EPD(SAS),∴PC=PE,∠CPH=∠EPD,∴∠CPE=∠HPD=90°,∴PC⊥PE;故答案为:PC⊥PE,PC=PE;③解:当α=135°时,AD⊥AC,过点D作DF⊥BC于F,连接CD,过点C作CN⊥BD于N,如图④所示:则四边形ACFD是矩形,∴CF=AD=AE=2,DF=AC=4,∴CD===2,BF=BC﹣CF=4﹣2=2,∴BD===2,∵DF•BC=CN•BD,∴CN===,BN===,∴PN=BD﹣BN=×2﹣=,∴PC===.。
2020届中考数学复习专题:三角形(含答案)

2020届中考数学复习专题:三角形1.定义:如果一个三角形一边上的中线与这条边上的高线之比为,那么称这个三角形为“神奇三角形”.(1)已知:Rt△ABC中,∠ACB=90°.①当AC=BC时,求证:△ABC是“神奇三角形”;②当AC≠BC时,且△ABC是“神奇三角形”,求tan A的值;(2)如图,在△ABC中,AB=AC,CD是AB边上的中线,若∠DCB=45°,求证:△ABC 是“神奇三角形”.2.如图,在等边三角形ABC中,BC=8,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D与点E.(1)在图中找出与∠EPC始终相等的角,并说明理由;(2)若△PDE为正三角形时,求BD+CE的值;(3)当DE∥BC时,请用BP表示BD,并求出BD的最大值.3.在等腰直角△ABC中,AB=AC,∠BAC=90°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)如图2,作AH⊥BC,垂足为H,作AG⊥EC,垂足为G,连接HG,判断△GHC的形状,并说明理由.4.(1)发现如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.填空:①∠DCE的度数是;②线段CA、CE、CD之间的数量关系是.(2)探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.(3)应用如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.5.如图1,在平面直角坐标系中,已知点A (a ,0),B (b ,0),C (2,7),连接AC ,交y 轴于D ,且a =,()2=5.(1)求点D 的坐标.(2)如图2,y 轴上是否存在一点P ,使得△ACP 的面积与△ABC 的面积相等?若存在,求点P 的坐标,若不存在,说明理由.(3)如图3,若Q (m ,n )是x 轴上方一点,且△QBC 的面积为20,试说明:7m +3n 是否为定值,若为定值,请求出其值,若不是,请说明理由.6.如图,以直角三角形AOC 的直角顶点O 为原点,以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足.D 为线段AC 的中点.在平面直角坐标系中,以任意两点P (x 1,y 1)、Q (x 2,y 2)为端点的线段中点坐标为,.(1)则A点的坐标为;点C的坐标为.D点的坐标为.(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP =S△ODQ,若存在,请求出t的值;若不存在,请说明理由.(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.7.已知:如图,在平面直角坐标系中,点A(a,0)、B(0,b)、且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP;(1)求点A、B的坐标;(2)如图,在第一象限内作BC⊥AB且BC=AB,连接CP,当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度;(3)在第一象限内作BQ⊥BP且BQ=BP,连接PQ,设P(p,0),直接写出S△PCQ=(用含p的式子表示).8.在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=时,求的值.9.如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索主要过程:(1)经过多少时间后,P、Q两点的距离为5cm?的面积为15cm2?(2)经过多少时间后,S△PCQ(3)用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?10.我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“广益值”就等于AO2﹣BO2的值,可记为AB∇AC=OA2﹣BO2.(1)在△ABC中,若∠ACB=90°,AB∇AC=81,求AC的值.(2)如图2,在△ABC中,AB=AC=12,∠BAC=120°,求AB∇AC,BA∇BC的值.=24,AC=8,AB∇AC=﹣64,求(3)如图3,在△ABC中,AO是BC边上的中线,S△ABCBC和AB的长.11.已知:等边△ABC中.(1)如图1,点M是BC的中点,点N在AB边上,满足∠AMN=60°,求的值;(2)如图2,点M在AB边上(M为非中点,不与A、B重合),点N在CB的延长线上且∠MNB=∠MCB,求证:AM=BN.(3)如图3,点P为AC边的中点,点E在AB的延长线上,点F在BC的延长线上,满足∠AEP=∠PFC,求的值.12.如图,等边△ABC的边长为15cm,现有两点M,N分别从点A,点B同时出发,沿三角形的边顺时针运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M,N同时停止运动(1)点M、N运动几秒后,M,N两点重合?(2)点M、N运动几秒后,△AMN为等边三角形?(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M,N运动的时间.13.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比例相互唯一确定,因此,边长与角的大小之间可以相互转化.类似地,可以在等腰三角形中建立边角之间的关系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA==.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60°=.(2)对于0°<A<180°,∠A的正对值sadA的取值范围是.(3)如图②,已知∠C=90°,sin A=,其中∠A为锐角,试求sadA的值.14.如图,在Rt△ABC中,∠ACB=90°,BC=4,sin∠ABC=,点D为射线BC上一点,联结AD,过点B作BE⊥AD分别交射线AD、AC于点E、F,联结DF,过点A作AG∥BD,交直线BE于点G.(1)当点D在BC的延长线上时,如果CD=2,求tan∠FBC;(2)当点D在BC的延长线上时,设AG=x,S=y,求y关于x的函数关系式(不需△DAF要写函数的定义域);(3)如果AG=8,求DE的长.15.如图,点O为平面直角坐标系的原点,三角形ABC中,∠BAC=90°,AB=m.顶点A,C的坐标分别为(1,0),(n,0),且|m﹣3|+(n﹣5)2=0.(1)求三角形ABC的面积;(2)动点P从点C出发沿射线CA方向以每秒1个单位长度的速度运动,设点P的运动时间为t秒,连接PB,请用含t的式子表示三角形ABP的面积;(3)在(2)的条件下,当三角形ABP的面积为时,直线BP与y轴相交于点D,求点D的坐标.16.已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°.(1)若D为AB上一动点时(如图1),①求证:△ACD≌△BCE.②试求线段AD,BD,DE间满足的数量关系.(2)当点D在△ABC内部时(如图2),延长AD交BE于点F.①求证:AF⊥BE.②连结BD,当△BDE为等边三角形时,直接写出△DCE与△ABC的边长之比.17.如图,直角坐标系中,点A,B分别在x,y轴上,点B的坐标为(0,2),∠BAO=30°.以AB为边在第一象限作等边△ABC,MN垂直平分OA,MA⊥AB.(1)求AB的长.(2)求证:MB=OC.(3)如图2,连接MC交AB于点P.点P是否为MC的中点?请说明理由.18.在△ABC中,AB=BC,∠A=40°,BD⊥AC垂足为D.(1)填空:∠ABC=°;(2)E是线段BD上的动点,连结EC,将线段EC绕点E按顺时针方向旋转80°,点C 的对应点是点F,连接CF,得到△CEF.①如图1,若点F在直线BD上,AB=a,AC=b,求EB+EC的值.②连结AF,直线AF与直线BC是否平行,为什么?19.如图,在平面直角坐标系中,点A(0,a),B(b,0),且a,b满足2a2+2ab+b2﹣8a+16=0,点P为AB上一个动点(不与A,B)重合),连接OP.(1)直接写出a=,b=;(2)如图1,过点P作OP的垂线交过点A平行于x轴的直线于点C,若点,求点C的坐标;(3)如图2,以OP为斜边在OP右侧作等腰Rt△OPD,PD=OD.连接BD,当点P从B向A运动过程中,△BOD的面积是否发生变化,请判断并说明理由.20.(1)如图①,小明同学作出△ABC两条角平分线AD,BE得到交点I,就指出若连接CI,则CI平分∠ACB,你觉得有道理吗?为什么?(2)如图②,Rt△ABC中,AC=5,AC=12,AB=13,△ABC的角平分线CD上有一点I,设点I到边AB的距离为d.(d为正实数)小季、小何同学经过探究,有以下发现:小季发现:d的最大值为.小何发现:当d=2时,连接AI,则AI平分∠BAC.请分别判断小季、小何的发现是否正确?并说明理由.参考答案1.解:(1)①证明:如图,作AC边上的中线BM,设CM=AM=a,则BC=AC=2a,∵∠ACB=90°,∴BM===a,∴,∴△ABC是“神奇三角形”;②当AC边上的中线与AC边上的高的比为时,设BM=a,BC=2a,∵∠ACB=90°,∴CM==a,∴AC=2a,∴AC=BC,不合题意,舍去;同理,当BC边上的中线与BC边上的高的比为时,也不符合题意,舍去;当AB边上的中线与AB边上的高的比为时,当BC>AC时,如图,作AB边上的中线CM,作AB边上的高线CD,设CM=a,CD=2a,则DM=a,∵∠ACB=90°,∴CM=AB=AM,∴AD=(﹣1)a,∴tan A==,当BC<AC时,如图,作AB边上的中线CM,作AB边上的高线CD,同理可得,tan A=.综合可得tan A的值为或.(2)证明:如图,作CH⊥AB于点H,AE⊥BC于点E,AE交CD于K,连接BK,∵AB=AC,∴E是BC的中点,∵CD是AB边上的中线,∴点K是△ABC的重心,∴KC=2DK,∵AE是BC的垂直平分线,∴KC=KB,∴∠KBC=∠KCB=45°,∴∠CKB=90°,即BK⊥CD,∴=tan∠CDH==2,∴,∴△ABC是“神奇三角形”.2.解:(1)∠BDP=∠EPC,理由如下:∵△ABC为等边三角形,∴∠B=60°,∵∠DPE=60°,∴∠DPE=∠B,∵∠DPC是△BDP的外角,∴∠DPE+∠EPC=∠B+∠BDP,∴∠EPC=∠BDP;(2)∵△PDE为正三角形,∴PD=PE,在△BDP和△CPE中,,∴△BDP≌△CPE(AAS),∴BD=CP,BP=CE,∴BD+CE=CP+BP=BC=8;(3)∵DE∥BC,△ABC为等边三角形,∴△ADE为等边三角形,∴AD=AE,∴BD=CE,∵∠B=∠C,∠EPC=∠BDP,∴△BDP∽△CPE,∴=,即=,整理得,BD=,﹣BP2+8BP=﹣(BP﹣4)2+16,∴BD的最大值为4.3.(1)解:∠ADE=45°.∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠ACM=∠ACB,∴∠ACM=∠ABC,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴AD=AE,∠CAE=∠BAD,∴∠DAE=∠BAC=90°,∴∠ADE=45°;(2)(1)中的结论成立证明:∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°.∵∠ACM=∠ACB,∴∠B=∠ACM=45°.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).∴AD=AE,∠BAD=∠CAE.∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=90°.即∠DAE=90°.∵AD=AE,∴∠ADE=∠AED=45°.(3)△CGH为等腰直角三角形.理由如下:∵∠BCA=∠ACE=45°,∴∠GCH=90°,又∵AH⊥BC,AG⊥CE,∴AG=AH,∵∠ACG=∠AGC=45°,∴AG=CG,∵AB=AC,AH⊥BC,∴∠HCA=∠HAC=45°,∴AH=HC,∴CH=CG,∴△CGH为等腰直角三角形.4.(1)发现解:①∵在△ABC中,AB=AC,∠BAC=60°,∴∠BAC=∠DAE=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴∠ACE=∠B=60°,∴∠DCE=∠ACE+∠ACB=60°+60°=120°;故答案为:120°,②∵△BAD≌△CAE,∴BD=CE,∴BC=BD+CD=EC+CD,∴CA=BC=CE+CD;故答案为:CA=CE+CD.(2)探究∠DCE=90°;CA=CD+CE.理由:∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.∴△BAD≌△CAE(SAS).∴BD=CE,∠B=∠ACE=45°.∴∠DCE=∠ACB+∠ACE=90°.在等腰直角三角形ABC中,CB=CA,∵CB=CD+DB=CD+CE,∴CA=CD+CE.(3)应用DA=5或.作DE⊥AB于E,连接AD,∵在Rt△ABC中,AB=6,AC=4,∠BAC=90°,∴BC===2,∵∠BDC=90°,DB=DC,∴DB=DC=,∠BCD=∠CBD=45°,∵∠BDC=∠BAC=90°,∴点B,C,A,D四点共圆,∴∠DAE=45°,∴△ADE是等腰直角三角形,∴AE=DE,∴BE=6﹣DE,∵BE2+DE2=BD2,∴DE2+(6﹣DE)2=26,∴DE=1,DE=5,∴AD=或AD=5.5.解:(1)∵a=,()2=5,∴a=﹣5,b=5,∵A(a,0),B(b,0),∴A(﹣5,0),B(5,0),∴OA=OB=5.如图1,连接OC,设OD=x,∵C(2,7),∴S△AOC=×5×7=17.5,∵S△AOC =S△AOD+S△COD,∴5x•=17.5,∴x=5,∴点D的坐标为(0,5);(2)如图2,∵A(﹣5,0),B(5,0),C(2,7),∴S△ABC=×(5+5)×7=35,∵点P在y轴上,∴设点P的坐标为(0,y),∵S△ACP =S△ADP+S△CDP,D(0,5),∴5×|5﹣y|×+2×|5﹣y|×=35,解得:y=﹣5或15,∴点P的坐标为(0,﹣5)或(0,15);(3)7m+3n是定值.∵点Q在x轴的上方,∴分两种情况考虑,如图3,当点Q在直线BC的左侧时,过点Q作QH⊥x轴,垂足为H,连接CH,∵S△QBC =S△QHC+S△HBC﹣S△QHB,且S△QBC=20,∴,∴7m+3n=﹣5.如图4,当点Q在直线BC的右侧时,过点Q作QH⊥x轴,垂足为H,连接CH,∵S△QBC =S△QHC+S△HBC﹣S△QHB,且S△QBC=20,∴=20,∴7m+3n=75,综上所述,7m+3n的值为﹣5或75.6.解:(1)∵.∴a﹣2b=0,b﹣2=0,解得a=4,b=2,∴A(0,4),C(2,0);∴x==1,y==2,∴D(1,2).故答案为(0,4),(2,0),(1,2).(2)如图1中,由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,∴0<t≤2时,点Q在线段AO上,即CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,∴S△DOP =OP•y D=(2﹣t)×2=2﹣t,S△DOQ=OQ•x D=×2t×1=t,∵S△ODP =S△ODQ,∴2﹣t=t,∴t=1;(3)的值不变,其值为2.理由如下:如图2中,∵∠2+∠3=90°,又∵∠1=∠2,∠3=∠FCO,∴∠GOC+∠ACO=180°,∴OG∥AC,∴∠1=∠CAO,∴∠OEC=∠CAO+∠4=∠1+∠4,如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,∴∠PHO=∠GOF=∠1+∠2,∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,∴=,=,=2.7.解:(1)∵|a+2|+(b+2a)2=0,∴a+2=0,b+2a=0,解得a=﹣2,b=4,∴A(﹣2,0),B(0,4);(2)如图1所示,过C作CE⊥OB于E,与PB交于F,∵BC⊥AB,∴∠ABO+∠EBC=90°,在Rt△BCE中,∠EBC+∠BCE=90°,∴∠ABO=∠BCE,在△AOB和△BEC中,,∴△AOB≌△BEC(AAS),∴BE=AO=2,又∵OB=4,∴E为OB的中点,∵EC∥OP,∴EF为△BOP的中位线,则F为BP的中点,在Rt△BCP中,CF为斜边上的中线,∴CF=PB=BF,∴∠BCE=∠CBD=∠ABO,在△AOB和△CDB中,∴△AOB≌△CDB(AAS),∴CD=AO=2;(3)如图2所示,过B作BG⊥CQ于点G,延长QC与x轴交于H,∵∠ABP+∠PBC=90°,∠PBC+CBQ=90°,∴∠ABP=∠CBQ,在△ABP与△CBQ中,,∴△ABP≌△CBQ(SAS),∴∠BPO=∠BQG,CQ=AP=2+p,在△BOP和△BGQ中,,∴△BOP≌△BGQ(AAS),∴∠OBP=∠GBQ,BG=BO=4,又∵∠GBQ+∠PBG=90°,∴∠OBP+∠PBG=90°,即∠OBG=90°,在四边形OBGH中,∠OBG=∠BOG=∠BGH=90°,∴∠OHG=90°,∴PH是△PCQ中CQ边上的高,PH=OH﹣OP=4﹣p,=•(2+p)(4﹣p)=﹣+p+4.∴S△PCQ故答案为:.8.(1)证明:∵CA=CB,EB=ED,∠ABC=∠DBE=60°,∴△ABC和△DBE都是等边三角形,∴AB=BC,DB=BE,∠A=60°.∵∠ABC=∠DBE=60°,∴∠ABD=∠CBE,∴△ABD≌△CBE(SAS).∴∠A=∠ECB;(2)证明:∵∠ABC=∠DBE=45°,CA=CB,EB=ED,∴△ABC和△DBE都是等腰直角三角形,∴∠CAB=45°,∴,∴,∵∠ABC=∠DBE,∴∠ABD=∠CBE,∴△ABD∽△CBE,∴∠BAD=∠BCE=45°,∵∠ABC=45°,∴∠ABC=∠BCE,∴CE∥AB;(3)解:过点D作DM⊥CE于点M,过点D作DN∥AB交CB于点N,∵∠ACB=90°,∠BCE=45°,∴∠DCM=45°,∴∠MDC=∠DCM=45°,∴DM=MC,设DM=MC=a,∴a,∵DN∥AB,∴△DCN为等腰直角三角形,∴DN=DC=2a,∵tan∠DEC=,∴ME=2DM,∴CE=a,∴,∵CE∥DN,∴△CEF∽△DNF,∴.9.解:(1)连接PQ ,设经过ts 后,P 、Q 两点的距离为5cm ,ts 后,PC =7﹣2tcm ,CQ =5tcm ,根据勾股定理可知PC 2+CQ 2=PQ 2, 代入数据(7﹣2t )2+(5t )2=(5)2;解得t =1或t =﹣(不合题意舍去);(2)设经过ts 后,S △PCQ 的面积为15cm 2ts 后,PC =7﹣2tcm ,CQ =5tcm ,S △PCQ =×PC ×CQ =×(7﹣2t )×5t =15解得t 1=2,t 2=1.5,经过2或1.5s 后,S △PCQ 的面积为15cm 2.(3)设经过ts 后,△PCQ 的面积最大,ts 后,PC =7﹣2tcm ,CQ =5tcm ,S △PCQ =×PC ×CQ =×(7﹣2t )×5t =×(﹣2t 2+7t ).=﹣5.∴当t =s 时,△PCQ 的面积最大,最大值为cm 2.10.解:(1)如图1,AO 是BC 边上的中线,∵∠ACB=90°,∴AO2﹣OC2=AC2,∵AB∇AC=81,∴AO2﹣OC2=81,∴AC2=81,∴AC=9;(2)①如图2,取BC的中点O,连接AO,∵AB=AC,∴AO⊥BC,∵∠BAC=120°,∴∠ABC=30°,在Rt△AOB中,∴==6,∴AB∇AC=AO2﹣BO2=36﹣108=﹣72;②如图3,取AC的中点D,连接BD,∴AC=6,过点B作BE⊥AC交CA的延长线于点E,∴∠BAE=180°﹣∠BAC=60°,∴∠ABE=30°,∵AB=12,∴AE=6,∴BE===6.∴DE=AD+AE=12,∴==6,∴BA∇BC=BD2﹣CD2==216;(3)作BD⊥CD,如图4,=24,AC=8,∵S△ABC∴=6,∵AB∇AC=﹣64,AO是BC边上的中线,∴AO2﹣OC2=﹣64,∴OC2﹣AO2=64,又∵AC2=82=64,∴OC2﹣AO2=AC2,∴∠AOC=90°,∴OA=2×=3,∴==.∴,在Rt△BCD中,==16,∴AD=CD﹣AC=16﹣8,∴==10.11.解:(1)∵△ABC为等边三角形,∴∠B=∠BAC=60°,AB=AC,∵点M是BC的中点,∴∠MAN=30°,∠AMB=90°,∵∠AMN=60°,∴∠BMN=30°,∴BM=2BN,AB=2BM,设BN=x,则BM=2x,AB=4x,∴AN=3x,∴;(2)证明:如图2,过点M作MG∥NC交AC于点G,∴∠A=∠AMG=∠AGM=60°,∴△AMG为等边三角形,∴AM=AG,∴BM=CG,∵∠AGM=∠ABC=60°,∴∠MGC=∠NBM=120°,∵MG∥BC,∴∠GMC=∠MCB,∵∠MNB=∠MCB,∴∠GMC=∠MNB,∴△MGC≌△NBM(AAS),∴MG=BN,∵△AMG为等边三角形,∴AM=MG,∴AM=BN;(3)如图3,过点P作PM∥BC交AB于点M,∴△AMP为等边三角形,∴AP=MP,∠AMP=60°,∵P为AC的中点,∴AP=PC,∴MP=PC,∵∠ACB=60°,∴∠EMP=∠PCF=120°,∵∠AEP=∠PFC,∴△PCF≌△PME(AAS),∴CF=ME,∴BF﹣BE=BC+CF﹣ME+MB,又∵P为AC的中点,MP∥BC,∴MB=,∴BF﹣BE=BC+BC=,∴.12.解:(1)设运动t秒,M、N两点重合,根据题意得:2t﹣t=15,∴t=15,答:点M,N运动15秒后,M、N两点重合;(2)如图1,设点M、N运动x秒后,△AMN为等边三角形,∴AN=AM,由运动知,AN=15﹣2x,AM=x,∴15﹣2x=x,解得:x=5,∴点M、N运动5秒后,△AMN是等边三角形;(3)假设存在,如图2,设M、N运动y秒后,得到以MN为底边的等腰三角形AMN,∴AM=AN,∴∠AMN=∠ANM,∵△ABC是等边三角形,∴AB=AC,∠C=∠B=60°,∴△ACN≌△ABM(AAS),∴CN=BM,∴CM=BN,由运动知,CM=y﹣15,BN=15×3﹣2y,∴y﹣15=15×3﹣2y,∴y=20,故点M,N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M,N运动的时间为20秒.13.解:(1)根据正对定义,当顶角为60°时,等腰三角形底角为60°,则三角形为等边三角形,则sad60°==1.故答案为:1.(2)当∠A接近0°时,sadA接近0,当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.于是sadA的取值范围是0<sadA<2.故答案为:0<sadA<2.(3)在AB上取点D,使AD=AC,过点D作DE⊥AC于E,连接CD,如图.∵在Rt△ADE中,=sin A=,设AD=AC=5x,则DE=3x,AE=4x.∴CE=x.∴在Rt△CDE中,CD==x.∴sad A===.14.解:(1)∵∠ACB=90°,BC=4,sin∠ABC=,∴设AC=3x,AB=5x,∴(3x)2+16=(5x)2,∴x=1,即AC=3,∵BE⊥AD,∴∠AEF=90°,∵∠AFE=∠CFB,∴∠DAC=∠FBC,∴tan∠FBC=tan∠DAC==;(2)∵AG∥BD,∴∠AGF=∠CBF,∴tan∠AGF=tan∠CBF,∴,,∴,∴.∴=.∵∠EAF=∠CBF,∴,∴,∴S==;△DAF(3)①当点D在BC的延长线上时,如图1,∵AG=8,BC=4,AG∥BD,∴,∴AF=2CF,∵AC=3,∴AF=2,CF=1,∴,∴,设AE=x,GE=4x,∴x2+16x2=82,解得x=,即AE=.同理tan∠DAC=tan∠CBF,∴,∴DC=,∴AD===.∴=.②当点D在BC的边上时,如图2,∵AG∥BD,AG=8,BC=4,∴.∴AF=6,∵∠EAF=∠CBF=∠ABC,∴cos∠EAF=cos∠ABC,∴,∴,同理,∴,∴.∴DE=AE﹣AD=.综合以上可得DE的长为或.15.解:(1)∵|m﹣3|+(n﹣5)2=0.∴|m﹣3|=0,(n﹣5)2=0.∴m=3,n=5,∴B(1,3),C(5,0),∴AB=3,AC=4,∴三角形ABC的面积=;(2)①如图1,当点P在线段AC上时,PC=t,AP=4﹣t,三角形ABP的面积为==6﹣.②如图2,当点P在线段AC的延长线上时,PC=t,AP=t﹣4,三角形ABP的面积为3=.(3)①当点P在线段AC上时,6﹣.解得t=﹣1(舍去).②如图3,当点P在线段AC的延长线上时,.解得t=9.∴OP=4,PA=5,∵∠BAC=90°=∠DOA,∴OD∥AB,∴.解得OD=.∵点D在y轴上且在原点O的上方,∴点D的坐标为(0,).16.(1)①证明:如图1,∵△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°.∴AC=BC,CD=CE,∠A=∠ABC=45°,∠ACB﹣∠DCB=∠ECD﹣∠DCB,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS).②解:∵△ACD≌△BCE.∴AD=BE,∠CBE=∠A=45°,∴∠DBE=90°,∴BD2+BE2=DE2,即BD2+AD2=DE2,(2)①证明:如图2,∵△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°.∴由(1)易知△ACD≌△BCE.∴∠DAC=∠CBE,∴∠ABF+∠BAF=∠ABC+∠CBE+∠BAF=∠ABC+∠BAF+∠DAC=∠ABC+∠BAC=90°.∴∠AFB=90°,即AF⊥BE.②如图3,∵△BDE为等边三角形,DF⊥BE,∴∠DEF=60°,设EF=BF=a,则DE=2a,∴a,∵BD=BE,DC=CE,∴BC是DE的垂直平分线,∴NE=a,BN=a,∴BC=.∴.即△DCE与△ABC的边长之比为.17.(1)解:∵B(0,2),∴OB=2,在Rt△AOB中,∠BAO=30°,∴AB=2OB=4;(2)证明:,∵AM⊥AB,∴∠BAM=90°,∴∠MAN=90°﹣∠BAO=60°,∵MN垂直平分OA,∴∠ANM=90°,∴∠AMN=30°,∴MA=2AN=OA,∵△ABC是等边三角形,∴AC=AB,∠BAC=60°,∴∠OAC=90°=∠MAB,∴△MAB≌△OAC(SAS),∴MB=OC;(3)解:P是MC的中点.理由如下:如图2,过点C作CH⊥AB于H,∴∠AHC=90°=∠HAM,∵△ABC是等边三角形,∴BC=AB,∠BCH=∠ACH=30°=∠BAO,∴△BCH≌△BAO(AAS),∴OA=CH,由(2)知,AM=OA,∴AM=CH,∵∠CPH=∠MPA,∴△CHP≌△MAP(AAS),∴CP=MP,即点P为MC的中点.18.解:(1)∵AB=BC,∴∠A=∠BCA=40°,∴∠ABC=180°﹣∠A﹣∠BCA=180°﹣40°﹣40°=100°故答案为:100.(2)①在△ABC中,AB=BC,BD⊥AC,∴AD=DC,∠ABF=50°,∵EC=EF,∠CEF=80°,点F在BD上,∴∠DFC=50°,又∠ADB=∠CDF=90°,∴△ABD≌△CFD(AAS),∴BD=DF,∴BE+EC=BE+EF=2BD=2=2=2.②连结AE并延长交BC于M.若点F在直线BD上,BF是AC的垂直平分线,∵∠AFD=∠DFC=50°,又∠ABF=50°,∴AF∥BC,若点F在直线BD的左侧,如图2,∵EC=EF=AE,∴∠MEF=2∠EAF,∵∠MEC=2∠EAD,∴2∠DAF=∠CEF,∴∠DAF=40°,∠BCA=40°.∴AF∥BC.若点F在直线BD的右侧,如图3.∵EC=EF=AE,∴∠MEF=2∠EAF,∵∠MEC=2∠EAD,∴2∠DAF=∠CEF,∴∠DAF=40°,∠BCA=40°.∴AF∥BC.19.解:(1)∵2a2+2ab+b2﹣8a+16=0,∴(a+b)2+(a﹣4)2=0,∴a+b=0,a﹣4=0,即a=4,b=﹣4,故答案为:4,﹣4;(2)过点P作PM⊥AP交y轴于点M,过P作PN⊥y轴于点N,∵∠OPC=∠MPA=∠OAC=90°,∴∠OPM=∠APC,∠POM=∠C,∵∠PAM=45°,∴PA=PM,∴△ACP≌△MOP(AAS),∴AC=MO,又∵,∴,∴AC=MO=1,∴C(1,4);(3)△BOD的面积不发生变化,理由,∵点A(0,4),B(﹣4,0),∴直线AB的解析式为y=x+4,①当点P的横坐标大于等于﹣2而小于0时,设D(m,n)如图2,过点D作DF⊥x轴于F,过点P作PE⊥DF,交FD的延长线于E,∴∠PED=∠DFO=90°,OF=m,DF=n,∴∠DPE+∠PDE=90°,∵∠ODP=90°,∴∠PDE+∠ODF=90°,∴∠DPE=∠ODE,∵DP=OD,∴△PDE≌△DOF(AAS),∴DE=OF=m,PE=DF=n,∴EF=DE+DF=m+n,PE﹣OF=n﹣m,∴P(m﹣n,m+n),而点P在线段AB上,∴m+n=m﹣n+4,∴n=2,∴点D的纵坐标为2,②当点P的横坐标小于﹣2而大于﹣4时,如图3,同①的方法得出点D的纵坐标为2,即:点P从点B向点A运动的过程中,点D的纵坐标始终为2,∴S=OB•|y D|=×4×2=4,△BOD即:点P从点B向点A运动的过程中,△BOD的面积始终不变,是4.20.解:如图1,过I点分别作IM,IN,IK垂直于AB,BC,AC于点M,N,K,连接IC,∵AI平分∠BAC,IM⊥AB,IK⊥AC,∴IM=IK,同理IM=IN,∴IK=IN,又∵IK⊥AC,IN⊥BC,∴CI平分∠BCA;(2)如图2,过C点作CE⊥AB于点E,则d的最大值为CE长,∵AC=5,BC=12,∴=,又∵=30,∴CE=,∴d的最大值为.∴小季正确;假设此时AI平分∠BAC,如图3,连接BI,过I点作IG,IH,IF分别垂直于AC,BC,AB 于点G,H,F,∵AI平分∠BAC,CD平分∠ACB,∴BI平分∠CBA,∵IG⊥AC,IH⊥BC,ID⊥AB,∴IG=IH=IF=d,∵S△ACB =S△AIC+S△BIC+S△ABI,∴,∴=,∴d=2,∴假设成立,当d=2时,连接AI,则AI平分∠BAC,∴小何正确.。
2020年中考数学专题 相似三角形综合练习(含答案)

2020年中考数学专题 相似三角形综合(含答案)一、单选题(共有10道小题)1.如图,在△ABC 中,∠ACB= 90,CD ⊥AB ,垂足为D ,点E 是AB 的中点,CD=DE=a ,则AB 的长为( )A .2aB .a 22C .3aD . 2.根据下列条件,△ABC 和△111C B A 不相似的是()A.∠A=68°,∠B=40°,∠A 1=68°,∠B 1=72°B.∠B=∠B 1,BC=2,BC:A 1 B 1= A B: B 1C 1C.AB=1,BC=2, CA=1.5,A 1 B 1=4, B 1 C 1 =8,D.AB=12,BC=15,CA=24,A 1 B 1=24,A 1 B 1=20,B 1 C 1 =25,A 1 C 1=32 3.用作位似图形的方法,可以将一个图形放大或缩小,位似中心( ) A.只能选在原图形的外部B.只能选在原图形的内部C.只能选在原形的边上D.可以选择任意位置4.如图,AB ,CD 都是BD 的垂线,AB=4,CD=6,BD=14。
P 是BD 上一点,连接AP ,CP ,所得两个三角形相似,则BP 的长是( )A.2B.5.6C.12D.上述都有可能5.如图,是一束平行的光线从教室窗户射入教室的示意图,测得光线与地面所成的角∠AMC=30°,窗户的高在教室地面上的影长MN=32m ,窗户的下沿到教室地面的距离BC=1m (点M ,N ,CC 在同一直线上),则窗户的高CAA B CD a 3346.如图,在□ABCD 中,EF ∥AB 交AD 于点E ,交BD 于点F ,DE:EA=3:4,EF=3,则CD 的长为( )A.4B.7C.3D.127.如图1,已知在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,且AD:DB = 3:5,那么CF ∶CB 等于( ) A. 5:8 B. 3:8 C. 3:5 D.8.如图,如果点C 是线段AB 的黄金分割点(AC>BC ),则下列比例式正确的是( )A.AB ACAC BC= B.AB BC BC AC = C. AC BC BC AB = D. AC ABAB BC=9.如图,P 为平行四边形ABCD 的边AD 上的一点,E 、F 分别为PB ,PC 的中点,△PEF ,△PDC ,△PAB 的面积分别为12,,S S S ,若3S =,则12S S +的值为()A.24B.12C.6D.3 10.如图,在□ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF:FC 等于( ) A.3:2 B.3:1 C.1:1 D.1:2 二、填空题(共有8道小题)11.如图,梯形ABCD 的对角线相交于O ,G 是BD 的中点.若AD = 3,BC = 9,则GOBG=A B C DE F A B C P A BCDE F E F A B CD12.如图,平行四边形中,是边上的点,交于点,如果, 那么 .13.如图,正五边形ABCDE 与五边形A ’B ’C ’D ’E ’是位似图形,且相似比为21。
2020年九年级数学中考复习题型 解直角三角形(带答案)

解直角三角形题型一 利用勾股定理求面积例 1.在Rt AED ∆中,90E ∠=︒,3AE =,4ED =,以AD 为边在AED ∆的外侧作正方形ABCD ,则正方形ABCD 的面积是( )A .5B .25C .7D .10【解析】根据勾股定理得到225AD AE DE =+=,根据正方形的面积公式即可得到结论.【答案】解:在Rt AED ∆中,90E ∠=︒,3AE =,4ED =,225AD AE DE ∴=+=,四边形ABCD 是正方形,∴正方形ABCD 的面积22525AD ===,故选:B .变式训练1.如图,图中所有的三角形都是直角三角形,四边形都是正方形,其中最大正方形E 的边长为10,则四个正方形A ,B ,C ,D 的面积之和为( )A .24B .56C .121D .100【解析】根据正方形的性质和勾股定理的几何意义解答即可.【答案】解:根据勾股定理的几何意义,可知:E F G S S S =+A B C D S S S S =+++100=;即四个正方形A ,B ,C ,D 的面积之和为100;故选:D .题型二 勾股定理逆定理的应用例2-1.在以线段a ,b ,c 的长三边的三角形中,不能构成直角三角形的是( )A .4a =,5b =,6c =B .::5:12:13a b c =C .2a =,3b =,5c =D .4a =,5b =,3c =【解析】知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【答案】解:A .222456+≠,不能构成直角三角形,故本选项符合题意;B .设三角形三边为5k ,12k ,13k ,2(5)(k +2212)(13)k k =,能构成直角三角形,故本选项不符合题意;C .(22)(+23)(=25),能构成直角三角形,故本选项不符合题意;D .222345+=,能构成直角三角形,故本选项不符合题意;故选:A .例2-2.如图,已知在四边形ABCD 中,20AB cm =,15BC cm =,7CD cm =,24AD cm =,90ABC ∠=︒.(1)连结AC ,求AC 的长;(2)求ADC ∠的度数;(3)求出四边形ABCD 的面积【解析】(1)连接AC ,利用勾股定理解答即可;(2)利用勾股定理的逆定理解答即可;(3)根据三角形的面积公式解答即可.【答案】解:(1)连接AC ,在Rt ABC ∆中,90ABC ∠=︒,20AB cm =,15BC cm =,∴由勾股定理可得:2222201525AC AB BC cm ++=;(2)在ADC ∆中,7CD cm =,24AD cm =,222CD AD AC ∴+=,90ADC ∴∠=︒;(3)由(2)知,90ADC ∠=︒,∴四边形ABCD 的面积2112015724234()22ABC ACD S S cm ∆∆=+=⨯⨯+⨯⨯=. 变式训练1.下列说法中,正确的有( )①如果0A B C ∠+∠-∠=,那么ABC ∆是直角三角形;②如果::5:12:13A B C ∠∠∠=,则ABC ∆是直角三角形; 71017ABC ∆为直角三角形;④如果三角形三边长分别是24n -、4n 、24(2)n n +>,则ABC ∆是直角三角形;A .1个B .2个C .3个D .4个【解析】根据直角三角形的判定进行分析,从而得到答案.【答案】解:①正确,由三角形内角和定理可求出C ∠为90度;②不正确,因为根据三角形的内角和得不到90︒的角;7x ,10x 17x ,则有2271017x +=;④正确,因为222(4)(4)(4)n n n -+=+.所以正确的有三个.故选:C .变式训练2.如图,在四边形ABCD 中,已知12AB =,9BC =,90ABC ∠=︒,且39CD =,36DA =.求四边形ABCD 的面积.【解析】连接AC ,在Rt ADC ∆中,已知AB ,BC 的长,运用勾股定理可求出AC 的长,在ADC ∆中,已知三边长,运用勾股定理逆定理,可得此三角形为直角三角形,故四边形ABCD 的面积为Rt ACD ∆与Rt ABC ∆的面积之差.【答案】解:连接AC ,90ABC ∠=︒,12AB =,9BC =,15AC ∴=,39CD =,36DA =,222215361521AC DA +=+=,22391521CD ==,ADC ∴∆为直角三角形,ACD ABC ABCD S S S ∆∆∴=-四边形1122AC AD AB BC =⨯-⨯ 11153612922=⨯⨯-⨯⨯ 27054=-216=.故四边形ABCD 的面积为216.题型三 利用勾股定理求最短路径例3.如图,一圆柱高BC 为20cm ,底面周长是10cm ,一只蚂蚁从点A 爬到点P 处吃食,且35PC BC =,则最短路线长为( )A.20cm B.13cm C.14cm D.18cm【解析】根据题意画出图形,连接AP,则AP就是蚂蚁爬行的最短路线长,根据勾股定理求出AP即可.【答案】解:如图展开,连接AP,则AP就是蚂蚁爬行的最短路线长,则90C∠=︒,11052AC cm cm=⨯=,20BC cm=,35PC BC=,12CP cm∴=,由勾股定理得:222251213()AP AC CP cm=+=+=,即蚂蚁爬行的最短路线长是13cm,故选:B.变式训练1.如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为()A.15 dm B.17 dm C.20 dm D.25 dm【解析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【答案】解:三级台阶平面展开图为长方形,长为8dm,宽为(23)3dm+⨯,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到B 点最短路程为xdm ,由勾股定理得:22228[(23)3]17x =++⨯=,解得17x =.故选:B .变式训练 2.如图,长方体的底面边长为1cm 和3cm ,高为6cm .如果用一根细线从点A 开始经过4个侧面缠绕一圈到达B ,那么所用细线最短需要( )A .12cmB .11cmC .10cmD .9cm【解析】要求所用细线的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.【答案】解:将长方体展开,连接A 、B ',则13138()AA cm '=+++=,6A B cm ''=,根据两点之间线段最短,228610AB cm '=+=.故选:C .变式训练3.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A 处有一滴蜜糖,在玻璃杯的外壁,A 的相对方向有一小虫P ,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖A 处的最短距离是( )A .73厘米B .10厘米C .82厘米D .8厘米【解析】由于小虫从外壁进入内壁,要先到杯子上沿,再进入杯子,故先求出到杯子沿的最短距离即可解答.【答案】解:如图所示:最短路径为:P A '→,将圆柱展开,2222(162)(6 1.5 1.5)10PA PE EA cm ''=+=÷+-+=,最短路程为10PA cm '=.故选:B .题型四 利用勾股定理解折叠问题例4.如图,有一块直角三角形纸片,两直角边6AC cm =,8BC cm =,将纸片沿AD 折叠,直角边AC 恰好落在斜边上,且与AE 重合,求BDE ∆的面积.【解析】由勾股定理可求AB 的长,由折叠的性质可得6AC AE cm ==,90DEB ∠=︒,由勾股定理可求DE 的长,由三角形的面积公式可求解.【答案】解:6AC cm =,8BC cm =2210AB AC CB cm ∴=+=将纸片沿AD 折叠,直角边AC 恰好落在斜边上,且与AE 重合,6AC AE cm ∴==,90DEB ∠=︒1064BE cm ∴=-=设CD DE x ==,则在Rt DEB ∆中,2224(8)x x +=-解得3x =,即DE 等于3cmBDE ∴∆的面积14362=⨯⨯= 答:BDE ∆的面积为26cm变式训练1.如图,把长为12cm 的纸条ABCD 沿EF ,GH 同时折叠,B 、C 两点恰好落在AD 边的P 点处,且90FPH ∠=︒,3BF cm =,求FH 的长.【解析】由翻折不变性可知:BF PF =,CH PH =,设FH x cm =,则(9)PH x cm =-,在Rt PFH ∆中,根据222FH PH PF =+,构建方程即可解决问题.【答案】解:由翻折不变性可知:BF PF =,CH PH =,设FH x cm =,则(9)PH x cm =-,在Rt PFH ∆中,90FPH ∠=︒,222FH PH PF ∴=+,222(9)3x x ∴=-+,5x ∴=,FH ∴的长是5cm .变式训练 2.如图,把长方形ABCD 沿AC 折叠,AD 落在AD '处,AD '交BC 于点E ,已知2AB cm =,4BC cm =.(长方形的对边相等,四个角都为直角)(1)求证:AE EC =;(2)求EC 的长;(3)求重叠部分的面积.【解析】(1)根据轴对称的性质和矩形的性质就可以得出EAC ECA ∠=∠,就可以得出AE CE =,(2)设EC x =,就有AE x =,4BE x =-,在Rt ABE ∆中,由勾股定理就可以求出结论;(3)根据(2)的结论直接根据三角形的面积公式就可以求出结论.【答案】解:(1)四边形ABCD 是矩形,AB CD ∴=,AD BC =,90B ∠=︒,//AD BC ,DAC BCA ∴∠=∠.ADC ∆与△AD C '关于AC 成轴对称ADC ∴∆≅△AD C ',DAC D AC ∴∠=∠',D AC ACB ∴∠'=∠,AE EC ∴=;(2)2AB cm =,4BC cm =,2CD cm ∴=,4AD cm =.设EC x =,就有AE x =,4BE x =-,在Rt ABE ∆中,由勾股定理,得224(4)x x +-=,解得: 2.5x =.答:EC 的长为2.5cm ;(3)2AEC EC AB S ∆=, 22.52 2.52AEC S cm ∆⨯==. 答:重叠部分的面积为22.5cm .题型五 勾股定理的实际应用例5.数学综合实验课上,同学们在测量学校旗杆的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开8米后,下端刚好接触地面,如图,根据以上数据,同学们准确求出了旗杆的高度,你知道他们是如何计算出来的吗?【解析】由题可知,旗杆,绳子与地面构成直角三角形,根据题中数据,用勾股定理即可解答.【答案】解:设旗杆高xm ,则绳子长为(2)x m +,旗杆垂直于地面,∴旗杆,绳子与地面构成直角三角形,由题意列式为2228(2)x x +=+,解得15x m =,∴旗杆的高度为15米.变式训练1.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC 的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D 的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)【解析】在Rt ABC ∆中,利用勾股定理计算出AB 长,再根据题意可得CD 长,然后再次利用勾股定理计算出AD 长,再利用BD AB AD =-可得BD 长.【答案】解:在Rt ABC ∆中:90CAB ∠=︒,17BC =米,8AC =米, 2215AB BC AC ∴=-=(米),此人以1米每秒的速度收绳,7秒后船移动到点D 的位置,171710CD ∴=-⨯=(米),22100646AD CD AC ∴=-=-=(米),1569BD AB AD ∴=-=-=(米),答:船向岸边移动了9米.变式训练 2.勾股定理是几何学中的明珠,它充满魅力,在现实世界中有着广泛的应用.请你尝试应用勾股定理解决下列问题:一架2.6m 长的梯子AB 斜靠在一竖直的墙AO 上,这时AO 为2.4m ,如果梯子的顶端A 沿墙下滑0.5m ,那么梯子底端B 向外移了多少米?(注意:3.15 1.77)≈【解析】先根据勾股定理求出OB 的长,再根据梯子的长度不变求出OD 的长,根据BD OD OB =-即可得出结论.【答案】解:Rt OAB ∆中, 2.6AB m =, 2.4AO m =,222226241OB AB AO m ∴=-=-=;同理,Rt OCD ∆中,2.6CD m =, 2.40.5 1.9OC m =-=,22222619 3.15 1.77OD CD OC m ∴=-=-=,1.7710.77()BD OD OB m ∴=-=-=.答:梯子底端B 向外移了0.77米.题型六 锐角三角函数定义例1.在Rt ABC ∆中,90C ∠=︒,3AB BC =,则sin B 的值为( )A.12B.22C.32D.223【解析】设BC为x,根据题意用x表示出AB,根据勾股定理求出BC,运用正弦的定义解答即可.【答案】解:设BC为x,则AB=3x,由勾股定理得,AC===2x,∴sin B===,故选:D.变式训练1.如图,在Rt ABC∆中,90ACB∠=︒,CD是斜边AB上的高,下列线段的比值等于cos A的值的有()个(1)ADAC(2)ACAB(3)BDBC(4)CDBC.A.1 B.2 C.3 D.4【解析】根据锐角三角函数关系的定义分析得出答案.【答案】解:∵在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,∴∠A=∠BCD,∴cos A===,故(1),(2),(4)正确.故选:C.题型七网格中的锐角三角函数值例7.如图,A,B,C是正方形网格中的格点(小正方形的顶点),则sin ACB∠的值为( )A .55B .255C .12D .33【解析】由勾股定理可求AC ,BC 的长,由三角形的面积公式可求BD 的长,即可求sin ∠ACB 的值.【答案】解:设小正方形的边长为1,过点B 作BD ⊥AC 于D ,过点B 作BF ⊥AE 于点F , ∵S △ABC =2×7﹣=5 由勾股定理可知:AC ==5, ∵AC •BD =5,∴BD =,由勾股定理可知:BC ==, ∴sin ∠ACB === 故选:A .变式训练 1.如图,在22⨯正方形网格中,以格点为顶点的ABC ∆的面积等于32,则sin (CAB ∠= )A.332B.35C.105D.310【解析】根据勾股定理,可得AC、AB、BC的长,根据三角形的面积公式,可得CD的长,根据正弦函数的定义,可得答案.【答案】解:如图:作CD⊥AB于D,AE⊥BC于E,由勾股定理,得AB=AC=,BC=.由等腰三角形的性质,得BE=BC=.由勾股定理,得AE==,由三角形的面积,得AB•CD=BC•AE.即CD==.sin∠CAB===,故选:B.题型八特殊角三角函数值的计算例8.计算:2sin60cos45sin30tan60︒+︒-︒︒.【解析】首先代入特殊角的三角函数值,再计算乘方,后算乘除,最后算加减即可.【答案】解:原式=+﹣×,=+﹣,=.变式训练1.计算:(1)222sin 30sin60sin 45cos 30︒+︒-︒+︒;(2)tan30tan 45tan 60tan 45︒+︒︒︒. 【解析】(1)直接利用特殊角的三角函数值代入求出答案;(2)直接利用特殊角的三角函数值代入求出答案.【答案】解:(1)原式=()2+﹣()2+()2=+﹣+ =+; (2)原式==.变式训练2.22cos30tan30cos60(1tan60)︒+︒︒--︒【解析】把特殊角的三角函数值代入原式,根据二次根式的加减运算法则计算.【答案】解:原式=2×+×﹣+1=+1. 题型九 解直角三角形例9.如图,在ABD ∆中,AC BD ⊥于点C ,32BC CD =,点E 是AB 的中点,tan 2D =,1CE =,求sin ECB ∠的值和AD 的长.【解析】利用已知表示出BC ,CD 的长,再利用勾股定理表示出AB 的长,进而求出sin ∠ECB 的值和AD 的长.【答案】解:∵AC ⊥BD ,∴∠ACB =∠ACD =90°.∵点E 是AB 的中点,CE =1,∴BE =CE =1,AB =2CE =2,∴∠B =∠ECB .∵=,∴设BC =3x ,CD =2x .在Rt △ACD 中,tan D =2,∴=2,∴AC =4x .在Rt △ACB 中,由勾股定理得AB ==5x , ∴sin ∠ECB =sin B ==. 由AB =2,得x =,∴AD ===2x =2×=.变式训练1.如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=. (1)求AD 的长;(2)求sin DBC ∠的值.【解析】(1)过点D 作DH ⊥AB 于点H ,根据等腰直角三角形的性质,勾股定理以及锐角三角形函数的定义即可求出答案.(2)由(1)可求出CD =4,根据勾股定理可求出BD 的长度,然后根据锐角三角函数的定义即可求出答案.【答案】解:(1)过点D 作DH ⊥AB 于点H ,∵等腰三角形ABC ,∠C =90°∴∠A =45°,∴AH =DH ,设AH =x ,∴DH =x ,∵tan∠DBA=,∴BH=5x,∴AB=6x,∵AC=6,∴由勾股定理可知:AB=6,∴x=,∴AH=DH=,∴由勾股定理可知:AD=2;(2)由于AD=2∴DC=4,∴由勾股定理可知:DB=2,∴,变式训练 2.如图,已知Rt ABC∠=︒,CD是斜边AB上的中线,过点A作∆中,90ACB=.AH CH⊥,AE分别与CD、CB相交于点H、E,2AE CD(1)求sin CAH∠的值;(2)如果5CD=,求BE的值.【解析】(1)由勾股定理得出AC==CH,由锐角三角函数定义即可得出答案;(2)根据sinB的值,可得出AC:AB=1:,由AB=2,得AC=2,设CE=x(x>0),则AE=x,由勾股定理得出方程,求出CE=1,从而得出BE.【答案】解:(1)∵AE⊥CD,∴∠AHC=90°,∵AH=2CH,∴由勾股定理得:AC==CH,∴sin∠CAH===;(2)∵∠ACB=90°,CD是斜边AB上的中线,∴AB=2CD=2,∴∠B=∠BCD,∵AE⊥CD,∴∠CAH+∠ACH=90°,又∵∠ACB=90°,∴∠BCD+∠ACH=90°,∴∠B=∠BCD=∠CAH,∵sinB==sin∠CAH==,∴AC:AB=1:,∴AC=2.设CE=x(x>0),则AE=x,在Rt△ACE中,由勾股定理得:x2+22=(x)2,解得:x=1,∴CE=1,在Rt△ABC中,由勾股定理得:BC===4,∴BE=BC﹣CE=3.题型十解直角三角形的应用之坡度坡角问题例10.如图,扶梯AB坡比为1:2,滑梯CD坡比为3.若40=,某人BC mAE m=,30m≈,从扶梯上去,经过顶部BC,再沿滑梯滑下,共经过多少路径?(结果精确到0.1)(2 1.41≈3 1.73≈5 2.24)【解析】首先在直角△ABE中根据AE=40m和坡比求得AB和BE,然后得出CF的长,最后在直角△CFD中求得CD的长即可,继而求出经过的路径=AB+BC+CD的长度即可.【答案】解:∵扶梯AB的坡比为1:2,即BE:AE=1:2,AE=40m,∴BE=20m,∴AB===20(m),∵CF=BE=20米,CF:DF=1:,∴FD=CF=20(m),∴CD===40(m),∴经过的路径=AB+BC+CD=20+30+40=70+20≈114.8(m).答:共经过路径长114.8m.变式训练1.今年“五一”假期,某教学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示,斜坡AB的长为20013米,斜坡BC的长为2002米,坡度是1:1,已知A点海拔121米,C点海拔721米(1)求B点的海拔;(2)求斜坡AB的坡度;(3)为了方便上下山,若在A到C之间架设一条钢缆,求钢缆AC的长度.【解析】(1)根据题意和图形,可以求得点B的海波,本题得以解决;(2)根据题目中的数据可以求得AF和BF的长度,从而可以求得斜坡AB的坡度;(3)根据题目中的数据可以求得AD和CD的长度,然后根据勾股定理即可求得AC的长度.【答案】解:(1)作CD⊥AM于点D,作BE⊥CD于点E,作BF⊥AM于点F,连接AC,∵斜坡BC的长为200米,坡度是1:1,∴BE=CE=200米,∵A点海拔121米,C点海拔721米,∴CD=600米,∴BF=400米,∵121+400=521(米),∴点B的海拔是521米;(2)∵斜坡AB的长为200米,BF=400米,∴AF==600米,∴BF:AF=400:600=2:3,即斜坡AB的坡度是2:3;(3)∵CD=600米,AD=AF+FD=AF+BE=600+200=800(米),∴AC==1000米,即钢缆AC的长度是1000米.题型十一解直角三角形的应用之仰角俯角问题例11.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53︒,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45︒,已知山坡AB的坡度1:3,10AB=米,21AE=米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:4tan533︒≈,cos530.60)︒≈【解析】过B作DE的垂线,设垂足为G,BH⊥AE.在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE﹣DE即可求出宣传牌的高度.【答案】解:过B作BG⊥DE于G,BH⊥AE,Rt△ABF中,i=tan∠BAH==,∴∠BAH=30°,∴BH=AB=5米;∴AH=5米,∴BG=AH+AE=(5+21)米,Rt△BGC中,∠CBG=45°,∴CG=BG=(5+21)米.Rt△ADE中,∠DAE=53°,AE=21米,∴DE=AE=28米.∴CD=CG+GE﹣DE=26+5﹣28=(5﹣2)m.答:宣传牌CD高为(5﹣2)米.变式训练1.如图(1),在豫西南邓州市大十字街西南方,耸立着一座古老建筑-福胜寺梵塔,建于北宋天圣十年(公元1032年),当地民谚云:“邓州有座塔,离天一丈八.”学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45︒,王华在高台上的点D处测得塔顶B的仰角为40︒,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin400.64︒≈,︒≈,cos400.77︒≈,tan400.84结果保留整数)【解析】作DM⊥AB于M,交CB于F,CG⊥DM于G,根据矩形的性质得到CG=DE=5,DG=EC=1.3,设FM=x米,根据正切的定义用x表示出DM、BM,结合图形列出方程,解方程得到答案.【答案】解:作DM⊥AB于M,交CB于F,CG⊥DM于G,则四边形DECG为矩形,∴CG=DE=5,DG=EC=1.3,设FM=x米,由题意得,∠BDM=40°,∠BFM=∠BCA=45°,∴∠CFG=45°,BM=FM=x,∴GF=GC=5,∴DF=DG+GF=5+1.3=6.3,在Rt△BDM中,tan∠BDM=,∴DM=≈,由题意得,DM﹣DF=FM,即﹣6.3=x,解得,x≈33.2,则BA=BM+AM=38.2≈38(米),答:该塔AB的高度约为38米.四、易错点辨析1.三角形构成问题中,忘记对构成三角形的前提(三边关系)进行检验.2.忽视直角三角形致错,题中没有说明角是直角,而直接应用正弦、余弦函数的定义.3.边角关系理解不透致错.4.记忆特殊三角函数值不准确,造成计算错误.五、直击中考1.(2017河北(11))如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的( ).【答案】A.【解析】试题分析:正方形的对角线的长是10214.14,所以正方形内部的每一个点,到正方形的顶点的距离都有小于14.14,故答案选A.2.(2015河北(16))如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )A.甲、乙都可以B.甲、乙都不可以C.甲不可以,乙可以D.甲可以,乙不可以【答案与解析】所作图形如图所示,甲乙都可以拼一个与原来面积相等的正方形.故选A.3.(2014河北(8))如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n≠【】A.2B.3C.4D.5【答案】A.【解析】4.(2019河北(19))勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.(1)A,B间的距离为km;(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为km.【答案】(1)20;(2)13;【解析】解:(1)由A、B两点的纵坐标相同可知:AB∥x轴,∴AB=12﹣(﹣8)20;(2)过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交直线l于点D,由(1)可知:CE=1﹣(﹣17)=18,AE=12,设CD=x,∴AD=CD=x,由勾股定理可知:x2=(18﹣x)2+122,∴解得:x=13,∴CD=13.5.(2013河北(26))一透明的敞口正方体容器ABCD -A′B′C′D′装有一些液体,棱AB 始终在水平桌面上,容器底部的倾斜角为α(∠CBE = α,如图1所示).探究如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.解决问题:(1)CQ与BE的位置关系是___________,BQ的长是____________dm;(2)求液体的体积;(参考算法:直棱柱体积V液 = 底面积SBCQ×高AB)(3)求α的度数.(注:sin49°=cos41°=34,tan37°=34)拓展在图1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出,图3或图4是其正面示意图.若液面与棱C′C或CB交于点P,设PC = x,BQ = y.分别就图3和图4求y与x的函数关系式,并写出相应的α的范围.图1图2图3图4延伸在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM = 1 dm,BM = CM,NM⊥BC.继续向右缓慢旋转,当α = 60°时,通过计算,判断溢出容器的液体能否达到4 dm3.图5【答案与解析】。
2020年九年级数学中考几何图形综合题专题训练(含答案)

2020年九年级数学中考几何图形综合题专题训练1、如图,在▱ABCD 中,点E 在边BC 上,点F 在边AD 的延长线上,且DF=BE ,BE 与CD 交于点G(1)求证:BD ∥EF ;(2)若=,BE=4,求EC 的长.2、如图,在Rt △ABC 中,∠C =90°,AC =6,∠BAC =60°,AD 平分∠BAC 交BC 于点D ,过点D 作DE ∥AC 交AB 于点E .点M 是线段AD 上的动点,连接BM 并延长分别交DE ,AC 于点F ,G .(1)求CD 的长;(2)若点M 是线段AD 的中点,求EF DF的值;(3)请问当DM 的长满足什么条件时,在线段DE 上恰好只有一点P ,使得∠CPG =60°?3、如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△AC D∽△BFD;(2)当tan∠ABD=1,AC=3时,求BF的长.4、如图,▱ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.5、如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF(1)根据题意,补全原形;(2)求证:BE=DF.6、如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.(1)猜想并证明线段FG与CG的数量关系;(2)若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段FG与CG之间的数量关系是否改变?请证明你的结论;(3)若将图①中的正方形改成平行四边形,其他条件不变,如图③,那么线段FG与CG 之间的数量关系是否会改变?请证明你的结论.7、如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.8、如图,□A BCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。
2020年九年级中考数学复习专题训练:《三角形》综合(含答案)

2020年九年级中考数学复习专题训练:《三角形》综合1.在△ABC与△ABD中,∠DBA=∠CAB,AC与BD交于点F(1)如图1,若∠DAF=∠CBF,求证:AD=BC;(2)如图2,∠D=135°,∠C=45°,AD=2,AC=4,求BD的长.(3)如图3,若∠DBA=18°,∠D=108°,∠C=72°,AD=1,直接写出DB的长.2.如图,已知CD是△ABC的高,AD=1,BD=4,CD=2.直角∠AEF的顶点E是射线CB上一动点,AE交直线CD于点G,EF所在直线交直线AB于点F.(1)判断△ABC的形状,并说明理由;(2)若G为AE的中点,求tan∠EAF的值;(3)在点E的运动过程中,若,求的值.3.如图,在平面直角坐标中,点O为坐标原点,△ABC的三个顶点坐标分别为A(0,m),B(﹣m,0),C(n,0),AC=5且∠OBA=∠OAB,其中m,n满足.(1)求点A,C的坐标;(2)点P从点A出发,以每秒1个单位长度的速度沿y轴负方向运动,设点P的运动时间为t秒.连接BP、CP,用含有t的式子表示△BPC的面积为S(直接写出t的取值范围);(3)在(2)的条件下,是否存在t的值,使得S△PAB =S△POC,若存在,请求出t的值,并直接写出BP中点Q的坐标;若不存在,请说明理由.4.一副三角板直角顶点重合于点B ,∠A =∠C =45°,∠D =60°,∠E =30°. (1)如图(1),若∠AFE =75°,求证:AB ∥DE ;(2)如图(2),若∠AFE =α,∠BGD =β,则α+β= 度.(3)如图(3),在(1)的条件下,DE 与AC 相交于点H ,连接CE ,BH ,若DG =2CG =2GH ,BC =10,S △CEH =S △BEH ,求△BDH 的面积.5.在△ABC中,∠BAC=120°,AB=AC,PC=PA,设∠APB=α,∠BPC=β.(1)如图1,当点P在△ABC内,①若β=153°,求α的度数;小明同学通过分析已知条件发现:△ABC是顶角为120°的等腰三角形,且PC=PA,从而容易联想到构造一个顶角为120°的等腰三角形.于是,他过点A作∠DAP=120°,且AD=AP,连接DP,DB,发现两个不同的三角形全等:≌再利用全等三角形及等腰三角形的相关知识可求出α的度数.请利用小王同学分析的思路,通过计算求得α的度数为;②小王在①的基础上进一步进行探索,发现α、β之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.(2)如图2,点P在△ABC外,那么a、β之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.6.在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB 于点E,DF∥AB交边AC于点F.(1)如图1,试判断四边形AEDF的形状,并说明理由;(2)如图2,若AD=4,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.(i)求EN•EG的值;(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上7.如图1,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE=α,且点A、D、E在同一直线上,连结BE(1)求证:AD=BE.(2)如图2,若α=90°,CM⊥AE于E.若CM=7,BE=10,试求AB的长.(3)如图3,若α=120°,CM⊥AE于E,BN⊥AE于N,BN=a,CM=b,直接写出AE的值(用a,b的代数式表示).8.已知,点A(t,1)是平面直角坐标系中第一象限的点,点B,C分别是y轴负半轴和x 轴正半轴上的点,连接AB,AC,BC.(1)如图1,若OB=1,OC=,且A,B,C在同一条直线上,求t的值;(2)如图2,当t=1,∠ACO+∠ACB=180°时,求BC+OC﹣OB的值;(3)如图3,点H(m,n)是AB上一点,∠A=∠OHA=90°,若OB=OC,求m+n的值.9.在平面直角坐标系中,点A(a,0),B(0,b),且a,b满足a2﹣2ab+b2+(b﹣4)2=0,点C为线段AB上一点,连接OC.(1)直接写出a=,b=;(2)如图1,P为OC上一点,连接PA,PB,若PA=BO,∠BPC=30°,求点P的纵坐标;(3)如图2,在(2)的条件下,点M是AB上一动点,以OM为边在OM的右侧作等边△OMN,连接CN.若OC=t,求ON+CN的最小值(结果用含t的式子表示)10.如图,在Rt△ABC中,∠ACB=90°,AC=16,BC=12,点D、E分别为边AB、BC中点,点P从点A出发,沿射线AB方向以每秒5个单位长度的速度向点B运动,到点B停止.当点P不与点A重合时,过点P作PQ∥AC,且点Q在直线AB左侧,AP=PQ,过点Q作QM ⊥AB交射线AB于点M.设点P运动的时间为t(秒)(1)用含t的代数式表示线段DM的长度;(2)求当点Q落在BC边上时t的值;(3)设△PQM与△DEB重叠部分图形的面积为S(平方单位),当△PQM与△DEB有重叠且重叠部分图形是三角形时,求S与t的函数关系式;(4)当经过点C和△PQM中一个顶点的直线平分△PQM的内角时,直接写出此时t的值.11.如图,平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,点B在x轴的正半轴上,以AB为斜边向上作等腰直角△ABC,BC交y轴于点D,C(﹣2,4).(1)如图1,求点B的坐标;(2)如图2,动点E从点O出发以每秒1个单位长度的速度沿y轴的正半轴运动,设运动时间为t秒,连接CE,设△ECD的面积为S,请用含t的式子来表示S;(3)如图3,在(2)的条件下,当点E在OD的延长线上时,点F在直线CE的下方,且CF⊥CE,CF=CE.连接AD,取AD的中点M,连接FM并延长交AO于点N,连接FO,当S△NFO =10S△AMN时,求S的值.12.如图,在平面直角坐标系中,O为坐标原点,△ABC的顶点A(﹣2,0),点B,C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°(1)求点B的坐标;(2)点P为AC延长线上一点,过P作PQ∥x轴交BC的延长线于点Q,若点P的横坐标为t,线段PQ的长为d,请用含t的式子表示d;(3)在(2)的条件下,点E是线段CQ上一点,连接OE、BP,若OE=PB,∠APB﹣∠OEB =30°,求PQ的长.13.在平面直角坐标系中,点A(0,m),C(n,0).(1)若m,n满足.①直接写出m=,n=;②如图1,D为点A上方一点,连接CD,在y轴右侧作等腰Rt△BDC,∠BDC=90°,连接BA并延长交x轴于点E,当点A上方运动时,求△ACE的面积;(2)如图2,若m=n,点D在边OA上,且AD=11,G为OC上一点,且OG=8,连接CD,过点G作CD的垂线交CD于点F,交AC于点FH.连接DH,当∠ADH=∠ODC,求点D的坐标.14.如图,平面直角坐标系中,A(a,0),B(0,b)分别为x、y轴正半轴上一点,其中a、b满足:b﹣8=+,C为AB的中点.(1)求A、B两点坐标;(2)E为OB上一点,连CE交x轴于D,若BE=AD,如图1,求D点坐标;(3)F为x轴上的点,连FC,在(2)的条件下,若∠ACF=45°,求F点坐标.15.如图所示,M为等腰三角形ABD的底边AB的中点,过D作DC∥AB,连接BC,AB=6cm,DM=3cm,DC=3﹣cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.(1)当点P在线段AM上运动时,PM=.(用t的代数式表示)(2)求BC的长度;(3)当点P在MB上运动时,求S与t之间的函数关系式.16.如图,射线AN上有一点B,AB=5,tan∠MAN=,点C从点A出发以每秒3个单位长度的速度沿射线AN运动,过点C作CD⊥AN交射线AM于点D,在射线CD上取点F,使得CF=CB,连结AF.设点C的运动时间是t(秒)(t>0).(1)当点C在点B右侧时,求AD、DF的长.(用含t的代数式表示)(2)连结BD,设△BCD的面积为S平方单位,求S与t之间的函数关系式.(3)当△AFD是轴对称图形时,直接写出t的值.17.阅读下面材料,完成(1)﹣(3)题.数学课上,老师出示了这样一道题:如图1,点E是正△ABC边AC上一点以BE为边做正△BDE,连接CD.探究线段AE与CD 的数量关系,并证明.同学们经过思考后,交流了自已的想法:小明:“通过观察和度量,发现∠ABE与∠DBC相等.”小伟:“通过全等三角形证明,再经过进一步推理,可以得到线段BC平分∠ACD.”…老师:“保留原题条件,连接AD,F是AB的延长线上一点,AD=DF(如图2),如果BD =BF,可以求出CE、CB、EB三条线段之间的数量关系.”(1)求证:∠ABE=∠DBC;(2)求证:线段BC平分∠ACD;(3)探究CE、CB、EB三条线段之间的数量关系,并加以证明.18.在△ABC中,AC=BC,点G是直线BC上一点,CF⊥AG,垂足为点E,BF⊥CF于点F,点D为AB的中点,连接DF.(1)如图1,如果∠ACB=90°,且G在CB边上,设CF交AB于点R,且E为CR的中点,若CG=1,求线段BG的长;(2)如图2,如果∠ACB=90°,且G在CB边上,求证:EF=DF;(3)如图3,如果∠ACB=60°,且G在CB的延长线上,∠BAG=15°,请探究线段EF、BD之间的数量关系,并直接写出你的结论.19.如图,△ABC和△ADE都是等腰三角形,其中AB=AC,AD=AE,且∠BAC=∠DAE.(1)如图①,连接BE、CD,求证:BE=CD;(2)如图②,连接BE、CD,若∠BAC=∠DAE=60°,CD⊥AE,AD=3,CD=4,求BD的长;(3)如图③,若∠BAC=∠DAE=90°,且C点恰好落在DE上,试探究CD2、CE2和BC2之间的数量关系,并加以说明.20.已知△ABC中,AB=AC.(1)如图1,在△ADE中,AD=AE,连接BD、CE,若∠DAE=∠BAC,求证:BD=CE;(2)如图2,在△ADE中,AD=AE,连接BE、CE,若∠DAE=∠BAC=60°,CE⊥AD于点F,AE=4,,求BE的长;(3)如图3,在△BCD中,∠CBD=∠CDB=45°,连接AD,若∠CAB=45°,求的值.参考答案1.(1)证明:∵∠DFA=∠CFB,∠DAF=∠CBF,∴∠D=∠C,在△DAB和△CBA中,,∴△DAB≌△CBA(AAS),∴AD=BC;(2)解:在FC上取一点E,使得∠FBE=∠DAF,如图2所示:由(1)知,△DAB≌△EBA(AAS),∴BE=AD=2,DB=EA,∠BDA=∠AEB=135°,∴∠BEC=45°,∵∠C=45°,∴∠BEC=∠C,∴BC=BE=2,∠EBC=90°,∴EC=BE=2,∵AC=4,∴AE=AC﹣EC=4﹣2,∴BD=AE=4﹣2.(3)解:在FC上取一点E,使得∠FBE=∠DAF,如图3所示:由(1)知△DAB≌△EBA(AAS),∴BE=AD=1,DB=AE,∠BEA=∠BDA=108°,∠DBA=∠EAB=18°,∴∠BEC=72°=∠C,∠EFB=∠DBA+∠EAB=36°,∴BC=BE=1,∠EBC=36°,∴∠C=∠BEA﹣∠EBC=72°,∴∠FBC=72°,∴∠C=∠FBC,∠EFB=∠EBF=36°,∴EF=EB=1,FB=FC,∵∠DBA=∠CAB,∴AF=FB=FC=1+EC,∵∠EBC=∠EFB,∠∠C=∠C,∴△CBE~△CFB,∴,∴BC2=CE•CF,∴CE•CF=1,∴CE(CE+1)=1,即CE2+CE﹣1=0,解得:(负值已舍去),∴,∴,∴.2.解:(1)结论:△ABC是直角三角形.理由:∵CD⊥AB,∴∠CDA=∠CDB=90°,∵AD=1,CD=2,BD=4,∴CD2=AD•BD,∴=,∴△ADC∽△CDB,∴∠ACD=∠B,∵∠B+∠DCB=90°,∴∠ACD+∠BCD=90°,∴∠ACB=90°,∴△ABC是直角三角形.(2)如图1中,作EH⊥AB于H.∵AD⊥AB,EH⊥AB,∴DG∥HE,∵AG=GE,∵AD=DH=1,∵DB=4,∴BH=DB﹣DH=3,∵EH∥CD,∴=,∴=,∴EH=,∴tan∠EAF===.(3)如图2中,作EH⊥AB于H.∵CD⊥AB,EH⊥AB,∴EH∥CD,∴===,∵CD=2,BD=4,∴EH=,BH=,∴AH=AB﹣BH=5﹣=,DH=AH﹣AD=,在Rt△AEH中,AE===,∵DG∥EH,∴=,∴=,∴EG=,∵AE⊥EF,EH⊥AF,∴△AEH∽△EFH,∴=,∴=,∴EF=∴==.3.解:(1)由,解得,∴A(0,4),C(3,0).(2)如图1中,当0<t<4时,S=•BC•OP=×5×(4﹣t)=﹣t+10.如图2中,当t>4时,S=•BC•OP=×5×(t﹣4)=t﹣10.综上所述,S=.(3)当0<t<4时,由题意,×t×4=××(4﹣t)×3,解得t=.此时,OP=4﹣=,∴P(0,),∵B(﹣4,0),∴BQ的中点Q的坐标为(﹣2,)当t>4时,由题意,×t×4=××(t﹣4)×3,解得t=36,此时OP=36﹣4=32,∴P(0,﹣32),∵B(﹣4,0),∴BP的中点Q的坐标为(﹣2,﹣16).综上所述,满足条件的t的值为或36.点Q的坐标为(﹣2,)或(﹣2,﹣16).4.(1)证明:如图(1),∵∠AFE=75°,∠A=45°,∴∠ABE=75°﹣45°=30°,∵∠E=30°,∴∠E=∠ABE,∴AB∥DE;(2)解:如图(2),△ABF中,∠AFE=∠A+∠ABE=α①,△BGE中,∠BGD=∠E+∠CBF=β②,①+②得:α+β=∠A+∠E+∠CBF+∠ABE=45°+30°+90°=165°;故答案为:165;(3)解:∵DE∥AB,∴∠CGH=∠ABC=90°,∵S△CEH =S△BEH,∴,∴CG=BG,∵BC=10,∴CG=2,BG=8,∵DG=2CG=2GH,∴DG=4,GH=2,∴△BDH的面积===24.5.解:(1)①如图1,过点A作AH⊥DP于H,∵∠DAP=∠BAC=120°,∴∠DAB=∠PAC,且AD=AP,AB=AC,∴△ADB≌△APC(SAS)∴BD=PC=PA,∠ADB=∠APC,∵∠DAP=120°,AD=AP,AH⊥DP,∴∠ADP=∠APD=30°,DH=PH,∴AP=2AH,HP=AH,∴DP=AP,∴DB=DP,∴∠DBP=∠DPB=∠APB﹣∠APD=α﹣30°,∴∠BDP=180°﹣2(α﹣30°)=240°﹣2α,∴∠ADB=∠BDP+∠ADP=270°﹣2α=∠APC,∵∠APB+∠APC+∠BPC=360°,∴270°﹣2α+α+β=360°,∴β﹣α=90°,当β=153°时,α=63°,故答案为:△ADB,△APC,63°;②β﹣α=90°,理由如上;(2)α+β=90°,理由如下:如图2,作∠PAN=120°,且PA=NA,连接PN,BN,∵∠PAN=∠BAC=120°,∴∠BAN=∠PAC,且AB=AC,AP=AN,∴△ABN≌△ACP(SAS)∴∠BNA=∠APC,PC=BN=AP,∵∠PAN=120°,PA=NA,∴∠APN=∠ANP=30°,∴PN=AP=BN,∴∠BPN=∠PBN=α+30°,∵∠BPN+∠PBN+∠BNP=180°,∴2(α+30°)+β﹣α+30°=180°,∴α+β=90°.6.(1)解:四边形AEDF的形状是菱形;理由如下:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∵AD平分∠BAC,∴∠EAD=∠FAD,∵DE∥AC,∴∠EDA=∠FAD,∴∠EAD=∠EDA,∴AE=DE,∴四边形AEDF是菱形;(2)(i)解:连接EF交AD于点Q,如图2所示:∵∠BAC=60°,四边形AEDF是菱形,∴∠EAD=30°,AD、EF相互垂直平分,△AEF是等边三角形,∴∠EAF=∠AEF=∠AFE=60°,∵AD=4,∴AQ=2,在Rt△AQE中,cos∠EAQ=,即cos30°=,∴AE===4,∴AE=AF=EF=4,在△AEG和△EFH中,,∴△AEG≌△EFH(SAS),∴∠AEG=∠EFH,∴∠ENH=∠EFH+∠GEF=∠AEG+∠GEF=60°,∴∠ENH=∠EAG,∵∠AEG=∠NEH,∴△AEG∽△NEH,∴=,∴EN•EG=EH•AE=3×4=12;(ii)证明:如图3,连接FM',∵DE∥AC,∴∠AED=180°﹣∠BAC=120°,由(1)得:△EDF是等边三角形,∴DE=DF,∠EDF=∠FED=∠EFD=60°,由旋转的性质得:∠MDM'=60°,DM=DM',∴∠EDM=∠FDM',在△EDM和△FDM'中,,∴△EDM≌△FDM'(SAS),∴∠MED=∠DFM',由(i)知,∠AEG=∠EFH,∴∠DFM'+∠EFH=∠MED+∠AEG=∠AED=120°,∴∠HFM'=∠DFM'+∠HFE+∠EFD=120°+60°=180°,∴H,F,M′三点在同一条直线上.7.(1)证明:∵∠ACB=∠DCE,∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE;(2)解:设AE交BC于点H,如图2所示:由(1)得:△ACD≌△BCE,∴∠CAD=∠CBE,AD=BE=10,∵∠AHC=∠BHE,∴∠AEB=∠ACH=90°,∵∠ACB=∠DCE=α=90°,CD=CE,∴△CDE是等腰直角三角形,∵CM⊥DE,∴CM=DM=ME=7,∴DE=2CM=14,∵AE=AD+DE=10+14=24,∠AEB=90°,∴AB===26;(3)解:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,∴∠CDM=∠CEM=×(180°﹣120°)=30°.∵CM⊥DE,∴∠CMD=90°,DM=EM.在Rt△CMD中,∠CMD=90°,∠CDM=30°,∴DE=2DM=2×=2×=2b.∵∠BEC=∠ADC=180°﹣30°=150°,∠BEC=∠CEM+∠AEB,∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°,∴∠BEN=180°﹣120°=60°.在Rt△BNE中,∠BNE=90°,∠BEN=60°,∴BE===a.∵AD=BE,AE=AD+DE,∴AE=BE+DE=a+2b.8.解:(1)过点A作AD⊥x轴于D,如图1所示:∵点A(t,1),∴AD=1,OD=t,∵A,B,C在同一条直线上,∴∠OCB=∠DCA,∵tan∠OCB===,∴tan∠OCB=tan∠DCA==,即=,解得:CD=,∴t=OD=OC+CD=+=3;(2)作AD⊥y轴于D,AM⊥x轴于M,AN⊥BC于N,如图2所示:则∠ADB=∠ANB=90°,∵t=1,∴点A(1,1),∴AD=AM=OM=1,∵∠ACO+∠ACB=180°,∠ACN+∠ACB=180°,∴∠ACO=∠ACN,∵AM⊥x轴于M,AN⊥BC于N,∴AN=AM=AD=1,在Rt△ABD和Rt△ABN中,,∴Rt△ABD≌Rt△ABN(HL),∴BN=BD=OB+1,同理:Rt△ACM≌Rt△ACN(HL),∴CM=CN,∵BC=BN﹣CN,OC=OM+CM=1+CM,∴BC+OC﹣OB=BN﹣CN+1+CM﹣OB=OB+1﹣CN+1+CM﹣OB=2;(3)作HG⊥OC于G,如图3所示:∵OB=OC,∠BOC=90°,∴△BOC是等腰直角三角形,∠OCB=45°,∵∠OHA=90°,∴OH⊥AB,∴△OCH是等腰直角三角形,∵HG⊥OC,∴△OGH是等腰直角三角形,∴OG=GH,即m=﹣n,∴m+n=0.9.解:(1)∵a2﹣2ab+b2+(b﹣4)2=0,∴(a﹣b)2+(b﹣4)2=0,∵(a﹣b)2≥0,(b﹣4)2≥0,∴a=b.b﹣4=0,∴a=4,b=4,故答案为4,4.(2)如图1中,分别过A,B作OC的垂线,垂足分别为D,E.∵∠BEO=∠ADO=∠AOB=90°,∴∠BOE+∠OBE=90°,∠BOE+∠AOD=90°,∴∠AOD=∠OBE,∵BO=AO,∴△ADO≌△OEB(AAS),∴OD=BE,∵∠BPC=30°,∴PB=2BE=2OD,∵AP=BO=AO,AD⊥OP,∴OD=DP,∴PB=PO,过P作PF⊥OB,∴OF=OB=2,即点P的纵坐标的为2.(3)如图2中,以OA为边在x轴下方作等边△OAG,连接GN.∵∠MON=∠AOG=60°,∴∠MOA=∠NOG,∵OM=ON,OA=OG,∴△OMA≌△ONG(SAS),∴∠OGN=∠OAM=45°,即点N在y轴与OG夹角为45°的直线GN上运动,作OH⊥OC交CA的延长线于H,连接NH.GH.由(2)可知∠ACO=60°,在四边形ACOG中,∠COG=360°﹣60°﹣60°﹣45°﹣60°=135°,∴OC∥NG,∵OC⊥OH,∴OH⊥NG,∵∠OHC=30°=∠AGO,∴点G在以G为圆心GO为半径的⊙G上,∴GO=GA,∴NH垂直平分线段OH,∴O,H关于GN对称,∴ON+NC=NH+NC≥CH,∵CH=2OC=2t,∴ON+NC≥2t,∴ON+CN的最小值为2t.10.解:(1)如图1中,在RtABC中,∵AC=16,BC=12,∠C=90°,∴AB===20,∵PQ∥AC,∴∠A=∠QPM,∵∠C=∠PMQ=90°,∴△ACB∽△PMQ,∴==,∴==,∴PM=4t,MQ=3t,当0<t≤时,DM=AD﹣AM=10﹣5t﹣4t=﹣9t+10.当<t≤4时,DM=AM﹣AD=9t﹣10.(2)如图2中,当点Q落在BC上时,∵PQ∥AC,∴=,∴=,解得t=,∴当点Q落在BC边上时t的值为s.(3)如图3﹣1中,当<t≤时,重叠部分是△DMK,S=×DM×MK=×(9t﹣10)×(9t﹣10)=t2﹣t+.如图3﹣2中,当≤t≤4时,重叠部分是△PBK,S=•PK•BK=×(20﹣5t)•(20﹣5t)=6t2﹣48t+96.(4)如图4﹣1中,当直线CQ平分∠PQM时,设直线CQ交AB于G,作GK⊥PQ于K.∵∠QKG=∠QMG=90°,∠GQK=∠GQM,QG=QG,∴△QGK≌△QGM(AAS),∴QK=QM=3t,PK=PQ﹣QK=5t﹣3t=2t,∴PG=PK=t,∵PQ∥AC,∴=,∴=,∴t=.如图4﹣2中,当CM平分∠QMP时,作CG⊥AB于G.∵•AC•BC=•AB•CG,∴CG===,AG===,∵∠CMG=∠GCM=45°,∴CG=GM=,∴AM=9t=+,解得t=,综上所述,满足条件的t的值为s或s.11.解:(1)如图1中,作CH⊥AB于H.∵C(﹣2,4),∴CH=4,OH=2,∵AC﹣BC,∠ACB=90°,∴AH=CH=BH=4,∴OB=OH=2,∵OD∥CH,∴CD=DB,∴OD=CH=2,∴D(0,2),B(2,0).(2)由(1)可知D(0,2),所以当0≤t<2时,当t>2时,,综上所述,S=.(3)如图3中,延长AC交y轴于H,连接FD,AF.FO.∵C(﹣2,4),△ABC是等腰直角三角形,∴AB=8,由(1)知B(2,0),∴OB=2,OA=6,∵△ABC是等腰直角三角形,∴∠ACB=90°,∴∠CAB=45°,∵∠AOH=90°,∴∠CHE=∠CAB=45°,∴OH=OA=6,∵∠ACB=90°,∴∠DCH=90°,∵∠CHE=45°,∴∠CDH=∠CHE=45°,∴CH=CD,∵CF⊥CE,∴∠DCF+∠ECD=90°,∵∠ACB=90°,∴∠HCE+∠ECD=90°,∴∠HCE=∠DCF,又∵CF=CE,∴△HCE≌△DCF(SAS),∴HE=FD=6﹣t,∠CDF=∠CHE=45°,∵∠CBA=45°,∴∠CDF=∠CBA,∴FD∥AB,∴∠FDM=∠NAM,∵M是AD中点,∴DM=AM,又∵∠FMD=∠NMA,∴△DMF≌AMN(ASA),∴AN=FD=6﹣t,∵DM=AM,∴S△DMF =S△AMF∵△DMF≌△AMN,∴S△DMF =S△AMN,∴S△NFA =2S△AMN∵S△NFO =10S△AMN∴S△NFO =5S△NFA,∴5AN=ON,∵OA=6,∴AN=1,∴AN=6﹣t=1,∴t=5,∴S=t﹣2=5﹣2=3.12.解:(1)在Rt△AOC中,A(﹣2,0),∠A=60°,∴OA=2,∠ACO=∠ABC=30°∴AC=2OA=4,在Rt△ABC中,∠ABC=30°,∴AB=2AC=8,即OB=AB﹣OA=8﹣2=6,则B(6,0);(2)如图1所示,在Rt△MCP中,MP=t,∠MCP=30°,∴CP=2MP=2t,在Rt△CQP中,∠CQP=30°,CP=2t,∴PQ=4t,即d=4t;(3)如图2所示,过P作PM∥y轴,交BC于M,∴∠APM=∠DCP=∠ACO=30°,∵∠APB﹣∠OEB=30°,∴∠APB﹣30°=∠OEB=∠BPM,∵∠BMP=180°﹣60°=120°=∠OCE,∵OE=PB,∴△OCE≌△BMP(AAS),∴OC=BM=2,∵BC=4,∴CM=4﹣2=2,Rt△PCM中,∠CPM=30°,CP=2t,∴PM=4,∴PC2+CM2=PM2,∴,4t2+12=48,t=3或﹣3(舍),∴PQ=4t=12.13.解:(1)①由,解得,故答案为4,4.②如图1中,∵A(0,4),C(4,0),∴OA=OC=4,∴△AOC是等腰直角三角形,∴AC=OC,∠ACO=45°,∵△DCB是等腰直角三角形,∴BC=CD,∠DCB=45°,∴∠OCD=∠ACB,==,∴∠OCD∽△ACB,∴∠BAC=∠DOC=90°,∴∠AEC=∠ACE=45°,∴AE=AC,∵AO⊥EC,∴EO=OC=AO=4,=•EC•AO=×8×4=16.∴S△ACE(2)如图2中,作CP∥OA交DH的延长线于P,作DK⊥CP于K.∵PC∥OA,∴∠P=∠ADH,∠DCP=∠ODC,∵∠ADH=∠ODC,∴∠P=∠PCD,∴DP=DC,∴△DPC是等腰三角形,∵∠DKC=∠KCO=∠DOC=90°,∴四边形ODKC是矩形,∴OD=CK,∵DK⊥PC,∴PK=CK=OD,设OD=x,则PK=CK=x,PC=2x,∵OA=OC,AD=11,OG=8,∴CG=OC﹣OG=x+3,∵GH⊥DC,∴∠CFG=∠COD=90°,∴∠ODC+∠OCD=90°,∠CGF+∠FCG=90°,∴∠ODC=∠CGF,∴∠CGH=∠P,∵CH=CH,∠HCG=∠HCP=45°,∴△HCG≌△HCP(AAS),∴CG=CP,∴x+3=2x,∴x=3,∴D(0,3)14.解:(1)根据题意得:,解得:a=4,∴b=8,∴A(4,0),B(0,8);(2)∵C为AB的中点,∴C(2,4),设OE=b,∵BE=AD,∴AD=8﹣b,∵OA=4,∴OD=4﹣b,设直线CD的解析式为:y=kx+b,把C(2,4)代入得:2k+b=4,∴k=,∴直线CD的解析式为:y=x+b,∵D(b﹣4,0),则﹣+b=0,解得:b=2或8(舍),∴D(﹣2,0);(3)由(2)知:直线CD的解析式为:y=x+2分两种情况:①当F在点A的左侧时,如图2,过F作FG⊥AB于G,∵∠BAO=∠FAG,∴tan∠BAO=tan∠FAG===2,设AG=x,则FG=2x,∵∠ACF=45°,∠CGF=90°,∴CG=FG=2x,∵AC=AB==2,∴AG=2﹣2x=x,x=,∴AF=x=,∴OF=4﹣=,∴F(,0);②当点F在点A的右侧时,如图3,过C作CP⊥CF,交x轴于点P,CH⊥x轴于H,过A 作AG⊥CF于G,∵∠ACF=45°,∴△ACG是等腰直角三角形,∵AC=2,∴CG=AG=,由(2)知:AP=,∵AH=2,∴PH=﹣2=,∵CH=OB=4,∴PC==,∵AG∥PC,∴,即=,∴AF=10,∴F(14,0),综上,点F的坐标为(,0)或(14,0).15.解:(1)如图1中,PM=3﹣t.故答案为3﹣t.(2)过点C作CE⊥AB,垂足为E,如图2,∵DA=DB,AM=BM,∴DM⊥AB.∵CE⊥AB,∴∠CEB=∠DMB=90°.∴CE∥DM.∵DC∥ME,CE∥DM,∠DME=90°,∴四边形DCEM是矩形.∴CE=DM=3,ME=DC=.∵AM=BM,AB=6,∴AM=BM=3.∴BE=BM﹣ME=.∵∠CEB=90°,CE=3,BE=,∴CB===2.(3)①当3<t≤时,点P在线段BM上,点Q在线段BC上,过点Q作QF⊥AB,垂足为F,如图3,∵QF⊥AB,CE⊥AB,∴∠QFB=∠CEB=90°.∴QF∥CE.∵BQ=t,∴QF=∵PM=AP﹣AM=t﹣3,∴S=PM•QF=(t﹣3)•=;②当<t≤时,点P在线段BM上,点Q在线段DC上,过点Q作QF⊥AB,垂足为F,如图4,此时QF=DM=3.∵PM=AP﹣AM=t﹣3,∴S=PM•QF=(t﹣3)×3=.综上所述:当3<t≤时,S=;当<t≤时,S=.16.解:(1)在Rt△ACD中,AC=3t,tan∠MAN=,∴CD=4t.∴AD===5t,当点C在点B右侧时,CB=3t﹣5,∴CF=CB.∴DF=4t﹣(3t﹣5)=t+5.(2)当0<t<时,S=•(5﹣3t)•4t=﹣6t2+10t.当t>时,S=•(3t﹣5)•4t=6t2﹣10t.(3)①如图1中,当DF=AD时,△ADF是轴对称图形.则有5﹣3t﹣4t=5t,解得t=,②如图2中,当AF=DF时,△ADF是轴对称图形.作FH⊥AD.∵FA=DF,∴AH=DH=t,由cos∠FDH=,可得=,解得t=.③如图3中,当AF=DF时,△ADF是轴对称图形.作FH⊥AD.∵FA=DF,∴AH=DH=t,由cos∠FDH=,可得=,解得t=.综上所述,满足条件的t的值为或或.17.(1)证明:∵△ABC,△DEB都是等边三角形,∴∠ABC=∠EBD=60°,∴∠ABE+∠EBC=∠EBC+∠CBD,∴∠ABE=∠CBD.(2)证明:∵△ABC,△DEB都是等边三角形,∴BA=BC,BE=BD,∠BAC=∠ACB=60°,∵∠ABE=∠CBD,∴△ABE≌△CBD(SAS),∴∠BAE=∠BCD=60°,∴∠ACB=∠BCD=60°,∴CB平分∠ACD.(3)解:结论:EC+BE=BC.理由:∵DA=DF,∴可以将△DBF绕点D顺时针旋转,使得DF与DA重合,得到△DMA,连接AM.∵DA=DF,BD=BF,∴∠DAF=∠F=∠BDF,∵∠BCD=∠ABC=60°,∴CD∥AB,∴∠CDF=∠DAF,∵∠MDA=∠BDF=∠F=∠DAB,∴∠MDA=∠CDA,∴D,C,M共线,∵∠AMD=∠DBF=∠CDB,∠ACM=∠BCD=60°,AM=DM=BD=BF,∴△AMC≌△BDC(AAS),∴CM=DC=BD=BE,∵△ABE≌△CBD,∴AE=CD,∴BC=AC=EC+AE=CE+CD=CE+BE,∴EC+BE=BC.18.(1)解:如图1中,在CA上取一点H,使得CH=CG.∵CA=CB,∠ACB=90°,∴∠CAB=45°,∵AE⊥CR,CE=ER,∴AC=AR,∴∠CAG=∠GAB=22.5°∵CG=CH=1,∴GH===,∠CHG=45°,∵∠CHG=∠HAG+∠HGA,∴∠HAG=∠HGA=22.5°,∴HA=HG=,∵CB=CA,CG=CH,∴BG=AH=.(2)解:如图2中,连接CD,DE.∵CF⊥AG,BC⊥CF,∴∠BCF=∠CAE=90°﹣∠ACE在△AEC和△CFB,,∴△AEC≌△CFB(AAS),∴AE=CF,CE=BF,∵等腰Rt△ABC中,∠ACB=90°,AC=BC,∴CD=BD,∠CDB=90°,∵∠CDB=∠CFB=90°,∴∠FBD=∠DCE,在△BFD与△CED中,,∴△BFD≌△CED(SAS),∴DF=DE,∠FDB=∠EDC,∴∠EDC+∠EDB=∠BDF+∠BDE=90°,∴△DEF是等腰直角三角形,∴EF=DF.(3)如图3中,结论:=.理由:连接AF,在EC上取一点H,使得CH=AH,连接AH.∵AC=BC,∠ACB=60°,∴△ABC是等边三角形,∴∠CAB=60°,AB=AC=BC,∵∠BAG=15°,∴∠CAE=75°,∵CE⊥AG,∴∠CEA=90°,∴∠ACE=15°,∴∠BCF=∠ACB﹣∠ACE=45°,∵BF⊥CE,∴∠FCB=∠FBC=45°,∴FB=FC,∵AB=AC,∴AF垂直平分线段BC,∴AF平分∠CAB,∴∠FAB=∠CAB=30°,∴∠EAF=∠EFA=45°,∴EF=AE,设EF=AE=m,∵HC=HA,∴∠HCA=∠HAC=15°,∴∠EHA=∠HCA+∠HAC=30°,∴AH=2AE=2m,EH=m,∴EC=2m+m,∴AC===(+)m,∵BD=AB=AC=m,∴=.19.(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.又∵AB=AC,AD=AE,∴△ACD≌△ABE(SAS),∴CD=BE.(2)如图2,连结BE,∵AD=AE,∠DAE=60°,∴△ADE是等边三角形,∴DE=AD=3,∠ADE=∠AED=60°,∵CD⊥AE,∴∠CDA=∠ADE=×60°=30°,∵由(1)得△ACD≌△ABE,∴BE=CD=4,∠BEA=∠CDA=30°,∴∠BED=∠BEA+∠AED=30°+60°=90°,即BE⊥DE,∴BD===5.(3)CD2、CE2、BC2之间的数量关系为:CD2+CE2=BC2,理由如下:解法一:如图3,连结BE.∵AD=AE,∠DAE=90°,∴∠D=∠AED=45°,∵由(1)得△ACD≌△ABE,∴BE=CD,∠BEA=∠CDA=45°,∴∠BEC=∠BEA+∠AED=45°+45°=90°,即BE⊥DE,在Rt△BEC中,由勾股定理可知:BC2=BE2+CE2.∴BC2=CD2+CE2.解法二:如图4,过点A作AP⊥DE于点P.∵△ADE为等腰直角三角形,AP⊥DE,∴AP=EP=DP.∵CD2=(CP+PD)2=(CP+AP)2=CP2+2CP•AP+AP2,CE2=(EP﹣CP)2=(AP﹣CP)2=AP2﹣2AP•CP+CP2,。
2020年九年级数学中考三轮复习:《三角形综合训练》(解析版)

∴
,
∴
,
解得 y= .
∴BE﹣OE=(BO﹣OE)﹣OE=BO﹣2OE=3﹣2× =﹣c=OC,
∴
=1.
(3)∠G 与∠H 之间的数量关系为:∠G=2∠H﹣180°. 如图,设 AH 与 CD 交于点 Q,过 H,G 分别作 DF 的平行线 MN,KJ,
4 / 49
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
解得:
,
∴A(﹣4,0),B(0,3). (2)设 C(0,c),E(0,y), ∵将线段 AB 平移得到 CD,A(﹣4,0),B(0,3). ∴由平移的性质得 D(4,3+c), 过 D 作 DP⊥x 轴于 P,
∴AO=4=OP,DP=3+c,OE=y,OC=﹣c,
∵S△ADP=S△AOE+S 梯形 OEDP,
的值;
(3)如图 2,点 F,G 分别在 CD,BD 的延长线上,连结 FG,∠BAC 的角平分线与∠DFG 的角平分线交于点 H,求∠能照亮一个人,也能照亮无数的人。--培根
解:(1)∵(2a+b+5)2≥0,
且(2a+b+5)2+
=0,
∴
,
≥0,
(4)由题意点 P 在线段 AB 的垂直平分线上, ∴PA=PB, 在 Rt△PBD 中,∵PB2=PD2+BD2, ∴t2=(8﹣t)2+62, 解得 t= . ∴满足条件的 t 的值为 .
6.如图 1,△ABC 是边长为 8 的等边三角形,AD⊥BC 下点 D,DE⊥AB 于点 E (1)求证:AE=3EB; (2)若点 F 是 AD 的中点,点 P 是 BC 边上的动点,连接 PE,PF,如图 2 所示,求 PE+PF 的最小值及此时 BP 的长; (3)在(2)的条件下,连接 EF,若 AD= ,当 PE+PF 取最小值时,△PEF 的面积是 2.
2020年中考数学复习《三角形综合》练习(含解析)
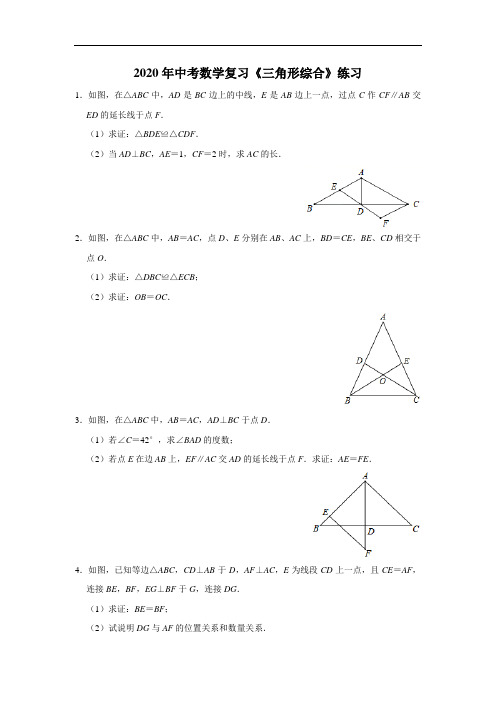
2020年中考数学复习《三角形综合》练习1.如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.(1)求证:△BDE≌△CDF.(2)当AD⊥BC,AE=1,CF=2时,求AC的长.2.如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BD=CE,BE、CD相交于点O.(1)求证:△DBC≌△ECB;(2)求证:OB=OC.3.如图,在△ABC中,AB=AC,AD⊥BC于点D.(1)若∠C=42°,求∠BAD的度数;(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.4.如图,已知等边△ABC,CD⊥AB于D,AF⊥AC,E为线段CD上一点,且CE=AF,连接BE,BF,EG⊥BF于G,连接DG.(1)求证:BE=BF;(2)试说明DG与AF的位置关系和数量关系.5.例2 如图,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G,求证:==证明:连结ED.请根据教材提示,结合图①,写出完整的证明过程.结论应用:在▱ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD交于点F.(1)如图②,若▱ABCD为正方形,且AB=6,则OF的长为.(2)如图③,连结DE交AC于点G,若四边形OFEG的面积为,则▱ABCD的面积为.6.如图,在△ABC中,内角A、B、C所对的边分别为a、b、c.(1)若a=6,b=8,c=12,请直接写出∠A与∠B的和与∠C的大小关系;(2)求证:△ABC的内角和等于180°;(3)若=,求证:△ABC是直角三角形.7.如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.(1)若∠C=36°,求∠BAD的度数;(2)求证:FB=FE.8.已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD 为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.(1)如图1,当BC=AC,CE=CD,DF=AD时,求证:①∠CAD=∠CDF,②BD=EF;(2)如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.9.如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC 交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.(1)求证:∠BAD=∠CAE;(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.10.在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN =AM.11.如图,是具有公共边AB的两个直角三角形,其中,AC=BC,∠ACB=∠ADB=90°.(1)如图1,若延长DA到点E,使AE=BD,连接CD,CE.①求证:CD=CE,CD⊥CE;②求证:AD+BD=CD;(2)若△ABC与△ABD位置如图2所示,请直接写出线段AD,BD,CD的数量关系.12.如图,△ABC是等腰直角三角形,∠ACB=90°,D是射线CB上一点(点D不与点B 重合),以AD为斜边作等腰直角三角形ADE(点E和点C在AB的同侧),连接CE.(1)如图①,当点D与点C重合时,直接写出CE与AB的位置关系;(2)如图②,当点D与点C不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)当∠EAC=15°时,请直接写出的值.13.如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),△CDE关于DE的轴对称图形为△FDE.(1)当点F在AC上时,求证:DF∥AB;(2)设△ACD的面积为S1,△ABF的面积为S2,记S=S1﹣S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;(3)当B,F,E三点共线时.求AE的长.14.如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.(1)求证:DE=EF;(2)判断BD和CF的数量关系,并说明理由;(3)若AB=3,AE=,求BD的长.15.如图,△ABC中,AB=AC,DE垂直平分AB,交线段BC于点E(点E与点C不重合),点F为AC上一点,点G为AB上一点(点G与点A不重合),且∠GEF+∠BAC=180°.(1)如图1,当∠B=45°时,线段AG和CF的数量关系是.(2)如图2,当∠B=30°时,猜想线段AG和CF的数量关系,并加以证明.(3)若AB=6,DG=1,cos B=,请直接写出CF的长.16.如图,在△ABC中,AB=7.5,AC=9,S△ABC=.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.(1)求cos A的值;(2)当△PQM与△QCN的面积满足S△PQM=S△QCN时,求t的值;(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.17.(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①的值为;②∠AMB的度数为.(2)类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD =1,OB=,请直接写出当点C与点M重合时AC的长.18.(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是;位置关系是.(2)类比思考:如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.(3)深入研究:如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.19.如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E.点M为BD中点,CM的延长线交AB于点F.(1)求证:CM=EM;(2)若∠BAC=50°,求∠EMF的大小;(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.20.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD =CE.(1)如图1,求证:∠CAE=∠CBD;(2)如图2,F是BD的中点,求证:AE⊥CF;(3)如图3,F,G分别是BD,AE的中点,若AC=2,CE=1,求△CGF的面积.答案与解析一.解答题(共20小题)1.如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.(1)求证:△BDE≌△CDF.(2)当AD⊥BC,AE=1,CF=2时,求AC的长.【分析】(1)根据平行线的性质得到∠B=∠FCD,∠BED=∠F,由AD是BC边上的中线,得到BD=CD,于是得到结论;(2)根据全等三角形的性质得到BE=CF=2,求得AB=AE+BE=1+2=3,于是得到结论.【解答】(1)证明:∵CF∥AB,∴∠B=∠FCD,∠BED=∠F,∵AD是BC边上的中线,∴BD=CD,∴△BDE≌△CDF(AAS);(2)解:∵△BDE≌△CDF,∴BE=CF=2,∴AB=AE+BE=1+2=3,∵AD⊥BC,BD=CD,∴AC=AB=3.2.如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BD=CE,BE、CD相交于点O.(1)求证:△DBC≌△ECB;(2)求证:OB=OC.【分析】(1)根据等腰三角形的性质得到∠ECB=∠DBC根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到∠DCB=∠EBC根据等腰三角形的判定定理即可得到OB=OC【解答】(1)证明:∵AB=AC,∴∠ECB=∠DBC,在△DBC与△ECB中,∴△DBC≌△ECB(SAS);(2)证明:由(1)知△DBC≌△ECB,∴∠DCB=∠EBC,∴OB=OC.3.如图,在△ABC中,AB=AC,AD⊥BC于点D.(1)若∠C=42°,求∠BAD的度数;(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.【分析】(1)根据等腰三角形的性质得到∠BAD=∠CAD,根据三角形的内角和即可得到∠BAD=∠CAD=90°﹣42°=48°;(2)根据等腰三角形的性质得到∠BAD=∠CAD根据平行线的性质得到∠F=∠CAD,等量代换得到∠BAD=∠F,于是得到结论.【解答】解:(1)∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD,∠ADC=90°,又∠C=42°,∴∠BAD=∠CAD=90°﹣42°=48°;(2)∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD,∵EF∥AC,∴∠F=∠CAD,∴∠BAD=∠F,∴AE=FE.4.如图,已知等边△ABC,CD⊥AB于D,AF⊥AC,E为线段CD上一点,且CE=AF,连接BE,BF,EG⊥BF于G,连接DG.(1)求证:BE=BF;(2)试说明DG与AF的位置关系和数量关系.【分析】(1)由等边三角形的性质可得AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,BD=AD,∠BCD=30°,由“SAS”可证△ABF≌△CBE,可得BF=BE;(2)通过证明△BEF是等边三角形,可得BG=GF,由三角形中位线定理可得AF=2GD,AF∥DG.【解答】证明:(1)∵△ABC是等边三角形∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°∵CD⊥AB,AC=BC∴BD=AD,∠BCD=30°,∵AF⊥AC∴∠F AC=90°∴∠F AB=∠F AC﹣∠BAC=30°∴∠F AB=∠ECB,且AB=BC,AF=CE∴△ABF≌△CBE(SAS)∴BF=BE(2)AF=2GD,AF∥DG理由如下:连接EF,∵△ABF≌△CBE∴∠ABF=∠CBE,∵∠ABE+∠EBC=60°∴∠ABE+∠ABF=60°,且BE=BF∴△BEF是等边三角形,且GE⊥BF∴BG=FG,且BD=AD∴AF=2GD,AF∥DG5.教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.例2 如图,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G,求证:==证明:连结ED.请根据教材提示,结合图①,写出完整的证明过程.结论应用:在▱ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD交于点F.(1)如图②,若▱ABCD为正方形,且AB=6,则OF的长为.(2)如图③,连结DE交AC于点G,若四边形OFEG的面积为,则▱ABCD的面积为6.【分析】教材呈现:如图①,连结ED.根据三角形中位线定理可得DE∥AC,DE=AC,那么△DEG∽△ACG,由相似三角形对应边成比例以及比例的性质即可证明==;结论应用:(1)如图②.先证明△BEF∽△DAF,得出BF=DF,那么BF=BD,又BO=BD,可得OF=OB﹣BF=BD,由正方形的性质求出BD=6,即可求出OF =;(2)如图③,连接OE.由(1)易证=2.根据同高的两个三角形面积之比等于底边之比得出△BEF与△OEF的面积比==2,同理,△CEG与△OEG的面积比=2,那么△CEG的面积+△BEF的面积=2(△OEG的面积+△OEF的面积)=2×=1,所以△BOC的面积=,进而求出▱ABCD的面积=4×=6.【解答】教材呈现:证明:如图①,连结ED.∵在△ABC中,D,E分别是边BC,AB的中点,∴DE∥AC,DE=AC,∴△DEG∽△ACG,∴===2,∴==;结论应用:(1)解:如图②.∵四边形ABCD为正方形,E为边BC的中点,对角线AC、BD交于点O,∴AD∥BC,BE=BC=AD,BO=BD,∴△BEF∽△DAF,∴==,∴BF=DF,∴BF=BD,∵BO=BD,∴OF=OB﹣BF=BD﹣BD=BD,∵正方形ABCD中,AB=6,∴BD=6,∴OF=.故答案为;(2)解:如图③,连接OE.由(1)知,BF=BD,OF=BD,∴=2.∵△BEF与△OEF的高相同,∴△BEF与△OEF的面积比==2,同理,△CEG与△OEG的面积比=2,∴△CEG的面积+△BEF的面积=2(△OEG的面积+△OEF的面积)=2×=1,∴▱ABCD的面积=4×=6.故答案为6.6.如图,在△ABC中,内角A、B、C所对的边分别为a、b、c.(1)若a=6,b=8,c=12,请直接写出∠A与∠B的和与∠C的大小关系;(2)求证:△ABC的内角和等于180°;(3)若=,求证:△ABC是直角三角形.【分析】(1)根据三角形中大角对大边,即可得到结论;(2)画出图形,写出已知,求证;过点A作直线MN∥BC,根据平行线性质得出∠MAB =∠B,∠NAC=∠C,代入∠MAB+∠BAC+∠NAC=180°即可求出答案;(3)化简等式即可得到a2+c2=b2,根据勾股定理的逆定理即可得到结论.【解答】解:(1)∵在△ABC中,a=6,b=8,c=12,∴∠A+∠B<∠C;(2)如图,过点B作MN∥AC,∵MN∥AC,∴∠MBA=∠A,∠NBC=∠C(两直线平行,内错角相等),∵∠MBA+∠ABC+∠NBC=180°(平角的定义),∴∠A+∠ABC+∠C=180°(等量代换),即:三角形三个内角的和等于180°;(3)∵=,∴ac=(a+b+c)(a﹣b+c)=[(a2+2ac+c2)﹣b2],∴2ac=a2+2ac+c2﹣b2,∴a2+c2=b2,∴△ABC是直角三角形.7.如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.(1)若∠C=36°,求∠BAD的度数;(2)求证:FB=FE.【分析】(1)利用等腰三角形的三线合一的性质证明∠ADB=90°,再利用等腰三角形的性质求出∠ABC即可解决问题.(2)只要证明∠FBE=∠FEB即可解决问题.【解答】(1)解:∵AB=AC,∴∠C=∠ABC,∵∠C=36°,∴∠ABC=36°,∵BD=CD,AB=AC,∴AD⊥BC,∴∠ADB=90°,∴∠BAD=90°﹣36°=54°.(2)证明:∵BE平分∠ABC,∴∠ABE=∠CBE=∠ABC,∵EF∥BC,∴∠FEB=∠CBE,∴∠FBE=∠FEB,∴FB=FE.8.已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD 为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.(1)如图1,当BC=AC,CE=CD,DF=AD时,求证:①∠CAD=∠CDF,②BD=EF;(2)如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.【分析】(1)①根据同角的余角相等证明;②作FH⊥BC交BC的延长线于H,证明△ACD≌△DHF,根据全等三角形的性质得到DH=AC,结合图形证明即可;(2)作FG⊥BC交BC的延长线于G,证明△ACD∽△DGF,根据相似三角形的性质得到DG=2AC,证明结论.【解答】(1)证明:①∵∠ACB=90°,∴∠CAD+∠ADC=90°,∵∠CDF+∠ADC=90°,∴∠CAD=∠CDF;②作FH⊥BC交BC的延长线于H,则四边形FECH为矩形,∴CH=EF,在△ACD和△DHF中,,∴△ACD≌△DHF(AAS)∴DH=AC,∵AC=CB,∴DH=CB,∴DH﹣CD=CB﹣CD,即HG=BD,∴BD=EF;(2)BD=EF,理由如下:作FG⊥BC交BC的延长线于G,∵∠CAD=∠GDF,∠ACD=∠DGF=90°,∴△ACD∽△DGF,∴===2,即DG=2AC,GF=2CD,∵BC=2AC,CE=2CD,∴BC=DG,GF=CE,∴BD=CG,∵GF∥CE,GF=CE,∠G=90°,∴四边形FECG为矩形,∴CG=EF,∴BD=EF.9.如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC 交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.(1)求证:∠BAD=∠CAE;(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.【分析】(1)由条件易证△ABC≌△ADE,得∠BAC=∠DAE,∴∠BAD=∠CAE.(2)PD=AD﹣AP=6﹣x,∵点P在线段BC上且不与B、C重合,∴AP的最小值即AP⊥BC时AP的长度,此时PD可得最大值.(3)I为△APC的内心,即I为△APC角平分线的交点,应用“三角形内角和等于180°“及角平分线定义即可表示出∠AIC,从而得到m,n的值.【解答】解:(1)在△ABC和△ADE中,(如图1)∴△ABC≌△ADE(SAS)∴∠BAC=∠DAE即∠BAD+∠DAC=∠DAC+∠CAE∴∠BAD=∠CAE.(2)∵AD=6,AP=x,∴PD=6﹣x当AD⊥BC时,AP=AB=3最小,即PD=6﹣3=3为PD的最大值.(3)如图2,设∠BAP=α,则∠APC=α+30°,∵AB⊥AC∴∠BAC=90°,∠PCA=60°,∠P AC=90°﹣α,∵I为△APC的内心∴AI、CI分别平分∠P AC,∠PCA,∴∠IAC=∠P AC,∠ICA=∠PCA∴∠AIC=180°﹣(∠IAC+∠ICA)=180°﹣(∠P AC+∠PCA)=180°﹣(90°﹣α+60°)=α+105°∵0<α<90°,∴105°<α+105°<150°,即105°<∠AIC<150°,∴m=105,n=150.10.在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN =AM.【分析】(1)根据等腰三角形的性质、直角三角形的性质得到AD=BD=DC=,求出∠MBD=30°,根据勾股定理计算即可;(2)证明△BDE≌△ADF,根据全等三角形的性质证明;(3)过点M作ME∥BC交AB的延长线于E,证明△BME≌△AMN,根据全等三角形的性质得到BE=AN,根据等腰直角三角形的性质、勾股定理证明结论.【解答】(1)解:∵∠BAC=90°,AB=AC,AD⊥BC,∴AD=BD=DC,∠ABC=∠ACB=45°,∠BAD=∠CAD=45°,∵AB=2,∴AD=BD=DC=,∵∠AMN=30°,∴∠BMD=180°﹣90°﹣30°=60°,∴∠MBD=30°,∴BM=2DM,由勾股定理得,BM2﹣DM2=BD2,即(2DM)2﹣DM2=()2,解得,DM=,∴AM=AD﹣DM=﹣;(2)证明:∵AD⊥BC,∠EDF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(ASA)∴BE=AF;(3)证明:过点M作ME∥BC交AB的延长线于E,∴∠AME=90°,则AE=AM,∠E=45°,∴ME=MA,∵∠AME=90°,∠BMN=90°,∴∠BME=∠AMN,在△BME和△NMA中,,∴△BME≌△NMA(ASA),∴BE=AN,∴AB+AN=AB+BE=AE=AM.11.如图,是具有公共边AB的两个直角三角形,其中,AC=BC,∠ACB=∠ADB=90°.(1)如图1,若延长DA到点E,使AE=BD,连接CD,CE.①求证:CD=CE,CD⊥CE;②求证:AD+BD=CD;(2)若△ABC与△ABD位置如图2所示,请直接写出线段AD,BD,CD的数量关系.【分析】(1)①根据四边形的内角和得到∠DAC+∠DBC=180°,推出∠DBC=∠EAC,根据全等三角形的性质得到CD=CE,∠BCD=∠ACE,求得∠DCE=90°,根据垂直的定义得到结论;②由已知条件得到△CDE是等腰直角三角形,求得DE=CD,根据线段的和差即可得到结论;(2)如图2,在AD上截取AE=BD,连接CE,根据等腰直角三角形的性质得到∠BAC =∠ABC=45°,求得∠CBD=∠CAE,根据全等三角形的性质得到CD=CE,∠BCD =∠ACE,求得∠DCE=90°,根据线段的和差即可得到结论.【解答】(1)证明:①在四边形ADBC中,∠DAC+∠DBC+∠ADB+∠ACB=360°,∵∠ADB+∠ACB=180°,∴∠DAC+∠DBC=180°,∵∠EAC+∠DAC=180°,∴∠DBC=∠EAC,∵BD=AE,BC=AC,∴△BCD≌△ACE(SAS),∴CD=CE,∠BCD=∠ACE,∵∠BCD+∠DCA=90°,∴∠ACE+∠DCA=90°,∴∠DCE=90°,∴CD⊥CE;②∵CD=CE,CD⊥CE,∴△CDE是等腰直角三角形,∴DE=CD,∵DE=AD+AE,AE=BD,∴DE=AD+BD,∴AD+BD=CD;(2)解:AD﹣BD=CD;理由:如图2,在AD上截取AE=BD,连接CE,∵AC=BC,∠ACB=90°,∴∠BAC=∠ABC=45°,∵∠ADB=90°,∴∠CBD=90°﹣∠BAD﹣∠ABC=90°﹣∠BAD﹣45°=45°﹣∠BAD,∵∠CAE=∠BAC﹣∠BAD=45°﹣∠BAD,∴∠CBD=∠CAE,∵BD=AE,BC=AC,∴△CBD≌△CAE(SAS),∴CD=CE,∠BCD=∠ACE,∵∠ACE+∠BCE=∠ACB=90°,∴∠BCD+∠BCE=90°,即∠DCE=90°,∴DE===CD,∵DE=AD﹣AE=AD﹣BD,∴AD﹣BD=CD.12.如图,△ABC是等腰直角三角形,∠ACB=90°,D是射线CB上一点(点D不与点B 重合),以AD为斜边作等腰直角三角形ADE(点E和点C在AB的同侧),连接CE.(1)如图①,当点D与点C重合时,直接写出CE与AB的位置关系;(2)如图②,当点D与点C不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)当∠EAC=15°时,请直接写出的值.【分析】(1)根据等腰直角三角形的性质、平行线的判定定理解答;(2)在AF上截取AF=CD,连接EF,证明△EAF≌△EDC,根据全等三角形的性质得到EF=EC,∠AEF=∠DEC,根据平行线的判定定理证明;(3)分图②、图③两种情况,根据全等三角形的性质、等腰直角三角形的性质计算,得到答案.【解答】解:(1)当点D与点C重合时,CE∥AB,理由如下:∵△ABC是等腰直角三角形,∴∠CAB=45°,∵△ADE是等腰直角三角形,∴∠ADE=45°,∴∠CAB=∠ADE,∴CE∥AB;(2)当点D与点C不重合时,(1)的结论仍然成立,理由如下:在AC上截取AF=CD,连接EF,∵∠AED=∠ACB=90°,∴∠EAF=∠EDC,在△EAF和△EDC中,,∴△EAF≌△EDC(SAS),∴EF=EC,∠AEF=∠DEC,∵∠AED=90°,∴∠FEC=90°,∴∠ECA=45°,∴∠ECA=∠CAB,∴CE∥AB;(3)如图②,∠EAC=15°,∴∠CAD=30°,∴AD=2CD,AC=CD,∴FC=(﹣1)CD,∵△CEF为等腰直角三角形,∴EC=FC=CD,∵△ABC是等腰直角三角形,∴AB=AC=CD,∴==,如图③,∠EAC=15°,由(2)得,∠EDC=∠EAC=15°,∴∠ADC=30°,∴CD=AC,AB=AC,延长AC至G,使AG=CD,∴CG=AG﹣AC=DC﹣AC=AC﹣AC,在△EAG和△EDC中,,∴△EAG≌△EDC(SAS),∴EG=EC,∠AEG=∠DEC,∴∠CEG=90°,∴△CEG为等腰直角三角形,∴EC=CG=AC,∴=,综上所述,当∠EAC=15°时,的值为或.13.如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),△CDE关于DE的轴对称图形为△FDE.(1)当点F在AC上时,求证:DF∥AB;(2)设△ACD的面积为S1,△ABF的面积为S2,记S=S1﹣S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;(3)当B,F,E三点共线时.求AE的长.【分析】(1)由折叠的性质和等边三角形的性质可得∠DFC=∠A,可证DF∥AB;(2)过点D作DM⊥AB交AB于点M,由题意可得点F在以D为圆心,DF为半径的圆上,由△ACD的面积为S1的值是定值,则当点F在DM上时,S△ABF最小时,S最大;(3)过点D作DG⊥EF于点G,过点E作EH⊥CD于点H,由勾股定理可求BG的长,通过证明△BGD∽△BHE,可求EC的长,即可求AE的长.【解答】解:(1)∵△ABC是等边三角形∴∠A=∠B=∠C=60°由折叠可知:DF=DC,且点F在AC上∴∠DFC=∠C=60°∴∠DFC=∠A(2)存在,过点D作DM⊥AB交AB于点M,∵AB=BC=6,BD=4,∴CD=2∴DF=2,∴点F在以D为圆心,DF为半径的圆上,∴当点F在DM上时,S△ABF最小,∵BD=4,DM⊥AB,∠ABC=60°∴MD=2∴S△ABF的最小值=×6×(2﹣2)=6﹣6∴S最大值=×2×3﹣(6﹣6)=﹣3+6(3)如图,过点D作DG⊥EF于点G,过点E作EH⊥CD于点H,∵△CDE关于DE的轴对称图形为△FDE∴DF=DC=2,∠EFD=∠C=60°∵GD⊥EF,∠EFD=60°∴FG=1,DG=FG=∵BD2=BG2+DG2,∴16=3+(BF+1)2,∴BF=﹣1∵EH⊥BC,∠C=60°∴CH=,EH=HC=EC∵∠GBD=∠EBH,∠BGD=∠BHE=90°∴△BGD∽△BHE∴∴∴EC=﹣1∴AE=AC﹣EC=7﹣14.如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.(1)求证:DE=EF;(2)判断BD和CF的数量关系,并说明理由;(3)若AB=3,AE=,求BD的长.【分析】(1)只要证明EA=ED,EA=EF即可解决问题;(2)结论:BD=CF.如图2中,在BE上取一点M,使得ME=CE,连接DM.想办法证明DM=CF,DM=BD即可;(3)如图3中,过点E作EN⊥AD交AD于点N.设BD=x,则DN=,DE=AE =,由∠B=45°,EN⊥BN.推出EN=BN=x+=,在Rt△DEN中,根据DN2+NE2=DE2,构建方程即可解决问题;【解答】(1)证明:如图1中,∵∠BAC=90°,∴∠EAD+∠CAE=90°,∠EDA+∠F=90°,∵∠EAD=∠EDA,∴∠EAC=∠F,∴EA=ED,EA=EF,∴DE=EF.(2)解:结论:BD=CF.理由:如图2中,在BE上取一点M,使得ME=CE,连接DM.∵DE=EF.∠DEM=∠CEF,EM=EC.∴△DEM≌△FEC,∴DM=CF,∠MDE=∠F,∴DM∥CF,∴∠BDM=∠BAC=90°,∵AB=AC,∴∠DBM=45°,∴BD=DM,∴BD=CF.(3)如图3中,过点E作EN⊥AD交AD于点N.∵EA=ED,EN⊥AD,∴AN=ND,设BD=x,则DN=,DE=AE=,∵∠B=45°,EN⊥BN.∴EN=BN=x+=,在Rt△DEN中,∵DN2+NE2=DE2,∴()2+()2=()2解得x=1或﹣1(舍弃)∴BD=1.15.如图,△ABC中,AB=AC,DE垂直平分AB,交线段BC于点E(点E与点C不重合),点F为AC上一点,点G为AB上一点(点G与点A不重合),且∠GEF+∠BAC=180°.(1)如图1,当∠B=45°时,线段AG和CF的数量关系是AG=CF.(2)如图2,当∠B=30°时,猜想线段AG和CF的数量关系,并加以证明.(3)若AB=6,DG=1,cos B=,请直接写出CF的长.【分析】(1)如图1,连接AE,根据线段垂直平分线的性质得到AE=BE,根据等腰直角三角形的性质得到∠BAE=∠B=45°,BE=EC=AE,∠BAE=∠EAC=∠C=45°,根据全等三角形的性质即可得到结论;(2)如图2,连接AE,根据等腰三角形的性质和三角形的内角和得到∠BAC=120°,根据线段垂直平分线的性质得到AE=BE,求得∠BAE=∠B=30°,根据相似三角形的性质得到,解直角三角形即可得到AG=CF;(3)①当G在DA上时,如图3,连接AE,根据线段垂直平分线的性质得到AD=BD =3,AE=BE,由三角函数的定义得到BE===4,根据相似三角形的性质得到=,过A作AH⊥BC于点H由三角函数的定义即可得到结论.②当点G在BD 上,如图4,方法同(1).【解答】解:(1)相等,理由:如图1,连接AE,∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B=45°,∴AE⊥BC,∵AB=AC,∴BE=EC=AE,∠BAE=∠EAC=∠C=45°,∵∠GEF+∠BAC=180°,∴∠AGE+∠AFE=360°﹣180°=180°,∵∠AFE+∠CFE=180°,∴∠AGE=∠CFE,∵∠GAE=∠C=45°,∴△AEG≌△CEF(AAS),∴AG=CF;故答案为:AG=CF;(2)AG=CF,理由:如图2,连接AE,∵AB=AC,∴∠B=∠C=30°,∴∠BAC=120°,∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B=30°,∴∠CAE=90°,∠BAE=∠C,∵∠GEF+∠BAC=180°,∴∠AGE+∠AFE=180°,∵∠CFE+∠AFE=180°,∴∠AGE=∠CFE,∴△AGE∽△CFE,∴,在Rt△ACE中,∵∠C=30°,∴=sin C=,∴=,∴AG=CF;(3)①当G在DA上时,如图3,连接AE,∵DE垂直平分AB,∴AD=BD=3,AE=BE,∵cos B=,∴BE===4,∴AE=BE=4,∴∠BAE=∠B,∵AB=AC,∴∠B=∠C,∴∠C=∠BAE,∵∠GEF+∠BAC=180°,∴∠AGE+∠AFE=360°﹣180°=180°,∵∠AFE+∠CFE=180°,∴∠CFE=∠AGE,∴△CFE∽△AGE,∴=,过A作AH⊥BC于点H,∵cos B=,cos45°=,∵>,∴∠B<45°,∴E在H的左侧,∵cos B=,∴BH=AB=×6=,∵AB=AC,∴BC=2BH=9,∵BE=4,∴CE=9﹣4=5,∵AG=AD﹣DG=3﹣1=2,∴=,∴CF=2.5;②当点G在BD上,如图4,同(1)可得,△CFE∽△AGE,∴=,∵AG=AD+DG=3+1=4,∴=,∴CF=5,综上所述,CF的长为2.5或5.16.如图,在△ABC中,AB=7.5,AC=9,S△ABC=.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.(1)求cos A的值;(2)当△PQM与△QCN的面积满足S△PQM=S△QCN时,求t的值;(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.【分析】(1)如图1中,作BE⊥AC于E.利用三角形的面积公式求出BE,利用勾股定理求出AE即可解决问题;(2)如图2中,作PH⊥AC于H.利用S△PQM=S△QCN构建方程即可解决问题;(3)分两种情形:①如图3中,当点M落在QN上时,作PH⊥AC于H.②如图4中,当点M在CQ上时,作PH⊥AC于H.分别构建方程求解即可;【解答】解:(1)如图1中,作BE⊥AC于E.∵S△ABC=•AC•BE=,∴BE=,在Rt△ABE中,AE==6,∴coaA===.(2)如图2中,作PH⊥AC于H.∵P A=5t,PH=3t,AH=4t,HQ=AC﹣AH﹣CQ=9﹣9t,∴PQ2=PH2+HQ2=9t2+(9﹣9t)2,∵S△PQM=S△QCN,∴•PQ2=וCQ2,∴9t2+(9﹣9t)2=×(5t)2,整理得:5t2﹣18t+9=0,解得t=3(舍弃)或.∴当t=时,满足S△PQM=S△QCN.(3)①如图3中,当点M落在QN上时,作PH⊥AC于H.易知:PM∥AC,∴∠MPQ=∠PQH=60°,∴PH=HQ,∴3t=(9﹣9t),∴t=.②如图4中,当点M在CQ上时,作PH⊥AC于H.同法可得PH=QH,∴3t=(9t﹣9),∴t=,综上所述,当t=s或s时,△PQM的某个顶点(Q点除外)落在△QCN 的边上.17.(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①的值为1;②∠AMB的度数为40°.(2)类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD =1,OB=,请直接写出当点C与点M重合时AC的长.【分析】(1)①证明△COA≌△DOB(SAS),得AC=BD,比值为1;②由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理得:∠AMB=180°﹣(∠DBO+∠OAB+∠ABD)=40°;(2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则=,由全等三角形的性质得∠AMB的度数;(3)正确画图形,当点C与点M重合时,有两种情况:如图3和4,同理可得:△AOC ∽△BOD,则∠AMB=90°,,可得AC的长.【解答】解:(1)问题发现①如图1,∵∠AOB=∠COD=40°,∴∠COA=∠DOB,∵OC=OD,OA=OB,∴△COA≌△DOB(SAS),∴AC=BD,∴=1,②∵△COA≌△DOB,∴∠CAO=∠DBO,∵∠AOB=40°,∴∠OAB+∠ABO=140°,在△AMB中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD)=180°﹣(∠DBO+∠OAB+∠ABD)=180°﹣140°=40°,故答案为:①1;②40°;(2)类比探究如图2,=,∠AMB=90°,理由是:Rt△COD中,∠DCO=30°,∠DOC=90°,∴,同理得:,∴,∵∠AOB=∠COD=90°,∴∠AOC=∠BOD,∴△AOC∽△BOD,∴=,∠CAO=∠DBO,在△AMB中,∠AMB=180°﹣(∠MAB+∠ABM)=180°﹣(∠OAB+∠ABM+∠DBO)=90°;(3)拓展延伸①点C与点M重合时,如图3,同理得:△AOC∽△BOD,∴∠AMB=90°,,设BD=x,则AC=x,Rt△COD中,∠OCD=30°,OD=1,∴CD=2,BC=x﹣2,Rt△AOB中,∠OAB=30°,OB=,∴AB=2OB=2,在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,,x2﹣x﹣6=0,(x﹣3)(x+2)=0,x1=3,x2=﹣2,∴AC=3;②点C与点M重合时,如图4,同理得:∠AMB=90°,,设BD=x,则AC=x,在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,+(x+2)2=x2+x﹣6=0,(x+3)(x﹣2)=0,x1=﹣3,x2=2,∴AC=2;综上所述,AC的长为3或2.18.(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是MG=NG;位置关系是MG⊥NG.(2)类比思考:如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.(3)深入研究:如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.【分析】(1)利用SAS判断出△ACD≌△AEB,得出CD=BE,∠ADC=∠ABE,进而判断出∠BDC+∠DBH=90°,即:∠BHD=90°,最后用三角形中位线定理即可得出结论;(2)同(1)的方法即可得出结论;(3)同(1)的方法得出MG=NG,最后利用三角形中位线定理和等量代换即可得出结论.【解答】解:(1)连接BE,CD相交于H,∵△ABD和△ACE都是等腰直角三角形,∴AB=AD,AC=AE,∠BAD=∠CAE=90°∴∠CAD=∠BAE,∴△ACD≌△AEB(SAS),∴CD=BE,∠ADC=∠ABE,∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°,∴∠BHD=90°,∴CD⊥BE,∵点M,G分别是BD,BC的中点,∴MG CD,同理:NG BE,∴MG=NG,MG⊥NG,故答案为:MG=NG,MG⊥NG;(2)连接CD,BE相交于点H,同(1)的方法得,MG=NG,MG⊥NG;(3)连接EB,DC,延长线相交于H,同(1)的方法得,MG=NG,同(1)的方法得,△ABE≌△ADC,∴∠AEB=∠ACD,∴∠CEH+∠ECH=∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE=∠ACD﹣45°+180°﹣∠ACD﹣45°=90°,∴∠DHE=90°,同(1)的方法得,MG⊥NG,∴△MGN是等腰直角三角形.19.如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E.点M为BD中点,CM的延长线交AB于点F.(1)求证:CM=EM;(2)若∠BAC=50°,求∠EMF的大小;(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.【分析】(1)利用直角三角形斜边中线的性质定理即可证明;(2)利用四边形内角和定理求出∠CME即可解决问题;(3)首先证明△ADE是等腰直角三角形,△DEM是等边三角形,设FM=a,则AE=CM=EM=a,EF=2a,推出=,=,由此即可解决问题;【解答】(1)证明:如图1中,∵DE⊥AB,∴∠DEB=∠DCB=90°,∵DM=MB,∴CM=DB,EM=DB,∴CM=EM.(2)解:∵∠AED=90°,∠A=50°,∴∠ADE=40°,∠CDE=140°,∵CM=DM=ME,∴∠MCD=∠MDC,∠MDE=∠MED,∴∠CME=360°﹣2×140°=80°,∴∠EMF=180°﹣∠CME=100°.(3)证明:如图2中,设FM=a.∵△DAE≌△CEM,CM=EM,∴AE=ED=EM=CM=DM,∠AED=∠CME=90°∴△ADE是等腰直角三角形,△DEM是等边三角形,∴∠DEM=60°,∠MEF=30°,∴AE=CM=EM=a,EF=2a,∵CN=NM,∴MN=a,∴=,=,∴=,∴EM∥AN.(也可以连接AM利用等腰三角形的三线合一的性质证明)20.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD =CE.(1)如图1,求证:∠CAE=∠CBD;(2)如图2,F是BD的中点,求证:AE⊥CF;(3)如图3,F,G分别是BD,AE的中点,若AC=2,CE=1,求△CGF的面积.【分析】(1)直接判断出△ACE≌△BCD即可得出结论;(2)先判断出∠BCF=∠CBF,进而得出∠BCF=∠CAE,即可得出结论;(3)先求出BD=3,进而求出CF=,同理:EG=,再利用等面积法求出ME,进而求出GM,最后用面积公式即可得出结论.【解答】解:(1)在△ACE和△BCD中,,∴△ACE≌△BCD,∴∠CAE=∠CBD;(2)如图2,记AE与CF的交点为M,在Rt△BCD中,点F是BD的中点,∴CF=BF,∴∠BCF=∠CBF,由(1)知,∠CAE=∠CBD,∴∠BCF=∠CAE,∴∠CAE+∠ACF=∠BCF+∠ACF=∠ACB=90°,∴∠AMC=90°,∴AE⊥CF;(3)如图3,记AE与CF的交点为M,∵AC=2,∴BC=AC=2,∵CE=1,∴CD=CE=1,在Rt△BCD中,根据勾股定理得,BD==3,∵点F是BD中点,∴CF=DF=BD=,同理:EG=AE=,连接EF,过点F作FH⊥BC,∵∠ACB=90°,点F是BD的中点,∴FH=CD=,∴S△CEF=CE•FH=×1×=,由(2)知,AE⊥CF,∴S△CEF=CF•ME=×ME=ME,∴ME=,∴ME=,∴GM=EG﹣ME=﹣=,∴S△CFG=CF•GM=××=.。
2020年九年级中考数学专题复习几何:三角形综合(含答案)

2020中考数学专题复习几何:三角形综合(含答案)一、选择题(本大题共6道小题)1. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于()A.5B.6C.7D.82. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.AD=3,BE=1.则DE的长是 ()A.B.2 C.2D.3. 如图,等边三角形OAB的边长为2,则点B的坐标为 ()A.(1,1)B.(1,)C.(,1)D.()4. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC 交AB于M,交AC于N.若△AMN的周长为18,BC=6,则△ABC的周长为()A.21B.22C.24D.265. 如K19-6,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为 ()A.35°B.40°C.45°D.50°6. 公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形的面积是25,则(sinθ-cosθ)2= ()A.B.C.D.二、填空题(本大题共5道小题)7. 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD 绕点A逆时针旋转45°得到△ACD',且点D',D,B在同一直线上,则∠ABD的度数是.8. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是.9. 如图,△ABC中,∠ABC=90°,BA=BC=2,将△ABC绕点C逆时针旋转60°得到△DEC,连接BD,则BD2的值是.10. 如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC 的面积是.11. 《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是步.三、解答题(本大题共6道小题)12. 已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.13. 如图,AB=AD,BC=DC,点E在AC上.(1)求证:AC平分∠BAD;(2)求证:BE=DE.14. 如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,且BD=CE.求证:(1)点D在BE的垂直平分线上;(2)∠BEC=3∠ABE.15. 如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF 的位置,使得∠CAF=∠BAE.连接EF,EF与AC交于点G.(1)求证:EF=BC;(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.16. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B 不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.17. 如图,Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D.过点D 作☉O的切线交BC于点E,连接OE.(1)求证:△DBE是等腰三角形;(2)求证:△COE∽△CAB.2020中考数学几何:三角形综合-答案一、选择题(本大题共6道小题)1. 【答案】B[解析]∵DE∥BC,∴△ADE∽△ABC,∴=,即=,解得BC=6,故选B.考点:相似三角形及其应用2. 【答案】B[解析]∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°,∴∠DAC+∠DCA=90°,∵∠ACB=90°,∴∠ECB+∠DCA=90°,∴∠DAC=∠ECB,又∵AC=CB,∴△ACD≌△CBE,∴AD=CE=3,CD=BE=1,∴DE=CE-CD=3-1=2,故选B.考点:全等三角形3. 【答案】B[解析]过点B作BH⊥AO于点H,∵△OAB是等边三角形,∴OH=1,BH=,∴点B的坐标为(1,).考点:等腰三角形4. 【答案】C[解析]∵MN∥BC,∴∠MEB=∠EBC.∵BE平分∠ABC,∴∠MBE=∠EBC,∴∠MEB=∠MBE,∴△MBE是等腰三角形,∴ME=MB.同理,EN=CN,∵AM+AN+MN=18,MN=ME+EN=BM+CN,∴AM+AN+BM+CN=18,∴AB+AC=18,∴AB+AC+BC=24.即△ABC的周长为24.考点:等腰三角形5. 【答案】C[解析]因为BD平分∠ABC,AE⊥BD,BF=BF,所以△ABF≌△EBF,易得BD是线段AE的垂直平分线,∠BAF=∠BEF,所以AD=ED,所以∠DEA=∠DAE,所以∠BAD=∠BED=180°-35°-50°=95°,所以∠CDE=∠BED-∠C=95°-50°=45°,故选C.考点:等腰三角形6. 【答案】A[解析]∵大正方形的面积是125,小正方形面积是25,∴大正方形的边长为5,小正方形的边长为5,∴5cosθ-5sinθ=5,∴cosθ-sinθ=,∴(sinθ-cosθ)2=.故选A.考点:直角三角形与勾股定理二、填空题(本大题共5道小题)7. 【答案】22.5°[解析]根据题意可知△ABD≌△ACD',∴∠BAC=∠CAD'=45°,AD'=AD,∴∠ADD'=∠AD'D==67.5°.∵D',D,B三点在同一直线上,∴∠ABD=∠ADD'-∠BAC=22.5°.考点:等腰三角形8. 【答案】(2,2)[解析]如图,作AE⊥x轴于E,∵∠OCD=90°,∠AOB=60°,∴∠ABO=∠OAE=30°.∵点B的坐标是(6,0),∴AO=OB=3,∴OE=OA=,∴AE===,∴A.∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∴点C的坐标为,即(2,2).考点:相似三角形及其应用9. 【答案】8+4[解析]如图,连接AD,设AC与BD交于点O,由题意得CA=CD,∠ACD=60°,∴△ACD为等边三角形,∴AD=CD,∠DAC=∠DCA=∠ADC=60°.∵∠ABC=90°,AB=BC=2,∴AC=CD=2.∵AB=BC,CD=AD,∴BD垂直平分AC,∴BO=AC=,OD=CD·sin60°=,∴BD=,∴BD2=()2=8+4.考点:直角三角形与勾股定理10. 【答案】8[解析]∵DC⊥BC,∴∠BCD=90°.∵∠ACB=120°,∴∠ACD=30°.延长CD到H使DH=CD,∵D为AB的中点,∴AD=BD.在△ADH与△BDC中,∴△ADH≌△BDC(SAS),∴AH=BC=4,∠H=∠BCD=90°.∵∠ACH=30°,∴CH=AH=4,∴CD=2,∴△ABC的面积=2S△BCD=2××4×2=8.考点:全等三角形11. 【答案】[解析]如图①,∵四边形CDEF是正方形,∴CD=ED=CF.设ED=x,则CD=x,AD=12-x.∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,∴△ADE∽△ACB,∴=,∴=,∴x=.如图②,四边形DGFE是正方形,过C作CP⊥AB于P,交DG于Q,∵S△ABC=AC·BC=AB·CP,则12×5=13CP,∴CP=.设ED=y,同理得:△CDG∽△CAB,∴=,∴=,y=<,∴该直角三角形能容纳的正方形边长最大是步,故答案为:.考点:相似三角形及其应用三、解答题(本大题共6道小题)12. 【答案】证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,∴∠BAC=∠DAE.在△ABC和△ADE中,∴△ABC≌△ADE(SAS),∴∠E=∠C.考点:全等三角形13. 【答案】证明:(1)在△ABC与△ADC中,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,即AC平分∠BAD.(2)由(1)知∠BAE=∠DAE.在△BAE与△DAE中,∴△BAE≌△DAE(SAS),∴BE=DE.考点:全等三角形14. 【答案】证明:(1)如图,连接DE.∵CD是AB边上的高,∴CD⊥AB.∴∠ADC=90°.∵AE=CE,∴DE=AC=CE=AE.∵BD=CE,∴DE=BD.∴点D在线段BE的垂直平分线上.(2)∵BD=DE,∴∠ADE=2∠ABE.∵DE=AE,∴∠A=∠ADE=2∠ABE.∴∠BEC=∠ABE+∠A=3∠ABE.考点:等腰三角形15. 【答案】解:(1)证明:∵线段AC绕点A旋转到AF的位置,∴AC=AF.∵∠CAF=∠BAE,∴∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.在△ABC和△AEF中,AB=AE,∠BAC=∠EAF,AC=AF,∴△ABC≌△AEF(SAS),∴EF=BC.(2)∵AE=AB,∴∠AEB=∠ABC=65°.∵△ABC≌△AEF,∴∠AEF=∠ABC=65°,∴∠FEC=180°-∠AEB-∠AEF=180°-65°-65°=50°.∵∠FGC是△EGC的外角,∠ACB=28°,∴∠FGC=∠FEC+∠ACB=50°+28°=78°.考点:等腰三角形16. 【答案】解:(1)证明:∵线段CD绕点C按逆时针方向旋转90°得到线段CE,∴∠DCE=90°,CD=CE.又∵∠ACB=90°,∴∠ACB=∠DCE,∴∠ACD=∠BCE.在△ACD和△BCE中,∵∴△ACD≌△BCE.(2)∵∠ACB=90°,AC=BC,∴∠A=45°,∵△ACD≌△BCE,∴AD=BE,∠CBE=∠A=45°.又AD=BF,∴BE=BF,∴∠BEF=∠BFE==67.5°.考点:等腰三角形17. 【答案】证明:(1)连接OD.∵DE是☉O的切线,∴∠ODE=90°,∴∠ADO+∠BDE=90°.又∵∠ACB=90°,∴∠A+∠B=90°,∵OA=OD,∴∠A=∠ADO,∴∠BDE=∠B,∴EB=ED,∴△DBE是等腰三角形.(2)∵∠ACB=90°,AC是☉O的直径,∴CB是☉O的切线,又∵DE是☉O的切线,∴DE=EC.∵DE=EB,∴EC=EB.∵OA=OC,∴OE∥AB.∴△COE∽△CAB.考点:相似三角形及其应用与圆有关的位置关系。
2020年九年级数学典型中考压轴题训练:《三角形综合》(含答案)

2020年九年级数学典型中考压轴题训练:《三角形综合》1.(1)已知:如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C重合),以AD为边作等边△ADE,连接CE.求证:①BD=CE,②∠DCE=120°;(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:①∠DCE的度数;②线段BD、CD、DE之间的关系,并说明理由;(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE.①则题(2)的结论还成立吗?请直接写出,不需论证;②连结BE,若BE=10,BC=6,直接写出AE的长.证明:(1)①如图1,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠ACB=∠B=60°,∠BAC=∠DAE=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠BAD=∠EAC.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE;②∵△ABD≌△ACE,∴∠ACE=∠B=60°,∴∠DCE=∠ACE+∠ACB=60°+60°=120°;(2)∠DCE=90°,BD2+CD2=DE2.证明:如图2,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE=45°,BD=CE,∴∠B+∠ACB=∠ACE+∠ACB=90°,∴∠BCE=90°,∴Rt△DCE中,CE2+CD2=DE2,∴BD2+CD2=DE2;(3)①(2)中的结论还成立.理由:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABC=∠ACE=45°,BD=CE,∴∠ABC+∠ACB=∠ACE+∠ACB=90°,∴∠BCE=90°=∠ECD,∴Rt△DCE中,CE2+CD2=DE2,∴BD2+CD2=DE2;②∵Rt△BCE中,BE=10,BC=6,∴CE===8,∴BD=CE=8,∴CD=8﹣6=2,∴Rt△DCE中,DE===,∵△ADE是等腰直角三角形,∴.2.【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线L上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.【探究发现】(1)如图2,某数学兴趣小组运用从特殊到一般的数学思想,发现当点D 移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;【数学思考】(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程.【探究发现】证明:(1)∵∠ACB=90°,AC=BC∴∠CAB=∠CBA=45°∵CD∥AB∴∠CBA=∠DCB=45°,且BD⊥CD∴∠DCB=∠DBC=45°∴DB=DC即DP=DB;【数学思考】证明:(2)∵DG⊥CD,∠DCB=45°∴∠DCG=∠DGC=45°∴DC=DG,∠DCP=∠DGB=135°,∵∠BDP=∠CDG=90°∴∠CDP=∠BDG,在△CDP和△GDB中,,∴△CDP≌△GDB(ASA)∴DP=DB.3.在△ABC中,AB=AC,D、E分别在BC和AC上,AD与BE相交于点F.(1)如图1,若∠BAC=60°,BD=CE,求证:∠1=∠2;(2)如图2,在(1)的条件下,连接CF,若CF⊥BF,求证:BF=2AF;(3)如图3,∠BAC=∠BFD=2∠CFD=90°,若S△ABC =2,求S△CDF的值.(1)证明:∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∴AB=BC,∠ABC=∠C=60°,在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),∴∠1=∠2;(2)如图2,过B作BH⊥AD,垂足为H,∵△ABD≌△BCE,∴∠BAD=∠CBE,∵∠ABF+∠CBE=60°,∴∠BFD=∠ABF+∠BAD=60°,∴∠FBH=30°,∴BF=2FH,在△AHB和△BFC中,∴△AHB≌△BFC(AAS),∴BF=AH=AF+FH=2FH,∴AF=FH,∴BF=2AF;(3)如图3,过C作CM⊥AD交AD延长线于M,过C作CN⊥BE交BE延长线于N,∵∠BFD=2∠CFD=90°,∴∠EFC=∠DFC=45°,∴CF是∠MFN的角平分线,∴CM=CN,∵∠BAC=∠BFD=90°,∴∠ABF=∠CAD,在△AFB和△CMA中,∴△AFB≌△CMA(AAS)∴BF=AM,AF=CM,∴AF=CN,∵∠FMC=90°,∠CFM=45°,∴△FMC为等腰直角三角形,∴FM=CM,∴BF=AM=AF+FM=2CM,∴S△BDF =2S△CDF,∵AF=CM,FM=CM,∴AF=FM,∴F是AM的中点,∴S△AFC =S△AMC=S△AFB,∵AF⊥BF,CN⊥BF,AF=CN,∴S△AFB =S△BFC,设S△CDF =x,则S△BDF=2x,∴S△AFB =S△BFC=3x∴S△AFC =S△AFB=x,则3x+3x+x=2,解得,x=,即S△CDF=.4.在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.(1)如图①,若∠BAC=110°,则∠MAN=40 °,若△AMN的周长为9,则BC=9 .(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2;(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA 的延长线于点H.若AB=5,CB=12,求AH的长.解:(1)∵∠BAC=110°,∴∠B+∠C=180°﹣110°=70°,∵AB边的垂直平分线交BC边于点M,∴AM=BM,∴∠BAM=∠B,同理:NA=NC,∴∠NAC=∠C,∴∠MAN=110°﹣(∠BAM+∠NAC)=40°,∵△AMN的周长为9,∴MA+MN+NA=9,∴BC=MB+MN+NC=MA+MN+NA=9,故答案为:40;9;(2)如图②,连接AM、AN,∵∠BAC=135°,∴∠B+∠C=45°,∵点M在AB的垂直平分线上,∴AM=BM,∴∠BAM=∠B,同理AN=CN,∠CAN=∠C,∴∠BAM+∠CAN=45°,∴∠MAN=∠BAC﹣(∠BAM+∠CAN)=90°,∴AM2+AN2=MN2,∴BM2+CN2=MN2;(3)如图③,连接AP、CP,过点P作PE⊥BC于点E,∵BP平分∠ABC,PH⊥BA,PE⊥BC,∴PH=PE,∵点P在AC的垂直平分线上,∴AP=CP,在Rt△APH和Rt△CPE中,,∴Rt△APH≌Rt△CPE(HL),∴AH=CE,在△BPH和△BPE中,,∴△BPH≌△BPE(AAS)∴BH=BE,∴BC=BE+CE=BH+CE=AB+2AH,∴AH=(BC﹣AB)÷2=3.5.5.(1)问题发现:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试写出线段DE,BD和CE之间的数量关系为DE=BD+CE;(2)思考探究:如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.解:(1)如图1,∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE,故答案为:DE=BD+CE;(2)(1)中结论成立,理由如下:如图2,∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠DBA=∠CAE,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(3)△DEF是等边三角形,理由如下:如图3,由(2)可知,△ADB≌△CEA,∴BD=AE,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,BF=AF,∴∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠AFE,∵在△DBF和△EAF中,,∴△DBF≌△EAF(SAS)∴DF=EF,∠BFD=∠AFE,∴∠DFE =∠DFA +∠AFE =∠DFA +∠BFD =60°,∴△DEF 为等边三角形.6.如图所示,直线AB 交x 轴于点A (4,0),交y 轴于点B (0,﹣4).(I )如图①,若C 的坐标为(﹣1,0),且AH ⊥BC 于点H ,AH 交OB 于点P ,试求点P 的坐标;(II )如图②,在(I )的条件下,连接OH ,求∠OHC 的度数;(III )如图③,若点D 为AB 的中点,点M 为y 轴正半轴上一动点,连接MD ,过D 作DN ⊥DM 交x 轴于N 点,当M 点在y 轴正半轴上运动的过程中,式子S △BDM ﹣S △ADN 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.解:(I )由题意,OA =OB =4,∵∠AHC =90°,∠BOC =90°,∴∠CAH =∠CBO ,在△OAP 和△OBC 中,,∴△OAP ≌△OBC (ASA ),∴OP =OC =1,则点P 的坐标为(0,﹣1);(II )如图②,过O 分别作OM ⊥BC 于M ,作ON ⊥AH 于N ,则四边形MONH 为矩形,∴∠MON =90°,∵∠COP =90°,∴∠COM =∠PON ,在△COM 和△PON 中,,∴△COM ≌△PON (AAS )∴OM =ON ,又OM ⊥BC ,作ON ⊥AH ,∴HO 平分∠MHN ,∴∠OHC =∠MHN =45°;(III )式子S △BDM ﹣S △ADN 的值不发生改变,等于4.理由如下:如图③,连接OD ,∵∠AOB =90°,OA =OB ,点D 为AB 的中点,∴OD ⊥AB ,OD =AD =BD =,∠OAB =45°,∴∠BOD =45°,∴∠MOD =135°,∴∠MOD =∠NAD =135°,∵∠ODA =90°,∠MDN =90°,∴∠MDO =∠NDA ,在△MOD 和△NAD 中,,∴△MOD ≌△NAD (ASA )∴S △MDO =S △NDA ,∴S △BDM ﹣S △ADN =S △BDM ﹣S △ODM =S △BDO =××4×4=4.7.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.(1)求证:AE=BD;(2)试探究线段AD、BD与CD之间的数量关系;(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2,CD=,求线段AB的长.(1)证明:∵△ACB和△ECD都是等腰直角三角形∴AC=BC,EC=DC,∠ACB=∠ECD=90°∴∠ACB﹣∠ACD=∠ECD﹣∠ACD∴∠ACE=∠BCD,∴△ACE≌△BCD(SAS),∴AE=BD.(2)解:由(1)得△ACE≌△BCD,∴∠CAE=∠CBD,又∵△ABC是等腰直角三角形,∴∠CAB=∠CBA=∠CAE=45°,∴∠EAD=90°,在Rt△ADE中,AE2+AD2=ED2,且AE=BD,∴BD2+AD2=ED2,∵ED=CD,∴BD2+AD2=2CD2,(3)解:连接EF,设BD=x,∵BD:AF=1:2,则AF=2x,∵△ECD都是等腰直角三角形,CF⊥DE,∴DF=EF,由(1)、(2)可得,在Rt△FAE中,EF===3x,∵AE2+AD2=2CD2∴,解得x=1,∴AB=2+4.8.如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)如图1,若点D是AC的中点,求证:AD=CE;(2)如图2,若点D不是AC的中点,AD=CE是否成立?证明你的结论;(3)如图3,若点D在线段AC的延长线上,试判断AD与CE的大小关系,并说明理由.(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∵D为AC中点,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°∵∠ACB=∠E+∠CDE,∴∠CDE=30°=∠E,∴CD=CE,∵AD=DC,∴AD=CE;(2)成立,如图2,过D作DF∥BC,交AB于F,则∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等边三角形,∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°﹣60°=120°,∵DF∥BC,∴∠FDB=∠DBE=∠E,在△BFD和△DCE中,∴△BFD≌△DCE(AAS),∴CE=DF=AD,即AD=CE.(3)AD=CE.证明:如图3,过点D作DP∥BC,交AB的延长线于点P,∵△ABC是等边三角形,∴△APD也是等边三角形,∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,∵DB=DE,∴∠DBC=∠DEC,∵DP∥BC,∴∠PDB=∠CBD,∴∠PDB=∠DEC,在△BPD和△DCE中,,∴△BPD≌△DCE(AAS),∴PD=CE,∴AD=CE.9.如图(a),△ABC、△DCE都为等腰直角三角形,B、C、E三点在同一直线上,连接AD.(1)若AB=2,CE=,求△ACD的周长;(2)如图(b),点G为BE的中点,连接DG并延长至F,使得GF=DG,连接BF、AG.(i)求证:BF∥DE;(ii)探索AG与FD的位置关系,并说明理由.(1)解:∵△ABC、△DCE都是等腰直角三角形,∴AB=AC,∠ACB=45°,DC=DE,∠DCE=45°,∴∠ACD=180°﹣45°﹣45°=90°,在Rt△DCE中,DC2+DE2=CE2=()2=2,∴DC=DE=1,由勾股定理得,AD===,∴△ACD的周长=AC+CD+AD=3+;(2)(i)证明:在△BGF和△EGD中,,∴△BGF≌△EGD(SAS)∴∠GBF=∠E,∴BF∥DE;(ii)AG⊥FD,理由如下:如图(b)连接AF,∵△DEG≌△FBG,∴BF=DE=CD,∠GBF=∠E=45°,∵∠ABF=∠ABC+∠GBF=90°,∴∠ABF=∠ACD,在△ACD和△ABF中,,∴△ACD≌△ABF(SAS),∴AF=AD,又∵DG=FG,∴AG⊥FD.10.如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,(1)M点如图1的位置时,如果AM=5,求BN的长;(2)M点在如图2位置时,线段AB、BM、BN三者之间的数量关系AB+BM=BN;(3)M点在如图3位置时,当BM=AB时,证明:MN⊥AB.(1)解:∵△PAB,△PMN都是等边三角形,∴∠APB=MPN=60°,PA=PB,PM=PN,∴∠APB﹣∠MPB=MPN﹣∠MPB,即∠APM=∠BPN,在△PAM和△PBN中,∴△PAM≌△PBN(SAS)∴AM=BN=5;(2)解:AB+BM=BN,理由如下:∵△PAB,△PMN都是等边三角形,∴∠APB=MPN=60°,PA=PB,PM=PN,∴∠APB+∠MPB=MPN+∠MPB,即∠APM=∠BPN,在△PAM和△PBN中,∴△PAM≌△PBN(SAS)∴AM=BN,∴BN=AM=AB+BM,故答案为:AB+BM=BN;(3)证明:∵△PAB是等边三角形,∴AB=PB,∠ABP=60°,∵BM=AB,∴PB=BM,∴∠BPM=∠PMB,∵∠ABP=60°,∴∠BPM=∠PMB=30°,∵△PMN是等边三角形,∴∠PMN=60°,∴∠AMN=90°,∴MN⊥AB.11.如图1,张老师在黑板上画出了一个△ABC,其中AB=AC.让同学们进行探究.(1)探究一:如图2,小明以BC为边在△ABC内部作等边△BDC,连接AD.请直接写出∠ADB的度数150°;(2)探究二:如图3,小彬在(1)的条件下,又以AB为边作等边△ABE,连接CE.判断CE与AD的数量关系,并说明理由;(3)探究三:如图3,小聪在(2)的条件下,连接DE.若∠DEC=60°,DE=2,求AE 的长.解:(1)探究一:∵△BDC是等边三角形,∴BD=DC,∠BDC=60°,在△ADB和△ADC中,,∴△ADB≌△ADC(SSS),∴∠ADB=∠ADC,∵∠ADB+∠ADC=360°﹣60°,∴∠ADB=150°,故答案为:150°.(2)探究二:结论:CE=AD.理由:∵△BDC、△ABE都是等边三角形∴∠ABE=∠DBC=60°,AB=BE,BD=DC.∴∠ABE﹣∠DBE=∠DBC﹣∠DBE∴∠ABD=∠EBC,在△ABD和△EBC中,∴△ABD≌△EBC(SAS).∴AD=CE.(3)探究三:∵△ABD≌△EBC,∴∠BDA=∠ECB=150°,∵∠BCD=60°,∴∠DCE=90°,∵∠DEC=60°,∴∠CDE=30°,∵DE=2,∴CE=1,由勾股定理得,DC=BC=,∵∠BDE=60°+30°=90°,DE=2,BD=.由勾股定理得,BE==.∵△ABE是等边三角形∴AE=BE=.12.(1)发现:如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E,由∠1+∠2=∠2+∠D=90°,得∠1=∠D,又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE,进而得到AC=DE,BC=AE.我们把这个数学模型称为“K 字”模型或“一线三等角”模型;(2)应用:如图2,在△ABC中,D是BC上一点,AC=AD=BD,∠CAD=90°,AB=6,请求出△ABC的面积;(3)拓展:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣1,﹣4),点B为平面内一点.若△AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标.解:(1)AC=DE,BC=AE;故答案为:DE,AE;(2)作AE⊥CD于E,如图2所示:∵AC=AD,∠CAD=90°,∴AE=CD=DE=CE,∴AD=AC=AE,设AE=DE=CE=x,则AC=AD=BD=x,∴BE=x+x,BC=2x+x,∴AB2=(x+x)2+x2=62,解得:x2=18﹣9,∴△ABC的面积=BC×AE=(2x+x)×x=×(2+)×x2=×(2+)×(18﹣9)=18;(3)分两种情况:①过A作AC⊥y轴于D,过B作BE⊥x轴于E,DA与EB相交于C,如图3所示:则∠C=90°,∵点A的坐标为(﹣1,﹣4),∴AD=1,OD=CE=4,∵∠OBO=90°,∴∠OBE+∠ABC=90°,∵∠ABC+∠BAC=90°,∴∠BAC=∠OBE,在△ABC与△BOE中,,∴△ABC≌△BOE(AAS),∴AC=BE,BC=OE,设OE=x,则BC=OE=CD=x,∴AC=BE=x+1,∴CE=BE+BC=x+1+x=OD=4,∴x=,x+1=,∴点B的坐标(,);②如图4,同理可得,点B的坐标(﹣,﹣),综上所述,点B的坐标为(,)或(﹣,﹣).13.模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C 的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为 5 .模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC =3+2=5,∵AE=BD,∴线段AE长的最大值为5,故答案为:5;模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.14.已知,平面直角坐标系中,A在x轴正半轴,B(0,1),∠OAB=30°.(1)如图1,已知AB=2.点C在y轴的正半轴上,当△ABC为等腰三角形时,直接写出点C的坐标为(0,3);(2)如图2,以AB为边作等边△ABE,AD⊥AB交OA的垂直平分线于D,求证:BD=OE;(3)如图3,在(2)的条件下,连接DE交AB于F,求的值.(1)解:∵B(0,1),∴OB=1,∵AB=2,点C在y轴的正半轴上,△ABC为等腰三角形,∴BC=AB=2,∴OC=OB+BC=3,∴点C的坐标为(0,3),故答案为:(0,3);(2)证明:连接OD,如图2所示:∵△ABE是等边三角形,∴AB=AE,∠BAE=60°,∵∠OAB=30°,∴∠OAE=30°+60°=90°,∵AD⊥AB,∴∠DAB=90°=∠OAE,∠OAD=90°﹣30°=60°,∵MN是OA的垂直平分线,∴OD=AD,∴△OAD是等边三角形,∴AO=AD,在△ABD和△AEO中,,∴△ABD≌△AEO(SAS),∴BD=OE;(3)解:作EH⊥AB于H,如图3所示:∵△ABE是等边三角形,EH⊥AB,∴AH=AB,∵∠AOB=90°,∠OAB=30°,∴OB=AB,∴AH=OB,在Rt△AEH和Rt△BAO中,,∴Rt△AEH≌Rt△BAO(HL),∴EH=AO=AD,在△HFE和△AFD中,,∴△HFE≌△AFD(AAS),∴EF=DF,∴DE=2DF,∴=.15.在平面直角坐标系中,M(m,n)且m、n满足m2+2n2﹣2mn+4n+4=0,B(0,b)为y轴上一动点,绕B点将直线BM顺时针旋转45°交x轴于点C,过C作AC⊥BC交直线BM于点A(a,t).(1)求点M的坐标;(2)如图1,在B点运动的过程中,A点的横坐标是否会发生变化?若不变,求a的值;若变化,写出A点的横坐标a的取值范围;(3)如图2,过T(a,0)作TH⊥BM(垂足H在x轴下方),在射线HB上截取HK=HT,连OK,求∠OKB的度数.解:(1)m2+2n2﹣2mn+4n+4=0,m2+n2﹣2mn+n2+4n+4=0,(m﹣n)2+(n+2)2=0,则m﹣n=0,n+2=0,解得,m=﹣2,n=﹣2,∴点M的坐标为(﹣2,﹣2);(2)过A作AT⊥x轴,MD⊥x轴于D,连接OM,CM,在Rt△ACB中,∠ABC=45°,∴CA=CB,∵∠ACB=90°,∴∠ACT+∠TCB=90°,∵∠BOC=90°,∴∠BCO+∠TCB=90°,∴∠ACT=∠CBO,在△CBO和△ACT中,,∴△CBO≌△ACT(AAS),∴CT=BO=﹣b,AT=CO=t,∴a=b+t,∵DO=DM,∴∠DOM=45°,∴∠MOC=135°,∴∠MOC+∠ABC=180°,∴O、M、B、C四点共圆,∴∠CMB=∠COB=90°,∵CA=CB,∴M为AB中点,∴b+t=﹣4,∴a=﹣4;(3)连TM、OM,过O作ON⊥BM于N,由(2)可知T(﹣4,0),∴OT=4,又点M的坐标为(﹣2,﹣2),∴△TMO为等腰直角三角形,∴MT=MO,∵∠THM=90°,∠TMO=90°,∴∠TMH=∠MON,在△HTM和△NMO中,,∴△HTM≌△NMO(AAS),∴HT=MN,HM=ON,∴HK=KN,∴KN=ON,∴∠OKB=45°.16.在等边三角形ABC中,点P从点B出发沿射线BA运动,同时点Q从点C出发沿线段AC 的延长线运动,P、Q两点运动的速度相同,PQ与直线BC相交于点D.(1)如图①,过点P作PE∥AC交BC于点E,求证:EP=CQ.(2)如图②,过点P作直线BC的垂线,垂足为F.①当点P在线段BA上运动时,求证:BF+CD=BC.②当点P在线段BA延长线上运动时,直接写出BF、CD与BC之间的数量关系.(1)证明:由题意得:BP=CQ,∵△ABC是等边三角形,∴∠BAC=∠BCA=∠ABC=60°,∵PE∥AC,∴∠BPE=∠BAC=60°,∠BEP=∠BCA=60°,∴∠B=∠BPE=∠BEP,∴△BPE是等边三角形,∴EP=BP,∴EP=CQ.(2)①证明:过点P作PE∥AC交BC于点E,如图②所示:由(1)得:EP=CQ,∠BEP=∠ACB=60°,△BPE是等边三角形,∴∠DEP=∠DCQ=120°,∵PF⊥BC,∴BF=EF,在△DPE和△DQC中,,∴△DPE≌△DQC(AAS),∴ED=CD,∴BF+CD=EF+ED=BC.②解:当点P在线段BA延长线上运动时,BC+2CD=2BF,理由如下:过点P作PE∥AC交BC于点E,如图③所示:同①得:△BPE是等边三角形,△DPE≌△DQC,∴ED=CD,∵PF⊥BC,∴BF=EF,∵BC﹣BF=CF,∴BC﹣BF=EF﹣2CD=BF﹣2CD,∴BC+2CD=2BF.17.问题情境:我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.问题初探:如图1,在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一个动点(D与A,B 不重合),连接CD,以CD为直角边作等腰直角三角形CDE,连接BE.(1)当点D在线段AB上时,AD与BE的数量关系是AD=BE;位置关系是AD⊥BE;AB,BD,BE三条线段之间的关系是AB=BD+BE.类比再探:(2)如图2,当点D运动到AB的延长线上时,AD与BE还存在(1)中的位置关系吗?若存在,请说明理由.同时探索AB,BD,BE三条线段之间的数量关系,并说明理由.能力提升:(3)如图3,当点D运动到BA的延长线上时,若AB=7,AD=2,则AE=9 .解:(1)∵∠ACB=90°,AC=BC,∴∠A=∠ABC=45°,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS)∴AD=BE,∠CBE=∠A=45°,∴∠ABE=90°,即AD⊥BE,∴AB=BD+AD=BD+BE;故答案为:AD=BE;AD⊥BE;AB=BD+BE;(2)AD⊥BE,理由如下:∵∠ACB=90°AC=BC,∴∠A=∠ABC=45°,∵△CDE是等腰直角三角形,∴CD=CE,∠DCE=90°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,在△ACD与△BCE中,,∴△ACD≌△BCE(SAS)∴∠CBE=∠A=45°,∵∠ABC=45°,∴∠ABE=∠ABC+∠CBE=90°,∴AB⊥BE,即AD⊥BE,∵△ACD≌△BCE,∴AD=BE,∵AD=AB+BD,∴BE=AB+BD;(3)∵△ABC、△CDE是等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,在△ACE与△BCD中,,∴△ACE≌△BCD(SAS)∴AE=BD=AD+AB=9,故答案为:9.18.已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.(1)如图1,若∠BAC=60°,点F与点C重合,求证:△ADC≌△BEC;(2)如图1,若∠BAC=60°,点F与点C重合,求证:AD∥BC;(3)如图2,若AD=AB,已知AF=10,AE=4,求BC的长.证明:(1)∵∠BAC=∠EDF=60°,△ABC和△DEF为等腰三角形,∴△ABC、△DEF为等边三角形,∴BC=AC,CD=CE,∠B=∠ACB=∠DCE=60°,∴∠BCE+∠ACE=∠ACD+∠ACE=60°,∴∠ACD=∠BCE,在△ADC和△BEC中,,∴△ADC≌△BEC(SAS);(2)证明:由(1)得:△ADC≌△BEC,∴∠DAC=∠EBC=60°,∴∠DAC=∠ACB,∴AD∥BC;(3)解:在FA上截取FM=AE,连接DM,如图2所示:∵∠BAC=∠EDF,∴∠AED=∠MFD,在△AED和△MFD中,,∴△AED≌△MFD(SAS),∴DA=DM=AB=AC,∠ADE=∠MDF,∴∠ADE+∠EDM=∠MDF+∠EDM,即∠ADM=∠EDF=∠BAC,在△ABC和△DAM中,,∴△ABC≌△DAM(SAS),∴AM=BC,∴AE+BC=FM+AM=AF.∴BC=AF﹣AE=10﹣4=6.19.如图,在△ABC中,AB=AC,点D,E分别是BC,AC上的点,AD,BE相交于点P,∠EBC=∠BAD.(1)如图1,求证:∠APE=∠C;(2)作AF∥BC交DE延长线于点F,PE=EC.①如图2,求证:AD=AF;②如图3,过点E作EG⊥BC于点G,若DP=1,DC=7,直接写出DG的长为 4 .(1)证明:∠APE=∠ABP+∠BAD,∠ABC=∠ABP+∠EBC,∵∠EBC=∠BAD,∴∠APE=∠ABC,∵AB=AC,∴∠C=∠ABC,∴∠APE=∠C;(2)①证明:如图2,作EG⊥DC于G,EH⊥AD于H,在△EHP和△EGC中,,∴△EHP≌△EGC(AAS)∴EH=EG,又EG⊥DC,EH⊥AD,∴∠ADF=∠CDF,∵AF∥BC,∴∠F=∠CDF,∴∠F=∠ADF,∴AD=AF;②解:如图3,作EH⊥AD于H,由(2)①可知,△EHP≌△EGC,∴PH=GC,在△DEH和△DEG中,,∴△DEH≌△DEG(AAS)∴DH=DG,∴DG=DH=DP+PH=1+GC,∴1+GC+GC=7,解得,GC=3,∴DG=DC﹣GC=7﹣3=4,故答案为:4.20.Rt△ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点E.△ACD与△CBE是否全等,并说明理由;(2)当AC=9cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF,点M 在AC上,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为C,点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F,点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.①当△CMN为等腰直角三角形时,求t的值;②当△MDC与△CEN全等时,求t的值.解:(1)△ACD与△CBE全等.理由如下:∵AD⊥直线l,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB,在△ACD和△CBE中,,∴△ACD≌△CBE(AAS);(2)①由题意得,AM=t,FN=3t,则CM=8﹣t,由折叠的性质可知,CF=CB=6,∴CN=6﹣3t,点N在BC上时,△CMN为等腰直角三角形,当点N沿C→B路径运动时,由题意得,9﹣t=3t﹣6,解得,t=,当点N沿B→C路径运动时,由题意得,9﹣t=18﹣3t,解得,t=,综上所述,当t=秒或秒时,△CMN为等腰直角三角形;②由折叠的性质可知,∠BCE=∠FCE,∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,∴∠NCE=∠CMD,∴当CM=CN时,△MDC与△CEN全等,当点N沿F→C路径运动时,9﹣t=6﹣3t,解得,t=﹣(不合题意),当点N沿C→B路径运动时,9﹣t═3t﹣6,解得,t=,当点N沿B→C路径运动时,由题意得,9﹣t=18﹣3t,解得,t=,当点N沿C→F路径运动时,由题意得,9﹣t=3t﹣18,解得,t=,综上所述,当t=秒或秒或6秒时,△MDC与△CEN全等.。
2020中考数学 三角形 综合训练(含答案)

2020中考数学三角形综合训练(含答案)一、选择题(本大题共6道小题)1. 如图,在△ABC中,AD平分△BAC交BC于点D,△B=30°,△ADC=70°,则△C的度数是()A.50°B.60°C.70°D.80°2. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD 的面积为()A.√3B.3C.√5D.53. 如图所示,线段AC的垂直平分线交线段AB于点D,△A=50°,则△BDC=()A.50°B.100°C.120°D.130°4. 如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是()A.2B.3C.4D.55. 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=22,BD=3,则AB的长为()A. 2B. 3C. 4D. 56. △ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A. 120°B. 125°C. 135°D. 150°二、填空题(本大题共6道小题)7. 如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=度.8. 已知:∠AOB,求作:∠AOB的平分线.作法:①以点O为圆心,适当长为半径画MN的长为半弧,分别交OA,OB于点M,N;②分别以点M,N为圆心,大于12径画弧,两弧在∠AOB内部交于点C;③画射线OC.射线OC即为所求.上述作图用到了全等三角形的判定方法,这个方法是.9. 如图,已知Rt△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=.10. 长为4 m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了________m.。
2020年九年级数学典型中考压轴题训练:《三角形综合》(含答案)

2020年九年级数学典型中考压轴题训练:《三角形综合》1.(1)已知:如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C重合),以AD为边作等边△ADE,连接CE.求证:①BD=CE,②∠DCE=120°;(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:①∠DCE的度数;②线段BD、CD、DE之间的关系,并说明理由;(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE.①则题(2)的结论还成立吗?请直接写出,不需论证;②连结BE,若BE=10,BC=6,直接写出AE的长.证明:(1)①如图1,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠ACB=∠B=60°,∠BAC=∠DAE=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠BAD=∠EAC.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE;②∵△ABD≌△ACE,∴∠ACE=∠B=60°,∴∠DCE=∠ACE+∠ACB=60°+60°=120°;(2)∠DCE=90°,BD2+CD2=DE2.证明:如图2,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE=45°,BD=CE,∴∠B+∠ACB=∠ACE+∠ACB=90°,∴∠BCE=90°,∴Rt△DCE中,CE2+CD2=DE2,∴BD2+CD2=DE2;(3)①(2)中的结论还成立.理由:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABC=∠ACE=45°,BD=CE,∴∠ABC+∠ACB=∠ACE+∠ACB=90°,∴∠BCE=90°=∠ECD,∴Rt△DCE中,CE2+CD2=DE2,∴BD2+CD2=DE2;②∵Rt△BCE中,BE=10,BC=6,∴CE===8,∴BD=CE=8,∴CD=8﹣6=2,∴Rt△DCE中,DE===,∵△ADE是等腰直角三角形,∴.2.【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线L上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.【探究发现】(1)如图2,某数学兴趣小组运用从特殊到一般的数学思想,发现当点D 移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;【数学思考】(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程.【探究发现】证明:(1)∵∠ACB=90°,AC=BC∴∠CAB=∠CBA=45°∵CD∥AB∴∠CBA=∠DCB=45°,且BD⊥CD∴∠DCB=∠DBC=45°∴DB=DC即DP=DB;【数学思考】证明:(2)∵DG⊥CD,∠DCB=45°∴∠DCG=∠DGC=45°∴DC=DG,∠DCP=∠DGB=135°,∵∠BDP=∠CDG=90°∴∠CDP=∠BDG,在△CDP和△GDB中,,∴△CDP≌△GDB(ASA)∴DP=DB.3.在△ABC中,AB=AC,D、E分别在BC和AC上,AD与BE相交于点F.(1)如图1,若∠BAC=60°,BD=CE,求证:∠1=∠2;(2)如图2,在(1)的条件下,连接CF,若CF⊥BF,求证:BF=2AF;(3)如图3,∠BAC=∠BFD=2∠CFD=90°,若S△ABC =2,求S△CDF的值.(1)证明:∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∴AB=BC,∠ABC=∠C=60°,在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),∴∠1=∠2;(2)如图2,过B作BH⊥AD,垂足为H,∵△ABD≌△BCE,∴∠BAD=∠CBE,∵∠ABF+∠CBE=60°,∴∠BFD=∠ABF+∠BAD=60°,∴∠FBH=30°,∴BF=2FH,在△AHB和△BFC中,∴△AHB≌△BFC(AAS),∴BF=AH=AF+FH=2FH,∴AF=FH,∴BF=2AF;(3)如图3,过C作CM⊥AD交AD延长线于M,过C作CN⊥BE交BE延长线于N,∵∠BFD=2∠CFD=90°,∴∠EFC=∠DFC=45°,∴CF是∠MFN的角平分线,∴CM=CN,∵∠BAC=∠BFD=90°,∴∠ABF=∠CAD,在△AFB和△CMA中,∴△AFB≌△CMA(AAS)∴BF=AM,AF=CM,∴AF=CN,∵∠FMC=90°,∠CFM=45°,∴△FMC为等腰直角三角形,∴FM=CM,∴BF=AM=AF+FM=2CM,∴S△BDF =2S△CDF,∵AF=CM,FM=CM,∴AF=FM,∴F是AM的中点,∴S△AFC =S△AMC=S△AFB,∵AF⊥BF,CN⊥BF,AF=CN,∴S△AFB =S△BFC,设S△CDF =x,则S△BDF=2x,∴S△AFB =S△BFC=3x∴S△AFC =S△AFB=x,则3x+3x+x=2,解得,x=,即S△CDF=.4.在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.(1)如图①,若∠BAC=110°,则∠MAN=40 °,若△AMN的周长为9,则BC=9 .(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2;(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA 的延长线于点H.若AB=5,CB=12,求AH的长.解:(1)∵∠BAC=110°,∴∠B+∠C=180°﹣110°=70°,∵AB边的垂直平分线交BC边于点M,∴AM=BM,∴∠BAM=∠B,同理:NA=NC,∴∠NAC=∠C,∴∠MAN=110°﹣(∠BAM+∠NAC)=40°,∵△AMN的周长为9,∴MA+MN+NA=9,∴BC=MB+MN+NC=MA+MN+NA=9,故答案为:40;9;(2)如图②,连接AM、AN,∵∠BAC=135°,∴∠B+∠C=45°,∵点M在AB的垂直平分线上,∴AM=BM,∴∠BAM=∠B,同理AN=CN,∠CAN=∠C,∴∠BAM+∠CAN=45°,∴∠MAN=∠BAC﹣(∠BAM+∠CAN)=90°,∴AM2+AN2=MN2,∴BM2+CN2=MN2;(3)如图③,连接AP、CP,过点P作PE⊥BC于点E,∵BP平分∠ABC,PH⊥BA,PE⊥BC,∴PH=PE,∵点P在AC的垂直平分线上,∴AP=CP,在Rt△APH和Rt△CPE中,,∴Rt△APH≌Rt△CPE(HL),∴AH=CE,在△BPH和△BPE中,,∴△BPH≌△BPE(AAS)∴BH=BE,∴BC=BE+CE=BH+CE=AB+2AH,∴AH=(BC﹣AB)÷2=3.5.5.(1)问题发现:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试写出线段DE,BD和CE之间的数量关系为DE=BD+CE;(2)思考探究:如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.解:(1)如图1,∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE,故答案为:DE=BD+CE;(2)(1)中结论成立,理由如下:如图2,∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠DBA=∠CAE,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(3)△DEF是等边三角形,理由如下:如图3,由(2)可知,△ADB≌△CEA,∴BD=AE,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,BF=AF,∴∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠AFE,∵在△DBF和△EAF中,,∴△DBF≌△EAF(SAS)∴DF=EF,∠BFD=∠AFE,∴∠DFE =∠DFA +∠AFE =∠DFA +∠BFD =60°,∴△DEF 为等边三角形.6.如图所示,直线AB 交x 轴于点A (4,0),交y 轴于点B (0,﹣4).(I )如图①,若C 的坐标为(﹣1,0),且AH ⊥BC 于点H ,AH 交OB 于点P ,试求点P 的坐标;(II )如图②,在(I )的条件下,连接OH ,求∠OHC 的度数;(III )如图③,若点D 为AB 的中点,点M 为y 轴正半轴上一动点,连接MD ,过D 作DN ⊥DM 交x 轴于N 点,当M 点在y 轴正半轴上运动的过程中,式子S △BDM ﹣S △ADN 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.解:(I )由题意,OA =OB =4,∵∠AHC =90°,∠BOC =90°,∴∠CAH =∠CBO ,在△OAP 和△OBC 中,,∴△OAP ≌△OBC (ASA ),∴OP =OC =1,则点P 的坐标为(0,﹣1);(II )如图②,过O 分别作OM ⊥BC 于M ,作ON ⊥AH 于N ,则四边形MONH 为矩形,∴∠MON =90°,∵∠COP =90°,∴∠COM =∠PON ,在△COM 和△PON 中,,∴△COM ≌△PON (AAS )∴OM =ON ,又OM ⊥BC ,作ON ⊥AH ,∴HO 平分∠MHN ,∴∠OHC =∠MHN =45°;(III )式子S △BDM ﹣S △ADN 的值不发生改变,等于4.理由如下:如图③,连接OD ,∵∠AOB =90°,OA =OB ,点D 为AB 的中点,∴OD ⊥AB ,OD =AD =BD =,∠OAB =45°,∴∠BOD =45°,∴∠MOD =135°,∴∠MOD =∠NAD =135°,∵∠ODA =90°,∠MDN =90°,∴∠MDO =∠NDA ,在△MOD 和△NAD 中,,∴△MOD ≌△NAD (ASA )∴S △MDO =S △NDA ,∴S △BDM ﹣S △ADN =S △BDM ﹣S △ODM =S △BDO =××4×4=4.7.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.(1)求证:AE=BD;(2)试探究线段AD、BD与CD之间的数量关系;(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2,CD=,求线段AB的长.(1)证明:∵△ACB和△ECD都是等腰直角三角形∴AC=BC,EC=DC,∠ACB=∠ECD=90°∴∠ACB﹣∠ACD=∠ECD﹣∠ACD∴∠ACE=∠BCD,∴△ACE≌△BCD(SAS),∴AE=BD.(2)解:由(1)得△ACE≌△BCD,∴∠CAE=∠CBD,又∵△ABC是等腰直角三角形,∴∠CAB=∠CBA=∠CAE=45°,∴∠EAD=90°,在Rt△ADE中,AE2+AD2=ED2,且AE=BD,∴BD2+AD2=ED2,∵ED=CD,∴BD2+AD2=2CD2,(3)解:连接EF,设BD=x,∵BD:AF=1:2,则AF=2x,∵△ECD都是等腰直角三角形,CF⊥DE,∴DF=EF,由(1)、(2)可得,在Rt△FAE中,EF===3x,∵AE2+AD2=2CD2∴,解得x=1,∴AB=2+4.8.如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)如图1,若点D是AC的中点,求证:AD=CE;(2)如图2,若点D不是AC的中点,AD=CE是否成立?证明你的结论;(3)如图3,若点D在线段AC的延长线上,试判断AD与CE的大小关系,并说明理由.(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∵D为AC中点,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°∵∠ACB=∠E+∠CDE,∴∠CDE=30°=∠E,∴CD=CE,∵AD=DC,∴AD=CE;(2)成立,如图2,过D作DF∥BC,交AB于F,则∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等边三角形,∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°﹣60°=120°,∵DF∥BC,∴∠FDB=∠DBE=∠E,在△BFD和△DCE中,∴△BFD≌△DCE(AAS),∴CE=DF=AD,即AD=CE.(3)AD=CE.证明:如图3,过点D作DP∥BC,交AB的延长线于点P,∵△ABC是等边三角形,∴△APD也是等边三角形,∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,∵DB=DE,∴∠DBC=∠DEC,∵DP∥BC,∴∠PDB=∠CBD,∴∠PDB=∠DEC,在△BPD和△DCE中,,∴△BPD≌△DCE(AAS),∴PD=CE,∴AD=CE.9.如图(a),△ABC、△DCE都为等腰直角三角形,B、C、E三点在同一直线上,连接AD.(1)若AB=2,CE=,求△ACD的周长;(2)如图(b),点G为BE的中点,连接DG并延长至F,使得GF=DG,连接BF、AG.(i)求证:BF∥DE;(ii)探索AG与FD的位置关系,并说明理由.(1)解:∵△ABC、△DCE都是等腰直角三角形,∴AB=AC,∠ACB=45°,DC=DE,∠DCE=45°,∴∠ACD=180°﹣45°﹣45°=90°,在Rt△DCE中,DC2+DE2=CE2=()2=2,∴DC=DE=1,由勾股定理得,AD===,∴△ACD的周长=AC+CD+AD=3+;(2)(i)证明:在△BGF和△EGD中,,∴△BGF≌△EGD(SAS)∴∠GBF=∠E,∴BF∥DE;(ii)AG⊥FD,理由如下:如图(b)连接AF,∵△DEG≌△FBG,∴BF=DE=CD,∠GBF=∠E=45°,∵∠ABF=∠ABC+∠GBF=90°,∴∠ABF=∠ACD,在△ACD和△ABF中,,∴△ACD≌△ABF(SAS),∴AF=AD,又∵DG=FG,∴AG⊥FD.10.如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,(1)M点如图1的位置时,如果AM=5,求BN的长;(2)M点在如图2位置时,线段AB、BM、BN三者之间的数量关系AB+BM=BN;(3)M点在如图3位置时,当BM=AB时,证明:MN⊥AB.(1)解:∵△PAB,△PMN都是等边三角形,∴∠APB=MPN=60°,PA=PB,PM=PN,∴∠APB﹣∠MPB=MPN﹣∠MPB,即∠APM=∠BPN,在△PAM和△PBN中,∴△PAM≌△PBN(SAS)∴AM=BN=5;(2)解:AB+BM=BN,理由如下:∵△PAB,△PMN都是等边三角形,∴∠APB=MPN=60°,PA=PB,PM=PN,∴∠APB+∠MPB=MPN+∠MPB,即∠APM=∠BPN,在△PAM和△PBN中,∴△PAM≌△PBN(SAS)∴AM=BN,∴BN=AM=AB+BM,故答案为:AB+BM=BN;(3)证明:∵△PAB是等边三角形,∴AB=PB,∠ABP=60°,∵BM=AB,∴PB=BM,∴∠BPM=∠PMB,∵∠ABP=60°,∴∠BPM=∠PMB=30°,∵△PMN是等边三角形,∴∠PMN=60°,∴∠AMN=90°,∴MN⊥AB.11.如图1,张老师在黑板上画出了一个△ABC,其中AB=AC.让同学们进行探究.(1)探究一:如图2,小明以BC为边在△ABC内部作等边△BDC,连接AD.请直接写出∠ADB的度数150°;(2)探究二:如图3,小彬在(1)的条件下,又以AB为边作等边△ABE,连接CE.判断CE与AD的数量关系,并说明理由;(3)探究三:如图3,小聪在(2)的条件下,连接DE.若∠DEC=60°,DE=2,求AE 的长.解:(1)探究一:∵△BDC是等边三角形,∴BD=DC,∠BDC=60°,在△ADB和△ADC中,,∴△ADB≌△ADC(SSS),∴∠ADB=∠ADC,∵∠ADB+∠ADC=360°﹣60°,∴∠ADB=150°,故答案为:150°.(2)探究二:结论:CE=AD.理由:∵△BDC、△ABE都是等边三角形∴∠ABE=∠DBC=60°,AB=BE,BD=DC.∴∠ABE﹣∠DBE=∠DBC﹣∠DBE∴∠ABD=∠EBC,在△ABD和△EBC中,∴△ABD≌△EBC(SAS).∴AD=CE.(3)探究三:∵△ABD≌△EBC,∴∠BDA=∠ECB=150°,∵∠BCD=60°,∴∠DCE=90°,∵∠DEC=60°,∴∠CDE=30°,∵DE=2,∴CE=1,由勾股定理得,DC=BC=,∵∠BDE=60°+30°=90°,DE=2,BD=.由勾股定理得,BE==.∵△ABE是等边三角形∴AE=BE=.12.(1)发现:如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E,由∠1+∠2=∠2+∠D=90°,得∠1=∠D,又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE,进而得到AC=DE,BC=AE.我们把这个数学模型称为“K 字”模型或“一线三等角”模型;(2)应用:如图2,在△ABC中,D是BC上一点,AC=AD=BD,∠CAD=90°,AB=6,请求出△ABC的面积;(3)拓展:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣1,﹣4),点B为平面内一点.若△AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标.解:(1)AC=DE,BC=AE;故答案为:DE,AE;(2)作AE⊥CD于E,如图2所示:∵AC=AD,∠CAD=90°,∴AE=CD=DE=CE,∴AD=AC=AE,设AE=DE=CE=x,则AC=AD=BD=x,∴BE=x+x,BC=2x+x,∴AB2=(x+x)2+x2=62,解得:x2=18﹣9,∴△ABC的面积=BC×AE=(2x+x)×x=×(2+)×x2=×(2+)×(18﹣9)=18;(3)分两种情况:①过A作AC⊥y轴于D,过B作BE⊥x轴于E,DA与EB相交于C,如图3所示:则∠C=90°,∵点A的坐标为(﹣1,﹣4),∴AD=1,OD=CE=4,∵∠OBO=90°,∴∠OBE+∠ABC=90°,∵∠ABC+∠BAC=90°,∴∠BAC=∠OBE,在△ABC与△BOE中,,∴△ABC≌△BOE(AAS),∴AC=BE,BC=OE,设OE=x,则BC=OE=CD=x,∴AC=BE=x+1,∴CE=BE+BC=x+1+x=OD=4,∴x=,x+1=,∴点B的坐标(,);②如图4,同理可得,点B的坐标(﹣,﹣),综上所述,点B的坐标为(,)或(﹣,﹣).13.模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C 的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为 5 .模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC =3+2=5,∵AE=BD,∴线段AE长的最大值为5,故答案为:5;模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.14.已知,平面直角坐标系中,A在x轴正半轴,B(0,1),∠OAB=30°.(1)如图1,已知AB=2.点C在y轴的正半轴上,当△ABC为等腰三角形时,直接写出点C的坐标为(0,3);(2)如图2,以AB为边作等边△ABE,AD⊥AB交OA的垂直平分线于D,求证:BD=OE;(3)如图3,在(2)的条件下,连接DE交AB于F,求的值.(1)解:∵B(0,1),∴OB=1,∵AB=2,点C在y轴的正半轴上,△ABC为等腰三角形,∴BC=AB=2,∴OC=OB+BC=3,∴点C的坐标为(0,3),故答案为:(0,3);(2)证明:连接OD,如图2所示:∵△ABE是等边三角形,∴AB=AE,∠BAE=60°,∵∠OAB=30°,∴∠OAE=30°+60°=90°,∵AD⊥AB,∴∠DAB=90°=∠OAE,∠OAD=90°﹣30°=60°,∵MN是OA的垂直平分线,∴OD=AD,∴△OAD是等边三角形,∴AO=AD,在△ABD和△AEO中,,∴△ABD≌△AEO(SAS),∴BD=OE;(3)解:作EH⊥AB于H,如图3所示:∵△ABE是等边三角形,EH⊥AB,∴AH=AB,∵∠AOB=90°,∠OAB=30°,∴OB=AB,∴AH=OB,在Rt△AEH和Rt△BAO中,,∴Rt△AEH≌Rt△BAO(HL),∴EH=AO=AD,在△HFE和△AFD中,,∴△HFE≌△AFD(AAS),∴EF=DF,∴DE=2DF,∴=.15.在平面直角坐标系中,M(m,n)且m、n满足m2+2n2﹣2mn+4n+4=0,B(0,b)为y轴上一动点,绕B点将直线BM顺时针旋转45°交x轴于点C,过C作AC⊥BC交直线BM于点A(a,t).(1)求点M的坐标;(2)如图1,在B点运动的过程中,A点的横坐标是否会发生变化?若不变,求a的值;若变化,写出A点的横坐标a的取值范围;(3)如图2,过T(a,0)作TH⊥BM(垂足H在x轴下方),在射线HB上截取HK=HT,连OK,求∠OKB的度数.解:(1)m2+2n2﹣2mn+4n+4=0,m2+n2﹣2mn+n2+4n+4=0,(m﹣n)2+(n+2)2=0,则m﹣n=0,n+2=0,解得,m=﹣2,n=﹣2,∴点M的坐标为(﹣2,﹣2);(2)过A作AT⊥x轴,MD⊥x轴于D,连接OM,CM,在Rt△ACB中,∠ABC=45°,∴CA=CB,∵∠ACB=90°,∴∠ACT+∠TCB=90°,∵∠BOC=90°,∴∠BCO+∠TCB=90°,∴∠ACT=∠CBO,在△CBO和△ACT中,,∴△CBO≌△ACT(AAS),∴CT=BO=﹣b,AT=CO=t,∴a=b+t,∵DO=DM,∴∠DOM=45°,∴∠MOC=135°,∴∠MOC+∠ABC=180°,∴O、M、B、C四点共圆,∴∠CMB=∠COB=90°,∵CA=CB,∴M为AB中点,∴b+t=﹣4,∴a=﹣4;(3)连TM、OM,过O作ON⊥BM于N,由(2)可知T(﹣4,0),∴OT=4,又点M的坐标为(﹣2,﹣2),∴△TMO为等腰直角三角形,∴MT=MO,∵∠THM=90°,∠TMO=90°,∴∠TMH=∠MON,在△HTM和△NMO中,,∴△HTM≌△NMO(AAS),∴HT=MN,HM=ON,∴HK=KN,∴KN=ON,∴∠OKB=45°.16.在等边三角形ABC中,点P从点B出发沿射线BA运动,同时点Q从点C出发沿线段AC 的延长线运动,P、Q两点运动的速度相同,PQ与直线BC相交于点D.(1)如图①,过点P作PE∥AC交BC于点E,求证:EP=CQ.(2)如图②,过点P作直线BC的垂线,垂足为F.①当点P在线段BA上运动时,求证:BF+CD=BC.②当点P在线段BA延长线上运动时,直接写出BF、CD与BC之间的数量关系.(1)证明:由题意得:BP=CQ,∵△ABC是等边三角形,∴∠BAC=∠BCA=∠ABC=60°,∵PE∥AC,∴∠BPE=∠BAC=60°,∠BEP=∠BCA=60°,∴∠B=∠BPE=∠BEP,∴△BPE是等边三角形,∴EP=BP,∴EP=CQ.(2)①证明:过点P作PE∥AC交BC于点E,如图②所示:由(1)得:EP=CQ,∠BEP=∠ACB=60°,△BPE是等边三角形,∴∠DEP=∠DCQ=120°,∵PF⊥BC,∴BF=EF,在△DPE和△DQC中,,∴△DPE≌△DQC(AAS),∴ED=CD,∴BF+CD=EF+ED=BC.②解:当点P在线段BA延长线上运动时,BC+2CD=2BF,理由如下:过点P作PE∥AC交BC于点E,如图③所示:同①得:△BPE是等边三角形,△DPE≌△DQC,∴ED=CD,∵PF⊥BC,∴BF=EF,∵BC﹣BF=CF,∴BC﹣BF=EF﹣2CD=BF﹣2CD,∴BC+2CD=2BF.17.问题情境:我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.问题初探:如图1,在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一个动点(D与A,B 不重合),连接CD,以CD为直角边作等腰直角三角形CDE,连接BE.(1)当点D在线段AB上时,AD与BE的数量关系是AD=BE;位置关系是AD⊥BE;AB,BD,BE三条线段之间的关系是AB=BD+BE.类比再探:(2)如图2,当点D运动到AB的延长线上时,AD与BE还存在(1)中的位置关系吗?若存在,请说明理由.同时探索AB,BD,BE三条线段之间的数量关系,并说明理由.能力提升:(3)如图3,当点D运动到BA的延长线上时,若AB=7,AD=2,则AE=9 .解:(1)∵∠ACB=90°,AC=BC,∴∠A=∠ABC=45°,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS)∴AD=BE,∠CBE=∠A=45°,∴∠ABE=90°,即AD⊥BE,∴AB=BD+AD=BD+BE;故答案为:AD=BE;AD⊥BE;AB=BD+BE;(2)AD⊥BE,理由如下:∵∠ACB=90°AC=BC,∴∠A=∠ABC=45°,∵△CDE是等腰直角三角形,∴CD=CE,∠DCE=90°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,在△ACD与△BCE中,,∴△ACD≌△BCE(SAS)∴∠CBE=∠A=45°,∵∠ABC=45°,∴∠ABE=∠ABC+∠CBE=90°,∴AB⊥BE,即AD⊥BE,∵△ACD≌△BCE,∴AD=BE,∵AD=AB+BD,∴BE=AB+BD;(3)∵△ABC、△CDE是等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,在△ACE与△BCD中,,∴△ACE≌△BCD(SAS)∴AE=BD=AD+AB=9,故答案为:9.18.已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.(1)如图1,若∠BAC=60°,点F与点C重合,求证:△ADC≌△BEC;(2)如图1,若∠BAC=60°,点F与点C重合,求证:AD∥BC;(3)如图2,若AD=AB,已知AF=10,AE=4,求BC的长.证明:(1)∵∠BAC=∠EDF=60°,△ABC和△DEF为等腰三角形,∴△ABC、△DEF为等边三角形,∴BC=AC,CD=CE,∠B=∠ACB=∠DCE=60°,∴∠BCE+∠ACE=∠ACD+∠ACE=60°,∴∠ACD=∠BCE,在△ADC和△BEC中,,∴△ADC≌△BEC(SAS);(2)证明:由(1)得:△ADC≌△BEC,∴∠DAC=∠EBC=60°,∴∠DAC=∠ACB,∴AD∥BC;(3)解:在FA上截取FM=AE,连接DM,如图2所示:∵∠BAC=∠EDF,∴∠AED=∠MFD,在△AED和△MFD中,,∴△AED≌△MFD(SAS),∴DA=DM=AB=AC,∠ADE=∠MDF,∴∠ADE+∠EDM=∠MDF+∠EDM,即∠ADM=∠EDF=∠BAC,在△ABC和△DAM中,,∴△ABC≌△DAM(SAS),∴AM=BC,∴AE+BC=FM+AM=AF.∴BC=AF﹣AE=10﹣4=6.19.如图,在△ABC中,AB=AC,点D,E分别是BC,AC上的点,AD,BE相交于点P,∠EBC=∠BAD.(1)如图1,求证:∠APE=∠C;(2)作AF∥BC交DE延长线于点F,PE=EC.①如图2,求证:AD=AF;②如图3,过点E作EG⊥BC于点G,若DP=1,DC=7,直接写出DG的长为 4 .(1)证明:∠APE=∠ABP+∠BAD,∠ABC=∠ABP+∠EBC,∵∠EBC=∠BAD,∴∠APE=∠ABC,∵AB=AC,∴∠C=∠ABC,∴∠APE=∠C;(2)①证明:如图2,作EG⊥DC于G,EH⊥AD于H,在△EHP和△EGC中,,∴△EHP≌△EGC(AAS)∴EH=EG,又EG⊥DC,EH⊥AD,∴∠ADF=∠CDF,∵AF∥BC,∴∠F=∠CDF,∴∠F=∠ADF,∴AD=AF;②解:如图3,作EH⊥AD于H,由(2)①可知,△EHP≌△EGC,∴PH=GC,在△DEH和△DEG中,,∴△DEH≌△DEG(AAS)∴DH=DG,∴DG=DH=DP+PH=1+GC,∴1+GC+GC=7,解得,GC=3,∴DG=DC﹣GC=7﹣3=4,故答案为:4.20.Rt△ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点E.△ACD与△CBE是否全等,并说明理由;(2)当AC=9cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF,点M 在AC上,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为C,点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F,点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.①当△CMN为等腰直角三角形时,求t的值;②当△MDC与△CEN全等时,求t的值.解:(1)△ACD与△CBE全等.理由如下:∵AD⊥直线l,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB,在△ACD和△CBE中,,∴△ACD≌△CBE(AAS);(2)①由题意得,AM=t,FN=3t,则CM=8﹣t,由折叠的性质可知,CF=CB=6,∴CN=6﹣3t,点N在BC上时,△CMN为等腰直角三角形,当点N沿C→B路径运动时,由题意得,9﹣t=3t﹣6,解得,t=,当点N沿B→C路径运动时,由题意得,9﹣t=18﹣3t,解得,t=,综上所述,当t=秒或秒时,△CMN为等腰直角三角形;②由折叠的性质可知,∠BCE=∠FCE,∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,∴∠NCE=∠CMD,∴当CM=CN时,△MDC与△CEN全等,当点N沿F→C路径运动时,9﹣t=6﹣3t,解得,t=﹣(不合题意),当点N沿C→B路径运动时,9﹣t═3t﹣6,解得,t=,当点N沿B→C路径运动时,由题意得,9﹣t=18﹣3t,解得,t=,当点N沿C→F路径运动时,由题意得,9﹣t=3t﹣18,解得,t=,综上所述,当t=秒或秒或6秒时,△MDC与△CEN全等.。
2020江苏省中考数学选择填空压轴题专题:《三角形综合问题》(含答案)

专题: 三角形综合问题例1.如图所示,矩形ABCD 中,AB =4,BC =4 3 ,点E 是折线ADC 上的一个动点(点E 与点A 不重合),点P 是点A 关于BE 的对称点.在点E 运动的过程中,使△PCB 为等腰三角形的点E 的位置共有( )A .2个B .3个C .4个D .5个同类题型1.1 如图,在钝角△ABC 中,分别以AB 和AC 为斜边向△ABC 的外侧作等腰直角三角形ABE 和等腰直角三角形ACF ,EM 平分∠AEB 交AB 于点M ,取BC 中点D ,AC 中点N ,连接DN 、DE 、DF .下列结论:①EM =DN ;②S △CDN =13S 四边形ABDN ;③DE =DF ;④DE ⊥DF .其中正确的结论的个数是( )A .1个B .2个C .3个D .4个同类题型1.2 如图,D ,E 分别是△ABC 的边BC ,AC 上的点,若∠B =∠C ,∠ADE =∠AED ,则( )A .当∠B 为定值时,∠CDE 为定值 B .当∠1为定值时,∠CDE 为定值C .当∠2为定值时,∠CDE 为定值D .当∠3为定值时,∠CDE 为定值同类题型1.3 如图,在△ABC 中,AB =AC =2 3 ,∠BAC =120°,点D 、E 都在边BC 上,∠DAE =60°.若BD =2CE ,则DE 的长为______________.例2.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,AB =BC ,E 为AB 边上一点,∠BCE =15°,且AE =A D .连接DE 交对角线AC 于H ,连接BH .下列结论: ①ACD ≌△ACE ;②△CDE 为等边三角形;③EH =2EB ;④S △AEH S △CEH = EHCD.其中正确的结论是________.同类题型2.1 如图所示,已知:点A(0,0),B( 3 ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于____________.同类题型2.2 如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为_________.例3.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+12∠A;②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;③EF是△ABC的中位线;④设OD=m,AE+AF=n,则S△AEF=12mn.其中正确的结论是()A.①②③B.①③④C.②③④D.①②④同类题型3.1 如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为()A.14 B.15 C.3 2 D.2 3同类题型3.2 如图,在Rt △ABC 中,BC =2,∠BAC =30°,斜边AB 的两个端点分别在相互垂直的射线OM 、ON 上滑动,下列结论:①若C 、O 两点关于AB 对称,则OA =23;②C 、O 两点距离的最大值为4; ③若AB 平分CO ,则AB ⊥CO ;④斜边AB 的中点D 运动路径的长为π2 ;其中正确的是______________(把你认为正确结论的序号都填上).同类题型3.3 如图,直角△ABC 中,∠B =30°,点O 是△ABC 的重心,连接CO 并延长交AB 于点E ,过点E 作EF ⊥AB 交BC 于点F ,连接AF 交CE 于点M ,则MOMF的值为( )A .12B .54C .23D .33例4.如图,在△ABC 中,4AB =5AC ,AD 为△ABC 的角平分线,点E 在BC 的延长线上,EF ⊥AD 于点F ,点G 在AF 上,FG =FD ,连接EG 交AC 于点H .若点H 是AC 的中点,则AGFD的值为________.同类题型4.1 如图,已知CO 1 是△ABC 的中线,过点O 1 作O 1E 1 ∥AC 交BC 于点E 1 ,连接AE 1 交CO 1 于点O 2 ;过点O 2 作O 2E 2 ∥AC 交BC 于点E 2 ,连接AE 2 交CO 1 于点O 3 ;过点O 3 作O 3E 3 ∥AC 交BC 于点E 3 ,…,如此继续,可以依次得到点O 4 ,O 5 ,…,O n 和点E 4 ,E 5 ,…,E n ,则O 2016E 2016 =_________A C .同类题型4.2 如图,过锐角△ABC 的顶点A 作DE ∥BC ,AB 恰好平分∠DAC ,AF 平分∠EAC 交BC 的延长线于点F .在AF 上取点M ,使得AM = 13 AF ,连接CM 并延长交直线DE 于点H .若AC =2,△AMH 的面积是112,则1tan ∠ACH的值是___________.例5. 如图,△ABC 的面积为S .点P 1 ,P 2 ,P 3 ,…,P n -1 是边BC 的n 等分点(n ≥3,且n 为整数),点M ,N 分别在边AB ,AC 上,且AM AB= AN AC = 1n,连接MP 1 ,MP 2 ,MP 3 ,…,MP n -1 ,连接NB ,NP 1 ,NP 2 ,…,NP n -1 ,线段MP 1 与NB 相交于点D 1 ,线段MP 2 与NP 1 相交于点D 2 ,线段MP 3 与NP 2 相交于点D 3 ,…,线段MP n -1 与NP n -2 相交于点D n -1 ,则△ND 1P 1 ,△ND 2P 2 ,△ND 3P 3 ,…,△ND n -1P n -1 的面积和是 ____________.(用含有S 与n 的式子表示)同类题型5.1如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B ′处,点A 对应点为A ′,且B ′C =3,则AM 的长是 ( )A .1.5B .2C .2.25D .2.5同类题型5.2 如图,△ABC 中,∠BAC =90°,AB =3,AC =4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,连CE ,则线段CE 的长等于 ( )A .2B .54C .53D .75同类题型5.3 如图,在Rt △ABC 中,∠A =90°,AB =AC ,BC = 2 +1,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠∠B ,使点B 的对应点B ′始终落在边AC 上,若△MB ′C 为直角三角形,则BM 的长为____________.同类题型5.4 如图,在矩形ABCD 中,∠B 的平分线BE 与AD 交于点E ,∠BED 的平分线EF 与DC 交于点F ,若AB=9,DF=2FC,则BC=_________________.(结果保留根号)参考答案例1.如图所示,矩形ABCD中,AB=4,BC=4 3 ,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有()A.2个 B.3个 C.4个 D.5个解:①BP为等腰三角形一腰长时,符合点E的位置有2个,是BC的垂直平分线与以B为圆心BA为半径的圆的交点即是点P;②BP为底边时,C为顶点时,符合点E的位置有2个,是以B为圆心BA为半径的圆与以C为圆心BC为半径的圆的交点即是点P;③以PC为底边,B为顶点时,这样的等腰三角形不存在,因为以B为圆心BA为半径的圆与以B为圆心BC 为半径的圆没有交点.选C.同类题型1.1 如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=13S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是()A.1个 B.2个 C.3个 D.4个解:∵D是BC中点,N是AC中点,∴DN 是△ABC 的中位线, ∴DN ∥AB ,且DN =12AB ;∵三角形ABE 是等腰直角三角形,EM 平分∠AEB 交AB 于点M , ∴M 是AB 的中点, ∴EM =12 AB ,又∵DN =12 AB ,∴EM =DN , ∴结论①正确;∵DN ∥AB , ∴△CDN ∽ABC , ∵DN =12 AB ,∴S △CDN =14S △ABC ,∴S △CDN =13 S _(四边形ABDN ),∴结论②正确;如图1,连接MD 、FN ,∵D 是BC 中点,M 是AB 中点, ∴DM 是△AB C 的中位线, ∴DM ∥AC ,且DM =12AC ;∵三角形ACF 是等腰直角三角形,N 是AC 的中点, ∴FN =12 AC ,又∵DM =12AC ,∴DM =FN ,∵DM ∥AC ,DN ∥AB ,∴四边形AMDN 是平行四边形, ∴∠AMD =∠AND ,又∵∠EMA =∠FNA =90°, ∴∠EMD =∠DNF , 在△EMD 和△DNF 中,⎩⎪⎨⎪⎧EM =DN∠EMD =∠DNF MD =NF ,∴△EMD ≌△DNF , ∴DE =DF , ∴结论③正确;如图2,连接MD ,EF ,NF ,∵三角形ABE 是等腰直角三角形,EM 平分∠AEB , ∴M 是AB 的中点,EM ⊥AB ,∴EM =MA ,∠EMA =90°,∠AEM =∠EAM =45°,∴EM EA =sin45°=22, ∵D 是BC 中点,M 是AB 中点, ∴DM 是△ABC 的中位线,∴DM ∥AC ,且DM =12AC ;∵三角形ACF 是等腰直角三角形,N 是AC 的中点, ∴FN =12 AC ,∠FNA =90°,∠FAN =∠AFN =45°,又∵DM =12 AC ,∴DM =FN =22FA , ∵∠EMD =∠EMA +∠AMD =90°+∠AMD , ∠EAF =360°-∠EAM -∠FAN -∠BAC =360°-45°-45°-(180°-∠AMD ) =90°+∠AMD ∴∠EMD =∠EAF ,在△EMD 和△∠EAF 中,⎩⎪⎨⎪⎧EM EA =DM FA =22∠EMD =∠EAF∴△EMD ∽△∠EAF , ∴∠MED =∠AEF ,∵∠MED +∠AED =45°, ∴∠AED +∠AEF =45°, 即∠DEF =45°, 又∵DE =DF , ∴∠DFE =45°,∴∠EDF =180°-45°-45°=90°, ∴DE ⊥DF , ∴结论④正确.∴正确的结论有4个:①②③④. 选D .同类题型1.2 如图,D ,E 分别是△ABC 的边BC ,AC 上的点,若∠B =∠C ,∠ADE =∠AED ,则( ) A .当∠B 为定值时,∠CDE 为定值 B .当∠1为定值时,∠CDE 为定值 C .当∠2为定值时,∠CDE 为定值 D .当∠3为定值时,∠CDE 为定值解:在△CDE 中,由三角形的外角性质得,∠AED =∠CDE +∠C ,在△ABD 中,由三角形的外角性质得,∠B +∠1=∠ADC =∠ADE +∠CDE , ∵∠B =∠C ,∠ADE =∠AED ,∴∠B +∠1=∠CDE +∠C +∠CDE =2∠CDE +∠B , ∴∠1=2∠CDE ,∴当∠1为定值时,∠CDE 为定值. 选B .同类题型1.3 如图,在△ABC 中,AB =AC =2 3 ,∠BAC =120°,点D 、E 都在边BC 上,∠DAE =60°.若BD =2CE ,则DE 的长为______________.解:将△ABD 绕点A 逆时针旋转120°得到△ACF ,取CF 的中点G ,连接EF 、EG ,如图所示.∵AB =AC =2 3 ,∠BAC =120°, ∴∠ACB =∠B =∠ACF =30°, ∴∠ECG =60°. ∵CF =BD =2CE , ∴CG =CE ,∴△CEG 为等边三角形, ∴EG =CG =FG ,∴∠EFG =∠FEG =12∠CGE =30°,∴△CEF 为直角三角形.∵∠BAC =120°,∠DAE =60°, ∴∠BAD +∠CAE =60°,∴∠FAE =∠FAC +∠CAE =∠BAD +∠CAE =60°.在△ADE 和△AFE 中,⎩⎪⎨⎪⎧AD =AF∠DAE =∠FAE =60°AE =AE,∴△ADE ≌△AFE (SAS ),∴DE =FE .设EC =x ,则BD =CD =2x ,DE =FE =6-3x , 在Rt △CEF 中,∠CEF =90°,CF =2x ,EC =x ,EF =CF 2-EC 2= 3 x ,∴6-3x = 3 x , x =3- 3 ,∴DE =3x =3 3 -3.例2.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,AB =BC ,E 为AB 边上一点,∠BCE =15°,且AE =A D .连接DE 交对角线AC 于H ,连接BH .下列结论: ①ACD ≌△ACE ;②△CDE 为等边三角形;③EH =2EB ;④S △AEH S △CEH = EHCD.其中正确的结论是________.解:①∵∠ABC =90°,AB =BC , ∴∠BAC =∠ACB =45°, 又∵∠BAD =90°, ∴∠BAC =∠DAC , 在△ACD 和△ACE 中,⎩⎪⎨⎪⎧AD =AE∠EAC =∠DAC AC =AC ,∴△ACD ≌△ACE (SAS );故①正确;②同理∠AED =45°,∠BEC =90°-∠BCE =90°-15°=75°, ∴∠DEC =60°, ∵△ACD ≌△ACE , ∴CD =CE ,∴△CDE 为等边三角形.故②正确.③∵△CHE 为直角三角形,且∠HEC =60° ∴EC =2EH∵∠ECB =15°, ∴EC ≠4EB ,∴EH ≠2EB ;故③错误. ④∵AE =AD ,CE =CD ,∴点A 与C 在DE 的垂直平分线上, ∴AC 是DE 的垂直平分线, 即AC ⊥DE , ∴CE >CH , ∵CD =CE , ∴CD >CH ,∵∠BAC =45°, ∴AH =EH ,∵S △AEH S △CEH =AH CH =EH CH, ∴S △AEH S △CEH >EHCD,故④错误. 答案为:①②.同类题型2.1 如图所示,已知:点A (0,0),B ( 3 ,0),C (0,1)在△ABC 内依次作等边三角形,使一边在x 轴上,另一个顶点在BC 边上,作出的等边三角形分别是第1个△AA 1B 1 ,第2个△B 1A 2B 2 ,第3个△B 2A 3B 3 ,…,则第n 个等边三角形的边长等于____________.解:∵OB = 3 ,OC =1, ∴BC =2,∴∠OBC =30°,∠OCB =60°.而△AA 1B 1 为等边三角形,∠A 1AB 1 =60°, ∴∠COA 1 =30°,则∠CA 1 O =90°. 在Rt △CAA 1 中,AA 1=32OC =32, 同理得:B 1A 2=12A 1B 1=322,依此类推,第n 个等边三角形的边长等于32n.同类题型2.2 如图,点P 在等边△ABC 的内部,且PC =6,PA =8,PB =10,将线段PC 绕点C 顺时针旋转60°得到P 'C ,连接AP ',则sin ∠PAP '的值为_________.解:连接PP ′,如图,∵线段PC 绕点C 顺时针旋转60°得到P 'C ,∴CP =CP ′=6,∠PCP ′=60°,∴△CPP ′为等边三角形,∴PP ′=PC =6,∵△ABC 为等边三角形,∴CB =CA ,∠ACB =60°,∴∠PCB =∠P ′CA ,在△PCB 和△P ′CA 中⎩⎪⎨⎪⎧PC =P ′C∠PCB =∠P ′CA CB =CA, ∴△PCB ≌△P ′CA ,∴PB =P ′A =10,∵62+82=102 ,∴PP ′2+AP 2=P ′A 2 ,∴△APP ′为直角三角形,∠APP ′=90°,∴sin ∠PAP ′=PP ′P ′A =610=35.同类题型2.4例3.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,过点O 作EF ∥BC 交AB 于E ,交AC 于F ,过点O 作OD ⊥AC 于D .下列四个结论:①∠BOC =90°+ 12∠A ; ②以E 为圆心、BE 为半径的圆与以F 为圆心、CF 为半径的圆外切;③EF 是△ABC 的中位线;④设OD =m ,AE +AF =n ,则S △AEF = 12mn . 其中正确的结论是( )A .①②③B .①③④C .②③④D .①②④解:∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =12 ∠ABC ,∠OCB =12 ∠ACB ,∠A +∠ABC +∠ACB =180°,∴∠OBC +∠OCB =90°-12 ∠A ,∴∠BOC =180°-(∠OBC +∠OCB )=90°+12 ∠A ;故①正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于N ,连接OA ,∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴ON =OD =OM =m ,∴S △AEF =S △AOE +S △AOF =12AE ﹒OM +12AF ﹒OD =12OD ﹒(AE +AF )=12 mn ;故④正确;∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠EBO =∠OBC ,∠FCO =∠OCB ,∵EF ∥BC ,∴∠EOB =∠OBC ,∠FOC =∠OCB ,∴∠EBO =∠EOB ,∠FOC =∠FCO ,∴EB =EO ,FO =FC ,∴EF =EO +FO =BE +CF ,∴以E 为圆心、BE 为半径的圆与以F 为圆心、CF 为半径的圆外切,故②正确,根据已知不能推出E 、F 分别是AB 、AC 的中点,故③正确,∴其中正确的结论是①②④选D .同类题型3.1 如图所示,四边形ABCD 中,DC ∥AB ,BC =1,AB =AC =AD =2.则BD 的长为()A .14B .15C .3 2D .2 3解:以A 为圆心,AB 长为半径作圆,延长BA 交⊙A 于F ,连接DF .∵DC ∥AB ,∴⌒DF =⌒BC ,∴DF =CB =1,BF =2+2=4,∵FB 是⊙A 的直径,∴∠FDB =90°,∴BD =BF 2-DF 2=15 . 选B .同类题型3.2 如图,在Rt △ABC 中,BC =2,∠BAC =30°,斜边AB 的两个端点分别在相互垂直的射线OM 、ON 上滑动,下列结论:①若C 、O 两点关于AB 对称,则OA =2 3 ;②C 、O 两点距离的最大值为4;③若AB 平分CO ,则AB ⊥CO ;④斜边AB 的中点D 运动路径的长为π2; 其中正确的是______________(把你认为正确结论的序号都填上).解:在Rt △ABC 中,∵BC =2,∠BAC =30°,∴AB =4,AC =42-22=2 3 ,①若C 、O 两点关于AB 对称,如图1,∴AB 是OC 的垂直平分线, 则OA =AC =2 3 ;所以①正确;②如图1,取AB 的中点为E ,连接OE 、CE ,∵∠AOB =∠ACB =90°,∴OE=CE=12AB =2, 当OC 经过点E 时,OC 最大,则C 、O 两点距离的最大值为4;所以②正确;③如图2,当∠ABO =30°时,∠OBC =∠AOB =∠ACB =90°,∴四边形AOBC 是矩形,∴AB 与OC 互相平分,但AB 与OC 的夹角为60°、120°,不垂直,所以③不正确;④如图3,斜边AB 的中点D 运动路径是:以O 为圆心,以2为半径的圆周的14,则:90π×2180 =π, 所以④不正确;综上所述,本题正确的有:①②.同类题型3.3 如图,直角△ABC 中,∠B =30°,点O 是△ABC 的重心,连接CO 并延长交AB 于点E ,过点E 作EF ⊥AB 交BC 于点F ,连接AF 交CE 于点M ,则MO MF的值为( ) A .12 B .54 C .23 D .33解:∵点O 是△ABC 的重心,∴OC =23CE , ∵△ABC 是直角三角形,∴CE =BE =AE ,∵∠B =30°,∴∠FAE =∠B =30°,∠BAC =60°,∴∠FAE =∠CAF =30°,△ACE 是等边三角形,∴CM =12CE , ∴OM =23CE -12CE =16 CE ,即OM =16AE , ∵BE =AE ,∴EF =33AE , ∵EF ⊥AB ,∴∠AFE =60°,∴∠FEM =30°,∴MF=36AE,∴MOMF=16AE36AE=33.选D.例4.如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则AGFD的值为________.解:已知AD为角平分线,则点D到AB、AC的距离相等,设为h.∵BDCD=S△ABDS△ACD=12AB﹒h12AC﹒h=ABAC=54,∴BD=54C D.如右图,延长AC,在AC的延长线上截取AM=AB,则有AC=4CM.连接DM.在△ABD与△AMD中,⎩⎪⎨⎪⎧AB=AM∠BAD=∠MADAD=AD∴△ABD≌△AMD(SAS),∴MD=BD=54C D.过点M作MN∥AD,交EG于点N,交DE于点K.∵MN∥AD,∴CK =14CD , ∴KD =54C D . ∴MD =KD ,即△DMK 为等腰三角形,∴∠DMK =∠DKM .由题意,易知△EDG 为等腰三角形,且∠1=∠2;∵MN ∥AD , ∴∠3=∠4=∠1=∠2,又∵∠DKM =∠3(对顶角)∴∠DMK =∠4,∴DM ∥GN ,∴四边形DMNG 为平行四边形,∴MN =DG =2F D .∵点H 为AC 中点,AC =4CM ,∴AH MH =23. ∵MN ∥AD , ∴AG MN =AH MH ,即AG 2FD =23, ∴AG FD =43 .同类题型4.1 如图,已知CO 1 是△ABC 的中线,过点O 1 作O 1E 1 ∥AC 交BC 于点E 1 ,连接AE 1 交CO 1 于点O 2 ;过点O 2 作O 2E 2 ∥AC 交BC 于点E 2 ,连接AE 2 交CO 1 于点O 3 ;过点O 3 作O 3E 3 ∥AC 交BC 于点E 3 ,…,如此继续,可以依次得到点O 4 ,O 5 ,…,O n 和点E 4 ,E 5 ,…,E n ,则O 2016E 2016 =_________A C .解:∵O 1E 1 ∥AC ,∴∠BO 1E 1 =∠BAC ,∠BE 1O 1 =∠BCA ,∴△BO 1E 1 ∽△BAC ,∴BO 1BA =O 1E 1AC.∵CO 1 是△ABC 的中线, ∴BO 1BA =O 1E 1AC =12 . ∵O 1E 1 ∥AC ,∴∠O 1E 1O 2=∠CAO 2 ,∠E 1O 1O 2=∠ACO 2 ,∴△E 1O 1O 2∽△ACO 2 ,∴E 1O 1AC =E 1O 2AO 2=12. ∵O 2E 2 ∥AC ,∴E 1O 2E 1A =O 2E 2AC =13, ∴O 2E 2=13A C . 同理:O n E n =1n +1A C . ∴O 2016E 2016=12016+1=12017.同类题型4.2 如图,过锐角△ABC 的顶点A 作DE ∥BC ,AB 恰好平分∠DAC ,AF 平分∠EAC 交BC 的延长线于点F .在AF 上取点M ,使得AM = 13 AF ,连接CM 并延长交直线DE 于点H .若AC =2,△AMH 的面积是112,则1tan ∠ACH的值是___________.解:过点H 作HG ⊥AC 于点G ,∵AF 平分∠CAE ,DE ∥BF ,∴∠HAF =∠AFC =∠CAF ,∴AC =CF =2,∵AM =13AF ,∴AM MF =12, ∵DE ∥CF ,∴△AHM ∽△FCM ,∴AM MF =AH CF, ∴AH =1,设△AHM 中,AH 边上的高为m ,△FCM 中CF 边上的高为n ,∴m n =AM MF =12, ∵△AMH 的面积为:112, ∴112=12AH ﹒m ∴m =16, ∴n =13, 设△AHC 的面积为S ,∴S S △AHM =m +n m=3, ∴S =3S △AHM =14, ∴12AC ﹒HG =14, ∴HG =14, ∴由勾股定理可知:AG =154 , ∴CG =AC -AG =2-154 ∴1tan ∠ACH =CG HG=8-15 .例5. 如图,△ABC 的面积为S .点P 1 ,P 2 ,P 3 ,…,P n -1 是边BC 的n 等分点(n ≥3,且n 为整数),点M ,N 分别在边AB ,AC 上,且AM AB = AN AC = 1n,连接MP 1 ,MP 2 ,MP 3 ,…,MP n -1 ,连接NB ,NP 1 ,NP 2 ,…,NP n -1 ,线段MP 1 与NB 相交于点D 1 ,线段MP 2 与NP 1 相交于点D 2 ,线段MP 3 与NP 2 相交于点D 3 ,…,线段MP n -1 与NP n -2 相交于点D n -1 ,则△ND 1P 1 ,△ND 2P 2 ,△ND 3P 3 ,…,△ND n -1P n -1 的面积和是 ____________.(用含有S 与n 的式子表示)解:连接MN ,设BN 交MP 1 于O 1 ,MP 2 交NP 1 于O 2 ,MP 3 交NP 2 于O 3 .∵AM AB =AN AC =1n, ∴MN ∥BC , ∴MN BC =AM AB =1n , ∵点P 1 ,P 2 ,P 3 ,…,P n -1 是边BC 的n 等分点,∴MN =BP 1=P 1P 2=P 2P 3 ,∴四边形MNP 1 B ,四边形MNP 2P 1 ,四边形MNP 3P 2 都是平行四边形,易知S △ABN =1n ﹒S ,S △BCN =n -1n ﹒S ,S △MNB =n -1n 2 ﹒S , ∴S △BP 1O 1=S △P 1P 2O 2=S △P 3P 2O 3=n -12n 2 ﹒S ,∴S 阴=S △NBC -(n -1)﹒S △BP 1O 1-S △NPn -1C =n -1n ﹒S -(n -1)﹒n -12n 2﹒S -n -1 n 2S =(n -1)22n 2 ﹒S .同类题型5.1如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B ′处,点A 对应点为A ′,且B ′C =3,则AM 的长是( )A .1.5B .2C .2.25D .2.5解:设AM =x ,连接BM ,MB ′,在Rt △ABM 中,AB 2+AM 2=BM 2 ,在Rt △MDB ′中,B ′M 2=MD 2+DB ′2 ,∵MB =MB ′,∴AB 2+AM 2=BM 2=B ′M 2=MD 2+DB ′2 ,即92+x 2=(9-x )2+(9-3)2 ,解得x =2,即AM =2,故选B .同类题型5.2 如图,△ABC 中,∠BAC =90°,AB =3,AC =4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,连CE ,则线段CE 的长等于( )A .2B .54C .53D .75解:如图连接BE 交AD 于O ,作AH ⊥BC 于H .在Rt △ABC 中,∵AC =4,AB =3,∴BC =32+42 =5,∵CD =DB ,∴AD =DC =DB =52 , ∵12﹒BC ﹒AH =12﹒AB ﹒AC , ∴AH =125, ∵AE =AB ,∴点A 在BE 的垂直平分线上.∵DE =DB =DC ,∴点D 在BE 使得垂直平分线上,△BCE 是直角三角形, ∴AD 垂直平分线段BE ,∵12﹒AD ﹒BO =12﹒BD ﹒AH , ∴OB =125, ∴BE =2OB =245, 在Rt △BCE 中,EC =BC 2-BE 2=52-(245)2=75, 选D .同类题型5.3 如图,在Rt △ABC 中,∠A =90°,AB =AC ,BC = 2 +1,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠∠B ,使点B 的对应点B ′始终落在边AC 上,若△MB ′C 为直角三角形,则BM 的长为____________.解:①如图1,当∠B ′MC =90°,B ′与A 重合,M 是BC 的中点,∴BM =12BC =122+12; ②如图2,当∠MB ′C =90°,∵∠A =90°,AB =AC ,∴∠C =45°,∴△CMB ′是等腰直角三角形, ∴CM = 2 MB ′,∵沿MN 所在的直线折叠∠B ,使点B 的对应点B ′,∴BM =B ′M ,∴CM = 2 BM ,∵BC = 2 +1,∴CM +BM =2BM +BM = 2 +1,∴BM =1,综上所述,若△MB ′C 为直角三角形,则BM 的长为122+12或1.同类题型5.4 如图,在矩形ABCD 中,∠B 的平分线BE 与AD 交于点E ,∠BED 的平分线EF 与DC 交于点F ,若AB =9,DF =2FC ,则BC =_________________.(结果保留根号)解:延长EF 和BC ,交于点G∵矩形ABCD 中,∠B 的角平分线BE 与AD 交于点E ,∴∠ABE =∠AEB =45°,∴AB =AE =9,∴直角三角形ABE 中,BE =92+92=9 2 ,又∵∠BED 的角平分线EF 与DC 交于点F ,∴∠BEG =∠DEF∵AD∥BC∴∠G=∠DEF∴∠BEG=∠G∴BG=BE=9 2由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC∴CGDE=CFDF=CF2CF=12设CG=x,DE=2x,则AD=9+2x=BC ∵BG=BC+CG∴92=9+2x+x解得x=3 2 -3∴BC=9+2(32-3)=6 2 +3.。
2020年九年级数学中考专题复习 全等三角形 (包含答案)
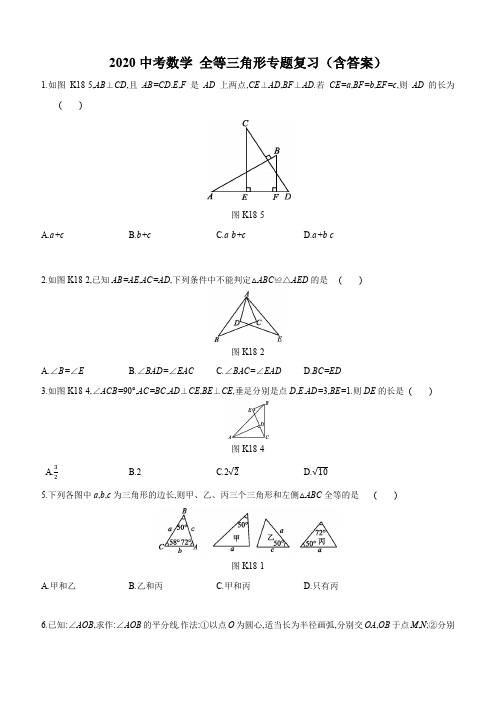
2020中考数学全等三角形专题复习(含答案)1.如图K18-5,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为()图K18-5A.a+cB.b+cC.a-b+cD.a+b-c2.如图K18-2,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是()图K18-2A.∠B=∠EB.∠BAD=∠EACC.∠BAC=∠EADD.BC=ED3.如图K18-4,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.AD=3,BE=1.则DE的长是()图K18-4A.3B.2C.2√2D.√1025.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()图K18-1A.甲和乙B.乙和丙C.甲和丙D.只有丙6.已知:∠AOB,求作:∠AOB的平分线.作法:①以点O为圆心,适当长为半径画弧,分别交OA,OB于点M,N;②分别MN的长为半径画弧,两弧在∠AOB内部交于点C;③画射线OC.射线OC即为所求.上述以点M,N为圆心,大于12作图用到了全等三角形的判定方法,这个方法是.图K18-78.已知,在如图K18-10所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.图K18-1011.如图K18-11,在△ABC中,D是BC边上一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.(1)求证:△ABE≌△DBE;(2)若∠A=100°,∠C=50°,求∠AEB的度数.图K18-1112.[2019·桂林]如图K18-12,AB=AD,BC=DC,点E在AC上.(1)求证:AC平分∠BAD;(2)求证:BE=DE.图K18-1213.[2019·菏泽]如图K18-13,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是.图K18-1314.如图K18-14,在△ABC中,AB=AC,∠BAC=90°,点D是射线BC上一动点,连接AD,以AD为直角边,在AD的上方作等腰直角三角形ADF.(1)如图①,当点D在线段BC上时(不与点B重合),求证:△ACF≌△ABD;(2)如图②,当点D在线段BC的延长线上时,猜想CF与BD的数量关系和位置关系,并说明理由.图K18-14【参考答案】1.D [解析]∵AB ⊥CD ,CE ⊥AD ,BF ⊥AD , ∴∠CED=∠AFB=90°,∠A=∠C , 又∵AB=CD ,∴△CED ≌△AFB , ∴AF=CE=a ,DE=BF=b ,DF=DE -EF=b -c , ∴AD=AF +DF=a +b -c ,故选D .2.A [解析]∵AB=AE ,AC=AD ,∴当∠BAD=∠EAC 或∠BAC=∠EAD 时,依据SAS 即可得到△ABC ≌△AED ; 当BC=ED 时,依据SSS 即可得到△ABC ≌△AED ; 当∠B=∠E 时,不能判定△ABC ≌△AED.3.B [解析]∵CF ∥AB , ∴∠A=∠FCE ,∠ADE=∠F . 在△ADE 和△CFE 中,{∠A =∠FCE ,∠ADE =∠F ,DE =FE ,∴△ADE ≌△CFE (AAS),∴AD=CF=3. ∵AB=4,∴DB=AB -AD=4-3=1,故选B . 4.B [解析]∵AD ⊥CE ,BE ⊥CE , ∴∠ADC=∠CEB=90°, ∴∠DAC +∠DCA=90°, ∵∠ACB=90°,∴∠ECB +∠DCA=90°,∴∠DAC=∠ECB , 又∵AC=CB ,∴△ACD ≌△CBE , ∴AD=CE=3,CD=BE=1, ∴DE=CE -CD=3-1=2,故选B .5.B [解析]依据SAS 全等判定可得乙三角形与△ABC 全等;依据AAS 全等判定可得丙三角形与△ABC 全等,不能判定甲三角形与△ABC 全等.故选B .6.B [解析]过点D 作DH ⊥AB 交BA 的延长线于H. ∵BD 平分∠ABC ,∠BCD=90°, ∴DH=CD=4,∴四边形ABCD 的面积=S △ABD +S △BCD =12AB ·DH +12BC ·CD=12×6×4+12×9×4=30.7.SSS[解析]由作图可得OM=ON,MC=NC,而OC=OC,∴根据“SSS”可判定△MOC≌△NOC.8.AB=DE或∠A=∠D或∠ACB=∠DFE或AC∥DF[解析]已知条件已经具有一边一角对应相等,需要添加的条件要么是夹已知角的边,构造SAS全等,要么添加另外的任一组角构造ASA或AAS,或者间接添加可以证明这些结论的条件即可.9.120°[解析]如图,设AC,DB的交点为H.∵△ACD,△BCE都是等边三角形,∴CD=CA,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,{CD=CA,∠DCB=∠ACE, CB=CE,∴△DCB≌△ACE,∴∠CAE=∠CDB,又∵∠DCH+∠CHD+∠BDC=180°,∠AOH+∠AHO+∠CAE=180°,∠DHC=∠OHA,∴∠AOH=∠DCH=60°,∴∠AOB=180°-∠AOH=120°.10.证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,∴∠BAC=∠DAE.在△ABC和△ADE中,{AB=AD,∠BAC=∠DAE, AC=AE,∴△ABC≌△ADE(SAS),∴∠E=∠C.11.解:(1)证明:∵BE平分∠ABC,∴∠ABE=∠DBE,在△ABE和△DBE中,{AB=DB,∠ABE=∠DBE, BE=BE,∴△ABE ≌△DBE (SAS). (2)∵∠A=100°,∠C=50°, ∴∠ABC=30°, ∵BE 平分∠ABC ,∴∠ABE=∠DBE=12∠ABC=15°,在△ABE 中,∠AEB=180°-∠A -∠ABE=180°-100°-15°=65°. 12.证明:(1)在△ABC 与△ADC 中,{AB =AD ,AC =AC ,BC =DC ,∴△ABC ≌△ADC (SSS),∴∠BAC=∠DAC ,即AC 平分∠BAD. (2)由(1)知∠BAE=∠DAE.在△BAE 与△DAE 中,{BA =DA ,∠BAE =∠DAE ,AE =AE ,∴△BAE ≌△DAE (SAS), ∴BE=DE.13.8√3 [解析]∵DC ⊥BC , ∴∠BCD=90°. ∵∠ACB=120°, ∴∠ACD=30°.延长CD 到H 使DH=CD , ∵D 为AB 的中点, ∴AD=BD.在△ADH 与△BDC 中,{DH =CD ,∠ADH =∠BDC ,AD =BD ,∴△ADH ≌△BDC (SAS), ∴AH=BC=4,∠H=∠BCD=90°. ∵∠ACH=30°,∴CH=√3AH=4√3,∴CD=2√3,∴△ABC 的面积=2S △BCD =2×12×4×2√3=8√3.14.解:(1)证明:∵∠BAC=90°,△ADF是等腰直角三角形,∴∠BAD+∠CAD=90°,∠CAF+∠CAD=90°,∴∠CAF=∠BAD.在△ACF和△ABD中,{AC=AB,∠CAF=∠BAD, AF=AD,∴△ACF≌△ABD(SAS).(2)CF=BD且CF⊥BD,理由如下:∵∠CAB=∠DAF=90°,∴∠CAB+∠CAD=∠DAF+∠CAD,即∠CAF=∠BAD.在△ACF和△ABD中,{AC=AB,∠CAF=∠BAD, AF=AD,∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠ABD.∵AB=AC,∠BAC=90°,∴∠ABD=∠ACB=45°,∴∠BCF=∠ACF+∠ACB=∠ABD+∠ACB=45°+45°=90°,∴CF⊥BD.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020中考数学专题复习几何:三角形综合(含答案)一、选择题(本大题共6道小题)1. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于()A.5B.6C.7D.82. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.AD=3,BE=1.则DE的长是 ()A.B.2 C.2D.3. 如图,等边三角形OAB的边长为2,则点B的坐标为 ()A.(1,1)B.(1,)C.(,1)D.()4. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC 交AB于M,交AC于N.若△AMN的周长为18,BC=6,则△ABC的周长为()A.21B.22C.24D.265. 如K19-6,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为 ()A.35°B.40°C.45°D.50°6. 公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形的面积是25,则(sinθ-cosθ)2= ()A.B.C.D.二、填空题(本大题共5道小题)7. 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD 绕点A逆时针旋转45°得到△ACD',且点D',D,B在同一直线上,则∠ABD的度数是.8. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是.9. 如图,△ABC中,∠ABC=90°,BA=BC=2,将△ABC绕点C逆时针旋转60°得到△DEC,连接BD,则BD2的值是.10. 如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC 的面积是.11. 《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是步.三、解答题(本大题共6道小题)12. 已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.13. 如图,AB=AD,BC=DC,点E在AC上.(1)求证:AC平分∠BAD;(2)求证:BE=DE.14. 如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,且BD=CE.求证:(1)点D在BE的垂直平分线上;(2)∠BEC=3∠ABE.15. 如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF 的位置,使得∠CAF=∠BAE.连接EF,EF与AC交于点G.(1)求证:EF=BC;(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.16. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B 不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.17. 如图,Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D.过点D 作☉O的切线交BC于点E,连接OE.(1)求证:△DBE是等腰三角形;(2)求证:△COE∽△CAB.2020中考数学几何:三角形综合-答案一、选择题(本大题共6道小题)1. 【答案】B[解析]∵DE∥BC,∴△ADE∽△ABC,∴=,即=,解得BC=6,故选B.考点:相似三角形及其应用2. 【答案】B[解析]∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°,∴∠DAC+∠DCA=90°,∵∠ACB=90°,∴∠ECB+∠DCA=90°,∴∠DAC=∠ECB,又∵AC=CB,∴△ACD≌△CBE,∴AD=CE=3,CD=BE=1,∴DE=CE-CD=3-1=2,故选B.考点:全等三角形3. 【答案】B[解析]过点B作BH⊥AO于点H,∵△OAB是等边三角形,∴OH=1,BH=,∴点B的坐标为(1,).考点:等腰三角形4. 【答案】C[解析]∵MN∥BC,∴∠MEB=∠EBC.∵BE平分∠ABC,∴∠MBE=∠EBC,∴∠MEB=∠MBE,∴△MBE是等腰三角形,∴ME=MB.同理,EN=CN,∵AM+AN+MN=18,MN=ME+EN=BM+CN,∴AM+AN+BM+CN=18,∴AB+AC=18,∴AB+AC+BC=24.即△ABC的周长为24.考点:等腰三角形5. 【答案】C[解析]因为BD平分∠ABC,AE⊥BD,BF=BF,所以△ABF≌△EBF,易得BD是线段AE的垂直平分线,∠BAF=∠BEF,所以AD=ED,所以∠DEA=∠DAE,所以∠BAD=∠BED=180°-35°-50°=95°,所以∠CDE=∠BED-∠C=95°-50°=45°,故选C.考点:等腰三角形6. 【答案】A[解析]∵大正方形的面积是125,小正方形面积是25,∴大正方形的边长为5,小正方形的边长为5,∴5cosθ-5sinθ=5,∴cosθ-sinθ=,∴(sinθ-cosθ)2=.故选A.考点:直角三角形与勾股定理二、填空题(本大题共5道小题)7. 【答案】22.5°[解析]根据题意可知△ABD≌△ACD',∴∠BAC=∠CAD'=45°,AD'=AD,∴∠ADD'=∠AD'D==67.5°.∵D',D,B三点在同一直线上,∴∠ABD=∠ADD'-∠BAC=22.5°.考点:等腰三角形8. 【答案】(2,2)[解析]如图,作AE⊥x轴于E,∵∠OCD=90°,∠AOB=60°,∴∠ABO=∠OAE=30°.∵点B的坐标是(6,0),∴AO=OB=3,∴OE=OA=,∴AE===,∴A.∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∴点C的坐标为,即(2,2).考点:相似三角形及其应用9. 【答案】8+4[解析]如图,连接AD,设AC与BD交于点O,由题意得CA=CD,∠ACD=60°,∴△ACD为等边三角形,∴AD=CD,∠DAC=∠DCA=∠ADC=60°.∵∠ABC=90°,AB=BC=2,∴AC=CD=2.∵AB=BC,CD=AD,∴BD垂直平分AC,∴BO=AC=,OD=CD·sin60°=,∴BD=,∴BD2=()2=8+4.考点:直角三角形与勾股定理10. 【答案】8[解析]∵DC⊥BC,∴∠BCD=90°.∵∠ACB=120°,∴∠ACD=30°.延长CD到H使DH=CD,∵D为AB的中点,∴AD=BD.在△ADH与△BDC中,∴△ADH≌△BDC(SAS),∴AH=BC=4,∠H=∠BCD=90°.∵∠ACH=30°,∴CH=AH=4,∴CD=2,∴△ABC的面积=2S△BCD=2××4×2=8.考点:全等三角形11. 【答案】[解析]如图①,∵四边形CDEF是正方形,∴CD=ED=CF.设ED=x,则CD=x,AD=12-x.∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,∴△ADE∽△ACB,∴=,∴=,∴x=.如图②,四边形DGFE是正方形,过C作CP⊥AB于P,交DG于Q,∵S△ABC=AC·BC=AB·CP,则12×5=13CP,∴CP=.设ED=y,同理得:△CDG∽△CAB,∴=,∴=,y=<,∴该直角三角形能容纳的正方形边长最大是步,故答案为:.考点:相似三角形及其应用三、解答题(本大题共6道小题)12. 【答案】证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,∴∠BAC=∠DAE.在△ABC和△ADE中,∴△ABC≌△ADE(SAS),∴∠E=∠C.考点:全等三角形13. 【答案】证明:(1)在△ABC与△ADC中,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,即AC平分∠BAD.(2)由(1)知∠BAE=∠DAE.在△BAE与△DAE中,∴△BAE≌△DAE(SAS),∴BE=DE.考点:全等三角形14. 【答案】证明:(1)如图,连接DE.∵CD是AB边上的高,∴CD⊥AB.∴∠ADC=90°.∵AE=CE,∴DE=AC=CE=AE.∵BD=CE,∴DE=BD.∴点D在线段BE的垂直平分线上.(2)∵BD=DE,∴∠ADE=2∠ABE.∵DE=AE,∴∠A=∠ADE=2∠ABE.∴∠BEC=∠ABE+∠A=3∠ABE.考点:等腰三角形15. 【答案】解:(1)证明:∵线段AC绕点A旋转到AF的位置,∴AC=AF.∵∠CAF=∠BAE,∴∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.在△ABC和△AEF中,AB=AE,∠BAC=∠EAF,AC=AF,∴△ABC≌△AEF(SAS),∴EF=BC.(2)∵AE=AB,∴∠AEB=∠ABC=65°.∵△ABC≌△AEF,∴∠AEF=∠ABC=65°,∴∠FEC=180°-∠AEB-∠AEF=180°-65°-65°=50°.∵∠FGC是△EGC的外角,∠ACB=28°,∴∠FGC=∠FEC+∠ACB=50°+28°=78°.考点:等腰三角形16. 【答案】解:(1)证明:∵线段CD绕点C按逆时针方向旋转90°得到线段CE,∴∠DCE=90°,CD=CE.又∵∠ACB=90°,∴∠ACB=∠DCE,∴∠ACD=∠BCE.在△ACD和△BCE中,∵∴△ACD≌△BCE.(2)∵∠ACB=90°,AC=BC,∴∠A=45°,∵△ACD≌△BCE,∴AD=BE,∠CBE=∠A=45°.又AD=BF,∴BE=BF,∴∠BEF=∠BFE==67.5°.考点:等腰三角形17. 【答案】证明:(1)连接OD.∵DE是☉O的切线,∴∠ODE=90°,∴∠ADO+∠BDE=90°.又∵∠ACB=90°,∴∠A+∠B=90°,∵OA=OD,∴∠A=∠ADO,∴∠BDE=∠B,∴EB=ED,∴△DBE是等腰三角形.(2)∵∠ACB=90°,AC是☉O的直径,∴CB是☉O的切线,又∵DE是☉O的切线,∴DE=EC.∵DE=EB,∴EC=EB.∵OA=OC,∴OE∥AB.∴△COE∽△CAB.考点:相似三角形及其应用与圆有关的位置关系。
