完整版对勾函数的性质.ppt

合集下载

对勾函数的性质及应用

对勾函数的性质及应用一、对勾函数by ax x=+)0,0(>>b a 的图像与性质：1. 定义域：),0()0,(+∞⋃-∞2. 值域：),2[]2,(+∞⋃--∞ab ab3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即0)()(=-+x f x f 4. 图像在一、三象限, 当0x >时，by ax x=+≥ab 2（当且仅当b x a =取等号），即)(x f 在x=ab 时，取最小值ab 2由奇函数性质知：当x<0时，)(x f 在x=ab -时，取最大值ab 2-5. 单调性：增区间为（∞+,a b ），（a b -∞-,）,减区间是（0，ab ），（a b -,0）二、对勾函数的变形形式类型一：函数by axx=+)0,0(<<b a 的图像与性质 1.定义域：),0()0,(+∞⋃-∞ 2.值域：),2[]2,(+∞⋃--∞ab ab3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，)(x f 在x=ab 时，取最小值ab 2；当0x >时，)(x f 在x=ab -时，取最大值ab 2-5.单调性：增区间为（0，a b ），（a b -,0）减区间是（∞+,ab ），（a b -∞-,）,类型二：斜勾函数by ax x =+)0(<ab①0,0<>b a 作图如下1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-∞，0），（0，+∞）.②0,0><b a 作图如下：1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-∞，0），（0，+∞）.类型三：函数)0()(2>++=ac xc bx ax x f 。

对勾函数的图像及其性质ppt课件

ab
值域
在- ，-
b a
和
b a
，
单调递减
在 -
b a
，0 和 0
，
b a
单调递增
y / y 2 ab 或 y 2 ab
12
4、当a 0 , b 0时，
定义域
(-∞,0) ∪(0 ,+∞)
奇偶性
b a
, 0
b a
, 0
奇函数
单调性在- ，0 , 0，单调递减
减函数
如果对于定义域内某个区间D上，任意两个自变量 x1、x2，当 x1<x2 都有 f(x1)>f(x2) ，就称函数f(x) 在区间D上是减函数.
(6).用定义法（作差法）证明函数在定义域区间D上是单调函数时,过程为:
任取自变量 x1、x2 D ,令 x1<x2；作差 f(x2)-f(x1)；分解因式；判断正负；下结论.
9
探究函数 f (x) ax bx的图像和性质.
1、当a 0 , b 0时，
定义域
(-∞,0) ∪(0 ,+∞)
b a
,2
ab
b a
,2
ab
奇偶性单调性
值域
奇函数
在 - ,
b a
和
b a
，
单调递增
在 -
b a
，0
和
0
，
b a
单调递减
y / y 2 ab 或 y 2 ab
x
4
7
3. 值域 , 4 3 (4 3 , )
4. 单调性
在
0
，
3 4
上
单调递减
f (x) 4x 3 x

新人教版高中数学必修第一册反比例函数对勾函数ppt课件及课时作业

则 f(x1)－f(x2)＝x1＋xa1－x2－xa2＝(x1－x2)·1－x1ax2.
因为 0<x1<x2≤ a，所以x1－x2<0,0<x1x2<a，所以x1ax2>1，所以 1－x1ax2<0，所以f(x1)－f(x2)>0，即f(x1)>f(x2). 所以 f(x)在(0， a]上单调递减.
任取 x1，x2∈( a，＋∞)，且 x1<x2，
则 f(x1)－f(x2)＝(x1－x2)1－x1ax2. 因为x1－x2<0，x1x2>a，所以x1ax2<1，所以 1－x1ax2>0，所以f(x1)－f(x2)<0，所以f(x1)<f(x2). 所以 f(x)在( a，＋∞)上单调递增. 同理，f(x)在(－∞，－ a)上单调递增，在(－ a，0)上单调递减. 其图象如图所示.
反思感悟
研究反比例函数的几个方面 (1)函数的定义域和值域可以由图象直接得到. (2)由图象或者单调性的定义可以判断函数的单调性，但一定要注意两个单调递增(减)区间的连接方法. (3)由图象或者奇偶性的定义可以判断函数的奇偶性. (4)函数图象关于(0,0)中心对称.
跟踪训练1 作出y＝2x (－2≤x<1且x≠0)的图象，并指出其值域和单调区间.
当 0<a≤4 时，0< a≤2，函数 f(x)在[2，＋∞)上单调递增， f(x)min＝f(2)＝a2；当 a>4 时， a>2，函数 f(x)在[2， a)上单调递减，在( a，＋∞)上单调递增，
f(x)min＝f( a)＝2 a－2. 设f(x)的最小值为g(a)， ∴g(a)＝2a，0<a≤4，
∵f(x)在[1,3]上单调递增，∴f(x)的最小值为f(1)＝2.

对勾函数的性质及应用(史上上最完整版)

对勾函数的性质及应用一、概念：【题型1】函数()(0,0)af x x a k =+>≠【例1】函数1()f x x =+的值域为【例2】函数3()x f x x +=+的值域为【题型2】函数()(0)ax bx cf x ac ++=>。

【例3】函数1()x x f x ++=的值域为【题型3】函数2()(0,0)axf x a b =≠>。

【例4】函数2()1xf x x =+的在区间[)2,+∞上的值域为【解析】2x ≥，∴，函数15222≥+=【例5】如2214xa x +=-+，(1,2)x ∈，则实数a 的取值范围是(1,2)x ∈4y x x =+1144x x <+，7352a <-<【题型4】函数2()(0)ax bx cf x a ++=≠.【例6】已知1x >-，求函数710()1x x f x x ++=+的最小值。

，1x >-，7101x ++的最小值【例7】已知1x <，求函数299()x x f x +-=的最大值。

，1x <，2991x x +--的最大【题型5】函数2()(0)x mf x a +=≠ 【例8】求函数21()2x f x x x -=++在区间(1,)+∞上的最大值。

【例9】求函数2223()x x f x ++=在区间[0,)+∞上的最大值。

【例10】求函数()f x =的最小值。

类型九：函数2()0)f x a>。

【例12】求函数2()f x=的最小值。

【解析】由题可知，函数22()f x===2t=，则1()()f xg t tt==+，显然在[)2,+∞上单调递增，故min15()(2)222g t g==+=，此时0x=，故函数2()f x=的最小值为52。

【例13】求函数()f x=的值域.。

对勾函数的图象和性质

＋。）。．
的况似证所函．ｎ睾两渐情类可．以数，有条近）＋一
线：直线ｘ＝Ｏ和直线 —ｎ．
６ａｂ的值对图象的影响．．、在第一象限内，ｂ当不
３奇偶性．．对勾函数定义域关于原点对称，且并
心对称
）原距离点越
远．第ｉ象限也存在类似情况．
从图象卜看．勾甬舯县斤例对的一个征
４单调性．．设ｌ ∈ （．、２０＋一）且ｌ＜２则，
，，ｚａ＋一。ｂｎ（一（一鲁ｎ一 —（ｚ））ｉ
以要加以注意和学习．
ｆｌ＜ｘ
以时数（上，当．在，］函０ √
单递 ’√ ，× 单递．函调减［＋）调增由数在Ｃ。上
，
函数厂（一“ 了）＋ｂ
（＞Ｏ６）大致图象如ｎ，＞Ｏ的
／
－
称性知，当＜Ｏ日，寸函数在（ ×，一Ｃ。
直ｎ的离则ＰＰ一， —时函线＝ｚ距，Ｍ＜Ｑ睾当ｏ，
数值一＋。；一＋ｏ时，ＰＯ即在第一象限，。当ｏＭ — ，
）一２ ≤
（当且仅
－卿一一
一
时
函数图象无限接近于Ｙ轴与直线Ｙ—ａ．在第三象限等号成立）所以值域为（．一一，／Ｕ［／，一２ｖ］２ｖ
的图象和性质．ｔ甬数一（与，ｊ的图象关于『于１厂） ’ ’ （）轴对称，们很容易得到函数，）ｚ我（一ｃ一（＜ “ ０ｂＯ的图象（图２和性质．于 “ ｂ异号的情．＜）如）至、

对勾函数的图像及其性质课件

不等式证明
在证明某些不等式时，可以利用对勾函数的单调性、奇偶性等性质进行推导。例如，在证明与根号相关的不等式时，通过构造函数并利用对勾函数的性质，可以更加简洁地证明不等式。
数列求和与极限计算
数列求和
对勾函数在数列求和中也有广泛应用。例如，在某些含有根号的数列求和问题中，可以通过对勾函数的变换将问题转化为等比数列或等差数列求和，从而简化计算过程。
极限计算
在求解某些极限问题时ቤተ መጻሕፍቲ ባይዱ可以利用对勾函数的连续性、可导性等性质进行推导。通过构造函数并利用洛必达法则等工具，可以更加便捷地求解极限问题。
积分变换与微分方程求解
积分变换
对勾函数在积分变换中也有重要作用。例如，在某些含有根号的积分问题中，可以通过对勾函数的变换将问题转化为更易于求解的形式。此外，对勾函数还可以用于构建某些特殊的积分公式，为积分计算提供便利。
对勾函数拟合
利用对勾函数对需求数据进行拟合，得到需求曲线方程。
预测未来需求
基于拟合得到的需求曲线方程，预测未来不同价格水平下的需求量。
供给曲线建模与预测
供给分析
收集历史数据，分析生产者在不同价格水平下愿意提供的商品或服务的数量。
对勾函数拟合
利用对勾函数对供给数据进行拟合，得到供给曲线方程。
单调性与增减性
单调性
对勾函数在其定义域内不是单调函数。它在某些区间内是增函数，而在另一些区间内是减函数。
增减性
具体来说，当x从负无穷大增加到0时，对勾函数从0增加到正无穷大；当x从0增加到正无穷大时，对勾函数从正无穷大减少到0。因此，对勾函数在x=0处达到极大值。
凸凹性与拐点
凸凹性
对勾函数在其定义域内既不是凸函数也不是凹函数。它在某些区间内是凸函数，而在另一些区间内是凹函数。

对勾函数(目前最全面的版本了吧)

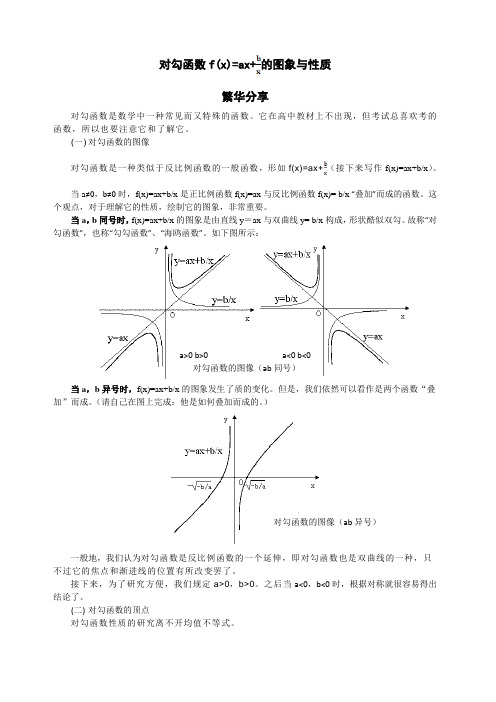
对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x）。

当a≠0，b≠0时，f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a，b同号时，f(x)=ax+b/x的图象是由直线y＝ax与双曲线y= b/x构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：a>0 b>0 a<0 b<0对勾函数的图像（ab同号）当a，b异号时，f(x)=ax+b/x的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）对勾函数的图像（ab异号）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，。

当x<0时，。

即对勾函数的定点坐标：(三)对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到：(六)对勾函数的奇偶性对勾函数在定义域内是奇函数，yXOy=ax。

(完整版)对勾函数详细分析

对勾函数的性质及应用、对勾函数 y ax b (a 0,b 0) 的图像与性 x质：1. 定义域： ( ,0) (0, )2. 值域： ( , 2 ab] [2 ab, )原点呈中心对称，即 f(x) f( x) 0即 f (x) 在 x= b时，取最小值 2 ab a、对勾函数的变形形式2. 值域： ( , 2 ab] [2 ab, )3.奇偶性：奇函数，函数图像整体呈两个对勾”的形状，且函数图像关于4.图像在一、三象限 , 当 x 0 时， y axb2 ab (当且仅当 x b取等号)，由奇函数性质知：当x <0 时， f (x) 在 x= b时，取最大值 2 ab a 5.单调性：增区间为(,b) ,a, 减区间是( 0 ，类型一：函数 y ax b (a 0,b x 质1. 定义域： ( ,0) (0, )0)的图像与性3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状4. 图像在二、四象限, 当x<0时，f （x）在x= b时，取最小值 2ab；当x 0时，af（x）在x= b时，取最大值 2 aba5. 单调性：增区间为（0，b），（b,0 ）减区间是（b, a a a,b a)类型二：斜勾函数y ax b（ab 0）x① a 0,b 0 作图如下1. 定义域：（ ,0）（0, ）2. 值域：R3. 奇偶性：奇函数4. 图像在二、四象限，无最大值也无最小值.5. 单调性：增区间为（- ，0），（0，+ ）② a 0,b 0 作图如下：1. 定义域：( ,0) (0, )2. 值域：R3. 奇偶性：奇函数4. 图像在二、四象限，无最大值也无最小值5. 单调性：减区间为（- ，0），（0，+ ）2此类函数可变形为 f(x) ax cb ，可由对勾函数 y axc 上下平移得到 x x2练习 1.函数 f(x) x x 1 的对称中心为x类型四：函数 f (x) x a (a 0,k 0)xk此类函数可变形为 f (x) (x k a ) k ，则 f ( x)可由对勾函数 y x a 左右平移， x k x 上下平移得到练习 1. 作函数 f(x) x 1 与 f(x) x 3 x 的草图x 2 x 22. 求函数 f (x) x 1 在 (2, )上的最低点坐标2x 4 3. 求函数 f(x) x x 的单调区间及对称中心x1a. 若 a 0 ，图像如下：1．定义域：( , ) 2. 值域：[ a 2 b ,a 2 b ]3. 奇偶性：奇函数 .4. 图像在一、三象限 . 当 x 0时， f (x) 在x b 时，取最大值 a ，当 x<0 时， f(x)在 x= b 时，取最小值 a2 b 2 b5. 单调性：减区间为( b, )，( , b )；增区间是 [ b, b]类型三函数 f(x)ax 2 bx c(ac 0)x类型五：函数 af(x) 2 xbx( )axf (x)2xa b xxb (a 0,b 0) 。

[课件]探究对勾函数的图象与性质说课课件-人教A版(2019)必修第一册

初步形成了从“图象视角” 和“运算视角” 来探究函数的习惯.
学生对两个基本初等函数相加所得的新函数接触不多，探究意识不够强，自主探究能力不够高.
教学背景分析
重点
探究函数 f (x) = x+ 1 的图象和性质， x
在此基础上，进一步学会研究函数的方法.
目标与目标解析
归纳“研究函数图象”的方法，渗透数形结合的思想.
迁移创新
教学过程设计
学生自主发现以下结论：
明确对象
确定目标探索路径探究过程迁移创新
在区间 (0,1) 上，
11
1
x0 0,
f
(x0 )
x0
x0
x0
x0
f
x0
根据这个结论, 就可以更合理的取点.
事实上，这也是函数的一个性质.
明确对象确定目标探索路径探究过程迁移创新
几何画板演示描点法
能用描点法画函数的草图.
能借助原来函数的图象画出新函数的图象.
能从函数解析式出发研究函数的性质.
能证明函数的单调性、奇偶性等.
02
探究函数的性质，通过证明结论，发展数学推理能力..
通过合作探究能直观感知函数的图象变化趋势，并能用代数方法进行证明.
能自主发现问题和提出问题.
体会探究活动的价值，合作交流的意义，发展直观想象、数学运算、逻辑推理等核心素养.
确定目标
探索路径
探究过程迁移创新
发展学生逻辑推理、数学运算核心素养
教学过程设计
明确对象确定目标
观察和实验是数学探究式教学的有效手段.
看图、作图是典型的观察和实验.
探索路径探究过程迁移创新
Euler （1707年——1783年）

探究对勾函数的单调性PPT课件

探究函数 f x x a a 0 的 x 单调性 2019年10月27日
1
一、创设情境
问题：学校准备建造一个长方形的花坛,面积设计为 16平方米,由于周围环境的限制,每边的长度均不能超过8米,也不能少于2米,求花坛长与宽两边之和的最小值.
2
二、探索研究
问题：学校准备建造一个长方形的花坛,面积设计为 16平方米,由于周围环境的限制,每边的长度均不能超过8米,也不能少于2米,求花坛长与宽两边之和的最小值.
你能证明f x x a a 0的单调性，
x
并画出f x的简图吗？
11
三、感悟与分享
1.本节课你学到了什么？对勾函数的图象及单调性
2.你能说说探究函数性质的一般思维过程吗？
计算、作出函数图像猜测、探究结论或规律
观察图像特征解释、证明
12
四、作业
补充题(略)
13
再见！
4xx221??????设??????????????????????????????????????????221121x16xx16xxfxf则????????212121xx16xxxx??????4xx221???????016xx16xx40xx212121???????????????????????????2121xfxf0xfxf???????即????????
6
二、探索研究
探究1：函数f x x 16 x 0的单调性如何？
x
证明：设0 x1 x2 4,
则f
x1 f x2 x1 16 x1 x2 x1x2 16
x1 ,

x2

16
x2

对勾函数

对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x ）。

当a≠0，b≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

a>0 b>0 a<0 b<0 对勾函数的图像（ab 同号）对勾函数的图像（ab 异号）(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，。

当x<0时，。

即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到：(六) 对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、类耐克函数性质探讨函数xbax y +=，在时或00==b a 为简单的单调函数，不予讨论。

数学对勾函数知识讲解

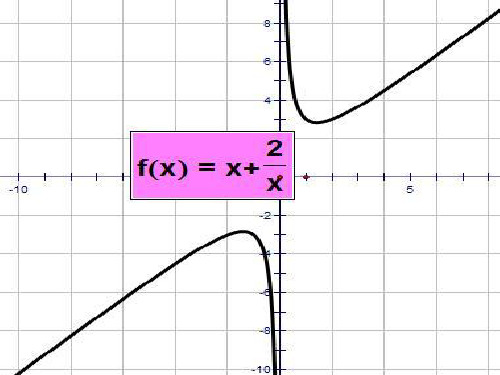
图象二
ቤተ መጻሕፍቲ ባይዱ
图像三
图像四
件下载可自行编辑修改，仅供参考！感谢您的支持，我们努力做得更好！
性质简介
1.对号函数是双曲线旋转得到的，所以也有渐近线、焦点、顶点等等
2.对号函数永远是奇函数，关于原点呈中心对称 3.对号函数的两条渐进线永远是y轴和y=ax 4.当a、b>0时，图像分布在第一、三象限两条渐近线的锐角之间部分，由于其对称性，只讨论第一象限中的情形。利用平均值不等式（a>0，b>0且ab 的值为定值时，a+b≥2√ab）可知最小值是2倍根号 ab，在x=根号下b/a的时候取得，所以在（0，负根号下b/a）上单调递减，在（根号下b/a，正无穷）上单调递增
性质一
➢ 函数y=ax+b/x的性质 ➢ Ⅰ当a、b均大于零时，性质： ➢ ⑴定义域：x≠0 ➢ ⑵值域：（-∞，-2 根号ab）∪（2根号ab ，
+∞） ⑶奇偶性：奇函数 ➢ ⑷单调性：当x﹥0时，当0﹤x﹤根号b/a 时，
y为减函数当x﹥根号b/a 时，y为增函数当x﹤0时，当- 根号b/a﹤x﹤0时，y 为减函数当x﹤根号b/a- 时，y为增函数
简介
对勾函数：图像，性质，单调性对勾函数是数学中一种常见而又特殊的函数，见图示。
对勾函数是一种类似于反比例函数的一般函数，又被称为“双勾函数”、"勾函数"等。也被形象称为“耐克函数”
所谓的对勾函数（双曲线函数），是形如 f(x)=ax+b/x的函数。由图像得名。
当x>0时，f(x)=ax+b/x有最小值（这里为了研究方便，规定a>0，b>0），也就是当x=sqrt(b/a) 的时候（sqrt表示求二次方根）

完整版对勾函数的性质.ppt

对勾函数的性质及应用

对勾函数的图像及其性质ppt课件

新人教版高中数学必修第一册反比例函数对勾函数ppt课件及课时作业

对勾函数的性质及应用(史上上最完整版)

对勾函数的图象和性质

对勾函数的图像及其性质课件

对勾函数(目前最全面的版本了吧)

(完整版)对勾函数详细分析

[课件]探究对勾函数的图象与性质 说课课件-人教A版(2019)必修第一册

探究对勾函数的单调性PPT课件

对勾函数

数学 对勾函数知识讲解

[课件]探究对勾函数的图象与性质说课课件-人教A版(2019)必修第一册

数学对勾函数知识讲解