基于Simulink模型的数据定标问题研究
基于Simulink可视化混沌模型的研究

基于Simulink可视化混沌模型的研究
混沌模型是目前非线性科学研究的重点之一,其表现出的随机性、确定性和极度敏感性使其在信息加密、通信技术、生态学、金融、天气预报等领域得到了广泛应用。
本文基于Simulink平台,探讨了几种常用的混沌模型,并进行了可视化仿真研究。
首先,本文介绍了三个经典的混沌模型:Logistic映射、Henon映射和Lorenz系统,分别介绍了其数学表达式和特征。
Logistic映射是一维非线性映射,其具有周期倍增的特征,可以用来生成随机数序列;Henon映射是二维非线性映射,其表现出的奇特轨迹使其被广泛应用于图像加密、压缩等领域;Lorenz系统是三维非线性动力学系统,其奇妙的漩涡结构与天气系统之间的联系被广泛研究。
接着,本文用Simulink实现了以上三个混沌模型,并进行了仿真分析。
通过对Logistic映射的仿真结果分析,可以看出当初始值接近3.57时,其混沌性质最为明显,即使微小的改变也能导致结果的不可预测性。
通过对Henon映射的仿真结果分析,可以看出其二维奇特的轨迹,进一步证实了其在图像加密、压缩等领域的应用价值。
通过对Lorenz系统的仿真结果分析,可以看出其漩涡结构的特征,说明其在天气预报、气候学等领域的重要性。
最后,通过对以上仿真结果的分析,证明了Simulink平台在混沌模型的研究中的优越性,其可视化的特点使得模型的仿真分析更加生动、直观。
在未来的研究中,可以通过优化模型参数,进一步探讨混沌模型的特性,应用于更多的领域。
实验六 基于Simulink的位置式和增量式PID仿真
实验六基于Simulink的位置式和增量式PID仿真一、实验目的:1、用Matlab的仿真工具Simulink分别做出数字PID控制器的两种算法(位置式和增量式)进行仿真;2、被控对象为一阶惯性环节 D(s) = 1 / (5s+1);3、采样周期 T = 1 s;4、仿真结果:确定PID相关参数,使得系统的输出能够很快的跟随给定值的变化,给出例证,输入输出波形,程序清单及必要的分析。
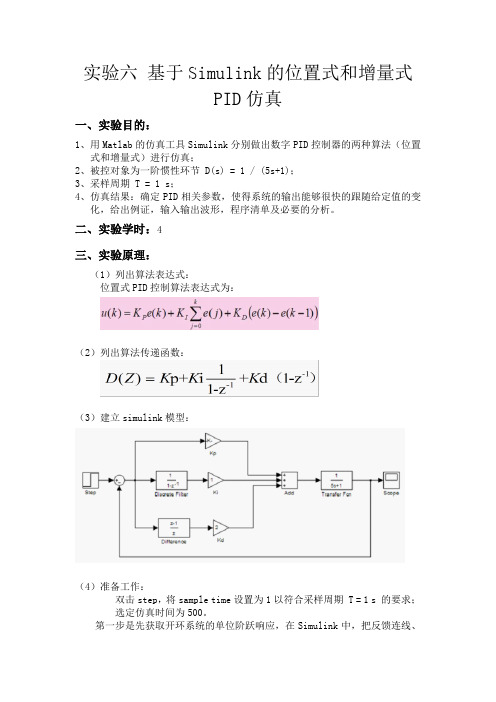
二、实验学时:4三、实验原理:(1)列出算法表达式:位置式PID控制算法表达式为:(2)列出算法传递函数:(3)建立simulink模型:(4)准备工作:双击step,将sample time设置为1以符合采样周期 T = 1 s 的要求;选定仿真时间为500。
第一步是先获取开环系统的单位阶跃响应,在Simulink中,把反馈连线、微分器、积分器的输出连线都断开,并将’Kp’的值置为1,调试之后获取响应值。
再连上反馈线,再分别接上微分器、积分器,仿真,调试仿真值。
2、增量式PID:(1)列出算法表达式:增量式PID控制算法表达式为:(2)列出算法传递函数:(3)建立simulink模型:(4)准备工作:双击step,将sample time设置为1以符合采样周期 T = 1 s 的要求;选定仿真时间为500。
第一步是先获取开环系统的单位阶跃响应,在Simulink中,把反馈连线、微分器、积分器的输出连线都断开,并将’Kp’的值置为1,调试之后获取响应值。
再连上反馈线,再分别接上微分器、积分器,仿真,调试仿真值。
四、实验内容:1、位置式:(1)P控制整定仿真运行完毕,双击“scope”得到下图将Kp的值置为0.5,并连上反馈连线。
仿真运行完毕,双击“scope”得到下图效果不理想,再将Kp的值置为0.2,并连上反馈连线。
P控制时系统的单位阶跃响应图如下:(2)PI控制整定(比例放大系数仍为Kp=0.2)经多次输入Ki的值,发现Ki=1时,系统的输出最理想,选定仿真时间,仿真运行,运行元毕后. 双击" Scope " 得到以下结果(3)PID控制整定经多次输入调试,Kd的值置为0.5时,系统能最快地趋向稳定。
基于Simulink—TargetLink的AMT电控系统软件开发

基于Simulink—TargetLink的AMT电控系统软件开发【摘要】利用Simulink-TargetLink开发AMT电控系统软件,具有模块功能定义明确、算法实现与验证方便快捷、模型数据统一管理、自动定标、代码自动生成等优点,极大地提高系统软件开发效率和开发质量。
【关键词】TargetLink;AMT;软件开发前言现代汽车电控系统功能越来越复杂,要求电控单元开发周期越来越短,采用传统的开发方式已难以满足车辆电控系统软件开发的要求。
因此应采用规范的软件开发平台,以提高软件开发效率和质量。
Simulink基于模型的设计以及Targetlink代码生成工具,目前在汽车电控单元开发中广泛使用。
本文主要介绍应用Simulink和TargetLink进行的AMT电控系统(以下简称TCU)软件开发的方法和流程。
1.AMT电控系统底层驱动软件AMT电控系统硬件采用Freescale公司的MC9S12DP256微处理器,电控系统底层驱动软件主要是对MCU寄存器操作,得到最底层输入信号并控制最末级输出信号,在电控系统开发周期内它们变化不大,且用Simulink不容易实现,故采用传统方法用手工编写,它们包括:I/O,A/D,转速,定时器,中断,CAN 通信等。
2.信号处理与控制策略信号输入、控制策略以及控制量输出在Simulink环境下进行编写。
2.1 模拟输入信号处理为了保证电控系统稳定可靠运行,必须对信号(数字I/O,模拟输入等)进行处理,如开关输入信号消抖以减小外界干扰、模拟输入信号高低限检查以判断是否故障,在出现故障时用什么值来替代输入信号等,它也是系统故障诊断的依据。
对于任何数字输入信号,由I/O信号处理状态机得到处理后的I/O值。
采用stateflow可以方便地实现模拟输入和数字输入的信号处理算法建模。
2.2 基于Simulink的控制策略车辆行驶时,TCU根据当前车辆运行状态确定变速箱的目标档位,并控制执行机构完成下面动作:离合器分离→摘空挡→选档→换档→离合器结合,实现自动换档,同时控制发动机的扭矩和转速以提高AMT的换档品质。
基于simulink信号与系统的建模与仿真

安康学院学年论文﹙设计﹚题目基于simulink信号与系统的建模与仿真学生姓名学号所在院(系)专业班级指导教师年月日基于simulink的信号与系统建模和仿真()指导教师:【摘要】本文着重论述了如何利用MATLAB Simulink工具在计算机上实现信号与系统分析,通过程序使一些运算量较大、抽象问题简单而直观,详细介绍了利用系统框图模拟实际系统的分析方法,该方法对连续或离散时不变因果系统具有普遍性,借助Matlab/Simulink 仿真工具对基本结构实现了建模和仿真分析。
【关键词】信号与系统、建模、仿真、SimulinkBased on simulink modeling and simulation of signaland systemAuthor: ZhangXiu(Grade2011,Class1,Major Electronic information engineering,Ankang University,Ankang 725000,Shaanxi)Directed by YushunyuanAbstract:This article discusses the methods of realizing signal and system analysis by MATLAB and making complicated arithmetic and abstract problems easy and direct by programs.It introduces an analysis method of simulating actual system by system diagram,which is universal to continuous and discrete time invariable causal system.It realizes modeling and simulation analysis on the basic structures based on Matlab /Simulink simulation tools.Keywords: signal and system; modeling; simulation; Matlab /Simulink0引言信号与分析系统是自动化、通信、电信、测控、电子类专业基础课,信号与系统分析就在给定系统的情况下,研究系统在输入不同信号时所产生的响应,由获得的参数,达到对系统的功能和特性的认知。
matlab simulink计算机领域故障数据生成

在MATLAB Simulink中,可以使用"Fault Detection and Diagnosis Toolbox"来生成故障数据。
以下是一个简单的步骤:1. 打开Simulink并创建一个新的模型。
2. 在模型中添加所需的组件,例如传感器、执行器和控制器等。
3. 从"Fault Detection and Diagnosis Toolbox"中将"Fault Detection"和"Fault Diagnosis"模块添加到模型中。
4. 使用"Fault Detection"模块来定义故障类型和故障位置。
可以选择的故障类型包括常数偏移、增益变化、非线性等。
5. 使用"Fault Diagnosis"模块来设置故障诊断参数,例如阈值、置信度等。
6. 运行模型并生成故障数据。
可以通过观察输出信号或保存结果来进行进一步的分析。
以下是一个示例代码,演示如何在MATLAB Simulink中使用"Fault Detection and Diagnosis Toolbox"生成故障数据:```matlab创建一个新的Simulink模型model = 'Model';open_system(model);添加所需的组件到模型中add_block('From Workspace', 'DataIn');add_block('Gain', 'Gain1');add_block('From Workspace', 'DataOut');添加"Fault Detection"模块add_block('Fault Detection', 'FD1');set_param('FD1', 'Type', 'gain'); % 设置故障类型为增益变化set_param('FD1', 'Location', '1/SamplingTime'); % 设置故障位置为采样时间添加"Fault Diagnosis"模块add_block('Fault Diagnosis', 'FD2');set_param('FD2', 'Threshold', 0.5); % 设置阈值为0.5set_param('FD2', 'ConfidenceLevel', 0.95); % 设置置信度为0.95连接组件和模块connect_block('DataIn', 'Gain1/Input');connect_block('Gain1/Output', 'FD1/Input');connect_block('FD1/Output', 'FD2/Input');connect_block('FD2/Output', 'DataOut');运行模型并生成故障数据simulate(model);。
基于Simulink仿真的标准映射的研究

基金项目:国防工业技术基础科研项目(FEBG27100001)收稿日期:2006-03-01 修回日期:2006-04-08第24卷 第5期计 算 机 仿 真2007年5月文章编号:1006-9348(2007)05-0291-04基于Si m uli nk 仿真的标准映射的研究张辉,李志成,翟国富(哈尔滨工业大学军用电器研究所,黑龙江哈尔滨150001)摘要:人们对于弹跳球模型的研究由来已久,标准映射是弹跳球模型在高弹跳情形下的二维映射,也是研究混沌现象最重要的物理模型之一。
以往对于标准映射的研究主要集中在理论分析,而对于标准映射中的混沌产生过程研究较少。
首先推导了标准映射的数学模型。
之后基于S i m u li nk 建立了标准映射的模型,并以此模型为基础,仿真分析了倍周期分叉到混沌的实现途径,给出了周期分叉过程中的不同周期运动的参数区间及混沌出现条件,并计算得到了分叉图,从而计算出Fei gen bau m 常数,与公认值比较误差很小。
最后在混沌带中发现了周期运动,进而揭示了混沌的复杂性。
关键词:标准映射;弹跳球;混沌;分叉图中图分类号:TP319 文献标识码:BR esearch on StandardM ap B ased on Si m uli nkZ HANG H u,i L I Zh i-cheng ,Z HA IGuo-fu(Instit ute o fM ilitary A pparatusH a rbin Institute o f T echno l ogy ,H arbi n H elong jiang 150001,China)ABSTRACT :Bounc i ng ba ll proble m has been resea rched f o r a long ti m e ,the standa rd map is the t w o di m ensi onal m app i ng of bounc i ng ba ll mode lwhen the balls 'he i ght i s greater than a m plit ude of table ,and i s t he mo st i m portant m odel f o r researching chaos .T he prev i ous researches concentrated on analysis of the standard map in t heory .The process of chaos i n the standard m ap w as researched rare ly .T he m athe m atica l model o f the standard map is derived firstly ,and t hen a model o f the standard map based on Si m uli nk is estab lished .The process fro m periodic b if urcation to chaos ,is observed and the bifurca te m ap is go t for ca lcu l ating t he F e i genbaum constant .L astly t he period m otion i n chaos stri ps i s found wh ich opens out the com plex ity o f the chaos .KEY W ORDS :S tandard m ap ;Bounc i ng ba l;l Chaos ;B ifurcation m ap1 引言人们对于弹跳球模型的研究由来已久,标准映射是弹跳球模型在高弹跳情形下的二维映射。
基于Matlab-Simulink的仿真模型库技术研究的开题报告

基于Matlab-Simulink的仿真模型库技术研究的开题报告一、选题背景和意义近年来,控制系统在现代制造业中占有很高的地位。
仿真模型库是一个非常重要的工具,用于设计和评估控制系统的性能。
基于仿真的设计与分析有助于减少试错成本,提供更好的控制策略,并帮助工程师更好地了解控制系统的动态特性。
此外,基于仿真技术可以加速系统开发周期、提高系统可靠性,并有助于工程师进行各种控制策略的比较和分析。
二、选题内容和目标该研究的主要目标是开发一个基于Matlab-Simulink的仿真模型库。
这个仿真模型库将包括各种控制系统的模型,如电子电路、机械系统、液压系统、热力学系统等。
这个库将帮助工程师更好地了解控制系统的特性,并提供一个平台,用于测试和比较不同的控制策略。
此外,该库还将提供一些工具,帮助工程师更快地创建他们自己的仿真模型,并与其它模型进行集成和共享。
三、研究方法和技术路线该研究主要包括以下步骤:1. 收集不同控制系统的仿真模型,并进行分类和整合。
2. 制定标准的仿真模型库架构和接口,以确保其适用于各种控制系统。
3. 开发一个Matlab-Simulink的仿真模型库,支持各种控制系统的建模和仿真。
4. 针对不同应用场景,进行实验测试,并检验仿真结果的准确性。
5. 针对用户的需求,开发用户界面和工具,方便用户进行建模、仿真与分析。
四、预期结果和成果根据以上研究方法和技术路线,预期结果和成果包括:1. 发展出一个基于Matlab-Simulink的仿真模型库,包括各种控制系统的模型。
2. 提供一个标准的仿真模型库架构和接口,方便用户定制和集成各种控制系统的模型。
3. 支持用户进行自定义建模和仿真,并提供用户界面和工具。
4. 验证仿真结果的准确性。
5. 发表相关论文和申请相关专利。
五、预期结论和贡献该研究预期结论是可以开发出一个基于Matlab-Simulink的仿真模型库,可以提供各种控制系统的模型,并支持用户定制和集成各种控制系统的模型。
simulink parameter estimation 原理 -回复

simulink parameter estimation 原理 -回复S i m u l i n k P a r a m e t e r E s t i m a t i o n原理S i m u l i n k是一款基于M A T L A B的模拟和仿真环境,广泛应用于系统建模和控制设计等领域。
其中的参数估计功能允许用户通过对实际数据进行分析,对模型的参数进行估计和优化。
本文将介绍S i m u l i n k参数估计的原理,包括相关算法和步骤。
第一步:系统建模在进行参数估计之前,首先需要建立待估参数的数学模型。
S i m u l i n k提供了丰富的模块库和工具箱,可以用于构建各种系统模型。
用户可以根据实际情况选择相应的模块,并通过连接这些模块来描述系统的输入、输出和状态变量关系。
在建模过程中,用户可以设置待估参数的初始值,以便后续的参数估计。
第二步:数据采集参数估计需要依赖实际的数据进行分析和计算。
因此,在进行参数估计之前,需要采集系统的输入和输出数据。
数据的采集可以通过实际试验、传感器测量或仿真等方式进行。
在实际采集数据时,要注意数据的采样率和精度,以及避免噪声和干扰的影响。
第三步:建立目标函数参数估计的目标是通过最小化误差函数的方法,找到最优的参数值。
为了实现这个目标,需要建立一个适当的目标函数。
目标函数的选择根据具体问题而定,常用的包括均方误差、最大似然估计和最小二乘估计等。
第四步:选择参数估计算法S i m u l i n k提供了多种参数估计算法,包括经典的最小二乘法、渐进随机搜索和基因算法等。
用户可以根据实际需求选择合适的算法。
一般来说,最小二乘法适用于线性参数估计问题,而进化算法则更适用于复杂的非线性问题。
第五步:进行参数估计一旦建立了目标函数和选择了参数估计算法,就可以进行参数估计了。
参数估计的过程是通过将实际数据输入到模型中进行仿真,并将仿真结果与实测数据进行比较,从而确定最优的参数值。
浮点,simulink 定标指导,定点

Simulink代码生成系列(定点数)82010-04-11 21:21:41| 分类:项目4_高性能DSP | 标签: |举报 |字号大中小订阅李会先(整理MATLAB)关于定点数定点数和它们的数据类型以字长、二进制小数点、有符号还是无符号为特征,SIMULINK定点软件支持整数和定点数,它们的主要区别是小数点。
一般的二进制定点数表示为:定点数的标度对于同等字长度,定点数的动态范围远小于浮点数,为了避免溢出和最小化量化误差,定点数需要标度,因此用如下方法来表示一个定点数。
∙V是任意精度的实数∙是实数的近似∙Q是一个存储值,用来编码V∙S=F是斜率∙B是偏差(基准)斜率被分成两个部分:∙确定二进制小数点,E是2的幂指数∙F是斜率调整因子,规范化时1≤F﹤2只有缩放标度的二进制小数∙F=1∙S=F=∙B=0一个被量化的实数的标度用斜率S定义,这被严格的限制为2的幂,负的2的幂指数被称为分数长度,分数长度是二进制小数点右边的比特数。
对于仅有缩放的二进制小数,定点数据类型表示为:∙signed types —fixdt(1, WordLength, FractionLength)∙unsigned types —fixdt(0, WordLength, FractionLength)整数是定点数类型的特殊情况,整数的用斜率为1直接标度,偏差为0,或者相当于分数长度为0,整数表达为:∙signed integer —fixdt(1, WordLength, 0)∙unsigned integer —fixdt(0, WordLength, 0)斜率和偏差(基准)标度当用斜率和偏差标度,被量化的实数的斜率S和偏差B可以使任何值,斜率必须是正数,用S和B定点数被表达为:∙fixdt(Signed, WordLength, Slope, Bias)范围和精度数的范围给出了表达的限制,精度给出了表达连续两数之间的距离,定点数的范围和精度取决于字的长度和标度。
基于MATLABSimulink的控制系统建模与仿真实践

基于MATLABSimulink的控制系统建模与仿真实践控制系统是现代工程领域中一个至关重要的研究方向,它涉及到对系统的建模、分析和设计,以实现对系统行为的控制和调节。
MATLAB Simulink作为一款强大的工程仿真软件,在控制系统领域有着广泛的应用。
本文将介绍基于MATLAB Simulink的控制系统建模与仿真实践,包括建立系统模型、进行仿真分析以及设计控制算法等内容。
1. 控制系统建模在进行控制系统设计之前,首先需要建立系统的数学模型。
MATLAB Simulink提供了丰富的建模工具,可以方便快捷地搭建系统模型。
在建模过程中,可以利用各种传感器、执行器、控制器等组件来描述系统的结构和功能。
通过连接这些组件,并设置其参数和初始条件,可以构建出一个完整的系统模型。
2. 系统仿真分析建立好系统模型后,接下来就是进行仿真分析。
MATLABSimulink提供了强大的仿真功能,可以对系统进行各种不同条件下的仿真实验。
通过改变输入信号、调节参数值等操作,可以观察系统在不同工况下的响应情况,从而深入理解系统的动态特性和性能指标。
3. 控制算法设计在对系统进行仿真分析的基础上,可以针对系统的性能要求设计相应的控制算法。
MATLAB Simulink支持各种常见的控制算法设计方法,如PID控制、状态空间法、频域设计等。
通过在Simulink中搭建控制算法,并与系统模型进行联合仿真,可以验证算法的有效性和稳定性。
4. 系统优化与调试除了基本的控制算法设计外,MATLAB Simulink还提供了优化工具和调试功能,帮助工程师进一步改进系统性能。
通过优化算法对系统参数进行调整,可以使系统响应更加迅速、稳定;而通过调试功能可以检测和排除系统中可能存在的问题,确保系统正常运行。
5. 实例演示为了更好地说明基于MATLAB Simulink的控制系统建模与仿真实践,接下来将通过一个简单的倒立摆控制系统实例进行演示。
基于Matlab/Simulink模型实现车载网络测试及其数据分析方法的研究及实践

主的测试 环境构建。同时也通过实例交待 了基于 Ma t l a b / S i m u l i n k平 台 的测试 数据 的处理方 法 , 展示 了 Ma t l a b /
S i mu l i n k强 大 的建 模 计 算 能 力 。
【 A b s t r a c t 】 F o c u s e d o n t h e i m p l e m e n t a t i o n , t h e t e s t e n v i r o n m e n t b a s e d o n M a t l a b p l a t f o r m i s
l i n k可 以凭借其 图形 化 描 述语 言 、 支持 代 码 生 成 、
强 大 的数 据处 理能 力 3大 优势 在 网络测 试 方 面 发 挥 出重 复作用 。
1 车载 网络测 试及 常用 测试 环境 简
介
目前 , 零 部 件 及 整 车 厂 对 于 车 载 网络 测 试 主
使用MATLAB和Simulink开发嵌入式软件之模型质量目标

使用MATLAB和Simulink开发嵌入式软件之模型质量目标模型质量目标(Model Quality Objectives,以下简称 MQO)的标准是由一流的汽车厂商和MathWorks 公司共同制定,目的是当在嵌入式软件开发中 OEM 和供应商进行 Simulink 模型共享时,可以清晰定义并简化双方的协作,并最终提高软件产品的质量和完整性。
首先,基于软件开发生命周期的四个不同阶段用到的四种设计模型,本文定义了一套软件开发方法。
然后,针对每种模型,提出了一个名为MQO 的特定质量目标。
每个目标被定义为一组质量特征和一些可衡量的标准,称为模型质量要求(Model Quality Requirement,MQR)。
此外还提供了一些额外的规范,来管理与 MQO 和 MQR 相关的计划和质量评估活动。
在文章最后也对汽车工业采用MQO 的预期影响进行了总结。
◆◆◆◆为什么制定模型质量目标为了加速嵌入式软件的开发,用 Simulink 软件开发的设计模型在业界广泛使用。
这些模型使工程师能够完成各种工程任务,如频域分析、桌面仿真、形式验证和自动代码生成。
这个开发过程被称为基于模型设计。
出于验证需求和快速地探索设计方案的目的,可以在非常早期的阶段开发设计模型。
这些模型也可以逐步改进,直到它们达到一定成熟度,可生成符合国际软件安全标准的代码。
为了逐步增加设计模型的成熟度,需要涉及到系统工程、控制工程和软件工程等不同的工程学科。
使用相同的语言、工具和模型进行协作,是提高工程师之间的沟通、降低工程费用和缩短开发时间的好方法。
然而,由于在不同的项目阶段使用设计模型有不同的规程,可能会出现关于模型的作用和它们代表的内容间的混乱。
对模型代表的内容的错误解释会导致错误地使用这些模型,并最终影响所产生的软件的质量。
参与制定MQO 的OEM 和一级供应商分享了许多关于成熟度不够或存在漏洞的模型被过早地确定为“可用于编码”的惨痛案例。
基于Simulink浮点模型和定点模型的问题研究

10.16638/ki.1671-7988.2019.04.045基于Simulink浮点模型和定点模型的问题研究邹凡,朱宏翔,袁凯(陕西汽车集团有限责任公司技术中心,陕西西安710200)摘要:文章介绍了MA TLAB/Simulink的自动代码生成的实现方法和过程。
以某新能源汽车油门控制模型为例,重点解释了浮点模型和定点模型之间的区别,并通过自动生成的代码和CodeWarrior编译生成的可执行文件证明定点模型相对于浮点模型所占内存少。
关键词:MATLAB/Simulink;自动代码生成;浮点;定点中图分类号:U462 文献标识码:A 文章编号:1671-7988(2019)04-131-03The research on Floating-Point model and Fixed-Point model based on SimulinkZou Fan, Zhu Hongxiang, Yuan Kai( Shaanxi Automobile Group Co., Ltd. Technical Center, Shaanxi Xi’an 710200 )Abstract: The paper introduces the realization method and process of automatic code generation of MATLAB/Simulink. Taking the throttle control model of a new energy vehicle as an example, the differences between floating-point model and fixed-point model are explained emphatically. The executable files complied by CodeWarrior and automatically generated code prove that fixed-point model occupies less memory than floating-point model.Keywords: MATLAB/Simulink; automatic code generation; floating point; fixed pointCLC NO.: U462 Document Code: A Article ID: 1671-7988(2019)04-131-03前言随着电动汽车的快速发展,企业对电子控制系统的性能与开发效率提出了越来越高的要求,传统手写代码的开发方式周期长、调试难度大,已经很难适用于现代电控系统的开发。
基于Simulink_AMESim控制系统仿真研究

基于Simulink/AMESim控制系统仿真研究薛 玮(中航工业航空动力控制系统研究所,无锡,214063)摘要:利用基于M A T L A B平台的Simulink和A M ESim软件的各自特点,将用Simulink建立的控制系统模型转化成A M ESim模型,在AM ESim软件中建模仿真,并与Simulink的模型进行对比验证一致性。
关键词:Simulink;M A T L A B;AM ESim;仿真引 言AM ESim是当今世界先进的流体、传动系统和液压/机械系统建模,仿真和动力学分析软件。
基于M ATLAB平台的Sim ulink是动态系统仿真领域中著名的仿真集成环境。
目前在航空发动机控制系统和燃机控制系统中,液压机械系统的仿真基本使用AM ESim平台进行建模仿真,控制系统一般使用M AT LAB/ Simulink进行系统仿真。
但是在M AT LAB/ Simulink下对液压机械系统进行建模和仿真需要做很多简化工作,模型的简化使得仿真结果往往出现较大的误差。
AM Esim-Simulink接口提供了一个使用便捷和行之有效的工具用于将Sim ulink模型转为AM Esim模型,在A MESim平台进行仿真很好的解决了上述的问题。
1 仿真设置(1)确认系统已安装VC++6.0或更高版本(2)在MAT LAB基本环境下输入m ex—setup选择VC++编译器。
(3)将%AM E%\scriping\matlab\amesim 和%AM E%\interface\sl2ame增加到MAT LAB 的路径中如图1和图2所示。
注:%AM E%是指在机器上的AM ESim安装目录。
(4)在AMESim软件中AMESim->tools->o ptions->A MESim Preferences->Compilation/Parametes中设置编译器为VC ++,见图3。
simulink 函数t-t到t之间的数据 -回复

simulink 函数t-t到t之间的数据-回复题目:Simulink函数tt到t之间的数据摘要:Simulink是一种功能强大的模型基于工具,用于设计、模拟和实现各种动态系统。
在Simulink模型中,tt到t之间的数据是指在指定的模拟时间范围内,模型输出的各种信号和参数。
本文将逐步回答关于Simulink 函数tt到t之间的数据的问题,以帮助读者更好地了解和使用Simulink。
引言:在工程系统设计和开发过程中,模拟和仿真是非常重要的步骤。
通过模拟和仿真可以预测系统的性能,验证设计的正确性,并进行系统优化。
Simulink作为一种流行且功能强大的模型基于工具,被广泛应用于各个领域。
本文将探讨Simulink函数tt到t之间的数据,介绍如何获取模型的输出信号和参数。
一、模型时间范围设置在开始使用Simulink进行仿真之前,我们首先需要设置模拟的时间范围。
在Simulink模型中,可以通过打开仿真配置参数对话框来设置。
在这个对话框中,可以指定仿真开始时间tt、仿真结束时间t和仿真步长等参数。
设置好时间范围后,Simulink会在指定的时间范围内模拟系统的动态行为。
二、信号输出设置在Simulink模型中,信号输出是指模型内部生成的信号值,可以用来表示系统的各种状态和动态行为。
在模型中,我们可以通过信号源块来产生各种输入信号,这些信号可用于模拟系统对不同输入的响应。
根据模型的设计需求,可以选择将信号输出到显示块,保存到MATLAB工作空间或输出到其他外部设备。
三、获取信号数据获取信号数据是了解模型动态行为的关键。
在Simulink中,可以通过以下几种方式获取信号数据:1. 使用显示块:可以通过在模型中添加显示块来实时监视和分析信号数据。
例如,Scope块可以实时显示信号值随时间变化的曲线。
使用这种方式,可以直观地观察信号的波形并进行定性分析。
2. 导出到MATLAB工作空间:Simulink提供了将信号数据导出到MATLAB工作空间的功能。
浮点,simulink 定标指导,定点

Simulink代码生成系列(定点数)82010-04-11 21:21:41| 分类:项目4_高性能DSP | 标签: |举报 |字号大中小订阅李会先(整理MATLAB)关于定点数定点数和它们的数据类型以字长、二进制小数点、有符号还是无符号为特征,SIMULINK定点软件支持整数和定点数,它们的主要区别是小数点。
一般的二进制定点数表示为:定点数的标度对于同等字长度,定点数的动态范围远小于浮点数,为了避免溢出和最小化量化误差,定点数需要标度,因此用如下方法来表示一个定点数。
∙V是任意精度的实数∙是实数的近似∙Q是一个存储值,用来编码V∙S=F是斜率∙B是偏差(基准)斜率被分成两个部分:∙确定二进制小数点,E是2的幂指数∙F是斜率调整因子,规范化时1≤F﹤2只有缩放标度的二进制小数∙F=1∙S=F=∙B=0一个被量化的实数的标度用斜率S定义,这被严格的限制为2的幂,负的2的幂指数被称为分数长度,分数长度是二进制小数点右边的比特数。
对于仅有缩放的二进制小数,定点数据类型表示为:∙signed types —fixdt(1, WordLength, FractionLength)∙unsigned types —fixdt(0, WordLength, FractionLength)整数是定点数类型的特殊情况,整数的用斜率为1直接标度,偏差为0,或者相当于分数长度为0,整数表达为:∙signed integer —fixdt(1, WordLength, 0)∙unsigned integer —fixdt(0, WordLength, 0)斜率和偏差(基准)标度当用斜率和偏差标度,被量化的实数的斜率S和偏差B可以使任何值,斜率必须是正数,用S和B定点数被表达为:∙fixdt(Signed, WordLength, Slope, Bias)范围和精度数的范围给出了表达的限制,精度给出了表达连续两数之间的距离,定点数的范围和精度取决于字的长度和标度。
基于MATLABSIMULINK开发自动驾驶系统第二讲之地面真值标签与验证

基于MATLABSIMULINK开发自动驾驶系统第二讲之地面真值标签与验证展开全文2.1 开始使用Ground Truth LabelerGround Truth Labeler 应用使能够在视频、图像序列或激光雷达点云中交互式地标示地面真值数据。
使用该应用程序,可以同时标记多个信号,例如从安装在车辆上的摄像头和激光雷达传感器获得的数据。
本示例通过这些步骤引导完成多信号地真值标签工作流程。
1 "加载要标记的地面真值信号" - 将多个信号加载到应用程序中,并配置这些信号的显示。
1 "为多个信号标记地面真值"--创建标签定义,并使用自动化算法对信号进行标记。
2 "导出和探索多个信号的地面真值标签" - 从应用程序中导出标签并探索数据。
可以使用这些导出的标签以及相关的信号帧,作为深度学习应用的训练数据。
2.2 将接地真值信号加载到标签上Ground Truth Labeler应用提供了两种类型信号的标签选项。
- 图像信号是基于图像的。
可以从视频或图像序列等来源加载这些信号。
- 点云信号是基于激光雷达的信号。
可以从诸如点云文件序列等来源加载这些信号。
在本例中,将一个视频和一个点云序列加载到应用程序中。
这些信号来自安装在车辆上的摄像头传感器和激光雷达传感器。
这些信号代表了同一个驾驶场景。
2.2.1 加载时间戳加载点云序列的时间戳。
时间戳是一个持续时间向量,与序列在同一文件夹中。
要加载时间戳,必须将此文件夹临时添加到MATLAB® 搜索路径中。
pcSeqFolder = fullfile(toolboxdir('driving'),'drivingdata','lidarSequence');addpat h(pcSeqFolder)loadtimestamps.mat rmpath(pcSeqFolder)该应用还提供了一个选项来为视频源指定时间戳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Simulink模型的数据定标问题研究
数据定标是指通过移位、缩放、线性变换等数学方法,将原始数据映射到新的取值范围内的过程。
在科学与工程领域中,数据定标是非常重要的环节,它能够帮助研究人员更好地理解数据,从而更准确地进行分析、建模和预测等工作。
本文将基于Simulink模型,对数据定标问题进行研究和分析。
Simulink是一种基于图形化编程语言的数学建模和仿真工具,
在工程领域中广泛应用于控制系统、信号处理、图像处理等方面。
对于数据定标问题而言,Simulink可以提供直观的图形界面,使得用户能够快速有效地构建定标模型,并进行仿真验证。
在本文中,我们以一个具体的例子来说明Simulink模型下的
数据定标问题。
假设我们有一组温度传感器数据,其数值范围在-40℃到100℃之间,为了更好地展示这些数据,我们需要
将其映射到0到255之间的整数值范围内。
在Simulink模型中,我们可以采取以下步骤来构建定标模型:
1. 选择数据和定标范围
选取所需定标的数据和新的取值范围区间。
对于本例,我们选择传感器数据和0到255的整数值范围。
2. 缩放和平移数据
对原始数据进行缩放和平移处理,并将其映射到新的取值范围内。
在Simulink模型中,我们可以使用“Gain”模块来进行缩放
处理,使用“Add”模块来进行平移处理。
具体而言,这里我们
可以将原始数据加上40℃,然后将结果乘以255/(100+40),
即可完成缩放和平移处理。
3. 取整输出
将缩放和平移后的数据取整,得到最终的定标数据。
在Simulink模型中,我们可以使用“Round”模块来进行取整处理。
以上三个步骤即是Simulink模型下的数据定标过程。
通过构
建定标模型,我们可以将原始数据准确而有效地映射到新的取值范围内,从而提高其可读性和可理解性,并且方便后续数据分析和应用。
总之,在科学与工程领域中,数据定标是至关重要的一环。
通过Simulink模型,我们可以更快捷、更直观地进行数据定标
处理,并为后续的数据分析和建模工作提供更有力的支持。
除了上述的基本步骤外,Simulink模型还提供了其他实用的模块
来处理数据定标问题。
比如,我们可以使用“Lookup Table”模
块来进行数据映射,即建立一张字典表,将原始数据作为输入,将映射后的数据作为输出。
此外,我们还可以使用“Saturate”
模块来进行数据截断,即将超出定标范围的数据设置为上限或下限的取值。
在实际应用过程中,数据的定标往往不仅仅是一个简单的缩放和平移操作。
例如,对于传感器数据,我们需要进行校准、补偿等复杂的任务,以获得更加准确的测量结果。
在这种情况下,
我们可以使用Simulink中的“System Identification Toolbox”等
工具包,结合数据建模和识别技术,来构建更加精细和高级的定标模型。
此外,在实际的应用中,我们还需要考虑如何处理数据缺失或异常值等问题。
对于数据缺失的情况,我们可以利用Simulink 模型中的“Interpolation”模块,通过插值方式较为准确地估算
丢失的数据值。
对于异常值的情况,我们可以采用滤波、平滑等技术对数据进行处理,以消除噪音和异常干扰,提高数据的可信度和可靠性。
综上所述,Simulink模型提供了丰富的、灵活的工具和方法,
能够帮助我们有效地解决数据定标问题。
无论是简单的缩放和平移操作,还是复杂的数据建模和识别任务,Simulink都能够
提供合适的工具和方法,以满足各种科学和工程领域的需求。
在今后的实际应用中,我们可以继续探索其更多的优势和潜力,以优化数据分析和决策的效率和准确性。
除了在数据定标问题上的广泛应用,Simulink模型在其他领域也有实用价值。
例如,在控制系统设计中,Simulink模型可以用来模拟和优化各种控
制策略。
通过建立模型、仿真测试和参数调节,我们可以在计算机环境下快速有效地评估不同控制方法的性能,并从中筛选出最佳方案。
与传统的试验方法相比,Simulink模型具有周期性、可重复性和可预测性的优势,有助于提升控制系统设计的效率和准确性。
此外,在系统建模和仿真方面,Simulink模型也有广泛应用。
例如,在信号处理和通信领域,模型可以用来模拟和测试各种
信号处理算法和通信协议的性能。
通过建立模型、仿真测试和数据分析,我们可以全面地评估算法和协议的可靠性、带宽效率、处理速度等指标,为实际应用提供重要的参考和支撑。
同样,在机电一体化系统设计中,Simulink模型也可以用来模拟
和优化各种机械电子系统的性能。
通过建立模型、仿真测试和参数调节,我们可以预测系统的工作状态、优化系统参数、改进系统结构,从而实现系统的更高效、更可靠、更安全的运行。
除此之外,Simulink模型也被广泛应用于科学研究和教育培训。
在科学研究方面,模型可以用来模拟和分析各种物理、化学、生物等系统的动态行为。
通过建立模型、仿真测试和数据分析,我们可以更好地理解物理原理、预测系统行为、验证理论假设、探索新的科学问题。
在教育培训方面,Simulink模型可以用来
教授科学原理、工程思维和计算方法。
通过基础的建模、仿真、调试操作,我们可以帮助学生掌握物理、工程、计算机等领域的核心概念和技能,培养学生的创新能力、解决问题的能力和团队合作精神。
综上所述,Simulink模型在各种领域有着广泛的应用和需求。
无论是在工程设计中优化系统性能、在科学研究中探索新的科学问题,还是在教育培训中培养学生的技能和素质,Simulink
都可以提供具有实用价值和创新潜力的工具和方法。
在今后的应用和发展中,我们可以继续挖掘其更多的优势和潜力,以推动科技进步和社会发展。
