不完整非对称性曲线线型优化及其坐标计算20页PPT

电力系统不对称故障的分析和计算.ppt

2)
I
fa(1)

(8

9)

Vfa(0) jX I ff (0) fa(0) 0

2019/10/11
8-1 简单不对称短路的分析 2. 两相(b相和c相)短路—复合序网
I fa(1)
jX ff (1) V (0)
f
V fa(1) I fa(2)
jX ff (2)
V fa(2)
8-1 简单不对称短路的分析 1. 单相(a相)接地短路—序分量边界条件
(1)相量表示的边界条件：Vfa 0, I fb 0, I fc 0
(2)对称分量表示的边界条件 Vfa V fa(1) V fa(2) V fa(0) 0 I fb I fb(1) I fb(2) I fb(0) 0 I fc I fc(1) I fc(2) I fc(0) 0
a b c Vfa 0
I fa V fb
I fb 0
I fc 0 V fc
(3)以a相为参考相 V fa V fa(1) V fa(2) V fa(0) 0
I fb 2 I fa(1) I fa(2) I fa(0) 0 I fc I fa(1) 2 I fa(2) I fa(0) 0
I fc(2)
I fa(0) I fb(0) I fc(0)
V fc
2019/10/11
V fa (1)
Vfa 0 V fa ( 2) V fa(0)
V fa (1)
V fc ( 2 )
V fb(2)
V fc (1) V fb
V fa(2) V fa ( 0 )
V fb (1)

非对称非完整缓和曲线推算公式

RL R L R R R L R R y p R L L R L R L R R L L R x m R L L x R L R L y L R L L R L y L R L L R L dLdy R L L L x R L L dL dx RL L R L RL dL L R dL d L R L R R L R L s s s hy ss ss s hy shy ss hy s xs x s xs x s xx s xxs sxx s xx x x x xs x s x x *24))*81((*6)cos (*2402)*482(**40sin **40*336*6**336**6)**48*2(sin *sin **40)**4*21(cos *cos *2**2****22220233323s 023s 3423373336222522402=---=--=-=---=-=-=-=-=-≈=-=-≈=======βββββββββ缓和曲线综合要素则缓圆点独立坐标标缓和曲线上任意一点坐缓和曲线性质：1121112213111221'12'11'11'1'11'12122211'212123221221111'*2轴正方向建立坐标系X 为JD 为原点ZH 以'*sin 1cot '*''*6'*40'*2*)(*轴X 为JD'为原点ZH'以)cos (sin 1tan tan sin cos cos sin sin cos cos cos )cos(cos cos cos cos *240)(2*24)(tan *)(R L Y E HH Y X E ZH R L Y R L L X R L RR L R L L L R L R p R p R p R p R p R p R R L L L L m RL L p m p R T HH HH HH xHH xx HH x x x x x x x ==∙-=∙=-==-=∴+=-++=∴+=+=-==+++=+∴=+=+-+=+=++=ββββααθθααθθαθαθθαθθθθαθθβθθ 正方向建立坐标系非对称非完整缓和曲线JDA A ZH T AF JD A E HH EF A HH AF E JD EF E ZH JD ZH E JD R L L Y A HH Y X A ZH R L Y R L L X x HHHH HH HH HH∙+∙=∴=∙∙-+∙=∙=∙-∙=∙--=-=-=-=-=∴+==∙-=∙=-=3664'''236354112155212212121311sin sin *中F -JD -A 在三角形sin sin *'||||'中F -JD'-E 在三角形*2*sin 1cot **6*40ββββββπβαπββαβββββββββ 改正数切线标高设计标高改正值：里程差为任一点与起点或终点）（变坡点标高切线标高设计标高变坡点高程又变坡点竖曲线起点±==-±=-==∴-==∴===-=Rx y x i x T TK E R E R E R L T R T E i i *2*K *88*2*2*2竖曲线222221ωωωω。

一不对称问题分析方法和应用 77页PPT文档

m 主绕组，工作绕组
a 辅助绕组，起动绕组
转子为鼠笼式绕组
2。对称分量法应用
2.2 单相感应电动机原理分析
双旋转理论分析
当作不对称状态的三相电机
2、分析方法
1 对称分量法
I m I m I m I 0 F m F m F m 0
一、结构：定子为单相绕组（有起动和工作绕组）；转子为鼠笼式。
二、工作原理
单相交流绕组通入单相交流电流产生脉动磁动势，其可分解为F+、F-，建
立起正转和反转磁场Φ+、Φ-，这两个磁场切割转子导体，产生感应电动
势和感应电流，从而形成正反向电磁转矩T+、T-，叠加后即为推动转子转
动的合成转矩T。
定子两相绕组：
1。对称分量法的基本原理
1.3 物理解释例2
设有一不对称三相电压请将其分解为对称分量。
iA 2 I cost
iB 0 iC 0
I A I 0 I B 0 IC 0
注意其物理含义
I ? I ? I 0 ?
1。对称分量法的基本原理
1。对称分量法的基本原理
1.1 三相对称系统的概念、表达，不对称问题引入
正序、负
序均是对
称系统
三相对称系统的瞬态表达式：
大小相等、相差120度
UUBA

UC
2U cos(t) 2U cos(t 120) 2U cos(t 240)
正序：A－B－C A 负序：A－C－B
U UB AU UB AU UB AU UB A00＝＝aU2UU aUU 0 U0 UC UC UCUC0＝aUa2UU0

优化方法的数学基础PPT课件

第26页/共50页
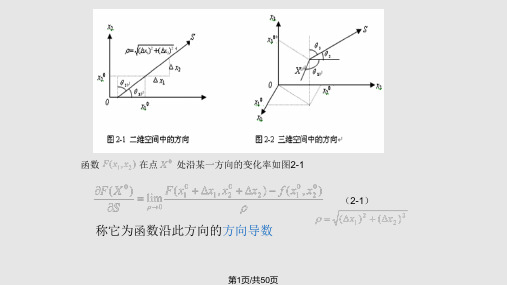
2.
处取得极值充分条件
x*
2F
x12
2F
2
F
(
x*
)
x2x1
2F
xnx1
2F x1x2 2F
x22
2F xnx2
2F
x1xn
2F
x2xn
正定或负定
2F
xn2 x*
第27页/共50页
各阶主子式均大于零:
，
，
，..
则海色（Hessian）矩阵H(x) 是正定则X*为极小点。的,
第30页/共50页
§2-4 有约束优化问题的极值条件
• 不等式约束的多元函数极值的必要条件是著名的库恩--塔克（Kuhn-Tucker）条件，它是非线性优化问题的重要理论Байду номын сангаас
1 库恩—塔克条件 (K-T条件）
• 对于多元函m数in 不F等( x式) 的约束优化问题：
•
s.t. g j (x) 0 ( j 1, 2, , m)
f
( x(1) )
2x1 4
2 x2
x(1)
2 4
第11页/共50页
例2-3：试求目标函数 f x1, x2 3x12 4x1x2 x22 在点X 0 0,1T 处
的最速下降方向。
解：由于
f X
f X
x1 6x1 4x2 , x2 4x1 2x2
则函数在 X 0 0,1T 处的最速下降方向是
3）任何一组凸集的积（或交）仍是凸集。
第15页/共50页
二、凸函数
具有凸性（表现为单峰性）或只有唯一的局部最优值亦即全域最优值的函数，称为凸函数或单峰函数。其数学定义是：

解析几何中“非对称”韦达定理的处理策略公开课教案教学设计课件资料

解析几何中“非对称”韦达定理的处理策略公开课教案教学设计课件资料第一章：韦达定理的基本概念与性质1.1 韦达定理的定义及几何意义1.2 韦达定理的适用范围及条件1.3 韦达定理与其他定理的联系与区别第二章：非对称韦达定理的提出2.1 非对称韦达定理的背景及意义2.2 非对称韦达定理的表述及证明2.3 非对称韦达定理与传统韦达定理的对比第三章：非对称韦达定理的处理策略3.1 转换法：将非对称问题转化为对称问题3.2 参数法：引入参数，简化非对称问题3.3 举例解析：运用非对称韦达定理解决实际问题第四章：非对称韦达定理在解析几何中的应用4.1 直线与圆的位置关系4.2 椭圆、双曲线、抛物线与直线的交点问题4.3 几何图形的面积、距离、角度等问题的求解第五章：课堂练习与拓展5.1 课堂练习题：巩固非对称韦达定理的基本应用5.2 拓展题目：探讨非对称韦达定理在更复杂问题中的应用5.3 答案与解析：对练习题及拓展题目进行解答和分析本教案旨在帮助学生掌握解析几何中非对称韦达定理的基本概念、性质和应用，培养学生运用非对称韦达定理解决实际问题的能力。

通过转换法、参数法等策略，使学生更好地理解和运用非对称韦达定理，提高解析几何解题水平。

第六章：非对称韦达定理与线性方程组6.1 线性方程组与非对称韦达定理的关系6.2 利用非对称韦达定理求解线性方程组6.3 实例分析：线性方程组在实际问题中的应用第七章：非对称韦达定理与函数性质7.1 非对称韦达定理与函数零点的关系7.2 利用非对称韦达定理分析函数的单调性、奇偶性7.3 实例分析：函数性质在实际问题中的应用第八章：非对称韦达定理与不等式8.1 非对称韦达定理与不等式的关系8.2 利用非对称韦达定理解决不等式问题8.3 实例分析：不等式在实际问题中的应用第九章：非对称韦达定理与解析几何中的优化问题9.1 解析几何中的优化问题概述9.2 利用非对称韦达定理解决优化问题9.3 实例分析：优化问题在实际问题中的应用第十章：总结与展望10.1 非对称韦达定理在解析几何中的地位与作用10.2 非对称韦达定理的进一步研究与发展10.3 课程回顾与拓展建议本教案后续五章旨在深入探讨非对称韦达定理在线性方程组、函数性质、不等式以及优化问题中的应用，帮助学生更好地理解和运用非对称韦达定理解决更广泛的数学问题。

第七章不对称故障分析ppt课件

加拿大C.L.Fortescue在1918年提出的，任意一组不对称的三相向量（三相电压或三相电流）均可由三相对称分量合成。
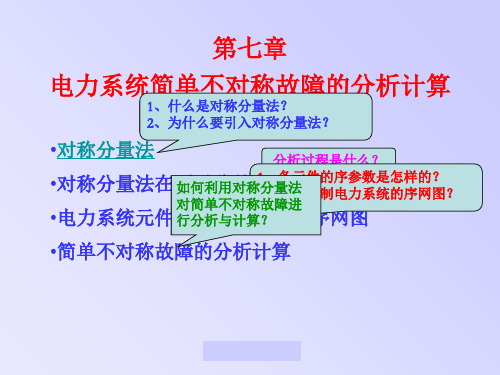
正序分量
负序分量
零序分量
合成
• 正序分量：三相量大小相等，互差1200，且与系统正常运行相序相同。超前 120°
• 负序分量：三相量大小相等，互差1200，且与系统正常运行相序相反。滞后 120°
➢ 负序网
0 I a 2 ( Z G 2 Z 1)2 V a 2
Ia2 Ib2 Ic2
Ia2 Ia2 2Ia2
0
三、对称分量法在不对称短路计算中的应用 ➢ 零序网
I a 0 I b 0 I c0 3 I a 0
0 I a 0 ( Z G 0 Z L 0 ) 3 I a 0 Z n V a 0
• 零序分量：三相量大小相等，相位一致。
逆时针旋转1200
正序负序
Fb1 Fb2
a2Fa1,Fc1 aFa2,Fc2
aFa1 a2Fa2
引入因子
aej1 20
零序 Fb0 Fc0 Fa0
一、对称分量法
• 三相量用三序量表示
Fa Fa1Fa2 Fa0 Fb Fb1Fb2 Fb0 a2Fa1aFa2
•简单不对称故障的分析计算
7.1 对称分量法在不对称短路计算中的应用
• 系统中发生最多的故障是不对称故障，即单相短路、两相短路、单相断线等，与三相比最大的区别就是不对称故障时三相电路时不对称的，因此不能采用前面的“对称相分析法”分析。采用将不对称问题对称化的处理方法
7.1.1、对称分量法
不含中性点阻抗
E 0
Ia1Z1 Ia2 Z 2
Va1 Va 2
0 Ia0 Z 0 Va0

非对称缓和曲线坐标计算程序

非对称缓和曲线坐标计算程序CASIO fx-4800P QXZB曲线坐标计算CASIO4800 QXZB可计算不等缓和曲线、圆曲线上的任意中、边桩坐标：该程序适用于计算器 CASIO fx-4800P，可计算与线路中心成任意夹角的缓和曲线、圆曲线中、边桩坐标及待测点方位角和距离。

1、DK(JD)？输入交点桩号2、X(JD)？输入交点坐标X3、Y(JD)？输入交点坐标Y4、T1？输入第一切线长(如果只有一条切线两者都输入一致)5、T2？输入第二切线长(如果只有一条切线两者都输入一致)6、FWJ？输入直线方位角(ZH→JD)7、A？输入转角：左转为负，右转为正8、R？输入圆曲线半径9、LS1？输入第一缓和曲线长(如果只有一条缓和曲线两者都输入一致)10、LY？输入圆曲线长(L-LS1-LS2)11、LS2？输入第二缓和曲线长(如果只有一条缓和曲线两者都输入一致)12、X(ZJD)？输入置镜点坐标X13、Y(ZJD)？输入置镜点坐标Y14、JSDK？输入前视点里程15、PL？输入偏距16、PA？输入偏角程序下载地址：/blog/post/QXZB-4800.html评价答案好:18不好:1原创:18非原创:0菲メ帆ぅ回答采纳率:52.8% 2010-06-02 17:37满意答案好评率：57%（for Casio-fx4850）扩展变量操作（15个）：Defm 15←┚ ( O为字母、0为数字)J-PQX (平面数据输入，自行切换到J-JSMS)Defm 15←┚A“JD” B“JDX” C“JDY” F“FWJ” O“A0：Z-，Y+” RE“LS1” K“LS2”：E<1=>E=1E-9⊿K<1=>K=1E-9⊿Z[1]=EE÷24R-E∧4÷2688RRR:Z[2]=E÷2-EEE÷240RR:X=(EE-KK)÷24R÷sin Abs O :“T1=”:Z[3]=(R+Z[1])tan(Abs O÷2)+Z[2]-X◢“T2=”:Z[4]=(R+KK÷24R-K∧4÷2688RRR)tan(Abs O ÷2)+K÷2-KKK÷240RR+X◢“L=”:L=Abs OπR÷180+(E+K)÷2◢J=tan-1((R+Z[1])÷(Z[3]-Z[2]):“E=”:X=(R+Z[1])÷sin J-R◢X=A-Z[3]:Y=X+E:E<1=>“ZY=”:X◢≠=> “ZH=”:X◢“HY=”:Y◢⊿ “QZ=”:Y =X+(L-K-E)÷2+E◢Y=X+L-K:X=X+L:K<1=> “YZ=”:X◢≠=> “YH=”:Y◢“HZ=”:X◢⊿Prog“J-JSMS” ←┚J-JSMS（放样模式主程序）“1-ZS, FY,3-FS”: Lb1 0:{Z}: Z“MS”≤2=>Goto 1: ≠=> Z≤4=> Goto2⊿⊿←┚Lb1 1 :Q“X-YIQI”S“Y-YIQI”T“X-HOUSI”U“Y-HOUSI”:{PDW}:P“F=”D“BZ=”W“BJ=”: Prog“JP”: Prog“FY”: Goto 1←┚Lb1 2 :{XYW}:XYW“BJ”: Prog“JF”: “P=”: P◢“BZ=”: D◢JP（平曲线正算子程序）Fixm←┚Lb1 1 :J=F:X= B-Z[3]cos F :Y= C-Z[3]sin F :G=E←┚P≤A-Z[3]=>I=A-Z[3]-P:M=-I:N=0:H=F+W:Goto 5←┚≠=>P≤A-Z[3]+E=>I=P-A+Z[3]:H=90II÷REπ:O<0=>H=-H⊿H=H+W+F:Goto 3←┚≠=>P≤A-Z[3]+L-K=>I=P-A+Z[3]-E:Goto 4: ≠=>Goto 2⊿⊿←┚Lb1 2 :X= B+Z[4]cos(F+O :Y= C+Z[4]sin(F+O :J=F+O+180:G=K←┚P≤A-Z[3]+L=>I=A-Z[3]+L-P:H=90II÷RKπ:O>0=>H=-H⊿H=H+J+W+180:Goto 3 ←┚≠=>I=P-A+Z[3]-L:M=-I:N=0:H=J+W+180:Goto 5 ←┚Lb1 3 :M=I-I∧5÷40RRGG:N=III÷6GR-I∧7÷336RRRGGG:Goto 5 ←┚Lb1 4 :H=(E+2I)×90÷πR:M=R sin H+Z[2]:N=R(1-cos H)+Z[1]:O<0=>H=-H⊿H=J+H+W: Goto 5←┚Lb1 5 :P≤A-Z[3]+L-K=> O<0=>N=-N⊿≠=>O>0=>N=-N⊿⊿Goto 6←┚Lb1 6 :X =X+M cos J-N sin J+D cos H:Y =Y+M sin J+N cos J+D sin H“X=”: X ◢“Y=”: Y ◢JF（平曲线反算子程序）Fixm←┚U=X:V=Y:D=0:J=F-W:P=A+(Y-C)cos J-(X-B)sin J←┚Lb1 1:Prog“JP”:J=H-180:I=(V-Y)cos J-(U-X)sin J:Abs I<1E-4=>Goto 2:≠=>P=P+I:Goto 1⊿←┚Lb2: D=(V-Y)÷sinHFY(放样计算子程序)Pol(T-Q,U-S):“HOUSI D=”:I◢J<0=>J=J+360⊿J>360=>J=J-360⊿“HOUSI J=”:J→DMS◢Pol(X-Q,Y-S):“I=”:I◢J<0=>J=J+360⊿J>360=>J=J-360⊿“J=”:J→DMS◢一、程序简介本套程序是共有2个主程序，3个子程序。

电力系统分析电力系统不对称故障的分析和计算PPT课件

)2
I
fa(1)
令
m(1.1)
3
1
(
X
X
ff
ff (0) X ff (2) (0) X ff (2)
)2
则
I
(1.1) f
m(1.1) I
fa(1)
m(1,1)的数值与比值Xff(0)/Xff(2)有关，
其变化范围为1.5 m(1,1) 3 。
（Xff(0)/Xff(2)=1.0时, m(1,1)有极小值1.5。）
(3)当Xff(0)0时，Vfa(0) 0, V fb 与 Vfc 正
好反相，电压的绝对值为
。 3
2
V
(0) f
z(1)=z(2)=zs–zm 如果 z(1)=z(2)=z(0)
z(0)=zs+2zm a 那么 zm=0a
b
三相独
立解耦 Xff(0)由
c
0，非故
XS
Ea Ec XS
Eb XS
XS
XS
I fa(0)
V
(0) f
j( X ff (1) X ff (2) X ff (0) )
Vfa(1)
V (0) f
jX ff (1)I fa(1)
j(X ff (2)
X ff (0) )I fa(1)
单相接地短路
I z(2) fa(2)
I z(0) fa(0)
Vfa(2)
Vfa(0)
单相短路的复合序网
I
fa(2)
X
ff
X
(2)
ff (0)
X
ff
(0)
I
fa(1)
I
fa(0)
X
ff

不完整非对称性曲线线型优化及其坐标计算

螺旋角β
R新 =
J0 W F
∞
ZH 31 新 +4 6 YK
6 .9
6
800 2 = R起
5911 . 7 3 3 1 R=
a
0
原ZH 96.605 5 YK6+
b
1 T0 计算 J W F
T1
HY .605 6 7 7 + 6 YK
c
JD0
图－2
R=1 337
PJ0
JD1
PJ右

e
11
.59
YH YK6 +
虽然设计中提供的参数不同，但是所涉及到的线型是一样，我们所设计优化的过程是一样的。对于此类曲线的优化设计中，曲线测设计算是影响线路平面测设进度和质量的重要因素，而对不完整非对称缓和曲线的设计更是增加了曲线测设坐标计算的难度。 1 概念综述对于不完整非对称性缓和曲线的坐标计算，过去经常采用的方法是用CAXIO－fx5800计算程序将此段曲线分解为多段（至少3段）进行分别计算，且所需的坐标计算要素繁多，输入要素不断变换。

4.2.3 计算恢复完整后平曲线的起算方位角FWJ0及线路偏角PJ0 FWJ0=FWJ计算-β0=132°6′32″－ 1°41′4.19″=130°25′27.81″。 PJ0=PJ 右 +β0=16°37′45″+1°41′4.19″=18°18′49.19″。 4.2.4 计算恢复后平曲线切线长To1和To2 前后半曲线圆曲线内移值为：P01=L01*L01/(24R) －L014/(2688R³ )=3.700 P02=L02*L02/(24R) －L024/(2688R³ )=0.900
YJD -----交点的Y坐标 DKJD -----交点的计算里程 FWJ计算----不完整曲线的起算方位 A1 ------第一缓和曲线参数 A2 ------第二缓和曲线参数 4.2 计算步骤及过程 4.2.1 缓和曲线参数计算第一段缓和曲线完整长度 Lo1=A1*A1/R=678.962/1337.5911=344.639> Lh1=180 第二段缓和曲线完整长度 Lo2=A2*A2/R=476.8502/1337.5911=169.997≈ Lh2=170

3.1不对称缓和曲线加圆曲线逐桩坐标计算讲解

β1 = l1 180 2R π
β2 = l2 180 2R π
主点里程
kZH = K JD T1
K HY K ZH l1
K YH K ZH L l 2
K HZ K ZH L
二、不等长的缓和曲线逐桩坐标计算 1、已知条件： (1)设计文件所给已知条件：
交点坐标及里程、曲线半径R、第一缓和曲线长、第二缓和曲线长、转向角、ZH点切线方位角。
CF DF ( R P2 ) tan
T 1 AJ AG

2
m1

2
m2
P1 P2 sin
P1 P2 sin
T 2 DJ DF
则切线长
l1 l m1 = 2 240R 2
3 1
l1 p1 = 24R
2 2
2
l2 l m2 = 2 240R 2
子情境3：特殊曲线测量
3.1 不等长的缓和曲线+圆曲线逐桩坐标计算
3.1不等长缓和曲线逐桩坐标计算
JD
T1
缓和曲线
T2
圆曲线
直线
ZH
1 l0
HY
YH
缓和曲线
l02
HZ
直线
不等长的缓和曲线+圆曲线通常敷设在地形复杂地
区以及铁路旧线改造中（如图）。其组成为：直线-缓和曲线（A1)-圆曲线-缓和曲线（A2)-直线
X P X HZ x P cos ky P sin P sin ky P cos YP YHZ x
k 1曲线右偏时 K 1曲线左偏时
360 HZ切
(2)地面上的已知条件：
导线点坐标及高程、导线控制点的实际位置。

非完整缓和曲线参数与坐标计算

道路工程测量中非完整缓和曲线参数与坐标计算中建八局第三建设有限公司张涛摘要：在道路工程测量中，非完整缓和曲线的参数、坐标计算和测设是一个常见的难点和重点，掌握其特性及公式推导原理，对从业者非常重要和必要。

关键词：非完整缓和曲线曲线参数计算公式八匝道互通式立交一、概论工程测量学科是一门应用科学，它直接为国民经济建设和国防建设服务，紧密与生产实践相结合。

在大中型建设项目中，工程测量是一项极其重要的、专业性较强的基础性工作。

特别是在道路工程建设中，经常会遇到道路线形较为复杂，线元变化较多的情况，而测量成果的精度高低，直接影响到工程质量的好坏，测量工作的任何一次失误，都可能导致工程施工出现较大的偏差，从而引起工程局部返工甚至报废，并会延误工期，造成巨大地工程损失。

因此，在施工过程中，如何控制好工程测量的施作质量，从而使工程建设顺利优质地完成，是每一个工程测量工作者的首要职责。

当前，全国各地基础设施工程建设快速发展。

在一些高等级公路建设时，既要保证行车的安全性、便捷性和舒适性，保证道路线形平滑流畅，保证道路景观效果，同时又受到地形条件限制，必须最大限度地节约土地资源，所以设计者经常采用较为复杂的平曲线、竖曲线线形设计。

如在作者近期参建的重庆市渝中区环道隧道工程和机场专用快速路工程中，设计者就采用了多条非对称、非完整缓和曲线线形。

特别是机场专用快速路工程的桃子湾互通式立交桥八条匝道（匝道A---匝道H），包含多个非完整缓和曲线线元及小半径（最小半径R=55m）回头曲线。

在上述较为复杂的线形测设中，作者结合非完整缓和曲线特性和理论计算，利用LEICA TS06全站仪后处理软件系统及CASIO fx-5800P计算器，较为精确地进行了施测，计算坐标值与设计逐桩坐标表给定值互差小于2mm。

二、非完整缓和曲线特性及参数计算在直线与圆曲线之间插入的一段半径由∞逐渐变化到R的曲线称做缓和曲线，它的形式有螺旋线（又称回旋线，我国普遍采用）、三次抛物线和双纽线。

浅谈不完整非对称性曲线在高速公路线型控制中的优化应用

浅谈不完整非对称性曲线在高速公路线型控制中的优化应用摘要：针对目前山区高速公路设计中出现的不完整非对称性线型的控制难点，结合现有的工程测量曲线计算理论和在工程实例中的应用，提出一种经过分析处理和优化设计改进后的方法，最终将不完整非对称性的线型计算补强后变得简单易操作，进而为施工现场提供了一种简捷易懂的计算方法。

关键词：不完整非对称性；补强；线型控制0引言在平面线型优化设计中，曲线组合类型比较多，所占线路总长的比例也是很大的。

近年来在山区高速公路曲线设计过程中，传统的曲线设计已经远远不能满足地形复杂的山区公路的选线设计要求，设置不完整非对称曲线来优化保证线路设计参数，进一步满足行车设计需要。

但这种线型的设计给现场施工的线路平面测设进度和质量的控制方面带来较大难度，本文结合现有的工程测量曲线计算理论和在工程实例中的应用，提出一种经过分析处理和优化设计后的改进方法，最终将不完整非对称性的线型计算补强后变得简单易操作。

1山区路段线型选择的技术规定为满足山区公路困难地段线型选择和设计的技术指标的均衡性与连续性，需要满足以下几点：（1）长直线尽头尽量不要接以小半径曲线，特别是在长下坡段尽头。

若由于地形所限小半径曲线难免时，中间应插入中等曲率的过渡性曲线。

使纵坡不应过大。

（2）高、低标准之间要有过渡。

而在高速公路线型设计基本要素中主要由直线、圆曲线、缓和曲线三个要素构成。

《规范》规定，基本型也可以使用非对称性的缓和曲线或者具有不完整性质的曲线特性，以适应周围的地形地物，也即是圆心位置不变而通过调整缓和曲线参数A或者截取一段距离的缓和曲线的方法来实现不完整非对称缓和曲线的设计。

对高速公路线路上不完整非对称性缓和曲线的线型控制，过去常采用的方法是用CAXIO-fx5800计算软件或计算机辅助技术将此段曲线分解为多段（至少3段）进行分别计算，且所需的计算要素繁多，输入要素不断变换。

下面通过对该线型通过一定的方法将该特点进行优化设计，并通过实例对优化设计思路进行透析，从而避免了变换曲线要素所带来的烦琐。

非线性规划基础PPT课件

f
(
xk
tkdk
)
min t 0
f(xk
tdk
)，
令 xk 1 xk tk dk ；k=k+1，转第1步。
第32页/共35页
• 一维搜索的方法很多，归纳起来，可分为试探法和函数逼近法。试探法中包括如黄金分割法、 Fibonacci法等；函数逼近法中包括如牛顿法、割线法等。
第33页/共35页
x (3,1)T
• 例13.6：
是下列优化问题的最优解，验
证x满足Fmrixitnzf-(Jxo) h(nx1定 7理)2 。 (x2 3)2
s.t.gg12((xx))
x12 x1
x22 x2
10 0, 4 0,
g
3
(
x)
x2
0,
第23页/共35页
紧指标集 I={1,2}
f(x)
-
• 在x点取到局部最优值的条件为：F0 G0
g f
i (x)T (x)T
d d
0 0
无解
第21页/共35页
• 定理13.11（Gorden）：
设 A (A1,, Am ), Ai Rn ,i 1,, m ，则Ax<0有解
y( Rm ) 0
的充A分T y必 0要(i 条 1件,为, m：) 不存在非零向量
G {d | d 0, x D, 0, (0, ), x d D}
定理13.6 若f(x)在点 x 可微，如果存在方向d，
使 f (x)T d 0 ，则 0 使 (0, ) 有
f (x d) f (x)
第17页/共35页
一、无约束优化的最优性条件
• 在无约束规划问题中，由于不涉及到可行域的问题，因此，只涉及下降方向。不涉及可行方向的问题。

非对称基本型曲线坐标计算

非对称基本型曲线要素计算
非对称基本型平曲线如图ｌ所示，图
２
、
嘉一，譬譬一
＝
ｌ为第一缓和曲线上任意点至ＺＨ点的曲线长。（）圆曲线（ＹＨ）任意点坐２ＨＹ标：
ｃｏ
中Ｐ，、Ｐ分别为左右两侧曲线的内移值，ｑ、ｑ，分别为左右两侧曲线的切线增值。通过圆心０作与ＪＤ的连线ＯＣ，将四边形ＯＡＣＢ分成两个直角三角形，通过圆心０作左右两侧切线的平行线分别交ＡＣ、ＢＣ
（￡ｓ＋８一）秽｛曲线长．置）ｋ０＋】一∞ ｏ
式中：ｌ为圆曲线上任意点至ＨＹ点的（）第二缓和曲线（３ＨＺ—ＹＨ）任
÷ ＋）ｓｌｓ一９），（Ｅ∞ｋ￣ｏ，】宾０１・０
最ｍｘｃｃ岛越删ｔ鲁
（）第一缓和曲线（１ＺＨ—ＨＹ）任意点坐标：
半径圆曲线时，会突然产生离心力的变化，使行车安全感和舒适受到影响。为了抵消突然产生离心力变化的作用，需要在直线与圆曲线间加设一段半径由无穷大逐渐变化到圆曲线半径（或反之）的缓和曲线。在路线设计中，对于圆曲线，使用时两端的缓和曲线长度取相等值，该组合两端切线长相等，称之为对称基本型曲线；相反，如果圆曲线两端的缓和曲线长度取值不相等，该组合两端切线长不相等，称之为非对称基本型曲线。本文针对非对称基本型曲线的问题，利用非对称基本型曲线交点大地坐标，计算出圆曲线圆心点大地坐标，从而推导出非对称基本型曲线上任意点坐标。

非线性优化算法(韦增欣,陆莎)PPT模板

非线性优化算法(韦增欣，陆莎)
演讲人
2 0 2 X - 11 - 11
01
封面
封面
02
非线性优化算法
非线性优化算法
03
内容简介
内容简介
04
前言
前言
05
第1章引论
第1章引论
1.1引言
1
1.3优化算法结构
1.3.1初始点的选取
1.3.2终止准则
3
1.3.3收敛速度 1.3.4迭代点的产生
牛顿公式
0 2
3.1.2新Ak公
式的性质
0 3
3.1.3三个算法
0 4
3.1.4全局收敛
性分析
0 5
3.1.5超线性收
敛分析
第3章拟牛顿方法
3.2一类非单调BFGS单调BFGS算法
2
3.2.2算法的超线性收敛性
第3章拟牛顿方法
3.3一个新的非单调MBFGS 算法
3.3.1全局收敛性
1
3.3.2超线性收敛
2
08
第4章邻近点方法
第4章邻近点方法
4.1非光滑凸优化的模式算法与收敛性分析 4.2近似方法 4.3求解非光滑凸优化的非单调线搜索Barzilai-Borwein梯度法
第4章邻近点方法
4.1非光滑凸优化的模式算法与收敛性分析
01
4.1.1模式算法
2
1.2数学基础 1.2.1凸集和凸函数 1.2.2最优性条件
4
1.4数值试验
06
第2章共轭梯度法
第2章共轭梯度法
2.1一些基本的共轭梯度法及收敛性质
2.1.1共轭梯度法 2.1.2一些基本共轭梯度法的收敛性分析

不完整缓和曲线坐标算法 (1)

不完整缓和曲线坐标计算式整理修正版（鉴于网络上关于不完整缓和曲线坐标计算的错误公式繁多，特此修正）①如上图所示，以大半径R 1（R 1=r ）建立切线支距坐标系则有:弧长l 处，切线角β=l r ﹢l 22×A 2坐标（X,Y ）计算如下：X=l ﹣l 36×r 2 ﹣l 48×r ×A 2﹣l 540×A 4﹢l 5120×r 4﹢l 672×r 3×A 2﹢l 7112×r 2×A 4﹢l 8384×r ×A 6﹢l 93456×A 8﹢… Y= l 22×r ﹢l 36×A 2﹣l 424×r 3﹣l 520×r 2×A 2﹣l 648×r ×A 4﹣l 7336×A 6﹢l 6720×r 5﹢l 7336×r 4×A 2﹢l 8384×r 3×A 4﹢l 9864×r 2×A 6﹢l 103840×r ×A 8﹢l 1142240×A 10﹢…②以小半径R 2（R 2=r ）建立切线支距坐标系:弧长l 处，切线角β=l r ﹣l 22×A 2坐标（X,Y ）计算如下： X=l ﹣l 36×r 2 ﹢l 48×r ×A 2﹣l 540×A 4﹢l 5120×r 4﹣l 672×r 3×A 2﹢l 7112×r 2×A 4﹣l 8384×r ×A 6﹢l 93456×A 8﹢…Y= l 22×r ﹣l 36×A 2﹣l 424×r 3﹢l 520×r 2×A 2﹣l 648×r ×A 4﹢l 7336×A 6﹢l 6720×r 5﹣l 7336×r 4×A 2﹢ l 8384×r 3×A 4﹣l 9864×r 2×A 6﹢l 103840×r ×A 8﹣l 1142240×A 10﹢…补充：如果嫌输入程序麻烦，下面是现成的C语言代码，复制粘贴即可：/*不完整缓和曲线坐标计算（小半径到大半径）*/void Hxd(double l,double r,double A,double *p,double *q){*p=l-pow(l,3)/(6*r*r)+pow(l,4)/(8*r*A)-pow(l,5)/(40*A*A)+pow(l,5)/(120*pow(r,4))-pow(l, 6)/(72*r*r*r*A)+pow(l,7)/(112*r*r*A*A)-pow(l,8)/(384*r*A*A*A)+pow(l,9)/(3456*pow(A,4));*q=l*l/(2*r)-pow(l,3)/(6*A)-pow(l,4)/(24*r*r*r)+pow(l,5)/(20*r*r*A)-pow(l,6)/(48*r*A*A)+pow( l,7)/(336*A*A*A)+pow(l,6)/(720*pow(r,5))-pow(l,7)/(336*pow(r,4)*A)+pow(l,8)/(384*r*r*r*A*A)-pow(l,9)/(864*r*r*A*A*A)+pow(l,10)/(3840*r*pow(A,4))-pow(l,11)/(42240*pow(A,5));}/*不完整缓和曲线坐标计算（大半径到小半径）*/void Hdx(double l,double r,double A,double *p,double *q){*p=l-pow(l,3)/(6*r*r)-pow(l,4)/(8*r*A)-pow(l,5)/(40*A*A)+pow(l,5)/(120*pow(r,4))+pow(l, 6)/(72*r*r*r*A)+pow(l,7)/(112*r*r*A*A)+pow(l,8)/(384*A*A*A*r)+pow(l,9)/(3456*pow(A,4));*q=l*l/(2*r)+pow(l,3)/(6*A)-pow(l,4)/(24*r*r*r)-pow(l,5)/(20*r*r*A)-pow(l,6)/(48*r*A*A)-pow( l,7)/(336*A*A*A)+pow(l,6)/(720*pow(r,5))+pow(l,7)/(336*pow(r,4)*A)+pow(l,8)/(384*r*r*r*A*A)-pow(l,9)/(864*r*r*pow(A,3))+pow(l,10)/(3840*r*pow(A,4))+pow(l,11)/(42240*pow(A,5));}A=A*A; /*这一条一定要补上，因为上面程序段为了输入简化对A进行了降阶处理，所以要对其还原*/。

创新设计高考政治总复习课件必修第单元课时曲线坐标图专项讲座

第二十二页，共23页。
内容(nèiróng)总结
曲线坐标图专项讲座。1、找出题中的变量与应变量。2、结合书本知识，概括变量与应变量之间的关系。3、运用函数知识，用图像表示变量与应变量之间的关
No 系。价格变动对生产的影响：调节生产规模。区分两个概念(gàiniàn)——需求量和
需求水平。C。2.下列示意图反映的是通常情况下价格与相关因素的关系。1、正确分析每个图像中的变量与应变量分别是谁。3.下面函数图像描述的是某商品在半年中的价格走势，根据该
3.选项分析
A．X为汽车的价格，Y为汽油的需求量
图示反映的是正相
B．X为物价总水平，Y为货币的实际购买关关系。汽车与汽油
力 C．X为居民可支配收入，Y为恩格尔系数
是互补商品，如果汽
D．X为出口额，Y为外汇收入
车的价格上涨，那么，
汽油的需求量会减少；
如果物价总水平上涨，
第十三页，共23页。
经济曲线图解读方法(fāngfǎ) 归纳
示意图中正确反映价格与相关因素关系的是（ C ）
A.①②
B.③④
C.①③
D.①④
①
②
③
④
1、正确分析(fēnxī)每个图像中的变量与应变量分别是谁； 2、分析(fēnxī)错误图像的错误原因；
第二十页，共23页。
3.下面函数图像描述的是某商品在半年中的价格走势，根据该图下列理解正确的是（）C
①该商品很可能处于卖方市场 ②该商品很可能处于买方市场 ③该商品的替代(tìdài)商品需求量会有所减少 ④生产者可能会扩大该商品生产 A．①③ B . ②③ C．①④ D．③④
第十一页，共23页。
三、典例剖析(pōuxī)
➢3.典例剖析

完整及不完整缓和曲线

转载自测量空间！本帖最后由 wenyajun 于 2010-9-30 16:30 编辑关于不同类型缓和曲线的起点、终点曲率半径判断方法目前在匝道或线路施工坐标计算中经常遇到缓和曲线，实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算，这就牵涉到线元的起点终点曲率半径判断的问题，一般的直线元，圆曲线元的起点终点半径判断，比较容易，可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题，缓和曲线有时候判断算对了，有时候却坐标算不对，究其原因，其实问题出于该缓和曲线是否是完整缓和曲线引起的。

关于这点，相关的课本教材上没有明确的讲述，网上对此问题的解释也是散见于不同的论文著作中，对于测量新手来说，线元法程序是非常适用上手的，但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误，的确是件令人恼火的事情，在此我就把自己的判断经验做一论述，给用线元法程序的测友们一同分享，当然高手们请一笑而过，也可留下你的经验与大家一起分享交流学习。

第一：先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的概念问题，以免混为一谈.1.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类；当对于一个单交点内的两段缓和曲线（即常说的第一缓和曲线和第二缓和曲线而言）又有对称缓和曲线与不对称缓和曲线之分。

由此看来，完整与对称与否是针对缓和曲线两个方面来看待区分的。

2.缓和曲线我们的测量教材上讲述的其实就是完整缓和曲线，也可以知道缓和曲线上：各个点的半径是不同的，起点到终点的半径值过度是从正无穷大到所接圆曲线半径之过度如从ZH向HY方向；或者是从所接圆曲线半径值向正无穷大过度的，如从YH向HZ方向。

那么由此可以不难判断出来，完整缓和曲线就是符合上述特征的，那么不完整的缓和曲线就是不符合上述特征的，但是线路上的平曲线设计时候一般缓和曲线不单独存在的，整体上缓和曲线前或后一般都是要连接一个圆曲线的，那么不完整缓和曲线其实就是在完整缓和曲线上截取的一段，一般就是去掉了半径无穷大的那端而是从某个点开始的半径值向所接圆曲线半径值过度的。