公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析
非完整缓和曲线起始点曲率半径问题

非完整缓和曲线起始点曲率半径问题
一、是否为非完整缓和曲线?
用A^2=R*Ls公式来验证
A为已知缓和曲线参数;
R为缓和曲线所接圆曲线的半径;
Ls为已知该段缓和曲线的长度;
当等式成立即为完整缓和曲线,否则即为非完整缓和曲线;
二、非完整缓和曲线起始点曲率半径计算(起点与终点计算方法相同):
1、计算第一线元终点对应的完整缓和曲线长度:
L=A^2/R
2、计算对应的第一线元完整缓和曲线舍弃段的长度L1:
L1=L-L S
3、计算得出第一线元缓和曲线(非完整)起点曲率半径R1:
R1=A^2/L1
A为已知缓和曲线参数;
R为已知缓和曲线所接圆曲线的半径;
Ls为已知该段缓和曲线的长度;
L为计算该段完整缓和曲线的长度;
L1该段完整缓和曲线舍弃段的长度;
R1第一线元缓和曲线起点(非完整)曲率半径。
缓和曲线超高计算

公路缓和曲线知识与计算公式未知2010-04-04 17:34:42 本站一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的 0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , l h=s 则 l h=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,a s= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在 3°—— 29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
圆曲线、缓和曲线计算方法

● 圆曲线方法一:sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二:11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三:180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角,A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段:先由JD1以及JD2的坐标算出JD1到JD2的方位角,即直线段方位角A ,故可算出HZ 、ZH 坐标及其直线段各点坐标。
2、缓和曲线:以HZ 、ZH 为起点,缓和曲线上任意一点离HZ 、ZH 距离为l ,利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标,利用arctan y x算出该点相对起点的方位角B ,再根据线路走向及直线段方位角可算出该点的方位角C (顺时针加,逆时针减),用可求出该点相对起点的距离D ,最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。
(00(,)x y 为缓和曲线起点的坐标)3、圆曲线:用上述方法求出圆曲线两端点HY 、YH 坐标,算出HY 到YH 的方位角F ,以及两点间的距离E ,用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ,根据线路走向求出起点到圆心的方位角H (H=F+/-G ),00(,)x y 圆曲线为起点坐标,根据00cos sin x x R H y y R H=+⎧⎨=+⎩,求出圆心坐标。
公路曲线要素计算公式

公路曲线要素计算公式
公路基本型曲线(回旋缓和曲线)要素及计算公式(FYL)缓和曲线:在直线与圆曲线之间加入一段半径由无穷大逐渐变化到圆曲线半径的曲线,这种曲线称为缓和曲线。
缓和曲线的主要曲线元素有ZH、HY、QZ、YH、HZ 5个主点。
圆曲线内移值P:()m R L P S 242=切线增长值q:)(240223m R L L q S S-=缓和曲线切线长:q P R q T T h++=+=2tan)(α缓和曲线外矢距:R P R E h-+=2sec)(α缓和曲线中曲线总长:s h L R L 2180)2(0+-=πβα缓和曲线中圆曲线长度:180)2(0R L yπβα-=缓和曲线与圆曲线区别:1.因为缓和曲线起始端分别和直线与圆曲线顺滑的相接,因此必须将原来的圆曲线向内移动一段距离才能够接顺,故曲线发生了内移(即设置缓和曲线后有内移值P产生)2.缓和曲线的一部分在直线段,另一部分插入了圆曲线,因此有切线增长值q;3.由于有缓和曲线的存在,因此有缓和曲线角0β:R L S 2/0=β(弧度)=RL Sπ90(度)S L-缓和曲线两端各自的缓和曲线长。
R-缓和曲线中的主圆曲线半径α-偏转角缓和曲线主点桩号:ZH桩号=JD桩号-h THY桩号=ZH桩号+S LQZ桩号=HY 桩号+2yLYH桩号=QZ桩号+2yLHZ桩号=ZH桩号+h L另外、QZ桩号、YH桩号、HZ桩号还可以用以下方式推导:QZ桩号=ZH桩号+2h。
公路缓和曲线原理及缓和曲线计算公式

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
发布日期:2012-01-31 作者:李秋生浏览次数:1494)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路缓和曲线段原理及缓和曲线计算公式

程序使用说明Fx9750、9860系列程序包含内容介绍:程序共有24个,分别是:1、0XZJSCX2、1QXJSFY3、2GCJSFY4、3ZDJSFY5、4ZDGCJS6、5SPJSFY7、5ZDSPFY8、5ZXSPFY9、6ZPJSFY 10、7ZBZFS 11、8JLHFJH 12、9DBXMJJS13、9DXPCJS 14、9SZPCJS 15、GC-PQX 16、GC-SQX17、PQX-FS 18、PQX-ZS 19、ZD-FS 20、ZD-PQX21、ZD-SQX 22、ZD-ZS 23、ZDSP-SJK 24、ZXSP-SJK其中,程序2-14为主程序,程序15-24为子程序。
每个主程序都可以单独运算并得到结果,子程序不能单独运行,它是配合主程序运行所必需的程序。
刷坡数据库未采用串列,因为知道了窍门,数据库看起很多,其实很少。
程序1为调度2-8程序;程序2为交点法主线路(含不对称曲线)中边桩坐标正反计算及极坐标放样程序;程序3为主线路中边桩高程计算及路基抄平程序;程序4为线元法匝道中边桩坐标正反计算及极坐标放样程序;程序5为匝道线路中边桩高程计算及路基抄平程序;程序6为任意线型开口线及填筑边线计算放样程序;程序7专为主线路开口线及填筑边线计算放样程序,只需测量任意一点三维数据,即可马上计算出该点相对于中桩法线上的偏移量;程序8专为匝道线路开口线及填筑边线计算放样程序,只需测量任意一点三维数据,即可马上计算出该点相对于中桩法线上的偏移量;程序9为桥台锥坡计算放样程序;程序10为计算两点间的坐标正反算程序;程序11为距离后方交会计算测站坐标程序;程序12为任意多边形面积周长计算程序;程序13为导线近似平差计算程序;程序14为水准近似平差计算程序;程序2-8所用数据库采用的串列,匝道用的File 1;主线用的File 2。
第一步:先用Excel按照文字说明输入完整条线路对应数据;第二步:保存为CSV格式,然后设置单元格格式、数字格式、科学计数、小数位数设置10位以上并保存;第三步:用FA-124导入,匝道数据列表文件选择“File 1”,主线数据列表文件选择“File 2”。
(建筑工程管理)道路工程测量(圆曲线缓和曲线计算公式)

(建筑工程管理)道路工程测量(圆曲线缓和曲线计算公式)道路工程测量(圆曲线缓和曲线计算公式)内容:理解线路勘测设计阶段的主要测量工作(初测控制测量、带状地形图测绘、中线测设和纵横断面测量);掌握路线交点、转点、转角、里程桩的概念和测设方法;掌握圆曲线的要素计算和主点测设方法;掌握圆曲线的切线支距法和偏角法的计算公式和测设方法;了解虚交的概念和处理方法;掌握缓和曲线的要素计算和主点测设方法;理解缓和曲线的切线支距法和偏角法的计算公式和测设方法;掌握路线纵断面的基平、中平测量和横断面测量方;了解全站仪中线测设和断面测量方法。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§9.1交点转点转角及里程桩的测设道路工程测量概述分为:路线勘测设计测量(routereconnaissanceanddesignsurvey)和道路施工测量(roadconstructionsurvey)。
勘测设计测量(routereconnaissanceanddesignsurvey)分为:初测(preliminarysurvey)和定测(locationsurvey)初测内容:控制测量(controlsurvey)、测带状地形图(topographicalmapofazone)和纵断面图(profile)、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:于选定设计方案的路线上进行路线中线测量(centerlinesurvey)、测纵断面图(profile)、横断面图(cross-sectionprofile)及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
(二)道路施工测量(roadconstructionsurvey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
公路缓和曲线计算公式讲解

公路缓和曲线计算公式讲解公路缓和曲线是指在设计公路线形时为了使车辆在曲线上能够顺利转弯而采用的一种曲线形式。
在公路设计中,缓和曲线的设计是非常重要的,因为它直接关系到车辆在曲线上的安全行驶和舒适性。
在本文中,我们将对公路缓和曲线的计算公式进行详细的讲解,希望能够帮助大家更好地理解和应用这一知识。
一、缓和曲线的类型。
在公路设计中,常见的缓和曲线类型有三种,分别是圆曲线、过渡曲线和螺旋曲线。
圆曲线是一种由圆弧组成的曲线形式,它的曲率是恒定的。
过渡曲线是一种由直线段和圆弧段组成的曲线形式,它的曲率是逐渐变化的。
螺旋曲线是一种由圆弧和直线段交替组成的曲线形式,它的曲率也是逐渐变化的。
在实际的公路设计中,我们需要根据具体的情况选择合适的缓和曲线类型,以确保车辆在曲线上的安全行驶和舒适性。
二、缓和曲线的计算公式。
1. 圆曲线的计算公式。
在公路设计中,圆曲线的计算是非常常见的。
圆曲线的计算公式如下:L = (V^2) / (127R)。
其中,L表示圆曲线的长度(单位,米),V表示车辆的设计速度(单位,公里/小时),R表示圆曲线的半径(单位,米)。
根据这个公式,我们可以计算出圆曲线的长度,从而确定圆曲线的位置和形状。
2. 过渡曲线的计算公式。
过渡曲线是一种由直线段和圆弧段组成的曲线形式,它的计算公式如下:L = (V^2) / (a)。
其中,L表示过渡曲线的长度(单位,米),V表示车辆的设计速度(单位,公里/小时),a表示过渡曲线的加速度(单位,米/秒^2)。
根据这个公式,我们可以计算出过渡曲线的长度,从而确定过渡曲线的位置和形状。
3. 螺旋曲线的计算公式。
螺旋曲线是一种由圆弧和直线段交替组成的曲线形式,它的计算公式比较复杂。
螺旋曲线的计算需要考虑曲线的曲率变化和车辆的行驶轨迹,因此通常需要借助计算机软件来进行精确计算。
三、缓和曲线的设计原则。
在公路设计中,缓和曲线的设计需要遵循一些基本原则,以确保车辆在曲线上的安全行驶和舒适性。
道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
完整及不完整缓和曲线 (1)

关于不同类型缓和曲线的起点、终点曲率半径判断方法目前在匝道或线路施工坐标计算中经常遇到缓和曲线,实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算,这就牵涉到线元的起点终点曲率半径判断的问题,一般的直线元,圆曲线元的起点终点半径判断,比较容易,可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题,缓和曲线有时候判断算对了,有时候却坐标算不对,究其原因,其实问题出于该缓和曲线是否是完整缓和曲线引起的。
关于这点,相关的课本教材上没有明确的讲述,网上对此问题的解释也是散见于不同的论文著作中,对于测量新手来说,线元法程序是非常适用上手的,但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误,的确是件令人恼火的事情,在此我就把自己的判断经验做一论述,给用线元法程序的测友们一同分享,当然高手们请一笑而过,也可留下你的经验与大家一起分享交流学习。
第一:先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的概念问题,以免混为一谈 .1.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类;当对于一个单交点内的两段缓和曲线(即常说的第一缓和曲线和第二缓和曲线而言)又有对称缓和曲线与不对称缓和曲线之分。
由此看来,完整与对称与否是针对缓和曲线两个方面来看待区分的。
2.缓和曲线我们的测量教材上讲述的其实就是完整缓和曲线,也可以知道缓和曲线上:各个点的半径是不同的,起点到终点的半径值过度是从正无穷大到所接圆曲线半径之过度如从 ZH 向 HY 方向;或者是从所接圆曲线半径值向正无穷大过度的,如从 YH 向 HZ 方向。
那么由此可以不难判断出来,完整缓和曲线就是符合上述特征的,那么不完整的缓和曲线就是不符合上述特征的,但是线路上的平曲线设计时候一般缓和曲线不单独存在的,整体上缓和曲线前或后一般都是要连接一个圆曲线的,那么不完整缓和曲线其实就是在完整缓和曲线上截取的一段,一般就是去掉了半径无穷大的那端而是从某个点开始的半径值向所接圆曲线半径值过度的。
缓和曲线)计算公式
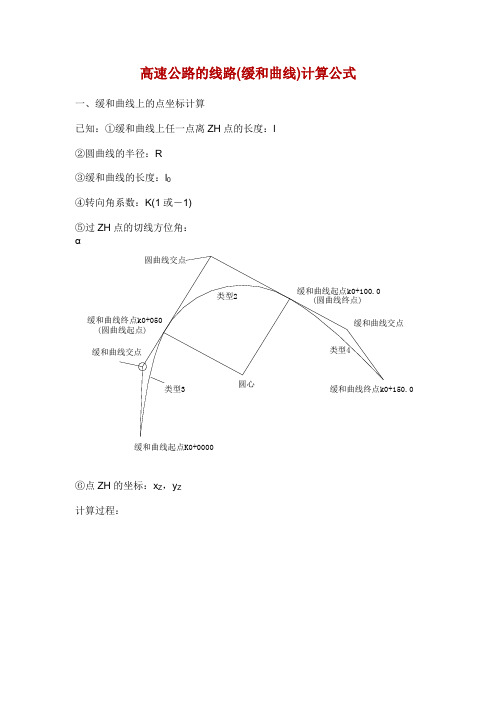
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
缓和曲线和圆曲线的有关计算

缓和曲线和圆曲线的计算与测设一、缓和曲线的性质缓和曲线是直线与圆曲线间的一种过渡曲线。
它与直线分界处半径为∞,与圆曲线相接处半径与圆曲线半径R 相等。
缓和曲线上任一点的曲率半径ρρ∝l1 或ρl=C式中,C 变更率。
当l =0l 时,ρ=R ,所以0Rl =C式中,0l 为缓和曲线总长。
ρl=C 是缓和曲线的必要条件,实用中能满足这一条件的曲线可以作为缓和曲线,如辐射螺旋线、三次抛物线等。
我国缓和曲线均采用辐射螺旋线。
二、缓和曲线方程式按照ρl=C 为必要条件导出的缓和曲线方程为:X=l -2540C l +493456C l +…Y=Cl 63-37336C l +51142240C l + (1)根据测设要求的精度,实际应用中可将高次项舍去,并顾及到0Rl =C ,则上式变为X=l -202540l R l +40493456l R lY=036Rl l -337336l R l (2)式中,x 、y 为缓和曲线上任一点的直角坐标,坐标原点为直缓点(ZH )或缓直点(HZ );通过该点的缓和曲线切线为x 轴,如图2:l 为缓和曲线上任一点P 到ZH (或HZ )的曲线长;0l 为缓和曲线总长度。
当l =0l 时,x=x 0,y=y 0,代入式(2)得:X 0=0l -23040R l+4503456R lY 0=Rl 62-340336Rl (3)式中,x 0 、y 0 为缓圆点(HY )或圆缓点(YH )的坐标。
三、缓和曲线常数计算β0、δ0、m 、p 、 x 0、y 0 等称为缓和曲线常数。
其物理意义及几何关系由下图,图3可得知:β0——缓和曲线的切线角,即HY (或YH )点的切线与ZH (或HZ )点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
δ0——缓和曲线的总偏角;m —切垂距,即ZH (或HZ )到由圆心O 向切线所作垂线垂足的距离; p —圆曲线内移量,为垂线长与圆曲线半径R 之差。
公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析
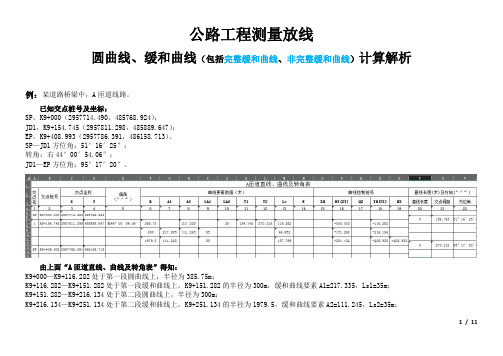
公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线)计算解析例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714.490,485768.924);JD1,K9+154.745(2957811.298,485889.647);EP,K9+408.993(2957786.391,486158.713)。
SP—JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″。
由上面“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151.282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282—K9+216.134处于第二段圆曲线上,半径为300m;K9+216.134—K9+251.134处于第二段缓和曲线上,K9+251.134的半径为1979.5,缓和曲线要素A2=111.245,Ls2=35m;1 / 11K9+251.134—K9+408.933处于第三段圆曲线上,半径为1979.5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算的计算公式,就可以直接求出未知点的坐标。
那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。
下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
2 / 113 / 11y 轴。
过圆曲线上任意点P 的切线与ZY —JD 相交,夹角(切线角)为β,ZY —P 与ZY —JD 的夹角(弦切角)为α,ZY —P 的弧长为L ,ZY —P 的直线距离为d ,圆曲线的半径为R 。
缓和曲线长度计算公式

缓和曲线长度计算公式
1缓和曲线(Horizontal Curve)
缓和曲线(Horizontal Curve)是指在道路曲线设计中,既要满足视距要求,又要满足最小转弯半径等安全要求的曲线。
它包括各种圆弧和椭圆曲线。
曲线体系是构成道路设计、规划和施工的重要一环,它能减少驾驶员的视距,同时能增加可用轨道宽度。
2缓和曲线长度计算
缓和曲线长度的计算可以用三种椭圆曲线公式来完成,即Purvisky贴合曲线(Purvisky tangent Curve)、Stull抛物线(Stull Parabolic Curve)和Camelback立体线(Camelback Vertical Curve)。
缓和曲线长度的计算并不是一个十分复杂的过程,可以按照以下几个步骤简单地计算:
(1)计算曲线横坡。
主要参数含义分别为曲线中心角、曲线中心距、曲线转角以及曲线上两端的交叉距离;
(2)根据横坡、曲线中心角和交叉距离,通过上述三种不同的椭圆公式来计算曲线长度。
(3)计算曲线长度时,若范围较大,需要将曲线分成多段,重复(2)步骤对每一段曲线分别计算,最后累加结果和得出最终的缓和曲线长度。
3总结
缓和曲线(Horizontal Curve)是道路曲线设计中重要的一环,能达到视距要求和最小转弯半径安全要求,它包括各种圆弧和椭圆曲线。
由于椭圆曲线的复杂性,缓和曲线长度的计算并不是一个复杂的过程,通常应该按照横坡、曲线中心角和交叉距离等参数来进行,再通过Purvisky贴合曲线、Stull抛物线和Camelback立体线三种不同的椭圆公式来实现。
高速公路线路缓和曲线竖曲线圆曲线匝道坐标计算公式

高速公路线路缓和曲线、竖曲线、圆曲线、匝道坐标计算公式_★★高速公路的一些线路坐标、高程计算公式缓和曲线、竖曲线、圆曲线、匝道一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K1或-1⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K1或-1⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度或缓曲上任意点到缓曲起点的长度l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1上坡为“+”,下坡为“-”②第二坡度:i2上坡为“+”,下坡为“-”③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点过渡段终点的距离:x求:待求处的横坡:i解:d=x/Li=i2-i11-3d2+2d3+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0左转为“-”,右转为“+”⑦曲线终点处曲率:P1左转为“-”,右转为“+”求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgnx函数是取符号函数,当x<0时sgnx=-1,当x>0时sgnx=1,当x=0时sgnx=0;在计算器中若无此函数可编一个小子程序代替;转载自:。
缓和曲线

关于缓和曲线的见解我国公路与铁路均使用回旋线作为缓和曲线,回旋线的几何意义是:曲线上任意点P的曲率半径ρ与该点至ZH的曲线长L成反比,曲线方程式为ρ=A2/L,即A=√Ls*R。
其余曲线要素值有:圆曲线内移值P, 切线增量q, 切线长T, 回旋线在P点的偏角β;缓和曲线的计算式祥见5800《书3-公路与铁路施工测量程序》公路与铁路施工测量程序(10022),33-35页。
以实例及图比较容易看懂。
所有线形按其形式可分直线、圆曲线、缓和曲线、单交点对称型曲线、单交点非对称型曲线、S型曲线、C型曲线、卵形曲线、凸型曲线、复曲线、回头曲线等。
缓和曲线根据设计给定参数方法的不同,可按交点法和线元法进行计算。
交点法与线元法都需要缓和曲线参数A(线元法一般给定缓和曲线长,则A=√(LS*R),),与圆曲线半径R,其余所需已知数据差异为:交点法需要已知1、JDn的桩号与坐标,2、JDn-1的坐标,3、JDn 的转角Δn或JDn+1的坐标。
线元法(即积木法)需要已知1、ZH、HY、YH、HZ的桩号及坐标,2、走向方位角。
实例:交点法给定参数形式如FX-5800公路高铁测量程序里面C匝道的参数数据,线元法给定参数形式如FX-5800公路高铁测量程序里面D、E、F匝道的线元数据(一)直线主要控制参数为直线段起点桩号,坐标,方位角。
(二)一般曲线一般曲线主要包括圆曲线、完整缓和曲线、单交点对称型曲线、单交点非对称型曲线:1、圆曲线主要组合为圆曲线起点~圆曲线上任一点。
2、完整缓和曲线与非完整缓和曲线主要组合为ZH(HZ)起点~缓和曲线上任一点。
“完整缓和曲线”是指起点直缓点或缓直点已知的缓和曲线,“非完整缓和曲线”是指起点直缓点或缓直点未知,仅知道缓和曲线上的任意一点或两点的缓和曲线,计算时需推算缓和曲线起点。
“非完整缓和曲线”与“完整缓和曲线”的区别,如上图,QD与ZD为非完整缓和曲线与其它线元相连接的两端点,QD(起点)为桩号较小的端点,ZD(终点)为桩号较大的端点,有R2不等于0为非完整缓和曲线(即实际缓和曲线长L1为Ls的一部分A2 /R=Ls),R2等于0就为完整缓和曲线。
道路工程测量(圆曲线缓和曲线计算公式)

道路工程测量( 圆曲线缓和曲线计算公式)内容:理解线路勘测设计阶段的主要测量工作 (初测控制测量、带状地形图测绘、中线测设和纵横断面测量);掌握路线交点、转点、转角、里程桩的概念和测设方法;掌握圆曲线的要素计算和主点测设方法;掌握圆曲线的切线支距法和偏角法的计算公式和测设方法;了解虚交的概念和处理方法;掌握缓和曲线的要素计算和主点测设方法;理解缓和曲线的切线支距法和偏角法的计算公式和测设方法;掌握路线纵断面的基平、中平测量和横断面测量方;了解全站仪中线测设和断面测量方法。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法—难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§ 9.1交点转点转角及里程桩的测设一、道路工程测量概述 6 x:分为:路线勘测设计测量(route reconnaissance and design survey) 和道路施工测量(road construction survey) 。
(一)勘测设计测量(route reconnaissance and design survey)分为:初测(preliminary survey) 和定测(location survey)1 、初测内容:控制测量(control survey) 、测带状地形图(topographical map of a zone)和纵断面图(profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、2、定测内容:在选定设计方案的路线上进行路线中线测量(center line survey) 、测纵断面图(profile) 、横断面图(cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
[整理]圆曲线缓和曲线计算公式
![[整理]圆曲线缓和曲线计算公式](https://img.taocdn.com/s3/m/95863d5910661ed9ac51f31d.png)
圆曲线缓和曲线计算公式内容:理解线路勘测设计阶段的主要测量工作(初测控制测量、带状地形图测绘、中线测设和纵横断面测量);掌握路线交点、转点、转角、里程桩的概念和测设方法;掌握圆曲线的要素计算和主点测设方法;掌握圆曲线的切线支距法和偏角法的计算公式和测设方法;了解虚交的概念和处理方法;掌握缓和曲线的要素计算和主点测设方法;理解缓和曲线的切线支距法和偏角法的计算公式和测设方法;掌握路线纵断面的基平、中平测量和横断面测量方;了解全站仪中线测设和断面测量方法。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§ 9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为:路线勘测设计测量(route reconnaissance and design survey) 和道路施工测量(road construction survey) 。
(一)勘测设计测量(route reconnaissance and design survey)分为:初测(preliminary survey) 和定测(location survey)1、初测内容:控制测量(control survey) 、测带状地形图(topographical map of a zone) 和纵断面图(profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、定测内容:在选定设计方案的路线上进行路线中线测量(center line survey) 、测纵断面图(profile) 、横断面图(cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
(二)道路施工测量(road construction survey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线)计算解析例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714.490,485768.924);JD1,K9+154.745(2957811.298,485889.647);EP,K9+408.993(2957786.391,486158.713)。
SP—JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″。
.由上面“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151.282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282—K9+216.134处于第二段圆曲线上,半径为300m;K9+216.134—K9+251.134处于第二段缓和曲线上,K9+251.134的半径为1979.5,缓和曲线要素A2=111.245,Ls2=35m;K9+251.134—K9+408.933处于第三段圆曲线上,半径为1979.5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算.的计算公式,就可以直接求出未知点的坐标。
那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。
下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
..圆曲线:建立圆曲线直角坐标系,以起点直圆ZY 的切点方向(也是直圆ZY 至交点JD 的方向)作为x 轴,以过直圆ZY 垂直于直圆ZY 切线的方向作为y 轴。
过圆曲线上任意点P 的切线与ZY —JD 相交,夹角(切线角)为β,ZY —P 与ZY —JD 的夹角(弦切角)为α,ZY —P 的弧长为L ,ZY —P 的直线距离为d ,圆曲线的半径为R 。
那么,α=RL2(弧度) 【注:这里计算出来的α是弧度,不是以度分秒表示的角度,转化为角度,需要换算,换算公式为,1(弧度)=π180︒(度)】所以如果以度表示,那么α=R L2×π180︒; 弦切角等于切线角的一半,所以β=2α; ZY 到P 的直线距离为:d=2Rsin α;ZYJDOPL d αβxyYZ.缓和曲线:建立缓和曲线直角坐标系,以起点直缓ZH 的切点方向(也是直缓ZH 至交点JD 的方向)作为x 轴,以过直缓ZH 垂直于直缓ZH 切线的方向作为y 轴。
过缓和曲线上任意点P 的切线与ZH —JD 相交,夹角(切线角)为β,ZH —P 与ZH —JD 的夹角(弦切角)为α,ZH —P 的弧长为L , L s 为缓和曲线起点ZH —缓和曲线终点HY 的里程,ZH —P 的直线距离为d ,R 为缓和曲线终点HY 点处的圆曲线半径。
那么,缓和曲线参数:A=s ·L R; β=s 22RL L 转化为角度为β=s 22RL L ×π180︒;当L=L s 时,β=R L 2s ×π180︒; α=31β; 在完整的缓和曲线坐标系中,缓和曲线上任一点P 的坐标为(x ,y ),则缓和曲线的参数方程为:x = L -2s 2540L R L +4s 493456L R L -6s 613599040L R L y =s 36RL L -3s 37336L R L +5s 51142240L R L -7s7159676800L R L 当L=L s 时,则缓和曲线终点HY 点或YH 点 坐标(x 0,y 0)为:ZHJDOPL dαβxyHY Rx 0= s L -23s 40RL +45s 3456R L -67s599040R L y 0=R L 62s -34s 336R L +56s 42240R L -78s9676800RL ZH 到P 的直线距离为:d=22y x ;935°17′20″K 9+000X =2957714936.391.713.分析:首先,从主线示意图上可以看出,这条线路是具有多段圆曲线和非完整缓和曲线组成的线路。
在计算时,需要分开推算,圆曲线段用圆曲线的推到公式计算,缓和曲线段用缓和曲线的推到公式计算。
我们需要计算的桩号为K9+130,K9+200,K9+230,K9+300,这四个桩号分别处于第一段缓和曲线,第二段圆曲线,第二段缓和曲线,第三段圆曲线上,需要注意的是,这里的缓和曲线是非完整缓和曲线。
【注意:一定要清楚,缓和曲线是从半径为+∞—R 。
】 解:① ,求K9+130的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
K9+130在第一段非完整缓和曲线上,在第一段圆曲线,我们只需要计算出K9+116.282的中桩坐标和切线方位角。
由于是圆曲线,且已知起止桩号、半径、K9+000—JD 的方位角,K9+000的坐标,所以计算非常简单。
K9+000的坐标为(2957714.490,485768.924),L=116.282,R=385.75,K9+000—JD 的方位角为51°16′25″,由圆曲线的相关公式推导, α=R L 2×π180=8°38′8.64″ K9+000—K9+116.282的方位角为: F=51°16′25″+α51°16′25″K9+116.282βαL d=59°54′33.64″K9+000—K9+116.282的距离为:d=2Rsinα=115.842K9+116.282的坐标为:X=2957714.490+d×cosF=2957772.570Y=485768.924+d×sinF=485869.154【利用坐标正算公式直接计算即可,这里不在推导。
】K9+116.282的切线方位角为:=51°16′25″+βF切=51°16′25″+2α=68°32′42.28″【注:我们推导下一段缓和曲线的时候,需要用到K9+116.282的坐标和切线方位角。
】在完整缓和曲线的计算中,通常以直线线元与缓和曲线线元衔接点(ZH点)为原点建立平面直角坐标系进行计算,而非完整缓和曲线只是完整缓和曲线中的一段,其与上一线元的衔接点并非是ZH点,而是缓和曲线上的任意一点,也就是说它的起点半径不是∞,而是一个具体的数值,其曲率半径变化时由R1到R2(R1>R2),但是它仍然是回旋线,所以仍具有回旋线的一切特性。
要解决非完整缓和曲线的计算问题,可以将其.一端延伸至曲率半径为∞的ZH 点处,将其转换为相对应的完整缓和曲线,然后通过相应的坐标转换,就可以计算出非完整缓和曲线上任意里程的坐标数据了。
如图1所示:已知第一段缓和曲线要素A1=217.335,起点曲率半径为R1=385.75,终点曲率半径为R2=300,且R1>R 2,非完整缓和曲线长Ls=35m ,将其曲率半径较大的一端O1(K9+116.282)端顺延至曲率半径为∞的O 处,形成完整缓和曲线,就可以完整缓和曲线公式来推导非完整缓和曲线计算公式了。
图中:eO 至O 1(K9+116.282)缓和曲线长为: L S1= A 2R 1=122.448O 至O 2(K9+151.282)缓和曲线长为: L S2=A 2R 2=157.448O 1至O 2非完整缓和曲线长为:L S = L S2− L S1=35我们要推算K9+130的中桩坐标,需要先推算出在完整缓和曲线中O 点的坐标和切线方位角。
所以需要先算出K9+116.282—O 点方位角和距离d1。
β1=s221s 2RL L ×π180=9°5′37.09″ 82.28″.α1=31β1=3°1′52.36″K9+116.282—O 点方位角为: F=68°32′42.28″+180°-γ =68°32′42.28″+180°-(β1-α1) =242°28′57.55″K9+116.282—O 点距离d1为: d1=22y x =122.311(x ,y 可由缓和曲线的参数方程x = L -2s 2540L R L +4s 493456L R L -6s 613599040L R L ,y =s 36RL L -3s 37336L R L +5s 51142240L R L -7s7159676800L R L 推导出来) 所以:O 点的坐标为(2957716.060,485760.680),O 点的切线方位角为68°32′42.28″-β1=59°27′5.19″;要计算K9+130的中桩及边桩坐标,需要计算出O 点到K9+130的方位角和距离d2,以及K9+130的切线方位角。
.O 点到K9+130的弧长为L=(9130-9116.282)+122.448=136.166β2=s222RL L ×π180︒=11°14′43.13″α2=31β2=3°44′54.38″O 点到K9+130的方位角为:F=59°27′5.19″+α2=63°11′59.57″ O 点到K9+130的距离d2为:d 2=22y x +=135.933(方法同上,此处不再列出计算过程) K9+130的中桩坐标为:(2957777.349,485882.012) K9+130的切线方位角为: F 切=59°27′5.19″+β2 =70°41′48.32″【推算切线方位角,是为了后面推算边桩方位角做铺垫。
】 K9+130左侧5米边桩方位角为: F 左= F 切-90°82=70°41′48.32″-90°=-19°18′11.68″这里计算出来的边桩方位角为负数,所以我们需要加上360°,所以,F左=340°41′48.32″,K9+130左侧5米边桩坐标为:(2957782.068,485880.359);K9+130右侧10米边桩方位角为:F右= F切+90°=70°41′48.32″+90°=160°41′48.32″K9+130右侧10米边桩坐标为:(2957767.911,485885.318)..②,求K9+200的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
