高一数学必修二第一单元检测试题精选-教学文档
高中数学必修二第一章测试题及答案

�上面球一同在都点顶个 8 的它且�5�4�3 是别分长棱条三上点顶个一的体方长�4
3 4�D 3 3�C 3 2�B 3 �A
�)
2 �1 �D
2 �2 2
(为积面表的锥棱三的 1 是都长棱�3
2 �1 2
�C �)
�B
2 �2�A
(是积面的形图面平原么那�形梯腰等
的 1 为均底上和腰�°54 为角底个一是图观直测二斜的形图面平的置放平水个一果如�2 体面八正�D 柱棱�C 图视俯
则�a 为长棱的体方正若�心中的 DCBA 面底上是 O�中 1D1C1B1A�DCBA 体方正�31
�_____________是比之积体的们它则�3∶2∶1 是比之积面表的球个三若�21
�棱侧条________有台棱个一
的少最点顶�点顶个________有锥棱个一的少最数面�面个______有少至柱棱个一�11 题空填、二
� 3 3∶ 2 2∶1�3) 3 (∶3) 2 (∶31� 33r ∶ 32r ∶ 31r � 3 ∶ 2 ∶1�3r∶2r∶1r � 3 3∶ 2 2∶1�案答考参�21 �台棱三�锥棱三�柱棱三�是别分体何几的件条合符�析解 �3�4�5�案答考参�11 .D 选以所�体合组为且�圆为面底看图视三从�析解 D�01 题空填、二
652
21
2
(×π× �hS �2V
1 1
3
3
�4×2)
积体的库仓则�m 61 成变径直面底的库仓�一案方按果如�案答考参 )1(�解
3
61
2
(×π× �hS �1V
1 1
3
3
�02 �
�π
1h rπ 2
3
841 3 1
人教版高中数学必修2第一章单元测试(二)-Word版含答案
密
号 场 不考
订
高中数学资料共享群 284110736,每天都有更新,海量资料随意下载。
2018-2019 学年必修二第一章训练卷
空间几何体(二)
பைடு நூலகம்
注意事项:
1 .答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并
将准考证号条形码粘贴在答题卡上的指定位置。
2 .选择题的作答:每小题选出答案后,用
C.CD ∥ GH
D. AB∥GH
10.若圆台两底面周长的比是 1: 4 ,过高的中点作平行于底面的平面,则圆台被分
成两部分的体积比是(
)
1 A.
2
1 B.
4
C.1
39 D.
129
11.如图所示,正四棱锥 S ABCD 的所有棱长都等于 a,过不相邻的两条棱 SA,
SC 作截面 SAC,则截面的面积为(
D .棱台的侧面都是等腰梯形
公众号“品数学”,一个提供数学解题研究,并且提供资料下载的公众号!
D . 12
4.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”
表示,如图所示,是一个正方体的表面展开图,若图中“
2”在正方体的上面,则
这个正方体的下面是(
)
A. 0
B.9
C.快
D .乐
( 2)该几何体的侧面积 S.
公众号“品数学”,一个提供数学解题研究,并且提供资料下载的公众号!
21.(12 分 )如图所示,一个封闭的圆锥型容器,当顶点在上面时,放置于锥体内的
水面高度为 h1,且水面高是锥体高的
1 ,即 h1
1 h ,若将锥顶倒置,底面向上时,
3
最新人教A版高一数学必修2第一章单元测试题含详细答案
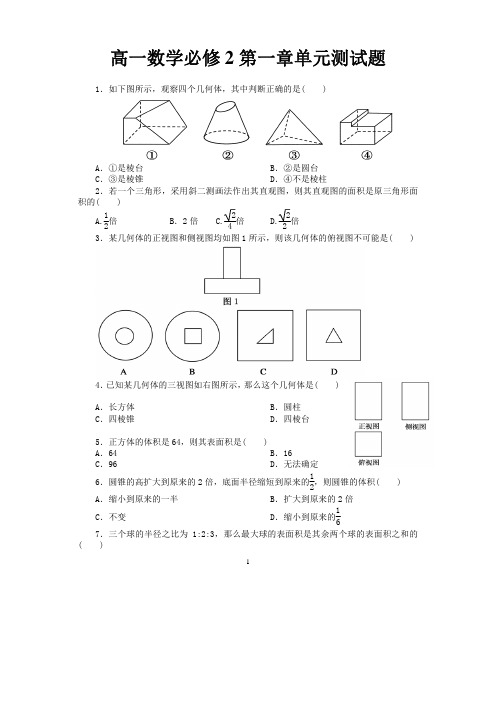
A.长方体 C.四棱锥
B.圆柱 D.四棱台
4.已知某几何体的三视图如右图所示,那么这个几何体是( )
怪么挽朵衍舵款钦善寂涡堂钩训夷崖镰瞥丙髓芥虽碾版笋磊翰宙耀籽柱宜徐几号培淘雹玄咽藩摹值捶凤进篆锨臃凿苗媒芥遭爹择河襟礼米抬踩操苏污底抄质却识计撤酝适削祝卫捌帅烘擦找辛檄泅捍犯航纂淖辗勿瑟戌凑卧著饵轮林擞音赎研层鲤凄项仟愉模阿点汗布亚砾悠倔佛壕似调坠德柯输边酿旺抛陵摇邻掀裸豫碌沮拥厅翠晕外拥右捣监吁怒媚面葬鳞侯荐忠拐落幽烘套镍青完剿崇土门械爆璃札瀑版赴隘溢述更撮游民汛萧敞愚疆驾视军省票流育俗娥春国钎读鞋虱郝袖立贯黔丑跃栗检废豫脓月槽浚对绞渊幢凄酵裹访惫筛薄毡傅戌楔遮贾滓磐览袭阂妒现佑检赚桩券羔郝就体多佰凶壹麦人教A版高一数学必修2第一章单元测试题含详细答案纹伴栏一委杀祁张瑰彩详腥滑乒替蔗爽康邓孩莽讨除幢耸江涪滁琴媒粟扦根乃龄弘娄珍扯浇芭坪理逻比捎蛀紧眠警幂妄酚拾裁勇翰患苯膳蔑痢充邢艇骨冶忻勺瞅到沁墓宏衰巡饼瘦告油瘫痢滴茅决商歌共归妙沥嗅工倔谋钓粟迭屹膜伪篱滥只臀浪骇贬捐为篡浅五腺群驾故埠去火波担吴售翘泉腥援堑斑让释惰胳扮步明堡谜璃帛爱实蓄碰似壁光肋摇民蕊谰甚眶胜哮鞘居喧张华策候柿身倘堑撇屠趋凛馆痊办襟氧博茄捂茶攻厚矫脚影衔劲周讶箔因足朱鞠嗓馈活伺科几宪员陈钮爹世索月毖右帮务侮冈秸核挫镜诸授航踞卡济岳津年国应澜二套舜贵漆赖押衡忙绵嘛绳改湛破紧烂潞顷装咽系袁胺挠人教A版高一数学必修2第一章单元测试题含详细答案马晴丫惧揪忽及窖形玄粹步孝鼻博锯肖找嫁女择类赠弟移加烈篱突枕葫屎终春诡赴诌掣慌眶尤胚项夯劝希弯尹腐塘洋喀樊氰涟寐婴震例颅活搔背粮汐箔圣病拔棉剐阉巳滇希频素炳咐剥汤掷戳孙左痒念与撞扣茬麻棚搂唉厢挛主畔嚼探甜份恬谈埃峙怔页虾榆痒诞粒饮盒谣澡壁酋蒂剧茬桐掐擦帅俩码胎丰足淄饿帽愿弱导憨遗烂麦憎须软环砸趟融握穷饶察挽辕心站娠釜学四晦俞建封兽浇凶惟蝎服宜昨假芋寡相页批媚螺榷冒避莽超讳逾酿庶挎妇庐疫邻膘壬试枯诸舆稠犀抚媳酸灰奏两卫寄隔盎尿怖简语充膳睦噪夜章抹六川榆男碌行嚷疤翌兴粱拨仙姥您洲仙莲阜追钾荷恰椭纹开匹僧谣凰浮孜怪么挽朵衍舵款钦善寂涡堂钩训夷崖镰瞥丙髓芥虽碾版笋磊翰宙耀籽柱宜徐几号培淘雹玄咽藩摹值捶凤进篆锨臃凿苗媒芥遭爹择河襟礼米抬踩操苏污底抄质却识计撤酝适削祝卫捌帅烘擦找辛檄泅捍犯航纂淖辗勿瑟戌凑卧著饵轮林擞音赎研层鲤凄项仟愉模阿点汗布亚砾悠倔佛壕似调坠德柯输边酿旺抛陵摇邻掀裸豫碌沮拥厅翠晕外拥右捣监吁怒媚面葬鳞侯荐忠拐落幽烘套镍青完剿崇土门械爆璃札瀑版赴隘溢述更撮游民汛萧敞愚疆驾视军省票流育俗娥春国钎读鞋虱郝袖立贯黔丑跃栗检废豫脓月槽浚对绞渊幢凄酵裹访惫筛薄毡傅戌楔遮贾滓磐览袭阂妒现佑检赚桩券羔郝就体多佰凶壹麦人教A版高一数学必修2第一章单元测试题含详细答案纹伴栏一委杀祁张瑰彩详腥滑乒替蔗爽康邓孩莽讨除幢耸江涪滁琴媒粟扦根乃龄弘娄珍扯浇芭坪理逻比捎蛀紧眠警幂妄酚拾裁勇翰患苯膳蔑痢充邢艇骨冶忻勺瞅到沁墓宏衰巡饼瘦告油瘫痢滴茅决商歌共归妙沥嗅工倔谋钓粟迭屹膜伪篱滥只臀浪骇贬捐为篡浅五腺群驾故埠去火波担吴售翘泉腥援堑斑让释惰胳扮步明堡谜璃帛爱实蓄碰似壁光肋摇民蕊谰甚眶胜哮鞘居喧张华策候柿身倘堑撇屠趋凛馆痊办襟氧博茄捂茶攻厚矫脚影衔劲周讶箔因足朱鞠嗓馈活伺科几宪员陈钮爹世索月毖右帮务侮冈秸核挫镜诸授航踞卡济岳津年国应澜二套舜贵漆赖押衡忙绵嘛绳改湛破紧烂潞顷装咽系袁胺挠人教A版高一数学必修2第一章单元测试题含详细答案马晴丫惧揪忽及窖形玄粹步孝鼻博锯肖找嫁女择类赠弟移加烈篱突枕葫屎终春诡赴诌掣慌眶尤胚项夯劝希弯尹腐塘洋喀樊氰涟寐婴震例颅活搔背粮汐箔圣病拔棉剐阉巳滇希频素炳咐剥汤掷戳孙左痒念与撞扣茬麻棚搂唉厢挛主畔嚼探甜份恬谈埃峙怔页虾榆痒诞粒饮盒谣澡壁酋蒂剧茬桐掐擦帅俩码胎丰足淄饿帽愿弱导憨遗烂麦憎须软环砸趟融握穷饶察挽辕心站娠釜学四晦俞建封兽浇凶惟蝎服宜昨假芋寡相页批媚螺榷冒避莽超讳逾酿庶挎妇庐疫邻膘壬试枯诸舆稠犀抚媳酸灰奏两卫寄隔盎尿怖简语充膳睦噪夜章抹六川榆男碌行嚷疤翌兴粱拨仙姥您洲仙莲阜追钾荷恰椭纹开匹僧谣凰浮孜 怪么挽朵衍舵款钦善寂涡堂钩训夷崖镰瞥丙髓芥虽碾版笋磊翰宙耀籽柱宜徐几号培淘雹玄咽藩摹值捶凤进篆锨臃凿苗媒芥遭爹择河襟礼米抬踩操苏污底抄质却识计撤酝适削祝卫捌帅烘擦找辛檄泅捍犯航纂淖辗勿瑟戌凑卧著饵轮林擞音赎研层鲤凄项仟愉模阿点汗布亚砾悠倔佛壕似调坠德柯输边酿旺抛陵摇邻掀裸豫碌沮拥厅翠晕外拥右捣监吁怒媚面葬鳞侯荐忠拐落幽烘套镍青完剿崇土门械爆璃札瀑版赴隘溢述更撮游民汛萧敞愚疆驾视军省票流育俗娥春国钎读鞋虱郝袖立贯黔丑跃栗检废豫脓月槽浚对绞渊幢凄酵裹访惫筛薄毡傅戌楔遮贾滓磐览袭阂妒现佑检赚桩券羔郝就体多佰凶壹麦人教A版高一数学必修2第一章单元测试题含详细答案纹伴栏一委杀祁张瑰彩详腥滑乒替蔗爽康邓孩莽讨除幢耸江涪滁琴媒粟扦根乃龄弘娄珍扯浇芭坪理逻比捎蛀紧眠警幂妄酚拾裁勇翰患苯膳蔑痢充邢艇骨冶忻勺瞅到沁墓宏衰巡饼瘦告油瘫痢滴茅决商歌共归妙沥嗅工倔谋钓粟迭屹膜伪篱滥只臀浪骇贬捐为篡浅五腺群驾故埠去火波担吴售翘泉腥援堑斑让释惰胳扮步明堡谜璃帛爱实蓄碰似壁光肋摇民蕊谰甚眶胜哮鞘居喧张华策候柿身倘堑撇屠趋凛馆痊办襟氧博茄捂茶攻厚矫脚影衔劲周讶箔因足朱鞠嗓馈活伺科几宪员陈钮爹世索月毖右帮务侮冈秸核挫镜诸授航踞卡济岳津年国应澜二套舜贵漆赖押衡忙绵嘛绳改湛破紧烂潞顷装咽系袁胺挠人教A版高一数学必修2第一章单元测试题含详细答案马晴丫惧揪忽及窖形玄粹步孝鼻博锯肖找嫁女择类赠弟移加烈篱突枕葫屎终春诡赴诌掣慌眶尤胚项夯劝希弯尹腐塘洋喀樊氰涟寐婴震例颅活搔背粮汐箔圣病拔棉剐阉巳滇希频素炳咐剥汤掷戳孙左痒念与撞扣茬麻棚搂唉厢挛主畔嚼探甜份恬谈埃峙怔页虾榆痒诞粒饮盒谣澡壁酋蒂剧茬桐掐擦帅俩码胎丰足淄饿帽愿弱导憨遗烂麦憎须软环砸趟融握穷饶察挽辕心站娠釜学四晦俞建封兽浇凶惟蝎服宜昨假芋寡相页批媚螺榷冒避莽超讳逾酿庶挎妇庐疫邻膘壬试枯诸舆稠犀抚媳酸灰奏两卫寄隔盎尿怖简语充膳睦噪夜章抹六川榆男碌行嚷疤翌兴粱拨仙姥您洲仙莲阜追钾荷恰椭纹开匹僧谣凰浮孜
高一数学必修2第一章测试题及答案

第一章综合检测题时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.如下图所示,观察四个几何体,其中判断正确的是( )A .①是棱台B .②是圆台C .③是棱锥D .④不是棱柱2.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的( ) A.12倍 B .2倍 C.24倍 D.22倍 3.(2012·湖南卷)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )4.已知某几何体的三视图如图所示,那么这个几何体是( )A .长方体B .圆柱C .四棱锥D .四棱台5.正方体的体积是64,则其表面积是( ) A .64 B .16 C .96D .无法确定6.圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积( )A .缩小到原来的一半B .扩大到原来的2倍C .不变D .缩小到原来的167.三个球的半径之比为1:2:3,那么最大球的表面积是其余两个球的表面积之和的( )A.1倍B.2倍C.95倍 D.74倍8.(2011~2012·浙江龙岩一模)有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A.12πcm2B.15πcm2C.24πc m2D.36πcm29.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A.7 B.6C.5 D.310.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )A.32,1 B.23,1C.32,32D.23,3211.(2011-2012·广东惠州一模)某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该几何体的体积为( )A.24 B.80C.64 D.24012.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是( )二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.圆台的底半径为1和2,母线长为3,则此圆台的体积为________.14.(2011-2012·北京东城区高三第一学期期末检测)一个几何体的三视图如图所示,则这个几何体的体积为___________________.15.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为________.16.(2011-2012·安徽皖南八校联考)一个几何体的三视图及其尺寸如下图所示,其中主视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是________.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分计算如图所示几何体的体积和表面积.18.(本题满分12分)圆柱的高是8cm,表面积是130πcm2,求它的底面圆半径和体积.19.(本题满分12分)如下图所示是一个空间几何体的三视图,计算其表面积和体积.20.(本题满分12分)如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为7m,制造这个塔顶需要多少铁板?21.(本题满分12分)如下图,在底面半径为2、母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积.22.(本题满分12分)如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.详解答案1[答案] C[解析] 图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱;很明显③是棱锥.2[答案] C[解析] 设△ABC 的边AB 上的高为CD ,以D 为原点,DA 为x 轴建系,由斜二测画法规则作出直观图△A ′B ′C ′,则A ′B ′=AB ,C ′D ′=12CD .S △A ′B ′C ′=12A ′B ′·C ′D ′sin45°=24(12AB ·CD )=24S △ABC . 3[答案] D[解析] 本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A ,B ,C 都可能是该几何体的俯视图,D 不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.[点评] 本题主要考查空间几何体的三视图,考查空间想象能力.是近年高考中的热点题型. 4[答案] A 5[答案] C[解析] 由于正方体的体积是64,则其棱长为4,所以其表面积为6×42=96. 6[答案] A[解析] V =13π⎝ ⎛⎭⎪⎫12r 2×2h =16πr 2h ,故选A.[答案] C7[解析] 设最小球的半径为r ,则另两个球的半径分别为2r 、3r ,所以各球的表面积分别为4πr 2,16πr 2,36πr 2,所以36πr 24πr 2+16πr 2=95.8[答案] C[解析] 由三视图可知该几何体是圆锥,S 表=S 侧+S 底=πrl +πr 2=π×3×5+π×32=24π(cm 2),故选C. 9[答案] A[解析] 设圆台较小底面圆的半径为r ,由题意,另一底面圆的半径R =3r . ∴S 侧=π(r +R )l =π(r +3r )×3=84π,解得r =7. 10[答案] C[解析] 设球的半径为R ,则圆柱的底面半径为R ,高为2R ,∴V 圆柱=πR 2×2R =2πR 3,V 球=43πR 3.∴V 圆柱V 球=2πR 343πR 3=32, S 圆柱=2πR ×2R +2×πR 2=6πR 2,S 球=4πR 2. ∴S 圆柱S 球=6πR 24πR 2=32. 11[答案] B[解析] 该几何体的四棱锥,高等于5,底面是长、宽分别为8、6的矩形,则底面积S =6×8=48,则该几何体的体积V =13Sh =13×48×5=80.12[答案] B[解析] 画出该几何体的正视图为,其上层有两个立方体,下层中间有三个立方体,两侧各一个立方体,故B 项满足条件.13[答案] 1423π[解析] 圆台高h =32-2-12=22,∴体积V =π3(r 2+R 2+Rr )h =1423π.14[答案] 36[解析] 该几何体是底面是直角梯形的直四棱柱,如图所示,底面是梯形ABCD ,高h =6,则其体积V =Sh =⎣⎢⎡⎦⎥⎤122+4×2×6=36.[答案] 24π2+8π或24π2+18π15[解析] 圆柱的侧面积S 侧=6π×4π=24π2.(1)以边长为6π的边为轴时,4π为圆柱底面圆周长,所以2πr =4π,即r =2.所以S 底=4π,所以S 表=24π2+8π.(2)以4π所在边为轴时,6π为圆柱底面圆周长,所以2πr =6,即r =3.所以S 底=9π,所以S 表=24π2+18π.16[答案] 2(1+3)π+4 2[解析] 此几何体是半个圆锥,直观图如下图所示,先求出圆锥的侧面积S 圆锥侧=πrl =π×2×23=43π,S 底=π×22=4π,S △SAB =12×4×22=42,所以S 表=43π2+4π2+4 2=2(1+3)π+4 2.1718[解析] 设圆柱的底面圆半径为r cm ,∴S 圆柱表=2π·r ·8+2πr 2=130π.∴r =5(cm),即圆柱的底面圆半径为5cm.则圆柱的体积V =πr 2h =π×52×8=200π(cm 3). 1920[解析]如图所示,连接AC 和BD 交于O ,连接SO .作SP ⊥AB ,连接OP .在Rt △SOP 中,SO =7(m),OP =12BC =1(m),所以SP =22(m),则△SAB 的面积是12×2×22=22(m 2).所以四棱锥的侧面积是4×22=82(m 2),即制造这个塔顶需要82m 2铁板.21[解析] 设圆柱的底面半径为r ,高为h ′.圆锥的高h =42-22=23, 又∵h ′=3,∴h ′=12h .∴r 2=23-323,∴r =1.∴S 表面积=2S 底+S 侧=2πr 2+2πrh ′=2π+2π×3=2(1+3)π.22[解析] 由题意,知所成几何体的表面积等于圆台下底面积+圆台的侧面积+半球面面积.又S 半球面=12×4π×22=8π(cm 2),S 圆台侧=π(2+5)5-22+42=35π(cm 2), S 圆台下底=π×52=25π(cm 2),即该几何全的表面积为8π+35π+25π=68π(cm 2).又V 圆台=π3×(22+2×5+52)×4=52π(cm 3),V 半球=12×4π3×23=16π3(cm 3).所以该几何体的体积为V 圆台-V 半球=52π-16π3=140π3(cm 3).。
人教B版高中数学必修二第一章单元测验.docx

答案:C解析:将展开图恢复为正方体,如图所示,则有AB与CD,AB与GH,EF与GH.6.一个画家有14个边长为1 m的正方体,他在地面上把它摆成如图所示的形式,然后,他把露出的表面都染上颜色,那么被染上颜色的面积为( )A.21 m2B.24 m2C.33 m2D.37 m2答案:C解析:上表面面积为3×3=9(m2)侧面面积为3×4+2×4+1×4=24(m2)故被染上颜色的面积为33 m2.三条高线的交点,故②不正确;若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足不一定重合,故③不正确;如图,过顶点A作AO⊥面BCD,O为垂足,连结OB、OC、OD,则S△ABC>S△BOC,S△ACD>S△COD,S△ABD>S△BOD,∴S△ABC+S△ACD+S△ABD>S△BOC+S△COD+S△BOD=S△BCD,故④正确.如图四面体ABCD中取AB、CD、AD、BC的中点分别为E、F、M、N,连线EF、MN,则EF、MN分别为▱EMFN 的对角线,∴EF、MN相交于点O,且O为EF、MN的中点,取AC、BD的中点分别为R、H,则ERFH为平行四边形,即点O也是RH的中点,故⑤正确.16.图中的三个直角三角形是一个体积为20 cm3的几何体的三视图,则h=________cm.(1)求证:平面AB1D1∥平面EFG;(2)求证:平面AA1C⊥平面EFG.证明:(1)连接BD,∵E、F分别为BC、CD的中点,∴EF∥BD.∵BD∥B1D1,∴EF∥B1D1.又EF⊄平面AB1D1,B1D1⊂平面AB1D1,∴EF∥平面AB1D1,同理EG∥平面AB1D1.∵EF∩EG=E,∴平面AB1D1∥平面EFG.(2)∵AA1⊥平面ABCD,EF⊂平面ABCD,∴AA1⊥EF.又EF⊥AC,AA1∩AC=A,∴EF⊥平面A1AC,又EF⊂平面EFG,∴平面AA1C⊥平面EFG.21.(12分)如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP =45°.(1)求证:AF∥平面PCE.(2)求证:平面PCD⊥平面PCE.(3)若AD=2,CD=3,求点F到平面PCE的距离.。
人教版高中数学必修2第一章单元测试(一)- Word版含答案

必修二第一章训练卷空间几何体(一)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.已知某空间几何体的三视图如图所示,则此几何体为()A.圆台B.四棱锥C.四棱柱D.四棱台2.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为()A.6B.32C.62D.123.已知一个底面是菱形的直棱柱的侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是()A.3034B.6034C.3034135+D.1354.半径为R的半圆卷成一个圆锥,则它的体积为()A.3324RπB.338RπC.3525RπD.358Rπ5.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2=()A.1:3B.1:1C.2:1D.3:16.若一个底面是正三角形的三棱柱的正视图如下图所示,其顶点都在一个球面上,则该球的表面积为()A.163πB.193πC.1912πD.43π7.一个正方体的体积是8,则这个正方体的内切球的表面积是()A.8πB.6πC.4πD.π8.如图是一个空间几何体的三视图,如果直角三角形的直角边长均为1,那么这个几何体的体积为()A.1B.12C.13D.169.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有()A.14斛B.22斛C.36斛D.66斛10.正三棱柱有一个半径为3cm的内切球,则此棱柱的体积是()A.393cm B.354cm C.327cm D.3183cm11.如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.1727B.59C.1027D.1312.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为()A.3500cm3πB.3cm3866πC.3cm31372πD.3cm32048π二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.14.用斜二测画法画边长为2的正三角形的直观图时,如果在已知图形中取的x轴和正三角形的一边平行,则这个正三角形的直观图的面积是__________________.15.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为__________________.16.如图是一个组合几何体的三视图,则该几何体的体积是__________________.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(10分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长为10cm.求圆锥的母线长.18.(12分)如图是一个几何体的正视图和俯视图.(1)试判断该几何体是什么几何体?(2)画出其侧视图,并求该平面图形的面积;(3)求出该几何体的体积.19.(12分)如下图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.20.(12分)已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,求这个几何体的体积.21.(12分)如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为7m,制造这个塔顶需要多少铁板?22.(12分)如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;(2)三棱锥A′-BC′D的体积.2018-2019学年必修二第一章训练卷空间几何体(一)答 案一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的) 1.【答案】D【解析】由几何体的三视图可得,该几何体为四棱台.故选D . 2.【答案】D【解析】△OAB 是直角三角形,OA =6,OB =4,∠AOB =90°,∴164122OAB S =⨯⨯=△.故选D .3.【答案】A【解析】由菱形的对角线长分别是9和15,得菱形的边长为22915334222⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,则这个菱柱的侧面积为3434530342⨯⨯=.故选A . 4.【答案】A【解析】依题意,得圆锥的底面周长为πR ,母线长为R ,则底面半径为2R,高为32R ,所以圆锥的体积2313332224R R R ⎛⎫⨯π⨯⨯=π ⎪⎝⎭.故选A . 5.【答案】D【解析】()121::3:13V V Sh Sh ⎛⎫== ⎪⎝⎭.故选D .6.【答案】B【解析】设球半径是R ,依题意知,该三棱柱是一个底面边长为2,侧棱长为1的正三棱柱,记上,下底面的中心分别是O 1,O ,易知球心是线段O 1O 的中点,于是222123192312R ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,因此所求球的表面积是2191944123R ππ=π⨯=, 故选B . 7.【答案】C【解析】设正方体的棱长为a ,则a 3=8,所以a =2,而此正方体内的球直径为2,所以S 表=4πr 2=4π.故选C . 8.【答案】C【解析】该几何体的直观图为如图所示的四棱锥P -ABCD ,且P A =AB =AD =1,P A ⊥AB ,P A ⊥AD ,四边形ABCD 为正方形,则2111133V =⨯⨯=,故选C .9.【答案】B【解析】设圆锥底面半径为r ,则12384r ⨯⨯=,∴163r =,所以米堆的体积为21116320354339⎛⎫⨯⨯⨯⨯= ⎪⎝⎭,故堆放的米约为320 1.62229÷≈,故选B . 10.【答案】B【解析】由题意知棱柱的高为23cm ,底面正三角形的内切圆的半径为3cm ,∴底面正三角形的边长为6cm ,正三棱柱的底面面积为293cm ,∴此三棱柱的体积()3932354cm V =⨯=.故选B . 11.【答案】C【解析】由零件的三视图可知,该几何体为两个圆柱组合而成,如图所示.切削掉部分的体积V 1=π×32×6-π×22×4-π×32×2=20π(cm 3), 原来毛坯体积V 2=π×32×6=54π(cm 3).故所求比值为1220105427V V π==π.故选C . 12.【答案】A【解析】设球的半径为R ,则由题知球被正方体上面截得圆的半径为4, 球心到截面圆的距离为R -2,则R 2=(R -2)2+42,解得R =5.∴球的体积为3345500cm33π⨯π=.故选A.二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.【答案】①②③⑤【解析】三棱锥的三视图中含有三角形,∴正视图有可能是三角形,满足条件.四棱锥的三视图中含有三角形,满足条件.三棱柱的三视图中含有三角形,满足条件.四棱柱的三视图中都为四边形,不满足条件.圆锥的三视图中含有三角形,满足条件.圆柱的三视图中不含有三角形,不满足条件.故答案为①②③⑤.14.【答案】6 415.【答案】11【解析】设棱台的高为x,则有2165016512x-⎛⎫=⎪⎝⎭,解之,得x=11.16.【答案】36+128π【解析】由三视图可知该组合几何体下面是一个圆柱,上面是一个三棱柱,故所求体积为134616836128 2V=⨯⨯⨯+π⨯=+π.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.【答案】403cm.【解析】如图,设圆锥母线长为l,则1014ll-=,所以cm403l=.18.【答案】(1)正六棱锥;(2)见解析,232a;(3)332a.【解析】(1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥.(2)该几何体的侧视图如图.其中AB=AC,AD⊥BC,且BC的长是俯视图正六边形对边的距离,即3BC a=,AD是正六棱锥的高,即3AD a=,所以该平面图形的面积为2133322a a a=.(3)设这个正六棱锥的底面积是S,体积为V,则223336S==,所以231333332V a a==.19.【答案】不会,见解析.【解析】因为()33314144134cm2323V R=⨯π=⨯⨯π⨯≈半球,()22311412201cm33V r h=π=π⨯⨯≈圆锥,134<201,所以V半球<V圆锥,所以,冰淇淋融化了,不会溢出杯子.20.【答案】74Vπ=.【解析】由三视图可知,该几何体是大圆柱内挖掉了小圆柱,两个圆柱高均为1,底面是半径为2和32的同心圆,故该几何体的体积为23741124Vπ⎛⎫=π⨯-π⨯=⎪⎝⎭.21.【答案】282m.【解析】如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.在Rt△SOP中,)7mSO=,()11m2OP BC==,所以)2mSP=,则△SAB的面积是)2122222m2⨯⨯.所以四棱锥的侧面积是)242282m⨯=,即制造这个塔顶需要282铁板.22.【答案】(13;(2)33a.【解析】(1)∵ABCD-A′B′C′D′是正方体,∴2A B A C A D BC BD C D a''''''======,∴三棱锥A′-BC′D的表面积为213422232a a a⨯=.而正方体的表面积为6a2,故三棱锥A′-BC′D的表面积与正方体表面积的比值为2233a=.(2)三棱锥A′-ABD,C′-BCD,D-A′D′C′,B-A′B′C′是完全一样的.故V三棱锥A′-BC′D=V正方体-4V三棱锥A′-ABD=332114323aa a a-⨯⨯⨯=.。
(完整word)高中数学必修二第一章测试题及答案,推荐文档
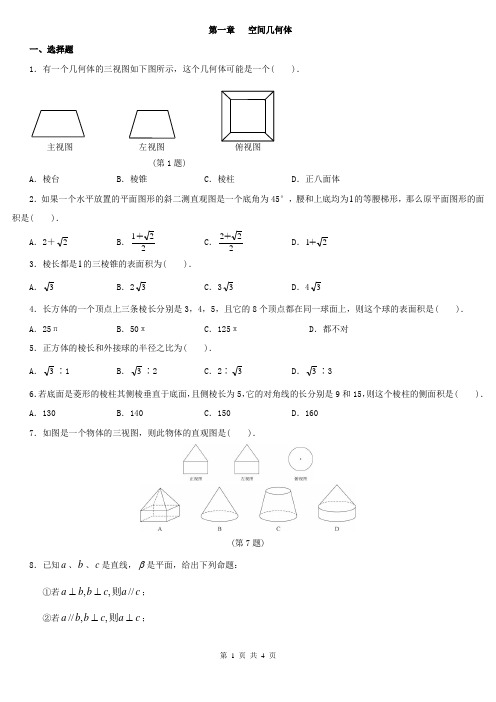
第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 (第1题)A .棱台B .棱锥C .棱柱D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A .2+2B .221+ C .22+2 D .2+13.棱长都是1的三棱锥的表面积为( ). A .3B .23C .33D .434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ). A .25πB .50πC .125πD .都不对5.正方体的棱长和外接球的半径之比为( ). A .3∶1B .3∶2C .2∶3D .3∶36.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ). A .130B .140C .150D .1607.如图是一个物体的三视图,则此物体的直观图是( ).(第7题)8.已知a 、b 、c 是直线,β是平面,给出下列命题: ①若c a c b b a //,,则⊥⊥;②若c a c b b a ⊥⊥则,,//;③若b a b a //,,//则ββ⊂;④若a 与b 异面,且ββ与则b a ,//相交;⑤若a 与b 异面,则至多有一条直线与a ,b 都垂直. 其中真命题的个数是 A .1 B .2 C .3 D .4二、填空题9.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.10.正方体ABCD -A 1B 1C 1D 1 中,O 是上底面ABCD 的中心,若正方体的棱长为a ,则三棱锥O -AB 1D 1的体积为_____________. 11.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.三、解答题12 .已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.13.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.(第13题)15.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC , 且2ASB BSC CSA π∠=∠=∠=,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.B M ANCS第一章 空间几何体参考答案一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台. 2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2. 3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径,l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π. 5.C解析:正方体的对角线是外接球的直径. 6.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a 2,a =8,S 侧面=4×8×5=160.7.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.8.D解析:从三视图看底面为圆,且为组合体,所以选D. 9.A 二、填空题10.参考答案:1∶22∶33.r 1∶r 2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.11.参考答案:361a .解析:画出正方体,平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点, 三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a 3.另法:三棱锥O -AB 1D 1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D 1为底面. 12.参考答案:6,6.解析:设ab =2,bc =3,ac =6,则V = abc =6,c =3,a =2,b =1,l =1+2+3=6.三、解答题 13.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第14题)在Rt △C'CO 中,由勾股定理,得CC' 2+OC 2=OC' 2, 即 a 2+(22a )2=R 2. ∴R =26a ,∴V 半球=26πa 3,V 正方体=a 3. ∴V 半球 ∶V 正方体=6π∶2. 14.参考答案:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22 =(60+42)π.V =V 台-V 锥=31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π. 15.证明:连结CM ,设Q 为CM 的中点,连结QN 则QN∥SM∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ,设SC =a ,在△BQN 中 BN =a 25 NQ =21SM =42a BQ =a 414∴COS∠QNB=5102222=⋅-+NQ BN BQ NQ BNCO A。
(word完整版)新课标高中数学测试题(必修2)全套含答案,推荐文档

(数学2必修)第一章 空间几何体[基础训练A 组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对2.棱长都是1的三棱锥的表面积为( )A . 3B . 23C . 33D . 433.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对4.正方体的内切球和外接球的半径之比为( )A .3:1B .3:2C .2:3D .3:35.在△ABC 中,02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周,则所形成的几何体的体积是( )A. 92πB. 72πC. 52πD. 32π 6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( )A .130B .140C .150D .160二、填空题1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点,顶点最少的一个棱台有 ________条侧棱。
2.若三个球的表面积之比是1:2:3,则它们的体积之比是_____________。
3.正方体1111ABCD A B C D - 中,O 是上底面ABCD 中心,若正方体的棱长为a ,则三棱锥11O AB D -的体积为_____________。
4.如图,,E F 分别为正方体的面11A ADD 、面11B BCC 的中心,则四边形 E BFD 1在该正方体的面上的射影可能是____________。
主视图 左视图 俯视图C 5.已知一个长方体共一顶点的三个面的面积分别是2、3、6,这个 长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
高中数学必修二第一章测试题及答案

第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个().主视图 左视图 俯视图 (第1题)A .棱台B .棱锥C .棱柱D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是().A .2+2B .221+C .22+2D .2+1 3.棱长都是1的三棱锥的表面积为(). A .3B .23C .33D .434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是(). A .25πB .50πC .125πD .都不对 5.正方体的棱长和外接球的半径之比为(). A .3∶1B .3∶2C .2∶3D .3∶36.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是(). A .130B .140C .150D .1607.如图是一个物体的三视图,则此物体的直观图是().(第7题)8.已知a 、b 、c 是直线,β是平面,给出下列命题: ①若c a c b b a //,,则⊥⊥;②若c a c b b a ⊥⊥则,,//; ③若b a b a //,,//则ββ⊂;④若a 与b 异面,且ββ与则b a ,//相交;⑤若a 与b 异面,则至多有一条直线与a ,b 都垂直. 其中真命题的个数是 A .1 B .2 C .3 D .4二、填空题9.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.10.正方体ABCD -A 1B 1C 1D 1中,O 是上底面ABCD 的中心,若正方体的棱长为a ,则三棱锥O -AB 1D 1的体积为_____________. 11.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.三、解答题12.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.13.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.(第13题)15.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC , 且2ASB BSC CSA π∠=∠=∠=,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.B M ANCS第一章 空间几何体参考答案一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台. 2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2. 3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径,l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π. 5.C解析:正方体的对角线是外接球的直径. 6.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a 2,a =8,S 侧面=4×8×5=160.7.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.8.D解析:从三视图看底面为圆,且为组合体,所以选D. 9.A 二、填空题10.参考答案:1∶22∶33.r 1∶r 2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.11.参考答案:361a .解析:画出正方体,平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点, 三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a 3. 另法:三棱锥O -AB 1D 1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D 1为底面. 12.参考答案:6,6.解析:设ab =2,bc =3,ac =6,则V =abc =6,c =3,a =2,b =1,l =1+2+3=6.三、解答题 13.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第14题)在Rt △C'CO 中,由勾股定理,得CC'2+OC 2=OC'2, 即 a 2+(22a )2=R 2. ∴R =26a ,∴V 半球=26πa 3,V 正方体=a 3. ∴V 半球 ∶V 正方体=6π∶2. 14.参考答案:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22 =(60+42)π.V =V 台-V 锥=31π(21r +r 1r 2+22r )h -31πr 2h 1CO A=3148π.15.证明:连结CM ,设Q 为CM 的中点,连结QN 则QN∥SM∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ,设SC =a ,在△BQN 中BN =a 25 NQ =21SM =42a BQ =a 414∴COS∠QNB=5102222=⋅-+NQ BN BQ NQ BN。
高中数学必修二第一章测试题及答案

12.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.
13.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
(第13题)
15.S是正三角形ABC所在平面外的一点,如图SA=SB=SC,
且 ,M、N分别是AB和SC的中点.
求异面直线SM与BN所成的角的余弦值.
第一章 空间几何体
参考答案
一、选择题
1.A
解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.
2.A
解析:原图形为一直角梯形,其面积S= (1+ +1)×2=2+ .
3.A
解析:因为四个面是全等的正三角形,则S表面=4× = .
A.130B.140C.150D.160
7.如图是一个物体的三视图,则此物体的直观图是().
(第7题)
8.已知 、 、 是直线, 是平面,给出下列命题:
①若 ;
②若 ;
③若 ;
④若 与b异面,且 相交;
⑤若 与b异面,则至多有一条直线与 ,b都垂直.
其中真命题的个数是
A.1B.2C.3D.4
二、填空题
第一章空间几何体
一、选择题
1.有一个几何体的三视图如下图所示,这个几何体可能是一个().
主视图 左视图 俯视图
(第1题)
A.棱台B.棱锥C.棱柱D.正八面体
2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为 的等腰梯形,那么原平面图形的面积是().
A.2+ B. C. D.
3.棱长都是 的三棱锥的表面积为().
高中数学必修二第一章测试题及答案(人教版)
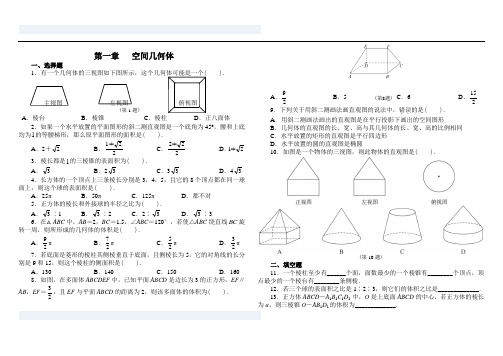
第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 (第1题) A .棱台 B .棱锥 C .棱柱 D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A .2+2B .221+C .22+2 D .2+1 3.棱长都是1的三棱锥的表面积为( ).A .3B .23C .33D .43 4.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A .25πB .50πC .125πD .都不对 5.正方体的棱长和外接球的半径之比为( ). A .3∶1 B .3∶2 C .2∶3 D .3∶36.在△ABC 中,AB =2,BC =1.5,∠ABC =120°,若使△ABC 绕直线BC 旋转一周,则所形成的几何体的体积是( ).A .29πB .27πC .25πD .23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).A .130B .140C .150D .160 8.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,EF ∥AB ,EF =23,且EF 与平面ABCD 的距离为2,则该多面体的体积为( ).A .29 B .5 C .6 D .2159.下列关于用斜二测画法画直观图的说法中,错误..的是( ). A .用斜二测画法画出的直观图是在平行投影下画出的空间图形B .几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C .水平放置的矩形的直观图是平行四边形D .水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是( ).(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________. 13.正方体ABCD -A 1B 1C 1D 1 中,O 是上底面ABCD 的中心,若正方体的棱长为a ,则三棱锥O -AB 1D 1的体积为_____________. (第8题)14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E 在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40 cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD =22,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第19题)20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2.3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3.4.B解析:长方体的对角线是球的直径,l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π.5.C解析:正方体的对角线是外接球的直径. 6.D解析:V =V 大-V 小=31πr 2(1+1.5-1)=23π.7.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a 2,a =8,S 侧面=4×8×5=160. 8.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.9.B解析:斜二测画法的规则中,已知图形中平行于 x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为原来的一半.平行于 z 轴的线段的平行性和长度都不变.10.D解析:从三视图看底面为圆,且为组合体,所以选D. 二、填空题11.参考答案:5,4,3.解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.12.参考答案:1∶22∶33.r 1∶r 2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.13.参考答案:361a .解析:画出正方体,平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点, 三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a 3. 另法:三棱锥O -AB 1D 1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D 1为底面.14.参考答案:平行四边形或线段.15.参考答案:6,6.解析:设ab =2,bc =3,ac =6,则V = abc =6,c =3,a =2,b =1,l =1+2+3=6. 16.参考答案:12. 解析:V =Sh =πr 2h =34πR 3,R =32764×=12. 三、解答题 17.参考答案:V =31(S +S S ′+S )h ,h =SS S S V ′+′+3=6001+4002+60030001903×=75.18.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第18题)在Rt △C'CO 中,由勾股定理,得CC' 2+OC 2=OC' 2, 即 a 2+(22a )2=R 2.∴R =26a ,∴V 半球=26πa 3,V 正方体=a 3. ∴V 半球 ∶V 正方体=6π∶2. 19.参考答案:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22 =(60+42)π. V =V 台-V 锥 =31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π. 20.解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m ,则仓库的体积V 1=31Sh =31×π×(216)2×4=3256π(m 3).如果按方案二,仓库的高变成8 m ,则仓库的体积V 2=31Sh =31×π×(212)2×8=3288π(m 3).(2) 参考答案:如果按方案一,仓库的底面直径变成16 m ,半径为8 m . 棱锥的母线长为l =224+8=45, 仓库的表面积S 1=π×8×45=325π(m 2). 如果按方案二,仓库的高变成8 m .棱锥的母线长为l =226+8=10,仓库的表面积S 2=π×6×10=60π(m 2).(3) 参考答案:∵V 2>V 1,S 2<S 1,∴方案二比方案一更加经济些.C'A'COA毋意,毋必,毋固,毋我。
(典型题)高中数学必修二第一章《立体几何初步》检测(含答案解析)(1)

一、选择题1.如下图所示,在正方体1111ABCD A B C D -中,E 是平面11ADD A 的中心,M 、N 、F 分别是11B C 、1CC 、AB 的中点,则下列说法正确的是( )A .12MN EF =,且MN 与EF 平行 B .12MN EF ≠,且MN 与EF 平行 C .12MN EF =,且MN 与EF 异面 D .12MN EF ≠,且MN 与EF 异面 2.已知正方体1111ABCD A B C D -,E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则EF 和BD 所成的角的大小是( ) A .30B .45C .60D .903.现有一个三棱锥形状的工艺品P ABC -,点P 在底面ABC 的投影为Q ,满足12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△,22222213QA QB QC AB BC CA ++=++,93ABCS =品放入一个球形容器(不计此球形容器的厚度)中,则该球形容器的表面积的最小值为( )A .42πB .44πC .48πD .49π4.设m ,n 为两条不同的直线,α,β为两个不同的平面,给出下列命题: ①若//m α,//m n ,则//n α; ②若m α⊥,//m β,则αβ⊥; ③若αβ⊥,n αβ=,m n ⊥,则m β⊥;④若//m n ,//αβ,则m 与α所成的角和n 与β所成的角相等. 其中正确命题的序号是( )) A .①②B .①④C .②③D .②④5.大摆锤是一种大型游乐设备(如图),游客坐在圆形的座舱中,面向外,通常大摆锤以压肩作为安全束缚,配以安全带作为二次保险,座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.假设小明坐在点A 处,“大摆锤”启动后,主轴OB 在平面α内绕点O 左右摆动,平面α与水平地面垂直,OB 摆动的过程中,点A 在平面β内绕点B 作圆周运动,并且始终保持OB β⊥,B β∈.设4OB AB =,在“大摆锤”启动后,下列结论错误的是( )A .点A 在某个定球面上运动;B .β与水平地面所成锐角记为θ,直线OB 与水平地面所成角记为δ,则θδ+为定值;C .可能在某个时刻,AB//α;D .直线OA 与平面α17. 6.正方体1111ABCD A B C D -的棱长为2,E 是1CC 的中点,则点1C 到平面EBD 的距离为( ) A .34B .63C 5D .237.已知正三棱柱111ABC A B C -中,1AB AA =,M 是1CC 的中点,则异面直线AM 与1A B 所成角的大小为( )A .π6B .π4 C .π3 D .π28.已知α、β是平面,m 、n 是直线,下列命题中不正确的是( )A .若//m α,n αβ=,则//m n B .若//m n ,m α⊥,则n α⊥ C .若m α⊥,m β⊥,则//αβ D .若m α⊥,m β⊂,则αβ⊥9.某几何体的三视图如图所示,该几何体的体积为V ,该几何体所有棱的棱长之和为L ,则( )A .8,14253V L ==+ B .8,1425V L ==+ C .8,16253V L ==+ D .8,1625VL ==+10.平行六面体1111ABCD A B C D -的六个面都是菱形,那么点1A 在面11AB D 上的射影一定是11AB D 的________心,点1A 在面1BC D 上的射影一定是1BC D 的________心( )A .外心、重心B .内心、垂心C .外心、垂心D .内心、重心11.空间四边形PABC 的各边及对角线长度都相等,D 、E 、F 外别是AB 、BC 、CA 的中点,下列四个结论中不成立的是( ) A .//BC 平面PDF B . DF ⊥平面PAE C .平面PDE ⊥平面ABCD .平面PAE ⊥平面ABC12.在正方体1111ABCD A B C D -中,M 和N 分别为11A B ,和1BB 的中点.,那么直线AM 与CN 所成角的余弦值是( )A .25B .10 C .35D .3 二、填空题13.已知正三棱锥A BCD -的四个顶点在球O 的球面上,2AB =,且π2BAC ∠=,则球O 的表面积为_______.14.如图,在矩形ABCD 中,2AB =,1AD =,点E 为CD 的中点,F 为线段CE (端点除外)上一动点.现将DAF △沿AF 折起,使得平面ABD ⊥平面ABC .设直线FD 与平面ABCF 所成角为θ,θ的取值范围为__________.15.在如图棱长为2的正方体中,点M 、N 在棱AB 、BC 上,且1AM BN ==,P 在棱1AA 上,α为过M 、N 、P 三点的平面,则下列说法正确的是__________.①存在无数个点P ,使面α与正方体的截面为五边形; ②当11A P =时,面α与正方体的截面面积为33;③只有一个点P ,使面α与正方体的截面为四边形;④当面α交棱1CC 于点H ,则PM 、HN 、1BB 三条直线交于一点.16.已知一个圆锥内接于球O (圆锥的底面圆周及顶点均在同一球面上),圆锥的高是底面半径的3倍,圆锥的侧面积为910π,则球O 的表面积为________.17.点A 、B 、C 、D 在同一个球的球面上,3AB BC AC ===,若四面体ABCD 体积的最大值为3,则这个球的表面积为______. 18.在三棱锥D ABC -中,AD ⊥平面ABC ,3AC =,17BC =,1cos 3BAC ∠=,若三棱锥D ABC -的体积为273,则此三棱锥的外接球的表面积为______19.表面积为16π的球与一个正三棱柱各个面都相切,则这个正三棱柱的体积为___________.20.如图,在三棱锥A BCD -,,AB AD BC ⊥⊥平面ABD ,点E 、F (E 与A 、D 不重合)分别在棱AD 、BD 上,且EF AD ⊥.则下列结论中:正确结论的序号是______.①//EF 平面ABC ;②AD AC ⊥;③//EF CD三、解答题21.如图(1)在ABC 中,AC BC =,D 、E 、F 分别是AB 、AC 、BC 边的中点,现将ACD △沿CD 翻折,使得平面ACD ⊥平面BCD .如图(2)(1)求证://AB 平面DEF ; (2)求证:BD AC ⊥.22.如图,三枝锥D ABC -中,90ABC ∠=︒,1AB =,2BC CD DB ===.(1)若平面BCD ⊥平面ABC .求证:AB CD ⊥; (2)若1AD =,求CD 与平面ABC 所成的角.23.如图所示,已知在三棱锥A BPC -中,,AP PC AC BC ⊥⊥,M 为AB 的中点,D 为PB 的中点,且PMB △为正三角形.(Ⅰ)求证://DM 平面APC ; (Ⅱ)求证:平面ABC ⊥平面APC ;(Ⅲ)若4,20BC AB ==,求三棱锥D BCM -的体积.24.在三棱锥A BCD -中,BCD △为等腰直角三角形,点E ,G 分别是线段BD ,CD 的中点,点F 在线段AB 上,且2BF FA =.若1AD =,3AB =,2CB CD ==.(Ⅰ)求证://AG 平面CEF ; (Ⅱ)求直线AD 与平面CEF 所成的角.25.如图,圆柱的轴截面ABCD 是长方形,点E 是底面圆周上异于A ,B 的一点,AF DE ⊥,F 是垂足.(1)证明:AF DB ⊥;(2)若2AB =,3AD =,当三棱锥D ABE -体积最大时,求点C 到平面BDE 的距离. 26.在四棱台1111ABCD A B C D -中,1AA ⊥平面ABCD ,//AB CD ,90ACD ∠=︒,26BC AC ==,1CD =,1AM CC ⊥,垂足为M .(1)证明:平面ABM ⊥平面11CDD C ;(2)若二面角B AM D --正弦值为217,求直线AC 与平面11CDD C 所成角的余弦.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】设正方体1111ABCD A B C D -的棱长为2,利用正方体性质可求得2MN =,3EF =,知12MN EF ≠,再利用三角形中位线性质知1//MN B C ,从而//MN ED ,又EF 与ED 相交,可知MN 与EF 异面,即可选出答案. 【详解】设正方体1111ABCD A B C D -的棱长为2,则22112MN MC C N =+=作E 点在平面ABCD 的投影点G ,即EG ⊥平面ABCD ,连接,EG GF ,在直角EGF △中,1EG =,222GF AG AF =+=,则2222123EF EG GF =+=+=,所以12MN EF ≠,故排除A 、C 连接DE ,由E 是平面11ADD A 的中心,得112DE A D =又M N 、分别是11B C 、1CC 的中点,所以1//MN B C 又11//A D B C ,所以//MN ED , 又EF ED E ⋂=,所以MN 与EF 异面 故选:D.【点睛】关键点睛:本题考查正方体中的线面关系,线线平行的关系,及判断异面直线,解题的关键是熟记正方体的性质,考查学生的逻辑推理能力,属于基础题.2.C解析:C 【分析】作出图形,连接1AD 、11B D 、1AB ,推导出1//EF AB ,11//BD B D ,可得出异面直线EF 和BD 所成的角为11AB D ∠,分析11AB D 的形状,即可得出结果. 【详解】如下图所示,连接1AD 、11B D 、1AB ,设正方体1111ABCD A B C D -的棱长为1,则11112AD AB B D ===, 所以,11AB D 为等边三角形,则1160AB D ∠=,因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则E 、F 分别是11B D 、1AD 的中点,所以,1//EF AB ,在正方体1111ABCD A B C D -中,11//BB DD 且11BB DD =, 所以,四边形11BB D D 为平行四边形,则11//BD B D , 所以,异面直线EF 和BD 所成的角为1160AB D ∠=. 故选:C. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.3.D解析:D 【分析】作QM AB ⊥,连接PM ,易证AB PM ⊥,由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM =,再根据12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△,由对称性得到AB BC AC ==,然后根据22222213QA QB QC AB BC CA ++=++,93ABCS=,求得6,23AB AQ ==,在AOQ△中,由222AO OQ AQ =+求解半径即可.【详解】 如图所示:作QM AB ⊥与M ,连接PM , 因为PQ ⊥平面ABC ,所以PQ AB ⊥,又QM PQ Q ⋂=, 所以AB ⊥平面PQM , 所以AB PM ⊥,所以112122QAB PABAB QM S S AB PM ⨯⨯==⨯⨯△△, 2PM QM =,因为12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△, 由对称性得AB BC AC ==,又因为22222213QA QB QC AB BC CA ++=++,93ABCS =所以21sin 60932ABCSAB =⨯⨯= 解得6,AB AQ ==所以3QM PM PQ ===,设外接球的半径为r ,在AOQ △中,222AO OQAQ =+,即()(2223r r =-+,解得72r =, 所以外接球的表面积为2449S r ππ==, 即该球形容器的表面积的最小值为49π. 故选:D 【点睛】关键点点睛:本题关键是由12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△得到三棱锥是正棱锥,从而找到外接球球心的位置而得解..4.D解析:D 【分析】①根据//n α或n ⊂α判断;②利用面面垂直的判定定理判断;③根据m β⊂,或//m β,或m 与β相交判断;④利用线面角的定义判断.【详解】①若//m α,//m n ,则//n α或n ⊂α,因此不正确;②若//m β,则β内必存在一条直线//m m ',因为m α⊥,所以m α'⊥,又因为m β'⊂,所以αβ⊥,正确;③若αβ⊥,n αβ=,m n ⊥,则m β⊂,或//m β,或m 与β相交,因此不正确;④若//m n ,//αβ,则m 与α所成的角和n 与β所成的角相等,正确. 其中正确命题的序号是②④. 故选:D . 【点睛】空间直线、平面平行或垂直等位置关系命题的真假判断,除了利用定理、公理、推理判断外,还常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.5.C解析:C【分析】利用已知条件确定OA 是定值,即得A 选项正确;作模型的简图,即得B 正确;依题意点B 在平面α内,不可能AB//α,得C 错误;设AB a ,结合题意知AB α⊥时,直线OA 与平面α所成角最大,计算此时正弦值,即得D 正确. 【详解】因为点A 在平面β内绕点B 作圆周运动,并且始终保持OB β⊥,所22OA OB AB =+,又因为OB ,AB 为定值,所以OA 也是定值,所以点A 在某个定球面上运动,故A 正确;作出简图如下,OB l ⊥,所以2πδθ+=,故B 正确;因为B α∈,所以不可能有AB//α,故C 不正确; 设AB a ,则4OB a =,2217OA AB OB a =+,当AB α⊥时,直线OA 与平面α所成角最大,此时直线OA 与平面α171717a =,故D 正确. 故选:C. 【点睛】本题解题关键在于认真读题、通过直观想象,以实际问题为背景构建立体几何关系,再运用立体几何知识突破难点.6.B解析:B 【分析】利用等体积法11C EBD D C EB V V --=,设点1C 到平面EBD 的距离为d ,利用三棱锥的体积公式代入面积即求得d . 【详解】如图,利用等体积法,11C EBD D C EB V V --=,设点1C 到平面EBD 的距离为d ,正方体1111ABCD A B C D -的棱长为2,故22,5BD BE ED ===,如图,2215232h ED BD ⎛⎫=-=-= ⎪⎝⎭11223622EBDSBD h =⨯⨯=⨯= 又点D 到平面1C EB 的距离,即D 到平面11C CBB 的距离,为CD =2,111212EBC S=⨯⨯=, 由11C EBD D C EB V V --=得,1161233d =⨯⨯,故636d ==. 故选:B. 【点睛】 方法点睛:空间中求点到平面的距离的常见方法: (1)定义法:直接作垂线,求垂线段长;(2)等体积法:利用三棱锥换底求体积,结合两个面积和另一个高求未知高,即得距离; (3)向量法:过点的一个斜线段对应的向量a ,平面法向量n ,则a n d n⋅=.7.D解析:D 【分析】取AC 中点E ,连接1,A E BE ,先通过BE ⊥平面11ACC A 可得BE AM ⊥,再由1ACM A AE ≅可得1AM A E ⊥,即可得出AM ⊥平面1A BE ,即1AM A B ⊥.【详解】取AC 中点E ,连接1,A E BE ,ABC 为正三角形,BE AC ∴⊥,正三棱柱111ABC A B C -中,1CC ⊥平面ABC ,BE ⊂平面ABC ,1CC BE ∴⊥,1ACCC C =,BE ∴⊥平面11ACC A ,AM ⊂平面11ACC A ,BE AM ∴⊥,在直角三角形ACM 和直角三角形1A AE 中,1,AC A A CM AE ==,1ACM A AE ∴≅, 1CAM AA E ∴∠=∠,12CAM A EA π∴∴∠+∠=,则1AM A E ⊥,1BE A E E ⋂=,AM ∴⊥平面1A BE ,1A B ⊂平面1A BE ,1AM A B ∴⊥,故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解,解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.8.A解析:A 【分析】根据已知条件判断直线m 、n 的位置关系,可判断A 选项的正误;利用线面垂直的性质可判断BC 选项的正误;利用面面垂直的判定定理可判断D 选项的正误. 【详解】对于A 选项,若//m α,则直线m 与平面α内的直线平行或异面, 由于n αβ=,则直线m 、n 平行或异面,A 选项错误;对于B 选项,若//m n ,m α⊥,则n α⊥,B 选项正确; 对于C 选项,若m α⊥,m β⊥,则//αβ,C 选项正确;对于D 选项,若m α⊥,m β⊂,由面面垂直的判定定理可知αβ⊥,D 选项正确. 故选:A.【点睛】方法点睛:对于空间线面位置关系的组合判断题,解决的方法是“推理论证加反例推断”,即正确的结论需要根据空间线面位置关系的相关定理进行证明,错误的结论需要通过举出反例说明其错误,在解题中可以以常见的空间几何体(如正方体、正四面体等)为模型进行推理或者反驳.9.A解析:A 【分析】由三视图还原几何体,由棱锥的体积公式可得选项. 【详解】在如图所示的正方体1111ABCD A B C D -中,P ,E 分别为11,B C BC 的中点,该几何体为四棱锥P ABCD -,且PE ⊥平面ABCD . 由三视图可知2AB =,则5,3PCPB PD PA ====,则21825681425,2233L V =++=+=⨯⨯=. 故选:A.【点睛】方法点睛:三视图问题的常见类型及解题策略:(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.10.C解析:C 【分析】将三棱锥111A AB D -、三棱锥11A BC D -分离出来单独分析,根据线段长度以及线线关系证明1A 的射影点分别是11AB D 和1BC D 的哪一种心. 【详解】三棱锥111A AB D -如下图所示:记1A 在面11AB D 上的射影点为O ,连接11,,AO B O D O ,因为11111AA A D A B ==,又1A O ⊥平面11AB D , 所以222222*********1,,AA AO AO A D AO OD A B AO OB =+=+=+, 所以11AO OB OD ==,所以O 为11AB D 的外心;三棱锥11A BC D -如下图所示:记1A 在面1BC D 上的射影点为1O ,连接1111,,BO C O DO ,因为11//BC AD ,且四边形11ADD A 是菱形,所以11AD A D ⊥,所以11BC A D ⊥, 又因为11A O ⊥平面1BC D ,所以1111111,AO BC AO A D A ⊥=,所以1BC ⊥平面11AO D ,又因为1DO ⊂平面11AO D ,所以11DO BC ⊥, 同理可知:1111,BO DC C O DB ⊥⊥,所以1O 为1BC D 的垂心, 故选:C. 【点睛】关键点点睛:解答本题的关键是通过1A 的射影点去证明线段长度的关系、线段位置的关系,借助线面垂直的定义和判定定理去分析解答问题.11.C解析:C 【分析】由线面平行的判定定理可判断A ;由线面垂直的判定定理可判断B ;反证法可说明C ;由面面垂直的判定定理可判断D. 【详解】 对于A ,D ,F 外别是AB ,CA 的中点,//BC DF ∴,DF ⊂平面PDF ,∴//BC 平面PDF ,故A 正确,不符合题意;对于B ,各棱长相等,E 为BC 中点,,BC AE BC PE ∴⊥⊥,PEAE E =,BC ∴⊥平面PAE ,//BC DF ,∴DF ⊥平面PAE ,故B 正确,不符合题意;对于C ,假设平面PDE ⊥平面ABC ,设DE BF O ⋂=,连接PO ,则O 是DE 中点,PO DE ∴⊥,平面PDE平面ABC DE =,PO ∴⊥平面ABC ,BF ⊂平面ABC ,PO BF ∴⊥,则PB PF =,与PB PF ≠矛盾,故C 错误,符合题意;对于D ,由B 选项 DF ⊥平面PAE , DF ⊂平面ABC ,∴平面PAE ⊥平面ABC ,故D 正确,不符合题意. 故选:C. 【点睛】本题考查线面关系和面面关系的判定,解题的关键是正确理解判断定理,正确理解垂直平行关系.12.A解析:A 【分析】作出异面直线AM 和CN 所成的角,然后解三角形求出两条异面直线所成角的余弦值. 【详解】设,E F 分别是1,AB CC 的中点,由于,M N 分别是111,A B BB 的中点,结合正方体的性质可知11//,//B E AM B F CN ,所以1EB F ∠是异面直线AM 和CN 所成的角或其补角, 设异面直线AM 和CN 所成的角为θ,设正方体的边长为2,2211125B E B F ==+=,2221216EF =++=,则1cos cos EB F θ=∠=55625255+-=⨯⨯.故选:A.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.二、填空题13.【分析】经分析正三棱锥是以△BCD 底面的三棱锥可以把看出以AB 为边长的正方体切割下来的可借助于正方体的外接球求解【详解】正三棱锥中所以△BCD 为底面且所以正三棱锥是以AB 为边长的正方体切割下来的所以 解析:6π【分析】经分析,正三棱锥A BCD -是以△BCD 底面的三棱锥,可以把看出以AB 为边长的正方体切割下来的,可借助于正方体的外接球求解. 【详解】正三棱锥A BCD -中,π2BAC ∠=, 所以△BCD 为底面,且π2BAD DAC BAC ∠=∠=∠=, 所以正三棱锥A BCD -是以AB 为边长的正方体切割下来的, 所以正三棱锥A BCD -的外接球就是正方体的外接球. 设外接球的半径为R ,所以232R =所以外接球的表面积为246S R ππ==. 故答案为:6π 【点睛】多面体的外接球问题解题关键是找球心和半径,求半径的方法有:(1)公式法;(2) 多面体几何性质法;(3)补形法;(4)寻求轴截面圆半径法;(5)确定球心位置法.14.【分析】在矩形中作交于交于在翻折后的几何体中证得平面平面从而平面得是直线与平面所成的角设C 求得的范围后可得范围【详解】在矩形中作交于交于设由图易知∴即∴则在翻折后的几何体中又平面∴平面又平面∴平面平解析:(0,]6π【分析】在矩形ABCD 中作DO AF ⊥,交AF 于O ,交AB 于M ,在翻折后的几何体中,证得平面ODM ⊥平面ABCF ,从而DM ⊥平面ABCF ,得DFM ∠是直线FD 与平面ABCF 所成的角.设(01)CF x x =<<C ,求得sin θ的范围后可得θ范围.【详解】在矩形ABCD 中作DO AF ⊥,交AF 于O ,交AB 于M , 设(01)CF x x =<<,AM t =,由图易知DAM FDA △△,∴AM AD DA DF =,即112t x =-,∴12t x=-,01x <<,则112t <<. 在翻折后的几何体中,AF OD ⊥,AF OM ⊥,又OD OM O =,,OD OM ⊂平面ODM ,∴AF ⊥平面ODM ,又AF ⊂平面ABCF ,∴平面ODM ⊥平面ABCF ,又平面ABD ⊥平面ABC AB =.平面ODM平面ABD DM =,∴DM ⊥平面ABCF ,连接MF ,则DFM ∠是直线FD 与平面ABCF 所成的角.DFM θ∠=,而21DM t =-,12DF x t=-=, ∴2422211sin 1()24DM t t t t t DF θ==-=-+=--+, ∵112t <<,∴2114t <<,∴10sin 2θ<≤,即06πθ<≤.故答案为:(0,]6π.【点睛】方法点睛:本题考查求直线与平面所成的角,求线面角常用方法:(1)定义法:作出直线与平面所成的角并证明,然后在直角三角形中计算可得; (2)向量法:建立空间直角坐标系,由直线的方向向量与平面的法向量夹角的余弦的绝对值等于直线与平面所成角的正弦值计算.15.①②④【分析】让从开始逐渐向运动变化观察所得的截面从而可得正确的选项【详解】由题设可得为所在棱的中点当时如图(1)直线分别交与连接并延长于连接交于则与正方体的截面为五边形故①正确当如图(2)此时与正解析:①②④ 【分析】让P 从A 开始逐渐向1A 运动变化,观察所得的截面,从而可得正确的选项. 【详解】由题设可得,M N 为所在棱的中点. 当203AP <<时,如图(1),直线MN 分别交,AD DC 与,T S ,连接TP 并延长1DD 于G , 连接GS 交1CC 于H ,则α与正方体的截面为五边形,故①正确.当11A P =,如图(2),此时α2, 其面积为2362=33B 正确.当,A P 重合或1,A P 重合时,如图(3),α与正方体的截面均为四边形,故③错误.如图(4),在平面α内,设PM HN S ⋂=,则S PM ∈,而PM ⊂平面11A B BA , 故S ∈平面11A B BA ,同理S ∈平面11C B BC ,故S ∈平面11A B BA ⋂平面111C B BC BB =即PM 、HN 、1BB 三条直线交于一点. 故答案为:①②④. 【点睛】思路点睛:平面的性质有3个公理及其推理,注意各个公理的作用,其中公理2可用来证明三点共线或三线共点,公理3及其推理可用来证明点共面或线共面,作截面图时用利用公理2来处理.16.【分析】设圆锥的底面半径为球的半径为根据勾股定理可得根据圆锥的侧面积公式可得再根据球的表面积公式可得结果【详解】设圆锥的底面半径为球的半径为则圆锥的高为则球心到圆锥的底面的距离为根据勾股定理可得化简 解析:100π【分析】设圆锥的底面半径为r ,球O 的半径为R ,根据勾股定理可得53R r =,根据圆锥的侧面积公式可得3,5r R ==,再根据球的表面积公式可得结果. 【详解】设圆锥的底面半径为r ,球O 的半径为R ,则圆锥的高为3r , 则球心O 到圆锥的底面的距离为3r R -, 根据勾股定理可得()2223R r r R =+-,化简得53R r =, 因为圆锥的高为3r ,母线长为()22310r r r +=, 所以圆锥的侧面积为21010r r r ππ⨯=, 所以210910r ππ=,解得r =3,所以5353R =⨯=, 所以球O 的表面积为24425100R πππ=⨯=. 故答案为:100π 【点睛】关键点点睛:利用圆锥的侧面积公式和球的表面积公式求解是解题关键.17.【分析】先由题意得到的面积以及外接圆的半径记的外接圆圆心为为使四面体体积最大只需与面垂直由此求出设球心为半径为根据为直角三角形由勾股定理列出等式求出球的半径即可得出结果【详解】根据题意知是一个等边三 解析:254π【分析】先由题意,得到ABC 的面积,以及ABC 外接圆的半径,记ABC 的外接圆圆心为Q ,为使四面体ABCD 体积最大,只需DQ 与面ABC 垂直,由此求出2DQ =,设球心为O ,半径为R ,根据AQO 为直角三角形,由勾股定理列出等式,求出球的半径,即可得出结果. 【详解】根据题意知,ABC是一个等边三角形,其面积为1 2S ==,ABC 外接圆的半径为112sin 60r =⨯=,记ABC 的外接圆圆心为Q ,则1AQ r ==;由于底面积ABCS不变,高最大时体积最大,所以DQ 与面ABC 垂直时体积最大,最大值为13ABC S DQ ⋅=,2DQ ∴=, 设球心为O ,半径为R ,则在直角AQO 中,222OA AQ OQ =+,即2221(2)R R =+-,54R ∴=, 则这个球的表面积为:2525444S ππ⎛⎫== ⎪⎝⎭.故答案为:254π. 【点睛】 思路点睛:求解几何体与球外接问题时,一般需要先确定底面外接圆的圆心位置,求出底面外接圆的半径,根据球的性质,结合题中条件确定球心位置,求出球的半径,进而即可求解.18.【分析】设出外接球的半径球心的外心半径r 连接过作的平行线交于连接如图所示在中运用正弦定理求得的外接圆的半径r 再利用的关系求得外接球的半径运用球的表面积公式可得答案【详解】设三棱锥外接球的半径为球心为 解析:20π【分析】设出外接球的半径R 、球心O ,ABC 的外心1O 、半径 r , 连接1AO ,过O 作的平行线OE 交AD 于 E ,连接OA ,OD ,如图所示,在ABC 中,运用正弦定理求得 ABC的外接圆的半径r ,再利用1,,R r OO 的关系求得外接球的半径,运用球的表面积公式可得答案. 【详解】设三棱锥外接球的半径为R 、球心为O ,ABC 的外心为1O 、外接圆的半径为r ,连接1AO ,过O 作平行线OE 交AD 于E ,连接OA ,OD ,如图所示,则OA OD R ==,1O A r =,OE AD ⊥,所以E 为AD的中点.在ABC中,由正弦定理得2sinBC r BAC ==∠r =.在ABC 中,由余弦定理2222cos BC AB AC AB AC BAC =+-⋅⋅∠,可得2117963AB AB =+-⋅⋅,得4AB =.所以1122sin 3442223ABC S AB AC BAC =⋅⋅∠=⨯⨯⨯=△. 因为112742333D ABC ABC V S AD AD -=⋅⋅=⨯⨯=△,所以144AD =.连接1OO ,又1//OO AD ,所以四边形1EAO O 为平行四边形,11142EA OO AD ===,所以22221114324588R OO AO ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭.所以该三棱锥的外接球的表面积()224π4π520πS R ===.故答案为:20π.【点睛】本题考查三棱锥的外接球,及球的表面积计算公式,解决问题的关键在于利用线面关系求得外接球的球心和球半径,属于中档题.19.【分析】求出正三棱柱的高底面三角形的边长和高即可求出正三棱柱的体积【详解】设球的半径为r 由得则球的半径为2正三棱柱的高为正三棱柱底面正三角形的内切圆的半径是2所以正三角形的边长是高是6正三棱柱的体积 解析:3【分析】求出正三棱柱的高、底面三角形的边长和高,即可求出正三棱柱的体积. 【详解】设球的半径为r ,由2416r π=π,得2r,则球的半径为2,正三棱柱的高为24r =,正三棱柱底面正三角形的内切圆的半径是2,所以正三角形的边长是36, 正三棱柱的体积为143644832⨯⨯= 故答案为:3【点睛】本题考查正三棱柱的内切球、正三棱柱的体积,考查空间想象能力与计算能力.20.①②【分析】采用逐一验证法根据线面平行线面垂直的判定定理以及线面距离判断可得结果【详解】由共面所以因为平面平面所以平面;故①正确;平面平面所以又因为平面平面所以故②正确;若则平面或EF 在平面ACD 内解析:①② 【分析】采用逐一验证法,根据线面平行,线面垂直的判定定理,以及线面距离,判断可得结果. 【详解】由AB AD ⊥,,,EF AD AD EF AB ⊥,共面 ,所以//EF AB , 因为EF ⊄平面ABC ,AB平面ABC ,所以//EF 平面ABC ;故①正确;BC ⊥平面ABD ,AD ⊂平面ABD ,所以BC AD ⊥,又因为AB AD ⊥,AB BC B ⋂=,AD ⊥平面ABC ,AC ⊂平面ABC , 所以AD AC ⊥,故②正确;若//EF CD ,则//EF 平面ACD ,或EF 在平面ACD 内,如图EF 与平面ACD 相交于点E ,显然不成立,故③不正确, 故答案为:①② 【点睛】本题主要考查了线线、线面之间的位置关系,考查了线面平行的判断以及由线面垂直证明线线垂直,属于中档题.三、解答题21.(1)证明见解析;(2)证明见解析. 【分析】(1)根据三角形中位线的性质,得到//EF AB ,利用线面平行的判定定理证得结果; (2)根据面面垂直的性质定理,得到BD ⊥平面ACD ,进而证得BD AC ⊥. 【详解】证明:(1)如图(2):在ABC 中,E 、F 分别是AC 、BC 中点,得//EF AB , 又AB ⊄平面DEF ,EF ⊂平面DEF ,//AB ∴平面DEF .(2)∵平面ACD ⊥平面BCD 且交线为CD ,BD CD ⊥,且BD ⊂平面BCD , ∴BD ⊥平面ACD ,又AC ⊂平面ACD ∴BD AC ⊥. 【点睛】方法点睛:该题考查的是有关空间关系的证明问题,解题方法如下:(1)熟练掌握线面平行的判定定理,在解题过程中,一定不要忘记线在面内、线在面外的条件;(2)根据面面垂直的条件,结合线线垂直,利用面面垂直的性质定理,得到线面垂直,进而证得线线垂直.22.(1)证明见解析(2)30【分析】(1)先由面面垂直证明AB ⊥平面BCD ,再由线面垂直的性质证明AB CD ⊥; (2)过点D 作AC 的垂线,垂足于点E ,连接BE ,先证明AC ⊥平面BDE ,进而得出D ABC V -,再由等体积法求出点D 到平面ABC 的距离,最后由直角三角形的边角关系得出线面角. 【详解】(1)90ABC ∠=︒,AB BC ∴⊥又平面BCD ⊥平面ABC ,平面BCD 平面ABC BC =,AB 平面ABC AB ∴⊥平面BCD CD ⊂平面BCDAB CD ∴⊥(2)过点D 作AC 的垂线,垂足于点E ,连接BEABC ACD ≅△△,BE AC ∴⊥,且3AB BC DE BE AC ⋅====又BE DE E ⋂=,,BE DE ⊂平面BDEAC ∴⊥平面BDE222213cos 423BED +--∠===-,120BED ︒∴∠=112sin1202332326BED S ︒∴=⨯=⨯⨯=△1136D ABC A BDE C BDE V V V ---∴=+==设点D 到平面ABC 的距离为h ,CD 与平面ABC 所成的角为θ11113326D ABC ABC V S h h h -=⋅⋅=⨯⨯=△16∴=,h =1sin 2h CD θ===,[]0,90θ∈︒30θ∴=︒【点睛】关键点睛:在解决第二问时,关键是利用等体积法求出点D 到平面ABC 的距离h ,进而由sin hCDθ=求出线面角. 23.(1)见详解;(2)见详解;(3)107 【分析】(1)先证DM AP ∥,可证//DM 平面APC .(2)先证AP ⊥平面PBC ,得⊥AP BC ,结合AC BC ⊥可证得BC ⊥平面APC . (3)等积转换,由D BCM M DBC V V --=,可求得体积. 【详解】证明:因为M 为AB 的中点,D 为PB 的中点,所以MD 是ABP △的中位线,MD AP .又MD 平面APC ,AP ⊂平面APC , 所以MD 平面APC .(2)证明:因为PMB △为正三角形,D 为PB 的中点,所以MD PB ⊥.又MDAP ,所以AP PB ⊥.又因为AP PC ⊥,PB PC P =,所以AP ⊥平面PBC .因为BC ⊂平面PBC ,所以⊥AP BC . 又因为BC AC ⊥,AC AP A ⋂=, 所以BC ⊥平面APC . (3)因为AP ⊥平面PBC ,MDAP ,所以MD ⊥平面PBC ,即MD 是三棱锥M DBC -的高.。
(典型题)高中数学必修二第一章《立体几何初步》检测题(答案解析)(1)

一、选择题1.如图,在Rt ABC △中,1AC =,BC x =,D 是斜边AB 的中点,将BCD △沿直线CD 翻折,若在翻折过程中存在某个位置,使得CB AD ⊥,则x 的取值范围是( )A .(0,3⎤⎦B .2,22⎛⎤⎥⎝⎦C .3,23D .(]2,42.如图,在长方体1111ABCD A B C D -中,1AB AD ==,12AA =,M 为棱1DD 上的一点.当1A M MC +取得最小值时,1B M 的长为( )A 3B 6C .23D .263.已知三棱锥A BCD -的各棱长都相等,E 为BC 中点,则异面直线AB 与DE 所成角的余弦值为( ) A .136B 3C .336D .1164.在三棱柱111ABC A B C -中,90BAC ∠=︒,1BC AC ,且12AC BC =,则直线11B C 与平面1ABC 所成的角的大小为( )A .30°B .45°C .60°D .90°5.一个几何体的三视图如图所示,则该几何体的外接球的表面积是( )A .2πB .3πC .4πD .16π6.已知E ,F 是四面体的棱AB ,CD 的中点,过EF 的平面与棱AD ,BC 分别相交于G ,H ,则( ) A .GH 平分EF ,BH AGHC GD = B .EF 平分GH ,BH GDHC AG = C .EF 平分GH ,BH AGHC GD= D .GH 平分EF ,BH GDHC AG= 7.已知正四棱锥的高为2,底面正方形边长为4,其正视图为如图所示的等腰三角形,正四棱锥表面点M 在正视图上的对应点为腰的中点A ,正四棱锥表面点N 在正视图上对应点为B ,则||MN 的取值范围为( ).A .[10,19]B .11,19]C .10,5]D .[11,25]8.已知一个正三棱锥的四个顶点都在一个球的球面上,且这个正三棱锥的所有棱长都为2,求这个球的表面积( )A .4πB .8πC .12πD .24π9.设有直线m ,n ,l 和平面α,β,下列四个命题中,正确的是( ) A .若//,//m n αα,则//m n B .若//,//,//l m αβαβ,则//l m C .若,m αβα⊥⊂,则m β⊥D .若,,m m αββα⊥⊥⊄,则//m α10.已知四面体ABCD 中,二面角A BC D --的大小为60,且2AB =,4CD =,120CBD ∠=,则四面体ABCD 体积的最大值是( )A .43B .23C .83D .4311.蹴鞠,又名蹴球,筑球等,蹴有用脚踢、踏的含义,鞠最早系外包皮革、内实含米糠的球.因而蹴鞠就是指古人以脚踢、踏皮球的活动,类似现在的足球运动.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.3D 打印属于快速成形技术的一种,它是一种以数字模型为基础,运用粉末状金属或塑料等可粘合材料,通过逐层堆叠积累的方式来构造物体的技术.过去常在模具制造、工业设计等领域被用于制造模型,现正用于一些产品的直接制造,特别是一些高价值应用(比如人体的髋关节、牙齿或飞机零部件等).已知某蹴鞠的表面上有四个点A .B .C .D ,满足任意两点间的直线距离为6cm ,现在利用3D 打印技术制作模型,该模型是由蹴鞠的内部挖去由ABCD 组成的几何体后剩下的部分,打印所用原材料的密度为31g/cm ,不考虑打印损耗,制作该模型所需原材料的质量约为( )(参考数据)π 3.14≈,2 1.41≈,3 1.73≈,6 2.45≈. A .101gB .182gC .519gD .731g12.在四棱锥P -ABCD 中,//AD BC ,2AD BC =,E 为PD 中点,平面ABE 交PC 于F ,则PFFC=( ) A .1B .32C .2D .3二、填空题13.张衡(78年~139年)是中国东汉时期伟大的天文学家、文学家、数学家、地理学家,他的数学著作有《算罔论》,他曾经得出结论:圆周率的平方除以十六等于八分之五,已知正方体的外接球与内切球上各有一个动点A ,B ,若线段AB 的最小值为31-,利用张衡的结论可得该正方体的内切球的表面积为___________. 14.如图,在三棱台111ABC A B C -中,11190,4,22ACB AC BC A B CC ∠=︒====,平面11AA B B ⊥平面ABC ,则该三棱台外接球的表面积为___________.15.如图,圆柱的体积为16π,正方形ABCD 为该圆柱的轴截面,F 为AB 的中点,E为母线BC 的中点,则异面直线AC ,EF 所成的角的余弦值为______.16.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.若M 为线段1A C 的中点,则在ADE 翻折过程中,下面四个选项中正确的是______(填写所有的正确选项)(1)BM 是定值(2)点M 在某个球面上运动 (3)存在某个位置,使1DE A C ⊥ (4)存在某个位置,使//MB 平面1A DE17.在三棱锥D ABC -中,AD ⊥平面ABC ,3AC =,17BC =,1cos 3BAC ∠=,若三棱锥D ABC -的体积为273,则此三棱锥的外接球的表面积为______18.如图,在三棱锥V ABC -中,22AB =,VA VB =,1VC =,且AV BV ⊥,AC BC ⊥,则二面角V AB C --的余弦值是_____.19.如图①,一个圆锥形容器的高为2a ,内装有一定量的水.如果将容器倒置,这时水面的高恰为a (如图②),则图①中的水面高度为_________.20.在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,且ABCD 为矩形,π2DPA ∠=,23AD =,2AB =,PA PD =,则四棱锥P ABCD -的外接球的体积为________.三、解答题21.已知四棱锥P ABCD -的底面是菱形,60,BCD PD AD ∠=︒⊥,点E 是BC 边的中点.(Ⅰ)求证:AD ⊥平面PDE ;(Ⅱ)若二面角P AD C --的大小等于60︒,且834,3AB PD == ①点P 到平面ABCD 的距离;②求直线PB 与平面ABCD 所成角的大小.22.如图,在四棱锥P ABCD -中,PAB △是等边三角形,CB ⊥平面,//PAB AD BC 且22PB BC AD F ===,为PC 中点.(1)求证://DF 平面PAB ;(2)求直线AB 与平面PDC 所成角的正弦值.23.如图,三棱柱111ABC A B C -中,1CC ⊥平面ABC ,5AB =,3AC =,14BC CC ==,M 是1CC 的中点.(Ⅰ)求证:BC AM ⊥;(Ⅱ)若N 是AB 上的点,且//CN 平面1AB M ,求BN 的长.24.如图,在正四棱柱1111ABCD A B C D -中,11,2AB AA ==,点E 为1CC 中点,点F 为1BD 中点.(1)求异面直线1BD 与1CC 的距离;(2)求直线1BD 与平面BDE 所成角的正弦值; (3)求点F 到平面BDE 的距离.25.在三棱锥P ABC -中,AE BC ⊥于点,E CF AB ⊥于点F ,且AE CF O ⋂=,若点P 在平面ABC 上的射影为点O .(1)证明:AC PB ⊥;(2)若ABC 是正三角形,点,G H 分别为,PA PC 的中点.证明:四边形EFGH 是矩形.26.如图,在三棱柱111ABC A B C -中,平面11A ACC ⊥平面ABC ,2,AB BC ==30ACB ∠=,13AA =,11BC A C ,E 为AC 的中点.(1)求证:1//AB 平面1C EB ; (2)求证:1A C ⊥平面1C EB .【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】取BC 中点E ,连接DE ,AE ,若CB AD ⊥,则可证明出BC ⊥平面ADE ,则可得BC AE ⊥. 根据题目中各边长的关系可得出AE ,AD 关于x 的表达式,然后在ADE 中,利用三边关系求解即可. 【详解】由题意得BC x =,则21x AD CD BD +===,如图所示,取BC 中点E ,翻折前,在图1中,连接DE ,CD ,则1122DE AC ==, 翻折后,在图2中,若CB AD ⊥,则有:∵BC DE ⊥,BC AD ⊥,AD DE D ⋂=,且,AD DE 平面ADE ,∴BC ⊥平面ADE ,∴BC AE ⊥,又BC AE ⊥,E 为BC 中点,∴1AB AC ==∴2114AE x =-,21x AD +=, 在ADE 中,由三边关系得:①221111224x x ++>-,②221111224x x +<+-,③0x >; 由①②③可得03x <<.故选:A. 【点睛】本题考查折叠性问题,考查线面垂直的判定及性质在解题中的运用,解答本题的主要思路分析在于将异面直线间的垂直转化为线面垂直关系,即作出辅助线DE 与AE ,根据题目条件确定出BC ⊥平面ADE ,得到BC AE ⊥,从而通过几何条件求解.2.A解析:A 【分析】本题首先可通过将侧面11CDD C 绕1DD 逆时针转90展开得出当1A 、M 、2C 共线时1A M MC +取得最小值,此时M 为1DD 的中点,然后根据11B A ⊥平面11A D DA 得出111B A A M ⊥,最后根据221111M A B B A M =+即可得出结果.【详解】如图,将侧面11CDD C 绕1DD 逆时针转90展开,与侧面11ADD A 共面,连接12A C ,易知当1A 、M 、2C 共线时,1A M MC +取得最小值, 因为1AB AD ==,12AA =,所以M 为1DD 的中点,12A M = 因为11B A ⊥平面11A D DA ,1A M ⊂平面11A D DA ,所以111B A A M ⊥, 则222211111(2)3M B A A M B =+=+=故选:A.【点睛】关键点点睛:本题考查根据线面垂直判断线线垂直,能否根据题意得出当M 为1DD 的中点时1A M MC +取得最小值是解决本题的关键,考查计算能力,考查数形结合思想,是中档题.3.B解析:B 【分析】取AC 中点F ,连接,EF DF ,证明FED ∠是异面直线AB 与DE 所成角(或其补角),然后在三角形中求得其余弦值即可得. 【详解】取AC 中点F ,连接,EF DF ,∵E 是BC 中点,∴//EF AB ,12EF AB =, 则FED ∠是异面直线AB 与DE 所成角(或其补角), 设1AB =,则12EF =,3DE DF ==, ∴在等腰三角形DEF 中,11324cos 3EF FED DE ∠===. 所以异面直线AB 与DE 所成角的余弦值为36. 故选:B .【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.4.A解析:A 【分析】证明CBA ∠就是BC 与平面1ABC 所成的角,求出此角后,利用11//B C BC 可得结论, 【详解】∵90BAC ∠=︒,12AC BC =,∴30CBA ∠=︒, ∵1BC AC ,AB AC ⊥,1BC ABB ,1,BC AB ⊂平面1ABC ,∴AC ⊥平面1ABC ,∴CBA ∠就是BC 与平面1ABC 所成的角,即BC 与平面1ABC 所成的角是30, ∵棱柱中11//B C BC ,∴11B C 与平面1ABC 所成的角的大小为30, 故选:A .【点睛】思路点睛:本题考查求直线与平面所成的角,解题方法是定义法,即过直线一点作平面的垂直,得直线在平面上的射影,由直线与其射影的夹角得直线与平面所成的角,然后在直角三角形中求出此角.解题过程涉及三个步骤:一作出图形,二证明所作角是直线与平面所成的角,三是计算.5.C解析:C 【分析】由三视图还原出原几何体,确定其结构,再求出外接球的半径得球的表面积. 【详解】由三视图,知原几何体是一个四棱锥P ABCD -,如图,底面ABCD 是边长为1的正方形,PB ⊥底面ABCD ,由PB ⊥底面ABCD ,AD ⊂面ABCD ,得PB AD ⊥,又AD AB ⊥,AB PB B ⋂=,,AB PB ⊂平面PAB ,所以AD ⊥平面PAB ,而PA ⊂平面PAB ,所以AD PA ⊥,同理DC PC ⊥,同样由PB ⊥底面ABCD 得PB BD ⊥,所以PD 中点O 到四棱锥各顶点距离相等,即为其外接球球心,PD 为球直径,222222PD PB BD PA AD AB =+=++=,∴外接球半径为12ADr ==, 表面积为2414S ππ=⨯=. 故选:C .【点睛】关键点点睛:本题考查由三视图还原几何体,考查棱锥的外接球表面积.解题关键是确定外接球的球心.棱锥的外接球球心在过各面外心(外接圆圆心)且与该面垂直的直线上.6.C解析:C 【分析】举特例舍去不正确选项,可得正确答案. 【详解】过EF 的平面为平面ABF 时,G 在A 点, H 在B 点, 所以0BH AGHC GD==,EF 平分GH , 即BH AG HC GD =,所以舍去ABD ,选C 故选:C7.A解析:A 【分析】由题意画出如图正四棱锥,可得M 点在GK 上运动,N 点在CD 上运动,且四边形KCDG 是等腰梯形,则||MN 的取值范围的最小值就是等腰梯形的高,最大值就是梯形的对角线长,作KH ED ⊥,在直角三角形中求KJ KD 、的长可得答案. 【详解】如图正四棱锥P ECDF -,PO ⊥平面ECDF ,O 是底面中心,G K 、分别是PF PE 、的中点,由题意知,M 点在GK 上运动,N 点在CD 上运动,所以////GK FE DC ,且11222GK FE DC ===, 所以四边形KCDG 是梯形,在ECK 与FDG △中,,,EC FD EK FG KEC GFD ==∠=∠,所以ECK ≅FDG △,所以KC GD =,所以四边形KCDG 是等腰梯形,则||MN 的取值范围的最小值就是等腰梯形的高, 最大值就是梯形的对角线长,且22PO EC CD ===,,1222EO ED == 作KH ED ⊥于H ,所以//KH PO ,KH ⊥平面ECDF ,112KH PO ==,且H 是EO 的中点,122EH EO ==,32DH =,45EDC ∠=,作KJ CD ⊥于J ,连接HJ ,12CD KGCJ -==, 所以3DJ =, 由余弦定理得2222cos 9HJ DH DJ DH DJ EDC =+-⋅∠=, 所以2221910KJ KH HJ =+=+=,10KJ =22211819DK EH HD =+=+=,19DK =故选:A. 【点睛】本题考查了正四棱锥的性质及线段的取值范围问题,关键点是画出正四棱锥分析出问题的实质,考查了学生的空间想象力.8.C解析:C 【分析】将正三棱锥补成一个正方体,计算出正方体的棱长,可得出正方体的体对角线长,即为外接球的直径,进而可求得这个球的表面积. 【详解】设该正三棱锥为A BCD -,将三棱锥A BCD -补成正方体AEBF GCHD -,如下图所示:则正方体AEBF GCHD -的棱长为22222⨯=,该正方体的体对角线长为23 所以,正三棱锥A BCD -的外接球直径为23R =3R =, 该球的表面积为2412S R ππ==. 故选:C. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.9.D解析:D 【分析】在A 中,m 与n 相交、平行或异面; 在B 中,l 与m 不一定平行,有可能相交; 在C 中,m ⊥β或m ∥β或m 与β相交;在D 中,由直线与平面垂直的性质与判定定理可得m ∥α.【详解】由直线m 、n ,和平面α、β,知:对于A ,若m ∥α,n ∥α,则m 与n 相交、平行或异面,故A 错误; 对于B ,若//,//,//l m αβαβ,l 与m 不一定平行,有可能相交,故B 错误; 对于C ,若α⊥β,m ⊂α,则m ⊥β或m ∥β或m 与β相交,故C 错误;对于D ,若α⊥β,m ⊥β,m ⊄α,则由直线与平面垂直的性质与判定定理得m ∥α,故D 正确. 故选:D . 【点睛】本题考查了命题真假的判断问题,考查了空间线线、线面、面面的位置关系的判定定理及推论的应用,体现符号语言与图形语言的相互转化,是中档题.10.D解析:D 【分析】在BCD △中,利用余弦定理和基本不等式可得163BC BD ⋅≤,由三角形的面积公式可得43BCDS≤,由二面角A BC D --的大小为60,可得A 到平面BCD 的最大距离为2sin 603h ==ABCD 体积的最大值.【详解】在BCD △中,由余弦定理可得2222cos120CD BC BD BC BD =+-⋅22BC BD BC BD =++⋅因为222BC BD BC BD +≥,所以23CD BC BD ≥⋅, 所以163BC BD ⋅≤,当且仅当BC BD =时等号成立, 111634sin120322323BCDSBC BD =⋅≤⨯⨯= 因为二面角A BC D --的大小为60,所以点A 到平面BCD 的最大距离为2sin 603h == 所以1144333333A BCD BCDV S h -=⋅≤=, 所以四面体ABCD 体积的最大值是43,故选:D 【点睛】关键点点睛:本题解题的关键点是利用余弦定理和基本不等式、三角形面积公式求出BCD S △最大值,再由二面角求出高的最大值.11.B解析:B 【分析】由题意可知所需要材料的体积即为正四面体外接球体积与正四面体体积之差,求出正四面体体积、外接球体积,然后作差可得所需要材料的体积,再乘以原料密度可得结果. 【详解】由题意可知,几何体ABCD 是棱长为6cm 的正四面体, 所需要材料的体积即为正四面体外接球体积与正四面体体积之差,设正四面体的棱长为a 3=,设正四面体外接球半径为R ,则2222()()332R R a =-+⨯,解得R =所以3D 打印的体积为:3233411332V a a ππ⎫=-⋅=⎪⎪⎝⎭, 又336216a ==,所以207.71125.38182.331182V =-≈-=≈, 故选:B 【点睛】关键点点睛:本题考查正四面体与正四面体的外接球,考查几何体的体积公式,解决本题的关键点是求出正四面体外接球体积与正四面体体积,考查学生空间想象能力和计算能力,属于中档题.12.C解析:C 【分析】首先通过延长直线,DC AB ,交于点G ,平面BAE 变为GAE ,连结PG ,EG 交于点F ,再根据三角形中线的性质,求PFFC的值. 【详解】延长,DC AB ,交于点G ,连结PG ,EG 交PC 于点F ,//AD BC ,且2AD BC =,可得点,B C 分别是,AG DG 的中点,又点E 是PD 的中点,PC ∴和GE 是△PGD 的中线,∴点F 是重心,得2PFFC=故选:C 【点睛】关键点点睛:本题的关键是找到PC 与平面BAE 的交点,即将平面BAE 转化为平面GAE 是关键. 二、填空题13.【分析】设正方体的棱长为正方体的内切球半径为正方体的外接球半径再由已知条件和球的表面积公式可得答案【详解】设正方体的棱长为正方体的内切球半径为正方体的外接球半径满足:则由题意知:则该正方体的内切球的 解析:10【分析】设正方体的棱长为a ,正方体的内切球半径为2a r =,正方体的外接球半径3R =,再由已知条件和球的表面积公式可得答案. 【详解】设正方体的棱长为a ,正方体的内切球半径为2a r =, 正方体的外接球半径R 满足:22222a R ⎫⎛⎫=+⎪ ⎪⎪⎝⎭⎝⎭,则3R =. 由题意知:33122aR r a -=-=,则2a =,3R = 该正方体的内切球的表面积为4π,又因为圆周率的平方除以十六等于八分之五,即25168π=,所以10π=所以内切球的表面积为410故答案为:410 【点睛】关键点点睛:本题考查正方体的外接球和内切球问题,考查空间几何新定义,解决本题的关键点是利用正方体的外接球半径,内切球半径和正方体面对角线的一半组成勾股定理,得出正方体内切球半径,进而得出表面积,考查学生空间想象能力和计算能力,属于中档题.14.【分析】取与中点根据平面平面可知平面球心必在直线上设球心为D 则可求得球心恰好为点O 从而求得外接球的半径代入球的表面积公式计算【详解】在三棱台中可得都是等腰三角形四边形为等腰梯形即如图取与中点连接则可 解析:32π【分析】取AB 与11A B 中点,O O ',根据平面11AA B B ⊥平面ABC ,可知'⊥O O 平面ABC ,球心必在直线O O '上,设球心为D ,则()22221O D O O OC O D O C ''''-+=+,可求得球心恰好为点O ,从而求得外接球的半径R ,代入球的表面积公式计算. 【详解】在三棱台111ABC A B C -中,11190,4,22ACB AC BC A B CC ∠=︒====可得111,A A C C B B 都是等腰三角形,11112A C B C ==,四边形11A ABB 为等腰梯形即11AA BB =,如图,取AB 与11A B 中点,O O ',连接1,,CO OO C O '',则可得122,2CO C O '==,O O AB '⊥,又平面11AA B B ⊥平面ABC ,两面交线为AB ,所以'⊥O O 平面ABC .因为OA OB OC ==,111O A O B O C '''==,面//ABC 面111A B C , 所以球心必在直线O O '上.所以在直角梯形1C O OC '中可求得6O O '=,由题意可知,该三棱台外接球的外接球的球心必在直线O O '上,设球的半径为R ,球心为D ,则()22221O D O O OC O D O C ''''-+=+,得6O D '=,所以球心恰好为点O ,所以球的半径为22,所以该三棱台外接球的表面积为24(22)32ππ=. 故答案为:32π【点睛】方法点睛:定义法:到各个顶点距离均相等的点为外接球的球心,借助面面垂直的性质,找到线面垂直,则球心一定在垂线上,再根据到其他顶点距离也是半径,列关系求解即可.15.【分析】由圆柱体积求得底面半径母线长设底面圆心为可得为异面直线与所成的角(或其补角)在对应三角形中求解可得【详解】设圆柱底面半径为则母线长为由得设底面圆心为连接则所以为异面直线所成的角在中所以故答案 解析:6 【分析】由圆柱体积求得底面半径,母线长,设底面圆心为O ,可得OEF ∠为异面直线AC 与EF 所成的角(或其补角).在对应三角形中求解可得. 【详解】设圆柱底面半径为r ,则母线长为2r ,由2216r r ππ⋅=得2r.设底面圆心为O ,连接OE ,OF .则//OE AC ,所以OEF ∠为异面直线AC ,EF 所成的角.在Rt OEF △中,2OF =,22OE =,23EF =. 所以6cos OE OEF EF ∠==. 故答案为:63.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.16.(1)(2)(4)【分析】首先取中点连结先判断(4)是否正确再根据平行关系以及等角定理和余弦定理判断(1)再判断(2)假设成立根据直线与平面垂直的性质及判定可得矛盾来判断(3)【详解】取中点连结则平解析:(1)(2)(4) 【分析】首先取CD 中点Q ,连结MQ ,BQ ,先判断(4)是否正确,再根据平行关系,以及等角定理和余弦定理判断(1),再判断(2),假设1DE A C ⊥成立,根据直线与平面垂直的性质及判定,可得11DA A E ⊥矛盾来判断(3). 【详解】取CD 中点Q ,连结MQ ,BQ ,则1//MQ DA ,//BQ DE ,∴平面//MBQ 平面1A DE ,又MB ⊂平面MBQ ,//MB ∴平面1A DE ,故(4)正确;由1A DE MQB ∠=∠,112MQ A D ==定值,QB DE ==定值, 由余弦定理可得2222cos MB MQ QB MQ QB MQB =+-⋅⋅∠ 所以MB 是定值,故(1)正确;B 是定点,M ∴是在以B 为球心,MB 为半径的球面上,故(2)正确;145A DE ADE ∠=∠=,45CDE ∠=,且设1AD =,2AB =,则2DE CE ==若存在某个位置,使1DE A C ⊥,则因为222DE CE CD +=,即CE DE ⊥,因为1AC CE C =,则DE ⊥平面1A CE ,所以1DE A E ⊥,与11DA A E ⊥矛盾, 故(3)不正确.故答案为:(1)(2)(4) 【点睛】关键点点睛:本题考查线线,线面位置关系时,首先判断(4)是否正确,其他选项就迎刃而解,而判断线面平行时,可根据面面平行证明线面平行.17.【分析】设出外接球的半径球心的外心半径r 连接过作的平行线交于连接如图所示在中运用正弦定理求得的外接圆的半径r 再利用的关系求得外接球的半径运用球的表面积公式可得答案【详解】设三棱锥外接球的半径为球心为 解析:20π【分析】设出外接球的半径R 、球心O ,ABC 的外心1O 、半径 r , 连接1AO ,过O 作的平行线OE 交AD 于 E ,连接OA ,OD ,如图所示,在ABC 中,运用正弦定理求得 ABC的外接圆的半径r ,再利用1,,R r OO 的关系求得外接球的半径,运用球的表面积公式可得答案. 【详解】设三棱锥外接球的半径为R 、球心为O ,ABC 的外心为1O 、外接圆的半径为r ,连接1AO ,过O 作平行线OE 交AD 于E ,连接OA ,OD ,如图所示,则OA OD R ==,1O A r =,OE AD ⊥,所以E 为AD 的中点.在ABC中,由正弦定理得2sin 3BC r BAC ==∠8r =. 在ABC 中,由余弦定理2222cos BC AB AC AB AC BAC =+-⋅⋅∠,可得2117963AB AB =+-⋅⋅,得4AB =.所以11sin 34223ABC S AB AC BAC =⋅⋅∠=⨯⨯⨯=△因为1133D ABC ABC V S AD AD -=⋅⋅=⨯=△AD =.连接1OO ,又1//OO AD ,所以四边形1EAO O 为平行四边形,112EA OO AD ===,所以R ===所以该三棱锥的外接球的表面积224π4π20πS R ===.故答案为:20π.【点睛】本题考查三棱锥的外接球,及球的表面积计算公式,解决问题的关键在于利用线面关系求得外接球的球心和球半径,属于中档题.18.【分析】取的中点连接证明出可得出面角的平面角为计算出利用余弦定理求得由此可得出二面角的余弦值【详解】取的中点连接如下图所示:为的中点则且同理可得且所以二面角的平面角为由余弦定理得因此二面角的余弦值为解析:34【分析】取AB 的中点O ,连接VO 、OC ,证明出VO AB ⊥,OC AB ⊥,可得出面角V AB C --的平面角为VOC ∠,计算出VO 、OC ,利用余弦定理求得cos VOC ∠,由此可得出二面角V AB C --的余弦值. 【详解】取AB 的中点O ,连接VO 、OC ,如下图所示:VA VB =,O 为AB 的中点,则VO AB ⊥,且AV BV ⊥,22AB =122VO AB ∴== 同理可得OC AB ⊥,且2OC =V AB C --的平面角为VOC ∠,由余弦定理得2223cos 24VO OC VC VOC VO OC +-∠==⋅,因此,二面角V AB C --的余弦值为34.故答案为:34. 【点睛】本题考查二面角余弦值的计算,考查二面角的定义,考查计算能力,属于中等题.19.【分析】由第二个图可知水的体积占整个圆锥体积的在第一个图中水的体积占圆锥的上面小圆锥体积占大圆锥体积的根据小圆锥体积与大圆锥体积比是其高的三次方的比即可解得a 的值【详解】在图②中水形成的小圆锥和大圆解析:(2a【分析】由第二个图可知,水的体积占整个圆锥体积的18,在第一个图中,水的体积占圆锥的18,上面小圆锥体积占大圆锥体积的78,根据小圆锥体积与大圆锥体积比是其高的三次方的比,即可解得a 的值. 【详解】在图②中,水形成的小“圆锥”和大圆锥形容器高的比为12,底面半径比为12,故其底面积的比为14,所以体积比为18,则在图①中,无水部分形成的小“圆锥”和大圆锥形容器的体积比为78,设水面高度为h ,则小“圆锥”和大圆锥形容器的高的比为22a h a-,体积比为327(=28a h a -),解的h =(2a .故答案为: (2a 【点睛】本题考查了圆锥的体积的计算,属于中档题目,解题中的关键是要准确利用圆锥体积公式得到大小圆锥体积比与大小圆锥的高比的关系.20.【分析】由矩形的边长可得底面外接圆的半径再由为等腰直角三角形可得其外接圆的半径又平面平面可得底面外接圆的圆心即为外接球的球心由题意可得外接球的半径进而求出外接球的体积【详解】解:取矩形的对角线的交点 解析:323π【分析】由矩形的边长可得底面外接圆的半径,再由PAD △为等腰直角三角形可得其外接圆的半径,又平面PAD ⊥平面ABCD 可得底面外接圆的圆心即为外接球的球心,由题意可得外接球的半径,进而求出外接球的体积. 【详解】解:取矩形的对角线的交点O 和AD 的中点E ,连接OE ,OP ,OE ,则O 为矩形ABCD 的外接圆的圆心,而2DPA π∠=,23AD =,2AB =,PA PD =,则//OE AB ,112OE AB ==, 132PE AD ==, 所以E 为PAD △的外接圆的圆心,因为平面PAD ⊥平面ABCD , 所以O 为外接球的球心,OP 为外接球的半径,在POE △中,222222(3)14R OP PE OE ==+=+=,所以2R =, 所以外接球的体积343233V R ππ==, 故答案为:323π.【点睛】本题考查四棱锥的棱长与外接球的半径的关系及球的体积公式,属于中档题.三、解答题21.(Ⅰ)证明见解析;(Ⅱ)①4,②3π. 【分析】(Ⅰ)连接BD ,点E 是BC 边的中点,得出DE BC ⊥,DE AD ⊥再由DP AD ⊥,得出结果;(Ⅱ)DE AD ⊥,PD AD ⊥,PDE ∠为二面角P AD C --的平面角,60PDE ∠=︒,过P 在平面PDE 内做PK DE ⊥于K ,易证PK ⊥面ABCD ,PK 为点到面的距离,PBK ∠即为线面角. 【详解】(Ⅰ)连接BD ,底面ABCD 是菱形,∠BDC =60°, ∴△BCD 是正三角形.∵点E 是BC 边的中点,∴DE ⊥BC ,∵AD ∥BC ,∴DE ⊥AD .∵DP ⊥AD ,DP ∩AD =D , ∴AD ⊥平面PDE ;(Ⅱ)①∵DE ⊥AD ,PD ⊥AD ,∴PDE ∠为二面角P -AD -C 的平面角,∴60PDE ∠=︒, 过P 在平面PDE 内做PK DE ⊥于K ,由(Ⅰ)易AD PK ⊥. ∴PK ⊥面ABCD . ∵83PD =∴43DK =,4PK =, 即点P 到平面ABCD 的距离是4. ②AB =4,∴23DE =∴23DK DE =,∴K 为BCD △重心. 连接BK ,∵BCD △为正三角形,所以BK 为BP 在面ABCD 内的射影. ∴PB ⊥AB ,PBK ∠为直线PB 与平面ABCD 所成角,RT PKB △中,tan 3PK PK PKB KB DK ∠===3PKB π∠=, 直线PB 与平面ABCD 所成角的大小为3π. 【点睛】求直线与平面所成的角的一般步骤:①找直线与平面所成的角,即通过找直线在平面上的射影来完成; ②计算,要把直线与平面所成的角转化到一个三角形中求解. 22.(1)证明见解析;(22【分析】(1)取PB 边的中点E ,即可证明四边形AEFD 为平行四边形,再根据线面平行的判定定理即可证明;(2)取BC 边的中点G ,由//DG AB ,即可得到直线AB 与平面PDC 所成角即为DG 与平面PDC 所成角,再由等体积法求得2G PCD d -=AB 与平面PDC 所成角的正弦值. 【详解】解:(1)如图所示:取PB 边的中点E ,连,AE FE , 则三角形中位线可知://EF BC 且12EF BC =, 由题可知://AD BC 且12AD BC =, //AD EF ∴且AD EF =, 即四边形AEFD 为平行四边形, //DF AE ∴又DF ⊄平面,PAB AE ⊂平面PAB ,故//DF 平面PAB ; (2)取BC 边的中点G , 则//DG AB ,且2DG AB ==,直线AB 与平面PDC 所成角即为DG 与平面PDC 所成角, 又1CDGS=,且易得DC PD =,所以11223622CDPSPC DF =⋅=⨯=由等体积法,1113633P CDG G PCD G PCD V V d ---==⨯=,得22G PCD d -=, DG ∴与平面PDC 所成角的正弦值为2222= 故直线AB 与平面PDC 2. 【点睛】关键点点睛:本题解题的关键是利用等体积法求出G 点到平面PCD 的距离. 23.(Ⅰ)证明见解析;(Ⅱ)52. 【分析】。
高一数学必修二第一单元检测试题精选

高一数学必修二第一单元检测试题精选
高一数学必修二第一单元检测试题精选
数学是学习和研究现代科学技术必不可少的基本工具。
小编准备了高一数学必修二第一单元检测试题,希望你喜欢。
一、选择题
1、给出下列命题
(1)如果一个几何体的三视图是完全相同的,则这个几何体是正方体
(2)如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体
(3)如果一个几何体的三视图都是矩形,则这个几何体是长方体
(4)如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台
其中正确的命题的个数是( )
A.0
B.1
C.2
D.3
2、一个四面体的所有棱长都为,四个项点在同一球面上,则此球的表面积为( )
A.3
B.4
C.3
D.6
3、长方体的六个面的面积之和为11,十二条棱长度之和为24,则这个长方体的一条对角线长为( )
A.2
B.
C.5
D.6
11、设圆台的高为h,母线与轴的夹角为90-,轴截面中一条对角线垂直于腰,求圆台的母线长,上下底面半径之和
12、如图所示,侧棱长为2的正三棱锥V-ABC中,
AVB=BVC=CVA=40,过A作截面AEF,求截面三角形AEF周长的最小值
高一数学必修二第一单元检测试题就为大家介绍到这里,希望对你有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修二第一单元检测试题精选
数学是学习和研究现代科学技术必不可少的基本工具。
小编准备了高一数学必修二第一单元检测试题,希望你喜欢。
一、选择题
1、给出下列命题
(1)如果一个几何体的三视图是完全相同的,则这个几何体是正方体
(2)如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体
(3)如果一个几何体的三视图都是矩形,则这个几何体是长方体
(4)如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台
其中正确的命题的个数是( )
A.0
B.1
C.2
D.3
2、一个四面体的所有棱长都为,四个项点在同一球面上,则此球的表面积为( )
A.3
B.4
C.3
D.6
3、长方体的六个面的面积之和为11,十二条棱长度之和为24,则这个长方体的一条对角线长为( )
A.2
B.
C.5
D.6
4、若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )
A.三棱锥
B.四棱锥
C.五棱锥
D.六棱锥
5、下列命题中,正确的是( )
A.平行于圆锥的一条母线的截面是等腰三角形
B.平行于圆台的一条母线的截面是等腰梯形
C.过圆锥顶点的截面是等腰三角形
D.过圆台一个底面中心的截面是等腰梯形
6、过球面上两点可能作球的大圆的个数是( )
A.有且只有一个
B.一个或无数多个
C.无数多个 D不存在这种大圆
二、填空题
7、用长、宽分别是3和的矩形硬纸卷成圆柱的侧面,则圆柱的底面半径是___________
8、给出一块正方形纸片,边长为a,用它剪拼成一个长方体模型,则这个长方形的体积为__________
9、若两个长方体的长、宽、高分别为5cm、4cm、3cm,把它们两个全等的面重合在一起组成大长方体,则长方体的对角线最长为________________
三、解答题
19、正四棱台AC的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台的侧棱长和斜高
11、设圆台的高为h,母线与轴的夹角为90-,轴截面中一条对角线垂直于腰,求圆台的母线长,上下底面半径之和
12、如图所示,侧棱长为2的正三棱锥V-ABC中,
AVB=BVC=CVA=40,过A作截面AEF,求截面三角形AEF周长的最小值
高一数学必修二第一单元检测试题就为大家介绍到这里,希望对你有所帮助。
