1000000以内的完全平方数
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位.之巴公井开创作2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位罕见分数、小数互化表罕见的分数、小数及百分数的互化经常使用平方数罕见立方数罕见特殊数的乘积错位相加/减例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25 A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合 11~99 所有平方的计算.11X11=121 21X21=4141 31X31=961 41X41=168112X12=148 22X22=484 32X32=1024 42X42=1764 52X52=2704从上面的计算我们可以得出公式:个位=个位×个位所得数的个位,如果满几十就向前进几,十位=个位×(十位上的数字×2)+进位所得数的末位,如果满几十就向前进几,百位=两个十位上的数字相乘+进位.例:26×26=个位=6×6=36,满 30 向前进 3;十位=6×(2×2)+3=27,满 20 向前=进 2;百位=2×2+2=6由此可见26×26=67623×23个位=3×3=9十位=3×(2×2)=12,写 2 进 1百位=2×2+进 1=5所以23×23=52946×46 个位=6×6= 36,写6进3十位=6×(4×2)+进 3= 5 1,写 1 进 5百位=4×4+进 5= 21,写 1 进 2所以46×46=2116如果没有满十就不用进位,计算更简便.例:13×13个位=3×3=9 十位=3×(1×2)=6 百位=1×1所以13×13=169规律:(1)完全平方数的个位数字只能是 0,1,4,5,6,9.(没有 2,3,7,8)两个整数的个位数字之和为 10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是 6;反之,如果完全平方数的个位数字是 6,则它的十位数字一定是奇数.(4)偶数的平方是 4 的倍数;奇数的平方是 4 的倍数加 1.(5)奇数的平方是 8n+1 型;偶数的平方为 8n 或 8n+4 型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被 5 整除的数的平方为5n±1 型,能被 5 整除的数的平方为 5n 型.(8)平方数的形式具有下列形式 16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有 2,5,8)(10)如果质数 p 能整除 a,但 p 的平方不能整除 a,则 a 不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数 n 是完全平方数的充沛需要条件是 n 有奇数个因数(包括 1 和 n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它自己乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如 0,1,8,27,64,125,216,343,512,729,1000 等.如果正整数 x,y,z 满足不定方程 x2+y2=z2 ,就称 x,y,z 为一组勾股数.x,y 肯定是一个为奇数另一个为偶数,不成能同时为奇数或同时为偶数.z 和z² 肯建都是奇数.五组罕见的勾股数:3²+4²=5²;5²+12²=13²;7²+24²=25²;8²+15²=17²;20²+21²=29²9+16=25;25+144=169;49+576=625; 64+225=289; 400+441=841记忆技巧:(a+b)²= a² + b² + 2ab (a-b)²=a² + b² -2ab|| | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:13²=(10+3) ²=10²+3²+2×10×3=100+9+60=16988²=(90-2)²=90²+2²-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较年夜的数 n 是不是质数时可以缩小其可能因子的筛选范围,只需检查 3 到n 之间的所有质数是不是 n 的因子即可, 超越n的都不用检查了例如:判定2431是否为质数,因为49²=2401<2431<2500=50²,所以 49<2431.<50,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到 47之间的所有质数能否整除2431即可,而53,59,61,67……等更年夜的质数都不用检查了,实际上2431=11×13×17③增加对数字的熟悉水平,比如16²=256=28,32²=1024=210,64²=4096=212,另外一些特殊结构的数字应该牢记,如88²=7744, 11²=121,22²=484,(121 和 484 从左到右与从右到左看是一样的) 12²=144,21²=441,13²=169,31²=961,(a 左右倒置后a² 也左右倒置).小学单元换算一、长度(一) 什么是长度?长度是一维空间的怀抱.(二) 长度经常使用单元* 公里(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) * 微米(um)(三) 单元之间的换算1 微米=1000 纳米 1 毫米 =1000 微米 1 厘米=10 毫米1 分米 =10 厘米1 米 =1000 毫米1 千米 =1000 米1 米=10 分米=100 厘米二、面积(一)什么是面积面积,就是物体所占平面的年夜小.对峙体物体的概况的几多的丈量一般称概况积.(二)经常使用的面积单元* 平方毫米 * 平方厘米 * 平方分米 * 平方米 * 平方千米(三)面积单元的换算1 平方厘米 =100 平方毫米 1 平方分米=100 平方厘米1 平方米=100 平方分米1 公倾 =10000 平方米 1 平方公里 =1 平方千米=100 公顷1 公顷=0.01 平方千米≈15 亩 1 平方千米=1000000 平方米1 平方米=100 平方分米=10000 平方厘米三、体积和容积(一)什么是体积、容积体积,就是物体所占空间的年夜小.容积,箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积.(二)经常使用单元1 体积单元* 立方米 * 立方分米 * 立方厘米2 容积单元* 升 * 毫升(三)单元换算1 体积单元1 平方米 =100 平方分米 1 平方分米=100 平方厘米 1 平方厘米=100 平方毫米1 立方米=1000 立方分米 1 立方分米=1000 立方厘米2 容积单元1 升=1 立方米 1 升=1000 毫升1 毫升=1 立方厘米1 立方米=1000 升1 立方分米=1 升 1 立方厘米=1 毫升四、质量(一)什么是质量质量,就是暗示暗示物体有多重.(二)经常使用单元* 吨 t * 千克 kg * 克 g(三)经常使用换算1 吨(t)=1000 千克(kg)1 千克=1000 克(g)重量单元换算1 吨=1000 千克1 千克=1000 克1 千克=1 公斤五、时间(一)什么是时间是指有起点和终点的一段时间(二)经常使用单元世纪、年、月、日、时、分、秒(三)单元换算* 1 世纪=100 年 1 年=12 月 1 年=365 天平年一年=366 天闰年.一、三、五、七、八、十、十二是年夜月年夜月有 31 天四、六、九、十一是小月小月有 30 天平年 2 月有 28 天闰年 2 月有 29 天1 天= 24 小时 1 小时=60 分 1 分=60 秒 1秒=1000毫秒(ms) 1时=3600秒货币(一)什么是货币货币是充任一切商品的等价物的特殊商品.货币是价值的一般代表,可以购买任何另外商品.(二)经常使用单元* 元 * 角 * 分(三)单元换算1 元=10 角 1 角=10 分 1 元=100 分四则运算关系加法:一个加数=和-另一个加数减法:被减数=差+减数减数=被减数-差乘法:一个因数=积÷另一个因数除法:被除数=商×除数除数=被除数÷商两个规律1、除法的商不变规律:被除数和除数同时乘或除以相同的数(0 除外),商不变.2、乘法的积不变规律:如果一个因数乘几,另一个因数则除以几,那么它们的积不变.数学简便运算方法归类一、同级运算(没有括号),可以带着符号搬场a+b+c=a+c+ba-b-c=a-c-ba+b-c=a-c+b a-b+c=a+c-ba×b×c=a×c×b a÷b÷c=a÷c÷ba×b÷c=a÷c×ba÷b×c=a×c÷b二、有括号的同级运算,可以根据去括号的性质把括号去失落1、括号前面是“+”号或“×”号,去失落括号不变号.a+(b+c)=a+b+c a+(b-c)=a+b-c a×(b×c)=a×b×c a×(b÷c)=a×b÷c2、括号前面是“-”号或“÷”号,去失落括号要变号.a-(b+c)=a-b-c a-(b-c)=a-b+c a÷(b×c)=a÷b÷c a÷(b÷ c)=a÷b×c上面的式子从左到右可以去括号,那么从右到左就是添括号的方法了.自己认真观察发现没有括号的同级运算中添括号的性质哦. 三、乘法分配律:(a+b)×c=a×c+b×c 或(a-b)×c=a×c-b×c 乘法分配律的逆运用:a×c+a×b=(a+b)×c 或a×c-b×c=(a-b)×c两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律.1.分配法(从左到右的用法) 括号里是加或减运算,与另一个数相乘,注意分配.2.提取公因式(从右到左的用法)注意相同因数的提取.3.注意构造,让算式满足乘法分配律的条件.四、借来还去法看到名字,就知道这个方法的含义.用此方法时,需要注意观察,发现规律.还要注意还哦 ,有借有还, 再借不难嘛.例:9999+999+99+9五、拆分法顾名思义,拆分法就是为了方便计算把一个数拆成几个数.这需要掌握一些“好朋友”,如:2 和 5,4 和 5,2 和 2.5,4 和 2.5,8 和 1.25 等.分拆还要注意不要改变数的年夜小哦. 例:3.2×12.5×25 1.25×88 3.6×0.25以上几种方法包括了小学数学罕见的简便运算的方法, 在选择简便方法的时候一定要注意简便方法的依据,千万不能没有依据的胡拉乱扯一通,有时候是出题者故意挖的陷阱,看似可以运用简便算法,实际上找不出可以简便运算的依据,这样的题只能依照运算顺序计算的.(例如 2.5×4÷ 2.5×4,看似加括号很简便,结果即是1,而实际上括号加在除号的后面是要变号的,所以本道题的简便方法是“没有括号的同级运算,可以带着符号搬场.2.5÷ 2.5×4×4)简便计算简便运算重在找依据1、运算定律:运算定律用字母暗示加法交换律 a+b=b+a加法结合律(a+b)+c=a+(b+c)乘法交换律a×b=b×a乘法结合律(a×b)×c=a×(b×c)乘法分配律(a+b)×c=a×c+b×c减法运算规律 a-b-c=a-(b+c)除法运算规律a÷b÷c=a÷(b×c)2、乘、除法的互化.(小技巧:符号是相反的;两个数相乘得“1”)(1)A÷0.1=A×10 (7)A÷0.01=A×100(2)A×0.1=A÷10 (8)A×0.01=A÷100(3)A÷0.2=A×5 (9)A÷0.25=A×4(4)A×0.2=A÷5 (10)A×0.25=A÷4(5)A÷0.5=A×2 (11)A÷0.125=A×8(6)A×0.5=A÷2 (12)A×0.125=A÷83、求近似数的方法.(1)四舍五入法. (2)进一法.(3)去尾法4、积与因数、商与被除数的年夜小比力:第 2 个因数>1,积>第 1 个因数;除数>1,商<被除数;第 2 个因数=1,积=第 1 个因数;除数=1,商=被除数;第 2 个因数<1,积<第 1 个因数. 除数<1,商>被除数;。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位.之迟辟智美创作2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位罕见分数、小数互化表罕见的分数、小数及百分数的互化经常使用平方数罕见立方数罕见特殊数的乘积错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;A÷5型速算技巧:A÷5=0.1A×2;A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算.11X11=121 21X21=4141 31X31=961 41X41=168112X12=148 22X22=484 32X32=1024 42X42=1764 52X52=2704从上面的计算我们可以得出公式:个位=个位×个位所得数的个位,如果满几十就向前进几,十位=个位×(十位上的数字×2)+进位所得数的末位,如果满几十就向前进几,百位=两个十位上的数字相乘+进位.例:26×26=个位=6×6=36,满30 向前进3;十位=6×(2×2)+3=27,满20 向前=进2;百位=2×2+2=6由此可见26×26=67623×23个位=3×3=9十位=3×(2×2)=12,写2 进1百位=2×2+进1=5所以23×23=52946×46 个位=6×6= 36,写6进3十位=6×(4×2)+进3= 5 1,写1 进5百位=4×4+进5= 21,写1 进2所以46×46=2116如果没有满十就不用进位,计算更简便.例:13×13个位=3×3=9 十位=3×(1×2)=6 百位=1×1所以13×13=169规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4 的倍数;奇数的平方是4 的倍数加1.(5)奇数的平方是8n+1 型;偶数的平方为8n 或8n+4 型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5 整除的数的平方为5n±1 型,能被5 整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p 能整除a,但p 的平方不能整除a,则a 不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n 是完全平方数的充沛需要条件是n 有奇数个因数(包括1 和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它自己乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000 等.如果正整数x,y,z 满足不定方程x2+y2=z2 ,就称x,y,z 为一组勾股数.x,y 肯定是一个为奇数另一个为偶数,不成能同时为奇数或同时为偶数.z 和z²肯建都是奇数.五组罕见的勾股数:3²+4²=5²;5²+12²=13²;7²+24²=25²;8²+15²=17²;20²+21²=29²9+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)²= a² + b² + 2ab (a-b)²=a² + b²-2ab|| | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:13² =(10+3) ²=10²+3²+2×10×3=100+9+60=16988²=(90-2)²=90²+2²-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较年夜的数n 是不是质数时可以缩小其可能因子的筛选范围,只需检查3 到n之间的所有质数是不是n 的因子即可,超越n的都不用检查了例如:判定2431是否为质数,因为49²=2401<2431<2500=50²,所以49<2431.<50,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更年夜的质数都不用检查了,实际上2431=11×13×17③增加对数字的熟悉水平,比如16²=256=28,32²=1024=210,64²=4096=212,另外一些特殊结构的数字应该牢记,如88²=7744, 11²=121,22²=484,(121 和484 从左到右与从右到左看是一样的) 12²=144,21²=441,13²=169,31²=961,(a 左右倒置后a²也左右倒置).小学单元换算一、长度(一) 什么是长度?长度是一维空间的怀抱.(二) 长度经常使用单元* 公里(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) * 微米(um)(三) 单元之间的换算1 微米=1000 纳米1 毫米=1000 微米1 厘米=10 毫米1 分米=10 厘米1 米=1000 毫米1 千米=1000 米1 米=10 分米=100 厘米二、面积(一)什么是面积面积,就是物体所占平面的年夜小.对峙体物体的概况的几多的丈量一般称概况积.(二)经常使用的面积单元* 平方毫米* 平方厘米* 平方分米* 平方米* 平方千米(三)面积单元的换算1 平方厘米=100 平方毫米1 平方分米=100 平方厘米 1 平方米=100 平方分米1 公倾=10000 平方米1 平方公里=1 平方千米=100 公顷1 公顷=0.01 平方千米≈15 亩1 平方千米=1000000 平方米1 平方米=100 平方分米=10000 平方厘米三、体积和容积(一)什么是体积、容积体积,就是物体所占空间的年夜小.容积,箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积.(二)经常使用单元1 体积单元* 立方米* 立方分米* 立方厘米2 容积单元* 升* 毫升(三)单元换算1 体积单元1 平方米=100 平方分米 1 平方分米=100 平方厘米1 平方厘米=100 平方毫米1 立方米=1000 立方分米 1 立方分米=1000 立方厘米2 容积单元1 升=1 立方米1 升=1000 毫升1 毫升=1 立方厘米1 立方米=1000 升1 立方分米=1 升 1 立方厘米=1 毫升四、质量(一)什么是质量质量,就是暗示暗示物体有多重.(二)经常使用单元* 吨t * 千克kg * 克g(三)经常使用换算1 吨(t)=1000 千克(kg)1 千克=1000 克(g)重量单元换算1 吨=1000 千克1 千克=1000 克1 千克=1 公斤五、时间(一)什么是时间是指有起点和终点的一段时间(二)经常使用单元世纪、年、月、日、时、分、秒(三)单元换算* 1 世纪=100 年1 年=12 月1 年=365 天平年一年=366 天闰年.一、三、五、七、八、十、十二是年夜月年夜月有31 天四、六、九、十一是小月小月有30 天平年2 月有28 天闰年2 月有29 天1 天= 24 小时 1 小时=60 分 1 分=60 秒1秒=1000毫秒(ms)1时=3600秒货币(一)什么是货币货币是充任一切商品的等价物的特殊商品.货币是价值的一般代表,可以购买任何另外商品.(二)经常使用单元* 元* 角* 分(三)单元换算1 元=10 角1 角=10 分1 元=100 分四则运算关系加法:一个加数=和-另一个加数减法:被减数=差+减数减数=被减数-差乘法:一个因数=积÷另一个因数除法:被除数=商×除数除数=被除数÷商两个规律1、除法的商不变规律:被除数和除数同时乘或除以相同的数(0 除外),商不变.2、乘法的积不变规律:如果一个因数乘几,另一个因数则除以几,那么它们的积不变.数学简便运算方法归类一、同级运算(没有括号),可以带着符号搬场a+b+c=a+c+ba-b-c=a-c-ba+b-c=a-c+b a-b+c=a+c-ba×b×c=a×c×b a÷b÷c=a÷c÷ba×b÷c=a÷c×ba÷b×c=a×c÷b二、有括号的同级运算,可以根据去括号的性质把括号去失落1、括号前面是“+”号或“×”号,去失落括号不变号.a+(b+c)=a+b+c a+(b-c)=a+b-c a×(b×c)=a×b×c a×(b÷c)=a×b÷c2、括号前面是“-”号或“÷”号,去失落括号要变号.a-(b+c)=a-b-c a-(b-c)=a-b+c a÷(b×c)=a÷b÷c a÷(b÷ c)=a÷b×c 上面的式子从左到右可以去括号,那么从右到左就是添括号的方法了.自己认真观察发现没有括号的同级运算中添括号的性质哦.三、乘法分配律:(a+b)×c=a×c+b×c 或(a-b)×c=a×c-b×c乘法分配律的逆运用:a×c+a×b=(a+b)×c 或a×c-b×c=(a-b)×c两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律.1.分配法(从左到右的用法) 括号里是加或减运算,与另一个数相乘,注意分配.2.提取公因式(从右到左的用法)注意相同因数的提取.3.注意构造,让算式满足乘法分配律的条件.四、借来还去法看到名字,就知道这个方法的含义.用此方法时,需要注意观察,发现规律.还要注意还哦,有借有还,再借不难嘛.例:9999+999+99+9五、拆分法顾名思义,拆分法就是为了方便计算把一个数拆成几个数.这需要掌握一些“好朋友”,如:2 和5,4 和5,2 和2.5,4 和2.5,8 和1.25 等.分拆还要注意不要改变数的年夜小哦. 例:3.2×12.5×25 1.25×883.6×0.25以上几种方法包括了小学数学罕见的简便运算的方法,在选择简便方法的时候一定要注意简便方法的依据,千万不能没有依据的胡拉乱扯一通,有时候是出题者故意挖的陷阱,看似可以运用简便算法,实际上找不出可以简便运算的依据,这样的题只能依照运算顺序计算的.(例如2.5×4÷ 2.5×4,看似加括号很简便,结果即是1,而实际上括号加在除号的后面是要变号的,所以本道题的简便方法是“没有括号的同级运算,可以带着符号搬场.2.5÷ 2.5×4×4)简便计算简便运算重在找依据1、运算定律:运算定律用字母暗示加法交换律a+b=b+a加法结合律(a+b)+c=a+(b+c)乘法交换律a×b=b×a乘法结合律(a×b)×c=a×(b×c)乘法分配律(a+b)×c=a×c+b×c减法运算规律a-b-c=a-(b+c)除法运算规律a÷b÷c=a÷(b×c)2、乘、除法的互化.(小技巧:符号是相反的;两个数相乘得“1”)(1)A÷0.1=A×10 (7)A÷0.01=A×100(2)A×0.1=A÷10 (8)A×0.01=A÷100(3)A÷0.2=A×5 (9)A÷0.25=A×4(4)A×0.2=A÷5 (10)A×0.25=A÷4(5)A÷0.5=A×2 (11)A÷0.125=A×8(6)A×0.5=A÷2 (12)A×0.125=A÷83、求近似数的方法.(1)四舍五入法. (2)进一法.(3)去尾法4、积与因数、商与被除数的年夜小比力:第2 个因数>1,积>第1 个因数;除数>1,商<被除数;第2 个因数=1,积=第1 个因数;除数=1,商=被除数;第2 个因数<1,积<第1 个因数. 除数<1,商>被除数;。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技巧:A×9= A×10—A;例:743×9=743×10—743=7430—743=6687A×9。
9型速算技巧:A×9。
9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430—74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739。
45×5=8739.45×10÷2=87394。
5÷2=43697。
25A÷5型速算技巧:A÷5=0。
1A×2;例:36。
843÷5=36.843×0。
1×2=3。
6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0。
沪科版数学七年级下完全平方公式与平方差公式(第1课时,完全平方公式)课件

+(
=
)2
(4)原式=(2a)2-2·2a·5+52
2
y +y+
=4a2-20a+25
注意每一项系数
例2.运用完全平方公式计算:
(1)(-2s+t)2
解:
(2) (-2x-1)2
(1)(-2s+t)2= (t-2s)²
= t² -2·2s·t +(2s)2
=t2-4st+4s2
=(2x+1)2
2
2
口诀:首平方,尾平方,首尾两倍中间放
( a b) a 2ab b
2
2
2
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不
丢项、不弄错符号、2ab时不少乘2;
巩固练习
(1) ( 2a
3)
2
(2)
1
(3
t)2
3
(3)
(b 3)
思考: (1)完全平方展开有几项?
2
(4)
( 2 a 3 y ) 2
(5)
(0.5m 0.2n) 2
(6)
(1 3x)(3x 1)
(2)每一项的符号特征?
相信你能行
课堂练习:
1、计算:
(1)(a
2
1 2
沪科版数学七年级下
8.3完全平方公式与平方差公式
第一课时
完全平方公式
知识回顾
1、多项式乘以多项式的 根据是什么?
——分配率
2、如何进行多项式与多项式乘法运算?
(m+b)(n+a)= mn
+ ma + bn + ba
小学数学单位换算及面积公式总结

小学数学单位换算及面积公式总结①.长度单位换算:1公里=1千米; 1千米=1000米; 1米=10分米; 1分米=10厘米; 1厘米=10毫米;1米=10分米=100厘米=1000毫米②.面积单位有:平方千米(km2)、公顷、平方米(m2)、平方分米(dm2)、平方厘米(cm2)、平方毫米(mm2)1公顷=10000平方米;1平方千米=100公顷=1000000平方米; 1平方米=100平方分米=10000平方厘米=1000000平方毫米; 1平方分米=100平方厘米10000平方毫米; 1平方厘米=100平方毫米③.比较图形的面积的方法有:(1)直接比较;(2)借助参照物比较;(3)数方格;(4)重叠法、转化法(经旋转、平移、分割、拼补、重组等将图形转换)④.地毯上的图形面积大小:(1)数方格计算面积;(2)“化整为零”即将整体的图案分割为若干个小图案面积不变;(3)“大面积减小面积”⑤.平行四边形两条平行的对边之间的垂直线段就是平行四边形的高,与它垂直的那组对边就是平行四边形的底。
平行四边形有两种不相同的高,每组对边之间有无数条高;三角形的一个顶点到对边的垂直线段就是三角形的高,这条对边是三角形的底。
三角形有三种不同的高而且只有三条高;梯形两条平行线之间的垂直线段就是梯形的高,梯形的高只有一种但有无数条。
每种图形的底和高都是相互对应的。
⑥正方形的面积(s)=边长(a)×边长(a) 公式 S= a2 长方形的面积(s)=长(a)×宽(b) 公式 S= a×b= ab⑦将平行四边形沿高剪开能拼成一个长方形:长方形的长=平行四边形的底,长方形的宽=平行四边形的高,所以平行四边形的面积(s)=底(a)×高(h) 公式s=a×h =ah 平行四边形的底=面积÷高公式a=s÷h 平行四边形的高=面积÷底公式h=s÷a;等底等高的平行四边形面积相等,但周长不一定相等,形状不一定相同。
完全平方公式与平方差公式(第1课时)-2022-2023学年七年级数学下册教材配套教学课件(沪科版)

方法总结:两数的平方和加上或减去它们积的 2倍,就构成了一个完全平方式.注意积的2倍的 符号,避免漏解.
二 完全平方公式的运用
思考:怎样计算1022,992更简便呢?
完全平方公式:
(a+b)2=a2 + 2ab + b2
(a-b)2=a2- 2ab + b2
语言表述:两数和(差)的平方,等于它 们的平方和加上(减去)它们乘积的两倍.
公式的结构特征:
首平方,尾平方,首尾二倍在中央,符号 看前方.
【例2】用完全平方公式计算:
(1)(5+3p)2;
(2) (2x-7y)2; (3) (-2a-5)2.
用语言叙述为:两项和的平方,等于这两个项的平 方和加上它们的积的2倍.
9.4 乘法公式(1)——完全平方公式
议一议
【例1】计算:(a-b)2.
解:(a-b)2 = [a+(-b)]2
= a 2 + 2 a (-b) + (-b) 2 =a2- 2ab+ b2.
(a-b)2=a2-2ab+b2
也称为完全平方公式.
公式特征: 1.积为二次三项式; 2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同. 4.公式中的字母a,b可以表示数,单项式和多项式.
想一想: 你能根据图1和图2中的面积解释完全平方公式吗?ba ab 图1b ab a 图2
几何解释:
b
a
=
+
a
b
a2
ab
(完整版)常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
常见分数、小数及百分数互化-常用平方数、立方数及各种计算方法
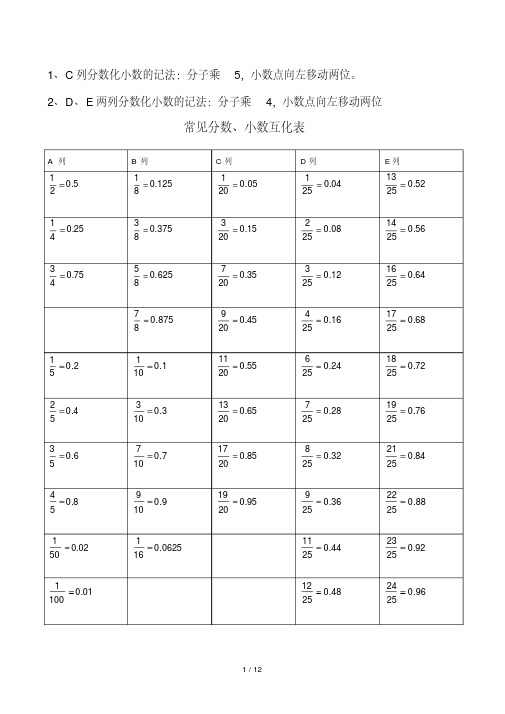
1、C 列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D 、E 两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表A 列B 列C 列D 列E 列5.021125.08105.020104.025152.0251325.041375.08315.020308.025256.0251475.043625.08535.020712.025364.02516875.08745.020916.025468.025172.0511.010155.0201124.025672.025184.0523.010365.0201328.025776.025196.0537.010785.0201732.025884.025218.0549.010995.0201936.025988.0252202.05010625.016144.0251192.0252301.0100148.0251296.02524常见的分数、小数及百分数的互化除法除不尽(按四舍五入计算)除法比分数小数百分除法比分数小数百分1÷2 1:2 1/2 0.5 50% 1÷3 1:3 1/3 0.33 33% 1÷4 1:4 1/4 0.25 25% 2÷3 2:3 2/3 0.67 67% 1÷5 1:5 1/5 0.2 20% 1÷6 1:6 1/6 0.17 17% 2÷5 2:5 2/5 0.4 40% 5÷6 5:6 5/6 0.83 83% 3÷5 3:5 3/5 0.6 60% 1÷7 1:7 1/7 0.14 14% 4÷5 4:5 4/5 0.8 80% 2÷7 2:7 2/7 0.29 29% 1÷8 1:8 1/8 0.125 12.5% 3÷7 3:7 3/7 0.43 43% 3÷8 3:8 3/8 0.375 37.5% 4÷7 4:7 4/7 0.57 57% 5÷8 5:8 5/8 0.625 62.5% 5÷7 5:7 5/7 0.71 71% 7÷8 7:8 7/8 0.875 87.5% 6÷7 6:7 6/7 0.86 86% 1÷10 1:10 1/10 0.1 10% 1÷9 1:9 1/9 0.11 11% 3÷10 3:10 3/10 0.3 30% 2÷9 2:9 2/9 0.22 22% 7÷10 7:10 7/10 0.7 70% 4÷9 4:9 4/9 0.44 44% 9÷10 9:10 9/10 0.9 90% 5÷9 5:9 5/9 0.56 56% 3÷2 3:2 3/2 1.5 150% 7÷9 7:9 7/9 0.78 78% 5÷4 5:4 5/4 1.25 125% 8÷9 8:9 8/9 0.89 89% 7÷5 7:5 7/5 1.4 140% 4÷3 4:3 4/3 1.33 133% 备注除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无限循环)小数;除不尽与除尽相反,是无限循环小数。
小学奥数25完全平方数

2.7完全平方数2.7.1相关概念完全平方即用一个整数乘以自己例如1*1,2*2,3*3等等,依此类推。
若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数。
完全平方数是非负数。
2.7.2性质推论例如:0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,529…观察这些完全平方数,可以获得对它们的个位数、十位数、数字和等的规律性的认识。
下面我们来研究完全平方数的一些常用性质:性质1:末位数只能是0,1,4,5,6,9。
此为完全平方数的必要不充分条件,且定义为“一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数”,0为整数,故0是完全平方数性质2:奇数的平方的个位数字一定是奇数,十位数字为偶数;偶数的平方的个位数字一定是偶数。
证明奇数必为下列五种形式之一:10a+1,10a+3,10a+5,10a+7,10a+9分别平方后,得(10a+1)2=100a2+20a+1=20a(5a+1)+1(10a+3)2=100a2+60a+9=20a(5a+3)+9(10a+5)2=100a2+100a+25=20 (5a+5a+1)+5(10a+7)2=100a2+140a+49=20 (5a+7a+2)+9(10a+9)2=100a2+180a+81=20 (5a+9a+4)+1综上各种情形可知:奇数的平方,个位数字为奇数1,5,9;十位数字为偶数。
性质3:如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
证明已知m2=10k+6,证明k为奇数。
因为k的个位数为6,所以m的个位数为4或6,于是可设m=10n+4或10n+6。
则10k+6=(10n+4)2=100+(8n+1)x10+6或10k+6=(10n+6)2=100+(12n+3)x10+6即k=10+8n+1=2(5+4n)+1或k=10+12n+3=2(5+6n)+3∴k为奇数。
小学数学必须背诵记忆的数值

小学数学必备数值一、常用分数、小数的互化1/2 =0.5=50%1/3 ≈0.333 =33.3% 2/3 ≈0.667=66.7% 1/4 =0.25=25%3/4 =0.75=75%1/5 =0.2=20%2/5 =0.4=40%3/5 =0.6=60%4/5 =0.8=80%1/6 ≈0.167=16.7% 5/6 ≈ 0.833=83.3% 1/8 =0.125=12.5% 3/8 =0.375=37.5% 5/8 =0.625=62.5% 7/8 =0.875=87.5% 1/9 ≈ 0.111=11.1% 1/10 =0.1=10%1/20=0.05=5%3/20=0.15=15%7/20=0.35=35%9/20=0.45=45%11/20=0.55=55%13/20=0.65 =65%17/20=0.85=85%19/20=0.95=95%1/16 =0.0625=6.25%1/32 =0.03125=3.125%1/64 =0.015625=1.5625%1/7 =0.142857142857…≈0.143 =14.3%2/7 =0.285714285714…≈0.286=28.6%3/7 =0.428571428571…≈0.429=42.9%4/7 =0.57142857142…≈0.571=57.1%5/7 =0.714285714285…≈0.714=71.4%6/7 =0.857142857142…≈0.857=85.7%熟记:142857二、常用圆周率的计算3.14×1=3.14 3.14×2=6.28 3.14×3=9.42 3.14×4=12.56 3.14×5=15.70 3.14×6=18.84 3.14×7=21.98 3.14×8=25.12 3.14×9=28.26 3.14×10=31.40 3.14×11=34.543.14×12=37.68 3.14×16=50.24 3.14×18=56.52 3.14×20=62.80 3.14×25=78.50 3.14×32=100.48 3.14×36=113.04 3.14×49=153.86 3.14×64=200.96 3.14×81=254.34 3.14×121=379.94三、常用的完全平方数1² =12² =43² =94² =16 5² =25 6² =36 7 ²=49 8² =64 9² =81 10² =10011² =121 12² =144 13² =169 14² =196 15² =225 16² =256 17² =289 18² =324 19² =361 20² =400四、常用的立方数1³=12³=83³=274³=645³=125 6³=216 7³=343 8³=512 9³=729 10³=100011³=133112³=172813³=219714³=274415³=337516³=409617³=491318³=583219³=685920³=8000五、常用单位换算长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米1米=100厘米1千米=100000厘米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方千米=1000000平方米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升1升=1000立方厘米1立方分米=1000毫升质量单位换算1吨=1000 千克1千克=1000克人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有:1、3、5、7、8、10、12月小月(30天)的有:4、6、9、11月平年2月28天,闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒。
1-6 完全平方公式(第二课时) 22-23北师大版数学七年级下册

(2) 992.
解: 1042 = (100+4)2
992 = (100 –1)2
=10000+800+16 =10000 -200+1
=10816.
=9801.
方法总结:运用完全平方公式进行简便计算,要熟 记完全平方公式的特征,将原式转化为能利用完全 平方公式的形式.
ZYT
巩固练习
利用乘法公式计算: (1)982-101×99; (2)20162-2016×4030+20152. 解:(1)原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1=-395; (2)原式=20162-2×2016×2015+20152
=(2016-2015)2=1.
ZYT
典例精析
例2 计算:(1)( x + 3 ) 2 - x 2 ;(2)( a + b + 3 ) ( a + b - 3 );
(3)( x + 5 ) 2 -(x-2)(x-3)
方法总结:要把其中两项看 成一个整体,再按照完全平 方公式进行计算.
ZYT
典例精析
例4 化简:(x-2y)(x2-4y2)(x+2y). 解:原式=(x-2y)(x+2y)(x2-4y2)
=(x2-4y2)2 =x4-8x2y2+16y4.
方法总结:先运用平方差公式,再运用完全平方公式.
典例精析 例4 已知a+b=7,ab=10,求a2+b2,(a-b)2
解:原式=2x2-2y2+[x2+y2 +2xy-xy]+[x2+y2 -2xy+xy] =2x2-2y2+x2+y2 +xy+x2+y2 -xy =2x2-2y2+2x2+2y2=4x2.
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
宇文皓月A 列B列C列D列E列2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位罕见分数、小数互化表罕见的分数、小数及百分数的互化除法除不尽(按四舍五入计算) 除法 比分数小数百分除法比分数小数百分1÷2 1:21/20.550%1÷31:31/30.3333%1÷1:41/40.2525%2÷32:32/30.6767%41÷51:5 1/5 0.2 20% 1÷6 1:6 1/6 0.17 17%2÷52:5 2/5 0.4 40% 5÷6 5:6 5/6 0.83 83% 3÷53:5 3/5 0.6 60% 1÷7 1:7 1/7 0.14 14% 4÷54:5 4/5 0.8 80% 2÷7 2:7 2/7 0.29 29%1÷81:8 1/8 0.125 12.5% 3÷7 3:7 3/7 0.43 43% 3÷83:8 3/8 0.375 37.5% 4÷7 4:7 4/7 0.57 57% 5÷85:8 5/8 0.625 62.5% 5÷7 5:7 5/7 0.71 71% 7÷87:8 7/8 0.875 87.5% 6÷7 6:7 6/7 0.86 86%1÷101:10 1/10 0.1 10% 1÷9 1:9 1/9 0.11 11% 3÷103:10 3/10 0.3 30% 2÷9 2:9 2/9 0.22 22% 7÷107:10 7/10 0.7 70% 4÷9 4:9 4/9 0.44 44% 9÷109:10 9/10 0.9 90% 5÷9 5:9 5/9 0.56 56% 3÷23:2 3/2 1.5 150% 7÷9 7:9 7/9 0.78 78%5÷45:4 5/4 1.25 125% 8÷9 8:9 8/9 0.89 89% 7÷57:5 7/5 1.4 140% 4÷3 4:3 4/3 1.33 133%备注除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无限循环)小数;除不尽与除尽相反,是无限循环小数。
常见的分数小数及百分数的互化经常使用平方数立方数及各类计算方式
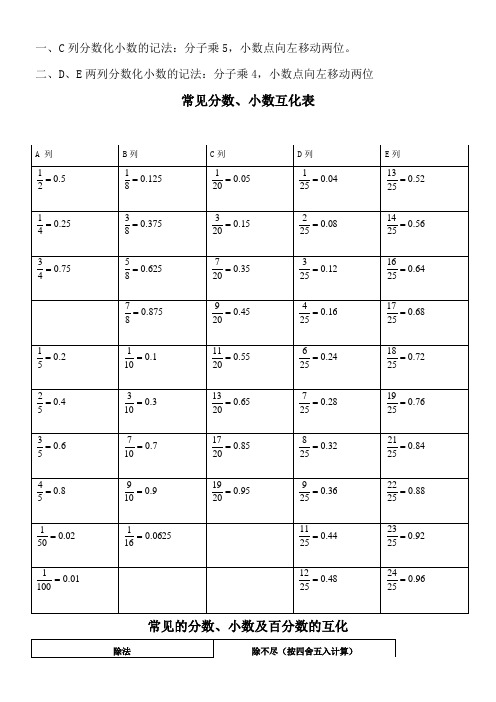
一、C列分数化小数的记法:分子乘5,小数点向左移动两位。
二、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技术:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技术:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技术:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技术:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以五、2五、125的速算技术:A×5型速算技术:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技术:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技术:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技术:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技术:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技术:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技术:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技术:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补因此乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方式适合11~99 所有平方的计算。
常见分数小数及百分数互化常用平方数立方数及各种计算方法
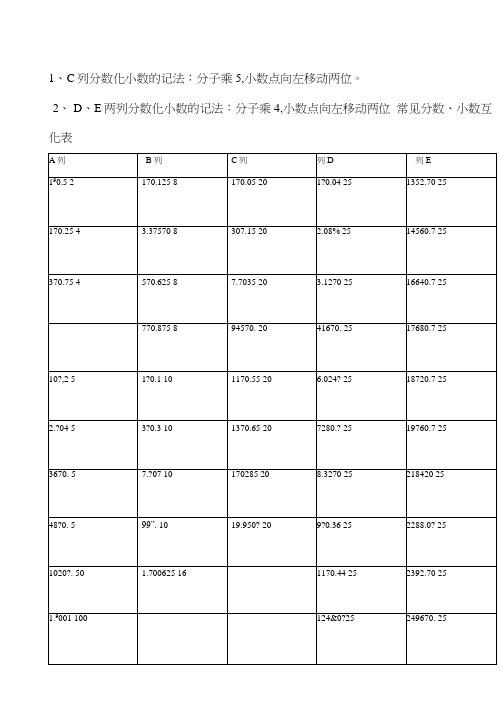
1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表1/12常见的分数、小数及百分数的互化减错位相加/ ;9=AX10-AX9 型速算技巧:AXA10-743=7430-743=6687 X743 X 9=743 例:;4-1OAX 9.9= A X 10+AAX 9.9 型速算技巧:10=7430-74.3=7355.7 4-X 10-743 例:743X9.9=74310+A; 11=A 型速算技巧:AX XAX1110+743=7430+743=8173 11=743X例:743 X100+A; X101=AXAAX101 型速算技巧:100+743=75043 101=743X例:743X的速算技巧:25、125除以乘/5、;5=10A4-2X5型速算技巧:AXA2=43697.25 一十2=87394.58739.45 X 5=8739.45 X 10 例:2: A4-5=0.1AX5A4-型速算技巧:2=7.3686 X2=3.6843 X0.1 X例:36.843三5=36.843;4-4AX25 型速算技巧:X25=100AA4=l80850 4=72340025=7234X 1004- 7234 例:X4: 25=0.01 A254-型速算技巧:AFXA4=148.564=37.140.0125=37143714 例:4-X X X3/12AX125 型速算技巧:AX5=1000A4-8;例:8736X 125=8736X 10004-8=87360004-8= 1092000A4-125 型速算技巧:A-rl255=0.001AX8;例:41154-125=4115X0.001X8=4.115X8=32.92减半相加:AX1.5 型速算技巧:AX1.5=A+A4-2;例:3406 X 1.5=3406+3406 4- 2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:X (头+1);积的尾=尾乂尾头=积的头例:23X27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2X (2+1) =6,尾数为3X7=21,即23X27=621本方法适合11〜99所有平方的计算。
数的改写和求近似数的方法

数的改写和求近似数的方法数的改写和求近似数是数学中常见的操作和技巧。
在实际问题中,我们常常需要对给定的数进行改写或者求出其近似值,以便更好地理解和应用数学知识。
一、数的改写方法数的改写是指将一个数用不同的形式或表达方式表示出来。
常见的数的改写方法有以下几种:1. 分数形式:将一个数表示为两个整数的比值,分子和分母都是整数,并且分母不为零。
例如,将小数形式的数1.5改写为分数形式,可以表示为3/2。
2. 百分数形式:将一个数表示为百分数的形式,其中分子是一个数,分母是100。
例如,将小数形式的数0.75改写为百分数形式,可以表示为75%。
3. 科学计数法形式:将一个数表示为一个实数与10的幂的乘积的形式。
例如,将大数1000000改写为科学计数法形式,可以表示为1.0 × 10^6。
二、数的求近似方法数的求近似是指将一个数用一个与之相近的数来表示。
常见的数的求近似方法有以下几种:1. 舍入法:将一个数四舍五入到某个位数。
例如,将小数形式的数1.3467近似到小数点后两位,可以表示为1.35。
2. 截断法:将一个数截断到某个位数。
例如,将小数形式的数1.3467截断到小数点后两位,可以表示为1.34。
3. 估算法:根据数的特点和给定的精度要求,通过估算计算出一个近似值。
例如,估算根号3的值,可以先找到离3最近的完全平方数,即2的平方等于4,然后根据平方根的性质,估算出根号3的值约为1.7。
为了更好地理解和应用数学知识,我们需要熟练掌握数的改写和求近似的方法,并在实际问题中灵活运用。
这样,我们就能够更准确地描述和计算数,更好地解决实际问题。
总结:数的改写和求近似数的方法是数学中常见的操作和技巧。
通过将一个数用不同的形式或表达方式表示出来,可以更好地理解和应用数学知识。
通过将一个数用一个与之相近的数来表示,可以更准确地描述和计算数,解决实际问题。
熟练掌握数的改写和求近似的方法,对于数学学习和实际问题的解决都具有重要的意义。
【易错题精析】第5讲 公顷、平方千米及组合图形的面积 小学数学五年级上册易错专项练(知识梳理易错汇

第5讲公顷、平方千米及组合图形的面积(讲义)小学数学五年级上册易错专项练(知识梳理+易错汇总+易错精讲+易错专练)1.公顷和平方千米。
边长是100米的正方形的面积是1公顷,测量或计量土地面积,通常用公顷作单位。
公顷可以写成hm2。
边长是1000米的正方形的面积是1平方千米,测量或计量大面积的土地,通常用平方千米作单位,平方千米可以写成km2。
2.公顷、平方米、平方千米之间的关系。
1公顷=10000平方米,1平方千米=100公顷=1000000平方米。
3.平方千米、公顷、平方米之间的转化。
把低级单位的数改写成高级单位的数要除以进率,把高级单位的数改写成低级单位的数要乘进率。
4.规则组合图形的面积。
观察上图可知:计算组合图形的面积时,可以先把它分割成已经学过的简单的基本图形,分别计算出面积,再相加;也可以先添补成学过的图形,计算出添补后整个图形的面积,再减去添补图形的面积。
5.不规则图形的面积。
方法一:借助方格纸用数格子的方法进行估计。
方法二:根据图形的特点转化为近似的规则图形来估计。
1. 平方米和公顷之间的进率是10000,而不是100。
2. 在对组合图形进行分解时,一定要考虑到分别求面积时所需要的数据条件下是否充分。
3. 将组合图形分成几个简单图形,计算每个简单图形的面积时要找准数据。
4. 利用添补法计算图形的面积时,不要忘记减去补上的图形的面积。
5. 用数方格的方法计算面积时,不满一格的按半格计算【易错一】国家体育场“鸟巢”的占地面积大约是()。
A.21平方分米B.21平方米C.21公顷D.21平方千米【解题思路】根据生活经验,对面积单位和数据的大小认识,可知国家体育场“鸟巢”的占地面积21公顷。
【完整解答】国家体育场“鸟巢”的占地面积大约是21公顷。
答案:C【易错点】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
【易错二】一架直升机在一片梯形松树林(如下图)上空喷洒药水。
四年级上数学公顷和平方千米

公顷和平方千米1平方千米=1000000平方米 1公顷=10000平方米一、填上合适的数字或单位锦州世界园艺博览会的陆地面积约为330()。
一本字典封面约为150()。
台湾日月潭的面积约为770()。
二、单位转化38000000平方米=()公顷=()平方千米5公顷2000平方米=()平方米3平方千米58公顷=()公顷=()平方米85平方米=()平方分米=()平方厘米三、简单的面积计算1、一块长方形的耕地,长250米,宽160米,这块耕地有()公顷。
2、一块长方形草地,长是398米,宽204米,这草坪的面积约是()公顷。
3、有两块长方形的地,第一块地的面积是9公顷,第二块地的长是150米,宽是60米,这两块地的面积比较,()面积大。
四、判断1、相邻面积单位之间的进率为100. ()2、2、面积是1公顷的土地只能是边长是100米的正方形。
()3、长度单位比面积单位大。
()4、平方千米比平方米大。
()五、应用题1.一块长方形菜地面积是2公顷,它的长是200米,如果在这块菜地的周围围上篱笆,篱笆长多少米?2.一个桃园长500米,宽140米,平均每公顷栽300棵桃树,每棵桃树每年产桃子50千克,桃园最多能产多少桃子?3.算出图中表示的土地面积是多少公顷。
4.一个占地1公顷的正方形苗圃,每条边各增加100米,苗圃的面积增加多少公顷?举一反三:有一块长方形土地,长400米,宽300米,如果把它的长增加200米,宽不变,那么它的面积增加多少公顷?举一反三:有一块长方形林地,如果长增加5千米,宽不变,则面积增加15平方千米。
如果宽增加6千米,长不变,面积增加48平方千米,这块林地的面积是多少平方千米?5.城市广场有一块长方形草坪,草坪中有两面花墙(下图空白部分),你能求出草坪的面积吗?(单位米)6.某地规划防护林呈长方形,长8千米,宽5千米,先划下一个最大的正方形种白杨树,再从剩下的长方形中,又划出最大的正方形种红松,最后剩下的一个小长方形的面积是多少公顷?7.右图是由7个完全相同的长方形拼成的图形。
