每周一测-学易试题君之每日一题君2019学年上学期九年级数学人教版 (4)
每周一测-学易试题君之每日一题君2019学年上学期九年级数学人教版

【解析】∵tan30°= ,∴tan30°−1<0,∴原式=1− .故选A.
9.【答案】
【解析】∵Rt△ABC中,∠ACB=90°,CD⊥AB于D,∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠A=∠BCD=α,∴cosα= = = .故答案为: .
10.【答案】
【解析】∵∠ACB=120°,∴∠ACD=60°,又AC=4,∴CD=AC·cos60°=4×cos60°= =2,AD=AC·sin60°= ,∴BD=BC+CD=6+2=8,tanB= .故答案为: .
14.如图,已知 是坐标原点, 、 的坐标分别为 , .
(1)在 轴的左侧以 为位似中心作 的位似 ,使新图与原图的相似比为 ;
(2)分别写出 、 的对应点 、 的坐标.
1.【答案】B
【解析】cos45°= ,故选B.学&科网
2.【答案】A
【解析】∵Rt△ABC中,∠C=90°,sinA= ,∴A=30°,∴B=60°,∴sinB= .故选A.
11.【解析】(1)原式=
+3 .
(2)原式=
= .
12.【解析】(1)∵在Rt△ABC中,∠C=90°,a=8,∠B=60°,
∴∠A=90°-60°=30°,
, .
(2)∵在Rt△ABC中,∠C=90°,∠A=45°,b= ,
∴∠B=45°, ,
∴ .
14.【解析】(1)如图所示:
(2)如图所示: , .
(2)cos260°-tan45°+sin60°·tan60°.
12.根据下列条件,解直角三角形:ቤተ መጻሕፍቲ ባይዱ
(1)在Rt△ABC中,∠C=90°,a=8,∠B=60 °;
中心对称-学易试题君之每日一题君2019学年上学期九年级数学人教版

1 9月11日 中心对称
中考频度:★★★☆☆ 难易程度:★★☆☆☆
若两个图形关于某点成中心对称,则以下说法:
①这两个图形一定全等;
②对称点的连线一定经过对称中心;
③对称点与旋转中心的连线所成的角都是旋转角;
④一定存在某条直线,沿该直线折叠后的两个图形能互相重合.
正确的是
A .①②③
B .①③④
C .①②④
D .①②③④
【参考答案】
A
【解题必备】
1.中心对称
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
2.中心对称与轴对称的不同点与相同点。
每周一测-学易试题君之每日一题君2018学年中考九年级数学人教版(一轮复习) (5)

一、选择题
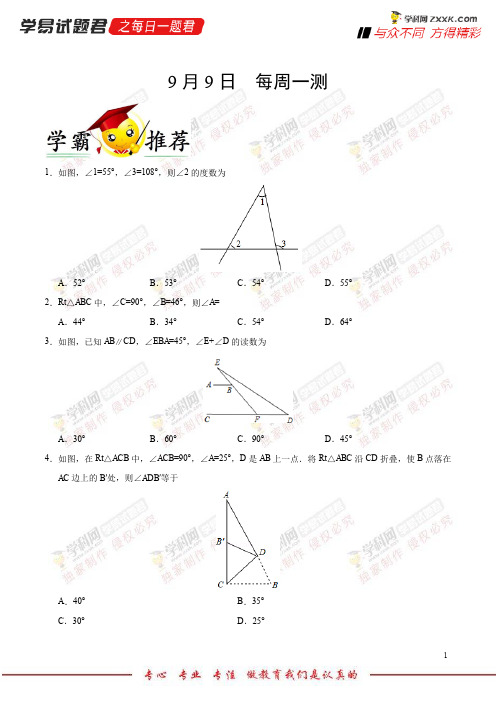
1.若∠1=25°,则∠1的余角的大小是
A.55°B.65°C.75°D.155°
2.已知 、 、 、为 的三条边,则化简 的结果为
A. B.
C. D.
3.如图,下列各组角是内 错角
A.∠1和∠2B.∠3和∠4C.∠2和∠3D.∠1和∠4
4.如图,将一块直角三角尺的直角顶点放在直尺的一边上,如果∠1=50°,那么∠2的度数是
(2)若AD=3.5cm,DE=2.7cm,求BE的长.
10.如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)求直线OA和二次函数的解析式;学&科网
(2)当点P在直线OA的上方时,
①当PC的长最大时,求点P的坐标;
A.40°B.50°C.60°D.30°
5.已知二次函数 的图象如图所示,则下列结论:① ;② 随 的增大而增大;③方程 的两根之和大于 ;④ .其中正确的个数
A. 个B. 个C. 个D. 个
二、填空题
6.如图,△ABC中,点D、E分别是BC,AD的中点,且△ABC的面积为8,则阴影部分的面积是__________.
7.在一个直角三角形中,有一个锐角等于30°,则另一个锐角的大小为__________度.
8.已知∠AOB=40°,OC平分∠AOB,则∠AOC的补角等于__________.
三、解答题
9.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D、E.
(1)求证:CD=BE;学+科网
4.【答案】A
【解析】如图所示:
周末培优-学易试题君之每日一题君2019学年上学期九年级数学人教版 (4)

A.x<-1或x>1B.x<-1或0<x<1
C.-1<x<0或x>1D.-1<x<0或0<x<1
2.一次函数y=kx+b(k≠0)的图象 经过点A(2,-6),且与反比例函数y=- 的图象交于点B(a,4).
(1)求一次函数的解析式;
11月3日周末培优
中考频度:★★☆☆☆难易程度:★★☆☆☆
如图,一次函数y1=kx+b的图象与反比例函数y2= 的图象交于A(2,3),B(6,n)两点.
(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.
【参考答案】(1)y=- x+4;(2)8.
(2)如图,设直线y=- x+4与x轴交于C,则C(8,0).
解得 或 ,
∴直线l与反比例函数图象的交点坐标为(1,6)和(3,2).
画出函数图象,如图所示.
观察函数图象可知:当0<x<1或x>3时,反比例函数图象在直线l的上方,
∴使y1<y2成立的x的取值范围为0<x<1或x>3.
(2)当y=0时,-x-1=0,解得x=-1,
则S△AOB= ×1×1+ ×1×2=0.5+1=1.5;
(3)若点P是y轴上的点,请直接写出能使△PAC为等腰三角形的点P的坐标.
1.【答案】C
【解析】观察图象可知当-1<x<0或x>1时,直线在双曲线的上方,
所以y1>y2的x取值范围是-1<x<0或x>1,故选C.
(2)直线AB向上平移10个单位后得到直线l的解析式为:y1=-2x+8.
解一元二次方程——配方法-学易试题君之每日一题君2019学年上学期九年级数学人教版

A.2(x–1)2=1B.2(x–1)2=5
C.(x–1)2= D.(x–2)2=
2.用配方法解方程 +2x–1=0时,配方结果正确的是
A. B.
C. D.
3.解方程:(1)2x2–4x+1=0;(2)y2-2y-15=0.
4.大家知道在用配方法解一般形式的一元二次方程时,都要先把二次解答过程,并按照此方法解方程( ).
方程( ) .
解: ,
,
,
,
, .学!科网
方程( ) .
2.【答案】A
【解析】用配方法解方程: ,
移项得: ,
配方得: ,即 .
故选A.
(2) ,
,
,
∴ .学科!网
4.【解析】原方程可化为: ,
∴ ,∴ ,
∴ , .
8月21日解一元二次方程——配方法
中考频度:★★★☆☆难易程度:★★★☆☆
把方程x2–2x–4=0用配方法化为(x+m)2=n的形式,则m=_______,n=________.
【参考答案】(1)–1;(2)5.
【解题必备】
把一般形式的一元二次方程ax2+bx+c=0(a≠0)左端配成一个含有未知数的完全平方式,右端是一个非负常数,进而可用直接开平方法来求解,这种通过配成完全平方形式来解一元二次方程的方法,叫做配方法.配方的目的是降次,把一个一元二次方程转化成两个一元一次方程来解.
每周一测-学易试题君之每日一题君2018学年中考九年级数学人教版(一轮复习) (4)

C.体育场离早餐店4千米D.张强从早餐店回家的平均速度是 千米/小时
二、填空题
6.在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有__________的值与其对应,那么我们就说y是x的函数.
7.一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表:
1.【答案】B
【解析】A.a<b,a+2<b+2,故A成立;B.a<b,–3a>–3b,故B错误;
C.a<b,2–a>2–b,故C正确;D.a<b,3a<3b,故D成立;故选B.
2.【答案】B
【解析】由题意得a=–(–2)=2,b=1.∴N(–2,1),∴点N在第二象限.故选B.
4.【答案】A
【解析】当点P从D到C的过程中,如下图所示,
3月18日每周一测
一、选择题
1.若a<b,则下列各式中不成立的是
A.a+2<b+2B.–3a<–3b
C.2–a>2–bD.3a<3b
2.已知点M(a,1)和点N(–2,b)关于y轴对称,则点N在
A.第一象限B.第二象限
C.第三象限D.第四象限
3.已知直线y=kx+b,若k+b=–5,kb=6,那么该直线不经过
链接打开方法:
1、按住ctrl键单击链接即可打开专题链接
2、复制链接到网页
A.第一象限B.第二象限
C.第三象限D.第四象限
4.如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是
每周一测-学易试题君之每日一题君2018学年九年级数学人教版(上学期期末复习) (2)

1 1月21日 每周一测
一、选择题
1.如图,用放大镜将图形放大,这种图形的改变是
A .相似
B .平移
C .轴对称
D .旋转
2.我国国土面积约为960万平方千米,画在比例尺为1∶1000万的地图上的面积约是
A .960平方千米
B .960平方米
C .960平方分米
D .960平方厘米
3.若△ABC ∽△A ′B ′C ′,相似比为1∶3,则△ABC 与△A ′B ′C ′的面积的比为
A .1∶3
B .3∶1
C .4∶1
D .1∶9
4.下列说法错误的是
A .两个等边三角形一定相似
B .两个等腰三角形一定相似
C .两个等腰直角三角形一定相似
D .两个全等三角形一定相似 5.如图,点G ,F 分别是△BCD 的边BC ,CD 上的点,BD 的延长线与GF 的延长线相交于点A ,D
E ∥BC 交GA 于点E ,则下列结论错误的是。
每周一测-学易试题君之每日一题君2019学年上学期七年级数学人教版 (7)

1 9月2日 每周一测
一、选择题
1.–13
的相反数是 A .3 B .–3 C .–13 D .13
2.|–3|的相反数是
A .–3
B .–13
C .13
D .3
3.一个数a 在数轴上表示的点是A ,当点A 在数轴上向左平移了3个单位长度后到点B ,点A 与点B 表示的数恰好互为相反数,则数a 是
A .–3
B .–1.5
C .1.5
D .3
4.相反数等于本身的数是
A .正数
B .负数
C .0
D .1
5.下列各对数中,互为相反数的是
A .+(–3)与–3
B .+(+3)与–3
C .–(–3)与3
D .3与+(+3) 二、填空题
6.写出一个数,使这个数的绝对值等于它的相反数:__________.
7.–2的绝对值是__________,–2的相反数是__________.
8.如图所示,有理数a ,b 在数轴上对应的点分别为A ,B ,则a ,–a ,b ,–b 按由小到大的顺序排列是__________.
9.若450a b -++=,则a b -=_________.学——科网
10.绝对值大于5并且小于8的所有整数是________,绝对值小于3.5的非负整数有________.
三、解答题
11.比较下列各组数的大小:(1)56-和67-;(2)15⎛⎫-- ⎪⎝⎭和16--.。
第24章 圆学易试题君之单元测试君20182019学年九年级数学人教版(上)(考试版)-2019年精选教育文档

第 1 页绝密★启用前|试题命制中心2019-2019学年九年级数学人教版(上)(第24章)章末检测(考试时间:90分钟 试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若⊙A 的半径为5,点A 的坐标为(3,4),点P 的坐标为(5,8),则点P A .在⊙A 内 B .在⊙A 上 C .在⊙A 外D .不确定2.如图,在⊙O 中,圆心角∠BOC =60°,则圆周角∠BAC 等于 A .60° B .50° C .40°D .30°3.下列四个命题:①等边三角形是中心对称图形;②在同圆或等圆中,相等的弦所对的圆周角相等; ③三角形有且只有一个外接圆; ④垂直于弦的直径平分弦所对的两条弧. 其中真命题的个数有 A .1个 B .2个 C .3个D .4个4.如图,直线PA PB ,是O 的两条切线,A B ,分别为切点,120APB ∠=︒,10OP =厘米,则弦AB的长为A.厘米 B .5厘米C.D厘米 5.下列四个命题中正确的是①与圆有公共点的直线是该圆的切线; ②垂直于圆的半径的直线是该圆的切线; ③到圆心的距离等于半径的直线是该圆的切线; ④过圆直径的端点,垂直于此直径的直线是该圆的切线. A .①② B .②③ C .③④D .①④6.小丽要制作一个圆锥模型,要求圆锥的母线长为9 cm ,底面圆的直径为10 cm ,那么小丽要制作的这个圆锥的侧面展开扇形的纸片的圆心角度数是 A .150° B .200° C .180°D .240°7.如图,P A ,PB 是⊙O 的切线,A ,B 是切点,点C 是劣弧AB 上的一点,若∠P =40°,则∠ACB 等于 A .80°B .110°C .120°D .140°8.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A 点到B 点,甲虫沿ADA 1、A 1EA 2、A 2F A 3、A 3GB 路线爬行,乙虫沿ACB 路线爬行,则下列结论正确的是 A .甲先到B 点B .乙先到B 点C .甲、乙同时到BD .无法确定9.如图,点A,B,C 在⊙O 上,若∠BAC =45°,OB =2,则图中阴影部分的面积为 A .π-4B .23π-1 C .π-2 D .2π3-2 10.如图,直线CD 与以线段AB 为直径的圆相切于点D 并交BA 的延长线于点C ,且AB =2,AD =1,P 点在切线CD 上移动.当∠APB 的度数最大时,则∠ABP 的度数为 A .15° B .30° C .60°D .90°第Ⅱ卷二、填空题(本题共8小题,每小题3分,共24分)11.一个多边形的每一个外角都等于72°,则这个多边形是__________边形. 12.如图, ⊙O 是△ABC 的外接圆,∠AOB =70°,AB =AC,则∠ABC =__________.13.如图,已知⊙O与△ABC的边AB,AC,BC分别相切于点D,E,F,若AB=4,AC=5,AD=1,则BC=__________.14.已知,⊙O的直径为10 cm,点O到直线a的距离为d:①若直线a与⊙O相切,则d=__________;②若d=4 cm,则直线a与⊙O有__________个交点;③若d=6 cm,则直线a与⊙O的位置关系是__________.15.如图,⊙O的半径为6,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则弧BC的长为__________.16.如图,已知AB是⊙O的直径,PB是⊙O的切线,P A交⊙O于点C,AB=3 cm,PB=4 cm,则BC=__________cm.17.如图,水平放置的圆柱形排水管道的截面直径是1 m,其中水面的宽AB为0.8 m,则排水管内水的深度为__________m.18.如图是考古学家发现的古代钱币的一部分,合肥一中的小明正好学习了圆的知识,他想求其外圆半径,连接外圆上的两点A,B,并使AB与内圆相切于点D,作CD⊥AB交外圆于点C.测得CD= 10 cm,AB=60 cm,则这个钱币的外圆半径为__________cm.三、解答题(本题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤)19.(本小题满分6分)如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D,AB=24 cm,CD= 8 cm.(1)求作此残片所在的圆(不写作法,保留作图痕迹);(2)求(1)中所作圆的半径.20.(本小题满分6分)如图,在△ABC中,AB=AC,内切圆O与边BC,AC,AB分别相切于点D,E,F.(1)求证:BF=CE;(2)若∠C=30°,CEAC.21.(本小题满分6分)如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O 上.(1)若∠AOD=52°,求∠DEB的度数;(2)若CD=2,BA=8,求半径的长.22.(本小题满分8分)如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)求AE的长.23.(本小题满分8分)如图,P A,PB是⊙O的切线,A,B为切点.连接AO并延长交PB的延长线于点C,连接PO交⊙O于点D.(1)求证:PO平分∠APC;(2)连接BD,若∠C=30°,求证:DB∥AC.24.(本小题满分10分)如图,平面直角坐标系中,⊙P与x轴分别交于A,B两点,点P的坐标为(3,-1),AB=.(1)求⊙P的半径长;(2)将⊙P向下平移,求⊙P与x轴相切时平移的距离.25.(本小题满分10分)中华民族的科学文化历史悠久、灿烂辉煌,我们的祖先几千年前就能在生产实践中运用数学.1300多年前,我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图).经测量,桥拱下的水面距拱顶6 m时,水面宽34.64 m,已知桥拱跨度是37.4 m,运用你所学的知识计算出赵州桥的大致拱高.(运算时取,26.(本小题满分12分)如图,点P是正方形ABCD内的一点,连接P A,PB,PC.将△P AB绕点B顺时针旋转90°到P'CB△的位置.(1)设AB的长为a,PB的长为b(b<a),求△P AB旋转到△P'CB的过程中边P A所扫过区域(图中阴影部分)的面积;(2)若P A=2,PB=4,∠APB=135°,求PC的长.。
每周一测-学易试题君之每日一题君2019学年上学期九年级数学人教版 (8)

= π (平方米);
2
360
8
90π 2
(2)设底面圆的半径为 r,则
2 =2πr,
180
5
∴r= 2 m,圆锥的底面圆的半径长为 2 m.
8
8
(2)如图,作 AF⊥DE 于点 F,则 AF=OD=6, ∵AB∥DE,∠OAD=45°, ∴∠ADF=∠OAD=45°, ∴DF=AF=6, ∵∠ACB=90°,AC=6,AB=12, ∴∠CBA=30°, ∴∠CAB=60°, ∵AB∥DE, ∴∠E=∠CAB=60°, ∵AF=6,∠AFE=90°,
12.如图,⊙O 的直径 AB=12,弦 AC=6,∠ACB 的平分线交⊙O 于 D,过点 D 作 DE∥AB 交 CA 的延长线 于点 E,连接 AD,BD.
(1)由 AB,BD, »AD 围成的阴影部分的面积是__________;
(2)求线段 DE 的长.
3
1.【答案】B
【解析】360°÷n= (n 2) 180 .故这个正多边形的边数为 4.故选 B.学科&网 n
B.60°
C.40°
D.20°
4.已知扇形的圆心角为 30°,面积为 3πcm2,则扇形的半径为
A.6cm
B.12cm
C.18cm
D.36cm
5.如图,在 Rt△AOB 中,∠AOB=90°,OA=3,OB=2,将 Rt△AOB 绕点 O 顺时针旋转 90°后得 Rt△FOE,
将线段 EF 绕点 E 逆时针旋转 90°后得线段 ED,分别以 O,E 为圆心,OA、ED 长为半径画弧 AF 和弧
10 月 7 日 每周一测
一、选择题
1.若一个正多边形的中心角等于其内角,则这个正多边形的边数为
应用举例(4)-学易试题君之每日一题君2019学年上学期九年级数学人教版

1 12月7日 应用举例(4)
中考频度:★★★☆☆ 难易程度:★★☆☆☆
如图,沿AC 方向修隧道,为了加快施工进度,要在小山的另一边同时施工,从AC 上的一点B 取∠ABD =145°,BD =500米,∠D =55°,使A 、C 、E 在一条直线上,那么开挖点E 与D 的距离是
A .500sin55°米
B .500cos35°米
C .500cos55°米
D .500tan55°米
【参考答案】
C
【解题必备】
利用解直角三角形的知识解决实际问题的一般步骤:
(1)将实际问题抽象为数学问题;
(2)根据问题中的条件,选用合适的锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.学科&网
1.一座楼梯的示意图如图所示,BC 是铅垂线,CA 是水平线,BA 与CA 的夹角为 ,现要在楼梯上铺一条。
每周一测-学易试题君之每日一题君2018学年九年级数学人教版(上学期期末复习)

1 1月14日 每周一测
一、选择题
1.下面的等式中,y 是x 的反比例函数的是
A .y =21x
B .y =12x
C .y =2x
D .y =12
x + 2.下列事件中是必然事件的是
A .任意画一个正五边形,它是中心对称图形
B .实数x 使式子3x -有意义,则实数x >3
C .a ,b 均为实数,若a =38,b =4,则a >b
D .5个数据分别是:6,6,3,2,1,则这组数据的中位数是3
3.下列事件中,不可能事件是
A .抛掷一枚骰子,出现4点向上
B .五边形的内角和为540°
C .实数的绝对值小于0
D .明天会下雨 4.点P (–3,1)在双曲线y =
k x 上,则k 的值是 A .–3 B .3 C .13- D .13
5.若双曲线1k y x -=
位于第二、四象限,则k 的取值范围是 A .k <1 B .k ≥1 C .k >1 D .k ≠1
6.一个不透明的布袋里装有5个红球,2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为
A .12
B .15
C .310
D .710
7.反比例函数y =3x
的图象在 A .第一,三象限
B .第二,四象限
C .第一,二象限
D .第三,四象限 8.袋内装有标号分别为1、2、3、4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3。
每周一测-学易试题君之每日一题君2018学年中考九年级数学人教版(二轮复习) (3)

将B(2,0)代入y=kx–4(k≠0)中得2k–4=0,解得k=2,
∴一次函数的解析式为y=2x–4,
当x=4时,y=4,∴C(4,4),∴m=4×4=16,
∴反比例函数的解析式为y= ;
(2)点D在反比例函数图象上,当y=6时,x= ,∴D( ,6),
5.【答案】–6<x<0或x>2
【解析】观察图象可得不等式kx+b> 的 解集为:–6<x<0或x>2.故答案为:–6<x<0或x>2.
7.【解析】(1)根据题意得
∵ 且
∴
(2)∵
∴当 时, 取得最大值,最大值为6125.
答:当降价2.5元时,每星期的利润最大,最大利润是6125元.
9.【解析】(1)在y=kx–4(k≠0)中,当x=0时y=–1,∴A(0,–4).
A. < < B. < <
C. < < D. <y <
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①abc<0;
②2a+b=0;
③当x=–1或x=3时,函数y的值都等于0;
④4a+2b+c>0,
其中正确结论的个数是
A.1个B.2个
C.3个D.4个
5.如图,在平面直角坐标系中,函数y=kx+b(k≠0)与 (m≠0)的图象相交于点A(2,3),B(−6,−1),则关于x的不等式kx+b> 的解集是____________.
3.【答案】B
每周一测-学易试题君之每日一题君2018学年中考九年级数学人教版(一轮复习)

1 3月11日 每周一测1.方程组13x y x y -=⎧⎨+=⎩的解是 A .12x y =⎧⎨=⎩ B .13x y =⎧⎨=⎩ C .31x y =⎧⎨=⎩ D .21x y =⎧⎨=⎩2.方程x 2+x =0的解是A .x =±1B .x =0C .x 1=0,x 2=-1D .x =13.x =-1是方程x 2+mx +1=0的一个实数根,则m 的值是A .0B .1C .2D .-24.若方程mx +ny =6的两个解是11x y =⎧⎨=⎩,21x y =⎧⎨=-⎩,则m ,n 的值为 A .42m n =⎧⎨=⎩ B .2 4m n =⎧⎨=⎩ C .24m n =-⎧⎨=-⎩ D .42m n =-⎧⎨=-⎩5.食堂的存煤计划用若干天,若每天用130 kg ,则缺少60 kg ;若每天用120 kg ,则还剩余60 kg .设食堂的存煤共有x kg ,计划用y 天,则下面所列方程组正确的是A .6013060120x y x y +=⎧⎨-=⎩B .6013060120x y x y -=⎧⎨+=⎩C .6013060120y x y x +=⎧⎨-=⎩D .6013060120y x y x-=⎧⎨+=⎩ 6.已知一元二次方程x 2-3x -3=0的两根为α与β,则11+αβ的值为 A .-1 B .1 C .-2D .2 7.关于x 的一元二次方程x 2-3x +m =0有两个不相等的实数根,则实数m 的取值范围为A .94m >B .94m <C .94m =D .94m <- 8.某特快列车在最近一次的铁路大提速后,速度提高了30千米/小时,则该列车行驶350千米所用的时问。
每周一测-学易试题君之每日一题君2018学年九年级数学人教版(上学期期末复习) (3)

1 1月28日 每周一测
一、选择题
1.Rt ABC △中的各边都扩大2倍,则A 的余弦值
A .扩大2倍
B .缩小2倍
C .不变
D .不能确定
2.在Rt △ABC 中,∠C =90°,AB =10,AC =6,则cos A 的值等于
A .
35 B .45 C .43 D .34
3.如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是
A .矩形
B .线段
C .平行四边形
D .一个点 4.图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的
A .主视图相同
B .俯视图相同
C .左视图相同
D .主视图、俯视图、左视图都相同
5.如图,A ,B ,C 三地在同一直线上,D 地在A 地北偏东30°方向、在C 地北偏西45°方向,C 地在A 地北偏东75°方向.且BD =BC =30 m .从A 地到D 地的距离是
A .303 m
B .205 m
C .302 m
D .156 m。
圆-学易试题君之每日一题君2019学年上学期九年级数学人教版

1 9月17日 圆
中考频度:★★★☆☆ 难易程度:★★☆☆☆
在以下所给的命题中,正确的个数为
①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的弧是等弧.
A .1
B .2
C .3
D .4
【参考答案】
C
【解题必备】
1.圆的概念及表示方法
(1)圆的描述性定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆.其固定的端点O 叫做圆心,线段OA 叫做半径.
(2)圆的集合性定义:将圆心为O ,半径为r 的圆看成是所有到定点O 的距离等于定长r 的点的集合.
(3)圆的表示方法:以点O 为圆心的圆,记作⊙O ,读作“圆O ”.
2.圆的特性
(1)圆上各点到定点(圆心O )的距离都等于定长(半径r );
(2)到定点的距离等于定长的点都在同一个圆上.
3.圆的有关概念
(1)弦:连接圆上任意两点的线段叫做弦.
(2)直径:经过圆心的弦叫做直径.
(3)弧、半圆:圆上任意两点间的部分叫做圆弧,简称弧.圆的任意一条直径的两个端点把圆分成两。
周末培优-学易试题君之每日一题君2019学年上学期九年级数学人教版

中考频度:★★☆☆☆难易程度:★★☆☆☆
已知 ,且 ,则锐角 等于
A. B.
C. D.无法求值
【解题必备】
1. .
2. .
3.在△ABC中,如果∠A+∠B=90°,那么sinA=cosB,cosA=sinB,即一个锐角的正弦值等于它的余角的余弦值,一个锐角的余弦值等于它的余角的正弦值.
①sinA>cosA;②sin2A+cos2A=1;③tanA·tanB=1;④tanA= .
A.①②③B.②③④C.① ③④D.①②③④
4.已知cosA= ,且∠B=90°-∠A,则sinB=__________.
5.观察下列等式:
①sin30°= ,cos60°= ;②sin45°= ,cos45°= ;③sin60°= ,cos30°= .
4.【答案】
【解析】∵cosAinB= .故答案为: .
5.【解析】(1)∵根据已知的式子可以得到sin(90°-α)=cosα,
∴sin2α+sin2(90°-α)=sin2α+cos2α=1.故答案为:1.
(1)根据上述规律,计算sin2α+sin2(90°-α)=__________.
(2)计算:sin21°+sin22°+sin23°+…+sin289°.
1.【答案】C
【解析】∵ ,sin25°=cosα,α是锐角,∴90°-α=25°,∴α=65°.故选C.
2.【答案】B
【解析】根据题意得:sin2A+cos2A=1,解得cosA= ,或cosA=- (舍去).故选B.
4.在△ABC中,如果∠A+∠B=90°,那么tanA·tanB=1.学科*网
一元二次方程-学易试题君之每日一题君2019学年上学期九年级数学人教版

1 12月17日 一元二次方程
中考频度:★★★☆☆ 难易程度:★★☆☆☆
已知关于x 的一元二次方程x 2+ax +b =0有一个非零根b ,则a +b 的值为
A .1
B .-1
C .0
D .-2
【参考答案】B
【试题解析】把x =b 代入x 2+ax +b =0得b 2+ab +b =0,而b ≠0,所以b +a +1=0,所以a +b =-1,故选B .
【解题必备】
1.应用一元二次方程的定义求字母参数的方法
首先正确判断两个字母中哪一个是未知数,哪一个是参数,然后根据一元二次方程的定义,需满足二次项系数不为0,未知数的最高次数为2这些条件,求出参数的值.
2.一元二次方程的根的应用方法
与一元二次方程的根相关的题目多以填空题、选择题的形式出现.利用方程根的概念,将方程的根代入原方程再解方程,就可以求出参数的值.
1.若关于x 的一元二次方程(m -1)x 2+x +m 2-5m +3=0有一个根为1,则m 的值为
A .1
B .3
C .0
D .1或3
2.下列方程中,一元二次方程的是
A .21x -=0
B .x 2+1=0
C .y +x 2=1
D .2
1x =1 3.方程3(1)2(1)x x x -=+化成一般形式后,二次项系数、一次项系数、常数项分别为
A .23x ,5x -,2-
B .23x ,5x -,2
C .3,-5,-2
D .3,-5。
每周一测-学易试题君之每日一题君2019学年上学期八年级.数学人教版 (3)
7.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=_________度.
8.已知:在△ABC中,AD⊥BC,BE平分∠ABC交AD于F,∠ABE=23°.求∠AFE的度数.
6.【答案】55°
【解析】∵∠B=50°,∠BAD=60°,∠ADC是△ABD的外角,∴∠ADC=∠B+∠BAD=110°,
又∵DE是∠ADC角平分线,∴∠CDE= ∠ADC=55°.故答案为:55°.
8.【解析】∵在△ABC中,AD⊥BC,
∴∠BDF=90°.
∵BE平分∠ABC交AD于F,∠ABE=23°,
9.在△ABC中,∠A=40°.
(1)如图1,BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;
(2)如图2,若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
(3)如图3,若BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;
(4)根据上述三问的结果,当∠A=n°时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).
4.如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于
A.40°B.35°
C.30°D.25°
5.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F等于
A.360°B.720°C.540°D.240°
∴2∠BOC=180°-∠A,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 11月4日 每周一测
1.反比例函数3k y x +=
的图象在二、四象限,则k 的取值范围是 A .3k ≤ B .3k ≥- C .3k > D .3k <-
2.点(23)-,在反比例函数k y x =的图象上,则下列各点在此函数图象上的是 A .(23),
B .(32)-,
C .(23)--,
D .(61)--,
3.函数y =mx 229m m --的图象是双曲线,且在每个象限内函数值y 随x 的增大而减小,则m 的值是
A .-2
B .4
C .4或-2
D .-1 4.如图,点B 是反比例函数k y x
=(k ≠0)在第一象限内图象上的一点,过点B 作BA ⊥x 轴于点A ,BC ⊥y 轴于点C ,矩形AOCB 的面积为6,则k 的值为
A .3
B .6
C .-3
D .-6
5.反比例函数k y x =
中,当1x =-时,4y =-,如果y 的取值范围为41y -≤≤-,则x 的取值范围是 A .14x << B .41x << C .14x -<<-
D .41x -≤≤- 6.如图,已知关于x 的函数(1)y k x =-和(0)k y k x
=≠,它们在同一坐标系内的图象大致是 A . B .。
