平行线分线段成比例测试题
初三数学平行线分线段成比例专题练习题

平行线分线段成比例专题练习题
3.如图,l 1∥l 2∥l 3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A.
AD CE BC DF = B. AD BC BE AF = C. AB CD CD EF = D. AD DF BC CE =
5.如图,已知EF CD AB ////,5:3:=AF AD ,12=BE ,那么CE 的长等于( ).
A .536
B .524
C .215
D .29
9.如图所示,△ABC 中,DE ∥BC ,若1
2AD
DB =,则下列结论中
正确的是( )
A .1
2AE
EC = B .1
2DE
BC =
C .1
=3ADE ABC △的周长△的周长 D .1
=3ADE ABC △的面积△的面积
11.如图,已知:△ABC 中,DE ∥BC ,AD=3,DB=6,AE=2,则
EC=_______.
14.在平行四边形ABCD 中,E 为BC 边上的一点.连结AE .
E D
C
B A
(1)若AB=AE , 求证:∠DAE=∠D ;
(2)若点E 为BC 的中点,连接BD ,交AE 于F ,求EF ︰FA 的值.
16.如图,在△ABC 中,已知DE ∥BC ,AD=4,DB=8,DE=3.
(1)求的值;
(2)求BC的长.
19.如图,梯形ABCD中,DC//EF//AB,AC交EF于G.若AE=2ED,CF=2cm,那么CB的长是多少?
20.如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20㎝,求FC的长.
3。
平行线分线段成比例经典例题与变式练习(精选题目)

平行线分线段成比例 【2 】平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,假如1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,假如DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的剖断定理:如上图,假如有BCDEAC AE AB AD ==,那么DE ∥BC .专题一.平行线分线段成比例定理及其推论根本运用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长.EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分离为B .D ,AC 和BD 订交于点E ,EF BD ⊥,垂足为F .证实:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆.BED S ∆.BCD S ∆之间的关系,并证实你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长.OFED CBA【巩固】(上海市数学比赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分离是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长.QPFED CBA专题二.定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 衔接EM 并延伸,交BC 的延伸线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 订交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中测验题)如图,在ABC ∆中,D 为BC 边的中点,E 为AC 边上的随意率性一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值; (2)当11A 34AE C =、时,求AOAD 的值; E D CBAO(3)试猜想1A 1AE C n =+时AOAD 的值,并证实你的猜想.【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延伸线与AC 的交点. (1)假如E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上随意率性一点(E 与A .D 不重合),上述结论是否仍然成立,若成立请写出证实,若不成立,请解释来由.F E DCA【巩固】(天津市比赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延伸BE 交AC 于F .求证:AF EF =.FEDCBA【例7】 (宁德市中考题)如图,ABC ∆中,D 为BC 边的中点,延伸AD 至E , 延伸AB 交CE 的延伸线于P .若2AD DE =,求证:3AP AB =.PEDCBA【巩固】(济南市中考题;安徽省中考题)如图,ABC ∆中,BC a =,若11D E ,分 别是AB AC ,的中点,则1112D E a =;若22D E 、分离是11D B E C 、的中点,则2213224a D E a a ⎛⎫=+= ⎪⎝⎭; 若33D E 、分离是22D B E C 、的中点,则33137248D E a a a ⎛⎫=+= ⎪⎝⎭;…………若n n D E 、分离是-1-1n n D B E C 、的中点,则n n D E =_________.E n D n E 3D 3E 2D 2E 1D 1CBA专题三.运用平行线转化比例【例8】 如图,在四边形ABCD 中,AC 与BD 订交于点O ,直线l 平行于BD ,且 与AB .DC .BC .AD 及AC 的延伸线分离订交于点M .N .R .S 和P . 求证:PM PN PR PS ⋅=⋅lSR PNMODC BA【巩固】已知,如图,四边形ABCD ,两组对边延伸后交于E .F ,对角线BD EF ∥,AC 的延伸线交EF 于G .求证:EG GF =.G FECDBA【例9】 已知:P 为ABC ∆的中位线MN 上随意率性一点,BP .CP 的延伸线分离交对 边AC .AB 于D .E ,求证:1AD AEDC EB+= PNME D CBA【例10】 在ABC ∆中,底边BC 上的两点E .F 把BC 三等分,BM 是AC 上的中线,AE .AF 分离交BM 于G .H 两点,求证:::5:3:2BG GH HM =MH G FECBA【例11】 如图,M .N 为ABC ∆边BC 上的两点,且知足BM MN NC ==,一条平行于AC 的直线分离交AB .AM 和AN 的延伸线于点D .E 和F . 求证:3EF DE =.F NMED CBA【例12】 已知:如图,在梯形ABCD 中,//AB CD ,M 是AB 的中点,分离连接AC .BD .MD .MC ,且AC 与MD 交于点E ,DB 与MC 交于F . (1)求证://EF CD(2)若AB a =,CD b =,求EF 的长.FEMDCBA【巩固】(山东省初中数学比赛题)如图,在梯形ABCD 中,AD BC ∥,396AD BC AB ===,,,4CD =,若EF BC ∥,且梯形AEFD 与梯形EBCF 的周长相等,求EF 的长.F E DCBA【例13】(山东省比赛题)如图,ABCD 的对角线订交于点O ,在AB 的延长线上任取一点E ,衔接OE 交BC 于点F ,若AB a AD c BE b ===,,,求BF 的值.OFE DCBA【例14】已知等腰直角ABC ∆中,E .D 分离为直角边BC .AC 上的点,且CE CD =,过E .D 分离作AE 的垂线,交斜边AB 于L ,K .求证:BL LK =.L KEDC BA【习题1】 如已知DE AB ∥,2OA OC OE =⋅,求证:AD BC ∥.DOECB【习题2】 在ABC ∆中,BD CE =,DE 的延伸线交BC 的延伸线于P ,求证:AD BP AE CP ⋅=⋅.PE D CBA【习题3】 如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =, 直线DE 和BC 的延伸线订交于P ,求证:BP BDCP CE=PEDCBA专题讲授1.选择题(1)如图5-27,△ABC 中,D 在AB 上,E 在AC 上,下列前提中,能剖断DE ∥BC 的是( )图5-27A .AB AE AC AD ⋅⋅= B .DB EC AE AD ⋅⋅= C .AC AE AB AD ⋅⋅= D .AB AE AC BD ⋅⋅=(2)如图5-28,321////l l l ,4l 与5l 交于点P ,P A =a ,AB =b ,BC =c ,PD =d ,DE =e ,EF =f ,则bf =( )图5-28A .abB .bdC .aeD .ce (3)如图5-29,△ABC 中,21==AC AE AB AD ,则OE ∶OB =( )图5-29A .21 B .31 C .41 D .51 (4)如图5-30,已知BN ∥AM ,ND ∥MC ,那么有( )图5-30A .NM PN DA PD = B .PD PCPB PA = C .MCNDPB PA = D .以上答案都不对 (5)如图5-31,H 为□ABCD 中AD 边上一点,且AH =21DH ,AC 和BH 交于点K ,则AK ∶KC 等于( )图5-31A .1∶2B .1∶1C .1∶3D .2∶3 2.填空题(1)如图5-32,梯形ABCD 中,AD ∥BC ,延伸两腰交于点E ,若AD =2,BC =6,AB =4,则ECED=________,DCDE=________;图5-32(2)如图5-33,梯形ABCD 中,DC ∥AB ,DC =4,AB =7,且MN ∥PQ ∥AB ,DM =MP =P A ,则MN =________,PQ =________;图5-33(3)如图5-34,梯形ABCD 中,AB ∥CD ,M 为AB 中点,分离贯穿连接AC .BD .MD .MC ,且AC 与MD 交于E ,BD 与MC 交于F ,则EF 与AB 的地位关系是________;3.如图5-35,△ABC 中,M 为AC 的中点,E 为AB 上一点,且AB AE 41=,贯穿连接EM 并延伸,交BC 的延伸线于D ,求证:BC =2CD .4.如图5-36,在△ABC 中,EF ∥CD ,DE ∥BC ,求证:DBADFD AF =.5.如图5-37,△ABC 中,AF ∶FD =1∶5,BD =DC ,求:AE ∶EC .6.如图5-38,M 为□ABCD 的边BC 的中点,F 为DC 边上的点,BF 交AM 于N ,交AC 于E ,且AN =3MN ,求FC∶AB的值.7.如图5-39,已知D是△ABC中AB边上一点,DE∥BC交AC于E,贯穿连接CD,过E作EF∥CD交AB于F,求证:AD是AF和AB的比例中项.8.如图5-40,已知△ABC中,AB>AC,AD⊥BC于D,F为BC中点,过F作BC垂线交AB于E,BD=6cm,DC=4cm,AB=8cm,求AE.BE的长.9.如图5-41,已知△ABC 中,∠ACB =90°,BFC S ∆∶AFC S ∆=1∶3,BC =12cm,FE ⊥BC 于E ,求EB 的长.10.如图5-42,已知:□ABCD 对角线交于O ,OE ⊥BC 于E ,交AB 的延伸线于F ,若AB =a ,BC =b ,BF =c ,求BE 的长.参考答案1.(1)A (2)D (3)A (4)B (5)C 2.(1)31,21(2)5,6 (3)平行 3.提醒:过点C 作CN ∥DE 交AB 于N .4.略 5.1∶10 6.32 7.略 8.cm 34,cm 320 9.3cm 10.ca bc2。
平行线分线段成比例经典例题与变式练习(精选题目)
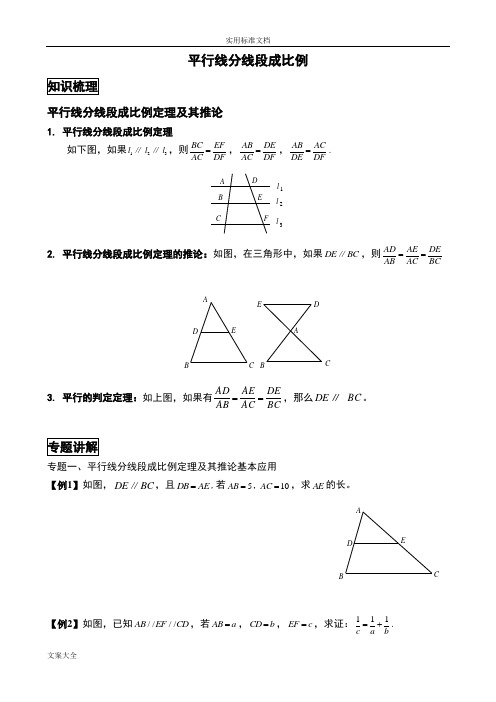
平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点. (1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D E D CBAO不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例经典例题与变式练习(题目)(教育相关)
A
E
D
M
N
P
B
C
【例10】 在 ABC 中,底边 BC 上的两点 E 、 F 把 BC 三等分, BM 是 AC 上的中 线, AE 、 AF 分别交 BM 于 G 、 H 两点,求证: BG :GH : HM 5:3: 2
A
M GH
BE
【例11】 如图, M 、 N 为 ABC 边 BC 上的两点,且满足 BM MN NC ,一条 平行于 AC 的直线分别交 AB 、 AM 和 AN 的延长线于点 D 、 E 和 F . 求证: EF 3DE .
AB AC BC
A D
E E
D A
B
CB
C
3. 平行的判定定理:如上图,如果有 AD AE DE ,那么 DE ∥ BC 。 AB AC BC
专题讲解
专题一、平行线分线段成比例定理及其推论基本应用 【例1】如图, DE ∥BC ,且 DB AE ,若 AB 5,AC 10 ,求 AE 的长。
(1)如图(1),在 ABC 中, M 是 AC 的中点, E 是 AB 上一点,且 AE 1 AB ,
4
连接 EM 并延长,交 BC 的延长线于 D ,则 BC _______.
CD
(2)如图(2),已知 ABC 中, AE : EB 1: 3, BD: DC 2:1, AD 与 CE 相交于 F ,则 EF AF
A
F E
B
D
C
【例7】(宁德市中考题)如图, ABC 中, D 为 BC 边的中点,延长 AD 至 E , 延长 AB 交 CE 的延长线于 P 。若 AD 2DE ,求证: AP 3AB 。
A
B P
(完整版)平行线分线段成比例经典例题与变式练习(含标准答案)

平行线分线段成比例知识梳理1. 平行线分线段成比例定理2. 平行线分线段成比例定理的推论:如图,在三角形中,如果 AD AE DE3. 平行的判定定理:如上图,如果有 A A D B A A C E B D C E ,那么DE ∥ BC专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】如图, DE ∥ BC ,且 DB AE ,若AB 5,AC 10,求 AE 的长。
如下图,如果 l 1∥ l 2∥ l 3,则BC ACAB DEAC DFABDE AC 1 2DFEFDFDE ∥ BC ,则A A DB A A EC BD C E例2】如图,已知 AB / /EF //CD ,若 AB a ,CD b ,EF c ,求证:1 1ca【巩固】如图, AB BD ,CD BD ,垂足分别为 B 、 D ,AC 和 BD 相交于点 E ,EFBD ,垂足为 F .证明: A 1B C 1D E 1F .【例3】如图,在梯形 ABCD 中, AB ∥CD , AB 12,CD 9 ,过对角线交点 O 作EF ∥ CD 交AD ,BC 于E ,F ,求 EF 的长。
AE巩固】如图,找出 S ABDS BEDS BCD 之间的关系,并证明你的结论1 b【巩固】(上海市数学竞赛题)如图,在梯形 ABCD 中, AD ∥BC , AD a ,BC b ,E ,F 分别 是AD ,BC 的中点, AF 交 BE 于 P , CE 交 DF 于 Q ,求 PQ 的长。
专题二、定理及推论与中点有关的问题 【例4】( 2007 年北师大附中期末试卷)1(1)如图( 1),在 ABC 中, M 是 AC 的中点, E 是 AB 上一点,且 AE 1AB ,4的值为( )5A. B.1 C.2 【例5】( 2001 年河北省中考试卷)如图,在 AC 边上的任意一点, BE 交 AD 于点O . (1)当 AE 1时,求 AO的值;AC 2 AD3 / 14连接 EM 并延长, 交 BC 的延长线于 D ,则 BCCD2)如图( 2),已知 ABC 中, AE : EB 1:3 , B D :DC 2:1 , AD 与CE 相交于 F ,则 EF FC AFFDD.2A2)当AE 1、1时,求AO的值;AC 3 4 AD3)试猜想AE 1时AO的值,并证明你的猜想AC n 1 AD【例6】(2003年湖北恩施中考题)如图,AD是ABC的中线,点E在AD上,F是BE 延长线与AC 的交点.(1)如果E是AD的中点,求证:AF 1;FC 2(2)由(1)知,当E是AD中点时,AF 1 AE成立,若E是AD上任意一点(E与A、D FC 2 ED 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC中,AD是BC边上的中线,E是AD 上的一点,且BE AC ,延长BE 交AC 于 F 。
高一数学平行线分线段成比例定理试题

高一数学平行线分线段成比例定理试题1.如图所示,l1∥l2∥l3,下列比例式正确的是()A.=B.=C.=D.=【答案】D【解析】根据平行线分线段成比例定理得出相应的线段对应成比例,进而逐一判断四个答案的正误,可得答案.解:∵直线l1∥l2∥l3,∴=,故A错误;=,故B错误;=,故C错误;=,故D正确;故选:D点评:本题考查了平行线分线段成比例定理,注意:一组平行线截两条直线,所截的线段对应成比例.2.如图,在梯形ABCD中,AB∥CD∥EF,若AB=5,CD=2,EF=4,则梯形ABFE与梯形EFDC的面积比是()A.B.C.D.【答案】D【解析】过D作DG∥BC交AB于G,交EF于H,根据平行四边形的性质先求出BG=FH=CD,从而得到EH,AG的长,再根据平行线分线段成比例定理可求出梯形ABFE与梯形EFDC的高的比,即可求出梯形ABFE与梯形EFDC的面积比.解:过D作DG∥BC交AB于G,交EF于H.则BG=FH=CD=2,∴EH=EF﹣FH=2,AG=3,∵AB∥EF,∴DE:AE=2:1,∴梯形ABFE与梯形EFDC的高的比为1:2,∴梯形ABFE与梯形EFDC的面积比是=故选:D.点评:本题考查平行线分线段成比例定理,考查梯形的面积公式是一个基础题,解题的时候容易出的一个错误是把两个梯形看成相似梯形,根据相似多边形的面积之比等于相似比的平方.3.如图,已知平行四边形ABCD中,E、F分别为边AB、AD上的点,EF与对角线AC交于点P.若=,=(a、b、m、n均为正数),则的值为()A. B. C. D.【答案】C【解析】过点E作EG∥AD,交AC于点O,利用平行线分线段成比例及三角形相似就可以表示出AO、CO的比值,进而表示出,AP+PO比PC﹣PO的比值,再表示出EO、BC的比值,从而表示出EO,利用△APF∽△OPE可以表示出PO,代入第一个比例式就可以求出结果.解:过点E作EG∥AD,交AC于点O,∵四边形ABCD是平行四边形,∴AD∥EG∥BC,AD=BC,∴,△AEO∽△ABC,△APF∽△OPE,∴,,,∵∴令AE=ax,BE=bx,AF=my,DF=ny,∴,∴EO=,∴,∴AP(a+b)bm+AP(m+n)ab+AP(m+n)a2=PC(a+b)am,∴AP(bm+an+am)(a+b)=PC(a+b)am,∴,∴C答案正确,故选C.点评:本题考查了相似三角形的判定及性质,平行四边形的性质,平行线分线段成比例定理的运用.4.如图,平行四边形ABCD中,AE:EB=m:n,若△AEF的面积等于a,则△CDF的面积等于()A.a B.a C.a D.a【答案】C【解析】根据平行四边形对边平行,得到两个三角形相似,根据两个三角形相似,知道这两个三角形的面积之比等于边长之比的平方,做出两个三角形的边长之比,根据△AEF的面积,得到要求的三角形的面积.解:平行四边形ABCD中,有△AEF∽△CDF∴△AEF与△CDF的面积之比等于对应边长之比的平方,∵AE:EB=m:n,∴AE:CD=m:(m+n)∵△AEF的面积等于acm2,∴△CDF 的面积等于acm 2故选:C .点评:本题考查三角形相似的性质,两个三角形相似,对应的高线,中线和角平分线之比等于边长之比,两个三角形的面积之比等于边长比的平方,这种性质用的比较多.5. 在△ABC 中,D ,E 分别为AB ,AC 上的点,且DE ∥BC ,△ADE 的面积是2cm 2,梯形DBCE 的面积为6cm 2,则DE :BC 的值为( )A .1:B .1:2C .1:3D .1:4【答案】B【解析】根据相似三角形的性质,由已知可证S △ADE :S △ABC =1:4,所以相似比是1:2,故DE :BC=1:2.解:根据题意,△ADE 的面积是2cm 2,梯形DBCE 的面积为6cm 2,则S △ADE :S △ABC =1:4∵DE ∥BC则△ADE ∽△ABC设相似比是k则面积的比是k 2=1:4因而相似比是1:2∴DE :BC=1:2.故选:B .点评:本题主要考查了相似三角形的性质,相似三角形面积的比等于相似比的平方.6. 如图,在△ABC 中,M 是AC 的中点,点E 在AB 上,且AE=AB ,连接EM 并延长交BC 的延长线于点D ,则BC :CD=( )A .2:1B .3:1C .3:2D .4:1【答案】A【解析】如图所示,过点C 作CF ∥AB 交DE 于点F .可得=1,由,可得.又.即可得出.解:如图所示,过点C 作CF ∥AB 交DE 于点F .∴=1, 又, ∴. ∵CF ∥AB ,∴=.∴.故选:A.点评:本题考查了平行线分线段成比例定理、相似三角形的性质,考查了推理能力,属于基础题.7.如图,四边形ABCD是等腰梯形,AB∥CD,且AD=CD=1.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则该平行四边形的面积为.【答案】3【解析】由于上底和两腰长已知,故要求梯形面积,关键是要找出底边上和高,由于图形中无法再分析出边与边的关系,所以我们可以从角的方向入手,求梯形的内角,进一步求出梯形的其它未知边长,进而求解平行四边形的面积.解:设等腰梯形的底角为θ,则由图可知,θ+θ+θ=180°,即θ=60°.由AD=CD=1知,AB=CD+2AD•cos60°=2,故梯形的面积为=,故平行四边形的面积为.故答案为:.点评:本小题主要考查梯形与平行四边形的有关知识,以及分析问题和解决问题的能力,以及转化与化归的思想方法.本题的切入点是求梯形的内角,如何由已知分析出该点,是解题的关键.8.(2009•惠州模拟)如图,在△ABC中,DE∥BC,DF∥AC,AE:AC=3:5,DE=6,则BF= .【答案】4【解析】因为已知中有两个平行关系,我们可以大胆猜想,本题的解答过程一定与平行线分线段成比例定理有关,因此可以根据平行线分线段成比例定理,构建比例式,列出已知线段与未知线段之间的关系式,解方程进行求解.解:因为DE∥BC,则△ADE~△ABC,所以,即,所以BC=10.又DF∥AC,则四边形DECF是平行四边形,故BF=BC﹣FC=BC﹣DE=10﹣6=4.点评:当题目中出现有多个平行关系时,我们可以使用平行线分线段成比例定理构造比例式,表示已知线段与未知线段之间的关系,解方程即可求解.解题思路是:分析已知量与未知量之间的关系,选择适合的性质构建方程,解方程求解.9.(几何证明选讲选做题)如图,在△ABC中,DE∥BC,EF∥CD,若BC=4,DE=2,DF=1,则AB的长为.【答案】4【解析】在△ABC中,利用平行线分线段成比例定理,得AD=BD=AB,AE=CE.然后在△ADC中,根据EF∥CD且AE=CE得到AF=DF=1,从而得出AD的长,最终得出AB的长.解:∵△ABC中,DE=BC,且DE∥BC,∴AD=BD,AE=CE∵△ADC中,EF∥CD,AE=CE∴AF=DF=1,得AD=2结合AD=BD=AB,可得AB=4故答案为:4点评:本题给出三角形中的中位线,求三角形的边长,着重考查了平行线的性质和三角形相似的判定等知识,属于基础题.10.(2010•佛山模拟)如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF=.【答案】【解析】根据两条直线平行,得到三角形相似,根据相似三角形对应边成比例,得到一系列比例式,根据三角形全等,得到边长相等,利用等量代换变化出要求的量,根据方程思想,得到结果.解:∵BF∥AE∴,∴=,即.故答案为:点评:本题考查三角形相似对应边成比例,考查等量代换思想,考查方程思想的应用,是一个比较典型的题目,本题是平面几何中常见的类型.。
平行线分线段成比例经典例题与变式练习(精选题目)
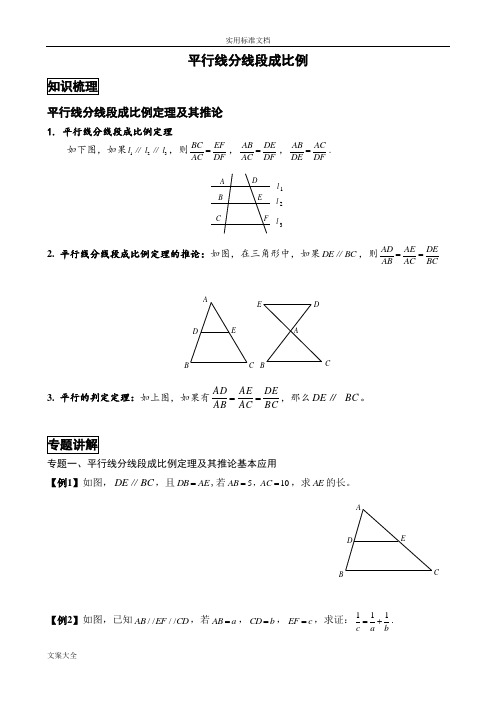
平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D E D CBAO不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例专题练习

平行线分线段成比例专题练习内部编号:(YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128)《平行线分线段成比例》专题练习1. 如图,平行四边形ABCD 中,E 是AB 中点,F 在AD 上,且AF =12FD ,EF 交AC 于G ,则AG ︰AC =________。
A. 14B. 15C. 16D.18(第1题图) (第2题图)(第3题图)2.如图,在△ABC 中,M 是AC 边中点,E 是AB 上一点,且AE =14AB ,连结EM 并延长,交BC 的延长线于D ,此时 BC ︰CD 为( )A .2︰1B .3︰2C .3︰1D .5︰23.如图,直线a∥b,AF ︰FB =3︰5,BC ︰CD =3︰1,则AE ︰EC 为( )A .5︰12B .9︰5C .12︰5D .3︰24.如图,在Rt△ABC 内有边长分别为a 、b 、c 的三个正方形,则a 、b 、c 满足的关系式是( )A. b=a+cB.b=acC. b2=a2+ c2 D .b=2a=2c5.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O )20米的点A 处,沿OA 所在的直线行走14 米到点B 时,人影长度( )A .变短3.5米B .变长1.5米C .变长3.5米D .变短1.5米(第4题图) (第5题图) (第6题图)6.已知:如图,平行四边形ABCD,E为BC的中点,BF︰FA=1︰2,EF与对角线BD相交于G,求BG︰BD。
7.已知:如图,F是四边形ABCD对角线AC上一点,EF∥BC,FG∥AD。
8.如图,在ΔABC中,EF//DC,DE//BC,求证:(1)AF︰FD=AD︰DB;(2)AD2=AF·AB。
9.如图,AB∥EF∥CD,(1)AB=10,CD=15,AE∶ED=2∶3,求EF的长。
(2)AB=a,CD=b,AE∶ED=k,求EF的长。
10. 一位同学想利用有关知识测旗杆的高度,他在某一时刻测得高为0.5m的小木棒的影长为0.3m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0m,又测地面部分的影长BC=3.0m,你能根据上述数据帮他测出旗杆的高度吗?11.小芳同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1m长的标杆测得其影长为1.2m,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6m和2m,你能帮助小芳同学算出学校旗杆的高度?12.如图所示,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB是多少?13.如图,花丛中有一路灯杆AB在灯光下,小明在D点处的影长DE=3米,沿BD 方向行走到达G点,DG=5米,这时小明的影长GH=5米。
平行线分线段成比例经典例题与变式练习题目

平行线分线段成比率知识梳理平行线分线段成比率定理及其推论1.平行线分线段成比率定理以以下列图,若是 l 1∥ l2∥ l3,则BCEF,AB DE,AB AC .AC DF AC DFDE DFA Dl 1B El 2C Fl 32.平行线分线段成比率定理的推论:如图,在三角形中,若是DE∥ BC ,则ADAE DE AB AC BCAE DD E AB C B C3. 平行的判判断理:如上图,若是有ADAEDE,那么 DE∥ BC。
AB AC BC专题解说专题一、平行线分线段成比率定理及其推论基本应用【例 1】如图,DE∥BC,且DB AE ,若AB5,AC 10 ,求AE的长。
ADEBC【例 2】如图,已知AB / / EF / /CD,若AB a , CD b , EF c ,求证:11 1.CAE BFD【坚固】 如图, AB BD ,CDBD ,垂足分别为 B 、D ,AC 和BD 订交于点 E , EFBD ,垂足为 F .证明:11 1 .ABCDEFCAEBFD【坚固】 如图,找出 S ABD 、 S BED 、 S BCD 之间的关系,并证明你的结论 .CAE BFD【例 3】如图,在梯形 ABCD 中, AB ∥ CD , AB12 ,CD 9 ,过对角线交点 O 作EF ∥CD 交 AD ,BC 于E ,F ,求 EF 的长。
D CEFOA B【坚固】(上海市数学竞赛题)如图,在梯形 ABCD 中, AD ∥ BC , AD a ,BC b ,E ,F 分别是 AD ,BC 的中点, AF 交BE 于P ,CE 交DF 于Q ,求 PQ 的长。
EADPQBCF专题二、定理及推论与中点相关的问题【例 4】( 2012 年北师大附中期末试题)(1)如图( 1),在 ABC 中, M 是 AC 的中点, E 是 AB 上一点,且 AE 1AB ,4连结 EM 并延伸,交 BC 的延伸线于 D ,则BC_______.CD2:1 ,AD 与CE 订交于 F ,则EFAF (2)如图( 2),已知 ABC 中, AE : EB 1:3 , BD : DCFCFD的值为()5C.3A.22AAEEMFBCD BD C(2)(1)【例 5】( 2011 年河北省中考试题)如图,在 ABC 中, D 为 BC 边的中点, E 为AC 边上的随意一点, BE 交 AD 于点 O .A(1)当AE1时,求AO的值;A C 2ADE(2)当AE 1 1AO时,求的值;OA C、AD3 4(3)试猜想AE1 时AO的值,并证明你的猜想 .A C n 1ADB D C【例 6】( 2013 年湖北恩施中考题)如图, AD 是 ABC 的中线,点 E 在 AD 上, F 是 BE 延伸线与 AC 的交点 .(1)若是 E 是 AD 的中点,求证:AF1 ;FC2(2)由(1)知,当 E 是 AD 中点时,AF1AE建立,若 E 是 AD 上随意一点( E 与 A 、D精选文库不重合),上述结论可否仍旧建立,若建立请写出证明,若不建立,请说明原因.AFEB D C【坚固】(天津市竞赛题)如图,已知ABC 中,AD是BC边上的中线,E是AD上的一点,且BE AC,延伸BE交AC于F。
平行线分线段成比例经典例题与变式练习

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如以下图,若是1l ∥2l ∥3l ,那么BC EF AC DF =,AB DE AC DF =,AB ACDE DF=.2. 平行线分线段成比例定理的推论:如图,在三角形中, 若是DE BC ∥,那么AD AE DEAB AC BC==3. 平行的判定定理:如上图,若是有BCDEAC AE AB AD ==,那么DE ∥ BC 。
1、如图,DE BC ∥,且DB AE =,假设510AB AC ==,,求AE 的长。
2、 如图,已知////AB EF CD ,假设AB a =,CD b =,EF c =,求证:111c a b=+.3、如图,AB BD ⊥,CD BD ⊥,垂足别离为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.4、如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.l 3l 2l 1FE D C BA ABCDEEDC B AEDCBAFE DCBAFEDCBAFEDCBAOFED C5、如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对 角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
六、(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,别离是AD BC,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
7、(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,那么BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,那么EF AFFC FD+ 的值为( ) A.52 B.1 C.32D.2八、如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.九、如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)若是E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,假设E 是AD 上任意一点(E 与A 、D 不重合),上述结论是不是仍然成立,假设成立请写出证明,假设不成立,请说明理由.10、如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例证明题

例2:已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD
求证:
例3、已知:△ABC中,AD为BC边上的中线,过C任作一直线交AD于E,交AB于F。
求证:
例4:如图,已知:D为BC的中点,AG∥BC,求证:例5:已知△ABC中,AD平分∠BAC,
求证: (过C作CE∥AD交BA的延长线于E).
例6:△ABC中,AD平分∠BAC,CM⊥AD交AD于E,交AB于M,
求证:
练习:1、已知:如图,EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2
BD=3.6,求CD的长。
2、已知:如图,四边形AEDF为菱形,AB=12,BC=10,AC=8,
求:BD、DC及AF的长。
3、已知:如图,B在AC上,D在BE上,且AB:BC=2:1,ED:DB=2:1
求AD:DF
4、已知,如图,E在BC上,F在AC的延长线上,且AF=BE,
求证:
方法1:过E作EG∥AF交AB于G
方法2:过E作EF∥AB交AC于F
5、已知:如图,平行四边形 ABCD中,EF∥AD求证:GH∥AB
平行线分线段成比例经典例题与变式练习(精选题目)

平行线分线段成比例知识梳理平行线分线段成比例定理及其推论1.平行线分线段成比例定理如下图,如果h // I2 // I3,则BCACABDEACDF2.平行线分线段成比例定理的推论:3.平行的判定定理:AB DEAC12DF,EFDF如图,在三角形中,如果ADDE // BC,贝U --ABAEACDEBC 如上图,如果有ADABAEACDEBC,那么DE // BC专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】如图,DE // BC,且DB AE,若AB 5, AC 10,求AE的长。
【例2】如图,已知AB//EF//CD,若AB a , CD b , EF c ,求证:111. cab 【巩固】如图,AB BD,CD BD,垂足分别为B、D,AC和【巩固】如图,找出S ABD、S BED、S BCD之间的关系,并证明你的结论BD相交于点E,EF BD,垂足为F .证明:1 1AB CD1EFA连接EM 并延长,交BC 的延长线于D , 则CC (2)如图(2),已知 ABC 中,AE:EB 1:3,BD :DC 2:1,AD 与CE 相交于F ,则EF FCAF FD的值为()A.|B.1C.【例5】(2001年河北省中考试题)如图,在 AC 边上的任意一点,BE 交AD 于点O .【例3】如图,在梯形ABCD 中,AB // CD , AB 12 , CD 9,过对角线交点0作EF // CD 交 AD , BC 于 E , F ,求 EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形 ABCD 中,AD // BC ,AD a ,BC b ,E ,F 分别 是AD ,BC 的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
专题二、定理及推论与中点有关的问题 【例4】(2007年北师大附中期末试题)1(1)如图(1),在 ABC 中,M 是AC 的中点,E 是AB 上一点,且AE - AB ,43 2D.2A(1)当AE-时,求AO的值;AC2AD(2)当AE 1 1 口」、—求A0的值;AC 3 4AD(3)试猜想AE 1AC n 1时A0的值,并证明你的猜想AD【例6】(2003年湖北恩施中考题)如图,AD是ABC的中线,点E在AD上,F 是BE延长线与AC的交点.(1)如果E是AD的中点,求证:圧 -;FC 2(2)由(1)知,当E是AD中点时,圧-成立,若E是AD上任意一点(E与A、DFC 2 ED不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC中,AD是BC边上的中线,E是AD 上的一点,且BE AC,延长BE交AC于F。
平行线分线段成比例-学生版

平行线分线段成比例一、选择题(本大题共13小题,共39.0分)1.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是()A. B. 3 C. 5 D.2.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=()A. B. C. D. 13.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=()A. 1:4B. 1:3C. 1:2D. 1:14.如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果,那么等于()A. B. C. D.5.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是()A. B. C. D.6.如图,△ABC是等腰三角形,AB=AC=3,BC=1.点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为()A. B. C. D. 17.如图,AD是△ABC的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于()A. 1:2B. 2:3C. 1:3D. 2:58.已知:如图,在▱ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=BG;(4)S△ABE=3S△AGE.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个9.AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=()A. 1:3B. 1:4C. 1:5D. 1:610.如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC于点F,则下列结论错误的是()A. B. C. D.11.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是()A. B. C. D.12.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为()A. B. C. D.13.如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则的值为()A. B. C. D.二、计算题(本大题共1小题,共6.0分)14.如图,已知△ABC中,AB=AC=,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.(1)求线段BF的长;(2)求AE:EC的值.三、解答题(本大题共1小题,共8.0分)15.如图1,已知四边形ABCD是菱形,G是线段CD上的任意一点时,连接BG交AC于F,过F作FH∥CD交BC于H,可以证明结论成立.(考生不必证明)(1)探究:如图2,上述条件中,若G在CD的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(2)计算:若菱形ABCD中AB=6,∠ADC=60°,G在直线CD上,且CG=16,连接BG交AC所在的直线于F,过F作FH∥CD交BC所在的直线于H,求BG与FG的长.(3)发现:通过上述过程,你发现G在直线CD上时,结论还成立吗?。
《平行线分线段成比例》练习题

《平行线分线段成比例》练习题平行线分线段成比例练题问题一已知在平行线AB和CD上,线段AE与CF相交于点P,线段BE与FD相交于点Q。
求证:如果AP与CQ互相延长所交于的点为O,那么O是平行线AB和CD上任意线段的分割点。
问题二在平行线AB和CD上,线段AE与CF相交于点P,线段BE 与FD相交于点Q,且已知AP和PB的比例为2:3,求证:线段CQ和QD的比例也为2:3。
问题三在平行线AB和CD上,线段AE与CF相交于点P,且已知线段AP与CQ的比例为3:4,线段PE与QF的比例为2:3,求证:线段BE和FD的比例为6:4。
问题四在平行线AB和CD上,线段AE与CF相交于点P,且已知线段AP与CQ的比例为3:5,线段PE与QF的比例为4:9,求证:线段BE和FD的比例为12:5。
问题五在平行线AB和CD上,线段AE与CF相交于点P,且已知线段AP与CQ的比例为1:2,线段PE与QF的比例为2:5,求证:如果线段BE和FD的比例为4:3,那么线段AE和CF的比例为8:15。
问题六在平行线AB和CD上,线段AE与CF相交于点P,且已知线段AP与CQ的比例为2:3,线段BE与FD的比例为3:5,求证:如果线段AF和DE的比例为6:7,那么线段EB和FC的比例为15:14。
问题七在平行线AB和CD上,已知AP与CQ互相延长所交于的点为O,且已知线段EO和FO的比例为3:4,线段DO和BO的比例为5:6,求证:线段AD和BC的比例为9:10。
问题八在平行线AB和CD上,已知线段AP与CQ的比例为7:8,线段PE与QF的比例为2:3,线段FO与EO的比例为5:7,求证:如果线段DE和AF的比例为9:10,那么线段EB和FC的比例为15:14。
以上是关于平行线分线段成比例的练习题,请根据给定的已知条件进行证明或运算,以验证分割点和比例的正确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D B
E F 4.1-4.2平行线等分线段定理与 平行线分线段成比例定理
考纲要求:
1.探索并理解平行线分线段定理的证明过程;
2.能独立证明平行线分线段定理的推论1、推论2; 3.平行线分线段成比例定理与推论的区别
4.能应用定理和推论解决相关的几何计算问题和证明问题
一:知识梳理
1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段
推论1:经过三角形一边的中点与另一边平行的直线必
推论2:经过梯形一腰的中点,且与底边平行的直线
2.三条平行线截两条直线,所得的对应线段 推论:平行于三角形的一边,并且和其他两边相交的直线。
所截得的三角形的三边与原三角形的三边
二:基本技能:
判断下列命题是否正确
1. 如图△ABC 中点D 、E 三等分AB ,DF ∥EG ∥BC ,DF 、EG 分别
交AC 于点F 、G ,则点F 、G 三等分AC ( )
2. 四边形ABCD 中,点M 、N 分别在AB 、CD 上若AM=BM 、
DN=CN 则AD ∥MN ∥BC ( )
3. 一组平行线,任意相邻的两平行线间的距离都相等,则这组
平行线能等分线段。
( )
4. 如图l 1//l 2// l 3且AB=BC ,那么AB=BC=DE=EF ( )
5.如图,DE ∥BC ,分别交AB 、AC 于点D 、E 则:
BC DE
AC AE AB AD =
=
( )
三:典型例题
1 已知线段AB ,求作:线段AB 的五等分点。
2 如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,E 是CD 的中点.求证EA =EB 。
4
3. 如图,在△ABC 中,AD 是BC 边上的中线,M 是AD 的中
点,BM 的延长线交AC 于N ,求证:AN=
2
1
CN 。
4.如下图,梯形ABCD 中,AD//BC ,∠B=60°,AB=BC,E 为AB 的中点,求证:△ECD 为等边三角形。
5:已知:△ABC 中,E 、G 、D 、F 分别是边AB 、CB 上的一点,且GF ∥ED ∥AC ,EF ∥AD
求证:.BC BD
BE BG =
A C
G
C
B E D F
l 3
l 2 l 1 A
6.已知:△ABC 中,AD 为BC 边上的中线,过C 任作一直线交AD 于E ,交AB 于F 。
求证:FB AF
ED AE 2=
7:如图,已知:D 为BC 的中点,AG ∥BC ,求证:FC
AF
ED EG =
DC
AG
8.已知:△ABC 中,AD 平分∠BAC , 求证:
DC
BD
AC AB =
(提示:过C 作CE ∥AD 交BA 的延长线于E )
9:△ABC 中,AD 平分∠BAC ,CM ⊥AD 交AD 于E ,交AB 于M ,
求证:AM AB
DC BD =
四:能力提升
1.如图1所示,F 为AB 的中点,FG ∥BC ,EG ∥CD ,则AG = ,AE = .
2.如图2,直线l 过梯形ABCD 一腰AB 的中点E ,且平行于BC ,l 与BD ,AC 、CD 分别交于F 、G 、H ,那么,BF = ,CG = ,DH = .
3.如图3,已知CE 是△ABC 的中线,CD=
2
1
AD,EF ∥BD ,EG ∥AC ,若EF=10cm ,则BG = cm ,若CD=5cm ,则AF= cm.
4.已知:如图,B 在AC 上,D 在BE 上,且AB:BC=2:1,ED:DB=2:1
求AD:DF
5. △ABC 中,DE ∥BC ,F 是BC 上一点。
AF 交DE 于点G ,AD:BD=2:1,BC=8.4cm 求(1)DE 的长
(2)AF
AG
(3)ADE ABC S S ∆∆。
