西电《数字信号处理》大作业
西安电子科技大学数字信号处理上机作业

数字信号处理MATLAB上机作业M 2.21.题目The square wave and the sawtooth wave are two periodic sequences as sketched in figure ing the function stem. The input data specified by the user are: desired length L of the sequence, peak value A, and the period N. For the square wave sequence an additional user-specified parameter is the duty cycle, which is the percent of the period for which the signal is positive. Using this program generate the first 100 samples of each of the above sequences with a sampling rate of 20 kHz ,a peak value of 7, a period of 13 ,and a duty cycle of 60% for the square wave.2.程序% 用户定义各项参数参数A = input('The peak value =');L = input('Length of sequence =');N = input('The period of sequence =');FT = input('The desired sampling frequency =');DC = input('The square wave duty cycle = ');% 产生所需要的信号t = 0:L-1;T = 1/FT;x = A*sawtooth(2*pi*t/N);y = A*square(2*pi*(t/N),DC);% Plotsubplot(2,1,1)stem(t,x);ylabel('幅度');xlabel('n');subplot(2,1,2)stem(t,y);ylabel('幅度');xlabel('n');3.结果4.结果分析M 2.41.题目(a)Write a matlab program to generate a sinusoidal sequence x[n]= Acos(ω0 n+Ф) and plot thesequence using the stem function. The input data specified by the user are the desired length L, amplitude A, the angular frequency ω0 , and the phase Фwhere 0<ω0 <pi and 0<=Ф<=2pi. Using this program generate the sinusoidal sequences shown in figure 2.15. (b)Generate sinusoidal sequences with the angular frequencies given in Problem 2.22.Determine the period of each sequence from the plot and verify the result theoretically. 2.程序%用户定义的参数L = input('Desired length = ');A = input('Amplitude = ');omega = input('Angular frequency = ');phi = input('Phase = ');%信号产生n = 0:L-1;x = A*cos(omega*n + phi);stem(n,x);xlabel('n');ylabel('幅度');title(['\omega_{o} = ',num2str(omega)]);3.结果(a)ω0=0ω0=0.1πω0=0.8πω0=1.2π(b)ω0=0.14πω0=0.24πω0=0.34πω0=0.68πω0=0.75π4.结果分析M 2.51.题目Generate the sequences of problem 2.21(b) to 2.21(e) using matlab.2.程序(b)n = 0 : 99;x=sin(0.6*pi*n+0.6*pi);stem(n,x);xlabel('n');ylabel('幅度');(c)n = 0 : 99;x=2*cos(1.1*pi*n-0.5*pi)+2*sin(0.7*pi*n);stem(n,x);xlabel('n');ylabel('幅度');(d)n = 0 : 99;x=3*sin(1.3*pi*n-4*cos(0.3*pi*n+0.45*pi));stem(n,x);xlabel('n');ylabel('幅度');(e)n = 0 : 99;x=5*sin(1.2*pi*n+0.65*pi)+4*sin(0.8*pi*n)-cos(0.8*pi*n);stem(n,x);xlabel('n');ylabel('幅度');(f)n = 0 : 99;x=mod(n,6);stem(n,x);xlabel('n');ylabel('幅度');3.结果(b)(c)(d)(e)(f)4.结果分析M 2.61.题目Write a matlab program to plot a continuous-time sinusoidal signal and its sampled version and verify figure 2.19. You need to use the hold function to keep both plots.2.程序%用户定义的参数fo = input('Frequency of sinusoid in Hz = ');FT = input('Samplig frequency in Hz = ');%产生信号t = 0:0.001:1;g1 = cos(2*pi*fo*t);plot(t,g1,'-')xlabel('时间t');ylabel('幅度')holdn = 0:1:FT;gs = cos(2*pi*fo*n/FT);plot(n/FT,gs,'o');hold off3.结果4.结果分析M 3.11.题目Using program 3_1 determine and plot the real and imaginary parts and the magnitude and phase spectra of the following DTFT for various values of r and θ:G(e jω)=1, 0<r<1.1−2r(cosθ)e−jω+r2e−2jω2.程序%program 3_1%discrete-time fourier transform computatition%k=input('Number of frequency points = ');num=input('Numerator coefficients= ');den=input('Denominator coefficients= ');%computer the frequency responsew=0:pi/k:pi;h=freqz(num,den,w);%plot the frequency responsesubplot(221)plot(w/pi,real(h));gridtitle('real part')xlabel('\omega/\pi');ylabel('Amplitude') subplot(222)plot(w/pi,imag(h));gridtitle('imaginary part')xlabel('\omega/\pi');ylabel('Amplitude') subplot(223)plot(w/pi,abs(h));gridtitle('magnitude spectrum')xlabel('\omega/\pi');ylabel('magnitude') subplot(224)plot(w/pi,angle(h));gridtitle('phase spectrum')xlabel('\omega/\pi');ylabel('phase,radians')3.结果(a)r=0.8 θ=π/6(b)r=0.6 θ=π/34.结果分析M 3.41.题目Using matlab verify the following general properties of the DTFT as listed in Table 3.2:(a) Linearity, (b) time-shifting, (c) frequency-shifting, (d) differentiation-in-frequency, (e) convolution, (f) modulation, and (g) Parseval’s relation. Since all data in matlab have to be finite-length vectors, the sequences to be used to verify the properties are thus restricted to be of finite length.2.程序%先定义两个信号N = input('The length of the sequence = ');k = 0:N-1;%g为正弦信号g = 2*sin(2*pi*k/(N/2));%h为余弦信号h = 3*cos(2*pi*k/(N/2));[G,w] = freqz(g,1);[H,w] = freqz(h,1);%*************************************************************************%% 线性性质alpha = 0.5;beta = 0.25;y = alpha*g+beta*h;[Y,w] = freqz(y,1);figure(1);subplot(211),plot(w/pi,abs(Y));xlabel('\omega/\pi');ylabel('|Y(e^j^\omega)|');title('线性叠加后的频率特性');grid;% 画出Y 的频率特性subplot(212),plot(w/pi,alpha*abs(G)+beta*abs(H));xlabel('\omega/\pi');ylabel('\alpha|G(e^j^\omega)|+\beta|H(e^j^\omega)|');title('线性叠加前的频率特性');grid;% 画出alpha*G+beta*H 的频率特性%*************************************************************************% % 时移性质n0 = 10;%时移10个的单位y2 = [zeros([1,n0]) g];[Y2,w] = freqz(y2,1);G0 = exp(-j*w*n0).*G;figure(2);subplot(211),plot(w/pi,abs(G0));xlabel('\omega/\pi');ylabel('|G0(e^j^\omega)|');title('G0的频率特性');grid;% 画出G0的频率特性subplot(212),plot(w/pi,abs(Y2));xlabel('\omega/\pi');ylabel('|Y2(e^j^\omega)|');title('Y2的频率特性');grid;% 画出Y2 的频率特性%*************************************************************************% % 频移特性w0 = pi/2; % 频移pi/2r=256; %the value of w0 in terms of number of samplesk = 0:N-1;y3 = g.*exp(j*w0*k);[Y3,w] = freqz(y3,1);% 对采样的512个点分别进行减少pi/2,从而生成G(exp(w-w0))k = 0:511;w = -w0+pi*k/512;G1 = freqz(g,1,w);figure(3);subplot(211),plot(w/pi,abs(Y3));xlabel('\omega/\pi');ylabel('|Y3(e^j^\omega)|');title('Y3的频率特性');grid;% 画出Y3的频率特性subplot(212),plot(w/pi,abs(G1));xlabel('\omega/\pi');ylabel('|G1(e^j^\omega)|');title('G1的频率特性');grid;% 画出G1 的频率特性%*************************************************************************% % 频域微分k = 0:N-1;y4 = k.*g;[Y4,w] = freqz(y4,1);%在频域进行微分y0 = ((-1).^k).*g;G2 = [G(2:512)' sum(y0)]';delG = (G2-G)*512/pi;figure(4);subplot(211),plot(w/pi,abs(Y4));xlabel('\omega/\pi');ylabel('|Y4(e^j^\omega)|');title('Y4的频率特性');grid;% 画出Y4的频率特性subplot(212),plot(w/pi,abs(delG));xlabel('\omega/\pi');ylabel('|delG(e^j^\omega)|');title('delG的频率特性');grid;% 画出delG的频率特性%*************************************************************************% % 相乘性质y5 = conv(g,h);%时域卷积[Y5,w] = freqz(y5,1);figure(5);subplot(211),plot(w/pi,abs(Y5));xlabel('\omega/\pi');ylabel('|Y5(e^j^\omega)|');title('Y5的频率特性');grid;% 画出Y5的频率特性subplot(212),plot(w/pi,abs(G.*H));%频域乘积xlabel('\omega/\pi');ylabel('|G.*H(e^j^\omega)|');title('G.*H的频率特性');grid;% 画出G.*H的频率特性%*************************************************************************% % 帕斯瓦尔定理y6 = g.*h;%对于freqz函数,在0到2pi直接取样[Y6,w] = freqz(y6,1,512,'whole');[G0,w] = freqz(g,1,512,'whole');[H0,w] = freqz(h,1,512,'whole');% Evaluate the sample value at w = pi/2% and verify with Y6 at pi/2H1 = [fliplr(H0(1:129)') fliplr(H0(130:512)')]';val = 1/(512)*sum(G0.*H1);% Compare val with Y6(129) i.e sample at pi/2 % Can extend this to other points similarly% Parsevals theoremval1 = sum(g.*conj(h));val2 = sum(G0.*conj(H0))/512;% Comapre val1 with val23.结果(a)(b)(c)(d)(e)4.结果分析M 3.81.题目Using matlab compute the N-point DFTs of the length-N sequences of Problem 3.12 for N=3, 5, 7, and 10. Compare your results with that obtained by evaluating the DTFTs computed in Problem 3.12 at ω= 2pik/N, k=0, 1,……N-1.2.程序%用户定义N的长度N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);w = 0:2*pi/255:2*pi;Y1 = freqz(y1, 1, w);%对y1做傅里叶变换Y1dft = fft(y1);k = 0:1:2*N;plot(w/pi,abs(Y1),k*2/(2*N+1),abs(Y1dft),'o');grid;xlabel('归一化频率');ylabel('幅度');(a)clf;N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);w = 0:2*pi/255:2*pi;Y1 = freqz(y1, 1, w);Y1dft = fft(y1);k = 0:1:2*N;plot(w/pi,abs(Y1),k*2/(2*N+1),abs(Y1dft),'o');xlabel('Normalized frequency');ylabel('Amplitude');(b)%用户定义N的长度N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);y2 = y1 - abs(k)/N;w = 0:2*pi/255:2*pi;Y2 = freqz(y2, 1, w);%对y1做傅里叶变换Y2dft = fft(y2);k = 0:1:2*N;plot(w/pi,abs(Y2),k*2/(2*N+1),abs(Y2dft),'o');grid;xlabel('归一化频率');ylabel('幅度');(c)%用户定义N的长度N = input('The value of N = ');k = -N:N;y3 =cos(pi*k/(2*N));w = 0:2*pi/255:2*pi;Y3 = freqz(y3, 1, w);%对y1做傅里叶变换Y3dft = fft(y3);k = 0:1:2*N;plot(w/pi,abs(Y3),k*2/(2*N+1),abs(Y3dft),'o');grid;xlabel('归一化频率');ylabel('幅度');3.结果(a)N=3N=5 N=7N=10 (b)N=3N=5 N=7N=10 (c)N=3N=5 N=7N=104.结果分析M 3.191.题目Using Program 3_10 determine the z-transform as a ratio of two polynomials in z-1 from each of the partial-fraction expansions listed below:(a)X1(z)=−2+104+z−1−82+z−1,|z|>0.5,(b)X2(z)=3.5−21−0.5z−1−3+z−11−0.25z−2,|z|>0.5,(c)X3(z)=5(3+2z−1)2−43+2z−1+31+0.81z−2,|z|>0.9,(d)X4(z)=4+105+2z−1+z−16+5z−1+z−2,|z|>0.5.2.程序% Program 3_10% Partical-Fraction Expansion to rational z-Transform %r = input('Type in the residues = ');p = input('Type in the poles = ');k = input('Type in the constants = ');[num, den] = residuez(r,p,k);disp('Numberator polynominal coefficients');disp(num) disp('Denominator polynomial coefficients'); disp(den)4.结果分析M 4.61.题目Plot the magnitude and phase responses of the causal IIR digital transfer functionH(z)=0.0534(1+z−1)(1−1.0166z−1+z−2) (1−0.683z−1)(1−1.4461z−1+0.7957z−2).What type of filter does this transfer function represent? Determine the difference equation representation of the above transfer function.2.程序b=[0.0534 -0.00088644 -0.00088644 0.0534];a=[1 -2.1291 1.7833863 -0.5434631];figure(1)freqz(b,a);figure(2)[H,w]=freqz(b,a);plot(w/pi,abs(H)),grid;xlabel('Normalized Frequency (\times\pi rad/sample)'),ylabel('Magnitude');幅度化成真值之后:4.结果分析H(z)=0.0534−0.00088644z−1−0.00088644z−2+0.0534z−31−2.1291z−1+1.7833863z−2−0.5434631z−3M 4.71.题目Plot the magnitude and phase responses of the causal IIR digital transfer functionH(z)=(1−z−1)4(1−1.499z−1+0.8482z−2)(1−1.5548z−1+0.6493z−2).2.程序b=[1 -4 6 -4 1];a=[1 -3.0538 3.8227 -2.2837 0.5472]; figure(1)freqz(b,a);figure(2)[H,w]=freqz(b,a);plot(w/pi,abs(H)),grid;xlabel('Normalized Frequency (\times\pi rad/sample)'), ylabel('Magnitude');3.结果4.结果分析。
西安电子科技大学数字信号处理大作业

数字信号处理大作业班级:021231学号:姓名:指导老师:吕雁一写出奈奎斯特采样率和和信号稀疏采样的学习报告和体会1、采样定理在进行A/D信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍;采样定理又称奈奎斯特定理。
(1)在时域频带为F的连续信号 f(t)可用一系列离散的采样值f(t1),f(t1±Δt),f(t1±2Δt),...来表示,只要这些采样点的时间间隔Δt≤1/2F,便可根据各采样值完全恢复原始信号。
(2)在频域当时间信号函数f(t)的最高频率分量为fmax时,f(t)的值可由一系列采样间隔小于或等于1/2fo的采样值来确定,即采样点的重复频率fs ≥2fmax。
2、奈奎斯特采样频率(1)概述奈奎斯特采样定理:要使连续信号采样后能够不失真还原,采样频率必须大于信号最高频率的两倍(即奈奎斯特频率)。
奈奎斯特频率(Nyquist frequency)是离散信号系统采样频率的一半,因哈里·奈奎斯特(Harry Nyquist)或奈奎斯特-香农采样定理得名。
采样定理指出,只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽,就可以真实的还原被测信号。
反之,会因为频谱混叠而不能真实还原被测信号。
采样定理指出,只要离散系统的奈奎斯特频率高于采样信号的最高频率或带宽,就可以避免混叠现象。
从理论上说,即使奈奎斯特频率恰好大于信号带宽,也足以通过信号的采样重建原信号。
但是,重建信号的过程需要以一个低通滤波器或者带通滤波器将在奈奎斯特频率之上的高频分量全部滤除,同时还要保证原信号中频率在奈奎斯特频率以下的分量不发生畸变,而这是不可能实现的。
在实际应用中,为了保证抗混叠滤波器的性能,接近奈奎斯特频率的分量在采样和信号重建的过程中可能会发生畸变。
《数字信号处理》第三版课后答案

数字信号处理(西电科大第三版)课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数; (2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
21秋西南大学[1077]《数字信号处理》作业辅导资料
![21秋西南大学[1077]《数字信号处理》作业辅导资料](https://img.taocdn.com/s3/m/162bf4991eb91a37f0115c5a.png)
1、按时间抽选基-2FFT算法蝶形单元中,后一半的公式为。
A.√B.×2、对FS在时域抽样,可得到DFS。
A.√B.×3、Matlab下调用Butter()函数,可设计模拟与数字的巴特沃思滤波器。
A.√B.×4、已知序列x(n)={1 2 1 1}与h(n)={1 0},则两序列3点的圆周卷积为{2 2 1}。
A.√B.×5、已知因果系统的差分方程为,则其冲激响应为。
A.√B.×6、对单位阶跃序列进行一阶后向差分,可得到单位冲激序列。
A.√B.×7、FFT的算法是库利(cooley)和图基(Tukey)在1965年首先提出的。
A.√B.×8、对信号进行采样,其奈奎斯特采样间隔为0.05秒。
A.√B.×9、汉宁窗,其阻带衰减大约可达到40dB。
A.√B.×10、全通系统可作为相位均衡器。
A.√B.×11、已知,且,则k=0.5。
A.√B.×12、若,则系统是因果稳定的。
A.√B.×13、基-2FFT的算法,可以按时间抽选,也可按频率抽选,二者的流图可看作相互转置。
A.√B.×14、IIR滤波器的设计,通常可先进行模拟原型滤波器的设计,再数值化为数字滤波器,称之为间接法。
A.√B.×15、窗函数设计法中,一般总是通过增加主瓣宽度来换取对旁瓣的抑制。
从而方差与分辨力存在矛盾。
A.√B.×16、按频率抽样法设计FIR滤波器,误差大小取决于理想频率响应曲线形状。
A.√B.×17、共轭对称的序列,满足x(n) = x*(-n)。
A.√B.×18、任一从s到z的映射,都应该满足s平面的虚轴到z平面的单位圆、s左半平面到z平面单位圆内部。
A.√B.×19、周期信号经采样后,所得序列也为周期序列。
A.√B.×20、利用留数法求解z反变换,围线c必然位于X(z)的解析域内。
西电DSP大作业任务报告

DSP实验课程序设计报告学院:电子工程学院学号:1202121013姓名:赵海霞指导教师:苏涛DSP实验课大作业设计一实验目的在DSP上实现线性调频信号的脉冲压缩、动目标显示(MTI)和动目标检测(MTD),并将结果与MATLAB上的结果进行误差仿真。
二实验内容2.1 MATLAB仿真设定带宽、脉宽、采样率、脉冲重复频率,用MATLAB产生16个脉冲的LFM,每个脉冲有4个目标(静止,低速,高速),依次做2.1.1 脉压2.1.2 相邻2脉冲做MTI,产生15个脉冲2.1.3 16个脉冲到齐后,做MTD,输出16个多普勒通道2.2 DSP实现将MATLAB产生的信号,在visual dsp中做脉压,MTI、MTD,并将结果与MATLAB作比较。
三实验原理3.1 线性调频线性调频脉冲压缩体制的发射信号其载频在脉冲宽度内按线性规律变化即用对载频进行调制(线性调频)的方法展宽发射信号的频谱,在大时宽的前提下扩展了信号的带宽。
若线性调频信号中心频率为f,脉宽为τ,带宽为B,幅度为A,μ为调频斜率,则其表达式如下:]212cos[)()(20t t f t rect A t x μπτ+••=;)(为矩形函数rect 在相参雷达中,线性调频信号可以用复数形式表示,即)]212(exp[)()(20t t f j t rect A t x μπτ+••= 在脉冲宽度内,信号的角频率由220μτπ-f 变化到220μτπ+f 。
3.2 脉冲压缩原理脉冲雷达信号发射时,脉冲宽度τ决定着雷达的发射能量,发射能量越大, 作用距离越远;在传统的脉冲雷达信号中,脉冲宽度同时还决定着信号的频率宽度B ,即带宽与时宽是一种近似倒数的关系。
脉冲越宽,频域带宽越窄,距离分辨率越低。
脉冲压缩的主要目的是为了解决信号的作用距离和信号的距离分辨率之间的矛盾。
为了提高信号的作用距离,我们就需要提高信号的发射功率,因此,必须提高发射信号的脉冲宽度,而为了提高信号的距离分辨率,又要求降低信号的脉冲宽度。
西电数字信号处理大作业
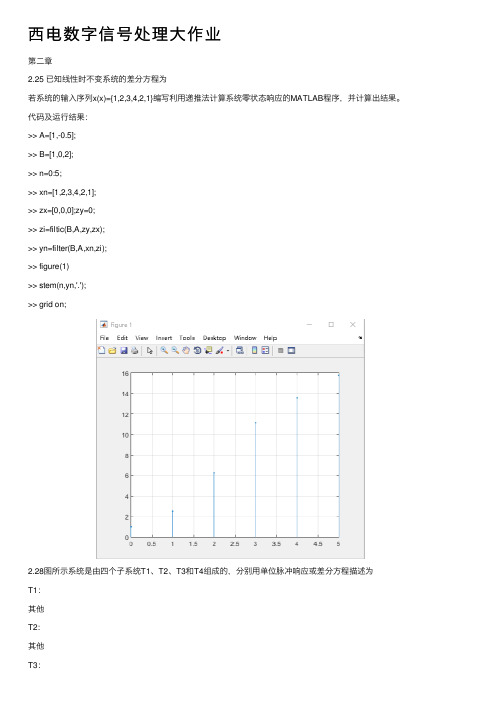
西电数字信号处理⼤作业第⼆章2.25 已知线性时不变系统的差分⽅程为若系统的输⼊序列x(x)={1,2,3,4,2,1}编写利⽤递推法计算系统零状态响应的MATLAB程序,并计算出结果。
代码及运⾏结果:>> A=[1,-0.5];>> B=[1,0,2];>> n=0:5;>> xn=[1,2,3,4,2,1];>> zx=[0,0,0];zy=0;>> zi=filtic(B,A,zy,zx);>> yn=filter(B,A,xn,zi);>> figure(1)>> stem(n,yn,'.');>> grid on;2.28图所⽰系统是由四个⼦系统T1、T2、T3和T4组成的,分别⽤单位脉冲响应或差分⽅程描述为T1:其他T2:其他T3:T4:编写计算整个系统的单位脉冲响应h(n),0≤n≤99的MATLAB程序,并计算结果。
代码及结果如下:>> a=0.25;b=0.5;c=0.25;>> ys=0;>> xn=[1,zeros(1,99)];>> B=[a,b,c];>> A=1;>> xi=filtic(B,A,ys);>> yn1=filter(B,A,xn,xi);>> h1=[1,1/2,1/4,1/8,1/16,1/32]; >> h2=[1,1,1,1,1,1];>> h3=conv(h1,h2);>> h31=[h3,zeros(1,89)]; >> yn2=yn1+h31;>> D=[1,1];C=[1,-0.9,0.81]; >> xi2=filtic(D,C,yn2,xi); >> xi2=filtic(D,C,ys);>> yn=filter(D,C,yn2,xi); >> n=0:99;>> figure(1)>> stem(n,yn,'.');>> title('单位脉冲响应'); >> xlabel('n');ylabel('yn');2.30 利⽤MATLAB画出受⾼斯噪声⼲扰的正弦信号的波形,表⽰为其中v(n)是均值为零、⽅差为1的⾼斯噪声。
数字信号处理西电

数字信号处理上机第一次实验实验一:设给定模拟信号()1000t a x t e -=,的单位是ms 。
(1) 利用MATLAB 绘制出其时域波形和频谱图(傅里叶变换),估计其等效带宽(忽略谱分量降低到峰值的3%以下的频谱)。
(2) 用两个不同的采样频率对给定的进行采样。
○1。
○2 。
比较两种采样率下的信号频谱,并解释。
实验一MATLAB 程序:(1)○1 clc; fs=5000;ts=1/fs;N=1000;t=(-N:N)*ts;s=exp(-abs(t));plot(t,s,'linewidth',1.5)xlabel('时间')ylabel('幅度')set(gca,'fontweight','b','fontsize',12)SPL=N*100;figuresp=fftshift(fft(s,SPL));sp=sp/max(sp)*100;freqb=-fs/2:fs/SPL:fs/2-fs/SPL;plot(freqb,abs(sp))xlabel('频率')ylabel('频谱幅度')set(gca,'fontweight','b','fontsize',12)yy=abs(abs(sp)-3);[aa,freqind]=min(yy);(freqind-SPL/2)*fs/SPLt ()a x t ()()15000s a f x t x n =以样本秒采样得到。
()()11j x n X e ω画出及其频谱()()11000s a f x t x n =以样本得到。
()()11j x n X e ω画出及其频谱○2 clc;fs=1000;ts=1/fs;N=1000;t=(-N:N)*ts;s=exp(-abs(t));plot(t,s,'linewidth',1.5)xlabel('时间')ylabel('幅度')set(gca,'fontweight','b','fontsize',12) SPL=N*100;figuresp=fftshift(fft(s,SPL));sp=sp/max(sp)*100;freqb=-fs/2:fs/SPL:fs/2-fs/SPL;plot(freqb,abs(sp))xlabel('频率')ylabel('频谱幅度')set(gca,'fontweight','b','fontsize',12)yy=abs(abs(sp)-3);[aa,freqind]=min(yy);(freqind-SPL/2)*fs/SPL实验三:设,,编写MATLAB 程序,计算:(1) 5点圆周卷积;(2) 6点圆周卷积;(3) 线性卷积;(4) 画出的,和时间轴对齐。
数字信号处理实验报告(西电)

数字信号处理实验报告班级:****姓名:郭**学号:*****联系方式:*****西安电子科技大学电子工程学院绪论数字信号处理起源于十八世纪的数学,随着信息科学和计算机技术的迅速发展,数字信号处理的理论与应用得到迅速发展,形成一门极其重要的学科。
当今数字信号处理的理论和方法已经得到长足的发展,成为数字化时代的重要支撑,其在各个学科和技术领域中的应用具有悠久的历史,已经渗透到我们生活和工作的各个方面。
数字信号处理相对于模拟信号处理具有许多优点,比如灵活性好,数字信号处理系统的性能取决于系统参数,这些参数很容易修改,并且数字系统可以分时复用,用一套数字系统可以分是处理多路信号;高精度和高稳定性,数字系统的运算字符有足够高的精度,同时数字系统不会随使用环境的变化而变化,尤其使用了超大规模集成的DSP 芯片,简化了设备,更提高了系统稳定性和可靠性;便于开发和升级,由于软件可以方便传送,复制和升级,系统的性能可以得到不断地改善;功能强,数字信号处理不仅能够完成一维信号的处理,还可以试下安多维信号的处理;便于大规模集成,数字部件具有高度的规范性,对电路参数要求不严格,容易大规模集成和生产。
数字信号处理用途广泛,对其进行一系列学习与研究也是非常必要的。
本次通过对几个典型的数字信号实例分析来进一步学习和验证数字信号理论基础。
实验一主要是产生常见的信号序列和对数字信号进行简单处理,如三点滑动平均算法、调幅广播(AM )调制高频正弦信号和线性卷积。
实验二则是通过编程算法来了解DFT 的运算原理以及了解快速傅里叶变换FFT 的方法。
实验三是应用IRR 和FIR 滤波器对实际音频信号进行处理。
实验一●实验目的加深对序列基本知识的掌握理解●实验原理与方法1.几种常见的典型序列:0()1,00,0(){()()(),()sin()j n n n n u n x n Aex n a u n a x n A n σωωϕ+≥<====+单位阶跃序列:复指数序列:实指数序列:为实数 正弦序列:2.序列运算的应用:数字信号处理中经常需要将被加性噪声污染的信号中移除噪声,假定信号 s(n)被噪声d(n)所污染,得到了一个含噪声的信号()()()x n s n d n =+。
(1077)数字信号处理大作业1

h=fft(x,1024);%做1024点的快速傅里叶变换,满足频域抽样定理
ff=1000*(0:511)/1024;%将数字频率转换为模拟频率,单位为Hz
plot(ff,abs(h(1:512)));%显示信号的幅度谱,由于对称性,只显示一半
答:
\
西南大学网络与继续教育学院课程考试答题卷
2016年6月
课程名称【编号】:数字信号处理【1077】类别:网教专升本
专业:电气工程及其自动化
(横线以下为答题区)
答题不需复制题目,写明题目编号,按题目顺序答题
一、简答题。
1.答:
二、计算题。
1.答:
三、编程题。
1.答:t= -1:0.01:1;%以0.01秒周期进行抽样,并加矩形窗截断,满足抽样定理
《数字信号处理》第三版课后实验答案_西安电子科技大学出版社
程序清单及波形显示: clc;close all;clear all;%======内容1:调用filter 解差分方程,由系统对u(n)的响应判断稳定性======A=[1,-0.9];B=[0.05,0.05]; %系统差分方程系数向量B 和A x1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号x1(n)=R8(n) x2n=ones(1,128); %产生信号x2(n)=u(n)y1n=filter(B,A,x1n); %求系统对x1(n)的响应y1(n) n=0:length(y1n)-1;subplot(2,2,1);stem(n,y1n,'.'); title('(a) 系统对R8(n)的响应y1(n)');xlabel('n');ylabel('y1(n)');y2n=filter(B,A,x2n); %求系统对x2(n)的响应y2(n) n=0:length(y2n)-1;subplot(2,2,2);stem(n,y2n,'.'); title('(b) 系统对u(n)的响应y2(n)');xlabel('n');ylabel('y2(n)');hn=impz(B,A,58); %求系统单位脉冲响应h(n) n=0:length(hn)-1;subplot(2,2,3);y=hn;stem(n,hn,'.'); title('(c) 系统单位脉冲响应h(n)');xlabel('n');ylabel('h(n)');(a) 系统对R8(n)的响应y1(n)ny 1(n )(b) 系统对u(n)的响应y2(n)ny 2(n )(c) 系统单位脉冲响应h(n)nh (n )%===内容2:调用conv 函数计算卷积============================x1n=[1 1 1 1 1 1 1 1 ]; %产生信号x1(n)=R8(n) h1n=ones(1,10); h2n=[1 2.5 2.5 1 ];y21n=conv(h1n,x1n); y22n=conv(h2n,x1n); figure(2)n=0:length(h1n)-1;subplot(2,2,1);stem(n,h1n); title('(d) 系统单位脉冲响应h1n');xlabel('n');ylabel('h1(n)'); n=0:length(y21n)-1;subplot(2,2,2);stem(n,y21n); title('(e) h1(n)与R8(n)的卷积y21n');xlabel('n');ylabel('y21(n)'); n=0:length(h2n)-1;subplot(2,2,3);stem(n,h2n); title('(f) 系统单位脉冲响应h2n');xlabel('n');ylabel('h2(n)'); n=0:length(y22n)-1;subplot(2,2,4);stem(n,y22n); title('(g) h2(n)与R8(n)的卷积y22n');xlabel('n');ylabel('y22(n)');nh 1(n )ny 21(n )(f) 系统单位脉冲响应h2nnh 2(n)(g) h2(n)与R8(n)的卷积y22nny 22(n )%=========内容3:谐振器分析======================== un=ones(1,256); %产生信号u(n) n=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49]; %系统差分方程系数向量B 和Ay31n=filter(B,A,un); %谐振器对u(n)的响应y31(n) y32n=filter(B,A,xsin); %谐振器对u(n)的响应y31(n) figure(3)n=0:length(y31n)-1;subplot(2,1,1);stem(n,y31n,'.'); title('(h) 谐振器对u(n)的响应y31n');xlabel('n');ylabel('y31(n)'); n=0:length(y32n)-1;subplot(2,1,2);stem(n,y32n,'.'); title('(i) 谐振器对正弦信号的响应y32n');xlabel('n');ylabel('y32(n)');050100150200250300(h) 谐振器对u(n)的响应y31nny 31(n )(i) 谐振器对正弦信号的响应y32nny 32(n )程序清单及波形显示:% DTMF 双频拨号信号产生6位电话号码 %clear all;clc;tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; % DTMF 信号代表的16个数N=205;K=[18,20,22,24,31,34,38,42];f1=[697,770,852,941]; % 行频率向量 f2=[1209,1336,1477,1633]; % 列频率向量 TN=input('键入6位电话号码= '); % 输入6位数字TNr=0; %接收端电话号码初值为零for l=1:6;d=fix(TN/10^(6-l)) TN=TN-d*10^(6-l); for p=1:4; for q=1:4;if tm(p,q)==abs(d); break,end % 检测码相符的列号q endif tm(p,q)==abs(d); break,end % 检测码相符的行号p endn=0:1023; % 为了发声,加长序列x = sin(2*pi*n*f1(p)/8000) + sin(2*pi*n*f2(q)/8000);% 构成双频信号sound(x,8000); % 发出声音 pause(0.1)% 接收检测端的程序X=goertzel(x(1:205),K+1); % 用Goertzel 算法计算八点DFT样本val = abs(X); % 列出八点DFT向量subplot(3,2,l);stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|') % 画出DFT(k)幅度axis([10 50 0 120])limit = 80; %for s=5:8;if val(s) > limit, break, end % 查找列号endfor r=1:4;if val(r) > limit, break, end % 查找行号endTNr=TNr+tm(r,s-4)*10^(6-l);enddisp('接收端检测到的号码为:') % 显示接收到的字符disp(TNr)显示结果:键入6位电话号码= 123456d = 1d = 2d = 3d = 4d = 5d = 6接收端检测到的号码为:123456050100|X (k )||X (k )|050100k|X (k )|050100k|X (k )|050100k|X (k )|050100k|X (k )|% DTMF 双频拨号信号产生8位电话号码 %clear all;clc;tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; % DTMF 信号代表的16个数 N=205;K=[18,20,22,24,31,34,38,42];f1=[697,770,852,941]; % 行频率向量 f2=[1209,1336,1477,1633]; % 列频率向量 TN=input('键入8位电话号码= '); % 输入8位数字TNr=0; %接收端电话号码初值为零for l=1:8;d=fix(TN/10^(8-l)) TN=TN-d*10^(8-l); for p=1:4; for q=1:4;if tm(p,q)==abs(d); break,end % 检测码相符的列号q endif tm(p,q)==abs(d); break,end % 检测码相符的行号p endn=0:1023; % 为了发声,加长序列 x = sin(2*pi*n*f1(p)/8000) + sin(2*pi*n*f2(q)/8000);% 构成双频信号 sound(x,8000); % 发出声音 pause(0.1)% 接收检测端的程序X=goertzel(x(1:205),K+1); % 用Goertzel 算法计算八点DFT 样本val = abs(X); % 列出八点DFT 向量 subplot(4,2,l);stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|') % 画出DFT(k)幅度axis([10 50 0 120])limit = 80; % for s=5:8;if val(s) > limit, break, end % 查找列号 endfor r=1:4;if val(r) > limit, break, end % 查找行号 endTNr=TNr+tm(r,s-4)*10^(8-l); enddisp('接收端检测到的号码为:') % 显示接收到的字符 disp(TNr) 显示结果:键入8位电话号码= 12345678 d = 1 d = 2 d = 3 d = 4 d = 5 d = 6 d = 7 d = 8接收端检测到的号码为:12345678|X (k )||X (k )||X (k )||X (k )||X (k )||X (k )|k|X (k )|k|X (k )|程序清单及波形显示: % 时域采样理论验证程序Tp=64/1000; %观察时间Tp=64微秒Fs=1000;T=1/Fs; M=Tp*Fs;n=0:M-1;t=n*T;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xat=A*exp(-alph*t).*sin(omega*t);Xk=T*fft(xat,M); %M点FFT[xat)]subplot(3,2,1); stem(n,xat,'.'); xlabel('n');ylabel('x1(n)'); title('(a) Fs=1000Hz');k=0:M-1;fk=k/Tp;subplot(3,2,2);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz');xlabel('\omega/hz');ylabel('(H1(ejw))');axis([0,Fs,0,1.2*max(abs(Xk))]);Fs=300;T=1/Fs; M=Tp*Fs;n=0:M-1;t=n*T;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xat=A*exp(-alph*t).*sin(omega*t);Xk=T*fft(xat,M); %M点FFT[xat)]subplot(3,2,3); stem(n,xat,'.'); xlabel('n');ylabel('x2(n)'); title('(b)Fs=300Hz');k=0:M-1;fk=k/Tp;subplot(3,2,4);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=300Hz');xlabel('\omega/hz');ylabel('(H2(ejw))');axis([0,Fs,0,1.2*max(abs(Xk))]);Fs=200;T=1/Fs; M=Tp*Fs;n=0:M-1;t=n*T;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xat=A*exp(-alph*t).*sin(omega*t);Xk=T*fft(xat,M); %M点FFT[xat)]subplot(3,2,5); stem(n,xat,'.'); xlabel('n');ylabel('x3(n)'); title('(c) Fs=200Hz');k=0:M-1;fk=k/Tp;subplot(3,2,6);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=200Hz');xlabel('\omega/hz');ylabel('(H3(ejw))');axis([0,Fs,0,1.2*max(abs(Xk))])nx 1(n )(a) Fs=1000Hz(a) T*FT[xa(nT)],Fs=1000Hzω/hz(H 1(e j w ))nx 2(n )(b) Fs=300Hz(a) T*FT[xa(nT)],Fs=300Hzω/hz(H 2(e j w ))nx 3(n )(c) Fs=200Hz(a) T*FT[xa(nT)],Fs=200Hzω/hz(H 3(e j w ))%频域采样理论验证程序 clc;clear;close all; M=27;N=32;n=0:M; xa=0:(M/2); xb= ceil(M/2)-1:-1:0; xn=[xa,xb]; %产生M 长三角波序列x(n) Xk=fft(xn,1024); %1024点FFT[x(n)], 用于近似序列x(n)的TF X32k=fft(xn,32) ;%32点FFT[x(n)] x32n=ifft(X32k); %32点IFFT[X32(k)]得到x32(n) X16k=X32k(1:2:N); %隔点抽取X32k 得到X16(K) x16n=ifft(X16k,N/2); %16点IFFT[X16(k)]得到x16(n) subplot(3,2,2);stem(n,xn,'.'); title('(b) 三角波序列x(n)');xlabel('n');ylabel('x(n)');axis([0,32,0,20]) k=0:1023;wk=2*k/1024; subplot(3,2,1);plot(wk,abs(Xk));title('(a)FT[x(n)]'); xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');axis([0,1,0,200]) k=0:N/2-1; subplot(3,2,3);stem(k,abs(X16k),'.'); title('(c) 16点频域采样');xlabel('k');ylabel('|X_1_6(k)|');axis([0,8,0,200]) n1=0:N/2-1; subplot(3,2,4);stem(n1,x16n,'.'); title('(d) 16点IDFT[X_1_6(k)]');xlabel('n');ylabel('x_1_6(n)');axis([0,32,0,20]); k=0:N-1; subplot(3,2,5);stem(k,abs(X32k),'.'); title('(e) 32点频域采样');xlabel('k');ylabel('|X_3_2(k)|');axis([0,16,0,200]);n1=0:N-1; subplot(3,2,6);stem(n1,x32n,'.');box on title('(f) 32点IDFT[X_3_2(k)]');xlabel('n');ylabel('x_3_2(n)');axis([0,32,0,20])(b) 三角波序列x(n)nx (n )0100200(a)FT[x(n)]ω/π|X (e j ω)|(c) 16点频域采样k|X 16(k)|102030(d) 16点IDFT[X 16(k)]nx 16(n)(e) 32点频域采样k|X 32(k )|(f) 32点IDFT[X 32(k)]nx 32(n )程序清单及波形显示:% 用FFT 对信号作频谱分析 clear all;close all %实验内容(1)=================================================== x1n=[ones(1,4)]; %产生序列向量x1(n)=R4(n) M=8;xa=1:(M/2); xb=(M/2):-1:1; x2n=[xa,xb]; %产生长度为8的三角波序列x2(n) x3n=[xb,xa]; X1k8=fft(x1n,8); %计算x1n 的8点DFT X1k16=fft(x1n,16); %计算x1n 的16点DFT X2k8=fft(x2n,8); %计算x1n 的8点DFT X2k16=fft(x2n,16); %计算x1n 的16点DFT X3k8=fft(x3n,8); %计算x1n 的8点DFT X3k16=fft(x3n,16); %计算x1n 的16点DFT %以下绘制幅频特性曲线 subplot(1,2,1);stem(X1k8,'.'); %绘制8点DFT 的幅频特性图 title('(1a) 8点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度'); subplot(1,2,2);stem(X1k16,'.'); %绘制16点DFT 的幅频特性图 title('(1b)16点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');figure(2)subplot(2,2,1);stem(X2k8,'.'); %绘制8点DFT 的幅频特性图 title('(2a) 8点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');subplot(2,2,2);stem(X2k16,'.'); %绘制16点DFT 的幅频特性图 title('(2b)16点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,3);stem(X3k8,'.'); %绘制8点DFT 的幅频特性图 title('(3a) 8点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');subplot(2,2,4);stem(X3k16,'.'); %绘制16点DFT 的幅频特性图 title('(3b)16点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');-2.5-2-1.5-1-0.500.511.522.5(1a) 8点DFT[x 1(n)]ω/π幅度-2.5-2-1.5-1-0.500.511.522.5(1b)16点DFT[x 1(n)]ω/π幅度2468-4-2024(2a) 8点DFT[x 2(n)]ω/π幅度5101520-20-1001020(2b)16点DFT[x 2(n)]ω/π幅度2468-4-2024(3a) 8点DFT[x 3(n)]ω/π幅度-10-50510(3b)16点DFT[x 3(n)]ω/π幅度%实验内容(2) 周期序列谱分析==================================N=8;n=0:N-1; %FFT 的变换区间N=8 x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n); %计算x4n 的8点DFT X5k8=fft(x5n); %计算x5n 的8点DFT N=16;n=0:N-1; %FFT 的变换区间N=16 x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k16=fft(x4n); %计算x4n 的16点DFT X5k16=fft(x5n); %计算x5n 的16点DFT figure(3)subplot(2,2,1);stem(X4k8,'.'); %绘制8点DFT 的幅频特性图 title('(4a) 8点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');subplot(2,2,3);stem(X4k16,'.'); %绘制16点DFT 的幅频特性图 title('(4b)16点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');subplot(2,2,2);stem(X5k8,'.'); %绘制8点DFT 的幅频特性图 title('(5a) 8点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');subplot(2,2,4);stem(X5k16,'.'); %绘制16点DFT 的幅频特性图title('(5b)16点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');2468-1012x 10-15(4a) 8点DFT[x 4(n)]ω/π幅度5101520-4-2024x 10-15(4b)16点DFT[x 4(n)]ω/π幅度2468-4-2024(5a) 8点DFT[x 5(n)]ω/π幅度5101520-4-2024x 10-15(5b)16点DFT[x 5(n)]ω/π幅度%实验内容(3) 模拟周期信号谱分析=============================== figure(4) Fs=64;T=1/Fs; N=16;n=0:N-1; %FFT 的变换区间N=16 x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t)16点采样 X6k16=fft(x6nT); %计算x6nT 的16点DFT X6k16=fftshift(X6k16); %将零频率移到频谱中心 Tp=N*T;F=1/Tp; %频率分辨率F k=-N/2:N/2-1;fk=k*F; %产生16点DFT 对应的采样点频率(以零频率为中心) subplot(3,1,1);stem(fk,abs(X6k16),'.');box on %绘制8点DFT 的幅频特性图 title('(6a) 16点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度'); axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k16))])N=32;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t)32点采样X6k32=fft(x6nT); %计算x6nT的32点DFTX6k32=fftshift(X6k32); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F; %产生16点DFT对应的采样点频率(以零频率为中心)subplot(3,1,2);stem(fk,abs(X6k32),'.');box on %绘制8点DFT的幅频特性图title('(6b) 32点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k32))])N=64;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t)64点采样X6k64=fft(x6nT); %计算x6nT的64点DFTX6k64=fftshift(X6k64); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F; %产生16点DFT对应的采样点频率(以零频率为中心)subplot(3,1,3);stem(fk,abs(X6k64),'.'); box on%绘制8点DFT的幅频特性图title('(6a) 64点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k64))])-30-20-1001020300510(6a) 16点|DFT[x 6(nT)]|f(Hz)幅度010(6b) 32点|DFT[x 6(nT)]|f(Hz)幅度020(6a) 64点|DFT[x 6(nT)]|f(Hz)幅度程序清单及波形显示: clc;clear all;close all;fc1=250; fm1=15; fc2=500; fm2=50; fc3=1000; fm3=100;N=800; Fs=10000;Ts=1/Fs; n=[0:N-1];t=n*Ts;x11=cos(2*pi*fc1*t); x12=cos(2*pi*fm1*t); x1=x11.*x12; subplot(3,1,1);plot(t,x11,'g');plot(t,x12,'r');plot(t,x1,'b'); legend('载波','调制波 ','已调 ');xlabel('t/s');ylabel('波形')x=cos(2*pi*fc1*t).*cos(2*pi*fm1*t)+cos(2*pi*fc2*t).*cos(2*pi*fm2*t)+cos(2*pi*fc3*t).*cos(2*pi*fm3*t); subplot(3,1,2);plot(t,x);X=fft(x)subplot(3,1,3)k=[0:(N-1)/2]stem(k*2/N,abs(X(k+1))/max(abs(X(k+1))),'.');axis([0,0.3,0,1]);xlabel('\omeg a/\pi');ylabel('幅度');wp=[0.04,0.06];ws=[0.03,0.07];rp=0.1;rs=60;[N1,wp]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N1,rp,rs,wp);y1=filter(B,A,x);figuresubplot(3,1,1);plot(t,x);xlabel('t/s');title('3路混合信号波形')subplot(3,1,2);[H1,w1]=freqz(B,A,N);plot(w1/pi,20*log10(abs(H1)));axis([0,0.5,-80,1]);xlabel('\omega/\pi');ylabel('|H(e^j\omega)|');title('中心频率为250Hz的频率响应');subplot(3,1,3);plot(t,y1);xlabel('t/s');ylabel('y1(t)');title('中心频率为250H的滤波信号')wp=[0.08,0.12];ws=[0.07,0.13];rp=0.1;rs=60;[N1,wp]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N1,rp,rs,wp);y1=filter(B,A,x);figuresubplot(3,1,1);plot(t,x);xlabel('t/s');title('3路混合信号波形');subplot(3,1,2)[H1,w1]=freqz(B,A,N);plot(w1/pi,20*log10(abs(H1)));axis([0,0.5,-90,2]);xlabel('\omega/\pi');ylabel('|H(e^j\omega)|');title('中心频率为500Hz的频率响应')subplot(3,1,3);plot(t,y1);xlabel('t/s');ylabel('y1(t)');title('中心频率为500H的滤波信号')wp=[0.17,0.23];ws=[0.16,0.24];rp=0.1;rs=60;[N1,wp]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N1,rp,rs,wp);y1=filter(B,A,x);figuresubplot(3,1,1);plot(t,x);xlabel('t/s');title('3路混合信号波形');subplot(3,1,2);[H1,w1]=freqz(B,A,N);plot(w1/pi,20*log10(abs(H1)));axis([0,0.5,-100,10]);xlabel('\omega/\pi');ylabel('|H(e^j\omega)|');title('中心频率为1000Hz的频率响应')subplot(3,1,3);plot(t,y1);xlabel('t/s');ylabel('y1(t)');title('中心频率为1000H的滤波信号')00.010.020.030.040.050.060.070.08-101t/s波形00.010.020.030.040.050.060.070.08-505ω/π幅度-505t/s3路混合信号波形-80-60-40-200ω/π|H (e j ω)|中心频率为250Hz 的频率响应-202t/sy 1(t )中心频率为250H 的滤波信号0.010.020.030.040.050.060.070.08-505t/s3路混合信号波形0.050.10.150.20.250.30.350.40.450.5-80-60-40-200ω/π|H (e j ω)|中心频率为500Hz 的频率响应0.010.020.030.040.050.060.070.08-202t/sy 1(t )中心频率为500H 的滤波信号0.010.020.030.040.050.060.070.08-505t/s3路混合信号波形0.050.10.150.20.250.30.350.40.450.5-100-500ω/π|H (e j ω)|中心频率为1000Hz 的频率响应0.010.020.030.040.050.060.070.08-202t/sy 1(t )中心频率为1000H 的滤波信号程序清单及波形显示: clc;clear;clear allN=1000; Fs=1000;T=1/Fs;Tp=N*T; t=0:T:(N-1)*T;fc=Fs/10;f0=fc/10; %载波频率fc=Fs/10,单频调制信号频率为f0=Fc/10; mt=cos(2*pi*f0*t); %产生单频正弦波调制信号mt ,频率为f0 ct=cos(2*pi*fc*t); %产生载波正弦波信号ct ,频率为fc xt=mt.*ct; %相乘产生单频调制信号xt nt=2*rand(1,N)-1; %产生随机噪声ntfp=150; fs=200;Rp=0.1;As=70; % 滤波器指标fb=[fp,fs];m=[0,1]; % 计算remezord 函数所需参数f,m,devdev=[10^(-As/20),(10^(Rp/20)-1)/(10^(Rp/20)+1)];[n,fo,mo,W]=remezord(fb,m,dev,Fs); % 确定remez 函数所需参数hn=remez(n,fo,mo,W); % 调用remez 函数进行设计,用于滤除噪声nt 中的低频成分yt=filter(hn,1,10*nt); %滤除随机噪声中低频成分,生成高通噪声yt xt=xt+yt; %噪声加信号 fst=fft(xt,N);k=0:N-1;f=k/Tp;subplot(2,1,1);plot(t,xt);grid;xlabel('t/s');ylabel('x(t)');axis([0,Tp/5,min(xt),max(xt)]);title('(a) 信号加噪声波形')subplot(2,1,2);plot(f,abs(fst)/max(abs(fst)));grid;title('(b) 信号加噪声的频谱')axis([0,Fs/2,0,1.2]);xlabel('f/Hz');ylabel('幅度')-10-50510t/sx (t )(a) 信号加噪声波形0501001502002503003504004505000.51(b) 信号加噪声的频谱f/Hz幅度%==调用xtg 产生信号xt, xt 长度N=1000,并显示xt 及其频谱,========= N=1000;xt=xtg(N);fp=120; fs=150;Rp=0.2;As=60;Fs=1000; % 输入给定指标% (1) 用窗函数法设计滤波器wc=(fp+fs)/Fs; %理想低通滤波器截止频率(关于pi归一化)B=2*pi*(fs-fp)/Fs; %过渡带宽度指标Nb=ceil(11*pi/B); %blackman窗的长度Nhn=fir1(Nb-1,wc,blackman(Nb));Hw=abs(fft(hn,1024)); % 求设计的滤波器频率特性ywt=fftfilt(hn,xt,N); %调用函数fftfilt对xt滤波subplot(4,1,1);plot(f,Hw);xlabel('f/Hz');ylabel('幅度'); title('(a)低通滤波器幅频特性');subplot(4,1,2);plot(t,ywt); title('(b)滤除噪声后的信号波形');xlabel('t/s');ylabel('ywt');% (2) 用等波纹最佳逼近法设计滤波器fb=[fp,fs];m=[1,0]; % 确定remezord函数所需参数f,m,dev dev=[(10^(Rp/20)-1)/(10^(Rp/20)+1),10^(-As/20)];[Ne,fo,mo,W]=remezord(fb,m,dev,Fs); % 确定remez函数所需参数hn=remez(Ne,fo,mo,W); % 调用remez函数进行设计Hw=abs(fft(hn,1024)); % 求设计的滤波器频率特性yet=fftfilt(hn,xt,N); % 调用函数fftfilt对xt滤波subplot(3,1,1);plot(f,Hw);xlabel('f/Hz');ylabel('幅度'); title('(c)低通滤波器幅频特性');subplot(3,1,2);plot(t,yet);title('(d)滤除噪声后的信号波形');xlabel('t/s');ylabel('yet');。
数字信号处理-西安电子科技大学出版(_高西全丁美玉)第三版_课后习题答案(全)
18
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
28
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章 时域离散信号和时域离散系统
解法(二) 采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
5. 设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输 出, 判断系统是否是线性非时变的。
(1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) n0 (4)y(n)=x(-n)
15
第 1 章 时域离散信号和时域离散系统
非零区间如下:
0≤m≤3 -4≤m≤n
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
西安电子科技大学(高西全丁美玉第三版)数字信号处理第6章

道, 设计巴特沃斯滤波器时, 对于3 dB截止频率λc进行归
一化最方便。
第5章
无限脉冲响应(IIR)数字滤波器的设 计
图5.1.5中①、 ②、 ③、 ④对应的4组频率变换公式:
p 频率变换公式: p 归一化低通边界频率: 1, s p s p
通过关系式(5.1.2)可由Ha(jΩ)指标确定数字滤波器
H(ejω)的指标(如ωp, ωs, αp, αs等); 利用频率转换关系ω=ΩT 容易求出H(ejω)的各边界频率; 选用适当的设计方法可得到数 字滤波器的系统函数H(z)。 由(5.1.3)式知, 也可以采用脉冲响应不变法将等效
模拟滤波器Ha(s)转换成采样数字系统中数字滤波器的系统函
第5章
无限脉冲响应(IIR)数字滤波器的设 计
第5章 无限脉冲响应(IIR)数字 滤波器的设计
5.1 5.2 5.3 学习要点 例题 教材第6章习题与上机题解答
第5章
无限脉冲响应(IIR)数字滤波器的设 计
5.1 学 习 要 点
5.1.1 IIR数字滤波器设计的基本概念及基本设计方法 1. 滤波器设计指标参数定义及其描述 滤波器设计指标参数定义及其描述在教材中有详细的 介绍, 下面仅给出低通滤波器幅频特性函数和损耗函数描 述的滤波器指标参数的示意图, 如图5.1.1所示, 并给出 二者的换算关系。
为了使初学者对IIR数字滤波器设计方法有一个整体概念, 先抛开繁杂的设计过程和设计公式, 用图5.1.3归纳IIR数字滤 波器的一般设计方法。
第5章
无限脉冲响应(IIR)数字滤波器的设 计
图5.1.3
第5章
无限脉冲响应(IIR)数字滤波器的设 计
下面对图5.1.3中给出的五种设计方法及其学习要点进行简
西电数字信号处理大作业-浅谈奈奎斯特频率采样和压缩感知概要

浅谈奈奎斯特频率采样和压缩感知信息技术的飞速发展使得人们对信息的需求量剧增。
现实世界的模拟化和信号处理工具的数字化决定了信号采样是从模拟信源获取数字信息的必经之路。
在信号和图像处理领域,凡是涉及到计算机作为处理工具的场合,所面临的首要问题就是模拟信号的数字化问题,然后再对得到的离散的样本进行各种处理。
连续信号转化为离散的数字化信号的过程称为采样。
对模拟信号采样所得的离散数字信号能否代表并恢复成原来的连续模拟信号呢?如能恢复应具备什么样的条件呢?这个问题直接关系到是否可以用数字处理工具和数字化的方法处理模拟信号。
一奈奎斯特频率采样奈奎斯特采样定理给我们提供了如何采样的重要理论基础。
它指出,如果信号是带限的,采样速率必须达到信号带宽的两倍以上才能精确重构信号。
事实上,在音频和可视电子设备、医学图像设备、无线接收设备等设备中的所有信号采样协议都隐含了这样的限制。
奈奎斯特采样定理至出现以来一直是数字信号和图像处理领域的重要理论基础,它支撑着几乎所有的信号和图像处理过程,包括信号和图像的获取、存储、处理、传输等。
采样定理,又称香农采样定理,奈奎斯特采样定理,是信息论,特别是通讯与信号处理学科中的一个重要基本结论.E.T.Whittaker (1915年发表的统计理论),克劳德·香农与Harry Nyquist都对它作出了重要贡献。
另外,V. A. Kotelnikov 也对这个定理做了重要贡献。
采样是将一个信号(即时间或空间上的连续函数)转换成一个数值序列(即时间或空间上的离散函数)。
采样定理指出,如果信号是带限的,并且采样频率高于信号带宽的一倍,那么,原来的连续信号可以从采样样本中完全重建出来。
带限信号变换的快慢受到它的最高频率分量的限制,也就是说它的离散时刻采样表现信号细节的能力是有限的。
采样定理是指,如果信号带宽小于奈奎斯特频率(即采样频率的二分之一),那么此时这些离散的采样点能够完全表示原信号。
西电数字信号处理上机实验
实验一1-1、a=[-2 0 1 -1 3];b=[1 2 0 -1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);xlabel('n');ylabel('幅度');title('离散卷积’);1-2、N=41;a=[0.8 -0.44 0.36 0.22]; b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=filter(a,b,x);stem(k,y)xlabel('n');ylabel('幅度'); title('差分方程');1-3、k=256;num=[0.8 -0.44 0.36 0.02];den=[1 0.7 -0.45 -0.6];w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部');xlabel('\omega/\pi');ylabel('幅度'); subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部');xlabel('\omega/\pi');ylabel('Amplitude'); subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱');xlabel('\omega/\pi');ylabel('幅值'); subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱');xlabel('\omega/\pi');ylabel('弧度');实验二2-1、N=16;n=0:1:15;p=8;q=4;a=0.1;f=0.0625;xa=exp(-((n-p).^2)./q);figure(1)stem(n, xa,'.');title('xa(n)序列')xlabel('n')ylabel('xa(n)')grid on[H, w] = freqz(xa, 1, [], 'whole', 1); Hamplitude = abs(H);Hphase = angle(H);Hphase = unwrap(Hphase);figure(2)subplot(2, 1, 1)plot(w, Hamplitude)title('幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|') grid onsubplot(2, 1, 2)plot(w, Hphase)title('相频响应')xlabel('w/(2*pi)')ylabel('fai(H(exp(jw)))') grid on2-2、n=0:1:15;a=0.1;f1=0.0625;f2=0.04375;f3=0.05625;xb1=exp(-a*n).*sin(2*pi*f1*n);figuresubplot(3,2,1)stem(n, xb1,'.');title('f=0.0625的时域特性')xlabel('n')ylabel('xb1(n)')grid on[H, w] = freqz(xb1, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,2)plot(w, Hamplitude)title('f=0.0625的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid onxb2=exp(-a*n).*sin(2*pi*f2*n);subplot(3,2,3)stem(n, xb2,'.');title('f=0.04375的时域特性')xlabel('n')ylabel('xb2(n)')grid on[H, w] = freqz(xb2, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,4)plot(w, Hamplitude)title('f=0.04375的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid onxb3=exp(-a*n).*sin(2*pi*f3*n);subplot(3,2,5)stem(n, xb3,'.');title('f=0.05625的时域特性')xlabel('n')ylabel('xb3(n)')grid on[H, w] = freqz(xb3, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,6)plot(w, Hamplitude)title('f=0.05625的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid on2-3、n1=0:1:3;xc1=n1+1;n2=4:7;xc2=8-n2;xc=[xc1,xc2];n =[n1,n2];figurestem(n,xc);xlabel('n'); ylabel('xc');title('三角序列');n1=0:1:3;xd1=4-n1;n2=4:7;xd2=n2-3;xd=[xd1,xd2];n =[n1,n2];figurestem(n,xd);xlabel('n'); ylabel('xd');title('反三角序列');N = 16;[H1,w1] = freqz(xc,1, 256, 'whole', 1); Hamplitude1 = abs(H1);figureplot(2*w1, Hamplitude1)title('xc幅频响应')xlabel('w/pi')ylabel('|H(exp(jw))|')grid on[H2,w2] = freqz(xd,1, 256, 'whole', 1); Hamplitude2 = abs(H2);figureplot(2*w2, Hamplitude2)title('xd幅频响应')xlabel('w/pi')ylabel('|H(exp(jw))|')grid on[H3, w3] = freqz(xc, 1, N, 'whole', 1); Hamplitude3 = abs(H3);figuresubplot(2, 1, 1)h3 = stem(2*w3, Hamplitude3, '*');title('xc幅频响应进行N点FFT’);xlabel('n')ylabel('|H(exp(jw))|')grid on[H4, w4] = freqz(xd, 1, N, 'whole', 1); Hamplitude4 = abs(H4);subplot(2, 1, 2)h4 = stem(2*w4, Hamplitude4, '*');title('xd幅频响应进行N点FFT');xlabel('n')ylabel('|H(exp(jw))|')grid on2-4、N = 128;f1 = 1/16;n = 0:N-1;xn = sin(2*pi*0.125.*n)+ cos(2*pi*(0.125+f1).*n); figurestem(n,xn);figuresubplot(2,1,1),plot(n,abs(fft(xn)));title('f =1/16 幅频响应');f2 = 1/64;xn = sin(2*pi*0.125.*n)+ cos(2*pi*(0.125+f2).*n); subplot(2,1,2),plot(n,abs(fft(xn)));title('f =1/64 幅频响应');2-5、N=16;n=0:1:15;p=8;q=2;a=0.1;f=0.0625;xa=exp(-((n-p).^2)./q);xb=exp(-a*n).*sin(2*pi*f*n);%线性卷积x=conv(xa,xb);XDft= fft(x, 32);XDftR = abs(XDft);XDftPhase = angle(XDft);XDftPhase = unwrap(XDftPhase);figure(1);stem(x,'.');title('x(n)序列');xlabel('n')ylabel('x(n)')grid onfigure(2)subplot(2, 1, 1)stem(XDftR, '.');title('X(k)的幅度’);xlabel('k')ylabel('|X(k)|')grid onsubplot(2, 1, 2)stem(XDftPhase, '.');title('X(k)的相角')xlabel('k')ylabel('fai((X(k)))')grid on%圆周卷积XDft161 = fft(xa, N);XDft16R1 = abs(XDft161);XDft16Phase1 = angle(XDft161);XDft16Phase1 = unwrap(XDft16Phase1); XDft162 = fft(xb, N);XDft16R2 = abs(XDft162);XDft16Phase2 = angle(XDft162);XDft16Phase2 = unwrap(XDft16Phase2); XDft16=XDft161.*XDft162;XDft16R=XDft16R1.*XDft16R2;XDft16Phase=XDft16Phase2 +XDft16Phase1 ; x = ifft(XDft16, N);figure(3)stem(x,'.')title('x(n)序列')xlabel('n')ylabel('x(n)')grid onfigure(4)subplot(2, 1, 1)t= 0 : 1 : N - 1;stem(t, XDft16R, '.');title('X(k)的幅度')xlabel('k')ylabel('|X(k)|')grid onsubplot(2, 1, 2)stem(t,XDft16Phase, '.');title('X(k)的相角')xlabel('k')ylabel('fai((X(k)))')grid on2-6、xe=rand(1,512);n1=0:1:3;xc1=n1+1;n2=4:7;xc2=8-n2;xc=[xc1,xc2];%重叠相加法yn=zeros(1,519);for j=0:7xj=xe(64*j+1:64*(j+1));xak=fft(xj,71);xck=fft(xc,71);yn1=ifft(xak.*xck);temp=zeros(1,519);temp(64*j+1:64*j+71)=yn1; yn=yn+temp;end;n=0:518;figure(1)subplot(2,1,1);plot(n,yn);xlabel('n');ylabel('y(n)');title('xc(n)与xe(n)的线性卷积的时域波形-重叠相加法'); subplot(2,1,2);plot(n,abs(fft(yn)));xlabel('k');ylabel('Y(k)');axis([0,600,0,300]);title('xc(n)Óëxe(n)的线性卷积的幅频特性-重叠相加法'); %重叠保留法k=1:7;xe1=k-k;xe_1=[xe1,xe];yn_1=zeros(1,519);for j=0:7xj_1=xe_1(64*j+1:64*j+71);xak_1=fft(xj_1);xck_1=fft(xc,71);yn1_1=ifft(xak_1.*xck_1);temp_1=zeros(1,519);temp_1(64*j+1:64*j+64)=yn1_1(8:71);yn_1=yn_1+temp_1;end;n=0:518;figure(2)subplot(2,1,1);plot(n,yn_1);xlabel('n');ylabel('y(n)');title(' xc(n)的线性卷积的时域波形-重叠保留法'); subplot(2,1,2);plot(n,abs(fft(yn_1)));xlabel('k');ylabel('Y(k)');axis([0,600,0,300]);title('xc(n)Óëxe(n)的线性卷积的幅频特性-重叠保留法');实验三3-1、Wp=0.3;Ws=0.2;Rp=0.8;Rs=20;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo,'high');w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('Chebyshev高通滤波器');3-2、Wp=0.2;Ws=0.3;Rp=1;Rs=25;[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bs,As]=butter(N,Wc,'s');[Bz,Az]=impinvar(Bs,As);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(211);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('脉冲响应不变法')[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(212);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('双线性变换法')3-3、Wp=1.2/8;Ws=2/8;Rp=0.5;Rs=40;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(311);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('切比雪夫')[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(312);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('巴特沃斯')[N,Wpo]=ellipord(Wp,Ws,Rp,Rs);[Bz,Az]=ellip(N,Rp,Rs,Wpo);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(313);plot(w/pi,H),grid ontitle('椭圆')xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB')3-4、Wp1=2/15;Wpu=0.2;Ws1=0.1;Wsu=0.4;Rp=3;Rs=20;Wp=[Wp1,Wpu];Ws=[Ws1,Wsu];[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('双线性变换法Butterworth型数字带通滤波器')。
数字信号处理大作业语音信号提取程序加噪声程序

% 数字信号处理大作业语音信号提取程序加噪声程序
% 功能:从文件名为''语音文件中提取出数据,并加入声音最大音量五分之一的噪声% 参数:name-原始信号;Y-加噪声后的信号;
% 大作业内容:请自己录音,编写FIR滤波程序,消减噪声的影响。
% 作者:西安电子科技大学雷达信号处理国家重点实验室李军
% 时间:2015年
close all;clear all;clc;
namex=1e5;
% 读取原始声音文件
[name,fs0,bit]=wavread('',[100,namex]); %读取源文件
sound(name,fs0,bit);
namex=length(name);
noise=(max(name(:,1))/5)*randn(namex,2);
Y=name+noise; % 加入噪声
wavwrite(Y,fs0,bit,'mingyun_'); % 写入噪声文件
sound(Y,fs0,bit);
% 作图分析声音信号的时域特性和频域特性
figure(1)
subplot(2,1,1);
plot(abs(name));
title('(a)原声音信号的时域特性');
subplot(2,1,2);
plot(abs(Y));
title('(b)含有噪声声音信号的时域特性');。
西电-数字信号处理大作业

数字信号处理上机大作业实验一:信号、系统及系统响应(1) 简述实验目的及实验原理。
1.实验目的●熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解。
●熟悉时域离散系统的时域特性。
●利用卷积方法观察分析系统的时域特性。
●掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。
2.实验原理与方法●时域采样。
● LTI系统的输入输出关系。
(2)按实验步骤附上实验过程中的信号序列、系统单位脉冲响应及系统响应序列的时域和幅频特性曲线,并对所得结果进行分析和解释。
Matlab源程序如下:A=1;T1=1/1000;T2=1/300;T3=1/200;a=25*pi;w0=30*pi;n=0:99;x1=A*exp(-a*n*T1).*sin(w0*n*T1);x2=A*exp(-a*n*T2).*sin(w0*n*T2);x3=A*exp(-a*n*T3).*sin(w0*n*T3);m=linspace(-pi,pi,10000);X1=x1*exp(-j*n'*m);%n'与m构造矩阵,xi向量与矩阵每一列相乘对应元素相加,构成DTFT后的矩阵X2=x2*exp(-j*n'*m);X3=x3*exp(-j*n'*m);figure(1);subplot(3,2,1)plot(m/pi,abs(X1));xlabel('\omega/π');ylabel('|H(e^j^\omega)|');title('采样频率为1000Hz时的幅度谱');subplot(3,2,3)plot(m/pi,abs(X2));xlabel('\omega/π');ylabel('|H(e^j^\omega)|');title('采样频率为300Hz时的幅度谱');subplot(3,2,5)plot(m/pi,abs(X3));xlabel('\omega/π');ylabel('|H(e^j^\omega)|');title('采样频率为200Hz时的幅度谱');subplot(3,2,2)plot(n,abs(x1));xlabel('n');ylabel('x1(t)');title('采样频率为1000Hz时的时域波形');subplot(3,2,4)plot(n,abs(x2));xlabel('n');ylabel('x2(t)');title('采样频率为300Hz时的时域波形');subplot(3,2,6)plot(n,abs(x3));xlabel('n');ylabel('x3(t)');title('采样频率为200Hz时的时域波形');波形图如下:-1-0.8-0.6-0.4-0.200.20.40.60.81ω/π|H (e j ω)|采样频率为1000Hz 时的幅度谱ω/π|H (e j ω)|采样频率为300Hz 时的幅度谱ω/π|H (e j ω)|采样频率为200Hz 时的幅度谱102030405060708090100nx 1(t )采样频率为1000Hz 时的时域波形nx 2(t )采样频率为300Hz 时的时域波形nx 3(t )采样频率为200Hz 时的时域波形② 时域离散信号、 系统和系统响应分析。
西安电子科技大学-数字信号处理-试卷C答案

Answer to “Digital Signal Processing of 2005”Problem 1(a) even part: };5.0,1,7,7,5,7,7,1,5.0{---=e X odd part: };5.0,1,3,1,0,1,3,1,5.0{----=o X(b) };20,16,11,94,36,40,31,16,12,0{-----=y (c) MATLAB Programn=-4:2;x=[1 -2 4 6 -5 8 10]; [x11,n11]=sigshift(x,n,2); [x12,n12]=sigshift(x,n,-1); [x13,n13]=sigfold(x,n); [x13,n13]=sigshift(x13,n13,-2); [x12,n12]=sigmult(x,n,x12,n12); [y,n]=sigadd(2*x11,n11,x12,n12); [y,n]=sigadd(y,n,-1*x13,n13)Problem 2(a)w j w j w j w j jw jw e e e e e e X 65424210124)(-----++++++=,()j X e ωis periodic in ω with period 2π(b) MATLAB Program :clear; close all;n = 0:6; x = [4,2,1,0,1,2,4]; w = [0:1:1000]*pi/1000;X = x*exp(-j*n'*w); magX = abs(X); phaX = angle(X); % Magnitude Response Plotsubplot(2,1,1); plot(w/pi,magX);grid;xlabel('frequency in pi units'); ylabel('|X|'); title('Magnitude Response'); % Phase response plotsubplot(2,1,2); plot(w/pi,phaX*180/pi);grid;xlabel('frequency in pi units'); ylabel('Degrees'); title('Phase Response'); axis([0,1,-180,180])(c) Because the given sequence x (n)={4,2,1,0,1,2,4} (n=0,1,2,3,4,5,6) is symmetric about 132N α-==,the phase response ()j H e ω< satisfied the condition :()3j H e ωαωω<=-=- so the phase response is a linear function in ω.(d) 150,350Hz Hz Ω=-;(e) The difference of amplitude and magnitude response:Firstly, the amplitude response is a real function, and it may be both positive and negative. The magnitude response is always positive.Secondly, the phase response associated with the magnitude response is a discontinuous function. While the associated with the amplitude is a continuous linear function.Problem 3(a) )9.09.01/()1()(211------=z z z z HZero:0 and 1; Pole:-0.6 and 1.5; (b)1116151()212110.61 1.5H z z z--=⨯+⨯+-, 165()((0.6)(1.5))()2121n nh n u n =-+ (c) ROC : 0.6 1.5Z <<,()()()163531215212n nh n u n u n ⎛⎫⎛⎫=⨯--⨯--- ⎪ ⎪⎝⎭⎝⎭ Problem 4(a) y(n)={50,44,34,52};(b) y(n)={5,16,34,52,45,28,0}; (c) N=6;(d) MATLAB Program :Function y=circonv(x1,x2,N) If (length(x1)>N)error(“N must not be smaller than the length of sequence ”) elsex1=[x1,zeros(1,N-length(x1))]; endif(length(x2)>N)error(“N must not be smaller than the length of sequence ”)elsex2=[x2,zeros(1,N-length(x2))]; endy1=dft(x1,N).*dft(x2,N); y=idft(y,N);(e) DTFT is discrete in time domain, but continuous in frequency domain. The DFT is discrete both in time and frequency domain.The FFT is a very efficient method for calculating DFT.Problem 5(a) Direct form II uses the little delay and it can decrease the space of the compute. (b)The advantage of the linear-phase form:1. For frequency-selective filters, linear-phase structure is generally desirable to have a phase-responsethat is a linear function of frequency.2. This structure requires 50% fewer multiplications than the direct form. (c) Block diagrams are shown as under:1z -1z -1z -1z -1z -1z -()x n )n()x n1-1-Problem 6(a) we use Hamming or Blackman window to design the bandpass filter because it can provide us attenuationexceed 60dB .(b) According to Blackman window :first, Determine transition width =p s W W - ;second, Determine the type of the window according to s A ;third, Compute M using the formula MW W p s π2=- ; fourth, Compute ideal LPF2sp W W Wc +=;fifth, design the window needed, multiply point by point; sixth, determines p A R ,(c) MATLAB Program :%% Specifications about Blackman window: ws1 = 0.2*pi; % lower stopband edge wp1 = 0.3*pi; % lower passband edge wp2 = 0.6*pi; % upper passband edge ws2 = 0.7*pi; % upper stopband edge Rp = 0.5; % passband ripple As = 60; % stopband attenuation %tr_width = min((wp1-ws1),(ws2-wp2));M = ceil(6.6*pi/tr_width); M = 2*floor(M/2)+1, % choose odd M n = 0:M-1;w_ham = (hamming(M))';wc1 = (ws1+wp1)/2; wc2 = (ws2+wp2)/2; hd = ideal_lp(wc2,M)-ideal_lp(wc1,M); h = hd .* w_ham;[db,mag,pha,grd,w] = freqz_m(h,1); delta_w = pi/500;Asd = floor(-max(db([1:floor(ws1/delta_w)+1]))), % Actual AttnRpd = -min(db(ceil(wp1/delta_w)+1:floor(wp2/delta_w)+1)), % Actual passband ripple (5) %%% Filter Response Plotssubplot(2,2,1); stem(n,hd); title('Ideal Impulse Response: Bandpass'); axis([-1,M,min(hd)-0.1,max(hd)+0.1]); xlabel('n'); ylabel('hd(n)') set(gca,'XTickMode','manual','XTick',[0;M-1],'fontsize',10) subplot(2,2,2); stem(n,w_ham); title('Hamming Window'); axis([-1,M,-0.1,1.1]); xlabel('n'); ylabel('w_ham(n)')set(gca,'XTickMode','manual','XTick',[0;M-1],'fontsize',10) set(gca,'YTickMode','manual','YTick',[0;1],'fontsize',10)subplot(2,2,3); stem(n,h); title('Actual Impulse Response: Bandpass'); axis([-1,M,min(hd)-0.1,max(hd)+0.1]); xlabel('n'); ylabel('h(n)') set(gca,'XTickMode','manual','XTick',[0;M-1],'fontsize',10)subplot(2,2,4); plot(w/pi,db); title('Magnitude Response in dB');axis([0,1,-As-30,5]); xlabel('frequency in pi units'); ylabel('Decibels') set(gca,'XTickMode','manual','XTick',[0;0.3;0.4;0.5;0.6;1])set(gca,'XTickLabelMode','manual','XTickLabels',['0';'0.3';'0.4';'0.5';'0.6';'1'],... 'fontsize',10)set(gca,'TickMode','manual','YTick',[-50;0])set(gca,'YTickLabelMode','manual','YTickLabels',['-50';'0']);gridProblem 7Firstly, we use the given specifications ofs p s p A R ,,,ωω to design an analog lowpass IIR filter.Secondly, we change the analog lowpass IIR filter into the analog highpass IIR filter. Thirdly, we change the analog highpass IIR filter into the digital highpass IIR filter.。
西电数字信号处理大作业
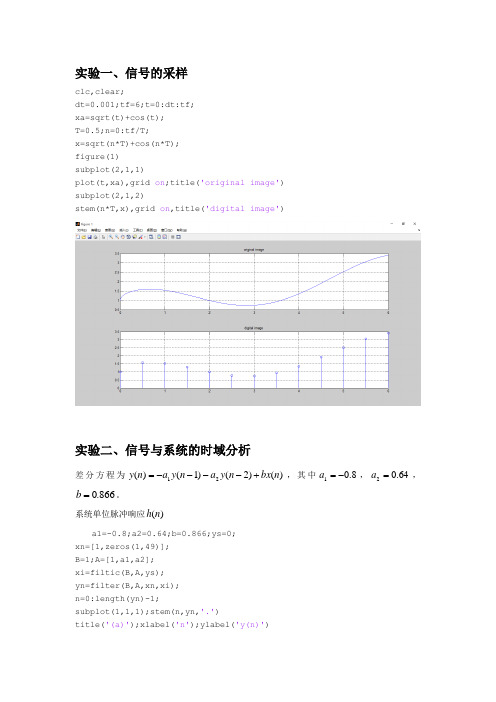
实验一、信号的采样clc,clear;dt=0.001;tf=6;t=0:dt:tf;xa=sqrt(t)+cos(t);T=0.5;n=0:tf/T;x=sqrt(n*T)+cos(n*T);figure(1)subplot(2,1,1)plot(t,xa),grid on ;title('original image')subplot(2,1,2)stem(n*T,x),grid on ,title('digital image')实验二、信号与系统的时域分析差分方程为)()2()1()(21n bx n y a n y a n y +----=,其中8.01-=a ,64.02=a ,866.0=b 。
系统单位脉冲响应)(n ha1=-0.8;a2=0.64;b=0.866;ys=0;xn=[1,zeros(1,49)];B=1;A=[1,a1,a2];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')title('(a)');xlabel('n');ylabel('y(n)')输入x(n)=cos(n)T=0.1;z=cos(n*T);zn=conv(yn,z); figure(2);n1=1:99;stem(n1,zn,'.')实验三、系统的频域和Z域分析程序代码(画出dtft的幅度和频率谱)clc,clear;n=0:1:7;x=(0.9*exp(j*pi/3)).^n;w=0:pi/200:pi;X=x*exp(-j).^(n'*w);realX=real(X);imagX=imag(X);angX=angle(X);magX=abs(X);subplot(2,2,1);plot(w/pi,magX);grid xlabel('frequency in pi unit');title('magnitude part');subplot(2,2,2);plot(w/pi,realX);grid xlabel('frequency in pi unit');title('real part');subplot(2,2,3);plot(w/pi,imagX);grid xlabel('frequency in pi unit');title('imaginary part');subplot(2,2,4);plot(w/pi,angX);grid xlabel('frequency in pi unit');title('angel part');clc,clear;a=[1,-0.5,0.06];b=[1,1,0];m=0:length(b)-1;l=0:length(a)-1;w=0:pi/500:pi;num=b*exp(-j*m'*w);den=a*exp(-j*l'*w);H=num./den;magH=abs(H);angH=angle(H);H1=freqz(b,a,w);magH1=abs(H1);angH1=angle(H1);subplot(2,2,2);plot(w/pi,angH);grid;xlabel('w(frequency in pi units)');ylabel('Ïàλrad/w');subplot(2,2,1);plot(w/pi,magH);grid;xlabel('w(frequency in pi units)');ylabel('·ù¶È|H|');subplot(2,2,3);plot(w/pi,magH1);grid;xlabel('w(frequency in pi units)');ylabel('·ù¶È|H1|');subplot(2,2,4);plot(w/pi,angH);grid;xlabel('w(frequency in pi units)');ylabel('Ïàλrad/w');axis([0,1,-0.8,0]); figure(2);zplane(b,a);实验四、信号的频谱分析程序代码clc,clear;n=0:7;k=0:7;N=8;w=n*(2*pi)/8;x=(0.9*exp(j*pi/3)).^n;X1=[x zeros(1,8)];X2=[X1 zeros(1,16)];XK=x*exp(-j*k'*w);k1=0:15;n1=0:15;w1=n1*(2*pi)/16;XK1=X1*exp(-j*k1'*w1);k2=0:31;n2=0:31;w2=n2*(2*pi)/16;XK2=X2*exp(-j*k2'*w2);w3=0:pi/200:2*pi;X=x*exp(-j*n'*w3);magX=abs(X);angX=angle(X);magXK=abs(XK);angXK=angle(XK);magXK1=abs(XK1);angXK1=angle(XK1);magXK2=abs(XK2);angXK2=angle(XK2);subplot(4,2,1);plot(w3/pi,magX);xlabel('w/pi');ylabel('·ù¶È|X|');grid on;subplot(4,2,2);plot(w3/pi,angX);xlabel('w/pi');ylabel('Ïàλrad/pi'); subplot(4,2,3);stem(n,magXK);xlabel('K');ylabel('·ù¶È|XK|');subplot(4,2,4);stem(n,magXK);xlabel('K');ylabel('Ïàλrad/pi'); subplot(4,2,5);stem(n1,magXK1);xlabel('K1');ylabel('·ù¶È|XK1|'); subplot(4,2,6);stem(n1,magXK1);xlabel('K1');ylabel('Ïàλrad/pi'); subplot(4,2,7);stem(n2,magXK2);xlabel('K2');ylabel('·ù¶È|XK2|'); subplot(4,2,8);stem(n2,magXK2);xlabel('K2');ylabel('Ïàλrad/pi');实验五、IIR数字滤波器设计IIR汉宁窗低通高通低通巴特沃斯通带截止频率wp=0.2pi 通带最大衰减R=1dB阻带截止频率wp=0.35pi 阻带最大衰减R=10dBclc,clear;Wp=0.2;Ws=0.35;Rp=1;Rs=100;[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc)w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);;ang=angle(H);H=20*log10(abs(H))subplot(4,2,1); plot(w/pi,H) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('µÍͨÂ˲¨Æ÷')subplot(4,2,2);plot(w/pi,ang);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')[Bz1,Az1]=butter(N,Wc,'high')w=0:0.1:pi;[H1,w2]=freqz(Bz1,Az1,w);ang1=angle(H1);H1=20*log10(abs(H1))subplot(4,2,3); plot(w/pi,H1) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('¸ßͨÂ˲¨Æ÷')subplot(4,2,4);plot(w/pi,ang1);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wc1]=buttord(Wp1,Ws1,Rp,Rs);[Bz2,Az2]=butter(N2,Wc1,'stop')w=0:0.1:pi;[H2,w3]=freqz(Bz2,Az2,w);ang2=angle(H2);H2=20*log10(abs(H2))subplot(4,2,5); plot(w/pi,H2) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´ø×èÂ˲¨Æ÷')subplot(4,2,6);plot(w/pi,ang2);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wc1]=buttord(Wp1,Ws1,Rp,Rs);[Bz3,Az3]=butter(N2,Wc1)w=0:0.1:pi;[H3,w4]=freqz(Bz3,Az3,w);ang3=angle(H3);H3=20*log10(abs(H3))subplot(4,2,7); plot(w/pi,H3) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´øͨÂ˲¨Æ÷')subplot(4,2,8);plot(w/pi,ang3);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')切比雪夫1型通带截止频率wp=0.7pi 通带最大衰减R=1dB阻带截止频率wp=0.5pi 阻带最大衰减R=40dBclc,clear;Wp=0.7;Ws=0.5;Rp=1;Rs=40;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo)w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);ang=angle(H);H=20*log10(abs(H))subplot(4,2,1); plot(w/pi,H) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('µÍͨÂ˲¨Æ÷')subplot(4,2,2);plot(w/pi,ang);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')[Bz1,Az1]=cheby1(N,Rp,Wpo,'high');w=0:0.1:pi;[H1,w2]=freqz(Bz1,Az1,w);ang1=angle(H1);H1=20*log10(abs(H1))subplot(4,2,3); plot(w/pi,H1) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('¸ßͨÂ˲¨Æ÷')subplot(4,2,4);plot(w/pi,ang1);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wpo1]=cheb1ord(Wp1,Ws1,Rp,Rs);[Bz2,Az2]=cheby1(N2,Rp,Wpo1,'stop')w=0:0.1:pi;[H2,w3]=freqz(Bz2,Az2,w);ang2=angle(H2);H2=20*log10(abs(H2))subplot(4,2,5); plot(w/pi,H2) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´ø×èÂ˲¨Æ÷')subplot(4,2,6);plot(w/pi,ang2);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wpo1]=cheb1ord(Wp1,Ws1,Rp,Rs);[Bz3,Az3]=cheby1(N2,Rp,Wpo1)w=0:0.1:pi;[H3,w4]=freqz(Bz3,Az3,w);ang3=angle(H3);H3=20*log10(abs(H3))subplot(4,2,7); plot(w/pi,H3) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´øͨÂ˲¨Æ÷')subplot(4,2,8);plot(w/pi,ang3);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')实验六、FIR数字滤波器设计FIR汉宁窗低通高通低通% 采用Hamming窗设计一个带阻FIR滤波器阻带:0~0.5pi,阻带最小衰减Rs=40dB;通带:0.5~pi,通带最大衰减:Rp=1dB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s.t y
l1 最小范数下最优化问题又称为基追踪(BP),其常用实现算法有:内
点法和梯度投影法。内点法速度慢,但得到的结果十分准确:而梯度投影法速 度快,但没有内点法得到的结果准确。二维图像的重构中,为充分利用图像的 梯度结构。可修正为整体部分(Total Variation,TV)最小化法。由于 l1 最小范数 下的算法速度慢,新的快速贪婪法被逐渐采用,如匹配追踪法(MP)和正交匹配 追踪法(OMP)。此外,有效的算法还有迭代阈值法以及各种改进算法。
图 2 传统编解码理论的框图
5
压缩感知理论对信号的采样、压缩编码发生在同一个步骤,利用信号的稀 疏性,以远低于 Nyquist 采样率的速率对信号进行非自适应的测量编码。测量 值并非信号本身,而是从高维到低维的投影值,从数学角度看,每个测量值是 传统理论下的每个样本信号的组合函数,即一个测量值已经包含了所有样本信 号的少量信息。解码过程不是编码的简单逆过程,而是在盲源分离中的求逆思 想下。利用信号稀疏分解中已有的重构方法在概率意义上实现信号的精确重构 或者一定误差下的近似重构。解码所需测量值的数目远小于传统理论下的样本 数。
1924 年奈奎斯特(Nyquist)就推导出在理想低通信道的最高码元传输速率的 公式: 理想低通信道的最高码元传输速率 B=2W Baud (其中 W 是带宽) 理想信道的极限信息速率(信道容量),其公式如下:
C = B * log2 N ( bps )
采样过程所应遵循的规律,又称取样定理、抽样定理。采样定理说明采样 频率与信号频谱之间的关系,是连续信号离散化的基本依据。采样定理是 1928 年由美国电信工程师 H.奈奎斯特首先提出来的,因此称为奈奎斯特采样定理。 1933 年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理,因此在苏 联文献中称为科捷利尼科夫采样定理。1948 年信息论的创始人 C.E.香农对这一 定理加以明确地说明并正式作为定理引用,因此在许多文献中又称为香农采样 定理。采样定理有许多表述形式,但最基本的表述方式是时域采样定理和频域
频域采样定理 对于时间上受限制的连续信号 f(t)(即当│t│>T 时,f(t)=0,这里 T=T2-T1 是 信号的持续时间),若其频谱为 F(ω),则可在频域上用一系列离散的采样值 来表示,只要这些采样点的频率间隔ω≦π / tm 。 传统采样的依据是奈奎斯特采样定理,即信号的采样频率必须是信号带宽 的 2 倍以上。然而随着信号的带宽越来越宽,据此定理进行信号采样,必然对 采样率提出更高的要求,对信号处理和硬件系统也带来了巨大的压力。能否降 低信号的采样率?能否寻找新的信号描述方式与信号处理的方法?能否减少信号 处理的成本?引起人们越来越大的研究兴趣。 目前,Candes,Romberg,Tao 和 Donoho 等人提出了一种全新的理论一 压缩感知理论(Compressed Sensing)。该理论是一种崭新的信号采样、信号编码 和信号解码理论。采样速率不再像 Nyquist 速率一样,与信号的带宽密切相 关,而是与信息在信号中的结构和位置息息相关。编码过程是围绕观测器即观 测矩阵展开的,而解码过程是一个优化计算过程。该理论已经被证明能够用较 低采样速率准确的进行信号采样,并且能够以很高的概率重构原始信号。目前 国内已经有科研单位的学者对其展开研究。
4
当前,压缩感知理论主要涉及三个核心问题: (1) 具有稀疏表示能力的过完备字典设计; (2) 满足非相干性或等距约束性准则的测量矩阵设计; (3) 快速鲁棒的信号重建算法设计。 压缩感知理论必将给信号采样方法带来一次新的革命。这一理论的引人之 处还在于它对应用科学的许多领域具有重要的影响,如统计学、信息论、编码 等。目前,学者们已经在模拟-信息采样、合成孔径雷达成像、遥感成像、核磁 共振成像、深空探测成像、无线传感器网络、信源编码、人脸识别、语音识 别、探地雷达成像等诸多领域对压缩感知展开了广泛的应用研究。Rice 大学已 经成功设计出了一种基于压缩感知的新型单像素相机,在实践中为取代传统相 机迈出了实质性的一步。
图 3 压缩感知理论的编解码框图
压缩感知的基本理论及核心问题
N 假设有一信号 f ( f R ) ,长度为 N ,基向量为 i (i 1,2,..., N ) ,对信号进
行变换:
f ai i 或 f
i 1 N
显然 f 是信号在时域的表示, 是信号在 域的表示。信号是否具有稀疏 性或者近似稀疏性是运用压缩感知理论的关键问题,若式中的 只有 K 个是非 零值 ( N K ) 者仅经排序后按指数级衰减并趋近于零,可认为信号是稀疏的。 信号的可稀疏表示是压缩感知的先验条件。在已知信号是可压缩的前提下,压 缩感知过程可分为两步:
6
(1)设计一个与变换基不相关的 M N ( M N ) 维测量矩阵对信号进行观 测,得到 M 维的测量向量。 (2)由 M 维的测量向量重构信号。
信号的稀疏表示
T 稀疏的数学定义:信号 X 在正交基 下的变换系数向量为 X ,假如
对于 0 p 2 和 R 0 ,这些系数满足:
7
学的石光明教授也对稀疏表示问题进行了认真研究,并基于多组正交基级联而 成的冗余字典提出一种新的稀疏分解方法。
信号的观测矩阵 用一个与变换矩阵不相关的 M N ( M N ) 测量矩阵 对信号进行线性投 影,得到线性测量值 y :
y f
测量值 y 是一个 M 维向量,这样使测量对象从 N 维降为 M 维。观测 过程是非自适应的即测量矩阵少的选择不依赖于信号 f 。测量矩阵的设计要求 信号从 f 转换为 y 的过程中,所测量到的 K 个测量值不会破坏原始信号的信 息,保证信号的精确重构。 由于信号 f 是是可稀疏表示的,上式可以表示为下式:
压缩感知理论框架 传统的信号采集、编解码过程如图所示:编码端先对信号进行采样,再对 所有采样值进行变换,并将其中重要系数的幅度和位置进行编码,最后将编码 值进行存储或传输:信号的解码过程仅仅是编码的逆过程,接收的信号经解压 缩、反变换后得到恢复信号。采用这种传统的编解码方法,由于信号的采样速 率不得低于信号带宽的 2 倍,使得硬件系统面临着很大的采样速率的压力。此 外在压缩编码过程中,大量变换计算得到的小系数被丢弃,造成了数据计算和 内存资源的浪费。
《数字信号处理》大作业
学
院
专
业
学生姓名
学
号
导师姓名
吕
雁
1
1、查找资料,写一篇关于奈奎斯特采样率与稀疏采样的学习报 告。
奈奎斯特采样定理即采样定理 。 在进行模拟/数字信号的转换过程中,当采样频率 fs.max 大于等于信号中最 高频率 fmax 的 2 倍时(fs.max 2fmax),采样之后的数字信号完整地保留了原始 信号中的信息,一般实际应用中保证采样频率为信号最高频率的 5~10 倍;采 样定理又称奈奎斯特定理。表达式为: C = B * logM N 矩阵。上式中,方程的个数远小于未知数的个数,方 程无确定解,无法重构信号。但是,由于信号是 K 稀疏,若上式中的 满足有 限等距性质(Restricted Isometry Property,简称 RIP),即对于任意 K 稀疏信号 f 和常数 k (0,1) ,矩阵 满足:
1 k
|| f ||2 2 1 k || f ||2 2
则 K 个系数能够从 M 个测量值准确重构。RIP 性质的等价条件是测量矩阵
和稀疏基 不相关。目前,用于压缩感知的测量矩阵主要有以下几种:高斯
随机矩阵,二值随机矩阵(伯努力矩阵),傅立叶随机矩阵,哈达玛矩阵,一致 球矩阵等。
从而得到稀疏系数的估计。由于上式的求解是个 NP—HARD 问题。而该 最优化问题与信号的稀疏分解十分类似,所以有学者从信号稀疏分解的相关理 论中寻找更有效的求解途径。表明, l1 最小范数下在一定条件下和 l0 最小范数具 有等价性,可得到相同的解。那么上式转化为 l1 最小范数下的最优化问题:
|| || min
2
采样定理。采样定理在数字式遥测系统、时分制遥测系统、信息处理、数字通 信和采样控制理论等领域得到广泛的应用。
时域采样定理 频带为 F 的连续信号 f(t)可用一系列离散的采样值 f(t1),f(t1±Δt),f(t1±2 Δt),...来表示,只要这些采样点的时间间隔Δt≤1/(2F),便可根据各采样值完 全恢复原来的信号 f(t)。 这是时域采样定理的一种表述方式。 时域采样定理的另一种表述方式是:当时间信号函数 f(t)的最高频率分量 为 fM 时,f(t)的值可由一系列采样间隔小于或等于 1/(2fM)的采样值来确定,即采 样点的重复频率 f≥(2fM)。图为模拟信号和采样样本的示意图。 时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基 础。
信号的重构算法
8
当矩阵 满足 RIP 准则时。压缩感知理论能够通过对上式的逆问题先求解
T 稀疏系数 x ,然后将稀疏度为 K 的信号 x 从 M 维的测量投影值 y 中正确
地恢复出来。解码的最直接方法是通过 l0 范数下求解的最优化问题:
|| || min
l0
s.t y
3
其 CS 理论如图 1 所示:
图 1 压缩感知 CS 理论
稀疏采样,也被称为压缩感知、压缩传感或压缩采样,是一种利用稀疏的 或可压缩的信号进行信号重构的技术。或者可以说是信号在采样的同时被压 缩,从而在很大程度上降低了采样率。稀疏采样跳过了采集 N 个样本这一步 骤,直接获得压缩的信号的表示。其理论利用到了许多自然信号在特定的基上 具有紧凑的表示。即这些信号是“稀疏”的或“可压缩”的。由于这一特性, 稀疏采样理论的信号编解码框架和传统的压缩过程大不一样,主要包括信号的 稀疏表示、编码测量和重构算法等三个方面。简单地说,压缩感知理论指出: 只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不 相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后通过求解一 个优化问题就可以从这些少量的投影中以高概率重构出原信号,可以证明这样 的投影包含了重构信号的足够信息。在该理论框架下,采样速率不再取决于信 号的带宽,而在很大程度上取决于两个基本准则:稀疏性和非相干性,或者稀 疏性和等距约束性。 显然,在压缩感知理论中,图像/信号的采样和压缩同时以低速率进行,使 传感器的采样和计算成本大大降低,而信号的恢复过程是一个优化计算的过 程。因此,该理论指出了将模拟信号直接采样压缩为数字形式的有效途径。从 理论上讲任何信号都具有可压缩性,只要能找到其相应的稀疏表示空间,就可 以有效地进行压缩采样。
