小学数学 最短路线问题
小学数学思维训练之最短线路问题

5.A、B两村中间隔了一条小河(如 下图),现在要在小河上架一座小木 桥,使它垂直于河岸,请你在河的两 岸选择合适的架桥地点,使A、B两村 之间路程最短。
3.如下图,要在两条街道OA、OB上 设立两个邮筒,M处是邮局,问邮筒设 在哪里,能使邮递员从邮电局出发, 先到OA上的邮筒取信,再到OB上的 邮筒取信,然后再回到邮电所的路程 最短?
友选择了三条不同的路线(如图),试问 哪条线最短?
2.小马倌要从A处出发(如图),到河 边打水,并把水送到B处的马棚中,这 附近没有固定的路,也没有什么障碍, 那么,小马倌选择怎样的路线最好呢? 请你在图中标出来.
例2.一牧人带马群从营房A点出发,到 草地MN(设其边界也叫MN)放牧。傍 晚到营房B点之前;先带马群到小河PQ去 给马饮水(如下图).想想看,牧人应走
7.如下图,在圆柱形桶外有一只蚂蚁, 要从桶外A点爬到桶内B点去寻找食物。 如果蚂蚁爬行的是最短路线,应该怎 么走?
例5.一个邮递员投递信件的街道如图, 他从邮局出发,走遍各街道,最后回到 邮局,怎样走,才能使他走的路程最短?
6.四班组织了一次有趣的赛跑,规则 是从A点出发(如下图),跑到墙边, 用手触摸墙壁,然后跑到B点,接着, 从B点再次跑到墙边,用手触摸墙壁后, 跑到C点。问选择怎样的路线最节省时 间?请在图中标出来。
哪条路线,才能使整个放牧的路程(即从 A→MN→PQ→B)最短?
例3.小猴子的家在河的左岸A点(如 图),隔河相望看到对岸远远的B点有一 棵果实累累的桃树,鲜嫩可口的桃子吸引 着猴子,可是河面上没有桥,它又不会游 泳,于是它想出一个好主意,用躺在河岸 旁的一棵枯树干搭一座桥,请小朋友想想, 这个独木桥搭在什么地方,使A、B两点 的通路最短?(假设河宽度不变,而枯木 的长度仅够搭一个垂直于河岸的桥)
小学奥数系列8-8-1最短路线及参考答案

小学奥数系列8-8-1最短路线一、小学奥数系列8-8-1最短路线1. 一只蚂蚁在长方形格纸上的点,它想去点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢?2. 如图所示,从点沿线段走最短路线到点,每次走一步或两步,共有多少种不同走法?3. 从A到B的最短路线有几条呢?4. 有一只蜗牛从点出发,要沿长方形的边或对角线爬到点,中间不许爬回点,也不能走重复的路,那么,它有多少条不同的爬行路线?最短的是哪条呢?5. 阿呆和阿瓜到少年宫参加北京奥运会志愿者培训.如果他们从学校出发,共有多少种不同的最短路线?6. 方格纸上取一点作为起点,再在的右上方任取一点作为终点,画一条由到的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?7. 如图,从点出发到点,走最短的路程,有多少种不同的走法?8. 小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!【分析】9. “五一”长假就要到了,小新和爸爸决定去黄山玩.聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?10. 从甲到乙的最短路线有几条?11. 古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.人一天一位将军向他请教一个问题:如下图,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为了使行走的路线最短,应该让马在什么地方饮水?12. 学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图).爱动脑筋的嘟嘟就在想,从学校到李家村共有多少种不同的最短路线呢?13. 亲爱的小朋友们,你们觉得从到共有几条最短路线呢?14. 阿花和阿红到少年宫参加北京奥运会志愿者培训.他们从学校出发到少年宫最多有多少种不同的行走路线?15. 小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?16. 阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行.咱们学而思的小朋友都很聪明,请你们帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?17. 大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院最短路线共有几条呢?聪明的小朋友,请你们快想想吧!18. 如图,从到最短路线总共有几种走法?19. 如图,从到沿网格线不经过线段和的最短路径的条数是多少条?20. 下图为某城市的街道示意图,处正在挖下水道,不能通车,从到处的最短路线共有多少条?21. 按图中箭头所指的方向行走,从到共有多少条不同的路线?22. 按图中箭头方向所指行走,从到有多少种不同的路线?23.(1)按下图左箭头方向所指,从到有多少种不同的路线?(2)如下图所示,这个问题有一个规则:只能沿着箭头指的方向走,你能否根据规则算出所有从入口到出口的路径共有多少条?24.(1)如下图,如果只允许向下移动,从点到点共有多少种不同的路线?(2)如下图,要从点到点,要求每一步都是向右,向上或者斜上方,问共有多少种不同的走法?25. 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间,从1号房间走到10号房间共有多少种不同走法?26. 一只密蜂从处出发,回到家里处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?27. 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“ ”的路线共有多少条?28. 图中的“我爱希望杯”有多少种不同的读法.29. 如下图左所示,科学家“爱因斯坦”的英文名拼写为“ ”,按图中箭头所示方向有多少种不同的方法拼出英文单词“ ”.注意图中的三个字母“ ”,左、右的两个字母“ ”只能由一个字母“ ”去到达.参考答案1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.。
小学数学《最短路线》练习题

小学数学《最短路线》练习题【例1】甲、乙两村之间隔一条河,如图.现在要在小河上架一座桥,使得这两村之间的行程最短,桥应修在何处?【例2】如下图,A、B两个学校都在公路的同侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?【例3】如图是一个长、宽、高分别为4分米、2分米、1分米的长方体纸盒.一只蚂蚁要从A点出发在纸盒表面上爬到B点运送食物,求蚂蚁行走的最短路程。
【例4】如下图,在圆柱形的木桶外,有一个小甲虫要从桶外的A点爬到桶内的B点.已知A 点到桶口C点的距离为14厘米,B点到桶口D点的距离是10厘米,而C、D两点之间的弧长是7厘米.如果小甲虫爬行的是最短路线,应该怎么走?路程是多少?【例5】一个邮递员投送信件的街道如图,图上数字表示各段街道的千米数.他从邮局出发,要走遍各街道,最后回到邮局.问走什么样的路线最合理,全程要走多少千米?【例6】下图是一个城市道路图,数字表示各段路的路程(单位:千米),求出图中从A到F 的最短路程。
【例7】仍取上面拓展训练的图中八个行政村的位置和线路图,乡政府要在全乡沿村与村之间的道路挖渠修道,建立排灌系统.全乡的地势是西高东低,即A村最高,依次为B、F、G、H、E、C、D,水源在A村,问沿什么路线修道最合理?【例8】有八栋居民楼A1、A2、…、A8分布在公路的两侧,如下图,由一些小路与公路相连,要在公路上设一个汽车站,使汽车站到各居民楼的距离之和最小,车站应设在哪里?【例9】有两条通讯路线A和B,如下图,通讯员从C处出发,查完两条线后到D处,作图表示他怎样走路程最短(假设到达通讯线路的任何一处都可完成查线工作)?【例10】要在两条街道(如下图)A和B上各设立一个邮筒,M处是邮局,问邮筒设在哪里才能使邮递员从邮局出发,到两个邮筒取完信再回到邮局的路程最短?【作1】如下图,A、B、C三点分别是正方体三条棱的中点.假设一只蚂蚁沿着正方体的表面从中点A爬到中点C,图中所示路线是否为蚂蚁爬行的最短路线,为什么?【作2】一个小虫从圆柱体(如下图)的A点处绕圆柱体侧面一周,最后爬到顶点B处.请画出小虫从A点绕到圆柱体侧面到达B点的最短路线。
四年级下册数学讲义-奥数讲练: 最短路线问题
在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
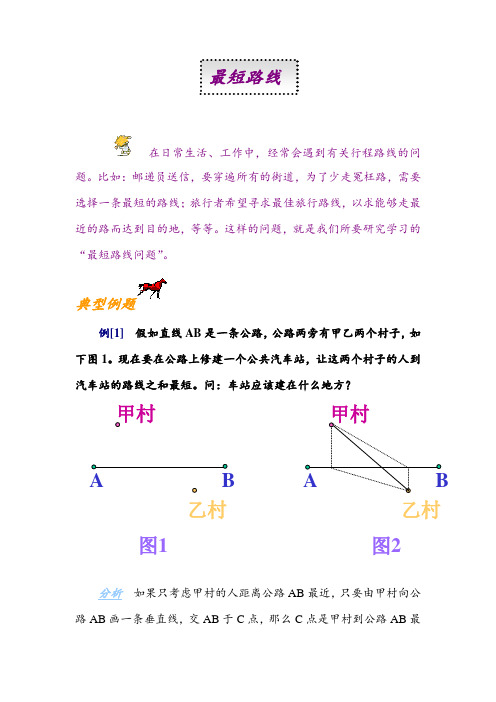
典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最甲村 乙村AB 甲村乙村 图1图2最短路线近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?3分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
小学数学《最短路线》练习题(含答案)

小学数学《最短路线》练习题(含答案)【例1】甲、乙两村之间隔一条河,如图.现在要在小河上架一座桥,使得这两村之间的行程最短,桥应修在何处?分析:设甲、乙两村分别用点A、B表示.要在河上架桥,关键是要选取一个最佳建桥的位置,使得从甲村出发经过桥到乙村的路程最短.即从甲村到甲村河边的桥头的距离加上桥长(相当于河的宽度),再加上乙村到乙村河边的桥头的距离尽可能短,这是一个求最短折线的问题.直接找出这条折线很困难,能否可以把它转化为直线问题呢?由于河的宽度不变,不论桥修在哪里,桥都是必经之路,且桥长相当于河宽,是一个定值,所以可以预先把这段距离扣除,只要使两镇到河边桥头的距离最短就可以了。
所谓预先将桥长扣除,就是假设先走完桥长,即先把桥平移到甲村,先过了桥,到C点,如下图,找出C到B的最短路线,实际上求最短折线问题转化为直线问题。
解:如下图.过A点作河岸的垂线,在垂线上截取AC的长等于河宽.连BC交与乙村的河岸于F点,作EF垂直于河的另一岸于E点,则EF为架桥的位置,也就是AE+EF+FB是两村的最短路线。
【例2】如下图,A、B两个学校都在公路的同侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?分析:车站建在哪里,使得A到车站与B到车站的距离之和最小,仍然是求最短折线问题,同例1一样关键在于转化成直线问题就好办了.采用轴对称(直线对称)作法。
答案:作点B关于公路(将公路看作是一条直线)的对称点B′,如下图,即过B点作公路(直线)的垂线交直线于O,并延长BO到B′,使BO=OB′.连结AB′交直线于点E,连BE,则车站应建在E处,并且折线AEB为最短。
为什么这条折线是最短的呢?分两步说明:(1)因为B与B′关于直线对称,根据对称点的性质知,对称轴上的点到两个对称点的距离相等,有BE=B′E,所以AB′=AE+EB′=AE+EB(2)设E′是直线上不同于E的任意一点,如图13—5,连结AE′、E′B、E′B′,可得AE′+E′B=AE′+E′B′>AB′(两点之间线段最短)上式说明,如果在E点以外的任意一点建车站,所行的路程都大于折线AEB.所以折线AEB最短。
小学奥数-最短路线

最短路线
1、请你画出从小明家去图书馆的最短路线,并说出理由。
2、一只小蚂蚁想从下图中的点A爬到对边BC。
沿怎样的路线爬行需要的时间最少?在图中画一画。
3、如图,三角形ABC的三条边AB,AC,BC分别表示三条公路。
在D点处有一名士兵接到一个紧急任务,需要他先到达BC公路,然后再到达AB公路。
他怎样走才能以最短的时间完成任务呢?在图中画出路线。
(假设士兵的速度一定)
4、如图,三角形ABC的三条边AB,AC,BC分别表示三条公路。
在D处有一个村庄,现准备修一条通往公路的小路,在图中画出最短的小路。
5、一只小蚂蚁想从下图中的点A爬到对边CD。
你能帮它开辟一条最短的路线,使它尽快到达吗?在图中画一画。
6、一个邮递员投送信件的街道如下图所示,你能帮他设计一条最短路线,使自己从邮局出发,走遍每一条街道并回到邮局吗?
7、如右图,每个小方格的边长是1厘米,一条贪吃的蛇从左下角出发,沿着格线爬行,如果它想吃掉图中的3个“”,最少要爬多远?请你画出路线。
8、下图是一个公园的平面图,A点是出入口,B,C,D,E,F,G,H,I,J是各个景点,你能帮游客设计一条最短路线,使他从出入口出发,走遍每一条路后,最终回到出入口吗?。
最短路径的十二个基本问题

两点之间线段最短. PA+PB 最小值为 A B'.
原理
分别作点 P 关于两直 线的对称点 P'和 P'', 在直线 l1 、l2 上分别求 连 P'P'',与两直线交 点 M、N,使△PMN 的 点即为 M,N. 周长最小.
两点之间线段最短. PM+MN+PN 的最小值为 线段 P'P''的长.
【十二个基本问题】
【问题 1】
作法
图形
原理
连 AB,与 l 交点即为
P.
在直线 l 上求一点 P,
使 PA+PB 值最小.
【问题 2】“将军饮马”
作法
作 B 关于 l 的对称点
B'连 A B',与 l 交点
在直线 l 上求一点 P,
即为 P.
使 PA+PB 值最小.
【问题 3】
作法
图形 图形
两点之间线段最短. PA+PB 最小值为 AB.
原理
将点 A 向下平移 MN 的
长度单位得 A',连 A'
B,交 n 于点 N,过 N 作
直线 m ∥ n ,在 m 、n , NM⊥ m 于 M.
上分别求点 M、N,使
MN⊥ m ,且 AM+MN+BN
的值最小.
【问题 6】
作法
图形
将点 A 向右平移 a 个
长度单位得 A',作 A'
关于 l 的对称点 A'',连 在直线 l 上求两点 M、N
对称点 B',连 A'B' l2 上一定点,在 l2 上求 交l2 于 M,交 l1 于 N.
点 M,在 l1 上求点 N,
使 AM+MN+NB 的 值 最
小.
六年级下册奥数试题——最短路线.(含答案)人教版

1. 准确运用“标数法”解决题目.2. 培养学生的实际操作能力.知识点说明从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最近的路走,也就是指要选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?亲爱的小朋友们,你要记住两点:⑴两点之间线段最短.⑵尽量不走回头路和重复路,这样的话,你就做到了省时省力.【例 1】一只蚂蚁在长方形格纸上的A 点,它想去B 点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢?BA11613321BA IHG F E DC【解析】 (方法一)从A 点走到B 点,不论怎样走,最短也要走长方形AHBD 的一个长与一个宽,因此,在水平方向上,所有线段的长度和应等于AD ;在竖直方向上,所有线段的长度和应等于DB .这样我们走的这条路线才是例题精讲知识精讲教学目标8-8最短路线最短路线.为了保证这一点,我们就不应该走“回头路”,只能向右和向下走.所有最短路线:→→→→→→→→、A E F G B→→→→、A C F G BA C D G B→→→→→→→→、A E H I BA C F I B→→→→、A E F I B这种方法不能保证“不漏”.如果图形再复杂些,做到“不重”也是很困难的.(方法二)遵循“最短路线只能向右和向下走”,观察发现这种题有规律可循.①看C点:只有从A到C的这一条路线.同样道理:从A到D、从A到E、从A到H也都只有一条路线.我们把数字“1”分别标在C D E H、、、这四个点上.②看F点:从A点出发到F,可以是A C F→→,也可以是→→,共有两种走法.那么我们在F点标上数字“2”(2=11+).③A E F看G点:从A G→→→、A C F G→→→、→有三种走法,即:A C D G→→→.在G点标上数字“3”(3=12+).④看I点:共有三种走A E F G法,即:A C F I→→→,在I点标上“3”→→→、A E H I→→→、A E F I(3=12+).⑤看B点:从上向下走是G B→,那么从→,从左向右走是I B 出发点A B→→→→、→→→→、A C F G B→有六种走法,即:A C D G B→→→→、A E H I B→→→→、A E F I B→→→→,→→→→、A C F I BA E F G B在B点标上“6”(633=+),观察发现每一个小格右下角上标的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点A到这点的所有最短路线的条数.此法能够保证“不重”也“不漏”,这种方法叫“对角线法”或“标号法”.【巩固】如图所示,从A点沿线段走最短路线到B点,每次走一步或两步,共有多少种不同走法?AB【解析】 这是一个较复杂的最短路线问题,我们退一步想想,先看看简单的情况.从A 到B 的各种不同走法中先选择一条路线来分析:如果按路线A →C →D →E →F →B 来走,这条路线共有5条线段,每次走一步或两步,要求从A 走到B ,会有几种走法?这不是“上楼梯”问题吗.根据“上楼梯”问题的解法可得在A →C →D →E →F →B 这条路线中有8种符合条件的走法.而对于从A 到B 的其他每条最短路线而言,每一条路线都有5条线段,所以每条路线都有8种走法. 进一步:从A 到B 共有多少条最短路线?这正是“最短路线”问题!用“标数法”来解决,有10条.综上所述,满足条件的走法有81080⨯=种.1032463111111B A BF ED CA BA【巩固】 从A 到B 的最短路线有几条呢?BA【解析】 图中从A 到B 的最短路线都为6条.【巩固】 有一只蜗牛从A 点出发,要沿长方形的边或对角线爬到C 点,中间不许爬回A 点,也不能走重复的路,那么,它有多少条不同的爬行路线?最短的是哪条呢?ODC BA【解析】 共有9种,即:A O C →→、 A O D C A O B C →→→→→→、 、 A B C →→A B O C →→→、 A B O D C →→→→、 A D C →→、 A D O C →→→ A D O B C →→→→,最短的路是:A O C →→.【例 2】阿呆和阿瓜到少年宫参加2008北京奥运会志愿者培训.如果他们从学校出发,共有多少种不 同的最短路线?少年宫学校J I HGF EDC B A 410633211111少年宫学校【解析】 从学校到少年宫的最短路线,只能向右或向下走.我们可以先看A 点:从学校到A 点最短路线只有1种走法,我们在A 点标上1.B 、E 、F 、G 点同理.再看J 点:最短路线可以是A J →、E J →共2条,我们在J 点标上2.我们发现211=+正好是对角线A 点和E 点上的数字和.所有的最短路线都符合这个规律,最终从学校到少年宫共有10种走法.【巩固】 方格纸上取一点A 作为起点,再在A 的右上方任取一点B 作为终点,画一条由A 到B 的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?BA【解析】 根据“标号法”可知共有10种,如图.【巩固】 如图,从F 点出发到G 点,走最短的路程,有多少种不同的走法?GF【分析】 共有115种.【巩固】 小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!南村北村【分析】 根据“对角线法”知共有126种,如图.12656703535216152015105541111南村北村410633211111【例 3】“五一”长假就要到了,小新和爸爸决定去黄山玩.聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?黄山北京2黄山北京211410331111722【解析】 采用对角线法(如图)这道题的图形与前几题的图形又有所区别,因此,在解题时要格外注意是由哪两点的数之和来确定另一点的.从北京到黄山最近的道路共有10条.【巩固】 从甲到乙的最短路线有几条?乙甲【解析】 有11条.【例 4】古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.人一天一位将军向他请教一个问题:如下图,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为了使行走的路线最短,应该让马在什么地方饮水?乙地甲地河流【解析】 本题主要体现最值思想和对称的思想,教师应充分引导孩子观察行走路线的变化情况甲地逐步引导学生通过对称来找到相应的点,进一步了解图形最值问题中应该如何解决问题.【例 5】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图).爱动脑筋的嘟嘟就在想,从学校到李家村共有多少种不同的最短路线呢?李家村学校81461025李家村学校235216151051114106331111【解析】 我们采用对角线法(如图),从学校到李家村共有81种不同的最短路线.[拓展] 亲爱的小朋友们,你们觉得从A 到B 共有几条最短路线呢?BA【解析】 此题与上题不同,但方法相同.我们采用对角线法(如图)可知:可以选择的最短路线共有41条.【例 6】阿花和阿红到少年宫参加2008北京奥运会志愿者培训.他们从学校出发到少年宫最多有多少种不同的行走路线?少年宫学校904214482814少年宫学校2651143111114952052【解析】 采用对角线法(如图).可得从学校到少年宫共有90种走法.[铺垫] 小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?小猪家游乐场149小猪家游乐场2551114321【解析】 “对角线”法(如图),共14 条.【例 7】阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行.咱们学而思的小朋友都很聪明,请你们帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?【解析】仍然用对角线法求解.第一天(无限制条件)共有16条;第二天(必须经过公园)共有8条;第三天(必须不经过公园)共有8条.【巩固】大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院最短路线共有几条呢?聪明的小朋友,请你们快想想吧!【解析】(方法一)用“对角线法”求出:从学校到养老院共126条.必经过市中心的60 条,所以可行的路有:1266066-=(条).养老院(方法二)可以直接求,即把含有市中心的田字格挖去,共有66条.664026111010养老院学校2526155111463311115155411【例 8】如图,从X 到Y 最短路线总共有几种走法?【分析】 如图,共有716种.71637434217017220285511536212815218364115878536492836211515101077666554432YX1111111111111【例 9】如图,从A 到B 沿网格线不经过线段CD 和EF 的最短路径的条数是多少条?A C DE FB【解析】 由于不能经过线段CD 和EF ,所以我们必须先在网络图中拆除CD 和EF ,然后再在拆除了CD 和EF 以后的网络图中进行标数(如下图所示).运用标数法可求出满足条件的最短路径有78条.【巩固】 下图为某城市的街道示意图,C 处正在挖下水道,不能通车,从A 到B 处的最短路线共有多少条?【解析】 从A 到B 的最短路线有431条.CBA174551999558325743117411030552518121211C BA836410776543211111111【例 10】 按图中箭头所指的方向行走,从A 到I共有多少条不同的路线?CF H DIGE B A【解析】 本题中的运动方向已经由箭头标示出来,所以关键要分析每一点的入口情况.通过标数法我们可以得出从A 到I 共有29条不同的路径.【例 11】 按图中箭头方向所指行走,从A 到G 有多少种不同的路线?GF E DC B A【解析】 运用标数法原理进行标数,整个标数流程如下图2181AB CD EF G 2351313532GF ED CB A1881AB CDE F G2355332GF E D CB A11AB CDE F G22GF E DC B A11AB C DE F G从A 到G 共有21条不同的路线.【巩固】 ⑴按下图左箭头方向所指,从X到Y 有多少种不同的路线?⑵如下图右所示,这个问题有一个规则:只能沿着箭头指的方向走,你能否根据规则算出所有从入口到出口的路径共有多少条?[分析]⑴利用标数法求得X到Y有34种不同的路线,如下图左所示.⑵由题将路线图转化为下图右所示,根据标数法求得从入口到出口的路径共有10条.出口1【例 12】⑴如下图左,如果只允许向下移动,从A点到B点共有多少种不同的路线?⑵如下图右,要从A点到B点,要求每一步都是向右,向上或者斜上方,问共有多少种不同的走法?ABBA【解析】⑴按题目要求,只能向下移动,利用标数法求得A到B共有路线68种,如下图左所示.⑵按题目要求,只能走下图右的3个方向,利用标数法求得共有22种不同的走法,如下图右.2622166111201010644143468341444332111111A BB A 42622166111B A【巩固】 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间,从1号房间走到10号房间共有多少种不同走法?10987654321【分析】 图中并没有标出行走的方向,但题中“你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间”这句话实际上就规定了行走的方向.如下图所示,我们可以把原图转化成常见的城市网络图,然后再根据标数法的思想标数:从图中可以看出,从1号走到10号房间共有22种不同的走法.【例 13】 一只密蜂从A 处出发,A 回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?BA864297531【解析】 蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房.明确了行走路径的方向,就可运用标准法进行计算.如图所示,小蜜蜂从A 出发到B 处共有89种不同的回家方法.【例 14】 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“APPLE ”的路线共有多少条?AAPPLELPPA A P L P P P A A P P P A A P A[分析] 要想拼出英语“APPLE ”的单词,必须按照“A P P L E →→→→”的次序拼写.在图中的每一种拼写方式都对应着一条最短路径.如下图所示,运用标数法原理标数不难得出共有31种不同的路径.131127211224154112283184411AAPPLELPPA A P L P P P A A P P P A A P A[铺垫] 图中的“我爱希望杯”有多少种不同的读法.望杯望杯希杯爱望希杯杯望希爱我 杯杯杯杯杯望望望希希希爱爱我644332111111111[分析] 从我(1个)、爱(2个)、希(3个)、望(4个)、杯(5个)中组成“我爱希望杯”即相同的字只能选一个而且不能重复选,所以共有1464116++++=(种).[拓展] 如下图左所示,科学家“爱因斯坦”的英文名拼写为“Einstein ”,按图中箭头所示方向有多少种不同的方法拼出英文单词“Einstein ”.i111111i[分析] 因为“Einstein ”的拼读顺序为“E i n s t e i n →→→→→→→”,每一种拼法都对应着网络图中的一条最短路径,所以可以运用标数法来解决. 如上图右所示,从E 点到n 点的最短路径有30条,所以共有303060+=(种)不同拼法.注意图中的三个字母“i ”,左、右的两个字母“i ”只能由一个字母“e ”去到达.。
小学三年级奥数最短路线问题【三篇】

【导语】海阔凭你跃,天⾼任你飞。
愿你信⼼满满,尽展聪明才智;妙笔⽣花,谱下锦绣第⼏篇。
学习的敌⼈是⾃⼰的知⾜,要使⾃⼰学⼀点东西,必需从不⾃满开始。
以下是为⼤家整理的《⼩学三年级奥数最短路线问题【三篇】》供您查阅。
【第⼀篇】
练习题:
图4-18是某城市的主要公路⽰意图,今在C、D、E、F、G、H路⼝修建⽴交桥,车辆不能通⾏,那么从A到B的最近路线共有⼏条?
答案解析:
【第⼆篇】
练习题:
如图4-17所⽰是⼀个街道的平⾯图,在不⾛回头路、不⾛重复路的条件下,可以有多少种不同的⾛法?
答案解析:
【第三篇】
练习题:
图4-16为某城市的街道⽰意图,C处正在挖下⽔道,不能通车,从A到B处的最短路线共有多少条?
答案解析:。
四年级 数学最短路线问题

第四讲最短路线【例1】甲、乙两村之间隔一条河,如图.现在要在小河上架一座桥,使得这两村之间的行程最短,桥应修在何处?分析:设甲、乙两村分别用点A、B表示.要在河上架桥,关键是要选取一个最佳建桥的位置,使得从甲村出发经过桥到乙村的路程最短.即从甲村到甲村河边的桥头的距离加上桥长(相当于河的宽度),再加上乙村到乙村河边的桥头的距离尽可能短,这是一个求最短折线的问题.直接找出这条折线很困难,能否可以把它转化为直线问题呢?由于河的宽度不变,不论桥修在哪里,桥都是必经之路,且桥长相当于河宽,是一个定值,所以可以预先把这段距离扣除,只要使两镇到河边桥头的距离最短就可以了。
所谓预先将桥长扣除,就是假设先走完桥长,即先把桥平移到甲村,先过了桥,到C点,如下图,找出C到B的最短路线,实际上求最短折线问题转化为直线问题。
解:如下图.过A点作河岸的垂线,在垂线上截取AC的长等于河宽.连BC交与乙村的河岸于F点,作EF垂直于河的另一岸于E点,则EF为架桥的位置,也就是AE+EF+FB是两村的最短路线。
【例2】如下图,A、B两个学校都在公路的同侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?分析:车站建在哪里,使得A到车站与B到车站的距离之和最小,仍然是求最短折线问题,同例1一样关键在于转化成直线问题就好办了.采用轴对称(直线对称)作法。
答案:作点B关于公路(将公路看作是一条直线)的对称点B′,如下图,即过B点作公路(直线)的垂线交直线于O,并延长BO到B′,使BO=OB′.连结AB′交直线于点E,连BE,则车站应建在E处,并且折线AEB为最短。
为什么这条折线是最短的呢?分两步说明:(1)因为B与B′关于直线对称,根据对称点的性质知,对称轴上的点到两个对称点的距离相等,有BE=B′E,所以AB′=AE+EB′=AE+EB(2)设E′是直线上不同于E的任意一点,如图13—5,连结AE′、E′B、E′B′,可得AE′+E′B=AE′+E′B′>AB′(两点之间线段最短)上式说明,如果在E点以外的任意一点建车站,所行的路程都大于折线AEB.所以折线AEB最短。
小学数学典型应用题之最短路线问题

小学数学典型应用题之最短路线问题一、含义在日常生活和工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地等等。
这样的问题,就是所要学习的“最短路线问题”。
二、解题思路和方法(1)两点之间线段最短。
(2)尽量不走回头路和重复路,这样的话才能做到省时省力。
三、例题例题(一):一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们,你能给它找到几条这样的最短路线呢?解析一:(1)从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽。
(2)因此在水平方向上,所有线段的长度和应等于AD;在竖值方向上,所有线段的长度和应等于DB。
(3)这样我们走的这条路线才是最短路线,为了保证这一点,我们就不应该走“回头路”,只能向右和向下走。
(4)因此所有的最短路线为:A→C→D→G→B 、A→C→F→G→B、A→E→F →G→B;A→C→F→l →B、A→E→F→l→B、A→E→H→l→B。
解析二:(1)看C点∶只有从A到C的这一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1"分别标在C、D、E、H 这四个点上。
(2)看F点:从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法。
那么我们在F点标上数字"2"(2=1+1)。
(3)看G点:从A→G有三种走法,即A→C→D→G、A→C→F→G、A→E→F →G,在G点标上数字"3"(3=1+2)。
(4)看I点:共有三种走法,即A→C→F→l、A→E→F→l、A→E→H→l,在Ⅰ点标上"3”(3=1+2)。
(5)看B点:从上向下走是G→B,从左向右走是l→B,那么从出发点A→B 有六种走法,即A→C→D→G→B、A→C→F→G→B、A→E→F→G→B、A→C→F→l →B、A→E→F→l→B、A→E→H→l→B ,在B点标上"6"( 6=3+3 )。
小学奥数最短路线问题(有答案)

小学六年级奥数教案—运筹学初步本讲主要讲统筹安排问题、排队问题、最短路线问题、场地设置问题等。
这些都是人们日常生活、工作中经常碰到的问题,怎样才能把它们安排得更合理,多快好省地办事,就是这讲涉及的问题。
当然,限于现有的知识水平,我们仅仅是初步探索一下。
1.统筹安排问题例1星期天妈妈要做好多事情。
擦玻璃要20分钟,收拾厨房要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。
妈妈干完所有这些事情最少用多长时间?分析与解:如果按照题目告诉的几件事,一件一件去做,要95分钟。
要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。
最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃和收拾厨房,最后晾衣服,共需60分钟(见下图)。
例1告诉我们,当有许多事要做时,科学地安排好先后顺序,就能用较少的时间完成较多的事情。
2.排队问题例2理发室里有甲、乙两位理发师,同时来了五位顾客,根据他们所要理的发型,分别需要10,12,15,20和24分钟。
怎样安排他们的理发顺序,才能使这五人理发和等候所用时间的总和最少?最少要用多少时间?分析与解:一人理发时,其他人需等待,为使总的等待时间尽量短,应让理发所需时间少的人先理。
甲先给需10分钟的人理发,然后15分钟的,最后24分钟的;乙先给需12分钟的人理发,然后20分钟的。
甲给需10分钟的人理发时,有2人等待,占用三人的时间和为(10×3)分;然后,甲给需 15分钟的人理发,有 1人等待,占用两人的时间和为(15×2)分;最后,甲给需 24分钟的人理发,无人等待。
甲理发的三个人,共用(10×3+15×2+24)分,乙理发的两个人,共用(12×2+20)分。
总的占用时间为(10×3+15×2+24)+(12×2+20)=128(分)。
小学三年级奥数最短路线问题(下学期教案)

小学三年级奥数最短路线问题(下学期教案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN小学三年级奥数最短最短路线问题(下学期教案)在日常工作、生活和娱乐中,经常会遇到有关行程路线的问题.在这一讲里,我们主要解决的问题是如何确定从某处到另一处最短路线的条数。
例1 下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B处共有多少条最短路线?分析为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B通过验证,我们确信这六条路线都是从A到B的最短路线.如果按照上述方法找,它的缺点是不能保证找出所有的最短路线,即不能保证“不漏”.当然如果图形更复杂些,做到“不重”也是很困难的。
现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A 到C只有一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1”分别标在C、D、E、H这四个点上,如图4—2。
2.看F点:从上向下走是C→F,从左向右走是E→F,那么从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法.我们在图4—2中的F点标上2数字“2”.2=1+1.第一个“1”是从A→C的一种走法;第二个“1”是从A→E的一种走法。
小学数学 最短路线问题

最短路线问题大家一定记得,教科书上有这样一个问题:一条河流的两边有A,B两个村庄,现准备在河上建一座桥(当然,桥应与河岸垂直,这样可以减少造价),问桥应建在何处才能使由A到B的路程最短?作出图形,并说明理由.探索如果没有可行的思路,不妨在同一个图上随便画几个方案,观察并比较这些方案各自路程的长短,也不难估计出一个大致的位置。
如图,通过测量不难发现,在C2D2位置桥建比在C1D1位置建桥,路程短一些。
实际工作中对精确度要求不高时,这倒也不失是一种方法。
但一点点的误差,也会造成实际问题中的巨大浪费,因此,我们更希望得到一个精确的结果。
到底桥应建在什么地方呢?我们还是回到上面两个方案的比较。
不管哪个方案中,路程都包括3个部分,AC,CD,DB,可以发现所有的CD都是相等的(等于河流的宽),因此,只要考虑AC+DB取得最小值就可以了。
可是,这两段线段分散着,能否将它们集中到一起呢?在前面的讲解中我们遇到过这样的问题,平移使得C,D重合就可以了,得到下面左图。
在左图中更容易看出:在C2D2位置桥建,路程短一些。
而要使得AC+DB最小,也不难发现,C,D应与A,B共线。
把这个过程反过来,就得到了具体的方案设计思路,如下中图。
拓展1如果A,B两个村庄中间有两条平行的河流(如上右图),准备在两条河上各建一座桥(桥仍然与河岸垂直),那么,要使由A到B的路程最短,两座桥又应建在何处呢?两座桥,问题当然变复杂了,画图发现需要计算5条线段的长度和,当然其中有两条长度是固定的,我们也可以暂时不考虑这两条线段,通过平移,将其他三条线段集中起来,不难类似地得到右面的草图,只要A1,D,E,B1 四点共线即可。
拓展2如果A,B两个村庄中间有两条不平行的河流,两座桥又应建在何处呢?有了拓展1,不难得到拓展2的解答:如图,将点A沿与甲河河岸垂直的方向向下平移与甲河河宽相等的距离,得点A′;将点B沿与乙河河岸垂直的方向向上平移与乙河河宽相等的距离,得点B′;连接A′,B′,分别交甲河、乙河于M点,P点,MN,PQ即为所建桥.小结最短路问题的实质是,把路径中的固定部分(桥的长度)用平移的方法去除掉,再利用两点之间线段最短来解决。
三年级下册数学试题-思维训练:最短路线(练习含答案)全国通用
【前铺1】如图,3条路可走,哪条路最短?知识要点一、基本思路⑴两点之间线段最短。
⑵尽量不走回头路和重复路,二、综合运用标数法(加法原理)1.标记方向2.方向沿线最外侧标13.对角相加(方向相加)马房将军家1最短路线将军家AC 马房【例1】假如直线AB是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子,乙村河 A B DB【例2】如图,已知牧马营地在P处,牧童每天要赶着马群先到河边饮水,再到草地吃草,然后回到营地,。
河流【拓展1】路线:A——草地——河——B草地营房P点BA草地河2【例3】一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们你能给总结1.标记方向2.方向沿线最外侧标13.对角相加(方向相加)【拓展2】小虎和小羊是好朋友,它们居住的小区的平面图如下。
星期天,两人相约去博物馆看展,,问小虎去小羊家的最短路线有多少条?【例4】寒假到了,小新和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共黄山3【例5】阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;咱们学而思的小朋友都很,的最短路线分别有多少种不同的走法?学校【例6】大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从朋友,请你们快想想吧!养老院学校图书馆【例7】在图中的“我爱春蕾杯”我爱春蕾杯有种不同的读法。
爱春蕾杯春蕾杯蕾杯杯4市中心测试题1.从 A 到 B 的最短路线有几条呢?A2.阿呆和阿瓜到少年宫参加 2008 北京奥运会志愿者培训。
如果他们从学校出发,共有多少种不同的最短路线?学校3.下图是小明家和学校的示意图,亲爱的同学们,你们觉得小明从家到学校共有几条最短路线呢?学校小明家4.从甲到乙的最短路线有几条?5.小明家所在的小镇街道线路图如下,若医院禁止通行的话,从小明家到学校的最短路线有几条?6.图中的“我爱希望杯”有多少种不同的读法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路线
【例1】
如右图,直线AB表示一条公路,公路两侧有甲、乙两村。
(1)甲村要修一条通往AB的小路,最短是哪一条?在图上表示出来。
(2)如果在公路上AB上修一个加油站,使两个村子到加油站的距离之和最短,加油站该建在哪里?在图上画出路线,用N表示加油站。
【例2】A、B两村来往很多,AB两村村民想在河上建一座桥。
请问,桥建在何处,才能使两村村民来往路程最近?
【例3】小华和妈妈每天在小区里散步,小区的道路如右图,图上的数据表示各街道长度的米数。
一天,妈妈给小华出了道难题:要求从家出发,要走遍各条道路,最后回到家。
什么样的路线最短?最短是多少米?
【例4】如图,从A点到B点,不走回头路,不走重复路的条件下,可以有多少种不同的路线?请用在交叉点上标数的方法算一下。
【例5】如右图是一个景点的路线图,从入口甲出发游览景点的最短路线,有多少不同的走法?从入口乙出发游览景点的最短路线,有多少不同走法?
【强化训练】
1、一种游戏,所有队员都必须从A地出发,先到河边,再到点。
张老师在小河边做了一个记号M,请队员们直接到河边的记号处,再出发到B点,这样总路程最近。
请在小河边标出M点。
2、下图是一个街区平面图,AB=300米,BE=600米,CH=450米。
一辆电影宣传车从电影院出发,到每条街上宣传至少一次,宣传车最短路线是多少米?
3、养兔专业户养殖场内安置了5个兔笼(如下图)。
在饲料房配好食物后,为了节省每次喂食的时间,他必须走一条最短的路,但又不能漏掉一个兔笼,喂完食后还要回到原出发点。
你能替他设计一条最短的路线吗?算出每喂食一次,至少要走多少路。
4、某迷宫从A点到B点有很多道路,其中C点不通。
从A点出发到B点的最短路线有多少种?
5、如右图,从小明家到学校,最短的路线有多少条?。
