物理化学知识点归纳
北京理工大学物理化学A(南大版)上册知识点总结
物理化学上册公式总结 第一章.气体 一、理想气体适用 ①波义耳定律：定温下，一定量的气体，其体积与压力成反比 pV=C ②盖·吕萨克定律：对定量气体，定压下，体积与T成正比 V t=C`T ③阿伏伽德罗定律：同温同压下，同体积的各种气体所含分子数相同。 ④理想气体状态方程式 pV=nRT 推导：气体体积随压力温度和气体分子数量改变，即： V=f（p,T,N） 对于一定量气体，N为常数dN=0，所以 dV=（?V/?p）T,N dp+（?V/?T）p,N dT 根据波义耳定律，有V=C/P，∴（?V/?p）T,N=-C/p2=-V/p 根据盖·吕萨克定律，V=C`T，有（?V/?T）p,N=C`=V/T 代入上式，得到 dV/V=-dp/p+dT/T 积分得 lnV+lnp=lnT+常数
若所取气体为1mol，则体积为V m，常数记作lnR，即得 pV m=RT 上式两边同时乘以物质的量n，则得 pV=nRT ⑤道尔顿分压定律：混合气体的总压等于各气体分压之和。 ⑥阿马格分体积定律：在一定温度压力下，混合气体的体积等于组成该气体的各组分分体积之和。 ⑦气体分子在重力场的分布 设在高度h处的压力为p，高度h+dh的压力为p-dp，则压力差为 dp=-ρgdh 假定气体符合理想气体状态方程，则ρ=Mp/RT，代入上式， -dp/p=Mgdh/RT 对上式积分，得lnp/p0=-Mgh/RT ∴p=p0exp（-Mgh/RT） ρ=ρ0exp（-Mgh/RT）或n=n0exp（-Mgh/RT） 二、实际气体适用 ①压缩因子Z Z=pV m/RT 对于理想气体，Z=1，对实际气体，当Z大于1，表明同温度同压力下，实际气体体积大于理想气体方程计算所得结果，即实际气体的可压缩性比理想气体小。当Z小于1，情况则相反。 ②范德华方程式
初中物理化学知识点总结.doc
化学知识点的归纳总结。 一、初中化学常见物质的颜色 （一）、固体的颜色 1、红色固体：铜，氧化铁 2、绿色固体：碱式碳酸铜 3、蓝色固体：氢氧化铜，硫酸铜晶体 4、紫黑色固体：高锰酸钾 5、淡黄色固体：硫磺 6、无色固体：冰，干冰，金刚石 7、银白色固体：银，铁，镁，铝，汞等金属 8、黑色固体：铁粉，木炭，氧化铜，二氧化锰，四氧化三铁，（碳黑，活性炭） 9、红褐色固体：氢氧化铁 10、白色固体：氯化钠，碳酸钠，氢氧化钠，氢氧化钙，碳酸钙，氧化钙，硫酸铜，五氧化二磷，氧化镁 （二）、液体的颜色 11、无色液体：水，双氧水 12、蓝色溶液：硫酸铜溶液，氯化铜溶液，硝酸铜溶液 13、浅绿色溶液：硫酸亚铁溶液，氯化亚铁溶液，硝酸亚铁溶液 14、黄色溶液：硫酸铁溶液，氯化铁溶液，硝酸铁溶液 15、紫红色溶液：高锰酸钾溶液 16、紫色溶液：石蕊溶液 （三）、气体的颜色 17、红棕色气体：二氧化氮 18、黄绿色气体：氯气 19、无色气体：氧气，氮气，氢气，二氧化碳，一氧化碳，二氧化硫，氯化氢气体等大多数气体。 二、初中化学之三 1、我国古代三大化学工艺：造纸，制火药，烧瓷器。 2、氧化反应的三种类型：爆炸，燃烧，缓慢氧化。 3、构成物质的三种微粒：分子，原子，离子。 4、不带电的三种微粒：分子，原子，中子。 5、物质组成与构成的三种说法： （1）、二氧化碳是由碳元素和氧元素组成的； （2）、二氧化碳是由二氧化碳分子构成的； （3）、一个二氧化碳分子是由一个碳原子和一个氧原子构成的。 6、构成原子的三种微粒：质子，中子，电子。 7、造成水污染的三种原因： （1）工业“三废”任意排放， （2）生活污水任意排放 （3）农药化肥任意施放 8、收集方法的三种方法：排水法（不容于水的气体），向上排空气法（密度 比空气大的气体），向下排空气法（密度比空气小的气体）。
物理化学知识点总结(热力学第一定律)
物理化学知识点总结 (热力学第一定律) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
热力学第一定律 一、基本概念 1.系统与环境 敞开系统：与环境既有能量交换又有物质交换的系统。 封闭系统：与环境只有能量交换而无物质交换的系统。（经典热力学主要研究的系统） 孤立系统：不能以任何方式与环境发生相互作用的系统。 2.状态函数：用于宏观描述热力学系统的宏观参量，例如物质的量n、温度 T、压强p、体积V等。根据状态函数的特点，我们 把状态函数分成：广度性质和强度性质两大类。 广度性质：广度性质的值与系统中所含物质的量成 正比，如体积、质量、熵、热容等，这种性质的函数具 有加和性，是数学函数中的一次函数，即物质的量扩大 a倍，则相应的广度函数便扩大a倍。 强度性质：强度性质的值只与系统自身的特点有关，与物质的量无关，如温度，压力，密度，摩尔体积等。 注：状态函数仅取决于系统所处的平衡状态，而与此状态的历史过程无关，一旦系统的状态确定，其所有的状态函数便都有唯一确定的值。
二、热力学第一定律 热力学第一定律的数学表达式： 对于一个微小的变化状态为： dU= 公式说明：dU表示微小过程的内能变化，而δQ和δW则分别为微小过程的热和功。它们之所以采用不同的符号，是为了区别dU是全微分，而δQ和δW不是微分。或者说dU与过程无关而δQ和δW却与过程有关。这里的W既包括体积功也包括非体积功。 以上两个式子便是热力学第一定律的数学表达式。它们只能适用在非敞开系统，因为敞开系统与环境可以交换物质，物质的进出和外出必然会伴随着能量的增减，我们说热和功是能量的两种传递形式，显然这种说法对于敞开系统没有意义。 三、体积功的计算 1.如果系统与环境之间有界面，系统的体积变化时，便克服外力做功。将一 定量的气体装入一个带有理想活塞的容器中，活塞上部施加外压。当气体膨胀微小体积为dV时，活塞便向上移动微小距离dl，此微小过程中气
物理化学复习知识点归纳
第二章热力学第一定律 1． 系统 ①隔离系统（孤立系统）：没有物质和能量交换 ②封闭系统：只有能量交换 ③敞开系统（开放系统）：既有物质交换，又有能量交换 2． 状态函数分类 ①广度量（广度性质）：与物质数量成正比，有加和性，数学上是一次齐函数 ②强度量（强度性质）：与物质数量无关的性质，不具有加和性 *任何两个广度性质之比得出的物理量则为强度量 3．过程分类 ①恒温过程：T=T 环境=定值 ②恒压过程：P=P 环境=定值（过程中压强均相等且不变） ③等压过程：P 1 = P 2 = P amb = 常数 ④恒容过程：V=定值 ⑤绝热过程：系统与环境无热交换，Q=0 ⑥循环过程：系统从始态出发经一系列变化又回到始态的过 ⑦自由膨胀过程（向真空膨胀）：P amb （环境压强）=0 ，δW=0 ⑧可逆过程：将推动力无限小、系统内部及系统与环境之间在无限接近平衡条件下进行的过程。即P amb =P 系统+dp ，且d p ≈0 4．功和热 （1）功：途径函数 ①体积功 W=? -2 V 1 V amb dV p ，系统得到环境所作功，W ＞0；系统对环境作功，W ＜0 ②可逆功W=? - 2 V 1 V pdV （2）热：途径函数，若系统从环境吸热，Q ＞0；若系统向环境放热，Q ＜0 5．热力学能（内能）：指系统内部的所有粒子全部能量的总和，包括系统内分子平动、转动、振动能和势能等，即内能，用U 表示，U=f （T,V ），则有：dV )V U (dT )T U ( dU T V ??+??= *理想气体时，U=f （T ），恒温过程，0)V U ( T =??，即△U=0
物理化学知识点(全)
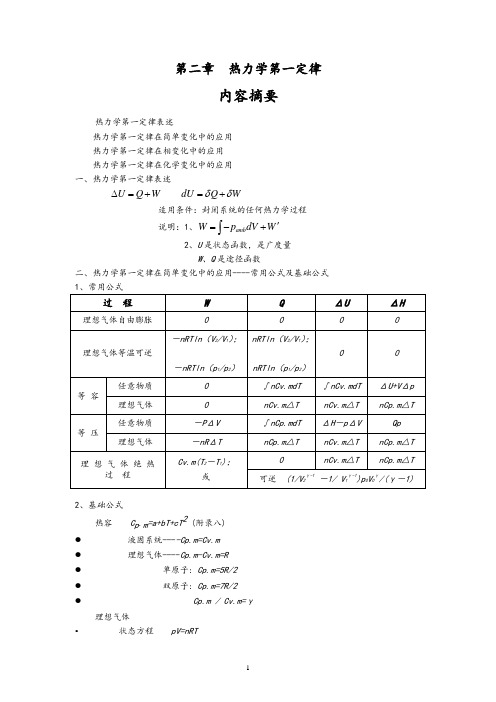
第二章 热力学第一定律 内容摘要 ?热力学第一定律表述 ?热力学第一定律在简单变化中的应用 ?热力学第一定律在相变化中的应用 ?热力学第一定律在化学变化中的应用 一、热力学第一定律表述 U Q W ?=+ d U Q W δδ=+ 适用条件：封闭系统的任何热力学过程 说明：1、amb W p dV W '=-+? 2、U 是状态函数，是广度量 W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 2、基础公式 热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ 理想气体 ? 状态方程 pV=nRT
? 过程方程 恒温:1122p V p V = ? 恒压: 1122//V T V T = ? 恒容: 1122/ / p T p T = ? 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--= 1111 22 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程 1、 可逆相变化 Q p =n Δ 相变 H m W = -p ΔV 无气体存在: W = 0 有气体相,只需考虑气体,且视为理想气体 ΔU = n Δ 相变 H m － p ΔV 2、相变焓基础数据及相互关系 Δ 冷凝H m (T) = －Δ蒸发H m (T) Δ凝固H m (T) = －Δ熔化H m (T) Δ 凝华 H m (T) = －Δ 升华 H m (T) (有关手册提供的通常为可逆相变焓) 3、不可逆相变化 Δ 相变 H m (T 2) = Δ 相变 H m (T 1) +∫Σ(νB C p.m )dT 解题要点： 1.判断过程是否可逆; 2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤; 3.除可逆相变化,其余步骤均为简单变化计算. 4.逐步计算后加和。 四、热力学第一定律在化学变化中的应用 1、基础数据 标准摩尔生成焓 Δf H θm,B (T) （附录九） 标准摩尔燃烧焓 Δc H θ m.B (T)（附录十） 2、基本公式 ?反应进度 ξ=△ξ= △n B /νB = (n B -n B.0) /νB ?由标准摩尔生成焓计算标准摩尔反应焓 Δr H θm.B (T)= ΣνB Δf H θ m.B (T) ?由标准摩尔燃烧焓计算标准摩尔反应焓 Δr H θ m.B (T)=-Σ νB Δc H θ m.B (T) (摩尔焓---- ξ=1时的相应焓值) ?恒容反应热与恒压反应热的关系 Q p =Δr H Q v =Δr U Δr H =Δr U + RT ΣνB (g) ?Kirchhoff 公式 微分式 d Δr H θ m (T) / dT=Δr C p.m 积分式 Δr H θm (T 2) = Δr H θ m (T 1)+∫Σ(νB C p.m )dT 本章课后作业： 教材p.91-96（3、4、10、11、16、17、38、20、23、24、28、30、33、34）
物理化学重点超强总结归纳
第一章热力学第一定律 1、热力学三大系统： （1）敞开系统：有物质和能量交换； （2）密闭系统：无物质交换，有能量交换； （3）隔绝系统（孤立系统）：无物质和能量交换。 2、状态性质（状态函数）： （1）容量性质（广度性质）：如体积，质量，热容量。 数值与物质的量成正比；具有加和性。 （2）强度性质：如压力，温度，粘度，密度。 数值与物质的量无关；不具有加和性，整个系统的强度性质的数值与各部分的相同。 特征：往往两个容量性质之比成为系统的强度性质。 3、热力学四大平衡： （1）热平衡：没有热隔壁，系统各部分没有温度差。 （2）机械平衡：没有刚壁，系统各部分没有不平衡的力存在，即压力相同 （3）化学平衡：没有化学变化的阻力因素存在，系统组成不随时间而变化。 （4）相平衡：在系统中各个相（包括气、液、固）的数量和组成不随时间而变化。 4、热力学第一定律的数学表达式： ?U = Q + W Q为吸收的热（+），W为得到的功（+）。
12、在通常温度下，对理想气体来说，定容摩尔热容为： 单原子分子系统 ,V m C =32 R 双原子分子（或线型分子）系统 ,V m C =52R 多原子分子（非线型）系统 ,V m C 6 32 R R == 定压摩尔热容： 单原子分子系统 ,52 p m C R = 双原子分子（或线型分子）系统 ,,p m V m C C R -=,72 p m C R = 多原子分子（非线型）系统 ,4p m C R = 可以看出： ,,p m V m C C R -= 13、,p m C 的两种经验公式：,2p m C a bT cT =++ （T 是热力学温度，a,b,c,c ’ 是经 ,2' p m c C a bT T =++ 验常数，与物质和温度范围有关） 14、在发生一绝热过程时，由于0Q δ=，于是dU W δ= 理想气体的绝热可逆过程，有：,V m nC dT pdV =- ? 22 ,11 ln ln V m T V C R T V =- 21,12ln ,ln V m p V C Cp m p V ?= ,,p m V m C pV C γγ=常数 =>1. 15、-焦耳汤姆逊系数：J T T =( )H p μ??- J T μ-＞0 经节流膨胀后，气体温度降低； J T μ-＜0 经节流膨胀后，气体温度升高； J T μ-=0 经节流膨胀后，气体温度不变。 16、气体的节流膨胀为一定焓过程，即0H ?=。 17、化学反应热效应：在定压或定容条件下，当产物的温度与反应物的温度相同而在反应过程中只做体积功不做其他功时，化学反应所 吸收或放出的热，称为此过程的热效应，或“反应热”。 18、化学反应进度：()()() n B n B B ξ ν-= 末初 （对于产物v 取正值，反应物取负值） 1ξ=时，r r m U U ξ ??= ，r r m H H ξ ??= 19、（1）标准摩尔生成焓（0 r m H ?）：在标准压力和指定温度下，由最稳定的单质生成单位物质的量某物质的定压反应热，为该物质的 标准摩尔生成焓。 （2）标准摩尔燃烧焓（0 c m H ?）：在标准压力和指定温度下，单位物质的量的某种物质被氧完全氧化时的反应焓，为该物质的标 准摩尔燃烧焓。 任意一反应的反应焓0 r m H ?等于反应物燃烧焓之和减去产物燃烧焓之和。 20、反应焓与温度的关系-------基尔霍夫方程
(完整版)生物化学知识点重点整理
一、蛋白质化学 蛋白质的特征性元素（N），主要元素：C、H、O、N、S，根据含氮量换算蛋白质含量：样品蛋白质含量=样品含氮量*6.25 （各种蛋白质的含氮量接近，平均值为16%）， 组成蛋白质的氨基酸的数量（20种），酸性氨基酸/带负电荷的R基氨基酸：天冬氨酸（D）、谷氨酸（E）； 碱性氨基酸/带正电荷的R基氨基酸：赖氨酸（K）、组氨酸（H）、精氨酸（R） 非极性脂肪族R基氨基酸：甘氨酸（G）、丙氨酸（A）、脯氨酸（P）、缬氨酸（V）、亮氨酸（L）、异亮氨酸（I）、甲硫氨酸（M）； 极性不带电荷R基氨基酸：丝氨酸（S）、苏氨酸（T）、半胱氨酸（C）、天冬酰胺（N）、谷氨酰胺（Q）； 芳香族R基氨基酸：苯丙氨酸（F）、络氨酸（Y）、色氨酸（W） 肽的基本特点 一级结构的定义：通常描述为蛋白质多肽链中氨基酸的连接顺序，简称氨基酸序列（由遗传信息决定）。维持稳定的化学键：肽键（主）、二硫键（可能存在）， 二级结构的种类：α螺旋、β折叠、β转角、无规卷曲、超二级结构， 四级结构的特点：肽键数≧2，肽链之间无共价键相连，可独立形成三级结构，是否具有生物活性取决于是否达到其最高级结构 蛋白质的一级结构与功能的关系：1、蛋白质的一级结构决定其构象 2、一级结构相似则其功能也相似3、改变蛋白质的一级结构可以直接影响其功能因基因突变造成蛋白质结构或合成量异常而导致的疾病称分子病，如镰状细胞贫血（溶血性贫血），疯牛病是二级结构改变 等电点（pI）的定义：在某一pH值条件下，蛋白质的净电荷为零，则该pH值为蛋白质的等电点（pI）。 蛋白质在不同pH条件下的带电情况（取决于该蛋白质所带酸碱基团的解离状态）：若溶液pH
初三物理化学中考知识点
园丁教育培训中心初三物理化学知识手册 姓名_________________ 年级_________________ 园丁教育王老师制作
化学部分 一、物质的学名、俗名及化学式 1、单质：金刚石、石墨、炭黑： C 汞、水银：Hg 硫、硫磺：S 2、氧化物：固体二氧化碳、干冰：CO2 氧化钙、生石灰：CaO 氧化铁、铁锈的主要成份：Fe2O3 3、酸：盐酸：HCI的水溶液碳酸（汽水）：H2CO3 4、碱：氢氧化钠、苛性钠、火碱、烧碱：NaOH 氢氧化钙、熟石灰、消石灰：Ca（OH）2 氨水、一水合氨：NH3H2O （为常见的碱，具有碱的通性，是一种不含金属离子的碱） 5、盐：碳酸钠、苏打、纯碱（不是碱，是盐）：Na2CO3, 碳酸钠晶体、纯碱晶体N32CO3 1OH2O 碳酸氢钠、小苏打：NaHCO3 大理石，石灰石的主要成份是CaCO3 食盐的主要成分是NaCI 亚硝酸钠、工业用盐：NaNO2 （有毒） 硫酸铜晶体、胆矶、蓝矶：CuSO4 5H2O 碳酸钾、草木灰的主要成份：K2CO3 碱式碳酸铜、铜绿、孔雀石：Cu2（OH）2CO3 （分解生成三种氧化物的物质） 6、有机物：甲烷、CNG、沼气、天然气的主要成份：CH4 乙醇、酒精：C2H5OH 葡萄糖：C6H12O6 甲醇：CH3OH 有毒、致失明、死亡 乙酸、醋酸（16.6 'C冰醋酸）CH3COOH （具有酸的通性） 二、常见物质的颜色和状态 1、白色固体：MgO、P2O5、CaO、NaOH、Ca（OH） 2、KCIO 3、KCI、Na2CO3、NaCI、无水 CuSO4、铁、镁为银白色（汞为银白色液态） 2、黑色固体：石墨、炭粉、铁粉、CuO、MnO2、Fe3O4 ▲KMnO 4为紫黑色 3、红色固体：Cu、Fe2O3、HgO、红磷▲ Fe（OH）3为红褐色 4、蓝色固体：硫酸铜晶体（胆矶）、氢氧化铜 ▲硫：淡黄色▲ 碱式碳酸铜CU2（OH）2CO3为绿色 5、溶液的颜色：凡含Cu2+的溶液呈蓝色；凡含Fe2+的溶液呈浅绿色；凡含Fe3+的溶液呈棕黄色，高锰酸钾溶液为紫红色；其余溶液一般无色。 6、沉淀（即不溶于水的盐和碱）：
物理化学考前复习基础知识重点考前必备
物理化学考前复习：基础知识+重点（考前必备）第一章热力学第一定律 1、热力学三大系统： （1）敞开系统：有物质和能量交换； （2）密闭系统：无物质交换，有能量交换； （3）隔绝系统（孤立系统）：无物质和能量交换。 2、状态性质（状态函数）： （1）容量性质（广度性质）：如体积，质量，热容量。 数值与物质的量成正比；具有加和性。 （2）强度性质：如压力，温度，粘度，密度。 数值与物质的量无关；不具有加和性，整个系统的强度性质的数值与各部分的相同。 特征：往往两个容量性质之比成为系统的强度性质。 3、热力学四大平衡： （1）热平衡：没有热隔壁，系统各部分没有温度差。 （2）机械平衡：没有刚壁，系统各部分没有不平衡的力存在，即压力相同
（3）化学平衡：没有化学变化的阻力因素存在，系统组成不随时间而变化。（4）相平衡：在系统中各个相（包括气、液、固）的数量和组成不随时间而变化。 4、热力学第一定律的数学表达式： ?U = Q + W Q为吸收的热（+），W为得到的功（+）。
12、在通常温度下，对理想气体来说，定容摩尔热容为： 单原子分子系统 ,V m C =32 R 双原子分子（或线型分子）系统 ,V m C =52 R 多原子分子（非线型）系统 ,V m C 632R R == 定压摩尔热容： 单原子分子系统 ,52 p m C R = 双原子分子（或线型分子）系统 ,,p m V m C C R -=,72 p m C R = 多原子分子（非线型）系统 ,4p m C R = 可以看出：,,p m V m C C R -= 13、,p m C 的两种经验公式：,2p m C a bT cT =++ （T 是热力学温度，a,b,c,c ’ 是经 ,2 ' p m c C a bT T =++ 验常数，与物质和温度范围有关） 14、在发生一绝热过程时，由于0Q δ=，于是dU W δ=
物理化学界面现象知识点
279 界面现象 1. 表面张力、表面功及表面吉布斯函数 表面张力γ：引起液体或固体表面收缩的单位长度上的力，单位为N·m -1。 表面功：'δ/d r s W A ，使系统增加单位表面所需的可逆功，单位为J·m -2。 表面吉布斯函数：B ,,()(/)s T p n G A α??，恒温恒压下系统增加单位表面时所增加的吉布斯 函数，单位为J·m -2。 表面吉布斯函数的广义定义： B()B()B()B(),,,,,,,,( )()()()S V n S p n T V n T p n s s s s U H A G A A A A ααααγ????====???? ',r s T p s W dA dG dA γδ== 表面张力是从力的角度描述系统表面的某强度性质，而表面功及表面吉布斯函数则是从能量角度和热力学角度描述系统表面的某一性质。三者虽为不同的物理量，但它们的数值及量纲等同的，均可化为N·m -1。 在一定温度、压力下，若系统有多个界面，其总界面吉布斯函数： s i i s i G A γ=∑ 2. 弯曲液面的附加压力、拉普拉斯方程 附加压力：Δp =p 内-p 外 拉普拉斯方程：2p r γ?= 规定弯曲液面凹面一侧压力位p 内，凸面一侧压力位p 外；γ为表面张力；r 为弯曲液面的曲率半径，△p 一律取正值；附加压力方向总指向凹面曲率半径中心。 3. 毛细现象 毛细管内液体上升或下降的高度 2cos h r g γθρ= 式中：γ为表面张力；ρ为液体密度；g 为重力加速度；θ为接触角；r 为毛细管半径。当液体不能润湿管壁，θ>90°即0cos θ<时，h 为负值，表示管内凸液体下降的深度。 4. 微小液滴的饱和蒸汽压——开尔文公式
物理化学知识点总结(热力学第一定律)
热力学第一定律 一、基本概念 1、系统与环境 敞开系统:与环境既有能量交换又有物质交换的系统。 封闭系统:与环境只有能量交换而无物质交换的系统。(经典热力学 主要研究的系统) 孤立系统:不能以任何方式与环境发生相互作用的系统。 2、状态函数:用 于宏观描述热力学系 统的 宏观 参量,例如物质的量n、温度T、压强p、体积V等。根据状态函数的特点,我们把状 态函数分成:广度性质与强度性质两大类。 广度性质:广度性质的值与系统中所含物质的量成正比,如体积、质量、熵、热容等,这种性质的函数具有加与性,就是数学函数中的一次函数,即物 质的量扩大a倍,则相应的广度函数便扩大a倍。 强度性质:强度性质的值只与系统自身的特点有关,与物质的量无关,如温度,压力,密度,摩尔体积等。 注:状态函数仅取决于系统所处的平衡状态,而与此状态的历史过程无关,一旦系统的状态确定,其所有的状态函数便都有唯一确定的值。 二、热力学第一定律 热力学第一定律的数学表达式: 对于一个微小的变化状态为: dU= 公式说明:dU表示微小过程的内能变化,而δQ与δW则分别为微小过程的热与功。它们之所以采用不同的符号,就是为了区别dU就是全微分,而δQ与δW不就是微分。或者说dU与过程无关而δQ与δW却与过程有关。这里的W既包括体积功也包括非体积功。 以上两个式子便就是热力学第一定律的数学表达式。它们只能适用在非敞开系统,因为敞开系统与环境可以交换物质,物质的进出与外出必然会伴随着能量的增减,我们说热与功就是能量的两种传递形式,显然这种说法对于敞开系统没有意义。 三、体积功的计算 1、如果系统与环境之间有界面,系统的体积变化时,便克服外力做功。将一定量的气体装入 一个带有理想活塞的容器中,活塞上部施加外压。当气体膨胀微小体积为dV 时,活塞便向上移动微小距离dl,此微小过程中气体克服外力所做的功等于作用
物理化学简明教程(重点内容)
第一章 【理想气体的能与焓只是温度的函数，与体积或压力的变化无关，所以对理想气体 定温过程：dU=0，dH=0，△U=0，△H=0变温过程：△U=nC v,m △T ；△H=nC p,m △T 节流膨胀：（特点）绝热、定焓，∴Q=0，△H=0，无论是理想气体还是实际气体均成立】 1.理想气体的状态方程可表示为： pV=nRT 2.能量守恒定律：自然界的一切物质都具有能量，能量有各种不同形式，能够从一种形式转化为另一种形式，但在转化过程中，能量的总值不变。 3.第一定律的数学表达式：△U=Q+W ；对微小变化：dU=δQ +δW （因为热力学能是状态函数，数学上具有全微分性质，微小变化可用dU 表示；Q 和W 不是状态函数，微小变化用δ表示，以示区别。） 4.膨胀作功：①自由膨胀：W=0；②等外压膨胀：W=-P 外(V 2-V 1)=P 2（V 1-V 2）； ③可逆膨胀：W=nRT ln 2 1V V =nRT ln 1 2P P ；④多次等外压膨胀，做 的功越多。 5.①功与变化的途径有关。不是状态函数。 ②可逆膨胀，体系对环境作最大功；可逆压缩，环境对体系作最小功。 6.恒温恒压的可逆相变 W=RT V P dV dP P dV P i V V i V V e n )(2 1 2 1 -=-=--=-??△(恒温恒压的可 逆相变,气体符合理想气体方程) 7.焓的定义式：H=U+PV ，等压效应H =Q p △，焓是容量性质。 8.理想气体的热力学能和焓仅是温度的函数：在恒温时，改变体积或压力，理想气体的热力学能和焓保持不变。还可以推广为理想气体的Cv,Cp 也仅为温度的函数。
硅物化知识点整理
第一章相平衡习题与解答1. 解释下列名词：凝聚系统，介稳平衡，低共熔点，双升点，双降点，马鞍点，连线规则，切线规则，三角形规则，重心规则。 解：凝聚系统：不含气相或气相可以忽略的系统。 介稳平衡：即热力学非平衡态，能量处于较高状态，经常出现于硅酸盐系统中。 低共熔点：是一种无变量点，系统冷却时几种晶相同时从熔液中析出，或加热时同时融化。 双升点：处于交叉位的单转熔点。 双降点：处于共轭位的双转熔点。 马鞍点：三元相图界线上温度最高点，同时又是二元系统温度的最低点。 连线规则：将一界线（或其延长线）与相应的连线（或其延长线）相交，其交点是该界线上的温度最高点。 切线规则：将界线上某一点所作的切线与相应的连线相交，如交点在连线上，则表示界线上该处具有共熔性质；如交点在连线的延长线上，则表示界线上该处具有转熔性质，远离交点的晶相被回吸。 三角形规则：原始熔体组成点所在副三角形的三个顶点表示的物质即为其结晶产物；与这三个物质相应的初初晶区所包围的三元无变量点是其结晶结束点。 重心规则：如无变点处于其相应副三角形的重心位，则该无变点为低共熔点：如无变点处于其相应副三角形的交叉位，则该无变点为单转熔点；如无变点处于其相应副三角形的共轭位，则该无变点为双转熔点。 2、在三元系统的相图分析中，切线规则与连线规则分别是如何在相图中应用的？分析两个规则的应用原理与范围。 解：切线规则用在判断三元系统相图中，各界线的性质即界线上的任一点在析晶过程中发生什么反应，是一致熔过 程还是转熔过程。 过界线上任一点切线，与对应的连线相 交，则是低共熔过程。与延长线相交， 为转熔过程。连线规则用在判断三元系 统相图中，各界线上的温度变化。即连 线与相应界线相交，交点是连线上的温 度最低点，又是界线上的温度最高点。 4. SiO2具有很高的熔点，硅酸盐玻璃的 熔制温度也很高。现要选择一种氧化物 与SiO2在800℃的低温下形成均一的 二元氧化物玻璃，请问，选何种氧化 物？加入量是多少？ 解：根据Na2O－SiO2系统相图可知最 低共熔点为799℃。故选择Na2O能与 SiO2在800℃的低温下形成均一的二 元氧化物玻璃。 10．相律应用必须注意哪几点？ 答：(1)相律是根据热力学平衡条件推 导而得，因而只能处理真实的热力学平 衡体系。 (2)相律表达式中的“2”是代表外 界条件温度和压强。如果电场、磁场或 重力场对平衡状态有影响，则相律中的 “2”应为“3”、“4”、“5”。如果 研究的体系为固态物质，可以忽略压强 的影响，相律中的“2”应为“1”。 (3)必须正确判断独立组分数、独 立化学反应式、相数以及限制条件数， 才能正确应用相律。 (4)自由度只取“0”以上的正值。 如果出现负值，则说明体系可能处于非 平衡态。 12．淬冷法的最大优点有哪些？适用的 对象是什么？ 答：最大优点：准确度高。因为长时间 保温较接近平衡状态，淬冷后在室温下 又可对试样中平衡共存的相数、各相的 组成、形态和数量直接进行测定。 适用对象：适用于相变速度慢的系 统，如果快则在淬冷时发生相变。 14．稳定相与介稳相的区别是什么？ 答：(1) 每一个稳定相有一个稳定存在 的温度范围，超过这个范围就变成介稳 相。 (2) 在一定温度下，稳定相具有最 小蒸汽压。 (3) 介稳相有向稳定相转变的趋 势，但从动力学角度讲，转变速度很慢， 能长期保持自己的状态。 15．在耐火材料硅砖的生产中，为什么 鳞石英含量越多越好，而方石英越少越 好？ 答：石英、鳞石英和方石英三种变体的 高低温型转变中，方石英?V变化最 大，石英次之，而鳞石英最小。如果制 品中方石英含量大，则在冷却到低温 时，由于α-方石英转变成β -方石英有 较大的体积收缩而难以获得致密的硅 砖制品。 16．三元系统组成的表示方法？在三元 系统组成中有哪些关系？ 答：表示方法：在三元系统中用等边三 角形来表示组成。 关系：⑴等含量规则；⑵定比例规 则；⑶杠杆规则；⑷重心规则；⑸交叉 位置规则；⑹共轭位置规则。 17.在三元系统中有哪几条重要规则？ 它们的用途和定义分别是什么？ 答：⑴连线规则： 用途：用来判断界线的温度走向。 定义：将界线(或延长线)与相应的 连线相交，其交点是该界线上的温度最 高点；温度走向是背离交点。 ⑵切线规则： 用途：用于判断三元相图上界线的性 质。 定义：将界线上的某一点所作的切线 与相应的组成的连线相交，如交点在连 线上，则表示界线上该处具有共熔性 质；如交点在连线的延长线上，则表示 界线上该处具有转熔性质，远离交点的 晶相被回吸。 ⑶重心规则： 用途：用于判断无变量点的性质。
大学物理化学知识点归纳
第一章气体的pvT关系 一、理想气体状态方程 pV=（m/M）RT=nRT （1.1） 或pV m =p（V/n）=RT （1.2） 式中p、V、T及n的单位分别为 P a 、m3、K及mol。V m =V/n称为气 体的摩尔体积，其单位为m3·mol。R=8.314510J·mol-1·K-1称为摩尔气体常数。 此式适用于理想，近似于地适用于低压下的真实气体。 二、理想气体混合物 1．理想气体混合物的状态方程（1.3） pV=nRT=（∑ B B n）RT pV=mRT/M mix （1.4） 式中M mix 为混合物的摩尔质量，其可表示为 M mix def ∑ B B y M B (1.5) M mix =m/n=∑ B B m/∑ B B n （1.6） 式中M B 为混合物中某一种组分B 的摩尔质量。以上两式既适用于各种 混合气体，也适用于液态或固态等均 匀相混合系统平均摩尔质量的计算。 2.道尔顿定律 p B =n B RT/V=y B p （1.7） P=∑ B B p (1.8) 理想气体混合物中某一种组分B 的分压等于该组分单独存在于混合气 体的温度T及总体积V的条件下所具 有的压力。而混合气体的总压即等于 各组分单独存在于混合气体的温度、 体积条件下产生压力的总和。以上两 式适用于理想气体混合系统，也近似 适用于低压混合系统。
3.阿马加定律 V B *=n B RT/p=y B V （1.9） V=∑V B * （1.10） V B *表示理想气体混合物中物质B 的分体积，等于纯气体B在混合物的温度及总压条件下所占有的体积。理想气体混合物的体积具有加和性，在相同温度、压力下，混合后的总体积等于混合前各组分的体积之和。以上两式适用于理想气体混合系统，也近似适用于低压混合系统。 三、临界参数 每种液体都存在有一个特殊的温度，在该温度以上，无论加多大压力，都不可能使气体液化，我们把 这个温度称为临界温度，以T c 或t c 表 示。我们将临界温度T c 时的饱和蒸气 压称为临界压力，以p c 表示。在临界温度和临界压力下，物质的摩尔体积 称为临界摩尔体积，以V m,c 表示。临 界温度、临界压力下的状态称为临界 状态。 四、真实气体状态方程 1.范德华方程 （p+a/V m 2）(V m -b)=RT (1.11) 或（p+an2/V2）(V-nb)=nRT (1.12) 上述两式中的a和b可视为仅与 气体种类有关而与温度无关的常数， 称为范德华常数。a的单位为Pa·ｍ ６·mol，b的单位是m3mol.-1。该方 程适用于几个兆帕气压范围内实际气 体p、V、T的计算。 2.维里方程 Z(p，T)=1+Bp+Cp+Dp+… （1.13） 或Z(V m, ,T)=1+B/V m +C / V m 2 +D/ V m 3 +… （1.14）
初中物理化学知识点
初中物理重要知识点总结
记住的常量
1．光（电磁波）在真空中传播得最快，c=3×105Km/s=3×108m /s。光在其它透明物质中传播比在 空气中传播都要慢 2．15℃的空气中声速：340m／s，振动发声 ，声音传播需要介质，声音在真空中不能传播。一般声 音在固体中传播最快，液体中次之，气体中最慢。 3．水的密度：1．0×103Kg／m3=1g／cm3=1．0Kg／dm3。 1 个标准大气压下的水的沸点：100℃，冰的熔点 O℃， 水的比热容 4．2×103J／(Kg·℃)。 4．g=9．8N/Kg，特殊说明时可取 10 N/Kg 5．一个标准大气压=76cmHg==760mmHg=1．01×105Pa=10.3m 高水柱。 6．几个电压值：1 节干电池 1.5V，一只铅蓄电池 2V。 照明电路电压 220V，安全电压不高于 36V。 7．1 度=1 千瓦·时（kwh）=3．6×106J。 8．常见小功率用电器：电灯、电视、冰箱、电风扇； 常见大功率用电器：空调、电磁炉、电饭堡、微波炉、电烙铁。
物理量的国际单位
长度（L 或 s） ：米（m） 时间（t） ：秒（s）面积（S） ：米 2（m2）体积（V） ：米 3（m3）速度（v） ：米/秒（m/s）温度（t） ： 摄氏度（℃） （这是常用单位） 质量（m） ：千克（Kg）密度（ρ ） ：千克/米 3（Kg/m3） 。力（F） ：牛顿（N）功（能，电功，电能） （W） ：焦耳（J） 功率（电功率） （P） ：瓦特（w）压强（p） ：帕斯卡（Pa）机械效率（η ）热量（电热） （Q） ：焦耳（J） 比热容（c） ：焦耳/千克 摄氏度（J/Kg℃）热值（q） ：J/kg 或 J/m3 电流（I） ：安培（A）电压（U） ：伏特（V） 电阻（R） ：欧姆（Ω ） 。
单位换算
1nm=10-9m,1mm=10-3m,1cm=10-2m;1dm=0.1m,1Km=103m,1h=3600s,1min=60s, 1Kwh=3.6×106J.1Km/h=5/18m/s=1/3.6m/s,1g/cm3=103Kg/m3,1cm2=10-4m2, 1cm3=1mL=10-6m3,1dm3=1L=10-3m3, 词冠：m 毫(10-3)，μ 微(10-6)，K 千（103） ，M 兆(106)
公式
1.速度 v=s/t； 2.密度ρ =m/v； 3.压强 P=F/s=ρ gh； 4.浮力 F=G 排=ρ 液 gV 排=G（悬浮或漂浮）=F 向上-F 向下=G-F’ ； 5.杠杆平衡条件：F1L1=F2L2；6.功 w=Fs=Gh（克服重力做功）=Pt；7.功率 p=W/t=Fv； 8.机械效率η =W 有/W 总=Gh/Fs=G/nF=G/(G+G 动) =fL/Fs(滑轮组水平拉物体克服摩擦力作功)； 9.热量：热传递吸放热 Q=cm△t；燃料完全燃烧 Q=mq=Vq；电热：Q= I2Rt 10．电学公式：电流：I=U/R=P/U 电阻：R=U/I=U2/P 电压：U=IR=P/I 电功：W=Pt =UIt =I2Rt=U2t/R 电热：Q= I2Rt（焦耳定律）=UIt==U2t/R 电功率：P=W/t= UI=I2R=U2/R 串联电路特点：I=I1=I2,U=U1+U2,R=R1+R2 U1:U2=P1:P2=Q1:Q2=W1:W2=R1:R2 并联电路特点：I=I1+I2,U=U1=U2,1/R=1/R1+1/R2 I1:I2=P1:P2=Q1:Q2=W1:W2=R2:R1
1
物理化学复习资料
《物理化学》课程期末复习资料 《XXX》课程讲稿章节目录： 绪论 第一章热力学第一定律 第一节热力学概论 第二节热力学基本概念 第三节热力学第一定律 第四节体积功与可逆过程 第五节热、热容与焓 第六节热力学第一定律应用 第七节热化学 第八节化学反应热效应计算 第二章热力学第二定律 第一节卡诺循环与卡诺定律 第二节热力学第二定律的表述 第三节熵函数 第四节熵变的计算 第五节熵函数的物理意义 第六节热力学第三定律 第七节吉布斯能和亥姆霍兹能 第八节热力学函数间关系 第九节吉布斯能和亥姆霍兹能计算 第三章多组分系统热力学 第一节多组分系统组成表示法 第二节偏摩尔量 第三节化学势 第四节液相多组分体系两个经验定律 第五节气体化学势 第六节液体混合物和稀溶液组分化学势
第七节稀溶液的依数性 第八节分配定律 第四章化学平衡 第一节化学反应等温方程 第二节化学反应平衡常数 第三节平衡常数计算和化学转化率 第四节反应标准吉布斯自由能和化合物标准生成吉布斯自由能第五节温度对平衡常数的影响 第六节其他因素对平衡常数的影响 第七节反应耦合 第五章相平衡 第一节相率 第二节单组份系统 第三节双组份系统（1） 第四节双组份系统（2） 第五节双组份系统（3） 第六章电化学 第一节电化学基本概念 第二节电解质溶液电导测定与应用 第三节电解质溶液活度与活度系数 第四节可逆电池 第五节电极电势和电池电动势 第六节可逆电池热力学 第七节电池种类 第八节电池电动势测量与应用 第九节电极极化和过点位 第七章化学动力学 第一节反应速率的表示与测量 第二节反应速率方程 第三节简单级数反应的速率方程
2020高考物理化学知识点归纳
2020高考物理化学知识点归纳 第一章气体的pvT关系 一、理想气体状态方程 pV=（m/M）RT= nRT （1.1）或pV m=p（V/n）=RT （1.2）式中p、V、T及n的单位分别为P a、m3、K及mol。V m=V/n称为气体的摩尔体积，其单位为m3·mol。R=8.314510J·mol-1·K-1称为摩尔气体常数。 此式适用于理想，近似于地适用于低压下的真实气体。 二、理想气体混合物 1．理想气体混合物的状态方程（1.3） pV=nRT=（∑ B B n）RT pV=mRT/M mix （1.4）式中M mix为混合物的摩尔质量，其可表示为 M mix def∑ B B y M B (1.5) M mix=m/n=∑ B B m/∑ B B n （1.6） 式中M B为混合物中某一种组分B的摩尔质量。以上两式既适用于各种混合气体，也适用于液态或固态等均匀相混合系统平均摩尔质量的计算。 2.道尔顿定律 p B=n B RT/V=y B p （1.7） P=∑ B B p(1.8) 理想气体混合物中某一种组分B的分压等于该组分单独存在于混合气体的温度T及总体积V的条件下所具有的压力。而混合气体的总压即等于各组分单独存在于混合气体的温度、体积条件下产生压力的总和。以上两式适用于理想气体混合系统，也近似适用于低压混合系统。 3.阿马加定律 V B*=n B RT/p=y B V （1.9）V=∑V B* （1.10）V B*表示理想气体混合物中物质B的分体积，等于纯气体B在混合物的温度及总压条件下所占有的体积。理想气体混合物的体积具有加和性，在相同温度、压力下，混合后的总体积等于混合前各组分的体积之和。以上两式适用于理想气体混合系统，也近似适用于低压混合系统。 三、临界参数 每种液体都存在有一个特殊的温度，在该温度以上，无论加多大压力，都不可能使气体液化，我们把这个温度称为临界温度，以T c或t c表示。我们将临界温度T c时的饱和蒸气压
物理化学知识点总结
第一章 热力学第一定律 一、基本概念 系统与环境，状态与状态函数，广度性质与强度性质，过程与途径，热与功，内能与焓。 二、基本定律 热力学第一定律：ΔU =Q +W 。 焦耳实验：ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式 1、体积功的计算 δW = －p e d V 恒外压过程：W = －p e ΔV 可逆过程：12 21ln ln p p nRT V V nRT W == 2、热效应、焓 等容热：Q V =ΔU （封闭系统不作其他功） 等压热：Q p =ΔH （封闭系统不作其他功） 焓的定义：H =U +pV ; d H =d U +d(pV ) 焓与温度的关系：ΔH =?2 1 d p T T T C 3、等压热容与等容热容 热容定义：V V )(T U C ??=；p p )(T H C ??=
定压热容与定容热容的关系：nR C C =-V p 热容与温度的关系：C p =a +bT +c’T 2 四、第一定律的应用 1、理想气体状态变化 等温过程：ΔU =0 ; ΔH =0 ; W =－Q =?-p e d V 等容过程：W =0 ; Q =ΔU =?T C d V ; ΔH =?T C d p 等压过程：W =－p e ΔV ; Q =ΔH =?T C d p ; ΔU =?T C d V 可逆绝热过程：Q =0 ; 利用p 1V 1γ=p 2V 2γ 求出T 2, W =ΔU =?T C d V ;ΔH =?T C d p 不可逆绝热过程： Q =0 ; 利用C V (T 2-T 1)=－p e (V 2-V 1)求出T 2, W =ΔU =?T C d V ;ΔH =?T C d p 2、相变化 可逆相变化：ΔH =Q =n Δ＿H ； Ｗ＝－p (V 2-V 1)=－pV g =－nRT ; ΔU =Q +W 3、热化学 物质的标准态；热化学方程式；盖斯定律；标准摩尔生成焓。 摩尔反应热的求算：)298,()298(B H H m f B m r θθν?=?∑