桁架的有限元分析
桁架有限元分析ppt课件

以图26所示的空间 桁架节点 3 为例,说 明总刚矩阵及总刚方 程的建立。该桁架共 有9个单元,5个节点, 单元及节点编号如图 示。相交于节点3的杆 件有⑥⑦⑧⑨。
图3.26 单元及节点编号
➢ 变形协调条件为连于同一节点上的杆端位移相 等 ,即:
➢ 内外力平衡条件为汇交于同一节点的杆端内力 之和等于该节点上的外荷载,即:
➢ (10)按杆件内力调整杆件截面,并重新计算, 迭代次数宜不超过4~5次。
➢
Ec——K支cx承柱3的EH材c料3Ic弹y 性模量K;cy
3E c I cx H3
➢ Icy、Icx——分别为支承柱绕截面y、x轴的截面惯 性矩;
➢ H——支承悬臂柱长度。
(3)斜边界处理 ➢ 斜边界是指与整体坐标斜交的方向有约束的边界。 ➢ 建筑平面为圆形或多边形的网架会存在斜边界( 图3.27a)。 ➢ 矩形平面网架利用对称性时,对称面也存在斜边 界(图3.27b,c)。
基本未知量
节点平衡及变形协调条件
总刚度矩阵 总刚度方程
引入边界条件
节点位移值
单元内力与节点位移间关系
杆件内力
3.4.1网架计算基本假定
➢ 网架的节点为空间铰接节点,杆件只承受轴 力;
➢ 结构材料为完全弹性,在荷载作用下网架变 形很小,符合小变形理论。
奥运会场馆
鸟巢
3.4.2单元刚度矩阵
一等截面空间桁架杆件ij如图所示,设局部直角坐
图3.27 网架的斜边界约束
➢ 斜边界有两种处理方法,一种是根据边界点的 位移约束情况设置具有一定截面积的附加杆, 如节点沿边界法线方向位移为零,则该方向设 一刚度很大的附加杆,截面积A=106~108(图 3.27b);如该节点沿边界法线方向为弹性约束, 则调节附加杆的截面积,使之满足弹性约束条 件。这种处理方法有时会使刚度矩阵病态。
桁架的有限元分析w

桁架的有限元分析问题:已知模型由轨座,桁架以及垫块三个部分组成。
载荷为186吨,加载与距中间400mm 处的轨座上。
材料为Q345钢,密度为33/108.7m kg ⨯,弹性模量为5102⨯MPa ,泊松比为0.3,摩擦系数为0.05。
要求对模型使用ANSYS 进行有限元分析,分析其安全性。
问题分析:模型是对称的,可以简化模型,用模型的四分之一进行ANSYS 有限元分析,可以减少计算量。
需要在两个剖面处施加对称约束,从而保证中间部分不发生位移。
垫块的底部需要添加一个全约束以防止刚体位移。
图1为简化的模型。
图1 模型建模以及运算1将模型导入将所给的模型文件dggl.sat 导入到ANSYS 中,补充完整模型,即添加垫块。
再将模型分割,得到简化后的模型,即图1。
2 划分网格将轨座和桁架分割成规整的方体,使用映射网格来将轨座和桁架划分成六面体网格,可以得到比较规整的网格。
使用扫掠划分将垫块划分成六面体网格,网格大小设定为15mm。
划分结果如图2。
图2 网格化分3 设置单元类型对于实体模型分析,我们可选用8节点SOLID185单元。
整个分析过程有关于非线性接触的问题,所以要设置接触对单元类型。
选择TARGET170和CONTACT174单元。
4接触对创建使用设置接触对向导Contact Manager来设置。
设置轨座下表面和垫块上表面作为接触面,桁架为两接触面所对应的目标面。
其中轨座与桁架的接触对需设置成绑定接触,以防止发生滑移。
创建的接触对如图3所示。
图3 接触对的创建图4 边界条件5 添加约束施加约束,要在整体模型的中间部分施加对称约束以及对垫块施加全约束,从而保证无刚体位移。
如图4所示。
6 添加载荷选择距YOZ平面400毫米处的线,加集中载荷力为1860KN,方向为竖直向下,即Y的负向。
加载结果如图5所示。
图5 添加集中力载荷7 设置材料参数和载荷步在Material Models中,设置弹性模量EX为2e5(单位为兆帕),泊松比PRXY 为0.3;材料的密度Density为7.8e-9(单位为千克每立方毫米);摩擦系数Friction coefficient为0.05。
第9章 桁架和梁的有限元分析

第9章桁架和梁的有限元分析第1节基本知识一、桁架和梁的有限元分析概要1.桁架杆系的有限元分析概要桁架杆系系统的有限元分析问题是工程中最常见的结构形式之一,常用在建筑的屋顶、机械的机架及各类空间网架结构等多种场合。
桁架结构的特点是,所有杆件仅承受轴向力,所有载荷集中作用于节点上。
由于桁架结构具有自然离散的特点,因此可以将其每一根杆件视为一个单元,各杆件之间的交点视为一个节点。
2.梁的有限元分析概要梁的有限元分析问题也是是工程中最常见的结构形式之一,常用在建筑、机械、汽车、工程机械、冶金等多种场合。
梁结构的特点是,梁的横截面均一致,可承受轴向、切向、弯矩等载荷。
根据梁的特点,等截面的梁在进行有限元分析时,需要定义梁的截面形状和尺寸,用创建的直线代替梁,在划分网格结束后,可以显示其实际形状。
二、桁架和梁的常用单元桁架和梁常用的单元类型和用途见表9-1。
通过对桁架和梁进行有限元分析,可得到其在各个方向的位移、应力并可得到应力、位移动画等结果。
第2节 桁架的有限元分析实例一、案例1——2D 桁架的有限元分析图9-1 人字形屋架的示意图 问题人字形屋架的几何尺寸如图9-1所示。
杆件截面尺寸为0.01m 2,试进行静力分析,对人字形屋架进行静力分析,给出变形图和各点的位移及轴向力、轴力图。
条件人字形屋架两端固定,弹性模量为2.0×1011 N/m 2,泊松比为0.3。
解题过程制定分析方案。
材料弹性材料,结构静力分析,属2D 桁架的静力分析问题,选用Link1单元。
建立坐标系及各节点定义如图9-1所示,边界条件为1点和5点固定,6、7、8点各受1000 N 的力作用。
1.ANSYS 分析开始准备工作(1)清空数据库并开始一个新的分析 选取Utility>Menu>File>Clear & Start New ,弹出Clears database and Start New 对话框,单击OK 按钮,弹出Verify 对话框,单击OK 按钮完成清空数据库。
桁架结构的有限元法

桁架结构的有限元法单元坐标系下的单元平衡方程为单元坐标系下的单元平衡方程为图1. i u v {u v u v u u v v {}u v e u v q u v图2.与位移不同的是,杆的轴向力U 和总体系下的力{,}TU V 是等价的(如图U V eU V U Vq ee K q P K l所示的简单桁架结构。
进行整体桁架结构分析?为说明分析方法,考虑图3所示的简单桁架结构。
总体系下的节点位移和力向量为总体系下的节点位移和力向量为总体平衡方程具有如下形式:总体平衡方程具有如下形式:是数学上定义的,它的重要性质是:只于坐标, (1+注意,本问题中的坐标, (1,,)ix i n = 相当于函数()u x 的定义区间图4 解:单元1的单刚的单刚113133333[]413133333e EA K l éù--êú--êú=êú--êúêú--ëû单元2的单刚的单刚213133333[]413133333e EA K l éù--êú--êú=êú--êúêú--ëû 总刚阵总刚阵1313330033001313[]4003333131320333306EA K l éù--êú--êúêú--êú=êú--êúêú---êú---ëû节点位移向量节点位移向量33{}{0000}T u u v =节点力向量节点力向量22{}{}22T P PP =´´´´故有故有332020642u P EA v P l ìüéùìü=íýíýêúëûîþîþ2Pl62)62)36262) 3。
弹性力学与有限元分析第二章-平面桁架有限元分析及程序设计

x
由单元①的刚度方程:
Fj
①
k
① ji
i
①
k
① jj
j
①
k
① ji
2
k
① jj
1
由单元③的刚度方程:
Fj
③
k
③ ji
i
③
k
③ jj
j
③
k
③ ji
3
k
③ jj
1
§2.3 结点平衡与整体刚度矩阵的集成
代入结点1的平衡条件:
k
l
xi
)
(dx j
dxi
)
(
yj
l
yi )
(dy j
dyi )
(dx j dxi ) (dy j dyi )
cos sin
由于杆件的变形产生位移:
ui dxi vi dyi
u j dxj v j dy j
因此,杆件应变为:
dl l
l
(ui
uj)
l
(vi
vj)
杆件轴力为:
(2k1 k2 )v4 P
结构的整体刚度系数
v4
P 2k1
k2
12 3
l2 l1 l1
4 P
N1
N1y
cos
k1v4
cos
k1P
(2k1 k2 ) cos
N2
k2v4
k2P 2k1 k2
位移法求解超静定结构。
§2.1 平面桁架单元的离散
结构的离散化:尽量将结构离散成数量最少的等截面直 杆单元
kki③ ③jii
ki③j
k
③ jj
3 3 3 3
§2.3 结点平衡与整体刚度矩阵的集成
实例1 四杆桁架结构有限元分析
(2)计算支反力: 将求得的节点位移代入整体刚度方程 得:
四杆桁架结构有限元分析(5)
ANSYS求解
基于图形界面(GUI)的交互式操作(step by step) 命令流方式
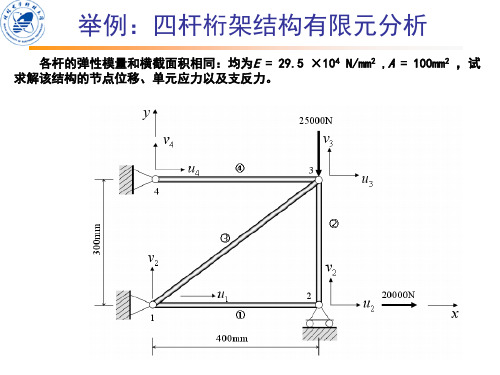
举例:四杆桁架结构有限元分析
各杆的弹性模量和横截面积相同:均为E = 29.5 ×104 N/mm2 ,A = 100mm2 ,试 求解该结构的节点位移、单元应力以及支反力。
四杆桁架结构有限元分析(1)
Step1.结构的离散化与编号
节点及坐标(对该结构进行自然离散)
节点
1 2 3 4
x
0 400 400 0
Step3.组装整体刚度方程
各个单元刚度矩阵/节点载荷按节点编号进行组装。
四杆桁架结构有限元分析(4)
Step4.处理边界条件求解
边界条件BC(u):
代入整体方程并化简得:
所有节点位移:
四杆桁架结构有限元分析(5)
Step5.计算其他力学分量
(1)计算单元应力:
杆单元的转换矩阵及节点位移(此处省 略了上角标)
yห้องสมุดไป่ตู้
0 0 300 300
单元编号及对应节点 单元 ① ② 节点 1 3 2 2 2
各单元的长度及轴线方向余弦
单元 ① ② ③ ④ l 400 300 500 400 nx 1 0 0.8 1 ny 0 -1 0.6 0
③
④
1
4
3
3
四杆桁架结构有限元分析(2)
Step2.单元描述
四杆桁架结构有限元分析(3)
基于ANSYS的平面桁架有限元分析.

PREP7 !* ET,1,LINK180 !* R,1,10, ,0 !* !* MPTEMP,,,,,,,, MPTEMP,1,0 MPDATA,EX,1,,2.0e6 MPDATA,PRXY,1,,0.3 WPSTYLE,,,,,,,,0 WPSTYLE,,,,,,,,1 WPSTYLE,,,,,,,,0 WPSTYLE,,,,,,,,1 FLST,3,1,8 FITEM,3,0,0,0 N, ,P51X FLST,3,1,8 FITEM,3,30,0,0 N, ,P51X FLST,3,1,8 FITEM,3,0,30,0 N, ,P51X FLST,3,1,8 FITEM,3,30,30,0 N, ,P51X FLST,3,1,8 FITEM,3,60,30,0
5
数值解与解析解的比较与分析
求出了平面桁架的数值解与解析解,现将两 者的结果进行列表对比
数值解与解析解的比较与分析
表2 整体坐标系下各节点的位移(in)
节点 解析解
U1x 0 0
U1y 0 0
U2x -0.0029 -0.002925
U2y -0.0085 -0.0084404
U3x 0 0
U3y 0 0
基于AN限元分析
平面桁架是工程中常见的结构,本文基于ANSYS平台对平面桁架进行有 限元分析。 首先通过有限元法的理论知识求得平面桁架在一定工况下的理论值,然 后利用ANSYS进行分析得到数值解,最后通过比较理论解与数值解得出结论。 利用ANSYS对平面桁架进行有限元分析,可以提取其他分析结果,对深 入研究平面桁架问题提供了强有力手段,也对其他结构问题的有限元分析具 有指导性意义与价值。
数值解与解析解的比较与分析
表4 单元①的内力与正应力(lb)
桁架结构及有限元分析MATLAB

桁架结构及有限元分析MATLAB桁架结构是一种由杆件和节点连接而成的结构系统。
它的主要特点是具有良好的刚性和承载能力,适用于跨度较大的建筑物或桥梁。
桁架结构的设计和分析是工程领域中重要的课题。
有限元分析是一种常用的方法,用于对桁架结构进行力学和结构分析。
MATLAB是一种强大的数学建模和计算工具,可以方便地进行有限元分析。
在进行桁架结构的有限元分析之前,首先需要进行结构的建模。
可以使用MATLAB中的节点和杆件来建立桁架结构的几何模型。
节点代表结构中的连接点,杆件代表连接节点的杆件。
接下来,需要将结构分割为有限元网格。
在MATLAB中,可以使用二维和三维有限元网格生成函数来生成网格。
生成的网格可以根据需要的精度进行调整。
每个有限元包含一个或多个节点和杆件,用于描述局部的力学行为。
在有限元分析中,需要考虑材料的力学性质。
可以通过定义材料的模量、泊松比和密度等参数来描述材料的本构关系。
在MATLAB中,可以使用材料库函数来定义不同材料的力学性质。
进行有限元分析时,需要考虑结构的边界条件和加载条件。
边界条件包括固定边界和位移约束,加载条件可以是力、压力或扭矩等。
在MATLAB中,可以使用边界条件函数来定义结构的边界条件和加载条件。
在有限元分析的过程中,需要对结构进行求解。
可以使用线性或非线性求解算法来计算结构的位移和应力等。
MATLAB中提供了多种求解器和求解方法,可以根据需要选择适合的求解算法。
完成有限元分析后,可以进行结果的后处理。
可以使用MATLAB中的可视化工具来绘制结构的位移和应力云图,以及显示结构的反应力和形变等。
可以通过对结果进行分析和比较,评估结构的可靠性和安全性。
总之,使用MATLAB进行桁架结构的有限元分析可以帮助工程师深入了解结构的力学行为和性能。
它可以为结构的设计和优化提供依据,并帮助工程师制定提高结构性能的策略。
同时,MATLAB提供了丰富的功能和工具,使得桁架结构的分析和设计更加高效和准确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入axis-Force(用户定义)选择“By sequence num”,“SMISC”,输入SMISC,1
输入axis-stress(用户定义)选择“By sequence num”,“LS”,输入LS,1
显示的轴向力 和轴向应力的结 果。
Axis-FOR=Axis-STR*A A为杆的截面面积。
定量分析 1)查看各节点位移值
Main menu>General postproc>List Results> Nodal Solution 同理也可查询单元的位移的物理量。
2)查看各支反力值
Main menu>General postproc>List Results>Reaction Solu 3)轴向力和轴力图:需要先定义单元数据表(Element Table),用ANSYS帮助文件,查看LINK1单元的输出数据, 如MFORX表示轴力,SAXL表示轴向应力,然后到 LINK1 Item and Sequence Numbers 表中查其对应的项目名称和序 列号, MFORX为SMISC ,1, SAXL为SL,1,进入Main menu>General postproc> Element Table>define Table 具体操作如下:
施加约束:单击“nodes”,在弹出的选择框中,按 “PICK ALL”,再在弹出的选择框中约束选“ALL DOF”,按“OK”完成施加约束。
Select>Everything选择全图,Plot>Multi-Plots显示 全图。
施加荷
求解 后处理均同2-D桁架分析。
THE END
桁架的有限元分析
2006年10月
桁架——2D问题
人字形屋架的几何尺寸、边界条件如图所示。材料的弹性模 量为207×109N/m2,泊松比为0.3,杆件截面尺寸为0.01m2, 试进行静力分析,求人字形屋架的变形图和各点的位移及轴 向力、轴力图。
以人字形屋架左支撑点为坐标原点,水平为X 轴,垂直方向为Y轴,建立直角坐标系,求出 各点坐标。 选择分析类型
确定单元类型
输入实常数
输入材料常数
创建各节点
以各节点为节点创建单元
施加约束,选择1,5点,在弹出的对话框中 选“ALL DOF”
施加载荷,选择6,7,8点,在弹出的对话框 中,选择“FY”,输入“-1000”。
求解。 进入后处理,查看结果 定性分析。 1)变形图Main menu>General postproc>Plot Result>deformed Shape; 2)彩色云图Main menu>General postproc>Plot Result>Contour Plot>Nodal Solu 3) Main menu>General postproc>Plot Result>Vector Plot>predefine 4)可到结果观察器(Result Viewer)中观察变形云图 和变形、变形结果的动画图。
显示轴力(应力图)
轴力(应力图)
桁架——3D问题
杆的截面面积为 4.91X10-4m2 材料密度为 7800kg/m3
选择分析类型,确定单元类型
定义实常数
定义材料常数
建立坐标系如图所示,创建模型
上弦平面的x坐标分别为0,1,2,3,4,5; y坐标分别为0,1,2,3,4,5,z坐标均为 0,共36个点。下弦平面的x坐标分别为0.5, 1.5,2.5,3.5,4.5; y坐标分别为0.5,1.5, 2.5,3.5,4.5 ,z坐标均为-0.7,共25个点。 先创建节点(nodes),然后由节点创建单元 创建模型如图所示。
施加约束。
Select>entities,选 “nodes”,”By location”。 先选“X location”, 在输入框 中输入“-0.1,0.1”,选“From Full”,按”Select All”,在输入 框中输入“4.9,5.1”,选“Also Select”,按”Apply”; 再选“Y location”, 在输入框 中输入“-0.1,0.1”,选“Also Select”,按”Apply”,在输入 框中输入“4.9,5.1”,选“Also Select”,按”Apply”。按 “PLOT”,”OK”,完成选择。
