北京邮电大学国际学院线性代数讲义Lecture 02汇总
北京邮电大学国际学院线性代数讲义Lecture 02

1 0 0 0 0
and we end up with
1 0 0 0 0
1 1 0 0 0 1 0 0 0 0
1 1 0 0 0 1 0 0 0 0
1 1 2 0 1 3 pivotal row 1 1 1 0 1 1 0 0 0 1 1 0 0 0 1 1 2 0 1 3. 0 4 0 3
in row k 1 is greater that the number of leading zero entries in row k . nonzero entries.
Row Echelon Form
Definition: The process of using row operation I, II and III to transform a linear system into one whose augmented matrix is in row echelon form is called Gaussian elimination. Remark: Row operation II is necessary in order to scale the rows so that lead coefficients are all 1. Remark: If the row echelon form of the augmented matrix contains a row of the form 0 0 0 1 The system has no solution set. Otherwise, the system will have solution set. Definition: If a system has solution set, we will be referred as consistent and if a system has no solution, we will be referred as inconsistent.
线性代数北京邮电大学出版社§2.4

结束
λx2 + 2x3 =1 λx1 + ) 3x3 =1 例2 问线性方程组 λx1 +(2λ −1 x2 + λx1 + λx2 +(λ +3)x3 = 2λ −1 中λ 取何值时, 方程组无解, 有唯一解 或有无穷多解. 解法2 解法 . 对增广矩阵作行初等变换
分析: 分析 对应齐次方程组基础解系含 4 – 2 = 2 个解向量,
备用题
−1 0 r r r r 2 x − x = 1 x1 −x3 = , 2 3 1 0 1 2 为对应齐次方程的解, 且线性无关
返回 上页 下页 结束
返回
上页
下页
结束
r2 ÷3 1 −2 5 12 5 7 10 0 1 −3 −3 − 3 0 0 0 0 0
1 0 1 −1 − 5 3 3 3 r +2r2 1 0 1 − 7 − 2 −10 3 3 3 0 0 0 0 0
ቤተ መጻሕፍቲ ባይዱ
R(A) = A(A) = 2 < 4
解: 对增广矩阵作初等行变换 1 −2 5 1 5 r −r 1 −2 5 1 5 2 −1 3 0 0 3 1 0 3 −7 −2 −10 A= 1 −5 12 3 15 r2 −2r 0 −3 7 2 10 1 r +r2 1 −2 5 1 5 3 0 3 −7 −2 −10 0 0 0 0 0
r r Ax = b的通解为
齐次方程通解 非齐次方程特解
作业: P97 11(2),(3);
12
返回 上页 下页 结束
1 0 1 r 2 r 1 r 0 设A为3×4 矩阵, 秩(A) = 2, x1 = , x2 = , x3 = 0 1 0 3 2 1 r r r r 是方程组 Ax = b (b ≠ 0)的三个特解, 则它的通解为 r r r r r r x = x1 +C1(x1 − x2) +C2(x1 − x3)
北京邮电大学国际学院线性代数讲义Lecture 03

2 A B 3 2 3
4 4 5 ( 1) 1 2 3 4 4 5 2 3 . 1
2 1 1 2
10
Matrix addition
Note: Let O denote a matrix, with the same dimensions as A , whose entries are all 0. Then
entry of A . Thus, if A is an m n matrix, then
a11 a12 a1n a a22 a2 n A 21 am 1 am 2 amn We will sometimes shorten the to A (aij ) .
Ax b
where A is an 1 1 matrix and x is an unknown vector in R1 , and b is in R1 . How about the case of one equation in several unknowns?
12
Matrix multiplication and linear systems
A a1 ,a 2 , ,a n .
6
Equality
Definition: Two m n matrix A and B are said to be equal if aij bij for each
i and j .
Note: The definition of equality of two matrix means that if two matrix is equal, then (1) These two matrices must have same rows and columns; (2) If two entries of each matrices is at the same position of each matrices, they are equll refer to an n -tuple of real numbers as a vector. If an n -tuple is represented in terms of a 1 n matrix, then we will refer to it as a row vector. Alternatively, if the n -tuple is represented by an n 1 matrix, then we will refer to it as a column vector. In working with matrix equations, it is generally more convenient to represent the solutions in terms of column vectors ( n 1 matrices). The set of all n 1 matrices of real numbers is called Euclidean n -space and is usually denoted by R n . We will always refer to a column vectors or elements of R n as simply vectors.
北京邮电大学出版社_线性代数习题答案(习题1-6)

线性代数习题及答案(北京邮电大学出版社 戴斌祥主)编习题一 (A 类)1. 求下列各排列的逆序数.(1) 341782659; (2) 987654321;(3) n (n 1)…321; (4) 13…(2n 1)(2n )(2n 2)…2.【解】(1) τ(341782659)=11;(2) τ(987654321)=36; (3) τ(n (n 1)…3〃2〃1)= 0+1+2 +…+(n 1)=(1)2n n -; (4) τ(13…(2n 1)(2n )(2n 2)…2)=0+1+…+(n 1)+(n 1)+(n 2)+…+1+0=n (n1).2. 求出j ,k 使9级排列24j157k98为偶排列。
解:由排列为9级排列,所以j,k 只能为3、6.由2排首位,逆序为0,4的逆序数为0,1的逆序数为3,7的逆序数为0,9的为0,8的为1.由0+0+3+0+1=4,为偶数.若j=3,k=6,则j 的逆序为1,5的逆序数为0,k 的为1,符合题意;若j=6,k=3,则j 的逆序为0,5的逆序数为1,k 的为4,不符合题意. 所以j=3、k=6.3. 写出4阶行列式中含有因子2234a a 的项。
解:D 4=1234()11223344(1)j j j j j j j j a a a a τ-由题意有:232,4.j j == 故1234141243243241j j j j j j ⎧==⎨⎩D 4中含的2234a a 项为:(1243)(3241)1122344313223441(1)(1)a a a a a a a a ττ-+-即为:1122344313223441a a a a a a a a -+4. 在6阶行列式中,下列各项应带什么符号?(1)233142561465a a a a a a ;解:233142561465142331425665a a a a a a a a a a a a = 因为(431265)6τ=,(431265)6(1)(1)1τ-=-= 所以该项带正号。
线性代数讲义(基础版)

1 2 3 1
2 0 2 1 a2
4 2 0 2 a3 a3 a3 − x a3 a4 a4 a4 a4 − x
a1 − x
例2 求 D=
a2 − x a2 a2
a0 1
例3 求 Dn +1 = 1
1 a1
1 a2
1 (ai ≠ 0) an
1
a1 + x a2 a3 a4 0 0 x −x 例 3 求 D4 = 0 −x x 0 0 0 −x x a1
n
6
线性代数基础班 09
合肥工业大学考研辅导中心(共创考研)
7
例1. 设
⎛1 0 1⎞ ⎜ ⎟ A = ⎜0 1 0⎟ ⎜0 0 1⎟ ⎝ ⎠
, 求A
n
例2. 设
⎛3 1 0⎞ ⎜ ⎟ A = ⎜0 3 0⎟ , ⎜0 0 2⎟ ⎝ ⎠
求 A
n
例3. 设
α = (1 2 3)T β = αT β
,
线性代数基础班 09
合肥工业大学考研辅导中心(共创考研)
1
第四篇:线性代数
第一章 行列式
考试要求 1.了解行列式的概念,掌握行列式的性质。 2. 会应用行列式的性质和行列式按行(列)展开定理计算行列式。
一、内容提要
1.行列式的定义
n 2 个数 ai j (i, j = 1,2,
a11 a 21 a n1 a12 a 22 an2
练习 求 Dn =
b1 a2
b2 an −1 bn −1
bn
an
1
练习
−1 −1 x −1 −1
1 x +1 1 1
x −1 −1 −1 −1
3
1 1 x +1
北京邮电大学国际学院线性代数讲义Lecture 01

a21 x1 a22 x2 a2 n xn b2 am 1 x1 am 2 x2 amn xn bm
where aij ’s and bi ’s are all real number. We will call this system as m n linear systems.
16
n×n Systems
Example: The system
3 x1
2 x2 x2
x3 x3 2 x3
1 2 4
is in triangular form. It is easy to solve this system. Actually, from the last equation, we have x3 2 . Using this value in the second equation×n Systems
We will restrict ourselves to n n systems. Definition: A system is said to be in triangular form if in the kth equation the coefficient of the first k-1 variables are all zero and the coefficient of xk is nonzero ( k 1, , n) .
6
Systems of Linear Equations
Example: Some linear systems
(a) x1 2 x1 (b) x1 2 x1 2 x2 3 x2 x2 x2 5 8 x3 x3 2 4
北京邮电大学国际学院高等数学(下)幻灯片讲义(无穷级数)Le.

1(x 2
−
2) +
1(x 4
−
2)2
=
3−
3x 2
+
x2 4
#
8
Convergence of Power Series
Abel’s Theorem (1)
(2)
∞
∑ Consider the series an xn. n=0
If it converges at x0 , x0 ≠ 0 , then it must converge
but converges for| x − x0 |< R. The series may or may not converge at either of the endpointsx = x0 − Randx = x0 + R. 2. The series converges for every x(R = ∞) . 3. The series converges at x = x0 and diverges elsewhere (R = 0).
n=1
13
Finding the Interval of Convergence Using the Ratio Test
∑ Solution Apply the Ratio Test to the series | un | , where un
is the nth term of the series in question.
divergence points is called the divergence domain of the series.
1
2
Series of Functions
Definition (Sum function and Convergence)
考研数学之线性代数讲义(考点知识点+概念定理总结)

收集自网络,不以任何盈利为目的。
欢迎考研的同学,下载学习。
线性代数讲义目录第一讲基本概念线性方程组矩阵与向量初等变换和阶梯形矩阵线性方程组的矩阵消元法第二讲行列式完全展开式化零降阶法其它性质克莱姆法则第三讲矩阵乘法乘积矩阵的列向量和行向量矩阵分解矩阵方程逆矩阵伴随矩阵第四讲向量组线性表示向量组的线性相关性向量组的极大无关组和秩矩阵的秩第五讲方程组解的性质解的情况的判别基础解系和通解第六讲特征向量与特征值相似与对角化特征向量与特征值—概念,计算与应用相似对角化—判断与实现附录一内积正交矩阵施密特正交化实对称矩阵的对角化第七讲二次型二次型及其矩阵可逆线性变量替换实对称矩阵的合同标准化和规范化惯性指数正定二次型与正定矩阵附录二向量空间及其子空间附录三两个线性方程组的解集的关系附录四06,07年考题第一讲基本概念1.线性方程组的基本概念线性方程组的一般形式为:a11x1+a12x2+…+a1n x n=b1,a21x1+a22x2+…+a2n x n=b2,…………a m1x1+a m2x2+…+a mn x n=b m,其中未知数的个数n和方程式的个数m不必相等.线性方程组的解是一个n维向量(k1,k2, …,k n)(称为解向量),它满足:当每个方程中的未知数x i都用k i替代时都成为等式.线性方程组的解的情况有三种:无解,唯一解,无穷多解.对线性方程组讨论的主要问题两个:(1)判断解的情况.(2)求解,特别是在有无穷多接时求通解.b1=b2=…=b m=0的线性方程组称为齐次线性方程组.n维零向量总是齐次线性方程组的解,称为零解.因此齐次线性方程组解的情况只有两种:唯一解(即只要零解)和无穷多解(即有非零解).把一个非齐次线性方程组的每个方程的常数项都换成0,所得到的齐次线性方程组称为原方程组的导出齐次线性方程组,简称导出组.2.矩阵和向量(1)基本概念矩阵和向量都是描写事物形态的数量形式的发展.由m n个数排列成的一个m行n列的表格,两边界以圆括号或方括号,就成为一个m n型矩阵.例如2 -1 0 1 11 1 1 0 22 5 4 -2 93 3 3 -1 8是一个45矩阵.对于上面的线性方程组,称矩阵a11 a12… a1n a11 a12… a1n b1A= a21 a22… a2n 和(A|β)= a21 a22… a2n b2…………………a m1 a m2… a mn a m1 a m2… a mnb m为其系数矩阵和增广矩阵.增广矩阵体现了方程组的全部信息,而齐次方程组只用系数矩阵就体现其全部信息.一个矩阵中的数称为它的元素,位于第i行第j列的数称为(i,j)位元素.元素全为0的矩阵称为零矩阵,通常就记作0.两个矩阵A和B相等(记作A=B),是指它的行数相等,列数也相等(即它们的类型相同),并且对应的元素都相等.由n个数构成的有序数组称为一个n维向量,称这些数为它的分量.书写中可用矩阵的形式来表示向量,例如分量依次是a1,a2, ,a n的向量可表示成a1(a1,a2, ,a n)或 a2 ,┆a n请注意,作为向量它们并没有区别,但是作为矩阵,它们不一样(左边是1n矩阵,右边是n1矩阵).习惯上把它们分别称为行向量和列向量.(请注意与下面规定的矩阵的行向量和列向量概念的区别.) 一个m n的矩阵的每一行是一个n维向量,称为它的行向量; 每一列是一个m维向量, 称为它的列向量.常常用矩阵的列向量组来写出矩阵,例如当矩阵A的列向量组为α1, α2, ,αn时(它们都是表示为列的形式!)可记A=(α1, α2, ,αn).矩阵的许多概念也可对向量来规定,如元素全为0的向量称为零向量,通常也记作0.两个向量α和β相等(记作α=β),是指它的维数相等,并且对应的分量都相等.(2) 线性运算和转置线性运算是矩阵和向量所共有的,下面以矩阵为例来说明.加(减)法:两个m n的矩阵A和B可以相加(减),得到的和(差)仍是m n矩阵,记作A+B (A-B),法则为对应元素相加(减).数乘: 一个m n的矩阵A与一个数c可以相乘,乘积仍为m n的矩阵,记作c A,法则为A的每个元素乘c.这两种运算统称为线性运算,它们满足以下规律:①加法交换律:A+B=B+A.②加法结合律:(A+B)+C=A+(B+C).③加乘分配律:c(A+B)=c A+c B.(c+d)A=c A+d A.④数乘结合律: c(d)A=(cd)A.⑤ c A=0 c=0 或A=0.转置:把一个m n的矩阵A行和列互换,得到的n m的矩阵称为A的转置,记作A T(或A).有以下规律:① (A T)T=A.② (A+B)T=A T+B T.③ (c A)T=c A T.转置是矩阵所特有的运算,如把转置的符号用在向量上,就意味着把这个向量看作矩阵了.当α是列向量时, α T表示行向量, 当α是行向量时,α T表示列向量.向量组的线性组合:设α1, α2,…,αs是一组n维向量, c1,c2,…,c s是一组数,则称c1α1+c2α2+…+c sαs为α1, α2,…,αs的(以c1,c2,…,c s为系数的)线性组合.n维向量组的线性组合也是n维向量.(3) n阶矩阵与几个特殊矩阵行数和列数相等的矩阵称为方阵,行列数都为n的矩阵也常常叫做n阶矩阵.把n阶矩阵的从左上到右下的对角线称为它对角线.(其上的元素行号与列号相等.)下面列出几类常用的n阶矩阵,它们都是考试大纲中要求掌握的.对角矩阵: 对角线外的的元素都为0的n阶矩阵.单位矩阵: 对角线上的的元素都为1的对角矩阵,记作E(或I).数量矩阵: 对角线上的的元素都等于一个常数c的对角矩阵,它就是c E.上三角矩阵: 对角线下的的元素都为0的n阶矩阵.下三角矩阵: 对角线上的的元素都为0的n阶矩阵.对称矩阵:满足A T=A矩阵.也就是对任何i,j,(i,j)位的元素和(j,i)位的元素总是相等的n阶矩阵.(反对称矩阵:满足A T=-A矩阵.也就是对任何i,j,(i,j)位的元素和(j ,i)位的元素之和总等于0的n阶矩阵.反对称矩阵对角线上的元素一定都是0.)3. 矩阵的初等变换和阶梯形矩阵矩阵有以下三种初等行变换:①交换两行的位置.②用一个非0的常数乘某一行的各元素.③把某一行的倍数加到另一行上.(称这类变换为倍加变换)类似地, 矩阵还有三种初等列变换,大家可以模仿着写出它们,这里省略了. 初等行变换与初等列变换统称初等变换.阶梯形矩阵:一个矩阵称为阶梯形矩阵,如果满足:①如果它有零行,则都出现在下面.②如果它有非零行,则每个非零行的第一个非0元素所在的列号自上而下严格单调递增.把阶梯形矩阵的每个非零行的第一个非0元素所在的位置称为台角.简单阶梯形矩阵:是特殊的阶梯形矩阵,特点为:③台角位置的元素为1.④并且其正上方的元素都为0.每个矩阵都可以用初等行变换化为阶梯形矩阵和简单阶梯形矩阵.这种运算是在线性代数的各类计算题中频繁运用的基本运算,必须十分熟练.请注意: 1.一个矩阵用初等行变换化得的阶梯形矩阵并不是唯一的,但是其非零行数和台角位置是确定的.2. 一个矩阵用初等行变换化得的简单阶梯形矩阵是唯一的.4. 线性方程组的矩阵消元法线性方程组的基本方法即中学课程中的消元法:用同解变换把方程组化为阶梯形方程组(即增广矩阵为阶梯形矩阵的方程组).线性方程组的同解变换有三种:①交换两个方程的上下位置.②用一个非0的常数乘某个方程.③把某个方程的倍数加到另一个方程上.以上变换反映在增广矩阵上就是三种初等行变换.线性方程组求解的基本方法是消元法,用增广矩阵或系数矩阵来进行,称为矩阵消元法. 对非齐次线性方程组步骤如下:(1)写出方程组的增广矩阵(A|β),用初等行变换把它化为阶梯形矩阵(B|γ).(2)用(B|γ)判别解的情况:如果最下面的非零行为(0,0, ,0|d),则无解,否则有解.有解时看非零行数r(r不会大于未知数个数n),r=n时唯一解;r<n时无穷多解.(推论:当方程的个数m<n时,不可能唯一解.)(3)有唯一解时求解的初等变换法:去掉(B|γ)的零行,得到一个n×(n+1)矩阵(B0|γ0),并用初等行变换把它化为简单阶梯形矩阵(E|η),则η就是解.对齐次线性方程组:(1)写出方程组的系数矩阵A,用初等行变换把它化为阶梯形矩阵B.(2)用B判别解的情况:非零行数r=n时只有零解;r<n时有非零解(求解方法在第五章讲). (推论:当方程的个数m<n时,有非零解.)讨论题1.设A是n阶矩阵,则(A) A是上三角矩阵A是阶梯形矩阵.(B) A是上三角矩阵A是阶梯形矩阵.(C) A是上三角矩阵A是阶梯形矩阵.(D) A是上三角矩阵与A是阶梯形矩阵没有直接的因果关系.2.下列命题中哪几个成立?(1) 如果A是阶梯形矩阵,则A去掉任何一行还是是阶梯形矩阵.(2) 如果A是阶梯形矩阵,则A去掉任何一列还是是阶梯形矩阵.(3) 如果(A|B)是阶梯形矩阵,则A也是阶梯形矩阵.(4) 如果(A|B)是阶梯形矩阵,则B也是阶梯形矩阵.(5) 如果 A 是阶梯形矩阵,则A和B都是阶梯形矩阵.B第二讲行列式一.概念复习1. 形式和意义形式:用n2个数排列成的一个n行n列的表格,两边界以竖线,就成为一个n阶行列式:a11 a12 (1)a21 a22 (2)……… .a n1 a n2… a nn如果行列式的列向量组为α1, α2, … ,αn,则此行列式可表示为|α1, α2, … ,αn|.意义:是一个算式,把这n2个元素按照一定的法则进行运算,得到的数值称为这个行列式的值.请注意行列式和矩阵在形式上和意义上的区别.当两个行列式的值相等时,就可以在它们之间写等号! (不必形式一样,甚至阶数可不同.)每个n阶矩阵A对应一个n阶行列式,记作|A|.行列式这一讲的的核心问题是值的计算,以及判断一个行列式的值是否为0.2. 定义(完全展开式)2阶和3阶行列式的计算公式:a 11 a 12a 21 a 22 = a 11a 22-a 12a 21 .a 11 a 12 a 13a 21 a 22 a 23 = a 11a 22a 33+ a 12a 23a 31+ a 13a 21a 32-a 13a 22a 31- a 11a 23a 32-a 12a 21a 33.a 31 a 32 a 33一般地,一个n 阶行列式a 11 a 12 … a 1na 21 a 22 … a 2n… … …a n1 a n2 … a nn 的值是许多项的代数和,每一项都是取自不同行,不同列的n 个元素的乘积,其一般形式为:n nj j j a a a 2121,这里把相乘的n 个元素按照行标的大小顺序排列,它们的列标j 1j 2…j n 构成1,2, …,n 的一个全排列(称为一个n 元排列),共有n!个n 元排列,每个n 元排列对应一项,因此共有n!个项. 所谓代数和是在求总和时每项先要乘+1或-1.规定τ(j 1j 2…j n )为全排列j 1j 2…j n 的逆序数(意义见下面),则项n nj j j a a a 2121所乘的是.)1()(21n j j j τ-全排列的逆序数即小数排列在大数右面的现象出现的个数.逆序数可如下计算:标出每个数右面比它小的数的个数,它们的和就是逆序数.例如求436512的逆序数: 002323215634, τ(436512)=3+2+3+2+0+0=10.至此我们可以写出n 阶行列式的值:a 11 a 12 … a 1na 21 a 22 … a 2n =.)1(21212121)(n n n nj j j j j j j j j a a a τ-∑ … … …a n1 a n2 … a nn这里∑n j j j 21表示对所有n 元排列求和.称此式为n 阶行列式的完全展开式.用完全展开式求行列式的值一般来说工作量很大.只在有大量元素为0,使得只有少数项不为0时,才可能用它作行列式的计算.例如对角行列式,上(下)三角行列式的值就等于主对角线上的元素的乘积,因为其它项都为0.2. 化零降阶法把n 阶行列式的第i 行和第j 列划去后所得到的n-1阶行列式称为(i,j)位元素a ij 的余子式,记作M ij .称A ij =(-1)i+j M ij 为元素a ij 的代数余子式.定理(对某一行或列的展开)行列式的值等于该行(列)的各元素与其代数余子式乘积之和.命题 第三类初等变换(倍加变换)不改变行列式的值.化零降阶法 用命题把行列式的某一行或列化到只有一个元素不为0,再用定理.于是化为计算一个低1阶的行列式.化零降阶法是实际计算行列式的主要方法,因此应该熟练掌握.3.其它性质行列式还有以下性质:① 把行列式转置值不变,即|A T |=|A | .② 某一行(列)的公因子可提出.于是, |c A |=c n |A |.③ 对一行或一列可分解,即如果某个行(列)向量α=β+γ ,则原行列式等于两个行列式之和,这两个行列式分别是把原行列式的该行(列)向量α换为β或γ 所得到的行列式.例如|α,β1+β2,γ |=|α,β1,γ |+|α,β2,γ |.④把两个行(列)向量交换, 行列式的值变号.⑤如果一个行(列)向量是另一个行(列)向量的倍数,则行列式的值为0.⑥某一行(列)的各元素与另一行(列)的对应元素的代数余子式乘积之和=0.⑦如果A与B都是方阵(不必同阶),则A * = A O =|A||B|.O B * B范德蒙行列式:形如1 1 1 (1)a1 a2 a3 … a na12 a22 a32… a n2…………a1n-i a2n-i a3n-i… a n n-i的行列式(或其转置).它由a1,a2 ,a3,…,a n所决定,它的值等于因此范德蒙行列式不等于0 a1,a2 ,a3,…,a n两两不同.对于元素有规律的行列式(包括n阶行列式),常常可利用性质简化计算,例如直接化为三角行列式等.4.克莱姆法则克莱姆法则应用在线性方程组的方程个数等于未知数个数n (即系数矩阵为n阶矩阵)的情形.此时,如果它的系数矩阵的行列式的值不等于0,则方程组有唯一解,这个解为(D1/D, D2/D,,D n/D),这里D是系数行列式的值, D i是把系数行列式的第i个列向量换成常数列向量所得到的行列式的值.说明与改进:按法则给的公式求解计算量太大,没有实用价值.因此法则的主要意义在理论上,用在对解的唯一性的判断,而在这方面法则不够. 法则的改进:系数行列式不等于0是唯一解的充分必要条件.实际上求解可用初等变换法:对增广矩阵(A|β)作初等行变换,使得A变为单位矩阵:(A|β)(E|η),η就是解.用在齐次方程组上 :如果齐次方程组的系数矩阵A是方阵,则它只有零解的充分必要条件是|A|0.二. 典型例题1.利用性质计算元素有规律的行列式例1① 2 a a a a ② 1+x 1 1 1 ③ 1+a 1 1 1a 2 a a a 1 1+x 1 1 2 2+a 2 2a a 2 a a . 1 1 1+x 1 . 3 3 3+a 3 .a a a 2 a 1 1 1 1+x 4 4 4 4+aa a a a 2例2 1 2 3 4 52 3 4 5 13 4 5 1 2 .4 5 1 2 35 1 2 3 4例3 1+x1 1 1 11 1+x2 1 1 .1 1 1+x3 11 1 1 1+x4例4 a 0 b c0 a c b .b c a 0c b 0 a例5 1-a a 0 0 0-1 1-a a 0 00 -1 1-a a 0 . (96四)0 0 -1 1-a a0 0 0 -1 1-a2. 测试概念与性质的题例6 x 3-3 1 -3 2x+2多项式f(x)= -7 5 -2x 1 ,求f(x)的次数和最高次项的系数.X+3 -1 3 3x 2-29 x 3 6 -6例7 求 x-3 a -1 4f(x)= 5 x-8 0 –2 的x 4和x 3的系数.0 b x+1 12 2 1 x例8 设4阶矩阵A =(α, γ1, γ2 ,γ3),B =(β, γ1, γ2 ,γ3),|A | =2, |B |=3 ,求|A +B | .例9 a b c d已知行列式 x -1 -y z+1 的代数余子式A 11=-9,A 12=3,A 13=-1,A 14=3,求x,y,z.1 -z x+3 yy-2 x+1 0 z+3例10 求行列式 3 0 4 0 的第四行各元素的余子式的和.(01)2 2 2 20 -7 0 05 3 -2 23.几个n 阶行列式两类爪形行列式及其值:例11 a 1 a 2 a 3 … a n-1 a nb 1c 2 0 … 0 0证明 0 b 2 c 3 0 0 =11111(1)n i i i i n i b b a c c --+=-∑.… … … …0 0 0 … b n-1 c n提示: 只用对第1行展开(M 1i 都可直接求出).例12 a 0 a 1 a 2 … a n-1 a nb 1c 1 0 … 0 0证明 b 2 0 c 2 … 0 0 =011111n n ii i i i n i i a c c c a b c c -+==-∑∏.… … … …b n 0 0 … 0c n提示: 只用对第1行展开(M 1i 都可直接求出).另一个常见的n 阶行列式:例13 证明a+b b 0 … 0 0a a+b b … 0 0… … … … = 110n n n n i i i a b a b a b ++-=-=-∑(当a b 时).0 0 0 … a+b b0 0 0 a a+b提示:把第j 列(行)的(-1)j-1倍加到第1列(行)上(j=2,…,n),再对第1列(行)展开.4.关于克莱姆法则的题例14设有方程组x 1+x 2+x 3=a+b+c,ax 1+bx 2+cx 3=a 2+b 2+c 2,bcx 1+acx 2+abx 3=3abc.(1)证明此方程组有唯一解的充分必要条件为a,b,c 两两不等.(2)在此情况求解.参考答案例1 ①(2+4a)(2-a)4.② x 3(x+4). ③ a 3(a+10).例2 1875.例3 x 1x 2x 3x 4+x 2x 3x 4+x 1x 3x 4+x 1x 2x 4+x 1x 2x 3.例4 (a+b+c)(a+b-c)(a-b+c)(a-b-c).例5 1-a+a 2-a 3+a 4-a 5.例6 9,-6例7 1,-10.例8 40.例9 x=0,y=3,z=-1.例10 -28.例14 x 1=a,x 2=b,x 3=c..第三讲 矩阵一.概念复习1. 矩阵乘法的定义和性质定义2.1 当矩阵A 的列数和B 的行数相等时,和A 和B 可以相乘,乘积记作AB . AB 的行数和A 相等,列数和B 相等. AB 的(i,j)位元素等于A 的第i 个行向量和B 的第j 个列向量(维数相同)对应分量乘积之和. 设 a 11 a 12 … a 1n b 11 b 12 … b 1s c 11 c 12 … c 1sA = a 21 a 22 … a 2nB = b 21 b 22 … b 2sC =AB = c 21 c 22 … c 2s… … … … … … … … …a m1 a m2 … a mn ,b n1 b n2 … b ns ,c m1 c m2 … c ms ,则c ij =a i1b 1j +a i2b 2j +…+a in b nj .矩阵的乘法在规则上与数的乘法有不同:① 矩阵乘法有条件.② 矩阵乘法无交换律.③ 矩阵乘法无消去律,即一般地由AB =0推不出A =0或B =0.由AB =AC 和A 0推不出B =C .(无左消去律)由BA =CA 和A 0推不出B =C . (无右消去律)请注意不要犯一种常见的错误:把数的乘法的性质简单地搬用到矩阵乘法中来.矩阵乘法适合以下法则:① 加乘分配律 A (B +C )= AB +AC , (A +B )C =AC +BC .② 数乘性质 (c A )B =c(AB ).③ 结合律 (AB )C = A (BC ).④ (AB )T =B T A T .2. n 阶矩阵的方幂和多项式任何两个n 阶矩阵A 和B 都可以相乘,乘积AB 仍是n 阶矩阵.并且有行列式性质:|AB |=|A ||B |.如果AB =BA ,则说A 和B 可交换.方幂 设k 是正整数, n 阶矩阵A 的k 次方幂A k 即k 个A 的连乘积.规定A 0=E .显然A 的任何两个方幂都是可交换的,并且方幂运算符合指数法则:① A k A h = A k+h .② (A k )h = A kh .但是一般地(AB )k 和A k B k 不一定相等!n 阶矩阵的多项式设f(x)=a m x m +a m-1x m-1+…+a 1x+a 0,对n 阶矩阵A 规定f(A )=a m A m +a m-1A m-1+…+ a 1A +a 0E .称为A 的一个多项式.请特别注意在常数项上加单位矩阵E .乘法公式 一般地,由于交换性的障碍,小代数中的数的因式分解和乘法公式对于n 阶矩阵的不再成立.但是如果公式中所出现的n 阶矩阵互相都是乘法交换的,则乘法公式成立.例如当A 和B 可交换时,有:(A B )2=A 22AB +B 2;A 2-B 2=(A +B )(A -B )=(A +B )(A -B ).二项展开式成立: B AC B A -=∑=+1)(等等.前面两式成立还是A 和B 可交换的充分必要条件.同一个n 阶矩阵的两个多项式总是可交换的. 一个n 阶矩阵的多项式可以因式分解.3. 分块法则矩阵乘法的分块法则是简化矩阵乘法的一种方法.对两个可以相乘的矩阵A 和B ,可以先用纵横线把它们切割成小矩阵(一切A 的纵向切割和B 的横向切割一致!),再用它们来作乘法.(1)两种常见的矩阵乘法的分块法则 A 11 A 12 B 11 B 12 = A 11B 11+A 12B 21 A 11B 12+A 12B 22A 21 A 22B 21 B 22 A 21B 11+A 22B 21 A 21B 12+A 22B 22要求A ij 的列数B jk 和的行数相等.准对角矩阵的乘法:形如A 1 0 0A = 0 A 2 0… … …0 0 … A n的矩阵称为准对角矩阵,其中A 1,A 2,…,A k 都是方阵.两个准对角矩阵A 1 0 ... 0 B 1 0 0A = 0 A 2 ... 0 , B = 0 B 2 0… … … … … …0 0 … A k 0 0 … B k如果类型相同,即A i 和B i 阶数相等,则A 1B 1 0 0AB = 0 A 2B 2 … 0 .… … …00 …A k B k(2)乘积矩阵的列向量组和行向量组设A是m n矩阵B是n s矩阵. A的列向量组为α1,α2,…,αn,B的列向量组为β1, β2,…,βs, AB的列向量组为γ1, γ2,…,γs,则根据矩阵乘法的定义容易看出(也是分块法则的特殊情形):①AB的每个列向量为:γi=Aβi,i=1,2,…,s.即A(β1, β2,…,βs)=(Aβ1,Aβ2,…,Aβs).②β=(b1,b2,…,b n)T,则Aβ= b1α1+b2α2+…+b nαn.应用这两个性质可以得到:如果βi=(b1i,b2i,…,b ni)T,则γi=AβI=b1iα1+b2iα2+…+b niαn.即:乘积矩阵AB的第i个列向量γi是A的列向量组α1, α2,…,αn的线性组合,组合系数就是B的第i个列向量βi的各分量.类似地, 乘积矩阵AB的第i个行向量是B的行向量组的线性组合,组合系数就是A的第i个行向量的各分量.以上规律在一般教材都没有强调,但只要对矩阵乘法稍加分析就不难得出.它们无论在理论上和计算中都是很有用的.(1) 当两个矩阵中,有一个的数字很简单时,直接利用以上规律写出乘积矩阵的各个列向量或行向量,从而提高了计算的速度.(2) 利用以上规律容易得到下面几个简单推论:用对角矩阵Λ从左侧乘一个矩阵,相当于用Λ⎤®↵X !Ξδ矩阵的各行向量; 用对角矩阵Λ从右侧乘一个矩阵,相当于用Λ⎤®↵X !Ξδ矩阵的各列向量.数量矩阵k E乘一个矩阵相当于用k乘此矩阵;单位矩阵乘一个矩阵仍等于该矩阵.两个同阶对角矩阵的相乘只用把对角线上的对应元素相乘.求对角矩阵的方幂只需把对角线上的每个元素作同次方幂.(3) 矩阵分解:当一个矩阵C的每个列向量都是另一个A的列向量组的线性组合时,可以构造一个矩阵B,使得C=AB.例如设A=(,,), C=(+2-,3-+,+2),令1 3 1B= 2 -1 0 ,则C=AB.-1 1 2(4) 初等矩阵及其在乘法中的作用对单位矩阵E作一次初等(行或列)变换,所得到的矩阵称为初等矩阵.有三类初等矩阵:E(i,j):交换E的i,j两行(或列)所得到的矩阵.E(i(c)):用非0数c乘E的第i行(或列)所得到的矩阵.也就是把E的对角线上的第i个元素改为c.E (i,j(c))(i j):把E的第j行的c倍加到第i行上(或把第i列的c倍加到第j列上)所得到的矩阵, 也就是把E的(i,j)位的元素改为c.命题对矩阵作一次初等行(列)变换相当于用一个相应的初等矩阵从左(右)乘它.4. 矩阵方程和可逆矩阵(伴随矩阵)(1) 矩阵方程矩阵不能规定除法,乘法的逆运算是解下面两种基本形式的矩阵方程:(I) AX=B.(II) XA=B.这里假定A是行列式不为0的n阶矩阵,在此条件下,这两个方程的解都是存在并且唯一的.(否则解的情况比较复杂.)当B只有一列时,(I)就是一个线性方程组.由克莱姆法则知它有唯一解.如果B有s列,设 B=(β1, β2,…,βs),则 X也应该有s列,记X=(X1,X2,…,X s),则有AX i=βi,i=1,2,…,s,这是s个线性方程组.由克莱姆法则,它们都有唯一解,从而AX=B有唯一解.这些方程组系数矩阵都是A,可同时求解,即得(I)的解法:将A和B并列作矩阵(A|B),对它作初等行变换,使得A变为单位矩阵,此时B变为解X.(A|B)(E|X)(II)的解法:对两边转置化为(I)的形式:A T X T=B T.再用解(I)的方法求出X T,转置得X..(A T|B T)(E|X T)矩阵方程是历年考题中常见的题型,但是考试真题往往并不直接写成(I)或(II)的形式,要用恒等变形简化为以上基本形式再求解.(2) 可逆矩阵的定义与意义定义设A是n阶矩阵,如果存在n阶矩阵B,使得AB=E, BA=E,则称A为可逆矩阵.此时B是唯一的,称为A的逆矩阵,通常记作A-1.如果A可逆,则A在乘法中有消去律:AB =0B=0;AB=AC B=C.(左消去律);BA=0B=0;BA=CA B=C. (右消去律)如果A可逆,则A在乘法中可移动(化为逆矩阵移到等号另一边):AB=C B=A-1C. BA=C B=CA-1.由此得到基本矩阵方程的逆矩阵解法:(I) AX=B的解X=A-1B .(II) XA=B的解X= BA-1.这种解法想法自然,好记忆,但是计算量比初等变换法大(多了一次矩阵乘积运算).(3) 矩阵可逆性的判别与性质定理 n阶矩阵A可逆|A|0.证明“”对AA-1=E两边取行列式,得|A||A-1|=1,从而|A|0. (并且|A-1|=|A|-1.)“”因为|A|0,矩阵方程AX=E和XA=E都有唯一解.设B,C分别是它们的解,即AB=E, CA=E. 事实上B=C(B=EB=CAB=CE=C),于是从定义得到A可逆.推论如果A和B都是n阶矩阵,则AB=E BA=E.于是只要AB=E(或BA=E)一式成立,则A和B都可逆并且互为逆矩阵.可逆矩阵有以下性质:①如果A可逆,则A-1也可逆,并且(A-1)-1=A.A T也可逆,并且(A T)-1=(A-1)T.当c0时, c A也可逆,并且(c A)-1=c-1A-1.对任何正整数k, A k也可逆,并且(A k)-1=(A-1)k.(规定可逆矩阵A的负整数次方幂A-k=(A k)-1=(A-1)k.)②如果A和B都可逆,则AB也可逆,并且(AB)-1=B-1A-1.(请自己推广到多个可逆矩阵乘积的情形.)初等矩阵都是可逆矩阵,并且E(i,j)-1= E(i,j), E(i(c))-1=E(i(c-1)), E(i,j(c))-1= E(i,j(-c)).(4) 逆矩阵的计算和伴随矩阵①计算逆矩阵的初等变换法当A可逆时, A-1是矩阵方程AX=E的解,于是可用初等行变换求A-1:(A|E)(E|A-1)这个方法称为求逆矩阵的初等变换法.它比下面介绍的伴随矩阵法简单得多.②伴随矩阵若A是n阶矩阵,记A ij是|A|的(i,j)位元素的代数余子式,规定A的伴随矩阵为A11 A21… A n1A*= A12 A22… A n2 =(A ij)T.………A1n A2n… A mn请注意,规定n阶矩阵A的伴随矩阵并没有要求A可逆,但是在A可逆时, A*和A-1有密切关系.基本公式: AA*=A*A=|A|E.于是对于可逆矩阵A,有A-1=A*/|A|, 即A*=|A|A-1.因此可通过求A*来计算A-1.这就是求逆矩阵的伴随矩阵法.和初等变换法比较, 伴随矩阵法的计算量要大得多,除非n=2,一般不用它来求逆矩阵.对于2阶矩阵a b * d -bc d = -c a ,因此当ad-bc0时,a b -1 d -bc d = -c a (ad-bc) .伴随矩阵的其它性质:①如果A是可逆矩阵,则A*也可逆,并且(A*)-1= A/|A|=(A-1)*.② |A*|=|A|n-1.③ (A T)*=(A*)T.④ (c A)*=c n-1A*.⑤ (AB)*=B*A*;(A k)*=(A*)k.⑥当n>2时,(A*)*=|A|n-2A; n=2时,(A*)*=A.二典型例题1.计算题例1 α=(1,-2,3) T,β=(1,-1/2,1/3)T, A=αβ T,求A6.讨论:(1)一般地,如果n阶矩阵A=αβ T,则A k=(βTα)k-1A=(tr(A ))k-1A .(2)乘法结合律的应用:遇到形如βTα的地方可把它当作数处理.① 1 -1 1ααT= -1 1 -1 ,求αTα.(2003一)1 -1 1②设α=(1,0,-1)T, A=ααT,求|a E-A n|.③ n维向量α=(a,0,,0,a)T, a<0, A=E-ααT, A-1=E+a-1αα T,求a. (03三,四)④ n维向量α=(1/2,0,,0,1/2)T, A=E-αα T, B=E+2αα T,求AB. (95四)⑤ A=E-αβ T,其中α,β都是n维非零列向量,已知A2=3E-2A,求αTβ.例2(1999三) 1 0 1设A = 0 2 0 ,求A n-2A n-1.(n>1)1 0 1例3 1 0 0设A = 1 0 1 ,(1)证明当n>1时A n=A n-2+A2-E. (2) 求A n.0 1 0例4 −A为3阶矩阵, α1,α2,α3是线性无关的3维列向量组,满足Aα1=α1+α2+α3, Aα2=2α2+ α3, Aα3=2α2+3α3.求作矩阵B,使得A(α1,α2,α3)=(α1,α2,α3)B. (2005年数学四)例5设3阶矩阵A=(α1,α2,α3),|A|=1,B=(α1+α2+α3,α1+2α2+3α3,α1+4α2+9α3),求|B|.(05)例6 3维向量α1, α2, α3, β1, β2, β3满足α1+α3+2β1-β2=0, 3α1-α2+β1-β3=0, -α2+α3-β2+β3=0,已知|α1, α2, α3|=a,求| β1, β2, β3|.例7设A是3阶矩阵, α是3维列向量,使得P=(α,Aα,A2α)可逆,并且A3α=3Aα-2A2α.又3阶矩阵B满足A=PBP-1.(1)求B.(2)求|A+E|.(01一)2 1 0例8 3阶矩阵A,B满足ABA*=2BA*+E,其中A= 1 2 0 ,求|B|.(04一)0 0 1例9 3 -5 1设3阶矩阵A= 1 -1 0 , A-1XA=XA+2A,求X.-1 0 2例10 1 1 -1设3阶矩阵A= -1 1 1 , A*X=A-1+2X,求X.1 -1 1例11 4阶矩阵A,B满足ABA-1=BA-1+3E,已知1 0 0 0A*= 0 1 0 0 ,求B. (00一)1 0 1 00 -3 0 8例12 3 0 0 1 0 0已知A= 2 1 0 , B= 0 0 0 , XA+2B=AB+2X,求X11.2 13 0 0 -1例13设α1=(5,1,-5)T, α2=(1,-3,2)T, α3=(1,-2,1)T,矩阵A满足Aα1=(4,3) T, Aα2=(7,-8) T, Aα3=(5,-5) T,求A.2.概念和证明题例14 设A是n阶非零实矩阵,满足A*=A T.证明:(1)|A|>0.(2)如果n>2,则 |A|=1.例15 设矩阵A=(a ij)33满足A*=A T,a11,a12,a13为3个相等的正数,则它们为(A) 3/3.(B) 3. (C)1/3. (D) 3. (2005年数学三)例16 设A和B都是n阶矩阵,C= A 0 ,则C*=0 B(A) |A|A* 0 . (B) |B|B * 0 .0 |B|B * 0 |A|A*(C) |A|B* 0 . (D ) |B|A* 0 .0 |B|A* 0 |A|B*例17 设A是3阶矩阵,交换A的1,2列得B,再把B的第2 列加到第3 列上,得C.求Q,使得C=AQ. 例18 设A是3阶可逆矩阵,交换A的1,2行得B,则(A) 交换A*的1,2行得到B*.(B) 交换A*的1,2列得到B*.(C) 交换A*的1,2行得到-B*.(D) 交换A*的1,2列得到-B*.(2005年)例19 设A是n阶可逆矩阵, 交换A的i,j行得到B.(1) 证明B可逆.(2) 求AB-1.例20设n阶矩阵A满足A2+3A-2E=0.(1)证明A可逆,并且求A-1.(2)证明对任何整数c,A-c E可逆.讨论: 如果f(A)=0,则(1) 当f(x)的常数项不等于0时,A可逆.(2) f(c)0时,A-c E可逆.(3) 上述两条的逆命题不成立.例21设α是n维非零列向量,记A=E-ααT.证明(1) A2=AαTα =1.(2) αTα =1 A不可逆. (96一)讨论: (2)的逆命题也成立.例22 设A,B都是n阶矩阵,证明E-AB可逆 E-BA可逆.例23设3阶矩阵A,B满足AB=A+B.(1) 证明A-E可逆.(2) 设 1 -3 0B= 2 1 0 ,求A.0 0 2 (91)例24设A,B是3阶矩阵, A可逆,它们满足2A-1B=B-4E.(1) 证明A-2E可逆.(2) 设 1 -2 0B= 1 2 0 ,求A.0 0 2 (2002)例25设n阶矩阵A,B满足AB=a A+b B.其中ab0,证明(1) A-b E和B-a E都可逆.(2) A可逆 B可逆.(3) AB=BA.例26设A,B都是n阶对称矩阵, E+AB可逆,证明(E+AB)-1A也是对称矩阵.例27 设A,B都是n阶矩阵使得A+B可逆,证明(1) 如果AB=BA,则B(A+B)-1A=A(A+B)-1B.(2) 如果A.B都可逆,则B(A+B)-1A=A(A+B)-1B.(3) 等式B(A+B)-1A=A(A+B)-1B总成立.例28设A,B,C都是n阶矩阵,满足B=E+AB,C=A+CA,则B-C为(A) E.(B) -E. (C) A. (D) -A. (2005年数学四)参考答案1 -1/2 1/3例135A=35 -2 1 –2/3 .3 -3/2 1① 3.② a2(a-2n). ③ -1. ④ E. ⑤ 4.例2 O.例3 (1)提示: A n=A n-2+A2-E A n-2(A2-E)=A2-E A(A2-E)=A2-E.(2)n=2k时, 1 0 0A n = k 1 0 .k 0 1n=2k+1时, 1 0 0A n = k+1 0 1 .k 1 0例 4 1 0 0B= 1 2 2 .1 1 3例5 2.例 6 –4a.例 7 0 0 0B= 1 0 3 . |E+A|=-40 1 -2例8 1/9.例 9 -6 10 4X= -2 4 2 .-4 10 0例 10 1 1 0(1/4) 0 1 1 .1 0 1例 11 6 0 0 0B= 0 6 0 0 .6 0 6 00 3 0 -1例 12 1 0 02 0 0 .6 -1 -1例 13 2 -1 1-4 -2 -5 .例15 (A).例16 (D).例 17 0 1 1Q= 1 0 0 .0 0 1例18 (D).例19 E(i,j).例22 提示:用克莱姆法则.例如证明,即在E-AB可逆时证明齐次方程组(E-BA)X=0只有零解.例23 1 1/2 0A= -1/3 1 0 .0 0 2例 24 0 2 0A= -1 -1 0 .0 0 -2例25 提示:计算(A-b E)(B-a E).例28 (A).第四讲向量组的线性关系与秩一.概念复习1. 线性表示关系设α1,α2,…,αs是一个n维向量组.如果n维向量β等于α1,α2,…,αs的一个线性组合,就说β可以用α1,α2,…,αs线性表示.如果n维向量组β1, β2,…,βt -∉ *⎬⎪∑可以用α1,α2,…,αs线性表示,就说向量β1,β2,…,βt可以用α1,α2,…,αs线性表示.判别“β是否可以用α1, α2,…,αs线性表示? 表示方式是否唯一?”就是问:向量方程x1α1+ x2α2+…+x sαs=β是否有解?解是否唯一?用分量写出这个向量方程,就是以(α1, α2,…,αs |β):⎡5↵∍≠⊗.反之,判别“以(A|β):⎡5↵∍≠⊗/&©©/&/ ”的问题又可转化为“β是否可以用A的列向量组线性表示? 表示方式是否唯一?”的问题.向量组之间的线性表示问题与矩阵乘法有密切关系: 乘积矩阵AB的每个列向量都可以表示为A的列向量组的线性组合,从而AB的列向量组可以用A的列向量组线性表示;反之,如果向量组β1,β2,…,βt可以用α1,α2,…,αs 线性表示,则矩阵(β1,β2,…,βt)等于矩阵(α1,α2,…,αs)和一个s t矩阵C的乘积. C可以这样构造: 它的第i 个列向量就是βi对α1,α2,…,αs的分解系数(C不是唯一的).向量组的线性表示关系有传递性,即如果向量组β1,β2,…,βt可以用α1,α2,…,αs线性表示,而α1,α2,…,αs 可以用1,2,…,r线性表示,则β1,β2,…,βt可以用1,2,…,r线性表示.当向量组α1,α2,…,αs β1,β2,…,βt互相都可以表示时,就说它们等价,ϖ︒∴{α1,α2,…,αs }≅{β1,β2,…,βt}.等价关系也有传递性.2. 向量组的线性相关性(1) 定义(从三个方面看线性相关性)线性相关性是描述向量组内在关系的概念,它是讨论向量组α1, α2,…,αs -ϒ∉⎪∑(ϖs-1个向量线性表。
北京邮电大学国际学院高等数学(下)幻灯片讲义(无穷级数)-Lecture 1

is called the partial sum of the series. The partial sum of the series form a sequence
s1 = a1 , s2 = a1 + a2 ,
, sn = ∑ ak ,
k =1 n
n approaching infinite, we say that the series converges to the sum S, and we write
1+ 1 1 1 1 + + + + 2 4 8 16
Infinite Series
∑a
n =1
∞
n
=1 +
1 1 1 1 + + + + 2 4 8 16
Partial Sum First: Second: Third:
…
Value
s1 = 1
1 s2 = 1 + 2
21
2 2 1 2 1 4
The way to do so is not to try to add all the terms at once (we cannot) but rather to add the terms one at a time from the beginning and look for a pattern in how these "partial sum" grow.
k =1 n
Convergence and Divergence
Definition (Convergence and Divergence of a series) If the sequence of partial sums of a series
线性代数讲义正式版

3:行列式——由 n2 个数组成的下列记号
a11 a12 ... a1n
D
a21
a22
...
a2 n
,称为 n 阶行列式,规定
an1 an2 ... an2
D 1 a a a j1 j2 jn
( j1 j2 jn )
1 j1 2 j2
njn
4:余子式与代数余子式——把行列式
1
郑老师线代核心讲义 第五节:线性方程组的性质........................................................................................................ 29 第六节:典型例题:.................................................................................................................... 31 第五章 特征值与特征向量................................................................................................................ 39 第一节:基本概念........................................................................................................................ 39 第二节:特征值与特征向量的性质............................................................................................... 40 第三节:矩阵相似........................................................................................................................ 43 第四节:相似及对角化性质........................................................................................................ 43 第五节:非实对称阵对角化步骤................................................................................................ 43 第六节:求特征值的方法............................................................................................................ 44 第七节:典型例题........................................................................................................................ 46 第六章 二次型.................................................................................................................................... 56 第一节 二次型及其标准型.......................................................................................................... 56 第二节:如何化二次型为标准二次型........................................................................................ 58 第三节 矩阵之间的三大关系.................................................................................................... 59 第四节 正定矩阵与正定二次型.................................................................................................. 63
(精品2011考研数学线性代数冲刺课程讲义

2011考研数学线性代数冲刺课程讲义2011考研冲刺班线性代数讲义主讲:尤承业欢迎使用新东方在线电子教材目录第一部分矩阵 (1)一. n阶行列式的计算 (1)二. 矩阵的初等变换和初等变换法 (4)三.矩阵乘法的两个规律,矩阵分解 (8)四. 可逆矩阵的充分必要条件 (10)第二部分向量组和线性方程组 (13)一.线性表示 (13)二. 向量组的线性相关性 (18)三. 秩的有关等式与不等式 (22)四. 线性方程组 (26)第三部分特征向量与特征值相似和对角化二次型 (33)一. 特征值的计算 (33)二. 相似对角化问题 (37)三. 实对称矩阵的相似对角化 (42)四. 实二次型的标准化 (44)五. 判断两个实对称矩阵是否合同(判断两个二次型是否可用可逆线性变量替换互相转化) (45)六. 正定问题 (46)什么是串讲: 串讲就是总复习.在系统复习和做了大量题目的基础上,对全课程的理论和解题的方法进行整理和总结.串讲的特点:(1) 全局性,宏观性.对命题不看证明, 关心作用和应用.(2) 不求全面,突出要点,重点,考点.(3) 强调纵向联系,不顾及先后顺序.第一部分矩阵本部分是全课程的基础,特别是计算的基础.本部分概念多,因此考点也多.关键性概念:矩阵的初等变换,矩阵的乘法,可逆矩阵.一. n阶行列式的计算计算n阶行列式不一定用递推法或数学归纳法,一些简单的n阶行列式可对某行(列)展开直接求得值;有些可化为三角行列式;还有的可用特征值计算.例1 1 0 0 …… tt 1 0 00 t 1 …… 0 .…………00 0 … t 1例2 证明a1 a2a3b 1c 2 0 … 0 0 0 b 2 c 3 0 0 =11111(1)ni i i i n i b b a c c --+=-∑.… … … …0 0 0 … b n-1 c n(就是要证明M 1i=b 1…b i-1 c i+1…c n .)例3 证明 a 0 a 1 a 2 … a n-1 a nb 1c 1 0 … 0 0b 2 0c 2 … 0 0 =011111nni i i i i n i i a c c c a b c c -+==-∑∏.… … … … b n… 0 c n例4 ① 2 a a a a ② 1+x 1 1 1 ③ 1+a 1 1 1a 2 a a a 1 1+x 1 1 2 2+a 2 2a a 2 a a . 1 1 1+x 1 . 3 3 3+a3 .a a a 2 a 1 1 1 1+x 4 4 4 4+aa a a a 2这些行列式都可以先求出相应矩阵的特征值来求值.例5 计算444342414433332313423222212413121111x b a b a b a b a b a x b a b a b a b a b a x b a b a b a b a b a x b a ++++ ,其中12340x x x x ≠.解444342414433332313423222212413121111x b a b a b a b a b a x b a b a b a b a b a x b a b a b a b a b a x b a ++++13111214123423212224123412343132333412344341424412341111a b a b a b a b x x x x a b a b a b a b x x x x x x x x a b a b a b a b x x x x a b a b a b a b x x x x ++=++矩阵⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛++++1111444334224114443333223113442332222112441331221111x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a x b a E xb x b x b x b a a a a +⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=),,,(443322114321 特征值为4443332221111,1,1,1x b a x b a x b a x b a ++++相应行列式为4443332221111x b a x b a x b a x b a ++++原行列式的值43122432114321x x x b a x x x b a x x x x ++=3214442133x x x b a x x x b a ++例6 证明2222121212a a a a aa a()1n n a =+证明 222222121321012221122aa a a aa aa aA aaa a ==2130124034(1)2(1)3231(1)0n a a a a a n aa n a nn a n+ ==⋅⋅⋅=++ 二. 矩阵的初等变换和初等变换法问题:①什么时候可用列变换?②如果两类变换都可以用,能否交替使用?1.初等变换的作用除了计算行列式,矩阵的初等变换应用在两个方面: (1) 用在线性方程组类问题上对线性方程组的增广矩阵作初等行变换反映了方程组的同解变换. 这方面的应用只可用行变换,决不可用列变换. (2) 计算矩阵和向量组的秩初等行变换和初等列变换都保持矩阵的秩.因此两类变换都可以用,并且可交替使用.(但是如果要求极大无关组,则只可用行变换) 每一种应用都要用到下面的基本运算:用初等(行)变换把一个矩阵化为阶梯形矩阵或简单阶梯形矩阵. 用初等行变换把可逆矩阵化为单位矩阵.2. 初等变换法(1)求方程组的唯一解当A是可逆矩阵时, AX=β唯一解,求解的初等变换法:对增广矩阵(A|β)作初等行变换,使得A变为单位矩阵:(A|β)→(E|η),则η就是解.(2) 解矩阵方程有两种基本矩阵方程:(I) AX=B.(II) XA=B.在A是可逆矩阵这两个方程都是且唯一解.(I) AX=B是线性方程组的推广,求解方法:将A和B并列作矩阵(A|B),对它作初等行变换,使得A变为单位矩阵,此时B变为解X:(A|B)→(E|X)(II)的解法:对两边转置化为(I)的形式:A T X T=B T.再用解(I)的方法求出X T..(A T|B T)→(E|X T)(3) 当A可逆时, A-1是矩阵方程AX=E的解,于是可用初等行变换求A-1:(A|E)→(E|A-1)近几年考题中常见的一类求矩阵的题, 可利用矩阵方程求解:给定了3阶矩阵A的3个线性无关的特征向量α1,α2,α3,和它们的特征值,求A,(给定6个3维列向量α1,α2,α3,β1,β2,β3,求一个3阶矩阵A,使得Aα1=β1,Aα2=β2, Aα3=β3.)例7 A是3阶矩阵的向量α1=(-1,2,-1)T,α2=(0,-1,1)T都是齐次线性方程组AX=0的解,(1) A的各行元素之和都为3, 求A.(06)(2)A是3阶实对称矩阵,求A.解 根据题意有100020101010A A -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭,.(1)A 的各行元素之和都为3,则 ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛333111A .建立矩阵方程 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛---000000333110121111A再用初等变换法求出111111111A ⎛⎫⎪= ⎪ ⎪⎝⎭.(2)0=Ax 有两个线性无关的解,,21αα则 32r A -()≥. ()1r A ≤. 再由()3()1tr A r A =⇒=. 所以A 的特征值为0,0,3.由于A 是实对称矩阵,属于3的特征向量与21,αα都相交,即满足⎩⎨⎧=+-=-+-00232321x x x x x 求得一个非零解,1113⎪⎪⎪⎭⎫ ⎝⎛=α即333αα=A建立矩阵方程 )0,0,3(),,(3213αααα=A .例8二次型f(x 1,x 2,x 3)= X T AX 在正交变换X =QY 下化为y 12+y 22, Q 的第3列为(22,0,22)T.求A . 解 有⎪⎪⎪⎭⎫ ⎝⎛=000010001AQ Q T . 即⎪⎪⎪⎭⎫⎝⎛=-0000100011AQ Q .则A 的特征值为0,1,1.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛22022是A 的特征向量,特征值为0,从而⎪⎪⎪⎭⎫ ⎝⎛101也是A 的特征向量,特征值为0.求A 的属于1的两个无关特征向量,即()0A E x -=的非零解它们都与⎪⎪⎪⎭⎫ ⎝⎛101相交,即满足方程组 031=+x x .(实际上它和()0A E x -=同解),求出两个无关解 ⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛101,010.建立矩阵方程 ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-000101010101101010A⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-010001010110001110A ⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛--100010100201010001010001010110001110⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--→2102101021021100010001 ⎪⎪⎪⎭⎫⎝⎛--=10102010121A*设3阶实对称矩阵A 的特征值为1,1,-1,(0,1,1)T是属于-1的特征向量,求A .(1995). *设3阶实对称矩阵A 的特征值为1,2,3,(1,1,-1)T 和(-1,2,1)T分别是属于1和2的特征向量,求A .(1997)*设3阶实对称矩阵A 的秩为2,又6是它的二重特征值,向量(1,1,0)T 和(2,1,1)T和(-1,2,-3)T都是属于6的特征向量.求A .(2004).*3阶实对称矩阵A 的特征值为1,2,-2, (1,-1,1)T 是A 的属于1的特征向量.记B =A 5-4A 3+E .(1) 求B 的特征值和特征向量. (2) 求B .(07)三.矩阵乘法的两个规律,矩阵分解① A (α1,α2,…, αs )= (Aα1,Aα2,…,Aαs ).② 若A =(α1,α2,…, αn ), B =(β1, β2,…, βn )T ,则A B =α1β1 +α2β2 +…+αn βn .乘积矩阵AB 的第i 个列向量是A 的列向量组的线性组合,组合系数就是B 的第i 个列向量的各分量.(从而AB 的列向量组可以用A 的列向量组线性表示.)乘积矩阵AB 的第i 个行向量是B 的行向量组的线性组合,组合系数就是A 的第i 个行向量的各分量. (AB 的行向量组可以用B 的行向量组线性表示.)近几年考题中常见的又一类求矩阵的题是利用矩阵分解求解. 设A 为3阶矩阵, α1, α2, α3是3维列向量组,知道了A α1,A α2,A α3对α1,α2, α3的分解,求矩阵B ,使得A P =P B . P =(α1, α2, α3).例9(2005) 设A 为3阶矩阵, α1, α2, α3是线性无关的3维列向量组,满足A α1=α1+ α2+ α3, A α2=2α2+α3, A α3=2α2+3α3.求作矩阵B ,使得A (α1, α2, α3)=( α1,α2, α3)B .解:三种方法对照方法一:设,332313322212312111⎪⎪⎪⎭⎫⎝⎛=b b b b b b bb b B 则 B A ),,(),,(321321αααααα=可化为)32,2,(3232321ααααααα++++),,,(333223113332222112331221111αααααααααb b b b b b b b b +++++= 得,331221111321ααααααb b b ++=++ 由于321,,ααα无关,得1,1,1312111===b b b .用同样方法求得1222320,2,1b b b ===, 3,2,0332313===b b b .⎪⎪⎪⎭⎫ ⎝⎛=320120111B方法二:AP P B 1-=.⎪⎪⎪⎭⎫⎝⎛==----100010001),,(,3121111αααP P P E P P 有得1111231000,1,0001P P P ααα---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭于是,)32,2,(32323211ααααααα++++=-P B)32,2,31213121312111ααααααα-------++++=P P P P P P P ⎪⎪⎪⎭⎫⎝⎛=320120111.方法三(矩阵分解法)B A ),,(),,(321321αααααα=.)32,2,(3232321ααααααα++++⎪⎪⎪⎭⎫⎝⎛=320120111),,(321ααα. ⎪⎪⎪⎭⎫⎝⎛=320120111B .方法三是直接求出了B ,并且不必要求321ααα线性无关!例10(2008)已知α1,α2,都是3阶矩阵A的特征向量,特征值分别为-1和1,又3维向量α3满足Aα3=α2+α3.(1) 证明α1,α2, α3线性无关.(2) 记P=(α1,α2, α3),求P-1A P.(3) 证明A不相似于对角矩阵.(4) 求A的所有特征向量.例11(2001)设A是3阶矩阵,α是3维列向量,使得P=(α,Aα,A2α)可逆,并且A3α=3Aα-2A2α.(1)求3阶矩阵B使得A=P B P-1.(2)计算|A+E|.(3)求A的特征值.用矩阵分解求行列式用矩阵分解估计秩和判断向量组的相关性(C矩阵法)四. 可逆矩阵的充分必要条件n阶矩阵A可逆⇔A的行列式|A|≠0⇔ r(A)=n⇔A的列(行)向量组线性无关.⇔AX=0只有零解(AX=β有唯一解)⇔ 0不是A的特征值.(A-c E可逆⇔c不是A的特征值.)例12 设n阶矩阵A满足A2+3A-2E=0.对任何有理数c, 证明A-c E可逆.解:方法一:令cEA+=,则B=,即cEB-A02)(3)(2=-+++E cE B cE B 0)23()32(22=-++++E c c B c B . E c c E c B B )23(])32([2-+-=++.0232=-+x x 的两根为21732893±-=+±-, 因此当c 是有理数时,0232≠-+c c . 则E c c )23(2-+-可逆,从而B 可逆. 方法二:只用说明有理数c 不是A 的特征值. 由0232=-+E A A ,A 的特征值满足 0232=-+λλ. 而有理数c 不满足此式,因此不是A 的特征值.例13 设n 阶矩阵A ,B 满足AB =a A +b B +c E ,其中0ab c +≠,证明A -b E 和B -a E 都可逆.解 方法一:只用证))((aE B bE A --可逆.abE bB aA AB aE B bE A +--=--))((=E c ab )(+∵0ab c +≠,E c ab )(+∴可逆,得)(),(aE B bE A --都可逆. 方法二:先证a 不是B 的特征值,从而aE B -可逆. 用反证法,若有向量0≠η,值得,ηηa B =则ηηηηc bB aA AB ++=, ηηηηc ab aA aA ++=得0)(=+ηc ab ,与条件0≠+c ab 矛盾要证b 不是A 的特征值,只用证b 不是T A 的特征值. 对cE bB aA AB ++=两侧转置,得cE bB aA A B T T T T ++=,用上法可证b 不是T A 的特征值,从而不是A 的特征值.例14 设α是n 维非零列向量,记A =E -T αα.证明1T αα=⇔ A 不可逆. (96)证明 T αα的特征值为0,,0,T αα.A 不可逆⇔1是T αα的特征值⇔1T αα=.例15 已知n 阶矩阵A ,B 满足E -AB 可逆,证明E -BA 也可逆,并且(E -BA )-1=E +B (E -AB )-1A .证明 1()[()]E BA E B E AB A --+-1()()E BA E BA B E AB A -=-+--1()()E BA B BAB E AB A -=-+-- 1()()E BA B E AB E AB A -=-+--.E BA BA E =-+=例16 设A ,B 都是n 阶矩阵,证明c E -AB 可逆⇔ c E -BA 可逆. 证明 当0=c 时,即AB -可逆BA -⇔可逆. 而||||||)1(||BA B A AB n -=-=-.结论显然 下设0≠c .方法一:左⇒右,即设AB cE -可逆,证BA cE -可逆.构选BA cE -的逆矩阵11[()]E B cE AB A c-+-11[][()]cE BA E B cE AB A c--+-])()([11A AB cE B BA cE BA cE c ---+-= 11[()()]cE BA B cE AB cE AB A c-=-+--E =. 方法二:用特征值,要证的是c 不是AB 的特征值⇔c 不是BA 的特征值 逆否为c 是AB 的特征值c ⇔是BA 的特征值.“⇒”设ηηηc AB =≠,0. 则ηηcB BAB =.0,0,0≠⇒≠≠ηηB c .于是ηB 是BA 的特征向量,特征值为c .第二部分 向量组和线性方程组本部分全课程的理论基础,理论制高点, 特点是概念性强,抽象,因此是最难的部分,也是考试的重点和难点.关键性概念:线性表示,线性相关性,向量组和矩阵的的秩.齐次线性方程组的基础解系.对这些概念要准确理解,并熟悉有关的性质,并且注意它们的联系,以及和其他章节的概念的联系.应该特别充分注意秩的作用. 一.线性表示1. 线性表示的意义(1)一个向量β可用α1,α2,…,αs 线性表示,即n 维向量β是α1,α2,…,αs 的一个线性组合.也就是:线性方程组AX =β有解,其中A =(α1, α2,…,αs ).一个向量是齐次方程组AX =0的解⇔它可以用AX =0的基础解系线性表示. (2) β1,β2,…,βt 可以用α1,α2,…,αs 线性表示,即每个βi 都可以用α1,α2,…,αs 线性表示. 这个概念和矩阵乘积有联系: 当AB =C 时 , C 的列向量组可以用A 的列向量组线性表示,C 的行向量组可以用B 的行向量组线性表示.反之,当 β1,β2,…,βt 可用α1,α2,…,αs 线性表示时,存在矩阵C (称为表示矩阵)使得: ( β1,β2,…,βt )=(α1,α2,…,αs )C .(3) 向量组α1,α2,…,αs 和β1,β2,…,βt 等价,即它们互相都可以表示,记作{α1,α2,…,αs }≅{β1,β2,…,βt }.如果A 用初等行变换化为B ,则A 和B 的行向量组等价; 如果A 用初等列变换化为B ,则A 和B 的列向量组等价.向量组和它的每个极大无关组都等价;因此它的任何两个极大无关组等价. 一个齐次方程组AX =0的任何两个基础解系等价.2.用秩判断线性表示(1) β可用α1,α2,…,αs 线性表示⇔r(α1,α2,…,αs ,β)=r(α1,α2,…,αs ). (2) β可用α1,α2,…,αs 唯一线性表示⇔r(α1,α2,…,αs ,β)=r(α1,α2,…,αs )= s.(3) β1,β2,…,βt 可以用α1,α2,…,αs 线性表示⇔r(α1,α2,…,αs ,β1,β2,…,βt )=r(α1,α2,…,αs ).(4) α1,α2,…,αs 和β1,β2,…,βt 等价⇔r(α1,α2,…,αs )= r(α1,α2,…,αs , β1,β2,…,βt )= r(β1,β2,…,βt ).例1设α1=(1,2,0,1) , α2 =(1,1,-1,0),α3=(0,1,a,1),γ1=(1,0,1,0),γ2=(0,1,0,2).a 和k 取什么值时, γ1+k γ2可用α1,α2,α3线性表示?解 ),,(),,,(32121321αααγγγαααγ=+k)|,,(21321γγαααk +⎪⎪⎪⎪⎪⎭⎫⎝⎛-=k k a 21111001111021行⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----1212111011110001k k a 行⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+----1321011000110001k kk a 1,1≠-=a k例2 已知r(α1,…,αs )=r(α1,…,αs , β)=k,r(α1,…,αs , β,γ)=k+1,求r(α1,…,αs , β-γ ).解 看γβ-是否可用s αα,,1 线性表示.β可以用s αα,,1 线性表示,γ不可用βαα,,,1s 表示,因此也不可用s αα,,1 表示.于是γβ-不可用s αα,,1 线性表示.11(,,,)(,,)11s s k γααβγγαα-=+=+例3设(1,2,3)T,(2,3,5)T和(1,a,b-1)T,(2,a 2,b)T都是AX =0的基础解系,求a,b.解 ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛b a b a 22,11532,321与等价,即221121153232122=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-b a b a b a b a γγ. 222121212122301243510022a a a a b b b a b a ⎛⎫⎛⎫ ⎪ ⎪→--- ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭得⎩⎨⎧=--=--02022a b a b 即⎩⎨⎧+==22a b a a ⎩⎨⎧==3210或或b a .当2,0==b a 时⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-2022,101112b a b a 秩为1,不合要求当3,1==b a 时⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-3122,211112b a b a ,秩为2,此时这两个向量组等价,符合题目要求.例4设AX=β的通解为 (1,-1,1,-1)T +c 1(1,-3,1,,0)T +c 2(-2,1,-1,2)T , c 1,c 2任意.(a,1,b,3)T 是AX=β的解, 求a,b.解 的解是的解是011113131=⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⇔=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛Ax b a Ax b a β线性表示可用⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⇔2112,01314121b a 221120131412121120131=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----⇔γγb a . ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+--→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----2932100120001213111520001412121120131a b a a a b a a b a 则1,302093-=-=⎩⎨⎧=--=+b a a b a .例5 α1=(1,1,0,-1)T , α2=(0,2,1,1)T . 求β=(c 1, c 2, c 3, c 4)T 可用α1,α2线性表示的条件.解 2),(,,2121==)(ααγβααγ.⎪⎪⎪⎪⎪⎭⎫⎝⎛-+--→⎪⎪⎪⎪⎪⎭⎫⎝⎛-=3143123143212120010111201011),,(c c c c c c c c c c c c βαα得:β可用⎩⎨⎧=-+=--⇔002,31431221c c c c c c 线性表示αα⎩⎨⎧=-+=--⇔002314312x x x x x x 是β的解. (即⎩⎨⎧=+-=+-02431321x x x x x x 是β的解).说明⎩⎨⎧=+-=+-002431321x x x x x x 以21,αα为基础解系.例6设α1,α2 ,…,αs 是n 维向量组.证明r(α1,α2 ,…,αs )= n 的充分必要条件为:任何n 维向量都可用α1,α2,…,αs 线性表示.解 必要性:对任何n 维向量β,,),,,()(11n n s s ≤≤=βααγααγ得),,,(),,,(11s s ααγβααγ =从而β可用s αα 1表示充分性:当任何n 维向量都可用s αα 1表示时,任何n 维向量组都可用s ααα,,,21 表示.取n ηηη,,,21 是一个线性无关的n 维向量组(如一个n 阶可逆矩阵的列向量组),则n n s n ≤≤=)()(11ααγηηγ . 得n s =)(1ααγ .例7 设A 是m ⨯n 矩阵, C 是m ⨯s 矩阵.证明矩阵方程AX =C 有解⇔r(A |C )=r(A ).证明 记),(),,,(11s n C A γγαα ==则AX C =有解⇔存在s n ⨯矩阵H 使得 C AH =⇔n s ααγγ 11可用线性表示⇔)(),(111n s n ααγγγααγ = 即)()|(A C A γγ=.例8 设(Ⅰ)和(Ⅱ)都是3元非齐次线性方程组,(Ⅰ)有通解ξ1+c 1η1+c 2η2,其中ξ1=(1,0,1)T ,η1=(1,1,0)T ,η2=(1,2,1)T ;(Ⅱ)有通解ξ2+c η, ξ2=(0,1,2)T ,η=(1,1,2)T .求(Ⅰ)和(Ⅱ)的公共解.解 公共解都可写成ηξc +2,我们来求当c 取什么值时它又是(I )的解?ηξc +2是(I )的解⇔是12ξηξ-+c (I )的导出组的解 ⇔12ξηξ-+c ,可用21,ηη线性表示.⎪⎪⎪⎭⎫ ⎝⎛++-=-+1211121011),,(1221c c c c ξηξηη⎪⎪⎪⎭⎫ ⎝⎛--→1221011001c c得21=c ,公共解为:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=+32321212ηξ二. 向量组的线性相关性1.定义和意义意义线性无关就是每个 αI都不能用其它向量线性表示; 线性相关就是有向量(不必每个)可以用其它向量线性表示.定义设α1,α2,…,αs 是n维向量组,如果存在不全为0的一组数c1,c2,…,c s 使得c 1α1+c2α2+…+csαs=0,则说α1,α2,…,αs 线性相关,否则(即要使得c1α1+c2α2+…+c sαs=0,必须c1,c2,…,c s全为0)就说它们线性无关.和齐次线性方程组的关系记A=(α1,α2,…,αs ),则:α1,α2,…,αs 线性相关(无关) ⇔齐次线性方程组AX=0有(没有)非零解.2.线性相关性的判别在考试真题中,相关性的判别是常见的,许多情形可用一些简单性质完成,甚至直接可用定义判别.因此熟记有关的性质是重要的.例如α1-α2,α2-α3,α3-α1线性相关,(2,1,a+4),(2,1,a+6)无关.对考场上也出现过一些证明题,常用的思路有3个:①定义法:用定义证明一个向量组α1,α2,…,αs 线性无关,就是由c1α1+c2α2+…+cs αs=0推出ci都为0.②扩大法:利用性质:如果α1,α2,…,αs 线性无关, 则α1,α2,…,αs ,β线性无关⇔β不能用α1,α2,…,αs 线性表示.推论如果αi≠0,并且每个αi都不能用前面的i-1个向量线性表示,则α1,α2,…,αs 线性无关.③秩法:α1,α2,…,αs 线性无关⇔ r(α1,α2,…,αs)=s.例9 设A 为n 阶矩阵, α为n 维列向量,正整数k 使得A k α=0,但是A k-1α≠0,证明α, A α,…, A k-1α线性无关.证明 方法一:用定义证设0121=+++-αααk k A c A c c (1) 用1-k A 乘(1)式得00111=⇒=-c A c k α 再用2-k A 乘(1)式,得0,0212=⇒=-c A c k α 这样逐个得出i c 都为0.方法二:用扩大法的推论,这个向量组是: 最后一个01≠-αk A .每一个都不能用后边的线性表示,如α1-i A 不可用αα1,,-k i A A 表示,因为αα1,,-k i A A 用i k A -乘都为0,即它们都是0=-αi k A 的解,而αi k A -不是:0)(1≠=---ααk i i i k A A A .由推论,得ααα1,,,-k A A 无关.例10设α1,α2,…,αs ,β1,β2,…,βt 线性无关,其中α1,α2,…,αs 是齐次方程组AX =0的基础解系.证明A β1,A β2,…,A βt 线性无关.证明 用定义法设,02211=+++t t A c A c A c βββ 而,0)(2211=+++t t c c c A βββ于是t t c c ββ++ 11是0=Ax 的解,从而可用0=Ax 的基础解系s αα,,1 线性表示,即有 s s t t k k c c c ααβββ++=+++ 112211但是11,,,,,s t ααββ线性无关,得)(11s t k k c c 和都为0.例11 设α1,α2,…,αs 和β1,β2,…,βt 是两个线性无关的n 维实向量组,并且每个αi 和βj 都正交,证明α1,α2,…,αs ,β1,β2,…,βt 线性无关.证明 用定义法,设,01111=+++++t t s s k k c c ββαα 记)(1111t t s s k k c c ββααγ++-=++= 则0))(,(),(1111=++-++=t t s s k k c c ββααγγ 即0=γ,于是s s k k c c 11和全都为0.例12 设α1,α2,…,αs 和β1,β2,…,βt 都是线性无关的n 维向量组,证明α1,α2,…,αs ,β1,β2,…,βt 线性相关⇔存在非零向量η,它既可用α1,α2,…,αs 线性表示,又可用β1,β2,…,βt 线性表示.证明 “⇒”存在t s k k c c 11,不全为0使得01111=+++++t t s s k k c c ββαα . 令t t s s k k c c ββααη---=++= 1111, 则0≠η(∵t s k k c c 11和不能全为0!) 且η既可用s αα 1表示,又可用t ββ 1表示.“⇐”设0≠η,既可用s αα 1表示,又可用t ββ 1表示, 证s s s c c c c 111,ααη++=不全为0,t t t p p p p ,,,111 ββη++=-也不全为0, 则,01111=++++t t s s p p c c ββαα ∴t s ββαα 11,相关.例13 已知n 元非齐次方程组AX =β有解, n-r(A )=3. (1)证明AX =β有4个线性无关的解. (2)证明AX =β的任何5个解都线性相关.(n 元非齐次方程组AX =β有解时,解集合的秩= n-r(A )+1.) 证明 (1)设0ξ是β=Ax 的一个解321,,ηηη是0=Ax 的基础的解系,321,,ηηη线性无关,而0ξ不可用321,,ηηη线性表示,从而这个向量线性无关.易见,,,,,,32103020100ηηηξηξηξηξξ≅+++,它们的秩相等,为4,从而3020100,,ηξηξηξξ+++,也无关,它们都是β=Ax 的解.(2)设54321,,,,ξξξξξ都是β=Ax 的解,则它们都可用(1)中的4210,,,ηηηξ这4个向量表示,所以必相关. 三. 秩的有关等式与不等式秩是讨论向量组线性相关性的深入,它把抽象的概念数量化了, 从而可用数量的形式来处理线性表示和线性相关性问题,显得简单化了.譬如, 有一个性质:如果β1,β2,…,βt 可用α1,α2,…,αs 线性表示,并且t>s,则β1,β2,…,βt 线性相关.从秩看,r(β1,β2,…,βt )≤ r(α1,α2,…,αs )≤s<t,从而β1,β2,…,βt 线性相关.例14 n 维向量组(I) α1,α2,…,αr 可以用n 维向量组(II) β1, β2,⋯, βs 线性表示.(A) 如果(I)线性无关,则r ≤s. (B) 如果(I)线性相关,则r>s.(C) 如果(II)线性无关,则r≤s. (D) 如果(II)线性相关,则r>s.这题可以用上面那个性质解决: (A)是它的逆否命题, (B)是否命题.如果用秩做: r=r(α1,α2,…,αr)≤r(β1, β2,⋯, βs)≤s.例15 已知β可用α1,α2,…,αs线性表示,但不可用α1,α2,…,αs-1线性表示.证明⑴αs不可用α1,α2,…,αs-1线性表示;⑵αs可用α1,α2,…,αs-1,β线性表示.这题可以用定义做,叙述起来有点罗嗦. 下面用秩做:r(α1,α2,…,αr-1)+1=r(α1,α2,…,αr-1,β)≤r(α1,α2,…,αr,β)=r(α1,α2,…,αr)≤ r(α1,α2,…,αr-1)+1于是r(α1,α2,…,αr-1,β)=r(α1,α2,…,αr,β), r(α1,α2,…,αr)=r(α1,α2,…,αr-)+1.1例16 已知α1,α2,α3线性相关,而α2,α3,α4线性无关,则α1,α2,α3,α4中, 能用另外3个向量线性表示,而不能用另外3个向量线性表示.r(α1,α2,α3)<3, r(α2,α3,α4)=3, r(α1,α2,α3,α4)=3.①如果α1,α2,…,αs是n维向量组, 0≤r(α1,α2,…,αs)≤ Min{s,n}.如果A是m⨯n矩阵,则0≤r(A)≤Min{m,n}.② r(α1,α2,…,αs)+1.若β不可用α1,α2,…,αs 线性表示.r(α1,α2,…,αs,β)=r(α1,α2,…,αs).若β可用α1,α2,…,αs 线性表示.③ 如果β1,β2,…,βt可以用α1,α2,…,αs线性表示,则r(β1,β2,…,βt )≤r(α1, α2,⋯ ,αs ). ④ r(A ±B )≤r(A )+r(B ).⑤ r(AB )≤Min{r(A ),r(B )}.⑥ 当A (或B )可逆时,r(AB )=r(B )(或r(A )). ⑦ 如果A 列满秩(r(A )等于列数),则r(AB )=r(B ). ⑧ 如果AB =0,n 为A 的列数(B 的行数),则r(A )+r(B )≤n. ⑨ 设A *为n 阶矩阵A 的伴随矩阵,则 n, 若r(A )=n,r(A *)= 1, 若r(A )=n-1,0, 若r(A )<n-1.⑩ r(A |B )≤r(A )+r(B ).例17设A 是n 阶矩阵, α1,α2,⋯,αs 是一组n 维向量,βi =A αi , i=1,2,⋯,s.证明:(1) r(β1, β2,⋯, βs )≤r(α1,α2,⋯,αs ).(2) 如果A 可逆,则r(α1,α2,⋯,αs )=r(β1, β2,⋯, βs ). 证明 (1)矩阵),,(),,(11s s A ααββ = ∴11(,,)min{(),()}s s r r A r ββαα≤(2)若A 可逆,则11()()s s r r ββαα=例18设α1,α2,α3,α4都是n 维向量.判断下列命题成立的为 ① 如果α1,α2,α3线性无关,α4不能用α1,α2,α3线性表示,则α1,α2,α3,α4线性无关.② 如果α1,α2线性无关,α3,α4都不能用α1,α2线性表示,则α1,α2,α3,α4线性无关.③ 如果存在n 阶矩阵A ,使得A α1,A α2,A α3,A α4线性无关,则α1,α2,α3,α4线性无关.④ 如果α1=A β1,α2=A β2,α3=A β3,α4=A β4,其中A 可逆,β1,β2,β3,β4线性无关,则α1,α2,α3,α4线性无关.解 ①√.② 不对,例如43αα=.③ 123412344(,,,)(,,,)4r A A A A r αααααααα=≤≤. ④ √. 4),,,(),,,(43214321==ββββααααA .例19,例20 都可用C 矩阵法解.C 矩阵法:若s αα 1无关,t ββ 1可用s αα 1线性表示,表示矩阵为C ,则1()()t r r C ββ=.如果s t =,则t ββ 1无关0||≠⇔C .例19 设 α1,α2,…,αs 是齐次方程组AX =0的基础解系, β1=α1+t α2,β2=α2+t α3,…,βs-1=αs-1+t αs ,βs =αs +t α1.t 取什么值时β1,β2,…,βs 也是AX =0的基础解系?解 s ββ,,1 确定都是0=Ax 的解,个数也合要求,看1s ββ是否无关,由于s αα 1无关,可用C 矩阵法,s βββ 21,对s αα 1的表示矩阵C 为10010000000001t t C t⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭s s t C 1)1(1||+-+= s s t C )1(0||-≠⇔≠当s s t )1(-≠时s ββ,,1 线性无关,从而构成基础解系.例20 设α1,α2,α3是齐次方程组AX =0的基础解系,则( )也是AX =0的基础解系.(A) α1,α2-α3 . (B) α1+α2, α2+α3,α3-α1. (C) α1+α2+α3,α1-α2-2α3,α1+3α2+4α3. (D) α1+2α2-α3,2α1+α2+α3, α2+α3.解 (A )个数2个,不对.×(B )0)()()(133221=-++-+αααααα相关.×(C )表示矩阵⎪⎪⎪⎭⎫ ⎝⎛--=431211111C111111||1130220124033C =-=-=--,32132132143,2,ααααααααα++--++相关.×(D )√ 此时⎪⎪⎪⎭⎫⎝⎛-=110112121C ,120120||2113006111111C ===---.四. 线性方程组线性方程组是课程的最主要部分,是考试的最大重点,但是考点很集中(解的情况的判别和通解的计算),有关的结论又十分明确,因此从方法上看不困难,大家也比较熟悉.但是近年来考题的发展趋势应该重视:考试重点转向概念化,考题渐渐脱离传统题型,出现许多有新意的题.1. 线性方程组解的情况的判别(1)对于方程组AX=β,判别其解的情况用三个数:未知数的个数n,r(A),r(A|β).①无解⇔r(A)<r(A|β).②有唯一解⇔r(A)=r(A|β)=n.(当A是方阵时,就推出克莱姆法则.)③有无穷多解⇔r(A)=r(A|β)<n.方程的个数m虽然在判别公式中没有出现,但它是r(A)和r(A|β)的上界,因此当r(A)=m时, AX=β一定有解.当m<n时,一定不是唯一解.(2)对于齐次方程组AX=0,判别解的情况用两个数: n,r(A).有非零解⇔ r(A)<n(即:只有零解⇔r(A)=n).2. 基础解系和通解(1) 齐次方程组的基础解系如果齐次方程组AX=0有非零解,则它的解集(全部解的集合)是无穷集,称解集的每个极大无关组为AX=0的基础解系.η1, η2,…,ηs是AX=0的基础解系的条件为:①η1, η2,…,ηs是AX=0的一组解.②η1, η2,…,ηs线性无关.③ s=n-r(A).(2) 通解当η1, η2,…,ηl是AX=0的基础解系时, AX=0的通解为:c 1η1+c 2η2+…+c s ηs , c 1,c 2,…,c s 任意.如果ξ0是非齐次方程组AX =β的一个解, η1, η2,…,η s 是AX =0的基础解系时,AX =β的通解为:ξ0+c 1η1+c 2η2+…+c l ηs , c 1,c 2,…,c s 任意.例21 已知 ξ1=(1,-1,0,1)T ,ξ2=(2,0,1,1)T ,ξ3=(3,0,1,2)T 都是线性方程组AX=β (β≠0)的解,并且r(A )=2,求通解.解 4,()2,()2n r A n r A ==-=.0=Ax 的基础解系由2个解构成0111201111312=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-Ax 是和ξξξξ两个无关的解,构成基础解系.通解:2121,,111201111011c c c c ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-任意.例22 已知 ξ1,ξ2,ξ3都是线性方程组AX=β (β≠0)的解, ξ1=(1,2,3,4)T , ξ2+ξ3=(0,1,2,3)T ,并且r(A )=3,求通解.解 4,()3,()1n r A n r A ==-=.123232()45ξξξ⎛⎫⎪⎪-+= ⎪ ⎪⎝⎭是0=Ax 的一个非零解,通解为c c ,54324321⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛任意例23 已知ξ=(0,1,0)T是方程组123123123322213x x x x bx x ax x cx d+-=⎧⎪-++=⎨⎪++=⎩的解,求通解.解 以ξ代入第2,3两个方程,得⎩⎨⎧==,31d b 不能确定c a 与.系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=c a A 2131213 ()2r A ≥若()3r A =,此时方程组有唯一解,它就是ξ.若()2r A =,则⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛--−→−011010001052051001021012013行A 0=Ax 的同解方程组为⎩⎨⎧-==3231x x x x ,得基础解系⎪⎪⎪⎭⎫⎝⎛-111,通解为c c ,111010⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛任意例24有两个3元方程组x 1+x 2+x 3=1, 2x 1+3x 2+ax 3=4,(I) 3x 1+5x 2+x 3=7, (II) 2x 1+4x 2+(a-1)x 3=b+4 (1) 已知它们同解,求a,b.(2) 已知它们有公共解,求a,b ,并求所有公共解. 解 (1)思路:解出(I )的通解,代入(II )求出b a ,.⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫ ⎝⎛211210014121210171115131 ⎩⎨⎧+=--=2123231x x x x ,通解⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-112021c . 用⎪⎪⎪⎭⎫ ⎝⎛-021代入(II )的第2个方程得2,482=⇒+=+-b b .取,1=c 得(I )的另一个解⎪⎪⎪⎭⎫ ⎝⎛-133,代入(II )的第1个方程1496=⇒=++-a a .(2)即联立方程组有解:1111111111113517022401122340122001024140110002a a a a b b b ⎛⎫⎛⎫⎛⎫⎪⎪⎪-- ⎪ ⎪ ⎪→→ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎪ ⎪ ⎪-+--⎝⎭⎝⎭⎝⎭得a b ,2=任意.i )当2,1==b a 时⎪⎪⎪⎪⎪⎭⎫⎝⎛--→⎪⎪⎪⎪⎪⎭⎫⎝⎛-=00210012001000010021001100110001公共解为c c ,112021⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-任意.ii )当2,1=≠b a 时 ⎪⎪⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎪⎪⎭⎫⎝⎛-→0021010000100010021011100110001,得唯一解⎪⎪⎪⎭⎫⎝⎛-021.例25 设(Ⅰ)和(Ⅱ)是两个齐次线性方程组,(Ⅰ)的一个基础解系(1,-1,0,2)T,(0,1,1,a)T ,(Ⅱ)的一个基础解系为(-2,0,a,-2)T ,(1,1,1,0)T.已知(Ⅰ)和(Ⅱ)有公共非零解,求a,并求出它们的全部公共解.解 (用例12结果)(1)(I )与(II )有公共非零解⇔这4个向量线性相关.⎪⎪⎪⎪⎪⎭⎫⎝⎛--+-+--→⎪⎪⎪⎪⎪⎭⎫⎝⎛---→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---a a a a a a a 2222001200221012012201102210120102211010111201⎪⎪⎪⎪⎪⎭⎫⎝⎛+---→⎪⎪⎪⎪⎪⎭⎫⎝⎛---+--→2)1(000100221012012200120022101201a a a a 得:1-=a 时,有非零解.(2)此时(I )的基础解系为,1110201121⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛-=ηη(II )的基础解系为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=0111,210221γγ.(II )的解为21121221212211,,2201112102c c c c c c c c c c c c ⎪⎪⎪⎪⎪⎭⎫⎝⎛-+-+-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=+γγ任意 它要成为公共解⇔它可用21,ηη表示.⎪⎪⎪⎪⎪⎭⎫⎝⎛-+-+-+-→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+---212121211212212001012211102011c c c c c c c c c c c c c c当21c c =时2211γγc c +是公共解,得公共解为1211()02c c γγ-⎛⎫⎪ ⎪+= ⎪ ⎪-⎝⎭,c 任意例26 设(Ⅰ)和(Ⅱ)是两个齐次线性方程组,(Ⅰ)的一个基础解系为(2,-1,-1,0)T,(t,1-t,0,1)T,(Ⅱ)为123412341242023300x x x x x x x x x px x -++=⎧⎪-++=⎨⎪++=⎩已知(Ⅰ)和(Ⅱ)有公共非零解,求p 和t,并求出它们的全部公共解.解 (1)记⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=132********,101,011221p A t t ηη (I )和(II )有公共非零解⇔存在21,c c 不全为0,使得2211ηηc c +也是(II )的解 ⇔存在21,c c 不全为0,使得0)(2211=+ηηc c A ⇔存在21,c c 不全为0,使得02211=+ηηA c A c ⇔21,ηηA A 相关122216,521t A A t p t p pt ηη+⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪-+-+⎝⎭⎝⎭21ηηA A 与相关,得3,36)12(35-=+=+=t t t t⎪⎪⎪⎭⎫ ⎝⎛---=241552p A η, 22542p p -=--84510,36,2p p p p -=-=-=-(2)⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛=10155,46221ηηA A .2211ηηc c +也是(II )的解⇔0)(2211=+ηηc c A,520101554622121c c c c =⇔=⎪⎪⎪⎭⎫⎝⎛---+⎪⎪⎪⎭⎫ ⎝⎛ 即当25∶21∶=c c 时,2211ηηc c +是公共解. 整理后:公共解为c c ),25(321ηη+任意.注:关于两个齐次方程组有公共非零解的判断.(1)如果都给出了方程组的具体形式, 有公共非零解就是联立方程组有非零解.(2)如果一个给了系数矩阵A,另一个给出了基础解系η1, η2,…,ηs,则有公共非零解⇔Aη,Aη2,…,Aηs线性相关.1(3)两个都给出了基础解系η1, η2,…,ηs和γ1, γ2,…,γt, 则有公共非零解⇔η1, η2,…,ηs,γ1, γ2,…,γt线性相关.第三部分特征向量与特征值相似和对角化二次型本部分包含了线性代数的应用方面的两部分.特点是:概念多,考点多,但是题型确定,变化小.特征值是本部分的关键, 本部分的各类问题几乎都和特征值有关. 因此特征值的计算是应该关注的重点,还应该总结这部分的各个题型和解法的思路.一. 特征值的计算特征值不仅在这两章中被广泛应用,还可以用来计算行列式和判断n阶矩阵的可逆性:λ1λ2…λn=|A|;λ不是A的特征值⇔|A-λE|≠0⇔A-λE可逆.0不是A的特征值⇔A可逆.因此应该关注特征值的计算方法.除了用定义,一般都会想到用特征多项式|λE-A|来计算特征值,但是这样做不仅计算量大,并且因为一般的多项式求根并不总是可行的,所以不是任何矩阵都可求特征值的.事实上,考试题里都是给出都是特殊的矩阵,或者给了特殊的条件让求特征值.因此应该总结这些特殊方法.1.两类特殊矩阵的特征值①对角矩阵和上下三角矩阵的特征值就是对角线上的元素.②当r(A)=1时,特征值为 0,0,…,0,tr(A).(例如:αβT的特征值为0,0,…,0,βTα.)2.利用相关矩阵的特征值的关系:如果A的特征值为λ1,λ2,…,λn,则①A的多项式f(A)的特征值是f(λ1),f(λ2),…,f(λn).特别地, A+c E的特征值是λ1+c,λ2+c,…,λn+c.②如果A可逆,则A-1的特征值是1/λ1,1/λ2,…,1/λn;A*的特征值是|A|/λ1,|A|/λ2,…,|A|/λn.③A T的特征值也是λ1,λ2,…,λn.④相似于A的特征值也是λ1,λ2,…,λn.3.利用特征值的性质:①λ1+λ2+…+λn=tr(A).②A的特征值λ的重数≥n-r(A-λE).A是实对称矩阵时, A的特征值λ的重数=n-r(A-λE).③如果f(A)=0,则A的每个特征值λ满足f(λ)=0.例1 设A =(α1,α2,α3)是3阶矩阵,满足|A |=0,它的各列元素之和都为3, α1-α2=(2,-2,0)T .求A 的特征值.解 A 有3个特征值,||A =0,则0是特征值各列元素之和为3,则1311331131T A ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,从而3是T A 的特征值,也是A 的一个特征值又12220αα⎛⎫ ⎪-=- ⎪ ⎪⎝⎭,而12110A αα⎛⎫ ⎪-=- ⎪ ⎪⎝⎭,则⎪⎪⎪⎭⎫⎝⎛-011是A 的特征向量,特征值为2.因此A 的特征值为0,3,2。
北京邮电大学国际学院线性代数讲义Lecture 04

0 1 0 a11 a12 a13 a21 a22 a23 E1 A 1 0 0 a21 a22 a23 a11 a12 a13 0 0 1 a 31 a32 a33 a31 a32 a33 a11 a12 a13 0 1 0 a12 a11 a13 AE1 a21 a22 a23 1 0 0 a22 a21 a23 a 31 a32 a33 0 0 1 a32 a31 a33
11
Elementary Matrices
Definition: A matrix B is row equivalent to A if there exists a finite sequence E1 , E2 ,, Ek of elementary matrices such
6
Elementary Matrices
Type II. Type II elementary matrices are obtained by multiplying a row of I by a nonzero constant.
1 0 0 Example: E 2 0 1 0 is an elementary matrix of type II. Then 0 0 3 a12 a13 1 0 0 a11 a12 a13 a11 0 1 0 a a22 a23 a21 a22 a23 21 0 0 3 a 31 a32 a33 3a31 3a32 3a33 a11 a12 a13 1 0 0 a11 a12 3a13 a21 a22 a23 0 1 0 a21 a22 3a23 a 0 0 3 a 31 a32 3a33 31 a32 a33
北京邮电大学版线性代数课后题答案解析

习题 六(A 类)1. 检验以下集合对于所指的线性运算是否构成实数域上的线性空间. (1) 2阶反对称(上三角)矩阵,对于矩阵的加法和数量乘法; (2) 平面上全体向量,对于通常的加法和如下定义的数量乘法: k ·αα=;(3) 2阶可逆矩阵的全体,对于通常矩阵的加法与数量乘法;(4) 与向量(1,1,0)不平行的全体3维数组向量,对于数组向量的加法与数量乘法. 【解】(1)是.由于矩阵加法和数量乘法满足线性空间定义中的18条性质,因此只需考虑反对称(上三角)矩阵对于加法和数量乘法是否封闭即可.下面仅对反对称矩阵验证:设A ,B 均为2阶反对称矩阵,k 为任一实数,则(A +B )′=A ′+B ′=A B =(A +B ), (k A )′=k A ′=k (A )=(k A ),所以2阶反对称矩阵的全体对于矩阵加法和数量乘法构成一个线性空间.(2) 否.因为(k +l )·αα=,而2k l ⋅+⋅=+=ααααα,所以这种数量乘法不满足线性空间定义中的第7条性质.(3) 否.因为零矩阵不可逆(又因为加法和数量乘法都不封闭). (4) 否.因为加法不封闭.例如,向量(1,0,0),(0,1,0)都不平行于(1,1,0),但是它们之和(1,0,0)+(0,1,0)=(1,1,0)不属于这个集合. 2. 设U 是线性空间V 的一个子空间,试证:若U 与V 的维数相等,则U =V. 【证明】设U 的维数为m ,且m ,,,ααα 21是U 的一个基,因U ⊂V ,且V 的维数也是m ,自然m ,,,ααα 21也是V 的一个基,故U =V .3. 在R 4中求向量α=(0,0,0,1)在基1ε=(1,1,0,1),2ε=(2,1,3,1), 3ε=(1,1,0,0), 4ε=(0,1,-1,-1)下的坐标.【解】设向量α在基1234,,,εεεε下的坐标为(1234,,,x x x x ),则11223344x x x x +++=εεεεα即为123412100111100301011011x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦解之得(1234,,,x x x x )=(1,0,1,0). 4. 在R 3中,取两个基1α=(1,2,1),2α=(2,3,3),3α=(3,7,1); 1β=(3,1,4),2β=(5,2,1),3β=(1,1,-6),试求123,,ααα到123,,βββ的过渡矩阵与坐标变换公式.【解】取R 3中一个基(通常称之为标准基)1ε=(1,0,0), 2ε=(0,1,0), 3ε=(0,0,1).于是有1231231231231123123123(,,)(,,)237,131351(,,)(,,)121,416123351(,,)(,,)237121,131416αααεεεβββεεεβββααα-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦所以由基123,,ααα到基123,,βββ的过渡矩阵为11233512771412371219209.1314164128----⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A坐标变换公式为1122332771419209,4128x x x x x x '---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥'=⎢⎥⎢⎥⎢⎥'⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中(123,,x x x )与(123,,x x x ''')为同一向量分别在基123,,ααα与123,,βββ下的坐标.5. 设α1,α2,α3与β1,β2,β3为R 3的两个基,且由基α1,α2,α3到基β1,β2,β3的过渡矩阵为121012111A ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,(1) 求由基β1,β2,β3到基α1,α2,α3的过渡矩阵B ;(2) 若向量α在基β1,β2,β3下的坐标为(2,3,1)′,求α在基α1,α2,α3下的坐标.解(1)123123(,,)(,,)A βββααα=,由于A 又逆,所以得1123123(,,)(,,)A αααβββ-=,可见A -1为从123,,βββ到123,,ααα的过渡矩阵B 利用求逆矩阵方法133312026131B A --⎛⎫⎪==- ⎪⎪-⎝⎭(2)由定理3知,123212129301235111110x x A x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪=== ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭6. 在R 4中取两个基11223344(1,0,0,0),(2,1,1,1),(0,1,0,0),(0,3,1,0),(0,0,1,0),(5,3,2,1),(0,0,0,1).(6,6,1,3).εαεαεαεα==-⎧⎧⎪⎪==⎪⎪⎨⎨==⎪⎪⎪⎪==⎩⎩(1) 求由前一个基到后一个基的过渡矩阵; (2) 求向量(1234,,,x x x x)在后一个基下的坐标;(3) 求在两个基下有相同坐标的向量.【解】(1)1234123420561336(,,,)(,,,),11211013ααααεεεε⎡⎤⎢⎥⎢⎥==⎢⎥-⎢⎥⎣⎦A A这里A 就是由基1234,,,εεεε到基1234,,,αααα的过渡矩阵.(2) 设1234(,,,)x x x x α=,由于(1234,,,εεεε)=(1234,,,αααα)A 1,所以11221123412343344(,,,)(,,,),a A εεεεαααα-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x x x x x x x x 因此向量α在基1234,,,αααα下的坐标为12113412927331129231,.900182773926A A ----⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥=⎢⎥⎢⎥-⎢⎥⎢⎥--⎣⎦⎣⎦x x x x(3) 设向量ξ在这两个基下有相同的坐标1234(,,,)k k k k ,那么 1122123412343344(,,,)(,,,),k k k k k k k k ξεεεεαααα⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦11223344,A ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦k k k k k k k k 即 1234(),A E ⎡⎤⎢⎥⎢⎥-=⎢⎥⎢⎥⎣⎦k k k k 0也就是134123412341345602360020++=⎧⎪+++=⎪⎨-+++=⎪⎪++=⎩k k k k k k k k k k k k k k解得1234(,,,)(,,,)=-k k k k c c c c ,其中c 为任一非零实数. 7. 说明xOy 平面上变换A ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦x x T y y 的几何意义,其中 (1)1001-⎡⎤=⎢⎥⎣⎦A ; (2)0001⎡⎤=⎢⎥⎣⎦A ; (3) 0110⎡⎤=⎢⎥⎣⎦A ; (4)0110⎡⎤=⎢⎥-⎣⎦A . 【解】10(1)01--⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦x x x T y y y ,T 把平面上任一点变到它关于y 轴对称的点. 000(2)01⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦x x T y y y ,T 把平面上任一点变到它在y 轴的投影点.01(3)10⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦x x y T y y x ,T 把平面上任一点变到它关于直线x=y 对称的点. 01(4)10⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦x x y T y y x ,T 把平面上任一点变到它绕原点按顺时针方向旋转90°后所对应的点.8. 设V 是n 阶对称矩阵的全体构成的线性空间[维数为(1)2n n +],给定n 阶方阵P ,变换T (A )=P ′AP , ∀A ∈V称为合同变换,试证合同变换T 是V 中的线性变换.【证明】因为∀A ,B ∈V ,k ∈R ,有T (A+B )=P ′(A+B )P =P ′AP+P ′BP =T (A )+T (B ),T (k A )=P ′(k A )P =k (P ′AP )=kT (A ).所以T 是线性空间V 的一个线性变换.9. 在R 3中取两个基:α1=(-1,0,-2),α2=(0,1,2),α3=(1,2,5); β1=(-1,1,0),β2=(1,0,1),β3=(0,1,2).定义线性变换T :T(α1)=(2,0,-1),T(α2)=(0,0,1),T(α3)=(0,1,2),求线性变换T 在基β1,β2,β3下的矩阵. 解:设123(1,0,0),(0,1,0),(0,0,1)ξξξ===则123123(,,)(,,)001112T αααξξξ ⎪= ⎪⎪-⎝⎭ 123123101(,,)(,,)012225αααξξξ-⎛⎫ ⎪= ⎪⎪-⎝⎭()()123123101(),(),()(),(),()012225T T T T T T αααξξξ-⎛⎫⎪= ⎪ ⎪-⎝⎭所以()()1123123101(),(),()(),(),()012225T T T T T T ξξξααα--⎛⎫⎪= ⎪ ⎪-⎝⎭ 故()()()123123123200121242(),(),(),,001432,,221112221111T T T ξξξξξξξξξ--⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪==--==- ⎪⎪ ⎪ ⎪⎪ ⎪----⎝⎭⎝⎭⎝⎭又()()123123110,,,,101012βββξξξ-⎛⎫⎪== ⎪ ⎪⎝⎭ , 所以T 在基123,,βββ下的矩阵为1110242110221101221101421012111012211-----⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪-=- ⎪ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪----⎝⎭⎝⎭⎝⎭⎝⎭10. 函数集合V 3={α=(a 2x 2+a 1x +a 0)e x |a 2,a 1,a 0∈R }对于函数的加法与数乘构成3维线性空间,在其中取一个基α1=x 2e x , α2=2x e x , α3=3e x , 求微分运算D 在这个基下的矩阵. 【解】211222333()e 2e ,2()2e 2e ,3()3e .D D D αααααααα=+=+=+=+==x x x x x x x x即123123110(,,)(,,),2013αααααα⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦T因此D 在基123,,ααα下的矩阵为1001102013⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦. 11. 2阶对称矩阵的全体12312323,,,A ⎧⎫⎡⎤⎪⎪==∈⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭a a V a a a a a R对于矩阵的加法与数乘构成3维线性空间,在V n 中取一个基123100100,,.001001⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A A A(1) 在V 3中定义合同变换31110(),0111T V ⎡⎤⎡⎤=∀∈⎢⎥⎢⎥⎣⎦⎣⎦A A A 求在基123,A A ,A 下的矩阵及T 的秩与零度.(2) 在V 3中定义线性变换31111(),,1111T V ⎡⎤⎡⎤=∀∈⎢⎥⎢⎥⎣⎦⎣⎦A A A 求T 在基123,A A ,A 下的矩阵及T 的像空间与T 的核.【解】(1)11212312311101010(),0100110011011021()2,0110111011001011().01011111A A A A A A A A A ⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤===+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤===++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦T T T由此知,T 在基123,A A ,A 下的矩阵为121011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦M显然M 的秩为3,故这线性变换T 的秩为3,零度为0. (2)11232123312311101111(),1100111111011122()222,1110112211001111().11011111A A A A A A A A A A A A ⎡⎤⎡⎤⎡⎤⎡⎤===++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤===++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤===++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦T T T即 T (123,A A ,A )=(123,A A ,A )M ,其中121121121⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦M 就是T 在基123,A A ,A 下的矩阵.显然有 2131()2(),()(),A A A A ==T T T T所以T (V 3)=L (T (A 1))=L (A 1+A 2+A 3).最后求出T 1(0).设A =x 1A 1+x 2A 2+x 3A 3∈T 1(0),那么T (A )=0,即123123(,),(,,),A A ,A '==T X X x x x 0也就是(123,A A ,A )MX =0,它等价于齐次方程组MX =0,解之得基础解系(2,1,0), (1,0,1).故T 1(0)=L (2A 1A 2,A 1A 3).(B 类)1. A2. A3. 设α1,α2是线性无关的n 维向量,那么V={λα1+μα2|λ,μ∈R}的维数为 . 解:由于V 中任何元素都可由12,αα线性表示,且12,αα线性无关,所以12,αα的维数为2.4. 在R 3中线性变换T(x 1,x 2,x 3)=(2x 1-x 2,x 2+x 3,x 1),那么T 关于基ε1=(1,0,0)′, ε2=(0,1,0)′,ε3=(0,0,1)′的矩阵为 . 解:由于12312231(,,)(2,,)T x x x x x x x x =-+,故1()(2,0,1)T ξ=,2()(1,1,0)T ξ=-,3()(0,1,0)T ξ=所以123123210(,,)(,,)011100T ξξξξξξ-⎛⎫ ⎪= ⎪ ⎪⎝⎭ 故T 在123,,ξξξ下的矩阵为210011100-⎛⎫ ⎪⎪⎪⎝⎭5. 在R 3中,已知向量α在基α1=(1,1,0),α2=(1,1,1),α3=(1,0,1)下的坐标为(2,1,0)′,向量β在基β1=(1,0,0),β2=(0,1,-1),β3=(0,1,1)下的坐标为(0,-1,1)′,求: (1) 由基α1,α2,α3到基β1,β2,β3的过渡矩阵; (2) 向量α+β在基α1,α2,α3下的坐标. 解:(1)由11232133123,,2βαααβααβααα=-+=-=-+-所以123123111(,,)(,,)102111βββααα-⎛⎫ ⎪=- ⎪ ⎪--⎝⎭ ,故过渡矩阵为111102111-⎛⎫ ⎪- ⎪⎪--⎝⎭ (2)1232(,,)10αααα⎛⎫ ⎪= ⎪⎪⎝⎭, 123123123011102(,,)1(,,)1021(,,)2111110ββββαααααα--⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪=-=--= ⎪ ⎪⎪⎪ ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭所以1230(,,)30αβααα⎛⎫ ⎪+= ⎪⎪⎝⎭,故αβ+在123,,ααα下坐标为030⎛⎫⎪⎪ ⎪⎝⎭6. 设B 是秩为2的5×4矩阵,α1=(1,1,2,3)′,α2=(-1,1,4,-1)′,α3=(5,-1,-8,9)′是齐次线性方程组Bx=0的解向量,求Bx=0的解空间的一个规范正交基. 解:由B 的秩为2知,Bx=0的解空间的维数为2.由13,αα线性无关令[][]13123111,(1,1,2,3),(4,2,10,6),βαββαβββ'==-=--单位化得121211,2533γγ-⎛⎫⎛⎫ ⎪ ⎪⎪⎪==⎪⎪⎪⎪-⎝⎭⎝⎭ 为解空间的规范正交基.7. 设3维线性空间V 3的线性变换T 在基ε1,ε2,ε3下的矩阵为112011101A ⎛⎫ ⎪= ⎪⎪--⎝⎭(1) 求T 在基η1=ε1+ε3,η2=-ε3,η3=ε1-ε2下的矩阵; (2) 求T 的像空间及维数; (3) 求T 的核及维数.解:(1)123123101(,,)(,,)001110ηηηξξξ⎛⎫ ⎪=- ⎪⎪-⎝⎭ ,所以T 在123,,ηηη下的矩阵为1101112101431001011001640110101110111---⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪--=- ⎪ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪-----⎝⎭⎝⎭⎝⎭⎝⎭(2)123123112(,,)(,,)011101T ξξξξξξ⎛⎫ ⎪= ⎪⎪--⎝⎭即1132123123(),(),()2,T T T ξξξξξξξξξξ=-=+=+-又312()()()T T T ξξξ=+,12()()T T ξξ与线性无关,所以()()31231312()(),(),(),T V L T T T L ξξξξξξξ==-+故3dim ()2T V =(3)设()1122330T k k k ξξξ++=即1132123123()()(2)0k k k ξξξξξξξ-++++-=得12323132000k k k k k k k ++=⎧⎪+=⎨⎪--=⎩可得基础解系111-⎛⎫⎪- ⎪⎪⎝⎭ ,故()1123(0)T L ξξξ-=--+,1dim (0)1T -=。
线性代数_北京邮电大学出版社(戴斌祥_主编)习题答案(全)

线性代数习题及答案习题一 (A 类)T2. 求出j ,k 使9级排列24j157k98为偶排列。
解:由排列为9级排列,所以j,k 只能为3、6.由2排首位,逆序为0,4的逆序数为0,1的逆序数为3,7的逆序数为0,9的为0,8的为1.由0+0+3+0+1=4,为偶数.若j=3,k=6,则j 的逆序为1,5的逆序数为0,k 的为1,符合题意;若j=6,k=3,则j 的逆序为0,5的逆序数为1,k 的为4,不符合题意. 所以j=3、k=6.T3. 写出4阶行列式中含有因子2234a a 的项。
解:D 4=1234()11223344(1)j j j j j j j j a a a a τ-由题意有:232,4.j j ==故1234141243243241j j j j j j ⎧==⎨⎩ D 4中含的2234a a 项为:(1243)(3241)1122344313223441(1)(1)a a a a a a a a ττ-+- 即为:1122344313223441a a a a a a a a -+5. 用定义计算下列各行列式.(1)0200001030000004; (2)1230002030450001. (3)0100002000100n n -【解】(1) D =(1)τ(2314)4!=24; (2) D =12.(3)由题意知:12231,,11210n nn ij a a a n a n a -=⎧⎪=⎪⎪⎪⎨=-⎪⎪=⎪=⎪⎩其余所以12()112233(2341)1223341,111(1)(1)(1)123(1)(231)1(1)!n j j j n j j j njn n n n n n n D a a a a a a a a a n n n n n τττ---=-=-=-⋅⋅⋅⋅⋅-⋅=-=-⋅6. 计算下列各行列式.(1)214131211232562-----; (2)abac ae bd cdde bfcfef-------;(3)10011001101a b c d ---; (4)1234234134124123.【解】(1) 125062312101232562r r D+---=--;(2) 1114111111Dabcdef abcdef--==------;21011111(3)(1)11101100111;b c D a a b cd c c d d dd abcd ab ad cd --⎡--⎤=+-=+++--⎢⎥⎣⎦=++++ 321221133142144121023410234102341034101130113(4)160.1041202220044101231114r r c c r r c c r r r r c c r r D -+-+-++---====-------7. 证明下列各式.(1)22322()111a ab b a a b b a b +=-; (2)2222222222222222(1)(2)(3)(1)(2)(3)0(1)(2)(3)(1)(2)(3)a a a a b b b b c c c c d d d d ++++++=++++++;(3) 232232232111()111a a a a bb ab bc ca b b c c cc =++(4)2000()000n n a ba b D ad bc c d cd==-;(5)121111111111111nni i i i na a a a a ==++⎛⎫=+ ⎪⎝⎭+∑∏. 【证明】(1)1323223()()()2()2001()()()()()2()21c c c c a b a b b a b b a b a b b a b a b b a b a b b a b a b a b a b--+--=--+--+==-=-=--左端右端.(2) 32213142412222-2-2232221446921262144692126021446921262144692126c c c c c c c c c c a a a a a a b b b b b b c c c c c cd d d d d d ---++++++++====++++++++左端右端. (3) 首先考虑4阶范德蒙行列式:2323232311()()()()()()()(*)11x x x a a a f x x a x b x c a b a c b c b b b c c c ==------从上面的4阶范德蒙行列式知,多项式f (x )的x 的系数为2221()()()()(),11a a ab bc ac a b a c b c ab bc ac b b cc ++---=++但对(*)式右端行列式按第一行展开知x 的系数为两者应相等,故231123231(1),11a a b b c c +- (4) 对D 2n 按第一行展开,得22(1)2(1)2(1)0000000(),n n n n ab aba ba bD abc dc dc d c d dc ad D bc D ad bc D ---=-=⋅-⋅=-据此递推下去,可得222(1)2(2)112()()()()()()n n n n n nD ad bc D ad bc D ad bc D ad bc ad bc ad bc ----=-=-==-=--=-2().n n D ad bc ∴=-(5) 对行列式的阶数n 用数学归纳法.当n =2时,可直接验算结论成立,假定对这样的n 1阶行列式结论成立,进而证明阶数为n 时结论也成立. 按D n 的最后一列,把D n 拆成两个n 阶行列式相加:112211211111011111110111111101111111.n n nn n n a a a a D a a a a a a D ---++++=++=+但由归纳假设11121111,n n n i i D a a a a ---=⎛⎫+= ⎪⎝⎭∑ 从而有11211211121111111111.n n n n n i i n n nn n i i i i i i D a a a a a a a a a a a a a a a ---=-===⎛⎫+=+ ⎪⎝⎭⎛⎫⎛⎫++== ⎪ ⎪⎝⎭⎝⎭∑∑∑∏8. 计算下列n 阶行列式.(1) 111111nx xD x=(2) 122222222232222n D n=;(3)0000000000nx y x y D x y yx=. (4)2100012100012000002100012nD =.【解】(1) 各行都加到第一行,再从第一行提出x +(n 1),得11111[(1)],11n x D x n x =+-1)后分别加到其余各行,得1111110[(1)](1)(1).01n n x D x n x n x x --=+-=+---(2) 213111222210000101001002010002n r r nr r r r D n ---=-按第二行展开222201002(2)!.00200002n n =---(3) 行列式按第一列展开后,得1(1)(1)(1)10000000000000(1)0000000(1)(1).n n n n n n n n xy y x y x y D xy x y x y yxx yx x y y x y +-+-+=+-=⋅+⋅-⋅=+-(4) 210002000001000121001210012100012000120001200000210002100021000120001200012n D ==+122n n D D --=-.即有 112211n n n n D D D D D D ----=-==-= 由()()()112211n n n n D D D D D D n ----+-++-=- 得11,121n n D D n D n n -=-=-+=+.9. 计算n 阶行列式.121212111n n n na a a a a a D a a a ++=+【解】各列都加到第一列,再从第一列提出11ni i a=+∑,得232323123111111,11n nnn i n i na a a a a a D a a a a a a a =+⎛⎫=++ ⎪⎝⎭+∑1)后加到其余各行,得23111010011.001001nnnn i i i i a a a D a a ==⎛⎫=+=+ ⎪⎝⎭∑∑10. 计算n 阶行列式(其中0,1,2,,ia i n ≠=).1111123222211223322221122331111123n n n n n n n n n n nn n n n n n nn n n n na a a a ab a b a b a b D a b a b a b a b b b b b ----------------=.【解】行列式的各列提取因子1(1,2,,)n ja j n -=,然后应用范德蒙行列式.3121232222312112123111131212311211111()().n nn n n n n n n n n n n j i n n j i n ij b b b b a a a a b b b b D a a a a a a a b b b b a a a a b b a a a a a ------≤<≤⎛⎫⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫-= ⎪⎝⎭∏11. 已知4阶行列式D 中第3列元素依次为-1,2,0,1,它们的余子式依次为8,7,2,10,求行列式D 的值。
北京邮电大学版_线性代数_课后题答案2
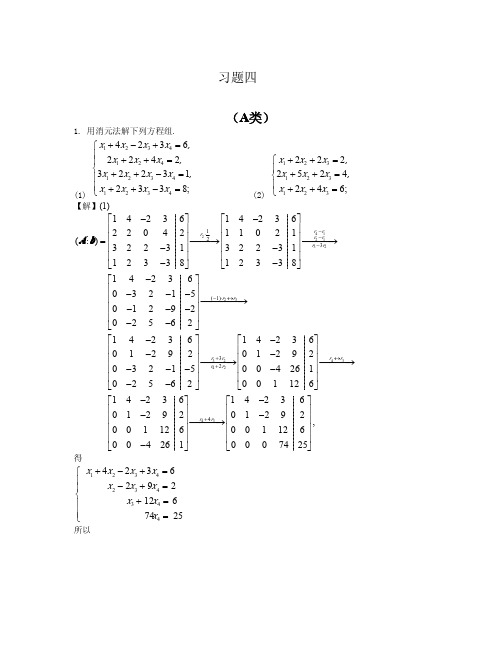
⎤ ⎡ 3⎤ − x4 ⎥ ⎢− 2 ⎥ ⎡ −1⎤ ⎥ ⎢ ⎥ ⎢ −2 ⎥ 7 −2 x4 ⎥ = x3 ⎢ ⎥ + x4 ⎢ ⎥ ⎥ ⎢ 2 ⎥ ⎢0⎥ ⎥ ⎢ 1 ⎥ ⎢ ⎥ ⎥ ⎢ ⎥ ⎣1⎦ ⎢ 0 ⎦ ⎥ x4 ⎥ ⎣ ⎦
⎡ 3⎤ ⎢− 2 ⎥ ⎢ ⎥ ⎢ 7 ⎥, ⎢ 2 ⎥ ⎢ 1 ⎥ ⎢ ⎥ ⎢ ⎣ 0 ⎥ ⎦
⎡ 1 2 −2 2 −1⎤ ⎡ 1 2 −2 2 −1⎤ r2 − r1 ⎢ ⎥ ⎥ A = 1 2 −1 3 −2 ⎯⎯⎯ →⎢ ⎢ ⎥ r3 −2 r1 ⎢ 0 0 1 1 −1⎥ ⎢ ⎢ ⎣ 2 4 −7 1 1 ⎥ ⎦ ⎣ 0 0 −3 −3 3 ⎥ ⎦ ⎡1 2 −2 2 −1⎤ r3 + 3r2 ⎥ ⎯⎯⎯ →⎢ R( A) = 2, ⎢0 0 1 1 −1⎥ ⎢ ⎣0 0 0 0 0 ⎥ ⎦
习题四 (A类)
1. 用消元法解下列方程组.
⎧ x1 + 4 x2 − 2 x3 + 3 x4 = 6 , ⎪ 2 x + 2 x + 4 x = 2, ⎪ 1 2 4 ⎨ ⎪3 x1 + 2 x2 + 2 x3 − 3 x4 = 1, ⎪ x + 2 x2 + 3x3 − 3x4 = 8; (1) ⎩ 1
⎧ x1 − x2 + 5 x3 − x4 = 0, ⎪ x + x − 2 x + 3x = 0, ⎪ 1 2 3 4 ⎨ 3 x − x + 8 x + x 2 3 4 = 0, ⎪ 1 ⎪ x + 3x2 − 9 x3 + 7 x4 = 0; (2) ⎩ 1 ⎧ x1 + 2 x2 − 2 x3 + 2 x4 − x5 = 0, ⎪ ⎨ x1 + 2 x2 − x3 + 3x4 − 2 x5 = 0, ⎪ 2 x + 4 x − 7 x + x + x = 0. ⎩ 1 2 3 4 5
北京邮电大学版 线性代数 课后题答案

习题五(A 类)1. 计算[],αβ.(1)(1,0,3,5),(4,2,0,1);12(2),.,123423αβαβ=--=-⎤⎡⎤==----⎥⎢⎥⎣⎦⎣⎦ 【解】[][](1)(1)40(2)30(5)19,21(2)(2)(1)0,33αβαβ=-⨯+⨯-+⨯+-⨯=-⎛⎛⎫=⨯+-⨯+⨯-=- ⎪ ⎝⎭⎝2. 把下列向量单位化.(1) α=(3,0,-1,4); (2) α=(5,1,-2,0).【解】(1)(3,0,1,4);(2)2,0).====∴=-====⎫==-=⎪⎭a e a ae a a e a3. 在R 4中求一个单位向量,使它与以下三个向量都正交:α1=(1,1,-1,1), α2=(1,-1,-1,1), α3=(2,1,1,3). 解:设向量a=(x 1,x 2,x 3,x 4)与a 1,a 2,a 3都正交,则12341234123400230x x x x x x x x x x x x +-+=⎧⎪--+=⎨⎪+++=⎩ 得:13243403x x x x x=⎧⎪=⎨⎪=-⎩令x 3=1得a=(4,0,1,-3)单位化可得单位向量为3)-.4. 利用施密特正交化方法把下列向量组正交化.(1) α1 =(0,1,1)′, α2 =(1,1,0)′, α3 =(1,0,1)′; (2) α1 =(1,0,-1,1), α2 =(1,-1,0,1), α3 =(-1,1,1,0) 【解】[][][][][][][][]112122111313233121122112122111(1)(0,1,1),,111(1,1,0)(0,1,1),1,,2,22,,222;,,,,333(2)(1,0,1,1),,2121(1,1,0,1)(1,0,1,1),1,,3,333βααββαβββαβαββαβββββββααββαβββ'=='⎛⎫''=-=-=- ⎪⎝⎭'⎛⎫=--=- ⎪⎝⎭'==-⎛''=-=---=-[][][][]313233121122,,,1334.,,,,,5555αβαββαββββββ'⎫ ⎪⎝⎭'⎛⎫=--=- ⎪⎝⎭5. 试证,若n 维向量α与β正交,则对于任意实数k ,l ,有k α与l β正交. 【证】α与β正交[]0,αβ⇒=.[],.(,)0,k l R k l kl αβαβ∀∈==∴ αk 与βl 正交.6. 下列矩阵是否为正交矩阵.111101023101011(1);(2).10101222110101132⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥-⎢⎥⎣⎦【解】(1) A ′A ≠E , ∴A 不是正交矩阵 (2) A ′A =E ⇒A 为正交矩阵7. 设x 为n 维列向量,x ′x =1,令H =E -2xx ′.求证H 是对称的正交矩阵. 【证】2(2)2()2()H E xx H E xx E xx E xx H '=-''''''=-=-=-= ∴ H 为对称矩阵.22(2)(2)2()2()4()()4()4()H H E xx E xx E E xx xx E xx xx E xx x xx x E'''=--''''=--+'''=-+=∴ H 是对称正交矩阵.8. 设A 与B 都是n 阶正交矩阵,证明AB 也是正交矩阵. 【证】A 与B 为n 阶正交矩阵⇒A ′A =EB ′B =E(AB )(AB )′=AB ·(B ′A ′)=A (BB ′)A ′=AEA ′=AA ′=E∴ AB 也是正交矩阵.9. 判断下列命题是否正确.(1) 满足Ax =λx 的x 一定是A 的特征向量;(2) 如果x 1,…,x r 是矩阵A 对应于特征值λ的特征向量.则k 1x 1+k 2x 2+…+k r x r 也是A 对应于λ的特征向量;(3) 实矩阵的特征值一定是实数. 【解】(1) ╳.Ax =λx ,其中当x =0时成立,但x =0不是A 的特征向量.(2) ╳.例如:E 3×3x =λx 特征值λ=1, λ的特征向量有11,2233-⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦ 则1100,22003300-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦不是E 3×3的特征向量. (3) ╳.不一定.实对称矩阵的特征值一定是实数. 10. 求下列矩阵的特征值和特征向量.62423(1),(2),2323142623142200121(3),(4).21201220200112⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦--⎡⎤-⎡⎤⎢⎥--⎢⎥⎢⎥--⎢⎥⎢⎥-⎢⎥-⎢⎥⎣⎦⎣⎦【解】(1)223(2)(1)9037031E A λλλλλλλλ-==---=⇒--=--=当32λ+=时,()E A x λ-=0为1233x x ⎤⎥⎡⎤⎢=⎢⎥⎢⎣⎦⎢⎣得解121⎡⎡⎤⎢=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦x x 对应的特征向量为,1⎡⎢⋅∈≠⎢⎥⎢⎥⎣⎦且k k R k 0.当λ=时,12132132x x ⎡⎤-⎢⎥⎡⎤⎢=⎢⎥⎢-⎣⎦⎢⎣⎦0其基础解系为11,16ξ'⎛⎫= ⎪⎝⎭,对应的特征向量为,01k k R k ⋅∈≠⎢⎥⎢⎥⎣⎦且.2624624(2)2322324260422(2)(11)0,A E λλλλλλλλλλ--==-----+-=--=∴ 特征值为1232,11.λλλ===(i) 当122λλ==时, 121233424220,212424⎡⎤⎡⎤⎢⎥⎢⎥=⇒++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x x x x x x 0其基础解系为112,.0110⎡⎤--⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦∴ 对应于λ=2的特征向量为1212112,0110⎡⎤--⎡⎤⎢⎥⎢⎥⎢⎥+∈⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦k k k k R且使得特征向量不为0.(ii)当311λ=时,123524282425-⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦x x x 0,解得方程组的基础解系为T1231(,,).1,,12'⎛⎫= ⎪⎝⎭x x x∴ 对应于311λ=的特征向量为T1,0.1,,12⎛⎫∈≠ ⎪⎝⎭且k k R k220(3)(2)(4)(1)212020A E λλλλλλλ--==-+--=------0⇒特征值为1232,4, 1.λλλ=-== (i) 当12λ=-时, 123420232022-⎡⎤⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦x x x 0 得基础解系为1.,112'⎛⎫ ⎪⎝⎭, 12λ=-对应的特征向量为120.11⎡⎤⎢⎥⎢⎥⋅∈≠⎢⎥⎢⎥⎣⎦且k k R k(ii) 当24λ=时,123220232024--⎡⎤⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦x x x 0其基础解系为(2,-2,1)′,所以与24λ=对应的特征向量为2,0.21⎡⎤⎢⎥⋅∈≠-⎢⎥⎢⎥⎣⎦且k k R k(iii) 当31λ=时,123120020200210-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦x x x 其基础解系为(2,1,-2)′∴ 与31λ=对应的特征向量为2,0.12⎡⎤⎢⎥⋅∈≠⎢⎥⎢⎥-⎣⎦且k k R k3123423141210121(4)(2)12201221120112(1)(2)01,2A E λλλλλλλλλλλλλλλ---------==-⋅-------=--⋅-=⇒====∴ A 的特征值为1,2. (i) 当1231λλλ===时,123413140022100112001110--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x x x其基础解系为(4,-1,1,0)′.∴ 其对应的特征向量为k ·(4,-1,1,0)T ,k ∈R 且k ≠0. (ii) 当42λ=时,12340314003210,0102001100--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x x x其基础解系为:(1,0,0,0)′. ∴ 其对应的特征向量为10,0.00⎡⎤⎢⎥⎢⎥⋅∈≠⎢⎥⎢⎥⎣⎦且k k R k11.设3阶方阵A 的特征值为λ1=1,λ2=0,λ3=-1,对应的特征向量依次为123122,,,221212-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x x求矩阵A .【解】111222333112311223312323,,00(,,)(,,)(,,)0000Ax x Ax x Ax x A x x x x x x x x x λλλλλλλλλ===⎡⎤⎢⎥⇒==⎢⎥⎢⎥⎣⎦由于1231,0,1λλλ===-为不同的特征值123,,x x x ⇒线性无关,则有123122(,,)221212x x x -⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦可逆11221001221021.2210002210123212001212220A ----⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⇒==----⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦12. 设3阶实对称矩阵A 的特征值为-1,1,1,与特征值-1对应的特征向量x =(-1,1,1)′,求A .【解】11λ=-对应的特征向量为x 1=(-1,1,1)T ,设21λ=对应的特征向量为x 2=(x 1,x 2,x 3)T ,A 为实对称矩阵,所以(x 1,x 2)=0,即有-x 1+x 2+x 3=0. 得方程组的基础解系为1211,,1001ξξ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 可知12,ξξ为21λ=对应的特征向量.将112,,x ξξ正交化得11x β==(-1,1,1)T ,单位化:T111e ββ==;21βξ= =(1,1,0)T ,T222e ββ⎫==⎪⎭;[][][][]T T3132331231122,,11,.,,1,,22e αβαββαββββββ⎛⎫=--==- ⎪⎝⎭0P ⎤⎥⎥=⎥⎥⎦ 则有1100.010001P AP --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1122333100212.010*******210333A -⎤⎤⎡⎤⎥⎥⎢⎥⎥⎥-⎡⎤⎢⎥⎢⎥⎢⎥⇒==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎥⎥⎢⎥-⎥⎥⎢⎥⎣⎦⎦⎦13. 若n 阶方阵满足A 2=A ,则称A 为幂等矩阵,试证,幂等矩阵的特征值只可能是1或者是零.【证明】设幂等矩阵的特征值为λ,其对应的特征向量为x .22;()();Ax x A Ax A x A x Ax x λλλλ==⇒==由A 2=A 可知22;Ax x x x λλλ⇒=⇒= 所以有20λλλ=⇒=或者λ=1.14. 若A 2=E ,则A 的特征值只可能是±1. 【证明】设λ是A 的特征值,x 是对应的特征向量. 则Ax =λx A 2x =λ(Ax )=λ2x 由A 2=E 可知 x =Ex =A 2x =λ2x⇒(λ2-1)x =0,由于x 为λ的特征向量,∴ x ≠0⇒λ2-1=0⇒λ=±1.15. 设λ1,λ2是n 阶矩阵A 的两个不同的特征根,α1,α2分别是A 的属于λ1, λ2的特征向量,证明α1+α2不是A 的特征向量.证明:假设α1+α2是A 的属于特征根λ的特征向量,则 A (α1+α2)=λ(α1+α2)=λα1+λα2.又 A (α1+α2)= A α1+ A α2=λ1α1+λ2α2 于是有 (λ-λ1)α1+(λ-λ2)α2 =0由于12λλ≠,α1与α2线性无关,故λ-λ1=λ-λ2=0. 从而12λλ=与12λλ≠矛盾,故α1+α2不是A 的特征向量.16. 设矩阵20022211x -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A 与10002000y -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B 相似. (1) 求x 与y ;(2) 求可逆矩阵P ,使P -1AP =B .【解】(1)由A ~B 可知,A 有特征值为-1,2,y .[]200(2)022()(1)2211A E λλλλλλλ--⎡⎤⎢⎥==-+⋅=-----⎢⎥⎢⎥-⎣⎦x x由于-1为A 的特征值,可知[](21)00(1)22A+E =--=⇒=+-x x .将x =0代入|A -λE |中可得[](2)0()(1)2(2)(2)(1)0,λλλλλλλ=-+=----⇒-+-+=A E1232,2,1λλλ⇒=-==-可知y = -2.(2) (i) 当1λ=-1时,123100212212-⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x x x 0其基础解系为1ξ=(0,-2,1)T ,1λ= -1对应的特征向量为 1ξ=(0,-2,1)T .(ii) 当2λ=2时,123400022202110-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦x x x 其基础解系为 2ξ=(0,1,1)T所以2λ=2对应的特征向量为 2ξ=(0,1,1)T (ⅲ) 当3λ=-2时,123000022202130⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x x , 其基础解系为 3ξ=(-2,1,1)T ,取可逆矩阵123002(,,)211111p ξξξ-⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦则1.p AP B -=17. 设111001023-⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦A , 求A 100. 【解】111(1)(1)(2)00123A E λλλλλλλ--==---=----⇒特征值为1231, 2.λλλ===(i) 当121λλ==时,123011001100220x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦其基础解系为01,.1111⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(ii) 当32λ=时,123111021021--⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦x x x 0其基础解系为(-1,1,2)T .令011111112p -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则1112p AP -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 1001100110010011001001001001001001001001()12011101111111111122112011113211111111122011121120222102221p AP p A P A ---⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⇒=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦--=----.⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦18. 求正交矩阵T ,使T-1AT 为对角矩阵.022124(1),(2),23422224342141013201410(3),(4).22201410211014-⎡⎤⎡⎤⎢⎥⎢⎥==---⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦-⎡⎤-⎡⎤⎢⎥-⎢⎥⎢⎥==--⎢⎥⎢⎥-⎢⎥-⎢⎥⎣⎦-⎣⎦A A A A【解】212322(1)(1)(8)02342431,8.A E λλλλλλλλλ--==--+=------⇒===-(i)当121λλ==时,123122024402440--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦x x x 方程组的基础解系为(-2,1,0)T ,(2,0,1)T .(ii) 当38λ=-时,123822254245-⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x x x 0其基础解系为T1,1,12⎛⎫-- ⎪⎝⎭. 取T11,1,12α⎛⎫-- ⎪⎝⎭,单位化为,T111122,,333p αα⎛⎫==-- ⎪⎝⎭取()T 22,1,0α-,取()T32,0,1α=,使23,a a 正交化.令[][]T32T2233222,24(2,1,0),,,,1,55αββαβαβββ⎛⎫==-=-⋅= ⎪⎝⎭ 单位化TT322332,15153ββββ⎛⎫====⎪ ⎭⎝⎭p p13152.315203T ⎡-⎢⎢⎢=⎢-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2124(2)(3)(6)222421A E λλλλλλ-==-+-----得1233, 6.λλλ==-=.(i) 当123λλ==-时,1234240,21204240⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x x 其基础解系为1211.2001αα--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦正交化得[][]T21T122111,42(1,2,0),,,,1,55αβββαβββ⎛⎫=-=-=-- ⎪⎝⎭单位化得TT121212,.p p ββββ⎛⎫====⎪ ⎭⎝ (ii) 当36λ=时,1235240,28204250-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦x x x 其基础解系为 3α=(2,1,2)T .单位化得()T3331,2,1,23p αα==231.315203T ⎡⎢⎢⎢=⎢-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 22123441011410(3)(4)(812)0014112144,2, 6.A E λλλλλλλλλλλλ----==-⋅-+=-----====(i) 当124λλ==时,12340101101001011010-⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦x x x x 0其基础解系为121001,.1001ξξ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 由于(12,ξξ)=0,所以12,ξξ正交.将它们单位化得1200,.00p p ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦(ii) 当32λ=时,12342101012100,0121010120-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦x x x x其基础解系为3ξ=(1,-1,-1,1)T,单位化得3331212.1212p ξξ⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦ (iii) 当46λ=时,12342101012100,0121010120--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦x x x x其基础解系为4ξ=(-1,-1,1,1)T ,单位化为T4441111,,,,2222p ξξ⎛⎫==-- ⎪⎝⎭1110224110422,.112022611022T T AT -⎤-⎥⎥⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎥-⎢⎥⎥⎣⎦⎥⎢⎥⎢⎥⎣⎦123320(4)(2)(5)(1)0,2220212,5,1,A E λλλλλλλλλλ--==--+=------===-(i) 当1λ=2时,123120202021-⎡⎤⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦x x x 0其基础解系为1ξ=(2,1,-2)T ,单位化得T111212,,333ξξ⎛⎫==- ⎪⎝⎭p ,(ii) 当2λ=5时,123220232024--⎡⎤⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦x x x 0其基础解系为2ξ=(2,-2,1)T .单位化得T222221,,333p ξξ⎛⎫==- ⎪⎝⎭.(iii) 当3λ=-1时,123420023200220-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦x x x , 其基础解系为3ξ=(1,2,2)T ,单位化得T333122,,333p ξξ⎛⎫== ⎪⎝⎭,得正交阵12213332122,.53331212333T T AT -⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦19.将下列二次型用矩阵形式表示.(1) 222123123122331(,,)25262=-++++f x x x x x x x x x x x x ;(2) 123412233441(,,,)=+++f x x x x x x x x x x x x ;(3) 2212341121314224(,,,)63252=+-++-f x x x x x x x x x x x x x x .【解】(1)112312323111(,,)(,,);123135⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x f x x x x x x x x (2)121234123434110022110022(,,,)(,,,);110022110022⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦x x f x x x x x x x x x x(3)12 12341234343561223120 (,,,)(,,,).221000510022xxf x x x x x x x xxx⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦20.写出下列各二次型的矩阵.(1)222123123121323 (,,)4424f x x x x x x x x x x x x=+++++;(2)2221231231223 (,,)724f x x x x x x x x x x=+---.解:(1)由1 12312323121 (,,)(,,)242121x f x x x x x x xx⎛⎫⎛⎫⎪⎪= ⎪⎪⎪ ⎪⎝⎭⎝⎭所以二次型的矩阵为121 242 121⎛⎫ ⎪ ⎪ ⎪⎝⎭(2)由1 12312323110 (,,)(,,)112027x f x x x x x x xx--⎛⎫⎛⎫⎪⎪=-- ⎪⎪⎪ ⎪--⎝⎭⎝⎭所以二次型的矩阵为110112027 --⎛⎫ ⎪--⎪ ⎪--⎝⎭21. 当t为何值时,二次型222 123112132233 (,,)642=+++++f x x x x x x x x x x x tx的秩为2.【解】112312323132(,,)(,,)31121xf x x x x x x xxt⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦23121128313213231108521054rr rr rt t⎛⎫⋅-⎪-⎝⎭-⎡⎤⎡⎤⎢⎥⎢⎥=−−−→−−−→--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦A32513213255010188250540048r r t t +⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥−−−→⎢⎥⎢⎥⎢⎥⎢⎥---+⎢⎥⎣⎦⎣⎦ 7()2.8R t ⇒=⇒=A22.用正交变换把下列二次型化为标准形,并写出所作的变换. (1) f (x 1,x 2,x 3,x 4)=2x 1x 2-2x 3x 4; (2)2221231231223(,,)2344f x x x x x x x x x x =++--.解:(1)f 的正交矩阵1001000001010A ⎛⎫ ⎪⎪= ⎪- ⎪-⎝⎭0 0 0 ,A 的特征多项式 22100100(1)0001001A E λλλλλλ---==-=---- ,于是A 的全部特征值为121(),1().λλ==-二重二重11,λ=解(A-E )x=0,得基础解系121010,0101αα⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪==⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭正交化得121010,0101ββ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭,单位化得1200,00γγ⎛⎫ ⎪⎪⎪== ⎪ ⎪ ⎪ ⎝⎭⎝21λ=-解(A+E )x=0,得基础解系341010,0101αα-⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭正交化341010,0101ββ-⎛⎫⎛⎫⎪ ⎪⎪ ⎪==⎪ ⎪⎪ ⎪⎝⎭⎝⎭,单位化得:34,γγ⎛⎛⎫⎪⎪⎪==⎪⎪⎝⎭取正交矩阵12340000 (,,,)0000Tγγγγ⎫-⎪⎪⎪⎪⎪==-⎪⎪⎝⎭令x=Ty,得22221233()f x Ax y T AT y y y y y'''===+--(2)f的矩阵120222023 A-⎛⎫⎪=--⎪⎪-⎝⎭特征多项式A Eλ-=,得特征值1231,2,5λλλ=-==当11λ=-,解(A+E)x=0,得基础解系1221α⎛⎫⎪= ⎪⎪⎝⎭当22λ=,解(A-2E)x=0,得基础解系2212α-⎛⎫⎪= ⎪⎪⎝⎭当35λ=,解(A-5E)x=0,得基础解系31211α⎛⎫⎪⎪=- ⎪⎪⎪⎝⎭单位化得123221333212,,333122333βββ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 取正交矩阵123(,,)T βββ=,令x=Ty ,得222123()25f x Ax y T AT y y y y '''===-++23. 用配方法把下列二次型化为标准型,并求所作变换.221231213231231213(1)(,,)248;(2)(,,)24.f x x x x x x x x x f x x x x x x x =+--=+【解】2212312132322222121113322221133(1)(,,)248;(2)48()(2)12f x x x x x x x x x x x x x x x x x x x x x x =+--=--+++-=--++-令11212321321233333222=-+=-⎧⎧⎪⎪=+⇒=+-⎨⎨⎪⎪==⎩⎩y x x x y y y x x x y y y y x x y由于1100102001-≠ ∴ 上面交换为可逆变换. 得222123123(,,)12.=-+-f x x x y y y1231213(2)(,,)24.=+f x x x x x x x令11221233=+⎧⎪=-⎨⎪=⎩x y y x y y x y为可逆线性变换12112233,22,22.⎧=+⎪⎪⇒⎨=-⎪⎪=⎩x x y x x y y x 222212312123121323222211332233221323(,,)2()4()22442(2)2422()2()f x x x y y y y y y y y y y y y y y y y y y y y y y y =-++=-++=++-+-=+--令11322333y y y y y ωωω=+⎧⎪=-⎨⎪=⎩为可逆线性交换2212312(,,)22f ωωωωω=-所作线性交换为121133********,2,2.x x y y x x x y y x x ωωω+⎧=+=+⎪⎪-⎨=-=-⎪⎪=⎩24. 用初等变换法化下列二次型为标准型,并求所作变换.1234121314232434212311223(1)(,,,);(2)(,,)54.f x x x x x x x x x x x x x x x x f x x x x x x x x =++++-=+-【解】(1)211212211212111101112222111111002222221111101022222111110102222211000111001001010001r r r r c c c c -++-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥−−−→−−−→⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 314131411011100111000000441310000122131001002211100110221110011022001000100010001----⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥−−−→−−−→⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦r r r r c c c c41413232100010001100000044300100012500034000211111221112111112211123001001020010001--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥−−−→⎢⎥⎢⎥--⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦r r c c2222123415()44f x y y y y =--+1111221111.22300120001⎡⎤--⎢⎥⎢⎥⎢⎥-⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦x pyp(2) 二次型矩阵为21213255228255510102255251002022245020020022100100020010010001001100250240205102010001r r c c r r ---⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥−−−→−−−→⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦32825100100252500024416160000252554511025280100125001001c c -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥−−−→−−−−→⎢⎥⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦5412580125001x pyp ⎡⎤-⎢⎥⎢⎥∴==⎢⎥-⎢⎥⎢⎥⎣⎦2221232516().425=-+f x y y y25. 判断下列二次型的正定性.22212312232221231223222112132233(1)26422;(2)34544;(3)9912481306071.f x x x x x x x f x x x x x x x f x x x x x x x x x =---++=+++-=-++-+【解】(1) 矩阵为2102120121016116014210420161014-⎡⎤-⎢⎥-<=->-⎢⎥-⎢⎥-⎣⎦-⎡⎤⎢⎥=-<-⎢⎥⎢⎥-⎣⎦∴ 二次型为负定二次型. (2) 矩阵32032308024224025320280242025⎡⎤⎢⎥>=>-⎢⎥⎢⎥-⎣⎦⎡⎤⎢⎥=>-⎢⎥⎢⎥-⎣⎦∴ 二次型为正定二次型. (3) 矩阵为9962499699006130306130243071996240673030243071-⎡⎤-⎢⎥>>--⎢⎥-⎢⎥-⎣⎦-⎡⎤⎢⎥>--⎢⎥⎢⎥-⎣⎦∴ 为正定二次型.26. t 满足什么条件时,下列二次型是正定的.2221231213222(1)4222;(2)23222.f x x x tx x x x f x y z xy xz tyz =++++=+++-+【解】(1) 二次型的矩阵为22111104040410211420.40102t t t t t t t t ⎡⎤⎢⎥>=->⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=->⎢⎥⎢⎥⎣可知t <<. (2)二次型的矩阵为211111,10101212131112(1)0111213t t t t t t -⎡⎤⎢⎥>=>⎢⎥⎢⎥-⎣⎦-⎡⎤⎢⎥=-+>⇒--<⎢⎥⎢⎥-⎣⎦当t满足11t -<<时,二次型为正定二次型. 27. 试证:如果A,B 都是n 阶正定矩阵,则A+B 也是正定的. 【证】A ,B 是正定矩阵,则存在正定二次型12(,,,)n f x x x = x T Ax12(,,,)n f x x x = x T Bx且A ′=A , B ′=B ⇒(A +B )′=(A ′+B ′)=A +B1n R ⨯∀∈≠x x 0有12(,,,)n f x x x = x T (A +B )x =x T Ax +x T Bx >0∴ A +B 为正定.28. 试证:如果A 是n 阶可逆矩阵,则A ′A 是正定矩阵.【证】A 可逆 (A ′A )′= A ′·(A ′)′= A ′A A ′A = A ′E A可知A ′A 与E 合同 ⇒A ′A 正定.29. 试证:如果A 正定,则A ′,A -1,A *都是正定矩阵. 【证】A 正交,可知A ′=A∀可逆阵C ,使得A =C ′EC .(i) A =C ′EC ⇒A ′=(C ′EC )′⇒A ′=C ′E ′(C ′)′=C ′EC ∴ A ′与E 合同,可知A ′为正定矩阵.(ii) (A -1)′=(A ′)-1=A -1可知A -1为对称矩阵. 由A 正交可知,A 为点对称矩阵 其特征值设为12,,,n λλλ 且有i λ>0(i =1,2,…,n )Ax i =i λx i ⇒x i =i λA -1x i ⇒A -1x i =1i λx i可知A -1的特征值为10i λ> , (i =1,2,…,n )∴ A -1正定.(iii) 由A *=|A |·A -1可知(A ′)1=|A |·(A -1)′=|A |·A -1=A *由(ii)可知A -1为正定矩阵即存在一个正定二次型12(,,,)n f x x x = x T A -1x1n x R ⨯∀∈≠x 且0有12(,,,)n f x x x >0 ∵ A 正交⇒|A |>012(,,,)n f x x x = x T A *x =x T ·|A |·A -1x =|A |·(x T A -1x )即有1n x R ⨯∀∈≠x 且0时,x T A -1x >0∵ |A |>0,即有12(,,,)n f x x x = x T A *x >0 ∴ A *为正定矩阵.(B 类)1. D2. B3. B4. 已知矩阵201A x ⎛⎫ ⎪= ⎪ ⎪⎝⎭ 0 00 0 1 与2000000B y ⎛⎫ ⎪= ⎪⎪⎝⎭ -1相似,则x = ,y = . 解:因为A 与B 相似,所以A ,B 有相同的特征值,又B 的特征值为2,y ,-1,而|A-λE |=(2-λ)(λ2-x λ-1),所以y,-1是λ2-x λ-1=0的两根,故 -y=-1,y-1=x 所以y=1,x=0 5. 二次型22212311223(,,)2f x x x x x x x x ==-++的符号差为 .解:22212311223(,,)2f x x x x x x x x ==-++化为标准形2212313(,,)x Tyf x x x y y ==+,所以符号差为2.6. 已知实二次型()222123123121323(,,)444f x x x a x x x x x x x x x ==+++++经正交变换x=Py 可化为标准形216f y =,则a .解:f 的矩阵为222222a A a a ⎛⎫⎪= ⎪ ⎪⎝⎭ ,又A 与600⎛⎫ ⎪ ⎪ ⎪⎝⎭ 相似,所以6,0是A 的特征值.故|A-0E |=0,|A-6E |=0,得:a=2.7. 设A,B 为n 阶正交矩阵,且|A |≠|B |,证明A+B 为不可逆矩阵.证明:因为A ,B 为正交矩阵,所以|A |·|A+B |=|A ′|·|A+B |=|E+A ′B |=|B ′B+A ′B |=|B ′+A ′|·|B |=|A+B |·|B |即 (|A |-|B |)(A+B )=0,因为|A |≠|B |,所以 |A+B |=0,所以A+B 为不可逆矩阵.8. 设1333366A a b -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦有特征值λ1=-2,λ2=4,求a ,b 的值.解:因为λ1=-2,λ2=4为A 的特征值,所以333323662a b -+=-+3333430664a b ---=-- ,得:a=-5,b=49. 设有4阶方阵A 满足条件|3E+A |=0,AA ′=2E,|A |<0,求方阵A 的伴随矩阵A *的一个特征值.解:由例11知1Aλ是A*的特征值,由|3E+A|=0,知-3是A的一个特征值,又|AA′|=24,|A|<0,所以,|A|=-4,故43是A*的一个特征值.10. 已知3阶方阵A的特征值为1,-1,2,设B=A3-5A2,试求:(1) B的特征值;(2) 与B相似的对角矩阵;(3) |B|;(4) |A-5E|.解:(1)设ξ(x)=x3-5x2,则B=ξ(A),所以ξ(1),ξ(-1),ξ(2)为B的特征值,即-4,-6,-12为B的全部特征值.(2)由相似矩阵有相同的特征值,知所求矩阵为4612 -⎛⎫ ⎪-⎪ ⎪-⎝⎭.(3)由|B|=λ1λ2λ3知,|B|=-288.(4)因为|A|=λ1λ2λ3=-2,则|B|=|A3-5A2|=|A|2|A-5E|,得|A-5E|=-72.11. 设A为3阶实对称矩阵,λ1=8,λ2=λ3=2是其特征值,已知对应于λ1=8的特征向量α1=11k⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,对应于λ2=λ3=2的一个特征向量α2=11-⎛⎫⎪⎪⎪⎝⎭,试求:(1) 参数k;(2) 对应于λ2=λ3=2的另一个特征向量;(3) 矩阵A.解:(1)由α1与α2正交得-1+k=0,即k=1.(2)设它的正交特征向量为(a1,a2,a3),则121230,0, a aa a a-=⎧⎨++=⎩得一个正交特征向量112⎛⎫ ⎪ ⎪ ⎪-⎝⎭.(3)单位化,0 ⎪⎪⎝⎭822A'⎛⎫⎪= ⎪⎪⎝⎭⎪⎪⎪⎪⎭⎭⎫⎪=⎪⎪⎪⎪⎝⎭则422242224⎪⎪⎛⎫⎪ ⎪=⎪ ⎪⎪⎪⎝⎭12. 已知二次型22212312312(,,)(1)(1)22(1)f x x x a x a x x a x x=-+-+++的秩为2.(1) 求a的值;(2) 求正交变换x=Py,求f(x1,x2,x3)化成标准形;(3) 求方程f(x1,x2,x3)=0的解.解:(1)f的矩阵1111002a aA a a-+⎛⎫⎪=+-⎪⎪⎝⎭,由f的秩为2故|A|=0,得a=0.(2)从110110002A⎛⎫⎪= ⎪⎪⎝⎭,由|A-λE|=0,得特征值为2,2,0.解得相应特征向量:11⎛⎫⎪⎪⎪⎝⎭,010110⎛⎫⎛⎫⎪⎪-⎪⎪⎪⎪⎝⎭⎝⎭正交单位化得:1⎛⎫⎪⎪⎪⎝⎭⎪⎪⎝⎭.⎛-⎪⎪⎝⎭,取010T⎫⎪⎪=-⎪⎪⎝⎭.令x=Ty则2212312(,,)()22f x x x x Ax y T AT y y y'''===+(3)由(2)知,对00y k ⎛⎫ ⎪= ⎪ ⎪⎝⎭,k 为任意常数,使123(,,)0f x x x =从而010100x T k k ⎛ -⎛⎫⎛⎫⎪ ⎪'=== ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎪ ⎪⎝⎭ ,k ′为任意常数.13. 设A=(a ij )是n 阶正定矩阵,证明:a ii >0(i=1,2,…,n).证明:设二次型f(x)=x ′Ax ,因为A 是n 阶正定矩阵,则对任何x ≠0,都有f(x)>0.令x=e i =(0,…,0,1,0, …,0) ′≠0(i=1,2,…,n)则f(x)=x ′Ax=( a i1, …, a ii , …, a in ) 00100⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭=a ii >0(i=1,2,…,n)14. 证明:若A 是n 阶正定矩阵,则存在n 阶正定矩阵B,使A=B 2. 证明:设二次型f(x)=x ′Ax,则存在正交矩阵P ,使得 P ′AP=diag(λ1, λ2,…, λn ), λi >0(i=1,2,…,n),从而得,12(,,,)n A Pdiag P Pdiag diag P Pdiag P Pdiag P λλλ''==''=令B Pdiag P '= ,可见B 为正定矩阵,从而A=B2。
北邮通信原理课件C通信原理经典讲义02

s
(
t
)
=
⎧⎪⎨s1 ⎪⎩
(
பைடு நூலகம்
t
)
= s2
g (t ) cos (t) = 0
ωct
发1
,
发0
(3)
其中 g (t ) 是基带脉冲形状。有脉冲/无脉冲谁对应 1,谁对应 0 无关紧要。对于 NRZ 矩形脉
冲,上式又可写成
s
(
t
)
=
⎧⎪⎨s1 ⎪⎩
(
t) = s2 (
A
t)
cos =0
ωct
发1 发0 , 0 ≤ t ≤ Tb
(4)
1/6
欢迎访问北邮通信原理学习与考研网 下载更多北邮通信原理复习资料
Lecture Notes for 04116~04118
#24
2006/12/03
注意(3)或(4)的模型与(1)有一点细微的差别。例如按照(4),第 1 个码元(时间在
Tb ≤ t ≤ 2Tb 内 ) 是 Aa1 cosωc (t − Tb ) , a1 ∈{0,1} 。 但 按 照 (1) , 第 1 个 码 元 应 该 是
如果把图中的 BPF 改成匹配滤波器,则成为图 6.2.13,这实际就是用包络检波器检出图 6.2.6 所示波形的包络。非相干解调的误码率分析方法见课本 203 页。对于图 6.2.13 所示的最佳非 相干,误码率分析也和 203 页一样。注意 MF 和 BPF 的差别仅在于 MF 可以改善抽样点的 信噪比,其他都是一样的。
4. OOK 的解调及误码率
把(3)中的 g (t ) cosωct 整体当作发送脉冲,则 OOK 其实还是一种 2PAM 信号(两个电
(8)北京邮电大学2009年版课程简介(理学院)

一、公共基础课高等数学A(上)课程编号: 4110011课程名称:高等数学A(上) ( 96学时)Advanced Mathematics(I)内容提要:高等数学是高等工科院校最重要的基础课程之一。
高等数学A(上)的教学内容包含一元函数微分学,一元函数积分、微积分的应用、常微分方程及空间解析几何与向量代数初步等内容。
通过该课程的学习,不但使学生具备学习后续课程所需要的基本数学知识,而且还使学生在数学的抽象性、逻辑性与严密性方面受到必要的训练和熏陶,使他们具有理解和运用数学知识解决实际问题的初步能力。
因此,高等数学教学不仅关系到学生在整个大学期间甚至研究生期间的学习质量,而且还关系到学生的思辨能力、创造潜能等科学素养和文化素养。
先修课程:适用专业:计算机科学与技术、网络工程、智能科学与技术、信息安全、通信工程、电子信息工程、信息工程、电子信息科学与技术、电子科学与技术、光信息科学与技术、机械工程及自动化、测控技术与仪器、物流工程、自动化、软件工程、电信工程及管理、电子商务及法律选用教材:《高等数学》(上) 同济大学数学教研室主编高等教育出版社第六版2008年2月高等数学A(下)课程编号:4110021课程名称:高等数学A (下) ( 80学时)Advanced Mathematics(II)内容提要:高等数学是高等工科院校最重要的基础课程之一。
高等数学A (下)的教学内容包含多元函数微分学及其应用,重积分、曲线积分和曲面积分,级数与傅立叶级数等内容。
通过该课程的学习,不但使学生具备学习后续课程所需要的基本数学知识,而且还使学生在数学的抽象性、逻辑性与严密性方面受到必要的训练和熏陶,使他们具有理解和运用数学知识解决实际问题的初步能力。
因此,高等数学教学不仅关系到学生在整个大学期间甚至研究生期间的学习质量,而且还关系到学生的思辨能力、创造潜能等科学素养和文化素养。
先修课程:适用专业:计算机科学与技术、网络工程、智能科学与技术、信息安全、通信工程、电子信息工程、信息工程、电子信息科学与技术、电子科学与技术、光信息科学与技术、机械工程及自动化、测控技术与仪器、物流工程、自动化、软件工程、电信工程及管理、电子商务及法律选用教材:《高等数学》(下) 同济大学数学教研室主编高等教育出版社第六版2008年2月高等数学B(上)课程编号: 4110012课程名称:高等数学B (上) ( 80学时)Advanced Mathematics(I)内容提要:高等数学是高等工科院校最重要的基础课程之一。
北京邮电大学版 线性代数 课后题答案

习题 三 (A 类)1. 设α1=(1,1,0),α2=(0,1,1),α3=(3,4,0).求α1-α2及3α1+2α2-α3.解:α1-α2=(1,1,0)-(0,1,1)=(1,0,-1),3α1+2α2-α3=(3,3,0)+(0,2,2)-(3,4,0)=(0,1,2)2. 设3(α1-α)+2(α2+α)=5(α3+α),其中α1=(2,5,1,3),α2=(10,1,5,10),α3=(4,1,-1,1).求α.解:由3(α1-α)+2(α2+α)=5(α3+α)整理得:α=16(3α1+2α2-5α3),即α=16 (6,12,18,24)=(1,2,3,4)3.(1)× (2)× (3)√ (4)× (5)×4. 判别下列向量组的线性相关性.(1)α1=(2,5), α2=(-1,3);(2) α1=(1,2), α2=(2,3), α3=(4,3);(3) α1=(1,1,3,1),α2=(4,1,-3,2),α3=(1,0,-1,2);(4) α1=(1,1,2,2,1),α2=(0,2,1,5,-1),α3=(2,0,3,-1,3),α4=(1,1,0,4,-1). 解:(1)线性无关;(2)线性相关;(3)线性无关;(4)线性相关.5. 设α1,α2,α3线性无关,证明:α1,α1+α2,α1+α2+α3也线性无关. 证明:设112123123()()0,k k k αααααα+++++=即123123233()()0.k k k k k k ααα+++++=由123,,ααα线性无关,有1232330,0,0.k k k k k k ++=⎧⎪+=⎨⎪=⎩所以1230,k k k ===即112123,,αααααα+++线性无关.6.问a 为何值时,向量组'''123(1,2,3),(3,1,2),(2,3,)a ααα==-=线性相关,并将3α用12,αα线性表示.解:1322137(5),32A a a=-=-当a =5时,312111.77ααα=+7. 作一个以(1,0,1,0)和(1,-1,0,0)为行向量的秩为4的方阵. 解:因向量(1,0,0,0)与(1,0,1,0)和(1,-1,0,0)线性无关,所以(1,0,0,0)可作为方阵的一个行向量,因(1,0,0,1)与(1,0,1,0),(1,-1,0,0),(1,0,0,0)线性无关,所以(1,0,0,1)可作为方阵的一个行向量.所以方阵可为1010110010001001⎛⎫⎪- ⎪ ⎪⎪⎝⎭.8. 设12,,,sααα的秩为r 且其中每个向量都可经12,,,rααα线性表出.证明:12,,,rααα为12,,,sααα的一个极大线性无关组.【证明】若 12,,,rααα (1)线性相关,且不妨设12,,,tααα (t <r ) (2)是(1)的一个极大无关组,则显然(2)是12,,,sααα的一个极大无关组,这与12,,,sααα的秩为r 矛盾,故12,,,rααα必线性无关且为12,,,sααα的一个极大无关组.9. 求向量组1α=(1,1,1,k ),2α=(1,1,k ,1),3α=(1,2,1,1)的秩和一个极大无关组.【解】把123,,ααα按列排成矩阵A ,并对其施行初等变换.1111111111111120010010101101001000111011001000k k k k kk k k ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥=→→→⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦A当k =1时,123,,ααα的秩为132,,αα为其一极大无关组.当k ≠1时,123,,ααα线性无关,秩为3,极大无关组为其本身.10. 确定向量3(2,,)a b =β,使向量组123(1,1,0),(1,1,1),==βββ与向量组1α=(0,1,1),2α=(1,2,1),3α=(1,0,1)的秩相同,且3β可由123,,ααα线性表出.【解】由于123123011120(,,);120011111000112112(,,),11010102a b b a ⎡⎤⎡⎤⎢⎥⎢⎥==→--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥==→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦A B αααβββ而R (A )=2,要使R (A )=R (B )=2,需a 2=0,即a =2,又12330112120(,,,),12001121110002a a b b a ⎡⎤⎡⎤⎢⎥⎢⎥==→⎢⎥⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦c αααβ要使3β可由123,,ααα线性表出,需b a +2=0,故a =2,b =0时满足题设要求,即3β=(2,2,0).11. 求下列向量组的秩与一个极大线性无关组.(1) α1=(1,2,1,3),α2=(4,-1,-5,-6),α3=(1,-3,-4,-7); (2) α1=(6,4,1,-1,2),α2=(1,0,2,3,-4),α3=(1,4,-9,-6,22),α4=(7,1,0,-1,3);(3) α1=(1,-1,2,4),α2=(0,3,1,2),α3=(3,0,7,14),α4=(1,-1,2,0),α5=(2,1,5,6). 解:(1)把向量组作为列向量组成矩阵Α,应用初等行变换将Α化为最简形矩阵B ,则1114110141141913951115409500000036701810000000A B⎛⎫-⎛⎫ ⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪---- ⎪ ⎪ ⎪=→→→= ⎪ ⎪ ⎪ ⎪---- ⎪ ⎪ ⎪ ⎪ ⎪----⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭⎝⎭ 52 0 50 0 99可知:R (Α)=R (B )=2,B 的第1,2列线性无关,由于Α的列向量组与B 的对应的列向量有相同的线性组合关系,故与B 对应的Α的第1,2列线性无关,即α1,α2是该向量组的一个极大无关组.(2)同理,61701714010810111201201312438⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪→→ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭ 1 -1 55 2 -9 0 4 40 - 55 7 -9 -9 0 -8 40 1 -6 0 5 -15 -10 5 -15 22 0 40 1111010101⎛⎫ ⎪ ⎪ ⎪→ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎪⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪→→ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭-10 0 0 0 2 -9 07 2 -9 0 0 0 0 -5 -11 -5 0 0 0450 0 0 -0 0 10 00 0 1 0110 0 0 10 0 0 240 0 10 0 0 0 0110 0 0 0B⎛⎫⎪⎪ ⎪= ⎪ ⎪ ⎪⎝⎭10 0 0 0可知R(Α)=R(B)=4,Α的4个列向量线性无关,即α1,α2,α3,α4是该向量组的极大无关组. (3)同理,A ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪=→→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1 0 3 1 2 1 0 3 1 2 1 0 3 1 2 1 0 3 1 2-1 3 0 -1 10 3 3 0 30 1 1 0 10 1 1 0 12 1 7 2 50 1 1 0 10 0 0 -4 -40 0 0 1 14 2 14 0 60 2 2 -4 -20 0 0 0 00 ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭0 0 0,可知R(Α)=R(B)=3,取线性无关组α1,α3,α5为该向量组的一个极大无关组.12.求下列向量组的一个极大无关组,并将其余向量用此极大无关组线性表示. (1) α1=(1,1,3,1),α2=(-1,1,-1,3),α3=(5,-2,8,-9),α4=(-1,3,1,7);(2) α1=(1,1,2,3),α2=(1,-1,1,1),α3=(1,3,3,5),α4=(4,-2,5,6),α5=(-3,-1,-5,-7). 解:(1)以向量组为列向量组成Α,应用初等行变换化为最简形式.11111100101A ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=→→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3 -1 5 -1 0 11 - 5 -1 -1 5 -127 -2 3 2 -7 47 - 2 - 2223 -1 8 10 2 -7 40 0 0 00 0 0 01 3 -9 70 4 -14 8 0 0 0 00 0 0 0B ⎛⎫ ⎪⎪ ⎪= ⎪ ⎪⎪ ⎪⎝⎭,可知,α1,α2为向量组的一个极大无关组.设α3=x 1α1+x 2α2,即12121212523839x x x x x x x x -=⎧⎪+=-⎪⎨-=⎪⎪+=-⎩解得,1237,22x x ==- 设α4=x 3α1+x 4α2,即12121212133137x x x x x x x x -=-⎧⎪+=⎪⎨-=⎪⎪+=⎩解得,121,2x x ==所以31241237,2.22a a a a a a =-=+(2)同理, 1111111A B ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪=→→= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1 1 4 -3 1 1 4 -3 1 0 2 1 -21 - 3 -2 -10 -2 2 -6 20 -1 3 -12 3 5 -50 - 1 -3 10 0 0 0 03 5 6 -70 -2 2 -6 20 0 0 0 0可知, α1、α2可作为Α的一个极大线性无关组,令α3=x 1α1+x 2α2可得:121213x x x x +=⎧⎨-=⎩即x 1=2,x 2=-1,令α4=x 3α1+x 4α2,可得:121242x x x x +=⎧⎨-=-⎩即x 1=1,x 2=3,令α5=x 5α1+x 6α2,可得:121231x x x x +=-⎧⎨-=-⎩即x 1=-2,x 2=-1,所以α3=2α1-α2α4=α1+3α2,α5=-2α1-α213. 设向量组12,,,mααα与12,,,sβββ秩相同且12,,,mααα能经12,,,sβββ线性表出.证明12,,,m ααα与12,,,sβββ等价.【解】设向量组12,,,m ααα (1)与向量组12,,,sβββ (2)的极大线性无关组分别为12,,,r ααα (3)和12,,,rβββ (4)由于(1)可由(2)线性表出,那么(1)也可由(4)线性表出,从而(3)可以由(4)线性表出,即1(1,2,,).ri ij jj a i r ===∑αβ因(4)线性无关,故(3)线性无关的充分必要条件是|a ij |≠0,可由(*)解出(1,2,,)j j r =β,即(4)可由(3)线性表出,从而它们等价,再由它们分别同(1),(2)等价,所以(1)和(2)等价.14. 设向量组α1,α2,…,αs 的秩为r 1,向量组β1,β2,…,βt 的秩为r 2,向量组α1,α2,…,αs ,β1,β2,…,βt 的秩为r 3,试证:max{r 1,r 2}≤r 3≤r 1+r 2. 证明:设αs1,…,1r Sα为α1,α2,…,αs 的一个极大线性无关组, βt1,βt2,…,2r tβ为β1,β2,…,βt 的一个极大线性无关组. μ1,…,3rμ为α1, α2,…,αs ,β1,β2,…,βt 的一个极大线性无关组,则αs1, …,1r Sα和βt1,…,βtr2可分别由μ1,…,3rμ线性表示,所以,r 1≤r 3,r 2≤r 3即max{r 1,r 2}≤r 3,又μ1,…,3r μ可由αs1, …,αsr1,βt1,…,βtr2线性表示及线性无关性可知:r 3≤r 1+r 2.15. 已知向量组α1=(1,a ,a ,a )′,α2=(a ,1,a ,a )′,α3=(a ,a ,1,a )′,α4=(a ,a ,a ,1)′的秩为3,试确定a 的值.解:以向量组为列向量,组成矩阵A ,用行初等变换化为最简形式:1113110a a a a a a a a a a a a a a a a a a a a a a a a a a a a +⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ -1 0 0 1- 0 0 1 -1 0 1- 00 0 1- 0 1-1 0 0 1-0 0 0 1-由秩A=3.可知a ≠1,从而1+3a =0,即a =-13.16. 求下列矩阵的行向量组的一个极大线性无关组.(1)2531174375945313275945413425322048⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; (2)11221021512031311041⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦.【解】(1) 矩阵的行向量组1234⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦αααα的一个极大无关组为123,,ααα; (2) 矩阵的行向量组1234⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦αααα的一个极大无关组为124,,ααα.17. 集合V 1={(12,,,nx x x )|12,,,nx x x ∈R 且12n+++x x x =0}是否构成向量空间?为什么?【解】由(0,0,…,0)∈V 1知V 1非空,设121122(,,,),(,,,),n n V V k =∈=∈∈x x x y y y αβR)则112212(,,,)(,,,).n n n x y x y x y k kx kx kx +=+++=αβα因为112212121212()()()()()0,()0,n n n n n n x y x y x y x x x y y y kx kx kx k x x x ++++++=+++++++=+++=+++=所以11,V k V +∈∈αβα,故1V 是向量空间.18. 试证:由123(1,1,0),(1,0,1),(0,1,1)===ααα,生成的向量空间恰为R 3.【证明】把123,,ααα排成矩阵A =(123,,ααα),则11020101011==-≠A ,所以123,,ααα线性无关,故123,,ααα是R 3的一个基,因而123,,ααα生成的向量空间恰为R 3.19. 求由向量12345(1,2,1,0),(1,1,1,2),(3,4,3,4),(1,1,2,1),(4,5,6,4)=====ααααα所生的向量空间的一组基及其维数.【解】因为矩阵12345(,,,,)113141131411314214150121301213,113260001200012024140241400000=⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--------⎢⎥⎢⎥⎢⎥=→→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A ααααα∴124,,ααα是一组基,其维数是3维的.20. 设1212(1,1,0,0),(1,0,1,1),(2,1,3,3),(0,1,1,1)===-=--ααββ,证明:1212(,)(,)L L =ααββ.【解】因为矩阵1212(,,,)1120112010110131,0131000001310000=⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=→⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦A ααββ由此知向量组12,αα与向量组12,ββ的秩都是2,并且向量组12,ββ可由向量组12,αα线性表出.由习题15知这两向量组等价,从而12,αα也可由12,ββ线性表出.所以1212(,)(,)L L =ααββ.21. 在R 3中求一个向量γ,使它在下面两个基123123(1)(1,0,1),(1,0,0)(0,1,1)(2)(0,1,1),(1,1,0)(1,0,1)==-==-=-=αααβββ下有相同的坐标.【解】设γ在两组基下的坐标均为(123,,x x x ),即111232123233112233(,,)(,,),110011001110101101x x x x x x x x x x x x ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦γαααβββ即1231210,111000x x x --⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦求该齐次线性方程组得通解123,2,3x k x k x k===- (k 为任意实数)故112233(,2,3).x x x k k k =++=-γεεε22. 验证123(1,1,0),(2,1,3),(3,1,2)=-==ααα为R 3的一个基,并把1(5,0,7),=β2(9,8,13)=---β用这个基线性表示.【解】设12312(,,),(,),==A B αααββ又设11112123132121222323,x x x x x x =++=++βαααβααα,即11121212321223132(,)(,,),x x x x x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ββααα记作 B =AX .则2321231235912359()111080345170327130327131235910023032713010330022400112r r r r r r -+↔--⎡⎤⎡⎤⎢⎥⎢⎥=−−−→−−−→---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥−−−−−→--⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦A B 作初等行变换因有↔A E,故123,,ααα为R 3的一个基,且1212323(,)(,,),3312⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦ββααα即1123212323,332=+-=--βαααβααα.(B 类)1.A2.B3.C4.D5.a=2,b=46.abc ≠07.设向量组α1,α2,α3线性相关,向量组α2,α3,α4线性无关,问: (1) α1能否由α2,α3线性表示?证明你的结论. (2) α4能否由α1,α2,α3线性表示?证明你的结论.解:(1)由向量组α1,α2,α3线性相关,知向量组α1, α2, α3的秩小于等于2,而α2, α3, α4线性无关,所以α2, α3线性无关,故α2, α3是α1, α2, α3的极大线性无关组,所以α1能由α2, α3线性表示.(2)不能.若α4可由α1,α2,α3线性表示,而α2,α3是α1,α2,α3的极大线性无关组,所以α4可由α2,α3线性表示.与α2,α3,α4线性无关矛盾.8.若α1,α2,…,αn,αn+1线性相关,但其中任意n个向量都线性无关,证明:必存在n+1个全不为零的数k1,k2,…,k n,k n+1,使k1α1+k2α2+…+k n+1αn+1=0.证明:因为α1,α2,…,αn,αn+1线性相关,所以存在不全为零的k1,k2,…,k n,k n+1使k1α1+k2α2+…+k n+1αn+1=0若k1=0,则k2α2+…+k n+1αn+1=0,由任意n个向量都性线无关,则k2=…=k n+1=0,矛盾.从k1≠0,同理可知k i≠0,i=2, …,n+1,所以存在n+1个全不为零的数k1,k2,…,k n,k n+1,使k1a1+k2a2+…+k n+1a n+1=0.9. 设A是n×m矩阵,B是m×n矩阵,其中n<m,E为n阶单位矩阵.若AB=E,证明:B的列向量组线性无关.证明:由第2章知识知,秩A≤n,秩B≤n,可由第2章小结所给矩阵秩的性质,n=秩E≤min{秩A,秩B}≤n,所以秩B=n,所以B的列向量的秩为n,即线性无关.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 0 0 0 0
1 0 0 0 0
1 1 2 1 1
1 1 2 1 1
1 1 2 0 pivotal row 5 3 3 1 3 0
Row Echelon Form
Example: (continue) Continue the eliminating process, we have
1 1 0 0 0
1 1 0 0 0
1 1 2 0 1 3 0 4 0 3
0 x5 0 x5 4 3
0 x3 0 x3
0 x4 0 x4
Since, there are no 5-tuples that could possibly satisfy these equations, the system
Row Echelon Form
If we change the right hand of equations in last example, so as to obtain a system has solution set, such as
1 1 1 1 2 2 0 0 1 1 1 0 0 0 0 1 0 0 0 0
Lecture 2
Row Echelon Form
Row Echelon Form
In last Lecture, we had seen that a n n system may be reduced to triangular form. But this progress may be broken if at any step, all the possible choices for a pivot element are 0. Since, the progress of reducing a system to triangular form is a progress of eliminating variables, at the stage of the reduction breaks down, it seems natural to move over the next column and eliminate the rest variables. By doing this, it is clear that the equations system can not be reduced to triangular form.
Using row operation III to eliminate the nonzero entries in the last four rows of the first column, the resulting matrix will be
Row Echelon Form
Example: (continue)
Row Echelon Form
Example: (continue) By augmented matrix
1 0 0 0 0
The last two rows mean that 0 x1 0 x2 0 x1 0 x2 has no solution.
1 0 0 0 0
1 0 0 2 1 1
1 1 2 1 1
1 1 2 0 pivotal row 5 3 3 1 3 0
It is easy to be seen that all possible choices of pivot are 0 in the second column. It is nature to continue our reduction process from the next column.
Row Echelon Form
Example: Consider the system represented by the augmented matrix
1 1 1 1 2 2 0 0 1 1
1 0 0 1 2
1 0 0 1 2
1 1 pivotal row 1 1 3 1 3 1 4 1
1 0 0 0 0
and we end up with
1 0 0 0 0
1 1 0 0 0 1 0 0 0 0
1 1 0 0 0 1 0 0 0 0
1 1 2 0 1 3 pivotal row 1 1 1 0 1 1 0 0 0 1 1 0 0 0 1 1 2 0 1 3. 0 4 0 3
x2
x3 x3
x4 x4
x5 2 x5 x5
1 0 3
Definition: The variables corresponding to the first nonzero elements in each row of the augmented matrix will be referred to as the lead variables and the remaining variables corresponding to the columns skipped in the reduction process will be referred to as free variables.
Will be satisfied for any 5-tuple.
Row Echelon Form
and the solution set will be the solution set of all 5-tuples satisfying the first three equations
x1
1 0 0 1 2 1 1 0 0 0
1 0 0 1 2 1 1 0 0 0
1 1 1 1 3 1 3 3 4 4 1 2 1 0 0 1 0 3 0 0
Then, the reduction process will yield the augmented matrix
