现代控制理论基础答案(黄辉先主编)
现代控制理论基础第三章习题答案

第三章 线性控制系统的能控性和能观性3-3-1 判断下列系统的状态能控性。
(1)⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=01,0101B A (2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=111001,342100010B A (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020011,100030013B A (4)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1110,0000000011111B A λλλλ 【解】:(1)[]2,1011==⎥⎦⎤⎢⎣⎡-==n rankU AB BU c c ,所以系统完全能控。
(2)[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==7111111010012B A ABBU c 前三列已经可使3==n rankU c ,所以系统完全能控(后续列元素不必计算)。
(3)A 为约旦标准型,且第一个约旦块对应的B 阵最后一行元素全为零,所以系统不完全能控。
(4)A 阵为约旦标准型的特殊结构特征,所以不能用常规标准型的判别方法判系统的能控性。
同一特征值对应着多个约旦块,只要是单输入系统,一定是不完全能控的。
可以求一下能控判别阵。
[]2,111321031211312113121121132=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡==c c rankU B A BA AB BU λλλλλλλλλλλ,所以系统不完全能控。
3-3-2 判断下列系统的输出能控性。
(1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=xy u x x 011101020011100030013 (2) []⎪⎪⎩⎪⎪⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x y u x x 0011006116100010【解】: (1)已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020011,100030013B A ,⎥⎦⎤⎢⎣⎡-=011101C ,⎥⎦⎤⎢⎣⎡=0000D []⎥⎦⎤⎢⎣⎡--=111300002B CA CAB CB D前两列已经使[]22==m B CA CAB CB D rank ,所以系统输出能控。
现代控制理论基础chapter1答案(第一版黄辉先主编)

现代控制理论基础chapter1答案(第一版黄辉先主编): 1.1(a )解法一:根据基尔霍夫电压、电流定律,对最大回路和左网孔列写两个回路方程如下:()⎪⎩⎪⎨⎧-+=++=⎰⎰⎰Ri i dt i C u Ri dt i C dt i C u i i 211221111, 对上述两个方程两边求导可得:()⎪⎩⎪⎨⎧-+=++=R i ii C u i R i C i C u i i 211221111 ,定义状态变量2211, 2Ri u x R i u x i i -=-=, 则得到两个状态变量的一阶微分方程如下:⎪⎪⎩⎪⎪⎨⎧+--=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+=+--=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=i i i i i i u RC x RC x RC R x u C R x u C i C i C x u RCx RC x RC R x u C R x u C x 31112111512122212121221211 输出方程i o u x Ri u y +-===22 写成矩阵形式的状态空间表达式为:iu RC RC x x RC RC RC RC x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎦⎤⎢⎣⎡3511122121i u x x y +⎥⎦⎤⎢⎣⎡-=21]1 0[状态变量图或模拟结构图略。
解法二:根据基尔霍夫电压、电流定律,对最大回路和左网孔列写两个回路方程及输出方程如下:()⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+=++=⎰⎰⎰2211221111Ri u i i R dt i C u Ri dt i C dt i C u o i i ,定义状态变量 1 , 12211⎰⎰==dt i C x dt i C x ,则可得到()⎪⎩⎪⎨⎧==-+=++=2211221x RC u y x xCR x u x RC x x u o i i ,求出基于状态变量和输入量表达的状态变量一阶微分方程和输出方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+--=+--=+--=i i i u x x y u RC x RC x RC x u RCx RC x RC x 21212211111212 ,写成矩阵形式的状态空间表达式为: []iiu x x y uRC RC x x RC RCRC RC x x +⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎦⎤⎢⎣⎡21212111351112 解法三:根据基尔霍夫电压、电流定律,对最大回路和左网孔列写两个回路方程如下:()⎪⎩⎪⎨⎧-+=++=⎰⎰⎰211221111i i R dt i C u Ri dt i C dt i C u i i , 对上述两个方程两边求导可得:()⎪⎩⎪⎨⎧-+=++=211221111i iR i C u i R i C i C u i i ,定义状态变量()22211, Ri u x i i R u x i i -=--=, 则得到两个状态变量的一阶微分方程如下:⎪⎪⎩⎪⎪⎨⎧+--=⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+--=+=+--=⎪⎭⎫ ⎝⎛+--==i i i i i u RC x RC x RC R u x C R u x x C i C i C x u RC x RC x RC R u x x C i C x 3211211121121121221212212111 输出方程i o u x Ri u y +-===22 写成矩阵形式的状态空间表达式为:iu RC RC x x RC RC RC RC x x⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎦⎤⎢⎣⎡3221112121i u x x y +⎥⎦⎤⎢⎣⎡-=21]1 0[1.1(b )(解法一)根据基尔霍夫电压、电流定律,列写回路方程和输出方程如下:⎪⎩⎪⎨⎧===++⎰idtC u y u u dt di L Ri o i o 1,选取状态变量⎰===idt C u i x o 1 x , 21, 则可得到状态方程和输出方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧==+--=212211111x y x C xu Lx L x L R x i 写成矩阵形式为:[]⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡2121211001011x x y u L x x C LL R x x i(解法二)根据基尔霍夫电压、电流定律,列写回路方程和输出方程如下:⎪⎩⎪⎨⎧===++⎰⎰idtC u y u idt C dt di L Ri o i 11,对第一个方程求导并两边同除以L 可得: i u Li LC i L R i 11=++ 选取状态变量i i i u u iu i x 10201- x , -βββ-== , 由系数 ;0 , 1, 0;1 ,21021=====b Lb b LC a L R a 可计算出 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=--==-===21102220111001010L R L L R a a b L a b b ββββββ ()()21102011Lx Rx u u u x L u x R i L Ri u idt Cu y i i i i i o --=+++-+-=--===⎰βββ 其状态空间表达式为:[]⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡21221211110x x L R y u L R L x x L R LCx x i 状态变量图或模拟结构图略。
现代控制理论基础习题解答
+ +
y
1
1
x3
s
3
1-4 已知系统的传递函数,试列写出状态空间表达式,并画出状态变量图。 (1)解
a 3 1, a 2 0,
G (s)
a 1 0,
s 2 2s 3 s3 1
b 0 0,
+
b1 1,
b 2 2,
b3 3
状态变量图为
1
U ( s) E ( s) 1
y 1 0 0x
状态变量图:
u
3
_
3 1 x3 1 x 2 1 x1 y x s s s5
5
+
3
作业和课堂练习
课堂练习: 已知系统的传递函数, 试列写出状态空间表达式, 并画出状态变量图。
G (s)
3s 4 s(s 1)(s 3)
s1 0 , s 2 -1, s 3 -3
y 1 0 0x
状态变量图:
u
2
3 1 x3 x _ s5
5
+
+
2 s x
1
x 2 1 x1 y
s
3
方法二: 状态空间表达式:
0 0 x a 3 1 0 -a2 0 0 1 x 0 u a1 1
u _
L2
i2
C22
x1 i1
R1 1 1 x1 x4 u L1 L`1 L1 1 1 2 x x3 x4 L2 L2 1 3 x x2 C2 1 x 4 x 1 1 x1 x2 C1 C1
设状态变量
x 2 i2 x3 1 i2 dt c2
现代控制理论课后题及答案

第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
1图P2.2解 这是一个物理系统,采用机理分析法求状态空间表达式会更为方便。
令()f t 为输入量,即u f =,1M ,2M 的位移量1y ,2y 为输出量, 选择状态变量1x =1y ,2x = 2y ,3x =1dy dt,24dyx dt =。
《现代控制理论》课后习题答案1.pdf

《现代控制理论》第一章习题解答1.1 线性定常系统和线性时变系统的区别何在? 答:线性系统的状态空间模型为:xAx Bu y Cx Du=+=+线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和中的各分量均为常数,而对线性时变系统,其系数矩阵D A ,B ,C 和中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的一类系统,而线性时变系统的参数则随时间的变化而变化。
D 1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别? 答: 传递函数模型与状态空间模型的主要区别如下:传递函数模型(经典控制理论)状态空间模型(现代控制理论) 仅适用于线性定常系统 适用于线性、非线性和时变系统用于系统的外部描述 用于系统的内部描述基于频域分析基于时域分析1.3 线性系统的状态空间模型有哪几种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。
对于阶传递函数n 1212101110()n n n n n n n b s b s b s b G s d s a s a s a −−−−−−++++=+++++"",分别有[]012101210100000100000101n n n xx ua a a a yb b b b x du−−−⎧⎡⎤⎪⎢⎥⎪⎢⎥⎪⎢⎥=+⎪⎢⎥⎨⎢⎥⎪⎢⎥⎪−−−−⎣⎦⎪=+⎪⎩"" ###%##"""⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⑴ 能控标准型:[]0011221100010********001n n n b a b a xa x ub a b y xdu −−−⎧−⎡⎤⎡⎤⎪⎢⎥⎢⎥−⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=−+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪−⎣⎦⎣⎦⎪=+⎪⎩"" "######""⑵ 能观标准型:[]1212001001001n n p p x x up y c c c x du⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎣⎦⎣⎦⎪⎪=+⎩"" ##%##""⑶ 对角线标准型: 式中的和可由下式给出,12,,,n p p p "12,,,n c c c "12121012111012()n n n n n n n n nb s b s b s bc c c G sd d s a s a s a s p s p s p −−−−−−++++=+=++++++−−−"""++能控标准型的特点:状态矩阵的最后一行由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分子多项式系数,输入矩阵中的元素除了最后一个元素是1外,其余全为0。
现代控制理论第二章答案

et
2e 2t
4e2t 2et
4e2t
et
0 1
2 3
(4)
(t)(t)
1
2
(et
e3t
)
(et e3t )
141((eet tee33t t))
1 (et 2 (et
e3t ) e3t )
2
141((eet tee33t t)) I
2
(t)
d dt
1 2
(t)
et
e2t
2e2t 2et
2e2t
et
(4)
(t )
1
2
(et
e3t
)
(et e3t )
141((eet tee33t t))
2
【解】 主要验证矢量不变性:
(t)(t) I
和组合性质: (t2 t1)(t1 ) (t2 )
(1)
1
(t)(t) 0
0
0 sin t cost
8
8
(
z
1 8
3)(z
5)
8
8
(
z
z1 2
3)(z
5)
8
8
x(z) (zI G) 1 zx(0) Hu(z)
(
z
z1 2
3)(z
5)
8
8
1 8
(
z
3)(z
5)
8
8
( (
z z
1 8
3)(z 8 z1
2 3)(z
5 8
5
) )
z
1
3
1 0
8
8
zT
(et
(et
现代控制理论基础(习题)
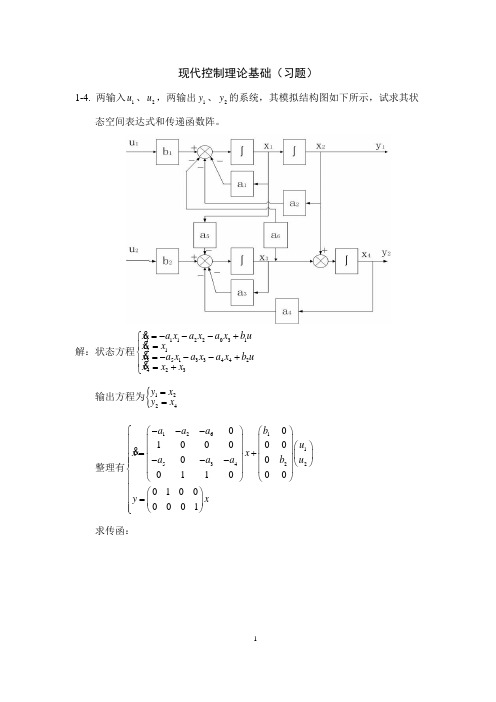
现代控制理论基础(习题)1-4. 两输入1u 、2u ,两输出1y 、2y 的系统,其模拟结构图如下所示,试求其状态空间表达式和传递函数阵。
解:状态方程111220312135133442423x a x a x a x b u x x x a x a x a x b u xx x =---+⎧⎪=⎨=---+⎪=+⎩输出方程为{1224y xy x ==整理有1261125342001000000001100001000001a a a b u x x u a a a b y x ⎧---⎛⎫⎛⎫⎪⎪ ⎪⎛⎫⎪ ⎪ ⎪=+ ⎪⎪ ⎪ ⎪---⎪⎝⎭⎪ ⎪⎨⎝⎭⎝⎭⎪⎪⎛⎫⎪= ⎪⎪⎝⎭⎩求传函:1121126153420010000()()00010000001001000000010001100b G s sI A b s a a a b s a s a a b s --⎛⎫ ⎪⎛⎫ ⎪=-⎪ ⎪⎝⎭ ⎪⎝⎭+⎛⎫⎛⎫ ⎪ ⎪-⎛⎫ ⎪ ⎪=⎪⎪ ⎪+⎝⎭⎪ ⎪--⎝⎭⎝⎭125342616122234534213415622346242260100det()det 001100(1)(1)det 0(1)det 1101()()()()s a a a s sI A a s a a s a a s a a s a a s a s a a s s a s s a a a a a s s a s a a s a s a a sa s a +++⎛⎫ ⎪- ⎪-= ⎪+ ⎪--⎝⎭+⎛⎫⎛⎫ ⎪ ⎪=-⋅-⋅++-⋅⋅+ ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭=+-++++++-=+432222346241313441564221313562414232446()()()()a s a a a a s a a s a a s a s a a s a a s s a a s a a a a a a s a a a a s a a a a -+++++++-=+++-+++++-121223141243()b a b a G s b a b a ⎛⎫= ⎪⎝⎭322134a s a s a s =++ 4153(1)a a s a=-+ 236a a s =- 243126a s a s a a =++- 213141622511321222621()det()(1)b s a b s a b a b s G s sI A a b s b a b s a b s a b a b ⎛⎫++-= ⎪--+++-⎝⎭1-5. 系统的动态特性由下列微分方程描述(1)5732y y y y u u +++=+(2)57332y y y y u u u +++=++列写其相应的状态空间表达式,并画出相应的模拟结构图。
现代控制理论习题解答

现代控制理论习题解答《现代控制理论》第1章习题解答1.1 线性定常系统和线性时变系统的区别何在?答:线性系统的状态空间模型为:xAx Bu y Cx Du=+=+&线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和D 中的各分量均为常数,⽽对线性时变系统,其系数矩阵A ,B ,C 和D 中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的⼀类系统,⽽线性时变系统的参数则随时间的变化⽽变化。
1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别?答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪⼏种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对⾓线标准型。
对于n 阶传递函数1212101110()n n n n n n n b s b s b s b G s d s a s a s a ------++++=+++++L L ,分别有⑴能控标准型: []012101210100000100000101n n n xx u a a a a y b b b b x du---=+??----????=+LL &M M M O M M L LL⑵能观标准型: []001122110001000100010001n n n b a b a xa x ub a b y xdu ---?--=-+?????-????=+??L L &%%L M M M M M M L %L ⑶对⾓线标准型: []1212001001001n n p p x x u p y c c c x du=+??????=+?L L &M M O M M L L 式中的12,,,n p p p L 和12,,,n c c c L 可由下式给出,12121012111012()n n n n n n n n nb s b s b s bc c c G sd d s a s a s a s p s p s p ------++++=+=++++++++---L L L 能控标准型的特点:状态矩阵的最后⼀⾏由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分⼦多项式系数,输⼊矩阵中的元素除了最后⼀个元素是1外,其余全为0。
现代控制理论基础第二章习题答案

第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1) (2) (3) (4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:(5)为结构四重根的约旦标准型。
(6)虽然特征值相同,但对应着两个约当块。
或}0100010000{])[()(1111----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=-=Φλλλλs s s s L A sI L t 3-2-2 已知系统的状态方程和初始条件 (1)用laplace 法求状态转移矩阵; (2)用化标准型法求状态转移矩阵; (3)用化有限项法求状态转移矩阵; (4)求齐次状态方程的解。
【解】:(1) (2)特征方程为: 特征值为:2,1321===λλλ。
由于112==n n ,所以1λ对应的广义特征向量的阶数为1。
求满足0)(11=-P A I λ的解1P ,得:0110000000312111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0011P 再根据0)(22=-P A I λ,且保证1P 、2P 线性无关,解得:对于当23=λ的特征向量,由0)(33=-P A I λ容易求得: 所以变换阵为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==110010001321P P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-1100100011P 线性变换后的系统矩阵为:(3)特征值为:2,1321===λλλ。
现代控制理论基础(第一版黄辉先主编)Chapter3答案

现代控制理论基础(第一版黄辉先主编)Chapter3答案: Chapter3 3.4 解:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=1111, 1111, 3113C B A 方法一:分别用能控性矩阵C Q 的秩以及能观性矩阵O Q 的秩来判别。
能控性判别。
[]212-2-112-2-11rank rank rank =<=⎥⎦⎤⎢⎣⎡==n AB B Q C , 所以系统是不完全能控的。
能观性判别。
n CA C Q O==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=244-2-2-1-111rankrank rank , 所以系统是完全能观的。
综上,系统是不完全能控但完全能观的。
方法二:用PBH 秩判据。
能控性判别。
求矩阵A 的特征值λ,有()()()[]()。
, , , 2 , 1 ,rank 4 , 2042861331132122则系统是完全能控的如果n i n B AI A I i ==--=-=∴=++=++=-+=+--+=-λλλλλλλλλλλ[][]21111-1-111-1-rank ,rank ,21111-111-1rank ,rank 2211=<=⎥⎦⎤⎢⎣⎡=-==⎥⎦⎤⎢⎣⎡=-n B AI ,n B A I ,λλλλ对对所以系统是不完全能控的。
能观性判别。
().2111111111rank rank ,211111111rank rank 。
, , , 2 , 1 rank 2211=<=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=⎥⎦⎤⎢⎣⎡-==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=⎥⎦⎤⎢⎣⎡-==⎥⎦⎤⎢⎣⎡-n A I C n A I C n i n A I C i λλλλλ有对有对则系统是完全能观的如果所以系统是完全能观的。
综上,系统是不完全能控但完全能观的。
方法三:分别根据()()11----A sI C B A sI 和的行线性相关性和列线性相关性来判别系统的能控与能观性。
现代控制理论第一章答案
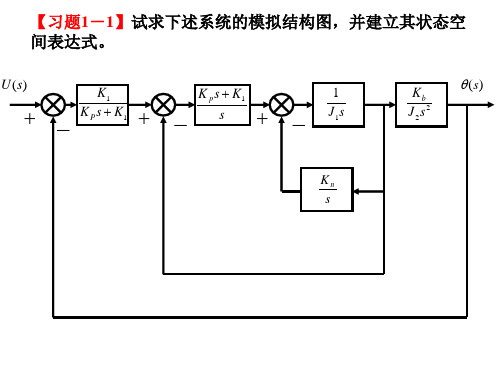
a0 3 a1 7 a2 5 b0 2 b1 1 b2 0 b3 0
标准型实现
1 0 0 0 x 0 u 0 x 0 1 3 7 5 1
y (b0 a 0 b3 ) (b1 a1b3 ) (b2 a 2 b3 )x 2 1 0x
1 0 0 0 x 0 0 1 x 0 u 3 7 5 1
y (b0 a 0 b3 ) (b1 a1b3 ) (b2 a 2 b3 )x 2 3 1x
【习题1-6】已知系统传递函数
10( s 1) (1) W ( s ) s ( s 1)(s 3) 6( s 1) (2) W ( s ) s ( s 2)(s 3) 2
x1
0 0 0 x 0 K1 Kp 0
1
0 Kb 0 J2 Kp 0 J1 0 K1 0 0 0 Kn
0 0 1 J1 0 0 0
0 0 Kp J1 K1 K1 Kp 0
0 0 0 0 1 0 J1 x 0 0 K1 Kp 0 0 0
y 0 0 1x
【解】(1)画模拟结构图的步骤 第一步:画出三个积分器 第二步:画出各增益系数和信号综合点 第三步:根据各变量的相互关系用信号线连接起来 (2)求系统的传递函数矩阵
Y ( s) 2s 2 7 s 3 1 W ( s) c( sI A) b U ( s) ( s 1)(s 2)(s 3) 2s 1 ( s 1)(s 2)
1 0
4 3
【习题1-10】已知两个子系统的传递函数分别为:
《现代控制理论》课后习题全部答案最完整打印版.pdf
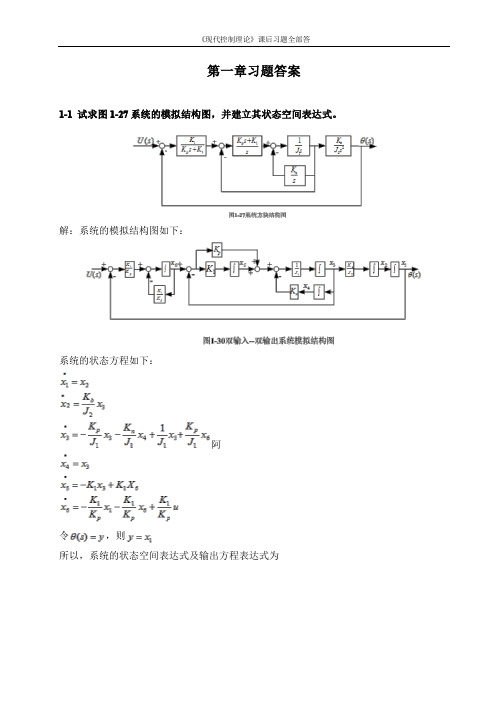
第一章习题答案
1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:
系统的状态方程如下:
阿
令,则
所以,系统的状态空间表达式及输出方程表达式为
状态变量的状态方程,和以电阻上的电压作为输出量的输出方程。
解:由图,令,输出量
有电路原理可知:既得
写成矢量矩阵形式为:
1-3参考例子1-3(P19).
1-4两输入,,两输出,的系统,其模拟结构图如图1-30所示,试求其状态空
间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:
1-5系统的动态特性由下列微分方程描述
列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令,则有
相应的模拟结构图如下:
1-6(2)已知系统传递函数,试求出系统的约旦标准型的实现,并画出相应的模拟结构图
解:
1-7给定下列状态空间表达式
(1)画出其模拟结构图
(2)求系统的传递函数
解:
(2)
1-8求下列矩阵的特征矢量
(3)
解:A的特征方程
解之得:
当时,
解得:令得
(或令,得)
当时,
解得:令得(或令,得)
当时,
解得:令得
1-9将下列状态空间表达式化成约旦标准型(并联分解)
(2)
解:A的特征方程
当时,
解之得令得
当时,
解之得令得
当时,
解之得令得。
现代控制理论课后题答案(第二章-第六章)

1
R R2C1 1 1 1 1 x1 x2 u1 x R1 R2C1 R2C1 R2C1 1 1 1 2 x1 x2 u1 x R2C2 R2C2 R2C2 y u2 u1 x1
即:
R1 R2C1 1 R1 R2C1 x x 2 1 R2C2
x2
u
R1
R3
y
R2
图 P2.8 RL 电网络
解 采用机理分析法求状态空间表达式。由电路原理可得到如下微分方程
2 x1 x2 R3 R2 x2 L2 x
1 x1 x2 R3 u x1 L1 x / R1
y x1 x2 R3
(2) 解 采用拉氏变换法求取状态空间表达式。对微分方程 (2)在零初试条件 下取拉氏变换得:
2s 3Y ( s ) 3sY ( s ) s 2U ( s ) U ( s ) 1 2 1 s Y (s) s 1 2 2 U ( s ) 2s 3 3s s 3 3 s 2
dy1 dy , x4 2 。 dt dt
3 Kx1 B1 M1 x
2
d ( x2 x1 ) dt
对 M 2 有:
4 f (t ) B M2x
经整理得:
1
d ( x2 x 1) dx B 2 dt dt
2
状态方程为:
1 x3 x x 2 x4 B B K 3 x1 1 x3 1 x4 x M1 M1 M1 B B B 1 4 1 x3 ( 1 2 ) x4 u x M2 M2 M2 M2
1 1 R2C1 x1 R2C1 u1 x2 1 1 R C R2C2 2 2
《现代控制理论》第版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有 相应的模拟结构图如下:1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图(2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P (或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ) 当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为 (1)⎥⎦⎤⎢⎣⎡=11b 解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论基础第二章习题答案
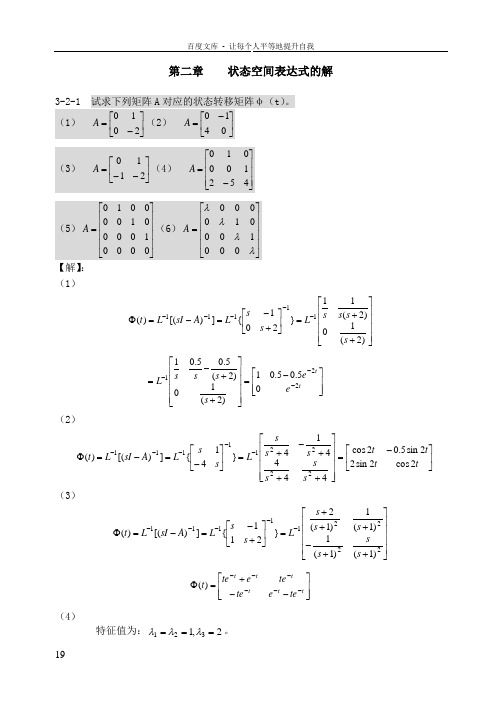
第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----)2(10)2(11}201{])[()(11111s s s s L s s L A sI L t ⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-=---t t e e s s s s L 22105.05.01)2(10)2(5.05.01(2)⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎦⎤⎢⎣⎡-=-=Φ-----t tt ts s s s s sL s s L A sI L t 2cos 2sin 22sin 5.02cos 444414}41{])[()(222211111(3)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-+++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----222211111)1()1(1)1(1)1(2}211{])[()(s s s s s s L s s L A sI L t ⎥⎥⎦⎤⎢⎢⎣⎡--+=Φ------t t tt tt te e te te e te t )((4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-200010011~1AP P A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=t t t t tA e e te e e2~0000 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===Φ-1211321200000421211101)(21~t t t ttA At e te e eP Pe e t ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++-----++-----++--=Φt t t tt t t t t t t t t t t tt t t t t t t t tt e te e e te e e te e e te e e te e e te e e te e e te e te e t 34838424225342222322)(222222222 (5)为结构四重根的约旦标准型。
现代控制理论课后习题答案

前言本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答,可帮助同学学习和理解教材的内容。
由于习题数量较多,难易程度不同,虽然主要对象是研究型大学自动化专业本科学生,但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答;第4、7 章由井元伟教授组织编选和解答,第1、2章由郑艳副教授组织编选和解答。
由于时间比较仓促,可能存在错误,请读者批评、指正。
另外有些题目解法和答案并不唯一,这里一般只给出一种解法和答案。
编者 2005年5月第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
现代控制理论习题答案

现代控制理论习题答案现代控制理论是控制工程领域中的一个重要分支,它涉及到系统建模、分析和设计,旨在提高系统性能、稳定性和鲁棒性。
以下是一些现代控制理论习题的典型答案。
习题1:状态空间表示法考虑一个线性时不变系统,其传递函数为:\[ G(s) = \frac{1}{s^2 + 3s + 2} \]解答:首先,我们需要找到系统的差分方程。
对于上述传递函数,差分方程可以表示为:\[ y[n] - 2y[n-1] - y[n-2] = 3x[n] - 6x[n-1] \]接下来,我们定义状态变量 \( x_1[n] = y[n] \) 和 \( x_2[n] =y[n-1] \),状态空间表示法可以写为:\[ \begin{bmatrix} x_1[n+1] \\ x_2[n+1] \end{bmatrix} =\begin{bmatrix} -2 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} x_1[n] \\ x_2[n] \end{bmatrix} + \begin{bmatrix} 3 \\ -3\end{bmatrix} x[n] \]\[ y[n] = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_1[n] \\ x_2[n] \end{bmatrix} \]习题2:极点配置给定一个系统的状态空间表示:\[ \dot{x}(t) = Ax(t) + Bu(t) \]\[ y(t) = Cx(t) \]其中:\[ A = \begin{bmatrix} 0 & 1 \\ -3 & -2 \end{bmatrix}, B =\begin{bmatrix} 0 \\ 1 \end{bmatrix}, C = \begin{bmatrix} 1 & 1 \end{bmatrix} \]解答:要实现极点配置,我们需要设计一个状态反馈控制器 \( u(t) = -Kx(t) \),使得闭环系统的特征值位于指定的位置。
现代控制理论(A卷)答案

《现代控制理论》参考答案(A 卷)一、填空(本题20 分,每空2分)1、稳态 ; G(jω)为G(s)中的s 用jω代替的结果2、不一定稳定 ; 不一定稳定3、欠阻尼状态 ;单位阶跃输入4、⎰+∞-=0)()(dt e t f s F st;0()()st f t F s e dt +∞=⎰5、(00.707)r M ξ=≤≤;(00.707)r ωωξ=≤≤二、选择题(本题20分,每题2分) 1~5 BCDDD 6~10 CABCC 三、(12分)R 、L 、C 串联电路的微分方程 解:方法一:LC 22()o d u t dt+ RC dt t du o )( + u o (t) = u i (t) (6分) 则 G(s) =11)()(20++=RCs LCs s U s U i (6分) 方法二:利用复阻抗,令 Z 1 = R + Ls , Z 2 = 1/Cs (4分) 则 G(s) =11)()(22120++=+=RCs LCs Z Z Z s U s U i (8分) 四、(12分)求一阶系统的频率特性及在正弦信号()sin i i x t X t ω=作用下的频率响应。
解:(4分)(4分)其稳态响应为:(4分)五、(12分)某二阶系统如图所示, 其中系统的结构参数ζ=0.6, ωn =5rad/s 。
输入信号为单位阶跃函数, 求性能指标r t 、p t 的数值。
解: 二阶系统闭环传函数(4分)因0< <1,所以系统处于欠阻尼状态。
根据给定的参数可以得出 (4分) 222()()()2n n nC s s R s s s ωξωωΦ==++ξ0.8,4,0.93drad ωωϕ====o x (t)arctan Tw)=-i 022i o 22X w K X (s)Ts 1s w X KTwx (t)arctan Tw)exp(t /T)1T w =⋅++=-+-+所以 (2分)(2分)六、(10分)考虑图所示的系统, 确定使系统稳定的K 的取值范围。
