优化方法大作业
最优化方法大作业答案

1.用薄钢板制造一体积5m 3,长度不小于4m ,无上盖的货箱,要求钢板耗量最小。
确定货箱的长x 1、宽x 2和高x 3。
试列出问题的数学模型。
解:min 32312122x x x x x x z ++= s.t 5321=x x x 41≥x 0,,321≥x x x2.将下面的线性规划问题表示为标准型并用单纯形法求解max f=x 1+2x 2+x 3s .t .2x 1+x 2-x 3≤2 -2x 1+x 2-5x 3≥-6 4x 1+x 2+x 3≤6 x i ≥0 i=1,2,3 解:先化标准形:Min 321x x x z -+=224321=+-+x x x x 6525321=++-x x x x646321=+++x x x x列成表格:121610011460105122001112-----可见此表已具备1°,2°,3°三个特点,可采用单纯形法。
首先从底行中选元素-1,由2/2,6/2,6/4最小者决定选第一行第一列的元素2,标以记号,迭代一次得121210231040116201002121211--------再从底行中选元素-2/3,和第二列正元素1/2,迭代一次得12123230210231040116201002121211-------再从底行中选元素-3,和第二列正元素2,迭代一次得4233410120280114042001112---再迭代一次得1023021062210231010213000421021013--选取最优解:01=x 42=x 23=x3. 试用DFP 变尺度法求解下列无约束优化问题。
min f (X )=4(x 1-5)2+(x 2-6)2取初始点X=(8,9)T ,梯度精度ε=0.01。
解:取IH=0,初始点()TX 9,8=2221)6()5(4)(-+-=x x x f⎥⎦⎤⎢⎣⎡--=∇122408)(21x x x f⎪⎪⎭⎫⎝⎛=∇624)()0(xfTx f d )6,24()()0()0(--=-∇=)0(0)0()1(dxxα+=T)69,248(00αα--=])669()5248(4min[)(min 2020)0(0)0(--+--⨯=+αααdxf 0)6()63(2)24()2458(8)(00)0(0)0(=-⨯-+-⨯--=+ααααd d xdf13077.0130170≈=α⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--⨯+⎪⎪⎭⎫ ⎝⎛=21538.886153.462413077.098)1(x⎪⎪⎭⎫⎝⎛-=∇43077.410784.1)()1(xf进行第二次迭代:⎥⎦⎤⎢⎣⎡--=-=78463.013848.31)0()1(xxδ⎥⎦⎤⎢⎣⎡--=∇-∇=56924.110783.25)()(1)0()1(xf xf γ101011011101γγγγγδδδH HH H H TTTT-+=03172.8011=γδT86614.6321101==γγγγH T⎥⎦⎤⎢⎣⎡=61561.046249.246249.285005.911Tδδ⎥⎦⎤⎢⎣⎡==46249.240022.3940022.3940363.630110110TTHH γγγγ所以:⎪⎪⎭⎫⎝⎛--=0038.103149.003149.012695.01H⎪⎪⎭⎫⎝⎛-⨯⎪⎪⎭⎫⎝⎛---=∇-=43076.410784.10038.103149.003149.012695.0)()1(1)1(xf H d⎪⎪⎭⎫⎝⎛-=48248.428018.0令 )1(1)1()2(dx x α+=利用)()1()1(=+ααd dxdf ,求得49423.01=α,所以⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫⎝⎛=+=21538.213848.021538.886152.449423.0)1()1()2(dxx⎪⎪⎭⎫ ⎝⎛=65因)()2(=∇xf ,于是停,)2(x 即为最优解。
2016年大连理工大学优化方法上机大作业

2016年理工大学优化方法上机大作业学院:专业:班级:学号::上机大作业1:1.最速下降法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = steepest(x0,eps)gk = grad(x0);res = norm(gk);k = 0;while res > eps && k<=1000dk = -gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;gk = grad(xk);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x=steepest(x0,eps)2.牛顿法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad2(x)g = zeros(2,2);g(1,1)=2+400*(3*x(1)^2-x(2));g(1,2)=-400*x(1);g(2,1)=-400*x(1);g(2,2)=200;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = newton(x0,eps)gk = grad(x0);bk = [grad2(x0)]^(-1);res = norm(gk);k = 0;while res > eps && k<=1000dk=-bk*gk;xk=x0+dk;k = k+1;x0 = xk;gk = grad(xk);bk = [grad2(xk)]^(-1);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x1=newton(x0,eps)--The 1-th iter, the residual is 447.213595--The 2-th iter, the residual is 0.000000x1 =1.00001.00003.BFGS法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = bfgs(x0,eps)g0 = grad(x0);gk=g0;res = norm(gk);Hk=eye(2);k = 0;while res > eps && k<=1000dk = -Hk*gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;fa0=xk-x0;x0 = xk;go=gk;gk = grad(xk);y0=gk-g0;Hk=((eye(2)-fa0*(y0)')/((fa0)'*(y0)))*((eye(2)-(y0)*(fa0)')/((fa0)'*( y0)))+(fa0*(fa0)')/((fa0)'*(y0));res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;End>> clear>> x0=[0,0]';>> eps=1e-4;>> x=bfgs(x0,eps)4.共轭梯度法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star =CG(x0,eps)gk = grad(x0);res = norm(gk);k = 0;dk = -gk;while res > eps && k<=1000ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;g0=gk;gk = grad(xk);res = norm(gk);p=(gk/g0)^2;dk1=dk;dk=-gk+p*dk1;fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk; end>> clear>> x0=[0,0]'; >> eps=1e-4; >> x=CG(x0,eps)上机大作业2:function f= obj(x)f=4*x(1)-x(2)^2-12;endfunction [h,g] =constrains(x) h=x(1)^2+x(2)^2-25;g=zeros(3,1);g(1)=-10*x(1)+x(1)^2-10*x(2)+x(2)^2+34;g(2)=-x(1);g(3)=-x(2);endfunction f=alobj(x) %拉格朗日增广函数%N_equ等式约束个数?%N_inequ不等式约束个数N_equ=1;N_inequ=3;global r_al pena;%全局变量h_equ=0;h_inequ=0;[h,g]=constrains(x);%等式约束部分?for i=1:N_equh_equ=h_equ+h(i)*r_al(i)+(pena/2)*h(i).^2;end%不等式约束部分for i=1:N_inequh_inequ=h_inequ+(0.5/pena)*(max(0,(r_al(i)+pena*g(i))).^2-r_al(i).^2) ;end%拉格朗日增广函数值f=obj(x)+h_equ+h_inequ;function f=compare(x)global r_al pena N_equ N_inequ;N_equ=1;N_inequ=3;h_inequ=zeros(3,1);[h,g]=constrains(x);%等式部分for i=1:1h_equ=abs(h(i));end%不等式部分for i=1:3h_inequ=abs(max(g(i),-r_al(i+1)/pena));endh1 = max(h_inequ);f= max(abs(h_equ),h1); %sqrt(h_equ+h_inequ);function [ x,fmin,k] =almain(x_al)%本程序为拉格朗日乘子算法示例算法%函数输入:% x_al:初始迭代点% r_al:初始拉格朗日乘子N-equ:等式约束个数N_inequ:不等式约束个数?%函数输出% X:最优函数点FVAL:最优函数值%============================程序开始================================ global r_al pena ; %参数(全局变量)pena=10; %惩罚系数r_al=[1,1,1,1];c_scale=2; %乘法系数乘数cta=0.5; %下降标准系数e_al=1e-4; %误差控制围max_itera=25;out_itera=1; %迭代次数%===========================算法迭代开始============================= while out_itera<max_iterax_al0=x_al;r_al0=r_al;%判断函数?compareFlag=compare(x_al0);%无约束的拟牛顿法BFGS[X,fmin]=fminunc(alobj,x_al0);x_al=X; %得到新迭代点%判断停止条件?if compare(x_al)<e_aldisp('we get the opt point');breakend%c判断函数下降度?if compare(x_al)<cta*compareFlagpena=1*pena; %可以根据需要修改惩罚系数变量elsepena=min(1000,c_scale*pena); %%乘法系数最大1000disp('pena=2*pena');end%%?更新拉格朗日乘子[h,g]=constrains(x_al);for i=1:1%%等式约束部分r_al(i)= r_al0(i)+pena*h(i);endfor i=1:3%%不等式约束部分r_al(i+1)=max(0,(r_al0(i+1)+pena*g(i)));endout_itera=out_itera+1;end%+++++++++++++++++++++++++++迭代结束+++++++++++++++++++++++++++++++++ disp('the iteration number');k=out_itera;disp('the value of constrains'); compare(x_al)disp('the opt point');x=x_al;fmin=obj(X);>> clear>> x_al=[0,0];>> [x,fmin,k]=almain(x_al)上机大作业3:1、>> clear alln=3; c=[-3,-1,-3]'; A=[2,1,1;1,2,3;2,2,1;-1,0,0;0,-1,0;0,0,-1];b=[2,5,6,0,0,0]'; cvx_beginvariable x(n)minimize( c'*x)subject toA*x<=bcvx_endCalling SDPT3 4.0: 6 variables, 3 equality constraints------------------------------------------------------------num. of constraints = 3dim. of linear var = 6*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime-------------------------------------------------------------------0|0.000|0.000|1.1e+01|5.1e+00|6.0e+02|-7.000000e+01 0.000000e+00| 0:0:00| chol 1 11|0.912|1.000|9.4e-01|4.6e-02|6.5e+01|-5.606627e+00 -2.967567e+01| 0:0:01| chol 1 12|1.000|1.000|1.3e-07|4.6e-03|8.5e+00|-2.723981e+00 -1.113509e+01| 0:0:01| chol 1 13|1.000|0.961|2.3e-08|6.2e-04|1.8e+00|-4.348354e+00 -6.122853e+00| 0:0:01| chol 1 14|0.881|1.000|2.2e-08|4.6e-05|3.7e-01|-5.255152e+00 -5.622375e+00| 0:0:01| chol 1 15|0.995|0.962|1.6e-09|6.2e-06|1.5e-02|-5.394782e+00 -5.409213e+00| 0:0:01| chol 1 16|0.989|0.989|2.7e-10|5.2e-07|1.7e-04|-5.399940e+00 -5.400100e+00| 0:0:01| chol 1 17|0.989|0.989|5.3e-11|5.8e-09|1.8e-06|-5.399999e+00 -5.400001e+00| 0:0:01| chol 1 18|1.000|0.994|2.8e-13|4.3e-11|2.7e-08|-5.400000e+00 -5.400000e+00| 0:0:01| stop: max(relative gap, infeasibilities) < 1.49e-08-------------------------------------------------------------------number of iterations = 8primal objective value = -5.39999999e+00dual objective value = -5.40000002e+00gap := trace(XZ) = 2.66e-08relative gap = 2.26e-09actual relative gap = 2.21e-09rel. primal infeas (scaled problem) = 2.77e-13rel. dual " " " = 4.31e-11rel. primal infeas (unscaled problem) = 0.00e+00rel. dual " " " = 0.00e+00norm(X), norm(y), norm(Z) = 4.3e+00, 1.3e+00, 1.9e+00norm(A), norm(b), norm(C) = 6.7e+00, 9.1e+00, 5.4e+00Total CPU time (secs) = 0.71CPU time per iteration = 0.09termination code = 0DIMACS: 3.6e-13 0.0e+00 5.8e-11 0.0e+00 2.2e-09 2.3e-09-------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval): -5.42、>> clear alln=2; c=[-2,-4]'; G=[0.5,0;0,1]; A=[1,1;-1,0;0,-1]; b=[1,0,0]'; cvx_beginvariable x(n)minimize( x'*G*x+c'*x)subject toA*x<=bcvx_endCalling SDPT3 4.0: 7 variables, 3 equality constraintsFor improved efficiency, SDPT3 is solving the dual problem.------------------------------------------------------------num. of constraints = 3dim. of socp var = 4, num. of socp blk = 1dim. of linear var = 3******************************************************************* SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime-------------------------------------------------------------------0|0.000|0.000|8.0e-01|6.5e+00|3.1e+02| 1.000000e+01 0.000000e+00| 0:0:00| chol 1 1 1|1.000|0.987|4.3e-07|1.5e-01|1.6e+01| 9.043148e+00 -2.714056e-01| 0:0:00| chol 1 1 2|1.000|1.000|2.6e-07|7.6e-03|1.4e+00| 1.234938e+00 -5.011630e-02| 0:0:00| chol 1 1 3|1.000|1.000|2.4e-07|7.6e-04|3.0e-01| 4.166959e-01 1.181563e-01| 0:0:00| chol 1 1 4|0.892|0.877|6.4e-08|1.6e-04|5.2e-02| 2.773022e-01 2.265122e-01| 0:0:00| chol 1 1 5|1.000|1.000|1.0e-08|7.6e-06|1.5e-02| 2.579468e-01 2.427203e-01| 0:0:00| chol 1 1 6|0.905|0.904|3.1e-09|1.4e-06|2.3e-03| 2.511936e-01 2.488619e-01| 0:0:00| chol 1 1 7|1.000|1.000|6.1e-09|7.7e-08|6.6e-04| 2.503336e-01 2.496718e-01| 0:0:00| chol 1 1 8|0.903|0.903|1.8e-09|1.5e-08|1.0e-04| 2.500507e-01 2.499497e-01| 0:0:00| chol 1 19|1.000|1.000|4.9e-10|3.5e-10|2.9e-05| 2.500143e-01 2.499857e-01| 0:0:00| chol 1 1 10|0.904|0.904|4.7e-11|1.3e-10|4.4e-06| 2.500022e-01 2.499978e-01| 0:0:00| chol 2 2 11|1.000|1.000|2.3e-12|9.4e-12|1.2e-06| 2.500006e-01 2.499994e-01| 0:0:00| chol 2 2 12|1.000|1.000|4.7e-13|1.0e-12|1.8e-07| 2.500001e-01 2.499999e-01| 0:0:00| chol 2 2 13|1.000|1.000|2.0e-12|1.0e-12|4.2e-08| 2.500000e-01 2.500000e-01| 0:0:00| chol 2 2 14|1.000|1.000|2.6e-12|1.0e-12|7.3e-09| 2.500000e-01 2.500000e-01| 0:0:00|stop: max(relative gap, infeasibilities) < 1.49e-08-------------------------------------------------------------------number of iterations = 14primal objective value = 2.50000004e-01dual objective value = 2.49999996e-01gap := trace(XZ) = 7.29e-09relative gap = 4.86e-09actual relative gap = 4.86e-09rel. primal infeas (scaled problem) = 2.63e-12rel. dual " " " = 1.00e-12rel. primal infeas (unscaled problem) = 0.00e+00rel. dual " " " = 0.00e+00norm(X), norm(y), norm(Z) = 3.2e+00, 1.5e+00, 1.9e+00norm(A), norm(b), norm(C) = 3.9e+00, 4.2e+00, 2.6e+00Total CPU time (secs) = 0.36CPU time per iteration = 0.03termination code = 0DIMACS: 3.7e-12 0.0e+00 1.3e-12 0.0e+00 4.9e-09 4.9e-09------------------------------------------------------------------------------------------------------------------------------- Status: SolvedOptimal value (cvx_optval): -3。
北航最优化大作业
图 18: 前两行为迭代点 xk, 后面一行为梯度的 2 范数,显然,前两行行都趋于无穷大,发散,梯度的 2 范数 趋于 13.4536(从 matlab 变量表格中得到)。 4: 初始点 x(0) = (10, 20)T 前两行为迭代点 xk, 后面一行为梯度的 2 范数,显然,前两行行都趋于无穷大,发散,梯度的 2 范数 趋于 13.4536(从 matlab 变量表格中得到)。
33
图 57: 7、9、11、13 迭代停止测试。
当 n=50 时,解 x*=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1] 判断矩阵:
图 58: 可以发现,没有发现负曲率的情况,第 1 和第 2 次的迭代到了边界,第 4、6、8、10、12、14、16 次 迭代到了边界。
▽f (x) = g = −400x1(x2 − x21) + 2x1 − 2
200(x2 − x21)
[
]
▽2f (x) = G = 1200x21 − 400x2 + 2 −400x1
−400x1
200
14
4.1 最速下降法
代码和流程图:
图 33:
图 34: 15
4.1.1 初始点为 (1.2,1.2)
++
)
x1 + x12 − 100
x11
x1
−
50 1
−
x2
−10 − µ(
++
)
x1 + x2 − 100 x2 −x1 + 50 + x2
大连理工大学优化方法上机作业

大连理工大学优化方法上机作业本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March优化方法上机大作业学院:电子信息与电气工程学部姓名:学号:指导老师:上机大作业(一)%目标函数function f=fun(x)f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;end%目标函数梯度function gf=gfun(x)gf=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)]; End%目标函数Hess矩阵function He=Hess(x)He=[1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1), 200;];end%线搜索步长function mk=armijo(xk,dk)beta=0.5; sigma=0.2;m=0; maxm=20;while (m<=maxm)if(fun(xk+beta^m*dk)<=fun(xk)+sigma*beta^m*gfun(xk)'*dk) mk=m; break;endm=m+1;endalpha=beta^mknewxk=xk+alpha*dkfk=fun(xk)newfk=fun(newxk)%最速下降法function [k,x,val]=grad(fun,gfun,x0,epsilon)%功能:梯度法求解无约束优化问题:minf(x)%输入:fun,gfun分别是目标函数及其梯度,x0是初始点,% epsilon为容许误差%输出:k是迭代次数,x,val分别是近似最优点和最优值maxk=5000; %最大迭代次数beta=0.5; sigma=0.4;k=0;while(k<maxk)gk=feval(gfun,x0); %计算梯度dk=-gk; %计算搜索方向if(norm(gk)<epsilon), break;end%检验终止准则m=0;mk=0;while(m<20) %用Armijo搜索步长if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk) mk=m;break;endm=m+1;endx0=x0+beta^mk*dk;k=k+1;endx=x0;val=feval(fun,x0);>> x0=[0;0];>> [k,x,val]=grad('fun','gfun',x0,1e-4)迭代次数:k =1033x =0.99990.9998val =1.2390e-008%牛顿法x0=[0;0];ep=1e-4;maxk=10;k=0;while(k<maxk)gk=gfun(x0);if(norm(gk)<ep)x=x0miny=fun(x)k0=kbreak;elseH=inv(Hess(x0));x0=x0-H*gk;k=k+1;endendx =1.00001.0000miny =4.9304e-030迭代次数k0 =2%BFGS方法function [k,x,val]=bfgs(fun,gfun,x0,varargin) %功能:梯度法求解无约束优化问题:minf(x)%输入:fun,gfun分别是目标函数及其梯度,x0是初始点,% epsilon为容许误差%输出:k是迭代次数,x,val分别是近似最优点和最优值N=1000;epsilon=1e-4;beta=0.55;sigma=0.4;n=length(x0);Bk=eye(n);k=0;while(k<N)gk=feval(gfun,x0,varargin{:});if(norm(gk)<epsilon), break;enddk=-Bk\gk;m=0;mk=0;while(m<20)newf=feval(fun,x0+beta^m*dk,varargin{:});oldf=feval(fun,x0,varargin{:});if(newf<=oldf+sigma*beta^m*gk'*dk)mk=m;break;endm=m+1;endx=x0+beta^mk*dk;sk=x-x0;yk=feval(gfun,x,varargin{:})-gk;if(yk'*sk>0)Bk=Bk-(Bk*sk*sk'*Bk)/(sk'*Bk*sk)+(yk*yk')/(yk'*sk);endk=k+1;x0=x;endval=feval(fun,x0,varargin{:});>> x0=[0;0];>> [k,x,val]=bfgs('fun','gfun',x0)k =20x =1.00001.0000val =2.2005e-011%共轭梯度法function [k,x,val]=frcg(fun,gfun,x0,epsilon,N)if nargin<5,N=1000;endif nargin<4, epsilon=1e-4;endbeta=0.6;sigma=0.4;n=length(x0);k=0;while(k<N)gk=feval(gfun,x0);itern=k-(n+1)*floor(k/(n+1));itern=itern+1;if(itern==1)dk=-gk;elsebetak=(gk'*gk)/(g0'*g0);dk=-gk+betak*d0; gd=gk'*dk;if(gd>=0),dk=-gk;endendif(norm(gk)<epsilon),break;endm=0;mk=0;while(m<20)if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk) mk=m;break;endm=m+1;endx=x0+beta^m*dk;g0=gk; d0=dk;x0=x;k=k+1;endval=feval(fun,x);>> x0=[0;0];[k,x,val]=frcg('fun','gfun',x0,1e-4,1000)k =122x =1.00011.0002val =7.2372e-009上机大作业(二)%目标函数function f_x=fun(x)f_x=4*x(1)-x(2)^2-12;%等式约束条件function he=hf(x)he=25-x(1)^2-x(2)^2;end%不等式约束条件function gi_x=gi(x,i)switch icase 1gi_x=10*x(1)-x(1)^2+10*x(2)-x(2)^2-34;case 2gi_x=x(1);case 3gi_x=x(2);otherwiseend%求目标函数的梯度function L_grad=grad(x,lambda,cigma)d_f=[4;2*x(2)];d_g(:,1)=[-2*x(1);-2*x(2)];d_g(:,2)=[10-2*x(1);10-2*x(2)];d_g(:,3)=[1;0];d_g(:,4)=[0;1];L_grad=d_f+(lambda(1)+cigma*hf(x))*d_g(:,1);for i=1:3if lambda(i+1)+cigma*gi(x,i)<0L_grad=L_grad+(lambda(i+1)+cigma*gi(x,i))*d_g(:,i+1);continueendend%增广拉格朗日函数function LA=lag(x,lambda,cee)LA=fun(x)+lambda(1)*hf(x)+0.5*cee*hf(x)^2;for i=1:3LA=LA+1/(2*cee)*(min(0,lambda(i+1)+cee*gi(x,i))^2-lambda(i+1)^2); endfunction xk=BFGS(x0,eps,lambda,cigma)gk=grad(x0,lambda,cigma);res_B=norm(gk);k_B=0;a_=1e-4;rho=0.5;c=1e-4;length_x=length(x0);I=eye(length_x);Hk=I;while res_B>eps&&k_B<=10000dk=-Hk*gk;m=0;while m<=5000if lag(x0+a_*rho^m*dk,lambda,cigma)-lag(x0,lambda,cigma)<=c*a_*rho^m*gk'*dkmk=m;break;endm=m+1;endak=a_*rho^mk;xk=x0+ak*dk;delta=xk-x0;y=grad(xk,lambda,cigma)-gk;Hk=(I-(delta*y')/(delta'*y))*Hk*(I-(y*delta')/(delta'*y))+(delta*delta')/(delta'*y);k_B=k_B+1;x0=xk;gk=y+gk;res_B=norm(gk);end%增广拉格朗日法function val_min=ALM(x0,eps)lambda=zeros(4,1);cigma=5;alpha=10;k=1;res=[abs(hf(x0)),0,0,0];for i=1:3res(1,i+1)=norm(min(gi(x0,i),-lambda(i+1)/cigma)); endres=max(res);while res>eps&&k<1000xk=BFGS(x0,eps,lambda,cigma);lambda(1)=lambda(1)+cigma*hf(xk);for i=1:3lambda(i+1)=lambda(i+1)+min(0,lambda(i+1)+gi(x0,1)); endk=k+1;cigma=alpha*cigma;x0=xk;res=[norm(hf(x0)),0,0,0];for i=1:3res(1,i+1)=norm(min(gi(x0,i),-lambda(i+1)/cigma)); endres=max(res);endval_min=fun(xk);fprintf('k=%d\n',k);fprintf('fmin=%.4f\n',val_min);fprintf('x=[%.4f;%.4f]\n',xk(1),xk(2));>> x0=[0;0];>> val_min=ALM(x0,1e-4)k=10fmin=-31.4003x=[1.0984;4.8779]val_min =-31.4003上机大作业(三)A=[1 1;-1 0;0 -1];n=2;b=[1;0;0];G=[0.5 0;0 2];c=[2 4];cvx_solver sdpt3cvx_beginvariable x(n)minimize (x'*G*x-c*x)subject toA*x<=bcvx_enddisp(x)Status: SolvedOptimal value (cvx_optval): -2.40.40000.6000A=[2 1 1;1 2 3;2 2 1;-1 0 0;0 -1 0;0 0 -1]; n=3;b=[2;5;6;0;0;0];C=[-3 -1 -3];cvx_solver sdpt3cvx_beginvariable x(n)minimize (C*x)subject toA*x<=bcvx_enddisp(x)Status: SolvedOptimal value (cvx_optval): -5.40.20000.00001.600011。
优化方法作业第二版

优化方法上机大作业院系:化工与环境生命学部姓名:李翔宇学号:31607007 指导教师:肖现涛第一题:编写程序求解下述问题min y(z) = (1 —xi)2+ 100(x2 —xj)2.初始点取/ = 0,精度取s = le - 4,步长由Armijo线捜索生成,方向分别由下列方法生成:最速下降法BFGS方法共辄梯度法1.最速下降法源程序如下:function x_star = ZSXJ (x0,eps) gk = grad(xO);res = norm(g k);k = 0;while res > eps && k<=10000 dk = -gk;ak =1; f0 = fun(xO);f1 = fun(xO+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.0001*ak*slope ak = ak/2;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;gk = grad(xk);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res);end x_star = xk; end function f = fun(x)f = (1-x(1))A2 + 100*以(2)咲(1)八2)八2;end function g = grad(x) g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)A2-x(2)); g(2) = 200*(x(2)-x(1)A2);end 运行结果:>> x0=[0,0]';>> esp=1e-4;>> xk= ZSXJ(x0,eps)--The 1-th iter, the residual is 13.372079 --The 2-th iter, the residual is 12.079876 --The 3-th iter, the residual is 11.054105 --The 9144-th iter, the residual is 0.000105 --The 9145-th iter, the residual is 0.000102 --The 9146-th iter, the residual is0.000100 xk =0.99990.9998MATLAB 截屏:>> xO= [Qj 01’ :>> esp=le-4:>> xk=ZSXJ txOj eps)一The I-th it er?the residual is13.372075一The2-th it er j the residual is12,07&876一Iht3-th it亡「■the residual is11. 054105一The Wh it er j the residual is10. 421221一一Ih?5-th it er^the residual is10. 020369Tl_ -■:丄一一丄ll_ ______ I; Ji ___ '1J _一The9142-th iter,the residual is0.000111-- The9143-th iterj the residual is0.000108一一The9144-th iter>the匸esidual is D. 000105一-The9145-th iter f th?residual is0. 000102一Th?9143-th iter,the residual is0. 0001000.99990.99932. 牛顿法源程序如下:function x_star = NEWTON (x0,eps) gk = grad(x0);bk = [grad2(xO)]A(-1);res = norm(gk);k = 0;while res > eps && k<=1000dk=-bk*gk; xk=x0+dk;k = k+1;x0 = xk;gk = grad(xk);bk = [grad2(xk)]A(-1);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); end x_star = xk;endfunction f = fun(x)f = (1-x(1))A2 + 100*(x(2)-x(1)A2)A2;end function g = grad2(x)g = zeros(2,2); g(1,1)=2+400*(3*x(1)A2-x(2));g(1,2)=-400*x(1);g(2,1)=-400*x(1);g(2,2)=200;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)A2-x(2));g(2) = 200*(x(2)-x(1)A2);end运行结果:>> xO=[O,O]';eps=1e-4;>> xk= NEWTON (x0,eps)--The 1-th iter, the residual is 447.213595--The 2-th iter, the residual is 0.000000xk =1.00001.0000MATALB 截屏;»x0= [0, DY :>> esp=1;»xk^NEirONtaO, eps)—The 1-th iter, the residual is 447,213595 一The 2-th iter, the residual is0.OOQOQOxk =L 0000|L 00003. BFGS 方法源程序如下:function x_star = Bfgs(x0,eps) g0 = grad(x0);gk=g0;res = norm(gk);Hk=eye(2);k = 0;while res > eps && k<=1000dk = -Hk*gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/2;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;fa0=xk-x0;x0 = xk;g0=gk;gk = grad(xk); y0=gk-g0;Hk=((eye(2)-fa0*(y0)')/((fa0)'*(y0)))*((eye(2)-(y0)*(fa0)')/((fa0)'*(y0)))+(fa0*(fa0)')/((fa0)'*(y0));res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); end x_star = xk; end function f=fun(x)f=(1-x(1))A2 + 100*債(2)咲(1)八2)八2;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)A2-x(2));g(2) = 200*(x(2)-x(1)A2);end运行结果:>> x0=[0,0]';>> esp=1e-4;>> xk= Bfgs(x0,eps)--The 1-th iter, the residual is 3.271712--The 2-th iter, the residual is 2.381565--The 3-th iter, the residual is 3.448742--The 1516-th iter, the residual is 0.000368 --The 1517-th iter, the residual is0.000099 xk =1.00011.0002MATLAB 截屏:x0= [0, 0]J:esp=le-4: xk=Bfgs (xOj eps)一The1th it erj the residual is3. 271712一The2th it erj the residual is2.381565一The3th it the residual is3.448742一The4th it er,the residual is3, 162431— The5th it erj the residual is2. 989084—The 1515-th iter, the residual is 0.000108—The 1516-th iter, the residual is 0.000368—The 1517-th iter, the residual is 0. 0000991.00011.00024. 共轭梯度法源程序如下:function x_star =Conj (x0,eps)gk = grad(x0);res = norm(gk);k = 0;dk = -gk;while res > eps && k<=1000ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/2;xk = x0 + ak*dk;f1 = fun(xk);endd0=dk;g0=gk;k=k+1;xO=xk;gk=grad(xk);f=(norm(gk)/norm(gO))A2;res=norm(gk);dk=-gk+f*d0;fprintf('--The %d-th iter, the residual is %f\n',k,res);endx_star = xk;endfunction f=fun(x)f=(1-x(1))A2+100*(x(2)-x(1)A2)A2;endfunction g=grad(x)g=zeros(2,1);g(1)=400*x(1)A3-400*x(1)*x(2)+2*x(1)-2;g(2)=-200*x(1)A2+200*x(2);end运行结果:>> xO=[O,O]';>> eps=1e-4;>> xk=Conj(xO,eps)--The 1-th iter, the residual is 3.271712--The 2-th iter, the residual is 1.380542--The 3-th iter, the residual is 4.527780--The 4-th iter, the residual is 0.850596--The 73-th iter, the residual is 0.001532 --The 74-th iter, the residual is 0.000402 --The 75-th iter, the residual is0.000134 --The 76-th iter, the residual is 0.000057 xk =0.99990.9999MATLAB 截屏:» ito= O]T:>> esp=l*-4 :>> xk=Conj eps)—The l-th it efj the residual is 3. 271712~Ihe2-th it erj the residual IS 1. 3805423-th it er^the residual IS 4. 527780—I he4-th it er^the residual IS0.8505&6—I he5-th it erj the residual is0.559005——Tin 尺一+ Vi■i十戶T十Ha■r 戶 uT H IT-al H QRR7J.il■■丄丄比U 3^111丄LBL,LILS丄M th UUUUZJ一The70-th iter,the residual is0. 001423一The71-th iter,the residual is0. 002841---The72-th iter^the residual is0. 002945一The73-th itetj the residual is0. 001532—Th?74-th iter,the residual is0. 000403—The75-th it the residual is0. 000134一Iht76-th iter,the r*sidual is0.0000570.99990-9999第二题:编写程序利用增广拉格朗日方法求解下述问题初始点取= 0,精度取s= lc-4.解:目标函数文件fl.mfunction f=f1(x)f=4*x(1)-x(2)A2-12;等式约束函数文件hl.mfunction he=h1(x)he=25-x(1)A2-x(2)A2;不等式约束函数文件gl.mfunction gi=g1(x)gi=10*x(1)-x(1)A2+10*x(2)-x(2)A2-34;目标函数的梯度文件dfl.mfunction g=df1(x)g = [4, 2.0*x(2)]';等式约束(向量)函数的Jacobi矩阵(转置)文件dhl.mfunction dhe=dh1(x)dhe = [-2*x(1), -2*x(2)]';不等式约束(向量)函数的Jacobi矩阵(转置)文件dg1.mfunction dgi=dg1(x)dgi = [10-2*x(1), 10-2*x(2)]';然后在Matlab命令窗口输入如下命令:x0=[0,0]';[X,mu,lambda,output]=multphr('f1','h1','g1','df1','dh1','dg1',x0);得到如下输出:x =4.898717426488211.00128197198571算法编程利用程序调用格式function [x, mu, lambda, out put ] =mul t phr (furij hf, gf, dfun, dhfj dgf, xO)paxk=500;si gma=2* 0; eta z2. 0; theta z O* 8;k=0; ink=0;epsilon=le-4;x=xO; he-feval (hf f x); gi=feval (gf> x);n=length(K); 1=1 eng th (he); nFlength(gi),rru=O> l*ones(lj 1); lairbda=O» l*ones(n A 1); btak=10; btaold=10;^hile(btak>epsilon & k<maxk)[爲ival, ik]=bfgsC 叩si"," dirpsi", xO* fun, hf, gf, dfun, dhf, dgf, m f 1 ambda, sigma); ink二ink+ik;he=feval (h£ x); gi=feval (gf, x);btak-0,0; 丹for (1=1:1)^ btak=btak+he(i) "2; endfor i=l:mteitp=min(gi (i), lairbda(i)/sigma); btak-btak+temp"2;end btak z sqrt(btak); if btak>epsilon if(k>=2 & btak > theta*btaold) sig^eta+sigma, end for iDu[i)z mu(i)-sigina*he(i); endfor (i=l:nOlambda(i)z max(0.0, lairbda(i)-signia*gi(i));endendk二k+1;btaold=btak;xO=x;endf=f eval (fun, x);output. fral=f; output. iter=k;output* inner_iter-ink;output,bta-btak;function [x, val, k]=bfgs (fun^ gfun, xO, varargin) maxk=500;rho=0. 55; sigmal=O. 4; epsi1onl = le—5;k=0; n=length(xO);Bk=eye (n) ; %Bk=feval (' Hess^ , xO);while(k<maxk)gk=feval (gfun, xO, varargin {: });if(norm(gk)<epsilonl), break; enddk=-Bk\gk;n»=0; ink=O;while(m<20) 亠newf=feval (fun, xO+rho^irF^dk, varacrgin {: }); oldf=feval (fun, xO, varargin {: });i f (newf <ol df+si gir)al*rho m*gk,*dk) rnk=m; break;endm=irrH;endx= xO+rho ^ink*dk;sk=x—xO; yk=feval (gfun^ x, varargin {: } ) -gk;i f (yk^ *sk>0)Bk=Bk—(Bk*sk*sk J *Bk)/(sk‘ *Bk*sk)+(yk*yk J )/(yk‘ *sk); end k=k+l;xO=x;endval = f eval (fun, xO, v ar argin {: });第三题:■下载安装 CVX h http: /cvx/■利用CVX 编写代码求解下述问题迟1 + 牝 一 1 < 0. xi > 0.工2 > 0 ■利用CVX 编写代码求解下述问题min —3J :I — X2 — 3帀S.t. 2淤]十念2 +②3 W 2x\ + 2x2 + 3x3 < 5 2叭 +2x 2 + 巧 W6 37 > 0.1.解:将目标函数改写为向量形式:x'*a*x-b*x程序代码:n=2;a=[0.5,0;0,1];b=[2 4];c=[1 1];cvx_beginvariable x(n)minimize( x'*a*x-b*x)subject toc * x <= 1x>=0cvx_end运算结果:Calling SDPT3 4.0: 7 variables, 3 equality constraintsFor improved efficiency, SDPT3 is solving the dual problem.nun 1-2—2x1 —■4J *2 subject tonum. of constraints = 3dim. of socp var = 4, num. of socp blk = 1dim. of linear var = 3*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime0|0.000|0.000|8.0e-001|6.5e+000|3.1e+002| 1.000000e+001 0.000000e+000| 0:0:00| chol 1 1 1|1.000|0.987|4.3e-007|1.5e-001|1.6e+001| 9.043148e+000 -2.714056e-001| 0:0:01| chol 1 1 2|1.000|1.000|2.6e-007|7.6e-003|1.4e+000| 1.234938e+000 -5.011630e-002| 0:0:01| chol 1 1 3|1.000|1.000|2.4e-007|7.6e-004|3.0e-001| 4.166959e-001 1.181563e-001| 0:0:01| chol4|0.892|0.877|6.4e-008|1.6e-004|5.2e-002| 2.773022e-001 2.265122e-001| 0:0:01| chol5|1.000|1.000|1.0e-008|7.6e-006|1.5e-002| 2.579468e-001 2.427203e-001| 0:0:01| chol6|0.905|0.904|3.1e-009|1.4e-006|2.3e-003| 2.511936e-001 2.488619e-001| 0:0:01| chol7|1.000|1.000|6.1e-009|7.7e-008|6.6e-004| 2.503336e-001 2.496718e-001| 0:0:01| chol8|0.903|0.903|1.8e-009|1.5e-008|1.0e-004| 2.500507e-001 2.499497e-001| 0:0:01| chol9|1.000|1.000|4.9e-010|3.5e-010|2.9e-005| 2.500143e-001 2.499857e-001| 0:0:01| chol10|0.904|0.904|5.7e-011|1.3e-010|4.4e-006| 2.500022e-001 2.499978e-001| 0:0:01| chol11|1.000|1.000|5.2e-013|1.1e-011|1.2e-006| 2.500006e-001 2.499994e-001| 0:0:01| chol12|1.000|1.000|5.9e-013|1.0e-012|1.8e-007| 2.500001e-001 2.499999e-001| 0:0:01| chol13|1.000|1.000|1.7e-012|1.0e-012|4.2e-008| 2.500000e-001 2.500000e-001| 0:0:01| chol14|1.000|1.000|2.3e-012|1.0e-012|7.3e-009| 2.500000e-001 2.500000e-001| 0:0:01|stop: max(relative gap, infeasibilities) < 1.49e-008number of iterations = 14primal objective value = 2.50000004e-001dual objective value = 2.49999996e-001gap := trace(XZ) = 7.29e-009relative gap = 4.86e-009actual relative gap = 4.86e-009rel. primal infeas (scaled problem) = 2.33e-012rel. dual " " " = 1.00e-012rel. primal infeas (unscaled problem) = 0.00e+000rel. dual " " " = 0.00e+000norm(X), norm(y), norm(Z) = 3.2e+000, 1.5e+000, 1.9e+000norm(A), norm(b), norm(C) = 3.9e+000, 4.2e+000, 2.6e+000 Total CPU time (secs) = 0.99CPU time per iteration = 0.07termination code = 0DIMACS: 3.3e-012 0.0e+000 1.3e-012 0.0e+000 4.9e-009 4.9e-009Status: SolvedOptimal value (cvx_optval): -32. 程序代码:n=3; a=[-3 -1 -3];b=[2;5;6];C=[2 1 1;1 2 3;2 2 1]; cvx_beginvariable x(n) minimize( a*x)subject toC * x <= bx>=0 cvx_end 运行结果:Calling SDPT3 4.0: 6 variables, 3 equality constraintsnum. of constraints = 3dim. of linear var = 6*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime0|0.000|0.000|1.1e+001|5.1e+000|6.0e+002|-7.000000e+001 0.000000e+000| 0:0:00| chol 1 1 1|0.912|1.000|9.4e-001|4.6e-002|6.5e+001|-5.606627e+000 -2.967567e+001| 0:0:00| chol 1 1 2|1.000|1.000|1.3e-007|4.6e-003|8.5e+000|-2.723981e+000 -1.113509e+001| 0:0:00| chol 1 1 3|1.000|0.961|2.3e-008|6.2e-004|1.8e+000|-4.348354e+000 -6.122853e+000| 0:0:00| chol 1 1 4|0.881|1.000|2.2e-008|4.6e-005|3.7e-001|-5.255152e+000 -5.622375e+000| 0:0:00| chol 1 1 5|0.995|0.962|1.6e-009|6.2e-006|1.5e-002|-5.394782e+000 -5.409213e+000| 0:0:00| chol 1 1 6|0.989|0.989|2.7e-010|5.2e-007|1.7e-004|-5.399940e+000 -5.400100e+000| 0:0:00| chol 1 1 7|0.989|0.989|5.3e-011|5.8e-009|1.8e-006|-5.399999e+000 -5.400001e+000| 0:0:00| chol 1 1 8|1.000|0.994|2.8e-013|4.3e-011|2.7e-008|-5.400000e+000 -5.400000e+000| 0:0:00|stop: max(relative gap, infeasibilities) < 1.49e-008 number of iterations = 8primal objective value = -5.39999999e+000 dual objective value = -5.40000002e+000 gap := trace(XZ) = 2.66e-008 relative gap = 2.26e-009 actual relative gap = 2.21e-009 rel. primal infeas (scaled problem) = 2.77e-013 rel. dual " " " = 4.31e-011 rel. primal infeas (unscaled problem) = 0.00e+000norm(X), norm(y), norm(Z) = 4.3e+000, 1.3e+000, 1.9e+000norm(A), norm(b), norm(C) = 6.7e+000, 9.1e+000, 5.4e+000Total CPU time (secs) = 0.11CPU time per iteration = 0.01termination code = 0DIMACS: 3.6e-013 0.0e+000 5.8e-011 0.0e+000 2.2e-009 2.3e-009Status: Solvedrel. dual = 0.00e+000Optimal value (cvx_optval): -5.4。
最优化方法与应用大作业(一)最速下降法

最优化方法与应用大作业(一)
---最速下降法部分:
1.问题描述:
用梯度下降法求解以下优化问题
min f(x)=(x1+10*x2)^2+5(x3-x4)^2+(x2-2*x3)^4+10*(x1-x4)^4
2.编程感想:
该算法需要计算Hesse矩阵,C语言在向量运算时没有Matlab方便,所以手工完成了理论计算,再输入,破坏了程序的移植性。
同时,实验表明当初始值离理想点较远且精度要求较高时,最速下降法的收敛速率极慢,迭代几乎不可能完成,这对初值的选取提出了一定限制。
3.结果分析:
编译界面(Mac os X,Xcode环境)
输入参数(设定为(0.1,0.2,0.3,0.4)):
结果(此处列出每次迭代结果)。
明显的看到,最速下降法的收敛较慢,最终结果接近理论值(F(0,0,0,0)=0)所以该结果可以满意。
4.算法代码见下页
西安电子科技大学电子工程学院020951
李骏昊02095005。
大连理工大学 秋季优化方法大作业

m=m+1; end x0=x0+rho^mk*d; val=feval(fun,x0); g0=g; d0=d; k=k+1; end x=x0; val=feval(fun,x);
//f(x)//
function f=fun(x) x1=[1 0]*x; x2=[0 1]*x; f=(1-x1)^2+100*(x2-x1^2)^2; //梯度函数// function g=gfun(x) x1=[1 0]*x; x2=[0 1]*x; g=[-2*(1-x1)-400*x1*(x2-x1^2); 200*(x2-x1^2)]; //运行过程// >> x0=[0 0]'
k=k+1; btaold=btak; x0=x; end f=feval(fun,x); output.fval=f; output.iter=k; output.inner_iter=ink; output.bta=btak;
//增广拉格朗日函数//
function psi=mpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma) f=feval(fun,x); he=feval(hf,x); gi=feval(gf,x); l=length(he); m=length(gi); psi=f; s1=0.0; for(i=1:l) psi=psi-he(i)*mu(i); s1=s1+he(i)^2; end psi=psi+0.5*sigma*s1; s2=0.0; for(i=1:m) s3=max(0.0, lambda(i) - sigma*gi(i)); s2=s2+s3^2-lambda(i)^2; end psi=psi+s2/(2.0*sigma); //增广拉格朗日函数// function dpsi=dmpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma) dpsi=feval(dfun,x); he=feval(hf,x); gi=feval(gf,x); dhe=feval(dhf,x); dgi=feval(dgf,x); l=length(he); m=length(gi); for(i=1:l) dpsi=dpsi+(sigma*he(i)-mu(i))*dhe(:,i); end for(i=1:m) dpsi=dpsi+(sigma*gi(i)-lambda(i))*dgi(:,i); end //f(x)// function f=f1(x) f=4*x(1)-x(2)^2-12; //等式约束// function he=h1(x) he=25-x(1)^2-x(2)^2;
北航最优化方法大作业参考
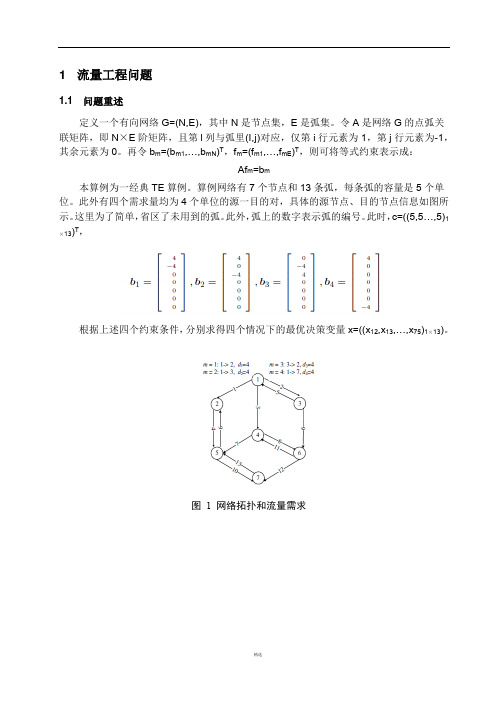
1 流量工程问题1.1 问题重述定义一个有向网络G=(N,E),其中N是节点集,E是弧集。
令A是网络G的点弧关联矩阵,即N×E阶矩阵,且第l列与弧里(I,j)对应,仅第i行元素为1,第j行元素为-1,其余元素为0。
再令b m=(b m1,…,b mN)T,f m=(f m1,…,f mE)T,则可将等式约束表示成:Af m=b m本算例为一经典TE算例。
算例网络有7个节点和13条弧,每条弧的容量是5个单位。
此外有四个需求量均为4个单位的源一目的对,具体的源节点、目的节点信息如图所示。
这里为了简单,省区了未用到的弧。
此外,弧上的数字表示弧的编号。
此时,c=((5,5…,5)1 )T,×13)。
根据上述四个约束条件,分别求得四个情况下的最优决策变量x=((x12,x13,…,x75)1×13图 1 网络拓扑和流量需求1.2 7节点算例求解1.2.1 算例1(b1=[4;-4;0;0;0;0;0]T)转化为线性规划问题:Minimize c T x1Subject to Ax1=b1x1>=0利用Matlab编写对偶单纯形法程序,可求得:最优解为x1*=[4 0 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x1=201.2.2 算例2(b2=[4;0;-4;0;0;0;0]T)Minimize c T x2Subject to Ax2=b2X2>=0利用Matlab编写对偶单纯形法程序,可求得:最优解为x2*=[0 4 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x2=201.2.3 算例3(b3=[0;-4;4;0;0;0;0]T)Minimize c T x3Subject to Ax3=b3X3>=0利用Matlab编写对偶单纯形法程序,可求得:最优解为x3*=[4 0 0 0 4 0 0 0 0 0 0 0 0]T对应的最优值c T x3=401.2.4 算例4(b4=[4;0;0;0;0;0;-4]T)Minimize c T x4Subject to Ax4=b4X4>=0利用Matlab编写对偶单纯形法程序,可求得:最优解为x4*=[4 0 0 4 0 0 0 0 0 4 0 0 0]T对应的最优值c T x4=601.3 计算结果及结果说明1.3.1 算例1(b1=[4;-4;0;0;0;0;0]T)算例1中,由b1可知,节点2为需求节点,节点1为供给节点,由节点1将信息传输至节点2的最短路径为弧1。
北航最优化方法大作业参考

北航最优化方法大作业参考旅行商问题是一个经典的组合优化问题,目标是找到一条最短路径,使得旅行商能够在访问所有城市后回到起始城市。
在实际应用中,旅行商问题有着广泛的应用,例如物流配送、城市规划等领域。
为了解决旅行商问题,我们可以采用启发式算法,其中一个常用的方法是遗传算法。
遗传算法是一种模拟自然进化过程的优化算法,通过模拟生物遗传的选择、交叉和变异等操作,逐步优化问题的解。
首先,我们需要对问题进行建模。
假设有N个城市,我们可以通过一个N*N的距离矩阵来表示各个城市之间的距离。
同时,我们需要定义一个染色体表示一条路径,其中每个基因表示一个城市的编号。
接下来,我们可以采用遗传算法来求解最优解。
遗传算法一般包括以下几个步骤:1.初始化种群:随机生成初始的染色体种群,每个染色体都表示一条路径。
2.适应度评价:根据染色体的路径长度来评估每个染色体的适应度,路径越短适应度越高。
3.选择操作:选择适应度较高的染色体作为父代,采用轮盘赌选择算法确定父代。
4.交叉操作:采用部分映射交叉算子对父代进行交叉操作,生成新的子代。
5.变异操作:对子代进行变异操作,以增加种群的多样性。
6.环境选择:根据适应度选择下一代种群,同时保留精英个体,避免解的丢失。
7.终止条件:当达到预设的迭代次数或者达到最优解时,终止算法。
通过以上步骤的迭代,我们可以逐步优化路径的长度,最终得到一条最短路径。
除了遗传算法,我们还可以尝试其他的优化算法,例如模拟退火算法、蚁群算法等。
这些算法在求解旅行商问题时都有一定的优势和适用性。
总结起来,旅行商问题是一个经典的组合优化问题,在北航最优化方法大作业中可以选择使用启发式算法来解决。
我们可以尝试使用遗传算法来求解最优路径,并根据实际情况选择合适的算法参数和终止条件。
通过不断地迭代和优化,我们可以得到一条最短路径,满足旅行商的需求。
以上是关于北航最优化方法大作业的参考内容,希望对你的写作有所帮助。
如果有其他疑问,欢迎继续提问。
国开幼儿园课程与活动设计大作业的迭代与优化

国开幼儿园课程与活动设计大作业的迭代与优化在国开幼儿园的课程与活动设计大作业中,我们经常需要不断地进行迭代与优化,以确保教学内容与方法能够紧跟幼儿的成长需求,让他们在愉快的游戏中学习,得到全面发展。
我们需要对幼儿园的课程进行深入的了解,明确每个学科的教学目标,以及幼儿阶段的认知特点和学习规律。
针对不同芳龄段的儿童,我们可以根据其认知发展水平,逐步设置相应的教学内容与方法。
1. 对于3-4岁幼儿,我们可以以简单的生活常识和认知启蒙为主,通过游戏、歌谣和手工活动,引导幼儿感知周围世界,培养他们的观察力和动手能力。
2. 随着芳龄的增长,5-6岁幼儿可以逐渐接触一些基础的数学、语言和科学知识。
通过多种形式的活动,如实验、角色扮演和小组合作,让幼儿在实践中学习,并提高他们的问题解决能力和团队协作意识。
3. 而对于6岁以上的儿童,我们可以加入更多的综合性学科内容,如艺术、体育和音乐等,培养他们的审美情趣和综合运用能力。
除了根据芳龄段设置不同的教学内容外,我们还需要不断优化课程活动设计,确保其能够贴近幼儿的实际生活经验和情感需求。
在活动设计中,我们要注重培养幼儿的动手能力和创造力,让他们在参与游戏和活动的过程中,不断探索、发现和创造。
在优化课程与活动设计时,我们也需要充分考虑幼儿的个体差异,尊重他们的兴趣和需要,给予他们自主选择的空间,并提供个性化的辅导和指导,使每个孩子都能够在快乐中茁壮成长。
对于课程与活动设计的迭代与优化,我们还需要不断总结经验,收集家长和教师的反馳意见,并结合幼儿的实际表现,进行反思与调整。
只有不断地完善与提升,才能够让幼儿园的课程与活动设计更加精准与有效,为幼儿的全面发展奠定坚实基础。
国开幼儿园课程与活动设计的迭代与优化是一个不断探索与实践的过程,需要我们不断关注幼儿的成长需求,深入了解他们的认知特点,灵活运用教学理论和方法,以确保幼儿在快乐中学习、在游戏中成长。
这也是我们作为幼儿园老师的责任与使命,值得我们不断努力与探索。
西电最优化大作业

p0 f x0 , 当 搜 索 到
xk 1
时
,
共
轭
方
向
为
pk 1 f xk 1 k pk , k 0,1,...,n 2 ,此时, pk 1 与 pk A 共轭,用 Apk 右乘上式得
T pk 1 Apk f xk 1 Apk k pk Apk
m 2 理解为拉格朗日乘子法: minT X ; M min f x M min0, g i x i 1
其中
min0, g i x 2
g i 0,i 1 ~ m
当g i x 0,
,
由
T pk 1 Apk 0
得
f x k 1 Ap k k k 0,1,...,n 2 ,若不满足条件,进行下一次迭代。 pT p Ap k
T
1.2.2 问题求解 本程序编程语言为 MATLAB,终止条件为 f x k x0 =[1 1]。 程序代码见附件conjugate.m 1.2.3 计算结果如下:
三、此次实验的收获
经过几个晚上的艰苦奋斗,努力学习,不断调试程序,最终才得以成功运行 程序并得到满意的结果。 有过山重水复疑无路的困境,但最终迎来的还是柳暗花 明又一村的喜悦。通过此次实验,我的收获主要有以下几点: 以前自己在求解函数最优化问题时都是通过求导、画图等方法,而这几个算法都 是通过不断迭代寻找最优解, 相对来说更有利于电脑编程的实现和推广,对函数 本身性质的要求也不是太高。 在最速下降法中, 沿负梯度方向函数值很快的说法容易使我们相信这一定是 最理想的搜索方向, 沿该方向搜索时收敛速度应该很快,然而在算法实现过程中 发现,梯度法的收敛速度并不快(迭代次数为 45 次) ,比其它算法收敛速度都要 慢。而共轭梯度法仅需要利用一阶导数信息,也不再要求精确的直线搜索,进而 克服了最速下降法收敛慢的缺点(迭代次数为 2 次) 。 内点法和外点法的实质都是构造 “惩罚函数” 或者 “围墙函数 (或障碍函数) ” , 将约束函数其转化为非约束函数, 其中外点法在将函数转化为非约束函数后调用 了“牛顿法”来求解,内点法也尝试过用“牛顿法”来求解非约束函数,但由于 障碍函数为倒数形式, 导致了程序在求矩阵逆的时候产生了无穷大的量,函数无 解,所以内点法采用“直接求导”来求解非约束函数。此外,我也尝试了用求极 限的方法来求解最优点,根据手算的步骤,在求得偏导数为 0 的点后,令障碍因 子 mk→0,求得最优解,方法简单,算法易于实现。 这门课在学习过程中多以理论学习为主,如果平时不注重实践,将自己所学 运用到实际中, 就很难会有太大的收获,通过自己的努力用课堂上的算法解决了 实际问题,无疑加深了自己对算法理论的理解。
优化方法作业第二版解读

优化方法上机大作业院系:化工与环境生命学部姓名:李翔宇学号:31607007指导教师:肖现涛第一题:1.最速下降法源程序如下:function x_star = ZSXJ(x0,eps)gk = grad(x0);res = norm(gk);k = 0;while res > eps && k<=10000dk = -gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.0001*ak*slopeak = ak/2;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;gk = grad(xk);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res);endx_star = xk;endfunction f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);end运行结果:>> x0=[0,0]';>> esp=1e-4;>> xk=ZSXJ(x0,eps)--The 1-th iter, the residual is 13.372079 --The 2-th iter, the residual is 12.079876 --The 3-th iter, the residual is 11.054105 ……………………………………………--The 9144-th iter, the residual is 0.000105 --The 9145-th iter, the residual is 0.000102 --The 9146-th iter, the residual is 0.000100 xk =0.99990.9998MATLAB截屏:2.牛顿法源程序如下:function x_star = NEWTON(x0,eps)gk = grad(x0);bk = [grad2(x0)]^(-1);res = norm(gk);k = 0;while res > eps && k<=1000dk=-bk*gk;xk=x0+dk;k = k+1;x0 = xk;gk = grad(xk);bk = [grad2(xk)]^(-1);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;endfunction f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2;endfunction g = grad2(x)g = zeros(2,2);g(1,1)=2+400*(3*x(1)^2-x(2));g(1,2)=-400*x(1);g(2,1)=-400*x(1);g(2,2)=200;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);end运行结果:>> x0=[0,0]';eps=1e-4;>> xk=NEWTON(x0,eps)--The 1-th iter, the residual is 447.213595 --The 2-th iter, the residual is 0.000000 xk =1.00001.0000MATALB截屏;3.BFGS方法源程序如下:function x_star = Bfgs(x0,eps)g0 = grad(x0);gk=g0;res = norm(gk);Hk=eye(2);k = 0;while res > eps && k<=1000dk = -Hk*gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/2;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;fa0=xk-x0;x0 = xk;g0=gk;gk = grad(xk);y0=gk-g0;Hk=((eye(2)-fa0*(y0)')/((fa0)'*(y0)))*((eye(2)-(y0)*(fa0)')/((fa0)'*(y0)))+(fa0*(fa0)')/((fa0)'*(y0)); res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;endfunction f=fun(x)f=(1-x(1))^2 + 100*(x(2)-x(1)^2)^2;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2));g(2) = 200*(x(2)-x(1)^2);end运行结果:>> x0=[0,0]';>> esp=1e-4;>> xk=Bfgs(x0,eps)--The 1-th iter, the residual is 3.271712--The 2-th iter, the residual is 2.381565--The 3-th iter, the residual is 3.448742…………………………--The 1516-th iter, the residual is 0.000368 --The 1517-th iter, the residual is 0.000099 xk =1.00011.0002MATLAB截屏:4.共轭梯度法源程序如下:function x_star =Conj (x0,eps)gk = grad(x0);res = norm(gk);k = 0;dk = -gk;while res > eps && k<=1000ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/2;xk = x0 + ak*dk;f1 = fun(xk);endd0=dk;g0=gk;k=k+1;x0=xk;gk=grad(xk);f=(norm(gk)/norm(g0))^2;res=norm(gk);dk=-gk+f*d0;fprintf('--The %d-th iter, the residual is %f\n',k,res);endx_star = xk;endfunction f=fun(x)f=(1-x(1))^2+100*(x(2)-x(1)^2)^2;endfunction g=grad(x)g=zeros(2,1);g(1)=400*x(1)^3-400*x(1)*x(2)+2*x(1)-2;g(2)=-200*x(1)^2+200*x(2);end运行结果:>> x0=[0,0]';>> eps=1e-4;>> xk=Conj(x0,eps)--The 1-th iter, the residual is 3.271712--The 2-th iter, the residual is 1.380542--The 3-th iter, the residual is 4.527780--The 4-th iter, the residual is 0.850596………………………………--The 73-th iter, the residual is 0.001532--The 74-th iter, the residual is 0.000402--The 75-th iter, the residual is 0.000134--The 76-th iter, the residual is 0.000057xk =0.99990.9999MATLAB截屏:第二题:解:目标函数文件 f1.mfunction f=f1(x)f=4*x(1)-x(2)^2-12;等式约束函数文件 h1.mfunction he=h1(x)he=25-x(1)^2-x(2)^2;不等式约束函数文件 g1.mfunction gi=g1(x)gi=10*x(1)-x(1)^2+10*x(2)-x(2)^2-34;目标函数的梯度文件 df1.mfunction g=df1(x)g = [4, 2.0*x(2)]';等式约束(向量)函数的Jacobi矩阵(转置)文件dh1.m function dhe=dh1(x)dhe = [-2*x(1), -2*x(2)]';不等式约束(向量)函数的Jacobi矩阵(转置)文件dg1.m function dgi=dg1(x)dgi = [10-2*x(1), 10-2*x(2)]';然后在 Matlab 命令窗口输入如下命令:x0=[0,0]’;[x,mu,lambda,output]=multphr('f1','h1','g1','df1','dh1','dg1',x0);得到如下输出:x =4.898717426488211.00128197198571算法编程利用程序调用格式第三题:1.解:将目标函数改写为向量形式:x'*a*x-b*x程序代码:n=2;a=[0.5,0;0,1];b=[2 4];c=[1 1];cvx_beginvariable x(n)minimize( x'*a*x-b*x)subject toc * x <= 1x>=0cvx_end运算结果:Calling SDPT3 4.0: 7 variables, 3 equality constraintsFor improved efficiency, SDPT3 is solving the dual problem.------------------------------------------------------------num. of constraints = 3dim. of socp var = 4, num. of socp blk = 1dim. of linear var = 3*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime-------------------------------------------------------------------0|0.000|0.000|8.0e-001|6.5e+000|3.1e+002| 1.000000e+001 0.000000e+000| 0:0:00| chol 1 1 1|1.000|0.987|4.3e-007|1.5e-001|1.6e+001| 9.043148e+000 -2.714056e-001| 0:0:01| chol 1 1 2|1.000|1.000|2.6e-007|7.6e-003|1.4e+000| 1.234938e+000 -5.011630e-002| 0:0:01| chol 1 1 3|1.000|1.000|2.4e-007|7.6e-004|3.0e-001| 4.166959e-001 1.181563e-001| 0:0:01| chol 1 1 4|0.892|0.877|6.4e-008|1.6e-004|5.2e-002| 2.773022e-001 2.265122e-001| 0:0:01| chol 1 1 5|1.000|1.000|1.0e-008|7.6e-006|1.5e-002| 2.579468e-001 2.427203e-001| 0:0:01| chol 1 1 6|0.905|0.904|3.1e-009|1.4e-006|2.3e-003| 2.511936e-001 2.488619e-001| 0:0:01| chol 1 1 7|1.000|1.000|6.1e-009|7.7e-008|6.6e-004| 2.503336e-001 2.496718e-001| 0:0:01| chol 1 1 8|0.903|0.903|1.8e-009|1.5e-008|1.0e-004| 2.500507e-001 2.499497e-001| 0:0:01| chol 1 1 9|1.000|1.000|4.9e-010|3.5e-010|2.9e-005| 2.500143e-001 2.499857e-001| 0:0:01| chol 1 1 10|0.904|0.904|5.7e-011|1.3e-010|4.4e-006| 2.500022e-001 2.499978e-001| 0:0:01| chol 2 2 11|1.000|1.000|5.2e-013|1.1e-011|1.2e-006| 2.500006e-001 2.499994e-001| 0:0:01| chol 2 2 12|1.000|1.000|5.9e-013|1.0e-012|1.8e-007| 2.500001e-001 2.499999e-001| 0:0:01| chol 2 2 13|1.000|1.000|1.7e-012|1.0e-012|4.2e-008| 2.500000e-001 2.500000e-001| 0:0:01| chol 2 2 14|1.000|1.000|2.3e-012|1.0e-012|7.3e-009| 2.500000e-001 2.500000e-001| 0:0:01|stop: max(relative gap, infeasibilities) < 1.49e-008-------------------------------------------------------------------number of iterations = 14primal objective value = 2.50000004e-001dual objective value = 2.49999996e-001gap := trace(XZ) = 7.29e-009relative gap = 4.86e-009actual relative gap = 4.86e-009rel. primal infeas (scaled problem) = 2.33e-012rel. dual " " " = 1.00e-012rel. primal infeas (unscaled problem) = 0.00e+000rel. dual " " " = 0.00e+000norm(X), norm(y), norm(Z) = 3.2e+000, 1.5e+000, 1.9e+000norm(A), norm(b), norm(C) = 3.9e+000, 4.2e+000, 2.6e+000Total CPU time (secs) = 0.99CPU time per iteration = 0.07termination code = 0DIMACS: 3.3e-012 0.0e+000 1.3e-012 0.0e+000 4.9e-009 4.9e-009 -------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval): -32. 程序代码:n=3;a=[-3 -1 -3];b=[2;5;6];C=[2 1 1;1 2 3;2 2 1];cvx_beginvariable x(n)minimize( a*x)subject toC * x <= bx>=0cvx_end运行结果:Calling SDPT3 4.0: 6 variables, 3 equality constraints------------------------------------------------------------num. of constraints = 3dim. of linear var = 6*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime-------------------------------------------------------------------0|0.000|0.000|1.1e+001|5.1e+000|6.0e+002|-7.000000e+001 0.000000e+000| 0:0:00| chol 1 1 1|0.912|1.000|9.4e-001|4.6e-002|6.5e+001|-5.606627e+000 -2.967567e+001| 0:0:00| chol 1 1 2|1.000|1.000|1.3e-007|4.6e-003|8.5e+000|-2.723981e+000 -1.113509e+001| 0:0:00| chol 1 1 3|1.000|0.961|2.3e-008|6.2e-004|1.8e+000|-4.348354e+000 -6.122853e+000| 0:0:00| chol 1 1 4|0.881|1.000|2.2e-008|4.6e-005|3.7e-001|-5.255152e+000 -5.622375e+000| 0:0:00| chol 1 1 5|0.995|0.962|1.6e-009|6.2e-006|1.5e-002|-5.394782e+000 -5.409213e+000| 0:0:00| chol 1 1 6|0.989|0.989|2.7e-010|5.2e-007|1.7e-004|-5.399940e+000 -5.400100e+000| 0:0:00| chol 1 1 7|0.989|0.989|5.3e-011|5.8e-009|1.8e-006|-5.399999e+000 -5.400001e+000| 0:0:00| chol 1 1 8|1.000|0.994|2.8e-013|4.3e-011|2.7e-008|-5.400000e+000 -5.400000e+000| 0:0:00|stop: max(relative gap, infeasibilities) < 1.49e-008-------------------------------------------------------------------number of iterations = 8primal objective value = -5.39999999e+000dual objective value = -5.40000002e+000gap := trace(XZ) = 2.66e-008relative gap = 2.26e-009actual relative gap = 2.21e-009rel. primal infeas (scaled problem) = 2.77e-013rel. dual " " " = 4.31e-011rel. primal infeas (unscaled problem) = 0.00e+000rel. dual " " " = 0.00e+000norm(X), norm(y), norm(Z) = 4.3e+000, 1.3e+000, 1.9e+000norm(A), norm(b), norm(C) = 6.7e+000, 9.1e+000, 5.4e+000Total CPU time (secs) = 0.11CPU time per iteration = 0.01termination code = 0DIMACS: 3.6e-013 0.0e+000 5.8e-011 0.0e+000 2.2e-009 2.3e-009 -------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval): -5.4。
机械优化设计大作业(长江大学)

机械优化设计大作业姓名:**班级:机械11005班序号:11目录第一题.........................................................................................1-4第二题........................................................................................4-5第三题........................................................................................5-7第四题........................................................................................8-10 第五题.......................................................................................10-11 心得体会...................................................................................11-13 草稿....................................................................... ....14-181.⎪⎩⎪⎨⎧≥=++≥++⋅++=0,20521532min 21321321321x x x x x x x x t s x x x f解法一:将可行域化为对应的函数的标准形式:-x 1-2x 2-3x 3≤-15s.t 2x 1+x 2+5x 3=20x 1,x 2≥0程序清单如下: f=[1,1,1]; A=[-1,-2,-3]; Aeq=[2,1,5]; b=[-15]; beq=[20]; lbnd=[0,0];[x,minf]=linprog(f,A,b,Aeq,beq,lbnd,[]) 程序运行结果整理: x 1=0.0000 x 2=2.1429 x 3=3.5714 minf=5.7143解法二:构造新的函数求解 由2x 1+x 2+5x 3=20可知x 3=3(20−x 2−2x 1)5所以f= x 1+x 2+x 3= x 1+x 2+3(20−x 2−2x 1)5=﹣15x 1+25x 2+4令F=5(f-4)=3x 1+4 x 2,则可行域可化为:-x 1-2x 2-3x 3≤-15 x 1-7x 2≤-15s.t 2x 1+x 2+5x 3=20 s.tx 1,x 2≥0 x 1,x 2≥0 所以欲求minf 即求minF 程序清单如下: f=[3,4]; A=[1,-7]; b=[-15]; lbnd=[0,0];[x,minF]=linprog(f,A,b,[],[],lbnd,[]) 程序运行结果整理: x 1=0.0000; x 2=2.1429 minF=8.5714 因此minf=F5+4=8.57145+4=5.7143解法三:将解法二的可行域转化x 1-7x 2≤-15 x 1-7x 2≤-15s.t - x 1≤0x 1,x 2≥0 - x 2≤0此时不等式的约束关系可表示为:1 -7 x 1 -15 -1 0 ≤ 0 0 -1 x2 0程序清单如下: f=[3,4];A=[1,-7;-1,0;0,-1]; b=[-15,0,0];[x,minF]=linprog(f,A,b) 程序运行结果整理: x 1=0.0000 x 2=2.1429 minF=8.5714 因此minf=F5+4=8.57145+4=5.7143注:Ⅰ.由以上三种方法的运行结果可知,三种方法均可行。
最优化方法大作业

学号《最优化方法》课程实践完成时间:2015年5月30日星期六选择题目:题目一使用优化软件,编写重要算法的程序1.第一大题:(1)学习最优流量工程问题,nonsmooth_MCFP.pdf(2)问题重述:Figure 1一个简单的网络拓扑和流量需求如Figure 1所示,网络有7 个节点,13 条弧,每条弧的容量是5 个单位. 此外有四个需求量均为4个单位的源-目的对(M=4),具体的源节点、目的节点信息如图所示. 这里为了简单,省去了未用到的弧,此外弧上的数字表示弧的编号。
(3)极小化MAU设定变量x,为531⨯的向量,其中(53)x即为变量z。
使用linprog 函数求解极小化问题得到x。
之前确定三个约束条件。
1、Ax b⨯的矩阵,b为131⨯的向量。
≤,其中A为13532、eq eq x b A =,其中eq A 为2853⨯的矩阵,eq b 为281⨯的向量。
3、x lb ≥,其中lb 为153⨯的向量 编程计算后得到结果如下:(4) 极小化FT 成本函数设定变量x ,为651⨯的向量,其中(53:65)x 即为变量l z 。
使用linprog 函数求解极小化问题得到x 。
之前确定三个约束条件。
1、Ax b ≤,其中A 为7865⨯的矩阵,b 为781⨯的向量。
2、eq eq x b A =,其中eq A 为2865⨯的矩阵,eq b 为281⨯的向量。
3、x lb ≥,其中lb 为165⨯的向量 编程计算后得到结果如下:2. 第二大题: 2.1. 习题5.6 2.1.1. 问题分析问题2112212()(101810)/241513q x x x x x x x =-++-+ 通过matlab 画出其等高线为:2.1.2. 最速下降法最速下降法中,取值:k k p g =-==()()k k k kk T k k T k g p g g p Gp g Ggα- x1x 2等高线-224681012(1)()k x k x k p α+=+2.1.3. 算法流程图如下图所示:2.1.4. 初始值(0,0)编程运行结构为:收敛过程曲线为:2.1.5. 初始值(-0.4,0)编程运行结构为:收敛过程曲线为:x1x 2等高线-2246810122.1.6. 初始值(10,0)编程运行结构为:收敛过程曲线为:x1x 2-2246810122.1.7. 初始值(11,0)编程运行结构为:收敛过程曲线为:x1x 2-2246810122.2. 习题5.7 2.2.1. 问题分析问题()94ln(7)f x x x =--497g x =-- 24(7)G x =- Matlab 画出在区间(7 10)的函数、一阶导数、二阶导数的变化曲线为x1x 2-22468101277.588.599.510707274767880828486xf函数变化曲线77.588.599.510-35-30-25-20-15-10-50510xg一阶导数g 变化曲线2.2.2. 牛顿法牛顿法中,取值:k k k G s g =- 1k k k s xx +=+其中,如果G 不是半正定,则采用修正牛顿法(+)k k k G I s g λ=-77.588.599.51050100150200250300350400xg二阶导数G 变化曲线2.2.3.算法流程图如下图所示:2.2.4.初始值7.40编程运行结构为:收敛过程曲线为:2.2.5. 初始值7.20编程运行结构为:收敛过程曲线为:7.397.47.417.427.437.447.457.4670.24570.2570.25570.2670.265xf2.2.6. 初始值7.01编程运行结构为:收敛过程曲线为:7.17.27.37.47.57.67.770.270.470.670.87171.271.471.6xf2.2.7. 初始值7.80编程运行结构为:收敛过程曲线为:6.856.9 6.9577.057.17.157.27.257.37.35727476788082xf2.2.8. 初始值7.88编程运行结构为:收敛过程曲线为:7.17.27.37.47.57.67.77.87.97070.57171.572xf2.2.9. 分析函数在区间(7,7.8888)内是凸函数,G 恒大于零,所以单纯牛顿法保证收敛。
最优化方法课程设计-最优化大作业-用优化算法求解函数最值问题

最优化方法大作业---------用优化算法求解函数最值问题摘要最优化(optimization) 是应用数学的重要研究领域.它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。
最优化问题一般包括最小化问题和最大化问题,而最大化问题可以通过简单的转化使之成最最小化问题。
最小化问题分为两类,即约束最小化和无约束最小化问题。
在此报告中,前两个问题属于无约束最小化问题的求解,报告中分别使用了“牛顿法”和“共轭梯度法”。
后两个问题属于有约束最小化问题的求解,报告中分别用“外点法”和“内点法”求解。
虽然命名不一样,其实质都是构造“惩罚函数”或者“障碍函数”,通过拉格朗日乘子法将有约束问题转化为无约束问题进行求解。
再此报告中,“外点法”和“内点法”分别用了直接求导和调用“牛顿法”来求解无约束优化问题。
在此实验中,用“共轭梯度法”对“牛顿法”所解函数进行求解时出现错误,报告中另取一函数用“共轭梯度法”求解得到正确的结果。
此实验中所有的函数其理论值都是显见的,分析计算结果可知程序正确,所求结果误差处于可接受范围内。
报告中对所用到的四种方法在其使用以前都有理论说明,对“外点法”中惩罚函数和“内点法”中障碍函数的选择也有相应的说明,另外,对此次试验中的收获也在报告的三部分给出。
本报告中所用程序代码一律用MATLAB编写。
【关键字】函数最优化牛顿法共轭梯度法内点法外点法 MATLAB一,问题描述1,分别用共轭梯度发法和牛顿法来求解一下优化问题()()()()()441432243221102510min x x x x x x x x x f -+-+-++=2, 分别用外点法和内点发求解一下优化问题⎩⎨⎧≥-++01.min 212231x x t s x x二、问题求解1.1 用牛顿法求解()()()()()441432243221102510min x x x x x x x x x f -+-+-++=1.1.1问题分析:取步长为1而沿着牛顿方向迭代的方法称为牛顿法,在牛顿法中,初始点的取值随意,在以后的每次迭代中,()[]()k k k k x f x f x x ∇∇-=-+121,直到终止条件成立时停止。
大连理工大学优化方法上机大作业

学院:专业:班级:学号:姓名:上机大作业1:1.最速下降法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = steepest(x0,eps) gk = grad(x0);res = norm(gk);k = 0;while res > eps && k<=1000dk = -gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + *ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;gk = grad(xk);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x=steepest(x0,eps)2.牛顿法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad2(x)g = zeros(2,2);g(1,1)=2+400*(3*x(1)^2-x(2));g(1,2)=-400*x(1);g(2,1)=-400*x(1);g(2,2)=200;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = newton(x0,eps)gk = grad(x0);bk = [grad2(x0)]^(-1);res = norm(gk);k = 0;while res > eps && k<=1000dk=-bk*gk;xk=x0+dk;k = k+1;x0 = xk;gk = grad(xk);bk = [grad2(xk)]^(-1);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x1=newton(x0,eps)--The 1-th iter, the residual is--The 2-th iter, the residual isx1 =法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = bfgs(x0,eps) g0 = grad(x0);gk=g0;res = norm(gk);Hk=eye(2);k = 0;while res > eps && k<=1000dk = -Hk*gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + *ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;fa0=xk-x0;x0 = xk;go=gk;gk = grad(xk);y0=gk-g0;Hk=((eye(2)-fa0*(y0)')/((fa0)'*(y0)))*((eye(2)-(y0)*(fa0)')/((fa0)'*(y0)))+(fa0*(fa 0)')/((fa0)'*(y0));res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res);endx_star = xk;End>> clear>> x0=[0,0]';>> eps=1e-4;>> x=bfgs(x0,eps)4.共轭梯度法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star =CG(x0,eps) gk = grad(x0);res = norm(gk);k = 0;dk = -gk;while res > eps && k<=1000 ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + *ak*slope ak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;g0=gk;gk = grad(xk);res = norm(gk);p=(gk/g0)^2;dk1=dk;dk=-gk+p*dk1;fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x=CG(x0,eps)上机大作业2:function f= obj(x)f=4*x(1)-x(2)^2-12;endfunction [h,g] =constrains(x) h=x(1)^2+x(2)^2-25;g=zeros(3,1);g(1)=-10*x(1)+x(1)^2-10*x(2)+x(2)^2+34;g(2)=-x(1);g(3)=-x(2);endfunction f=alobj(x) %拉格朗日增广函数%N_equ等式约束个数?%N_inequ不等式约束个数N_equ=1;N_inequ=3;global r_al pena;%全局变量h_equ=0;h_inequ=0;[h,g]=constrains(x);%等式约束部分?for i=1:N_equh_equ=h_equ+h(i)*r_al(i)+(pena/2)*h(i).^2;end%不等式约束部分for i=1:N_inequh_inequ=h_inequ+pena)*(max(0,(r_al(i)+pena*g(i))).^2-r_al(i).^2); end%拉格朗日增广函数值f=obj(x)+h_equ+h_inequ;function f=compare(x)global r_al pena N_equ N_inequ;N_equ=1;N_inequ=3;h_inequ=zeros(3,1);[h,g]=constrains(x);%等式部分for i=1:1h_equ=abs(h(i));end%不等式部分for i=1:3h_inequ=abs(max(g(i),-r_al(i+1)/pena));endh1 = max(h_inequ);f= max(abs(h_equ),h1); %sqrt(h_equ+h_inequ);function [ x,fmin,k] =almain(x_al)%本程序为拉格朗日乘子算法示例算法%函数输入:% x_al:初始迭代点% r_al:初始拉格朗日乘子N-equ:等式约束个数N_inequ:不等式约束个数?%函数输出% X:最优函数点FVAL:最优函数值%============================程序开始================================ global r_al pena ; %参数(全局变量)pena=10; %惩罚系数r_al=[1,1,1,1];c_scale=2; %乘法系数乘数cta=; %下降标准系数e_al=1e-4; %误差控制范围max_itera=25;out_itera=1; %迭代次数%===========================算法迭代开始============================= while out_itera<max_iterax_al0=x_al;r_al0=r_al;%判断函数?compareFlag=compare(x_al0);%无约束的拟牛顿法BFGS[X,fmin]=fminunc(@alobj,x_al0);x_al=X; %得到新迭代点%判断停止条件?if compare(x_al)<e_aldisp('we get the opt point');breakend%c判断函数下降度?if compare(x_al)<cta*compareFlagpena=1*pena; %可以根据需要修改惩罚系数变量elsepena=min(1000,c_scale*pena); %%乘法系数最大1000disp('pena=2*pena');end%%?更新拉格朗日乘子[h,g]=constrains(x_al);for i=1:1%%等式约束部分r_al(i)= r_al0(i)+pena*h(i);endfor i=1:3%%不等式约束部分r_al(i+1)=max(0,(r_al0(i+1)+pena*g(i)));endout_itera=out_itera+1;end%+++++++++++++++++++++++++++迭代结束+++++++++++++++++++++++++++++++++ disp('the iteration number');k=out_itera;disp('the value of constrains'); compare(x_al)disp('the opt point');x=x_al;fmin=obj(X);>> clear>> x_al=[0,0];>> [x,fmin,k]=almain(x_al)上机大作业3: 1、>> clear alln=3; c=[-3,-1,-3]'; A=[2,1,1;1,2,3;2,2,1;-1,0,0;0,-1,0;0,0,-1];b=[2,5,6,0,0,0]';cvx_beginvariable x(n)minimize( c'*x)subject toA*x<=bcvx_endCalling SDPT3 : 6 variables, 3 equality constraints------------------------------------------------------------num. of constraints = 3dim. of linear var = 6*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime -------------------------------------------------------------------0|||+01|+00|+02|+01 +00| 0:0:00| chol 1 11|||||+01|+00 +01| 0:0:01| chol 1 12|||||+00|+00 +01| 0:0:01| chol 1 13|||||+00|+00 +00| 0:0:01| chol 1 14||||||+00 +00| 0:0:01| chol 1 15||||||+00 +00| 0:0:01| chol 1 16||||||+00 +00| 0:0:01| chol 1 17||||||+00 +00| 0:0:01| chol 1 18||||||+00 +00| 0:0:01|stop: max(relative gap, infeasibilities) <------------------------------------------------------------------- number of iterations = 8primal objective value = +00dual objective value = +00gap := trace(XZ) =relative gap =actual relative gap =rel. primal infeas (scaled problem) =rel. dual " " " =rel. primal infeas (unscaled problem) = +00rel. dual " " " = +00norm(X), norm(y), norm(Z) = +00, +00, +00norm(A), norm(b), norm(C) = +00, +00, +00Total CPU time (secs) =CPU time per iteration =termination code = 0DIMACS: +00 +00-------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval):2、>> clear alln=2; c=[-2,-4]'; G=[,0;0,1]; A=[1,1;-1,0;0,-1]; b=[1,0,0]'; cvx_beginvariable x(n)minimize( x'*G*x+c'*x)subject toA*x<=bcvx_endCalling SDPT3 : 7 variables, 3 equality constraintsFor improved efficiency, SDPT3 is solving the dual problem.------------------------------------------------------------num. of constraints = 3dim. of socp var = 4, num. of socp blk = 1dim. of linear var = 3*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime -------------------------------------------------------------------0||||+00|+02| +01 +00| 0:0:00| chol 1 11|||||+01| +00 | 0:0:00| chol 1 12|||||+00| +00 | 0:0:00| chol 1 13|||||| | 0:0:00| chol 1 14|||||| | 0:0:00| chol 1 15|||||| | 0:0:00| chol 1 16|||||| | 0:0:00| chol 1 17|||||| | 0:0:00| chol 1 18|||||| | 0:0:00| chol 1 19|||||| | 0:0:00| chol 1 110|||||| | 0:0:00| chol 2 211|||||| | 0:0:00| chol 2 212|||||| | 0:0:00| chol 2 213|||||| | 0:0:00| chol 2 214|||||| | 0:0:00|stop: max(relative gap, infeasibilities) <------------------------------------------------------------------- number of iterations = 14primal objective value =dual objective value =gap := trace(XZ) =relative gap =actual relative gap =rel. primal infeas (scaled problem) =rel. dual " " " =rel. primal infeas (unscaled problem) = +00rel. dual " " " = +00norm(X), norm(y), norm(Z) = +00, +00, +00norm(A), norm(b), norm(C) = +00, +00, +00Total CPU time (secs) =CPU time per iteration =termination code = 0DIMACS: +00 +00-------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval): -3。
机械优化设计大作业

一、问题描述1.1结构特点(1)体积小、重量轻、结构紧凑、传递功率大、承载能力高;(2传)动效率高,工作高;(3)传动比大。
1.2用途和使用条件某行星齿轮减速器主要用于石油钻采设备的减速,其高速轴转速为1300r/min;工作环境温度为-20°C〜60°C,可正、反两向运转。
按该减速器最小体积准则,确定行星减速器的主要参数。
二、分析传动比u=4・64,输入扭矩T=1175・4N・m,齿轮材料均选用38SiMnMo钢,表面淬火硬度HRC45〜55,行星轮个数为3。
要求传动比相对误差A u<0.02。
弹性影响系数Z E=189.8MPa i/2;载荷系数k=1.05;齿轮接触疲劳强度极限[°]H=1250MPa;齿轮弯曲疲劳强度极限[。
]F=1000MPa;齿轮的齿形系数Y Fa=2・97;应力校正系数Y Sa=1.52;小齿轮齿数z取值范围17--25;模数m取值范围2—6。
注:优化目标为太阳轮齿数、齿宽和模数,初始点[24,52,5]T三、数学建模建立数学模型见图1,即用数学语言来描述最优化问题,模型中的数学关系式反映了最优化问题所要达到的目标和各种约束条件。
3.1设计变量的确定影响行星齿轮减速器体积的独立参数为中心轮齿数、齿宽、模数及行星齿轮的个数,将他们列为设计变量,即:x=[xxxx]T=[zbmc]T[1]12341式中:Z]_太阳轮齿数;b—齿宽(mm);m一模数(mm);行星轮的个数。
通常情况下,行星轮个数根据机构类型以事先选定,由已知条件c=3。
这样,设计变量为:x=[xxx]T=[Z bm】T[i]12313.2目标函数的确定为了方便,行星齿轮减速器的重量可取太阳轮和3个行星轮体积之和来代替,即:V=n/4(d2+Cd2)b12式中:d「-太阳轮1的分度圆直径,mm;d2--行星轮2的分度圆直径,mm。
将d=mzd=mz,z=z(u—2)/2代入(3)式整理,目标函11,2221数则为:F(x)=0.19635m2z2b[4+(u-2)2c][1]式中U--减速器传动比;C--行星轮个数由已知条件c=3,u=4.64,因此目标函数可简化为:F(x)=4.891x2x2x3123.3约束条件的建立3.3.1限制齿宽系数b/m的范围5W b/m W17,得:g(x)=5x—xWO[1]132g(x)=x—17WO[1]223.3.2保证太阳轮z1不发生跟切,得:g(x)=17—xWO[1]313.3.3限制齿宽最小值,得:g(x)=10—xWO】i]423.3.4限制模数最小值,得:g(x)=2—xWO】i]533.3.5按齿面接触疲劳强度条件,有:g(x)=750937.3/(xxx1/2)—[o]W0〔i]6123H式中:[。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
function [x,val,k]=frcg(fun,gfun,x0)%输入: x0是初始点, fun, gfun分别是目标函数和梯度%输出: x, val分别是近似最优点和最优值, k是迭代次数.maxk=200; %最大迭代次数rho=0.6;sigma=0.4;k=0; epsilon=1e-4;n=length(x0);while(k<maxk)g=feval(gfun,x0); %计算梯度itern=k-(n+1)*floor(k/(n+1));itern=itern+1;%计算搜索方向if(itern==1)d=-g;elsebeta=(g'*g)/(g0'*g0);d=-g+beta*d0; gd=g'*d;if(gd>=0.0)d=-g;endendif(norm(g)<epsilon), break; end%检验终止条件m=0; mk=0;while(m<20) %Armijo搜索if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d) mk=m; break;endm=m+1;endx0=x0+rho^mk*d;val=feval(fun,x0);g0=g; d0=d;k=k+1;endx=x0;val=feval(fun,x);x=reshape(x,10,10);x=double(x);disp('final x='),disp(x)disp('final y='),disp(val)最速下降clc;clear;x0=[-1.2;1;-1.2;1];syms x1x2x3x4xx=[ x1;x2;x3;x4];fun=(x1-1)^2+(x3-1)^2+100*(x2-x1^2)^2+100*(x4-x3^2)^2;gfun=[2*(x1-1)-400*x1*(x2-x1^2);...200*(x2-x1^2);...2*(x3-1)-400*x3*(x4-x3^2);...200*(x4-x3^2)];maxk=10; %最大迭代次数rho=0.5;sigma=0.4;k=0; epsilon=1e-5;xx=x0;k2=0;while(k2<maxk)g=subs(gfun,{x1 x2 x3 x4},{xx(1) xx(2) xx(3) xx(4)}); %计算梯度d=-g; %计算搜索方向if(norm(d)<epsilon), break; endm=0; mk=0;while(m<20) %Armijo搜索xz=xx+rho^m*d;if(subs(fun,{x1 x2 x3 x4},{xz(1) xz(2) xz(3) xz(4)})<subs(fun,{x1 x2 x3 x4},{xz(1) xz(2) xz(3) xz(4)})+sigma*rho^m*g'*d)mk=m; break;endm=m+1;endxx=xx+rho^mk*d;k=k+1;end%%%%牛顿function [x,val,k]=dampnm(fun,gfun, Hess,x0)k2=0;maxk=100; rho=0.55;sigma=0.4;k=0; epsilon=1e-5;while(k2<maxk)gk=feval(gfun,x0); %计算梯度Gk=feval(Hess,x0); %计算Hesse阵dk=-Gk\gk; %解方程组Gk*dk=-gk, 计算搜索方向if(norm(gk)<epsilon), break; end%检验终止准则m=0; mk=0;while(m<20) % 用Armijo搜索求步长if(feval(fun,x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk)mk=m; break;endm=m+1;endx0=x0+rho^mk*dk;k2=k2+1;endx2=x0;%%%%BFGSBk=eye(n);K3=0;while(k3<maxk)gk=feval(gfun,x0); %计算梯度if(norm(gk)<epsilon1)break;end%检验终止准则dk=-Bk\gk; m=0; mk=0;while(m<20) % 用Armijo搜索求步长newf=feval(fun,x0+rho^m*dk);oldf=feval(fun,x0);if(newf<oldf+sigma1*rho^m*gk'*dk)mk=m; break;endm=m+1;endx=x0+rho^mk*dk;det_xk=x-x0;det_gk=feval(gfun,x)-gk;if(det_gk'*det_xk>0)Bk=Bk-(Bk*det_xk*det_xk'*Bk)/(det_xk'*Bk*det_xk)+(det_gk*det_gk')/(de t_gk'*det_xk);endk3=k3+1; x0=x;Endx3=x;disp('the solution for gradient is '); disp(xx');disp(' gradient iteration is '); disp(k);disp('the solution for newton is '); disp(x2');disp('newton iteration is'); disp(k2);disp('the solution for BGFS is '); disp(x3’);disp('BFGS iteration is'); disp(k3);(三)惩罚函数法clcclearm=zeros(1,50);a=zeros(1,50);b=zeros(1,50);f0=zeros(1,50); syms x1syms x2syms em(1)=1;c=10;a(1)=6;b(1)=6;imax=100;for k=1:imax xi=a(k);yi=b(k);e=m(k);fx=4*x1-x2^2-12;hx=25-x1^2-x2^2;gx=-10*x1+x1^2-10*x2+x2^2+34;gx1=subs(gx,{x1 x2},{xi yi});if gx1<=0f=fx+M*hx^2;elsef=fx+M*(hx^2+gx^2);endfx1=diff(f,'x1');fx2=diff(f,'x2');fx1x1=diff(fx1,'x1');fx1x2=diff(fx1,'x2');fx2x1=diff(fx2,'x1');fx2x2=diff(fx2,'x2');for n=1:100f1=subs(fx1,{x1 x2},{xi yi}); f2=subs(fx2,{x1 x2},{xi yi});f11=subs(fx1x1,{x1 x2},{xi yi});f12=subs(fx1x2,{x1 x2},{xi yi});f21=subs(fx2x1,{x1 x2},{xi yi});f22=subs(fx2x2,{x1 x2},{xi yi});if(double(sqrt(f1^2+f2^2))<=1e-6) %a(k+1)=double(x1);b(k+1)=double(x2);f0(k+1)=double(subs(f));break;elseX=[x1 x2]'-inv([f11 f12;f21 f22])*[f1 f2]';xi=X(1);yi=X(2);endendendffinal=double(subs(fi,{x1 x2},{xi yi}));disp('x1='),disp(xi)disp('x2='),disp(yi)disp('objective function value f='),disp(ffinal)乘子法function [x,mu,lambda,output]=multphr(fun,hf,gf,dfun,dhf,dgf,x0)maxk=500; %最大迭代次数sigma=2.0; %罚因子eta=2.0; theta=0.8; %PHR算法中的实参数k=0; ink=0; %k, ink分别是外迭代和内迭代次数epsilon=1e-5; %终止误差值x=x0; he=feval(hf,x); gi=feval(gf,x);n=length(x); l=length(he); m=length(gi);%选取乘子向量的初始值mu=0.1*ones(l,1); lambda=0.1*ones(m,1);btak=10; btaold=10; %用来检验终止条件的两个值while(btak>epsilon & k<maxk)%调用BFGS算法程序求解无约束子问题[x,ival,ik]=bfgs('mpsi','dmpsi',x0,fun,hf,gf,dfun,dhf,dgf,mu,lambda,s igma);ink=ink+ik;he=feval(hf,x); gi=feval(gf,x);btak=0.0;for (i=1:l), btak=btak+he(i)^2; endfor i=1:mtemp=min(gi(i),lambda(i)/sigma);btak=btak+temp^2;endbtak=sqrt(btak);if btak>epsilonif(k>=2 & btak > theta*btaold)sigma=eta*sigma;end%更新乘子向量for (i=1:l), mu(i)=mu(i)-sigma*he(i); endfor (i=1:m)lambda(i)=max(0.0,lambda(i)-sigma*gi(i));endendk=k+1;btaold=btak;x0=x;endf=feval(fun,x);disp('x1='),disp(x(1))disp('x2='),disp(x(2))disp('objective function value f='),disp(f)。
