平行四边形的判定测试题.doc
平行四边形的判定习题-含答案

证明:∵CE∥AB,
∴∠DAO=∠ECO,
∵OA=OC,
∴△ADO≌△ECO,
∴AD=CE,
∴四边形ADCE是平行四边形,
∴CD AE.
6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.
求证:四边形MFNE是平行四边形.
证明:∵▱ABCD中,对角线AC交BD于点O,
∴OB=OD,
又∵四边形AODE是平行四边形,
∴AE∥OD且AE=OD,Fra bibliotek∴AE∥OB且AE=OB,
∴四边形ABOE是平行四边形,
同理可证,四边形DCOE也是平行四边形.
13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD的中点,并且点E、F、G、H有在同一条直线上.
证明:如答图所示,
∵点O为平行四边形ABCD对角线AC,BD的交点,
∴OA=OC,OB=OD.
∵G,H分别为OA,OC的中点,
∴OG= OA,OH= OC,
∴OG=OH.
又∵AB∥CD,
∴∠1=∠2.
在△OEB和△OFD中,
∠1=∠2,OB=OD,∠3=∠4,
∴△OEB≌△OFD,
∴OE=OF.
∴四边形EHFG为平行四边形.
平行四边形的判定
1.如图所示,□AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.
2如图,已知,□ABCD中,AE=CF,M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形.
3如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.
平行四边形的判定

20.1 平行四边形的判定1.四边形ABCD,从(1)AB∥CD;(2)AB=CD;(3)BC∥AD;(4)BC=AD这四个条件中任选两个,其中能使四边形ABCD是平行四边形的选法有()A.3种 B.4种 C.5种 D.6种2.四边形的四条边长分别是a,b,c,d,其中a,b为一组对边边长,c,d•为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd,则这个四边形是()A.任意四边形 B.平行四边形 C.对角线相等的四边形 D.对角线垂直的四边形 3.下列说法准确的是()A.若一个四边形的一条对角线平分另一条对角线,则这个四边形是平行四边形B.对角线互相平分的四边形一定是平行四边形C.一组对边相等的四边形是平行四边形D.有两个角相等的四边形是平行四边形4.在□ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动,点F从C•向B运动,点E的速度m与点F的速度n满足_______关系时,四边形BFDE为平行四边形.5.如图1所示,平行四边形ABCD中,E,F分别为AD,BC边上的一点,连结EF,若再增加一个条件_______,就能够推出BE=DF.6.如图2所示,AO=OC,BD=16cm,则当OB=_____cm时,四边形ABCD是平行四边形.7.如图所示,四边形ABCD中,对角线BD=4,一边长AB=5,其余各边长用含有未知数x 的代数式表示,且AD⊥BD于点D,BD⊥BC于点B.问:四边形ABCD•是平行四边形吗?为什么?D AC FE B8.如图所示,在□ABCD中,点E,F都在对角线AC上,且AE=CF,连结DE,BE,DF,BF,则四边形DEBF是平行四边形吗?9.如图所示,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P,Q分别是线段AD,BC上两动点,P,Q分别从A,C出发,P以1cm/s的速度由A向D运动,Q•以2cm/s的速度由C 向B运动,P,Q两点同时开始运动,且开始运动的时刻是0.P,Q•运动到顶点处即停止运动,问:第几秒时,四边形ABQP是平行四边形?10.如图所示,某城市中心有一个小公园,在它的四个角A,B,C,D•处均有一棵古树,城建部门准备扩建公园,要求使公园的面积扩大一倍,•而且必须保持四棵古树不动,并要求建成以后的公园呈平行四边形形状.问:该城市能否实现这个设想?若能,请你设计方案并画出图;若不能,请说明理由.11.如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红,黄,紫,白四种花卉,种植面积依次是S1,S2,S3,S4.若MN•∥AB•∥DC,EF∥DA∥CB,则有()A.S1=S4B.S1+S4=S2+S3C.S1S4=S2S3D.都不对12.实际生活中,我们常碰到这样的例子:对一个物体M•同时施加两个成某个角度的力F1和F2,这个物体的实际受力效果并不是F1与F2的简单叠加,它们的合力F•的大小和方向由以F1和F2为边的平行四边形的对角线决定,如图1所示.•对于既有大小又有方向的量求和时,一般都采用上面的方法,我们把这种方法叫做平行四边形法则,•实际上求两个分为F1,F2的合力F的大小,就是求□F1MF2F的对角线MF的长.下面请利用平行四边形法则来解决一个实际问题:如图2,一条小河缓缓地流着,河水的流速是2km/h,一艘船从A点出发以4km/h的速度向垂直于对岸的方向行驶,实际上,它以怎样的速度向对岸行驶?图1 图220.2 矩形的判定一、选择题1.矩形具有而一般平行四边形不具有的性质是()A.对角相等 B.对边相等 C.对角线相等 D.对角线互相垂直2.下列叙述中能判定四边形是矩形的个数是()①对角线互相平分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线互相平分且相等的四边形.A.1 B.2 C.3 D.43.下列命题中,准确的是()A.有一个角是直角的四边形是矩形 B.三个角是直角的多边形是矩形C.两条对角线互相垂直且相等的四边形是矩形 D.有三个角是直角的四边形是矩形D A CF O E B4.如图1所示,矩形ABCD 中的两条对角线相交于点O ,∠AOD=120°,AB=4cm ,则矩形的对角线的长为_____.图1 图25.若四边形ABCD 的对角线AC ,BD 相等,且互相平分于点O ,则四边形ABCD•是_____形,若∠AOB=60°,那么AB :AC=______.6.如图2所示,已知矩形ABCD 周长为24cm ,对角线交于点O ,OE⊥DC 于点E , OF⊥AD 于点F ,OF-OE=2cm ,则AB=______,BC=______.7.如图所示,□ABCD 的四个内角的平分线分别相交于E ,F ,G ,H 两点,试说明四边形EFGH 是矩形.8.如图所示,△ABC 中,CE ,CF 分别平分∠ACB 和它的邻补角∠ACD.AE ⊥CE 于E ,AF⊥CF 于F ,直线EF 分别交AB ,AC 于M ,N 两点,则四边形AECF 是矩形吗?为什么?9.如图所示,△ABC 为等腰三角形,AB=AC ,CD⊥AB 于D ,P•为BC 上的一点,过P 点分别作PE⊥AB,PF⊥CA,垂足分别为E ,F ,则有PE+PF=CD ,你能说明为什么吗?D A C F P EB10.如图所示,△ABC 中,AB=AC ,AD 是BC 边上的高,AE•是∠CAF 的平分线且∠CAF 是△ABC 的一个外角,且DE∥BA,四边形ADCE 是矩形吗?为什么?11.已知AC 为矩形ABCD 的对角线,则下图中∠1与∠2一定不相等的是( )20.3 菱形的判定一、选择题1.下列四边形中不一定为菱形的是( )A .对角线相等的平行四边形B .每条对角线平分一组对角的四边形C .对角线互相垂直的平行四边形D .用两个全等的等边三角形拼成的四边形2.四个点A ,B ,C ,D 在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD= BC; ⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD 是菱形的选法有( ).A .1种B .2种C .3种D .4种3.菱形的周长为32cm ,一个内角的度数是60°,则两条对角线的长分别是( )A .8cm 和3cmB .4cm 和3cmC .8cm 和3.4cm 和34.如图1所示,已知□ABCD,AC,BD相交于点O,•添加一个条件使平行四边形为菱形,添加的条件为________.(只写出符合要求的一个即可)图1 图25.如图2所示,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是________.(只写出符合要求的一个即可)6.菱形ABCD的周长为48cm,∠BAD: ∠ABC= 1:•2,•则BD=•_____,•菱形的面积是______.7.在菱形ABCD中,AB=4,AB边上的高DE垂直平分边AB,则BD=_____,AC=_____.三、解答题8.如图所示,在四边形ABCD中,AB∥CD,AB=CD=BC,四边形ABCD是菱形吗?•说明理由.9.如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD,PC相交于点P,四边形PCOD是菱形吗?试说明理由.10. 如图所示,已知△ABC中,AB=AC,D是BC的中点,过点D•作DE⊥AB,DF⊥AC,垂足分别为E,F,再过E,F作EG⊥AC,FH⊥AB,垂足分别为G,H,且EG,•FH相交于点K,试说明EF和DK之间的关系.K D AC F H G EB11.已知:如图所示,菱形ABCD 中,E ,F 分别是CB ,CD 上的点,且BE=DF .(1)试说明:AE=AF ;(2)若∠B=60°,点E ,F 分别为BC 和CD 的中点,试说明:△AEF 为等边三角形.20.4 正方形的判定1.下列命题准确的是( )A .两条对角线互相平分且相等的四边形是菱形B .两条对角线互相平分且垂直的四边形是矩形C .两条对角线互相垂直,平分且相等的四边形是正方形D .一组邻边相等的平行四边形是正方形2.矩形四条内角平分线能围成一个( )A .平行四边形B .矩形C .菱形D .正方形3.已知点D ,E ,F 分别是△ABC 的边AB ,BC ,CA 的中点,连结DE ,EF ,•要使四边形ADEF 是正方形,还需要添加条件_______.4.如图1所示,直线L 过正方形ABCD 的顶点B ,点A ,C 到直线L•的距离分别是1和2,则正方形ABCD 的边长是_______.D A C FE B图1 图2 图35.如图2所示,四边形ABCD 是正方形,点E 在BC 的延长线上,BE=BD 且AB=2cm ,则∠E 的度数是______,BE 的长度为____.6.如图3所示,正方形ABCD 的边长为4,E 为BC 上一点,BE=1,F•为AB•上一点,AF=2,P 为AC 上一动点,则当PF+PE 取最小值时,PF+PE=______.7.如图所示,在Rt△ABC 中,CF 为∠ACB 的平分线,FD⊥AC 于D ,FE⊥BC 于点E ,试说明四边形CDFE 是正方形.8.已知如图所示,在正方形ABCD 中,E ,F 分别是AB ,BC边上的点,且AE=BF ,•请问:(1)AF 与DE 相等吗?为什么?(2)AF 与DE 是否垂直?说明你的理由.9.如图所示,P ,Q ,R ,S 分别是正方形ABCD 各边的中点,•要使中间阴影部分小正方形的面积为5,求大正方形ABCD 的边长.10.如图所示,在△ABC中,点O是边AC上的一个动点,过点O作直线MN∥BC,设MN与∠BCA的平分线CE相交于点E,与∠BCA的外角平分线CF•相交于点F.(1)EO与FO的长度相等吗?说明理由;(2)当点O运动到何处时,四边形AECF是矩形?说明理由;(3)若要使四边形AECF成为正方形,则∠ACB的度数应为多大?11.如图所示,正方形ABCD的对角线相交于O点,点O•是正方形A′B′C′O的一个顶点,如果两个正方形的边长都等于1,那么正方形A′B′C ′O绕顶点O转动,两个正方形重叠部分的面积大小有什么规律?说明理由.12.如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F.(1)求证:DE=DF;(2)只添加一个条件,使四边形EDFA是正方形(不另外添加辅助线,无需证明).13.如图所示,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去……(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4, …,a n,请求出a2,a3,a4的值.(2)根据以上规律写出a n的表达式.20.5 等腰梯形的判定1.下列结论中,准确的是()A.等腰梯形的两个底角相等 B.两个底角相等的梯形是等腰梯形C.一组对边平行的四边形是梯形 D.两条腰相等的梯形是等腰梯形2.如图所示,等腰梯形ABCD的对角线AC,BD相交于点O,则图中全等三角形有()A.2对 B.3对 C.4对 D.5对3.课外活动课上,•老师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm,则两条对角线所用的竹条长度之和至少为()A.2cm B.30cm C.60cm D.2cm4.等腰梯形上底,下底和腰分别为4,•10,•5,•则梯形的高为_____,•对角线为______. 5.一个等腰梯形的上底长为5cm,下底长为12cm,一个底角为60°,则它的腰长为____cm,周长为______cm.6.在四边形ABCD中,AD∥BC,但AD≠BC,若使它成为等腰梯形,则需要添加的条件是__________(填一个准确的条件即可).7.如图所示,AD是∠BAC的平分线,DE∥AB,DE=AC,AD≠EC.求证:•四边形ADCE是等腰梯形.8.如图所示,四边形ABCD中,有AB=DC,∠B=∠C,且AD<BC,四边形ABCD是等腰梯形吗?为什么?9.如图所示,等腰梯形ABCD中,AD∥BC,AB=CD=•12cm,•上底AD=15cm,∠BAD=120°,求下底BC的长.10.如图所示,在矩形ABCD中,AC,BD相交于点O,E,•F•分别是OA,OD的中点,且EF≠AD,试判断四边形EBCF的形状,并说明你的理由.11.如图所示,小军将两根长度相等的木条AC,BD•交叉摆放,•并使木条AC,BD分别与水平线所成的夹角∠1,∠2相等,然后在交点O处钉一个钉子固定,OA<OC,•再用一根彩带沿AD,DC,CB,BA围起来,小军得到的四边形ABCD是等腰梯形吗?请说明你的理由.12.如图所示,在直角梯形纸片ABCD中,AB ∥DC, ∠A=90°,CD>AD,将纸片沿过点D 的直线折叠,使点A落在边CD上的点E,折痕为DF,连结EF并展开纸片.(1)求证:四边形ADEF是正方形;(2)取线段AF的中点G,连结EG,结果BG=CD,试说明四边形GBCE是等腰梯形.13.如图20-5-8所示,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB,BC于点F,E,若AD=2,BC=8,求BE的长.14.如图所示,在等腰梯形ABCD中,AD∥BC,M,N分别为AD,BC的中点,E,F•分别是BM,CM的中点.(1)试说明△ABM≌△DCM;(2)四边形MENF是什么图形?请说明理由.(3)若四边形MENF是正方形,则梯形的高与底边BC的长有何数量关系?请说明理由.F B E D C A H F E D C B A第20章 平行四边形的判定测试一、认认真真选,沉着应战!1. 正方形具有菱形不一定具有的性质是 ( )(A )对角线互相垂直 (B )对角线互相平分 (C )对角线相等 (D )对角线平分一组对角2. 如图(1),EF 过矩形ABCD 对角线的交点O ,且分别交AB 、CD 于E 、F ,那么阴影部分的面积是矩形ABCD 的面积的( )(A )51 (B )41 (C )31 (D )103(1) (2) (3)3.在梯形ABCD 中,AD ∥BC ,那么:::A B C D ∠∠∠∠能够等于( )(A )4:5:6:3 (B )6:5:4:3 (C )6:4:5:3 (D )3:4:5:64.如图(2),平行四边形ABCD 中,DE ⊥AB 于E ,DF ⊥BC 于F ,若ABCD 的周长为48,DE =5,DF =10,则ABCD 的面积等于( )(A )87.5 (B )80 (C )75 (D )72.55. A 、B 、C 、D 在同一平面内,从①AB ∥CD; ②AB=CD; ③BC ∥AD; ④BC=AD 这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有( )(A )3种 (B )4种 (C )5种 (D )6种6.如图(3),D 、E 、F 分别是ABC 各边的中点,AH 是高,如果5ED cm =,那么HF 的长为( )(A )5cm (B )6cm (C )4cm (D )不能确定 7. 如图(4):E 是边长为1的正方形ABCD 的对角线BD 上一点,且BE =BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ +PR 的值是( )(A )22 (B )21 (C )32 (D )23 8.如图(5),在梯形ABCD 中,AD ∥BC ,AB CD =,60C ∠=︒,BD 平分ABC ∠,如果这个梯形的周长为30,则AB 的长 ( )(A )4 (B )5 (C )6 (D )7E D CB A R PD B A (5)A B C D lC A9.右图是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm ,墙上悬挂晾衣架的两个铁钉A 、B 之间的距离为203cm ,则∠1等于( ) (A )90° (B)60° (C)45° (D)30° 10.某校数学课外活动探究小组,在老师的引导下进一步研究了完全平方公式.结合实数的性质发现以下规律:对于任意正数a 、b , 都有a+b ≥2ab 成立.某同学在做一个面积为3 600cm 2,对角线相互垂直的四边形风筝时,使用上述规律,求得用来做对角线用的竹条至少需要准备x cm . 则x 的值是( )(A) 1202 (B) 602 (C) 120 (D) 60二、仔仔细细填,记录自信!11.一个四边形四条边顺次是a 、b 、c 、d ,且bd ac d c b a 222222+=+++,则这个四边形是_______________.12.在四边形ABCD 中,对角线AC 、BD 交于点O ,从(1)AB CD =;(2)AB CD ∥;(3)OA OC =;(4)OB OD =;(5)AC BD ⊥;(6)AC 平分BAD ∠这六个条件中,选择三个推出四边形ABCD 是菱形.如(1)(2)(5)⇒ABCD 是菱形,再写出符合要求的两个: ⇒ABCD 是菱形;⇒ABCD 是菱形.13. 如图,已知直线l 把ABCD 分成两部分,要使这两部分的面积相等,直线l 所在位置需满足的条件是____________________.(只需填上一个你认为合适的条件)(第13题) (第16题14. 梯形的上底长为6cm ,过上底的一顶点引一腰的平行线,与下底相交,所构成的三角形周长为21cm ,那么梯形的周长为_________cm 。
平行四边形的判定含答案

平行四边形的判定一.选择题(共15小题)1.如图,▱ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是()A.10B.8C.7D.62.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是()A.OA=OC B.AB=CD C.AD=BC D.∠ABD=∠CBD 3.如图,平行四边形OABC的顶点A,B坐标分别为(﹣6,0),(﹣8,2),则点C的坐标是()A.(1,2)B.(﹣1,2)C.(2,2)D.(﹣2,2)4.如图,在平行四边形ABCD中,AC、BD相交于点O,AB⊥AC,若AB=4,AC=6,则△COD的周长是()A.8B.10C.12D.165.如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是()A.AB∥DC,AD∥BC B.AB=DC,AD=BCC.AO=CO,BO=DO D.AB=DC,AD∥BC6.如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD 是平行四边形的是()A.AB∥DC,AD∥BC B.AB=DC,AD=BCC.AB∥DC,AD=BC D.OA=OC,OB=OD7.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是()A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CDC.∠ABC=∠ADC,AD∥BC D.∠ABD=∠BDC,∠BAD=∠DCB 8.满足下列条件的四边形,不一定是平行四边形的是()A.两组对边分别平行B.两组对边分别相等C.一组对边平行且相等D.一组对边平行,另一组对边相等9.下列四个选项中,能判断四边形ABCD是平行四边形的是()A.AB=CD,AC=BD B.∠A=∠B,∠B=∠CC.AB=CD,AD∥BC D.AB∥CD,∠A=∠C10.从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD,这四个条件中选取两个,使四边形ABCD成为平行四边形,下面不能说明是平行四边形的是()A.①②B.①③C.②④D.①④11.在下列条件中,能判定四边形为平行四边形的是()A.两组邻边相等B.一组对边平行且另一组对边相等C.两组对边分别平行D.对角线互相垂直12.不能判定四边形ABCD为平行四边形的条件是()A.AB∥CD,AD=BC B.AB∥CD,∠A=∠CC.AD∥BC,AD=BC D.∠A=∠C,∠B=∠D13.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是()A.AD=BC B.AB=CD C.AD∥BC D.∠A=∠C 14.下列给出的条件中,能判断四边形ABCD是平行四边形的是()A.AB∥CD,AD=BC B.∠B=∠C;∠A=∠DC.AB=CD,CB=AD D.AB=AD,CD=BC15.下列条件中,能判定四边形ABCD为平行四边形的个数是()①AB∥CD,AD=BC;②AB=CD,AD=BC;③∠A=∠B,∠C=∠D;④AB=AD,CB=CDA.1个B.2个C.3个D.4个二.解答题(共15小题)16.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.(1)求证:△ABC≌△DEF;(2)连接AD,求证:四边形ABED是平行四边形.17.如图,在四边形ABCD中,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF.求证:四边形ABCD是平行四边形.18.已知:如图,在四边形ABCD中,∠BAC=∠ACD=90°,AB=CD,点E是CD的中点.(1)求证:四边形ABCE是平行四边形;(2)若AC=4,AD=4,求四边形ABCE的面积.19.如图,四边形ABCD的对角线AC、BD相交于点O,BO=DO,点E、F分别在AO,CO上,且BE∥DF,AE=CF.求证:四边形ABCD为平行四边形.20.如图:已知∠B=∠E=90°,点B、C、F、E在一条直线上AC=DF,BF=EC.求证四边形ACDF是平行四边形.21.如图,在四边形ABCD中,AD∥BC且AD=9cm,BC=6cm,点P、Q分别从点A、C 同时出发,点P以1cm/s的速度由A向D运动,点Q以2cm/s的速度由C向B运动.问几秒后直线PQ将四边形ABCD截出一个平行四边形?22.已知:如图,A,B,C,D在同一直线上,且AB=CD,AE=DF,AE∥DF.求证:四边形EBFC是平行四边形.23.如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.求证:四边形ABDF是平行四边形.24.如图,已知,AE⊥BD于E点,CF⊥BD于F点,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.25.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.连接AF、BD,求证:四边形ABDF是平行四边形.26.如图,AD是△ABC边BC上的中线,AE∥BC,BE交AD于点F,F是BE的中点,连结CE.求证:四边形ADCE是平行四边形.27.如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若F A=FC.求证:四边形ADCE是平行四边形;28.如图,在四边形ABCD中,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE =BF.求证:(1)AE=CF;(2)四边形ABCD是平行四边形.29.如图,已知△ABC是等边三角形,点D在BC边上,△ADF是以AD为边的等边三角形,过点F作BC的平行线交线段AC于点E,连接BF.求证:(1)△AFB≌△ADC;(2)四边形BCEF是平行四边形.30.如图,点B、E、C、F在一条直线上,AB∥DF,AC∥DE,BE=FC,连接BD、AF.求证:四边形ABDF是平行四边形.平行四边形的判定参考答案与试题解析一.选择题(共15小题)1.如图,▱ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是()A.10B.8C.7D.6解:∵四边形ABCD是平行四边形,∴OA=AC=3,OB=BD=4,在△AOB中:4﹣3<AB<4+3,即1<AB<7,∴AB的长可能为6.故选:D.2.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是()A.OA=OC B.AB=CD C.AD=BC D.∠ABD=∠CBD 解:A、∵平行四边形ABCD的对角线AC、BD相交于点O,∴OA=OC,故此选项不符合题意;B、∵四边形ABCD是平行四边形,∴AB=CD,故此选项不符合题意;C、∵四边形ABCD是平行四边形,∴AD=BC,故此选项不符合题意;D、当四边形ABCD是菱形时,∠ABD=∠CBD,故此选项符合题意;故选:D.3.如图,平行四边形OABC的顶点A,B坐标分别为(﹣6,0),(﹣8,2),则点C的坐标是()A.(1,2)B.(﹣1,2)C.(2,2)D.(﹣2,2)解:∵A(﹣6,0),∴OA=6,∵四边形OABC是平行四边形,∴BC∥OA,BC=OA=6,∵B(﹣8,2),∴C(﹣2,2),故选:D.4.如图,在平行四边形ABCD中,AC、BD相交于点O,AB⊥AC,若AB=4,AC=6,则△COD的周长是()A.8B.10C.12D.16解:∵在平行四边形ABCD中,AC、BD相交于点O,AB⊥AC,若AB=4,AC=6,∴BO=,∴BD=10,∴△COD的周长=OD+OC+CD=5+3+4=12,故选:C.5.如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是()A.AB∥DC,AD∥BC B.AB=DC,AD=BCC.AO=CO,BO=DO D.AB=DC,AD∥BC解:A、∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,故此选项不符合题意;B、∵AB=DC,AD=BC,∴四边形ABCD是平行四边形,故此选项不符合题意;C、∵AO=CO,BO=DO,∴四边形ABCD是平行四边形,故此选项不符合题意;D、AB=DC,AD∥BC无法得出四边形ABCD是平行四边形,故此选项符合题意;故选:D.6.如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD 是平行四边形的是()A.AB∥DC,AD∥BC B.AB=DC,AD=BCC.AB∥DC,AD=BC D.OA=OC,OB=OD解:∵AB∥DC,AD∥BC,∴四边形ABCD是平行四边形,故选项A中条件可以判定四边形ABCD是平行四边形;∵AB=DC,AD=BC,∴四边形ABCD是平行四边形,故选项B中条件可以判定四边形ABCD是平行四边形;∵AB∥DC,AD=BC,则无法判断四边形ABCD是平行四边形,故选项C中的条件,不能判断四边形ABCD是平行四边形;∵OA=OC,OB=OD,∴四边形ABCD是平行四边形,故选项D中条件可以判定四边形ABCD是平行四边形;故选:C.7.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是()A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CDC.∠ABC=∠ADC,AD∥BC D.∠ABD=∠BDC,∠BAD=∠DCB 解:A、∵∠ABD=∠BDC,OA=OC,又∠AOB=∠COD,∴△AOB≌△COD,∴DO=BO,∴四边形ABCD是平行四边形,故此选项不合题意;B、∠ABC=∠ADC,AB=CD不能判断四边形ABCD是平行四边形,故此选项符合题意;C、∵AD∥BC,∴∠ABC+∠BAD=180°,∵∠ABC=∠ADC,∴∠ADC+∠BAD=180°,∴AB∥CD,∴四边形ABCD是平行四边形,故此选项不合题意;D、∵∠ABD=∠BDC,∠BAD=∠DCB,∴∠ADB=∠CBD,∴AD∥CB,∵∠ABD=∠BDC,∴AD∥CB,∴四边形ABCD是平行四边形,故此选项不合题意;故选:B.8.满足下列条件的四边形,不一定是平行四边形的是()A.两组对边分别平行B.两组对边分别相等C.一组对边平行且相等D.一组对边平行,另一组对边相等解:A、∵两组对边分别平行的四边形是平行四边形,∴选项A不符合题意;B、∵两组对边分别相等的四边形是平行四边形,∴选项B不符合题意;C、∵一组对边平行且相等的四边形是平行四边形,∴选项C不符合题意;D、∵一组对边平行,另一组对边相等的四边形可能是等腰梯形或平行四边形,∴选项D符合题意;故选:D.9.下列四个选项中,能判断四边形ABCD是平行四边形的是()A.AB=CD,AC=BD B.∠A=∠B,∠B=∠CC.AB=CD,AD∥BC D.AB∥CD,∠A=∠C解:A、AB=CD,AC=BD不能判定四边形ABCD是平行四边形,故此选项错误;B、∠A=∠B,∠B=∠C不能判定四边形ABCD是平行四边形,故此选项错误;C、AB=CD,AD∥BC不能判定四边形ABCD是平行四边形,故此选项错误;D、∵AB∥CD,∴∠A+∠D=∠B+∠C=180°,∵∠A=∠C,∴∠B=∠D,∴四边形ABCD是平行四边形,故此选项正确;故选:D.10.从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD,这四个条件中选取两个,使四边形ABCD成为平行四边形,下面不能说明是平行四边形的是()A.①②B.①③C.②④D.①④解:根据平行四边形的判定,符合条件的有4种,分别是:①②、③④、①③、②④.故选:D.11.在下列条件中,能判定四边形为平行四边形的是()A.两组邻边相等B.一组对边平行且另一组对边相等C.两组对边分别平行D.对角线互相垂直解:A、两组邻边相等的四边形是筝形,故本选项不符合题意;B、一组对边平行且另一组对边相等的四边形可能是等腰梯形或平行四边形,故本选项不符合题意;C、两组对边分别平行的四边形是平行四边形,故本选项符合题意;D、对角线互相平分的四边形才是平行四边形,故本选项不符合题意;故选:C.12.不能判定四边形ABCD为平行四边形的条件是()A.AB∥CD,AD=BC B.AB∥CD,∠A=∠CC.AD∥BC,AD=BC D.∠A=∠C,∠B=∠D解:A、AB∥CD,AD=BC,不能判定四边形ABCD为平行四边形,错误;B、∵AB∥CD,∴∠A+∠D=180°,∵∠A=∠C,∴∠C+∠D=180°,∴AD∥BC,∴四边形ABCD为平行四边形,正确;C、∵AD∥BC,AD=BC,∴四边形ABCD为平行四边形,正确;D、∵∠A=∠C,∠B=∠D,∴∠A+∠D=∠C+∠D=180°,∴AD∥BC,AB∥CD,∴四边形ABCD为平行四边形,正确;故选:A.13.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是()A.AD=BC B.AB=CD C.AD∥BC D.∠A=∠C解:D、当AB∥CD,AD=BC时,四边形ABCD可能为等腰梯形,所以不能证明四边形ABCD为平行四边形;B、AB∥CD,AB=DC,一组对边分别平行且相等,可证明四边形ABCD为平行四边形;C、AB∥CD,AD∥BC,两组对边分别平行,可证明四边形ABCD为平行四边形;D、∵AB∥CD,∴∠A+∠D=180°,∵∠A=∠C,∴∠C+∠D=180°,∴AD∥BC,∴四边形ABCD为平行四边形;故选:A.14.下列给出的条件中,能判断四边形ABCD是平行四边形的是()A.AB∥CD,AD=BC B.∠B=∠C;∠A=∠DC.AB=CD,CB=AD D.AB=AD,CD=BC解:A、根据AD∥CD,AD=BC不能判断四边形ABCD是平行四边形,故本选项错误;B、根据∠B=∠C,∠A=∠D不能判断四边形ABCD是平行四边形,故本选项错误;C、根据AB=CD,AD=BC,得出四边形ABCD是平行四边形,故本选项正确;D、根据AB=AD,BC=CD,不能判断四边形ABCD是平行四边形,故本选项错误;故选:C.15.下列条件中,能判定四边形ABCD为平行四边形的个数是()①AB∥CD,AD=BC;②AB=CD,AD=BC;③∠A=∠B,∠C=∠D;④AB=AD,CB=CDA.1个B.2个C.3个D.4个解:①AB∥CD,AD=BC,不能判定四边形ABCD为平行四边形;②AB=CD,AD=BC;能判定四边形ABCD为平行四边形;③∠A=∠B,∠C=∠D;不能判定四边形ABCD为平行四边形;④AB=AD,CB=CD;不能判定四边形ABCD为平行四边形;能判定四边形ABCD为平行四边形的个数有1个,故选:A.二.解答题(共15小题)16.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.(1)求证:△ABC≌△DEF;(2)连接AD,求证:四边形ABED是平行四边形.(1)证明:∵BE=CF,∴BE+EC=CF+EC,∴BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SSS);(2)证明:由(1)得:△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE,又∵AB=DE,∴四边形ABED是平行四边形.17.如图,在四边形ABCD中,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF.求证:四边形ABCD是平行四边形.证明:∵DE⊥AC于点E,BF⊥AC于点F,∴∠DEC=∠BF A=90°,在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL),∴∠DCE=∠BAF,∴AB∥CD,又∵AB=CD,∴四边形ABCD是平行四边形.18.已知:如图,在四边形ABCD中,∠BAC=∠ACD=90°,AB=CD,点E是CD的中点.(1)求证:四边形ABCE是平行四边形;(2)若AC=4,AD=4,求四边形ABCE的面积.(1)证明:∵∠BAC=∠ACD=90°,∴AB∥EC,∵点E是CD的中点,∴,∵,∴AB=EC,∴四边形ABCE是平行四边形;(2)解:∵∠ACD=90°,AC=4,,∴,∵,∴AB=2,∴S平行四边形ABCE=AB•AC=2×4=8.19.如图,四边形ABCD的对角线AC、BD相交于点O,BO=DO,点E、F分别在AO,CO上,且BE∥DF,AE=CF.求证:四边形ABCD为平行四边形.证明:∵BE∥DF,∴∠BEO=∠DFO,在△BEO与△DFO中,,∴△BEO≌△DFO(ASA),∴EO=FO,∵AE=CF,∴AE+EO=CF+FO,即AO=CO,∵BO=DO,∴四边形ABCD为平行四边形.20.如图:已知∠B=∠E=90°,点B、C、F、E在一条直线上AC=DF,BF=EC.求证四边形ACDF是平行四边形.证明:∵BF=EC,∴BF﹣CF=EC﹣CF,即BC=EF,在Rt△ABC和Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL),∴∠ACB=∠DFE,∴∠ACF=∠DFC,∴AC∥DF,又∵AC=DF,∴四边形ACDF是平行四边形.21.如图,在四边形ABCD中,AD∥BC且AD=9cm,BC=6cm,点P、Q分别从点A、C 同时出发,点P以1cm/s的速度由A向D运动,点Q以2cm/s的速度由C向B运动.问几秒后直线PQ将四边形ABCD截出一个平行四边形?解:设点P,Q运动的时间为ts.依题意得:CQ=2t,BQ=6﹣2t,AP=t,PD=9﹣t.①当BQ=AP时,四边形APQB是平行四边形.即6﹣2t=t,解得t=2.②当CQ=PD时,四边形CQPD是平行四边形,即2t=9﹣t,解得:t=3.所以经过2或3秒后,直线PQ将四边形ABCD截出一个平行四边形.22.已知:如图,A,B,C,D在同一直线上,且AB=CD,AE=DF,AE∥DF.求证:四边形EBFC是平行四边形.证明:连接AF,ED,EF,EF交AD于O.∵AE=DF,AE∥DF.∴四边形AEDF为平行四边形,∴EO=FO,AO=DO,又∵AB=CD,∴AO﹣AB=DO﹣CD,∴BO=CO,又∵EO=FO,∴四边形EBFC是平行四边形.23.如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.求证:四边形ABDF是平行四边形.证明:∵△ABC是等边三角形,∴AC=BC=AB,∠ACB=60°;∵将AC绕点E旋转∴ED=CE,EF=AE∴△EDC是等边三角形,∴DE=CD=CE,∠DCE=∠EDC=60°,∴FD=AC=BC,∴△ABC、△AEF、△DCE均为等边三角形,∴∠CDE=∠ABC=∠EF A=60°,∴AB∥FD,BD∥AF,∴四边形ABDF是平行四边形.24.如图,已知,AE⊥BD于E点,CF⊥BD于F点,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.证明:∵AE⊥BD于E点,CF⊥BD于F点,∴∠AED=∠BFC=90°,∵BE=DF,∴BE+EF=DF+EF,即:BF=DE又∵∠1=∠2,∴△ADE≌△CBF(ASA),∴AD=BC,又∵∠1=∠2,∴AD∥BC,∴四边形ABCD是平行四边形.25.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.连接AF、BD,求证:四边形ABDF是平行四边形.解:∵BE=FC,∴BE+EC=FC+EC,∴BC=FE,在△ABC和△DFE中,,∴△ABC≌△DFE(SSS),∴∠ABC=∠DFE,∴AB∥DF,又∵AB=DF,∴四边形ABDF是平行四边形.26.如图,AD是△ABC边BC上的中线,AE∥BC,BE交AD于点F,F是BE的中点,连结CE.求证:四边形ADCE是平行四边形.证明:∵AD是△ABC边BC上的中线,F是BE的中点,∴BF=EF,BD=CD,∴DF∥CE,∴AD∥CE,∵AE∥BC,∴四边形ADCE是平行四边形.27.如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若F A=FC.求证:四边形ADCE是平行四边形;证明:∵CE∥AB,∴∠BAC=∠ECA,在△DAF和△ECF中,∴△DAF≌△ECF(ASA),∴CE=AD,∴四边形ADCE是平行四边形;28.如图,在四边形ABCD中,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE =BF.求证:(1)AE=CF;(2)四边形ABCD是平行四边形.证明:(1)∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFC=90°,在Rt△DEC和Rt△BFC中,,∴Rt△DEC≌Rt△BFC(HL),∴EC=AF,∴EC﹣EF=AF﹣EF即AE=FC;(2)∵Rt△DEC≌Rt△BFC,∴∠DCE=∠BAF,∴AB∥DC,又∵AB=DC,∴四边形ABCD是平行四边形.29.如图,已知△ABC是等边三角形,点D在BC边上,△ADF是以AD为边的等边三角形,过点F作BC的平行线交线段AC于点E,连接BF.求证:(1)△AFB≌△ADC;(2)四边形BCEF是平行四边形.证明:(1)∵△ABC和△ADF都是等边三角形,∴AF=AD,AB=AC,∠F AD=∠BAC=60°,又∵∠F AB=∠F AD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,∴∠F AB=∠DAC,且AF=AD,AB=AC∴△AFB≌△ADC(SAS);(2)∵△AFB≌△ADC,∴∠ABF=∠C=60°.又∵∠BAC=∠C=60°,∴∠ABF=∠BAC,∴FB∥AC,又∵BC∥EF,∴四边形BCEF是平行四边形;30.如图,点B、E、C、F在一条直线上,AB∥DF,AC∥DE,BE=FC,连接BD、AF.求证:四边形ABDF是平行四边形.证明:∵BE=FC,∴BE+CE=FC+CE,即BC=FE,∵AB∥DF,AC∥DE,∴∠ABC=∠DFE,∠ACB=∠DEF,在△ABC和△DFE中,,∴△ABC≌△DFE(ASA),∴AB=DF,∵AB∥DF,∴四边形ABDF是平行四边形.。
(完整版)平行四边形的性质判定练习题

第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ,两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中,∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图,在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,求∠DAC 与∠D 的度数。
例题3.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延长线于F ,∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
1、如图,四边形ABCD 是平行四边形,AB=6cm,BC=8cm ,∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.3、平行四边形得周长为50cm ,两邻边之差为5cm,则长边是________ ,短边是__________.4、平行四边形ABCD 中,∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中,∠A+∠C=200°.则:∠A= _______,∠B= _________ .7、如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
平行四边形的判定练习题(含答案)

平行四边形的判定练习题(含答案)(1)因为AD∥BC,AB=CD,所以ABCD是平行四边形.()(2)因为AB∥CD,AD=BC,所以ABCD是平行四边形.()(3)因为AD∥BC,AD=BC,所以ABCD是平行四边形.()(4)因为AB∥CD,AD∥BC,所以ABCD是平行四边形.()(5)因为AB=CD,AD=BC,所以ABCD是平行四边形.()(6)因为AD=CD,AB=AC,所以ABCD是平行四边形.()5.已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件________.6.如图所示,∠1=∠2,∠3=∠4,问四边形ABCD是不是平行四边形.7.如图所示,在四边形ABCD中,AB=CD,BC=AD,E,F 为对角线AC上的点,且AE=CF,求证:BE=DF.8.如图所示,D为△ABC的边AB上一点,DF交AC于点E,且AE=CE,FC∥AB.求证:CD=AF.9.如图所示,已知四边形ABCD是平行四边形,在AB 的延长线上截取BE=•AB,BF=BD,连接CE,DF,相交于点M.求证:CD=CM.10.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC•交EB于F,求证:EF=FB.知能点2 三角形的中位□线11.如图所示,已知E为□ABCD中DC边的延长线上的一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF,求证:AB=2OF.12.如图所示,在ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF•交于点M,连接CF,DE交AD.于点N,求证:MN∥AD且MN=1213.如图所示,DE是△ABC的中位线,BC=8,则DE=_______.14.如图所示,在□ABCD中,对角线AC,BD交于点O,OE∥BC交CD•于E,•若OE=3cm,则AD的长为(). A.3cm B.6cm C.9cm D.12cm 15.如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,•则四边形EFGH是平行四边形吗?为什么?16.如图所示,在△ABC中,AC=6cm,BC=8cm,AB=10cm,D,E,F分别是AB,BC,CA的中点,求△DEF的面积.规律方法应用17.如图所示,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,•并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离是多少?18.如图所示,在□ABCD中,AB=2AD,∠A=60°,E,F 分别为AB,CD的中点,EF=1cm,那么对角线BD的长度是多少?你是怎样得到的?19.如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.•(BC-AC).试说明:(1)DE∥BC.(2)DE=12开放探索创新20.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD•于E,EF∥BC交AC于F,那么AE与CF相等吗?请验证你的结论.中考真题实战21.(长沙)如下左图所示,在四边形ABCD中,AB∥CD,要使四边形ABCD•为平行四边形,则应添加的条件是________.(添加一个即可)22.(呼和浩特)如上右图所示,已知E,F,G,H是四边形ABCD各边的中点,•则S四边形EFGH :S四边形ABCD的值是_________.23.(南京)已知如图19-1-55所示,在Y ABCD中,E,F分别是AB,CD的中点.求证:(1) △AFD≌△CEB.(2)四边形AECF是平行四边形.答案:1.C 2.C 3.D4.(1)× (2)× (3)∨ (4)∨ (5)∨ (6)×5.AD=BC或AB∥CD6.解:∵∠1=∠2,∴AD∥BC.又∵∠3=∠4,∴AB∥CD.∴四边形ABCD是平行四边形.7.证明:∵AB=CD,BC=AD,∴四边形ABCD是平行四边形.∴AB∥CD,∴∠BAE=∠DCF.又∵AE=CE,∴△ABE≌△CDF(SAS),∴BE=EF.8.证明:∵FC∥AB,∴∠DAC=∠ACF,∠ADF=∠DFC.又∵AE=CE,∴△ADE≌△CFE(AAS),∴DE=EF.∵AE=CE,∴四边形ADCF为平行四边形.∴CD=AF.9.证明:∵四边形ABCD是平行四边形.∴AB//DC.又∵BE=AB,∴BE//DC,∴四边形BDCE是平行四边形.∵DC∥BF,∴∠CDF=∠F.同理,∠BDM=∠DMC.∵BD=BF,∴∠BDF=∠F.∴∠CDF=∠CMD,∴CD=CM.10.证明:过点B作BG∥AD,交DC的延长线于G,连接EG.∵DC∥AB,∴ABGD是平行四边形,∴BG// AD.在□ACED中,AD//CE,∴CE//BG.∴四边形BCEG为平行四边形,∴EF=FB.11.证明:∵四边形ABCD是平行四边形,∴AB//CD,AD=BC.∵CE=CD,∴AB//CE,∴四边形ABEC为平行四边形.∴BF=FC,∴OF//1AB,即AB=2OF.212.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.又∵EF∥AB,∴EF∥CD.∴四边形ABEF,ECDF均为平行四边形.又∵M,N分别为Y ABEF和Y ECDF对角线的交点.∴M为AE的中点,N为DE的中点,即MN为△AED的中位线.∴MN∥AD且MN=12AD.13.4 14.B15.解:EFGH是平行四边形,连接AC,在△ABC中,∵EF是中位线,∴EF//12AC.同理,GH//12AC.∴EF//GH,∴四边形EFGH为平行四边形.16.解:∵EF,DE,DF是△ABC的中位线,∴EF=12AB,DE=12AC,DF=12BC.又∵AB=10cm,BC=8cm,AC=6cm,∴EF=5cm,DE=3cm,DF=4cm,而32+42=25=52,即DE2+DF2=EF2.∴△EDF为直角三角形.∴S△EDF =12DE·DF=12×3×4=6(cm2).17.解:∵M,N分别是AC,BC的中点.∴MN是△ABC的中位线,∴MN=12AB.∴AB=2MN=2×20=40(m).故A,B两点间的距离是40m.18.解:连接DE.∵四边形ABCD是平行四边形,∴AB//CD.∵DF=12CD,AE=12AB,∴DF//AE.∴四边形ADFE是平行四边形.∴EF=AD=1cm.∵AB=2AD,∴AB=2cm.∵AB=2AD,∴AB=2AE,∴AD=AE.∴∠1=∠4.∵∠A=60°,∠1+∠4+∠A=180°,∴∠1=∠A=∠4=60°.∴△ADE是等边三角形,∴DE=AE.∵AE=BE,∴DE=BE,∴∠2=∠3.∵∠1=∠2+∠3,∠1=60°,∴∠2=∠3=30°.∴∠ADB=∠3+∠4=90°.=cm).19.解:延长AD交BC于F.(1)∵AD⊥CD,∴∠ADC=∠FDC=90°.∵CD平分∠ACB,∴∠ACD=∠FCD.在△ACD与△FCD中,∠ADC=∠FDC,DC=DC,∠ACD=∠FCD.∴△ACD≌△FCD,∴AC=FC,AD=DF.又∵E为AB的中点,∴DE∥BF,即DE∥BC.(2)由(1)知AC=FC,DE=12BF.∴DE=12(BC-FC)=12(BC-AC).20.解:AE=CF.理由:过E作EG∥CF交BC于G,∴∠3=∠C.∵∠BAC=90°,AD⊥BC,∴∠ABC+∠C=90°,∠ABD+∠BAD=90°.∴∠C=∠BAD,∴∠3=∠BAD.又∵∠1=∠2,BE=BE,∴△ABE≌△GBE(AAS),∴AE=GE.∵EF∥BC,EG∥CF,∴四边形EGCF是平行四边形,∴GE=CF,∴AE=CF.21.答案不唯一,如AB=CD或AD∥BC.22.1223.解:(1)在□ABCD中,AD=CB,AB=CD,∠D=∠B.∵E,F分别为AB,CD的中点,∴DF=12CD,BE=12AB,∴DF=BE,∴△AFD≌△CEB.(2)在□ABCD中,AB=CD,AB∥CD.由(1)得BE=DF,∴AE=CE,∴四边形AECF是平行四边形.。
平行四边形的判定常考题(含详细解析)

一、选择题<共14小题)1、<2003•广西)如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是< )A、5B、10C、15D、202、在四边形ABCD中,AB∥CD,若ABCD不是梯形,则∠A:∠B:∠C:∠D可能为< )A、2:3:6:7B、3:4:5:6C、3:5:7:9D、4:5:4:53、<2006•佛山)如图,平面上两颗不同高度、笔直的小树,同一时刻在太阳光线照射下形成的影子分别是AB、DC,则< )b5E2RGbCAPA、四边形ABCD是平行四边形B、四边形ABCD是梯形C、线段AB与线段CD相交D、以上三个选项均有可能4、<2005•柳州)不能判断四边形ABCD是平行四边形的是< )A、AB=CD,AD=BCB、AB=CD,AB∥CDC、AB=CD,AD∥BCD、AB∥CD,AD∥BC5、<2004•聊城)如图,有两块全等的含30°角的三角板拼成形状不同的平行四边形,最多可以拼成< )p1EanqFDPwA、1个B、2个C、3个D、4个6、<2002•山西)A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个中任选两个作为条件,能使四边形ABCD为平行四边形的选法有< )DXDiTa9E3dA、6种B、5种C、4种D、3种7、<1998•内江)能判定四边形是平行四边形的条件是< )A、一组对边平行,另一组对边相等B、一组对边相等,一组邻角相等C、一组对边平行,一组邻角相等D、一组对边平行,一组对角相等8、已知四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下四种说法正确的是< )RTCrpUDGiT①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;②如果再加上条件∠BAD=∠BCD,那么四边形ABCD一定是平行四边形;③如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;④如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.A、①②B、①③④C、②③D、②③④9、已知四边形ABCD的对角线相交于O,给出下列5个条件①AB∥CD;②AD∥BC;③AB=CD;④∠BAD=∠DCB.从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有< )5PCzVD7HxAA、6组B、5组C、4组D、3组10、在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有jLBHrnAILg< )A、3B、4C、5D、611、四边形ABCD中,AD∥BC,当满足下列< )条件时,四边形ABCD是平行四边形.A、∠A+∠C=180°B、∠B+∠D=180°C、∠A+∠B=180°D、∠A+∠D=180°12、以不在同一直线上的三个点为顶点作平行四边形,最多能作< )A、4个B、3个C、2个D、1个13、在下列给出的条件中,能判定四边形ABCD为平行四边形的是< )A、AB=BC,CD=DAB、AB∥CD,AD=BCC、AB∥CD,∠A=∠CD、∠A=∠B,∠C=∠D14、下列哪组条件能判别四边形ABCD是平行四边形< )A、AB∥CD,AD=BCB、AB=CD,AD=BCC、∠A=∠B,∠C=∠DD、AB=AD,CB=CD二、填空题<共4小题)15、<2018•常德)如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是_________.<添加一个条件即可,不添加其它的点和线).xHAQX74J0X16、<2009•郴州)如图,在四边形ABCD中,已知AB=CD,再添加一个条件_________ <写出一个即可),则四边形ABCD是平行四边形.<图形中不再添加辅助线)LDAYtRyKfE17、如图,△ABC、△ACE、△ECD都是等边三角形,则图中的平行四边形有哪些_________ _________ .Zzz6ZB2Ltk18、把边长为3,5,7的两个全等三角形拼成四边形,一共能拼成_________ 种不同的四边形,其中有_________ 个平行四边形.dvzfvkwMI1三、解答题<共8小题)19、<2018•贵阳)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.rqyn14ZNXI求证:<1)△AFD≌△CEB;<2)四边形ABCD是平行四边形.20、<2018•本溪)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:EmxvxOtOco<1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;<2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.SixE2yXPq521、<2006•镇江)已知:如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.6ewMyirQFL求证:四边形ABCD是平行四边形.22、<2004•万州区)已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于,若MA=MC,求证:CD=AN.kavU42VRUs23、如图,在△ABC中,D是BC边的中点,F、E分别是AD及其延长线上的点,CF∥BE.<1)求证:△BDE≌△CDF;<2)请连接BF,CE,试判断四边形BECF是何种特殊四边形,并说明理由.24、如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE、BD,求证:四边形ABDE是平行四边形.y6v3ALoS8925、<2006•泰安)已知:如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.M2ub6vSTnP<1)BC与⊙O是否相切?请说明理由;<2)当△ABC满足什么条件时,以点O,B,E,D为顶点的四边形是平行四边形?并说明理由.26、<2007•南宁)如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.0YujCfmUCw<1)请指出图中哪些线段与线段CF相等;<2)试判断四边形DBCF是怎样的四边形,证明你的结论.答案与评分标准一、选择题<共14小题)1、<2003•广西)如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是< )eUts8ZQVRdA、5B、10C、15D、20考点:平行四边形的性质;等腰三角形的性质;平行四边形的判定。
平行四边形判定专项练习30题

平行四边形的判定专项练习30题(有答案)求证:四边形ABCD 为平行四边形.I __ D ZX73 .已知四边形 ABCD 的对角线 AC 与BD 交于点0,现给出四个条件: ①0A=0C ;②AB=CD ;③/BAD= ZDCB ;④AD //BC •请你从中选择两个,推出四边形ABCD 为平行四边形,并写出你的推理过程.(1 )从以上4个条件中任意选取 2个条件,能推出四边形 ABCD 是平行四边形的有(用序号表示) __________________ . (2 )从(1 )中选出一种情况,写出你的推理过程.4 .如图,已知:点 B 、E 、F 、D 在一条直线上,DF=BE , AE=CF .请从下列三个条件中选择一个合适的条件,添 加到已知条件中,使四边形 ABCD 是平行四边形,并说明理由,供选择的三个条件(请从其中选择一个):2 .如图,四边形 ABCD 中,/ BAC=90,AB=11 ABCD 是平行四边形.-x , BC=5 , CD=x - 5 , AD=x - 3, AC=4.AD //BC , ED //BF , AF=CE ,求证:①AB=DC :② BC=AD ;③/AED= /CFB .5 .如图,在? ABCD中,AC交BD于点0,点E,点F分别是OA , OC的中点,请判断线段BE,7 .如图,已知BE丄AD , CF丄AD,且BE=CF .求证:(1 ) AD是△ABC的中线;(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.DF的位置关6.如图所示, 以△ABC的三边为边在BC的同侧分别作三个等边三角形厶ABD、ABCE、△XCF ,猜想: 四边形ADEFA8 .如图,矩形ABCD的两条对角线AC和BD相交于点O, E、F是BD上的两点,且/ AEB= /CFD .求证:四边形AECF是平行四边形.9 .如图:在四边形ABCD 中,AD //BC, AB=CD , E 是BC 上一点,DE=AB .10 .如图,已知AB //DC, E是BC的中点,AE , DC的延长线交于点F;(1 )求证:△ ABE 也£CE;11 .等边△ ABC 中,点D 在BC 上,点E 在AB 上,且CD=BE ,以AD 为边作等边△ ADF ,如图.求证:四边形 CDFE 是平行四边形.足为F ,连结DF . 求证:(1 )MBC 也△AF ; (2)四边形ADFE 是平行四边形.别从A 、C 同时出发,点 P 以2cm/秒的速度由A 向D 运动,点Q 以3cm/秒的速度由C 向B 运动.12 •如图,分别以 Rt △ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD 、等边△ ABE .若/BAC=30,EF 丄 AB ,垂13 .已知:如图,在△ ABC 中,中线BE , CD 交于点O , F , G 分别是OB , OC 的中点.求证:四边形 DFGE 是平14 •如图所示:在四边形ABCD 中,AD //BC 、BC=18cm , CD=15cm , AD=10cm , AB=12cm ,动点P 、Q 分行四边形.实用标准文案(1 )几秒钟后,四边形ABQP为平行四边形?并求出此时四边形ABQP的周长PDCQ的周长.15 •求证:顺次连接四边形各边中点所得的四边形是平行四边形.16 .△ABC中,中线BE、CF相交于0 , M是BO的中点,N是CO的中点, 求证:四边形MNEF是平行四边形.17 .如图,AD=DB , AE=EC , FG //AB, AG //BC.(1 )证明:△ AGE ^/CFE;(2)说明四边形ABFG是平行四边形;(3)研究图中的线段DE, BF, FC之间有怎样的位置关系和数量关系.18 .如图,△ ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB.(1 )求证:△ ABE 也△CD ;19 .已知在△ ABC中,D、E分别是AB、AC的中点,点F在DE的延长线上,且EF=DE ,图中有几个平行四边形? 请说明你的理由.20 .如图,在△ ABC中,AD是中线,点E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF. 求证:四边形AFBD是平行四边形.21 .如图:在四边形ABCD中,AD //BC, E是BC的中点,BC=2AD .找出图中所有的平行四边形,并选择一个22 •求证:两组对角分别相等的四边形是平行四边形.23 .已知:如图,A、B、C、D在同一条直线上,且AB=CD , AE //DF , AE=DF .求证:四边形 EBFC 是平行四边形.24 .如图,在△ ABC 中,D 是BC 边的中点,E 、F 分别在 AD 及其延长线上,CE//BF ,连接BE 、CF .形BFCE 是平行四边形吗?为什么?25 .已知点E 、F 、G 、H 分别为四边形 ABCD 四边的中点,试问四边形 EFGH 的形状并说明理由.26 .如图,已知四边形 ABCD 中AD=BC ,点A 、B 、E 在同一条直线上,且/ B= /EAD ,试说明四边形平行四边形.图中的四边ABCD 是28 .已知:△ ABC 的中线BD 、CE 交于点O , F 、G 分别是OB 、OC 的中点.求证:四边形 29 .如图,△ ACD 、MBE>ABCF 均为直线 BC 同侧的等边三角形.当 AB 丰AC 时,求证: 边形.30 .已知:在四边形 ABCD 中,AD //BC ,且 AB=DC=5 , AC=4 , BC=3 .求证:四边形ABCD 为平行四边形.ABCD 是平行四边形.DEFG 是平行四边形.四边形 ADFE 为平行四平行四边形的判定30题参考答案:1.TAD //BC,•••/DAE= ZBCF,TED //BF,•••/DEF= ZBFE,•••厶ED= ZCFB,又T AF=CE ,•••AE=CF ,在△ADE和ACBF中:T/DAE= ZBCF,ZAED= ZCFB,AE=CF ,.•.念DE 也zCBF (AAS ),•••AD=CB ,即:AD //CB , AD=CB ,•四边形ABCD是平行四边形,2.T/BAC=90° , AB=11 - x , BC=5 , AC=4 . •••(11 - x) 2+4 2=5 2,解得:x i =8 , X2=14 > 11 (舍去),当x=8 时,BC=AD=5 , AB=CD=3 ,•四边形ABCD为平行四边形.3. (1 )解:能推出四边形ABCD是平行四边形的有①④、③④;故答案是:①④、③④;(2 )以①④为例进行证明.如图,在四边形ABCD中,OA=OC , AD //BC .证明:T AD //BC, •••/DAO= ZBCO .•••在△KOD 与△COB 中,r ZDA0-ZBC0{DA=0CZAOD-ZDOB (对顶角相等)•••ZAOD 也ZCOB (ASA ),•••AD=BC ,•••在四边形ABCD中,AD二BC, •四边形ABCD为平行四边形.4.选择①,VDF=BE , AE=CF, AB=CD ,•ZABE也/CDF ( sss),•ZABE= /CDF ,•••AB //CD,又TAB=CD ,•四边形ABCD是平行四边形.5. BE=DF , BE //DF因为ABCD是平行四边形,所以OA=OC , OB=OD ,因为E, F分别是OA, OC的中点,所以OE=OF ,36 •四边形ADEF是平行四边形.连接ED、EF,•••念BD 'ABCE'^ACF分别是等边三角形, •••AB=BD,BC=BE,/DBA= /EBC=60 °•••/DBE= /ABC ••••念BC 也QBE.同理可证厶ABC也/EEC,•••AB=EF , AC=DE .VAB=AD , AC=AF ,•••AD=EF , DE=AF .•••/BED= ZCFD .VZBDE= /CDF , BE=CF ,•••/BED也EFD .•••BD=CD .•••AD是EABC的中线.(2)四边形BECF是平行四边形,由(1)得:BD=CD , ED=FD .•四边形BECF是平行四边形8 •四边形ABCD是矩形•••AB //CD , AB=CD , •••/ABE= /CDF ,又v/AEB= ZCFD , /•ZABE也EDF ,•••BE=DF ,又•••四边形ABCD是矩形,•••OA=OC , OB=OD , •••OB - BE=OD - DF , •••OE=OF ,•四边形AECF是平行四边形9.TAD //BC, AB=CD , •四边形ABCD是等腰梯形,•••/B= ZC ,VDE=AB ,•••DE=CD ,•ZDEC= ZC ,•ZDEC= ZB ,•••AB //DE,•四边形ABED是平行四边形.10. (1 )证明:T AB //DC, •/= Z , ZFCE= ZEBA , •••E为BC中点,•••CE=BE, 所以BFDE是平行四边形,所以BE=DF , BE//DFT在ZABE 和AFCE 中,Z1= Z , ZFCE= ZEBA , CE=BE ,(2)四边形ABFC是平行四边形;理由:由(1 )知:AABE^△CE,•••EF=AE ,VCE=BE,•四边形ABFC是平行四边形11 •连接BF,•••念DF和AABC是等边三角形,/FAD=60 • /FAD -Z EAD= /CAB -ZEAD , •••/FAB= /CAD , 在AFAB和ADAC中;AF=AD彳ZFAB=ZCAD ,I AB=AC• △AB BAAC (SAS), •••BF=DC , ZABF= ZACD=60 VBE=CD ,•••BF=BE ,•ZBFE是等边三角形,•••ZACD BABE ( SAS),•••AD=CE=DF ,VEF=CD ,•四边形CDFE是平行四边形.5 D C12• (1 )vAABE为等边三角形,EF±AB ,•••EF 为ZBEA 的平分线,Z AEB=60 °,AE=AB , •••ZFEA=30。
18_2 平行四边形的判定(重点练)原卷版 (1)

18.2 平行四边形的判定(重点练)一.选择题(共10小题)1.(2021秋•杜尔伯特县期末)下列不能判定一个四边形是平行四边形的是()A.两组对边分别平行的四边形是平行四边形B.两组对边分别相等的四边形是平行四边形C.一组对边平行另一组对边相等的四边形是平行四边形D.对角线互相平分的四边形是平行四边形2.(2021春•大名县期末)下列条件中,不能判定四边形是平行四边形的是()A.两组对边分别平行B.一组对边平行,另一组对边相等C.两组对边分别相等D.一组对边平行且相等3.(2021•奉贤区三模)已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是()A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B 4.(2021春•满洲里市期末)四边形ABCD中,AD∥BC.要判别四边形ABCD是平行四边形,还需满足条件()A.∠A+∠C=180°B.∠B+∠A=180°C.∠A=∠D D.∠B=∠D 5.(2021春•越秀区校级期中)如图,D、E、F是△ABC各边的中点,连接DE、EF、FD,则图中共有()个平行四边形.A.1B.2C.3D.46.(2021•广州模拟)如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且BE∥DF,AC分别交BE、DF于点G、H.下列结论:①四边形BFDE是平行四边形;②△AGE≌△CHF;③BG=DH;④S△AGE:S△CDH=GE:DH,其中正确的个数是()A.1个B.2个C.3个D.4个7.(2021秋•龙凤区期末)下面关于平行四边形的说法中,不正确的是()A.对角线互相平分的四边形是平行四边形B.有一组对边平行,一组对角相等的四边形是平行四边形C.有一组对边相等,一组对角相等的四边形是平行四边形D.有两组对角相等的四边形是平行四边形8.(2021•河北)如图1,▱ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案()A.甲、乙、丙都是B.只有甲、乙才是C.只有甲、丙才是D.只有乙、丙才是9.(2021春•扶沟县期末)已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是()A.AB∥CD,AD=BC B.AB=CD,AD=BCC.AO=CO,BO=DO D.∠ABD=∠CDB,∠ADB=∠CBD 10.(2021•烈山区模拟)已知,凸四边形ABCD,给出下列四个条件:①AB=CD,AD=BC②AB=CD,AD∥BC③AB∥CD,∠A=∠C④AB=CD,∠A=∠C能判断四边形ABCD是平行四边形的个数是()A.1B.2C.3D.4二.填空题(共10小题)11.(2021春•海淀区校级期中)如果四边形ABCD中∠A、∠B、∠C、∠D的大小之比是2:3:2:3,那么四边形ABCD是平行四边形,判定的依据是.12.(2021春•德惠市期末)如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是.13.(2020秋•东坡区期末)在△ABC中,AB=3,AC=4,点D是BC边的中点,则中线AD的长度的取值范围是.14.(2021春•綦江区期中)在四边形ABCD中,AB∥CD,AD∥BC,如果∠B=50°,则∠D =.15.(2021春•乾安县期末)四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需满足的条件是(横线只需填一个你认为合适的条件即可)16.(2021春•准格尔旗期末)如图,方格纸中每个最小正方形的边长为l,则两平行直线AB、CD之间的距离是.17.(2021春•遂宁期末)如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止).在运动以后,当t =时以P、D、Q、B四点组成的四边形为平行四边形.18.(2021春•平阴县期末)如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=s时,以A、C、E、F为顶点四边形是平行四边形.19.(2021春•淮北期末)如图,在四边形ABCD中,AD∥BC,AD=5,BC=18,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动,当运动时间t秒时,以点P,Q,E,D为顶点的四边形是平行四边形,则t的值为.20.(2021春•夏津县期末)如图,在▱ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF =CE.这些结论中正确的是.三.解答题(共10小题)21.(2021春•汉阳区期末)如图,E,F分别是平行四边形ABCD的边AD、BC边上的点,且AE=CF,连接BE,DF.求证:四边形BFDE是平行四边形.22.(2021春•邯郸期末)如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE.(1)若∠BCF=65°,求∠ABC的度数;(2)求证:四边形AECF是平行四边形.23.(2021春•宜兴市期中)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.24.(2021春•甘孜州期末)如图,▱ABCD的对角线AC、BD交于点O,M,N分别是AB、AD 的中点.(1)求证:四边形AMON是平行四边形;(2)若AC=6,BD=4,∠AOB=90°,求四边形AMON的周长.25.(2021秋•任城区期末)如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.(1)求证:四边形ABCD为平行四边形;(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.26.(2021•内江)如图,点A、D、C、B在同一条直线上,AC=BD,AE=BF,AE∥BF.求证:(1)△ADE≌△BCF;(2)四边形DECF是平行四边形.27.(2021春•越秀区校级期中)如图,平行四边形ABCD中,E、F分别是AD,BC的中点,求证:四边形BFDE是平行四边形.28.(2021•陕西模拟)如图,在四边形ABCD中,AD∥BC、点E为CD边上的中点,连接AE并延长,与BC的延长线交于点F,连接AC、DF,求证:四边形ACFD是平行四边形.29.(2021春•滕州市期末)已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.(1)求证:四边形EGFH是平行四边形.(2)连接BD交AC于点O,若BD=12,AE=EF﹣CF,求EG的长.30.(2021•永嘉县校级模拟)在▱ABCD中,E、F分别在DC、AB上,且DE=BF,求证:四边形AFCE是平行四边形.。
平行四边形测试题及答案

平行四边形测试题及答案一、选择题1. 平行四边形的定义是什么?A. 两组对边分别平行的四边形B. 两组对边分别相等的四边形C. 对角线互相平分的四边形D. 四边形的对角线互相垂直答案:A2. 平行四边形的对角线具有什么性质?A. 互相垂直B. 互相平分C. 相等D. 互相平行答案:B3. 下列哪个图形不是平行四边形?A. 矩形B. 菱形C. 梯形D. 正方形答案:C4. 平行四边形的对边具有什么性质?A. 相等B. 平行C. 垂直D. 互相垂直答案:B5. 平行四边形的对角线将平行四边形分成几个全等的三角形?A. 1B. 2C. 4D. 8答案:B二、填空题6. 平行四边形的对角线互相________。
答案:平分7. 平行四边形的对边互相________。
答案:平行8. 如果一个四边形的对角线互相平分且相等,那么这个四边形一定是________。
答案:矩形9. 平行四边形的面积可以通过底和高的乘积来计算,公式为________。
答案:面积 = 底× 高10. 菱形是特殊的平行四边形,它的四条边都________。
答案:相等三、简答题11. 请描述平行四边形的判定定理。
答案:一个四边形是平行四边形,如果满足以下任一条件:(1)两组对边分别平行;(2)两组对边分别相等;(3)对角线互相平分;(4)一组对边平行且相等。
12. 在平行四边形中,如果一组对边是垂直的,那么这个平行四边形是什么形状?答案:如果一组对边垂直,那么这个平行四边形是矩形。
四、计算题13. 已知平行四边形的底为10cm,高为5cm,求其面积。
答案:面积= 10cm × 5cm = 50平方厘米14. 已知平行四边形的对角线长度分别为8cm和6cm,且对角线互相平分,求平行四边形的面积。
答案:设平行四边形的面积为S,对角线交点为O,那么OA=4cm,OB=3cm,根据三角形面积公式,S = 2 × (1/2) × OA × OB = 2 × (1/2) × 4cm × 3cm = 12平方厘米。
平行四边形的判定典型题

平行四边形的判定例题1:BD是平行四边形ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需要添加的一个条件是_________练习:1、如图,已知:E、F是平行四边形ABCD对角线AC 上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形。
2.如图所示,在平行四边形ABCD中,P1、P2是对角线BD的三等分点,求证:•四边形AP1CP2是平行四边形.3、如图所示,在四边形ABCD中,M是BC中点,AM、BD互相平分于点O,那么请说明AM=DC 且AM∥DC例题2:(2013•镇江)如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.(1)求证:△ABE≌△DCF;OMAB CD(2)试证明:以A 、F 、D 、E 为顶点的四边形是平行四边形. 练习:1、11、如图,在□ABCD 中,已知两条对角线相交于点O ,E 、F 、G 、H 分别是AO 、BO 、CO 、DO 的中点,以图中的点为顶点,尽可能多地画出平行四边形2.(2012•惠城区模拟)如图,D 是AB 上的一点,DF 与AC 相交于E ,DE=EF ,CF∥BA.求证:四边形ADCF 是平行四边形.3、已知:如图所示,平行四边形ABCD 的对角线AC 、BD•相交于点O ,EF 经过点O 并且分别和AB 、CD 相交于点E 、F ,又知G 、H 分别为OA 、OC 的中点.求证:四边形EHFG 是平行四边形.例题3:、如图4.4-17,等边三角形ABC 的边长为a ,P 为△ABC 内一点,且PD ∥AB ,PE ∥BC ,PF ∥AC ,那么,PD+PE+PF 的值为一个定值.这个定值是多少?请你说出这个定值的来历.H GFE O A BCDHGFEO A BC DHGFE O ABCD HG FE O ABCD练习1:如图,平行四边形ABCD中,AF=CH,DE=BG。
求证:EG和HF互相平分。
平行四边形的性质与判定练习题

E D C OF B A一、选择题1、下面各条件中,能判定四边形是平行四边形的是 〔 〕A 、对角线互相垂直B 、对角线互相平分C 、一组对角相等D 、一组对边相等2、以下四个命题:①一组对边平行且相等的四边形;②两组对角分别相等的四边形;③对角线相等的四边形;④对角线互相平分的四边形。
其中能判定平行四边形的命题的个数为 〔 〕A 、1个B 、2个C 、3个D 、4个3、以下说法中错误的选项是〔 〕A .平行四边形的对角线互相平分B .有两对邻角互补的四边形为平行四边形C .对角线互相平分的四边形是平行四边形D .一组对边平行,一组对角相等的四边形是平行四边形4、平行四边形的两条对角线及一边的长可依次取 〔 〕A 、6、6、6B 、6、4、3C 、6、4、6D 、3、4、55、以不共线三点为三个顶点作平行四边形,一共可作平行四边形的个数是 〔 〕A 、2个B 、3个C 、4个D 、5个6、 四边形ABCD 的四个角∠A ∶∠B ∶∠C ∶∠D 满足以下哪一条件时,四边形ABCD 是平行四边形?〔 〕A 、1∶2∶2∶1B 、2∶1∶1∶1C 、1∶2∶3∶4D 、2∶1∶2∶17、四边形ABCD 中,AD ∥BC ,要判定四边形ABCD 是平行四边形,还应满足〔 〕A 、∠A +∠C =180°B 、∠B +∠D =180°C 、∠A +∠B =180°D 、∠A +∠D =180°8、根据以下条件,得不到平行四边形的是〔 〕A 、AB =CD ,AD =BC B 、AB ∥CD ,AB =CD C 、AB =CD ,AD ∥BC D 、AB ∥CD ,AD ∥BC9、如图,在□ABCD 中,EF 过对角线的交点,假设AB =4,BC =7,OE =3,那么四边形EFDC 的周长是〔 〕A 、14B 、11C 、10D 、179题图 10题图 11题图 12题图10、如图,线段a 、b 、c 的端点分别在直线l 1、l 2上,那么以下说法中正确的选项是〔 〕A .假设l 1∥l 2,那么a=bB .假设l 1∥l 2,那么a=cC .假设a∥b,那么a=bD .假设l 1∥l 2,且a∥b,那么a=b11、如图,△ABC 中,AB=AC=15,D 在BC 边上,DE∥BA,DF∥CA,那么四边形AFDE 的周长是〔 〕A .30B . 25C . 20D .1512、如图,AB=CD ,BF=ED ,AE=CF ,由这些条件能得出图中互相平行的线段共有〔 〕A .1组 B . 2组 C . 3组 D . 4组13、假设□ABCD 的周长为40cm ,ΔABC 的周长为27cm ,那么AC 的长是〔 〕A 、13cmB 、3cmC 、7cmD 、14、平行四边形的对角线长分别是x 和y ,一边长为12,那么以下各组数据可能是x 与y 的值的是〔 〕A 、8与14B 、10与14C 、18与20D 、10与3615、□ABCD 中,∠A:∠B=13:5,那么∠A 和∠B 的度数分别为〔 〕A .80° ,100°B .130°,50°C .160°,20°D .60°,120°16、一个平行四边形的两条对角线把它分成的全等三角形的对数是( )A.2B.4 C17、E 、F 分别是□ABCD 的边AB 、DC 中点,DE 、BF 交AC 于M 、N ,那么( )⊥MD18、在□ABCD 中假设∠A >∠B ,那么∠A 的补角与∠B 的余角之和( )°°°19、从等腰三角形底边上任意一点分别作两腰的平行线与两腰所围成的平行四边形的周长等于三角形( )A B E C F DO A B D C20、平行四边形两条邻边的长分别是6厘米和4厘米,它们的夹角是60°,那么它的面积是( )A.123cm 2B.73cm 2C.63cm 2D.43cm 221、以下说法正确的有〔 〕①平行四边形的对角线相等;②平行四边形的对边相等;③平行四边形的对角线互相垂直;④平行四边形的对角线互相平分;⑤两组对边分别相等的四边形是平行四边形;⑥一组对边平行而且另一组对边相等的四边形是平行四边形.A .4个 B . 3个 C . 2个 D . 1个22、平行四边形的一条对角线与一边垂直,且此对角线为另一边的一半,那么此平行四边形两邻角之比为( )∶∶3 C.1∶∶523、如图,□ABCD 和□EAFC 的顶点D 、E 、F 、B 在一条直线上,那么以下关系中一定正确的选项是( )A.DE >BFB.DE=BFC.DE <BFD.DE=EF=BF23题图 24题图 25题图24、如图,□ABCD 中,∠ABC=60°,AE∥BD,EF⊥BC 交BC 的延长线于点F ,DF=2,那么EF 的长为〔 〕 A .2 B . 2 C . 4 D . 425、如图,∠BAC=120°,AD⊥AC,BD=CD ,那么以下结论正确的选项是〔 〕A . A D=ACB . A B=AC C . A B=2ACD . A B=AC二、填空题1、□ABCD 中,∠B -∠A =40°,那么∠D =________.2、□ABCD 的周长是44cm ,AB 比AD 大2cm ,那么AB =________cm ,AD =________cm.3、平行四边形的两个相邻内角的平分线相交所成的角的度数是________.4、平行四边形的两条邻边的比为2∶1,周长为60cm ,那么这个四边形较短的边长为________.5、如右上图,在□ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F ,∠BAD =120°,BE =2,FD =3,那么∠EAF =________,□ABCD 的周长为________.6、假设平行四边形的两邻边的长分别为16和20,两长边间的距离为8,那么两短边间的距离为________.7、□ABCD 中,AB=6cm,BC=8cm ,∠B=70°,那么AD=__________,CD=__________, ∠D=__________,∠A=__________,∠C=__________.8、平行四边形周长为50cm ,两邻边之差为5cm,各边长为 . 9、如右图,平行四边形ABCD 的周长为30cm,它的对角线AC 和BD 相交于O,且△AOB 的周长比△BOC 的周长大5cm,那么AB=________,BC=________. 10、□ABCD 的对角线AC 和BD 相交于O,那么其中全等的三角形有________对.(1)由平行四边形的一个顶点在形内向两边引垂线,二垂线夹角为65°,那么这个平行四边形各内角的度数分别为________.(2)在□ABCD 中,∠A 的补角与∠B 的和等于210°,那么∠A=________,∠B=________.(3)在□ABCD 中,AB ∶BC=1∶2,∠D=30°,AE ⊥BC 于E ,AE=3cm,那么AB=________cm.这个平行四边形的周长是________cm.(4)平行四边形周长是40cm ,二邻边的比为3∶2,那么两邻边长分别是________.(5)在□ABCD 中,两邻边AB 、AD 的比是1∶2,M 是大边AD 的中点,那么∠BMC 的度数是________.(6)平行四边形的周长为50厘米,那么它两邻边之和是______cm ,每条对角线的长不能超过______cm.(7)□ABCD 中,周长为50厘米,AB=15cm ,∠A=30°,那么此平行四边形的面积为______cm 2.(8)□ABCD 的周长为50厘米,对角线交于O 点,△AOB 的周长比△BOC 的周长大5厘米,那么AB 、BC 的长分别是______、______.(9)有五条平行的直线,每相邻两条的距离相等,有一条直线和这组平行线相交成30°角,它介于相邻两条平行线之间的线段长是10厘米,那么这一组平行线最外面两条之间的距离是______厘米.(10)平行四边形周长为68厘米,被两条对角线分成两个不同的三角形的周长的和等于82厘米,两条对角线A BF CD EA BE CFDA BFOC DE的长度比为2∶1,那么两条对角线的长分别为______厘米,______厘米.11、等腰△ABC底边上任意一点D,AB=AC=5cm,过D作DE∥AC交AB于E,DF∥AB交AC于F,那么四边形AEDF的周长为.12、如图〔在下页〕,等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AD,PF∥BC,点D,E,F分别在AB,BC,AC上,那么PD+PE+PF= .第12题第13题第14题13、如图,在□ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,那么图中共有个平行四边形.14、如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的选项是.15、如图,梯形ABCD,AD∥BC,∠B+∠C=90°,EF=10,E,F分别是AD,BC的中点,那么BC﹣AD= .第15题第16题第17题16、如图,六边形ABCDEF的每个内角都是120°,AB∥DE,BC∥EF,CD∥FA,且AB=4,BC=5,CD=6,DE=7,那么,六边形ABCDEF的周长是.17、如图,△ABC中,如果AB=30,BC=24,AC=27,DN∥GM∥AB,EG∥DF∥BC,FM∥EN∥AC,那么图中阴影局部的三个三角形周长之和为.18、如右图所示,木工师傅把曲尺的一边紧靠木板边缘,从曲尺的另一边上可以读出木板另一边缘的刻度,然后将曲尺移动到另一处〔紧靠木板边缘〕,如果两次读数一样,说明木板两个边缘平行,其中道理是 .三、解答题与证明题1、在□ABCD中,E、F分别在DC、AB上,且DE=BF。
平行四边形的判定2

平行四边形的判定21.以下四个命题:(D两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形.其中正确的命题个数有( )A.4个B.3个C.2个D.1个2.能判定四边形是平行四边形的条件是( )A.一组对边平行,另一组对边相等B.一组对边相等,一组邻角相等C.一组对边平行,一组邻角相等D.一组对边平行,一组对角相等3.不能判定四边形4¾笫为平行四边形的题设是()A.AB=CD,AB//CDB.AA=AC,/B=ZDC.AB=AD,BC=CDD.AB=CD,AD=BC4一四边形4¾力中,4。
交勿于点Q,如果只给条件’,那么还不能判定四边形4腼为平行四边形,给出以下四种说法:(1)如果再加上条件«BC=AU',那么四边形/1阅9一定是平行四边形;(2)如果再加上条件"ZBAD=ZBCD",那么四边,形4%力一定是平行四边形;(3)如果再加上条件"AO=OC',那么四边形月时一定是平行四边形;(4)如果再加上条件"ND班=Ne46",那么四边形力AR一定是平行四边形其中正确的说法有()个.D. 1 B.2 C.3 D.A5.如图,在平行四边形/发力中,点反尸分别在边8。
、上,请添加一个条件,使四边形力的是平行四边形(只填一个即可).6.如图,在四边形力中,对角线4G加交于点0,49〃%,请添加一个条件:,使四边形力犯9为平行四边形(不添加任何辅助线).7.:如图,□ABCD中,E、〃分别是边被09的中点.(1)求证:四边形能叨是平行四边形;⑵假设力〃刃生2,/住60°,求四边形砌力的周长.8.:如图,点£,尸是5阅9中科,如边上的点,且AE=CF,蛛结DE,BF.求证:DE=BF.1.以下命题中,真命题的个数有().①对角线互相平分的四边形是平行四边形;②两组对角分别相等的四边形是平行四边形;③一组对边平行,另一组对边相等的四边形是平行四边形.A.3个B.2个C.1个D.O个2.能判定四边形力版是平行四,边形的是( )A.AB//CD t AD=BCB./A=/B,/C=ZDC.AB=CD,AD=BCD.AB=AD,CB=CD3.在四边形4ra中,根据下面选项中N4N反NG 的度数比,可以判定四边形4¾力是平行四边形的是()A.1:2:3:4B.2:3:2:3C.2:2:3:3D.1:2:2:34.四边形/腼中,对角线力C、协相交于『点0,给出以下四个条件.:①AAC戾②AD=BC•,③曲=玄;®0B=OD.从中任选两个条件,能使四边形川?如为平行四边形的选法有( )A.1种B.2种C.3种D.4种5.四边形4¾力中,力,请补充一个条件,使得四边形/1腼是平行四边形.7.如图,在四边形力比9中M8=6Z?"C交加于点0,如果想使该四边形成为平行四边形,那么只需添加的条件是(添一个即可).8.如图,在平行四边形4¾券中,E、厂分别在力反刃边上,且丝=6F.(1)求证:4ADEq2CBF∙,(2)求证:四边形皮,泥、是平行四边形。
平行四边形的判定测试题(含答案)

19.1.2 平行四边形的判定一、选择题1.不能判断四边形ABCD是平行四边形的是( )A.AB=CD,AD=BCB.AB=CD,AB∥CDC.AB=CD,AD∥BCD.AB∥CD,AD∥BC2.下列给出的条件中,能判定四边形ABCD是平行四边形的是( )A.AB∥CD,AD=BCB.AB=AD,CB=CDC.AB=CD,AD=BCD.∠B=∠C,∠A=∠D3.如图1,已知AD∥BC,要使四边形ABCD为平行四边形,需添加一个条件为______________.图1 图2 图34.如图2,在△ABC中,D、E分别是AB、AC边的中点,且DE=6 cm,则BC=____________.二、填空题1.如图3,在ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB2.如图4,AB DC,DC=EF=10,DE=CF=8,则图中的平行四边形有_________________,理由分别是_________________、____________________.图4 图5 图63.如图5,E、F是平行四边形ABCD对角线BD上的两点,请你添加一个适当的条件:__________,使四边形AECF是平行四边形.4.如图6,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件是:______ ________.5.如图,在ABCD中,已知M和N分别是边AB、DC的中点,试说明四边形BMDN也是平行四边形.三、综合题1.以不在同一直线上的三个点为顶点作平行四边形最多能作( )A.4个B.3个C.2个D.1个2.下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD 是平行四边形的是( )A.1∶2∶3∶4B.2∶2∶3∶3C.2∶3∶3∶2D.2∶3∶2∶33.九根火柴棒排成如右图形状,图中_____个平行四边形,你判断的根据是________________.4.已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC.(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示):_____________________________;(2)对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举出反例说明.5.若三条线段的长分别为20 cm,14 cm,16 cm,以其中两条为对角线,另一条为一边,是否可以画平行四边形?6.如图,E 、F 是四边形ABCD 的对角线AC 上的两点,AF=CE ,DF=BE ,DF ∥BE.求证:(1)△AFD ≌△CEB; (2)四边形ABCD 是平行四边形.7.如图,已知DC ∥AB ,且DC=21AB ,E 为AB 的中点. (1)求证:△AED ≌△EBC ;(2)观察图形,在不添加辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形(直接写出结果,不要求证明):______________________________.8.如图,已知ABCD中DE⊥AC,BF⊥AC,证明四边形DEBF为平行四边形.9.如图,已知ABCD中,E、F分别是AB、CD的中点.求证:(1)△AFD≌△CEB;(2)四边形AECF是平行四边形.参考答案一、课前预习(5分钟训练)1.不能判断四边形ABCD是平行四边形的是( )A.AB=CD,AD=BCB.AB=CD,AB∥CDC.AB=CD,AD∥BCD.AB∥CD,AD∥BC答案:C2.下列给出的条件中,能判定四边形ABCD是平行四边形的是( )A.AB∥CD,AD=BCB.AB=AD,CB=CDC.AB=CD,AD=BCD.∠B=∠C,∠A=∠D答案:C3.如图,已知AD∥BC,要使四边形ABCD为平行四边形,需添加一个条件为______________.答案:提示:添加AB∥DC,AD=BC等都可以.4.如图,在△ABC中,D、E分别是AB、AC边的中点,且DE=6 cm,则BC=____________.解析:根据三角形的中位线平行于第三边,并且等于第三边的一半,可知BC=2DE=12 cm.答案:12 cm二、课中强化(10分钟训练)1.如图,在ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F 满足下列哪个条件时,四边形DEBF不一定是平行四边形( )A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB解析:当E、F满足AE=CF时,由平行四边形的对角线相等知OB=OD,OA=OC,故OE=OF.可知四边形DEBF是平行四边形.当E、F满足∠ADE=∠CBF时,因为AD∥BC,所以∠DAE=∠BCF.又AD=BC,可证出△ADE≌△CBF,所以DE=BF,∠DEA=∠BFC.故∠DEF=∠BFE.因此DE∥BF,可知四边形DEBF是平行四边形.类似地可说明D也可以.答案:B2.如图,AB DC,DC=EF=10,DE=CF=8,则图中的平行四边形有_________________,理由分别是_________________、____________________.解析:因为AB DC,根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形;DC=EF,DE=CF,根据两组对边分别相等的四边形是平行四边形可判定四边形CDEF是平行四边形.答案:四边形ABCD,四边形CDEF 一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形3.如图,E、F是平行四边形ABCD对角线BD上的两点,请你添加一个适当的条件:__________,使四边形AECF是平行四边形.解析:根据平行四边形的定义和判定方法可填BE=DF;∠BAE=∠CDF等.答案:BE=DF或∠BAE=∠CDF等任何一个均可4.如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件是:______ ________.解析:根据平行四边形的判定定理,知可填①AD ∥BC,②AB=CD,③∠A+∠B=180°,④∠C+∠D=180°等. 答案:不唯一,以上几个均可. 5.如图,在ABCD 中,已知M 和N 分别是边AB 、DC 的中点,试说明四边形BMDN 也是平行四边形.答案:证明:∵ABCD,∴AB CD.∵M 、N 是中点, ∴BM=21AB,DN=21CD. ∴BM DN.∴四边形BMDN 也是平行四边形. 三、课后巩固(30分钟训练)1.以不在同一直线上的三个点为顶点作平行四边形最多能作( )A.4个B.3个C.2个D.1个解析:要求最多能作几个,只要连结起三个顶点后构成三角形,分别以其中一边作为对角线,另两边作为平行四边形的邻边作图,即可得出三种. 答案:B2.下面给出了四边形ABCD 中∠A 、∠B 、∠C 、∠D 的度数之比,其中能判定四边形ABCD 是平行四边形的是( )A.1∶2∶3∶4B.2∶2∶3∶3C.2∶3∶3∶2D.2∶3∶2∶3 解析:由两组对角分别相等的四边形是平行四边形易知,要使四边形ABCD 是平行四边形需满足∠A=∠C ,∠B=∠D ,因此∠A 与∠C ,∠B 与∠D 所占的份数分别相等. 答案:D3.九根火柴棒排成如右图形状,图中_____个平行四边形,你判断的根据是________________.答案:有3 两组对边分别相等的四边形是平行四边形4.已知四边形ABCD 的对角线AC 、BD 相交于点O ,给出下列5个条件:①AB ∥CD ;②OA=OC ;③AB=CD ;④∠BAD=∠DCB ;⑤AD ∥BC.(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示):_____________________________;(2)对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举出反例说明.解析:本题是条件开放性试题,要使四边形ABCD是平行四边形,从边、角、对角线上考虑共有5种判定方法,因此只需将任意两个条件组合加以评砼卸?答案:(1)①与②;①与③;①与④;①与⑤;②与⑤;④与⑤(2)③与⑤两个条件不能推出四边形ABCD是平行四边形.如图,AB=CD且AD∥BC,而四边形ABCD不是平行四边形.5.若三条线段的长分别为20 cm,14 cm,16 cm,以其中两条为对角线,另一条为一边,是否可以画平行四边形?解析:由平行四边形对角线互相平分,能否画平行四边形,应以任两条的一半和第三边为三边,看是否能构成三角形即可.20,16或20,14为对角线,另一条为一边可画平行四边形.6.如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.答案:证明:(1)∵DF∥BE,∴∠AFD=∠CEB.又∵AF=CE,DF=BE,∴△AFD≌△CEB.(2)由(1)△AFD≌△CEB知AD=BC,∠DAF=∠BCE,∴AD∥BC.∴四边形ABCD是平行四边形.7.如图,已知DC ∥AB ,且DC=21AB ,E 为AB 的中点. (1)求证:△AED ≌△EBC ;(2)观察图形,在不添加辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形(直接写出结果,不要求证明):______________________________.答案:证明:(1)∵E 为AB 的中点, ∴AE=EB=21AB. ∵DC=21AB ,DC ∥AB , ∴AE DC ,EB DC.∴四边形AECD 和四边形EBCD 都是平行四边形. ∴AD=EC ,ED=BC. 又∵AE=BE , ∴△AED ≌△EBC.(2)△ACD ,△ACE ,△CDE(写出其中两个三角形即可) 8.如图,已知ABCD 中DE ⊥AC,BF ⊥AC,证明四边形DEBF 为平行四边形.答案:证明:在ABCD 中,AD=BC,AD ∥BC,∴∠DAC=∠BCA. 又∵∠DEA=∠BFC=90°, ∴Rt △ADE ≌Rt △CBF. ∴DE=BF. 同理,可证DF=BE.∴四边形DEBF 为平行四边形. 9.(2010江苏南京模拟,19)如图,已知ABCD 中,E 、F 分别是AB 、CD 的中点.求证:(1)△AFD ≌△CEB;(2)四边形AECF 是平行四边形.答案:证明:(1)在ABCD 中,AD=CB,AB=CD,∠D=∠B.∵E 、F 分别是AB 、CD 的中点, ∴DF=21CD,BE=21AB. ∴DF=BE. ∴△AFD ≌△CEB. (2)在ABCD 中,AB=CD,AB ∥CD.由(1)得BE=DF,∴AE=CF. ∴四边形AECF 是平行四边形.。
平行四边形判定练习题

平行四边形判定练习题在几何学中,平行四边形是指具有两对相互平行的对边的四边形。
要判定一个四边形是否为平行四边形,我们需要检查四边形的特性和属性。
下面是一些平行四边形判定的练习题,通过解答这些题目,你可以巩固对平行四边形的理解并提升你的几何技巧。
练习题一:已知四边形ABCD,其中AB ∥ CD,AC ⊥ CD,AD ⊥ AB。
判断四边形ABCD是否为平行四边形。
解答:根据题干已知条件,我们可以得到以下推理:1. AB ∥ CD:对于平行四边形,对边是相互平行的,所以该条件满足。
2. AC ⊥ CD:平行四边形的两条对边不仅平行,还相互垂直,所以该条件不满足。
因此,根据已知条件,四边形ABCD不是平行四边形。
练习题二:在四边形EFGH中,EF ∥ GH,FG ⊥ GH,EG ⊥ EF。
已知EF = 5 cm,FG = 8 cm,EG = 4 cm。
求EH的长度。
解答:根据题干已知条件,我们可以得到以下推理:1. EF ∥ GH:对于平行四边形,对边是相互平行的,所以该条件满足。
2. FG ⊥ GH:平行四边形的两条对边不仅平行,还相互垂直,所以该条件不满足。
3. EG ⊥ EF:平行四边形的两条对边不仅平行,还相互垂直,所以该条件满足。
根据已知条件,我们可以将四边形EFGH划分成两个直角三角形EFG和EGH。
根据直角三角形的性质,我们可以使用勾股定理求解:EG² + GH² = EH²代入已知值,得到:4² + 8² = EH²16 + 64 = EH²80 = EH²通过开方运算,得到:EH = √80 ≈ 8.94 cm所以,四边形EFGH中EH的长度约为8.94 cm。
练习题三:在平行四边形IJKL中,已知IJ = 6 cm,JK = 8 cm,KL = 6 cm,IL = 8 cm。
判断平行四边形IJKL的类型。
(完整版)平行四边形性质与判定测试题

《平行四边形的性质与判定》测试卷5.如图,在口 ABC 冲,/ B=110° 则/ E+Z F 的值为().A.110 °B.30 °C.507. 平行四边形ABCD 勺周长32, 5AB=3BC,则对角线AC 的取值范围为()A. 6<AC<10B. 6<AC<16C. 10<AC<16D. 4<AC<168. 如图,平行四边形ABCD 中, E,F 是对角线BD 上的两点,若添加一个条件使△ ABE^A CDF 则添加的条件不能是()A.AE=CFB.BE=FDC.BF=DED. Z 1=Z 29. 若口 ABCD 勺周长为28,A ABC 的周长为17cm,则AC 的长为 ( )(满分120 分) 姓名: _________ 班级: 一.选择题(每题3分共30分) 1.如下右图,下列条件中,不能判定四边形ABCD 是平行四边形的是(A 、心 CO B8 DOB A 吐 DC ,/ BAD=Z BCDC 、A 吐 CD / 1 = /2 D A 吐 CD BO AD 2. 在以下平行四边形的性质中,错误的是() A.对边平行 B. 对角相等 C. 对边相等D.对角线互相垂直 3. 如右图,四边形 ABCD 是平行四边形,Z D=120°,ZCAD=32 . 则Z ABC ZCAB 的度数分别为( A . 28°,120° B O c o C . 32°, 120° D 4.如图,在平行四边形 A. 1 2 180 B. ) .120°,28°.120°,32° ABCD 中, 2 3 F 列各式不 180 C . 3 4 180 D . 2 4 180E 、 6.如上右图所示,在□ ABCDK 则图中平行四边形共有 ( 、4个F 分别AB CD 的中点,连结DE EF 、BF,)C 、6个A 二 D C,延长AD 至F,延长CD 至E,连接EF, D.70A.11cmB.5.5cmC.4cmD.3cm10. 如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是()①图甲,DEL AC, BF丄AC②图乙,DE平分/ ADC BF平分/ ABC③图丙,E是AB的中点,F是CD的中点④图丁,E是AB上一点,EF L ABA.3个B.4 个C.1个D.2 个二•填空题(每题3分,共30分)11. ________________________________________________________________ 用两根长40 cm的木条,作为四边形的一组对边,再用两根长为30cm的木条作为四边形的另一组对边,拼成一个四边形,这个四边形是__________________________________________________ 其根据___________________ .12. 平行四边形的周长为36cm相邻两边的比为1:2,则它的两邻边长分别是13. 如图,在平行四边形ABCD中, EF 〃AD,GH 〃AB,EF、GH相交于点0,则图中共有________ 平行四边形.14. 如图,平行四边形ABCDK BC=2CD CAL AB AC=3cm 则平行四边形ABCD的面积为________ .15. 如图,P是四边形ABCD的DC边上的一个动点,当四边形ABCD满足条件:_______________________ 时,△ PAB的面积始终保持不变.(注:只需填上你认为正确的一种条件即可,不必考虑所有可能的情形.)16. □ ABCD勺周长36cm AB=8cm 贝U BC= cm ;当/ B=60°时,AD为BC间的距离AE= cm ,□ ABCD勺面积S^ABC=cm17. ___________________________________________ 如图□ ABC冲,点E在边AD上,以BE为折痕,将厶ABE向上翻折,点A正好落在CD上的点卩,若厶FDE 的周长为8,A FCB的周长为22,则FC的长为___________________ .218. 在平面直角坐标系中,口 ABCD 勺顶点,A , B , D 的坐标分别是(0, 0) (5, 0), (2, 3),则顶点C 的坐标是 ______ .19. 女口图,在二ABCD 中, AB= 6, AD- 9,Z BAD 的平分线交BC 于点E ,交DC 的 延长线于点F , BGL AE 垂足为G, AF = 5, BG 4匹,则厶CEF 的周长为 __________ .20. 如图,□ ABCC 中,/ ABC=60 , E , F 分别在CD 和BC 的延长线上,AE// BDEF 丄BC , EF= 3,则AB 的长是22. (8分)如图,四边形ABCD 是平行四边形,AB=10, AD=8, AC BC 求AC 、OA以及平行四边形ABCD 的面积23. (8 分)如图,△ ABC D 是 AB 的中点,E 是 AC 上一点,EF / AB DF / BE 证明:DF 与AE互相平分21. (8 分) 求证:(1)BExC如图,二ABCDK E 、-DF; (2)BE // DF.24. ( 8 分) 如图,△ ABC 中,AB = AC, E 是AB 上一点,以点 E 为圆心,EB 为半径画弧 交BC 于点D ,连接ED ,并延长ED 到F ,使EF = AB ,连接FC,问/ F 和/ A 是否相等?为什27. (12 分)如图,在四边形 ABCDh AD// BC 且 AD<BC BC=18cm CD=15cm AD=10cm AB=12cm 动点P 、Q 分别从A 、C 同时出发,点P 以2cm/秒的速度由A 向D 运动,点Q 以3cm/秒的速度由C 向B 运动。
(完整版)平行四边形的判定练习题

行四边形的判定习题精选一、你能填对吗1.在四边形ABCD 中,若AB=CD ,再添加一个条件为_____________ ,就可以判定四边形ABCD 为平行四边形。
2. 延长△ ABC的中线AD至E,使DE=AD,连接BE, CE,贝U AB ____________ C E ,AC ________ BE 。
3. 若四边形ABCD中,AC , BD相交于点O,要判定它为平行四边形,从角的关系看应满足___________ ,从对角线的关系看应满足___________________ 。
4. 已知E、F、G、H 分别为Y ABCD 各边的中点, 贝四边形EFGH 为 __________________ 。
二、选一选5. 能识别四边形ABCD 是平行四边形的题设是()A . AB // CD , AD=BCB. Z A= / B ,Z C= / DC.AB=CD , AD=BCD.AB=AD , CB=CD6. 点A , B, C, D 在同一平面内,从① AB // CD,② AB=CD,③ BC // AD,④ BC=AD 这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有()A. 3种B. 4种C. 5种D. 6种7. 下列结论正确的是()A .对角线相等且一组对角相等的四边形是平行四边形B •一边长为5cm,两条对角线长分别是4cm和6cm的四边形是平行四边形C. 一组对边平行且一组对角相等的四边形是平行四边形D .对角线相等的四边形是平行四边形8. 不能判定四边形ABCD 是平行四边形的条件是()A. AB=CD , AD=BCB. AB / CD, AB=CDC. AB=CD , AD / BCD. AB / CD , AD / BC9. 如图19- 1 —26,在Y ABCD中,E, F分别在BC , AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是()。
平行四边形的判定基础练习
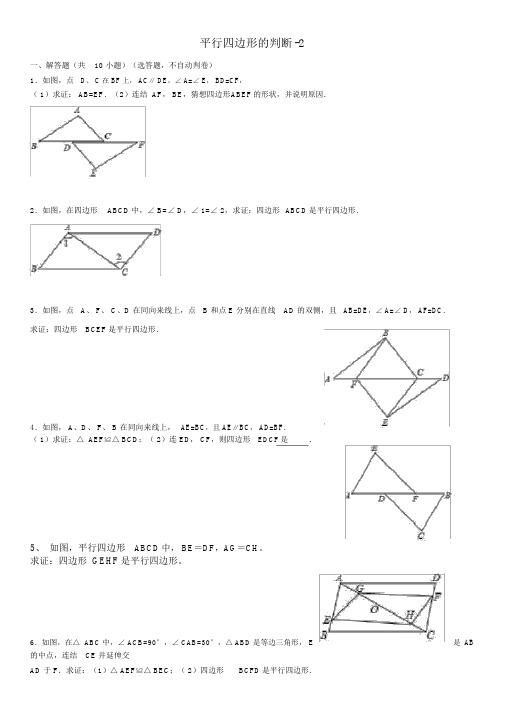
平行四边形的判断 -2一、解答题(共10 小题)(选答题,不自动判卷)1.如图,点D、 C 在 BF 上, AC∥ DE,∠ A=∠ E, BD=CF,( 1)求证: AB=EF.(2)连结 AF, BE,猜想四边形A BEF的形状,并说明原因.2.如图,在四边形ABCD中,∠ B=∠ D,∠ 1=∠ 2,求证:四边形ABCD是平行四边形.3.如图,点A、 F、 C、D 在同向来线上,点 B 和点 E 分别在直线AD 的双侧,且AB=DE,∠ A=∠ D, AF=DC.求证:四边形BCEF是平行四边形.4.如图, A、D、 F、 B 在同向来线上,AE=BC,且 AE∥BC, AD=BF.( 1)求证:△ AEF≌△ BCD;( 2)连 ED, CF,则四边形EDCF是.5、如图,平行四边形ABCD中, BE=DF,AG=CH。
求证:四边形 GEHF是平行四边形。
6.如图,在△ ABC 中,∠ ACB=90°,∠ CAB=30°,△ ABD 是等边三角形,E是AB 的中点,连结CE并延伸交AD 于 F.求证:(1)△ AEF≌△ BEC;( 2)四边形BCFD是平行四边形.7.已知:如图,在四边形ABCD中, AB∥ CD,E, F 为对角线AC 上两点,且AE=CF, DF∥ BE.求证:四边形ABCD为平行四边形.8.如图, AB∥ CD, AB=CD,点 E、F 在 BC 上,且 BE=CF.( 1)求证:△ ABE≌△ DCF;( 2)试证明:以A、F、 D、 E 为极点的四边形是平行四边形.9.如图,已知BE∥ DF,∠ ADF=∠ CBE, AF=CE,求证:四边形DEBF是平行四边形.10.如图,已知: AB∥CD, BE⊥ AD,垂足为点 E, CF⊥AD,垂足为点 F,而且 AE=DF.求证:四边形 BECF是平行四边形.【考点训练】平行四边形的判断-2参照答案与试题分析一、解答题(共10 小题)(选答题,不自动判卷)1.如图,点D、 C 在 BF 上, AC∥ DE,∠ A=∠ E, BD=CF,(1)求证: AB=EF.(2)连结 AF, BE,猜想四边形 ABEF的形状,并说明原因.【剖析】(1)利用AAS证明△ ABC≌△ EFD,再依据全等三角形的性质可得AB=EF;( 2)第一依据全等三角形的性质可得∠B=∠ F,再依据内错角相等两直线平行可获得AB∥ EF,又AB=EF,可证出四边形 ABEF为平行四边形.【解答】(1)证明:∵ AC∥DE,∴∠ ACD=∠EDF,∵BD=CF,∴BD+DC=CF+DC,即BC=DF,又∵∠ A=∠E,∴△ ABC≌△ EFD(AAS),∴ AB=EF;(2)猜想:四边形 ABEF为平行四边形,原因以下:由( 1)知△ ABC≌△ EFD,∴∠ B=∠ F,∴ AB∥ EF,又∵ AB=EF,∴四边形 ABEF为平行四边形.【评论】本题主要考察了全等三角形的判断与性质,平行四边形的判断,解决问题的重点是证明△ ABC ≌△ EFD.2.如图,在四边形ABCD中,∠ B=∠D,∠ 1=∠2,求证:四边形 ABCD是平行四边形.【剖析】依据三角形内角和定理求出∠ DAC=∠ACB,依据平行线的判断推出 AD∥ BC,AB∥CD,依据平行四边形的判断推出即可.【解答】证明:∵∠ 1+∠B+∠ACB=180°,∠ 2+∠D+∠ CAD=180°,∠ B=∠D,∠1=∠ 2,∴∠ DAC=∠ACB,∴AD∥ BC,∵∠ 1=∠ 2,∴AB∥ CD,∴四边形 ABCD是平行四边形.【评论】本题考察了平行线的判断和平行四边形的判断的应用,主要考察学生的推理能力.3.如图,点 A、F、C、D 在同向来线上,点 B 和点 E 分别在直线 AD 的双侧,且 AB=DE,∠ A=∠D,AF=DC.求证:四边形 BCEF是平行四边形.【剖析】第一证明△ AFB≌△ DCE(SAS),从而得出 FB=CE,FB∥CE,从而得出答案.【解答】证明:在△ AFB和△ DCE中,,∴△ AFB≌△ DCE(SAS),∴FB=CE,∴∠ AFB=∠DCE,∴FB∥CE,∴四边形 BCEF是平行四边形.【评论】本题主要考察了平行四边形的判断以及全等三角形的判断与性质,得出△ AFB≌△ DCE 是解题重点.4.如图, A、D、F、B 在同向来线上, AE=BC,且 AE∥ BC, AD=BF.(1)求证:△ AEF≌△ BCD;(2)连 ED,CF,则四边形 EDCF是.(从平行四边形,矩形,菱形,正方形中选填).【剖析】(1)依据 AE∥BC 可得∠ A=∠ B,再由 AD=BF可得 AF=BD,再加上条件 AE=CB,可依据SAS 定理证明△ AEF≌△ BCD;(2)依据△ AEF≌△ BCD,可得 EF=CD,∠ EFA=∠ CDB,从而证明出 EF∥ DC,再依据一组对边平行且相等的四边形 EDCF是平行四边形.【解答】解:(1)证明:∵AE∥BC,∴∠ A=∠ B,∵AD=BF,∴AF=DB,∵ AE=BC,在△ AEF和△ BCD中,∴△ AEF≌△ BCD(SAS);(2)平行四边形.∵△AEF≌△BCD,∴ EF=CD,∠ EFA=∠CDB,∴ EF∥DC,∴四边形 EDCF是平行四边形.【评论】本题主要考察了全等三角形的判断与性质,以及平行四边形的判断,重点是掌握一组对边平行且相等的四边形是平行四边形.5.如图,在 ABCD中, AC 交 BD 于点 O,点 E,点 F 分别是 OA, OC的中点,请判断线段BE,DF 的地点关系和数目关系,并说明你的结论.【剖析】依据平行四边形的性质对角线相互均分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判断定理“对角线相互均分的四边形是平行四边形”判断BFDE是平行四边形,从而得出 BE=DF, BE∥DF.【解答】解: BE=DF,BE∥ DF由于 ABCD是平行四边形,因此OA=OC,OB=OD,由于 E,F 分别是 OA,OC的中点,因此OE=OF,因此 BFDE是平行四边形,因此BE=DF,BE∥DF【评论】主要考察了平行四边形的基天性质和判断定理的运用.性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线相互均分.判断:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线相互均分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.6.如图,在△ ABC中,∠ ACB=90°,∠ CAB=30°,△ ABD 是等边三角形, E 是 AB 的中点,连结CE并延伸交 AD 于 F.求证:(1)△ AEF≌△ BEC;(2)四边形 BCFD是平行四边形.【剖析】(1)利用等边三角形的性质得出∠DAB=60°,即可得出∠ ABC=60°,从而求出△ AEF≌△ BEC (ASA);(2)利用平行线的判断方法以及直角三角形的性质得出 CF∥BD,从而求出答案.【解答】证明(1)∵ E 是 AB 中点,∴ AE=BE,∵△ABD 是等边三角形,∴∠ DAB=60°,∵∠CAB=30°,∠ACB=90°,∴∠ ABC=60°,在△ AEF和△ BEC中,∴△ AEF≌△ BEC(ASA);(2)∵∠ DAC=∠DAB+∠ BAC,∠ DAB=60°,∠ CAB=30°,∴∠ DAC=90°,∴AD∥ BC,∵E 是 AB 的中点,∠ACB=90°,∴ EC=AE=BE,∴∠ ECA=30°,∠ FEA=60°,∴∠ EFA=∠BDA=60°,∴CF∥BD,∴四边形 BCFD是平行四边形.【评论】本题主要考察了平行四边形的判断以及全等三角形的判断方法,得出∠ ABC=60°是解题重点.7.已知:如图,在四边形ABCD中, AB∥ CD,E,F 为对角线 AC上两点,且 AE=CF,DF∥BE.求证:四边形 ABCD为平行四边形.【剖析】第一证明△ AEB≌△ CFD可得 AB=CD,再由条件 AB∥CD 可利用一组对边平行且相等的四边形是平行四边形证明四边形 ABCD为平行四边形.【解答】证明:∵ AB∥ CD,∴∠ DCA=∠BAC,∵DF∥BE,∴∠DFA=∠BEC,∴∠AEB=∠DFC,在△ AEB和△ CFD中,∴△ AEB≌△ CFD(ASA),∴AB=CD,∵ AB∥ CD,∴四边形 ABCD为平行四边形.【评论】本题主要考察了平行四边形的判断,重点是掌握一组对边平行且相等的四边形是平行四边形.8.如图, AB∥CD,AB=CD,点 E、F 在 BC上,且 BE=CF.(1)求证:△ ABE≌△ DCF;(2)试证明:以 A、 F、 D、 E 为极点的四边形是平行四边形.【剖析】(1)由全等三角形的判断定理SAS证得△ ABE≌△ DCF;( 2)利用( 1)中的全等三角形的对应角相等证得∠AEB=∠DFC,则∠ AEF=∠DFE,因此依据平行线的判断能够证得AE∥ DF.由全等三角形的对应边相等证得AE=DF,则易证得结论.【解答】证明:(1)如图,∵ AB∥CD,∴∠ B=∠ C.∵在△ ABE与△ DCF中,,∴△ ABE≌△ DCF(SAS);(2)如图,连结 AF、DE.由( 1)知,△ ABE≌△ DCF,∴ AE=DF,∠ AEB=∠DFC,∴∠ AEF=∠DFE,∴ AE∥DF,∴以 A、F、D、E 为极点的四边形是平行四边形.【评论】本题考察了平行四边形的判断、全等三角形的判断与性质.在证明(2)题时,利用了“一组对边平行且相等的四边形是平行四边形”的判断定理.9.如图,已知 BE∥DF,∠ ADF=∠CBE,AF=CE,求证:四边形D EBF是平行四边形.【剖析】第一依据平行线的性质可得∠ BEC=∠ DFA,再加上条件∠ ADF=∠CBE,AF=CE,可证明△ADF ≌△ CBE,再依据全等三角形的性质可得 BE=DF,依据一组对边平行且相等的四边形是平行四边形进行判断即可.【解答】证明:∵ BE∥ DF,∴∠ BEC=∠DFA,在△ ADF和△ CBE中,∴△ ADF≌△ CBE(AAS),∴BE=DF,又∵ BE∥ DF,∴四边形 DEBF是平行四边形.【评论】本题主要考察了平行四边形的判断,重点是掌握一组对边平行且相等的四边形是平行四边形.10.如图,已知: AB∥ CD, BE⊥AD,垂足为点 E, CF⊥AD,垂足为点 F,而且 AE=DF.求证:四边形 BECF是平行四边形.【剖析】经过全等三角形(△ AEB≌△ DFC)的对应边相等证得 BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得 BE∥CF.则四边形 BECF是平行四边形.【解答】证明:∵BE⊥ AD,CF⊥AD,∴∠ AEB=∠DFC=90°,∵AB∥ CD,∴∠ A=∠ D,在△ AEB与△ DFC中,,∴△ AEB≌△ DFC(ASA),∴BE=CF.∵BE⊥AD,CF⊥AD,∴ BE∥CF.∴四边形 BECF是平行四边形.【评论】本题考察了平行四边形的判断、全等三角形的判断与性质.一组对边平行且相等的四边形是平行四边形.。
平行四边形的判定测试题

第十八章平行四边形18.1.2平行四边形的判定一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,DE是△ABC的中位线,且△ADE的周长为20,则△ABC的周长为A.30 B.40C.50 D.无法计算【答案】B2.如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为A.60°B.70°C.80°D.90°【答案】A【解析】∵AB=CD,BC=AD,∴四边形ABCD是平行四边形,∴AD∥BC,∴∠C+∠D=180°,∵∠D=120°,∴∠C=60°.故选A.3.四边形ABCD中,从∠A,∠B,∠C,∠D的度数之比中,能判定四边形ABCD是平行四边形的是A.1∶2∶3∶4 B.2∶3∶2∶3C.2∶2∶3∶3 D.1∶2∶2∶3【答案】B【解析】根据对角相等的四边形是平行四边形,A.1∶2∶3∶4,对角不相等,不能;B.2∶3∶2∶3,对角相等,能;C.2∶2∶3∶3,对角不相等,不能;D.1∶2∶2∶3,对角不相等,不能,故选B.4.依次连接任意四边形各边的中点,得到一个特殊图形,则这个图形一定是A.平行四边形B.矩形C.菱形D.梯形【答案】A【解析】如图,连接AC,∵四边形ABCD各边中点是E、F、G、H,∴HG∥AC,HG=12AC,EF∥AC,EF=12AC,∴EF=GH,EF∥GH,∴四边形EFGH是平行四边形.故选A.5.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是A.AB∥CD,AD∥BC B.OA=OC,OB=ODC.AD=BC,AB∥CD D.AB=CD,AD=BC【答案】C6.如图,ABCD的对角线AC,BD相交于点O,E是AB中点,且AE+EO=4,则ABCD的周长为A.20 B.16 C.12 D.8【答案】B【解析】∵四边形ABCD是平行四边形,∴OA=OC,∵AE=EB,∴OE =12BC,∵AE+EO=4,∴2AE+2EO=8,∴AB+BC=8,∴平行四边形ABCD的周长=2×8=16,故选B.7.如图,在ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形A.AE=CF B.DE=BFC.∠ADE=∠CBF D.∠AED=∠CFB【答案】BD选项:∵∠AED=∠CFB,∴∠DEO=∠BFO ,∴DE∥BF,在△DOE和△BOF中,DOE BOF DEO BFO OD OB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DOE≌△BOF,∴DE=BF,∴四边形DEBF是平行四边形.故选项正确.故选B.8.如图,E,F分别是□ABCD的边AB,CD的中点,则图中平行四边形的个数共有A.2个B.3个C.4个D.5个【答案】C【解析】∵四边形ABCD是平行四边形,∴DC∥AB,DC=AB,∵E、F分别是边AB、CD的中点,∴DF=FC=12DC,AE=EB=12AB,∵DC=AB,∴DF=FC=AE=EB,∴四边形DFBE和CFAE都是平行四边形,∴DE∥FB,AF∥CE,∴四边形FHEG是平行四边形,故选C.二、填空题:请将答案填在题中横线上.9.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是__________.【答案】三角形的中位线等于第三边的一半10.如图,在四边形ABCD中,AD∥BC,点E是BC边的中点,连接DE并延长,交AB的延长线于F点.已知AB=4,∠F=∠CDE,则BF的长为__________.【答案】4【解析】因为∠F=∠CDE,所以AB∥CD,因为AD∥BC,所以四边形ABCD是平行四边形,所以AB=CD,因为点E是BC边的中点,所以ED=EF,又因为∠F=∠CDE,∠DEC=∠FEB,所以△ECD≌△EBF,所以BF=CD,所以BF=AB,因为AB=4,所以BF=4,故答案为:4.11.如图,四边形ABCD中,AD∥BC,E是DC上一点,连接BE并延长交AD的延长线于点F,连接CF,BD,请你只添加一个条件:__________,使得四边形BDFC为平行四边形.【答案】DE=EC(答案不唯一)【解析】答案不唯一,比如:BD∥CF,构成两组对边分别平行的四边形是平行四边形;DF=BC,构成一组对边平行且相等的四边形是平行四边形;DE=EC,可以证明BE=EF,构成对角线相互平分的四边形是平行四边形,等等.故答案:DE=EC(答案不唯一).12.如图,在平行四边形ABCD中,对角线交于点O,点E、F在直线AC上(不同于A、C),当E、F的位置满足__________的条件时,四边形DEBF是平行四边形.【答案】AE=CF(答案不唯一)三、解答题:解答应写出文字说明、证明过程或演算步骤.13.如图,已知D、E、F分别是△ABC各边的中点,求证:AE与DF互相平分.【解析】∵D、E、F分别是△ABC各边的中点,根据中位线定理知:DE∥AC,DE=AF,EF∥AB,EF=AD,∴四边形ADEF为平行四边形,故AE与DF互相平分.14.如图,ABCD中,E、F分别是AB、CD上的点,AE=CF,M、N分别是DE、BF的中点.求证:四边形ENFM是平行四边形.【解析】∵四边形ABCD是平行四边形,∴AB∥CD.∵AE=CF,∴FD=EB,∴四边形DEBF是平行四边形,∴DE∥FB,DE=FB.∵M、N分别是DE、BF的中点,∴EM=FN.∵DE∥FB,∴四边形MENF是平行四边形.15.如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD.求证:∠1=∠2.16.如图1,平行四边形ABCD中,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.(1)在旋转过程中,线段AF与CE的数量关系是__________.⊥,当旋转角至少为__________︒时,四边形ABEF是平行四边形,并证明(2)如图2,若AB AC此时的四边形是ABEF是平行四边形.【解析】(1)相等,理由如下: 如图,在ABCD 中,AD ∥BC ,OA =OC ,∴∠1=∠2,在△AOF 和△COE 中,1234OA OC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOF ≌△COE (ASA ), ∴AF =CE .(2)当旋转角为90︒时,90COE ∠=︒,如图,又∵AB ⊥AC , ∴∠BAO =90°, ∠AOF =90°, ∴∠BAO =∠AOF , ∴AB ∥EF ,∵四边形ABCD 是平行四边形, ∴AD ∥BC , 即:AF ∥BE , ∵AB ∥EF ,AF ∥BE ,∴四边形ABEF 是平行四边形.人教版七年级上册期末测试卷一、选择题(每题3分,共30分)1.某天的最高气温是8℃,最低气温是-3℃,那么这天的温差是() A.-3℃B.8℃C.-8℃D.11℃2.下列立体图形中,从上面看能得到正方形的是()3.下列方程是一元一次方程的是()A.x-y=6 B.x-2=xC.x2+3x=1 D.1+x=34.今年某市约有108 000名应届初中毕业生参加中考,108 000用科学记数法表示为() A.0.108×106B.10.8×104C.1.08×106D.1.08×1055.下列计算正确的是()A.3x2-x2=3 B.3a2+2a3=5a5C.3+x=3x D.-0.25ab+14ba=06.已知ax=ay,下列各式中一定成立的是()A.x=y B.ax+1=ay-1C.ax=-ay D.3-ax=3-ay7.某商品每件标价为150元,若按标价打8折后,再降价10元销售,仍获利10%,则该商品每件的进价为()A.100元B.105元C.110元D.120元8.如果一个角的余角是50°,那么这个角的补角的度数是()A.130°B.40°C.90°D.140°9.如图,C,D是线段AB上的两点,点E是AC的中点,点F是BD的中点,EF=m,CD =n,则AB的长是()A.m-n B.m+nC .2m -nD .2m +n10.下列结论:①若a +b +c =0,且abc ≠0,则a +c 2b =-12;②若a +b +c =0,且a ≠0,则x =1一定是方程ax +b +c =0的解; ③若a +b +c =0,且abc ≠0,则abc >0; ④若|a |>|b |,则a -ba +b >0.其中正确的结论是( ) A .①②③ B .①②④ C .②③④D .①②③④二、填空题(每题3分,共24分)11.-⎪⎪⎪⎪⎪⎪-23的相反数是________,-15的倒数的绝对值是________.12.若-13xy 3与2x m -2y n +5是同类项,则n m =________.13.若关于x 的方程2x +a =1与方程3x -1=2x +2的解相同,则a 的值为________. 14.一个角的余角为70°28′47″,那么这个角等于____________.15.下列说法:①两点确定一条直线;②两点之间,线段最短;③若∠AOC =12∠AOB ,则射线OC 是∠AOB 的平分线;④连接两点之间的线段叫做这两点间的距离;⑤学校在小明家南偏东25°方向上,则小明家在学校北偏西25°方向上,其中正确的有________个. 16.在某月的月历上,用一个正方形圈出2×2个数,若所圈4个数的和为44,则这4个日期中左上角的日期数值为________.17.规定一种新运算:a △b =a ·b -2a -b +1,如3△4=3×4-2×3-4+1=3.请比较大小:(-3)△4________4△(-3)(填“>”“=”或“<”).18.如图是小明用火柴棒搭的1条“金鱼”、2条“金鱼”、3条“金鱼”……则搭n 条“金鱼”需要火柴棒__________根.三、解答题(19,20题每题8分,21~23题每题6分,26题12分,其余每题10分,共66分) 19.计算:(1)-4+2×|-3|-(-5);(2)-3×(-4)+(-2)3÷(-2)2-(-1)2 018.20.解方程:(1)4-3(2-x)=5x;(2)x-22-1=x+13-x+86.21.先化简,再求值:2(x2y+xy)-3(x2y-xy)-4x2y,其中x=1,y=-1. 22.有理数b在数轴上对应点的位置如图所示,试化简|1-3b|+2|2+b|-|3b-2|.23.如图①是一些小正方体所搭立体图形从上面看得到的图形,方格中的数字表示该位置的小正方体的个数.请在如图②所示的方格纸中分别画出这个立体图形从正面看和从左面看得到的图形.24.已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.25.为鼓励居民节约用电,某市电力公司规定了电费分段计算的方法:每月用电不超过100度,按每度电0.50元计算;每月用电超过100度,超出部分按每度电0.65元计算.设每月用电x度.(1)当0≤x≤100时,电费为________元;当x>100时,电费为____________元.(用含x的整式表示)(2)某用户为了解日用电量,记录了9月前几天的电表读数.该用户9月的电费约为多少元?(3)该用户采取了节电措施后,10月平均每度电费0.55元,那么该用户10月用电多少度?26.如图,O为数轴的原点,A,B为数轴上的两点,点A表示的数为-30,点B表示的数为100.(1)A,B两点间的距离是________.(2)若点C也是数轴上的点,点C到点B的距离是点C到原点O的距离的3倍,求点C表示的数.(3)若电子蚂蚁P从点B出发,以6个单位长度/s的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/s的速度向左运动,设两只电子蚂蚁同时运动到了数轴上的点D,那么点D表示的数是多少?(4)若电子蚂蚁P从点B出发,以8个单位长度/s的速度向右运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/s的速度向右运动.设数轴上的点N到原点O的距离等于点P到原点O的距离的一半(点N在原点右侧),有下面两个结论:①ON+AQ的值不变;②ON-AQ的值不变,请判断哪个结论正确,并求出正确结论的值.(第26题)答案一、1.D 2.A 3.D 4.D 5.D 6.D7.A8.D9.C10.B二、11.23;512.-813.-514.19°31′13″15.316.717.>18.(6n+2)三、19.解:(1)原式=-4+2×3+5=-4+6+5=7;(2)原式=12+(-8)÷4-1=12-2-1=9.20.解:(1)去括号,得4-6+3x=5x.移项、合并同类项,得-2x=2.系数化为1,得x=-1.(2)去分母,得3(x-2)-6=2(x+1)-(x+8).去括号,得3x-6-6=2x+2-x-8.移项、合并同类项,得2x=6.系数化为1,得x=3.21.解:原式=2x2y+2xy-3x2y+3xy-4x2y=(2x2y-3x2y-4x2y)+(2xy+3xy)=-5x2y+5xy.当x=1,y=-1时,原式=-5x2y+5xy=-5×12×(-1)+5×1×(-1)=5-5=0.22.解:由题图可知-3<b<-2.所以1-3b>0,2+b<0,3b-2<0.所以原式=1-3b-2(2+b)+(3b-2)=1-3b-4-2b+3b-2=-2b-5.23.解:如图所示.24.解:(1)设∠COF=α,则∠EOF=90°-α.因为OF 是∠AOE 的平分线,所以∠AOE =2∠EOF =2(90°-α)=180°-2α.所以∠BOE =180°-∠AOE =180°-(180°-2α)=2α.所以∠BOE =2∠COF .(2)∠BOE =2∠COF 仍成立.理由:设∠AOC =β,则∠AOE =90°-β,又因为OF 是∠AOE 的平分线,所以∠AOF =90°-β2.所以∠BOE =180°-∠AOE =180°-(90°-β)=90°+β,∠COF =∠AOF +∠AOC =90°-β2+β=12(90°+β).所以∠BOE =2∠COF .25.解:(1)0.5x ;(0.65x -15)(2)(165-123)÷6×30=210(度),210×0.65-15=121.5(元).答:该用户9月的电费约为121.5元.(3)设10月的用电量为a 度.根据题意,得0.65a -15=0.55a ,解得a =150.答:该用户10月用电150度.26.解:(1)130(2)若点C 在原点右边,则点C 表示的数为100÷(3+1)=25; 若点C 在原点左边,则点C 表示的数为-[100÷(3-1)]=-50. 故点C 表示的数为-50或25.(3)设从出发到同时运动到点D 经过的时间为t s ,则6t -4t =130, 解得t =65.65×4=260,260+30=290,所以点D 表示的数为-290.(4)ON -AQ 的值不变.设运动时间为m s,则PO=100+8m,AQ=4m. 由题意知N为PO的中点,得ON=12PO=50+4m,所以ON+AQ=50+4m+4m=50+8m,ON-AQ=50+4m-4m=50.故ON-AQ的值不变,这个值为50.。
平行四边形重难点考点真题(word+答案)

专题平行四边形1.平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
2.平行四边形的性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分。
3.平行四边形的判定:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)对角线互相平分的四边形是平行四边形;(5)两组对角分别相等的四边形是平行四边形。
4.平行四边形的面积:S平行四边形=底边长×高=ah【例题1】(2019▪广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是()A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF【例题2】(2018湖北黄石)如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.专题知识回顾专题典型题考法及解析一、选择题1. (福建福州)平面直角坐标系中,已知□ABCD的三个顶点坐标分别是A(m,n),B ( 2,-l ),C(-m,-n),则点D的坐标是()A.(-2 ,l ) B.(-2,-l ) C.(-1,-2 ) D .(-1,2 )2.(河北省)关于□ABCD的叙述,正确的是()A.若AB⊥BC,则□ABCD是菱形 B.若AC⊥BD,则□ABCD是正方形C.若AC=BD,则□ABCD是矩形 D.若AB=AD,则□ABCD是正方形3.(湖南湘西)下列说法错误的是()A.对角线互相平分的四边形是平行四边形B.两组对边分别相等的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.一组对边相等,另一组对边平行的四边形是平行四边形4.(2019•山东临沂)如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是()A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND5.(山东淄博)如图,△ABC的面积为16,点D是BC边上一点,且BD=14BC,点G是AB上一点,点H 在△ABC内部,且四边形BDHG是平行四边形.则图中阴影的面积是()专题典型训练题A. 3B. 4C. 5D. 6 二、填空题6.(2019广西百色)四边形具有不稳定性.如图,矩形ABCD 按箭头方向变形成平行四边形A 'B 'C 'D ',当变形后图形面积是原图形面积的一半时,则∠A '= .6.(2019湖南娄底)如图,平行四边形ABCD 的对角线 AC 、BD 交于点 O ,点 E 是 AD 的中点,△BCD 的周长为 18,则△DEO 的周长是 .7.( 2019河南省)如图,在□ABCD 中,BE⊥AB交对角线AC 于点E ,若∠1=20°,则∠2的度数是_________.8.( 2019湖北省十堰市)如图,在平行四边形ABCD 中,AB=213cm,AD=4cm,A C ⊥BC,则△DBC 比△ABC 的周长长__________cm.9.(2019浙江金华)如图,已知AB △CD ,BC △DE .若△A =20°,△C =120°,则△AED 的度数是 .BF10.(江苏省无锡市)如图,已知□OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为_______.11. (2019•湖北武汉)如图,在▱ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为.三、解答题12.(2019徐州)如图,将平行四边形纸片ABCD沿一条直线折叠,使点A与点C重合,点D落在点G处,折痕为EF.求证:(1)∠ECB=∠FCG;(2)△EBC≌△FGC.13.(2019湖南郴州)如图,平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.求证:四边形ACDF是平行四边形.14. (湖南省永州市)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.(1)求证:BE=CD.(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.15.(2019安徽)如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;(2)设▱ABCD的面积为S,四边形AEDF的面积为T,求的值.16.(2019湖南张家界)如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC交于点F,G.(1)求证:BF=CF;(2)若BC=6,DG=4,求FG的长.17. (2019•南京)如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.求证:△ADF≌△CEF.18.(2018海南)如图,将▱ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.(1)求证:四边形CEDF是平行四边形;(2)若AB=3,AD=4,∠A=60°,求CE的长.19.(2019辽宁本溪)如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.(1)求证:AE=BC;(2)若AB=3,CD=1,求四边形ABCE的面积.20.(江苏省扬州市)如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M 处,将边CD沿CF折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)若AB=6,AC=10,求四边形AECF的面积.21.(2019四川省凉山州)如图,□ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD 分别交于点E、F。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《平行四边形的判定》练习卷
一.选择题
1.能判定四边形ABCD为平行四边形的题设是().
(A)AB∥CD,AD=BC; (B)∠A=∠B,∠C=∠D;(C)AB=CD,AD=BC; (D)AB=AD,CB=CD
2.在给定的条件中,能画出平行四边形的是().
(A)以60cm为一条对角线,20cm.34cm为两条邻边;
(B)以6cm.10cm为对角线,8cm为一边;
(C)以20cm.36cm为对角线,22cm为一边;
(D)以6cm为一条对角线,3cm.10cm为两条邻边
3.正方形具有而菱形不一定具有的性质是()
(A)对角线互相平分; (B)对角线相等;(C)对角线平分一组对角;(D)对角线互相垂直
4.在下列说法中不正确的是()
(A)两条对角线互相垂直的矩形是正方形;
(B)两条对角线相等的菱形是正方形;
(C)两条对角线垂直且相等的平行四边形是正方形;
(D)两条对角线垂直且相等的四边形是正方形
5.下列说法不正确的是()
(A)对角线相等且互相平分的四边形是矩形;
(B)对角线互相垂直平分的四边形是菱形;
(C)一组对边平行且不等的四边形是梯形;
(D)一边上的两角相等的梯形是等腰梯形
6.不能判定四边形ABCD为平行四边形的题设是()
(A)AB=CD,AD=BC (B)AB//CD (C)AB=CD,AD∥BC (D)AB∥CD,AD∥BC
7.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的题设是()
(A)AO=CO,BO=DO;(B)AO=CO=BO=DO;(C)AO=CO,BO=DO,AC⊥BD; (D)AO=BO=CO=DO,AC⊥BD
8.对角线互相垂直平分的四边形一定是()
A.矩形
B. 菱形
C.等腰梯形
D.直角梯形
9.下列说法不正确的是()
(A)只有一组对边平行的四边形是梯形;
(B)只有一组对边相等的梯形是等腰梯形;
(C)等腰梯形的对角线相等且互相平分;
(D)在直角梯形中有且只有两个角是直角
10.下列说法中,错误的是()
A.一组对边平行且相等的四边形是平行四边形
B.两条对角线互相垂直且平分的四边形是菱形
C.四个角都相等的四边形是矩形
D.邻边相等的四边形是正方形
11.下列判断中正确的是()
(A)四边相等的四边形是正方形(B) 对角线互相垂直平分且相等的四边形是正方形
(C) 对角线互相垂直的平行四边形是正方形(D) 四角相等的四边形是正方形
二.填空题
1.顺次连接一个任意四边形四边的中点,得到一个四边形.
2.命题“平行四边形的对角线互相平分”的逆命题是.
3.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20cm,则其对角线长为_______,矩形的面积为________.
4.一个菱形的两条对角线长分别为6cm,8cm,这个菱形的边长为_______,•面积S=______.
5.如图,□ABCD中,AE.CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是(只需写出一个即可,图中不能再添加别的“点”和“线”).
6.如图,在平行四边形ABCD中,
E.F是对角线BD上的两点,要
使△ADF≌△CBE,还需添加一个什么
条件?。
(只需添加一个条件)
三.证明题
1.已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于, A
B C
D
F
B
D
1 / 1
1 / 1 若MA=MC,求证:(1)四边形ADCN 是平行四边形 (2)CD=AN.
2.已知:如图,D 是△ABC 的BC 边上的中点,DE ⊥AC,DF ⊥AB,垂足分别是E.F,且BF=CE.求证:(1)△ABC 是等腰三角形;
(2)当∠A=90°时,试判断四边形AFDE
是怎样的四边形,证明你的结论.
3.如图,在△ABC 中,D 为BC 边的中点,过D 点分别作DE ∥AB 交AC 于点E ,
DF ∥AC 交AB 于点F .
(1)证明:△BDF ≌△DCE ;
(2)如果给△ABC 添加一个条件,使四边形AFDE 成为菱形,则该条件是 ;
如果给△ABC 添加一个条件,使四边形AFDE 成为矩形,则该条件是 .
(均不再增添辅助线) 请选择一个结论进行证明.
4.已知:如图7,在梯形ABCD 中A D ∥BC,AB=DC 。
点E.F.G 分别在边AB.BC.CD 上,AE=GF=GC 。
(1) 求证:四边形AEFG 是平行四边形;
(2) 当∠FGC=2∠EFB 时,求证:四边形AEFG 是矩形。
5.如图,在Rt ABC △与Rt ABD △中,90ABC BAD ∠=∠=,AD BC AC BD =,,相交于点G ,过点A 作AE DB ∥交CB 的延长线于点E ,过点B 作BF CA ∥交DA 的延长线于点F AE BF ,,相交于点H .
(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)
(2)证明四边形AHBG 是菱形;
(3)若使四边形AHBG 是正方形,还需在Rt ABC △的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)
图7
A
D G C B
E
A
B D F E C
(第3题图) D
G
C
A
6.如图,等腰梯形ABCD中,AD BC
∥.
M、N分别是AD、BC的中点,E、F分别是BM、
CM的中点.
(1)求证:四边形MENF是菱形;
(2)若四边形MENF是正方形,请探索等腰梯形
ABCD的高和底边BC的数量关系并证明你的结论.
7.如图10,在四边形ABCD中,A D∥BC,A E⊥BC于E,且AE=8cm,AD=24cm,CD=10cm,动点P从点A开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB 边以2cm/s的速度运动,P、Q分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t秒,t为何值时,四边形PQCD为等腰梯形?
知识改变命运
A
B
E
M
N
F
C
D
1 / 1。
