哈工大机械原理大作业24题
哈尔滨工业大学机械原理大作业_连杆26题
1.运动分析题目如图所示机构，已知机构各构件的尺寸为AB=108mm，EF=320mm，BC=CE=CD=200mm，FG=162mm，AD=258mm，AG=514mm，DG=384mm，β=80º，构件1的角速度为ω1=10rad/s，试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度，并对计算结果进行分析。
2.机构的结构分析，组成机构的基本杆组划分3.各基本杆组的运动分析数学模型（1）RR基本杆组：delt=0xB = xA + AB * Cos(f + delt)yB = yA + AB* Sin(f + delt)vxB = vxA - w * AB * Sin(f + delt)vyB = vyA + w * AB* Cos(f + delt)axB = axA - w ^ 2 * AB * Cos(f + delt):ayB = ayA - w ^ 2 * AB* Sin(f + delt)(2)RRR基本杆组Ci = lbc * Cos(fbc)Si = lbc * Sin(fbc)Cj = lcd * Cos(fcd)Sj = lcd * Sin(fcd)G1 = Ci * Sj - Cj * Siwbc = (Cj * (vxD - vxB) + Sj * (vyD - vyB)) / G1wcd = (Ci * (vxD - vxB) + Si * (vyD - vyB)) / G1vxC = vxB - wbc * lbc * Sin(fbc)vyC = vyB + wbc * lbc * Cos(fbc)G2 = axD - axB + wbc ^ 2 * Ci - wcd ^ 2 * CjG3 = ayD - ayB + wbc ^ 2 * Si - wcd ^ 2 * Sjebc = (G2 * Cj + G3 * Sj) / G1ecd = (G2 * Ci + G3 * Si) / G1axC = axB - ebc * lbc * Sin(fbc) - wbc ^ 2 * lbc * Cos(fbc)ayC = ayB + ebc * lbc * Cos(fbc) - wbc ^ 2 * lbc * Sin(fbc)EB = 2 * BC * Cos(febc)xE = xB + EB* Cos(fbc + febc)yE = yB + EB * Sin(fbc + febc)vxE = vxB – wbc * EB* Sin(fbc + febc)vyE = vyB + wbc * EB* Cos(fbc + febc)axE = axB - wbc ^ 2 * EB * Cos(fbc + delt) - ebc * EB * Sin(fbc + febc)ayE = ayB - wbc ^ 2 * leb * Sin(fbc + delt) + ebc * leb * Sin(fbc + febc) Ci = lef * Cos(fef)Si = lef * Sin(fef)Cj = lfg * Cos(ffg)Sj = lfg * Sin(ffg)G1 = Ci * Sj - Cj * Siwef = (Cj * (vxG - vxE) + Sj * (vyG - vyE)) / G1wfg = (Ci * (vxG - vxE) + Si * (vyG - vyE)) / G1vxF = vxE - wef * lef * Sin(fef)vyF = vyE + wef * lef * Cos(fef)G2 = axG - axE + wef ^ 2 * Ci - wfg ^ 2 * CjG3 = ayG - ayE + wef ^ 2 * Si - wfg ^ 2 * Sjeef = (G2 * Cj + G3 * Sj) / G1efg = (G2 * Ci + G3 * Si) / G1axF = axE - eef * lef * Sin(fef) - wef ^ 2 * lef * Cos(fef)ayF = ayE + eef * lef * Cos(fef) - wef ^ 2 * lef * Sin(fef)4.计算编程Dim xA As DoubleDim yA As DoubleDim vxA As DoubleDim vyA As DoubleDim axA As Double 'A '点加速度x轴分量Dim ayA As Double 'A '点加速度y轴分量Dim xB As Double 'B'点'x轴坐标Dim yB As Double 'B点y轴坐标Dim vxB As Double 'B点速度x轴分量Dim vyB As Double 'B点速度y轴分量Dim axB As Double 'B点加速度x轴分量Dim ayB As Double 'B点加速度y轴分量Dim xC As Double 'C点x轴坐标Dim yC As Double C'点y轴坐标Dim vxC As Double 'C点速度x轴分量Dim vyC As Double 'C点速度y轴分量Dim axC As Double 'C点加速度x轴分量Dim ayC As Double 'C点加速度y轴分量Dim xD As Double 'D点x轴坐标Dim yD As Double 'D点y轴坐标Dim vxD As Double 'D点速度x轴分量Dim vyD As Double 'D点速度y轴分量Dim axD As Double 'D点加速度x轴分量Dim ayD As Double 'D点加速度y轴分量Dim xE As Double 'E点x轴坐标Dim yE As Double 'E点y轴坐标Dim vxE As Double 'E点速度x轴分量Dim vyE As Double 'E点速度y轴分量Dim axE As Double 'E点加速度x轴分量Dim ayE As Double 'E点加速度y轴分量Dim xF As Double 'F点x轴坐标Dim yF As Double 'F点y轴坐标Dim vxF As Double 'F点速度x轴分量Dim vyF As Double 'F点速度y轴分量Dim axF As Double 'F点加速度x轴分量Dim ayF As Double 'F点加速度y轴分量Dim xG As Double 'G点x轴坐标Dim yG As Double 'G点y轴坐标Dim vxG As Double 'G点速度x轴分量Dim vyG As Double 'G点速度y轴分量Dim axG As Double 'G点加速度x轴分量Dim ayG As Double 'G点加速度y轴分量Dim delt As Double ' AB杆初始转角Dim lab As Double 'AB杆长Dim lbc As Double 'BC杆长Dim lcd As Double ' CD杆长Dim lce As Double 'CE杆长Dim lef As Double 'EF杆长Dim lfg As Double 'FG杆长Dim leb As Double 'ED杆长Dim f As Double 'AB杆转角Dim fbc As Double 'BC杆转角Dim fcd As Double 'CD杆转角Dim fce As Double 'CE杆转角Dim fef As Double 'EF杆转角Dim ffg As Double 'FG杆转角Dim fge As Double 'ge杆转角Dim w As Double 'AB杆角速度Dim wbc As Double ' BC角速度Dim wcd As Double 'CD角速度Dim wce As Double 'CE角速度Dim wef As Double 'EF角速度Dim wfg As Double 'FG角速度Dim e As Double 'AB杆角加速度Dim ebc As Double ' BC杆角加速度Dim ecd As Double 'CD杆角加速度Dim ece As Double 'CE杆角加速度Dim eef As Double 'EF杆角加速度Dim efg As Double 'FG杆角加速度Dim LBD As Double 'BD距离Dim leg As Double 'EG距离Dim JCBD As Double '角CBDDim jfeg As Double '角FEGDim fBD As Double 'BD转角Dim feg As Double 'EG转角Dim Ci As DoubleDim Cj As DoubleDim Si As DoubleDim Sj As DoubleDim G1 As DoubleDim G2 As DoubleDim G3 As DoubleDim val As DoubleDim pi As DoubleDim pa As DoubleDim febc As Double '角EBCDim i As DoubleDim fj1 As DoublePrivate Sub Command1_Click() '求点E的轨迹Picture1.Scale (-300, 400)-(10, -15)Picture1.Line (-300, 0)-(10, 0) 'XPicture1.Line (0, 400)-(0, -15) 'YFor i = -300 To 0 Step 50 'X轴坐标Picture1.DrawStyle = 2Picture1.Line (i, 400)-(i, 0)Picture1.CurrentX = i - 10: Picture1.CurrentY = 0 Picture1.Print iNext iFor i = 0 To 350 Step 50 'Y轴坐标Picture1.DrawStyle = 2Picture1.Line (0, i)-(-400, i)Picture1.CurrentX = -20: Picture1.CurrentY = i + 7 Picture1.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Picture1.PSet (xE, yE)Next fj1End SubPrivate Sub Command2_Click() '求构件5的角位移Picture2.Scale (-20, 5)-(380, -0.5)Picture2.Line (-20, 0)-(380, 0) 'XPicture2.Line (0, 3)-(0, -0.5) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture2.DrawStyle = 2Picture2.Line (i, 3)-(i, 0)Picture2.CurrentX = i - 10: Picture2.CurrentY = 0 Picture2.Print iNext iFor i = -0.5 To 3 Step 0.5 'Y轴坐标Picture2.Line (0, i)-(380, i)Picture2.CurrentX = -25: Picture2.CurrentY = i Picture2.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Picture2.PSet (fj1, ffg)Next fj1End SubPrivate Sub Command3_Click() '求构件5的角速度Picture3.Scale (-20, 10)-(380, -10)Picture3.Line (-20, 0)-(380, 0) 'XPicture3.Line (0, 10)-(0, -10) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture3.DrawStyle = 2Picture3.Line (i, 10)-(i, -10)Picture3.CurrentX = i - 10: Picture3.CurrentY = 0 Picture3.Print iNext iFor i = -8 To 8 Step 2 'Y轴坐标Picture3.Line (0, i)-(380, i)Picture3.CurrentX = -20: Picture3.CurrentY = i Picture3.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Picture3.PSet (fj1, wfg)Next fj1End SubPrivate Sub Command4_Click() '求构件5的角加速度Picture4.Scale (-20, 300)-(380, -200)Picture4.Line (-20, 0)-(380, 0) 'XPicture4.Line (0, 300)-(0, -200) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture4.DrawStyle = 2Picture4.Line (i, 300)-(i, -200)Picture4.CurrentX = i - 10: Picture4.CurrentY = 0 Picture4.Print iNext iFor i = -200 To 300 Step 50 'Y轴坐标Picture4.Line (0, i)-(380, i)Picture4.CurrentX = -25: Picture4.CurrentY = i + 5 Picture4.Print iNext iFor fj1 = 0 To 360 Step 0.01f = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Picture4.PSet (fj1, efgNext fj1End SubPrivate Sub Form_Load() '赋初值lab = 108lce = 200lbc = 200lcd = 200lef = 320lfg = 162w = 10e = 0delt = 0xA = 0yA = 0vyA = 0axA = 0ayA = 0xD = -178.311284yD = 186.464704vxD = 0vyD = 0axD = 0ayD = 0xG = -514yG = 0vxG = 0vyG = 0axG = 0ayG = 0pi = 3.1415926pa = pi / 180febc = pa * 50End SubPrivate Sub RR1() 'RR基本杆组xB = xA + lab * Cos(f + delt)yB = yA + lab * Sin(f + delt)vxB = vxA - w * lab * Sin(f + delt)vyB = vyA + w * lab * Cos(f + delt)axB = axA - w ^ 2 * lab * Cos(f + delt) - e * lab * Sin(f + delt)ayB = ayA - w ^ 2 * lab * Sin(f + delt) + e * lab * Sin(f + delt)End SubPrivate Sub RR2() 'RR基本杆组leb = 2 * lbc * Cos(febc)xE = xB + leb * Cos(fbc + febc)yE = yB + leb * Sin(fbc + febc)vxE = vxB - wbc * leb * Sin(fbc + febc)vyE = vyB + wbc * leb * Cos(fbc + febc)axE = axB - wbc ^ 2 * leb * Cos(fbc + delt) - ebc * leb * Sin(fbc + febc) ayE = ayB - wbc ^ 2 * leb * Sin(fbc + delt) + ebc * leb * Sin(fbc + febc) End SubPrivate Sub RRR1() 'RRR基本杆组LBD = Sqr((xD - xB) ^ 2 + (yD - yB) ^ 2)If LBD > lbc + lcd And LBD < Abs(lbc - lcd) ThenIf MsgBox("RRR杆组杆长不符合要求", vbOKOnly, "提示") = 1 Then EndEnd IfElseEnd IfIf LBD < lbc + lcd And LBD > Abs(lbc - lcd) Then val = (lbc ^ 2 + LBD ^ 2 - lcd ^ 2) / (2 * lbc * LBD) JCBD = Atn(-val / Sqr(-val * val + 1)) + 2 * Atn(1) ElseEnd IfIf LBD = lbc + lcd ThenJCBD = 0ElseEnd IfIf LBD = Abs(lbc - lcd) ThenIf lbc > lcd ThenJCBD = 0ElseEnd IfIf lbc < lcd ThenJCBD = piElseEnd IfElseEnd IfIf xD > xB And yD >= yB Then '第一象限fBD = Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD = xB And yD > yB ThenfBD = pi / 2ElseEnd IfIf xD < xB And yD >= yB Then '第二象限fBD = pi + Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD < xB And yD < yB Then '第三象限fBD = pi + Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD = xB And yD < yB ThenfBD = 3 * pi / 2ElseEnd IfIf xD > xB And yD <= yB Then '第四象限fBD = 2 * pi + Atn((yD - yB) / (xD - xB))ElseEnd Iffbc = fBD - JCBDxC = xB + lbc * Cos(fbc)yC = yB + lbc * Sin(fbc)If xC > xD And yC >= yD Then '第一象限fcd = Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC = xD And yC >= yD Thenfcd = pi / 2ElseEnd IfIf xC < xD And yC >= yD Then '第二象限fcd = pi + Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC < xD And yC < yD Then '第三象限fcd = pi + Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC = xD And yC < yD Thenfcd = 3 * pi / 2ElseEnd IfIf xC > xD And yC <= yD Then '第四象限fcd = 2 * pi + Atn((yC - yD) / (xC - xD))ElseEnd IfCi = lbc * Cos(fbc)Si = lbc * Sin(fbc)Cj = lcd * Cos(fcd)Sj = lcd * Sin(fcd)G1 = Ci * Sj - Cj * Siwbc = (Cj * (vxD - vxB) + Sj * (vyD - vyB)) / G1 wcd = (Ci * (vxD - vxB) + Si * (vyD - vyB)) / G1 vxC = vxB - wbc * lbc * Sin(fbc)vyC = vyB + wbc * lbc * Cos(fbc)G2 = axD - axB + wbc ^ 2 * Ci - wcd ^ 2 * CjG3 = ayD - ayB + wbc ^ 2 * Si - wcd ^ 2 * Sj ebc = (G2 * Cj + G3 * Sj) / G1ecd = (G2 * Ci + G3 * Si) / G1axC = axB - ebc * lbc * Sin(fbc) - wbc ^ 2 * lbc * Cos(fbc)ayC = ayB + ebc * lbc * Cos(fbc) - wbc ^ 2 * lbc * Sin(fbc)End SubPrivate Sub RRR2() 'RRR基本杆组leg = Sqr((xG - xE) ^ 2 + (yG - yE) ^ 2)If leg > lef + lfg And leg < Abs(lef - lfg) ThenIf MsgBox("RRR杆组杆长不符合要求", vbOKOnly, "提示") = 1 Then EndElseEnd IfElseEnd IfIf leg < lef + lfg And leg > Abs(lef - lfg) Thenval = (lef ^ 2 + leg ^ 2 - lfg ^ 2) / (2 * lef * leg)jfeg = Atn(-val / Sqr(-val * val + 1)) + 2 * Atn(1)ElseEnd IfIf leg = lef + lfg Thenjfeg = 0ElseEnd IfIf leg = Abs(lef - lfg) ThenIf lef > lfg Thenjfeg = 0ElseEnd IfIf lef < lfg Thenjfeg = piElseEnd IfElseEnd IfIf xG > xE And yG >= yE Then '第一象限feg = Atn((yG - yE) / (xG - xE))ElseEnd IfIf xG = xE And yG > yE Thenfeg = pi / 2ElseEnd IfIf xG < xE And yG >= yE Then '第二象限feg = pi + Atn((yG - yE) / (xG - xE))ElseEnd IfIf xG < xE And yG < yE Then '第三象限feg = pi + Atn((yG - yE) / (xG - xE)) ElseEnd IfIf xG = xE And yG < yE Thenfeg = 3 * pi / 2ElseEnd IfIf xG > xE And yG <= yE Then '第四象限feg = 2 * pi + Atn((yG - yE) / (xG - xE)) ElseEnd Iffef = feg - jfegxF = xE + lef * Cos(fef)yF = yE + lef * Sin(fef)If xF > xG And yF >= yG Then '第一象限ffg = Atn((yF - yG) / (xF - xG))ElseEnd IfIf xF = xG And yF >= yG Thenffg = pi / 2ElseEnd IfIf xF < xG And yF >= yG Then '第二象限ffg = pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfIf xF < xG And yF < yG Then '第三象限ffg = pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfIf xF = xG And yF < yG Thenffg = 3 * pi / 2ElseEnd IfIf xF > xG And yF <= yG Then '第四象限ffg = 2 * pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfCi = lef * Cos(fef)Si = lef * Sin(fef)Cj = lfg * Cos(ffg)Sj = lfg * Sin(ffg)G1 = Ci * Sj - Cj * Siwef = (Cj * (vxG - vxE) + Sj * (vyG - vyE)) / G1wfg = (Ci * (vxG - vxE) + Si * (vyG - vyE)) / G1vxF = vxE - wef * lef * Sin(fef)vyF = vyE + wef * lef * Cos(fef)G2 = axG - axE + wef ^ 2 * Ci - wfg ^ 2 * CjG3 = ayG - ayE + wef ^ 2 * Si - wfg ^ 2 * Sjeef = (G2 * Cj + G3 * Sj) / G1efg = (G2 * Ci + G3 * Si) / G1axF = axE - eef * lef * Sin(fef) - wef ^ 2 * lef * Cos(fef)ayF = ayE + eef * lef * Cos(fef) - wef ^ 2 * lef * Sin(fef)End Sub5．结果及分析图1 E点的运动轨迹（1）由图1所示，E点的运动轨迹呈稍倾斜“8字形”。
哈工大、机械原理大作业、凸轮机构设计20题
Harbin Institute of Technology机械原理大作业二课程名称：机械原理设计题目：凸轮机构设计院系：能源科学与工程学院班级：1102301设计者：刘平成学号：1110200724指导教师：唐德威设计时间：2013年6月7日凸轮机构设计1．设计题目(1) 凸轮机构运动简图：(2)凸轮机构的原始参数表2-1.凸轮机构原始参数 序号 升程（mm ）升程运动角 升程运动规律升程许用压力角20 110 120° 正弦加速度35°回程运动角回程运动规律 回程许用压力角 远休止角近休止角 90°正弦加速度 65°90°60°（二）凸轮运动方程及相关图像、程序凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图： ○1 凸轮推杆升程、回程方程 πϕπϕϕs)650(πϕ≤≤140)(2=ϕs 511()69πφπ≤≤pi))*5708)/(23.2289)/1.-(sin(2+57083.2289)/1.-(-140(1)(3ϕπϕϕ=s1116()99πφπ≤≤)2914(πϕπ≤≤ 0)(4=ϕs ○2速度方程/2.0944;/2.09440))cos(2-140(1)(1πϕϕ=v 16(2)9πφπ≤≤ 0)(2=ϕv 511()69πφπ≤≤ 708;5708))/1.53.2289)/1.-(cos(2-140(1)(3ϕπϕ=v 1116()99πφπ≤≤ 0)(4=ϕv 16(2)9πφπ≤≤○3加速度方程 .0944^2;/2.0944)/2sin(2280)(1πϕπϕ=a )650(πϕ≤≤0)(2=ϕa 511()69πφπ≤≤08^25708)/1.573.2289)/1.-(sin(2280)(3ϕππϕ=a 1116()99πφπ≤≤ 0)(4=ϕa 16(2)9πφπ≤≤推杆位移、速度、加速度线图matlab编程clear,clcpu=0*pi/180:0.0001:120*pi/180; %升程运动角范围pf=120*pi/180:0.0001:210*pi/180; %远休止角范围pd=210*pi/180:0.0001:300*pi/180; %回程运动角范围pn=300*pi/180:0.0001:2*pi; %近休止角范围h=110e-3; %升程w=10; %凸轮角速度p0=120*pi/180; %升程运动角p01=90*pi/180; %回程运动角ps=90*pi/180; %远休止角%----------推程-----------------------------------------su=h.*(pu./p0-sin(2.*pi.*pu./p0)/(2*pi)); %推杆位移vu=h*w/p0*(1-cos(2*pi*pu./p0)); %推程速度au=2*pi*h*w^2/p0^2*sin(2*pi*pu./p0); %推程加速度%------------远休止----------------------------nf=size(pf);sf=h*ones(nf); %推杆位移vf=zeros(nf); %推程速度af=zeros(nf); %推程加速度%---------------回程------------------------------T=pd-(p0+ps);sd=h/2*(1+cos(pi/p01*T)); %回程位移vd=-pi*h*w/(2*p01)*sin(pi/p01*T); %回程速度ad=-pi^2*h*w^2/(2*p01^2)*cos(pi/p01*T); %回程加速度%--------------------近休止---------------------------------nn=size(pn);sn=zeros(nn); %推杆位移vn=zeros(nn); %推程速度an=zeros(nn); % 推程加速度%------画出推杆位移、速度、加速度线图---------------p=[pu,pf,pd,pn];s=[su,sf,sd,sn];subplot(2,3,1),hold onplot(p,s*1e3,'linewidth',2),xlabel('\phi/rad'),ylabel('s/mm'),grid on,title('推杆位移'),axis([0,2*pi,1.1*min(s)*1e3,1.1*max(s)*1e3]) subplot(2,3,2) v=[vu,vf,vd,vn];plot(p,v,'linewidth',2),xlabel('\phi/rad'),ylabel('v/m/s'),grid on,title('推杆速度'),axis([0,2*pi,1.1*min(v),1.1*max(v)]) subplot(2,3,3) a=[au,af,ad,an];plot(p,a,'linewidth',2),xlabel('\phi/rad'),ylabel('a/m/s^2'),grid on,title('推杆加速度'),axis([0,2*pi,1.1*min(a),1.1*max(a)]) hold off（三）凸轮机构s d ds-ϕ图像及程序代码 %--------------------求ds/d_phi-------------------subplot(2,3,4),plot(v/w*1e3,s*1e3,'linewidth',2),xlabel('ds/d\phi/mm'),ylabel('s/mm'),axis equal,grid on,title('ds/d\phi —s')%---------------------凸轮轴心许用区域--------------------------- alpha_up=35*pi/180; %升程许用压力角 alpha_down=65*pi/180; %回程许用压力角 p1=pi/2-alpha_up; %推程斜率角 p2=alpha_down-pi/2; %回程斜率角 ku=tan(p1); %推程切线斜率 kd=tan(p2); %回程切线斜率 R2=[cos(-p2),-sin(-p2);sin(-p2),cos(-p2)];%推程旋转矩阵 R1=[cos(-p1),-sin(-p1);sin(-p1),cos(-p1)];%推程旋转矩阵 nu=size(pu); for i=1:nu(2)Temp=R1*[vu(i)/w;su(i)];vut(i)=Temp(1); %旋转推程ds/dp-s 曲线 sut(i)=Temp(2); endnd=size(pd); for i=1:nd(2)Temp=R2*[vd(i)/w;sd(i)];vdt(i)=Temp(1); %旋转回程ds/dp-s 曲线 sdt(i)=Temp(2); endfor j=1:nu(2)if sut(j)==min(sut)temu=j; %旋转推程ds/dp-s 曲线后求最低点 end endfor j=1:nd(2)if sdt(j)==min(sdt)temd=j; %旋转回程ds/dp-s曲线后求最低点endendt1=1.2*min(vd/w):0.01:1.2*max(vu/w); %切线定义域t2=min(vd/w)/6:0.01:1.2*max(vu/w);t3=0:0.01:1.2*max(vu/w);s1=ku*(t2-vu(temu)/w)+su(temu); %推程切线s2=kd*(t1-vd(temd)/w)+sd(temd); %回程切线s3=tan(-p1)*t3; %推程起点压力角限制线subplot(2,3,5) %画图hold on,axis equal,grid onplot(v/w*1e3,s*1e3,'linewidth',2)plot(t2*1e3,s1*1e3,'linewidth',1,'color','r')plot(t1*1e3,s2*1e3,'linewidth',1,'color','r')plot(t3*1e3,s3*1e3,'linewidth',1,'color','r')xlabel('ds/d\phi/mm'),ylabel('s/mm'),hold off,title('ds/d\phi—s，轴向许用范围')（四）确定凸轮的基圆半径和偏距、绘制凸轮机圆、偏距圆、理论轮廓曲线---------------画理论廓线图-------------------------e=36e-3;s0=52e-3;r0=sqrt(s0^2+e^2);x=(s0+s).*cos(p)-e.*sin(p);y=(s0+s).*sin(p)+e.*cos(p);x1=r0*cos(p);y1=r0*sin(p);subplot(2,3,6)plot(x*1e3,y*1e3,'linewidth',1),axis equal,grid on,hold on,title('廓线图')plot(x1*1e3,y1*1e3,'linewidth',1,'color','r')%-------------求最小曲率半径-----------------------nx=size(x);nx1=nx(2)-2;dydp=diff(y)./diff(p);%求微分dxdp=diff(x)./diff(p);d2ydp2=diff(dydp)./diff(p(1:nx1+1));d2xdp2=diff(dxdp)./diff(p(1:nx1+1));rho=(dxdp(1:nx1).^2+dydp(1:nx1).^2).^1.5./abs((dxdp(1:nx1).*d2ydp2(1:nx1)-dydp(1:nx1).*d2x dp2(1:nx1)));%理论廓线曲率半径rhomin=min(rho);%最小曲率半径rr=rhomin-3e-3;%----------------实际廓线图----------------X=x(1:nx(2)-1)-rr*dydp./(dxdp.^2+dydp.^2).^0.5;%求实际廓线坐标Y=y(1:nx(2)-1)+rr*dxdp./(dxdp.^2+dydp.^2).^0.5;plot(X*1e3,Y*1e3,'linewidth',2,'color','k')%画实际廓线图Legend('理论廓线','基圆','实际廓线'),axis([1.1*min(x)*1e3,1.1*max(x)*1e3,1.1*min(y)*1e3,1.1*max(y)*1e3])得到基圆半径311mm、偏距36mm。
哈工大机械原理连杆和凸轮大作业24题
班级学号机械原理大作业说明书题目 1、连杆机构运动分析2、凸轮机构设计学生姓名1连杆机构运动分析1.设计题目：一、先建立如下坐标系：二、划分杆组如下，进行结构分析：该机构由I级杆组RR（如图1）、II级杆组RPR（如图2、3）和II级杆组RRP（如图4）组成。
（1）（2）（3）（4）三、运动分析数学模型：（1）同一构件上点的运动分析：如右图所示的原动件1,已知杆1的角速度=10/rad s ω，杆长1l =170mm,A y =0，A x =110mm 。
可求得下图中B 点的位置B x 、B y ，速度xB v 、yB v ，加速度xB a 、yB a 。
θcos 1l xB =，θsin 1l yB =θωυsin 1l xB -=，θωυcos 1l yB =，222B2==-cos =-BxB i d x a l x dt ωϕω2222==-sin =-B yB i B d y a l y dtωϕω。
（2）RPRII 级杆组的运动分析：a. 如右图所示是由2个回转副和1个移动副组成的II 级组。
已知两个外运动副C 、B 的位置（B x 、B y 、c x =110mm 、C y =0）、速度（xB υ，yB υ，xC υ=0，yC υ=0）和加速度（0,0,,==yC xC yB xB a a a a ）。
可确定下图中D 点的位置、速度和加速度。
确定构件3的角位移1ϕ、角速度1ω、角加速度1α。
1sin 31..ϕϕl x dt dx C B -= 1s i n 131c o s 13.....2ϕϕϕϕl l x dt x d C B --= 1cos 31..ϕϕl y dt dy C B += 1c o s 131s i n 13.....2ϕϕϕϕl l y dty d C B +-= 根据关系：1111d 122..11.αϕϕωϕϕ====dtd dt ， 故可得出： D x =)1cos(4βϕ++l x CD y =)1sin(4βϕ++l y Cb. 如右图所示是由2个回转副和1个移动副组成的II级组。
哈工大-机械原理大作业-连杆机构运动分析
机械原理大作业（一）作业名称：连杆机构运动分析设计题目： 20院系：英才学院班级： XXXXXXX设计者：邵广斌学号： XXXXXXXXXX指导教师：林琳设计时间： 2013年05月19日哈尔滨工业大学机械设计1.运动分析题目如图所示机构，已知机构各构件的尺寸为150AB mm =，97β=︒，400BC mm =，300CD mm =，320AD mm =，100BE mm =，230EF mm =，400FG mm =，构件1的角速度为110/rad s ω=,试求构件2上点F 的轨迹及构件5上点G 的位移、速度和加速度，并对计算结果进行分析。
2. 机构分析该机构由原动件AB （Ⅰ级杆组）、BCD （RRR Ⅱ级杆组）和FG （RRP Ⅱ级杆组）组成。
3. 建立坐标系如图3，建立以定点A 为原点的平面直角坐标系A-xy 。
图1 运动机构结构图4. 运动分析数学模型4.1 原动件AB原动件AB 的转角： 10~2ψπ= 原动件AB 的角速度：110/rad s ω=原动件AB 的角加速度： 10α= 运动副A 的位置坐标： 0A x = 0A y =运动副A 的速度： 0xA v = 0yA v = 运动副A 的加速度： 0xA a = 0yA a =原动件AB 长度：150AB l mm =运动副B 的位置坐标： 1B A AB x x l cos ψ=+1B A AB y x l sin ψ=+运动副B 的速度： 11 xB xA AB v v l sin ωψ=-11 yB yA AB v v l cos ωψ=+运动副B 的加速度： 2 1111 xBxA AB AB a a l cos l sin ωψαψ=--21111yB yA AB AB a a l sin l cos ωψαψ=-+4.2 RRR Ⅱ级杆组BCD运动副D 的位置坐标： 320D x mm = 0D y = 运动副D 的速度： 0xD v = 0yD v = 运动副D 的加速度： 0xD a = 0yD a = 杆BC 长度： 400BC l mm = 杆CD 长度：300CD l mm =BC 相对于x 轴转角：200ψ=其中02BC D B A l x x =-（） 0 2 BC D B B l y y =-（）2220B B C C l C l D l D =+- 222())(BDD B D B l x x y y =-+- CD 相对于x 轴转角： 3C DC Dy y arctanx x ψ-=-求导可得BC 角速度2ω、角加速度2α以及CD 角速度3ω、角加速度3α。
哈工程机械原理题库
哈工程机械原理题库一、是非题，判断下列各题,对的画“√”，错的画“×”（每题2分，共10分）1、Ⅱ级机构的自由度不能大于2；（）2、铰链四杆机构中，若存在曲柄，其曲柄一定是最短杆。
（）3、当凸轮机构的压力角过大时，机构易出现自锁现象。
（）4、国产标准斜齿圆柱齿轮的端面齿顶高等于法面齿顶高；（）5、棘轮机构和槽轮机构都是间歇运动机构。
（）1、机构中与机架相联的每个主动件相对机架可以有两个以上的独立运动。
（）2、摆动导杆机构中的导杆一定具有急回特性（曲柄为原动件）。
（）3、直动从动件盘形凸轮机构可以用增大基圆半径的方法减小其推程压力角。
（）4、与标准齿轮相比，负变位齿轮的分度圆变大。
（）5、标准直齿圆柱齿轮外啮合时，只能有1对轮齿啮合。
（）1、机构是具有确定运动的运动链。
（）2、直动从动件盘形凸轮机构中进行合理偏置是为了减小推程压力角和回程压力角。
（）3、平面四杆机构有无急回特性取决于极位夹角是否大于零。
（）4、用成形铣刀加工渐开线直齿圆柱齿轮时，一定会发生根切现象。
（）5、直齿圆锥齿轮的标准模数是指中间截面的模数；（）二、单项选择题（每小题2分，共10分）1、在铰链四杆机构中，取（）杆作为机架，则可得到双摇杆机构。
A ．最短杆； B ．最短杆的对边； C ．最长杆； D ．连杆2、下列为空间齿轮机构的是（）机构。
A ．圆锥齿轮；B ．人字齿轮； C ．平行轴斜齿圆柱齿轮；D ．直齿圆柱齿轮3、表征蜗杆传动的参数和几何尺寸关系的平面应为（）。
A ．轴面；B ．端面；C ．中间平面；D ．法面4、在机构中原动件数目（）机构自由度时，该机构具有确定的运动。
A ．小于；B ．等于；C ．大于；D ．大于等于5、作连续往复移动的构件，在行程的两端极限位置处，其运动状态必定是（）。
A ．0=v ，0=a ； B ．0≠v ，0=a ； C ．0=v ，0≠a ； D ．0≠v ，0≠a 。
1、平面连杆机构是由若干构件和（）组成的平面机构。
(完整word版)哈工大机械原理试卷
一.填空题（本大题共7小题，每空1分， 共15分）1. 按照两连架杆可否作整周回转，平面连杆机构分为 、 和 。
2. 平面连杆机构的 角越大，机构的传力性能越好。
3. 运动副按接触形式的不同，分为 和 。
4．直齿圆柱齿轮正确啮合条件是两齿轮的 和 分别相等。
5. 凸轮从动件按其端部的形状可分为 从动件、 从动件和从动件动件。
6. 机构具有确定运动的条件是： 。
7．通过将铰链四杆机构的转动副之一转化为移动副时，则可得到具有移动副的 机构、 机构、摇块机构和 机构。
二．选择题（本大题共15小题，每小题1分，共15分）1. 要实现两相交轴之间的传动，可采用 传动。
A ．直齿圆柱齿轮B ．斜齿圆柱齿轮C ．直齿锥齿轮D ．蜗杆蜗轮2. 我国标准规定，对于标准直齿圆柱齿轮，其ha*= 。
A ．1B ．0.25C ．0.2D ．0.83. 在机械传动中，若要得到大的传动比，则应采用 传动。
A. 圆锥齿轮B. 圆柱齿轮C. 蜗杆D. 螺旋齿轮4. 当四杆机构处于死点位置时，机构的压力角为 。
A ．0°B ．90°C ．45°D ．15°5. 一般情况凸轮机构是由凸轮、从动件和机架三个基本构件组成的 机构。
A ．转动副B ．移动副C ．高副D ．空间副6. 齿轮的渐开线形状取决于它的 直径。
A ．齿顶圆B ．分度圆C ．基圆D ．齿根圆7. 对于滚子从动件盘形凸轮机构，滚子半径 理论轮廓曲线外凸部分的最小曲率半径。
A ．必须小于B ．必须大于C ．可以等于D ．与构件尺寸无关8. 渐开线直齿圆柱齿轮中，齿距p ，法向齿距n p ，基圆齿距b p 三者之间的关系为 。
A.p p p n b <=B.p p p n b <<C.p p p n b >>D. p p p n b =>9. 轻工机械中常需从动件作单向间歇运动，下列机构中不能实现该要求的是 。
哈工大机械原理凸轮大作业-24江湖青衫版
实用标准H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业（二）课程名称：机械原理设计题目：凸轮机构设计-24院系：机电工程学院班级： 1108***班设计者：江湖青衫学号： 11108*****指导教师：×××设计时间： 2013年6月哈尔滨工业大学机电工程学院一、设计题目 如右图所示直动从动件盘形凸轮机构，选择一组凸轮机构的原始参数，据此设计该凸轮机构。
二. 凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图凸轮推杆正弦加速度升程运动方程：)]2sin(21[s oo h Φ-Φ=πϕπϕ)2sin(2)]2cos(1[v 2121ϕππϕπωωo oh a oo h ΦΦ=Φ-Φ=凸轮推杆余弦加速度回程运动方程：[]})('cos1{2s s o o hΦ+Φ-Φ+=ϕπ[])('cos '2)](['sin'2v 21221s o o o h a s o o o hΦ+Φ-ΦΦ-=Φ+Φ-ΦΦ-=ϕππϕππωω1、推杆位移线图% t表示转角 ，s表示位移t=0:0.01:5*pi/6; %升程阶段s=120*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)]; hold onplot(t,s);t= 5*pi/6:0.01:10*pi/9; %远休止阶段s=120;hold onplot(t,s);t=10*pi/9:0.01:5*pi/3; %回程阶段s=60*[1+cos(9*(t-10*pi/9)/5)];hold onplot(t,s);t=5*pi/3:0.01:2*pi; %近休止阶段s=0;hold onplot(t,s);grid onhold offtitle('推杆位移线图','FontSize',20);2、推杆速度线图% t表示转角 ，令ω1=1t=0:0.01:5*pi/6; %升程阶段v=144*1*[1-cos(12*t/5)]/pihold onplot(t,v);t= 5*pi/6:0.01:10*pi/9; %远休止阶段v=0hold onplot(t,v);t=10*pi/9:0.01:5*pi/3; %回程阶段v=-108*1*sin(9*(t-10*pi/9)/5)hold onplot(t,v);t=5*pi/3:0.01:2*pi; %近休止阶段v=0hold ontitle('推杆速度线图','FontSize',20);3、推杆加速度线图% t表示转角 ，令ω1=1t=0:0.001:5*pi/6; %升程阶段a=345.6*sin(12*t/5)/pi;hold onplot(t,a);t=5*pi/6:0.01:10*pi/9; %远休止阶段a=0;hold onplot(t,a);t=10*pi/9:0.001:5*pi/3; %回程阶段a=-194.4*cos(9*(t-10*pi/9)/5);hold onplot(t,a);t=5*pi/3:0.001:2*pi; %近休止阶段a=0;hold ontitle('推杆加速度线图','FontSize',20);三. 绘制凸轮机构的sdds-ϕ线图% t表示转角ϕ，x(横坐标)表示速度ds/dϕ，y（纵坐标）表示位移s t=0:0.001:5*pi/6; % 升程阶段x= 144/pi-144*cos(12*t/5)/pi;y= 120*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)];hold onplot(x,y,'-r');t= 5*pi/6:0.01:10*pi/9; %远休止阶段x=0;y=120;hold onplot(x,y,'-r');t=10*pi/9:0.001:5*pi/3; % 回程阶段x=-180*1*sin(9*(t-10*pi/9)/5);y=60*[1+cos(9*(t-10*pi/9)/5)];hold onplot(x,y,'-r');t=14*pi/9:0.01:2*pi; %近休止阶段x=0;y=0;hold onplot(x,y,'-r');grid onhold offtitle('凸轮机构的ds/dφ-s线图','FontSize',20);四.按许用压力角确定凸轮基圆半径和偏距1. 求切点转角（1）在图-4中，右侧曲线为升程阶段的类速度-位移图，作直线D t d t与其相切，且位移轴正方向呈夹角[α1]=400,但是为了安全起见，可缩小需用压力角至[α1]=300，则切点处的斜率与直线D t d t的斜率相等，故右侧曲线斜率可以表示为k Dtdt=tan600, 通过编程求其角度。
哈工大—机械原理凸轮大作业
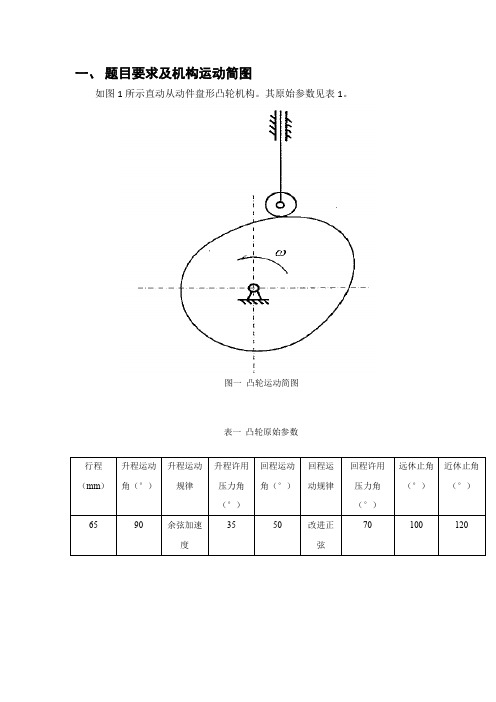
一、题目要求及机构运动简图如图1所示直动从动件盘形凸轮机构。
其原始参数见表1。
图一凸轮运动简图表一凸轮原始参数二、计算流程框图凸轮机构分析建立数学模型位移方程速度方程加速度方程速度线图位移线图加速线图ds/dΨ-s曲线升程压力角回程压力角确定轴向及基圆半径压力角图确定滚子半径实际轮廓理论轮廓轮廓图结束三、建立数学模型1.从动件运动规律方程首先，由于设计凸轮轮廓与凸轮角速度无关，所以不妨设凸轮运动角速度为w = 1rad/s。
（1）推程运动规律(0 < φ < 90°)s=φ）v=φφ）a=φφ）式中：h=65mm，Φ0=π/2（2）远休程运动规律(90°< φ < 190°)s = 65mmv = 0a = 0（3）回程运动规律(190°< φ < 240°)(190°< φ < 196.25°)(196.25°< φ < 233.75°)(233.75°< φ < 240°) 回程运动中的速度和加速度为位移对时间t的倒数：（4）近休程运动规律(240°< φ < 360°)s = 0v = 0a = 02.从动件位移、速度、加速度线图（1）位移线图（2）速度线图（3）加速度线图（4）位移、速度、加速度线图MATLAB源程序%% 已知条件h = 65; %mmphi_0 = 90./180*pi; %radalpha_up_al = 35./180*pi; %升程许用压力角phi_00 = 50./180*pi;alpha_down_al = 70./180*pi; %回程许用压力角phi_s = 100./180*pi;phi_ss = 120./180*pi;w = 1;%% 绘制从动件位移、速度、加速度线图% 推程阶段t_up = 0 : 0.5 : 90;t_up1 = t_up./180*pi;syms t_up1phi_up s_up v_up a_upphi_up = w.*t_up1;s_up = h./2.*(1 - cos(pi.*phi_up./phi_0));v_up = diff(s_up,t_up1);a_up = diff(v_up,t_up1);s_up1 = double(subs(s_up,t_up./180*pi));v_up1 = double(subs(v_up,t_up./180*pi));a_up1 = double(subs(a_up,t_up./180*pi));% 远休程t_s = 90 : 0.5 : (90+100);t_s1 = t_up./180*pi;s_s(1:201) = h;v_s(1:201) = 0;a_s(1:201) = 0;% 回程阶段1t_down1 = (90+100) : 0.5 : (90+100+50/8);t_down11 = t_down1./180*pi;syms t_down11phi_down1s_down1v_down1a_down1phi_down1 = w.*t_down11;s_down1 = h - h./(4+pi).*(pi.*(phi_down1 - phi_0 - phi_s)./phi_00 - ...sin(4.*pi.*(phi_down1 - phi_0 - phi_s)./phi_00)./4);v_down1 = diff(s_down1,t_down11);a_down1 = diff(v_down1,t_down11);s_down11 = double(subs(s_down1,t_down1./180*pi));v_down11 = double(subs(v_down1,t_down1./180*pi));a_down11 = double(subs(a_down1,t_down1./180*pi));% 回程阶段2t_down2 = (90+100+50/8) : 0.5 : (90+100+7*50/8);t_down22 = t_down2./180*pi;syms t_down22phi_down2s_down2v_down2a_down2phi_down2 = w.*t_down22;s_down2 = h - h./(4+pi).*(2+pi.*(phi_down2 - phi_0 - phi_s)./phi_00 - 9.*sin(pi./3 + 4.*pi.*(phi_down2 - phi_0 - phi_s)./(3.*phi_00))./4);v_down2 = diff(s_down2,t_down22);a_down2 = diff(v_down2,t_down22);s_down22 = double(subs(s_down2,t_down2./180*pi));v_down22 = double(subs(v_down2,t_down2./180*pi));a_down22 = double(subs(a_down2,t_down2./180*pi));% 回程阶段3t_down3 = (90+100+7*50/8) : 0.5 : (90+100+50);t_down33 = t_down3./180*pi;syms t_down33phi_down3s_down3v_down3a_down3phi_down3 = w.*t_down33;s_down3 = h - h./(4+pi).*(4+pi.*(phi_down3 - phi_0 - phi_s)./phi_00 - …sin(4.*pi.*(phi_down3 - phi_0 - phi_s)./phi_00)./4);v_down3 = diff(s_down3,t_down33);a_down3 = diff(v_down3,t_down33);s_down33 = double(subs(s_down3,t_down3./180*pi));v_down33 = double(subs(v_down3,t_down3./180*pi));a_down33 = double(subs(a_down3,t_down3./180*pi));% 近休程t_ss = (90+100+50) : 0.5 : 360;s_ss(1:241) = 0;v_ss(1:241) = 0;a_ss(1:241) = 0;% 绘图位移t = [t_up t_s t_down1 t_down2 t_down3 t_ss];phi = w .* t ./ 180 .*pi;s = [s_up1 s_s s_down11 s_down22 s_down33 s_ss];v = [v_up1 v_s v_down11 v_down22 v_down33 v_ss];a = [a_up1 a_s a_down11 a_down22 a_down33 a_ss];figure('Name','从动件位移-时间线图');plot(t,s,'k','linewidth',1.0);grid on;title('从动件位移-时间线图');xlabel('转角\phi / 度');ylabel('位移h/mm');% 绘图速度figure('Name','从动件速度-时间线图');plot(t,v,'k','linewidth',1.0);grid on;title('从动件速度-时间线图');xlabel('转角\phi / 度');ylabel('速度v/mm*s^{-1}');% 绘图加速度figure('Name','从动件加速度-时间线图');plot(t,a,'k','linewidth',1.0);grid on;title('从动件加速度-时间线图');xlabel('转角\phi / 度');ylabel('加速度a/mm*s^{-2}');3.绘制ds/dΦ线图并确定基圆半径和偏距（1）绘制ds/dΦ线图及源程序①MATLAB源程序：%% 绘制ds/dphi-s线图，确定基圆半径和偏距ds_dphi = v ./ w;figure('Name','凸轮ds/dphi - s线图');plot(ds_dphi,s,'k','linewidth',1.5);hold on;axis([-150 150 -70 70]);grid on;title('凸轮ds/dphi - s线图');xlabel('ds/dphi / (mm*s^{-2})');ylabel('s/mm');% 三条临界线x = linspace(-150,150,301);k_up = tan(pi/2 - alpha_up_al);y_up = k_up.*x - 66;plot(x,y_up,'linewidth',1.5);k_down = - tan(pi/2 - alpha_down_al);y_down = k_down.*x - 24.7;plot(x,y_down,'linewidth',1.5);x0 = linspace(0,150,151);k0 = - tan(alpha_up_al);y0 = k0.*x0;plot(x0,y0,'--');% 由图像选取凸轮基圆半径为r0 = sqrt(23^2 + 34^2) = 41 mm,偏距e = 23mm plot(23,-34,'or');r0 = 41;e = 23;plot(linspace(0,23,10),linspace(0,-34,10),'r',linspace(0,23,10),linspace(-34,-34,10),'r',li nspace(23,23,10),linspace(0,-34,10),'r','linewidth',1.0);（2）确定基圆半径和偏距在凸轮机构的ds/d φ-s 线图里再作斜直线Dt-dt 与升程的[ds/d φ-s]曲线相切并使与纵坐标夹角为升程许用压力角[α]，则Dt-dt 线的右下方为选择凸轮轴心的许用区。
哈工大—机械原理凸轮大作业
一、题目要求及机构运动简图如图1所示直动从动件盘形凸轮机构。
其原始参数见表1。
图一凸轮运动简图表一凸轮原始参数二、计算流程框图凸轮机构分析建立数学模型位移方程速度方程加速度方程速度线图位移线图加速线图ds/dΨ-s曲线升程压力角回程压力角确定轴向及基圆半径压力角图确定滚子半径实际轮廓理论轮廓轮廓图结束三、建立数学模型1.从动件运动规律方程首先，由于设计凸轮轮廓与凸轮角速度无关，所以不妨设凸轮运动角速度为w = 1rad/s。
（1）推程运动规律(0 < φ < 90°)s=h2×[1−cos(πφ0×φ）]v=πhw2φ0×sin(πφ0×φ）a=π2ℎw22φ02×cos(πφ0×φ）式中：h=65mm，Φ0=π/2（2）远休程运动规律(90°< φ < 190°)s = 65mmv = 0a = 0（3）回程运动规律(190°< φ < 240°)s1=h−h4+π∗(π∗(φ−φ0−φs)φ0′−sin(4∗π∗φ−φ0−φsφ0′)4)(190°< φ < 196.25°)s2=h−h4+π∗(2+π∗(φ−φ0−φs)φ0′−9∗sin(π3+4∗π∗φ−φ0−φs3∗φ0′)4)(196.25°< φ < 233.75°)s3=h−h4+π∗(4+π∗(φ−φ0−φs)φ0′−sin(4∗π∗φ−φ0−φsφ0′)4)(233.75°< φ < 240°)回程运动中的速度和加速度为位移对时间t的倒数：v=ds dta=dv dt（4）近休程运动规律(240°< φ < 360°)s = 0v = 0a = 02.从动件位移、速度、加速度线图（1）位移线图（2）速度线图（3）加速度线图（4）位移、速度、加速度线图MATLAB源程序%% 已知条件h = 65; %mmphi_0 = 90./180*pi; %radalpha_up_al = 35./180*pi; %升程许用压力角phi_00 = 50./180*pi;alpha_down_al = 70./180*pi; %回程许用压力角phi_s = 100./180*pi;phi_ss = 120./180*pi;w = 1;%% 绘制从动件位移、速度、加速度线图% 推程阶段t_up = 0 : 0.5 : 90;t_up1 = t_up./180*pi;syms t_up1phi_up s_up v_up a_upphi_up = w.*t_up1;s_up = h./2.*(1 - cos(pi.*phi_up./phi_0));v_up = diff(s_up,t_up1);a_up = diff(v_up,t_up1);s_up1 = double(subs(s_up,t_up./180*pi));v_up1 = double(subs(v_up,t_up./180*pi));a_up1 = double(subs(a_up,t_up./180*pi));% 远休程t_s = 90 : 0.5 : (90+100);t_s1 = t_up./180*pi;s_s(1:201) = h;v_s(1:201) = 0;a_s(1:201) = 0;% 回程阶段1t_down1 = (90+100) : 0.5 : (90+100+50/8);t_down11 = t_down1./180*pi;syms t_down11phi_down1s_down1v_down1a_down1phi_down1 = w.*t_down11;s_down1 = h - h./(4+pi).*(pi.*(phi_down1 - phi_0 - phi_s)./phi_00 - ...sin(4.*pi.*(phi_down1 - phi_0 - phi_s)./phi_00)./4);v_down1 = diff(s_down1,t_down11);a_down1 = diff(v_down1,t_down11);s_down11 = double(subs(s_down1,t_down1./180*pi));v_down11 = double(subs(v_down1,t_down1./180*pi));a_down11 = double(subs(a_down1,t_down1./180*pi));% 回程阶段2t_down2 = (90+100+50/8) : 0.5 : (90+100+7*50/8);t_down22 = t_down2./180*pi;syms t_down22phi_down2s_down2v_down2a_down2phi_down2 = w.*t_down22;s_down2 = h - h./(4+pi).*(2+pi.*(phi_down2 - phi_0 - phi_s)./phi_00 - 9.*sin(pi./3 + 4.*pi.*(phi_down2 - phi_0 - phi_s)./(3.*phi_00))./4);v_down2 = diff(s_down2,t_down22);a_down2 = diff(v_down2,t_down22);s_down22 = double(subs(s_down2,t_down2./180*pi));v_down22 = double(subs(v_down2,t_down2./180*pi));a_down22 = double(subs(a_down2,t_down2./180*pi));% 回程阶段3t_down3 = (90+100+7*50/8) : 0.5 : (90+100+50);t_down33 = t_down3./180*pi;syms t_down33phi_down3s_down3v_down3a_down3phi_down3 = w.*t_down33;s_down3 = h - h./(4+pi).*(4+pi.*(phi_down3 - phi_0 - phi_s)./phi_00 - …sin(4.*pi.*(phi_down3 - phi_0 - phi_s)./phi_00)./4);v_down3 = diff(s_down3,t_down33);a_down3 = diff(v_down3,t_down33);s_down33 = double(subs(s_down3,t_down3./180*pi));v_down33 = double(subs(v_down3,t_down3./180*pi));a_down33 = double(subs(a_down3,t_down3./180*pi));% 近休程t_ss = (90+100+50) : 0.5 : 360;s_ss(1:241) = 0;v_ss(1:241) = 0;a_ss(1:241) = 0;% 绘图位移t = [t_up t_s t_down1 t_down2 t_down3 t_ss];phi = w .* t ./ 180 .*pi;s = [s_up1 s_s s_down11 s_down22 s_down33 s_ss];v = [v_up1 v_s v_down11 v_down22 v_down33 v_ss];a = [a_up1 a_s a_down11 a_down22 a_down33 a_ss];figure('Name','从动件位移-时间线图');plot(t,s,'k','linewidth',1.0);grid on;title('从动件位移-时间线图');xlabel('转角\phi / 度');ylabel('位移h/mm');% 绘图速度figure('Name','从动件速度-时间线图');plot(t,v,'k','linewidth',1.0);grid on;title('从动件速度-时间线图');xlabel('转角\phi / 度');ylabel('速度v/mm*s^{-1}');% 绘图加速度figure('Name','从动件加速度-时间线图');plot(t,a,'k','linewidth',1.0);grid on;title('从动件加速度-时间线图');xlabel('转角\phi / 度');ylabel('加速度a/mm*s^{-2}');3.绘制ds/dΦ线图并确定基圆半径和偏距（1）绘制ds/dΦ线图及源程序①MATLAB源程序：%% 绘制ds/dphi-s线图，确定基圆半径和偏距ds_dphi = v ./ w;figure('Name','凸轮ds/dphi - s线图');plot(ds_dphi,s,'k','linewidth',1.5);hold on;axis([-150 150 -70 70]);grid on;title('凸轮ds/dphi - s线图');xlabel('ds/dphi / (mm*s^{-2})');ylabel('s/mm');% 三条临界线x = linspace(-150,150,301);k_up = tan(pi/2 - alpha_up_al);y_up = k_up.*x - 66;plot(x,y_up,'linewidth',1.5);k_down = - tan(pi/2 - alpha_down_al);y_down = k_down.*x - 24.7;plot(x,y_down,'linewidth',1.5);x0 = linspace(0,150,151);k0 = - tan(alpha_up_al);y0 = k0.*x0;plot(x0,y0,'--');% 由图像选取凸轮基圆半径为r0 = sqrt(23^2 + 34^2) = 41 mm,偏距e = 23mm plot(23,-34,'or');r0 = 41;e = 23;plot(linspace(0,23,10),linspace(0,-34,10),'r',linspace(0,23,10),linspace(-34,-34,10),'r',li nspace(23,23,10),linspace(0,-34,10),'r','linewidth',1.0);（2）确定基圆半径和偏距在凸轮机构的ds/d φ-s 线图里再作斜直线Dt-dt 与升程的[ds/d φ-s]曲线相切并使与纵坐标夹角为升程许用压力角[α]，则Dt-dt 线的右下方为选择凸轮轴心的许用区。
哈尔滨工业大学机械原理大作业凸轮设计
大作业1连杆机构运动分析1.题目（8）如图所示机构，已知机构各构件的尺寸为==100AC CE l l mm ，==200BC CD l l mm ，90BCD ∠=︒，构件1的角速度为1=10/w rad s ，试求构件5的角位移、角速度和角加速度，并对计算结果进行分析。
1.1机构的运动分析AB 为原动件，AB 转动通过转动导杆机构带动杆BCD 转动，BCD 转动通过转动导杆机构带动杆DE 摆动。
1.2 机构的结构分析杆组可以划分为一个RR I级杆组（杆1）、RRPII级杆组（滑块2,杆3）、RPRII 级杆组（滑块4,杆5）（1）RRI级杆组1：（2）RRPII级杆组2,3：（3）RPRII级杆组4,5：2．分析过程 2.1 建立坐标系建立以点E 为原点的固定平面直角坐标系x-E-y ，如图所示。
2.2 建立数学模型（1）构件1、2、3的分析原动件杆1的转角：1θ=0--360。
原动件杆1的角速度：1ω=.1θ=10/rad s 原动件杆1的角加速度：..1αθ==0运动副A 的坐标：0200A A x y mm =⎫⎬=⎭运动副A 的速度及加速度都为零。
构件1为BC （RRP Ⅱ级杆组）上滑块B 的导路 滑块B 的位置为：132cos cos B A C x x s x l θθ=+=+132sin sin B A C y y s x l θθ=+=+消去s,得：0212arcsinA l θθ=+式中：011()sin ()cos C A C A A x x y y θθ=---构件3的角速度i ω和滑块B 沿导路的移动速度D υ：.211213(Q sin Q cos )/Q ωϕθθ==-+ 1322323(Q cos Q sin )/Q D s l l υθθ⋅==-+式中：..11111211321212Q sin ;Q cos ;Q sin sin cos sin l l l θθθθθθθθ=-==+构件3的角加速度和滑块B 沿导路移动的加速度：..241513(Q sin Q cos )/Q αθθθ==-+..4325323(Q cos Q sin )/Q B s l l υθθ==-+式中：122......21142211111Q cos sin cos 2sin l l l s θθθθθθθθ=---- 122......21152211111Q sin cos sin 2cos l l l s θθθθθθθθ=+-+（2）构件3,4,5的分析构件3,4,5,由1个Ⅰ级基本杆组和一个RRP Ⅱ级杆组组成，与构件1,2,3结构相同，只运动分析过程与其相反。
哈工大机械原理大作业2-29
设计说明书1 设计题目如图所示直动从动件盘形凸轮机构，其原始参数见表2-1。
从表2-1中选择一组凸轮机构的原始参数，据此设计该凸轮机构。
2、推杆升程、回程运动方程及位移、速度、加速度线图2.1凸轮运动分析 推程运动方程; 01cos 2h s πϕ⎡⎤⎛⎫=-⎢⎥ ⎪Φ⎝⎭⎣⎦100sin 2h v πωπϕ⎛⎫=⎪ΦΦ⎝⎭221200cos 2h a πωπϕ⎛⎫= ⎪ΦΦ⎝⎭回程运动方程：()'1s s hϕ-Φ+Φ⎡⎤=-⎢⎥Φ⎣⎦1'hvω=-Φa=2.2求位移、速度、加速度线图MATLAB源程序pi=3.1415926;c=pi/180;h=140;f0=120;fs=45;f01=90;fs1=105;%升程阶段f=0:1:360;for n=0:f0s(n+1)=h/2*(1-cos(pi/f0*f(n+1)));v(n+1)=pi*h/(2*f0*c)*sin(pi/f0*f(n+1));a(n+1)=pi^2*h/(2*f0^2*c^2)*cos(pi/f0*f(n+1));end%远休止阶段for n=f0:f0+fss(n+1)=140;v(n+1)=0;a(n+1)=0;end%回程阶段for n=f0+fs:f0+fs+f01s(n+1)=h*(1-(f(n+1)-(f0+fs))/f01);v(n+1)=-h/(f01*c);a(n+1)=0;end;%近休止阶段for n=f0+fs+f01:360;s(n+1)=0;v(n+1)=0;a(n+1)=0;endfigure(1);plot(f,s,'r');xlabel('\phi/\circ');ylabel('s/mm');grid on;title('推杆位移线图')figure(2);plot(f,v,'r');xlabel('\phi/\circ');ylabel('v/\ommiga');grid on;title('推杆速度线图') figure(3);plot(f,a,'r');xlabel('\phi/\circ');ylabel('a/\ommiga');grid on;title('推杆加速度线图')2.3位移、速度、加速度线图3 凸轮机构的dssdϕ-线图，确定基圆半径和偏心距3.1理论分析机构压力角α应按下式计算：以d s/dφ为横坐标，以s(φ)为纵坐标，可作出d s/dφ-s(φ)曲线如图4-16所示，再作斜直线D t d t 与升程的[d s/dφ-s(φ)]曲线相切并使与纵坐标夹角为升程[α]，则D t d t线的右下方为选择凸轮轴心的许用区。
哈尔滨工业大学《机械原理》期末考试试题与答案
哈尔滨工业大学《机械原理》期末考试试题与答案第一篇：哈尔滨工业大学《机械原理》期末考试试题与答案机械原理期末考试试题与答案一、问答题（15分）1．什么是连杆机构的压力角、传动角？（2分）答：不考虑运动副中的摩擦力、构件的惯性力，运动副中力的作用线与受力点速度方向所夹的锐角称为压力角，压力角的余角称为传动角。
2．什么是基本杆组？机构的组成原理是什么？（2分）答：机构中，结构最简单、不可再分的、自由度为零的构件组称为基本杆组。
任一机构都可以看作是由若干个基本杆组依次连接于原动件和机架上所组成的，这就是机构的组成原理。
3．常用的间歇运动机构有几种？其主动件与从动件的运动转换各有什么特点？（2分）答：常用的间歇运动机构有：棘轮机构、槽轮机构和不完全齿轮机构。
棘轮机构把一个往复摆动转换为间歇单向转动；槽轮机构把一个连续单向转动转换为间歇单向转动；不完全齿轮机构把一个连续单向转动转换为间歇单向转动。
4．什么是槽轮机构的运动系数？（2分）答：槽轮的运动时间与拨盘的运动时间的比值称为槽轮机构的运动系数。
5．通常，机器的运转过程分为几个阶段？各阶段的特征是什么？（3分）答：机器的运转过程分为三个阶段：启动阶段，稳定运转阶段和停车阶段。
启动阶段的特点：原动件速度由零上升到稳定运转速度，系统驱动力所做的功大于阻抗力所消耗的功。
稳定运转阶段的特点：在一个周期内，系统驱动力所做的功等于阻抗力所消耗的功。
停车阶段的特点：系统驱动力所做的功小于于阻抗力所消耗的功，原动件速度由稳定运转速度下降为零。
6．利用飞轮进行机器的周期性速度波动调节时，飞轮一般安装在高速轴还是低速轴上？为什么？（2分）答：安装在高速轴上。
这样可以使飞轮的质量减小。
（2分）7．平行轴外啮合斜齿圆柱齿轮的正确啮合条件是什么？答：模数相等、压力角相等、螺旋角大小相等旋向相反。
二、下图机构中，已知JK//LM//NO，并且JK=LM=NO，EG=GH=FG，EF⊥FH，求该机构的自由度。
哈工大机械原理大作业1
420.636249
198
-25.780027
-7.408008
448.711622
19
17.496096
11.511568
389.280068
199
-27.066134
-7.329197
454.399338
20
19.511173
11.576658
356.588380
200
-28.338399
-6.837081
484.309157
26
31.792111
11.837106
133.586249
206
-35.672384
-6.752179
488.602299
27
33.860111
11.856813
92.240035
207
-36.843419
-6.666544
492.701606
28
35.930920
（4）利用导数的定义与其物理意义
利用上述公式，选取适当的步长h，利用F点位移就可以得出速度与加速度
5、用VC编程
#include <stdio.h>
#include <math.h>
#define pi 3.14159265358979323846
//定义全局变量
double Lab,Lbc,Lcd,Xf,Xd,Yd;//定义已知位置量
11.079883
-670.906136
223
-53.471235
-5.223053
533.839546
44
68.312705
10.958430
机械原理大作业齿轮24题
Harbin Institute of Technology机械原理大作业一课程名称：机械原理设计题目：齿轮传动机构设计院系：班级：设计者：学号：指导教师：设计时间： 2013/05/291、设计题目机构运动简图：械传动系统原始参数：序号 电机转速（r/min ）输出轴转速（r/min ）带传动最大传动比 滑移齿轮传动定轴齿轮传动 最大传动比模数圆柱齿轮 圆锥齿轮 一对齿轮最大传动比模数一对齿轮最大传动比模数24 745 33 37 41 5.2≤ 4≤ 2 4≤ 3 4≤ 32、传动比的分配计算电动机转速n=745r/min ，输出转速n 1=33 r/min ，n 2=37 r/min ，n 3=41 r/min ，带传动的最大传动比max p i =2.5,滑移齿轮传动的最大传动比max v i =4，定轴齿轮传动的最大传动比max d i =4。
根据传动系统的原始参数可知，传动系统的总传动比为：171.184174511===n n i 135.203774522===n n i 576.223374533===n n i传动系统的总传动比由带传动、滑移齿轮传动和定轴齿轮传动三部分实现。
设带传61,15,60,17,58,181098765======z z z z z z 1*=ah 动的传动比为5.2max =p i ，滑移齿轮的传动比为321,v v v i i i 和，定轴齿轮传动的传动比为f i ，则总传动比：fv p i i i i 1max 1= fv p i i i i 2max 2= f v p i i i i 3max 3=令：4max 3==v v i i则可得定轴齿轮传动部分的传动比： 258.245.2576.22max max 3=⨯==v p f i i i i滑移齿轮传动的传动比： 219.3258.25.2171.18max 11=⨯==fp v i i i i567.3258.25.2135.20max 22=⨯==fp v i i i i定轴齿轮传动由3对齿轮传动组成，则每对齿轮的传动比为 4312.1258.2max 33=≤===d f d i i i3、齿轮齿数的确定根据滑移齿轮变速传动系统中对齿轮齿数的要求，可大致选择齿轮5、6、7、8、9角度变位齿轮，其齿数：它们的齿顶高系数径向间隙系数25.0*=c ，分和10为度圆压力角α=20°，实际中心距77'=a 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
班级1013102学号 6机械原理大作业说明书题目 1、连杆机构运动分析2、凸轮机构设计3、齿轮传动设计学生姓名1连杆机构运动分析1.设计题目：一、先建立如下坐标系：二、划分杆组如下，进行结构分析：该机构由I级杆组RR（如图1）、II级杆组RPR（如图2、3）和II级杆组RRP（如图4）组成。
（1）（2）（3）（4）三、运动分析数学模型：（1）同一构件上点的运动分析：如右图所示的原动件1,已知杆1的角速度=10/rad s ω，杆长1l =170mm,A y =0，A x =110mm 。
可求得下图中B 点的位置B x 、B y ，速度xB v 、yB v ，加速度xB a 、yB a 。
θcos 1l xB =，θsin 1l yB =θωυsin 1l xB -=，θωυcos 1l yB =，222B2==-cos =-BxB i d x a l x dt ωϕω2222==-sin =-B yB i B d y a l y dtωϕω。
（2）RPRII 级杆组的运动分析： a. 如右图所示是由2个回转副和1个移动副组成的II 级组。
已知两个外运动副C 、B 的位置（B x 、B y 、c x =110mm 、C y =0）、速度（xB υ，yB υ，xCυ=0，yCυ=0）和加速度（0,0,,==yC xC yB xB a a a a ）。
可确定下图中D 点的位置、速度和加速度。
确定构件3的角位移1ϕ、角速度1ω、角加速度1α。
1sin 31..ϕϕl x dtdx C B-= 1sin 131cos 13.....2ϕϕϕϕl l x dt x d C B --= 1cos 31..ϕϕl y dtdy C B+=1cos 131sin 13.....2ϕϕϕϕl l y dt y d C B +-= 根据关系：1111d 122..11.αϕϕωϕϕ====dtd dt ， 故可得出： D x =)1cos(4βϕ++l x CD y =)1sin(4βϕ++l y Cb. 如右图所示是由2个回转副和1个移动副组成的II 级组。
已知杆5的长度5l =650mm,E 点的坐标（320,0-）， 可确定下图中F 点的位置、速度和加速度。
确定构件5的角位移2ϕ、角速度2ω、角加速度2α。
2sin 42.ϕϕl x dtdx E D -= 2cos 42.ϕϕl y dtdy E D+= 2sin 422cos 42..2...ϕϕϕϕl l x dtdx E D --= 2cos 422sin 42..2...22ϕϕϕϕl l x dty d E D +-= 根据关系：222,22222...αϕϕωϕϕ====dt d dt d 故可得出： 2cos 5ϕl x x E F +=2sin 5ϕl y y E F +=（3）RRPII 级杆组的运动分析;如右图所示是由2个回转副和1个移动副组成的II 级组。
已知杆6的长度为6l =500mm ，可确定下图中G 点的位置、速度和加速度。
确定构件6的角位移3ϕ、角速度3ω、角加速度3α。
1）G 点的位置方程3sin 63cos 6ϕϕl y y l x x F G F G +=+=为求解上式，应先求出3ϕ。
3cos 6sina 3ϕϕF x k l krc -== 为保证机构能够存在；应满足装配条件3ϕ≤k ，求出3ϕ后可按上式求出G G y x ,。
2）G 点的速度方程6l 杆的角速度3ω和滑块7移动的速度7υ：262666.66.66.7.33cos 3sin 3)3sin 3cos (32)3cos 3sin (313/)3sin 23cos 1(63/3cos 23sin 13ϕϕϕϕϕϕϕϕϕϕυϕϕϕωl l Q l l y Q l l x Q Q l Q l Q l Q Q Q F F +=-+=+-=+-==+-==式中：）（G 点速度可表示为：3cos 3sin 3sin 3cos ..36.6.36.6..ϕϕυϕϕυϕϕl l y y l l x x F D yD F D xD ++==-+==3）G 点的加速度方程6l 杆的角加速度3α和滑块7沿导轨的移动加速度a: 3/)3sin 53cos 4(3/)3cos 53sin 4(3366..Q l Q l Q a Q Q Q ϕϕϕϕϕα--=+-==式中：3cos 32)3cos 3sin (3)3sin 3cos (33sin 353sin 2)3sin 3cos (3)3cos 3sin (33cos 34..6662.66..62....6662.66..62...2ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕl l l l l l y Q l l l l l l x Q F F ++--++-=---+-+-=G 点的加速度yG xG a a ,为3cos 323sin 33cos 33sin 3sin 323cos 33sin 33cos ..62.6..6..6.......662...6..6....ϕϕϕϕϕϕϕϕϕϕϕϕϕϕl l l l y y a l l l l x x a F D yD F D xD +-++==---+==四、结果：（1）G点的运动参数计算结果如下：对结果的分析：实线分别表示表示点G的在x方向上的坐标、速度、加速度随AB角位移的变化，虚线表示其在y方向上的坐标、速度、加速度随AB角位移的变化。
2 凸轮机构设计1、设计题目：如图（2）直动从动盘形凸轮机构，其原始数据见表1，据此原始数据设计凸轮机构。
图（2）表一 直动推杆盘形凸轮机构的已知参数2、凸轮机构的设计要：（1）计算推杆的位移s 、速度υ和加速度a 线图； （2）绘制凸轮机构的S d s-ϕd 线图；（3）确定凸轮的基圆半径0r 和偏距e ； （4）绘制凸轮的理论轮廓线；（5）确定滚子半径r r 并绘制凸轮实际轮廓线。
一、首先计算推杆的位移s 、速度υ和加速度a 线图 1、推杆位移s 的方程：升程运动 加速：20)(2s Φ=ϕh ）（40ππ≤≤减速：)(2s 002ϕ-ΦΦ-=hh ）（24πϕπ≤≤ 回程运动 ⎥⎦⎤⎢⎣⎡Φ+Φ-=)2sin(211s 0'0'2T T h ππ 其中）（s -0Φ+Φ=ϕT ）（913πϕπ≤≤ 推杆位移线图：2、推杆速度υ的方程：升程运动： 加速：ϕωυ201h 4Φ=（40πϕ≤≤） 减速：)(40201ϕωυ-ΦΦ=h ）（24πϕπ≤≤回程运动 )]2cos(1[h -'0'01T Φ-Φ=πωυ 其中）（s -0Φ+Φ=ϕT （913πφπ≤≤） 推杆速度线图：3、推杆加速度a 的方程：升程运动 加速：2124Φ=ωh a ）（40ππ≤≤ 减速：2014Φ-=ωh a回程运动 )2sin(2'2'2001ΦΦ-=T h a πωπ 其中）（s -0Φ+Φ=ϕT （913πφπ≤≤）推杆加速度线图：附MATLB 程序：h=100;x = 0:pi/100:(pi/4); s1 = 8*h*x.^2/pi^2; v1=16*h*x./pi^2; a1 = 16*h/pi^2;k=(pi/4):pi/100:(pi/2);sk=h-8*h*(pi^2/4-k.*pi+k.^2)/pi^2; vk=(8*h*pi-k*16*h)/pi^2; ak=-(16*h/pi^2);y = (pi/2):(pi/100):(pi); s2 =h; v2=0; a2 = 0;q=4*pi/9;z = pi:(pi/100):(13*pi/9);s3 = h*(1-(z-pi)/q+sin(2*pi*(z-pi)/q)/(2*pi)); v3 = -h/q*(1-cos(2*pi*(z-pi)/q)); a3 = -2*pi*h*sin(2*pi*(z-pi))/q^2;c = (13*pi/9):(pi/100):( 2*pi); s4 = 0; v4 = 0; a4 = 0;plot(x,s1,'g.',k,sk,'g.',y,s2,'g.',z,s3,'g. ',c,s4,'g.') xlabel('转角/rad') ylabel('位移/(m/s)') title('位移与转角曲线')plot(x,v1,'g.',k,vk,'g.',y,v2,'g.',z,v3,'g. ',c,v4,'g.') xlabel('转角/rad') ylabel('速度/(m/s)') title('速度与转角曲线')plot(x,a1,'g.',k,ak,'g.',y,a2,'g.',z,a3,'g. ',c,a4,'g.') xlabel('转角/rad') ylabel('加速度/(m/s)') title('加速度与转角曲线') 二、绘制凸轮机构的s d ds-ϕ线图：附MATLAB 程序：h=100;x=0:(pi/100):(pi/4); s1= 8*h*x.^2/pi^2; news1=16*h*x/pi^2;k=pi/4:pi/100:pi/2;sk=h-8*h*(pi^2/4-k.*pi+k.^2)/pi^2; newsk=16*h*(pi/2-k)/pi^2;y = (pi/2):(pi/100):(pi); s2 = h; news2 = 0;q=4*pi/9;z = (pi ):(pi/100):(13*pi/9);s3 = h*(1-(z-pi)/q+sin(2*pi*(z-pi)/q)/(2*pi)); news3 =h*cos(2*pi*(z-pi)/q)/q-h/q;c = (13*pi/9):(pi/100):( 2*pi); s4 = 0; news4 = 0;plot(news1,s1,'r',newsk,sk,'r',news2,s2,'r',news3,s3,'r',news4,s4,'r') grid onxlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s 曲线')三、确定凸轮的基圆半径0r 和偏距e ：)tan 2arctan tan 2(00αφπαφππ-=h r 其中压力角分别取o 70,402o 1==αα。